Andhra Pradesh BIEAP AP Inter 2nd Year Chemistry Study Material Lesson 3(b) Chemical Kinetics Textbook Questions and Answers.
AP Inter 2nd Year Chemistry Study Material Lesson 3(b) Chemical Kinetics
Very Short Answer Questions
Question 1.
Define the speed or rate of a reaction.
Answer:
The change in the concentration of a reactant (or) product in unit time is called the speed or rate of a reaction.
(or)
The decrease in the concentration of a reactant (or) increases in the concentration of product per unit time.
Question 2.
Assuming that the volume of the system is constant, derive the expression for the average rate of the system R → P in terms of R and R [time = ‘t’ sec] [R = reactant, P = product].
Answer:
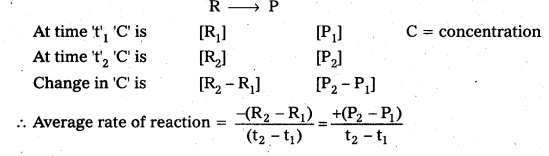
![]()
Question 3.
What are the units of rate of reaction?
Answer:
Units of rate of reaction – moles/Lit × sec – moles. Lit-1 . sec-1
Question 4.
Draw the graphs that relate the concentrations .(C) of the reactants and the reaction times (t) and the concentrations of the products (C) and the reaction times (t) in chemical reactions.
Answer:
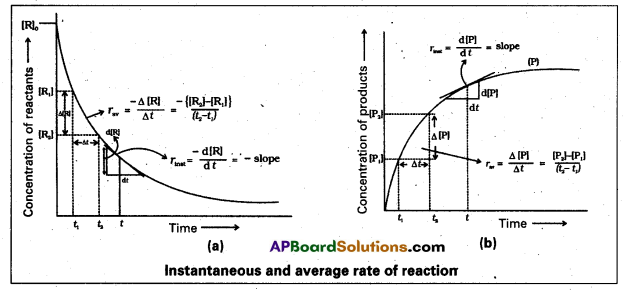
Question 5.
Write the equation for the rate of the reaction.
\(5 \mathrm{Br}_{(\mathrm{aq})}^{-}+\mathrm{BrO}_{3(\mathrm{aq})}^{-}+6 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 3 \mathrm{Br}_{2(\mathrm{aq})}+3 \mathrm{H}_2 \mathrm{O}_{(\text {) }}\)
Answer:
Given reaction is
\(5 \mathrm{Br}_{(\mathrm{aq})}^{-}+\mathrm{BrO}_{3(\mathrm{aq})}^{-}+6 \mathrm{H}_{(\mathrm{aq})}^{+} \longrightarrow 3 \mathrm{Br}_{2(\mathrm{aq})}+3 \mathrm{H}_2 \mathrm{O}_{(\text {) }}\)
Rate of reaction = \(=-\frac{1}{5} \frac{\Delta\left[\mathrm{Br}^{-}\right]}{\Delta \mathrm{t}}=\frac{-\Delta\left[\mathrm{BrO}_3^{-}\right]}{\Delta \mathrm{t}}=\frac{-1}{6} \frac{\Delta\left[\mathrm{H}^{+}\right]}{\Delta \mathrm{t}}=\frac{-1}{3} \frac{\Delta\left[\mathrm{Br}_2\right]}{\Delta \mathrm{t}}=\frac{1}{3} \frac{\Delta\left[\mathrm{H}_2 \mathrm{O}\right]}{\Delta \mathrm{t}}\)
Question 6.
What is rate law ? Illustrate with an example.
Answer:
The equation that describes mathematically the dependence of the rate of a reaction on the concentration terms of the reactions is known as the rate equation (or) rate law.
Eg : 2A + 3B → 3C
Rate, of the given reaction ∝ [A]2 [B]3
![]()
Question 7.
Mention a reaction for which the exponents of concentration terms are not the same as their stoichiometric coefficients in the rate equation.
Answer:
The following are the reactions for which the exponents of concentration terms are not the same as their stoichiometric coefficients in the rate equation.
CHCl3 + Cl2 → CCl4 + HCl
rate = k[CHCl3] [Cl2]1/2
CH3COOC2H5 + H2O → CH3COOH + C2H5OH
rate = k[CHCOOC2H5] [H2O]1/2
Question 8.
Define Order of a reaction. Illustrate your answer with an example. [T.S. Mar. 15]
Answer:
Order of a reaction : The sum of the powers of the concentration terms of the reactants present in the rate equation is called order of a reaction.
Order of a reaction can be 0, 1, 2, 3, and even a fraction
Eg. : 1) N2O5 → N2O4 + \(\frac{1}{2}\) O2
rate ∝ [N2O5]
∴ It is a first order reaction.
2) 2N2O → 2N2 + O2
rate ∝ [N2O]2
∴ It is 2nd order reaction.
Question 9.
What are elementary reactions ?
Answer:
The reactions taking place in one step are called elementary reactions.
Question 10.
What are complex reactions ? Name one Complex reaction.
Answer:
A sequence of elementary reactions, reactants give the products, the reactions are called complex reactions.
Eg: Oxidation of Ethane to CO2 and H2O passes through a series of intermediate steps in which alcohol, aldehyde and acid are formed.
![]()
Question 11.
Give the units of rate constants for Zero, first order and second order reactions.
Answer:
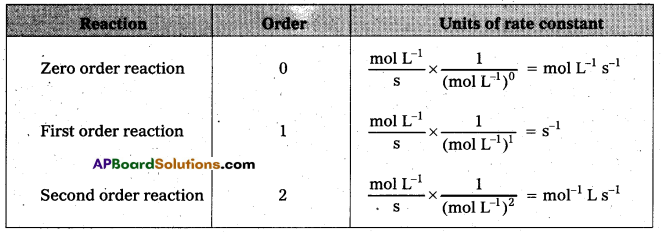
Question 12.
Define molecularity of a reaction. Illustrate with an example.
Answer:
The number of reacting species (atoms, ions or molecules) taking parts in an elementary reaction, which must colloid simultaneously to bring about a chemical reaction is called molecularity of a reaction.
NH4NO2 → N2 + 2H2O (Unimolecular)
2HI → H2 + I2 (Bimolecular)
2NO + O2 → 2NO2 (Trimolecular)
Question 13.
What is rate determining step in a complex reaction ?
Answer:
The overall rate of a reaction is controlled by the slowest step in a reaction is called the rate determining step in a complex reaction.
Question 14.
Give the mechanism for the decomposition reaction of H2O2 in alkaline medium catalysed by I– ions.
Answer:
Chemical equation of decomposition of H2O2 in alkaline medium is
![]()
Mechanism:
- It is a first order reaction w.r.t. both H2O2, I–
- This reaction takes place is two steps
- H2O2 + I– → H2O + IO–
- H2O2 + IO– → H2O + I– + O2
![]()
Question 15.
Write the equation relating [R], [R]0 and reaction time ‘t’ for a zero order reaction. [R] = concentration of reactant at time ‘t’ and [R]0 = initial concentration of reactant.
Answer:
Zero order reaction Rate constant k = \(\frac{[R]_0-[R]}{t}\)
Eg : Decomposition of NH3
![]()
Rate = k [NH3]0 = k
∴ \(\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\) = k ⇒ ∆x = ∆t × k
Question 16.
Draw the graph that relates the concentration ‘R, of the reactant and ‘t’ the reaction time for a zero Order reaction.
Answer:
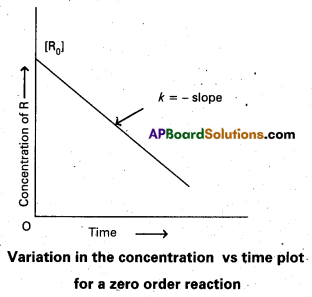
Question 17.
Give two examples for zero Order reactions. [A.P. Mar. 19]
Answer:
Examples for zero order reactions
Question 18.
Write the Integrated equation for a first order reaction in terms of [R], [R]0 and ‘t’.
Answer:
[Rl = Concentration of reaction after time ‘t
[R]0 = Initial concentrations of reactant
∴ k = \(\frac{2.303}{t} \log \frac{[R]_0}{[R]}\)
This is the integrated Equation for a first order reaction.
Question 19.
Give two examples for gaseous first order reactions. [Mar. 14]
Answer:
The following are the examples for gaseous first order reactions
N2O5(g) → N2O4(g)g + \(\frac{1}{2}\) O2(g)
SO2Cl2(g) → SO2(g) + Cl2(g)
![]()
Question 20.
For the reaction A(g) → B(g) + C(g), write the integrated rate equation in terms of total pressure ‘P and the partial pressures pApBpC.
Answer:
Given
A(g) → B(g) + C(g)
p = pA + pB + pC
k = (\(\frac{2.303}{t}\)) log (\(\frac{\mathrm{p}_0}{\mathrm{p}_{\mathrm{A}}}\))
k = (\(\frac{2.303}{t}\)) log (\(\frac{\mathrm{p}_0}{2 \mathrm{p}_{\mathrm{i}}-\mathrm{p}_{\mathrm{t}}}\))
p0 = initial pressure
Pi = Total pressure
pA, pB, pC are partial pressures.
Question 21.
What is half-life of a reaction ? Illustrate your answer with an example. .
Answer:
The time required for the initial concentration of the reactants to become half of it’s value during the progress of the reaction is called half life (t1/2) of reaction.
Eg : The radio active of C-14 is exponential with a half life of 5730 years.
Question 22.
Write the equation relating the half-life (t1/2) of a reaction and the rate constant ‘k’ for first order reaction.
Answer:
Half life of first order reaction (t1/2) = \(\frac{0.693}{k}\)
k = rate constant
Question 23.
Write the equation useful to calculate half-life (t1/2) values for zero and first order reactions.
Answer:
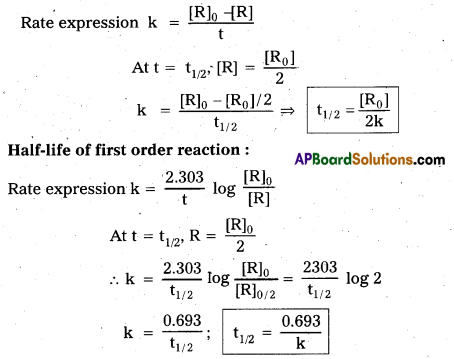
Half life (t1/2) of zero order reaction
At half life (t1/2) [R] = \(\frac{[\mathrm{R}]_0}{2}\)
∴ t1/2 = \(\frac{[\mathrm{R}]_0 / 2}{\mathrm{k}}\)
∴ t1/2 = \(\frac{\left[\mathrm{R}_0\right]}{2 \mathrm{k}}\)
Half life of a first order reaction
t1/2 = \(\frac{0.693}{\mathrm{k}}\)
k = rate constant
![]()
Question 24.
What are pseudo first order reactions ? Give one example.
Answer:
First order reactions whose molecularity is more than one are called pseudo first order reactions.

Order = 1
molecularity = 2
Question 25.
Write the Arrhenius equation for the rate constant (k) of a reaction.
Answer:
Arrhenius equation is
k = A × e-Ea/RT
k = Rate constant
Ea = activation energy
R = gas constant
T = Temperature (K)
Question 26.
By how many times the rate constant increases for a rise of reaction temperature by 10°C ?
Answer:
For every 10°C rise of temperature rate constant of chemical reactions may be doubled (some times tripled).
Question 27.
Explain the term ‘activation energy’ of a reaction with a suitable diagram.
Answer:
Activation Energy : The energy required to for an intermediate called activated complex (C) during a chemical reaction is called activation energy.
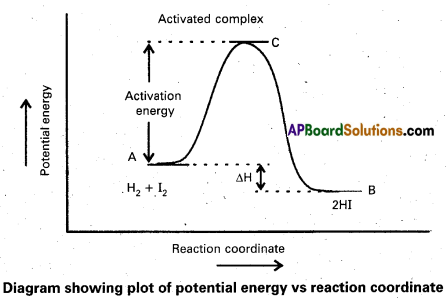
Question 28.
Write the equation which relates the rate constants k1 and k2 at temperatures T1 and T2 of a reaction.
Answer:
\(\log \left(\frac{\mathrm{k}_2}{\mathrm{k}_1}\right)=\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\left[\frac{1}{\mathrm{~T}_1}-\frac{1}{\mathrm{~T}_2}\right]\)
Ea = activation energy; R = Universal gas constant.
![]()
Question 29.
What is collision frequency (Z) of a reaction ? How is rate related to it for the reaction A + B → Products.
Answer:
The number of collisions per second per unit volume of the reaction mixture is called collision frequency (Z). Fora bimolecular elementary reactions.
A + B → products; Rate = ZAB.e – Ea/RT.
Question 30.
Draw the graphs between potential energy – reaction coordinates for catalysed and uncatalysed reactions.
Answer:
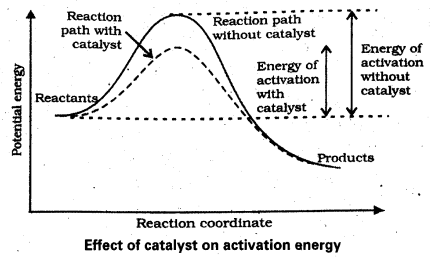
Question 31.
What is the effect of temperature on the rate constant ?
Answer:
Most of the chemical reactions are accelerated by increase of temperature.
For a chemical reaction with rise of temperature by 10°C the rate constant is nearly doubled k = A.e-Ea/RT
Short Answer Questions
Question 1.
Define average rate of a reaction. How is the rate of reaction expressed in terms of change in the concentration of reactants and products for the following reactions.
1) 2HI(g) → H2(g) + I2(g)
2) Hg(l) + Cl2(g) → HgCl2(g)
3) 5 Br(aq) + \(\mathrm{BrO}_{3(\mathrm{aq})}^{-}\) + \(6 \mathrm{H}_{(\mathrm{aq})}^{+}\) → 3 Br2(aq) + 3 H2O(l)
Answer:
Average rate of a reaction: The change in the concentration of any one of the reactants or products per unit time is called average rate of a reaction.

Question 2.
What is rate equation ? How is it obtained ? Write the rate equations for
1) 2NO(g) + O2 (g) → 2NO2 (g)
2) CHCl3 + Cl2 → CCl4 + HCl
3) CH3COOC2H5 (l) + H2O(l) → CH3COOH (aq) + C2H5OH(aq)
Answer:
The equation that describes mathematically the dependence of the rate of a reaction on the concentration terms of the reactions is known as the rate equation (or) rate law.
Eg, : 2A + 3B → 3C
Rate of the given reaction ∝ [A]2 [B]3
How to obtain: Each concentration term is raised to some power which may or may not be same as the stoichiometric coefficient of the reacting species
i) 2NO(g) + O2(g) → 2NO2(g)
\(\frac{\Delta[\mathrm{R}]}{\Delta t}\) = k [NO]2 [O2]
ii) CHCl3 + Cl2 → CCl4 + HCl
\(\frac{\Delta[\mathrm{R}]}{\Delta t}\) = k [CHCl3] [Cl2]1/2
iii) CH3COOC2H5(l) + H2O(l) → CH3COOH(aq) + C2H5OH(aq)
\(\frac{\Delta[\mathrm{R}]}{\Delta t}\) = k [CH3COOC2H5].
![]()
Question 3.
Define and explain the order of a reaction. How is it obtained experimentally?
Answer:
Order of a reaction :. The sum of the powers of the concentration terms of the reactants
present in the rate equation is called order of a reaction.
Order of a reaction can be 0, 1, 2, 3, and even a fraction
Eg. : 1) N2O5 → N2O4 + \(\frac{1}{2}\) O2
rate ∝ [N2O5]
∴ It is a first order reaction.
2) 2N2O → 2N2 + O2
rate ∝ [N2O]2
∴ It is 2nd order reaction.
Order of a reaction can be determined experimentally
Half – Time (t1) method : The time required for the initial concentration (a) of the reactant to become half its value (a/2) during the progress of the reaction is called half-time (t1/2) of the reaction.
A general expression for the half life, (t1/2) is given by
t1/2 ∝ \(\frac{1}{a^{n-1}}\)
Therefore, for a given reaction two half time values (t’1/2and t”1/2) with initial concentrations a’ and a” respectively are determined experimentally and the order is established from the equation.
\(\left(\frac{t_{1 / 2}^{\prime}}{t_{1 / 2}^n}\right)=\left(\frac{a^n}{a^{\prime}}\right)^{n-1}\)
Where ‘n’ is the order of the reaction.
Question 4.
What is “moleculartiy” of a reaction ? How is it different from the ‘order’ of a reaction ? Name one bimolecular and one trimolecular gaseous reactions. [T.S. Mar. 17] [Mar. 14]
Answer:
The number of reacting species (atoms, ions or molecules) taking parts in an elementary reaction, which must colloid simultaneously to bring about a chemical reaction is called molecularity of a reaction.
NH4NO2 → N2 + 2H2O (Unimolecular)
2HI → H2 + I2 (Bimolecular)
2NO + O2 → 2NO2 ( Trimolecular)
- Molecularity has only integer values (1, 2, 3 )
- It has nop zero, non fraction values while order has zero, 1, 2, 3 and fractional values.
- It is determined by reaction mechanism, order is determined experimentally.
Question 5.
Derive the integrated rate equation for a zero order reaction.
Answer:
Zero order reaction is the reaction in which rate of reaction does not depends on the concentration of reactants.
R → P
Rate = \(\frac{-\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\) = k [R]°
Rate = \(\frac{-\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\); d[R] = – k. dt
Integrating on both sides
[RJ = -kt + I …………….. (1)
I – Integration constant
At t = 0 → R = [R]0 initial concentration
I = [R]0
Substituting I = [R]0 in the above equation (1)
[R] = – kt + [R]0
k = \(\frac{\left[R_0\right]-[R]}{t}\)
This is the integrated rate equation for a zero order reaction.
![]()
Question 6.
Derive an integrated rate equation for a first order reaction.
Answer:
In first order reactions rate depends on only one concentration term.
R → P
Rate = k [R]; -M = – k. dt
Integration on both sides
ln [R] = – kt + I
I = Integration constant
At t = 0, [R] = [R]0 ⇒ ln[R]0 = I
Substituting I = ln [R] in the above equation (1)
ln [R] = – kt + ln [R]0
ln \(\frac{[\mathrm{R}]}{\left[\mathrm{R}_0\right]}\) = -kt ………………. (2)
k = \(\frac{1}{\mathrm{t}} \ln \frac{\left[\mathrm{R}_0\right]}{[\mathrm{R}]}\)
Taking antilog on both sides of eq. (2)
R = [R]0. e-kt
This is first order rate equation.
Question 7.
Derive an integrated rate equation in terms of total pressure (P) and the partial pressures pA, pB, pC for the gaseous reaction A(g) → B(g) + C(g).
Answer:
Given first order gas phase equations
A(g) → B(g) + C(g)
Let pi be the initial pressure of A and pt the total pressure at time’t’. Integrated rate equation for such a reaction can be derived as
Total pressure pt = pA + pB + pC (pressure units)
pA, pB and pC are the partial pressures of A, B and C, respectively.
If x atm be the decrease in pressure of A at time t and one mole each of B and C is being formed, the increase in pressure of B and C will also be x atm each.

Thus the rate expression for 1st order gaseous phase reaction derived.
Question 8.
What is half-life (t1/2) of a reaction ? Derive the equations for the ‘half-life’ value of zero and first order reactions.
Answer:
The time required for the initial concentration of the reactants to become half of it’s value during the progress of the reaction is called half life (t1/2) of reaction.
Eg : The radio active of C-14 is exponential with a half life of 5730 years.
Half life of zero order reaction :
Question 9.
What is Arrhenius equation ? Derive an equation which describes the effect of rise of temperature (T) on the rate constant (k) of a reaction.
Answer:
The temperature dependence of the rate of reaction can be explained by Arrhenius equation.
k = A.e-Ea/KT
A = Arrhenius factor.
Ea = activation Energy
R = gas constant
T = Temperature. (K)
k = A.e-Ea/KT
ln k = ln A – Ea/RT
2.303 log k = 2.303 log A – Ea/RT
T1, T2 are Temperatures
k1 is rate constant at temperature T1
k2 is rate constant at temperature T2
∴ 2.303 (log k2 – log k1) = \(\frac{-\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\left(\frac{1}{\mathrm{~T}_2}-\frac{1}{\mathrm{~T}_1}\right)\)
\(\log \frac{\mathrm{k}_2}{\mathrm{k}_1}=\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\left[\frac{1}{\mathrm{~T}_1}-\frac{1}{\mathrm{~T}_2}\right]\)
The above equation describes the effect of temperature (T) on rate constant (k)
![]()
Question 10.
Discuss the effect of catalyst on the kinetics of a chemical reaction with a suitable diagram. [T.S. Mar. 15]
Answer:
The substance which increases the rate of reaction without being consumed in the chemical reaction is called a catalyst.
In presence of catalyst the reaction proceeds in a new path which lowers the activation energy.
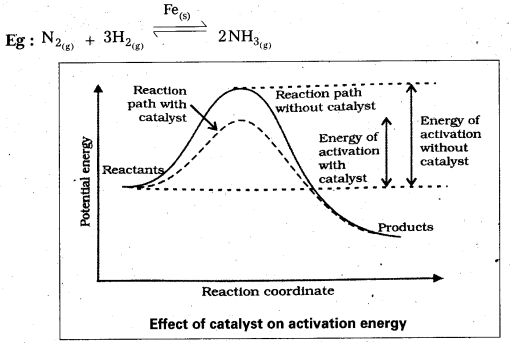
Question 11.
Describe the salient features of the collision theory of reaction rates of bimolecular reactions. [T.S. Mar. 18, 16; A.P. Mar. 17]
Answer:
Collision theory of reaction rate bimolecular reactions salient features.
- The reaction molecules are assumed to be hard spheres
- The reaction is postulated to occur when molecules collide with each other.
- The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z).
- For a bimolecular elementary reaction
A + B → products
Rate = ZAB. e-Ea/RT ; ZAB = collision frequency. - All collisions do not lead to product formation.
- The collisions with sufficient kinetic energy (Threshold energy) are responsible for product formation. These are called as effective collisions.
- To account for effective collisions a factor p called to probability factor or steric factor is introduced.
Rate = P ZAB. e-Ea/RT
Question 12.
Explain the terms
a) Activation energy (Ea)
b) Collision frequency (Z) :
c) Probability factor (P) with respect to Arrhenius equation.
Answer:
a) Activation Energy: The energy required to for an intermediate called activated complex (C) during a chemical reaction is called activation energy.
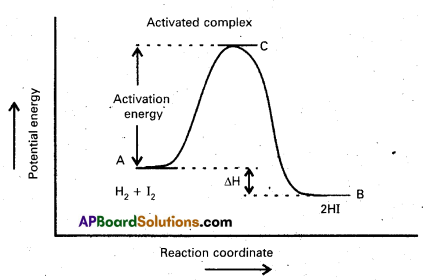
Diagram showing plot of potential energy vs reaction coordinate
b) Collision frequency: The number of collisions per second per unit volume of the reaction mixture is called collision frequency (Z). For a bimolecular elementary reactions
A + B → products
Rate = ZAB. e-Ea/RT
c) Probability factor (P) with respect to Arrhenius equation : To account for effective collisions a factor p called to probability factor or steric factor is introduced.
Rate = P ZAB. e-Ea/RT
Long Answer Questions
Question 1.
Explain the following terms with suitable examples.
a) Average rate of a reaction
b) Slow and fast reactions
c) Order of a reaction
d) Molecularity of a reaction
e) Activation energy of reaction.
Answer:
a) Average rate of a reaction : The change in the concentration of any one of the reactants or products per unit time is called average rate of a reaction.
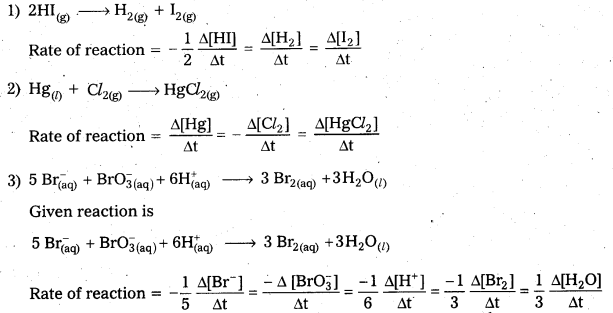
b)
- Fast Reactions : In case pf ionic compounds reactions takes place fastly i.e., rate is high
NaCl + AgNO3 → NaNO3 + AgCl - Slow reactions : In case of covalent compounds reactions takes place slowly i.e., rate is low.
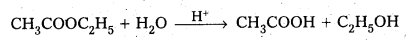
c) Order of reaction : The number of reacting species (atoms, ions or molecules) taking parts in an elementary reaction, which must colloid simultaneously to bring about a chemical reaction is called molecularity of a reaction.
NH4NO2 → N2 + 2H2O (Unimolecular)
2HI → H2 + I2 (Bimolecular)
2NO + O2 → 2NO2 (Trimolecular)
Molecularity has only integer values (1, 2, 3 …………..)
It has non zero, non fraction values while order has zero, 1, 2, 3 ……….. and fractional values.
It is determined by reaction mechanism, order is determined experimentally.
d) Molecularity of a reaction: Zero order reaction is the reaction in which rate of reaction does not depends on the concentration of reactants.
R → P
Rate = \(\frac{-\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\) = k [R]°
Rate = \(\frac{-\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\); d[R] = – k. dt
Integrating on both sides
[RJ = -kt + I …………….. (1)
I – Integration constant
At t = 0 → R = [R]0 initial concentration
I = [R]0
Substituting I = [R]0 in the above equation (1)
[R] = – kt + [R]0
k = \(\frac{\left[R_0\right]-[R]}{t}\)
This is the integrated rate equation for a zero order reaction.
e) Activation energy of reaction: The energy required to for an intermediate called activated complex (C) during a chemical reaction is called activation energy
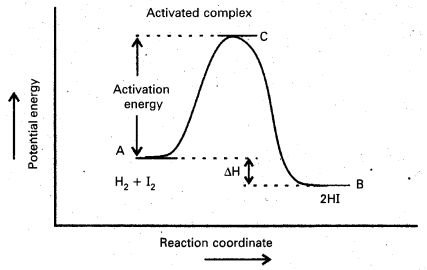
Diagram showing plot of potential energy vs reaction co-ordinate
![]()
Question 2.
Give two examples for each of zero order and first order reactions. Write the equations for the rate of a reaction in terms of concentration changes of reactants and products for the following reactions.
1) A(g) + B(g) → C(g) + D(g)
2) A(g) → B(g) + C(g) 3) A(g) + B(g) – C(g)
Answer:
Examples of zero order reaction :
Examples of first order reaction :
N2O5(g) → N2O4(g) + \(\frac{1}{2}\) O2(g)
SO2Cl2(g) → SO2(g) + Cl2(g)

Question 3.
Discuss the effect of temperature on the rate of a reaction. Derive necessary equations in this context. [T.S. Mar. 15]
Answer:
Most of the chemical reactions are accelerated by increase of temperature.
For a chemical reaction with rise of temperature by 10°C the rate constant is nearly doubled
k = A.e-Ea/RT
The temperature dependence of the rate of reaction can be explained by Arrhenius equation.
k = A.e-Ea/RT
A = Arrhenius factor.
Ea = activation Energy
T = Temperature (°K)
R = gas constant
k = A.e-Ea/RT
In k = ln A – Ea/RT
2.303 log k = 2.303 log A – Ea/RT
T1, T2 are Temperatures
k1 is rate constant at temperature T1
k2 is rate constant at temperature T2
∴ 2.303 (log k2 – log k1) = \(\frac{-\mathrm{E}_{\mathrm{a}}}{\mathrm{R}}\left(\frac{1}{\mathrm{~T}_2}-\frac{1}{\mathrm{~T}_1}\right)\)
\(\log \frac{\mathrm{k}_2}{\mathrm{k}_1}=\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}\left[\frac{1}{\mathrm{~T}_1}-\frac{1}{\mathrm{~T}_2}\right]\)
The above equation describes the effect of temperature (T) on rate constant (k)
Question 4.
Give a detailed account of the collision theory of reaction rates of bimolecular gaseous reactions. [A.P. Mar. 17, 16]
Answer:
Collision theory of reaction rate bimolecular reactions salient features.
- The reaction molecules are assumed to be hard spheres
- The reaction is postulated to occur when molecules collide with each other.
- The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z).
- For a bimolecular elementary reaction
A + B → products - Rate = ZAB.e-Ea/RT; ZAB = collision frequency.
- All collisions do not lead to product formation.
- The collisions with Sufficient kinetic energy (Threshold eriergy) are responsible for product formation. These are called as effective collisions.
- To account for effective collisions a factor p called to probability factor or steric factor is introduced.
Rate = PZAB.e-Ea/RT - The proper orientation of reactant molecular lead to bond formation where as improper orientation makes them back and no product are formed.
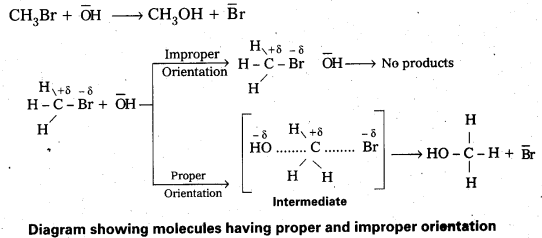
In this theory activation energy and proper orientation of the molecules to gather determine the creteria for an effective collision and hence the rate of a chemical reaction.
![]()
Problems
Numerical Data Based And Concept Oriented Questions
Question 1.
A reaction is 50% completed in 2 hours and 75% completed in 4 hours. What is the order of the reaction ? [T.S. Mar. 16]
Solution:
Given that a reaction is 50% completed in 2 hrs.
75% completed in 4 hrs.
From the data half life is independent of initial concentration so it is a first order reaction.
Question 2.
A reaction has a half – life of 10 minutes. Calculate the rate constant for the first order reaction. [T.S. Mar. 16]
Solution:
In case of fist order reaction t1/2 = \(\frac{0.693}{k}\)
∴ k = \(\frac{0.693}{t_{1 / 2}}=\frac{0.693}{10}\) = 0.0693 min-1
Question 3.
In a first order reaction, the concentration of the reactant is reduced from 0.6 mol/L to 0.2 mol/L in 5 min. Calculate the rate constant (k).
Solution:
a = 0.6mol L-1; a – x = 0.2 mol L-1; t = 5 min.
Since it is a first order reaction.
k = \(\frac{2.303}{t} \log _{10} \frac{a}{(a-x)}\)
k = \(\frac{2.303}{t}\) log \(\frac{0.6}{0.2}\) = 0.2197 min-1.
Question 4.
The rate constant for a zero order reaction in A is 0.0030 mol L-1 s-1. How long it will take for the initial concentration of A to fall from 0.10 M to 0.075 M.
Solution:
In case of zero order reaction
k = \(\frac{1}{t}\) [[A0] – [A]]
[A]0 = Initial concentration
[A] = concentration after time t
k = 0.0030 mol L-1s-1
[A]0 = 0.10 M
[A] = 0.075 M
0.0030 = \(\frac{1}{t}\) [0.10 – 0.075]
t = \(\frac{0.025}{0.0030}\) = 8.33 seconds.
![]()
Question 5.
A first order decomposition reaction takes 40 min. for 30% decomposition. Calculate it’s t1/2 value.
Solution:
Given t = 40 min, a = 100
a – x = 100 – 30 = 70
In case of first order reaction
k = \(\frac{2.303}{t} \log \frac{a}{(a-x)}\)
k = \(\frac{2.303}{40} \log \frac{100}{70}\) = 0.0576 [2.0000 – 1.8451]
= 0.0576 (0.1549) = 8.922 × 10-3
\(\mathrm{t}_{\frac{1}{2}}=\frac{0.693}{\mathrm{k}}=\frac{0.693}{8.922 \times 10^{-3}}\) = 77.673 min.
Question 6.
Calculate the half-life of first order réaction whose rate constant is 200 s-1.
Solution:
Half – life period for first order reaction
\(\mathrm{t}_{\frac{1}{2}}=\frac{0.693}{\mathrm{k}}\)
\(\mathrm{t}_{\frac{1}{2}}=\frac{0.693}{200 \mathrm{~s}^{-1}}\) = 0.346 × 10-2s = 3.46 × 10-3s
Question 7.
The thermal decomposition of HCOOH is a first order reaction. The rate constant is 2.4 × 10-3 s-1 at a certain temperature. Calculate how long will it take for 3/4 of initial quantity of HCOOH to decompose. ‘
Solution:
Given reaction is a first order reaction.
\(\mathrm{t}_{\frac{1}{2}}=\frac{0.693}{\mathrm{k}}=\frac{0.693}{2.4 \times 10^{-3}}\)
= 288.75 sec.
To convert into \(\frac{3}{4}\) of the original, two half lifes are required.
Time to decompose = 2 × 288.75
= 577.5 sec.
= 5.775 × 102 sec.
Question 8.
The decomposition of a compound is found to follow first order rate law. If it takes 15 minutes for 20% of original material to react, calculate the rate constant.
Solution:
Given t = 15 min., a = 100
a – x = 100 – 20 = 80
k = \(\frac{2.303}{t} \log \frac{\mathrm{a}}{\mathrm{a}-\mathrm{x}}\)
k = \(\frac{2.303}{15} \log \frac{100}{80}\) = 0.1535 [2.0000 – 1.9031] = 0.1535 × 0.0969
k = 0.0148 min-1.
![]()
Question 9.
In a pseudo first order hydrolysis of ester in water, the following results are obtained

Calculate the average rate of reaction between the time interval 30 to 60 s.
Solution:

Question 10.
The half-life for a first order reaction is 5 × 10-6s. What percentage of the initial reactant will react in 2 hours ?
Solution:
Given t1/2 = 5 × 10-6 sec.
k = \(\frac{0.693}{1_{1 / 2}}=\frac{0.693}{5 \times 10^{-6}}\) = 0.1386 × 106 sec-1
k = 0.1386 × 106 sec-1 = 1.386 × 105 sec-1
Here a = 100, t = 2 hrs. = 2 × 60 × 60 sec, (a – x) = ?

Question 11.
H2O2(aq) decomposes to H2O(l) and O2(g) in a first order reaction w.r.t. H2O2. The rate constant is k = 1.06 × 10-3 min-1. How long it will take 15% of the sample to decompose?
Solution:
k = 1.06 × 10-3 min-1
a = 100 .
a – x = 100 – 15 = 85
k = \(\frac{2.303}{t} \log \frac{a}{a-x}\)
1.06 x 10 = \(\frac{2.303}{t} \log \frac{100}{85}\)
t = \(\frac{2.303}{1.06 \times 10^{-3}} \log \frac{100}{85}\) = 153.4 min
Question 12.
Show that in the case of first order reaction, the time required for 99.9% completion of the reaction is 10 times that required for 50% completion. (log 2 = 0.30 10)
Solution:
t1/2 = \(\frac{0.693}{k}\)
For 99.9% → a = 100
a – x = 100 – 99.9 = 0.1
k = \(\frac{2.303}{\mathrm{k}} \log \frac{100}{0.1}\)
But k = \(\frac{0.693}{\mathrm{t}_{1 / 2}}=\frac{2.303}{0.693}\) × t1/2 log 1000 = 3.33 × t1/2 × 3 = 9.99 × t1/2
t99.9% is 10 times t1/2
![]()
Question 13.
The rate constant of a reaction is doubled when the temperature is raised from 298 K to 308 K. Calculate the activation energy.
Solution:
Ea = ? k2 = 2k1; T1 = 298 K; T2 = 308 K

Question 14.
The first order rate constant ‘k’ for the reaction C2H5I(g) → C2H4 (g) + HI(g) at 600 K is 1.60 × 10-5 s-1. The energy of activation is 209 kJ/mol. Calculate ‘k’ at 700 K.
Solution:
k1 = 1.60 × 10-5 s-1
k2 = ?
T1 = 600 K
T2 = 700 K
Ea = 209 kJ mol-1 = 209000 J mol-1

Question 15.
The activation energy for the reaction 2HI(g) → H2(g) + I2(g) at 581 K is 209.5 kJ/mol. Calculate the fraction of molecules having energy equal to or greater than activation energy. [R = 8.31 JK-1 mol-1] .
Solution:
Fraction of molecules [x] having energy equal to or more than activation energy may be calculated as fallows:
x – n/N = e-Ea/RT
In x = \(\frac{-\mathrm{E}_{\mathrm{a}}}{\mathrm{RT}}\) or log x = \(\frac{-\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
or log x = –\(\frac{209.5 \times 10^3 \mathrm{~J} \mathrm{~mol}^{-1}}{2.303 \times\left[8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\right] \times 581 \mathrm{~K}}\) = -18.8323
x = Antilog [-18.8324] = Antilog \(\overline{19} .1677\) = 1.471 × 10-19
Fraction of molecules = 1.471 × 10-19
Question 16.
For the reaction R → P, the concentration of a reactant changes from 0.03M to 0.02M in 25 minutes. Calculate the average rate of reaction using units seconds.
Solution:
R→ P
0.03M to 0.02 M in 25 minutes.
0.03M – 0.02M in 25 × 60 sec.
Average rate \(\frac{0.03-0.02}{25 \times 60}=\frac{0.01}{25 \times 60}\)
= \(\frac{0.01}{1500}\) = 6.66 × 10-6 ms-1
Question 17.
In a reaction 2A → Products, the concentration of A decreases from 0.5 mol L-1 to 0.4 mol L-1 in 10 minutes. Calculate the rate during this interval.
Solution:
2A → products
0.5 – 0.4 moI lit rate ∝ [A]2
rate = \(\frac{-1}{2} \frac{\mathrm{d}}{\mathrm{dt}}\) [A] = \(\frac{1}{2}\left[\frac{(0.5-0.4)}{10}\right]\) = 0.5 × 10-2
rate = 5 × 10-3 mol Lit-1 min-1
![]()
Question 18.
For a reaction, A + B → Product : the rate law is given by r = k [A]1/2 [B]2 What is the order of the reaction?
Solution:
A + B → product
r = k [A]1/2 [B]2
Rate of the reaction r = \(\frac{1}{2}\) + 2 = 2.5
Question 19.
The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased by three times, how will it affect the rate of formation of Y.
Solution:
x → y It is a second order reaction
r ∝ [x]2
If x = 1 r = 1
If x = 3 r = 32 = 9
The rate of formation of y increases by 9 times.
Question 20.
A first order reaction has a rate constant 1.15 × 10-3 s-1. How long will 5g of this reactant take to reduce to 3 g?
Solution:
Rate constant [k] = 1.15 × 10-3 s-1
Initial amount [R]0 = 5g; Final amount [R] = 3g

Question 21.
Time required to decompose SO2Cl2 to half of its initial amount Is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
Solution:
For the first order reaction
Rate constant (k) = \(\frac{0.693}{60 \mathrm{~min}}=\frac{0.693}{(60 \times 60) \mathrm{s}}\) = 1.925 × 10-4 s-1
k = 1.925 × 10-4 s-1
Question 22.
From the rate expression for the following reactions, determine their order of reaction . and the dimensions of the rate constants.
i) 3NO(g) → N2O(g) Rate = k[NO]2
ii) H2O2 (aq) + 3I– (aq) + 2H+ → 2H2O(l) + I3 Rate = k[H2O2] [I–]
iii) CH3CHO(g) → CH4 (g) + CO(g) Rate = k[CH3CHO]3/2
iv) C2H5Cl(g) → C2H2 .(g) + HCl(g) Rate = k[C2H5Cl]
Solution:
i) Rate = k [NO]2
order of reaction = 2 .
units (dimensions) of rate constant
[k] = \(\frac{\text { Rate }}{[\mathrm{NO}]^2}=\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}^{-1}}{\left(\mathrm{~mol} \mathrm{~L}^{-1}\right)^2}\) = mol-1 L s-1
ii) Rate = k[H2O2] [I–]
order of reaction = 1 + 1 = 2
Dimensions of k = \(\) = mol-1 L s-1
iii) Rate = k[CH3CHO]3/2
order of reaction = \(\frac{3}{2}\)
Dimensions of k = \(\frac{\text { Rate }}{\left[\mathrm{CH}_3 \mathrm{CHO}\right]^{3 / 2}}=\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}^{-1}}{\left(\mathrm{~mol} \mathrm{~L}^{-1}\right)^{3 / 2}}\) = mol-1/2 L1/2 s-1
iv) Rate = k[C2H5Cl]
order of reaction = 1
Dimensions of k = \(\frac{\text { Rate }}{\mathrm{C}_2 \mathrm{H}_5 \mathrm{Cl}}=\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}^{-1}}{\mathrm{~mol} \mathrm{~L}^{-1}}\) = s-1
![]()
Question 23.
For the reaction 2A + B → A, B, the rate = K[A] [B]2 with k = 2.0 × 10-6 v mol-2 L2 s-1. Calculate the initial rate of the reaction when [A] = 0.1 mol L-1, [B] = 0.2 mol L-1, Calculate the rate of reaction after [A] is reduced to 0.06 mol L-2.
Solution:
i) Case I:
Rate = k [A] [B]2
= [2.0 × 10-6 mol2 L-2 s-1] × (0.1 mol L-1) × (0.2 mol L-1)2
= 8.0 × mol L-1 s-1
ii) Case II:
Concentration of A at a particular time = 0.06 mol L-1
Amount of A reacted = (0.1 – 0.06) = 0.04 mol L-1
Amount of B reacted = \(\frac{1}{2}\) × 0.04 mol L-1 = 0.02 mol L-1
Concentration of B at a particular time = [0.2 – 0.02] mol L-1 = 0.18 mol L-1.
Rate = k [A] [B]2
= [2.0 × 10-6 mol-2 L2 s-1] × [0.06 mol L-1] × (0.18 mol L-1)2
= 3.89 × 10-9 mol L-1 s-1.
Question 24.
The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10-4 mol-1 Ls-1.
Solution:
For a zero order reaction
rate = \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = k.
dx = change in the concentration
dt = difference in time
k = rate constant
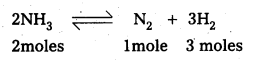
Rate of production of N2 = k = 2.5 × 10-14 mol L-1 s-1
Rate of production of H2 = 3 × 2.5 × 10-14 = 7.5 × 10-14 mol L-1 s-1
Question 25.
The rate expression for the decomposition of dimethyl ether in terms of partial pressures is given as Rate = k (pCH3 O CH3)3/2. If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constant ?
Solution:
Unit of rate = bar min-1
unit of k = \(\frac{\text { Rate }}{\left[\left(\mathrm{PCH}_3 \mathrm{OCH}_3\right]^{3 / 2}\right.}\)
= \(\frac{\text { bar } \min ^{-1}}{[\mathrm{bar}]^{3 / 2}}\) = bar-1/2 min-1
Question 26.
A reaction is second order with respect to a reactant. How is the rate of reaction is affected if the concentration of the reactant is
i) doubled
ii) reduced to half
Solution:
For a reaction A → products
Rate = k[A]2 = ka2
i) When concentration of A is doubled
i.e., [A] = 2a
Rate = k[2a]2 = 4ka2
Rate of reaction becomes 4 times
ii) When concentration of A is reduced to \(\frac{1}{2}\) i.e., [A] = \(\frac{1}{2}\) a
Rate = k [latex]\frac{a}{2}[/latex]2 = \(\frac{1}{4}\) ka2
Rate of reaction becomes \(\frac{1}{2}\) times i.e reduced to one fourth.
![]()
Question 27.
A reaction is first order in A and second order in B.
- Write the differential rate equation
- How is the rate affected on increasing the concentrations of B there times?
- How is the rate affected when the concentrations of both A and B are doubled ?
Solution:
- Rate k [A] [B]2
- Rate = k [A] [3B]2 = 9k [A] [B]2 Rate of reaction becomes 9 times
- Rate = k [2A] [2B]2 = 8k [A] [B]2 Rate of reaction becomes 8 times
Question 28.
In a reaction between A and B, the initial rate of reaction (ro) was measured for different initial concentrations of A and B as given below:

What is the order of the reaction with respect to A and B ?
Solution:
Rate law states that
Rate = k [A]x [B]y
(Rate)1 = k[0.20]x [0.30]y = 5.07 × 10-5 ………………. (i)
(Rate)2 = k[0.20]x [0.10]y = 5.07 × 10-5 …………….. (ii)
(Rate)3 = k[0.40]x [0.05]y = 1.43 × 10-4 …………… (iii)
Dividing equation (i) by equation (ii)

x log 2 = log 2.82
x = 1.4957 = 1.5
∴ order with respect to A = 1.5
order with respect to B = 0.
Question 29.
The following results have been obtained during the kinetic studies of the reaction: 2A + B → C + D
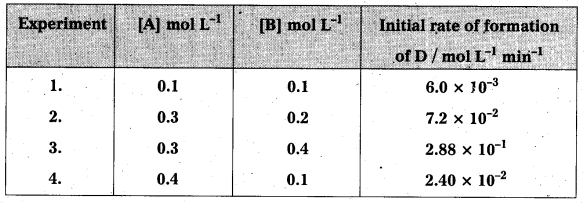
Determine the rate law and rate constant for the reaction.
Solution:
Rate law may be expressed. as
Rate = k [A]x [B]y
[Rate]1 = 6.0 × 10-3 = k (0.1)x (0.1)y …………….. (i)
[Rate]2 = 7.2 × 10-2 = k (0.3)x (0.2)x …………….. (ii)
[Rate]3 = 2.88 × 10-1 = k (0.3)x (0.4)x ……………. (iii)
[Rate]4 = 2.40 × 10-2 = k (0.4)x (0.l)x …………….. (iv)

∴ Rate law expression is given by Rate = k [A] [B]2
Rate constant k, can be determined by placing the values of A,B and rate of formation of D.
By taking the values from experimant II.
Rate k[A] [B]2
k = \(\frac{\text { Rate }}{[\mathrm{A}][\mathrm{B}]^2}=\frac{7.2 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}}{\left(0.3 \mathrm{molL}^{-1}\right)\left(0.2 \mathrm{molL}^{-1}\right)^2}\) = 6.0 mol-2 L2 min-1
∴ k = 6.0 mol-2 L2 min-1
Question 30.
The rate constant for a first order reaction is 60 s-1. How much time will it take to reduce. the initial concentration of the reactant to its 1/ 16th value?
Solution:
For 1st order reaction
t = \(\frac{2.303}{k} \log \frac{a}{(a-x)}\) …………….. (i)
Given (a – x) \(\frac{a}{16}\), k = 60 s-1
Placing the values in eq. (i)
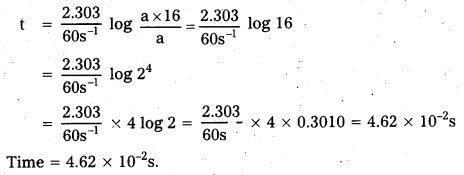
![]()
Question 31.
For a first order reaction, show that the time required for 99% completion is twice the time required for completion of 90% of reaction.
Solution:
Case I:
If a = 100; (a – x) = (100 – 99) = 1
For 99% completion of the reaction
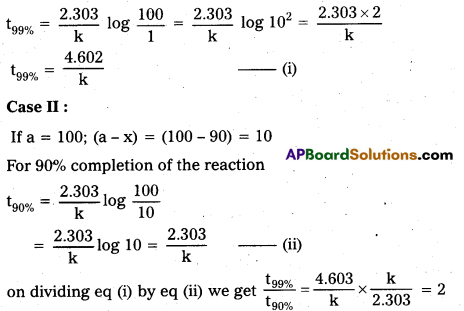
It means that time required for 99% completion of the reaction is twice the time required to complete 90% of the reaction.
Question 32.
Here the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
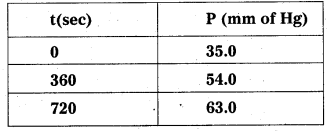
Calculate the rate constant.
Solution:
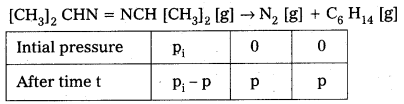
Total pressure after time t,
i e., [pt] = [pi – p] + p + p = pi + p
Or p = pt – pi
a = pi [a – x] = pi – p on substituting the values of pi
[a – x] = pi – [pt – pi]
i. e., [a – x] = 2pi – pi
The decomposition reaction is of gaseous nature and the rate constant k can be calculate as :

Average rate constant k = \(\frac{(2.17+2.24) \times 10^{-3} \mathrm{~s}^{-1}}{2}\)
k = 2.21 × 10-3 s-1
Question 33.
The following data were obtained during the first order thermal decomposition of SO2C2 at a constant volume.
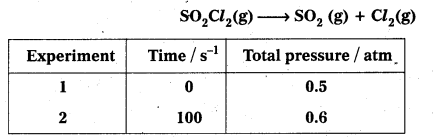
Calculate the rate of reaction when total pressure is 0.65 atm.
Solution:

Total presstce after time t
i.e., pt = pi – p + p + p = pi + p
So, a = pi
a – x = pi – (pt – pi) pi – pt + pi = 2pi – pt
Substitutions of the value of a and (a – x) gives
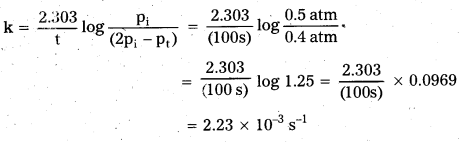
b. Calculation of reaction rate when total pressure is 0.65 atm.
PSO2Cl2 = 0.5 – (0.65 – 0.50) = (1 – 0.65) = 0.35atm
k = 2.23 × 10-3 s-1
Rate = k × PSO2Cl2 = (2.23 × 10-3 s-1) × (0.35 atm)
Rate = 7.3 × 10-4 atm s-1
![]()
Question 34.
The rate constant for the decomposition of hydrocarbons is 2.418 × 10-5 s-1 at 546 K. If the energy of activation is 179.9 kJ/mol. What will be the value of pre-exponential factor ?
Solution:
According to Arrhenius equation,
log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
k = 2.418 × 10-5 s-1
Ea = 179.9 KJ mol-1 or 179900 J mol-1
R = 8.314 JK-1 mol-1
T = 546K
log A = log k + \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
= log (2.418 × 10-5 s-1) + \(\frac{179900 \mathrm{Jmol}^{-1}}{2.303 \times\left(8.314 \mathrm{Jk}^{-1} \mathrm{~mol}^{-1}\right) \times 546 \mathrm{k}}\)
= -4.6184 + 17.21 = 12.5916
A = Antilog 12.5916 = 3.9 × 1012s-1
A = 3.9 × 1012 s-1
Question 35.
Consider a certain reaction A → Products with k = 2.0 × 10-2s-1. Calculate the concentration of A remaining after 100 s If the initial concentration of A is 1.0 mol L-1.
Solution:
For the first order reaction

Question 36.
Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t\(\frac{1}{2}\) = 3.00 hours. What fraction of sample of sucrose remains 8 after 8 hours?
Solution:

Question 37.
The decomposition of hydrocarbon follows the equation K = (4.5 × 1011 s-1) e-28000K/T. Calculate Ea.
Solution:
According to Arrhenius equation
k = Ae-Ea/RT ………………. (i)
According to the available data
k = (4.5 × 10 s-1)e-28000k/T ………………….. (ii)
on comparing both equations
\(-\frac{E_{\mathrm{a}}}{\mathrm{RT}}=\frac{-28000 \mathrm{k}}{\mathrm{T}}\)
Ea = (28000 k) × R
= (28000 k) × (8.314 K-1 J mol-1)
= 232792 Jk mol-1
Ea = 232.792 kJ-1 mol-1
![]()
Question 38.
The rate constant for the first order decomposition of H2O2 is given by the following equation: log k = 14.34 – 1.25 × 104 K/T. Calculate Ea for this reaction and at what temperature will its half-life period be 256 minutes?
Solution:
a) Calculation of activation energy Ea
According to Arrhenius equation; k = Ae-Ea/RT
log k = log A – \(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\) …………………. (i)
log K = 14.34 – \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\) …………………. (ii)
on comparing both equations.
\(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}=\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
Ea = 1.25 × 104 K × 2.303 × 8.314 (JK-1 mol-1)
= 23.93 × 104 J mol-1 = 239.3 kJ mol-1
b) Calculation of required temperature
If t1/2 = 256 min. for 1st order reaction;

Question 39.
The decomposition of A into product has value of k as 4.5 × 103 s-1 at 10°C and energy of activation 60 kJ mol-1. At what temperature would k be 1.5 × 104 s-1?
Solution:
According to Arrhenius equation
\(\log \frac{\mathrm{k}_2}{\mathrm{k}_1}=\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}} \times \frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\)
k1 = 4.5 × 103 s-1
k2 = 1.5 × 104 s-1
T1 = 10°C = 283 K

T2 = 297.19 K = (297.19 – 273.0) = 24.19°C
Temperature = 24.19°C
Question 40.
The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 × 1010 s-1. calculate k at 318K andE .
Solution:
Calculation of activation energy (Ea)
For 1st order reaction :

According to Arrhenius theory
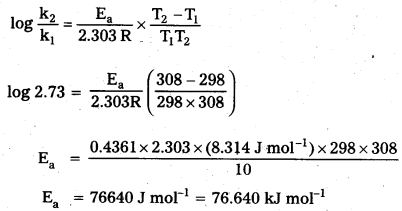
b) Calculation of rate constant (k)
According to Arrhenius equation
log k = log A \(\frac{-\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}\)
log k = log (4 × 1010) – \(\frac{76640 \mathrm{~J} \mathrm{~mol}^{-1}}{2.303 \times\left(8.314 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\right) \times(318 \mathrm{~K})}\)
log k = 10.6021 – 12.5870 = – 1.9849
k = Antilog (-1.9849) = Antilog \((\overline{2} .0151)\) = 1.035 × 10-2 s-1
Ea = 76.640 kJ mol-1
k = 1.035 × 10-2 s-1
![]()
Question 41.
The rate of a reaction quadruples when the temperature changes from 293 K to 313K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Solution:
According to Arrhenius equation

Textual Examples
Question 1.
From the concentrations of C4H9Cl (butyl chloride) at different times given below, calculate the average rate of the reaction :
C4H9Cl + H2O → C4H9OH + HCl
during different intervals of time.

Solution:
We can determine the difference in concentration over different intervals of time and thus determine the average rate by dividing ∆ [R] by ∆t
Average rates of hydrolysis of butyl chloride
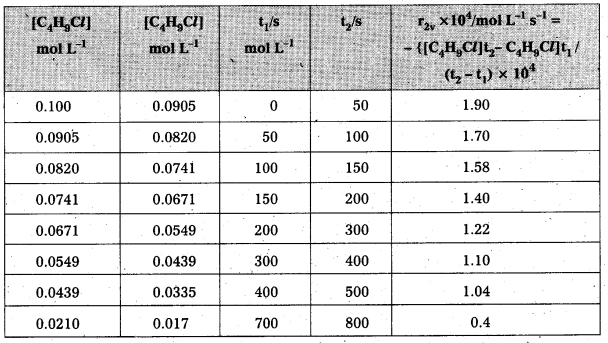
Question 2.
The decomposition of N2O5 in CCl4 at 318K has been studied by monitoring the concentration of N2O5 in the solution. Initially the concentration of N2O5 is 2.33 mol L-1 and after 184 minutes, it is reduced to 2.08 mol L-1. The reaction takes place according to the equation
2 N2O5 (g) → 4 NO2 (g) + O2 (g)
Calculate the average rate of this reaction in terms of hours, minutres and seconds. What is the rate of production of NO2 during this period?
Solution:
Average Rate = \(\frac{1}{2}\left\{-\frac{\Delta\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta \mathrm{t}}\right\}=-\frac{1}{2}\left[\frac{(2.08-2.33) \mathrm{mol} \mathrm{L}^{-1}}{184 \mathrm{~min}}\right]\)
= 6.79 × 10-4 mol L-1/min
= (6.79 × 10-4 mol L-1 min-1) × (60 min / 1h)
=4.07 × 10-2 mol L-1/h .
= 6.79 × 10-4 mol L-1 × 1mm / 60s = 1.13 × 10-5 mol L-1s-1
It may be remembered that
Rate = \(\frac{1}{4}\left\{\frac{\Delta\left[\mathrm{NO}_2\right]}{\Delta \mathrm{t}}\right\}\)
\(\frac{\Delta\left[\mathrm{NO}_2\right]}{\Delta \mathrm{t}}\) = 6.79 × 10-4 × 4 mol L-1 min-1
= 2.72 × 10-3 mol L-1 min-1
![]()
Question 3.
Calculate the overall order of a reaction which has the rate expression
a) Rate = k [A]1/2 [B]3/2
b) Rate = k [A]3/2 [B]-1
Solution:
a) Rate = k [A]x [B]y
order = x + y
So order = 1/2 + 3/2 = 2, i.e., second order
b) order = 3/2 + (- 1) = 1/2, i.e., half order.
A balanced chemical equation never gives us a true picture of how a reaction takes place since rarely a reaction gets completed in one step. The reactions taking place in one step are called elementary reactions. If a sequence of elementary reactions (called mechanism), reactants give in the products, the reactions are called complex reactions. These may be consecutive reactions (e.g., oxidation of ethane to CO2 and H2O passes through a series of intermediate steps in which alcohol, aldehyde and acid are formed), reversible reactions and parallel reactions (e.g., nitration of phenol yields o-nitrophenol and p-nitrophenol).
Question 4.
Identify the reaction order from each of the following rate constants.
- k = 2.3 × 10-5 L mol-1 s-1
- k = 3 × 10-4 s-1
Solution:
- The unit of second order rate constant is L mol-1 s-1, therefore k = 2.3 × 10-5 L mol-1 s-1represents a second order reaction.
- The unit of a first order rate constant is s-1 therefore k = 3 × 10-4 s-1 represents a first order reaction.
Question 5.
The initial concentration of N2O5 in the following first order reaction
N2O5(g) → 2 NO2(g) + \(\frac{1}{2 \mathrm{O}_2}\) (g) was 124 × 10-2 mol L-1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20 × 10-2 mol L-1 . Calculate the rate constant of the reaction at 318 K.
Solution:
For a first order reaction
\(\log \frac{[\mathrm{R}]_1}{[\mathrm{R}]_2}=\frac{\mathrm{k}\left(\mathrm{t}_2-\mathrm{t}_1\right)}{2.303}\)

k = 0.0304 min-1.
Question 6.
The following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
2N2O5 (g) → 22 O4 (g) + O2 (g)
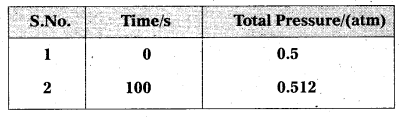
Calculate the rate constant.
Solution:
Let the pressure of N2O5 (g) decrease by 2x atm. As two moles of N2O5 decompose to give two moles of N2O4 (g) and one mole of O2 (g), the pressure of N2O4 (g) increases by 2x atm and that of O2 (g) increases by x atm.

Question 7.
A first order reaction is found to have a rate constant, k = 5.5 × 10-14 s-1. Find the half¬life of the reaction.
Solution:
Half-life for a first order reaction is
t1/2 = \(\frac{0.693}{k}\)
t1/2 = \(\frac{0.693}{5.5 \times 10^{-14} \mathrm{~S}^{-1}}\) = 1.26 × 1013 s
![]()
Question 8.
Show that in a first order reaction, time required for completion of 99.9% is 10 times of half-life (t1/2) of the reaction.
Solution:
When reaction is completed 99.9%, [R]n = [R]0 – 0.999 [R]0

Question 9.
Hydrolysis of methyl acetate in aqueous solution has been studied by titrating the liberated acetic acid against sodium hydroxide. The concentration of the ester at different times is given below.

Show that it follows a pseudo first order reaction, as the concentration of water remains nearly constant (55 mol L-1), during the course of the reaction. What is the value of k’ in this equation ?
Rate = k’ [CH3 COOCH3] [H2O]
Solution:
For pseudo first order reaction, the reaction should be first order with respect to ester when [H2O] is constant. The rate constant k for pseudo first order reaction is
k = \(\frac{2.303}{t} \log \frac{C_0}{C}\) where k = k’ [H2O]
From the above data we note
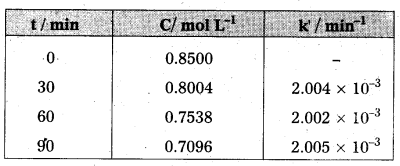
It can be seen that k’ [H2O] is constant and equal to 2.004 × 10-3 min-1 and hence, it is pseudo first order reaction. We can now determine k from
k’ [H2O] = 2.004 × 10-3 min-1
k'[55 mol L-1] = 2.004 × 10-3 min-1
k’ = 3.64 × 10-5 mol-1 L min-1
Question 10.
The rate constants of a reaction at 500 K and 700 K are 0.02s-1 and 0.07s-1 respectively. Calculate the values of Ea and A.
Solution:

![]()
Question 11.
The first order rate constant for the decomposition of ethyl iodide by the reaction.
C2H5I(g) → C2H4 (g) + HI(g) at 600K is 1.60 × 10-5 s-1. It is energy of activation is 209 kj/mol. Calculate the rate constant of the reaction at 700 K.
Solution:
We know that

Intext Questions
Question 1.
For the reaction, R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 min. Calculate the average rate of reaction using units of time both in minutes and seconds.
Solution:
For the reaction R → P

Question 2.
In a reaction, 2A → products, concentration of A decreases from 0.5 mol L-1 to 0.4 to mol L-1 in 10 min. Calculate the rate during this interval.
Solution:
Rate of reaction = rate of disappearance of A
= \(-\frac{1}{2} \frac{\Delta[\mathrm{A}]}{\Delta \mathrm{t}}\)
= \(-\frac{1}{2} \frac{(0.4-0.5) \mathrm{mol} \mathrm{L}^{-1}}{10 \mathrm{~min}}\)
= 0.005 mol L-1 m-1
Question 3.
For a reaction, A + B → product; the rate law is given by, r = k[A]1/2 [B]2. What is the order of the reaction ?
Solution:
Order of reaction = \(\frac{1}{2}\) + 2 = \(\frac{1}{2}\)
Order = \(\frac{5}{2}\)
![]()
Question 4.
The conversion of molecules X to Y follows second order kinetics. If concentration of x is increased to three times how will it affect the rate of formation of y ?
Solution:
For the reaction x → y
Reaction rate (r) = k[x]2 …………….. (i)
If the concentration of x is increased three times, then
Reaction rate (r’) = k[3x]2 = kx [9x]2 ……….. (ii)
Dividing Eq. (ii) by Eq. (i) .
\(\frac{\mathrm{r}^{\prime}}{\mathrm{r}}=\frac{\mathrm{k} \times[9 \mathrm{x}]^2}{\mathrm{k} \times[\mathrm{x}]^2}=9\)
It means that the rate of formation of y will increase by nine times.
Question 5.
What will be the effect of temperature on rate constant ?
Solution:
The rate constant for a reaction is nearly doubled with about 10° rise in temperature. The reason is that the number of effective collision becomes almost double. The exact dependence of the rate of reaction can be given by Arrhenius equation; k = Ae-Ea/RT. Where, A is called the frequency factor and Ea is the activation energy of the reaction.