AP Inter 2nd Year Maths 2B Important Questions Chapter 3 పరావలయం

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 3 పరావలయం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 3 పరావలయం

ప్రశ్న 1.
(కింద పరావలయాలకు శీర్షం, నాభు నిరూపకాలు, నియతరీఖ, అక్షరేఖల సమీకరణాలు కనుక్కోండి.
(i) y²=16 x
(ii) x²=-4y
(iii) 3 x²-9 x+5 y-2=0
(iv) y²-x+4 y+5=0
సాధన:
(i) y²=16 x, ను y²=4 a xతో ఏోల్చగా
4a=1.6 ⇒ a=4
శీర్షం నిరూపకాలు =(0,0)
నాభి నిరూపకాలు =(a, 0)=(4,0)
నియతరేఖ సమీకరణము : x+a=0, i.e., x+4=0
అక్షం సమీకరణము y=0

(ii) x²=-4y, ను x²=-4 ay, తో పోల్చగా
4a = 4 ⇒ a=1
శీర్షం నిరూపకాలు =(0,0)
నాభి నిరూపకాలు =(0,-a)=(0,-1)
నియతరేఖ సమీకరణము y-a =0
i.e., y-1=0
అక్షం సమీకరణము x=0

(iii) 3 x²-9 x+5 y-2=0
3(x²-3x)=2-5y

నియతరేఖ సమీకరణము y-k-a=0
i.e. 6y-13=0
అక్షం సమీకరణము x-h=0
i.e., 2 x-3=0

(iv) y²-x+4 y+5=0 ⇒ (y-(-2))²=(x-1) ను
(y-k)² =4 a(x-h), తో పోల్చగా
(h, k)=(1,-2) మరియు a=\(\frac{1}{4}\)
శీర్షం నిరూపకాలు (h, k)=(1,-2)
నాభి నిరూపకాలు (h+a, k) \(=\left(\frac{5}{4},-2\right)\)
నియతరేఖ సమీకరణము x-h+a=0
i.e., 4x-3=0
అక్షం సమీకరణము y-k=0.
i.e., y+2=0

ప్రశ్న 2.
(3,-2) శీర్షంగాను, (3,1) నాభిగాను గల పరావలయ సమీకరణం కనుక్రోండి.
సాధన:
నాభి శీర్షాల x నిరూపకాలు 3 తో సమానం. పరావలయ అక్షం X=3.
ఇది Y – అక్షానికి సమాంతరంగా శీర్షానికి ఎగువస (పైన) నాభి ఉంటుంది.
a = నాభి, శీర్షాల మధ్యదూరం = 3
∴ పరావలయ సమీకరణం
(x-3)²=4(3)(y+2)
i.e., (x-3)²=12(y+2).

ప్రశ్న 3.
y² =2x పరావలయంపై నాభి దూరం \(\frac{5}{2}\) గల బిందువులు కనుక్కోండి.
సాధన:
P (x₁,y₁) బిందువు పరావలయం మీద ఉంది
y²=2x నాభి నుండి దూరం \(\frac{5}{2}\) కనుక
y₁² = 2x₁ మరియు x₁+a= \(\frac{5}{2}\)
⇒ x₁+\(\frac{1}{2}=\frac{5}{2}\) ⇒ x₁=2
∴ y₁² = 2(2) = 4 ⇒ y₁=±2
∴  కావలసిన బిందువులు (2,2) మరియు (2,-2)

ప్రశ్న 4.
(-1, 2), (1, -1),(2, 1) బిందువుల గుండా హోతూ x – అక్షానికి సమాంతరంగా అక్షరేఖ గల పరావలయ సమీకరణాన్ని, కనుక్రోండి.
సాధన:
పరావలయం అక్షం X-అక్షానికి సమాంతరం కనుక దాని సమీకరణము.
x =ly²+my+n రూపంలో ఉంటుంది.
పరావలయం (-1,2) గుండా పోతుంది. కనుక -1
= 1(2)²+m(2)+n ⇒ 4l+2 m+n=-1 …………. (1)
పరావలయం (1,-1),(2,1) ల గుండా పోతుంది.
l- m+n =1 …………. (2)
l+m+n = 2 …………. (3)
(1), (2) మరియు (3) సాధించగా
\(l=-\frac{7}{6}, m=\frac{1}{2} \text { మరియు } \mathrm{n}=\frac{8}{3}\)
పరావలయ సమీకరణము
(లేదా) 7y² – 3y + 6x – 16 = 0.

ప్రశ్న 5.
పరావలయం y²=4 ax పై ద్వి y – నిరూపకం పాడవా 8 అయితే, ద్వి y – నిరూపక కొనలను శీర్షానికి కలిపితే వచ్చే రేఖలు లంబంగా ఉంటాయని చూపండి.
సాధన:
P = (at², 2at) మరియు P’ = (at²,-2 at) లు PP’ కానలు
8a = PP’ =\(\sqrt{0+(4 a t)^2}\) + (4at)2 = 4at ⇒ t = 2.
∴ P=(4a,4a), P’ = (4a,-4a)

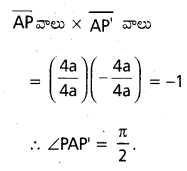
ప్రశ్న 6.
(i) y²=4 ax నాఖి జ్లా అగగాలు (x₁, y₁),(x₂, y₂) అయితే x₁ x₂=a², y₁ y₂=-4 a² అని రుజువ చేయండ.
(ii) y²=4 ax నాభి జ్యా PQ, SP=l, SQ=l’ అ అయతే \(\frac{1}{l}+\frac{1}{l^{\prime}}=\frac{1}{a}\) అని చూపండి.
సాధన:
(i) P(x₁, y₁)=(a t²₁, 2 at₁) మరియు Q(x₂, y₂)
=(a t²₂, 2at²) నాభి జ్యా కొనలు
P, S, Q లు సరేఖీయాలు

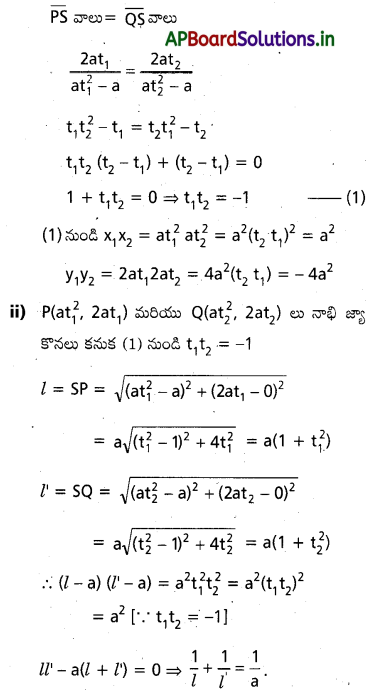
ప్రశ్న 7.
నాఖిగా గల పరావలయం y²=8(x-3) పై, బిందువు P నుంచి నియతరేఖ పైకి గీసిన లంబపాదము Q. SPQ సమబాహు తిిభుజం అయితే భజం పొడవు కనుక్రోండి.
సాధన:
దత్త పరావలయము y²=8(x-3) అయితే,
శీర్షం A=(3,0) నాభి =(5,0)
[∵ 4 a=8 ⇒ a=2] PQS సమబాహు తిరిభుజము కనుక

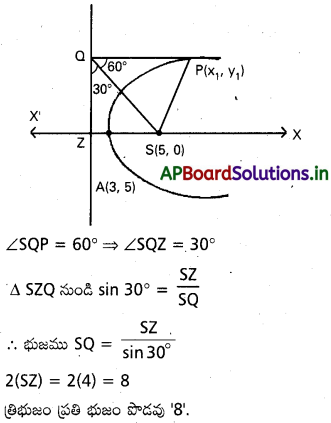
ప్రశ్న 8.
72 మీటర్ల పొడవు గల ఒక క్షితిజ సమాంతర వంతెన రోడ్డు, ఏకరూప భారవాహక శక్తి గలిగిన పరావలయ ఆకారపు ప్రధాన తీగకు అనుసంధానం చేసిన ఊర్థ్ సహాయ తీగలకు వేలాడుతున్నది. సహాయ తీగ గరిష్ఠ పొడవు 30 మీ, కనిష్ఠ పొడవు 6 మీ. అయితే వంతెన మధ్య పిందువు నుంచి 18 మీ. దూరంలో గల బిందువుల వద్ద గల సహాయక తీగ పౌడవు కనుక్కోండి.

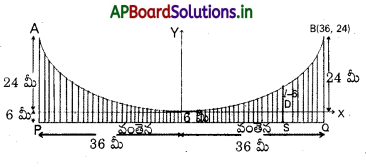
సాధన:
AOBను ప్రధాన తీగ అనుకొందాం. (కనిష్ఠ ఎత్తులోనున్న బిందువు O, గరిష్ఠ ఎత్తులోనున్న బిందువులు A, Be PRQ అనేది వంతెన PR = RQ = 36 మీ.
PA=QB=30 మీ (గరిష్ఠ ఊర్థ్ తీగలు).
OR=6 మీ (వంతెన మధ్య బిందువు R నుంచి నిట్టనిలువుగా ఉండే ఊర్మ్వ తీగ కనిష్ఠ ఎత్తులో ఉండే ఊర్థవీ తీగ అవుతుంది)
O ను మూలబిందువుగాను, (పధాన తీగకు O వద్ద నున్న స్పర్శ రేఖను, X-అక్షంగాను, \(\overleftrightarrow{\mathrm{RO}}\) ను Y- అక్షంగాను తీసుకొందాం.
పరావలయాకారంలో నున్న ప్రధాన తీగ యొక్క సమీకరణం x²=4 ay (a>0) రూపంలో ఉంటుంది.
B=(36,24) కాబట్టి 36²=4a 24 అవుతుంది.
4a=\(\frac{36 \times 36}{24}\)=54 మీ. RS =18 మీ. అనుకొందాం.
S గుండా పోమే ఊర్వ్వ రేఖ X-అక్షాన్ని D వద్ద, ప్రధాన తీగను C వద్ద ఖండిస్తూందనుకొంటే, SC అనేది కావలసిన అనుసంధానం చేసిన ఊర్ధ్వ తీగ అవుతుంది.
అంటే SC పొడపును కనుక్కోవాలి.
SC =l మీ అనుకొంటే, DC =(l-6) మీ అవుతుంది.
అప్పుడు C = (18, l-6) అవుతుంది.
C అనేది పరావలయం మీద పిందువు కాబట్టి
18=4 a(l-6) కావాలి.
l-6=\(\frac{18^2}{4 a}=\frac{18 \times 18}{54}\)=6మీ.
l-12 మీ.

ప్రశ్న 9.
పరావలయం y²=4 a x కు సరళరీఖ
lx+m y+n=0 స్రర్రేేఖ కావడానికి నియమం కనుక్రోండి. స్పర్శ బిందువు నిరూపకాలను కూడా కనుక్రోండి.
సాధన:
lx+m y+n=0 రేఖ y²=4 a x, వద్ద స్పర్శేేఖ.
(at², 2at) P(t) వద్ద స్పర్శరేఖ సమీకరణము
x-y t+a t²=0
కాబట్టి l x+m y+n=0, x-y t+a t²=0 లు ఒకే  రేఖను సూచిస్తాయి.

ప్రశ్న 10.
y²-7 x-8 y+14=0 పరావలయాన్ని, సరళరీఖ 7 x+6 y=13 స్పృశిస్తుందని.మూపి, స్ర్శబిందువు నిరాపకాలు కనుక్రోండి.
సాధన.
దత్తరీఖ సమీకరణము 7 x+6 y=13, పరావలయం
సమీకరణము y²-7 x-8 y+14=0.
x ను ఠౌలగిస్తే పరావలయం, రేఖల ఖండన బిందువుల నిరూపకాలు వస్తాయి.
కూడగా y²-2 y+1=0. i.e., (y-1)²=0 ⇒ y=1,1.
∴ దత్తరేఖ పరావలయానికి స్పర్శరేఖ,
y=1 అయితే x=1 స్ర్యబిందువు (1,1)

ప్రశ్న 11.
పరావలయం x, y- నిరాపకాలా సమానంగా గల మాల బిందువు కాని బిందువు వద్ద అభిలంబ జ్యా, నాష్ధి వద్ద లంబకోణం ేస్తందని చాపండి.
సాధన.
పరావలయ సమీకరణము
y²=4 a x పై P(at², 2at) ఏదైనా బిందువు …………….. (1)
పరావలయం మీద x, y నిరూపకాలు సమానము.
i.e., a t²=2 a t  ⇒ t=0
లేదా t=2. కాని t ≠ 0. బిండువు (4a, 4a) వద్ద అభిలంబరేఖ
y+2 x=2 a(2)+a(2)³  (లేదా)
y=(12 a – 2x) …………….. (2)
y=12 a-2 x(1) లో పతక్షపంచగా
(12 a-2x)²=4 ax (లేదా)
x²-13 a x+36 a²=(x-4 a)(x-9 a)=0
⇒ x=4 a, 9a
వీటికి అనుబంధ y విలువలు  4 a,-6 a . పరావలయం P వద్ద అభిలంబ రేఖల ఖండన బిందువు Q(9 a,-6 a),
S(a, 0) అని తెలుసు.

ప్రశ్న 12.
పరావలయం y²=4 a x కు బాహ్య బిందువు P నుంచి గీసిన స్రశశరేఖలు అక్షరీఖతో θ₁, θ₂ కోణాలు జేస్త్నాన్నాయి.  tanθ₁ + tanθ₂  విలువ స్థిరం b అయితే y=b x రేఖపై P ఉంటుందని చూపండ.
సాధన.
P నిరూపకాలు (x₁, y₁) పరావలయం సమీకరణము. y²=4 ax. ఏదైనా స్పర్యరేఖ సమీకరణము

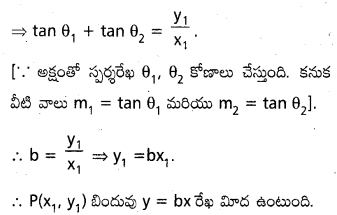
ప్రశ్న 13.
y²=4 a x, x²=4 b y పాాలయాలకు ఉమ్మడి స్ర్శరీఖ x a^1/3+y b^1/3+a^2/3 b^/3 =0 అని చాహండి.
సాధన:
దత్త పరావలయాల సమీకరణాలు y²=4 ax మరియు ………….. (1)
x²=4 by ………….. (2)
(1) యొక్క స్పర్యరేఖ రూపము y =m x+\(\frac{a}{m}\) ………….. (3)
(3) సూచించే రేఖ (2) కు స్ర్శరేఖ అయితే వీటికి ఒకే ఖండన బిందువు ఉంటుంది.
(3) నుండి y విలువను (2) లో (ప్రతిక్షేపించగా

ప్రశ్న 14
పరావలయం y²=4 a x(a>0) పై (x₁, y₁), (x₂, y₂), (x₃, y₃) ఐిందువుల వద్ద గీసిన స్పర్శరేఖలతో ఏర్పడే (తరిభుజ వైశాల్యం \(\frac{1}{16 a} \mid\left(y_1-y_2\right)\left(y_2-y_3\right)\left(y_3-y_1\right) \mid\) అని రుజువు చేయండి.
సాధన:

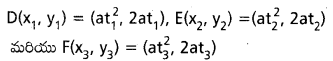
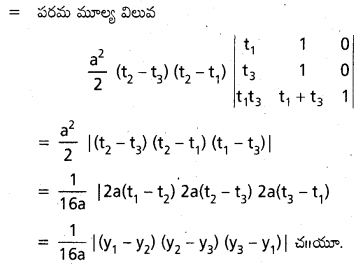
ప్రశ్న 15.
y²=4 a x, x²=4 by అనే పరావలయాల (మూలబిందువు వద్ద కాకుండా) వ్యతిచ్చేదక కోణం
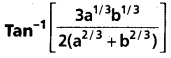అని చూపండి.
సాధన:
సార్వతతికికానికి భంగం లేకుండా a>0, b>0 అనుకుండాం. పరావలయాలు P(x, y) అనే మూలబిందువు కాని బిందువు వద్ద ఖండించుకొంటాయనుకొందాం. అప్పుడు y⁴=16 a² x²

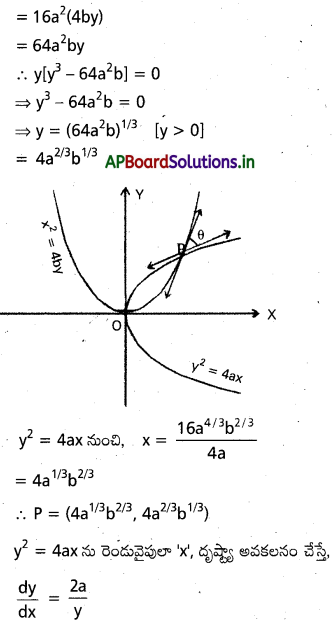
ప్రశ్న 16.
పరావలయం మీది మూడు బిందువుల వద్ద ఉండే స్ర్శరీఖలతో ఏర్పడే కతిియజం లంబకేంద్రం పరావలయం నియత రీఖపై ఉంటుందని చాపండి.
సాధన:
\(A=\left(a t_1^2, 2 a t_1\right), B=\left(a t_2^2, 2 a t_2\right), C=\left(a t_3^2, 2 a t_3\right)\)
అనేవి y²=4 ax అనే పరావలయం మీద బిందువులు.
A, B, C ల వద్ద పరావలయానికి గల స్పర్శరేఖలతో ఏర్పడిన త్రిభుజాన్ని PQR అనుకొంటే,

కాబట్టి PQR, త్రిభుజం యొక్క లంబకేంద్ర – x నిరూపకం -a, అవటం చేత, అది పరావలయ నియతరేఖపై ఉంటుంది.