AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Ex 1(e)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 1 వృత్తం Exercise 1(e) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Exercise 1(e)

అభ్యాసం – 1 (ఇ)

I.

ప్రశ్న 1.
కింది ఇచ్చిన వృత్తాల జతల సాపేక్ష స్థితిని తెలపండి.
i) x² + y² – 4x – 6y – 12 = 0
x² + y² + 6x + 18y + 26 = 0.
సాధన:
వృత్తాల కేంద్రాలు A (2, 3), B(-3, – 9)
వ్యాసార్ధాలు r₁ = \(\sqrt{4+9+12}\) = 5
r₂ = \(\sqrt{9+81-26}\) = 8
AB = \(\sqrt{(2+3)^2+(3+9)^2}\)
= \(\sqrt{25+144}\) = 13 = r₁ + r₂
∴ వృత్తాలు బాహ్యంగా స్పృశించుకుంటాయి.

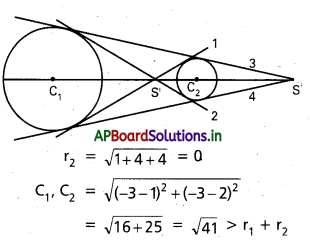
ii) x² + y² + 6x + 6y + 14 = 0,
x² + y² – 2x – 4y – 4 = 0.
సాధన:
కేంద్రాలు A (-3, -3), B (1, 2)
r₁ = \(\sqrt{9+9-14}\) = 2
r₂ = \(\sqrt{1+4+4}\) = 3
AB = \(\sqrt{(-3-1)^2+(-3-2)^2}\)
= \(\sqrt{16+25}\) = \(\sqrt{41}\) > r₁ + r₂
∴ వృత్తాలు ఒకదానికొకటి బాహ్యంగా ఉంటాయి.

iii) (x – 2)² + (y + 1)² = 9, (x + 1)² + (y – 3)² = 4
సాధన:
కేంద్రాలు A( 2 – 1), B(−1, 3)
r₁ = \(\sqrt{4+1+4}\) = 3
r₂ = \(\sqrt{1+9-6}\) = 2
AB = \(\sqrt{(2+1)^2+(-1-3)^2}\)
= \(\sqrt{9+16}\)
= 5 = r₁ + r₂
∴ వృత్తాలు బాహ్యంగా స్పృశించుకుంటాయి.

iv) x² + y² – 2x + 4y – 4 = 0,
x² + y² + 4x – 6y – 3 = 0
సాధన:
కేంద్రాలు A (1, -2), B (-2, 3)
r₁ = \(\sqrt{1+4+4}\) = 3
r₂ = \(\sqrt{4+9+3}\) = 4
AB = \(\sqrt{(1+2)^2+(-2-3)^2}\)
= \(\sqrt{9+25}\) = \(\sqrt{34}\) < r₁ + r₂
r₁ – r₂ < AB < r₂ + r₁
∴ వృత్తాలు ఖండించుకుంటాయి.

ప్రశ్న 2.
కింద వృత్తాల జతలకు ఎన్ని ఉమ్మడి స్పర్శ రేఖలు గీయవచ్చో తెలపండి.
సాధన:
i) x² + y²+ 6x + 6y+ 14 = 0,
x² + y² – 2x – 4y – 4 = 0
సాధన:
c₁ (-3, -3) c₂ = (1, 2)
r₁ = \(\sqrt{9+9-14}\) = 2,

ii) x² + y² – 4x – 2y + 1 = 0;
x² + y² – 6x – 4y + 4 = 0
సాధన.
C₁ = (2,1)
C₂ = (3,2)
r₁ = \(\sqrt{4+1-1}\)
= 2
r₂ = \(\sqrt{9+4-4}\)
= 3

C₁C₂ = \(\sqrt{(2-3)^2+(1-2)^2}\) = \(\sqrt{2}\)
C₁C₂ < r₁ + r₂
2 ఉమ్మడి స్పర్శరేఖలు

iii) x² + y² – 4x + 2y – 4 = 0;
x² + y² + 2x – 6y + 6 = 0
సాధన:
C₁ (2, 1)
C₂ = (-1, 3)
r₁ = \(\sqrt{4+1+4}\)
= 3
r₂ = \(\sqrt{1+9-6}\)
= 2

C₁ C₂ = r₁ + r₂ బాహ్యంగా స్పృశించుకుంటాయి.
ఉమ్మడి స్పర్శరేఖలు – 3.

iv) x² + y² = 4; x² + y² – 6x – 8y + 16 = 0
సాధన:
C₁ = (0, 0)
C₂ = (3, 4)
r₁ = 2
r₂ = \(\sqrt{9+16-16}\) = 3
C₁C₂ = \(\sqrt{(0-3)^2+(0-4)^2}\) = 5
r₁ + r₂ = C₁ C₂
వృత్తాలు బాహ్యంగా స్పృశించుకుంటాయి.
2 – ప్రత్యక్ష స్పర్శరేఖ
1 – తిర్యక్ స్పర్శరేఖ
ఉమ్మడి స్పర్శరేఖలు = 3.

v) x² + y² + 4x – 6y – 3 = 0;
x² + y²+4x – 2y + 4 = 0.
సాధన:
C₁ = (-2, 3)
C₂ = (-2, 1)
r₁ = \(\sqrt{4+9+3}\)
= 4
r₂ = \(\sqrt{4+1-4}\)
= 1
C₁C₂ = \(\sqrt{(-2+2)^2+(3-1)^2}\)
C₁C₂ = 2 < 3 = r₁ – r₂
ఒక వృత్తానికి అంతరంగా రెండో వృత్తం ఉంటుంది.
∴ ఉమ్మడి స్పర్శరేఖలు లేవు.

ప్రశ్న 3.
x² + y²+ 6x – 2y + 1 = 0, x² + y² – 2x – 6y + 9 = 0 వృత్తాలకు అంతర సరూప కేంద్రం కనుక్కోండి.
సాధన:
C₁ = (-3, 1)
C₂ = (1, 3)
r₁ = \(\sqrt{9+1-1}\)
= 3
r₂ = \(\sqrt{1+9-9}\)
= 1

ప్రశ్న 4.
x² + y² – 2x – 6y + 9 = 0, x² + y² = 4 వృత్తాల బాహ్య సరూప -కేంద్రం కనుక్కోండి.
సాధన:
వృత్తాల కేంద్రాలు C₁ (1, 3), C₂ (0, 0)
r₁ = \(\sqrt{1+9-9}\)
= 1
r₂ = 2
బాహ్య నిరూపక కేంద్రం S¹, C₁, C₂ ను బాహ్యంగా, r₁ : r₂ = 1 : 2 నిష్పత్తిలో విభజిస్తుంది.

II.

ప్రశ్న 1.
i) x² + y² – 6x – 2y + 1 = 0; x² + y² + 2x – 8y + 13 = 0 స్పృశిస్తాయని చూపిస్తూ, స్పర్శబిందువును, ఆ బిందువు దగ్గర దత్త వృత్తాలకు ఉమ్మడి స్పర్శ రేఖ సమీకరణాలను కనుక్కోండి. [A.P. Mar. ’16 (Mar. ’11)]
సాధన:
వృత్త కేంద్రాలు C₁ = (3, 1), C₂ = (-1, 4)
వాటి వ్యాసార్ధాలు r₁ = \(\sqrt{9+1-1}\) = 3
r₂ = \(\sqrt{1+16-13}\) = \(\sqrt{4}\)= 2

∵ C₁C₂ = r₁ + r₂
⇒ రెండు వృత్తాలు బాహ్యంగా స్పృశించుకుంటాయి.
స్పర్శ బిందువు P అనుకుంటే, P బిందువు C₁ C₂ రేఖాఖండాన్ని అంతరంగా r₁ : r₂ (i.e.,) 3 : 2 నిష్పత్తిలో విభజిస్తుంది. కనుక
P = \(\left(\frac{3(-1)+2(3)}{5}, \frac{3(4)+2(1)}{5}\right)\)
= \(\left(\frac{3}{5}, \frac{14}{5}\right)\)
P వద్ద ఏదేని ఒక వృత్తానికి గీచిన స్పర్శరేఖయే ఉమ్మడి స్పర్శరేఖ అవుతుంది.
∴ P \(\left(\frac{3}{5}, \frac{14}{5}\right)\) వద్ద x² + y² – 6x – 2y + 1 = 0
వృత్తానికి స్పర్శరేఖా సమీకరణము
S₁ = 0
(i.e.,) x \(\left(\frac{3}{5}\right)\) + y \(\left(\frac{14}{5}\right)\) – 3 \(\left(x+\frac{3}{5}\right)\) – 1 \(\left(y+\frac{14}{5}\right)\) + 1 = 0
⇒ 3x + 14y – 15x – 9 – 5y – 14 + 5 = 0
⇒ -12x + 9y – 18 = 0
4x – 3y + 6 = 0

ii) x² + y² – 6x – 9y + 13 = 0;
x² + y² – 2x – 16y = 0 వృత్తాలు పరస్పరం స్పృశిస్తాయని చూపిస్తూ, స్పర్శబిందువును, ఆ బిందువు దగ్గర దత్త వృత్తాలకు ఉమ్మడి స్పర్శరేఖ సమీకరణాలను కనుక్కోండి.
సాధన:
వృత్తాల సమీకరణాలు x² + y² – 6x – 9y + 13 = 0,
x² + y² – 2x – 16y = 0
వృత్త కేంద్రాలు C₁ = (3, \(\frac{9}{2}\)), C₂ = (1, 8)
r₁ = \(\sqrt{9+\frac{81}{4}-13}=\sqrt{\frac{36+81-52}{4}}=\frac{\sqrt{65}}{2}\)
r₂ = \(\sqrt{1+64}=\sqrt{65}\)

దత్త వృత్తాలు అంతరంగా స్పృశించుకుంటాయి.
సర బిందువు P, C₁ C₂ ని బాహ్యంగా 2 : 1 నిష్పత్తిలో విభజిస్తుంది.

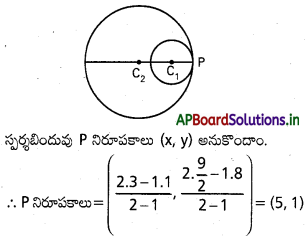
రెండవ వృత్తానికి స్పర్శరేఖ సమీకరణం
x.5 + y.1 – 1(x + 5) − 8(y + 1) = 0
5x + y – x – 5 – 8y – 8 = 0
4x – 7y – 13 = 0

ప్రశ్న 2.
x² + y² – 2x – 4y – 20 = 0 (5, 5) బిందువు వద్ద బాహ్యంగా స్పృశిస్తూ 5 యూనిట్ల వ్యాసార్ధం ఉన్న వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
x² + y² – 2x – 4y – 20 = 0
C = (1, 2)
r = \(\sqrt{1+4+20}\) = 5

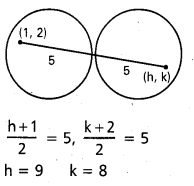
వృత్త సమీకరణం
(x – 9)² + (y – 8)² = 25
x² + y² – 18x – 16y + 120 = 0
కావలసిన వృత్త కేంద్రం (h, k) అయితే (3, 2) మరియు (h, k) ల మధ్య బిందువు (5, 5).

ప్రశ్న 3.
3x² + y² + 22x – 4y – 100 = 0; x + y – 22x + 4y + 100 = 0 వృత్తాల ప్రత్యక్ష ఉమ్మడి స్వర్య రేఖలు కనుక్కోండి.
సాధన:
C₁ = (-11, 2)
C₂ = (11, -2)
r₁ = \(\sqrt{121+4+100}\) = 15
r₂ = \(\sqrt{121+41-100}\) = 5
y = mx + c స్పర్శరేఖ అనుకొనుము.
mx – y + c = 0

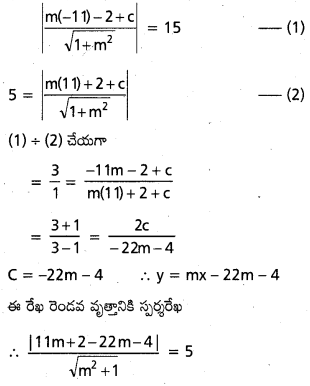
వర్గీకరించి అడ్డ గుణకారము చేయగా
25 (1 + m²) = (11m + 2 – 22m – 4)²
96m² + 44m – 21 = 0
⇒ 96m² + 72m – 28m – 21 = 0
m = \(\frac{7}{24}\), \(\frac{-3}{4}\)
C = \(\frac{25}{2}\)
స్పర్శరేఖ సమీకరణము
y = – \(\frac{3}{4}\)x + \(\frac{25}{2}\)
4y + 3x = 50 ⇒ 3x + 4y – 50 = 0
C = -22m – 4
= – 22(\(\frac{7}{24}\)) – 4
= \(\frac{-77-48}{12}\) = \(\frac{-125}{12}\)
y = \(\frac{7}{24}\) x – \(\frac{125}{12}\)
స్పర్శరేఖ సమీకరణము
⇒ 24y = 7x – 250
⇒ 7x – 24y – 250 = 0

ప్రశ్న 4.
x² + y² – 4x – 10y + 28 = 0; x² + y²+ 4x – 6y+ 4 = 0 55 ఉమ్మడి స్పర్శరేఖలు కనుక్కోండి.
సాధన:
C₁ = (2, 5), C₂ = (−2, 3)
r₁ = \(\sqrt{4+25-28}\) = 1, r₂ = \(\sqrt{4+9-4}\) = 3
r₁ + r₂ = 4
C₁C₂ = \(\sqrt{(2+2)^2+(5-3)^2}\)
= \(\sqrt{16+4}=\sqrt{20}\)
‘C’ బిందువు C₁C₂ ని 5 : 3 నిష్పత్తిలో విభజిస్తుంది.

-2x – y + 7)² = (x² + y² – 4x − 10y + 28)
4x² + y² + 4xy – 28x – 14y + 49 = x² + y² – 4x – 10y + 28
3x² + 4xy – 24x – 4y + 21
(3x + 4y – 21); (x – 1) = 0
3x + 4y – 21 = 0; x – 1 = 0

ప్రశ్న 5.
P (4,10) నుంచి x² + y² = 25 వృత్తానికి గల స్పర్శరేఖ యుగ్మ సమీకరణాన్ని కనుక్కోండి.
సాధన:
SS₁₁ = S₁²,
(x² + y² – 25) (16 + 100 – 25) = (4x + 10 y – 25)² 91x² + 91y² – 2275
= [16x² + 100y² + 625 + 80 xy – 200x – 500y] 75x² – 9y² – 80 xy + 500y + 200 x – 2900 = 0

ప్రశ్న 6.
(0, 0) x² + y² + 10x + 10y + 40 = 0 వృత్తానికి గల స్పర్శ రేఖాయుగ్మ సమీకరణాన్ని కనుక్కోండి.
సాధన:
SS₁₁ = S₁²
(x² + y² + 10x + 10y + 40) (40)
= [5x + 5y + 40]²
8(x² + y² + 10x + 10y + 40) = 5(x + y + 8)²
8x² + 8y² + 80x + 80y + 320 = 5x² + 5y² + 10xy + 80x + 80y +
3x² + 3y² – 10xy = 0

III.

ప్రశ్న 1.
x² + y² – 4x + 6y – 12 = 0 వృత్తాన్నీ (-1, 1) వద్ద అంతరంగా స్పృశిస్తూ, 2 యూనిట్లు వ్యాసార్ధం ఉన్న వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణం x² + y² – 4x + 6y – 12 = 0
కేంద్రం C₁ (+2, -3)
వ్యాసార్ధం (r₁) = \(\sqrt{4+9+12}\) = \(\sqrt{25}\) = 5
కావలసిన వృత్త వ్యాసార్ధం (r) = 2
కావలసిన వృత్త కేంద్రం C₂ (α, β) అనుకుందాం.

∴ కావలసిన వృత్త సమీకరణం
\(\left(x-\frac{1}{5}\right)^2\) + \(\left(y+\frac{-3}{5}\right)^2\) = 2²
⇒ x² + \(\frac{2x}{5}\) + y² + \(\frac{6}{5}\)y + \(\frac{9}{25}\) = 4
⇒ 25(x² + y²) – 10x + 1+ 30y + 9 = 100
⇒ 25(x² + y²) – 10x + 30y – 90 = 0
⇒ 5(x² + y²) – 2x + 6y – 18 = 0

ప్రశ్న 2.
కింది వృత్త యుగ్మాలకు అన్ని ఉమ్మడి స్పర్శ రేఖలు కనుక్కోండి. (i) x² + y² = 9, x² + y² – 16x + 2y + 49 = 0
సాధన:
వృత్త సమీకరణాలు x² + y² = 9
x² + y² – 16x + 2y + 49 = 0
కేంద్రలు A (0, 0), B(8, -1)
r₁ = 3, r₂ = \(\sqrt{64+1-49}\) = 4
AB = \(\sqrt{(0-8)^2+(0+1)^2}\)
= \(\sqrt{64+1}\) = \(\sqrt{65}\) > r₁ + r₂
వృత్తాలు ఒకదానికొకటి బాహ్యంగా ఉంటాయి.
A(0, 0), B(8, -1)
బాహ్యసరూప కేంద్రం S, AB ని బాహ్యంగా 3 : 4 నిష్పత్తిలో విభజిస్తుంది.
నిరూపకాలు (-24, + 3)
ప్రత్యక్ష స్పర్శరేఖ వాలు m అనుకొనుము.
y – 3 = m(x + 24)
= mx + 24m
mx – y + (24m + 3) = 0 ……………. (1)
ఇది x² + y² = 9 వృత్తానికి స్పర్శరేఖ సమీకరణము
3 = \(\frac{|24 m+3|}{\sqrt{m^2+1}}\)
9(m² + 1) = 9(8m + 1)²
= 64m² + 10m + 1
63m² + 16m = 0
m(63m+10) = 0
m = 0 లేదా \(\frac{-16}{63}\)

సందర్భం (i) : m = 0
(1) లో ప్రతిక్షేపిస్తే స్పర్శరేఖ సమీకరణము
-y + 3 = 0
y – 3 = 0
సందర్భం (ii): m = \(\frac{-16}{63}\)
స్పర్శరేఖ సమీకరణము
\(\frac{-16}{63}\) x – y + (\(\frac{-384}{63}\) + 3) = 0
\(\frac{-16}{63}\) x – y + \(\frac{195}{63}\) = 0
16x + 63y + 195 = 0
అంతర సరూప కేంద్రము S’, AB ని అంతరంగా 3:4 నిష్పత్తిలో విభజిస్తుంది.
S’ నిరూపకాలు
తిర్యక్ ప్రత్యక్ష స్పర్శరేఖా సమీకరణము
y + \(\frac{3}{7}\) = m(x – \(\frac{24}{7}\))
\(\frac{7 y+3}{7}=\frac{m(7 x-24)}{7}\)
7y + 3 = 7mx – 24m
7mx – 7y – (24m + 3) = 0 ……………. (2)
స్పర్శరేఖా సమీకరణము x² + y² = 9
3 = \(\frac{|24 m+3|}{\sqrt{49 m^2+49}}=\frac{3}{7} \frac{|28 m+1|}{\sqrt{m^2+1}}\)
49 (m² + 1) = (8m + 1)²
49m² +49 = 64m² + 16m + 1
15m² + 16m – 48 = 0
(3m – 4) (5m + 12) = 0
m = \(\frac{4}{3}\) లేదా \(\frac{-12}{5}\)

సందర్భం (i) : : (2) లో ప్రతిక్షేపిస్తే స్పర్శరేఖా సమీకరణము
\(\frac{28}{x}\) x – 7y – (\(\frac{96}{3}\) + 3) = 0
\(\frac{28}{x}\) x – 7y – \(\frac{105}{3}\) = 0
\(\frac{7}{3}\) (4x – 3y – 15) = 0
4x – 3y – 15 = 0
సందర్భం (ii) : : m = \(\frac{-12}{5}\)
తిర్యక్ ఉమ్మడి స్పర్శరేఖాసమీకరణము
\(\frac{-84}{5}\) x – 7y – (\(\frac{-288}{5}\) + 3) = 0
\(\frac{-84}{4}\) x – 7y + \(\frac{273}{5}\) = 0
\(\frac{-7}{5}\) (12x + 5y – 39) = 0
i.e., 12x + 5y – 39 = 0
∴ ప్రత్యక్ష స్పర్శరేఖల సమీకరణాలు
y – 3 = 0 మరియు 16x + 63y+ 195 = 0
తిర్యక్ స్పర్శరేఖల సమీకరణాలు
4x – 3y – 15 = 0 మరియు 12x + 5y – 39 = 0

ii) x² + y² + 4x + 2y – 4 = 0, x² + y² – 4x – 2y + 4 = 0.
సాధన:
కేంద్రాలు A (-2, -1), B(2, 1)
r₁ = \(\sqrt{4+1+4}\) = 3, r₂ = \(\sqrt{4+1-4}\) = 1
బాహ్య సరూప కేంద్రము S, AB ని 3 : 1 నిష్పత్తిలో బాహ్యంగా విభజిస్తుంది.

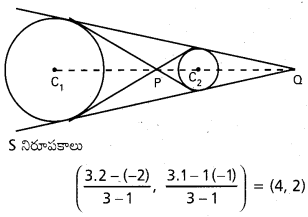
స్పర్శరేఖ వాలు m అనుకొందాం
స్పర్శరేఖ సమీకరణము
y – 2 = m (x – 4)
= mx – 4m
mx – y + (2 – 4m) = 0 …………… (1)
ఈ రేఖ వృత్తాన్ని స్పృశిస్తుంది.
x² + y² + 4x + 2y – 4 = 0
\(\frac{|-2 m+1+2-4 m|}{\sqrt{m^2+1}}\) = 3
\(\frac{3|1-2 m|}{\sqrt{m^2+1}}\) = 3
వర్గీకరించి, అడ్డ గుణకారము చేయగా
(1 – 2m)² = (m² + 1)
4m² – 4m + 1 = m² + 1
3m² – 4m = 0
m(3m – 4) = 0
m = 0 లేదా \(\frac{4}{3}\)

సందర్భం (i) : m = 0
(1) లో ప్రతిక్షేపిస్తే, స్పర్శరేఖ సమీకరణము
y + 2 = 0 లేదా
y – 2 = 0

సందర్భం (ii) : m = \(\frac{4}{3}\)
(1) లో ప్రతిక్షేపిస్తే, స్పర్శరేఖ సమీకరణము
\(\frac{4}{3}\) x – y + (2 – \(\frac{1}{3}\)) = 0
⇒ \(\frac{4}{3}\) x – y + \(\frac{10}{3}\) = 0
4x – 3y – 10 = 0
అంతర సరూప కేంద్రము S’, AB ని 3 : 1 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
S’ నిరూపకాలు \(\left(\frac{6-2}{3+1}, \frac{3-1}{3+1}\right)=\left(1, \frac{1}{2}\right)\)
స్పర్శరేఖ సమీకరణము
y – \(\frac{1}{2}\) = m (x – 1)
= mx – m
mx – y + (\(\frac{1}{2}\) – m) = 0 ………………. (2)
ఇది వృత్తానికి స్పర్శరేఖ
x² + y² + 4x + 2y – 4 = 0
\(\frac{\left|-2 m+1+\frac{1}{2}-m\right|}{\sqrt{m^2+1}}\) = 3
\(\frac{3}{2} \frac{|1-2 m|}{\sqrt{m^2+1}}\) = 3
వర్గీకరించి, అడ్డ గుణకారము చేయగా
(1 – 2m)² = 4(m² + 1)
1 + 4m² – 4m = 4m² + 4
m విలువ ∞, కనుక స్పర్శరేఖ, ఊర్థ్వరేఖ స్పర్శరేఖ సమీకరణము
x = 1
x – 1 = 0
4m + 3 = 0
m = \(\frac{-3}{4}\)
(2) లో ప్రతిక్షేపిస్తే, స్పర్శరేఖ సమీకరణము
⇒ \(\frac{-3}{4}\)x – y + (\(\frac{1}{2}\) + \(\frac{3}{4}\)) = 0
– 3x + 4y + 5 = 0
3x + 4y – 5 = 0
ప్రత్యక్ష స్పర్శరేఖల సమీకరణాలు
y – 2 = 0, 4x – 3y – 10 = 0
తిర్యక్ స్పర్శరేఖల సమీకరణాలు
x – 1 = 0, 3x + 4y – 5 = 0

ప్రశ్న 3.
(3, 2) o x² + y² – 6x + 4y – 2 = 0 వృత్తానికి గల స్పర్శ రేఖా యుగ్య సమీకరణాన్ని కనుక్కోండి.
సాధన:
S.S₁₁ = S₁²,
(x² + y² – 6x + 4y – 2) (9 + 4 – 6 × 3 + 4 × 2 – 2)
= (3x + 2y – 3(x + 3) + 2(y + 2) – 2)²
(x² + y² – 6x + 4y – 2) = (4y – 7)²
x² + y² – 6x + 4y – 2 = 16y² – 56y + 49
x² – 15y² – 6x + 60y – 51 = 0

ప్రశ్న 4.
(1, 3) నుంచి x² + y² – 2x + 4y – 11 = 0 వృత్తానికి గల స్వద్య లేఖా యుగ్య సమీకరణాన్ని కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
S.S₁₁ = S₁²
(x² + y² – 2x + 4y – 11) (1 + 9 – 2 + 12 – 11) = (x + 3y – 1(x + 1) + 2(y + 3) – 11]²
(x² + y² – 2x + 4y – 11) 9 = [5y – 6]²
9x² + 9y² – 18x + 36y – 99 = 25y² + 36 – 60y
9x² – 16y² – 18x + 96y – 135 = 0

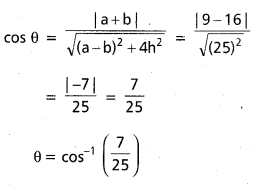
ప్రశ్న 5.
మూల బిందువు నుంచి x² + y² + 2gx +2fy +c = 0 వృత్తానికి స్పర్శ రేఖాయుగ్మ సమీకరణాన్ని కనుక్కోండి. దీని నుంచి ఆ స్పర్శ రేఖలు లంబంగా ఉండటానికి నియమాన్ని రాబట్టండి.
సాధన:
S.S₁₁ = S₁²
(x² + y² + 2gx + 2fy + c) (c) = [gx + fy + c]² = g²x² + f²y²+ 2gfxy + 2gcx + 2fyc + c²
(gx + fy)² = c(x² + y²)
g²x² + f²y² + 2fg xy = cx² + cy²
(g² – c)x² + 2fgxy + (f² – c) y² = 0
స్పర్శరేఖలు లంబంగా ఉన్నాయి. కనుక
x² గుణకం + y² గుణకం = 0
g² – c + f² – c = 0
g² + f² = 2c

ప్రశ్న 6.
x² + y² + 2gx + 2fy + c = 0 వృత్తం మీద ఏదైనా బిందువు నుంచి x² + y² + 2gx + 2fy + c sin² α + (g² + f²) cos² α = : 0 (0 < α < π/2) వృత్తానికి స్పర్శరేఖలు గీసినట్లెతే ఆ స్పర్శరేఖా యుగ్మ రేఖల మధ్య కోణం 2α అని చూపండి.
సాధన:
(x² + y² + 2gx₁ + 2fy₁ + c sin² α + (g² + f²) cos² α ] (s)
= (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c sin² α + (g² + f²) cos² α)² [(-c + c sin² α) + (g² + f²) cos² α ]S
= (x (x₁ + g) + y (y₁ + f) + gx₁ + fy₁ + c sin² α + (g² + f²) cos² α)² [cos² α (g² + f² – c)] S
= [x (x₁ + g) + y (y₁ + f) + gx₁ + fy₁ + c sin² α + (g² + f²) cos² α)²
g² + f² – c = r²
[(cos² α)r²] S = [x (x₁ + g) + y (y₁ + f)
+ gx₁ + fy₁ + c + (cos² α).r²)²
x² యొక్క గుణకము r² cos² α – (x₁ + g)²
y² యొక్క గుణకము r² cos² α – (y₁ + f)²
xy యొక్క గుణకము
h. cos¹α r¹ – 2 (x₁ + g) (y₁ + f)
cos θ = \(\frac{a+b}{\sqrt{(a-b)^2+4 h^2}}\)

cos θ = cos 2α
θ = 2α కనుక ఫలితము నిరూపంచబడింది.