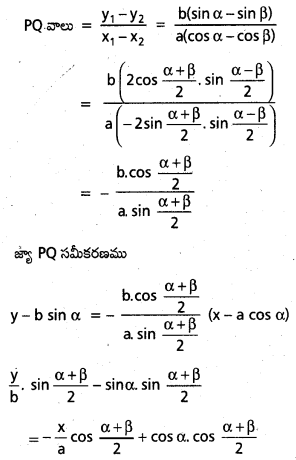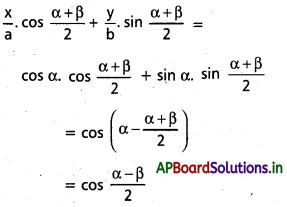AP Inter 2nd Year Maths 2B Solutions Chapter 4 దీర్ఘవృత్తం Ex 4(a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 4 దీర్ఘవృత్తం Exercise 4(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 4 దీర్ఘవృత్తం Exercise 4(a)

అభ్యాసం – 4(ఎ)

I.

ప్రశ్న 1.
నియత రేఖ x + y + 2 = 0 గాను, e = \(\frac{2}{3}\), ఒక నాభి (1, −1) వద్ద గల దీర్ఘవృత్త సమీకరణం కనుక్కోండి. [Mar. ’05]
సాధన:
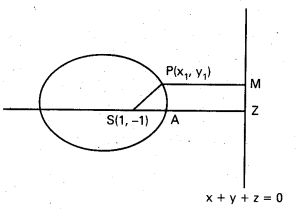
P(x₁, y₁) దీర్ఘవృత్తం మీద బిందువు
నియత రేఖ సమీకరణం
x + y + 2 = 0
ZM కు లంబంగా PM ను గీద్దాం. SP ని కలుపుదాం.
నిర్వచనం ప్రకారం SP = e. PM
SP² = e² . PM²
(x₁ – 1)² + (y₁ + 1)² = \(\left(\frac{2}{3}\right)^2\left[\frac{x_1+y_1+2}{\sqrt{1+1}}\right]^2\)
(x₁ – 1)² + (y₁ + 1)² = \(\frac{4}{9} \frac{\left(x_1+y_1+2\right)^2}{2}\)
9[(x₁ – 1)² + (y₁ + 1)²] = 2[x₁ + y₁ + 2]²
9[x₁² – 2x₁ + 1 + y₁² + 2y₁ +1] = 2[x₁² + y₁² + 4 + 2x₁y₁ + 4x₁ + 4y₁]
9x₁² + 9y₁² – 18x₁ + 18y₁ + 18 = 2x₁² + 2y₁² +4x₁y₁ + 8x₁ + 8y₁ + 8
7x₁² – 4x₁y₁ + 7y₁² – 26x₁ + 10y₁ + 10 = 0
P (x₁, y₁)
7x² – 4xy + 7y² – 26x + 10y + 10 = 0
ఇది కావలసిన దీర్ఘవృత్తం సమీకరణం.

ప్రశ్న 2.
నాభిలంబం పొడవు \(\frac{15}{2}\). నాభుల మధ్యదూరం 2 గా గల దీర్ఘవృత్తం సమీకరణం ప్రామాణిక రూపంలో కనుక్కోండి.
సాధన:
నాభి లంబము పొడవు = \(\frac{15}{2}\)
నాభుల మధ్య దూరము = 2
\(\frac{2 b^2}{a}=\frac{15}{2}\) ; 2ae = 2
⇒ b² = a² – a²e²
⇒ b² = a² – 1
⇒ \(\frac{15}{2}\) a = a² – 1
⇒ 4a² – 15a – 4 = 0
b² = a² – 1
= 16 – 1
a = 4 లేదా a = –\(\frac{1}{4}\)
దీర్ఘవృత్తం సమీకరణం \(\frac{x^2}{16}+\frac{y^2}{15}\) = 1

ప్రశ్న 3.
నాభుల మధ్య దూరం 8, నియత రేఖల మధ్యదూం 32 గా గల దీర్ఘవృత్తం సమీకరణం ప్రామాణిక రూపంలో కనుక్కోండి. [May ’07; Mar. ’06]
సాధన:
నాభుల మధ్యదూరము = 8
నియత రేఖల మధ్యదూరము = 32
2ae = 8
ae = 4
\(\frac{2 a}{\mathrm{e}}\) = 32
\(\frac{\mathrm {a}}{\mathrm{e}}\) = 16
(ae) \(\frac{\mathrm {a}}{\mathrm{e}}\) = 64
a² = 64
b² = a² – a²e²
= 64 – 16 = 48
దీర్ఘవృత్తము సమీకరణము
∴ \(\frac{x^2}{64}+\frac{y^2}{48}\) = 1

ప్రశ్న 4.
ప్రామాణిక రూపంలో దీర్ఘవృత్తపు నాభిలంబం పొడవు దీర్ఘాక్షం పొడవులో సగం ఉంటే, ఉత్కేంద్రత కనుక్కోండి.
సాధన:
నాభి లంబము = \(\frac{2 b^2}{a}\)
దీర్ఘాక్షము = 2a
దత్తాంశం ప్రకారం \(\frac{2 b^2}{a}=\frac{1}{2}\) . 2a
2b² = a²
b² = a²(1 – e²) కనుక
2a²(1 – e²) = a²
1 – e² = \(\frac{1}{2}\)
e² = \(\frac{1}{2}\) ⇒ e = \(\frac{1}{\sqrt{2}}\)

ప్రశ్న 5.
x² + 3y² = 6 దీర్ఘవృత్తంపై గల బిందువుకు, కేంద్రం నుంచి దూరం 2. ఆ బిందువు ఉత్కేంద్రీయ కోణాలు కనుక్కోండి.
సాధన:
దీర్ఘవృత్తం సమీకరణం
x² + 3y² = 6
\(\frac{x^2}{6}+\frac{y^2}{2}\) = 1
a = \(\sqrt{6}\), b = \(\sqrt{2}\)
దీర్ఘ వృత్తం మీది బిందువు
P(\(\sqrt{6}\) cos θ, \(\sqrt{2}\) sin θ)
CP = 2 ⇒ CP² = 4
6 cos² θ + 2 sin² θ = 4
6(1 – sin² θ) + 2 sin² θ = 4
6 – 6 sin² θ + 2 sin² θ
4 sin² θ = 2 ⇒ sin² θ = \(\frac{2}{4}\) = \(\frac{1}{2}\)
sin θ = ± \(\frac{1}{\sqrt{2}}\)
sin θ = \(\frac{1}{\sqrt{2}}\) ⇒ θ = \(\frac{\pi}{4}\), \(\frac{3\pi}{4}\)
sin θ = –\(\frac{1}{\sqrt{2}}\) ⇒ θ = \(\frac{5\pi}{4}\), \(\frac{7\pi}{4}\)
∴ ఉత్కేంద్రీయ కోణాలు \(\frac{\pi}{4}\), \(\frac{3\pi}{4}\), \(\frac{5\pi}{4}\), \(\frac{7\pi}{4}\)

ప్రశ్న 6.
(-2, 2), (3, – 1) బిందువుల గుండా పోయే దీర్ఘవృత్తం సమీకరణం ప్రామాణిక రూపంలో కనుక్కోండి.
సాధన:
ప్రామాణిక రూపంలో దీర్ఘవృత్తము సమీకరణము

∴ దీర్ఘవృత్తం సమీకరణము
3x² + 5y² = 32

ప్రశ్న 7.
దీర్ఘాక్షం కొనలు (5, 0), (-5, 0)1, అయినాభి 3x – 5y – 9 = 0 పై ఉంటే దీర్ఘవృత్తం సమీకరణం ప్రామాణిక రూపంలో కనుక్కోండి.
సాధన:
(a, 0) : (5, 0), (-a, 0) : (-5, 0)
a = 5,
b² = a²(1 – e²)
నాభి 3x – 5y – 9 = 0 రేఖపై ఉంది.
3(ae) – 5(0) – 9 – 0
3(5e) – 9 = 0
5e = \(\frac{9}{3}\) లేదా e = \(\frac{3}{5}\)
b² = 25 (1 – \(\frac{9}{25}\))
= 25 (\(\frac{16}{26}\)) = 16
∴ దీర్ఘవృత్తం సమీకరణం
\(\frac{x^2}{25}+\frac{y^2}{16}\) = 1

ప్రశ్న 8.
దీర్ఘ వృత్తం యొక్క దీర్ఘాక్షం పొడవు, హ్రస్వాక్షం పొడవుకు మూడు రెట్లు ఉంటే ఉత్యేంద్రత కనుక్కోండి.
సాధన:
దీర్ఘాక్షము = 3 హ్రస్వాక్షము
2a = 3(2b) ⇒ a = 3b
a² = 9b² ⇒ a² = 9a²(1 – e²)
1 – e² = \(\frac{1}{9}\) ⇒ e² = 1 – \(\frac{1}{9}\) = \(\frac{8}{9}\)
e = \(\frac{2 \sqrt{2}}{3}\)
దీర్ఘవృత్త ఉత్కేంద్రత = \(\frac{2 \sqrt{2}}{3}\)

II.

ప్రశ్న 1.
క్రింది దీర్ఘవృత్తాలకు దీర్ఘాక్షం, హ్రస్వాక్షం, నాభిలంబం పొడవులు, ఉత్కేంద్రత, కేంద్రం, నాభులు నిరూపకాలు, నియత రేఖల సమీకరణాలు కనుక్కోండి. [T.S. Mar. ’16]
i) 9x² + 16y² = 144
ii) 4x² + y² – 8x + 2y + 1 = 0
iii) x² + 2y² – 4x + 12y + 14 = 0 [May ’07]
సాధన:
i) దత్త సమీకరణం 9x² + 16y² = 144
\(\frac{x^2}{16}+\frac{y^2}{9}\) = 1
∴ a = 4, b = 3
దీర్ఘాక్షం పొడవు = 2a = 2 . 4 = 8
హ్రస్వాక్షం పొడవు = 2b = 2 . 3 = 6
నాభిలంబం పొడవు = \(\frac{2 b^2}{a}=\frac{2.9}{4}=\frac{9}{2}\)
ఉత్కేంద్రత = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{16-9}{16}}=\frac{\sqrt{7}}{4}\)
కేంద్రం C(0,0)
నాభులు (±ae, 0) (±\(\sqrt{7}\), 0)
నియత రేఖా సమీకరణాలు x = ± \(\frac{a}{e}\)
x = ± 4 . \(\frac{4}{\sqrt{7}}\) = ± \(\frac{16}{\sqrt{7}}\)
\(\sqrt{7}\) x = ± 16

ii) దత్త సమీకరణము 4x² + y² – 8x + 2y + 1 = 0
4(x² – 2x) + (y² + 2y) = -1
4(x – 1)² + (y + 1)² = 4 + 1 – 1 = 4
\(\frac{(x-1)^2}{1}+\frac{(y+1)^2}{4}\) = 1
a < b కనుక ⇒ Y – అక్షం దీర్ఘాక్షము
a = 1, b = 2
దీర్ఘాక్షం పొడవు = 2b = 4
హ్రస్వాక్షం పొడవు = 2a = 2
నాభిలంబం పొడవు = \(\frac{2 a^2}{b}=\frac{2}{2}\) = 1
ఉత్కేంద్రత = \(\sqrt{\frac{b^2-a^2}{b^2}}=\sqrt{\frac{4-1}{4}}=\frac{\sqrt{3}}{2}\)
కేంద్రం C (-1, 1)
be 2 . \(\frac{\sqrt{3}}{2}\) = \(\sqrt{3}\)
నాభులు (−1, 1 ± \(\sqrt{3}\))
నియత రేఖల సమీకరణాలు y + 1 = ± \(\frac{b}{e}\) = ± \(\frac{4}{\sqrt{3}}\)
\(\sqrt{3}\) y + \(\sqrt{3}\) = ± 4
\(\sqrt{3}\) y + \(\sqrt{3}\) ± 4 = 0

iii) x² + 2y² – 4x + 12y + 14 = 0
x² – 4x + 2(y² – 4x + 2(y² + 6y) = – 14
⇒ (x² – 4x + 4) + 2(y² + 6y + 9) = 4 + 18 – 14
⇒ (x – 2)² + 2(y + 3)² = 8
⇒ \(\frac{(x-2)^2}{8}+\frac{(y+3)^2}{4}\) = 1
⇒ \(\frac{(x-2)^2}{(2 \sqrt{2})^2}+\frac{(y+3)^2}{2^2}\) = 1
a = 2\(\sqrt{2}\), b = 2, h = 2, k = – 3
దీర్ఘాక్షం పొడవు = 2a = 2(2\(\sqrt{2}\)) = 4\(\sqrt{2}\)
హ్రస్వాక్షం పొడవు = 2b = 2(2) = 4
నాభిలంబం పొడవు = \(\frac{2 b^2}{a}=\frac{2(4)}{2 \sqrt{2}}=2 \sqrt{2}\)
ఉత్కేంద్రత = \(\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{4}{8}}=\frac{1}{\sqrt{2}}\)
కేంద్రం C = (h, k) = (2, – 3)
నాభులు = (h ± ae, k) = (2 ± 2, -3)
= (4, -3), (0, -3)
నియత రేఖల సమీకరణాలు x – h = ± \(\frac{a}{e}\)
x – 2 = ± \(\frac{2 \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right)}\)
x – 2 = ± 4
i.e., x = 6, x = -2

ప్రశ్న 2.
క్రింది వివరాలను తృప్తిపరచే దీర్ఘవృత్తాల సమీకరణాలను \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 రూపంలో కనుక్కోండి.
i) కేంద్రం (2, −1), e = 3, దీర్ఘాక్షం కొన (2, -5),
సాధన:
కేంద్రం (2, -1) ⇒ h = 2, k = -1
దీర్ఘాక్షం కొన (2, -5), k – a = -5
-1 – a = -5
a = 4
b² = a²(1 – e²)
= 16 (1 – \(\frac{1}{9}\)) = \(\frac{128}{9}\)
దీర్ఘవృత్తం సమీకరణం
\(\frac{(x-2)^2}{16}+\frac{9(y+1)^2}{128}\) = 1
i.e., 8(x – 2)² + 9(y + 1)² = 128

ii) కేంద్రం (4, -1), దీర్ఘాక్షం ఒక కొన (−1, −1) అయి (8, 0) గుండా పోతుంది.
సాధన:
a = \(\sqrt{(4+1)^2+(-1+1)^2}\)
a = 5
దీర్ఘవృత్తం (8, 0) గుండా పోతుంది
\(\frac{(8-4)^2}{25}+\frac{(0+1)^2}{b^2}\) = 1
\(\frac{1}{b^2}=1-\frac{16}{25}\)
\(\frac{1}{b^2}=\frac{9}{25}\)
∴ కావలసిన దీర్ఘవృత్తం సమీకరణం
\(\frac{(x-4)^2}{25}+\frac{9}{25}\) (y + 1)² = 1
(x – 4)² + 9 (y + 1)² = 25

iii) కేంద్రం (0, -3), e = \(\frac{2}{3}\) అర్థ హ్రస్వాక్షం పొడవు 5.
సాధన:
b = 5
⇒ b² = a² – a²e²
⇒ 25 = a² – a² . \(\frac{4}{9}\) = a² (\(\frac{5}{9}\))
⇒ 45 = a²
\(\frac{(x-0)^2}{45}+\frac{(y+3)^2}{25}\) = 1
⇒ \(\frac{x^2}{45}+\frac{(y+3)^2}{25}\) = 1

iv) కేంద్రం (2, -1); e = \(\frac{1}{2}\), నాభిలంబం పొడవు 4.
సాధన:
b² = a² – a²e²
\(\frac{2 b^2}{a}\) = 4
b² = 2a
⇒ b² = a² – a² . \(\frac{1}{4}\)
⇒ b² = \(\frac{3}{4}\) a
⇒ 2a = \(\frac{3}{4}\) a²
⇒ \(\frac{8}{3}\) = a లేదా a² = \(\frac{64}{9}\)
⇒ b² = \(\frac{16}{3}\)
దీర్ఘవృత్తం సమీకరణం
\(\frac{9(x-2)^2}{64}+\frac{3(y+1)^2}{16}\) = 1
9(x – 2)² + 12(y + 1)² = 64

ప్రశ్న 3.
దీర్ఘ వృత్తం 9x² + 16y² = 144 యొక్క నాభుల గుండా పోతూ కనిష్ఠ వ్యాసార్ధం గల వృత్త వ్యాసార్ధం కనుక్కోండి.
సాధన:
దీర్ఘవృత్త సమీకరణము 9x² + 16y² = 144

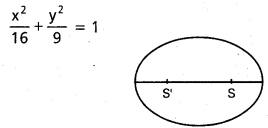
a² = 16, b² = 9
a = 4, b = 3
వృత్తం SS’ ల గుండా పోతూ కనిష్ట వ్యాసార్ధము కలిగి ఉంది.
∴ S, S’ వ్యాసం అవుతుంది.
a²e² = a² – a²(1 – e²) = a² – b² = 16 – 9 = 7
కావలసిన వృత్త సమీకరణము x² + y² = 7.

ప్రశ్న 4.
రేసుకోర్సులో పరిగెడుతున్న మనిషి, రెండు జెండా కొయ్యల నుంచి తనకు గల దూరాల మొత్తం ఎప్పుడూ 10 మీ అని, జెండా కొయ్యల మధ్య దూరం 8 మీ. అని గమనించాడు. అయితే ఆ మనిషి పరిగెత్తే రేసు కోర్సు మార్గం సమీకరణం కనుక్కోండి.
సాధన:
S, S’ లు జెండాలు. మనిషి ఉన్న స్థానము P.

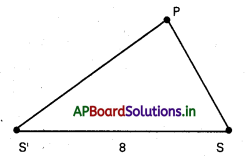
SP + S’P = 10 మరియు SS’ = 8
S మరియు S’ లు నాభులుగా కలిగిన దీర్ఘవృత్తంలో
ప్రయాణిస్తున్నప్పుడు
2a = 10 ⇒ a = 5
SS’ = 8 ⇒ 2ae = 8 = ae = 4
e = \(\frac{4}{5}\)
b² = a²(1 – e²) = 25 (1 – \(\frac{16}{25}\)) = 9
దీర్ఘవృత్తం సమీకరణం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
\(\frac{x^2}{25}+\frac{y^2}{9}\) = 1

III.

ప్రశ్న 1.
a + b స్థిరంగా గల ఒక సరళరేఖ కొనలు ఎప్పుడూ రెండు పరస్పర లంబరేఖలపై చలిస్తున్నాయి. సరళరేఖ పొడవును (a), (b) భాగాలుగా విభజించే నిర్దేశించిన బిందువు ఎప్పుడూ ఒక దీర్ఘవృత్తాన్ని అనుసరిస్తుందని చూపండి. a = 8, b = 12 అయితే దీర్ఘవృత్తం ఉత్యేంద్రత కనుక్కోండి.
సాధన:
లంబ రేఖలను నిరూపకాక్షాలుగా తీసుకుందాం.
AB స్థిరరేఖ.
OA = α, OB = β అనుకుంటే
AB సమీకరణము \(\frac{x}{\alpha}+\frac{y}{\beta}\) = 1
(∵ α² + β² = (a + b)²) ………….. (1)
P(x, y) బిందువు AB ని a = b నిష్పత్తితో విభజిస్తుంది

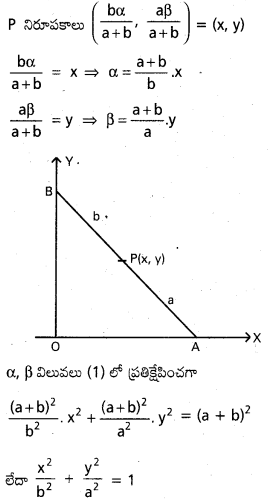
P దీర్ఘవృత్తాన్ని అనుసరిస్తుంది..
a = 8, b = 12, కనుక b > a
ఉత్కేంద్రత = \(\sqrt{\frac{b^2-a^2}{b^2}}=\sqrt{\frac{144-64}{144}}=\sqrt{\frac{80}{144}}=\frac{\sqrt{5}}{3}\)

ప్రశ్న 2.
దీర్ఘవృత్త \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 పై బిందువులు ‘α’, ‘β’ లను కలిపే జ్యా సమీకరణం \(\frac{x}{a} \alpha \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \beta \sin \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right)\) అని చూపండి.
సాధన:
దీర్ఘవృత్తం మీద బిందువులు
P(a cos α, b sin α) మరియు Q(a cos β, b sin β).