Students get through AP Inter 2nd Year Physics Important Questions 6th Lesson Current Electricity which are most likely to be asked in the exam.
AP Inter 2nd Year Physics Important Questions 6th Lesson Current Electricity
Short Answer Questions
Question 1.
Derive an expression for the effective resistance when three resistors are connected in
(i) series
(ii) parallel.
Answer:
Effective resistance when three resistors are connected :
(i) In series :
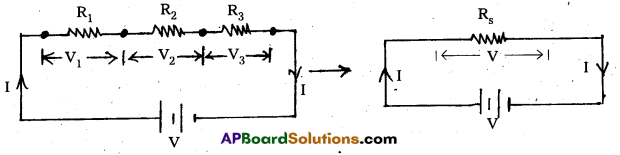
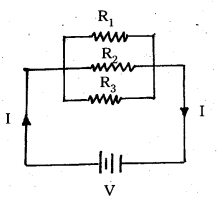
- Three resistors R1, R2 and R3 are connected in series as shown in fig. V1, V2, V3 are the potential differences across R1, R2 and R3. I is the current flowing through them.
- Applying Ohm’s law to R1, R2 and R3, Then V1 = IR1, V2 = IR2, V3 = IR3
- In series, V = V1 + V2 + V3
IRs = IR1 + IR2 + IR3 [∵V = IRs]
∴ Rs = R1 + R2 + R3
ii) In parallel :
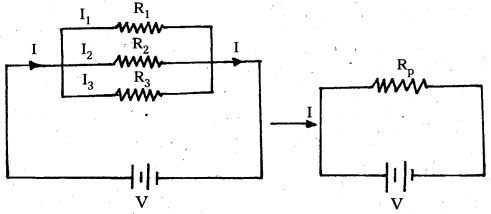
- Three resistors, R1, R2 and R3 are connected in parallel as shown in fig. Potential differences across each resistor is V.I1, I2, I3 are the currents flowing through them.
- Applying Ohm’s law to R1, R2 and R3, then
V = I1R1 = I2R2 = I3R3
⇒ I1 = \(\frac{\mathrm{V}}{\mathrm{R}_1}\); I2 = \(\frac{\mathrm{V}}{\mathrm{R}_2}\); I3 = \(\frac{\mathrm{V}}{\mathrm{R}_3}\) - In parallel, I = I1 + I2 + I3
⇒ \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{p}}}=\frac{\mathrm{V}}{\mathrm{R}_1}+\frac{\mathrm{V}}{\mathrm{R}_2}+\frac{\mathrm{V}}{\mathrm{R}_3}\) [∵ I = \(\frac{V}{R_P}\)]
∴ \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)
![]()
Question 2.
On what factors does the resistance of a conductor depend ? Define electric resistance and write its S.I unit. How does the resistance of a conductor vary if (a) Conductor is stretched to 4 times of its length (b) Temperature of conductor is increased ? [Board Model Paper]
Answer:
Dependence of Resistance on geometry :
- Resistance is directly proportional to length of the conductor (R ∝ l)
- Resistance is inversely proportional to area of cross-section (R ∝ 1/A)
i.e., R ∝ l/A ⇒ R = ρl / A; ρ is called specific resistance or resistivity of the material.
Dependence of Resistance on temperature : R1 = R1[1 + α(∆T)] & α = \(\frac{\Delta R / R}{\Delta T}\)
α is called temperature coefficient of resistance and its SI unit: K-1.
Definition of electrical resistance (R) : The ratio between the potential difference (V) across the ends of the conductor and the current (i) flowing through the conductor is called its electrical resistance, R = V/i; S.I unit of electrical resistance is ohm (Ω)
a) Resistance of the conductor, R = ρ \(\frac{l}{\mathrm{~A}}\) = ρ \(\frac{l^2}{V}\) ⇒ R ∝ l2 (∵ ρ and V constant)
⇒ R1/R2 = (l1/l1)2 ∴ R1/R2 = (l/4l)
⇒ R2 = 16R
Hence resistance of the conductor increases by 16 times.
b) The value of the electrical resistance of a conductor increases with increase of temperature. Because, temperature coefficient of resistance is positive for metals.
Long Answer Questions
Question 1.
State Kirchhoffs law for an electrical network. Using th&se laws deduce the condition for balance in a Wheatstone bridge. [T.S. Mar. 16; 15; Mar. 14]
Answer:
- Kirchhoffs first law (Junction rule or KCL) : The algebraic sum of the currents at any junction is zero.
∴ ΣI = 0
(or)
The sum of the currents flowing towards a junction is equal to the sum of currents away from the junction. - Kirchhoffs second law (Loop rule or KVL) : The algebraic sum of potential around any closed loop is zero.
∴ Σ(IR) + ΣE = 0
Wheatstone bridge : Wheatstone’s bridge circuit consists of four resistances R1, R2, R3 and R4 are connected to form a closed path. A cell of emf is connected between the point A and C and a galvanometer is connected between the points B and D as shown in fig. The current through the various branches are indicated in the figure. The current through the galvanometer is Ig and the resistance of the galvanometer is G.
Applying Kirchhoffs first law at the junction D, I1 – I3 – Ig = 0 ………………. (1)
at the junction B, I2 + Ig – I4 = 0 ……………. (2)
Applying Kirchhoff s second law to the closed path ADBA,
-I1R1 – IgG + I2R2 = 0
or
⇒ I1R1 + IgG = I2R2 …………….. (3)
applying kirchhoft’s second law to the closed path DCBD,
-I3R3 + I4R4 + IgG = 0
⇒ I3R3 – IgG = I4R4 ……………….. (4)
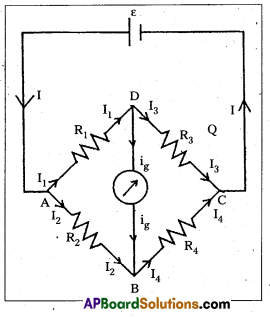
When the galvanometer shows zero deflection the points D and B are at the same potential. So Ig = 0.
Substituting this value in (1), (2), (3) and (4).
I1 = I3 ………………. (5)
I2 = I4 ……………… (6)
I1R1 = I2R2 ……………….. (7)
I3R3 = I4R4 …………….. (8)
Dividing (7) and (8)
\(\frac{I_1 R_1}{I_3 R_3}=\frac{I_2 R_2}{I_4 R_4} \Rightarrow \frac{R_1}{R_3}=\frac{R_2}{R_4}\) [∵ I1 = I3 & I2 = I4]
∴ Wheatstone’s Bridge principle : R4 = R3 × \(\frac{\mathrm{R}_2}{\mathrm{R}_1}\)
![]()
Question 2.
State the working principle of potentiometer explain with the help of circuit diagram how the emf of two primary cells are compared by using the potentiometer. [A.P. Mar. 16]
Answer:
Working principle of potentiometer : The potential difference across a length of the potentiometer wire is directly proportional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant,
i.e. ε ∝ l ⇒ ε = Φl where Φ is potential gradient.
Comparing the emf of two cells ε1 and ε2 :
- To compare the emf of two cells of emf E1 and E2 with potentiometer is shown in diagram.
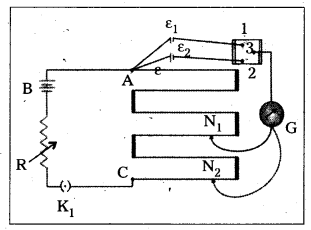
- The points marked 1, 2, 3 form a two way key.
- Consider first a position of the key where 1 and 3 are connected so that the galvanometer is connected to ε1.
- The Jockey is moved along the wire till at a point N1 at a distance l1 from A, there is no deflection in the galvanometer. Then ε1 ∝ l1 ⇒ ε1 = Φl1 ………………. (1)
- Similarly, if another emf ε2 is balanced against
l2 (AN2), then ε2 ∝ l2 ⇒ ε2 = Φl2 ……………. (2) - \(\frac{(1)}{(2)} \Rightarrow \frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2}\)
Question 3.
State the working principle of potentiometer. Explain with the help of circuit diagram how the potentiometer is used to determine the internal resistance of the given primary cell. [A.P. & T.S. Mar. 17, 15]
Answer:
Working principle of potentiometer : The potential difference across a length of the potentiometer wire is directly proportional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant.
i.e. ε ∝ l ⇒ ε = Φl
where Φ is potential gradient.
Measurement of internal resistance (r) with potentiometer :
- Potentiometer to measure internal resistance (r) of a cell (ε) is shown in diagram.
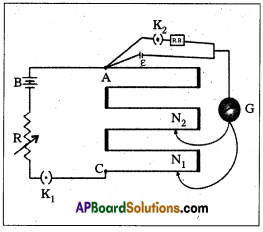
- The cell (emf ε) whose internal resistance (r) is to be determined is connected across a resistance box (R.B) through a key K2.
- With key K2 open, balance is obtained at length l1 (AN1). Then ε = Φl1 …………… (1)
- When key K2 is closed, the cell sends a current (I) through the resitance box (R.B).
- If V is the terminal potential difference of the cell and balance is obtained at length l2 (AN2).
Then V = Φ l2 ………………… (2) - \(\frac{(1)}{(2)} \Rightarrow \frac{\varepsilon}{V}=\frac{l_1}{l_2}\) ……………. (3)
- But ε = I (r + R) and V = IR. This gives
\(\frac{\varepsilon}{V}=\frac{(r+R)}{R}\)
\(\frac{l_1}{l_2}=\left(\frac{r}{R}+1\right)\) [∵ from (3)]
∴ r = \(\mathrm{R}\left(\frac{l_1}{l_2}-1\right)\)
![]()
Question 4.
Under what condition is the heat produced in an electric circuit a)directly proportional b) inversely proportional to the resistance of the circuit ? Compute the ratio of the total quantity of heat produced in the two cases.
Answer:
Expression of heat produced by electric current:
Consider a conductor AB of resistance R.
Let V = P.D applied across the ends of AB.
I = current flowing through AB.
t = time for which the current is flowing.
∴ Total charge flowing from A to B in time t is q = It. By definition of P.D, work done is carrying unit charge from A to B = V
Total work done in carrying a charge q from A to B is
W = V × q = V It = I2 Rt (∵V = IR)
This work done is called electric work done. If this electric work done appears as heat, then amount of heat produced (H) is given by
H = W = I2 Rt Joule.
This is a statement of Joule’s law of heating.
a) If same current flows through an electric circuit, heat is developed.
i.e., H ∝ R.
b) If same P.D applied across the the electric circuit heat is developed.
i.e., H2 ∝ \(\frac{1}{R}\)
c) The ratio of H1 and H2 is given by
\(\frac{\mathrm{H}_1}{\mathrm{H}_2}=\frac{\mathrm{R}}{\frac{1}{\mathrm{R}}}\)
∴ \(\frac{\mathrm{H}_1}{\mathrm{H}_2}\) = R2
Problems
Question 1.
A 10Ω thick wire is stretched so that its length becomes three times. Assuming that there is no change in its density on stretching, calculate the resistance of the stretched wire.
Solution:
Given R1 = 10 Ω,
l1 = l
l2 = 3l, R2 ?
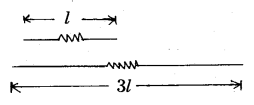
R1 = \(\frac{\rho}{\mathrm{V}} l_1^2\)
R2 = \(\frac{\rho}{\mathrm{V}} l_2^2\)
\(\frac{\dot{\mathrm{R}}_2}{\mathrm{R}_1}=\left(\frac{l_2}{l_1}\right)^2 \Rightarrow \frac{\mathrm{R}_2}{10}=\left(\frac{3 l}{l}\right)^2\)
∴ R2 = 10 × 9 = 90Ω.
![]()
Question 2.
A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter ? [T.S. Mar. 16; Mar. 14]
Solution:
Resistance of long wire = 4R
Hence the resistance of half wire = \(\frac{4 R}{2}\) = 2R
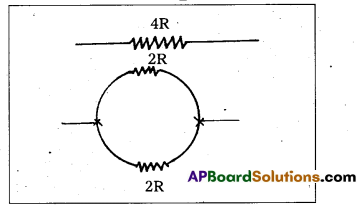
Now these two wire are connected in parallel. Hence the effective resistance between the ends of the diameter
RP = \(\frac{\mathrm{R}_1 \mathrm{R}_2}{\mathrm{R}_1+\mathrm{R}_2}\) ⇒ RP = \(\frac{2 R \times 2 R}{2 R+2 R}\)
∴ RP = R.
Question 3.
Three resistors 3Ω, 6Ω and 9Ω are connected to a battery. In which of them will the power of dissipation be maximum if:
a) They all are connected in parallel
b) They all are connected in series ? Give reasons.
Solution:
Given R1 = 3Ω, R2 = 6Ω, R3 = 9Ω
a) Effective resistance in parallel is given by
\(\frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}=\frac{1}{3}+\frac{1}{6}+\frac{1}{9}\)
\(\frac{1}{R_P}=\frac{6+3+2}{18}\)
∴ RP = \(\frac{18}{11}\) Ω
∴ Dissipated power in parallel,
PP ∝ \(\frac{1}{R_P}\) ⇒ PP ∝ \(\frac{1}{\left(\frac{18}{11}\right)}\)
∴ PP ∝ \(\frac{11}{18}\) …………….. (1)
b) Effective resistance in series is given by
Rs = R1 + R2 + R3 = 3 + 6 + 9 = 18 Ω
∴ Dissipated power in series, PS ∝ RS ⇒ PS ∝ 18
From equations (1) and (2) power dissipation is maximum in series and minimum in parallel.
Reasons:
- In series connection, P ∝ R and V ∝ R. Hence dissipated power (P) and potential difference (V) is more because current is same across each resistor.
- In parallel connection, P ∝ \(\frac{1}{R}\) and I ∝ \(\frac{1}{R}\) Hence dissipated power (P) and potential difference (V) is less because voltage is same across each resistor.
![]()
Question 4.
A silver wire has a resistance of 2.1Ω at 27.5°C and a resistance of 2.7Ω at 100°C. Determine the temperature coeff. of resistivity of silver.
Solution:
For silver wire, R1 = 2.1Ω, t1 = 27.5°C
R2 = 2.7 Ω, t2 = 100°C, α = ?
α = \(\frac{R_2-R_1}{R_1 \mathrm{t}_2-\mathrm{R}_2 \mathrm{t}_1}=\frac{2.7-2.1}{2.1 \times 100-2.7 \times 27.5}=\frac{0.6}{210-74.25}=\frac{0.6}{135.75}\)
∴Temperature coefficient of resistivity
α = 0.443 × 10-2/°C
Question 5.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm. what is the emf of the second cell ? [A.P. Mar. 15
Solution:
Here ε1 = 1.25 V, l1 = 35.0 cm, ε2 = ?. l2 = 63.0 cm.
As \(\frac{\varepsilon_2}{\varepsilon_1}=\frac{l_2}{l_1}\) or
ε2 = \(\frac{\varepsilon_1 \times l_2}{l_1}=\frac{1.25 \times 63}{35}\) = 2.25 V
Question 6.
A battery of emf 2.5 V and internal resistance r is connected in series with a resistor of 45 ohm through an ammeter of resistance 1 ohm. The ammeter reads a current of 50 mA Draw the circuit diagram and calculate the value of r. [T.S. Mar. 17]
Solution:
Circuit diagram for the given data is shown below.
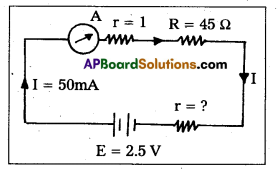
Given, E = 2.5 V; R = 45Ω;
rA = 1A; I = 50mA;
r = ?
E = I (R + rA + r)
2.5 = 50 × 10-3 (45 + 1 + r)
46 + r = \(\frac{2.5}{50 \times 10^{-3}}=\frac{2.5 \times 10^3}{50}\) = 50
∴ r = 50 – 46 = 4Ω.
![]()
Question 7.
The balancing point in meter bridge experiment is obtained at 30 cm from the left. If the right gap contains 3.5 £2, what is the resistance in the left gap? [BMP]
Solution:
\(\frac{x}{R}=\frac{I_1}{100-I_1} \Rightarrow \frac{x}{3.5}=\frac{30}{70} \Rightarrow x=\frac{30 \times 3.5}{70}=1.5\)
∴ x = 1.5 Ω
The resistance in the left gap in meter bridge is, x = 1.5 Ω
Question 8.
The storage battery of a car has an emf of 12 V If the internal resistance of the battery is 0.4Q, what is the maximum current that can be drawn from the battery ?
Solution:
Here E = 12 V, r = 0.4Ω
Maximum Current, Imax = \(\frac{E}{r}=\frac{12}{0.4}\) = 30 A
Question 9.
A battery of emf 10V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor ? What is the terminal voltage of the battery when the circuit is closed ? [T.S. Mar. 15]
Solution:
Here E = 10 V, r = 3Ω,1 = 0.5 A, R = ?, V = ?
I = \(\frac{E}{(R+r)}\) or (R + r) = \(\frac{\mathrm{E}}{\mathrm{I}}=\frac{10}{0.5}\)= 20 or
R = 20 – 3 = 17Ω
Terminal voltage V = IR = 0.5 × 17 = 8.5 Ω.
![]()
Question 10.
If the balancing point in a meter bridge from the left is 60 cm, compare the resistance in the left and right gaps of meter bridge.
Solution:
\(\frac{R_1}{R_2}=\frac{I_1}{100-I_1}=\frac{60}{100-60}=\frac{60}{40}=\frac{3}{2} \Rightarrow \frac{R_1}{R_2}=\frac{3}{2}\)
Question 11.
A potentiometer wire is 5m long and a potential difference of 6 V is maintained between its ends. Find the emf of a cell which balances against a length of 180cm of the potentiometer wire. [A.P. Mar. 17, 16]
Solution:
Length of potentiometer wire L = 5m
Potential difference V = 6 Volt
Potential gradient Φ = \(\frac{V}{L}=\frac{6}{5}\) = 1.2V/m
Balancing length l = 180cm
= 1.80m
Emf of the cell E = Φl
= 1.2 × 1.8 = 2.16V.