AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration InText Questions
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration InText Questions and Answers.
10th Class Maths 10th Lesson Mensuration InText Questions and Answers
Try this
(Page No. 245)
Question 1.
Consider the following situations. In each find out whether you need volume or area and why?
i) Quantity of water inside a bottle.
ii) Canvas needed for making a tent.
iii) Number of bags inside the lorry.
iv) Gas filled in a cylinder.
v) Number of match sticks that can be put in the match box.
Answer:
i) Volume: 3-d shape
ii) Area: L.S.A. / T.S.A.
iii) Volume: 3-d shape
iv) Volume: 3-d shape
v) Volume: 3-d shape
![]()
Question 2.
Write 5 more such examples and ask your friends to choose what they need?
Answer:
Student’s Activity.
Question 3.
Break the pictures in the previous figure into solids of known shapes. (Page No. 246)
Answer:
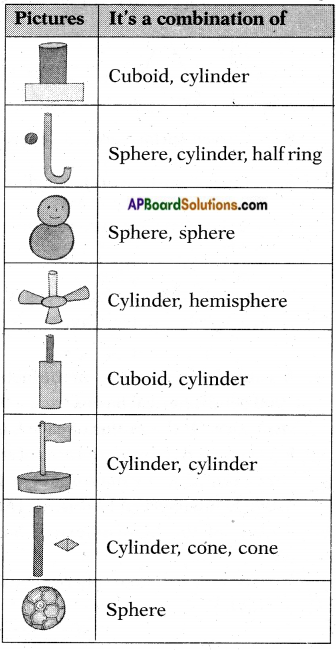
Question 4.
Think of 5 more objects around you that can be seen as a combination of shapes. Name the shapes that combined to make them. (Page No. 246)
Answer:
Student’s Activity.
![]()
Try this
Question 1.
Use known solid shapes and make as many objects (by combining more than two) as possible that you come across in your daily life.
[Hint: Use clay, or balls, pipes, paper cones, boxes like cube, cuboid etc] (Page No. 252)
Answer:
Student’s Activity.
Think & Discuss
Question 1.
A sphere is inscribed in a cylinder. Is the surface of the sphere equal to the curved surface of the cylinder? If yes, explain how. (Page No. 252)
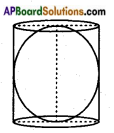
Answer:
Yes, the surface area of the sphere is equal to the curved surface area of the cylinder.
Let the radius of the “cylinder be ‘r’ and its height ‘h’.
Then radius of sphere = r.
Then curved surface area of cylinder = 2πrh = 2πr (r + r)
[∵ height = diameter of the sphere = diameter of the cylinder = 2r]
= 2πr (2r) = 4πr2
And surface area of the sphere = 4πr2
∴ C.S.A. of cylinder = Surface area of sphere.
Try This
(Page No. 257)
Question 1.
If the diameter of the cross – section of a wire is decreased by 5%, by what percentage should the length be increased so that the volume remains the same ?
Answer:
Let the radius of wire = r
(if diameter = 2r)
and length of wire = h = l (say)
then volume of wire = πr2l1 = v1 ….(1)
Now the diameter after decreasing 5%
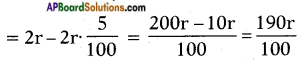
then radius of wire after decreasing
= \(\frac{190r}{100}\) × \(\frac{1}{2}\) = \(\frac{95r}{100}\)
and let the length of wire = (l2)

So it length is increased by 24.22%. Its volume remains same.
![]()
Question 2.
Surface area of a sphere and cube are equal. Then find the ratio of their volumes.
Answer:
Let a cube with side ‘a’.
Then its surface area = 6a2
By problem, surface area of the sphere = 4πr2
Surface area of the cube = 6a2

Do This
(Page No. 263)
Question 1.
A copper rod of diameter 1 cm. and length 8 cm; is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Answer:
Volume of the copper rod (cylinder)
= πr2h
= \(\frac{22}{7}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × 8
= \(\frac{44}{7}\) m2
If V is the radius of the wire, then its volume = πr2h
∴ The volume of rod is equal to the volume of the wire. We have

∴ Thickness = d = 2 × 0.03 ≃ 0.06 cm.
![]()
Question 2.
Pravali house has a water tank in the shape of a cylinder on the roof. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 9.5 cm. The water tank has radius 60 cm. and height 95 cm. Find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water. Compare the capacity of the tank with that of the sump, (π = 3.14)
Answer:
Volume of the water in the sump = 1.57 × 1.44 × 0.95 [∵ V = lbh]
= 2.14776 m3 = 2147760 cm3
Volume of the tank on the roof = πr2h
= 3.14 × 60 × 60 × 95
= 1073880 cm3
∴ Volume of the water left in the sump after filling the tank
= 2147760 – 1073880 = 1073880 cm3
Let the height of the water in the tank be h.
∴ 157 × l44h = 1073880
h = \(\frac{1073880}{157 \times 144}\) = 47.5 cm.
∴ Ratio of the volume of the sump and tank = 2147760 : 1073880 = 2 : 1
∴ Sump can hold two times the water that can be hold in the tank.
![]()
Think & Discuss
(Page No. 262)
Question 1.
Which barrel shown in the below figure can hold more water? Discuss with your friends.
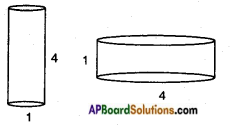
Answer:
r1 = \(\frac{1}{2}\) = 0.5 cm; h1 = 4 cm
Volume of the 1st barrel = πr2h
= \(\frac{22}{7}\) × 0.5 × 0.5 × 4 = 3.142 cm3
r2 = \(\frac{4}{2}\) = 2 cm
∴ h = 1 cm
Volume of the 2nd barrel
V = πr2h = \(\frac{22}{7}\) × 2 × 2 × 1 = 12.57 cm3
Hence the volume of the 2nd barrel is more than the first barrel.