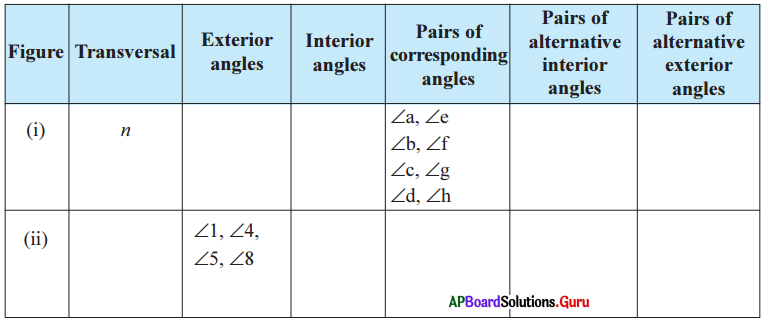
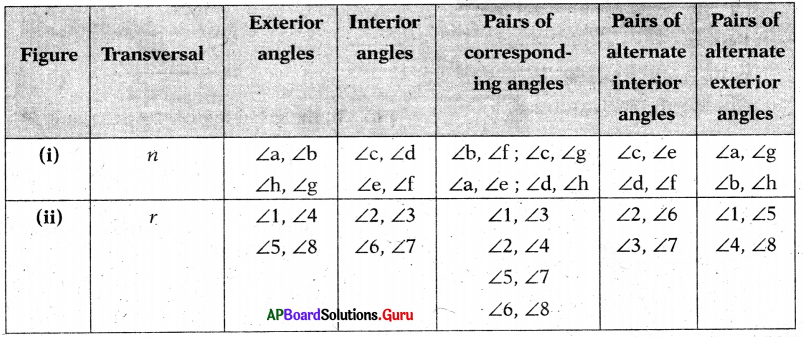
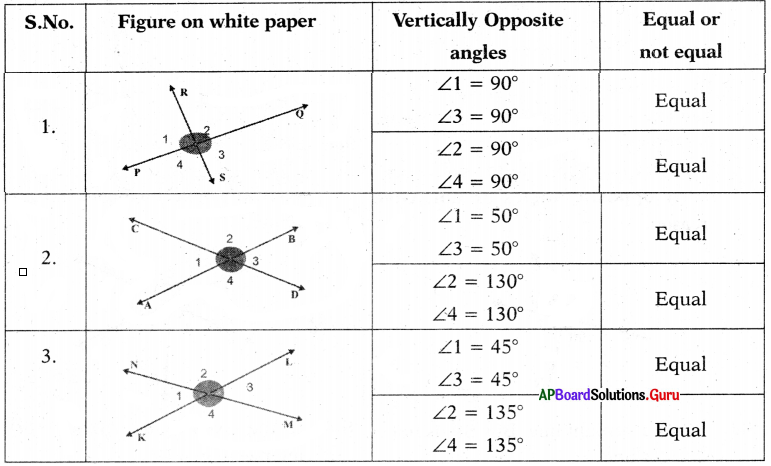
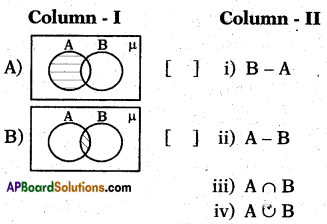
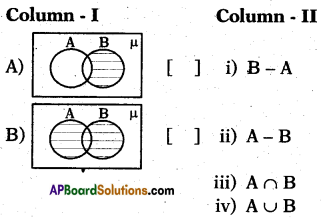
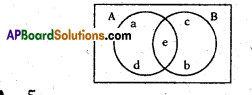
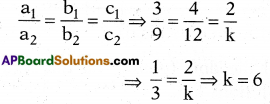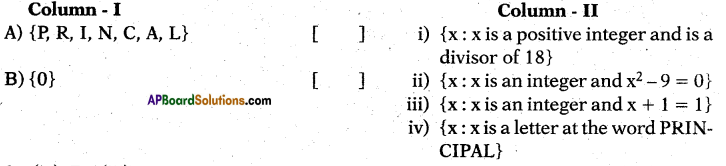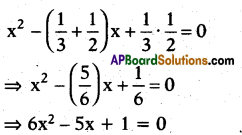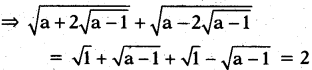These AP 7th Class Social Important Questions 8th Lesson భక్తి – సూఫీ will help students prepare well for the exams.
AP Board 7th Class Social 8th Lesson Important Questions and Answers భక్తి – సూఫీ
ప్రశ్న 1.
భక్తి అంటే ఏమిటి? భక్తి ఉద్యమం గురించి క్లుప్తంగా రాయండి.
జవాబు:
- భక్తి అంటే దేవుని యందు ప్రేమ.
- అనగా భక్తులు తనను తాను ఏ విధమైన సందేహం లేకుండా దేవునితో అనుబంధాన్ని కలిగియున్నటువంటి
- హిందూ మతం కర్మ, జ్ఞానం మరియు భక్తుని మోక్ష సాధన మార్గాలుగా చెబుతుంది.
- భక్తి ఉద్యమం 8వ శతాబ్దంలో మొదలై 17వ శతాబ్దం వరకు కొనసాగింది. ఈ ఉద్యమం దేశవ్యాప్తంగా విస్తరించింది.
- ఆయా మతాలలోని మూఢనమ్మకాలు, దురాచారాలు, ఆ మత సంస్కరణలకు కారణమయ్యాయని సంస్కరణవాదుల అభిప్రాయం.
- సంస్కరణవాదులు కీర్తనలతో, దేవుణ్ణి స్తుతిస్తూ, తమ స్థానిక భాషలలో గీతాలు పాడటం వంటి వాటిని అవలంబించారు.
- సమాజంలో వివిధ వర్గాల ప్రజలు వీరికి శిష్యులుగా మారారు. వీరు సమాజంలో చాలా సంస్కరణలు తీసుకొచ్చారు.
- కుల, మత, వర్గ భేదాలు లేకుండా అందరికీ తమ బోధనలను అందించారు.
ప్రశ్న 2.
భక్తి ఉద్యమ నేపథ్యం గురించి విశదీకరించండి.
జవాబు:
భక్తి ఉద్యమ నేపథ్యం :
- భక్తి ఉద్యమాన్ని ఆదిశంకరాచార్యులు ప్రారంభించారు.
- తరువాత రామానుజాచార్యులు విశిష్టాద్వైతాన్ని ప్రబోధించారు.
- మధ్వాచార్యుడు ద్వైత సిద్ధాంతాన్ని ప్రతిపాదించాడు.
- ఆ తరువాత బసవేశ్వరుడు కర్ణాటకలో, తుకారాం, సమర్థ రామదాసు, నామ్ దేవ్ మొదలగువారు మహారాష్ట్రలో, రామానందుడు, మీరాబాయి, సూర్దాస్, రవిదాస్ మరియు కబీర్ ఉత్తర భారతదేశంలో భక్తి ఉద్యమాన్ని ప్రాచుర్యంలోకి తెచ్చారు.
- అదే విధంగా చైతన్య మహా ప్రభు బెంగాల్ లో, గురునానక్ దేవ్ పంజాబ్ లో మరియు శంకరదేవుడు అస్సాంలో భక్తి ఉద్యమాన్ని కొనసాగించారు.
![]()
ప్రశ్న 3.
భక్తి ఉద్యమ సాధువులైన ఆదిశంకరాచార్యులు, రామానుజాచార్యుల గురించి వ్రాయండి.
జవాబు:
ఆదిశంకరాచార్య :
కేరళలోని కాలడి గ్రామంలో ఆదిశంకరాచార్యులు జన్మించారు. వీరు ఐదు సంవత్సరముల వయస్సులో సన్యాసం స్వీకరించారు. వీరు అద్వైత సిద్ధాంతాన్ని ప్రబోధించారు. ఆదిశంకరాచార్యులు భారతదేశ నలుదిక్కులా అనగా, ఉత్తరాన బదరీ, దక్షిణాన శృంగేరి, తూర్పున పూరీ, పడమర ద్వారకలలో నాలుగు శక్తి పీఠాలను ఏర్పాటు చేశారు. వివేక చూడామణి, సౌందర్యలహరి, శివానందలహరి, ఆత్మబోధ మున్నగున్నవి వీరి రచనలు. 32వ సంవత్సరములో వీరు నిర్యాణం చెందారు. భారత సనాతన ధర్మంలో వీరిని గొప్ప మత సంస్కర్తగా భావిస్తారు.
రామానుజాచార్య :
రామానుజాచార్యులు తత్వవేత్త మరియు సంఘ సంస్కర్త. వీరు దక్షిణ భారతదేశంలోని శ్రీపెరంబుదూలో క్రీ.శ. 1017వ సంవత్సరంలో జన్మించారు. వీరు వైష్ణవ సిద్ధాంతానికి తాత్విక విచార పునాదులను అందించారు. వీరు విశిష్టాద్వైతాన్ని ప్రబోధించారు. సంపూర్ణ సమర్పణ భావంతో మోక్షాన్ని సాధించవచ్చునని ప్రతి ఒక్కరికి బోధించారు. రామానుజాచార్యులు “శ్రీ భాష్యం” అనే పేరుతో బ్రహ్మసూత్రాలను వ్యాఖ్యానించారు.
ప్రశ్న 4.
మధ్వాచార్యులు మరియు వల్లభాచార్యుల గురించి వివరించండి.
జవాబు:
మధ్వాచార్యులు :
13వ శతాబ్దంలో మధ్వాచార్యులు కర్ణాటక రాష్ట్రంలోని పశ్చిమ తీరంలో జన్మించారు. వీరు ద్వైత సిద్ధాంతాన్ని ప్రాచుర్యంలోకి తెచ్చారు. ద్వైతమనగా రెండు అని అర్థం. దీని ప్రకారం బ్రహ్మ మరియు ఆత్మ రెండూ వేరు వేరు అంశాలు. మోక్ష మార్గానికి భక్తి ప్రధాన ఆధారం. ద్వైత సిద్ధాంతం ప్రకారం ఈ ప్రపంచం అనేది భ్రమ కాదు వాస్తవం. బ్రహ్మ, ఆత్మ మరియు పదార్థాలనేవి ప్రకృతిలో ప్రత్యేకమైనవి.
వల్లభాచార్య :
దక్షిణ భారతదేశంలో వల్లభాచార్యులు మరో ముఖ్యమైన వైష్ణవ సన్యాసి. వీరు తెలుగు ప్రాంతానికి సంబంధించినవారు. తత్వశాస్త్రంలో అపార జ్ఞానం, ప్రతిభ పాండిత్యము కలిగినవారు. వీరి ఆలోచనా విధానాన్ని శుద్ధ అద్వైతం అంటారు. ఈ సాంప్రదాయం ప్రకారం దేవుడు ఒక్కడే. వల్లభాచార్యుని బోధనలను పుష్టి మార్గం లేదా భగవదనుగ్రహ మార్గంగా చెప్పవచ్చు. వీరికి భగవాన్ శ్రీకృష్ణుని యందు అపార భక్తి, అద్వితీయ ప్రేమ ఉండేది. బ్రహ్మ సూత్రాలకు వీరు భాష్యం రచించారు.
ప్రశ్న 5.
ఈ క్రింది భక్తి సాధువుల గురించి వ్రాయండి.
ఎ) బసవేశ్వరుడు
బి) రామానందుడు
జవాబు:
ఎ) బసవేశ్వరుడు :
బసవేశ్వరుడు కర్ణాటక రాష్ట్రానికి చెందిన రాజనీతిజ్ఞుడు, తత్వవేత్త, కవి మరియు సామాజిక సంస్కర్త. అతను వీర శైవ సంప్రదాయాన్ని ప్రచారం చేశాడు. ఆయన రచనలను వచనములు అంటారు. అతను పుట్టుకతో లేదా సామాజిక స్థితితో సంబంధం లేకుండా ప్రజలందరికి బోధించాడు. అతని ప్రసిద్ధ సూక్తి “మానవులంతా సమానమే, కులం లేదా ఉప కులం లేదు”.
బి) రామానందుడు :
ఉత్తర భారతదేశంలో వైష్ణవ మతాన్ని ప్రచారం చేసిన ఘనత రామానందునికి చెందుతుంది. వీరు ప్రయాగలో జన్మించారు. బనారస్లో వీరి విద్యాభ్యాసం కొనసాగింది. ఉత్తర భారతదేశంలోని అనేక ఆధ్యాత్మిక ప్రదేశాలలో సంచరిస్తూ వైష్ణవ సిద్ధాంతాన్ని బోధించారు. రామానుజాచార్యుల వారి విశిష్టాద్వైతం పట్ల వీరికి విశ్వాసం. అతని బోధనలను ఈయన బహుళ ప్రచారంలోకి తీసుకొచ్చాడు. సమాజం వివిధ వర్గాలుగా విభజించబడి ఉండడాన్ని ఈయన వ్యతిరేకించాడు. ఇతను హిందీ భాషలో బోధనలను చేశాడు.
ప్రశ్న 6.
కబీర్ మరియు సంత్ రవిదాస్ గురించి నీకేమి తెలియును?
జవాబు:
కబీర్ :
ఉత్తర భారతదేశంలోని ప్రముఖ భక్తి ఉద్యమ సాధువులలో కబీర్ ఒకరు. “నీరు” అనే ఇస్లాం చేనేతకారుని ఆదరణలో పెరిగారు. బాల్యం నుంచి కబీరు దైవ భక్తి ఎక్కువ. యవ్వన ప్రాయానికి వచ్చాక రామానందుని శిష్యునిగా మారి ఎక్కువ కాలం బనారస్లో గడిపాడు. రామానందుని ద్వారా ఆధునికీకరించబడిన మరియు బహుళ ప్రాచుర్యం పొందిన వేదాంత తత్వాన్ని కబీర్ సంగ్రహించాడు. అన్ని మతాలు, వర్గాలు, కులాల మధ్య ఐకమత్యాన్ని పెంపొందింపచేసేలా ప్రేమతత్వాన్ని ఒక మతంగా ప్రచారం చేశాడు. దేవుని ఎదుట అందరూ సమానమే అని బోధించాడు. హిందూ ముస్లింల సమైక్యత కొరకు ప్రయత్నించిన మొదటి సాధువుగా కబీర్ ని చెప్పవచ్చు.
సంత్ రవిదాస్ :
సంత్ రవిదాస్ బెనారస్ లో నివసించారు. వీరు నిరాడంబర జీవితాన్ని గడుపుతూ సంతృప్తిగా జీవించేవారు. ఆయన రచనలలో ఎంతో సామరస్యం కనిపించేది. ప్రతి వారు భగవంతునికి తనను పరిపూర్ణంగా సమర్పించుకోవాలని బోధించాడు. “హరిలో అందరూ, అందరిలోనూ హరి” అనేది వీరి బోధనల సారాంశం.
![]()
ప్రశ్న 7.
సిక్కు మత స్థాపకుడయిన గురునానక్ గురించి తెల్పండి.
జవాబు:
గురునానక్ :
సిక్కు మత స్థాపకుడు అయిన గురునానక్ మరొక ముఖ్య సాధువు. కబీర్ బోధనలను ఈయన విశేషంగా అభిమానించాడు. లాహోర్ సమీపంలోని తల్వండి గ్రామంలో గురునానక్ క్రీ.శ. 1469లో జన్మించాడు. చిన్నతనం నుండే మత గురువులతో, సాధువులతో మతపరమైన చర్చలు జరుపుతూ ఉండేవాడు. సత్యం, సోదర భావం, సరైన జీవన విధానం, సామాజిక విలువలైన పని పట్ల గౌరవం మరియు దాతృత్వం పట్ల నమ్మకాన్ని కలిగి వుండేవాడు.
ప్రశ్న 8.
చైతన్య మహాప్రభు మరియు శంకర దేవుడు భక్తి సాధువుల గురించి వివరించండి.
జవాబు:
చైతన్య మహాప్రభు :
ఇతనిని శ్రీగౌరంగ అని కూడా పిలుస్తారు. ఇతను బెంగాల్ కి చెందిన ప్రముఖ వైష్ణవ సాధువు మరియు సంస్కర్త. భారతదేశంలోని దక్షిణ, పశ్చిమ ప్రాంతాలైన పండరీపురం, సోమనాథ్ మరియు ద్వారకలను సందర్శించి తన బోధనలను ప్రచారం చేశాడు. ఉత్తర దిక్కున ఉన్న బృందావన్, మధుర మరియు ఇతర తీర్థయాత్రా ప్రదేశాలను సందర్శించి చివరిగా పూరీలో స్థిర నివాసం ఏర్పరచుకొని, చైతన్యుడు తుది శ్వాస వరకు అక్కడే నివసించాడు. “దేవుడు ఒక్కడే” అని, ఆయన కృష్ణుడు లేదా హరి అని విశ్వసించాడు. ప్రేమ, భక్తి, గానం మరియు నృత్యం ద్వారా దేవుని సన్నిధి చేరుకోవచ్చు అని ప్రబోధించాడు మరియు ఆత్మ పరిశీలనకు ప్రాముఖ్యతను ఇచ్చాడు. ఇది గురువు ద్వారా మాత్రమే సాధించవచ్చునని అతను నమ్మాడు.
శంకర దేవుడు :
శంకర దేవుడు అస్సాం ప్రాంత సాధువు. అతను కవి, నాటక కర్త మరియు సంఘ సంస్కర్త. సాంఘిక, ఆధ్యాత్మిక కార్యక్రమాలకు అన్ని వర్గాల ప్రజలు సమావేశమవడానికి సత్రాలు లేక మఠములు మరియు నామ్ ఘర్లను ప్రారంభించాడు. శంకరదేవుడు గిరిజనులతో సహా అందరికి వైష్ణవ మతాన్ని ప్రబోధించడంలో విజయం సాధించాడు.
ప్రశ్న 9.
నామ్ దేవ్ మరియు జ్ఞానేశ్వర్ల గురించి మీకు తెలిసినది వ్రాయండి.
జవాబు:
నామ్ దేవ్ :
ఈయన పండరీపురానికి చెందిన విరోభా భక్తుడు. సమాజంలోని అన్ని వర్గాల ప్రజలతో భజనలను నిర్వహించేవాడు. నామ్ దేవ్ ప్రకారం దేవుణ్ణి ప్రార్థించడానికి క్రతువులు, విస్తృతమైన పూజా విధానం అనుసరించాల్సిన అవసరం లేదు. ఏకాగ్రతతో మనస్సుని దైవానికి సమర్పించడం ద్వారా మోక్షాన్ని సాధించవచ్చు అని బోధించారు.
జ్ఞానేశ్వర్ :
జ్ఞానేశ్వరుడు “భగవత్ దీపిక” పేరుతో భగవద్గీతకు వ్యాఖ్యానాన్ని రాశారు. దీనినే జ్ఞానేశ్వరి అని కూడా అంటారు. జ్ఞానేశ్వర్ మరాఠీ భాషలో బోధనలు చేశాడు. సమాజంలోని అన్ని కులాలను భగవద్గీత గ్రంథ పఠనానికి అనుమతించాలని బోధించాడు.
ప్రశ్న 10.
తెలుగు భక్తి ఉద్యమకారులు ఎవరైనా ఇద్దరి గురించి వ్రాయండి.
జవాబు:
తెలుగు భక్తి ఉద్యమకారులు :
సాహిత్యంలోను మరియు సామాజిక అంశాలలోను బహుళ ప్రాచుర్యం పొందిన కొందరు తెలుగు కవులు, పండితులు.
మొల్ల :
ఈమెను మొల్లమాంబ అని కూడా పిలుస్తారు. మొల్ల ప్రసిద్ధ తెలుగు కవయిత్రి. రామాయణాన్ని తెలుగులో వ్రాసిన మొల్ల శ్రీకృష్ణదేవరాయలకి సమకాలీకురాలని పరిశీలకుల అభిప్రాయం. ఈమె శైలి సరళంగాను, ఆకర్షణీయంగాను ఉంటుంది.
అన్నమయ్య :
తాళ్ళపాక అన్నమాచార్యగా ప్రసిద్ధి గాంచిన అన్నమయ్య కడప జిల్లాలోని తాళ్ళపాక గ్రామంలో జన్మించాడు. వీరిని పద కవితా పితామహుడు అంటారు. ఈయన శ్రీవేంకటేశ్వరుడిని కీర్తిస్తూ 32 వేల సంకీర్తనలు రాశారని ప్రతీతి. తెలుగు వారందరిలో అన్నమయ్య కీర్తనలు బాగా ప్రాచుర్యాన్ని పొందాయి. సమాజంలోని అసమానతలను తన పద్యాలలో నిరసించారు.
ప్రశ్న 11.
సూఫీ ఉద్యమం అంటే ఏమిటి? సూఫీయిజం యొక్క విశిష్ట లక్షణాలు ఏవి?
జవాబు:
సూఫీ ఉద్యమం :
ఇస్లాం మతంలోని సాంఘిక మత సంస్కరణ ఉద్యమాన్ని సూఫీ ఉద్యమం అని అంటారు. సూఫీతత్వం విశ్వ మానవ ప్రేమ మరియు సమతావాదాన్ని ప్రచారం చేసింది. సూఫీ అనే పదం ‘సాఫ్’ అనే అరబిక్ పదం నుంచి గ్రహించబడింది. సాఫ్ అనగా స్వచ్ఛత లేదా శుభ్రత. సూఫీ సన్యాసులు నిరంతరం ధ్యానంలో గడుపుతూ, సాధారణ జీవనం గడిపేవారు.
సూఫీయిజం యొక్క విశిష్ట లక్షణాలు :
- దేవుడు ఒక్కడే. అందరూ దేవుని సంతానమే.
- సాటి మానవుడిని ప్రేమించడం అంటే భగవంతుడిని ప్రేమించడమే.
- భక్తితో కూడిన సంగీతం దేవుని సన్నిధిని చేరడానికి ఉన్న మార్గాలలో ఒకటి.
- వహదాత్-ఉల్-ఉజూద్ అనగా ఏకేశ్వరోపాసనని సూఫీతత్వం విశ్వసిస్తుంది.
![]()
ప్రశ్న 12.
సూఫీ ఉద్యమ ప్రభావం గురించి తెల్పండి.
జవాబు:
సూఫీ ఉద్యమ ప్రభావం :
- సూఫీలు దేశ వ్యాప్తంగా పర్యటించి నిరుపేదలకి, గ్రామీణ ప్రాంతాలవారికి తమ బోధనలను చేర్చగలిగారు.
- వారు స్థానిక భాషలలో తమ బోధనలను చేసేవారు.
- వీరు అతి సాధారణ నిరాడంబర జీవనాన్ని గడిపేవారు.
ప్రశ్న 13.
భక్తి, సూఫీ ఉద్యమానికి చెందిన సాహిత్యంలోని అంశాలేవి? వివరణాత్మకంగా తెల్పండి.
జవాబు:
భక్తి, సూఫీ ఉద్యమానికి చెందిన సాహిత్యంలోని అంశాలు :
- భక్తి, సూఫీ ఉద్యమాలు ప్రజల జీవన విధానం, సంస్కృతి సాంప్రదాయాలు, ఆచార వ్యవహారాలను ప్రభావితం చేశాయి.
- అప్పటి సమాజంలో ఉన్న మత, కుల అసమానతలను భక్తి ఉద్యమ సాధువులు మరియు వారి అనుచరులు తీవ్రంగా వ్యతిరేకించారు.
- వ్యవసాయం, చేనేత, హస్త కళలలో శ్రమ విలువకు గౌరవం పెంపొందింది.
- భక్తి ఉద్యమ ప్రేరణతో కొత్త సామ్రాజ్యాలు స్థాపించబడ్డాయి. ఉదా : విద్యారణ్య స్వామి ప్రేరణతో విజయనగర సామ్రాజ్యం, సమర్థ రామదాస్ స్వామి ప్రేరణతో శివాజీచే మరాఠా సామ్రాజ్యం.
- సాధారణ ప్రజలను ఆకట్టుకొనేలా పాటలని, పద్యాలని భక్తి ఉద్యమ సాధువులు రచించారు. ఇవి ప్రాంతీయ భాషలలో సాహిత్యాన్ని వికసింపజేసేలా చేశాయి.
ఉదా : అక్క మహాదేవి రచనలు, మీరాబాయి భజనలు, గోదాదేవి రచించిన తిరుప్పావై. - సూఫీ సాధువులు ఏకేశ్వరోపాసనను, నిరాడంబర పూజా విధానాన్ని ప్రచారం చేశారు. మూఢనమ్మకాలను నిరసించారు. ఈ అంశాలను వారి పాటలు, పద్యాలలో ప్రముఖంగా ప్రస్తావించేవారు. దైవాన్ని స్తుతించడంలో సంగీతానికి విశేష ప్రాధాన్యత ఉండేది.
ఉదా : ఖవ్వాలీ - నిరాడంబరత, క్రమశిక్షణతో కూడిన జీవనం, ఇస్లాం మతం పట్ల నిబద్దత మొదలగునవి సమాజాన్ని సూఫీయిజం పట్ల ఆకర్షితులయ్యేలా చేసింది.
ప్రశ్న 14.
ఆది శంకరాచార్యుని రచనలు ఏవి?
జవాబు:
ఆది శంకరాచార్యుని రచనలు :
- వివేక చూడామణి,
- సౌందర్యలహరి,
- శివానందలహరి,
- ఆత్మబోధలు,
ప్రశ్న 15.
ఉత్తర భారతదేశానికి చెందిన భక్తి సాధువులను వ్రాయండి. వారు పీఠాలను ఎక్కడ నెలకొల్పారు?
జవాబు:
ఉత్తర భారతదేశానికి చెందిన భక్తి సాధువులు, వారి పీఠాలు :
1) రామానందుడు :
ఉత్తర భారతదేశంలో వైష్ణవ మతాన్ని ప్రచారం చేసారు. వీరు ప్రయాగలో జన్మించారు. రామానుజాచార్యుల విశిష్టాద్వైతం పట్ల వీరికి విశ్వాసం, హిందీ భాషలో బోధనలు చేశారు.
2) కబీర్ :
రామానందుల వారి శిష్యులు. “నీరు” అనే ఇస్లాం చేనేతకారుని ఆదరణలో పెరిగారు. హిందూ ముస్లింల సమైక్యత కొరకు ప్రయత్నించిన మొదటి సాధువుగా కబీర్ ని చెప్పవచ్చు.
3) సంత్ రవిదాస్ :
వీరు బెనారస్ లో నివసించారు. వీరు నిరాడంబర జీవితాన్ని గడుపుతూ సంతృప్తిగా జీవించేవారు. ‘హరిలో అందరూ, అందరిలోనూ హరి” అనేది వీరి బోధనల సారాంశం.
4) మీరాబాయి :
బాల్యం నుంచి ఈమె శ్రీకృష్ణ భక్తురాలు. ఈమె సంత్ రవిదాస్ శిష్యురాలు. శతాబ్దాలుగా మీరాబాయి భజనలు జన బాహుళ్యంలో చిరస్థాయిగా నిలిచిపోయాయి.
5) చైతన్య మహాప్రభు :
ఇతనిని శ్రీ గౌరంగ అని కూడా పిలుస్తారు. పూరిలో స్థిర నివాసం ఏర్పరచుకున్నారు. దేవుడు ఒక్కడే అని, ఆయన శ్రీకృష్ణుడు లేదా హరి అని విశ్వసించాడు. ప్రేమ, భక్తి, గానం మరియు నృత్యం ద్వారా దేవుని సన్నిధి చేరుకోవచ్చు అని ప్రబోధించాడు మరియు ఆత్మపరిశీలనకు ప్రాముఖ్యతను ఇచ్చాడు. ఇది గురువు ద్వారా మాత్రమే సాధించవచ్చునని నమ్మాడు.
6) శంకర దేవుడు :
అస్సాం ప్రాంత సాధువు. ఇతను కవి, నాటక కర్త మరియు సంఘ సంస్కర్త. సాంఘిక, ఆధ్యాత్మిక కార్యక్రమాలకు అన్ని వర్గాల ప్రజలు సమావేశమవడానికి సత్రాలు లేక మఠములు మరియు నామ మర్లను ప్రారంభించాడు.
7) నామ్ దేవ్ :
ఈయన పండరీపురానికి చెందిన విరోభా భక్తుడు. దేవుణ్ణి ప్రార్ధించటానికి క్రతువులు, విస్తృతమైన పూజా విధానం అనుసరించాల్సిన అవసరం లేదు అని అన్నారు.
8) జ్ఞానేశ్వర్ :
వీరు భగవత్ దీపిక పేరుతో భగవద్గీతకు వ్యాఖ్యానాన్ని రాశారు. దీనినే జ్ఞానేశ్వరి అని కూడా అంటారు. వీరు మరాఠీ భాషలో బోధనలు చేశారు.
ప్రశ్న 16.
సమాజంపై భక్తి ఉద్యమ ప్రభావం ఏమిటి?
జవాబు:
భారతీయ సమాజంపై భక్తి ఉద్యమ ప్రభావం :
- భక్తి ఉద్యమకారులు కుల వివక్షతను తిరస్కరించటం అనేది భక్తి ఉద్యమం వలన కలిగిన అతి ముఖ్య సామాజిక ప్రభావం.
- ఈ ఉద్యమం మత సహనాన్ని ప్రోత్సహించింది.
- భక్తి ఉద్యమ సాధకులు సహనాన్ని, ఏకేశ్వరోపాసనను బోధించారు.
- సమాజంలోని విభిన్న వర్గాల మధ్య సామరస్య భావాన్ని పెంపొందించింది.
- ఇది మానవతా దృక్పథాన్ని పెంపొందించే ప్రయత్నం చేసింది.
ప్రశ్న 17.
వివిధ మత సాధువులు మీరా భజనలకు ఎందుకు ఆకర్షితులయ్యారు?
జవాబు:
- భక్తి పారవశ్యంతో నిండిన మీరాబాయి పాడే భజనలు వినడానికి అన్ని మతాలకు చెందిన సాధువులు ఆకర్షితులయ్యారు.
- ఈమె భజనలు సరళ భాషలో ఉండి అందరూ పాడుకోగలిగేవిగా ఉండేవి.
- శ్రీకృష్ణుని మనస్ఫూర్తిగా ప్రార్థిస్తూ, ఆమె పాడే పాటలు అందరిని ఆకట్టుకునేవి.
- శ్రీకృష్ణునిపై మీరాబాయి పాడిన సంకీర్తనలు శ్రావ్యంగా, రాగయుక్తంగా యుండి వినెడి వారి మనస్సులు భగవంతునిలో లీనమయ్యేవి.
![]()
ప్రశ్న 18.
ఉపాధ్యాయుని సహకారంతో మీ పాఠశాలలోని లైబ్రరీలో కానీ, అంతర్జాలంలో కాని అన్వేషించి అన్ని మతాలలోని సగుణ మరియు నిర్గుణ భక్తి సాధకుల పట్టిక తయారుచేయండి.
జవాబు:
భక్తి సాధకుల జాబితా :
| శ్రీ ఆదిశంకరాచార్యులు | శ్రీ సూరదాస్ | గురునానక్ |
| శ్రీ రామానుజాచార్యులు | మీరాబాయి | గురుఅంగద్ |
| శ్రీ మధ్వాచార్యులు | తులసీదాస్ | గురు గోవింద్ సింగ్ |
| శ్రీ నింబార్కుడు | కబీర్ (నిర్గుణ) | గురు అర్జున్ |
| శ్రీ వల్లభాచార్యులు | రవిదాస్ | షేక్ ఇస్మాయిల్ (నిర్గుణ) |
| శ్రీ రామానందుడు | నరహరిదాస్ | ఖ్వాజా మొయినుద్దీన్ చిస్తీ (నిర్గుణ) |
| శ్రీ చైతన్యుడు | జ్ఞానదేవ్ | బహుద్దీన్ జకారియా (నిర్గుణ) |
| శ్రీ తుకారామ్ | ఏకనాథుడు | నిజాముద్దీన్ ఔలియా (నిర్గుణ) |
| శ్రీ బసవేశ్వరుడు | అన్నమయ్య | మాణిక్కవసగర్ |
| శ్రీ పురంధరదాసు | శ్రీ నమ్మాళ్వారు | శ్రీరామదాసు |
| శ్రీ శంకరదేవుడు | నర్సి మెహతా | ఆండాళ్ మొదలగువారు |
మీకు తెలుసా?
7th Class Social Textbook Page No. 37
భక్తి రెండు రకాలుగా ఉంటుంది. అవి సగుణ భక్తి. నిర్గుణ భక్తి. సగుణ భక్తి అనగా భగవంతుని ఒక ఆకారంలో పూజించడం, నిర్గుణ భక్తి అనగా భగవంతుని నిరాకారంగా పూజించడం.
7th Class Social Textbook Page No. 41
బ్రహ్మసూత్రాలనేది ఒక సంస్కృత గ్రంథం. వీటిని వ్యాసుడు లేదా బాదరాయణుడు రచించాడు. బ్రహ్మసూత్రాలనే వేదాంత సూత్రం అని కూడా అంటారు.
![]()
7th Class Social Textbook Page No. 49
మొయినుద్దీన్ చిస్తీ దర్గా భారతదేశంలో రాజస్థాన్ లోని అజ్మీర్ లో ఉన్నది. ఈ పవిత్ర స్థలంలో ఖ్వాజా మొయినుద్దీన్ చిస్తీ పవిత్ర సమాధి ఉంది.