AP 10th Class Maths Bits Chapter 3 Polynomials with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 3 Polynomials on a regular basis so that you can attempt exams with utmost confidence.

AP SSC 10th Class Maths Bits 3rd Lesson Polynomials with Answers

Question 1.
Write the sum of zeroes of
bx² + ax + c.
Answer:
\(\frac{-a}{b}\)

Question 2.
Find product of the zeroes of
p(x) = (x-2).(x + 3)
Answer:
= -6
Explanation:
p(x) = x² + x – 6,
Product of zeroes = \(\frac{\mathrm{c}}{\mathrm{a}}\) = – 6.

Question 3.
5x – 3 represents which type of poly¬nomial ?
Answer:
Linear.

Question 4.
Find the value of ‘x’ which satisfies 2(x – 1) – (1 – x) = 2x + 3 ?
Answer:
6
Explanation:
2x – 2 – 1 + x = 2x + 3
⇒ 3x – 2x = 3 + 3 = 6
⇒ x = 6.

Question 5.
Write the degree of the polynomial
\(\sqrt{2}\)x² – 3x + 1.
Answer:
2

Question 6.
Write order of the polynomial 5x⁷ – 6x⁵ + 7x – 6.
Answer:
7

Question 7.
Find the product of zeroes of 2x² – 3x + 6.
Answer:
3
Explanation:
Product of zeroes = \(\frac{c}{a}=\frac{6}{2}\) = 3.

Question 8.
Find sum of zeroes of a polynomial x³ – 2x² + 3x – 4.
Answer:
2
Explanation:
Sum of zeroes = α + β + γ
= \(\frac{-b}{a}=\frac{-(-2)}{1}\) = 2

Question 9.
Find a quadratic polynomial, the sum of whose zeroes is zero and one zero is 4, is
Answer:
x² – 16 = 0
Explanation:
Sum of zeroes = \(\frac{-b}{a}\) = 0,
α + β = 0, β = 4
⇒ α = -4 x2 – (α + β)x + αβ = 0
⇒ x² – 0(x) -16 = 0
⇒ x² – 16 = 0.

Question 10.
If p(x) = x² – ax – 3 and p(2) = – 3, then find Answer:
Answer:
2
Explanation:
p(x) = (2)² – 2a – 3 = – 3
⇒ 1 — 2a = — 3
⇒ 4 – 2a = 0
⇒ 4 = 2a ⇒ a = 2

Question 11.
Write the zero value of polynomial px + q.
Answer:
\(\frac{-\mathrm{q}}{\mathrm{p}}\)

Question 12.
In a division, if divisor is x + 1, quo¬tient is x and remainder is 4, then find dividend.
Answer:
x (x + 1) + 4 = x² + x + 4
Explanation:
Dividend = Divisor x Quotient
+ Remainder
= (x + 1) x + 4 = x² + x + 4.

Question 13.
Find the zero value of linear polynomial ax – b.
Answer:
\(\frac{\mathrm{b}}{\mathrm{a}}\)

Question 14.
Find the sum of the zeroes of the poly-nomial x² + 5x + 6.
Answer:
– 5

Question 15.
4y² – 5y + 1 is an example for this type of polynomial.
Answer:
Quadratic polynomial.

Question 16.
Write the degree of the polynomial 5x⁷ – 6x⁵ + 7x – 4.
Answer:
7

Question 17.
How much the sum of zeroes of the polynomial 2x² – 8x + 6 ?
Answer:
4

Question 18.
f α,β are the zeroes of x² + x +1, then find \(\frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:
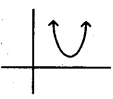
-1
Explanation:
α + β = -1, αβ = 1
⇒ \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\alpha+\beta}{\alpha \beta}=\frac{-1}{1}\) = -1

Question 19.
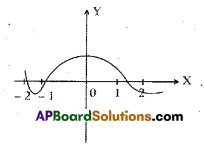
Write the number of zeroes of the poly¬nomial in the given graph.

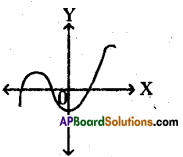
Answer:
3

Question 20.
Write product of zeroes of the cubic polynomial 3x³ – 5x² – 11x – 3.
Answer:
1
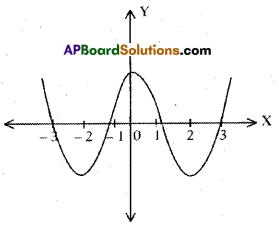
Explanation:
Product of zeroes = αβγ
= \(\frac{-d}{a}=\frac{-(-3)}{3}=\frac{3}{3}\) = 1

Question 21.
The following is the graph of a poly¬nomial. Find the zeroes of the poly¬nomial from the given graph.

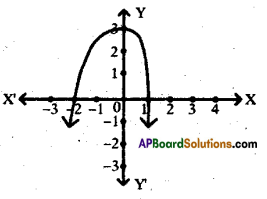
Answer:
– 2,1

Question 22.
Find the value of p(x) = 4x² + 3x + 1 at x = -1.
Answer:
2

Question 23.
If α, β, γ are the zeroes of the cubic polynomial ax³ + bx² + cx + d and (a ≠ 0), then find αβγ

Question 24.
4x + 6y = 18 doesn’t pass through ori-gin, then its graph indicates
Answer:
A straight line

Question 25.
If ‘3’ is one of the zeroes of
p(x) = x² + kx – 9, then find the value of k.
Answer:
0
Explanation:
p(3) = 3² + 3k – 9 = 0
⇒ 3k = 0 ⇒ k = 0

Question 26.
When p(x) = x² – 8x + k leaves a re-mainder when it is divided by (x – 1), then find k.
Answer:
k > 7
Explanation:
p(1) = 1 – 8 + k = 0
⇒ k > 7

Question 27.
If α, β, γ are zeroes of x³ + 3x² – x + 2, then find the value of αβγ.
Answer:
-2

Question 28.
Make a quadratic polynomial having 2, 3 as zeroes.
Answer:
x² – 5x + 6 = 0
Explanation:
x² – (2 + 3)x + 2 . 3 = 0
⇒ x² – 5x + 6 = 0.

Question 29.
Write a quadratic polynomial, whose zeroes are \(\sqrt{2}\) and –\(\sqrt{2}\).
Answer:
x² – 2 = 0
Explanation:
x² – \((\sqrt{2}-\sqrt{2}) x+\sqrt{2}(-\sqrt{2})\) = 0
⇒ x² – 0(x) -2 = 0
⇒ x² – 2 = 0.

Question 30.
Find the coefficient of x7 in the poly¬nomial 7x¹⁷ – 17x¹¹ + 27x⁵ – 7.
Answer:
0

Question 31.
If α, β are the zeroes of the polyno¬mial x² – x – 6, then find α²β²
Answer:
36
Explanation:
αβ = \(\frac{\mathrm{c}}{\mathrm{a}}\) = – 6 ⇒ (αβ)² = (-6)² = 36

Question 32.
If ‘4’ is one of the zeroes of p(x) = x² + kx – 8, then the value of k.
Answer:
-2

Question 33.
If the polynomial p(x) = x³ – x² + 3x + k is divided by (x – 1), the remainder obtained is 3, then find the value of k.
Answer:
0
Explanation:
p(1) = 1-1 + 3 + k = 3 ⇒ k = 0

Question 34.
If one zero of the polynomial f(x) = 5x² + 13x + k is reciprocal of the other, then find the value of k.
Answer:
5
Explanation:
α = x, β = 1/x
⇒ α . β = x . 1/x = k/5 ⇒ k = 5

Question 35.
Find the number of zeroes of the po!y: nomial, whose graph is given below.
Answer:

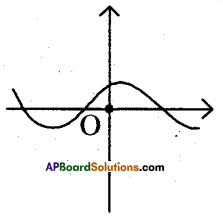
Question 36.
Number of zeroes that can be identi¬fied by the given figure.
Answer:

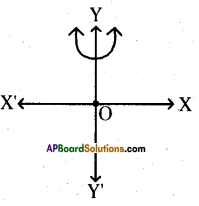
Question 37.
Observe the given rectangular figure, then write its area in polynomial func-tion.

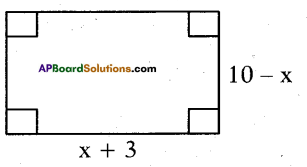
Answer:
x² – 7x – 30 = 0
Explanation:
(10 – x)(x + 3) = 10x + 30 – x² – 3x = 0
⇒ x² – 7x – 30 = 0

Question 38.
f(x) = x + 3, then find zero of f(x).
Answer:
-3

Question 39.
One zero of the polynomial 2x² + 3x + k is 1/2, then find k.
Answer:
-2
Explanation:
im 19
α + β + γ = \(\frac{-b}{a}\) = -3
\(\sqrt{5}-\sqrt{5}+\gamma\) = -3
γ = -3

Question 40.
Find factors of x² + x(a + b) + ab.
Answer:
x + a and x + b

Question 41.
f(x) = 4x² + 4x – 3, then find f(\(\frac{-3}{2}\))
Answer:
0

Question 42.
If \(\sqrt{5}\) and \(-\sqrt{5}\) are two zeroes of the polynomial x³ + 3x² – 5x – 15, then find its third zero.
Answer:
-3
Explanation:

Question 43.
If \(\sqrt{3}\) and – \(\sqrt{3}\) are the zeroes of a polynomial p(x), then find p(x).
Answer:
x² – 3

Question 44.
If ‘m’ and ‘n’ are zeroes of the polyno-mial 3x² + 11x – 4, then find the value \(\frac{\mathbf{m}}{\mathbf{n}}+\frac{\mathbf{n}}{\mathbf{m}}\)
Answer:
\(\frac{-145}{12}\)
Explanation:
3x² + 11x – 4 = 3x² + 12x – x – 4 = 0
⇒(x + 4)(3x – 1)= 0
⇒x = -4, \(\frac { 1 }{ 2 }\)

Question 45.
In the product (x + 4) (x + 2). Write the constant term.
Answer:
8

Question 46.
Find the polynomial whose zeroes are – 5 and 4.
Answer:
x² + x – 20

Question 47.
Flnd product of zeroes of 3x² = 1
Answer:
\(-\frac{1}{3}\)

Question 48.
Find the sum of the zeroes of x² + 7x + 10.
Answer:
-7

Question 49.
If one root of the polynomial
fix) = 5x² + 13x + k is reciprocal of the other, then find ‘k’.
Answer:
5

Question 50.
f(x) = 3x – 2. then find zero of f(x).
Answer:
\(\frac{2}{3}\)

Question 51.
Write the zeroes from the below graph.

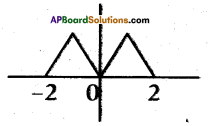
Answer:
-2, 0 and 2

Question 52.
Make a quadratic polynomial whose zeroes are 5 and -2.
Answer:
x² – 3x – 10.

Question 53.
If α, β are (1w zero ai polynomial
f(x) = x² – p(x + 1) – c then find (α + 1)(β + 1).
Answer:
1 – c
Explanation:
α + β = \(\frac{-b}{a}=\frac{+p}{1}\) = +p
αβ = \(\frac{c}{a}=\frac{-p-c}{1}\) = -(p+c)
(α + 1) (β + 1) = αβ + α + β + 1
= -p – c + p + 1
= 1 – c

Question 54.
Write number of constant polynomial x² + 7x – 7.
Answer:
1

Question 55.
Write the quadratic polynomial, whose sum and product of zeroes are 1 and – 2 respectively.
Answer:
x² – x – 2

Question 56.
Find the product of the zeroes of x³ + 4x² + x – 6.
Answer:
6

Question 57.
p(x) = \(\frac{x+1}{1-x}\) , then find p(0).
Answer:
1

Question 58.
Write the maximum number of zeroes that a polynomial of degree 3 can have.
Answer:
Three

Question 59.
If x + 2 is a factor of x² + ax + 2 b and a 4 b = 4, then find Answer:
Answer:
3
Explanation:
(- 2)² – 2a + 2b = 0
⇒ 4 – 2a + 2b = 0
⇒ -a + b = -2

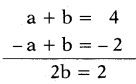
⇒ b = 1,a = 4- b = 4 – 1 = 3.

Question 60.
The graph of ax + b represents which type of polynomial ?
Answer:
linear polynomial.

Question 61.
If ‘1’ is the zero of the quadratic poly- nomlal x² + kx – 5, then find the value ofk.
Answer:
4
Explanation:
1 + k – 5 = 0 ⇒ k = 4.

Question 62.
Find a quadratic polynomial, the sum of whose zeroes is W and product of zero is 3.
Answer:
x² – 9

Question 63.
If y = p(x) is represented by the given pqih, then find die number of zeroes.

Answer:
4

Question 64.
If α + β = 0, αβ = \(\sqrt{3}\), then write the quadratic polynomial.
Answer:
x² + \(\sqrt{3}\)

Question 65.
Find the degree of the polynomial ax⁴ + bx³ + cx² + dx + e.
Answer:
4.

Question 66.
If α, β, γ are the zeroes of the polyno- mid f(x) = x³ – px² + qx – r, then find
\(\frac{1}{\alpha \beta}+\frac{1}{\beta \gamma}+\frac{1}{\gamma \alpha}\)
Answer:
\(\frac{\mathbf{p}}{\mathrm{r}}\)
Explanation:
\(\frac{1}{\alpha \beta}+\frac{1}{\beta \gamma}+\frac{1}{\gamma \alpha}=\frac{\alpha+\beta+\gamma}{\alpha \beta \gamma}=\frac{\frac{p}{1}}{\frac{r}{1}}=\frac{p}{r}\)

Question 67.
If α and β are the zeroes of the poly¬nomial p(x) = 2x² + 5x + k satisfying the relation α² + β² + αβ = \(\frac{21}{4}\), then find k.
Answer:
2
Explanation:
α² + β² + αβ

Question 68.
If p(t) = t³ , then find p(- 2).
Answer:
– 9

Question 69.
If the polynomial f(x) = ax³ – bx – a is divisible % the polynomial g(x) = x² + bx + c, then find ah.
Answer:
1

Question 70.
Write degree of a linear polynomial.
Answer:
1

Question 71.
If the sum off the zeroes off die polyno¬mial fix) = 2x³ – 3kx² + 4x – 5 is 6, then find k.
Answer:
4.

Question 72.
If p and q are the zeroes of the poly¬nomial t² – 4t + 3, then find \(\frac{1}{p}+\frac{1}{9}-2 p q+\frac{14}{3}\)
Answer:
0
Explanation:
t² – 3t – t + 3
= t(t – 3) – 1(t-3)
= (t – 3) (t – 1)
t = 3,1
p = 3, q = 1

Question 73.
If the inudnct of zeroes rf9x2+3x + p is 7, then find p”.
Answer:
63

Question 74.
If α, β, γ are the zeroes of the polyno-mial f(x) = ax³ + hx² + cx + d, then find α² + β² + γ²
Answer:
\(\frac{b^{2}-2 a c}{a^{2}}\)

Question 75.
p(x) = x² + 5x + 6, then find zeroes of p(x).
Answer:
-2,-3.

Question 76.
If one of the zeroes of the quadratic polynomial ax² + bx + c is ‘0’, then find the other zero.
Answer:
-b

Question 77.
α = a – b, β = a 4 b, then make the quadratic polynomial.
Answer:
x² – 2ax + a² – b²

Question 78.
Find the quadratic polynomial whose zeroes are \(4+\sqrt{5}\) and \(4-\sqrt{5}\)
Answer:
x² – 8x + 11

Question 79.
Find die remainder when
3x³ + x² + 2x + 5 is divided by x² + 2x + 1.
Answer:
9x + 10

Question 80.
What must be subtracted or added to p(x) = 8x⁴ + 14x³ – 2x² + 8x – 12, so that 4x² + 3x – 2 is a factor off p(x) ?
Answer:
15x – 14

Question 81.
Prepare a quadratic polynomial whose zeroes are \(\sqrt{15}\) and \(-\sqrt{15}\).
Answer:
x² – 15

Question 82.
Divide(x³ – 6x² + 11x – 12) by (x² – x + 2)r then find quotient.
Answer:
x – 5

Question 83.
If -1 is a zero of the polynomial f(x) = x² – 7x – 8, then find the other zero.
Answer:
8

Question 84.
If a > 0, dim draw the shape off ax² + bx + c = 0.
Answer:

Question 85.
If 2x + 3 is a factor of 2x³ – x – b + 9x², then find the value erf b.
Answer:
-15

Question 86.
If the order erf ax⁵ + 3x⁴ + 4x³ + 3x² + 2x + 1 is 4, then find Answer:
Answer:
0
Explanation:
If a = 0, then given equation order becomes 4.

Question 87.
Find the zeroes erf the polynomial p(x) = 4x² – 12x + 9.
Answer:
\(\frac{3}{2}, \frac{3}{2}\)

Question 88.
If α, β, γ are roots erf a cubic polynomial ax³ + bx² + cx + d, then find αβ + βγ + γα
Answer:
\(\frac{\mathbf{c}}{\mathbf{a}}\)

Question 89.
If one of the zeroes of the quadratic polynomial f(x) = 14x² – 42k²x – 9 is negative of the other, then find k.
Answer:
0
Explanation:
Let α = x, β = – x
α + β = \(-\frac{b}{a}\)
x – x = \(\frac{-\left(-42 \mathrm{k}^{2}\right)}{14}\)
⇒ + 3k² = 0
⇒ k² = \(\frac{0}{3}\) = 0 ⇒ k = 0

Question 90.
p(x) = 4x² + 3x – 1, then find P(\(\frac{1}{4}\))
Answer:
0

Question 91.
Find the sum of zeroes of the polynomial 3x² – 8x + 1 = 0.
Answer:
\(\frac{8}{3}\)
Explanation:
3x² – 8x + 1 = 0
Sum of zeroes = \(-\frac{b}{a}\)
= \(\frac{-(-8)}{3}=\frac{8}{3}\)

Question 92.
If the product of zeroes of the polynomial f(x) = ax³ – 6x² + 11x – 6 is 4, then find Answer:
Answer:
\(\frac{3}{2}\)
Explanation:
αβγ = \(\frac{-\mathrm{d}}{\mathrm{a}}\) = 4
\(\frac{-(-6)}{a}\) = 4 ⇒ 4a = 6 ⇒ a = \(\frac{6}{4}=\frac{3}{2}\)

Question 93.
Name a polynomial of degree ‘3’.
Answer:
Cubic polynomial.

Question 94.
Is the below graph represents a polynomial ?

Answer:
No, it is not a polynomial.

Question 95.
Find the quotient when x⁴ + x³ + x² – 2x – 3 is divided by x² – 2.
Answer:
x² + x + 3

Question 96.
If α, β, γ are roots of a cubic polyno-mial ax³ + bx² + cx + d, then find α + β + γ
Answer:
\(\frac{-b}{a}\)

Question 97.
If one zero of the quadratic polynomial 2x² + kx – 15 is 3, then find the other zero.
Answer:
\(\frac{-5}{2}\)

Question 98.
If α, β, γ are the zeroes of the polynomial f(x) = ax³ + bx² + cx + d, then
find \(\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}\)
Answer:
\(-\frac{c}{d}\)

Question 99.
The graph

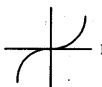
represents, which type of polynomial ?
Answer:
Cubic polynomial.

Question 100.
Write the product and sum of the zeroes of the quadratic polynomial ax² + bx + c respectively.
Answer:
\(\frac{c}{a}, \frac{-b}{a}\)

Question 101.
Write the number of zeroes of the poly¬nomial in the given graph.

Answer:
0

Question 102.
If f(x) = ax² + bx + c has no real zeroes and a + b + c < 0, then write the condition.
Answer:
c < 0

Question 103.
Which type of polynomial ax² + bx + c?
Answer:
Quadratic polynomial.

Question 104.
If one zero of the polynomial
f(x) = (k² + 4)x2 + 13x + 4k is recip¬rocal of the other, then find k.
Answer:
2
Explanation:
\(x \cdot \frac{1}{x}=\frac{4 k}{k^{2}+4}\)
⇒ k² + 4 = 4k
=» k² – 4k + 4 = 0
⇒ (k – 2)² = 0
⇒ k = 2

Question 105.
Write the number of zeroes of the poly-nomial function p(x), whose graph is given below.

Answer:
3

Question 106.
If two zeroes of x³ + x² – 5x – 5 are \(\sqrt{5}\) and \(-\sqrt{5}\) then find its third zero.
Answer:
-1

Question 107.
If one zero of the quadratic polynomial x² – 5x – 6 is 6, then find the other zero.
Answer:
– 1

Question 108.
Find the degree of the polynomial \(a_{0} x^{n}+a_{1} x^{n-1}+a_{2} x^{n-2}+\ldots .+a_{n} x^{n}\)
Answer:
n

Question 109.
If α and β are the zeros of the polyno-mial f(x) = x² + px + q, then find a
polynomial having \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\) as its a p
zeroes.
Answer:
qx² + px + 1

Question 110.
If both the zeroes of a quadratic poly-nomial ax² + bx + c are equal and opposite in sign, then find ‘b’.
Answer:
0

Question 111.
Write the number of zeroes of the poly-nomial in the given graph.

Answer:
1

Question 112.
Find the sum and product of the ze¬roes of polynomial x² – 3 respectively.
Answer:
0,-3

Question 113.
If a < 0, then draw the shape of ax² + bx + c = 0.
Answer:

Question 114.
From the graph write the number of zeroes of the polynomial.

Answer:
2

Question 115.
If α and β are zeroes of the polynomial p(x) = x² – 5x + 6, then find the value of α + β – 3αβ.
Answer:
– 13
Explanation:
α + β = \(\frac{-b}{a}=\frac{-(-5)}{1}\) = 5
αβ = \(\frac{\mathrm{c}}{\mathrm{a}}\) = 6
= α + β – 3αβ = 5 – 3(6)
= 5- 18 = – 13.

Question 116.
What should be subtracted from the polynomial x² – 16x + 30 so that 15 is the zero of the resulting polynomial ?
Answer:
15

Question 117.
Find the number of zeroes lying be-tween – 2 and 2 of the polynomial f(x) whose graph is given below.

Answer:
2

Question 118.
If the zeroes of a quadratic polynomial are equal in magnitude but opposite in sign, then write the relation be¬tween zeroes.
Answer:
Sum of its zeroes is 0.

Question 119.
Find where the graph of the polyno¬mial f(x) = 2x – 5 is a straight line which intersects the x – axis.
Answer:
[\(\frac{5}{2}\),0]

Question 120.
If α,β are the zeroes of the polyno¬mial f(x) = ax² + bx + c, then find \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}=\)
Answer:
\(\frac{b^{2}-2 a c}{c^{2}}\)

Choose the correct answer satis¬fying the following statements.

Question 121.
Statement (A): (2 – \(\sqrt{3}\))is °ne zero of the quadratic polynomial, then other zero will be (2 + \(\sqrt{3}\)).
Statement (B) : Irrational zeroes (roots) always occurs in pairs.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
As irrational roots / zeroes always oc¬curs in pairs therefore, when one, zero
is 2 – √3 , then other will be 2 + √3
So, both A and B are correct and B explains A.
Hence, (i) is the correct option.

Question 122.
Statement (A) : If both zeroes of the quadratic polynomial x² – 2kx + 2 are equal in magnitude but opposite in sign, then value of k is \(\frac { 1 }{ 2 }\).
Statement (B) : Sum of zeroes of a quadratic polynomial ax² + bx + c is \(\frac{-b}{a}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
As the polynomial is x² – 2kx + 2 and
its zeros are equal but opposition sign.
∴ Sum of zeroes = 0 = \(\frac{-(-2 \mathrm{k})}{1}\) = 0
⇒ 2k = 0 ⇒ k = 0
So, A is incorrect but B is correct.
Hence, (iii) is the correct option.

Question 123.
Statement (A): p(x) = 14x³ – 2x² + 8x⁴ + 7x – 8 is a polynomial of degree 3. Statement (B) : The highest power of x in any polynomial p(x) is the degree of the polynomial.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
The highest power of x in the polyno¬mial p(x) = 14x³ – 2x² + 8x⁴ + 7x – 8 is 4.
∴ Degree of p(x) is 4.
So, A is incorrect but B is correct.
Hence, (iii) is the correct option.

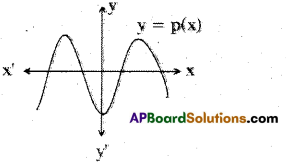
Question 124.

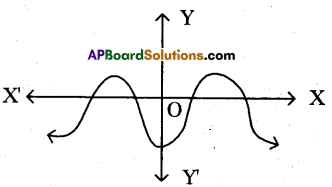
Statement (A) : The graph y = f(x) is shown in figure, for the polynomial f(x). The number of zeroes of f(x) is 4.
Statement (B): The number of zero of polynomial f(x) is the number of point of which f(x) cuts or touches the axes.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
As the number of zero of polynomial f(x) is the number of {mints at which f(x) cuts (intersects) the x-axis and number of zero in the given figure is 4. So A is correct but B is incorrect Hence, (ii) is the correct option.

Question 125.
Statement (A) : The sum and product of the zeroes of a quadratic polynomial
are – \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 4 }\) respectively. Then the
quadratic polynomial is 4x² + x + 1.
Statement (B): The quadratic polyno-mial whose sum and product of zeroes are given is x² – (sum of zeroes)x + product of zeroes.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false,
Answer:
(i)
Explanation:
Sum of zeroes = –\(\frac { 1 }{ 4 }\) and
Product of zeroes = \(\frac { 1 }{ 4 }\)
∴ Quadratic polynomial be

∴ Quadratic polynomial be 4x² + x + 4.
So, both A and B are correct and B explains A. Hence, (i) is the correct option.

Question 126.
Statement (A) : If α, β are zeroes of x² – 3x + p and 2α + 3β = 15, then p – 54.
Statement (B) : If α, β are the zeroes of the polynomial ax² + bx + c, then
α + β = \(\frac{-b}{a}\) and αβ = \(\frac{c}{a}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)

Question 127.
Statement (A) : A quadratic polyno¬mial having 4 and – 2 as zeroes is 2x² – 4x – 16.
Statement (B): The quadratic polyno-mial having a and (3 as zeroes is given by p(x) = x² – (α + β)x + αβ
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)

Question 128.
Statement (A) : The polynomial p(x) = x³ + x has one real zero.
Statement (B) : A polynomial of nth degree has at most n zeroes.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)

Question 129.
Statement (A): If α, β, γ are the zeroes of x³ – 2x² – qx – r and α + β = 0, then 2q= r.
Statement (B) : If α, β, γ are the ze¬roes of ax³ + bx² + cx + d, then
α + β + γ = \(\frac{-b}{a}\), αβ, βγ, γα = \(\frac{c}{a}\), αβγ = \(\frac{-d}{a}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
Clearly, (B) is true, [standard result] cc + p + y = -(-2) = 2 ⇒ 0 + y = 2 ‘ Y – 2 ‘
α + β + γ = – (- 2) = 2=
o + γ = 2
γ = 2
αβγ = -(-r) = r
∴ αβ(2) = r
⇒ αβ = \(\frac{r}{2}\)
⇒ αβ + βγ + γα = -q
⇒\(\frac{r}{2}\) + γ(α+β) = -q
⇒\(\frac{r}{2}\) + 2(0) = -q
⇒ r = 2q
∴ (A) is false
Hence, (iii) is the correct option.

Question 130.
Statement (A) : If one zero of polyno¬mial p(x) = (k² + 4)x² + 13x + 4k is reciprocal of other, then k = 2.
Statement (B) : If x – a is a factor of p(x), then p(α) = 0 i.e., a is a zero of p(x).
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
(B) is true
Let α, 1/α be the zeroes of p(x), then
\(\alpha \cdot \frac{1}{\alpha}=\frac{4 \mathbf{k}}{\mathbf{k}^{2}+4} \Rightarrow \mathbf{1}=\frac{4 \mathbf{k}}{\mathbf{k}^{2}+4}\)
∴ k² -4k + 4 = 0 ⇒ (k- 2)² = 0
∴ k = 2
∴ (A) is true. So, (i) is correct option.

Question 131.
Statement (A) : The polynomial x⁴ + 4x² + 5 has four zeroes. Statement (B) : If p(x) is divided by (x – k), then the remainder = p(k).
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
(B) is true by remainder theorem. Again, x⁴ + 4x² + 5
= (x² + 2)² + 1 > 0 for all x.
∴ Given polynomial has no zeroes.
∴ (A) is not true.
Hence, (iii) is the correct option.

Question 132.
Statement (A) : x³ + x has only one real zero.
Statement (B) : A polynomial of nth degree must have ‘n’ real zeroes.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
(B) is false [v a polynomial of n<sup<th degree has at most x zeroes]
Again, x³ + x = x (x² + 1) which has only one real zero (x = 0)
[∵ x² + 1 ≠ 0 for all x ∈ R]
(A) is true.
Hence, (ii) is the correct option.

Question 133.
Statement (A) : If 2, 3 are the zeroes of a quadratic polynomial, then poly¬nomial is x² – 5x + 6.
Statement (B) : If a, P are the zeroes of a monic quadratic polynomial, then polynomial is x² – (a + p)x + ap.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)

Question 134.
Statement (A): Degree of a zero poly-nomial is not defined.
Statement (B) : Degree of a non-zero constant polynomial is ‘0’.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)

Question 135.
Statement (A) : Zeroes of f(x) = x³ – 4x – 5 are 5, – 1.
Statement (B): The polynomial whose zeroes are \(2+\sqrt{3}, 2-\sqrt{3}\) is x² – 4x + 7.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)

Question 136.
Statement (A) : x² + 4x + 5 has two zeroes.
Statement (B) : A quadratic polyno¬mial can have at the most two zeroes.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)

Read the below passages and an¬swer to the following questions.

If α, β are the zeroes of the quadratic polynomial f(x) = ax² + bx + c, then
α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)

If α, β are the zeroes of the quadratic polynomial f(x) = x² – px + q, then find \(\frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:
\(\frac{p}{q}\)
Explanation:
α + β = p, αβ = q
∴ \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\alpha+\beta}{\alpha \beta}=\frac{p}{q}\)

Question 138.
If α, β are the zeroes of the quadratic polynomial fix) = x² + x – 2, then find \(\left(\frac{1}{\alpha}-\frac{1}{\beta}\right)^{2}\)
Answer:
\(\frac{9}{4}\)
Explanation:
α + β = -1, αβ = -2

Question 139.
If α, β are the zeroes of the quadratic polynomial fix) = x² – 5x + 4, then
find \(\frac{1}{\alpha}+\frac{1}{\beta}-2 \alpha \beta\)
Answer:
–\(\frac{27}{4}\)

If α, β, γ are the zeroes of ax³ + bx² + cx + d, then \(\Sigma \alpha=\frac{-b}{a}\), \(\Sigma \alpha \beta=\frac{\mathbf{c}}{\mathbf{a}}, \Sigma \alpha \beta \gamma=\frac{-\mathbf{d}}{\mathbf{a}}\)
Explanation:
α + β = 5, αβ = 4

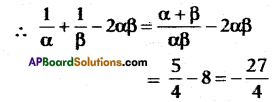
Question 140.
If α, β, γ are the zeroes of x³ – 5x² – 2x + 24 and ap = 12, then
find αβ = 12, then find ‘γ’
Answer:
-2

Question 141.
If a – b, a, a + b are the roots of x³ – 3x² + x + 1, then find a + b².
Answer:
3

Question 142.
If two zeroes of the polynomial x³ – 5x² – 16x + 80 are equal in magni¬tude but opposite in sign, then find ze¬roes.
Answer:
4,-4, 5.

Manow says that the order of the polynomial (x² – 5) (x³ + 1) is 6.

Question 143.
Do you agree with Manow ?
Answer:
No.

Question 144.
Which mathematical concept is used to judge Manow ?
Answer:
Polynomial.

Question 145.
How much the actual order of given problem ?
Answer:
Degree is 5.

The length of a rectangle is ’5’ more than its breadth.

Question 146.
Express the information in the form of polynomial.
Answer:
(x + 5 + x) = 2x + 5.

Question 147.
Find the perimeter of the rectangle given above.
Answer:
(4x + 10)m

Question 148.
To solve this given problem which mathematical concept was used by you?
Answer:
Polynomial.

Question 149.
Write the correct matching option.

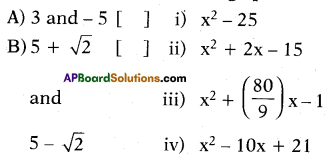
Answer:
A – (ii), B – (iv).

Question 150.
Write the correct matching option.

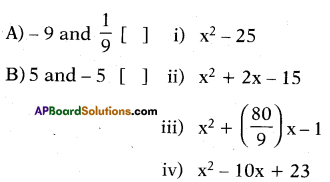
A – (iii), B – (i).

Question 151.
Write the correct matching option.

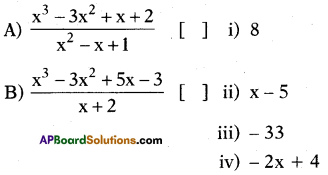
Answer:
A – (iv), B – (iii).

Question 152.
Write the correct matching option.

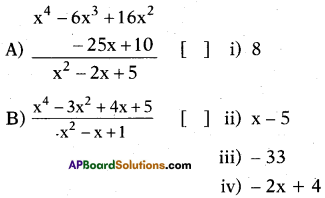
Answer:
A – (ii), B – (i).

Question 153.
Write the correct matching option.

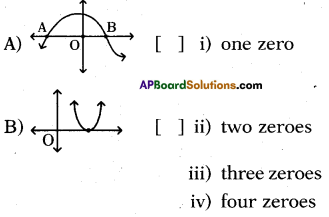
Answer:
A – (iii), B – (i).

Question 154.
Write the correct matching option.

Answer:
A – (iii), B – (v).

Question 155.
Write the correct matching option.

Answer:
A – (iv), B – (i).

Question 156.
If α, β, γ are the zeroes of the polyno-mial px³ + qx² + rx + s then, which of the following matching is correct ?

a) A(i), B(ii), C(iii)
b) A(ii), B(iii), C(i)
c) A(iii), B(i), C(ii)
d) A(ii), B(i), C(iii)
Answer:
(b)

Question 157.
What is the zero of the polynomial 3x – 2 ?
Solution:
f(x) = 3x – 2; f(x) = 0
3x – 2 = 0 ⇒ 3x = 2
⇒ x = 2/3

Question 158.
Write the polynomial in variable ‘x’ whose zero is \(\frac{-k}{a}\).
Solution:
x – \(\frac{-k}{a}\) = 0 ⇒ x + \(\frac{k}{a}\) = 0
⇒ ax + k = 0
∴ ax + k = 0 is a polynomial with degree T in variable ‘x’ whose zero is \(\frac{-k}{a}\).