Mahesh

Students can go through AP Board 7th Class Maths Notes Chapter 12 Quadrilaterals to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 12 Quadrilaterals

→ Quadrilateral: A closed figure bounded by four line segments is called a quadrilateral.
In the figure, ABCD is a quadrilateral.

→ A quadrilateral divides a plane into three parts.
i) Interior of the quadrilateral
ii) Exterior of the quadrilateral
iii) Boundary of the quadrilateral

→ In the figure the points P, Q are in the interior of the quadrilateral. i3r In the figure the points R, S are in the exterior of the quadrilateral.

→ In the figure the points A, B, C, D are on the boundary of the quadrilateral.

→ A quadrilateral is said to be a convex quadrilateral if all line segments joining points in the interior of it also lie in its interior completely.
□ BELT is a convex quadrilateral.

→ A quadrilateral is said to be a concave quadrilateral if all line segments joining points in the interior of it do not necessarily lie in its interior completely.

In □ RING, the line segment \(\overline{\mathrm{AB}}\) does not lie completely in its interior, as such the quadrilateral RING is a concave quadrilateral.

→ Sum of the interior angles of a quadrilateral is 360°.
∠A + ∠B + ∠C + ∠D = 360°

→ A quadrilateral in which one pair of opposite sides are parallel is called a trapezium.
In □ ABCD ; AB // CD

→ A kite has four sides. There are exactly two distinct pairs of equal length.
In quadrilateral KITE,

KI = KE and IT = ET

→ A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram. In quadrilateral ABCD,
AB // CD and AD // BC. Hence □ ABCD is a parallelogram.

→ In a parallelogram,

• Opposite sides are parallel and equal [AB = CD and AD = BC]
• Diagonals bisect each other (AO = OC and BO = OD)
• Opposite angles are equal (∠A = ∠C and ∠B = ∠D)
• Adjacent angles are supplementary (∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A = 180°)

→ A parallelogram in which adjaœnt sides are equal is called a Rhombus.
In quadrilateral ABCD,
AB = BC = CD = DA and hence □ ABCD is a Rhombus.

In a rhombus diagonals bisect each other at right angles,
(i.e.) AC ⊥ BD and AO = OC, BO = OD

→ A rectangle is a parallelogram with equal angles (OR)
A parallelogram in which one angle is a right angle is called a rectangle.

In fig. ∠A = ∠B = ∠C = ∠D = 90° and □ ABCD is a rectangle.
In a rectangle the diagonals are equal.
In a rectangle the diagonals bisect each other.

(AC = BD and AO = OC; BO = OD)

→ A square is a rectangle with equal adjacent sides.

In the figure AB = BC = CD = DA
∠A = ∠B = ∠C = ∠D = 90°
In a square the diagonals are equal and bisect at right angles. Also they are equal.
[(AO = OC ; BO = OD), (AC ⊥ BD) and (AC = BD)]

Flow chart of family of quadrilaterals

SCERT AP 7th Class Social Study Material Pdf 8th Lesson Bhakthi – Sufi Textbook Questions and Answers.

AP State Syllabus 7th Class Social 8th Lesson Questions and Answers Bhakthi – Sufi

7th Class Social 8th Lesson Bhakthi – Sufi Textbook Questions and Answers

Review Of Your Previous Knowledge

Question 1.
What do you observe in the picture 8.1?
Answer:
I observe Jagadguru Adi Sankaracharya, his disciples and his devotees in the left picture. In the right side picture, I observe Muslim priest and his disciples. In both the pictures the gurus are preaching their disciples.

Question 2.
What are they teaching?
Answer:

1. In the first picture Adi Shankara Charya preached equality of all humans.
2. In the second picture Sufi Saints emphasised on an egalitarian society based on Universal love.

Improve Your Learning

I. Answer the following questions.

Question 1.
What are the salient features of Bhakti movement?
Answer:
Salient features of Bhakti Movement:

1. Oneness of God.
2. One of the ways to Moksha is Bhakti.
3. Bhakti means to surrender to God.
4. Emphasized equality of all humans.
5. No discrimination of caste, creed, sect.
6. The Bhakti saints travelled to various places to speak about the path of Bhakti and preached in the local languages.

Question 2.
Who is Mira Bai? What was her contribution to the Bhakthi movement?
Answer:

1. Mira Bai was woman saint of the medieval times.
2. Mira became a devotee of Krishna right from her childhood.
3. Mira Bai’s contribution to the Bhakti movement was primarily in her music.
4. She wrote hundreds of songs and initiated a mode of singing the songs a raga.
5. About 200 400 songs are accepted by scholars as being written by Mirabai.
6. Mirabai wrote her songs in Rajasthani and Braj Bhasha languages, and they were translated into Hindi and Gujarathi.
7. Mirabai’s songs express her love and devotion to Krishna, almost always as Krishna’s wife.

Question 3.
What can the present society learn from the bhakthi movement and the sufi movement?
Answer:

1. The songs and the teachings of the Sufi and the Bhaki saints are relevant even today.
2. The two movements brought a new form of religious expression amongst Muslims and Hindus.
3. Worship, or singing bhajans, kirtans or qawwalis, or even repeating the name of God in silence, and noticed that some of them are moved to tears. Such intense devotion or love of God is the legacy of various kinds of bhakti and Sufi movements that have evolved even today.

Question 4.
Read the topic in page number 46 under the heading ‘Impact of bhakti movement onthe medieval Indian society’ and comment in your own words.
Answer:
Impact of the Bhakti Movement on the Medieval Indian Society :

1. The most important social impact of the Bhakti movement was that the followers of the Bhakti movement rejected caste discrimination.
2. This movement encouraged religious tolerance.
3. The bhakti saints preached religous tolerance and monotheism
4. A spirit of harmony developed among different sections of the society.
5. It tried to develop humanitarian attitude.

Iitipact of Sufi movement :

1. Sufis travelled all over the country to reach the poor and rural communities.
2. They preached in the local languages.
3. They lived a modest simple life.

Question 5.
Who was the founder of Sikhism and what were the main principles of Sikhism?
Answer:
Guru Nanak was the founder of Sikh religion.
Main Principles:

1. Truthful living,
2. Serving to humanity,
3. Uphold the values of honesty,
4. Compassion, generosity, humanity, integrity, servi-e and spirituality on a daily basis.

Question 6.
Write an essay appreciating the social services rendered by bhakti saints.
Answer:

1. The Bhakti movement empowered the underbelly of Indian society in fundamental ways and also provided the required impetus for the growth of vernacular literature.
2. This tradition of those deemed “low” singing and writing did not, however, end with
   the Bhakti movement comingling into the mainstream. ‘
3. They emphasized the virtues of love and devotion, brotherhood and equality etc. This helped to bring the two communities nearer.
4. It also helped to harmonise the conflicting interests. The saints of the Bhakti movement rejected the differences of caste system.

Question 7.
Decribe the prominent saints of South India.
Answer:
Prominent Saints of South India :
1. Ramanujacharya:
Ramanuja gave a philosophical basis to the teachings of Vaishnavism. His commentaries on the Brahma Sutras are popularly known as “Sri Bhasya”.

2. Nimbarka :
He was a younger contemporary of Ramanuja, who also rendered great service to the spread of Bhakti movement.

3. Madhwacharya :
Madhwacharya propagated Dvaita philosophy.
Madhwacharya divides the Universe into two parts.
i) Swatantra (independent being) and
ii) Aswatantra (dependent being).

4. Vallbhacharya :
He advocated a system of pure non-dualism devoid of the concept of Maya.

5. Basaveswara:
He popularised the Veerasaivism. His literary works are named Vachanas.

6. Adi Shankaracharya :
1) He preached Advaita Philosophy.
2) He established four Shakthi Peethas in all the four corners of India.

Question 8.
Write about Sufi saints and their teachings.
Answer:

1. The Sufi saints were always in meditation and they led a simple life.
2. They wore woollen clothes.

The main teachings of Sufism are ;

1. There is only one God.
2. All are children of God.
3. Devotional music is one of the ways to move nearer to God.
4. Sufi believes. Wahdat-ul-Wujud means worship for a single God.
5. Fasts and rituals are not essential to reach God.
6. Different religions are different ways to reach God.

II. Choose the correct answer.

1. Who preached the Vishishtadvaitha philosophy?
a) Ramanuja
b) Sankaracharya
c) Ramananda
d) Kabir
Answer:
a) Ramanuja

2. Who of the following preached Saguna Bhakti?
a) Mira bai
b) Shankara Deva
c) Basaveswgra
d) All the above
Answer:
a) Mira bai

3. Who is the founder of Sikh religion?
a) Gurunanak
b) Sankaracharya
c) Ramananda
d) Akbar
Answer:
a) Gurunanak

4. What does it mean “oneness of god”?
a) Only one god
b) Belief in one god
c) Unity of god
d) All the above
Answer:
d) All the above

5. In which century did the Bhakti movement begin?
a) 6^th CE
b) 7^th CE
c) 8^th CE
d) 9^th CE
Answer:
c) 8^th CE

III. Match the following.

Answer:

7th Class Social 8th Lesson Bhakthi – Sufi InText Questions and Answers

7th Class Social Textbook Page No. 19

Question 1.
With the help of your teacher/parents collect some preachings of Adi Sankaracharya from your school library and discuss in classroom.
Answer:
The preachings of Adi Sankaracharya :

1. He taught that supreme Brahman in Nirguna (without the Gunas), Nirakara (formless), Nirvisesha (without attributes) and Akarta (non-agent).
2. Brahman is above all needs and desires.
3. Brahman is alone real,
4. This world is unreal,
5. and the jiva or the individual soul is non-different from Brahman.

7th Class Social Textbook Page No. 22

Question 2.
Collect the information regarding the holy texts Guru Grandh Sahib.
Answer:
The text consists of 1,430 angs (pages) and 5,894 sabads (line compositions), which are poetically rendered and set to a rhythmic ancient north Indian classical form of music.

The bulk of the scripture is divided into 31 main ragas, with each Granth raga subdivided according to length and author.

7th Class Social Textbook Page No. 25

Question 3.
List out the similarities in the preachings of Hindu and Islamic reformers.
Answer:
Similarities :

1. Both Islam and Hinduism are based on divine revelation and in essence both worship the Supreme being is generally ignored.
2. Both are followed the words of Prophets and Rishis.
3. Hinduism and Islam share some ritual practices such as fasting and pilgrimage.

Think & Respond

7th Class Social Textbook Page No. 21

Question 1.
Kabir said that “All are equal before God”? Do you agree with this statement? Mention your reasons.
Answer:
Yes, “I agree with the statement, because he preached a religion of love which aimed at promoting unity amongst all castes and creeds.

He was the first saint who tried to reconcile Hinduism and Islam.

7th Class Social Textbook Page No. 23

Question 2.
Namdev preached no need to follow rituals and elaborated process to worship god.Why did he say?
Answer:
According to Namdev we have to concentrate our mind on God to attain moksha.

7th Class Social Textbook Page No. 24

Question 3.
Bhakti inculcates honesty, kindness, love, service-mindedness, etc. Discuss
Answer:
Honesty, kindness, love, service mindedness are interconnnected with each other. Without these a soul cannot walk through the Bhakti Path.

Explore

7th Class Social Textbook Page No. 19

Question 1.
What are the contributions of Ramanujacharya to attain social equality?
Answer:
Sri Ramanujacharya is considered as the first Acharya, who devoted his entire life for the upliftment of the equality in the society.

He gave perfect commentaries to the Brahma Sutras and Upanishads and made a perfect bridge between different sections of society.

He established 74 authoritative acharyas to spread the message of equality across the world.

7th Class Social Textbook Page No. 20

Question 2.
Why did Ramananda oppose sectarianism? Know from your teacher.
Answer:
Ramananda perceived that there is only one God. Who is the origin of all, all the distinctions of caste and creed vanished for him and he saw humanity as one large family, and all men as brothers.
One man is higher than another, not through birth, but only through his love and sympathy.

Question 3.
Collect the information about Basaveswara from internet, discuss with your teacher.
Answer:

Basaveshwara, colloquially known as Basavanna, was a 12th-century CE

Indian statesman, philosopher, poet, social reformer and Lingayat saint in the Shiva-focussed bhakti movement, and a Hindu Shaivite social reformer during the reign of the Kalyani Chalukya/Kalachuri dynasty.

7th Class Social Textbook Page No. 22

Question 4.
Collect the names of ten Sikh gurus with the help of your teacher.
Answer:

1. Guru Nanak
2. GuruAngad
3. Guru Amardas
4. Guru Ramdas
5. Guru Arjan
6. Guru Hargobind
7. Guru Har Rai
8. Guru Har Krishan
9. Guru Tegh Bahadur
10. Guru Gobind Singh

Project Work

Collect the pictures of various Bhakthi and Sufi saints.
Answer:

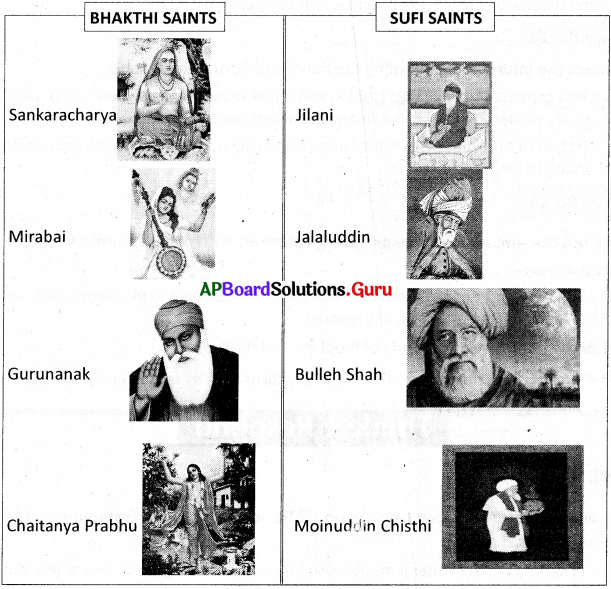
Students can go through AP Board 6th Class Maths Notes Chapter 6 Basic Arithmetic to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 6 Basic Arithmetic

→ If a comparison is made by finding the difference between two quantities, it is called comparison by difference.
Eg: Age of Harshita is 11 years and age of Srija is 8 years. Harshita is (11 – 8 = 3) 3 years older than Srija or Srija is 3 years younger than Harshita.

→ If a comparison is made by division it makes more sense than the comparison made by taking the difference.
Eg: If cost a key pad cell phone is Rs. 3000 and another smart phone is Rs. 15000, then the cost of the second phone is five times the cost of the first phone.

→ Ratio: Comparison of two quantities of the same type by virtue of division is called ratio. Eg: The weight of Ramu is 24 kg and the weight of the Gopi is 36 kg., then the ratio of weights is 24/36. It can also be written as 24:36 and read as 24 is to 36.
The ratio of two numbers ‘a’ and ‘b’ (b ≠ 0) is a ÷ b or a/b or \(\frac{a}{b}\) and is denoted as a : b and is read as a is to b.
In the ratio a : b the quantities a and b are called the terms of the ratio.
In the ratio a : b the quantity a is called the first term or antecedent and b is called the second term or the consequent of the ratio.
The value of a fraction remains the same if the numerator and the denominators are multiplied or divided by the same non-zero number so is the ratio.
That is if the first term and the second term of a ratio are multiplied or divided by . the same non-zero number.
3 : 4 = 3 × 5 : 4 × 5 = 15 : 20
Also 36 : 24 = 36 – 4 : 24 – 4 = 9 : 6.

→ Ratio in the simplest form or in the lowest terms:
A ratio a : b is said to be in its simplest form if its terms have no factors in common other than 1. A ratio in the simplest form is also called the ratio in its lowest terms. Generally ratios are expressed in their lowest terms.
To express a given ratio in its simplest term, we cancel H.C.F. from both its terms. To find the ratio of two terms, we express the both terms in the same units.
Eg: Ratio of 3 hours and 120 minutes is 3 : 2 (as 120 minutes = 2 hours) or 180 : 120 (as 3 hours = 180 minutes)
A ratio has no units or it is independent of units used in the quantities compared. The order of terms in a ratio a : b is important a : b ≠ b : a.

→ Equivalent ratio:
A ratio obtained by multiplying or dividing the antecedent and consequent of a given ratio by the same number is called its equivalent ratio.
Eg: 3 : 4 = 3 × 5 : 4 × 5 = 15 : 20. Here 3 : 4 & 15 : 20 are called equivalent ratios.
Also 36 : 24 = 36 ÷ 4 : 24 ÷ 4 = 9 : 6. Here 36 : 24 & 9 : 6 are called equivalent ratios.

→ Comparison of ratios: To compare two ratios
a) First express them as fractions
b) Now convert them to like fractions
c) Compare the like fractions

→ Proportion:
If two ratios are equal, then the four terms of these ratios are said to be in proportion. If a : b = c : d, then a, b, c and d are said to be in proportion.
This is represented as a : b :: c : d and read as a is b is as c is d.
The equality of ratios is called proportion.
Conversely in the proportion a : b :: c : d , the terms a and d are called extremes and b and c are called means.
If four quantities are in proportion, then
Product of extremes = Product of means .
If a : b :: c : d, then a × d = b × c
From this we have

→ Unitary method:
The method in which first we find the value of one unit and then the value of required number of units is known as unitary method.
Eg: If the cost of 8 books Rs.96, then find the cost of 15 books.
Cost of one book = 96/8 = 12 Cost of 15 books = 12 × 15 = 180
Distance travelled in a given time = speed × time From this we have

→ Percentage:
The word per cent means for every hundred or out of hundred. The word percentage is derived from the Latin language. The % symbol is uses to represent percent.
Eg: 5% is read as five percent
5% = \(\frac{5}{100}\) = 0.05
38% = \(\frac{38}{100}\) = 0.38

→ To convert a percentage into a fraction:
a) Drop the % symbol
b) Divide the number by 100
Eg: 25% = \(\frac{25}{100}\) = 0.25 = \(\frac{1}{4}\)

→ To convert a fraction into percentage:
a) Assign the percentage symbol %
b) Multiply the given fraction with 100
Eg: \(\frac{3}{4}\) = \(\frac{3}{4}\) × 100% = 75% = 0.75

Students can go through AP Board 9th Class Maths Notes Chapter 15 Proofs in Mathematics to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 15 Proofs in Mathematics

→ The sentences that can be judged on some criteria, no matter by what process for their being true or false are statements.

→ Mathematical statements are of a distinct nature from general statements. They cannot be proved or justified by getting evidence while they can be disproved by finding a counter example.

→ Making mathematical statements through observing patterns and thinking of the rules that may define such patterns.
A hypothesis is a statement of idea which gives an explanation to a sense of observation.

→ A process which can establish the truth of a mathematical statement based purely on logical arguments is called a mathematical proof.

→ Axioms are statements which are assumed to be true without proof.

→ A conjecture is a statement we believe is true based on our mathematical intuition, but which we are yet to prove.

→ A mathematical statement whose truth has been established or proved is called a theorem.

→ The prime logical method in proving a mathematical statement is deductive reasoning.

→ A proof is made up of a successive sequence of mathematical statements.

→ Beginning with given (Hypothesis) of the theorem and arrive at the conclusion by means of a chain of logical steps is mostly followed to prove theorems.

→ The proof in which, we start with the assumption contrary to the conclusion and arriving at a contradiction to the hypothesis is another way that we establish the original conclusion is true is another type of deductive reasoning.

→ The logical tool used in the establishment of the truth of an un-ambiguous statement is called deductive reasoning.

→ The reasoning which is based on examining of variety of cases or sets of data discovering pattern and forming conclusion is called Inductive reasoning.

Students can go through AP Board 9th Class Maths Notes Chapter 14 Probability to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 14 Probability

→ If in an experiment all the possible outcomes are known in advance and none of the outcomes can be predicted with certainty, then such an experiment is called a random experiment.
Eg: Tossing a coin; throwing a die, drawing a card from deck of cards.

→ The possible outcomes of a trial are called events.

→ Events are said to be equally likely if there is no reason to expect any one in preference to other. Thus equally likely events mean outcome is as likely to occur as any other outcome.

→ To measure the chance of its happening numerically we classify them as follows.

→ Certain: Something that must happen

→ More likely: Something that would occur with great chance

→ Equally likely: Something that have the same chance of occurring

→ Less likely: Something that would occur with less chance

→ Impossible: Something that cannot happen

→ Probability of an event = \(\frac{\text { Number of favourable outcomes for the event }}{\text { Number of total possible outcomes }}\)

Students can go through AP Board 9th Class Maths Notes Chapter 12 Circles to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 12 Circles

→ A collection of all points in a plane which are at a fixed distance from a fixed point in the sapie plane is called a circle. The fixed point is called the centre and the fixed distance is called the radius of the circle.

→ A line segment joining any two points on the circle is called a chord.

→ The longest of all chords which passes through the centre is called a diameter.

→ Circles with same radii are called congruent circles.

→ Circles with same centre and different radii are called concentric circles.

→ Diameter of a circle divides it into two semi-circles.

→ The part between any two points on the circle is called an arc.

→ The area enclosed by a chord and an arc is called a segment. If the arc is a minor arc then it is called the minor segment and if the arc is major arc then it is called the major segment.

→ The area enclosed by an arc and the two radii joining the end points of the arc with centre is called a sector.

→ Equal chords of a circle subtend equal angles at the centre.

→ Angles in the same segment are equal.

→ An angle in a semi circle is a right angle.

→ If the angles subtended by two chords at the centre are equal, then the chords are congruent.

→ The perpendicular from the centre of a circle to a chord bisects the chords. The converse is also true.

→ There is exactly one circle that passes through three non-collinear points.

→ The circle passing through the three vertices of a triangle is called a circumcircle.

→ Equal chords are at equal distance from the centre of the circle, conversely chords at equidistant from the centre of the circle are equal in length.

→ Angle subtended by an arc at the centre of the circle is twice the angle subtended by it at any other point on the circle.

→ If the angle subtended by an arc at a point on the remaining part of the circle is 90°, then the arc is a semi circle.

→ If a line segment joining two points subtends same angles at two other points lying on the same side of the line segment, the four points lie on the circle.

→ The sum of pairs of opposite angles of a cyclic quadrilateral are supplementary.

Students can go through AP Board 8th Class Maths Notes Chapter 4 Exponents and Powers to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 4 Exponents and Powers

Laws of Exponents:

→ a × a × a …… m times = a^m

In a^m, a is called base; m is called exponent/ power.

→ a^m × aⁿ = a^m+n

→ \(\frac{\mathrm{a}^{\mathrm{m}}}{\mathrm{a}^{\mathrm{n}}}\) = a^m-n (m > n)
⇒ \(\frac{1}{a^{n-m}}\) (m < n)

→ (ab)^m = a^m . b^m

→ a⁰ = 1

→ a^-n = \(\frac{1}{a^{n}}\)

→ aⁿ = \(\frac{1}{a^{-n}}\)

→ \(\left(\frac{a}{b}\right)^{m}\) = \(\frac{a^{m}}{b^{m}}\)

→ \(\left(a^{m}\right)^{n}\) = a^mn

→

→ \(\sqrt[n]{a}\) = \((\mathrm{a})^{1 / \mathrm{n}}\)

Students can go through AP Board 9th Class Maths Notes Chapter 11 Areas to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 11 Areas

→ The part of a plane enclosed by a simple closed figure is called a planar region corresponding to that figure.

→ The magnitude of a planar region is its area.

→ The unit area is the area enclosed by a unit square i.e. a square of side 1 unit.

→ Area is always expressed in square units.

→ The areas of two congruent figures are equal.

→ Converse of the above is not true, i.e., if two figures have same area, they need not be congruent.

→ The area of a whole figure is equal to sum of the areas of finite parts of it.

→ Area of a rectangle is equal to the product of its length and breadth.

→ Area of a parallelogram is the product of a side and its corresponding altitude.

→ Parallelograms on the same base and between same parallels are equal in area.

→ If a parallelogram and a triangle lie on a same base and between same parallels, then the area of the triangle is half the area of parallelogram.

→ Triangles between same base and between same parallels are equal in area.

Students can go through AP Board 9th Class Maths Notes Chapter 10 Surface Areas and Volumes to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 10 Surface Areas and Volumes

→ Cuboid and cube may be treated as regular prisms having six faces.

→ Solids whose lateral surfaces are parallelograms are called prisms,

→ Solids whole lateral surfaces are triangles are called pyramids.

→ Cube and cuboid are also prisms.

→ Volume of a pyramid = \(\frac{1}{3}\) Area of the base × height
= \(\frac{1}{3}\) of the volume of right prism.

Students can go through AP Board 8th Class Maths Notes Chapter 3 Construction of Quadrilaterals to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 3 Construction of Quadrilaterals

→ A closed four sided polygon is called a quadrilateral.

→ A quadrilateral has 4 sides, 4 vertices, 4 angles and 2 diagonals.

→ The sum of the 4 angles of a quadrilateral is 360°.

→ Quadrilateral and their types:

→ Five independent measurements are required to draw a unique quadrilateral.

→ A quadrilateral can be constructed uniquely, if
a) The lengths of four sides and one angle are given
b) The lengths of four sides and one diagonal are given
c) The lengths of three sides and two diagonals are given
d) The lengths of two adjacent sides and three angles are given
e) The lengths of three sides and two included angles are given

→ The two special quadrilaterals, namely rhombus and square can be constructed when two diagonals are given.

Students can go through AP Board 8th Class Maths Notes Chapter 15 Playing with Numbers to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 15 Playing with Numbers

→ Place value of the digits:
12, 34, 56, 789

→ Expanded form of the number:
7843 = 7 × 1000 + 8 × 100 + 4 × 10 + 3 × 1
= 7 × 10³ + 8 × 10² + 4 × 10¹ + 3 × 10⁰

→ Prime numbers: Numbers which are having the factors 1 and itself are called primes.
Ex: 2, 3, 5, 7, 11, 13, …. etc.

→ Divisibility Rules:
(i) Divisibility by 10: If the units digit of a number is ‘0’ then it is divisible by 10.
Ex: 10, 50, 100, 150, 1000 etc.

(ii) Divisibility by 5: If the units digit of a number is either ‘0 ‘or ‘5’ then it is divisible by 5.
Ex: 15, 20, 50, 90 …. etc.

(iii) Divisibility by 2: If the units digit of a number is 0, 2, 4, 6, 8 then it is divisible by 2.
Ex: 0, 16, 32, 48, 22 …. etc.

(iv) Divisibility by 3: If the sum of the digits of a number is divisible by 3 then the number is also divisible by 3.
Ex: 126 → 1 + 2 + 6 → \(\frac{9}{3}\) (R = 0) then 126 is divisible by 3.

(v) Divisibility by 6: If a number is divisible 2 and 3 then it is divisible by 6.

(vi) Divisibility by 4: If the last two digits of a number is divisible by 4, then the entire number is divisible by 4.

∴ 496 is divisible by 4.

(vii) Divisibility by 8: If the last 3 digits of a number is divisible by 8 then it is divisible by 8.

∴ 80952 is divisible by 8.

(viii) Divisibility by 7: If a number is divisible by 7 (2a + 3b + c) must be divisible by 7.
Where a = digit at the hundreds place, b = digit at the tens place and c = digit at ones place.

(ix) Divisibility by ’11’: If the difference of the sum of digits in odd places and sum of digits in even places of a number is divisible by 11. Then the number is divisible by 11.
Ex: 1234321

⇒ (1 + 3 + 3 + 1) – (2 + 4 + 2) = 8 – 8 = 0 → \(\frac{0}{11}\) (R = 0)
∴ 1234321 is divisible by 11.

Students can go through AP Board 8th Class Maths Notes Chapter 2 Linear Equations in One Variable to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 2 Linear Equations in One Variable

→ An algebraic equation is equality of algebraic expressions involving variables and constants.

→ If the degree of an equation is one then it is called a linear equation.

→ If a linear equation has only one variable then it is called a linear equation in one variable or simple equation. ‘

→ The value which when substituted for the variable in the given equation makes L.H.S. = R.H.S. is called a solution or root of the given equation.

→ Just as numbers, variables can also be transposed from one side of the equation to the other side.
Note: When we transpose terms
‘+’ quantity becomes ’-‘ quantity,
‘-‘ quantity becomes ‘+’ quantity.
‘×’ quantity becomes ‘÷’ quantity.
‘÷’ quantity becomes ‘×’ quantity.
Also
Also,
(+) × (+) = +
(+) × (-) = –
(-) × (+) = –
(-) × (-) = +