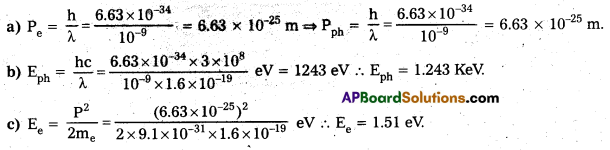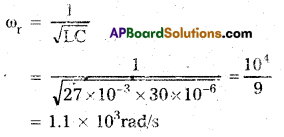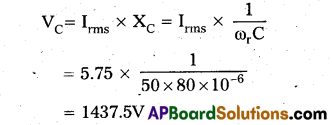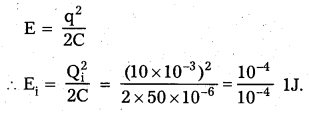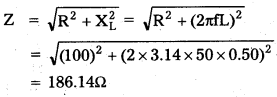Andhra Pradesh BIEAP AP Inter 1st Year Zoology Study Material Lesson 8 Ecology and Environment Textbook Questions and Answers.
AP Inter 1st Year Zoology Study Material Lesson 8 Ecology and Environment
Very Short Answer Type Questions
Question 1.
Define the term “ecology” and its branches.
Answer:
The word ‘ecology’ was derived from the Greek terms (‘Oikos house and ‘logos’ – ‘study’) and it can be defined as “the study of the relationship of organisms with their environment”.
Question 2.
What is an ecological population?
Answer:
A population is a group of organisms of the same species living in a specific area at a specific time.
Question 3.
Define a community.
Answer:
It is an association of the interacting members of populations of different autotrophic and heterotrophic species in a particular area.
Question 4.
What is an ecosystem?
Answer:
An ecosystem is a functional unit of the biosphere in which members of the community interact among themselves and with the surrounding environment.
![]()
Question 5.
Distinguish between ecosystem and biome.
Answer:
| Ecosystem | Biome |
| 1. Level of organization above the level of the biological community landscape. | 1. Level of organization above the level. |
| 2. It can be as small as an aquarium/tiny puddle. | 2. It occupies a vast region. |
| 3. Functional unit of the biosphere. | 3. Large community of plants and animals. |
Question 6.
What is a biome? Name any two biomes you studied.
Answer:
A ‘biome’ is a large community of plants and animals that occupies a vast region.
Ex: Tropical rain forest, desert, tundra (terrestrial biomes) Freshwater biomes, marine biome (aquatic biomes).
Question 7.
What is meant by ecosphere?
Answer:
It is the part of the Earth that supports ‘life’. It extends several kilometers above the Earth’s surface into the atmosphere and extends several kilometers below the ocean’s surface.
Question 8.
Explain the difference between the ‘nich’ of an organism and its ‘habitat’.
Answer:
| Habitat | Nich |
| 1. It is the place in which an organism lives. | 1. Functional role of an organism in an ecosystem. |
| 2. It is comparable to the address of a person. | 2. It is comparable to the profession of a person. |
Question 9.
A population has more genetically similar organisms than a biotic community. Justify the statement.
Answer:
A population is a group of organisms of the same species, living in a specific area at a specific time.
Ex: The fish belongs to the species Catla. catla living at a given time.
Question 10.
How do the fish living in Antarctic waters manage to keep their body fluids from freezing?
Answer:
During the course of millions of years of their existence, many species (fish) would have evolved a relatively constant internal (within body) environment so it permits all biochemical reactions and physiological reactions to proceed with maximal efficiency and thus, enhance the overall “fitness” of the species.
Question 11.
How does your body solve the problem of altitude sickness, when you ascend tall mountains?
Answer:
The body compensates for low oxygen availability by increasing red blood cell production and increasing the rate of breathing.
Question 12.
What is the effect of light on body pigmentation?
Answer:
Light influences the colour of the skin. The animals which live in the regions of low intensity of light have less pigmentation than the animals exposed to light.
Question 13.
Distinguish the terms phototaxis and photokinesis.
Answer:
Phototaxis is the oriented locomotion of an organism towards or away from the direction of light.
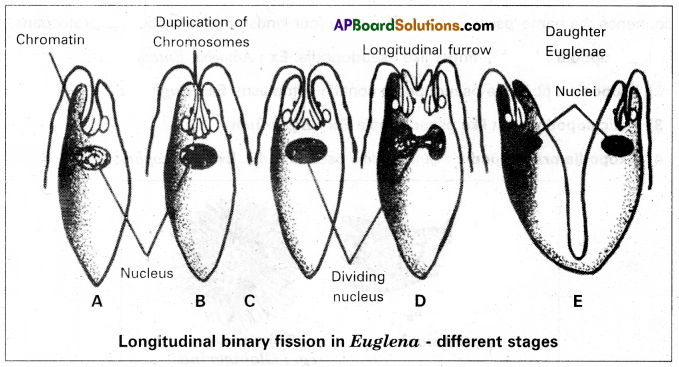
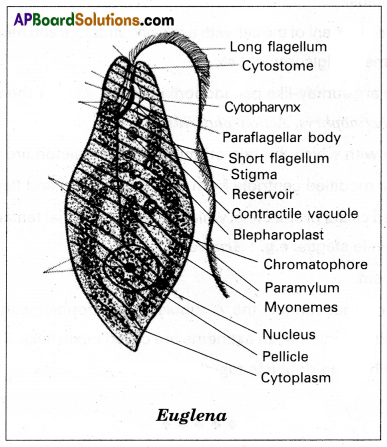
Ex: As seen in Euglena
Photokinesis is the influence of light on the non-directional movement of organisms.
Ex: Mussel crab
Question 14.
What are circadian rhythms?
Answer:
Biological rhythms that occur in a time period of 24 hours are called circadian rhythms.
![]()
Question 15.
What is photoperiodism?
Answer:
The response of organisms to the photoperiod is called photoperiodism.
Ex: Reproduction of flowers, migration of birds.
Question 16.
Distinguish between photoperiod and critical photoperiod.
Answer:
Photoperiod: The duration of light hours is known as a photoperiod.
Critical photoperiod: The specific day length which is essential for the initiation of seasonal events is called critical photoperiod.
Question 17.
Mention the advantages of some UV rays to us.
Answer:
- UV radiation kills the microorganisms present on the body surface of animals.
- UV radiation helps in the conversion of sterols present in the skin into vitamin D in mammals.
Question 18.
What is cyclomorphosis? Explain its importance in Daphnia.
Answer:
The cyclic seasonal morphological variations among certain organisms are called “Cyclomorphosis”. In the case of Daphnia, it is an adaptation to “stabilize the movement” in water and can “resist the water currents better” to stay in the water rich in food materials.
Question 19.
What are ‘regulators’?
Answer:
Organisms that are able to maintain homeostasis by physiological means which ensure constant body temperature, and constant osmotic concentration are called, “regulators”.
Ex: Mammals, Birds
Question 20.
What are conformers?
Answer:
Living organisms that cannot maintain 3 constant internal environments are described as “conformers”.
Question 21.
Define commensalism. Give one example.
Answer:
This is the interaction in which one species benefits and the other is neither harmed nor benefited.
Ex: Barnacles growing on the back of a whale benefit while the whale derives no noticeable benefit.
Question 22.
Define mutualism. Give one example.
Answer:
This is the interaction that benefits both the interacting species.
Ex: Lichens represent an intimate mutualistic relationship between a fungus and photosynthesizing algae.
Question 23.
Define amensalism. Give one example.
Answer:
Amensalism is an interaction in which one species is harmed whereas the other one is unaffected.
![]()
Question 24.
What is meant by interspecific competition? Give one example.
Answer:
A process in which the fitness of one species is significantly lower in the presence of another species is called interspecific competition.
Ex: Competition between visiting flamingos and resident fishes in shallow South American lakes.
Question 25.
What is camouflage? Give its significance.
Answer:
Some species of insects and frogs are cryptically coloured to avoid being detected easily by the predator. This phenomenon is called “Camouflage”.
Question 26.
What is Gause’s principle? When does it applicable?
Answer:
When the resources are limited, the competitively superior species will eventually eliminate the other species. It is relatively easy to demonstrate in laboratory experiments.
Question 27.
Name the association that exists in mycorrhiza.
Answer:
The association that exists in mycorrhiza is called “Mutualism”.
Question 28.
Distinguish between lotic and lentic habitats.
Answer:
| Lotic habitat | Lentic habitat |
| The still water bodies fall under the lotic community. Ex: Lakes, ponds | Flowing water bodies are called lentic habitats. Ex: River, canals, streams |
Question 29.
What is a zone of compensation in an aquatic ecosystem?
Answer:
The imaginary line that separates the limnetic zone from the profundal zone in a lake is called the zone of compensation (or) compensation point.
Question 30.
Distinguish between phytoplankton and zooplankton.
Answer:
| Phyto plankton | Zooplankton |
| Microscopic organisms bear chlorophyll and form producers in the lakes. Ex: Diatoms, Green algae, Euglenoids | Microscopic organisms that do not bear chlorophyll move through water currents and form primary consumer levels in the lakes. Ex: Daphnia, rotifers and ostracods |
Question 31.
Distinguish between neuston and nekton.
Answer:
| Neuston | Nekton |
| The animals living at the air-water interface constitute the “neuston”. Ex: Water strides beetles, the larva of mosquitoes. | The animals capable of swimming constitute the “nekton”. Ex: Water scorpion, back swimmer, diving beetles. |
Question 32.
What is periphyton?
Answer:
The animals that are attached to/creeping on the aquatic plants are called “periphyton”.
Ex: Water snails, hydras, nymphs of insects, etc.
Question 33.
Write three examples of man-made ecosystems.
Answer:
Cropland ecosystems, Aquaculture ponds, Aquaria.
Question 34.
What is meant by osmotrophic nutrition?
Answer:
The state of pre-digested food material through the body surface is known as osmotrophic nutrition.
![]()
Question 35.
Explaining the process of “leaching”.
Answer:
When the water-soluble inorganic nutrients go down into the soil and get precipitated as unavailable salts that entire process is called “leaching”.
Question 36.
What is PAR?
Answer:
PAR means “Photosynthetically Active Radiation”.
Question 37.
What is the percentage of PAR, in the incident solar radiation?
Answer:
Of the incident solar radiation, less than 50% of it is PAR.
Question 38.
Define entropy.
Answer:
As per the second law of thermodynamics, the energy dispersed is in the form of unavailable heat energy and constitutes entropy.
Question 39.
What is a standing crop?
Answer:
Each trophic level has a certain mass of living material at a particular time and it is called the “Standing crop”.
Question 40.
Explain the terms GPP and NPP.
Answer:
GPP means Gross primary productivity.
NPP means Net primary productivity.
Question 41.
Distinguish between upright and inverted ecological pyramids.
Answer:
| Upright Pyramid | Inverted Pyramid |
| Producers (I – trophic level Biomass) are more in number than other trophic levels. Ex: Grazing food chain | Producers are less in number biomass than other trophic levels. Ex: Parasitic food chain |
Question 42.
Distinguish between litter and detritus.
Answer:
Litter: Litter is just like manure that is formed by dead (Either plant (or) Animal clusters) organic matter. It is the primary food source in the detritus food chain.
Detritus: It is a decaying organic matter being decomposed into detritivores organisms.
Question 43.
Distinguish between primary and secondary productivity.
Answer:
| Primary Productivity | Secondary Productivity |
| 1. The amount of biomass produced per unit area over a period of time by plants. | 1. The rate formation of new organic matter by consumers. |
| 2. It can be divided into gross primary productivity (GPP), net primary productivity (NPP) | 2. It also can be divided into two types cross secondary productivity, and net secondary productivity. |
Question 44.
Which air pollutants are chiefly responsible for acid rains?
Answer:
Sulphur dioxide (SO2) and nitrogen oxides are the major causes of acid rain.
Question 45.
What is BOD?
Answer:
BOD means Biological Oxygen Demand. It is a measure of the content of biologically degradable substances in sewage.
![]()
Question 46.
What is biological magnification?
Answer:
An increase in the concentration of the pollutant (or) toxicant at successive trophic levels in an aquatic food chain is called ‘Bio-magnification’.
Question 47.
Why are incinerators used in hospitals?
Answer:
Disposal of hospital wastes that contain disinfectants, harmful chemicals, and also pathogenic micro-organisms incinerators are used in hospitals.
Short Answer Type Questions
Question 1.
Considering the benefits of a constant internal environment to the organism we tend to ask ourselves why the conformers had not evolved to become regulators.
Answer:
Thermoregulation is energetically expensive for many organisms. This is particularly true in small animals like shrews and hummingbirds. Heat loss or heat gain is a function of the surface area. Since small animals have a larger surface area relative to their volume, they tend to lose body heat very fast when it is cold outside. Then they have to spend much energy to generate body heat through metabolism. This is the main reason why very small animals are rarely found in polar regions. During the course of evolution, the costs and benefits of maintaining a constant internal environment are taken into consideration. Some species have evolved the ability to regulate, but only over a limited range of environmental conditions, beyond which they simply conform.
Question 2.
The individuals who have fallen through the ice and been submerged under cold water for long periods can sometimes be revived – explain.
Answer:
Temperature variations occur with seasonal changes. These differences in the temperature form thermal layers in water. Water shows maximum density at 4°C decrease its density. Generally, during the winter season the surface water cools down in the upper water phases in the temperature reaches 0°C. below the upper icy layer, the cool water occupies the lake. The aquatic animals continue their life below the icy layer at lower temperatures the activity of bacteria and the rate of oxygen consumption by aquatic animals decrease. Hence organisms can survive below the frozen (icy) upper water without being subject to hypoxia.
Question 3.
What is summer stratification? Explain.
Answer:
During summer in temperate lakes, the density of the surface water decreases because of an increase in its temperature (21-25°C). This ‘uppermost warm layer’ of a lake is called the epilimnion. Below the epilimnion, there is a zone in which the temperature decreases at the rate of 1°C per meter in-depth, and it is called thermocline or metalimnion. The bottom layer is the hypolimnion, where water is relatively cool, stagnant, and with low oxygen content (due to the absence of photosynthetic activity).
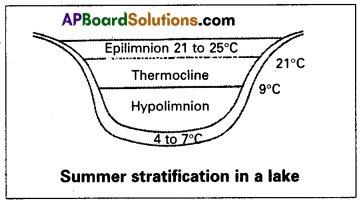
During autumn (also called fall). The epilimnion cools down, and the surface water becomes heavy when the temperature is 4°C and sinks to the bottom of the lake overturns bringing about a ‘uniform temperature’ in lakes during that period, this circulation during the autumn is known as fall. The upper oxygen-rich water reaches the hypolimnion and the nutrient-rich bottom water comes to the Surface. Thus there is a uniform distribution of nutrients and oxygen in the lake.
Question 4.
What is the significance of stratification in lakes?
Answer:
Temperature variations occur with seasonal changes in temperature regions. These differences in the temperature form thermal layers in water. These phenomena are called thermal stratification.
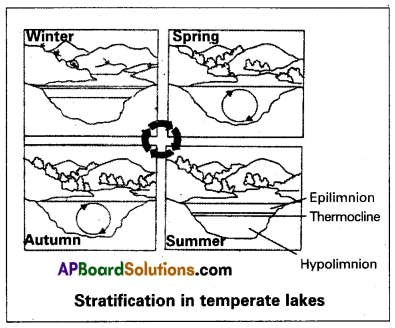
During autumn (also called fall), the epilimnion cools down and the surface water becomes heavy when the temperature is 4°C and sinks to the bottom of the lake. Overturns bring about uniform temperatures in lakes during that period. This circulation during autumn is known as the fall or autumn overturn. The upper oxygen-rich water reaches the hypolimnion and the nutrient-rich bottom water comes to the surface. Thus there is a uniform distribution of nutrients and oxygen in the lake. In the spring season the temperatures start rising when it reaches 4°C, the water becomes more dense and heavy and sinks to the bottom, taking oxygen-rich sinks down and bottom nutrient-rich water reaches the surface.
![]()
Question 5.
Explain Vant’ Hoff’s rule.
Answer:
Van’t Hoff, a Nobel Laureate in thermo chemistry proposed that, with the increase of every 10°C, the rate of metabolic activities doubles. This rule is referred to as Van’t Hoff’s rule. Van’t Hoffs rule can also be stated in reverse saying that the reaction rate is halved with the decrease of every 10°C. The effect of temperature on the rate of a reaction is expressed in terms of the temperature coefficient of the Q10 value. Q10 values are estimated by taking the ratio between the rate of a reaction at X°C and the rate of reaction at (X – 10°C). In the living systems, the Q10 value is about 2.0. If the Q10 value is 2.0, it means, for every 10°C increase, the rate of metabolism doubles.
Question 6.
Unlike mammals, reptiles cannot tolerate environmental fluctuations in temperature. How do they adapt to survive in desert conditions?
Answer:
Some organisms show behavioural responses to cope with variations in their environment. Desert lizards manage to keep their body temperature fairly constant by behavioural means. They ‘bask’ (staying in the warmth of sunlight) in the sun and absorb heat when their body temperature drops below the comfort zone, but move into the shade when the temperature starts increasing. Some species are capable of burrowing into the soil to escape from the excessive heat above the ground level.
Question 7.
How do terrestrial animals protect themselves from the danger of being dehydration of bodies?
Answer:
In the absence of an external source of water, the kangaroo rat of the North American deserts is capable of meeting all its water requirements through oxidation of its internal fat (in which water is a by-product – of metabolic water). It also has the ability to concentrate its urine, so that minimal volume of water is lost in the process of removal of its excretory products.
Question 8.
How do marine animals adapt to hypertonic seawater?
Answer:
To overcome the problem of water loss, marine fishes have glomerular kidneys with less number of nephrons. Such kidneys minimize the loss of water through urine. To compensate for water loss marine fish drink more water and along with this water, salts are added to the body fluids and disturb the internal equilibrium. To maintain salt balance (salt homeostasis) in the body they have salt-secreting chloride cells in their gills. Marine birds like seagulls and penguins eliminate salts in the form of salty fluid that drips through their nostrils. In turtles, the ducts of chloride-secreting glands open near the eyes. Some cartilaginous fishes retain urea and trimethylamine oxide (TMO) in their blood to keep the body fluids isotonic to the seawater and avoid dehydration of the body due to exosmosis.
Question 9.
Discuss the various type of adaptations in freshwater animals.
Answer:
Animals living in fresh waters have to tackle the problem of endosmosis. The osmotic pressure of freshwater is very low and that of the body fluids of freshwater organisms is much higher. So water tends to enter into bodies by endosmosis. To maintain the balance of water in the bodies, the freshwater organisms acquired several adaptations such as contractile vacuoles in the freshwater protozoans, and large glomerular kidneys in fishes, etc., They send out large quantities of urine along which some salts are also lost. To compensate for the ‘salt loss’ through urine freshwater fishes have ‘salt absorbing chloride cells’ in their gills.
The major problem in freshwater ponds is in summer most of the ponds dry up. To overcome this problem most of the freshwater protists undergo encystment. The freshwater sponges produce asexual reproductive bodies, called gemmules, to tide over the unfavourable conditions of the summer. The African lungfish Protopterus burrows into the mud and forms a gelatinous cocoon around it, to survive, in summer.
Question 10.
Compare the adaptations of animals with fresh water and seawater mode of life.
Answer:
| Adaptations in freshwater | Adaptations in seawater |
| 1. Freshwater fishes have glomerular kidneys with more nephrons. | 1. Marine water fishes have glomerular kidneys with a number of nephrons. |
| 2. They send out large quantities of urine. | 2. They minimize the loss of water through urine. |
| 3. To compensate for the salt loss through urine freshwater fishes have salt-absorbing chloride cells in their gills. | 3. To maintain salt balance in the body they have salt-secreting chloride cells. |
| 4. They undergo encystment to overcome the problems. | 4. Some fishes retain urea in their blood to keep the body fluid isotonic to the seawater. |
Question 11.
Distinguish between euryhaline and stenohaline animals.
Answer:
| Euryhaline | Stenohaline |
| Organisms that are adapted to stand wide fluctuations in salinity are called Euryhaline animals. Ex: Salmon fish, eel fish, etc. | Those that cannot stand wild fluctuations in salinity are known as steno haline animals. Ex: Aromatic insects, Aromatic insects |
Question 12.
Many tribes living at high altitudes in the Himalayas normally have higher red blood cell count (or) total haemoglobin than the people living in the plains. Explain?
Answer:
Some organisms possess adaptations that are physiological and allow them to respond quickly to a stressful situation. If you had ever been to any high-altitude place (e.g. > 3,500 M Rohtang pass near Manali and Manasarovar, in Tibet) you must have experienced what is called altitude sickness. Its symptoms include nausea (vomiting sense), fatigue (tiredness), and heart palpitations (abnormality in heartbeat). This is because, in the low atmospheric pressure of high altitudes, the body does not get enough oxygen. But, you gradually get acclimatized and overcome the altitude sickness. How did your body solve this problem? The body compensates for low oxygen availability by increasing red blood cell production and increasing the rate of breathing.
![]()
Question 13.
An orchid plant is growing on the branch of the mango tree. How do you describe this interaction between the orchid and mango tree?
Answer:
An orchid growing as an epiphyte on a mango branch gets the benefit of exposure to light, while the mango tree does not drive any noticeable benefit. So in this interaction, one species (arched) get benefitted the other (Mango) is neither armed nor benefitted. So the interactions between orchids and mango trees are commensalism.
Question 14.
Predation is not an association. Support the statement.
Answer:
Predation is not an association (it is a feeding strategy), it is an interaction between two different species. The predator gets benefits at the cost of the prey. Besides acting as) pipelines for energy transfer across trophic levels predators play other important roles. They keep the prey populations under control. In the absence of predators, the prey species could achieve very high population densities and cause instability in the ecosystem.
Question 15.
What is the biological principle behind the biological control method of managing pest insects?
Answer:
The prickly pear cactus introduced in Australia in the early 1920s caused havoc by spreading rapidly into millions of hectares of Rangel and (vast natural grasslands). Finally, the invasive cactus was brought under control only after a cactus-feeding predator (a moth) was introduced into the country. Biological control methods adopted in agricultural pest control are based on the ability of the predators to regulate prey populations.
Question 16.
Discuss competitive release.
Answer:
Another evidence for the occurrence of competition in nature comes from what is called competitive releases. Competitive release occurs when one of the two competing species is removed from an area, thereby releasing the remaining species from one of the factors that limited its distributional range dramatically when the competing species is experimentally removed. This is due to the phenomenon called competitive release, Connells field experiments showed that on the rocky sea coasts of Scotland the larger and competitively superior barnacle Balanus dominates the intertidal area, and excludes the smaller barnacle chathamalus from that zone. When the dominant one is experimentally removed, the population of the smaller one’s increases. In general, herbivores and plants appear to be more adversely affected by competition than carnivores.
Question 17.
Write a short note on the parasitic adaptations.
Answer:
In order to lead successful parasitic life, parasites evolved special adaptations such as:
- Loss of sense organs (which are not necessary for most parasites).
- Presence of adhesive organs such as suckers, and hooks to cling to the host’s body parts.
- Loss of digestive system and presence of high reproductive capacity.
- The life cycles of parasites are often complex, involving one or two intermediate hosts or vectors to facilitate the parasitization of their primary hosts.
Examples:
- The human liver fluke depends on two intermediates (secondary) hosts (a snail and a fish) to complete its life cycle.
- The malaria parasite needs a vector (mosquito) to spread to other hosts. The majority of the parasites harm the host: they may reduce the survival, growth, and reproduction of the host and reduce its population density. They might render the host more vulnerable to predation by making it physically weak.
Question 18.
Explain brood parasitism with a suitable example.
Answer:
Certain birds are fascinating examples of a special type of parasitism, in which the parasitic bird lays its eggs in the nest of its host and lets/allows the host incubates them. During the course of evolution, the eggs of the parasitic bird have evolved to resemble the host’s egg in size and colour to reduce the chances of the host bird detecting the foreign eggs and ejecting them from the nest.
Question 19.
How do predators act as biological control?
Answer:
The prickly pears cactus introduced in Australia in the early 1920s caused havoc by spreading rapidly into millions of hectares of Rangel and (vast natural grasslands) Finally, the invasive cactus was brought under control only after a cactus-feeding predator (a moth) was introduced into the country. Biological control methods adopted in agricultural pest control are based on the ability of the predators to regulate prey populations.
Question 20.
Write notes on the structure and functioning of an ecosystem.
Answer:
‘An ecosystem’ is a functional unit of nature, where living organisms interact among themselves and also with the surrounding physical environment.
Ecosystem varies greatly in size from a small pond to a large forest or a sea. Many ecologists regard the entire biosphere as a global ecosystem as a composite of all local ecosystems on Earth. Since this system is too big and complex to be studied at one time it is convenient to divide it into two basic categories, namely natural and artificial. The natural ecosystems include aquatic ecosystems of water and terrestrial ecosystems of the land. Both types of natural and artificial ecosystems have several subdivisions.
The Natural Ecosystem: These are naturally occurring ecosystems and there is no role of humans in the formation of such types of ecosystems. These are categorized mainly into two types – aquatic and terrestrial ecosystems. These are man-made ecosystems such as agricultural or agroecosystems. They include cropland ecosystems, aquaculture ponds, and aquaria.
![]()
Question 21.
Explain the different types of aquatic ecosystems.
Answer:
Based on the salinity of water, three types of aquatic ecosystems are identified marine, fresh water, and estuarine.
- The marine ecosystem: It is the largest of all the aquatic ecosystems. It is the most stable ecosystem.
- Estuarine ecosystem: Estuary is the zone where the river joins the sea, and seawater ascends up into the river twice a day (effect of high tides and low tides). The salinity of water in an estuary also depends on the seasons. During the rainy season outflow of river water makes the estuary saline and the opposite occurs during the summer. Estuarine organisms are capable of withstanding the fluctuations in salinity.
- The freshwater ecosystem: The freshwater ecosystem is the smallest aquatic ecosystem. It includes rivers, lakes, ponds, etc., It is divided into two groups the lentic and lotic. The still water bodies like ponds, lakes reservoirs, etc., fall under the category of lentic ecosystems, whereas streams, rivers, and flowing water bodies are called lotic ecosystems. The communities of the above two types are called lentic and lotic communities respectively. The study of freshwater ecosystems is called limnology.
Question 22.
Explain the different types of terrestrial ecosystems.
Answer:
The ecosystems of land are known as terrestrial ecosystems. Some examples of terrestrial ecosystems are the forest, grass, and desert.
- The forest ecosystem: The two important types of forests seen in India are tropical rain forests and tropical deciduous forests.
- The grassland ecosystems: These are present in the Himalayan region of India. They occupy large areas of sandy and saline soils in western Rajasthan.
- Desert ecosystem: The areas having less than 25 cm of rainfall per year are called deserts. They have characteristic flora and fauna. The deserts can be divided into two types – hot type and cold type deserts, the desert in Rajasthan is an example of the hot type of desert. Cold-type desert is seen in Ladakh.
Question 23.
Discuss the main reason for the low productivity of the ocean.
Answer:
The Primary productivity is very low in the ocean ecosystem compared with the terrestrial ecosystem.
Unlike terrestrial ecosystems, the majority of primary production in the ocean is performed by feel living microscopic organisms called Phytoplankton, large autotrophs such as the seagrasses and macroalgae or seaweeds are generally confined to the littoral zone.
The sunlight zone of the ocean is called the photic zone or euphotic zone, it is a thin layer upto 10 to 100 m near the Ocean’s surface where there is sufficient light for photosynthesis to occur. Light is attenuated down the water column by its absorption or scattering by the water itself. Net photosynthesis in the water column is determined by the interaction between the photic zone and the mixed layer. In the deep water of the ocean (Demersal) there is no light penetration for photosynthesis.
Another factor relatively recently discovered to play a significant role in oceanic primary production is the micronutrient iron. The factors limiting primary production in the ocean are also very different from those on land. However, the availability of light, the source of energy for photosynthesis, and mineral nutrients, building the blocks for new growth, play a crucial role in regulating primary production in the ocean.
Question 24.
Explain the terms saprotrophs detritivores and mineralizers.
Answer:
Saprotrophs are microorganisms such as fungi and bacteria which live on dead organic matter. Detritivores ingest small fragments of decomposing organic materials, termed detritus mineralizers affect the mineralization of humans.
Question 25.
Define decomposition and describe the process and products of decomposition.
Answer:
When organisms die, their bodies and the waste materials passed from the bodies of living organisms form a source of energy and nutrient for the decomposer organisms like saprotrophs detritivores, and mineralizers. Saprotrophs absorb substances through the general body surface of the dead bodies. Detritivores ingest detritus as food. Mineralized mineralize humus these decomposers are referred to as micro consumers of the ecosystem. The decomposition of organic matter includes three phases. In the first phase, particulate detritus is formed by the action of saprotrophs. The second stage is the rapid action of saprotrophs and detritivores to convert detritus into humic substances. The third process is the slower mineralization of the hummus.
Decomposers also play an important role in an ecosystem by converting complex molecules of dead organisms into simpler and reusable molecules. The breakdown products of the dead organisms and waste materials are recycled in the ecosystem and are made available to the producers. The producers cannot continue to exist forever in the absence of the decomposers (as minerals are not returned to the environment).
Question 26.
Write a note on DFC. Give its significance in a terrestrial ecosystem.
Answer:
The detritus food chain (DFC) begins with dead organic matter (such as leaf litter, and bodies of dead organisms). It is made up of decomposers which are heterotrophic organisms ‘mainly’ the fungi’ and ‘bacteria’. They meet their energy and nutrient requirements by degrading dead organic matter to detritus. These are also known as saprotrophs.
Decomposers secrete digestive enzymes that break down dead and waste materials (such as feces i) into simple absorbable substances. Some examples of detritus food chains are:
- Detritus – Earthworm – Frogs – Snakes
- Dead animals – Flies and maggots – Frogs – Snakes
In an aquatic ecosystem. GFC is the major conduit for the energy flow. As against this, in a terrestrial ecosystem, a much larger fraction of energy flows through the detritus food chain than through the GFC. The Detritus food chain may be connected with the grazing food chain at some levels. Some of the organisms of DFC may form the prey of the GFC animals. For example, in the detritus food chain given above, the earthworms of the DFC may become the food of the birds of the GFC. It is to be understood that food chains are not ‘isolated1 always.
![]()
Question 27.
What is primary productivity? Give a brief description of the factors that affect primary productivity.
Answer:
Primary productivity is defined as the amount of biomass or organic matter produced per unit area over a period of time by plants, during photosynthesis. It can be divided into Gross Primary Productivity (GPP) and Net Primary Productivity (NPP).
(a) Gross Primary Productivity: Of an ecosystem is the rate of production of organic matter
during photosynthesis. A considerable amount of GPP is utilized by plants for their catabolic process (respiration).
(b) Net Primary Productivity: Gross Primary Productivity minus respiratory loss (R), is the Net Primary Productivity (NPP). On average about 20-25 percent of GPP is used for catabolic (respiratory) activity.
GPP – R = NPP
The Net Primary productivity is the biomass available for the consumption of the heterotrophs (herbivores and decomposers).
Question 28.
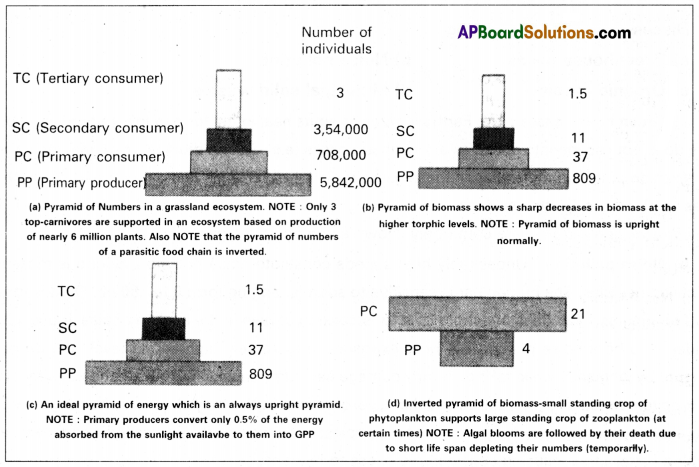
Define ecological pyramids and describe with examples, pyramids of numbers and biomass.
Answer:
It is a graphical representation of the trophic structure and function of an ecosystem. The base of each pyramid represents the producers of the first trophic level, while the apex represents the tertiary or top-level/top-order consumers. The three types of ecological pyramids that are usually studied are (a) pyramid of numbers (b) pyramid of biomass and (c) pyramid of energy. These pyramids were first represented by Elton, hence the name ELTONIANpyramids/Ecological pyramids.
Any calculations of energy content, biomass, or numbers have to include all organisms at that trophic level. No generalizations we make will be true if we take only a few individuals of any trophic level into account. In most ecosystems, all the pyramids – of numbers, energy, and biomass are uprights. i.e., producers are more in number and biomass than the herbivores, and herbivores are more in number and biomass than the carnivores. Also, energy (available) at a lower trophic level is always more than that at a higher level.
There are exceptions to this generalization. In the case of a parasitic food chain, the pyramid of numbers is inverted. A large tree (single producer) may support many herbivores like squirrels and fruit-eating birds. On these herbivores, many ectoparasites such as ticks, mites, and lice (secondary consumers) may live. These secondary consumers may support many more top-level consumers and also the hyper-parasites. Thus in each trophic level from the bottom to the top, the numbers of organisms increase and form an ‘inverted pyramid’ of numbers.
The pyramid of biomass in the sea is also generally inverted because the biomass of fishes far exceeds that of phytoplankton.
Question 29.
What are the deleterious effects of depletion of ozone in the stratosphere?
Answer:
The depletion of ozone is particularly marked over the Antarctic region. This has resulted in the formation of a large area of thinned ozone layer commonly called the ‘ozone hole.
UV radiation with wavelengths shorter than that of UV-B is almost completely absorbed by Earth’s atmosphere, provided that the ozone layer is intact. But IJV-B damages DNA and may induce mutations. It causes aging of the skin, damage to skin cells, and various types of skin cancers. In the human eye, the cornea absorbs UV-B radiation, and a high dose of UV-B causes inflammation of the cornea called snow-blindness, cataract, etc., such exposure may permanently damage the cornea.
Question 30.
Describe the ‘Green House’ Effect.
Answer:
The term Green House effect’ has been derived from a phenomenon that occurs in a greenhouse. The greenhouse is a small glasshouse and is used for growing plants, especially during winter. In a greenhouse, the glass panel allows the passage of light into it but does not allow heat to escape (as it is reflected back). Therefore, the greenhouse warms up, very much like inside a car that has been parked in the sun for a few hours.
The greenhouse effect is a naturally occurring phenomenon that is responsible for heating the Earth’s surface and atmosphere. It would be surprising to know that without the greenhouse effect the average temperature of the Earth’s surface would have been chilly – 18°C rather than the present average of 15°C.
When sunlight reaches the outermost layer of the atmosphere, clouds and gases reflect about one-fourth of the incoming solar radiation and absorb some of it. Almost half of the incoming solar radiation falls on the Earth’s surface and heats it up. While a small proportion is reflected back.
Question 31.
Discuss briefly the following:
(a) Greenhouse gases
(b) Noise pollution
(c) Organic farming
(d) Municipal solid wastes
Answer:
(a) Greenhouse gases: The Earth’s surface re-emits heat in the form of infrared radiation but part of this does not escape into space as atmospheric gases (e.g. carbon dioxide, methane, etc.) absorb a major fraction of it. The molecules of these gases radiate heat energy, a major part of which again comes back to the Earth’s surface, thus heating it up once again. The above-mentioned gases- Carbon dioxide and methane are commonly known as greenhouse gases.
(b) Noise pollution: Undesirably high sounds constitute noise pollution. Sound is measured in units called decibels. The human ear is sensitive to sounds ranging from 0 to 180 dB. 0 dB is the threshold limit of hearing and 120 dB is the threshold limit for the sensation of pain in the ear. Any noise above 120 dB is considered to be noise pollution. Brief exposure to the extremely high sound level. 150 dB or more generated by jet planes while taking off may damage eardrums causing permanent hearing impairment. Even long-term exposure to a relatively higher level of noise in cities may also cause hearing impairment. Noise also causes auditory fatigue, anxiety, sleeplessness/msommaj, increased heartbeat, and altered breathing pattern thus causing considerable stress to humans.
(c) Organic farming: Integrated organic farming is a zero waste procedure, where the recycling of waste products is efficiently carried out. This allows the maximum utilization of resources and increases the efficiency of production. A method practiced by Ramesh Chandra Dagar, all these processes support one another and allow an extremely economical and sustainable venture. Natural – biogas generated in the process can be used for meeting the energy needs of the farm. Enthusiastic about spreading information and helping in the practice of integrated organic farming, Dagar has created the Haryana Kisan welfare club.
(d) Municipal Solid waste: Anything (substance/material/articles/goods) that is thrown out as waste in solid form is referred to as solid waste. The municipal solid wastes generally consist of paper, food wastes, plastics, glass, metals, rubber, leather, textile, etc., The wastes are burnt to reduce the volume of the waste. As a substitute for open-burning dumps, sanitary landfills are adopted. There is a danger of seepage of chemicals and pollutants from these landfills, which may contaminate the underground water resources.
![]()
Question 32.
Discuss the causes and effects of global warming. What measures need to be taken to control ‘Global warming’?
Answer:
An increase in the level of greenhouse gases has led to considerable heating of the “Earth leading to global warming. During the past century, the temperature of the earth has increased by 0.6°C most of it during the last three decades. Scientists believe that this rise in temperature is leading to severe changes in the environment. Global warming is causing climatic changes (e.g. as El Nino effect) and is also responsible for the melting of polar ice caps and other snow caps of mountains such as the Himalayas. Over many years, this will result in a rise in sea levels, all over the world, that can submerge many coastal areas. The total spectrum of changes that global warming can bring about is a subject that is still under active research.
Global warming: Control measures
- The measures include cutting down the use of fossil fuels.
- Improving the efficiency of energy usage.
- Planting trees and avoiding deforestation.
Question 33.
Write critical notes on the following:
(a) Eutrophication
(b) Biological magnification
Answer:
(a) Eutrophication: Natural ageing of a lake by nutrient enrichment of its water is known as eutrophication. In a young lake, the water is cold and clear supporting little life. Gradually nutrients such as nitrates and phosphates are carried into the lake via streams, in course of time. This encourages the growth of aquatic algae and other plants. Consequently, animal life proliferates and organic matter gets deposited on the bottom of the lake. Over centuries, as silt and organic debris pile up the lake grows shallower and warmer. As a result, the aquatic organisms thriving in the cold environment are gradually replaced by warm-water organisms. Marsh plants appear by taking root in the shallow regions of the lake. Eventually, the lake gives way to large masses of floating plants (bog) and is finally converted into land.
(b) Biological magnification: Increase in the concentration of the pollutant or toxicant at successive trophic levels in an aquatic food chain is called biological magnification or Bio-magnification. This happens in the instance where a toxic substance accumulated by an organism is not metabolized or excreted and thus passes on to the next higher trophic level. This phenomenon is well known regarding DDT and mercury pollution.
As shown in the above example, the concentration of DDT is increased at successive trophic levels. Starting at a very low concentration of 0.003 PPb (PPb part per billion) in water, which ultimately reached an alarmingly high concentration of 25 ppm (ppm = parts per million) in fish-eating birds through biomagnification. High concentrations of DDT disturb calcium metabolism in birds, which causes thinning of eggshells and their premature breaking, eventually causing a decline in bird populations.
(c) Groundwater depletion and ways for its replenishment: Sewage arising from homes and hospitals may contain undesirable pathogenic microorganisms. If it is released untreated into water courses, there is a likelihood of an outbreak of serious diseases, such as dysentery, typhoid, jaundice, cholera, etc.
Untreated industrial effluents released into water bodies pollute most of the rivers, freshwater streams, etc. Effluents contain a wide variety of both inorganic and organic pollutants such as oils, greases, plastics, metallic wastes, suspended solids, and tonics. Most of them are non-degradable. Arsenic, Cadmium, Copper, Chromium, Mercury, Zinc, and Nickel are the common heavy metals discharged from industries.
Effects: Organic substances present in the water deplete the dissolved oxygen content in water by increasing the BOD (Biological Oxygen Demand) and COD (Chemical Oxygen Demand). Most of the inorganic substances render the water unit for drinking.
Removal of dissolved salts such as nitrates, phosphates, and other nutrients and toxic metal ions and organic compounds is much more difficult. Domestic sewage primarily contains biodegradable organic matter, which will be readily decomposed by the action of bacteria and other microorganisms.
Water-logging and soil salinity: Irrigation without proper drainage of water leads to water logging in the soil. Besides affecting the crops, water logging draws salt to the surface of the soil (salinization of the topsoil). The salt then is deposited as a thin crust on the land surface or starts collecting at the roots of the plants. This increased salt content is inimical (unfavourable) to the growth of crops and is extremely damaging to agriculture. Water logging and soil salinity are some of the problems that have come in the wake of the Green Revolution.
Long Answer Type Questions
Question 1.
Write an essay on temperature as an ecological factor.
Answer:
Temperature is a measure of the intensity of heat. The temperature on land or in water is not uniform. On land, the temperature variations are more pronounced when compared to the aquatic medium because land absorbs or loses heat much more quickly than water. The temperature on land depends on seasons and the geographical area on this planet. Temperature decreases progressively when we move from the equator to the poles. Altitude also causes variations in temperature. For instance, the temperature decreases gradually as we move to the top of the mountains.
Biological effects of Temperature:
Temperature Tolerance: A few organisms can tolerate and thrive in a wide range of temperatures they are called eurythermal, but, a vast majority of organisms are restricted to a narrow range of temperatures such organisms are called stenothermal. The levels of thermal tolerance of different species determine their geographical distribution.
Temperature and Metabolism: Temperature affects the working of enzymes and through it, the basal metabolism, and other physiological functions of the organism. The temperature at which the metabolic activities occur at the climax level is called the optimum temperature. The lowest temperature at which an organism can live indefinitely is called minimum effective temperature. It an animal or plant is subjected to a temperature below the minimum effective limit, enters into a condition of inactivity called a chill coma. The metabolic rate increases with the rise of temperature from the minimum effective temperature to the optimum temperature.
The maximum temperature at which a species can live indefinitely in an active state is called maximum effective temperature, the animals enter into a ‘heat coma’. The maximum temperature varies much in different animals.
Vant Hoffs’s rule: Vant Hoff, a Nobel Laureate the thermochemistry proposed that, with the increase of every 10°C, the rate of metabolic activities doubles. This rule is referred to as the Vant Hoffs rule. Vant Hoffs’s rule can also be stated in reverse saying that the reaction rate is halved with the decrease of every 10°C. The effect of temperature on the rate of a reaction is expressed in terms of temperature coefficient or Q10 value. Q10 values are estimated by taking the ratio between the rate of a reaction at X°C and the rate of reaction at (X-10°C). In the ‘living systems’ the Q10 value is about 2.0. If the Q10 value is about 20, it means, for every 10°C increase, the rate of metabolism doubles.
Cyclomorphosis: The cyclic seasonal morphological variations among certain organisms are called cyclomorphosis. This phenomenon has been demonstrated in the Cladoceran (a subgroup of Crustacea) and Daphnia (water flea). In the winter season, the head of Daphnia is ’round’ in shape (typical or non helmet morph). With the onset of the spring season, a small ‘helmet’/’hood’ starts developing on it. The helmet attains the maximum size in summer. In ‘autumn’ the helmet starts receding. By the winter season, the head becomes round. Some scientists are of the opinion that Cyclomorphosis is a seasonal adaptation to changing densities of the water in lakes. In summer as the water is less dense Daphnia requires a larger body surface to keep floating easily. During winter the water is denser, so it does not require a larger surface area of the body to keep floating.
Temperature adaptations: Temperature adaptations in animals can be dealt with under three heads:
(a) Behavioural adaptations
(b) Morphological and Anatomical adaptations and
(c) Physiological adaptations.
(a) Behavioural adaptations: Some organisms show behavioural responses to cope with variations in their environment. Desert lizards manage to keep their body temperature fairly constant by behavioural means. They bask (staying in the warmth of sunlight) in the sun and absorb heat when their body temperature drops below the comfort zone, but move into the shade when the temperature starts increasing. Some species are capable of burrowing into the soil to escape from the excessive heat above the ground level.
(b) Morphological and anatomical adaptations: In the polar seas, aquatic mammals such as the seals have a thick layer of fat (blubber) that acts as an insulator and reduces the loss of body heat, underneath their skin. The animals which inhabit the colder regions have larger body sizes with greater mass. The body mass is useful to generate more heat. As per Bergmann’s rule mammals and other warm-blooded living in colder regions have less surface area to body volume ratio. Then their counterparts live in the tropical regions. The small surface area helps to conserve heat. For instance, the body size of American moose/Eurasian elk (Alces alces), increases with the latitudes in which they live. Moose in the northern part of Sweden show 15-20% more body moss than the same species (counterparts) living in southern Sweden.
Mammals from colder climates generally have shorter earlobes and limbs (extremities of the body) to minimize heat loss. Large earlobes and long limbs increase the surface area without changing the body volume. This is known as Allen’s rule. For instance, the polar fox, Vulpes lagopus (formerly called Alopex lagopus) has short extremities to minimize the heat loss from the body. In contrast, the desert fox has short extremities to minimize heat loss from the body. In contrast, the desert fox, Vulpes zerda, has large ear lobes and limbs to facilitate better heat loss from the body.
(c) Physiological adaptations: In most animals, all the physiological functions proceed ‘optimally’ in a narrow temperature range (in humans, it is 37°C). But there are microbes (archaebacteria) that flourish in hot springs and in some parts of deep seas, where temperatures far exceed 100°C. Many fish thrive in Antarctic waters where the temperature is always below zero. Having realized that the abiotic conditions of many habitats may vary over a time period, we now ask. How do the organisms living in such habitats manage stressful conditions?
One would expect that during the course of millions of years of their existence, many species would have evolved a relatively constant internal (within the body) environment. It permits all biochemical reactions and physiological functions to proceed with maximal efficiency and thus, enhance the overall fitness of the species. This constancy could be chiefly in terms of optimal temperature and osmotic concentration of body fluids. So the organism should try to maintain the constancy of its internal environment (homeostasis) despite varying external environmental conditions that tend to upset its homeostasis. This is achieved by the processes described below.
Thermal migration: The organism can move away temporarily from the stressful habitat to a more hospitable (comfortable) area and return when the stressful period is over. In human analogy comparison, this strategy is comparable to a person moving from Delhi to Shimla for the duration of summer. Many animals, particularly birds, during winter undertake long-distance migrations to more hospitable areas. Every winter, many places in India including the famous Keoladeo Ghana National Park (Formerly – Bharatpur bird sanctuary) in Rajastan and Pulicat Lake in Andhra Pradesh host thousands of migratory birds coming from Siberia and other extremely cold northern regions.
Diapause: Certain organisms show a delay in development, during periods of unfavourable environmental conditions and spend periods in a state of inactiveness called diapause. This dormant period in animals is a mechanism to survive extremes of temperature drought, etc. It is seen mostly in insects and embryos of some fish. Under unfavourable conditions, many zooplankton species in Lakes and ponds are known to enter diapause.
![]()
Question 2.
Write an essay on water as an ecological factor.
Answer:
Water is another important factor influencing the life of organisms. Life is unsustainable without water. Its availability is so limited in deserts that only certain special adaptations make it possible for them to live there. You might think that organisms living in oceans, lakes, and rivers should not face any water-related problems, but It is not true. For aquatic organisms the quality (chemical composition, pH, etc.) of water becomes important. The salt concentration is less than 5 percent in inland waters and 30-35 percent in seawater. Some organisms are tolerant to a wide range of salinities (euryhaline) but others are restricted to a narrow range (stenohaline) Many freshwater animals cannot live for long in seawater and vice versa because of the osmotic problems, they would face.
Adaptations in freshwater habitat: Animals living in freshwater have to tackle the problem of endosmosis. The osmotic pressure of freshwater is very low and that of the body fluids of freshwater organisms is much higher. So water tends to enter into bodies by endosmosis. To maintain the balance of water in the bodies, the freshwater organisms acquired several adaptations such as contractile vacuoles in the freshwater protozoans, large glomerular kidneys in fishes, etc… They send out large quantities of urine freshwater fishes have salt-absorbing ‘chloride cells’ in their gills. The major problem in freshwater ponds is – in summer most of the ponds dry up. To overcome this problem, most of the freshwater protists undergo encystment. The freshwater sponges produce asexual reproductive bodies, called gemmules to tide over the unfavorable conditions of the summer. The African lungfish, Protopterus, burrows into the mud and forms a gelatinous cocoon around it, to survive, in summer.
Adaptations in marine habitat: Seawater is high in salt content compared to that body fluids. So, marine animals continuously tend to lose water from their bodies by exosmosis and face the problem of dehydration. To overcome the problem of water loss marine fishes have glomerular kidneys with less number of nephrons. Such Kidneys minimize the loss of water through urine. To compensate for water loss marine fish drink more water, and along with this water, salts are added to the body fluids and disturb the internal equilibrium.
To maintain salt balance (salt homeostasis) in the body they have salt-secreting chloride cells in their gills. Marine birds like seagulls and penguins eliminate salts in the form of salty fluid that drips through their nostrils. In turtles, the ducts of chloride-secreting glands open near the eyes. Some cartilaginous fishes retain urea and trimethylamine oxide (TMO) in their blood to keep the body fluid isotonic to the seawater and avoid dehydration of the body due to exosmosis.
Water-related adaptations in brackish water animals: The animals of brackish water are adapted to withstand wide fluctuations in salinity. Such organisms are called euryhaline animals and those that cant with stand is known as stenohaline. The migratory fishes such as salmon and Hilsa are anadromous fishes i.e. they ‘migrate from the sea to freshwater, for breeding; Anguilla bengalensis is a catadromous fish i.e. it migrates from the river to sea, for breeding. In these fishes, their glomerular kidneys are adjusted to changing salinities. The chloride cells are adapted to excrete or absorb salts depending on the situation. On entering the river they drink more freshwater to maintain the concentration of body fluids equal to that of the surrounding water.
Water-related adaptations for terrestrial life: In the absence of an external source of water, the Kangaroo rat of the North American deserts is capable of meeting all its water requirements through oxidation of its internal fat (in which water is a by-product – of metabolic water). It also has the ability to concentrate its urine, so that minimal volume of water is lost in the process of removal of its excretory products.
Question 3.
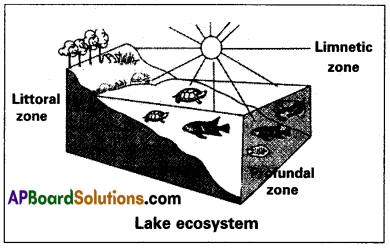
Describe the lake as an ecosystem giving examples for the various zones and the biotic components in it.
Answer:
Deep water lakes contain three distinct zones namely
- Littoral zone
- Limnetic zone
- Profundal zone
Littoral Zone: It is the shallow part of the lake closer to the shore. Light penetrates up to the bottom. It is euphotic (having good light) and has rich vegetation and a higher rate of photosynthesis, hence rich in oxygen.
Limnetic Zone: It is the open water zone away from the shore. It extends up to the effective light penetration level, vertically. The imaginary line that separates the limnetic zone from the profundal zone is known as the zone of compensation/compensation point light compensation level. It is the zone of effective light penetration. Here the rate of photosynthesis is equal to the rate of respiration. The limnetic zone has no contact with the bottom of the lake.
Profundal Zone: It is the deep water area present below the limnetic zone and beyond the depth of effective light penetration. Light is absent. Photosynthetic organisms are absent and so the water is poor in oxygen content. It includes mostly the anaerobic organisms which feed on detritus. The organisms living in lentic habitats are classified into pedantic forms, which live at the bottom of the lake and those living in the open waters of lakes, away from the shore vegetation are known as limnetic forms.
Biota (animal and plant life of a particular region) of the littoral zone: Littoral zone is rich with pedantic flora (especially up to the depth of the effective light penetration). At the shore, proper emergent vegetation is abundant with firmly fixed roots at the bottom of the lake, and shoots and leaves are exposed above the level of water. These are amphibious plants. Certain emergent rooted plants of the littoral zone are the cattails (Typha), bulrushes (Scirpus) arrowheads (Sagittaria),. Slightly deeper are the rooted plants with floating leaves, such as the water lilies (Nymphaea), Nelumbo, Trapa, etc., still deeper are the submerged plants such as Hydrilla – Chara, Potamogeton, etc… The free-floating vegetation includes pistia, Wolffia, Lemna (duckweed), Azolla, Eichhornia, etc.
The phytoplankton of the littoral zone is composed of diatoms (Coscinodiscus, Nitzschia, etc) green algae (Volvox, spirogyra, etc), euglenoids (Euglena, phacus, etc), and dinoflagellates (Gymnodinium, Cystodinium, etc ….)
Animals, the consumers of the littoral zone, are abundant in this zone of the lake, these are categorized into zooplankton, neuston, nekton, periphyton, and benthos. The Zoo-plankton of the littoral zone consists of water fleas such as Daphnia, rotizers, and ostracods.
The animals living at the air-water interface constitute the neuston. They are of two types. The epineuston and hyponeuston. Water striders (Gerris), beetles, and water bugs (Dineutes) form the epineuston/ supraneuston and the hyponeuston/infraneuston includes the larvae of mosquitoes.
The animals such as fishes, amphibians, water-snakes, terrapins, insects like water scorpion (Ranatra), back swimmer (Notonecta), diving beetles (Dytiscus), capable of swimming constitute the nekton.
The animals that are attached to/creeping on the aquatic plants, such as the ‘water snails’, nymphs of insects, bryozoans, turbellarians, hydras, etc, constitute the periphyton. The animals that rest on or move on the bottom of the lake constitute the ‘benthos’, e.g.: red annelids, chironomid larvae, crayfishes, some isopods amphipods, clams, etc.
Biota of the limnetic zone: Limnetic zone is the largest zone of a lake. It is the region of rapid variations of the level of the water, temperature, oxygen availability, etc., from time to time. The limnetic zone has autotrophs (photosynthetic plants) in abundance. The chief autotrophs of this region are the phytoplankton such as the euglenoids, diatoms, cyanobacteria, dinoflagellates, and green algae. The consumers of the limnetic zone are the zooplanktonic organisms such as the copepods, Fisher frogs, water snakes, etc., which form the limnetic nekton.
Biota of the profundal zone: It includes the organisms such as decomposers (bacteria), chironomid larvae, Chaoborus (phantom larva), red annelids, clams, etc., that are capable of living in low oxygen levels. The decomposers of this zone decompose the dead plants and animals and release nutrients that are used by the biotic communities of both littoral and limnetic zones.
The lake ecosystem performs all the functions of any ecosystem and of the biosphere as a whole, i.e., conversion of inorganic substances into organic material, with the help of the radiant solar energy by the autotrophs, consumption of the autotrophs by the heterotrophs; decomposition and mineralization of the dead matter to release them back for reuse by the autotrophs (recycling of minerals).
![]()
Question 4.
Describe different types of food chains that exist in an ecosystem.
Answer:
The food energy passes from one trophic level to another trophic level mostly from the lower to higher trophic levels. When the path of food energy is ‘linear’ the components resemble the ‘links’ of a chain and it is called a ‘food chain’. Generally, a food chain ends with decomposers. The three major types of food chains in an ecosystem are the Grazing Food Chain, Parasitic Food Chain, and Detritus Food Chain.
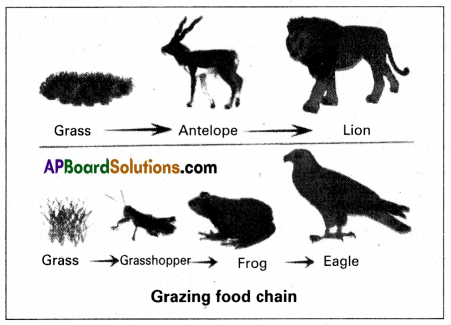
(i) Grazing food chain: It is also known as the predatory food chain, it begins with the green plants (producers), and the second third, and fourth trophic levels are occupied by the herbivores, primary carnivores, and secondary carnivores respectively. In some food chains, these are yet another trophic level – the climax carnivores. The number of trophic levels in food chains varies from 3 to 5 generally. Some examples from the grazing food chain (GFC) are given below.
| I trophic level | II trophic level | III trophic level | IV trophic level | V trophic level |
| Rosebush → | Aphids → | Spiders → | Small birds → | Hawk |
| Grass → | Grasshopper → | Frog → | Snake → | Hawk |
| Plants → | Caterpillar → | Lizard → | Snake | |
| Phytoplankton → | Zooplankton → | Fish → | Bird | |
| Grass → | Goat → | Man |
(ii) Parasitic food chain: Some authors included the Parasitic Food Chains as a part of the GFC. As in the case of GFC’s, it also begins with the producers, the plants (directly or indirectly). However, the food energy passes from large organisms to small organisms in the parasitic chains. For instance, a tree that occupies the 1st trophic level provides shelter and food for many birds. These birds host many ectoparasites and endo parasites. Thus, unlike in the predator food chain, the path of the flow of energy includes fewer, large-sized organisms in the lower trophic levels and numerous, small-sized organisms in the successive higher trophic levels.
(iii) Detritus Food Chain: The detritus food chain (DFC) begins with dead organic matter (such as leaf litter, and bodies of dead organisms). It is made up of decomposers which are heterotrophic organisms, mainly fungi’ and ‘bacteria’. They meet their energy and nutrient requirements by degrading dead organic matter or detritus. These are also known as saprotrophs (sappro: to decompose).
Decomposers: Secrete digestive enzymes that break down dead and waste materials (such as feces) into simple absorbable substances. Some examples of detritus food chains are:
- Detritus (formed from leaf litter) – Earthworms – Frogs – Snakes
- Dead animals – Flies and maggots – Frogs – Snakes.
In an aquatic ecosystem, GFC is the major ‘conduit for the energy flow. As against this in a terrestrial ecosystem, a much larger fraction of energy flows through the detritus food chain than through the GFC. The Detritus food chain may be connected with the grazing food chain at some levels. Some of the organisms of DFC may form the prey of the GFC animals. For example, in the detritus food chain given above, the earthworms of the DFC may become the food of the birds of the GFC. It is to be understood that food chains are not ‘isolated’ always.
Question 5.
Give an account of the flow of energy in an ecosystem.
Answer:
Except for the deep sea hydro-thermal ecosystem, the sun is the only source of energy for all ecosystems on Earth. Of the incident solar radiation, less than 50 percent of it is photosynthetically active radiation (PAR). We know that plants and photosynthetic bacteria (autotrophs), fix the sun’s radiant energy to synthesize food from simple inorganic materials. Plants capture only 2-10 percent of the PAR and this small amount of energy sustains the entire living world. So, it is very important to know how the solar energy captured by plants flows through different organisms of an ecosystem. All heterotrophs are dependent on the producers for their food, either directly or indirectly. The law of conservation of energy is the first law of thermodynamics. It states that energy may transform from one form into another form, but it is neither created nor destroyed. The energy that reaches the earth is balanced by the energy that leaves the surface of the earth as invisible heat radiation.
The energy transfers in an ecosystem are essential for sustaining life. Without energy transfers, there could be no life and ecosystem. Living beings are the natural proliferations that depend on the continuous inflow of concentrated energy. Further, ecosystems are not exempted from the Second Law of thermodynamics. It states that no process involving energy transformation will spontaneously occur unless there is the degradation of energy. As per the second law of thermodynamics – the energy dispersed is in the form of unavailable heat energy and constitutes the entropy (energy lost or not available for work in a system).
The organisms need a constant supply of energy to synthesize the molecules they require. The transfer of energy through a food chain is known as energy flow. A constant input of mostly solar energy is the basic requirement for any ecosystem to function. The important point to note is that the amount of energy available decreases at successive trophic levels. When an organism dies, it is converted to detritus or dead biomass that serves as a source of energy for the decomposers. Organisms at each trophic level depend on those at the lower trophic level, for their energy demands.
Each trophic level has a certain mass of living material at a particular time and it is called the standing crop. The standing crop is measured as the mass of living organisms (biomass) or the number of organisms per unit area. The biomass of a species is expressed in terms of fresh or dry weight (dry weight is more accurate because water contains no usable energy).
The 10 percent Law: The 10 percent law for the transfer of energy from one trophic level to the next was introduced by Lindeman (the Founder of modern Ecosystem Ecology). According to this law, during the transfer of energy from one trophic level to the next, only about 10 percent of the energy is stored/converted as body mass/biomass. The remaining is lost during the transfer or broken down in catabolic activities (Respiration). Lindeman’s rule of trophic efficiency/Gross ecological efficiency is one of the earliest and most widely used measures of ecological efficiency. For example: If the NPP (Net Primary Production) in a plant is 100 kJ, the organic substance converted into the body mass of the herbivore which feeds on it is 10 kJ only. Similarly, the body mass of the carnivore-I is 1 kJ only.
![]()
Question 6.
List out the major air pollutants and describe their effects on human beings.
Answer:
Air pollutants cause injury to all living organisms. They reduce the growth and yield of crops. They are harmful to the respiratory system of humans and animals. An increase in the concentration of pollutants or duration of exposure increases the harmful effects on the organisms.
The major air pollutants:
1. Carbon monoxide (CO): It is produced mainly due to incomplete combustion of fossil fuels. Automobiles are a major cause of CO pollution in larger cities and towns. Automobile exhausts, fuels from factories, emissions from power plants, forest fires and even burning of firewood contribute to CO pollution. Haemoglobin has a greater affinity for CO and SO, and CO competitively interferes with oxygen transport. CO symptoms such aS headache and blurred vision at lower concentrations. In higher concentrations, it leads to coma and death.
2. Carbon Dioxide (CO2): Carbon dioxide is the main pollutant that is leading to global warming. Plants utilize CO2 for photosynthesis and all living organisms emit carbon dioxide in the process of respiration. With rapid urbanization, automobiles, aeroplanes, power plants, and other human activities that involve the burning of fossil fuels such as gasoline, carbon dioxide is turning out to be an important pollutant of concern.
3. Sulphur Dioxide (SO2): It is mainly produced by burning fossil fuels. Melting of sulphur ores is another important source of SO2 pollution. The metal smelting and other industrial processes also contribute to SO2 pollution. Sulfur dioxide and nitrogen oxides are the major causes of acid rains, which cause acidification of soils, lakes, and streams and also accelerated corrosion of buildings and monuments. High concentrations of sulphur dioxide (SO2) can result in breathing problems in asthmatic children and adults. Other effects associated with long-term exposure to sulphur dioxide, include respiratory illness, alterations in the lungs defenses, and aggravation of existing cardiovascular problems.
To control SO2 pollution, the emissions are filtered through scrubbers. Scrubbers are devices that are used to clean the impurities in exhaust gases. Gaseous pollutants such as SO2 are removed by scrubbers.
4. Nitrogen Oxides: Nitrogen oxides are considered to be major primary pollutants. The source is mainly automobile exhaust. The air polluted by nitrogen oxide is not only harmful to humans and animals but also dangerous for the life of plants. Nitrogen oxide pollution also results in acid rain and the formation of photochemical smog. The effect of nitrogen oxides on plants includes the occurrence of necrotic spots on the surface of leaves. Photosynthesis is affected in crop plants and the yield is reduced. Nitrogen oxides combine with volatile organic compounds by the action of sunlight to form secondary pollutants called Peroxyacetyl nitrate (PAN) which are found especially in photochemical smog. They are powerful irritants to the eyes and respiratory tract.
5. Particulate matter/Aerosols: Tiny particles of solid matter suspended in a gas or liquid constitute the particulate matter. Aerosols refer to particles and /or liquid droplets and the gas together (a system of colloidal particles dispersed in a gas) Combustion of “fossil fuels” (petrol, diesel, etc) fly ash produced in thermal plants, forest fires, cement factories, asbestos mining, and manufacturing units, spinning and ginning mills, etc., are the main sources of particulate matter pollution. According to the Central Pollution Control Board (CPCB) particles of 2.5 micrometers or less in diameter are highly harmful to man and other air-breathing organisms.
An electrostatic precipitator is a widely used filter’ for removing particulate matter from the exhaust of thermal power plants. It can remove 99% of particulate matter. It has high voltage electrodes which produce a ‘corona’ that releases electrons. These are collected by collecting plates that attract charged particles. The air flowing between the plates is kept at a low velocity so as to allow the dust particles to fall. Thus clean air is released into the atmosphere.
![]()
Question 7.
What are the causes of water pollution and suggested measures for control of water pollution?
Answer:
Domestic Sewage: Sewage is the major source of water pollution in large cities and towns. It mainly consists of human and animal excreta and other waste materials. It is usually released into freshwater bodies or the sea directly. As per the regulations the sewage has to be passed through treatment plants before it is released into the water sources. Only 0.1 percent of impurities from domestic sewage are making these water sources unfit for human consumption. In the treatment of sewage, solids are easy to remove. Removal of dissolved salts such as nitrates, phosphates, and other nutrients and toxic metal ions and organic compounds is much more difficult. Domestic sewage primarily contains biodegradable organic matter, which will be readily decomposed by the action of bacteria and other microorganisms.
Biological Oxygen Demand (BOD): BOD is a measure of the content of biologically degradable substances in sewage. The organic degradable substances are broken down by microorganisms using oxygen. The demand for oxygen is measured in terms of the oxygen consumed by microorganisms over a period of 5 days (BOD 5) or seven days (BOD 7). BOD forms an index for measuring pollution load in the sewage. Microorganisms involved in the biodegradation of organic matter in water bodies consume a lot of oxygen and as a result, there is a sharp decline in dissolved oxygen causing the death of fish and other aquatic animals.
Algal blooms: The presence of large amounts of nutrients in waters also causes excessive growth of plankton algae and the phenomenon is commonly called “algal blooms1′. Algal blooms impart distinct colour to the bodies and deteriorate the quality of water. It also causes the mortality of fish. Some algae which are involved in algal blooms are toxic to human beings and animals.
Excessive growth of aquatic plants such as the common water hyacinth (Eichhornia crassipes), the world’s most problematic aquatic weed which is also called “Terror of Bengal” causes blocks in our waterways. They grow faster than our ability to remove them. They grow abundantly in eutrophic water bodies (water bodies rich in nutrients) and lead to an imbalance in the ecosystem dynamics of the water body.
Sewage arising from homes and hospitals may contain undesirable pathogenic microorganisms. If it is released untreated into water courses, there is a likelihood of an outbreak of serious diseases, such as dysentery, typhoid, jaundice, cholera, etc.
2. Industrial Effluents: Untreated industrial effluents released into water bodies pollute most of the rivers, freshwater streams, etc. Effluents contain a wide variety of both inorganic and organic pollutants such as oils, greases, plastics, metallic wastes, suspended solids, and toxins. Most of them are non-degradable. Arsenic, Cadmium, Copper, Chromium, Mercury, Zinc, and Nickel are the common heavy metals discharged from industries.
Effects: Organic substances present in the water deplete the dissolved oxygen content in water by increasing the BOD (Biological Oxygen Demand) and COD (Chemical Oxygen Demand). Most of the inorganic substances render the water unfit for drinking. Outbreaks of dysentery, typhoid, jaundice, cholera, etc., are caused by sewage pollution.
Biomagnification: Increase in the concentration of the pollutant or toxicant at successive trophic levels in an aquatic food chain is called Biological Magnification or Bio-magnification. This happens in the instances where a toxic substance accumulated by an organism is not metabolized or excreted and thus passes on to the next higher trophic level. This phenomenon is well known regarding DDT and mercury pollution.
As shown in the above example, the concentration of DDT is increased at successive trophic levels starting at a very low concentration of 0.003 ppb (ppb = parts per billion) in water, which ultimately reached an alarmingly high concentration of 25 ppm (ppm = parts per million) in fish-eating birds, through biomagnification. High concentrations of DDT disturb calcium metabolism in birds, which causes thinning of eggshells and their premature breaking, eventually causing a decline in bird populations.
Eutrophication: Natural ageing of a lake by nutrient enrichment of its water is known as eutrophication. In a young lake, the water is cold and clear, supporting little life. Gradually nutrients such as nitrates and phosphates are carried into the lake via streams, in course of time. This encourages the growth of aquatic algae and other plants. Consequently, animal life proliferates and organic debris piles up, the lake grows shallower and warmer. As a result, the aquatic organisms thriving in the cold environment are gradually replaced by warm-water organisms. Marsh plants appear by taking root in the shallow regions of the lake. Eventually, the lake gives way to large masses of floating plants (bog) and is finally covered in land.