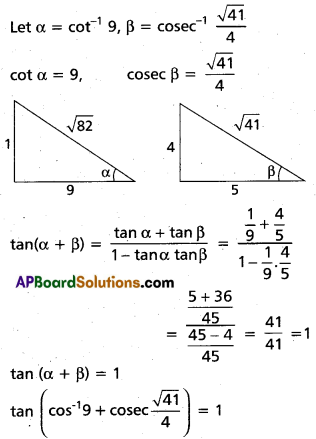
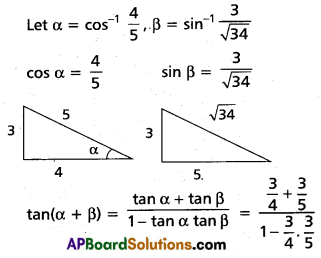
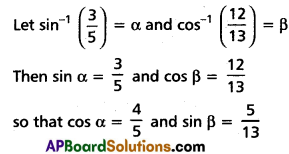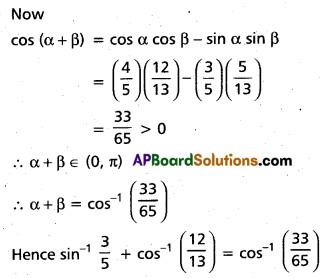These AP 9th Biology Important Questions and Answers 6th Lesson జ్ఞానేంద్రియాలు will help students prepare well for the exams.
AP Board 9th Class Biology 6th Lesson Important Questions and Answers జ్ఞానేంద్రియాలు
9th Class Biology 6th Lesson జ్ఞానేంద్రియాలు 1 Mark Important Questions and Answers
ప్రశ్న 1.
మనకు ఇంద్రియ జ్ఞానం ఏ విధంగా కలుగుతుంది?
జవాబు:
నాడీ సంకేతాల వలన ఇంద్రియ జ్ఞానం కలుగుతుంది.
ప్రశ్న 2.
ఆకు ఆకుపచ్చగా కనబడుటకు కారణమేది?
జవాబు:
ఆకుపచ్చని ఆకు నుండి పరావర్తనం చెందిన కాంతి గ్రాహకాలను చేరి నాడీ సంకేతాలుగా మారి అవి మెదడుకు చేరి, అది ఒక ఆకుపచ్చని ఆకారంగా రూపకల్పన చేయబడుతుంది.
ప్రశ్న 3.
దృష్టి ఎందుకు సహాయపడుతుంది?
జవాబు:
మన భౌతిక పరిసరాల్లో కోరుకున్న ‘గమ్యాలు, భయాలు, మార్పులను గుర్తించి వాటికి అనుగుణంగా ఉండడానికి దృష్టిలో (చూపు) ఉపయోగపడుతుంది.
ప్రశ్న 4.
కంటిలోని మూడు ముఖ్యమైన పొరలు ఏవి?
జవాబు:
దృఢస్తరం, రక్తపటలం మరియు నేత్రపటలం కంటిలోని మూడు ముఖ్యమైన పొరలు.
ప్రశ్న 5.
కటకం కంటి గుడ్డు లోపలి భాగాల్ని ఎన్ని భాగాలుగా విడగొడుతుంది?
జవాబు:
రెండు భాగాలు, అవి నేత్రోదక కక్ష మరియు కాచావత్ కగా విడగొడుతుంది.

ప్రశ్న 6.
నేత్రోదక కక్ష మరియు కాచావత్ కక్ష వేటితో నింపబడి ఉంటాయి?
జవాబు:
నేత్రోదక కక్ష నీరు వంటి ద్రవంతోను, కాచావత్ కక్ష జెల్లి వంటి ద్రవంతోను నిండి ఉంటాయి.
ప్రశ్న 7.
కంటిని మనము ఏ విధంగా భావించవచ్చు?
జవాబు:
ప్రపంచంలోని దృశ్యాలను చలన చిత్రాలుగా తీయడానికి మెదడు ఉపయోగించే ఒక రకమైన వీడియో కెమెరాగా కంటిని భావించవచ్చు.
ప్రశ్న 8.
కన్ను ప్రతిబింబాన్ని ఎక్కడ ఏర్పరుస్తుంది?
జవాబు:
కన్ను కాంతిని సేకరించి కుంభాకార కటకం ద్వారా కేంద్రీకరించి కంటిలో వెనుక భాగాన ఉండే నేత్రపటలంపై ప్రతిబింబాన్ని ఏర్పరుస్తుంది.
ప్రశ్న 9.
కుంభాకార కటకం వల్ల ఏర్పడే ప్రతిబింబం ఏ విధంగా ఉంటుంది?
జవాబు:
కటకం వల్ల ఏర్పడే ప్రతిబింబంలో ఎడమ కుడిగాను, కుడి ఎడమగాను, తలకిందులుగాను ఏర్పడుతుంది.
ప్రశ్న 10.
నేత్రపటలం మధ్యభాగంలో ఉండే ఫోవియో యొక్క ఉపయోగమేమిటి?
జవాబు:
ఫోవియో నందు శంకువులు గుమికూడి ఉంటాయి. ఇవి , దృష్టి స్పష్టంగా ఉండేలా చేస్తాయి. మరియు మనం చూడాలనుకున్న దానిని సూక్ష్మంగా పరిశీలించడానికి ఉపయోగపడుతుంది.
ప్రశ్న 11.
అంధచుక్క అనగా నేమి?
జవాబు:
నేత్రపటలంలో ఒక చిన్న ప్రాంతంలో కాంతి గ్రాహకాలు ఉండవు. దానితో ఆ ప్రాంతం అంధకారంగా ఉంటుంది. దీనిని అంధచుక్క అంటారు.
ప్రశ్న 12.
కంటిని, కంటి భాగాల్ని యాంత్రిక అఘాతాల నుండి రక్షించేవి ఏవి?
జవాబు:
నేత్రోదక కక్ష, కచావత్ కక్షలో ఉండే ద్రవాలు కంటిని, కంటి భాగాల్ని రక్షిస్తాయి.
ప్రశ్న 13.
కంటిలోని ద్వికుంభాకారంలో ఉండే కటకం యొక్క ఆకారాన్ని మార్చేవి ఏవి?
జవాబు:
కటకాల యొక్క నాభ్యంతరం శైలికామయ కండరాలు, అవలంబిత స్నాయువుల సహాయంతో మార్పుచేయబడుతుంది. అవి కటకం యొక్క ఆకారాన్ని కావలసిన విధంగా మార్చగలవు.
ప్రశ్న 14.
భ్రమలు మనకు దృష్టి జ్ఞానం గురించి ఏమి తెలుపుతాయి?
జవాబు:
భ్రమలు మనం చూస్తున్న దానికి బాహ్యంగా ఉన్న సత్యానికి మధ్య ఉన్న తేడాల్ని అవగాహన చేసుకోడానికి, తార్కికతను తెలుసుకోవడానికి ఉపయోగపడతాయి.
ప్రశ్న 15.
కళ్ళకు ప్రధానంగా వచ్చే కొన్ని వ్యాధులు ఏవి?
జవాబు:
రేచీకటి, పొడిబారిన కళ్ళు, హ్రస్వదృష్టి దీర్ఘదృష్టి, గ్లూకోమా, కంటి శుక్లం, వర్ణాంధత మొదలగునవి కళ్ళకు వచ్చే వ్యాధులు.

ప్రశ్న 16.
చెవుల యొక్క ఉపయోగమేమిటి?
జవాబు:
వినడంతోబాటు మన శరీరం యొక్క సమతాస్థితిని సక్రమంగా ఉంచడానికి చెవులు ఉపయోగపడతాయి.
ప్రశ్న 17.
చెవినందలి మూడు భాగాలు ఏవి?
జవాబు:
వెలుపలి చెవి, మధ్యచెవి మరియు అంతర చెవి
ప్రశ్న 18.
వెలుపలి చెవినందుండే గ్రంథులు ఏవి?
జవాబు:
వెలుపలి చెవినందు మైనాన్ని స్రవించే సెరుమినస్ గ్రంథులు, తైలాన్ని స్రవించే తైల గ్రంథుల్ని కలిగి ఉంటుంది.
ప్రశ్న 19.
మధ్య చెవినందలి మూడు ఎముకలు ఏవి?
జవాబు:
కూటకము లేక సుత్తి, దాగలి లేక పట్టెడ, కర్ణాంతరాస్థి లేక అంకవన్నె అనే మూడు ఎముకలు మధ్య చెవిలో ఉంటాయి.
ప్రశ్న 20.
అంతర చెవినందు ఉండే పేటికా ఉపకరణం యొక్క ఉపయోగమేమిటి?
జవాబు:
పేటికా ఉపకరణం శరీరస్థితి, సమతులనం సక్రమంగా ఉండేలా చూసి, శరీర సమతాస్థితిని నిర్వహిస్తుంది.
ప్రశ్న 21.
చెవికి సాధారణంగా వచ్చే వ్యాధులు ఏవి?
జవాబు:
బాక్టీరియా, ఫంగస్ వల్ల చీము, కర్ణభేరికి ఇన్ఫెక్షన్ సాధారణంగా చెవికి వచ్చే వ్యాధులు.
ప్రశ్న 22.
ముక్కు జంతువులను ఏ విధంగా సంరక్షిస్తోంది?
జవాబు:
ప్రమాదకరమైన ఆహారం, పరభక్షుల నుండి వచ్చే వాసనను గ్రహించుట ద్వారా ముక్కు జంతువులను సంరక్షిస్తోంది.
ప్రశ్న 23.
నాలుక కలిగించే రుచి జ్ఞానంలో ఉన్న నాలుగు ప్రాథమిక రుచులు ఏవి?
జవాబు:
తీపి, పులుపు, చేదు, ఉప్పు నాలుక కలిగించే రుచి రకాలు.
ప్రశ్న 24.
ఉమామి రకపు రుచి గురించి తెలపండి. ఏయే ఆహారపదార్థాలలో ఉంటుంది?
జవాబు:
మాంసం, సముద్రం నుండి లభించే ఆహారం, జున్ను వంటి మాంసకృత్తులు పుష్కలంగా ఉండే ఆహారం నుండి వచ్చే వాసనను ‘ఉమామి’ అంటారు.
ప్రశ్న 25.
ఆహారపు రుచిని ఏవిధంగా తెలుసుకోగలం?
జవాబు:
ఆహారం నమిలిన, కొరికిన, చప్పరించిన వెలువడే రసాయనాలు రుచికణికల్ని ప్రేరేపిస్తాయి. దాంతో అవి ప్రేరణను మెదడుకు పంపి రుచిని తెలుసుకునేలా చేస్తాయి.

ప్రశ్న 26.
నాలుక మీద ఉండే నిర్మాణాలు ఎన్ని రకాలు? అవి ఏవి?
జవాబు:
నాలుగు రకాలు. అవి :
- ఫిలిఫార్మ్ పాపిల్లే
- ఫంగిఫార్మ్ పాపిల్లే
- సర్కంవేలేట్ పాపిల్లే
- ఫోలియేట్ పాపిల్లే.
ప్రశ్న 27.
చర్మంలోని రెండు ముఖ్యమైన పొరలు ఏవి?
జవాబు:
బహిశ్చర్మం మరియు అంతశ్చర్మం అనేవి చర్మంలోని పొరలు.
ప్రశ్న 28.
బహిశ్చర్మం ఎన్ని పొరలను కలిగి ఉంటుంది? అవి ఏవి?
జవాబు:
బహిశ్చర్మం మూడు పొరలను కలిగి ఉంటుంది. అవి వెలుపలి కార్నియం పొర, జీవకణాలుండే గ్రాన్యులర్ పొర మరియు స్థిరంగా విభజనలు చెందే మాల్ఫీజియన్ పొర.
ప్రశ్న 29.
అంతశ్చర్మంలో ఏమి ఉంటాయి?
జవాబు:
అంతశర్మంలో స్వేదగ్రంథులు, తైలగ్రంథులు, రోమపుటికలు, రక్తనాళాలు, కొవ్వులు ఉంటాయి.
ప్రశ్న 30.
కంటి చూపులో బలహీనులయిన ప్రత్యేక అవసరాలు కలిగిన విద్యార్ధులు స్పర్శ ద్వారా బ్రెయిలీ లిపిని ఎందుకు చదవగలరు?
జవాబు:
బ్రెయిలీ లిపిలో అక్షరాలు ఉబ్బెత్తులు, పల్లాలు కలిగి ఉంటాయి. అందువలన కంటి చూపులో బలహీనులయిన ప్రత్యేక అవసరాలు గల విద్యార్థులు బ్రెయిలీ లిపిని చదువగలరు.
ప్రశ్న 31.
జ్ఞానేంద్రియాలు పనిచేయని ప్రత్యేక అవసరాలు గల పిల్లలకు మీరు ఎలాంటి ప్రోత్సాహం ఇస్తారు?
జవాబు:
వారు మామూలు మనుష్యులలాగానే జీవించడానికి అవసరమైన ఆత్మవిశ్వాసమును వారిలో నింపుతాను. ప్రత్యేక అవసరాలు గల పిల్లలు తమకు ఎటువంటి కొరత లేదనే భావనను మరియు వారికి కొదువ లేదనే తృప్తిని అందిస్తాను.
ప్రశ్న 32.
ప్రకృతి సౌందర్యాన్ని ఆస్వాదించడానికి సహాయపడే జ్ఞానేంద్రియాల పనులు నీకు ఎలాఉపయోగపడుతున్నాయి?
జవాబు:
మనం ప్రకృతి సౌందర్యాన్ని కళ్ళతో, వీనుల విందైన సంగీతాన్ని చెవులతో, పూల సువాసనలను ముక్కుతో మరియు చల్లని చిరుగాలిని చర్మంతో స్పర్శిస్తున్నాము మరియు ఆహార పదార్థాల రుచిని నాలుకతో ఆస్వాదిస్తున్నాము.
ప్రశ్న 33.
కాంతి యొక్క హానికర ప్రభావానికి లోనుగాకుండా శరీరపు పొరలను చర్మం ఏ విధముగా కాపాడుతుంది?
జవాబు:
చర్మంలో ఉండే వర్ణద్రవ్యం మెలనిన్ సూర్యకాంతి చేత ఉత్తేజితమవుతుంది. అటువంటప్పుడు చర్మం నల్లబడి మిగిలిన పొరల్ని కాంతి యొక్క హానికర ప్రభావానికి లోనుగాకుండా చూస్తుంది.
ప్రశ్న 34.
కన్నీరు మనకు ఏ విధముగా ఉపయోగపడుతుంది?
జవాబు:
ఎప్పుడైనా, ఏదైనా అవసరం లేని పదార్థం కనుక కంటిలో పడితే వెంటనే అశ్రుగ్రంథులు ప్రేరేపితమై ఆ పదార్థాన్ని బయటకు పంపించివేస్తాయి.
ప్రశ్న 35.
మనకు వెలుపలి చెవి లేకుండా ఉంటే ఏం జరుగుతుంది?
జవాబు:
మనకు వెలుపలి చెవి లేకుండా ఉంటే శబ్దతరంగాలు సేకరించబడవు తద్వారా మనకు ఏమీ వినపడదు.
ప్రశ్న 36.
మీరు జలుబుతో బాధపడుతున్నప్పుడు మామూలుగా పదార్థాలను వాసన చూడగలరా? (పేజీ నెం. 89)
జవాబు:
జలుబుగా ఉన్నప్పుడు నాసికామార్గాలు మూయబడి ఉండుట చేత మనకు ఆహారము యొక్క వాసన తెలియదు.

ప్రశ్న 37.
వాసనకి, రుచికి ఏమైనా సంబంధం ఉందని మీరు అనుకుంటున్నారా? (పేజీ నెం. 89)
జవాబు:
వాసన, రుచి కూడా ఆహారంలో ఉండే రసాయనాలను గుర్తించడం పైన ఆధారపడిన ఇంద్రియ జ్ఞానము. ఇవి ఒకదానితో ఒకటి దగ్గర సంబంధాన్ని కలిగి ఉన్నాయి.
ప్రశ్న 38.
మనకు దోమ కుట్టగానే దానిని ఎలా చంపగలం?
జవాబు:
కాలిమీద దోమ కుట్టగానే జ్ఞాన నాడులు దోమకుట్టే సమాచారాన్ని మెదడుకు చేరవేస్తాయి. మెదడు దోమను చంపాల్సిందిగా చాలకనాడుల ద్వారా చేతికి సమాచారం పంపుతుంది. అప్పుడు చేతితో దోమను చంపుతాం.
ప్రశ్న 39.
మానవులలో జ్ఞానేంద్రియములు ఎన్ని? అవి ఏవి?
జవాబు:
మానవులలో ఐదు జ్ఞానేంద్రియాలు కలవు. అవి :
- కన్ను
- చెవి
- ముక్కు
- నాలుక
- చర్మం.
ప్రశ్న 40.
కంటిలోని ప్రధాన భాగాలేవి?
జవాబు:
కంటిరెప్పలు, కనురెప్ప రోమాలు, కనుబొమ్మలు, అశ్రుగ్రంథులు, కంటిగుడ్డు కంటిలోని ప్రధాన భాగాలు.

ప్రశ్న 41.
అరచేయిలో ఎక్కడ స్పర్శ జ్ఞానం ఎక్కువగా ఉంటుంది? (పేజీ నెం. 93)
జవాబు:
అరచేయి మధ్యలో స్పర్శజ్ఞానం ఎక్కువ.
9th Class Biology 6th Lesson జ్ఞానేంద్రియాలు 2 Marks Important Questions and Answers
ప్రశ్న 1.
మీరు జ్వరంతో బాధపడుతున్నప్పుడు నోటికి ఆహారం రుచిగా ఉండదు. ఎందువల్ల?
జవాబు:
రుచి కణికల్లో ఉండే ఎంజైములు 77°F నుండి 98.6°F వరకు మాత్రమే పనిచేస్తాయి. ఎంజైములు పనిచేయక పోవడం వలన రుచి కణికలో ఉండే కణాలు మెదడు నందలి రుచి భాగములకు సమాచారమును పంపకపోవడం వలన జ్వరంగా ఉన్నప్పుడు రుచి తెలియదు.
ప్రశ్న 2.
కన్ను ఇతర జ్ఞానేంద్రియాల కంటే ఏ విధముగా భిన్నమైనది?
జవాబు:
కాంతి తరంగాల నుండి సమాచారాన్ని తీసుకొని మెదడు, తన ప్రక్రియను నిర్వర్తించడానికి వీలుగా వాటి కాంతి లక్షణాలను నాడీ సంకేతాలుగా మార్చే సామర్థ్యం ఇతర జ్ఞానేంద్రియాలకు లేకుండా కంటికి మాత్రమే ఉన్న లక్షణం.
ప్రశ్న 3.
నేత్రపటలంలోని దందాల గురించి క్లుప్తంగా రాయండి.
జవాబు:
- మన కంటిలో రొడాప్సిన్ అనే వర్ణద్రవ్యం కలిగిన దండాలు సుమారుగా 125 మిలియన్లు ఉన్నాయి.
- అవి అతి తక్కువ కాంతిలో అంటే చీకటిలో వస్తువుల్ని చూడగలవు. కానీ వివిధ రంగులకు సంబంధించిన నిశితమైన తేడాలను మాత్రం గుర్తించలేవు.
ప్రశ్న 4.
కన్ను గురించి ఇటీవల కనుగొనిన విషయాలు ఏమిటి?
జవాబు:
వస్తువుల అంచులు, సరిహద్దులను సునిశితంగా చూపేవి, వెలుతురుకు, నీడకు, కదలికలకు స్పందించే ప్రత్యేక గ్రాహక కణాల్ని నేత్రపటలంలో ఇటీవల కనుగొన్నారు.
ప్రశ్న 5.
ఆధార్ కార్లను ఇవ్వడంలో కంటిపాపలు ఎలా ఉపయోగపడతాయి?
జవాబు:
- కంటిపాపలు ఎవరికి వారికే ప్రత్యేకంగా ఉంటాయి.
- అందుకే వేలిముద్రల మాదిరిగానే కంటిపాపలను కూడా గుర్తింపు కోసం ఉపయోగిస్తారు.
ప్రశ్న 6.
చెవులు నిర్వహించే విధులు ఏమిటి?
జవాబు:
చెవుల యొక్క విధులు :
- శబ్ద ప్రకంపనాలను నాడీ ప్రేరణలుగా మార్చి మెదడుకు అందించడం.
- సమతాస్థితిని కాపాడుతాయి.
ప్రశ్న 7.
నాసికా కుహరమునందలి శ్లేష్మము మరియు వెంట్రుకల ఉపయోగం ఏమిటి?
జవాబు:
ముక్కు కుహరంలో ఉండే వెంట్రుకలు, మ్యూకస్, దుమ్ము, సూక్ష్మక్రిములు ఇంకా అవసరములేని ఇతర పదార్థాలను ముక్కు ద్వారా శరీరంలోకి చేరకుండా కాపాడతాయి.

ప్రశ్న 8.
చర్మము యొక్క గ్రాహక స్వభావమెటువంటిది?
జవాబు:
- స్పర్శకు, ఉష్ణోగ్రతకు, పీడనానికి చర్మం సూక్ష్మ గ్రాహకత్వాన్ని చూపుతుంది.
- స్పర్శకు స్పర్శ గ్రాహకాలు, పీడనానికి పెసిమియన్ గ్రాహకాలు, ఉష్ణోగ్రతకి నాసిష్టారులు వంటి ప్రత్యేక గ్రాహకాలను కలిగి ఉంటుంది.
ప్రశ్న 9.
చర్మానికి వచ్చే కొన్ని వ్యాధులను తెలపండి.
జవాబు:
- పొంగు, ఆటలమ్మ వంటివి వైరస్ వల్ల వచ్చే వ్యాధులు.
- చర్మానికి బ్యాక్టీరియా వలన వచ్చే వ్యాధి కుష్టు.
- మెలనిన్ లోపం వలన చర్మానికి వచ్చే వ్యాధి బొల్లి.
- ఫంగస్ వలన చర్మానికి తామర వస్తుంది.
- విటమిన్ల లోపం వలన చర్మానికి పెల్లాగ్రా వ్యాధి వస్తుంది.
ప్రశ్న 10.
మెలనిన్ అనగానేమి? మెలనిన్ యొక్క విధులేమిటి?
జవాబు:
- చర్మానికి రంగునిచ్చే వర్ణద్రవ్యము మెలనిన్.
- ఈ వర్ణద్రవ్యం సూర్యకాంతి చేత ఉత్తేజితమవుతుంది.
- అటువంటప్పుడు చర్మం నల్లబడి మిగిలిన పొరల్ని కాంతి యొక్క హానికర ప్రభావానికి లోను కాకుండా చేస్తుంది.
ప్రశ్న 11.
మనకు వెలుపలి చెవి లేకుండా ఉంటే ఏం జరుగుతుంది? (పేజీ నెం. 87)
జవాబు:
- చెవి ద్వారా శబ్దతరంగాలు సేకరించబడవు.
- మధ్య చెవిని తాకే శబ్ద తరంగాలను మాత్రమే వినగలము.
- అందువలన వెలుపలి చెవి శబ్ద తరంగాలను సేకరించకపోతే మనకు ఏమీ వినపడదు.
ప్రశ్న 12.
ప్రేరణలు లేదా ఉత్తేజకాలు అనగానేమి? పరిసరాల నుండి సమాచారం మెదడుకు ఎట్లా చేరుతుంది?
జవాబు:
- ప్రకృతిలోని కొన్ని పరిస్థితులు, పదార్థాలు ఇంద్రియ జ్ఞానం మన శరీరంలో కలిగేలా ప్రేరేపిస్తాయి. వాటిని ప్రేరకాలు లేదా ఉత్తేజకాలు అంటారు.
- ఈ ఉత్తేజకాలు తీసుకెళ్ళే సమాచారాన్ని మన జ్ఞానేంద్రియాలలోని గ్రాహకాలు గ్రహించి నాడీ సంకేతాలుగా మారుస్తాయి.
- ఇవి మెదడుకు అందించబడి, ఇంద్రియ జ్ఞానంగా రూపొందుతాయి.
9th Class Biology 6th Lesson జ్ఞానేంద్రియాలు 4 Marks Important Questions and Answers
ప్రశ్న 1.
జ్ఞానేంద్రియాలు చేసే పనికి కేంద్రం ఎవరు? అది ఏ విధముగా సమాచారాన్ని విశ్లేషిస్తుంది? ఉదాహరణ ఇవ్వండి.
జవాబు:
- జ్ఞానేంద్రియాలు చేసే పనులన్నింటికి కేంద్రం మెదడు.
- అది జ్ఞానేంద్రియాల నుండి నాడీ సంకేతాలు తెచ్చే జ్ఞాననాడులు ద్వారా సమాచారాన్ని అందుకుంటుంది.
- తరువాత వాటిని విశ్లేషించి చాలకనాడులు అని పిలువబడే నాడుల ద్వారా ప్రతిచర్యను చూపాల్సిన భాగాలకు సంకేతాలు పంపుతుంది.
- ఉదాహరణకు మన కాలి మీద దోమ కుట్టగానే జ్ఞాననాడులు దోమ కుట్టిన సమాచారాన్ని మెదడుకు చేరవేస్తాయి.
- మెదడు దోమను చంపాల్సిందిగా చాలకనాడుల ద్వారా చేతికి సమాచారం పంపుతుంది. అపుడు చేతితో దోమను చంపేస్తాం.
ప్రశ్న 2.
కంటి నిర్మాణమును పటము సహాయముతో వివరించండి.
జవాబు:
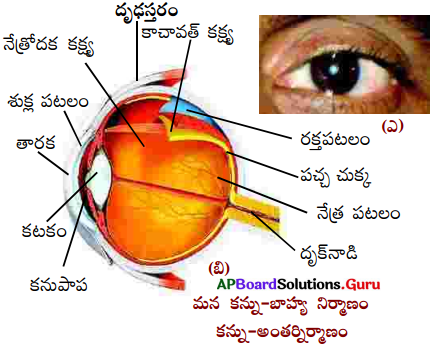
- మన కంటిలో కంటిరెప్పలు, కనురెప్ప రోమాలు, కనుబొమ్మలు, అశ్రుగ్రంథులు ఉంటాయి.
- కంటి ముందు భాగాన్ని పలుచటి కంటిపొర కప్పి ఉంటుంది.
- కంటి గుడ్డు కంటి గుంతలో అమరి ఉంటుంది.
- కంటిగ్రుడ్డులో కేవలం 1/6వ వంతు భాగం మాత్రమే మన కంటికి కన్పిస్తుంది.
- కంటిలో మూడు ముఖ్యమైన పొరలు ఉన్నాయి. అవి దృఢస్తరం, రక్తపటలం నేత్రపటలం.
- దృఢస్తరం ఉబ్బి శుక్లపటలంను ఏర్పరుస్తుంది.
- దృఢస్తరం యొక్క కొనభాగంలో దృక్నడి కలుపబడుతుంది.
- రక్తపటలం నలుపురంగులో ఉండి అనేక రక్తనాళాలను కలిగి ఉంటుంది.
- తారక భాగాన్ని తప్ప కంటి యొక్క అన్ని భాగాల్ని రక్తపటలం ఆవరించి ఉంటుంది.
- తారక చుట్టూ రక్తపటలం నుండి ఏర్పడిన భాగము కంటిపాప.
- తారకకు వెనుక ద్వికుంభాకారంలో ఉండే కటకం ఉంటుంది.
- కంటిగుడు లోపలి భాగమును నేత్రోదక కక్ష, కాచావత్ కక్ష అనే రెండు భాగాలుగా కటకం విడగొడుతుంది.
- నేత్రపటలంలో దండాలు, శంకువులు ఉంటాయి.
- దృష్టి జానంలేని అంధచుక్క, మంచి దృష్టి జ్ఞానాన్ని కలిగిన పచ్చచుక్క నేత్రపటలంలో ఉంటాయి.
- పచ్చచుక్కను మేక్యులా అని, ఫోవియా అని కూడా అంటారు.
ప్రశ్న 3.
కన్ను పనిచేసే విధానమును వివరించండి.
జవాబు:
- కన్ను కాంతిని సేకరించి కుంభాకార కటకం ద్వారా కేంద్రీకరించి, కంటిలో వెనుకభాగాన ఉండే నేత్రపటలంపై ప్రతిబింబాన్ని ఏర్పరుస్తుంది.
- కటకం వల్ల ఏర్పడే ప్రతిబింబంలో ఎడమ కుడిగాను, తలకిందులుగాను ఉంటుంది.
- ఈ తలకిందులైన ప్రతిబింబం మెదడు నిర్మాణంపై ప్రభావం చూపి జ్ఞానకేంద్రాలలో దాన్ని సక్రమంగా చేయడానికి మార్గాన్ని ఏర్పరచుకుంటుంది.
- అందువల్ల జ్ఞానేంద్రియాల నుండి వచ్చే సమాచారం చాలా వరకు మెదడులో వ్యతిరేకదిశ నుండి దాటిపోతుంది.
- మెదడులోని జ్ఞానకేంద్రాలలో పటాలన్నీ సాధారణముగా తిరగబడి, తలకిందులుగా అవుతాయి.
- కన్ను ఏర్పరచే ప్రతిబింబం మెదడులో మరొక పెద్ద ప్రక్రియకు లోనవుతుంది.
ప్రశ్న 4.
కాంతి గ్రాహకాలు అనగానేమి? అవి కాంతిని ఏ విధముగా గ్రహిస్తాయి?
జవాబు:
- నేత్రం పటలంలో ఉండే సున్నితమైన కాంతిని గ్రహించే కణములను కాంతి గ్రాహకాలు అంటారు.
- కాంతి గ్రాహకాలలో కాంతి శక్తిని శోషించుకోగలిగి, నాడీ ప్రేరణలను సృష్టించి ప్రత్యుత్తరమివ్వగలిగే దండాలు, శం అనే రెండు రకాల ప్రత్యేక కణాలు ఉంటాయి.
- మన కళ్ళు కొన్నిసార్లు చిమ్మచీకటిలోను, కొన్నిసార్లు కాంతివంతమైన వెలుతురులోనూ పనిచేస్తుంటాయి.
- అందుకనే ఈ రెండు రకాల కణాలు తగిన ప్రక్రియలను నిర్వహిస్తాయి.
ప్రశ్న 5.
నేత్రపటలం నందలి శంకువుల గురించి క్లుప్తంగా రాయండి.
జవాబు:
- రంగుల్లో స్వల్ప ప్రత్యేకతల్ని చూడగలిగే లక్షణం శంకువుల్లో ఉంది.
- దాదాపు ఏడు మిలియన్ల శంకువులు కంటిలో ఉంటాయి.
- అవి అయొడాప్సిన్ అనే వర్గపదార్థాన్ని కలిగి కాంతివంతమైన వెలుతురులో రంగుల్ని గుర్తిస్తాయి.
- నేత్రపటలం మధ్యభాగంలో ఉండే ఫోవియా అనే చిన్నభాగంలో శంకువులు గుమిగూడి ఉండి దృష్టి స్పష్టంగా ఉండేలా చేస్తాయి.
ప్రశ్న 6.
కన్నులు ఏ విధంగా సంరక్షించబడతాయి?
జవాబు:
- కనురెప్పలు, రెప్ప వెంట్రుకలు, కనుబొమ్మలు అశ్రుగ్రంథులతో కన్ను నిరంతరం రక్షించబడుతూ ఉంటుంది.
- కంటి ముందు భాగాన ఉన్న కంటిపొర కంటికి రక్షణ కల్పిస్తుంది.
- ఏదైనా అవసరం లేని పదార్థం కనుక కంటిలో పడితే వెంటనే ఆశ్రుగ్రంథులు ప్రేరేపితమై ఆ పదార్థాన్ని బయటకు పంపించివేసాయి.
- కంటిలో నేత్రక, కాచావత్ కక్షలో ఉండే ద్రవాలు కటకాన్ని, కంటి యొక్క ఇతర భాగాల్ని యాంత్రిక అఘాతాల నుండి రక్షిస్తాయి.
- కంటిపాపకు ముందుండే శుక్లపటలం, దృఢస్తరం ఒక పరిశుభ్రమైన కిటికీలా పనిచేస్తుంది. అది కంటిని కాంతికి ప్రత్యక్షంగా గురికాకుండా రక్షిస్తుంది.

ప్రశ్న 7.
వెలుపలి చెవి గురించి క్లుప్తంగా వివరించండి.
జవాబు:
- వెలుపలి చెవి ఒక గొప్ప మాదిరిగా ఉంటుంది. దీన్నే పిన్నా అని అంటారు.
- పిన్నా మగాన్ని స్రవించే సెరుమినస్ గ్రంథుల్ని, తైలాన్ని స్రవించే తైలగ్రంథుల్ని కలిగి ఉంటుంది.
- ఇవి శ్రవణ కుహరాన్ని మృదువుగా ఉండేలా చేస్తాయి. ఇంకా దుమ్ము, ధూళి శ్రవణ కుహరంలోకి చేరకుండా ఆపుతాయి.
- శ్రవణ కుహరాన్ని ఆడిటరీ మీటస్ అని కూడా అంటారు.
- శ్రవణ కుహరం చివరలో కర్ణభేరి అనే పలుచని పొర ఉంటుంది.
- ఇది వెలుపలి చెవికి, మధ్య చెవికి మధ్యలో ఉంటుంది. ఇది ఒక శంకువు ఆకారంలో ఉంటుంది.
- కర్ణభేరి సన్నటి భాగం మధ్యచెవి యొక్క మొదటి ఎముక కూటకం లేక సుత్తికి కలుపబడి ఉంటుంది.
ప్రశ్న 8.
మధ్య చెవి గురించి క్లుప్తంగా రాయండి.
జవాబు:
- కరభేరిపై కలిగిన ప్రకంపనాలకు పెంచడంలో మధ్యచెవి ముఖ్యమైన పాత్రను పోషిస్తుంది.
- మూడు ఎముకల గొలుసు కూటకము లేక సుత్తి, దాగలి లేక పట్టెడ, కర్ణాంతరాస్థి లేక అంకవన్నె ఈ పనికి సహకరిస్తాయి.
- మధ్య చెవి చివరిభాగాన్ని కప్పుతూ అండాకార కిటికీ అనే పొర ఉంటుంది.
- మధ్య చెవి, లోపలి చెవిలోకి వర్తులాకార కిటికీ ద్వారా తెరచుకుంటుంది.
ప్రశ్న 9.
అంతరచెవి నిర్మాణమును వివరించండి.
జవాబు:
- లోపలి చెవిలో త్వచాగహనంను ఆవరించి అస్లి గహనం ఉంటుంది.
- త్వచాగహనంలో పేటిక, అర్ధవర్తుల కుల్యలు, కర్ణావర్తం అనే భాగాలుంటాయి.
- పేటిక యొక్క ముందుభాగాన్ని సేక్యులస్ అని, వెనుకభాగాన్ని యుట్రిక్యులస్ అనీ అంటాం.
- వాటి నుండి వచ్చే నాడీ తంతువులు పేటికానాడిని ఏర్పరుస్తాయి.
- అర్ధవర్తులాకార కుల్యలు, పేటికకు కలుపబడి ఉండి అంతరలసిక అనే ద్రవాన్ని కలిగి ఉంటాయి.
- పేటిక, అర్థవర్తుల కుల్యలు కలిసి పేటికా ఉపకరణంను ఏర్పరుస్తాయి.
- ఇది శరీరస్థితి, సమతులనం సక్రమంగా ఉండేలా చూసి శరీర సమతాస్థితిని నిర్వహిస్తుంది.
- కర్ణావర్తం ఒక సర్పిలాకార నిర్మాణం. ఇది స్కాలావెస్టిబులై, స్కాలామీడియా, స్కాలాటింపాని అనే మూడు సమాంతర నాళాల్ని కలిగి ఉంటుంది.
- స్కాలా వెస్టిబులై, స్కాలాటింపాని పరలసిక ద్రవంతోనూ, స్కాలామీడియా అంతరలసిక ద్రవంతోనూ నిండి ఉంటాయి.
- ఇది కార్టి అంగాన్ని, ఇంకా చిన్న ప్రాథమిక జ్ఞాన కణాల్ని కలిగి ఉంటుంది.
- పేటికానాడి, కర్ణావర్తన నాడి కలిసి శ్రవణ నాడి ఏర్పడుతుంది.
ప్రశ్న 10.
శ్రవణ జ్ఞానం కలిగే విధమును వ్రాయుము
జవాబు:
- వెలుపలి చెవి శబ్ద తరంగాలను సేకరిస్తుంది. అవి శ్రవణకుల్యను చేరతాయి.
- అప్పుడు కర్ణభేరిని తాకుతాయి. కర్ణభేరి నుండి వచ్చే ప్రకంపనాలు కూటకము, దాగలి, కర్ణాంతరాస్థిలను చేరతాయి.
- కూటకము, దాగలి, కర్ణాంతరాస్థి శబ్ద ప్రకంపనాల తీవ్రతను పెంచుతాయి.
- కర్ణాంతరాస్థి ప్రకంపనాలను అండాకార కిటికీకి చేరుస్తుంది.
- అక్కడ నుండి అవి కర్ణావర్తం చేరుతాయి.
- త్వచాగహనం కదులుతుంది. దాంతో ప్రకంపనాలు కార్టె అంగాన్ని చేరుతాయి.
- ప్రేరణలు శ్రవణనాడి ద్వారా మెదడుకు చేరతాయి.
- మెదడు ఇచ్చిన ప్రతిస్పందనలను బట్టి వినడం జరుగుతుంది.
ప్రశ్న 11.
ముక్కు నిర్మాణమును గురించి వివరించండి.
జవాబు:
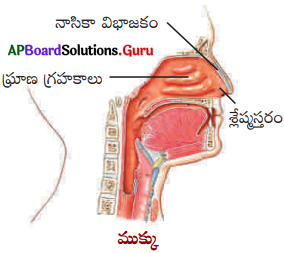
- మనకు బాహ్యంగా కనిపించే ముక్కు రెండు నాసికా రంధ్రాలను కలిగి ఉంటుంది.
- అవి నాసికా కుహరంలోకి తెరచుకుంటాయి.
- నాసికా విభాజకం నాసికా కుహరాన్ని రెండుగా విభజిస్తుంది.
- నాసికా కుహరం గోడలు శ్లేష్మస్తరాన్ని, చిన్న వెంట్రుకలని కలిగి ఉంటాయి.
- శ్లేష్మస్తరంలో ఋణ గ్రాహకాలు ఉంటాయి.
ప్రశ్న 12.
మన నాలుక మీద ఉండే వివిధ రకాల నిర్మాణముల గురించి రాయండి.
జవాబు:
- నాలుక మీద పొలుసుల వంటి నిర్మాణాలను ఫిలిఫార్మ్ పాపిల్లే అంటారు.
- గుండ్రంగా కనిపించే వాటిని ఫంగి ఫార్మ్ పాపిల్లే అంటారు.
- నాలుక వెనుకవైపు గుండ్రంగా ఉండే పెద్ద పాపిల్లే ఉంటాయి. వాటిని సర్కం వేలేట్ పాపిల్లే అంటారు.
- నాలుకకు ఇరువైపులా ఉబ్బెత్తుగా ఉండే నిర్మాణాలను ఫోలియేట్ పాపిల్లే అంటారు.
- అన్ని రకాల పాపిల్లేల్లోనూ రుచి కణికలు ఉంటాయి. ఒక్క ఫిలి ఫార్మ్ పాపిల్లేలో మాత్రం ఉండవు.
ప్రశ్న 13.
చర్మమును గురించి సంక్షిప్తంగా వివరించండి.
జవాబు:
- మన శరీరంలో అన్నింటికంటే వెలుపల ఉండే పొర చర్మం.
- చర్మం శరీర ఉష్ణోగ్రతను క్రమపరుస్తుంది.
- చర్మం స్పర్శ జ్ఞానేంద్రియం.
- స్పర్శ గ్రాహకాలు స్పర్శజ్ఞానాన్ని కలిగిస్తాయి.
- అన్ని అవయవాల కంటే చర్మం పెద్దది.
- మన శరీరానికి ప్రాథమిక రక్షణను చర్మం ఇస్తుంది.
ప్రశ్న 14.
మన జ్ఞానేంద్రియాలు ఉమ్మడిగా పనిచేస్తాయా? ఎందుకు? ఎందువలన పనిచేయవు?
జవాబు:
- అవును, మన జ్ఞానేంద్రియాలు కలిసి పనిచేస్తాయి.
- మన శరీరంలో జరిగే పనులన్నింటిని మెదడు నిర్వహిస్తుంది మరియు నియంత్రిస్తుంది. జ్ఞానేంద్రియాలను కూడా మెదడు సమన్వయపరుస్తుంది.
- మెదడు. ఈ విధముగా చేయకపోయినట్లైతే ప్రేరణలకు సంబంధించిన విశ్లేషణ మనను తికమకకు గురిచేస్తుంది.
- మెదడు నిరంతరం జ్ఞానేంద్రియాల నుండి ప్రేరణలను గ్రహించుట ద్వారా అవయవాలు కలిసి పనిచేయుటకు అవకాశం కల్పిస్తుంది.
- సమాచారమును సమన్వయము చేయుట ద్వారా మెదడు అన్ని భాగాలను కలిపి ఉంచుతుంది.

ప్రశ్న 15.
కనురెప్పలకు వెంట్రుకలు లేకపోతే ఏం జరుగుతుంది?
జవాబు:
- కనురెప్పల యొక్క ముఖ్యవిధి కంటిని ఎల్లప్పుడు తడిగా ఉంచడం.
- కనురెప్పల వెంట్రుకలు కంటిని దుమ్ము, ధూళి నుండి కాపాడతాయి.
- కనురెప్పలకు వెంట్రుకలు కనుక లేకపోయినట్లైతే కంటిగుడ్డు ఎల్లప్పుడూ తేమగా ఉండే అవకాశం లేదు.
- దుమ్ము, ధూళి నుండి రక్షణ ఉండదు.
ప్రశ్న 16.
మన చర్మం స్పర్శ జ్ఞానాన్ని ఎలా కలిగి ఉంటుంది?
జవాబు:
- మన శరీరపు వివిధ భాగాలలో స్పర్శ జ్ఞానం వేరుగా ఉంటుంది.
- మెడచుట్టూ మరియు వేళ్ళ చివరన స్పర్శ జ్ఞానం ఎక్కువగా ఉంటుంది. అరచేయి, మోకాలు, చేతుల మీద స్పర్శ జ్ఞానం తక్కువగా ఉంటుంది.
- మన శరీరపు స్పర్శ జ్ఞానం ఈ క్రింది వాటిపై ఆధారపడి ఉంటుంది.
a)మన శరీరపు చర్మం మందం మీద.
b) స్పర్శ గ్రాహకాల సంఖ్య మీద.
9th Class Biology 6th Lesson జ్ఞానేంద్రియాలు Important Questions and Answers
ప్రశ్న 1.
కింది పటాన్ని పరిశీలించి భాగాలు గుర్తించండి. అడిగిన ప్రశ్నలకు సమాధానాలు రాయండి.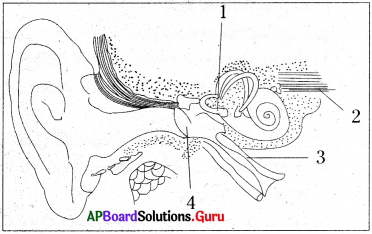
ఎ) చెవిని స్థూలంగా ఎన్ని భాగాలుగా విభజిస్తారు?
జవాబు:
3 భాగాలుగా విభజిస్తారు.
1) బాహ్యచెవి, 2) మధ్యచెవి, 3) లోపలిచెవి
బి) చెవి ఎముకలను సరైన క్రమంలో తెలపండి.
జవాబు:
కూటకము, దాగలి, కర్ణాంతరాస్థి
సి) ధ్వని తరంగాల వల్ల చెవిలో కంపించే భాగం ఏది?
జవాబు:
కర్ణభేరి
డి) సమతాస్థితిని కలిగించే చెవిలోని భాగం ఏది?
జవాబు:
పేటికా ఉపకరణం
ప్రశ్న 2.
కర్ణభేరికి రంధ్రాలు పడితే ఏమవుతుంది?
జవాబు:
- కర్ణభేరికి రంధ్రం పడితే, శబ్ద ప్రకంపనాలు సరియైన ప్రేరణలుగా మార్చబడలేవు.
- ఇందువల్ల ఈ ప్రేరణలను శ్రవణ నాడి మెదడుకు చేర్చలేదు.
- అందువల్ల వినపడదు. చెవుడు వస్తుంది (Deafness).
ప్రశ్న 3.
కన్ను పటము గీచి భాగాలు గుర్తించండి. కంటిలో శంఖువులు లేకపోతే ఏమవుతుంది?
జవాబు:

- శంఖువులు ఎక్కువ కాంతిలో చూడడానికి, రంగులను గుర్తించడంలో ముఖ్యపాత్ర పోషిస్తాయి.
- శంఖువులు లేకపోతే ఎక్కువ వెలుతురులో చూడడానికి, రంగులను గుర్తించడానికి వీలుకాదు.
ప్రశ్న 4.
చర్మం తన స్పర్శజ్ఞానంను కోల్పోతే ఏమి జరుగుతుందో ఊహించి వ్రాయండి.
జవాబు:
a) శరీరాన్ని వేడి నుండి చలి నుండి కాపాడుకోలేము.
b) శరీర ఉష్ణోగ్రత క్రమబద్దం కాదు
c) స్పర్శ కోల్పోనపుడు చర్మానికి తగిలే గాయాలు, దెబ్బలు మనం గుర్తించలేము. అందువల్ల తీవ్ర రక్తస్రావం జరిగే మరణించే అవకాశం ఉన్నది.
d) నడవటం చాలా కష్టమవుతుంది.

ప్రశ్న 5.
కంటిలో శంకు కణాలు లోపిస్తే ఏమౌతుంది?
జవాబు:
రంగులను శక్తివంతమైన వెలుతురులో స్పష్టంగా గుర్తించలేము.
ప్రశ్న 6.
చర్మం ఒక జ్ఞానేంద్రియంగా పనిచేస్తుందని నీవెట్లా చెప్పగలవు?
జవాబు:
- చర్మం అన్నింటికన్నా పెద్దదైన జ్ఞానేంద్రియం
- ఇది మనకు స్పర్శను కలుగజేస్తుంది.
- మనశరీరంలో స్పర్శ జ్ఞానం వేరుగా ఉంటుంది.
- మెడచుట్టూ మరియూ వేళ్ళ చివరన స్పర్శజ్ఞానం ఎక్కువగా ఉంటుంది. అరచేయి, మోకాలు చేతుల మీద స్పర్శజ్ఞానం తక్కువగా ఉంటుంది.
- స్పర్శకు, ఉష్ణోగ్రతకు, పీడనానికి చర్మం సూక్ష్మగ్రాహ్యతను కలిగి ఉంటుంది.
- స్పర్శకు స్పర్శ గ్రాహకాలు, పీడనానికి పెసినియన్ గ్రాహకాలు, ఉష్ణోగ్రతకు నాసిప్టారులు వంటి ప్రత్యేక గ్రాహకాల్ని కలిగి ఉంటుంది.
- పై కారణాల వలన చర్మం ఒక జ్ఞానేంద్రియంగా పనిచేస్తుందని చెప్పవచ్చు.
ప్రశ్న 7.
1. A, B, C ల భాగాల పేర్లను రాయండి.
2. కంటిలో కటకం చేసే పని ఏమిటి?
3. నేత్రపటలంలో ఉండే ప్రత్యేకమైన కణాలేవి?
4. కంటికి వచ్చే ఏవైనా రెండు వ్యాధుల పేర్లు వ్రాయండి.
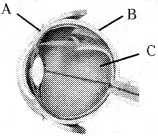
జవాబు:
- A) ధృడసరం, B) రక్తపటలం, C) నేత్రపటలం
- కన్ను కాంతిని సేకరించీ కుంభాకార కటకం ద్వారా కేంద్రీకరించి కంటి వెనుక భాగాన ఉండే నేత్ర పటలంపై ప్రతిబింబాన్ని ఏర్పరుస్తుంది.
- దండాలు, కొనులు
- రేచీకటి, కండ్లకలక, శుక్లాలు ఏర్పడటం, Dry Eye మొదలగునవి.
9th Class Biology 6th Lesson జ్ఞానేంద్రియాలు 1 Mark Bits Questions and Answers
లక్ష్యాత్మక నియోజనము
1. ఇంద్రియజ్ఞానం మన శరీరంలో కలిగేలా ప్రేరేపించే కొన్ని పరిస్థితులు, పదార్థాలు
A) ఉత్తేజితాలు
B) క్రియాత్మకాలు
C) ఉత్ర్పేరకాలు
D) ఎంజైములు
జవాబు:
A) ఉత్తేజితాలు
2. పరిసరాల నుండి ప్రేరణలను గ్రహించే మన శరీర భాగాలు
A) కన్ను, చెవి
B) ముక్కు, నాలుక
C) చర్మం
D) అన్నీ
జవాబు:
D) అన్నీ
3. జ్ఞానేంద్రియాలు చేసే పనులన్నింటికి కేంద్రం
A) వెన్నుపాము
B) మెదడు
C) హృదయము
D) కన్ను
జవాబు:
B) మెదడు
4. జ్ఞానేంద్రియాల నుండి నాడీ ప్రచోదనలను తీసుకొనివచ్చేవి
A) చాలకనాడులు
B) వెన్నునాడులు
C) జ్ఞాననాడులు
D) అన్నీ
జవాబు:
C) జ్ఞాననాడులు
5. కంటి ముందుభాగంలో ఉండే పలుచని పొర
A) దృఢస్తరం
B) రక్తపటలం
C) కటకం
D) కంజెక్టివ్ (కంటిపొర)
జవాబు:
D) కంజెక్టివ్ (కంటిపొర)
6. కంటిగుద్దులో కేవలం ఎన్నవ వంతు భాగం మాత్రమే మనకు కన్పిస్తుంది?

జవాబు:
B
7. కంటినందుండే ఈ పొరలో ఎక్కువ సంఖ్యలో రక్తనాళాలుంటాయి.
A) కంటిపొర
B) దృఢస్తరం
C) రక్తపటలం
D) నేత్రపటలం
జవాబు:
C) రక్తపటలం
8. జెల్లీ వంటి ద్రవంతో నిండి ఉండే కంటి గుడ్డు భాగం
A) కాచావత్ క
B) నేత్రోదక కక్ష
C) రక్తపటలం
D) దృఢస్తరం
జవాబు:
B) నేత్రోదక కక్ష

9. కన్ను కాంతిని సేకరించి కుంభాకార కటకం ద్వారా కేంద్రీకరించి దీనిపై ప్రతిబింబాన్ని ఏర్పరుస్తుంది.
A) దృఢస్తరం
B) కనుపాప
C) తారక
D) నేత్రపటలం
జవాబు:
D) నేత్రపటలం
10. నేత్రపటలం నందలి దండాలలో ఉండే వర్ణద్రవ్యం
A) రొడాప్సిన్
B) అయొడాప్సిస్
C) ఫోటాప్సిన్
D) కీటాప్సిన్
జవాబు:
A) రొడాప్సిన్
11. శంకువుల ఉపయోగం
A) చీకటిలో చూడడానికి
B) రంగులలోని తేడాలు గుర్తించలేకపోవుట
C) రంగులు గుర్తించడం
D) అశ్రువులను ఉత్పత్తిచేయటం
జవాబు:
C) రంగులు గుర్తించడం
12. నేత్రపటలంలోని ఈ భాగమునందు కాంతిగ్రాహకాలు ఉండవు.
A) అంధ చుక్క
B) పసుపు చుక్క
C) ఆకుపచ్చ చుక్క
D) నల్ల చుక్క
జవాబు:
A) అంధ చుక్క
13. కంటిలోని గ్రంథులు
A) లాక్రిమల్ గ్రంథులు
B) సెరుమినస్ గ్రంథులు
C) సెబేషియస్ గ్రంథులు
D) శ్లేష్మ గ్రంథులు
జవాబు:
A) లాక్రిమల్ గ్రంథులు
14. కంటిలోని ఈ భాగమును సరిచేయవచ్చును.
A) కంటిగ్రుడ్డు
B) ద్వికుంభాకార కటకం
C) నేత్ర పటలం
D) శుక్ల పటలం
జవాబు:
B) ద్వికుంభాకార కటకం
15. పిన్నా అని దీనిని అంటారు.
A) బాహ్య చెవి
B) మధ్య చెవి
C) లోపలి చెవి
D) కర్ణభేరి
జవాబు:
A) బాహ్య చెవి
16. మధ్య చెవిలోని ఎముకల గొలుసునందు ఉండేవి
A) కూటకము
B) దాగలి
C) కర్ణాంతరాస్థి
D) అన్నియు
జవాబు:
D) అన్నియు
17. మధ్య చెవి అంతరచెవిలోకి దీని ద్వారా తెరుచుకుంటుంది.
A) గుండ్రని కిటికి
B) అండాకార కిటికి
C) వర్తులాకార కిటికి
D) దీర్ఘవృత్తాకార కిటికి
జవాబు:
C) వర్తులాకార కిటికి
18. నాలికయందు గల రుచి కణికల సంఖ్య
A) 100
B) 1000
C) 10000
D) 5000
జవాబు:
C) 10000
19. ఋణ గ్రాహకాలు గల జ్ఞానేంద్రియం
A) చర్మం
B) కన్ను
C) చెవి
D) ముక్కు
జవాబు:
D) ముక్కు
20. మెటాలిక్ టేస్ట్ ఈ క్రింది. ఆహార పదార్థాలలో ఉంటుంది.
A) సహజ ఆహార పదార్థాలు
B) కృత్రిమంగా తయారైన ఆహార పదార్థాలు
C) పచ్చి ఆహార పదార్థాలు
D) వండిన ఆహార పదార్థాలు
జవాబు:
B) కృత్రిమంగా తయారైన ఆహార పదార్థాలు

21. నాలుక యందు రుచికలు ఈ నిర్మాణాలలో ఉంటాయి.
A) ఫంగి ఫార్మ్ పాపిల్లే
B) ఫోలియేట్ పాపిల్లే
C) ఫంగి ఫార్మ్ మరియు ఫోలియేట్ పాపిల్లే
D) ఫిలి ఫార్మ్ పాపిల్లో
జవాబు:
C) ఫంగి ఫార్మ్ మరియు ఫోలియేట్ పాపిల్లే
22. స్పర్శగ్రాహకాలు గల జ్ఞానేంద్రియం
A) చెవి
B) నాలుక
C) ముక్కు
D) చర్మం
జవాబు:
D) చర్మం
23. చర్మము నందలి అంతశ్చర్మంలో ఉండేవి
A) స్వేదగ్రంథులు
B) సెబేషియస్ గ్రంథులు, రక్తనాళాలు
C) రోమపుటికలు, కొవ్వులు
D) పైవి అన్నీ
జవాబు:
D) పైవి అన్నీ
24. చర్మము నందు స్పర్శకు గల ప్రత్యేక గ్రాహకాలు
A) టార్టెల్ రిసెప్టార్స్
B) పెసిమియన్ గ్రాహకాలు
C) నాసి రిసెప్టారులు
D) అన్నీ
జవాబు:
A) టార్టెల్ రిసెప్టార్స్
25. విటమిన్ లోపం వలన చర్మానికి వచ్చే వ్యాధి
A) కుష్టు
B) పెల్లాగ్రా
C) బొల్లి
D) తామర
జవాబు:
B) పెల్లాగ్రా
26. మెలనిన్ అనే వర్ణద్రవ్యం దీనిలో ఉంటుంది.
A) చెవి
B) నాలుక
C) ముక్కు
D) చర్మం
జవాబు:
D) చర్మం
27. ఈ క్రింది వాటిలో చర్మ వ్యాధిని గుర్తించండి.
A) శుక్లం
B) జిరాఫాల్మియా
C) లూకోడెర్మా
D) గ్లూకోమా
జవాబు:
C) లూకోడెర్మా
28. 2,300 సంవత్సరాల క్రిందట మన ఇంద్రియ జ్ఞానాలను గూర్చి తెలియచేసినది
A) అరిస్టాటిల్
B) ప్లాటో
C) A మరియు B
D) పైవేవీ కావు
జవాబు:
C) A మరియు B
29. స్పర్శజ్ఞానంలో నాడుల పాత్రను గూర్చి మొదటిసారిగా తెలిపినది
A) ఆల్బర్టస్ మేగ్నస్
B) అరిస్టాటిల్
C) ప్లాటో
D) కెప్లర్
జవాబు:
A) ఆల్బర్టస్ మేగ్నస్
30. భూభ్రమణం, భూపరిభ్రమణం గురించి వివరించి జ్ఞానేంద్రియంగా కన్ను పాత్రను వివరించే ప్రయత్నం చేసినవాడు
A) ఆల్బర్టస్ మేగ్నస్
B) అరిస్టాటిల్
C) ప్లాటో
D) జోహన్స్ కెప్లర్
జవాబు:
D) జోహన్స్ కెప్లర్

31. జ్ఞానేంద్రియాలు చేసే పన్నులన్నింటికి కేంద్రం
A) మెదడు
B) వెన్నుపాము
C) A మరియు B
D) పైవేవీ కావు
జవాబు:
C) A మరియు B
32. ఈ క్రింది వానిలో అసత్య వాక్యం
A) అధిక స్థాయిలో ఉండే ప్రేరణ అల్ప స్థాయిలో ఉండే ప్రేరణని కప్పివేస్తుంది.
B) బాహ్య ప్రపంచంలోని మార్పులను గుర్తించటం జ్ఞానేంద్రియాల ప్రధాన పని.
C) మార్పులేని ప్రేరణలకు మన జ్ఞానేంద్రియాలు అలవాటు పడవు.
D) ప్రేరణలు స్థిరంగా ఉంటే వాటి గురించి పట్టించుకోవటం తగ్గుతుంది.
జవాబు:
C) మార్పులేని ప్రేరణలకు మన జ్ఞానేంద్రియాలు అలవాటు పడవు.
33. మెటాలిక్ టేస్ట్ ఈ క్రింది ఆహార పదార్థాల్లో ఉంటుంది.
A) సహజ ఆహార పదార్థాలు
B) కృత్రిమంగా తయారయిన ఆహార పదార్థాలు
C) పచ్చి ఆహార పదార్థాలు
D) వండిన ఆహార పదార్థాలు
జవాబు:
B) కృత్రిమంగా తయారయిన ఆహార పదార్థాలు
34. కంటిలో ఉండే ముఖ్యమైన పొరల సంఖ్య
A) 1
B) 2
C) 3
D) 4
జవాబు:
C) 3
35. కంటిలోని కటకం
A) ద్విపుటాకార
B) ద్వికుంభాకార
C) పుటాకార
D) కుంభాకార
జవాబు:
B) ద్వికుంభాకార
36. దండాలు, శంఖువులు అనే కణాలు ఇక్కడ ఉంటాయి.
A) దృఢస్తరం
B) రక్తపటలం
C) నేత్రపటలం
D) పైవేవీ కావు
జవాబు:
C) నేత్రపటలం
37. నేత్ర పటలంలో దండాలు, శంఖువులు లేని ప్రాంతం
A) అంధచుక్క
B) పసుపుచుక్క
C) పచ్చచుక్క
D) తెల్లచుక్క
జవాబు:
A) అంధచుక్క
38. పసుపు చుక్కలో ఉండేవి
A) దండాలు
B) శంఖువులు
C) దండాలు మరియు శంఖువులు
D) పైవేవీ కావు
జవాబు:
B) శంఖువులు
39. కంటిలో ఏర్పడే ప్రతిబింబ లక్షణం
A) మామూలుగా నిలువుగా
B) మామూలుగా తలక్రిందులుగా
C) ఎడమ కుడిగా నిలువుగా
D) ఎడమ కుడిగా తలక్రిందులుగా
జవాబు:
D) ఎడమ కుడిగా తలక్రిందులుగా
40. హ్రస్వదృష్టి ఉన్నవారిలో ప్రతిబింబం ఏర్పడే ప్రదేశం
A) నేత్ర పటలానికి ముందు
B) నేత్రపటలంపై
C) నేత్ర పటలంకు వెనుక
D) పైవేవీ కావు
జవాబు:
A) నేత్ర పటలానికి ముందు
41. కంటిలో ఉండే గ్రాహకాలు
A) నాసిప్టారులు
B) టాక్టయిల్ రిసెప్టర్స్
C) పాసీనియన్ రిసెప్టర్స్
D) ఫోటో, రిసెప్టర్స్
జవాబు:
D) ఫోటో, రిసెప్టర్స్

42. కంటిలో ఉండే శంఖువుల సంఖ్య
A) 7 మిలియన్లు
B) 125 మిలియన్లు
C) 14 మిలియన్లు
D) 100 మిలియన్లు
జవాబు:
A) 7 మిలియన్లు
49. కంటిలో ఉండే దందాల సంఖ్య
A) 7 మిలియన్లు
B) 125 మిలియన్లు
C) 14 మిలియన్లు
D) 100 మిలియన్లు
జవాబు:
B) 125 మిలియన్లు
44. తక్కువ కాంతిలో వస్తువుల్ని చూడడానికి ఉపయోగపడేవి సంయోగ పదార్థాలుంటాయి?
A) దండాలు
B) కోనులు
C) A మరియు B
D) పైవేవీ కావు
జవాబు:
A) దండాలు
45. రంగుల్ని గుర్తించడానికి ఉపయోగపడే వర్ణద్రవ్యం
A) రొడాప్సిన్
B) అయోడాప్సిన్
C) పై రెండూ
D) పైవేవీ కావు
జవాబు:
B) అయోడాప్సిన్
46. అంధచుక్క ఉండే ప్రదేశం
A) నేత్రపటలం
B) దృక్మడి
C) నేత్రపటలం నుండి దృక్ నాడి వెలువడే చోటు
D) నేత్రపటలంలో కోనులు ఎక్కువగా ఉండే ప్రదేశం
జవాబు:
C) నేత్రపటలం నుండి దృక్ నాడి వెలువడే చోటు
47. ఆధార్ గుర్తింపుకార్డు ఇచ్చేటప్పుడు ఫోటో తీసే కంటి భాగం
A) కంటికటకం
B) కంటిపాప
C) తారక
D) రెటీనా
జవాబు:
B) కంటిపాప
48. శరీరం యొక్క సమతాస్థితి నిర్వహించే అవయవం
A) కన్ను
B) ముక్కు
C) చెవి
D) చర్మం
జవాబు:
C) చెవి
49. గుబిలిని స్రవించే గ్రంథులు
A) సెబేషియస్ గ్రంథులు
B) స్వేదగ్రంథులు
C) క్షీరగ్రంథులు
D) సెరుమినస్ గ్రంథులు
జవాబు:
D) సెరుమినస్ గ్రంథులు
50. శ్రవణ కుహరం చివరలో ఉండే నిర్మాణం
A) కర్ణభేరి
B) మూడు ఎముకల గొలుసు
C) అర్ధవర్తుల కుల్యలు
D) పేటిక
జవాబు:
A) కర్ణభేరి

51. మధ్యచెవిలో ఉండే ఎముకల గొలుసులోని మూడు ఎముకలు వరుసగా
A) కూటకం, దాగలి, కర్ణాంతరాస్థి
B) దాగలి, కూటకం, కర్ణాంతరాస్థి
C) కూటకం, కర్ణాంతరాస్థి, దాగలి
D) కర్ణాంతరాస్థి, దాగలి, కూటకం
జవాబు:
A) కూటకం, దాగలి, కర్ణాంతరాస్థి
52. పేటిక యొక్క ముందు భాగాన్ని ఏమంటారు?
A) యుట్రిక్యులస్
B) శాక్యులస్
C) కాక్లియ
D) అర్ధవర్తుల కుల్యలు
జవాబు:
B) శాక్యులస్
53. స్కాలా వెస్టిబ్యులై, స్కాలా మీడియా, స్కాలాటింపాని వీనిలోని భాగాలు.
A) త్వచాగహనం
B) అస్థి గహనం
C) పేటిక
D) కర్ణావర్తం
జవాబు:
D) కర్ణావర్తం
54. అంతరలసికా ద్రవంతో నిండి ఉండేది
A) స్కాలా వెస్టిబ్యులై
B) స్కాలాటింపాని
C) స్కాలామీడియా
D) పైవేవీ కావు
జవాబు:
C) స్కాలామీడియా
55. పేటికానాడి, కర్ణావర్తనాడి కలసి ఏర్పడేది
A) జిహ్వనాడి
B) దృక్నడి
C) శ్రవణనాడి
D) వాగన్నడి
జవాబు:
C) శ్రవణనాడి
56. అపుడే తయారయిన కాఫీలో వెంటనే ఆవిరయ్యే ఎన్ని
A) 500
B) 600
C) 700
D) 800
జవాబు:
B) 600
57. ఇప్పటివరకు శాస్త్రవేత్తలు ఎన్ని రకాల వాసనలను ఉత్పత్తి చేయగలిగే రసాయనాలను వర్గీకరించారు?
A) 1000
B) 1500
C) 2,000
D) 2,500
జవాబు:
B) 1500
58. మెదడులోని దేని ద్వారా వాసన సంకేతాలు ప్రసారం చెందవు?
A) మెడుల్లా
B) హైపోథాలమస్
C) ద్వారగొర్ధం
D) మస్తిష్కం
జవాబు:
B) హైపోథాలమస్
59. MSG అనగా
A) మోనోసోడియం గ్లుటామేట్
B) మెగ్నీషియం సోడియం గ్లుటామేట్
C) మోనోసల్ఫర్ గ్లుటామేట్
D) మెగ్నీషియం సల్ఫర్ గ్లుటామేట్
జవాబు:
A) మోనోసోడియం గ్లుటామేట్
60. రుచికణికలు దీనిలో ఉండవు.
A) ఫిలి ఫార్మ్ పాపిల్లే
B) ఫంగి ఫార్మ్ పాపిల్లే
C) సర్కం వాలేట్ పాపిల్లే
D) ఫోలియేట్ పాపిల్లే
జవాబు:
A) ఫిలి ఫార్మ్ పాపిల్లే
61. ప్రాచీన కాలం నుండి ఉన్నతమైన జ్ఞానంగా గుర్తించినది
A) దృష్టి జ్ఞానం
B) ఋణ జ్ఞానం
C) జిహ్వ జ్ఞానం
D) స్పర్శ జ్ఞానం
జవాబు:
D) స్పర్శ జ్ఞానం

62. నిర్జీవ కణాలుండే పొర
A) కార్నియం పొర
B) గ్రాన్యులర్ పొర
C) మాల్ఫీజియన్ పొర
D) అంతశ్చర్యం
జవాబు:
A) కార్నియం పొర
63. స్థిరంగా విభజనలు చెందుతూ ఉండే పొర
A) కార్నియం పొర
B) గ్రాన్యులర్ పొర
C) మాల్ఫీజియన్ పొర
D) అంతఃశ్చర్శం
జవాబు:
C) మాల్ఫీజియన్ పొర
64. స్వేదగ్రంథులు, తైలగ్రంథులుండే పొర
A) కార్నియం పొర
B) గ్రాన్యులర్ పొర
C) మాల్ఫీజియన్ పొర
D) అంతఃశ్చర్మం
జవాబు:
D) అంతఃశ్చర్మం
65. శరీర ఉష్ణోగ్రతను క్రమపరిచేది
A) కన్ను
B) ముక్కు
C) చెవి
D) చర్మం
జవాబు:
D) చర్మం
66. అన్ని అవయవాల కంటే పెద్దది
A) చర్మం
B) హృదయం
C) మూత్రపిండం
D) మెదడు
జవాబు:
A) చర్మం
67. యుక్తవయసు వచ్చిన వారిలో శరీరాన్ని కప్పి ఉంచే చర్మ ఉపరితల వైశాల్యం

జవాబు:
A
68. చర్మంను కాంతి నుంచి రక్షించేది
A) టానిన్
B) మెలనిన్
C) టైలిన్
D) హి మోగ్లోబిన్
జవాబు:
B) మెలనిన్
69. ఈ క్రింది వానిలో పీడన గ్రాహకాలు
A) టార్టెల్ రిసెప్టర్స్
B) ఫోటో రిసెప్టర్స్
C) పాసీనియన్ రిసెప్టర్స్
D) నాసిస్టర్స్
జవాబు:
C) పాసీనియన్ రిసెప్టర్స్
70. ఈ క్రింది వానిలో స్పర్శ గ్రాహకాలు
A) టార్టెల్ రిసెప్టర్స్
B) ఫోటో రిసెప్టర్స్
C) పాసీనియన్ రిసెప్టర్స్
D) నాసిస్టర్స్
జవాబు:
A) టార్టెల్ రిసెప్టర్స్
71. ఈ క్రింది వానిలో ఉష్ణ గ్రాహకాలు
A) టార్టెల్ రిసెప్టర్స్
B) ఫోటో రిసెప్టర్స్
C) పాసీనియన్ రిసెస్టర్స్
D) నాసిస్టర్స్
జవాబు:
D) నాసిస్టర్స్
72. ఈ క్రింది వానిలో విటమిన్ల లోపం వలన చర్మానికి వచ్చే వ్యాధి
A) బొల్లి
B) పెల్లాగ్రా
C) తామర
D) పొంగు
జవాబు:
B) పెల్లాగ్రా
73. కంటి ఆరోగ్యా నికి అవసరమైన విటమిన్
A) విటమిన్ ‘ఎ’
B) విటమిన్ ‘బి’
C) విటమిన్ ‘సి’
D) విటమిన్ ‘డి’
జవాబు:
A) విటమిన్ ‘ఎ’
74. ఇంద్రియ జ్ఞానమన్నది ఒక సంక్లిష్టమైన విధానం. దీనిలో పాల్గొనేవి
A) జ్ఞానేంద్రియాలు
B) జ్ఞానేంద్రియాలు, నాడీ ప్రేరణలు
C) జ్ఞానేంద్రియాలు, నాడీ ప్రేరణలు, మెదడు
D) మెదడు, నాడీప్రేరణలు
జవాబు:
C) జ్ఞానేంద్రియాలు, నాడీ ప్రేరణలు, మెదడు

75. వెలుపలి చెవిగనుక శబ్ద తరంగాలని కేంద్రీకరించకపోతే శ్రవణకుల్య
A) అనేక రకాల శబ్దాలను గట్టిగా వినగలదు
B) ఏమీ వినలేదు
C) కొద్దిగా వినగలదు
D) శబ్దం పుట్టుకని, రకాన్ని తెలుసుకోలేదు
జవాబు:
B) ఏమీ వినలేదు
76. ఒక వ్యక్తి యొక్కకంటి గుడ్డు కండరాలు పనిచేయకుండా పాడైతే, తప్పనిసరిగా కలిగే ప్రభావం
A) ఆ వ్యక్తి కళ్ళు మూసుకోలేడు.
B) కన్ను కదపలేడు, రంగుల్ని బాగా చూడగలడు.
C) కంటిలో నొప్పి వస్తుంది. కళ్ళు మూసుకోలేడు.
D) ఆ కండరాలకు చేరే నాడులు పనిచేయవు.
జవాబు:
B) కన్ను కదపలేడు, రంగుల్ని బాగా చూడగలడు.
77. ఒక వ్యక్తి నాలుక ఎక్కువ ఉప్పగా ఉన్న పదార్థం రుచి చూసింది. అపుడు ఆ వ్యక్తి
A) ఉప్పటి పదార్థాలను తినడం నేర్చుకుంటాడు.
B) ఉప్పటి పదార్థాలను తినడానికి ఇష్టపడతాడు.
C) ఉప్పటి పదార్థాలను తినడానికి ఇష్టపడడు.
D) అంతకంటే తక్కువ ఉప్పదనం కలిగిన పదార్థాల రుచి తెలుసుకోలేడు.
జవాబు:
D) అంతకంటే తక్కువ ఉప్పదనం కలిగిన పదార్థాల రుచి తెలుసుకోలేడు.
78. మధ్య చెవి అంతర చెవిలోకి దీని ద్వారా తెరుచుకుంటుంది.
A) గుండ్రని కిటికి
B) అండాకార కిటికి
C) వర్తులాకార కిటికి
D) దీర్ఘవృత్తాకార కిటికి
జవాబు:
C) వర్తులాకార కిటికి
79. సరియైన జతను గుర్తించండి.
1) పిన్నా – వెలుపలి చెవి
2) కర్ణభేరి – సెరుమినస్ గ్రంథులు
3) మైనం ఉత్పత్తి – కర్ణభేరి
A) 1 మాత్రమే
B)3 మాత్రమే
C) 2, 3
D) 1, 3
జవాబు:
C) 2, 3
80. క్రింది వాక్యాలను చదవండి.
a) పోవియా అనే చిన్న భాగంలో శంకువుల గుమిగూడి ఉండి దృష్టిని స్పష్టంగా ఉండేలా చేస్తాయి.
b) కనుపాపకు ముందుండే శుక్లపటలం ఒక పరిశుభ్రమైన కిటికీలా పనిచేస్తుంది.
A) a సరియైనది, b సరియైనది కాదు
B) b సరియైనది, a సరియైనది కాదు
C) a, b లు రెండూ సరియైనవి కావు
D) a, b లు రెండూ సరియైనవి
జవాబు:
D) a, b లు రెండూ సరియైనవి
81. సరిగా గుర్తించిన జతను గుర్తించండి.
1) బొల్లి – చర్మం
2) గ్లూకోమా – ముక్కు
3) చెవుడు – చెవి
A) 1, 3
B) 2, 3
C) 1 మాత్రమే
D) 2 మాత్రమే
జవాబు:
D) 2 మాత్రమే
82. ఈ క్రింది వాక్యాలను చదవండి.
a) అంధచుక్క దృక్ నాడి కంటి నుండి బయటకు పోయే చోట ఉంటుంది.
b) చెవిలోని సెరుమిన్ గ్రంథులు తైలాన్ని స్రవిస్తాయి.
A) a మరియు b లు సరియైనవే
B) a మరియు b లు సరియైనవి కావు
C) a సరియైనది, b సరియైనది కాదు
D) b సరియైనది, a సరియైనది కాదు
జవాబు:
C) a సరియైనది, b సరియైనది కాదు
83. సరిగా జతపరచని జతను గుర్తించండి.
1) వాసన – గ్రాహక కణాలు
2) కన్నీళ్ళు – అశ్రు గ్రంథులు
3) మైనము – సెరుమిన్ గ్రంథులు
A) 1, 2
B) 2,3
C) 2 మాత్రమే
D) పైవన్నీ
జవాబు:
D) పైవన్నీ
| కంటి వ్యాధి పేరు, దోషము పేరు | లక్షణాలు |
| 1. వయసు సంబంధిత మాక్యులా (పచ్చచుక్క) క్షీణత | ఈ వ్యాధి పరిస్థితిలో నేత్రపటలం నందలి మధ్యభాగమైన మాక్యులా లేదా ఫోవియా క్షీణించిపోతుంది. అంధత్వము వస్తుంది. |
| 2. ఎస్టిగ్మాటిజమ్ | నేత్రపటలం నందలి వంపు అసంపూర్ణంగా ఉండడం. |
| 3. కంటిశుక్లం (కెటరాక్ట్) | కంటి ముందరభాగంలో ఉండే పొర ఉబ్బి మెత్తగా అయి పగులుతుంది. కళ్ళు సరిగా కనపడవు. |
| 4. సెంట్రల్ రెటినల్ వీన్ ఆక్లుసన్ | నేత్రపటం నందలి సిరలో రక్తప్రవాహానికి ఆటంకం ఏర్పడడం. |
| 5. కలర్ బ్లైండ్ నెస్ (వర్ణాంధత) | సాధారణ పరిస్థితులలో రంగులను గుర్తించకపోవటం, చూడలేకపోవడం. |
పై పట్టికను పరిశీలించి ఈ క్రింది ప్రశ్నకు సరియైన సమాధానాన్ని ఎన్నుకోండి.
84. నేత్రపటలం నందలి వంపులో మార్పు రావటం వలన కలిగే వ్యాధి.
A) ఎస్టిగ్మాటిజమ్
B) కంటిశుక్లం
C) సింట్రల్ రెటినల్ లీన్ ఆక్లుసన్
D) వర్ణాంధత
జవాబు:
| కంటి వ్యాధి పేరు, దోషము పేరు | లక్షణాలు |
| 1. కండ్ల కలక | కంటి ముందర పొర ఉబ్బుతుంది. కన్ను ఎరుపెక్కుతుంది, మండుతుంది, నీరు కారుతుంది. |
| 2. శుక్లపటలం మార్పు చెందడం | శుక్లపటలం మీద మచ్చలు, ఉబ్బటం వలన లేదా అక్రమాకారం ఉండడం వలన కళ్ళు మెరవడం, చూపు చెదరడం జరుగుతుంది. |
| 3. డయాబెటిక్ రెటినోపతి | మధుమేహం వలన కంటికి వచ్చు వ్యాధి నేత్రపటలం నందలి రక్తనాళాలలో మార్పు వలన కలుగుతుంది. |
| 4. పొడికళ్ళు లేదా జిరాఫ్తాల్మియా | కంటిలోని అశ్రుగ్రంథులు అశ్రువులను ఉత్పత్తి చెయ్యవు. కంటిపొర పొడిగా అవుతుంది. |
| 5. దీర్ఘదృష్టి (హైపర్ మెట్రోపియా) | ఇది వక్రీభవన దోషము. కన్ను సరిగ్గా కాంతిని వక్రీభవించదు. అందువలన ప్రతిబింబాలు నేత్రపటలం వెనుక ఏర్పడతాయి. దూరపు వస్తువులు కనపడతాయి. దగ్గర వస్తువులు సరిగ్గా కనపడవు. |
| 6. గ్లూకోమా | కంటిలోని దృక్మడి పాడయిపోతుంది. దీనివలన కంటిలో ఎక్కువ పీడనము కలుగుతుంది. |
| 7. కెరోలైటిస్ | శుక్లపటలం ఉబ్బుతుంది. అందువలన కన్ను ఎర్రగా మారి నొప్పి కలిగిస్తుంది. చూచునపుడు నొప్పి ఉంటుంది. |
పై పట్టికను పరిశీలించి ఈ క్రింది ప్రశ్నకు సరియైన సమాధానాన్ని ఎన్నుకోంది.
85. ఈ వ్యాధిలో ప్రతిబింబాలు రెటీనా వెనుక ఏర్పడతాయి.
A) పొడికళ్ళు లేదా జిరాపాల్మియా
B) దీర్ఘదృష్టి
C) గ్లూకోమా
D) కెరోలైటిస్
జవాబు:
B) దీర్ఘదృష్టి
86. ఈ చిత్రం సూచించినది ఏమి?
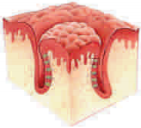
A) చర్మం
B) కన్ను
C) నాలుక
D) చెవి
జవాబు:
C) నాలుక
87. పటంలోని A, B, C భాగాల పేర్లు.
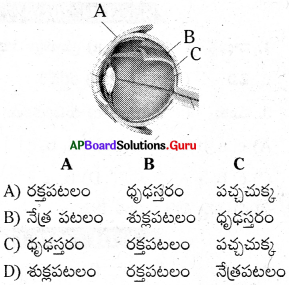
జవాబు:
C
88. కంటికి సంబంధిత వ్యాధులను అరికట్టడానికి నీవు ఏమి చేస్తావు.
A) కంటిని 3-4 సార్లు కడుగుతాను
B) విటమిన్ – A ఉన్న ఆహారం తింటాను
C) కళ్ళను నలపనుత
D) పైవన్నియూ
జవాబు:
D) పైవన్నియూ

89. సరిగా జతపరచండి.
1) ఫోవియా ( ) a) నాలుక
2) ఫోలియట్ పాపిల్లె ( ) b) ఆడిటరీమీటన్
3) శ్రవణ కుహరం ( ) c) పచ్చచుక్క
A) 1 – a, 2 – b, 3-c
B) 1-b, 2 – a, 3-c
C) 1 – c, 2 – b, 3- a
D) 1-c, 2-a, 3-b
జవాబు:
D) 1-c, 2-a, 3-b
90. మెలనిన్ వర్ణకం యొక్క లోపం దేనికి దారితీస్తుంది.
A) ల్యూకోడెర్మా
B) పెల్లాగ్రా
C) రింగ్ వార్మ్
D) టానింగ్
జవాబు:
A) ల్యూకోడెర్మా
91. అశ్రుగ్రంధులచే విడుదలయ్యే అశ్రువుల విధి
A) రంగులను గుర్తించుట
B) కంటిలోకి ప్రవేశించే కాంతిని నియంత్రించుట
C) కంటిని తడిగా, తేమగా వుంచుట
D) ఏ విధి లేదు
జవాబు:
C) కంటిని తడిగా, తేమగా వుంచుట
92. కంటిని నేత్రోదయ కక్ష్య కచావత్ కక్ష్యగా విభజించునది
A) కటకము
B) కనుపాప
C) తారక
D) రక్తపటలము
జవాబు:
A) కటకము
93. శరీరస్థితి సమతులనం (సమతాస్థితి)ని క్రమబద్ధం చేయునది
A) యుట్రిక్యులస్ మాత్రమే
B) యుట్రిక్యులస్, సేక్యులస్
C) యుట్రిక్యులస్, సేక్యులస్, అర్ధవృత్త కుల్యాలు
D) యుట్రిక్యులస్, సేక్యులస్, అర్ధవృత్త కుల్యాలు మరియు కర్ణావర్తనం
జవాబు:
C) యుట్రిక్యులస్, సేక్యులస్, అర్ధవృత్త కుల్యాలు
94. జీవశాస్త్రీయంగా వాసన ఇలా ప్రారంభమవుతుంది.
A) ఆహారాన్ని చూడడం వలన
B) ఆహారపు వాసన గురించి ఆలోచించడం వలన
C) ఆహారాన్ని రుచి చూడడం వలన
D) ముక్కులోని రసాయన సంఘటన వలన
జవాబు:
D) ముక్కులోని రసాయన సంఘటన వలన
95. మెలనిన్ అనునది
A) పీడన గ్రాహకము
B) గోర్లు, వెంట్రుకలను ఏర్పరుస్తుంది
C) చర్మం రంగు నిర్ధారిస్తుంది
D) ఉష్ణాన్ని క్రమబద్ధం చేస్తుంది.
జవాబు:
C) చర్మం రంగు నిర్ధారిస్తుంది
96. P : రవి కొన్ని రంగులను గుర్తించలేకున్నాడు.
Q: రవి కంటి నందు కోన్ కణాలు లోపించినవి.
A) P, Q లు రెండూ సరియైనవి
B) P కి Q సరియైన వివరణ కాదు
C) P కి ఏ సంబంధము లేదు
D) P Q సరైన వివరణ
జవాబు:
A) P, Q లు రెండూ సరియైనవి
97. ఆధార్ గుర్తింపు కార్డులు జారీ చేసేందుకు కంటిపాప ఫోటోలను తీయుటకు కారణము.
A) కంటిపాపలు ప్రతి వ్యక్తికి వేరు వేరుగా ఉంటాయి
B) కంటి రంగులు వేరు వేరుగా ఉంటాయి
C) దృష్టి దోషములను గుర్తించుటకు
D) సమయాభావంను పాటించుటకు
జవాబు:
A) కంటిపాపలు ప్రతి వ్యక్తికి వేరు వేరుగా ఉంటాయి
98. చెవి నిర్మాణంలో ఎముకల వరుస క్రమము
A) సుత్తి, పట్టెడ, అంకవన్నె
B) అంకవన్నె, పట్టెడ, సుత్తి
C) పట్టెడ, అంకవన్నె, సుత్తి
D) సుత్తి, అంకవన్నె, పట్టెడ
జవాబు:
A) సుత్తి, పట్టెడ, అంకవన్నె

99. P: జ్ఞానేంద్రియాలు ప్రేరణలను మాత్రమే గ్రహిస్తాయి.
Q: మెదడు ప్రేరణలను విశ్లేషించి ప్రతి స్పందనలను ఏర్పరుస్తుంది.
A) P మాత్రమే సరియైనది
B) Q మాత్రమే సరియైనది
C) P మరియు Q సరియైనది
D) P మరియు Q సరియైనవి కావు
జవాబు:
C) P మరియు Q సరియైనది
100. వృద్ధులు రుచిని గ్రహించలేకపోవడానికి కారణం ఏమైవుంటుందో ఊహించండి.
A) ఘ్రాణగ్రాహకాల సామర్థ్యం తగ్గడం
B) రుచి కళికల సామర్థ్యం తగ్గడం
C) నాళికా కుహరం మూసుకుపోవడం
D) A మరియు B
జవాబు:
D) A మరియు B
101. అధిక ఉప్పు కలిగిన ఆహారపదార్థమును తీసికొన్న తరువాత ఆవ్యక్తి.
A) ఉప్పు రుచి తెలుసుకుంటాడు
B) ఉప్పు రుచిని ఇష్టపడతారు
C) ఉప్పు కలిగిన పదార్థములను ఇష్టపడడు
D) తక్కువ ఉప్పు కలిగిన రుచిని గుర్తించలేడు
జవాబు:
D) తక్కువ ఉప్పు కలిగిన రుచిని గుర్తించలేడు
102. కింది వాటిని జతపరచండి.
1. నాలుక ( ) a) ఘాణగ్రాహకాలు
2. చెవి ( ) b) కర్ణభేరి
3. ముక్కు ( ) c) రుచికణికలు
A) c, a, b
B) a, b, c
C) c, b, a
D) b, a, c
జవాబు:
C) c, b, a
103. చెవిలో ఉన్న చిన్న ఎముక పేరు
A) సుత్తి
B) అంకవన్నె
C) పట్టెడ
D) కర్ణభేరి
జవాబు:
B) అంకవన్నె
104. కంటి సంబంధిత వ్యాధులను అరికట్టడానికి నీవు ఏమి చేస్తావు?
A) కంటిని 3-4 సార్లు కడుగుతాను
B) విటమిన్-A ఉన్న ఆహారం తింటాను
C) కళ్ళను నలపను
D) పైవన్నీ
జవాబు:
D) పైవన్నీ
మీకు తెలుసా?
“ఆధార్” లాంటి గుర్తింపు కార్డులను ఇచ్చేటప్పుడు వారు మీ కళ్ల ఫోటోలను తీసుకుంటారు. మీ కంట్లో వారు దీన్ని ఫోటోగా తీసుకుంటారో మీకు తెలుసా ? కంటిపాప (Iris) ఎవరికి వారికే ప్రత్యేకంగా ఉంటాయి. అందుకే వేలిముద్రల మాదిరిగానే వాటిని కూడా గుర్తింపు కోసం ఉపయోగిస్తారు.
ప్రతి రుచికణికలోనూ ఒక కుహరం, రంధ్రాన్ని కలిగి ఉంటుంది. ఆ రంధ్రాన్ని రుచిరంధ్రం అంటాం. రుచికణిక దగ్గర ఉండే ఉపకళా కణాలు రుచికణాలు లేక గ్రాహకాలను ఏర్పరుస్తాయి. ఈ గ్రాహక కణాలు, వాటికి ఆధారం ఇచ్చే కణాలు, కుహరంలో ఉంటాయి. ప్రతి గ్రాహక కణం, ఒక నాడీ తంతువుకు కలుపబడి ఉంటుంది. అన్ని నాడి తంతువులు కలిసి ప్రధాన నాడులుగా ఏర్పడతాయి. అవి మెదడుకు, వెన్నుపాముకి వార్తలను అందిస్తాయి.
జ్ఞానేంద్రియాలు జ్ఞానానికి ద్వారాలు, మనం ఈ జ్ఞానేంద్రియాల ద్వారా ప్రకృతిని చూస్తాం, వింటాం, ఆస్వాదిస్తాం. జ్ఞానేంద్రియాల గురించి జాగ్రత్తలు తీసుకుంటే ఆరోగ్యం బాగా ఉంటుంది. అదే మంచి జీవనానికి దారితీస్తుంది.

ఆల్బర్టస్ మేగ్నస్ ఇటలీలో ఒక చర్చి బిషప్. ప్రకృతి పరిశీలకుడు. అరిస్టాటిల్ ఆలోచనలను అనుసరిస్తూ విజ్ఞానశాస్త్రాన్ని ఇష్టపడే వ్యక్తి. మొదటిసారిగా వాటిని విమర్శిస్తూ, విస్తృతమైన విద్యా విషయక చర్చనీయాంశాలుగా అందరికీ అందుబాటులో ఉంచిన వ్యక్తి. స్పర్శజ్ఞానంలో నాడుల పాత్రను మొదటిసారిగా తెలిపిన వ్యక్తి ఆయన.
17వ శతాబ్దం నుండి జ్ఞానేంద్రియాలకు సంబంధించిన శరీర ధర్మశాస్త్రం బాగా అధ్యయనం చేయబడింది. ఆ సమయంలోనే బాగా దగ్గరగా చూడడం కోసం కంటికి సంబంధించి, అనేక ఉపకరణాలను కనుగొనడం జరిగింది. క్రీ. శ. 1600వ సంవత్సరంలో భూమి భ్రమణం – పరిభ్రమణం గురించి తెలిపిన ప్రముఖ ఖగోళశాస్త్రవేత్త జోహాన్స్ కెప్లర్ (Johannes Kepler) జ్ఞానేంద్రియంగా కన్ను పాత్రను వివరించే ప్రయత్నం చేశారు.
ఇటీవల కాలంలో శాస్త్రవేత్తలు జ్ఞానేంద్రియాలను గురించి ఎన్నో విషయాలు కనుగొన్నారు. జ్ఞానేంద్రియాలు ఇంకా మనకు తెలిసీ తెలియని ఎన్నో రకాల ఆశ్చర్యకరమైన క్లిష్టమైన, నమ్మశక్యంకాని పనులను చేయగలవని తెలిపారు. నాడీ సంకేతాల విద్యుత్ రసాయనిక ఆధార ప్రకారం మెదడులో జ్ఞానానికి సంబంధించిన ప్రత్యేక కేంద్రాలు, అవి చేసే పనుల గురించి సరైన అవగాహనను కూడా పెంపొందించారు.

అరిస్టాటిల్ కాలం నుండి 19వ శతాబ్దం వరకు ఇంద్రియాల వరకు పొందే జ్ఞానాలు ఐదుగా పేర్కొనేవారు. అయితే ఆధునిక కాలంలో ఆ సంఖ్య (5), మన శరీరంలోని జ్ఞానేంద్రియాల సంఖ్యను తెలియజేసేదిగా మారింది.
మనం లెక్కకు ఐదు జ్ఞానేంద్రియాలనే కలిగి ఉన్నా, ఇంద్రియ జ్ఞానాలు మాత్రం చాలా ఎక్కువే ఉంటాయి. ఉదాహరణకి మనం పీడనాన్ని తెలుసుకునేందుకు ఒక స్పర్శజ్ఞానాన్ని, వేడిమి, చల్లదనాన్ని తెలుసుకునేందుకు మరొకటి, కంపనాలు, తరచుదనం తెలుసుకునేందుకు ఇంకొకటి ‘అలా ఎన్నో ఉన్నా లెక్కకి మాత్రం అన్నీ ఒకే రకమైన స్పర్శజ్ఞానంగా భావించడం జరుగుతుంది.
పునరాలోచన
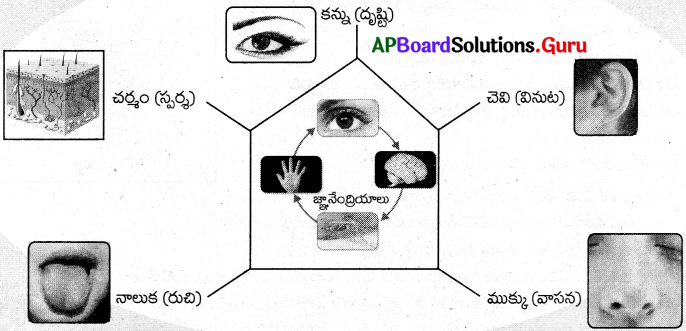
![]()
![]()
![]()



![]()


![]()



![]()


![]()