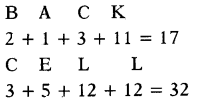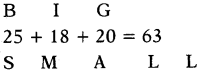Class 7

SCERT AP 7th Class Maths Solutions Pdf Chapter 10 Construction of Triangles InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Construction of Triangles InText Questions

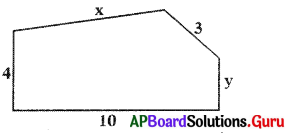
[Page No. 67]

Look at the picture and answer the following questions

Question 1.
Name some things from your daily life that look like triangles.
Answer:
Samosa, chapathi, window elevations, house tops, bridge trusses, floor tessellations.

Question 2.
What are the types of triangles can see in the picture?
Answer:
Right triangles,
Equilateral triangles.

Question 3.
Do you think all triangles shown are similar with their properties? What are they?
Answer:
Yes. All right triangles are similar.

All triangles are similar because they have
(a) right angle
(b) equal side and
(c) equal hypotenuse.

Check Your Progress [Page No. 69]

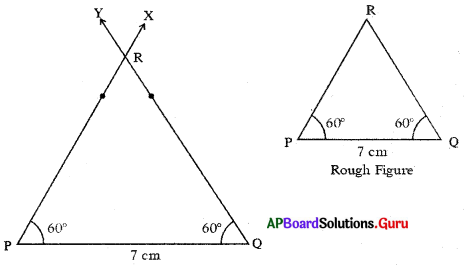
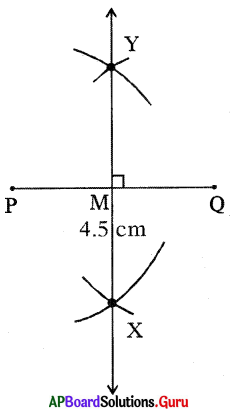
Question 1.
Construct an equilateral triangle ∆XYZ with XY = 4 cm.
Answer:
Given sides of an equilateral triangle ∆XYZ is XY = 4 cm.
In equilateral triangle all sides ,gresequal in length
∴ XY = YZ = ZX = 4 cm.

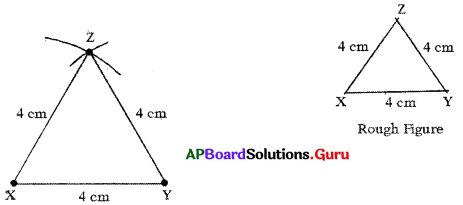
Steps of Construction:

1. Draw a rough sketch of the triangle and label it with the given measurements.
2. Draw a line segment with XY = 4 cm,
3. Draw an arc with centre X and radius 4 cm.
4. Draw another arc with centre Y and radius 4 cm to intersecting the previous arc at Z.
5. Join XZ andYZ.

Hence, required ∆XYZ is constructed with the given measurements.

Question 2.
Construct an isosceles triangle ∆PQR With PQ = PR = 3 cm, QR = 5 cm.
Answer:
Given sides of an isosceles triangle ∆PQR are PQ = PR = 3 cm and QR = 5 cm
In isosceles triangle two sides are equal.
∴ PQ = PR = 3 cm

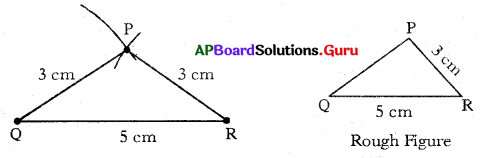
Steps of construction:

1. Draw a rough sketch of the triangle and label it with the given measurements.
2. Draw a line segment QR = 5 cm.
3. Draw an arc with centre Q and radius 3 cm.
4. Draw another arc with centre R and same radius (3 cm) to intersect the previous arc at P.
5. Join PQ and PR.

Hence, required APQR is constructed with the given measurements.

Let’s Think [Page No. 69]

Can you construct ∆ABC with AB = 4 cm, BC = 5 cm and CA =10 cm? Why? Justify your answer.
Answer:
Given sides of a ∆ABC are AB = 4 cm, BC = 5 cm and CA =10 cm.
In any triangle sum of any two sides is always greater than the third side.
AB + BC = 4 cm + 5 cm = 9 cm <10 cm.
Sum of AB + BC < AC
So, with the given measurements construction of ∆ABC is not possible.

Check Your Progress [Page No. 72]

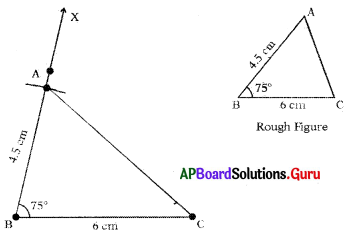
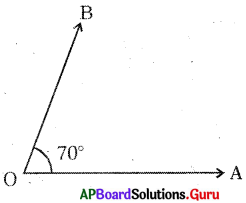
Question 1.
Construct ∆MAT with measurements MA = 5.5 cm, MT = 4 cm and ∠M=70°.
Answer:
Given measurements of ∆MAT are MA = 5.5 cm, MT = 4 cm and ∠M = 70°.

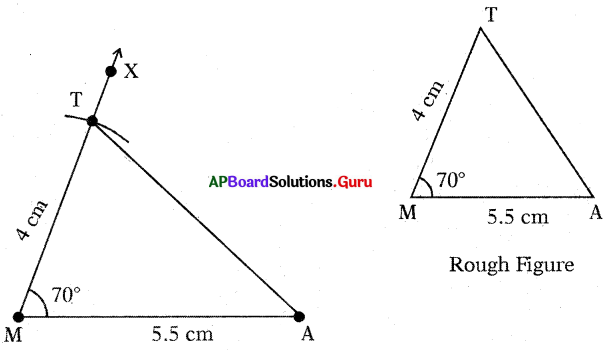
Steps of Construction:

1. Draw a rough sketch of the triangle and label it with the given measurements.
2. Draw a line segment with MA = 5.5 cm.
3. Draw a ray \(\overrightarrow{\mathrm{MX}}\) such that ∠AMX = 70°
4. Draw an arc with centre M and radius 4 cm, to intersect the \(\overrightarrow{\mathrm{MX}}\) at point T.
5. Join AT.

Hence, required ∆MAT is constructed with the given measurements.

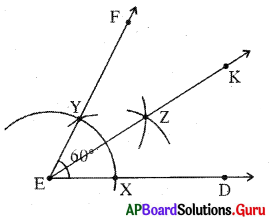
Let’s Explore [Page No. 72]

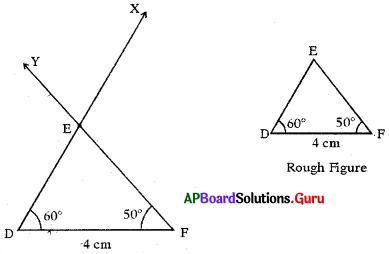
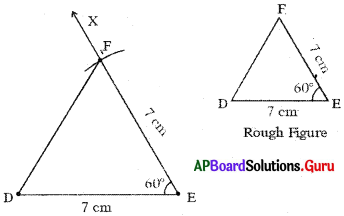
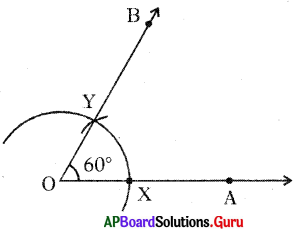
Question 1.
Construct the triangle with the measurements of AB = 7cm, ∠B = 60° and ∠C = 70°.
Answer:
Given measurements of ∆ABC are AB = 7 cm, ∠B = 60° and ∠C = 70°.
In ∆ABC, ∠A + ∠B + ∠C = 180°
∠A + 60° + 70° = 180° .
∠A + 130° = 180°
∠A = 180° – 130° = 50°

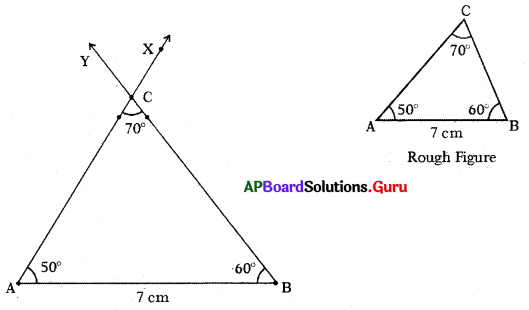
Steps of Construction:

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with AB = 7 cm.
3. Draw a ray BY such that ABY = 60°.
4. Draw another ray AX such that BAX = 50°.
5. Name the intersecting of rays AX and BY is C.

Hence, required ∆ABC is constructed with the given measurements.

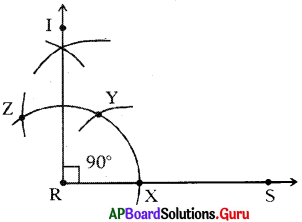
Check Your Progress [Page No. 73]

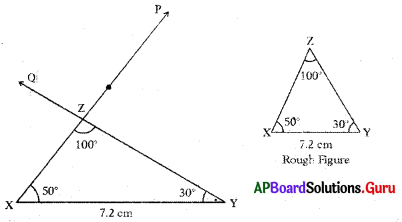
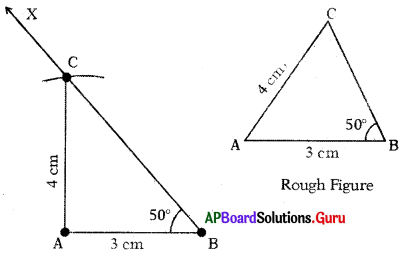
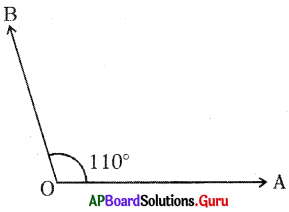
Question 1.
Construct ∆ABC with the measurements ∠A = 90°, ∠C = 50° and AC = 8 cm.
Answer:
Given measurements of ∆ABC are ∠A = 90°, ∠C = 50° and AC = 8 cm.

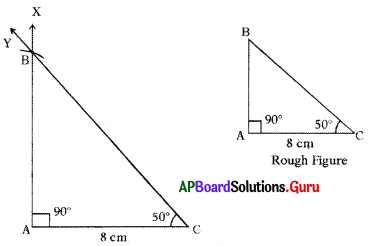
Steps of Construction:

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with AC = 8 cm.
3. Draw a ray AX such that ∠CAX = 90°.
4. Draw another ray CY such that ∠ACY = 50°.
5. Name the intersecting point of AX and CY as B.

Thus, required ∆ABC is constructed with the given measurements.

Let’s Think [Page No. 73]

Construct a triangle with angles 100°, 95° and a side of length of your choice. Can1 you construct the triangle?
Answer:
No. It is not possible. We know that the sum of the angles of a triangle is 180°.
But, given two angles are 100° and 95°. Their sum is greater than 180°.
So, we cannot construct the triangle.

Examples:

Question 1.
Construct ∆ABC with slides AB = 6 cm, BC = 4 cm and AC = 5 cm.
Answer:

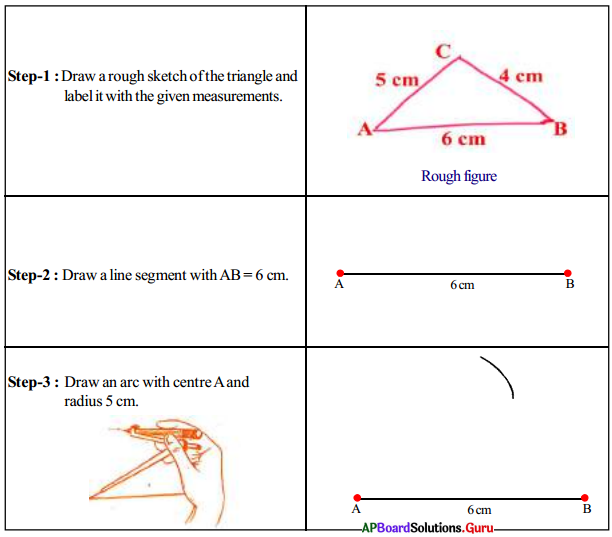
Question 2.
Construct ∆EFD with the measurements ∠F = 70°, EF = 4 cm and FD = 5 cm.
Answer:

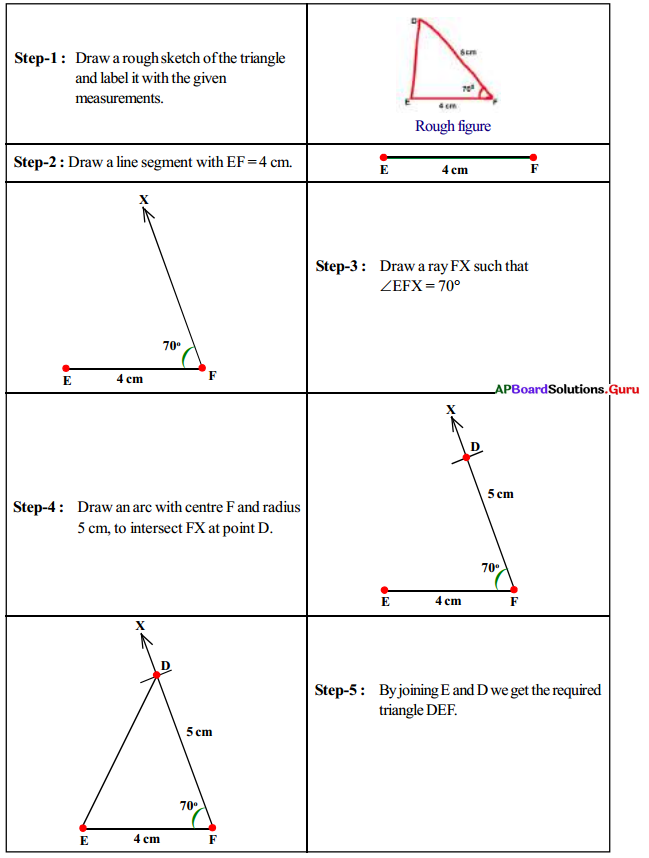
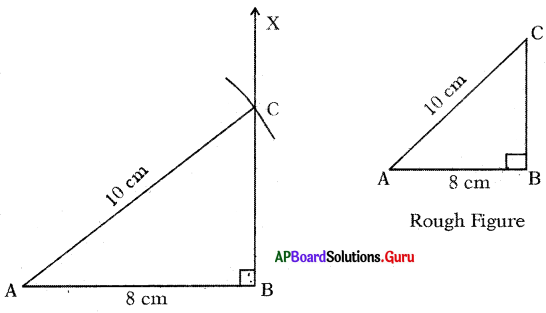
Question 3.
Construct ∆ABC with AB = 6 cm, BC = 7 cm, ∠BAC = 80°.
Answer:

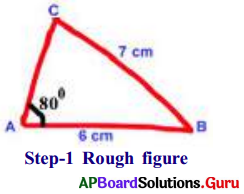
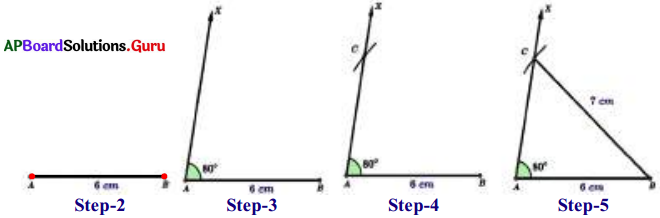
• Step-1: Draw a rough sketch of ∆ABC and label it with the given measurements.
• Step-2: Draw a line segment AB of length 6 cm.
• Step-3: Draw a ray AX such that ∠BAX = 80°.
• Step-4: Draw an arc with center B and radius 7 cm to Intersect the ray AX at C.
• Step-5: Join B and C to get the required ∆ABC.

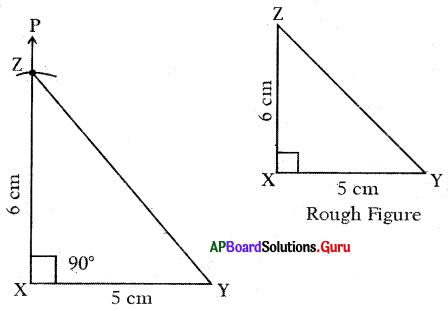
Question 4.
Construct a right angled triangle ∆XYZ, XY = 4 cm, XZ = 6.5 cm and ∠Y = 90°.
Answer:

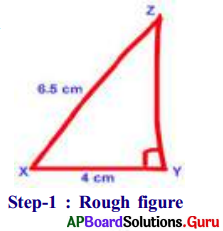
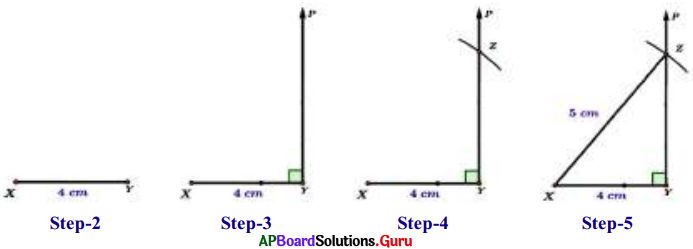
• Step-1: Draw a rough sketch of ∆XYZ and label it with given measurements.
• Step-2: Draw a line segment with XY = 4 cm.
• Step-3: Draw a ray YP such that ∠XYP = 90°.
• Step-4: Draw an arc with center X and radius 6.5 cm to intersect the Ray YP at Z.
• Step-5: Join X and Z to get the required ∆XYZ.

Question 5.
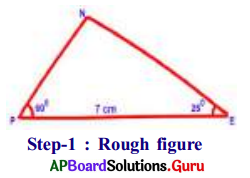
Construct ∆PEN with measurements PE. = 7 cm, ∠PEN = 25° and ∠EPN = 60°
Answer:

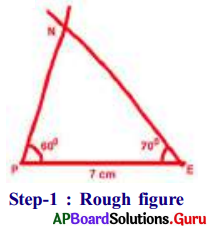
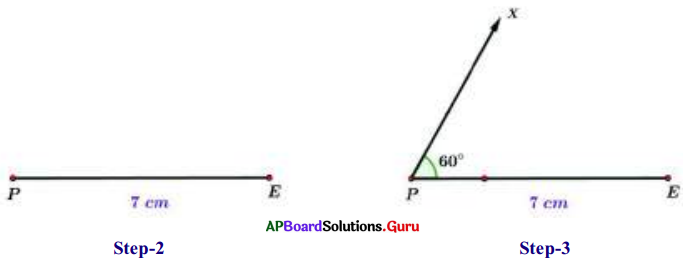
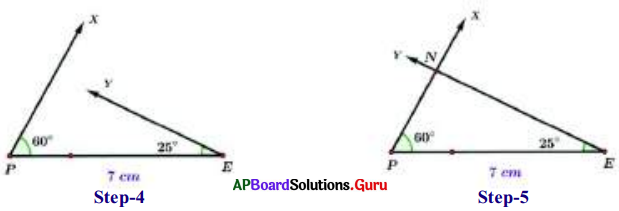
• Step-1: Draw a rough sketch of the triangle and label it with given measurements.
• Step-2: Draw a line segment with PE = 7 cm,
• Step-3: Draw a ray PX such that ∠EPX = 60°.
• Step-4: Draw another ray EY such that ∠PEY = 25°.
• Step-5: Rays PX and EY intersect each other at N.

Hence, we get the required ∆PEN.
(If necessary, extend the rays to form a triangle.)

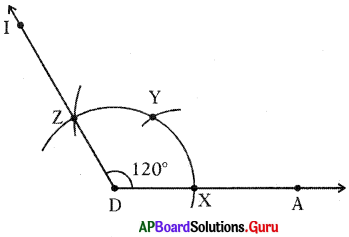
Question 6.
Construct ∆MPC the triangle with the measurements MP = 4 cm, ∠P = 45° arid ∠C = 80°.
Answer:
Now we have to find out the third angle.
We know that the sum of three angles in a triangle is 1800.
So, ∠M + ∠P + ∠C = 180°
⇒ ∠M + 450 + 80° = 180°
⇒ ∠M + 125° = 180°
⇒ ∠M = 180 – 125 = 55°

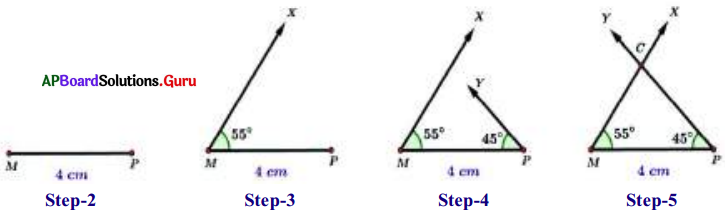
• Step-1: Draw a rough sketch of the triangle and label it with given measurements.
• Step-2: Draw a line segment with MP = 4 cm.
• Step-3: Draw a ray MX such that ∠PMX = 55°.
• Step-4: Draw another ray PY such that ∠MPY = 45°.
• Step-5: Rays MX and PY intersect each other at C. (If necessary extend the rays to ‘ form a triangle.)

Hence, we get the required ∆MPC.
Verification: By using the protractor and check whether ∠C is equal to 80° or not.

Practice Questions [Page No. 78]

Find the number of triangles in the given figures.

Question 1.

(a) 8
(b) 9
(c) 10
(d) 12
Answer:
(b) 9

Explanation:

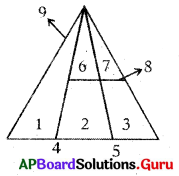
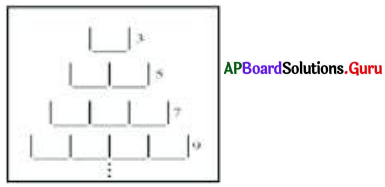
Question 2.

(a) 60
(b) 65
(c) 84
(d) 90
Answer:
(a) 60

Explanation:

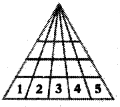
Number of rows = 4
Sum of numbers in each row = 1 + 2 + 3 + 4 + 5 = 15
Number of triangles in the picture = 4 × 15 = 60

Question 3.

(a) 12
(b) 13
(c) 14
(d) 15
Answer:
(b) 13

Explanation:
Formula to count number of triangles = 4n + 1
Here n = number of embedded triangles in outer triangle
In the figure n = 3
So, number of triangles = 4(3) + 1 = 12 + 1 = 13

Question 4.

(a) 16
(b) 13
(c) 9
(d) 7
Answer:
(a) 16

Question 5.

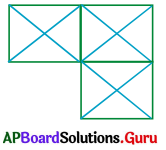
(a) 21
(b) 23
(c) 25
(d) 29
Answer:
(d) 29

Explanation:

Question 6.

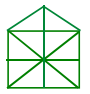
(a) 10
(b) 19
(c) 21
(d) 23
Answer:
(c) 21

Explanation:

Question 7.

Answer:
(a) 5
(b) 6
(c) 8
(d) 10
Answer:
(c) 8

Question 8.

(a) 9
(b) 10
(c) 11
(d) 12
Answer:
(a) 9

Explanation:

Question 9.

(a) 19
(b) 20
(c) 16
(d) 14
Answer:
(a) 19

Question 10.

(a) 56
(b) 48
(c) 32
(d) 60
Answer:
(b) 48

Explanation:
Formula to count number of triangles = \(\frac{\mathrm{n}(\mathrm{n}+2)(2 \mathrm{n}+1)}{8}\)
Where n = number of the angles formed in a side
Here in the given figure n = 5
Number of triangles = \(\frac{5(5+2)(2 \times 5+1)}{8}=\frac{5 \times 7 \times 11}{8}\) = 48.1
So, the total number of triangles = 48.

SCERT AP 7th Class Maths Solutions Pdf Chapter 10 Construction of Triangles Ex 10.3 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Construction of Triangles Ex 10.3

Question 1.
Construct ∆DEF with measurements ∠D = 60°, ∠F = 50° and DF = 4 cm.
Answer:
Given measurements of ∆DEF are ∠D = 60°, ∠F = 50° and DF = 4 cm.

Steps of Construction :

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with DF = 4 cm.
3. Draw a ray DX such that ∠FDX = 60°.
4. Draw another ray FY such that ∠DFY = 50° which intersects the previous ray at E. Thus, required ∆DEF is constructed with the given measurements.

Question 2.
Construct the triangle with the measurements XY = 7.2 cm, ∠Y = 30° and ∠Z = 100°.
Answer:
Given measurements of ∆XYZ are XY = 7.2 cm, ∠Y = 30° and ∠Z = 100°.
We know stun of angles of triangle is 180°
So, ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 30° + 100° = 180°
⇒ ∠X= 180°-130°
∴ ∠X = 50°

Steps of Construction:

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with XY = 7.2 cm.
3. Draw a ray \(\overrightarrow{\mathrm{XP}}\) such that ∠YXP = 50°
4. Draw another ray \(\overrightarrow{\mathrm{YQ}}\) such that ∠XYQ = 30° which intersects the previous ray at Z. Thus, required ∆XYZ is constructed with the given measurements.

Question 3.
Construct ∆PQR with the measurements ∠P = ∠Q = 60° and PQ = 7 cm.
Answer:
Given measurements of ∆PQR are ∠P = ∠Q = 60° and PQ = 7 cm.

Steps of Construction:

1. Draw a rough sketch of the triangle and label it with given measurements.
2. Draw a line segment with PQ = 7 cm.
3. Draw a ray PX such that ∠QPX — 60°
4. Draw another ray QY such that ∠PQY = 60° which intersects the previous ray at R. Thus, required ∆PQR is constructed with the given measurements.

SCERT AP 7th Class Maths Solutions Pdf Chapter 10 Construction of Triangles Ex 10.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Construction of Triangles Ex 10.2

Question 1.
Construct ∆ABC with measurements AB = 4.5 cm, BC = 6 cm and ∠B=75°
Answer:
Given measurements of ∆ABC are AB = 4.5 cm, BC = 6 cm and ∠B = 75°.

Steps of Construction :

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with BC = 6 cm.
3. Draw a ray \(\overrightarrow{\mathrm{BX}}\) such that ∠CBX = 15°.
4. Draw an arc with centre B and radius 4.5 cm, to intersect \(\overrightarrow{\mathrm{BX}}\) at point A.
   Thus, required ∆ABC is constructed with the given measurements.

Question 2.
Construct an isosceles triangle with measurements DE = 7 cm, EF = 7 cm and ∠E = 60°
Answer:
Given measurements of ∆DEF are DE = 7 cm, EF = 7 cm and ∠E = 60°.

Steps of Construction:

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with DE = 7 cm.
3. Draw a ray \(\overrightarrow{\mathrm{EX}}\) such that ∠DEX = 60°.
4. Draw an arc with centre E and radius 7 cm to intersect \(\overrightarrow{\mathrm{EX}}\) at point F.
5. Join DF.
   Hence, required ∆DEF is constructed with the given measurements.

Question 3.
Draw a triangle with,measurements ∠B = 50°, AB = 3 cm and AC = 4 cm.
Answer:
Given measurements of a triangle are ∠B = 50°, AB = 3 cm and AC = 4cm..

Steps of Construction:

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with AB = 3 cm.
3. Draw a ray \(\overrightarrow{\mathrm{BX}}\) such that ∠ABX = 50°.
4. Draw an arc with centre A and radius 4 cm to intersect \(\overrightarrow{\mathrm{BX}}\) at point C.
5. Join AC.
   Hence, required ∆ABC is constructed with the given measurements.

Question 4.
Construct a right angled triangle in which, XY = 5 cm, XZ = 6 cm and right tingle at X.
Answer:
Given measurements of ∆XYZ are XY = 5 cm, XZ = 6 cm and ZX = 90° (∠YXZ = 90°)

Steps of Construction:

1. Draw a rough sketch of triangle arid label it with given measurements.
2. Draw a line segment with XY = 5 cm.
3. Draw a ray \(\overrightarrow{\mathrm{XP}}\) such that ∠YXP = 90°.
4. Draw an arc with centre X and radius 6 cm to intersect XP at point Z.
5. Join YZ.
   Hence, required triangle ∆XYZ is constructed with the given measurements.

Question 5.
Construct a right angled with measurements ABC, ∠B = 90°, AB = 8 cm and AC = 10 cm.
Answer:
Given measurements of ∆ABC are ∠B = 90°, AB = 8 cm and AC = 10 cm.

Steps of Construction :

1. Draw a rough sketch of triangle and label it with given measurements.
2. Draw a line segment with AB = 8 cm.
3. Draw a ray \(\overrightarrow{\mathrm{BX}}\) such that ∠ABX = 90°.
4. Draw an arc with centre A and radius 10 cm to intersect \(\overrightarrow{\mathrm{BX}}\) at point C.
5. Join AC.
   Thus, the required ∆ABC is constructed with the given measurements.

SCERT AP 7th Class Maths Solutions Pdf Chapter 10 Construction of Triangles Review Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Construction of Triangles Review Exercise

Question 1.
Draw the angles 70° and 110° by using a protractor,
(i) ∠AOB = 70°
Answer:
∠AOB = 70°

1. Draw a ray \(\overrightarrow{\mathrm{OA}}\)
2. At ‘O’ erect a ray OB such that ∠AOB = 70°

(ii) ∠AOB = 110°
Answer:
∠AOB = 110°

1. Draw a ray \(\overrightarrow{\mathrm{OA}}\).
2. At ‘O’ erect a ray \(\overrightarrow{\mathrm{OB}}\) such that ∠AOB = 110°

Question 2.
Construct the angles 60° and 120° by using ruler and compass.
(i) ∠AOB = 60°
Answer:
∠AOB = 60°

1. Draw a ray \(\overrightarrow{\mathrm{OA}}\).
2. Draw an arc with any radius (convenient) taking ‘O’ as a centre and cutting \(\overrightarrow{\mathrm{OA}}\) at X.
3. Draw an arc with the same radius – taking X as a centre and meeting the previous arc at Y.
4. Join OY and produce it to B.
5. ∠AOB is formed.
6. ∠AOB = 60°

(ii) ∠ADI = 120°
Answer:
∠ADI = 120°

1. Draw a ray \(\overrightarrow{\mathrm{DA}}\).
2. Draw an arc with any radius taking ‘D’ as centre intersecting \(\overrightarrow{\mathrm{DA}}\) at X.
3. Now draw two successive arcs from X intersecting the previous arc at Y and Z.
4. Join D and Z and produce DZ to I.
5. Now the angle formed ∠ADI is equal to 120°.

Question 3.
Draw a line segment PQ = 4.5 cm and construct its perpendicular bisector by using ruler and compass.
Answer:

∠PMY = ∠QMY = 90°
So, PQ ⊥ XY

1. Draw a line segment PQ of length 4.5 cm.
2. Draw two arcs with centre P and radius > \(\frac{1}{2}\)PQ on both sides of PQ.
3. Repeat step 2 with centre ‘Q’ intersecting the previous arc at X and Y.
4. Join X and Y and produce it on either sides to form \(\overrightarrow{\mathrm{XY}}\).
5. XY is the perpendicular bisector of PQ.

Question 4.
Construct ∠DEF = 60° and its angular bisector by using ruler and compass.
Answer:

∠DEF = 60°
∠DEK = ∠FEK = \(\frac{\angle \mathrm{DEF}}{2}=\frac{60^{\circ}}{2}\) = 30°

1. Construct ∠DEF = 60°
2. Draw an arc with a convenient radius taking E as centre intersecting ED at X and EF at Y.
3. Draw two arcs with the same radius taking X and Y as centres intersecting at Z.
4. Join E, Z and produce it to K.
5. ∠DEK = ∠KEF = 30°.

Question 5.
Construct an angle of 90° without using a protractor.
Answer:
∠SRI = 90°

1. Draw a ray \(\overrightarrow{R S}\).
2. Draw an arc of convenient radius taking R as a centre and intersecting \(\overrightarrow{R S}\) at X.
3. With the same radius draw two successive arcs from X intersecting the previous arc at Y & Z.
4. Draw bisector to \(\widehat{\mathrm{YZ}}\) intersecting at I.
5. Join R, I.

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions InText Questions

Check your progress [Page No. 49]

Question 1.
How many number of terms are there in each of the following expressions ?
(i) 5x² + 3y + 7
Answer:
Given expression is 5x² + 3y + 7 Number of terms = 3

(ii) 5x²y + 3
Answer:
Given expression is 5x²y + 3
Number of terms = 2

(iii) 3x²y
Answer:
Given expression is 3x²y
Number of terms = 1

(iv) 5x – 7
Answer:
Given expression is 5x – 7
Number of terms = 2

(v) 7x³ – 2x
Answer:
Given expression is 7x³ – 2x
Number of terms = 2

Question 2.
Write numeric and algebraic terms in ‘ the above expressions.
(i) 5x² + 3y + 7
Answer:
Given expression is 5x² + 3y + 7
Numerical terms = 7
Algebraic terms = 5x², 3y

(ii) 5x²y + 3
Answer:
Given expression is 5x²y + 3
Numerical terms = 3
Algebraic terms = 5x²y

(iii) 3x²y
Answer:
Given expression is 3x²y
Numerical terms = No
Algebraic terms = 3x²y

(iv) 5x – 7
Answer:
Given expression is 5x – 7
Numerical terms = – 7
Algebraic terms = 5x

(v) 7x³ – 2x
Answer:
Given expression is 7x³ – 2x
Numerical terms = No
Algebraic terms = 7x³, – 2x

Question 3.
Write the terms in the following expressions.
– 3x + 4, 2x – 3y, \(\frac{4}{3}\)a² + \(\frac{5}{2}\)b,
1.2ab + 5.1b – 3.2a
Answer:

Let’s Explore (Page No: 50)

Question 1.
Identify the terms which contain m² and write the coefficients of m².
(i) mn² + m²n
Answer:
Given expression is mn² + m²n

(ii) 7m² – 5m – 3
Answer:
Given expression is 7m² – 5m – 3

(iii) 11 – 5m² + n + 8 mn
Answer:
Given expression is 11 – 5m² + n + 8 mn

Check Your Progress [Page No. 52]

Question 1.
Write like terms from the following :
– xy², – 4yx, 8x, 2xy², 7y, – 11x², – 100x, – 11yx, 20x²y, – 6x², y, 2xy, 3x
Answer:
Given – xy², – 4yx, 8x, 2xy², 7y, – 11x², – 100x, – 11yx, 20x²y, – 6x², y, 2xy, 3x

• – xy², 2xy² are like terms because they contain same algebraic factor xy².
• – 4yx, – 11yx, 2xy are like terms because they contain same algebraic factor xy.
• 8x, – 100x, 3x are like terms because they contain same algebraic factor x.
• 7y, y are like terms because they contain same algebraic factor y.
• – 11x², – 6x². are like terms because they contain same algebraic factor x².

Question 2.
Write 3 like terms for
(i) 3x²y
Answer:
Like terms of 3x²y are – 8x²y, \(\frac{5}{3}\) x²y, 2.9 x²y

(ii) – ab²c
Answer:
Like terms of – ab²c are 3ab²c, 5.8 ab²c, \(\frac{-1}{4}\) ab²c.

Let’s Explore [page No: 52]

Question 1.
Jasmin says that 3xyz is a trinomial. Is she right ? Give reason.
Answer:
Given expression 3xyz.
In this expression only one term is there. So, it is a monomial only. But, not trinomial.
So, Jasmin is wrong.

Question 2.
Give two examples each for Monomial and Binomial algebraic expression.
Answer:

Check Your progress [Page No. 54]

Question 1.
Add the following like terms.
(i) 12ab, 9ab, ab
Answer:
Sum of 12ab, 9ab, ab
= 12ab + 9ab + ab
= (12 + 9 + 1) ab
= 22 ab.

(ii) 10x², – 3x², 5x²
Answer:
Sum of 10x², – 3x², 5x²
= 10x² + (- 3x²) + 5x²
= 10x² – 3x² + 5x²
= (10 – 3 + 5) x²
= 12x²

(iii) – y², 5y², 8y², – 14y²
Answer:
Sum of – y², 5y², 8y², – 14y²
= – y² + 5y² + 8y² + (- 14y²)
= – 1y² + 5y² + 8y² – 14y²
= (- 1 + 5 + 8 – 14) y²
= – 2y²

(iv) 10mn, 6mn, – 2mn, – 7mn
Answer:
Sum of 10mn, 6mn, – 2mn, – 7mn
= 10mn + 6mn + (- 2mn) + (- 7mn)
= 10mn + 6mn – 2mn – 7mn
= (10 + 6 – 2 – 7) mn
= 7mn

Let’s Think [Page No: 54]

Reshma simplified the expression
4p + 6p + p like this.
4p + 6p + p = 10p. Is she correct ?
Answer:
4p + 6p + p = (4 + 6 + 1)p
= 11p ≠ 10p
So, Reshma simplified is wrong.

Check Your Progress [Page No: 54]

Question 1.
Write the standard form of the following expressions :
(i) – 5l + 2l² + 4
Answer:
2l² – 5l + A

(ii) 4b² + 5 – 3b
Answer:
4b² – 3b + 5

(iii) z – y – x
Answer:
– x – y + z.

Check Your Progress [Page No. 56]

Question 1.
Add the following expressions in both Row and Column methods:
(i) x – 2y, 3x + 4y
Answer:

(ii) 4m² – 7n² + 5mn, 3n² + 5m² – 2mn
Answer:

(iii) 3a – 4b, 5c – 7a + 2b
Answer:

Let’s Explore [Page No. 56]

Think of at least two situations in each of which you need to form two algebraic expressions and add them.

(i) Aditya and Madhu went to a store. Aditya bought 6 books and Madhu bought 2 books. All the books are same cost. How much money did both spend ₹
Answer:
Let the cost of each book ₹a.
Number of books Aditya bought = 6
Cost of 6 books = 6 × a = ₹ 6a
Number of books Madhu bought = 2
Cost of 2 books = 2 × a = ₹ 2a
Money spend on books bought by Aditya and Madhu
= 6a + 2a
= (6 + 2)a
= ₹ 8a

(ii) Sreeja and Sreekari went to icecream parlour. Sreeja bought Vineela icecreams 2 and Sreekari bought Butter Scotch 3. Cost of icecreams are different. How much money they gave to the shop keeper ₹
Answer:
Let the cost of Vineela is ₹x and cost of Butter Scotch is ₹y.
Number of Vineela icecreams Sreeja bought = 2
Cost of 2 iceqreams = 2 × x = ₹ 2x
Number of Butter Scotch icecreams Sreekari bought = 3
Cost of 3 icecreams = 3 × y = ₹ 3y
Money given to shopkeeper = 2x + 3y
= ₹(2x + 3y)

Check Your Progress [Page No. 57]

Question 1.
Subtract the first term from second term :
(i) 2xy, 7xy
Answer:
7xy – 2xy
= (7 – 2) xy
= 5xy

(ii) 4a², 10a²
Answer:
10a² – 4a² = (10 – 4)a² = 6a²

(iii) 15p, 3p
Answer:
3p – 15p = (3 – 15)p = – 12p

(iv) 6m²n, – 20m²n
Answer:
– 20 m²n – 6m²n = (- 20 – 6) m²n
= – 26m²n

(v) a²b², – a²b²
Answer:
– a²b² – a²b² = (- 1 – 1)a²b² = – 2a²b²

Let’s Explore [Page No. 58]

Add and subtract the following expressions in both Horizontal and Vertical method x – 4y + z, 6z – 2x + 2y
Answer:
Addition

Subtraction:

Let’s Explore [Page No. 60]

Question 1.
Write an expression whose value is – 15 when x = – 5.
Answer:
Given x = – 5 and value = – 15
Value = – 15 ,
= 3 × – 5 ,
= – 3 × x (∵ x = – 5)
∴ Expression = 3x

Question 2.
Write an expression whose value is 15 when x = 2.
Answer:
Given x = 2 and value = 15
Value = 15
= \(\frac{30}{2}\)
= \(\frac{1}{2}\) × 15 × 2
= \(\frac{1}{2}\) × 15 × x (∵ x = 2)
∴ Expression = \(\frac{15 x}{2}\)

Lets Think [Page No. 60]

While finding the value of an algebraic expression 5x when x = – 2, two stu¬dents solved as follows:

Can you guess who has done it correctly? Justify!
Answer:
Given expression is 5x when x = – 2
5x = 5(- 2) = – 10
Chaitanya is correct.
Here we have to multiply 5 and,- 2.
But Reeta subtracted.
So, Reeta is wrong.

Examples

Question 1.
How many number of terms are there in each of the following expressions ?
(i) a + b
Answer:
a + b ……….. 2 terms

(ii) 3t²
Answer:
3t² ……….. 1 term

(iii) 9p³ + 10q – 15
Answer:
9p³ + 10q – 15 ……….. 3 terms

(iv) \(\frac{5 \mathrm{~m}}{3 \mathrm{n}}\)
Answer:
\(\frac{5 \mathrm{~m}}{3 \mathrm{n}}\) ……….. 1 term

(v) 4x + 5y – 3z – 1
Answer:
4x + 5y – 3z – 1 ……….. 4 terms

Question 2.
In the following expressions, write the number of terms and identify numeri¬cal and algebraic expressions in them.
(i) 8p
Answer:
8p = 1 term – Algebraic expression

(ii) 5c + s – 7
Answer:
5c + s – 7 = 3 terms – Algebraic expression

(iii) – 6
Answer:
– 6 = 1 term – Numerical expression

(iv) (2 + 1) – 6
Answer:
(2 + 1) – 6 = 2 terms – Numerical expression

(v) 9t + 15
Answer:
9t + 15 = 2 terms – Algebraic expression

Question 3.
Write the coefficients of
(i) p in 8pq
Answer:
8pq = p(8q)
so, coefficient of p in 8pq is 8q.

(ii) x in \(\frac{x y}{3}\)
Answer:
\(\frac{x y}{3}\) = x\(\left(\frac{\mathrm{y}}{3}\right)\)
so, coefficient of x in \(\frac{x y}{3}\) is \(\left(\frac{\mathrm{y}}{3}\right)\)

(iii) abc in (- abc)
Answer:
(- abc) = – (abc)
so, coefficient of abc is – 1.

Question 4.
Identify like terms among the following and group them:
10ab, 7a, 8b, – a²b², – 7ba, – 105b, 9b²a², – 5a², 90a.
Answer:
(7a, 90a) are like terms because they
contain same algebraic factor ‘a’.
(10ab, – 7ba) are like terms as they have same algebraic factor ’ab’.
(8b, -105b) are like terms because they contain same algebraic factor ‘b’.
(- a²b², 9b²a²) are like terms because they contain same algebraic factor ‘a²b²‘.

Question 5.
State with reasons, classify the following expressions into monomials, binomials, trinomials.
a + 4b, 3x²y, px² + qx + 2, qz², x² + 2y, 7xyz, 7x² + 9y³ – 10z⁴, 3l² – m², x, – abc.
Answer:

Question 6.
Find the sum of the following like terms :
(i) 3a, 9a
Answer:
Sum of 3a, 9a = 3a + 9a
= (3 + 9)a = 12a

(ii) 5p²q, 2p²q
Answer:
Sum of 5p²q, 2p²q = 5p²q + 2p²q
= (5 – 2) p²q = 7p²q

(iii) 6m, – 15m, 2m
Answer:
Sum of 6m, – 15m, 2m
= 6m + (- 15m) + 2m
= 6m – 15m + 2m
= (6 – 15 + 2)m = – 7m

Question 7.
Write the perimeter of the given figure.

Answer:
The perimeter of the figure
= 10 + 4 + x + 3+ y
= x + y + (10 + 4 + 3)
= x + y + 17

Question 8.
Simplify:
6a² + 3ab + 5b² – 2ab – b² + 2a² + 4ab + 2b² – a²
Answer:
6a² + 3ab + 5b² – 2ab – b² + 2a² + 4ab + 2b² – a²
= (6a² + 2a² – a²) + (3ab – 2ab + 4ab) + (5b² – b² + 2b²)
= [(6 + 2 – 1) a²] + [(3 – 2 + 4)ab] + [(5 – 1 + 2)b²]
= 7a² + 5ab + 6b²

Question 9.
Add 2x² – 3x + 5 and 9 + 6x² in vertical method.

Answer:

Question 10.
Find the additive inverse of the follow-ing expressions:
(i) 35
Answer:
Additive inverse of 35 = – 35

(ii) – 5a
Answer:
Additive inverse of – 5a = – (-5a) = 5a

(iii) 3p – 7
Answer:
Additive inverse of 3p – 7 = – (3p – 7) = – 3p + 7

(iv) 6x² – 4x + 5
Answer:
Additive inverse of 6x² – 4x + 5
= (6x² – 4x + 5) = – 6x² + 4x – 5

Question 11.
Subtract 2p² – 3 from 9p² – 8.
Answer:
9p² – 8 – (2p² – 3) = 9p² – 8 – 2p² + 3
= (9 – 2) p² – 8 + 3
= 7p² – 5

Question 12.
Subtract 3a + 4b – 2c from 6a – 2b + 3c in row method.
Answer:
Let A = 6a – 2b + 3c, B = 3a + 4b – 2c
Subtracting 3a + 4b – 2c from 6a – 2b + 3c is equal to adding additive inverse of 3a + 4b – 2c to 6a – 2b + 3c
i.e., A – B = A + (-B)
additive inverse of (3a + 4b – 2c) = – (3a + 4b – 2c) = – 3a – 4b + 2c
A – B = A + (-B)
= 6a – 2b + 3c + (- 3a – 4b + 2c)
= 6a – 2b + 3c – 3a – 4b +2c = (6 – 3)a – (2 + 4)b + (3 + 2)c
Thus, the required answer = 3a – 6b + 5c

Question 13.
Subtract 3m³ + 4 from 6m³ + 4m² + 7m – 3 in stepwise method.
Answer:
Let us solve this in stepwise.
Step 1: 6m³ + 4m² + 7m – 3 – (3m³ + 4)
Step 2: 6m³ + 4m² + 7m – 3 – 3m³ – 4
Step 3: 6m³ – 3m³ + 4m² + 7m – 3 – 4 (rearranging like terms)
Step 4: (6 – 3)m³ + 4m² + 7m – 7 (distributive law)
Thus, the required answer = 3m³ + 4m² + 7m – 7

Question 14.
Subtract 4m² – 7n² + 5mn from 3n² + 5m² – 2mn.
(For easy understanding, same colours are taken to like terms)
Answer:

Question 15.
Find the value of the following expressions, when x = 3.
(i) x + 6
Answer:
When x = 3, the value of x + 6
(substituting 3 in the place of x) is
(3) + 6 = 9

(ii) 8x – 1
Answer:
When x = 3,
the value of 8x – 1 = 8(3) – 1
= 24 – 1 = 23

(iii) 14 – 5x
Answer:
When x = 3,
the value of 14 – 5x = 14 – 5(3)
= 14 – 15 = – 1

Practice Questions [Page No: 65]

Question 1.
In a certain code BOARD: CNBQE, how ANGLE will be written in that code?
(a) BMHKF
(b) CNIJE
(c) BLGIF
(d) CMIKF
Answer:
(a) BMHKF

Explaination:
Each letter in a word is shifted to 1 position is alphabetical order and went 1 position is backward like this.

ANGLE = BMHKF

Question 2.
In a certain code, MOBILE: 56, how PHONE will be written in that code?
(a) 52
(b) 54
(c) 56
(d) 58
Answer:
(d) 58

Explaination:
Taking sum of positions of letters in for ward direction.

So, PHONE = 16 + 8 + 15 + 14 + 5 = 58

Question 3.
If BEAN: ABNE, then NEWS ?
(a) WSNE
(b) WSEN
(c) WNSE
(d) WNES
Answer:
(c) WNSE

Explaination:
Follow the same to decode the given word.

Question 4.
If ROSE : 6821, CHAIR : 73456, PREACH : 961473, then SEARCH ?
(a) 241673
(b) 214673
(c) 216473
(d) 216743
Answer:
(b) 214673

Explaination:
By comparing each letter with the symbol, by writing one below the other.

Question 5.
If COMPUTER: RFUVQNPC, then MEDICINE?
(a) EDJOJMEF
(b) EOJDJEFM
(c) EOJJDFEM
(d) EDJJOFME
Answer:
(b) EOJDJEFM

Explaination:
In the coded form the first & last letters have been interchanged while the rem¬aining letters are coded by taking their immediate next letters in the reverse order.

Question 6.
If LAKE = 7@$5, WALK = %@7$, then WAKE = ?
(a) @%75
(b) %@$5
(c) %5@7
(d) %@57
Answer:
(b) %@$5

Explaination:
By comparing each letter with symbol, by writing One below the other.

Question 7.
If MANY = OCPA, then LOOK = ?
(a) NQQM
(b) MQQN
(c) QMQN
(d) QNQM
Answer:
(a) NQQM

Explaination:
Each letter in a word is shifted to 2 position forward in alphabetical order.

∴ LOOK = NQQM

Question 8.
If SOME = PUB, then BODY ?‘
(a) LABY
(b)YBAL
(c) YLAV
(d) ABLY
Answer:
(c) YLAV

Explaination:
Bach letter in a word is shifted to 3 position backward in alphabetical order.

So, BODY = YLAV

Question 9.
If ARC = CVI, then RAY?
(a) TEU
(b) TEE
(c) TED
(d) TEF
Answer:
(b) TEE

Explaination:
Each letter in a word is forwarded alphabetical order as follows.

So, RAY = TEE

Question 10.
If MEAN = KGYI, then MODE = ?
(a) QBGK
(b) KBQC
(c) KGBQ
(d) kQBG
Answer:
(d) kQBG

Explaination:
Each letter in the word is shifted to 2 position backward and 2 position forward as following.

So, MODE = KQBG

Question 11.
If FIND = DNIF, then DONE ?
(a) ENOD
(b) ENDO
(c) NEOD
(d) ONED
Answer:
(a) ENOD

Explaination:
By reversing the word from left to right.
So, DONE = ENOD .

Question 12.
If BASE = SBEA, then AREA = ?
(a) AARE
(b) EAAR
(c) EARA
(d) REAA
Answer:
(b) EAAR

Explaination:
Follow the same to decode the given word.

Question 13.
If LESS = 55, then MORE = ?
(a)54
(b)50
(c) 51
(d) 52
Answer:
(c) 51

Explaination:
Taking sum of positions of letters in forward direction.

Question 14.
If BACK = 17, then CELL =?
(a) 33
(b) 30
(c) 31
(d) 32
Answer:
(d) 32

Explaination:
Taking sum of positions of letters in for ward direction.

3 + 5 + 12 + 12 = 32

Question 15.
If BIG = 63, then SMALL =?
(a) 76
(b) 78
(c) 74
(d) 72
Answer:
(b) 78

Explaination:
Taking sum of positions of letters in reverse direction.

8 + 14 + 26 + 15 + 15 = 78

SCERT AP 7th Class Maths Solutions Pdf Chapter 6 Algebraic Expressions Unit Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 6th Lesson Algebraic Expressions Unit Exercise

Question 1.
Fill in the blanks:
(i) The constant term in the expression a + b + 1 is ………………..
Answer:
1.

(ii) The variable in the expression 3x – 8 is ………………..
Answer:
x

(iii) The algebraic term in the expression 2d – 5 is ………………..
Answer:
2d

(iv) The number of terms in the expression ……………….. p² – 3pq + q is
Answer:
3

(v) The numerical coefficient of the term – ab is …………………..
Answer:
– 1

Question 2.
Write below statements are True or False:
(i) \(\frac{3 x}{9 y}\) is a binomial.
Answer:
False

(ii) The coefficient of b in – 6abc is – 6a.
Answer:
False

(iii) 5pq and – 9qp are like terms.
Answer:
True

(iv) The sum of a + b and 2a + 7 is 3a + 7b.
Answer:
False

(v) When x = – 2, then the value of x + 2 is 0.
Answer:
True.

Question 3.
Identify like terms among the following:
3a, 6b, 5c, – 8a, 7c, 9c, – a, \(\frac{2}{3}\)b, \(\frac{7 c}{9}\), \(\frac{a}{2}\).
Answer:
Given terms are
3a, 6b, 5c, – 8a, 7c, 9c, – a, \(\frac{2}{3}\)b, \(\frac{7 c}{9}\), \(\frac{a}{2}\)
Like terms: 3a, – 8a, – a, \(\frac{a}{2}\)
6b, \(\frac{2}{3}\)b
5c, 7c, 9c, \(\frac{7 c}{9}\)

Question 4.
Arjun and his friend George went to a stationary shop. Arjun bought 3 pens and 2 pencils whereas George bought one pen and 4 pencils. If the price of each pen and pencil is ₹ x and ₹ y respectively, then find the total bill amount in x and y.
Answer:
Given cost of each pen is ₹ x and cost of each pencil is ₹ y .
Arjun bought 3 pens and 2 pencils. Cost of 3 pens = 3 × ₹ x = ₹ 3x
Cost of 2 pencils = 2 × ₹y = ₹ 2y
Amount paid by Arjun = 3x + 2y = ₹ (3x + 2v)
George bougth one pen and 4 pencils.
Cost of 1 pen = 1 × ₹ x = ₹ x
Cost of 4 pencils = 4 × ₹ y = ₹ 4y
Amount paid by George = x + 4y = ₹(x + 4y)
Total bill amount
= Arjun amout + George amount
= (3x + 2y) + (x + 4y)
= 3x + 2y + x + 4y
= 3x + x + 2y + 4y
= (3 + 1)x + (2 +4)y
∴ Total bill amount = ₹ (4x + 6y)

Question 5.
Find the errors and correct the following :
(i) 7x + 4y = 11xy
Answer:
7x and 4y are not like terms and different variables x, y.
So, we should not add the coefficients.

(ii) 8a² + 6ac = 14a³c
Answer:
8a² and 6ac are not like terms. So, we should not add the coefficients.

(iii) 6pq² – 9pq² = 3pq2
Answer:
6pq² – 9pq² = (6 – 9)pq²
= – 3pq²

(iv) 15mn – mn = 15
Answer:
15mn – mn = (15 – 1) mn
= 14 mn

(v) 7 – 3a = 4a
Answer:
7 and 3a are not like terms.
So, we should not subtract the coefficient 7 and 3.

Question 6.
Add the expressions
(i) 9a + 4, 2 – 3a
Answer:
Given expressions are 9a + 4; 2 – 3a
Write the given expressions in standard form.
9a + 4, – 3a + 2.
The sum = (9a + 4) + (- 3a + 2)
= 9a + 4 – 3a + 2
= (9a – 3a) + (4 + 2)
= (9 – 3)a + 6
= 6a + 6

(ii) 2m – 7n, 3n + 8m, m + n
Answer:
Given expressions are
2m – 7n, 3n + 8m, m + n
Write the given expressions in standard form.
2m – 7n, 8m + 3n, m + n
The sum
= (2m 7n) + (8m + 3n) + (m + n)
= 2m – 7n + 8m + 3n + m + n
= (2m + 8m + m) + (- 7n + 3n + n)
= (2 + 8 + 1)m + (- 7 + 3 + 1)n
= 11 m + (- 3)n
= 11 m – 3n

Question 7.
Subtract:
(i) – y from y
Answer:
– y from y = y – (-y) = y + y = 2y

(ii) 18 pq from 25pq
Answer:
18pq from 2 5pq
= 25 pq – 18 pq
= (25 – 18) pq = 7pq

(iii) 6t + 5 from 1 – 9t
Answer:
Given expressions are (6t + 5), (1 – 9t)
Write the given expressions in the standard form (6t + 5); (- 9t + 1)
(6t + 5) from (- 9t + 1)
= (- 9t + 1) – (6t + 5)
= – 9t + 1 – 6t – 5
= (- 9t – 6t) + (1 – 5)
= (- 9 – 6) t + (- 4) = – 15t – 4

Question 8.
Simplify the following :
(i) t + 2 + t + 3 + t + 6- t- 6 + t
Answer:
Given t + 2 + t + 3+ t + 6 – t – 6 + t

= 3t + 5

(ii) (a + b + c) + (2a + 3b – c) – (4a + b – 2c)
Answer:
Given (a + b + c) + (2a + 3b – c) – (4a + b – 2c)
= a + b + c + 2a + 3b – c – 4a – b + 2c
= (a + 2a – 4a) + (b + 3b – b) + (c – c + 2c)
= (1 + 2 – 4)a + (1 + 3 – 1)b + (1 – 1 + 2)c
= (- 1) a + 3b + 2c
= – a + 3b + 2c

(iii) x + (y + 1) + (x + 2) + (y + 3) + (x + 4) + (y + 5)
Answer:
Given x + (y + 1) + (x + 2) + (y + 3) + (x + 4) + (y + 5)
= x + y + 1 + x + 2 + y + 3 + x + 4 + y + 5
= (x + x + x) + (y + y + y) + (1 + 2 + 3 + 4 + 5)
= 3x + 3y + 15

Question 9.
The perimeter of a triangle is 8x² + 7x – 9 and two of its sides are x² – 3x + 4, 2x² + x – 9 respectively, then find third side.
Answer:
Let the sides of triangle are A, B, C.
A = x² – 3x + 4; B = 2x² + x – 9 ; C = ?
Perimeter = 8x² + 7x – 9
Perimeter of the triangle = A + B + C
To get the third side (C). subtract sum of A and B from the perimeter.
∴ C = Perimeter – (A + B)
So,
A + B = (x² – 3x + 4) + (2x² + x – 9)
= x² – 3x + 4 + 2x² + x – 9
= x² + 2x² – 3x + x +4 – 9
= (1 + 2) x² + (- 3 + 1) x – 5
A + B = 3x² – 2x – 5
Additive inverse of A + B is – (A + B)
– (A + B) = – (3x² – 2x – 5) .
– (A + B) = – 3x² + 2x + 5
C = perimeter + [- (A + B)]
= (8x² + 7x – 9) + (- 3x² + 2x + 5)
= 8x² + 7x – 9 – 3x² + 2x + 5
= 8x² – 3x² + 7x + 2x – 9 + 5
= (8 – 3) x² + (7 + 2) x – 4
C = 5x² + 9x – 4
∴ Third side is 5x² + 9x – 4.

Question 10.
The perimeter of a rectangle is 2a³ – 4a² – 12a + 10, if length is 3a² – 4, find its breadth.
Answer:
Given length of rectangle l = 3a² – 4 and breadth b = ?
Perimeter of a rectangle = 2a³ – 4a² – 12a + 10
Perimeter of a rectangle
= 2(l + b)
= 2a³ – 4a² – 12a + 10

= \(\frac{1}{2}\) × 2(a³ – 2a² – 6a + 5)
⇒ l + b = (a³ – 2a² – 6a + 5)
⇒ l + b – l = (a³ – 2a² – 6a + 5) – l
∴ b = (a³ – 2a² – 6a + 5) – l
Additive inverse of 1 is – 1 = – (3a² – 4)
∴ – l = – 3a² + 4 .
b = (a³ – 2a² – 6a + 5) + (- 1)
= (a³ – 2a² – 6a + 5) + (- 3a² + 4)
= a³ – 2a² – 6a + 5 – 3a² + 4
= a³ – 2a² – 3a² – 6a + 5 + 4
= a³ + (- 2 – 3) a² – 6a + 9
= a³ + (- 5) a² – 6a + 9
∴ Breadth of rectangle
= a³ – 5a² – 6a + 9

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Ex 9.4 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Ex 9.4

Question 1.
Find the value of the expression
2x² – 4x + 5 when
(i) x = 1
(ii) x = – 2
(iii) x = 0.
Answer:
Given expression is 2x² – 4x + 5

(i) When x = 1, then
= 2(1)² – 4(1) + 5
= 2 × 1 – 4 + 5
= 2 – 4 + 5 = 3
When x = 1, then 2x² – 4x + 5 = 3

(ii) When x = – 2, then
= 2(- 2)² – 4(- 2) + 5
= 2(4) + 8 + 5
= 8 + 8 + 5 = 21
When x = – 2, then 2x² – 4x + 5 = 21

(iii) When x = 0, then
= 2(0)² – 4(0) + 5
= 2(0) – 0 + 5
= 0 – 0 + 5 = 5
When x = 0, then 2x² – 4x + 5 = 5

Question 2.
Find the value of Expressions when m = 2, n = – 1.
(i) 2m + 2n
Answer:
Given expression is 2m + 2n
If m = 2, n = – 1, then
2m + 2n = 2(2) + 2(- 1) = 4 – 2 = 2
∴ If m = 2, n = – 1, then 2m + 2n = 2

(ii) 3m – n
Answer:
Given expression is 3m – n
If m = 2, n = – 1, then
3m – n = 3(2) -(-1) = 6 + 1 = 7
∴ If m = 2, n = – 1, then 3m – n = 7

(iii) mn – 2.
Answer:
Given expression is mn – 2
If m = 2, n = – 1, then
mn – 2 = 2 × (-1)-2
= – 2 – 2 = – 4
∴ If m = 2, n = – 1, then mn – 2 = – 4

Question 3.
Simplify and find the value of the expression 5x² – 4 – 3x² + 6x + 8 + 5x – 13 when x = – 2.
Answer:
Given expression is
5x² – 4 – 3x² + 6x + 8 + 5x – 13
= (5x² – 3x²) + (6x + 5x) + (-4 + 8 – 13)
= (5 – 3)x² + (6 + 5)x + (- 9)
= 2x² + 11x – 9
If x = – 2, then 2x² + 11x – 9
= 2(- 2)² + 11 (- 2) – 9
= 2(4) – 22 – 9
= 8 – 22 – 9
∴ If x = – 2, then 2x² + 11x – 9 = – 23

Question 4.
Find the length of the line segment PQ when a = 3 cm.

Answer:
From the figure,
Given PR = 3a and RQ = 2a
PQ = PR + RQ
= 3a + 2a
= (3 + 2)a
PQ = 5a
If a = 3 cm, then PQ = 5(3)
∴ PQ = 15 cm

Question 5.
The area of a square field of side ‘s’ meters is s2 sq. m. Find the area of square field, when
(i) s = 5m
(ii) s =12m
(iii) s = 6.5m

Answer:
From the figure,
Area of square = s2 sq.m.
(i) If s = 5m, then
s² = (5)² = 5 × 5 = 25 sq.m

(ii) If s = 12 m, then
s² = (12)² = 12 × 12 = 144 sq.m

(iii) If s = 6.5m, then
s² = (6.5)² = 6.5 × 6.5 = 42.25 sq.m

Question 6.
The area of triangle is given by \(\frac{1}{2}\) ∙ b ∙ h and if b = 12 cm, h = 8 cm, then find the area of triangle.
Answer:
Given area of the triangle = \(\frac{1}{2}\) ∙ b ∙ h
If b = 12 cm, h = 8 cm

= 6 × 8 = 48 sq.cm.

Question 7.
Simple interest is given by I = \(\frac{\text { PTR }}{100}\), If P = ₹ 900, T = 2 years and R = 5%, then find the simple interest.
Answer:
Given simple interest I = \(\frac{\text { PTR }}{100}\)
If P = ₹ 900, T= 2 and R = 5% then

= 9 × 2 × 5 = 90

Question 8.
Find the errors and correct them in the following:
The value of following when a = – 3.
(i) 3 – a = 3 – 3 = 0
Answer:
3 – a = 3 – (- 3) (when a = – 3)
= 3 + 3 = 6
(Error is – (- 3) = – 3)

(ii) a² + 3a = (- 3)² + 3(- 3) = 9 + 0 = 9
Answer:
a² + 3a = (- 3)² + 3(- 3) (when a = – 3)
= (- 3 × – 3) – 9
(Error is 3(- 3) = 0)
= 9 – 9 = 0

(iii) a² – a – 6 = (- 3)² – (- 3) – 6 = 9 – 3 – 6 = 0
Answer:
a² – a – 6
= (- 3)² – (- 3) – 6 (when a = – 3)
= (- 3 × – 3) + 3 – 6
(Error is – (- 3) = – 3)
= 9 + 3 – 6
= 12 – 6 = 6

(iv) a² + 4a + 4 = (- 3)² + 4(-3) + 4 = 9 + 1 + 4 = 14
Answer:
a² + 4a + 4
= (- 3)² + 4(- 3) + 4 (when a = – 3)
= (- 3 × – 3)- 12 + 4
(Error is 4 (- 3) = 1)
= 9 – 12 + 4 = 13 – 12 = 1

(v) a³ – a² – 3 = (- 3)³ – (-3)² – 3 = – 9 + 6 – 3 = – 6
Answer:
a³ – a² – 3
= (- 3)³ – (- 3)² – 3 (when a = – 3)
= (- 3 × – 3 × – 3) – (- 3 × – 3) – 3
= – 27 – (9) – 3
(Error is (- 3)³ = – 9 and (- 3)² = 6)
= – 27 – 9 – 3 = – 39

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Ex 9.3 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Ex 9.3

Question 1.
Write standard form and additive inverse of the following expressions.
(i) – 6a
Answer:
Additive inverse of – 6a = – (- 6a) = 6a

(ii) 2 + 7c²
Answer:
Standard form of 2 + 7c² = 7c² + 2
Additive inverse of 7c² + 2
= – (7c² + 2)
= – 7c² – 2

(iii) 6x² + 4x – 5
Answer:
Given expression is in standard form.
Additive inverse of 6x² + 4x – 5
= – (6x² + 4x – 5)
= – 6x² – 4x + 5

(iv) 3c + 7a – 9b
Answer:
Standard form of 3c + 7a – 9b = 7a – 9b + 3c
Additive inverse of 7a – 9b + 3c
= – (7a – 9b + 3c)
= – 7a + 9b – 3c

Question 2.
Write the following expressions in standard form:
(i) 6x + x² – 5
Answer:
Standard form of 6x + x² – 5
= x² + 6x – 5

(ii) 3 – 4a² – 5a
Answer:
Standard form of 3 – 4a² – 5a
= – 4a² – 5a + 3

(iii) – m + 6 + 3m²
Answer:
Standard form of – m + 6 + 3m²
= 3m² – m + 6

(iv) c³ + 1 + c + 2c²
Answer:
Standard form of
c³ + 1 + c + 2c² = c³ + 2c² + c + 1

(v) 9 – p²
Answer:
Standard form of 9 – p² = – p² + 9

Question 3.
Add the following algebraic expressions using both horizontal and vertical methods. Did you get the same answer with both the methods? Verify.
(i) 2x² – 6x +3; 4x² + 9x + 5
Answer:

(ii) a² + 6ab + 8; – 3a² – ab – 2
Answer:

(iii) – p² + 2p – 10; 4 – 5p – 2p²
Answer:

Question 4.
Subtract the second expression from the first expression:
(i) 2x + y , x – y
Answer:
Let A = 2x + y and B = x – y
A – B = A + (- B) Additive inverse of B is
-B = – (x – y) = – x + y
∴ A – B = A + (- B)
= 2x + y + (- x + y)
= 2x + y – x + y
= 2x – x + y + y
= (2 – 1)x + (1 + 1)y
∴ A – B = x + 2y

(ii) a + 2b + c, – a – b – 3c
Answer:
Let A = a + 2b + c and B = – a – b – 3c
A – B = A + (- B)
Additive inverse of B is
– B = – (- a – b – 3c)
= a + b + 3c
∴ A – B = A + (- B)
= a + 2b + c + (a + b + 3c)
= a + 2b + c + a + b + 3c
= (a + a) + (2b + lb) + (c + 3c)
∴ A – B = 2a + 3b + 4c

(iii) 2l² – 3lm + 5m², 3l² – 4lm + 6m²
Answer:
Let A = 2l² – 3lm + 5m² and
B = 3l² – 4lm + 6m²
A – B = A + (- B)
Additive inverse of B is
– B = – (3t² – 4lm + 6m²)
= – 3l² + 4lm – 6m²
∴ A – B = A + (- B)
= (2l² – 3lm + 5m²) + (- 3l² + 4lm – 6m²)
= 2l² – 3lm + 5m² – 3l² + 4lm – 6m²
= 2l² – 3l² – 3lm + 4lm + 5m² – 6m²
= (2 – 3)l² + (- 3 + 4)lm + (5 – 6)m²
= (- 1) l² + 1 lm + (- 1)m²
∴ A – B = – l² + lm – m²

(iv) 7 – x – 3x², 2x² – 5x – 3
Answer:
Let A = 7 – x – 3x² and B = 2x² – 5x – 3
Write the given expressions in standard form.
∴ A = – 3x² – x + 7 and B = 2x² – 5x – 3
A – B = A + (- B)
Additive inverse of B is
– B = – (2x² – 5x – 3)
= – 2x² + 5x + 3
∴ A – B = A + (- B)
= (- 3x² – x + 7) + (- 2x² + 5x + 3)
= – 3x² – x + 7 – 2x² + 5x + 3
= (- 3x² – 2x²) + (- x + 5x) + (7 + 3)
= (- 3 – 2)x² + (- 1 + 5)x + 10
∴ A – B = – 5x² + 4x + 10

(v) 6m³ + 4m² + 7m – 3, 2m³ + 4
Answer:
Let A = 6m³ + 4m² + 7m – 3 and
B = 2 m² + 4
A – B = A + (- B)
Additive inverse of B is
– B = – (2m³ + 4)
= – 2m³ – 4
∴ A – B = A + (- B)
= (6m³ + 4m² + 7m – 3) + (- 2m³ – 4)
= 6m³ + 4m² + 7m – 3 – 2m³ – 4
= (6m³ – 2m³) + 4m² + 7m + (- 3 – 4)
= (6 – 2)m³ + 4m² + 7m + (- 7)
∴ A – B = 4m³ + 4m² + 7m – 7

Question 5.
Find the perimeter of the beside rect¬angle whose length is 6x + y and breadth is 3x – 2y.

Answer:
Given length of rectangle l = 6x + y
breadth b = 3x – 2y
Perimeter of Rectangle = 2 (l + b)
= 2[(6x + y) + (3x – 2y)]
= 2[6x + y + 3x – 2y]
= 2[(6 + 3)x + (1 – 2)y]
= 2[9x + (- 1) y]
= 2[9x – 1y]
= 2 × (9x) – 2 × (1y)
∴ Perimeter of rectangle = (18x – 2y) units.

Question 6.
Find the perimeter of triangle whose sides are a + 3b, a – b and 2a – b.

Answer:
Let the sides of triangle are
x = a + 3b, y = a – b and z = 2a – b
Perimeter of triangle = x + y + z
= (a + 3b) + (a – b) + (2a – b)
= a + 3b + a – b + 2a – b
= (a + a + 2a) + (3b – b – b)
= (1 + 1 + 2)a + (3 – 1 – 1)b
Perimeter of triangle.
= (4a + b) units.

Question 7.
Subtract the sum of x² – 5xy + 2y² and y² – 2xy – 3x² from the sum of 6x² – 8xy – y² and 2xy – 2y² – x².
Answer:
Given expressions are
x² – 5xy + 2y² and y² – 2xy – 3x² and 6x² – 8xy – y² and 2xy – 2y² – x²
Write the given expressions in the standard form
x² – 5xy + 2y² and – 3x² – 2xy + y² and 6x² – 8xy – y² and – x² + 2xy – 2y²
Let the Sum
A = (x² – 5xy + 2y²) + (- 3x² – 2xy + y²)
= x² – 5xy + 2y² – 3x² – 2xy + y²
= x² – 3x² – 5xy – 2xy + 2y² + y²
= (1 – 3)x² + (- 5 – 2)xy + (2 + 1)y²
A = – 2x² – 7xy + 3y²

Let the Sum
B = (6x² – 8xy – y²) + (- x² + 2xy – 2y²)
= 6x² – 8xy – y² – x² + 2xy – 2y²
= (6 – 1 )x² + (- 8 + ²)xy + (- 1 – 2)y²
B = 5x² – 6xy – 3y²
B – A = B + (- A)
Additive inverse of A is
– A = – (A)
= – (- 2x² – 7xy + 3y²)
∴ – A = 2x² + 7xy – 3y²
B – A = B + (- A)
= (5x² – 6xy – 3y²) + (2x² + 7xy – 3y²)
= (5 + 2)x² + (- 6 + 7)xy + (- 3 – 3)y²
∴ B – A = 7x² + xy – 6y²

Question 8.
What should be added to 1 + ²p – 3P² to get p² – p – 1 ?
Answer:
Given expressions are
1 + 2p – 3p² and p² – p – 1
Write the given expressions in the standard form.
– 3p² + ²p + 1 and p² – p – 1
Let A should be added to B to get C.
i.e. A + B = C
∴ A = C – B
Let B = – 3p² + 2p + 1 and
C = p² – p – 1
A = C + (- B )
Additive inverse B is
– B = – (- 3p² + 2p + 1) .
– B = 3p² – 2p – 1 .
A = (p² – p – 1) + (3p² – 2p – 1)
= p² – p – 1 + 3p² – 2p – 1
= (1 + 3)p² + (- 1 – 2)p + (- 1 – 1)
∴ A = 4p² – 3p – ²
∴ 4p² – 3p – ² is added to 1 + 2p – 3p² to get p² – p – 1.

Question 9.
What should be taken away from 3a² – 4b² + 5ab + 20 to get – a² – b² + 6ab + 3 ?
Answer:
Given expressions are
3a² – 4b² + 5ab + 20 and – a² – b² + 6ab +3
Let A be taken away from B to get C. that is A = B – C = B + (- C)
Let B = 3a² – 4b² + 5ab + 20 and C = – a² – b² + 6ab + 3 Additive inverse of C is
(- C) = – (- a² – b² + 6ab + 3)
= a² + b² – 6ab – 3
A = B + (- C)
= (3a² – 4b² + 5ab + 20) + (a² + b² – 6ab – 3)
= 3a² – 4b² + 5ab + 20 + a² + b² – 6ab – 3
= 3a² + a² – 4b² + b² + 5ab – 6ab + 20 – 3
= (3 + 1)a² + (- 4 + 1)b² + (5 – 6) ab + (20 – 3)
A = 4a² – 3b² – 1 ab + 17
So, 4a² – 3b² – 1 ab + 17 is taken away from 3a² – 4b² + 5ab + 20 to get – a² – b² + 6ab + 3.

Question 10.
If A = 4x² + y² – 6xy;
B = 3y² + 12x² + 8xy;
C = 6x² + 8y² + 6xy then,
find(i) A + B + C (ii) (A – B) – C
Answer:
Given A = 4x² + y² – 6xy
B = 3y² + 12x² + 8xy
C = 6x² + 8y² + 6xy
Write the given expressions in standard form.
A = 4x² – 6xy + y²
B = 12x² + 8xy + 3y²
C = 6x² + 6xy + 8y²

(i) A + B + C = (4x² – 6xy + y²) + (12x² + 8xy + 3y²) + (6x² + 6xy + 8y²)
= 4x² – 6xy + y² + 12x² + 8xy + 3y² + 6x² + 6xy + 8y²
= (4x² + 12x² + 6x²) + (- 6xy + 8xy + 6xy) + (y² + 3y² + 8y²)
= (4 + 12 + 6) x² + (- 6 + 8 + 6) xy + (1 + 3 + 8)y²
∴ A + B + C = 22x² + 8xy + 12y²

(ii) (A – B) – C
A + (- B) + (- C)
Additive inverse of B is
– B = – (12x² + 8xy + 3y²)
∴ – B = – 12x² – 8xy – 3y²
Additive inverse of C is
– C = -(6x² + 6xy + 8y²)
∴ – C = – 6x² – 6xy – 8y²
A + (- B) + (- C)
= (4x² – 6xy + y²) + (- 12x² – 8xy – 3y²) + (- 6x² – 6xy – 8y²)
= 4x² – 6xy + y² – 12x² – 8xy – 3y² – 6x² – 6xy – 8y²
= (4x² – 12x² – 6x²) + (- 6xy – 8xy – 6xy) + (y² – 3y² – 8y²)
= (4 – 12 – 6)x² + (- 6 – 8 – 6)xy + (1 – 3 – 8)y²
∴ (A – B) – C = – 14x² – 20xy – 10y²

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Ex 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Ex 9.2

Question 1.
State True or False and give reasons for your answer.
(i) 7x² and 2x are unlike terms.
Answer:
True.
7x² and 2x have different algebraic factors and terms contain variables with different exponents.

(ii) pq² arid – 4pq² are like terms.
Answer:
True.
pq² and – 4pq² are contain variables with same exponents. So, they are like terms.

(iii) xy, – 12x²y and 5xy² are like terms.
Answer:
False.
xy, – 12x²y and 5xy² are contain variables with different exponents. So, they are unlike terms.

Question 2.
Write like terms in the following :
(i) a², b², 2a², c²
Answer:
Given a², b², 2a², c²
Like terms: a², 2 a².

(ii) 5x, yz, 3xy, \(\frac{1}{9}\)yz
Answer:
Given 5x, yz, 3xy, \(\frac{1}{9}\)yz
Like terms : yz, \(\frac{1}{9}\)yz.

(iii) 4m²n, n²p, – m²n, m²n²
Answer:
Given 4m²n, n²p, – m²n, m²n²
Like terms: 4m²n, – m²n.

(iv) acb², 2c²ab, 5b²ac, 3cab²
Answer:
Given acb², 2c²ab, 5b²ac, 3cab²
Like terms: acb², 5b²ac, 3cab².

Question 3.
Write number of terms and name of the expression for the following algebraic expressions.
(i) p²q²p
(ii) 2020
(iii) 3ab – \(\frac{a}{2}\) + \(\frac{b}{5}\)
Answer:

Question 4.
Classify the following into monomials, binomilas and trinomials:
(i) 8a + 7b²
(ii) 15xyz
(iii) p + q – 2r
(iv) l²m²n²
(v) cab²
(vi) 3t – 5s + 2u
(vii) 1000
(viii) \(\frac{\mathbf{c d}}{2}\) + ab
(ix) 5ab – 9a
(x) 2p²q² + 4qr³
Answer:

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Ex 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Ex 9.1

Question 1.
Write numerical and algebraic coefficients of the following terms.
(i) 4xy
Answer:
Given the term is 4xy
Numerical coefficient: 4
Algebraic coefficient: xy

(ii) – 7a² b³ c
Answer:
Given term is – 7a² b³ c
Numerical coefficient: – 7
Algebraic coefficient: a²b³c

(iii) \(\frac{p q}{2 r}\)
Answer:
Given terra is \(\frac{p q}{2 r}\)
Numerical coefficient: \(\frac{1}{2}\)
Algebraic coefficient: \(\frac{p q}{r}\)

(iv) – 6mn
Answer:
Given term is – 6mn
Numerical coefficient: – 6
Algebraic coefficient: mn

Question 2.
Write the number of terms in each of the following expressions and write ’ them:
(i) 5 – 3t²
(ii) 1 + t² + t³
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) – p²q² + 7pq
Answer:

Question 3.
In – 5ab²c write the coefficients of
(i) b²c
(ii) – b²c
(iii) – 5abc
(iv) 5ac
(v) ab²
(vi) – 5ab
Answer:
Given term is – 5ab²c
(i) Coefficient of b²c is – 5a
(ii) Coefficient of – b²c is 5a
(iii) Coefficient of – 5abc is b
(iv) Coefficient of 5ac is – b²
(v) Coefficient of ab² is – 5c
(vi) Coefficient of – 5ab is bc

Question 4.
Write term containing x and coefficient of x for the following algebraic expressions.
(i) 2x + 5y
(ii) -x + y + 3
(iii) 6y² – 7xy
Answer:

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Review Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Review Exercise

Question 1.
Identify constants and variables in the following terms:
0, – x, 3t, – 5, 5ab, – m, 700, – n, 2pqr, – 1, ab, 10, – 6z
Answer:
Given, 0, – x, 3t, – 5, 5ab, – m, 700, – n, 2pqr, – 1, ab, 10, – 6z
Constants = 0, – 5, 700, – 1, 10
Variables = – x, 3t, 5ab, – m, – n, 2pqr, ab, – 6z.

Question 2.
Observe the pattern the side and express the pattern in the form of an algebraic expression.

Answer:
In row = 1, 2(1) + 1 = 3
In row = 2, 2(2) + 1 = 5
In row = 3, 2(3) + 1 = 7
In row = 4, 2(4) + 1 = 9
In row = n, 2(n) + 1 = 2n + 1

Question 3.
Write the following statements as expressions
(i) x reduced by 5
Answer:
Given x reduced by 5 = x – 5

(ii) 8 more than twice of k
Answer:
Given 8 more than twice of k = 2k + 8

(iii) Half of y
Answer:
Given Half of y = \(\frac{1}{2}\) of y = \(\frac{y}{2}\)

(iv) One fourth of product of b and c
Answer:
Given One fourth of product of b and c
= \(\frac{1}{4}\) of b × c
= \(\frac{1}{4}\) × bc = \(\frac{b c}{4}\)

(v) One less than three times of p
Answer:
Given One less than three times of p
= 3 times of p – 1
= 3 ∙ p – 1

Question 4.
Write the following expressions as statements :
(i) s + 3
Answer:
Given s + 3 = 3 added to s.

(ii) 3p + 10
Answer:
Given 3p + 10
= 10 more than thrice of p.

(iii) 5c – 8
Answer:
Given 5c – 8 = 8 less than 5 times of c.

(iv) 10z
Answer:
Given 10z = 10 times of z.

(v) \(\frac{b}{9}\)
Answer:
Given \(\frac{b}{9}\) = one nineth of b.

Question 5.
Write the following situations into algebraic expressions :
(i) Cost of one pen is double the cost of pencil.
Answer:
Let the cost of pencil = ₹x
then the cost of pen = double the cost of pencil = 2 × ₹ x
∴ The cost of pen = ₹ 2x

(ii) Age of John is 10 more than age of Yusuf.
Answer:
Let the age of Yusuf = a years
then the age of John = (a + 10) years

(iii) Height of Siri is 15 cm less than height of Giri.
Answer:
Let the height of Giri = x cm
then the height of Siri = (x – 15) cm

(iv) Length of a rectangle is 2 more than three times of it’s breadth.
Answer:
Let the breadth = b units
then the length of rectangle
= 3 times b + 2
= (3 ∙ b + 2) units.

SCERT AP Board 7th Class Hindi Study Material 4th Lesson हम नन्हें बच्चे Textbook Questions and Answers.

AP State Syllabus 7th Class Hindi 4th Lesson Questions and Answers हम नन्हें बच्चे

7th Class Hindi 4th Lesson हम नन्हें बच्चे Textbook Questions and Answers

सोचिए-बोलिए

प्रश्न 1.
चित्र में क्या-क्या दिखाई दे रहे हैं? (చిత్రంలో ఏమేమి కన్పించుచున్నావి?)
उत्तर:
चित्र में भारत देश के कुछ सैनिक हैं। भारत देश का तिरंगा झंडा एक सैनिक के हाथ में है। सैनिकों के हाथों में बंदूक और सैनिक हिम से ढके पहाड़ों पर खड़े हुए हैं। वे कुछ नारा लगा रहे हैं।
(చిత్రంలో భారతదేశ సైనికులు కొంతమంది ఉన్నారు. భారతదేశ జాతీయ పతాకం మూడు రంగుల జెండా ఒక సైనికుని చేతిలో ఉన్నది. సైనికుల చేతుల్లో తుపాకులు ఉన్నాయి. మరియు సైనికులు మంచు కొండలపై నిలుచుని ఉన్నారు. వారు ఏదేని నినాదం చేస్తున్నారు.)

प्रश्न 2.
सैनिक क्या कर रहे हैं? (సైనికులు ఏమి చేయుచున్నారు?)
उत्तर:
सैनिक मातृभूमि की रक्षा कर रहे हैं।
(సైనికులు మాతృభూమిని రక్షిస్తున్నారు.)

कविता

1. हम नन्हें – नन्हें बच्चे हैं, మేము చిన్న చిన్న పిల్లలం.
नादान, उमर के कच्चे हैं, అమాయకులం, తక్కువ వయస్సు ఉన్నవాళ్ళం,
पर अपनी धुन के सच्चे हैं। కానీ మా సంకల్పానికి నిజమైన వారము.
जननी की जय-जय गाएँगे, జన్మభూమికి జయజయలు పాడుతాం,
भारत की ध्वजा फहराएँगे। భారతదేశ పతాకం ఎగురవేస్తాం.

2. अपना पथ कभी न छोडेंगे, మా దారిని ఎప్పుడూ విడవం,
अपना प्रण कभी न तोड़ेंगे, మా ప్రతిభ ఎప్పటికీ వదలం,
हिम्मत से नाता जोड़ेंगे, ధైర్యంతో బంధుత్వం కలుపుతాం,
हम हिमगिरि पर चढ़ जाएँगे, మేము హిమాలయాలను ఎక్కుతాం,
भारत की ध्वजा फहराएँगे। భారతదేశ జెండాను ఎగురవేస్తాం.

3. हम भय से कभी न डोलेंगे, మేము భయంతో ఎప్పుడూ ఊగిసలాడం,
अपनी ताकत को तोलेंगे, మా శక్తిని నిరూపిస్తాం,
जननी की जय – जय बोलेंगे। జన్మభూమికి జయజయలు పలుకుతాం,
अपना सिर भेंट चढ़ाएँगे, మా ‘తలను’ కానుకగా అర్పిస్తాం,
भारत की ध्वजा फहराएंगे। భారతదేశ జాతీయ జెండాను ఎగురవేస్తాం.

POEM

1. हम नन्हें – नन्हें बच्चे हैं, We are children,
नादान, उमर के कच्चे हैं, We are innocent, we are kids,
पर अपनी धुन के सच्चे हैं। But we are true to our will.
जननी की जय-जय गाएँगे, We sing songs of praise of the motherland,
भारत की ध्वजा फहराएँगे। We hoist the Indian flag.

2. अपना पथ कभी न छोडेंगे, We never leave our path,
अपना प्रण कभी न तोड़ेंगे, We never forsake our talent,
हिम्मत से नाता जोड़ेंगे, We establish relationship with courage,
हम हिमगिरि पर चढ़ जाएँगे, We climb the Himalayas,
भारत की ध्वजा फहराएँगे We hoist the Indian flag.

3. हम भय से कभी न डोलेंगे, We never oscillate with fear,
अपनी ताकत को तोलेंगे, We prove our power,
जननी की जय – जय बोलेंगे। We sing songs of praise of the motherland,
अपना सिर भेंट चढ़ाएँगे, We offer our head as a gift,
भारत की ध्वजा फहराएंगे। We hoist the Indian flag.

Intext Questions & Answers

प्रश्न 1.
बच्चों में कौन – कौन से गुण होते हैं? (పిల్లలలో ఎలాంటి గుణాలు ఉంటాయి?)
उत्तर:
बच्चे नादान होते हैं, उमर के कच्चे होते हैं। छोटे – छोटे होते हैं। और धुन के सच्चे होते हैं।
(పిల్లలు అమాయకంగా ఉంటారు. తక్కువ వయస్సు కలవారై ఉంటారు. చిన్న చిన్న వారై ఉంటారు మరియు నిజమైన సంకల్పం కలిగినవారై ఉంటారు.)

प्रश्न 2.
शहीद किसे कहते हैं? (శహీద్ అని ఎవరిని అంటారు?)
उत्तर:
देश के लिए जो अपने प्राणों को खो देते हैं उन्हें शहीद कहते हैं।
(దేశం కొరకు తమ ప్రాణాలను ఎవరైతే అర్పిస్తారో వారిని శహీద్ అని అందురు. )

Improve Your Learning

सुनिए-बोलिए

प्रश्न 1.
बच्चे कैसे होते हैं? (పిల్లలు ఎలా ఉంటారు?)
उत्तर:
बच्चे नन्हें, नादान और उमर के कच्चे होते हैं।
(పిల్లలు చిన్నవారు, అమాయకులు, వయస్సులో చిన్నవారుగను ఉందురు.)

प्रश्न 2.
बच्चे क्या तोडना नहीं चाहते हैं? (పిల్లలు దేనిని తప్పకుడదని కోరుకుంటున్నారు?)
उत्तर:
बच्चे अपना प्रण तोडना नहीं चाहते हैं।
(పిల్లలు తమ ప్రతిన తప్పకూడదని కోరుకొనుచుండిరి.)

प्रश्न 3.
बच्चे क्या फहराना चाहते हैं? (పిల్లలు దేనిని ఎగురవేయాలని కోరుచుండిరి?)
उत्तर:
बच्चे भारत ध्वजा (झंडे) को फहराना चाहते हैं।
(పిల్లలు భారతదేశ పతాకం (జెండాను) ఎగురవేయాలని కోరుచుండిరి.)

पढ़िए

अ) जोड़ी बनाइए।

आ) पाठ में वाक्यों के सही क्रम को पहचानकर क्रम संख्या कोष्ठक में लिखिए।

1. हम भय से कभी न डोलेंगे। [ 3 ]
2. जननी की जय – जय गाएँगे। [ 4 ]
3. अपना सिर भेंट चढ़ाएँगे। [ 5 ]
4. नादान, उमर के कच्चे हैं। [ 1 ]
5. अपना प्रण कभी न तोड़ेंगे। [ 2 ]

इ) सही वर्तनी वाले शब्दों पर गोला “O” बनाइए।

ई) चित्रों से संबंधित शब्दों पर गोला “O” बनाइए।

लिखिए

अ) नीचे दिये गये प्रश्नों के उत्तर छोटे – छोटे वाक्यों में लिखिए।
క్రింది ఇవ్వబడిన ప్రశ్నలకు సమాధానములు చిన్న – చిన్న వాక్యములలో ఇవ్వండి.)

1. बच्चे अपनी धुन के कैसे हैं? (పిల్లలు తమ సంకల్పములో ఎటువంటివారు?)
उत्तर:
बच्चे अपनी धुन के सच्चे हैं।
(పిల్లలు తమ సంకల్పములో నిజమైనవారు.)

2. बच्चे किससे नाता जोड़ना चाहते हैं? (పిల్లలు ఎవరితో బంధుత్వం కలుపకోరుచున్నారు?)
उत्तर:
बच्चे हिम्मत से नाता जोडना चाहते हैं।
(పిల్లలు ధైర్యముతో బంధుత్వం కలుపకోరుచున్నారు.)

3. भारत की शान कब बढ़ेगी?(భారతదేశ ప్రతిష్ఠ ఎప్పుడు పెరుగును?)
उत्तर:
बच्चे धैर्य से रहकर ताकत दिखाकर देश की रक्षा में अपने प्राणों को अर्पण करने पर भारत की शान बढेगी।
(పిల్లలు ధైర్యముతో నుండి తమ శక్తిని చూపించి దేశ రక్షణలో తమ ప్రాణాలను అర్పించిన భారతదేశ ప్రతిష్ఠ పెరుగును.)

आ) नीचे दिये गये प्रश्न का उत्तर पाँच – छह वाक्यों में लिखिए।
(క్రింది ఇవ్వబడిన ప్రశ్నకు సమాధానము చిన్న – చిన్న వాక్యములలో ఇవ్వండి.)

→ “हम नन्हें बच्चे” – कविता का सारांश लिखिए। (‘మేము చిన్న పిల్లలం’ కవిత సారాంశమును వ్రాయండి.)
उत्तर:
कवि कहते हैं कि – हम छोटे बच्चे हैं। हम नादान हैं। हम कम उम्र के हैं। हम सच बोलते हैं। हम भारतमाता की जय गाते हैं। हम भारत का झंडा फहराते हैं। हम अच्छे रास्ते पर चलते हैं। हम अपना वादा नहीं तोड़ते हैं। हम धैर्य से रहते हैं। हम कभी नहीं डरते हैं। जरूरत पड़ने पर हम अपनी ताकत
दिखाते हैं।
(మేము చిన్న పిల్లలం. మేము అమాయకులం. మేము తక్కువ వయస్సు కలవాళ్ళం. మేము నిజము మాట్లాడతాము. మేము భారతమాతకు జయగీతం పాడతాం. మేము భారతదేశ జెండా ఎగురువేస్తాం. మేము మంచి దారిలో నడుస్తాం. మేము ప్రతిజ్ఞను విడనాడం. మేము ధైర్యంతో ఉంటాం. మేము ఎప్పటికీ భయపడం. అవసరం వచ్చినప్పుడు మేము మా శక్తిని ప్రదర్శిస్తాము.)

इ) उचित शब्दों से खाली जगह भरिए।

1. बच्चे नादान उम्र के कच्चे होते हैं। (कच्चे / सच्चे)
उत्तर:
कच्चे

2. वे अपना ……… कभी न तोडेंगे। (प्रण | वन)
उत्तर:
प्रण

3. सब मिलकर भारत की …….. उड़ाएँगे। (ध्वजा / धुन)
उत्तर:
ध्वजा

4. बच्चे …….. से नाता जोड़ेंगे। (हिम्मत / हिमगिरि)
उत्तर:
हिम्मत

5. बालक अपनी …… को तोलेंगे। (ताकत / उमर)
उत्तर:
ताकत

ई) संकेतों के आधार पर शब्द बनाइए।

उ) वर्ण विच्छेद कीजिए।

1. बच्चे : ब् + अ + च् + च् + ए
2. नन्हें : …………………………
उत्तर:
न् + अ + न् + इ + एं

3. धुन : …………………………
उत्तर:
ध् + उ + न् + अ

4. ध्वजा : …………………………
उत्तर:
ध् + व् + अ + ज् + आ

5. ताकत : …………………………
उत्तर:
त् + आ + क् + अ + त् + अ

भाषांश

अ) अंत्याक्षरी विधि के अनुसार नीचे दिये गये शब्दों के आधार पर चार शब्द बनाइए।

उत्तर:

आ) पर्यायवाची शब्द लिखिए।
1. रास्ता : राह, पथ
2. ताकत : …………………………………
3. जननी : …………………………………
4. प्रण : …………………………………
5. ध्वजा : …………………………………
उत्तर:
1. रास्ता : राह, पथ
2. ताकत : शक्ति, बल
3. जननी : माँ, माता
4. प्रण : प्रतिज्ञा, संकल्प
5. ध्वजा : झंडा, पताका

सृजनात्मकता

अ) चित्र देखकर दो शब्द लिखिए।

उत्तर:
मोर, पंख

आ) परियोजना कार्य :

→ देशभक्ति से संबंधित दो नारे लिखकर कक्षा में दिखाइए।
(దేశభక్తికి సంబంధించిన రెండు నినాదములు వ్రాసి తరగతిలో చూపించండి.)
उत्तर:
1. “भारत माता की जय।”
2. “जय हिंद”।
3. “जन गण – मन अधिनायक जय है’।

इ) अनुवाद कीजिए।

1. झंडा राष्ट्र की शान है।
उत्तर:
झंडा राष्ट्र की शान है। జెండా దేశ ప్రతిష్ఠ.

2. मैं भारत का नागरिक हूँ।
उत्तर:
मैं भारत का नागरिक हूँ। నేను భారతదేశ పౌరుడను.

3. हिमालय ऊँचा पर्वत है।
उत्तर:
हिमालय ऊँचा पर्वत है। హిమాలయము ఎత్తైన పర్వతము.

4. बच्चे खेलना पसंद करते हैं।
उत्तर:
बच्चे खेलना पसंद करते हैं। పిల్లలు ఆడడం ఇష్టపడెదరు.

5. हम सब गीत गाते हैं।
उत्तर:
हम सब गीत गाते हैं। మేమందరము పాటలు పాడుతాము.

व्याकरणांश

अ) नीचे दिये गये संकेतों के आधार पर शब्द लिखिए।
उत्तर:
प्रताप, प्रयोग, प्रकाश
सूर्य, आर्य, कार्य

आ) नीचे दिए गए वाक्यों में से “रेफ” शब्दों के नीचे रेखांकित कीजिए।

1. हमारे झंडे के बीच में अशोक चक्र है।
उत्तर:
हमारे झंडे के बीच में अशोक चक्र है।

2. सुरेश ड्रामा देखने गया।
उत्तर:
सुरेश ड्रामा देखने गया।

3. सूर्य की किरणें तेज़ होती हैं।
उत्तर:
सूर्य की किरणें तेज़ होती हैं।

4. चंद्र को चाँद भी कहते है।
उत्तर:
चंद्र को चाँद भी कहते हैं।

5. कर्ण को दान कर्ण कहते हैं।
उत्तर:
कर्ण को दान कर्ण कहते हैं।

अध्यापकों के लिए सूचना : ఉపాధ్యాయులకు సూచన :

→ सोहनलाल द्विवेदी जी के द्वारा लिखित देशभक्ति से संबंधित कविता को गाकर सुनाइए।
(సోహలాల్ ద్వివేదీ గారి ద్వారా రచించబడిన దేశభక్తికి సంబంధించిన కవిత పాడి వినిపించండి.)
उत्तर:
(मेरा देश)

ऊँचा खड़ा हिमालय आकाश चूमता है।
नीचे पखार पग तल, नित सिंधू झूमता है
गंगा पवित्र यमुना, नदियाँ लहर रही हैं।
पल – पल नई छटाएँ पग – पग छहर रही हैं।

वह पुण्य भूमि मेरी
वह जन्म भूमि मेरी
वह स्वर्ण भूमि मेरी
वह मात्रु भूमि मेरी

झरने अनेक झरते, जिसकी पहाड़ियों में
चिड़ियाँ चहक रही है, हो मस्त झाड़ियों में
अमराइयाँ घनी हैं, कोयल पुकारती है।
बहती मलय पवन है, तन – मन सँवारती है।

वह धर्म भूमि मेरी
वह कर्म भूमि मेरी,
वह जन्म भूमि मेरी
वह मात्रु भूमि मेरी।

जन्म जहाँ ये रघुपति, जन्मी जहाँ थी सीता,
श्रीकृष्ण ने सुनाई वंशी पुनीत गीता,
गौतम ने जन्म लेकर, जिसका सुयश बढ़ाया
जग को दया दिखाई, जग को दिया दिखाया।

वह युद्ध भूमि मेरी
वह बुद्ध भूमि मेरी
वह जन्म भूमि मेरी
वह मात्रुभूमि मेरी। – सोहनलाल द्विवेदी

पाठ का सारांश

कवि कहते हैं कि – हम छोटे बच्चे हैं। हम नादान हैं। हम कम उम्र के हैं। हम सच बोलते हैं। हम भारतमाता की जय गाते हैं। हम भारत का झंडा फहराते हैं। हम अच्छे रास्ते पर चलते हैं। हम अपना वादा नहीं तोड़ते हैं। हम धेर्य से रहते हैं। हम कभी नहीं डरते हैं। ज़रूरत पड़ने पर हम अपनी ताकत दिखाते हैं।

పాఠ్య సారాంతం

మేము చిన్న పిల్లలం. మేము అమాయకులం. మేము తక్కువ వయస్సు కలవాళ్ళం. మేము నిజము మాట్లాడతాము. మేము భారతమాతకు జయగీతం పాడతాం. మేము భారతదేశ జెండా ఎగురవేస్తాం. మేము మంచి దారిలో నడుస్తాం. మేము ప్రతిజ్ఞను విడనాడం. మేము ధైర్యంతో ఉంటాం. మేము ఎప్పటికీ భయపడం. అవసరం వచ్చినప్పుడు మేము మా శక్తిని ప్రదర్శిస్తాము.

Summary

We are children. We are innocent. We are youngers. We speak truth. We sing songs of praise for the Mother India. We hoist the Indian flag. We follow the good path. We do not break the vow. We will be courageous. We will ever be fearless. In times of needs we will show our power.

व्याकरणांश (వ్యాకరణాంశాలు)

लिंग बदलिए (లింగములను మార్చండి)

बच्चा – बच्ची
सेवक – सेविका
नर्तक – नर्तकी
नायक – नायकी
युवक – युवती
माँ – बाप
सिंह – सिंहनी
ऋषि – ऋषि पत्नी
सखा – सखी

वचन बदलिए (వచనములను మార్చండి)

जवान – जवान
कर्तव्य – कर्तव्य
कविताएँ – कविता
बच्चा – बच्चे
जननी – जननी
पथ – पथ

विलोम शब्द (వ్యతిరేక పదములు)

रक्षा × नाश
देश × विदेश
जय × अपजय/पराजय
छोडना × पकडना
भय × निर्भय
छोटे × बड़े
अच्छे × बुरे
डर × निडर
धैर्य × अधैर्य

शब्दार्थ (అర్థాలు) (Meanings)

उम्र = आयु, వయస్సు, age
धुन = लगन, లీనమగుట, determined
ताकत = शक्ति, శక్తి, strength, power
नाता = संबंध, సంబంధము, relationship
पथ = मार्ग, దారి, way
शान = प्रतिष्ठा, వైభవం, grandeur
प्रण = वादा, ప్రతిజ్ఞ, vow
हिम्मत = धैर्य, ధైర్యము, couarge
ध्वजा = झंडा, జెండా, flag.
नन्हें = छोटे, చిన్న, small
नादान = नासमझ, ఏమీ తెలియని, senseless
जननी = माँ, తల్లి, mother
हिमगिरि = हिमालय पहाड, హిమాలయ పర్వతములు, Himalayas
भय = डर, భయము, fear
सिर = सर, తల, head
भेंट = उपहार, కానుక, gift

श्रुत लेख : శ్రుతలేఖనము : Dietations

अध्यापक या अध्यापिका निम्न लिखित शब्दों को श्रुत लेख के रूप में लिखवायें। छात्र अपनी – अपनी नोट पुस्तकों में लिखेंगे। अध्यापक या अध्यापिका इन्हें जाँचे।
ఉపాధ్యాయుడు లేదా ఉపాధ్యాయిని క్రింద వ్రాయబడిన శబ్దములను శ్రుతలేఖనంగా డిట్ చేయును. విద్యార్థులు వారి వారి నోట్ పుస్తకాలలో వ్రాసెదరు. ఉపాధ్యాయుడు లేదా ఉపాధ్యాయిని వాటిని దిద్దెదరు.