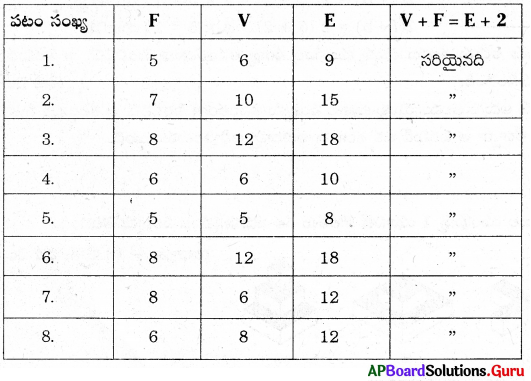
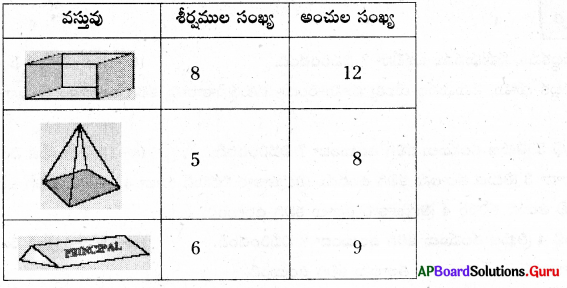
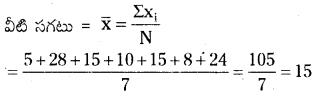AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Ex 14.2 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం Exercise 14.2
ప్రశ్న 1.
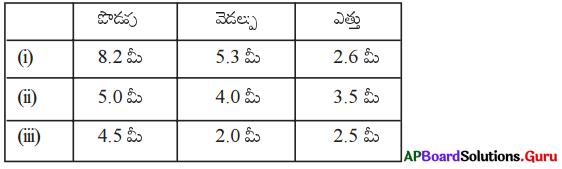
ఈ క్రింది కొలతలు కలిగిన దీర్ఘఘనము యొక్క ఘనపరిమాణమును కనుగొనుము.
సాధన.
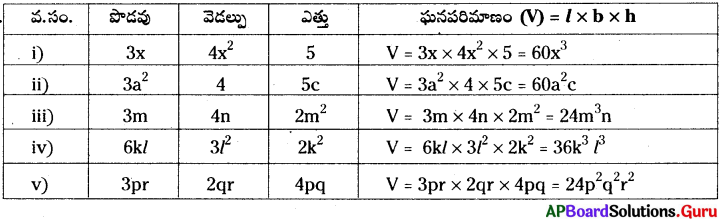
| పొడవు | వెడల్పు | ఎత్తు | ఘనపరిమాణము (V) = lbh |
| 1. 8.2 మీ | 5.3 మీ | 2.6 మీ | V = 8.2 × 5.3 × 2.6 = 112.99 ఘ.మీ. |
| 2. 5.0 మీ | 4.0 మీ | 3.5 మీ | V = 5 × 4 × 3.5 = 70 ఘ.మీ. |
| 3. 4.5 మీ | 2.0 మీ | 2.5 మీ | V = 4.5 × 2 × 2.5 = 22.5 ఘ.మీ. |
![]()
ప్రశ్న 2.
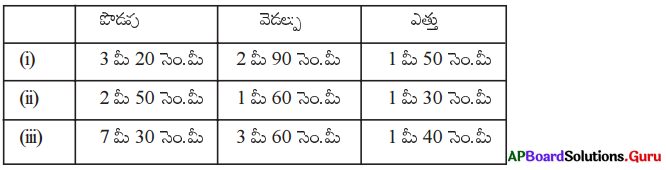
ఈ క్రింది కొలతలు కలిగిన బ్యాంకు యొక్క సామర్థ్యమును ఘనపు మీటర్లు మరియు లీటర్లలో కనుగొనుము.
సాధన.
| పొడవు | వెడల్పు | ఎత్తు | ఘనపరిమాణము (V) = lbh |
| 1. 3 మీ 20 సెం.మీ. | 2 మీ 90 సెం.మీ. | 1 మీ 50 సెం.మీ. | V = 3.20 × 2.90 × 1.50 = 13.92 ఘ.మీ. = 13.92 × 1000 = 13920 లీ |
| 2. 2 మీ 50 సెం.మీ. | 1 మీ 60 సెం.మీ. | 1 మీ 30 సెం.మీ. | V = 2.5 × 1.6 × 1.3 = 5.2 ఘ.మీ. = 5.2 × 1000 = 5200 లీ |
| 3. 7 మీ 30 సెం.మీ. | 3 మీ 60 సెం.మీ. | 1 మీ 40 సెం.మీ. | V = 7.3 × 3.6 × 1.4 = 36.792 ఘ.మీ. = 36.792 × 1000 = 36792 లీ |
ప్రశ్న 3.
ఒక సమఘనము యొక్క భుజమును సగము చేస్తే దాని ఘనపరిమాణము తగ్గుతుందా ? మారినచో ఎంత తగ్గును?
సాధన.
సమఘనం యొక్క భుజం (s) = a యూ. అనుకొనుము సమఘనం యొక్క ఘన పరిమాణం
(V1) = (s)3 = a × a × a = a3
భుజాన్ని సగం చేయగా, 5 – 2
∴ సమఘనం యొక్క ఘనపరిమాణం
V2 = (s)3 = (\(\frac {a}{2}\))3 = \(\frac {a3}{8}\)
V2 = \(\frac {V}{8}\) లీక V1 = 8V2
∴ సమఘనం యొక్క ముజాన్ని సగం చేయగా దాని ఘనపరిమాణం ఆసలు ఘనపరిమాణంలో \(\frac {1}{8}\) వ వంతు తగ్గును.
![]()
ప్రశ్న 4.
ఈ క్రింది కొలతలు భుజంగా కలిగిన సమఘనముల యొక్క ఘనపరిమాణము కనుక్కోండి.
(i) 6.4 సెం.మీ. (ii) 1.3 మీ. (iii) 1.6 మీ.
సాధన.
సమఘన ఘనపరిమాణం (V) = a3
| భుజం | సమఘనం ఘనపరిమాణం (V) = a3 |
| 1. a = 6.4 సెం.మీ. | V = (6.4)3; = 6.4 × 6.4 × 6.4 = 262.144 ఘ. సెం.మీ. |
| 2. a = 1.3 సెం.మీ. | V = (1.3)3; = 1.3 × 1.3 × 1.3 = 2.197 ఘ. మీ. |
| 3. a = 1.6 సెం.మీ. | V = (1.6)3; = 1.6 × 1.6 × 1.6 = 4.096 ఘ. మీ. |
ప్రశ్న 5.
8 మీ. × 22.5 సెం.మీ. × 6 మీ. కొలతలుగా గల ఒక గోడను నిర్మించుటకు 25 సెం.మీ. × 11.25 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల ఇటుకలెన్ని అవసరము?
సాధన.
8 మీ. × 22.5 సెం.మీ. × 6 మీ కొలతలు గల గోడ ఘనపరిమాణం (V1) = l1 b1 h1
= 8మీ × 22.5 సెం.మీ. × 6 మీ
= 800 × 22.5 × 600 సెం.మీ.
25 సెం.మీ. × 11.25 సెం.మీ. × 6 సెం.మీ.లు కొలతలుగా గల ఇటుక ఘనపరిమాణం (V2) = l2 b2 h2
= 25 × 11.25 × 6
∴ కావలసిన ఇటుకల సంఖ్య
= \(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{800^{32} \times 22.5^{2} \times 600^{100}}{25_{1} \times 11.25_{1} \times 6_{1}}\)
= 32 × 2 × 100 = 6400
![]()
ప్రశ్న 6.
25 సెం.మీ. పొడవు, 16 సెం.మీ. వెడల్పు మరియు 8 సెం.మీ. ఎత్తు కొలతలుగా గల దీర్ఘమన ఘనపరిమాణము, ప్రతీ భుజము 16 సెం.మీ.గా గల సమఘనము ఘనపరిమాణముతో ఎంత తేడా కలదు?
సాధన.
l = 25 సెం.మీ., b = 15 సెం.మీ., h = 8 సెం.మీ.
∴ దీర్ఘఘనం యొక్క ఘనపరిమాణం (V1) = lbh
⇒ V1 = 25 × 15 × 8 = 3000 సెం.మీ.
సమఘనం యొక్క ఘనపరిమాణం (V2) = s3
⇒ V2 = (16)3 = 16 × 16 × 16 = 4096 ఘ. సెం.మీ.
∴ V2 – V1 = 4096 – 3000 = 1096 ఘ. సెం.మీ.
∴ సమఘనం, దీర్ఘఘనాల పరిమాణాల మధ్య తేడా 1096 ఘ. సెం.మీ. ఉండును.
ప్రశ్న 7.
1సెం.మీ. మందము కలిగిన చెక్కతో 5 సెం.మీ. × 4 సెం.మీ. × 7 సెం.మీ. కొలతలు కలిగిన మూతగల పెట్టెను తయారుచేయడానికి ఎంత ఘనపరిమాణము గల చెక్క అవసరము?
సాధన.
బయటి కొలతలు 5 సెం.మీ. × 4 సెం.మీ × 7 సెం.మీ
గల చెక్క పెట్టి ఘనపరిమాణం V1 = l × b × h
V1 = 5 × 4 × 7
V1 = 140 ఘ. సెం.మీ
లోపలి కొలతలు = l – 2w, b – 2w, h – 2w
= (5 – 2 × 1), (4 – 2 × 1), (7 – 2 × 1)
= (5 – 2), (4 – 2), (7 – 2)
= 3 సెం.మీ., 2 సెం.మీ., 5 సెం.మీ.
∴ 3 సెం.మీ., 2 సెం.మీ., 5 సెం.మీ.లతో ఏర్పడు చెక్క పెట్టె ఘనపరిమాణం
(V2) = (l – 2w) (b – 2w) (h – 2w)
= 3 × 2 × 5
= 30 ఘ, సెం.మీ.
∴ కావలసిన చెక్క పెట్టి తయారుచేయుటకు అవసరమగు చెక్క ఘనపరిమాణం
= V1 – V2 = 140 – 30 = 110 ఘ. సెం.మీ.
ప్రశ్న 8.
20 సెం.మీ. × 18 సెం.మీ. × 16 సెం.మీ. కొలతలుగా గల దీర్ఘఘనం నుండి 4 సెం.మీ. భుజంగా గల ఎన్ని సమఘనములను ఏర్పరచవచ్చు?
సాధన.
20 సెం.మీ. × 18 సెం.మీ. × 16 సెం.మీ.
కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం . V1 = lbh
∴ V1 = 20 × 18 × 16
4 సెం.మీ. భుజంగా గల సమఘన ఘనపరిమాణం
⇒ V2 = (s)3 = 4 × 4 × 4
∴ కావలసిన సమఘనాల సంఖ్య
= \(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{26^{5} \times 18 \times 16}{A \times A \times A}\) = 90
![]()
ప్రశ్న 9.
12 సెం.మీ. × 9 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల దీర్ఘఘనం నుండి 4 సెం.మీ. × 3 సెం.మీ. × 2 సెం.మీ. కొలతలుగా గల దీర్ఘఘనాలను ఎన్నింటిని తయారుచేయవచ్చు?
సాధన.
12 సెం.మీ. × 9 సెం.మీ. × 6 సెం.మీ. కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం
V1 = l1 × b1 × h1 = 12 × 9 × 6
4 సెం.మీ. × 3 సెం.మీ. × 2 సెం.మీ. కొలతలుగా గల దీర్ఘఘన ఘనపరిమాణం
V2 = l2 × b2 × h2 = 4 × 3 × 2
∴ కావలసిన సమఘనాల సంఖ్య
= \(\frac{V_{1}}{V_{2}}=\frac{12^{3} \times 9 \times 6}{A_{1} \times \beta^{\prime} \times 2}\) = 27
ప్రశ్న 10.
దీర్ఘఘనాకృతిలో ఉన్న ఒక పాత్ర 30 సెం.మీ. పొడవు, 25 సెం.మీ. వెడల్పు కలిగియున్నది. దానిలో 4.5 లీటర్ల నీటిని నింపుటకు ఎంత ఎత్తును కలిగి ఉండాలి?
సాధన.
దీర్ఘఘనాకార పాత్ర పొడవు (l) = 30 సెం.మీ.
వెడల్పు (b) = 25 సెం.మీ.
ఎత్తు (h) = ?
దీర్ఘఘనాకార పాత్రలో నీటి పరిమాణం (ఘనపరిమాణం) = 4.5 లీటర్లు
= 4.5 x 1000 ఘ. సెం.మీ.
= 4500 ఘ. సెం.మీ.
∴ l × b × h = 45000
⇒ 30 × 25 × h = 4500
⇒ h = \(\frac {4500}{30 × 25}\)
∴ h = 6 సెం.మీ