Inter 1st Year Maths 1A Addition of Vectors Important Questions

Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Addition of Vectors Important Questions which are most likely to be asked in the exam.

Intermediate 1st Year Maths 1A Addition of Vectors Important Questions

Question 1.
Find unit vector in the direction of vector a = 2i + 3j + k. (Mar. 14)
Solution:
The unit vector in the direction of a vector a is given by \(\hat{a}\) = \(\frac{1}{|a|} a\)
Now |a| = \(\sqrt{2^{2}+3^{2}+1^{2}}\) = \(\sqrt{14}\).
∴ \(\hat{a}\) = \(\frac{1}{\sqrt{14}}\)(2i + 3j + k)
= \(\frac{2}{\sqrt{14}} i\) + \(\frac{3}{\sqrt{14}} \mathrm{j}\) + \(\frac{1}{\sqrt{14}} k\)

Question 2.
Find a vector in the direction of vector a = i – 2j that has magnitude 7 units.
Solution:
The unit vector in the direction of the given vector a is
\(\hat{a}\) = \(\frac{1}{|\mathrm{a}|} \mathrm{a}\) = \(\frac{1}{\sqrt{5}}(i-2 j)\) = \(\frac{1}{\sqrt{5}} \mathrm{i}\) – \(\frac{2}{\sqrt{5}} \mathrm{j}\)
Therefore, the vector having a magnitude equal to 7 and in the direction of a is
7a = 7\(\left(\frac{1}{\sqrt{5}} \mathrm{i}-\frac{2}{\sqrt{5}} \mathrm{j}\right)\) = \(\frac{7}{\sqrt{5}} \mathrm{i}\) – \(\frac{14}{\sqrt{5}} j\)

Question 3.
Find the unit vector in the direction of the sum of the vectors.
a = 2i + 2j – 5k and b = 2i + j + 3k.
Solution:
The sum of the given vectors is
a + b (= c, say) = 4i + 3j – 2k and
|c| = \(\sqrt{4^{2}+3^{2}+(-2)^{2}}\) = \(\sqrt{29}\).
∴ \(\hat{c}\) = \(\frac{a+b}{|a+b|}\) = \(\frac{4 i+3 j-2 k}{\sqrt{29}}\)

Question 4.
Write direction ratios of the vector a = i + j – 2k and hence calculate its direction cosines.
Solution:
Note that direction ratios a, b, c of a vector r = xi + yj + zk are just the respective components x. y and z of the vector. So, for the given vector, we have a = 1, b = 1, c = – 2, Further, if l, m and n the direction cosines of the given vector, then
l = \(\frac{a}{|r|}\) = \(\frac{1}{\sqrt{6}}\), m = \(\frac{b}{|r|}\) = \(\frac{1}{\sqrt{6}}\),
n = \(]\frac{c}{|r|}\) = \(\frac{2}{\sqrt{6}}\) as |r| = \(\sqrt{6}\).
Thus, the direction cosines are
(\(\frac{1}{\sqrt{6}}\), \(\frac{1}{\sqrt{6}}\), \(-\frac{2}{\sqrt{6}}\)).

Question 5.
Consider two points P and Q with position vectors OP = 3a – 2b and OQ = a + b. Find the position vector of a point R which divides the line joining P and Q in the ratio 2 :1,
(i) internally and
(ii) externally.
Solution:
i) The position vector of the point R dividing the join of P and Q internally in the ratio 2 : 1 is
OR = \(\frac{2(a+b)+(3 a-2 b)}{2+1}\) = \(\frac{5 a}{3}\)

ii) The position vector of the point R dividing the join of P and Q externally in the ratio 2 : 1 is
OR = \(\frac{2(a+b)-(3 a-2 b)}{2-1}\) = 4b – a.

Question 6.
Show that the points A (2i – j + k), B(i – 3j – 5k), C(3i – 4j – 4k) are the vertices of a right angled triangle.
Solution:
We have AB = (1 – 2)i + (-3 + 1)j + (-5 – 1)
k = -i – 2j – 6k
BC = (3 – 1)i + (-4 + 3)j + (-4 + 5)k
= 2i – j + k. and CA = (2 – 3)i + (-1 + 4)j + (1 +4)k = -i + 3j + 5k.
we have |AB|² = |BC|² + |CA|².

Question 7.
Let A. B, C, D be four points with position vectors \(\overline{\mathbf{a}}\) + 2\(\overline{\mathbf{b}}\), 2\(\overline{\mathbf{a}}\) – \(\overline{\mathbf{b}}\), \(\overline{\mathbf{a}}\) and 3\(\overline{\mathbf{a}}\) + \(\overline{\mathbf{b}}\) respectively. Express the vectors \(\overline{\mathbf{A C}}\), \(\overline{\mathbf{D A}}\), \(\overline{\mathbf{B A}}\) and \(\overline{\mathbf{B C}}\) interms of \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\).
Solution:
The position vectors of A, B, C, D with respect to the origin O are

Question 8.
Let ABCDEF be a regular hexagon with centre O. Show that \(\overline{\mathbf{A B}}\) + \(\overline{\mathbf{A C}}\) + \(\overline{\mathbf{A D}}\) + \(\overline{\mathbf{A E}}\) + \(\overline{\mathbf{A F}}\) = 3\(\overline{\mathbf{A D}}\) = 6\(\overline{\mathbf{A O}}\) (Mar. ’16, ’15)
Solution:
Let ABCDEF be a regular hexagon with centre O.
Then \(\overline{\mathbf{A B}}\) = \(\overline{\mathbf{B C}}\) = \(\overline{\mathbf{C D}}\) = \(\overline{\mathbf{D E}}\) = \(\overline{\mathbf{E F}}\) = \(\overline{\mathbf{F A}}\)

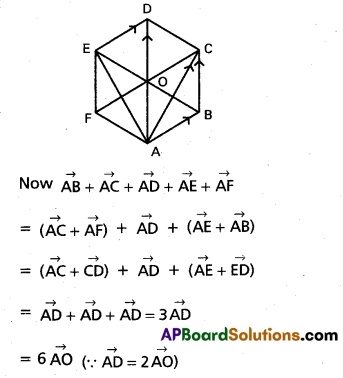
Question 9.
In ΔABC, If \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) are position vectors of the vertices A, B and C respectively, then prove that the position vector of the centroid G is \(\frac{1}{3}(\bar{a}+\bar{b}+\bar{c})\).
Solution:
Let G be the centroid of ΔABC and AD is the median through the vector A.
Then AG : GD = 2 : 1. Let ‘O’ be the origin \(\overline{\mathrm{OA}}\) = \(\bar{a}\), \(\overline{\mathrm{OB}}\) = \(\bar{b}\), \(\overline{\mathrm{OC}}\) = \(\bar{c}\) ∵ D is Mid point of BC, the P.V. of D is \(\overline{O D}\) = \(\frac{1}{2}(\bar{b}+\bar{c})\)

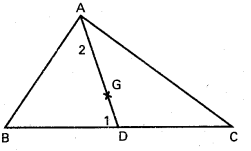
G divides the median AD in the ratio 2 : 1
∴ The P.V. of G is

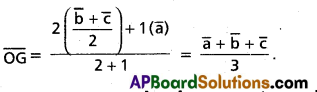
Question 10.
In ΔABC, if ‘O’ is the circum centre and H is the orthocentre, then show that
i) \(\overline{O A}\) + \(\overline{O B}\) + \(\overline{O C}\) = \(\overline{O H}\)
ii) \(\overline{H A}\) + \(\overline{H B}\) + \(\overline{H C}\) = 2\(\overline{H O}\)
Solution:
Let D be the midpoint of BC

i) Take’O’as the origin, let \(\overline{O A}\) = \(\bar{a}\) \(\overline{O B}\) = \(\bar{b}\) and \(\overline{O C}\) = \(\bar{c}\)

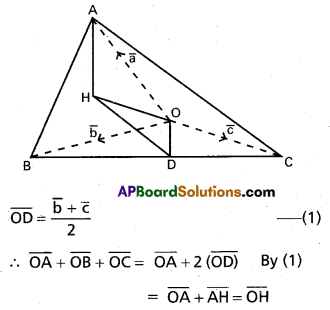
(∵ AH =2 R cos A, OD = R cos A, R is the circum radius of Δ ABC and hence AH = 2 (OD))

ii) \(\overline{\mathrm{HA}}\) + \(\overline{\mathrm{HB}}\) + \(\overline{\mathrm{HC}}\) = \(\overline{\mathrm{HA}}\) +2\(\overline{\mathrm{HD}}\)
= \(\overline{\mathrm{HA}}\) + 2(\(\overline{\mathrm{HO}}\) + \(\overline{\mathrm{OD}}\))
= \(\overline{\mathrm{HA}}\) + 2\(\overline{\mathrm{HO}}\) + 2\(\overline{\mathrm{OD}}\)
= \(\overline{\mathrm{HA}}\) + 2\(\overline{\mathrm{HO}}\) + \(\overline{\mathrm{AH}}\) = 2\(\overline{\mathrm{HO}}\)

Question 11.
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) be the position vectors of A, B,C and D respectively which are the vertices of a tetrahedron. Then Prove that the lines joining the vertices to the centroids of the opposite faces are concurrent (this point is called the centroid or the centre of the tetrahe dron)
Solution:
Let ‘O’ be the origin of reference
Let G₁, G₂, G₃ and G₄ be the centroids of ΔBCD, ΔCAD, ΔABD and ΔABC, respectively then OG₁ = \(\frac{\overline{\mathrm{b}}+\overline{\mathrm{c}}+\overline{\mathrm{d}}}{3}\)

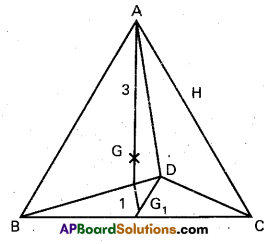
Consider the point P that divides AG₁ in the ratio 3 : 1

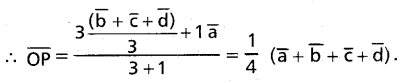
Similarly we can show that the P.vs. of the points dividing BG₂, CG₃ and DG₄ in the ratio 3 : 1 are equal to \(\frac{1}{4}\) (\(\overline{\mathrm{a}}\) + \(\overline{\mathrm{b}}\) + \(\overline{\mathrm{c}}\) + \(\overline{\mathrm{d}}\)). Therefore P lies on each of AG₁, BG₂, CG₃ and DG₄.

Question 12.
Let OABC be a parallelogram and D the mid point of OA. Prove that the segment CD trisects the diagonal OB and is trisected by the diagonal OB.
Solution:
Let \(\overline{\mathrm{OA}}\) = \(\bar{a}\), \(\overline{\mathrm{OC}}\) = \(\bar{b}\), So that
\(\overline{\mathrm{OB}}\) = \(\bar{a}\) + \(\bar{b}\), \(\overline{\mathrm{OD}}\) = \(\frac{1}{2}\)(\(\bar{a}\))

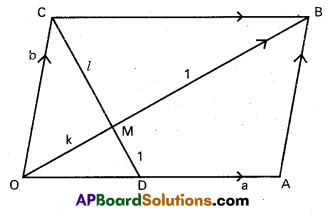
Let M be the intersection of OB and CD.
Let OM : MB = k : 1 and CM : MD = l : 1

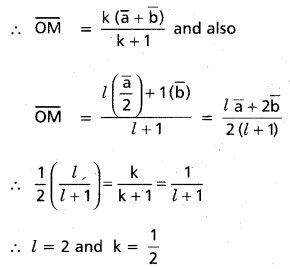
∴ l = 2 and k = \(\frac{1}{2}\)
∴ CD trisects OB and OB trisects CD

Question 13.
Let \(\bar{a}\), \(\bar{b}\) be non – collinear vectors, if \(\bar{\alpha}\) = (x + 4y)\(\bar{a}\) + (2x + y + 1)\(\bar{b}\) and \(\bar{\beta}\) = (y – 2x + 2)\(\bar{a}\) + (2x – 3y – 1)\(\bar{b}\) are such that 3\(\bar{\alpha}\) = \(\bar{\beta}\), then find x andy.
Solution:
Given 3\(\bar{\alpha}\) = 2\(\bar{\beta}\)
⇒ 3(x + 4y)\(\bar{a}\) + 3(2x + y + 1)\(\bar{b}\) = 2(y – 2x + 2)\(\bar{a}\) + 2(2x – 3y – 1)\(\bar{b}\)
On comparing the coeffs. of \(\bar{a}\) and \(\bar{b}\), we get
3x + 12y = 2y – 4x + 4 ⇒ 7x + 10y = 4 ——–— (1)
and 6x + 3y + 3 = 4x – 6y – 2 ⇒
2x + 9y = -5 ——–—(2)
Solve (1) and (2), we get
x = 2 and y = -1

Question 14.
Show that the points whose position vectors are
-2\(\bar{a}\) + 3\(\bar{b}\) + 5\(\bar{c}\), \(\bar{a}\) + 2\(\bar{b}\) + 3\(\bar{c}\), 7\(\overline{\mathrm{a}}\) + \(\overline{\mathrm{c}}\) are non – collinear when \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are non – coplanar vectors.
Solution:
Let O be the origin and let P, Q, R be the P.Vs. of the given points

⇒ The points P, Q, R are collinear.

Question 15.
If the points whose position vectors are 3\(\bar{i}\) – 2\(\bar{j}\) – \(\bar{k}\), 2\(\bar{i}\) + 3\(\bar{j}\) – 4\(\bar{k}\), –\(\bar{i}\) + \(\bar{j}\) + 2\(\bar{k}\) and 4\(\bar{i}\) + 5\(\bar{j}\) + λ\(\bar{k}\) are coplanar, then show that λ = \(\frac{-146}{7}\)
Solution:
Let ‘O’ be the origin and Let A, B, C and D be the given points. Then

Equating the corresponding coeffs.
-x – 4y = 1, 5x + 3y = 7, -3x + 3y = λ + 1
Solving x + 4y + 1 = 0 and 5x + 3y – 7 = 0

Question 16.
In the two dimensional plane, Prove by using vector methods, the equation of the line whose intercepts on the
axes are ‘a’ and ’b’ is \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1.
Solution:
Let A = (a, 0), B = (0, b)
∴ A = a\(\overline{\mathbf{i}}\), B = b\(\overline{\mathbf{j}}\)
The equation of the line is
\(\overline{\mathbf{r}}\) = (1 – t)a\(\overline{\mathbf{i}}\) + t(b\(\overline{\mathbf{j}}\))
If \(\overline{\mathbf{r}}\) = x\(\overline{\mathbf{i}}\) + y\(\overline{\mathbf{j}}\), then x = (1 – t)a and y = t b
By eliminating ‘t’
x = \(\left(1-\frac{y}{b}\right) a\)
⇒ \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1

Question 17.
Using the vector equation of the straight line passing through two points, prove that the points whose position vectors are \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and (3\(\overline{\mathbf{a}}\) – 2\(\overline{\mathbf{b}}\)) are collinear.
Solution:
The vector equation of the st. line passing through two pt.s \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\) is
\(\overline{\mathbf{r}}\) = (1 – t) \(\overline{\mathbf{a}}\) + t\(\overline{\mathbf{b}}\) ; for some t ∈ R
This line also passes through the pt. which
P.v. is 3\(\overline{\mathbf{a}}\) – 2\(\overline{\mathbf{b}}\) then
3\(\overline{\mathbf{a}}\) – 2\(\overline{\mathbf{b}}\) = (1 – t)\(\overline{\mathbf{a}}\) + t\(\overline{\mathbf{b}}\)
Equating the corresponding coeffs,
1 – t = 3 and t = -2
∴ The three given points are collinear.

Question 18.
Find the equation of the line parallel to the vector 2\(\overline{\mathbf{i}}\) – \(\overline{\mathbf{j}}\) + 2\(\overline{\mathbf{k}}\) and which passes through the point A whose position vector is 3\(\overline{\mathbf{i}}\) + \(\overline{\mathbf{j}}\) – \(\overline{\mathbf{k}}\). If P is a point on this line such that AP = 15, find the position vector of R
Solution:
The vector equation of the line passing through the point A whose P.v is

Question 19.
Show that the line joining the pair of points 6\(\overline{\mathbf{a}}\) – 4\(\overline{\mathbf{b}}\) + 4\(\overline{\mathbf{c}}\) and the line joining the pair of points –\(\overline{\mathbf{a}}\) – 2\(\overline{\mathbf{b}}\) – 3\(\overline{\mathbf{c}}\), \(\overline{\mathbf{a}}\) + 2\(\overline{\mathbf{b}}\) – 5\(\overline{\mathbf{c}}\) intersect at the point -4\(\overline{\mathbf{c}}\) when \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) are non-coplanar vectors. (T.S) (Mar. ’16)
Solution:
The vector equation o+ the-line joining the pair of points \(\bar{q}\) = 6\(\bar{a}\) – 4\(\bar{b}\) + 4\(\bar{c}\), and \(\bar{p}\) = -4\(\bar{c}\) is \(\bar{r}\) = (1 – t)\(\bar{p}\) + t\(\bar{q}\) for t ∈ R

Let \(\bar{r}\) be the point of intersection of (1) and (2) then equating the coeffs of \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\), we get
6t = 2s – 1 ⇒ 6t – s = -1 ——- (3)
– 4t = 4s – 2 ⇒ 4t + 4s = 2 —— (4)
-4 + 8t = -2s – 3 ⇒ 8t + 2s = 1 —— (5)
From (3) and (4)

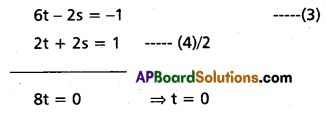
From (1) s = \(\frac{1}{2}\)
Substitute t = 0 and s = \(\frac{1}{2}\) in (5)
8(0) + 2(\(\frac{1}{2}\)) = 1 ⇒ 1 = 1
Hence the lines (1) and (2) point of intersection put t = 0 in (1)
(i.e) \(\bar{r}\) = -4\(\bar{c}\)
∴ The two lines intersect at the point whose P.v. is -4\(\bar{c}\)

Question 20.
Find the point of intersection of the line \(\bar{r}\) = 2\(\bar{a}\) + \(\bar{b}\) + t(\(\bar{b}\) – \(\bar{c}\)) and the plane \(\bar{r}\) = \(\bar{a}\) + x(\(\bar{b}\) + \(\bar{c}\)) + y(\(\bar{a}\) + 2\(\bar{b}\) – \(\bar{c}\)) where \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are non — coplanar vectors.
Solution:
Let \(\bar{r}\) be the P.v. of the point P, the intersection of the line and the plane.
Then
2\(\bar{a}\) + \(\bar{b}\) + t(\(\bar{b}\) – \(\bar{c}\)) = \(\bar{a}\) + x(\(\bar{b}\) + \(\bar{c}\)) + y(\(\bar{a}\) + 2\(\bar{b}\) – \(\bar{c}\))
∵ \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are non – coplanar vectors.
Equation th coeffs. of \(\bar{a}\), \(\bar{b}\), \(\bar{c}\)
2 = 1 + y ⇒ y = 1
1 + t = x + 2y
⇒ 1 + t = x + 2(1)
⇒ t – x = 1 ——— (1)
and -t = x – y
x + t = y
⇒ x + t = 1 ——— (2)
From (1),(2) t = 1, x = 0, y = 1
∴ Point of intersection is
\(\bar{r}\) = 2\(\bar{a}\) + \(\bar{b}\) + 1(\(\bar{b}\) – \(\bar{c}\))
⇒ \(\bar{r}\) = 2\(\bar{a}\) + \(\bar{b}\) + 1(\(\bar{b}\) – \(\bar{c}\))
⇒ \(\bar{r}\) = 2\(\bar{a}\) + 2\(\bar{b}\) – \(\bar{c}\)
∴ P.v. of the point of intersection is 2\(\bar{a}\) + 2\(\bar{b}\) – \(\bar{c}\)