Inter 1st Year Maths 1A Products of Vectors Important Questions

Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Products of Vectors Important Questions which are most likely to be asked in the exam.

Intermediate 1st Year Maths 1A Products of Vectors Important Questions

Question 1.
If \(\bar{a}\) = 6\(\bar{i}\) + 2\(\bar{j}\) + 3\(\bar{k}\) and \(\bar{b}\) = 2\(\bar{i}\) – 9\(\bar{j}\) + 6\(\bar{k}\), then find \(\bar{a}\) . \(\bar{b}\) and the angle between \(\bar{a}\) and \(\bar{b}\).
Solution:

Question 2.
If a = i + 2j – 3k, b = 3i – j + 2k then show that a + b and a – b are perpendicular to each other. (A.P) (Mar. ’15, May ’11)
Solution:
a + b = (1 + 3)i + (2 – 1)j+ (-3 + 2) k
= 4i + j – k
Similarly a – b = – 2i + 3j – 5k
(a + b). (a – b) = 4(-2) + 1(3) + (-1)(-5) = 0
Hence (a + b) and (a – b) are mutually perpendicular.

Question 3.
Let \(\bar{a}\) and \(\bar{b}\) be non- zero, non-collinear vectors. If |\(\bar{a}\) + \(\bar{b}\) | = | \(\bar{a}\) – \(\bar{b}\) |, then find the angle between \(\bar{a}\) and \(\bar{b}\).
Solution:
| \(\bar{a}\) + \(\bar{b}\) |² = | a – b |².
⇒ |\(\bar{a}\)|² + |\(\bar{b}\)|² + 2 (\(\bar{a}\). \(\bar{b}\))
⇒ |\(\bar{a}\)|² + |\(\bar{b}\)|² – 2 (\(\bar{a}\). \(\bar{b}\))
⇒ 4(\(\bar{a}\) . \(\bar{b}\)) = 0 ⇒ \(\bar{a}\) . \(\bar{b}\) = 0
⇒ Angle between \(\bar{a}\) and \(\bar{b}\) is 90°.

Question 4.
If |\(\bar{a}\)| = 11, |\(\bar{b}\)| = 23 and | \(\bar{a}\) – \(\bar{b}\) | = 30, then find the angle between the vectors \(\bar{a}\), \(\bar{b}\) and also find | \(\bar{a}\) + \(\bar{b}\) |.
Solution:
Given that | \(\bar{a}\) | = 11, | \(\bar{b}\) | = 23 and | \(\bar{a}\) – \(\bar{b}\) | = 30, Let (\(\bar{a}\), \(\bar{b}\)) = θ.

Question 5.
If \(\bar{a}\) = \(\bar{i}\) – \(\bar{j}\) – \(\bar{k}\) and \(\bar{b}\) = 2\(\bar{i}\) – 3\(\bar{j}\) + \(\bar{k}\), then find the projection vector of \(\bar{b}\) on \(\bar{a}\) and its magnitude.
Solution:

Question 6.
If P, Q, R and S are points whose position vectors are \(\bar{i}\) – \(\bar{k}\), –\(\bar{i}\) +2\(\bar{j}\), 2\(\bar{i}\) – 3\(\bar{k}\) and 3\(\bar{i}\) – 2\(\bar{j}\) – \(\bar{k}\) respectively, then find the component of \(\overline{\mathbf{R S}}\) on \(\overline{\mathbf{P Q}}\).
Solution:
Let ‘O’ be the origin.
\(\overline{\mathrm{OP}}\) = \(\overline{\mathbf{i}}\) – \(\overline{\mathbf{k}}\), \(\overline{\mathrm{OQ}}\) = –\(\overline{\mathbf{i}}\) + 2\(\overline{\mathbf{j}}\), \(\overline{\mathrm{OR}}\) = 2\(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{k}}\) and \(\overline{\mathrm{OR}}\) = 3\(\overline{\mathbf{i}}\) – 2\(\overline{\mathbf{j}}\) – \(\overline{\mathbf{k}}\)

The component of \(\overline{\mathrm{RS}}\) and \(\overline{\mathrm{PQ}}\)

Question 7.
If the vectors λ\(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) + 5\(\overline{\mathbf{k}}\) and 2 λ\(\overline{\mathbf{i}}\) – λ\(\overline{\mathbf{j}}\) + \(\overline{\mathbf{k}}\) are perpendicular to each other, find λ. (T.S) (Mar. ’16)
Solution:
Since the vectors are perpendicular
⇒ (λ\(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) + 5\(\overline{\mathbf{k}}\)) . (2λ\(\overline{\mathbf{i}}\) – λ\(\overline{\mathbf{j}}\) – \(\overline{\mathbf{k}}\)) = 0
⇒ λ(2λ) + (-3)(-λ) + 5(-1) = 0
⇒ 2λ² + 3λ – 5 = 0
⇒ (2λ + 5)(λ – 1) = 0
∴ λ = 1 (or) \(\frac{-5}{2}\)

Question 8.
Let \(\overline{\mathbf{a}}\) = 2\(\overline{\mathbf{i}}\) + 3\(\overline{\mathbf{j}}\) + \(\overline{\mathbf{k}}\), \(\overline{\mathbf{b}}\) = 4\(\overline{\mathbf{i}}\) + \(\overline{\mathbf{j}}\) and \(\overline{\mathbf{c}}\) = \(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) – 7\(\overline{\mathbf{k}}\). Find the vector \(\overline{\mathbf{r}}\) such that \(\overline{\mathbf{r}}\) . \(\overline{\mathbf{a}}\) = 9, \(\overline{\mathbf{r}}\) . \(\overline{\mathbf{b}}\) = 7 and \(\overline{\mathbf{r}}\) . \(\overline{\mathbf{c}}\) = 6.
Solution:
Let \(\overline{\mathbf{r}}\) = x\(\overline{\mathbf{i}}\) + y\(\overline{\mathbf{j}}\) + z\(\overline{\mathbf{k}}\)
∴ \(\overline{\mathbf{r}}\) . \(\overline{\mathbf{a}}\) = 9 ⇒ 2x + 3y + z = 9
\(\overline{\mathbf{r}}\) . \(\overline{\mathbf{b}}\) = 7 ⇒ 4x + y = 7 and \(\overline{\mathbf{r}}\) . \(\overline{\mathbf{c}}\) = 6 ⇒ x – 3y – 7z = 6
By solving these equations, we get x = 1, y = 3 and z = -2
∴ \(\overline{\mathbf{r}}\) = \(\overline{\mathbf{i}}\) + 3\(\overline{\mathbf{j}}\) – 2\(\overline{\mathbf{k}}\)

Question 9.
Show that the points 2\(\overline{\mathbf{i}}\) – \(\overline{\mathbf{j}}\) + \(\overline{\mathbf{k}}\), \(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) – 5\(\overline{\mathbf{k}}\) and 3\(\overline{\mathbf{i}}\) – 4\(\overline{\mathbf{j}}\) – 4\(\overline{\mathbf{k}}\) are the vertices of a right angle triangle. Also, find the other angles.
Solution:
Let ‘O’ be the origin and A, B, C be the given points, then

Question 10.
Prove that the angle θ between any two diagonals of a cube is given by cos θ = \(\frac{1}{3}\). (May ’11)
Solution:
Let us suppose that the cube is a unit cube

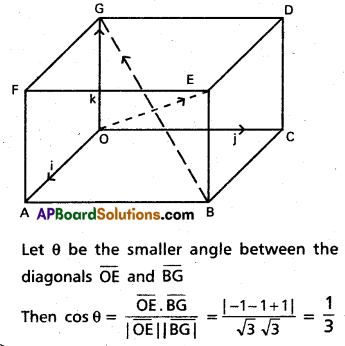
Question 11.
Let \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) be non—zero mutually orthogonal vectors, if x \(\overline{\mathbf{a}}\) + y\(\overline{\mathbf{b}}\) + z = 0, then x = y = z = 0.
Solution:
x\(\overline{\mathbf{a}}\) + y\(\overline{\mathbf{b}}\) + z\(\overline{\mathbf{c}}\) = 0
⇒ \(\overline{\mathbf{a}}\) • (x\(\overline{\mathbf{a}}\) + y\(\overline{\mathbf{b}}\) + z\(\overline{\mathbf{c}}\)) = 0
⇒ x(\(\overline{\mathbf{a}}\) • \(\overline{\mathbf{a}}\)) = 0
⇒ x = 0 (∵ \(\overline{\mathbf{a}}\) • \(\overline{\mathbf{a}}\) ≠ 0)
Similarly y = 0, z = 0.

Question 12.
Let \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) be mutually orthogonal vectors of equal magnitudes. Prove that the vector \(\overline{\mathbf{a}}\) + \(\overline{\mathbf{b}}\) + \(\overline{\mathbf{c}}\) is equally inclined to each of \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\), the angle of inclination being cos^-1\(\left(\frac{1}{\sqrt{3}}\right)\).
Solution:

Similarly, it can be proved that \(\overline{\mathbf{a}}\) + \(\overline{\mathbf{b}}\) + \(\overline{\mathbf{c}}\) inclines at an angle of cos^-1\(\left(\frac{1}{\sqrt{3}}\right)\) with \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\).

Question 13.
The vectors \(\overline{\mathbf{A B}}\) = 3\(\bar{i}\) – 2\(\bar{j}\) + 2\(\bar{k}\) and \(\overline{\mathbf{A D}}\) = \(\bar{i}\) – 2\(\bar{k}\) represent the adjacent sides of a parallelogram ABCD. Find the angle between the diagonals.
Solution:

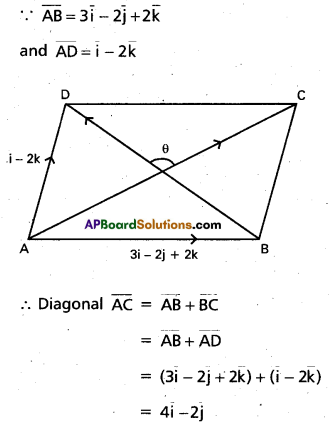
Question 14.
For any two vectors a and b, show that
i) |a • b| (Cauchy – Schwartz inequality)
ii) || a + b | ≤ ||a|| + ||b| (triangle inequality
Solution:
i)
If a = 0 or b = 0, the inequalities hold trivially.

ii)

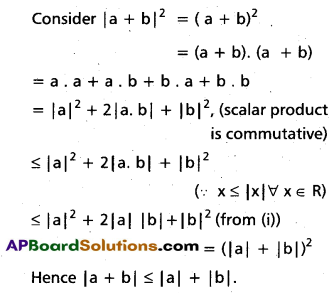
Question 15.
Find the cartesian equation of the plane passing through the point (-2, 1, 3) and perpendicular to the vector 3\(\bar{i}\) + \(\bar{j}\) + 5\(\bar{k}\).
Solution:
Let A = -2\(\bar{i}\) + \(\bar{j}\) + 3\(\bar{k}\) and \(\bar{r}\) = x\(\bar{i}\) + y\(\bar{j}\) + z\(\bar{k}\) be any point in the plane
∴ \(\overline{\mathrm{AP}}\) = (x + 2)\(\bar{i}\) + (y – 1)\(\bar{j}\) + (z – 3)\(\bar{k}\)
∴ \(\overline{\mathrm{AP}}\) is perpendicular to 3\(\bar{i}\) + \(\bar{j}\) + 5\(\bar{k}\)
⇒ (x + 2)3 + (y – 1)1 + (z – 3)5 = 0
⇒ 3x + y + z – 10 = 0

Question 16.
Find the cartesian equation of the plane through the point A (2, -1, -4) and parallel to the plane 4x – 12y – 3z – 7 = 0.
Solution:
The equation of the plane parallel to
4x – 12y – 3z – 7 = 0 be
4x -12y – 3z = p
∴ If passes through the point A(2, -1, -4)
⇒ 4(2) – 12(-1) – 3(-4) = p
⇒ p = 32
∴ The equation of the required plane is
4x – 12y – 3z = 32

Question 17.
Find the angle between the planes 2x – 3y – 6z = 5 and 6x + 2y – 9z = 4.
Solution:
Equation to the planes is 2x – 3y – 6z = 5
⇒ \(\overline{\mathbf{r}}\) .(2\(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) – 6\(\overline{\mathbf{k}}\)) = 5 ———- (1)
and 6x + 2y – 9z = 4 —— (2)
∴ The angle between the planes \(\overline{\mathbf{r}} \cdot \overline{\mathbf{n}}_{1}\) = p, and \(\overline{\mathbf{r}} \cdot \overline{\mathbf{n}}_{2}\) = q is θ, then

Question 18.
Find unit vector orthogonal to the vector 3\(\bar{i}\) + 2\(\bar{j}\) +6\(\bar{k}\) and coplanar with thevectors 2\(\bar{i}\) + \(\bar{j}\) + \(\bar{k}\) and \(\bar{i}\) – \(\bar{j}\) + \(\bar{k}\).
Solution:

⇒ (2x + y)3 + (x – y)2 + (x + y)6 = 0
⇒ 6x + 3y + 2x – 2y + 6x + 6y = 0
⇒ 14x + 7y = 0
⇒ y = -2x —— (1)
∵ |\(\overline{\mathbf{r}}\)| = 1
⇒ (2x + y)² + (x – y)² + (x + y)² = 1
⇒ 4x² + 4xy + 9 + 2(x² + y²) = 1
⇒ 6x² + 4x (-2x) + 3(-2x)² = 1 (By using (1))
⇒ 10x² = 1

Question 19.
If \(\overline{\mathbf{a}}\) = 2\(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) + 5\(\overline{\mathbf{k}}\), \(\overline{\mathbf{b}}\) = –\(\overline{\mathbf{i}}\) + 4\(\overline{\mathbf{j}}\) + 2\(\overline{\mathbf{k}}\), then find \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\) and unit vector perpendicular to both \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\).
Solution:
\(\overline{\mathbf{a}}\) = 2\(\overline{\mathbf{i}}\) – 3\(\overline{\mathbf{j}}\) + 5\(\overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}\) = –\(\overline{\mathbf{i}}\) + 4\(\overline{\mathbf{j}}\) + 2\(\overline{\mathbf{k}}\)

Question 20.
If \(\bar{a}\) = 2\(\bar{i}\) – 3\(\bar{j}\) + 5\(\bar{k}\), \(\bar{b}\) = –\(\bar{i}\) + 4\(\bar{j}\) + 2\(\bar{k}\), then find (\(\bar{a}\) + \(\bar{b}\)) × (\(\bar{a}\) – \(\bar{b}\)) and unit vector perpendicular to both \(\bar{a}\) + \(\bar{b}\) and \(\bar{a}\) – \(\bar{b}\).
Solution:

Question 21.
Find the area of the parallelogram for which the vectors \(\bar{a}\) = 2\(\bar{i}\) – 3\(\bar{j}\) and \(\bar{b}\) = 3\(\bar{i}\) – \(\bar{k}\) are adjacent sides. (Mar. ; May ‘08)
Solution:
The vector area of the given parallelogram

Question 22.
If \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) and \(\overline{\mathbf{d}}\) are vectors such that \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\) = \(\overline{\mathbf{c}}\) × \(\overline{\mathbf{d}}\) and \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{c}}\) = \(\overline{\mathbf{b}}\) × \(\overline{\mathbf{d}}\) then show that the vectors \(\overline{\mathbf{a}}\) – \(\overline{\mathbf{d}}\) and \(\overline{\mathbf{b}}\) – \(\overline{\mathbf{c}}\) are parallel.
Solution:

Question 23.
If \(\overline{\mathbf{a}}\) = \(\overline{\mathbf{i}}\) + 2\(\overline{\mathbf{j}}\) + 3\(\overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}\) = 3\(\overline{\mathbf{i}}\) + 5\(\overline{\mathbf{j}}\) – \(\overline{\mathbf{k}}\) are two sides of a triangle, then find
its area.
Solution:
Area of the triangle = \(\frac{1}{2}|\bar{a} \times \bar{b}|\)

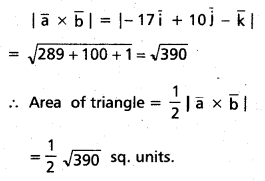
Question 24.
In Δ ABC, if \(\overline{\mathrm{BC}}\) = \(\bar{a}\), \(\overline{\mathrm{CA}}\) = \(\bar{b}\), \(\overline{\mathrm{AB}}\) = \(\bar{c}\) then show that \(\bar{a}\) × \(\bar{b}\) = \(\bar{b}\) × \(\bar{c}\) = \(\bar{c}\) × \(\bar{a}\).
Solution:

Question 25.
Let \(\bar{a}\) = 2\(\bar{i}\) – \(\bar{j}\) + \(\bar{k}\) and \(\bar{b}\) = 3\(\bar{i}\) + 4\(\bar{j}\) – \(\bar{k}\). If θ is the angle between \(\bar{a}\) and \(\bar{b}\) then find sin θ.
Solution:

Question 26.
Let \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\) be such that \(\bar{c}\) ≠ 0,
\(\bar{a}\) × \(\bar{b}\) = \(\bar{c}\), \(\bar{b}\) × \(\bar{c}\) = \(\bar{a}\). Show that \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are pair wise orthogonal vectors and |\(\bar{b}\)| = 1, |\(\bar{c}\)| = |\(\bar{a}\)|.
Solution:

Question 27.
Let \(\overline{\mathbf{a}}\) = 2\(\overline{\mathbf{i}}\) + \(\overline{\mathbf{j}}\) – 2\(\overline{\mathbf{k}}\) ; \(\overline{\mathbf{b}}\) = \(\overline{\mathbf{i}}\) + \(\overline{\mathbf{j}}\). If \(\overline{\mathbf{c}}\) is a vector such that \(\overline{\mathbf{a}}\) . \(\overline{\mathbf{c}}\) = |\(\overline{\mathbf{c}}\)|, |\(\overline{\mathbf{c}}\) – \(\overline{\mathbf{a}}\)| = \(2 \sqrt{2}\) and the angle between \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\) = \(2 \sqrt{2}\) and the angle between \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) is 30°, then find the value of |(\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\)) × \(\overline{\mathbf{c}}\)|
Solution:

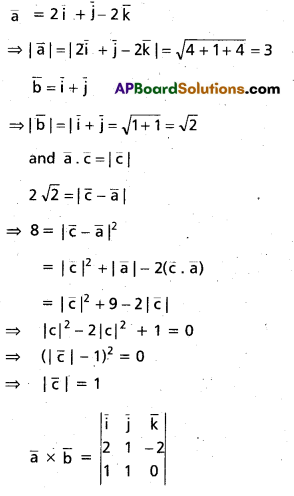
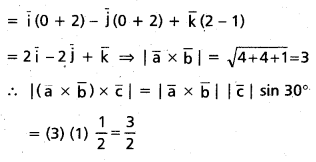
Question 28.
Let \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) be two non-collinear unit vectors. If \(\bar{\alpha}\) = \(\overline{\mathbf{a}}\) – (\(\overline{\mathbf{a}}\) • \(\overline{\mathbf{b}}\))\(\overline{\mathbf{b}}\) and \(\bar{\beta}\) =
= \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\), then show that |\(\overline{\boldsymbol{\beta}}\)| = |\(\bar{\alpha}\)|.
Solution:

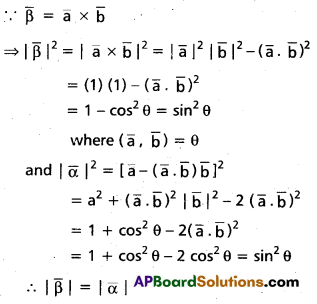
Question 29.
A non-zero vector \(\bar{a}\) is parallel to the line of intersection of the plane determined by the vectors \(\bar{i}\), \(\bar{i}\) + \(\bar{j}\) and the plane determined by the vectors \(\bar{i}\) – \(\bar{j}\), \(\bar{i}\) + \(\bar{k}\). Find the angle between \(\bar{a}\) and the vector \(\bar{i}\) – 2\(\bar{j}\) + 2\(\bar{k}\).
Solution:
Let l be the line of intersection of the planes determined by the pairs \(\bar{i}\), \(\bar{i}\) + \(\bar{j}\) and \(\bar{i}\) – \(\bar{j}\), \(\bar{i}\) + \(\bar{k}\)

∴ \(\bar{n}_{1}\) is perpendicular to l and \(\bar{n}_{2}\) is also perpendicular to l.
∴ \(\bar{a}\) is parallel to the line l, follows that \(\bar{a}\) is perpendicularto both \(\bar{n}_{1}\), and \(\bar{n}_{2}\)

Question 30.
Let \(\overline{\mathbf{a}}\) = 4\(\overline{\mathbf{i}}\) + 5\(\overline{\mathbf{j}}\) – \(\overline{\mathbf{k}}\), \(\overline{\mathbf{b}}\) = \(\overline{\mathbf{i}}\) – 4\(\overline{\mathbf{j}}\) + 5\(\overline{\mathbf{k}}\) and \(\overline{\mathbf{c}}\) = 3\(\overline{\mathbf{i}}\) + \(\overline{\mathbf{j}}\) – \(\overline{\mathbf{k}}\). Find the vector \(\bar{\alpha}\) which is perpendicular to both \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\) and \(\bar{\alpha} \cdot \mathbf{c}\) = 21.
Solution:

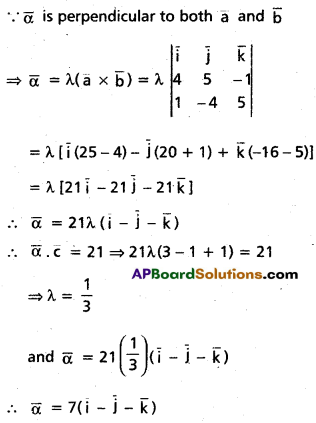
Question 31.
For any vector a, show that |a × i|² + |a × j|² + |a × k|² = 2|a|².
Solution:
Let a = x i + y j + z k.
Then a × i = -yk + zj.
∴ |a × i|² = y² + z²
Similarly |a × j|² = z² + x² and |a × k|² = x²
+ y²
∴ |a × i|² + |a × j|² + |a × k|² = 2(x² + y² + z²) = 2|a|²

Question 32.
If \(\overline{\mathbf{a}}\) is a non-zero vector and \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) are two vector such that \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\) = \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{c}}\) and \(\overline{\mathbf{a}}\) • \(\overline{\mathbf{b}}\) = \(\overline{\mathbf{a}}\) • \(\overline{\mathbf{c}}\), then prove that \(\overline{\mathbf{b}}\) = \(\overline{\mathbf{c}}\).
Solution:

Question 33.
Prove that the vectors \(\bar{a}\) = 2\(\bar{i}\) – \(\bar{j}\) + \(\bar{k}\), \(\bar{b}\) = \(\bar{i}\) – 3\(\bar{j}\) – 5\(\bar{k}\) and \(\bar{c}\) = 3\(\bar{i}\) – 4\(\bar{j}\) – 4\(\bar{k}\) are coplanar.
Solution:

Question 34.
Find the volume of the parallelopiped whose cotersminus edges are represented by the vectors 2\(\bar{i}\) – 3\(\bar{j}\) + \(\bar{k}\), \(\bar{i}\) – \(\bar{j}\) + 2\(\bar{k}\) and 2\(\bar{i}\) + \(\bar{j}\) – \(\bar{k}\).
Solution:
Let \(\bar{a}\) = 2\(\bar{i}\) – 3\(\bar{j}\) + \(\bar{k}\)

Question 35.
If the vectors \(\bar{a}\) = 2\(\bar{i}\) – \(\bar{j}\) + \(\bar{k}\), \(\bar{b}\) = \(\bar{i}\) + 2\(\bar{j}\) – 3\(\bar{k}\) and \(\bar{c}\) = 3\(\bar{i}\) + p\(\bar{j}\) + 5\(\bar{k}\) are coplanar, then find p.
Solution:

Question 36.
Show that
\(\overline{\mathbf{i}}\) × (\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{i}}\)) + \(\overline{\mathbf{j}}\) × (\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{j}}\)) + k × (\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{k}}\)) = 2\(\overline{\mathbf{a}}\) for any vector \(\overline{\mathbf{a}}\).
Solution:

Question 37.
Prove that for any three vectors \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\), [\(\overline{\mathbf{b}}\) + \(\overline{\mathbf{c}}\) \(\overline{\mathbf{c}}\) + \(\overline{\mathbf{a}}\) \(\overline{\mathbf{a}}\) + \(\overline{\mathbf{b}}\)] = 2[\(\overline{\mathbf{a}}\) \(\overline{\mathbf{b}}\) \(\overline{\mathbf{c}}\)]
Solution:

Question 38
For any three vectors \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) prove that [\(\overline{\mathbf{b}}\) × \(\overline{\mathbf{c}}\) \(\overline{\mathbf{c}}\) × \(\overline{\mathbf{a}}\) \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\)] = [\(\overline{\mathbf{a}}\) \(\overline{\mathbf{b}}\) \(\overline{\mathbf{c}}\)]²
Solution:

Question 39.
Let \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) be unit vectors such that \(\overline{\mathbf{b}}\) is not parallel to \(\overline{\mathbf{c}}\) and \(\overline{\mathbf{a}}\) × (\(\overline{\mathbf{b}}\) × \(\overline{\mathbf{c}}\)) = \(\frac{1}{2} \bar{b}\). Find the angles made by \(\overline{\mathbf{a}}\) with each of \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\).
Solution:

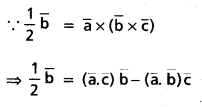
Since \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) are non—collinear vectors. Equating corresponding coeffs. on both sides

Question 40.
Let \(\overline{\mathbf{a}}\) = \(\overline{\mathbf{i}}\) + \(\overline{\mathbf{j}}\) + \(\overline{\mathbf{k}}\), \(\overline{\mathbf{b}}\) = 2\(\overline{\mathbf{i}}\) – \(\overline{\mathbf{j}}\) + 3\(\overline{\mathbf{k}}\), \(\overline{\mathbf{c}}\) = \(\overline{\mathbf{i}}\) – \(\overline{\mathbf{j}}\) and \(\overline{\mathbf{d}}\) = 6\(\overline{\mathbf{i}}\) + 2\(\overline{\mathbf{j}}\) + 3\(\overline{\mathbf{k}}\). Express \(\overline{\mathbf{d}}\) interms of \(\overline{\mathbf{b}}\) × \(\overline{\mathbf{c}}\), \(\overline{\mathbf{c}}\) × \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\)  (May. ’12)
Solution:

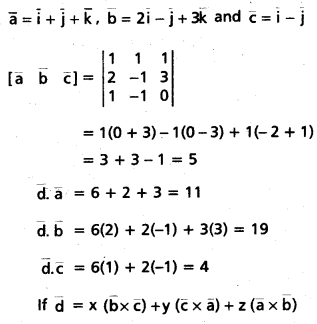
Then from the above problem,

Question 41.
For any four vectors \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) and \(\overline{\mathbf{d}}\) prove that
(\(\overline{\mathbf{b}}\) × \(\overline{\mathbf{c}}\)) . (\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{d}}\)) + (\(\overline{\mathbf{c}}\) × \(\overline{\mathbf{a}}\)) . (\(\overline{\mathbf{b}}\) × \(\overline{\mathbf{d}}\)) + (\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\)) . (\(\overline{\mathbf{c}}\) × \(\overline{\mathbf{d}}\)) = 0.
Solution:

Question 42.
Find the equation of the plane passing through the points A = (2, 3, -1), B = (4, 5, 2) and C = (3, 6, 5).
Solution:
Let ‘O’ be the origin

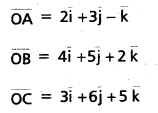
Let P be any point on the plane passing through the points A, B, C.

Hence, equation of the required plane is

Question 43.
Find the equation of the plane passing through the point A (3, -2, -1) and parallel to the vector \(\bar{b}\) = \(\bar{i}\) – 2\(\bar{j}\) + 4\(\bar{k}\) and \(\bar{c}\) = 3\(\bar{i}\) + 2\(\bar{j}\) – 5\(\bar{k}\).
Solution:
The required plane passes through A = (3, -2, -1) and is parallel to the vectors
\(\bar{b}\) = \(\bar{i}\) – 2\(\bar{j}\) + 4\(\bar{k}\) and \(\bar{c}\) = 3\(\bar{i}\) + 2\(\bar{j}\) – 5\(\bar{k}\). Hence if P is a point in the plane, then AP, b and C are coplanar and [AP b c] = 0.

i.e., 2x + 17y + 8z + 36 = 0 is the equation of the required plane.

Question 44.
Find the vector equation of the plane passing through the intersection of the planes r. (i + j + k) = 6 and r. (2i + 3j+ 4k) = -5 and the point (1, 1, 1).
Solution:

Substituting this value of λ in equation (1), we get

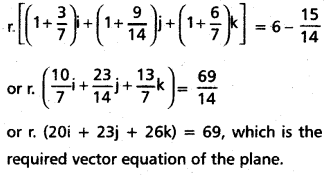
Question 45.
Find the distance of a point (2, 5, -3) from the plane r. (6i – 3j + 2k) = 4.
Solution:
Here a = 2i + 5j – 3k, N = 6i – 3j + 2k and d = 4.
∴ The distance of the point (2, 5, -3) from the given plane is

Question 46.
Find the angle between the line \(\frac{x+1}{2}\) = \(\frac{y}{3}\) = \(\frac{z-3}{6}\) and the plane 10x + 2y – 11z = 3.
Solution:
Let φ be the angle between the given line and the normal to the plane.
Converting the given equations into vector form, we have
r = (-i + 3k) + λ(2i + 3j + 6k)
and r. (10i + 2j – 11k) = 3
Here b = 2i + 3j + 6k and n = 10i + 2j – 11k

Question 47.
For any four vectors a, b, c and d, (a × b) × (c × d) = [a c d]b – [b c d]a and (a × b) × (c × d) = [a b d]c – [a b c]d.
Solution:
Let m = c × d
∴ (a × b) × (c × d) = (a × b) × m
= (a.m)b – (b.m)a
= (a. (c × d))b – (b. (c × d))a
= [a c d]b – [b c d]a.
Again Let a × b = n.
Then(a × b) × (c × d) = n × (c × d)
= (n .d)c – (n.c)d
= ((a × b). d) c – ((a × b). c)d
= [a b d]c – [a b c]d.

Question 48.
Find the shortest distance between the skew line r = (6i + 2j + 2k) + t(i – 2j + 2k) and r = (-4i – k) + s (3i – 2j – 2k).
Solution:
The first line passes through the point
A(6, 2, 2) and is parallel to the vector b = i – 2j + 2k. Second line passes through the point C(-4, 0, -1) and is parallel to the vector d = 3i – 2j – 2k

Question 49.
The angle ¡n a semi circle is a right angle. (May ’08)
Solution:
Let O be the centre and AOB be the diameter of the given šemi circle. Let P be a point on the semi circle. With reference to O as the origin, if the position vectors of A and P are taken as \(\overline{\mathrm{a}}\) and \(\overline{\mathrm{p}}\),then

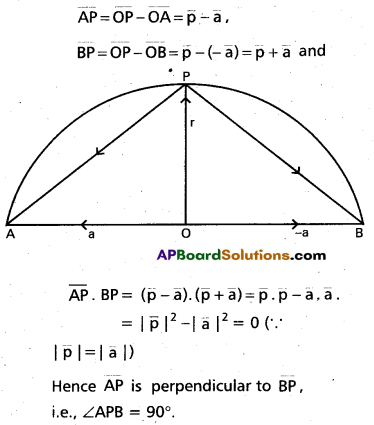
Question 50.
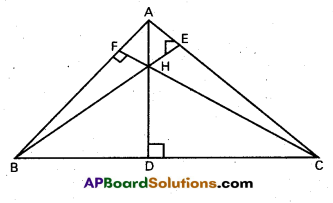
The altitude of a triangle are concurrent.
ii) The perpendicular bisectors of the sides of a triangle are concurrent.
Solution:
i) In the given triangle ABC, let the altitudes from A, B drawn to BC. CA respectively intersect them at D, E. Assume that AD and BE intersect at O, join CO and produce it to meet AB at F. With reference to O, let the position vectors of A, B and C be a, b and c respectively.

From Fig. we have

ii) In the given ABC, let the mid-points of BC, CA and AB be D, E and F respectively. Let the perpendicular bisectors drawn to BC and CA at D and E meet at O. Join OF. With respect to O, let the position vectors of A, B and C be \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\) respectively.


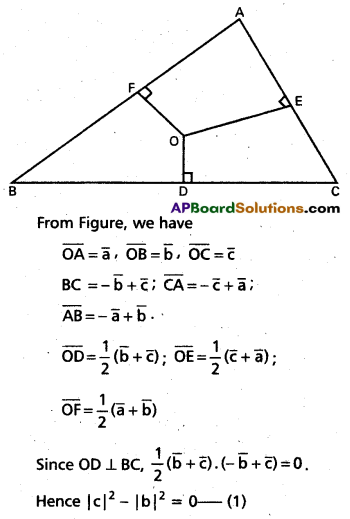
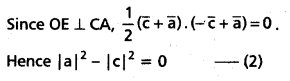
On adding equations (1) and (2), we obtain

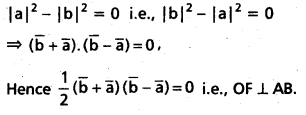
Question 51.
Show that the vector area of the quadrilateral ABCD having diagonals \(\overline{\mathbf{A C}}\), \(\overline{\mathbf{B D}}\) is \(\frac{1}{2}(\overline{A C} \times \overline{B D})\)
Solution:
If the point of intersection of the diagonals AC, BD of the given quadrilateral ABCD is assumed as Q, the vector area of the quadrilateral ABCD.

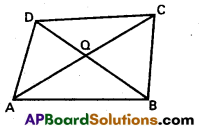
= Sum of the vector areas of ΔQAB, ΔQBC, ΔQCD and ΔQDA.

Question 52.
For any vectors a, b and c (a × b) × c = (a.c) b – (b.c) a (AP) (Mar. 15 May ‘06; June ’04)
Solution:
Equation (1) is evidently true if a and b are parallel.
Now suppose that a and b are non-parallel.
Let O denote the origin. Choose points A and B such that \(\overline{\mathrm{OA}}\) = \(\overline{\mathbf{a}}\) and \(\overline{\mathrm{OB}}\) = \(\overline{\mathbf{b}}\). Since \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\) are non-parallel, the points O, A and B are non-collinear. Hence they determine a plane.
Let i denote the unit vector along \(\overline{\mathrm{OA}}\).
Let j be a unit vector in the OAB plane perpendicular to i. Let k = i × j. Then

Question 53.
For any four vectors a, b, c and d(a × b). (c × d) = \(\left|\begin{array}{cc}
a \cdot c & a \cdot d \\
b . c & b . d
\end{array}\right|\) and in particular (a × b)² = a²b² – (a. b)².
Solution:

Question 54.
In the above fou rmula if \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\), \(\overline{\mathbf{c}}\) and \(\overline{\mathbf{d}}\)(\(\overline{\mathbf{a}}\) × \(\overline{\mathbf{b}}\)). (\(\overline{\mathbf{c}}\) × \(\overline{\mathbf{d}}\)) = (\(\overline{\mathbf{a}}\) . \(\overline{\mathbf{c}}\))(\(\overline{\mathbf{b}}\) . \(\overline{\mathbf{d}}\)) – (\(\overline{\mathbf{a}}\) . \(\overline{\mathbf{d}}\))(\(\overline{\mathbf{b}}\) . \(\overline{\mathbf{c}}\)) = \(\left|\begin{array}{ll}
\overline{\mathbf{a}} \cdot \overline{\mathbf{c}} & \overline{\mathbf{a}} \cdot \overline{\mathbf{d}} \\
\overline{\mathbf{b}} \cdot \overline{\mathbf{c}} & \bar{b} \cdot \overline{\mathbf{d}}
\end{array}\right|\).
Solution:

Since this is a scalar, this is also called the scalar product of four vectors.