Inter 1st Year Maths 1A Matrices Solutions Ex 3(e)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(e) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(e)

I.

Question 1.
Find the adjoint and inverse of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & -3 \\
4 & 6
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 1 & 0 \\
3 & 2 & 1
\end{array}\right]\)
Solution:

(iv) \(\left[\begin{array}{lll}
2 & 1 & 2 \\
1 & 0 & 1 \\
2 & 2 & 1
\end{array}\right]\)
Solution:

Question 2.
If A = \(\left[\begin{array}{cc}
a+i b & c+i d \\
-c+i d & a-i b
\end{array}\right]\), a² + b² + c² + d² = 1, then find the inverse of A.
Solution:

Question 3.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), then find A^-1
Solution:

Question 4.
If A = \(\left|\begin{array}{ccc}
-1 & -2 & -2 \\
2 & 1 & -2 \\
2 & -2 & 1
\end{array}\right|\), then show that the adjoint of A = 3A’ find A^-1.
Solution:

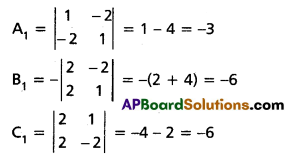
Question 5.
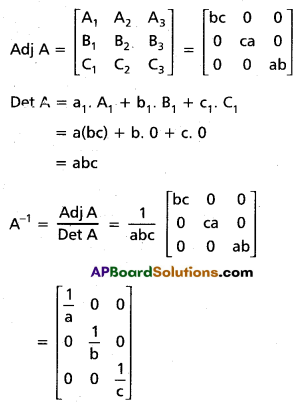
If abc ≠ 0, find the inverse of \(\left[\begin{array}{lll}
a & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right]\)
Solution:

II.

Question 1.
If A = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\) and B = \(\frac{1}{2}\left[\begin{array}{lll}
b+c & c-a & b-a \\
c-b & c+a & a-b \\
b-c & a-c & a+b
\end{array}\right]\) then show that ABA^-1 is a diagonal matrix.
Solution:

Question 2.
If 3A = \(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
-2 & 2 & -1
\end{array}\right]\) then show that A^-1 = A’
Solution:

Question 3.
If A = \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\), then show that A^-1 = A³
Solution:

∴ A⁴ = I
det A = 3(1) – 3(-2) + 4(-2) = 1
∵ A ≠ 0 ⇒ A^-1 exists
∵ A⁴ = I
Multiply with A^-1
A⁴ (A^-1) = I (A^-1)
⇒ A³ (AA^-1) = A^-1
⇒ A³ (I) = A^-1
∴ A^-1 = A³

Question 4.
If AB = I or BA = I, then prove that A is invertible and B = A^-1
Solution:
Given AB = I
⇒ AB| = |1|
⇒ |A| |B| = 1
⇒ |A| ≠ 0
∴ A is a non-singular matrix and BA = I
⇒ |BA| = |I|
⇒ |B| |A| = 1
⇒ |A| ≠ 0
∴ A is a non-singular matrix.
AB = I or BA = I, A is invertible.
∴ A^-1 exists.
AB = I
⇒ A^-1AB = A^-1I
⇒ IB = A^-1
⇒ B = A^-1
∴ B = A^-1