Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(e) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(e)
I.
Question 1.
Prove that sin 50° – sin70° + sin 10° = 0
Solution:
LHS = sin 50° – sin 70° + sin 10°
= 2 cos(\(\frac{50^{\circ}+70^{\circ}}{2}\)) . sin(\(\frac{50^{\circ}-70^{\circ}}{2}\)) + sin 10°
= 2 cos 60° . sin (-10°) + sin 10°
= 2(\(\frac{1}{2}\)) (-sin 10°) + sin 10°
= -sin 10° + sin 10°
= 0
= RHS
∴ sin 50° – sin 70° + sin 10° = 0
![]()
Question 2.
Prove that \(\frac{\sin 70^{\circ}-\cos 40^{\circ}}{\cos 50^{\circ}-\sin 20^{\circ}}=\frac{1}{\sqrt{3}}\)
Solution:

Question 3.
Prove that cos 55° +cos 65° + cos 175° = 0
Solution:
LHS = cos 55° + cos 65° + cos 175°
= cos 65° + cos 55° + cos (180° – 5°)
= 2 cos(\(\frac{65^{\circ}+55^{\circ}}{2}\)) . cos(\(\frac{65^{\circ}-55^{\circ}}{2}\)) – cos 5°
= 2 cos (60°) . cos (5°) – cos 5°
= 2(\(\frac{1}{2}\)) cos 5° – cos 5°
= cos 5° – cos 5°
= 0
= RHS
∴ cos 55° + cos 65° + cos 175° = 0
Question 4.
Prove that 4(cos 66° + sin 84°) = √3 + √15
Solution:

Question 5.
Prove that cos 20° cos 40° – sin 5° sin 25° = \(\frac{\sqrt{3}+1}{4}\)
Solution:
cos 20° cos40° – sin 5° sin 25°
= \(\frac{1}{2}\) [2 cos 20° cos 40° – 2 sin 5° sin 25°]
= \(\frac{1}{2}\) [cos (20° + 40°) + cos (20° – 40°) – {cos (5° – 25°) – cos (5° + 25°)}]
= \(\frac{1}{2}\) [cos 60° + cos 20° – cos 20° + cos 30°]
= \(\frac{1}{2}\left[\frac{1}{2}+\frac{\sqrt{3}}{2}\right]\)
= \(\frac{\sqrt{3}+1}{4}\)
= RHS
∴ cos 20° cos 40° – sin 5° sin 25° = \(\frac{\sqrt{3}+1}{4}\)
![]()
Question 6.
Prove that cos 48° . cos 12° = \(\frac{3+\sqrt{5}}{8}\)
Solution:
LHS = cos 48° . cos 12°
= \(\frac{1}{2}\) (2 cos 48°. cos 12°)
= \(\frac{1}{2}\) [cos (48° + 12°) + cos (48° – 12°)]
= \(\frac{1}{2}\) [cos 60° + cos 36°]
= \(\frac{1}{2}\left[\frac{1}{2}+\frac{\sqrt{5}+1}{4}\right]\)
= \(\frac{1}{2}\left[\frac{2+\sqrt{5}+1}{4}\right]\)
= \(\frac{3+\sqrt{5}}{8}\)
= RHS
∴ cos 48° . cos 12° = \(\frac{3+\sqrt{5}}{8}\)
II.
Question 1.
Prove that cos θ + cos[\(\frac{2 \pi}{3}\) + θ] + cos[\(\frac{4 \pi}{3}\) + θ] = 0
Solution:

Question 2.
Prove that sin2(α – π/4) + sin2(α + π/2) – sin2(α – π/2) = \(\frac{1}{2}\)
Solution:

Question 3.
If sin x + sin y = \(\frac{1}{4}\) and cos x + cos y = \(\frac{1}{3}\), then show that
(i) \(\tan \left(\frac{x+y}{2}\right)=\frac{3}{4}\)
(ii) cot (x + y) = \(\frac{7}{24}\)
Solution:

Question 4.
If neither [A – \(\frac{\pi}{12}\)] nor [A – \(\frac{5 \pi}{12}\)] is an integral multiple of π. Prove that cot(π/2 – A) + tan(π/12 + A) = \(\frac{4 \cos 2 A}{1-2 \sin 2 A}\)
Solution:


Question 5.
Prove that 4 cos 12° cos 48° cos 72° = cos 36°.
Solution:
LHS = 4 cos 12° cas 48° cos 72°
= 2 cos 12° {2 cos 72° cos 48°}
= 2 cos 12° {cos (72° + 48°) + cos (72° – 48°)}
= 2 cos 12° {cos (120°) + cos 24°)
= 2 cos 12° {\(\frac{1}{2}\) + cos 24°}
= 2 cos 12° \(\left\{\frac{-1+2 \cos 24^{\circ}}{2}\right\}\)
= -cos 12° + 2 cos 24° cos 12°
= -cos 12° + {cos(24° + 12°) + cos (24° – 12°))
= -cos 12° + cos 36° + cos 12°
= cos 36°
= RHS
∴ 4 cos 12° cos 48° cos 72° = cos 36°
![]()
Question 6.
Prove that sin 10° + sin 20° + sin 40° + sin 50° = sin 70° + sin 80°
Solution:
LH.S. = sin 10° + sin 20° + sin 40° + sin 50°
= (sin 50°+ sin 10°) + (sin 40° + sin 20°)
= 2 sin(\(\frac{50^{\circ}+10^{\circ}}{2}\)) . cos(\(\frac{50^{\circ}-10^{\circ}}{2}\)) + 2 sin(\(\frac{40^{\circ}+20^{\circ}}{2}\)) . cos(\(\frac{40^{\circ}-20^{\circ}}{2}\))
= 2 . sin (30°) . cos 20° + 2 sin 30° . cos 10°
= 2 sin 30° (cos 20° + cos 10°)
= 2(\(\frac{1}{2}\)) [cos(90° – 70°) + cos(90° – 80°)]
= sin 70° + sin 80°
= RHS
∴ sin 10° + sin 20° + sin 40° + sin 50° = sin 70° + sin 80°
III.
Question 1.
If cos x + cos y = \(\frac{4}{5}\) and cos x – cos y = \(\frac{2}{7}\) find the value of \(14 \tan \left(\frac{x-y}{2}\right)+5 \cot \left(\frac{x+y}{2}\right)\)
Solution:

Question 2.
If none of the denominators is zero, prove that
\(\left(\frac{\cos A+\cos B}{\sin A-\sin B}\right)^{n}+\left(\frac{\sin A+\sin B}{\cos A-\cos B}\right)^{n}\) = \(\begin{cases}2 \cot ^{n}\left(\frac{A-B}{2}\right), & \text { if } n \text { is even } \\ 0, & \text { if } n \text { is odd }\end{cases}\)
Solution:
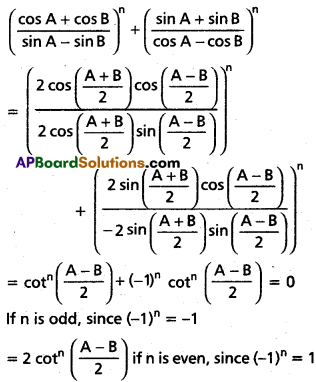
Question 3.
If sin A = sin B and cos A = cos B, then prove that A = 2nπ + B for some integer n.
Solution:

![]()
Question 4.
If cos nα ≠ 0 and cos \(\frac{\alpha}{2}\) ≠ 0. then show that \(\frac{\sin (n+1) \alpha-\sin (n-1) \alpha}{\cos (n+1) \alpha+2 \cos n \alpha+\cos (n-1) \alpha}\) = tan \(\frac{\alpha}{2}\)
Solution:

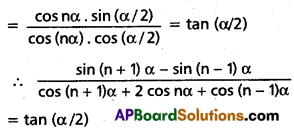
Question 5.
If sec (θ + α) + sec (θ – α) = 2 sec θ and cos α ≠ 1, then show that cos θ = ±√2 cos \(\frac{\alpha}{2}\).
Solution:

Question 6.
If none of x, y, z is an odd multiple of \(\frac{\pi}{2}\) and if sin (y + z – x), sin (z + x – y), sin (x + y – z) are in A.P., then prove that tan x, tan y, tan z are also in A.P.
Solution:
sin (y + z – x), sin (z + x – y), sin (x + y – z) are in A.P.
⇒ sin (z + x – y) – sin (y + z – x) = sin (x + y – z) – sin (z + x – y)
⇒ 2 cos z sin (x – y) = 2 cos x sin (y – z)
⇒ cos z [sin x cos y – cos x sin y] = cos x [sin y cos z – cos y sin z]
Dividing with cos x cos y cos z, we get
\(\frac{\sin x}{\cos x}-\frac{\sin y}{\cos y}=\frac{\sin y}{\cos y}-\frac{\sin z}{\cos z}\)
⇒ tan x – tan y = tan y – tan z
⇒ tan x + tan z = 2 tan y
∴ tan x, tan y, tan z are in A.P.
![]()
Question 7.
If x, y, z are non zero real numbers and if x cos θ = y cos (θ + \(\frac{2 \pi}{3}\)) = z cos (θ + \(\frac{2 \pi}{3}\)) for some θ ∈ R, then show that xy + yz + zx = 0.
Solution:


Question 8.
If neither A nor A + B is an odd multiple of \(\frac{\pi}{2}\) and if m sin B = n sin(2A + B), then prove that (m + n) tan A = (m – n) tan (A + B).
Solution:
Neither A nor (A + B) is an odd multiple of \(\frac{\pi}{2}\)
Given that m sin B = n sin (2A + B)

![]()
Question 9.
If tan (A + B) = λ tan (A – B), then show that (λ + 1) sin 2B = (λ – 1) sin 2A.
Solution:
