Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Solutions Exercise 6(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Solutions Exercise 6(a)
I.
Question 1.
A line makes angles 90°, 60° and 30° with positive directions of X, Y, Z – axes respectively. Find the direction cosines.
Solution:
Suppose l, m, n are the direction cosines of the line.
l = cos α = cos 90° = 0
m = cos β = cos 60° = \(\frac{1}{2}\)
n = cos γ = cos 30° = \(\frac{\sqrt{3}}{2}\)
Direction cosines of the line are (0, \(\frac{1}{2}\), \(\frac{\sqrt{3}}{2}\))
Question 2.
If a line makes angles α, β, γ with the positive direction of x, y, z axes, what is the value of sin² α + sin² β + sin² γ?
Solution:
We know that cos² α + cos² β + cos² γ = 1
1 – sin² α + 1 – sin² β + 1 – sin² γ = 1
sin² a + sin² P + sin² γ = 3 – 1 = 2.
![]()
Question 3.
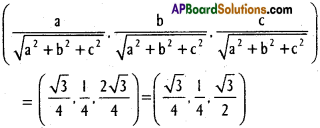
If P(√3, 1, 2√3) is a point in space, find the direction cosines of \(\overrightarrow{O P}\).
Solution:
Direction ratios of P are (√3, 1, 2√3)
a² + b² + c² = 3 + 1 + 12 = 16
⇒ \(\sqrt{a^{2}+b^{2}+c^{2}}\) = 4
Direction cosines of \(\overrightarrow{O P}\) are
Question 4.
Find the direction cosines of the line joining the points (-4, 1, 7) are (2, -3, 2).
Solution:
A(- 4, 1, 2) and B(2, -3, 2) are the given points
d.rs of PQ are (x2 – x1, y2 – y1, z2 – z1)
(2 + 4, 1 + 3, 2 – 7) ie., (6, 4, -5)
Dividing with
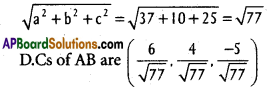
II.
Question 1.
Find the direction cosines of the sides of the triangle whose vertices are (3, 5, -4), (-1, 1, 2) and (-5, -5, -2).
Solution:
A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2) are the vertices of ∆ABC
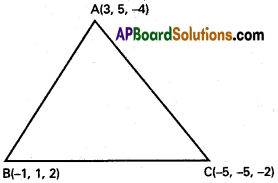
d.rs of AB are (-1 -3, 1 – 5, 2 + 4) (-4, -4, 6)
Dividing with \(\sqrt{16+16+36}=\sqrt{68}=2 \sqrt{17}\)
D.Rs of AB are \(\frac{-4}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}}\)
ie., \(\frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}\)
D.Rs of BC are (-5 + 1, -5 -1, -2 -2)
i.e., (-4, -6, -4)
Dividing with \(\sqrt{16+16+36}=\sqrt{68}=2 \sqrt{17}\)
d.cs of BC are \(\frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}\)
ie., \(\frac{-2}{\sqrt{17}}, \frac{-3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}\)
d.rs of CA are 3 + 5, 5 + 5, -4 + 2
= 8, 10, -2
Dividing with \(\sqrt{64+100+4}=\sqrt{168}=2 \sqrt{42}\)
d.cs of CA are \(\frac{8}{2 \sqrt{42}}, \frac{10}{2 \sqrt{42}}, \frac{-2}{2 \sqrt{42}}\)
ie., \(\frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}}, \frac{-1}{\sqrt{42}}\)
![]()
Question 2.
Show that the lines \(\stackrel{\leftrightarrow}{P Q}\) and \(\stackrel{\leftrightarrow}{R S}\) are parallel where P, Q, R, S are two points (2, 3, 4), (4, 7, 8), (-1, -2, 1) and (1, 2, 5) respectively.
Solution:
P(2, 3, 4), Q(4, 7, 8), R(-1, -2, 1)
and S(1, 2, 5) are the given points.
d.rs of PQ are 4 -2, 7 -3, 8 – 4 i.e., 2, 4, 4
d.rs of RS are 1 + 1, 2 + 2, 5 – 1 i.e., 2, 4, 4
d.rs of PQ are RS are proportional
∴ PQ and RS are parallel.
III.
Question 1.
Find the direction cosines of two lines which are connected by the relations l – 5m + 3n = 0 and 7l² + 5m² – 3n² = 0.
Solution:
Given l – 5m + 3n = 0
⇒ l = 5m – 3n ………….. (1)
7l² + 5m² – 3n² = 0 …………. (2)
Substituting the value of l in (2)
7(5m – 3n)² + 5m² – 3n² = 0
7(25m² + 9n² – 30 mn) + 5m² – 3n² = 0
175 m² + 63n² – 210 mn + 5m² – 3n² = 0
180m² – 210mn + 60n² = 0
Dividing with 30.
6m² – 7mn + 2n² = 0
(3m – 2n) (2m – n) = 0
3m = 2n or 2m = n
Case (i): 3m1 = 2n1 ⇒ \(\frac{m_{1}}{2}=\frac{n_{1}}{3}\)
and m1 = \(\frac{2}{3}\) n1
From (1) l1 = 5m1 – 3n1 = \(\frac{10}{3}\)n1 – 3n1
d.rs of the first line are (1, 2, 3)
Dividing with \(\sqrt{1+4+9}=\sqrt{14}\)
d.cs of the first line are (\(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\))
Case (ii): 2m2 = n2
From (1) l2 – 5m2 + 3n2 = 0
l2 – 5m2 + 6m2 = 0
l2 = m2
∴ \(\frac{l_{2}}{-1}=\frac{m_{2}}{1}=\frac{n_{2}}{2}\)
d.rs of the second line are -1, 1, 2
Dividing with \(\sqrt{1+1+4}=\sqrt{6}\)
d.cs of the second line are (\(\frac{-1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{2}{\sqrt{6}}\))