Inter 1st Year Maths 1B Three Dimensional Coordinates Solutions Ex 5(b)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(b)

I.

Question 1.
Find the ratio in which the XZ-plane divides the line joining A(-2, 3, 4) and B(l, 2,3).
Solution:
Ratio in which XZ plane divides
AB = -y₁ : y₂
= -3 : 2

Question 2.
Find the co-ordinates of the vertex ‘C’ of ∆ABC if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively.
Solution:
A(1, 1, 1) B(-2, 4, 1) and (x, y, z) are the vertices of ∆ABC.
G is the centroid of ∆ABC
Co-ordinates of G are
(\(\frac{1-2+x}{3}\), \(\frac{1+4+y}{3}\), \(\frac{1+1+z}{3}\)) = (0, 0, 0)
\(\frac{x-1}{3}\) = 0, \(\frac{y+5}{3}\) = 0, \(\frac{z+2}{3}\) = 0
x – 1 = 0, y +5 =0, z + 2 = 0
x = 1, y = – 5, z = -2
∴ Co-ordinates of c are (1, -5, -2)

Question 3.
If (3, 2, -1), (4, 1, 1) and (6, 2, 5) are three vertices and (4, 2, 2) is the centroid of a tetrahedron, find the fourth vertex.
Solution:
A(3, 2, -1), B(4, 1, 1), C(6, 2, 5), D(x, y, z) are the vertices of the tetrahedron.
Co-ordinates of the centroid G are

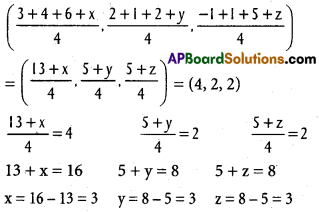
Co-ordinates of D are (3, 3, 3)

Question 4.
Find the distance between the mid point of the line segment \(\overline{\mathrm{A B}}\) and the point (3, -1, 2) where A = (6, 3, -4) and B = (-2, -1, 2).
Solution:
A(6, 3, – 4) B(-2, -1,2) are the given points.
Q is the midpoint of AB.
Co-ordinates of Q are (\(\frac{6-2}{2}\), \(\frac{3-1}{2}\), \(\frac{-4+2}{2}\)) = (2, 1, -1)
Co-ordinates of P are (3, -1, 2)

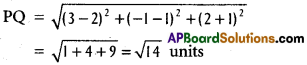
II.

Question 1.
Show that the points (5, 4,2) (6,2, -1) and (8, -2, -7) are collinear.
Solution:
A(5, 4, 2), B(6, 2, -1) c(8, -2, -7) are the given points.
AB = \(\sqrt{(5-6)^{2}+(4-2)^{2}+(2+1)^{2}}\)

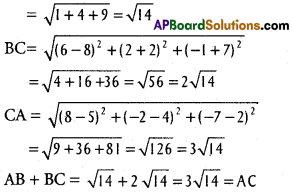
∴ A, B, C are collinear.

Question 2.
Show that the points A(3, 2, -4), B(5, 4, -6) and C(9, 8, -10) are collinear and find the ratio in which B divides \(\overline{\mathrm{A C}}\).
Solution:
A(3, 2, -4), B(5, 4, -6) and C(9, 8, -10) are the given points.

A, B, C are collinear
Ratio in which B divides AC = AB : BC
= 2√3 : 4√3 = 1 : 2

III.

Question 1.
If A(4, 8, 12) B(2, 4, 6) C(3, 5, 4) and D(5, 8, 5) are four points, show that the line \(\stackrel{\leftrightarrow}{A B}\) and \(\stackrel{\leftrightarrow}{C D}\) intersect.
Solution:
A(4, 8, 12), B(2, 4, 6) C(3, 5, 4) and D(5, 8, 5) are the given points
Co-ordinates of the point dividing AB in the ratio λ : 1 is
\(\left[\frac{2 \lambda+4}{\lambda+1} \cdot \frac{4 \lambda+8}{\lambda+1} \cdot \frac{6 \lambda+12}{\lambda+1}\right]\) ……….. (1)
Co-ordinates of the point dividing CD in the ratio p : 1 is
\(\left[\frac{5 \mu+3}{\mu+1}, \frac{8 \mu+5}{\mu+1}, \frac{5 \mu+4}{\mu+1}\right]\) ……….. (2)
If the given lines intersects these two points must coincide.
\(\frac{2 \lambda+4}{\lambda+1}=\frac{5 \mu+3}{\mu+1}\)
(2λ + 4) (µ + 1) = (5µ + 3) (λ + 1)
2λµ + 2λ + 4µ + 4 = 5λµ + 5µ + 3λ + 3
3λ + λ + µ – 1 = 0
λ(3µ+1) = -(µ – 1)
λ = –\(\frac{(\mu-1)}{3 \mu+1}\)
\(\frac{4 \lambda+8}{\lambda+1}=\frac{8 \mu+5}{\mu+1}\)
(4λ + 8) (µ + 1) = (8µ + 5) (λ + 1)
4λµ + 4λ + 8µ + 8 = 8λµ + 8µ + 5λ + 5
4Aµ + λ – 3 = 0
(4µ + 1) λ = 3
\(-\frac{(4 \mu+1)(\mu-1)}{3 \mu+1}=3\)
4µ2 – 4µ + µ – 1 = -9µ – 3
4µ2 4- 6µ + 2 = 0
2µ2 + 3µ + 1=0
(2µ + 1) (µ – 1) = 0
µ = – \(\frac{1}{2}\) or – 1
µ = -1 is not possible
µ = – \(\frac{1}{2}\)

Co-ordinates of (2) are

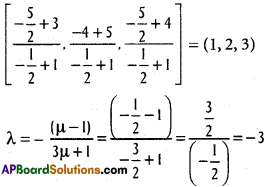
Co-ordinates of (1) are
\(\frac{-6+4}{-3+1}, \frac{-12+8}{-3+1}, \frac{-18+12}{-3+1}\) = (1, 2, 3)
Since these two points coincide the given lines intersect.

Question 2.
Find the point of instersection of the lines \(\stackrel{\leftrightarrow}{A B}\) and \(\stackrel{\leftrightarrow}{C D}\) where A = (7, -6, 1) B = (17, -18, -3), C = (1, 4, -5) and D = (3, -4, 11)

Solution:
A(7, -6, 1), B(17, -18, -3), C(1, 4, -5) and D(3, -4, 11) are the given points.
Co-ordinates of the point dividing AB in the ratio λ: 1 are

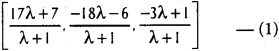
Co-ordinates of the point dividing CD in the ratio µ : 1 are

(17λ + 7) (µ + 1) = (3µ + 1) (λ + 1)
17λµ + 17λ + 7µ + 7 = 3λµ + 3µ + λ + 1
14λµ + 16λ + 4µ + 6 = 0.

-18λµ – 6µ – 18λ – 6
= -4λµ + 4λ – 4µ + 4
14λµ + 22λ + 2µ + 10 = 0
14λµ + 16λ + 4µ + 6 = 0 ………. (1)
14λµ + 22λ + 2µ + 10 = 0……….(2)
Subtraction – 6λ + 2µ – 4 = 0
2µ = 6λ + 4
µ = 3λ + 2
Substituting in (3)
14λ(3λ + 2) + 16λ + 4(3λ + 2) + 6 = 0
42λ² + 28λ + 16λ + 12λ+ 8 + 6 = 0
42λ² + 56λ + 14 = 0
3λ² + 4λ + 1 = 0
(λ + 1) (3λ + 1) = 0
λ = -1 or λ = –\(\frac{1}{3}\)
λ = -1 is not possible
λ = –\(\frac{1}{3}\)

µ = 3λ + 2 = -1 + 2 = 1
µ = 1 ⇒
\(\frac{3+1}{1+1}, \frac{-4+4}{1+1}, \frac{11-5}{1+1}\) = (2, 0, 3)
∴ These two points coincide
⇒ The given lines AB and CD intersect
Point of intersection is (2, 0, 3)

Question 3.
A(3, 2, 0), B(5, 3, 2), C(-9, 6, -3) are vertices of a triangle. \(\overline{\mathrm{A D}}\), the bisector of ∠BAC meets \(\overline{\mathrm{B C}}\) at D. Find the co-ordinates of D.
Solution:
A(3, 2, 0),B(5, 3, 2) C(-9, 6, -3) are the vertices of ∆ABC


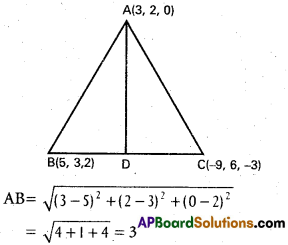
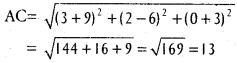
AB is the bisector of ∠DAC
‘D’ divides BC in the ratio 3 : 13
Co-ordinates of D are

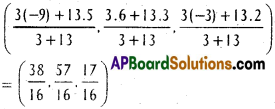
Question 4.
Show that the points 0(0,0,0), A(2, -3, 3), B(-2, 3, -3) are collinear. Find the ratio in which each point divides the segment joining the other two.
Solution:
0(0, 0, 0), A(2, -3, 3), B(-2, 3, -3) are the given points.

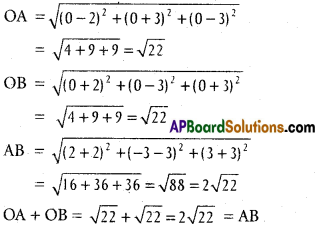
∴ O, A, B are collinear.

Ratio in which ‘O’ divides AB
= OA : OB = √22 : √22 = 1 : 1
Ratio is which A divides OB
= OA:AB = -√22 : √22 = -1 : 2
Ratio in which B divides OA
= AB : BO = -2√22 : √22 =-2 : 1
A and B divide externally.