Use these Inter 1st Year Maths 1B Formulas PDF Chapter 4 Pair of Straight Lines to solve questions creatively.
Intermediate 1st Year Maths 1B Pair of Straight Lines Formulas
→ If ax2 + 2hxy + by2 = 0 represents a pair of lines, then the sum of the slopes of lines is \(-\frac{2 h}{b}\) and the product of the slopes of lines is \(\frac{a}{b}\).
→ If ‘θ’ is an angle between the lines represented by ax2 + 2hxy + by2 = 0
then cos θ = \(\frac{a+b}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
tan θ = \(\frac{2 \sqrt{h^{2}-a b}}{a+b}\)
If ‘θ’ is accute, cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^{2}+4 h^{2}}}\); tan θ = \(\frac{2 \sqrt{h^{2}-a b}}{|a+b|}\)
→ If h2 = ab, then ax2 + 2hxy + by2 = 0 represents coincident or parallel lines.
→ ax2 + 2hxy + by2 = 0 represents a pair of ⊥lr lines ⇒ a+ b = 0 i.e., coeft. of x2 + coeff. of y2 = 0.
→ The equation of pair of lines passing through origin and perpendicular to ax2 + 2hxy + by2 = 0 is bx2 – 2hxy + ay2 = 0.
→ The equation of pair of lines passing through (x1, y1) and perpendicular to ax2 + 2hxy + by2 = 0 isb (x – x1)2 – 2h(x – x1) (y – y1) + a(y – y1)2 = 0.
→ The equation of pair of lines passing through (x1, y1) and parallel to ax2 + 2hxy + by2 = 0 is a(x-x,)2 + 2h(x-x1)(y-y1) + b(y – y1)2 = 0.
→ The equations of bisectors of angles between the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0, is \(\frac{a_{1} x+b_{1} y+c_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \frac{\left(a_{2} x+b_{2} y+c_{2}\right)}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
→ The equation to the pair of bisectors of angles between the pair of lines ax2 + 2hxy + by2 = 0 is h(x2 – y2) = (a – b)xy.
![]()
→ The product of the perpendicular is from (α, β) to the pair of lines ax2 + 2hxy + by2 = 0 is \(\frac{\left|a \alpha^{2}+2 h \alpha \beta+b \beta^{2}\right|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
→ The area of the triangle formed by ax2 + 2hxy + by2 = 0 and lx + my + n = 0 is \(\frac{n^{2} \sqrt{h^{2}-a b}}{\left|a m^{2}-2 h / m+b\right|^{2} \mid}\)
→ The line ax + by + c = 0 and pair of lines (ax + by)2 – 3(bx – ay)2 =0 form an equilateral triangle and the area is \(\frac{c^{2}}{\sqrt{3}\left(a^{2}+b^{2}\right)}\) sq.units
→ If ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of lines, then
- abc + 2fgh – af2 – bg2 – ch2 = 0
- h2 ≥ ab
- g2 ≥ ac
- f2 ≥ be
→ If ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of lines and h2 > ab, then the point of intersection of the lines is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)
→ If ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of parallel lines then h2 = ab and af2 = bg2
The distance between the parallel lines = \(2 \sqrt{\frac{g^{2}-a c}{a(a+b)}}=2 \sqrt{\frac{f^{2}-b c}{b(a+b)}}\)
Pair of Straight Lines:
Let L1 = 0, L2 = 0 be the equations of two straight lines. If P(x1, y1) is a point on L1 then it satisfies the equation L1 = 0. Similarly, if P(x1, y1) is a point on L2 = 0 then it satisfies the equation.
If P(x1, y1) lies on L1 or L2, then P(x1,y1) satisfies the equation L1L2= 0.
L1L2 = 0 represents the pair of straight lines L1 = 0 and L2 = 0 and the joint equation of L1 = 0 and L2 = 0 is given by L1 L2= 0. ……………(1)
On expanding equation (1) we get and equation of the form ax2 + 2hxy + by2 + 2 gx + 2 fy + c = 0 which is a second degree (non – homogeneous) equation in x and y.
Definition: If a, b, h are not all zero,then ax2 + 2hxy + by2 = 0 is the general form of a second degree homogeneous equation in x and y.
Definition: If a, b, h are not all zer, then ax2 + 2hxy + by2 + 2gx + 2 fy + c = 0 is the general form of a second degree non – homogeneous equation in x and y.
Theorem:
If a, b, h are not all zero and h2 ≥ ab then ax2 + 2hxy + by2 = 0 represents a pair of straight lines passing through the origin.
Proof:
Case (i) : Suppose a = 0.
Given equation ax2 + 2hxy + by2 = 0 reduces to 2hxy + by2 = 0 ^ y(2hx + by) = 0 .
Given equation represents two straight lines y = 0 ………..(1) and 2hx + by = 0 ………(2) which pass through the origin.
Case (ii): Suppose a ≠ 0.
Given equation ax2 + 2hxy + by2 = 0
⇒ a2x2 + 2ahxy + aby2 = 0
⇒ (ax)2 + 2(ax)(hy) + (hy)2 – (h2 – ab)y2 = 0
⇒ (ax + hy)2 – (y\(\sqrt{h^{2}-a b}\))2 = 0
[ax + y (h + \(\sqrt{h^{2}-a b}\))][ax + y (h – \(\sqrt{h^{2}-a b}\)] = 0
∴ Given equation represents the two lines
ax + hy + y\(\sqrt{h^{2}-a b}\) = 0, ax + hy – y\(\sqrt{h^{2}-a b}\) = 0 which pass through the origin.
Note 1:
- If h2 > ab , the two lines are distinct.
- If h2 = ab , the two lines are coincident.
- If h2 < ab , the two lines are not real but intersect at a real point (the origin).
- If the two lines represented by ax2 + 2hxy + by2 = 0 are taken as l1x + m1y = 0 and l2x + m2y = 0 then
ax2 + 2kxy + by2 = (4 x + m1y) (x + m2y) = 2 x2 + (l1m2 + l2m1) xy + m1m2 y2 - Equating the coefficients of x2, xy and y2 on both sides, we get l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
![]()
Theorem:
If ax2 + 2hxy + by2 = 0 represent a pair of straight lines, then the sum of slopes of lines is \(\frac{-2 h}{b}\) product of the slopes is \(\frac{a}{b}\).
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1x + m1y = 0 ………….(1) and l2x + m2y = 0 ………….(2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
Slopes of the lines (1) and (2) are –\(\frac{l_{1}}{m_{1}}\) and \(-\frac{l_{2}}{m_{2}}\).
sum of the slopes = \(\frac{-l_{1}}{m_{1}}+\frac{-l_{2}}{m_{2}}=-\frac{l_{1} m_{2}+l_{2} m_{1}}{m_{1} m_{2}}=-\frac{2 h}{b}\)
Product of the slopes = \(\left(\frac{-l_{1}}{m_{1}}\right)\left(-\frac{l_{2}}{m_{2}}\right)=\frac{l_{1} l_{2}}{m_{1} m_{2}}=\frac{a}{b}\)
Angle Between A Pair of Lines:
Theorem :
If θ is the angle between the lines represented by ax2 + 2hxy + by2 = 0, then cos θ = ±\(\frac{a+b}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1 x + m1 y = 0 ………..(1) and l2x + m2 y = 0 …………..(2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
Let θ be the angle between the lines (1) and (2). Then cos θ = ±\(\frac{l_{1} l_{2}+m_{1} m_{2}}{\sqrt{\left(l_{1}^{2}+m_{1}^{2}\right)\left(l_{2}^{2}+m_{2}^{2}\right)}}\)
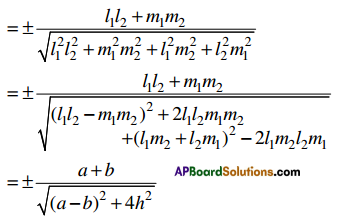
Note 1:
If θ is the accute angle between the lines ax2 + 2hxy + by2 = 0 then cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
If θ is the accute angle between the lines ax2 + 2hxy + by2 = 0 then tan θ = ±\(\frac{2 \sqrt{h^{2}-a b}}{a+b}\) and sin θ = \(\frac{2 \sqrt{h^{2}-a b}}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
Conditions For Perpendicular And Coincident Lines:
- If the lines ax2 + 2hxy + by2 = 0 are perpendicular to each other then θ = π/ 2 and cos θ = 0 ⇒ a + b = 0 i.e., co-efficient of x2 + coefficient of y2 = 0.
- If the two lines are parallel to each other then 0 = 0.
⇒ The two lines are coincident ⇒ h2 = ab
Bisectors of Angles:
Theorem:
The equations of bisectors of angles between the lines a1 x + b1 y + c1 = 0, a2 x + b2 y + c2 = 0 are \(\frac{a_{1} x+b_{1} y+c_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\) = ±\(\frac{a_{2} x+b_{2} y+c_{2}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
Pair of Bisectors of Angles:
The equation to the pair bisectors of the angle between the pair of lines ax2 + 2hxy + by2 = 0 is h(x2 – y2) = (a – b)xy (or) \(\frac{x^{2}-y^{2}}{a-b}=\frac{x y}{h}\).
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1x + m1y = 0 ……….(1)
and l2x + m2y = 0 ………(2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
The equations of bisectors of angles between (1) and (2) are \(\frac{l_{1} x+m_{1} y}{\sqrt{l_{1}^{2}+m_{1}^{2}}}-\frac{l_{2} x+m_{2} y}{\sqrt{l_{2}^{2}+m_{2}^{2}}}\) = 0 and
\(\frac{l_{1} x+m_{1} y}{\sqrt{l_{1}^{2}+m_{1}^{2}}}+\frac{l_{2} x+m_{2} y}{\sqrt{l_{2}^{2}+m_{2}^{2}}}\) = 0
The combined equation of the bisectors is
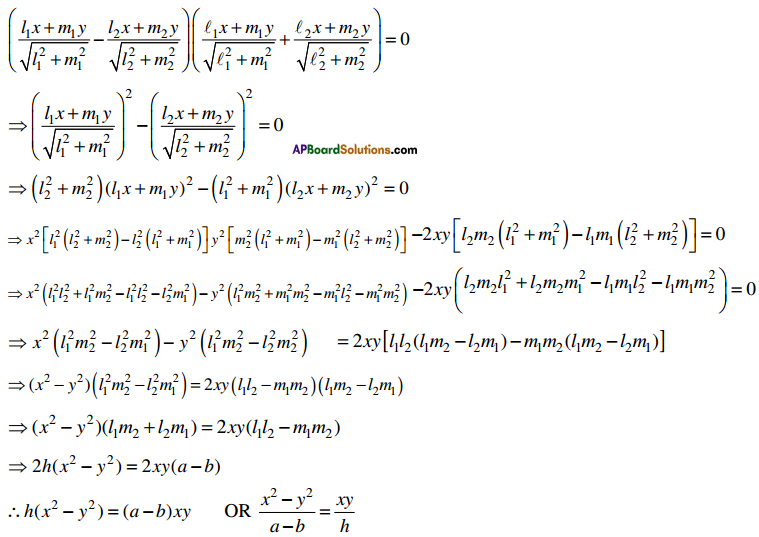
Theorem
The equation to the pair of lines passing through (x0, y0) and parallel ax2 + 2hxy + by2 = 0
is a( x – x0)2 + 2h( x – x0)(y – y0) + b( y – y0)2 = 0
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1x + m1y = 0 ……(1) and l2x + m2 y = 0 …….. (2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
The equation of line parallel to (1) and passing through (x0, y0) is l2(x – x0) + m2(y – y0) = 0 ………(3)
The equation of line parallel to (2) and passing through (x0, y0) is l2(x – x0) + m2(y – y0) = 0 ………(4)
The combined equation of (3), (4) is
[l1( x – x0) + m1( y – y0)][l2( x – x0) + m2(y – y0)] = 0
⇒ l1l2(x – x0)2 + (l1m2 + l2m1)(x – x0)(y – y0) + m1m2(y – y0)2 = 0
⇒ a( x – x0)2 + 2h( x – x0)( y – y0) + b( y – y0)22 = 0
Theorem:
The equation to the pair of lines passing through the origin and perpendicular to ax2 + 2hxy + by2 = 0 is bx2 – 2hxy + ay2 = 0 .
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1x + m1y = 0 ………(1) and l2x + m2y = 0 ……..(2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
The equation of the line perpendicular to (1) and passing through the origin is m1x – l1y = 0 ……….(3)
The equation of the line perpendicular to (2) and passing through the origin is m2 x – l2 y = 0 — (4)
The combined equation of (3) and (4) is
⇒ (m1x – l1 y)(m2 x – l2 y) = 0
⇒ m1m2x – (l1m2 + l2m1 )ny + l1l2 y = 0
bx2 – 2hxy + ay2 = 0
![]()
Theorem:
The equation to the lines passing through (x0, y0) and Perpendicular to ax2 + 2hxy + by2 = 0 is b(x – x0)2 – 2h(x – x0)(y – y0) + a(y – y0)2 = 0
Area of the triangle:
Theorem:
The area of triangle formed by the lines ax2 + 2hxy + by2 = 0 and lx + my + n = 0 is \(\frac{n^{2} \sqrt{h^{2}-a b}}{\left|a m^{2}-2 h \ell m+b \ell^{2}\right|}\)
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1x + m1y = 0 ………(1) and l2x + m2y = 0 ……..(2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
The given straight line is lx + my + n = 0 ………(3)
Clearly (1) and (2) intersect at the origin.
Let A be the point of intersection of (1) and (3). Then
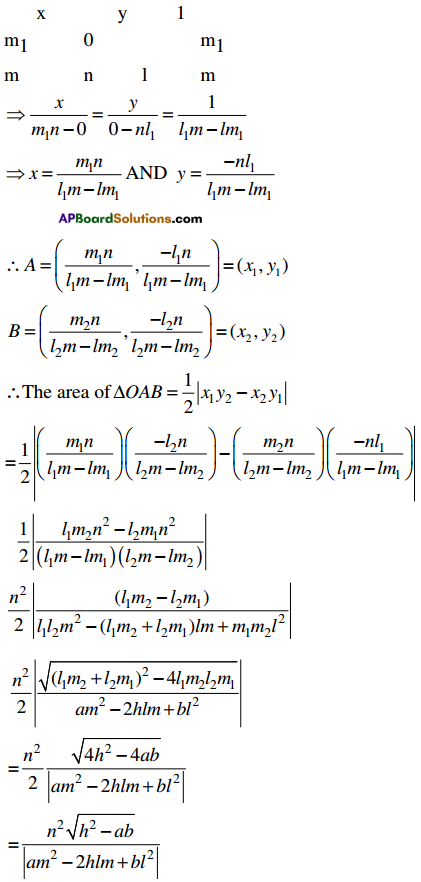
Theorem:
The product of the perpendiculars from (α, β) to the pair of lines ax2 + 2hxy + by2 = 0 is \(\frac{\left|a \alpha^{2}+2 h \alpha \beta+b \beta^{2}\right|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines l1x + m1y = 0 — (1) and l2x + m2 y = 0 …………..(2).
Then l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b.
The lengths of perpendiculars from (α, β) to
the line (1) is p = \(\frac{\left|l_{1} \alpha+m_{1} \beta\right|}{\sqrt{l_{1}^{2}+m_{1}^{2}}}\)
and to the line (2) is q = \(\frac{\left|l_{2} \alpha+m_{2} \beta\right|}{\sqrt{l_{2}^{2}+m_{2}^{2}}}\)
∴ The product of perpendiculars is

Pair of Lines-Second Degree General Equation:
Theorem:
If the equation S ≡ ax2 + 2hxy + by2 + 2 gx + 2 fy + c = 0 represents a pair of straight lines then
(i) Δ ≡ abc + 2fgh – af2 – bg2 – ch2 =0 and
(ii) h2 ≥ ab, g2 ≥ ac, f2 ≥ bc
Proof:
Let the equation S = 0 represent the two lines l1x + m1 y + n1 = 0 and l2 x + m2 y + n2 = 0. Then
ax2 + 2hxy + by2 + 2 gx + 2 fy + c
≡ (l1x + m1y + n1)(l2 x + m2 y + n2) = 0
Equating the co-efficients of like terms, we get
l1l2 = a, l1m2 + l2m1 = 2h , m1m2 = b, and l1n2 + l2n1 = 2g , m1n2 + m2n1 = 2 f , n1n2 = c
(i) Consider the product(2h)(2g)(2f)
= (l1m2 + l2m1)(l1n2 + l2n1)(m1n2 + m2n1)
= l1l2 (m12n2 + m22n12) + m1m2 (l12n22 + l22n12) + n1n2 (l12m22 + l22m12) + 2l1l2m1m2n1n2
= l1l2[(m1n2 + m2n1) – 2m1m2n1n2] + m1m2[(l1n2 + l2n1) – 2l1l2n1n2] + n1n2[(l1m2 + l2m1) – 2l1l2m1m2] + 2l1l2m1m2n1n2
= a(4 f2 – 2bc) + b(4g2 – 2ac) + c(4h2 – 2ab)
8 fgh = 4[af2 + bg2 + ch2 – abc]
abc + 2 fgh – af2 – bg2 – ch2 = 0
(ii) h2 – ab = \(\left(\frac{l_{1} m_{2}+l_{2} m_{1}}{2}\right)^{2}\) – l1l2m1m2 = \(\frac{\left(l_{1} m_{2}+l_{2} m_{1}\right)^{2}-4-l_{1} l_{2} m_{1} m_{2}}{4}\)
= \(\frac{\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}{4}\) ≥ 0
Similarly we can prove g2 > ac and f2 ≥ bc
Note :
If A = abc + 2 fgh – af2 – bg2 – ch2 = 0 , h2 ≥ ab, g2 ≥ ac and f2 ≥ bc, then the equation S ≡ ax2 + 2hxy + by2 + 2 gx + 2 fy + c = 0 represents a pair of straight lines
![]()
Conditions For Parallel Lines-Distance Between Them:
Theorem:
If S = ax2 + 2hxy + by2 + 2 gx + 2 fy + c = 0 represents a pair of parallel lines then h2 = ab and bg2 = af2. Also the distance between the two parallel lines is 2\(\sqrt{\frac{g^{2}-a c}{a(a+b)}}\) (or) 2\(\sqrt{\frac{f^{2}-b c}{b(a+b)}}\)
Proof:
Let the parallel lines represented by S = 0 be
lx + my + n1 = 0 ……….(1) lx + my + n2 = 0 ………..(2)
ax2 + 2hxy + 2gx + 2 fy + c
= (lx + my + n1)(lx + my + n2)
Equating the like terms
l2 = a ………(3)
2lm = 2h …………(4)
m2 = b ………..(5)
l(n1 + n2) = 2g …….(6)
m(n1 + n2) = 2 f ….(7)
n1n2 = c …….(8)
From (3) and (5), l2m2 = ab and from (4) h2 = ab .

Point of Intersection of Pair of Lines:
Theorem:
The point of intersection of the pair of lines represented by
a2 + 2hxy + by2 + 2gx + 2fy + c = 0 when h2 > ab is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)
Proof:
Let the point of intersection of the given pair of lines be (x1, y1).
Transfer the origin to (x1, y1) without changing the direction of the axes.
Let (X, Y) represent the new coordinates of (x, y). Then x = X + x1 and y = Y + y1.
Now the given equation referred to new axes will be
a( X + x1)2 + 2h( X + x1)(Y + y1) +b(Y + y1)2 + 2 g (X + x1) + 2 f (Y + y1) + c = 0
⇒ aX2 + 2hXY + bY2 + 2 X (ax1 + hy1 + g) + 2Y(hx1 + by1 + f) +(ax12 + 2hx1y1 + by2 + 2 gx1 + 2 fy1 + c) = 0
Since this equation represents a pair of lines passing through the origin it should be a homogeneous second degree equation in X and Y. Hence the first degree terms and the constant term must be zero. Therefore,
ax1 + hy1 + g = 0
hx1 + by1 + f = 0
ax12 + 2hx1 y1 + by12 + 2 gx1 + 2 fyx + c = 0
But (3) can be rearranged as
x1(ax1 + hy + g) + y (hx1 + byx + f) + (gx1 + fq + c) = 0
⇒ gx1 + fy1 + c = 0 ………..(4)
Solving (1) and (2) for x1 and y1
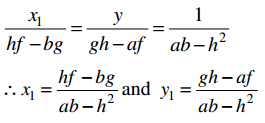
Hence the point of intersection of the given pair of lines is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)
Theorem:
If the pair of lines ax2 + 2hxy + by2 = 0 and the pair of lines ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 form a rhombus then (a – b) fg+h(f2 – g2) = 0.
Proof:
The pair of lines ax2 + 2hxy + by2 = 0 …………(1) is parallel to the lines ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ……….. (2)
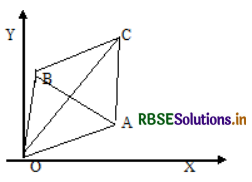
Now the equation
ax2 + 2hxy + by2 + 2gx + 2 fy + c + λ(ax2 + 2hxy + by2) = 0
Represents a curve passing through the points of intersection of (1) and (2).
Substituting λ = -1, in (3) we obtain 2gx + 2fy + c = 0 …(4)
Equation (4) is a straight line passing through A and B and it is the diagonal \(\overline{A B}\)
The point of intersection of (2) is C = \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)
⇒ Slope of \(\overline{O C}=\frac{g h-a f}{h f-b g}\)
In a rhombus the diagonals are perpendicular ⇒ (Slope of \(\overline{O C}\)) (Slope of \(\overline{A B}\)) = -1
⇒ \(\left(\frac{g h-a f}{h f-b g}\right)\left(-\frac{g}{f}\right)\) = -1
⇒ g2h – afg = hf2 – bfg
⇒ (a – b)fg + h(f2 – g2) = 0
\(\frac{g^{2}-f^{2}}{a-b}=\frac{f g}{h}\)
![]()
Theorem:
If ax2 + 2hxy + by2 = 0 be two sides of a parallelogram and px + qy = 1 is one diagonal, then the other diagonal is y(bp – hq) = x(aq – hp)
proof:
Let P(x1, y1) and Q(x2, y2) be the points where the digonal
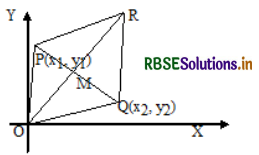
px + qy = 1 meets the pair of lines.
\(\overline{O R}\) and \(\overline{P Q}\) biset each other at M(α, β)
∴ α = \(\frac{x_{1}+x_{2}}{2}\) and β = \(\frac{y_{1}+y_{2}}{2}\)
Eliminating y from ax2 + 2hxy+by2 = 0
and px + qy = 1 ………..(2)
ax2 + 2hx\(\left(\frac{1-p x}{q}\right)\) + b\(\left(\frac{1-p x}{q}\right)^{2}\) = 0
⇒ x2 (aq2 – 2hpq + bp2) + 2 x(hp – bp) + b = 0
The roots of this quadratic equation are x1 and x2 where
x1 + x2 = \(-\frac{2(h q-b p)}{a q^{2}-2 h p q-b p^{2}}\)
⇒ α = \(\frac{(b p-h q)}{\left(a q^{2}-2 h p q+b p^{2}\right)}\)
Similarly, by eliminating x from (1) and (2) a quadratic equation in y is obtained and y1,
y2 are its roots where
y1 + y2 = \(-\frac{2(h p-a q)}{a q^{2}-2 h p q-n p^{2}}\) ⇒ β = \(\frac{(a q-h p)}{\left(a q^{2}-2 h p q+b p^{2}\right)}\)
Now the equation to the join of O(0, 0) and M(α, β) is (y – 0)(0 – α) = (x – 0)(0 – β)
⇒ αy = βx
Substituting the values of α and β, the equation of the diagonal OR
is y(bp – hq) = x(aq – hp).