AP Board 7th Class Maths Solutions Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు Ex 8.2

SCERT AP 7th Class Maths Solutions Pdf Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు Ex 8.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు Exercise 8.2

ప్రశ్న 1.
ఘాతాంక న్యాయాలనుపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
(i) 3⁷ × 3⁸
సాధన.
3⁷ × 3⁸ = 3^{7 + 8} = 3¹⁵ (∵ a^m × aⁿ = a^{m + n})

(ii) 9² × 9⁰ × 9³
సాధన.
9² × 9⁰ × 9³ = 9^{2 + 0 + 3} = 9⁵
(∵ a^m × aⁿ × a^p = a^{m + n + p}
(లేదా)
9² × 1 × 9³ = 9² × 9³ = 9^{2 + 3} = 9⁵ (∴ a⁰ = 1)
∴ 9² × 9⁰ × 9³ = 9⁵

(iii) (2⁸)³
సాధన.
(2⁸)³ = 2^{8 × 3} = 2²⁴ (∵ (a^m)ⁿ = a^mn)

(iv) (a⁵)⁴
సాధన.
(a⁵)⁴ = a^{5 × 4} = a²⁰ (∵ (a^m)ⁿ = a^mn)

(v) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{2}{5}\right)^{3} \times\left(\frac{2}{5}\right)^{8}\)
సాధన.
\(\left(\frac{2}{5}\right)^{4} \times\left(\frac{2}{5}\right)^{3} \times\left(\frac{2}{5}\right)^{8}\)
= \(\left(\frac{2}{5}\right)^{4+3+8}\)
= \(\left(\frac{2}{5}\right)^{15}\) (∴ a^m ∙ aⁿ ∙ a^p = a^{m + n + p})

(vi) 7⁵ ÷ 7⁸
సాధన.
7⁵ ÷ 7⁸ = \(\frac{7^{5}}{7^{8}}=\frac{1}{7^{8-5}}=\frac{1}{7^{3}}\)
\(\left(\frac{a^{m}}{a^{n}}=\frac{1}{a^{n-m}}, n>m\right)\)

(vii) \(\frac{(-6)^{9}}{(-6)^{5}}\)
సాధన.
\(\frac{(-6)^{9}}{(-6)^{5}}\) = (- 6)^{9 – 5} = (- 6)⁴
(∵ \(\frac{a^{m}}{a^{n}}\) = a^{m – n}, m > n)

(viii) (6⁴ × 6²) ÷ 6⁵
సాధన.
(6⁴ × 6²) ÷ 6⁵
= (6^{4 + 2}) ÷ 6⁵ (∵ a^m × aⁿ = a^{m + n}
= 6⁶ ÷ 6⁵
= \(\frac{6^{6}}{6^{5}}\) = 6^{6 – 5} = 6¹ = 6
(∵ \(\frac{a^{m}}{a^{n}}\) = a^{m – n}, (m > n))

(ix) \(\frac{5^{3}}{2^{3}}\)
సాధన.
\(\frac{5^{3}}{2^{3}}\) = \(\left(\frac{5}{2}\right)^{3}\) \(\left(\frac{a^{m}}{b^{m}}=\left(\frac{a}{b}\right)^{m}\right)\)

(x) (- 3)³ × (- 3)¹⁰ × (- 3)⁷
సాధన.
(- 3)³ × (- 3)¹⁰ × (- 3)⁷ = (- 3)^{3 + 10 + 1}
= (- 3)²⁰
(∵ a^p ∙ a^q ∙ a^r = a^{p + q + r})

ప్రశ్న 2.
కింది వానిని సూక్ష్మీకరించి ఘాత రూపంలో వ్యక్తపరచండి.

(i) \(\left(\frac{a^{5}}{a^{3}}\right)\) × a⁸
సాధన.

(ii) 2⁰ + 3⁰ – 4⁰
సాధన.
2⁰ + 3⁰ – 4⁰ = 1 + 1 – 1 = 2 – 1 = 1
∴ 20 + 30 – 40 = 1 (∵ a⁰ = 1)

(iii) (2³ × 2)²
సాధన.
(2³ × 2)² = (2^{3 + 1})² = (2⁴)²
(∵ a^m × aⁿ = a^{m + n}; (a^m)ⁿ = a^mn)
∴ (2³ × 2)² = 2⁸
(లేదా )
(2³ × 2)² = (2³)² × 2²
(∵ (a × b)^m = a^m × b^m)
= 2⁶ × 2² (∵ (a^m)ⁿ = a^mn)
= 2^{6 + 2} = 2⁸ (∵ a^m × aⁿ = a^{m + n})

(iv) [(5²)³ × 5⁴] ÷ 5⁷.
సాధన.
[(5²)³ × 5⁴] ÷ 5⁷
= (5^{2 × 3} × 5⁴ ÷ 5⁷ (∵ (a^m)ⁿ = a^mn)
= [5⁶ × 5⁴] ÷ 5⁷(∵ a^m × aⁿ = a^{m + n})
= [5^{6 + 4}] ÷ 5⁷
= 5¹⁰ ÷ 5⁷ = \(\frac{5^{10}}{5^{7}}\)
= 5^{10 – 7} = 5³ (∵ \(\frac{a^{m}}{a^{n}}\) = a^{m – n}, m > n)
∴ [(5²)³ × 5⁴)] ÷ 5⁷ = 5³

ప్రశ్న 3.
\(\left(\frac{x^{a}}{x^{b}}\right) \times\left(\frac{x^{b}}{x^{c}}\right) \times\left(\frac{x^{c}}{x^{a}}\right)\) ను సూక్ష్మీకరించండి.
సాధన.

ప్రశ్న 4.
కింది వాటి విలువ కనుక్కోండి.
(i) (- 1)¹⁰⁰⁰
సాధన.
(- 1)¹⁰⁰⁰ = 1 (∵ 1000 సరిసంఖ్య)
[∵ (- 1)^m = – 1 (m బేసిసంఖ్య)
(- 1)^m = 1 (m సరిసంఖ్య)]

(ii) (1)²⁵⁰
సాధన.
(1)²⁵⁰ = 1. (∵ 250 సరిసంఖ్య)

(iii) (- 1)¹²¹
సాధన.
(- 1)¹²¹ = – 1 (∵ 121 బేసిసంఖ్య)

(iv) (10000)⁰
సాధన.
(100000)⁰ = 1 (∵ a⁰ = 1)

ప్రశ్న 5.
7⁵ × 7^3x = 7²⁰ అయితే ‘x’ విలువ కనుక్కోండి.
సాధన.
7⁵ × 7^3x = 7²⁰
7^{5 + 3x} = 7²⁰ (∵ a^m × aⁿ = a^{m + n})
సమీకరణంలో ఇరువైపులా భూములు సమానం కావున ఘాతాంకాలు సమానం అవుతాయి.
∴ 5 + 3x = 20
⇒ 3x = 20 – 5
⇒ 3x = 15
⇒ \(\frac{3 x}{3}\) = \(\frac{15}{3}\) = 5
∴ 7⁵ × 7^3x = 7²⁰ అయితే x = 5

సరిచూచుట:
x = 5 అయిన L.H.S.
7⁵ × 7^3x = 7⁵ × 7³⁽⁵⁾
= 7⁵ × 7¹⁵
= 7^{5 + 15}
= 7²⁰
= R.H.S.

ప్రశ్న 6.
10^y = 10000 అయితే 5y = ?
సాధన.
10^y = 10000
10^y = 10⁴
సమీకరణంలో ఇరువైపులా భూములు సమానం కావున ఘాతాంకాలు సమానం.
∴ y = 4
⇒ 5y = 5(4) = 20
∴ 10^y = 10000 అయిన 5y = 20

ప్రశ్న 7.
5^x = 100 అయితే కింది వాటి విలువలు కనుక్కోండి.
(i) 5^{x + 2}
సాధన.
5^x = 100 (ఇవ్వబడినది)
5^{x + 2} = 5^x × 5² = 100 × 25 = 2500
(∵ a^m × aⁿ = a^{m + n})

(ii) 5^{x – 2}
సాధన.
5^{x – 2} = \(\frac{5^{x}}{5^{2}}\) = \(\frac{100}{25}\) = 4
[∵ (a^m ÷ aⁿ = a^{m – n}]

ప్రశ్న 8.
3⁴ ను ఏ సంఖ్యచే గుణించిన లబ్దము
సాధన.

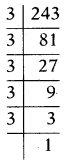
3⁴ ను x తో గుణించిన లబ్దం అనుకొనుము.
3⁴ × x = 243
3⁴ × x = 3⁵
∴ x = \(\frac{3^{5}}{3^{4}}\)
⇒ x = 3^{5 – 4}
∴ x = 3¹ = 3
3⁴ ను 3చే గుణించిన లబ్దం 243 అవుతుంది

ప్రశ్న 9.
ఆరుషి (5²)⁴ ను 5¹⁶ గా లెక్కించింది. ఆమె చేసినది సరియైనదేనా ? మీ జవాబును సమర్థించండి.
సాధన.
ఆరుషి చేసినది సరైనది కాదు. ఎందుకనగా
(5²)⁴ = 5^{2 × 4}
= 5⁸ [∵ (a^m)aⁿ = a^mn)

ప్రశ్న 10.
3⁵ × 4⁵ అనునది 12²⁵ కు సమానమా ? కానిచో ఎందుకు కాదు ? మీ జవాబును సమర్థించండి.
సాధన.
3⁵ × 4⁵ అనునది (12)²⁵ కు సమానం కాదు.
3⁵ × 4⁵ = (3 × 4)⁵
= (12)⁵
[∵ a^m × b^m = (a × b)^m]