Students can go through AP State Board 9th Class Physical Science Notes Chapter 7 Reflection of Light at Curved Surfaces to understand and remember the concept easily.
AP State Board Syllabus 9th Class Physical Science Notes Chapter 7 Reflection of Light at Curved Surfaces
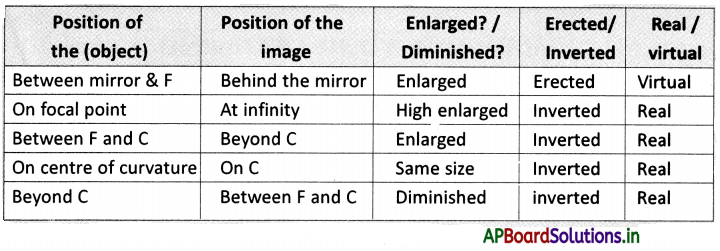
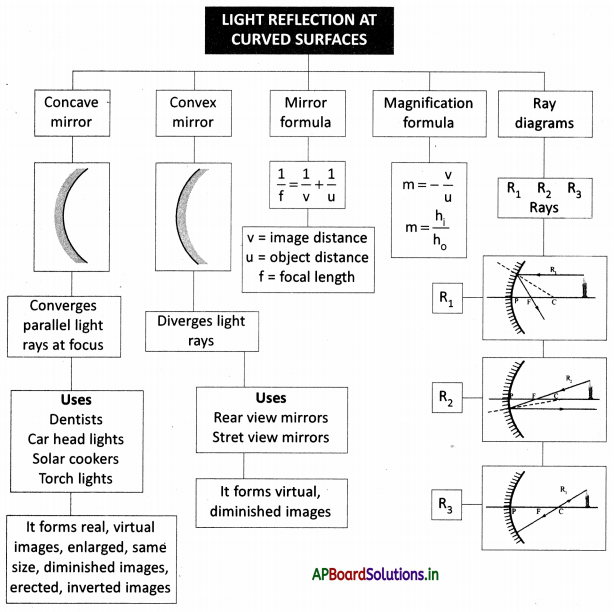
→ The concave mirror converges the parallel light beam at one point. So it is called a converging mirror.
→ Convex mirror diverges the parallel light beam. So it is called a diverging mirror.
→ We always get a virtual and diminished image due to a convex mirror.
→ Mirror formula is \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
f = focal length; u = object distance; v = image distance
→ Focal length is positive for a concave mirror and negative for a convex mirror.
→ The image distance is negative for a real image and positive for a virtual image.
→ The height of the object and height of the image is positive, if measured upward from the axis and negative if measured downwards.
→ Magnification is positive for erect images and negative for the inverted images.
→ Solar cooker works on the principle of converting sunlight at a point due to concave mirror.
![]()
→ Magnification: m = \(\frac{\text { size of the image }}{\text { size of the object }}\) (or) \(\frac{\mathrm{h}_{1}}{\mathrm{~h}_{\mathrm{o}}}\)
(OR)
m = – \(\frac{\text { image distance }}{\text { object distance }}=-\frac{v}{u}\)
→ We should use sign convention every time while using the formulae of the mirrors.
→ It is easy to understand the certain properties of light by drawing a ray diagram
→ Curved Surface: The surfaces which are not flat are called curved surface
→ The angle of incidence (∠i): The angle between the incident ray and normal is called the angle of incidence.
→ The angle of reflection (∠r): The angle between normal and reflected rays is called the angle of reflection.
→ Normal: The Pine perpendicular to the surface is called normal.
→ Centre of curvature (C): The normal from a concave mirror converges at a point that point is called the center of curvature.
→ The radius of curvature (R): The distance between vertex and center of curvature is called the radius of curvature.
→ Principal axis (or) Central axis: The horizontal line which passes through the center of curvature and pole.
![]()
→ Pole (P) (or) Vertex: The point where the central axis touches the mirror.
→ Focus or focal point (F): The rays coming from distinct objects parallel to the concave mirror will converge at a point called focus or focal point.
→ Focal length (f): The distance between vertex and focus.
→ Object distance (u): The distance between object and mirror is called object distance.
→ Image distance (v): The distance between image and mirror is called image distance.
→ Virtual image The Image formed in the mirror by extending the rays backward is called a virtual image.
→ Real image: The image formed due to the converging of light rays is a real image.
→ Ray diagram: A diagram showing the paths of selected rays through an optical system.
→ Magnification (m): Ratio of the size of the image to the size of the object.
→ Reflection: The bouncing back of the light is called reflection.
→ Incident ray: The ray which is an incident on a surface is called an Incident ray.
→ Reflected Ray: The ray which is reflected from the surface is called a reflected ray.
→ Virtual image: Virtual image ¡s the ¡mage formed due to diverging of light rays.
(OR)
The Image formed due to the extension of rays in the backward direction.
![]()
→ Spherical mirror: A mirror that has a curved reflective surface is a spherical mirror.
→ Concave mirror: A spherical mirror whose reflecting surface is curved inwards is called a concave mirror.
→ Convex mirror: A spherical mirror whose reflecting surface is curved outwards is called a convex mirror.
→ Pierre de Fermat:
- A French Lawyer at the Parliament of Toulouse, France, and an amateur mathematician.
- He made notable contributions to analytical geometry, probability, and optics.
- He proposed his principle on the light which states that light selects the path which takes the least time to travel. This principle was famous as the Fermat principle.