Andhra Pradesh BIEAP AP Inter 1st Year Chemistry Study Material 5th Lesson Stoichiometry Textbook Questions and Answers.
AP Inter 1st Year Chemistry Study Material 5th Lesson Stoichiometry
Very Short Answer Questions
Question 1.
How many number of moles of glucose are present in 540 gms of glucose?
Answer:
Formulae:
No. of moles = \(\frac{\text { Weight }}{\text { G.M. Wt }}\)
= \(\frac{540}{180}\)
= 3
Given
Weight of glucose = 540 gms
G.M. wt = 180 (C6H12O6)
No. of moles of glucose in 540 gms = 3 moles.
Question 2.
Calculate the weight of 0.1 mole of sodium carbonate.
Answer:
Formulae:
No. of moles = \(\frac{\text { Weight }}{\mathrm{GMWt}}\), 0.1 = \(\frac{\text { Weight }}{106}\)
Weight = 10.6 × 0.1 = 10.6 gms
Given
No. of moles = 0.1
G.M. Wt of Na2CO3 = 106
![]()
Question 3.
How many molecules of glucose are present in 5.23g of glucose (Molecular weight of glucose 180 u).
Answer:
Formulae:
No. of molecules = No. of moles × Avagadro no
No. of moles = \(\frac{\text { Weight }}{\text { GM Wt }}\) = \(\frac{5.23}{180}\) = 0.02906 moles
No. of molecules = 0.02906 × 6.023 × 1023
= 1.75 × 1022 molecules
Given
Wt of glucose = 5.23 gms
G.M. Wt = 180
Question 4.
Calculate the number of molecules present in 1.12 × 10-7 c.c. of a gas at STP (c.c. cubic centimeters = cm3).
Answer:
1 mole of any gas occupies 22400 cc of volume
1 mole of any gas contains 6.023 × 1023 molecules
∴ 22400 cc of gas at STP contains 6.023 × 1023 molecules
1.12 × 10-7 cc of a gas at STP contains ——–?
\(\frac{1.12 \times 10^{-7} \times 6.023 \times 10^{23}}{22400}\) = 3.015 × 1012 molecules
Question 5.
The empirical formula of a compound is CH2O. Its molecular weight is 90. Calculate the molecular formula of the compound. (A.P. Mar. ‘16) (Mar. 13)
Answer:
Formulae:
![]()
∴ Molecular formula = 3(CH2O) = Cr (NO3)3(aq) + Pb(s).
Given
Molecular wt = 90
Emperical formula = CH3O
∴ Emperical wt = 30
![]()
Question 6.
Balance the following equation by the oxidation number method
Cr(S) + Pb(NO3)2(aq) → Cr (NO3)3(aq) + Pb(s).
Answer:
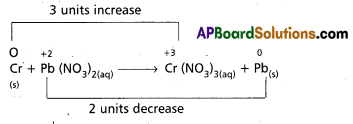
So the balanced equation is 2Cr + 3Pb(NO3)2 → 2Cr(NO3)3 + 3Pb
Question 7.
What volume of H2 at STP is required to reduce 0.795 g of CuO to give Cu and H2O.
Answer:
Balance equation is
CuO + H2 → Cu + H2O
79.5 gms → 1 mole H2 gas for reduction → 22.4 lit of volume at STP
∴ 79.5 gms of CuO require 22.4 lit of H2 at STP
Then 0.795 gms of CuO require ——-?
\(\frac{0.795 \times 22.4}{79.5}\) = 0.224 lit.
AP Inter 1st Year Chemistry Study Material Chapter 5 Stoichiometry
Question 8.
Calculate the volume of O2 at STP required to completely burn 100 ml of acetylene.
Answer:
Balanced chemical equation for combustion of acetylene is
2C2H2 + 5O2 → 4CO2 + 2H2O
2 moles of C2H2 require 5 moles of O2 for complete combustion at STP
2 × 22400 ml of C2H2 require 5 × 22400 ml of O2 at STP
Then 100 ml of C2H2 require ————?
\(\frac{100 \times 5 \times 22400}{2 \times 22400}\) = \(\frac{500}{2}\) = 250 ml
Question 9.
Now-a-days it is thought that oxidation is simply decrease in electron density and reduction is increase in electron density. How would you justify this?
Answer:
Oxidation : The process of removing electrons from an element is called oxidation. It is also called
as de-electronation.
- Oxidation means decrease in electron density
e.g. : 2Cl– → Cl2 + 2\(e^{\ominus}\) - Oxidation process occurs at anode in the electrolysis process.
- Reduction : The process of addition of electrons to an element is called reduction. It is also called as electronation.
- Reduction means increase in electron density.
e.g.: Mg2+ + 2e– → Mg - Reduction process occurs of cathode in the electrolysis process.
Question 10.
What is a redox concept? Give an example.
Answer:
Redox reactions are the reactions in which reduction and oxidation both takes place.
e.g.:
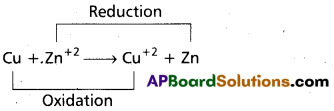
Question 11.
Calculate the mass per cent of the different elements present in sodium sulphate (Na2SO4).
Answer:
Given compound is sodium sulphate (Na2SO4)
Molecular weight of the compound = 2(23) + 1(32) + 4(16)
= 46 + 32 + 64
= 142
Step – I:
Mass percent of Na
142 gms of Na2SO4 → 46 gms of Na
100 gms of Na2SO4 → ?
\(\frac{100 \times 46}{142}\) = 32.39%
Step – II:
Mass percent of ‘S’
142 gms of Na2SO4 → 32 gms of ‘S’
100 gms of Na2SO4 → ?
\(\frac{100 \times 32}{142}\) = 22.53%
Step-III:
Mass percent of ‘0’
142 gms of Na2SO4 → 64 gms of oxygen
100 gms of Na2SO4 → ?
\(\frac{100 \times 64}{142}\) = 45.07%
∴ Mass percents of Na, S, O are 32.39, 22.53, 45.07.
Question 12.
What do you mean by significant figures?
Answer:
The meaningful digits which are known with certainty are called significant figures.
- The uncertainty in the experimental (or) calculated values is indicated by mentioning the number of significant figures.
![]()
Question 13.
If the speed of light is 3.0 × 108 ms-1. Calculate the distance covered by light in 2.00 ns.
Answer:
Given the speed of light 3 × 108 m/sec.
i.e., 1 sec → 3 × 108 m
In 2 nano seconds → ?
2 × 10-9 sec
\(\frac{2 \times 10^{-9} \times 3 \times 10^8}{1}\) = 6 × 10-1 = 0.6 m
Short Answer Questions
Question 1.
The approximate production of sodium carbonate per month is 424 × 108 g, while that of methyl alcohol is 320 × 106 g. Which is produced more in terms of moles?
Answer:
Given that weight of Na2CO3 produced per month = 424 × 106 gms
No. of moles of Na2CO3 = \(\frac{w t}{\text { GMwt }}\) = \(\frac{424 \times 10^6}{106}\) = 4 × 106 moles per month
Given weight of CH3OH produced per month = 320 × 106 gms
No. of moles of CH3OH = = \(\frac{320 \times 10^6}{32}\) = 107 moles per month
Methyl Alcohol is produced more (per month) in terms of moles.
Question 2.
How much minimum volume of CO at STP is needed to react completely with 0.112 L of O2 at 1.5 atm pressure and 127°C to give CO2.
Answer:
Formula \(\frac{P_1 V_1}{T_1}\) = \(\frac{P_2 V_2}{T_2}\)
At STP
P1 = 1 atm
V1 = ?
T1 = 0°C = 273 K
Given P2 = 1.5 at m
V2 = 0.112 lit
T2 = 127°C = 400 K
\(\frac{1 \times V_1}{273}\) = \(\frac{1.5 \times 0.112}{400}\)
V1 = \(\frac{1.5 \times 0.112 \times 273}{400}\)
= 0.1147 lit
Chemical equation
2CO + O2 → 2CO2
2 moles of CO → 1 mole of O2 at STP
2 × 22.4 lit → 1 × 22.4 lit
? ← 0.1147 lit
\(\frac{0.1147 \times 2 \times 22.4}{22.4}\) = 0.2294 lit
The volume of CO required at STP = 0.2294 lit = 229.4 ml
Question 3.
Chemical analysis of a carbon compound gave the following percentage composition by weight of the elements present, carbon = 10.06%, hydrogen = 0.84%. chlorine = 89.10%. Calculate the empirical formula of the compound.
Answer:
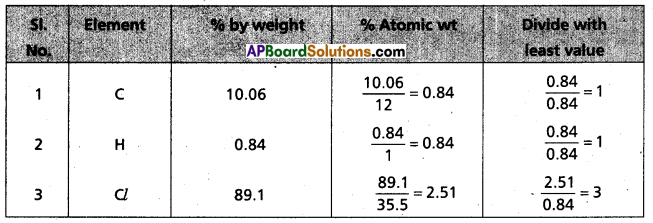
∴ Emperical formula of given compound = C1H1Cl3
= CHCl3
Question 4.
A carbon compound on analysis gave the following percentage composition, carbon 14.5%, hydrogen 1.8%, chlorine 64.46%, oxygen 19.24%. Calculate the empirical formula of the compound.
Answer:
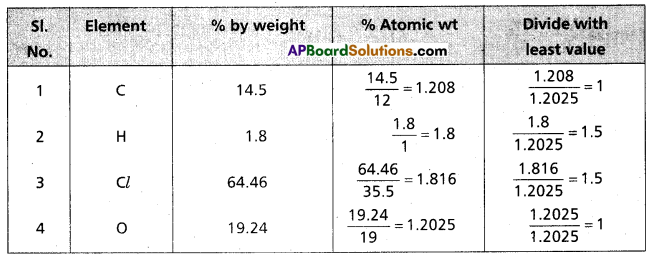
∴ The formula of the compound = C1 H1.5 Cl1.5 O1
Emperical formula of the compound = C2 H3 Cl3 O2
Question 5.
Calculate the empirical formula of a compound having percentage composition : Potassium (K) = 26.57, chromium (Cr) = 35.36; oxygen (0) 38.07. (Given the atomic weights of K. Cr and O as 39; 52 and 16 respectively).
Answer:

Formula of the compound = K1 Cr1 O3.5
Emperical formula of the compound = K2 Cr2 O7
Question 6.
A carbon compound contains 12.8% carbon, 2.1% hydrogen, 85.1% bromine. The molecular weight of the compound is 187.9. Calculate the molecular formula.
Answer:

∴ Emperical formula of the compound = C1 H2 Br
Molecular formula = n (Emperical formula)
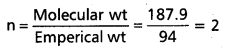
Given molecular wt = 187.9
Emperical wt = 94 (CH2 Br)
∴ Molecular formula = 2 (CH2Br)
= C2H4Br2
Question 7.
0.188 g of an organic compound having an empirical formula CH2Br displaced 24.2 cc. of air at 14 °C and 752 mm pressure. Calculate the molecular formula of the compound. (Aqueous tension at 14°C is 12mm).
Answer:
Given Emperical formula CH2Br
Wt. of compound = 0.188 gms
Volume of displaced air = 24.2 CC
Temperature = 14°C = 287 K
Pressure = 752 mm.
STP conditions
P1 = 760 mm
v1 = ?
T1 = 273 K
Given conditions
P2 = Pressure – aqueous tension
= 752 – 12mm = 740 mm
V2 = 24.2K
T2 = 287 K
Formula
\(\frac{P_1 V_1}{T_1}\) = \(\frac{P_2 V_2}{T_2}\) ⇒ \(\frac{760 \times V_1}{273}\) = \(\frac{740 \times 24.2}{287}\)
V1 = \(\frac{740 \times 24.2}{287} \times \frac{273}{760}\) = 22.414ml (or) 22.414 CC
∴ 0.188 gms of organic compound displaced 22.414 CC of air gms of organic compound displaced 22400 CC of air
\(\frac{22400}{22.414} \times 0.188\) = 188 ∴ Gram molecular wt of compound = 188
Molecular formula = n (Emperical formula)
= n (CH2Br)
n = \(\frac{\text { Molecular wt }}{\text { Emperical wt }}\) = \(\frac{188}{94}\) = 2 ∴ Molecular formula = C2 H4 Br2
Question 8.
Calculate the amount of 90% H2S04 required for the preparation of 420 kg HCl.
2 NaCl + H2SO4 → Na2SO4 + 2 HCl
Answer:
Given equation is
2NaCl + H2SO4 → 4 Na2SO4 + 2HCl
1 Mole H2SO4 → 2 Moles HCl
98 gms of H2SO4 → 2 × 36.5 = 73 gms of HCl
? → 420 × 103 gms of HCl
\(\frac{420 \times 10^3 \times 98}{73}\) = 563.84 × 103 gms
For 100% H2SO4 → 563.84 × 103
For 90% H2SO4 → 563.84 × 103 × \(\frac{100}{90}\)
= 626.5 × 103 gms of H2SO4
∴ 626.5 × 103 gms of 90% H2SO4 is required to produce 420 × 103 gms of HCl
Question 9.
An astronaut receives the energy required in his body by the combustion of 34g of sucrose per hour. How much oxygen he has to carry along with him for his energy requirement in a day ?
Answer:
Given sucrose quantity required per hour = 34 gms
Sucrose quantity required per a day = 34 × 24 gms
Chemical equation of combustion of sucrose
C12 H22 O11 + 12O2 → 12CO2 + 11 H2O + Energy
1 mole sucrose → 12 moles of Oxygen
342 gms of sucrose → 12 × 32 gms of oxygen
34 × 24 gs of sucrose → ?
\(\frac{34 \times 24}{342}\) × 12 × 32 = 916.21 gms
∴ The astronaut require 916.21 gms of Oxygen per a day
Question 10.
What volume of CO2 is obtained at STP by heating 4g of CaCO3 ?
Answer:
Chemical Equation is
CaCO3 ![]() CaO + CO2
CaO + CO2
1 mole CaCO3 → 1 mole CO2 at STP
100 gms of CaCO3 → 22.4 lit of CO2 at STP
4gms of CaCO3 → ?
\(\frac{4 \times 22.4}{100}\) = 0.896 lit
Question 11.
When 50g of a sample of sulphur was burnt in air 4% of the sample was left over. Calculate the volume of air required at STP containing 21% oxygen by volume.
Answer:
Given that when a 50 gms of sample of sulphur was burnt 4% of the sample was left over.
∴ 50 gms of S → 48 gms of ‘S’ burnt.
Chemical equation is S + O2 → SO2
32 gm of ‘S’ 22.4 lit of O2 at STP
48 gms of S →
100 ml air contains 21 ml of oxygen
100 lit of air contains 21 lit of oxygen
33.6 lit of oxygen is present in \(\frac{33.6 \times 100}{21}\) = 160 lit
∴ The volume of air needed for combustion = 160 lit
Question 12.
Calculate the volume of oxygen gas required at STP conditions for the complete combustion of 10 cc of methane gas at 20°C and 770 mm pressure.
Answer:
Given 10 cc of methane (CH4) undergoes combustion at 20°C and 770 mm pressure
STP Conditions
P1 = 760 mm
V1 = ?
T1 = 273 k
Given conditions
P2 = 770 mm
V2 = 10 cc
T2 = 20°C = 293 k
![]()
Formulae
\(\frac{P_1 V_1}{T_1}\) = \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\)
\(\frac{760 \times V_1}{273}\) = \(\frac{770 \times 10}{293}\)
V1 = \(\frac{770 \times 10 \times 273}{293 \times 760}\) = 9.44 cc ∴ Volume of methane (CH4) at STP = 9.44 cc.
Chemical equation is
CH4 + 2O2 → CO2 + 2H2O
1 mole CH4 → 2 moles of oxygen
22,400 cc of CH4 → 2 × 22400 cc of oxygen
9.44 cc of CH4 → ?
\(\frac{9.44}{22400}\) × 2 × 22400 = 18.88 cc ∴ Volume of oxygen gas required STP = 18.88 cc.
Question 13.
Calculate the volume of H2 liberated at 27°C and 760 mm of Hg pressure by action by 0.6g of magnesium with excess of dil HCl.
Answer:
Chemical equation is
Mg + 2HCl → MgCl2 +H2
24 gms. of Mg → 1 mole of H2 at STP
= 22.4 lit at STP
0.6 gms. of Mg → ?
\(\frac{0.6 \times 22.4}{24}\) = 0.56 lit = 560 ml
Formula
\(\frac{P_1 V_1}{T_1}\) = \(\frac{P_2 V_2}{T_2}\)
\(\frac{760 \times V_1}{300}\) = \(\frac{760 \times 560}{273}\)
V1 = \(\frac{560 \times 300}{273}\) = 615.4 ml
∴ volume of H2 liberated at 27°C and 760 mm of presence = 615.4 ml = 0.6154 Lit.
Given conditions
P1 = 760 mm
V1 = ?
T1 = 27° mm
STP conditions
P2 = 760 mm
V2 = 560 ml
T2 = 0° C = 273 k
Question 14.
Explain the role of redox reactions in titrimetre processes and galvanic cells.
Answer:
a) Redox reactions in titrimetric quantitative analysis : In titrimetric analysis the substance of known concentration is called the titrant and the substance being titrated is called the titrand. The standard solution is generally added from a long graduated tube called burette. The process of adding the standard solution until the reaction is just complete is called titration. The substance to be estimated is titrated. The point at which the titrand just completely reacts is called the equivalence point (or) the theoretical point (or) stoichiometric end point. In the redox reactions the completion of the titration is detected by a suitable method like
- Observing a physical change, for example, the light pink colour of KMnO4 titrations.
- By using a reagent known as indicator which gives a clear visual change like colour change, formation of turbidity etc. The point at wh’ch this is observed is called the end point of the titration which should coincide with theoretical end point.
Examples:
- In Cr2\(\mathrm{O}_7^{2-}\) titrations dippenyl amine is used as indicator and at the end poirtt it produces intense blue colour due to oxidation by Cr2\(\mathrm{O}_7^{2-}\).
- In the titration of Cu+2 with I–
2Cu2+ (aq) + 4I– (aq) → Cu2I2 (s) + I2 (aq)
A redox reaction I2 gives a deep blue colour with starch solution. - In the titration of I2 (aq) S2\(\mathrm{O}_3^{-2}\) as per the stoichiometric reduce equation.
In this way redox reactions are taken as the basis for titrimetric analysis with Mn\(\mathrm{O}_4^{-}\), Cr2\(\mathrm{O}_7^{-2}\) etc., as oxidising agents and S2\(\mathrm{O}_3^{-}\) etc., as a reducing agents,
b) Redox Reactions – Galvanic cells : Redox reaction (i.e) cell reaction that takes place in gavamic cell is
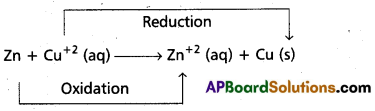
The process of transfer of electrons from Zn(s) to Cu+2 take place directly. To make this transfer indirectly, Zn rod is kept in ZnSO4 solution in one beaker and in the other beaker CuSO4 solution is taken and a copper rod is dipped in it. Now the redox reaction takes place in either of the beakers. Each beakers contains both oxidised and reduced forms of the respective species in the beakers containing CuSO4 solution & Cu rod at the interface Cu and Cu+2 and in the other beaker at the interface Zn and Zn+2. The two forms i.e., oxidised and reduced forms of a species participating in oxidation and reduction half reactions is called redox couple. Both the beakers contains each a redox couple. The oxidised form and reduced form are separated by a vertical line (or) a slash that represent an interface, e.g.: Zn (s) / Zn+2 (aq)
In the above arrangement, the two redox couples are represented by Zn+2 / Zn and Cu+2 / Cu.
halvamic cell is represented as : Zn/Zn2+//Cu+2/Cu.
Question 15.
Define and explain molar mass.
Answer:
Molar mass : The mass of one mole of any substance in gms is called its molar mass,
e.g. :
- Molar mass of sulphuric acid = 98 g
- Molar mass of hydrogen is one gram for gram atomic mass and two grams for gram molecular mass.
Question 16.
What are disproportionation reactions ? Give example. (T.S. Mar. ’16)
Answer:
Disproportionation Reaction : Reactions in which same element in the given form to undergo both oxidation and reduction simultaneously.

Here Cl2 undergoes both oxidation and reduction reactions. So, above reaction is disproportionation reaction.
Question 17.
What are comproportionation reactions ? Give example.
Answer:
Comproportionation reactions : In these reactions, two species with the same element in two different oxidation states form a single product in which the element is in an intermediate oxidation state. Reverse of disproportionation is comproportionation.
e.g.:
Question 18.
Determine the empirical formula of an oxide of iron which has 69.9% iron and 30.1% dioxygen by mass.
Answer:
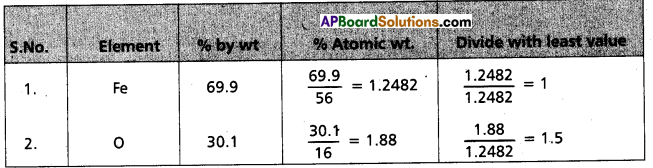
∴ Formula of compound = Fe1O1.5
Emperical formula = Fe2O3
![]()
Question 19.
Calculate the mass of sodium acetate (CH3COONa) required to make 500 ml of 0.375 molar aqueous solution. Molar mass of sodium acetate is 82.0245 g mol-1.
Answer:
Formula
Molarity = \(\frac{\mathrm{Wt}}{\mathrm{GMwt}}\) × \(\frac{1000}{V(m l)}\)
Molarity = 0.375M
V = 500 ml
GMwt of CH3COONa = 82.0245
0.375 = \(\frac{W t}{82.0245}\) × \(\frac{1000}{500}\)
Wt = \(\frac{82.0245 \times 0.375}{2}\)
= 15.3795 gms
∴ Mass of CH3COONa required = 15.3795 gms
Question 20.
What is the concentration of sugar (C12H22O11) in mol L-1 if 20g are dissolved in enough water to make a final volume up to 2L ?
Answer:
Formula
Molarity = \(\frac{W t}{G M W t} \times \frac{1}{V(\text { lit })}\)
= \(\frac{20}{342} \times \frac{1}{2}\)
= 0.02924 M
Wt = 20 gms
GMWt = 342
[C12H22OH]
V = 2 lit
Question 21.
How many significant figures are present in the following ?
- 0.0025
- 208
- 5005
- 126,000
- 500.0
- 2.0034
Answer:
- 0.0025 has 2 significant figures
- 208 has 3 significant figures
- 5005 has 4 significant figures
- 126000 has 3 significant figures
- 500.0 has 4 significant figures
- 2.0034 has 5 significant figures
Question 22.
Round up the following upto three significant figures :
- 34.216
- 10.4107
- 0.04597
- 2808
Answer:
- 34.216 becomes 34.2
- 10.4107 becomes 10.4
- 0.04597 becomes 0.046
- 2808 becomes 281
Question 23.
Calculate the molarity of a solution of ethanol in water in which the mole fraction of ethanol is 0.040 (assume the density of water to be one)
Answer:
The relation between Molarity and mole fraction is given by
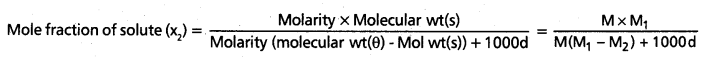
Given data, x2 = 0.040, M = ?
M1 = 18(H2O), M2 = 46 (C2H5OH), Cl = 1
0040 = \(\frac{M \times 18}{M(18-46)+1000 \times 1}\) = \(\frac{M \times 18}{-28 M+1000}\)
18 M = -0.040 × M × 28 + 0.040 × 1000
18 M = -1.12M + 40
(18 + 1.12)M = 40
19.12 M = 40
M = \(\frac{40}{19.12}\) = 2 09 M ∴ Molarity of Ethanol = 2.09 M
Given data

Question 24.
A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g of water and no other products. A volume of 10.0 L (measured at STP) of this welding gas is found to weigh 11.6 g. calculate
(i) empirical formula,
(ii) molar mass of the gas and
(iii) molecular formula.
Answer:
Assuming 1 gm. of gas is burnt
The weight % of ‘C’ = \(\frac{3.38 \times 12}{44}\) × 100 = 92.18%
The weight % of ‘H’ = \(\frac{0.69 \times 2}{18}\) = 7.67%
i)

Experical formula of compound = C1H1
ii) Given 10 lit of gas at STP weighs – 11.6 gas
22.44 lit of gas at STP weights = \(\frac{22.4 \times 11.6}{10}\) = 25.984
∴ Molecular weight of given gas = 25.984
iii) Molecular formula = n(emperical formula)
n = \(\frac{\text { Mol. wt }}{\text { Emp. wt }}\) = \(\frac{25.984}{13}\) = 2 ∴ Molecular formula = 2(CH) = C2H2.
Question 25.
Calcium carbonate reacts with aqueous HCl to give CaCl2 and CO2 according to the reaction CaCO3(5) + 2 HCl(aq) → CaCl2(aq) + CO2(g) + H2O (L). What mass of CaCO3 is required to react completely with 25 mL of 0.75 M HCl?
Answer:
Given chemical reaction
CaCO3(s) + 2HCl(aq) → CaCl2(aq) + CO2(g) + H2O(l)
Molarity = \(\frac{\mathrm{Wt}}{\mathrm{GMWt}} \times \frac{1000}{\mathrm{~V}(\mathrm{~m})}\)
0.75 = \(\frac{\mathrm{Wt}}{36.5} \times \frac{1000}{25}\)
M = 0.75 M
W = ?
Wt = \(\frac{0.75 \times 36.5 \times 25}{1000}\)
= 0.6844 gms of HCl
GMwt = 36.5
V = 25 ml
From the equation
1 mole of CaCO3 – 2 moles of HCl
100 gms of CaCO3 – 2 × 36.5 gms of HCl
? – 0.6844 gms of HCl
∴ Mass of CaCO3 = \(\frac{0.6844}{2 \times 36.5}\) × 100 = 0.937 5 gms
![]()
Question 26.
Chlorine is prepared in the laboratory by treating manganese dioxide (MnO2) with aqueous hydrochloric acid according to the reaction
4 HCl (aq) + MnO2(s) → 2 H2O (l) + MnCl2(aq) + Cl2(g)
How many grams of HCl react with 5.0 g of manganese dioxide?
Answer:
Given chemical reaction is
4HCl(aq) + MnO2(s) → MnCl2(aq) + 2H2O(l) + Cl2(g)
4 moles of HCl – 1 mole of MnO2
4 × 36.5 gms. of HCl – 87 gms. of MnO2
∴ Weight of HCl required = \(\frac{5 \times 4 \times 36.5}{87}\) = 8.39 gms.
Question 27.
To 50 ml of 0.1 N Na2CO3 solution 150 ml of H2O is added. Then calculate a normality of resultant solution.
Answer:
Formulae N1V1 = N2V2
0.1 × 50 = N2 × 200
N2 = \(\frac{0.1}{4}\)
= 0.025 N
N1 = 0.1 N
V1 = 50 ml
N2 = ?
V2 = 150 + 150 = 200 ml
Question 28.
Calculate the volume of 0.1 N H2SO4 required to neutralize 200 ml of 0.2 N NaOH solution. It is an acid base neutralisation reaction. Hence, at the neutralisation point. Number of equivalents of acid = Number of equivalents of base.
Answer:
Formula N1V1 = N2V2
0.1 × V1 = 0.2 × V2
V2 = 2 × 200
= 400 ml
N1 = 0.1 N
V1 = ?
V2 = 200 ml
N2 = 0.2 N
Question 29.
Calculate normality of H2SO4 solutions if 50 ml of it completely neutralises 250 ml of 0.1 N Ba(OH)2 solutions.
Solution:
Formulae N1V1 = N2V2
N × 50 = 0.1 × 250
N1 = 0.5 N
N1 = ?
V1 = 50 ml
N2 = 0.1 N
V2 = 250 ml
![]()
Question 30.
Calculate the volume of 0.1 M KMnO4 required to react with 100 ml of 0.1 M H2C2O4.2H2O solution in presence of H2SO4.
Answer:
Balanced chemical equation for the given data is
Formulae
\(\frac{M_1 V_1}{n_1}\) = \(\frac{M_2 V_2}{n_2}\)
\(\frac{0.1 \times V_1}{2}\) = \(\frac{0.1 \times 100}{8}\)
V1 = 40 ml
KMnO4
M1 = 0.1 M
V1 = ?
n1 = 2
Oxalic acid
M2 = 0.1 M
V2 = 100 ml
n2 = 5
Question 31.
Assign oxidation number to the underlined elements in each of the following species:
a) NaH2PO4
b) NaHSO4
c) H4P2O7
d) K2MnO4
e) CaO2
f) NaH4
g) H2S2O7
h) KAl(SO4)2.12 H2O
Answer:
a) NaH2PO4
1(+1) + 2(+1) + x + 4(-2) = 0
1 + 2 + x – 8 = 0
x – 5 = 0
x= + 5
Oxidation no. of ‘P in NaH2PO4 = + 5
b) NaHSO4
1(+1) + 1(+1) + x + 4(-2) = 0
1 + 1 + x – 8 = 0
x = +6
Oxidation no. of ‘S in NaHSO4 = + 6
c) H4P2O7
4(+1) + 2x + 7(-2) = 0
4 + 2x – 14 = 0
2x – 10 = 0.
x = +5
Oxidation no. of ‘P’ in H4P2O7 is +5
d) K2MnO4
2(+1) + x + 4(-2) = 0
2 + x – 8 = 0
x = + 6
Oxidation no of Mn is K2MnO4 = +6
e) CaO2
+ 2 + 2x = 0
2x = -2
x = -1
Oxidation no. of oxygen in CaO2 = -1
f) NaBH4
1(+1) + x + 4 (-1) = 0
1 + x – 4 = 0
x = +3
Oxidation no. of ‘B’ in NaBH4 = + 3
But B’ most probably exhibits – 3 oxidation state.
g) H2S2O7
2(1) + 2x + 7(-2) = 0
2 + 2x – 14 = 0
2x – 12 = 0
x = +6
Oxidation state of ‘S’ in H2S2O7 = + 6
h) K Al(SO4)2 12H2O :
General formula of above compound is K2SO4 Al2 (SO4)3 2 + H2O (Potash alum)
Consider Al2(SO4)3 from the above double salt
2x + 3 (-2) = 0
2x – 6 = 0
x = + 3
Question 32.
What are the oxidation number of the underlined elements in each of the following and how do you rationalise your results ?
a) KI3
b) H2SO4O6
c) Fe3O4
Answer:
a) KI3
It is formed by the combining KI, I2
∴ Oxidation no. of ‘I’ in KI = – 1
[1 + x = 0
x = – 1]
In I2 oxidation no. of. I = 0
b) H2S4O6
According to H2S4O6 structure
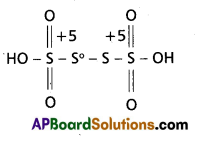
2(1) + 4x + 6(-2) = 0 ⇒ 4x – 10 = 0
x = 2.5
‘S’ average Ox. No = 2.5
c) Fe3O4
3x + 4(-2) = 0
3x – 8 = 0
x = \(\frac{8}{3}\)
In general Fe3O4 obtained by FeO + Fe2O3
∴ In FeO → x = + 2 [x – 2 = 0 ⇒ x = + 2]
In Fe2O3 → x = + 3 [2x – 6 = 0 ⇒ x = + 3]
Question 33.
Justify that the following reactions are redox reactions :
Answer:
a) CuO(s) + H2(g) → Cu(s) + H2O(g)
b) Fe2O3(s) + 3CO(g) → 2 Fe(s) + 3 CO2(g)
c) 4 BCl3(g) + 3 LiAlH4(s) → 2 B2H6(g) + 3 LiCl(s) + 3 AlCl3(s)
d) 2 K(s) + F2(g) → 2 K+F–(s)
e) 4 NH3(g) + 5 O2(g) → 4 NO(g) + 6 H2O(g)
a)
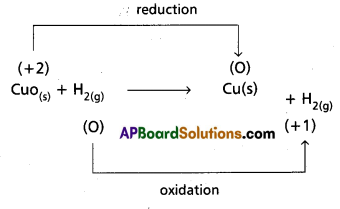
Hence it is a Redox reaction.
b)
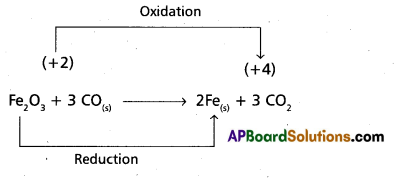
Hence it is a Redox reaction.
c) \(4 \mathrm{BCl}_{3_{(g)}}\) + \(3 \mathrm{LiAlH}_{4_{(s)}}\) → \(2 \mathrm{~B}_2 \mathrm{H}_{6_{(g)}}\) + \(3 \mathrm{LiCl}_{(s)}\) + \(4 \mathrm{AlCl}_{3_{(\mathrm{s})}}\)
Here in the above reaction the oxidation states of all elements doesnot changed. So it is not a redox reaction.
d)

Hence it is a redox reaction.
e)
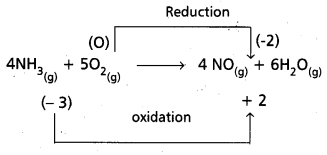
Hence it is a redox reaction.
![]()
Question 34.
Fluorine reacts with ice and results in the change
H2O(S) + F2(g) → HF(g) + HOF(g)
Justify that this reaction is a redox reaction.
Answer:
Given chemical equation
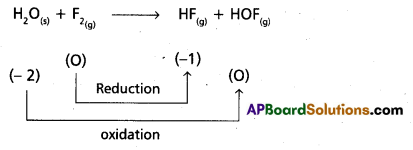
Hence it is a redox reaction.
Question 35.
Calculate the oxidation number of sulphur, chromium and nitrogen in H2SO5, Cr2\(O_7^{-2}\) and \(\mathrm{NO}_3^{-}\). Suggest structure of these compounds.
Answer:
a) H2SO5 Structure:

2(1) + x + 2(-1) + 3(-2) = 0 (One peroxy linkage)
2 + x – 2 – 6 = 0
x = +6
b) Cr2\(\mathrm{O}_7^{-2}\) Structure:
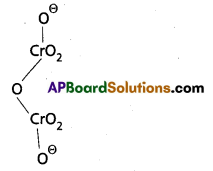
2(x) + 7(-2) = -2
2x – 14 = -2
x = +6
c) \(\mathrm{NO}_3^{-}\) Structure:

x + 3(-2) = -1
x – 6 = -1
x = +5
Question 36.
Write formulas for the following compounds: .
a) Mercury (II) chloride
b) Nickel (II) sulphate
c) Tin (IV) oxide
d) Thallium (I) sulphate
e) Iron (III) sulphate
f) Chromium (III) oxide
Answer:
Formula
a) Mercury (II) Chloride — HgCl2
b) Nickel (II) Sulphate — NiSO4
c) Tin (IV) Chloride — SnCl4
d) Thallium (I) Sulphate — Tl2SO4
e) Iron (III) Sulphate — Fe2(SO4)3
f) Chromium (III) Oxide — Cr2O3
![]()
Question 37.
Suggest a list of the substances where carbon can exhibit oxidation states from -4 to +4 and nitrogen from -3 to +5.
Answer:


Question 38.
While sulphur dioxide and hydrogen peroxide can act as oxidising as well as reducing agents in their reactions, ozone and nitric acid act only as oxidants. Why ?
Answer:
SO3 and H2O2 both acts as oxidising as well as reducing agents.
- Ozone acts as strong oxidising agent in acidic medium (Ozone acts as reducing agent also in some cases).
- HNO3 acts as strong oxidising agent because in HNO3. He H+ ion readily released and the oxidation state of ‘N’ is +5 in HNO3. So it is a good oxidising agent.
Question 39.
Consider the reactions :
a) 6 CO2(g) + 6 H2O (l) → C6H12O6 (aq) + 6 O2(g)
b) O3 (g) + H2O2 (l) → H2O () + 2 O2 (g)
Why it is more appropriate to write these reactions as :
a) 6 CO2 (g) + 12 H2O(l) → C6H12O6(aq) + 6 H2O(l) + 6 O2(g)
b) O3(g) + H2O2(l) → H2O2(l) + O2(g) + O2(g)
Also suggest a technique to investigate the path of the above (a) and (b) redox reactions.
Answer:
a) 6CO2 + 12 H2O → C6H12O6 + 6 H2O + 6 O2
This equation is more appropriate writing equation of photosynthesis.
Because of evolution of oxygen from H2O but not from CO2.
b) O3(g) + H2O2(l) → H2O(l) + O2(g) + O2(g)
This is the more appropriate equation to write because in this reaction clearly mentioned that which is oxidised and which is reduced.
Question 40.
The compounds AgF2 is unstable compound. However, if formed, the compound acts as a very strong oxidising agent. Why ?
Answer:
- AgF2 is an unstable compound.
- If suppose it is formed it acts as good oxidising agent.
Reason :
AgF2 releases fluorine gas which is a powerful oxidising agent.
∴ AgF2 is a good oxidising agent.
Question 41.
Whenever a reaction between an oxidising agent and a reducing agent is carried out, a compound of lower oxidation state is formed if the reducing agent is in excess and a compound of higher oxidation state is formed if the oxidising agent is in excess. Justify this statement giving three illustrations.
Answer:
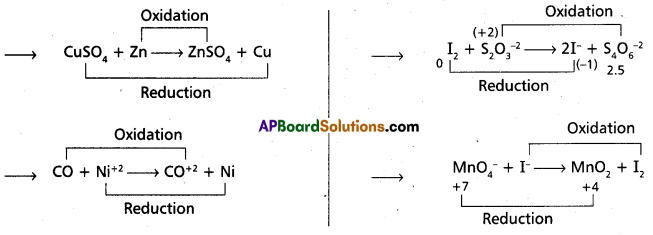
The above equations illustrates the given statement.
Question 42.
How do you count for the following observations ?
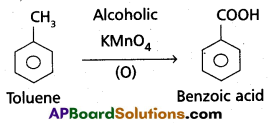
a) Though alkaline potassium permagnate and acidic potassium permanganate both are used as oxidants, yet in the manufacture of benzoic acid from toluene we use alcoholic potassium permanganate as an oxidant. Why ? Write a balanced redox equation for the reaction.
b) When concentrated sulphuric acid is added to an inorganic mixture containing chloride, we get colourless pungent smelling gas HCl, but if the mixture contains bromide then we get red vapour of bromine. Why ?
Answer:
a) Balanced equation of KMn04/H+ (Acidic medium)
Mn\(\mathrm{O}_4^{-}\) + 8 H+ + 5 e– → Mn+2 + 4 H2O
Balanced equation of KMnO4/ H+ (Basic medium)
Mn\(\mathrm{O}_4^{-}\) + 2 H2O + 3 e– → MnO2 + 4 OH–
- Toluene is oxidised to benzoic acid in alcoholic medium.
- Toluene is easily oxidised in presence of alcoholic KMnO4
b) When Conc. H2SO4 reacts with NaCl then HCl vapours are evolved.
2 NaCl + H2SO4 → Na2SO4 + 2 HCl
When Conc. H4SO4 reacts with KBr than HBr vapours are evolved which on further oxidation gives reddish brown Br2 vapours.
2 KBr + H2SO4 → Na2SO4 + 2 HBr
2MBr + H2SO4 → 2 H2O + SO2 + Br2 (Reddish brown)
Question 43.
Identify the substance oxidised, reduced, oxidising agent and reducing agent for each of the following reactions :
a) 2 AgBr (s) + C6H6O2 (aq) → 2 Ag (s) + 2 HBr (aq) + C6H6O2 (aq)
b) HCHO(l) + 2[Af(NH3)2]+(aq) + 3 OH–(aq) → 2 Ag(s) + HCOO–(aq) + 4 NH3(aq) + 2 H2O(l)
c) HCHO(l) + 2 Cu2+(aq) + 5 OH–(aq) → Cu2O(s) + HCOO–(aq) + 3 H2O(l)
d) N2H4 (l) + 2 H2O2(l) → N2(g) + 4 H2O(l)
e) Pb(s) + PbO2(s) + 2 H2SO4(aq) → 2 PbSO4(s) + 2 H2O(l)
Answer:
a) Given equation is
2 AgBr(s) + C6H6O2(aq)
- 2 Ag(s) + 2 HBr(aq) + C6H4O2 (aq)
- C6H6O2 oxidised to C6H4O2
- Ag+Br– reduced to Ag
- Oxidising agent is Ag+
- Reducing agent is C6H6O2
b) Given equation is HCHO(l) + \(2\left[\mathrm{Ag}\left(\mathrm{NH}_3\right)_2\right]_{(\mathrm{aq})}^{+}\) + \(3 \mathrm{OH}_{(\mathrm{aq})}^{-}\)
- 2 Ag(s) + \(3 \mathrm{OH}_{\text {(aq) }}^{-}\) + 4NH3(aq) + 2 H2O(l)
- HCHO oxidised to HCOO–
- [Ag(NH3)2]+ reduced to Ag
- [Ag(NH3)2]+ is oxidising agent
- HCHO is reducing agent
c) Given equation is
HCHO(l) + \(2 \mathrm{Cu}_{(\mathrm{aq})}^{+2}\) + 5OH– → Cu2O(s) + \(\mathrm{HCOO}_{(a q)}^{-}\) + 3H2O(l)
- HCHO oxidised to HCOO–
- Cu+2 reduced to Cu+(in Cu2O)
- Oxidising agent is Cu+2 ions (In Fehling’s reagent)
- Reducing agent is HCHO
d) Given equation is
N2H4(l) + 2K2O2(l) → N2(g) + 4H2O(l)
- \(N^{-2}\) oxidised to N2
- \(\mathrm{O}_2^{-2}\) reduced to O-2
- Oxidising agent is H2O2
- Reducing agent is N2H4
Pb(s) + pbO4(s) + 2H2SO4(aq)
e)
- 2PbSO4(s) + 2H2O
- Pb oxidised to Pb+2
- PbO2 reduced to Pb+2
- Oxidising agent is PbO2
- Reducing agent is Pb
Question 44.
Consider the reactions :
2S2\(\mathrm{O}_3^{-2}\) (aQ) + I2 (s) → S4\(\mathrm{O}_6^{-2}\) (aQ) + 2I– (aQ)
S2\(\mathrm{O}_3^{-2}\) (aQ) + I2(s) + 5H2O(l) → 2S\(\mathbf{O}_4^{-2}\) (aq) + 4\(\mathrm{Br}_{(\mathrm{aq})}^{-}\)(aq) + 10\(H_{(aq)}^{+}\)
Why does the same reductant, thiosulphate react differently with iodine and bromine ?
Answer:
- Thio sulphate ion is not a strong reducing agent.
- I2 is not a strong oxidising agent.
- The reaction between I2 and thio sulphate form tetrathionate (S4\(\mathrm{O}_6^{-2}\)) ion.
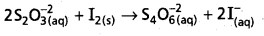
- The above reaction has high rate of reaction.
- The reaction between Thiosulphate and Bromine involves the formation of sulphate ion.
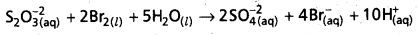
- Br2 is some what better oxidising agent than I2.
Hence the difference observed in the above reactions.
Question 45.
Justify giving reactions that among halogens, fluorine is the best oxidant and among hydrohalic compounds, hydroiodic acid is the best reductant.
Answer:
a)
- The oxidising capacity of any substance depends on the net result of several contributing energy factors like enthalpy change in a reaction, standard Electrode potential.
- With reference to Born-Haber type energy cycle the change in enthalpy value is greater for fluorine.
- Greater the magnitude of negative change in enthalpy greater is the oxidising power.
Supporting reaction :
- Fluorine reacts with carbon while the other elements of group do not combine even under drastic conditions.
C + 2 F2 → CF4 - Fluorine is also called as superhalogen.
b)
- Hydrohalic compounds acts as reducing agents. Their stability order is
HF >> HCl > HBr > HI - HI is least stable and acts as strons reducing agent among these halides.
H2 + I2 \(\rightleftharpoons\) 2 HI
Question 46.
Why does the following reaction occur ?
![]()
What conclusion about the compound Na4XeO6(of which ![]() is a part) can be drawn from the reaction.
is a part) can be drawn from the reaction.
Answer:
Given equation is
![]()
- In the above reaction ‘Xe’ under go reduction (+8 to +6)
- F– oxidised to F2 here perxenate ion acts as powerful oxidising agent.
- Perxenates are stable in alkali solutions.
- Na4XeO6 is a powerful oxidant.
![]()
Question 47.
Consider the reactions :
(a) H3PO2(aq) + 4 AgNO3(aq) + 2 H2O(1) → H3PO4(aq) + 4Ag(s) + 4HNO3(aq)
(b) H3PO2(aq) + 2 CuSO4(aq) + 2 H2O(1) → H3PO4(aq) + 2Cu(s) + H2SO4(aq)
(c) C6H5CHO(l) + 2[Ag (NH3)2]+(aq) + 3OH–(aq) → C6H5COO–(aq) + 2Ag(s) + 4NH3(aq) + 2H2O(l)
(d) C6H5CHO(l) + 2Cu2+(aq) + 5OH–(aq) → No Change observed.
what inference do you draw about the behaviour of Ag+ and Cu2+ from these reactions ?
Answer:
- H3PO2 is a strong reducing agent hence it reduce Ag+ to Ag and Cu+2 to Cu.
- C6H5CHO is also a reducing agent it just reduced.
Ag+ to Ag in tollen’s reagent but it does not reduced Cu+2 in alkaline solution.
Question 48.
Balance the following redox reactions by ion – electron method :
(a) Mn\(\mathrm{O}_4^{-}\) (aq) + I– (aq) → MnO2(s) + I2 (s) (in basic medium)
(b) Mn\(\mathrm{O}_4^{-}\) (aq) + SO2 (g) → Mn2+ (aq) + HSO4 (aq) (in acidic solution)
(c) H2O2 (aq) + Fe2+ (aq) → Fe3+ (aq) + H2O(l) (in acidic solution)
(d) Cr2\(\mathrm{O}_7^{2-}\)SO2 (g) → Cr3+ (aq) + S\(\mathrm{O}_4^{2-}\) (aq) (in acidic solution)
Answer:
a) Mn\(\mathrm{O}_{4 \text { (aq) }}^{-}\) + \(\mathbf{I}_{(\mathrm{aq})}^{-}\) → MnO2(s) + I2(s) (Basic medium)
Reduction half cell
\(\mathrm{MnO}_4^{-}\) → MnO2
\(\mathrm{MnO}_4^{-}\) → MnO2 + 2H2O (Oxygens balanced)
\(\mathrm{MnO}_4^{-}\) + 4H2O → MnO2 + 2H2O + 4OH–
(Hydrogens balanced)
\(\mathrm{MnO}_4^{-}\) + 2H2O → MnO2 + 4OH–
\(\mathrm{MnO}_4^{-}\) + 2H2O + 3e– → MnO2 +4OH–]
(Charge balanced)
2 × [Mn\(\mathrm{MnO}_4^{-}\) + 2H2O + 3e– → MnO2 + 4OH-1]
3 × [2 I– → I2 + 2e–]
Oxidation half cell
I– → I2
2 I– → I2 (Iodines balanced)
2 I– → I2 + 2 e– (Charge balanced)
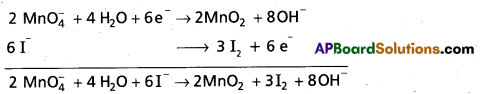
The above equation is balanced equation.
b)

Above equation is balanced chemical equation.
c)

d)

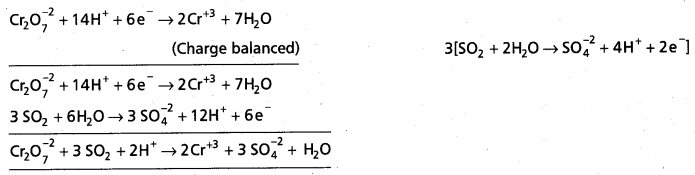
Question 49.
Balance the following equations in basic medium by ion-electron method and oxidation number methods and identify the oxidising agent and the reducting agent
(a) P4(s) + OH–(aq) → PH3(g) + HP\(\mathrm{O}_2^{-}\)
(b) N2H4(l) + Cl\(\mathrm{O}_3^{-}(\mathrm{aq})\)(aq) → NO(g) + Cl–(g)
(c) Cl2O7 (g) + H2O2 (aq) → ClO2 (aq) + O2 (g) + H+
Answer:
a) P4 + OH– → PH3 + HP\(\mathrm{O}_2^{-}\)
Reduction half cell
P4 → PH3
P4 → 4PH3
P4 + 12H2O → 4PH3 + 12 OH– (H balanced)
P4 + 12H2O + 12e– → 4PH3 + 12 OH–
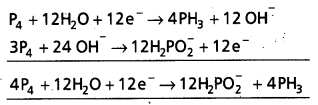
Oxidation half cell
P4 → H2P\(\mathrm{O}_2^{-}\)
P4 → 4H2P\(\mathrm{O}_2^{-}\) (‘P’ balanced)
P4 + 8H2O → 4H2\(\mathrm{PO}_2^{-}\) (Oxygen balanced)
P4 + 8H2O + 8 OH– → 4H2\(\mathrm{PO}_2^{-}\) + 8H2O
(Hydrogen balanced)
P4 + 8OH– → 4H2\(\mathrm{PO}_2^{-}\) + 4e–
(Charge balanced)
Here P4 is oxidising agent as well reducing agent.
b)
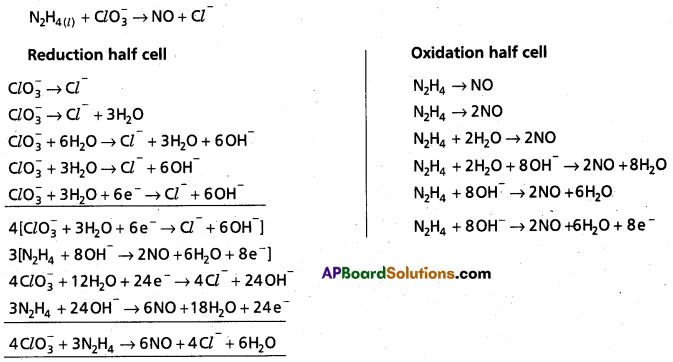
\(\mathrm{ClO}_3^{-}\) is oxidant
N2H4 is reductant
c)

![]()
Question 50.
What sorts of informations can you draw from the following reaction ?
(CN)2(g) + 20H(aq → CN–(aq) + CNO(aq) + H2O(1)
Answer:
(CN)2(g) + 2(OH–) → \(\mathrm{CN}_{(\mathrm{aq})}^{-}\) + \(\mathrm{CNO}_{(\mathrm{aq})}^{-}\) + \(\mathrm{H}_2 \mathrm{O}_{(l)}\)
(CN)2 + 2e– → 2 CN– (Reduction)
(CN)2 + 2H2O → 2 CNO– + 4H+ + 2e– (Oxidation)
Here (CN2) undergo oxidation as well as reduction.
It is a dis proportionation reaction.
Question 51.
The Mn3+ ion is unstable in solution and undergoes disproportionation to give Mn2+. MnO2+ and H+ ion. Write a balanced ionic equation for the reaction.
Answer:
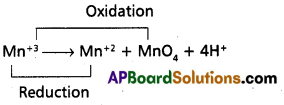
- Above equation is a dis proportionation reaction
Question 52.
Consider the elements :
Cs, Ne, I and F
(a) Identify the element that exhibits only negative oxidation state.
(b) Identify the element that exhibits only positive oxidation state.
(c) Identify the element that exhibits both postive and negative oxidation states.
(d) Identify the element which exhibits neither the negative nor does the positive oxidation state.
Answer:
a) ‘F’ Exhibits negative oxidation state i.e. ‘-1’
b) ‘Cs’ Exhibits only positive oxidation state
c) ‘I’ Exhibits positive as well as negative oxidation states
d) ‘Ne’ doesnot exhibit any oxidation state in ground state
(Neither positive nor negative)
Question 53.
Chlorine is used to purify drinking water. Excess of chlorine is harmful. The excess of chlorine is removed by treating with sulphur dioxide. Present a balanced equation for this redox change taking place in water.
Answer:
Balanced equations for the given data is
Cl2 + SO2 + H2O → SO3 + 2H+ + Cl–
Question 54.
Refer to the periodic table given in your book and now answer the following questions :
a) Select the possible non metals that can show disproportionation reaction.
b) Select three metals that can show disproportionation reaction.
Answer:
a) Non metals
Chlorine, Bromine, Oxygen, Sulphur, Phosphorous, Iodine undergo disproportionations
b) Metals Cr, Mn and pb undergo disproportionation.
Question 55.
In Ostwald’s process for the manufacture of nitric acid, the first step involves the oxidation of ammonia gas by oxygen gas to give nitric oxide gas and steam. What is the maximum weight of nitric oxide that can be obtained starting only with 10.00 g, of ammonia and 20.00 g of oxygen ?
Answer:
Chemical reaction is
4NH3 + 5O2 → 4NO + 6H2O
4 moles NH3 – 5 moles of O2
Given 10 gms of NH3
∴ No. of moles = \(\frac{10}{17}\) = 0.588 moles
Given 20 gms of NH3
∴ No. of moles = \(\frac{20}{32}\) = \(\frac{5}{8}\) = 0.4
4 moles of ammonia reacts with 5 moles of O2
0.588 moles of NH3 …. ?
\(\frac{0.588}{4}\) × 5 = 0.735 moles
5 moles of O2 reacts with 4 moles of NH3
0.4 moles of O2…. ?
\(\frac{0.4}{5}\) × 4 = \(\frac{1.6}{5}\) = 0.32
- Here O2 is not present in sufficient amount NH3 has sufficient in amount
5 moles of O2 → 4 moles of NO.
5 × 32 gms of O2 → 4 × 30 gms of NO.
20 gms of O2 → ?
\(\frac{20 \times 4 \times 30}{5 \times 32}\) = \(\frac{20 \times 24}{32}\) = \(\frac{120}{8}\) = 15 gms
![]()
Question 56.
Arrange the following metals in the order in which they displace each other from the solution of their salts.
Al, Cu, Fe, Mg and Zn.
Answer:
According to electro chemical series electrode potentials of given elements as follows
Al – -1.66 V
Cul – + 0.34 V
Fe – -0.40 V
Mg – -2.37 V
Zn – -0.76 V
∴ The order of the above metals in which they displace each other from the solution of their salts. Mg > AZ > Zn > Fe > Cu
Long Answer Questions
Question 1.
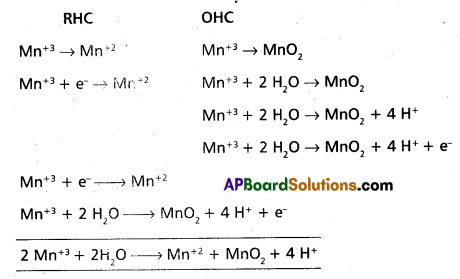
Wtire the balanced ionic equation which represents the oxidation of iodide (I-) ion by permanganate ion in basic medium at give iodine (I) and managanese dioxide (MnO2)
Answer:
Basic equation is

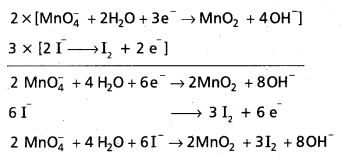
The above equation is balanced equation.
Question 2.
Write the balanced equation for the oxidation of suiphite ions to sulphate ions in acid medium by permanganate ion.
Answer:
![]()
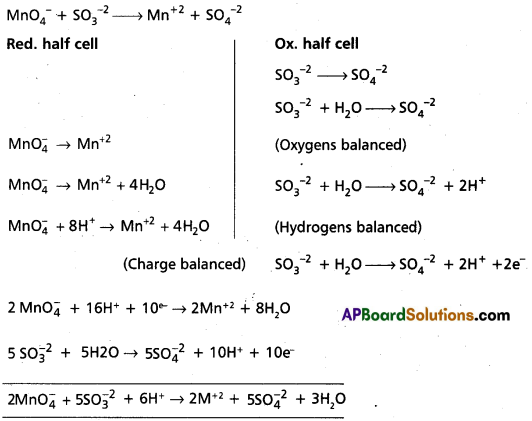
Question 3.
Oxalic acid is oxidised by permanganate ion is acid medium of Mn2+ balance the reaction by ion — electron method.
Answer:
![]()
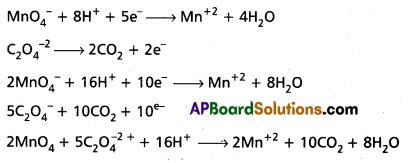
Question 4.
Phosphorus when heated with NaOH solution gives phosphine (PH3) and H2P\(\mathrm{O}_2^{-}\). Give the balanced equation.
Answer:
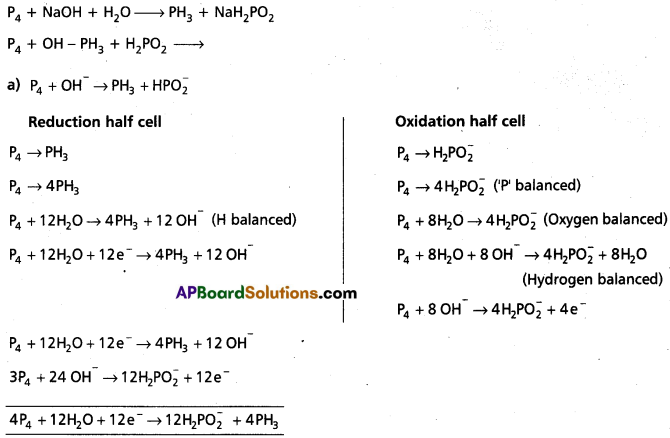
Here P4 is oxidising agent as well reducing agent.
Question 5.
Balance the following equation
![]()
Answer:
Oxidation half reaction Cr(OH)3 → \(\mathrm{CrO}_4^{2-}\)
(The ox. no of Cr changes from +3 to +6)
Reduction half reaction \(\mathrm{IO}_3^{-}\) → I– (The ox. no. of ‘I’ changes from +5 to —1)


Question 6.
Balance the following equation by the oxidation number method.
Mn\(\mathrm{O}_4^{-2}\) + Cl2 → Mn\(\mathrm{O}_4^{-2}\) + Cl–
Answer:
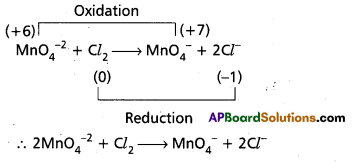
Question 7.
Exaplain the different types of redox reactions.
Answer:
Redox reaction : “The reaction that involves loss of electrons is called an oxidation reaction and that involving gain of electrons is called a reduction reaction. The overall reaction is called as oxidation – reduction reaction” or simply ‘redox reaction’.
Types of redox reactions:
a) Chemical combination reactions: In these reactions one species combine with another species to form product. In this conversion one species undergo oxidation and other species undergo reduction.
e.g.:
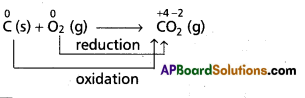
As the oxidation state of carbon increases from ‘0’ to ‘+4’ in the reaction. So, carbon undergoes oxidation.
Oxygen changes from ‘0’ to ‘-2’ oxidation state. So, it undergoes reduction. Therefore, the above overall combination reaction is redox reaction.
b) Decomposition reactions : Chemical compounds chemically split into two or more simpler substances during decomposition reactions. These are again redox reactions.
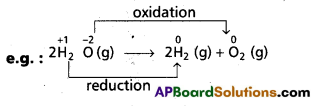
Here, water decomposes. H2 undergoes reduction from +1 to 0 in the reaction. Oxygen on the other hand changes its oxidation state from -2 to 0 (or) it undergoes oxidation.
Therefore, decomposition of H20 is a redox reaction.
c) Displacement reactions : In these reactions the place of one species in its compound is taken up by other species.
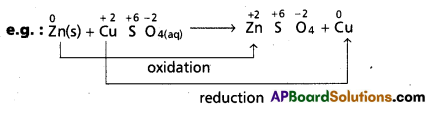
‘Zn’ displaces ‘Cu’ from CuSO4 solution. In this reaction Zn undergoes oxidation and Cu undergoes reduction. Therefore overall reaction is a redox reaction.
d) Disproportionation reactions : These reactions involve the same element in the given form to undergo both oxidation and reduction simultaneously.
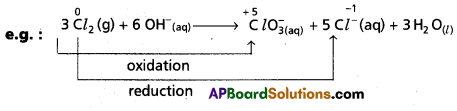
In the above reaction ‘Cl2‘ undergoes both oxidation and reduction. It is a special type of redox reaction.
e) Comproportionation reactions : Reverse of disproportionation is comproportionation. In comproportionation reactions, two species with the same element in two different oxidation states form a single product in which the element is in an intermediate oxidation state.
e.g.:
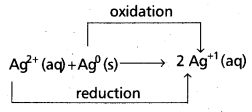
![]()
Question 8.
Calculate the amount of carbon dioxide that could be produced when
(i) 1 mole of carbon is burnt in air.
(ii) 1 mole of carbon is burnt in 16 g of dioxygen,
(iii) 2 moles of carbon are burnt in 16 g of dioxygen.
Answer:
i) C + O2 → CO2
1 mole of ‘C’ → 1 mole of CO2
∴ 44 gms of CO2
ii) C + O2 → CO2
Given 1 mole of O2 burnt in 16 gms of di oxygen
iii) C + O2 → CO2
2 moles of ‘C’ burnt in 16 gms of O2
∴ 1 mole of O2 → 44 gms of CO2
32 gms of O2 → 44 gms of CO2
16 gms of O2 → 22 gms of CO2
![]()
Question 9.
Dinitrogen and dihydrogen react with each other to produce ammonia according to the following chemical equation :
N2(g) + H2(g) → 2NH3 (g)
(i) Calculate the mass of ammonia produced if 2.00 × 103 g dinitrogen reacts with 1.00 × 103 g of dihydrogen.
(ii) Will any of the two reactants remain unreacted ?
(iii) If yes, which one and what would be its mass ?
Answer:
i) N2 + 3H2 → 2NH3
Given Nitrogen = 2 × 103 gms
No. of moles = \(\frac{2000}{28}\) = 71.4285
Given hydrogen = 1 × 103 gms
No. of moles = \(\frac{1000}{2}\) = 500 moles
N2 is limiting agent
∴28 gms of N2 → 2 × 17gms NH3
2000 gms of N2 →
\(\frac{2000 \times 17}{28}\) = 2428.57 gms
ii) Used amount of hydrogen
28 → 6 gms
100 gms → ?
\(\frac{1000 \times 6}{28}\) = 214.285 gms
iii) Remaining amount of hydrogens
= 1000 – 2140.285
= 785.715 gms
![]()
Question 10.
Assign oxidation number to the underlined elements in each of the following epecies :
(a) NaH2PO4
b) NaHSO4
c) H4P2O7
d) K2MnO4
(e) CaO2
(f) NaBH4
(g) H2S2O7
(h) KA1(SO4)2.12 H2O
Answer:
(a) NaH2PO4
1(+1) + 2(+1) + x + 4 (-2) = 0
1 + 2 + x – 8 = 0
x – 5 = 0
x = +5
Oxidation no. of ‘P’ in NaH2PO4 = + 5
b) NaHSO4
1(+1) +1(+1) + x + 4(-2) = 0
1 + 1 + x – 8 = 0
x = + 6
Oxidation no. of ‘S’ in NaHSO4 = + 6
c) H4P2O7
4(+1) + 2x + 7(-2) = 0
4 + 2x – 14 = 0
2x – 10 = 0
x = + 5
Oxidation no. of ‘P’ in H4P2O7 is +5
d) K2MnO4
2(+1) + x + 4(-2) = 0
2 + x + 8 = 0
x = + 6
Oxidation no of Mn is K2MnO4 = + 6
e) CaO2
+ 2 + 2x = 0.
2x = -2
x = -1
Oxidation no. of oxygen in CaO2 = -1
f) NaBH4
1(+1) + x+ 4(-1) = 0
1 + x – 4 = 0
x = +3
Oxidation no. of ‘B’ in NaBH4 = +3
But ‘B’ most probably exhibits -3 oxidation state.
g) H2S2O7
2(1) + 2x + 7(-2) = 0
2 + 2x – 14 = 0
2x – 12 = 0
x = +6
Oxidation state of ‘S’ in H2S2O7 = + 6
h) k Al(SO4)2 12H2O :
General formula of above compound is
k2SO4 Al2 (SO4) 24 H2O (Potash alum)
Consider Al2(SO4)3 from the above double salt
2x + 3(-2) = 0
2x – 6 = 0
x = +3
Question 11.
What are the oxidation number of the underlined elements in each of the following and how do you rationalise your results?
(a) H2S4O6
(b) Fe3O4
(c) CH3CH2OH
(d) CH3COOH
Answer:
a) 45 (b)
b) 45 (c)
c) CH3 CH2 – OH
C2H6O
2x + 6(1) + (-2) = 0
2x + 6 – 2 = 0
2x + 4 = 0
x = -2
d) CH3COOH
C2H4O2
2x + 4(+1) + 2(-2) = 0
2x + 4 – 4 = 0
x = 0
Solved Problems
Question 1.
Calculate molecular mass of glucose (C6H12O6) molecule.
Solution:
Molecular mass of glucose (C6H12O6)
= 6(12.011 u) + 12(1.008 u) + 6(16.00.u)
= (72.066 u) + (12.096 u) + (96.00 u)
= 180.162 u
Question 2.
A compound contains 4.07% hydrogen, 24.27% carbon and 71.65% chlorine. Its molar mass is 98.96 g. What are its empirical and molecular formulae ?
Solution:
Step 1.
Conversion of mass per cent to grams :
Since we are having mass percent, it is convenient to use 100 g of the compound as the starting material. Thus, in the 100 g sample of the above compound, 4.07 g hydrogen; 24.27 g carbon; and 71.65 g chlorine are present.
Step 2.
Convertion into number of moles of each element:
Divide the masses obtained above by respective atomic masses of various elements.
Moles of hydrogen = \(\frac{4.07 \mathrm{~g}}{1.008 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 4.04
Moles of carbon = \(\frac{24.27 \mathrm{~g}}{12.01 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 2.021 Moles of chlorine = \(\frac{71.65 \mathrm{~g}}{35.453 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 2.021
Step 3.
Divide the mole value obtained above by the smallest number:
Since 2.021 is smallest value, division by it gives a ratio of 2:1:1 for H:C:Cl.
In case the ratios are not whole numbers, then they may be converted into whole number by multiplying by the suitable coefficient.
Step 4.
These numbers indicate the relative number of atoms of the elements. Write empirical formula by mentioning the numbers after writing the symbols of respective elements :
CH2Cl is thus, the empirical formula of the above compound.
Step 5.
Writing molecular formula :
a) Determine empirical formula mass.
Add the atomic masses of various atoms present in the empirical formula.
For CH2Cl, empirical formula mass is 12.01 + 2 × 1.008 + 35.453 = 49.48 g
b) Divide Molar mass by empirical formula mass
![]()
= 2 = (n)
c) Multiply empirical formula by n obtained above to get the molecular formula.
Empirical formula = CH2Cl, n = 2. Hence molecular formula is C2H4Cl2.
![]()
Question 3.
Calculate the amount of water (g) produced by the combustion of 16 g of methane.
Solution:
The balanced equation for combustion of methane is :
CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)
- 16 g of CH4 corresponds to one mole.
- From the above equation, 1 mol of CH4(g) gives 2 mol of H2O(g).
2 mol of water (H2O) = 2 × (2 + 16)
= 2 × 18 = 36 g
1 mol H2O = 18g H2O ⇒ \(\frac{18 \mathrm{~g} \mathrm{H}_2 \mathrm{O}}{1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}}\) = 1
Hence 2 mol H2O × \(\frac{18 \mathrm{~g} \mathrm{H}_2 \mathrm{O}}{1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}}\)
= 2 × 18 g H2O = 36 g H2O
Question 4.
How many moles of methane are required to produce 22 g CO2(g) after combustion ?
Solution:
According to the chemical equation
CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)
44 g CO2 (g) is obtained from 16 g CH4(g).
[∵ 1 mol CO2(g) is obtained from 1 mol of CH4(g)]
Mole of CO2(g)
= 22 g CO2(g) × \(\frac{1 \mathrm{~mol} \mathrm{CO}_2(\mathrm{~g})}{44 \mathrm{gCO}_2(\mathrm{~g})}\)
= 0.5 mol CO2(g)
Hence 0.5 mol CO2(g) would be obtained from 0.5 mol CH4(g) or 0.5 mol of CH4(g) would be required to produce 22g CO2(g).
Question 5.
50.0 kg of N2(g) anfd 10.0 kg of H2(g) are mixed to produce NH3(g). Calculate the NH3 (g) formed. Identify the limiting reagent in the production of NH3 in this situation.
Solution:
A balanced equation for the above reaction is written as follows :
Calculation of moles:
N2 + 3H2(g) ⇌ 2HN3(g)
Moles of N2
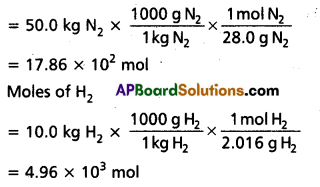
According to the above equation, 1 mol N2(g) requires 3 mol H2(g), for the reaction. Hence, for 17.86 × 102 mol N2, the moles of H2(g) required would be
17.86 × 102 mol N2 × \(\frac{3 \mathrm{~mol} \mathrm{H}_2(\mathrm{~g})}{1 \mathrm{molN}_2(\mathrm{~g})}\)
= 5.36 × 103 mol H2
But we have only 4.96 × 103 mol H2. Hence, dihydrogen is the limiting reagent in
this case. So NH3(g) would be formed only from that amount of available dihydrogen i.e.,
4.96 × 103 mol.
Since 3 mol H2(g) gives 2 mol NH3(g)
4.96 × 103 mol H2 (g) × \(\frac{2 \mathrm{~mol} \mathrm{NH}_3(\mathrm{~g})}{3 \mathrm{molH}_2(\mathrm{~g})}\)
= 3.30 × 103 mol NH3 (g)
3.30 × 103 mol NH3 (g) is obtained.
If they are to be converted to grams, it is done as follows :
1 mol NH3(g) = 17.0 g NH3(g)
3.30 × 103 mol NH3 (g) × \(\frac{17.0 \mathrm{~g} \mathrm{NH}_3(\mathrm{~g})}{1 \mathrm{~mol} \mathrm{NH}_3(\mathrm{~g})}\)
= 3.30 × 103 × 17 g NH3 (g)
= 56.1 × 103 g NH3 (g)
= 56.1 kg NH3
Question 6.
A solution ¡s prepared by adding 2 g of a substance A to 18 g water. Calculate the mass percent of the solute.
Solution:

Question 7.
Calculate the molarity of NaOH in the solution prepared by dissolving 4 g in enough water to form 250 mL of the solution.
Solution:
Since molarity

Note that molarity of a solution depends upon temperature because volume of a solution is temperature dependent.
![]()
Question 8.
The density of 3 M solution of NaCl is 1.25 g mL-1. Calculate molality of the solution.
Solution:
M = 3 mol L-1
Mass of NaCl in 1 L solution
= 3 × 58.5 = 175.5 g
Mass of
1 L solution = 1000 × 1.25 = 1250 g
(Since density = 1.25 gmL-1)
Mass of water of solution = 1250 – 175.5
= 1074.5 g = 1.0745 kg
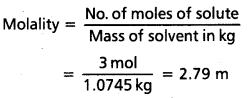
Often in a chemistry laboratory, a solution of a desired concentration is prepared by diluting a solution of known higher concentration. The solution of higher concentration is also known as stock solution. Note that molality of a solution does not change with temperature since mass remains unaffeoted with temperature.
Question 9.
Calculte the normality of oxalic acid solutions containing 6.3g of H2C2O4.2H2O in 500 ml of solutions.
Solution:
Weight of solute = 6.3 g
GEW of solute = \(\frac{126}{2}\) = 63
∴ Normality (N) = \(\frac{\omega}{\mathrm{GEW}} \times \frac{1000}{\mathrm{~V}(\mathrm{~mL})}\)
Normality (N) = \(\frac{6.3}{63} \times \frac{1000}{500}\) = 0.2 N
Question 10.
Calculate the mass of Na2CO3 required to prepare 250 ml of 0.5 N solution.
Solution:
Normality of required solution = 0.5 N
Volume of required solution = 250 ml
Equivalent wt.of. Na2CO3 = \(\frac{106}{2}\) = 53
Normality (N) = \(\frac{\mathrm{W}}{\mathrm{GEW}} \times \frac{1000}{\mathrm{~V}(\mathrm{~mL})}\)
wt. of solute = N × GEW × \(\frac{V(\mathrm{ml})}{1000}\)
= 0.5 × 53 × \(\frac{250}{1000}\) = \(\frac{53}{8}\) = 6.62 g
Question 11.
In the reactions given below, identify the species undergoing oxidation and reduction :
(i) H2S (g) + Cl2 (g) → 2HC (g) + S (s)
(ii) 3Fe3O4 (s) + 8Al (s) → 9Fe (s) + 4Al2O3 (s)
(iii) 2Na (s) + H2 (g) → 2NaH (s)
Solution:
(i) H2S is oxidised because a more electronegative element, chlorine is added to hydrogen (or a more electropositive element, hydrogen has been removed from S). Chlorine is reduced due to addition of hydrogen to it.
(ii) Aluminium is oxidised because oxygen is added to it. Ferrous ferric oxide (Fe3O4) is reduced because oxygen has been removed from it.
(iii) This reaction is very interesting. It may be said from the above definitions that the reaction is only a reduction reaction as it involves the addition of sodium (electropositive metal) or hydrogen whereas sodium undergoes oxidation and hydrogen undergoes reduction. It is to say that the above definitions for oxidation and reduction can not explain this and they have limitations like this. Therefore a new concept has to be considered for the oxidation and the reduction.
Question 12.
Justify that the reaction :
2Na (s) + H2 (g) → 2NaH (s) is a redox change.
Solution:
Since in the above reaction the compound formed is an ionic compound, which may also be represented as Na+H– (s), this suggests that one half reaction in this process is :
2Na (s) → 2Na+ (g) + 2e– and the other half reaction is H2 (g) + 2e– → 2H– (g)
This splitting of the reaction under examination into two half reactions automatically reveals that here sodium is oxidised and hydrogen is reduced, therefore, the complete reaction is a redox change.
Question 13.
Using stock notation, represent the following compounds : HAuCl4, Tl2O, FeO, Fe2O3, Cul, CuO, MnO and MnO2.
Solution:
By applying various rules of calculating the oxidation number of the desired element in a compound, the oxidation number of each metallic element in its compound is as follows:
HAuCl4 → Au has 3
Tl2O → Tl has 1
FeO → Fe has 2
Fe2O3 → Fe has 3
Cul → Cu has 1
CuO → Cu has 2
MnO → Mn has 2
MnO2 → Mn has 4
Therefore, these compounds may be represented as :
HAu (III) Cl4, Tl2(I)O, Fe(II)O, Fe2(III)O3, Cu(I)I, Cu(II)O, Mn(II)O, Mn(IV)O2.
Question 14.
Justify that the reaction :
2Cu2O(S) + Cu2S(s) → 6Cu(s) + SO2(g) is a redox reaction. Identify the species oxidised/reduced, which acts as an oxidant and which acts as a reductant.
Solution:
Let us assign oxidation number to each of the species in the reaction under examination. This results into :
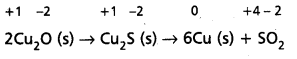
We therefore, conclude that in this reaction copper is reduced from +1 state to zero oxidation state and sulphur is oxidised from -2 state to +4 state. The above reaction is thus a redox reaction.
Further, Cu2O helps sulphur in Cu2S to increase its oxidation number, therefore Cu (I) is an oxidant; and sulphur of Cu2S helps copper both in Cu2S itself and Cu2O to decrease its oxidation number ; therefore, sulphur of Cu2S is reductant.
Question 15.
Which of the following species, do not show disproportionation reaction and why ? ClO–, Cl\(\mathrm{O}_2^{-}\), ClO3 and ClO4. Also write reaction for each of the species that disproportionates.
Solution:
Among the oxoanions of chlorine listed above, ClO4 does not disproportionate because in this oxoanion chlorine is present in its highest oxidation state that is, +7. The disproportionation reactions for the other three oxoanions of chlorine areas follows :

Question 16.
Suggest a scheme of classification of
the following redox reactions
(a) N2 (g) + O2 (g) → 2NO (g)
(b) 2Pb(NO3)2(s) → 2PbO(s) + 2NO2(g) + 1/2 O2(g)
(c) NaH(s) + H2O (l) → NaOH (aq) + H2(g)
(d) 2NO2(g) + 2OH–(aq) → N\(\mathrm{O}_2^{-}\) (aq) + N\(\mathrm{O}_3^{-}\) (aq) + H2O(l)
Solution:
In reaction
(a) the compound nitric oxide is formed by the combination of the elemental substances, nitrogen and oxygen ; therefore, this is an example of combination redox reactions. The reaction.
(b) involves the breaking down of lead nitrate into three components, therefore, this is categorised under decomposition redox reaction. In reaction.
(c) hydrogen of water has been displaced by hydride ion into dihydrogen gas. There-fore, this may be called as displacement redox reaction.
(d) The reaction involves disproportionation of NO2 (+4 state) into NO2 (+3 state) and NO3 (+5 state). Therefore reaction (d) is an example of disproportionation redox reaction.
Question 17.
Why do the following reactiolns proceed differently ?
Pb3O4 + 8HCl → 3PbCl2 + Cl2 + 4H2O and
Pb3O4 + 4HNO3 → 2Pb(NO3)3 + PbO2 + 2H2O
Solution:
Pb3O4 is actually a stoichiometric mixture of 2 mol. of PbO and 1 mol. of PbO2. In PbO2, lead is present in +4 oxidation state, whereas the stable oxidation state of lead in PbO is +2. PbO2 thus can act as an oxidant (oxidising agent) and, therefore, can oxidise Cl ion of HCl into chlorine. We may also keep in mind that PbO is a basic oxide. Therefore, the reaction
Pb3O4 + 8HCl → 3PbCl2 + Cl2 + 4H2O can be splitted into two reactions namely :
2 PbO + 4HCl → 2PbCl2 + 2H2O (acid base reaction)
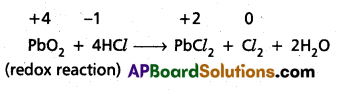
Question 18.
Write the net ionic equation for the reaction of potassium dichromate (VI) K2Cr2O7 with sodium sulphite, Na2SO3 in an acid solution to give chromium (III) ion and the sulphate ion.
Solution:
Step – 1 :
The skeletal ionic equation is :
Cr2\(\mathrm{O}_7^{2-}\) (aq) + S\(\mathrm{O}_3^{-2}\) (aq) → Cr3+ (aq) + S\(\mathrm{O}_4^{2-}\) (aq)
Step – 2 :
Assign oxidation numbers for Cr and S
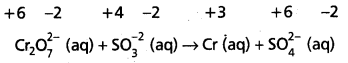
This indicates that the dichromate ion is the oxidant (it oxidises sulphite ion to sulphate ion) and the sulphite ion is the reductant. (it reduces dichromate ion to chromium (III).
Step – 3 :
Calculate the increase and decrease of oxidation numbers of respective species and make them equal.
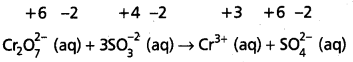
As reduction is total 6 units due to two Cr3+ formed, oxidation also must be 6 units. This is obtained by multiplying S\(\mathrm{O}_3^{-2}\) with 3.
Step – 4 :
Adjust the coefficients of the products accordingly
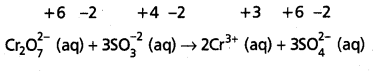
Step – 5 :
a) Add H+ ions in acid medium or H2O molecules in basic medium in the required number to hydrogen atoms deficient side.
b) Add H2O molecules in acid medium or OH– ions in basic medium in the required number to oxygen atoms diffident side, (a) and (b) may be repeated any number of times by hit and trial method until hydrogen and oxygen atoms are same in number on both the sides of the redox reaction.
The given reaction is in acid medium
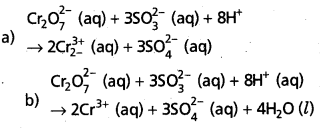
![]()
Question 19.
Permanganate ion reacts with bromide ion in basic medium to give manganese dioxide and bromate ion. Write the balanced ionic equation for the reaction.
Solution:
Step – 1 : The skeletal ionic equation is :
Mn\(\mathrm{O}_4^{-}\) (aq) + Br– (aq) → MnO2 (s) + Br\(\mathrm{O}_3^{-}\) (aq)
Step – 2 : Assign oxidation numbers for Mn and Br.
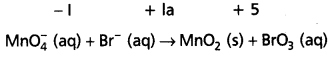
This indicates that permanganate ion is the oxidant and bromide ion is the reductant.
Step – 3 :
Calculate the increase or decrease in the oxidation number per atom and for the entire molecule/ion in which it occurs. The number units of oxidations change must be equal to the number units of reduction change. If this is not observed then multiply the oxidising agent with the number of units of oxidation and the reducing agent with the number of units of reduction i.e., multiply oxidant MnO4 by 2 and reductant Br– by I.
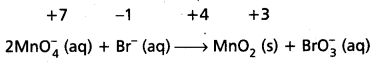
Know number of units oxidation number of units reduction.
Step – 4:
Adjust the coefficients of products accordingly.
2Mn\(\mathrm{O}_4^{-}\) (aq) + Br (aq) → 2MnO2 (s) + BrO3 (aq)
Step – 5 :
a) Add H+ ions in acid medium or H2O molecules in basic medium in the required number to hydrogen atoms deficient side.
b) Add H2O molecules in acid medium or OH– ions in basic medium in the required number to oxygen atoms dificient side, (a) and (b) may be repeated any number of times by hit and trial method until hydrogen and oxygen atoms are same in number on both the sides of the redox reaction. This reaction is basic medium.
2Mn\(\mathrm{O}_4^{-}\) (aq) + Br (aq) + H2O (I)
- 2MnO2 (s) + Br\(\mathrm{O}_3^{-}\) (aq) + 2OH– (aq)
Question 20.
Permanganate (VII) ion, MnO4 in basic solution oxidises iodide ion. I to produce molecular iodine (I2) and manganese (IV) oxide (MnO2). Write a balanced ionic equation to represent this redox reaction.
Solution:
Step – 1 :
First we write the skeletal ionic equation, which is
Mn\(\mathrm{O}_4^{-}\) (aq) + I– (aq) → MnO2 (s) + I2 (s)
Step – 2 :
The two half-reactions are :
-1 0
Oxidation half :
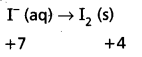
Reduction half : Mn\(\mathrm{O}_4^{-}\) (aq) → MnO2 (s)
Step – 3 :
To balance the I atoms in the oxidation half reaction, we rewrite it as:
2I– (aq) → I2 (s)
Step – 4:
As the reaction takes place to basic medium, to balance the 0 atoms in the reduction half reaction, we add OH– ions in required number.
Mn\(\mathrm{O}_4^{-}\) (aq) → MnO2 (s) + 2HO– (I)
To balance the H atoms, we add two H2O molecules on the left.
Mn\(\mathrm{O}_4^{-}\) (aq) + 2H2O (aq) → MnO2 (s) + 2 HO– (I)
Balance H and 0 atoms by bit and trial method even if it requires morethan once we haye to do it.
The resultant equation is :
Mn\(\mathrm{O}_4^{-}\) (aq) + 2H2O (I) → MnO2 (s) + 4OH– (aq)
Note : While balanceing H atom 0 atoms do not disturb the coefficients of other species (oxidant and reduCtant and the products).
Step-5 :
In this step we balance the charges of the two half-reactions in the manner depicted as:
2I– (aq) → I2 (s) + 2e–
Mn\(\mathrm{O}_4^{-}\) (aq) + 2H2O (I) + 3e– → MnO2 (s) + 4OH– (aq)
Now to equalise the number of electrons, in the two half reactions we multiply the oxidation hatf-reaction by 3 and the reduction half-reaction by 2.
6I– (aq) → 3I2 (s) + 6e–
2MnO4 (aq) + 4H4O (I) + 6e– → 2MnO2 (s) + 8OH–(aq)
Step-6:
Add two half-reactions to obtain the net reaction and canceel the electrons on both sides.
6I– (aq) + 2Mn\(\mathrm{O}_4^{-}\) (aq) + 4H2O (I) → 3I2 (s) + 2MnO2 (s) + 8 OH– (aq)
Step – 7:
A final verification shows that the equation is balanced in respect of the number of atoms and charges on both sides.
Question 21.
Calculate the normality of H2So4 solution. If 50 ml of it completely neutralised 250 ml of 0.2 N sodium hydroxide (NaoH) solution.
Answer:
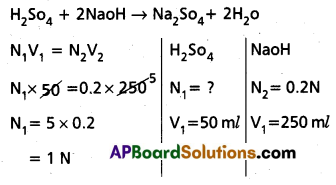
∴ Normality of H2So4 solution = 1 N.