AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(b)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(b)

I. కింది ప్రమేయాలకు ఆవర్తనాలు కనుక్కోండి.

Question 1.
cos(3x + 5) + 7
Solution:
f(x) = cos(3x + 5) + 7
g(x) = cos x, ∀ x ∈ R కు ఆవర్తనం 2π
f(x) = cos(3x + 5) + 7
f(x) ఆవర్తనం \(\frac{2 \pi}{|3|}=\frac{2 \pi}{3}\)

Question 2.
tan 5x
Solution:
f(x) = tan 5x
g(x) = tan x ఆవర్తనం π
∴ f(x) = tan 5x
\(\frac{\pi}{|5|}=\frac{\pi}{5}\)

Question 3.
\(\cos \left(\frac{4 x+9}{5}\right)\) [Mar. ’14]
Solution:

Question 4.
|sin x|
Solution:
f(x) = |sin x|
h(x) = sin x ∀ x ∈ R ఆవర్తనం 2π
f(x) = |sin x| ఆవర్తనం π
∵ f(x + π) = |sin(x + π)|
= |-sin x|
= sin x
∴ |sin x| ఆవర్తనం π

Question 5.
tan(x + 4x + 9x + ……. + n²x) (n ధన పూర్ణాంకం) [(A.P & T.S) Mar. ’15]
Solution:
tan(1² + 2² + 3² + ……. + n²)x
= \(\tan \left[\frac{n(n+1)(2 n+1)}{6}\right] x\)
ఆవర్తనం = \(\frac{6 \pi}{n(n+1)(2 n+1)}\)

Question 6.
ఆవర్తనం \(\frac{2}{3}\) గా గల ఒక sin ప్రమేయాన్ని కనుక్కోండి.
Solution:
\(\frac{2 \pi}{|k|}=\frac{2}{3}\)
3π = |k|
∴ sin kx = sin 3πx

Question 7.
ఆవర్తనం 7గా గల ఒక cos ప్రమేయాన్ని కనుక్కోండి. [Mar. ’13]
Solution:
\(\frac{2 \pi}{k}\) = 7
\(\frac{2 \pi}{7}\) = k
∴ cos kx = cos \(\frac{2 \pi}{7}\)x

II. కింది వాటికి రేఖాచిత్రాలను వేయండి.

Question 1.
0, \(\frac{\pi}{4}\) ల మధ్య tan x ప్రమేయం
Solution:

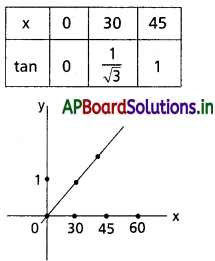
Question 2.
[0, π] అంతరంలో cos 2x ప్రమేయం
Solution:

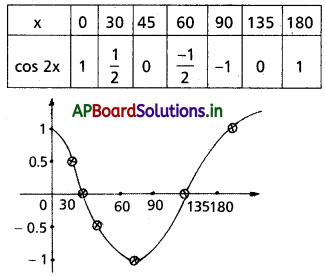
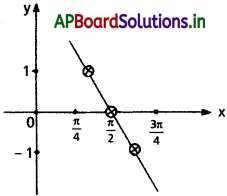
Question 3.
(0, π) అంతరంలో sin 2x ప్రమేయం
Solution:

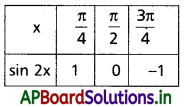
Question 4.
[-π + π] అంతరంలో sin x ప్రమేయం
Solution:

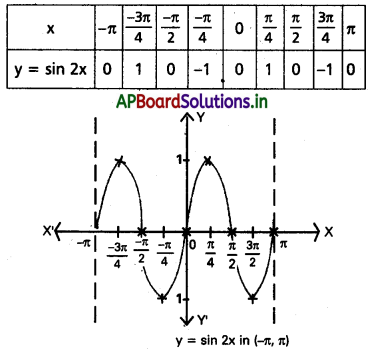
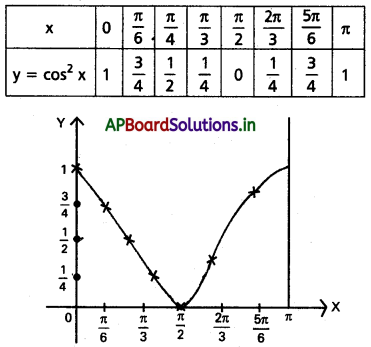
Question 5.
[0, π] అంతరంలో cos²x ప్రమేయం
Solution:

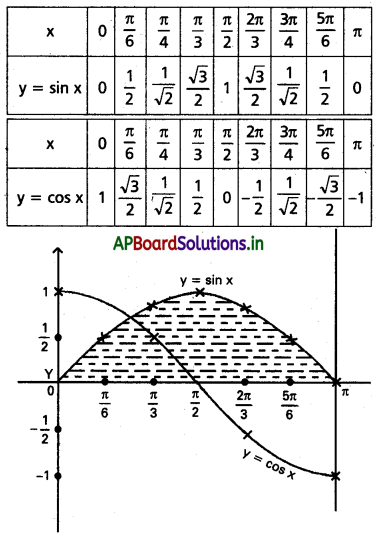
Question 6.
[0, π] అంతరంలో y = sin x, y = cos x, X-అక్షాల మధ్యభాగం.
Solution: