AP Inter 2nd Year Maths 2B Solutions Chapter 3 పరావలయం Ex 3(a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 3 పరావలయం Exercise 3(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 3 పరావలయం Exercise 3(a)

అభ్యాసం – 3(ఎ)

I.

ప్రశ్న 1.
4y² + 12x – 20y + 67 = 0 పరావలయం శీర్షం, నాభులు కనుక్కోండి.
సాధన:
దత్త సమీకరణము 4y² + 12x – 20y + 67 = 0
4y² – 20y = -12x – 67
y² – 5y = -3x – \(\frac{67}{4}\)
ఇరువైపులా \(\frac{25}{4}\) కూడగా

ప్రశ్న 2.
x² – 6x – 6y + 6 = 0 పరావలయం శీర్షం, నాభులు కనుక్కోండి.
సాధన:
దత్త సమీకరణము
x² – 6x – 6y + 6 = 0
x² – 6x = 6y – 6
ఇరువైపులా 9 కలుపగా
x² – 6x + 9 = 6y+ 3
(x – 3)² = 6\(\left(y+\frac{1}{2}\right)\)
= \(\left[y-\left(\frac{-1}{2}\right)\right]\)
∴h = 3, k = \(\frac{-1}{2}\), a = \(\frac{6}{4}\) = \(\frac{3}{2}\)
శీర్షం = (h, k) = (3, \(\frac{-1}{2}\))
నాభి = (h, k + a) = (3, \(\frac{-1}{2}\)–\(\frac{1}{2}\))
= (3, 1).

ప్రశ్న 3.
y² + 6y – 2x + 5 = 0 పరావలయం అక్షరేఖ, నియత రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
y² + 6y = 2x – 5
ఇరువైపులా 9 కలుపగా
y² + 6y + 9 = 2x – 5 + 9
[y – (-3)]² = 2x + 4
[y – (-3)]² = 2[x – (-2)]
(y – k)² = 4a (x – h) తో పోల్చగా
(h, k) = (-2,-3), a = \(\frac{1}{2}\)
అక్ష సమీకరణము y – k =  i.e. y + 3 = 0
నియత రేఖా సమీకరణము x – h + a = 0
i.e., x – (-2) + \(\frac{1}{2}\) = 0
2x + 5 = 0.

ప్రశ్న 4.
4x² + 12x – 20y + 67 = 0 పరావలయం అక్షరేఖ, నియత రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
4x² + 12x = 20y – 67
x² + 3x = 5y – \(\frac{67}{4}\)
ఇరువైపులా \(\frac{9}{4}\) కలుపగా
x² + 3x + \(\frac{9}{4}\) = 5y – \(\frac{67}{4}\) + \(\frac{9}{4}\)
(x + \(\frac{3}{2}\))² = 5y – \(\frac{58}{4}\)
= 5y – \(\frac{29}{2}\)
\(\left[x-\left(\frac{-3}{2}\right)\right]^2=5\left[y-\frac{29}{10}\right]\)
(x – h)² = 4a(y – k) తో పోల్చగా
(h, k) = (\(\frac{-3}{2}\), \(\frac{29}{10}\)) ; a = \(\frac{5}{4}\)
అక్ష సమీకరణము x – h = 0, i.e., x + \(\frac{3}{2}\) = 0
2x + 3 = 0
నియత రేఖా సమీకరణము, y – k + a = 0
у – \(\frac{29}{10}\) + \(\frac{5}{4}\) = 0
⇒ 20y – 33 = 0.

ప్రశ్న 5.
నాభి 5(1, -7), శీర్షం (1, 2) గా గల పరావలయం సమీకరణం కనుక్కోండి.
సాధన:
S = (1, -7), A(1, -2) అనుకుందాము.
h = 1, k = -2, a = -2 + 7 = 5
పరావలయం అక్షం Y – అక్షానికి సమాంతరము.
పరావలయ, సమీకరణము
(x – h)² = – 4a (y – k)
(x – 1)² = 20(y + 2)
x² – 2x + 1 = -20y – 40
⇒ x² – 2x + 20y + 41 = 0.

ప్రశ్న 6.
నాభి S(3, 5), శీర్షం (1, 3)గా గల పరావలయం సమీకరణం కనుక్కోండి.
సాధన:
అక్ష సమీకరణము y – 3 = \(\frac{3-5}{1-3}\) (x – 1)
= x – 1
x – y + 2 = 0
నియత రేఖ, అక్షానికి లంబంగా ఉంది.
నియత రేఖ సమీకరణము x + y + k = 0
Z నిరూపకాలు (x, y)
SZ మధ్య బిందువు A
A నిరూపకాలు \(\left(\frac{3+x}{2}, \frac{5+y}{2}\right)\) = (1, 3)
\(\frac{3+x}{2}\) = 1
3 + x = 2
x = 2 – 3 = -1

\(\frac{5+y}{2}\) = 3
5 + y = 6
y = 6 – 5 = 1

Z నిరూపకాలు (-1, 1).
నియత రేఖ Z (-1, 1) గుండా పోతుంది.
-1 + 1 + k = 0 ⇒ k = 0
నియతరేఖ సమీకరణము x + y = 0
పరావలయ సమీకరణము ( x – α)² + (y – β)²
= \(\frac{(l \mathrm{x}+\mathrm{my}+\mathrm{n})^2}{l^2+\mathrm{m}^2}\)
(x – 3)² + (y – 5)² = \(\frac{(x+y)^2}{1+1}\)
⇒ 2(x² – 6x + 9 + y² – 10y + 25)= (x + y)²
⇒ 2x² + 2y² – 12x – 20y + 68 = x² + 2xy + y²
i.e., x² – 2xy + y² – 12x – 20y+ 68 = 0.

ప్రశ్న 7.
(-3, 2), (-3, 1) బిందువులను కలిపే రేఖాఖండం నాభి లంబంగా గల పరావలయం సమీకరణం కనుక్కోండి.
సాధన:

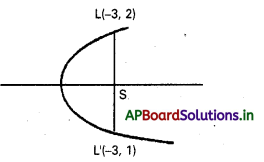
L (-3, 2) మరియు L’ (-3, 1) నాభి లంబము కొనలు S మధ్య బిందువు LL’
S నిరూపకాలు \(\left(-3, \frac{3}{2}\right)\)

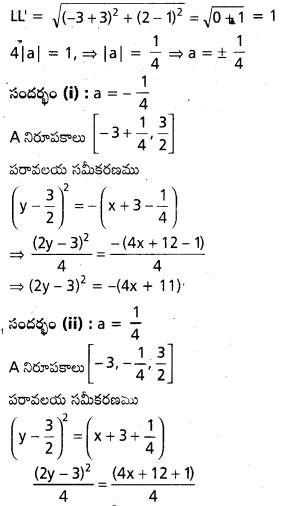
i.e., (2y – 3)² = 4x + 13.

ప్రశ్న 8.
y² = 6x పరావలయం దృష్ట్యా కింది బిందువుల స్థితి (అంతరంగా ఉన్నాయో, బాహ్యంగా ఉన్నాయో, పరిధిపై ఉన్నాయో) తెలపండి.
i) (6, -6)
ii) (0, 1)
iii) (2, 3)
సాధన:
i) (6, -6)
పరావలయ సమీకరణము y² = 6x
i.e., S = y – 6x
S₁₁ = (-6)² – 6.6 = 36 – 36 = 0
∴ (6, 6) బిందువు పరావలయం మీద ఉంది.

ii) (0, 1)
S₁₁ = 1² – 6.0 = 1 > 0
∴ (0, 1) బిందువు పరావలయానికి బాహ్యంగా ఉంది.

iii) (2, 3)
S = 9 – 6 (2) = 9 – 12 = 3
∴ (2, 3) బిందువు పరావలయానికి అంతరంగా ఉంది.

ప్రశ్న 9.
y² = 8x పరావలయంపై నాభిదూరం 10 గల బిందువుల నిరూపకాలు కనుక్కోండి. [(Mar. ’11) ‘T.S. Mar, ’17 A.P. Mar. ’17 A.P. Mar. ’16]
సాధన:
పరావలయ సమీకరణము y² = 8x
4a = 8 ⇒ a = 2

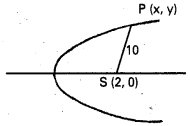
నాభి నిరూపకాలు (2, 0)
పరావలయం మీద పడని బిందువు P(x, y)
దత్తాంశం SP = 10 ⇒ SP² = 100
(x – 2)² + y² = 100 + 2
కనుక y² = 8X
⇒ (x – 2)² + 8x = 100
⇒ x² – 4x + 4 + 8x – 100 = 0
⇒ x + 4x – 96 = 0 ⇒ (x + 12) (x – 8) = 0
x + 12 = 0 లేదా × – 8 = 0
x = -12, లేదా 8
సందర్భం : (i) x = 8
y² = 8.x = 8.8 = 64
y = ±8
కావలసిన బిందువుల నిరూపకాలు (8, 8) మరియు (8, -8)
సందర్భం : (ii) x = -12
y² = 8(-12) = -96 < 0
y వాస్తవము కాదు.

ప్రశ్న 10.
y² = 8x పరావలయం, నాభి జ్యా ఒక కొన (\(\frac{1}{2}\), 2) అయితే రెండో కొన నిరూపకాలు కనుక్కోండి. [May ’06]
సాధన:
A = (\(\frac{1}{2}\), 2); S = (2, 0)
B = (x₁, y₁) ⇒ \(\left(\frac{y_1^2}{8}, y_1\right)\)
ASB నాభి జ్యా
∴ SA, SB వాలులు సమానము.

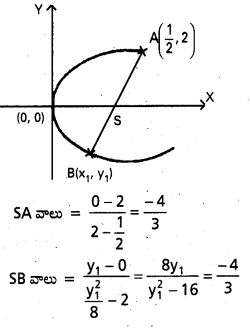
24y₁ = -4y₁² + 64
లేదా 4y₁² + 24y₁ – 64 = 0
⇒ y₁² + 6y₁ – 16 = 0 ⇒ (y₁ + 8) (y₁ – 2) = 0
y₁ = 2, -8
x₁ = \(\frac{1}{2}\) , 8; కావున (8, -8) రెండవ కొన.

ప్రశ్న 11.
y² = 4ax (a > 0) పై గల బిందువులలో నాభి నుంచి కనిష్ట దూరంలో గల బిందువు శీర్షం అని చూపండి.
సాధన:
P(at², 2at) పరావలయం మీది బిందువు

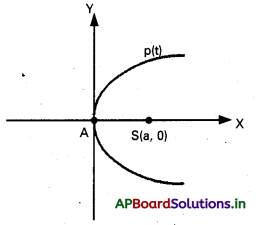
S(a, 0) కనిష్ఠ దూరంలో ఉంది.
[SP² = (at – a)² + (2at – 0)²]
f'(t) = a²2(t² − 1) (2t) + 4a²(2t).
= 4a²t(t² – 1 + 2) = 4a²t(t² + 1)
కనిష్ఠ విలువను’ f'(t) = 0 ⇒ t = 0
f” (t) = 4a²(3t² + 1)
f'(0) = 4a² > 0]
∴ t = 0, వద్ద f(t) కనిష్ఠం
P = (0, 0):
∴ y² = 4ax, మీద ఉంటుంది. ధృవానికి కనిష్ఠ దూరములో గల బిందువు A (0, 0).

ప్రశ్న 12.
సూర్యుడు నాభిగా గల పరావలయ కక్ష్యలో ఒక తోకచుక్క సంచరిస్తోంది. సూర్యుడు నుంచి తోకచుక్క దూరం 2 × 10⁷ కి.మీ. ఉన్నప్పుడు సూర్యుడిని, తోకచుక్కను కలిపే రేఖ, కక్ష్య యొక్క అక్షరేఖతో \(\frac{\pi}{2}\) కోణం చేస్తోంది. సూర్యుడికి ఎంత దగ్గరగా తోకచుక్క రాగలదో కనుక్కోండి.
సాధన:

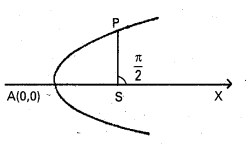
తోకచుక్క యొక్క పరావలయ కక్ష్య y² = 4ax అనుకుందాం.
తోకచుక్క ఉన్న స్థితి P
∠XSP = \(\frac{\pi}{2}\) అని ఇవ్వబడింది.
SP అక్షానికి లంబంగా ఉంది.
SP అర్థ నాభి లంబము
2a = 2 × 10⁷
⇒ a = 10⁷ కి . మీ
పరావలయము మీద నాభి నుండి అత్యంత సమీప బిందువు A
AS = a = 10⁷ కి . మీ
∴ సూర్యుని నుండి కనిష్ఠ దూరంలో గల పరావలయం మీది బిందువు 10⁷ కి.మీ దూరంలో ఉంది.

II.

ప్రశ్న 1.
పరావలయం y² = 4ax (a > 0) ద్విy నిరూపకం, త్రిథాకరణ బిందువుల బిందు పథాన్ని కనుక్కోండి.
సాధన:
పరావలయం సమీకరణము y⁷ = 4ax
P(x, y) మరియు Q(x, -y) నాభి జ్యా కొనలు.

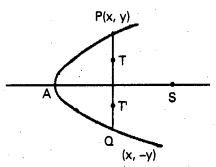
T బిందువు PQ ని 1 : 2 నిష్పత్తిలో విభజిస్తుంది.
T నిరూపకాలు \(\left(x, \frac{-y+2 y}{3}\right)\)
= \(\left(x, \frac{y}{3}\right)\)
T బిందువు PQ ని 2 : 1 నిష్పత్తిలో విభజిస్తుంది.
T నిరూపకాలు \(\left[x, \frac{-2 y+y}{3}\right]\)
= \(\left(x_1-\frac{y}{3}\right)\)
L, L’ల నిరూపకాలు (x₁, y₁) అయితే
y₁ = ± \(\frac{y}{3}\) ⇒ y₁² = \(\frac{y^2}{9}\)
y² = 9y₁²
4ax₁ = 9y₁²
బిందు పథము (x₁, y₁) = 9y² = 4ax.

ప్రశ్న 2.
ధన X – అక్షంపై మూలబిందువు నుంచి శీర్షం, నాభులు వరుసగా (a, a’) దూరాలలో గల పరావలయ సమీకరణం కనుక్కోండి.
సాధన:
A నిరూపకాలు (a, 0) మరియు
S నిరూపకాలు (a’, 0)
AS = a’ – a

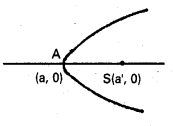
పరావలయ సమీకరణము y² = 4(a’ – a) (x – a).

ప్రశ్న 3.
x² = 6y పరావలయం నాభి లంబాగ్రాలు L,L’ లు అయితే OL, OL’ సమీకరణాలు, వాటి మధ్యకోణం -కనుక్కోండి. (‘O’ మూలబిందువు)
సాధన;
x² = 6y
Y – అక్షం దృష్ట్యా వక్ర సౌష్ఠవము
నాభి జ్యా కొనలు
(2a, a), (-2a, a)
4a = 6 ⇒ a = \(\frac{3}{2}\)
OL : x = 2y
∴ L = (3, \(\frac{3}{2}\))
OL’ : x = -2y
L’ = (-3, \(\frac{3}{2}\))
Tan θ = \(\left|\frac{\frac{1}{2}+\frac{1}{2}}{1-\frac{1}{4}}\right|=\frac{4}{3}\)
∴ θ =Tan^-1 \(\left(\frac{4}{3}\right)\)

ప్రశ్న 4.
(-2, 1), (1, 2), (-1, 3) బిందువుల గుండా పోతూ, X- అక్షానికి సమాంతరంగా అక్షరేఖ గల పరావలయ సమీకరణం కనుక్కోండి.
సాధన:
అక్షం X – అక్షానికి సమాంతరము
సాధారణ సమీకరణము
x = ay² + by + c
(−2, 1) (1, 2) (−1, 3) బిందువుల గుండా పోతుంది.
-2 = a + b + c ……………… (i)
1 = 4a + 2b + c ……………… (ii)
-1 = 9a + 3b + c ………………. (iii)

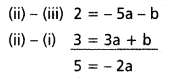
–\(\frac{5}{2}\) = a
\(\frac{21}{2}\) = b
– 10 = c
x = –\(\frac{5}{2}\)y² + \(\frac{21}{2}\)y – 10
5y² + 2x – 21y + 20 = 0

ప్రశ్న 5.
(4, 5), (-2, 11), (4, 21) బిందువుల గుండా పోతూ, Y – అక్షానికి సమాంతరంగా అక్షరేఖ గల పరావలయ సమీకరణం కనుక్కోండి.
సాధన:
సాధారణ సమీకరణము y = ax² + bx + C
(4, 5), (-2, 11), (-4, 21) ల గుండాపోతుంది.
5 = 16a + 4b + c ………………. (i)
11 = 4a – 2b + c …………….. (ii)
+ 21 = 16a – 4b + c ……………….. (iii)
(ii) – (i) చేయగా
6 = -12a – 6b
(iii) – (ii) 10 = 12a – 2b
సాధించగా
b = -2, a = 1/2, c = 5
y = \(\frac{1}{2}\) x² – 2x + 5
x² – 2y – 4x + 10 = 0

III.

ప్రశ్న 1.
నాభి (−2, 3) నియతరేఖ 2x + 3y + 4 = 0 గా గల పరావలయ సమీకరణం కనుక్కోండి. నాభిలంబం పొడవు, అక్షరేఖ సమీకరణాలు కూడా కనుక్కోండి.
సాధన:

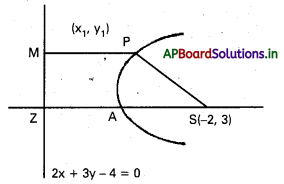
P(x₁, y₁) పరావలయం మీది బిందువు.
S(-2, 3) నాభి
SP² = (x₁ + 2)² +(y₁ – 3)²
నియత రేఖ సమీకరణము 2x + 3y – 4 = 0
PM = P నుండి నియత రేఖ మీదకు
PM = \(\frac{\left|2 x_1+3 y_1-4\right|}{\sqrt{4+9}}\)
పరావలయ నిర్వచనం ప్రకారం SP = PM ⇒ SP² = PM²
(x₁ + 2)² + (y₁ – 3)² = \(\frac{\left(2 x_1+3 y_1-4\right)^2}{13}\)
⇒ 13(x₁² + 4x₁ + 4 + y₁² – 6y₁ + 9) = (2x₁ + 3y₁ – 4)²
⇒ 13x₁² + 13y₁² + 52 x₁ – 78 y₁ + 169 = 4x₁² + 9y₁² + 16 + 12 x₁y₁ – 16x₁ – 24 y₁
⇒ 9x₁² – 12 x₁y₁ + 4y₁² + 68x₁ – 54y₁ + 153 = 0
బిందు పథము P(x₁, y₁)
9x² – 12xy +4y²+68x-54y+ 153 = 0
నాభి లంబము పొడవు. = 4a
S నుండి నియత రేఖ మీదకు లంబదూరము
= \(\frac{|2(-2)+3.3-4|}{\sqrt{4+9}}=\frac{1}{\sqrt{13}}\)
2a = \(\frac{1}{\sqrt{13}}\)
నాభి లంబం పొడవు
= 4a = \(\frac{2}{\sqrt{13}}\)
అక్షం, నియత రేఖకు లంబంగా ఉంటుంది.
నియత రేఖ సమీకరణాన్ని
3x – 2y + k = 0 గా తీసుకొనగలము.
ఈ రేఖ S (−2, 3) గుండా పోతుంది.
-6 – 6 + k = 0 ⇒ k = 12
అక్షం సమీకరణము 3x – 2y + 12 = 0

ప్రశ్న 2.
y² = 4ax పరావలయంలో అంతర్లిఖించిన త్రిభుజం శీర్షాల y నిరూపకాలు y₁, y₂, y₃ అయితే త్రిభుజ వైశాల్యం \(\frac{1}{8 a}\) (y₁ − y₂) (y₂ – y₃) (y₃ – y₁) | చ || యూ ॥ అని చూపండి.
సాధన:
P(at₁², 2at₁), Q(at₂², 2at₂),
R(at₃², 2at₃) లు ∆PQRశీర్షాలు .
∆ PQR వైశాల్యము = \(\frac{1}{2}\) |at₁² (2at₂ – 2at₃) + at₂² (2at₃ – 2at₁) + at₃² (2at₁ – 2at₂)|
= \(\frac{1}{2}\) . 2a² |t₁² (t₂ – t₃) + t₂² (t₃ – t₁) + t₃² (t₁ – t₂)|
= a² (t₁ – t₂) (t₂ – t₃) (t₃ – t₁)|
= \(\frac{1}{8 a}\) |(2at₁ – 2at₂) (2at₂ – 2at₃) (2at₃ – 2at₁)|
= \(\frac{1}{8 a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)|
P(x₁, y₁), Q(x₂, y₂), R(x₃, y₃) లు ∆PQRశీర్షాలు.

ప్రశ్న 3.
కింది పరావలయాలకు, శీర్షం, నాభి నిరూపకాలు, నియత రేఖ, అక్షరేఖల సమీకరణాలు కనుక్కోండి.
(i) y² + 4x + 4y – 3 = 0
(ii) x² – 2x + 4y – 3 = 0
సాధన:
i) y² + 4x + 4y – 3 = 0
⇒ y²+ 4y = -4x + 3
⇒ y² + 4y + 4 = -4x + 3+ 4
⇒ + (y + 2)² = – 4x + 7
⇒ [y − (−2)]² = -4[x – \(\frac{7}{4}\)]
h = \(\frac{7}{4}\), k = -2, a = 1
శీర్షం A(h, k) = \(\left(\frac{7}{4},-2\right)\)
నాభి (h-a, k) = \(\left(\frac{7}{4}-1,-2\right)\)
= \(\left(\frac{3}{4},-2\right)\)
నియత రేఖ సమీకరణము x – h- a = 0
x – \(\frac{7}{4}\) – 1 = 0
4x – 11 = 0
అక్షం సమీకరణము y – k = 0
y + 2 = 0

ii) x² – 2x + 4y – 3 = 0
x² – 2x = -4y + 3
⇒ x – 2x + 1 = -4y + 3 + 1
(x – 1)² = -4y + 4
= -4 [y – 1]
(x – 1)² = -4[y – 1]
h = 1; k = 1; a = 1
శీర్షం A(h, k) = (1, 1)
నాభి (h, k – a) = (1, 1 – 1) = (1, 0)
నియత రేఖ సమీకరణము y – k – a = 0
y – 1 – 1 = 0
y – 2 = 0
అక్షరేఖ సమీకరణము x – h = 0
x – 1 = 0