AP Inter 2nd Year Physics Study Material Chapter 4 విద్యుత్ ఆవేశాలు, క్షేత్రాలు

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 4th Lesson విద్యుత్ ఆవేశాలు, క్షేత్రాలు Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 4th Lesson విద్యుత్ ఆవేశాలు, క్షేత్రాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఆవేశం క్వాంటీకరణం చెందింది అనే ప్రవచనం అర్థం ఏమిటి?
జవాబు:
ఒక వస్తువు నుండి మరొక వస్తువుకు ప్రసారమగు కనీస ఆవేశం, ఎలక్ట్రాన్ ఆవేశం (e = 1.602 × 10^-19C) కు సమానము. ఆవేశం ఎల్లప్పుడు ఎలక్ట్రాన్ ఆవేశంనకు పూర్ణ గుణిజాలలో (q = ne) ఉండును. అప్పుడు ఆవేశం క్వాంటీకృతమైంది అంటారు.

ప్రశ్న 2.
ఆకర్షణ కంటే వికర్షణ ఏ ఆవేశానికి సరైన పరీక్ష, ఎందుకు?
జవాబు:
ఒక ఆవేశ వస్తువు, తటస్థ ఆవేశ వస్తువును మరియు వ్యతిరేక ఆవేశ వస్తువును ఆకర్షించును. కాని ఇది ఎల్లప్పుడు సజాతి ఆవేశ వస్తువును వికర్షించును. కావున విద్యుద్దీకరణకు ఆకర్షణకన్నా, వికర్షణ సరైన పరీక్ష.

ప్రశ్న 3.
1C ఆవేశం ఎన్ని ఎలక్ట్రాన్లతో ఏర్పడుతుంది?
జవాబు:

ప్రశ్న 4.
వస్తువును ధనావేశితం చేసినప్పుడు వస్తువు భారం ఏమవుతుంది?
జవాబు:
ఒక వస్తువును ధనావేశితం చేసినప్పుడు, అది కొన్ని ఎలక్ట్రాన్లను కోల్పోవును. కావున వస్తుభారం తగ్గును.

ప్రశ్న 5.
రెండు ఆవేశాల మధ్య దూరాన్ని a) సగానికి తగ్గిస్తే, b) రెట్టింపు చేస్తే వాటి మధ్య బలం ఏమవుతుంది?
జవాబు:
కూలుమ్ నియమము నుండి F ∝ \(\frac{1}{d^2}\)

ప్రశ్న 6.
విద్యుత్ బలరేఖలు (క్షేత్ర రేఖలు) పరస్పరం ఖండించుకోవు. ఎందుకు?
జవాబు:
విద్యుత్ బలరేఖలు (క్షేత్ర రేఖలు) ఖండించుకుంటే, ఖండన బిందువు, రెండు విద్యుత్ క్షేత్ర దిశలను తప్పక కలిగి ఉండాలి. ఇది అసంభవము. కావున విద్యుత్ బలరేఖలు ఖండించుకోవు.

ప్రశ్న 7.
ABC సమబాహు త్రిభుజంపై B, Cల వద్ద +q, -q ఆవేశాలు ఉన్నాయనుకోండి. ఈ వ్యవస్థకు మొత్తం ఆవేశం శూన్యం. కాని, B, C ల నుంచి సమదూరంలో ఉండే A వద్ద విద్యుత్ క్షేత్రం (తీవ్రత) శూన్యం కాదు. ఎందుకు?
జవాబు:
ఆవేశాలు అదిశలు. కాని విద్యుత్ తీవ్రతలు సదిశలు మరియు సదిశ సంకలనం చెందును.

ప్రశ్న 8.
స్థిర విద్యుత్ బల క్షేత్రరేఖలు సంవృత లూప్లను ఏర్పరచవు. ఒకవేళ సంవృత లూప్లను ఏర్పరిస్తే, సంవృత పథం వెంబడి ఆవేశాన్ని జరిపేందుకు చేసిన పని శూన్యం కాజాలదు. పై రెండు ప్రవచనాల నుంచి స్థిర విద్యుత్ బలం స్వభావాన్ని ఊహించగలరా?
జవాబు:
ఇది శక్తి నిత్యత్వ బలం.

ప్రశ్న 9.
స్థిర విద్యుత్ శాస్త్రంలోని గాస్ నియమాన్ని తెలపండి.
జవాబు:
గాస్ నియమము :
“సంవృత తలం ద్వారా పోవు మొత్తం విద్యుత్ అభివాహం తలం ఆవరించి ఉన్న నికర ఆవేశంకు \(\frac{1}{\varepsilon_0}\) రెట్లు ఉండును.

ప్రశ్న 10.
ఏయే సందర్భాల్లో విద్యుత్ అభివాహం రుణాత్మకం, ధనాత్మకం?
జవాబు:
విద్యుత్ అభివాహం Φ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{E}}\) మరియు \(\overrightarrow{\mathrm{A}}\) ల మధ్య కోణం 180° అయిన అభివాహం రుణ సంజ్ఞను కలిగి ఉండును. తలం నుండి అభివాహం వెలుపలకు ప్రవహిస్తే ధన మరియు అభివాహం తలంలోనికి ప్రవేశిస్తే రుణ సంజ్ఞను కలిగి ఉండును.

ప్రశ్న 11.
అనంతమైన పొడవు ఉండే ఆవేశిత తీగ నుంచి r త్రైజ్యా దూరంలో విద్యుత్ (క్షేత్ర) తీవ్రతకు సమాసాన్ని రాయండి.
జవాబు:
అనంతమైన పొడవు గల ఆవేశ తీగ వల్ల విద్యుత్ తీవ్రత E = \(\frac{\lambda}{2 \pi\varepsilon_0r}\), వాహకంనకు లంబంగా
λ = ఏకరీతి రేఖీయ ఆవేశ సాంద్రత
r = వాహకం నుండి బిందు దూరం

ప్రశ్న 12.
అనంతమైన వైశాల్యం గల ఆవేశిత పలకవల్ల ఏర్పడే విద్యుత్ (క్షేత్ర) తీవ్రతకు సమాసాన్ని రాయండి.
జవాబు:
అనంతమైన ఆవేశతలం పలక వల్ల విద్యుత్ క్షేత్ర తీవ్రత, E = \(\frac{\sigma}{2\varepsilon_0}\)

ప్రశ్న 13.
ఆవేశిత వాహక గోళాకార కర్పరం వల్ల దాని వెలుపల, లోపల బిందువుల వద్ద ఏర్పడే విద్యుత్ (క్షేత్ర) తీవ్రతకు సమాసాలను రాయండి.
జవాబు:
a) ఆవేశ గోళాకార కర్పరం లోపల బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత శూన్యం.

b) ఆవేశ గోళాకార కర్పరం వెలుపలి బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత, E = \(\frac{1}{4 \pi\varepsilon_0}.\frac{q}{r^2}\)

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
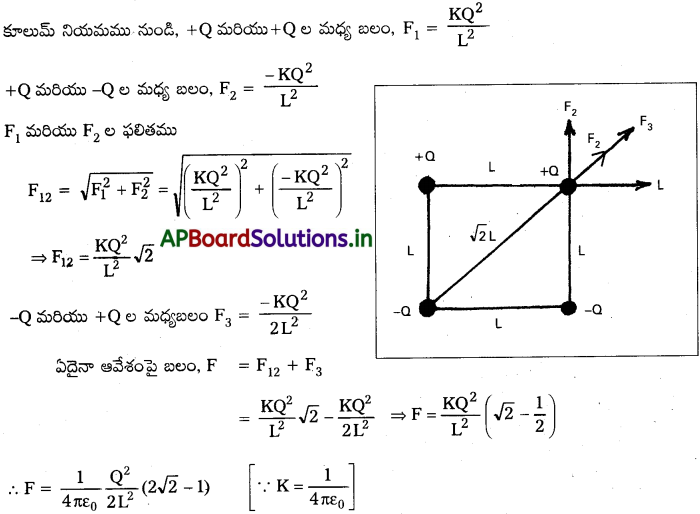
విద్యుత్లోని కూలుమ్ విలోమవర్గ నియమాన్ని తెలిపి, వివరించండి. [TS. Mar.’17; Mar.’14]
జవాబు:
కూలుమ్ నియమము-నిర్వచనం:
“రెండు ఆవేశాల మధ్య బలం, ఆవేశాల లబ్దంనకు అనులోమానుపాతంలో మరియు వాని మధ్య దూరం వర్గంనకు విలోమానుపాతంలో ఉండును. బలం రెండు ఆవేశాలను కలిపే రేఖపై పనిచేయును.

వివరణ :
q₁ మరియు q₂ అను రెండు ఆవేశాలు దూరంలో వేరుచేయబడి ఉన్నాయని భావిద్దాం. అప్పుడు

ఇక్కడ ε యానకం పెర్మిటి విటీ.

ప్రశ్న 2.
ఒక బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రతను నిర్వచించండి. బిందు ఆవేశం వల్ల ఏర్పడే తీవ్రతకు సమాసాన్ని ఉత్పాదించండి. [AP. Mar.’16]
జవాబు:
విద్యుత్ క్షేత్ర తీవ్రత (E) :
విద్యుత్ క్షేత్రంలో ఏదైనా బిందువు వద్ద ఉంచిన ప్రమాణ ధనావేశంపై పనిచేయు బలంను, ఆ బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రతగా నిర్వచిస్తారు.

సమాసము:

1. విద్యుత్ క్షేత్ర తీవ్రత ఒక సదిశ. దీని దిశ ప్రమాణ ధనావేశం కదిలే దిశలో ఉండును.
2. బిందు ఆవేశం q ను భావిద్దాం. ఆవేశం చుట్టు విద్యుత్ క్షేత్రం ఏర్పడును. ఆవేశం నుండి విద్యుత్ క్షేత్రంలో r దూరంలో బిందువు P ను భావిద్దాం. P వద్ద శోధన ఆవేశం q₀ ఉంచుదాము.
3. q వల్ల q₀ పై బలం F = \(\frac{1}{4 \pi\varepsilon_0}.\frac{qq_0}{r^2}\)
4. బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత, q₀ శోధన ఆవేశంపై పనిచేయు బలంనకు సమానం.
   విద్యుత్ క్షేత్ర తీవ్రత,
   

ప్రశ్న 3.
ఏకరీతి విద్యుత్ క్షేత్రంలోని విద్యుత్ డైపోల్పై పనిచేసే యుగ్మానికి లేదా టార్క్కు సమాసాన్ని ఉత్పాదించండి.
జవాబు:

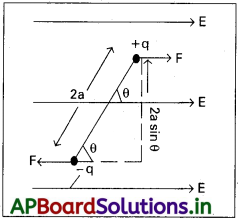
1. సమాన, వ్యతిరేక ఆవేశాల జంట స్వల్ప దూరంలో వేరుచేయబడితే, దానిని ద్విధ్రువం అంటారు.
2. −q మరియు+q కూలుమ్ ఆవేశాలను భావిద్దాం. వాటి మధ్యదూరం 2a.
3. ద్విధ్రువ భ్రామకం, P = q × 2a = 2a. ఇది ఒక సదిశ. దీని దిశ ద్విధ్రువ అక్షంపై – q నుండి + q వైపుకు.
4. పటంలో చూపినట్లు, ద్విధ్రువ అక్షం, క్షేత్రదిశలో 9 కోణము చేయునట్లు ఉంచామనుకుందాము.
5. విద్యుత్ క్షేత్రం వల్ల +q పై బలం F = +qE మరియు – q పై బలం
   F = -qE.
6. ఈ రెండు సమాన వ్యతిరేక బలాలు టార్క్ లేక యుగ్మ భ్రామకంను ఏర్పరుచును.
   i.e., టార్క్, τ = లంబదూరం × ఒక బలపరిమాణం
   ∴ τ (2a sin θ)qE = 2aqE sin θ = PE sin θ
   సదిశ రూపంలో, = \(\vec{\tau}=\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{E}}\)

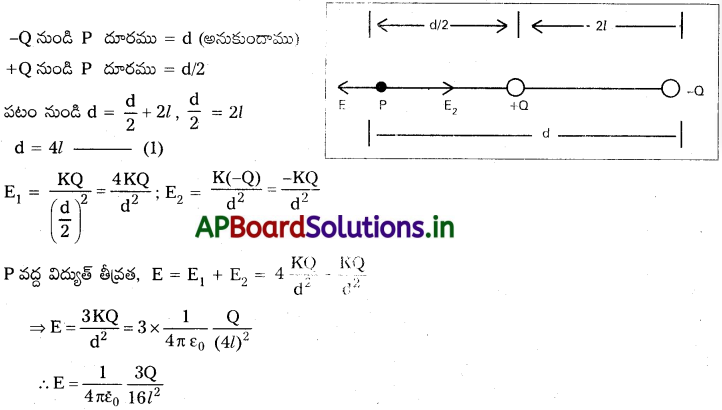
ప్రశ్న 4.
విద్యుత్ డైపోల్ అక్షంపై ఏదైనా బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రతకు సమాసాన్ని ఉత్పాదించండి. [TS. Mar.’16; AP. Mar.’17]
జవాబు:

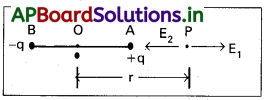
ద్విధ్రువం అక్షంపై ఏదైనా బిందువు వద్ద క్షేత్ర తీవ్రత :
1) ఒక విద్యుత్ ధృవంలో -q మరియు + q ఆవేశాలు గల ’24’ దూరంలో వేరుచేయబడినట్లు భావిద్దాం. ‘O’ కేంద్రం.

2) ద్విధ్రువం అక్షంపై OP = r దూరంలో P బిందువు వద్ద, విద్యుత్ క్షేత్ర తీవ్రత గణిద్దాం.

3) P వద్ద +q మరియు -q ఆవేశాల వల్ల విద్యుత్ క్షేత్ర తీవ్రతలు E₁ మరియు E₂.

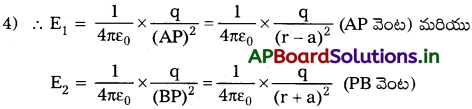
ప్రశ్న 5.
విద్యుత్ డైపోల్ మధ్య లంబ తలంపై ఏదైనా బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రతకు సమాసాన్ని ఉత్పాదించండి. [AP. Mar.’15]
జవాబు:
విద్యుత్ డైపోల్ లంబ తలంపై ఒక బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత :
1) ఒక విద్యుత్ ద్విధ్రువంలో -q మరియు +q ఆవేశంలు ‘2a’ దూరంలో వేరు చేయబడినట్లు భావిద్దాం. ‘O’ కేంద్రం.
2) ద్విధ్రువం లంబ సమద్విఖండన రేఖపై OP = r దూరంలో P బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత గణిద్దాం.
3) +q మరియు -q ఆవేశాల వల్ల P వద్ద విద్యుత్ క్షేత్ర తీవ్రతలు E₁ మరియు E₂.
4) లంబ అంశాలు (E₁ sin θ మరియు E₂ sin θ) లు సమానం మరియు వ్యతిరేకం. కావున అవి రద్దుపరుచుకుంటాయి. సమాంతర అంశాలు (E₁ cos θ మరియు E₂ cos θ) లు ఒకే దిశలో ఉండును. కావున వాటిని కలుపవచ్చును.

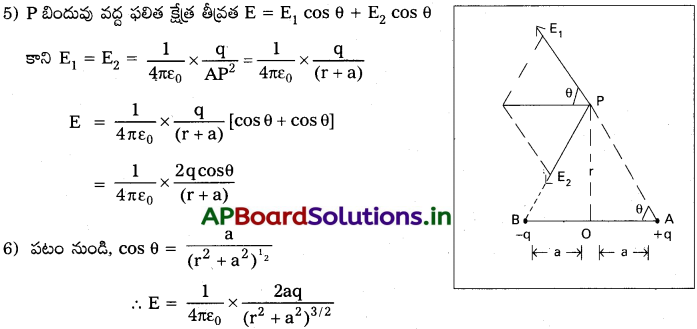
7) r >> a, అయితే అప్పుడు, a² ను r²తో పోల్చినపుడు విస్మరించవచ్చును. అప్పుడు

ప్రశ్న 6.
స్థిర విద్యుత్ శాస్త్రంలోని గాస్ నియమాన్ని తెలిపి, దాని ప్రాముఖ్యతను వివరించండి. [TS. Mar.’15]
జవాబు:
గాస్ నియమము :
“ఏదైనా సంవృత తలం ద్వారా పోవు మొత్తం విద్యుత్ అభివాహం, తలం ఆవరించి ఉన్న నికర ఆవేశంనకు \(\frac{1}{\varepsilon_0}\) రెట్లు ఉండును.

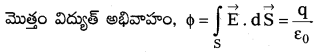
ఇక్కడ S తలముచే ఆవరించబడిన మొత్తం ఆవేశం q, \(\oint_S\) సంవృత తలము యొక్క తల సమాకలనంను సూచించును.

ప్రాముఖ్యత :

1. సంవృత తలము నిర్మించుటకు వీలున్న లెక్కలలో విద్యుత్ క్షేత్రం తీవ్రతను గణించుటకు గాస్ నియమం ఉపయోగపడుతుంది.
2. పదార్థం లేకపోయినా, దాని ఆకారం మరియు పరిమాణం ఎలా ఉన్నా, ఏదైనా సంవృత తలంనకు గాస్ నియమమును వర్తింపచేయవచ్చును,
3. సౌష్టవతను భావించి, గాస్ నియమ అనువర్తనంతో ఎక్కువ లెక్కలను చాలా తేలికగా చేయవచ్చును.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
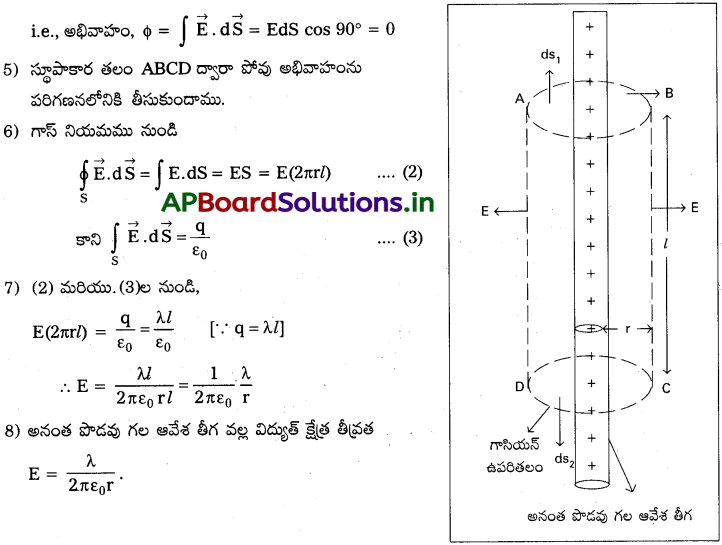
విద్యుత్ అభివాహాన్ని నిర్వచించండి. గాస్ నియమాన్ని అనువర్తించి అనంతమైన, తిన్నని పొడవాటి ఆవేశిత తీగ వల్ల కలిగే విద్యుత్ తీవ్రతకు సమాసాన్ని ఉత్పాదించండి. (విద్యుత్ క్షేత్రం ప్రతి బిందువు వద్ద రేడియల్ క్షేత్రమని, తీగనుంచి బిందువు ఉండే త్రైజ్యా దూరం పైనే ఆధారపడుతుందని అనుకోండి).
జవాబు:
విద్యుత్ అభివాహం :
వైశాల్యంనకు లంబంగా పోవు విద్యుత్ బలరేఖల సంఖ్యను విద్యుత్ అభివాహం (Φ) అంటారు.
విద్యుత్ అభివాహం Φ = \(\overrightarrow{E}.\overrightarrow{A}\) అభివాహం ఒక సదిశ.

అనంతమైన, తిన్నని పొడవాటి ఆవేశిత తీగవల్ల విద్యుత్ తీవ్రతకు సమాసము :
1) ఒక అనంతమైన తిన్నని పొడవాటి ఆవేశ తీగ, ఏకరీతి రేఖీయ ఆవేశ సాంద్రత ”గా భావిద్దాం.

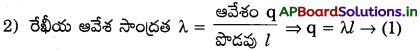
3) l పొడవు, r వ్యాసార్థము గల సహాక్ష స్థూపాకార గాసియన్ తలంను నిర్మిద్దాం. సౌష్టవము వల్ల విద్యుత్ క్షేత్రం, ఆవేశ తీగకు లంబంగా ఊహించవచ్చును.

4) AB మరియు CD సమతల తలాలు, తీగకు లంబంగా ఉండును. AB మరియు CD తలంపై ds,, మరియు ds చిన్న వైశాల్యాలు తీసుకుందాము. అవి \(\overrightarrow{E}\) కు లంబము. వాని నుండి వచ్చు అభివాహం శూన్యం.

ప్రశ్న 2.
స్థిర విద్యుత్ శాస్త్రంలోని గాస్ నియమాన్ని తెలపండి. గాస్ నియమాన్ని అనువర్తించి అనంత సమతల ఆవేశిత పలక వల్ల ఏర్పడే విద్యుత్ తీవ్రతకు సమాసాన్ని ఉత్పాదించండి.
జవాబు:
గాస్ నియమము :
“ఏదైనా సంవృత తలం ద్వారా పోవు మొత్తం విద్యుత్ అభివాహం, తలం ఆవరించి ఉన్న నికర ఆవేశంనకు \(\frac{1}{\varepsilon_0}\) రెట్లు ఉండును”.

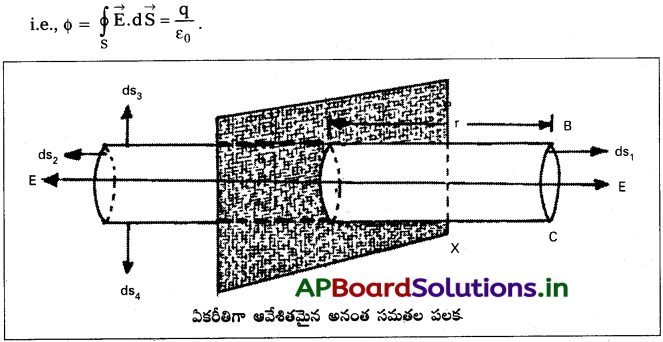
అనంత సమతల ఆవేశ పలక వల్ల Eకు సమాసము :
1) అనంత సమతల ఆవేశ పలకను భావిద్దాం. ఆ తలంపై ఆవేశం ఏకరీతి వితరణ కలిగి ఉందని భావిద్దాం.
2) ఆ తలంపై ఏకరీతి ఆవేశ సాంద్రత σ = \(\frac{dq}{dS}\). ఇక్కడ dq చిన్న వైశాల్యం ds పై ఆవేశము.
3) 2. పొడవు ఉన్న ABCD క్షితిజ సమాంతర స్థూపాకార గాసియన్ ఉపరితలంను, అనంత సమతల ఆవేశిత తలంనకు లంబంగా నిర్మిద్దాం.
4) AD మరియు BC సమతలాలు పలక తలంనకు సమాంతరంగా మరియు తలం నుండి సమాన దూరంలో ఉండును.
5) ఈ ఉపరితలాల వైశాల్యాలు ds₁ మరియు ds₂. ఇవి \(\overrightarrow{E}\) కు సమాంతరము. ఈ రెండు ఉపరితలాల ద్వారా పోవు అభివాహం శ్రీ \(\oint \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{S}}=\oint \mathrm{EdS}=\mathrm{E}(\mathrm{S}+\mathrm{S})=2 \mathrm{ES}\) ఇక్కడ AD లేక BC సమతల తల వైశాల్యం S. రెండు వైశాల్యాలు మరియు తీవ్రతలు సమానం.
6) AB మరియు CD స్థూపాకార ఉపరితలంను భావిద్దాం. వానిపై చిన్న వైశాల్యాలు ds₃ మరియు ds₄ తీసుకుందాం. ఈ ఉపరితలాలు విద్యుత్ క్షేత్ర తీవ్రత E కు లంబము.

ప్రశ్న 3.
గాస్ నియమాన్ని అనువర్తించి ఆవేశిత వాహక గోళాకార కర్పరం వల్ల ఏర్పడే విద్యుత్ క్షేత్రానికి సమాసాలను
(i) కర్పరం వెలుపలి బిందువు వద్ద, (ii) కర్పరం ఉపరితలంపై గల బిందువు వద్ద, (iii) కర్పరం లోపల బిందువు వద్ద ఉత్పాదించండి.
జవాబు:
ఆవేశ వాహక గోళాకార కర్పరం వల్ల E కు సమాసము:
1) ఏకరీతి ఆవేశ గోళాకార కర్పరంను భావిద్దాం. దానిపై ఆవేశం ‘q’ మరియు వ్యాసార్ధం R.

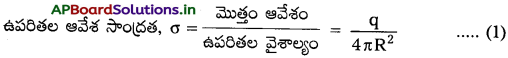
2) కర్పరంను ఏకరీతిగా ఆవేశపరిచినప్పుడు, ఏ బిందువు వద్దనైనా విద్యుత్ క్షేత్ర తీవ్రత ‘O’ నుండి రేడియల్ దూరం ‘I’ పై ఆధారపడును. E దిశ కేంద్రం నుండి వ్యాసార్థం వెంట దూరంగా ఉండును.

i) కర్పరం వెలుపల బిందువు వద్ద E :
1) గోళాకార కర్పరం వెలుపలఁదూరంలో ఉన్న బిందువుని భావిద్దాం. వ్యాసార్థంగల గాసియన్ ఉపరితలంను (r > R) నిర్మిద్దాం.

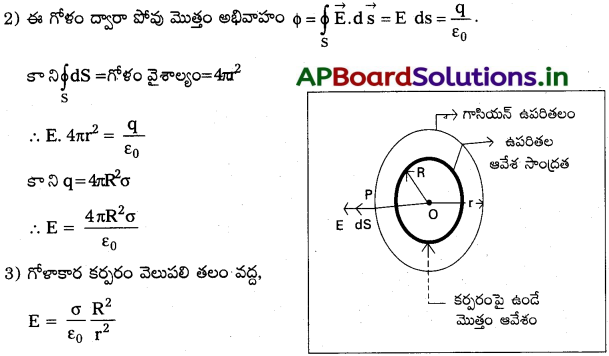
ii) కర్పరం ఉపరితలంపై బిందువు వద్ద E:

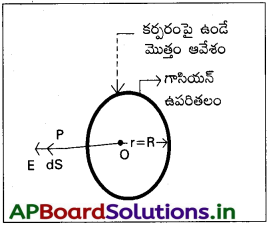
1) r = R వ్యాసార్థం ఉన్న గాసియన్ ఉపరితలంను నిర్మిద్దాం.
2) ఈ తలం ద్వారా పోవు మొత్తం అభివాహం.

3) ∴ గోళాకార కర్పరంపై ఏదైనా బిందువు వద్ద తీవ్రత
E = \(\frac{\sigma}{\varepsilon_0}\)

iii) కర్పరం లోపలి బిందువు వద్ద E :
1) కర్పరం లోపల ఒక బిందువును భావిద్దాం. r వ్యాసార్థం ఉన్న గాసియన్ ఉపరితలం (r < R) ను నిర్మిద్దాం. కర్పరము లోపల ఆవేశం శూన్యం.

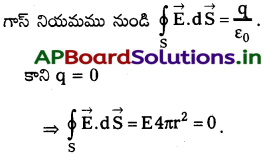
2) ఆవేశ గోళాకార కర్పరం లోపలి ఏదైనా బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత శూన్యం.

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
ఒక్కొక్కటి 0.20g ద్రవ్యరాశి గల రెండు చిన్నవైన, సర్వసమానమైన బంతులు సమాన ఆవేశాన్ని కలిగి ఉన్నాయి. వీటిని సమాన పొడవుగల రెండు దారాలతో వేలడదీశారు. దారాల మధ్య కోణం 60° ఉండే విధంగా ఆ బంతులు తమకుతామే సమతాస్థితిలోకి వచ్చాయి. బంతుల మధ్య దూరం 05 m అయితే బంతులపై ఉండే ఆవేశం ఎంత?
సాధన:
ఇచ్చినవి m = 0.20 g = 0.2 × 10^-3 kg; θ = 60°

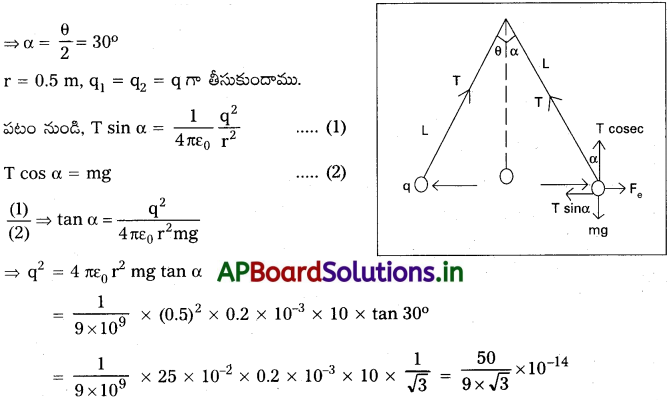
∴ ప్రతి బంతిపై ఆవేశం, q = 1.79 × 10^-7 C.

ప్రశ్న 2.
ఒక్కొక్కటి q ఆవేశం గల అనంతమైన ఆవేశాలను X-అక్షంపై మూల బిందువు నుంచి 1, 2, 4, 8, ……………. మీటర్ దూరాల వద్ద ఉంచారు. మూల బిందువు వద్ద విద్యుత్ క్షేత్రం ఎంత?
సాధన:
q₁ = q₂ = q₃ = q₄ = …………. = q గా తీసుకుందాము
r₁ = 1; r₂ = 2; r₃ = 4; r₄ = 8,
మూల బిందువు ‘O’ వద్ద ఫలిత విద్యుత్ క్షేత్రం

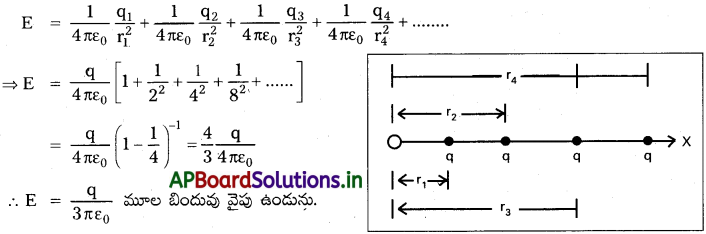
ప్రశ్న 3.
గడియారంలోని డయల్పై ఉండే అంకెల వద్ద -9, -24, -3q, ………… -12q ఆవేశాలను బిగించారు. బిందు ఆవేశాలు ఉత్పత్తి చేసే విద్యుత్ క్షేత్రాన్ని గడియారంలోని ముల్లులు ఆటంకపరచవు. ఏ సమయం వద్ద గంటల ముల్లు డయల్ కేంద్రం వద్ద ఉండే విద్యుత్ క్షేత్ర దిశలో ఉంటుంది?
సాధన:
‘O’ వద్ద ఉన్న ప్రమాణ ఆవేశం నుండి ప్రతి ఆవేశం దూరం = r.
ఫలిత క్షేత్ర తీవ్రత, E = \(\frac{1}{4 \pi \varepsilon_0} \frac{6 q}{r^2}\) [∵ -6q – (-12q)]
OX నిర్దేశ అక్షము. OX-అక్షంతో ఫలిత క్షేత్రాల కోణాలు పటంలో చూపబడినవి.


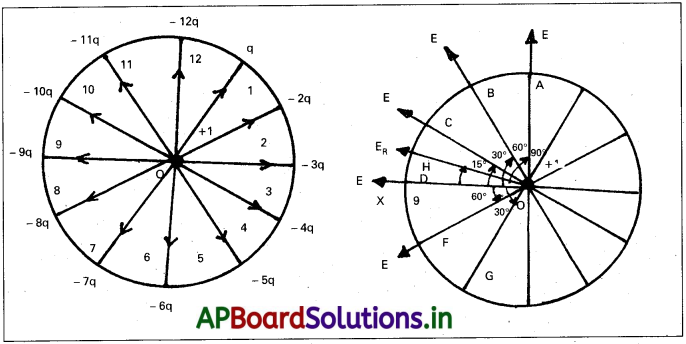
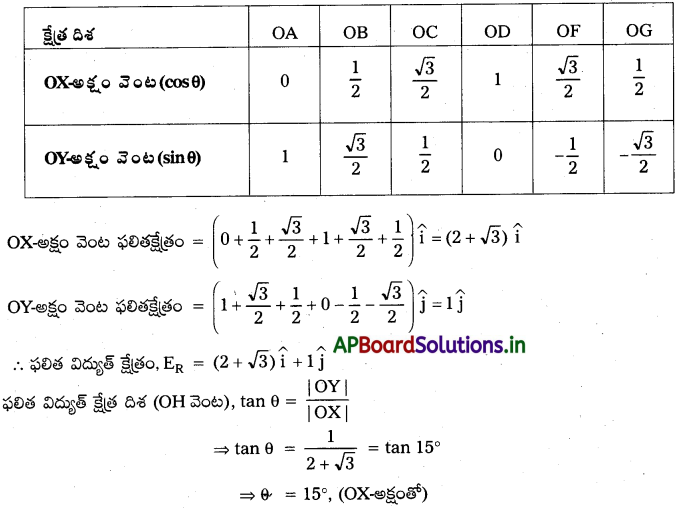
∴ గంటల ముల్లు డయల్ కేంద్రం వద్ద 9.30 చూపును.

ప్రశ్న 4.
E = 3 × 10³ N/C పరిమాణం గల ఏకరీతి విద్యుత్ క్షేత్రాన్ని పరిగణించండి. (a) yz తలాన్ని సమాంతరంగా తలాన్ని కలిగి ఉండే భుజానికి 10 cm పొడవు గల చతురస్రం ద్వారా క్షేత్ర అభివాహం ఎంత? (b) చతురస్రం తలానికి గీచిన లంబం X అక్షంతో 60° కోణం చేసే విధంగా ఉంటే చతురస్రం ద్వారా అభివాహం ఎంత?
సాధన:

a) ఇచ్చినవి E = 3 × 10³ N/C
S = 10²cm²
= 10² x (10^-2m)² = 10²m²
θ = 0°
Φ = ES cos θ
= 3 × 10³ × 10^-2 × cos 0°
∴ Φ = 30 Nm²C^-1
60° Φ = ES cos θ
× 10³ × 10^-2 × cos 60°
∴ Φ = 15 Nm²C^-1

ప్రశ్న 5.
Qపరిమాణం గల 4 ఆవేశాలు కలవు. వీటిలో రెండు ధనాత్మకం, రెండు రుణాత్మకం. వీటిని ‘ L’ భుజంగాగల చతురస్రం శీర్షాల వద్ద ప్రతి మూల వద్ద ఒకటి ఉండేట్లు ప్రతి ఆవేశంపై పనిచేసే బల దిశ కేంద్రం వైపు ఉండే విధంగా అమర్చారు. ప్రతి ఆవేశం అనుభవించే నికర విద్యుత్ బల పరిమాణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 6.
ఒక ప్రదేశంలోని విద్యుత్ క్షేత్రాన్ని \(\overrightarrow{E}\) = \(a\hat{i}+b\hat{j}\) సూచిస్తుంది. ఇక్కడ a, b లు స్థిరాంకాలు, y zతలానికి సమాంతరంగా ఉండే L భుజంగా గల చతురస్ర వైశాల్యం ద్వారా పోయే నికర అభివాహాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 7.
r వ్యాసార్థం గల బోలు గోళాకార కర్పరం ఆ ఏకరీతి ఆవేశ సాంద్రతను కలిగి ఉంది. కర్పరం కేంద్రం, ఘనం కేంద్రంతో ఏకీభవించే విధంగా దీన్ని 3 అంచుగల సమఘనంలో ఉంచారు. ఘనం తలం నుంచి బహిర్గతం అయ్యే విద్యుత్ అభివాహాన్ని లెక్కించండి.
సాధన:
గోళాకార కర్పరం, ఆవేశం = q అనుకుందాము.

ప్రశ్న 8.
ఒక విద్యుత్ డైపోల్ 2l దూరంలో ఉండే +Q, -Q అనే రెండు సమాన, వ్యతిరేక ఆవేశాలను కలిగి ఉంది. ఆవేశాలకు సరేఖీయంగా(collinear) P అనే బిందువు ఉంది. ధనావేశం నుంచి P దూరం, రుణావేశం నుంచి P ఉండే దూరంలో సగం అయితే P వద్ద విద్యుత్ తీవ్రత
సాధన:

ప్రశ్న 9.
λ, 2λ ఏకరీతి రేఖీయ ఆవేశ సాంద్రతలు గల రెండు అనంతమైన పొడవుతో ఉండే తిన్నని తీగలను r దూరంలో సమాంతరంగా అమర్చారు. రెండింటికి మధ్య దూరంలో ఉండే బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత,
సాధన:

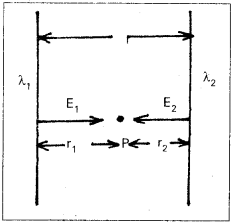
రెండు సమాంతర, అనంతమైన పొడవు గల తిన్నని తీగల మధ్యదూరం = r
అనంత పొడవు గల తిన్నని తీగవల్ల విద్యుత్ క్షేత్రం E = \(\frac{\lambda}{2 \pi\varepsilon_0r}\)


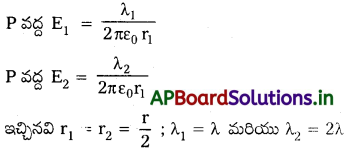
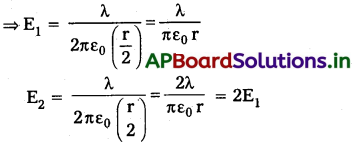
∴ మధ్య బిందువు వద్ద విద్యుత్ తీవ్రత, E = E₂ – E₁ = 2E₁ – E₁ = E
∴ E = \(\frac{\lambda}{\pi\varepsilon_0r}\)

ప్రశ్న 10.
λ, 3λ. ఏకరీతి రేఖీయ ఆవేశ సాంద్రతలు గల రెండు అనంతమైన పొడవుతో ఉండే తిన్నని తీగలను దూరంలో సమాంతరంగా అమర్చారు. రెండింటికి మధ్య దూరంలో ఉండే బిందువు వద్ద విద్యుత్ క్షేత్ర తీవ్రత.
సాధన:
ఇచ్చినవి λ₁ =λ, λ₂ = 3λ.

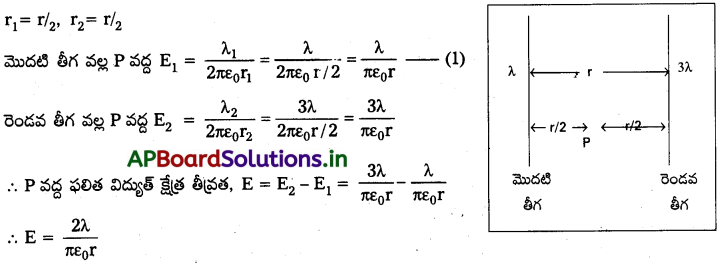
ప్రశ్న 11.
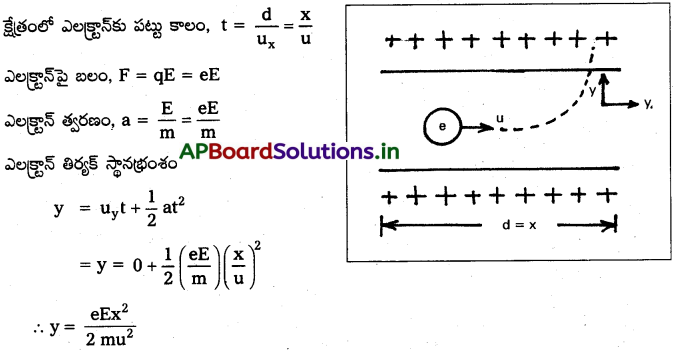
m ద్రవ్యరాశి, ఆ ఆవేశం గల ఎలక్ట్రాన్ను తొలివేగంతో E క్షేత్ర తీవ్రత గల ఏకరీతి విద్యుత్ క్షేత్రానికి లంబంగా తుపాకీతో పేల్చారు. పేల్చిన దిశలోనే ఎలక్ట్రాన్ క్షేత్రంలో X దూరం ప్రయాణిస్తే, అది పొందే తిర్యక్ స్థానభ్రంశం y విలువ ఎంత?
సాధన:
ఇచ్చినవి m_e = m; q = e; d = x; u_x = u; u_y = 0
పలకల మధ్య విద్యుత్ క్షేత్రం = E

అదనపు అభ్యాసాలు Additional Exercises

ప్రశ్న 1.
2 × 10^-7 C, 3 × 10^-7 C ఆవేశాలు గల రెండు చిన్న గోళాలను గాలిలో 30 cm ఎడంతో ఉంచారు. వాటి మధ్య పనిచేసే బలం ఎంత?
సాధన:
q₁ = 2 × 10^-7 C; q₂ = 3 × 10^-7 C; r = 30 cm = 30 × 10^-2m; F = ?

∴ F = 6 × 10^-3 N.

ప్రశ్న 2.
0.4µC ఆవేశం గల చిన్న గోళంపై -0.8 C ఆవేశం గల మరొక గోళం గాలిలో కలగచేసే స్థిర విద్యుత్ బలం 0.2N.. అయితే (a) రెండు గోళాల మధ్య దూరం ఎంత? (b) రెండో గోళంపై మొదటి గోళం వల్ల కలిగే బలం ఎంత?
సాధన:
a) q₁ = 0.4 µc = 0.4 × 10^-6 C
r₂ = – 0.8 µc = 0.8 × 10^-6 C
F = 0.2 N; r = ?

మొదటి గోళం వల్ల రెండవ గోళంపై బలం అంతే ఉండును.
i.e., 0.2 N.

ప్రశ్న 3.
ke²/G m_em_p అనే నిష్పత్తికి మితులు లేవని సరిచూడండి. భౌతిక స్థిరాంకాల పట్టికను పరిశీలించి, ఈ నిష్పత్తి విలువను నిర్ణయించండి. నిష్పత్తి డేన్ని తెలియచేస్తుంది?
సాధన:

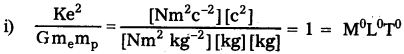
ఇచ్చిన నిష్పత్తి మితిరహితం.
K = 9 × 10⁹ Nm²c^-2, e = 1.6 × 10^-19 C;
G = 6.67 × 10^-11 N/m²/kg²
m_e = 9.1 × 10^-31 kg మరియు m_p = 1.66× 10^-27 kg
\(\frac{Ke^2}{Gm_em_p}\) = 2.29 × 10³⁹
ఇదియే ఎలక్ట్రాన్ మరియు ప్రోటాన్ ల మధ్య స్థిర విద్యుత్ బలం మరియు గురుత్వాకర్షణ బలంల మధ్య నిష్పత్తి.

ప్రశ్న 4.
a) ఒక వస్తువు విద్యుదావేశం క్వాంటీకరణం చెందింది అనే ప్రవచనం అర్థాన్ని వివరించండి.
b) స్థూల లేదా బృహధ్శాన ఆవేశాలతో వ్యవహరించేటప్పుడు క్వాంటీకరణాన్ని ఎందుకు ఉపేక్షిస్తారు ?
సాధన:
a) విద్యుత్ ఆవేశ వస్తువు క్వాంటీకృతమైనది అంటే ఆ వస్తువు ఆవేశం నిర్దిష్ట విలువలు కలిగి ఉండును. వస్తువుపై ఆవేశం ఎల్లప్పుడు ప్రాథమిక ఆవేశం అయిన ఎలక్ట్రాన్ ఆవేశంనకు పూర్ణాంక గుణిజాలుగా ఉండును. వస్తువుపై ఆవేశంనుq = ± ne గా వ్యక్తపరుస్తారు. ఇక్కడ n = సరఫరా అయిన ఎలక్ట్రాన్ల సంఖ్యకు సమానం మరియు e = ఎలక్ట్రాన్పై ఆవేశం. క్వాంటీకరణంనకు కారణం ఒక వస్తువు నుండి మరొక వస్తువుకు ఎలక్ట్రాన్లు పూర్ణాంక గుణిజాలుగా సరఫరా జరుగుటయే.

b) ఎలక్ట్రాన్ ఆవేశము 1.6 × 10^-19 C. ఈ విలువ స్వల్పము, కావున స్థూల లేదా బృహద్మాన ఆవేశాలతో వ్యవహరించేటప్పుడు క్వాంటీకరణంను ఉపేక్షిస్తారు.

ప్రశ్న 5.
గాజు కడ్డీని సిల్క్ గుడ్డతో రుద్దినప్పుడు రెండింటిపై ఆవేశాలు కనిపిస్తాయి. ఇదే దృగ్విషయాన్ని ఇంకా ఎన్నో జతల వస్తువుల విషయంలోనూ గమనించడమైంది. ఈ పరిశీలన ఆవేశ నిత్యత్వ నియమంతో ఏ విధంగా సుసంగతం అవుతుంది? వివరించండి.
సాధన:
ఆవేశ నిత్యత్వ నియమము ప్రకారము, ఆవేశం సృష్టించబడదు. మరియు నాశనం కాదు. కాని ఒక వస్తువు నుండి మరియొక వస్తువుకు బదిలీ జరుగును. రెండు వస్తువులు రుద్దక ముందు రెండు తటస్థముగా ఉండును. వ్యవస్థ మొత్తం ఆవేశం స్థిరం. గాజు కడ్డీని, సిల్క్ గుడ్డతో రుద్దితే, గాజుకడ్డీ నుండి సిల్క్ గుడ్లలోనికి ఎలక్ట్రాన్ లు బదిలీ జరుగును. కావున గాజుకడ్డీ ధనావేశంను, సిల్క్ గుడ్డ రుణావేశంను పొందును.

గాజు కడ్డీని సిల్క్ గుడ్డతో రుద్దిన తరువాత వ్యవస్థ మొత్తం ఆవేశం శూన్యం. ఇది ఆవేశ నిత్యత్వ నియమమును కలిగి ఉంటుంది. ఇక్కడ ఆవేశాలు సమానంగా మరియు విజాతి జంటలుగా సృష్టించబడును.

ప్రశ్న 6.
10cm భుజంగాగల ABCD చతురస్రం శీర్షాల వద్ద q_A = 2 µC, q_B = -5 µC, q_C = 2 µC, q_D = -5 µC అనే నాలుగు బిందు ఆవేశాలున్నాయి. చతురస్రం కేంద్రం వద్ద ఉంచిన 1 µC ఆవేశంపై పనిచేసే బలం ఎంత?
సాధన:


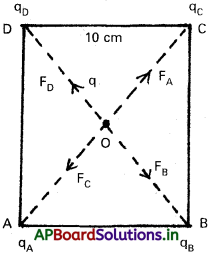
O వద్ద ఉన్న lµC ఆవేశంపై A మరియు C ల
వద్ద ఉన్న 2µC ఆవేశాల వల్ల ఆకర్షణ బలాలు సమానం మరియు వ్యతిరేకం. అందువల్ల అవి రద్దు అవుతాయి. ఇదే విధంగా, వద్ద ఉన్న 1µC ఆవేశంపై, B మరియు Dల వద్ద ఉన్న – 5µC ఆవేశాల వల్ల ఆకర్షణ బలాలు సమానం మరియు వ్యతిరేకం. అందువల్ల అవి రద్దు అవుతాయి. కావున O వద్ద 1µC ఆవేశంపై ఫలితబలం శూన్యం.

ప్రశ్న 7.
a) స్థిర విద్యుత్ క్షేత్రరేఖ ఒక అవిచ్ఛిన్న వక్రం. అంటే, క్షేత్ర రేఖ ఎలాంటి అంతరాలను కలిగి ఉండదు. ఎందుకు?
b) రెండు క్షేత్ర రేఖలు పరస్పరం ఏ బిందువు వద్ద అయిన ఎందుకు ఖండించుకోవో వివరించండి.
సాధన:
a) విద్యుత్ క్షేత్ర రేఖ, విద్యుత్ క్షేత్రంలో ప్రమాణ ధనావేశం ప్రయాణించి వాస్తవ పథము అవిచ్ఛిన్న వక్రంను సూచిస్తుంది. రేఖ అకస్మాత్తుగా తెగితే, ప్రమాణ ఆవేశం ఒక ప్రదేశం నుండి మరొక ప్రదేశంనకు దూకుటను తెలుపును. ఇది అసాధ్యం. దాని అర్ధం తెగిన ప్రదేశం వద్ద విద్యుత్ క్షేత్రం శూన్యం. ఇది అసాధ్యం. కావున క్షేత్ర రేఖ అంతరాలను కలిగి ఉండదు.

b) రెండు క్షేత్ర రేఖలు ఒక దానితో మరొకటి ఖండించుకొంటే ఖండన బిందువు వద్ద గీసిన రెండు స్పర్శ రేఖలు, రెండు విద్యుత్ క్షేత్ర దిశలను తెలుపవలెను. ఒక బిందువు ఒకేసారి రెండు దిశలను సూచించదు. కావున రెండు క్షేత్ర రేఖలు ఏ బిందువు వద్ద కూడా ఖండించుకోవు.

ప్రశ్న 8.
శూన్యంలో q_A = 3 µC, qg = -3 µC అనే రెండు బిందు ఆవేశాలు 20 cm దూరంలో ఉన్నాయి.
a) రెండు ఆవేశాలను కలిపే AB రేఖ మధ్య బిందువు వద్ద విద్యుత్ క్షేత్రం ఎంత?
b) ఈ బిందువు వద్ద 1.5 × 10^-19 C పరిమాణం గల శోధన రుణావేశాన్ని ఉంచితే, శోధన ఆవేశం అనుభూతికి లోనయ్యే బలం ఎంత?
సాధన:

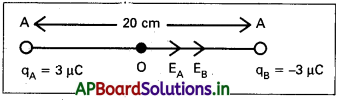
a) q_A = 3 µC = 3 × 10^-6
q_B = -3 µC = -3 × 10^-6 C, AB = 20 cm
r = OA = OB = 10 cm = 10^-1 m, E = ?

b) ‘O’ వద్ద ఉన్న q = -1.5 × 10^-9 C
ఆవేశంపై బలం, F = qE = -1.5 × 10^-9 × (5.4 × 10⁶) N
F = -8.1 × 10^-3 N, OA వెంట

ప్రశ్న 9.
ఒక వ్యవస్థలో A : (0, 0, -15 cm), B(0, 0, + 15 cm) బిందువుల వద్ద q_A = 2.5 × 10^-7 C, q_B = -2.5 × 10^-7 C అనే బిందు ఆవేశాలున్నాయి. ఈ వ్యవస్థ మొత్తం ఆవేశం, విద్యుత్ ద్విధ్రువ (డైపోల్) భ్రామకం ఎంత?
సాధన:

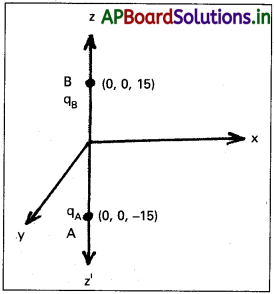
q_A మరియు q_B ఆవేశాలు Z – అక్షంపై (0, 0, -15) మరియు B (0, 0, 15) బిందువుల వద్ద పటంలో చూపినట్లు ఉన్నాయి. అవి విద్యుత్ (డైపోల్) ద్విధ్రువంను ఏర్పరచును. మొత్తం ఆవేశం
q = q = q_A + q_B = 2.5 × 10^-7 – 2.5 × 10^-7 = 0
AB = 15 + 15 = 30cm = 30 × 10^-2m.

విద్యుత్ ద్విధ్రువం (డైపోల్) భ్రామకం, P = ఒక ఆవేశం × AB
= 2.5 × 10^-7 × (30 × 10^-2)
= 7.5 × 10^-8 c – m
\(\overrightarrow{P}\) దిశ BA వెంట i. e., రుణాత్మక Z-అక్షం వెంట పనిచేయును.

ప్రశ్న 10.
4 × 10^-9 Cm డైపోల్ భ్రామకం గల విద్యుత్ డైపోల్ 5 × 10⁴ NC^-1 పరిమాణం గల ఏకరీతి విద్యుత్ క్షేత్రం దిశతో 30° కోణం చేసే విధంగా అమరి ఉంది. డైపోల్పై పనిచేసే టార్క్ పరిమాణాన్ని లెక్కించండి.
సాధన:

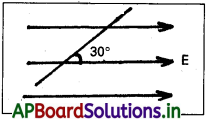
P = 4 × 10^-9 Cm; 6 = 30°, E = 5 × 10⁴ N C^-1, τ = ?
τ = PE sin θ = (4 × 10^-9) × (5 × 10⁴) sin 30°
= 4 × 5 × 10^-5 × \(\frac{1}{2}\) = 10^-4 N-m

ప్రశ్న 11.
ఉన్నితో రుద్దిన పాలిథీన్ ముక్కపై రుణావేశం 3 × 10^-7 C ఏర్పడినట్లు గుర్తించారు.
a) బదిలీ అయ్యే ఎలక్ట్రాన్ల సంఖ్యను అంచనా వేయండి (ఇవి దేని నుంచి దేనికి)
b) ఉన్ని నుంచి పాలిథీన్కు ద్రవ్యరాశి బదిలీ అవుతుందా?
సాధన:

a) q = -3 × 10^-7 C, ఎలక్ట్రాన్పై ఆవేశం,
e = -1.6 × 10^-19 C
∴ ఉన్ని నుండి పాలిథీన్ ముక్కలోకి బదిలీ అయిన ఎలక్ట్రాన్ల సంఖ్య,

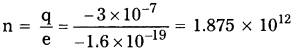
b) ద్రవ్యరాశి బదిలీ ఉండును.
ప్రతి ఎలక్ట్రాన్ ద్రవ్యరాశి = 9 × 10^-19 kg
పాలిథీన్ లోనికి బదిలీ అయిన ద్రవ్యరాశి = 2 × 10¹² × 9 × 10^-31 kg
= 1.8 × 10^-18 kg

ప్రశ్న 12.
a) రెండు విద్యుత్ బంధిత, ఆవేశిత రాగి గోళాలు A, B ల కేంద్రాల మధ్య దూరం 50 cm. ఒక్కొక్క దానిపై 6.5 × 10^-7 C ఆవేశం ఉంటే, వాటి మధ్య పనిచేసే స్థిర విద్యుత్ వికర్షణ బలం ఎంత? A, B ల మధ్య దూరంతో పోల్చితే వాటి వ్యాసార్థాలు ఉపేక్షణీయం.
b) వాటిపై ఆవేశాన్ని రెట్టింపు చేసి, మధ్య దూరాన్ని సగానికి తగ్గిస్తే వాటి మధ్య వికర్షణ బలం ఎంత?
సాధన:

ప్రశ్న 13.
అభ్యాసం 2లోని A, B గోళాల పరిమాణాలు సర్వసమానమని ఊహించండి. అంతే పరిమాణం గల, ఆవేశితం కాని మూడో గోళాన్ని మొదటి గోళంతో స్పర్శింపచేసి తిరిగి రెండో గోళాన్ని తాకించి, చివరకు రెండింటి నుంచి తొలగిస్తే A, B ల మధ్య పనిచేసే కొత్త వికర్షణ బలం విలువ ఎంత ?
సాధన:
A పై ఆవేశం = 6.5 × 10^-7 C
B పై ఆవేశం = 6.5 × 10^-7 C

వాని పరిమాణంలు సమానం. అంతే పరిమాణం ఉన్న ఆవేశంలేని మూడవగోళం C ను A కు దగ్గరగా తెచ్చి స్పృశించితే, వాని ఆవేశాలను
సమానంగా పంచుకొనును.
∴ A పై ఉన్న ఆవేశం, q₁ = \(\frac{6.5\times10^{-7}}{2}\) = 3.25 × 10^-7C
3.25 × 10^-7 C ఆవేశం ఉన్న గోళం Cను 6.5 × 10^-7 C ఆవేశం ఉన్న గోళం B దగ్గరకు తెచ్చి స్పృశించితే, వాని పరిమాణాలు సమానం కావున B మరియు C గోళాలు సమానంగా పంచుకుంటాయి.

ప్రశ్న 14.
ఏకరీతి స్థిర విద్యుత్ క్షేత్రంలో ప్రయాణించిన మూడు ఆవేశ కణాల పథాలను పటం చూపుతోంది. మూడు కణాల ఆవేశ సంజ్ఞలను ఇవ్వండి. ఏ కణం అత్యధిక ఆవేశ, ద్రవ్యరాశి నిష్పత్తిని కలిగి ఉంటుంది?

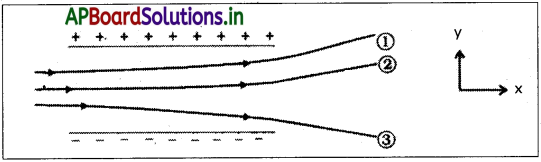
సాధన:
ఆవేశ కణాలు, వ్యతిరేక ఆవేశ పలకలవైపు అపవర్తనం చెందును. కావున కణాలు (1) మరియు (2) లు రుణావేశాలు మరియు కణం (3) ధనావేశం.

స్థానభ్రంశం y ∝ (\(\frac{e}{m}\)) . అన్ని కణాలు ఒకే వేగంతో విద్యుత్ క్షేత్రంలోనికి ప్రవేశిస్తే, కణం 3 గరిష్ట y విలువ అనగా ఎక్కువ ఆవేశం మరియు ద్రవ్యరాశి నిష్పత్తి కలిగి ఉండును.

ప్రశ్న 15.
ఏకరీతి విద్యుత్ క్షేత్రం E = 3 × 10³ \(\hat{i}\)N/C ని పరిగణించండి.
(a) yz తలానికి సమాంతరంగా ఉండే 10 cm భుజంగా గల చతురస్రం ద్వారా క్షేత్ర అభివాహం ఎంత?
(b) చతురస్రం తలానికి గీచిన లంబం X అక్షంతో 60° కోణం చేస్తే దాని ద్వారా అభివాహం ఎంత?
సాధన:

\(\overrightarrow{E}\) = 3 × 10³ \(\hat{i}\) N/C i. e., ధన X-అక్షం వెంట క్షేత్రం ఉండును.
ఉపరితల వైశాల్యం, S = (10cm)² = 10² cm²
= 10² × 10^-4 m² = 10^-2m²

a) తలం, YZ తలానికి సమాంతరంగా ఉంటే θ = 0°
Φ_E = ES cos θ° = 3 × 10³ × 10^-2 × cos 0°
= 30 Nc^-1 m²

b) X అక్షంతో తలానికి గీసిన లంబము చేయు కోణం 60,
అప్పుడు θ = 60°
Φ_E = ES cos θ = 3 × 10³ × 10^-2 × cos 60° = 30 × \(\frac{1}{2}\) = 15 NC^-1 m².

ప్రశ్న 16.
అభ్యాసం 15లో సూచించిన ఏకరీతి విద్యుత్ క్షేత్రంలో తలాలు నిరూపకతలాలకు సమాంతరంగా ఉండే విధంగా అమర్చితే 20 cm భుజంగాగల ఘనం నుంచి వచ్చే నికర అభివాహం ఎంత?
సాధన:
ఘనంలోనికి మరియు వెలుపలకు వెళ్ళు బలరేఖల సంఖ్య సమానం. కావున ఘనంపై నికర అభివాహం శూన్యం.

ప్రశ్న 17.
ఒక పెట్టె ఉపరితలం వద్ద విద్యుతక్షేత్రంపై జాగ్రత్తగా చేసిన కొలత, ఆ తలం నుంచి బహిర్గతం అయ్యే నికర అభివాహం 8.0 × 10³ Nm²/C అని సూచించింది.
(a) పెట్టెలోని నికర ఆవేశం ఎంత?
(b) పెట్టె ఉపరితలం ద్వారా బహిర్గతం అయ్యే నికర అభివాహం శూన్యం అయితే పెట్టెలోపల ఎలాంటి ఆవేశాలు లేవని మీరు నిశ్చయిస్తారా? ఎందుకు లేదా ఎందుకు కాదు?
సాధన:
a) Φ_E = 8.0 × 10³ N C^-1 m², q = ? Φ_E = \(\frac{q}{\varepsilon_0}\)
q = ε_o Φ_E = (8.85 × 10^-12) (8.0 × 10³)
= 0.07 × 10^-6 C = 0.07C

b) Φ_E =0, q=0; ∑q = 0ie, పెట్టె లోపల ఆవేశాల బీజీయ. మొత్తం శూన్యం లేక పెట్టె లోపల ఆవేశం ఉండదు.

ప్రశ్న 18.
పటంలో చూపిన విధంగా 10 cm భుజంగా ఉండే చతురస్రం కేంద్రం నుంచి 5 cm ఎత్తులో +10 µC ఆవేశం గల బిందు ఆవేశం ఉంది. చతురస్రం ద్వారా విద్యుత్ అభివాహం పరిమాణం ఎంత? (Hint : చతురస్రాన్ని 10 cm అంచుగా ఉండే ఘనం ఒక తలంగా భావించండి.)

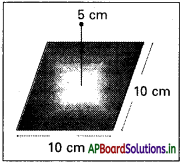
సాధన:

పటంలో చూపినట్లు, ABCD చతురస్ర భుజం పొడవు 10 cm.
ABCD చతురస్ర కేంద్రంపైన 5 cm వద్ద + 10 C బిందు ఆవేశం కలదు.
10 cm ప్రక్క భుజం ఉన్న ఘనం ఆరుభుజాలలో ABCD చతురస్రంను భావిద్దాం.
గాస్ సిద్ధాంతం ప్రకారము, ఘనం ఆరు తలాల ద్వారా
-మొత్తం విద్యుత్ అభివాహం = \(\frac{q}{\varepsilon_0}\)

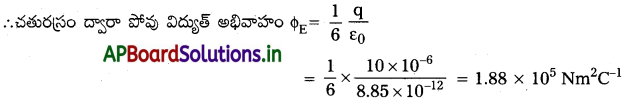
ప్రశ్న 19.
9.0 cm అంచుగాగల ఘనాకార గాసియన్ ఉపరితలం కేంద్రం వద్ద 2.0 pC బిందు ఆవేశం ఉంది. ఉపరితలం ద్వారా నికర విద్యుత్ అభివాహం ఎంత?
సాధన:

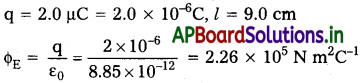
ప్రశ్న 20.
10am వ్యాసార్థం గల గోళాకార గాసియన్ ఉపరితలం కేంద్రం వద్ద ఉండే బిందు ఆవేశం, తలం నుంచి -1.0 × 10³Nm²/C విద్యుత్ అభివాహాన్ని వెలువరించడానికి కారణం అవుతోంది. (a) గాసియన్ ఉపరితలం వ్యాసార్థాన్ని రెట్టింపు చేస్తే, తలం ద్వారా ఎంత అభివాహం వెళుతుంది? (b) బిందు ఆవేశం విలువ ఎంత?
సాధన:
Φ_E = – 1.0 × 10³ N m²/C, r = 10.0cm

a) గాసియన్ తలం వ్యాసార్థం రెట్టింపు అయితే, తలం ద్వారా పోవు అభివాహం ఒకే విధంగా ఉండును. దీనికి కారణం ఆవేశం లోపల ఉన్న ఆవేశంపై అభివాహం ఆధారపడదు.

b) Φ_E = \(\frac{q}{\varepsilon_0}\)
∴ q_E = ε_o Φ_E = (8.85 × 10^-12) (-1.0 × 10³) = -8.85 × 10^-9C.

ప్రశ్న 21.
10 cm వ్యాసార్థంలో ఉండే వాహక గోళం కొంత ఆవేశాన్ని కలిగి ఉంది. గోళం కేంద్రం నుంచి 20 cm దూరంలో ఉండే విద్యుత్ క్షేత్రం 1.5 × 10³N/C. క్షేత్రం వ్యాసార్థం దిశలో లోపలికి పనిచేస్తే గోళంపైన ఉండే నికర ఆవేశం ఎంత?
సాధన:
గోళం వ్యాసార్థం = 10 cm
గోళం కేంద్రం నుండి బిందువు దూరం, r = 20 cm = 0.2 m
, విద్యుత్ క్షేత్రం, E =- 1.5 × 10³ N/C
(ఋణ సంజ్ఞ క్షేత్రంలోనికి వెళ్లుటను తెలుపును)
ఆవేశం, q = ?

ప్రశ్న 22.
2.4m వ్యాసం గల ఏకరీతి ఆవేశిత వాహక గోళం 80.0 µC/m² ఉపరితల ఆవేశ సాంద్రతను కలిగి ఉంది.
a) గోళంపై ఆవేశాన్ని కనుక్కోండి.
b) గోళం ఉపరితలాన్ని వదిలి వెళ్ళే ముందు మొత్తం విద్యుత్ అభివాహం ఎంత?
సాధన:
a) D = 2r = 2.4 m = 1.2 m
σ = 80 uc/m2 = 80 × 10^-6 C/m²
గోళంపై ఆవేశం, Q = σ × 4πr² 80 × 10^-6 × 4 × \(\frac{22}{7}\) × (1.2)² = 1.45 × 10^-3C

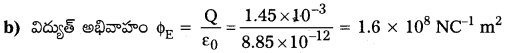
ప్రశ్న 23.
ఒక అనంత రేఖీయ ఆవేశం 2 cm దూరంలో 9 × 10⁴ N/C క్షేత్రాన్ని ఉత్పత్తి చేస్తోంది. రేఖీయ ఆవేశ సాంద్రతను లెక్కించండి.
సాధన:

ప్రశ్న 24.
రెండు పెద్ద, పలుచని లోహ పలకలు సమాంతరంగా, ఒకదానికి మరొకటి సమీపంగా ఉన్నాయి. వాటి లోపలివైపు ఉపరితలాలపై 17.0 × 10-22 C/m2 పరిమాణంగల సమాన, వ్యతిరేక ఉపరితల ఆవేశ సాంద్రతలున్నాయి.
a) మొదటి పలక వెలుపలి ప్రదేశంలో,
b) రెండవ పలక వెలుపలి ప్రదేశంలో, c) పలకల మధ్య విద్యుత్ క్షేత్రం E విలువలు ఎంత?
సాధన:

a) σ_A = 17.0 × 10^-22 Cm^-2
సిద్ధాంతంలో చెప్పినట్లు మొదటి పలక వెలుపలి ప్రదేశంలో E
E = 0

b) సిద్ధాంతంలో చెప్పినట్లు రెండవ పలక వెలుపలి ప్రదేశంలో
E = 0

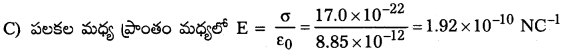
ప్రశ్న 25.
మిల్లికాన్ తైల బిందు ప్రయోగంలో 12 ఎలక్ట్రాన్లు అధికంగా ఉండే తైల బిందువుపై 2.55 × 10⁴ NC^-1 స్థిర విద్యుత్ క్షేత్రాన్ని ప్రయోగించి స్థిరంగా ఉంచారు. నూనె సాంద్రత 1.26 g cm^-3. ద్రవ బిందువు వ్యాసార్థాన్ని అంచనా వేయండి (g = 9.81 ms^-2; e = 1.60 × 10^-19C).
సాధన:

n = 12; E = 2.55 × 10⁴ Vm^-1
ρ = 1.26 gm/cm³ = 1.26 × 10³ kg/m³, r = ?
బిందువు నిశ్చలంగా ఉంటే,
బిందువు భారం = విద్యుత్ క్షేత్రం వల్ల బలం

ప్రశ్న 26.
పటంలో చూపిన వక్రాల్లో ఏవి స్థిర విద్యుత్ క్షేత్రరేఖలను సూచించవు?

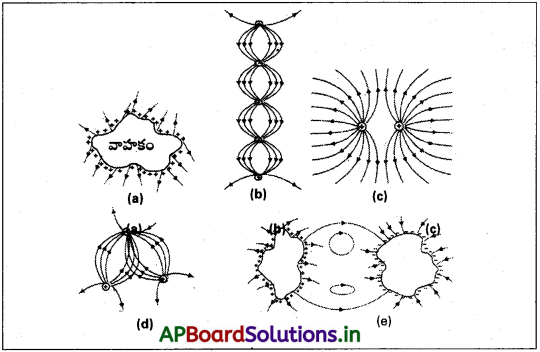
సాధన:
a) వాహక తలంనకు 90° వద్ద మాత్రమే స్థిర విద్యుత్ బలరేఖలు మొదలు లేక అంతమవుతున్నాయి. కావున పటం (a) అటువంటి రేఖలను సూచించదు.

b) స్థిర విద్యుత్ బలరేఖలు రుణావేశం నుండి మొదలుకావు. కావున అటువంటి రేఖలను పటం (b) సూచించదు.

c) పటం (c) స్థిర విద్యుత్ బలరేఖలను సూచించును.

d) విద్యుత్ బలరేఖలు ఒకదానికొకటి ఖండించుకోవు. కావున (d) ఇటువంటి రేఖలను సూచించదు.

ప్రశ్న 27.
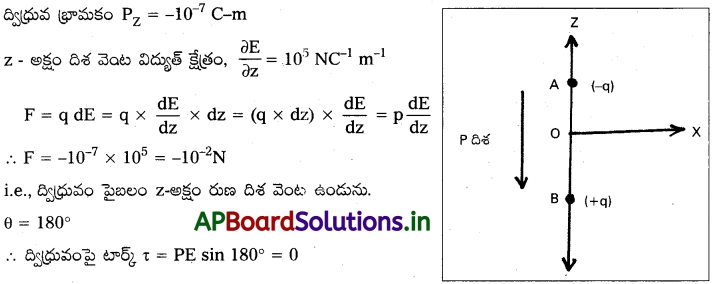
అంతరాళంలోని నియమిత ప్రాంతంలో అంతా విద్యుత్ క్షేత్రం z–దిశలో ఉంది. కాని, విద్యుత్ క్షేత్రం పరిమాణం మాత్రం స్థిరం కాదు. ఇది ధన z-దిశలో మీటర్ దూరానికి 10⁵ NC^-1చొప్పున ఏకరీతిగా పెరుగుతోంది. డైపోల్ (ద్విధ్రువ) భ్రామకం 10^-7 Cm తో రుణ Z-దిశలో ఉండే వ్యవస్థపై పనిచేసే బలం, టార్క్ల విలువ ఎంత?
సాధన:
z – అక్షం వెంట A వద్ద – q ఆవేశం మరియు B వద్ద +q ఆవేశం గల విద్యుత్ ధ్రువంను భావిద్దాం. రుణ Z దిశలో

ప్రశ్న 28.
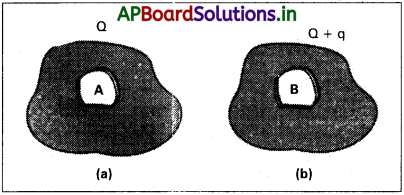
a) పటం (a) లో చూపిన విధంగా కోటరాన్ని కలిగి ఉండే వాహకం A కి ఇచ్చిన ఆవేశం Q. మొత్తం ఆవేశం వాహకం బాహ్య ఉపరితలంపైనే కనిపించాలని చూపండి.
b) q ఆవేశంతో ఉండే మరొక వాహకం B ని A తో విద్యుద్బంధితం అయ్యే విధంగా కోటరంలోకి ప్రవేశపెట్టారు. A బాహ్యం ఉండే మొత్తం ఆవేశం Q + q అని చూపండి. (పటం (b). (e) ఒక సున్నితమైన పరికరాన్ని దాని చుట్టూ ఉండే బలమైన స్థిర విద్యుత్ క్షేత్రాల నుంచి రక్షించవలసి ఉంది. సాధ్యమయ్యే ఒక మార్గాన్ని సూచించండి.

సాధన:
a) ఆవేశ వాహకం లోపల నికర క్షేత్రం శూన్యం. i. e., \(\overrightarrow{E}\) = 0.
వాహకం లోపల రంధ్రంను ఆవరించి ఉన్న గాసియన్ తలంను భావిద్దాం. గ్లాస్ నియమము ప్రకారము,

∴ q = 0_i.e., రంధ్రం లోపల ఆవేశం శూన్యం. వాహకంపై మొత్తం ఆవేశం Q, వాహకం వెలుపల తలంపై ఉండును.

b) వాహకం B రంధ్రము వద్ద +q ఆవేశం ఉంచితే, తలంపై -q ఆవేశం వాహకం A వెలుపల +q ప్రేరణ వల్ల ఏర్పడును. A వెలుపల తలం Q ఆవేశం మొదటే ఉంటే దానిపై మొత్తం ఆవేశం (Q + q).

c) పరిసరాలలోని బలమైన విద్యుత్ క్షేత్రం నుండి రక్షించుటకు సున్నితమైన పరికరమును లోహ కవచంలో ఉంచుతారు.

ప్రశ్న 29.
బోలు ఆవేశ వాహకం ఉపరితలంలోకి ఒక చిన్న రంధ్రం ఉంది. రంధ్రంలో విద్యుత్ క్షేత్రం (σ/2ε₀) \(\hat{n}\) అని చూపండి. ఇక్కడ \(\hat{n}\) బహిర్గత లంబ దిశలోని యూనిట్ సదిశ, ఆ రంధ్రం వద్ద ఉపరితల ఆవేశ సాంద్రత.
సాధన:
రంధ్రంనకు సమీపంన ఉపరితల ఆవేశ సాంద్రత = σ
బహిర్గత లంబదిశలో యూనిట్ సదిశ = \(\hat{n}\)
రంధ్రంపై బిందువు P.

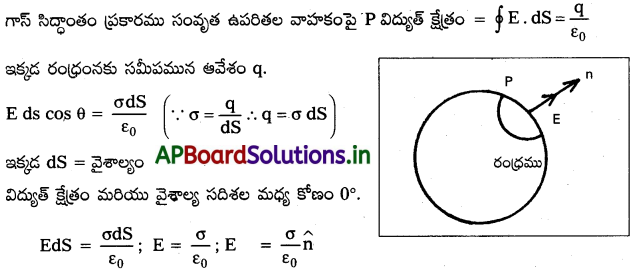
ఈ విద్యుత్ క్షేత్రం, వాహక విరామ ఆవేశం వల్ల ఏర్పడే విద్యుత్ క్షేత్రం మరియు రంధ్రంలో విద్యుత్ క్షేత్రంనకు సమానం. వాహకం లోపల రెండు క్షేత్రాలు సమానం మరియు వ్యతిరేకం.

వాహకం లోపల విద్యుత్ క్షేత్రం ఉండదు. వాహకం వెలుపల, విద్యుత్ క్షేత్రాలు సమానం మరియు ఒకే దిశలో ఉండును.

ప్రతి భాగం వల్ల, P వద్ద విద్యుత్ క్షేత్రం \(\frac{1}{2}\) E = E\(\frac{\sigma}{2 \varepsilon_0} \hat{\mathrm{n}}\)

ప్రశ్న 30.
గాస్ నియమాన్ని ఉపయోగించకుండా, 2. రేఖీయ ఆవేశ సాంద్రతను ఏకరీతిగా కలిగి ఉండే సన్నని, పొడవాటి తీగ వల్ల ఏర్పడే విద్యుత్ క్షేత్రానికి ఫార్ములాను రాబట్టండి.
[Hint : కూలుమ్ నియమాన్ని నేరుగా ఉపయోగించి అవసరమయిన సమాకలనం విలువ కట్టండి.]
సాధన:
సన్నని AB పొడవాటి తీగ. దాని రేఖీయ సాంద్రత 2. తీగ నుండి PC = r లంబదూరంలో P బిందువు వద్ద విద్యుత్ క్షేత్ర ఫార్ములాను గణిద్దాం.

తీగ మధ్య బిందువు O నుండి OC = x దూరంలో dx పొడవు ఉన్న చిన్న మూలకాన్ని భావిద్దాం.
మూలకంపై ఆవేశం, q = λdx

∆OCP = θ అయితే \(\overrightarrow{dE}\) ను రెండు అంశాలుగా విడదీయవచ్చును. P వెంట dE cos θ మరియు PF వెంట dE sin θ. క్షితిజ సమాంతర అంశాలు రద్దు అవుతాయి. రేడియల్ అంశాలు కలుస్తాయి.
∴ ఆవేశ మూలకం వల్ల తుల్య అంశ విద్యుత్ తీవ్రత, dE’ = dE cos θ

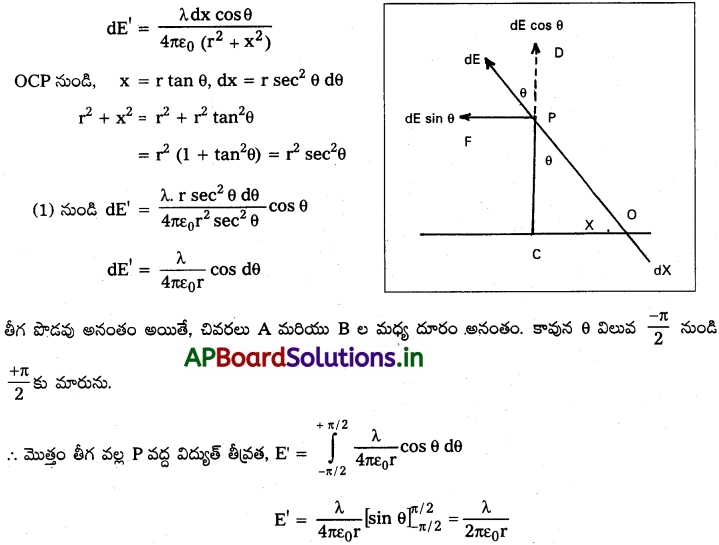
ప్రశ్న 31.
ప్రోటాన్లు, న్యూట్రాన్లు (సాధారణ ద్రవ్యం కేంద్రాలను ఏర్పరచేవి) కూడా మరింత ప్రాథమిక ప్రమాణాలైన క్వార్క్ నే వాటితో నిర్మితం అవుతాయని ఇప్పుడు నమ్ముతున్నారు. ప్రోటాన్, న్యూట్రాన్ ఒక్కొక్కటి మూడేసి క్వార్క్లను కలిగి ఉంటాయి. +(2/3)e ఆవేశం గల ఎగువ (up) క్వార్క్ (u తో సూచిస్తారు), -1/3 e ఆవేశం గల దిగువ (down) క్వార్క్ (d తో సూచిస్తారు) అని పిలిచే రెండు రకాల క్వార్క్లు, ఎలక్ట్రాన్లతో కలిసి సాధారణ ద్రవ్యం నిర్మితం అవుతుంది. (ఇతర రకాల క్వార్క్లను కూడా కనుక్కొన్నారు. ఇవి అసాధారణ రకాలైన ద్రవ్యాన్ని ఏర్పరుస్తాయి) ప్రోటాన్, న్యూట్రాన్లలో సాధ్యమయ్యే క్వార్క్ సంఘటనాన్ని సూచించండి.
సాధన:
ప్రోటాన్, ఊర్థ్వ క్వార్క్స్ n గా తీసుకుందాము.
∴ అథోక్వార్క్స్ సంఖ్య = (3 – n)

∴ ఊర్ధ్వ క్వార్క్స్ సంఖ్య (u) = 2, అథోక్వార్క్స్ సంఖ్య (d) = 3 – 2 = 1
∴ ఒక ప్రోటాను P గా సూచిస్తే= UUd.
ఒక న్యూట్రాన్లో క్వార్క్స్ సంఖ్య = n గా భావిద్దాం.
∴ అథో క్వార్క్స్ సంఖ్య = (3 – n)
న్యూట్రాన్్ప మొత్తం ఆవేశం= (\(\frac{2}{3}\)e)n – \(\frac{1}{3}\)e (3 – n) = 0
\(\frac{2}{3}\)en -e + \(\frac{1}{3}\)en = 0
en = e, n = 1
ఊర్ధ్వ క్వార్క్స్ (u) సంఖ్య = 1
అథో క్వార్క్స్ (d) సంఖ్య = 3 – 1 = 2
∴ ఒక న్యూట్రాన్ ను n గా సూచిస్తే = udd

ప్రశ్న 32.
a) అనియతమైన స్థిర విద్యుత్ క్షేత్ర ఆకృతిని పరిగణించండి. ఒక చిన్న శోధన ఆవేశాన్ని ఆకృతిలోని శూన్య బిందువు (E = 0 అయ్యే ప్రాంతం) వద్ద ఉంచారు. శోధన ఆవేశం సమతాస్థితి తప్పకుండా అస్థిరం అని చూపండి.
b) సమాన పరిమాణం, ఒకే సంజ్ఞతో కొంత దూరంలో ఉండే రెండు ఆవేశాల సరళ ఆకృతికి కూడా ఈ ఫలితాన్ని సరిచూడండి.
సాధన:
a) మొదట ఒక చిన్న శోధన ఆవేశంను శూన్య బిందువు (E = 0 అయ్యే ప్రాంతం) వద్ద ఉంచారని భావిద్దాం. శోధన ఆవేశంను శూన్య బిందువు నుండి స్థానభ్రంశం చెందిస్తే, శూన్య బిందువు వైపు పునఃస్థాపక బలంను ప్రయోగించును. శూన్య బిందువు చుట్టూ సంవృత తలం ద్వారా లోపలకు నికర అభివాహం ఉంటుందని దీని అర్థం. గాస్ సిద్ధాంతం ప్రకారం, ఆవేశంను ఆవరించి ఉన్న తలం ద్వారా నికర అభివాహం శూన్యం. కావున శోధన ఆవేశం సమతాస్థితి తప్పకుండా అస్థిరం.

b) సమాన పరిమాణం, ఒకే సంజ్ఞతో కొంత దూరంలో రెండు ఆవేశాలు భావిద్దాం. వాని మధ్య బిందువు వద్ద శూన్య బిందువు ఏర్పడును. శోధన ఆవేశంను శూన్య బిందువు నుండి రేఖపై ప్రక్కకు బరిశిత, పునఃస్థాపక బలం, శోధన ఆవేశంను శూన్య బిందువు తీసుకురావటానికి ప్రయత్నించును. రేఖకు లంబంగా శోధన ఆవేశంను జరిపితే, శూన్య బిందువు నుండి శోధన ఆవేశంను దూరంగా తీసుకువెళ్ళును. కావున సమతాస్థితి తప్పకుండా అస్థిరం.

ప్రశ్న 33.
m ద్రవ్యరాశి, (-q) ఆవేశంతో తొలుత x-అక్షం దిశలో v_x వేగంతో చలించే పటంలోని కణాన్ని పోలిన) కణం రెండు ఆవేశిత పలకల మధ్య ప్రదేశంలోకి ప్రవేశించింది. పలక పొడవు L, పలకల మధ్య ఏకరీతి విద్యుత్ క్షేత్రం E ని కొనసాగిస్తున్నారు. పలక చివరి అంచు వద్ద కణం పొందే అంబ అపవర్తనం qEL² (2m v_x²) అని చూపండి.
ఈ చలనాన్ని మొదటి సంవత్సరం భౌతికశాస్త్ర పాఠ్యాంశంలో చర్చించిన గురుత్వ క్షేత్రంలోని ప్రక్షేపకం చలనంతో పోల్చండి.
సాధన:


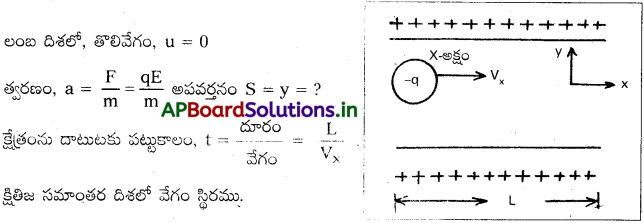
ఈ సందర్భం, గురుత్వ క్షేత్రంలో క్షితిజ ప్రక్షేపకం చలనము y = 7 gt ను ఖచ్చితంగా పోలియున్నది.

ప్రశ్న 34.
అభ్యాసం 33 లోని కణాన్ని v_x = 2.0 × 10⁶ ms^-1 వేగంతో ప్రక్షిప్తం చేసిన ఎలక్ట్రాన్ గా పరిగణించండి. 0.5 cm దూరంతో వేరుచేసిన పలకల మధ్య E విలువ 9.1 × 102 N/C అయితే, పైన ఉండే పలకను ఎలక్ట్రాన్ ఎక్కడ ఢీ కొడుతుంది? (|e| = 1.6 × 10^-19 C, m_e = 9.1 × 10^-31 kg.)
సాధన:

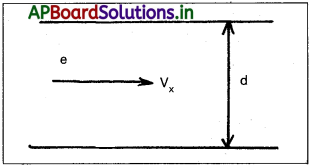
V = 2.0 × 10⁶ ms^-1
E = 9.1 × 10² N/C
d = 0.5cm 5 × 10^-3 m
q = e = 1.6 × 10^-19 C
m_e = 9.1 × 10^-31 kg
ఎలక్ట్రాన్ అపవర్తనంలో పై పలక రెండవ చివర X = L వద్ద తాకితే,

సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
ఒక లోహ గోళాన్ని స్పర్శించకుండా దాన్ని మీరెలా ధనావేశితం చేస్తారు?
సాధన:
విద్యుద్భంధక లోహ స్టాండ్పై ఉన్న అనావేశిత లోహ గోళాన్ని పటం చూపుతుంది. పటంలో చూపిన విధంగా రుణావేశిత లోహ కడ్డీని లోహ గోళం వద్దకు తీసుకొనిరండి. కడ్డీని గోళానికి సమీపంగా తీసుకొని రాగానే, వికర్షణతో గోళంలోని స్వేచ్ఛా ఎలక్ట్రాన్లు దూరంగా వెళ్ళి రెండో చివరన పోగవుతాయి. గోళం మొదటి చివర ఎలక్ట్రాన్ల లేమి వల్ల ధనావేశితం అవుతుంది. లోహ లోపలి స్వేచ్ఛా ఎలక్ట్రాన్లపై పనిచేసే నికర బలం శూన్యం కాగానే ఆవేశ వితరణ ప్రక్రియ ఆగిపోతుంది. వాహక తీగతో గోళాన్ని భూమికి అనుసంధానం చేయండి. ఎలక్ట్రాన్లు భూమిలోకి ప్రవహిస్తే, కడ్డీపై ఉండే రుణావేశాల ఆకర్షణ బలంతో గోళం సమీప చివర వద్ద ఉన్న ధనావేశాలు పటం (c)లో చూపిన విధంగా ఉండిపోతాయి. గోళం, భూమి అనుసంధానాన్ని తొలగించండి. సమీప కొన వద్ద ధనావేశాలు అలాగే ఉండిపోతాయి. పటం (d). విద్యుదీకృత కడ్డీని తొలగించండి. పటం (e) లో చూపిన విధంగా ధనావేశం గోళంపై వ్యాపిస్తుంది.

ఈ ప్రయోగంలో లోహ గోళం ప్రేరణ వల్ల ఆవేశాన్ని పొందుతుంది. కడ్డీ తన ఆవేశాన్ని ఎంతమాత్రం కోల్పోదు. ఇదే విధంగా ధనావేశిత కడ్డీని గోళం వద్దకు తెచ్చి దాన్ని ప్రేరణతో రుణావేశితం చేయవచ్చు. ఈ సందర్భంలో ఎలక్ట్రాన్లు భూమి నుంచి గోళానికి, భూమిని, గోళాన్ని సంధానం చేసిన తీగ ద్వారా ప్రవహిస్తాయి.

ప్రశ్న 2.
ఒక వస్తువు నుంచి మరో వస్తువుకు ప్రతి సెకనుకు 10⁹ ఎలక్ట్రాన్లు బయటకు వెళ్తే రెండో వస్తువుపై 1 C ఆవేశం చేరుకొనేందుకు ఎంత సమయం పడుతుంది?
సాధన:
ఒక సెకనులో బయటకు వెళ్ళిపోయే ఎలక్ట్రాన్లు 10⁹. కాబట్టి ఒక సెకన్లో ఇచ్చే ఆవేశం
1.6 × 10^-19 × 10⁹C = 1.6 × 10^-10 C. 1 C ఆవేశం పేరుకొనిపోయేందుకు కావలసిన సమయాన్ని ఈ విధంగా అంచనా వేయవచ్చు.

1 C ÷ (1.6 × 10^-10 C/s) = 6.25 × 10⁹ s = 6.25 × 10⁹ ÷ (365 × 24 × 3600 సంవత్సరాలు = 198 సంవత్సరాలు. కాబట్టి ఒక సెకన్కు 10° ఎలక్ట్రాన్లను ఇచ్చే వస్తువు నుంచి ఒక కూలుమ్ ఆవేశాన్ని సేకరించేందుకు మనకు సుమారు 200 సంవత్సరాలు అవసరం. కాబట్టి ఎన్నో ప్రాయోగిక ప్రయోజనాలకు, ఒక కులూమ్ అతి పెద్ద ప్రమాణం.

పదార్థపు ఒక ఘనపు సెంటీ మీటర్ ముక్కలో సుమారుగా ఎన్ని ఎలక్ట్రాన్లుంటాయో తెలుసుకోవడం కూడా అతి ముఖ్యమైందే. 1 cm భుజంగా ఉండే రాగి ఘనపు ముక్కలో సుమారు 2.5 × 10²⁴ ఎలక్ట్రాన్ల ఉంటాయి.

ప్రశ్న 3.
ఒక కప్పు నీటిలో ఉండే ధన, రుణావేశం ఎంత?
సాధన:
ఒక కప్పు నీటి ద్రవ్యరాశి 250 g అని అనుకొంటే, నీటి అణు ద్రవ్యరాశి 18g ఒక మోల్ (= 6.02 × 10²³ అణువులు) నీటి ద్రవ్యరాశి 18 g. కాబట్టి ఒక కప్పు నీటిలోని అణువుల సంఖ్య (250/18) × 6.02 × 10²³.

ప్రతి నీటి అణువులో రెండు హైడ్రోజన్ పరమాణువులు, ఒక ఆక్సిజన్ పరమాణువులుంటాయి. అంటే, దాన్లో 10 ఎలక్ట్రాన్లు, 10 ప్రోటాన్లుంటాయి. అందువల్ల మొత్తం ధానవేశం, మొత్తం ధనావేశం సమాన పరిమాణాన్ని కలిగి ఉంటాయి. ఆవేశ పరిమాణం (250/18) × 6.02 × 10²³ × 10 × 1.6 × 10^-19 C = 1.34 × 10^-7Cకి సమానం.

ప్రశ్న 4.
రెండు బిందు ఆవేశాల మధ్య పనిచేసే స్థిర విద్యుత్ బలానికి కూలుమ్ నియమం, అలాగే రెండు స్థిర (stationary) బిందు ద్రవ్యరాశుల మధ్య పనిచేసే గురుత్వాకర్షణ బలానికి న్యూటన్ నియమం రెండూ ఆవేశాలు/ద్రవ్యరాశుల మధ్య ఉండే దూరంపై విలోమ వర్గ ఆధారితమై ఉంటాయి.
(a) (i) ఎలక్ట్రాన్, ప్రోటాను (ii) రెండు ప్రోటాన్లకు వాటి పరిమాణాల నిష్పత్తిని కనుక్కోవడం ద్వారా ఈ బలాలను పోల్చండి.
(b) ఎలక్ట్రాన్, ప్రోటాన్లు 1 Å (= 10^-10 m) దూరంతో ఉన్నప్పుడు వాటి మధ్య పనిచేసే పరస్పర ఆకర్షణ వల్ల ఎలక్ట్రాన్, ప్రోటాన్లు పొందే త్వరణాలను అంచనా వేయండి?
(m_p = 1.67 × 10^-27 kg, m_e = 9.11 × 10^-31 kg).
సాధన:
a)

ii) ఇదే విధంగా r దూరంలో ఉండే రెండు ప్రోటాన్ల మధ్య ఉండే విద్యుత్, గురుత్వ బలాల పరిమాణాల నిష్పత్తి :

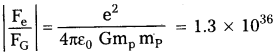
అయితే, ఇక్కడ రెండు రకాల బాల సంజ్ఞలు భిన్నమైనవని గమనించాలి. రెండు ప్రోటాన్లకు సంబంధించి గురుత్వ బలం ఆకర్షక స్వభావాన్ని కలిగి ఉంటే కూలుమ్ బలం వికర్షక స్వభావాన్ని కలిగి ఉంటుంది. కేంద్రకంలో ఉండే రెండు ప్రోటాన్ల మధ్య ఉండే (కేంద్రకంలో రెండు ప్రోటాన్ల మధ్య దూరం ~10^-15 m) ఈ బలాల నిజ విలువలు F_e ~ 230N అయితే F_G ~ 1.9 × 10^-34 N. విద్యుత్ బలాలు, గురుత్వాకర్షణ బలాల కంటే చాలా ప్రబలమైనవని రెండు బలాల నిష్పత్తి (మితులు లేనిది) సూచిస్తుంది.

b) ఎలక్ట్రాన్ పై ప్రోటాన్ కలుగచేసే విద్యుత్ బలం F పరిమాణం, ప్రోటాన్పై ఎలక్ట్రాన్ కలగచేసే బలం పరిమాణం రెండూ ఒకటే. అయితే, ఎలక్ట్రాన్, ప్రోటాన్ల ద్రవ్యరాశులు మాత్రం భిన్నమైనవి. కాబట్టి బల పరిమాణం

న్యూటన్ రెండవ గమన నియమం, F = ma ని ఉపయోగించి, ఎలక్ట్రాన్ పొందే త్వరణం
a = 2.3 × 10^-8 N/9.11 × 10^-31 kg = 2.5 × 10²² m/s²

దీన్ని గురుత్వ త్వరణం విలువతో పోల్చితే ఎలక్ట్రాన్ చలనంపై గురుత్వ కేక ప్రభావం ఉపేక్షణీయమని, ప్రోటాన్ వల్ల కలిగే కూలుమ్ బలం వల్ల ఎలక్ట్రాన్ చాలా అధిక త్వరణాలను పొందుతుందని మనం ముగించవచ్చు. ప్రోటాన్ త్వరణానికి విలువ 2.3 × 10^-8 N/1.67 × 10^-27 kg = 1.4 × 10⁹ m/s².

ప్రశ్న 5.
ఒక ఆవేశిత లోహ గోళం A ని నైలాన్ దారంతో వేలాడదీశారు. మరొక ఆవేశిత లోహ గోళం B ని విద్యుద్బంధక పిడితో పట్టుకుని పటం (a) లో చూపిన విధంగా (రెండు గోళాల కేంద్రాల మధ్య 10cm దూరం ఉండేట్లుగా) Aకి సమీపంలోకి తీసుకొని వచ్చారు. ఫలితంగా కలిగే A యొక్క వికర్షణను గుర్తించారు. (ఉదాహరణకు గోళాన్ని కాంతి పుంజంతో ప్రకాశింపచేసి తెరపై దాని నీడలో వచ్చే అపవర్తనాన్ని కొలవడం ద్వారా) పటం (b) లో చూపినట్లు A, B గోళాలను ఆవేశరహిత, సర్వసమానాలయిన మరో రెండు గోళాలు C, D లతో పటం (b) లో చూపినట్లు స్పర్శింపచేసారు. C, D లను తొలగించి, కేంద్రాల మధ్య దూరం 5.0 cm ఉండేట్లుగా, పటం (c) లో చూపిన విధంగా B ని సమీపంలోకి తీసుకొనివచ్చారు. కూలుమ్ నియమం ప్రకారం A వికర్షణ ఎంతని ఊహిస్తున్నారు? A, C గోళాలు, B, D గోళాలు ఒకే పరిమాణాలను కలిగి ఉన్నాయి. A, B ల కేంద్రకాల మధ్య దూరంతో పోల్చి, వాటి పరిమాణాలను ఉపేక్షించండి.

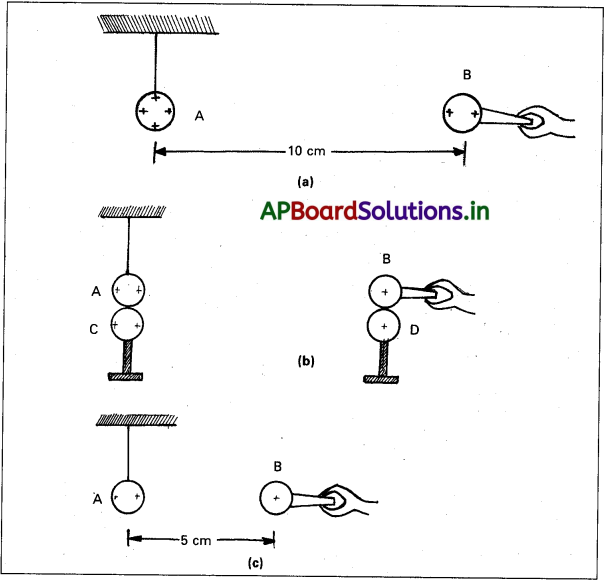
సాధన:
A గోళంపై ఉండే మౌలిక (లేదా సహజ) ఆవేశం q అనుకుంటే B పై q’ అనుకోండి. వాటీ కేంద్రాల మధ్య దూరం ఉన్నప్పుడు, ప్రతిదానిపై ఉండే స్థిర విద్యుత్ బలం పరిమాణంతో పోల్చితే A, B గోళాల పరిమాణాలను ఉపేక్షించినప్పుడు
F = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{qq}}{\mathrm{r}^2}\)

A ను పోలిన ఆవేశరహిత గోళం C, A ని తాకితే A, C లపై ఆవేశాలు పునర్వితరణ చెంది, సౌష్టవం వల్ల ప్రతి గోళం q/2 ఆవేశం కలిగి ఉంటుంది. ఇదేవిధంగా D, B ని తాకిన తరువాత ప్రతి గోళంపై పునర్వితరణ వల్ల కలిగే ఆవేశం q’/2. A, B ల మధ్య దూరం సగానికి తగ్గిస్తే, ప్రతిదానిపై స్థిర విద్యుత్ బలం పరిమాణం,

కాబట్టి B వల్ల A పై పనిచేసే స్థిర విద్యుత్ బలంలో మార్పులేదు.

ప్రశ్న 6.
l భుజంగా గల సమబాహు త్రిభుజ మూడు శీర్షాల వద్ద మూడు ఆవేశాలు q₁, q₂, q₃లు ప్రతీది q కు సమానంగా, ఉన్నాయనుకోండి. పటంలో చూపిన విధంగా త్రిభుజం కేంద్రాభం (centroid) వద్ద Q (q సంజ్ఞనే కలిగి ఉన్న) ఆవేశాన్ని ఉంచితే దానిపై పనిచేసే బలం ఎంత?

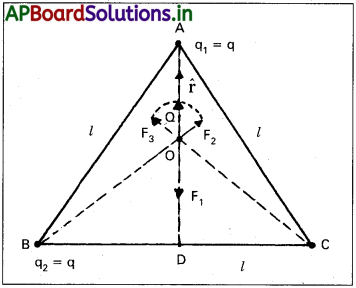
సాధన:
l భుజం పొడవు ఉండే సమబాహు త్రిభుజం ABC లో BC భుజానికి లంబం AD ని గీస్తే

ప్రశ్న 7.
పటంలో చూపిన విధంగా ఒక సమబాహు త్రిభుజం శీర్షాల వద్ద q, q, −q ఆవేశాలను ఉంచారు. ప్రతి ఆవేశంపై పనిచేసే బలం ఎంత?

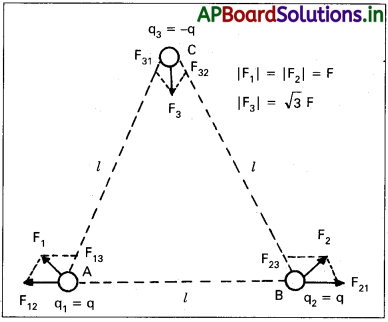
సాధన:
పటంలో చూపిన విధంగా, A వద్ద ఉండే ఆవేశం q పై B వద్ద ఉండే ఆవేశం q వల్ల, C వద్ద ఉండే q వల్ల పనిచేసే బలాలు వరసగా F12 (BA దిశలో), F13 (AC దిశలో). సమాంతర చతుర్భుజ నియమం ప్రకారం A వద్ద ఉండే ఆవేశం q పై పనిచేసే మొత్తం బలం F, అయితే,
F₁ = F \(\hat{r_1}\)1, ఇక్కడ \(\hat{r_1}\) BC దిశలో ఏకాంక సదిశ

ప్రతి జత ఆవేశాల మధ్య. పనిచేసే ఆకర్షణ లేదా వికర్షణ బలాల పరిమాణాలు సమానం, దీని విలువ F = \(\frac{q^2}{4 \pi\varepsilon_0l^2}\) B వద్ద ఉండే ఆవేశం q పై పనిచేసే మొత్తం బలం F₂ అయితే, F₂ = F\(\hat{r_2}\), ఇక్కడ \(\hat{r_2}\), AC దిశలో ఏకాంక సదిశ. ఇదే విధంగా C వద్ద ఉండే ఆవేశం -q పై పనిచేసే మొత్తం బలం F₃ = √3 F \(\hat{n}\), ఇక్కడ \(\hat{n}\), ∠BCA సమద్విఖండన దిశలోని ఏకాంక సదిశ.

మూడు ఆవేశాలపై పనిచేసే బలాల మొత్తం శూన్యం కావడం అనేది ఆసక్తి కలిగించే అంశం. అంటే,
F₁ + F₂ + F₃ = 0

ప్రశ్న 8.
2.0 × 10⁴ N C^-1 పరిమాణం గల ఏకరీతి విద్యుత్ క్షేత్రంలో ఎలక్ట్రాన్ 1.5cm దూరం పతనం చెందుతోంది. (పటం a). పరిమాణంలో మార్పులేకుండా క్షేత్ర దిశను వ్యతిరేక దిశలోకి మార్చడం వల్ల ప్రోటాన్ కూడా అంతే దూరం. పతనం చెందింది. (పటం (b)). రెండు సందర్భాల్లో పతన కాలాన్ని లెక్కించండి. దీన్ని గురుత్వ వల్ల స్వేచ్ఛా పతన సన్నివేశంతో భేదపర్చండి.

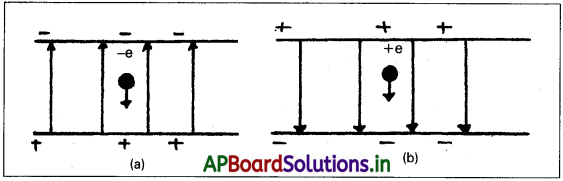
సాధన:
పటం (a) లో E పరిమాణం గల, క్షేత్రం ఊర్ధ్వ దిశలో ఉంది కాబట్టి రుణావేశిత ఎలక్ట్రాన్ eE పరిమాణం గల అథోబలానికి లోనవుతుంది. ఇక్కడ E విద్యుత్ క్షేత్ర తీవ్రత, ఎలక్ట్రాన్ త్వరణం a_e = eE/m_e.
ఇక్కడ m_e ఎలక్ట్రాన్ ద్రవ్యరాశి

కాబట్టి, భారయుత కణం (ప్రోటాన్) సమాన దూరాన్ని ప్రయాణించేందుకు ఎక్కువ కాలాన్ని తీసుకొంటుంది. ఇదే స్వేచ్ఛాపతన వుస్తువుకు, ఈ సన్నివేశానికి ఉండే ప్రాథమిక భేదం. స్వేచ్ఛాపతన వస్తువు పతన కాలం వస్తువు ద్రవ్యరాశిపై ఆధారపడదు. ఉదాహరణలో పతన కాలాన్ని లెక్కించడంలో గురుత్వ త్వరణాన్ని ఉపేక్షించామని గమనించండి. ఇది దోషరహితమేనా అని తెలుసుకొనేందుకు ఇచ్చిన విద్యుత్ క్షేత్రంలో ప్రోటాన్ త్వరణాన్ని లెక్కిద్దాం.

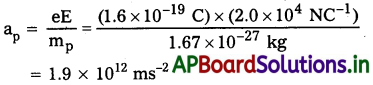
ఇది గురుత్వ త్వరణం g (9.8 ms^-2) విలువతో పోల్చితే అత్యధికం. ఎలక్ట్రాన్ త్వరణం మరీ ఎక్కువ కాబట్టి, ఈ ఉదాహరణలో గురుత్వ త్వరణాన్ని ఉపేక్షించవచ్చు.

ప్రశ్న 9.
+10^-8 C, -10^-8 C ఆవేశ పరిమాణం గల q₁, q₂, అనే రెండు బిందు ఆవేశాలను 0.1 m ఎడంతో అమర్చారు. పటంలో చూపిన A, B, C బిందువుల వద్ద విద్యుత్ క్షేత్రాలను లెక్కించండి.

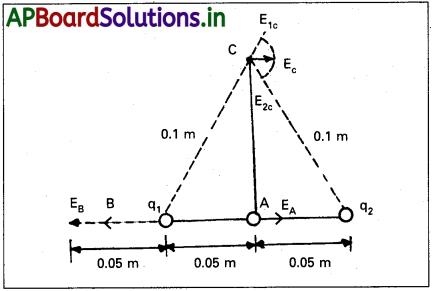
సాధన:
q₁ ధనావేశం వల్ల A వద్ద విద్యుత్ క్షేత్ర సదిశ E_1A. ఇది కుడివైపు చూపిస్తుంది. దాని పరిమాణం

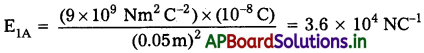
q₂ రుణావేశం వల్ల A వద్ద విద్యుత్ క్షేత్ర సదిశ E_2A కుడివైపు చూపిస్తుంది. మరియు పై పరిమాణాన్నే (ఒకే విధమైన) కలిగి ఉంటుంది. కాబట్టి, A వద్ద మొత్తం విద్యుత్ క్షేత్రం పరిమాణం
E_A = E_1A + E_2A = 7.2 × 10⁴ NC^-1
E_A కుడివైపు దిశలో ఉంటుంది.
q₁ ధనావేశం వల్ల B వద్ద విద్యుత్ క్షేత్ర సదిశ E_1B ఎడమవైపు చూపుతుంది. దీని పరిమాణం

B వద్ద మొత్తం విద్యుత్ క్షేత్రం పరిమాణం = E_B = E_1B – E_2B = 3.2 × 10⁴ N C^-1.
E_B దిశ ఎడమవైపు ఉంటుంది.

బిందువు C వద్ద, q₁, q₂ ఆవేశాల వల్ల కలిగే ప్రతి విద్యుత్ క్షేత్ర పరిమాణం

ప్రశ్న 10.
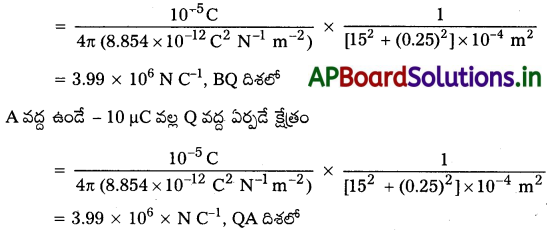
రెండు ఆవేశాలు ± 10 µC లను 5.0 mm దూరంలో ఉంచారు. పటం (a) లో చూపిన విధంగా కేంద్రం నుంచి ధనావేశం ఉన్న వైపు 15 cm దూరంలో అక్షంపై ఉండే బిందువు P వద్ద, (b) పటం (b) లో చూపినట్లు డైపోల్ అక్షానికిలంబంగా ఉంటూ ద్వారా పోయే రేఖపై Oనుంచి 15cm దూరంలో ఉండే బిందువు Qవద్ద విద్యుత్ క్షేత్రాలను కనుక్కోండి.

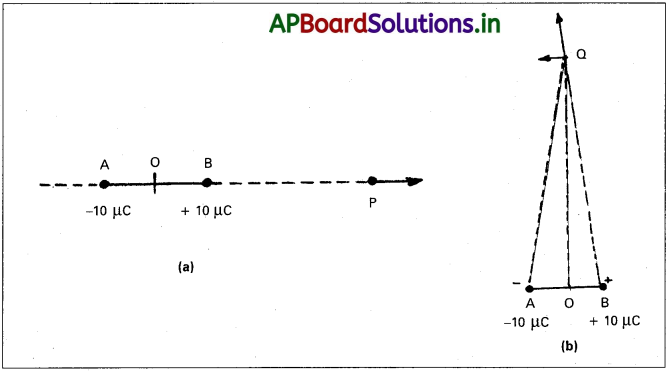
సాధన:
a) + 10 ±C ఆవేశం వల్ల బిందువు P వద్ద క్షేత్రం

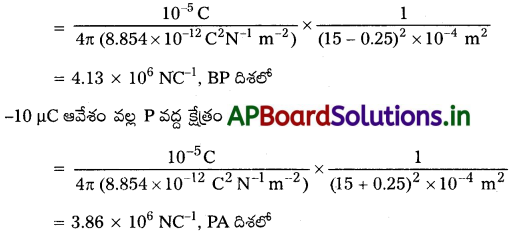
A, B ల వద్ద ఉండే ఆవేశాల వల్ల P వద్ద ఫలిత విద్యుత్ క్షేత్రం = 2.7 × 10⁵ NC^-1, BP దిశలో

OP/OB నిష్పత్తి విలువ చాలా అధికం (= 60). డైపోల్ అక్షంపై ఉండే చాలా దూర బిందువు వద్ద విద్యుత్ క్షేత్రానికి గల ” ఫార్ములాను ఉపయోగించి కూడా పైన పొందిన ఫలితాన్నే ఉజ్జాయింపుగా పొందవచ్చు. 22 దూరంతో ±q ఆవేశాలను కలిగి ఉండే డైపోల్ అక్షంపై కేంద్రం నుంచి దూరంలో విద్యుత్ క్షేత్రం పరిమాణం.
E = \(\frac{2p}{4 \pi\varepsilon_0r^3}\) (r/a >> 1)
ఇక్కడ p = 2aq డైపోల్ భ్రామకం పరిమాణం

డైపోల్ అక్షంపై ఏర్పడే విద్యుత్ క్షేత్రం దిశ ఎప్పుడూ డైపోల్ భ్రామకం సదిశ దిశలోనే (అంటే -q నుంచి q వైపు). ఉంటుంది. ఇక్కడ p = 10^-5 × C × 5 × 10^-3 m = 5 × 10^-8 C m

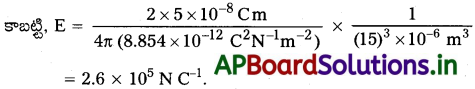
ఇది డైపోల్ భ్రామకం AB దిశలో ఉంటూ, దీని విలువ ఇంతకు ముందే పొందిన విలువకు దగ్గరగా ఉంది.

(b) B వద్ద ఉండే + 10 µC వల్ల Q వద్ద ఏర్పడే క్షేత్రం

ఈ రెండు బలాల సమాన పరిమాణం గల అంశాలు OQ దిశలో రద్దుపరచుకొంటే, BA కి సమాంతర దిశలో సంకలనం చెందుతాయి. కాబట్టి, A, B ల వద్ద ఉండే రెండు ఆవేశాల వల్ల Q వద్ద ఏర్పడే ఫలిత విద్యుత్ క్షేత్రం

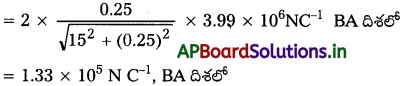
a) లో చూసిన విధంగానే డైపోల్ అక్షానికి లంబంగా ఒక బిందువు వద్ద ఏర్పడే క్షేత్రానికి గల ఫార్ములాను నేరుగా ఉపయోగించి కూడా ఇదే ఫలితాన్ని ఉజ్జాయింపుగా పొందవచ్చు :

ఈ సందర్భంలో విద్యుత్ క్షేత్రం దిశ డైపోల్ భ్రామకం సదిశ దిశకు వ్యతిరేకం. మళ్ళీ, ఫలితం ఇంతకు ముందే పొందిన దానితో ఏకీభవిస్తుంది.

ప్రశ్న 11.
పటం లోని విద్యుత్ క్షేత్ర అంశాలు E_x = ax^½, E_y = E_z = 0. ఇక్కడ a = 800 N/C m^½. (a) ఘనం ద్వారా అభివాహాన్ని, (b) ఘనంలోని ఆవేశాన్ని లెక్కించండి. a = 0.1 m అని అనుకోండి.

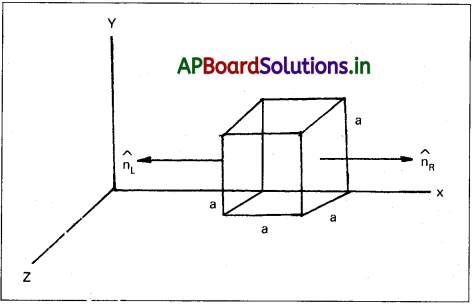
సాధన:
a) విద్యుత్ క్షేత్రం కేవలం x అంశాన్ని మాత్రమే కలిగి ఉంది. కాబట్టి, x-అక్షానికి లంబంగా ఉండే తలాలకు E, ∆S ల మధ్య కోణం ± π/2. కాబట్టి, అభివాహం Φ = E. ∆S రెండు నీలం రంగు తలాల్లో (ముఖాల్లో) (faces) తప్ప మిగతా అన్నింటికి విడివిడిగా శూన్యం. ఎడమ తలం (ముఖం) వద్ద విద్యుత్ క్షేత్రం పరిమాణంE_L = αx^½ = αa^½ (ఎడమ తలం వద్ద x = a). కుడి ఉపరితలం వద్ద విద్యుత్ క్షేత్రం పరిమాణం E_R = αx^½ = α[2a]^½ (కుడి తలం వద్ద X = 2a).
ఈ తలాల వద్ద అభివాహాలు

b) ఘనంలోని మొత్తం ఆవేశం q ని కనుక్కొనేందుకు గాస్ నియమాన్ని ఉపయోగించవచ్చు.
Φ = q/ε₀ లేదా q = Φε₀. కాబట్టి, q = 1.05 × 8.854 × 10^-12 C = 9.27 × 10^-27. C.

ప్రశ్న 12.
ఒక ఏకరీతి విద్యుత్ క్షేత్రం ధన x- విలువకు ధన x-అక్షం దిశలో, రుణ x విలువకు రుణ x అక్షం దిశలో అంతే పరిమాణంతో ఏకరీతి ఉంది. x > 0 కి E = 200 \(\hat{i}\) N/C, x <0 కి E = -200 \(\hat{i}\) N/C అని ఇచ్చారు. 20 cm పొడవు, వ్యాసార్థం 5 cm గల లంబ వృత్తాకార స్థూపం కేంద్రం మూల బిందువు వద్ద ఉంది. దాని ఒక తలం x = + 10 cm వద్ద మరొక తలం x = – 10 cm వద్ద ఉండే విధంగా దాని అక్షం (x-అక్షం దిశలో ఉంది. (a) దా ని ‘ప్రతి చదునైన తలం ద్వారా వెలువడే నికర అభివాహం ఎంత? (b) స్థూపం పక్క తలం ద్వారా అభివాహం ఎంత? (c) స్థూపం ద్వారా వెలువడే నికర అభివాహం ఎంత? (d) స్థూపం లోపల నికర ఆవేశం ఎంత?
సాధన:
a) ఎడమ తలం (ముఖం) పై E, ∆S లు సమాంతరం అని పటం నుంచి తెలుసుకోవచ్చు. కాబట్టి, వెలువడే అభివాహం
Φ_L = E. ∆S -200 \(\hat{i}\)
∆S = +200 ∆S,
ఎందుకంటే \(\hat{i}\). ∆S = – ∆S
= +200 × π(0.05)²
= +1.57 Nm²C^-1

కుడి తలంపై, E, ∆S లు సమాంతరాలు కాబట్టి,
Φ_R = E. ∆S = +1.57 Nm²C^-1.

b) స్థూపం పక్క (పార్శ్వ) తలంపై ఏ బిందువు వద్దనైనా, E, ∆S కి లంబం. కాబట్టి E. ∆S = 0 కాబట్టి, స్థూపం పక్క తలం నుంచి బయటకు వచ్చే అభివాహం శూన్యం.

c) స్థూపం ద్వారా వెలువడే నికర అభివాహం
Φ = 1.57 + 1.57 + 0 = 3.14 Nm²C^-1.

d) గాస్ నియమం నుంచి స్థూపం లోపల నికర ఆవేశాన్ని కనుక్కోవచ్చు. దాని ప్రకారం.
q = ε₀Φ
= 3.14 × 8.854 × 10^-12 C
= 2.78 × 10^-12 C

ప్రశ్న 13.
తొలి పరమాణు నమూనా ప్రకారం, Ze ఆవేశం గల ధనావేశిత బిందు కేంద్రకం ఉండి, దాని చుట్టూ ఏకరీతి సాంద్రతతో రుణావేశం వ్యాసార్థం R వరకు ఉంటుందని అనుకొనేవారు. పరమాణువు మొత్తంగా తటస్థం. ఈ నమూనాకు, కేంద్రకం నుంచి r దూరంలో విద్యుత్ క్షేత్రం ఎంత?

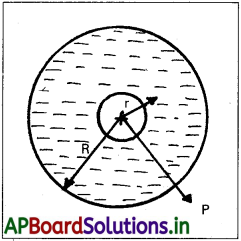
సాధన:
ఈ పరమాణు నమూనాకు సంబంధించిన ఆవేశ వితరణను పటంలో చూపించారు. R వ్యాసార్ధం గల ఏకరీతి గోళాకార ఆవేశ వితరణలో మొత్తం రుణావేశం -Ze కావాల్సిందే. ఎందుకంటే పరమాణువు తటస్థావేశాన్ని కలిగి ఉంది. కేంద్రకం Ze ఆవేశం + రుణావేశం) ఇది రుణావేశ సాంద్రత ρ ని ఇస్తుంది. కాబట్టి,

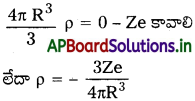
కేంద్రకం నుంచి దూరంలో ఉండే బిందువు P వద్ద విద్యుత్ క్షేత్రం E (r) ని కనుక్కొనేందుకు మనం గాస్ నియమాన్ని ఉపయోగిస్తాం. ఆవేశ వితరణ గోళీయ సౌష్టవాన్ని కలిగి ఉంది కాబట్టి r దిశతో సంబంధం లేకుండా విద్యుత్ క్షేత్రం E(r) పరిమాణం కేవలం త్రైజ్యా (రేడియల్) దూరంపై మాత్రమే ఆధారపడుతుంది. దీని దిశ మూల బిందువు నుంచి బిందువు P దిశలోని వ్యాసార్థ సదిశ r దిశలో (లేదా వ్యతిరేక దిశలో) ఉంటుంది. కేంద్రకం (nucleus) కేంద్రంగా ఉండే గోళాకార తలం గాసియన్ ఉపరితలం అని మనకు స్పష్టమౌతోంది. r < R, r > R అనే రెండు పరిస్థితులను చూద్దాం.

i) r < R : గోళాకార ఉపరితలంతో ఆవృతమైన విద్యుత్ అభివాహం Φ = E(r) × 4πr²
ఇక్కడ E(r), r వద్ద విద్యుత్ క్షేత్ర పరిమాణం. ఎందుకంటే, గోళాకార గాసియన్ ఉపరితలంపై ఉండే అన్ని బిందువుల వద్ద క్షేత్రం పరిమాణం సమానం. అలాగే ఏదైనా బిందువు వద్ద క్షేత్రం ఆ బిందువు వద్ద గీచిన లంబం దిశలోనే ఉంటుంది.

గాసియన్ ఉపరితలంతో ఆవృతమైన ఆవేశం q అనేది కేంద్రక ధనావేశం, r వ్యాసార్థం గల గోళంలోని రుణావేశాల మొత్తం. అంటే,

విద్యుత్ క్షేత్రం వ్యాసార్థం దిశలో వెలుపలివైపు ఉంటుంది.

ii) r > R : ఈ సందర్భంలో పరమాణువు తటస్థం కాబట్టి ఈ సందర్భంలో గోళాకార గాసియన్ ఉపరితలంతో ఆవృతం అయ్యే ఆవేశం శూన్యం. కాబట్టి, గాస్ నియమం నుంచి,
E(r) × 4 π r² = 0
లేదా E(r) = 0 ; r > R
r = R వద్ద రెండు సందర్భాలు ఒకే ఫలితాన్ని ఇస్తాయి : E = 0.