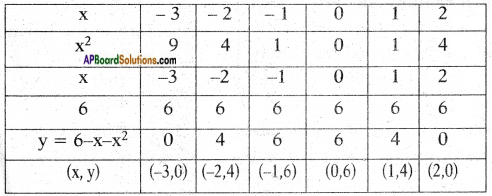
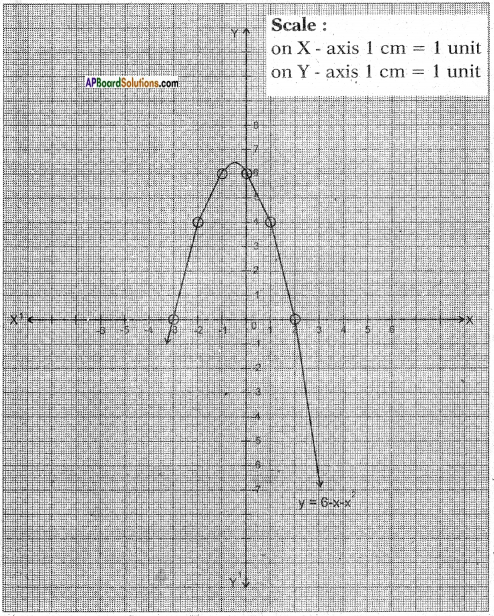
SCERT AP Board 7th Class Hindi Solutions 5th Lesson ईमानदारी का फल Textbook Questions and Answers.
AP State Syllabus 7th Class Hindi 5th Lesson Questions and Answers ईमानदारी का फल
7th Class Hindi 5th Lesson ईमानदारी का फल Textbook Questions and Answers
सोचिए-बोलिए

प्रश्न 1.
चित्र में क्या – क्या दिखाई दे रहे हैं? (చిత్రంలో ఏమేమి కనిపించుచున్నవి?)
उत्तर:
चित्र में कुछ पेड़ – पौधे, फूल, एक झोपडी, एक घर, घास, पर्वत, जड.पी. हाई स्कूल, एक आदमी और एक बालक दिखाई दे रहे हैं। बडे – बडे पत्थर भी दिखाई दे रहे हैं।
(చిత్రంలో కొన్ని చెట్లు, మొక్కలు, పూలు, ఒక గుడిసె, ఒక ఇల్లు, గడ్డి, పర్వతములు, జెడ్.పి స్కూల్, ఒక మనిషి మరియు ఒక బాలుడు కనిపించుచున్నారు.)

प्रश्न 2.
लड़का क्या कर रहा है? (బాలుడు ఏమి చేయుచుచున్నాడు?)
उत्तर:
लड़का एक आदमी को रुपयों का बंडल दे रहा है और वह आदमी उसे ले रहा है।
(బాలుడు ఒక మనిషికి రూపాయల కట్టను ఇచ్చుచున్నాడు. ఆ మనిషి దానిని తీసుకొనుచున్నాడు.)
Intext Questions & Answers
प्रश्न 1.
जंगल में क्या – क्या मिलते हैं? (అడవిలో ఏమేమి లభించును?)
उत्तर:
जंगल में तरह – तरह के पेड़, फल, फूल, पत्ते,वनस्पति, खनिज आदि मिलते हैं।
(అడవిలో రకరకాల చెట్లు, పండ్లు, పూలు, ఆకులు, వనస్పతి, ఖనిజ పదార్థములు మున్నగునవి లభించును.)
प्रश्न 2.
परियों के बारे में तुम क्या जानते हो? (దేవదూతల గురించి నీకు ఏమి తెలియును?)
उत्तर:
कहा जाता है कि परियाँ बहुत सुंदर होती हैं। अगर किसी पर महरबान हो जाए तो अपनी जादू की छड़ी से उसकी कोई कामना पूरी कर देती हैं। यों तो परियाँ कई प्रकार की होती हैं – जैसे जंगल परी, पर्वत परी, जल परी आदि।
(దేవతలు చాలా అందంగా ఉంటారని అంటూ ఉంటారు. ఎవరి మీదైనా ప్రేమ, ఇష్టం కల్గినట్లయితే అవి తమ మాయాజాలంతో వారి ఇష్టాన్ని తీరుస్తాయి. సాధారణంగా వీరు చాలా రకాలుగా ఉంటారు. ఉదా : వన దేవత, పర్వత మరియు జల దేవత.)
Improve Your Learning
सुनिए-बोलिए
प्रश्न 1.
नदी से क्या – क्या लाभ हैं? (నదుల వలన ఏమేమి లాభములు కలవు?)
उत्तर:
नदी से हमें कई लाभ मिलते हैं जैसे पीने का पानी मिलता है। नदियों के पानी से सिंचाई का प्रबंध किया जाता है। नदी यातायात का साधन भी हैं। नदियों के पानी को इकट्टा करके बिजली की उत्पत्ति की जाती है।
(నదుల నుండి మనకు అనేక లాభములు కలుగును ఉదాహరాణకి త్రాగునీరు లభించును. నదీ నీటిలో నీటి తడుపు ఏర్పాట్లు చేయబడును. నదులు ప్రయాణ మార్గాలు కూడా. నదీ నీటిని పోగు చేసి విద్యుత్ ఉత్పత్తి చేయవచ్చు.)
प्रश्न 2.
कुछ पेड़ों के नाम बताइए| (కొన్ని చెట్ల పేర్లను తెలపండి.)
उत्तर:
बरगद, पीपल, इमली, नीम, नींबू, जामून, नारियल और ताड़ आदि कुछ पेडों के नाम हैं।
(మర్రిచెట్టు, రావిచెట్టు, చింతచెట్టు, వేపచెట్టు, నిమ్మచెట్టు, నేరేడు చెట్టు, కొబ్బరి చెట్టు మరియు తాటిచెట్టు అనునవి కొన్ని చెట్ల పేర్లు)

प्रश्न 3.
ईमानदारी का फल कैसा होता है? (నిజాయితీ ఫలితము ఎలా ఉంటుంది?)
उत्तर:
ईमानदारी का फल मीठा होता है। (నిజాయితీ యొక్క ఫలితము తీయగా ఉంటుంది.)
पढिए
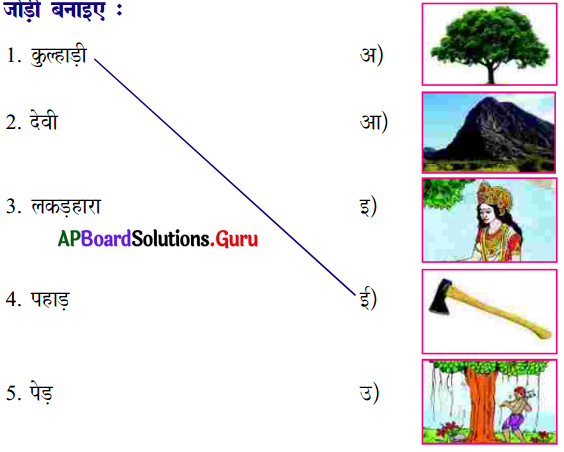
अ) जोड़ी बनाइए।
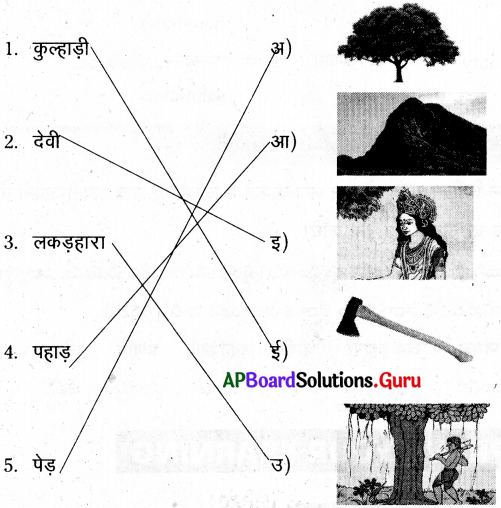
उत्तर:
आ) पाठ में नीचे दिये गये वाक्यों के सही क्रम को पहचानकर उनकी क्रम संख्या कोष्ठक में लिखिए।
1. उसने सोने की कुल्हाड़ी दिखाई। [ 3 ]
2. एक लकड़हारा था। [ 1 ]
3. हाँ, यही मेरी कुल्हाड़ी है। [ 5 ]
4. लकड़हारा रोने लगा। [ 2 ]
5. यह मेरी नहीं है। [ 4 ]
इ) सही वर्तनी वाले शब्दों पर गोला “O” बनाइए।

ई) नीचे दिये गये वाक्यों में चित्रों से संबंधित शब्दों पर “O” गोला बनाइए।

लिखिए
अ) नीचे दिये गये प्रश्नों के उत्तर छोटे – छोटे वाक्यों में लिखिए।
క్రింది ఇవ్వబడిన ప్రశ్నలకు సమాధానములు చిన్న – చిన్న వాక్యములలో ఇవ్వండి.)
1. लकड़हारा क्या करता था? (Sev Senyas Sansats?)
उत्तर:
लकड़हारा जंगल में लकडियाँ काटकर उन्हें बेचता था।
(కట్టెలు నరుకువాడు అడవిలో కట్టెలు నరికి వాటిని అమ్ముకునేవాడు.)
2. नदी की देवी क्यों खुश हुई? (568 vos 305220060?)
उत्तर:
लकडहारे की ईमानदारी को देखकर नदी की देवी खुश हुई।
(కట్టెలు నరుకువాని నిజాయితీని చూసి నదీ దేవత సంతోషించినది.)

आ) नीचे दिये गये प्रश्न का उत्तर पाँच – छह वाक्यों में लिखिए।
క్రింది ఇవ్వబడిన ప్రశ్నకు సమాధానము 5 -6 వాక్యములలో వ్రాయండి.)
“ईमानदारी का फल” कहानी का सारांश लिखिए। (“Resran 2080” s av5g dowon provis.)
उत्तर:
एक लकड़हारे की कुल्हाडी नदी में गिर गई। नदी की देवी ने उसे सोने और चाँदी की कुल्हाड़ियाँ दिखाई। लेकिन उसने ईमानदारी से अपनी कुल्हाड़ी ही माँगी। इससे उसे तीनों कुल्हाड़ियाँ ईनाम के रूप में मिलीं। इससे यह शिक्षा मिलती है कि ईमानदारी का फल मीठा होता है।
(ఒక కట్టెలు నరుకువాని గొడ్డలి నదిలో పడిపోయినది. నదీ దేవి అతనికి బంగారపు మరియు వెండి గొడ్డళ్ళు చూపినది. కానీ అతడు నిజాయితీతో తన గొడ్డలినే అడిగెను. అందువలన అతనికి బహుమతిగా మూడు గొడ్డళ్ళు లభించినవి. దీని నుండి మనకు నిజాయితీ ఫలితము తీయగా ఉంటుందన్న పాఠం లభించుచున్నది.)
इ) उचित शब्दों से खाली जगह भरिए।
1. वह ………. में लकड़ियाँ काटता था। (जंगल / मैदान)
उत्तर:
जंगल
2. नदी में ……….. जा गिरी। (कुल्हाड़ी / लकड़ी)
उत्तर:
कुल्हाड़ी
3. नदी की देवी ……….. आयी। (अंदर / बाहर)
उत्तर:
बाहर
4. देवी ने उसको ………. कुल्हाड़ियाँ दे दी। (एक | तीनों)
उत्तर:
तीनों
5. ईमानदारी का फल ……… होता है। (मीठा/ कडुआ)
उत्तर:
मीठा
ई) संकेतों के आधार पर शब्द लिखिए।

उत्तर:
नाम
धाम
काम
आम

उ) वर्ण विच्छेद कीजिए।
1. जंगल : ज् + अं + ग् + अ + ल् + अ
2. कुल्हाड़ी : ………………………….
उत्तर:
क् + उ + ल् + इ + आ + ड् + ई
3. आधार : ………………………………
उत्तर:
आ + ध् + आ + र् + अ
4. प्रणाम : ………………………………..
उत्तर:
प् + र् + अ + ण् + आ + म् + अ
5. कहानी : ………………………………….
उत्तर:
क् + अ + ह् + आ + न् + ई
भाषांश
अ) अंत्याक्षरी विधि के अनुसार नीचे दिये गये शब्दों के आधार पर चार शब्द बनाइए।
उदा : लकड़हारा – राम – मगर – रमेश – शरत

उत्तर:

आ) पर्यायवाची शब्द लिखिए।
1. जल : पानी, नीर
2. जंगल : …………
उत्तर:
कानन, वन
3. लकड़ी : ………………..
उत्तर:
डंडा, काठ
4. मीठा : ………………
उत्तर:
मधुर, रसीला
5. खुश : …………………
उत्तर:
आनंद, संतोष

इ) विलोम शब्द लिखिए।
1. बाहर × अंदर
2. आना × जाना
3. गिरना × उठना
4. ईमान × बेईमान
5. अपना × पराया
सृजनात्मकता
अ) चित्र को देखकर छोटे – छोटे शब्द लिखिए।

1. लड़का
उत्तर:
2. आशीश
3. चरण
4. रास्ता
5. अंधा
आ) परियोजना कार्य
कुछ नीति वाक्यों का संकलन कीजिए। (కొన్ని నీతి వాక్యాములను సంగ్రహించండి.)
उत्तर:
नीति वाक्य :
- पाप से घृणा करो, पापी से नहीं। – महात्मा गाँधी
- ईश्वर के हाथ देने के लिए खुले हैं, लेने के लिए तुम्हें प्रयत्न करना होगा : गुरु नानक देव।
- प्रार्थना करनेवाले होठों से सहायता करनेवाले हाथ कहीं अच्छे हैं – मदर तेरेसा
- मानव की सेवा ही माधव की सेवा है। – मदर तेरेसा।
- मूर्ख अपने घर में पूजा जाता, मुखिया अपने गाँव में परंतु विद्वान सर्वत्र पूजा जाता है। – चाणक्य
- रास्ते कभी खत्म नहीं होते, अकसर लोग हिम्मत हार जाते हैं।
- मीठा जबान, अच्छी आदतें, अच्छा व्यवहार और अच्छे लोग हमेशा सम्मानित होते हैं।
- कड़ी मेहनत ही आपको अच्छी किस्मत दे सकती है।
- कम बोलना एक अच्छी आदत है।
- घमंड पतन का लक्षण है।

इ) अनुवाद कीजिए।
1. लकड़हारा लकड़ियाँ काटता है। …………………………………………
उत्तर:
लकड़हारा लकड़ियाँ काटता है। కట్టెలు నరుకువాడు కట్టెలు నరుకుతాడు.
2. जंगल में अनेक जीव – जंतु रहते हैं। …………………………………………
उत्तर:
जंगल में अनेक जीव – जंतु रहते हैं। అడవిలో అనేక జంతు జీవములు ఉండును.
3. नदी में मछलियाँ रहती हैं। …………………………………………
उत्तर:
नदी में मछलियाँ रहती हैं। నదిలో చేపలు ఉండును.
4. सोना बहुत महँगा है। …………………………………………
उत्तर:
सोना बहुत महँगा है। బంగారము చాలా పిరుము.
5. बड़ों को प्रणाम करना चाहिए। …………………………………………
उत्तर:
बड़ों को प्रणाम करना चाहिए। పెద్దలకు నమస్కరించవలెను.
व्याकरणांश
अ) परिभाषा :
किसी व्यक्ति, स्थान, गुण या वस्तु के नाम को “संज्ञा” कहते हैं।
(ఎవరైనా ఒక వ్యక్తి, స్థానము, గుణము లేదా వస్తువు పేర్లను నామవాచకము (సంజ్ఞ) అని అందురు.)
उदाहरण : मोहन, लड़का, दिल्ली, पानी, मेज़, धर्म आदि।
आ) निम्न लिखित वाक्यों में संज्ञा शब्दों को पहचानकर लिखिए।
1. सब धर्म अच्छे होते हैं।
उत्तर:
धर्म
2. मैदान में घोड़ा है।
उत्तर:
मैदान, घोडा
3. दीपा गाती है।
उत्तर:
दीपा
4. वे विजयवाडा में रहते हैं।
उत्तर:
विजयवाडा
5. ‘हिंदी” सरल भाषा है।
उत्तर:
हिंदी, भाषा

इ) नीचे दिये गये वाक्यों में संज्ञा शब्दों को रेखांकित कीजिए।
1. वह जंगल में लकड़ियाँ काटता था।
उत्तर:
जंगल, लकड़ियाँ
2. नदी की देवी जल से बाहर आयी।
उत्तर:
नदी, देवी, जल
3. यह मेरी कुल्हाड़ी नहीं है।
उत्तर:
कुल्हाड़ी
4. एक लकड़हारा वन में गया।
उत्तर:
लकडहारा, वन
5. देवी को उस पर दया आयी।
उत्तर:
देवी, दया
अध्यापकों के लिए सूचना : ఉపాధ్యాయులకు సూచన :
ईमानदारी से संबंधित कुछ घटनाओं का वर्णन कीजिए।
उत्तर:
एक घटना :
एक बार मेरा दोस्त दिल्ली गया। उसके पास एक लाख रुपये थे। जिन्हें वह अपने पिता के इलाज के लिए लेकर जा रहा था। वह रेलगाडी में अपना पर्स खो दिया। अस्पताल पहुंचने पर उसने अपनी जेब देखी तो उसमें पर्स नहीं था। उसके चेहरे की हवाएँ उडने लगी।
इतने में एक व्यक्ति वहाँ पहुँचा। उसने मेरे दोस्त का पर्स लौटाते हुए कहा कि उसे यह पर्स रेलगाड़ी में पड़ा मिला था। मेरे दोस्त के यह पूछने पर कहा कि उसे यहाँ का पता किसने दिया तो उसने बताया था कि उसके पर्स में अस्पताल का नाम तथा डॉक्टर द्वारा लिखी गयी दवाइयों की पर्ची को पढ़कर वह यहाँ तक पहुंचा है। मेरा दोस्त उस अनजान व्यक्ति की ईमानदारी को आज भी याद करता है।
एक और घटना :
यह घटना तेलंगाणा की राजधानी हैदराबाद की है। बीते बुधवार को बाईस वर्षीय गोपाल अपने खाते में मौजूद कुल एक लाख रुपये में से हजार रुपये निकालने स्टेट बैंक आफ़ हैदराबाद के एक ए.टी.एम.पर गया। पैसे निकालने के क्रम में मशीन के किनारे का एक दरवाज़ा खुल गया और उसमें से सारे नोट बाहर गिर गए। वहाँ न कोई सुरक्षा गार्ड तैनात था न ही सी.सी.टी.वी कैमरा लगा था। यानी चुपचाप सुरक्षित तरीके ढेर सारी रकम ले जाने के लिए गोपाल के सामने पूरा मौका था। लेकिन उसके भीतर पल भर के लिए भी ऐसा ख्याल नहीं आया, और उसने बाहर खडे हुए अपने साथियों से सुरक्षा गार्ड को खोजने के लिए कहा। गार्ड के न मिलने पर पुलिस को फोन करके सारी स्थिति बताई। इतने सारे रुपये देखकर न गोपाल के भीतर लालच नहीं आया, बल्कि उसके बेरोजगार दोस्त भी उसे कुछ गलत करने के लिए उकसाने के बजाय उसकी ईमानदारी में सहभागी बने। यह पुलीस और सबसे ज्यादा उस बैंक के लिए भी राहत की बात थी। अंदाज़ा लगाया जा सकता है कि इन युवकों ने इससे उलट व्यवहार किया होता तो बैंक और उसके कर्मचारी की लापरवाही का अंजाम क्या हो सकता था। हैदराबाद पुलीस ने उचित ही गोपाल को सम्मानित करने का फैसला किया है।
पाठ का सारांश
एक लकड़हारे की कुल्हाड़ी नदी में गिर गई। नदी की देवी ने उसे सोने और चाँदी की कुल्हाड़ियाँ दिखाई। लेकिन उसने ईमानदारी से अपनी कुल्हाड़ी ही माँगी। इससे उसे तीनों कुल्हाड़ियाँ ईनाम के रूप में मिलीं। इससे यह शिक्षा मिलती है कि ईमानदारी का फल मीठा होता है।
పాఠ్య సారాంశం
ఒక కట్టెలు నరుకువాని గొడ్డలి నదిలో పడిపోయినది. నదీ దేవి అతనికి బంగారపు మరియు వెండి గొడ్డళ్ళు చూపినది. కానీ అతడు నిజాయితీతో తన గొడ్డలినే అడిగెను. అందువలన అతనికి బహుమతిగా మూడు గొడ్డళ్ళు లభించినవి. దీని నుండి మనకు నిజాయితీ ఫలితము తీయగా ఉంటుందన్న పాఠం లభించుచున్నది.
Summary
A woodcutter’s axe fell into a river. The river goddess showed him golden and silver axes. But he asked the goddess honestly for his own axe. Because of this, he was rewarded with three axes. From this, we learn a moral that the result of honesty would be sweet.
व्याकरणांश (వ్యాకరణాంశాలు)
लिंग बदलिए (లింగములను మార్చండి)
लड़का – लड़की
देवी – देव
भगवान – भगवती
चाचा – चाची
पुत्र – पुत्री
पति – पत्नी
आचार्य – आचार्या
सुनार – सुनारिन
श्रीमान – श्रीमती
अध्यापक – अध्यापिका
पोता – पोती
ग्वाला – ग्वालिन
अध्यक्ष- अध्यक्षा
दूल्हा – दुल्हन
साला – साली
वचन बदलिए (వచనములను మార్చండి)
फल – फल
सेवा – सेवाएँ
गुण – गुण
मार्ग – मार्ग
सीख – सीख
नदी – नदियाँ
लकडी – लकड़ियाँ
कुल्हाडी – कुल्हाड़ियाँ
खुशी – खुशियाँ
ईनाम – ईनाम
विलोम शब्द (వ్యతిరేక పదములు)
दया × निर्दया
विनय × अविनय
उपकार × अपकार
परोपकार × अपकार
नैतिक × अनैतिक
गुण × अगुण
ईमानदार × बेईमान
सही × गलत
जीवन × मरण
महान × अल्प/तुच्छ
बेचना × खरीदना
रोना × हँसना
आधार × निराधार
अंदर × बाहर
खुश × दुःख
मीठा × कडुवा
खुशी × दुःखी

शब्दार्थ (అర్థాలు) (Meanings)
जंगल = वन, అడవి, forest
मिठा = मधुर, తీయని, sweet
लकड़हारा = लकड़ियाँ काटनेवाला, కట్టెలు నరుకువాడు, wood cutter
नदी = सरिता, నది, river
ईमानदारी = सच्चाई, నిజాయితీ, honesty
सीख = नीति, నీతి, morality
चाँदी = रजत, వెండి, silver
सोना = कनक, బంగారం, gold
किनारा = तट, ఒడ్డు, bank
दिन = दिवस, రోజు, day
जल = पानी, నీరు, water
दया = कृपा, దయ, kindness
खुश = संतोष, సంతోషము, happiness
प्रणाम = नमस्कार, నమస్కారం, salutation
श्रुत लेख : శ్రుతలేఖనము : Dietations
अध्यापक या अध्यापिका निम्न लिखित शब्दों को श्रुत लेख के रूप में लिखवायें। छात्र अपनी-अपनी नोट पुस्तकों में लिखेंगे। अध्यापक या अध्यापिका इन्हें जाँचे।
ఉపాధ్యాయుడు లేదా ఉపాధ్యాయిని క్రింద వ్రాయబడిన శబ్దములను శ్రుతలేఖనంగా డిక్లేట్ చేయును. విద్యార్థులు వారి వారి నోట్ పుస్తకాలలో వ్రాసెదరు. ఉపాధ్యాయుడు లేదా ఉపాధ్యాయిని వాటిని దిద్దెదరు.
![]()
![]()

![]()


![]()

![]()