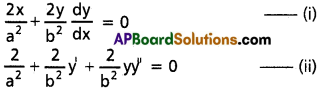Mahesh

Students get through AP Inter 2nd Year Physics Important Questions 7th Lesson Moving Charges and Magnetism which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 7th Lesson Moving Charges and Magnetism

Very Short Answer Questions

Question 1.
What is the importance of Oersted’s experiment? [T.S. Mar. 17]
Answer:
The importance of Oersted’s experiment is every current-carrying conductor produces a magnetic field around it which is perpendicular to the current-carrying conductor.

Question 2.
State Ampere’s law and Biot-Savart’s law.
Answer:
Ampere’s law : The line integral of the intensity of magnetic induction around a closed path is equal to g0 times the total current enclosed in it.
∴ \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} l\) = μ₀ i.
Biot – Savart’s laws : Biot – Savart’s law states that the intensity of magnetic induction (dB) due to a small element is directly proportional to the
i) current (i)
ii) length of the element (dZ)
iii) sine angle between radius vector (r) and dl and inversely proportional to the square of the point from current element.
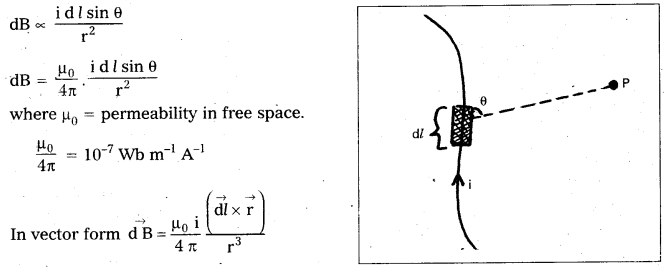
∴dB ∝ \(\frac{\mathrm{i} \mathrm{dl} \sin \theta}{\mathrm{r}^2}\)
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{i} \mathrm{d} l \sin \theta}{\mathrm{r}^2}\)

Question 3.
Write the expression for the magnetic induction at any point on the axis of a circular current-carrying coil. Hence, obtain an expression for the magnetic induction at the centre of the circular coil.
Answer:

1. Intensity of magnetic induction field on the axis of the circular coil B = \(\frac{\mu_0 \mathrm{ni} \mathrm{r}^2}{2\left(\mathrm{r}^2+\mathrm{x}^2\right)^{3 / 2}}\)
2. At the centre of the coil B = \(\frac{\mu_0 \mathrm{ni}}{2 \mathrm{r}}\)

Question 4.
A circular coil of radius T having N turns carries a current “i”. What is its magnetic moment ?
Answer:
Magnetic moment (M) = N i A
M = N i (πr²) (∵ A = πr²)
∴ M = π N i r²

Question 5.
What is the force on a conductor of length L carrying a current “i” placed in a magnetic field of induction B ? When does it become maximum ?
Answer:

1. Force on a conductor (F) = B i L sinθ
2. If θ = 90°,F_Max = BiL
   i.e., the direction of current and magnetic field are perpendicular to,each other, then force is maximum.

Question 6.
What is the force on a charged particle of charge “q” moving with a velocity “v” in a uniform magnetic field of induction B ? When does it become maximum ?
Answer:

1. Force on a charged particle (F) = B q v sin θ.
2. If θ = 90°, F_Max = B q v.

Question 7.
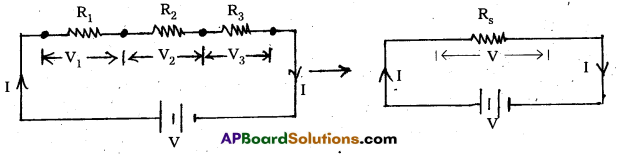
Distinguish between ammeter and voltmeter. [A.P. Mar. 17; A.P. Mar. 15]
Answer:
Ammeter

1. It is used to measure current.
2. Resistance of an ideal ammeter is zero.
3. It is connected in series in the circuits.

Voltmeter

1. It is used to measure RD between two points.
2. Resistance of ideal voltmeter is infinity.
3. It is connected in parallel in the circuits.

Question 8.
What is the principle of a moving coil galvanometer ?
Answer:
Moving coil galvanometer is based on the fact that when a current carrying coil is placed in a uniform magnetic field, it experiences a torque.
∴ current in the coil (i) ∝ deflecting angle (θ).

Question 9.
What is the smallest value of current that can be measured with a moving coil galvanometer ?
Answer:
Moving coil galvanometer is sensitive galvanometer, it is used to measure very small current upto 10^-9 A.

Question 10.
How do you convert a moving coil galvanometer into an ammeter ?
Answer:
A small resistance is connected in parallel to the moving coil galvanometer, then it converts to ammeter.

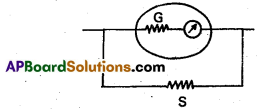
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)

Question 11.
How do you convert a moving coil galvanometer into a voltmeter ? [T.S. Mar. 16, 15, 14; A.P. Mar. 16]
Answer:
A high resistance is connected in series to the moving coil galvanometer, then it converts to voltmeter.

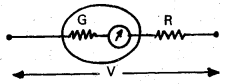
R = \(\frac{\mathrm{v}}{\mathrm{i}_g}\) – G

Question 12.
What is the relation between the permittivity of free space e₀, the permeability of free space m₀ and the speed of light In vaccum?
Answer:
Speed of light in vaccum (C) = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\)
Here μ₀ = m₀ = permeability in vaccum
ε₀ = permittivity in vaccum.

Question 13.
A current carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic Held be set up in such a manner that the loop turns about the vertical axis ?
Answer:
Torque (τ) = \(\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}=\mathrm{i} \overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\) (M = n i A)
where i is current, \(\overrightarrow{\mathrm{A}}\) is area vector, \(\overrightarrow{\mathrm{B}}\) is magnetic field. Area vector \(\overrightarrow{\mathrm{A}}\) acts normal to the loop, so torque \(\vec{\tau}\) cannot act along the vertical axis. The magnetic field is not set up to turn the loop around itself.

Question 14.
A current carrying circular loop is placed in a uniform external magnetic field. If the loop is free to turn, what is its orientation when it achieves stable equilibrium?
Answer:
The plane of the loop is perpendicular to the direction of magnetic field because the torque on the loop in this orientation is zero.

Question 15.
A wire loop of irregular shape carrying current is placed in an external magnetic field. If the wire is flexible, what shape will the loop change to ? Why ?
Answer:
For a given perimeter, a circle has maximum area among all geometrical shapes. So to maximise the magnetic flux through it will assume a circular shape with its plane normal to the field.

Question 16.
Consider a tightly wound 100 turn coil of radius 10 cm, carrying a current of 1 A. What is the magnitude of the magnetic field at the centre of the coil ?
Solution:
Since the coil is tightly wound we may take each circular element to have the same radius R = 10 cm = 0.1 m. The number of turns N = 100. The magnitude of the magnetic field is (From Eq.),
B₀ = \(\frac{\mu_0 \mathrm{I}}{2 \mathrm{R}} \hat{\mathrm{i}}\)
B = \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}=\frac{4 \pi \times 10^{-7} \times 10^2 \times 1}{2 \times 10^{-1}}\) = 2π × 10^-4 = 6.28 × 10^-4 T

Question 17.
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. What is the magnitude of the magnetic field inside the solenoid ?
Solution:
The number of turns per unit length is,
n = \(\frac{500}{0.5}\) = 1000 turns / m
The length l = 0.5m and radius r = 0.01 m. Thus, l/a = 50 i.e., l >> a.
Hence, we can use the long solenoid formula, namely, Eq. (B = μ₀nI)
B = μ₀ n I
= 4π × 10^-7 × 10³ × 5 = 6.28 × 10^-3 T

Question 18.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil ?
Solution:
Here, n = 100, r = 8cm = 8 × 10^-2 m and I = 0.40 A
The magnetic field B at the centre
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{In}}{\mathrm{r}}=\frac{10^{-7} \times 2 \times 3.14 \times 0.4 \times 100}{8 \times 10^{-2}}\) = 3.1 × 10^-4 T
The direction of magnetic field depends on the direction of current if the direction of current is anticlockwise. According to Maxwell’s right hand rule, the direction of magnetic field at the centre of coil will be perpendicular outwards to the plane of paper.

Question 19.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8A and making an angle of 30° with the direction of a uniform magnetic field of 0.15 T ?
Solution:
According to the question
I = 8 A, 6 = 30°, B = 0,15 T, l = 1 m

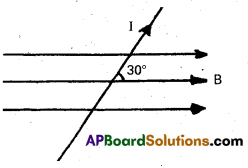
The magnitude of magnetic force
f = I (l × B) = I l B sin θ
= 8 × 1 × 0.15 × sin 30°
= \(\frac{8 \times 0.15}{2}\) = 4 × 0.15 = 0.6 N/m

Short Answer Questions

Question 1.
State and explain Biot-Savart’s law.
Answer:
Consider a very small element of length dl of a conductor carrying current (i). Magnetic induction due to small element at a point P distance r from the element.
Magnetic induction (dB) is directly proportional to i) current (i) ii) Length of the element (di) iii) sine angle between r and dl and inversely proportional to the square of the distance from small element to point P.

Question 2.
State and explain Ampere’s law.
Answer:
Ampere’s law : The line integral of the intensity of magnetic induction field around closed path is equal to μ₀ times the net current (i) enclosed by the path.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i
Proof: Consider a long straight conductor carrying current i as shown in figure. Magnetic induction at a distance r from the conductor is given by

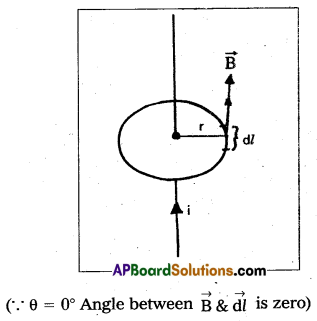
B = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) (From Biot-Savart’s law)
The value of B is same at all points on the circle.
\(\oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d} l}=\oint \mathrm{B} \mathrm{d} l \cos \theta\)
= \(\mathrm{B} \oint \mathrm{d} l\) = B × 2π
= \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) × 2πr
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i
This proves Ampere’s circuital laws.

Question 3.
Find the magnetic induction due to a long current carrying conductor.
Answer:
Consider a long straight conductor carrying a current i. Let P be a point at a distance r from the conductor. Let r be the radius of the circle passing through point p.

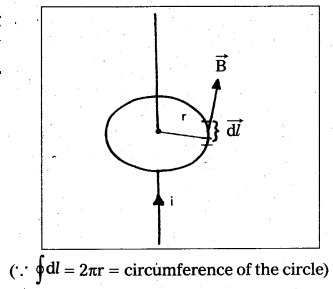
Magnetic induction is same at all points on the circle. Consider a small element of length dl.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}=\oint \mathrm{Bd} l \cos \theta\)
Angle between B and dl is zero i.e. θ = 0
= \(\mathrm{B} \oint \mathrm{d} l\)
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = B (2πr) ………………. (1)
According to Ampere’s laws
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i ……………. (2)
From equations (1) and (2), B (2πr) = μ₀i
= \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\)

Question 4.
Derive an expression for the magnetic induction at the centre of a current carrying circular coil using Biot-Savart’s law.
Answer:
Consider a circular coil of radius r and carry a current! Consider a small element ‘dl’. Let O is the centre of the coil. By using Biot – Savart’s law,

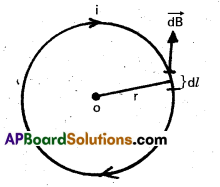
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
Here angle \(\overrightarrow{\mathrm{d} l}\) and \(\overrightarrow{\mathrm{r}}\) is 90° (i.e., θ = 90°)
dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{idl}}{\mathrm{r}^2}\) …………… (1)
As the field due to all elements of the circular loop have the same direction. The resultant magnetic field can be obtained by integrating equation (1)

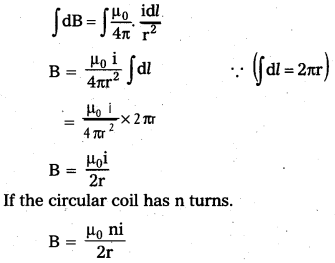
Question 5.
Derive an expression for the magnetic induction of a point on the axis of a current carrying circular coil using Biot-Savart’s law.
Answer:

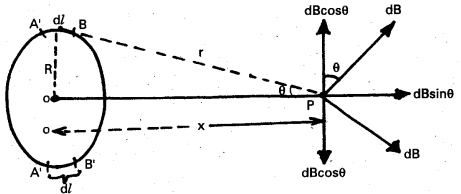
Consider a circular coil of radius R and carrying a current i. Let P is a point on the axis at a distance x from the centre O. Let r be the distance of small element (dl) from P.
From Biot – savart’s law
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l}{\mathrm{r}^2}\) ……………….. (1)
(∵ θ = 90° Angle between \(\overrightarrow{\mathrm{d} l}\) and \(\overrightarrow{\mathrm{r}}\))
dB can be resolved into two components dB cosθ and dB sinθ. If we consider another This also resolved into dB cosθ and dB sinθ.
The components along the axis will add up and perpendicular to the axis will cancel.
∴ Resultant magnetic induction at P is

Question 6.
Explain how crossed E and B fields serve as a velocity selector.
Answer:
When a charged particle q moving with a velocity v in presence of both electric and magnetic fields.
The force experienced due to electric field F_E = q\(\overrightarrow{\mathrm{E}}\)
The force experienced due to magnetic field F_B = q \((\vec{v} \times \vec{B})\)
Consider electric and magnetic fields are perpendicular to each other and also perpendicular to the velocity of the particle.

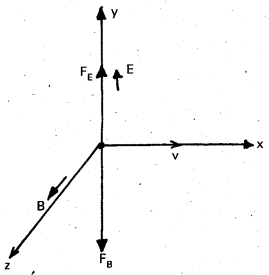
E = E\(\hat{\mathrm{j}}\),B = B\(\hat{\mathrm{k}}\), v = υ\(\hat{\mathrm{i}}\)
F_E = qE\(\hat{\mathrm{j}}\), F_B =q(v\(\hat{\mathrm{i}}\) × B\(\hat{\mathrm{k}}\)) = – qvB\(\hat{\mathrm{j}}\)
∴ F = F_E + F_B
F = q (E – υB)\(\hat{\mathrm{j}}\)
Thus electric and magnetic forces are in opposite directions.
We adjust E and B such that, the forces are equal
F_E = F_B
qE = q υ B
υ = \(\frac{E}{B}\)
This condition can be used to selefct charged particles of a particular velocity. The crossed field E and B serve as a velocity selector.

Question 7.
What are the basic components of a cyclotron ? Mention its uses ?
Answer:
Cyclotron is a device used to accelerate positively charged particles like protons, α – particles, deutrons etc.

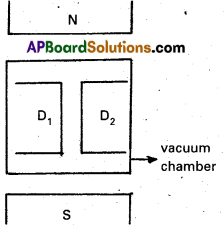
Cyclotron mainly consists of

1. Two hollow D-shaped metallic chambers D₁ and D₂
2. High-frequency oscillator
3. Strong electro magnet
4. Vaccum chamber.

Uses of cyclotron :

1. It is used for producing radioactive material for medical purposes i.e. diagnostics and treatment of chronic diseases. “
2. It is used to improve the quality of solids by adding ions.
3. It is used to synthesise fresh substances.
4. It is used to bombard the atoms with highly accelerated particles to study the nuclear reactions.

Question 8.
Derive an expression for the magnetic dipole moment of a revolving electron. [A.P. Mar. 16]
Solution:
Consider an electron revolving in a circular orbit of radius r with speed v and frequency υ. If the electron cross a point P on the circle in every revolution, then distance travelled by electron to complete one revolution = 2πr.
No. of revolutions in one second (υ) = \(\frac{\mathrm{v}}{2 \pi \mathrm{r}}\)
The electric current (i) = \(\frac{\text { Charge }}{\text { Time }}\) = charge × frequency
i = e × \(\frac{\mathrm{v}}{2 \pi \mathrm{r}}\)
∴ Magentic dipole moment (M) = iA (∵ N = 1)
M = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}}\) × πr² (∵ A = πr²)
M = \(\frac{\mathrm{evr}}{2}\)

Long Answer Questions

Question 1.
Deduce an expression for the force on a current carrying conductor placed in a magnetic field. Derive an expression for the force per unit length between two parallel current-carrying conductors.
Answer:
Expression for the Force acting on a current carrying conductor :
Consider a straight conductor (wire) of length T, area of cross section ’A1, carrying a current T, which is placed in a uniform magnetic field of induction ’B’ as shown in fig.

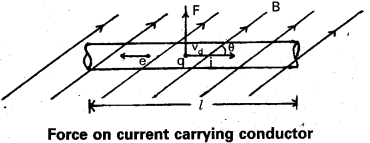
We know the external magnetic field exerts a force on the conductor.
The electrons in effect move with an average velocity called drift velocity ‘V_d‘. The direction of conventional current will be opposite to the direction of drift velocity.

Let us assume that the current flows through the conductor from left ‘B’ in the plane of the paper makes an angle ‘θ’ with the direction of current ‘i’ as shown in fig.
If F’ is the force acting on the charge ‘q’ in B.
∴ F’ = q V_d B sin θ
If ‘n’ represents number of moving electrons per unit volume (∵ n = \(\frac{N}{V}\))
∴ Current i = nq V_d A
If ‘N’ is the number of electrons in the length ‘l’
N = nlA
Total force on conductor F = F’.N (∵N = nV = n × A × l)
= (q V_d B sin θ) (nlA)
(nqV_dA) (lB sin θ)
∴ F = ilB sin θ
Case (i) : If θ = 0°, F_Min = 0
Case (ii) : If θ = 90°, F_Max = Bil
Expression for the force between two Parallel conductors carrying conductors :
Consider two straight parallel conductors AB and ‘CD’ carrying currents ‘ix’ and ‘i2’ and which are separated by a distance ‘r’ as shown in fig.

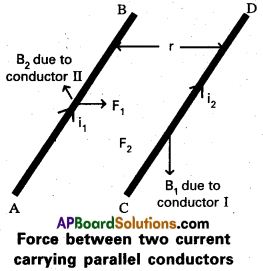
If B₁ and B₂ are magnetic inductions produced by the current carrying conductors AB and CD. Magnetic induction Bx at a distance ‘r’ from the conductor ‘AB’ can be written as B₁ = \(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\)
If ‘F’ is forœ acting on ‘CD’ clue to magnetic induction ‘B₁‘ then
F_CD = i₂lB₁
Where l = length of the conductor
F_CD = i₂l \(\left(\frac{\mu_0 i_1}{2 \pi \mathrm{r}}\right)=\frac{\mu_0 i_1 i_2 l}{2 \pi r}\) ……………. (1)
The direction of the force can be determined by using Flemings left hand rule.
Similarly we can find the force acting on the A conductor AB due to magnetic induction B₂.
F_AB = i₁lB₂
∴ F_AB = i₁l \(\left(\frac{\mu_0 i_2}{2 \pi r}\right)\) ………….. (2) [∵B₂ = \(\left(\frac{\mu_0 i_2}{2 \pi r}\right)\)]
From the equations (1) and (2) F_AB = F_CD = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
∴ Force between two parallel, straight conductors carrying currents,
F = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
Force per unit length \(\frac{\mathrm{F}}{l}=\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\)

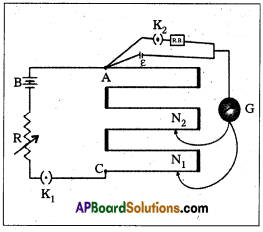
Question 2.
Obtain an expression for the torque on a current carrying loop placed in a uniform ‘ magnetic field. Describe the construction and working of a moving coil galvanometer.
Answer:
Torque acting on a coil carrying a current kept in a uniform magnetic field : Let a rectangular current loop ABCD of length l = AB = CD and width b = AD – BC carrying a current “i” be suspended in a magnetic field of flux density B.
The normal ON drawn to the plane of the coil makes an angle ‘θ’ with the magnetic field B.

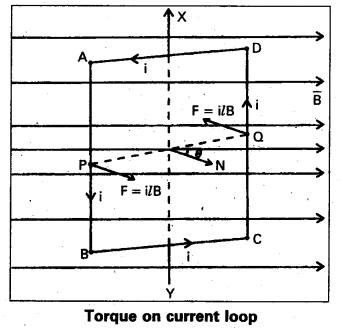
Force on arm AD = \(\mathrm{i} \overline{\mathrm{b}} \times \overline{\mathrm{B}}\) acting upwards along the axis of suspension
Force on arm BC = \(\mathrm{i} \overline{\mathrm{b}} \times \overline{\mathrm{B}}\) acting downwards along the axis of suspension
Hence these two forces cancel.

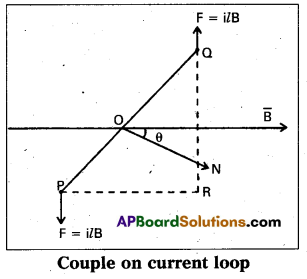
Force on arm AB = ilB acting perpendicular to the plane as shown.
Force on arm CD = ilB acting perpendicular to the plane as shown.
These two forces constitute a couple on the coil.
Moment of the couple = (Force) × (Perpendicular distance between the forces) = ilB (PQ sin θ)
Torque = ilB b sinθ
But l × b = Area of coil
∴ Torque = iAB sin θ
If the loop has ‘n’ turns the torque on the coil
τ = n i AB sin θ
If ‘Φ’ is the deflection of the coil, that is the angle between the plane of the coil and magnetic field B
τ = n i AB cos Φ

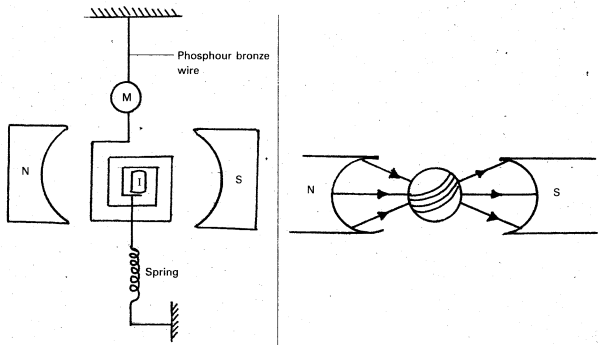
Moving coil galvanometer:
Principle : When a current carrying coil is placed in the uniform magnetic field, it experiences a torque.
Construction :

1. It consists of a coil wound on a non metallic frame.
2. A rectangular coil is suspended between two concave shaped magnetic poles with the help of phosphour Bronze wire.
3. The lower portion of the coil is connected to a spring.
4. A small plane mirror M is fixed to the phosphour Bronze wire to measure the deflection of the coil.
5. A small soft iron cylinder is placed within the coil without touching the coil. The soft iron cylinder increases the induction field strength.
6. The concave shaped magnetic poles render the field radial. So maximum torque acting on it.
7. The whole of the apparatus is kept inside a brass case provided with a glass window.
   

Theory:
Consider a rectangular coil of length l and breadth b and carrying current i suspended in the induction field strength B.
Deflecting torque (τ) = B i A N …………….. (5)
where A = Area of the coil
N = Total number of turns.
The restoring torque developed in the suspension = C θ …………….. (2)
Where C is the couple per unit twist and 9 is the deflection made by the coil.
When the coil is in equilibrium position
Deflecting torque = Restoring torque
B i A N = Cθ
i = \(\left(\frac{\mathrm{C}}{\mathrm{BAN}}\right) \theta\)
Where K = \(\frac{\mathrm{C}}{\mathrm{BAN}}\) = Galvanometer constant.
i = K θ ……………… (3)
i ∝ θ
Thus deflection of the coil is directly proportional to the current flowing through it. The deflection in the coil is measured using lamp and scale arrangement.

Question 3.
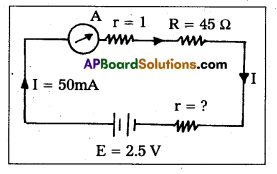
How can a galvanometer be converted to an ammeter ? Why is the parallel resistance smaller that the galvanometer resistance ? A moving coil galvanometer can measure a current of 10-6 A. What is the resistance of the shunt required if it is to measure 1A ?
Answer:
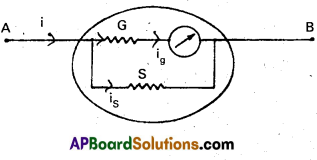
Conversion of Galvanometer into Ammeter :
Galvanometer is converted into an ammeter by connecting a suitable resistance is parallel to it:

This arrangement decreases the effective resistance.

Ammeter is used for measuring the current in an electric circuit and it is connected in series in circuit. The inclusion of the ammeter in the circuit should not alter the current or total resistance of the circuit so it has very low resistance.

The resistance of An ideal Ammeter is zero.
Let G and S be the Galvanometer and shunt resistances respectively.
Let ‘i’ be the total current, divided at A into i_g and i_s as shown in fig.
From Kirchhoffs I^st law, i = i_g + i_s
As ‘G’ and ‘S’ are parallel P.D. across
Galvanometer = P.D. across shunt
i_gG = i_sS
S = \(\frac{\mathrm{i}_{\mathrm{g}}}{\mathrm{i}_{\mathrm{s}}} \mathrm{G}\)
= \(\frac{\mathrm{Gi}_{\mathrm{g}}}{\mathrm{i}-\mathrm{i}_{\mathrm{g}}}\) [∵ i_s = i – i_g]
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)
If \(\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}\) = n ⇒ i_g = \(\frac{\mathrm{i}}{\mathrm{n}}\)
∴ The current flowing through the galvanometer be \(\left(\frac{1}{n}\right)^{\text {th }}\) of total current.
∴ S = \(\frac{\mathrm{G}}{\mathrm{n}-1}\)
If ‘R’ is the effective resistance between points ‘A’ and ‘B’ then

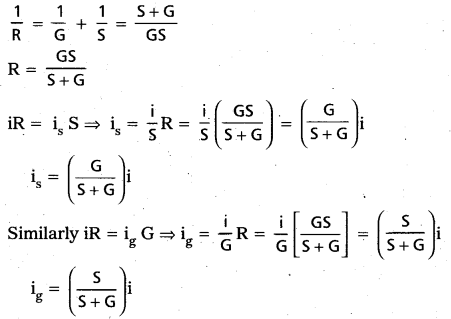
Hence current through galvanometer is proportional to the total current. Since ‘S’ is small major portion of the current flows through it and a small portion of current flows through G. So shunt protects the galvanometer from high currents. Parallel resistance is smaller than Galvanometer resistance because to protect the Galvanometer from high (large) current (or) to pass. Large currents through shunt and small current passes through the galvanometer.
Solution for the problem : Current in the circuit i = 1A;
Current through the galvanometer, i_g = 10^-6A
Shunt resistance, S = \(\frac{G}{n-1}=\frac{G}{\frac{i}{i_g}-1}=\frac{G}{10^6-1}=\frac{G}{99.999} \Omega\)

Question 4.
How can a galvanometer be converted to a voltmeter ? Why is the series resistance greater that the galvanometer resistance ? A moving coil galvanometer of resistance 5Ω can measure a current of 15mA. What is the series resistance required if it is to measure 1.5V ?
Answer:
Conversion of Galvanometer into Voltmeter : A galvanometer is converted into voltmeter by connecting a high resistance (R) in series with it. Voltmeter is used to measure the P.D. between any two points in circuit and it is connected in parallel to the component of the circuit.

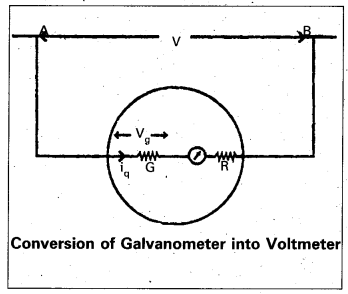
Let ‘V’ be the potential difference to be measured between the points ‘A’ and ‘B’.
∴ V = (R + G) i_g [∴ V = iR]
i_g = Current passing through the galvanometer
\(\frac{\mathrm{V}}{\mathrm{i}_{\mathrm{g}}}\) = R + G
R = \(\frac{\mathrm{V}}{\mathrm{i}_{\mathrm{g}}}\) – G ……………. (1)
The value of ‘R’ can be calculated by using the above formula. If V_g is the maximum P.D. across the galvanometer then V_g = i_g G
∴ i_g = \(\frac{V_g}{G}\) …………….. (2)
Substitute ‘i_g‘ in Equ (1)
R = \(\frac{V_G}{V_g}\) – G = \(\left(\frac{V}{V_g}-1\right)\)
If \(\frac{V}{V_g}\) = n ⇒ R = G(n – 1)
Note : n = \(\frac{V}{V_g}\) is the ratio of maximum voltage to be measured to the maximum voltage across the galvanometer.

Series resistance is greater than galvanometer resistance because the current in external resistance and potential difference will be decreased and to increase the resistance of the galvanometer.
Solution for the problem:

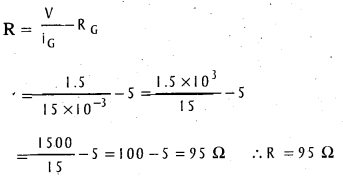
Problems

Question 1.
Two long and parallel straight wires A and B canying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Solution:
Given I₁ = 8A, I₂ = 5A and r = 4 cm = 0.4m
F = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}_1 \mathrm{I}_2}{\mathrm{r}}=\frac{10^{-7} \times 2 \times 8 \times 5}{0.04}\) = 2 × 10^-4 N
The force on A of length 10 cm is F¹ = F × 0.1 (∵ 1 m = 100 cm)
F¹ = 2 × 10^-4 × 0.1
F¹ = 2 × 10^-5 N.

Question 2.
A current of 10A passes through two very long wires held parallel to each other and separated by a distance of 1m. What is the force per unit length between them ? [A.P. & T.S. Mar. 15]
Answer:
i₁ = i₂ = 10A
r = 1m
\(\frac{\mathrm{F}}{l}=\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\)
= \(\frac{4 \pi \times 10^{-7} \times 10 \times 10}{2 \pi \times 1}\)
\(\frac{\mathrm{F}}{l}\) = 2 × 10^-5 Nm^-1.

Question 3.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B (Fig.). What is the magnitude of the magnetic field ?

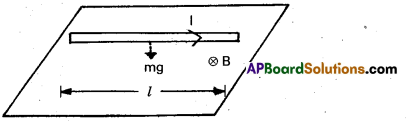
Solution:
From Eq F = Il × B we find that there is an upward force F, of magnitude IlB,. For mid-air suspension, this must be balanced by the force due to gravity.
m g = I lB mg
B = \(\frac{\mathrm{mg}}{\mathrm{I} l}\)
= \(\frac{0.2 \times 9.8}{2 \times 1.5}\) = 0.65 T
Note that it would have been sufficient to specify mll, the mass per unit length of the wire. The earth’s magnetic field is approximately 4 × 10^-5 T and we have ignored it.

Question 4.
The horizontal component of the earth’s magnetic field at a certain place is 3.0 × 10^-5 T and the direction of the field is from the geographic south to the geographic north. A very long straight conductor is carrying a steady current of 1 A. What is the force per unit length on it when it is placed on a horizontal table and the direction of the current is
(a) east to west;
(b) south to north ?
Solution:
F = Il × B
F = IlB sin θ
The force per unit length is
f = F/l = IB sinθ
a) When the current is flowing from east to west,
θ = 90°
Hence,
f = IB
= 1 × 3 × 10^-5 = 3 × 10^-5 Nm^-1
This is larger than the value 2 × 10^-7 Nm^-1 quoted in the definition of the ampere. Hence it is important to eliminate the effect of the earth’s magnetic field and other stray fields while standardising the ampere.
The direction of the force is downwards. This direction may be obtained by the directional property of cross product of vectors.

b) When the current is flowing from south to north, .
θ = 0°
f = 0
Hence there is no force on the conductor.

Textual Examples

Question 1.
A straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal niagnetic field B (Fig.). What is the magnitude of the magnetic field ?

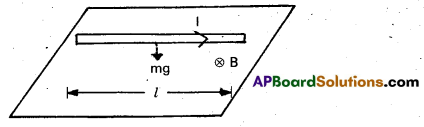
Solution:
From Eq F = Il × B we find that there is an upward force F, of magnitude IlB,. For mid-air suspension, this must be balanced by the force due to gravity, m g = I lB .
B = \(\frac{\mathrm{mg}}{\mathrm{I} l}\)
= \(\frac{0.2 \times 9.8}{2 \times 1.5}\) = 0.65 T
Note that it would have been sufficient to specify m/l, the mass per unit length of the wire. The earth’s magnetic field is approximately 4 × 10^-5 T and we have ignored it.

Question 2.
If the magnetic field is parallel to the positive y-axis and the charged particle is moving along the positive x-axis (Fig.), which way would the Lorentz force be for (a) an electron (negative charge), (b) a proton (positive charge).

Solution:
The velocity v of particle is along the x-axis, while B, the magnetic field is along the y-axis, so v × B is along the z-axis (screw rule or right-hand thumb rule). So, (a) for electron it will be along -z axis, (b) for a positive charge (proton) the force is along +z axis.

Question 3.
What is the radius of the path of ah electron (mass 9 × 10^-31 kg and charge 1.6 × 10^-19 C) moving at a speed of 3 × 10⁷ m/s in a magnetic field of 6 × 10^-4 T perpendicular to it ? What is its frequency ? Calculate its energy in keV. (1 eV = 1.6 × 10^-19 J).
Solution:
Using Eq. r = mυ/qb we find
r = mυ/(qB) = 9 × 10^-31 kg × 3 × 10⁷ m s^-1 / (1.6 × 10^-19 C × 6 × 10^-4 T)
= 26 × 10^-2 m = 26 cm
v = υ / (2 πr) = 2 × 10⁶ s^-1 = 2 × 10⁶ Hz = 2MHz.
E = (1/2)mυ² = (1/2) 9 × 10^-31 kg × 9 × 10¹⁴ m2/s = 40.5 × 10^-17 J
≈ 4 × 10^-16 J = 2.5 keV.

Question 4.
A cyclotron’s oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating protons ? If the radius of its does is 60 cm, what is the kinetic energy (in MeV) of the proton beam produced by the accelerator.
(e = 1.60 × 10^-19 C, m_p = 1.67 × 10^-27 kg, 1 MeV = 1.6 × 10^-13 J).
Solution:
The oscillator frequency should be same as proton’s cyclotron frequency.
Using Eqs. r = mυ/qb and ω = 2πυ = \(\frac{\mathrm{qB}}{\mathrm{M}}\) we have
B = 2π m υ/q = 6.3 × 1.67 × 10^-27 × 10⁷ / (1.6 × 10^-19) = 0.66 T
Final velocity of protons is
υ = r × 2π v = 0.6 m × 6.3 × 10⁷ = 3.78 × 10⁷ m/s.
E = 1/2 mv² = 1.67 × 10^-27 × 14.3 × 10¹⁴/ (2 × 1.6 × 10^-13) = 7 MeV

Question 5.
element ∆1 = ∆x\(\hat{\mathrm{i}}\) is placed at the origin and carries a large current I = 10 A (Fig.). Wat is the magnetic field on the y-axis at a distance of 0.5 m. ∆x = 1 cm.

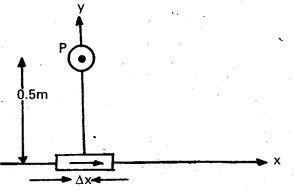
Solution:
|dB| = \(\frac{\mu_0}{4 \pi} \frac{I \mathrm{dl} \sin \theta}{\mathrm{r}^2}\)
dl = ∆x = 10^-2 m, I = 10 A, r = 0.5 m = y, μ₀/4π = 10^-7 \(\frac{\mathrm{Tm}}{\mathrm{A}}\)
θ = 90°; sin θ = 1
|dB| = \(\frac{10^{-7} \times 10 \times 10^{-2}}{25 \times 10^{-2}}\) = 4 × 10^-8 T
The direction of the field is in the +z-direction. This is so since,
dl × r = \(\Delta \mathrm{x} \hat{\mathrm{i}} \times \mathrm{y} \hat{\mathrm{j}}=\mathrm{y} \Delta \mathrm{x}(\hat{\mathrm{i}} \times \hat{\mathrm{j}}) \mathrm{y} \Delta \mathrm{x} \hat{\mathrm{k}}\)
We remind you of the following cyclic property of cross-products,
\(\hat{\mathrm{i}} \times \hat{\mathrm{j}}=\mathrm{k} ; \hat{\mathrm{j}} \times \hat{\mathrm{k}}=\hat{\mathrm{i}} ; \hat{\mathrm{k}} \times \hat{\mathrm{i}}=\hat{\mathrm{j}}\)
Note that the field is small in magnitude.

Question 6.
A straight wire carrying a current of 12 A is bent into a semi-circular arc of radius 2.0 cm as shown in Fig. Consider the magnetic field B at the centre of the arc. (a) What is the magnetic field due to the straight segments ? (b) In what way the contribution to B from the semicircle differs from that of a circular loop and in what way does it resemble ? (c) Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way as shown in Fig. (b) ?

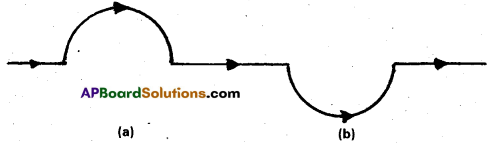
Solution:
a) dl and r for each element of the straight segments are parallel. Therefore, dl × r = 0. Straight segments do not contribute to |B|.

b) For all segments of the semicircular arc, dl × r are all parallel to each other (into the plane of the paper). All such contributions add up in magnitude. Hence direction of B for a semicircular arc is given by the right-hand rule and magnitude is half that of a circular loop. Thus B is 1.9 × 10^-4 T normal to the plane of the paper going into it.

c) Same magnitude of B but opposite in direction to that in (b).

Question 7.
Consider a tightly wound 100 turn coil of radius 10 cm, carrying a current of 1 A. What is the magnitude of the magnetic field at the centre of the coil?
Solution:
Since the coil is tightly wound we may take each circular element to have the same radius R = 10 cm = 0.1 m. The number of turns N = 100. The magnitude of the magnetic field is (From Eq.),
B₀ = \(\frac{\mu_0 \mathrm{I}}{2 \mathrm{R}} \hat{\mathrm{i}}\)
B = \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}=\frac{4 \pi \times 10^{-7} \times 10^2 \times 1}{2 \times 10^{-1}}\) = 2π × 10^-4 = 6.25 × 10^-4 T

Question 8.
Magnetic field due to a long current-carrying wire Oersted’s experiments showed that there is a magnetic field around a current-carrying wire. We determine the magnitude of magnetic field at some distance from a long striaght wire carrying a current I.
Solution:
The direction of the field is given by the right hand rule. The figure shows an element dl of the current-carrying wire. The point P, where the field is to be determined is at a perpendicular distance ‘S’ from the wire. The position vector of P from dl is r.

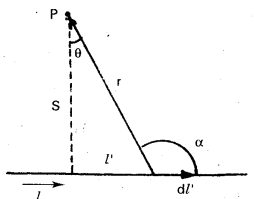
The magnitude dB of the magnetic field due to dl is given by Biot-Savart law to be

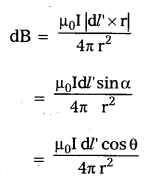
now from the figure S = r cosθ which gives l/r² = cos²θ/s²
and l’ = S tanθ which gives dl’ = S sec²θ dθ = S dθ/cos²θ
thus dB = \(\frac{\mu_0 I \cos \theta}{4 \pi S}\) dθ
we integrate this to get B at P If the wire is very long then the limits for 0 would be -π/2 to π/2
thus B = \(\frac{\mu_0 l}{2 \pi S}\) (emerging from the paper at P)

Question 9.
Find \(\oint\) B . dl for the paths shown in (a) and (b)

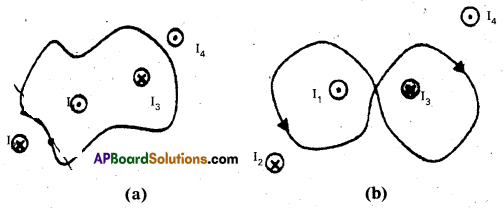
Solution:
a) Going around theKpath in the anticlockwise direction, I₁ is taken as positive while I₃ is negative. Currents I₂ and I₄ do not matter as they are NOT enclosed by the path.
\(\oint\) B . dl = μ₀(I₁ – I₃)
Note : Currents I₂ and I₄ create magnetic fields all around them and B due to them on any element of the path would be non-zero. However, the sum B.dZ due to them would be zero, b) Calculation of B. dl for the entire path can be broken up into two separate calculations, one covering all contributions from an anti-clockwise traversal around I₁ and the other covering all contributions from a clockwise traversal around I₃. Thus
\(\int_1 \mathrm{~B} . \mathrm{d} l\) = μ₀I₁ for all elements around I₁ traversed in an anti-clockwise direction
\(\int_2 \mathrm{~B} . \mathrm{d} l\) = μ₀I₃ for all elements around I₃ traversed in a clockwise direction; I₃ taken as positive because it is flowing into the plane. Thus the total \(\oint\) B.dl = μ₀ (I₁ – I₃)

Question 10.
Figure shows the circular cross-section of a long straight wire of radius a carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a (dashed inner circle) and r > a (dashed outer circle).

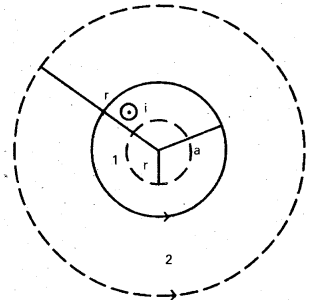
Solution:
a) Consider the case r > a. The Amperian loop, labelled 2, is a circle concentric with the cross-section. For this loop,
L = 2πr
I_e = Current enclosed by the loop = I
The result is the familiar expression for a long straight wire B(2πr) = μ₀I
B = \(\frac{\mu_0 I}{2 \pi \mathrm{r}}\) ……………… (1)
b) Consider the case r < a. The Amperian loop is a circle labelled 1 . For this loop, taking the radius of the circle to be r,
L = 2 π r
Now the current enclosed I_e is not I (because r < a), but is less than this value. Since the current distribution is uniform, the current enclosed is,

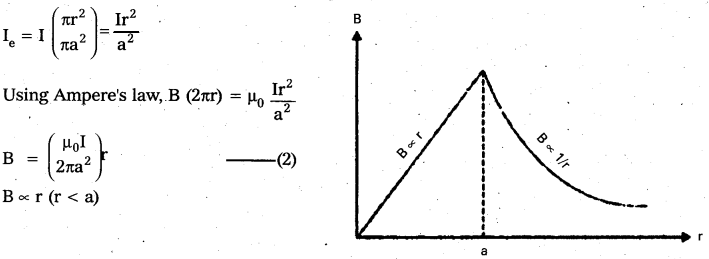
Figure shows a plot of the magnitude of B with distance r from the centre (axis) of the wire. The direction of the field is tangential to the respective circular loop (1 or 2) and given by the right-hand rule described earlier in this section.
This example possesses the required symmetry so that Ampere’s law can be applied readily.

Question 11.
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. What is the magnitude of the magnetic field inside the solenoid ?
Solution:
The number of turns per unit length is,
n = \(\frac{500}{0.5}\) = 1000 turns / m
The length l = 0.5m and radius r = 0.01 m. Thus, l/a = 50 i.e., l > >a.
Hence, we can use the long solenoid formula, namely, Eq. (B = μ₀nI)
B = μ₀ n I
= 4π × 10^-7 × 10³ × 5 = 6.28 × 10^-3 T

Question 12.
The horizontal componet of the earth’s magnetic field at a certain place is 3.0 × 10^-5 T and the direction of the field is from the geographic south to the geographic north. A very long straight conductor is carrying a steady current of 1A. What is the force per unit length on it when it is placed on a horizontal table and the direction of the current is
(a) east to west;
(b) south to north ?
Solution:
F = Il × B
F = IlB sin θ
The force per unit length is
f = F/l = IB sinθ
a) When the current is flowing from east to west,
θ = 90°
Hence,
f = IB
= 1 × 3 × 10^-5 = 3 × 10^-5 Nm^-1
This is larger than the value 2 × 10^-7 Nm^-1 quoted in the definition of the ampere. Hence it is important to eliminate the effect of the earth’s magnetic field and other stray fields while standardising the ampere.
The direction of the force is downwards. This direction may be obtained by the directional property of cross product of vectors.

b) When the current is flowing from south to north,
θ = 0°
f = 0
Hence there is no force on the conductor.

Question 13.
A 100 turn closely wound circular coil of radius 10 cm carries a current of 3.2A. (a) What is the field at the centre of the coil ? (b) What is the magnetic moment of this coil ?
The coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A uniform magnetic field of 2T in the horizontal direction exists such that initially the axis of the coil is in the direction of the field. The coil rotates through an angle of 90° under the influence of the magnetic field, (c) What are the magnitudes of the torques on the coil in the initial and final position ? (d) What is the angular speed acquired by the coil when it has rotated by 90° ? The moment of inertia of the coil is 0.1 kg m². [A.P. Mar. 19]
Solution:
a) From B = \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)
Here, N = 100; I = 3.2 A, and R = 0.1 m. Hence,
B = \(\frac{4 \pi \times 10^{-7} \times 10^2 \times 3.2}{2 \times 10^{-1}}=\frac{4 \times 10^{-5} \times 10}{2 \times 10^{-1}}\) (using π × 3.2 = 10)
= 2 × 10^-3 T
The direction is given by the right-hand thumb rule.

b) The magnetic moment is given by
m = N I A = N I π r² = 100 × 3.2 × 3.14 × 10^-2 = 10 A m²
The direction is once again given by the right hand thumb rule.

c) τ = |m × B|
= mBsin θ
Initially, θ = 0. Thus initial torque τ_i = 0. Finally, θ = π/2 (or 90°).
Thus, final torque τ_f = m B = 10 × 2 = 20 N m.

d) From Newton’s second law.
I\(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) = mBsin θ
where I is the moment of inertia of the coil. From chain rule,
\(\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d} \omega}{\mathrm{d} \theta} \frac{\mathrm{d} \theta}{\mathrm{dt}}=\frac{\mathrm{d} \omega}{\mathrm{d} \theta} \omega\)
Using this,
Iω dω = m B sinθ dθ
Integrating from θ = 0 to θ = π/2,
\(\mathrm{I} \int_0^{\omega \mathrm{I}} \omega \mathrm{d} \omega=\mathrm{mB} \int_0^{\pi / 2} \sin \theta d \theta\)
\(\mathrm{I} \frac{\omega_{\mathrm{I}}^2}{2}=-\left.\mathrm{mB}[\cos \theta]\right|_0 ^{\pi / 2}=\mathrm{mB}\)
ω_f = \(\left(\frac{2 \mathrm{mB}}{\mathrm{I}}\right)^{1 / 2}=\left(\frac{2 \times 20}{10^{-1}}\right)^{1 / 2}\) = 20 s^-1

Question 14.
a) A current-carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic field be set up in such a manner that the loop turns around it self (i.e. turns about the vertical axis).
Solution:
No, because that would require τ to the in the vertical direction. But τ = I A × B, and since A of the horizontal loop is in the vertical direction, τ would be in the plane of the loop for any B.

b) A current-carrying circular loop is located in a uniform external magnetic field. If the loop is free to turn, what is its. orientation of stable equilibrium ? Show that in this orientation, the flux of the total field (external field + field produced by the loop) is maximum.
Solution:
Orientation of stable equilibrium is one where the area vector A of the loop is in the direction of external magnetic field. In this orientation, the magnetic field produced by the loop is in the same direction as external field, both normal to the plane of the loop, thus giving rise to maximum flux of the total field.

c) A loop of irregular shape carrying current is located in an external magnetic field. If the wire is flexible, why does it change to a circular shape ? What could be the sense of current in the loop and the direction of magnetic field ?
Solution:
It assumes circular shape with its plane normal to the field to maximize flux, since for a given perimeter, a circle encloses greater area than any other shape.

Question 15.
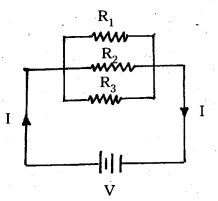
In the circuit (Fig.) the current is to be measured. What is the value of the current if the ammeter shown (a) is a galvanometer with a resistance R_G = 60.00 Ω; (b) is a galvanometer described in (a) but converted to an ammeter by a shunt resistance r_s = 0.02 Ω; (c) is an ideal ammeter with zero resistance ?

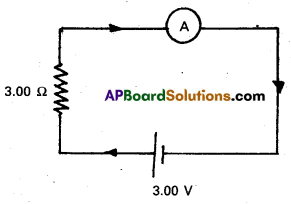
Solution:
a) Total resistance in the circuit is,
R_G + 3 = 63 Ω. Hence I = 3/63 = 0.048 A.

b) Resistance of the galvanometer converted to an ammeter is,
\(\frac{\mathrm{R}_{\mathrm{G}} \mathrm{r}_{\mathrm{s}}}{\mathrm{R}_{\mathrm{G}}+\mathrm{r}_{\mathrm{s}}}=\frac{60 \Omega \times 0.02 \Omega}{(60+0.02) \Omega}\) = 0.02 Ω
Total resistance in the circuit is,
0.02 Ω + 3 Ω = 3.02 Ω. Hence I = 3/3.02 = 0.99 A.

c) For the ideal ammeter with zero resistance,
1 = 3/3 = 1.00 A

Students get through AP Inter 2nd Year Physics Important Questions 6th Lesson Current Electricity which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 6th Lesson Current Electricity

Short Answer Questions

Question 1.
Derive an expression for the effective resistance when three resistors are connected in
(i) series
(ii) parallel.
Answer:
Effective resistance when three resistors are connected :
(i) In series :

1. Three resistors R₁, R₂ and R₃ are connected in series as shown in fig. V₁, V₂, V₃ are the potential differences across R₁, R₂ and R₃. I is the current flowing through them.
2. Applying Ohm’s law to R₁, R₂ and R₃, Then V₁ = IR₁, V₂ = IR₂, V₃ = IR₃
3. In series, V = V₁ + V₂ + V₃
   IR_s = IR₁ + IR₂ + IR₃ [∵V = IR_s]
   ∴ R_s = R₁ + R₂ + R₃

ii) In parallel :

1. Three resistors, R₁, R₂ and R₃ are connected in parallel as shown in fig. Potential differences across each resistor is V.I₁, I₂, I₃ are the currents flowing through them.
2. Applying Ohm’s law to R₁, R₂ and R₃, then
   V = I₁R₁ = I₂R₂ = I₃R₃
   ⇒ I₁ = \(\frac{\mathrm{V}}{\mathrm{R}_1}\); I₂ = \(\frac{\mathrm{V}}{\mathrm{R}_2}\); I₃ = \(\frac{\mathrm{V}}{\mathrm{R}_3}\)
3. In parallel, I = I₁ + I₂ + I₃
   ⇒ \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{p}}}=\frac{\mathrm{V}}{\mathrm{R}_1}+\frac{\mathrm{V}}{\mathrm{R}_2}+\frac{\mathrm{V}}{\mathrm{R}_3}\) [∵ I = \(\frac{V}{R_P}\)]
   ∴ \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)

Question 2.
On what factors does the resistance of a conductor depend ? Define electric resistance and write its S.I unit. How does the resistance of a conductor vary if (a) Conductor is stretched to 4 times of its length (b) Temperature of conductor is increased ? [Board Model Paper]
Answer:
Dependence of Resistance on geometry :

1. Resistance is directly proportional to length of the conductor (R ∝ l)
2. Resistance is inversely proportional to area of cross-section (R ∝ 1/A)
   i.e., R ∝ l/A ⇒ R = ρl / A; ρ is called specific resistance or resistivity of the material.

Dependence of Resistance on temperature : R₁ = R₁[1 + α(∆T)] & α = \(\frac{\Delta R / R}{\Delta T}\)
α is called temperature coefficient of resistance and its SI unit: K^-1.

Definition of electrical resistance (R) : The ratio between the potential difference (V) across the ends of the conductor and the current (i) flowing through the conductor is called its electrical resistance, R = V/i; S.I unit of electrical resistance is ohm (Ω)
a) Resistance of the conductor, R = ρ \(\frac{l}{\mathrm{~A}}\) = ρ \(\frac{l^2}{V}\) ⇒ R ∝ l² (∵ ρ and V constant)
⇒ R₁/R₂ = (l₁/l₁)² ∴ R₁/R₂ = (l/4l)
⇒ R₂ = 16R
Hence resistance of the conductor increases by 16 times.
b) The value of the electrical resistance of a conductor increases with increase of temperature. Because, temperature coefficient of resistance is positive for metals.

Long Answer Questions

Question 1.
State Kirchhoffs law for an electrical network. Using th&se laws deduce the condition for balance in a Wheatstone bridge. [T.S. Mar. 16; 15; Mar. 14]
Answer:

1. Kirchhoffs first law (Junction rule or KCL) : The algebraic sum of the currents at any junction is zero.
   ∴ ΣI = 0
   (or)
   The sum of the currents flowing towards a junction is equal to the sum of currents away from the junction.
2. Kirchhoffs second law (Loop rule or KVL) : The algebraic sum of potential around any closed loop is zero.
   ∴ Σ(IR) + ΣE = 0

Wheatstone bridge : Wheatstone’s bridge circuit consists of four resistances R₁, R₂, R₃ and R₄ are connected to form a closed path. A cell of emf is connected between the point A and C and a galvanometer is connected between the points B and D as shown in fig. The current through the various branches are indicated in the figure. The current through the galvanometer is I_g and the resistance of the galvanometer is G.

Applying Kirchhoffs first law at the junction D, I₁ – I₃ – I_g = 0 ………………. (1)
at the junction B, I₂ + I_g – I₄ = 0 ……………. (2)
Applying Kirchhoff s second law to the closed path ADBA,
-I₁R₁ – I_gG + I₂R₂ = 0
or
⇒ I₁R₁ + I_gG = I₂R₂ …………….. (3)
applying kirchhoft’s second law to the closed path DCBD,
-I₃R₃ + I₄R₄ + I_gG = 0
⇒ I₃R₃ – I_gG = I₄R₄ ……………….. (4)

When the galvanometer shows zero deflection the points D and B are at the same potential. So I_g = 0.
Substituting this value in (1), (2), (3) and (4).
I₁ = I₃ ………………. (5)
I₂ = I₄ ……………… (6)
I₁R₁ = I₂R₂ ……………….. (7)
I₃R₃ = I₄R₄ …………….. (8)
Dividing (7) and (8)
\(\frac{I_1 R_1}{I_3 R_3}=\frac{I_2 R_2}{I_4 R_4} \Rightarrow \frac{R_1}{R_3}=\frac{R_2}{R_4}\) [∵ I₁ = I₃ & I₂ = I₄]
∴ Wheatstone’s Bridge principle : R₄ = R₃ × \(\frac{\mathrm{R}_2}{\mathrm{R}_1}\)

Question 2.
State the working principle of potentiometer explain with the help of circuit diagram how the emf of two primary cells are compared by using the potentiometer. [A.P. Mar. 16]
Answer:
Working principle of potentiometer : The potential difference across a length of the potentiometer wire is directly proportional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant,
i.e. ε ∝ l ⇒ ε = Φl where Φ is potential gradient.

Comparing the emf of two cells ε₁ and ε₂ :

1. To compare the emf of two cells of emf E₁ and E₂ with potentiometer is shown in diagram.
   
2. The points marked 1, 2, 3 form a two way key.
3. Consider first a position of the key where 1 and 3 are connected so that the galvanometer is connected to ε₁.
4. The Jockey is moved along the wire till at a point N₁ at a distance l₁ from A, there is no deflection in the galvanometer. Then ε₁ ∝ l₁ ⇒ ε₁ = Φl₁ ………………. (1)
5. Similarly, if another emf ε₂ is balanced against
   l₂ (AN₂), then ε₂ ∝ l₂ ⇒ ε₂ = Φl₂ ……………. (2)
6. \(\frac{(1)}{(2)} \Rightarrow \frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2}\)

Question 3.
State the working principle of potentiometer. Explain with the help of circuit diagram how the potentiometer is used to determine the internal resistance of the given primary cell. [A.P. & T.S. Mar. 17, 15]
Answer:
Working principle of potentiometer : The potential difference across a length of the potentiometer wire is directly proportional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant.
i.e. ε ∝ l ⇒ ε = Φl
where Φ is potential gradient.

Measurement of internal resistance (r) with potentiometer :

1. Potentiometer to measure internal resistance (r) of a cell (ε) is shown in diagram.
   
2. The cell (emf ε) whose internal resistance (r) is to be determined is connected across a resistance box (R.B) through a key K₂.
3. With key K₂ open, balance is obtained at length l₁ (AN₁). Then ε = Φl₁ …………… (1)
4. When key K₂ is closed, the cell sends a current (I) through the resitance box (R.B).
5. If V is the terminal potential difference of the cell and balance is obtained at length l₂ (AN₂).
   Then V = Φ l₂ ………………… (2)
6. \(\frac{(1)}{(2)} \Rightarrow \frac{\varepsilon}{V}=\frac{l_1}{l_2}\) ……………. (3)
7. But ε = I (r + R) and V = IR. This gives
   \(\frac{\varepsilon}{V}=\frac{(r+R)}{R}\)
   \(\frac{l_1}{l_2}=\left(\frac{r}{R}+1\right)\) [∵ from (3)]
   ∴ r = \(\mathrm{R}\left(\frac{l_1}{l_2}-1\right)\)

Question 4.
Under what condition is the heat produced in an electric circuit a)directly proportional b) inversely proportional to the resistance of the circuit ? Compute the ratio of the total quantity of heat produced in the two cases.
Answer:
Expression of heat produced by electric current:
Consider a conductor AB of resistance R.
Let V = P.D applied across the ends of AB.
I = current flowing through AB.
t = time for which the current is flowing.
∴ Total charge flowing from A to B in time t is q = It. By definition of P.D, work done is carrying unit charge from A to B = V
Total work done in carrying a charge q from A to B is
W = V × q = V It = I² Rt (∵V = IR)
This work done is called electric work done. If this electric work done appears as heat, then amount of heat produced (H) is given by
H = W = I² Rt Joule.
This is a statement of Joule’s law of heating.

a) If same current flows through an electric circuit, heat is developed.
i.e., H ∝ R.

b) If same P.D applied across the the electric circuit heat is developed.
i.e., H₂ ∝ \(\frac{1}{R}\)

c) The ratio of H₁ and H₂ is given by
\(\frac{\mathrm{H}_1}{\mathrm{H}_2}=\frac{\mathrm{R}}{\frac{1}{\mathrm{R}}}\)
∴ \(\frac{\mathrm{H}_1}{\mathrm{H}_2}\) = R²

Problems

Question 1.
A 10Ω thick wire is stretched so that its length becomes three times. Assuming that there is no change in its density on stretching, calculate the resistance of the stretched wire.
Solution:
Given R₁ = 10 Ω,
l₁ = l
l₂ = 3l, R₂ ?

R₁ = \(\frac{\rho}{\mathrm{V}} l_1^2\)
R₂ = \(\frac{\rho}{\mathrm{V}} l_2^2\)
\(\frac{\dot{\mathrm{R}}_2}{\mathrm{R}_1}=\left(\frac{l_2}{l_1}\right)^2 \Rightarrow \frac{\mathrm{R}_2}{10}=\left(\frac{3 l}{l}\right)^2\)
∴ R₂ = 10 × 9 = 90Ω.

Question 2.
A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter ? [T.S. Mar. 16; Mar. 14]
Solution:
Resistance of long wire = 4R
Hence the resistance of half wire = \(\frac{4 R}{2}\) = 2R

Now these two wire are connected in parallel. Hence the effective resistance between the ends of the diameter
R_P = \(\frac{\mathrm{R}_1 \mathrm{R}_2}{\mathrm{R}_1+\mathrm{R}_2}\) ⇒ R_P = \(\frac{2 R \times 2 R}{2 R+2 R}\)
∴ R_P = R.

Question 3.
Three resistors 3Ω, 6Ω and 9Ω are connected to a battery. In which of them will the power of dissipation be maximum if:
a) They all are connected in parallel
b) They all are connected in series ? Give reasons.
Solution:
Given R₁ = 3Ω, R₂ = 6Ω, R₃ = 9Ω
a) Effective resistance in parallel is given by

\(\frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}=\frac{1}{3}+\frac{1}{6}+\frac{1}{9}\)
\(\frac{1}{R_P}=\frac{6+3+2}{18}\)
∴ R_P = \(\frac{18}{11}\) Ω
∴ Dissipated power in parallel,
P_P ∝ \(\frac{1}{R_P}\) ⇒ P_P ∝ \(\frac{1}{\left(\frac{18}{11}\right)}\)
∴ P_P ∝ \(\frac{11}{18}\) …………….. (1)

b) Effective resistance in series is given by
R_s = R₁ + R₂ + R₃ = 3 + 6 + 9 = 18 Ω
∴ Dissipated power in series, P_S ∝ R_S ⇒ P_S ∝ 18
From equations (1) and (2) power dissipation is maximum in series and minimum in parallel.
Reasons:

1. In series connection, P ∝ R and V ∝ R. Hence dissipated power (P) and potential difference (V) is more because current is same across each resistor.
2. In parallel connection, P ∝ \(\frac{1}{R}\) and I ∝ \(\frac{1}{R}\) Hence dissipated power (P) and potential difference (V) is less because voltage is same across each resistor.

Question 4.
A silver wire has a resistance of 2.1Ω at 27.5°C and a resistance of 2.7Ω at 100°C. Determine the temperature coeff. of resistivity of silver.
Solution:
For silver wire, R₁ = 2.1Ω, t₁ = 27.5°C
R₂ = 2.7 Ω, t₂ = 100°C, α = ?
α = \(\frac{R_2-R_1}{R_1 \mathrm{t}_2-\mathrm{R}_2 \mathrm{t}_1}=\frac{2.7-2.1}{2.1 \times 100-2.7 \times 27.5}=\frac{0.6}{210-74.25}=\frac{0.6}{135.75}\)
∴Temperature coefficient of resistivity
α = 0.443 × 10^-2/°C

Question 5.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm. what is the emf of the second cell ? [A.P. Mar. 15
Solution:
Here ε₁ = 1.25 V, l₁ = 35.0 cm, ε₂ = ?. l₂ = 63.0 cm.
As \(\frac{\varepsilon_2}{\varepsilon_1}=\frac{l_2}{l_1}\) or
ε₂ = \(\frac{\varepsilon_1 \times l_2}{l_1}=\frac{1.25 \times 63}{35}\) = 2.25 V

Question 6.
A battery of emf 2.5 V and internal resistance r is connected in series with a resistor of 45 ohm through an ammeter of resistance 1 ohm. The ammeter reads a current of 50 mA Draw the circuit diagram and calculate the value of r. [T.S. Mar. 17]
Solution:
Circuit diagram for the given data is shown below.

Given, E = 2.5 V; R = 45Ω;
r_A = 1A; I = 50mA;
r = ?
E = I (R + r_A + r)
2.5 = 50 × 10^-3 (45 + 1 + r)
46 + r = \(\frac{2.5}{50 \times 10^{-3}}=\frac{2.5 \times 10^3}{50}\) = 50
∴ r = 50 – 46 = 4Ω.

Question 7.
The balancing point in meter bridge experiment is obtained at 30 cm from the left. If the right gap contains 3.5 £2, what is the resistance in the left gap? [BMP]
Solution:
\(\frac{x}{R}=\frac{I_1}{100-I_1} \Rightarrow \frac{x}{3.5}=\frac{30}{70} \Rightarrow x=\frac{30 \times 3.5}{70}=1.5\)
∴ x = 1.5 Ω
The resistance in the left gap in meter bridge is, x = 1.5 Ω

Question 8.
The storage battery of a car has an emf of 12 V If the internal resistance of the battery is 0.4Q, what is the maximum current that can be drawn from the battery ?
Solution:
Here E = 12 V, r = 0.4Ω
Maximum Current, I_max = \(\frac{E}{r}=\frac{12}{0.4}\) = 30 A

Question 9.
A battery of emf 10V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor ? What is the terminal voltage of the battery when the circuit is closed ? [T.S. Mar. 15]
Solution:
Here E = 10 V, r = 3Ω,1 = 0.5 A, R = ?, V = ?
I = \(\frac{E}{(R+r)}\) or (R + r) = \(\frac{\mathrm{E}}{\mathrm{I}}=\frac{10}{0.5}\)= 20 or
R = 20 – 3 = 17Ω
Terminal voltage V = IR = 0.5 × 17 = 8.5 Ω.

Question 10.
If the balancing point in a meter bridge from the left is 60 cm, compare the resistance in the left and right gaps of meter bridge.
Solution:
\(\frac{R_1}{R_2}=\frac{I_1}{100-I_1}=\frac{60}{100-60}=\frac{60}{40}=\frac{3}{2} \Rightarrow \frac{R_1}{R_2}=\frac{3}{2}\)

Question 11.
A potentiometer wire is 5m long and a potential difference of 6 V is maintained between its ends. Find the emf of a cell which balances against a length of 180cm of the potentiometer wire. [A.P. Mar. 17, 16]
Solution:
Length of potentiometer wire L = 5m
Potential difference V = 6 Volt
Potential gradient Φ = \(\frac{V}{L}=\frac{6}{5}\) = 1.2V/m
Balancing length l = 180cm
= 1.80m
Emf of the cell E = Φl
= 1.2 × 1.8 = 2.16V.

Students get through AP Inter 2nd Year Physics Important Questions 2nd Lesson Ray Optics and Optical Instruments which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 2nd Lesson Ray Optics and Optical Instruments

Very Short Answer Questions

Question 1.
What is optical density and how is it different from mass density ?
Answer:
Optical density: Optical density is defined as the ratio of the speed of light in media. Mass density: Mass per unit volume is defined as mass density.
Mass density of an optically denser medium is less than that of optically rarer medium.

Question 2.
What are the laws of reflection through curved mirrors ?
Answer:

1. “The angle of reflection equals to the angle of incidence”.
2. “The incident ray, reflected ray and the normal to the reflecting surface at the point of incidence lie in the same plane”.

Question 3.
Define ‘power’ of a convex lens. What is its unit ? [A.P. Mar. 17, T.S. Mar. 16]
Answer:
Power of a lens : Power of a lens is defined as its bending ability and is measured as reciprocal of focal length in metre.
∴ Power of a lens = \(\frac{1}{f(\text { in metres) }}=\frac{100}{\mathrm{f}(\text { in cms) }}\)
Unit → Dioptre (D)

Problems

Question 1.
A concave mirror of focal length 10 cm is placed at a distance 35 cm from a wall. How far from the wall should an object be placed so that its real image is formed on the wall ?
Answer:
f = 10 cm, υ = 35 cm
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{-u}\) (using sign convention)
\(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}=\frac{1}{35}-\frac{1}{10}\)
\(\frac{1}{u}=\frac{10-35}{35 \times 10}=\frac{-1}{14}\)
U = – 14 cm.
Distance of the object from the wall = 35 – 14 = 21cm.

Question 2.
A concave mirror produces an image of a long vertical pin, placed 40cm from the mirror, at the position of the object. Find the focal length of the mirror. [T.S. Mar. 17, 16]
Answer:
Give u = υ = 40cm
\(\frac{1}{\mathrm{f}}=\frac{1}{v}+\frac{1}{u}\)
\(\frac{1}{f}=\frac{1}{40}+\frac{1}{40}\)
\(\frac{1}{\mathrm{f}}=\frac{2}{40}\)
f = 20 cm.

Question 3.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism.
Answer:
A = 4°, D_m = 2.48°
D_m = A (μ – 1)
μ – 1 = \(\frac{\mathrm{D}_{\mathrm{m}}}{\mathrm{A}}=\frac{2.48}{4}\) = 0.62
μ = 1 + 0.62
μ = 1.62

Question 4.
What is ‘dispersion’? Which colour gets relatively more dispersed ? [Mar. 14]
Answer:
Dispersion : The phenomenon of splitting of white light ipto its constituent colours, on passing through a prism is called dispersion of light.
The deviation is maximum for violet colour.

Question 5.
The focal length of a concave lens is 30 cm. Where should an object be placed so that its image is 1/10 of its size ?
Solution:
f = 30 cm, h₁ = h, h₂ = \(\frac{\mathrm{h}}{10}\)

Question 6.
What is myopia ? How can it be corrected ? [T.S. Mar. 15]
Answer:
Myopia (or) Near sightedness :
The light from a distant object arriving at the eye-lens may get converged at a point infront of the retina. This type of defect is called myopia.
To correct this, we interpose a concave lens between the eye and the object.

Question 7.
What is hypermetropia ? How can it be corrected ? [A.P. Mar. 16]
Answer:
Hypermetropia (or) Farsightedness :
The light from a distant object arriving at the eye-lens may get converged at a point behind the retina. This type of defect is called Hypermetropia.
To correct this, we interpose a convex lens (Convergent lens) between the eye and the object.

Question 8.
Draw neat labelled ray diagram of simple microscope. [PE 2015 (A.P.)]
Answer:

u = object distance
D = distance of near point.

Short Answer Questions

Question 1.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length. [A.P. Mar. 17]
Answer:
Focal length of concave mirror:
The distance between the focus F and the pole P of the mirror is called the focal length of the concave mirror.

Consider a ray AB parallel to principal axis incident on a concave mirror at B and is re-flected along BF. The line CB is normal to the mirror.
Let θ be the angle of incidence, ∠ABC = ∠BCP = θ
Draw BD ⊥ CP
In right angled ∆^le
Tan θ = \(\frac{\mathrm{BD}}{\mathrm{CD}}\) ……………. (1)
From ∆^le BFD, Tan 2θ = \(\frac{\mathrm{BD}}{\mathrm{FD}}\) ……………. (2)
Dividing eq (2) by eq (1), \(\frac{{Tan} 2 \theta}{{Tan} \theta}=\frac{\mathrm{CD}}{\mathrm{FD}}\) ………………….. (3)
If θ is very small, then tan θ ≈ θ and tan 2θ ≈ 2θ since the aperture of the lens is small
∴ The point B lies very close to p.
CD ≈ CP and FD ≈ FP
From eq (3), \(\frac{2 \theta}{\theta}=\frac{\mathrm{CP}}{\mathrm{FP}}=\frac{\mathrm{R}}{\mathrm{f}} \Rightarrow 2=\frac{\mathrm{R}}{\mathrm{f}}\)
R = 2f

Question 2.
Define critical angle. Explain total internal reflection using a neat diagram. [T.S. Mar. 15]
Answer:
Critical angle:
When light ray travelling from denser medium to rarer medium, then the angle of incidence for which angle of refraction in air is 90a is called critical angle.
C = sin^-1 \(\left(\frac{1}{\mu}\right)\)
Total internal reflection:
When a light ray travels from denser to rarer medium, the angle of incidence is greater than the critical angle, then it reflects into the same medium is called total internal reflection.

Explanation:
Consider an object in the denser medium. A ray OA incident on XY bends away from the normal. As the angle of incidence is increased, the angle of refraction goes on increasing. For certain angle of incidence, the refracted ray parallel to XY surface (r = 90°).

When the angle of incidence is further increased, the ray is not refracted but is totally reflected back in the denser medium. This phenomenon is called total internal reflection.

Question 3.
Explain the formation of a mirage. [A.P. Mar. 16]
Answer:
In a desert, the sand becomes very hot during the day time and it rapidly heats the layer of air which is in its contact. So density of air decreases. As a result the successive upward layers are denser than lower layers.

When a beam of light travelling from the top of a tree enters a rarer layer, it is refracted away from the normal. As a result at the surface of layers of air, each time the angle of incidence increases and ultimately a stage is reached, when the angle of incidence becomes greater than the critical angle between the two layers, the incident ray suffers total internal reflection.

So it appears as inverted image of the tree is formed and the same looks like a pool of water to the observer.

Question 4.
Explain the formation of a rainbow. [A.P. Mar. 15]
Answer:

Figure shows how sun light is broken into its segments in the process and a rainbow appears. The dispersion of the violet and the red rays after internal reflection in the drop is shown in figure.

The red rays emerge from the drops of water at one angle (43°) and the violet rays emerge at another angle (41°). The large number of water drops in the sky makes a rain-bow. The rainbow appears semicircular for an observer on earth.

Question 5.
Why does the setting sun appear red ? [T.S. Mar. 17, Mar. 14]
Answer:
As sunlight travels through the earths atmosphere, gets scattered by the large number of molecules present. This scattering of sun light is responsible for the colour of the sky, during sunrise and sunset etc.
The light of shorter wave length is scattered much more than light of larger wave-length. Scattering ∝ \(\frac{1}{\lambda^4}\).
Most of blue light is scattered, hence the bluish colour of sky predominates.

At sunset (or) sunrise, sun rays must pass through a larger atmospheric distance. More of the blue colour is scattered away only red colour which is least scattered ap-pears to come from sun. Hence it appears red.

Question 6.
With a neat labelled diagram explain the formation of image in a simple microscope. [T.S. Mar. 16, A.P. Mar. 15]
Answer:
Simple microscope: It consists a single short focus convex lens. It increases the visual angle to see an object clearly. It is also called magnifying glass (or) reading glass.

Working : The object is adjusted within the principal focus Of the convex lens to form the image at the near point. The image is formed on same side of the object and it is virtual, erect and magnified as shown in fig.

Magnifying power : The ratio of the angle subtended by the image at the eye to the angle subtended by the object at the eye is called magnifying power of a simple microscope.
It is denoted by ‘m’.
m = \(\frac{\alpha}{\beta} \simeq \frac{{Tan} \alpha}{{Tan} \beta}\)

Question 7.
What is the position of the object for a simple microscope ? What is the maximum magnifi-cation of a simple microscope for a realistic focal length ?
Answer:
When an object is placed between principal focus and optical centre of a convex lens, a virtual and erect image will be formed on the same side of the object.

Magnifying power: It is defined as the ratio of the angle subtended at the eye by the image to the angle subtended by the object at the eye.
m = \(\frac{\alpha}{\beta} \simeq \frac{{Tan} \alpha}{{Tan} \beta}\)
From figure OJ = IJ’, ∠IO’G = α and ∠IO’J’ = β

The above equation can be written as
m = 1 + \(\frac{\mathrm{D}}{\mathrm{f}}\) …………… (2)
This shows that smaller the focal length of the lens, greater will be the magnifying power of microscope.

Long Answer Questions

Question 1.
Draw a neat labelled diagram of a compound microscope and explain its working. Derive an expression for its magnification.
Answer:
Description : It consists of two convex lenses separated by a distance. The lens near the object is called objective and the lens near the eye is called eye piece. The objective lens has small focal length and eye piece has of larger focal length. The distance of the object can be adjusted by
means of a rack and pinion arrangement.

Working: The object OJ is placed outside the principal focus of the objective and the real image is formed on the other side of it. The image I₁ G₁ is real, inverted and magnified.
This image acts as the object for the eyepiece. The position of the eyepiece is so adjusted that the image due to the objective is between the optic centre and principal focus to form the final image at the near point. The final image IG is virtual, inverted and magnified.

Magnifying Power: It is defined as the ratio of the angle subtended by the final image at the eye when formed at near point to the angle subtended by the object at the eye when imagined to be at near point.

Imagining that the eye is at the optic centre, the angle subtended by the final image is a. When the object is imagined to be taken at near point it is represented by IJ’ and OJ – IJ’.
The angle made by I J’ at the eye is β. Then by the definition of magnifying power

Dividing and multiplying by I₁ G₁ on the right side, we get
m = \(\left(\frac{\mathrm{IG}}{\mathrm{I}_1 \mathrm{G}_1}\right)\left(\frac{\mathrm{I}_1 \mathrm{G}_1}{\mathrm{OJ}}\right)\)
Magnifying power of the objective (m₀) = I₁ G₁ / OJ = Height of the image due to the objective / Height of its object.
Magnifying power of the eye piece (m_e) = IG/I₁G₁ = Height of the final image / Height of the object for the eyepiece.
∴ m = m₀ × m_e ……………… (1)
To find m0: In figure OJ O’ and I₁ G₁ O’ are similar triangles. \(\left(\frac{\mathrm{I}_1 \mathrm{G}_1}{\mathrm{OJ}}\right)=\frac{\mathrm{O}^{\prime} \mathrm{I}_1}{\mathrm{O}^{\prime} \mathrm{O}}\)
Using sign convention, we find that O’I₁ = + v₀ and O’O = -u where v₀ is the image distance due to the objective and u is the object distance for the objective or the compound microscope. I₁G₁ is negative and OJ is positive.
∴ m₀ = \(\frac{\mathrm{v}_0}{\mathrm{U}}\) (∵ \(\frac{\mathrm{I}_1 \mathrm{G}_1}{\mathrm{OJ}}\) = m₀)
To find m_e : The eyepiece behaves like a simple microscope. So the magnifying power of the eye piece.
∴ m_e = (1 + \(\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\))
Where f_e is the focal length of the eyepiece.
Substituting m0 and me in equation (1),
m = \(+\frac{\mathrm{v}_0}{\mathrm{u}}\left(1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right)\)
When the object is very close to the principal focus F₀ of the objective, the image due to the objective becomes very close to the eyepiece,
u ≈ -f₀ and v₀ ≈ L
Where L is the length of the microscope. Then
m ≈ \(-\frac{L}{f_0}\left(1+\frac{D}{f_e}\right)\)

Question 2.
a) Define Snell’s Law. Using a neat labelled diagram derive an expression for the refractive index of the material of an equilateral prism.
b) A ray of light, after passing through a medium, meets the surface separating the medium from air at an angle of 45° and is just not refracted. What is the refractive index of the medium ?
Answer:
a) Snell’s law:
The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant, called the refractive index of the medium.
\(\frac{\sin i}{\sin r}\) = μ (constant).
Let ABC be the glass prism. Its angle of prism is A. The refractive index of the material of the prism is p. Let AB and AC be the two refracting surfaces PQ = incident ray, RS = emergent ray.
Let angle of incidence = i₁
angle of emergence = i₂
angle of refraction = r₁
angle of refraction at R = r₂
After travelling through the prism it falls on AC and emerges as RS.

The D angle of deviation.
From the ∆ QRT
r₁ + r₂ + ∠T = 180° ……………….. (1)
From the quadrilateral AQTR
∠A + ∠T = 180°
∠T = 180° – A ………………. (2)
From the equations (1) and (2)
r₁ + r₂ + ∠T = 180° we get
r₁ + r₂ + 180° – A = 180°
r₁ + r₁ = A ………………. (3)
from the ∆ QUR
i₁ – r₁ + i₂ – r₂ + 180° – D = 180°
i₁ + i₂ = (r₁ + r₂) = D
i₁ + i₂ – A = D [∵r₁ + r₂ = A]
i₁ + i₂ = A + D ……………… (4)
Minimum deviation : Experimentally it is found that as the angle of incidence increased the angle of deviation decreases till it reaches a minimum value and then it increases. This least value of deviation is called angle of minimum deviation ‘δ’ as shown in the fig.

When D decreases the two angles i₁ and i₂ become closer to each other at the angle of minimum deviation, the two angles of incidence are same i.e, i ₁ = i₂.
As i₁ = i₂, r₁ = r₂
∴ i₁ = i₂ = i, r₁ = r₂ = r
substituting this in (1) and (2) we get
2r = A ⇒ r = A/2
i + i = A + δ ⇒ i = \(\frac{\mathrm{A}+\delta}{2}\)
According to Snell’s law μ =
μ =
Note :The minimum deviation depends on the refractive index of the prism material and the angle of the prism.

b) Given that i = C = 45°
μ = \(\frac{1}{\sin \mathrm{c}}\) ⇒ μ = \(\frac{1}{\sin 45^{\circ}}\)
μ = \(\frac{1}{1 / \sqrt{2}}=\sqrt{2}\)
μ = 1.414

Textual Examples

Question 1.
Suppose that the lower half of the concave mirror’s reflecting surface in figure is covered with an opaque (non- reflective) material. What effect will this have on the image of an object p’ iced in front of the mirror ?

Solution:
You may think that the image will now show only half of the object, but taking the laws of reflection to be true for all points of the remaining part of the mirror, the image will be that of the whole object. However, as the area of the re-fleeting surface has been reduced, the intensity of the image will be low (in this case, half).

Question 2.
A mobile phone lies along the principal axis of a concave mirror, as shown in Fig. Show by suitable diagram, the formation of its image. Explain why the magnification is not uniform. Will the distortion of image depend on the location of the phone with respect to the mirror ?

Solution:
The ray diagram for the formation of the image of the phone is shown in fig. The image of the part which is on the plane perpendicular to principal axis will be on the same plane. It will be of the same size, i.e., B’C = BC. You can yourself realise why the image is distorted.

Question 3.
An object is placed at (i) 10 cm. (ii) 5 cm in front of a concave mirror of radius of curvature 15cm. Find the position, nature, and magnification of the image in each case.
Solution:
The focal length f = – 15/2 cm = – 7.5 cm
i) The object distance u = – 10 cm. Then
Eq. \(\frac{1}{v}+\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}}\) gives
\(\frac{1}{v}+\frac{1}{-10}=\frac{1}{-7.5}\)
or υ = \(\frac{10 \times 7.5}{-2.5}\) = -30 cm
The image is 30 cm from the mirror on the same side as the object.
Also, magnification
m = –\(\frac{v}{u}=-\frac{(-30)}{(-10)}\) = -3
The image is magnified, real and inverted.

ii) The object distance u = -5cm. Then
from Eq. \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{-5}=\frac{1}{-7.5}\)
or υ = \(\frac{5 \times 7.5}{(7.5-5)}\) = 15 cm
This image is formed at 15 cm behind the mirror. It is a virtual image.
Magnification m = – \(\frac{v}{u}=-\frac{15}{(-5)}\) = 3
The image is magnified, virtual and erect.

Question 4.
Suppose while sitting in a parked car, you notice a jogger approaching towards you in the side view mirror of R = 2 m. If the jogger is running at a speed of 5ms^-1, how fast the image of the jogger appear to move when the jogger is (a) 39 m, (b) 29m, (c) 19 m and (d) 9 m away.
Solution:
From the mirror equation, Eq. \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
we get
υ = \(\frac{\mathrm{fu}}{\mathrm{u}-\mathrm{f}}\)
For convex mirror, since R = 2m, f = 1 m.
Then for u = -39 m. v = \(\frac{(39) \times 1}{-39-1}\)
= \(\frac{39}{40}\)
Since the jogger moves at a constant speed of 5ms”1, after Is the position of the image u (for u = – 39 + 5 = – 34) is (34/35) m.
The shift in the position of image in 1 s is
\(\frac{39}{40}-\frac{34}{35}=\frac{1365-1360}{1400}=\frac{5}{1400}\)
Therefore, the average speed of the im-age when the jogger is between 39 m and 34 m from the mirror, is (1/280) ms^-1. Similarly, it can be seen that for u = – 29 m, -19 m and -9 m, the speed with which the image appears to move is \(\frac{1}{150}\)ms^-1, \(\frac{1}{60}\) ms^-1 and \(\frac{1}{10}\) ms^-1 respectively.

Question 5.
The earth takes 24 h to rotate once about its axis. How much time does the sun take to shift by 1° when viewed from the earth ?
Solution:
Time taken for 360° shift = 24h
Time taken for 1° shift = 24/360
h = 4 min.

Question 6.
Light from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
Solution:
We use the relation given by Eq.
\(\frac{\mathrm{h}_2}{v}-\frac{\mathrm{h}}{\mathrm{u}}=\frac{\mathrm{h}_2-\mathrm{h}_1}{\mathrm{R}}\) Here
u = – 100 cm, υ = ?. R = + 20 cm, n₁ = 1, and n₂ = 1.5. We then have
\(\frac{1.5}{v}+\frac{1}{100}=\frac{0.5}{20}\)
or υ = + 100 cm

Question 7.
A magician during a show makes a glass lens with n = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid ? Could the liquid be water ?
Answer:
The refractive index of the liquid must be equal to 1.47 in order to make the lens disappear. This means n₁ = n₂. This gives 1/f = 0 or f → ∞. The lens in the liquid will act like a plane sheet of glass. No, the liquid is not water. It could be glycerine.

Question 8.
(i) If f = 0.5 m for a glass lens, what is the power of the lens ? (ii) The radii of curvature 6f the faces of a double convex lens are 10 cm and 15cm. Its focal length is 12 cm. What is the refractive index of glass ? (iii) A convex lens has 20 cm focal length in air. What is focal length in water ?
(Refractive index of air-water = 1.33. Refractive index for air – glass = 1.5.)
Solution:
i) Power = + 2 dioptre.

ii) Here, we have f = + 12 cm,
R₁ = + 10 cm, R₂ = – 15 cm.
Refractive index of air is taken as unity.
We use the lens formula of Eq. \(\frac{\mathrm{h}_1}{\mathrm{DB}}+\frac{\mathrm{h}_1}{\mathrm{DB}}=\frac{\mathrm{h}_1}{\mathrm{f}}\). The sign convention has to be applied for f, R₁ and R₂.
Substituting the values, we have
\(\frac{1}{12}\) = (n – 1) (\(\frac{1}{10}\) – \(\frac{1}{-15}\))
This gives n = 1.5.

iii) For a glass lens in air, n₂ = 1.5, n: = 1, f = + 20cm. Hence, the lens formula gives.
\(\frac{1}{20}=0.5\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
For the same glass lens in water. n₂ = 1.5, n₁ = 1.33. Therefore,
\(\frac{1.33}{f}=(1.5-1.33)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
Combining the above two equations, we find f = + 78.2 cm.

Question 9.
Find the position of the image formed by the lens combination given in the fig.

Solution:
Image formed by the first lens
\(\frac{1}{v_1}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}_1}\)
\(\frac{1}{v_1}-\frac{1}{-30}=\frac{1}{10}\)
or v₁ = 15 cm
The image formed by the first lens serves as the object for the second. This is at a distance of (15 – 5) cm = 10 cm to the right of the second lens. Though the image is reeil, it serves as a virtual object for the second lens, which means that the rays appear to come from it for the second lens.
\(\frac{1}{v_3}-\frac{1}{10}=\frac{1}{-10}\) or v₂ ∞
The virtual image is formed at an infinite distance to the left of the second lens. This acts as an object for the third lens.
\(\frac{1}{v_3}-\frac{1}{\mathrm{u}_3}=\frac{1}{\mathrm{f}_3} \text { or } \frac{1}{v_3}-\frac{1}{\infty}+\frac{1}{30}\)
or v₃ = 30 cm
The final image is formed 30 cm to the right of the third lens.

Question 10.
What focal length should the reading spectacles have for a person for whom the least distance of distinct vision is 50 cm ?
Solution:
The distance of normal vision is 25cm. So if a book is at u= – 25 cm. Its image should be formed at υ = – 50 cm. There-fore, the desired focal length given by
\(\frac{1}{\mathrm{f}}=\frac{1}{v}-\frac{1}{\mathrm{u}} \text { or } \frac{1}{\mathrm{f}}=\frac{1}{-50}-\frac{1}{-25}=\frac{1}{50}\)
or f = + 50 cm (convex lens).

Question 11.
a) The far point of a myopic person is 80 cm in front of the eye. What is ,. the power of the lens required to enable him to see very distant objects clearly ?
b) In what way does the corrective lens help the above person ? Does the lens magnify very distant objects ? Explain carefully.
c) The above person prefers to remove his spectacles while reading a book. Explain why?
Solution:
a) Solving as in the previous example, we find that the person should use a concave lens of focal length = – 80 cm. i.e:, of power = – 1.25 dioptres.

b) No. The concave lens, in fact, reduces the size of the object, but the angle subtended by the image (at the far point) at the eye. The eye is able to see distant objects not because the corrective lens magnifies the object, but because it brings the (i.e., it produces virtual image of the object) at the far point of the eye which then can be focussed by the eye-lens on the retina.

c) The myopic person may have a normal near point, i.e., about 25 cm (or even less). In order to read a book with the spectacles, such a person must keep the book at a distance greater than 25cm so that the image of the book by the concave lens is produced not closer than 25cm. The angular size of the book (dr its image) at the greater distance is evidently less than the angular size when the book is placed at 25 cm and no spectacles are needed. Hence, the person prefers to remove the spectacles while reading.

Question 12.
a) The near point of a hypermetropic person is 75 cm from the eye. What is the power of the lens required to enable the person to read clearly a book held at 25cm from the eye ?
b) In what way does the corrective lens help the above person ? Does the lens magnify objects held near the eye ?
c) The above person prefers to remove the spectacles while looking at the sky. Explain why? .
Solution:
a) u = – 25 cm, υ = – 75 cm
1/f = 1/25 – 1/75, i.e., f = 37.5 cm.
The corrective lens- needs to have a converging power of +2.67 dioptres.

b) The corrective lens produces a virtual image (at 75 cm) of an object at 25 cm. The angular size of this image is the same as that of the object. In this sense the lens does not magnify the object but merely brings the object to the near point of the hypermetric eye, which then gets focussed on the retina. However, the angular size is greater than that of the same object at the near point (75 cm) viewed without the spectacles.

c) A hypermetropic eye may have normal far point i.e., it may have enough converging power to focus parallel rays from infinity on the retina of the shortened eyeball. Wearing spectacles of converging lenses (used for near vision) will amount to more converging power than needed for parallel rays. Hence the person prefers not to use the spectacles for far objects.

Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 14th Lesson Microbes in Human Welfare Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 14th Lesson Microbes in Human Welfare

Very Short Answer Questions

Question 1.
Why does ‘Swiss cheese’ have big holes? Name the Bacteria responsible for it.
Answer:
The large holes in ‘Swiss cheese’ are due to the production of large amount of CO₂ by Propionibacterium sharmanii.

Question 2.
What are fermenters?
Answer:
These are large vessels in which microbes are grown in large numbers as on industrial scale.

Question 3.
Name a microbe used for statin production. How do statins lower blood cholesterol level?
Answer:
Monascus purpureus statins act by competitively inhibiting the enzyme responsible for the synthesis of cholesterol.

Question 4.
Why do we prefer to call secondary waste water treatment as Biological treatment?
Answer:
The primary effluent is passed into large aeration tanks where it is constantly agitated mechanically and air is pumped into it. This allows vigorous growth of useful microbes into floes while growing these microbes consume the major part of the organic matter in the effluent, which reduces the BOD (Biochemical oxygen demand).

Question 5.
What is Nucleo polyhedro virus is being used for now-a-days?
Answer:
These viruses are excellent candidates for species-specific, narrow spectrum insecticidal applications. They have been shown to have no negative impacts on plants, mammals, birds, fish or even on non-target insects.

Question 6.
Write the most important characteristic that Aspergillus niger, Clostridium butylicum and Lactobacillus share.
Answer:
The microbes are acid producers. E.g. : Aspergillus niger (a fungus) produce citric acid, Clostridium butylicum (a bacterium) produce butyric acid and Lactobacillus (a bacterium) produce lactic acid.

Question 7.
Name any two genetically modified crops.
Answer:
Bt-cotton, Bt-brinjal.

Question 8.
Name any two industrially important Enzymes.
Answer:
Lipases, Streptokinase.

Question 9.
Name an Immuno suppressive Agent. From where it is obtained?
Answer:
Cyclosporin-A, Trichoderma polysporum.

Question 10.
What is the group of Bacteria found in both the rumen of cattle and sludge of sewage treatment?
Answer:
Methanogens – Methanobacterium.

Question 11.
Name the scientists who were credited for showing the role of Pencillin as an antibiotic. Ernst chain and Howard florey after Alexander Fleming.

Short Answer Questions

Question 1.
How do mycorrhizal fungi help the plants harbouring them?
Answer:
The symbiotic association between fungal members and roots of vascular plants is called mycorrihiza. Many members of the genus Glomus forms Mycorrhiza. The fungal symbiont in these associations facilitates absorption of phosphorous by the plant from the soil. Plants having such associations show resistance to root-borne pathogens, tolerance to salinity and drought and an overall increase in plant growth and development.

Question 2.
What is the chemical Nature of Biogas? Explain the process of Biogas production.
Answer:
Biogas is a mixture of methane (CH₄), Co₂, traces of H₂S and moisture. It is generated by the decomposition of excreta or dung of cattle, domestic waste material and industrial and agricultural sewage due to the activity of anaerobic bacteria (Methanococcus and Methanobacillus) present in them. It is used as fuel. The Bacteria which grow anaerobically on cellulosic material product large amount of Biogas, and the Bacteria are called Methariogens.

E.g : Methano bacterium commonly found in the anaerobic sludge during sewage treatment and also present in the food of cattle and in the rumen of cattle. In rumen, this bacteria help in the breakdown of cellulose and play an important role in the nutrition of cattle. The excreta or dung can be used for generation of Biogas (Gobar gas).

Question 3.
What ire Biofertilisers? Write a brief note on them.
Answer:
Organisms that enrich the nutrient quality of the soil are called Bio fertilisers.
E.g.: Bacteria, Fungi and Cyanobacteria.
1) Bacteria :
In symbiotic Bacteria, Rhizobium is present in the root nodules and legumes. These Bacteria fix atmospheric Nitrogen into organic forms which is used by the plant as a nutrient. Other Bacteria can fix atmospheric Nitrogen, while free living in the soil are Azospirillum and Azotobacter thus enriching the Nitrogen content of’the soil.

2) Fungi :
The symbiotic association between fungal members and roots of vascular plants is called mycorrhiza. Many members of the genus Glomus forms Mycorrhiza. The fungal symbiont in these associations facilitates absorption of phosphorous by the plant from the soil. Plants having such associations show resistance to root-borne pathogens, tolerance to salinity and drought and an overall increase in plant growth and development.

Long Answer Questions

Question 1.
Write brief essay on microbes in sewage treatments?
Answer:
Municipal waste-water is also called sewage. It contains large amount of organic matter and microbes, many of which are pathogenic. This sewage cannot be discharged into natural water bodies before disposal, sewage is treated in sewage treatment plants to make it less polluting treatment of waste water is done by heterotrophic microbes naturally present in the sewage. This treatment is carried out in two stages.

1) Primary treatment:
It involves physical removal of particles from the sewage through filteration and sedimentation. Floating debris is removed by seanential Alteration. Then the grit (soil & small pebbles) is removed by sedimentation.

All solids that settle form the primary sludge and the supernatant forms the effluent. The effluent is taken for the secondary treatment.

2) Sedbndary treatment or Biological treatment:
The primary effluent is taken into large tanks where it is constantly agitated mechanically and air is pumped into it. This allows vigorous growth of aerobic microbes into floes. While growing, these microbes consume the major of the organic matter in the effluent. This significantly reduces the BOD of the effluent. The sewage water is treated till the BOD is reduced. Now the effluent is passed into a settling tank where the bacterial floes are allowed to sediment. This sediment is called activated sludge.

This activated sludge is pumped into aeration tanks (small amount) and anaerobic sludge digesters (large amount). Here other kind of bacteria which grow anaerobically, digest the bacteria & fungi in the sludge. During this digestion bacteria produces a mixture of gases such as methane, H₂S & CO₂. The effluent from the secondary treatment plant is released into natural water bodies like rivers and streams.

Intext Questions

Question 1.
Bacteria cannot be seen with the naked eye, but these can be seen with the help of a microscope. If you have to carry a sample from your home to your biology laboratory to demonstrate the presence of microbes under a microscope, which sample would you carry and why?
Answer:
Curd can be used as a sample for the study of microbes. Curd contains numerous lactic acid bacteria (LAB) or lactobacillus. These bacteria produce acids that coagulate and digest milk proteins. A small cup of curd and contains millions of bacteria which can be easily observed under a microscope.

Question 2.
Give examples to prove that microbes release gases during metabolism.
Answer:
Bacteria and fungi carry out the process of Fermentation and during this process, they release CO₂. Fermentation is the process of converting a complex organic substances into a simples substance with the action of bacteria or yeast. Fermentation of sugar produces alcohol with the release of CO₂ and little energy. The dough used for making idli and dosa gives a pubbed appearance due to the release of CO₂.

Question 3.
Name the states involved in Ganga action plan.
Answer:
Uttarakhand, Uttar Pradesh.

Question 4.
Name some Indian traditional Indian foods made of wheat, rice and bengals gram (or their products). Which of these food involve the use of microbes?
Answer:
a) Wheat products – Bread, Cake
b) Rice products – Idli, Dosa
c) Bengal gram products – Dhokla, Khandvi

Question 5.
In which way have microbes played a major role in controlling diseases caused by harmful bacteria?
Answer:
Several microorganisms are used for preparing medicines. Antibiotics are medicines produced by certain microorganisms to kill other disease causing microorganisms. These medicines are commonly obtained from bacteria and fungi. They kill or stop the growth of microorganisms.
E.g.: Pencillium notatum produces, pencillin which checks the growth of staphylococci bacteria.

Question 6.
Do you think microbes can also be used as a source of energy? If yes, how?
Answer:
Yes, microbes can be used as a source of energy. Bacteria such as methane bacterium used for the generation of gobar gas. The dung is mixed with water to form the slurry and thrown into the tank. The tank is filled with numerous anaerobic methane bacteriun which produce bio gas from slurry. Bio gas can be removed through the pipe and is then used as a source of energy, while the spent slurry is removed from the outlet and js used as a fertilizer.

Question 7.
Microbes can be used to decrease the use of chemical fertilisers and pesticides. Explain how this can be accomplished?
Answer:
Microbes play an improtant role in organic farming, which is done without the use of chemical fertilizers and pesticides. Biofertilisers are living organisms which help increasing the fertility of soil. Biofertilisers are introduced in seeds, roots or soil to mobilize the availability of nutrients. Thus they are extremely beneficial in enriching the soil with organic nutrients. Thus cyanobacteria have the ability to fix free atmospheric nitrogen. Rhizobium is a symbiotic bacteria found in the root nodules of legumes.

Biofertilizers are ecofriendly microbes can also act as biopesticides to control insect pests in plants. E.g.: Bacillus thuringiensis which produce a toxin that kills the insect pests. Dried bacterial spores are mixed in water and sprayed in agricultural field, which larvae of insects feed on crops, these bacterial spore enter the gut of the larvae and release toxins, thereby it dies. Trichoderma are free living fungi. They live in the roots of higher plants and protect them from various pathogens. Baculoviruses is another biopesticide that is used as a biological control agent against insets and arthropods.

Question 8.
Three water samples namely river water, untreated sewage water and secondary effluent discharged from a sewage treatment plant were subjected to BOD test. The samples were labelled A, B and C; but the laboratory attendant did not note which was which’. The BOD values of the three samples A, B and C were recorded as 20 mg/L, 8 mg/L and 400 mg/L respectively. Which sample of the water is most polluted ? Can you assign the correct label to each assuming the river water is relatively clean?
Answer:
BOD (Biological Oxygen Demand) is the method of determining the amount of oxygen required by microorganisms to decompose the waste present in water supply. If the quantity of organic waste in the water supply is high, then the number of decomposing bacteria present in the water will also be high. As a result, the BOD value also will increase.

Therefore it can be concluded that if the water supply is more polluted, then it will have a higher BOD value out of the above three samples, sample C is most polluted since it has the maximum BOD value of 400 mg/L. After this, secondary effluent discharge from a sewage treatment plant is most polluted. Thus sample A has the BOD value of 20 mg/L while sample B is river water and has the BOD value of 8 mg/L. Hence correct label for each sample is.

A – 20 mg/L – Secondary effluent discharge from a sewage treatment plant
B – 8 mg/L – River water
C – 400 mg/L – Untreated sewage water.

Question 9.
Name of the microbes from which Cyclosporin A (an immunosuppressive drug) and Statins (blood cholesterol lowering agent) are obtained.
Answer:
Cyclosporin A – Trichoderma polysporum
Statin – Monascus purpureus

Question 10.
Find out the role of microbes in the following and discuss it with your teacher.
a) single cell protein (SCP) b) Soil.
Answer:
a) Single cell protein :
It is a protein obtained from contain microbes which forms an altenate source of proteins in animal feeds. The microbes involved are algae, fungi, yeast or bacteria. These microbes are grown On an industrial scale to obtain the desired protein. E.g.: Spirulina can be grown oh waste materials obtained from molasses, sewage and animal manures. It seves a rich supplement of dietary nutrients such as proteins, carbohydrates, fats, minerarls and vitamins. Methylophilous methylotrophus have a large rate of Biomass production, produce large amounts of proteins.

b) Soil:
Soil microbes play an important role in maintaining soil fertility. They help in the formation of nutrient rich humus by the process of decomposition. Many species of bacteria and cyanobacteria have the ability to fix atmospheric nitrogen into usable form. Rlizobium is a symbiotic bacteria found in the root nodules of legumes. Azospirillum and Azetobacter are free living nitrogen fixing bacteria.

Question 11.
Arrange the following in the decreasing order (most important first) of their importance, for the welfare of human society. Give reasons for your answer. Bio gas, Citric acid, Penicillin and Curd.
Answer:
Penicillin → Biogas → Citric acid → Curd
Pencillin:
It is the most important product (Antibiotic) for the welfare of Human society. It is used for controlling various bacterial diseases.

Biogas :
It is an eco-friendly source of energy.

Citric acid :
It is used as a food preservative.

Curd:
A food item obtained by the action of lactobacillus bacteria of milk.

Question 12.
What is sewage? In which way can sewage be harmful to us?
Answer:
Sewage is the municipal waste matter that is carried away in sewars and drains. It includes both liquid and solid wastes, rich in organic matter and microbes. Many of these microbes are pathogenic and can cause several water borne diseases. Sewage water is a major cause of polluting drinking water. Hence it is essential that sewage water is properly collected, treated and disposed.

Question 13.
What is the key difference between primary and secondary sewage treatment?
Answer:

Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 13th Lesson Strategies for Enhancement in Food Production Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 13th Lesson Strategies for Enhancement in Food Production

Very Short Answer Questions

Question 1.
What is meant by “hidden hunger”?
Answer:
It is a chronic lack of vitamins and minerals that often has no visible warning signs. It leads to mental impairment, poor health, and productivity or even death.

Question 2.
Name two Semi-Dwarf varieties of rice developed in India.
Answer:
Jaya and Ratna.

Question 3.
Give two examples of wheat varieties introduced in India, which are high-yielding and disease resistant.
Answer:
Sonalika and Kalyan Sona.

Question 4.
Give two examples of fungi used in SCP production.
Answer:
Candida utilis (Torula yeast), Saccharomyces cerevisiae (Baker’s yeast), Chaetomium cellulolyticum.

Question 5.
Which two species bf sugarcane were crossed for better yield?
Answer:
Saccharum barberi’and Saccharum officinarum were crossed for better yield, high sugar etc.

Question 6.
Define totipotency and explant.
Answer:
Totipotency:
The ability of a cell (or) an explant to regenerate into a complete plant is called totipotency.

Explant:
It is a part of a plant taken out and grown in a test tube under sterile conditions in special nutrient media.

Question 7.
Define micropropagation and somaclones.
Answer:
Micropropagation:
The production of large number of plants in a very short time and limited space is known as micropropagation.

Somaclones :
Plants grown through tissue culture which are genetically identical with the original plant are called somaclones.

Question 8.
What is meant by germplasm collection?
Answer:
The entire collection of plants/seeds, having all the diverse alleles for all genes in a given crop is called germplasm collection.

Question 9.
What is meant by Biofortification?
Answer:
Development of crops with higher levels of vitamins and minerals or higher protein and healthier fats to improve public health.

Question 10.
Which part of the plant is best suited for making virus-free plants and why?
Answer:
Meristem. Here the cells are in dividing state.

Short Answer Questions

Question 1.
Give few examples of biofortified crops. What benefits do they offer to the society?
Answer:
1) Wheat variety, Atlas 66, having a high protein content.
2) Rice variety, Golden Rice – β carotene containing variety.

6) Broad, lablab, French and garden peas – Protein enriched beans.

Benefits :

1. It aims at breeding crops with higher levels of vitamins and minerals.
2. Higher protein and healthier fats to improve public health.

Question 2.
Write a short note on SCR
Answer:
Dried biomass of a single cell species of microbes that can be used as proteins are called single cell protein.

1. SCP is an alternative sources of proteins for animal and human nutrition.
2. Microbes like algae, fungi and bacteria are used in SCP production.
3. Spirulina maxima, chlorella pyrenoidosa and scenedesmos acutus are the examples of Algal SCP.
4. Spirulina can be grown easily on materials like waste water from potato processing plants, straw, molasses and animal manure and can serve as food which is rich in protein, minerals, fats, carbohydrates & vitamins.
5. SCP utilization can reduces environmental pollution.
6. It is possible to produce large amount of protein in short period of time. For example 250 kg cow produces 200 g of protein per day. In the same period 250 g of a protein produces by methylophilus methylotrophus bacterial SCP.
7. Candida utilis, Bakers yeast, chaetomium cellulolyticum are good examples of Fungal SCP.

Long Answer Questions

Question 1.
You are a Botanist working in the area of plant breeding. Describe the various steps that you will undertake to release a new variety.
Answer:
The main steps in breeding a new genetic variety of a crop are :

1) Collection of Variability:
Genetic variability is the root of any breeding programme. Collection and preservation of all the different wild varieties, species and relatives of cultivated species is a prerequisite for effective exploitation of natural genes available in the populations.

The entire collection having all the diverse alleles for all genes in a given crop is called Germplasm collection.

2) Evaluation and selection of parents :
The germplasm is evaluated so as to identify plants with desirable characters. The selected plants are multiplied and are used. Purelines are created wherever desirable.

3) Cross Hybridisation among the selected parents :
After emasculation (Removal of Anthers from bisexual flower of a fpmale parent) the female flowers are enclosed in a polythene bag to prevent undesired cross pollination.

pollen grains are collected from the male parent with the help of a brush and are transferred to the surface of the stigma and thus cross pollination is affected artificially.

4) Selection and Testing of superior recombinants :
It involves selecting among the progeny of hybrids, those plants that have the desired character combination. The selection process requires careful scientific evaluation of the progeny. Due to this, plants that are superior to both the parents are obtained. These are self pollinated for several generations till they reach a homozygosity.

5) Testing, release and commercialisation of new characters :
The newly selected lines are evaluated for their yield and other traits of quality, disease resistance etc. It is done by growing these in research fields and recording their performance under ideal fertilizer application, irrigation and other crop management practices. It is followed by testing the materials in farmers fields for at least 3 growing seasons at several places in the country, in all agroclimatic zones. Finally they are distributed to farmers as a new variety.

Question 2.
Describe the tissue culture technique and what are the advantages of tissue culture over conventional method of plant breeding in crop improvement programmes?
Answer:
Tissue culture Technique : It involves
a) Preparation of Nutrient medium :
The nutrient medium is a mixture of various essential nutrients, aminoacids, vitamins and carbohydrates. These are mixed in distilled water and PH is adjusted to 5.6 to 6.0. Growth regulators like auxins, cytokinins are added to the medium. The nutrient medium is poured in glass vessels and closed tightly with cotton plugs before sterilizing them in an autoclave.

b) Sterilisation :
The nutrient medium is rich in nutrients and therefore attracts the growth of microorganisms. The culture medium is auto claved for 15 mins, at 121°c or 15 pounds of pressure to make aseptic.

c) Preparation of explant:
Any living part of plant can be used as explant. The explants must be cleaned with liquid detergent and in running water and surface sterilised with sodium hypo chlorite and rinsed with distilled water.

d) Inoculation of explants :
The transfer of explants on to the sterilized nutrient medium is called inoculation. It is carried out under sterilized conditions.

e) Incubation:
The culture vessels with inoculated explants are incubated in a culture room under controlled temperature, optimum light and humidity. The cultures are incubated for 3 – 4 weeks, the cells of the explant divide arid redivide, producing a mass of tissue called callus. The callus is transferred to another medium containing growth regulators to initiate the formation of roots and leafy shoot (organogenesis). Sometimes embryo like structures develop directly from the callus which are referred as somatic embryos. These can be encapsulated with sodium alginate to form synthetic or artificial seeds.

f) Acclamatization and transfer to pots :
The plants produced through tissue culture are washed gently and are planted in pots kept in glass house for 1-2 weeks. Finally they are transferred to field.

Advantages:

1. The production of exact copies of plants that produce particularly good flowers, fruits or have other desirable traits.
2. To quickly produce mature plants.
3. The production of multiples of plants in the absence of seeds or necessary pollinators to produce seeds.
4. The regeneration of whole plants froih plant cells that have been genetically modified.
5. The production of plants from seeds that otherwise have very low chances of germinating and growing i.e., orchids and nepenthes.
6. To clean particular plants of viral and other infections and to quickly multiply these plants as cleaned stock for Horticulture and Agriculture.

Intext Questions

Question 1.
Describe in brief, various steps involved in plant breeding.
Answer:
The main steps in breeding a’new genetic variety of a crop are :
1) Collection of Variability: Genetic variability is the root of any breeding programme . Collection and preservation of all the different wild varieties, species and relatives of cultivated species is a prerequisite for effective exploitation of natural genes available in the populations.

The entire collection haring all the diverse alleles for all genes in a given crop is called Germplasm collection.

2) Evaluation and selection of parents :
The germplasm is evaluated so as to identify plants with desirable characters. The selected plants are multiplied and are used. Purelines are created wherever desirable.

3) Cross Hybridisation among the selected parents :
After emasculation (Removal of Anthers from bisexual flower of a female parent) the female flowers are enclosed in a polythene bag to prevent uridesired cross pollination.

pollen grains are collected from the male parent with the help of a brush and are transferred to the surface of the stigma and thus cross pollination is affected artificially.

4) Selection and Testing of superior recombinants :
It involves selecting among the progeny of hybrids, those plants that have the desired character combination. The selection process requires careful scientific evaluation of the progeny. Due to this, plants that are superior to both the parents are obtained. These are self pollinated for several generations till they reach a homozygosity.

5) Testing, release and commercialisation of new characters :
The newly selected lines are evaluated for their yield and other traits of quality, .disease resistance etc. It is done by growing these in research fields and recording their performance under ideal fertilizer application, irrigation and other crop management practices. It is followed by testing the materials in farmers fields for at least 3 growing seasons at several places in the country, in all agroclimatic zones. Finally they are distributed to farmers as a new variety.

Question 2.
What is the major advantage of producing plants by micropropagation?
Answer:
Plants produced are genetically identical to the original source of plant.

Question 3.
Find out what are the various components of the medium used for propagation of an explant in vitro?
Answer:
Sucrose, Inorganic salts, vitamins, amino acids, growth regultaors like Auxins, Cytokinins, water, agar-agar.

Question 4.
Name any five hybrid varieties of crop plants which have been developed in India.
Answer:
Rice – Semidwarf varities – Jaya, Ratna.

Question 5.
The term ‘desirable trait’ can mean different things for different plants. Justify the statement with suitable examples.
Answer:
Different plants have different qualities in expressing desirable traits/characters. Eg.: Bacillus thermogenesis is used to kill other insect larvae acting as pesticide is a desirable trait. Another examples are Bt Cotton, Bt Com, rice, tomato, potato all have good qualities in increasing food production.

Question 6.
Is there any relationship between dedifferentiation and the higher degree of success achieved in plant tissue culture experiments?
Answer:
Yes, cultured tissue must certain competent cells or cells capable of reasoning competance (dedifferentiation).
Ex : an Explant → dedifferentiation → allay redifferentiation (whole plant) = cellular Totipotency.

Question 7.
“Give me a living cell of any plant and I will give you a thousand plants of the same type” is this only a slogan or is it scientifically possible? Write your comments and Justify them.
Answer:
It is possible to produce large number of plants from a living cell with in a short period is called micropropagation. Because each living cell of any plant has the capacity to develop into a new plant called totipotency. Based on this principle. It is possible to produce several plants which are identical to parents.

Question 8.
What are the physical barriers of a cell in the protoplast fusion experiment? How are the barriers overcome?
Answer:
Cell wall is the physical barrier of cell. To Isolate protoplast from the cells, the cells are to be treated with cellulages and pectinages to break the cell walls. Then protoplasts are taken and are fused with the help of polyethylene Glycol to obtain a hybrid plants.

Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 12th Lesson Biotechnology and its Applications Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 12th Lesson Biotechnology and its Applications

Very Short Answer Questions

Question 1.
Give different types of cry genes and pests which are controlled by the proteins encoded by these genes.
Answer:
The proteins encoded by the genes cry IAC and cry II Ab control the cotton bollworms, cry IAb controls com borer. [Cry protein is a protein toxin produced by Bacillus thuringiensis that kills insects]

Question 2.
Can a disease be detected before its symptoms appear? Explain the principle involved
Answer:
Yes. Very low concentration of a bacteria or virus (when the symptoms of the disease are not visible) can be detected by amplification of their nucleic acid through PCR. rDNA technology, Enzyme Linked Immunosorbent Assay are some of the techniques that serve the purpose of early diagnosis.

Question 3.
What is GEAC and what are its objectives?
Answer:
GEAC stands for Genetic Engineering Approval Committee. It make decisions regarding the validity of GM research and the safety of introducing GM organisms for public services.

Question 4.
Name the nematode that infects the roots of tobacco plants. Name the strategy adopted to prevent this infestation.
Answer:
Meloidegyne incognitia. A novel strategy adopted to prevent this infestation is process of RNA interference [RNj/fii]

Question 5.
For which variety of Indian rice, has a patent been filed by a USA company?
Answer:
Basmati Rice.

Question 6.
Give one example for each of transgenic plants which are suitable for food processing and those with improved nutritional quality.
Answer:
‘Flavr Savr’ – tomato, Golden Rice from Taipei is rich in vitamin A and prevent blindness.

Question 7.
What is green revolution? Who is regarded as father of green revolution?
Answer:
Green revolution: Substantial and dramatic increase in agricultural production which was termed as green revolution by William Gaud, the director of United States Agency for International development (USAID). Norman Borlaug is regarded as father of Green Revolution. Dr. M.S. Swaminathan and his team is the success of green revolution in our country.

Short Answer Questions

Question 1.
List out the beneficial aspects of transgenic plants.
Answer:
Plants with desirable characters created through gene transfer methods are called Transgenic plants. Beneficial aspects are :
a) Transgenic crop plants are efficient because they have many beneficial traits like virus resistance, insect resistance and herbicide resistance.

1. Papaya in resistant to papaya ring spot virus
2. Bt. cotton is resistant to insects.
3. Transgenic tomato plants are resistant to bacterial pathogen pseudomonas.
4. Transgenic potato plants are resistant to fungus phytophthora.

b) Transgenic plants which are suitable for food processing are produced with improved nutritional quality.
Eg: i) Transgenic tomato “Flavr Savr” are bruise resistant i.e., suitable for storage and transport due to delayed ripening and offers longer shelf life,
ii) Transgenic Golden Rice Taipei’is rich in vitamin A and prevents blindness.

c) Transgenic plants are used for hybrid seed production.
Eg., : Male sterile plants of Brassica napus are produced. This will eliminate the problem of manual emasculation and reduce the cost of hybrid seed production.
d) Transgenic plants have been shown to express the genes of insulin, interferon, human growth hormones, antibiotics, antibodies etc.
e) Transgenic plants are used as bio-reactors for obtaining, commercially useful products, specialised medicines and antibodies on large scale is called molecular farming.
f) Transgenic plants tolerant to abiotic stresses caused by chemicals, cold, drought, salt, heat etc.,
i) Basmati variety of rice was made resistant against biotic and abiotic stresses.
ii) Round up ready soyabean is herbicide tolerant.

Question 2.
What are some bio-safety issues concerned with genetically modified crops?
Answer:

1. There is fear of transferring allergins or toxins to humans and animals as side effects.
2. There is a risk of changing the fundamental nature of vegetables.
3. They may pose a harmful effect on biodiversity and have an adverse impact on environment.
4. There is a risk of gene pollution due to transfer of the new genes into related wild species through natural out crossing. This may result in the development of super weeds which may be fast growing than the crops and may be resistant to weedicides.
5. They may bring about changes in natural evolutionary pattern.

Question 3.
Give a brief account of Bt. Cotton
Answer:
Bt.Cotton : Some strains of Bacillus thuringiensis produce proteins that kill certain insects such as lepidopterans (tobacco budworm armyworm), coleopterans (beetles) and dipterans (flies, mosquitoes). Bacillus thuringiensis forms protein crystals which contain a toxic insecticidal protein. The gene responsible for the production of this toxic protein is introduced genetically into the cotton seeds, protects the plants from Bollworm, a major pest of cotton. The worm feeding on the leaves of Bt Cotton plant becomes lethargic and sleepy thereby causing less damage to the plant! Use of Bt Cotton has led to 3 – 27% increase in cotton yield in countries where it is grown.

The toxin is coded by a gene named ‘cry’. The proteins encoded by the genes cry IAc and cry II Ab control the cotton bollworms and Cry IAb controls com borer.

Question 4.
Give a brief account of pest resistant in plants.
Answer:
Pest resistant plants: Several nematodes parasitize a wide variety of plants and animals. A nematode. Meloidegyne incognitia infects the roots of tobacco plants and causes a great reduction in yield. To prevent this infestation, process of RNA interference was adopted. Using Agrobacterium vectors, nematode specific genes were introduced into the host plant. The introduction of DNA was such that it produced both sense and anti-sense RNAs in the host cells. These two RNAs formed a double stranded RNA that initiated RNAi and thus silenced the specific mRNA of the nematode. The parasite could not survive in a transgenic host expressing specific interfering RNA. The transgenic plant therefore got itself protected from the parasite.

Intext Questions

Question 1.
Crystals of Bt toxin produced by some bacteria do not kill the bacteria themselves because
a) Bacteria are resistant to the toxin
b) Toxin is immature
c) Toxin is inactive
d) Bacteria encloses toxin in a special sac
Answer:
c) Toxin is inactive

Question 2.
What are transgenic bacteria? Illustrate using any one example.
Answer:
Transgenic bacteria contain foreign gene that is intentionally introduced into its genome. They are manipulated to express the desirable gene for the production of various commercially important products. Eg.: E.coli. In the plasmid of E.coli, the two DNA sequences corresponding to A and B chain of human Insulin are inserted so as to produce human Insulin chains. Later on these chains are extracted from E.coli and combined to form human insulin.

Question 3.
Compare and contrast the advantages and disadvantages of production of genetically modified crops.
Answer:
Advantages :

1. Most of the GM crops have been developed for pest resistance which increases the crop productivity and therefore reduces the reliance on chemical pesticides.
2. Many varieties of GM food crops have been developed which Have enhanced nutritional quality. Eg.: Golden rice, rich in vitamin A.
3. These plants present the loss of fertility of soil by increasing the efficiency of mineral usage.
4. They are highly tolerant to unfavourable abiotic conditions.
5. The use of GM crops decreases the pest harvesting loss of crops.

Disadvantages :

1. They can affect the native biodiversity in an area.
2. They can cause genetic pollution in the wild relative of crop plants hence it is affecting our natural environment.
3. They are affecting human health.

Question 4.
What are Cry proteins? Name an organism that produces it. How has man exploited this protein to his benefit?
Answer:
It is a protein toxin produced by Bacillus thuningiensis that kills certain insects. Man by using there proteins, controls the insects and are minimising the usage of insecticides.

Question 5.
List out the advantages of recombinant Insulin.
Answer:

1. It is supplied continuously.
2. Stabilizes the market price.
3. Humulin is absorbed more rapidly.
4. Humulin is less expensive.

Question 6.
What is meant by the term Biopesticide? Name and explain the mode of action of a popular biopesticide?
Answer:
The organism which kills the other pathogenic organisms called Biopesticides. Eg. : Bacillus thuringiensis. It produces inactive crystals but once on insect in guts, it is converted into an active form due to alkaline pH of the gut and cause cell swelling and lysis finally the death of the insect.

Andhra Pradesh BIEAP AP Inter 2nd Year Botany Study Material 10th Lesson Molecular Basis of Inheritance Textbook Questions and Answers.

AP Inter 2nd Year Botany Study Material 10th Lesson Molecular Basis of Inheritance

Very Short Answer Questions

Question 1.
Distinguish between Heterochromatin and Euchromatin. Which of the two is transcriptionally active?
Answer:
The chromatin that is more densely packed and stains dark is called heterochromatin. The chromatin that is loosely packed and stain light is called Euchromatin. Euchromatin is transcriptionally active chromatin.

Question 2.
Who proved that DNA is Genetic Material? What is the organism they worked on?
Answer:
Alfred Hershey and Martha chase (1952). They worked with viruses that infect Bacteria, bacteriophages.

Question 3.
What is the function of DNA polymerase?
Answer:
DNA polymerise is a highly efficient enzyme which catalyse polymerisation of a large number of nucleotides in a very short time. It also catalyse the reaction with a high degree of accuracy.

Question 4.
What are the components of a nucleotide?
Answer:
A nucleotide has three components – a nitrogenous base, a pentose sugar and a phosphate group’.

Question 5.
Given below is the sequence of coding strand of DNA in a transcription unit.
5’AATGCAGCTATTAGG – 3 . Write the sequence of
a) Its complementary strand
b) The mRNA
Answer:
a) 5’TTACGTCGATAATCC-3′
b) 5’ AAUGCAGCUAUUAGG – 3’

Question 6.
Name any three viruses which have RNA as the Genetic Material.
Answer:
Tobacco mosaic virus, QB bacteriophage, HIV.

Question 7.
What are the components of a transcription unit?
Answer:
a) A promotor b) The structural Gene c) A terminator.

Question 8.
What is the difference between exons and Introns?
Answer:

Question 9.
What is meant by capping and tailing?
Answer:
Adding of an unusual nucleotide (methyl guanosine triphosphate) to the 5′ -end of heterogenous nuclear RNA [hnRNA) is called capping.

Adding of adenylate residues to the 3’ – end in a template independent manner is called tailing.

Question 10.
What is meant by point mutation? Give an example.
Answer:
Change of single base pair in the gene for betaglobin chain that results in the change of aminoacid residue glutamate to valine. It results in a diseased condition called sickle cell anaemia.

Question 11.
What is meant by charging of tRNA?
Answer:
Activation of aminoacids in the presence of ATP and linked to their cognate tRNA is known as charging of tRNA or amino acylation of tRNA.

Question 12.
What is the function of the codon AUG?
Answer:
It has dual functions. It codes for methionine and also act as the initiator codon.

Question 13.
Define stop codon. Write the codons.
Answer:
Codons which do not code for any aminoacids are called stop codons. They are UAA, UAG, UGA.

Question 14.
What is the difference between the template strand and a coding strand in a DNA molecule?
Answer:
The two strands have opposite polarity and the DNA-dependant RNA polymerise also catalyses the polymerisation in only one direction that is, 5′ → 3′, the strand that has the polarity 3′ → 5′ acts as a template and is also called template strand. The other strand which has polarity 5′ → 3′ and does not code for anything is called coding strand.

Question 15.
Write any two differences between DNA and RNA.
Answer:

Question 16.
In a typical DNA molecule the proportion of thymine is 30% of the N bases. Find out the percentages of other N bases.
Answer:
Adenine = 30%
Guanine = 20%
Cytosine = 20%

Question 17.
The proportion of nucleotides in a given nucleic acid are Adenine 18%, Guanine 30%, Cytosine 42% and uracil 10%. Name the nucleic acid and mention the number of strands in it.
Answer:
RNA. Only one strand is present.

Short Answer Questions

Question 1.
Define transformation in Griffith’s Experiment. Discuss how it helps in the identifi¬cation of DNA as genetic material.
Answer:
Frederick Griffith (1928) conducted experiments on streptococcus pneumoniae and observed a transformation in bacteria. When streptococcus were grown on a culture plate, some produced smooth shiny colonies (s) while others produced rough colonies (R). Mice injected with ‘s’ shain (mucous coat) die from pneumonia infection but mice injected with R strain do not develop pneumonia.

He injected heat killed ‘s’ strain bacteria to mice, It is healthy. Finally he injected heat killed S and R strains, the mice died. He concluded that the R strain bacteria had been transformed by heat killed ‘s’ strain bacteria. Some transforming principle transferred from heat killed strain to R strain to synthesize a mucous coat and become virulent. This is due to the transfer of genetic material.

Question 2.
Discuss the significance of heavy isotope of Nitrogen in Meselson and Stahl’s experiment.
Answer:
Matthew Meselson and Franklin Stahl, grow E.Coli in a medium containing ¹⁵NH₄Cl and observed 15_N was incorporated in newly synthesized DNA. This heavy DNA molecule could be distinguished from themormal DNA by centrifugation in a cesium chloride density gradient.

They transformed the cells into a medium with ¹⁵NH₄Cl (normal) and took samples at various time intervals and extracted the DNA that remained as double stranded helices. The various samples were separated independently on cesium chloride (cscl) gradients to measure the densities of DNA. Thus the DNA that was extracted from the culture, one generation after the transfer from ¹⁵N to ¹⁴N medium had a hybrid density. DNA extracted from the culture after another generation (40 mts) was composed of equal amounts of this hybrid DNA and of ‘Light’ DNA.

Question 3.
A single base mutation in a gene may not always result in loss or gain of function. Do you think the statement is correct? Defined your answer.
Answer:
A single base mutation in a gene may result in loss or gain of a gene and so a function.
E.g.: A change of single base pair in the gene for betaglobin chain that results in the change of aminoacid residue glutamate to valine. It results in a diseased condition called sickle cell anaemia.

E.g.: 2) Consider a statement that is made like a genetic code is – RAM HAS RED CAP.
If we remove a letter ‘S’ in HAS, it will be RAM HAR EDC AP.

Question 4.
How many types of RNA polymerases exist in cells ? Write their names and functions.
Answer:
Three RNA polymerases exist in Cells. They are :

1. RNA polymerase I – It transcribes r RNAs (28S, 18S, and 5.8S)
2. RNA polymerase II – It transcribes the precursor of RNA, the heterogeneous nuclear RNA (hn RNA)
3. RNA polymerase III – It is responsible for transcription of tRNA 5 Sr RNA and Sn RNAs (small nuclear RNAs)

Question 5.
What are the contributions of George Gamow, H.G. Khorana, Marshall Nirenberg in deciphering the genetic code?
Answer:
George Ganow, suggested that, in order to code for all the 20 Amino’ acids, the code should be made up of three nucleotides. This was a very bold proposition, because a permutation and combination of 4³ would generate 64 codons, generating more codons than required.

H.G. Khorana developed chemical method in synthesising RNA molecules with defined combinations of bases.

Marshall Nirenberg’s cell-free system for protein synthesis finally helped the code to be deciphered. The enzyme polynucleotide phosphorylase was also helpful in polymerising RNA with defined sequences in a template independent manner (enzymatic synthesis of RNA)

Question 6.
On the diagram of the secondary structure of tRNA shown below label the location
of the following parts.
Answer:

a) Anticodon
b) Acceptor stem
c) Anticodon stem
d) 5′ end
e) 3′ end

Question 7.
Draw the schematic / diagrammatic presentation of the lac operon.
Answer:

Question 8.
What are the differences between DNA and RNA.
Answer:

Question 9.
Write the important features of Genetic code?
Answer:

1. The codon is triplet. 61 codons code for aminoacids and 3 codons donot code for any aminoacids called stop codons.
2. One codon codes for only one aminoacid, hence it is unambiguous and specific.
3. Some aminoacids are coded by more than one codon, hence the code is degenerated.
4. The codon is read in mRNA in a contiguous fashion. There are no punctuations.
5. The code is nearly universal: For Ex: UUU code for phenylalanine (Phe) in Bacteria or Humans.
6. AUG has dual functions. It codes for methionine and also acts as initiator codon.

Question 10.
Write briefly on nucleosomes.
Answer:
Nucleosome is a bead like structure of chromosomes. It consists of eight histone molecules and a DNA segment of about 150 base pairs. Each Nucleosome is separated from one another by a linker DNA sequence of about 50 base pairs. Nucleosome helps to fold DNA into a compact form in the interphase nucleus. Otherwise the length of a chromosome, when linear is many orders of magnitude greater than the diameter of the nucleus.

Intext Questions

Question 1.
Group the following as nitrogenous bases and nucleosides : Adenine, Cytidine, Thymine, Guanosine, Uracil and Cytosine.
Answer:
Nitrogenous bases : Adenine, Thymine, Uracil, Cytosine,
Nucleosides : Cytidine, Guanosine.

Question 2.
If a double stranded DNA has 20% of cytosine, calculate the percent of adenine in the DNA.
Answer:
Cytosine = 20%
Guamine = 20%
Adenine = 30%
Thymine = 30%

Question 3.
If the sequence of one strand of DNA is written as follows : Write down the sequence of complementary strand in 3′ → 5′ direction.
5′ – ATGCATGCATGCATGCATGCATGCATGC – 3‘
Answer:
3′ – TACGTACGTACGTACGTACGTACGTACG – 5′

Question 4.
If the sequence of the coding strand in a transcription unit is written as follows.
5 – ATGCATGCATGCATGCATGCATGCATGC – 3 write down the sequence of m RNA
Answer:
3′ AUGC AUGC AUGC AUGC AUGC AUGC AUGC – 5

Question 5.
Which property of DNA double helix led Watson and Crick to hypothesise semi conservative mode of DNA replication? Explain.
Answer:
The two strands would separate and acts as a template for the synthesis of new complementary strands. After completion of replication, each DNA would have one parental and one newly synthesised strand.

Question 6.
Depending upon the chemical nature of the template [DNA or RNA] and the nature of nucleic acids synthesized from it [DNA or RNA], List the types of nucleic acid polymerases.
Answer:
DNA polymerases
RNA polymerases.

Question 7.
How did Hershey and Chase differentiate between DNA and protein in their experiment while proving that DNA is the genetic material?
Answer:
Hershey and chase purified biochemicals (proteins, DNA, RNA etc) from the heat killed ‘S’ cells. They discovered the DNA alone from S bacteria caused R bacteria to become transformed. They also discovered thal protein digesting enzymes and RNA digesting enzymes did not affect transformation. So the transforming principle was not a protein or RNA. Digestron with DNAse did inhibit transformation suggesting that the DNA caused the transformation.

Question 8.
Differentiate between the followings :
a) mRNA and tRNA
b) Template strand and Coding strand
Answer:

a)

b)

Question 9.
List two essential roles of ribosomes during translation.
Answer:

1. Ribosome acts as the site where protein synthesis takes place from individual aminoacids.
2. Ribosome acts a catalyst for forming peptide bond.
   E.g. : 23 S r-RNA in bacteria acts as ribozyme.

Question 10.
In the medium where E. coli was growing, lactose was added. Which induced the Lac operon. Then, why does Lac operon shut down some time after addition of lactose in the medium?
Answer:
Lac operon is a segment of DNA that is made up of three adjacent structural genes namely, an operator gene, a promoter gene and a regulator gene. It works in a coordinated manner to metabolise lactose into glucose and galactose. In Lac operon lactose acts as an inducer. It binds to the repressor and inactivates it. Once the lactose binds to the repressor, RNA polymerase binds to the promotor region.

Hence, three structural genes express their product and respective enzymes are produced. These enzymes act on lactose or metabolise it into glucose and galactose. After sometime, when the level of the inducer decreases, it causes the synthesis of the repressor from regulator gene. The repressor binds to the operator gene and prevents RNA polymerase from transcribing the operon. Hence the transcription is stopped.

Question 11.
Explain (in one or two lines) the functions of the followings :
a) Promoter b) tRNA c) Exons.
Answer:
a) Promoter:
It is a region of DNA that helps in initiating the process of transcription. It serves as the binding site for RNA polymerase. :

b) tRNA :
It is a small RNA that reads the genetic code present on mRNA it carries specific aminoacids to mRNA on ribosome during translation of proteins.

c) Exons:
Exons are coding sequences of DNA in Eukaryotes that transcribe for proteins.

Question 12.
Briefly describe the following :
a) Transcription b) Translation.
Answer:
a) Transcription:
It is the process of synthesis of RNA from DNA template. A segment of DNA gets copied into mRNA during the process. The process of transcription starts at the promotor region of the template DNA and terminates at the terminator region The segment of DNA between these two regions is known as transciption unit. The transcription requires RNA polymerase enzyme, a DNA template, four types of nucleotides, and certain cofactors such as Mg²⁺

During transcription, three events occur. They are : a)Initiations b)Elongation, c) Termination. The DNA dependant RNA polymerase and certain initiation factors bind at the double stranded DNA at the promotor region of the template strand and initiate the process of transcription, RNA polymerase moves along the DNA and leads to the unwinding of DNA duplex in two separate strands.

Then one of the strands, called sense strand acts as template for mRNA synthesis. The epzyme RNA polymerase utilises nucleoside triphosphates as raw material and polymerizes them to form m RNA according to the complimentary bases present on the template DNA. This process of opening of helix and elongation of polynucleotide chain continuous until the enzyme reaches terminator region. As RNA polymerase reaches the terminator region, the newly synthesized mRNA transcripted alpng with enzyme is released. Another factor called terminator factor (p) required for the termination of the transcription.

b) Translation :
It is the process of polymerizing amino acid to form a polypeptide chain. The triplet sequence of base pairs in mRNA defines the order and sequence of amino acids in a polypeptide chain. This process invoivs 3 steps, a) Initiation b) Elongation c) Termination. During the initiation, tRNA gets charged when the aminoacid binds by using ATR The start codon (AUG) present on mRNA is recognized only by the charged tRNA. The ribosome acts as an actual site for the process of translation and contains two separate sites in.a large subunit for the attachment of subsequent aminoacid.

The small subunit of ribosome binds to mRNA at the initiation codon (AUG) followed by the large subunit. Then, it initiates the process of translation. During the elongation process, the ribosome moves one codon dowonstream along with mRNA so as to leave the space for binding of another charged tRNA, The aminoacid brought by tRNA get linked with the previous aminoacid through a peptide bond and this process continues resulting in the formation of a polypeptide chain. When the ribosome reaches one or more STOP codon (UAA, UAG and UGA), the process of translation gets terminated. The polypeptide chain is released and ribosomes get detached from mRNA.

Question 13.
How the polymerization of nucleotides can be prevented in a DNA molecule?
Answer:
Due to Lack of Helicase enzyme, unwounding does not occurs. The single stranded Binding proteins cover the DNA strands preventing them from annealing into a double strand.

Question 14.
In an experiment, DNA is treated with a compound which trends to place itself amongst the stacks of nitrogenous base pairs. As a result of this, the distance between two consecutive base pairs increases. From 0.34 nm to 0.44 nm calculate the length of DNA double helix (which has 2 × 10⁹ bp) in the presence of saturating amount of this compound.
Answer:
2 × 10⁹ × 0.44 × 10^-9 bp.

Question 15.
Recall the experiments done by Frederick Griffith. Where DNA was speculated to be the genetic material. If RNA, instead of DNA was the genetic material, would the heat killed strain of pneumococcus have transformed the R – strain into virulent strain? Explain?
Answer:
RNA is more labile and prone to degradation (owing to the presence of 2’OH group in its ribose). Hence heat killed ‘s’ strain may not have retained its ability to transform the ‘R’ strain into virulent form if RNA was its genetic material.

Question 16.
You are repeating the Hershey – Chase experiment and are provided with two Isotopes : ³²P and ¹⁵N (in place of ³⁵S in the original experiment). How do you expect your results to be different?
Answer:
Use of ¹⁵N will be inappropriate because method of detection of ³⁵P and ¹⁵N is different (³²P being a radioactive Isotope while ¹⁵N is not radioactive but is the heavier Isotope of Nitrogen). Even if ¹⁵N was radioactive, them its presence would have been detected both inside the cell as well as in the supernatant because ¹⁵N would also get incorporated in amino group of aminoacids in proteins. Hence the use of ¹⁵N would not give any conclusive results.

Question 17.
Do you think that the alternate splicing of exons may enable a structural gene to code for several Isoproteins from one and the same gene? If yes, how? If not, why so?
Answer:
Functional m RNA of structural genes need not always include all of its exons. This alternate splicing of exons in sex-specific, tissue – specific, and even developmental stage specific. By such alternate splicing of exons a single gene may encode for several Isoproteins and/or proteins of similar class’. In absence of such a kind of splicing, there should have been new genes for every protein/Isoprotein. Such an extravagency has been avoided in natural phenomena by way of alternate splicing.

Question 18.
Can you recall what centrifugal force is, and think why a molecule with higher mass/ Density would sediment faster?
Answer:
Proteins have lower density when compared to others. So a molecule with higher mass would sediment faster than molecules with light weight (density).

Question 19.
Do Retroviruses follow central Dogma? Give one example.
Answer:
Genetic material of Retroviruses in RNA. At the time of synthesis of protein RNA is reverse transcribed to its complementary DNA first/which is opposite to the central Dogma. Hence Retroviruses are not known to follow central Dogma.

Question 20.
If there are 2.9 × 10⁹ complete turns in a DNA molecule. Estimate the length of the molecule (1 angstrom = 10^-8 cm).
Answer:
1 turn of DNA = 3.4 nm.
Number of turns are = 2.9 × 10⁹
The length of the DNA molecule = 2.9 × 10⁹ × 3.4 nm.

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(d)

I. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=-\frac{(12x+5y-9)}{5x+2y-4}\)
Solution:
A non-homogenous equation
\(\frac{dy}{dx}=-\frac{(ax+by-9)}{a’x+b’y-c’}\) where b = -a’
b = -5, a = 5 ⇒ b = -a
(5x + 2y-4)dy = -(12x + 5y-9) dx
(5x + 2y – 4)dy + (12x + 5y – 9) dx = 0
5 (x dy + y dx) + 2y dy – 4 dy + 12x dx – 9 dx = 0
integrating 5xy + y² – 4y + 6x² – 9x = c

Question 2.
\(\frac{dy}{dx}=-\frac{-3x-2y+5}{2x+3y+5}\)
Solution:
b = – 2, a = 2 ⇒ b = -a
(2x + 3y + 5) dy = (- 3x – 2y + 5) dx
2x dy + 3y dy + 5 dy = -3x dx- 2y dx + 5 dx
2(x.dy + y dx) + By dy + 3x dx + 5 dy – 5 dx = 0
Integrating
2xy + \(\frac{3}{2}\)y² + \(\frac{3}{2}\)x² + 5y – 5x = c
4xy + 3y² + 3x² – 10x + 10y = 2c = c’
Solution is
4xy + 3(x² + y²)- 10(x – y) = c

Question 3.
\(\frac{dy}{dx}=\frac{-3x-2y+5}{2x+3y-5}\)
Solution:
\(\frac{dy}{dx}=\frac{-(3x-2y+5)}{2x+3y-5}\)
Here b = – 2, a¹ = 2
∵ b = -a¹
(2x + 3y – 5) dy = (-3x – 2y + 5) dx „
⇒ 2(x dy + y dx) + (3y – 5) dy + (3x – 5) dx – 0
⇒ 2d (xy) + (3y- 5) dy + (3x- 5) dx = 0
Now integrating term by term, we get
⇒ 2 ∫d (xy) + ∫(3y – 5)dy + ∫(3x – 5)dx = 0
⇒ 2xy + 3.\(\frac{y^2}{2}\) – 5y + 3\(\frac{x^2}{2}\) – 5x = \(\frac{c}{2}\)
or) 3x² + 4xy + 3y² – 10x – 10y = c
Which is the required solution.

Question 4.
2(x – 3y + 1) \(\frac{dy}{dx}\) = 4x – 2y + 1
Solution:
(2x – 6y + 2) dy = (4x – 2y + 1) dx
(2x – 6y + 2) dy – (4x – 2y + 1) dx = 0
2 (x dy + y dx) – 6y dy + 2 dy – 4x dx – dx = 0
Integrating
2xy – 3y² – 2x² + 2y – x = c

Question 5.
\(\frac{dy}{dx}=\frac{x-y+2}{x+y-1}\)
Solution:
b = -1, a’ = 1 ⇒ b = -a’
(x + y – 1) dy = (x – y + 2) dx
(x + y – 1) dy = (x – y + 2) dx = 0
(x dy + y dx) + y dy – dy – x dx – 2 dx = 0
integrating
xy + \(\frac{y^2}{2}\) – \(\frac{x^2}{2}\) – y – 2x = c
2xy + y² – x² – 2y – 4x = 2c = c’

Question 6.
\(\frac{dy}{dx}=\frac{2x-y+1}{x+2y-3}\)
Solution:
b = -1, a = 1 ⇒ b = -a’
(x + 2y – 3) dy = (2x – y + 1) dx
(x + 2y – 3) dy – (2x – y + 1) dx = 0
(x dy + y dx) 4- 2y dy – 3 dy – 2x dx – dx = 0
Integrating
xy + y² – x² – 3y – x = c

II. Solve the following differential equations.

Question 1.
(2x + 2y + 3) \(\frac{dy}{dx}\) = x + y + 1
Solution:
\(\frac{dy}{dx}=\frac{x+y+1}{2x+2y+3}\)

Multiplying with 9
6v + log (3v + 4) = 9x + 9c
6(x + y) + log [3(x + y) + 4] = 9x + c
i.e., log (3x + 3y + 4) = 3x – 6y + c

Question 2.
\(\frac{dy}{dx}=\frac{4x+6y+5}{3y+2x+4}\)
Solution:

Multiplying with 64
8v + 9log (8v + 23) = 64x + 64c
8 (2x + 3y) – 64x + 9 log (16x + 24y + 23) = c’
Dividing with 8
2x + 3y – 8x + \(\frac{9}{8}\) log (16x + 24y + 23) = c”
3y – 6x + \(\frac{9}{8}\) log (16x + 24y + 23) = c”
Dividing with 3, solution is 3
y – 2x + \(\frac{3}{8}\) log (16x + 24y + 23) = k

Question 3.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0
Solution:

∫(2 + \(\frac{1}{v-1}\))dv = 3∫dx
2v + log (v – 1) = 3x + c
2v – 3x + log (v – 1) = c
2(2x + y) – 3x + log (2x + y – 1) = c
4x + 2y – 3x + log (2x + y – 1) = c
Solution is x + 2y + log (2x + y – 1) = c

Question 4.
\(\frac{dy}{dx}=\frac{2y+x+1}{2x+4y+3}\)
Solution:

Multiplying with 8
4v + log (4v + 5) = 8x + 8c
4(x + 2y) – 8x + log [4(x + 2y) + 5] = c’
Solution is
4x + 8y – 8x + log (4x + 8y + 5) = c’
8y – 4x + log (4x + 8y + 5) = c’

Question 5.
(x + y – 1) dy = (x + y + 1)dx
Solution:

v – log v = 2x + c
x + y – log (x + y) = 2x – c
(x – y) + log (x + y) = c is the required
solution.

III. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{3y-7x+7}{3x-7y-3}\)
Solution:
Let x = x + h, y = y + k so that \(\frac{dy}{dx}=\frac{dy}{dx}\)


3ln (v – 1) – 3ln (v + 1) – 7ln (v + 1) – 7ln (v – 1)
14ln x – ln c = – 10ln (v + 1) – 4 ln (v – 1)
ln (v + 1)⁵ + ln (v – 1)² + ln x⁷ = ln c
(v +1)⁵. (v – 1)². x⁷ = c
(\(\frac{y}{x}\) + 1)⁵ (\(\frac{y}{x}\) – 1)².x⁷ = c
(y – x)² (y + x)⁵ = c
[y – (x – 1 )]² (y + x – 1 )⁵ = c
Solution is [y-x + 1 ]² (y + x – 1)⁵ = c.

Question 2.
\(\frac{dy}{dx}=\frac{6x+5y-7}{2x+18y-14}\)
Solution:



Multiplying with (3V – 2)(2V + 1)
2 + 18V = A(2V + 1) + B(3V – 2)

2 log (3V- 2)+ log (2V+ 1) = – 3 log X + log c
log (3V – 2)².(2V + 1) + log X³ = log c
log X³(3V – 2)² (2V + 1) = log c
x³(3V – 2)² (2V + 1) = c

Solution is (3y – 2x – 1)² (x + 2y – 2) = 343c = c”.

Question 3.
\(\frac{dy}{dx}=\frac{10x+8y-12}{7x+5y-9}\) = 0
Solution:
\(\frac{dy}{dx}=\frac{10x+8y-12}{7x+5y-9}\) = 0
x = X + h, y = Y + k


5V + 7 = A(V + 2) + B (V + 1)
V = -1 ⇒ 2 = A(-1 + 2) = A ⇒ A = 2
V = -2 ⇒ -3 = B(-2 + 1) = -B, B = 3
∫(\(\frac{2}{(V+1)}+\frac{3}{(V+2)}\))dv = ∫\(\frac{dx}{X}\)
2 log (V + 1) + 3 log (V + 2) = – 5 log X + c
c = 2 log (V + 1) + 3 log (V + 2) + 5 log X
= log (V + 1)². (V + 2)³. X⁵
= log(\(\frac{2}{(V+1)})\))².(\(\frac{3}{(V+2)}\))³. X⁵
= log\(\frac{(Y+X)^2}{X^2}\) \(\frac{(Y+2X)^3}{X^3}\) . X⁵
⇒ (Y + X)² . (Y + 2X)³ = e^c = c’
(Y + 1 – X – 2)² (Y + 1 – 2x – 4)³ = c
Solution is (x + y – 1)² (2x + y – 3)³ = c.

Question 4.
(x – y – 2) dx + (x – 2y – 3) dy = 0
Solution:
Given equation is \(\frac{dy}{dx}=\frac{-x+y+2}{x-2y-3}\)
Let x = X + h, y = Y + k




is the required solution.

Question 5.
(x – y) dy = (x + y + 1) dx
Solution:

Question 6.
(2x + 3y – 8) dx = (x + y – 3) dy
Solution:

Question 7.
\(\frac{dy}{dx}=\frac{x+2y+3}{2x+3y+4}\)
Solution:
Let x = X + h, y = Y + k so that \(\frac{dY}{dX}=\frac{dy}{dx}\)

Choose h and k so that
h + 2k + 3 = 0
2h + 3k + 4 = 0

This is a homogeneous equation

Question 8.
\(\frac{dy}{dx}=\frac{2x+9y-20}{6x+2y-10}\)
Solution:
Given equation is \(\frac{dy}{dx}=\frac{2x+9y-20}{6x+2y-10}\)
Let x = X + h, y = Y + k so that \(\frac{dY}{dX}=\frac{dy}{dx}\)

∴ \(\frac{dY}{dX}=\frac{2X+9Y}{6X+2Y}\)
This is a homogeneous equation

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b)

I.

Question 1.
Find the general solution of \(\sqrt{1-x^2}\) dy + \(\sqrt{1-y^2}\) dx = 0.
Solution:
Given differential equation is

sin^-1 y = – sin^-1 x + c
Solution is sin^-1 x + sin^-1 y = c, where c is a constant.

Question 2.
Find the general solution of \(\frac{dy}{dx}=\frac{2y}{x}\).
Solution:
\(\frac{dy}{dx}=\frac{2y}{x}\)
∫\(\frac{dy}{dx}\) = 2∫\(\frac{2y}{x}\)
log c + log y = 2 log x
log cy = log x²
Solution is cy = x², where c. is a constant.

II. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{1+y^2}{1+x^2}\)
Solution:
\(\frac{dy}{dx}=\frac{1+y^2}{1+x^2}\)
∫\(\frac{dy}{1+y^2}\) = ∫\(\frac{dx}{1+x^2}\)
tan^-1 y = tan^-1 x + tan^-1c where c is a constant.

Question 2.
\(\frac{dy}{dx}\) = e^y-k
Solution:
\(\frac{dy}{dx}=\frac{e^y}{e^x}\)
\(\frac{dy}{e^y}=\frac{dx}{e^x}\)
∫e^-xdx = ∫e^-ydy
-e^-x = -e^-y + C
e^-y = e^-x + c where c is a constant.

Question 3.
(e^x + 1) y dy + (y + 1) dx = 0
Solution:
(e^x + 1 )y. dy = – (y + 1) dx

y – log (y + 1) = log (e^-x + 1) + log c
⇒ y – log (y + 1) = log c (e^-x + 1)
⇒ y = log (y + 1) + log c (e^-x + 1)
y = log c (y + 1) (e^-x +1)
Solution is
e^y = c(y + 1) (e^-x +1)

Question 4.
\(\frac{dy}{dx}\) = e^x-y + x²e^-y
Solution:
\(\frac{dy}{dx}\) = e^x-y + x² . e^-y
= \(\frac{e^x}{e^y}=\frac{x^2}{e^y}\)
∫e^y . dy = ∫(e^x + x²) dx
Solution is
e^y = e^x + \(\frac{x^3}{3}\) + c

Question 5.
tan y dx + tan x dy = 0
Solution:
tan y dx = – tan x dy

log sin x = – log sin y + log c
log sin x + log sin y = log c
log (sin x . sin y) = log c
⇒ sin x . sin y = c is the solution

Question 6.
\(\sqrt{1+x^2}\)dx + \(\sqrt{1+y^2}\)dy = 0
Solution:
\(\sqrt{1+x^2}\)dx = –\(\sqrt{1+y^2}\)dy
Integrating both sides we get
∫\(\sqrt{1+x^2}\)dx = -∫\(\sqrt{1+y^2}\)dy
Integrating both sides we get

Question 7.
y – x\(\frac{dy}{dx}\) = 5(y² + \(\frac{dy}{dx}\))
Solution:
y – 5y² = (x + 5)\(\frac{dy}{dx}\)
\(\frac{dx}{x+5}=\frac{dy}{y(1-5y}\)
Integrating both sides

Question 8.
\(\frac{dy}{dx}=\frac{xy+y}{xy+x}\)
Solution:

III. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{1+y^2}{(1+x^2)xy}\)
Solution:

log (1 + y²) = log x² – log (1 + x²) + log c
log (1 + x²) + log (1 + y²) = log x² + log c
Solution is (1 + x²) (1 + y²) = cx²

Question 2.
\(\frac{dy}{dx}\) + x² = x² e^3y
Solution:

log(1 – e^-3y) = x³ + c'(c’ = 3c)
Solution is
1 – e^-3y = e^x³ . k(k = e^c’)

Question 3.
(xy² + x)dx+(yx²+y)dy = 0.
Solution:
(xy² + x) dx + (yx² + y) dy = 0
x(y² + 1) dx + y (x² + 1) dy = 0
Dividing with (1 + x²) (1 + y²)
\(\frac{x dx}{1+x^2}+\frac{y dy}{1+y^2}\) = 0
Integrating
∫\(\frac{x dx}{1+x^2}\) + ∫\(\frac{y dy}{1+y^2}\) = 0
\(\frac{1}{2}\) [(log (1 + x²) + log (1 + y²)] = log c
log (1 + x²) (1 + y²) = 2 log c = log c²
Solution is (1 + x²) (1 + y²) = k when k = c².

Question 4.
\(\frac{dy}{dx}\) = 2y tanh x
Solution:
\(\frac{dy}{dx}\) = 2y tanh x
\(\frac{dy}{y}\) = 2 tanh x dx
Integrating both sides we get
∫\(\frac{dy}{y}\) = 2 ∫ tanh x dx
log y = 2 log |cosh x| + log c
lny = 2ln cosh x + In c
y = c cos²h x

Question 5.
sin^-1 \(\frac{dy}{dx}\) = x + y
Solution:
\(\frac{dy}{dx}\) = sin(x + y)
x + y = t
1 + \(\frac{dy}{dx}=\frac{dt}{dx}\)
\(\frac{dt}{dx}\) – 1 = sin t
\(\frac{dt}{dx}\) = 1 + sin t
Integrating both sides we get
∫\(\frac{dt}{1+\sin t}\) = ∫dx
∫\(\frac{1-\sin t}{\cos^2 t}\) dt = x + c
∫sec² t dt – ∫tan t . sec t dt = x + c
tan t – sec t = x + c
⇒ tan (x + y) – sec (x + y) = x + c

Question 6.
\(\frac{dy}{dx}+\frac{y^2+y+1}{x^2+x+1}\) = 0
Solution:
\(\frac{-dy}{y^2+y+1}=\frac{dx}{x^2+x+1}\)
Integrating both sides dy

Question 7.
\(\frac{dy}{dx}\) = tan² (x + y)
Solution:
\(\frac{dy}{dx}\) = tan² (x + y)
put v = x + y

2v + sin 2v = 4x + c’
2(x + y) + sin 2(x + y) = 4x + c’
x – y – \(\frac{1}{2}\)sin [2(x + y)] = c

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(a)

I.

Question 1.
Find the order of the differential equation obtained by eliminating the arbitrary constants b and c from xy = ce^x – be^-x + x².
Solution:
Given equation is xy = ce^x – be^-x + x²
Differentiating w.r.to x, we get
xy₁ + y = ce^x – be^-x + 2x.
Again differentiating w.r.to x, we get
xy₂ + y₁ + y₁ = ce^x – be^-x + 2
xy₂ + 2y₂ = xy – x² + 2
Arbitary constants a and b are eliminated.
∴ The order is 2.

Question 2.
Find the order of the differential equation of the family of all circles with their centres at the origin.
Solution:
Equation of the circle with centre at origin is x² + y² = r²
Order = no .of arbitrary constants = 1

II.

Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets.
i) y = c(x – c)² ; (c)
Solution:
y = c(x – c)² ………….. (1)
Differentiating w.r. to x
y₁ = c. 2(x – c) ………….. (1)
Dividing (2) by (1)
\(\frac{y_2}{y}=\frac{2c(x-c)}{c(x-c)^2}\)
x – c = \(\frac{2y}{y_1}\)
c = x – \(\frac{2y}{y_1}\)
Substituting in (1)
y = x – \(\frac{2y}{y_1}\)(x – \(\frac{2y}{y_1}\))²
= \(\frac{xy_1-2y}{y_1}.\frac{4y^2}{y_1^2}\)
y.y³₁ = 4y²(xy₁ – 2y)
i.e., y³₁ = 4y (xy₁ – 2y)
= 4xyy₁ – 8y²
(\(\frac{dy}{dx}\))³ – 4xy\(\frac{dy}{dx}\) + 8y² = 0

ii) xy = ae^x + be^-x; (a, b)
Solution:
xy = ae^x + b.e^-x
Differentiating w.r.t. x
x . y₁ + y = ae^x – b . e^-x
Differentiating again w.r.t. x
xy₂ + y₁ + y₁ = ae^x + be^-x = xy
\(\frac{d^2y}{dx^2}\) + 2\(\frac{dy}{dx}\) – xy = 0

iii) y = (a + bx)e^kx ; (a, b)
Solution:
y = (a + bx)e^kx
Differentiating w.r.t. x
y₁ = (a + bx) e^kx. k + e^kx . b
= k . y + b.e^kx
y₁ – ky = b.e^kx …………. (1)
Differentiating again w.r.t. x
y₂ – ky₁ = kb e^kx
= k(y₁ – ky) ………… (2)
= ky₁ – k²y
\(\frac{d^2y}{dx^2}\) – 2k\(\frac{dy}{dx}\) + k²y = 0

iv) y = a cos (nx + b); (a, b)
Solution:
y = a cos (nx + b)
y₁ = – a sin (nx + b) n
y₂ = – an. cos (nx + b) n
= – n² . y
\(\frac{d^2y}{dx^2}\)+n².y = 0

Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
i) The rectangular hyperbolas which have the co-ordinate axes as asymptotes.
Solution:
Equation of the rectangular hyperbolas is xy = c² where c is arbitrary constant
Differentiating w.r.t. x
x\(\frac{dy}{dx}\) + y = 0

ii) The ellipses with centres at the origin and having co-ordinate axes as axes.
Solution:
Equation of ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Differentiating w.r.to ‘x’ we get

Multiply (ii) by x and subtract from (i)

III.

Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets :
i) y = ae^3x + be^3x; (a, b)
Solution:
Differentiating w.r. to x
y₁ = 3ae^3x + 4be^4x
y₁ – 3a. e^3x = 4b.e^4x
= 4(y – a. e^3x)
= 4y – 4a. e^3x
y₁ – 4y = – a.e^3x ………… (1)
Differentiating again w.r.t. x
y₂ – 4y₁ = – 3a. e^3x
= 3 (y₁ – 4y) by (1)
= 3y₁ – 12y
\(\frac{d^2y}{dx^2}\) – 7\(\frac{dy}{dx}\) + 12y = 0

ii) y = ax² + bx; (a, b)
Solution:

Adding all three equations we get
x²\(\frac{d^2y}{dx^2}\) – 2x\(\frac{dy}{dx}\) + 2y = 0

iii) ax² + by² = 1; (a, b)
Solution:
ax² + by² = 1
by² = 1 – ax² ………….. (1)
Differentiating w.r.t. x
2by. y₁ = – 2ax ………….. (2)
Dividing (2) by (1)
\(\frac{by.y_1}{by^2}=\frac{-ax}{1-ax^2}\)

Differentiating w.r.t. x

iv) xy = ax² + \(\frac{b}{x}\); (a, b)
Solution:
xy = ax² + \(\frac{b}{x}\)
x²y = ax³ + b
Differentiating w.r.t. x
x²y₁ + 2xy = 3ax²
Dividing with x
xy₁ + 2y = 3ax ………… (1)
Differentiating w.r.t. x
xy₂ + y₁ + 2y₁ = 3a
xy₂ + 3y₁ = 3a ………… (2)
Dividing (1) by (2)
\(\frac{xy_1+2y}{xy_2+3y_1}=\frac{3ax}{3a}=x\)
Cross multiplying
xy₁ + 2y = x²y₂ + 3xy
x²y₂ + 2xy₁ – 2y = 0
x²\(\frac{d^2y}{dx^2}\) + 2x\(\frac{dy}{dx}\) – 2y = 0

Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
i) The circles which touch the Y – axis at the origin.
Solution:
Equation of the required circle is
x² + y² + 2gx = 0
x² + y² = – 2gx …………. (1)
Differentiating w.r. t x
2x + 2yy₁ = – 2g ……….. (2)
Substituting in (1)
x² + y² = x(2x + 2yy₁) by (2)
= 2x² + 2xyy₁
yy² – 2xyy₁ – 2x² = 0
y² – x² = 2xy\(\frac{dy}{dx}\)

ii) The parabolas each of which has a latus rectum 4a and whose axes are parallel to X – axis.
Solution:

Equation of the required parabola is
(y – k)² = 4a (x – h) …………. (1)
Differentiating w.r.t. x
2(y – k)y₁ = 4a …………. (2)
Differentiating w.r.t. x
(y – k) y₂ + y²₁ = 0 …………. (3)
From (2), y – k = \(\frac{2a}{y_1}\)
Substituting in (3)
\(\frac{2a}{y_1}\).y₂ = y²₁ = 0
2ay₂ + y³₁ = 0

iii) The parabolas have their foci at the origin and axis along the X – axis.
Solution:
Equation of parabola be y² = 4a(x + a)