Andhra Pradesh BIEAP AP Inter 2nd Year Chemistry Study Material 7th Lesson d and f Block Elements & Coordination Compounds Textbook Questions and Answers.
AP Inter 2nd Year Chemistry Study Material 7th Lesson d and f Block Elements & Coordination Compounds
Very Short Answer Questions
Question 1.
What are transition elements ? Give examples.
Answer:
Transition elements are the elements which contains partially filled d-subshells in their ionic state (or) in their elementary state.
Eg : Mn, Co, Ag etc.
Question 2.
Which elements of 3d, 4d, and 5d series are not regarded as transition elements and why ?
Answer:
Zn (3d-series), Cd (4d-series), Hg (5d-series) are not regarded as transition elements because these contains completely filled d-subshells.
![]()
Question 3.
Why are d-block elements called transition elements ?
Answer:
The name transition elements given to d-block is due to their properties which are transitioned between the electropositive s-block metals and electronegative p-block elements.
Question 4.
Write the general electronic configuration of transition elements.
Answer:
General electronic configuration of transition elements is (n – 1)d1-10 ns1-2.
Question 5.
In what way is the electronic configuration of transition elements different from non . transition elements ?
Answer:
- The general electronic configuration of transition elements is (n – 1) d1-10 ns1-2.
- The general electronic configuration of non-transition elements is (n – 1)d1-10 ns2.
Question 6.
Write the electronic configuration of chromium (Cr) and copper (Cu).
Answer:
- Electronic configuration of chromium (Cr) – [Ar]4s1d5.
- Electronic configuration of copper (Cu) – [Ar]4s13d10.
![]()
Question 7.
Why do transition elements exhibits characteristic properties ?
Answer:
Due to the presence of partially filled d-orbitals transition elements exhibit characteristic properties such as variable oxidation states, colour property, magnetic property, complex tendency etc.
Question 8.
Scandium is a transition element. But Zinc is not. Why
Answer:
Scandium has electronic configuration [Ar] 4s23d1.
Zinc has electronic configuration [Ar] 4s23d10.
Scandium has one unpaired d-electron where as Zinc has zero unpaired d-electrons so Scandium is transition element but Zinc is not.
Question 9.
Even though silver has d10 configuration, it is regarded as transition element. Why ?
Answer:
The outer electronic configuration of silver is – 4d105s1. It is having general electronic configuration of a transition element (n – 1) d1-10 ns1-2.
So silver is a transition element.
Question 10.
Write the electronic configuration of Co2+ and Mn2+.
Answer:
- The electronic configuration of Co+2 is [Ar] 4s0 3d7.
- The electronic configuration of Mn+2 is [Ar] 4s0 3d5.
Question 11.
Why are Mn2+ compounds more stable than Fe2+ towards oxidation to their +3 state ?
Answer:
- Mn+2 has electronic configuration [Ar] 4s0 3d5.
- Fe+2 has electronic configuration [Ar] 4s1 3d6.
- Mn+2 has half filled d-subshell which is more stable.
- Hence Mn+2 compounds are more stable than Fe+2 toward oxidation to their +3 state.
Question 12.
Which metal in the first series of transition metals exhibits +1 oxidation state most frequently and why ?
Answer:
Copper exhibits +1 oxidation state most frequently because Cu+ has electronic configuration [Ar] 4s03d10 which has a fulfilled d-subshell which is more stable.
![]()
Question 13.
Why do transition elements exhibit more than one oxidation state (variable oxidation states) ?
Answer:
Transition elements exhibits more than one oxidation state.
Reason:
The energy difference between (n -1) d subshell and ns subshell is very low. So both of these subshells compelete to lose the electrons.
Question 14.
Though Sc is a transition element, it does not exhibit variable oxidation state. Why ?
Answer:
Scandium has electronic configuration [Ar] 4s23d1. It has only one unpaired d-electron. So it does not exhibits variable oxidation state. It exhibits +3 stable oxidation state.
Question 15.
Why is it difficult to obtain M3+ oxidation state in Ni, Cu and Zn ?
Answer:
- Ni has electronic configuration [Ar] 4s23d8.
- Ni+2 has electronic configuration [Ar] 4s03d8
- It is difficult to remove an electron from 3d8. So, Ni+3 is difficult to obtain. (Ni has high negative enthalpy of hydration).
- Cu has electronic configuration [Ar] 4s13d10.
- Cu+ has electronic configuration [Ar] 3d10
- It is difficult to remove the electrons from 3d10 (stable). So, Cu+3 is difficult to obtain.
- Zn has electronic configuration [Ar] 4s23d10
- Zn+2 has electronic configuration [Ar] 4s03d10
- It is difficult to remove the electron from 3d10 (stable). So Zn+3 is difficult to obtain.
Question 16.
Why is Cr2+ reducing and Mn3+ oxidizing even though both have the same d4 electronic configuration.
Answer:
Cr+2 is reducing as its configuration changes from d4 to d3, the latter having a half filled t2g level. On the other hand the change from Mn+2 to Mn+3 results in the half filled (d5) configuration which has extra stability.
Question 17.
Although Cr, Mo and W belong to the same group (group 6) Cr (VI) is a strong oxidizing agent while Mo (VI) and W (VI) are not. Why ?
Answer:
In group 6, Mo (VI) and W (VI) are more stable than Cr (VI). Thus Cr (VI) in the form of dichromate in acidic medium is a strong oxidising agent. Where as MoO3 and WO3 are not.
Question 18.
What do you infer from the fact that M3+/M2+ standard electrode potential of Mn is comparatively higher and that of Fe is comparitively lower ?
Answer:
M3+/M2+ standard electrode potential of Mn is comparatively higher than that of Fe is comparatively lower. This is because much larger 3rd ionisation energy of Mn (d5 to d4).
![]()
Question 19.
Transition elements have high melting points. Why ?
Answer:
Transition elements have high melting points because of involvement of greater number of electrons from (n – 1)d in addition to ns electrons in the interatomic metallic bonding of these metals.
Question 20.
Among the first transition series (3d series) Chromium has highest melting point. Why? Ans. Among first transition series (3d-series) chromium has highest melting point.
Reason : In chromium one unpaired electron per d-orbital is particularly favourable for strong inter atomic interactions.
Question 21.
Compared to s-block elements, the transition elements exhibit higher enthalpy of atomization. Why ?
Answer:
Because of large no. of unpaired electrons in their atoms transition elements have stronger inter atomic interaction and hence stronger bonding between atoms resulting in higher enthalpies of atomisation.
Question 22.
Among the first transition series (3d series) zinc has lowest enthalpy of atomization. Why ?
Answer:
Among the first transition series zinc has lowest enthalpy of atomisation because zinc has no unpaired electrons in their atomic state or in ionic state.
Question 23.
How do you expect the density of transition elements to vary in a given series and why ?
Answer:
In a given series the density of transition elements increases.
Eg. : From Titanium to copper there is a significant increase in the density.
This is due to decrease in metallic radius coupled with increase in atomic mass.
Question 24.
How do the atomic and ionic sizes vary among transition metals in a given series ?
Answer:
In a given series of transition elements atomic and ionic sizes progressively decreased. This is due to entering of a new electron into d-orbital each time.
Question 25.
Why do Mn, Ni and Zn exhibit more negative E⊖ values than expected ?
Answer:
E0 values of Mn, Ni and Zn are more negative than expected from general trend. This is due to the stabilities of half filled d-subshell (d5) in Mn+2 and completely filled d-subshell (d10) in Zinc. For Nickel E0 value is related to the highest negative enthalpy of hydration.
![]()
Question 26.
Among the first transition series (3d series) only copper has positive E⊖M2+/M value. Why?
Answer:
Among the first transition series only copper has positive E⊖M2+/M value. This is due to high ∆aH0 and low ∆hydH0 values.
Question 27.
Cu+2 forms halides like CuF2, CuCl2 and CuBr2 but not CuI2. Why ?
Answer:
Cu+2 forms halides like CuF2, CuCl2 and CuBr2 but not CuI2 because Cu+2oxidises I– to I2
2Cu+2 + 4I– → Cu2I2 + I2
Question 28.
The highest Mn fluoride is MnF4 where as the highest oxide is Mn2O7 Why ?
Answer:
The ability of oxygen to stabilize the high oxidation states exceeds that of fluoride. Thus the highest Mn fluoride is MnF4 where as highest oxide is Mn2O7.
Question 29.
In its fluoride or Oxide, in which a transition metal exhibits highest oxidation state and why ?
Answer:
- In fluorides highest oxidation numbers are achieved in TiF4, VF5 and CrF6.
- The +7 state of Mn is represented in MnO3F.
- The highest oxidation number in oxides acheived from Sc2O3 to Mn2O7.
- In Mn2O7, Mn oxidation state is +7.
Question 30.
Why Zn2+ is diamagnetic whereas Mn2+ is paramagnetic ? [T.S. Mar. 15]
Answer:
- Zn+2 electronic configuration is [Ar] 4s03d10. It has no unpaired electrons. So it is dia magnetic.
- Mn+2 electronic configuration is [Ar] 4s03d5. It has five unpaired electrons so it is paramagnetic.
Question 31.
Write ‘spin only’ formula to calculate the magnetic moment of transition metal ions.
Answer:
Spin only formula to calculate the magnetic moment of transition metal ions is
μ = \(\sqrt{n(n+2)}\) BM
BM = Bohr Magneton.
![]()
Question 32.
Calculate the ‘spin only’ magnetic moment of Fe2+(aq) ion.
Answer:
Fe+2 ion has electronic configuration [Ar] 4s03d6
It has four unpaired electrons n = 4
Spin only magnetic moment μ = \(\sqrt{n(n+2)}\) BM = \(\sqrt{4(4+2)}\) = \(\sqrt{24}\) BM = 4.9 BM
Question 33.
What is meant by ‘disproportionation’ ? Give an example of disproportionation reaction in aqueous solution.
Answer:
The reactions in which only one element undergo both oxidation as well, as reduction are called disproportion reactions.
When a particular oxidation state becomes less stable relative to other oxidation states, one lower, one higher, it is said to undergo disproportionation.
Eg: Cu+ ion is not stable in aqueous solution because it undergo disproportionation in aqueous solution.
2Cu+(aq) → Cu+2(aq) + Cu(s)
Question 34.
Aqueous Cu2+ ions are blue in colour, where as Aqueous Zn2+ ions are colourless. Why ?
Answer:
- Electronic configuration of Cu+2 ion is [Ar] 4s03d9. If contains one unpaired electron due to presence of this unpaired electron aq. Cu+2 ions are blue in colour.
- Electronic configuration of Zn+2 ion is [Ar] 4s03d10. It contains no unpaired electrons, due to absence of unpaired electrons aq. Zn+2 ions are colourless.
Question 35.
What are complex compounds ? Give examples.
Answer:
Complex compounds: Transition metal atoms or ions form a large number of compounds in which anions or neutral groups are bound to metal atom or ion through co-ordinate covalent bonds. Such compounds are called co-ordination compounds (or) complex compounds.
Eg.: [Fe(CN)6]4-, [Co(NH3)6]3+.
Question 36.
Why do the transition metals form a large number of complex compounds ?
Answer:
Transition elements (metals) forms a large number of complex compounds this is due to
- Small size of these ions
- High effective nuclear charge,
- Possessing in completely filled d-orbitals.
![]()
Question 37.
How do transition metals exhibit catalytic activity ?
Answer:
Catalytic properties:
- Transition metals and their compounds form important catalysts in industry and in biological systems.
- The catalytic activity of transition metals depends on their ability to exist in different oxidation states of oxidation (or) to form co-ordination compounds.
Eg : 1) V2O5 is used as catalyst in manufacturing of SO3 from SO2.
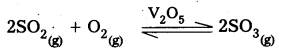
2) Fe is used as a catalyst in manufacturing of NH3.
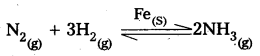
Question 38.
Give two reactions in which transition metals or their compounds acts as catalysts.
Answer:
1) V2O5 is used as catalyst in manufacturing of SO3 from SO2.
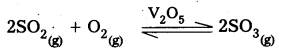
2) Fe is used as a catalyst in manufacturing of NH3.
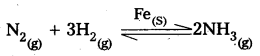
Question 39.
What is an alloy ? Give example.
Answer:
Alloy : An intimate mixture having physical properties similar to that of the metal formed by a metal with other metals or metalloids or sometimes a non metal is called as an alloy.
Eg.: Invar – 64% Fe, 35% Ni, Mn 8cc in traces
Nichrome – 60% Ni, 25% Fe, 15% Cr.
Question 40.
Why do the transition metals readily form alloys ?
Answer:
Because of similar atomic or ionic radii and similar characterstic properties of transition elements alloys are readily formed by these elements.
Question 41.
How do the ionic character and acidic nature vary among the oxides of first transition series ?
Answer:
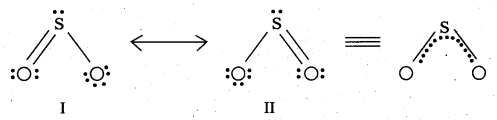
- As the oxidation number of a metal increases ionic character decreases in case of transition elements. Eg : Mn2O7 is a covalent green oil.
- In CrO3 and V2O5 the acidic character is predominant.
- V2O5 is however amphoteric though mainly acidic V2O5 reacts with alkali as well as acids to give V04-3 and VO+4.
- CrO is basic
- Mn2O7gives HMnO4 and CrO3 gives H2CrO4 and H2Cr2O7.
Question 42.
What is the effect of increasing pH on a solution of potassium dichromate ?
Answer:
On increasing pH of K2Cr2O7 (orange) it changes into K2CrO4 (yellow)
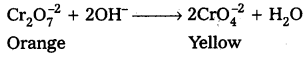
![]()
Question 43.
Name the oxometal anions of the first series of transition metals in which the metal exhibits the oxidation state equal to its group number.
Answer:
V4-3 ion exhibits ‘+5’ oxidation state which is equal to the V group number
V4-3 + 4(-2) = -3, x = +5
Question 44.
Permanganate titrations are carried out in the presence of sulphuric acid but not in presence of hydrochloric acid. Why ?
Answer:
Per manganate titrations are carried out in the presence of sulphuric acid but not in presence of hydrochloric acid because hydrochloric acid is oxidised to chlorine.
Question 45.
What is lanthanoid contraction ? [T.S. Mar. 19]
Answer:
The slow decrease of atomic and ionic radii in lanthanides with increase in atomic number is called lanthanide contraction.
Question 46.
What are the different oxidation states exhibited by the lanthanoids ?
Answer:
- Lanthanoids exhibits +2, +3 states majorly. Sometimes +2 and +4 states exhibited in solid compounds.
- The common oxidation state of lanthanoids is +3.
Question 47.
What is mischmetall ? Give its composition and uses. [A.P. Mar. 19, 16]
Answer:
- Mischmetall is an alloy which consists of a lanthanoid metal (~ 95%) and iron (~ 5%) and traces of S, C, Ca and Al.
- It is used in Mg- based alloy to produce bullets, shell and lighter flint.
Question 48.
What is actinoid contraction ?
Answer:
The gradual decrease in the size of atoms or M+3 ions across, the actinoid series is called actinoid contraction.
Question 49.
What are co-ordination compounds ? Give two examples.
Answer:
Co-ordination compounds : Transition metal atoms or ions form a large number of compounds in which anions or neutral groups are bound to metal atom or ion through coordinate covalent bonds. Such compounds are called co-ordination compounds (or) complex compounds.
Eg.: [Fe(CN)6]4-, [Co(NH3)6]+3.
![]()
Question 50.
What is a coordination polyhedron ?
Answer:
The spatial arrangement of the ligands which are directly bonded to the central atom or ions defines the geometry about the central atom is called co-ordination polyhedron
Eg. : Octahedral, tetrahedral etc.
Question 51.
What is a double salt ? Give example.
Answer:
The salts which contains two cations and one anion are called double salts.
These dissociates into simple ions completely when dissolved in water.
Eg : KCl.MgCl2.6H3O -Camallite.
Question 52.
What is difference between a double salt and a complex compound ?
Answer:
Double salts dissociate into simple ions completely when dissolved in water while complex compounds dissociate to give complex ion and the counter ions.
Question 53.
What is a ligand ?
Answer:
Ligand : A co-ordinating entity which is bound to the central atom by donating electron pairs is called a ligand.
Eg.: Cl–, NH3, CN– etc.
Question 54.
Give one example each for ionic and neutral ligands.
Answer:
Examples for ionic ligands – CN–, I–, Cl–
Examples for Neutral ligands – NH3, H2O
Question 55.
How many moles of AgCl is precipitated when 1 mole of CoCl3 is treated with AgNO3, solution ?
Answer:
3 moles of AgCl is precipitated by the reaction of 1 mole of CoCl3 with AgNO3 solution
3 AgNO3 + CoCl3 → CO(NO3)3 +3 AgCl ↓
Question 56.
What is a chelate ligand ? Give example.
Answer:
The ligands which can form two co-ordinate covalent bonds through two donar atoms are called bidentate ligands. These bidentate ligands are also called chelate ligands.
Eg.: C2O4-2, CO3;-2 etc.
![]()
Question 57.
What is an ambidentate ligand ? Give example. [A.P. Mar. 16]
Answer:
A unidentate ligand containing two possible donor atoms can co-ordinate through either of donor atoms. Such ligands are called ambidentate ligands.
Eg : NO2–
Question 58.
CUSO4.5H2O is blue in colour where as anhydrous CuSO4 is colourless. Why ?
Answer:
CUSO4.5H2O is blue in colour whereas anhydrous CuSO4 is colourless because in the absence of ligand, crystal field splitting does not occurs.
Question 59.
FeSO4 solution mixed with (NH4)2SO4 solution in 1:1 molar ratio gives the test for Fe2+ ion but CuS04 mixed with aqueous ammonia in 1 : 4 molar ratio does not give the test of Cu2+ ion. why ?
Answer:
- FeSO4 solution mixed with (NH4)2SO4 solution in 1 : 1 molar ratio gives the test for Fe2+ because of formation of double salt (FeSO4(NH4)2 SO4 6H2O Mohr’s salt).
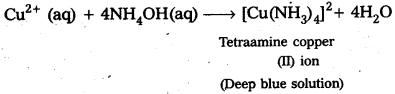
- CuSO4 mixed with aq.ammonia in 1 : 4 molar ratio does not give the test of Cu+2 ion because of formation of complex compound [Cu(NH3)4]SO4.
Question 60.
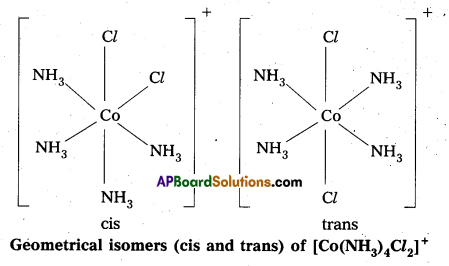
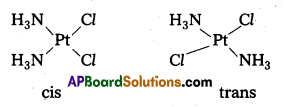
How many geometrical isomers are possible in the following coordination entities ?
- [Cr(C2O4)3]3-
- [CO(NH3)3Cl3]
Answer:
- [Cr(C2O4)3]3- : Two geometrical isomers are possible i) cis-isomer, ii) Trans-isomer.
- [CO(NH3)3Cl3] : Two geometrical isomers are possible i) cis-isomer, ii) Trans-isomer.
Question 61.
What is the coordination entity formed when excess of aqueous KCN is added to an aqueous solution copper sulphate ? Why ?
Answer:
When excess of aq. KCN is mixed with aq.CuSO4 a complex named potassium tetra cyano cuprate (II) is formal
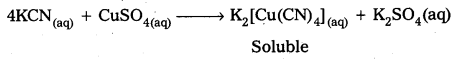
Question 62.
[Cr(NH3)6]3+ is paramagnetic while [Ni(CN)4]2- is diamagnetic Why ?
Answer:
[Cr(NH3)6]3+ is paramagnetic due to the presence of three unpaired electrons.
[Ni(CN)4]2- is diamagnetic due to the absence of unpaired electrons.
![]()
Question 63.
A solution of [Ni(H2O)6]2+ is green but a solution of [Ni(CN)4]2- is colourless. Why ?
Answer:
- In the complex [Ni(H2O)6]2+, H2O molecules are weak ligands they do not cause pairing.
So the complex has two unpaired electrons, d-d-transitions takes place due to absorption of red light radiation and emission of green colour occurs. - In the complex [Ni(CN)4]2-, CN– ions are strong ligands they cause pairing. So there is no unpaired electrons so, no d-d transition. Hence it is colourless.
Question 64.
[Fe(CN)4]2- and [Fe(H2O)6]2+ are of different colours in dilute solutions. Why ?
Answer:
In the given complexes Fe has + 2 oxidation state with 3d6 outer electronic configuration. It has four unpaired electrons in presence of weak ligand H2O. But in presence of strong ligand CN– the electrons are paired up. Due to the difference in the no. of unpaired electrons both complex have different colours in dilute solutions.
Question 65.
What is the oxidation state of cobalt in (i) K[Co(CO)4] and (ii) [Co(NH3)6]3+ ?
Answer:
- K[CO(CO)4] : 1 + x + 4(0) = 0, x = -1 .
- [CO(NH3)6]3+ : x + 6(0) = + 3, x = + 3
Short Answer Questions
Question 1.
Compared to 3d series the corresponding transition metals of 4d and 5d transition series show high enthalpy of atomization. Explain.
Answer:
Compared to 3d-series the corresponding transition metals of 4d and 5d transition series show high enthalpy of atomisation.
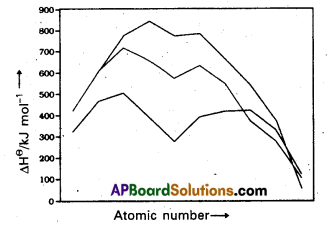
Reason : This is due to the occurrence of much more frequent metal-metal bonding in compounds of heavy transition metals.
Question 2.
Compared to the changes in atomic and ionic sizes of elements of 3d and 4d series, the change in radii of elements of 4d and 5d series is virtually the same Comment.
Answer:
Compared to the change in atomic and ionic sizes of elements 3d and 4d series, the change in radii of elements 4d and 5d series is virtually the same.
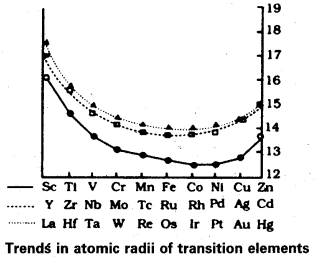
This is due to the intervention of the 4f orbitals which must be filled before the 5d series of elements begin. The filling of 4f before 5d orbitals results in a regular decrease in atomic radii called lanthanoid contraction. The consequence of lanthanoid contraction is that the 4d and 5d series exhibit same size of radii.
![]()
Question 3.
Account for the zero oxidation state of Ni and Fe in [Ni(CO)4] and [Fe(CO)5] respectively.
Answer:
In [Ni(CO)4] and [Fe(CO)5] the oxidation state of Ni and Fe is zero.
These low oxidation states found when the complex compound has ligands capable of π-acceptor character in addition to the σ-bonding.
Question 4.
Why do the transition metal ions exhibit characteristic colours in aqueous solution. Explain giving examples.
Answer:
Colour property of transition metal ions in aqueous solution is due to the presence of unpaired d-electrons. These unpaired d-electrons from a lower energy level of a metal ion in a complex is excited to a higher energy d-orbital of the same n value. The energy of excitation corresponds to the frequency of light absorbed and this frequency lies in visible region. The colour observed corresponds to the complementary colour of light obsorbed. The frequency of light absorbed is determined by the nature of the ligand. In aqueous solutions water molecules are ligands the colour of the ions observed are listed in the following table.
Colours of Some of the First Row (aquated) Transition Metal Ions
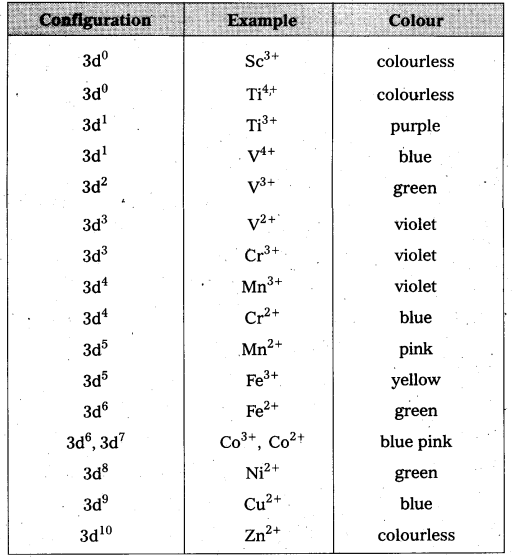
Question 5.
Explain the catalytic action of Iron(DI) in the reaction between I arid S2O82- ions.
Answer:
Transition metal ions can change their oxidation states and become more effective catalysts. Iron (III) Catalyses the reaction between iodide and per sulphate ions
![]()
Catalytic action explained as follows
2Fe+3 + 2I– → 2Fe+2 + I2
2Fe+2 + S2O8-2 → 2Fe+3 + 2SO4-2
Question 6.
What are interstitial compounds ? How are they formed ? Give two examples.
Answer:
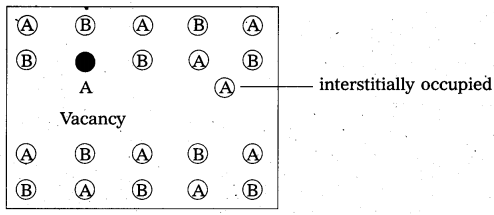
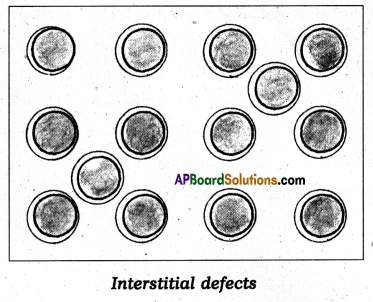
The compounds which are formed when small atoms like H, C or N are trapped inside the crystal lattices of metal are called interstitial compounds.
Eg : TiC, Fe3H, VH0.56 etc.
- These are non stoichiometric and are neither typically ionic nor covalent.
- They have high melting points, higher than of pure metals.
- They are very hard, some borides approach diamond in hardness.
- They retain metallic conductivity.
- They are chemically inert.
![]()
Question 7.
Write the characteristics of interstitial compounds.
Answer:
Characteristics of interstitial compounds :
- These are non stoichiometric and are neither typically ionic nor covalent.
- They have high melting points, higher than of pure metals.
- They are very hard, some borides approach diamond in hardness.
- They retain metallic conductivity.
- They are chemically inert.
Question 8.
Write the characteristic properties of transition elements. [A.P. Mar. 15]
Answer:
Transition elements exhibits typical characteristic properties.
- Electronic configurations.
- Para and ferro magnetic properties.
- Alloy forming ability
- Complex forming ability.
- Interstitial compounds.
- Variable oxidation states.
- Formation of coloured hydrated ions.
- Catalytic property.
- Metallic character.
Question 9.
Write down the electronic configuration of ‘
- Cr3+
- Cu+
- Co2+
- Mn2+
Answer:
- Cr3+ electronic configuration is [Ar] 4s03d3
- Cu+ electronic configuration is [Ar] 4s03d10
- Co2+ electronic configuration is [Ar] 4s03d7
- Mn2+ electronic configuration is [Ar] 4s03d5
Question 10.
What may be the stable oxidation state of the transition element with the following d electron configurations in the ground state of their atoms : 3d3 3d5 3d8 and 3d4 ?
Answer:
- 3d3-stable oxidation states are +2,+3,+4 and+5 (V)
- 3d5-stable oxidation states are +3, +4 and +6 (Cr)
- 3d5-stable oxidation states are +2, +4, +6 and +7 (Mn)
- 3d8-stable oxidation states are +2, +3 (Co)
- 3d4-This configuration does not exist.
![]()
Question 11.
What is lanthanoid contraction ? What are the consequences of lanthanoid contraction?
Answer:
Lanthanoid contraction : The overall decrease in atomic and ionic radii from lanthanum to leutetium is observed in the lanthanoids. This phenomenon is called lanthanoid contraction. It is due to the fact that with every additional proton in the nucleus, the corresponding electron goes into a 4f-subshell. This is too diffused to screen the nucleus as effectively as the more localised inner shell. Hence, the attraction of the nucleus for the outermost electrons increases steadily with the atomic number.
Consequences of Lanthanoid Contraction : The important consequences of lanthanoid contraction are as follows :
i) Basic character of oxides and hydroxides : Due to the lanthanoid contraction, the covalent nature of La-OH bond increases and thus, the basic character of oxides and hydroxides decreases from La(OH)3 to Lu(OH)3.
ii) Similarity in the size of elements of second and third transition series : Because of
lanthanoid contraction, elements which follow the third transition series are considerably smaller than would otherwise be expected. The normal size increases from Sc → Y → La and disappears after lanthanides. Thus, pairs of elements such as Zr/Hf, Nb/Ta and Mo/w are almost identical in size.
Due to almost similar size, such pairs have very sijnilar properties which makes their separation difficult.
iii) Separation of lathanoids : Due to lanthanoid contraction, there is a difference in some properties of lanthanoid like solubility, degree of hydration and complex formation. These difference enable the separation of lanthanoids by ion exchange method.
Question 12.
How is the variability in oxidation states of transition metals different from that of the non transition metals ? Illustrate with examples.
Answer:
- In transition elements the oxidation states vary by unity (due to incomplete filling of d- orbitals)
Eg : Mn exhibits +2, +3, +4, +5, +6 and +7 all differing by 1. - In non-transition element, this variation is selective, always differing by 2.
Eg : S exhibits 2, 4, 6 oxidation states. N exhibits 3, 5 etc.
Question 13.
Describe the preparation of potassium dichromate from iron chromite ore.
Answer:
Preparation of K2Cr2O7 from chromite ore :
i) a) Potassium dichromate is obtained by the fusion of chromite ore (FeCr2O4) with sodium (or potassium) carbonate in the presence of excess of air.

b) The solution is filtered and treated with sulphuric acid.

c) Now sodium dichromate is treated with potassium chloride. As a result, potassium dichromate is produced.
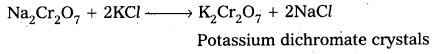
ii) Effect of increasing pH on K2Cr2O7 solution :
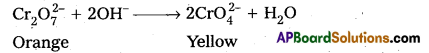
On increasing pH, K2Cr2O7 changes into K2CrO4 (orange to yellow).
Question 14.
Describe the oxidising action of potassium dichromate and write the ionic equations for its.
With (i) iodide (ii) iron (II) solution (iii) H2S and (iv) Sn(II)
Answer:
Potassium dichromate is a strong oxidising agent. In acidic solution, its oxidising action may be represented as :
Cr2O72- + 14H+ + 6e– → 2Cr3+ + 7H2O (E° = 1.33 V)
Ionic reactions :
- Reaction of K2Cr2O7 with I–
Cr2O72- + 14H+ + 6I– → 2Cr3+ + 3I2 + 7H2O - Reaction of K2Cr2O7 with Fe2+ (aq)
Cr2O72- + 14H+ + 6Fe2+ → 2Cr3+ + 6Fe3+ + 7H2O - Reaction of K2Cr2O7with H2S
Cr2O72- + 8H+ + 3H2S → 2Cr+3 + 3S + 7H2O
![]()
Question 15.
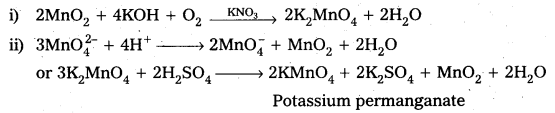
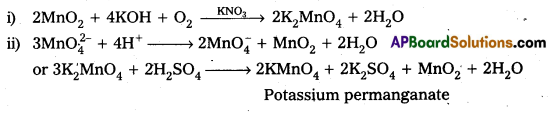
Describe the preparation of potassium permanganate.
Answer:
Preparation of KMnO4 Potassium permanganate is prepared by the fusion of MnO2 with an alkali metal hydroxide and an oxidising agent like KNO3. It forms dark green, K2MnO4 which disproportionates in a neutral or acidic solution to give permanganate.
Question 16.
How does the acidified permanganate solution react with
- iron (II) ions
- SO2 and
- oxalic acid.
Write the ionic equations for the reactions.
Answer:
Reactions of KMnO4 in acidic medium
MnO4– + 8H+ + 5e– → Mn2+ + 4H2O …………. (i)
1) Iron (II) ions : Ferrous is oxidised to ferric.
[Fe2+ → Fe3+ + e] × 5 ………………. (ii)
From equation (i) and (ii) 5Fe2+ + MnO4– + 8H+ → Mn2+ + 4H2O + 5Fe3+
2) SO2 : It is oxidised to SO42- by acidified KMnO4.
SO2 + 2H2O → SO42- + 4H+ + 2e– ……………….(iii)
From equation (i) and (iii) .
5SO2 + 2MnO4– + 2H2O → 2Mn2+ + 4H+ + 5SO42-
3) Oxalic acid : C2O42- → 2CO2 + 2e– ……………… (iv)
From equation (1) and (iv)
5C2O42- + 2MnO4– + 16H+ → 2Mn2+ + 8H2O + 10CO2
Question 17.
Predict which of the ions Cu+, Sc3+, Mn2+, Fe2+ are coloured in aqueous solution ? Give reasons.
Answer:
Only those ions will be coloured which have incomplete d-orbitals. Ions which has complete or vacant d-orbitals are colourless.

As Sc3+ and Cu+ have 3d0 and 3d10 configuration in their valence shell so their aqueous solutions are colourless. All others, i.e., Ti3+, V3+, Mn2+ Fe+2 and Co2+ are coloured in aqueous medium.
Question 18.
Compare the stability of +2 oxidation state of the elements of the first transition series.
Answer:
Element (+2 state) 21Sc2+ Ti2+ 22 22V2+ 24Cr2+ 25Mn2+,
Electronic configuration 3d1 3d2 3d3 3d4 3d5
In all the elements listed, the removal of two 4s. Electrons (in Cr2+, i.e., from 4s and 1e– from 3d), the 3d-orbitais get gradually occupied. Since, the number of empty d-orbitais decreases or the number unpaired electrons in 3d-orbitais increases with increase in atomic number of cations, so the stability of the cations (M2+) increases from Sc2+ to Mn2+.
![]()
Question 19.
Use Hund’s rule to derive the electronic configuration of Ce3+ ion and calculate its magnetic moment on the basis of ‘spin-only’ formula.
Answer:
Ce(Z = 58) = [Xe] = 4f1 5d1 6s2
Ce3+ = [Xe]4f1 (only one unpaired electron)
By ‘spin-only’ formula, Magentic moment of Ce3+(μ) = \(\sqrt{n(n+2)}\)
[∵ n = 1 (unpaired electron)] = \(\sqrt{1(1+2)}\) = \(\sqrt{3}\) = 1.73 BM
Question 20.
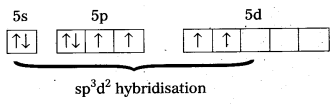
Write down the number of 3d electrons in each of the following ions : Ti2+, V2+ Cr3+ and Mn2+ Indicate how would you expect the five 3d orbitais to be occupied for these hydrated ions (octahedral).
Answer:
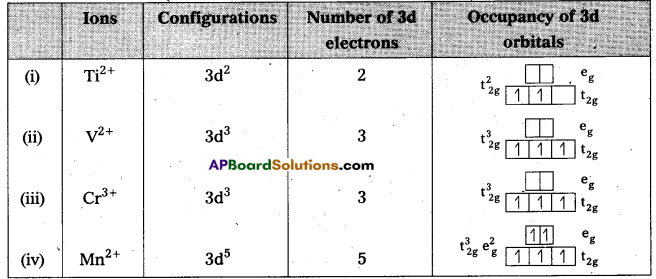
Question 21.
Explain Werner’s theory of coordination compounds with suitable examples. [A.P. Mar. 18; T.S. Mar. 18, 15] [Mar. 14]
Answer:
Werner’s theory:
Postulates :
1) Every complex compound has a central metal atom (or) ion.
2) The central metal shows two types of valencies namely primary valency and secondary valency.
A) Primary valency: The primary valency is numerically equal to the oxidation state of the
metal. Species or groups bound by primary valencies undergo complete ionization. These valencies are identical with ionic bonds and are non-directional. These valencies are represented by discontinuous lines (…..)
Eg- : CoCl3 contains Co3+ and 3Cl– ions. There are three Primary Valencies or three ionic bonds.
B) Secondary Valency : Each’ metal has a characteristic number of Secondary Valencies. They are directed in space around the central metal.
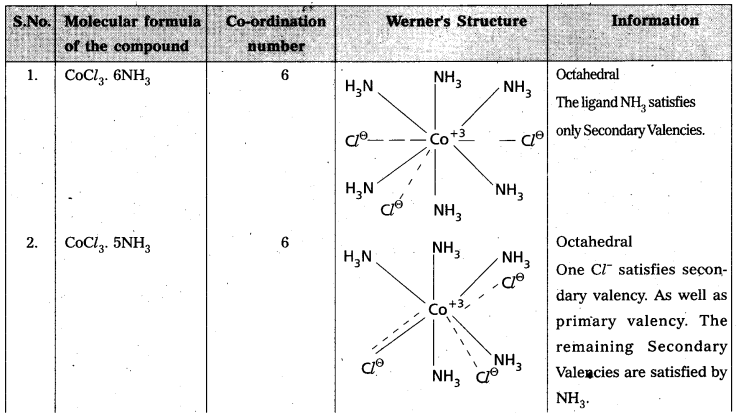
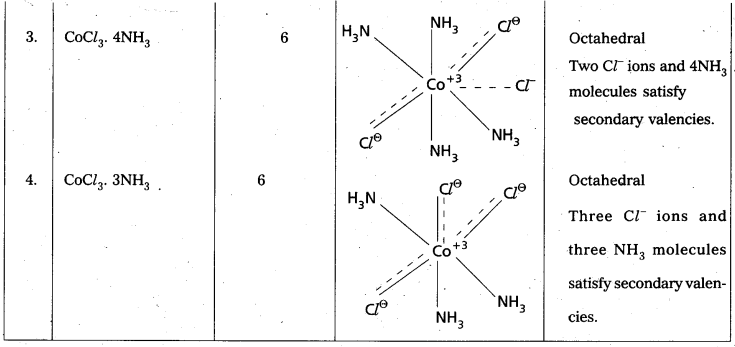
The number of Secondary Valencies is called Coordination numbe (C.N.) of the metal. These valencies are directional in Nature.
For example in CoCl3. 6NH3
Three Cl– ions are held by primary Valencies and 6NH3 molecules are held by Secondary Valencies. In CuSO4 . 4NH3 complex SO42- ion is held by two Primary Valencies and 4NH3 molecules are held by Secondary Valencies.
3) Some negative ligands, depending upon the complex, may satisfy both primary and secondary valencies. Such ligands, in a complex, which satisfy both primary as well as secondary valencies do not ionize.
4) The primary valency of a metal is known as its outer sphere of attraction or ionizable valency while the Secondary valencies are known as the inner sphere of attraction or coordination Sphere. Groups bound by secondary valencies do not undergo ionization in the complex.
Example to Clarify Werner’s Theory
![]()
Question 22.
Give the geometrical shapes of the following complex entities
- [Co(NH3)6]3+
- [Ni(CO)4]
- [Pt Cl4]2- and
- [Fe(CN)8]4-.
Answer:
- Geometrical shape of [Co(NH3)6]3+ is octahedral
- Geometrical shape of [Ni(CO)4] is tetrahedral
- Geometrical shape of [Pt Cl4]2- is square planar
- Geometrical shape of [Fe(CN)8]4- is octahedral
Question 23.
Explain the terms
(i) Ligand
(ii) Coordination number
(iii) Coordination entity
(iv) Central metal atom/ion.
Answer:
i) Ligand : The ions or molecules bound to the central atom/ion in the coordination entity are called ligands. These may be
a) simple ions such as Cl–
b) small molecules such as H2O or NH3
c) large molecules such as H2NCH2CH2NH2 or N(CH2CH2NH2)3 or even (d) macromolecules, such as proteins.
On the basis of the number of donor atoms available for coordination, the ligands can be classified as :
a) Unidentate : One donor atom, Eg.: ![]()
b) Bidentate : Two donor atoms, Eg. : H2NCH2CH2NH2
(ethane-1, 2-diamine or en), C2O42- (oxalate), etc.
c) Polydentate : More than two donor atoms, Eg. : N(CH2CH2NH2)3 EDTA, etc.
ii) Coordination number: The coordination number (CN) of metal ion in a complex can be defined as the number of ligands or donor atoms to which the metal is directly bonded.
Eg : In [PtCl6]2-, CN of Pt = 6, In [Ni(NH3/sub>)4]2+, CN of Ni 4.
iii) Coordination entity: A central metal atoms or ion bonded to a fixed number of molecules or ions (ligands) is known as coordination entity. For example [CoCl3(NH3)3. Ni(CO)4/sub>], etc.
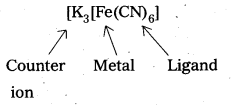
iv) Central metal atom/ion : In a coordination entity, the atom/ion to which a fixed no. of ions/groups are bound in a definite geometrical arrangement around it is called central metal atom or ion. Eg: K4[Fe(CN)6] ‘Fe’ is central metal.
Question 24.
Explain the terms (i) Unidentate ligand (ii) bidentate ligand (iii) polydentate ligand and (iv) ambidentate ligand giving one example for each.
Answer:
i) Unidentate : The negative ion or neutral molecule having only one donor atom is called unidentate ligand
Eg : ![]()
ii) Bidentate (or didentate) : The ions or molecules having two donor atoms are called bidentate ligands.
Eg: 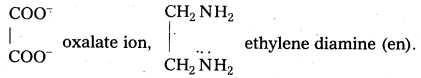
iii) Polydentate ligands : Ligands having more than one donor atom in the coordinating group and are capable of forming two or more coordinate bonds with same central atom simultaneously are called poly dentate ligands.
Eg : C2O4-2.
iv) Ambidentate: Ligand which can ligate through two different atoms is called ambidentate ligand. Eg: NO2–, SCN–ions, NO2– ion can coordinate either through nitrogen or through oxygen to a central metal atom/ion. Similarly, SCN– ion can coordinate through the sulphur or nitrogen atom.
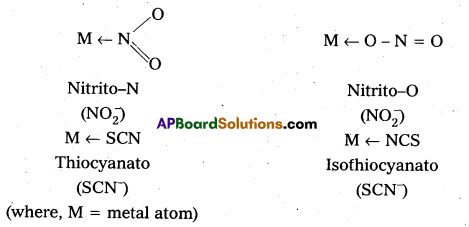
Question 25.
What is meant by chelate effect ? Give example.
Answer:
When a didentate or a polydentate ligand contains donor atoms positioned in such a way that when they coordinate with the central metal ion, a 5-or 6-membered ring is formed, the effect is known as chelate effect. Example
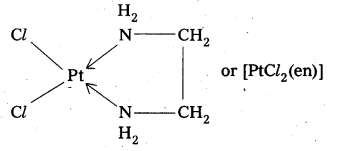
![]()
Question 26.
Give the oxidation numbers of the central metal atoms in the following complex entities
(i) [Ni(CO)4]
(ii) [CO(NH3)6]3+
(iii) [Fe(CN)6]4- and
(iv) [Fe(C2O4)3]3-
Answer:
i) [Ni(CO)4] :
x + 4(0) = 0
x = 0
‘Ni’ oxidation state is zero.
ii) [CO(NH3)6]3+
x + 6(0) = + 3
x = +3
‘Co’ oxidation state is + 3.
iii) [Fe(CN)6]4-
x + 6(-1) = -4
x = + 2
‘Fe’ oxidation state is + 2.
iv) [Fe(C2O4)3]3-
x + 3(-2) = -3
x = + 3
‘Fe’ oxidation state is + 3.
Question 27.
Using IUPAC norms write the formulas for the following.
- Tetrahydroxozincate (II)
- Hexaamminecobalt (III) sulphate
- Potassium tetrachloropalladate (II) and
- Potassium tri(oxalato) chromate (III)
Answer:
- Tetrahydroxozincate (II) – [Zn(OH)4]-2
- Hexa ammine cobalt (III) sulphate – [Co(NH3)6]2 (SO4)3
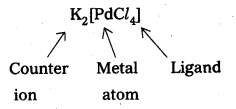
- Potassium tetrachloropalladate – K2[PdCl4]
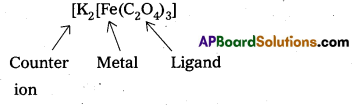
- Potassium tri(oxalato) chromate (III) – K3[Cr(C2O4)3]
Question 28.
Using IUPAC norms write the systematic names of the following. [A.P. Mar 19]
- [CO(NH3)6]Cl3
- [Pt(NH3)2Cl(NH2CH3)]Cl
- [Ti(H2O)6]3+ and
- [NiCl4]2-
Answer:
- Hexa ammine cobalt (III) chloride
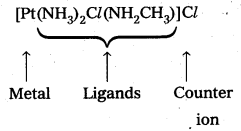
- Diammine chlorido (methyl amine) platinum (II) chloride
- Hexa aquo titanium (III) ion
- Tetra chloro nickelate (III) ion
![]()
Question 29.
Explain geometrical isomerism in Co-ordination compounds giving suitable examples. [A.P. Mar 19]
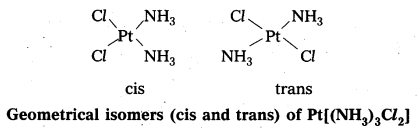
Answer:
- Geometrical isomerism arises in Co-ordination complexes due to different possible geometric arrangements of the ligands.
- This isomerism found in complexes with Co-ordination numbers 4 and 6.
- In a square planar complex of formula [MX2L2] the two ligands may be arranged in adjacent to each other in a cis isomer (or) opposite to each other in a trans isomer.
- Square planar complex of type [MAB XL] shows three isomers two-cis and one trans. (A, B, X, L are unidentate ligands is square planar complex).
- Geometrical isomerism is not possible in tetrahedral geometry.
- In octahedral complexes of formula [MX2L4] in which two ligands X may be oriented cis or trans to each other.
- Another type of geometrical isomerism occurs in octahedral Co-ordination compounds of type [Ma3b3] if three donar atoms of the same ligands occupy adjacent positions at the corners of an octahedral face then it is facial (fac) isomer. When the positions occupied are around the meridian of the octahedran then it is meridonial (mer). isomer.
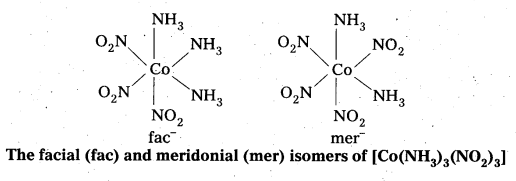
Question 30.
What are homoleptic and heteroleptic complexes ? Give one example for each.
Answer:
Homoleptic complexes : These are the complexes in which a metal is bound by only ore kind of ligands.
eg.: [Co(NH3)6]3+
Heteroleptic complexes: These are the complexes in which a metal is bound by more than one kind of ligends. eg.: [Co(NH3)4Cl2]+
Long Answer Questions
Question 1.
Explain giving reasons :
(i) Transition metals and many of their compounds show paramagnetic behaviour.
(ii) The enthalpies of atomisation of the transition metals are high.
(iii) The transition metals generally form coloured compounds.
(iv) Transition metals and their many compounds act as good catalysts.
Answer:
i) Transition elements have unpaired electrons. Each unpaired electron has a magnetic moment associated with its spin angular momentum and orbital angular momentum. This is the reason of paramagnetism in transition metals.
ii) The reason for the high enthalpy of atomisation is the presence of large number of unpaired electrons in their atoms. These atoms have strong interatomic interaction and hence, stronger bonding between them.
iii) Formation of coloured compounds by transition metals is due to partial adsorption of visible light. The electron absorbs the radiation of a particular frequency (of visible region) and jumps into next orbital.
iv) Catalysts, at the solid surface, involve the formation of bonds between reactants molecules and atoms of the surface of the catalyst (I row transition metals utilise 3d and 48- electrons for bonding). This has the effect of increasing the concentration of the reactants at the catalyst surface and also lowering of the activation energy.
Transition metal ions show variable oxidation states, so they are effective catalysts.
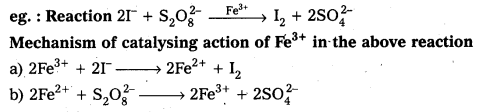
Question 2.
Describe the preparation of potassium permanganate. How does the acidified permanganate solution react with
(i) iron (II) ions
(ii) SO2 and
(iii) oxalic acid ?
Write the ionic equations.
Answer:
Preparation of KMnO4 Potassium permanganate is prepared by the fusion of MnO2 with an alkali metal hydroxide and an oxidising agent like KNO3. It forms dark green, K2MnO4 which disproportionates in a neutral or acidic solution to give permanganate.
Reactions of KMnO4 in acidic medium
MnO4– + 8H+ + 5e– → Mn2+ + 4H2O …………. (i)
i) Iron (II) ions : Ferrous is oxidised to ferric.
[Fe2+ → Fe3+ + e] × 5 ………………. (ii)
From equation (i) and (ii) 5Fe2+ + MnO4– + 8H+ → Mn2+ + 4H2O + 5Fe3+
ii) SO2 : It is oxidised to SO42- by acidified KMnO4.
SO2 + 2H2O → SO42- + 4H+ + 2e– ……………….(iii)
From equation (i) and (iii) .
5SO2 + 2MnO4– + 2H2O → 2Mn2+ + 4H+ + 5SO42-
iii) Oxalic acid : C2O42- → 2CO2 + 2e– ……………… (iv)
From equation (1) and (iv)
5C2O42- + 2MnO4– + 16H+ → 2Mn2+ + 8H2O + 10CO2
![]()
Question 3.
Compare the chemistiy of actinoids with that of the lanthanoids with special reference to :
(i) electronic configuration (ii) oxidation state (iii) atomic and ionic sizes and (iv) chemical reactivity.
Answer:


Question 4.
How would you account for the following.
(i) Of the d4 species, Cr2+ is strongly reducing while manganese (HI) is strongly oxidising.
(ii) Cobalt (II) is stable in aqueous solution but in the presence of complexing reagents it is easily oxidised,
(iii) The d1 configuration is very unstable in ions.
Answer:
i) E° value of Cr3+/Cr2+ is negative (-0.41 V) while that of Mn3+/Mn2+ is positive (+1.57 V). This means that Cr2+ ions can lose electrons to form Cr3+ ions and act as a reducing agent while Mn3+ ions can accept electrons and can act as an oxidising agent.
ii) Cobalt (III) ion has greater tendency to form complexes than cobalt (II) ion. Therefore, Co (II) ion, being stable in aqueous solution, changes to Co (III) ion, in the presence of complexing reagents and gets oxidised.
iii) Ions of transition metals with d1 configuration tend to lose one electron to acquire d0 configuration that is quite stable. Therefore, such ions (with d1) undergo either oxidation or disproportionation hence unstable.
Question 5.
Give examples and suggest reasons for the following features of the transition medals.
(i) The lowest oxide of transition metal is basic, the highest is amphoteric/acidic.
(ii) A transition metal exhibits highest oxidation state in oxides and fluorides.
(iii) The highest oxidation state is exhibited in oxoanions of a metal.
Answer:
i) Acidic strength of oxides increases with the increase in oxidation state of the element Eg.: MnO(Mn2+) is basic whereas Mn2O7(Mn7+) is acidic in nature.
ii) Both oxygen and fluorine being highly electronegative can increase the oxidation state of a particular transition metal. In certain oxides, the element oxygen is involved in multiple bonding with the metal .and this is responsible for the higher oxidation state of the metal.
iii) This is also due to high electronegativity of oxygen eg.: chromium exhibits oxidation states of +6 in oxoanion [CrO4]2- and manganese shows oxidation state of +7 in oxoanion [MnO4]–
![]()
Question 6.
Compare the chemistry of the actinoids with that of lanthanoids with reference to : (i) electronic configuration (ii) oxidation states and (iii) chemical reactivity
Answer:

Question 6.
Explain IUPAC nomenclature of Co-ordination compounds with suitable examples.
Answer:
IUPAC nomenclature : The formula of a compound is an abreviated description of the constitution of the compound. The fpllowing rules are prescribed by IUPAC for naming of Coordination compounds.
i) Positive ions are named first followed by negative ions,
eg.: Potassium hexacyanoferrate (II), K4[Fe(CN)6]
ii) Within the Co-ordination sphere ligands are named before the metal atom/ion. However, in formulae, metal ion is written first.
eg.: Tetraammine copper (II) sulphate [Cu(NH3)4]SO4
iii) Prefixes are used to denote the number of same ligands that the present in the Co¬ordination sphere. Complex ions are denoted in paranthesis ( ) and prefixed by bis, tris etc.
Examples:

eg. : [CO(NH2CH2CH2NH2)Cl2] Cl is named as dichloro bis (ethylenediamine) cobalt (III) chloride.
iv) Ligands are named in alphabetical order.
eg.: [PtCl2(NH3)2 diammine dichloro platinum (II)
v) Anionic ligands are denoted by a suffix ‘O’ and neutral ligands are denoted by their original names.
eg.: Cl– – Chloro, CN– – Cyano
Exception for the above are indicated below.
vi) Oxidation state of the metal ion is indicated by Roman numerical in parenthesis, eg.: [Ag(NH3)2] [Ag(CN)2] is named as diammine silver (I) dicyanoargentate (I).
vii) If the charge of the Co-ordination entity is negative, the name of the metal ends with a suffix-ate.
eg.: [CO(SCN)4]2- – tetrahiocyanato cobaltate (II)
Some metal ions are denoted by their names from which their symbols are derived
eg.: Fe – ferrate
Pb – plumbate
Sn – stannate .
Ag-argentate
Au-aurate
viii) Prefixes cis – and trans are used to designate adjacent and opposite geometric locations of the ligands, in a complex.
eg. :
ix) Bridging ligands between two metal ions in a Co-ordination entity are denoted by prefix p(greek letter’mu).
eg.: [(NH3)4 CO(OH) (NH2)Co(NH3)4]+ is named as μ-amido-μ hydroxo bis (tetraammine) cobalt (IV) .
- Tetrahydroxozincate (II) – [Zn(OH4]-2
- Hexa ammine cobalt (III) sulphate – [Co(NH3)6]2 (SO4)3
- Potassium tetrachloropalladate – K2[PdCl4)
- Potassium tri(oxalato) chromate (III) – K3[Cr(C2O4)3]
Question 7.
Explain different types of isomerism exhibited by Co-ordination compounds, giving suitable examples.
Answer:
Isomerism in Co-ordination compounds : Isomers are compounds that have the same chemical formula but different arrangement of atoms. Two principal types of isomerism are known among Co-ordination compounds namely stereo isomerism and structural isomerism.
a) Stereoisomengni: Stereoisomerism is a form of isomerism in which two substances have the same composition and structure but differ in the relative spatial positions of the ligands. This can be sub divided into two classes namely.
- Geomethcal isomerism and
- optical isomerism
b) Structural isomerism:
- Linkage isomerism
- Co-ordination isomerism
- Ionisation isomerism
- Hydrate isomerism
a) (1) Geometrical isomerism:
- Geometrical isomerism arises in Co-ordination complexes due to different possible geometric arrangements of the ligands.
- This isomerism found in complexes with Co-ordination numbers 4 and 6.
- In a square planar complex of formula [MX2L2] the two ligands may be arranged in adjacent to each other in a cis isomer (or) opposite to each other in a trans isomer.

- Square planar complex of type [MAB XL] shows three isomers two-cis and one trans. (A, B, X, L are unidentate ligands is square planar complex).
- Geometrical isomerism is not possible in tetrahedral geometry.
- In octahedral complexes of formula [MX2L4] in which two ligands X may be oriented cis or trans to each other.

- Another type of geometrical isomerism occurs in octahedral Co-ordination compounds of type [Ma3b3] if three donar atoms of the same ligands occupy adjacent positions at the corners of an octahedral face then it is facial (fac) isomer. When the positions occupied are around the meridian of the octahedran then it is meridonial (mer). isomer.

a(2) Optical isomerism : Optical isomerism arises when two isomers of a compound exist such that one isomer is a mirror image of the other isomer. Such isomers are called optical isomers or enantiomers. The molecules or ions that cannot be superimposed are called chiral. The two forms are called dextro (d) and laevo (1) depending upon the direction they rotate the plane of polarised light in a polarimeter (d rotates to the right, l to the left). Optical isomerism is common in octahedral complexes involving bidentate ligands.
b(1) Linkage isomerism: Linkage isomerism arises in Co-ordination compound containing ambidentate ligand. A simple example is provided by complexes containing the thiocyanate ligand-NCS–, which may bind through the nitrogen to give M-NCS or through sulphur to give M-SCN.
eg. : [Mn(CO)5SCN] and [Mn(CO)5NCS]
(2) Co-ordinate isomerism : This type isomerism arises from the interchange of ligands between cationic and anionic entities of different metal ions present in a complex.
eg. : [CO(NH3)6] [Cr(CN)6] and [Co(CN)6] [Cr(NH3)6]
(3) Ionisation isomerism: This form of isomerism arises when the counter ion in a complex salt is itself a potential ligand and can displace a ligand which can then become the counter ion
eg. : [CO(NH3)5SO4] Br and [Co(NH3)5Br]SO4
(4) Hydrate isomerism : This form of isomerism is known as ‘hydrate isomerism since water is involved as a solvent. Hydrate isomers differ by whether or not a hydrate molecule is directly bonded to the metal ion or merely present as free solvent molecules in the crystal lattice.
![]()
Question 8.
Discuss the nature of bonding and magnetic behaviour in the following Co-ordination entities on the basis of valence bond theory.
(i) [Fe(CN6)]4-
(ii) [FeF6]3-
(iii) [Co(C2O4)3]3- and
(iv) [CoF6]3-
Answer:
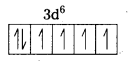
i) Fe(CN6)]4- : In this complex Fe is present as Fe2+.
Fe = [Ar] 3d64s2
Outer configuration of Fe2+ = 3d64s0
CN being strong field ligand, pair up the unpaired d electrons Thus, two 3d-orbital are now available for CN– ions.
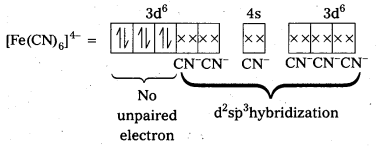
Since, all the electrons are paired, the complex is diamagnetic. Moreover (n – 1) d- orbitals are involved in bonding, so, it is an inner orbital or low spin complex.
ii) [FeF6]3- : In this complex, the oxidation state of Fe is + 3.
Fe3+ = 3d54s0
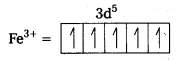
F- is not a strong field ligand. It is a weak field ligand, so no pairing occurs. Thus, 3d- orbitals are not available to take part in bonding.
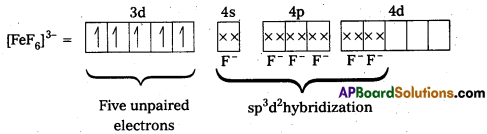
Because of the presence of five unpaired electrons, the complex is paramagnetic. Moreover, nd-orbitals are involved in bonding, so it is an outer orbital or high spin complex.
iii) [Co(C2O4)3]3- : In this complex, the oxidation state of Co is + 3.
Outer configuration of Co = 3d7 4s2
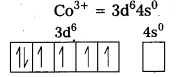
Oxalate ion being a strong field ligand pair up the 3d electrons, thus two out of the five 3d-orbitals are available for oxalate ions.
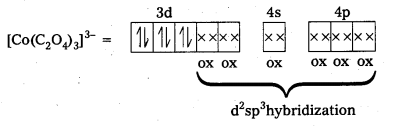
Since, all the electrons are paired, this complex is diamagnetic. It is an inner orbital complex because of the involvement of (n – 1) d-orbital for bonding.
iv) [CoF6]3- : In this complex, Co is present as Co3+.
Outer configuration of Co3+ = 3d6 4s0
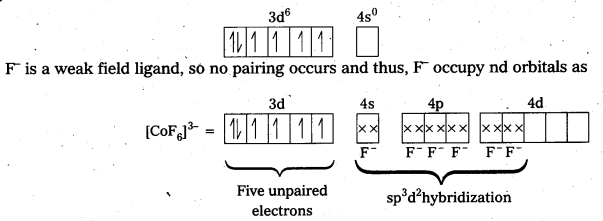
Because of the presence of four unpaired electrons, the complex is paramagnetic. Since, nd orbitals take part in bonding, it is an outer orbital complex or high spin complex.
Question 9.
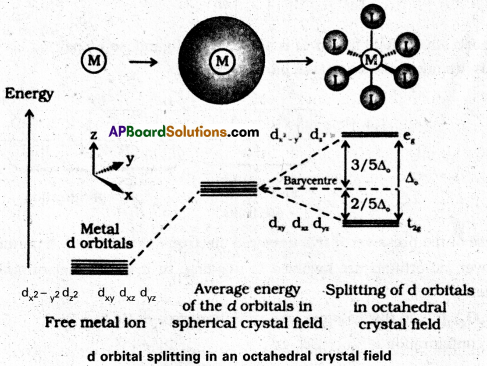
Sketch the spliting of d orbitals in an octahedral crystal field.
Answer:
Question 10.
What is spectrochemical series ? Explain the difference between a weak field ligand and a strong field ligand.
Answer:
The arrangement of ligands in order of their increasing field strengths, i.e., increasing crystal field splitting energy (CFSE) values is called spectrochemical series.
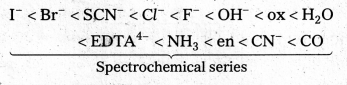
The ligands with a small value of CFSE (∆0) are called weak field ligands. For such ligands ∆0 < P where P is the pairing energy. Whereas the ligands with a large value of CFSE are called strong field ligands. In case of such ligands ∆0 > P.
When ligands approach a transition metal ion, the d-orbitals split into two sets (t2g and eg), one with lower energy and the other with higher energy. The difference of energy between the two sets of orbitals is called crystal field splitting energy, ∆0 for octahedral field (and ∆t for tetrahedral field)
If ∆0 < P (pairing energy), the 4th electron enters one of the eg orbitals giving the configuration \(t_{2 g}^{3} e_{g}^{1}\) thereby forming high spin complex. Such ligands for which ∆0 < P are known as weak field ligands.
If ∆0 > P, the 4th electron pairs up in one of the t2g orbitals giving the configuration \(\mathrm{t}_{2 \mathrm{~g}}^{4} \mathrm{e}_{\mathrm{g}}^{0}\), thus forming low spin complexes. Such ligands for which ∆0 > P are called strong field ligands.
![]()
Question 11.
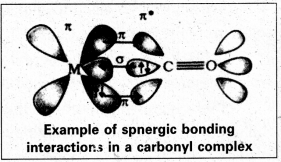
Discuss the nature of bonding in metal carbonyls.
Answer:
The metal-carbon bond in metal carbonyls have both sigma (σ) and pi (π) characters. The metal-carbon σ-bond is formed by the donation of lone pair of electrons of the carbonyl carbon to a vacant orbital of the metal. The metal- carbon re-bond is formed by the donation of a pair of electrons from a filled d-orbital of metal into the vacant
Question 12.
Explain the applications of Co-ordination compounds in different fields.
Answer:
Applications of Co-ordination compounds : Co-ordination compounds are of great importance. These compounds are widely present in the mineral, plant and animal worlds and are known to play many important functions in the area of analytical chemistry, metallurgy, biological systems, industry and medicine. These are described below.
Co-ordination compounds find use in many qualitative and quantitative chemical analysis. The familiar colour reactions given by metal ions with a number of ligands (especially chelating ligands), as a result of formation of co-ordination enitites, form the basis for their detection and estimation by classical and instrumental methods of analysis. Examples of such reagents include EDTA, DMG (dimethylglyoxime), oc-nitroso-p-naphtol, cupron etc.
Hardness of water is estimated by simple titration with Na2EDTA. The Ca2+ and Mg2+ ions form stable complexes with EDTA. The selective estimation of these ions can be done due to difference in the stability constants of calcium and magnesium complexes.
Some important extraction processes of metals, like those of silver and gold, make use of complex formation. Gold for example, combines with cyanide in the presence of oxygen and water to form the co-ordination entity [Au(CN)2]– in aqueous solution. Gold can be separated in metallic from this solution by the addition of zinc.
Similarly, purification of metals can be achieved through formation and subsequent decomposition of their coordination compounds. For example, impure nickel is converted to [Ni(CO)4], which is decomposed to yield pure nickel.
Co-ordination compounds are of great importance in biological systems. The pigment responsible for photosynthesis, chlorophyll, is a co-ordination compound of magnesium. Haemoglobin, the red pigment of blood which acts as oxygen carrier is a co-ordination compound of iron. Vitamin B12, cyanocobalamine, the anti-pernicious anaemia factor, is a coordination compound of cobalt. Among the other compounds of biological importance with coordinated metal ions are the enzymes like, carboxypeptidase A and carbonic anhydrase (catalysts of biological systems).
Co-ordination compounds are used as catalysts for many industrial processes. Examples include rhodium complex, [(Ph3P)3RhCl], a Wilkinson catalyst, is used for the hydrogenation of alkenes.
Articles can be electroplated with silver and gold much more smoothly and evenly fr6m solutions of the complexes, [Ag(CN)2]– and. [Au(CN)2]– than from a solution of simple metal ions.
In black and white photography, the developed film is fixed by washing with hypo solution which dissolves the undecomposed AgBr to form a complex ion, [Ag(S2O3)2]3-.
There is growing interest in the use of chelate therapy in medicinal chemisty. An example is the treatment of problems caused by the presence of metals in toxic proportions in plant/animal systems. Thus, excess of copper and iro are removed by the chelating ligands D-penicillamine and desferrioxime B via the formation of coordination compounds. EDTA is used in the treatment of lead poisoning. Some co-ordination compounds of platinum effectively inhibit the growth of tumours. Examples are : cis-platin and related compounds.
Textual Examples
Question 1.
On what ground can you say that scandium (Z = 21) is a transition element but zinc (Z = 30) is not ?
Solution:
On the basis of incompletely filled 3d orbitals in case of scandium atom in its atomic state (3d1), it is regarded as a transition element. On the other hand, zinc atom has completely filled d orbitals (3d10) in its ground state as well as in its oxidised state, hence it is not regarded as a transition element.
Question 2.
Why do the transition elements exhibit higher enthapies of atomisation ?
Solution:
Because of large number of unpaired electrons in their atoms they have stronger interatomic interaction and hence stronger bonding between atoms resulting in higher enthalpies of atomisation.
Question 3.
Name at transition element which does not exhibit variable oxidation states.
Solution:
Scandium (Z = 21) does not exhibit variable oxidation states.
![]()
Question 4.
Why is Cr2+ reducing and Mn3+ oxidising when both have d4 configuration ?
Solution:
Cr22+ is reducing as its configuration changes from d4 to d3, the latter having a half-filled t2g level. On the other hand; the change from Mn2+ to Mn3+ results in the half-filled (d<sup5) configuration which has extra stability.
Question 5.
How would you account for the increasing oxidising power in the series VO2+ < Cr2O72- < MnO4–?
Solution:
This is due to the increasing stability of the lower species to which they are reduced.
Question 6.
For the first row transition metals the E⊖ values are

Explain the non-regularity in the above values.
Solution:
The E⊖ (M2+/M) values are not regular which can be explained from the non-regular variation of ionisation enthalpies (∆iH1 + ∆iH2) and also the sublimation enthalpies which are relatively much less for manganese and vanadium.
Question 7.
Why is the E⊖ value for the Mn3+/Mn2+ couple much more positive than that for Cr3+/ Cr2+ or Fe3+/Fe2+ ? Explain.
Solution:
Much larger third ionisation energy of Mn (where the required change is d5 to d4) is mainly responsible for this. This also explains why the +3 state of Mn is of little importance.
Question 8.
Calculate the magnetic moment of a divalent ion in aqueous solution if its atomic number is 25. [A.P. Mar. 16]
Solution:
With atomic number 25, the divalent ion in aqueous solution will have d5 configuration (five unpaired electrons). The magnetic moment, μ is μ = \(\sqrt{5(5+2)}\) = 5.92 BM
![]()
Question 9.
What is meant by ‘disproportionation’ of an oxidation state ? Give an example.
Solution:
When a particular oxidation state becomes less stable relative to other oxidation states, one lower, one higher, it is said to undergo disproportionation. For example, manganese (VI) becomes unstable relative to manganese (VII) and manganese (TV) in acidic solution.
3MnVIO42- + 4H+ → 2MnVIIO4– + MnIVO2 + H2O
Question 10.
Name a member of the lanthanoid series which is well known to exhibit +4 oxidation state.
Solution:
Cerium (Z = 58)
Question 11.
On the basis of the following observations made with aqueous solutions, assign secondary valencies to metals in the following compounds.
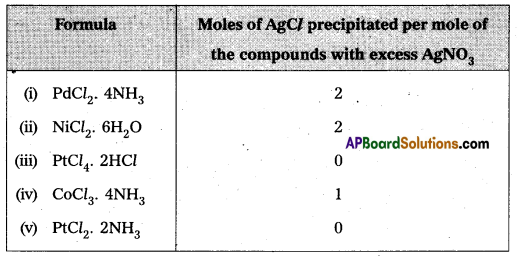
Solution:
i) Secondary 4 ii) Secondary 6 iii) Secondary 6 iv) Secondary 6 v) Secondary 4
Question 12.
Write the formulas for the following Co-ordination compounds
a) Tetraammineaquachloro cobalt (III) chloride
b) Potassium tetrahydroxozincate (II)
c) Potassium trioxalatoaluminate (III)
d) Dichlorobis (ethane-1, 2-diamine) cobalt (III)
e) Tetracarbonylnickel (0)
Solution:
a) [Co(NH3)4(H2O)Cl]Cl2
b) K2[Zn(OH)4]
c) K3[Al(C2O4)3]
d) [CoCl2(en)2]+
e) [Ni(CO)4]
Question 13.
Write the IUPAC names of the following coordination compounds.
a) [Pt(NH3)2Cl(NO2)]
b) K3[Cr(C2O<sub4)3]
c) [CoCl2(en)2]Cl
d) [Co(NH3)5(CO3)]Cl
e) Hg[Co(SCN)4]
Solution:
a) Diamminechloronitrito-N-platinum (II)
b) Potassium trioxalatochromate (III)
c) Dichlorobis (ethane-1, 2-diamine) cobalt (III) chloride
d) Pentaairuninecarbonatocobalt (III) chloride
e) Mercury tetrathiocyanocobaltate (III)
![]()
Question 14.
Why is geometrical isomerism not possible in tetrahedral complexes having two different types of unidentate ligands Co-ordinated with the central metal ion ?
Solution:
Tetrahedral complexes do not show geometrical isomerism because the relative positions of the unidentate ligands attached to the central metal atom are the same with respect to each other.
Question 15.
Draw structures of geometrical isomers of [Fe(NH3)2(CN)4]–
Solution:
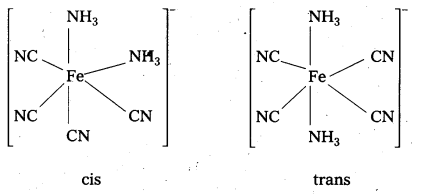
Question 16.
Out of the following two Co-ordination entities which is chiral (optically active) ?
a) cis-(CrCl2(ox)2]3-
b) trans-[CrCl2(ox)2]3-
Solution:
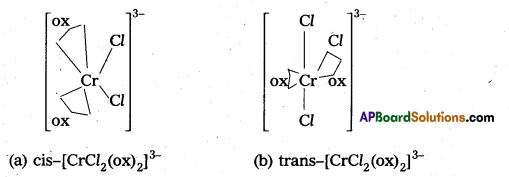
Out of the two, (a) cis-(CrCl2(ox)2]3- is chiral (optically active).
Question 17.
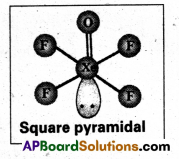
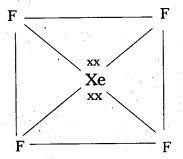
The spin only magnetic moment of [MnBr4]2- is 5.9 BM. Predict the geometry of the complexion?
Solution:
Since the Co-ordination number of Mn2+ ion in the complex ion is 4, it will be either tetrahedral (sp3 hybridisation) or square planar (dsp2 hybridisation). But the fact that the magnetic moment of the complex ion is 5.9 BM, it should be tetrahedral in shape rather than square planar because of the presence of five unpaired electrons in the d-orbitals.
Intext Questions
Question 1.
Silver atom has completely filled d-orbitals (4d10) in its ground State. How can you say that it is a transition element ?
Solution:
Silver (atomic no. = 47), in its +1 oxidation state exhibits 4d105s0 configuration. But in some compounds it also shows +2 oxidation state, i.e., 4d95s0 configuration. Here d-orbital is not completely filled. Therefore, silver is a transition element.
![]()
Question 2.
In the series Sc (Z = 21) to Zn (Z = 30), the enthalpy of atomisation of zinc is the lowest, i.e., 126 kJ mol-1, why ?
Solution:
In zinc (3d104s1) d-orbital is complete so the electrons of d-orbital are not involved in bonding. So, metallic bond is weaker than the other elements of the series, where the electrons of d-orbitals are involved in metallic bonds. So, enthalpy of atomisation of zinc is lowest in its transition series.
Question 3.
Which of the 3d series of the transition metals exhibits the largest number of oxidation states and why ?
Solution:
Manganese (atomic no. = 25) has electronic configuration [Ar] 3d54s2. It shows maximum number of oxidation states, i.e., from +2 to +7 (+2, +3, +4, +5, +6, +7) in its compounds.
Question 4.
The E°(M2+/M) value for copper is positive (+0.34 V). What is possibly the reason for this ?
Answer:
E° (M2+/M) value for any metal depends on three factors : •
i) ∆aH (Enthalpy of atomisation); M(s). + ∆aH → M(g)
ii) ∆iH (Enthalpy of ionisation); M(g) + ∆iH → M2+(g)
iii) ∆hydH (Hydration enthalpy); M2+(g) + (aq → M2+(aq)
Copper has high value of enthalpy of atomisation and low value of enthalpy of hydration. It means that ∆iH required is not compensated by the energy released. Therefore, E0(Cu2+/Cu) is positive.
Question 5.
How would you account for the irregular variation of ionisation enthalpies (first and second) in the first series of the transition elements ?
Solution:
In the first transition series, there is irregular variation of ionisation enthalpies because the stability of 3d configuration differs to some extent. Generally the ionisation enthalpy increases with increase in effective nuclear charge, Thus, it is lower for Cr due to absence of any change in the d-configuration while high for Zn as it represents an jonisation from the 4s level. Second ionisation energy, shows the removal of second. The configurations like d5 and d10 are exceptionally stable. So, they have high ionisation enthalpies.
Question 6.
Why is the highest oxidation state of a metal exhibited in its oxide or fluoride only ?
Solution:
Oxygen as well as fluorine both have high values of electronegativity. So, in their compounds (oxides and fluorides) they can oxidise the metal to their highest oxidation states.
Question 7.
Which is the stronger reducing agent Cr2+ or Fe2+ and why ?
Solution:
Cr2+ is a stronger reducing agent than Fe2+. The E° values are
E°Cr3+/Cr2+ = -0-41 V and E0Fe3+/Fe2+ = 0.77 V

Therefore, Cr2+ is stronger reducing agent (itself gets oxidised easily) than Fe2+.
![]()
Question 8.
Calculate the ‘spin only’ magnetic moment of M2+(aq) ion (Z = 27).
Solution:
Electronic configuration of M(Z = 27) is [Ar] 3d7 4s2
Electronic configuration of M2+ = [Ar]3d7 or ![]()
Three unpaired electrons are present in M2+ (aq) ion. i.e., n = 3. Applying ‘spin only1 formula for magnetic moment.
μ = \(\sqrt{n(n+2)}\) = \(\sqrt{3(3+2)}\) = \(\sqrt{15}\) BM = 3.87 BM
Note : Unit of magnetic moment is Bohr Magnetons (BM).
Question 9.
Explain why Cu+ ion is not stablein aqueous solutions ?
Solution:
In aqueous solution, Cu+(aq) undergoes disproportionation reaction as follows.
2Cu+(aq) → Cu2+(aq) + Cu(s)
The higher stability of Cu2+ (aq) in aqueous solution is due to higher negative enthalpy of hydration ∆hydH° than that of Cu+(aq). It compensates the second IE of Cu involved in the formation of Cu2+ ion. Hence, Cu+ ion changes to more stable Cu2+ ion in aqueous medium.
Question 10.
Actinoid contraction is greater from element to element than lanthanoid contraction ?
Solution:
The decrease in atomic (or ionic) radii in actinoid elements (actinoid contraction) is greater than lanthanoid contraction because 5f-electrons have poor shielding effect as compared to 4f- electrons. Therefore, the effect of increased nuclear charge leading to contraction in size is more in case of actinoid elements.
![]()
Question 11.
Write the formulae for the following Co-ordination compounds
i) Tetraamminediaquacobalt (III) chloride,
ii) Potassium tetracyanonickelate (II)
iii) Tris-(ethane-l, 2-diamine) chromium (m) chloride
iv) Amminebromidochloridonitrito-N-platinate (II)
v) Dichlorido bis-(ethane-1,2-diamine) platinum (IV) nitrate
Solution:
i)
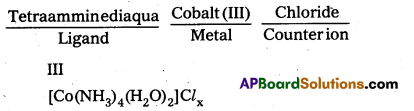
To find the value of x, we have to find the charge on the complex.
III
[CO(NH3)4 (H2O)2]x+ + 3 + 4 × 0 + 2 × 0 = x, × = +3
o, the formula of the complex is [CO(NH3)4 (H2O)2]Cl3.
ii)

To find the value of x, find the charge on the complex.
[Ni(CN)4]x- (as K+ is positive)
+2 + (-1) x 4 = – x
-x = -2 or x = + 2
So, the formula of the complex is K2[Ni(CN)4].
Similarly
iii) [Cr(en)3]Cl3
iv) [Pt(NH3) BrCl(NO2)]–
v) [PtCl2(en)2] (NO3)2
vi) Fe4[Fe(CN)6]3
Question 12.
Write the IUPAC names of the following Co-ordination compounds.
(i) [Co(NH3)6]Cl3
(ii) [Co(NH3)5Cl]Cl2
(iii) K3[Fe(CN)6]
(iv) K3[Fe(C2O4)3]
(v) K2[PdCl4]
(vi) [Pt(NH3)2Cl(NH2CH3)Cl.
Solution:
i)
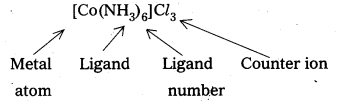
Let the oxidation state of Co be x.
x + (0)6 + (-1) × 3 = 0, x + 0 – 3 = 0, x = +3
So, the name of this complex is hexaamminecobalt (III) chloride,
ii) [CO(NH3)5Cl]Cl2
x + (0) × 5 + (-1) × 1 + (-1) × 2 = 0, x + 0 – 3 = 0, x =.+ 3
So, the name of the complex is pentaamminechloridocobalt (III) chloride
[K3[Fe(CN)6]
iii)
Let the oxidation state of Fe is x.
(+ 1) 3 + x + (-1) 6 = 0, + 3 + x – 6 = 0, x = + 3
So, the name of the complex is potassium hexacyanoferrate (III) .
iv)
Let the oxidation state of Fe is x.
(+ 1) 3 + x + (-2) 3 = 0 [∵ Oxalate ion (C2O42-) bears – 2 charge.]
3 + x- 6 = 0, x = +3
So, the name of the complex is potassium trioxalateferrate (III).
v)
Let the oxidation state of Pd is x.
(+ 1) 2 + x + (-1) 4 = 0, 2 + x – 4 = 0, x = + 2 .
So, the name of the complex is potassium tetrachloridopalladate (II).
vi)
Let the oxidation state of Pt is x.
x + (0) 2 + (-1) × 1 + 0 + (-1) × 1 = 0
x + 0- 1 + 0 -1 = 0, x – 2 = 0, x = + 2
So, the name of the complex is diamminechlorido (methylamine) platinum (II) chloride.
Question 13.
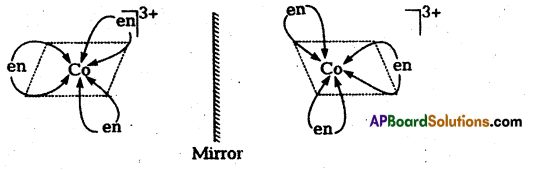
Indicate the types of isomerism exhibited by the following complexes and draw the structures for these isomers :
(i) K[Cr(H2O)2(C2O4)2]
(ii) [Co(en)3]Cl3
(iii) [Co(NH3)5(NO2)](NO3)2
(iv) [Pt(NH3)(H2O)Cl2]
Solution:
i) [Cr(H2O)2(C2O4)2] or K[Cr(H2O)2(ox)2] :
(where, ox = oxalate ion)
a) It exists as geometrical isomers : cis and trans forms.
(In cis form, the same groups occupy adjacent positions while in trans form, they are present at alternate positions.)
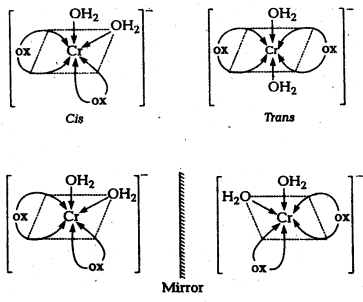
b) The cis isomer can also exist as a pair of optical isomers (i.e., d-and 1- forms) (due to absence of plane of symmetry).
ii) [Co(en)3]Cl3 : It has two optical isomers (i.e. d-and 1-forms)
iii) [Co(NH3)5(NO2)](NO3)2 : It can exist as a pair of ionization isomers as well as linkage iosmers.
Ionization isomers :
[Co(NH3)5(NO2)](NO3)2 and [Co(NH3)5(NO3)](NO2) (NO3) as they give different ions on ionization.

Linkage isomers : [Co(NH3)5(NO2)](NO3)2 and [CO(NH3)5ONO](NO3)2
iv) [Pt(NH3)(H2O)Cl2] : It can exist as two geometrical iosmers. .
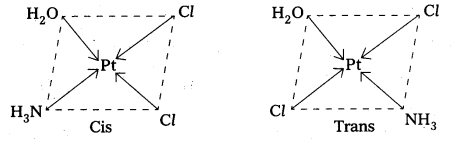
![]()
Question 14.
Give evidence that [Co(NH3)5Cl]SO4 and [CO(NH3)5SO4]Cl are ionization isomers.
Solution:
We dissolve both the compounds in water in separate test tubes. To the both test tube
I Step or I Test: Add BaCl2 solution One compound give white ppt., indicating the presence of SO42- ions.
The other compound does not give white ppt, indicating the absence of SO42- ions.
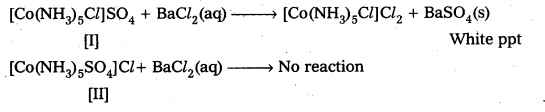
II Test: Add AgNO3 solution to both the Compounds in separate test tubes :
Only [II] compound gives white ppt, not the [I] one, due to absence of Cl– as counter ion.

These two tests prove that the given two compounds are a pair of ionization isomers.
Question 15.
Explain on the basis of valence bond theory that [Ni(CN)4]2- ion with square planar structure is diamagnetic and the [NiCl4] ion with tetrahedral geometry is paramagnetlc.
Solution:

(Cl– being weak field ligand, cannot cause pairing.)
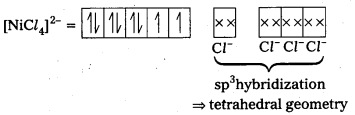
[NiCl4]2- ion is paramagnetic in nature as it has two unpaired electrons.
Question 16.
[NiCl4]2- is paramagnetic while [Ni(CO)4] is diamagnetic though both are tetrahedral.
Solution:
In the complex [NiCl4]2- Ni is in +2 oxidation state and has the configuration 3d84s0. The cr ion being a weak field ligand cannot pair the two unpaired electrons present in 3d-orbitals. This means that 3d-orbitals are not involved in hybridization. Thus, the complex is sp3 hybridized (tetrahedral) and.is paramagnetic in nature.
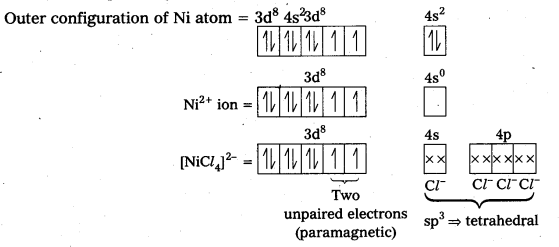
In the complex [Ni(CO)4], the oxidation state of nickel is zero and electronic configuration is 3d84s2. In the presence of the ligand CO, the 4s-electrons shift to the two half-filled 3d-orbitals and make all the electrons paired. The valence 4s and 4p-orbitals are involved in hybridization. Thus, the complex is tetrahedral but diamagnetic in nature.
Outer configuration of Ni atom = 3d8 4s2.
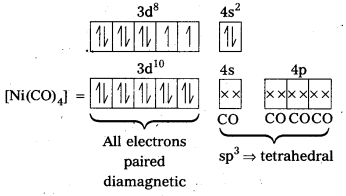
![]()
Question 17.
[Fe(H2O)6]3+ is strongly paramagnetic whereas [Fe(CN)6]3- is weakly paramagnetic Explain.
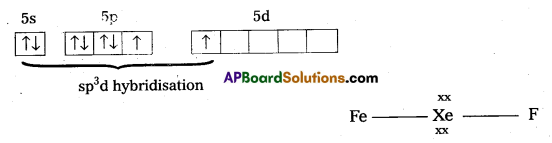
Solution:
Outer configuration of 26Fe = 3ds64s2. In both the complexes Fe is present as Fes3+ ion.
Fes3+ ion = 3d54s0
In the presence of CN– (a strong field ligand) the 3d-electrons pair up leaving only one unpaired electron. The hybridization is d2sp3 forming an inner orbital complex.
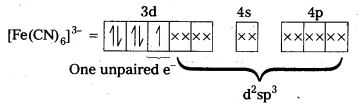
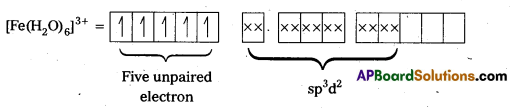
In the presence of H2O, (a weak field ligand), 3d-electrons do not pair up. The hybridization is sp3d2 forming an outer orbital complex containing five unpaired electrons. Hence, it is strongly paramagnetic.
Question 18.
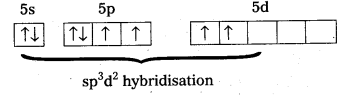
Explain [Co(NH3)6]3+ is an inner orbital complex whereas [Ni(NH3)6]2+ is an outer orbital complex.
Solution:
In [Co(NH3)6]3+, CO is present as Co3+ arid has 3d0 configuration.
In the presence of NH3, the 3d-electrons pair up leaving two d-orbitals empty to the involved in d2sp3 hybridization forming inner orbital complex in the case of [Co(NH3)6]3+.
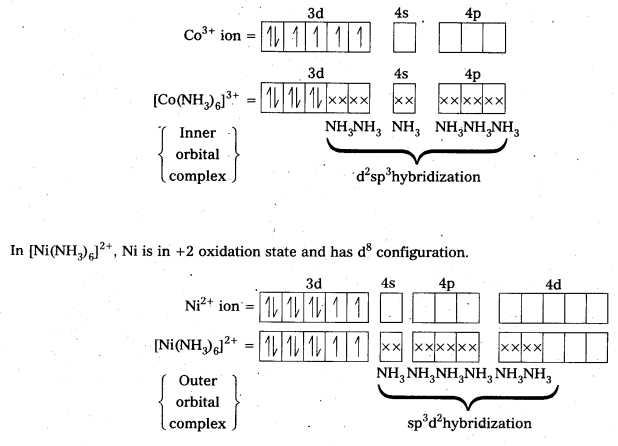
Since, (n – 1) d-orbitals are not available but the nd-orbitals are used in bond formation i.e., in hybridization, the complex is called outer orbital complex.
Question 19.
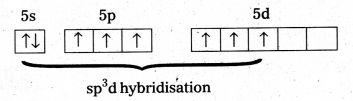
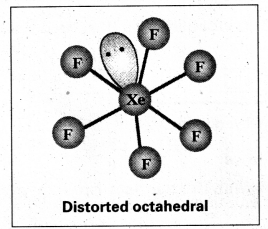
Predict the number of unpaired electrons in the square planar [Pt(CN)4]2- ion.
Solution:
78Pt is present in group 10 of the Periodic Table. Its outer configuration is 5d96s1.
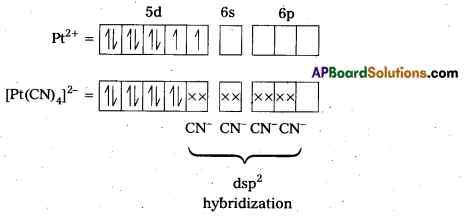
For square plannar shape, the hybridization is dsp2. Hence, the unpaired electrons in 5d- orbital pair up to make one d-orbital empty for dsp2 hybridization. Thus, there is no unpaired electron.
![]()
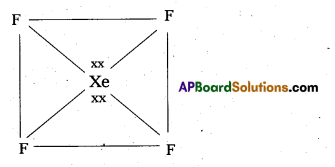
Question 20.
The hexaquo manganese (II) ion contains five unpaired electrons, while the hexacyano ion contains only one unpaired electron. Explain using crystal field theory.
Solution:
Mn(II) ion has 3d5 configuration. In the presence of H2O molecules (acting as weak field ligands), the distribution of these five electrons is \(\mathrm{t}_{2 \mathrm{~g}}^3 \mathrm{e}_{\mathrm{g}}^2\) all the electrons remain unpaired to form a high spin complex.
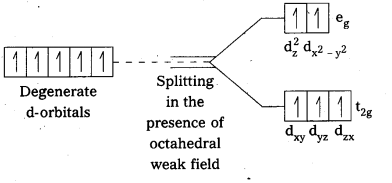
However, in the presence of CN– (acting as strong field ligands), the distribution of these electrons is \(\mathrm{t}_{2 \mathrm{~g}}^5 \mathrm{e}_{\mathrm{g}}^0\), i.e., two t2g orbitals contain paired electrons while the third t2g orbital contains one unpaired electron. The complex formed is a low spin complex.
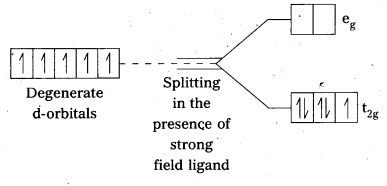
Question 21.
Calculate the overall complex dissociation equilibrium constant for the Cu(NH3)42+ ions, given that β4 for this complex is 2.1 × 1013.
Solution:
Overall complex dissociation equilibrium constant
= \(\frac{1}{\beta_4}\) = \(\frac{1}{2.1 \times 10^{13}}\)
= 4.7 × 10-14
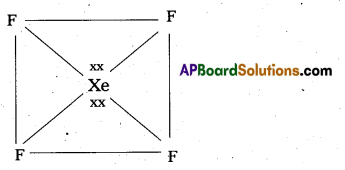
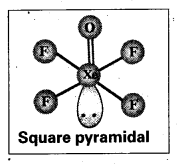

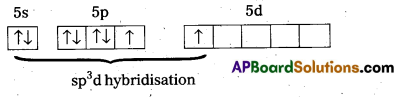
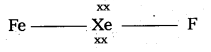

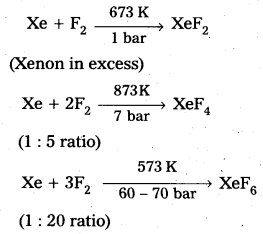
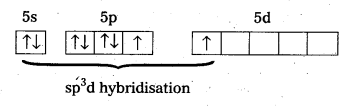
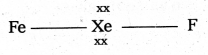
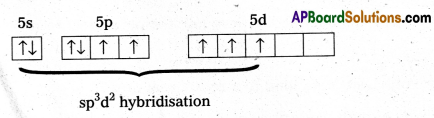


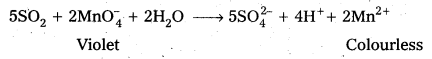
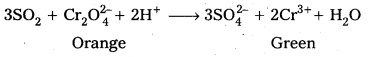

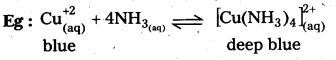
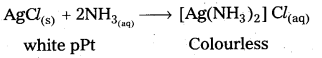
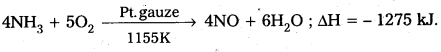
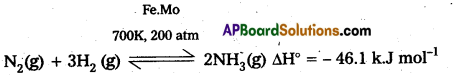






































































 × 100
× 100 × 106
× 106
 × 10
× 10 × 100
× 100