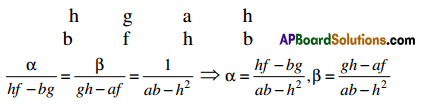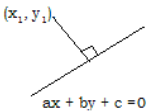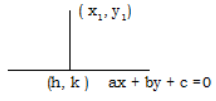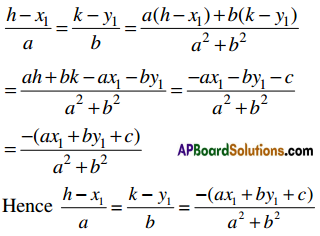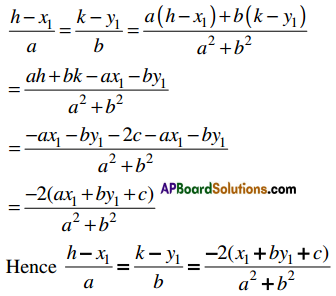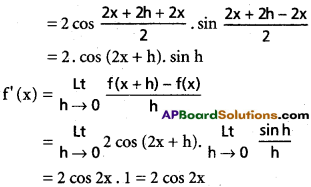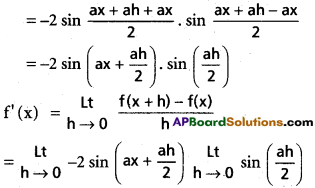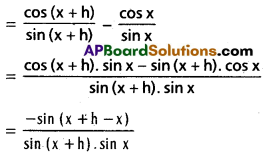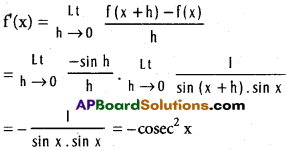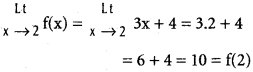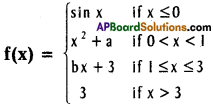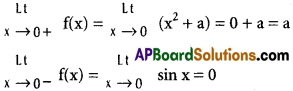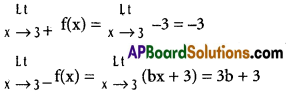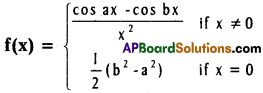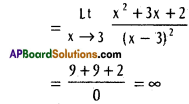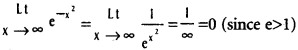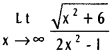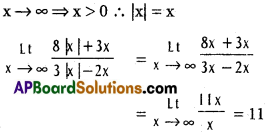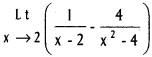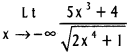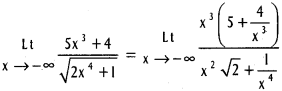Mahesh

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 10 Applications of Derivatives to solve questions creatively.

Intermediate 1st Year Maths 1B Applications of Derivatives Formulas

→ Error in y = Δy = f(x + Δx) – f(x)

→ Differential in y = dy = f’ (x) Δx

→ Relative error in y = \(\frac{\Delta y}{y}\)

→ Percentage error in y = \(\frac{\Delta y}{y}\) × 100

Circle:
if’ r’ is the radius, x is the diameter, p is the perimeter (circumference) and A is the area of a circle then

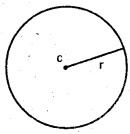
• A = πr or A = \(\frac{\pi x^{2}}{4}\)
• x = 2r
• p = 2πr (or) p = πx

Sector :
If ‘r’ is the radius, l is the length of arc and ‘θ’ is the angle then

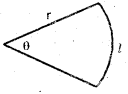
• Area = A = \(\frac{1}{2}\)r (or) A = \(\frac{1}{2}\)r²θ
• Perimeter = p = l + 2r (or) p = r (θ + 2)
• l = rθ

Cylinder :
If ‘r’ is the radius, h is the height then

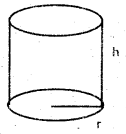
• Lateral surface area = 2πrh
• Total surface area = S = 2πrh + 2πr²
• Volume = V = πr²h

Cone:

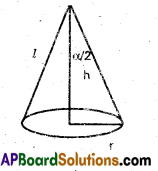
r is base radius, h is the height, ‘l’ is the slant height, a is the vertical angle then

• l² = r² + h²
• tan \(\frac{\alpha}{2}=\frac{r}{h}\)
• Lateral surface area = πrl (or) πr\(\sqrt{r^{2}+h^{2}}\)
• Total surface area = S = πrl + πr² (or) S = πr \(\sqrt{r^{2}+h^{2}}\) + πr²
• Volume = V = \(\frac{1}{3}\)πr²h

Simple pendulum:
If ‘l’ is the length, T is the period of oscillation of a simple pendulum and g is the acceleration due to gravity then T = 2π\(\sqrt{\frac{l}{g}}\)

Sphere :
‘r’ is the radius,

• Surface area = S = 4πr
• Volume = V = \(\frac{4}{3}\) πr³

Cube :
Let ‘x’ is the side

• Surface area = S = 6x²
• Volume = V = x³

→ Slope of the tangent = f'(x)

→ Equation of the tangent is (a, b) is y – b = f'(a) (x – a)

→ Equation of the normal at (a, b) is y – b = –\(\frac{1}{f^{\prime}(a)}\) (x – a)

→ Length of the tangent = \(\left|\frac{f(a) \sqrt{1+\left(f^{\prime}(a)\right)^{2}}}{f^{\prime}(a)}\right|\)

→ Length of the normal = \(\left|f(a) \sqrt{1+\left[f^{*}(a)\right]^{2}}\right|\)

→ Length of the sub-tangent = \(\left|\frac{f(a)}{f^{\prime}(a)}\right|\)

→ Length of the sub-normal = |f(a).f'(a)|

Angle between the curves is tan Φ = \(\left|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\right|\)

→ If m₁ = m₂, the curves touch each other and have a common tangent

→ If m₁m₂ = -1, the curves cut orthogonally

→ If a particle starts from a fixed point and moves a distance ‘s’ along a straight line during time ‘t’, then
v = velocity of the particle at the time t = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
a = acceleration of the particle at the time t = \(\frac{\mathrm{d}^{2} \mathrm{~s}}{\mathrm{dt}^{2}}\) = v\(\frac{\mathrm{dv}}{\mathrm{ds}}\)

• If v > 0, then the particle is moving away from the straight point.
• If v < 0, then the particle is moving towards the straight point.
• If v = 0, then the particle comes to rest.

→ Let O be a fixed in a plane and OX be a fixed ray in the same plane. Let P be the position of a particle on a curve C, at time ‘f and ∠XOP = θ.

• ω = Angular velocity of the particle around ‘O’ = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)
• Angular acceleration of the particle around ‘O’ = \(\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}{ }^{2}}\) (Where θ is in radian measure).

→ Increasing and Decreasing functions: A function f(x) is

• Increasing if f'(x) > 0
• Decreasing if f'(x) < 0′
• f(x) is stationary if f’ (x) = 0

→ A function f(x) has local maxima or local minima only at stationary points.

• f(x) has local maximum of f’(x) = 0, f”(x) < 0 f(x) has local minimum if
• f’(x) = 0, f”(x) > 0
  Absolute maximum = max. {local maxima}
  Absolute minimum = Min {local minima}.

Tangent To A Curve:
Definition :
Let y = f(x) be a curve and P be a point on the curve. If Q is a point on the curve other than P, then PQ is called a secant line of the curve. If the secant line \(\overline{P Q}\) approaches the same limiting position as Q approaches P along the curve from either side then the limiting position is called the tangent line to the curve at the point P. The point P is called the point of contact of the tangent line to the curve.

The tangent at a point to a curve, if it exists, is unique. Therefore, there exists at most one tangent at a point to a curve.

Geometrical Interpretation Of Derivative:
Let P be a point on the curve y = f(x). Then the slope of the tangent to the curve at P is equal to \(\left(\frac{d y}{d x}\right)_{P}\) i.e., (f'(x))_p

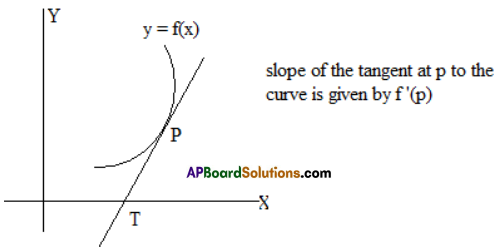
Gradent The slope of the tangent at a point to a curve is called the gradient of the curve at that point.

The gradient of the curve y = f(x) at P is \(\left(\frac{d y}{d x}\right)_{P}\)

Note:

• If \(\left(\frac{d y}{d x}\right)_{P}\) = o then the tangent to the curve at P is parallel to the x – axis. The tangent, in this case, is called a horizontal tangent.
• If \(\left(\frac{d y}{d x}\right)_{P}\) = +∞ or -∞ i.e., if \(\left(\frac{d y}{d x}\right)_{P}\) = 0 then the tangent to the curve at P is perpendicular to x – axis. The tangent, in this case, is called a vertical tangent.
• If \(\left(\frac{d y}{d x}\right)_{P}\) does not exist then there exists no tangent to the curve at P.

Equation of Tangent:
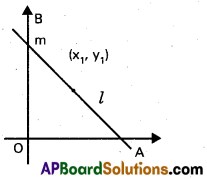
The equation of the tangent at the point P(x₁, y₁) to the curve y = f(x) is y – y₁ = m(x – x₁)
where m = \(\left(\frac{d y}{d x}\right)_{P}\)

Note:

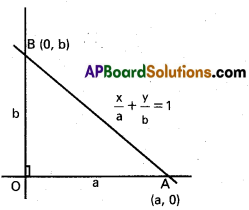
• x – intercept of the tangent = x₁ – \(\frac{y_{1}}{m}\) = x₁ – y₁m
• y – intercept of the tangent = y₁ – mx₁ = y₁ – x₁m

Normal To A Curve
Let P be a point in the curve y = f(x). The line passing through P and perpendicular to the tangent at P to the curve is called the normal to the curve at P.

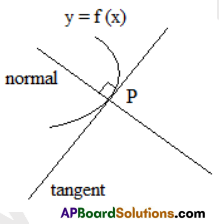
The slope of the normal to the curve y = f(x) at P is m’ = \(\frac{1}{m}=-\left(\frac{d x}{d y}\right)_{P}\) where m = \(\left(\frac{d y}{d x}\right)_{P}\) ≠ 0

The equation of the normal at p(x₁, y₁) to the curve y = f(x) is
y – y₁ = \(\frac{-1}{m}\)(x – x₁) where m = \(\left(\frac{d y}{d x}\right)_{P}\)
i.e., y – y₁ = \(\left(\frac{d y}{d x}\right)_{P}\)(x – x₁)

Infinitesimals:
Let x be a finite variable quantity and be a minute change in x. Such a quanitity , which is very small when compared to x and which is smaller than any pre-assigned small quantity, is called an infinitesimal or an infinitesimal of first order. If δX is an infinitesimal then (δX)² , (δX)³ , …….. are called infinitesimals respectively of 2nd order, 3rd order….

If A is a finite quantity and is an infinitesimal then A. δX , A. (δX)² , A. (δX)³, ………. are also infinitesimals and they are infinitesimals respectively of first order, second order, third order
Definition: A quantity α = α(x) is called an infinitesimal as x → a if \({Lt}_{x \rightarrow a} α(x)\) = 0

Theorem:
Let y = f (x) be a differentiable function at x and be a small change in x. Then f'(x) and \(\frac{δ}{δ x}\) differ by an infinitesimal G(δx) as δx → 0 , where δy = f (x + δx) – f (x).

Differential
Definition: If y = f (x) is a differentiable function of x then f ’(x)S is called the differential of f. It is denoted by df or dy.
dy = f'(x)δx or df = f'(x)δx.
Note: δf = df i.e., error in f is approximately equal to differential of f

Approximations:
We have δf = f (x + δx) – f (x) ………………(1)
⇒ df ≅ f (x + δx) – f (x)
⇒ f’ (x)δx ≅ f (x + δx) – f (x)
⇒ f (x + δx) ≅ f (x) + f’ (x)δx
If we know the value of f at a point x, then the approximate value of f at a very nearby point x + δX can be calculated with the help of above formula.

Errors
Definition: Let y=f(x) be a function defined in a nbd of a point x. Let δx be a small change in x and δy be the corresponding change in y.
If δx is considered as an error in x, then

• δf is called the absolute error or error in y,
• \(\frac{δy}{y}\) is called the relative error (or proportionate error) in y,
  \(\frac{δy}{y}\) × 100 is called the percentage error in y corresponding to the error ox in x.

Lengths Of Tangent, Normal, Subtangent And Sub Normal
Definition :
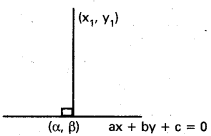
Let y = f (x) be a differentiable curve and P be a point on the curve.
Let the tangent and normal at P to the curve meet the x – axis in T and N respectively. Let M be the projection of P on the x – axis. Then
(i) PT is called the length of the tangent,
(ii) PN is called the length of the normal
(iii) TM is called the length of the subtangent,
(iv) MN is called and length of the subnormal at the point P.

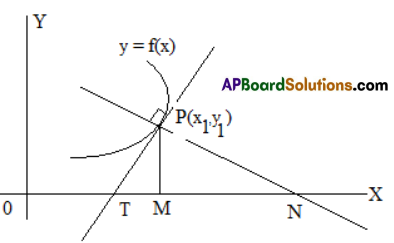
Let P(x₁, y₁) be a point on the curve y = f (x). Then

• The length of the tangent to the curve at P is \(\left|\frac{y_{1}}{m} \sqrt{1+m^{2}}\right|\)
• the length of the normal to the curve at P is |y₁\(\sqrt{1+m^{2}}\)|
• the length of the subtangent to the curve at P is \(\left|\frac{y_{1}}{m}\right|\)
  the length of the subnormal to the curve at P is |y₁m| where m = \(\left(\frac{d y}{d x}\right)_{P}\)

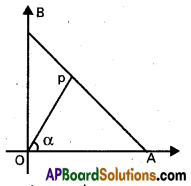
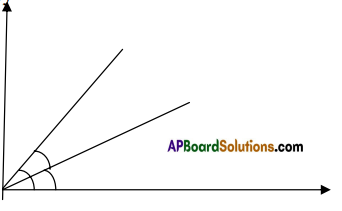
Angle between two curves:
If two curves intersect at P then the angle between the tangents to the curves at P is called the angle between the curves at P.

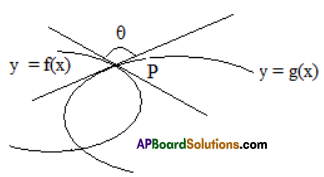
Angle between the curves:
Let y = f (x) and y = g(x) be two differentiable curves intersecting at a point P. Let m₁ = [ f'(x)]_P , m₂ = [g'(x)]_P be the slopes of the tangents to the curves at P. If θ is the acute angle between the curves at P then tan θ = \(\left|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\right|\)

Note:

• If m₁ = m₂ then θ = 0. In this case the two curves touch each other at P. Hence the curves have a common tangent and a common normal at P.
• If m₁m₂ = -1then θ = \(\frac{\pi}{2}\). In this case the curves cut each other orthogonally at P.
• If m₁ = 0 and \(\frac{1}{m_{2}}\) = 0 then the tangents to the curves are parallel to the coordinate axes.
• Therefore the angle between the curves is θ = \(\frac{\pi}{2}\)

Rate of Changes:
Let y = f(x) be defined on an interval (a,b). let δy be change in y corresponding to a change δx in x.
Then , \(\frac{\Delta y}{\Delta x}\) is called average rate of change of y. if \(\underset{δx \rightarrow 0}{L t} \frac{\Delta y}{\Delta x}\) exists finitely, the this limit (i.e., \(\frac{d y}{d x}\)) is called rate of change of y with respect to x .

Note:
\(\left(\frac{d y}{d x}\right)_{a t \mathrm{x}=\mathrm{c}}\) represents the rate of change of y with respect to x at x = c.

Rectilinear Motion:
Let a particle start at a point O on a line L and move along the line. After a time of t units, let the particle be at P and OP = s. Since s is dependent on time t, we write s=s(t). s is called the displacement of the particle during time t.
The rate of change of displacement s is called the velocity of the particle and it is denoted by v = \(\frac{d s}{d t}\).
The rate of change of velocity is called acceleration. It is denoted by a.
a = \(\frac{d v}{d t}=\frac{d}{d t}\left(\frac{d s}{d t}\right)=\frac{d^{2} s}{d t^{2}}\)

Angular Velocity:
At time t, let P be the position of a moving point, Q be the position of the point after an interval δt. Let ∠xop = 6 and ∠POQ = δθ

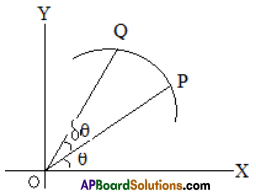
The angular velocity of P at O is\(\underset{x \rightarrow 0}{L t} \frac{δθ}{δt}=\frac{dθ}{d t}\)
Angular velocity w\(\frac{d \theta}{d t}\)
The angular acceleration of P at O is \(\frac{d \omega}{d t}=\frac{d}{d t}\left(\frac{d \theta}{d t}\right)=\frac{d^{2} \theta}{d t^{2}}\)

Maxima And Minima
Monotonic Functions Over An Internal
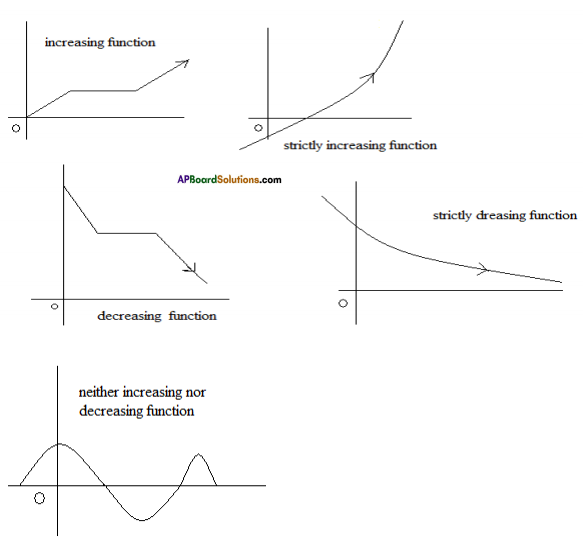
Definition: A function f :[a, b] → R is said to be
(i) Monotonically increasing (or non – decreasing) on [a, b] if x₁ < x₂ ⇒ f (x₁) ≤ f (x₂) ∀ x₁,x₂ ∈ [a, b]
(ii) Monotonically decreasing (or non – increasing) on [a, b] if x₁ < x₂ ⇒ (x₁) ≥ f (x₂) ∀ x₁,x₂ ∈ [a, b]
(iii) strictly increasing on [a, b] if x₁ < x₂ ⇒ (x₁) < f (x₂) ∀ x₁,x₂ ∈ [a, b]
(iv) strictly decreasing on [a, b] if x₁ < x₂ ⇒ (x₁) > f (x₂) ∀ x₁,x₂ ∈ [a, b]
(v) a monotonic function on [a, b] if f is either monotonically increasing or monotonically decreasing on [a, b].

Theorem:
Let f be a function defined in a nbd of a point a and f be differentiable at a. Then

• f'(a) > 0 ⇒ f is locally increasing at a.
• f >(a) < 0 ⇒ f is locally decreasing at a. Note: Let f be continuous on [a, b] and differentiable on (a, b). Then (i) f'(x) ≥ 0 ∀ x ∈ (a,b) ⇒ f (x) is increasing on [a, b]. (ii) f'(x) ≤ 0 ∀ x ∈ (a,b) ⇒ f (x) is decreasing on [a, b].
• f'(x) > 0 ∀ x ∈ (a,b) ⇒ f (x) is strictly increasing on [a, b].
• f'(x) < 0 ∀ x ∈ (a,b) ⇒ f (x) is strictly decreasing on [a, b].
• f'(x) = 0 ∀ x ∈ (a,b) ⇒ f (x) is a constant function on [a,b].

Greatest And Least Values
Definition: Let f be a function defined on a set A and l ∈ f (A). Then l is said to be
(i) the maximum value or the greatest value of f in A if f (x) ≤ l ∀ x ∈ A .
(ii) the minimum value or the least value of f in A if f (x ) ≥ l ∀ x ∈ A

Local Maximum And Local Minimum Values
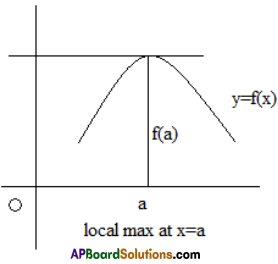
Let f be a function defined in a nbd of a point ‘a’ then f is said to have
(i)a local maximum (value) or a relative maximum at a if ∃ a δ > 0 such that f (x) < f (a) ∀ x ∈ (a – δ, a) ∪ (a, a + δ) . In this case a is called a point of local maximum of f and f (a) is its local maximum value.

(ii) a local minimum (value) or relative minimum at a if 3 a 5> 0 such that f (x) > f (a) ∀ x ∈ (a – δ, a) ∪ (a, a + δ). In this case a is called a point of local minimum and f (a) is its local minimum value.

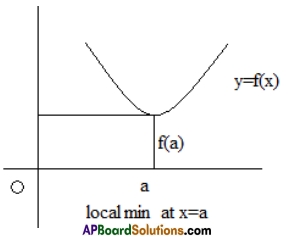
Theorem:
Let f be a differentiable function in a nbd of a point a. The necessary condition for f to have local maximum or local minimum at a is f ‘(a) = 0.

First Derivative Test
Let f be a differentiable function in a nbd of a point a and f'(a) = 0. Then

• f (x) has a relative maximum at x =a if ∃ a δ > 0 such that
  x ∈ (a – δ, a) ⇒ f'(x) > 0 and x ∈ (a, a + δ) ⇒ f'(x) < 0 .
• f(x) has a relative minimum at x= a if 3 a 8> 0 such that
  x ∈ (a – δ, a) ⇒ f'(x) < 0 and x ∈ (a, a +δ) ⇒ f'(x) < 0 .
• f (x) has neither a relative maximum nor a minimum at x=a if f'(x) has the same sign for all x ∈ (a – δ, a) ∪ (a, a + δ) .

Second Derivative Test
Let f (x) be a differentiable function in a nbd of a point ‘a’ and let f”(a) exist.

• If f'(a) = 0 and f”(a) < 0 then f (x) has a relative maximum at f (x) and the maximum value at a is f (a).
• If f'(a) = 0 and f”(a) > 0 then f (x) has a relative minimum at f (x) and the minimum value at a is f (a).

Absolute Maxima And Absolute Minima
Let f be a function defined on [a, b]. Then

• Absolute maximum of f on [a, b] = Max.{ f (a), f (b) and all relative maximum values of f in (a, b)}.
• Absolute minimum of f on [a, b] = Min.{ f (a), f (b) and all relative minimum values of f in (a,b)}.

Note :

• maximum and minimum values are called extrimities.
• If f'(a) = 0 , then f is said to be stationary at a and f(a) is called the stationary value of f. and (a, f(a)) is called a stationary point of f.

Mean Value Theorems
Rolle’sTheorem :If a function f : [a, b] → R is such that

• It is continuous on [a, b]
• It is derivable on (a, b) and i
• f(a) = f(b) then there exists at least one C ∈ (a,b) such that f ‘(C) = 0.

Lagrange’s mean -value theorem or first mean – value theorem :
If a function f : [a, b] → R is such that

• It is continuous on [a, b].
• It is derivable on (a, b) then there exists at least one C ∈ (a,b) such that \(\frac{f(b)-f(a)}{b-a}\) = f ‘(C)

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 9 Differentiation to solve questions creatively.

Intermediate 1st Year Maths 1B Differentiation Formulas

→ f'(x) = \({Lt}_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

→ Δy = f(x + Δx) – f(x)

→ \(\frac{d}{d x}\) (u ± v) = \(\frac{d u}{d x} \pm \frac{d v}{d x}\)

→ \(\frac{d}{d x}\)(uv) = u\(\frac{d v}{d x}\) + v\(\frac{d u}{d x}\)

→ \(\frac{d}{d x}\)(uvw) = uv\(\frac{d w}{d x}\) + uw\(\frac{d v}{d x}\) + vw\(\frac{d u}{d x}\)

→ \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^{2}}\)

→ \(\frac{d}{d x}\)(xⁿ) = nx^n-1

→ \(\frac{d}{d x}\)(x) = 1

→ \(\frac{d}{d x}\)(sin x) = cos x

→ \(\frac{d}{d x}\)(cos x) = -sin x

→ \(\frac{d}{d x}\)(tan x) = sec²x

→ \(\frac{d}{d x}\)(cot x) = -cosec²x

→ \(\frac{d}{d x}\)(sec x) = sec x tan x

→ \(\frac{d}{d x}\)(cosec x) = -cosec x cot x

→ \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\)

→ \(\frac{d}{d x}\)(cos^-1x) = –\(\frac{1}{\sqrt{1-x^{2}}}\)

→ \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^{2}}\)

→ \(\frac{d}{d x}\)(cot^-1x) = –\(\frac{1}{1+x^{2}}\)

→ \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{|x| \sqrt{x^{2}-1}}\)

→ \(\frac{d}{d x}\)(cosec^-1x) = \(\frac{-1}{|x| \sqrt{x^{2}-1}}\)

→ \(\frac{d}{d x}\)(e^x) = e^x

→ \(\frac{d}{d x}\)(a^x) = a^xlog a

→ \(\frac{d}{d x}\)(log x) = \(\frac{1}{x}\)

→ \(\frac{d}{d x}\)|x| = \(\frac{|x|}{x}\)

→ \(\frac{d}{d x}\)(log |x|) = \(\frac{1}{x}\)

→ \(\frac{d}{d x}\)(x^x) = x^x(1 + log x)

→ \(\frac{d}{d x}\)(sinh x) = cosh x

→ \(\frac{d}{d x}\)(cosh x) = sinh x

→ \(\frac{d}{d x}\)(tanh x) = sech²x

→ \(\frac{d}{d x}\)(coth x) = -cosech²x

→ \(\frac{d}{d x}\)(sech x) = -sech x tanh x

→ \(\frac{d}{d x}\)(cosech x) =-cosech x coth x

→ \(\frac{d}{d x}\)(sinh^-1x) = \(\frac{1}{\sqrt{1+x^{2}}}\)

→ \(\frac{d}{d x}\)(cosh^-1x) = \(\frac{1}{\sqrt{x^{2}-1}}\)

→ \(\frac{d}{d x}\)(tanh^-1x) = \(\frac{1}{1-x^{2}}\)

→ \(\frac{d}{d x}\)coth^-1x) = \(\frac{1}{1-x^{2}}\)

→ \(\frac{d}{d x}\)(sech^-1x) = \(\frac{-1}{|x| \sqrt{1-x^{2}}}\)

→ \(\frac{d}{d x}\)(cosech^-1x) = \(\frac{-1}{|x| \sqrt{x^{2}+1}}\)

→ \(\frac{\mathrm{d} y}{\mathrm{dx}}=\frac{\mathrm{d} y}{\mathrm{du}} \cdot \frac{\mathrm{d} u}{\mathrm{dx}}\)

→ \(\frac{d}{d x}\left(\frac{1}{x^{n}}\right)=\frac{-n}{x^{n+1}}\)

Parametric Differentiation
If x =g (t) and y =h (t) are two functions of t then y may be expressed as a function of x, say y = f(x), by eliminating the real variable t. Such a variable t is called a parameter. Also, x and y are said to be defined parametrically. The equations x =g (t), y =h (t) are called the parametric equations of y = f(x).

The process of finding \(\frac{d y}{d x}\) when x and y are defined parametrically, is called parametric differentiation.

Theorem:
Let x = g(t) and y = h(t) be two differentiable functions of t such that g^-1 exists.
Then \(\frac{d y}{d x}=\left(\frac{d y}{d t}\right) /\left(\frac{d x}{d t}\right)\)

Implicit Differentiation
Let y be an implicit function of x defined by a relation of the type f(x, y) = 0. Then the method of finding the derivative \(\frac{d y}{d x}\) of such an implicitly defined function is called implicit differentiation.
In this method, we differentiate f(x, y) = 0 w.r.t x (treating y as a function of x) to get an equation of the type F(x,y, \(\frac{d y}{d x}\)) = 0.
By solving this equation we find \(\frac{d y}{d x}\).

Logarithmic Differentiation
If a given function is of the form y = f(x) g(x) where f(x) and g(x) are differentiable functions of x, we apply logarithms to transform it into a suitable form so as to find . This method of finding \(\frac{d y}{d x}\) is called logarithmic differentiation.
This method is also useful in finding the derivatives of functions which are products of a number of functions.

Theorem:
If y = f(x) g(x) where f(x) and g(x) are differentiable functions then \(\frac{d y}{d x}\) = f (x)^g(x)[\(\frac{g(x)}{f(x)}\)f'(x) + g'(x)log f(x)]
Proof:
y = f(x)g(x), f(x) > 0
logy = g(x) log f(x)

Differentiating both sides w.r.t x,

Method of Substitution:
In the case of inverse trigonometric functions with typical arguments direct differentiation of the function to find the derivative may become quite tedious and cumbersome. In such cases the derivative can be easily found by using proper trigonometric substitutions and transformations. The application of this method is illustrated in the following examples.

Derivative Of One Function W.R.T Another Function
Let f(x) and g(x) be two differentiable functions with a common domain of differentiability then the derivative of u = f(x) w.r.t v = g(x) is given by
\(\frac{d u}{d v}=\left(\frac{d u}{d x}\right) /\left(\frac{d v}{d x}\right)=\frac{f^{\prime}(x)}{g^{\prime}(x)}\)

Second Order Derivatives:
If y = f(x) is a differentiable function of x then its derivative f ‘(x) is a function of x. If f ‘(x) is a differentiable function then its derivative is called the second order derivative of f(x). It is denoted by f ”(x) and f”(x) = \({Lt}_{h \rightarrow 0} \frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}\)
f ”(x) is also denoted by f”(x) = \({Lt}_{h \rightarrow 0} \frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}\) or \(\frac{d^{2} f}{d x^{2}}\) or D²y or y” or y₂.

Derivatives of Inverse Trignometric Functions
If y = sin^-1x, x ∈ (-1, 1) then \(\frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}\)
Proof:
y = sin^-1x ⇒ x = sin y

Theorem:
y = cos^-1x, x ∈(-1, 1) then \(\frac{d y}{d x}=\frac{-1}{\sqrt{1-x^{2}}}\)

Theorem:
y = Tan^-1x, x ∈(-1, 1) then \(\frac{d y}{d x}=\frac{1}{1+x^{2}}\)
Proof:
y = Tan^-1x ⇒ x = tan y where x ∈ R and y ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
x = tan y ⇒ \(\frac{d y}{d x}\) = sec²y = 1 + tan²y = 1 + x² > 0
∴ \(\frac{d y}{d x}=\left(\frac{d x}{d y}\right)^{-1}=\frac{1}{1+x^{2}}\), x ∈ R

Theorem:
y = Cot^-1x, x ∈ R then \(\frac{d y}{d x}=\frac{-1}{1+x^{2}}\)

Theorem:
y = Sec^-1x, x ∈ (-∞, -1) ∪ (1, ∞) then \(\frac{d y}{d x}=\frac{1}{|x| \sqrt{x^{2}-1}}\)

Theorem:
\(\frac{d}{d x}\)(Cosec^-1x) = \(\frac{-1}{|x| \sqrt{x^{2}-1}}\), |x| > 1

Derivatives of Hyperbolic Functions

1. \(\frac{d}{d x}\)(sinh x) = cosh x, x ∈ R
\(\frac{d}{d x}\)(sinh x) = \(\frac{d}{d x}\left(\frac{e^{x}-e^{-x}}{2}\right)\)
= \(\frac{1}{2}\)[\(\frac{d}{d x}\)(e^x) – \(\frac{d}{d x}\)(e^-x] = \(\frac{1}{2}\)[e^x + e^-x]
= cosh x, exists for all x.

2. \(\frac{d}{d x}\)(cosh x) = sinh x, x ∈ R
\(\frac{d}{d x}\)(cosh x) = \(\frac{d}{d x}\left(\frac{e^{x}+e^{-x}}{2}\right)\)
= \(\frac{1}{2}\)[\(\frac{d}{d x}\)(e^x) + \(\frac{d}{d x}\)(e^-x] = \(\frac{1}{2}\)[e^x – e^-x] = sinh x, ∀x

3. \(\frac{d}{d x}\)(tanh x) = sech²x, x ∈ R

4. \(\frac{d}{d x}\)(Coth x) = -cosec²x, x ∈ R

= \(\frac{-1}{\sinh ^{2} x}\) = -cosech²x exists for all x ≠ 0

Derivatives of Inverse Hyperbolic Functions:
1. \(\frac{d}{d x}\)(sinh^-1x) = \(\frac{1}{\sqrt{1+x^{2}}}\), x ∈ R
Let y = sinh^-1x, x, y ∈ R
Then x = sinh y, sinh y is differentiable for all y ∈ R
\(\frac{d x}{d y}\) = cosh y and cosh y > 0 ∀ x ∈ R
\(\frac{d y}{d x}=\left(\frac{d x}{d y}\right)^{-1}=\frac{1}{\cosh y}=\frac{1}{\sqrt{1+\sinh ^{2} y}} .=\frac{1}{\sqrt{1+x^{2}}}\) exists
\(\frac{d}{d x}\)(sinh^-1x) = \(\frac{1}{\sqrt{1+x^{2}}}\), x ∈ R

2. \(\frac{d}{d x}\)(cosh^-1x) = \(\frac{1}{\sqrt{x^{2}-1}}\), x ∈ (1, ∞)

3. \(\frac{d}{d x}\)(tanh^-1x) = \(\frac{1}{1-x^{2}}\), |x| < 1
Let y = Tanh^-1x, x ∈ (-1, 1), y ∈ R
Then x = tanhy. Tanh y is differetniable on R
∴ \(\frac{d x}{d y}\) = sech² ⇒ \(\frac{d y}{d x}=\frac{1}{{sech}^{2} y}=\frac{1}{1-\tanh ^{2} y}=\frac{1}{1-x^{2}}\) exists for all x ∈ (-1, 1)

4. \(\frac{d}{d x}\)(coth^-1x) = \(\frac{1}{1-x^{2}}\), |x| > 1

5. \(\frac{d}{d x}\)(sech^-1x) = \(\frac{-1}{x \sqrt{1-x^{2}}}\), x ∈ (0, 1)

6. \(\frac{d}{d x}\)(cosech^-1x) = \(\frac{-1}{x \sqrt{1+x^{2}}}\), x ≠ 0
Let y = cosech^-1x, x ∈ R – {0}, y ∈ R- {0}.
Then x = cosech y, cosech y is differentiable on R – {0}.

Partial Differentiation
Let u = f (x, y) be a function of two independent varaibles x and y.
(i) If \({Lt}_{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h}\) exists then the limit is called the partial derivatie of u with respect to x. It is denoted by \(\frac{\partial u}{\partial x}\) or u_x or \(\frac{\partial f}{\partial x}\) or f_x.

(ii) If \({Lt}_{k \rightarrow 0} \frac{f(x, y+k)-f(x, y)}{k}\) exists then the limit is called the partial derivative of u with respect to x. It is denoted by \(\frac{\partial u}{\partial y}\) or u_x or \(\frac{\partial f}{\partial y}\) or f_x.
∴ \(\frac{\partial u}{\partial x}={Lt}_{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h}\) and \(\frac{\partial u}{\partial y}=\underset{k \rightarrow 0}{L t} \frac{f(x, y+k)-f(x, y)}{k}\)

Note :

• The partial derivative of u w.r.t. x is the ordinary derivative of u w.r.t. x treating the other variable y (and its functions) as constant
• The partial derivative of u w.r.t. y is the ordinary derivative of u w.r.t. y treating the other variable x (and its functions) as constant.

Differentiation of Composite Functions
1. If V = g(U) and U = f(x, y) then (i) \(\frac{\partial V}{\partial x}=\frac{d V}{d U} \cdot \frac{\partial U}{\partial x}\) (ii) \(\frac{\partial V}{\partial y}=\frac{d V}{d U} \cdot \frac{\partial U}{\partial y}\)

2. If Z = f(x, y) and x = g(t); y = h(t) then \(\frac{d Z}{d t}=\frac{\partial Z}{\partial x} \cdot \frac{d x}{d t}+\frac{\partial Z}{\partial y} \frac{d y}{d t}\) is called the total differential coefficient of Z w.r.t. t.

3. If f(x, y) = c where c is constant, then \(\frac{d y}{d x}=-\frac{\partial f}{\partial x} / \frac{\partial f}{\partial y}\).

Partial Derivatives Of Second Order:
Definition : If U = f(x, y) then \(\frac{\partial \mathbf{U}}{\partial \mathrm{x}}, \frac{\partial \mathbf{U}}{\partial \mathbf{y}}\) are called the partial derivatives of first order and they are functions of x, y. The partial derivatives of \(\frac{\partial U}{\partial x}\) and \(\frac{\partial U}{\partial y}\), if they exist, are called the second order partial derivatives . They are denoted by

Homogeneous Functions:
A function u = f (x, y) is said to be a homogeneous function of degree n in the variables in x and y if f(kx, ky) = kⁿf(x, y) for all k or f (x, y) = xⁿ f\(\left(\frac{y}{x}\right)\) or f (x, y) = yⁿ f\(\left(\frac{y}{x}\right)\).

Euler’S Theorem:
If u = f (x, y) is a homogeneous function of degree n in the variables x,y then x\(\frac{\partial \boldsymbol{U}}{\partial x}\) + y \(\frac{\partial \boldsymbol{U}}{\partial y}\) = nU
Proof:
Since u = f (x, y) is a homogeneous function of degree n, we have U = xng (y / x) where g (y / x) is function of y/x.
\(\frac{\partial \boldsymbol{U}}{\partial x}\) = xⁿ.g'(y / x)\(\left(\frac{-y}{x^{2}}\right)\) + nx^n-1 .g (y / x) ………(1)
and \(\frac{\partial \boldsymbol{U}}{\partial y}\) = xⁿ .g'(y / x) \(\left(\frac{1}{x}\right)\)
x\(\frac{\partial \boldsymbol{U}}{\partial x}\) + y\(\frac{\partial \boldsymbol{U}}{\partial y}\) = x(x\(\left(\frac{-y}{x^{2}}\right)\)) + nxⁿg(y/x) + yx^n-1.g’9y/x)
= n.xⁿ.g (y / x) == nU.

Note :
If U = f (x, y, z) is a homogeneous function of degree n in x,y,z then
x\(\frac{\partial U}{\partial x}\) + y\(\frac{\partial U}{\partial y}\) + z\(\frac{\partial U}{\partial z}\) = nU

Theorem:
If U = f (x, y) is a homogeneous function of degree n in x,y then x²\(\frac{\partial^{2} U}{\partial x^{2}}\) + 2xy\(\frac{\partial^{2} U}{\partial x \partial y}\) + y²\(\frac{\partial^{2} U}{\partial y^{2}}\) = n(n – 1)U .
Proof:
Since U = f (x, y) is a homogeneous function of degree n, by Euler’s theorem, we have

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 7 The Plane to solve questions creatively.

Intermediate 1st Year Maths 1B The Plane Formulas

Definition: If F(x, y, z) is a polynomial of degree one, then the surface represented by F(x, y, z).= 0 is called a first degree

→ If A, B, C are three non-collinear points in space, then there exists exactly only one plane through A,

→ If a plane contains two points A and B, then the plane also contains the line \(\overleftrightarrow{A B}\).

→ If two planes intersect, then their intersection is a line.

→ If a plane π and a line L are perpendicular at a point P, then π contains every line that passes through P and is perpendicular to L.

→ Equation of a plane in the normal form is lx + my + nz = p. Hence (l, m, n) are D.C’s of the normal to the plane, and p( > 0) is the perpendicular distance of the plane from the origin.

→ If (a, b, c) & (0,0,0), then the equation ax + by + cz + d = 0 is called the general form of the equation of a plane.

→ Equation of the plane n which contains the point A(x₀, y₀, z₀) and perpendicular to the line L with direction ratios (a, b, c) is a(x – xQ) + b(y – y0) + c(z – z ) = 0.

→ Equation of the plane passing through three non-collinear point A(x₁, y₁; z₁), B(x₂, y₂, z₂) and C(x₃ y₃, z₃) is \(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{i}
\end{array}\right|\) = 0

→ Equation of the plane in the intercept form is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1.

→ The angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is cos^-1 \(\frac{\left|a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

→ The perpendicular distance of the plance ax + by + cz + d = 0 from the point P(x₀ , y₀ , z₀) is \(\frac{\left|a x_{0}+b y_{0}+c z_{0}+d\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

→ The distance between the parallel planes ax + by + cz + d₁ = 0 and ax + by + cz + d₂ = 0 is \(\frac{\left|d_{1} \cdot d_{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

Planes:
Definition:
A surface in space is said to be a plane surface or a plane if all the points of the straight line joining any two points of the surface lie on the surface.

Theorem:
The equation of the plane passing through a point (x₁, y₁, z₁) and perpendicular to a line whose direction ratios are a, b, c is a( x – x₁)+b( y – y₁)+c( z – z₁) = 0

Theorem:
The equation of the plane passing through a point (x₁, y₁, z₁) is a( x – x₁)+b( y – y₁)+c (z – z₁) = 0 where a,b,c are constants.

Theorem:
The equation of the plane containing three points (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) is \(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0

Normal Form of A Plane:
Theorem:
The equation of the plane which is at a distance of p from the origin and whose normal has the direction cosines (l, m, n) is lx + my + nz = p (or) x cos α+ y cos β + z cos γ = p.

Note:
Equation of the plane through the origin is lx + my + nz = 0
Note: The equation of the plane ax +by+cz+d=0 in the normal form is

where Σa² = a² + b² + c²

Perpendicular Distance From A Point to A Plane:
The perpendicular distance from the origin to the plane ax + by + cz + d = 0 is \(\frac{|d|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

Theorem
The perpendicular distance from P(x1, y1, z1) to the plane ax + by + cz + d = 0 is \(\frac{\left|a x_{1}+b y_{1}+c z_{1}+d\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

Theorem
Intercept form of the plane
The equation of the plane having a,b,c as x, y, z- intercepts respectively is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1

Theorem
The intercepts of the plane ax + by + cz + d = 0 are respectively \(\frac{-d}{a}, \frac{-d}{b}, \frac{-d}{c}\)

Angle Between Two Planes:
Definition: The angle between the normals to two planes is called the angle between the planes.

Theorem:
If θ is the angle between the planes a₁x + b₁ y + c₁z + d₁ = 0, a₂x + b₂y + c₂z + d₂ = 0 then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{1}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

Note:

• If θ is acute then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{1}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}} \mid\)
• The planes a₁x + b₁ y + c₁z + d₁ = 0, a₂x + b₂y + c₂z + d₂ = 0 are
  • parallel iff \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
  • Perpendicular iff . a₁a₂ + b₁b₂ + c₁c₂ = 0
• The given planes are perpendicular
  ⇔ θ = 90° ⇔ cos θ = 0 ⇒ a₁a₂ + b₁b₂ + c₁c₂ = 0

Theorem:
The equation of the plane parallel to the plane ax + by + cz + d = 0 is ax + by + cz + k = 0 where k is a constant.

Theorem:
The distance between the parallel planes ax + by + cz + d₁ = 0, ax + by + cz + d₂ = 0 is \(\frac{\left|d_{1}-d_{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 6 Direction Cosines and Direction Ratios to solve questions creatively.

Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Formulas

Formulae and Synopsis :
If a line PQ makes angles α, β, γ with the co – ordinate axes, then cos α, cos β, cos γ are called
direction cosines of the line PQ. We take
l = cos α, m = cos β and n = cos γ
Relation between direction cosines is l² + m² + n² = 1

Direction Ratios :
An ordered triple of numbers proportional to the direction cosines of a line are defined as ‘Direction ratios’ of that fine.

→ If \(\frac{1}{a}=\frac{m}{b}=\frac{n}{c}\) then a, b, c are called direction ratios of the line.

→ If a, b, c are the direction ratios of a line, then its direction cosines are \(\left(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\right)\)

→ Direction ratios of the line joining P(x₁, y₁, z₁) and Q (x₂, y₂, z₂) are (x₂ – x₁, y₂ – y₁, z₂ – z₁) or (x₁ – x₂, y₁ – y₂, z₁ – z₂)

→ D.cs of the above line \(\frac{x_{2}-x_{1}}{P Q}, \frac{y_{2}-y_{1}}{P Q}, \frac{z_{2}-z_{1}}{P Q}\) or \(\frac{x_{1}-x_{2}}{P Q}, \frac{y_{1}-y_{2}}{P Q}, \frac{z_{1}-z_{2}}{P Q}\)

→ Angle between the lines whose D.cs are (l₁ m₁, n₁) and (l₂, m₂, n₂) is given by cos θ = l₁l₂ + m₁m₂ + n₁n₂

→ If these lines are perpendicular, then l₁l₂ + m₁m₂ + n₁n₂ = 0

Angle Between Two Lines:
The angle between two skew lines is the angle between two lines drawn parallel to them through any point in space.

Direction Cosines:
If α, β, γ are the angles made by a directed line segment with the positive directions of the coordinate axes respectively, then cos α, cos β, cos γ are called the direction cosines of the given line and they are denoted by l, m, n respectively Thus l = cos α, m = cos β, n = cos γ

The direction cosines of \(\overline{o p}\) are l = cos α, m = cos β, n = cos γ.
If l, m, n are the d.c’s of a line L is one direction then the d.c’s of the same line in the opposite direction are -l, -m, -n.

Note :

• The angles α, β, γ are known as the direction angles and satisfy the condition 0 < α, β, γ < π.
• The sum of the angles α, β, γ is not equal to 2β because they do not lie in the same plane.
• Direction cosines of coordinate axes.

The direction cosines of the x-axis are cos0, cos\(\frac{\pi}{2}\), cos\(\frac{\pi}{2}\) i.e., 1, 0, 0
Similarly the direction cosines of the y-axis are (0, 1, 0) and z-axis are (0, 0, 1)

Theorem:
If P(x, y, z) is any point in space such that OP = r and if l, m, n are direction cosines of \(\overline{O P}\) then x = lr,y = mr, z = nr.
Note: If P(x, y, z) is any point in space such that OP = r then the direction cosines of \(\overline{O P}\) are
Note: If P is any point in space such that OP =r and direction cosines of OP are l,m,n then the point P =(lr,mr,nr)
Note: If P(x,y,z) is any point in space then the direction cosines of OP are \(\frac{x}{\sqrt{x^{2+} y^{2}+z^{2}}}, \frac{y}{\sqrt{x^{2+} y^{2}+z^{2}}}, \frac{z}{\sqrt{x^{2+} y^{2}+z^{2}}}\)

Theorem:
If l, m, n are the direction cosines of a line L then l² + m² + n² = 1.
Proof:

l = cos α = \(\frac{x}{r}\), m = cos β = \(\frac{y}{r}\), n = cos γ = \(\frac{z}{r}\) ⇒ cos²α + cos²β + cos²γ = \(\frac{x^{2}}{r^{2}}+\frac{y^{2}}{r^{2}}+\frac{z^{2}}{r^{2}}\)
= \(\frac{x^{2}+y^{2}+z^{2}}{r^{2}}=\frac{r^{2}}{r^{2}}\)
∴ l² + m² + n² = 1

Theorem:
The direction cosines of the line joining the points P(x₁, y₁, z₁),Q(x₂, y₂, z₂) are
\(\left(\frac{x_{2}-x_{1}}{r}, \frac{y_{2}-y_{1}}{r}, \frac{z_{2}-z_{1}}{r}\right)\) where r = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

Direction Ratios:
A set of three numbers a,b,c which are proportional to the direction cosines l,m,n respectively are called DIRECTION RATIOS (d.r’s) of a line.
Note : If (a, b, c) are the direction ratios of a line then for any non-zero real number λ , (λa, λb, λc) are also the direction ratios of the same line.
Direction cosines of a line in terms of its direction ratios
If (a, b, c) are direction ratios of a line then the direction cosines of the line are ±\(\left(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\right)\)

Theorem:
The direction ratios of the line joining the points are (x₂ – x₁, y₂ – y₁, z₂ – z₁)

Angle Between Two Lines:
If (l₁, m₁, n₁) and (l₂, m₂, n₂) are the direction cosines of two lines θ and is the acute angle between them, then cos θ = |l₁l₂ + m₁m₂ + n₁n₂|

Note.
If θ is the angle between two lines having d.c’s (l₁, m₁, n₁) and (l₂, m₂, n₂) then
sin θ = \(\sqrt{\sum\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}\) and tan θ = \(\frac{\sqrt{\sum\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}}{\left|l_{1} l_{2}+m_{1} m_{2}+n_{1} n_{2}\right|}\) where θ ≠ \(\frac{\pi}{2}\)

Note :
The condition for the lines to be perpendicular is l₁l₂ + m₁m₂ + n₁n₂ = 0
The condition for the lines to be parallel is \(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)

Theorem:
If (a₁, b₁, c₁) and (a₂, b₂, c₂) are direction ratios of two lines and θ is the angle
between them then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

Note:

• If the two lines are perpendicular then a₁a₂ + b₁b₂ + c₁c₂ = 0
• If the two lines are parallel then \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
• If one of the angle between the two lines is 0 then other angle is 180° – θ

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 5 Three Dimensional Coordinates to solve questions creatively.

Intermediate 1st Year Maths 1B Three Dimensional Coordinates Formulas

→ Distance from the origin to P(x, y, z) = OP = \(\sqrt{x^{2}+y^{2}+z^{2}}\)

→ Distance between the points P(x₁, y₁ z₁) and Q (x₂, y₂, z₂) is

→ PQ = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}}\)

→ Translation of axes : If the origin is shifted to the point (h, k, l) under translation of axes, then x = x’ + h, y = y’ + k, z = z’ + l where (x, y, z) are the old co-ordinates and (x’, y’, z’) are the new co-ordinates.

Coordinates of a Point In Space (3-D):
Let \(\overline{X^{\prime} O X}, \overline{Y^{\prime} O Y}\) and \(\overline{Z^{\prime} O Z}\) be three mutually perpendicular straight lines in space, intersecting at O. This point O is called origin.

Axes :
The three fixed straight lines \(\overline{X^{\prime} O X}, \overline{Y^{\prime} O Y}\) and \(\overline{Z^{\prime} O Z}\) are respectively called X-axis ,Y-axis and Z-axis. The three lines taken together are called rectangular coordinate axes.

Coordinate Planes:
The plane containing the axes of Y and Z is called yz-plane. Thus yoz is the yz plane. Similarly the plane zox containing the axes of z and x is called ZX-plane and the plane xoy is called the xy-plane and contains x axis and y axis.
The above three planes are together called the rectangular co ordinate plane.

Octants:
The three co ordinate planes divide the whole space into 8 parts called octants.

Coordinates of A Point:
Let P be any point in the space. Draw through P , three planes parallel to the three co ordinate planes meeting the axes of X,Y,Z in the points A,B and C respectively. Then if OA = x, OB = y and OC = z, the three numbers x,y,z taken in this order are called the co ordinates of the point P and we refer the point as (x,y,z) . Any one of these x,y,z will be positive of negative according as it is measured from O along the corresponding axis, in the positive or negative direction.
Another method of finding coordinates of a point.
The coordinates x,y,z of a point P are the perpendicular distances of P from the three co ordinate planes YZ,ZX and XY respectively.

From fig PN = z, PL = x and PM = y
Therefore point P =(x,y,z)
Note. On YZ- plane, a point has x coordinate as zero and similarly on zx-plane y coordinates and on xy-plane z coordinates are zero.

For any point on the

• X-axis, Y,Z coordinates are equal to zero,
• Y-axis, X,Z coordinates are equal to zero,
• Zaxis, X,Y coordinates are equal to zero.

Distance Between The Points:
The distance between the points and is given by PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

Note:
If is the origin and is a point in space, then
OP = \(\sqrt{(x-0)^{2}+(y-0)^{2}+(z-0)^{2}}=\sqrt{x^{2}+y^{2}+z^{2}}\)

Section Formula:
P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) be two points in space and let R be a point on the line segment joining P and Q such that it divides \(\overline{P Q}\) internally in the ratio m: n . Then the coordinate of are \(\left(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}, \frac{m z_{2}+n z_{1}}{m+n}\right)\)

(ii) P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) be two points in space and let R be a point on the line segment joining P and Q such that it divides \(\overline{P Q}\) externally in the ratio m: n . Then the coordinate of are \(\left(\frac{m x_{2}-n x_{1}}{m-n}, \frac{m y_{2}-n y_{1}}{m-n}, \frac{m z_{2}-n z_{1}}{m-n}\right)\), m ≠ n

Mid Point:
The mid point of the linesegment joining the points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right)\)

Centroid of a triangle:
The coordinates of the centriod of the triangle with vertices A(x₁, y₁, z₁) B(x₂, y₂, z₂) and C(x₃, y₃, z₃) is \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}+\frac{z_{1}+z_{2}+z_{3}}{3}\right)\)

Centroid of a tetrahydron:
The coordinates of the centriod of the tetrahedron with vertices A(x₁, y₁, z₁) B(x₂, y₂, z₂), C(x₃, y₃, z₃) and D(x₄, y₄, z₄) is \(\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}, \frac{z_{1}+z_{2}+z_{3}+z_{4}}{4}\right)\)

Translation of Axes :

Let P(x,y,z) and A(h,k,l) be two points is space w.r.t the frame of reference OXYZ. Now treating A as the origin, let \(\overline{A X^{1}}, \overline{A Y^{1}}, \overline{A Z^{1}}\) be the new axes parallel to
\(\overline{O X}, \overline{O Y}, \overline{O Z}\) respectively. If (x’, y’, z’) are the coordinates of P w.r.t
AX¹Y¹Z¹ then x¹ = x – h, y¹ = y – k, z¹ = z – l.

Example: Origin is shifted to the point (1,2 -3). Find the new coordinates of (1,0,-1)
Answer:
(x, y, z) = (1,0,-1) and( h, k, l) = (1,2 -3).
Now new coordinates are X = x – h = 1 -1 = 0
Y = y – k = 0 – 2 = -2
Z = z – l = -1 + 3 = 2
herefore new coordinates are ( 0,-2, 2)

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 3 The Straight Line to solve questions creatively.

Intermediate 1st Year Maths 1B The Straight Line Formulas

→ Equation of a horizontal line is y = k

→ Equation of a vertical line is x = h

→ If ‘θ ‘ is the inclination of a line then slope = m = tan θ

→ If m₁ m₂ are slopes of two lines and ‘θ ‘ is angle between them then tan θ = \(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\)

→ If two lines are parallel then their slopes are equal i.e., m₁ = m₂

→ If two lines are perpendicular, then m₁m₂ = -1

→ Equation of a line passing through (x₁, y₁) with slope ‘m’ is y – y₁ = m(x – x₁)

→ Equation of a line passing through origin with slope m is y = mx

→ Equation of the line passing through (x₁, y₁) and (x₂, y₂) is \(\) (or) (x – x₁)(y₁ – y₂) = (y – y₁)(x₁ – x₂)

→ Equation of the line with slope’m’ and having

• y-intercept ‘c’ is y = mx + c (slope intercept form)
• x-intercept ‘a’ is y = m(x – a)

→ Equation of a line in intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1

• Intersecting point on X – axis = (a, 0)
• Intersecting point on Y – axis = (0, b)

→ Area of Δ^le formed by the line with co-ordinate axis is = \(\frac{1}{2}\)|ab|

→ Area of Δ^le formed by the line ax + by + c = 0 with co-ordinate axis is \(\frac{c^{2}}{2|a b|}\)

→ If a point (x₁, y₁) divides the line segment between the co-ordinate axes in the ratio l: m then equation of the line is \(\frac{m x}{x_{1}}+\frac{l y}{y_{1}}\) = l + m

→ Equation of a line in normal form or perpendicular form is x cos α + y sin α = p where ‘α’ is the angle made by the perpendicular with +ve X – axis. ‘p’ is length of normal form origin to the line.

→ Perpendicular distance from (x₁, y₁) to the line ax + by + c = 0 is \(\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)

→ Perpendicular distance from origin to the line ax + by + c = 0 is \(\frac{|c|}{\sqrt{a^{2}+b^{2}}}\)

→ The ratio in which the line L ax + by + c = 0 (ab ≠ 0) divides the line segment AB joining the points A(x₁, y₁) and B(x₂, y₂) is –\(\left(\frac{a x_{1}+b y_{1}+c}{a x_{2}+b y_{2}+c}\right)\) or –\(\frac{L_{11}}{L_{22}}\)
where L₁₁ = a₁x + b₁y + c; L₂₂ = a₂x + b₂y + c

→ If L₁₁, L₂₂ are having same sign or opposite sign’s then those points lies same side or opposite sides of the line L = 0 respectively.

→ If the foot of the perpendicular from (x₁, y₁) to the line ax + by + c = 0 is (α, β) then \(\frac{\alpha-x_{1}}{a}=\frac{\beta-y_{1}}{b}=\frac{-\left(a x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\)

→ If the image of(x₁, y₁) w.r.t. the line ax +by + c = 0 is (α, β) then
\(\frac{\alpha-x_{1}}{a}=\frac{\beta-y_{1}}{b}=\frac{-2\left(a x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\)

→ The point of intersection of two lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 is
\(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}} \cdot \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)

→ If θ |0 ≤ θ ≤ π| is angle between the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
sin θ = \(\frac{a_{1} b_{2}-a_{2} b_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
and tan θ = \(\frac{a_{1} b_{2}-a_{2} b_{1}}{a_{1} a_{2}+b_{1} b_{2}}\)

• The lines are perpendicular ⇔ a₁a₂ + b₁b₂ = 0
• Then lines are parallel ⇔ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\)

→ The equation of a line passing through the point (x₁, y₁) and parallel to the line ax + by + c = 0 is a(x – x₁) + b(y – y₁) = 0

→ The equation of a line passing through the point (x₁, y₁) and perpendicular to ax + by + c = 0 is b(x – x₁) – a(y – y₁) = 0

→ The distance between the two parallel straight lines a₁x + b₁y + c₁ = 0 and a₁x + b₁y + c₂ = 0 is \(\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\)

→ Area of the parallelogram formed by the lines a₁x + b₁y + c₁ = 0,a ₂x + b₂y + d₁= 0, a₂x + b₂y + c₂ = 0 and a₂x + b₂y + d₂ = 0 is \(\left|\frac{\left(d_{1}-c_{1}\right)\left(d_{2}-c_{2}\right)}{a_{1} b_{2}-a_{2} b_{1}}\right|\)

→ Equation of the line parallel to X – axis and passing through (x₁, y₁) is y = y₁

→ Equation of the line parallel to Y- axis and passing through (x₁, y₁) is x = x₁

Concurrent lines-properties related to a Triangle
Theorem:
The medians of a triangle are concurrent.
Proof:
Let A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) be the vertices of the triangle

Let D,E,F be the mid points of BC, CA, AB respectively
∴ D = \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)
E = \(\left(\frac{x_{3}+x_{1}}{2}, \frac{y_{3}+y_{1}}{2}\right)\)
F = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

Slope of \(\overline{A D}\) is \(\frac{\frac{y_{2}+y_{3}}{2}-y_{1}}{\frac{x_{2}+x_{3}}{2}-x_{1}}=\frac{y_{2}+y_{3}-2 y_{1}}{x_{2}+x_{3}-2 x_{1}}\)

Equation of \(\overline{A D}\) is
y – y₁ = \(\frac{y_{2}+y_{3}-2 y_{1}}{x_{2}+x_{3}-2 x_{1}}\)(x – x₁)
⇒ (y – y₁)(x₂ + x₃ – 2x₁) = (x – x₁)(y₂ + y₃ – 2y₁)
⇒ L₁ = (x – x₁)(y₂ + y₃ – 2y₁) – (y – y₁)(x₂ + x₃ – 2x₁) = 0

Similarly, the equations to \(\overline{B E}\) and \(\overline{C F}\) respectively are L₂ s (x – x₂)(y₃ + y₁ – 2y₂) – (y – y₂) (x₃ + x₁ – 2x₂) = 0.
L₃ = (x – x₃)(y₁ + y₂ – 2y₃) – (y – y₃) (x₁ + x₂ – 2x₃) = 0.
Now 1. L₁ + 1.L₂ + 1. L₃ = 0
The medians L₁ = 0, L₂ = 0, L₃ = 0 are concurrent.

Theorem:
The altitudes of a triangle are concurrent.
Proof:
Let A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) be the vertices of the triangle ABC. Let AD, BE,CF be the altitudes.
Slope of \(\overline{B C}\) is \(\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\) and AD ⊥ BC

Slope of the altitude through A is – \(\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\)

Equation of the altitude through A is y – y₁ = \(\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\) (x – x₁)
(y – y₁) (y₃ – y₂) = -(x – x₁) (x₃ – x₂)
L₁ = (x – x₁)(x – x₃) + (y – y₁)(y – y₃) = 0.

Similarly equations of the altitudes through B,C are
L₂ = (x – x₂) (x₃ – x₁) + (y – y₂) (y₂ – y₃) = 0,
L₃ = (x – x₃) (x₁ – x₂) + (y – y₃) (y₁ – y₂) = 0.
Now 1.L₁ + 1.L₂ + 1.L₃ = 0
The altitudes L₁ = 0, L₂ = 0, L₃ = 0 are concurrent.

Theorem:
The internal bisectors of the angles of a triangle are concurrent.

Theorem:
The perpendicular bisectors of the sides of a triangle are concurrent

Point of Intersection of Two Straight Lines:
Theorem:
The point of intersection of the two non parallel lines
a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 is \(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}, \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)
Proof:
The lines are not parallel ^ Slopes are not equal
⇒ \(\frac{-a_{1}}{b_{1}} \neq \frac{-a_{2}}{b_{2}}\) ⇒ a₁b₂ ≠ a₂b₁ ⇒ a₁b₂ – a₂b₁ ≠ 0
Let P (α, β) be the point of intersection. Then a₁ α + b₁β + C₁ = 0 and a₂ α + b₂β + c₂ = 0.
Solving by the method of cross multiplication

Point of intersection is P = \(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}, \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)

Theorem:
The ratio in which the line L = ax + by + c = 0 divides the line segment joining A(x₁, y₁), B(x₂, y₂) is -L₁₁ : L₂₂, where L₁₁ = L(x₁, y₁) = ax₁ + by₁ + c and L₂₂ = L(x₂, y₂) = ax₂ + by₂ + c.
Proof:
Let k : 1 be the ratio in which the line divides the line segment.

The point which divides in the ratio k : 1 is P = \(\left(\frac{k x_{2}+x_{1}}{k+1}, \frac{k y_{2}+y_{1}}{k+1}\right)\)

Since P lies on the line ax + by + c = 0 ⇒ a\(\left(\frac{k x_{2}+x_{1}}{k+1}\right)\) + b\(\left(\frac{k y_{2}+y_{1}}{k+1}\right)\) + c = 0
⇒ a(kx₂ + x₁) + b(ky₂ + y₁) + c(k + 1) = 0
⇒ k(ax₂ + by₂ + c) = -(ax₁ + by₁ + c)
⇒ k = –\(\frac{\left(a x_{1}+b y_{1}+c\right)}{a x_{2}+b y_{2}+c}\)
Required Ratio = -(ax₁ + by₁ + c) : (ax₂ + by₂ + c)
= -L₁₁: L₂₂.

Note:
The points A,B lie in the same side or opposite side of the line L = 0 according as L₁₁, L₂₂ have the same sign or opposite signs.

• The points A,B are opposite sides of the line L = 0 iff L₁₁ and L₂₂ have opposite signs.
• The points A,B are same side of the line L = 0 iff L₁₁ and L₂₂ have same sign.

Concurrent Lines:
Three or more lines are said to be concurrent if they have a point in common. The common point is called the point of concurrence.

Condition for Concurrency of Three Straight Lines:
Theorem:
The condition that the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0, a₃x + b₃y + c₃ = 0 to be concurrent is a₃(b₁c₂ – b₂c₁) + b₃(c₁a₂ – c₂a₁) + c₃(a₁b₂ – a₂b₁) = 0.
Proof:
Suppose the given lines are concurrent.
Let P(α, β) be the point of concurrence.
Then a₁ α + b₁ β + c₁ = 0 ………..(1)
a₂ α + b₂ β + c₂= 0 ………..(2)
a₃ α + b₃ β + c₃= 0 ………….(3)

By solving (1) and (2) we get
α = \(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)
β = \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)

Therefore P = \(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}, \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)

Substituting P in eq.(3), we get
a₃\(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\) + b₃\(\left(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\) + c₃ = 0
a₃(b₁c₂ – b₂c₁) + b₃(c₁a₂ – c₂a₁) + C3 (a₁b₂ – a₂b₁) = 0 which is required Condition.

Above condition can be written in a determinant form as \(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|\) = 0

Problem:
Find the Condition that the lines ax + hy + g = 0, hx + by + f = 0, gx + fy + c = 0 to be Concurrent.
Answer:
Let P be the point of ConCurrenCe
aα + h β + g = 0 …………..(1)
hα + b β + f = 0 ………….(2)
gα + f β + c = 0 …………(3)

solving (1) and (2) we get

Sub these values in eq.(3)
g\(\left(\frac{h g-b g}{a b-h^{2}}\right)\) + f\(\left(\frac{g h-a f}{a b-h^{2}}\right)\) + c = 0
⇒ g(hf – bg) + f(gh – af) + C(ab – h²) = 0
⇒ fgh – bg² + fgh – af² + abc – ch² = 0
⇒ abc + 2fgh – af² – bg² – ch² = 0
The Condition is abc + 2fgh – af² – bg² – ch² = 0

Family of Straight Lines – Concurrent Straight Lines:
Theorem:
Suppose L₁ = a₁x + b₁y + c₁ = 0, L₂ = a₂x + b₂y + c₂ = 0 are two intersection lines.
(i) If (λ₁, λ₂) ≠ (0,0) then λ₁L₁ + λ₂L₂ = 0represents a straight line passing through the point of intersection of L₁ = 0 and L₂ = 0.
(ii) The equation of any line passing through the point of intersection of
L₁ = 0, L₂ = 0 is of the form where (λ₁, λ₂) ≠ (0,0).
Note: If L₁ = 0, L₂ = 0 are two intersecting lines, then the equation of any line other than L₂ = 0 passing through their point of intersection can be taken as L₁ + λL₂ = 0 where λ is a parameter.

Theorem:
If there exists three constants p,q,r not all zero such that
p(a₁x + b₁y + c₁) + q(a₂x + b₂y + c₂) + r(a₃x + b₃y + c₃) = 0 for all x and y then the three lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 and a₃x + b₃y + c₃ = 0 in which no two of them are parallel, are concurrent.

Theorem:
Let L₁ = a₁x + b₁y + c₁ = 0, L₂ = a₂x + b₂y + c₂ = 0 represent two parallel lines.Then the straight line represented by λ₁L₁ + λ₂L₂ = 0 is parallel to each of the straight line L₁ = 0 and L₂ = 0.

A Sufficient Condition for Concurrency of Three Straight Lines:
Theorem:
If L₁ = a₁x + b₁y + c₁ = 0, L₂ = a₂x + b₂y + c₂ = 0, L₃ = a₃x + b₃y + c₃ = 0 are three straight lines, no two of which are parallel, and
if non-zero real numbers λ₁, λ₂, λ₃ exist such that λ₁ L₁ + λ₂ L₂ + λ₃ L₃ = 0 then the straight lines L₁ = 0, L₂ = 0 and L₃ = 0are concurrent.

Length of The Perpendicular From A Point to A Straight Line and Distance Between Two Parallel Lines
Theorem:
The perpendicular distance from a point P(x₁, y₁) to the line ax + by + c = 0 is \(\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
Proof:

Let the axes be translated to the point P(x₁, y₁).
Let (X,Y) be the new coordinates of (x, y). Then x = X + x₁, y = Y + y₁
The transformed equation of the given line is
a(X + x₁) + b(Y + y₁) + c = 0
⇒ aX + bY + (ax₁ + by₁ + c) = 0
The perpendicular distance from the new origin P to the line is (from normal form) The perpendicular distance from a point
P(x₁, y₁) to the line ax+ by + c = 0 is \(\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)

Distance Between Parallel Lines Theorem:
The distance between the two parallel lines ax + by + c₁ = 0 and ax + by + c₂ = 0 is \(\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
Proof:
Given lines are ax + by + c₁ = 0 …………(1)
ax + by + c₂ = 0 …………(2)
Let P(x₁, y₁) be a point on the line (2).

Then
ax₁ + by₁ + c₂ = 0
ax₁ + by₁ = -c₂.
Distance between the parallel lines = Perpendicular distance from P to line (i)
= \(\frac{\left|a x_{1}+b y_{1}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)

Foot of The Perpendicular:
Theorem:
If (h, k) is the foot of the perpendicular from (x₁, y₁) to the line ax + by + c = 0 (a0, b0) then \(\frac{h-x_{1}}{a}=\frac{k-y_{1}}{b}=\frac{-\left(a x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\).
Proof:

Let A = (x₁, y₁) P = (h, k)
P lies on ax + by + c = 0
ah + bk + c = 0
ah + bk = – c
Slope of \(\overline{A P}\) is \(\frac{k-y_{1}}{h-x_{1}}\)
Slope of given line is \(-\frac{a}{b}\)

\(\overline{A P}\) is perpendicular to the given line
⇒ \(\left(\frac{k-y_{1}}{h-x_{1}}\right)\left(-\frac{a}{b}\right)\) = -1
⇒ \(\frac{k-y_{1}}{b}=\frac{h-x_{1}}{a}\)

By the law of multipliers in ratio and proportion

Image of A Point
Theorem:
If (h, k) is the image of (x₁, y₁) w.r.t the line ax + by + c = 0 (a ≠ 0, b ≠ 0), then \(\frac{h-x_{1}}{a}=\frac{k-y_{1}}{b}=\frac{-2\left(x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\).
Proof:
Let A(x₁, y₁), B(h, k)
Mid Point of is P = \(\left(\frac{x_{1}+h}{2}, \frac{y_{1}+k}{2}\right)\)
Since B is the image of A,therefore mid point P lies on ax + by + c = 0.
a\(\left(\frac{x_{1}+h}{2}\right)\) + b\(\left(\frac{y_{1}+k}{2}\right)\) + c = 0
⇒ ax₁ + by₁ + ah + bk + 2c = 0
⇒ ah + bk = -ax₁ + by₁ – 2c.

Slope of \(\overline{A B}\) is \(\frac{k-y_{1}}{h-x_{1}}\)
Slope of given line is \(-\frac{a}{b}\)
\(\overline{A B}\) is perpendicular to the given line a
⇒ \(\left(\frac{k-y_{1}}{h-x_{1}}\right)\left(-\frac{a}{b}\right)\) = -1
⇒ \(\frac{k-y_{1}}{b}=\frac{h-x_{1}}{a}\)

By the law of multipliers in ratio and proportion

Note :

• The image of (x₁, y₁) w.r.t the line x = y is (y₁, x₁)
• The image of (x₁, y₁) w.r.t the line x + y = 0 is (-y₁, -x₁)

Theorem:
If the four straight lines ax + by + p = 0, ax + by + q = 0, cx + dy + r = 0 and cx + dy + s = 0 form a parallelogram. Then the area of the parallelogram so formed is
\(\left|\frac{(p-q)(r-s)}{b c-a d}\right|\)
Proof:
Let L₁ = ax + by + p = 0
L₂ = ax + by + q = 0
L₃ = cx + dy + r = 0
L₄ = cx + dy + s = 0
Clearly
L₁ ∥ L₂ and L₃ ∥ L₄. So L₁ and L₃ are nonparallel. Let be the angle between L₁ and L₃.
Let d₁ = distance between L₁ and L₂= \(\frac{|p-q|}{\sqrt{a^{2}+b^{2}}}\)
Let d₂ = distance between L₃ and L₄ = \(\frac{|r-s|}{\sqrt{c^{2}+d^{2}}}\)
Now cos θ = \(\frac{|a c+b d|}{\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\) and sin θ = \(\sqrt{\frac{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)-(a c+b d)^{2}}{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\)
= \(\frac{|b c-a d|}{\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\)
Now area of the parallelogram is \(\frac{d_{1} d_{2}}{\sin \theta}=\left|\frac{(p-q))(r-s)}{b c-a d}\right|\)

Angle Between Two Lines
Theorem:
If θ is an angle between the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 then
cos θ = ±\(\frac{a_{1} a_{2}+b_{1} b_{2}}{\sqrt{a_{1}^{2}+b_{2}^{3}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
Proof:
The lines passing through the origin and parallel to the given lines are
a₁x + b₁y = 0, ……… (1)
a₂x + b₂y = 0. …………….(2)

Let θ₁, θ₂ be the inclinations of (1) and (2) respectively (θ1 > θ2)
Now θ is an angle between (1) and (2)
θ = θ₁ – θ₂
P(-b₁, a₁) satisfies eq(1), the point lies on (1)
Similarly, Q(-b₂, a₂) lies on (2)

Let L and M be the projection of P, Q respectively on the x – axis.

Note :

• If is the acute angle between the lines then cos θ = \(\frac{\left|a_{1} a_{1}+b_{1} b_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
• If is an angle between two lines, then is another angle between the lines.
• If is an angle between two lines are not a right angle then the angle between the lines means the acute angle between the lines.
• If 0 is an angle between the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 then tan θ = \(\frac{a_{1} b_{2}-a_{2} b_{1}}{a_{1} a_{2}+b_{1} b_{2}}\)
• If is the acute angle between the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 then
  tan θ = \(\left|\frac{a_{1} b_{2}-a_{2} b_{1}}{a_{1} a_{2}+b_{1} b_{2}}\right|=\left|\frac{a_{1} / b_{1}-a_{2} / b_{2}}{\left(a_{1} a_{2}\right) /\left(b_{1} b_{2}\right)+1}\right|\)
  = \(\left|\frac{\left(-a_{1} / b_{1}\right)-\left(-a_{2} / b_{2}\right)}{1+\left(-a_{1} / b_{1}\right)\left(-a_{2} / b_{2}\right)}\right|\) where mj, m2 are the slopes of the lines.

Theorem:
The equation of the line parallel to ax + by + c = 0 and passing through (x₁, y₁) is a(x – x₁) + b(y – y₁) = 0.
Proof:
Slope of the given line is -a/b.
⇒ Slope of the required line is -a/b.(lines are parallel)
Equation of the required line is
y – y₁ = –\(\frac{a}{b}\)(x – x₁)
b(y – y₁) = -a(x – x₁)
a(x – x₁) + b(y – y₁) = 0.

Note :

• The equation of a line parallel to ax + by + c = 0 may be taken as ax + by + k = 0.
• The equation of a line parallel to ax + by + c = 0 and passing through the origin is ax + by = 0.

Theorem:
The equation of the line perpendicular to ax + by + c = 0 and passing through (x₁, y₁) is b(x – x₁) – a(y – y₁) = 0.
Proof:
Slope of the given line is -a/b. ⇒ Slope of the required line is b/a. (since product of slopes = -1)
Equation of the required line is y – y₁ = \(\frac{b}{a}\) (x – x₁)
a(y – y₁) = b(x – x₁)
b(x – x₁) – a(y – y₁) = 0.

Note :

• The equation of a line perpendicular to ax + by + c = 0 may be taken as bx – ay + k = 0
• The equation of a line perpendicular to ax + by + c = 0 and passing through the origin is bx – ay = 0.

Concurrent Lines- Properties Related to A Triangle
Theorem:
The medians of a triangle are concurrent.
Proof:
Let A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) be the vertices of the triangle

Let D, E, F be the mid points of \(\overline{B C}, \overline{C A}, \overline{A B}\) respectively

Equation of \(\overline{A D}\)
y – y₁ = (x – x₁)
(y – y₁) (x₂ + x₃ – 2x₁) = (x – x₁)(y₂ + y₃ – 2y₁)
⇒ L₁ ≡ (x – x₁)(y₂ + y₃ – 2y₁) – (y – y₁) (x₂ + x₃ – 2x₁) = 0.

Similarly, the equations to \(\overline{B E}\) and \(\overline{C F}\) respectively are L₂ ≡ (x – x₂)(y₃ + y₁ – 2y₂) – (y – y₂) (x₃ + x₁ – 2x₂) = 0.
L₃ ≡ (x – x₃)(y₁ + y₂ – 2y₃) – (y – y₃) (x₁ + x₂ – 2x₃) = 0.
Now 1. L₁ + 1.L₂ + 1. L₃ = 0
The medians L₁ = 0, L₂ =0, L₃ = 0 are concurrent.

Theorem:
The altitudes of a triangle are concurrent.
Proof:
Let A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) be the vertices of the triangle ABC.
Let AD, BE,CF be the altitudes.
Slope of \(\overline{B C}\) is \(\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\) and AD ⊥ BC
Slope of the altitude through A is \(-\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\)

Equation of the altitude through A is y – y₁ = \(\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\)(x – x₁)
(y – y₁) (y₃ – y₂) = -(x – x₁) (x₃ – x₂)
L₁ = (x – x₁)(x₂ – x₃) + (y – y₁)(y₂ – y₃) = 0.

Similarly equations of the altitudes through B,C are
L₂ = (x – x₂) (x₃ – x₁) + (y – y₂) (y₂ – y₃) = 0
L₃ = (x – x₃) (x₁ – x₂) + (y – y₃) (y₁ – y₂) = 0.
Now 1.L₁ + 1.L₂ + 1.L₃ = 0
The altitudes L₁ = 0, L₂ =0, L₃ = 0 are concurrent.

Theorem:
The internal bisectors of the angles of a triangle are concurrent.

Theorem:
The perpendicular bisectors of the sides of a triangle are concurrent

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 2 Transformation of Axes to solve questions creatively.

Intermediate 1st Year Maths 1B Transformation of Axes Formulas

→ x = x’ + h ⇒ x’ = x – h

→ y = y’ + k ⇒ y’ = y – k

→ To make the first degree term absent, origin should be shifted to \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

→ If the equation is ax² + by² + 2gx + 2fy + c = 0, origin should be shifted to be \(\left(-\frac{g}{a},-\frac{f}{b}\right)\)

x = x’ cos θ – y’ sin θ
x’ = x cos θ + y sin θ
y = x’ sin θ + y’ cos θ
y’ = – x sin θ + y cos θ

→ To make the xy term absent, axes should be rotated through an angle θ given by
tan 2θ = \(\frac{2 h}{a-b}\)

Rotation Of Axes (Change Of Direction):
I. Definition: If thc axes are rotated through an angle in the same plane by keeping the origin constant, then the transformation is called Rotation of axes.

2. Theorem: To find the co-ordinates of a point (x,y)are transformed to (X, Y)when the axes are rotated through an angle ‘6’ about the origin in the same plane.
Proof: Let x’Ox, yOY’ are the original axes
Let P(x,y)be the co-ordinates of the point in the above axes.
After rotating the axes through an angle ‘θ’, then the co-ordinates of P be (X, Y) w.r.t the new axes X’OX and YOY’ as in figure.

Since θ is the angle of rotation, then ∠xOA = ∠yOY = θ as in the figure.
Since L, M is projections of P on Ox and OX respectively. We can see that ∠LPM = ∠xOA = θ
Let N be the projection to PL from M
Now x = OL = OQ – LQ = OQ – NM
= OM cos θ – PM sin θ
= A cos θ – Y sin θ
y = PL = PN + NL = PN + MQ
PM cos θ + OM sin θ = Ycos θ + X sin θ
x = X cos θ – Y sin θ and
y = Y cos θ + X sin θ ………….(1)
Solving the above equations to get X and Y, then X = x cos θ + y sin θ and Y = -x sin θ + y cos θ ………… (2)

From (1) and (2) we can tabulate

Note:

• If the axes are turned through an angle ‘ θ ’, then the equation of a curve f (x, y) = 0 is transformed to f (X cos θ – Y sin θ, X sin θ + Y cos θ) = 0
• If f (X, Y) = 0is the transformed equation of a curve when the axes are rotated through an angle ‘ θ ’ then the original equation of the curve is f (x cos θ + y sin θ, – x sin θ + y cos θ) = 0

Theorem:
To find the angle of rotation of the axes to eliminate xy term in the equation ax² + 2hxy + by² + 2 gx + 2 fy + c = 0
Proof: given equation is ax²+ 2hxy + by² + 2 gx + 2 fy + c = 0
Since the axes are rotated through an angle θ, then x = X cos θ – Y sin θ, y = X sin θ + Y cos θ

Now the transformed equation is
a (X cos θ – Y sinθ)² + 2h (X cos θ – Y sin θ)(X sin θ + Y cos θ) + b (X sin θ + Y cos θ)² + 2g (X cos θ – Y sin θ) + 2 f (X sin θ + Y cos θ) + c = 0

⇒ X²cos²θ + Y²sin²θ – 2XYcosθsinθ) + 2h [X²cos θ + XY(cos²θ – sin²θ) – Y sin²θ cos²θ] + b[X² sin²θ + Y² cos²θ + 2XY cos θ sin θ) + 2g (X cos θ – Y sin θ) + 2 f (X sin θ + Y cos θ) + c = 0

Since XY term is to be eliminated, coefficient of XY = 0.
⇒ 2 (b – a) cos θ sin θ + 2h (cos2 θ – sin2 θ) = 0
⇒ h cos 2θ + (b – a) sin 2θ = 0
⇒ 2hcos2θ = (a -b)sin 2θ
⇒ Angle of rotation (θ) = \(\frac{1}{2}\) Tan^-1\(\left(\frac{2 h}{a-b}\right)\)
Note: The angle of rotation of the axes to eliminate xy term in
ax² + 2hxy + ay² + 2 gx + 2 fy + c = 0 is \(\frac{\pi}{4}\)

Translation of Axes:
1. Definition: Without changing the direction of the axes, the transformation in which the origin is shifted to another position or point is called translation of axes.

2. Theorem: To find the co-ordinates of a point (x, y) are translated by shifting the origin to a point (x, y)
Proof :

Let xox¹ xox¹, yoy¹ be the original axes and A(x₁, y₁) be a point to which the origin is shifted
Let AX, AY be the new axes which are parallel to the original axes as in figure.
Let P be any point in the plane whose coordinates w.r.t old system are (x, y)
And w.r.t new axes are (X, Y) .
From figure, A = (x₁, y₁) then AL = y₁, OL = x₁,
P(x, y )then x = ON = OL + LN = OL + AM = x₁ + X = X + x₁
Hence x = X + x₁.
y = PN = PM +MN = X+ AL = X + y₁
therefore, y = Y + y₁
hence x = X + x₁ y = Y + y₁

3. Theorem: To find the point to which the origin is to be shifted by translation of axes to eliminate x, y terms(first degree terms) in the equation ax² + 2xhy + by² + 2gx + 2fy + c = 0 (2 = ab)
Proof : given equation is ax2 + 2 xhy + by2 + 2gx + 2fy + c = 0
Let (x1, y1) be a point to which the origin is shifted by translation Let (X ,Y) be the new co-ordinates of the point (x, y) .
the equations of the transformation are x = X + x₁, y = Y + y₁
Now the transformed equation is
a (X + x₁)² + 2h (X + x₁)(Y + y₁)+ b (Y + y₁)² + 2g (X + x₁) + 2f [Y + y₁] + c = 0
⇒ a(X² + 2x₁X + x₁²) + 2h(XY + x₁Y + y₁X + x₁y₁) + b(Y² + 2y₁Y + y₁²) + 2g(X + x₁) + 2f (Y + y₁) + c = 0
⇒ aX² + 2hXY + bY² + 2X [ax₁ + hy₁ + g) + 2Y(hx₁ + by₁ + f ) + (ax₁² + 2x₁ + by₁² + 2gx₁ + 2fy₁ + c) = 0

Since x, y terms (the first degree terms) are to be eliminated
ax₁ + hy₁ + g = 0
hx₁ + by₁ + f = 0
Solving these two equations by the method of cross pollination

\(\frac{x_{1}}{h f-b g}=\frac{y_{1}}{g h-a f}=\frac{1}{a b-h^{2}}\) ⇒ x₁ = \(\frac{h f-b g}{a b-h^{2}}\) y₁ = \(\frac{g h-a f}{a b-h^{2}}\)
New Origin is ⇒ (x₁, y₁) = \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

Note:
(i) The point to which the origin has to be shifted to eliminate x, y terms by translation in the equation ax2 + by2 + 2gx + 2 fy + c = 0is \(\left(\frac{-g}{a}, \frac{-f}{b}\right)\)
If b = a, then the new origin is \(\left(\frac{-g}{a}, \frac{-f}{b}\right)\)

(ii) The point to which the origin has to be shifted to eliminate x, y terms by translation of axes in the equation a(x + x₁)² + b(y + y₁)² = c is (-x₁, – y₁)

(iii) The point to which the origin has to be shifted to eliminate x, y terms by translation in the equation 2hxy + 2gx + 2 fy + c = 0 is \(\left(\frac{-f}{h}, \frac{-g}{h}\right)\)
l h ’ h I
Theorem : To find the condition that the equation ax² + 2hxy + by² + 2 gx + 2 fy + c = 0 to be in the form aX² + 2hXY + bY² = 0 when the axes are translated. (h² ≠ ab)
Proof : From theorem 3, we get
ax₁ + hy₁ + g = 0 ………..(1)
hx₁ + by₁ + f = 0 …………(2)

Solving (1) and (2),
(x₁, y₁) = \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g f-a f}{a b-h^{2}}\right)\)

Since the equation is to be in the form of aX² + 2hXY + bY² = 0 ,then for this we should have axj² + 2hx₁y₁ + by² + 2 gx₁ + 2 fy₁ + c = 0
⇒ (ax₁ + hyx + g) x₁ + (x₁ + byx + f) yx + (gx + fy₁ + c ) = 0
⇒ (0).x + (0), y + (gx₁ + fyx + c) = 0 from(1) and (2) ⇒ gx₁ + fyx + c = 0 …………..(3)

Substituting x₁, y₁ in (3), we get
g\(\left(\frac{h f-b g}{a b-h^{2}}\right)\) + f\(\left(\frac{g h-a f}{a b-h^{2}}\right)\) + c = 0
⇒ fgh – bg² + fgh – af² + abc + -ch² = 0
⇒ abc + 2 fgh – af² – bg² – ch² = 0

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 1 Locus to solve questions creatively.

Intermediate 1st Year Maths 1B Locus Formulas

→ PQ = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}\)

→ OP = \(\sqrt{x_{1}^{2}+y_{1}^{2}}\)

→ P divides A(x₁, y₁) and B(x₂, y₂) in the ratio m : n

→ Co-ordinates of P are \(\left(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}\right)\)

→ Midpoint = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

→ ΔABC = \(\frac{1}{2}\)[x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃(y₁ – y₂)] = \(\frac{1}{2}\)\(\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)

→ Area of the Quadrilateral = \(\frac{1}{2}\)|x₁(y₂ – y₄) + x₂(y₃ – y₁) + x₃(y₄ – y₂) + x₄(y₁ – y₃)|

→ Centroid G = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)

→ Incentre I = \(=\left(\frac{a x_{1}+b x_{2}+c x_{3}}{a+b+c}, \frac{a y_{1}+b y_{2}+c y_{3}}{a+b+c}\right)\)

→ Ex-centre I₁ = \(\left(\frac{-a x_{1}+b x_{2}+c x_{3}}{-a+b+c}, \frac{-a y_{1}+b y_{2}+c y_{3}}{-a+b+c}\right)\)

Distance Between two points:

• The distance between two points A(x₁, y₁) and B(x₂, y₂)
  AB (orBA) = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}\)
• The distance from origin O to the point A(x₁, y₁) OA = \(\sqrt{x_{1}^{2}+y_{1}^{2}}\)
• The distance between two points A(x₁, 0) and B(x₂, 0) lying on the X – axis is AB= \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+(0-0)^{2}}=\sqrt{\left(x_{1}-x_{2}\right)^{2}}\) = |x₁ – x₂|
• The distance between two points C(0, y₁) and D(0, y₂) lying on the Y-axis is CD = |y₁ – y₂|

Section Formula:

• The point P which divides the line segment joining the points A(x₁, y₁). B(x₂, y₂) in the ratio m : n internally is given by P = \(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}\)
• If P divides in the ratio m:n externally then P = \(\frac{m x_{2}-n x_{1}}{m-n}, \frac{m y_{2}-n y_{1}}{m-n}\) (m’ n)

Note: If the ratio m : n is positive then P divides internally and if the ratio is negative P divides externally.

Mid Point:
The mid point of the line segment joining A(x₁, y₁) and B(x₂, y₂) is \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

Points Of Trisection:
The points which divide the line segment \(\overline{A B}\) in the ratio 1: 2 and 2: 1 (internally) are called the points of trisection of \(\overline{A B}\)

Area Of A Triangle:
The area of the triangle formed by the points A(x₁, y₁), B(x₂, y₂) C(x₃, y₃) is
Area = \(\frac{1}{2}\)|(x₁y₂ – x₂y₁) +(x₂y₃ – x₃y₂) + (x₃y₁ – x₁y₃)|
i.e., Area of ABC = \(\frac{1}{2}\)|Σ(x₁y₂ – x₂y₁)|

Note:

• The area of the triangle formed by the points (x₁, y₁)(x₂, y₂).(x₃, y₃) is the positive value of the determinant \(\frac{1}{2}\)\(\left|\begin{array}{ll}
  x_{1}-x_{2} & y_{1}-y_{2} \\
  x_{2}-x_{3} & y_{2}-y_{3}
  \end{array}\right|\)
• The area of the triangle formed by the points (x₁, y₁)(x₂, y₂) and the origin is \(\frac{1}{2}\)|x₁y₂ – x₂y₁|

Area Of A Quadrilateral:
The area of the quadrilateral formed by the points (x₁, y₁) (x₂, y₂), (x₃, y₃), (x₄, y₄) taken in that order is
\(\frac{1}{2}\)|x₁y₂ – x₂y₁ + x₂y₃ – x₃y₂ + x₃y₄ – x₄y₃ + x₄y₁ – x₁y₄|

Note:
The area of the quadrilateral formed by the points (x₁, y₁) (x₂, y₂) (x₃, y₃),(x₄, y₄) taken in order is
Area = \(\frac{1}{2}\left|\begin{array}{ll}
x_{1}-x_{3} & y_{1}-y_{3} \\
x_{2}-x_{4} & y_{2}-y_{4}
\end{array}\right|\)

Centres Of A Triangle:
Median: In a triangle, the line segment joining a vertex and the mid point of its opposite side is called a median of the triangle. The medians of a triangle are concurrent.
The point of concurrence of the medians of a triangle is called the centroid (or) centre of gravity of the triangle. It is denoted by G.

In Centre Of A Triangle:
Internal bisector : The line which bisects the internal angle of a triangle is called an internal angle bisector of the triangle.
The point of concurrence of internal bisectors of the angles of a triangle is called the incentre of the triangle, it is denoted by I.
I = \(\left(\frac{a x_{1}+b x_{2}+c x_{3}}{a+b+c}, \frac{a y_{1}+b y_{2}+c y_{3}}{a+b+c}\right)\)

Ex-centres Of A Triangle:
The point of concurrence of internal bisector of angle A and external bisectors of angles B, C of ABC is called the ex-centre opposite to vertex A. It is denoted by I₁. The excentres of ABC opposite to the vertices B, C are respectively denoted by I₂, I₃.

• I₁ = Excentre opposite to A = \(\left(\frac{-a x_{1}+b x_{2}+c x_{3}}{-a+b+c}, \frac{-a y_{1}+b y_{2}+c y_{3}}{-a+b+c}\right)\)
• I₂ = Excentre oppposite to B = \(\left(\frac{a x_{1}-b x_{2}+c x_{3}}{a-b+c}, \frac{a y_{1}-b y_{2}+c y_{3}}{a-b+c}\right)\)
• I₃ = Excentre opposite to C = \(\left(\frac{a x_{1}+b x_{2}-c x_{3}}{a+b-c}, \frac{a y_{1}+b y_{2}-c y_{3}}{a+b-c}\right)\)

Ortho Centre Of A Triangle:
Altitude: The line passing through vertex and perpendicular to opposite side of a triangle is called an altitude of the triangle. Altitudes of a triangle are concurrent. The point of concurrence is called the ortho centre of the triangle. It is denoted by “O” or H’.

Circum centre of a Triangle:
Perpendicular bisector: The line passing through mid point of a side and perpendicular to the side is called the perpendicular bisector of the side.
The perpendicular bisectors of the sides of a triangle are concurrent. The point of concurrence is called the circurn centre or the triangle. It is denoted by S.

→ We have mentioned that the Coordinate Geometry unifies the ideas of Algebra and Geometry. Now, in this chapter, we study a set of points, which satisfies certain geometric conditions that can also be represented in the form of algebraic equation.

Definition of Locus :
Let us call a set of geometric conditions ‘consistent’ if there is atleast one point satisfying that set of conditions. For example when A = (1, 0) and B = (3,0), the condition ‘the sum of distances of a point P from A and B is equal to 2’ is consistent, where as the condition ‘the sum of distances of a point Q from A and B is equal to 1’ is not consistent, because there is no point Q such that QA + QB = 1 (since AB = 2)
By the locus of a point we mean the set of all positions that it can take when it is subjected to certain consistent geometric conditions.
Or
Locus:

• The set of all points (and only those points) which satisfy the given geometrical condition(s) (or properties) is called a locus.
  Eg. The set of points in a plane which are at a constant distance r from a given point C is a locus. Here the locus a circle.
• The set of points in a plane which are equidistant from two given points A and B is a locus. Here the locus is a straight line and it is the perpendicular bisector of the line segment joining A and B.

Equation of Locus :
It is clear that, every point on the locus satisfies the given conditions and every point which satisfies the given conditions lies on the locus.
By the equation of a locus we mean an algebraic description of the locus. It is obtained by translating the geometric conditions satisfied by the points on the locus, into equivalent algebraic conditions.

Algebraic descriptions give rise to algebraic equations which sometimes contain more than what is required by the geometric conditions. Thus locus may be a part of the curve represented by the algebraic equation. Usually we call this algebraic equation as the equation of locus. However, to get the full description of the locus, the exact part of the curve, points of which satisfy the given geometric description, must be specified.
or
Equation of a Locus:
An equation f(x, y) = O is said to be the equation of a locus S if every point of S satisfies f(x, y) = O and every point that satisfies f(x, y) = O belongs to S.

An equation of a locus is an algebraic description of the locus. This can be obtained in the following way

• Consider a point P(x, y) on the locus
• Write the geometric condition(s) to bc satisfied by P in terms of an equation or in equation in symbols.
• Apply the proper formula of coordinate geometry and translate the geometric condition(s) into an algebraic equation.
• Simplify the equation so that it is free from radicals. The equation thus obtained is the required equation of locus.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(d)

I.

Question 1.
If y = \(\frac{2x+3}{4x+5}\) then find y”
Solution:
y = \(\frac{2x+3}{4x+5}\)
Differentiating w.r.to x

Question 2.
y = ae^nx + be^-nx nx then prove that y” = n²y
Solution:
y = ae^nx + be^-nx
y₁ = na e^nx – nb e^-nx
y_{2 = n² . ae^nx + n² be^-nx
y”= n² (ae^nx + b.e^-nx)
= n²y}

II.

Question 1.
Find the second order derivatives of the following functions f(x)
i) cos³ x
Solution:
y = cos³ x = \(\frac{1}{4}\) [cos 3x + 3 cos x]
y’ = \(\frac{1}{4}\) [- 3 sin 3x – 3 sin x]
y” = \(\frac{1}{4}\) (- 9 cos 3x – 3 cos x)
= – \(\frac{1}{4}\) (3 cos x + 9 cos 3x)
= – \(\frac{3}{4}\) (cos x + 3 cos 3x)

ii) y = sin⁴ x
Solution:
y = sin⁴ x = (sin²x)² = (\(\frac{(1-\cos 2 x)^{2}}{2}\))
= \(\frac{1}{4}\) [1 – 2 cos 2x + cos² 2x]
= \(\frac{1}{4}\) [1 – 2cos 2x + \(\frac{1+\cos 4 x}{2}\)]
= \(\frac{1}{8}\) [2 – 4 cos 2x + 1 + cos 4x]
= \(\frac{1}{8}\)(3 – 4 cos 2x + cos 4x)
y’ = \(\frac{1}{8}\) (8 sin 2x – 4 sin 4x)
y” = \(\frac{1}{8}\) (16 cos 2x-16 cos 4x)
= 2 (cos 2x – cos 4x)

iii) log (4x² – 9)
Solution:
y = log (4x² – 9)
= log (2x – 3) (2x + 3)
= log (2x – 3) + log (2x + 3)

iv) y = e^-2x sin³ x
Solution:
y = e^-2x. sin³ x
y’ = e^-2x (3 sin² x. cos x) + sin3 x (e^-2x) (-2)
= e^-2x [3 sin² x. cos x – 2 sin³ x)
\(\frac{d^{2} y}{d x^{2}}\) = e^-2x [3 sin² x (- sin x) + 3 cos x (2 sin x) cos x – 6 sin² x cos x) – 2. e^-2x
[3 sin² x. cos x – 2 sin³ x]
= e^-2x [6 sin x. cos² x – 6 sin² x. cos x – 3 sin³ x. – 6 sin² x. cos x + 4 sin³ x)
= e^-2x [sin³ x – 12 sin² x. cos x + 6 sin x. cos² x)

v) e^x sin x cos 2x
Solution:
y = e^x. sin x. cos 2x = \(\frac{e^{x}}{2}\) (2 cos 2x. sin x)
= \(\frac{e^{x}}{2}\) (sin 3x – sin x)
y’ = \(\frac{1}{2}\) [e^x(3 cos 3x – cos x) + e^x (sin 3x – sin x)
y”= \(\frac{1}{2}\) [ex (- 9 sin 3x + sin x) + e^x (3 cos 3x – cos x) + e^x (3 cos 3x – cos x) + e^x (sin 3x – sin x)]
= \(\frac{e^{x}}{2}\) [- 9 sin 3x + sin x + 3 cos 3x – cos x + 3 cos 3x cos x + sin 3x – sin x]
= \(\frac{e^{x}}{2}\) [6 cos 3x – 8 sin 3x – 2 cos x]
= e^x [3 cos 3x – 4 sin 3x – cos x]

vi) Tan^-1\(\frac{1+x}{1-x}\)
Solution:
y = tan^-1\(\frac{1+x}{1-x}\)
Put x = tan θ

∴ f(x) = \(\frac{\pi}{4}\) + tan^-1 (x)
Diff. w.r.to x
f'(x) = 0 + \(\frac{1}{1+x^{2}}\)
f”(x) = (-1) (1 + x²)^-2 (2x)
f”(x) = \(\frac{-2 x}{\left(1+x^{2}\right)^{2}}\)

vii) tan^-1\(\frac{3x-x^{3}}{1-3x^{2}}\)
Solution:
f(x) = tan^-1\(\frac{3x-x^{3}}{1-3x^{2}}\) ; Put x = tan θ
f(x) = tan^-1\(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\)
= tan^-1(tan 3θ) = 3θ
∴ f(x) = tan^-1 (x)
f'(x) = 3\(\frac{1}{1+x^{2}}\) = \(\frac{3}{1+x^{2}}\)
Again Diff. w.r.to x
f”(x) = (3) (-1) (1 + x²)^-2 (2x)
⇒ f”(x) = \(\frac{-6 x}{\left(1+x^{2}\right)^{2}}\)

II. Prove the following.
If y = ax^{n + 1} + bx^-n
then x²y” = n(n + 1) y.
Solution:
y = ax^{n + 1} + bx^-n
y_{1 = (n + 1). axⁿ – n bx^-n-1
y2 = n(n + 1). ax^n-1 + n(n + 1) bx^-n-2
∴ x²y2 = n(n + 1) axⁿ⁺¹ + n(n + 1) bx^-n
= n(n + 1) (axn+1+bx_n) = n(n + 1) y
∴ x²y” = n(n + 1) y}

ii) If y = a cos x + (b + 2x) sin x, then y” + y = 4 cos x
Solution:
\(\frac{dy}{dx}\) = y’ = a(-sin x) + (b + 2x) \(\frac{d}{dx}\) (sin x) + sin x \(\frac{d}{dx}\) (b + 2x)
= – a sin x + (b + 2x) cos x + sin x.2
\(\frac{d^{2} y}{d x^{2}}\) = y” = – a cos x + (b + 2x) (- sin x) + cos x (2) + 2 cos x
L.H.S. = y” + y = – a cos x + (b + 2x) (- sin x) + 2 cos x + 2 cos x + a cos x+ (b + 2x) sinx = 4 cosx

iii) If y = 6 (x + 1) + (a + bx) e^3x then y” – 6y’ + 9y = 54 x + 18
Solution:
y’ = 6 \(\frac{d}{dx}\) (x + 1) + (a + bx) \(\frac{d}{dx}\) (e^3x) + e^3x \(\frac{d}{dx}\) (a + bx)
= 6(1) + (a + bx) 3e^3x + e^3x. b.
y” = 0 + 3 (a + bx) \(\frac{d}{dx}\) e^3x + 3e^3x \(\frac{d}{dx}\) (a + bx) + b \(\frac{d}{dx}\) (e^3x)
= 3(a + bx) 3e^3x + 3e^3x(b) + b. 3e^3x
= 9(a + bx) e^3x + 6b e^3x
Now L.H.S. = y” – 6y’ + 9y = 9(a + bx) e^3x + 6be^3x – 6[6 + 3(a + bx)e^3x + be^3x] + 9 [6(x + 1) + (a + bx)e^3x]
= 9(a + bx) e^3x + 6b e^3x – 36 – 18(a + bx)e^3x – 6be^3x + 54x + 54 + 9(a + bx) e^3x = 54x + 18

iv) If ay⁴ = (x + b)⁵ then 5y y” = (y’)²
Solution:
ay⁴ = (x + b)⁵ ; y⁴ = \(\frac{\left(x+b\right)^{2}}{a}\)

v) If y = a cos (sin x) + b sin (sin x) then y” + (tan x) y’ + y cos² x = 0
Solution:
y = a cos (sin x) + b sin (sin x) …………. (1)
Differentiating w.r.to x
y₁ = – a sin (sin x) cos x + b cos (sin x). cos x = [- a sin (sin x) + b cos (sin x)j cos x ………. (2)
Differentiating again w.r.to x.
y₂ = – sin x [-a sin (sin x) + b cos (sin x)] + cos x [- a cos (sin x) cos x – b sin (sin x) cos x]
= – sin x. \(\frac{y_{1}}{\cos x}\) = -cos² x.y
From (1) and (2),
⇒ y₂ + (tan x) y₁ + y cos² x = 0

III.

i) If y = 128 sin³ x cos⁴ x, then find y”.
Solution:
f(x) = 128 sin³ x. cos⁴ x
D.w.r. to x
f'(x)= 128 [sin³ x {4cos³ x (-sinx)} + cos⁴ x {3sin² x. cos x}]
= 128 [3sin² x cos⁵ x – 4sin⁴ x cos³ x]
Again D.w.r to x.
f”(x)= 128 {3 [sin² x 5cos⁴ x . (-sinx) + cos⁵ x. 2sinx cosx] – 4 [sin⁴ x. 3. cos2x (-sinx) + cos³ x. 4 sin³ x. cos x]}
= 128 [-15sin³ x . cos⁴ x + 6sin x cos⁶ x + 12 sin⁵ x cos² x- 16sin³ x cos⁴ x]
f”(x)= 128 [6sinx cos6x + 12sin⁵ x. cos² x – 31sin³ x. cos⁴ x]

ii) If y = sin 2x sin 3x sin 4x, then find y”.
Solution:
f(x) = sin 2x sin 3x sin 4x
= \(\frac{1}{2}\)sin 2x [2sin 4x. sin 3x]
= \(\frac{1}{2}\)sin 2x [cos x – cos 7x]
= \(\frac{1}{2}\) [sin 2x . cos x – cos 7x. sin 2x]
= \(\frac{1}{2}\)×\(\frac{1}{2}\) [2 sin2x. cosx – 2 cos7x. sin2x]
= \(\frac{1}{4}\) [(sin3x + sinx) – (sin9x – sin5x)]
= \(\frac{1}{4}\) [-sin9x + sin5x + sin3x + sinx]
D.w.r. to x
f'(x) = \(\frac{1}{4}\) [-9 cos 9x + 5 cos 5x + 3 cos 3x + cos x]
D.w.r. to x
f”(x) = \(\frac{1}{4}\) [81 sin 9x – 25sin 5x – 9sin 3x – sin x]

iii) If ax² + 2hxy + by² = 1 then prove that
\(\frac{d^{2} y}{d x^{2}}=\frac{h^{2}-a b}{(h x+b y)^{3}}\)
Solution:
Given ax² + 2hxy + by² = 1
Differentiating w.r. to x
a.2x + 2h(x. \(\frac{dy}{dx}\) + y) + b . 2y\(\frac{dy}{dx}\) = 0
2ax + 2hx. \(\frac{dy}{dx}\) + 2hy + 2by. \(\frac{dy}{dx}\) = 0
2(hx + by).\(\frac{dy}{dx}\) = -2(ax + hy)
\(\frac{dy}{dx}\) = \(\frac{-2(ax +hy)}{2(hx+by)}\) = \(\frac{(ax+hy)}{(hx+by)}\) ……… (1)
Differentiating again w.r. to x, \(\frac{d^{2} y}{d x^{2}}\)

iv) If y = ae^-bx cos(cx + d) then prove that y” + 2by’ + (b² + c²) y = 0.
Solution:
Given y = ae^-bx cos(cx + d) ……….. (1)
y₁ = a[e^-bx {- sin (cx + d)}. c. + cos (cx + d) e^-bx (-b)}
= – a. e^-bx [c sin (cx + d) + b cos (cx + d)]
= – ac.e^-bx sin (cx + d) – by
y₁ + by = – ac. e^-bx sin (cx + d) ………. (2)
Differentiating once w.r.to x
y₂ + by₁ = – ac(- b) e^-bx sin (cx + d) – ac e^-bx cos (cx + d) (+ c)
= abce^-bx sin (cx + d) -ac² e^-bx cos (cx + d)
= – b (y₁ + by) c²y [From (1) and (2)]
⇒ y₂ + by₁ + by₁ + b²y + c²y = 0.
⇒ y₂ + 2by₁ + (b² + c²) y = 0 (or)
y” + 2 by’ + (b² + c²) y = 0

v) If y = \(e^{\frac{-k}{2} x}\) (a cos nx + b sin nx) prove that then y” + ky’+ (n² + \(\frac{k^{2}}{4}\))y = 0
Solution:
Given y = \(e^{\frac{-k}{2} x}\) (a cos nx + b sin nx) ………… (1)
∴ y₁ = \(e^{\frac{-k}{2} x}\) (-n. a sin nx + n. b cos nx) + (a cos nx + b sin nx).\(e^{\frac{-k}{2} x}\) (-\(\frac{k}{2}\))
= –\(\frac{k}{2}\) . y – n.e^-kx/2 (a sin nx + b cos nx)
∴ y₁ + \(\frac{k}{2}\) y = – n.e^-kx/2 (a sin nx + b cos nx) …………. (2)
Differentiating w.r. to x k
y₂ + \(\frac{k}{2}\) y₁ = -n[{e^-kx/2 (- na cos nx – nb sin nx)}] + {(a sin nx +b cos nx).e^-kx/2 \(\frac{k}{2}\)}
= – n² e^-kx/2(a cos nx + b sin nx) – \(\frac{k}{2}\){-n.e^-kx/2 (a sin nx + b cos nx)}

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(a)

I. Compute the following limits.

Question 1.
Find the derivatives of the following functions f(x). 7286883416
i) \(\sqrt{x}+2 x^{\frac{3}{4}}+3 x^{\frac{5}{6}}\) (x > 0)
Solution:
y = \(\sqrt{x}+2 x^{\frac{3}{4}}+3 x^{\frac{5}{6}}\) (x>0)
\(\frac{dy}{dx}\) = \(\frac{1}{2}\).x^-1/2 + 2.\(\frac{3}{4}\).x^-1/4 + 3.\(\frac{5}{6}\).^x-1/6 dx
= \(\frac{1}{2}\)[x^-1/2 + 3.x^-1/4 + 5.x^-1/6]

ii) \(\sqrt{2 x-3}+\sqrt{7-3 x}\).
Solution:

iii) (x² – 3) (4x³ + 1)
Solution:
y = (x² – 3) (4x³ + 1)
\(\frac{dy}{dx}\) = (x² – 3) \(\frac{d}{dx}\) (4x³ + 1) + (4x³ + 1) \(\frac{d}{dx}\)(x² – 3)
= (x² – 3) (12x²) + (4x³ + 1) (2x)
= 12x⁴ – 36x² + 8x⁴ + 2x
= 20x⁴ – 36x² + 2x

iv) (√x – 3x) (x + \(\frac{1}{x}\))
Solution:
y = (√x – 3x) (x + \(\frac{1}{x}\))

v) (√x + 1) (x² – 4x + 2) (x > 0)
Solution:
y = (√x + 1) (x² – 4x + 2) (x > 0)
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (√x + 1) \(\frac{d}{dx}\)(x² – 4x + 2) + (x² – 4x + 2) \(\frac{d}{dx}\)(√x +1)
= (√x + 1) (2x – 4) + \(\frac{x^{2}-4 x+2}{2 \sqrt{x}}\)

vi) (ax + b)ⁿ. (cx + d)^m.
Solution:
y = (ax + b)ⁿ. (cx + d)^m
\(\frac{dy}{dx}\) = (ax + b)ⁿ \(\frac{d}{dx}\)(cx +d)^m + (cx + d)^m \(\frac{d}{dx}\)(ax + b)ⁿ
= (ax + b)ⁿ [m(cx + d)^m-1. c] + (cx + d)^m [n(ax + b)^n-1. a]
= (ax + b)^n-1 (cx + d)^m-1 [cm (ax + b) + an (cx + d)]
= (ax + b)ⁿ (cx + d)^m [\(\frac{an}{ax+b} + \frac{cm}{cx+d}\) ]

vii) 5 sin x + ex log x
Solution:
y = 5 sin x + e^x. log x
\(\frac{dy}{dx}\) = 5 cos x + e^x. \(\frac{d}{dx}\) (log x) + log x \(\frac{d}{dx}\)(e^x)
= 5 cos x + e^x. \(\frac{1}{x}\) + (log x) (e^x)

viii) 5^x + log x + x³ e^x
Solution:
y = 5^x + log x + x³ e^x
\(\frac{dy}{dx}\) = 5^x . log 5 + \(\frac{1}{x}\) + x³.e^x + e^x.3x²
= 5^x. log 5 + – + x³ e^x + 3x² e^x

ix) e^x + sin x cos x
Solution:
y = e^x + sin x . cos x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (e^x) + \(\frac{d}{dx}\) (sin x . cos x)
= e^x + sin x \(\frac{d}{dx}\) (cos x) + cos x \(\frac{d}{dx}\) (sin x)
= e^x – sin² x + cos² x
= e^x + cos 2x

x) \(\frac{p x^{2}+e x+r}{a x+b}\)(|a| + |b| ≠ 0)
Solution:

xi) log₇ (log x) (x > 0)
Solution:
y = log₇ (log x) (x > 0)

xii) \(\frac{1}{a x^{2}+b x+c}\) (|a| + |b| + |c| ≠ 0)
Solution:
\(\frac{1}{a x^{2}+b x+c}\) (|a| + |b| + |c| ≠ 0)

xiii) e^2x log (3x + 4) (x > –\(\frac{4}{3}\))
Solution:
y = e^2x. log (3x + 4) (x > –\(\frac{4}{3}\))
Differentiating w.r.to x
\(\frac{dy}{dx}\) = e^2x \(\frac{d}{dx}\)[log (3x + 4) + log (3x + 4) \(\frac{d}{dx}\) (e^2x)]
= e^2x.\(\frac{1}{3x+4}\) 3 + log (3x + 4). e^2x . 2
= e^2x (\(\frac{3}{3x+4}\) + 2 log (3x + 4))

xiv) (4 + x²) e²xy
Solution:
y = (4 + x²). e^2x
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (4 + x²) \(\frac{d}{dx}\) (e^2x) + e^2x \(\frac{d}{dx}\)(4 + x²)
= (4 + x²). 2e^2x + e^2x (0 + 2x)
= 2e^2x [4 + x² + x]
= 2e^2x (x² + x + 4)

xv) \(\frac{ax+b}{cx+d}\) [|c| + |d|≠0]
Solution:
y = \(\frac{ax+b}{cx+d}\) [|c| + |d|≠0]
Differentiating w.r.to x

xvi) a^x. e^x²
Solution:
y = a^x. e^x²
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (a^x) \(\frac{d}{dx}\)(e^x²) + (e^x²)\(\frac{d}{dx}\)(a^x)
= a^x. e^x². 2x + e^x². a^x. log a
= ax. ^x² (2x + log a)
= y(2x + log a)

Question 2.
If f(x) = 1 + x + x² + + x¹⁰⁰, then find f’ (1).
Solution:
f'(x) = 1 + 2x + 3x² + 100 x⁹⁹
f'(1) = 1+2 + 3 ….+ 100
= \(\frac{100 \times 101}{2}=5050\left(\Sigma x=\frac{x(x+1)}{2}\right)\)

Question 3.
If f (x) = 2x² + 3x – 5, then prove that f(0) + 3f (-1) = 0.
Solution:
f'(x) = 4x + 3
f'(0) = 0 + 3 = 3
f'(-1) = – 4 + 3 = -1
f'(0) + 3f'(-1) = 3 + 3(-1) = 3 – 3 = 0 n.

II.

Question 1.
Find the derivatives of the following functions from the first principles.
i) x³
Solution:


= 3x² + 0 + 0 = 3x²

ii) x⁴ + 4
Solution:
f(x + h) – f(x) = ((x + h)⁴ + 4) – (x⁴ + 4)
= (x + h)4 + 4 – x⁴ – 4 .
= x⁴ + 4x³h + 6x²h² + 4xh³ + h⁴ – x⁴

= 4x³ + 0 + 0 + 0 = 4x³

iii) ax² + bx + c
Solution:
f(x + h) = a(x + h)² + b(x + h) + c
= a(x² + 2hx + h²) + b(x + h) + c
= ax² + 2ahx + ah² + bx + bh +c

f(x + h) – f(x) = ax² + 2ahx + ah² + bx + bh + c – ax² – bx – c
= h [2ax + ah + b]

= 2ax + 0 + b = 2ax + b

iv) \(\sqrt{x+1}\)
Solution:

v) sin 2x
Solution:
f(x + h) – f(x) = sin 2(x + h) – sin 2x

vi) cos ax
Solution:
f(x + h) – f(x) = cos a (x + h) – cos ax

= – 2 sin ax. \(\frac{a}{2}\)
=-a. sin ax

vii) tan 2x
Solution:
f(x + h) – f(x) = tan 2(x + h) – tan 2x

viii) cot x
Solution:
f(x + h) – f(x) = cot (x + h) – cot x

ix) sec 3x
Solution:
f(x + h) – f(x)= sec 3(x + h) – sec 3x

x) x sin x
Solution:
f(x + h) – f(x) = (x + h) sin (x + h) – x sin x
= x (sin (x + h) – sin x) + h. sin (x + h)

xi) cos² x
Solution:
f(x + h) – f(x) = cos² (x + h) – cos² x
= -(cos² x – cos² (x + h))
= -sin (x + h + x) sin (x + h – x)

= -sin 2x. 1 = -sin 2x

Question 2.
Find the derivatives of the following function.
i) \(\frac{1-x \sqrt{x}}{1+x \sqrt{x}}\) (x > 0)
Solution:

ii) xⁿ n^x log (nx) (x > 0, n ∈ N)
Solution:
y = xⁿ. n^x. log nx
\(\frac{dy}{dx}\) = xⁿ. n^x (log nx) + nⁿ. log xn (xⁿ) + xⁿ. log nx (n^x)
= xⁿ. n^x \(\frac{n}{log nx}\) + n^x. log xⁿ (nx^n-1) + xⁿ . log nx. (n^x . log nx)
= x^n-1. n^x[\(\frac{nx}{log nx}\) + log nx. (nⁿ. log nx)]

iii) ax²ⁿ. log x + bxⁿ e^-x
Solution:
y = ax²ⁿ. log x + bxⁿ e^-x
\(\frac{dy}{dx}\) = a (x²ⁿ.\(\frac{1}{x}\) + log x (2nx^2n-1)) + b n (-e^-x) + e^-x. nx^n-1)
= a. x^2n-1 + 2an. x^2n-1. log x – bxⁿ e^-x + bn. x^n-1 . e^-x

iv) (\(\frac{1}{x}\) – x)³ e^x
Solution:
y = (\(\frac{1}{x}\) – x)³ . e^x
\(\frac{dy}{dx}\) = (\(\frac{1}{x}\) – x)³ \(\frac{d}{dx}\)(e^x) + e^x \(\frac{d}{dx}\){(\(\frac{1}{x}\) – x)³}

Question 3.
Show that the function f(x) = |x| + |x – 1|, x ∈ R is differentiable for all real numbers except for 0 and 1.
Solution:
f(x) = |x| + |x – 1| ∀ x ∈ R
f(x) = x + x – 1 = 2x – 1, x ≥ 1
= x – (x – 1) = x – x + 1, = 1, 0 < x < 1
= -x – (x – 1) =-x – x + 1 = 1 – 2x, x < 0 ∴ f(x) = 2x – 1, x > 1
= 1, 0 < x < 1 = 1 – 2x, x ≤ 0 If x > 1, then f(x) = 2x – 1 = polynomial in x f(x) is differentiable for all x > 1
If 0 < x < 1, then f(x) = 1 – constant
∴ f(x) is differentiable if 0 < x < 1.
If x < 1, then f(x) = 1 – 2x = polynomial in x.
∴ f(x) is differentiable for all x < 1

Case (i) : x = 0

R f'(0) ≠ Lf'(0)
∴ f'(0) does not exist.
f(x) is not differentiable at x = 0.

Case (ii): x = 1

R f'(1) ≠ L f'(1)
f(1) does not exist.
f(x) is not differentiable at x = 1
∴ f(x) is differentiable for all real x except zero and one.

Question 4.
Verify whether the following function is differentiable at 1 and 3.

Solution:
Case (i): x = 1

R f'(1) ≠ L f'(1)
f(x) is not differentiable at x = 1

Case (ii) : x = 3

f(3⁺) ≠ f'(3^–)
f(x) is not differentiable at x = 3.

Question 5.
Is the following function f derivable at 2?

Solution:

f'(2^–) ≠ f(2⁺); f(x) is not derivable at x = 2.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(e) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(e)

I.

Question 1.
Is the function f, defined by \(f(x)=\left\{\begin{array}{l}
x^{2} \text { if } x \leq 1 \\
x \text { if } x>1
\end{array}\right.\) continuous on R?
Solution:

f is continuous at x = 1
f is continuous on R.

Question 2.
Is f defined by f(x) = \(=\left\{\begin{array}{cc}
\frac{\sin 2 x}{x}, & \text { if } x \neq 0 \\
1 & \text { if } x=0
\end{array}\right.\) continuous at 0?
Solution:

f is not continuous at 0

Question 3.
Show that the function f(x) = [cos (x¹⁰ + 1)]^1/3, x ∈ R is a continuous function.
Solution:
We know that cos x is continuous for every x ∈ R
∴ The given function f(x) is continuous for every x ∈ R.

II.

Question 1.
Check the continuity of the following function at 2.

Solution:

f(x) is not continuous at 2.

Question 2.
Check the continuity of f given by f(x) = \(\begin{cases}\frac{\left[x^{2}-9\right]}{\left[x^{2}-2 x-3\right]} & \text { if } 0<x<5 \text { and } x \neq 3 \\ 1.5 & \text { if } x=3\end{cases}\) at the point 3.
Solution:

f(x) is continuous at x = 3.

Question 3.
Show that f, given by f(x) = \(\frac{x-|x|}{x}\) (x ≠ 0) is continuous on R – {0}.
Solution:
Case (i) : a > 0 ⇒ |a| = a

If x = 0, f(a) is not defined
f(x) is not continuous at ’0′
∴ f(x) is continuous on R – {0}

Question 4.
If f is a function defined by

then discuss the continuity of f.
Solution:
Case (i) : x = 1

f(x) is not continuous at x > 1

Case (ii) : x = -2

f(x) is not continuous at x = -2.

Question 5.
If f is given by f(x) = \(=\left\{\begin{array}{cl}
k^{2} x-k & \text { if } x \geq 1 \\
2 & \text { if } x<1
\end{array}\right.\) is a continuous function on R, then find the values of k.
Solution:

2 = k² – k
k² – k – 2 = 0
(k – 2) (k + 1) = 0
k = 2 or – 1

Question 6.
Prove that the functions ‘sin x’ and ‘cos x’ are continuous on R.
Solution:
i) Let a ∈ R

∴ f is continuous at a.

ii) Let a ∈ R

∴ f is continuous at a.

III.

Question 1.
Check the continuity of ‘f given by

at the points 0, 1 and 2.
Solution:
i)
∴ f(x) is continuous at x = 0

ii)
∴ f(x) is continuous at x = 1

iii)
∴ f(x) is continuous at x = 2

Question 2.
Find real constant a, b so that the function f given by

is continuous on R.
Solution:

Since f(x) is continuous on R
LHS = RHS ⇒ a = 0

Since f(x) is continuous on R.
LHS = RHS
3b + 3 = -3
3b = – 6 ⇒ b = -2

Question 3.
Show that

where a and b are real constants, is continuous at 0.
Solution:

∴ f(x) is continuous at x = 0

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(d)

I. Compute the following limits.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

II.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

III.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution: