Mahesh

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(c)

I. Computer the following limits.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:
As x → 0
⇒ 7x → 0

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

II.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:
By L. Hospital rule

III.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(b)

Find the right and left-hand limits of the functions in 1,2,3 of I and 1,2, of II at the point mentioned against them. Hence, check whether the functions have limits at those a’s.

I.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

II.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:
x → 2 – ⇒ x < 2
x – 2 < 0
|x – 2| = – (x – 2)

Question 4.

Solution:
x → 0 + ⇒ x > 0
|x| = x

Question 5.

Solution:

Question 6.

Solution:

III.

Question 1.

Solution:

∴ LHL ≠ RHL
Limit does not exists.

Question 2.

Solution:

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(a)

I. Compute the following limits.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Note : Text Book answer will come, when the problem changes like.
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Plane Solutions Exercise 7(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B The Plane Solutions Exercise 7(a)

I.

Question 1.
Find the equation of the plane if the foot of the perpendicular from origin to the plane is (1, 3, -5).
Solution:
OP is the normal to the plane D. Rs of op are 1, 3, -5
The plane passes through P( 1, 3, -5) equation of the plane is
1(x – 1) + 3(y – 3) – 5(z + 5) = 0
x – 1 + 3y – 9 – 5z – 25 = 0
x + 3y – 5z – 35 = 0

Question 2.
Reduce the equation x + 2y – 3z – 6 = 0 of the plane to the normal form.
Solution:
Equation of the plane is x + 2y – 3z – 6 = 0
i.e., x + 2y – 3z = 6
Dividing in the
\(\sqrt{1^{2}+2^{2}+(-3)^{2}}=\sqrt{1+4+9}=\sqrt{14}\)
The equation of the plane in the normal form is

Question 3.
Find the equation of the plane. Whose intercepts on X, Y, Z – axis are 1, 2, 4 respectively.
Solution:
Equation of the plane in the intercept form is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Given a = 1, b = 2, c = 4.
Equation of the required plane in the intercept form is
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{4}\) = 1
Multiplying with 4, we get
4x + 2y + z = 4

Question 4.
Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the co-ordinate axes.
Solution:
Equation of the plane is 4x + 3y – 2z + 2 = 0
– 4x – 3y + 2z = 2

x – intercept = -1/2, y – intercept = -2/3, z intercept =1.

Question 5.
Find the d.c.’s of the normal to the plane x + 2y + 2z – 4 = 0.
Solution:
Equation of the plane is x + 2y + z- 4 = 0
d.r.’s of the normal are (1, 2, 2)
Dividing with \(\sqrt{1+4+4}\) = 3,
d.c.’s of the normal to the plane are (\(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\))

Question 6.
Find the equation of the plane passing through the point (-2, 1, 3) and having (3, -5, 4) as d.r.’s of its normal.
Solution:
d.r.’s of the normal are (3, -5, 4) and the plane passes through (-2, 1, 3).
Equation of the plane is 3(x + 2) – 5(y – 1) + 4(z – 3) = 0
3x + 6 – 5y + 5 + 4z – 12 = 0
3x -5y+ 4z – 1 = 0.

Question 7.
Write the equation of the plane 4x – 4y + 2z + 5 = 0 in the intercept form.
Solution:
Equation of the plane is
4x – 4y + 2z + 5 = 0
– 4x + 4y – 2z = 5
\(-\frac{4x}{5}, \frac{4y}{5}, \frac{2z}{5}\)
Intercept form is

x – intercept = \(\frac{5}{4}\), y – intercept = \(\frac{5}{4}\), z – intercept = –\(\frac{5}{2}\)

Question 8.
Find the angle between the planes x + 2y + 2z-5 = 0 and 3x + 3y + 2z – 8 = 0.
Solution:
Equation of the planes are
x + 2y + 2z – 5 = 0
3x + 3y + 2z – 8 = 0

II.

Question 1.
Find the equation of the plane passing through the point (1,1,1) and parallel to the plane x +.2y + 3z – 7 = 0.
Solution:
Equation of the given plane is x + 2y + 3z – 7 = 0.
Equation of the parallel plane is x + 2y + 3z = k.
This plane passes through the point P (1, 1, 1)
1 + 2 + 3 = k ⇒ k = -6
Equation of the required plane is x + 2y + 3z = 6

Question 2.
Find the equation of the plane passing through (2, 3, 4) and perpendicular to x – axis.
Solution:
The plane is perpendicular to x – axis
∴ x – axis is the normal to the plane
d.c.’s of x -axis are 1, 0, 0
Equation of the required plane is x = k
This plane passes through the point P(2, 3, 4)
∴ 2 = k
Equation of the required plane is x = 2.

Question 3.
Show that 2x + 3y + 7 = 0 represents a plane perpendicular to XY – plane.
Solution:
Equation of the given plane is 2x + 3y + 7 = 0
Equation of xy – plane is z = 0
a₁a₂ + b₁b₂ + c₁c₂ = 2.0 + 3.0 + 0.1 = 0
+0+0=0
The plane 2x + 3y + 7 = 0 is perpendicular to XY – plane.

Question 4.
Find the constant k so that the planes x – 2y + kz = 0 and 2x + 5y – z = 0 are at right angles. Find the equation of the plane through (1, -1, -1) and perpen-dicular to these planes.
Solution:
Equations of the given planes are x – 2y + kz = 0 and 2x + 5y – z = 0
These the planes are perpendicular
1.2 – 2.5 + k (-1) = 0
2 – 10 = k ⇒ k = -8
Equation of the planes
x – 2y – 8z = 0 ………. (1)
2x + 5y – z = 0 ……….. (2)
The required plane passes through (1, -1, -1)
∴ Equation of the plane can be taken as
a(x – 1) + b(y + 1) + c(z + 1) = 0 ………… (3)
This plane is perpendicular to the planes (1) and (2)
a – 2b – 8c = 0
2a + 5b – c = 0

Substituting in (3), equation of the required planes
42 (x – 1) – 15(y + 1) + 9(z + 1) = 0
42x – 42 – 15y – 15 + 9z + 9 = 0
42x – 15y + 9z – 48 = 0.

Question 5.
Find the equation of the plane through (-1, 6, 2) and perpendicular to the join of (1, 2, 3) and (-2, 3, 4).
Solution:
The plane is perpendicular to the line joining A(1, 2, 3) and B(-2, 3, 4).
d.r.’s of AB are 1 + 2, 2 – 3, 3 – 4
i.e., 3, -1, -1

AB is normal to the plane and the plane passes through the point P(-1, 6, 2)
Equation of the required plane is 3(x + 1) – 1(y – 6) -1(z – 2) = 0
3x + 3 – y + 6- z + 2 = 0
3x – y – z + 11 = 0

Question 6.
Find the equation of the plane bisecting the line segment joining (2, 0, 6) and (-6, 2, 4) and perpendicular to it.
Solution:
A (2, 0, 1), B(-6, 2, 4) are the given points ‘o’ is the mid point of AB

Co-ordinates of O are
\(\left(\frac{2-6}{2}, \frac{0+2}{2}, \frac{6+4}{2}\right)\) = (-2, 1, 5)
The plane is perpendicular to AB
d.r.’s of the normal to the plane are
2 + 6, 0 – 2, 6 – 4
8, -2, 2
Equation of the required plane is
+8 (x + 2) – 2(y – 1) + 2 (z – 5) = 0
8x + 16 – 2y + 2 + 2z – 10 = 0
8x – 2y + 2z + 8 = 0

Question 7.
Find the equation of the plane passing through (0, 0, -4) and perpendicular to the line joining the points (1, -2, 2) and (-3, 1, -2).
Solution:
A(1, -2, 2), B(-3, 1, -2) are the given points
d.r.’s of AB are 1 + 3, -2 -1, 2 + 2 i.e., 4, -3, 4
AB is normal to the plane and the plane passes through the point P(0, 0, -4).
Equation of the required plane is
4(x – 0) – 3(y – 0) + 4(z + 4) = 0
4x – 3y + 4z + 16 = 0

Question 8.
Find the equation of the plane through (4, 4, 0) and perpendicular to the planes 2x + y + 2 z + 3 = 0 and 3x + 3y + 2z – 8 = 0.
Solution:
Equation of the plane passing through P(4, 4, 0) is
a(x – 4) + b(y – 4) + c(z – 0) = 0 ………. (1)
This plane is perpendicular to
2x + y + 2z – 3 = 0
3x + 3y + 2z – 8 = 0
∴ 2a + b + 2c = 0 ………… (2)
3a + 3b + 2c = 0 ………….(3)

Substituting in (1), equation of the required plane is
-4 (x – 4) + 2(y – 4) + 3(z – 0) = 0
-4x + 16 + 2y – 8 + 3z = 0
-4x + 2y + 3z + 8 = 0

III.

Question 1.
Find the equation of the plane through the points (2, 2, -1), (3, 4, 2), (7, 0, 6).
Solution:
A(2, 2, -1), B(3, 4, 2), C(7, 0, 6) are the given points.
Equation of the plane passing through A(2, 2, -1) is
a(x – 2) + b(y – 2) + c(z + 1) = 0
This plane passes through B(3, 4, 2) and C(7, 0, 6)
a(3 – 2) + b(4 – 2) +c(2 + 1) = 0
a + 2b + 3c = 0 ……….. (2)
a(7 – 2) + b(0 – 2) + c(6 + 1) = 0
5a – 2b + 7c = 0 ……….. (3)
From (2) and (3)

Substituting in (1) equation of the required plane is
5(x- 2) + 2(y- 2) – 3(z +1) = 0
5x – 10 + 2y – 4 – 3z – 3 = 0
5x + 2y – 3z -17 = 0 or 5x + 2y- 3z = 17

Question 2.
Show that the points (0, -1, 0), (2, 1, -1), (1, 1, 1), (3, 3, 0) are coplanar.
Solution:
Equation of the plane through A(0, -1, 0) is
ax + b(y + 1) + cz = 0 …….. (1)
This plane passes through B(2, 1, -1) and C(1, 1, 1)
2a + 2b – c = 0 …………. (2)
a + 2b + c = 0 ………….. (3)
(2) – (3) gives a – 2c = 0 ⇒ a = 2c ⇒ \(\frac{a}{2}=\frac{c}{1}\)
(2) + (3) gives 3a + 4b = 0 ⇒ 3a = – 4b
⇒ \(\frac{a}{4}=\frac{b}{-3}\)
∴ \(\frac{a}{4}=\frac{b}{-3}=\frac{c}{2}\)
Substitutes in (1) equation of the plane ABC is
4x – 3(y + 1) + 2(z – 0) = 0
4x – 3y + 2z – 3 = 0
4x – 3y + 2z – 3 = 4.3 – 3.3. + 0.3
= 12 – 9 – 3 = 0
The given points A, B, C, D are coplanar.

Question 3.
Find the equation of the plane through (6, – 4, 3), (0, 4, -3) and cutting of inter-cepts whose sum is zero.
Solution:
Suppose a, b, c are the intercepts of the plane.
Equation of the plane is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Given a + b + c = 0
c = – (a + b)
The plane passes through
P(6, -4, 3), Q(0, 4, -3)

c = -a – b = -3 – b
4(-3 – b) – 3b = b(-3 – b)
-12 – 4b – 3b = – 3b – b²
b² – 4b – 12 = 0
(b – 6) (b + 2) = 0 ⇒ b = 6 – 2

Case i) b = 6
c = -3 – b = -3 – 6 = -9
Equation of the plane is
\(\frac{x}{3}+\frac{y}{6}+\frac{z}{9}\) = 1
6x + 3y – 2z = 18

Case ii) b = -2
c = -3 – b = -3 + 2 = -1
Equation of the plane is
\(\frac{x}{3}+\frac{y}{-2}+\frac{z}{-1}\) = 1

Question 4.
A plane meets the co-ordinate axes in A, B, C. If the centroid of ∆ABC is (a, b, c). Show that the equation of the plane is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Solution:
Suppose α, β, γ are the intercepts of the plane ABC.
Equation of the plane is the intercept form is
\(\frac{x}{\alpha}+\frac{y}{\beta}+\frac{z}{\gamma}=1\) ………… (1)

Co-ordinates of A are (α, 0, 0), B are (0, β, 0) and C are (0, 0, γ)
G is the centroid of ∆ABC
Co-ordinates of Gare =

α = 3a, β = 3b, γ = 3c
Substituting in (1), equation of the plane ABC is

Question 5.
Show that the plane through (1, 1, 1) , (1, -1, 1) and (-7, -3, -5) is parallel . to Y-axis.
Solution:
Equation of the plane through A (1, 1, 1) can be taken as
a(x – 1) +b(y – 1) + c(z – 1) = 0 ……….. (1)
This plane passes through B(1, -1, 1) and C(-7, -3, -5)
0 – 2b + 0 = 0 ⇒ b – 0
Equation of zy – plane is y = 0
0.x + 1.y + 0.z = 0
a.0 + 0.1 + c.0 = 0
The required plane is perpendicular to zx – plane hence it is parallel to Y – axis.

Question 6.
Show that the equations ax + by + r =0, by + cz + p = 0, cz + ax + q = 0 represent planes perpendicular to xy,yz, zx planes respectively.
Solution:
Equation of the given plane is
ax + by + c = Q
d.rs of the normal are (a, b, c)
Equation of XY – plane is z = 0
d.rs of the normal are (0, 0, 1)
a.0 + b.0 + 0.1 = 0
∴ ax + by + r = 0 is perpendicular to xy – plane.
Similarly we can show that by + cz + p = 0 is perpendicular to yz – plane and cz + ax + q – 0 is perpendicular to zx – plane.

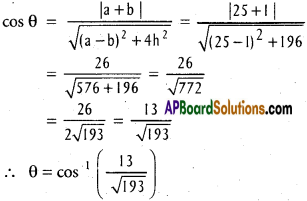
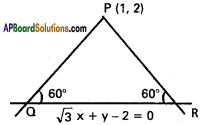
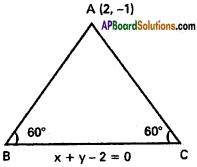
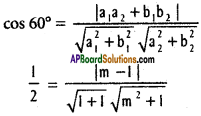
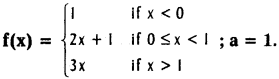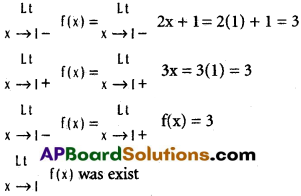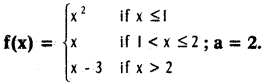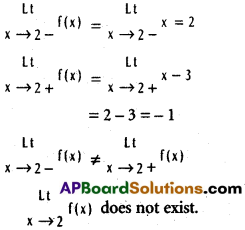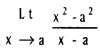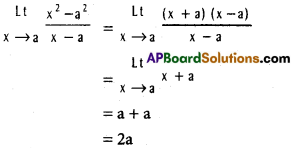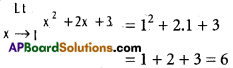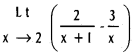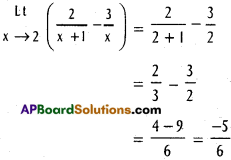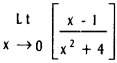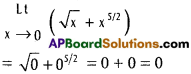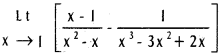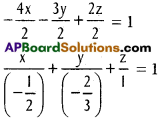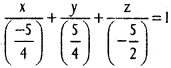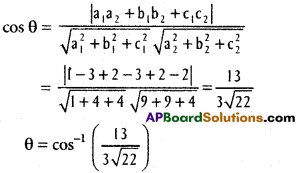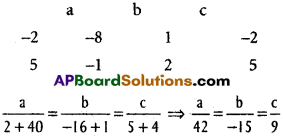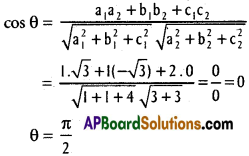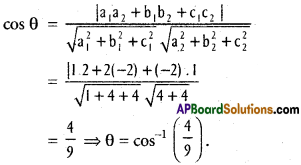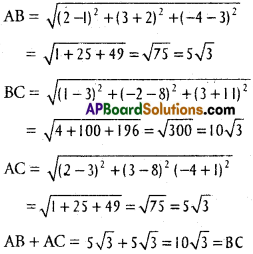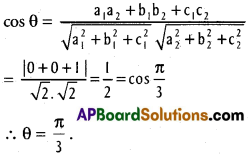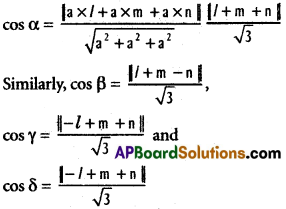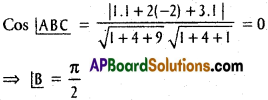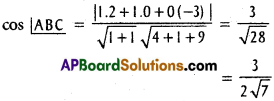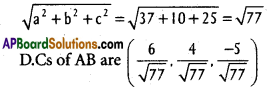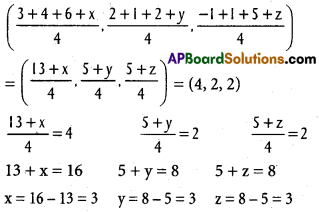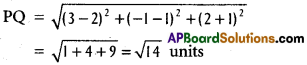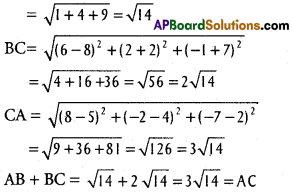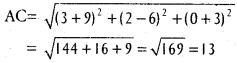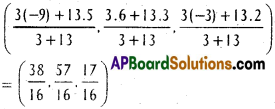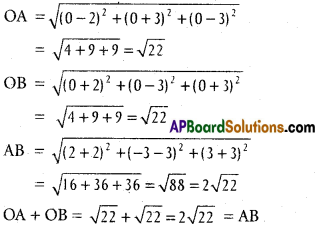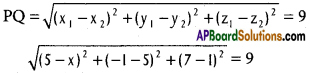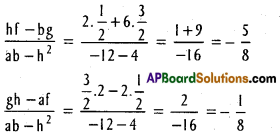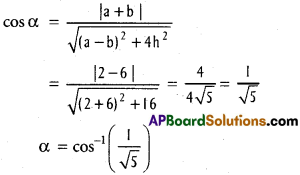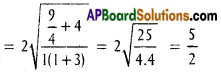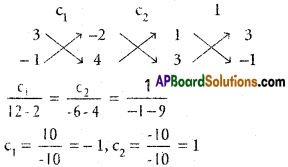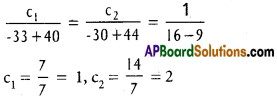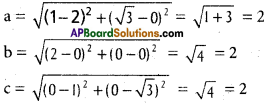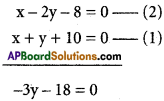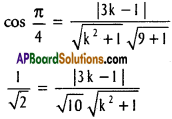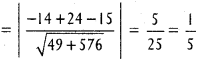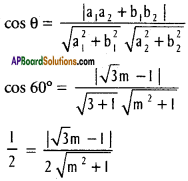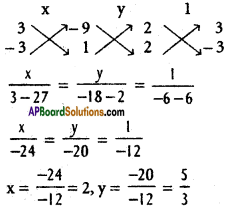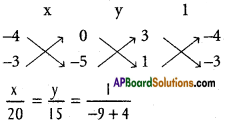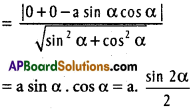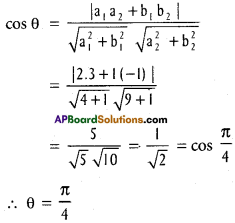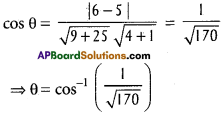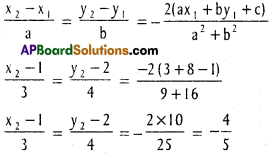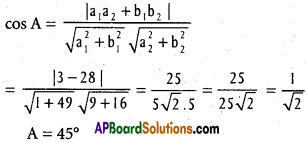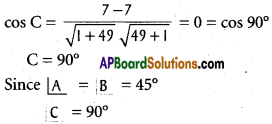Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Solutions Exercise 6(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Solutions Exercise 6(b)

I.

Question 1.
Find the direction ratios of the line joining the points (3, 4, 0) and (4, 4, 4).
Solution:
A(3, 4, 0) and B(4, 4, 4) are the given points.
d.rs of AB are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
(4-3, 4-4, 4-0) i.e.,(1, 0, 4)

Question 2.
The direction ratios of a line are (-6, 2, 3). Find its direction cosines.
Solution:
D.Rs of the line are -6, 2, 3
Dividing with \(\sqrt{36+4+9}\) = 7
Direction cosines of the line are – \(\frac{6}{7}, \frac{2}{7}, \frac{3}{7}\)

Question 3.
Find the cosine of the angle between the lines whose direction cosines are (\(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\)) and (\(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\), 0)
Solution:
cos θ = l₁ + l₂ + m₁ m₂ + n₁ n₂

Question 4.
Find the angle between the lines whose direction ratios are (1, 1, 2) (√3, -√3, 0).
Solution:

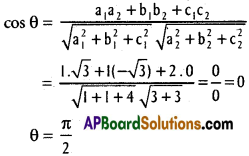
Question 5.
Show that the lines with direction cosines (\(\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13}\)) and (\(\frac{4}{13}, \frac{12}{13}, \frac{3}{13}\)) are perpendicular to each other.
Solution:
If two lines, are perpendicular, then
l₁l₂ + m₁m₂ + n₁n₂ = 0
l₁l₂ + m₁m₂ + n₁n₂
\(\frac{12}{13} \cdot \frac{4}{13}-\frac{3}{13} \cdot \frac{12}{13}-\frac{4}{13} \cdot \frac{3}{13}\)
∴ The given lines are perpendicular.

Question 6.
O is the origin, P(2, 3, 4) and Q(1, k, 1) are points such that \(\overline{\mathrm{O P}}\) ⊥ \(\overline{\mathrm{O Q}}\). Find k.
Solution:
d.rs of OP and 2, 3,4
d.rs of OQ are 1, k, 1
OP and OQ are perpendicular
⇒ a₁a₂ + b₁b₂ + c₁c₂ = 0
2 + 3k + 4 = 0
3k = -6
k = -2.

II.

Question 1.
If the direction ratios of a line are (3, 4, 0), find its direction cosines are also the angles made with the co-ordinate axes.
Solution:
Direction ratios of the line are (3, 4, 0)
Dividing with \(\sqrt{9+16+0}\) = 5
D.C’s of the line are (\(\frac{3}{5}, \frac{4}{5}\), 0)
If α_c, βc² are the angles made By the line with the co-ordinate axes, then
cos α = \(\frac{3}{5}\) cos β = \(\frac{4}{5}\) cos γ = 0
α = cos^-1\(\frac{3}{5}\), β = cos^-1\(\frac{4}{5}\), γ = \(\frac{\pi}{2}\)
Angles made with co-ordinate axes are
cos^-1\(\frac{3}{5}\), cos^-1\(\frac{4}{5}\), γ = \(\frac{\pi}{2}\)

Question 2.
Show that the line through the points (1, -1,2) (3, 4, -2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Solution:
A(1, -1 2) B(3, 4, -2) C(0,3,2) and D(3, 5,6) are the given points
d.rs of AB are 3 – 1, 4 + 1, -2 -2 i.e., 2, 5, -4
d.rs of CD are 3 – 0, 5 – 3, 6 – 2 i.e., 3, 2 4
a₁a₂ + b₁b₂ + c₁c₂ = 2.3 + 5.2 – 4.4
= 6 + 10 – 16 = 0
AB and CD are perpendicular.

Question 3.
Find the angle between \(\overline{\mathrm{D C}}\) and \(\overline{\mathrm{A B}}\) where A = (3, 4, 5), B =(4, 6, 3) C = (-1, 2, 4) are D(l, 0, 5).
Solution:
A(3, 4, 5), B(4, 6, 3), C(-1, 2, 4), D(1, 0, 5) are the given points.
d.rs of AB are 4 – 3, 6 – 4, 3 – 5 i.e., 1, 2, -2
d.rs of CD are 1 + 1, 0 – 2, 5 – 4 i.e., 2, -2, 1

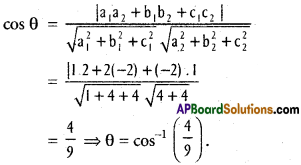
Question 4.
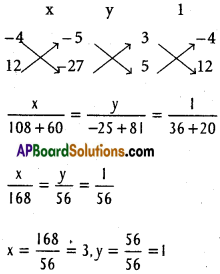
Find the direction cosines of a line which is perpendicular to the lines, whose direction ratios are (1, -1, 2) and (2, 1, -1).
Solution:
Let l, m, n be the d.cs of the required line it is perpendicular to the lines with
d.rs (1, -1, 2) and (2, 1, -1)
l – m + 2n = 0
2l + m – n = 0

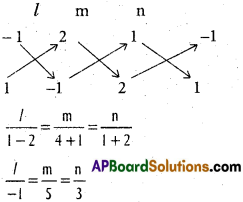
d.rs of the line are – 1, 5, 3
Dividing with \(\sqrt{1+25+9} =\sqrt{35}\)
d.cs of the required line are ’
– \(\frac{1}{\sqrt{35}}, \frac{5}{\sqrt{35}}, \frac{3}{\sqrt{35}}\)

Question 5.
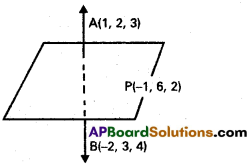
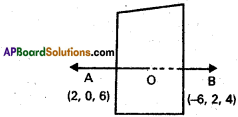
Show that the points (2, 3, -4), (1, -2, 3) and (3, 8, -11) are collinear.
Solution:
A(2, 3, -4),B( 1, -2, 3) and C(3, 8, -11) are the given points.

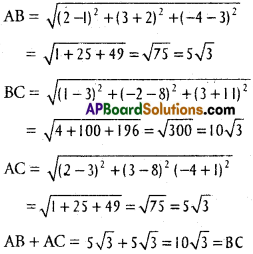
∴ A, B, C are collinear.

Question 6.
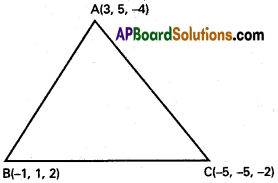
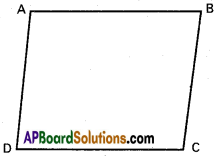
Show that the points (4, 7, 8), (2, 3, 4), (-1, -2,1), (1,2,5) are vertices of apare- llelogram.
Solution:
A(4, 7, 8), B(2, 3, 4), C(-1, -2, 1) and D (1, 2, 5) . are the given points.

∴ AB = CD and BC = DA
∴ A, B, C, D are the vertical of parallelogram.

III.

Question 1.
Show that the lines whose direction co – sines are given by l + m + n = 0, 2mn + 3nZ – 5Zm = 0 are perpendicular to each other.
Solution:
Given l + m + n = 0 ………… (1)
2mn + 3nl – 5lm = 0 …………… (2)
From (1), l = -(m + n)
Substituting in (2)
2mn – 3n(m + n) + 5m(m + n) = 0
2mn – 3mn – 3n2 + 5m2 + 5mn = 0
5m² + 4mn – 3n² = 0
\(\frac{m_{1} m_{2}}{n_{1} n_{2}}=-\frac{3}{5} \Rightarrow \frac{m_{1} m_{2}}{-3}=\frac{n_{1} n_{2}}{5}\) ………. (1)
From (1), n = -(l + m).
Substituting is (2)
-2m (l + m) – 3l(l + m) – 5lm = 0
– 2lm – 2m2 – 3l² – 3lm – 5lm = 0
3l² + 10lm + 2m² = 0
\(\frac{l_{1} l_{2}}{m_{1} m_{2}}=\frac{2}{3} \Rightarrow \frac{l_{1} l_{2}}{2}=\frac{m_{1} m_{2}}{3}\) ……… (2)
From (1) and (2) we get
\(\frac{I_{1} I_{2}}{2}=\frac{m_{1} m_{2}}{3}=\frac{n_{1} n_{2}}{-5}=1\)
l₁l₂ = 2k, m₁m₂ = 3k, n₁ n₂ = -5k
∴ l₁l₂ + m₁m₂ + n₁n₂ = 2k + 3k – 5k = 0
The two lines are perpendicular.

Question 2.
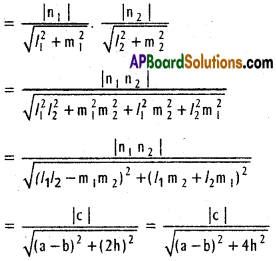
Find the angle between the lines whose direction cosines satisfy the equations l + m + n = 0, l² + m² – n² = 0.
Solution:
Given l + m + n = 0
l² + m² – n² = 0
From (1), l = – (m + n)
Substituting in (2)
(m + n)² + m² – n² = 0
m² + n² + 2mn + m² – n² = 0
2m² + 2mn = 0
2m(m + n) = 0
∴ m = 0 or m + n = 0

Case (i) : m = 0, Substituting in (1) l + n = 0
l = -n ⇒ \(\frac{l}{1}\) = \(\frac{n}{-1}\)
D.Rs of the first line l₁ are (1, 0, – 1)

Case (ii) :m + n = 0 ⇒ m = -n ⇒ \(\frac{m}{1}\) = \(\frac{n}{-1}\)
Substituting in (1) l = 0
D.Rs of the second line l₂ are (0, 1 – 1)
Suppose θ is the angle between the two lines

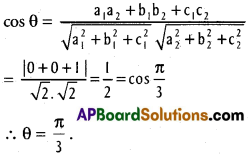
Question 3.
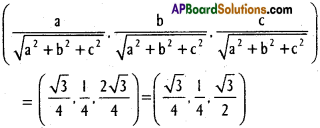
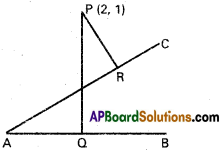
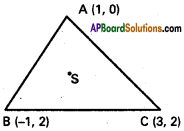
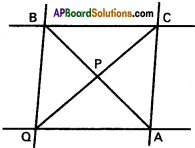
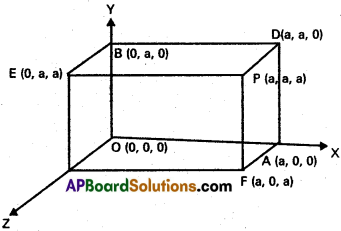
If a ray makes angles α, α, γ and δ with the four diagonals of a cube find cos² α + cos² β + cos² γ + cos² δ.
Solution:
Let each side of the cube be of length a. Let one of the vertices of the cube be the origin O and the co-ordinate axes be along the three edges \(\overline{\mathrm{O A}}\), \(\overline{\mathrm{O B}}\) and \(\overline{\mathrm{O C}}\) passing through the origin. The co-ordinates of the vertices of the cube with respect to the frame of reference OABC are as shown in figure. The diagonals of he cubeare \(\overline{\mathrm{O P}}\) \(\overline{\mathrm{C D}}\), \(\overline{\mathrm{A E}}\) and \(\overline{\mathrm{B F}}\) .(a, a, a), (a, a, -a), (-a, a, a) and (a, -a, a) are direction . ratios of these diagonals respectively.

Let the direction cosines of the given ray be (l, m, n). If this fay makes the angles α, β, γ and δ with the four diagonals of the cube, then

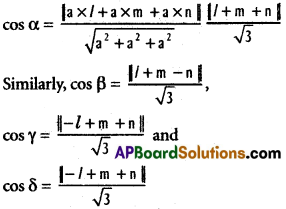
cos² α + cos² β + cos² γ + cos² δ
\(\frac{1}{3}\){|l + m + n|² +|l + m – n|² + |-l + m + n|² + |l – m + n|²}
\(\frac{1}{3}\)[(l + m + n)² + (l + m – n)² + (-l + m + n)² + (l – m + n)²]
\(\frac{1}{3}\)[4(l² + m² + n²)] = \(\frac{4}{3}\) (since l² + m² + n² = 1)

Question 4.
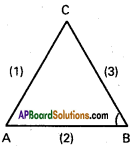
If (l₁, m₁, n₁), (l₂, m₂, n₂) are d.c.s of two intersecting lines, show that d.c.s of two lines, bisecting the angles between them are proportional to l₁ ± l₂, m₁ ± m₂ n₁ ± n₂.

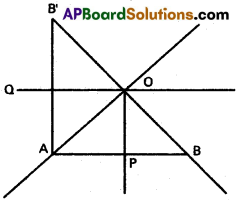
Solution:
OA and OB are the given lines
A and B are points at unit distances from O
Co-ordinates of A are (l₁, m₁, n₁)
Co-ordinates of B are (l₂, m₂, n₂)
P is the mid point of AB
Co-ordinates of P are \(\left(\frac{l_{1}+l_{2}}{2}, \frac{m_{1}+m_{2}}{2}, \frac{n_{1}+n_{2}}{2}\right)\)
∴ OP is the bisector of ∠AOB
D.Rs of OP are l₁ + l₂, m₁+ m₂, n₁+ n₂
Suppose B’ is a point are OB such that OB’ OB = 1
Co-ordinates of B’ are (-l₂, -m₂, -n₂)
Q is the mid point of AB’
Co-ordinates of Q are \(\left(\frac{l_{1}-l_{2}}{2}, \frac{m_{1}-m_{2}}{2}, \frac{n_{1}-n_{2}}{2}\right)\)
OQ is the other bisector of ∠AOB
D.Rs of OQ are l₁ – l₁, m₁ – m₂, n₁ – n₂

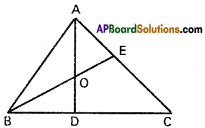
Question 5.
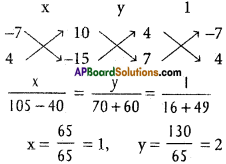
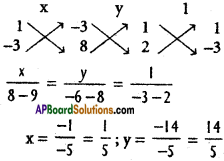
A (-1, 2, -3), B(5, 0, -6), C(0, 4, -1) are three points. Show that the direction cosines of the bisectors of ∠BAC are propotional to (25, 8, 5) and (-11, 20, 23).
Solution:
A (-1, 2, -3), B (5, 0, -6) and C (0, 4, -1) are the given points.
D.Rs of AB are 5 +1, 0 -2, -6 +3 ie., 6, -2, -3
D.Rs of AB are \(\frac{6}{7}, \frac{-2}{7}, \frac{-3}{7}\)
D.Rs of AC are 0 + 1, 4 – 2, -1 + 3 i.e., 1, 2, 2
D.Rs of AC are \(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\)
D.Rs of one of the bisectors are

D.Rs of one of the bisectos are (25, 8, 5)
D.Rs of the other bisectors are

D.Rs of the second bisector are (-11, 20, 23)

Question 6.
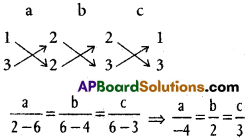
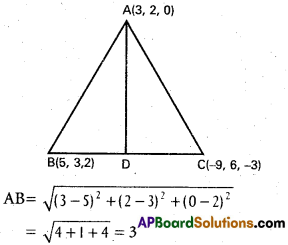
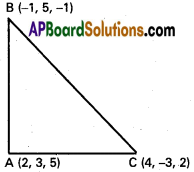
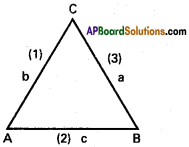
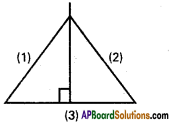
If (6,10,10), (1, 0, -5), (6, -10, 0) are vertices of a triangle, find the direction ratios of its sides. Determine whether it is right angled or isosceles.
Solution:
A (6, 10, 10), B (1, 0, -5), C (6, -10, 0) are the vertices of ∆ABC
D.Rs of AB are 5, 10, 15 i.e., 1, 2, 3
D.Rs of BC are -5, 10, -5 i.e., 1, -2, 1
D.Rs of AC are 0,20,10, i.e., 0, 2, 1

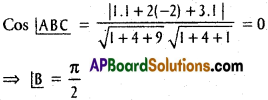
∴ The given triangle is right angle a.

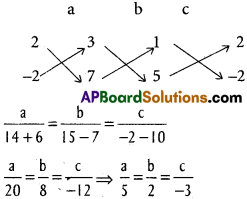
Question 7.
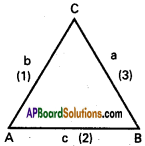
The vertices of a triangle are A (1, 4, 2), B (-2, 1, 2) C (2, 3, -4). Find ∠A, ∠B, ∠C.

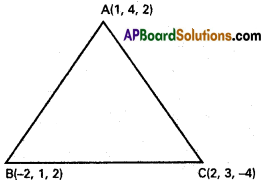
Solution:
A (1, 4, 2), B (-2, 1, 2), C (2, 3, -4) and the vertices of OABC.
D.Rs of AB are 3, 3, 0 i.e., 1, 1, 0
D.Rs of BC are -4, -2, 6 i.e., 2, 1, -3
D.Rs of AC are -1, 1, 6.

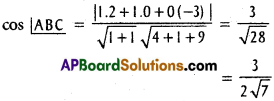
Question 8.
Find the angle between the lines whose direction cosines are given by the equation 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0
Solution:
Given 3l + m + 5n = 0 ……….. (1)
6mn – 2nl + 5lm = 0 …………. (2)
From (1), m = – (3l + 5n)
Substituting in (2)
-6n(3l + 5n) -2nl – 5l(3l + 5n) = 0
-18ln – 30n² – 2nl – 15l² – 25ln = 0
-15l² – 45ln – 30n² = 0
l² + 3ln + 2n² = 0
(l + 2n) (l + n) — 0
l + 2n = 0 or l + n = 0

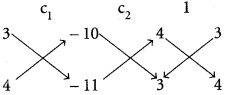
Case (i) : l₁ + n₁ = 0 ⇒ n₁ = – l₁; ⇒ \(\frac{l_{1}}{1}=\frac{n_{1}}{-1}\)
But m₁ = -(3l₁ + 5n₁) = -(-3n₁ + 5n₁) = -2n₁
∴ \(\frac{m_{1}}{+2}=\frac{n_{1}}{-1}\)
∴ \(\frac{l_{1}}{1}=\frac{m_{1}}{2}=\frac{n_{1}}{-1}\)
D.Rs of the first line lx are (1,2, -1)
Case (ii): l₂ + 2n₂ = 0
l₂ = —2n₂ ⇒ \(\frac{l_{2}}{-2}=\frac{n_{2}}{1}\)
m₂ = -(3l₂ + 5n₂) = – (-6n₂ + 5n₂) = n₂
\(\frac{m_{2}}{1}=\frac{n_{2}}{1}\)
∴ \(\frac{l_{2}}{-2}=\frac{m_{2}}{1}=\frac{n_{2}}{1}\)
D.Rs of the second line Z2 are (-2, 1, 1)
Suppose ‘θ’ is the angle between the lines l₁ and l₂

Question 9.
If a variable line in two adjecent positions has direction cosines (l, m, n) and (l + δl, m + δm, n + δn), show that the small angle δθ between two position. Is given by (δθ)² = (δl)² + (δm)² + (δn)².
Solution:
Since (l, m, n) and (l + δl, m + δm, n + δn) are direction cosines, we have
l² + m² + n² = 1 …………. (1)
(l + δl)² + (m + δm)² + (n + δn)² — 1 ………. (2)
(2) – (1) gives (l + δl)² + (m + δm)² + (n + 8n)² – (l² + m² + n²) = 0
2(l.δl + m.δm + n.δn) = -((δl)² + (δm)² + (δn)²) …………. (3)
cos θ . δθ = l(l + δl) + m(m + δm) + n(n + δn)
= (l² + m² + n²) + (l.δl + m.δm + n.δn)
= 1 – \(\frac{1}{2}\) [(δl)² + (δm)² + (δn)²]
(δl)² + (δm)² + (δn)² = 1 = ² (1 – cos θ.δ θ)
δθ being small, sin \(\frac{\delta \theta}{2}\) = \(\frac{\delta \theta}{2}\)
∴ sin²θ \(\frac{\delta \theta}{2}\) = 4(\(\frac{\delta \theta}{2}\))² = (δθ)²
∴ (δθ)² = (δl)² + (δm)² + (δn)².

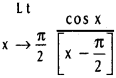
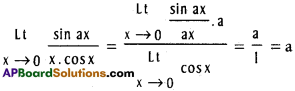
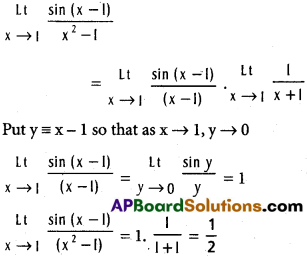
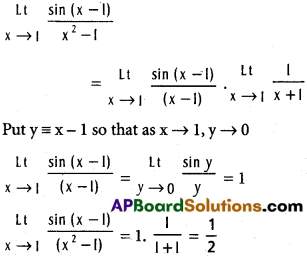
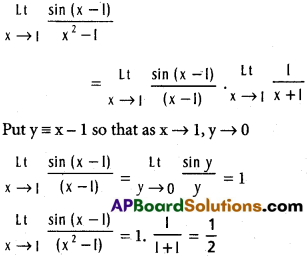
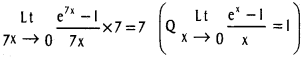
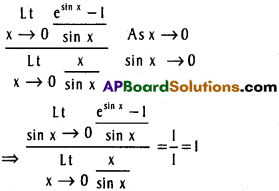
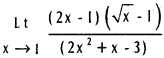
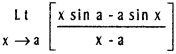
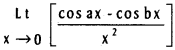
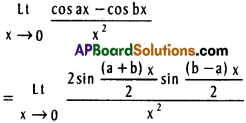
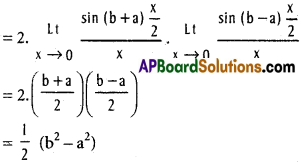
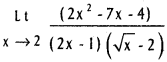
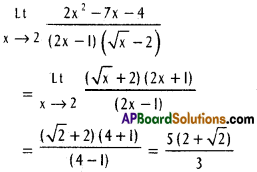
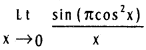
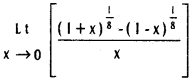
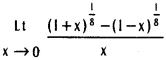
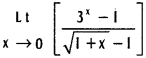
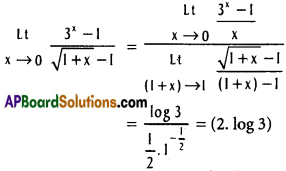
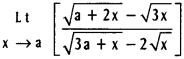
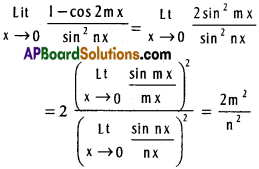
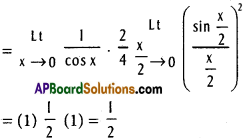
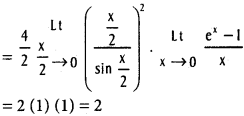
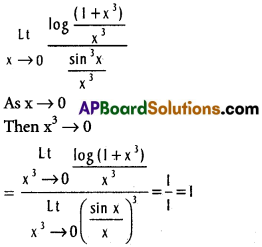
Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Solutions Exercise 6(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Solutions Exercise 6(a)

I.

Question 1.
A line makes angles 90°, 60° and 30° with positive directions of X, Y, Z – axes respectively. Find the direction cosines.
Solution:
Suppose l, m, n are the direction cosines of the line.
l = cos α = cos 90° = 0
m = cos β = cos 60° = \(\frac{1}{2}\)
n = cos γ = cos 30° = \(\frac{\sqrt{3}}{2}\)
Direction cosines of the line are (0, \(\frac{1}{2}\), \(\frac{\sqrt{3}}{2}\))

Question 2.
If a line makes angles α, β, γ with the positive direction of x, y, z axes, what is the value of sin² α + sin² β + sin² γ?
Solution:
We know that cos² α + cos² β + cos² γ = 1
1 – sin² α + 1 – sin² β + 1 – sin² γ = 1
sin² a + sin² P + sin² γ = 3 – 1 = 2.

Question 3.
If P(√3, 1, 2√3) is a point in space, find the direction cosines of \(\overrightarrow{O P}\).
Solution:
Direction ratios of P are (√3, 1, 2√3)
a² + b² + c² = 3 + 1 + 12 = 16
⇒ \(\sqrt{a^{2}+b^{2}+c^{2}}\) = 4
Direction cosines of \(\overrightarrow{O P}\) are

Question 4.
Find the direction cosines of the line joining the points (-4, 1, 7) are (2, -3, 2).
Solution:
A(- 4, 1, 2) and B(2, -3, 2) are the given points
d.rs of PQ are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
(2 + 4, 1 + 3, 2 – 7) ie., (6, 4, -5)
Dividing with

II.

Question 1.
Find the direction cosines of the sides of the triangle whose vertices are (3, 5, -4), (-1, 1, 2) and (-5, -5, -2).
Solution:
A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2) are the vertices of ∆ABC

d.rs of AB are (-1 -3, 1 – 5, 2 + 4) (-4, -4, 6)
Dividing with \(\sqrt{16+16+36}=\sqrt{68}=2 \sqrt{17}\)
D.Rs of AB are \(\frac{-4}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}}\)
ie., \(\frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}\)
D.Rs of BC are (-5 + 1, -5 -1, -2 -2)
i.e., (-4, -6, -4)

Dividing with \(\sqrt{16+16+36}=\sqrt{68}=2 \sqrt{17}\)
d.cs of BC are \(\frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}\)
ie., \(\frac{-2}{\sqrt{17}}, \frac{-3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}\)

d.rs of CA are 3 + 5, 5 + 5, -4 + 2
= 8, 10, -2
Dividing with \(\sqrt{64+100+4}=\sqrt{168}=2 \sqrt{42}\)
d.cs of CA are \(\frac{8}{2 \sqrt{42}}, \frac{10}{2 \sqrt{42}}, \frac{-2}{2 \sqrt{42}}\)
ie., \(\frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}}, \frac{-1}{\sqrt{42}}\)

Question 2.
Show that the lines \(\stackrel{\leftrightarrow}{P Q}\) and \(\stackrel{\leftrightarrow}{R S}\) are parallel where P, Q, R, S are two points (2, 3, 4), (4, 7, 8), (-1, -2, 1) and (1, 2, 5) respectively.
Solution:
P(2, 3, 4), Q(4, 7, 8), R(-1, -2, 1)
and S(1, 2, 5) are the given points.
d.rs of PQ are 4 -2, 7 -3, 8 – 4 i.e., 2, 4, 4
d.rs of RS are 1 + 1, 2 + 2, 5 – 1 i.e., 2, 4, 4
d.rs of PQ are RS are proportional
∴ PQ and RS are parallel.

III.

Question 1.
Find the direction cosines of two lines which are connected by the relations l – 5m + 3n = 0 and 7l² + 5m² – 3n² = 0.
Solution:
Given l – 5m + 3n = 0
⇒ l = 5m – 3n ………….. (1)
7l² + 5m² – 3n² = 0 …………. (2)
Substituting the value of l in (2)
7(5m – 3n)² + 5m² – 3n² = 0
7(25m² + 9n² – 30 mn) + 5m² – 3n² = 0
175 m² + 63n² – 210 mn + 5m² – 3n² = 0
180m² – 210mn + 60n² = 0
Dividing with 30.
6m² – 7mn + 2n² = 0
(3m – 2n) (2m – n) = 0
3m = 2n or 2m = n

Case (i): 3m₁ = 2n₁ ⇒ \(\frac{m_{1}}{2}=\frac{n_{1}}{3}\)
and m₁ = \(\frac{2}{3}\) n₁
From (1) l₁ = 5m₁ – 3n₁ = \(\frac{10}{3}\)n₁ – 3n₁
d.rs of the first line are (1, 2, 3)
Dividing with \(\sqrt{1+4+9}=\sqrt{14}\)
d.cs of the first line are (\(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\))

Case (ii): 2m₂ = n₂
From (1) l₂ – 5m₂ + 3n₂ = 0
l₂ – 5m₂ + 6m₂ = 0
l₂ = m₂
∴ \(\frac{l_{2}}{-1}=\frac{m_{2}}{1}=\frac{n_{2}}{2}\)
d.rs of the second line are -1, 1, 2
Dividing with \(\sqrt{1+1+4}=\sqrt{6}\)
d.cs of the second line are (\(\frac{-1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{2}{\sqrt{6}}\))

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(b)

I.

Question 1.
Find the ratio in which the XZ-plane divides the line joining A(-2, 3, 4) and B(l, 2,3).
Solution:
Ratio in which XZ plane divides
AB = -y₁ : y₂
= -3 : 2

Question 2.
Find the co-ordinates of the vertex ‘C’ of ∆ABC if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively.
Solution:
A(1, 1, 1) B(-2, 4, 1) and (x, y, z) are the vertices of ∆ABC.
G is the centroid of ∆ABC
Co-ordinates of G are
(\(\frac{1-2+x}{3}\), \(\frac{1+4+y}{3}\), \(\frac{1+1+z}{3}\)) = (0, 0, 0)
\(\frac{x-1}{3}\) = 0, \(\frac{y+5}{3}\) = 0, \(\frac{z+2}{3}\) = 0
x – 1 = 0, y +5 =0, z + 2 = 0
x = 1, y = – 5, z = -2
∴ Co-ordinates of c are (1, -5, -2)

Question 3.
If (3, 2, -1), (4, 1, 1) and (6, 2, 5) are three vertices and (4, 2, 2) is the centroid of a tetrahedron, find the fourth vertex.
Solution:
A(3, 2, -1), B(4, 1, 1), C(6, 2, 5), D(x, y, z) are the vertices of the tetrahedron.
Co-ordinates of the centroid G are

Co-ordinates of D are (3, 3, 3)

Question 4.
Find the distance between the mid point of the line segment \(\overline{\mathrm{A B}}\) and the point (3, -1, 2) where A = (6, 3, -4) and B = (-2, -1, 2).
Solution:
A(6, 3, – 4) B(-2, -1,2) are the given points.
Q is the midpoint of AB.
Co-ordinates of Q are (\(\frac{6-2}{2}\), \(\frac{3-1}{2}\), \(\frac{-4+2}{2}\)) = (2, 1, -1)
Co-ordinates of P are (3, -1, 2)

II.

Question 1.
Show that the points (5, 4,2) (6,2, -1) and (8, -2, -7) are collinear.
Solution:
A(5, 4, 2), B(6, 2, -1) c(8, -2, -7) are the given points.
AB = \(\sqrt{(5-6)^{2}+(4-2)^{2}+(2+1)^{2}}\)

∴ A, B, C are collinear.

Question 2.
Show that the points A(3, 2, -4), B(5, 4, -6) and C(9, 8, -10) are collinear and find the ratio in which B divides \(\overline{\mathrm{A C}}\).
Solution:
A(3, 2, -4), B(5, 4, -6) and C(9, 8, -10) are the given points.

A, B, C are collinear
Ratio in which B divides AC = AB : BC
= 2√3 : 4√3 = 1 : 2

III.

Question 1.
If A(4, 8, 12) B(2, 4, 6) C(3, 5, 4) and D(5, 8, 5) are four points, show that the line \(\stackrel{\leftrightarrow}{A B}\) and \(\stackrel{\leftrightarrow}{C D}\) intersect.
Solution:
A(4, 8, 12), B(2, 4, 6) C(3, 5, 4) and D(5, 8, 5) are the given points
Co-ordinates of the point dividing AB in the ratio λ : 1 is
\(\left[\frac{2 \lambda+4}{\lambda+1} \cdot \frac{4 \lambda+8}{\lambda+1} \cdot \frac{6 \lambda+12}{\lambda+1}\right]\) ……….. (1)
Co-ordinates of the point dividing CD in the ratio p : 1 is
\(\left[\frac{5 \mu+3}{\mu+1}, \frac{8 \mu+5}{\mu+1}, \frac{5 \mu+4}{\mu+1}\right]\) ……….. (2)
If the given lines intersects these two points must coincide.
\(\frac{2 \lambda+4}{\lambda+1}=\frac{5 \mu+3}{\mu+1}\)
(2λ + 4) (µ + 1) = (5µ + 3) (λ + 1)
2λµ + 2λ + 4µ + 4 = 5λµ + 5µ + 3λ + 3
3λ + λ + µ – 1 = 0
λ(3µ+1) = -(µ – 1)
λ = –\(\frac{(\mu-1)}{3 \mu+1}\)
\(\frac{4 \lambda+8}{\lambda+1}=\frac{8 \mu+5}{\mu+1}\)
(4λ + 8) (µ + 1) = (8µ + 5) (λ + 1)
4λµ + 4λ + 8µ + 8 = 8λµ + 8µ + 5λ + 5
4Aµ + λ – 3 = 0
(4µ + 1) λ = 3
\(-\frac{(4 \mu+1)(\mu-1)}{3 \mu+1}=3\)
4µ2 – 4µ + µ – 1 = -9µ – 3
4µ2 4- 6µ + 2 = 0
2µ2 + 3µ + 1=0
(2µ + 1) (µ – 1) = 0
µ = – \(\frac{1}{2}\) or – 1
µ = -1 is not possible
µ = – \(\frac{1}{2}\)

Co-ordinates of (2) are

Co-ordinates of (1) are
\(\frac{-6+4}{-3+1}, \frac{-12+8}{-3+1}, \frac{-18+12}{-3+1}\) = (1, 2, 3)
Since these two points coincide the given lines intersect.

Question 2.
Find the point of instersection of the lines \(\stackrel{\leftrightarrow}{A B}\) and \(\stackrel{\leftrightarrow}{C D}\) where A = (7, -6, 1) B = (17, -18, -3), C = (1, 4, -5) and D = (3, -4, 11)

Solution:
A(7, -6, 1), B(17, -18, -3), C(1, 4, -5) and D(3, -4, 11) are the given points.
Co-ordinates of the point dividing AB in the ratio λ: 1 are

Co-ordinates of the point dividing CD in the ratio µ : 1 are

(17λ + 7) (µ + 1) = (3µ + 1) (λ + 1)
17λµ + 17λ + 7µ + 7 = 3λµ + 3µ + λ + 1
14λµ + 16λ + 4µ + 6 = 0.

-18λµ – 6µ – 18λ – 6
= -4λµ + 4λ – 4µ + 4
14λµ + 22λ + 2µ + 10 = 0
14λµ + 16λ + 4µ + 6 = 0 ………. (1)
14λµ + 22λ + 2µ + 10 = 0……….(2)
Subtraction – 6λ + 2µ – 4 = 0
2µ = 6λ + 4
µ = 3λ + 2
Substituting in (3)
14λ(3λ + 2) + 16λ + 4(3λ + 2) + 6 = 0
42λ² + 28λ + 16λ + 12λ+ 8 + 6 = 0
42λ² + 56λ + 14 = 0
3λ² + 4λ + 1 = 0
(λ + 1) (3λ + 1) = 0
λ = -1 or λ = –\(\frac{1}{3}\)
λ = -1 is not possible
λ = –\(\frac{1}{3}\)

µ = 3λ + 2 = -1 + 2 = 1
µ = 1 ⇒
\(\frac{3+1}{1+1}, \frac{-4+4}{1+1}, \frac{11-5}{1+1}\) = (2, 0, 3)
∴ These two points coincide
⇒ The given lines AB and CD intersect
Point of intersection is (2, 0, 3)

Question 3.
A(3, 2, 0), B(5, 3, 2), C(-9, 6, -3) are vertices of a triangle. \(\overline{\mathrm{A D}}\), the bisector of ∠BAC meets \(\overline{\mathrm{B C}}\) at D. Find the co-ordinates of D.
Solution:
A(3, 2, 0),B(5, 3, 2) C(-9, 6, -3) are the vertices of ∆ABC


AB is the bisector of ∠DAC
‘D’ divides BC in the ratio 3 : 13
Co-ordinates of D are

Question 4.
Show that the points 0(0,0,0), A(2, -3, 3), B(-2, 3, -3) are collinear. Find the ratio in which each point divides the segment joining the other two.
Solution:
0(0, 0, 0), A(2, -3, 3), B(-2, 3, -3) are the given points.

∴ O, A, B are collinear.

Ratio in which ‘O’ divides AB
= OA : OB = √22 : √22 = 1 : 1
Ratio is which A divides OB
= OA:AB = -√22 : √22 = -1 : 2
Ratio in which B divides OA
= AB : BO = -2√22 : √22 =-2 : 1
A and B divide externally.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(a)

I.

Question 1.
Find the distance of P (3, -2,4) from the origin.
Solution:
OP = \(\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{9+4+16}\)
= √29 units

Question 2.
Find the distance between the points (3,4,¬2) are (1,0,7).
Solution:

II.

Question 1.
Find x if the distance between (5, -1,7) and (x, 5,1) is 9 units.
Solution:
P(5, -1, 7), Q(x, 5,1) are the given points
PQ = 9

(5 – x)² + 36 + 36 = 81
(5 -x)² = 81 – 72 = 9
5 – x = ± 3
5 – x = 3 or 5 – x = -3
x = 5 – 3 or x = 5 + 3
= 2 or 8

Question 2.
Show that the points (2,3,5), (-1,5, -1) and (4, -3, 2) form a right angled iso-sceles triangle.
Solution:
A(2, 3, 5) B(-1, 5, -1), C(4, -3, 2) are the given points
AB² = (2 + 1)² + (3 – 5)² + (5 + 1)²
= 9 + 4 + 36 = 49

BC² = (-1- 4)² + (5 + 3)² + (-1 – 2)²
= 25 + 64 + 9 = 98

CA² = (4 – 2)² + (-3 -3)² + (2 – 5)²
= 4 + 36 + 9 = 49

AB² = CA² ⇒ AB² + CA² = 49 + 49 = 98 = BC²
ABC is a right angled isosceles triangle.

Question 3.
Show that the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) form an equilateral triangle.
Solution:
A( 1, 2, 3), B(2, 3, 1) and C (3, 1, 2) are the given points
AB² = (1 – 2)² + (2 – 3)²+ (3 – 1)²
= 1 + 1+ 4 = 6

BC² = (2 – 3)² + (3 – 1)² + (1 – 2)²
= 1 + 4 + 1 = 6

CA² = (3 – 1)² + (1 – 2)² + (2 – 3)²
= 4 + 1 + 6

AB² = BC² = CA² ⇒ AB = BC = CA
∴ ABC is an equilateral triangle

Question 4.
P is a variable point which moves such that 3PA = 2PB. If A = (-2, 2,3) and B = (13, -3,13) prove that P satisfies the equation.
x² + y² + z² + 28x – 12y + 10z – 247 = 0.
Solution:
A(-2, 2, 3) and B(13, -3, 13) are the given points. P(x, y, z) is any point on the locus.
Given condition is 3P A = 2P B
⇒ 9 PA² = 4PA²
9[(x + 2)² + (y – 2)² + (z – 3)²] = 4[(x – 13)²+(y + 3)² + (z – 13)²]
⇒ 9(x² + 4x +4 + y² – 4y + 4 + z² – 6z + 9) = 4(x² – 26x + 169 + y² + 6y + 9 + z² – 26z + 169)
⇒ 9x² + 9y² + 9z² + 36x – 36y – 54z +153 = 4x² + 4y² + 4z² – 104x + 24y – 104z + 1388
5x² + 5f + 5z² + 140x – 60y + 50z – 1235 =0
Dividing with 5 locus of P is
x² + y² + z² + 28x – 12y + 10z – 247 = 0

Question 5.
Show that the points (1, 2, 3) (7, 0, 1) and (-2, 3, 4) are collinear.
Solution:
A (1, 2, 3), B(7, 0, 1) C(-2, 3, 4) are the given points.

AB + AC = 2√11 + √11 = 3√11 = BC
A, B, C are collinear

Question 6.
Show that ABCD is a square where A, B, C, D are the points (0, 4, 1), (2, 3 -1) (4, 5, 0) and (2, 6, 2) respectively.
Solution:
A(0, 4, 1), B(2, 3, -1) C(4, 5, 0), D(2, 6, 2) are the given points.
AB² = (0 – 2)² + (4 – 3)² + (1 + 1)²
=4 + 1 + 4 = 9

BC² = (2 – 4)² + (3 – 5)² + (-1 – 0)²
= 4 + 4 + 1 = 9

CD² = (4- 2) ²+ (5 – 6)² + (0 – 2)²
= 4 + 1 – 4 = 9

DA² = (2- 0) ²+ (6 – 4)² + (2 – 1)²
= 4 + 4 + 1 = 9

AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA
AC² = (0 – 4)² + (4 – 5)² + (1 – 0)² = 16 + 1 + 1 = 18
BD² = (2 – 2)² + (3 – 6)² + (-1 -2)² = 9 + 9 = 18
AC² = BD² ⇒ AC = BD
AB² + BC² = 9 + 9 = 18 = AC²
⇒ ∠ABC = 90°
A, B, C, D are the vertices of a square.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c)

I.

Question 1.
Find the equation of the lines joining the origin to the points of intersection of x² + y² = 1 and x + y = 1.
Solution:
The given curves are
x² + y² = 1 …….. (1)
x + y = 1 ……….. (2)
Homogenising (1) with the help of (2) Combined equation of OA and OB is

x² + y² = (x + y)²
= x² + y² + 2xy
i.e., 2xy = 0 ⇒ xy – 0

Question 2.
Find the angle between the lines joining the origin to the points of intersection of y2 = x and x + y = 1.
Solution:
Equation of the centre is y² = x …………. (1)
Equation of AB is x + y = 1 ………. (2)
Hamogonsing (1) with the help of O
Combined equation of A & OB is
y² = x(x + y) = x² + xy
x² + xy – y2 = 0
a + b = 1 – 1 = 0
OA, OB an perpendicular
∴ ∠AOB =90°

II.

Question 1.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – √2 = 0 are mutually perpendicular.
Solution:

Equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 ……….. (1)
Equation of AB is x – y – √2 = 0
x – y = √2
\(\frac{x-y}{\sqrt{2}}\) = 1 ………. (2)
Homogenising, (1) with the help of (2) combined equation of OA, OB is
x² – xy + y² + 3x.1 + 3y.1 – 2.1² = 0
x² – xy + y² + 3(x + y)\(\frac{x-y}{\sqrt{2}}\) – 2\(\frac{(x-y)^{2}}{2}\) = 0
x² – xy + y² + \(\frac{3}{\sqrt{2}}\)(x² – y²) – (x² – 2xy + y²) = 0
x² – xy + y² + \(\frac{3}{\sqrt{2}}\)x² – \(\frac{3}{\sqrt{2}}\)y² – x² + 2xy – y² = 0
\(\frac{3}{\sqrt{2}}\)x² + xy – \(\frac{3}{\sqrt{2}}\)y² = 0
a + b = \(\frac{3}{\sqrt{2}}\) – \(\frac{3}{\sqrt{2}}\) = 0
∴ OA, OB are perpendicular.

Question 2.
Find the values of k, if the lines joining the origin to the points of intersection of the curve 2x² – 2xy + 3y² + 2x – y – 1 = 0 and the line x + 2y = k are muiually perpendicular.
Solution:
Given equation of the curve is
S ≡ 2x² – 2xy + 3y² + 2x – y – 1 = 0 ……….. (1)
Equation of AB is x + 2y = k

\(\frac{x+2y}{k}\) = 1
Homogenising, (1) with the help of (2), combined equation of OA, OB is
2x² – 2xy + 3y² + 2x.1 – y.1 – 1² = 0
2x² – 2xy + 3y² + 2x\(\frac{x+2y}{k}\) – y\(\frac{x+2y}{k}\) – \(\frac{(x+2y)^{2}}{k^{2}}\) = 0
Multiplying with k²
2k²x² – 2k²xy + 3k²y² + 2kx(x + 2y) – ky(x + 2y) – (x + 2y)² = 0
2k²x² – 2k²xy + 3k²y² + 2kx² + 4kxy – kxy – 2ky² – x² – 4xy – 4y² = 0
(2k² + 2k – 1)x² + (-2k² + 3k – 4) xy + (3k² – 2k – 4) y² = 0
Since OA, OB are perpendicular.
Co-efficient x² + Co-efficient of y² = 0
2k² + 2k – 1 + 3k² – 2k – 4 = 0
5k² = 5 ⇒ k² = 1
∴ k = ± 1

Question 3.
Find the angle between the lines joining the origin to the points of intersection of the curve x² + 2xy + y² + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0
Solution:

Equation of the curve is
x² + 2xy + y² + 2x + 2y- 5 = 0 …….. (1)
Equation of AB is 3x – y + 1 = 0
y – 3x = 1…………. (2)
Homogenising (1) with the help of (2), combined equation of OA, OB is
x² + 2xy + y² + 2x.1 + 2y.1 – 5.1² = 0
x² + 2xy + y² + 2x(y – 3x) + 2y(y – 3x) – 5 (y – 3x)² = 0
x² + 2xy + y² + 2xy – 6x² + 2y² – 6xy – 5(y² + 9x² – 6xy) = 0
– 5x² – 2xy + 3y² – 5y² – 45x² + 30 xy = 0
-50x² + 28xy – 2y² = 0
i.e, 25x² – 14xy + y² = 0
Suppose θ is the angle between OA and OB

III.

Question 1.
Find the condition for the chord lx + my = 1 of the circle x² + y² = a² (whose centre is the origin) to subtend a right angle at the origin.
Solution:

Equation of the circle is x² + y² = a² ………. (1)
Equation of AB is lx + my = 1 ……….. (2)
Homogenising (1) with the help of (2)
Gombined equation of OA, OB is
x² + y² = a².l²
x² + y² = a² (lx + my)²
= a²(l²x² + m²y² + 2lmxy)
= a²l²x² + a²m²y² + 2a²lmxy
i.e., a²l²x² + 2a²lmxy + a²m²y² – x² – y² = 0
(a²l² – 1) x² + 2a² lmxy + (a²m² – 1)y² = 0
Since OA, OB are perpendicular
Co-efficient of x² + co-efficient of y² = 0
a²l² – 1 + a²m² – 1 = 0
a²(l² + m²) = 2
This is the required condition.

Question 2.
Find the condition for the lines joining the origin to the points of intersection of the circle x² + y² = a² and the line lx + my = 1 to coincide.
Solution:

Equation of the circle is
x² + y² = a² ………. (1)
Equation of AB is lx + my = 1 ……….. (2)
Homogenising (1) with the help of (2)
Combined equation of OA, OB is
x² + y² = a².l²
= a²(lx + my)²
= a²(l²x² + m²y² + 2lmxy)
i.e., x² + y² = a²l²x² + a²m²y² + 2a²lmxy
(a²l² – 1)x² + 2a²lmxy + (a²m² – 1)y² = 0
Since OA, OB are coincide
⇒ h² = ab
a⁴ l²m² = (a²l² – 1)(a²m² – 1)
a⁴ l²m² = a⁴ l²m² – a²l² – a² m² + 1
∴ a²l² – a²m² +1=0
a² (l² + m²) = 1
This is the required condition.

Question 3.
Write down the equation of the pair of straight lines joining the origin to the points of intersection of the line 6x – y + 8 = 0 with the pair of straight lines 3x² + 4xy – 4y² – 11x + 2y + 6 = 0. Show that the lines so obtained make equal angles with the coordinate axes.
Solution:
Given pair of lines is
3x² + 4xy – 4y² – 11x + 2y + 6 = 0 ……….. (1)
Given line is
6x – y + 8 = 0 ⇒ \(\frac{6x-y}{-8}\) = 1
⇒ \(\frac{y-6x}{8}\) = 1
Homogenising (1) w. r. t. (2)
3x² + 4xy – 4y² – (11x – 2y) (\(\frac{y-6x}{8}\)) = 6(\(\frac{y-6x}{8}\))² = 0
64[3x² + 4xy – 4y²] – 8[11xy – 66x² – 2y² + 12xy] + 6[y² + 36x² – 12xy] = 0
936x² + 256 xy – 256 xy – 234y² = 0
∴ 468x² – 117y² = 0 …….. (3)
⇒ 4x² – y² = 0
is eq. of pair of lines joining the origin to the point of intersection in.
The eq. pair of angle bisectors to (3) is
h(x² – y²) – (a – b)xy = 0
0(x² – y²) – f4 – l)xy = 0
⇒ xy = 0
x = 0 or y = 0 [Eqs. is of coordinate axes]
∴ The pair of lines are equally inclined to the co-ordinate axes.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(b)

I.

Question 1.
Find the angle between the lines represented by 2x² + xy – 6y² + 7y – 2 = 0.
Solution:
Comparing with
ax² + 2hxy + by² + 2gx + 2fy + c = 0
a = 2, 2g = 0, g = 0
b = – 6, 2f = 7, f = 7/2
c = – 2, 2h = 1, h = 1/2
Angle between the lines is given by

Question 2.
Prove that the equation 2x² + 3xy – 2y² + 3x + y + 1 = 0 represents a pair of perpendicular lines.
Solution:
Given a = 2, b = -2
a + b = 0 ⇒ cos α = 0 ⇒ α = π/2
∴ The given lines are perpendicular.

II.

Question 1.
Prove that the equation 3x² + 7xy + 2y² + 5x + 5y + 2 = 0 represents a pair of straight lines and find the co-ordinates of the’point of intersection.
Solution:
The given equation is
3x² + 7xy + 2y² + 5x + 5y + 2 = 0
Comparing a = 3 2f = 5 ⇒ f = \(\frac{5}{2}\)
b = 2 2g = 5 ⇒ g = \(\frac{5}{2}\)
c = 2 2h = 7 ⇒ h = \(\frac{7}{2}\)
∆ = abc + 2fgh – af² – bg² – ch²
= 3(2)(2) + 2.\(\frac{5}{2}\).\(\frac{5}{2}\).\(\frac{7}{2}\) – 3.\(\frac{25}{4}\) – 2.\(\frac{25}{4}\) – 2.\(\frac{49}{4}\) = 0
= \(\frac{1}{4}\)(48 + 175 – 75 – 50 – 98)
= \(\frac{1}{2}\)(223 – 223) = 0

∴ The given equation represents a pair of lines point of intersection is

Question 2.
Find the value of k, if the equation 2x² + kxy – 6y² + 3x + y + l = 0 represents a pair of straight lines. Find the point of intersection of the lines and the angle between the straight lines for this value of k.
Solution:
The given equation is
2x² + kxy – by² + 3x + y+ 1 = 0
a = 2 2f = 1 ⇒ f = \(\frac{1}{2}\)
b = -6 2g = 3 ⇒ g = \(\frac{3}{2}\)
c = 1 2h = k ⇒ h = \(\frac{k}{2}\)
The given equation represents a pair of straight lines abc + 2fgh – af² – bg² – ch² = 0
-12 + 2.\(\frac{1}{2}\).\(\frac{3}{2}\)(+\(\frac{k}{2}\) -2.\(\frac{1}{4}\) + 6.\(\frac{9}{4}\) – \(\frac{k^{2}}{4}\) = 0
– 48 + 3k – 2 + 54 – k² = 0
-k² + 3k + 4 = 0 ⇒ k² – 3k – 4 = 0
(k – 4) (k + 1) = 0
k = 4 or – 1.

Case (i): k = – 1
Point of’intersection is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

Point of intersection is (\(\frac{-5}{7}\), \(\frac{1}{7}\))
Angle between the lines

Case (ii): k = 4

Point of intersection is P(-\(\frac{5}{8}\), –\(\frac{1}{8}\))

Question 3.
Show that the equation x² – y² – x + 3y – 2 = 0 represents a pair of perpendicular lines and find their equations.
Solution:
Comparing a= 1, f = \(\frac{3}{2}\)
b = -1, g = –\(\frac{1}{2}\)
c = -2, h = 0
abc + 2fgh – af² – bg² – ch²
= 1 (-1) (-2) + 0- 1.\(\frac{9}{4}\) + 1.\(\frac{1}{4}\) + 0
= + 2 – \(\frac{9}{4}\) + \(\frac{1}{4}\) = 0
h² – ab = 0 – 1(-1) = 1 > 0,
f² – be = \(\frac{9}{4}\) – 2 = \(\frac{1}{4}\) = 1 > 0
g² – ac = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
a + b = 1 – 1 = 0
The given equation represent a pair of per-pendicular lines
Let x² – y² – x + 3y – 2
= (x + y + c₁) (x – y + c₂)
Equating the co-efficients of x
⇒ c₁ + c₂ = – 1
Equating the co-efficients of y
⇒ – c₁ + c₂ = 3
Adding 2c₂ = 2 ⇒ c₂ = 1
c₁ + c₂ = – 1 ⇒ c₁ + 1 = – 1
c₁ = – 2
Equations of the lines are x + y – 2 = 0 and x – y + 1 = 0

Question 4.
Show that the lines x² + 2xy – 35y² – 4x + 44y – 12 = 0 are 5x + 2y – 8 = 0 are concurrent.
Solution:
Equations of the given lines are
x² + 2xy- 35y² -4x + 44y- 12 = 0
a = 1, f = 22
b = – 35, g = – 2
c = – 12, h = 1
Point or intersection is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

Point of intersection of the given lines is P(\(\frac{4}{3}\), \(\frac{2}{3}\))
5x + 2y – 8 = 5.\(\frac{4}{3}\) + 2.\(\frac{2}{3}\) – 8
= \(\frac{20+4-24}{3}\) = 0
P lies on the third line 5x + 2y – 8 = 0
∴ The given lines are concurrent.

Question 5.
Find the distances between the following pairs of parallel straight lines :
i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
Solution:
Distance between parallel lines = \(2 \sqrt{\frac{g^{2}-a c}{a(a+b)}}\)

ii) x² + 2√3xy + 3y² – 3x – 3√3y – 4 = 0
Solution:
Distance between parallel lines = \(2 \sqrt{\frac{g^{2}-a c}{a(a+b)}}\)

Question 5.
Show that the two pairs of lines 3x² + 8xy – 3y² = 0 and 3x² + 8xy – 3y² + 2x – 4y – 1 = 0 form a square.

Solution:
Combined equation of CA and CB is
3x² + 8xy – 3y²
(x + 3y) (3x – y) = 0
3x – y = 0, x + 3y = 0
Equation of OA is 3x – y = 0 ………. (1)
Equation of OB is x + 3y = 0 ……….(2)
Combined equation of CA and CB is
3x² + 8xy – 3y² + 2x – 4y + 1 =0
Let 3x² + 8xy – 3y² + 2x – 4y + 1 = (3x – y + c₁) (x + 3y + c₂)
Equating the co-efficients of
x, we get c₁ + 3c₂ = 2
y, we have 3c₁ + c₂ = -4

Equation of BC is 3x – y – 1 = 0 ………. (3)
Equation of AC is x + 3y + 1 = 0 ………. (4)
OA and BC differ by a constant ⇒ OA parallel to BC
OB and CA differ by a constant ⇒ OB parallel to AC
From combined equation of OA and OB
OACB is a rectangle a + b = 3 – 3 = 0
OA = Length of the -L lar from O to AC = \(\frac{|0+0+1|}{\sqrt{1+9}}=\frac{1}{\sqrt{10}}\)
OB = Length of the perpendicular from O to BC = \(\frac{|0+0-1|}{\sqrt{9+1}}=\frac{1}{\sqrt{10}}\)
OA = OB and OACB is a rectangle
OACB is a square.

III.

Question 1.
Find the product of the lengths of the perpendiculars drawn from (2, 1) upon the lines
12x² + 25xy + 12y² + 10x + 11y + 2 = 0

Solution:
Combined equation of AB, AC is
12x² + 25xy+ 12y² + 10x + 11y + 2 = 0
12x² + 25xy +12y²
= 12x² + 16xy + 9xy + 12y² = 0
= 4x (3x + 4y) + 3y (3x + 4y)
= (3x + 4y) (4x + 3y)
Let 12x² + 25xy + 12y² + 10x + 11y + 2
= (3x + 4y + c₁) (4x + 3y + c₂)
Equating the co-efficients of x, we get
4c₁ + 3c₂ = 10 ………. (1)
Equating the co-efficients of y, we get
3c₁ + 4c₂ = 11 ………… (2)
i.e., 4c₁ + 3c₂ – 10 = 0
3c₁ + 4c₂ – 11 = 0


Equation of AB is 3x + 4y + 1 = 0
Equation of AC is 4x + 3y + 2 = 0
PQ = Length of the perpendicular from P(2, 1) on
AB = \(\frac{6+4+1}{\sqrt{9+16}}=\frac{11}{5}\)
PQ = Length of the perpendiculars from P(2, 1) on
AC = \(\frac{|8+3+2|}{\sqrt{16+9}}=\frac{13}{5}\)
Product of the length of the perpendiculars
= PQ × PR= \(\frac{11}{5}\) × \(\frac{13}{5}\) = \(\frac{143}{25}\)

Question 2.
Show that the straight lines y² – 4y + 3 = 0 and
x² + 4xy + 4y² + 5x + 10y + 4 = 0 form a parallelogram and find the lengths of its sides.

Solution:
Equation of the first pair of lines is
y² – 4y + 3 = 0
(y – 1) (y – 3) = 0
y – 1 = 0 or y – 3 = 0
Equation of AB is y – 1 = 0 ……….. (1)
Equation of CD is y – 3 = 0 ………. (2)
Equations of AB and CD differ by a constant.
∴ AB and CD are parallel.
Equation of the second pair of lines is
x² + 4xy + 4y² + 5x + 10y + 4 = 0
(x + 2y)² + 5(x + 2y) + 4 = 0
(x + 2y)² + 4 (x + 2y) + (x + 2y) + 4 = 0
(x + 2y)(x + 2y + 4) + 1(x + 2y + 4) = 0
(x + 2y + 1) (x + 2y + 4) = 0
x + 2y + 1 = 0, x + 2y + 4 = 0
Equation of AD is x + 2y + 1 = 0 ……… (3)
Equation of BC is x + 2y + 4 = 0 ……… (4)
AD and BC are parallel.
Solving (1), (3) x + 2 + 1 = 0
x = – 3
Co-ordinates of A are (-3, 1)
Solving (2), (3) x + 6 + 1 = 0
x = -7
Co-ordinates of DC are (-7, 3)
Solving (1), (4) x + 2 + 4 = 0
x = – 6
Co-ordinates of B are (-6, 1)

Lengths of the sides of the parallelogram are 3, 2√5.

Question 3.
Show that the product of the perpendicular distances from the origin to the pair of straight lines represented by ax² + 2hxy + by² + 2gx + 2fy + c = 0 is \(\frac{|c|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
Solution:
Let ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents the lines
l₁x + m₁y + n₁ = 0 ……….. (1)
l₂x + m₂y + n₂ = 0 ………. (2)
⇒ ax² + 2hxy + by² + 2gx + 2fy + c ≡ (l₁x + m₁y + n₁) (l₂x + m₂y + n₂)
l₁l₂ = a, m₁m₂ = b, l₁m₂ + l₂m₁ = 2h,
l₁n₂ + l₂n₁ = 2g, m₁n₂ + m₂n₁ = 2f, n₁n₂ = c
⊥^Ir distance from origin to (1) is = \(\frac{\left|n_{1}\right|}{\sqrt{l_{1}^{2}+m_{1}^{2}}}\)
⊥^Irdistance from origin to (2) is = \(\frac{\left|n_{2}\right|}{\sqrt{I_{2}^{2}+m_{2}^{2}}}\)
Product of perpendiculars

Question 4.
If the equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a pair of intersecting lines, then show that the square of the distance of their point of intersection from the origin is \(\frac{c(a+b)-f^{2}-g^{2}}{a b-h^{2}}\). Also slow that the square of this distance is \(\frac{f^{2}+g^{2}}{h^{2}+b^{2}}\) if the given lines are perpendicular.
Solution:
Let the equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0
represent the lines
l₁x + m₁y + n₁ = 0 …….. (1)
l₂x + m₂y + n₂ = 0 …….. (2)
(l₁x + m₁y + n₁)(l₂x + m₂y + n₂) = ax² + 2hxy + by² + 2gx + 2fy + c
l₁l₂ = a, m₁ m₂ = b, n₁n₂ = c
l₁m₂ + l₂m₁ = 2h, l₁n₂ + l₁₂n₁ = 2g, m₁n₂ + m₂n₁ = 2f
Solving (1) and (2)
\(\frac{x}{m_{1} n_{2}-m_{2} n_{1}}=\frac{y}{I_{2} n_{1}-l_{1} n_{2}}=\frac{1}{l_{1} m_{2}-I_{2} m_{1}}\)
The point of intersection, P


If the given pair of lines are perpendicular, then a + b = 0
∴ a = -b
\(\mathrm{OP}^{2}=\frac{0-r^{2}-g^{2}}{(-b) b-h^{2}}=\frac{r^{2}+g^{2}}{h^{2}+b^{2}}\)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(e) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(e)

I.

Question 1.
Find the incentre of the triangle whose vertices are (1, √3) (2, 0) and (0, 0)
Solution:
0(0, 0), A (1, √3), B (2, 0) are the vertices of ∆ ABC

∴ ABC is an equilateral triangle
Co-ordinates of the in centre are

Question 2.
Find the orthocentre of the triangle whose sides are given by x + y + 10 = 0, x – y – 2 = 0 and 2x + y – 7 = 0
Solution:
Equation of AB is x + y + 10 = 0 ………… (1)
Equation of BC is x – y – 2 = 0 ………… (2)
Equation of AC is 2x + y – 7 = 0 ………… (3)

Solving (1) and (2) co – ordinates of B are (-4, -6)
Solving (1) and (3) co – ordinates of A are (17, -27)
Equation of BC is x – y – 2 = 0
AD is perpendicular to BC.
Equation of AD is x + y + k = 0
AD passes through A (17, -27)
17 – 27 + k = 0 ⇒ k = 10
∴ Equation of AB is x + y + 10 = 0 ………….. (1)
Equation of AC is 2x + y – 7 = 0
BE is perpendicular to AC.
Equation of DE can be taken as x – 2y = k
BE passes through D (-4, -6)
-4 + 12 = k ⇒ k = 8
Equation of BE is x – 2y = 8

3y = -18 ⇒ y = – 6 x + y+10 = 0
⇒ x – 6+10 = 0
x = 6 – 10 = -4
Orthocentre of A ABC is (- 4, – 6)

Question 3.
Find the orthocentre of the triangle whose sides are given by 4x – 7y + 10 = 0, x + y = 5 and 7x + 4y = 15
Solution:
Equation of AB is. 4x – 7y + 10 = 0 …………. (1)
Equation of BC is x + y = 5 …………. (2)
Equation of AC is 7x + 4y – 15 = 0 …………. (3)
AB and AC are perpendicular and ∠A = 90°
∴ ABC is a right angled triangle
Right angled vertex A is the orthocentre
Solving (1) and (3)

Orthocentre is O (1,2)

Question 4.
Find the circumcentre of the triangle whose sides are x = 1, y = 1 and x + y = 1
Solution:
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1

AB and BC are perpendicular
∴ ABC is a right angled triangle and ∠B = 90°
Mid point of AC is the circumcentre
Co-ordinates of A are (1,0) and C are (0,1)
Circumcentre is (\(\frac{1}{2}\), \(\frac{1}{2}\))

Question 5.
Find the incentre of the triangle formed by the lines x = 1, y = 1 and x + y = 1
Solution:
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1
Solving the vertices are A(1, 0), B(1, 1), C (0, 1)

Question 6.
Find the circumcentre of the triangle whose vertices are (1,0),(-l, 2) and (3,2)
Solution:
A (1, 0), B (-1, 2), C (3, 2) are the vertices of ∆ ABC

S (x, y) is the circumcentre of ∆ ABC
SA = SB = SC
SA = SB ⇒ SA² = SB²
(x – 1)² + y² = (x + 1)² + (y – 2)²
x² – 2x + 1 + y² = x² + 2x + 1 + y² – 4y + 4
4x – 4y = – 4 ⇒ x – y = -1 …….. (1)
SB = SC ⇒ SB² = SC²
(x+ 1)² + (y – 2)² = (x-3)² + (y – 2)²
x² + 2x + 1 = x² – 6x + 9
8x = 8 ⇒ x = 1
From (1), 1 – y = -1
y = 2
∴ Circumcentre is (1, 2)

Question 7.
Find the value of k, if the angle between the straight lines kx + y + 9 =0 and 3x – y + 4 = 0 is π/4
Solution:
Equations of the given lines are
kx + y + 9 = 0
3x – y + 4 = 0

Squaring and cross-multiplying
5k² + 5 = (3k – 1)² = 9k² – 6k + 1
4k² – 6k – 4 = 0
2k² – 3 k – 2 = 0
(k – 2) (2k + 1) =0
k = 2 or -1/2

Question 8.
Find the equation of the straight line passing through the origin and also through the point of intersection of the lines 2x – y + 5 = 0 and x + y + 1 = 0.

Solution:
Equation of AB is L₁ = 2x – y + 5 = 0
Equation of AC is L₂ = x + y+ l = 0
Equation of any line passing through A is
L₁ + kL₂ = 0
(2x – y + 5) +k (x + y + 1) = 0 ……….. (1)
This line passes through O (0, 0)
5 + k = 0 ⇒ k = -5
Substituting in (1), equation of OA is
(2x – y + 5) – 5(x + y + 1) =0
2x – y + 5 – 5x – 5y – 5 = 0
-3x- 6y = 0 ⇒ x + 2y = 0

Question 9.
Find the equation of the straight line parallel to the line 3x + 4y = 7 and passing through the point of intersection of the lines x – 2y – 3 = 0 and x + 3y – 6 = 0.
Solution:
Equation of the given lines are
L₁ = x – 2y – 3 = 0 and
L₂ = x + 3y – 6 = 0
Equation of any line passing through the intersection is L₁ + kL₂ = 0
(x – 2y – 3) + k(x + 3y – 6) = 0
(1 + k)x + (-2 + 3k)y + (-3 – 6k) = 0
This line is parallel to 3x + 4y = 7
a₁b₂ = a₂b₁
3(-2 + 3k) = (1+ k) 4
-6 + 9k = 4 + 4k ⇒ 5k=10 ⇒ k = 2
Equation of the required line is 3x + 4y – 15 = 0

Question 10.
Find the equation of the straight line perpendicular to the line 2x + 3y = 0 and passing through the point of intersection of the lines x + 3y – 1 = 0 and x – 2y + 4 = 0.
Solution:
Equation of AB is x + 3y – 1 = 0
Equation of AC is x – 2y + 4 = 0

Equation of any line through A is
(x + 3y – 1) + k(x – 2y + 4) = 0
(1 + k)x + (3 – 2k)y + (4k – 1) = 0 ………… (1)
This line is perpendicular to 2x + 3y = 0
a₁a₂ + b₁b₂ = 0
2(1 +k) + 3(3 – 2k) = 0
2 + 2k + 9 – 6k = 0
4k = 11 ⇒ k = \(\frac{11}{4}\)
Substituting in (1), equation of the required line AD is
(1 + \(\frac{11}{4}\))x + (3 – \(\frac{11}{2}\))y + (11 – 1) = 0
\(\frac{15}{4}\) x – \(\frac{5}{2}\)y + 10 = 0
15x – 10y + 40 = 0
3x – 2y + 8 = 0

Question 11.
Find the equation of the straight line making non-zero equal intercepts on the coordinate axes and passing through the point of intersection of the lines 2x – 5y + 1 = 0 and x – 3y – 4 = 0.
Solution:
Equation of the given lines are
L₁ = 2x – 5y + 1 = 0
L₂ = x – 3y – 4 = 0
Equation of any line passing through the intersection of these lines is L₁ + kL2 = 0
(2x – 5y + 1) + k(x – 3y – 4) = 0
(2 + k)x – (5 + 3k)y + (1 – 4k) = 0 …………. (1)
Intercepts on co-ordinate axes are equal
2 + k = -5 – 3k
4k = – 7 ⇒ k = -7/4
Substituting in (1)
Equation of the required line is
(2 – \(\frac{7}{4}\))x – (s – \(\frac{21}{4}\))y+ (1 + 7) = 0
\(\frac{1}{4}\) x + \(\frac{1}{4}\)y + 8 = 0
⇒ x + y + 32 = 0

Question 12.
Find the length of the perpendicular drawn from the point of intersection of the lines 3x + 2y + 4 = 0 and 2x + 5y – 1 = 0 to the straight line 7x + 24y -15 = 0.
Solution:
Equation of the given lines
3x + 2y + 4 = 0
2x + 5y – 1 = 0

x = \(\frac{-22}{11}\) = -2, y = \(\frac{11}{11}\) = 1
Co-ordinates of P are (-2, 1)
Equation of the line is 7x + 24y- 15 = 0
Length of the perpendicular

Question 13.
Find the value of ‘a’ if the distances of the points (2, 3) and (-4, a) from the straight line 3x + 4y – 8 = 0 are equal.
Solution:
Equation of P’Q’ is 3x + 4y – 8 = 0 P (2, 3), Q (- 4, a) are the given points
PP’ and QQ’ are the perpendicular from P and Q.

PP’ = QQ’
\(\frac{|3.2+4.3-8|}{\sqrt{9+16}}=\frac{|3 .(-4)+4 a-8|}{\sqrt{9+16}}\)
10 = |4a – 20|
4a – 20 = ±10 ⇒ 4a = 20 ± 10 = 30 or 10
a = \(\frac{30}{4}\) or \(\frac{10}{4}\)
i.e., a = \(\frac{15}{2}\) oe \(\frac{5}{2}\)

Question 14.
Find the circumcentre of the triangle formed by the straight lines x + y = 0, 2x + y + 5 = 0 and x – y = 2.
Solution:
Equation of AB is x + y = 0 ………….. (1)
Equation of BC is 2x + y + 5 = 0 ………….. (2)
Equation of AC is x – y = 2 ………….. (3)

Solving (1) and (2) co-ordinates of D are (-5, 5)
Solving (2) and (3) co-ordinates of C are (-1, -3)
Solving (1) and (3) co-ordinates of A are (1, -1)
Suppose S(x, y) is the circumcentre
SA = SB = SC
SA = SB ⇒ SA² = SB²
(x + 5)² + (y – 5)² = (x + 1)² + (y + 3)²
x² + 10x + 25 + y² – 10y + 25
= x² + 2x + 1 + y² + 6y + 9
8x – 16y = -40
x – 2y = -5 ………… (1)
SB = SC ⇒ SB² = SC²
(x+ 1)² + (y + 3)² = (x -1)² + (y + 1)²
x² + 2x + 1 + y² + 6y+9
= x² – 2x + 1 + y² + 2y + 1
4x + 4y = -8
x + y = -2 …………… (2)
(2) – (1) gives 3y = 3 ⇒ y = 1
x + 1 = -2 ⇒ x = -3
Circumcentre is S(-3, 1)

Question 15.
If 6 is the angle between the lines \(\frac{x}{a}+\frac{y}{b}=1\) and \(\frac{x}{b}+\frac{y}{a}=1\) , find the value of sin 0 when a > b.
Solution:
Equation of AB is. \(\frac{x}{a}+\frac{y}{b}=1\) ⇒ bx + ay = ab
Equation of AC is. \(\frac{x}{b}+\frac{y}{a}=1\) ⇒ ax + by = ab

II.

Question 1.
Find the equation of the straight lines passing through the point (-10, 4) and making an angle 0 with the line x – 2y = 10 such that tan θ = 2.
Solution:
Equation of QR is x – 2y = 10

Suppose slope of PQ is m, PQ passes through P(-10, 4)
Equation Of PQ is y – 4 = m(x + 10)
= mx + 10m
i.e., mx-y + (10m + 4) = 0 …………… (1)
tan θ = 2 ⇒ cos θ = \(\frac{1}{\sqrt{5}}\)

Squaring and cross multiplying
m² + 1 = (m + 2)²
= m² + 4m + 4
4m + 3 = 0
m = –\(\frac{3}{4}\)

Case (i) : Co-efficient of m² = 0
⇒ One of the roots is ∞
Hence PR is a vertical line
∴ Equation of PR is x + 10 = 0

Case (ii): m = –\(\frac{3}{4}\)
Substituting in (1)
Equation of PQ is – \(\frac{3}{4}\)x – y + (\(\frac{30}{4}\) + 4) = 0
\(\frac{-3 x-4 y-14}{4}=0\)
⇒ 3x + 4y + 14 = 0

Question 2.
Find the equation of the straight lines pass-ing through the point (1, 2) and making an angle of 60° with the line √3x + y + 2 = 0.
Solution:
Equation of QR is √3x + y + 2 = 0

PQ and PR passes through P( 1, 2) and makes an angle of 60° with QR
Suppose slope of PQ is m.
Equation of PQ is
y – 2 = m(x – 1)
= mx – m
mx – y + (2 – m) = 0 ……………. (1)

Squaring and cross multiplying
m² + 1 = (√3 – 1)²
= 3m² + 1 – 2√3m
2m² – 2√3m = 0
2m(m – √3) = 0
m = 0 or √3

Case (i) : m = 0
Equation of PQ is -y+2 = 0 or y-2 = 0

Case (ii): m = √3
Equation of PQ is √3x – y + (2 – √3) = 0

Question 3.
The base of an equilateral triangle is x + y – 2 = 0 and the opposite vertex is (2, -1). Find the equation of the remaining sides.
Solution:
ABC is an equilateral triangle.
∴ ∠B = C = 60°

Equation of BC is x + y – 2 = 0
AB passes through A(2, -1)
Suppose slope of AB = m
Equation of AB is
y + 1 = m(x – 2)
= mx – 2m
mx – y – (2m + 1) = 0 …………. (1)

Squaring and cross multiplying
m² + 1 = 2 (m – 1)² = 2 (m² – 2m + 1)
= 2m² – 4m + 2
m² – 4m +1 = 0
\(m=\frac{4 \pm \sqrt{16-4}}{2}=\frac{4 \pm 2 \sqrt{3}}{2}=2 \pm \sqrt{3}\)
Substituting in (1)
Equation of AB is y + 1 = (2 + √3) (x – 2)
Equation of AC is y + 1 = (2 – √3) (x – 2)

Question 4.
Find the orthocentre of the triangle with following vertices.
i) (-2, -1), (6, -1) and (2, 5)
ii) (5,-2), (-1, 2) and (1, 4)
Solution:
i) A(-2, -1), B(6, -1), C(2,5) are the vertices of ∆ ABC.

Slope of BC = \(\frac{5+1}{2-6}=\frac{6}{-4}=-\frac{3}{2}\)
AD is perpendicular to BC
Slope of AD = \(\frac{2}{3}\)
Equation of AD is
y + 1 = \(\frac{2}{3}\) (x + 2)
2x – 3y + 1 = 0 …………….. (1)
Slope of AC = \(\frac{5+1}{2+2}=\frac{6}{4}=\frac{3}{2}\)
BE is ⊥^lr to AC
Slope of BE = –\(\frac{2}{3}\)
Equation of BE is
y + 1 = – \(\frac{2}{3}\)(x – 6)
2x + 3y – 9 = 0 …………. (2)
By solving (1),(2)

∴ Co-ordinates of the orthocentre
O are = (2, \(\frac{5}{3}\))

ii) (5, -2), (-1, 2) and (1, 4)
A(5, -2), B(-1, 2), C(1, 4) are the vertices of ∆ ABC.
Slope of BC = \(\frac{2-4}{-1-1}=\frac{-2}{-2}=1\)
AD is perpendicular to BC

Slope of AD = –\(\frac{1}{m}\) = -1 m
Equation of AD is
y + 2 = -(x – 5)
= -x + 5
x + y – 3 = 0 …………. (1)
Slope of AC = \(\frac{4+2}{1-5}=\frac{6}{-4}=-\frac{3}{2}\)
BE is perpendicular to AC
Slope of BE is –\(\frac{1}{m}\) = \(\frac{2}{3}\)
Equation of BE is y – 2 = j(x + 1)
3y – 6 = 2x + 2
2x – 3y + 8 = 0 ……….. (2)
From (1), (2) by cross – multiplication law

Co-ordinates of the Orthocentre O are (\(\frac{1}{5}\), \(\frac{14}{5}\))

Question 5.
Find the clrcumcentre of the triangle whose vertices are given below.
i) (-2, 3) (2, -1) and (4, 0)
ii) (1, 3), (0, -2) and (-3, 1)
Solution:
i) A(-2, 3), B(2, -1), C(4, 0) are the vertices of ∆ ABC.
D is the midpoint of BC

Co-ordinates of D are (\(\frac{2+4}{2}\), \(\frac{-1+0}{2}\)
= (3, \(\frac{-1}{2}\))
Slope of BC = \(\frac{-1-1}{2-4}=\frac{-1}{-2}=\frac{1}{2}\)
SD is perpendicular to BC
Slope of SD = –\(\frac{1}{m}\) = -2
Equation of SD is y + \(\frac{1}{2}\) = -2(x – 3)
2y + 1 = -4(x – 3)
= -4x+ 12
4x + 2y – 11 = 0 ………….. (1)
E is the midpoint of AC
Co-ordinates of E are (\(\frac{-2+4}{2}\), \(\frac{3+0}{2}\)) = (1, \(\frac{3}{2}\))
Slope of AC = \(\frac{3-0}{-2-4}=-\frac{3}{6}=-\frac{1}{2}\)
SE is perpendicular to AC
Slope of SE = –\(\frac{1}{m}\) = 2
Equation of SE is y – \(\frac{3}{2}\) = 2(x – 1)
2y- 3 = 4(x- 1)
= 4x – 4
4x – 2y – 1 = 0 ……………. (2)
4x + 2y – 11 = 0 ……………. (1)
Adding (1), (2) ⇒ 8x- 12 = 0
8x = 12
x = \(\frac{12}{8}\) = \(\frac{3}{2}\)
Substituting in (1)
2y = 11 – 4x = 11 – 4 . \(\frac{3}{2}\) = 11 – 6 = 5
y = \(\frac{5}{2}\)
∴ Co-ordinates of S are (\(\frac{3}{2}\), \(\frac{5}{2}\))

ii) (1, 3), (0, -2) and (-3, 1)

In ∆ ABC,
A = (1, 3), B = (0, -2), C = (-3, 1)
D is the midpoint of BC

SD is ⊥^lr to BC
Slope of SD = 1
Equation of SD is
y + \(\frac{3}{2}\) = 1(x + \(\frac{3}{2}\))
⇒ 2y + 1 = 2x + 3
⇒ 2x – 2y + 2 = 0
⇒ x – y + 1 = 0 …………… (1)
E is the midpoint of CA
⇒ E = (\(\frac{-3+1}{2}\), \(\frac{1+3}{2}\)) = (-1, 2)
Slope of CA = \(\frac{1-3}{-3-1}\) = \(\frac{1}{2}\)
SE is ⊥^lr to CA
Slope of SE = -2
Equation of SE is
y – 2 = -2(x + 1)
⇒ y – 2 = -2x – 2
⇒ 2x + y = 0 …………….. (2)
By solving (1), (2)

Question 6.
Let \(\overline{\mathrm{P S}}\) be the median of the triangle with vertices P(2, 2) Q(6, -1) and R(7, 3). Find the equation of the straight line passing through (1, -1) and parallel to the median \(\overline{\mathrm{P S}}\).

Solution:
P(2, 2), Q(6, -1), R(7, 3) are the vertices of ∆ ABC.
S is the mid point of QR

AB is parallel to PS and passes through A(1, -1)
Equation of AB is y + 1 = – \(\frac{2}{9}\) (x – 1)
9y + 9 = -2x + 2
2x + 9y + 7 = 0

III.

Question 1.
Find the orthocentre of the triangle formed by the lines.
x + 2y = 0, 4x + 3y – 5 = 0 and 3x + y = 0.

Solution:
Equation of AB is x + 2y = 0 ………….. (1)
Equation of BC is 4x + 3y – 5 = 0 ………….. (2)
Equation of AC is 3x + y = 0 ………….. (3)
Solving (1) and (2) Co-ordinates of A are (0, 0)

4x – 8 = 0 ⇒ 4x = 8, x=2
Co-ordinates of B are (2, -1)
Equation of BC is 4x + 3y – 5 = 0
AB is perpendicular to BC and passes through A(0, 0)
Equation of AB is 3x – 4y = 0 ……….. (1)
BE is perpendicular to AC
∴ Equation of BE is x – 3y = k
BE passes through B (2, -1)
2 + 3 = k ⇒ k = 5
Equation of BE is x – 3y – 5 = 0 …………………. (2)

x = – 4, y = -3
∴ Orthocentre is O (- 4, -3)

Question 2.
Find the circumcentre of the triangle whose sides are given by x + y + 2 = 0, 5x – y – 2 = 0 and x – 2y + 5 = 0.
Solution:
Given lines are
x + y + 2 = 0 ………………. (1)
5x – y – 2 = 0 ………………. (2)
x – 2y + 5 = 0 ……………… (3)
Point of intersection of (1) and (2) is A = (0, -2)
Point of intersection of (2) and (3) is B = (1, 3)
Point of intersection of (1) and (3) is C = (-3, 1)
Let S = (α, β) the orthocentre of ∆ ABC then
SA = SB = SC
⇒ SA² = SB² = SC²
⇒ (α – 0)² + (β + 2)² = (α – 1)² + (β – 3)² = (α + 3)² + (β – 1)²

(a) = (b) ⇒ α² + β² + 4β + 4 = α² + β² – 2α – 6β + 10
⇒ 2α + 10β – 6 = 0
⇒ α + 5β – 3 = 0 ………. (4)

(a) = (c) => α² + β² + 4β + 4 = α² + β² + 6α – 2β + 10
⇒ 6α – 6β + 6 = 0
⇒ α – β + 1 = 0 ………….. (5)
From (4) and (5)

Question 3.
Find the equation of the straight lines passing through (1, 1) and which are at a distance of 3 units from (-2, 3).
Solution:
AB passes through A(1, 1)
Suppose slope of AB is m
Equation of AB is y – 1 = m(x – 1)
= mx – m
mx – y + (1 – m) = 0 ………….. (1)
Distance from (-2, 3) on AB = 3
\(\frac{|-2 m-3+1-m|}{\sqrt{m^{2}+1}}=3\)
Squaring and cross multiplying
(3m + 2)² = 9(m² + 1)
9m² + 4 + 12m = 9m² + 9
12m = 5 ⇒ m = \(\frac{5}{12}\)
Co-efficient of m² = 0 ⇒ m = ∞

i) m = ∞
AB is a vertical line
Equation of AB is x = a
AB passes through A(1, 1)
∴ a = 1
Equation of AB is x = 1 S

ii) m = \(\frac{5}{12}\)
substituting in (1),
Equation of AB is \(\frac{5}{12}\)x – y + [1 – \(\frac{5}{12}\)] = 0
\(\frac{5}{12}\)x – y + \(\frac{7}{12}\) = 0
5x – 12y + 7 = 0

Question 4.
If P and q are the lengths of the perpen-diculars from the origin to the straight lines x sec α + y cosec α = a and x cos α – y sin α = a cos 2α, prove that 4p² + q² = a².
Solution:
Equation of AB is x sec α + y cosec α = a
\(\frac{x}{\cos \alpha}+\frac{y}{\sin \alpha}=a\)
x sin α + y cos α = a sin α cos α
x sin α + y cos α – a sin α cos α = 0
p = length of the perpendicular from O on AB

2p = asin 2α …………. (1)
Equation of CD is x cos α – y sin α = a cos 2α
x cos α – y sin α – a cos 2α = 0
q = Length of the perpendicular from O on CD
\(\frac{|0+0-a \cos 2 \alpha|}{\sqrt{\cos ^{2} \alpha+\sin ^{2} \alpha}}\) = cos2α ………. (2)
Squaring and adding (1) and (2)
4p² + q² = a² sin² 2α + a² cos² 2α
= a2 (sin² 2α + cos² 2α)
= a².1
= a²

Question 5.
Two adjacent sides of a parallelogram are given by 4x + 5y = 0 and 7x + 2y = 0 and one diagonal is 11x + 7y = 9. Find the equations of the remaining sides and the other diagonal.
Solution:
Let 4x + 5y = 0 ………… (1) and
7x + 2y – 0 ………… (2) respectively
denote the side \(\stackrel{\leftrightarrow}{O A}\) and \(\stackrel{\leftrightarrow}{O B}\) of the parallelo-gram OABC.
Equation of the diagonal \(\stackrel{\leftrightarrow}{A B}\) is 1 lx + 7y – 9 = 0 ………. (3)

Solving (1) and (2) vertex O = (0, 0)
Solving (1) and (3), we get
Solving (2) and (3), we get

Midpoint of AB is P (\(\frac{1}{2}\), \(\frac{1}{2}\)), Slope of OP is 1.
Equation to OC is y = (1)x = x – y = 0
x = y

Question 6.
Find the incenter of the triangle formed by the following straight line.
i) x + 1 = 0, 3x- 4y = 5 and 5x + 12y = 27
ii) x + y – 7 =0, x – y + 1 = 0 and x – 3y + 5 = 0
Solution:
i)

In ∆ ABC,
Equation of side AC is
x + 1 = 0 ……… (1)
Equation of side AB is
3x – 4y – 5 = 0 ……………. (2)
Equation of side BC is
5x + 12y – 27 = 0 ………… (3)
From (1), x = – 1
Substitute in (2) ⇒ 3 (-1) – 4y – 5 = 0
4y = -8
y = -2
The point of intersection of (1), (2) is A =(-1, -2)
By solving (2), (3)

The point of intersection of (2), (3) is B = (3, 1)
From (1) x = -1
Substitute in (3)
-5 + 12y – 27 =0
12y = 32
y = \(\frac{32}{12}=\frac{8}{3}\)
The point of intersection of (3), (1) is

Incentre = I =

ii)

In ∆ ABC,
Equation of AC is x + y – 7 = 0 ………… (1)
Equation of AB is x – y + 1 = 0 ………… (1)
Equation of BC is x – 3y + 5 = 0 ………… (1)
solving (1) (2) and (3)
verti and A (3, 4) B (1, 2) and C (4, 3)

Question 7.
A ∆^le is formed by the lines ax + by + c = 0, lx + my + n = 0 and px + qy + r = 0. Given that the ∆^le is not right angled, show that the straight line \(\frac{a x+b y+c}{a p+b Q}=\frac{l x+m y+n}{I p+m Q}\) passes through the orthocentre of the ∆^le.
Solution:
Given sides of triangle are

ax+by+c /x+mv+y
ax + by + c = 0 ………… (1)
lx + my + n = 0 ………… (2)
px + qy + r = 0 ………… (3)
Equation of line passing through intersecting points of (1), (2) is
ax + by + c + k (lx + my + n) = 0 ………… (4)
(a + ki) x + (b + km)y + (c + nk) = 0
It is ⊥^lr to (3), then
p(a + kl) + q(b + km) = 0
⇒ k = –\(\frac{a P+b Q}{l p+m Q}\)
Substitute in (4)

is the required straight line equation of AD This is the altitude passing through A.

Passes through the othrocentre of the triangle.

Question 8.
The Cartesian equations of the sides \(\overrightarrow{B C}\) , \(\overrightarrow{C A}\) and \(\overrightarrow{A B}\) of a ∆^le are respectively u₁ = a₁x + b₁y + c1 = 0, r = 1, 2, 3. Show that the equation of the straight line passing through A and bisecting the side \(\overline{\mathrm{B C}}\) is \(\frac{u_{3}}{a_{3} b_{1}-a_{1} b_{3}}=\frac{u_{2}}{a_{3} b_{1}-a_{1} b_{3}}\)
Solution:
A is a point of intersection of the lines u₂ = 0 and u₃ = 0
∴ The equation to a line passing through A is
u₂ + λu₃ = 0 ⇒ (a₂x + b₂y + c₂) + λ(a₃x + b₃y + c₃) = 0 ………….. (1)
⇒ (a₂ + λa₃)x + (b₂ + λb₃) y + (c₂ + λc₃) = 0
If this is parallel to a₁x + b₁y + c₁ = 0, we get
\(-\frac{\left(a_{2}+\lambda a_{3}\right)}{\left(b_{2}+\lambda b_{3}\right)}=-\frac{a_{1}}{b_{1}}\)
⇒ (a₂ + λa₃) b₁ = (b₂ + λb₃) a₁
⇒ a₂b₁ + λa₃b₁ = a₁b₂ + λa₁b₃
⇒ λ(a₃b₁ – a₁b₃) = – (a₂b₁ – a₁b₂) .
⇒ λ = \(\frac{\left(a_{2} b_{1}-a_{1} b_{2}\right)}{a_{3} b_{1}-a_{1} b_{3}}\)
Substituting this value of X in (1), the required equation is
(a₂x + b₂y + c₂) – \(\frac{\left(a_{2} b_{1}-a_{1} b_{2}\right)}{\left(a_{3} b_{1}-a_{1} b_{3}\right)}\) (a₃x + b₃y + c₃) = 0
⇒ (a₃b₁ – a₁b₃) (a₂x + b₂y + c₂) – (a₂b₁ – a₁b₂) (a₃x + b₃y + c₃) = 0
⇒ (a₃b₁ – a₁b₃)u₂ – (a₂b₁ – a₁b₂) u₃ = 0
⇒ (a₃b₁ – a₁b₃)u₂ = (a₂b₁ – a₁b₂)u₃
⇒ \(\frac{u_{3}}{\left(a_{3} b_{1}-a_{1} b_{3}\right)}=\frac{u_{2}}{\left(a_{2} b_{1}-a_{1} b_{2}\right)}\)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(d)

I. Find the angle between the following straight lines.

Question 1.
y = 4 – 2x, y = 3x + 7
Solution:
y = 4 – 2x ⇒ 2x + y – 4 = 0
3x – y + 7 = 0

Question 2.
3x + 5y = 7, 2x – y + 4 = 0
Solution:

Question 3.
y = – √3 + 5, y = \(\frac{1}{\sqrt{3}} x-\frac{2}{\sqrt{3}}\)
Solution:
m₁ = √3, m₂= \(\frac{1}{\sqrt{3}}\)
m₁m₂ = (-√3).\(\frac{1}{\sqrt{3}}\) = 1
The lines are perpendicular θ = \(\frac{\pi}{2}\)

Question 4.
ax + by = a + b, a(x-y) + b(x + y) = 2b
Solution:
ax + by = a + b, (a + b) x + (- a + b) y = 2b

Find the length of the perpendicular drawn from the point given against the following straight lines.

Question 5.
5x – 2y + 4 = 0, (-2, -3)
Solution:
Length of the perpendicular

Question 6.
3x – 4y + 10 = 0, (3, 4)
Solution:
Length of the perpendicular
\(=\frac{|3.3-4.4+10|}{\sqrt{9+16}}=\frac{3}{5}\)

Question 7.
x – 3y – 4 = 0, (0,0)
Solution:
Length of the perpendicular
\(=\frac{|0-0-4|}{\sqrt{1+9}}=\frac{4}{\sqrt{10}}\)

Find the distance between the following parallel lines.

Question 8.
3x – 4y = 12, 3x – 4y = 7
Solution:
Equation of the lines are
3x – 4y – 12 = 0
3x – 4y – 7 = 0

Distance between parallel lines
\(=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}=\frac{|-| 2+7 \mid}{\sqrt{9+16}}=\frac{5}{5}=1\)

Question 9.
5x – 3y – 4 = 0, 10x – 6y – 9 = 0
Solution:
Equations of the lines can be taken as
10x – 6y – 8 = 0
10x – 6y – 9 = 0

Distance between parallel lines
\(=\frac{|-8+9|}{\sqrt{100+36}}=\frac{1}{2 \sqrt{34}}\)

Question 10.
Find the equation of the straight line parallel to the line 2x + 3y 4- 7 = 0 and passing through the point (5, 4).
Solution:
Equation of the given line is 2x + 3y + 7 = 0
The required line is parallel to this line
Equation of the parallel line is 2x + 3y = k
This line passes through p (5, 4)
10 + 12 = k ⇒ k = 22
Equation of the required line is
2x + 3y = 22
2x + 3y — 22 = 0

Question 11.
Find the equation of the straight line per-pendicular to the line 5x – 3y + 1 = 0 and passing through the point (4, – 3).
Solution:
Equation of the given line is 5x – 3y + 1 = 0
Equation of the perpendicular line is 3x + 5y + k = 0
This line passes through P (4, -3)
12 – 15 + k = 0 ⇒ k = 3
Equation of the required line is
3x + 5y + 3 = 0

Question 12.
Find the value of k, if the straight lines 6x – 10y + 3 = 0 and kx – 5y + 8 = 0 are parallel.
Solution:
Equations of the given lines are
6x – 10y + 3 = 0
kx – 5y + 8 = 0
These lines are parallel
a₁b₂ = a₂b₁
-30 = -10 k
k = 3

Question 13.
Find the value of p, if the straight lines 3x 4- 7y – 1 = 0 and 7x – py + 3 = 0 are mutually perpendicular.
Solution:
Equations of the given lines are
3x + 7y – 1 = 0
7x – py + 3 = 0
These lines are perpendicular
⇒ a₁a₂ + b₁b₂ = 0
3.7 + 7(- p) = 0
7p = 21 ⇒ p = 3

Question 14.
Find the value of k, if the straight lines y – 3kx + 4 = 0 and (2k-1) x-(8k-1) y – 6 = 0 are perpendicular.
Solution:
Equations of the given lines are
-3kx + y + 4 = 0
(2k- 1)x- (8k- 1)y- 6 = 0
These lines are perpendicular
⇒ -3k(2k – 1) – 1(8k – 1) = 0
– 6k² +.3k – 8k +1 = 0
6k² + 5k – 1 = 0
(k + 1) (6k – 1) = 0
k = -1 or 1/6

Question 15.
(- 4,5) is a vertex of a square and one of its diagonal is 7x – y + 8 = 0. Find the equation of the other diagonal.

Solution:
ABCD is a square Equation of the diagonal AC is 7x – y + 8 = 0
The other diagonal BD is perpendicular to AC.
Equation of BD can be taken asx + 7y + k = 0
BD passes through D (- 4, 5)
-4 + 35 + k = 0 ⇒ k = 4-35 = -31
Equation of BD is x + 7y- 31 = 0

II.

Question 1.
Find the equations of the straight lines passing through (1, 3) and i) parallel to ii) perpendicular to the line passing through the points (3, -5) and (-6,1).

Solution:
A (3, -5), B(- 6, 1) are the given points
Slope of AB = \(\frac{-5-1}{3+6}=\frac{-6}{9}=\frac{-2}{3}\)

i) The required line is parallel to AB and passes through (1, 3)
Equation of the required line is
y – 3 = \(\frac{-2}{3}\)(x – 1)
3y – 9 = -2x + 2
2x + 3y – 11 = 0

ii) The required line AE is perpendicular to AD.
Equation of AE can be taken as 3x – 2y + k = 0
This line passes through A (1, 3)
3 – 6 + k = 0 ⇒ k = 6 – 3 = 3
Equation of AE is 3x – 2y + 3 = 0.

Question 2.
The line \(\frac{x}{a}-\frac{y}{b}\) = 1 meets the X-axis at P. Find the equation of the line perpen-dicular to this line at P.
Solution:

Equation of PQ is \(\frac{x}{a}-\frac{y}{b}\) = 1
Equation of X-axis is y = 0
\(\frac{x}{a}\) = 1 ⇒ x = a
Co-ordinates of P are (a, 0)
PR is perpendicular to PQ
Equation of PR = \(\frac{x}{b}+\frac{y}{a}\) = k
This line PR passes through P is (a, 0) a
\(\frac{a}{b}\) + 0 = k ⇒ k = a/b
Equation of PR is \(\frac{x}{b}+\frac{y}{a}=\frac{a}{b}\) = 1

Question 3.
Find the equation of the line perpendi-cular to the line 3x + 4y + 6 = 0 and making an intercept – 4 on X-axis.
Solution:
Equation of the given line is 3x + 4y + 6 = 0
Equation of the perpendicular line is
4x – 3y = k
\(\frac{4x}{k}-\frac{3y}{k}\) = 1
\(\frac{x}{\left(\frac{k}{4}\right)}+\frac{y}{\left(-\frac{k}{3}\right)}=1\)
x – intercept = \(\frac{k}{4}\) = – 4 ⇒ k = -16
Equation of the required line is 4x – 3y = -16
⇒ 4x – 3y + 16 = 0

Question 4.
A (-1,1), B (5, 3) are opposite vertices of a square in the XY plane. Find the equation of the other diagonal, (not passing through A, B) of the square.
Solution:
A (-1, 1), B (5, 3) are opposite vertices of the square.
Slope of AB \(\frac{1-3}{-1-5}=\frac{-2}{-6}=\frac{1}{3}\)

The other diagonal perpendicular to AB
Slope of CD = – \(\frac{1}{m}\) = -3 m
‘O’ is the point of intersection of the diagonals
Co-ordinates of O are\(\left(\frac{-1+5}{2}. \frac{1+3}{2}\right)\) = (2, 2)
CD passes through O (2, 2)
Equation of CD is y – 2 = -3 (x – 2)
= -3x + 6
3x + y – 8 = 0

Question 5.
Find the foot of the perpendicular drawn from (4, 1) upon the straight line 3x – 4y + 12 = 0.
Solution:
Equation of the line is 3x – 4y + 12 = 0
If (x₂, y₂) is the foot of the perpendicular from (x₁, y₁) on the line
ax + by + c = 0, then

Question 6.
Find the foot of the perpendicular drawn from (3, 0) upon the straight line 5x + 12y – 41 = 0.
Solution:
Equation of the line is 5x + 12y – 41 = 0
If (x₂, y₂) is the foot of the perpendicular from (x₁, y₁) on the line ax + by + c = 0,

Question 7.
x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining the points A, B. If A = (-1, -3), find the co-ordinates of B.

Solution:
If PQ is the perpendicular bisector of AB, then B is the image of A in the line PQ.
Equation of PQ is x – 3y – 5 = 0

Co-ordinates of A are (-1, -3)
If (x₂, y₂) is the image of (x₁, y₁) about the line ax + by + c = 0, then

Question 8.
Find the image of the point (1, 2) in the straight line 3x + 4y – 1 = 0,
Solution:
Equation of the line is 3x + 4y – 1 = 0 ‘
If (x₂, y₂) is the image of (x₁, y₁) in the line ax + by + c = 0, then

Question 9.
Show that the distance of the point (6, – 2) from the line 4x + 3y = 12 is half the distance of the point (3,4) from the line 4x – 3y = 12.
Solution:

Equation of AB is 4x + 3y – 12 = 0
PQ = Length of the perpendicular from
\(P=\frac{|24-6-12|}{\sqrt{16+9}}=\frac{6}{5}\)
Equation of CD is 4x – 3y – 12 = 0
RS = Length of the perpendicular from
\(R=\frac{|12-12-12|}{\sqrt{16+9}}=\frac{12}{5}\)
∴ PQ = \(\frac{1}{2}\)RS

Question 10.
Find the locus of the foot of the perpendi¬cular from the origin to a variable straight line which always passes through a fixed point (a, b).

Solution:
Suppose m is the slope of the line AB
Equation of AB is y – b = m (x – a)
= mx – ma
mx – y + (b – ma) = 0 ……………. (1)

OK is perpendicular to A B and passes through the origin O. Suppose co-ordinates of K are (x, y)
Equation of AB is x + my – 0 ……………. (2)

m = -x/y
Substituting in (1)
\(-\frac{x^{2}}{y}-y+b+\frac{x}{y} \cdot a=0\).
– x² – y² + by + ax = 0
or x² + y² – ax – by = 0
Locus of K is x² + y² – ax – by = 0

III.

Question 1.
Show that the lines x – 7y – 22 = 0, 3x + 4y + 9 = 0 and 7x + y – 54 = 0 form a right angled isosceles triangle.
Solution:
Given lines x – 7y – 22 = 0 …………. (1)
3x + 4y + 9 = 0 …………. (2)
7x + y – 54 = 0 …………. (3)

Let ‘A’ be the angle between (1), (2)

Let B be the angle between (2), (3)

Let ‘C’ be the angle between (3), (1)

∴ Given lines form a right angled isosceles triangle.

Question 2.
Find the equation of the straight lines passing through the point (-3, 2) and making an angle of 45° with the straight line 3x – y + 4 = 0.
Solution:
Given point
P(x₁, y₁) = (-3, 2)
Given line 3x – y + 4 = 0 ………….. (1)
Slope = m = – \(\frac{a}{b}\) = 3

m – 3 = -1 + 3m
2m = – 4 or m = -2
\(\frac{m-3}{1+3 m}\) = -1 ⇒ m – 3 = -1 – 3m
4m = 2 ⇒ m = 1/2
Case (i) m = – 2
Equation of the line PQ is
y – 2 = -2(x+3)
= -2x – 6
2x + y + 4 = 0

Case (ii) m =\(\frac{1}{2}\)
Equation of the line PR is
y – 2 = \(\frac{1}{2}\) (x + 3)
2y – 4 = x + 3
x – 2y + 7 = 0

Question 3.
Find the angles of the triangle whose sides are x + y- 4 = 0,2x + y- 6 = 0, 5x + 3y -15 = 0.
Solution:
Equation of AB is x + y – 4 = 0
Equation of BC is 2x + y – 6 = 0
Equation of AC is 5x + 3y – 15 = 0

Question 4.
Proye that the feet of the perpendiculars from the origin on the lines x + y = 4, x + 5y = 26 and 15x – 27y = 424 are collinear.
Solution:
Given lines
x + y – 4 = 0 ……… (1)
x + 5y – 26 = 0 ……… (2)
15x – 27y – 424 = 0 ……… (3)

Let P(x₂, y₂) be the foot of the ⊥^le of (x₁, y₁) = (0, 0) on (1)

⇒ x₂ – 0 = 2, y₂ – 0 = 2
⇒ x₂ = 2, y₂ = 2
∴ P = (2, 2)
Let Q(x₃, y₃) be the foot of the ⊥^le of (x₁ y₁) = (0, 0) on (2)

x₃ = 1, y₃ = 5 ⇒ Q = (1, 5)
Let R(x₄, y₄) be the foot of the ⊥^le of (x₁, y₁) = (0, 0) on (3)

Equation of the line through P,Q is
\(\frac{x-2}{1-2}=\frac{y-2}{5-2}\) ⇒ 3x + y – 8 = 0 ………. (4)
Substitute R (x₄, y₄) in (4)
⇒ 3\(\frac{1060}{159}\) – 12 – 8
= 20 – 20 = 0
∴ Foot of perpendiculars of origin on the lines lies on a straight line.

Question 5.
Find the equations of the straight lines passing through the point of intersection of the lines 3x + 2y + 4 = 0,2x + 5y = 1 and whose distance from (2, -1) is 2.
Solution:
Equations of the lines passing through the point of intersection of the line
L₁ ≡ 3x + 2y + 4 = 0, L₃ ≡ 2x + 5y – 1 = 0 is
L₁ + λL₂ = 0
(3x + 2y + 4) + λ (2x + 5y- 1) = 0
(3 + 2λ)x + (2 + 5λ) y + (4 – λ) = 0 ………….. (1)
Given distance from (2, -1) to (1) = 2

⇒ (-λ + 4)2 = 9 + 4λ2 + 12λ + 4 + 25λ2 + 20λ
⇒ 28λ2 + 40λ – 3 = 0
⇒ 28λ2 – 2λ + 42λ – 3 = 0
⇒ (2λ + 3) (14λ – 1) = 0
⇒ λ = \(\frac{1}{14}\), λ = – \(\frac{3}{2}\)
From (1)
If λ = \(\frac{1}{14}\) ⇒ 4x + 3y + 5 = 0
If λ = – \(\frac{3}{2}\)
⇒ y – 1 = 0 are the required line equations.

Question 6.
Each side of a square is of length 4 units. The centre of the square is (3, 7) and one of its diagonals is parallel to y = x. Find the co-ordinates of its vertices.
Solution:
Let ABCD be the square.
Point of intersection of the diagonals is the centre P(3, 7)

From P draw PM⊥AB. Then M is midpoint ofAB
∴ AM = MB = PM = 2
Since a diagonal is parallel to y = x, its sides are parallel to the co-ordinate axes.
M(3, 5) ⇒ A(1, 5), B(5, 5), C(5, 9), D(1, 9)

Question 7.
If ab > 0, find the area of the rhombus enclosed by the four straight lines ax ± by ± c = 0.
Solution:
Equation of AB is ax + by + c = 0 ………….. (1)
Equation of CD is ax + by – c = 0 ………….. (2)
Equation of BC is ax – by + c = 0 ………….. (3)
Equation of AD is ax – by – c = 0 ………….. (4)

Solving (1) and (3), co-ordinates of B are (-\(\frac{c}{a}\) 0)
Solving (1) and (4) co-ordinates of A are (0, –\(\frac{c}{b}\)
Solving (2) and (3) co-ordinates of C are (0, \(\frac{c}{b}\)
Solving (2) and (4) co-ordinates of D are (\(\frac{c}{a}\), 0)
Area of rhombus ABCD = \(\frac{1}{2}\)|∑x₁ (y₂ – y₄)|

Question 8.
Find the area of the parallelogram whose sides are 3x + 4y + 5 = 0, 3x + 4y – 2 = 0, 2x + 3y + 1 = 0 and 2x + 3y – 7 = 0
Solution:
Given sides are 3x + 4y + 5 = 0 ……….. (1)
3x + 4y – 2 = 0 ……….. (2)
2x + 3y + 1 = 0 ……….. (3)
2x + 3y – 7 = 0 ……….. (4)

Area of parallelogram formed by (1), (2), (3), (4)

Question 9.
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path the he should follow.
Solution:
By solving
2x – 3y + 4 = 0
3 x + 4y – 5 = 0

Given line 6x – 7y + 8 = 0
Required line is 7x + 6y + k = 0 …….. (1)

From (1) 7x + 6y – \(\frac{125}{17}\)
119x + 102y – 125 = 0

Question 10.
A ray of light passing through the point (1, 2) reflects on the X – axis at a point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Solution:
Let m be the slope then equation of line passing through (1, 2).
y – 2 = m(x – 1)
\(\frac{y-2}{x-1}=m\)
Let -m be the slope the equation of line passing through (5, 3)
y – 3 = -m(x – 5)