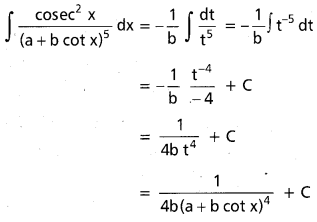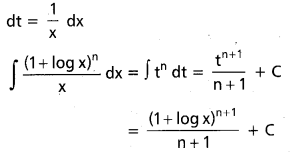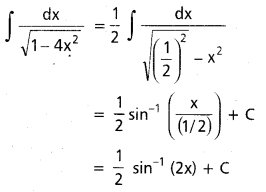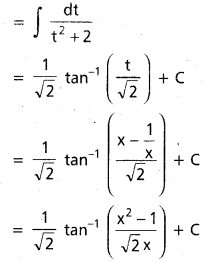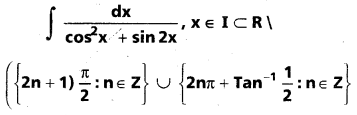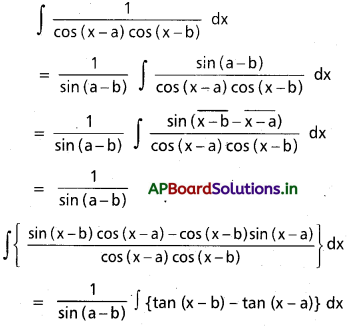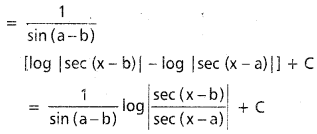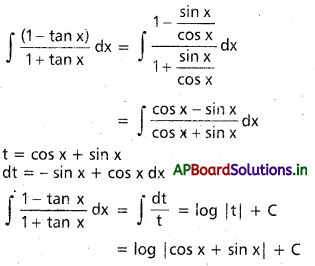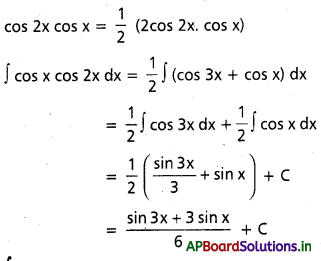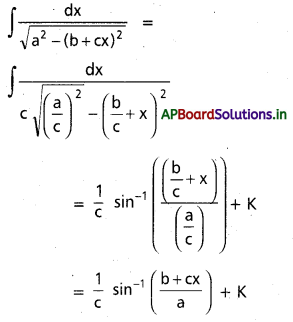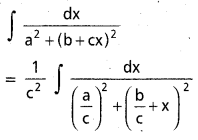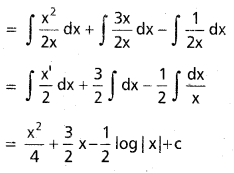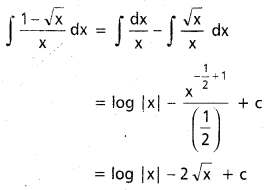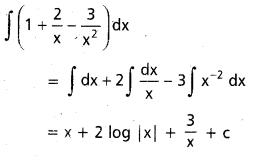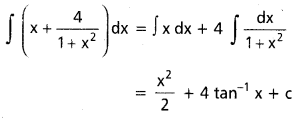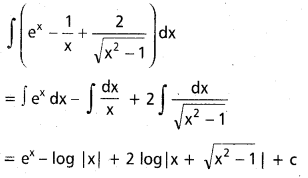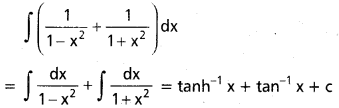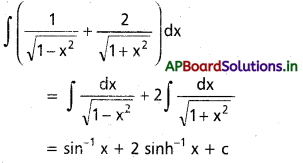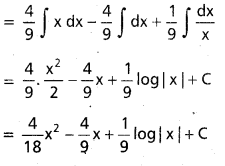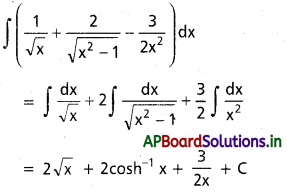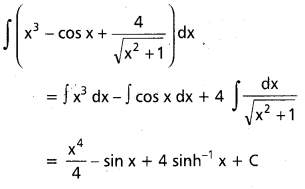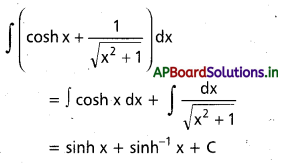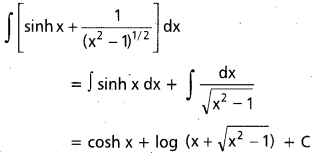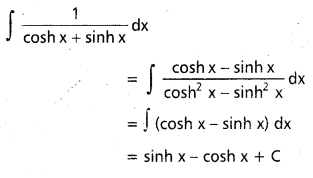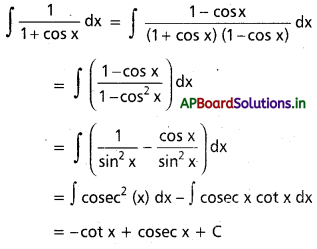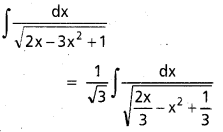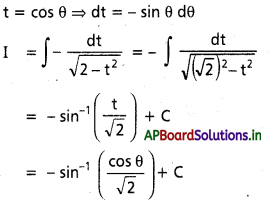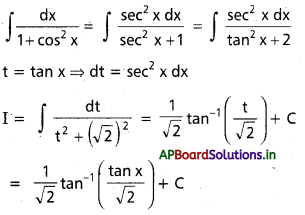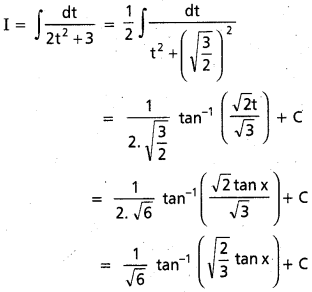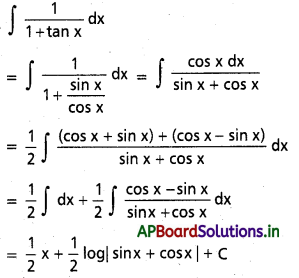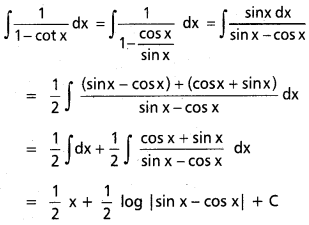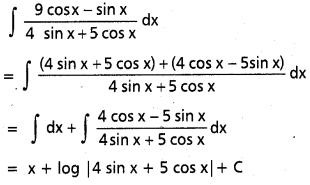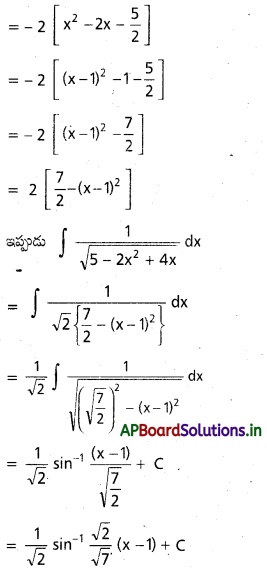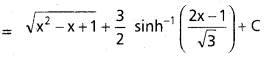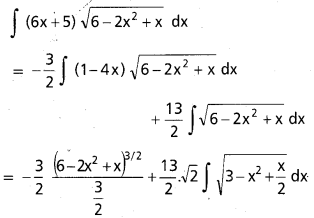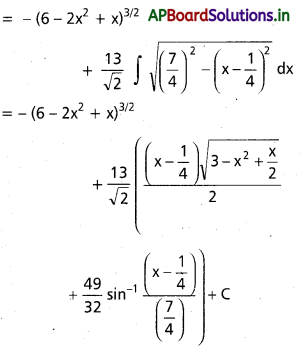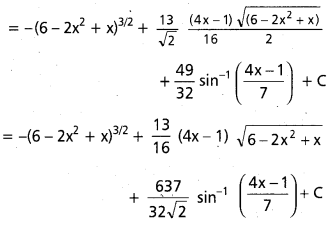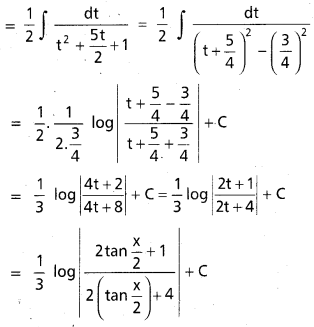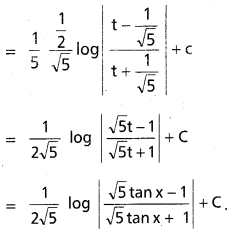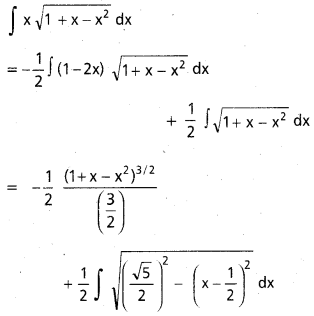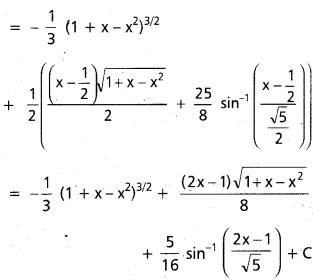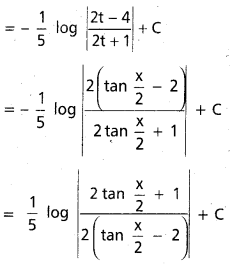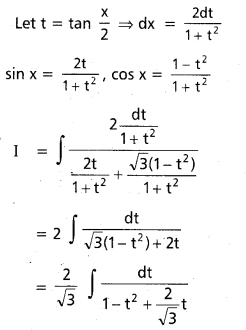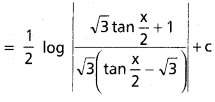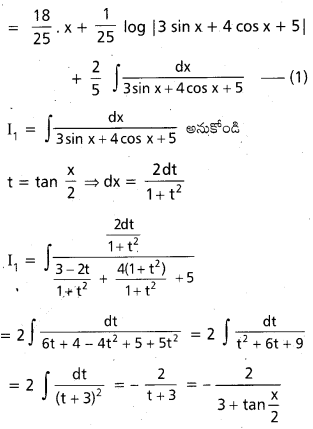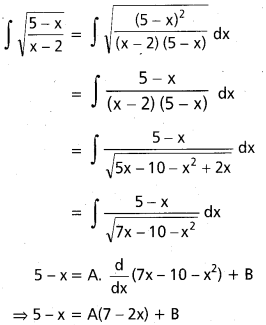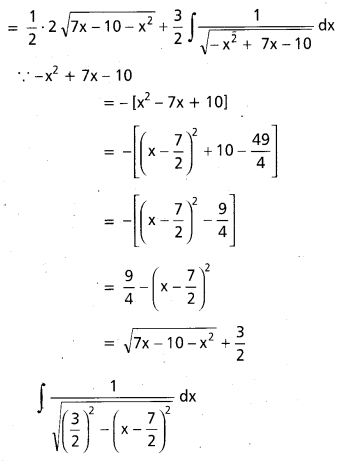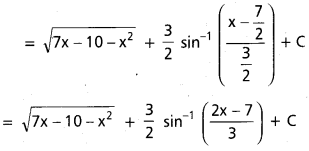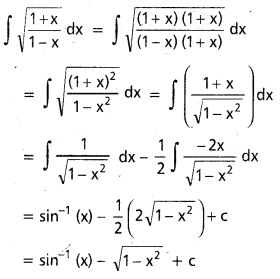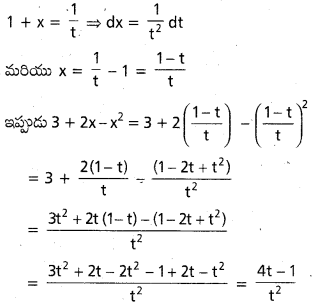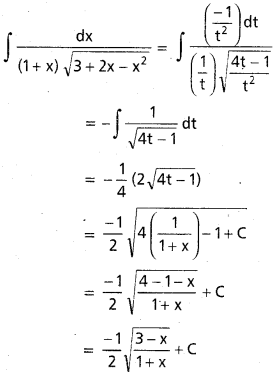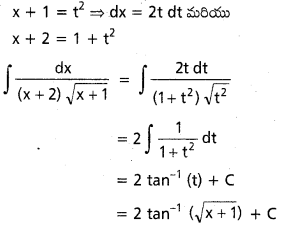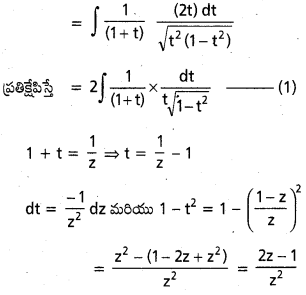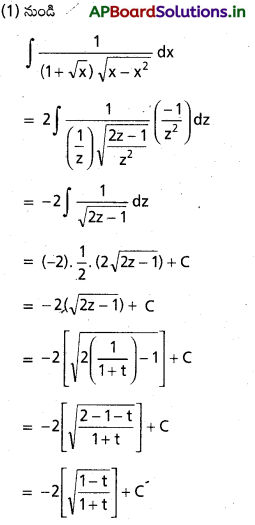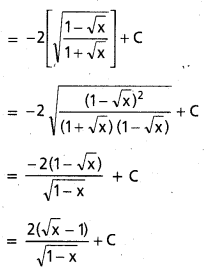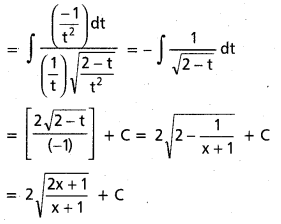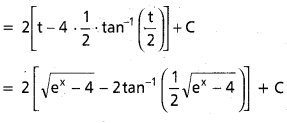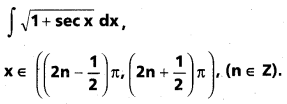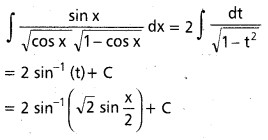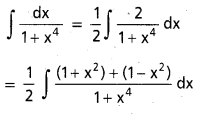Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 6 సమాకలనం Exercise 6(b) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Exercise 6(b)
అభ్యాసం – 6(బి)
I. కింది సమాకలనులను గణించండి.
ప్రశ్న 1.
∫ e2x dx, x ∈ R.
సాధన:
∫ e2x dx = \(\frac{e^{2 x}}{2}\) + C
ప్రశ్న 2.
∫ sin 7x dx, x ∈ R
సాధన:
∫ sin 7x dx = –\(\frac{\cos 7 x}{7}\) + C
ప్రశ్న 3.
∫\(\frac{x}{1+x^2}\) dx, x ∈ R
సాధన:
∫\(\frac{\mathrm{x} \cdot \mathrm{dx}}{1+\mathrm{x}^2}\) = \(\frac{1}{2} \int \frac{2 x d x}{1+x^2}\) = \(\frac{1}{2}\) log (1 + x2) + C

ప్రశ్న 4.
∫2x sin(x2 + 1) dx, x ∈ R
సాధన:
∫2x. sin(x2 + 1) dx
t = x2 + 1 ⇒ dt = 2x dx
∫2x. sin(x2 + 1) dx = ∫ sin t dt = – cos t + C
= -cos(x2 + 1) + C
ప్రశ్న 5.
∫\(\frac{(\log x)^2}{x}\)dx, x ∈ I ⊂ (0, ∞)
సాధన:

ప్రశ్న 6.
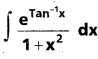 , x ∈ I ⊂ (0, ∞)
, x ∈ I ⊂ (0, ∞)
సాధన:

ప్రశ్న 7.
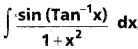 , x ∈ R.
, x ∈ R.
సాధన:
∫\(\frac{\sin \left(\tan ^{-1} x\right)}{1+x^2}\)dx
t = tan-1x ⇒ dt = \(\frac{d x}{1+x^2}\)
∫\(\frac{\sin \left(\tan ^{-1} x\right)}{1+x^2}\) dx = ∫sin t dt = – cos t + t
= -cos(tan-1 x) + C
ప్రశ్న 8.
∫\(\frac{1}{8+2 x^2}\)dx, x ∈ R.
సాధన:
∫\(\frac{1}{8+2 x^2}\)dx = \(\frac{1}{2} \int \frac{d x}{x^2+2^2}\)
= \(\frac{1}{2}\).\(\frac{1}{2}\) tan-1(\(\frac{x}{2}\)) + C
= \(\frac{1}{4}\) tan-1(\(\frac{x}{2}\)) + C
ప్రశ్న 9.
∫\(\frac{3 x^2}{1+x^6}\) x, x ∈ R.
సాధన:
∫\(\frac{3 x^2 d x}{1+x^6}\)
t = x3 ⇒ dt = 3x2 dt
∫\(\frac{3 x^2 d x}{1+x^6}\) = ∫\(\frac{d t}{1+t^2}\) = tan-1 (t) + C
= tan-1(x3) + C
ప్రశ్న 10.
∫\(\frac{2}{\sqrt{25+9 x^2}}\) dx, x ∈ R.
సాధన:
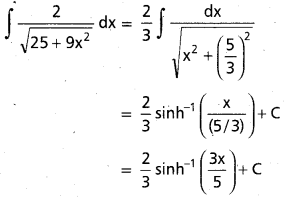

ప్రశ్న 11.
∫\(\frac{3}{\sqrt{9 x^2-1}}\) dx x ∈ (\(\frac{1}{3}\), ∞)
సాధన:
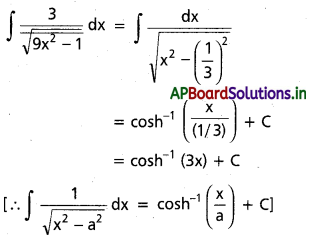
ప్రశ్న 12.
∫sin m x cos nx dx, x ∈ R, m ≠ n, m, n లు ధన పూర్ణాంకాలు.
సాధన:
∫sin m x cos nx dx = \(\frac{1}{2}\) ∫2 sin m x cos nx dx,
= \(\frac{1}{2}\) ∫(sin m + n)x + sin(m – n)x)dx
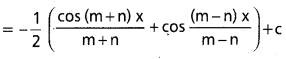
ప్రశ్న 13.
∫sin mx sin nx dx, x ∈ R, m ≠ n, m, n లు ధన పూర్ణాంకాలు.
సాధన:
∫sin mx. sin nx dx = \(\frac{1}{2}\)∫2 sin m x.sin nx dx
= \(\frac{1}{2}\)∫cos (m – n)x – cos (m + n)x dx
= \(\frac{1}{2}\)[\(\frac{\sin (m-n) x}{m-n}\) – \(\frac{\sin (m+n) x}{m+n}\)] + c
ప్రశ్న 14.
∫cos mx cos nx dx, x ∈ R, m ≠ n, m, n లు ధన పూర్ణాంకాలు.
సాధన:
∫cos m n. cos nx dx = \(\frac{1}{2}\)∫2 cos mx.cos nx dx
= \(\frac{1}{2}\) ∫(cos (m + n)x + cos (m – n)x) dx
= \(\frac{1}{2}\) sin (\(\frac{\sin (m+n) x}{m+n}\) + \(\frac{\sin (m-n) x}{m-n}\)) + c
ప్రశ్న 15.
∫ sin x sin 2x. sin 3x dx, x ∈ R.
సాధన:
sin 2x. sin 3x = \(\frac{1}{2}\)(2 sin 3x. sin 2x)
= \(\frac{1}{2}\) (cos x – cos 5x)
sin x sin 2x sin 3x


ప్రశ్న 16.
∫\(\frac{\sin x}{\sin (a+x)}\) dx x ∈ I ⊂ R\ {nπ – a : n ∈ Z}
సాధన:
sin x = sin (a + x − a)
= sin (a + x). cos a – cos (a + x) sin a
∫\(\frac{\sin x}{\sin (a+x)}\) dx = cos a ∫ dx – sin a ∫\(\frac{\cos (a+x)}{\sin (a+x)}\) dx
= x cos a – sin a. log sin (a + x) + c
II. కింది సమాకలనులను గణించండి.
ప్రశ్న 1.
∫(3x – 2)1/2dx, x ∈ (\(\frac{2}{3}\), ∞)
సాధన:
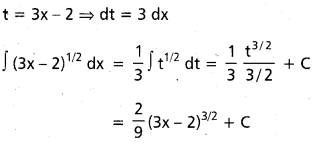
ప్రశ్న 2.
∫\(\frac{1}{7 x+3}\) dx, x ∈ I ⊂ R \ {-\(-\frac{3}{7}\)}
సాధన:
∫\(\frac{1}{7 x+3}\) dx
t = 7x + 3 ⇒ dt = 7 dx
= ∫\(\frac{1}{7 x+3} d x\) dx = \(\frac{1}{7} \int \frac{d t}{t}\)
= \(\frac{1}{7} \log |t|\) + C = \(\frac{1}{7}\) log |7x + 3| + C

ప్రశ్న 3.
∫\(\frac{\log (1+x)}{1+x}\) dx, x ∈ (-1, ∞)
సాధన:
∫\(\frac{\log (1+x)}{1+x}\) dx
t = 1 + x ⇒ dt = dx
∫\(\frac{\log (1+x)}{(1+x)}\) dx = ∫\(\frac{\log t}{t}\). dt = \(\frac{(\log \mathrm{t})^2}{2}\) + C
= \(\frac{1}{2}\)[log (1 + x)]2 + C
ప్రశ్న 4.
∫(3x2 – 4)x dx, x ∈ R.
సాధన:
∫(3x2 – 4)x dx
t = 3x2 – 4 ⇒ dt = 6x dx
∫(3x2 – 4)x dx = \(\frac{1}{6}\)∫t dt = \(\frac{1}{6}\) . \(\frac{\mathrm{t}^2}{2}\) + C
= \(\frac{\left(3 x^2-4\right)^2}{12}\) + C
ప్రశ్న 5.
∫\(\frac{d x}{\sqrt{1+5 x}}\), x ∈ (-\(\frac{1}{5}\), ∞)
సాధన:
∫\(\frac{d x}{\sqrt{1+5 x}}\)
1 + 5x = t2 అనుకొందాము
5dx = 2t dt
dx = \(\frac{2}{5} t d t\)
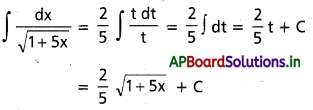
ప్రశ్న 6.
∫(1 – 2x3)x2 dx, x ∈ R.
సాధన:
∫(1 – 2x3)x2 dx
t = 1 – 2x3 ⇒ -6x2 dx
∫(1 – 2x3)x2 dx = –\(-\frac{1}{6} \int \mathrm{t} d t\)
= \(-\frac{1}{6} \cdot \frac{t^2}{2}\) + C
= \(\frac{-\left(1-2 x^3\right)^2}{12}\) + C
ప్రశ్న 7.
∫\(\frac{\sec ^2 x}{(1+\tan x)^3}\)dx, x ∈ I ⊂ R \ {nπ – \(\frac{\pi}{4}\) : n ∈ Z}.
సాధన:
∫\(\frac{\sec ^2 x}{(1+\tan x)^3}\) dx
t = 1 + tan x ⇒ dt = sec2 x dx
∫\(\frac{\sec ^2 x}{(1+\tan x)^3}\) dx = ∫\(\frac{d t}{t^3}\) = ∫t-3 dt
= \(\frac{\mathrm{t}^{-2}}{(-2)}\) + C = \(-\frac{1}{2 t^2}\) + C
= –\(\frac{1}{2(1+\tan x)^2}\) + C

ప్రశ్న 8.
∫x3 sin x4 dx, x ∈ R
సాధన:
∫x3. sin x4 dx
t = x4 ⇒ dt = 4x3 dx
∫x3.sin x4 dx = \(\frac{1}{4}\)∫sin t. dt = \(-\frac{1}{4}\) cos t + C
= \(-\frac{1}{4}\). cos x4 + C
ప్రశ్న 9.
∫\(\frac{\cos x}{(1+\sin x)^2}\)dx, x ∈ I ⊂ R \ {2nπ + \(\frac{3 \pi}{2}\) : n ∈ Z}.
సాధన:
∫\(\frac{\cos x d x}{(1+\sin x)^2}\)
t = 1 + sin x ⇒ dt = cos x dx
∫\(\frac{\cos x d x}{(1+\sin x)^2}\) = ∫\(\frac{\mathrm{dt}}{\mathrm{t}^2}\) = \(-\frac{1}{t}\) + C
= \(-\frac{1}{1+\sin x}\) + C
ప్రశ్న 10.
∫\(\sqrt[3]{\sin x}\) cos x dx, x ∈ [2nπ, (2n + 1)π], (n ∈ Z).
సాధన:
∫\(\sqrt[3]{\sin x}\) cos x
t = sin x ⇒ dt = cos x dx
∫\(\sqrt[3]{\sin x}\) .cos x dx = ∫\(\sqrt[3]{t}\) . dt
= \(\frac{t^{4 / 3}}{(4 / 3)}\) + C
= \(\frac{3}{4} t^{4 / 3}\) + C
= \(\frac{3}{4}\)(sin x)4/3 + C
ప్రశ్న 11.
∫2x ex2dx, x ∈ R
సాధన:
∫2x ex2dx
t = x2 ⇒ dt = 2x dx
∫2x ex2dt = ∫et dt = et + C
= ex2 + C
ప్రశ్న 12.
∫\(\frac{e^{\log x}}{x}\) dx, x ∈ (0, ∞)
సాధన:
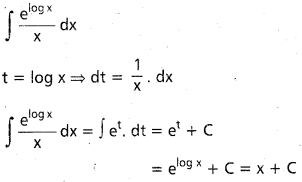
ప్రశ్న 13.
∫\(\frac{x^2}{\sqrt{1-x^6}}\) dx, x ∈ I = (-1, 1). (May. 05)
సాధన:
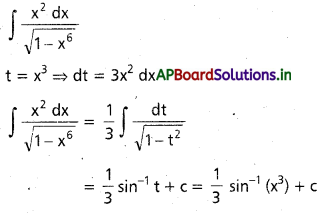
ప్రశ్న 14.
∫\(\frac{2 x^3}{1+x^8}\)dx, x ∈ R.
సాధన:
t = x4 ⇒ dt = 4x3 dx
∫\(\frac{2 x^3}{1+x^8}\) = \(\frac{1}{2} \int \frac{d t}{1+t^2}\) = \(\frac{1}{2}\)tan-1 t + C
= \(\frac{1}{2}\)tan-1(x4) + C

ప్రశ్న 15.
∫\(\frac{x^8}{1+x^{18}}\)dx, x ∈ R. (A.P. Mar. 16)
సాధన:

ప్రశ్న 16.
∫\(\frac{e^x(1+x)}{\cos ^2\left(x e^x\right)}\)dx, x ∈ I ⊂ R \ {x ∈ R : cos (xex) = 0}
సాధన:
t = x. ex
dt = (x. ex + ex) dx = ex (1 + x)dx
∫\(\frac{e^x(1+x)}{\cos ^2\left(x \cdot e^x\right)} d x\) = ∫\(\frac{\mathrm{dt}}{\cos ^2 t}\) = ∫sec2 t dt
= tan t + C
= tan (x. ex) + C
ప్రశ్న 17.
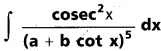 , x ∈ I ⊂ R \ {x ∈ R : a + b cot x = 0}, a, b ∈ R, b ≠ 0.
, x ∈ I ⊂ R \ {x ∈ R : a + b cot x = 0}, a, b ∈ R, b ≠ 0.
సాధన:
t = a + b cot x అనుకొనుము.
dt = -b cosec2 x dx
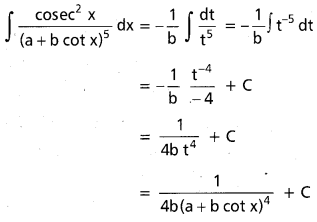
ప్రశ్న 18.
∫ex sin ex dx, x ∈ R.
సాధన:
t = ex ⇒ dt = ex dx
∫ex.sin ex dx = ∫sint dt = – cos t + C
= -cos(ex) + C
ప్రశ్న 19.
∫\(\frac{\sin (\log x)}{x}\) dx, x ∈ (0, ∞)
సాధన:
t = log x ⇒ dt = \(\frac{1}{x} d x\)
∫\(\frac{\sin (\log x)}{x} d x\) = ∫sint dt = – cos t + c
= -cos (log x) + c
ప్రశ్న 20.
∫\(\frac{1}{x \log x}\) dx, x ∈ (0, ∞).
సాధన:
t = log (log x)
dt = \(\frac{1}{\log x} \cdot \frac{1}{x}\) dx
∫\(\frac{1}{x \log x}\) dx = ∫ dt = t + C = log(log x) + C

ప్రశ్న 21.
∫\(\frac{(1+\log x)^n}{x}\)dx, x ∈ (e-1, ∞), n ≠ 1.
సాధన:
t = 1 + log x
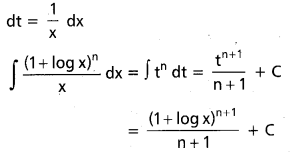
ప్రశ్న 22.
∫\(\frac{\cos (\log x)}{x}\)dx, x ∈ (0, ∞)
సాధన:
t = log x
dt = \(\frac{1}{x} d x\)
∫\(\frac{\cos (\log x) d x}{x}\) = ∫cos t dt = sin t + C
= sin (log x) + C
ప్రశ్న 23.
∫\(\frac{\cos \sqrt{x}}{\sqrt{x}}\)dx, x ∈ (0, ∞).
సాధన:

ప్రశ్న 24.
∫\(\frac{2 x+1}{x^2+x+1}\)dx, x ∈ R.
సాధన:
t = x2 + x + 1
dt = (2x + 1) dx
∫\(\frac{2 x+1}{x^2+x+1}\) dx = \(\int \frac{d t}{t}\)
= log |t| + C
= log |x2 + x + 1| + C
ప్రశ్న 25.
∫\(\frac{a x^{n-1}}{b x^n+c}\)dx, n ∈ N, a, b, c లు వాస్తవ సంఖ్యలు b ≠ 0, x ∈ I ⊂ {x ∈ R : xn ≠ –\(\frac{c}{b}\)}
సాధన:
t = bxn + C
dt = nbxn-1dx

ప్రశ్న 26.
∫\(\frac{1}{x \log x[\log (\log x)]}\)dx, x ∈ (1, ∞). (Mar. 11)
సాధన:
t = log (log x)
dt = \(\frac{1}{\log x} \cdot \frac{1}{x} d x\)
∫\(\frac{1}{x \log x[\log (\log x)]}\)dx = ∫\(\frac{\mathrm{dt}}{\mathrm{t}}\)
= log |t| + C
= log |log (log x)| + C

ప్రశ్న 27.
∫coth x dx = x ∈ R.
సాధన:
t = sinh x ⇒ dt = cosh x dx
∫coth x dx = \(\int \frac{d t}{t}\) = log |t| + C
= log |sinh x| + C
ప్రశ్న 28.
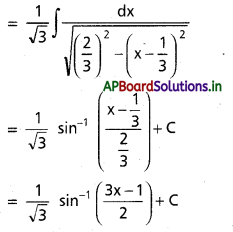
∫\(\frac{1}{\sqrt{1-4 x^2}}\)dx, x ∈ \(\left(-\frac{1}{2}, \frac{1}{2}\right)\)
సాధన:
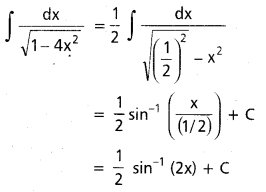
ప్రశ్న 29.
∫\(\frac{d x}{\sqrt{25+x^2}}\), x ∈ R
సాధన:
∫\(\frac{d x}{\sqrt{x^2+25}}\) = ∫\(\frac{d x}{\sqrt{x^2+5^2}}\)
= sinh-1 \(\left(\frac{x}{5}\right)\) + C
ప్రశ్న 30.
∫\(\frac{1}{(x+3) \sqrt{x+2}}\) dx, x ∈ I ⊂ (-2, ∞)
సాధన:
x + 2 = t2
dx = 2t dt
∫\(\frac{d x}{(x+3) \sqrt{x+2}}\) = ∫\(\frac{2 t d t}{t\left(t^2+1\right)}\)
= 2 ∫\(\frac{\mathrm{dt}}{\mathrm{t}^2+1}\)
= 2tan-1(t) + C
= 2tan-1\((\sqrt{x+2})\) + C
ప్రశ్న 31.
∫\(\frac{1}{1+\sin 2 x}\) dx
x ∈ I ⊂ R \ {\(\frac{n \pi}{2}\) + (-1)n\(\frac{\pi}{4}\) : n ∈ Z}
సాధన:

ప్రశ్న 32.
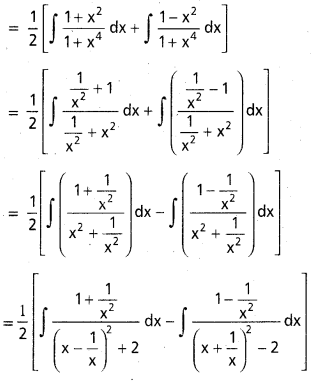
∫\(\frac{x^2+1}{x^4+1}\)dx, x ∈ R.
సాధన:
\(\int \frac{x^2+1}{x^4+1} d x\)
లవ హారాలను x2 తో భాగించగా

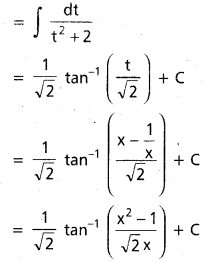
ప్రశ్న 33.
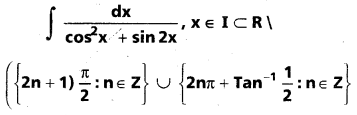
సాధన:
∫\(\frac{d x}{\cos ^2 x+\sin 2 x}\)
లవ హారాలను cos2 x తో భాగించగా


ప్రశ్న 34.
∫\(\sqrt{1-\sin 2 x}\) dx, x ∈ I ⊂ [2nπ – \(\frac{3 \pi}{4}\) + \(\frac{\pi}{4}\)], n ∈ Z.
సాధన:

ప్రశ్న 35.
∫\(\sqrt{1+\cos 2 x}\)dx, x ∈ I ⊂ [2nπ – \(\frac{\pi}{2}\), 2nπ + \(\frac{\pi}{2}\)], n ∈ Z.
సాధన:
∫\(\sqrt{1+\cos 2 x}\) dx = ∫\(\sqrt{2 \cos ^2 x}\) dx
= \(\sqrt{2} \int \cos x d x\)
= \(\sqrt{2}\) sin x + C
ప్రశ్న 36.
∫\(\frac{\cos x+\sin x}{\sqrt{1+\sin 2 x}} d x\), x ∈ I ⊂ (2nπ – \(\frac{\pi}{4}\), 2nπ + \(\frac{3 \pi}{4}\)), n ∈ Z
సాధన:

ప్రశ్న 37.
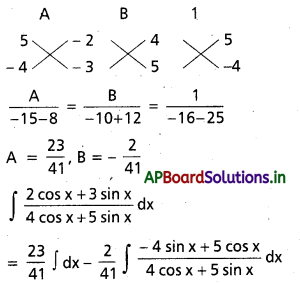
∫\(\frac{\sin 2 x}{(a+b \cos x)^2} d x\), x ∈ x ∈ R, |a| > |b| అయితే {x ∈ I { x ∈ R : a + b cos x ≠ 0}, |a| < |b| అయితే.
సాధన:
a + b cos x = t ⇒ cos x = \(\frac{\mathrm{t}-\mathrm{a}}{\mathrm{b}}\)
అయితే b(-sin x) dx = dt
⇒ sin x dx = \(\frac{-1}{b} d t\)

ప్రశ్న 38.
∫\(\frac{\sec x}{(\sec x+\tan x)^2}\)dx, x ∈ I ⊂ R \ ({a + nπ : n ∈ Z ∪ {b + nπ : n ∈ Z}).
సాధన:
sec x + tan x = t ప్రతిక్షేపిస్తే
(sec x tan x + sec2 x) dx = dt అవుతుంది.
sec x (sec x + tan x) dx = dt

ప్రశ్న 39.
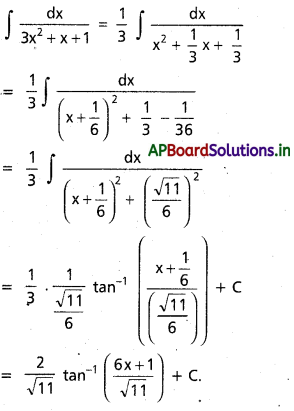
∫\(\frac{d x}{a^2 \sin ^2 x+b^2 \cdot \cos ^2 x}\) x ∈ R, a ≠ 0, b ≠ 0.
సాధన:

ప్రశ్న 40.
∫\(\frac{d x}{\sin (x-a) \sin (x-b)}\), x ∈ I ⊂ R \ ({a + nπ : n ∈ Z} ∪ {b + nπ : n ∈ Z})
సాధన:


ప్రశ్న 41.
∫\(\frac{1}{\cos (x-a) \cos (x-b)}\)dx, x ∈ I ⊂ R \ ({a + \(\frac{(2 n+1) \pi}{2}\) : n ∈ Z} ∪ {b + (2n + 1)\(\frac{\pi}{2}\) : n ∈ Z})
సాధన:
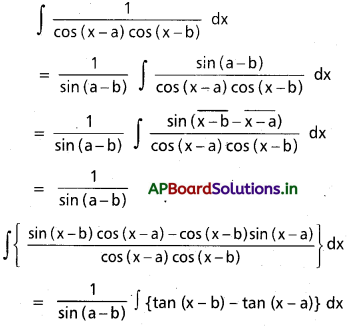
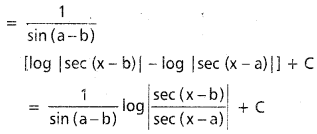
III. కింది సమాకలనులను గణించండి.
ప్రశ్న 1.
∫\(\frac{\sin 2 x}{a \cos ^2 x+b \sin ^2 x}\), x ∈ I ⊂ R \ {x ∈ R | a cos2x + b sin2x = 0}.
సాధన:
t = a cos2 x + b sin2 x
⇒ dt = (a (2cos x) (-sin x) + b(2 sin x cos x))dx
= sin 2x (b – a) dx
sin 2x. dx = \(\frac{1}{(b-a)}\)dt

ప్రశ్న 2.
∫\(\frac{1-\tan x}{1+\tan x}\)dx, x ∈ I ⊂ R \ {nπ – \(\frac{\pi}{4}\) : n ∈ Z}.
సాధన:
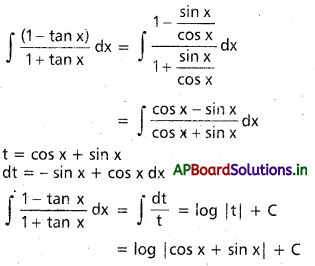
ప్రశ్న 3.
∫\(\frac{\cot (\log x)}{x}\)dx, x ∈ I ⊂ (0, ∞) \ {enπ : n ∈ Z} (Mar. 05)
సాధన:
t = log x ⇒ dt = \(\frac{\mathrm{dx}}{\mathrm{x}}\)
∫\(\frac{\cot (\log x)}{x}\)dx = ∫cos t dt = log(sin t) + C
= log |sin (log x)| + C
ప్రశ్న 4.
∫ex . cot ex dx, x ∈ I ⊂ R \ {log nπ : n ∈ Z}.
సాధన:
t = ex ⇒ dt = ex dx
∫ex. cot ex dx = ∫cot t dt = log |(sin t)| + C
= log (sin ex) + c
ప్రశ్న 5.
∫sec(tan x)sec2x dx, x ∈ I ⊂ {x ∈ E : ఏ k ∈ Z కైనా tan x ≠ \(\frac{(2 k+1) \pi}{2}\)} , ఇక్కడ E = R/ {\(\frac{(2 n+1) \pi}{2}\) : n ∈ Z}.
సాధన:
t = tan x dt = sec2 x dx
∫ sec (tan x) sec2 x dx = ∫ sec t. dt
= log tan (\(\frac{\pi}{4}\) + \(\frac{t}{2}\)) + C
= log(tan(\(\frac{\pi}{4}\) + \(\frac{\tan x}{2}\))) + C
ప్రశ్న 6.
∫\(\sqrt{\sin x}\) cos x dx, x ∈ [2nπ, (2n + 1)π], (n ∈ Z).
సాధన:
t = sin x ⇒ dt = cos x dx
∫\(\sqrt{\sin x}\). cos x dx = ∫\(\sqrt{t} d t\) = \(\frac{2}{3}\) t3/2 + C
= \(\frac{2}{3}\)(sin x)3/2 + C
ప్రశ్న 7.
∫tan4 sec2x dx, x ∈ I ⊂ R \ {\(\frac{(2 n+1) \pi}{2}\) : n ∈ Z}.
సాధన:
x = tan x ⇒ dt = sec2 x dx
∫tan4 x . sec2 x dx = ∫t4 dt
= \(\frac{t^5}{5}\) + C = \(\frac{\tan ^5 x}{5}\) + C
ప్రశ్న 8.
∫\(\frac{2 x+3}{\sqrt{x^2+3 x-4}}\)dx, x ∈ I ⊂ R \ [-4, 1].
సాధన:
t = x2 + 3x – 4
dt = (2x + 3) dx
∫\(\frac{2 x+3}{\sqrt{x^2+3 x-4}}\) = ∫\(\frac{\mathrm{dt}}{\sqrt{\mathrm{t}}}\) = 2\(\sqrt{t}\) + C
= 2\(\sqrt{x^2+3 x-4}\) + C

ప్రశ్న 9.
∫cosec2 x\(\sqrt{\cot x}\) dx, x ∈ \(\left(0, \frac{\pi}{2}\right]\)
సాధన:
t = cot x = dt = -cosec2 x dx
∫cosec2 x\(\sqrt{\cot }\) x dx = – ∫\(\sqrt{t}\) dt
= \(-\frac{2}{3} t \sqrt{t}\) + C
= \(-\frac{2}{3}\) cot(x)3/2 + C
ప్రశ్న 10.
∫sec x log (sec x + tan x) dx, x ∈ (0, \(\frac{\pi}{2}\))
సాధన:
t = log (sec x + tan x)
dt = \(\frac{\left(\sec x \cdot \tan x+\sec ^2 x\right) d x}{(\sec x+\tan x)}\)
= sec x dx
∫sec x log (sec x + tan x) dx = ∫t dt
= \(\frac{\mathrm{t}^2}{2}\) + C
= \(\frac{(\log (\sec x+\tan x))^2}{2}\) + C
ప్రశ్న 11.
∫sin3x dx, x ∈ R.
సాధన:
sin 3x = 3 sin x – 4 sin3 x
sin3 x = \(\frac{1}{4}\)(3 sin x – sin 3x)
∫sin3x dx = \(\frac{3}{4}\)∫sin x – \(\frac{1}{4}\)∫sin 3x dx
= –\(\frac{3}{4}\)cos x + \(\frac{1}{12}\) cos 3x + C
= \(\frac{1}{12}\)(cos 3x – 9 cos x) + C
ప్రశ్న 12.
∫cos3x dx, x ∈ R.
సాధన:
cos 3x = 4 cos3 x – 3 cos x
cos3 x = \(\frac{1}{4}\)(3 cos x + cos 3x)
∫cos3x dx = \(\frac{3}{4}\)∫cos x dx + \(\frac{1}{4}\)∫cos 3x dx
= \(\frac{3}{4}\)sin x + \(\frac{1}{12}\) sin 3x + C
= \(\frac{1}{12}\)(9 sin x + sin 3x) + C
ప్రశ్న 13.
∫cos x cos 2x dx, x ∈ R.
సాధన:
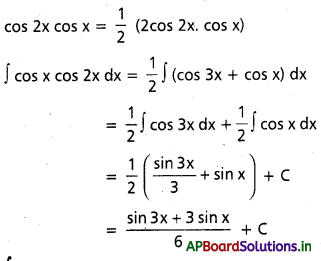
ప్రశ్న 14.
∫cos x cos 3x dx, x ∈ R.
సాధన:
cos 3x cos x = \(\frac{1}{2}\)(2cos 3x . cos x)
= \(\frac{1}{2}\)(cos 4x + cos 2x)
∫cos x cos 3x dx = \(\frac{1}{2}\)∫cos 4x dx + \(\frac{1}{2}\)∫cos 2x dx
= \(\frac{1}{2}\)(\(\frac{\sin 4 x}{4}\) + \(\frac{\sin 2 x}{2}\)) + C
= \(\frac{1}{8}\)(sin 4x + 2 sin 2x) + C
ప్రశ్న 15.
∫cos4x dx, x ∈ R.
సాధన:
cos4x = (cos2x)2 = \(\left(\frac{1+\cos 2 x}{2}\right)^2\)
= \(\frac{1}{4}\)(1 + 2 cos 2x + cos2 2x)
= \(\frac{1}{4}\)(1 + 2 cos 2x + \(\frac{1+\cos 4 x}{2}\))
= \(\frac{1}{8}\)(2 + 4 cos 2x + 1 + cos 4x)
= \(\frac{1}{8}\)(3 + 4 cos 2x + cos 4x)
= \(\frac{1}{8}\)(3∫dx + 4∫cos 2x dx + ∫cos 4x dx)
= \(\frac{1}{8}\)(3x + 4\(\frac{\sin 2 x}{2}\) + \(\frac{\sin 4 x}{4}\)) + C
= \(\frac{1}{32}\)(12x + 8 sin 2x + sin 4x) + C

ప్రశ్న 16.
∫x \(\sqrt{4 x+3}\) dx, x ∈ \(\left(-\frac{3}{4}, \infty\right)\)
సాధన:

ప్రశ్న 17.
∫\(\frac{d x}{\sqrt{a^2-(b+c x)^2}}\), x ∈ I ⊂ {x ∈ R : |b + c x| < a}, a, b, c లు వాస్తవ సంఖ్యలు c ≠ 0, a > 0.
సాధన:
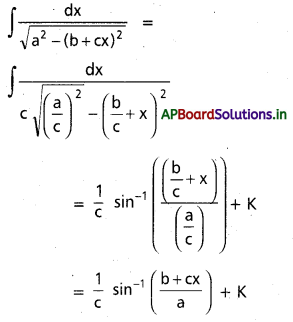
ప్రశ్న 18.
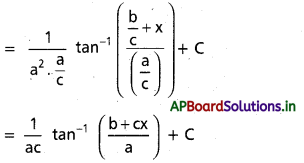
∫\(\frac{d x}{a^2+(b+c x)^2}\), x ∈ R, a, b, c లు వాస్తవ సంఖ్యలు c ≠ 0, a > 0.
సాధన:
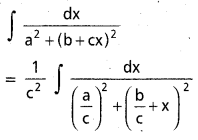
ప్రశ్న 19.
∫\(\frac{d x}{1+e^x}\), x ∈ R
సాధన:


ప్రశ్న 20.
∫\(\frac{x^2}{(a+b x)^2}\)dx, x ∈ I ⊂ R \ {-\(\frac{\mathbf{a}}{\mathbf{b}}\)}, a, b లు వాస్తవ సంఖ్యలు b ≠ 0.
సాధన:
t = a + bx అనుకోండి
dt = b dx ⇒ dx = \(\frac{1}{b}\) . dt

ప్రశ్న 21.
∫\(\frac{x^2}{\sqrt{1-x}}\)dx, x ∈ (-∞, 1).
సాధన:
1 – x = t2
-dx = 2t dt
∫\(\frac{x^2}{\sqrt{1-\dot{x}}}\)dx = ∫(1 – t2)2. \(\frac{-2 \mathrm{t}}{\mathrm{t}} \mathrm{dt}\)
= -2∫(1 – 2t2 + t4)dt
= -2(t – \(\frac{2}{3} t^3\) + \(\frac{t^5}{5}\)) + C
= -2(\(\sqrt{1-x}\) – \(\frac{2}{3}\)(1 – x)3/2 + \(\frac{1}{5}\)(1 – x)5/2) + C
![]()
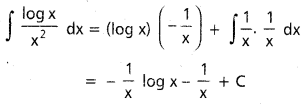
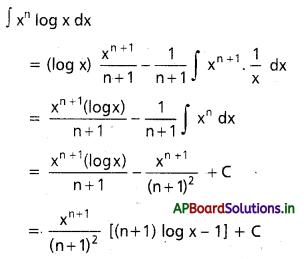






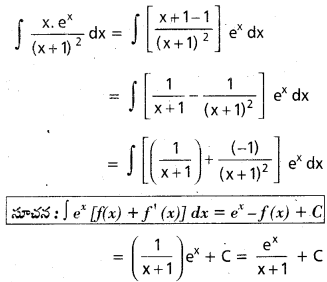






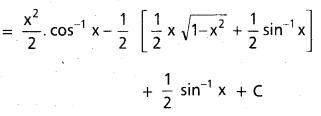



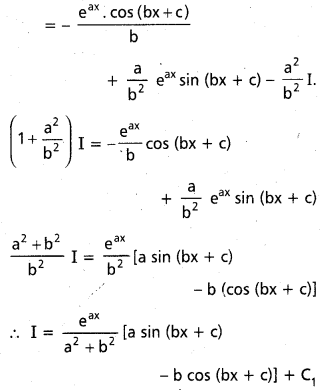
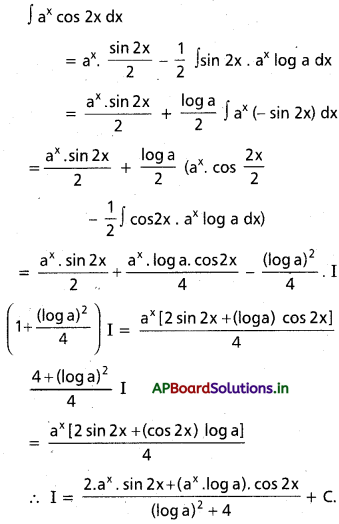

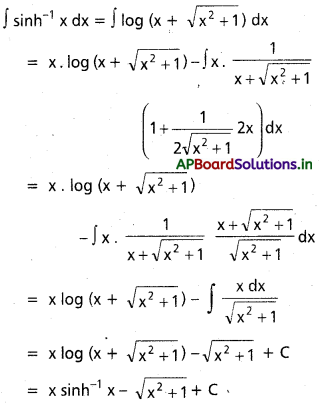
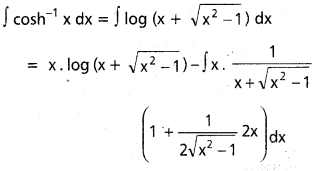
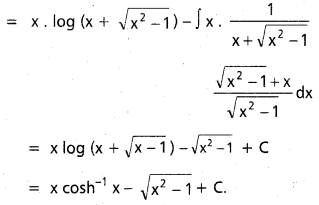
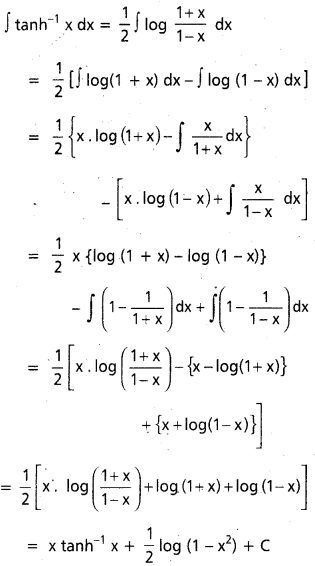

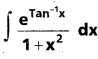 , x ∈ I ⊂ (0, ∞)
, x ∈ I ⊂ (0, ∞)
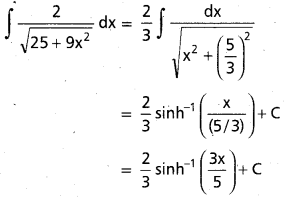

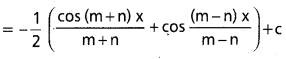

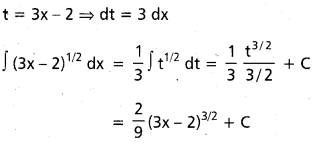
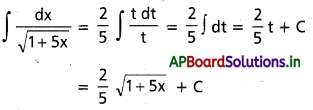
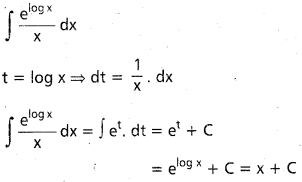
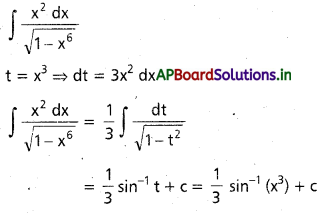

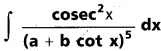 , x ∈ I ⊂ R \ {x ∈ R : a + b cot x = 0}, a, b ∈ R, b ≠ 0.
, x ∈ I ⊂ R \ {x ∈ R : a + b cot x = 0}, a, b ∈ R, b ≠ 0.