Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(e) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(e)
I.
Question 1.
If nC4 = 210, find n.
Solution:
nCr = \(\frac{n !}{(n-r) ! r !}\) = \(\frac{n(n-1)(n-2) \ldots \ldots[n-(r-1)]}{1.2 .3 \ldots \ldots \ldots . . . r}\)
Solution:
nC4 = 210
⇒ \(\frac{n(n-1)(n-2)(n-3)}{1.2 .3 .4}=10 \times 21^n C_{2 r-1}\)
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 21 × 1 × 2 × 3 × 4
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 7 × 3 × 2 × 3 × 4
⇒ n(n – 1) (n – 2) (n – 3) = 10 × 9 × 8 × 7
⇒ n = 10
Question 2.
If 12Cr = 495, find the possible values of r.
Solution:
Hint: nCr = nCn-r
12Cr = 495
= 5 × 99
= 11 × 9 × 5
= \(\frac{12 \times 11 \times 9 \times 5 \times 2}{12 \times 2}\)
= \(\frac{12 \times 11 \times 10 \times 9}{1.2 .3 .4}\)
= 12C4 or 12C8
∴ r = 4 or 8
![]()
Question 3.
If 10 . nC2 = 3 . n+1C3, find n.
Solution:
10 . nC2 = 3 . n+1C3
⇒ 10 × \(\frac{n(n-1)}{1.2}=\frac{3(n+1)(n-1)}{1.2 .3}\)
⇒ 10 = n + 1
⇒ n = 9
Question 4.
If nPr = 5040 and nCr = 210, find n and r.
Solution:
Hint: nPr = r! nCr and nPr = n(n – 1) (n – 2) ……. [n – (r – 1)]
nPr = 5040, nCr = 210
r! = \(\frac{{ }^n P_r}{{ }^n C_r}=\frac{5040}{210}=\frac{504}{21}\) = 24 = 4!
∴ r = 4
nPr = 5040
nP4 = 5040
= 10 × 504
= 10 × 9 × 56
= 10 × 9 × 8 × 7
= 10P4
∴ n = 10
∴ n = 10, r = 4
Question 5.
If nC4 = nC6, find n.
Solution:
nCr = nCs ⇒ r = s or r + s = n
nC4 = nC6
∴ n = 4 + 6 = 10, (∵ 4 ≠ 6)
Question 6.
If 15C2r-1 = 15C2r+4, find r.
Solution:
15C2r-1 = 15C2r+4
2r – 1 = 2r + 4 or (2r – 1) + (2r + 4) = 15
(2r – 1) + (2r + 4) = 15
⇒ 4r + 3 = 15
⇒ 4r = 12
⇒ r = 3
∴ 2r – 1 = 2r + 4
⇒ -1 = 4 which is impossible
∴ r = 3
![]()
Question 7.
If 17C2t+1 = 17C3t-5, find t.
Solution:
17C2t+1 = 17C3t-5
2t + 1 = 3t – 5 or (2t + 1) + (3t – 5) = 17
⇒ 1 + 5 = t or 5t = 21
⇒ t = 6 or t = \(\frac{21}{5}\) which is not an integer
∴ t = 6
Question 8.
If 12Cr+1 = 12C3r-5, find r.
Solution:
12Cr+1 = 12C3r-5
⇒ r + 1 = 3r – 5 or (r + 1) + (3r – 5) = 12
⇒ 1 + 5 = 2r or 4r – 4 = 12
⇒ 2r = 6 or 4r = 16
⇒ r = 3 or r = 4
∴ r = 3 or 4
Question 9.
If 9C3 + 9C5 = 10Cr then find r.
Solution:
nCr = nCn-r
10Cr = 9C3 + 9C5
∴ 9C3 + 9C5 = 9C3 + 9C5 = 10C6 or 10C4 = 10Cr (given)
⇒ r = 4 or 6
Question 10.
Find the number of ways of forming a committee of 5 members from 6 men and 3 ladies.
Solution:
Total number of persons = 6 + 3 = 9
∴ Number of ways of forming a committee of 5 members from 6 men and 3 ladies = 9C5
= \(\frac{9 \times 8 \times 7 \times 6 \times 5}{5 \times 4 \times 3 \times 2 \times 1}\)
= 126
![]()
Question 11.
In question no. 10, how many committees contain atleast two ladies?
Solution:
Since a committee contains atleast 2 ladies, the members of the committee may be of the following two types.
(i) 3 men, 2 ladies
(ii) 2 men, 3 ladies
The number of selections in the first type = 6C3 × 3C2
= 20 × 3
= 60
The number of selections in the second type = 6C2 × 3C3
= 15 × 1
= 15
∴ The required number of ways of selecting the committee containing atleast 2 ladies = 60 + 15 = 75.
Question 12.
If nC5 = nC6, then find 13Cn.
Solution:
∵ nC5 = nC6
⇒ n = 6 + 5 = 11
13Cn = 13C11 = 13C2
= \(\frac{13 \times 12}{1 \times 2}\)
= 78
II.
Question 1.
Prove that for 3 ≤ r ≤ n, (n-3)Cr . (n-3)C(r-1) + 3 . (n-3)C(r-2) + 3 . (n-3)C(r-3) = nCr
Solution:
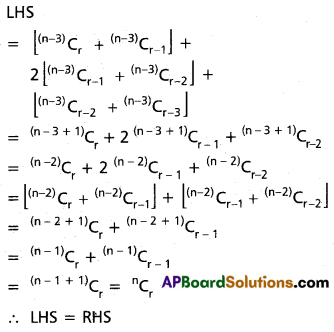
Question 2.
Find the value of 10C5 + 2 . 10C4 + 10C3
Solution:
Hint: nCr + nCr-1 = (n+1)Cr
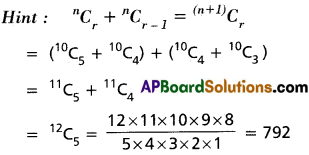
![]()
Question 3.
Simplify 34C5 + \(\sum_{r=0}^4{ }^{(38-r)} C_4\)
Solution:

Question 4.
In a class, there are 30 students. If each student plays a chess game with each of the other students then find the total number of chess games played by them.
Solution:
Number of students in a class = 30
Since each student plays a chess game with each of the other students, the total number of chess games played by them = 30C2 = 435
Question 5.
Find the number of ways of selecting 3 girls and 3 boys out of 7 girls and 6 boys.
Solution:
The number of ways of selecting 3 girls and 3 boys Out of 7 girls and 6 boys = 7C3 × 6C3
= 35 × 20
= 700
Question 6.
Find the number of ways of selecting a committee of 6 members out of 10 members always including a specified member.
Solution:
Since a specified member is always included in a committee, the remaining 5 members can be selected from the remaining 9 members in 9C5 ways.
∴ Required number of ways selecting a committee = 9C5 = 126
Question 7.
Find the number of ways of selecting 5 books from 9 different mathematics books such that a particular book is not included.
Solution:
Since a particular book is not included in the selection, the 5 books can be selected from the remaining 8 books in 8C5 ways.
∴ The required number of ways of selecting 5 books = 8C5 = 56
![]()
Question 8.
Find the number of ways of selecting 3 vowels and 2 consonants from the letters of the word EQUATION.
Solution:
The word EQUATION contains 5 vowels and 3 consonants.
The 3 vowels can be selected from 5 vowels in 5C3 = 10 ways.
The 2 consonants can be selected from 3 consonants in 3C2 = 3 ways.
∴ The required number of ways of selecting 3 vowels and 2 consonants = 10 × 3 = 30
Question 9.
Find the number of diagonals of a polygon with 12 sides.
Solution:
The number of diagonals of a polygon with sides = \(\frac{n(n-3)}{2}\)
= \(\frac{12(12-3)}{2}\)
= 54
Question 10.
If n persons are sitting in a row, find the number of ways of selecting two persons, who are sitting adjacent to each other.
Solution:
The number of ways of selecting 2 persons out of n persons sitting in a row, who are sitting adjacent to each other = n – 1
![]()
Question 11.
Find the number of ways of giving away 4 similar coins to 5 boys if each boy can be given any number (less than or equal to 4) of coins.
Solution:
The 4 similar coins can be divided into different groups as follows.
(i) One group containing 4 coins
(ii) Two groups containing 1, 3 coins respectively
(iii) Two groups containing 2, 2 coins respectively
(iv) Two groups containing 3, 1 coins respectively
(v) Three groups containing 1, 1, 2 coins respectively
(vi) Three groups containing 1, 2, 1 coins respectively
(vii) Three groups containing 2, 1, 1 coins respectively
(viii) Four groups containing 1, 1, 1, 1 coins respectively
these groups can given away to 5 boys in = \({ }^5 C_1+2 \times{ }^5 C_2+{ }^5 C_2+{ }^5 C_3 \times \frac{3 !}{2 !}+{ }^5 C_4\)
= 5 + 20 + 10 + 30 + 5
= 70 ways
III.
Question 1.
Prove that \(\frac{{ }^{4 n} C_{2 n}}{{ }^{2 n} C_n}=\frac{1.3 .5 \ldots \ldots(4 n-1)}{\{1.3 .5 \ldots \ldots(2 n-1)\}^2}\)
Solution:

Question 2.
If a set A has 12 elements, find the number of subsets of A having
(i) 4 elements
(ii) Atleast 3 elements
(iii) Atmost 3 elements
Solution:
Number of elements in set A = 12
(i) Number of subsets of A with exactly 4 elements = 12C4 = 495
(ii) The required subset contains atleast 3 elements.
The number of subsets of A with exactly 0 elements is 12C0
The number of subsets of A with exactly 1 element is 12C1
The number of subsets of A with exactly 2 elements is 12C2
Total number of subsets of A formed = 212
∴ Number of subsets of A with atleast 3 elements = (Total number of subsets) – (number of subsets contains 0 or 1 or 2 elements)
= 212 – (12C0 + 12C1 + 12C2)
= 4096 – (1 + 12 + 66)
= 4096 – 79
= 4017
(iii) The required subset contains atmost 3 elements
i.e., it may contain 0 or 1 or 2 or 3 elements.
The number of subsets of A with exactly 0 elements is 12C0
The number of subsets of A with exactly 1 element is 12C1
The number of subsets of A with exactly 2 elements is 12C2
The number of subsets of A with exactly 3 elements is 12C3
∴ Number of subsets of A with atmost 3 elements = 12C0 + 12C1 + 12C2 + 12C3
= 1 + 12 + 66 + 220
= 299
![]()
Question 3.
Find the number of ways of selecting a cricket team of 11 players from 7 batsmen and 6 bowlers such that there will be atleast 5 bowlers in the team.
Solution:
Since the team consists of at least 5 bowlers, the selection may be of the following types.
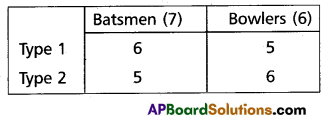
The number of selections in the first type = 7C6 × 6C5
= 7 × 6
= 42
The number of selections in the second type = 7C5 × 6C6
= 21 × 1
= 21
∴ The required number of ways selecting the cricket team = 42 + 21 = 63
Question 4.
If 5 vowels and 6 consonants are given, then how many 6-letter words can be formed with 3 vowels and 3 consonants?
Solution:
No. of vowels given = 5
No.of consonants given = 6
We have to form a 6-letter word with 3 vowels and 3 consonants from given letters.
3 vowels can select from 5 in 5C3 ways.
3 consonants can select from 6 in 6C3 ways.
Total No. of words = 5C3 × 6C3 × 6! = 1,44,000
Question 5.
There are 8 railway stations along a railway line. In how many ways can a train be stopped at 3 of these stations such that no two of them are consecutive?
Solution:
Number of ways of selecting 3 stations out of 8 = 8C3 = 56
Number of ways of selecting 3 out of 8 stations such that 3 are consecutive = 6
Number of ways of selecting 3 out of 8 stations such that 2 of them are consecutive = 2 × 5 + 5 × 4
= 10 + 20
= 30
∴ Number of ways for a train to be stopped at 3 of 8 stations such that no two of them are consecutive = 56 – (6 + 30) = 20
![]()
Question 6.
Find the number of ways of forming a committee of 5 members out of 6 Indians and 5 Americans so that always the Indians will be in majority in the committee.
Solution:
Since the committee contains the majority of Indians, the members of the committee may be of the following types.

The number of selections in type I = 6C5 × 5C0 = 6 × 1 = 6
The number of selections in type II = 6C4 × 5C1 = 15 × 5 = 75
The number of selections in type III = 6C3 × 5C2 = 20 × 10 = 200
∴ The required number ways of selecting a committee = 6 + 75 + 200 = 281.
Question 7.
A question paper is divided into 3 sections A, B, C Containing 3, 4, 5 questions respectively. Find the number of ways of attempting 6 questions choosing at least one from each section.
Solution:
First Method: The selection of a question may be of the following
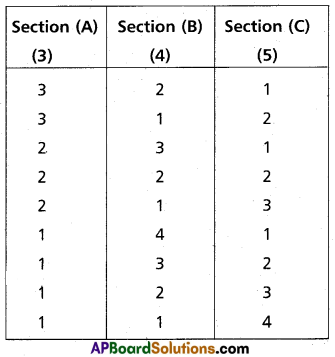
Total No. of ways of attempting 6 questions

Second Method:
Required No.of attempting 6 questions = Total no. of arrangements – selection except question from C – selection except Q from A – selection except Q from B
= 12C6 – 7C6 – 9C6 – 6C6
= 805
Question 8.
Find the number of ways in which 12 things be
(i) divided into 4 equal groups
(ii) distributed to 4 persons equally.
Solution:
(i) The number of ways in which 12 things be divided into 4 equal groups = \(\frac{12 !}{3 ! 3 ! 3 ! 3 ! 4 !}\) = \(\frac{12 !}{(3 !)^4 4 !}\)
(ii) The number of ways in which 12 things be distributed to 4 persons equally = \(\frac{12 !}{3 ! 3 ! 3 ! 3 !}\) = \(\frac{12 !}{(3 !)^4}\)
![]()
Question 9.
A class contains 4 boys and g girls. Every Sunday, five students with atleast 3boys go for a picnic. A different group is being sent every week. During the picnic, the class teacher gives each girl in the group a doll. If the total number of dolls distributed is 85, find g.
Solution:
No. of boys = 4
No. of girls = g
Since there should be atleast 3 boys it can be done in 2 ways as shown in the table

The number of girls in G1 = [4C3 × gC2] × 2
Since each group contains 2 girls
The number of girls in G2 = [4C3 × gC2] × 1
Since each group contains 1 girl.
Given no. of dolls distributed = 85
⇒ [4C3 × gC2] × 2 + [4C4 × gC1] × 1 = 85
⇒ 4 . \(\frac{g(g-1)}{2}\) × 2 + 1 . g . 1 = 85
⇒ 4g2 – 4g + g – 85 = 0
⇒ 4g2 – 3g – 85 = 0
⇒ 4g2 – 20g + 17g – 85 = 0
⇒ 4g(g – 5) + 17(g – 5) = 0
⇒ (g – 5)(4g + 17) = 0
Since g ≠ \(\frac{-17}{4}\)
∴ g = 5
Hence No. of girls = 5