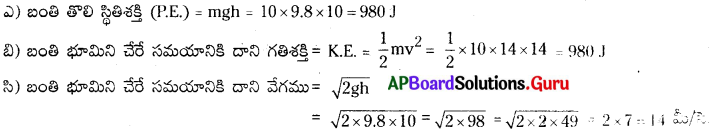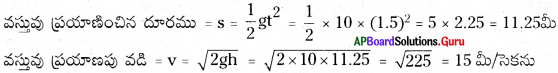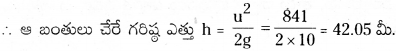Mahesh – Page 48 – AP Board Solutions

Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a)

Question 1.
Find the angle between the vectors \(\bar{i}+2 \bar{j}+3 \bar{k}\) and \(3 \bar{i}-\bar{j}+2 \bar{k}\).
Solution:
Let \(\overline{\mathrm{a}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}\) and \(\overline{\mathrm{b}}=3 \overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}\) and ‘θ’ be the angle between them (i.e.,) \((\bar{a}, \bar{b})\) = θ
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q1

Question 2.
If the vectors \(\mathbf{2} \overline{\mathbf{i}}+\lambda \overline{\mathbf{j}}-\overline{\mathbf{k}}\) and \(4 \bar{i}-2 \bar{j}+2 \bar{k}\) are perpendicular to each other, then find λ.
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q2

Question 3.
For what values of λ, the vectors \(\overline{\mathbf{i}}-\lambda \overline{\mathbf{j}}+2 \overline{\mathbf{k}}\) and \(8 \overline{\mathbf{i}}+6 \overline{\mathbf{j}}-\overline{\mathbf{k}}\) are at right angles?
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q3

Question 4.
\(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}-3 \overline{\mathbf{j}}-5 \overline{\mathbf{k}}\). Find the vector C such that \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) form the sides of a triangle.
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q4

Question 5.
Find the angle between the planes \(\bar{r} \cdot(2 \bar{i}-\bar{j}+2 \bar{k})=3\) and \(\overline{\mathrm{r}} \cdot(3 \overline{\mathrm{i}}+6 \bar{j}+\bar{k})=4\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q5

Question 6.
Let \(\overline{\mathbf{e}}_{1}\) and \(\overline{\mathbf{e}}_{2}\) be unit vectors makingangle θ. If \(\frac{1}{2}\left|\bar{e}_{1}-\bar{e}_{2}\right|=\sin \lambda \theta\), then find λ.
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q6

Question 7.
Let \(\overline{\mathbf{a}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}+3 \overline{\mathbf{j}}+\overline{\mathbf{k}}\). Find
(i) The projection vector of \(\overline{\mathbf{b}}\) on \(\overline{\mathbf{a}}\) and its magnitude.
(ii) The vector components of \(\overline{\mathbf{b}}\) in the direction of a and perpendicular to \(\overline{\mathbf{a}}\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q7

Question 8.
Find the equation of the plane through the point (3, -2, 1) and perpendicular to the vector (4, 7, -4).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q8

Question 9.
If \(\overline{\mathbf{a}}=2 \bar{i}+2 \bar{j}-3 \bar{k}\); \(\overline{\mathbf{b}}=3 \overline{\mathbf{i}}-\overline{\mathbf{j}}+2 \overline{\mathbf{k}}\), then find the angle between \(2 \overline{\mathbf{a}}+\overline{\mathbf{b}}\) and \(\bar{a}+2 \bar{b}\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) I Q9

II.

Question 1.
Find unit vector parallel to the XOY- plane and perpendicular to the vector \(4 \bar{i}-3 \bar{j}+\bar{k}\).
Solution:
Any vector parallel to XOY-plane will be of the form \(p \bar{i}+q \bar{j}\)
∴ The vector parallel to the XOY-plane and perpendicular to the vector \(4 \bar{i}-3 \bar{j}+\bar{k}\) is \(3 \bar{i}+4 \bar{j}\)
Its magnitude = \(|3 \bar{i}+\overline{4 j}|=\sqrt{9+16}=5\)
∴ Unit vector parallel to the XOY-plane and perpendicular to the vector \(4 \bar{i}-3 \bar{j}+\bar{k}\) is \(\pm \frac{(3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}})}{5}\)

Question 2.
If \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathrm{c}}=0,|\overline{\mathbf{a}}|=3,|\overline{\mathbf{b}}|=5\) and \(|\bar{c}|=7\), then find the angle between \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) II Q2

Question 3.
If \(|\overline{\mathbf{a}}|\) = 2, \(|\overline{\mathbf{b}}|\) = 3 and \(|\overline{\mathbf{c}}|\) = 4 and each of \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) is perpendicular to the sum of the other two vectors, then find the magnitude of \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) II Q3

Question 4.
Find the equation of the plane passing through the point \(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+3 \bar{j}-\overline{\mathbf{k}}\) and perpendicular to the vector \(3 \bar{i}-2 \bar{j}-2 \bar{k}\) and the distance of this plane from the origin.
Solution:
Equation of the plane passing through the point \(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+3 \bar{j}-\overline{\mathbf{k}}\) and perpendicular to the vector \(\bar{n}=3 \bar{i}-2 \bar{j}-2 \bar{k}\) is
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) II Q4

Question 5.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) and \(\overline{\mathbf{d}}\) are the position vectors of four coplanar points such that \((\mathbf{a}-\overline{\mathbf{d}}) \cdot(\bar{b}-\bar{c})=(\bar{b}-\bar{d}) \cdot(\bar{c}-\bar{a})=0\). Show that the point \(\bar{d}\) represents the orthocentre of the triangle with \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\) as its vertices.
Solution:
Position vectors of A, B, C, D are \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) respectively.
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) II Q5

⇒ BD is perpendicular to AC
∴ BD is another altitude of ∆ABC.
Altitudes AD and BD intersect at D.
∴ D is the orthocentre of ∆ABC.

III.

Question 1.
Show that the points (5, -1, 1), (7, -4, 7), (1, -6, 10) and (-1, -3, 4) are the vertices of a rhombus.
Solution:
Let A(5, -1, 1), B(7, -4, 7), C(1, -6, 10) and D(-1, -3, 4) are the given points.
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) III Q1
∵ AB = BC = CD = DA = 7 units
AC ≠ BD
∴ A, B, C, D points are the vertices of a rhombus.

Question 2.
Let \(\bar{a}=4 \bar{i}+5 \bar{j}-\bar{k}, \quad \bar{b}=\bar{i}-4 \bar{j}+5 \bar{k}\) and \(\overline{\mathbf{c}}=\mathbf{3} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\). Find the vector which is perpendicular to both \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\) and whose magnitude is twenty one times the magnitude of \(\overline{\mathbf{c}}\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) III Q2

Question 3.
G is the centroid of ΔABC and a, b, c are the lengths of the sides BC, CA and AB respectively prove that a² + b² + c² = 3 (OA² + OB² + OC²) – 9(OG)² where O is any point.
Solution:
Given that \(\overline{\mathrm{BC}}=\overline{\mathrm{a}}, \overline{\mathrm{CA}}=\overline{\mathrm{b}}, \overline{\mathrm{AB}}=\overline{\mathrm{c}}\)
Let ‘O’ be the origin and let \(\overline{\mathrm{OA}}=\overline{\mathrm{p}}, \overline{\mathrm{OB}}=\overline{\mathrm{q}} \text { and } \overline{\mathrm{OC}}=\overline{\mathrm{r}}\)
Then P.V. of the centroid of ΔABC is
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) III Q3
From (1) and (2)
∴ a² + b² + c² = 3(OA² + OB² + OC²) – 9(OG)².

Question 4.
A line makes angles θ₁, θ₂, θ₃, and θ₄ with the diagonals of a cube. Show that cos²θ₁ + cos²θ₂ + cos²θ₃ + cos²θ₄ = \(\frac{4}{3}\).
Solution:
Inter 1st Year Maths 1A Products of Vectors Solutions Ex 5(a) III Q4

Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b)

Question 1.
Find the vector equation of the line passing through the point \(2 \bar{i}+3 \bar{j}+\bar{k}\) and parallel to the vector \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) I Q1

Question 2.
OABC is a parallelogram. If \(\overline{O A}=\bar{a}\) and \(\overline{O C}=\bar{c}\), find the vector equation of the side BC.
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) I Q2

Question 3.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are the position vectors of the vertices A, B and C respectively of ∆ABC, theind the vector equation of the median through the vertex A.
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) I Q3

Question 4.
Find the vertor equation of the line joining the points \(2 \bar{i}+\bar{j}+3 \bar{k}\) and \(-4 \bar{i}+3 \bar{j}-\bar{k}\).
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) I Q4

Question 5.
Find the vector equation of the plane passing through the points \(\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+5 \overline{\mathbf{k}},-5 \overline{\mathbf{j}}-\overline{\mathbf{k}} \text { and }-3 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}\).
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) I Q5

Question 6.
Find the vector equation of the plane through the points (0, 0, 0), (0, 5, 0) and (2, 0, 1).
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) I Q6

II.

Question 1.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are noncoplanar find the point of intersection of the line passing through the points \(2 \bar{a}+3 \bar{b}-\bar{c}\), \(3 \bar{a}+4 \bar{b}-2 \bar{c}\) with the line joining the points \(\bar{a}-2 \bar{b}+3 \bar{c}, \bar{a}-6 \bar{b}+6 \bar{c}\).
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) II Q1

Question 2.
ABCD is a trapezium in which AB and CD are parallel. Prove by vector methods, that the mid points of the sides AB, CD and the intersection of the diagonals are collinear.
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) II Q2

⇒ M, P, N are collinear
Hence the midpoints of parallel sides of a trapezium and the point of intersection of the diagonals are collinear.

Question 3.
In a quadrilateral ABCD, if the midpoints of one pair of opposite sides and the point of intersection of the diagonals are collinear, using vector methods, prove that the quadrilateral ABCD is a trapezium.
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) II Q3

III.

Question 1.
Find the vector equation of the plane which passes through the points \(2 \bar{i}+4 \bar{j}+2 \bar{k}, 2 \bar{i}+3 \bar{j}+5 \bar{k}\) and parallel to the vector \(3 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\). Also find the point where this plane meets the line joining the points \(2 \overline{\mathbf{i}}+\overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) and \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) III Q1

Question 2.
Find the vector equation of the plane passing through points \(4 \overline{\mathbf{i}}-3 \overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(3 \overline{\mathbf{i}}+7 \overline{\mathbf{j}}-10 \overline{\mathbf{k}}\) and \(2 \bar{i}+5 \bar{j}-7 \bar{k}\), and show that the point \(\overline{\mathbf{i}}+2 \bar{j}-3 \overline{\mathbf{k}}\) lies in the plane.
Solution:
Inter 1st Year Maths 1A Addition of Vectors Solutions Ex 4(b) III Q2

Inter 1st Year Maths 1A Matrices Solutions Ex 3(i)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(i) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(i)

Solve the following systems of homogeneous equations.

Question 1.
2x + 3y – z = 0, x – y – 2z = 0, 3x + y + 3z = 0
Solution:
The Coefficient matrix is \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & -1 & -2 \\
3 & 1 & 3
\end{array}\right]\)
det of \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & -1 & -2 \\
3 & 1 & 3
\end{array}\right]=\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & -1 & -2 \\
3 & 1 & 3
\end{array}\right]\)
= 2(-3 + 2) – 3(3 + 6) – 1(1 + 3)
= -2 – 27 – 4
= -33 ≠ 0, ρ(A) = 3
Hence the system has the trivial solution x = y = z = 0 only.

Question 2.
3x + y – 2z = 0, x + y + z = 0, x – 2y + z = 0
Hint: If the determinant of the coefficient matrix ≠ 0 then the system has a trivial solution (i.e.) ρ(A) = 3.
Solution:
The coefficient matrix is \(\left[\begin{array}{ccc}
3 & 1 & -2 \\
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right]\)
\(\left|\begin{array}{ccc}
3 & 1 & -2 \\
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right|\)
= 3(1 + 2) – 1(1 – 1) – 2(-2 – 1)
= 9 + 6
= 15 ≠ 0, ρ(A) = 3
Hence the system has the trivial solutions x = y = z = 0 only.

Question 3.
x + y – 2z = 0, 2x + y – 3z = 0, 5x + 4y – 9z = 0
Solution:
The coefficient matrix is \(\left[\begin{array}{rrr}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right]\) = A (say)
|A| = \(\left|\begin{array}{rrr}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right|\)
= 1(-9 + 12) – 1(-18 + 15) – 2(8 – 5)
= 3 + 3 – 6
= 0
∴ Rank of A = 2 as the submatrix \(\left[\begin{array}{ll}
1 & 1 \\
2 & 1
\end{array}\right]\) is non-singular, ρ(A) < 3
Hence the system has a non-trivial solution.
A = \(\left[\begin{array}{lll}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right]\)
R₂ → R₂ – 2R₁, R₃ → R₃ – 3R₁
A ~ \(\left[\begin{array}{ccc}
1 & 1 & -2 \\
0 & -1 & 1 \\
0 & -1 & -1
\end{array}\right]\)
The system of equation is equivalent to the given system of equations are x + y – 2z = 0, -y + z = 0
Let z = k
⇒ y = k, x = k
∴ x = y = z = k for real number k.

Question 4.
x + y – z = 0, x – 2y + z = 0, 3x + 6y – 5z = 0
Solution:
Coefficient matrix A = \(\left[\begin{array}{ccc}
1 & 1 & -1 \\
1 & -2 & 1 \\
3 & 6 & -5
\end{array}\right]\)
R₂ → R₂ – R₁, R₃ → R₃ – 3R₁
A ~ \(\left[\begin{array}{ccc}
1 & 1 & -1 \\
0 & -3 & 2 \\
0 & 3 & -2
\end{array}\right]\)
⇒ det A = 0 as R₂, R₃ are identical.
and rank (A) = 2 as the submatrix \(\left[\begin{array}{cc}
1 & 1 \\
0 & -3
\end{array}\right]\) is non-singular.
Hence the system has a non-trivial solution, ∵ ρ(A) < 3
The system of equations equivalent to the given system of equations are
x + y – z = 0
3y – 2z = 0
Let z = k
⇒ y = \(\frac{2 k}{3}\)
x = \(\frac{k}{3}\)
∴ x = \(\frac{k}{3}\), y = \(\frac{2 k}{3}\), z = k for any real number of k.

Inter 1st Year Maths 1A Matrices Solutions Ex 3(h)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(h) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(h)

Solve the following systems of equations.
(i) by using Cramer’s rule and matrix inversion method, when the coefficient matrix is non-singular.
(ii) by using the Gauss-Jordan method. Also, determine whether the system has a unique solution or an infinite number of solutions, or no solution, and find the solutions if exist.

Question 1.
5x – 6y + 4z = 15
7x + 4y – 3z = 19
2x + y + 6z = 46
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
5 & -6 & 4 \\
7 & 4 & -3 \\
2 & 1 & 6
\end{array}\right|\)
= 5(24 + 3) + 6(42 + 6) + 4(7 – 8)
= 135 + 288 – 4
= 419
Δ₁ = \(\left|\begin{array}{ccc}
15 & -6 & 4 \\
19 & 4 & -3 \\
46 & 1 & 6
\end{array}\right|\)
= 15(24 + 3) + 6(114 + 138) + 4(19 – 184)
= 405 + 1512 – 660
= 1917 – 660
= 1257
Δ₂ = \(\left|\begin{array}{ccc}
5 & 15 & 4 \\
7 & 19 & -3 \\
2 & 46 & 6
\end{array}\right|\)
= 5(114 + 138) – 15(42 + 6) + 4(322 – 38)
= 1260 – 720 + 1136
= 1676
Δ₃ = \(\left|\begin{array}{ccc}
5 & -6 & 15 \\
7 & 4 & 19 \\
2 & 1 & 46
\end{array}\right|\)
= 5(184 – 19) + 6(322 – 38) + 15(7 – 8)
= 825 + 1704 – 15
= 2529 – 15
= 2514
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q1(i)
Solution is x = 3, y = 4, z = 6.

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q1(ii)

Solution is x = 3, y = 4, z = 6

(iii) Gauss-Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q1(iii)
∴ Unique solution exists.
Solution is x = 3, y = 4, z = 6.

Question 2.
x + y + z = 1
2x + 2y + 3z = 6
x + 4y + 9z = 3
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 3 \\
1 & 4 & 9
\end{array}\right|\)
= 1(18 – 12) – 1(18 – 3) + 1(8 – 2)
= 6 – 15 + 6
= -3
Δ₁ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
6 & 2 & 3 \\
3 & 4 & 9
\end{array}\right|\)
= 1(18 – 12) – 1(54 – 9) + 1(24 – 6)
= 6 – 45 + 18
= -21
Δ₂ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 6 & 3 \\
1 & 3 & 9
\end{array}\right|\)
= 1(54 – 9) – 1(18 – 3) + 1(6 – 6)
= 45 – 15
= 30
Δ₃ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 6 \\
1 & 4 & 3
\end{array}\right|\)
= 1(6 – 24) – 1(6 – 6) + 1(8 – 2)
= -18 – 0 + 6
= -12
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q2(i)
Solution is x = 7, y = -10, z = 4

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q2(ii)

∴ Solution is x = 7, y = -10, z = 4

(iii) Gauss-Jordan method:
Augmented matrix is A = \(\left[\begin{array}{llll}
1 & 1 & 1 & 1 \\
2 & 2 & 3 & 6 \\
1 & 4 & 9 & 3
\end{array}\right]\)
R₂ → R₂ – 2R₁, R₃ → R₃ – R₁
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q2(iii)
Unique solution exists.
∴ Solution is x = 7, y = -10, z = 4

Question 3.
x – y + 3z = 5
4x + 2y – z = 0
-x + 3y + z = 5
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
1 & -1 & 3 \\
4 & 2 & -1 \\
-1 & 3 & 1
\end{array}\right|\)
= 1(2 + 3) + 1(4 – 1) + 3(12 + 2)
= 5 + 3 + 42
= 50
Δ₁ = \(\left|\begin{array}{ccc}
5 & -1 & 3 \\
0 & 2 & -1 \\
5 & 3 & 1
\end{array}\right|\)
= 5(2 + 3) + 1(0 + 5) + 3(0 – 10)
= 25 + 5 – 30
= 0
Δ₂ = \(\left|\begin{array}{ccc}
1 & 5 & 3 \\
4 & 0 & -1 \\
-1 & 5 & 1
\end{array}\right|\)
= 1(0 + 5) – 5(4 – 1) + 3(20 – 0)
= 5 – 15 + 60
= 50
Δ₃ = \(\left|\begin{array}{ccc}
1 & -1 & 5 \\
4 & 2 & 0 \\
-1 & 3 & 5
\end{array}\right|\)
= 1(10 – 0) + 1(20 – 0) + 5(12 + 2)
= 10 + 20 + 70
= 100
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q3(i)
∴ Solution is x = 0, y = 1, z = 2.

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q3(ii)

Solution is x = 0, y = 1, z = 2

(iii) Gauss Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q3(iii)
Unique solution exists.
∴ Solution is x = 0, y = 1, z = 2

Question 4.
2x + 6y + 11 = 0
6x + 20y – 6z + 3 = 0
6y – 18z + 1 = 0
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & 6 & 0 \\
6 & 20 & -6 \\
0 & 6 & -18
\end{array}\right|\)
= 2(-360 + 36) – 6(-108 – 0)
= -648 + 648
= 0
∴ Cramer’s rule and matrix inversion method cannot be used.
∵ Δ = 0

(ii) Gauss Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q4(ii)
ρ(A) = 2, ρ(AB) = 3
ρ(A) ≠ ρ(AB)
∴ The given system of equations does not have a solution.

Question 5.
2x – y + 3z = 9
x + y + z = 6
x – y + z = 2
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
1 & 1 & 1 \\
1 & -1 & 1
\end{array}\right|\)
= 2(1 + 1) + 1(1 – 1) + 3(-1 – 1)
= 4 + 0 – 6
= -2
Δ₁ = \(\left|\begin{array}{ccc}
9 & -1 & 3 \\
6 & 1 & 1 \\
2 & -1 & 1
\end{array}\right|\)
= 9(1 + 1) + 1(6 – 2) + 3(-6 – 2)
= 18 + 4 – 24
= -2
Δ₂ = \(\left|\begin{array}{lll}
2 & 9 & 3 \\
1 & 6 & 1 \\
1 & 2 & 1
\end{array}\right|\)
= 2(6 – 2) – 9(1 – 1) + 3(2 – 6)
= 8 – 0 – 12
= -4
Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 9 \\
1 & 1 & 6 \\
1 & -1 & 2
\end{array}\right|\)
= 2(2 + 6) + 1(2 – 6) + 9(-1 – 1)
= 16 – 4 – 18
= -6
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q5(i)
Solution is x = 1, y = 2, z = 3.

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q5(ii)

Solution is x = 1, y = 2, z = 3.

(iii) Gauss-Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q5(iii)
∴ The given equations have a unique solution.
Solution is x = 1, y = 2, z = 3

Question 6.
2x – y + 8z = 13
3x + 4y + 5z = 18
5x – 2y + 7z = 20
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 8 \\
3 & 4 & 5 \\
5 & -2 & 7
\end{array}\right|\)
= 2(28 + 10) + 1(21 – 25) + 8(-6 – 20)
= 76 – 4 – 208
= -136
Δ₁ = \(\left|\begin{array}{ccc}
13 & -1 & 8 \\
18 & 4 & 5 \\
20 & -2 & 7
\end{array}\right|\)
= 13(28 + 10) + 1(126 – 100) + 8(-36 – 80)
= 494 + 26 – 928
= -408
Δ₂ = \(\left|\begin{array}{lll}
2 & 13 & 8 \\
3 & 18 & 5 \\
5 & 20 & 7
\end{array}\right|\)
= 2(126 – 100) – 13(21 – 25) + 8(60 – 90)
= 52 + 52 – 240
= -136
Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 13 \\
3 & 4 & 18 \\
5 & -2 & 20
\end{array}\right|\)
= 2(80 + 36) + 1(60 – 90) + 13(-6 – 20)
= 232 – 30 – 338
= -136
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q6(i)
∴ Solution is x = 3, y = 1, z = 1

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q6(ii)

∴ Solution is x = 3, y = 1, z = 1

(iii) Gauss Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q6(iii)
∴ The given equations have a unique solution and Solution is x = 3, y = 1, z = 1.

Question 7.
2x – y + 3z = 8
-x + 2y + z = 4
3x + y – 4z = 0
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
-1 & 2 & 1 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 1) + 1(4 – 3) + 3(-1 – 6)
= -18 + 1 – 21
= -38
Δ₁ = \(\left|\begin{array}{ccc}
8 & -1 & 3 \\
4 & 2 & 1 \\
0 & 1 & -4
\end{array}\right|\)
= 8(-8 – 1) + 1(-16 – 0) + 3(4 – 0)
= -72 – 16 + 12
= -76
Δ₂ = \(\left|\begin{array}{ccc}
2 & 8 & 3 \\
-1 & 4 & 1 \\
3 & 0 & -4
\end{array}\right|\)
= 2(-16 – 0) – 8(4 – 3) + 3(-0 – 12)
= -32 – 8 – 36
= -76
Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 8 \\
-1 & 2 & 4 \\
3 & 1 & 0
\end{array}\right|\)
= 2(0 – 4) + 1(0 – 12) + 8(-1 – 6)
= -8 – 12 – 56
= -76
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q7(i)
∴ Solution is x = 2, y = 2, z = 2.

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q7(ii)

Solution is x = 2, y = 2, z = 2

(iii) Gauss Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q7(iii)

∴ The given equations have a unique solution and solution is x = 2, y = 2, z = 2.

Question 8.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 5 & 7 \\
2 & 1 & -1
\end{array}\right|\)
= 1(-5 – 7) – 1(-2 – 14) + 1(2 – 10)
= -12 + 16 – 8
= -4
Δ₁ = \(\left|\begin{array}{ccc}
9 & 1 & 1 \\
52 & 5 & 7 \\
0 & 1 & -1
\end{array}\right|\)
= 9(-5 – 7) – 1(-52 – 0) + 1(52 – 0)
= -108 + 52 + 52
= -4
Δ₂ = \(\left|\begin{array}{ccc}
1 & 9 & 1 \\
2 & 52 & 7 \\
2 & 0 & -1
\end{array}\right|\)
= 1(-52 – 0) – 9(-2 – 14) + 1(0 – 104)
= -52 + 144 – 104
= -12
Δ₃ = \(\left|\begin{array}{ccc}
1 & 1 & 9 \\
2 & 5 & 52 \\
2 & 1 & 0
\end{array}\right|\)
= 1(0 – 52) – 1(0 – 104) + 9(2 – 10)
= -52 + 104 – 72
= -20
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q8(i)

(ii) Matrix inversion method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q8(ii)

Solution is x = 1, y = 3, z = 5

(iii) Gauss Jordan method:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(h) Q8(iii)
∴ The given equations have a unique solution and solution is x = 1, y = 3, z = 5.

Inter 1st Year Maths 1A Matrices Solutions Ex 3(g)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(g) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(g)

Examine whether the following systems of equations are consistent or inconsistent and if consistent find the complete solutions.

Question 1.
x + y + z = 4
2x + 5y – 2z = 3
x + 7y – 7z = 5
Solution:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q1
ρ(A) = 2, ρ(AB) = 3
ρ(A) ≠ ρ(AB)
∴ The given system of equations are in consistent.

Question 2.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Solution:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q2

Question 3.
x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1
Solution:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q3
ρ(A) = 2 = ρ(AB) < 3
The given system of equations are consistent and have infinitely many solutions.
The solutions are given by [(x, y, z) 1x = 1, y + z = 0].

Question 4.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q4
∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent have a unique solution.
∴ Solution is given by x = 1, y = 3, z = 5.

Question 5.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Solution:
Augmented matrix A = \(\left[\begin{array}{cccc}
1 & 1 & 1 & 6 \\
1 & 2 & 3 & 10 \\
1 & 2 & 4 & 1
\end{array}\right]\)
By R₂ → R₂ – R₁, R₃ → R₃ – R₂, we obtain
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q5
∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent.
They have a unique solution.
∴ Solution is given by x = -7, y = 22, z = -9.

Question 6.
x – 3y – 8z = -10
3x + y – 4z = 0
2x + 5y + 6z = 13
Solution:
The Augmented matrix
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q6
ρ(A) = ρ(AB) = 2 < 3
∴ The given system of equations are consistent have infinitely many solutions.
x + y = 2 and y + 2z = 3
Taking z = k, y = 3 – 2z = 3-2k
x = 2 – y
= 2 – (3 – 2k)
= 2 – 3 + 2k
= 2k – 1
∴ The solutions are given by x = -1 + 2k, y = 3 – 2k, z = k where ‘k’ is any scalar.

Question 7.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Solution:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q7
∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent have a unique solution.
∴ Solution is given by x = \(\frac{35}{18}\), y = \(\frac{29}{18}\), z = \(\frac{5}{18}\)

Question 8.
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Solution:
Inter 1st Year Maths 1A Matrices Solutions Ex 3(g) Q8
∴ ρ(A) = ρ(AB) = 3
∴ The given system of equations are consistent have a unique solution.
∴ Solution is given by x = 2, y = 2, z = \(\frac{1}{2}\)

Inter 1st Year Maths 1A Matrices Solutions Ex 3(f)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(f) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(f)

I. Find the rank of each of the following matrices.

Question 1.
\(\left[\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right|\) = 0 – 0 = 0
and |1| = 1 ≠ 0
∴ ρ(A) = 1

Question 2.
\(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1 ≠ 0
∴ ρ(A) = 2

Question 3.
\(\left[\begin{array}{ll}
1 & 1 \\
0 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 1 \\
0 & 0
\end{array}\right|\) = 0 – 0 = 0
|1| = 1 ≠ 0
∴ ρ(A) = 1

Question 4.
\(\left[\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right|\) = 0 – 1 = -1 ≠ 0
∴ ρ(A) = 2

Question 5.
\(\left[\begin{array}{ccc}
1 & 0 & -4 \\
2 & -1 & 3
\end{array}\right]\)
Solution:
\(\left|\begin{array}{cc}
1 & -4 \\
2 & 3
\end{array}\right|\) = 3 + 8 = -11 ≠ 0
∴ ρ(A) = 2

Question 6.
\(\left[\begin{array}{lll}
1 & 2 & 6 \\
2 & 4 & 3
\end{array}\right]\)
Solution:
\(\left|\begin{array}{ll}
2 & 6 \\
4 & 3
\end{array}\right|\) = 6 – 24 = -18 ≠ 0
∴ ρ(A) = 2

II.

Question 1.
\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
= 1(1 – 0) – 0(0 – 0) + 0(0 – 0)
= 1 – 0 + 0
= 1 ≠ 0
∴ ρ(A) = 3

Question 2.
\(\left[\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 0 \\
0 & 1 & 2
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 0 \\
0 & 1 & 2
\end{array}\right|\)
= 1(6 – 0) – 2(8 + 1) + 0(0 + 3)
= 6 – 18
= -12 ≠ 0
∴ ρ(A) = 3

Question 3.
\(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right|\)
= 1(6 – 4) – 2(4 – 3) + 0(8 – 9)
= 2 – 2 + 0
= 0
∴ ρ(A) ≠ 3, ρ(A) < 3
Take \(\left|\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right|\) = 3 – 4 = -1 ≠ 0
∴ ρ(A) = 2

Question 4.
\(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\), det A = 0, ρ(A) ≠ 3
All 2 × 2 sub-matrix det. is zero
∴ ρ(A) ≠ 2
|1| = 1 ≠ 0
∴ ρ(A) = 1

Question 5.
\(\left[\begin{array}{cccc}
1 & 2 & 0 & -1 \\
3 & 4 & 1 & 2 \\
-2 & 3 & 2 & 5
\end{array}\right]\)
Solution:
Take sub-matrix B = \(\left|\begin{array}{ccc}
1 & 2 & 0 \\
3 & 4 & 1 \\
-2 & 3 & 2
\end{array}\right|\)
= 1(8 – 3) – 2(6 + 2)
= 5 – 16
= -11 ≠ 0
Rank of the given matrix is 3.

Question 6.
\(\left[\begin{array}{cccc}
0 & 1 & 1 & -2 \\
4 & 0 & 2 & 5 \\
2 & 1 & 3 & 1
\end{array}\right]\)
Solution:
Take sub matrix A = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
4 & 0 & 2 \\
2 & 1 & 3
\end{array}\right]\)
= -1(12 – 4) + 1(4 – 0)
= -8 + 4
= -4 ≠ 0
∴ ρ(A) = 3

AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని

January 5, 2024January 4, 2024 by Mahesh

SCERT AP 9th Class Physics Study Material Pdf Download 11th Lesson ధ్వని Textbook Questions and Answers.

AP State Syllabus 9th Class Physical Science 11th Lesson Questions and Answers ధ్వని

9th Class Physical Science 11th Lesson ధ్వని Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
యానకంలో ధ్వని ప్రయాణిస్తుందని మనం ఎప్పుడు అంటాం?
A) యానకం ప్రయాణిస్తున్నప్పుడు
B) యానకంలోని కణాలు ప్రయాణిస్తున్నప్పుడు
C) ధ్వనిజనకం ప్రయాణిస్తున్నప్పుడు
D) అలజడి ప్రయాణిస్తున్నప్పుడు
జవాబు:
D) అలజడి ప్రయాణిస్తున్నప్పుడు

ప్రశ్న 2.
ధ్వని తరంగం కింది వాటిని కలిగి ఉంటుంది.
A) సంపీడనాలు మాత్రమే
B) విరళీకరణాలు మాత్రమే
C) సంపీడనాలను, విరళీకరణాలను ఒకదాని తర్వాత ఒకటి
D) శూన్యాన్ని
జవాబు:
శృంగాలను, ద్రోణులను ఒకదాని తర్వాత ఒకటి

ప్రశ్న 3.
హెర్ట్ అనగా
A) సెకనుకు ఉత్పత్తి అయ్యే తరంగాల సంఖ్య
B) నిమిషానికి ఉత్పత్తి అయ్యే తరంగాల సంఖ్య
C) గంటకు ఉత్పత్తి అయ్యే తరంగాల సంఖ్య
D) మిల్లీ సెకనుకు ఉత్పత్తి అయ్యే తరంగాల సంఖ్య
జవాబు:
A) సెకనుకు ఉత్పత్తి అయ్యే తరంగాల సంఖ్య

ప్రశ్న 4.
TV ధ్వనిని పెంచితే, ధ్వని యొక్క లక్షణాలలో మారేది.
A) కంపనపరిమితి
B) పౌనఃపున్యం
C) తరంగదైర్ఘ్యం
D) వేగం
జవాబు:
A) కంపనపరిమితి

ప్రశ్న 5.
ధ్వని వలన మెదడు పొందే అనుభూతిని తెలియజేసే ధ్వని లక్షణం
A) పిచ్ (స్థాయి)
B) తీవ్రత
C) నాణ్యత
D) ధ్వని
జవాబు:
A) పిచ్ (స్థాయి)

ప్రశ్న 6.
స్టెతస్కోప్ ట్యూబ్ గుండా ధ్వని ఎలా ప్రయాణిస్తుంది?
A) ట్యూబ్ తో పాటు వంగి ప్రయాణిస్తుంది
B) సరళరేఖా మార్గంలో ప్రయాణిస్తుంది
C) బహుళ పరావర్తనాల వల్ల
D) పైవన్నీ
జవాబు:
C) బహుళ పరావర్తనాల వల్ల

ప్రశ్న 7.
కింది పదాలను వివరించండి.
ఎ) కంపన పరిమితి
బి) తరంగ దైర్ఘ్యం
సి) పౌనఃపున్యము
జవాబు:
ఎ) కంపన పరిమితి :
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 1

తరంగ చలనములో ఏదైనా ఒక కణము పొందు గరిష్ఠ కంపన పరిమితి స్థానభ్రంశమును కంపన పరిమితి అంటారు.
దీనిని ‘a’ తో సూచిస్తారు.
దీనిని వివరించే అంశాలు సాంద్రత, పీడనం మరియు స్థానభ్రంశము.
దీనికి ప్రమాణాలు కి.గ్రా/మీ ‘, పాస్కల్ మరియు మీటర్.

బి) తరంగ దైర్ఘ్యం :

ఒకే కంపన దశలో ఉన్న రెండు వరుస కణముల (సంపీడనాలు లేక విరళీకరణాలు) మధ్య దూరమును తరంగ దైర్ఘ్యం అంటారు.
దీనిని “లాంబా (2)” తో సూచిస్తారు.
ఇది పొడవును సూచించును కావున దీనికి S.I పద్దతిలో ప్రమాణం మీటరు.

సి) పౌనఃపున్యము :

యానకములోని కణము ఒక సెకనులో చేయు డోలనముల సంఖ్యను (లేదా) జనకము నుండి ఒక సెకను కాలములో ప్రసారమయిన తరంగముల సంఖ్యను కూడా పౌనఃపున్యము అంటారు.
దీని ప్రమాణాలు హెర్లు (లేదా) సైకిల్స్/సెకను (లేదా) కంపనాలు / సెకను.

ప్రశ్న 8.
గాలిలో ధ్వని ప్రయాణిస్తున్నప్పుడు గాలిలో ఒకానొక ప్రదేశంలో కాలానుగుణంగా మారే రెండు రాశులను తెలపండి.
జవాబు:

గాలిలో ధ్వని ప్రయాణిస్తున్నపుడు ఒకానొక ప్రదేశంలో కాలానుగుణంగా సాంద్రత మరియు పీడనాలు మారతాయి.
గాలిలో ధ్వని అనుదైర్ఘ్య తరంగాల రూపంలో ప్రయాణిస్తుంది.
అనుదైర్ఘ్య తరంగాల యొక్క సంపీడనాల వద్ద సాంద్రత, పీడనాలు ఎక్కువగా ఉంటాయి.
అనుదైర్ఘ్య తరంగాల యొక్క విరళీకరణాల వద్ద సాంద్రత, పీడనాలు తక్కువగా ఉంటాయి.

ప్రశ్న 9.
ధ్వని తరంగం యొక్క తరంగదైర్ఘ్యాన్ని నిర్వచించండి. ఇది పౌనఃపున్యం మరియు ధ్వని వేగాలతో ఏ విధమైన సంబంధం కలిగి ఉంటుంది?
జవాబు:
తరంగదైర్ఘ్యం (λ) :
ఏవైనా రెండు వరుస సంపీడనాల (లేదా) విరళీకరణాల మధ్య దూరమును తరంగదైర్ఘ్యం (λ) అంటారు.

తరంగదైర్ఘ్యం (λ) = తరంగ వేగము (v) / పౌనఃపున్యము (η)
తరంగదైర్యాన్ని S.I. పద్ధతి నందు మీటర్లలో కొలుస్తారు.

ప్రశ్న 10.
గబ్బిలాలు తమకెదురుగా ఉన్న అవరోధాలను గుర్తించటంలో ప్రతిధ్వనులను ఎలా వినియోగించుకుంటాయి?
జవాబు:

గబ్బిలాలు వాటి నోటి ద్వారా అతిధ్వనులను ఉత్పత్తి చేస్తాయి.
ఈ ధ్వని అవి ప్రయాణించే మార్గంలో ఏవైనా అవరోధాలు ఉంటే వాటిని తాకి పరావర్తనం చెందుతాయి.
ఈ పరావర్తన ధ్వనులను గ్రహించిన గబ్బిలాలు వాటి మార్గదిశను మార్చుకుంటాయి.

ప్రశ్న 11.
సోనార్ పనిచేయు విధానాన్ని, ఉపయోగాలను వివరించండి. (లేదా) సోనార్ పనితీరును మరియు అనువర్తనాలను వివరించంది.
జవాబు:
సోనార్ అనగా సౌండ్ నావిగేషన్ అండ్ రేంజింగ్.
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 2

పనిచేయు విధానము :

ఈ వ్యవస్థలో ప్రసారిణి (transmitter) మరియు గ్రాహకం (receiver) అనే పరికరాలు ఓడలోని పరిశీలన కేంద్రంలో అమర్చబడి ఉంటాయి.
పరిశీలనా కేంద్రంలోని ప్రసారిణి ద్వారా దాదాపు 1000 Hz పౌనఃపున్యంగల అతిధ్వనులను నీటిలోని అన్ని దిశలకు ప్రసారం చేస్తారు.
ఈ తరంగాలు తమ మార్గంలో ఏదైనా అవరోధం తగిలే వరకు సరళరేఖా మార్గంలో ప్రయాణిస్తాయి.
పటంలో చూపినట్లుగా అవరోధానికి తగిలిన తరంగాలు పరావర్తనం చెంది ఓడ పరిశీలనా కేంద్రంలోని గ్రాహకాన్ని చేరతాయి.
పరిశీలనా కేంద్రానికి ఈ తరంగాలు ఏ దిశ నుండి వచ్చాయో ఆ దిశలో అవరోధ వస్తువున్నట్లు తెలుస్తుంది.
అతిధ్వనుల పరావర్తనం వల్ల వచ్చిన ప్రతిధ్వని ఓడను చేరడానికి పట్టే కాలం మరియు సముద్రనీటిలో అతిధ్వనుల వేగాన్ని బట్టి పరిశీలనా కేంద్రం నుండి వస్తువు ఎంత దూరంలో గలదో లెక్కిస్తారు.
ప్రతిధ్వనులు ఏర్పరచిన/వచ్చిన కోణాలను బట్టి ఆ వస్తువు ఆకృతి, పరిమాణాలను తెలుసుకుంటారు.

ఉపయోగాలు :

ఈ పద్ధతిని ఉపయోగించి సముద్రపు లోతును కనుగొనవచ్చును. దీనినే “ఈకోరేంజింగ్” అంటారు.
సముద్ర భూగర్భశాస్త్రవేత్తలు సముద్రంలోని పర్వతాలను కనుగొంటారు.
చేపల వేటకు వెళ్ళేవారు చేపల గుంపు ఉనికి కోసం వీటిని వాడుతారు.
సముద్రంలోని సబ్ మెరైన్స్, మునిగిన ఓడల జాడను తెలుసుకునేందుకు ఈ వ్యవస్థను వాడతారు.

ప్రశ్న 12.
400 Hz పౌనఃపున్యం గల ధ్వనితరంగం యొక్క ఆవర్తన కాలాన్ని కనుగొనండి.
జవాబు:
పౌనఃపున్యం = (η) = 400 Hz

ప్రశ్న 13.
ఒక ధ్వని తరంగ వేగం 340 మీ/సె మరియు తరంగదైర్ఘ్యం 2 సెం.మీ. అయిన ఆ తరంగం యొక్క పౌనఃపున్యం ఎంత? అది శ్రవ్య అవధిలో ఉంటుందా?
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 4
∴ ఇచ్చిన ధ్వని తరంగము శ్రవ్య అవధిలో కలదు.

ప్రశ్న 14.
పరశ్రావ్యాలు, అతిధ్వనులలో వేటి పౌనఃపున్యం ఎక్కువ?
జవాబు:
పరశ్రావ్యాల పౌనఃపున్యం 20 Hz కంటే తక్కువ, అతిధ్వనుల పౌనఃపున్యం 20,000 Hz కంటే ఎక్కువ. కావున అతిధ్వనుల పౌనఃపున్యం పరశ్రావ్యాల కంటే ఎక్కువ.

ప్రశ్న 15.
ఒక్కొక్కసారి మన పెంపుడు కుక్క దాని పరిసరాలలో ఎవరూ లేకపోయినా, ఏ శబ్దం వినపడకపోయినా అరుస్తూ ఉండటం చూస్తుంటాం. “శ్రవ్య అవధి” అనే భావన తెలిశాక మీరు గమనించిన కుక్క ప్రవర్తన గురించి మీకేమైనా సందేహాలు కలిగాయా? అయితే అవి ఏమిటి?
జవాబు:

కుక్క శ్రవ్య అవధి ఎంత?
మనము వినలేని ధ్వని దానికి స్పష్టంగా వినబడుతుందా?
ఇది ఈ కుక్క విషయంలోనేనా? అన్నింటి విషయంలలో కూడా ఇదే నియమమా?
కుక్క మన మాటలను ఎలా అర్థం చేసుకోగలదు?
దాని తక్కువ శ్రవ్య అవధి ఎంత?

ప్రశ్న 16.
ఒక ధ్వని జనకం సమీపంలోని గాలిలో సంపీడనాలు, విరళీకరణాలు ఎలా ఏర్పడతాయో పటం గీచి వివరించండి.
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 5

ఒక ధ్వని జనకం కంపించినపుడు అది సమీప యానకంలో అలజడి సృష్టిస్తుంది.
యానకంలో ఏర్పడే ఈ అలజడి ధ్వని జనకానికి దగ్గరగా ఉన్న చోట సంపీడన రూపంలోకి మారును.
ఈ సంపీడనము వలన ఆ యానకంలో కణాలకు సాంద్రత పెరిగి, తర్వాతి పొరలోని కణాలకు అందిస్తుంది.
తర్వాతి పొరలోని కణాలు ఒకదాని తర్వాత ఒకటి ఉత్పత్తి అయి యానకంలో అలజడిని ముందుకు తీసుకొని సాగిపోతాయి.
ఈ విధంగా యానకంలో ధ్వని ప్రసారం జరుగును.

ప్రశ్న 17.
రెండు సంవత్సరాల వయస్సు గల పాప యొక్క తల్లిదండ్రులు మరియు ఆ పాప యొక్క అవ్వ, తాత ఆ పాపతో పాటు ఒక గదిలో ఆటలాడుతున్నారు. ఒక శబ్దజనకం 28 KHz ధ్వనిని ఉత్పత్తి చేస్తే ఆ ధ్వనిని ఎవరు స్పష్టంగా వినగలరు?
జవాబు:
శబ్దజనక పౌనఃపున్యము 28 KHz అనగా 28000 Hz అర్ధము.

మానవుని శ్రవ్య అవధి 20 Hz – 20,000 Hz. పిల్లలు సుమారుగా 30,000 Hz వరకు వినగలరు. కావున ఆ గదిలో రెండు సంవత్సరాల వయస్సుగల పాప 28 KHz ధ్వనిని స్పష్టంగా వినగలదు. మిగిలిన వారికి ఈ ధ్వని అతిధ్వని అగును.

ప్రశ్న 18.
ఆడిటోరియంలలో, పెద్ద పెద్ద హాళ్ళలోని గోడలు, నేలభాగాలను నునుపుగా ఉంచరు. ఎందుకు?
జవాబు:

ధ్వని పరావర్తనం అనేది పరావర్తన తలంపై ఆధారపడి ఉంటుంది.
ధ్వని నునుపైన తలాల కంటే గరుకు తలాలపై అధిక పరావర్తనం చెందుతుంది.
సాధారణంగా సినిమాహాళ్ళు, ఆడిటోరియంలు, ఫంక్షన్‌హాళ్ళు నిర్మించేటప్పుడు ధ్వని పరావర్తనం చెందిన తర్వాత హాల్ మొత్తం ఏకరీతిలో విస్తరించేందుకు వీలుగా ఉండేందుకు గోడలు, నేల భాగాలు నునుపుగా ఉంచరు.

ప్రశ్న 19.
గాలిలో ధ్వనివేగం 340 మీ/సె. అయిన 20 KHz పౌనఃపున్యం గల ఒక ధ్వనిజనకం ఉత్పత్తి చేసే ధ్వని తరంగం యొక్క తరంగదైర్ఘ్యం కనుగొనండి. అదే ధ్వని జనకాన్ని నీటిలో ఉంచితే అది ఉత్పత్తి చేసే ధ్వనితరంగ తరంగదైర్ఘ్యం ఎంత ఉంటుంది? (నీటిలో ధ్వని వేగం = 1480 మీ/సె)
జవాబు:
గాలిలో ధ్వనివేగం = v = 340 మీ./సె. ; ధ్వని జనక పౌనఃపున్యం = η = 20 KHz = 20000 Hz
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 6

ప్రశ్న 20.
తరంగదైర్ఘ్యం, పౌనఃపున్యము, ధ్వనివేగాల మధ్య సంబంధాన్ని రాబట్టండి. (AS 1)
జవాబు:
తరంగదైర్ఘ్యం λ, డోలనావర్తన కాలము (T) మరియు పౌనఃపున్యము η గల తరంగము ఒక యానకంలో ప్రయాణించుచున్నదనుకొనుము.
T సెకనులలో తరంగము ప్రయాణించిన దూరము = λ మీటర్లు
ఒక సెకనులో తరంగం ప్రయాణించిన దూరము = λ/T మీటర్లు
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 7

ప్రశ్న 21.
కాంతి పరావర్తన నియమాలను ధ్వని పరావర్తనం కూడా పాటిస్తుందా? (AS 1)
జవాబు:
ధ్వని పరావర్తనం చెందిన తలంపై పతన బిందువు వద్ద గల లంబంతో పతన, పరావర్తన ధ్వని తరంగాలు సమాన కోణాలను ఏర్పరుస్తాయి. కావున ధ్వని పరావర్తనం కూడా కాంతి పరావర్తన నియమాలను పాటిస్తుంది.

ప్రశ్న 22.
ఎ, బి లనే శబ్ద జనకాలు ఒకే కంపన పరిమితితో కంపిస్తున్నాయి. అవి వరుసగా 1 KHz, 30 KHz పౌనఃపున్యాలు గల ధ్వనులను ఉత్పత్తి చేస్తున్నాయి. ఏ తరంగానికి అధిక శక్తి ఉంటుంది? (AS 1)
జవాబు:
శబ్ద జనకాల కంపన పరిమితులు స్థిరముగా ఉన్నవి. కావున ఏ జనక పౌనఃపున్యము అధికమో ఆ జనకము అధిక శక్తిగల తరంగమును విడుదలచేయును.
∴ 30 KHz పౌనఃపున్యంగల శబ్ద జనకము అధిక శక్తిగల తరంగమును విడుదలచేయును.

ప్రశ్న 23.
ధ్వని తరంగం గురించి మీరేం అవగాహన చేసుకున్నారు? (AS 1)
జవాబు:

ధ్వని తరంగం ఒక శక్తి వాహకము.
ధ్వని తరంగము అనుదైర్ఘ్య తరంగాల రూపంలో ఒక స్థానము నుండి మరొక స్థానమునకు ప్రయాణించును.
అనుదైర్ఘ్య తరంగాలలో వరుసగా సంపీడనాలు, విరళీకరణాలు ఏర్పడతాయి.
ధ్వని తరంగమునకు తరంగదైర్ఘ్యం, కంపన పరిమితి, పౌనఃపున్యం మరియు తరంగ వేగం అను లక్షణాలు కలవు.
ధ్వని యొక్క ఒక రకము సంగీత ధ్వనులు.
సంగీత ధ్వనుల అభిలక్షణాలు పిచ్, తీవ్రత, నాణ్యత.
ధ్వనులకు పరావర్తన లక్షణము కలదు.
ఈ పరావర్తన లక్షణము వలన ప్రతిధ్వని, ప్రతినాదములు ఏర్పడును.

ప్రశ్న 24.
పరశ్రావ్యాల (లేదా) అతిధ్వనుల ద్వారా భావ ప్రసారాలను చేసుకునే జంతువుల పేర్లను రాయండి. వాటి ఫోటోలను ఇంటర్నెట్ ద్వారా సేకరించి బుక్ తయారుచేయంది. (AS 4)
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 8

ప్రశ్న 25.
ఒక సంగీత వాయిద్యం నుండి ఉత్పత్తి అయిన ధ్వని యొక్క పౌనఃపున్యం, కంపనపరిమితులను ఏక కాలంలో నియంత్రిస్తూ శ్రావ్యమైన ధ్వనిని ఉత్పత్తి చేయడంలో సంగీత వాద్యకారుని కృషిని నీవెలా అభినందిస్తావు? (AS 6)
జవాబు:
ఒక సంగీత వాయిద్యం నుండి ఉత్పత్తయిన ధ్వనిని ఏక కాలంలో నిరంతరం నియంత్రిస్తూ మనకు శ్రావ్యమైన సంగీత స్వరంను వినిపిస్తున్న వాయిద్య కళాకారుని ప్రతిభాపాటవాలను నేను అభినందిస్తున్నాను.

ప్రశ్న 26.
ధ్వని యొక్క బహుళ పరావర్తనాల వల్ల డాక్టర్లకు, ఇంజనీర్లకు కలిగే ఉపయోగమేమిటి? (AS 7)
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 9

నిర్మాణ రంగంలో పనిచేయు ఇంజనీర్లు వారి కింద పనిచేయు పనివారికి సూచనలు ఇచ్చుటకు మెగా ఫోన్ వంటి పరికరాలను వాడతారు.
ఈ మెగాఫోన్లు ధ్వని యొక్క బహుళ పరావర్తనాలపై ఆధారపడి పనిచేస్తాయి.
వైద్యులు వాడే స్టెతస్కోపు ధ్వని యొక్క బహుళ పరావర్తనాలపై ఆధారపడి పనిచేస్తుంది.
ఏ విధముగా అంటే స్టెతస్కోపు ద్వారా శరీరం అంతర్భాగంలో ఉండే వివిధ భాగాలైన గుండె, ఊపిరితిత్తుల శబ్దాలు దానికి ఉండే గొట్టం ద్వారా అనేకమార్లు పరావర్తనం చెందుతూ వైద్యుని చెవికి చేరుతాయి.

ప్రశ్న 27.
సాధారణ గదులలో మనం వినే ధ్వని నాణ్యతపై ప్రతిధ్వనుల ప్రభావమేమిటి?
జవాబు:
సాధారణ గదులలో మనము విడుదల చేసే ధ్వని 0.1 సెకనులోపు మన చెవికి చేరాలి. లేనిచో ప్రతినాదం ఏర్పడి ధ్వని నాణ్యతలో తేడా వచ్చి, మాటల యొక్క స్పష్టతలో మార్పు వస్తుంది.

ప్రశ్న 28.
అర్ధగోళాకృతి కలిగి ఉన్న గదిలో, దాని కేంద్రం వద్ద తల ఉండేట్లుగా నేలపై ఒక వ్యక్తి పడుకున్నాడు. అతను ‘హలో’ అని అరచిన 0.2 సె. తర్వాత ప్రతిధ్వని వింటే ఆ అర్ధగోళాకృతి గది యొక్క వ్యాసార్థం ఎంత? (గాలిలో ధ్వ ని వేగం = 340 మీ/సె)
జవాబు:
ప్రతిధ్వని రావటానికి పట్టుకాలం = t = 0.2 సె. ; గాలిలో ధ్వని వేగం = 340 మీ./సె.
అర్ధగోళాకృతి ఆకారంలో ఉన్న గది వ్యాసార్ధం ‘d’ అయిన ప్రతిధ్వని ఇచ్చారు కాబట్టి ధ్వని ప్రయాణించిన దూరము ‘2d’ అగును.
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 10

ప్రశ్న 29.
“ధ్వని ఒక శక్తిస్వరూపమని తెలుసు. అయితే మహానగరాలలో ధ్వని కాలుష్యానికి కారణమవుతున్న ధ్వని ద్వారా ఉత్పత్తయిన శక్తిని నిత్యజీవితంలో మన శక్తి అవసరాలకు వాడుకోవచ్చు. ఇలా చేస్తే మహానగరాలలో జీవవైవిధ్యాన్ని కాపాడుటకు వీలవుతుంది. ” ఈ వాక్యాన్ని నీవు అంగీకరిస్తావా ? అంగీకరిస్తే ఎందుకో వివరించండి. (AS 7)
జవాబు:
ధ్వని ఒక శక్తి స్వరూపము. ధ్వని శక్తిని మన నిత్యజీవితంలో శక్తి అవసరాలకు ఉపయోగించుకొనవచ్చును. ప్రస్తుత రోజుల్లో ఈ ధ్వని శక్తిని వైద్యరంగంలో, పారిశ్రామిక రంగంలో విరివిగా ఉపయోగిస్తున్నాము.

పారిశ్రామిక రంగం :

లోహపు వస్తువులకు మరియు గాజు వస్తువులకు రంధ్రాలు వేయుటకు, కోరిన ఆకృతులలో కట్ చేయుటకు.
పాత్రలు, మురికి బట్టల వంటి సామాన్లలో మురికిని తొలగించలేని ప్రాంతాలలో మురికిని తొలగించుటకు.
యంత్రాలు, లోహ వంతెనలు, సైన్సు పరికరాలు మొదలగు లోహపు వస్తువులలో ఏర్పడు సన్నని పగుళ్ళు లేదా రంధ్రాలు ఉన్నట్లైతే వాటిని గుర్తించుటకు.

వైద్యరంగం:

ఇకోకార్డియోగ్రఫి ద్వారా గుండె యొక్క చిత్రాన్ని తీయుటకు.
అల్ట్రాసోనోగ్రఫి ద్వారా కాలేయం, పిత్తాశయం, గర్భాశయం వంటి శరీర భాగాలలో ఏర్పడే కణితులు, రాళ్ళను గుర్తించుటకు.
కంటిలోని శుక్లాలను తొలగించుటకు.
మూత్రపిండాలలో తయారైన రాళ్ళను తొలగించుటకు వాడతారు.
పై విధముగా మన నిత్యజీవితంలో శక్తి అవసరాలకు ధ్వనిని ఉపయోగించుకొనుచున్నాము.

9th Class Physical Science 11th Lesson ధ్వని Textbook InText Questions and Answers

9th Class Physical Science Textbook Page No. 189

ప్రశ్న 1.
ధ్వని తరంగంలో సంపీడనాలు, విరళీకరణాలు ఒకే దిశలో ప్రయాణిస్తాయా లేక ఒకదానికొకటి వ్యతిరేక దిశలో ప్రయాణిస్తాయా?
జవాబు:
ధ్వని తరంగంలో సంపీడనాలు, విరళీకరణాలు ఒకే దిశలో ప్రయాణిసాయి.
ఉదా :
ఒక తబలా కంపించినపుడు దాని పొర నిరంతరంగా ముందుకు, వెనుకకు కదులుతూ ఉండును.

9th Class Physical Science Textbook Page No. 193

ప్రశ్న 2.
ధ్వని తరంగపు పౌనఃపున్యం అది ప్రయాణించే యానకంపై ఆధారపడుతుందా? ఎలా?
జవాబు:
ధ్వని తరంగ ప్రసారంలో యానకపు సాంద్రత కణాలు ఒక సెకనులో చేయు డోలనాల సంఖ్య పౌనఃపున్యం. కావున యానకపు సాంద్రత పెరిగిన పౌనఃపున్యం మారును. యానకపు సాంద్రత తగ్గిన పౌనఃపున్యం మారును.

ఉదాహరణకు ధ్వని ప్రసారంలో సంపీడనాల వద్ద అధిక సాంద్రత, విరళీకరణాల వద్ద అల్ప సాంద్రత ఉండును.

ప్రశ్న 3.
ఒక ధ్వని జనకపు పౌనఃపున్యం 10 హెర్ట్ (Hz) అయితే ఒక నిమిషంలో అది ఎన్ని కంపనాలు చేస్తుంది?
జవాబు:
పౌనఃపున్యం = η = 10 Hz ; కాలము = T = 1 నిమిషం = 60 సెకనులు
పౌనఃపున్యం = కంపనాల సంఖ్య / కాలము
కంపనాల సంఖ్య = 10 x 60 = 600

ప్రశ్న 4.
ఒక గంటను మెల్లగా చేతితో కొట్టి దాని నుండి ఉత్పత్తి అయిన ధ్వనిని స్టెతస్కోప్ సహాయంతో వినడానికి ప్రయత్నించండి. స్టెతస్కోపు గంట యొక్క పైభాగం వద్ద, కింది భాగం వద్ద ఉంచి విన్నప్పుడు మీరు వినే ధ్వనిలో ఏం తేడాను గమనించారు? గంట యొక్క ఈ రెండు భాగాల నుండి ఉత్పత్తి అయిన ధ్వనుల కీచుదనం మరియు శబ్ద తీవ్రతలు ఒకే విధంగా ఉంటాయా? ఎందుకు?
జవాబు:
ఈ రెండు భాగాల నుండి ఉత్పత్తి అయిన ధ్వనుల కీచుదనం మరియు శబ్ద తీవ్రతలు వేరుగా ఉంటాయి. దీనికి కారణమేమనగా గంట యొక్క పై భాగంతో పోల్చగా క్రింది భాగము యొక్క పౌనఃపున్యం అధికము.

ప్రశ్న 5.
ఉరుములు వచ్చే ఒక సందర్భంలో మెరుపు కనబడిన 3 సెకన్ల తర్వాత ఉరుము శబ్దం వినిపిస్తే ఆ మెరుపు మీకు ఎంత దూరంలో ఉందో లెక్కించండి.
జవాబు:
మెరుపుకు, ఉరుముకు మధ్య గల సమయం = 3 సెకనులు
మెరుపు వేగము = కాంతి వేగము = 3 × 10⁸మీ/సె.
దూరము = వేగం × కాలం = 3 × 10⁸ × 3 = 9 × 10⁸ మీటర్లు
∴ మెరుపుకు నాకు గల దూరము = 9 × 10⁸ మీటర్లు.

9th Class Physical Science Textbook Page No. 196

ప్రశ్న 6.
ఇద్దరు అమ్మాయిలు ఒకే రకమైన తీగవాయిద్యాలతో ఆడుకుంటున్నారు. వాటి తీగలను ఒకే పిచ్ (pitch) గల స్వరాలను ఇచ్చే విధంగా సర్దుబాటు చేశారు. వాటి నాణ్యత కూడా సమానమౌతుందా? మీ జవాబును సమర్థించండి.
జవాబు:
ఆ రెండు తీగ వాయిద్యాల నాణ్యత సమానము కాదు ఎందుకనగా వాటి తరంగ రూపములో మార్పు ఉంటుంది కాబట్టి. ఒక సంగీత స్వరం యొక్క నాణ్యత దాని తరంగ రూపముపై ఆధారపడి ఉంటుంది.

ప్రశ్న 7.
ఒకసారి పౌనఃపున్యాన్ని, మరొకసారి కంపన పరిమితిని పెంచినపుడు సంగీతస్వరం యొక్క లక్షణములలో ఎలాంటి మార్పులను గమనించవచ్చు?
జవాబు:

ఒక సంగీత స్వరం యొక్క పౌనఃపున్యాన్ని పెంచితే దాని పిచ్ పెరుగును.
కంపన పరిమితిని పెంచితే సంగీత స్వరం యొక్క శబ్ద తీవ్రత పెరుగును.

9th Class Physical Science Textbook Page No. 197

ప్రశ్న 8.
ధ్వని నునుపైన తలాల కంటే గరుకు తలాలపై అధిక పరావర్తనం చెందటానికి కారణమేంటి?
జవాబు:
గరుకు తలాలపై ధ్వని అక్రమ పరావర్తనం చెందుతుంది కావున.

9th Class Physical Science Textbook Page No. 198

ప్రశ్న 9.
ధ్వని కన్నా ప్రతిధ్వని బలహీనంగా ఉంటుంది. ఎందుకు?
జవాబు:
సహజ ధ్వని ఒక పరావర్తన తలంను తాకినపుడు ఆ పరావర్తన తలం కొంత శక్తిని సంగ్రహించుకుంటుంది. దానితో ప్రతిధ్వని (పరావర్తన ధ్వని), నిజ ధ్వని కంటే బలహీనంగా ఉంటుంది.

ప్రశ్న 10.
ఒక మూసివున్న పెట్టెలో నీవు “హలో” అని అరిస్తే అది మీకు “హలో ……” అని ఎక్కువ సమయం వినిపిస్తుంది. ఎందువలన?
జవాబు:
ధ్వని మూసివున్న పెట్టెలో అనేక పర్యాయాలు పరావర్తనం చెందటం వలన ప్రతిధ్వని వచ్చేందుకు ఎక్కువ సమయం తీసుకుంటుంది.

9th Class Physical Science Textbook Page No. 199

ప్రశ్న 11.
మెగాఫోన్ వంటి పరికరాలకు శంఖాకారపు ముందు భాగాలు ఉండటం వల్ల ఏమి ఉపయోగం?
జవాబు:
శంఖాకారపు గొట్టం ద్వారా ప్రయోగించే ధ్వని అనేక పర్యాయాలు పరావర్తనం చెందడం ద్వారా ఉత్పత్తి అయిన ధ్వని తరంగాలు ఎదుటివారికి నేరుగా పంపబడతాయి.

ప్రశ్న 12.
సినిమా హాల్ లో కుర్చీలకు మెత్తని పదార్థాలు, నేలపై తివాచీలు, గోడపై రంపపు పొట్టుతో తయారైన అట్టలు ఎందుకు ఏర్పాటు చేస్తారు?
జవాబు:
సాధారణంగా ప్రతినాదము కనిష్టముగా ఉండేందుకు, సినిమా హాల్ లో కుర్చీలకు మెత్తని పదార్థాలు, నేలపై తివాచీలు, గోడపై రంపపు పొట్టుతో తయారైన అట్టలు ఏర్పాటు చేస్తారు.

9th Class Physical Science Textbook Page No. 187

ప్రశ్న 13.
కంపించే వస్తువు ధ్వనిని ఉత్పత్తి చేస్తుందనటానికి ఉదాహరణలిమ్ము.
జవాబు:
సైకిలు బెల్ ను మ్రోగించినప్పుడు, చేతితో కొట్టిన తబల, మీటిన వీణ తంత్రులు, తంబూరా మొ||వి.

ప్రశ్న 14.
మాట్లాడేటప్పుడు మన శరీరంలో ఏ అవయవం కంపిస్తుంది?
జవాబు:
మాట్లాడేటప్పుడు మన శరీరంలోని స్వరపేటిక కంపిస్తుంది.

ప్రశ్న 15.
కంపించే ప్రతి వస్తువు ధ్వనిని ఉత్పత్తి చేస్తుందా?
జవాబు:
కచ్చితముగా కంపనంలో ఉన్న వస్తువు దాని చుట్టుప్రక్కల గల యానకంలోనికి ధ్వని తరంగాలను ప్రసారం చేస్తుంది.

9th Class Physical Science Textbook Page No. 194

ప్రశ్న 16.
ఎ) దోమలు చేసే శబ్దం కీచుగా ఉంటుంది. కాని సింహాలు బిగ్గరగా గర్జిస్తాయి.
బి) ఆడవారి స్వరం మగవారి కంటే ఎక్కువ కీచుదనం కలిగి ఉంటుంది.
పైన తెలిపిన ధ్వనుల ఏ లక్షణం రెండు ధ్వనులు భిన్నమైనవి అని తెల్పుతుంది.
జవాబు:
పై ఉదాహరణలలో తెలిపిన ధ్వనుల యొక్క పిచ్ రెండు ధ్వనులు భిన్నమైనవి అని తెల్పుతుంది.

9th Class Physical Science Textbook Page No. 197

ప్రశ్న 17.
గట్టి తలాలు మెత్తని తలాల కంటే స్పష్టంగా ధ్వనిని పరావర్తనం చెందిస్తాయా?
జవాబు:
గట్టి తలాలు మెత్తని తలాల కంటే స్పష్టంగా ధ్వనిని పరావర్తనం చెందిస్తాయి.

ప్రశ్న 18.
0.1 సెకన్ల తర్వాత ప్రతిధ్వని రావాలంటే శబ్ద జనకానికి, అవరోధానికి (పరావర్తన తలానికి) మధ్య అవసరమైన కనీస దూరం ఎంత? ప్రతిధ్వని యొక్క వేగాన్ని కనుగొనటానికి ఒక సూత్రాన్ని రాబట్టండి.
జవాబు:
ధ్వని జనకం నుండి పరావర్తన తలం వరకు ధ్వని ప్రయాణించిన దూరము = d అవుతుంది.
పరావర్తన తలం నుండి ధ్వని జనకం వరకు ధ్వని ప్రయాణించిన దూరం కూడా ‘d’ అవుతుంది.
ధ్వని ప్రయాణించిన మొత్తం దూరం = 2d; ప్రతిధ్వని కాలం = t = 0.1 సె.
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 12
∴ దూరము = 344 x 0.1 = 34.4 మీ.
∴ 0.1 సెకన్ల తర్వాత ప్రతిధ్వని రావాలంటే శబ్దజనకానికి, అవరోధానికి మధ్య 34.4 మీటర్ల కనీస దూరం ఉండాలి.

ఉదాహరణ సమస్యలు

9th Class Physical Science Textbook Page No. 193

ప్రశ్న 1.
500 హెర్ట్ (Hz) పౌనఃపున్యం గల తరంగపు ఆవర్తన కాలాన్ని కనుగొనండి.
సాధన:

ప్రశ్న 2.
ఒక వాయువులో ధ్వని జనకం ఒక సెకనులో 40,000 సంపీడనాలను మరియు 40,000 విరళీకరణాలను ఉత్పత్తి చేసింది. రెండవ సంపీడనం ఏర్పడినపుడు మొదటి జనకము నుండి ఒక సెంటీమీటరు దూరంలో ఉన్నది. తరంగవేగాన్ని కనుగొనండి.
సాధన:
ఒక సెకనులో ప్రయాణించిన సంపీడన లేక విరళీకరణాల సంఖ్యను పౌనఃపున్యం అంటారు.
పౌనఃపున్యం = 40000 Hz
రెండు వరుస సంపీడన లేక విరళీకరణాల మధ్య దూరాన్ని తరంగ దైర్ఘ్యం అంటాం.
λ = 1 సెం.మీ.
తరంగ వేగం సూత్రం ప్రకారం V = ηλ
v= 40000 Hz x 1సెం.మీ. = 40000 సెం.మీ./సె. = 400 మీ/సె.

9th Class Physical Science Textbook Page No. 198

ప్రశ్న 3.
ఒక అబ్బాయి ఒక ఎత్తైన భవంతికి 132 మీటర్ల దూరంలో ఒక టపాకాయను పేల్చగా దాని ప్రతిధ్వని 0.8 సెకన్ల తర్వాత వినబడినది. అయితే ధ్వని వేగాన్ని కనుగొనండి.
సాధన:
ప్రతిధ్వని కాలం (t) = 0.8 సెకన్లు
ధ్వని ప్రయాణించిన మొత్తం దూరం 2d = 2 × 132 మీ. = 264 మీ.

9th Class Physical Science Textbook Page No. 202

ప్రశ్న 4.
సముద్రం లోతును కనుగొనడానికి సోనార్ నుండి తరంగం పంపబడింది. 6 సె. తర్వాత ప్రతిధ్వని సోనారను చేరితే సముద్రం లోతును కనుగొనండి. (సముద్రం నీటిలో ధ్వనివేగం 1500 మీ/సె)
సాధన:
సముద్రం లోతు = d మీ అనుకుందాం ; తరంగం ప్రయాణించిన మొత్తం దూరం = 20 మీ.
సముద్ర నీటిలో ధ్వని వేగం (u) = 1500 మీ./సె. ; పట్టిన కాలం (t) = 6 సె.
s = ut = 2d = 1500 మీ./సె. × 6 సె. ⇒ 2d = 9000 మీ.
⇒ d = 9000/2 = 4500 మీ. = 4.5 కి. మీ.

పరికరాల జాబితా

శృతిదండం, రాగి తీగ, తీగలు, స్ప్రింగ్, స్టెతస్కోపు

9th Class Physical Science 11th Lesson ధ్వని Textbook Activities (కృత్యములు)

కృత్యం – 1

ధ్వని ఒక శక్తి స్వరూపం :

ప్రశ్న 1.
ధ్వని ఒక శక్తి స్వరూపమని ప్రయోగపూర్వకముగా తెల్పుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 11

ఒక స్థూపాకార డబ్బాను తీసుకొనుము.
దానికి ఇరువైపులా గల మూతలను తొలగించి, ఒక బెలూనను పటంలో చూపినట్లు డబ్బా ఒక మూతకు తొడిగి అది కదలకుండా రబ్బరు బ్యాండు వేయండి.
చిన్న చతురస్రాకారపు సమతల దర్పణాన్ని తీసుకుని బెలూను పైభాగంలో అతికించండి.
పటంలో చూపినట్లు డబ్బాను స్టాండుకు అమర్చండి.
లేజర్ లైటును తీసుకొని దాని కాంతిని దర్పణంపై పడేటట్లు చేయండి.
పరావర్తనం చెందిన కాంతి గోడపై పడుతుంది.
ఇప్పుడు డబ్బా రెండవ రంధ్రం ద్వారా బిగ్గరగా మాట్లాడండి.
ధ్వని ప్రభావము వలన బెలూన్ పొర ముందుకు, వెనుకకు కదులుతుంది. దీనితో కాంతి బిందువు పైకి, కిందకు గాని లేక ప్రక్కలకు గాని కదలటం జరుగుతుంది.
దీనిని బట్టి ధ్వనికి యాంత్రికశక్తి కలదని చెప్పవచ్చును.

కృత్యం – 2

శృతిదండం కంపనాలను పరిశీలించడం :

ప్రశ్న 2.
శృతిదండం కంపనాలను ఏ విధముగా పరిశీలించవచ్చో ప్రయోగపూర్వకముగా తెల్పుము.
(లేదా)
ధ్వని యొక్క ఉత్పత్తిని ఒక కృత్యం ద్వారా తెల్పుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 15

ఒక సన్నని ఇనుప తీగను శృతిదండపు ఒక భుజంకు పటములో చూపినట్లుగా అతికించండి.
ఒక గాజు అద్దమునకు ఇరువైపులా మసిపూసి దానిపై కంపిస్తున్న శృతిదండానికి అతికించిన తీగ అద్దమునకు తాకే విధంగా పటంలో చూపినట్లు ఉంచాలి.
ముందుగా ఒక సరళరేఖను నిటారుగా గీసిన, ఆ తీగ అద్దంపై ఒక తరంగాన్ని ఏర్పరుస్తుంది.
ఇదే ప్రయోగాన్ని శృతిదండం కంపన స్థితిలో లేనపుడు చేయగా తీగ, గీతతో ఏకీభవించును.
పై రెండు సందర్భాల్లో అద్దంపై ఏర్పరచిన రేఖలలో తేడాను గమనించగా, శృతిదండం కంపనాలను చేస్తుందని మరియు కంపించే వస్తువులు ధ్వనిని ఉత్పత్తి చేస్తాయని తెలుసుకోవచ్చును.

కృత్యం – 3

ప్రశ్న 3.
తరంగ రకాలను పరిశీలిద్దాం :
ఎ) స్ప్రింగులో ఏర్పడే అనుదైర్ఘ్య తరంగాలను పరిశీలించే ప్రయోగంను వ్రాయుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 16

రంగు రంగుల ప్లాస్టిక్ స్ప్రింగ్ ను తీసుకోండి.
దీనిని సులభంగా కుదించడంగాని, సాగదీయడంగాని చేయవచ్చును.
ఈ స్ప్రింగును ఒక బల్లపై ఉంచి, మీ స్నేహితునితో ఆ స్ప్రింగు ఒకవైపు కొనను పట్టుకోమని చెప్పండి.
మీరు రెండవ కొనను పట్టుకొని స్ప్రింగ్ ను కొంత సాగదీయండి.
స్ప్రింగు యొక్క రెండవ కొనను దాని పొడవు వెంట ముందుకు, వెనుకకు కదిలించండి.
మీరు ఏకాంతరంగా సంపీడన, వీరళీకరణాలను స్ప్రింగు వెంబడి ముందుకు కదలడం గమనించవచ్చును.
ఈ సందర్భంలో స్ప్రింగ్ కంపనాలు తరంగ చలన దిశలోనే ఉన్నాయి. కావున ఈ తరంగాలను అనుదైర్ఘ్య తరంగాలు అంటారు.
అనుదైర్ఘ్య తరంగాలు ధ్వని తరంగాలకు ఉదాహరణ కాబట్టి ఇవి యానకంలో సాంద్రతలో మార్పును తెలియచేయును.

బి) స్ప్రింగులో ఏర్పడే తిర్యక్ తరంగాలను పరిశీలించే ప్రయోగంను వ్రాయుము.
(లేదా)
ఒక యానకంలో తిర్యక్ తరంగాలు ఏర్పడు కృత్యమును తెల్పుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 17

రంగు రంగుల ప్లాస్టిక్ స్ప్రింగును తీసుకోండి.
స్ప్రింగును ఒక స్టాండుకు పటంలో చూపినట్లు వ్రేలాడదీయండి.
స్ప్రింగు కింది కొనను పట్టుకొని కుడి, ఎడమలకు కదిలించండి.
ఇప్పుడు స్ప్రింగ్ కింది కొనలో ఒక అలజడి సృష్టించబడి పటంలో చూపిన విధంగా క్రమంగా పైకి ఎగబాకుతుంది.
స్ప్రింగ్ యొక్క కిందికొన పైకి పోవడం జరగదు. అలజడి మాత్రమే పైకి వెళుతుంది. స్ప్రింగ్లో తిర్యక్ దీనిద్వారా మనము ఒక తరంగం స్ప్రింగ్ ద్వారా పైకి కదిలిందని చెప్పవచ్చును.
ఇక్కడ స్ప్రింగ్ కంపనాలు తరంగ చలనదిశకు లంబముగా ఉన్నాయని గమనించవచ్చును.
ఈ విధమైన చలనాలు గల తరంగాలను తిర్యక్ తరంగాలు అంటారు.
ఈ చలనాలు యానకపు ఆకృతిలో మార్పునకు కారణమవుతాయి.

కృత్యం – 4

పరావర్తనం చెందిన ధ్వనిని విందాం :

ప్రశ్న 4.
ధ్వని పరావర్తనంను తెల్పు ప్రయోగంను వివరింపుము.
(లేదా)
ధ్వని పరావర్తనం కూడా కాంతి పరావర్తన నియమాలను పాటిస్తుందని తెల్పు ప్రయోగంను వ్రాయుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 11th Lesson ధ్వని 18

గోడకు దగ్గరగా, ఒక టేబుల్‌ నుంచి, ఒకే పొడవుగల రెండు పొడవైన గొట్టాలను పటంలో చూపినట్లు అమర్చుము.
ఒక గొట్టంద్వారా మాట్లాడమని మీ స్నేహితునితో చెప్పి, రెండవ గొట్టం ద్వారా వినండి.
మీరు ఒకవేళ ధ్వనిని స్పష్టంగా వినలేకపోతే, గొట్టాన్ని సర్దుబాటు చేయండి.
గమనించగా, రెండు గొట్టాలు గోడ యొక్క లంబంతో సమాన కోణాన్ని చేసేటప్పుడు మీ స్నేహితుని ధ్వనిని స్పష్టంగా వినగలరు.
దీనినిబట్టి ధ్వని పరావర్తనం చెందునని అవగాహన చేసుకోవచ్చును.
ధ్వని పరావర్తనం చెందిన తలంపై పతన బిందువు వద్దగల లంబంతో పతన, పరావర్తన ధ్వనులు సమానకోణాలను చేయుచున్నాయి.
అనగా ధ్వని పరావర్తనం కూడా కాంతి పరావర్తన నియమాలను పాటిస్తుందని చెప్పవచ్చును.

AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి

January 5, 2024January 4, 2024 by Mahesh

SCERT AP 9th Class Physics Study Material Pdf Download 10th Lesson పని మరియు శక్తి Textbook Questions and Answers.

AP State Syllabus 9th Class Physical Science 10th Lesson Questions and Answers పని మరియు శక్తి

9th Class Physical Science 10th Lesson పని మరియు శక్తి Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
పనిని నిర్వచించి, ప్రమాణాలు తెలపండి. (AS 1)
జవాబు:
ఒక వస్తువుపై బలాన్ని ప్రయోగించిన ఆ వస్తువు స్థానభ్రంశములో మార్పు వచ్చినట్లయితే వస్తువు విషయంలో పని జరిగినది అని అంటారు.
(లేదా)
ఒక వస్తువుపై ప్రయోగించబడిన బలము (F) మరియు బలప్రయోగ దిశలో వస్తువు ప్రయాణించిన దూరం (S)ల లబ్దాన్ని పని అంటారు.
∴ పని = బలము × స్థానభ్రంశం
W: F × s
ప్రమాణాలు : పనికి ప్రమాణాలు : న్యూటన్ – మీటర్ (లేదా) జెల్.

ప్రశ్న 2.
వస్తువు స్థానభ్రంశం దానిపై ప్రయోగింపబడిన బలానికి వ్యతిరేక దిశలో ఉండే సందర్భాలకు కొన్ని ఉదాహరణలివ్వండి. (AS 1)
జవాబు:
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 1

ఒక కొలనులో ఈత వేయుచున్న బాలుడి చేతుల కదలికల వలన ప్రయోగించబడిన బలం అతని శరీరాన్ని వ్యతిరేక దిశలో స్థానభ్రంశాన్ని కలిగిస్తుంది.
ఒక బంతిని మనము పైకి విసిరిన బంతి స్థానభ్రంశము పైకి ఉండును. గురుత్వ బలము దిశ క్రిందకు పనిచేయును.

ప్రశ్న 3.
క్రింది వాక్యాలలో తప్పు వాక్యాలను గుర్తించి సరిచేసి రాయండి. (AS 1)
ఎ) పనికి, శక్తికి ప్రమాణాలు వేర్వేరుగా ఉంటాయి.
బి) విమానం పైకెగిరినపుడు దాని ‘భారం’ చేసిన పని ధనాత్మకం.
సి) స్ప్రింగ్ ను సాగదీసినపుడు దాని స్థితిశక్తి పెరుగుతుంది. మరియు స్ప్రింగ్ ను దగ్గరగా అదిమినపుడు దాని స్థితిశక్తి తగ్గుతుంది.
డి) ఒక వ్యవస్థపై బాహ్యబలం వలన జరిగిన పని ఋణాత్మకమైతే ఆ వ్యవస్థ యొక్క శక్తి తగ్గుతుంది.
ఇ) కొంత ఎత్తు నుండి స్వేచ్ఛగా కిందపడే వస్తువుకు గతిశక్తి స్థిరంగా ఉంటుంది.
ఎఫ్) సామర్థ్యానికి ప్రమాణం వాటి.
జవాబు:
ఎ) పనికి, శక్తికి ప్రమాణాలు “ఒకే విధంగా” ఉంటాయి.
బి) విమానం పైకి ఎగిరినప్పుడు దాని భారం చేసిన పని “ఋణాత్మకం”.
సి) స్ప్రింగ్ ను సాగదీసినప్పుడు దాని స్థితిశక్తి తగ్గుతుంది మరియు స్ప్రింగును దగ్గరగా అదిమినపుడు దాని స్థితిశక్తి పెరుగుతుంది.
డి) ఒక వ్యవస్థపై బాహ్యబలం వలన జరిగిన పని ఋణాత్మకమైతే ఆ వ్యవస్థ యొక్క శక్తి తగ్గుతుంది.
ఇ) కొంత ఎత్తు నుండి స్వేచ్ఛగా కిందకు పడే వస్తువు గతిశక్తి క్రమేపి పెరుగుతుంది.
ఎఫ్) సామర్థ్యానికి ప్రమాణము వాట్.

ప్రశ్న 4.
యాంత్రిక శక్తి అంటే ఏమిటి? (AS 1)
జవాబు:
యాంత్రిక శక్తి :
ఒక వస్తువు యొక్క స్థితిశక్తి మరియు గతిశక్తుల మొత్తాన్ని యాంత్రిక శక్తి అంటారు.

ప్రశ్న 5.
శక్తి నిత్యత్వ సూత్రాన్ని తెలపండి. (AS 1)
జవాబు:
శక్తి నిత్యత్వ సూత్రం :
శక్తి సృష్టించబడదు, నాశనము కాదు. కాని అది ఒక రూపం నుండి మరొక రూపంలోకి మారుచుండును. దీనినే శక్తి నిత్యత్వ నియమం అంటారు.

ప్రశ్న 6.
కింద తెలుపబడిన సందర్భాలలో పని ధనాత్మకమా? ఋణాత్మకమా? శూన్యమా? తెలపంది. (AS 1)
ఎ) ఒక సూట్‌కేసును నేలపై నుండి ఎత్తి తన తలపై పెట్టుకోవడానికి ‘కూలీ’ ప్రయోగించిన బలం చేసిన పని
బి) కూలీ తలపై నుండి సూటికేస్ పడిపోవడానికి గురుత్వాకర్షణ బలం వల్ల సూట్‌కేస్ పై జరిగిన పని
సి) సూట్ కేసను తలపై పెట్టుకుని నిలుచున్న కూలీచేసే పని
డి) నిట్టనిలువుగా పైకి విసరబడిన బంతిపై గురుత్వాకర్షణ బలం చేసే పని
ఇ) ఈత కొట్టే వ్యక్తి చేతులతో ప్రయోగింపబడిన బలం చేసే పని
జవాబు:
ఎ) ధనాత్మకము
బి) ధనాత్మకము
సి) శూన్యము
డి) ఋణాత్మకము
ఇ) ఋణాత్మకము

ప్రశ్న 7.
స్థితిశక్తి అంటే ఏమిటి? ‘h’ ఎత్తులో ఉన్న, ‘m’ ద్రవ్యరాశి గల వస్తువు యొక్క గురుత్వాకర్షణ ‘g’ అయితే స్థితిశక్తికి సూత్రాన్ని ఉత్పాదించండి. (AS 1)
(లేదా)
P. E. = mgh ను ఉత్పాదించండి.
జవాబు:
స్థితిశక్తి లేదా గురుత్వాకర్షణ శక్తి :
ఒక వస్తువును కొంత ఎత్తు వరకు ఎత్తినప్పుడు, గురుత్వాకర్షణ బలమునకు వ్యతిరేకముగా ఆ వస్తువుపై పని జరగడం వలన కలిగిన మార్పునే గురుత్వాకర్షణ శక్తి లేదా స్థితిశక్తి అంటాము.
(లేదా)
ఒక వస్తువుకి దాని స్థితి వలన, ఆకారము వలన పొందే శక్తిని స్థితిశక్తి అంటారు.
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 2

సూత్ర ఉత్పాదన :
1) ‘m’ ద్రవ్యరాశి గల ఒక వస్తువును నేల నుండి ‘h’ ఎత్తు వరకు తీసుకెళ్ళడానికి కావల్సిన కనీస బలము ఆ వస్తున్న బరువు (mg) కు సమానం.

2) వస్తువుపై జరిగిన పనికి సమానమైన ఆ వస్తువు పొందినది అనుకొనుము.

3) వస్తువుపై గురుత్వాకర్షణ బలానికి వ్యతేరేకంగా జరిగిన పని (W) అనుకొనిన
వస్తువుపై జరిగిన పని = బలము × స్థానభ్రంశము
= mg × h = mgh
దీనినే ఎత్తు వద్ద వస్తువు యొక్క స్థితి శక్తి (PE) అంటాము.
∴ P. E = mgh

ప్రశ్న 8.
గతిశక్తి అంటే ఏమిటి? ‘v’ వేగంతో ప్రయాణిస్తున్న ‘m’ ద్రవ్యరాశి గల వస్తువు యొక్క గతిశక్తికి సూత్రాన్ని ఉత్పాదించండి. (AS 1)
(లేదా)
‘m’ ద్రవ్యరాశి కలిగిన వస్తువు ‘v’ వేగంతో ప్రయాణించుచున్న దాని యొక్క గతిశక్తి K.E. = \(\frac{1}{2}\) mv² ను ఉత్పాదించుము.
జవాబు:
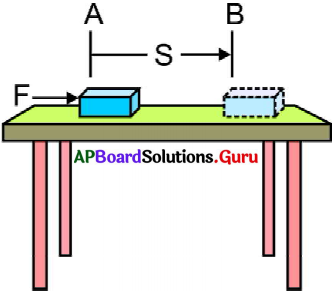
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 3
ఒక వస్తువుకు దాని గమనం వలన కలిగే శక్తిని గతిశక్తి అంటాం.
1) ‘m’ ద్రవ్యరాశి గల ఒక వస్తువు నునుపైన సమతలంపై నిశ్చలస్థితిలో ఉందనుకొనుము.

2) ఆ వస్తువుపై ‘F బలాన్ని ప్రయోగించిన ఆ వస్తువు బలప్రయోగ దిశలో ‘జై’ దూరంను అనగా ‘A’ బిందువు నుండి ‘B’ వరకు కదిలినది అనుకొనుము.

3) ఆ సందర్భంలో వస్తువుపై జరిగిన పని W = F_net . S = Fs ………….. (1)

4) వస్తువు పై పని జరగడం వల్ల దాని వేగము ‘u’ నుండి ‘v’ కి మారి, త్వరణము ‘a’ ను పొందినది అనుకొనుము.
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 4
6) ఈ జరిగిన పని వస్తువునకు గతిశక్తిగా మారును.
∴ K.E. = \(\frac{1}{2}\) mv²

ప్రశ్న 9.
స్వేచ్ఛాపతన వస్తువు భూమిని చేరి వెంటనే ఆగితే దాని గతిశక్తి ఏమవుతుంది? (AS 1)
జవాబు:
స్వేచ్ఛాపతన వస్తువు భూమిని చేరిన వెంటనే దాని గతిశక్తి, శక్తి నిత్యత్వ నియమం ప్రకారం గురుత్వ స్థితిశక్తిగా మారును.

ప్రశ్న 10.
25 కి.గ్రా. ద్రవ్యరాశి గల సంచిని మోస్తూ ఒక వ్యక్తి 50 సి. కాలంలో 10 మీ. ఎత్తుకు చేరుకున్నాడు. ఆ వ్యక్తి ఆ సంచిపై వినియోగించిన సామర్యం ఎంత? (AS 1)
జవాబు:
వస్తువు ద్రవ్యరాశి (m) = 25 కి.గ్రా. ; కాలం (t) = 50 సెకనులు ; ఎత్తు (b) = 10 మీ
గురుత్వత్వరణం (g) = 9.8 మీ/సె².

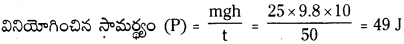
ప్రశ్న 11.
20 కి.గ్రా.ల ద్రవ్యరాశి గల ఒక వస్తువును 1 మీ. ఎత్తులో గల బల్లపై పెట్టడానికి ఒక వ్యక్తి చేయవలసిన పని ఎంత? (AS 1)
జవాబు:
వస్తువు ద్రవ్యరాశి (m) = 20 కి.గ్రా, ; ఎత్తు (b) = 1 మీ.
పని = బలం × స్థానభ్రంశము = mgh = 20 × 9.8 × 1 = 196 J

ప్రశ్న 12.
2 మీ/సె. వేగంతో కదులుతున్న వస్తువు యొక్క గతిశక్తి 5 జొళ్ళు అయిన దాని ద్రవ్యరాశి ఎంత? (AS 1)
జవాబు:
వస్తువు వేగము (v) = 2 m/s; గతిశక్తి (K.E.) = 5 J; ద్రవ్యరాశి (m) = ?
K.E. = \(\frac{1}{2}\) mv²
⇒ 5 = \(\frac{1}{2}\) × m × (2)²
⇒ 5 = \(\frac{1}{2}\) × m × 4
ద్రవ్యరాశి (m) = 5/2 = 2.5 kg

ప్రశ్న 13.
ఐంతి వడి రెట్టింపైన దాని గతిశక్తి (AS 1)
A) మారదు
B) రెట్టింపగును
C) సగమవుతుంది
D) నాలుగురెట్లగును
జవాబు:
D) నాలుగురెట్లగును

ప్రశ్న 14.
ఒకే ద్రవ్యరాశి గల రెండు వస్తువులు ఒకే ఎత్తు నుండి వదిలివేయబడ్డాయి. కింద తెలిపిన వాటిలో ఏది రెండు వస్తువులకూ ఏ సమయంలోనైనా సమానంగా ఉంటుంది? (AS 1, AS 2)
A)వడి
B) గురుత్వాకర్షణ బలం
C) స్థితిశక్తి
D) గతిశక్తి
జవాబు:
B) గురుత్వాకర్షణ బలం

ప్రశ్న 15.
ఒక వ్యక్తి తలపై సూట్‌కేస్‌తో నిచ్చెన ఎక్కుతున్నాడు. ఆ వ్యక్తి ఆ పెట్టెపై చేసిన పని (AS 1)
A) ధనాత్మకం
B) ఋణాత్మకం
C) శూన్యం
D) నిర్వచించలేము
జవాబు:
A) ధనాత్మకం

ప్రశ్న 16.
ఒక వ్యక్తి తలపై సూట్ కేస్ పెట్టుకుని మెట్లెక్కుతున్నాడు. ఆ సూట్ కేస్ పై ‘ఆ సూట్ కేస్ బరువు’ చేసే పని (AS 1)
A) ధనాత్మకం
B) ఋణాత్మకం
C) శూన్యం
D) నిర్వచించలేము
జవాబు:
B) ఋణాత్మకం

ప్రశ్న 17.
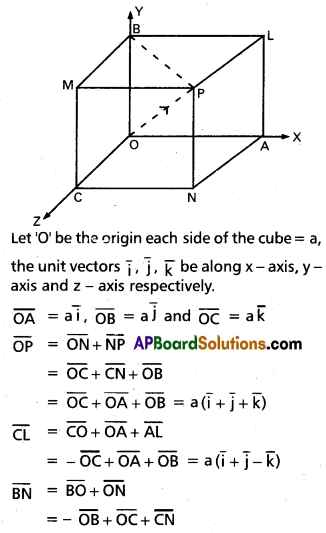
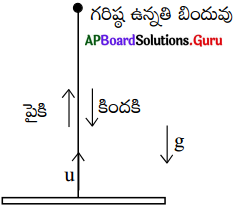
స్వేచ్ఛాపతన వస్తువులలో యాంత్రిక శక్తి నిత్యత్వంను చూపే పటం గీయండి. (AS 5)
జవాబు:
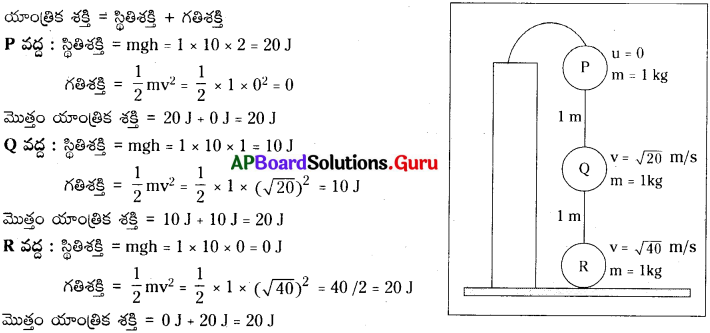
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 7
∴ ఈ విధంగా స్వేచ్ఛాపతన వస్తువు విషయంలో స్థితిశక్తి తగ్గుచూ, గతిశక్తి పెరుగుచూ ఉంటుంది. కాని వ్యవస్థలోని యాంత్రిక శక్తిలో ఎట్టి మార్పుండదు.

ప్రశ్న 18.
సైకిల్ ను నడుపుతున్నప్పుడు సైకిల్ ను వాలు తలం పైకి నెడుతూ పోతే సైకిల్ మరియు మీకు ఉండే స్థితిశక్తి పెరుగుతుంది. ఈ శక్తి ఎక్కడి నుండి వచ్చింది? (AS 7)
జవాబు:
సైకిలు చలనంలో ఉన్నది. సైకిలు యొక్క గతిశక్తి, రోడ్డు యొక్క ఘర్షణ బలం వలన స్థితిశక్తిగా మారును. కనుక నాకు మరియు సైకిల్‌కు స్థితిశక్తి పెరుగుతుంది. ఈ స్థితిశక్తి సైకిలు యొక్క గతిశక్తి నుండి లభిస్తుంది.

ప్రశ్న 19.
ఒక వ్యక్తి ఏ పనీ చేయక ఎక్కువ సేపు నిలుచున్నా ఎందుకు అలసిపోతాడు? (AS 7)
(లేదా)
ఒక వ్యక్తి ఒక ప్రదేశంలో ఎక్కువ సేపు నిలుచున్నా అలసిపోతాడు. ఎందుకో మీకు తెలుసా? సమాచారంను సేకరించండి.
జవాబు:

నిలుచున్న వ్యక్తి పనిచేస్తున్నట్లు మనకు కనిపించకపోయినా అతని శరీరంలో అనేక పనులు జరుగుతాయి.
అతను ఎక్కువ సేపు నిలుచున్నప్పుడు అతని శరీరంలో కండరాలు సంకోచ, వ్యాకోచాలు చెందుతాయి.
అదే విధంగా గుండె వివిధ అవయవాలకు రక్తాన్ని సరఫరా చేస్తుంది.
ఇటువంటి అనేక పనుల వలన శరీరంలోని శక్తి తరిగిపోతుంది. కాబట్టి ఆ వ్యక్తి అలసిపోతాడు.

ప్రశ్న 20.
అలమరాపై ఉంచబడిన ఒక పుస్తకం యొక్క స్థితిశక్తి 20 ఔళ్లని ఒక వ్యక్తి, 30 ఔళ్లని మరొక వ్యక్తి అన్నారు. వారిద్దరిలో ఎవరో ఒకరు తప్పు చేసినట్లేనా? కారణాలు తెలపండి. (AS 2, AS 1)
జవాబు:
ఎవరూ తప్పు చేసినట్లు కాదు. ఎందుకనగా రెండు సందర్భాలలో పుస్తకమునకు స్థితిశక్తి కలదు కాబట్టి.

ప్రశ్న 21.
10 కి.గ్రా. ద్రవ్యరాశి గల బంతి 10 మీ. ఎత్తు నుండి వదిలివేయబడింది. అయిన (AS 1)
ఎ) బంతి తొలి స్థితిశక్తి ఎంత?
బి) బంతి భూమిని చేరే సమయానికి దాని గతిశక్తి ఎంత?
సి) బంతి భూమిని చేరే సమయానికి దాని వేగమెంత?
జవాబు:
బంతి ద్రవ్యరాశి (m) = 10 కి.గ్రా. ; ఎత్తు (b) = 10 మీ ; గురుత్వత్వరణం (g) = 9.8 మీ/సె².
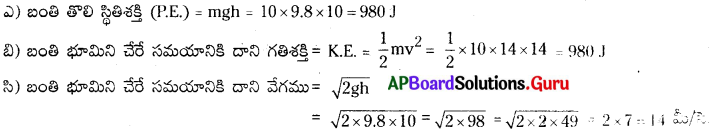
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 8

ప్రశ్న 22.
సైకిల్ తో సహా సైకిల్ పైనున్న వ్యక్తి ద్రవ్యరాశి 100 కి.గ్రా. అయిన ఆ సైకిల్ 3 మీ/సె. వేగంతో కడలాలంటే అతను ఎంత పని చేయాలి?
జవాబు:
వ్యక్తి ద్రవ్యరాశి (m) = 100 కి.గ్రా. ; సైకిల్ వేగం (v) = 3 మీ/సె.
చేయవలసిన పని = గతిశక్తి = \(\frac{1}{2}\) × mv² – \(\frac{1}{2}\) × 100 × (3)² = \(\frac{1}{2}\) × 100 × 9 = 450 J

ప్రశ్న 23.
మీరొక సూటికేస్ ను నేలపై నుండి ఎత్తి బల్లపై పెట్టారనుకుందాం. మీరు చేసిన పని కింది వాటిలో వేటిపై ఆధారపడుతుంది? వేటిపై ఆధారపడదు? ఎందుకు? (AS 2)
ఎ) సూటికేస్ కదిలిన మార్గం
బి) పనిచేయడానికి మీరు తీసుకున్న సమయం
సి) సూటికేస్ యొక్క బరువు
డి) మీ బరువు
జవాబు:
ఎ) జరిగిన పని సూట్కేస్ కదిలిన మార్గముపై ఆధారపడును.
బి) పని (W) = mgh కావున ఇది కాలముపై ఆధారపడదు.
సి) పని (W) = mgh కావున పని సూట్కే స్ పై ఆధారపడును.
డి) పని విషయంలో నా యొక్క బరువు లెక్కలోనికి తీసుకోదగినది కాదు.

ప్రశ్న 24.
ఒక వస్తువు దాని స్థితి వలన, స్థానము వలన పొందే స్థితిశక్తి చూపే సందర్భాలకు చిత్రపటాలను సేకరించి స్క్రిప్ బుక్ తయారు చేయండి. (AS 4)
జవాబు:
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 9

ప్రశ్న 25.
ప్రకృతి సిద్ధంగా జరిగే వివిధ శక్తి రూపాంతరాలు ప్రకృతి సమతుల్యతను కాపాడడంలో నిర్వహించే పాత్రను నీవెలా అభినందిస్తావు? (AS 6)
జవాబు:
ఈ ప్రకృతిలో అనేక రకాల శక్తి రూపాంతరాలను మనము గమనిస్తుంటాము.

ఉదాహరణకు పర్వతాలపై ఉన్నటువంటి మంచు కరిగి నీరుగా మారి, నదులుగా ప్రవహించును. ఈ విధముగా స్థితిశక్తి, గతిశక్తిగా మారును. జల విద్యుత్ కేంద్రాలలో నీటి గతిశక్తిని విద్యుత్ శక్తిగా మారుస్తాము.

ప్రశ్న 26.
ఒక పెట్టెను నేలపై నుండి ఎత్తి ఒక బీరువాపై పెడితే దాని స్థితిశక్తి పెరుగుతుంది. కానీ దాని గతిశక్తిలో మార్పురాదు. మరి ఇది శక్తి నిత్యత్వ నియమానికి విరుద్ధం కాదా? వివరించండి. (AS 7)
జవాబు:

ఇది శక్తి నిత్యత్వ నియమమునకు విరుద్ధము కాదు. ఎందుకనగా పెట్టె నేలపై ఉన్నప్పుడు దాని స్థితిశక్తి శూన్యము (కారణము h = 0). కాని వ్యవస్థ యొక్క మొత్తం శక్తి శూన్యము కాదు.
పెట్టెను బీరువాపై పెట్టిన గతిశక్తి శూన్యము. కాని వ్యవస్థ యొక్క మొత్తం శక్తి శూన్యము కాదు. ఈ విధముగా శక్తి నిత్యత్వము కాబడినది.

ప్రశ్న 27.
చెట్టు నుండి రాలిన ఆపిల్ పండు భూమికి చేరువగా ఉన్నప్పుడు దాని గురుత్వ స్థితిశక్తి ఏమవుతుంది? భూమికి తగలగానే దాని స్థితిశక్తి ఏమవుతుంది? (AS 7)
జవాబు:

ఆపిల్పండు భూమికి చేరువగా ఉన్నప్పుడు దాని గురుత్వ స్థితిశక్తి తగ్గును. ఎందుకనగా దాని ‘h’ విలువ తక్కువగా ఉన్నది కావున.
పండు భూమికి తగలగానే దాని స్థితిశక్తి పెరుగును. ఎందుకనగా దాని ‘h’ విలువ పెరుగును కనుక.

ప్రశ్న 28.
అంతర్జాతీయ శాంతి, సహకారం మరియు భద్రతలపై పెరుగుతున్న శక్తి అవసరాలు మరియు శక్తి నిత్యత్వంపై చర్చించండి. (AS 7)
జవాబు:
మానవ మనుగడకు శక్తి అధికముగా అవసరము. శక్తి లేని మానవ జీవితము, గాలి లేని బుడగ లాంటిది. ఈ ప్రకృతి శక్తి బదిలీకి వీలు కల్పించకపోయినట్లైతే మానవాళి మనుగడ ప్రశ్నారకమయ్యేది. ప్రపంచంలో రోజు రోజుకీ పెరిగిపోతున్న జనాభాకు ఎల్లప్పుడు శక్తి, శక్తి నిత్యత్వము అవసరము.

ఒక దేశము యొక్క శక్తి వనరులు అధికముగా ఉన్నట్లయితే, ఆ దేశము అభివృద్ధి పథములో పయనించును.

ఉదా :
అమెరికా, చైనా మరియు భారతదేశాలు. ఒక దేశము దాని యొక్క శక్తి వనరులను సరైన పద్ధతిలో వినియోగించుకోవాలి. తన తోటి దేశాలతో స్నేహసంబంధాలను, భద్రతా ఒప్పందాలను పాటించాలి. ఉదాహరణకు మనము కేంద్రక సంలీనంలో లేదా కేంద్రక విచ్ఛిత్తిలో వాడు యురేనియం థోరియం వంటి అధిక విలువైన వనరులను మానవాళికి ఉపయోగపడు పద్ధతిలో వాడాలి. అనగా విద్యుత్ శక్తిని ఉత్పత్తి చేయుటలో వాడాలి. కాని వాటిని అణుబాంబు తయారీలో వాడి ప్రపంచ జనాభా మనుగడను ప్రశ్నార్థకముగా చేయకూడదు. ఈ ప్రక్రియ వలన ప్రపంచశాంతి ప్రశ్నార్థకమగును.

9th Class Physical Science 10th Lesson పని మరియు శక్తి Textbook InText Questions and Answers

9th Class Physical Science Textbook Page No. 167

ప్రశ్న 1.
ఒక చెక్క కుర్చీని సమాంతర తలంపై వివిధ దిశలలో లాగి, దానిని తిరిగి యధాస్థానానికి తీసుకొచ్చారు. దానిపై తలం ప్రయోగించిన ఘర్షణ బలం (f) మరియు అది కదిలిన దూరం (s) అయిన ఆ ఘర్షణ బలం చేసిన పని ఎంత?
జవాబు:
ఘర్షణ బలం చేసిన పని శూన్యం, ఎందుకనగా వస్తువు స్థానభ్రంశములో మార్పు లేదు గనుక,

9th Class Physical Science Textbook Page No. 168

ప్రశ్న 2.
ఒక వస్తువును నేలపై నుండి కొంత ఎత్తుకు ఎత్తండి. మీరు ఉపయోగించిన బలం ఆ వస్తువును పై దిశలోకి కదిలించింది. అదే సమయంలో ఆ వస్తువుపై గురుత్వాకర్షణ బలం కూడా పని చేస్తున్నది కదా ! మరి
ఎ) వీటిలో ఏ బలం ధనాత్మకమైన పని చేసింది?
బి) ఏ బలం ఋణాత్మకమైన పని చేసింది? కారణాలను వివరించండి.
జవాబు:
ఎ) వస్తువును నేలపై నుండి పైకి ఎత్తినపుడు దానిపై పనిచేసిన బలం ధనాత్మకము. ఎందుకనగా వస్తువు అదే దిశలో పైకి స్థానభ్రంశం చెందినది కనుక.
బి) వస్తువుపై పనిచేసే గురుత్వ బలం ఋణాత్మకము. ఎందుకనగా అది వస్తువుకి వ్యతిరేక దిశలో క్రిందకి పనిచేయును కనుక.

9th Class Physical Science Textbook Page No. 171

ప్రశ్న 3.
శక్తి బదిలీకి ప్రకృతి వీలు కల్పించకపోతే ఏమి జరుగుతుంది? కొన్ని ఉదాహరణలతో చర్చించండి.
జవాబు:
శక్తి బదిలీకి ప్రకృతి వీలు కల్పించకపోతే మానవ జీవితం శూన్యమగును. మన నిత్యజీవితంలో వివిధ పనులు చేయడానికి మనము వివిధ రూపాలలో ఉన్న శక్తిని ఉపయోగిస్తుంటాము.
ఉదాహరణ :
కండర శక్తి, ఉష్ణశక్తి, కాంతి శక్తి, విద్యుత్ శక్తి, యాంత్రిక శక్తి, ధ్వని శక్తి, అయస్కాంత శక్తి, సౌరశక్తి, రసాయనిక శక్తి మొదలగునవి.

మనము సౌరశక్తి నుండి ఉష్ణశక్తిని, ఉష్ణశక్తి నుండి విద్యుత్ శక్తిని వినియోగించుకుంటున్నాము. ఇది అంతయూ ప్రకృతి శక్తి బదిలీకి వీలు కల్పించుటయే, లేనిచో ఏ జీవరసాయనిక చర్యలు జరగవు.

9th Class Physical Science Textbook Page No. 174

ప్రశ్న 4.
ఒకే వడితో ప్రయాణిస్తున్న రెండు లారీలలో తక్కువలోడ్ తో ఉన్న లారీని ఎక్కువ లోడ్ తో ఉన్న లారీతో పోల్చినపుడు సులభంగా ఆపగలం. ఎందుకు?
జవాబు:
తక్కువలోడ్ ఉన్న లారీ తక్కువ బరువుతో ఉంటుంది. అందువలన దానిని ఆపుటకు దానిపై పని చేయవలసిన నిరోధక బలం తక్కువగా ఉంటుంది.

ప్రశ్న 5.
ఒక కారు యొక్క వడి ఒక సందర్భంలో 10 మీ/సె. నుండి 20 మీ/సె. కు మారింది. మరొక సందర్భంలో 20 మీ/సె నుండి 30 మీ/సె. లోనికి మారింది. దాని గతిశక్తి మార్పు ఏ సందర్భంలో ఎక్కువ ఉంటుంది?
జవాబు:
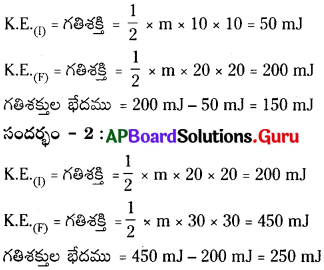
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 10

ప్రశ్న 6.
ఒక వ్యక్తి నేలపై నిశ్చలస్థితి నుండి పరుగెత్తడం ప్రారంభించాడు. అతడు తన ద్రవ్యవేగాన్ని కొంత పెంచుకుంటే నేల యొక్క ద్రవ్యవేగంలో ఏ మార్పు వస్తుంది? అతడు తన గతిశక్తిని కొంతమేర పెంచుకుంటే నేల యొక్క గతిశక్తిలో ఏ మార్పు వస్తుంది?
జవాబు:
ఇక్కడ రెండు సందర్భాలుంటాయి.

సందర్భం – 1 :
పరిశీలకుడి దృష్టిలో నేలకు ఎలాంటి వేగం లేదు. కనుక నేల యొక్క ద్రవ్యవేగం, గతిశక్తులు శూన్యము.

సందర్భం – 2 :
పరుగెత్తే వ్యక్తి దృష్టిలో నేల వేగం, అతని వేగం సమానం. నేల యొక్క ద్రవ్యవేగం మరియు గతిశక్తి, పరుగెత్తేవాని ద్రవ్యవేగం మరియు గతిశక్తులు సమానంగా ఉండి, వ్యతిరేక దిశలలో ఉంటాయి.

9th Class Physical Science Textbook Page No. 177

ప్రశ్న 7.
అంతరిక్షంలో ఉండే అంతర్జాతీయ అంతర కేంద్రానికి (Space station) గురుత్వ స్థితిశక్తి ఉంటుందా?
జవాబు:
అంతరిక్షంలో ఉండే అంతర్జాతీయ అంతర కేంద్రానికి గురుత్వ శక్తి ఉండదు.

9th Class Physical Science Textbook Page No. 180

ప్రశ్న 8.
బంతులను అమ్ముకొనే ఒక వ్యక్తి తన వద్ద ఒక అద్భుత బంతి ఉందని, దానిని ఒక ఎత్తు నుండి క్రిందికి జారవిడిస్తే, మనం జారవిడిచిన ఎత్తుకంటె ఎక్కువ ఎత్తుకు ఎగురుతుందని చెప్పాడు. మీరు ఆ బంతి అద్భుతమైనదని నమ్ముతారా? ఎందుకు? వివరించండి.
జవాబు:
నేను నమ్మను. ఎందుకనగా అది అసాధ్యము కనుక.

ప్రశ్న 9.
ఏటవాలుగా ఉండే ఒక ఎత్తైన ప్రదేశం వద్ద నిశ్చలస్థితి నుండి వదిలిన బంతి కింద దొర్లుతూ భూమిపైకి చేరేటప్పటికి 4 మీ/సె. వడిని కలిగి ఉంది. ఇదే బంతి తిరిగి అదే ఎత్తు నుండి 3 మీ/సె. వడితో వదిలితే భూమికి చేరేటప్పటికి దాని వేగం ఎంత?
జవాబు:
ఏటవాలుగా ఉండే ఒక ఎత్తైన ప్రదేశం నుండి బయలుదేరిన బంతి యొక్క u₁ = 0 మీ./సె.; v₁ = 4 మీ./సె.
త్వరణము ‘a’ మరియు దూరము ‘S’ అయిన
v₁² – u₁² = 2as ………………. (1)
తరువాత బంతి యొక్క వేగములు
u₂ = 3 మీ./సె. ; v₂ = ?
v₂² – u₂² = 2as
(1), (2) లను సాధించగా
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 11

9th Class Physical Science Textbook Page No. 181

ప్రశ్న 10.
F₁ బలం చేసిన పని F₂ బలం చేసిన పని కన్నా ఎక్కువ. అయితే F₁ యొక్క సామర్థ్యం F₂ యొక్క సామర్థ్యం కన్నా ఎక్కువని కచ్చితంగా చెప్పగలమా? కారణం తెలపండి.
జవాబు:
అవును చెప్పగలము. ఎందుకనగా సామర్థ్యము, పనికి అనులోమానుపాతంలో ఉంటుంది కావున.

9th Class Physical Science Textbook Page No. 167

ప్రశ్న 11.
i) వస్తువు పై ప్రయోగింపబడిన బలం శూన్యం (0) అయితే, అప్పుడు ఎంత పని జరిగినట్లు?
ii) వస్తువు కదిలిన దూరం శూన్యం (1) అయినపుడు వస్తువులో స్థాన మార్పు జరగకపోతే అపుడు ఎంత పని జరిగినట్లు?
జవాబు:
i) ప్రయోగించిన బలం శూన్యం కావున జరిగిన పని శూన్యం.
ii) దూరం శూన్యం కావున ఏ పని జరగనట్లే.

9th Class Physical Science Textbook Page No. 168

ప్రశ్న 12.
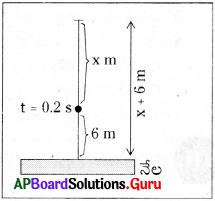
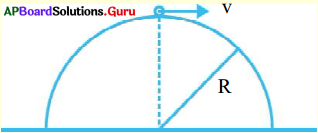
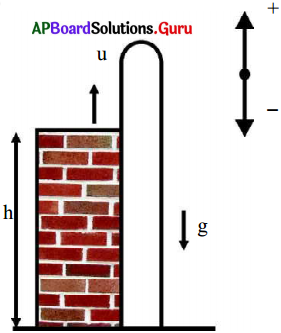
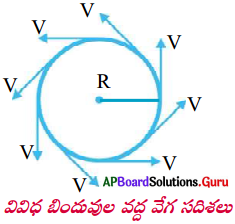
ప్రక్కన ఇవ్వబడిన పటంను పరిశీలించి, దానిపై మూడు వాక్యాలను వ్రాయుము.
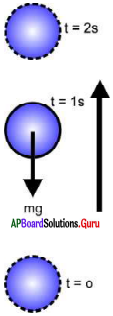
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 12
జవాబు:

ప్రక్క పటంలో ఒక బంతిని పైకి విసిరితే దాని గమనం ఏ దిశలో ఉంటుందో ఇవ్వబడినది.
బంతి పైకి వెళుతున్న కొద్ది దానిపై పనిచేసే గురుత్వాకర్షణ బలం వ్యతిరేక దిశలో పనిచేస్తుంది.
బంతి పైకి వెళుతుంటే వడి క్రమేపి తగ్గును. గరిష ఎత్తు వద్ద దాని వడి శూన్యము. బంతి తిరిగి కిందకు వస్తుంటే దాని వడి క్రమేపి పెరుగును.

9th Class Physical Science Textbook Page No. 169

ప్రశ్న 13.
శక్తి అంటే ఏమిటి? వివిధ రకాల శక్తి రూపాలను రాయుము.
జవాబు:
శక్తి :
పనిచేయు సామర్థ్యాన్నే శక్తి అంటారు.

శక్తి రూపాలు :
యాంత్రిక శక్తి, ఉష్ణశక్తి, కాంతి శక్తి, ధ్వని శక్తి, విద్యుత్ శక్తి, అయస్కాంత శక్తి, కేంద్రక శక్తి మొదలగునవి శక్తి యొక్క అనేక రూపాలు.

9th Class Physical Science Textbook Page No. 170

ప్రశ్న 14.
పని చేయడానికి శక్తి అవసరమని, ఒక వ్యక్తి పని చేస్తున్నప్పుడు శక్తి ఖర్చు చేస్తాడని అంటే శక్తిని కోల్పోతున్నాడని తెలుసుకున్నాం.
ఎ) మరి ఈ శక్తి ఎక్కడకు పోతుంది?
బి) పనిచేయడానికి అవసరమైన బలాన్ని ప్రయోగించే వస్తువుకు, పనిచేయబడిన వస్తువుకు మధ్య శక్తి బదిలీ అవుతుందా?
సి) శక్తి బదిలీ కాకుండా ఏ బలమైనా ఒక పనిని చేయడం సాధ్యమేనా?
జవాబు:
ఎ) ఈ శక్తి పని జరగడానికి ఉపయోగపడుతుంది.
బి) శక్తి మార్పిడి జరుగుతుంది.
సి) శక్తి బదిలీ కాకుండా పనిచేయడం జరుగదు.

9th Class Physical Science Textbook Page No. 171

ప్రశ్న 15.
మనకు శక్తి ఎక్కడ నుండి లభిస్తుంది?
జవాబు:
సూర్యుడు మనకు అతి పెద్ద సహజ శక్తి వనరు. మనకు అవసరమైన అనేక ఇతర శక్తి వనరులన్నీ సూర్యునిపై ఆధారపడి ఉంటాయి.

ప్రశ్న 16.
ఇతర శక్తి వనరుల గురించి రాయుము.
(లేదా)
సూర్యునిపై ఆధారపడని శక్తి జనకాలు ఉన్నాయా? ఉంటే అవి ఏమిటి?
జవాబు:
ప్రకృతిలో మనకు ముఖ్య శక్తి భాండాగారము సౌరశక్తి, ఈ సౌరశక్తిపై ఆధారపడని శక్తి వనరులు కొన్ని గలవు. అవి

భూ అంతర్భాగం నుండి వచ్చు శక్తి
సముద్ర అలల నుండి వచ్చు శక్తి
కేంద్రక శక్తి
రసాయనిక శక్తి
విద్యుత్ శక్తి నుండి ఉష్ణశక్తి ఏర్పడటం
ఇంధన శక్తి
బొగ్గు శక్తి
బయోగ్యాస్

9th Class Physical Science Textbook Page No. 178

ప్రశ్న 17.
ఆకుపచ్చని మొక్కలు ఆహారాన్ని ఎలా తయారుచేసుకుంటాయి?
జవాబు:
ఆకుపచ్చని మొక్కల యొక్క ఆకులు సౌరశక్తిని వినియోగించుకుని, వాటి ఆకులలో గల క్లోరోఫిల్ ను, ప్రకృతిలోని CO₂ తో కలిసి రసాయన చర్య (కిరణజన్య సంయోగ క్రియ)ను జరిపి పిండిపదార్థాలు మరియు O₂. ను తయారుచేసుకుంటాయి.

ప్రశ్న 18.
బొగ్గు, పెట్రోలియం వంటి ఇంధనాలు ఎలా ఏర్పడ్డాయి?
జవాబు:
భూ అంతర్భాగంలోకి చేరిన వృక్ష కళేబరాలు కొన్ని వేల సంవత్సరాల తర్వాత రసాయన శక్తి రూపాలైన బొగ్గు, పెట్రోలియం వంటి ఇంధనాలుగా మారతాయి.

ప్రశ్న 19.
ప్రకృతిలో జలచక్రం ఏర్పడడానికి ఏయే శక్తి రూపాంతరాలు దోహదపడతాయి?
జవాబు:
మనము ప్రకృతిలో వివిధ రకాల శక్తి రూపాంతరాలను చూస్తుంటాము.

పర్వతాలపై ఉన్న మంచు కరిగి నీరుగా మారి నదులుగా ప్రవహిస్తుంది.
ఈ క్రమంలో మంచు యొక్క స్థితిశక్తి గతిశక్తిగా మారుతుంది.
జల విద్యుత్ కేంద్రాలలో నీటి యొక్క గతిశక్తిని విద్యుత్ శక్తిగా మారుతుంది.
ఈ విధంగా స్థితిశక్తి → గతిశక్తి → విద్యుత్ శక్తి → కాంతిశక్తి

9th Class Physical Science Textbook Page No. 180

ప్రశ్న 20.
ఒక రిక్షా కూలీ నిర్ణీత మార్గాన్ని తోటి రిక్షా కూలీ కంటే త్వరగా చేరుకోగలవచ్చు. అదే విధంగా 1 కి.గ్రా. పిండి రుబ్బడానికి మన ఇంట్లోని గైండర్ పక్కింటి వారి గైండర్ కంటే ఎక్కువ సమయం తీసుకోవచ్చు.
ఎ) ఒక పనిని ప్రతివారూ ఒకే కాలవ్యవధిలో చేయగలరా?
బి) ఒక పనిని చేసే ప్రతిసారి ఆ పనిని చేసే, బలం చేత సమాన శక్తి వినియోగించబడుతుందా?
సి) ఒక నిర్ణీత పనిని చేసే ప్రతిసారి వివిధ యంత్రాలు సమానమైన శక్తిని ఖర్చు చేస్తాయా?
జవాబు:
ఎ) ఒక పనిని ప్రతివారూ ఒకే కాలవ్యవధిలో చేయలేరు.
బి) సమాన శక్తి వినియోగించబడదు.
సి) నిర్ణీత పనిని చేసే ప్రతిసారి వివిధ యంత్రాలు సమానమైన శక్తిని ఖర్చు చేస్తాయి.

ప్రశ్న 21.
రహీమ్ తన ఇంటిలోని ఒకటో అంతస్తులో కొన్ని రిపేర్లు చేయించాలనుకున్నాడు. సుతారి మేస్త్రి సలహా మేరకు అతను 100 ఇటుకలు తెప్పించి ఒక కూలీతో మొదటి అంతస్తుకు మోయించాడు. కూలీ ఒక గంటలో 100 ఇటుకలను మొదటి అంతస్తుకు మోసినందుకుగాను రూ. 150/- లను కూలీగా తీసుకున్నాడు. సుతారి మేన్ సూచన మేరకు రహీమ్ రెండవ రోజు కూడా మళ్ళీ 100 ఇటుకలు తెప్పించి మరొక కూలీతో మొదటి అంతస్తుకు మోయించాడు. అతను రెండు గంటల్లో ఇటుకలన్నీ పైకి మోసి రూ. 300/- కూలీ అడిగాడు. నిన్నటి కూలీకి రూ. 150/- మాత్రమే ఇచ్చానని రహీమ్ అన్నాడు. నేను ఎక్కువ గంటలు పని చేశాను. కాబట్టి నాకు ఎక్కువ కూలీ ఇవ్వాలని వాదించాడు.
ఎ) ఎవరి వాదన సరియైనది?
బి) ఇద్దరు కూలీలు చేసిన పని సమానమేనా?
సి) పని జరిగిన రేటులో తేడాకు కారణమేమిటి?
జవాబు:
ఎ) రహీమ్ వాదన సరియైనది.
బి) ఇద్దరు కూలీలు చేసిన పని సమానమే.
సి) పట్టిన కాలవ్యవధి సమానం కాకపోడమే.

ఉదాహరణ సమస్యలు

9th Class Physical Science Textbook Page No. 167

ప్రశ్న 1.
ఒక పిల్లవాడు బల్లపై ఉన్న పుస్తకంపై 4.5 న్యూటన్ల బలాన్ని ప్రయోగించి ఆ పుస్తకాన్ని బలప్రయోగ దిశలో 30 సెం.మీ. దూరం కదిలించినట్లయితే జరిగిన పని ఎంత?
సాధన:
పుస్తకంపై ప్రయోగించబడిన బలం (F) = 4.5 న్యూ
స్థానభ్రంశము (s) = 30 సెం.మీ = \(\frac{30}{100}\) మీ. = 0.3 మీ.
జరిగిన పని (W) = Fs = 4.5 న్యూ × 0.3 మీ. = 1.35 న్యూటన్ – మీ (లేదా) 1.35 బౌల్ (J)

ప్రశ్న 2.
ఒక విద్యార్థి 0.5 కి.గ్రా.ల బరువున్న పుస్తకాన్ని నేలపై నుండి ఎత్తి 1.5 మీ. ఎత్తు గల అలమరా పైకి చేర్చితే జరిగిన పని ఎంత?
సాధన:
పుస్తకం ద్రవ్యరాశి = 0.5 కి.గ్రా, ఈ పుస్తకంపై గురుత్వాకర్షణ బలం ‘mg’ అవుతుంది.
F = mg = 0.5 కి.గ్రా. × 9.8 మీ/సె² = 4.9 న్యూటన్లు
అంతే బలాన్ని ఆ విద్యార్థి పుస్తకాన్ని పైకి ఎత్తడానికి ప్రయోగించవలసి ఉంటుంది.
పుస్తకంపై విద్యార్థి ప్రయోగించిన బలం (F) = 4.9 న్యూటన్లు
బలప్రయోగ దిశలో వస్తువు స్థానభ్రంశం (s) = 1.5 మీ.
జరిగిని పని (W) = Fs = 4.9 న్యూటన్లు × 1.5 మీ. = 7.35 న్యూటన్ – మీటరు లేదా 7.35 జెల్

9th Class Physical Science Textbook Page No. 168

ప్రశ్న 3.
100 న్యూటన్ల ఘర్షణ బలం కలిగించే తలంపై ఒక పెట్టె 4 మీ. దూరం నెట్టబడితే ఘర్షణ బలం చేసిన పని ఎంత?
సాధన:
పెట్టెపై కలుగజేయబడిన ఘర్షణ బలం (F) = 100 న్యూటన్లు
పెట్టెలో జరిగిన స్థానభ్రంశం (s) = 4 m

బలం, వస్తువు స్థానభ్రంశం ఒకదానికొకటి వ్యతిరేక దిశలో ఉన్నాయి. కాబట్టి పెట్టెపై జరిగిన పని ఋణాత్మకం.
W= – Fs (F ఘర్షణబలం)
= -(100 న్యూటన్లు × 4 మీ) = – 400 న్యూటను – మీటరు (లేదా) – 400 జాల్

9th Class Physical Science Textbook Page No. 169

ప్రశ్న 4.
0.5 కి.గ్రా. ద్రవ్యరాశి గల ఒక బంతిని పైకి విసిరినప్పుడు అది 5 మీ. ఎత్తుకు చేరుకుంది. బంతి పై దిశలో కదులుతున్నప్పుడు దానిపై గురుత్వాకర్షణ బలం వల్ల జరిగిన పని ఎంత? (g = 10 మీ/సె²)
సాధన:
బంతిపై పనిచేసే గురుత్వాకర్షణ బలం (F) = mg = (0.5 కి.గ్రా) × (10 మీ/సె²) = 5 న్యూటన్లు
బంతి స్థానభ్రంశం = 5 మీ.
బంతిపై ప్రయోగింపబడిన బలం, బంతి స్థానభ్రంశం ఒకదానికొకటి వ్యతిరేక దిశలో ఉన్నందున పనిని ఋణాత్మకంగా పరిగణిస్తాం.
W = -F × s = – (5 న్యూటన్లు) × (5 మీటర్లు) = – 25 న్యూటన్ – మీటర్లు (లేదా) – 26 జౌల్

9th Class Physical Science Textbook Page No. 174

ప్రశ్న 5.
250 గ్రా. ద్రవ్యరాశి గల ఒక బంతి 40 సెం.మీ./సె. వేగంతో కదులుతుంటే, దాని కుండే గతిశక్తి ఎంత?
సాధన:
బంతి ద్రవ్యరాశి (m) = 250 గ్రా. = 0.25 కి.గ్రా. ,
బంతి వేగం (v) = 40 సెం.మీ/సె. = 0.4 మీ/సె.
బంతి గతిశక్తి K.E. = ½ (0.25) (0.4)² = 0.02 జెల్

ప్రశ్న 6.
సైకిల్ తొక్కే వ్యక్తి ద్రవ్యరాశి సైకిల్ ద్రవ్యరాశితో కలిపి 90 కి.గ్రా. సైకిల్ యొక్క వేగం 6 కి.మీ./గం. నుండి 12 కి.మీ/గం. కు పెరిగితే అతను చేసిన పని ఎంత?
సాధన:
సైకిల్ తో సహా వ్యక్తి యొక్క ద్రవ్యరాశి = 90 కి.గ్రా.
సైకిల్ తొలివేగం (u) = 6 కి.మీ./గం. = 6 × ( 5/18) = 5/3 మీ/సె.
సైకిల్ తుది వేగం (v) = 12 కి.మీ./గం. = 12 × (5/18) = 10/3 మీ./సె.
సైకిల్ యొక్క తొలి గతిశక్తి K.E_(i) = ½mu² = ½(90) (5/3)² = ½(90) (5/3) (5/3) = 125 జౌళ్ళు
సైకిల్ యొక్క తుది గతిశక్తి K.E_(f) = ½mv² = ½ (90) (10/3)² = ½(90) (10/3) (10/3) = 500 జౌళ్ళు
సైకిల్ తొక్కే వ్యక్తి చేసిన పని = గతిశక్తిలో కలిగిన మార్పు = K.E_(f) – K.E_(i)
= 500 జౌళ్ళు – 125 జౌళ్ళు = 375 జౌళ్ళు

9th Class Physical Science Textbook Page No. 177

ప్రశ్న 7.
2 కి.గ్రా. ద్రవ్యరాశి గల దిమ్మ భూమి నుండి 2 మీ. ఎత్తు వరకు ఎత్తబడింది. ఆ ఎత్తు వద్ద దిమ్మ యొక్క స్థితిశక్తిని లెక్కించండి. (గురుత్వత్వరణం (g) = 9.8 మీ/సె²).
సాధన:
దీమ్మ యొక్క ద్రవ్యరాశి (m) = 2 కి.గ్రా. ; దిమ్మ చేరుకున్న ఎత్తు (h) = 2 మీ.
గురుత్వత్వరణం (g) = 9.8 మీ/సె²
దిమ్మ యొక్క స్థితిశక్తి P.E. = mgh = (2) (9.8) (2) = 39.2 జౌళ్ళు

ప్రశ్న 8.
1 కి.గ్రా. ద్రవ్యరాశి గల పుస్తకం h ఎత్తు వరకు ఎత్తబడింది, ఆ పుస్తకం స్థితిశక్తి 49 జౌళ్ళు, అయిన అది ఎంత ఎత్తుకు ఎత్తబడిందో కనుక్కోండి.
సాధన:
పుస్తకం యొక్క స్థితిశక్తి = mgh
mgh = 49 జౌళ్ళు ⇒ (1) (9.8)h = 49 జౌళ్ళు
పుస్తకం ఎత్తబడిన ఎత్తు, h = (49)/(1 × 9.8) = 5 మీ.

9th Class Physical Science Textbook Page No. 181

ప్రశ్న 9.
ఒక వ్యక్తి 5 నిమిషాలలో 420 ఔళ్ల పని చేయగలిగితే అతని సామర్థ్యం ఎంత?
సాధన:
జరిగిన పని (W) = 420 జౌళ్లు ;
పనిచేయడానికి తీసుకున్న కాలం (t) = 5 నిమిషాలు = 5 × 60 సెకన్లు = 300 సెకన్లు
సామర్థ్యం (p) = W/t = 420/300 = 1.4 వాట్లు

ప్రశ్న 10.
ఒక స్త్రీ 10 సెకన్లలో 250 ళ్ల పని చేయగలదు. ఒక బాలుడు 4 సెకన్లలో 100 జోళ్ల పని చేయగలడు. వారిలో ఎవరి సామర్థ్యం ఎక్కువ?
సాధన:
సామర్థ్యం , P = W/U
స్త్రీ సామర్థ్యము = 250 / 10 = 25 వాట్లు
బాలుని సామర్థ్యము = 100/4 = 25 వాట్లు
ఇద్దరి సామర్థ్యమూ సమానమే. అంటే ఇద్దరూ పనిని సమాన వేగంతో చేయగలుగుతారు.

పరికరాల జాబితా

పింగాణి పాత్ర, లోహపు గోళం, కీ ఇచ్చే బొమ్మ కారు, స్ప్రింగ్, పొడవాటి స్థూపాకారపు గొట్టం, రబ్బరు బెలూను, అద్దం ముక్క లేజర్ లైట్, శక్తి వనరులను ప్రదర్శించే చార్టు, గతి శక్తి, స్థితి శక్తి ఉదాహరణలను చూపే చారు

9th Class Physical Science 10th Lesson పని మరియు శక్తి Textbook Activities (కృత్యములు)

కృత్యం – 1

విజ్ఞానశాస్త్ర ప్రకారం ‘పని’కి గల అర్థాన్ని అవగాహన చేసుకుందాం :

ప్రశ్న 1.
కింద ఇవ్వబడిన ఉదాహరణలలో విజ్ఞానశాస్త్ర ప్రకారం పని జరిగిందో, లేదో మీ స్నేహితులతో చర్చించి, ఏ కారణం ఆధారంగా పని జరిగిందని చెప్పారు? ఆ కారణాన్ని నమోదు చేయు విధంగా ఒక పట్టిక నమూనాను తయారు చేయండి.
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 13
జవాబు:

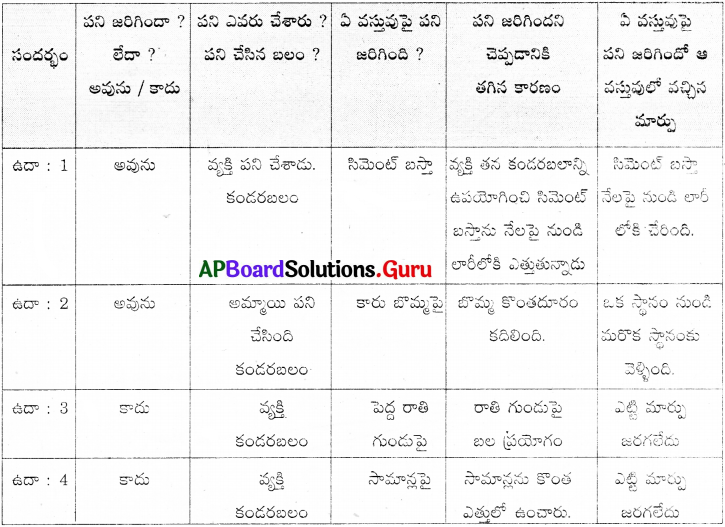
కృత్యం – 2

ఒక వస్తువు యొక్క శక్తిలో పెరుగుదల లేదా తగ్గుదలను అవగాహన చేసుకుందాం :

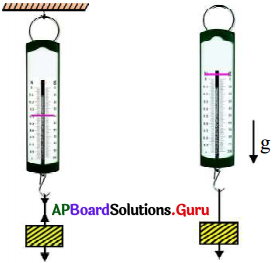
ప్రశ్న 2.
ఒక వస్తువు యొక్క శక్తిలో పెరుగుదల (లేదా) తగ్గుదలను ఏ విధంగా అవగాహన చేసుకోగలమో ప్రయోగపూర్వకంగా వ్రాయండి.
జవాబు:
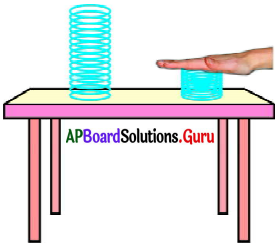
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 18

పటంలో చూపినట్లు ఒక గట్టి స్ప్రింగును బల్లపై ఉంచండి.
మీ చేతితో ఆ స్ప్రింగు పై భాగము నుండి గట్టిగా అదిమి కొద్దిసేపటి తర్వాత వదిలేయండి.
స్ప్రింగును అదిమి పట్టినప్పుడు, వదిలిన తర్వాత స్ప్రింగ్ లో జరిగిన మార్పులను పరిశీలించండి.
పని జరిగేందుకు బలాన్ని ప్రయోగించిన వస్తువు శక్తిని కోల్పోతుందని, ఏ వస్తువుపై అయితే పని జరిగిందో ఆ వస్తువు శక్తిని గ్రహిస్తుందని తెలుస్తుంది.

ఈ విధంగా ఒక వస్తువుపై బలం ప్రయోగించబడటం వలన దాని శక్తి పెరుగుదల లేదా తగుదల ఏ విధంగా ఉంటుందో అవగాహన చేసుకోవచ్చును.

కృత్యం – 3

శక్తి వనరుల జాబితా తయారుచేయడం :

ప్రశ్న 3.
శక్తి వనరుల జాబితాను తయారుచేయండి. అందులో ఏవి సూర్యునిపై ఆధారపడి ఉన్నాయో గుర్తించండి. అవి సూర్యునిపై ఆధారపడ్డాయని ఎలా చెప్పగలమో వ్రాయండి.
జవాబు:
శక్తి వనరులు :
సౌరశక్తి, వాయుశక్తి, జలశక్తి, బయోమాస్ శక్తి, నేలబొగ్గు, చమురు, సహజ వాయువులు, అలల శక్తి, సముద్ర ఉష్ణ మార్పిడి శక్తి, భూ ఉష్ణ శక్తి, గార్బేజి శక్తి, కేంద్రక శక్తి, మూలకాల శక్తి, మొదలగునవి.

ఈ శక్తి వనరులు కొన్ని సూర్యునిపై ఆధారపడతాయి. వాటిని ఒక శక్తి పరివర్తన ఛార్టు ద్వారా చూపడం జరుగుచున్నది.
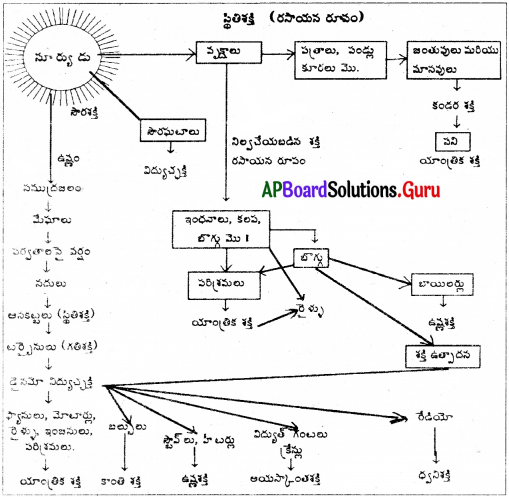
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 19

కృత్యం – 4

కదిలే వస్తువులకు గల శక్తిని తెలుసుకుందాం :

ప్రశ్న 4.
గతిశక్తిని నిరూపించు ప్రయోగాలను వ్రాయుము.
జవాబు:
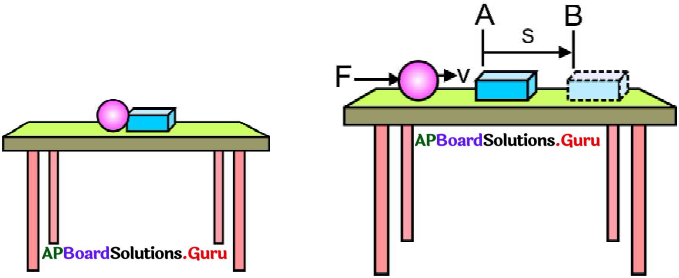
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 20

పటం (i)లో చూపినట్లు ఒక బల్లపై ఒక లోహపు గోళాన్ని, ఒక బోలుగా ఉన్న ప్లాస్టిక్ డబ్బాను పక్కపక్కనే ఉంచండి.
పటం (ii)లో చూపినట్లు లోహపు గోళాన్ని బల్ల అంచువరకు జరిపి, డబ్బావైపు ‘v’ వేగంతో దొర్లించండి.
గోళాన్ని దొర్లించినపుడు అది ‘v’ వేగంతో కదలడం ప్రారంభించి ప్లాస్టిక్ డబ్బాను ఢీకొన్నది.
డీకొనడం వల్ల పటం (ii)లో చూపినట్లు డబ్బా స్థానం ‘A’ నుండి ‘B’ కు మారింది.
దీని ఆధారంగా నిశ్చలస్థితిలో ఉన్న గోళం కంటే కదిలే గోళం శక్తివంతమైనదని చెప్పవచ్చును.
ఎందుకనగా నిశ్చలస్థితిలో ఉన్న గోళం ఎటువంటి పని చేయలేదు.
కానీ కదిలే గోళం ప్లాస్టిక్ డబ్బాను ముందుకు కదిలించింది.
దీనిని బట్టి నిశ్చలస్థితిలో ఉన్న వస్తువు కంటే కదిలే వస్తువుకు అధిక శక్తి గలదని తెలుసుకోవచ్చును.

కృత్యం – 5

స్థితిశక్తిని గురించి తెలుసుకుందాం :

ప్రశ్న 5.
స్థితిశక్తిని గురించి తెలుపు కృత్యాలను వ్రాయుము.
జవాబు:
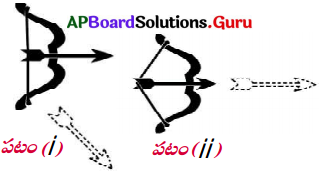
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 21

ఒక వెదురు కర్రను తీసుకుని ‘విల్లు’ తయారుచేయండి.
ఒక కర్ర పుల్లతో బాణాన్ని తయారుచేసి పటం (1)లో చూపినట్లు బాణం ఒక కొనను వింటినారికి ఆనించి కొద్దిగా లాగి బాణాన్ని వదలండి.
ఆ బాణం విల్లు నుంచి వేరుపడి, కొద్ది దూరంలో కిందపడిపోవడం గమనించవచ్చును.
ఇప్పుడు మరొక బాణాన్ని పటం (ii)లో చూపినట్లు అధిక బలాన్ని ఉపయోగించి బాగా లాగి వదలండి.
ఈ సందర్భంలో బాణం అతివేగంగా గాలిలో దూసుకుపోవడం గమనించవచ్చును.
రెండవ సందర్భంలో అధిక బలంను ప్రయోగించడం వలన విల్లుపై చేసిన పని, విల్లు ఆకారాన్ని మార్చడం వల్ల అధిక శక్తిని పొందింది.
ఇటువంటి శక్తిని స్థితిశక్తి అంటారు. ఈ శక్తి బాణాన్ని గాలిలో అతివేగంగా కదిలేట్లు చేసింది.

కృత్యం – 6

సాగదీయబడిన రబ్బరు బ్యాండ్ లోని శక్తిని పరిశీలిద్దాం :

ప్రశ్న 6.
సాగదీయబడిన రబ్బరు బ్యాండ్ లోని శక్తిని పరిశీలించు ప్రయోగాలను వ్రాయుము.
జవాబు:

ఒక రబ్బరు బ్యాండును తీసుకొనుము.
దాని రెండు చివరలా రెండు చేతులతో పట్టుకుని సాగదీయుము.
ఒక చేతి నుండి రబ్బరు బ్యాండను వదిలేయండి.
మీరు ఏమి జరిగిందో గమనించగా దాని ఆకారం పూర్వస్థితికి వచ్చింది. అనగా మారినది.
స్వతహాగా మీ ఫలితమేమనగా అది మీ చేతిపై శక్తిని ప్రయోగిస్తుంది.
దీనిని బట్టి వస్తువులు ఆకారం మారడం వల్ల శక్తిని పొందుతాయి అని గమనించవచ్చును.

కృత్యం – 7

కొంత ఎత్తులో ఉన్న వస్తువుకు ఉండే శక్తిని పరిశీలిద్దాం :

ప్రశ్న 7.
కొంత ఎత్తులో ఉన్న వస్తువుకు ఉండే శక్తిని గూర్చి ప్రయోగ పూర్వకంగా తెల్పుము.
జవాబు:

ఒక బరువైన లోహపు బంతిని తీసుకుని తడిమట్టి ఉన్న ప్రదేశంలో కొంత ఎత్తు నుండి వదలండి.
ఇదే విధముగా ఈ ప్రక్రియను వివిధ ఎత్తుల నుండి లోహపు బంతిని వదిలేస్తూ తడిమట్టిలో ఏర్పడే గుంతలను పరిశీలించండి.
ఆ గుంతలను పరిశీలించగా ఎత్తు పెరిగే కొలది దాని శక్తిలో మార్పును గమనించవచ్చును.
దీనిని బట్టి వస్తువుల స్థానం మారటం వల్ల కూడా అవి శక్తిని పొందుతాయని గమనించవచ్చును.

కృత్యం – 8

ప్రశ్న 8.
ప్రకృతిలో సహజమైన శక్తి మార్పులు, నిత్య జీవిత కార్యకలాపాలలో శక్తి మార్పుల జాబితా తయారు చేద్దాం
ఎ) ప్రకృతిలో సహజమైన శక్తి రూపాంతరాల యొక్క జాబితాను తయారుచేయండి.
జవాబు:

క్రమసంఖ్య	ప్రకృతిలో సహజంగా శక్తి రూపాంతరం చెందే సందర్భాలు
1.	చెట్లు ఆహారం తయారుచేసుకునే సందర్భంలో సౌరశక్తి రసాయన శక్తిగా మారుట.
2.	ఇస్త్రీ పెట్టెలో విద్యుత్ శక్తి ఉష్ణశక్తిగా మారడం.
3.	మొక్కల నుండి, మొక్కలను తినే జంతువుల నుండి మనకు ఆహారం వస్తుంది. వివిధ రసాయనచర్యల వల్ల ఆహారంలో రసాయన శక్తి రూపంలో దాగి ఉన్న శక్తి మనకు అవసరమైన రూపాలలోకి మారుతుంది.
4.	భూభ్రమణం జరగటం వలన నీటి అలలు ఏర్పడి తద్వారా వాటికి శక్తి వస్తుంది.
5.	పవనాలు అధికముగా రావటం వలన గాలి మరలు తిరిగి యాంత్రిక శక్తి, విద్యుత్ శక్తి ఉత్పత్తి అవుతుంది.

బి) మన నిత్య జీవిత కార్యకలాపాలలో శక్తి రూపాంతరాల జాబితాను తయారుచేయండి.
జవాబు:

శక్తి రూపాంతరం జరిగే సందర్భాలు	శక్తి రూపాంతరానికి కారణమైన పరికరాలు
1. విద్యుత్ శక్తి, యాంత్రిక శక్తిగా మారుట	ఫ్యాన్
2. ధ్వనిశక్తి, విద్యుత్ శక్తిగా మారుట	మైక్రోఫోన్
3. యాంత్రిక శక్తి, విద్యుత్ శక్తిగా మారుట	జలవిద్యుత్ కేంద్రం
4. సౌరశక్తి, విద్యుత్ శక్తిగా మారుట	సోలార్ బ్యాటరీ
5. రసాయనిక శక్తి, విద్యుత్ శక్తిగా మారుట	విద్యుత్ బ్యాటరీ
6. ఉష్ణశక్తి, యాంత్రిక శక్తిగా మారుట	ఆవిరి యంత్రము

కృత్యం – 9

యాంత్రిక శక్తి నిత్యత్వ నియమం :

ప్రశ్న 9.
యాంత్రిక శక్తి నిత్యత్వ నియమంను తెల్పు ప్రయోగాన్ని వ్రాయుము.
జవాబు:
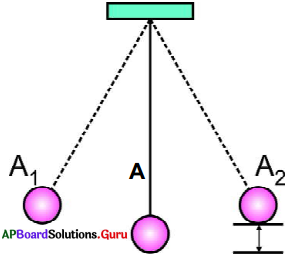
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 22

50 – 60 సెం||మీల పొడవు గల సన్నని దారాన్ని తీసుకోండి.
ఆ దారపు ఒక చివర చిన్న లోహపుగోళాన్ని కట్టండి.
దారం రెండవ కొనను పటంలో చూపినట్లు గోడకు స్థిరముగా కట్టుము.
ఇప్పుడు లోలకపు లోహపుగోళాన్ని కొంచెం (A₁ వైపుకు) లాగి వదలండి.
ఆ గోళం కంపిస్తూ వ్యతిరేకదిశకు అనగా A₂ స్థానానికి చేరును.
ఈ విధంగా ఆ గోళం A₁ , A₂ స్థానాల మధ్య కంపిస్తుండును.
గోళం యొక్క స్థితిశక్తి ‘A’ స్థానం వద్ద తక్కువ. ఎందుకనగా A₁, A₂ లతో పోల్చగా భూమి నుండి ఎత్తు తక్కువ కనుక.
గోళం A₁ నుండి బయలుదేరిన గోళానికి స్థితిశక్తి తగ్గుతూ గతిశక్తి పెరుగును.
గోళం A స్థానంకు చేరిన దాని స్థితిశక్తి – గతిశక్తి అగును.
గోళం A₁ నుండి A₂ కు కదులుతున్నపుడు దాని స్థితిశక్తి పెరుగుతూ, A₂ వద్ద గరిష్టానికి చేరుకుంటుంది.
గాలి నిరోధంను లెక్కలోనికి తీసుకొనకపోతే, లోలకం కంపించే మార్గంలోని ప్రతీ బిందువు వద్ద దాని స్థితిశక్తి మరియు గతిశక్తి ల మొత్తం స్థిరముగా ఉంటుంది.

ఈ విధంగా యాంత్రిక శక్తి నిత్యత్వమయినదని చెప్పవచ్చును.

కృత్యం – 10

వివిధ ఎత్తుల వద్ద స్వేచ్ఛాపతన వస్తువు యొక్క మొత్తం శక్తిని లెక్కించుట :

ప్రశ్న 10.
వివిధ ఎత్తుల వద్ద స్వేచ్ఛాపతన వస్తువు యొక్క మొత్తం శక్తిని లెక్కించే కృత్యంను వ్రాయుము.
జవాబు:
20 కి.గ్రా. ద్రవ్యరాశి గల ఒక వస్తువు 4 మీ. ఎత్తు నుండి స్వేచ్ఛగా వదిలి వేయబడింది. కింది పట్టికలో ఇవ్వబడిన వివిధ సందర్భాలలో దాని స్థితిశక్తి, గతిశక్తి మరియు ఆ రెండు శక్తుల మొత్తం కనుగొని పట్టికలో రాయండి. (g విలువ 10 మీ/సె². గా తీసుకోండి)
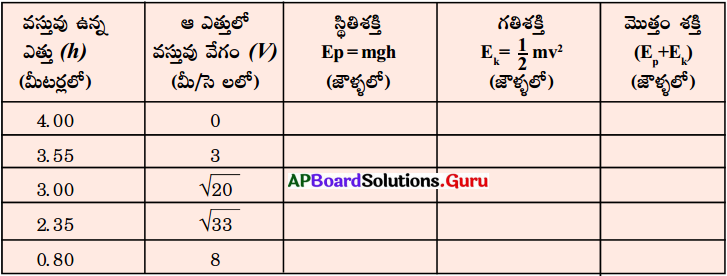
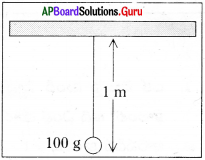
AP Board 9th Class Physical Science Solutions 10th Lesson పని మరియు శక్తి 23

AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ

January 5, 2024January 4, 2024 by Mahesh

SCERT AP 9th Class Physics Study Material Pdf Download 8th Lesson గురుత్వాకర్షణ Textbook Questions and Answers.

AP State Syllabus 9th Class Physical Science 8th Lesson Questions and Answers గురుత్వాకర్షణ

9th Class Physical Science 7th Lesson గురుత్వాకర్షణ Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
10 మీ. వ్యాసార్ధం గల వృత్తమార్గంలో 1000 కే.జీల కారు 10 మీ/సె. వడితో చలిస్తున్నది. దానికి కావలసిన అభికేంద్రబలాన్ని సమకూర్చేదెవరు? ఆ విలువ ఎంత? (AS 1)
జవాబు:
కారుకు కావలసిన అభికేంద్ర బలాన్ని వృత్తాకార మార్గములోని కేంద్రము సమకూరుస్తుంది.
విలువ:
కారు ద్రవ్యరాశి = m = 1000 కే.జీలు. ; వ్యాసారము = r = 10 మీ. ; కారు వడి = v = 10 మీ/సె.

ప్రశ్న 2.
భూ ఉపరితలం నుండి 40 మీ/సె వడితో ఒక వస్తువును నిట్టనిలువుగా పైకి విసిరితే, అది చేరే గరిష్ట ఎత్తు, పలాయన కాలంలను కనుగొనండి. పైకి విసిరిన 55 తర్వాత ఆ వస్తువేగం ఎంతుంటుంది? (g = 10 మీ/సె²) (AS 1)
జవాబు:
వస్తువు వడి = 1 = 40 మీ/సె ; గురుత్వ త్వరణం = g = 10 మీ/సె ; ఇచ్చిన కాలము = t = 5 సె||
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 2

ప్రశ్న 3.
50 మీ/సె.తో ఒక బంతిని నిట్టనిలువుగా పైకి విసిరాం. అది చేరే గరిష్ఠ ఎత్తు, ఆ ఎత్తు చేరడానికి పట్టే కాలం మరియు గరిష్ఠ ఎత్తు వద్ద దాని వేగాలను కనుక్కోండి. (g = 10 మీ/సె²) (AS 1)
జవాబు:
వస్తువు తొలి వేగం = 1 = 50 మీ/సె
గురుత్వ త్వరణం = g =10 మీ/సె²
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 3
గరిష్ఠ ఎత్తు వద్ద బంతి వేగము శూన్యముగా వుండును.

ప్రశ్న 4.
m₁ మరియు m₂ ద్రవ్యరాశులు గల రెండు కారులు వరుసగా r₁ మరియు r₂ వ్యాసార్థాలు గల వృత్తాకార మార్గాల్లో ప్రయాణిస్తున్నాయి. ఒక భ్రమణాన్ని పూర్తి చేయటానికి పట్టే సమయం రెండు కార్లకు సమానం. ఐతే వాటి వడులు మరియు అభికేంద్రత్వరణాల నిష్పత్తి ఎంత? (AS 1)
జవాబు:
కార్ల ద్రవ్యరాశులు వరుసగా m₁ మరియు m₂ ; వృత్తాకార మార్గాల వ్యాసార్ధాలు r₁ మరియు r₂.
ఒక భ్రమణాన్ని పూర్తి చేయుటకు పట్టు సమయం రెండు కార్లకు సమానము.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 4

ప్రశ్న 5.
10 కిలో గ్రాముల ద్రవ్యరాశి గల రెండు గోళాకార వస్తుకేంద్రాల మధ్య దూరం 10 సెం.మీ. వాటి మధ్యగల గురుత్వాకర్షణ బలం ఎంత? (AS 1)
జవాబు:
రెండు గోళాకార వస్తువుల ద్రవ్యరాశులు వరుసగా 10కి.గ్రా. మరియు 10 కి.గ్రా.
గోళాల మధ్య దూరము = d = 10 సెం.మీ
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 5
∴ వాటి మధ్య గల గురుత్వాకర్షణ బలము = 10G

ప్రశ్న 6.
ఏ ఏ సందర్భాల్లో మనిషి గురుత్వ కేంద్రం తన నుండి బయటకు వస్తుందో కొన్ని ఉదాహరణలతో వివరించంది. (AS 1)
జవాబు:
ఒక అథ్లెట్ ‘హైజంప్ చేయు సందర్భంలో, కొంత ఎత్తునుండి పారాచూట్ సహాయంతో విమానం నుండి దూకు సందర్భంలో గురుత్వ కేంద్రం బయటకు వచ్చును. ఎందుకనగా ఈ స్థితిలో వస్తువు అస్థిరత్వం మరియు భారరహితంగా ఉంటుంది కావున.

ప్రశ్న 7.
భూమి మరియు చంద్రుని మధ్య గురుత్వాకర్షణ బలం పనిచేయకపోతే చంద్రుని గమన మార్గం ఎలా ఉంటుంది? (AS 2)
జవాబు:
భూమి మరియు చంద్రునికి మధ్య గురుత్వాకర్షణ బలం పనిచేయకపోతే చంద్రుని గమన మార్గం భూమివైపు ఉండును.
(లేదా)
అసమరీతిలో చలన మార్గం ఉండును.

ప్రశ్న 8.
రెండు కణాల మధ్య గురుత్వాకర్షణ బలం పనిచేయని సందర్భం ఉంటుందా? ఎందుకు? (AS 2)
జవాబు:
రెండు కణాల మధ్య గురుత్వాకర్షణ బలం పనిచేయని సందర్భాలు ఉంటాయి. ఎందుకనగా ఆ వస్తువులు కాంతివేగంతో ఒకదానికొకటి వ్యతిరేక దిశలలో ప్రయాణించినపుడు గానీ, వాటి మధ్య లెక్కింపలేని దూరము ఉన్నపుడుగానీ సాధ్యపడును.

ప్రశ్న 9.
భూ వాతావరణం యొక్క గురుత్వకేంద్రం ఎక్కడ ఉంటుంది? (AS 2)
జవాబు:
భూ వాతారణపు మందం ఎంత ఉన్నప్పటికినీ, ఆ వాతావరణపు మందము యొక్క లక్షణము భూ ఉపరితలం నుండి 11 కి.మీ వరకు ఉండును. కావున భూ వాతావరణం యొక్క గురుత్వకేంద్రము భూ కేంద్రం వద్ద ఉండును. దీనికి కారణం భూమి గోళాకారంగా ఉండటమే.

ప్రశ్న 10.
స్టీలు ప్లేటుతో తయారుచేసిన భారతదేశ పట గురుత్వ కేంద్రం ఎలా కనుగొంటారు? వివరించండి. భారతదేశ పటం యొక్క గురుత్వ కేంద్రాన్ని నిర్ణయించడానికి ఏదైనా కృత్యాన్ని వివరింపుము. (AS 3)
జవాబు:
ఉద్దేశ్యం :
స్టీలు ప్లేటుతో తయారుచేసిన భారతదేశ పట గురుత్వ కేంద్రంను కనుగొనుట.

కావలసిన పరికరాలు :
స్టాండు, స్టీలుతో చేసిన భారతదేశ పటము, సన్నని పురిలేని త్రాడు.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 6

పద్దతి :

ఒక రిటార్డు స్టాండును తీసుకొనుము.
స్టాండుకు స్టీలు ప్లేటుతో చేసిన భారతదేశ పటం యొక్క ఒక బిందువు (దాదాపు మధ్య బిందువు)ను గుర్తించుము.
త్రాడును ఈ బిందువు నుండి వ్రేలాడదీయుము.
ఈ బిందువు ద్వారా ఒక వడంబకంను వ్రేలాడదీయుము.
వడంబకపు త్రాడు వెంట ఒక సరళరేఖను ప్లేటుపై గుర్తించుము.
ఈ విధముగా ప్లేటుపై రెండు లేక మూడు స్థానాలను పరీక్షించి సరళరేఖలను గీసిన అవి ఖండించుకొను బిందువు ఆ ప్లేటు యొక్క గురుత్వ కేంద్రం అగును.
ఈ విధముగా స్టీలు ప్లేటుపై గల భారతదేశ పటంను కనుగొనవచ్చును.

ప్రశ్న 11.
తాడుపై నడిచే వ్యక్తి పొడవైన, వంపు గల కర్రను ఎందుకు ఉపయోగిస్తాడు? వివరించండి. (AS 7)
జవాబు:
తాడుపై నడిచే వ్యక్తి పొడవైన కర్రను ఉపయోగించుటకు గల కారణము అతడు తాడుపై నడుచునపుడు ఆ కర్రను ఉపయోగించి అతని మొత్తం బరువు యొక్క చర్యారేఖను, తాడు ద్వారా పొవునట్లు జాగ్రత్త పడతాడు. ఈ ఫలితముగా అతడు పడిపోకుండా త్రాడుపై నడవగలుగుతాడు.

ప్రశ్న 12.
నీటితో నింపిన ఒక బకెట్ ను మోయటం కంటే నీటితో నింపిన రెండు బకెట్లను రెండు చేతులతో మోయటం సులభం ఎందుకు? (AS 7)
జవాబు:
నీటితో నింపిన ఒక బకెట్ ను మోయటం వలన మనిషి శరీరపు గురుత్వ కేంద్రంలో మార్పు వచ్చి అతను ప్రక్కకు వంగవలసి వచ్చును. కాని అదే మనిషి రెండు బకెట్లను రెండు చేతులతో పట్టుకోవడం వలన గురుత్వ కేంద్రంలో ఎట్టి మార్పు రాక స్థిరముగా ఉండుట వలన సులభముగా అనిపిస్తుంది.

ప్రశ్న 13.
ఒక వ్యక్తి తన కుడి భుజం మరియు కుడికాలు గోడకు ఆనించి ఉన్నాడు. ఈ స్థితిలో అతను గోడకు ఆనించకుండా ఉన్న తన ఎడమ కాలుని పైకి లేపగలదా? ఎందుకు? వివరించండి. (AS 7)
జవాబు:
పైకి లేపలేడు. ఎందుకనగా మనిషి యొక్క గురుత్వకేంద్రము అతని శరీరము మధ్యన ఉండును. ఒకవేళ అతను తన ఎడమకాలును పైకి లేపినట్లయితే అతని గురుత్వ కేంద్ర స్థానంలో మార్పు వచ్చి శరీరము స్థానంలో మార్పు వచ్చును.

ప్రశ్న 14.
మీరు గుంజీలు తీస్తున్నప్పుడు మీ శరీర గురుత్వ కేంద్రం ఏ విధంగా మారుతుందో వివరించండి. (AS 7)
జవాబు:
గురుత్వ కేంద్రము, వస్తు భారాల కేంద్రీకృత బిందువు కావున మన శరీరము యొక్క గరిమనాభి, గుంజీలు తీస్తున్నప్పుడు భూమి నుండి ఎత్తు మారినపుడల్లా మారును.

ప్రశ్న 15.
ఒక చెట్టుపై నుండి స్వేచ్ఛగా జారిపడిన ఆపిల్ 1.5 సెకనుల తర్వాత ఎంత వడిని కల్గి ఉంటుంది? మరియు ఈ కాలంలో అది ఎంత దూరం ప్రయాణిస్తుంది? (g = 10 మీ/సె² గా తీసుకోండి.) (AS 1)
జవాబు:
జారిపడిన కాలము = 1 = 1.5 సెకనులు ; గురుత్వత్వరణము = 9 = 10 మీ/సె²
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 7

ప్రశ్న 16.
ఒక బంతిని కొంత ఎత్తు నుండి జారవిడిచాం. అది నేలను తాకే ముందు చివరి 6మీ. దూరాన్ని 0.2 సెకనుల్లో దాటితే ఆ బంతిని ఎంత ఎత్తు నుండి జారవిడిచామో కనుక్కోండి. (g = 10 మీ/సె గా తీసుకొనండి.) (AS 1)
జవాబు:
ప్రయాణించిన దూరము S = 6 మీ ; కాలము = t = 0.2 sec ; తొలివేగం = u అనుకొనుము.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 8
S = ut + ½at² నుండి
6 = u × 0.2 + 12 × 10 × (0.2)²
6 = u × 0.2 + 5 × 0.04
u = \(\frac{5.8}{0.2}\) = 29 మీ/సె.
ఈ వేగము ‘x’ దూరాన్ని ప్రయాణించేటప్పుడు తుది వేగం అవుతుంది.
∴ s = x ; v = 29 మీ/సె. ; a = g = 10 మీ/సె² ; u = 0
v² – u² = 2as ⇒ v² = u² + 2as
v² = 841 + 2 × 10 × 6 = 841 + 120 = 961
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 9
మొత్తం దూరం = x + 6 = 42.05 + 6 = 48.05 మీ.

ప్రశ్న 17.
చంద్రుని వ్యాసార్థం మరియు ద్రవ్యరాశులు వరుసగా 1740 కి.మీ. మరియు 7.4 × 10²² కే.జీలు అయిన చంద్రునిపై గురుత్వత్వరణం ఎంత? (AS 1)
జవాబు:
చంద్రుని వ్యాసార్ధం = r = 1740 కి.మీ. ; చంద్రుని ద్రవ్యరాశి = m = 7.4 × 10²² కే.జీలు
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 10

ప్రశ్న 18.
30 మీ. వ్యాసార్థం గల వృత్తాకార మార్గంలో 36కి.మీ./గంట వడితో ఒక వ్యక్తి స్కూటర్ పై చలిస్తుంటే కావలసిన అభికేంద్రబలాన్ని సమకూర్చేదెవరు? ఆ బలమెంత? స్కూటరు మరియు వ్యక్తి యొక్క మొత్తం ద్రవ్యరాశి 150 కే.జీలు.
జవాబు:
వృత్త వ్యాసార్ధం = r = 30 మీ ; స్కూటర్ వడి = v = 10 కి.మీ/ గం.
స్కూటర్ మరియు వ్యక్తి ద్రవ్యరాశి = m = 150 కే.జీలు

ప్రశ్న 19.
1 మీ. పొడవు లఘులోలకంనకు గల గోళం యొక్క ద్రవ్యరాశి 100 గ్రా. దాని మార్గంలో సమతాస్థితి వద్ద గోళం 1.4 మీ/సె. వడితో చలిస్తుంటే లోలకం తాడులో గల తన్యత ఎంత? (g = 9.8 మీ/సె²) (AS 1)
జవాబు:
గోళం ద్రవ్యరాశి = 100 గ్రా. = 0.1 కేజి; లోలకం పొడవు = l = 1 మీ. ; గోళం యొక్క వడి (v) = 1.4 మీ/సె.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 12
తాడులో గల తన్యత = T అనుకొనుము.
గోళంలో పనిచేసే బలాలు :
1) గోళము బరువు mg (క్రింది దిశలో), 2) తాడులో తన్యత T (పై దిశలో)
గోళము బరువు = \(\frac{\mathrm{mv}^{2}}{l}\) ; తాడులో తన్యత = T = g cos θ
∴ న్యూటన్ మూడవ గమన నియమం ప్రకారం
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 13

ప్రశ్న 20.
R వ్యాసార్థం గల అర్ధగోళాకార పాత్రపై ఒక బిందువు వద్ద పటంలో చూపినట్లు ఒక చిన్న వాషర్‌ను ఉంచబడింది. ఆ బిందువు వద్ద నుండి వాషర్ అర్ధగోళాన్ని విడిచి ప్రయాణించాలంటే ఆ వాషర్‌కు అందించవలసిన కనీస వేగం ఎంత? (AS 7)
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 14
జవాబు:
అర్ధగోళపు వ్యాసార్ధము = R
వాషర్ చలనము వృత్తాకార చలనము కావున వాషర్ పై కేంద్రము ప్రయోగించు బలం అభికేంద్రబలం అగును.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 15

ప్రశ్న 21.
ఒక బాలుడు రెండు బంతులను గాలిలోకి నిట్టనిలువుగా విసిరి ఆడుకొనుచున్నాడు. మొదట విసరిన బంతి దాని గరిష్ట ఎత్తు వద్ద ఉన్నప్పుడు రెండవ బంతిని పైకి విసురుతున్నాడు. అతను ఒక సెకనుకు రెండు బంతులను విసురుతున్నట్లయితే ఆ బంతులు చేరే గరిష్ట ఎత్తు ఎంత? (AS 7)
జవాబు:
అతడు ఒక సెకనుకు రెండు బంతులను విసురుతున్నాడు.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 16

ప్రశ్న 22.
5మీ/సె. స్థిరవదితో పైకి వెళ్లే బెలూన్ నుండి అది 60 మీ. ఎత్తు వద్ద ఉన్నప్పుడు ఒక రాయిని జారవిడిచిన, అది ఎంత కాలంలో భూమిని చేరును?
జవాబు:
పైకి వెళ్ళే బెలూన్ వడి = 5 మీ/సె ; భూమి నుండి బెలూను గల దూరము = 60 మీ
కొంత ఎత్తు వద్ద వస్తువు వున్న సమీకరణం
h = – ut + ½gt²
60 = – 5t + ½ . 10. f²
5t² – 5t – 60 = 0
5(t² – 1 – 12) = 0
t² – t – 12 = 0
t² – 4t + 3t – 12 = 0
t(t – 4) + 3(t – 4) = 0
(t- 4) (t + 3) = 0
t = 4 sec
60 మీ|| ఎత్తు వద్ద నుండి ఒక రాయిని జారవిడిచిన అది భూమిని చేరుటకు 4 సెకనుల కాలం పట్టును.

ప్రశ్న 23.
ఒక చెట్టు నుండి ఆపిల్ జారిపడింది. ఆపిల్ పై నున్న ఒక చిన్న చీమ, భూమి తనవైపు ్వ త్వరణంతో చలిస్తుందని గమనించింది. భూమి నిజంగా చలిస్తుందా? ఒకవేళ చలిస్తే భూమికి ఈ త్వరణం పొందడానికి దానిపై పనిచేసే బిలం ఏమిటి? (AS 7)
జవాబు:
పై ప్రశ్నలో భూమి చలించుట జరుగదు. పండులో మాత్రమే చలనం గమనించగలము. ఒకవేళ భూమి గాని చలిస్తే న్యూటన్ 3వ గమన నియమం ప్రకారం ఆ పండుపై భూమి యొక్క గురుత్వాకర్షణ బలం పనిచేస్తూ ఉంటుంది.

9th Class Physical Science 8th Lesson గురుత్వాకర్షణ Textbook InText Questions and Answers

9th Class Physical Science Textbook Page No. 130

ప్రశ్న 1.
ఒక వస్తువుపై ఏ బలం పనిచేయకపోతే ఆ వస్తువు వక్రమారంలో చలించగలదా?
జవాబు:
వస్తువుపై ఏ బలం పనిచేయకపోతే వస్తువు వక్రమార్గంలో చలించదు.

ప్రశ్న 2.
వక్రమార్గంలో ప్రయాణించే సందర్భంలో కారు వడి పెరిగినట్లయితే దాని అభికేంద్రత్వరణం పెరుగుతుందా?
(మీ సమాధానాన్ని a = \(\frac{\mathrm{V}^{2}}{R}\) సమీకరణ సహాయంతో సమర్థించుకోండి).
జవాబు:
అభికేంద్ర త్వరణం (a_c) = \(\frac{\mathrm{V}^{2}}{R}\)
a ∝ V² కావున కారు వడి పెరిగినట్లయితే దాని అభికేంద్రత్వరణం పెరుగును.

ప్రశ్న 3.
1 మీ. పొడవు గల తాడు చివర 1 కి.గ్రా॥ ద్రవ్యరాశి గల బొమ్మను కట్టి క్షితిజ సమాంతరతలంలో 3 మీ./సె. వడితో త్రిప్పిన తాదులో ఉండే తన్యత ఎంత?
జవాబు:
బొమ్మ ద్రవ్యరాశి = m = 1 కి.గ్రా. ; వృత్త వ్యాసార్థం = తాడు పొడవు = R = 1 మీ. ; వడి = v = 3 మీ./సె.
తాడు క్షితిజ సమాంతర తలంలో తిరుగుచున్నది. కావున దానికి కావలసిన అభికేంద్రబలమే తాడు తన్యత అవుతుంది.

9th Class Physical Science Textbook Page No. 133

ప్రశ్న 4.
పటంలో చూపినట్లు చంద్రుడు భూమిచుట్టూ వృత్తాకార మార్గంలో చలిస్తూ ఉంటాడు. ఒకవేళ చంద్రుని వేగం శూన్యమయితే, చంద్రుడు చలనం ఏ విధంగా ఉంటుంది?
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 18
జవాబు:
చంద్రుని వేగం శూన్యమయితే, చంద్రుని యొక్క చలన దిశ భూమి వైపుకు ఉంటుంది.

ప్రశ్న 5.
రెండు వస్తువుల్లో ఒకదాని ద్రవ్యరాశి రెట్టింపయిన, వాటి మధ్య గురుత్వాకర్షణ బలం ఎంతుంటుంది?
జవాబు:
గురుత్వాకర్షణ బలం ద్రవ్యరాశికి అనులోమానుపాతంలో ఉండును. కావున గురుత్వాకర్షణ బలం రెట్టింపగును.

ప్రశ్న 6.
విశ్వంలో అన్ని వస్తువుల మధ్య గురుత్వాకర్వణ బలం ఉంటుందని మనకు తెలుసు. మరి మనం పెద్ద భవంతుల దగరగా నిలుచున్నప్పుడు వాటి వల్ల మనపై ప్రయోగింపబడే గురుత్వాకర్షణ బల ప్రభావాన్ని అనుభూతి పొందకపోవడానికి గల కారణమేమి?
జవాబు:

పెద్ద భవంతులతో పోల్చినపుడు మన ద్రవ్యరాశి లెక్కించదగినది కాదు.
భవంతుల ఎత్తుల మధ్య అధిక తేడా ఉంటుంది.
అందువలన మనం పెద్ద భవంతుల దగ్గరగా నిల్చున్నప్పుడు వాటివల్ల మనపై ప్రయోగింపబడే గురుత్వాకర్షణ బల ప్రభావ అనుభూతిని పొందలేము.

ప్రశ్న 7.
ఒకే ద్రవ్యరాశి గల చెక్కముక్క మరియు ఇనుప ముక్కలపై పనిచేసే భూమ్యాకర్షణ బలాల్లో దేనిపై పనిచేసే బలం అధికంగా ఉండును?
జవాబు:
ఒకే ద్రవ్యరాశి గల చెక్కముక్క మరియు ఇనుపముక్కలపై పనిచేసే భూమ్యాకర్షణ బాలాలు రెండింటిపైన సమానంగా ఉంటాయి. ఎందుకంటే అవి ఒకే ద్రవ్యరాశిని కలిగి ఉన్నాయి కనుక.

ప్రశ్న 8.
భూమి గురుత్వాకర్షణబలంతో ఆపిలను ఆకర్షించడం వలన అది భూమిపై పడుతుందని మనకు తెలుసు. ఆపిల్ కూడా భూమిని ఆకర్షిస్తుందా? ఒకవేళ ఆకర్షిస్తే అది ఎంత బలంతో భూమిని ఆకర్షిస్తుంది?
జవాబు:
ఆపిల్ కూడా భూమిని ఆకర్షించును. భూమి, ఆపిల్ పై ఎంత బలంను ప్రయోగించునో దానికి సమానమైన బలంతో వ్యతిరేక దిశలో ఆపిల్ భూమిపై బలాన్ని ప్రయోగించును.

9th Class Physical Science Textbook Page No. 135

ప్రశ్న 9.
వడి లేకుండా, త్వరణాన్ని కలిగి ఉండే వస్తు గమనాన్ని తెలిపే సందర్భానికి ఉదాహరణ యివ్వండి.
జవాబు:
నిట్టనిలువుగా పైకి విసిరిన వస్తువు వడి క్రమేపి తగ్గి శూన్యమై, గరిష్ఠ ఎత్తుకు చేరును. ఆ గరిష్ట ఎత్తు వద్ద వస్తువుకు వడి ఉండదు కానీ, గురుత్వత్వరణాన్ని కలిగి ఉండును.

ప్రశ్న 10.
20 మీ/సె. మరియు 40 మీ/సె. వేగాలతో గాలిలోనికి విసిరిన రెండు వస్తువుల యొక్క త్వరణాలను పోల్చండి.
జవాబు:
రెండు వస్తువులకు ఒకే త్వరణముండును.

9th Class Physical Science Textbook Page No. 137

ప్రశ్న 11.
నీ భారం ఎప్పుడు “mg” కు సమానం?
జవాబు:
మనము భూమి ఉపరితలముపై ఉన్నప్పుడు, మన భారం “mg” కు సమానమౌతుంది.

ప్రశ్న 12.
నీ భారం శూన్యమయ్యే సందర్భాలకు ఉదాహరణను ఇవ్వండి.
జవాబు:

స్విమ్మింగ్ పూల్ లో ఈతకొట్టేందుకు కొంత ఎత్తు నుండి దూకిన సందర్భంలో భారము శూన్యమగును.
పారాచూట్ సహాయంతో కొంత ఎత్తున గల విమానం నుండి దూకిన సందర్భంలో భారము శూన్యమగును.

9th Class Physical Science Textbook Page No. 140

ప్రశ్న 13.
పలుచని సమతల త్రిభుజాకార వస్తువు మరియు గోళాకార వస్తువుల గురుత్వ కేంద్రాలు ఎక్కడ ఉంటాయి?
జవాబు:

సమతల త్రిభుజాకార వస్తువు గురుత్వ కేంద్రము, ఆ వస్తువు భుజాల మధ్యగతరేఖల ఖండన బిందువు వద్ద ఉండును.
గోళాకార వస్తువుల విషయంలో దాని వ్యాసాల ఖండన బిందువు వద్ద గురుత్వ కేంద్రం ఉండును.

ప్రశ్న 14.
వస్తువుకి ఒకటి కంటే ఎక్కువ గురుత్వ కేంద్రాలు ఉండవచ్చా?
జవాబు:
ఉండవు, వస్తువుకి ఒకే ఒక్క గురుత్వకేంద్రం ఉండును.

ప్రశ్న 15.
“వీసా” అనే పట్టణంలో ఒక టవర్ కొంచెం వాలి ఉంటుంది. అయినా అది పడిపోవడం లేదు. ఎందుకు?
జవాబు:
గురుత్వ కేంద్రం స్థానంలో మార్పిడి, ఆ వస్తువు యొక్క స్థిరత్వంను పెంచును. కావున పీసా గోపురం పడిపోవడం లేదు.

ప్రశ్న 16.
వీపు పై అధిక భారాన్ని మోసే వ్యక్తి ఎందుకు కొంచెం ముందుకు వంగుతాడు?
జవాబు:
వీపుపై అధిక భారాన్ని మోసే వ్యక్తి స్థిరత్వం కొరకు కొంచెం ముందుకు వంగుతాడు.

9th Class Physical Science Textbook Page No. 129

ప్రశ్న 17.
సమవృత్తాకార చలనంను నిర్వచించుము. ఆ చలనంలో గల వస్తువు వేగం మారుతుందా? ఆ వస్తువుకు త్వరణం వుంటుందా? ఒకవేళ ఉంటే ఏ దిశలో ఉండును?
జవాబు:
నిర్వచనం : ఏదైనా ఒక వస్తువు స్థిరవడితో వృత్తాకార మార్గంలో చలిస్తూ ఉంటే ఆ వస్తువు చలనాన్ని “సమవృత్తాకార చలనము” అందురు.

సమవృత్తాకార చలనంలో గల వస్తువు వేగం మారును.
ఆ వస్తువుకు త్వరణం ఉండును.
దాని దిశ వస్తువేగ దిశలో ఉండును.

9th Class Physical Science Textbook Page No. 131

ప్రశ్న 18.
సర్ ఐజాక్ న్యూటన్ ఆపిల్ చెట్టు క్రింద కూర్చుని ఉన్నపుడు ఆపిల్, చెట్టు నుండి పడిందనే విషయం ద్వారా అతను గురుత్వాకర్షణ అనే భావనను కనుగొన్నాడని మనందరికీ సుపరిచితమే కదా ! ఈ సందర్భంలో న్యూటన్ మదిలో మెదిలిన ప్రశ్నలేమిటో మీకు తెలుసా?
జవాబు:

ఆపిల్ మాత్రమే భూమిపై పడింది. ఎందుకు?
ఆపిలను ఎవరో లాగి ఉంటారు (ఆకర్పించి)?
ఒకవేళ భూమి ఆపిల్ను లాగి ఉంటే ఆ బలం ఏమై ఉంటుంది?
ఈ నియమం ఆపిల్ కు మాత్రమేనా? ఏ వస్తువులకైనా వర్తిస్తుందా?

ఉదాహరణ సమస్యలు

9th Class Physical Science Textbook Page No. 133

ప్రశ్న 19.
భూ ఉపరితలానికి దగ్గరగా భూమి చుట్టూ భ్రమించే ఉపగ్రహ ఆవర్తన కాలమెంత? (భూ ఉపరితలం నుండి ఉపగ్రహ కక్ష్యకు గల ఎత్తు విస్మరించంది. భూమి ద్రవ్యరాశి, వ్యాసార్ధాలు వరుసగా 6 × 10^-24 కి.గ్రా. మరియు 6.4 × 10⁶ మీ.గా తీసుకోండి).
సాధన:
భూ ద్రవ్యరాశి మరియు వ్యాసార్ధాలు వరుసగా M మరియు R లు తీసుకుందాం. ఉపగ్రహ ద్రవ్యరాశి IT అనుకుందాం.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 19

పై సమీకరణంలో M, R మరియు G లు ప్రతిక్షేపించగా T = 84.75 ని. వచ్చును.

అనగా భూమి ఉపరితలానికి దగ్గరగా భూమి చుట్టూ వృత్తాకార మార్గంలో చలించే ఉపగ్రహం ఒక పూర్తి భ్రమణం చేయడానికి 1 గంట 24.7 నిముషాల సమయం (సుమారుగా) తీసుకుంటుంది.

9th Class Physical Science Textbook Page No. 135

ప్రశ్న 20.
ఒక వస్తువును నిట్టనిలువుగా పైకి విసిరారు. అది ఊర్ద్పదిశలో చలించేటప్పుడు ఆఖరి సెకనులో ప్రయాణించే దూరమెంత? S= 10 మీ/సె² గా తీసుకోండి.
సాధన:
ఊర్ధ్వ దిశలో చలించే వస్తువు ఆఖరి సెకనులో ప్రయాణించిన దూరం, అదే దిశలో మొదటి సెకనులో ప్రయాణించిన
దూరానికి సమానం.
కనుక u = 0 మరియు s = ut + \(\frac{1}{2}\)at², నుండి
వస్తువు ఊర్ధ్వ దిశలో ఆఖరి సెకనులో ప్రయాణించిన దూరం s = \(\frac{1}{2}\)gt² = \(\frac{1}{2}\) × 10 × 1 = 5 మీ.

ప్రశ్న 21.
వివిధ ఎత్తుల నుండి జారవిడిచిన రెండు స్వేచ్ఛా పతన వస్తువులు భూమికి ఒకేసారి చేరుకున్నవి. రెండు వస్తువుల ప్రయాణ కాలాలు వరుసగా 2సె. మరియు 1సె. అయిన 1సె. ప్రయాణించిన వస్తువును పతనం చెందడం ప్రారంభించేటప్పటికి 18 = 10 మీ/సె² గా తీసుకోండి). 2సె. ప్రయాణించిన వస్తువు ఏ ఎత్తులో ఉంటుంది?
సాధన:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 21
2సె|| ప్రయాణ కాలం గల వస్తువును మొదటిదని, 1 సె॥ ప్రయాణ కాలం గల వస్తువును రెండవదని అనుకుందాం. రెండవ వస్తువు 1 సెకను కాలంలో ప్రయాణించే దూరం
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 22
కావున రెండవ వస్తువు జారవిడిచే సమయంలో, మొదటి వస్తువు భూ ఉపరితలం నుండి 15 మీ. ఎత్తులో ఉంటుంది.

ప్రశ్న 22.
25మీ. ఎత్తు గల భవనం నుండి నిట్టనిలువుగా 20 మీ/సె వడితో ఒకరాయిని పైకి విసిరారు. ఆ రాయి భూమిని చేరడానికి ఎంత సమయం పడుతుంది? (g= 10 మీ/సె² గా తీసుకోండి.)
సాధన:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 23
ఈ లెక్కను సాధించడంలో ప్రక్క పటంలో చూపిన విధంగా సంజ్ఞా సాంప్రదాయాన్ని పాటించాలి.

రాయిని పైకి ఏ బిందువువద్ద నుంచైతే విసిరారో ఆ బిందువును నిర్దేశిత బిందువు (point of reference) గా తీసుకోండి. ఈ బిందువు నుండి పై దిశను ధనాత్మకం గాను, క్రింది దిశను ఋణాత్మకంగాను తీసుకుందాం. ఇచ్చిన విలువలు u = 20మీ/సె.
a = g = – 10 మీ/సె²
S = h = – 25 మీ. అవుతాయి.
చలన సమీకరణం, s = ut + \(\frac{1}{2}\) at²
– 25 = 20t – \(\frac{1}{2}\) × 10 × t²
– 25 = 20t – 5t²
– 5 = 4t – t²
⇒ t² – 4t – 5 = 0
దీనిని సాధించగా, (t- 5) (t + 1) = 0
కనుక t = 5 లేదా -1
కావున రాయి భూమిని చేరడానికి 5 సె|| సమయం పట్టును.

9th Class Physical Science Textbook Page No. 136

ప్రశ్న 23.
వడితో నిట్టనిలువుగా భూ ఉపరితలం నుండి పైకి విసిరిన వస్తువు భూమికి తిరిగిరావడానికి ఎంత సమయం పట్టును?
సాధన:
పైకి విసిరిన వస్తువు తిరిగి విసిరిన స్థానంకు చేరుకొనును. కావున స్థానభ్రంశం S = 0 అగును.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 24
తొలి వేగం u = u మరియు a = – g
చలన సమీకరణం, s = ut + \(\frac{1}{2}\) at² నుండి
0 = ut – \(\frac{1}{2}\)gt²
⇒ \(\frac{1}{2}\) gt² = ut
⇒ t = \(\frac{2u}{g}\)

పరికరాల జాబితా

చెక్కదిమ్మె, చెక్క స్టాండు, వడంబం, దారము, స్టీలు ప్లేటు, విద్యుత్ మోటారు, బ్యాటరీ, స్ప్రింగ్ త్రాసు, సమతాస్థితిని ప్రదర్శించే బొమ్మలు, నమూనాలు, మీటరు స్కేలు, అక్రమాకారపు వస్తువులు, రింగు

9th Class Physical Science 8th Lesson గురుత్వాకర్షణ Textbook Activities (కృత్యములు)

కృత్యం – 1

వృత్తాకార చలనంలో ఉన్న వస్తువును గమనించుట :

ప్రశ్న 1.
వృత్తాకార చలనంలో గల వస్తువును గమనించు కృత్యంను సోదాహరణంగా వివరించుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 25

ఒక విద్యుత్ మోటారు యొక్క కడ్డీకి ఒక వృత్తాకార ప్లేటును బిగించుము.
పటంలో చూపిన విధంగా ప్లేటు అంచు వద్ద చిన్న చెక్కదిమ్మను ఉంచుము.
ఇప్పుడు విద్యుత్ మోటారు స్విచ్ ను ఆన్ చేయుము.
కొంతసేపు తర్వాత చెక్కదిమ్మ పది భ్రమణాలు చేయుటకు పట్టే కాలాన్ని లెక్కించుము.
ఈ విధముగా రెండు లేక మూడు సార్లు చేయుము.

పై కృత్యం ద్వారా చెక్కదిమ్మ వృత్తాకార మార్గంలో స్థిర వడి, స్థిర భ్రమణ కాలములో తిరుగుచున్నది అని గమనించవచ్చును.

కృత్యం – 2

సమవృత్తాకార చలనంలో ఉన్న వస్తు వేగ సదిశలను గీయటం :

ప్రశ్న 2.
సమవృత్తాకార చలనంలో ఉన్న వస్తు వేగ సదిశలను గీయుటను వివరించుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 26

స్థిరవడి, స్థిరవేగంతో వృత్తాకార మార్గంలో ఒక చెక్కదిమ్మ భ్రమణం చేయుచున్నదనుకొనుము.
పటంలో చూపిన విధంగా చెక్కదిమ్మ చలించే మార్గాన్ని గీయుము.
ఈ మార్గంకు నిర్దిష్ట కాలవ్యవధుల వద్ద వేగ సదిశలను పటంలో చూపిన విధముగా గీయుము.
వేగ సదిశల తొలి బిందువులను ఒక బిందువు వద్దకు చేర్చుము.
ఈ వేగ సదిశలన్నీ వృత్తాకార మార్గం యొక్క కేంద్రం దగ్గర కలిసి వివిధ దిశల్లో ఉన్న వృత్త వ్యాసార్ధాలు కన్పిస్తాయి.

కృత్యం – 3

స్వేచ్ఛా పతన వస్తు త్వరణం దాని ద్రవ్యరాశిపై ఆధారపడదు

ప్రశ్న 3.
స్వేచ్ఛా పతన వస్తు త్వరణం దాని ద్రవ్యరాశిపై ఆధారపడదను చూపు కృత్యాన్ని రాయుము.
జవాబు:

పుస్తకంపై ఒక చిన్న కాగితాన్ని ఉంచి కొంత ఎత్తు నుండి రెండింటిని కలిపి ఒకేసారి వదలవలెను.
తర్వాత పుస్తకాన్ని మరియు కాగితాన్ని విడివిడిగా ఒకే ఎత్తు నుండి ఒకేసారి జారవిడవవలెను.

మొదటి సందర్భంలో కాగితం, పుస్తకంపైనున్నచో రెండునూ ఒకేసారి భూమి చేరినవి. రెండవ సందర్భంలో పుస్తకం ముందు భూమిని చేరి, కాగితం కొద్ది తేడాతో భూమిని చేరినది. దీనికి కారణం గాలి నిరోధక బలం కాగితంపై ఎక్కువగా పనిచేయటమే.

కృత్యం – 4

ప్రశ్న 4.
గురుత్వత్వరణం (g) ఏ దిశలో పనిచేస్తుంది?
జవాబు:
ఒక రాయిని నిట్టనిలువుగా పైకి విసరండి. అది భూమికి, తిరిగి చేరడానికి పట్టే సమయాన్ని లెక్కించండి.
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 27
రాయి పైకి చలించేటప్పుడు దాని వడి తగ్గుతూ ఉంటుంది. క్రిందకు చలించేటప్పుడు దాని వడి పెరుగుతూ ఉంటుంది. కనుక స్వేచ్చా పతన వస్తువు యొక్క త్వరణదిశ భూ ఉపరితలానికి లంబంగా పనిచేస్తుంది. వస్తువులను ఏవిధంగా విసిరినా వాటి గురుత్వత్వరణం ఎల్లప్పుడూ క్రిందకి పటంలో చూపిన విధంగా ఉంటుంది.

కృత్యం – 5

స్వేచ్ఛాపతన వస్తు భారంను కొలవగలమా?

ప్రశ్న 5.
స్వేచ్ఛాపతన వస్తు భారంను కొలిచే విధానాన్ని వివరించుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 28

ఒక స్ప్రింగ్ త్రాసును తీసుకొనుము.
ఆ త్రాసును పటంలో చూపిన విధంగా ఏదైనా ఆధారంకు వ్రేలాడదీయుము.
ఆ త్రాసు కొనకు కొంత భారాన్ని తగిలించుము.
ఈ సందర్భంలో త్రాసు రీడింగును గుర్తించుము.
భారం తగిలించి వున్న ఆ త్రాసును దాని ఆధారం నుండి వేరుచేసి స్వేచ్చగా వదిలివేయుము.
ఈ సందర్భంలో సూచీ సున్నా రీడింగును చూపుతుంది.
అనగా వస్తువు భార రహిత స్థితిలో కలదని గమనించవచ్చును.

కృత్యం – 6

స్వేచ్ఛాపతన వస్తువు – జరిగే మార్పులు :

ప్రశ్న 6.
స్వేచ్ఛాపతన వస్తువు విషయంలో జరిగే మార్పులను తెల్పు కృత్యంను వ్రాయుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 29

ఒక పారదర్శక టీ లాంటి పాత్రను తీసుకొనుము.
ఆ బ్రేకు ఎదురెదురు భుజాలపై రంధ్రాలను చేయుము.
2 లేక 3 రబ్బరు బ్యాండ్లను తీసుకుని రంధ్రాల మధ్య బిగుతుగా బిగించుము.
ఆ రబ్బరు బ్యాండ్లపై ఒక రాయిని పటం(ఎ)లో చూపిన విధంగా ఉంచండి.
రబ్బరు బ్యాండ్లలో వంపును గమనించవచ్చును.
ఈ స్థితిలో రాయితో సహా మొత్తం పాత్రను స్వేచ్చగా వదులుము.
పాత్రను స్వేచ్ఛగా వదిలినపుడు రాయి వలన రబ్బరు బ్యాండ్లలో ఏర్పడిన వంపు ఉండదు.
ఈ కృత్యం వలన వస్తుభారం శూన్యం కనుక భారం, ఆధారిత బలానికి సమానమైనదని తెలుసుకోవచ్చును.

కృత్యం – 7

ప్రశ్న 7.
కొన్ని వస్తువులను సమతాస్థితిలో (Balancing) ఉంచడం :
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 30
ఒక స్పూన్, ఒక ఫోర్క్ మరియు భారయుత కడ్డీలను ఒక గ్లాసు అంచుపై పటంలో చూపిన
విధంగా మొత్తం వ్యవస్థ సమతుల్య స్థితిలో ఉండేట్లు చేయండి. కొన్ని ప్రయత్నాల తర్వాత పటంలో చూపిన విధంగా సమతుల్య స్థితిలో ఉండిపోతాయి.

కృత్యం – 8

వంగకుండా మీరు పైకి లేవగలరా?

ప్రశ్న 8.
పటంలో చూపిన విధంగా కుర్చీలో కూర్చోండి. కాళ్లను మరియు వీపును, నడుము భాగాలను వంచకుండా పటంలో చూపిన స్థితిలోనే ఉండి పైకి లేవడానికి ప్రయత్నించండి.
పైన తెలిపిన విధంగా చేయగలరా? లేకపోతే ఎందుకు చేయలేరు?
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 31
జవాబు:
1) ఆ విధంగా పైకి లేవలేము.

కారణములు:

కుర్చీలో కూర్చున్నప్పుడు మనము భారరహిత స్థితిలో ఉంటాము.
ఆ స్థితిలో మనము కుర్చీ నుండి బలమును పొందవలసి ఉంటుంది.
దాని కొరకు మనము కాళ్ళను మరియు వీపును, నడుము భాగాలను వంచవలసి ఉంటుంది.

కృత్యం – 9

ప్రశ్న 9.
నిచ్చెనను సమతుల్య స్థితిలో ఉంచడం :
జవాబు:
నిచ్చెనను లేదా పొడుగాటి కర్రను నీ భుజంపై సమతాస్థితినందు ఉంచుటకు ప్రయత్నించండి. అతి కష్టం మీద సమతాస్థితి యందు ఉంచగలం.

కృత్యం – 10

ప్రశ్న 10.
గురుత్వ కేంద్రాన్ని కనుగొనుట :
ఎ) క్రమాకార వస్తువు యొక్క గురుత్వ కేంద్రంను కనుగొనుటను ఒక కృత్యం ద్వారా తెలుపుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 32

ఒక మీటరు పొడవుగల కొలబద్దను తీసుకొనుము.
ఆ బద్దపై వేర్వేరు బిందువుల వద్ద, దానిని వ్రేలాడదీయుము.
కొలబద్ద స్థిరముగా ఉండదు.
ఆ కొలబద్ద యొక్క మధ్యబిందువు నుండి వేలాడదీయుము.
ఈ బిందువు వద్ద కొలబద్ద క్షితిజ సమాంతరంగా ఉండును.
అనగా ఈ బిందువు వద్ద కొలబద్ద మొత్తంకు ఆధారము ఏర్పడింది. కావున ఈ బిందువునే ఆ వస్తువు యొక్క గురుత్వకేంద్రము అంటారు.
ఈ విధముగా క్రమాకార వస్తువు యొక్క గురుత్వ కేంద్రంను కనుగొనవచ్చును.

బి) ఒక అక్రమాకార వస్తువు యొక్క గురుత్వ కేంద్రంను ఏ విధముగా నిర్ణయించగలము?
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 33

స్వేచ్ఛగా వ్రేలాడదీసిన ఏ వస్తువు గురుత్వ కేంద్రమైననూ, ఈ వ్రేలాడదీసిన బిందువు నుండి గీయబడిన క్షితిజ లంబముపై ఉండును.
ఆ వస్తువు యొక్క వేరొక బిందువు గుండా మరలా వ్రేలాడదీయుము.
ఈ బిందువు నుండి క్షితిజ లంబాన్ని ఊహించుకొనుము.
ఈ రెండు రేఖల ఖండన బిందువును గురుత్వ కేంద్రముగా లెక్కించవచ్చును.

కృత్యం – 11

ఒక రింగు గురుత్వ కేంద్రాన్ని కనుగొనుట :

ప్రశ్న 11.
ఒక రింగు యొక్క గురుత్వ కేంద్రమును ఎట్లు కనుగొంటావో ప్రయోగపూర్వకంగా వివరించుము.
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 34

ఒక దళసరి కార్డుబోర్డు తీసుకొని, వేర్వేరు వ్యాసార్థాలతో ఏక కేంద్ర వృత్తాలు గీయుము.
వృత్తాకార రేఖల వెంబడి కార్డుబోర్డును కత్తిరించాలి. పటంలో చూపినట్లు రింగు ఆకారము ఏర్పడుతుంది.
AB అనే సన్నని తీగపై దీనిని ఉంచి దాని స్థానం సవరిస్తూ, అదిక్షితిజ సమాంతరంగా ఉండునట్లు చేయాలి.
ఆ తీగను టేపుతో ఆ స్థానంలో స్థిరంగా ఉండునట్లు చేయాలి.
మరల ఇదే ప్రయోగాన్ని CD అనే తీగపై చేయాలి.
AB మరియు CD తీగల ఖండన బిందువు ‘G’ గా గుర్తించుము.
‘G’ వద్ద త్రాడు సహాయముతో రింగును ‘G’ బిందువు నుండి వ్రేలాడదీసిన అది క్షితిజ సమాంతరంగా ఉంటుంది.
ఈ బిందువే గురుత్వ కేంద్రము లేక గరిమనాభి అవుతుంది.

కృత్యం – 12

ప్రశ్న 12.
గురుత్వ కేంద్రం స్థానంలో మార్పు – దాని ఫలితం :
జవాబు:
AP Board 9th Class Physical Science Solutions 8th Lesson గురుత్వాకర్షణ 35
మీరు నిటారుగా నిలబడినారనుకోండి. మీ శరీరం యొక్క గురుత్వ కేంద్రం మీ శరరము యొక్క మధ్యభాగము (గరిమినాభి).

మీరు నిలబడిన స్థానంలో ముందుకు వంగి పటం(ఎ)లో చూపినట్లు, మీ కాలివ్రేళ్లను పట్టుకోవడానికి ప్రయత్నించండి. తర్వాత ఒక గోడకు అనుకొని పటం(బి)లో చూపిన విధంగా కాళ్ళు గోడకు ఆనించి ఉంచి నడుము పై భాగంను ముందుకు వంచి మీ కాలివ్రేళ్లను పట్టుకోవడానికి ప్రయత్నించండి.

పటం(ఎ)లో వ్యక్తి ముందుకు వంగి కాలి వేళ్ళను పట్టుకోగలిగాడు. కారణం అతను తన శరీర గురుత్వ కేంద్రం వద్ద వంగాడు కాబట్టి.
పటం(బి)లో వ్యక్తి ముందుకు వంగి కాలివ్రేళ్ళను పట్టుకోలేకపోయాడు. కారణం అతను తన శరీర గురుత్వకేంద్రం వద్ద వంగలేదు కాబట్టి.

Inter 1st Year Maths 1A Functions Solutions Ex 1(c)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(c)

Question 1.
Find the domains of the following real-valued functions.
(i) f(x) = \(\frac{1}{\left(x^{2}-1\right)(x+3)}\)
Solution:
f(x) = \(\frac{1}{\left(x^{2}-1\right)(x+3)}\) ∈ R
⇔ (x² – 1) (x + 3) ≠ 0
⇔ (x + 1) (x – 1) (x + 3) ≠ 0
⇔ x ≠ -1, 1, -3
∴ Domain of f is R – {-1, 1, -3}

(ii) f(x) = \(\frac{2 x^{2}-5 x+7}{(x-1)(x-2)(x-3)}\)
⇔ (x – 1) (x – 2) (x – 3) ≠ 0
⇔ x ≠ 1, x ≠ 2, x ≠ 3
∴ Domain of f is R – {1, 2, 3}

(iii) f(x) = \(\frac{1}{\log (2-x)}\)
Solution:
f(x) = \(\frac{1}{\log (2-x)}\)
⇔ log (2 – x) ≠ 0 and 2 – x > 0
⇔ (2 – x) ≠ 1 and 2 > x
⇔ x ≠ 1 and x < 2
x ∈ (-∞, 1) ∪ (1, 2) (or) x ∈ (-∞, 2) – {1}
∴ Domain of f is {(-∞, 2) – {1}}

(iv) f(x) = |x – 3|
Solution:
f(x) = |x – 3| ∈ R
⇔ x ∈ R
∴ The domain of f is R

(v) f(x) = \(\sqrt{4 x-x^{2}}\)
Solution:
f(x) = \(\sqrt{4 x-x^{2}}\) ∈ R
⇔ 4x – x² ≥ 0
⇔ x(4 – x) ≥ 0
⇔ x ∈ [0, 4]
∴ Domain of f is [0, 4]

(vi) f(x) = \(\frac{1}{\sqrt{1-x^{2}}}\)
Solution:
f(x) = \(\frac{1}{\sqrt{1-x^{2}}}\) ∈ R
⇔ 1 – x² > 0
⇔ (1 + x) (1 – x) > 0
⇔ x ∈ (-1, 1)
∴ Domain of f is {x/x ∈ (-1, 1)}

(vii) f(x) = \(\frac{3^{x}}{x+1}\)
Solution:
f(x) = \(\frac{3^{x}}{x+1}\) ∈ R
⇔ 3^x ∈ R, ∀ x ∈ R and x + 1 ≠ 0
⇔ x ≠ -1
∴ Domain of f is R – {-1}

(viii) f(x) = \(\sqrt{x^{2}-25}\)
Solution:
f(x) = \(\sqrt{x^{2}-25}\) ∈ R
⇔ x² – 25 ≥ 0
⇔ (x + 5) (x – 5) ≥ 0
⇔ x ∈ (-∞, -5] ∪ [5, ∞)
⇔ x ∈ R – (-5, 5)
∴ Domain of f is R – (- 5, 5)

(ix) f(x) = \(\sqrt{x-[x]}\)
Solution:
f(x) = \(\sqrt{x-[x]}\) ∈ R
⇔ x – [x] ≥ 0
⇔ x ≥ [x]
⇔ x ∈ R
∴ Domain of f is R.

(x) f(x) = \(\sqrt{[x]-x}\)
Solution:
f(x) = \(\sqrt{[x]-x}\) ∈ R
⇔ [x] – x ≥ 0
⇔ [x] ≥ x
⇔ x ≤ [x]
⇔ x ∈ Z
∴ The domain of f is z (Where z denotes a set of integers)

Question 2.
Find the ranges of the following real-valued functions.
(i) log|4 – x²|
Solution:
Let y = f(x) = log|4 – x²|
f(x) ∈ R
⇔ 4 – x² ≠ 0
⇔ x ≠ ±2
∵ y = log|4 – x²|
⇒ |4 – x²| = e^y
∵ e^y > 0 ∀ y ∈ R
∴ The range of f is R.

(ii) \(\sqrt{[x]-x}\)
Solution:
Let y = f(x) = \(\sqrt{[x]-x}\)
f(x) ∈ R
⇔ [x] – x ≥ 0
⇔ x ≤ [x]
⇔ x ∈ z
∴ Domain of f is z. Then range of f is {0}

(iii) \(\frac{\sin \pi[x]}{1+[x]^{2}}\)
Solution:
Let f(x) = \(\frac{\sin \pi[x]}{1+[x]^{2}}\) ∈ R
⇔ x ∈ R
∴ The domain of f is R
For x ∈ R, [x] is an integer,
sin π[x] = 0, ∀ x ∈ R [∵ sin nπ = 0, ∀ n ∈ z]
∴ Range of f is {0}

(iv) \(\frac{x^{2}-4}{x-2}\)
Solution:
Let y = f(x) = \(\frac{x^{2}-4}{x-2}\) ∈ R
⇔ y = \(\frac{(x+2)(x-2)}{x-2}\)
⇔ x ≠ 2
∴ The domain of f is R – {2}
Then y = x + 2, [∵ x ≠ 2 ⇒ y ≠ 4]
Then its range R – {4}

(v) \(\sqrt{9+x^{2}}\)
Solution:
Let y = f(x) = \(\sqrt{9+x^{2}}\) ∈ R
The domain of f is R
When x = 0, f(0) = √9 = 3
For all values of x ∈ R – {0}, f(x) > 3
∴ The range of f is [3, ∞)

Question 3.
If f and g are real-valued functions defined by f(x) = 2x – 1 and g(x) = x² then find
(i) (3f – 2g)(x)
(ii) (fg) (x)
(iii) \(\left(\frac{\sqrt{f}}{g}\right)(x)\)
(iv) (f + g + 2) (x)
Solution:
(i) (3f – 2g)(x)
f(x) = 2x – 1, g(x) = x²
(3f – 2g) (x) = 3f(x) – 2g(x)
= 3(2x – 1) – 2x²
= -2x² + 6x – 3

(ii) (fg) (x)
= f(x) . g(x)
= (2x – 1) (x²)
= 2x³ – x²

(iii) \(\left(\frac{\sqrt{f}}{g}\right)(x)\)
\(\frac{\sqrt{f(x)}}{g(x)}=\frac{\sqrt{2 x-1}}{x^{2}}\)

(iv) (f + g + 2) (x)
= f(x) + g(x) + 2
= (2x – 1) + x² + 2
= x² + 2x + 1
= (x + 1)²

Question 4.
If f = {(1, 2), (2, -3), (3, -1)} then find
(i) 2f
(ii) 2 + f
(iii) f²
(iv) √f
Solution:
Given f = {(1, 2), (2, -3), (3, -1)}
(i) 2f = {(1, 2 × 2), (2, 2(-3), (3, 2(-1))}
= {(1, 4), (2, -6), (3, -2)}

(ii) 2 + f = {(1, 2 + 2), (2, 2 + (-3)), (3, 2 + (-1)}
= {(1, 4), (2, -1), (3, 1)}

(iii) f² = {(1, 22), (2, (-3)2), (3, (-1)2)}
= {(1, 4), (2, 9), (3, 1)}

(iv) √f = {(1, √2)}
∵ √-3 and √-1 are not real

II.

Question 1.
Find the domains of the following real-valued functions.
(i) f(x) = \(\sqrt{x^{2}-3 x+2}\)
Solution:
f(x) = \(\sqrt{x^{2}-3 x+2}\) ∈ R
⇔ x² – 3x + 2 ≥ 0
⇔ (x- 1) (x – 2) ≥ 0
⇔ x ∈ (-∞, 1 ] ∪ [2, ∞]
∴ The domain of f is R – (1, 2)

(ii) f(x) = log(x² – 4x + 3)
Solution:
f(x) = log(x² – 4x + 3) ∈ R
⇔ x² – 4x + 3 > 0
⇔ (x – 1) (x – 3) > 0
⇔ x ∈ (-∞, 1) ∪ (3, ∞)
∴ Domain of f is R – [1, 3]

(iii) f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\)
Solution:
f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\) ∈ R
⇔ 2 + x ≥ 0, 2 – x ≥ 0, x ≠ 0
⇔ x ≥ -2, x ≤ 2, x ≠ 0
⇔ -2 ≤ x ≤ 2, x ≠ 0
⇔ x ∈ [-2, 2] – {0}
Domain of f is [-2, 2] – {0}

(iv) f(x) = \(\frac{1}{\sqrt[3]{(x-2)} \log _{(4-x)} 10}\)
Solution:
f(x) = \(\frac{1}{\sqrt[3]{(x-2)} \log _{(4-x)} 10}\) ∈ R
⇔ 4 – x > 0, 4 – x ≠ 1 and x – 2 ≠ 0
⇔ x < 4, x ≠ 3, x ≠ 2
∴ Domain of f is (-∞, 4) – {2, 3}

(v) f(x) = \(\sqrt{\frac{4-x^{2}}{[x]+2}}\)
Solution:
f(x) = \(\sqrt{\frac{4-x^{2}}{[x]+2}}\) ∈ R
Case (i) 4 – x² ≥ 0 and [x] + 2 > 0 (or) Case (ii) 4 – x² ≤ 0 and [x] + 2 < 0
Case (i): 4 – x² ≥ 0 and [x] + 2 > 0
⇔ (2 – x) (2 + x) ≥ 0 and [x] > -2
⇔ x ∈ [-2, 2] and x ∈ [-1, ∞]
⇔ x ∈ [-1, 2] ……..(1)
Case (ii): 4 – x² ≤ 0 and [x] + 2 < 0
⇔ (2 + x) (2 – x) ≤ 0 and [x] < – 2
⇔ x ∈ (-∞, -2] ∪ [2, ∞] and x ∈ (-∞, -2)
⇔ x ∈ (-∞, -2) ……(2)
from (1) and (2),
Domain of f is (-∞, -2) ∪ [-1, 2]

(vi) f(x) = \(\sqrt{\log _{0.3}\left(x-x^{2}\right)}\)
Solution:
f(x) = \(\sqrt{\log _{0.3}\left(x-x^{2}\right)}\) ∈ R
Then log_0.3(x – x²) ≥ 0
⇒ x – x² ≤ (0.3)⁰
⇒ x – x² ≤ 1
⇒ -x² + x – 1 ≤ 0
⇒ x² – x + 1 ≥ 0
This is true for all x ∈ R ……..(1)
and x – x² ≥ 0
⇒ x² – x ≤ 0
⇒ x(x – 1) ≤ 0
⇒ x ∈ (0, 1) …….(2)
From (1) and (2)
Domain of f is R ^ (0, 1) = (0, 1)
∴ The domain of f is (0, 1)

(vii) f(x) = \(\frac{1}{x+|x|}\)
Solution:
f(x) = \(\frac{1}{x+|x|}\) ∈ R
⇔ x + |x| ≠ 0
⇔ x ∈ (0, ∞)
∵ |x| = x, if x ≥ 0
|x| = -x, if x < 0
∴ The domain of f is (0, ∞)

Question 2.
Prove that the real valued function f(x) = \(\frac{x}{e^{x}-1}+\frac{x}{2}+1\) is an even function on R \ {0}.
Solution:
f(x) ∈ R, e^x – 1 ≠ 0
⇒ e^x ≠ 1
⇒ x ≠ 0
Inter 1st Year Maths 1A Functions Solutions Ex 1(c) II Q2
⇒ f(x) is an even function on R – {0}

Question 3.
Find the domain and range of the following functions.
(i) f(x) = \(\frac{\tan \pi[x]}{1+\sin \pi[x]+\left[x^{2}\right]}\)
Solution:
f(x) = \(\frac{\tan \pi[x]}{1+\sin \pi[x]+\left[x^{2}\right]}\) ∈ R
⇔ x ∈ R, since [x] is an integer tan π[x] and sin π[x] each is zero for ∀ x ∈ R and f(x) ∈ R
Domain of f is R
Its range = {0}

(ii) f(x) = \(\frac{x}{2-3 x}\)
Solution:
Inter 1st Year Maths 1A Functions Solutions Ex 1(c) II Q3(ii)

(iii) f(x) = |x| + |1 + x|
Solution:
f(x) = |x| + |1 + x| ∈ R
⇔ x ∈ R
∴ Domain of f is R
∵ |x| = x, if x ≥ 0
= -x, if x < 0
|1 + x| = 1 + x, if x ≥ -1
= -(1 + x) if x < -1
For x = 0, f(0) = |0| + |1 + 0| = 1
x = 1, f(1) = |1| + |1 + 1| = 1 + 2 = 3
x = 2, f(2) = |2| + |1 + 2| = 2 + 3 = 5
x = -2, f(-2) = |-2| + |1 + (-2)| = 2 + 1 = 3
x = -1, f(-1) = |-1| + |1 +(-1)| = 1 + 0 = 1
∴ The range of f is [1, ∞]

Inter 1st Year Maths 1A Functions Solutions Ex 1(b)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(b)

Question 1.
If f(x) = e^x and g(x) = log_ex, then show that f o g = g o f and find f^-1 and g^-1.
Solution:
Given f(x) = e^x and g(x) = log_ex
Now (f o g) (x) = f(g(x))
= f(log_ex) [∵ g(x) = \(\log _{e} x\)]
= \(e^{\left(\log _{e} x\right)}\)
= x
∴ (fog) (x) = x ………(1)
and (g o f) (x) = g(f(x))
= g(e^x) [∵ f(x) = e^x]
= log_e (e^x) [∵ g(x) = log_ex]
= x log_e (e)
= x(1)
= x
∴ (g o f) (x) = x …….(2)
From (1) and (2)
f o g = g o f
Given f(x) = e^x
Let y = f(x) = e^x ⇒ x = f^-1(y)
and y = e^x ⇒ x = log_e (y)
∴ f^-1(y) = log_e (y) ⇒ f^-1(x) = log_e (x)
Let y = g(x) = log_e (x)
∵ y = g(x) ⇒ x = g^-1(y)
∵ y = log_e (x) ⇒ x = e^y
∴ g^-1(y) = e^y ⇒ g^-1(x) = e^x
∴ f^-1(x) = log_e (x) and g^-1(x) = e^x

Question 2.
If f(y) = \(\frac{y}{\sqrt{1-y^{2}}}\), g(y) = \(\frac{y}{\sqrt{1+y^{2}}}\) then show that (fog) (y) = y
Solution:
f(y) = \(\frac{y}{\sqrt{1-y^{2}}}\) and g(y) = \(\frac{y}{\sqrt{1+y^{2}}}\)
Now, (fog) (y) = f(g(y))
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) I Q2
∴ (fog) (y) = y

Question 3.
If f : R → R, g : R → R are defined by f(x) = 2x² + 3 and g(x) = 3x – 2, then find
(i) (fog)(x)
(ii) (gof) (x)
(iii) (fof) (0)
(iv) go(fof) (3)
Solution:
f : R → R, g : R → R and f(x) = 2x² + 3; g(x) = 3x – 2
(i) (f o g) (x) = f(g(x))
= f(3x – 2) [∵ g(x) = 3x – 2]
= 2(3x- 2)² + 3 [∵ f(x) = 2x² + 3]
= 2(9x² – 12x + 4) + 3
= 18x² – 24x + 8 + 3
= 18x² – 24x + 11

(ii) (gof) (x) = g(f(x))
= g(2x² + 3) [∵ f(x) = 2x² + 3]
= 3(2x² + 3) – 2 [∵ g(x) = 3x – 2]
= 6x² + 9 – 2
= 6x² + 7

(iii) (fof) (0) = f(f(0))
= f(2(0) + 3) [∵ f(x) = 2x² + 3]
= f(3)
= 2(3)² + 3
= 18 + 3
= 21

(iv) g o (f o f) (3)
= g o (f (f(3)))
= g o (f (2(3)² + 3)) [∵ f(x) = 2x² + 3]
= g o (f(21))
= g(f(21))
= g(2(21)² + 3)
= g(885)
= 3(885) – 2 [∵ g(x) = 3x – 2]
= 2653

Question 4.
If f : R → R, g : R → R are defined by f(x) = 3x – 1, g(x) = x² + 1, then find
(i) (f o f) (x² + 1)
(ii) f o g (2)
(iii) g o f (2a – 3)
Solution:
f : R → R, g : R → R and f(x) = 3x – 1 ; g(x) = x² + 1
(i) (f o f) (x² + 1)
= f(f(x² + 1))
= f[3(x² + 1) – 1] [∵ f(x) = 3x – 1]
= f(3x² + 2)
= 3(3x² + 2) – 1
= 9x² + 5

(ii) (f o g) (2)
= f(g(2))
= f(2² + 1) [∵ g(x) = x² + 1]
= f(5)
= 3(5) – 1
= 14 [∵ f(x) = 3x – 1]

(iii) (g o f) (2a – 3)
= g(f(2a – 3))
= g[3(2a – 3) – 1] [∵ f(x) = 3x – 1]
= g(6a – 10)
= (6a – 10)² + 1 [∵ g(x) = x² + 1]
= 36a² – 120a + 100 + 1
= 36a² – 120a + 101

Question 5.
If f(x) = \(\frac{1}{x}\), g(x) = √x for all x ∈ (0, ∞) then find (g o f) (x).
Solution:
f(x) = \(\frac{1}{x}\), g(x) = √x, ∀ x ∈ (0, ∞)
(g o f) (x) = g(f(x))
= g(\(\frac{1}{x}\)) [∵ f(x) = \(\frac{1}{x}\)]
= \(\sqrt{\frac{1}{x}}\)
= \(\frac{1}{\sqrt{x}}\) [∵ g(x) = √x]
∴ (gof) (x) = \(\frac{1}{\sqrt{x}}\)

Question 6.
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) for all x ∈ R, find (g o f) (x).
Solution:
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) ∀ x ∈ R
(g o f) (x) = g(f(x))
= g(2x – 1) [∵ f(x) = 2x – 1]
= \(\frac{(2 x-1)+1}{2}\)
= x [∵ g(x) = \(\frac{x+1}{2}\)]
∴ (g o f) (x) = x

Question 7.
If f(x) = 2, g(x) = x², h(x) = 2x for all x ∈ R, then find (f o (g o h)) (x).
Solution:
f(x) = 2, g(x) = x², h(x) = 2x, ∀ x ∈ R
[f o (g o h) (x)]
= [f o g (h(x))]
= f o g (2x) [∵ h(x) = 2x]
= f[g(2x)]
= f((2x)²) [∵ g(x) = x²]
= f(4x²) = 2 [∵ f(x) = 2]
∴ [f o (g o h) (x)] = 2

Question 8.
Find the inverse of the following functions.
(i) a, b ∈ R, f : R → R defined by f(x) = ax + b, (a ≠ 0).
Solution:
a, b ∈ R, f : R → R and f(x) = ax + b, a ≠ 0
Let y = f(x) = ax + b
⇒ y = f(x)
⇒ x = f^-1(y) ……..(i)
and y = ax + b
⇒ x = \(\frac{y-b}{a}\) ……..(ii)
From (i) and (ii)
f^-1(y) = \(\frac{y-b}{a}\)
⇒ f^-1(x) = \(\frac{x-b}{a}\)

(ii) f : R → (0, ∞) defined by f(x) = 5^x
Solution:
f : R → (0, ∞) and f(x) = 5^x
Let y = f (x) = 5^x
y = f(x) ⇒ x = f^-1(y) ……(i)
and y = 5^x ⇒ log₅ (y) = x ……..(ii)
From (i) and (ii)
f^-1(y) = log₅(y) ⇒ f^-1(x) = log5 (x)

(iii) f : (0, ∞) → R defined by f(x) = log₂ (x).
Solution:
f : (0, ∞) → R and f(x) = log₂ (x)
Let y = f(x) = log₂ (x)
∵ y = f(x) ⇒ x = f^-1(y) ……..(i)
and y = log₂(x) ⇒ x = 2y
From (i) and (ii)
f^-1(y) = 2y ⇒ f^-1(x) = 2x

Question 9.
If f(x) = 1 + x + x² + …… for |x| < 1 then show that f^-1(x) = \(\frac{x-1}{x}\)
Solution:
f(x) = 1 + x + x² + ……..
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) I Q9

Question 10.
If f : [1, ∞) ⇒ [1, ∞) defined by f(x) = \(2^{x(x-1)}\) then find f^-1(x).
Solution:
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) I Q10

II.

Question 1.
If f(x) = \(\frac{x-1}{x+1}\), x ≠ ±1, then verify (f o f^-1) (x) = x.
Solution:
Given f(x) = \(\frac{x-1}{x+1}\), x ≠ ±1
Let y = f(x) = \(\frac{x-1}{x+1}\)
∵ y = f(x) ⇒ x = f^-1(y) ……(i)
and y = \(\frac{x-1}{x+1}\)
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) II Q1

Question 2.
If A = {1, 2, 3}, B = {α, β, γ}, C = {p, q, r} and f : A → B, g : B → C are defined by f = {(1, α), (2, γ), (3, β)}, g = {(α, q), (β, r), (γ, p)}, then show that f and g are bijective functions and (gof)^-1 = f^-1 o g^-1.
Solution:
A = {1, 2, 3}, B = {α, β, γ},
f : A → B and f = {(1, α), (2, γ), (3, β)}
⇒ f(1) = α, f(2) = γ, f(3) = β
∵ Distinct elements of A have distinct f – images in B, f: A → B is an injective function.
Range of f = {α, γ, β} = B(co-domain)
∴ f : A → B is a surjective function.
Hence f : A → B is a bijective function.
B = {α, β, γ}, C = {p, q, r}, g : B → C and g : {(α, q), (β, r), (γ, p)}
⇒ g(α) = q, g(β) = r, g(γ) = p
∴ Distinct elements of B have distinct g – images in C, g : B → C is an injective function.
Range of g = {q, r, p} = C, (co-domain)
∴ g : B → C is a surjective function
Hence g : B → C is a bijective function
Now f = {(1, α), (2, γ), (3, β)}
g = {(α, q), (β, r), (γ, p)}
g o f = {(1, q), (2, p), (3, r)}
∴ (g o f)^-1 = {(q, 1), (r, 3), (p, 2)} ………(1)
g^-1 = {(q, α), (r, β), (p, γ)}
f^-1 = {(α, 1), (γ, 2),(β, 3)}
Now f^-1 o g^-1 = {(q, 1), (r, 3), (p, 2)} …….(2)
From eq’s (1) and (2)
(gof)^-1 = f^-1 o g^-1

Question 3.
If f : R → R, g : R → R defined by f(x) = 3x – 2, g(x) = x² + 1, then find
(i) (g o f^-1) (2)
(ii) (g o f)(x – 1)
Solution:
f : R → R, g : R → R and f(x) = 3x – 2
f is a bijective function ⇒ its inverse exists
Let y = f(x) = 3x – 2
∵ y = f(x) ⇒ x = f^-1(y) …….(i)
and y = 3x – 2
⇒ x = \(\frac{y+2}{3}\) ……..(ii)
From (i) and (ii)
f^-1(y) = \(\frac{y+2}{3}\)
⇒ f^-1(x) = \(\frac{x+2}{3}\)
Now (gof^-1) (2)
= g(f^-1(2))
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) II Q3
∴ (g o f^-1) (2) = \(\frac{25}{9}\)

(ii) (g o f) (x -1)
= g(f(x – 1))
= g(3(x – 1) – 2) [∵ f(x) = 3x – 2]
= g(3x – 5)
= (3x – 5)² + 1 [∵ g(x) = x² + 1]
= 9x² – 30x + 26
∴ (g o f) (x – 1) = 9x² – 30x + 26

Question 4.
Let f = {(1, a), (2, c), (4, d), (3, b)} and g^-1 = {(2, a), (4, b), (1, c), (3, d)} then show that (gof)^-1 = f^-1 o g^-1
Solution:
f = {(1, a), (2, c), (4, d), (3, b)}
∴ f^-1 = {(a, 1), (c, 2), (d, 4), (b, 3)}
g^-1 = {(2, a), (4, b), (1, c), (3, d)}
∴ g = {(a, 2), (b, 4), (c, 1), (d, 3)}
(g o f) = {(1, 2), (2, 1), (4, 3), (3, 4)}
∴ (gof)^-1 = {(2, 1), (1, 2), (3, 4), (4, 3)} ……….(1)
f^-1 o g^-1 = {(2, 1), (4, 3), (1, 2), (3, 4)} ……..(2)
From eq’s (1) and (2), we observe (gof)^-1 = f^-1 o g^-1

Question 5.
Let f : R → R, g : R → R be defined by f(x) = 2x – 3, g(x) = x³ + 5 then find (f o g)^-1 (x).
Solution:
f : R → R, g : R → R and f(x) = 2x – 3 and g(x) = x³ + 5
Now (fog) (x) = f(g(x))
= f(x³ + 5) [∵ g(x) = x² + 5]
= 2(x³ + 5) – 3 [∵ f(x) = 2x – 3]
= 2x³ + 7
∴ (f o g) (x) = 2x³ + 7
Let y = (f o g) (x) = 2x³ + 7
∵ y = (fog)(x)
⇒ x = (fog)^-1 (y) …….(1)
and y = 2x³ + 7
⇒ x³ = \(\frac{y-7}{2}\)
⇒ x = \(\left(\frac{y-7}{2}\right)^{\frac{1}{3}}\) …..(2)
From eq’s (1) and (2),
(f o g)^-1 (y) = \(\left(\frac{y-7}{2}\right)^{\frac{1}{3}}\)
∴ (f o g)^-1 (x) = \(\left(\frac{x-7}{2}\right)^{\frac{1}{3}}\)

Question 6.
Let f(x) = x², g(x) = 2^x. Then solve the equation (f o g) (x) = (g o f) (x)
Solution:
Given f(x) = x² and g(x) = 2^x
Now (f o g) (x) = f(g(x))
= f(2^x) [∵ g(x) = 2^x]
= (2^x)²
= 2^2x [∵ f(x) = x²]
∴ (f o g) (x) = 2^2x ……(1)
and (g o f) (x) = g(f(x))
= g(x²) [∵ f(x) = x²]
= \((2)^{x^{2}}\) [∵ g(x) = 2^x]
∴ (g o f) (x) = \((2)^{x^{2}}\)
∵ (f o g) (x) = (g o f) (x)
⇒ 2^2x = \((2)^{x^{2}}\)
⇒ 2^x = x²
⇒ x² – 2x = 0
⇒ x(x – 2) = 0
⇒ x = 0, x = 2
∴ x = 0, 2

Question 7.
If f(x) = \(\frac{x+1}{x-1}\), (x ≠ ±1) then find (fofof) (x) and (fofofof) (x).
Solution:
f(x) = \(\frac{x+1}{x-1}\), (x ≠ ±1)
(i) (fofof) (x) = (fof) [f(x)]
= (fof) \(\left(\frac{x+1}{x-1}\right)\) [∵ f(x) = \(\left(\frac{x+1}{x-1}\right)\)]
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) II Q7

(ii) (fofofof) (x) = f[(f o f o f) (x)]
= f [f(x)] {from (1)}
Inter 1st Year Maths 1A Functions Solutions Ex 1(b) II Q7.1
In the above problem if a number of f is even its answer is x and if a number of f is odd its answer is f(x).

Inter 1st Year Maths 1A Functions Solutions Ex 1(a)

January 5, 2024January 4, 2024 by Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(a)

Question 1.
If the function f is defined by
Inter 1st Year Maths 1A Functions Solutions Ex 1(a) I Q1
then find the values of
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(-2)
(v) f(-5)
Solution:
(i) f(3)
For x > 1, f(x) = x + 2
∴ f(3) = 3 + 2 = 5

(ii) f(0)
For -1 ≤ x ≤ 1, f(x) = 2
∴ f(0) = 2

(iii) f(-1.5)
For -3 < x < -1, f(x) = x – 1
∴ f(-1.5) = -1.5 – 1 = -2.5

(iv) f(2) + f(-2) For x > 1, f(x) = x + 2
∴ f(2) = 2 + 2 = 4
For -3 < x < -1, f(x) = x – 1
∴ f(-2)= -2 – 1 = -3
f(2) + f(-2) = 4 + (-3) = 1

(v) f(-5) is not defined, since domain of x is {X/X ∈ (-3, ∞)}

Question 2.
If f: R{0}R is defined by f(x) = \(x^{3}-\frac{1}{x^{3}}\); then show that f(x) + \(f\left(\frac{1}{x}\right)\) = 0.
Solution:
Given f(x) = \(x^{3}-\frac{1}{x^{3}}\) ……(i)
Now \(f\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)^{3}-\frac{1}{\left(\frac{1}{x}\right)^{3}}=\frac{1}{x^{3}}-x^{3}\) ……(2)
Add (1) and (2)
\(f(x)+f\left(\frac{1}{x}\right)=\left(x^{3}-\frac{1}{x^{3}}\right)+\left(\frac{1}{x^{3}}-x^{3}\right)\) = 0
∴ f(x) + \(f\left(\frac{1}{x}\right)\) = 0

Question 3.
If f : R → R is defined by f(x) = \(\frac{1-x^{2}}{1+x^{2}}\), then show that f(tan θ) = cos 2θ.
Solution:
Given f(x) = \(\frac{1-x^{2}}{1+x^{2}}\)
Inter 1st Year Maths 1A Functions Solutions Ex 1(a) I Q3
∴ f(tan θ) = cos 2θ

Question 4.
If f : R\{±1} → R is defined by f(x) = \(\log \left|\frac{1+x}{1-x}\right|\), then show that \(f\left(\frac{2 x}{1+x^{2}}\right)\) = 2f(x)
Solution:
f : R\{±1} → R and f(x) = \(\log \left|\frac{1+x}{1-x}\right|\)
Inter 1st Year Maths 1A Functions Solutions Ex 1(a) I Q4
∴ \(f\left(\frac{2 x}{1+x^{2}}\right)\) = 2f(x)

Question 5.
If A = {-2, -1, 0, 1, 2} and f : A → B is a surjection defined by f(x) = x² + x + 1, then find B.
Solution:
A = {-2, -1, 0, 1, 2} and f : A → B, f(x) = x² + x + 1
f : A → B is a surjection
f(-2) = (-2)² + (-2) + 1
= 4 – 2 + 1
= 3
f(-1) = (-1)² + (-1) + 1
= 1 – 1 + 1
= 1
f(0) = 0² + 0 + 1
= 0 + 0 + 1
= 1
f(1) = 1² + 1 + 1
= 1 + 1 + 1
= 3
f(2) = 2² + 2 + 1
= 4 + 2 + 1
= 7
∴ B = f(A) = {3, 1, 7}

Question 6.
If A = {1, 2, 3, 4} and f : A → R is a function defined by f(x) = \(\frac{x^{2}-x+1}{x+1}\), then find the range of f.
Solution:
A= {1, 2, 3, 4}
Inter 1st Year Maths 1A Functions Solutions Ex 1(a) I Q6
∴ Range of f = f(A) = \(\left\{\frac{1}{2}, 1, \frac{7}{4}, \frac{13}{5}\right\}\)

Question 7.
If f(x + y) = f(xy) ∀ x, y ∈ R then prove that f is a constant function.
Solution:
Given f(x + y) = f(x y), x, y ∈ R
take x = y = 0
⇒ f(0) = f(0) ………(1)
Let x = 1, y = 0
⇒ f(1) = f(0) ……..(2)
Let x = 1, y = 1
⇒ f(2) = f(1) ………(3)
from (1), (2), (3)
f(0) = f(1) = f(2)
⇒ f(0) = f(2)
Similarly f(3) = f(0)
f(4) = f(0)
and so on
f(n) = f(0)
∴ f is a constant function

II.

Question 1.
If A = {x | -1 ≤ x ≤ 1}, f(x) = x², g(x) = x³, which of the following are surjections?
(i) f : A → A
(ii) g : A → A
Solution:
(i) ∵ A = {x | -1 ≤ x ≤ 1} and f(x) = x²
This implies f(x) is a function from A to A
(i.e.,) f : A → A
Now let y ∈ A
If f(x) = y then x² = y
x = √y
So, if y = -1 then x = √-1 ∉ A
∴ f : A → A is not a surjection.

(ii) ∵ A = {x | -1 ≤ x ≤ 1} and g(x) = x³
⇒ g : A → A
Let y ∈ A. Then g(x) = y
⇒ x³ = y
⇒ x = \((y)^{1 / 3}\) ∈ A
So if y = -1 then x = -1 ∈ A
y = 0, then x = 0 ∈ A
y = 1, then x = 1 ∈ A
∴ g : A → A is a surjections.

Question 2.
Which of the following are injections or surjections or bijections? Justify your answers.
(i) f : R → R defined by f(x) = \(\frac{2 x+1}{3}\)
Solution:
f(x) = \(\frac{2 x+1}{3}\)
Let x₁, x₂ ∈ R
∵ f(x₁) = f(x₂)
⇒ \(\frac{2 x_{1}+1}{3}=\frac{2 x_{2}+1}{3}\)
⇒ 2x₁ + 1 = 2x₂ + 1
⇒ 2x₁ = 2x₂
⇒ x₁ = x₂
∵ f(x₁) = f(x₂) ⇒ x₁ = x₂, ∀ x₁, x₂ ∈ R
So f(x) = \(\frac{2 x+1}{3}\), f : R → R is an injection
If y ∈ R (co-domain) then y = \(\frac{2 x+1}{3}\)
⇒ x = \(\frac{3 y-1}{2}\)
Then f(x) = \(\frac{2 x+1}{3}=\frac{2\left(\frac{3 y-1}{2}\right)+1}{3}=y\)
∴ f is a surjection
∴ f : R → R defined by f(x) = \(\frac{2 x+1}{3}\) is a bijection

(ii) f : R → (0, ∞) defined by f(x) = 2x
Solution:
Let x₁, x₂ ∈ R
∵ f(x₁) = f(x₂)
⇒ \(2^{x_{1}}=2^{x_{2}}\)
⇒ x₁ = x₂
∴ f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁, x₂ ∈ R
∴ f(x) = 2x, f : R → (0, ∞) is injection
If y ∈ (0, ∞) and y = 2x ⇒ x = log₂ (y)
Then f(x) = 2x
= \(2^{\log _{2}(y)}\)
= y
∴ f is a surjection
Hence f is a bijection.

(iii) f : (0, ∞) → R defined by f(x) = log_ex
Solution:
Let x₁, x₂ e (0, ∞)
f(x₁) = f(x₂)
⇒ \(\log _{e}\left(x_{1}\right)=\log _{e}\left(x_{2}\right)\)
⇒ x₁ = x₂
∵ f(x₁) = f(x₂)
⇒ x₁ = x₂ ∀ x₁, x₂ ∈ (0, ∞)
∴ f(x) is injection.
Let y ∈ R.
y = log_ex ⇒ x = e^y
Then f(x) = log_ex
= log_e(e^y)
= y . log_ee
= y(1)
= y
∴ f is a surjection.
∴ f is a bijection.

(iv) f : [0, ∞) → [0, ∞) defined by f(x) = x².
Solution:
Let x₁, x₂ ∈ [0, ∞) (i.e.,) domain of f.
Now f(x₁) = f(x₂)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x₁ = x₂
∵ x₁, x₂ ≥ 0
∴ f(x) = x², f : {0, ∞) → {0, ∞) is injection
Let y ∈ (0, ∞), co-domain of f
Let y = x² ⇒ x = √y, ∵ y ≥ 0
Then f(x) = x²
= \((\sqrt{y})^{2}\)
= y
∴ f is surjection.
Hence f is a bijection.

(v) f : R → [0, ∞) defined by f(x) = x².
Solution:
Let x₁, x₂ ∈ R.
f(x₁) = f(x₂)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x₁ = ±x₂, ∵ x₁, x₂ ∈ R
Hence f is not injection
Let y ∈ [0, ∞)
y = x²
⇒ x = ±√y, where y ∈ [0, ∞)
Then f(x) = x²
= \((\sqrt{y})^{2}\)
= y
∴ f is surjection
Hence f is not a bijection

(vi) f : R → R defined by f(x) = x².
Solution:
Let x₁, x₂ ∈ R, (domain of f)
∴ f(x₁) = f(x₂)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x₁ = ±x₂, ∵ x₁, x₂ ∈ R
∴ f(x) is not injection
For elements that belong to (-∞, 0) codomain of f has no pre-image in f.
∴ f is not a surjection
Hence f is neither injection nor surjection.

Question 3.
Is g = {(1, 1) (2, 3) (3, 5) (4, 7)} is a function from A = {1, 2, 3, 4} to B = {1, 3, 5, 7}. If this is given by the formula g(x) = ax + b, then find a and b.
Solution:
A = {1, 2, 3, 4}; B = {1, 3, 5, 7}
g : {(1, 1), (2, 3), (3, 5), (4, 7)}
∵ g(1) = 1, g(2) = 3, g(3) = 5, g(4) = 7
So for each element a ∈ A, there exists a unique b ∈ B such (a, b) ∈ g
∴ g : A → B is a function
Given g(x) = ax + b, ∀ x ∈ A
g(1) = (a) + b = 1
⇒ a + b = 1 ……..(1)
g(2) = 2a + b = 3
⇒ 2a + b = 3 …….(2)
Solve (1) and (2)
a = 2, b = -1

Question 4.
If the function f : R → R defined by f(x) = \(\frac{3^{x}+3^{-x}}{2}\), then show that f(x + y) + f(x – y) = 2f(x) f(y).
Solution:
f : R → R and f(x) = \(\frac{3^{x}+3^{-x}}{2}\)
Inter 1st Year Maths 1A Functions Solutions Ex 1(a) II Q4
∴ f(x + y) + f(x – y) = 2 f(x).f(y)

Question 5.
If the function f : R → R defined by f(x) = \(\frac{4^{x}}{4^{x}+2}\), then show that f(1 – x) = 1 – f(x) and hence reduce the value of \(f\left(\frac{1}{4}\right)+2 f\left(\frac{1}{2}\right)+f\left(\frac{3}{4}\right)\)
Solution:
Inter 1st Year Maths 1A Functions Solutions Ex 1(a) II Q5

∴ f(1 – x) = 1 – f(x)

Question 6.
If the function f : {-1, 1} → {0, 2), defined by f(x) = ax + b is a surjection, then find a and b.
Solution:
f : {-1, 1} → {0, 2} and f(x) = ax + b is a surjection
Given f(-1) = 0 and f(1) = 2 (or) f(-1) = 2, f(1) = 0
Case (i):
f(-1) = 0 and f(1) = 2
a(-1) + b = 0 ⇒ -a + b = 0 ……..(1)
a(1) + b = 2 ⇒ a + b = 2 ……(2)
Solve eq’s (1) and (2), we get a = 1, b = 1
Case (ii):
f(-1) = 2 and f(1) = 0
a(-1) + b = 2 ⇒ -a + b = 2 ……(3)
a(1) + b = 0 ⇒ a + b = 0 ……….(4)
Solve eq’s (3) and (4), we get a = -1, b = 1
Hence a = ±1 and b = 1

Question 7.
If f(x) = cos (log x), then show that \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]=0\)
Solution:
Given f(x) = cos(log x)
\(f\left(\frac{1}{x}\right)=\cos \left(\log \left(\frac{1}{x}\right)\right)\)
= cos(log 1 – log x)
= cos(-log x)
= cos (log x) (∵ log 1 = 0)
Similarly
\(f\left(\frac{1}{y}\right)\) = cos (log y)
\(f\left(\frac{x}{y}\right)=\cos \log \left(\frac{x}{y}\right)\)
= cos (log x – log y)
and f(x y) = cos log (x y) = cos (log x + log y)
\(f\left(\frac{x}{y}\right)\) + f(x y) = cos (log x – log y) + cos (log x + log y)
= 2 cos (log x) cos (log y)
[∵ cos (A – B) + cos (A + B) = 2 cos A . cos B]
LHS = \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\)
= cos (log x) cos (log y) – \(\frac{1}{2}\) [2 cos (log x) cos (log y)]
= 0