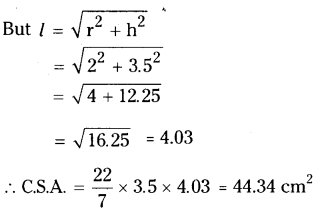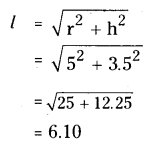Students can go through AP State Board 10th Class Biology Notes Chapter 9 Our Environment to understand and remember the concept easily.
AP State Board Syllabus 10th Class Biology Notes Chapter 9 Our Environment
→ The sum of physical and biological factors along with their chemical interactions that affect an organism is called environment.
→ The living organisms maintain balance with both biotic and abiotic factors.
→ The place where organisms live is called the biosphere.
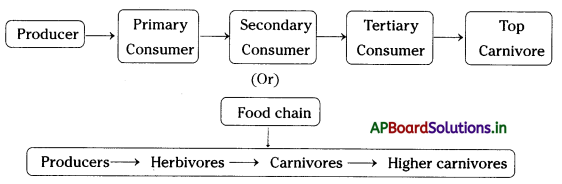
→ The food chain shows how energy is passed from one organism to another.
→ The terrestrial ecosystems are being determined largely by the variations in climatic conditions between the poles and equator.
→ The climatic factors that determine the ecosystems are rainfall, temperature, and availability of light from the sun.
→ Niche denotes not only the animals’ position in the food web and what it eats but also its mode of life.
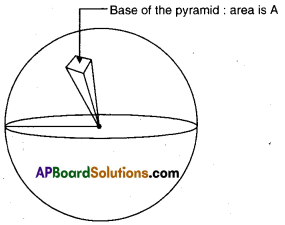
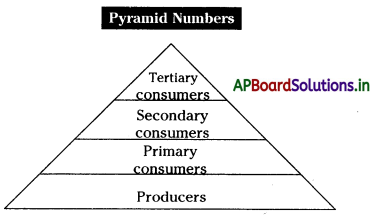
→ Graphic representation of the feeding level of an ecosystem by taking the shape of a pyramid is called an ecological pyramid.
→ The ecological pyramid was first introduced by Charles Elton in 1927.
![]()
→ Pyramid of numbers, the pyramid of biomass, and the pyramid of energy are other ways to show food relationships and flow of energy among living things.
→ A pyramid is a large stone building with four triangular walls that slope into a point at the top.
→ Each bar in the pyramid of numbers represents the number of individuals at each trophic level in the food chain.
→ Any type of plant or animal material that can be converted into energy is called biomass.
→ Biomass which can be used for energy production is called bio-fuels.
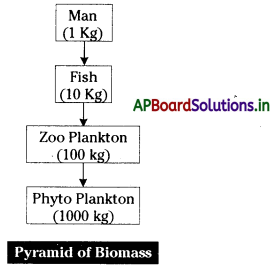
→ The pyramid of biomass represents the relationship that exists between the quantity of living matter at different trophic levels.
→ It is found that 10-20% of the biomass is transferred from one tropic level to the next in a food chain.
→ The food chains and food webs help in the transfer of food and energy from producers to different consumers.
→ The flow of materials between organisms and their environment is called the cycling of materials or biogeochemical cycles.
→ The ratio between energy flows at different tropic levels along the food chain expressed as a percentage is called “Ecological efficiency”.
![]()
→ Slobodkin (1959) suggested that the transfer of energy from one tropic level to the next is of the order of 10% and this is called “Gross ecological efficiency”.
→ 10 % law was originally observed by Lindeman (1942).
→ Steele (1974) proved that the gross ecological efficiency is about 20 to 30%.
→ In November 1999, the Government of Andhra Pradesh had declared the Kolleru Lake as Bird Sanctuary.
→ Using pesticides indiscriminately results in the killing of a vast number of other animals apart from pests.
→ The process of entry of pollutants into a food chain is known as bioaccumulation.
→ The tendency of pollutants to concentrate as they move from one tropic level to the next is known as biomagnification.
→ Minamata disease (Japan) was the result of bioaccumulation of the metal mercury in shellfish and fish that live in Minimata Bay.
→ There are several alternatives of pesticides through which we can get more crops with less harm like the rotation of crops, biological control, sterility of males, development of genetic resistant strains, etc.
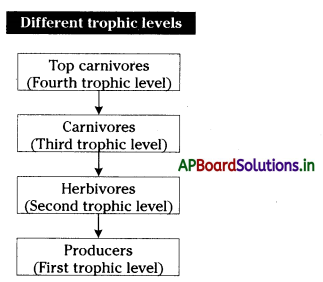
→ Food chain: It represents a single directional or unidirectional transfer of energy the pathway along which food is transferred from one tropic level to another beginning with producers.
![]()
→ Food web: The interlocking pattern of a number of food chains forms a web-like arrangement.
→ Niche: The functional role of an organism in a community.
→ Ecological pyramId: A graphical representation designed to show the biomass or number of organisms or energy at each tropic level in a given ecosystem.
→ Biomass: Any type of plant or animal material that can be converted into energy is called biomass.
→ PesticIdes: A chemical substance used to kill insects and small animals that destroy crops.
→ Bioaccumulation: The process of entry of pollutants into a food chain is known as bioaccumulatiorì.
→ Biomagnification: The tendency of pollutants to concentrate as they move from one tropic level to the next is known as biomagnification.
→ Eco-friendly activities: These are the activities to protect the environment.
→ Environmental ethics: These are concerned with the morality of human activities as they affect the environment.
→ Biosphere: It is the largest unit of organization of life. It includes all the biomes of the world i.e., Terrestrial, aquatic, or aerial where life exists.
→ Pyramid: A large stone building with four triangular walls that slope into a point at the top, especially in Egypt.
→ Biofuels: When biomass is used for energy production, it is known as biofuels. Fuel made from plant or animal sources.
![]()
→ Pyramid of number: A graphical representation designed to show the number of organisms at each tropic level in a given ecosystem.
→ Pyramid of biomass: A graphical representation designed to show the quantity of energy present at each tropic level in a given ecosystem.
→ DDT: “Dichloro Diphenyl Trichloro Ethane” is a chemical used to kill insects that harm crops.
→ Deciduous: (of tree or shrub) Shedding its leaves annually broad-leaved tree or shrub.
→ Environment: The sum of physical and biological factors along with their chemical interactions that affect an organism is called environment.
→ Biotic factor: A living thing, as an animal or plant, that influences or affects an ecosystem.
→ Abiotic factors: Non-living components of an ecosystem.
→ Dissipate: Disappear or cause to disappear.
→ Tropical rain forest: It is a forest of tall trees in a region of year-round warmth located in between the latitudes 28 degrees north and south of the equator.
→ Perpetual: Never ending or changing.
→ Phytoplankton: Microscopic plants that live in watery environments both salty and fresh.
→ Regurgitate: Bring up again to the mouth (swallowed food).
→ Substantial: Of considerable importance, size, or worth.
→ Rivulet: A small stream of water or another liquid.
![]()
→ Anthropogenic: Originating in human activity, chiefly of environmental pollution and pollutants.
→ Swarm: A large or dense group of flying insects.
→ Pyramid Numbers:
→ Pyramid of Biomass:
→ Different trophic levels:
![]()
→ Charles Sutherland Elton (1900 – 1991):
- Charles Elton of England was among the most important and influential ecologists of the twentieth century
- In the early 1920s, while still a student at Oxford, he took part in three expeditions to the Arctic island of Spitsbergen.
- He wrote three important books which are classics in ecology. Those are
1. Animal Ecology (1927),
2. Voles, Mice and Lemmings: Problems in Population Dynamics (1942),
3. The Ecology of Invasions by Animals and Plants (1958). - He was the founder and editor of the Journal of Animal Ecology.
- He is especially remembered for his studies on animal community patterns including the concepts of “Estonian niche” and the “Pyramid of numbers”.




 [Page No. 267]
[Page No. 267]