Inter 2nd Year

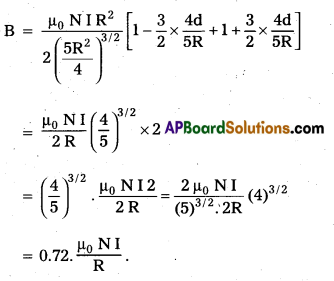
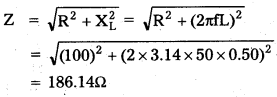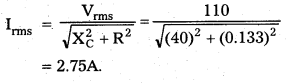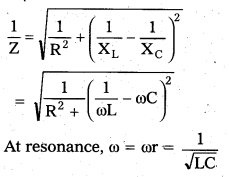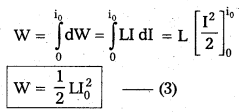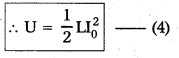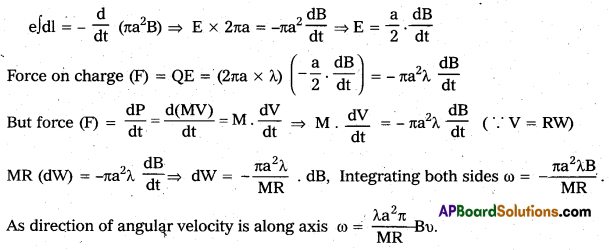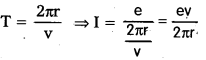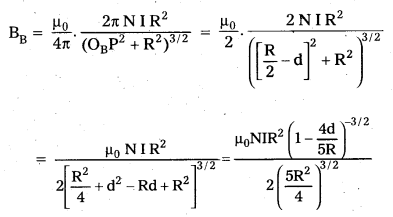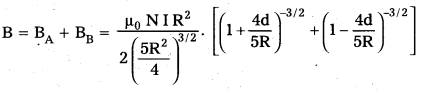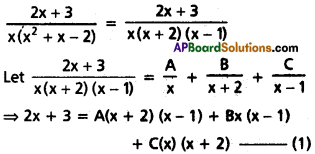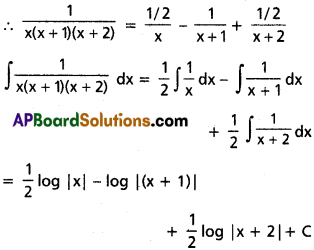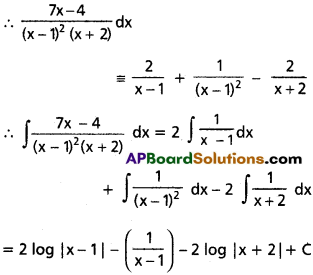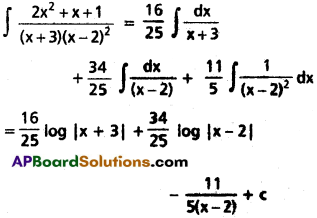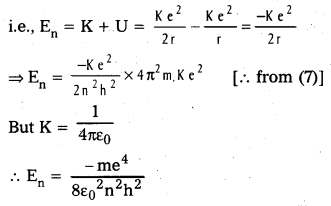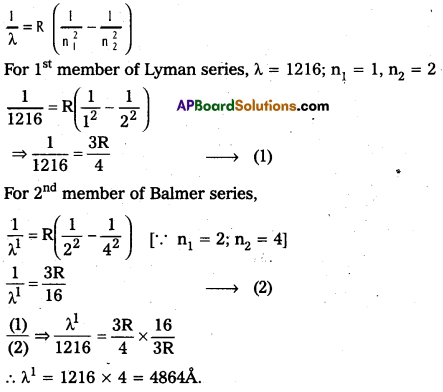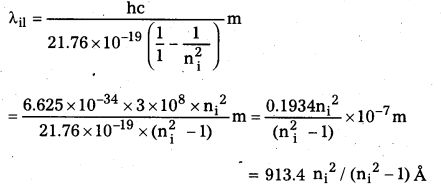Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 13th Lesson Atoms Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 13th Lesson Atoms

Very Short Answer Questions

Question 1.
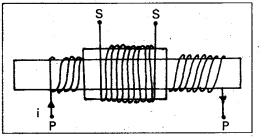
What is the angular momentum of electron in the second orbit of Bohr’s model of hydrogen atom ?
Answer:
Angular momentum of electron in second orbit of Hydrogen atom
L = \(\frac{2 \mathrm{~h}}{2 \pi}\) = \(\frac{h}{\pi}\) (∵ L = \(\frac{h h}{2 \pi}\))

Question 2.
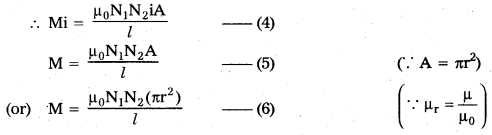
What is the expression for fine structure constant and what is its value ?
Answer:
Formula for fine structure constant
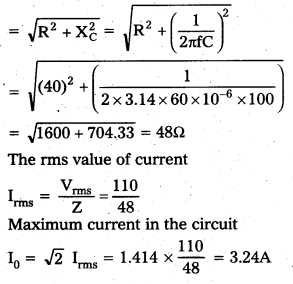
α = \(\frac{\mathrm{e}^2}{2 \varepsilon_0 \mathrm{ch}}\); value of α = \(\frac{1}{137}\)

Question 3.
What is the physical meaning of ‘negative energy of an electron’ ?
Answer:
The ‘negative energy of an electron’ indicates that the electron bound to the nucleus due to force of attraction.

Question 4.
Sharp lines are present in the spectrum of a gas. What does this indicate ?
Answer:
Sharp lines in the spectrum of gas indicates bright lines against dark background.

Question 5.
Name a physical quantity whose dimensions are the same as those of angular momentum.
Answer:
Planck’s constant.

Question 6.
What is the difference between α – particle and helium atom ?
Answer:
Alpha particle

1. It is a + 2e charged Helium nucleus.
2. It contains 2 protons and 2 neutrons.

Helium atom

1. It has no charge.
2. It contains 2 protons, 2 electrons and 2 neutrons.

Question 7.
How is impact parameter related to angle of scattering ?
Answer:
The impact parameter related to angle of scattering is given by b = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{\mathrm{Ze}^2}{\left(\frac{1}{2} m v^2\right)} \cot \theta_2\)

Question 8.
Among alpha, beta and gamma radiations, which get affected by the electric field ?
Answer:
Alpha and Beta radiations are get affected by the electric field.

Question 9.
What do you understand by the ‘phrase ground state atom’ ?
Answer:
If the electron is present in the ground state, it is called ground state atom.

Question 10.
Why does the mass of the nucleus not have any significance in scattering in Rutherford’s experiment ?
Answer:
The size of the atom is 10^-10 m and size of the nucleus is 10^-15 m. Hence atom has large empty space. So the mass of nucleus has no significance in Rutherford’s scattering experiment.

Question 11.
The Lyman series of hydrogen spectrum lies in the ultraviolet region. Why ? (A.P. Mar. ’15)
Answer:
The calculated values of wavelengths lie in the ultraviolet region of the spectrum well agree with the values of wavelengths observed experimentally by Lyman.

Question 12.
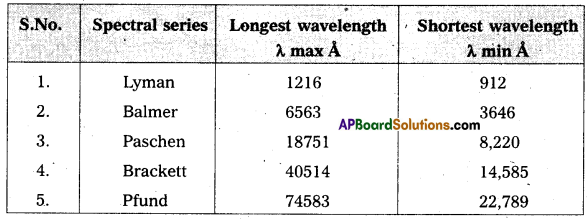
Write down a table giving longest and shortest wavelengths of different spectral series.
Answer:
Wavelength limits of some spectral series of hydrogen.

Question 13.
The wavelengths of some of the spectral lines obtained in hydrogen spectrum are 1216 A, 6463 A and 9546A. Which one of these wavelengths belongs to the Paschen series ?
Answer:
The wavelength of spectral line 9546A belongs to the Paschen series.

Question 14.
Give two drawbacks of Rutherford’s atomic model.
Answer:
Drawbacks of Rutherford’s atom model:

1. As the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. But matter is stable, we can not expect the atom collapse.
2. The atoms should emit continuous spectrum, but what we observe is only a line spectrum.

Short Answer Questions

Question 1.
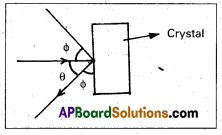
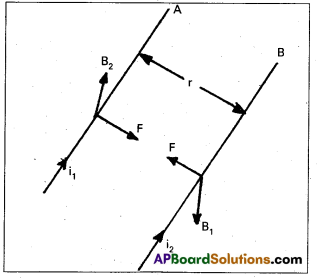
What is impact parameter and angle of scattering ? How are they related to each other ?
Answer:

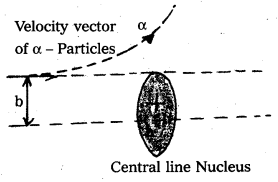
1. Impact parameter (b) : Impact parameter is defined as the perpendicular distance of the initial velocity vector of the alpha particle from the central line of the nucleus, when the particle is far away from the nucleus of the atom.
2. Scattering angle (θ): The scattering angle (θ) is the angle between the asymtotic direction of approach of the α – particle and the asymptotic direction in which it receeds.
3. The relation between b and θ is b = \(\frac{1}{4 \pi \varepsilon_0} \frac{Z \mathrm{e}^2}{E} \cot \frac{\theta}{2}\) where E = K.E. of α – particle = \(\frac{1}{2} \mathrm{mv}^2\)

Question 2.
Derive an expression for potential and kinetic energy of an electron in any orbit of a hydrogen atom according to Bohr’s atomic model. How does P.E change with increasing n. (T.S. Mar. ’15)
Answer:

1. According fo Bohr electrostatic force of attraction, F_e between the revolving electrons and nucleus provides the necessary centripetal force F_c to keep them in their orbits.
2. Thus for dynamically state orbit in a hydrogen atom.
   F_c = F_e ⇒ \(\frac{m v^2}{r}\) = \(\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r_2}\)
3. The relation between the orbit radius and the electron velocity is r = 2
   4e0 (m )
4. The kinetic energy (K) and electrostatic potential energy (υ) of the electron in hydrogen atom are
   K = \(\frac{1}{2} \mathrm{mv}^2\) = \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 r}\) and υ = \(\frac{-\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{r}}\)
5. The total energy E of the electron in a hydrogen atom is
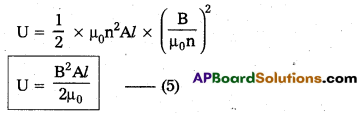
   E = K + U = \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) – \(\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{r}}\)
   ∴ E = \(\frac{-\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\)
6. With increase in ‘nr potential energy (U) also increases.

Question 3.
What are the limitations of Bohr’s theory of hydrogen atom ? (Mar. ’14)
Answer:
Limitations of Bohr’s theory of Hydrogen atom :

1. This theory is applicable only to simplest atom like hydrogen, with z = 1. The theory fails in case of atoms- of other elements for which z > 1.
2. The theory does not explain why orbits of electrons are taken as circular, while elliptlical orbits are also possible.
3. Bohr’s theory does not say anything about the relative intensities of spectral lines.
4. Bohr’s theory does not take into account the wave properties of electrons.

Question 4.
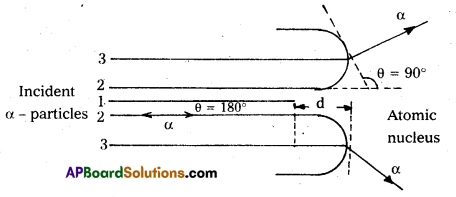
Explain the distance of closest approach and impact parameter.
Answer:
Distance of closest approach :

1. Suppose an α-particle with initial kinetic energy (K.E) is directed towards the centre of the nucleus of an atom.
2. On account of Coulomb’s repulsive force between nucleus and alpha particle, kinetic energy of alpha particle goes on decreasing and in turn, electric potential energy of the particle goes on increasing.
3. At certain distance ‘d’ from the nucleus, K. E of α-particle reduces to zero. The particle stops and it can not go closer to the nucleus. It is repelled by the nucleus and therefore it retraces its path, turning through 180°.
4. Therefore, the distance d is known as the distance of closest of approach.
   
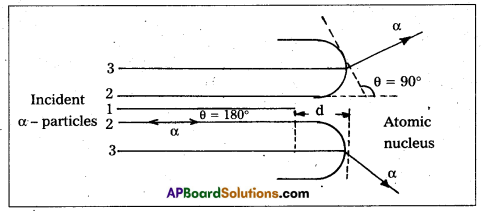
   The closest distance of approach,
   d = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{Z e^2}{\left(\frac{1}{2} m v^2\right)}\)
   
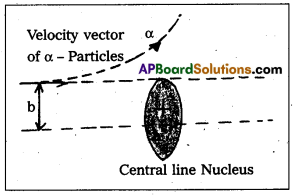
5. Impact parameter (b) : Impact parameter is defined as the ⊥^r distance of the initial velocity vector of the α – particle from the central line of the nucleus, when the particle is far away from the nucleus of the atom.

Question 5.
Give a brief account of Thomson model of atom. What are its limitations ?
Answer:
Thomson’s model of atom :

1. According to Thomson’s model, every atom consists of a positively charged sphere of radius of the order of 10^-10 m in which entire mass and positive charge of the atom are uniformly distributed.
   
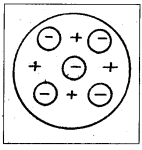
2. Inside this sphere, the electrons are embedded like seeds in a watermelon or like plums in a pudding.
3. The negative charge of electrons is equal to the positive charge of the atom. Thus atom is electrically neutral.

Limitations :

1. It could not explain the origin of spectral series of hydrogen and other atoms, observed experimentally.
2. It could not explain large angle scattering of a-particles from thin metal foils, as observed by Rutherford.

Question 6.
Describe Rutherford atom model. What are the draw backs of this model.
Answer:
Rutherford atom model: The essential features of Rutherford’s nuclear model of the atom or planetary model of the atom are as follows :

1. Every atom consists of tiny central core, called the atomic nucleus, in which the entire positive charge and almost entire mass of the atom are concentrated.
2. The size of nucleus is of the order of 10^-15m, which is very small as compared to the size of the atom which is of the order of 10^-10m.
3. The atomic nucleus is surrounded by certain number of electrons. As atom on the whole is electrically neutral, the total negative charge of electrons surrounding the nucleus is equal to total positive charge on the nucleus.
4. These electrons revolve around the nucleus in various circular orbits as do the planets around the sun. The centripetal force required by electron for revolution in provided by the electrostatic force of attraction between the electrons and the nucleus.

Draw backs : According to classical E.M. theory.

1. The revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. As matter is stable, we cannot expect the atoms to collapse.
2. Since the frequency of radiation emitted is the same as the frequency of revolution, the atom should radiate a continuous spectrum, but what we observe is only a line spectrum.

Question 7.
Distinguish between excitation potential and ionization potential.
Answer:
Excitation Potential:

1) When the electron jumps from lower orbit to higher orbit by absorbing energy is called excited electron and the process is known as excitation. The minimum accelerating potential which provides an electron energy sufficient to jump from the inner most orbit (ground state) to one of the outer orbits is called excitation potential or resonance potential.

2) a) For example, in case of hydrogen atom,
E₁ = -13.6 eV. E₂ = -3.4 eV E₃ = -1.51eV and soon, E_∞ = 0
∴ Energy required to raise an electron from ground state (n = 1) to first excited state
(n = 2) is E = E₂ – E₁ = -3.4 – (-13.6) = 10.2 eV.
The corresponding excitation potential = 10.2 Volt,

b) Similarly, energy required to raise an electron from ground state (n = 1) to second excited , state (n = 3) is
E = E₃ – E₁ = -1.51 – (-13.6) = -1.51 + 13.6 = 12.09 eV
The corresponding excitation potential = 12.09 Volt and so on.

3) The excitation potential of an atom is not one. It can have many values, depending on the state to which the atom is excited.

Ionisation potential:

1. The energy supplied is so large that it can remove an electron from the outer most orbit of an atom, the process is called Ionisation. Thus ionisation is the phenomenon of removal of an electron from the outer most orbit of an atom.
2. The minimum accelerating potential which would provide an electron energy sufficient just to remove it from the atom is called Ionisation potential.
3. For example, total energy of electron in ground state of hydrogen atom, + 13.6 eV energy is required.
   ∴ Ionisation energy of hydrogen atom = 13.6 eV.
   Ionisation potential of hydrogen atom = 13.6 Volts.
4. The general expression for ionisation potential of an atom is V = \(\frac{13.6 \mathrm{Z}^2}{\mathrm{n}^2}\) volt, Where Z is the charge number of the atom and n is number of orbit from which electron is to be removed.
5. For a given element, ionisation potential is fixed, but for different elements, ionisation potentials are different.

Question 8.
Explain the different types of spectral series in hydrogen atom. (A.P. Mar. ’19, ’15; T.S. Mar. ’16)
Answer:
The atomic hydrogen emits a line spectrum consisting of five series.

1. Lyman series : v = Rc \(\left(\frac{1}{1^2}-\frac{1}{n^2}\right)\) where n = 2, 3, 4, ……
2. Balmer series : v = Rc\(\left(\frac{1}{2^2}-\frac{1}{n^2}\right)\) where n = 3, 4, 5, ………
3. Paschen series : v = Rc\(\left(\frac{1}{3^2}-\frac{1}{n^2}\right)\) where n = 4, 5, 6, …….
4. Brackett series : v = Rc\(\left(\frac{1}{4^2}-\frac{1}{n^2}\right)\) where n = 5, 6, 7, ……
5. Pfund series : v = Rc\(\left(\frac{1}{5^2}-\frac{1}{n^2}\right)\) where n = 6, 7, 8,……..

Question 9.
Write a short note on Debroglie’s explanation of Bohr’s second postulate of quantization.
Answer:
Debroglie’s explanation of Bohr’s second postulate of quantization :

1. The second postulate of Bohr atom model says that angular momentum of electron orbiting around the nucleus is quantized i.e., mυr = \(\frac{\text { nh }}{2 \pi}\) where m = 1, 2, 3,….
2. According to Debroglie, the electron in its circular orbit, as proposed by Bohr, must be seen as a particle wave.
3. When a string fixed at two ends is plucked, a large number of wavelengths are excited and standing wave is formed.
4. It means that in a string, standing waves form when total distance travelled by a wave down the string and back is an integral number of wavelengths.
5. According to Debroglie, a stationary orbit is that which contains an integral number of Debrogile waves associated with the revolving electron.
6. For an electron revolving in nth circular orbit of radius r_n, total distance covered = circumference òf the orbit = 2πr_n
   ∴ For permissible orbit, 2πr_n = nλ
7. According to Debrogile, λ = \(\frac{h}{m v_n}\) Where υ_n is speed of electron revolving in n^th orbit
   ∴ mυ_nr_n = \(\frac{\mathrm{nh}}{2 \pi}\) = \(\mathrm{n}\left(\frac{\mathrm{h}}{2 \pi}\right)\)
   i.e., angular momentum of electron revolrmg in n^th orbit must be an integral multiple of \(\frac{\mathrm{h}}{2 \pi}\), which is the quantum condition proposed by Bohr in second postulate.

Long Answer Questions

Question 1.
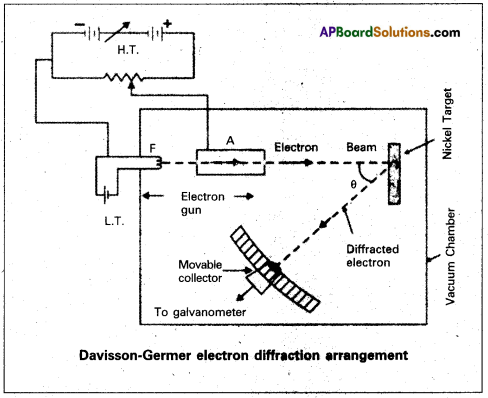
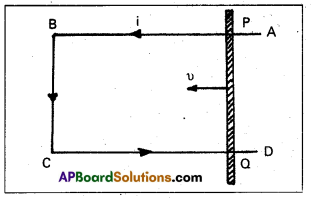
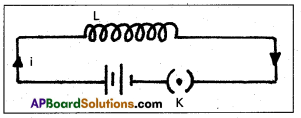
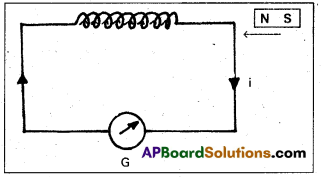
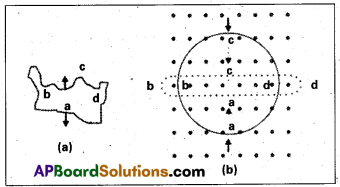
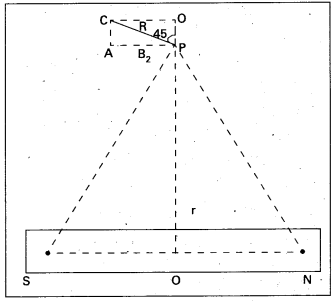
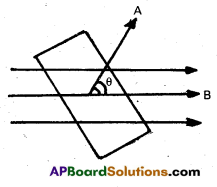
Describe Geiger-Marsden Experiment on scattering of α – particles. How is the size of the nucleus estimated in this experiment ?
Answer:

1. The experimental set up used by Rutherford and his colaborators, Geiger and Marsden is shown in fig.
   
2. The α-particles emitted by radio active source contained in a lead cavity are collimated into a narrow beam with the help of a lead slit (collimator).
3. The collimated beam is allowed to fall on a thin gold foil of thickness of the order of 2.1 × 10^-7m.
4. The α-particles scattered in different directions are observed through a rotatable detector consisting of zinc sulphide screen and a microscope.
5. The α-particles produce bright flashes or scintillations on the ZnS screen.
6. These are observed in the microscope and counted at different angles from the direction of incidence of the beam.
7. The angle θ of deviation of an α-particle from its original direction is called its scattering angle θ.

Observations : We find that

1. Most of the alpha particles pass straight through the gold foil. It means they do not suffer any collision with gold atoms.
2. Only about 0.14% of incident α-particles scatter by more than 1°.
3. About one α-particle in every 8000 α-particles deflect by more than 90°.

Estimation of size of the nucleus :

1. This led to Rutherford postulate, that the entire positive charge of the atom must be concentration in a tiny central core of the atom. This tiny central core of each atom was called atomic nucleus.
2. The electrons would be moving in orbits about the nucleus just as the planets do around the sun.
3. Rutherford’s experiments suggested the size of the nucleus to be about 10^-15m to 10^-14m. From kinetic theory, the size of an atom was known to be 10^-10m, about 10,000 to 1,00,000 times larger than the size of the nucleus.

Question 2.
Discuss Bohr’s theory of the spectrum of hydrogen atom.
Answer:

1. According to Bohr’s model an electron continuous to revolve round the nucleus in fixed, stationary orbits. This is called groupd state of the atom. In ground state there is no emission of radiation.
2. But when some energy is given to an atom the electron absorbs this energy. This is called excited state of the atom. In this state the electron jumps to the next higher orbit. But it can remain 10^-8 sec and it immediatly returns back to its ground state and the balance of the energy is emitted out as a spectral line.
3. According to Bohr’s third postulate, the emitted energy is given by E = hv = E₂ – E₁
   

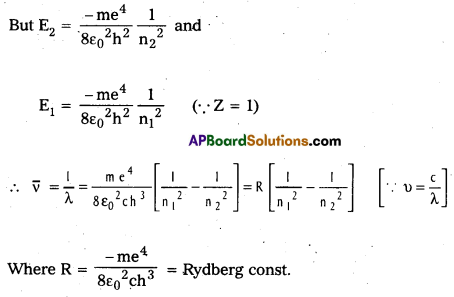
Spectral series of Hydrogen atom:

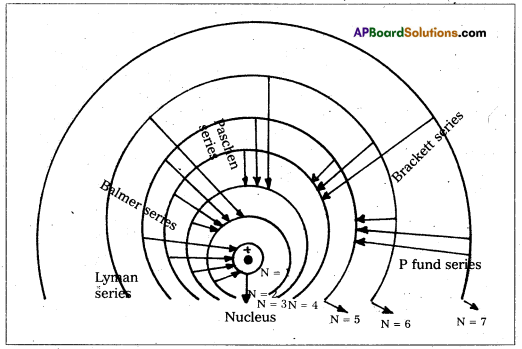
Hydrogen atom has five series of spectral lines: They are

1. Lyman series: When an electron jumps from the outer orbits to the first orbit, the spectral lines are in the ultra – violet region. Here n₁ = 1, n₂ = 2, 3, 4, 5….
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{\mathrm{n}_2^2}\right]\) = \(\mathrm{R}\left[1-\frac{1}{\mathrm{n}_2^2}\right]\)

2) Balmer Series : When an electron jumps from the outer orbits to the second orbit, the
spectral Lines are in the visible region. Here n₁ = 2, n₂ = 3, 4, 5…
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

3) Paschen series : When an electron jumps from the outer orbits to the third orbit, the spectral lines are in the near infrared region. Here n₁ = 3, n₂ = 4, 5, 6 ….
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{\mathrm{n}_2{ }^2}\right]\)

4) Brackett series : When an electron jumps from outer orbits to the forth orbit, the spectral lines are in the infrared region. Here n₁ = 4, n₂ = 5, 6, 7…….
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left[\frac{1}{4^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

5) Pfund series : When an electron jumps from outer orbits to the fifth orbit, the spectral lines are in the far infrared region. Here n₁ = 5, n₂ = 6, 7, 8, ………
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left[\frac{1}{5^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

Question 3.
State the basic postulates of Bohr’s theory of atomic spectra. Hence obtain an expression for the radius of orbit and the energy of orbital electron in a hydrogen atom.
Answer:
a) Basic postulates of Bohr’s theory are
1) The electron revolves round a nucleus is an atom in various orbits known as stationary orbits. The electrons can not emit radiation when moving in their own stationary levels.

2) The electron can revolve round the nucleus only in allowed, orbits whose angular momentum is the integral multiple of \(momentum is the integral multiple of
i.e., mυ_nr_n = [latex]\frac{\mathrm{nh}}{2 \pi}\) ———> (1)
where n = 1, 2, 3…..

3) If an electron jumps from higher energy (E₂) orbit to the lower energy (E₁) orbit, the difference of energy is radiated in the form of radiation.
i.e., E = hv = E₂ – E₁ ⇒ v = \(\frac{E_2-E_1}{h}\) ——> (2)

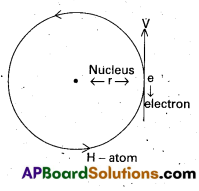
b) Energy of emitted radiation : In hydrogen atom, a single electron of charge — e, revolves around the nucleus of charge e in a ciccular orbit of radius r_n.

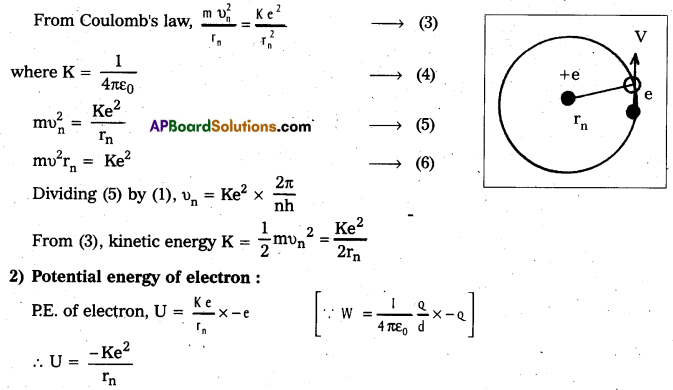
1) K.E. of electron : For the electron to be in circular orbit, centripetal force = The electrostatic force of attraction between the electron and nucleus,
From Coulomb’s law, \(\frac{\mathrm{m} \dot{v}_n^2}{r_n}\) = \(\frac{\mathrm{Ke}^2}{\mathrm{r}_{\mathrm{n}}^2}\) ——> (3)

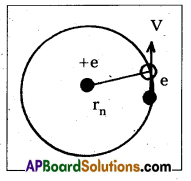
where K = \(\frac{1}{4 \pi \varepsilon_0}\) —–> (4)
\(m v_n^2\) = \(\frac{\mathrm{Ke}^2}{\mathrm{r}_{\mathrm{n}}}\) —–> (5)
\(m v^2 r_n\) = Ke² ——-> (6)
Dividing (5) by (1), υ_n = Ke² × \(\frac{2 \pi}{\mathrm{nh}}\)
From (3), kinetic energy K = \(\frac{1}{2} m v_n^2\) = \(\frac{\mathrm{Ke}^2}{2 r_{\mathrm{n}}}\)

2) Potential energy of electron:
P.E. of electron, U = \(\frac{\mathrm{Ke}}{\mathrm{r}_{\mathrm{n}}} \times-\mathrm{e}\) [∵ W = \(\frac{I^{\prime}}{4 \pi \varepsilon_0} \frac{Q}{d}\) × -Q]
∴ U = \(\frac{-\mathrm{Ke}^2}{\mathrm{r}_{\mathrm{n}}}\)

3) Radius of the orbit: Substituting the value of (6) in (2),

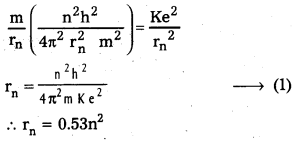
4) Total energy (E_n) : Revolving electron posses K.E. as well as P.E.

Textual Exercises

Question 1.
The radius of the first electron orbit of a hydrogen atom is 5.3 × 10^-11m. What is the radius of the second orbit ?
Solution:
r_n ∝ n²
\(\frac{\mathrm{r}_2}{\mathrm{r}_1}\) = \(\frac{2^2}{1^2}\) = \(\frac{4}{1}\) ⇒ r₂ = 4r₁

Question 2.
Determine the radius of the first orbit of the hydrogen atom. What would be the velocity and frequency of the electron in the first orbit ?
Solution:
Given: h = 6.62 × 10^-34 J-s,
m = 9.1 × 10^-31kg,
e = 1.6 × 10^-19 C,
k = 9 × 10⁹Nm²C^-2, n = 1

i)
r₁ = \(\frac{n^2 h^2}{4 \pi^2 \mathrm{mke}^2}\)
= \(\frac{(1)^2 \times\left(6.62 \times 10^{-34}\right)^2}{4 \times(3.14)^2 \times 9.1 \times 10^{-31} \times 9 \times 10^9\left(1.6 \times 10^{-19}\right)^2}\)
∴ r₁= 0.529 A \(\simeq\) 0.53 A

ii)

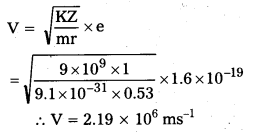
iii)

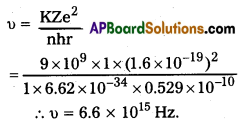
Question 3.
The total energy of an electron in the first excited state of the hydrogen atom is -3.4eV. What is the potential energy of the electron in this state ?
Solution:
In 1^st orbit, E = -3.4eV
Total energy E = \(\frac{\mathrm{KZe}^2}{2 \mathrm{r}}\) – \(\frac{\mathrm{KZe}^2}{\mathrm{r}}\)
\(\frac{\mathrm{KZe}^2}{\mathrm{r}}\) = U(say)
E = \(\frac{\mathrm{U}}{2}-\mathrm{U}\) = \(\frac{-\mathrm{U}}{2}\)
U = -2E
∴ U = -2 × -3.4 = 6.8 eV.

Question 4.
The total energy of an electron in the first excited state of hydrogen atom is -3.4eV. What is the kinetic energy of the electron in this state ?
Solution:
In Hydrogen like atom, we know that
K = – Total energy E
Here E = – 3.4eV
∴ K = -(-3.4) = 3.4 eV

Question 5.
Find the radius of the hydrogen atom in its ground state. Also calculate the velocity of the electron in n = 1 orbit. Given
h = 6.63 × 10^-34 J s, m = 9.1 × 10^-31 kg, e = 1.6 × 10^-19 C, K = 9 × 10⁹N m²C^-2
Solution:
n = 1, h = 6.63 × 10^-34 J-s,
m = 9.1 × 10^-31 kg
e = 1.6 × 10^-19C,
K = 9 × 10⁹ Nm²C^-2

Question 6.
Prove that the ionisation energy of hydrogen atom is 13.6 eV.
Solution:
n = 1 corresponds to ground state.
E = \(\frac{-13.6}{n^2} e V\)
E = \(\frac{-13.6}{1^2} \mathrm{eV}\)
E = -13.6 eV
∴ The minimum energy required to free the electron from the ground state of hydrogen atom
= 13.6 eV.
∴ Ionisation energy of hydrogen atom = 13.6 eV

Question 7.
Calculate the ionization energy for a lithium atom.
Solution:

∴ Ionization energy of Lithium = 30.6eV.

Question 8.
The wavelength of the first member of Lyman series is 1216 A. Calculate the wavelength of second member of Balmer series.
Solution:
\(\frac{1}{\lambda}\) = \(R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)
For 1^st member of Lyman series, λ = 1216; n₁ = 1, n₂ = 2

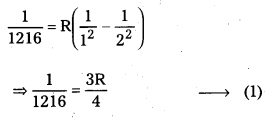
For 2^nd member of Balmer senes,

Question 9.
The wavelength of first member of Balmer series is 6563 A. Calculate the wavelength of second member of Lyman series.
Solution:
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)\)
For 1^st member of Balmer senes,
\(\frac{1}{6563}\) = \(\mathrm{R}\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)
\(\frac{1}{6563}\) = \(\frac{5 R}{36}\) —–> (1)
For 2^nd member of Lyman senes,
\(\frac{1}{\lambda^1}\) = \(\mathrm{R}\left(\frac{1}{1^2}-\frac{1}{3^2}\right)\)
\(\frac{1}{\lambda^1}\) = \(\frac{8 \mathrm{R}}{9}\) —–> (2)
\(\frac{(1)}{(2)}\) ⇒ \(\frac{\lambda^1}{6563}\) = \(\frac{5 \mathrm{R}}{36} \times \frac{9}{8 \mathrm{R}}\)
λ’ = \(\frac{5}{32} \times 6563\)
∴ λ’ = 1025.5A

Question 10.
The second member of Lyman series in hydrogen spectrum has wavelength 5400 A. Find the wavelength of first member.
Solution:
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)\)
For second member of Lyman senes,
\(\frac{1}{5400}\) = \(R\left(\frac{1}{1^2}-\frac{1}{3^2}\right)\) ⇒ \(\frac{1}{5400}\) = \(\frac{8 \mathrm{R}}{9}\) —-> (1)
For first member of Lyman series,
\(\frac{1}{\lambda^1}\) = \(\mathrm{R}\left(\frac{1}{1^2}-\frac{1}{2^2}\right)\)
\(\frac{1}{\lambda^1}\) = \(\frac{3 R}{4}\) —–> (2)
\(\frac{(1)}{(2)}\) ⇒ \(\frac{\lambda^1}{5400}\) = \(\frac{8 R}{9} \times \frac{4}{3 R}\)
∴ λ’ = \(\frac{32}{27}\) × 5400 = 6400A.

Question 11.
Calculate the shortest wavelength of Balmer series. Or Calculate the wavelength of the Balmer senes limit. Given : R = 10970000m^-1.
Solution:
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)\)
R = 10970000 = 1.097 × 10⁷ ms^-1
For Balmer senes limit n₁ = 2 and n₂ = ∞
\(\frac{1}{\lambda}\) = \(\mathrm{R}\left(\frac{1}{2^2}-\frac{1}{\infty}\right)\) ⇒ \(\frac{1}{\lambda}\) = \(\frac{R}{4}\)
λ = \(\frac{4}{\mathrm{R}}\) = \(\frac{4}{1.097 \times 10^7}\) = 3646.3A

Question 12.
Using the Rydberg formula, calcûlate the wavelength of the first four spectral lines in the Balmer series of the hydrogen spectrum.
Solution:

Additional Exercises

Question 1.
Choose the correct alternative from the clues given at the end of the each statement:
a) The size of the atom in Thomson’s model is ……… the atomic size in Rutherford’s model. (much greater than / no different from / much less than.)
b) In the ground state of ……. electrons are in stable equilibrium, while in …… electrons always experience a net force. (Thomson’s model / Rutherford’s model.)
c) A classical atom based on …… is doomed to collapse. (Thomson’s model / Rutherford’s model).
d) An atom has a nearly continuous mass distribution in a ……. but has a highly non-uniform mass distribution in ………. (Thomson’s model / Rutherford’s model.)
e) The positively charged part of the atom possesses most of the mass in …….. (Rutherford’s model / both the models.)
Answer:
a) No different from
b) Thomson’s model, Rutherford’s model
c) Rutherford’s model
d) Thomson’s model, Rutherford’s model
e) Both the models.

Question 2.
Suppose you are given a chance to repeat the alpha – particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What results do you expect ?
Answer:
The basic purpose of scattering experiment is defeated because solid hydrogen will be much lighter target compared to the alpha particle acting as projectile. According to theory of elastic the collisions, the target hydrogen will move much faster compared to alpha after collision. We cannot determine the size of hydrogen nucleus.

Question 3.
What is the shortest wavelength present in the Paschen series of spectral lines ?
Answer:
From Rydberg’s formula
\(\frac{\mathrm{hc}}{\lambda}\) = 13.6 × 1.6 × 10^-19\(\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)\)
For shortest wavelength in Paschen series n₂ = ∞ and n₁ = 3
\(\frac{\mathrm{hc}}{\lambda}\) = 21.76 × 10^-19\(\left[\frac{1}{3^2}-\frac{1}{\infty^2}\right]\)
= 2.42 × 10^-19
λ = \(\frac{\mathrm{hc}}{2.42 \times 10^{-19}}\) = \(\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{2.42 \times 10^{-19}} \mathrm{~m}\)
= 8.1818 × 10^-7m = 818.18nm.

Question 4.
A difference of 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom make a transition from the upper level to the lower level ?
Answer:
Here E = 2.3eV = 2.3 × 1.6 × 10^-19 J
As E = hv
∴ v = \(\frac{\mathrm{E}}{\mathrm{h}}\) = \(\frac{2.3 \times 1.6 \times 10^{-19}}{6.6 \times 10^{-34}}\) = 5.6 × 10⁴ Hz

Question 5.
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of the electron in this state ?
Answer:
Total energy E = -13.6 eV
K.E = -E = 13.6 eV
RE. = -2.K.E = -2 × 13.6
= -27.2eV.

Question 6.
A hydrogen atom initially in the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of photon.
Answer:
For ground state n₁ = 1 and n₂ = 4
Energy of photon absorbed E = E₂ – E₁

Question 7.
a) Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2 and 3 levels.
b) Calculate the orbital period in each of these levels.
Answer:
a) From v = \(\frac{c}{n} \alpha\), where α = \(\frac{2 \pi \mathrm{Ke}^2}{\mathrm{ch}}\) = 0.0073
v₁ = \(\frac{3 \times 10^8}{1}\) × 0.0073 = 2.19 × 10⁶ m/s
v₂ = \(\frac{3 \times 10^8}{2}\) × 0.0073 = 1.095 × 10⁶ m/s
v₃ = \(\frac{3 \times 10^8}{3}\) × 0.0073 = 7.3 × 10⁵ m/s

b) Orbital period, T = \(\frac{2 \pi r}{V}\), As r₁ = 0.53 × 10^-10m
T₁ = \(\frac{2 \pi \times 0.53 \times 10^{-10}}{2.19 \times 10^6}\) = 1.52 × 10^-16S
As r₂ = 4r₁ and V₂ = \(\frac{1}{2} V_1\)
T₂ = 8T₂ = 8 × 1.52 × 10^-6 S = 1.216 × 10^-15S
As r₃ = 9r₁ and V₃ = \(\frac{1}{3} \mathrm{~V}_1\)
T₃ = 27T₁= 27 × 1.52 × 10^-16 S = 4.1 × 10^-15S

Question 8.
The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10-^-11m. What are the radii of the n = 2 and n = 3 orbits?
Answer:
As r = n²r
∴ r² = 4r₁ = 4 × 5.3 × 10^-11 m = 2.12 × 10^-10m ,
and r₃ = 9r₁ = 9 × 5.3 × 10^-11 = 4.77 × 10^-10m.

Question 9.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelengths will be emitted?
Answer:
In ground state, energy of gaseous hydrogen at room temparature = -13.6eV, when it is bombarded with 12.5 eV electron beam, the energy becomes 13.6 + 12.5 = -1.1eV.
The electron would jump from n = 1 to n = 3 where E₃ = \(\frac{-13.6}{32}\) = -1.5eV
On de — excitation the electron may jump from n = 3 to n = 2 giving rise to Balmer series. It may also jump from n = 3 to n = 1 giving rise to Lýman series.

Question 10.
In accordance with the Bohr’s model, find the quantum number that characterises the earths revolution around the sun in an orbit of radius 1.5 × 10¹¹ m with orbital speed 3 × 10⁴m/s. (Mass of earth = 6.0 × 10²⁴ kg.)
Answer:
Here r = 1.5 × 10¹¹m, V = 3 × 10⁴m/s, m = 6.0 × 10²⁴kg
According to Bohrs model mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
n = \(\frac{2 \pi \mathrm{mvr}}{\mathrm{h}}\) = 2 × \(\frac{22}{7}\) × \(\frac{6.0 \times 10^{24} \times 3 \times 10^4 \times 1.5 \times 10^{11}}{6.6 \times 10^{-34}}\)
= 2.57 × 10⁷⁴, which is too large.

Question 11.
Answer the following questions, which help you understand the difference between Thomson’s model and Rutherford’s model better.
a) Is the average angle of deflection of α — particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
b) Is the probability of backward scattering (i.e., scattering of α – particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model ?
c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α – particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide ?
d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of a – particles by a thin foil ?
Answer:
a) About the same this is because we are talking of average angle of deflection.
b) Much less, because in Thomson’s model there is no such massive central core called the nucleus as in Rutherford’s model.
c) This suggests that scattering is predominantly due to a single collision increases with the number of target atoms which increases linearly with the thickness of the foil.
d) In Thomson model, positive charge is uniformly distributed in the spherical atom. Therefore a single collision causes very little deflection. Therefore average scattering angle can be explained only by considering multiple scattering may be ignored as a first approximation.

Question 12.
The gravitational attraction between electron and proton in a hydrogen atom is weaker than the coulomb attraction by a factor of about 10^-40. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
Answer:
The radius of the first Bohr orbit of a hydrogen atom is
r₀ = \(\frac{4 \pi \varepsilon_0(h / 2 \pi)^2}{m_e \mathrm{e}^2}\)
If we consider the atom bound by the gravitational force
= \(\left(\frac{\mathrm{Gm}_{\mathrm{p}} \mathrm{m}_{\mathrm{e}}}{\mathrm{r}^2}\right)\). We should replace \(\frac{\mathrm{e}^2}{4 \pi \varepsilon_0}\) by (Gm_pm_e). In that case radius of first Bohr orbit of hydrogen atom would be given by r₀ = \(\frac{(\mathrm{h} / 2 \pi)^2}{\mathrm{Gm}_p \mathrm{~m}^2 \mathrm{e}}\)
Putting the standard values we get
r₀ = \(\frac{\left(6.6 \times 10^{-34} / 2 \pi\right)^2}{6.67 \times 10^{-11} \times 1.67 \times 10^{-27} \times\left(9.1 \times 10^{-31}\right)^2}\)
= 1.2 × 10²⁹ metre.
This is much greater than the estimated size of the whole universe!

Question 13.
Obtain an expression for the frequency of radiation emitted when a hydrogen atom de- excites from level n to level (n – 1). For large n, show that this frequency equals the classical frequency of revolution of the electron in the orbit.
Answer:
The frequency v of the emitted radiation when a hydrogen atom de-excites from level n to level (n – 1) is
E = hv = E₂ – E₁

In Bohr’s Atomic model, velocity of electron in n^th orbit is v = \(\frac{\mathrm{nh}}{2 \pi \mathrm{mr}}\)
and radius of n^th orbital is v = \(\frac{n^2 h^2}{4 \pi^2 m K e^2}\)
Frequency of revolution of electron v = \(\frac{\mathrm{V}}{2 \pi \mathrm{r}}\) = \(\frac{\mathrm{nh}}{2 \pi \mathrm{mr}}\)
and radius of n^th orbital is r = \(\frac{n^2 h^2}{4 \pi^2 m K e^2}\)
Frequency of revolution of electron

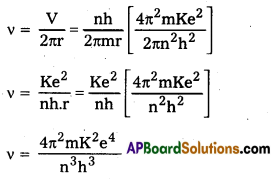
which is the same as (i) .
Hence for large values of n₁ classical frequency of revolution of electron in n^th orbit is the same as the frequency of radiation emitted when hydrogen atom de-excites from level (n) to level (n – 1)

Question 14.
Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size ? Why is an atom not, say, thousand times bigger than its typical size ? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text. To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~ 10¹⁰m).
a) Construct a quantity with the dimensions of length from the fundamental constants e, m_e, and c. Determine its numerical value.
b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non- relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the ‘Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognising that h, m_e, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
Answer:
a) Using fundamental constants e, me and c, we construct a quantity which has the dimensions of length. This quantity is \(\left(\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{~m}_{\mathrm{e}} \mathrm{c}^2}\right)\)
Now \(\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{~m}_{\mathrm{e}} \mathrm{c}^2}\) = \(\frac{\left(1.6 \times 10^{-19}\right)^2 \times 9 \times 10^9}{9.1 \times 10^{-31}\left(3 \times 10^8\right)^2}\) = 2.82 × 10^-15m
This is of the order of atom sizes.

b) However when we drop c and use hc, m_e and e to construct a quantity which has dimensions of length the quantity we obtain is
\(\frac{4 \pi \varepsilon_0(\mathrm{~h} / 2 \pi)}{\mathrm{m}_{\mathrm{e}} \mathrm{e}^2}\)

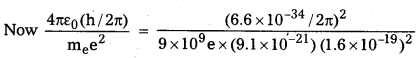
= 0.53 × 10^-10m
This is of the order of atom sizes.

Question 15.
The total energy of an electron in the first excited state of the hydrogen atom is about -3.4 eV
a) What is the kinetic energy of the electron in this state ?
b) What is the potential energy of the electron in this state ?
c) Which of the answers above would change if the choice of the zero of potential energy is changed ?
Answer:
We know kinetic energy of electron = \(\frac{K Z e^2}{2 r}\)
and P.E of electron = \(\frac{-\mathrm{KZe}^2}{\mathrm{r}}\)
P.E. = -2 (kinetic energy).
In this calculation electric potential and hence potential energy is zero at infinity.
Total energy = PE + KE = -2KE + KE = -KE
a) In the first excited state total energy = -3.4eV
∴ K.E = -(-3.4eV) = + 3.4 eV
b) P. E of electron in this first excited state = -2KE = -2 × 3.4 = -6.8eV.
c) If zero of potential energy is changed, KE does not change and continues to be +3.4 eV However, the P.E. and total energy of the state would change with the choice of zero of potential energy.

Question 16.
If Bohr’s quantisation postulate (angular momentum = nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantisation of orbits of planets around the sun ?
Answer:
Bohr’s quantisation postulate is in terms of Plank’s constant (h), But angular momenta associated with planetary motion are = 10⁷⁰ h (for earth). In terms of Bohr’s quantisation posulate this will correspond to n = 10⁷. For such large values of n the differences in successive energies and angular momenta of the quantised levels are so small, that the levels can be considered as continuous and not discrete.

Question 17.
Obtain the first Bohr’s radius and the ground state energy of a muonic hydrogen atom [i.e., an atom in which a negatively charged muon (µ^–) of mass about 207m_e orbits around a proton].
Answer:
A muonic hydrogen is the atom in which a negatively charged muon of mass about 207 m_e revolves around a proton.
In Bohr’s atom model as, r ∝ \(\frac{1}{\mathrm{~m}}\)
\(\frac{\mathrm{r}_\mu}{\mathrm{r}_{\mathrm{e}}}\) = \(\frac{\mathrm{m}_{\mathrm{e}}}{\mathrm{m}_\mu}\) = \(\frac{\mathrm{m}_{\mathrm{e}}}{207 \mathrm{~m}_{\mathrm{e}}}\) = \(\frac{1}{207}\)
Here r_e is radius of first orbit of electron in hydrogen atom = 0.53A = 0.53 × 10^-10m.
r_m = \(\frac{\mathrm{r}_{\mathrm{e}}}{207}\) = \(\frac{0.53 \times 10^{-10}}{207}\) = 2.56 × 10^-13m
Again in Bohr’s atomic model
E ∝ m
∴ \(\frac{\mathrm{E}_\mu}{\mathrm{E}_{\mathrm{e}}}\) = \(\frac{\mathrm{m}_\mu}{\mathrm{m}_{\mathrm{e}}}\) = \(\frac{207 \mathrm{~m}_{\mathrm{e}}}{\mathrm{m}_{\mathrm{e}}}\), E_μ = 207E_e
As ground state energy of electron in hydrogen atom is E_e = -13.6 eV
E_μ = 207(-13.6)eV = -2815.2eV
= -2.8152KeV.

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 12th Lesson Dual Nature of Radiation and Matter Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 12th Lesson Dual Nature of Radiation and Matter

Very Short Answer Questions

Question 1.
What are “cathode rays”?
Answer:
Cathode rays are streams of fast-moving electrons or negatively charged particles.

Question 2.
What important fact did Millikan’s experiment establish?
Answer:
Millikan’s experiment established that electric charge is quantised. That means the charge on anybody (oil drop) is always an integral multiple of the charge of an electron, i.e., Q = ne.

Question 3.
What is a “work function”? (A.P. Mar. ’19 & T.S. Mar. ’15)
Answer:
The minimum energy required to liberate an electron from a photo metal surface is called the work function, ϕ₀.

Question 4.
What is “photoelectric effect” ?
Answer:
When light of sufficient energy is incident on the photometal surface electrons are emitted. This phenomenon is called photoelectric effect.

Question 5.
Give examples of “photosensitive substances”. Why are they called so ?
Answer:
Examples of photosensitive substances are Li, Na, K, Rb and Cs etc.
The work function of alkali metals is very low. Even the ordinary visible light, alkali metals can produce photoelectric emission. Hence they are called photosensitive substances.

Question 6.
Write down Einstein’s photoelectric equation. (A.P. Mar. ’15)
Answer:
Einstein’s photoelectric equation is given by K_max = \(\frac{1}{2} \mathrm{mv}_{\max }^2\) = hυ – ϕ₀.

Question 7.
Write down de-Broglie’s relation and explain the terms there in. (A.P. & T.S. Mar. ’16)
Answer:
The de-Broglie wave length (λ) associated with a moving particle is related to its momentum (p) is λ = \(\frac{h}{p}\) = \(\frac{\mathrm{h}}{\mathrm{mv}}\), where h is planck’s constant.

Question 8.
State Heisenberg’s Uncertainly Principle. (A.P. Mar. ’19) (Mar. ’14)
Answer:
Uncertainity principle states that “it is impossible to measure both position (Δx) and momentum of an electron (Δp) [or any other particle] at the same time exactly”, i.e., Δx . Δp ≈ h where Δx is uncertainty in the specification of position and Δp is uncertainty in the specification of momentum.

Short Answer Questions

Question 1.
What is the effect of
(i) intensity of light
(ii) potential on photoelectric current ?
Answer:
(i) Effect of intensity of light on photoelectric current:

1) When the intensity (I) of incident light, with frequency greater than the threshold frequency (υ > υ₀) is increased then the number of photoelectrons emitted increases i.e. the value of photoelectric current (i) increases, ie. i ∝ I.

ii) The effect of potential on photoelectric current:

1. On increasing the positive potential on collecting electrode, the photoelectric current increases. At a particular positive potential, the photocurrent becomes maximum which is known as saturated current.
   
2. On increasing the value of negative potential on collecting electrode, the photoelectric current gradually goes on decreasing. At a particular negative potential the value of photoelectric current becomes zero. This is known as stopping potential.
3. Stopping potential does not depend on the intensity of incident light. On increasing intensity, the value of saturated current increases, whereas the stopping potential remains unchanged.

Question 2.
Describe an experiment to study the effect of frequency of incident radiation on ‘stopping potential’.
Answer:
Experimental study of the effect of frequency of incident radiation on stopping potential:

1. The experimental set up is shown in fig.
2. Monochromatic light of sufficient energy (E = hv) from source ‘s’ is incident on photosensitive plate ‘C’ (emitter), electrons are emitted by it.
3. The electrons are collected by the plate A (collector), by the electric field created by the battery.
4. The polarity of the plates C and A can be reversed by a commutator.
   
5. For a particular frequency of incident radiation, the minimum negative (retarding) potential V₀ given to the plate A for which the photo current stops or becomes zero is called stopping potential.
6. The experiment is repeated with different frequencies, and their different stopping potential are measured with voltmeter.
7. From graph, we note that
   1. The values of stopping potentials are different for different frequencies.
   2. The value of stopping potential is more negative for radiation of higher incident frequency.
   3. The value of saturation current depends on the intensity of incident radiation but it is independent of the frequency of the incident radiation.
      

Question 3.
Summarise the photon picture of electromagnetic radiation.
Answer:
We can summarise the photon picture of electromagnetic radiation as follows.

1. In interaction of radiation with matter, radiation behaves as if it is made up of particles called photons.
2. Each photon has energy E\(\left[\begin{array}{l}
   =\mathrm{hv} \\
   =\frac{\mathrm{hc}}{\lambda}
   \end{array}\right]\) and momentum P \(\left[\begin{array}{l}
   =\frac{h v}{c} \\
   =\frac{h}{\lambda}
   \end{array}\right]\) and speed c, the speed of light.
3. By increasing the intensity of light of given wave length, there is only an increase in the number of photons per second crossing a given area, with each photon having the same energy. Thus, photon energy is independent of intensity of radiation.
4. Photons are not deflected by electric and magnetic field. This shows that photons are electrically neutral.
5. In a photon-particle collision (such as photo-electron collision), the energy and momentum
   are conserved. However the number of photons may not be conserved in a collision. One photon may be absorbed or a new photon may be created.
6. The rest mass of photon is zero. According to theory of relativity, the mass of moving particle is given by m = \(\frac{\mathrm{m}_0}{\sqrt{1-\frac{v^2}{c^2}}}\) where v is velocity of particle and c is velocity of light.

Question 4.
What is the deBroglie wavelength of a ball of mass 0.12 Kg moving with a speed of 20 ms^-1 ? What can we infer from this result ?
Answer:
Given, m = 0.12 kg; υ = 20 m/s; h = 6.63 × 10^-34 J-s;
λ = \(\frac{h}{\mathrm{mv}}\) = \(\frac{6.63 \times 10^{-34}}{0.12 \times 20}\) = \(\frac{6.63 \times 10^{-34}}{2.4}\) ∴ λ = 2.762 × 10^-34 m = 2762 × 10^-21 A.

Long Answer Questions

Question 1.
How did Einstein’s photoelectric equation explain the effect of intensity and potential on photoelectric current ? How did this equation account for the effect of frequency of incident light on stopping potential ? (T.S. Mar. ’19)
Answer:

1. Einstein postulated that a beam of light consists of small energy packets called photons or quanta.
2. The energy of photon is E = hv. Where ‘h’ is Planck’s constant; v is frequency of incident light (or radiation).
3. If the absorbed energy of photon is greater than the work function (ϕ₀ = hυ₀), the electron is emitted with maximum kinetic energy i.e., k_max = \(\frac{1}{2} m_{\max }^2\) = eV₀ = hv – ϕ₀. This equation is known as Einstein’s photoelectric equation.
4. Effect of intensity of light on photoelectric current:
   When the intensity (I) of incident light, with frequency greater thanthe threshold frequency (υ > υ₀) is increased then the number of photoelectrons emitted decreases i.e. the value of photoelectric current (i) increases, le. i ∝ I.
   
5. The effect of potential on photoelectric current:
   1. On increasing the positive potential on collecting electrode, the photoelectric current increases. At a particular positive potential, the photocurrent becomes maximum which is known as saturated current.
   2. On increasing the value of negative potential on collecting electrode, the photoelectric current gradually goes on decreasing. At a particular negative potential the value of photoelectric current becomes zero. This is known as stopping potential (v₀).
      
   3. Stopping potential does not depend on the intensity of incident light. On increasing intensity, the value of saturated current increases, whereas the stopping potential remains unchanged.
6. The effect of frequency of incident radiation on stopping potential:
   On increasing the frequency of incident light, the value of stopping potential goes on increasing gradually as shown in fig. That means k_max increases eV₀ also increases.
   
7. From the graph, we note that
   1. For a given photosensitive metal, the cut off potential (v₀) varies linearly with the frequency of the incident radiation.
   2. For a given photosensitive metal, there is a certain minimum cut off frequency v₀ (called threshold frequency) for which the stopping potential is zero.
      
8. From the graph we note that
   1. The value of cut-off potential is different for radiation of different frequency.
   2. The value of stopping potential is more negative for radiation of higher incident frequency.
9. From above experiments, it is found that, if the incident radiation is of higher frequency than that of threshold frequency, the photoelectric emission is possible.

Question 2.
Describe the Davisson and Germer experiment. What did this experiment conclusively prove?
Answer:
Davisson and Germer experiment:

1. The experimental arrangement is schematically shown in fig.
2. Electrons from a filament F are rendered into a fine beam by applying a positive potential to the cylinder A.
3. A fine narrow beam of electrons is incident on the nickel crystal. The electrons are scattered in all directions by the atoms of the crystal.
4. The intensity of the electron beam scattered in a given direction, is measured by the electron detector (collector). The detector can be moved on a circular scale and is connected to a sensitive galvanometer, which records the current.
5. The deflection of the galvanometer is proportional to the intensity of the electron beam entering collector.
6. The apparatus is enclosed in an evacuated chamber.
7. The experiment was performed by varying the accelerating voltage from 44 V to 68 V. It is found that the intensity is maximum at 50° for a critical energy of 54 V
   
8. For θ = 50°, the glancing angle, ϕ (angle between the scattered beam of electron with the plane of atoms of the crystal) for electron beam will be given by
   ϕ + θ + ϕ = 180°
   ϕ = \(\frac{1}{2}\left[180^{\circ}-50^{\circ}\right]\) = 65°
   
9. According to Bragg’s law for first order diffraction maxima (n = 1), we have 2 d sin ϕ = 1 × λ ⇒ λ = 2 × 0.91 × sin 65° = 1.65A = 0.165 nm. (experimentally).
   [∵ for Nickel crystal interatomic separation d = 0.91 A]
10. According to de-Broglie hypothesis, the wavelength of the wave associated with electron is given by λ =
    = 1.67A = 0.167 nm, (Theoritically).
11. The experimentally measured wavelength was found to be in confirmity with proving the existence of de-Broglie waves.

Textual Exercises

Question 1.
Find the
(a) maximum frequency, and
(b) minimum wavelength of X-rays produced by 30 kV electrons.
Solution:
Given voltage V = 30 kV = 30 × 10³ V; e = 1.6 × 10^-19 C; h = 6.63 × 10^-34 j-s C = 3 × 10⁸ m/s
a) Maximum frequency, v = \(\frac{\mathrm{eV}}{\mathrm{h}}\) = \(\frac{1.6 \times 10^{-19} \times 30 \times 10^3}{6.63 \times 10^{-34}}\) = 7.24 × 10¹⁸ Hz

b) Minimum wavelength of X-ray, λ = \(\frac{\mathrm{C}}{\mathrm{v}}\) = \(\frac{3 \times 10^8}{7.24 \times 10^{18}}\) = 0.414 × 10^-10 Hz
∴ λ = 0.0414 × 10^-9m = 0.0414 nm.

Question 2.
The work function of caesium metal is 2.14 eV. When light of frequency 6 × 10¹⁴ Hz is incident on the metal surface, photoemission of electrons occurs. What is the
(a) maximum kinetic energy of the emitted electrons,
(b) stopping potential and
(c) maximum speed of the emitted photoelectrons ?
Solution:
Given ϕ₀ = 2.14 eV; v = 6 × 10¹⁴ Hz
a) KE_max = hv – ϕ₀ = \(\frac{6.63 \times 10^{-34} \times 6 \times 10^{14}}{1.6 \times 10^{-19}}\) – 2.14 ∴ KE_max = 0.35 eV

b) KE_max = eV0 ⇒ 0.35 eV = eV₀ ∴ V₀ = 0.35 V
c) KE_max = \(\frac{1}{2} m v_{\max }^2\) ⇒ \(v_{\max }^2\) = \(\frac{2 K_{\max }}{m}\) = \(\frac{2 \times 0.35 \times 1.6 \times 10^{-19}}{9.1 \times 10^{-31}}\) (∴ e = 1.6 × 10^-19 C)
\(v_{\max }^2\) = 0.123 × 10¹² ⇒ υ_max = \(\sqrt{1230 \times 10^8}\) = 35.071 × 10⁴ m/s ∴ υ_max = 350.71 km/s.

Question 3.
The photoelectric cut-off voltage in certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted ?
Solution:
Given, V₀ = 1.5 V; e = 1.6 × 10^-19 C, KE_max = eV₀ = 1.6 × 10^-19 × 1.5 = 2.4 × 10^-19 J.

Question 4.
Monochromatic light of wavelength 632.8 nm is produced by a helium-neon laser. The power emitted is 9.42 mW.
(a) Find the energy and momentum of each photon in the light beam,
(b) How many photons per second, on the average, arrive at a target irradiated by this beam ? (Assume the beam to have uniform cross-section which is less than the target area), and,
(c) How fast does a hydrogen atom have to travel in order to have the same momentum as that of the photon ?
Solution:
Given, λ = 632.8 nm = 632.8 × 10^-9m; p = 9.42 mW = 9.42 × 10^-3W
h = 6.63 × 10^-34 J-s; c = 3 × 10^-3 m/s

a) E = \(\frac{h c}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10}{632.8 \times 10^{-9}}\) = 3.14 × 10^-19 J.
Momentum of each photon, p = \(\frac{\mathrm{h}}{\lambda}\) = \(\frac{6.63 \times 10^{-34}}{632.8 \times 10^{-9}}\) = 1.05 × 10^-27kg \(\frac{\mathrm{m}}{\mathrm{s}}\)

b) No. of photons per second,

∴ N = 3 × 10¹⁶ photons/s
c) Since, P_Hydrogen = P_photon
⇒ mυ = p ⇒ υ = \(\frac{\mathrm{p}}{\mathrm{m}}\) = \(\frac{1.05 \times 10^{-27}}{1.66 \times 10^{-27}}\) [∴ m_H = 1.66 × 10^-27 kg] ∴ υ = 0.63 m/s.

Question 5.
The energy flux of sunlight reaching the surface of the earth is 1.388 × 10³ W/m². How many photons (nearly) per square metre are incident on the Earth per second ? Assume that the photons in the sunlight have an average wavelength of 550 nm.
Solution:
Given, P = 1.388 × 10³ W/m²; λ = 550 nm = 550 × 10^-9 m
h = 6.63 × 10^-34 J-s; e = 3 × 10⁸ m/s
Energy of each photon E = \(\frac{\mathrm{hc}}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{550 \times 10^{-9}}\) = 3.616 × 10^-19 J
No. of photons incident on the earths surface, N = \(\frac{\mathrm{P}}{\mathrm{E}}\) = \(\frac{1.388 \times 10^3}{3.66 \times 10^{-19}}\)
∴ N = 3.838 × 10²¹ photons/m² – s.

Question 6.
In an experiment on photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 × 10^-15 V s. Calculate the value of Planck’s constant.
Solution:
Given, slope of graph tan θ = 4.12 × 10^-15 V — s; .
e = 1.6 × 10^-19 c.

For slope of graph, tan θ = \(\frac{\mathrm{V}}{\mathrm{v}}\)
We know that hv = eV
\(\frac{\mathrm{V}}{\mathrm{v}}\) = \(\frac{h}{e}\) ⇒ \(\frac{\mathrm{h}}{\mathrm{e}}\) = 4.12 × 10^-15; h = 4.12 × 10^-15 × 1.6 × 10^-19 = 6.592 × 10^-34 J-s

Question 7.
A 100W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is 589 nm. (a) What is the energy per photon associated with the sodium light ?
(b) At what rate are the photons delivered to the sphere ?
Solution:
Given, P = 100 W; λ = 589 nm = 589 × 10,sup>-9 m; h = 6.63 × 10^-34 J – S; c = 3 × 10⁸ m/s
a) E = \(\frac{\text { hc }}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{589 \times 10^{-9}}\) = 3.38 × 10^-19J = \(\frac{3.38 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV = 2.11 eV.
b) No. of photons delivered per second, N = \(\frac{\mathrm{P}}{\mathrm{E}}\) = \(\frac{100}{3.38 \times 10^{-19}}\) = 3 × 10²⁰ photons/s

Question 8.
The threshold frequency for a certain metal is 3.3 × 10¹⁴ Hz. If light of frequency 8.2 × 10¹⁴ Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission.
Solution:
Given, v₀ = 3.3 × 10¹⁴ Hz; v = 8.2 × 10¹⁴ Hz; e = 1.6 × 10^-19 c; KE = eV₀ = hv – hv₀
V₀ = \(\frac{h\left(v-v_0\right)}{e}\) = \(\frac{6.63 \times 10^{-34} \times(8.2-3.3) \times 10^{14}}{1.6 \times 10^{-19}}\) = \(\frac{6.63 \times 10^{-34} \times 10^{14} \times 4.9}{1.6 \times 10^{-19}}\) ∴ V₀ = 2.03 V.

Question 9.
The work function for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm ?
Solution:
Given, ϕ₀ = 4.2 eV = 4.2 × 1.6 × 10^-19 J = 6.72 × 10~1S J
λ = 330 nm = 330 × 10^-9 m; h = 6.63 × 10^-34 J – s ⇒ c = 3 × 10⁸ m/s
E = \(\frac{\text { hc }}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{330 \times 10^{-9}}\) ∴ E = 6.027 × 10^-19J
As E < ϕ₀, no photoelectric emission takes place.

Question 10.
Light of frequency 7.21 × 10¹⁴ Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 10⁵ m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons ?
Solution:
Given, v = 7.21 × 10¹⁴ Hz; m = 9.1 × 10^-31 kg; υ_max = 6 × 10⁵ m/s
KE_max = \(\frac{1}{2} \mathrm{mv}_{\max }^2\) = hv – hv₀ = h(v – v₀)

Question 11.
Light of wavelength 488 nm is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut-off) potential of photoelectrons is 0.38 V. Find the work function of the material from which the emitter is made. .
Solution:
Given, λ = 488 nm = 488 × 10^-9 m; V₀ = 0.38 V; e = 1.6 × 10^-19 c; h = 6.63 × 10^-34 J – s
c = 3 × 10⁸ m/s ⇒ KE = eV₀ = \(\frac{\mathrm{hc}}{\lambda}\) – ϕ ⇒ 1.6 × 10^-19 × 0.38 = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{488 \times 10^{-9}}\) – ϕ₀
6.08 × 10^-20 = 40.75 × 10^-20 – ϕ₀ ⇒ (40.75 – 6.08) × 10^-20 = 34.67 × 10^-20 J
= \(\frac{34.67 \times 10^{-20}}{1.6 \times 10^{-19}} \mathrm{eV}\) ∴ ϕ₀ = 2.17 eV.

Question 12.
Calculate the
(a) momentum, and
(b) de Broglie wavelength of the electrons accelerated through a potential difference of 56 V
Solution:
Given, V = 56 V; e = 1.6 × 10^-19 c; m = 9 × 10^-31 kg
a) As KE = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\) ⇒ 2m (KE) = P² ⇒ P = \(\sqrt{2 \mathrm{~m}(\mathrm{KE})}\) = \(\sqrt{2 \mathrm{~m} \mathrm{eV}}\) [∵ KE = eV]
∴ P = \(\sqrt{2 \times 9 \times 10^{-31} \times 1.6 \times 10^{-31} \times 56}\) = 4.02 × 10^-24 kg – m/s
b) λ = \(\frac{12.27}{\sqrt{V}}\) A = \(\frac{12.27}{\sqrt{56}}\) A = 0.164 × 10^-9m ∴ λ = 0.164 nm.

Question 13.
What is the
(a) momentum,
(b) speed, and
(c) de Brogue wavelength of an electron with kinetic energy of 120 eV.
Solution:
Given, KE = 120 eV; m = 9.1 × 10^-3 kg; e = 1.6 × 10^-19 c
a) P = \(\sqrt{2 m(K E)}\) = \(\sqrt{2 \times 9.1 \times 10^{-31} \times\left(120 \times 1.6 \times 10^{-19}\right)}\) ∴ P = 5.91 × 10^-24 kg – m/s
b) υ = \(\frac{\mathrm{p}}{\mathrm{m}}\) = \(\frac{5.91 \times 10^{-24}}{9.1 \times 10^{-31}}\) = 6.5 × 10⁶ m/s .
c) λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\) A = \(\frac{12.27}{\sqrt{120}}\) A = 0.112 × 10^-9 m ∴ λ = 0.112 nm.

Question 14.
The wavelength of light from the spectral emission line of sodium is 589 nm Find the kinetic energy at which (a) an electron, and (b) a neutron, and would have the same de Brogue wavelength.
Solution:
Given, λ = 589 mn = 589 × 10^-9 m; m_e = 9.1 × 10^-31 kg.
m_n = 1.67 × 10^-27 kg; h = 6.62 × 10^-34 J – s.

Question 15.
What is the de Brogue wavelength of
(a) a bullet of mass 0.040 kg travelling at the speed of 1.0 km/s
(b) a ball of mass 0.060 kg moving at a speed of 1.0 m/s, and
(c) a dust particle of mass 1.0 × 10^-9 kg drifting with a speed of 2.2 m/s?
Solution:
a) Given, for bullet m = 0.040 kg and o = 1000 m/s = 10³ m/s
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{6.63 \times 10^{-34}}{0.040 \times 10^3}\) = 1.66 × 10^-35m
b)Given, for ball m = 0.060 kg and υ = 1 m/s ⇒ λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{6.63 \times 10^{-34}}{0.060 \times 1}\) = 1.1 × 10^-32 m
c) Given, for a dust particle m = 1 × 10^-9 kg and υ = 2.2 m/s
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{6.63 \times 10^{-34}}{1 \times 10^{-9} \times 2.2}\) = 3.0 × 10^-25 m.

Question 16.
An electron and a photon each have a wavelength of 1.00 nm. Find
(a) their momenta,
(b) the energy of the photon, and
(c) the kinetic energy of electron.
Solution:
Given, λ = 1 mm = 10^-9m; h = 6.63 × 10^-34 J-S; c = 3 × 10⁸ m/S

Question 17.
(a) For what kinetic energy of a neutron will the associated de Brogue wavelength be 1.40 × 10^-10 m?
(b) Also find the de Brogue wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of (3/2) k T at 300 K.
Solution:
(a) Given, for neutron, λ = 1.40 × 10^-10 m and m = 1.675 × 10^-27 kg
KE = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\) = \(\frac{h^2}{2 \mathrm{~m} \lambda^2}\) = \(\frac{\left(6.63 \times 10^{-34}\right)^2}{2 \times\left(1.40 \times 10^{-10}\right)^2 \times 1.675 \times 10^{-27}}\) ∴ KE = 6.686 × 10^-21J

b) Given, T = 300 k and K = 1.38 × 10^-23 J/K
KE = \(\frac{3}{2}\) KT = \(\frac{3}{2}\) × 1.38 × 10^-21 × 300 = 6.21 × 10^-21 J
λ = \(\frac{h}{\sqrt{2 m(K E)}}\) = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 1.675 \times 10^{-27} \times 6.21 \times 10^{-21}}}\) ∴ λ = 1.45 × 10^-10m = 1.45 A

Question 18.
Show that the wavelength of electromagnetic radiation is equal to the de Broglie wavelength of its quantum (photon).
Solution:
The momentum of a photon of frequency v, wavelength λ is given by p = \(\frac{\mathrm{hv}}{\mathrm{c}}\) = \(\frac{\mathrm{h}}{\lambda}\)
λ = \(\frac{\mathrm{h}}{\mathrm{p}}\) ⇒ de-Broglie wavelength of photon, λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{h}{p}\) = \(\frac{\frac{\mathrm{h}}{\mathrm{hv}}}{\mathrm{c}}\) = \(\frac{\mathrm{c}}{\mathrm{v}}\)
Thus, the wavelength of electromagnetic radiation is equal to the de-Broglie wavelength.

Question 19.
What is the de Broglie wavelength of a nitrogen molecule in air at 300 K ? Assume that the molecule is moving with the root-mean-square speed of molecules at this temperature. (Atomic mass of nitrogen = 14.0076 u)
Solution:
Given, T = 300 k; K = 1.38 × 10^-23 J/k; m = 28.0152u = 28.0152 × 1.67 × 10^-27 kg;
h = 6.63 × 10^-34 Js; Mean KE of molecules \(\frac{1}{2}\) mυ² = \(\frac{3}{2}\) KT
υ = \(\sqrt{\frac{3 \mathrm{KT}}{\mathrm{m}}}\) = \(\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 300}{28.0152 \times 1.66 \times 10^{-27}}}\)
∴ υ = 516.78 m/s
de-Broglie wavelength, λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{6.63 \times 10^{-34}}{28.0152 \times 1.66 \times 10^{-27} \times 516.78}\) = 2.75 × 10^-11 m
∴ λ = 0.0275 × 10^-19 m = 0.028 nm.

Additional Exercises

Question 1.
(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be 1.76 × 10¹¹ C kg^-1.
(b) Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong ? In what way is the formula to be modified ?
Solution:
a) Given, V = 500 V, \(\frac{\mathrm{e}}{\mathrm{m}}\) = 1.76 × 10¹¹ C/kg; KE = \(\frac{1}{2} \mathrm{mv}^2\) = eV

b) V = 10 MV = 10⁷ V; υ = \(\sqrt{\frac{\mathrm{e}}{\mathrm{m}} \times 2 \mathrm{~V}}\) = \(\sqrt{1.76 \times 10^{11} \times 2 \times 10^7}\) ∴ υ = 1.8762 × 10⁹ m/s
This speed is greater than speed of light, which is not possible. As o approaches to c, then mass m = \(\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\)

Question 2.
(a) A monoenergetic electron beam with electron speed of 5.20 × 10⁶ m s^-1 is subject to
a magnetic field of 1.30 × 10^-4 T normal to the beam velocity. What is the radius of the circle traced by the beam, given e/m for electron equals 1.76 × 10¹¹ C kg^-1.
(b) Is the formula you employ in (a) valid for calculating radius of the path of a 20 MeV electron beam ? If not, in what way is it modified ?
[Note : Exercises 20(b) and 21(b) take you to relativistic mechanics which is beyond the scope of this book. They have been inserted here simply to emphasise the point that the formulas you use in part (a) of the exercises are not valid at very high speeds or energies. See answers at the end to know what ‘very high speed or energy’ means.]
Solution:
a) Given, υ = 5.20 × 10⁶ m/s; B = 1.30 × 10^-4 T; \(\frac{\mathrm{e}}{\mathrm{m}}\) = 1.76 × 10¹¹ C/kg
Since centripetal force is balanced by Force due to magnetic field, \(\frac{\mathrm{m} v^2}{\mathrm{r}}\) = Bυ
[∵ (\(\vec{v} \times \vec{B}\)) = e υ B sin 90° = Beυ]

b) Given, E = 20 MeV = 20 × 1.6 × 10^-13J; m_e = 9.1 × 10^-31 kg
E = \(\frac{1}{2} \mathrm{mv}^2\)
⇒ v = \(\sqrt{\frac{2 E}{m}}\) = \(\sqrt{\frac{2 \times 20 \times 1.6 \times 10^{-13}}{9.1 \times 10^{-32}}}\) ∴ v = 2.67 × 10⁹ m/s

As υ > C, the formula used in (a) r = \(\frac{\mathrm{mv}}{\mathrm{eB}}\) is not valid for calculating the radius of path of 20 MeV electron beam because electron with such a high energy has velocity in relatistic domain i.e., comparable with the velocity of light and the mass varies with the increase in velocity but we have taken it a constant.
∴ m = \(\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\) ⇒ Thus, the modified formula will be r = \(\frac{\mathrm{mv}}{\mathrm{eB}}\) = \(\left[\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\right] \frac{v}{e B}\)

Question 3.
An electron gun with its collector at a potential of 100V fires out electrons in a spherical bulb containing hydrogen gas at low pressure (~ 10^-2 mm of Hg). A magnetic field of 2.83 × 10^-4 T curves the path of the electrons in a circular orbit of radius 12.0 cm. (The path can be viewed because the gas ions in the path focus the beam by attracting electrons and emitting light by electron capture; this method is known as the fine beam tube’ method.) Determine e/m from the data.
Solution:
Given, V = 100 V; B = 2.83 × 10^-4 T; m = 9.1 × 10^-31 kg; e = 1.6 × 10^-19 C;
r = 12 cm = 0.12m; KE = \(\frac{1}{2} \mathrm{mv}^2\) = eV ⇒ \(\frac{1}{2}\) × 9.1 × 10^-31 × υ² = 1.6 × 10^-19 × 100
υ² = \(\frac{2 \times 1.6 \times 10^{-17}}{9.1 \times 10^{-3.1}}\) = 3.516 × 10¹³ ∴ υ = \(\sqrt{3.516 \times 10^{13}}\) = 5.93 × 10⁶ m/s
Specific charge of electron, \(\frac{\mathrm{e}}{\mathrm{m}}\) = \(\frac{v}{r B}\) [∵ \(\frac{\mathrm{mv}^2}{\mathrm{r}}\) = Beυ] = \(\frac{5.93 \times 10^6}{2.83 \times 10^{-4} \times 0.12}\)
∴ \(\frac{\mathrm{e}}{\mathrm{m}}\) = 1.74 × 10¹¹ C/kg.

Question 4.
(a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.45 A. What is the maximum energy of a photon in the radiation ?
(b) From your answer to (a), guess what order of accelerating voltage (for electrons) is required in such a tube ?
Solution:
a) Given, λ = 0.45 A = 0.45 × 10^-10 m; E = \(\frac{\mathrm{hc}}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{0.45 \times 10^{-10} \times 1.6 \times 10^{-19}}\) eV
∴ E = 27.6 × 10³ eV = 27.6 KeV

b) In X-ray tube, accelerating voltage provides the energy to the electrons which produce X-rays. For getting X-rays, photons of 27.51 KeV is required that the incident electrons must posess kinetic energy of 27.61 KeV.
Energy = eV = E; eV = 27.6 KeV; V = 27.6 KV .
So, the order of accelerating voltage is 30 KV.

Question 5.
In an accelerator experiment on high-energy collisions of electrons with positrons, a certain event is interpreted as annihilation of an electron-positron pair of total energy 10.2 BeV into two γ-rays of equal energy. What is the wavelength associated with each γ-ray ? (1 BeV = 10⁹ eV)
Solution:
Given, energy of 2 γ-rays, 2E = 10.2 BeV

⇒ 2\(\frac{\mathrm{hc}}{\lambda}\) = 10.2 BeV [∵ E = \(\frac{\mathrm{hc}}{\lambda}\)] ⇒ λ = \(\frac{2 \mathrm{hc}}{10.2 \mathrm{BeV}}\)
Here h = 6.63 × 10^-34 J-S; c = 3 × 10⁸m/s, 1 BeV = 10⁹ eV = 10⁹ × 1.6 × 10^-19J
⇒ λ = \(\frac{2 \times 6.63 \times 10^{-34} \times 3 \times 10^8}{10.2 \times 10^9 \times 1.6 \times 10^{-19}}\) ∴ λ = 2.436 × 10^-16 m

Question 6.
Estimating the following two numbers should bé interesting. The first number will tell you why radio engineers do not need to worry much about photons ! The second number tells you why our eye can never count photons’, even in barely detectable light.
(a) The number of photons emitted per second by a Medium wave transmitter of 10 kW power, emitting radiowaves of wavelength 500 m.
(b) The number of photons entering the pupil of our eye per second corresponding to the minimum intensity of white light that we humans can perceive (~ 10^-10 W m^-2). Take the area of the pupil to be about 0.4 cm², and the average frequency of white light to be about 6 × 10¹⁴ Hz.
Solution:
a) Given, P = 10kW = 10 × 10³ W; λ = 500m; h = 6.63 × 10^-34 J – s; C = 3 × 10⁸
The no. of photons emitted per second, N = \(\frac{\mathrm{P}}{\mathrm{E}}\) = \(\frac{\mathrm{P}}{\frac{\mathrm{hc}}{\lambda}}\) = \(\frac{\mathrm{p} \lambda}{\mathrm{hc}}\) = \(\frac{10 \times 10^3 \times 500}{6.63 \times 10^{-34} \times 3 \times 10^8}\)
∴ N = 2.51 × 10³¹ photons/s

b) Given, v = 6 × 10^-4 Hz; I = \(\frac{E}{A-t}\) = 10^-10 W/m²; Area of pupil, A = 0.4 cm² = 0.4 × 10^-4 m².
Total energy falling on pupil in unit time, E’ = IA = 10^-10 × 0.4 × 10^-4 ∴ E’ = 4 × 10^-155 J/s
Energy of each photon, E” = hv = 6.63 × 10^-34 × 6 × 10¹⁴ = 3.978 × 10^-19 J
No. of photons per second, N = \(\frac{E^{\prime}}{E^{\prime \prime}}\) = \(\frac{4 \times 10^{-15}}{3.978 \times 10^{-19}}\) = 1.206 × 10⁴ photons/s
As this number is not so large a: in part (a), so it is large enough for us never to sense the individual photons by our eye.

Question 7.
Ultraviolet light of wavelength 2271 A from a 1oo W mercury source irradiates a photo cell made of molybdenum metal. If the stopping potential is -1.3 V, estimate the work function of the metal. How would the photo-cell respond to a high intensity (-10⁵ W m^-2) red light of wavelength 6328 A produced by a He-Ne laser?
Solution:
Given, for UV light, λ = 2271A = 2271 × 10^-10 m
V₀ = 1.3 V; P = 100W; h = 6.63 × 10^-34 J-s; c = 3 × 10⁸ m/s
From Einstein’s equation E = KE + ϕ₀, hυ = eV₀ + ϕ₀
ϕ₀ = \(\frac{\mathrm{hc}}{\lambda}\) – eV₀ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{2271 \times 10^{-10}}\) – 1.6 × 10^-19 × 1.3 = 8.758 × 10^-19 – 2.08 × 10^-19
ϕ₀ = \(\frac{6.678 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV = 4.17 eV ∴ ϕ₀ = 4.2 eV
Given, for red light, λ = 6328Å = 6328 × 10^-10m
E = \(\frac{\mathrm{hc}}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{6328 \times 10^{-10}}\) = \(\frac{3.143 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV ∴ E = 1.96 eV
Here, E < ϕ₀, So, the photocell will not respond to this red light. (It is independent of intensity).

Question 8.
Monochromatic radiation of wavelength 640.2 nm (1 nm = 10^-9 m) from a neon, lamp irradiates photosensitive material made of caesium on tungsten. The stopping voltage is measured to be 0.54 V. The source is replaced by an iron source and its 427.2 nm line irradiates the same photo-cell. Predict the new stopping voltage.
Solution:
Given, for Neon X = 640.2 nm = 640.2 × 10^-9 m ; V₀ = 0.54 V
h = 6.63 × 10^-34 J-s; c = 3 × 10⁸ m/s; e = 1.6 × 10^-19 C
ϕ = \(\frac{\mathrm{hc}}{\lambda}\) – eV₀ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{640.2 \times 10^{-9}}\) – 1.6 × 10^-19 × 0.54
= 3.1 × 10^-19 – 0.864 × 10^-19 = 2.236 × 10^-19J = \(\frac{2.236 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV ∴ ϕ = 1.4 eV
For iron; given ϕ₀ = 1.4eV; λ = 427.2 nm = 427.2 × 10^-9 m
Let V₀ be the new stopping potential, eV₀ = \(\frac{\mathrm{hc}}{\lambda}\) – ϕ₀
eV₀’ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{427.2 \times 10^{-9} \times 1.6 \times 10^{-19}}\) – 1.4 = 1.51 eV. Required stopping potential V₀‘ = 1.51 V.

Question 9.
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ₁ = 3650Å, λ₂ = 4047Å, λ₃ = 4358Å, λ₄ = 5461 Å, λ₅ = 6907Å,
The stopping voltages, respectively, were measured to be:
V₀₁ = 1.28 V, V₀₂ = 0.95 V, V₀₃ = 0.74 V, V₀₄ = 0.16 V, V₀₅ = 0V.
Determine the value of Plancks constant h, the threshold frequency and work function
for the material.
[Note : You will notice that, to get h from the data, you will need to know e(which you can take to be 1.6 × 10^-19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
Solution:
Given λ₁ = 3650 A = 3650 × 10^-10 m
λ₂ = 4047 A = 4047 × 10^-10 m
λ₃ = 4358 A = 4358 × 10^-10 m
λ₄ = 5461 A = 5461 × 10^-10 m
λ₅ = 6907 A = 6907 × 10^-10 m
V₀₁ = 1.28V, V₀₂ = 0.95, V₀₃ = 0.74 V; V₀₅ = 0

a) v₁ = \(\frac{\mathrm{c}}{\lambda_1}\) = \(\frac{3 \times 10^8}{3650 \times 10^{-10}}\) = 8.219 × 10¹⁴ Hz
v₂ = \(\frac{\mathrm{c}}{\lambda_2}\) = \(\frac{3 \times 10^8}{4047 \times 10^{-10}}\) = 7.412 × 10¹⁴ Hz
v₃ = \(\frac{\mathrm{c}}{\lambda_3}\) = \(\frac{3 \times 10^8}{4358 \times 10^{-10}}\) = 6.884 × 10¹⁴ Hz
v₄ = \(\frac{\mathrm{c}}{\lambda_4}\) = \(\frac{3 \times 10^8}{5461 \times 10^{-10}}\) = 5.493 × 10¹⁴ Hz
v₅ = \(\frac{\mathrm{c}}{\lambda_5}\) = \(\frac{3 \times 10^8}{6907 \times 10^{-10}}\) = 4.343 × 10¹⁴ Hz
As the graph between V₀ and frequency v is a straight line.
The slope of this graph gives the values of \(\frac{\mathrm{h}}{\mathrm{e}}\)

∴ \(\frac{\mathrm{h}}{\mathrm{e}}\) = \(\frac{V_{01}-V_{04}}{v_1-v_4}\) = \(\frac{1.28-0.16}{(8.219-5.493) \times 10^{14}}\)
h = \(\frac{1.12 \times 1.6 \times 10^{-19}}{2.726 \times 10^{14}}\) = 6.674 × 10^-34 J . s

b) ϕ₀ = hv₀ = 6.574 × 10^-34 × 5 × 10¹⁴
= 32.870 × 10^-20 J = \(\frac{32.870 \times 10^{-20}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 2.05 eV

Question 10.
The work function for the following metals is given:
Na : 2.75 eV; K: 2.30 eV; Mo : 4.17 eV; Ni : 5.15 eV. Which of these metals will not give photoelectric emission for a radiation of wavelength 3300 A from a He-Cd laser placed 1 m away from the photocell ? What happens if the laser is brought nearer and placed 50 cm away?
Solution:
Given λ = 3300 A = 3300 × 10^-10 m
Energy of incident photon, E = \(\frac{\mathrm{hc}}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{3300 \times 10^{-10} \times 1.6 \times 10^{-19}}\) ∴ E = 3.75 eV
Here Na, K has lesser work function than 3.75 eV. So, they produce photoelectric effect. If the laser is brought nearer then only the intensity change or the number of photoelctrons change.

Question 11.
Light of intensity 10^-5 W m^-2 falls on a sodium photo-cell of surface area 2 cm². Assuming that the top 5 layers of sodium absorb the incident energy, estimate time required for photoelectric emission in the wave-picture of radiation. The work function for the metal is given to be about 2 eV. What is the implication of your answer?
Solution:
Given, I = 10^-5 W/m²; A = 2 cm² = 2 × 10^-4 m²; ϕ₀ = 2eV
Let t be the time.
The effective atomic area of Na = 10^-20 m² and it contains one conduction electron per
atom.
No. of conduction electrons m five layers

We know that sodium has one free electron (or conduction electron) per atom.
Incident power on the surface area of photocell
= Incident intensity × Area on the surface area of photo cell
= 10^-5 × 2 × 10^-4 = 2 × 10^-9 W.
The electron present in all the 5 layers of sodium will share the incident energy equally.
Energy absorbed per second per electron, E =
= \(\frac{2 \times 10^{-9}}{10^{17}}\) = 2 × 10^-26 W.
Time required for emission by each electron,
which is about 0.5 yr.
The answer obtained implies that the time of emission of electron is very large and is not agreement with the observed time of emission. There is no time lag between the incidence of light and the emission of photoelectron.
Thus, it is implied that the wave theory cannot be applied in this experiment.

Question 12.
Crystal diffraction experiments can be performed using X-rays, or electrons accelerated through appropriate voltage. Which probe has greater energy? (For quantitative. comparison. take the wavelength of the probe equal to 1 A, which is of the order of interatomic spacing in the lattice) (m_e = 9.11 × 10^-31 kg).
Solution:
Given λ = 1 A = 10^-10 m ; m_e = 9.11 × 10^-31 kg; h = 6.63 × 10^-34 J – s; c = 3 × 10⁸ m/s

Thus, for the same wavelength a X-ray photon has much KE than an electron.

Question 13.
(a) Obtain the de Brogue wavelength of a neutron of kinetic energy 150 eV. As you have seen in Exercise 31, an electron beam of this energy is suitable for crystal diffraction experiments. Would a neutron beam of the same energy be equally suitable ? Explain. (m_n = 1.675 × 10^-27 kg)
(b) Obtain the de Brogue wavelength associated with thermal neutrons at room temperature (27 °C). Hence explain why a fast neutron beam needs to be thermalised with the environment before it can be used for neutron diffráction experiments.
Solution:
a) Given, KE = 150 eV; m = 1.675 × 10^-27 kg

The interatomic spacing is 10^-10 m, which is greater than this wavelength. So, neutron beam of 150 eV is not suitable for diffraction experiment.

b) T = t + 273 = 27 + 273 = 300 K; K = 1.38 × 10^-23 J/mol/K

This wavelength is order of interatomic spacing. So, the neutron beam first thermalised and then used for diffraction.

Question 14.
An electron microscope uses electrons accelerated by a voltage of 50 kV. Determine the de Broglie wavelength associated with the electrons. If other factors (such as numerical aperture, etc.) are taken to be roughly the same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light?
Solution:
Given, V = 50 KV s 50000 V
λ =

= 0.055 A ⇒ λ = 5.5 × 10^-12 m; For yellow light (λ) = 5.9 × 10^-7m
As resolving power (RP) ∝ \(\frac{1}{\lambda}\)
⇒

Question 15.
The wavelength of a probe is roughly a measure of the size of a structure that it can probe in some detail. The quark structure of protons and neutrons appears at the minute length-scale of 10^-15 m or less. This structure was first probed in early 1970’s using high energy electron beams produced by a linear accelerator at Stanford, USA. Guess what might have been the order of energy of these electron beams. (Rest mass energy of electron = 0.5 11 MeV.)
Solution:
Given λ = 10^-15 m; E = 0.5 11 MeV; P = \(\frac{\mathrm{h}}{\lambda}\) = \(\frac{6.63 \times 10^{-34}}{10^{-15}}\) = 6.63 × 10^-19 kg^m/s
Rest mass energy; E₀ = m₀c² = 0.511 MeV = 0.511 × 1.6 × 10^-13 T.
From relativistic theory, E² = p²c² + \(m_0^2 c^4\)
= (3 × 10⁸ × 6.63 × 10^-19)² + (0.511 × 10^-13 × 1.6)² = 9 × (6.63)² × 10^-22.
As the rest mass energy is negligible ∴ Energy E = \(\sqrt{p^2 c^2}\) = pc = 6.63 × 10^-19 × 3 × 10⁸
= \(\frac{1.989 \times 10^{-10}}{1.6 \times 10^{-19}}\)eV = 1.24 × 10⁹ eV = 1.24 BeV
Thus, to energies the electron beam, the energy should be of the order of BeV.

Question 16.
Find the typical de Brogue wavelength associated with a He atom in helium gas at room temperature (27 °C) and 1 atm pressure; and compare It with the mean separation between two atoms under these conditions.
Solution:
Given T = 27 + 273 = 300 K; K = 1.38 × 10^-23 J/mol/K; p = 1 atm = 1.01 × 10⁵ Pa

We can see that the wave length with mean separation r, it can be observed (r >> λ) that separation is larger than wave length.

Question 17.
Compute the typical de Broglie wavelength of an electron in a metal at 27 °C and compare it with the mean separation between two electrons in a metal which is given to be about 2 × 10^-10 m.
[Note : Exercise 35 and 36 reveal that while the wave-packets associated with gaseous molecules under ordinary conditions are non-overlapping, the electron wave-packets in a metal strongly overlap with one another. This suggests that whereas molecules in an ordinary gas can be distinguished apart, electrons in a metal cannot be distinguished apart from one another. This indistinguishibility has many fundamental implications which you will explore in more advanced Physics courses.]
Solution:
Given, T = 27 + 273 = 300 K; r = 2 × 10^-10m
Momentum, P = \(\sqrt{3 \mathrm{mKT}}\) = \(\sqrt{3 \times 9.11 \times 10^{-31} \times 1.38 \times 10^{-23} \times 300}\) = 1.06 × 10^-25 kg-m/s
λ = \(\frac{\mathrm{h}}{\mathrm{p}}\) = \(\frac{6.63 \times 10^{-34}}{1.06 \times 10^{-25}}\) = 62.6 × 10^-10m; Mean separation, r = 2 × 10^-10 m
\(\frac{\lambda}{r}\) = \(\frac{62.6 \times 10^{-10}}{2 \times 10^{-10}}\) = 31.3
We can see that de-Broglie wavelength is much greater than the electron separation.

Question 18.
Answer the following questions :
(a) Quarks inside protons and neutrons are thought to carry fractional charges [(+2/3)e; (-1/3)e]. Why do they not show up in Millikan’s oil-drop experiment ?
Solution:
The quarks have fractional charges. These quarks are bound by forces. These forces become stronger when the quarks are tried to be pulled apart. That is why, the quarks always remain’ together. It is due to this reason that tough fractional charges exists in nature but the observable charges are always integral multiple of charge of electron.

(b) What is so special about the combination e/m ? Why do we not simply talk of e and m separately ?
Solution:
The motion.of electron in electric and magnetic fields are governed by these two equations.
\(\frac{1}{2} \mathrm{mv}^2\) = eV or Beυ = \(\frac{m v^2}{\mathrm{r}}\)
In these equations, e and m both are together i.e. there is no equation in which e or m are alone. So, we always take e/m.

(c) Why should gases be insulators at ordinary pressures and start conducting at very low pressures ?
Solution:
At ordinary pressure, only very few positive ions and electrons are produced by the ionisation of gas molecules. They are not able to reach the respective electrodes and becomes insulators. At low pressure, density decreases and the mean free path becomes large. So, at high voltage, they acquire sufficient amount of energy and they collide with molecules for further ionisation. Due to this, the number of ions in a gas increases and it becomes a conductor.

(d) Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic ? Why is there an energy distribution of photoelectrons ?
Solution:
Because all the electrons in the metal do not belong to same level but they occupy a continuous band of levels, therefore for the given incident radiation, electrons come out from different levels with different energies.

(e) The energy and momentum of an electron are related to the frequency and wavelength of the associated matter wave by the relations :
E = h v, p = \(\frac{\mathbf{h}}{\lambda}\)
But while the value of λ is physically significant, the value of v (and therefore, the value of the phase speed v λ) has no physical significance. Why ?
Solution:
As λ = \(\frac{\mathrm{h}}{\mathrm{p}}\) = p = \(\frac{h}{\lambda}\) ⇒ E = hv = \(\frac{\mathrm{hc}}{\lambda}\)
Energy of moving particle E’ = \(\frac{p^2}{2 m}\) = \(\frac{1}{2} \frac{\left(\frac{h}{\lambda}\right)^2}{m}\) = \(\frac{1}{2} \frac{h^2}{\lambda^2 \mathrm{~m}}\). For the relation of E and p, we note that there is a physical significance of λ but not for frequency v.

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 11th Lesson Electromagnetic Waves Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 11th Lesson Electromagnetic Waves

Very Short Answer Questions

Question 1.
What is the average wavelength of X-rays? (A.P. Mar. ’16 )
Answer:
The wavelength range of X-rays is from 10^-8m(10nm) to 10^-13 m (10^-4 nm).
Average wavelength of X – rays = \(\frac{10+0.0001}{2}\) = 5.00005nm.

Question 2.
Give anyone use of infrared rays. (T.S. Mar. ’19)
Answer:

1. Infrared radiation plays an important role in maintaining the Earth warm.
2. Infrared lamps are used in physical therapy.
3. Infrared detectors are used in Earth Satellites.
4. These are used in taking photographs during conditions of fog, smoke, etc.

Question 3.
If the wavelength of electromagnetic radiation is doubled, what happens to the energy of photon? (T.S. Mar. ’16)
Answer:
Photon energy (E) = hv = \(\frac{\mathrm{hc}}{\lambda}\)
E ∝ \(\frac{1}{\lambda}\)
Given λ₁ = λ, λ₂ = 2λ, E₁ = E
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}\) = \(\frac{\lambda_2}{\lambda_1}\)
\(\frac{E}{\mathrm{E}_2}\) = \(\frac{2 \lambda}{\lambda}\)
E₂ = E/2
∴ The energy of photon reduces to half of its initial value.

Question 4.
What is the principle of production of electromagnetic waves ?
Answer:
If the charge is accelerated both the magnetic field and electric field will change with space and time, then electromagnetic waves are produced.

Question 5.
What is the ratio of speed of infrared rays and ultraviolet rays in vacuum ?
Answer:
The ratio of speed of infrared rays and ultraviolet rays in vacuum is 1 : 1.
All electromagnetic waves travel with same speed 3 × 10⁸ m /s in vacuum.

Question 6.
What is the relation between the amplitudes of the electric and magnetic fields in free space for an electromagnetic wave ?
Answer:
E₀ = CB₀
Where E₀ = Amplitude of electric field.
B₀ = Amplitude of magnetic field.
C = velocity of light.

Question 7.
What are the applications of microwaves ? (T.S. Mar. ’15)
Answer:

1. Microwaves are used in Radars.
2. Microwaves are used for cooking purposes.
3. A radar using microwave can help in detecting the speed of automobile while in motion.

Question 8.
Microwaves are used in Radars, why ? (Mar. ’14)
Answer:
As microwaves are of smaller wavelengths, hence they can be transmitted as a beam signal in a particular direction. Microwaves do not bend around the comers of any obstacle coming in their path.

Question 9.
Give two uses of infrared rays. (A.P. Mar. ’19)
Answer:

1. Infrared rays are used for producing dehydrated fruits.
2. They are used in the secret writings on the ancient walls.
3. They are used in green houses to keep the plants warm.

Question 10.
The charging current for a capacitor is 0.6 A. What is the displacement current across its plates?
Answer:
i = charging current for a capacitor = 0.6 A
i = id = \(\varepsilon_0 \frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
∴ i = i = i_d = 0.6A
∴ Displacement current (i_d) = 0.6 A.

Short Answer Questions

Question 1.
What does an electromagnetic wave consists of ? On what factors does its velocity in vacuum depend ?
Answer:
Maxwell concluded that the variation in electric and magnetic field vectors perpendicular to each other leads to the production of electromagnetic waves in space. They can travel in space even without any material medium. These waves are called electromagnetic waves.

According to Maxwell, electromagnetic waves are those waves in which there are sinusoidal variation of electric and magnetic field vectors at right angles to each other as well as at right angles to the direction of wave propagation. Thus electomagnetic waves have transverse nature.

Electric field E_x = E₀ Sin (kz – ωt)
Magnetic field B_y = B₀ sin (kz – ωt)
Where K is propagation constant (K = \(\frac{2 \pi}{\lambda}\))
The velocity of electromagnetic waves C = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\)

Velocity of E.M waves depends on

1. Permeability in free space (μ₀).
2. Permittivity in free space (ε₀).

Velocity of e.m waves is 3 × 10⁸ m / s.

Question 2.
What is Greenhouse effect and its contribution towards the surface temperature of earth ?
Answer:
Green house effect: Temperature of the earth increases due to the radiation emitted by the earth is trapped by atmospheric gases like CO₂, CH₄, N₂, Chlorofluoro carbons etc is called green house effect.

1. Radiation from the sun enters the atmosphere and heat the objects on the earth. These heated objects emit infrared rays.
2. These rays are reflected back to Earth’s surface and trapped in the Earth’s atmosphere. Due to this temperature of the earth increases.
3. The layers of carbon dioxide (CO₂) and low lying clouds prevent infrared rays to escape Earth’s atmosphere.
4. Since day-by-day the amount of carbondioxide in the atmosphere increases, more infrared rays are entrapped in the atmosphere.
5. Hence the temperature of the Earth’s surface increases day by day.

Long Answer Questions

Question 1.
Give the brief history of discovery of knowledge of electromagnetic waves.
Answer:

1. Faraday from his experimental study of electromagnetic induction magnetic field changing with time, gives rise to an electric field.
2. Maxwell in 1865 from his theoritical study concluded that, an electric field changing with time gives rise to magnetic field.
3. It is a consequence of the displacement current being a source of magnetic field.
4. It means a change in electric (or) magnetic field with time produces the other field.
5. Maxwell concluded that the variation in electric and magnetic field vectors perpendicular to each other leads to the production of electromagnetic waves in space.
6. These electromagnetic waves travel in space without any material medium.
7. Both electric and magnetic fields vary with time and space and have the same frequency.
   
8. The electric field vector \(\overrightarrow{\mathrm{E}}\) and magnetic field vector \(\overrightarrow{\mathrm{B}}\) are vibrating along y and z axis and propagation of electromagnetic waves along x – axis.
9. Maxwell found that the electromagnetic waves travel in vacuum with a speed is given by
   
   Where μ₀ = 4π × 10^-7 H/m = permeability in free space.
   ε₀ = 8.85 × 10^-12 c² N^-1 m^-2 = permittivity in free space.
10. The velocity of electromagnetic waves in a medium is given by v = \(\frac{1}{\sqrt{\mu \varepsilon}}\)
11. Maxwell also concluded that electromagnetic waves are transverse in nature.
12. In 1888 Hertz demonstrated experimentally the production and detection of E.M waves using spark oscillator.
13. In 1895 Jagadish Chandra Bose was able to produce E.M waves of wavelength 5m.m to 25 m.m.
14. 1899 Marconi was the first to establish a wireless communication at a distance of about 50 km.

Question 2.
State six characteristics of electromagnetic waves. What is Greenhouse effect ?
Answer:
Characteristics (or) properties of electromagnetic waves :

1. Electromagnetic waves do not require any material medium for their propagation. They propagate in vacuum as well as in a medium.
2. Speed of E.M. waves in free space (or) vacuum is given by
   C = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\) = 3 × 10⁸ m/s.
3. Speed of E.M waves in a medium is given by
   v = \(\frac{1}{\sqrt{\mu \varepsilon}}\)
4. Electromagnetic waves are transverse in nature.
   Electric field \(\overrightarrow{\mathrm{E}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\) which constitute the E.M waves an mutually perpendicular to each other as well as perpendicular to the direction of propagation of the wave.
5. Electromagnetic waves are self sustaining electric and magnetic field oscillations in space.
6. Electromagnetic waves transport energy.
   Poynting vector (\(\overrightarrow{\mathrm{P}}\)) = \(\frac{1}{\mu_0}(\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}})\)
7. Relation between electric field vector E and magnetic field vector g in vacuum is given by
   C = \(\frac{\mathrm{E}_0}{\mathrm{~B}_0}\)
8. Electromagnetic waves are not deflected by magnetic and electric fields.
9. Electromagnetic waves can be reflected, refracted, interferenced, diffracted and polarised.
10. Electromagnetic wave follow the superposition principle.
11. Average electric energy density of E.M wave is given by
    U_av = U_E + U_B
    U_av = \(\frac{1}{2} \varepsilon_0 \mathrm{E}^2\) + \(\frac{1}{2} \cdot \frac{\mathrm{B}^2}{\mu_0}\)
    U_av = 2U_E = 2U_B
12. Intensity of an E.M waves depends on its average energy density.
    I = \(\frac{1}{2} \varepsilon_0 \mathrm{C} \mathrm{E}_0^2\)
13. E.M. waves carry momentum and exert radiation pressure is given by
    P = \(\frac{\mathrm{F}}{\mathrm{A}}\) = \(\frac{1}{\mathrm{~A}} \frac{\mathrm{dp}}{\mathrm{dt}}\) = \(\frac{\text { Intensity (I) }}{C}\)

Green house effect:
The temperature of the Earth increases due to radiation emitted by the Earth.is trapped by atmospheric gases like CO₂, CH₄, N₂O, chlorofluoro carbons etc is called green house effect.

Textual Exercises

Question 1.
The figure shows a capacitor made of two circular plates each of radius 12cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A.
a) Calculate the capacitance and the rate of charge of potential difference between the plates.

b) Obtain the displacement current across the plates.
c) Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor ? Explain.
Answer:
Given ε₀ = 8.85 × 10^-12 C² N^-1 m^-2
Here, R = 12cm = 0.12m, d = 5.0mm = 5 × 10^-3m, I = 0.15A
Area, A = πR² = 3.14 × (0.12)²m²

a) We know that capacity of a parallel plate capacitor is given by

b) Displacement current is equal to conduction current i.e., 0.15 A.
c) Yes, Kirchhoffs first rule is valid at each plate of the capacitor provided. We take the current to be the sum of the conduction and displacement currents.

Question 2.
A parallel plate capacitor in the figure made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of 300 rad s^-1.
a) What is the rms value of the conduction current ?
b) Is the conduction current equal to the displacement current ?
c) Determine the amplitude of B at a point 3.0 cm from the axis between the plates.

Answer:
a) I_rms = \(\frac{E_{\mathrm{fms}}}{X_c}\) = \(\frac{E_{\mathrm{rms}}}{\frac{1}{\omega C}}\) = E_rms × ωC
∴ I_rms = 230 × 300 × 100 × 10^-12 = 6.9 × 10^-6A = 6.9µA

b) Yes, I = I_d where I is steady d.c or a.c. This is shown below

c) We know, B = \(\frac{\mu_0}{2 \pi} \times \frac{\pi}{R^2} \times I_d\)
The formula is valid even if I_d is oscillating. As I_d = I, therefore
B = \(\frac{\mu_0 r \mathrm{I}}{2 \pi \mathrm{R}^2}\)
If I = I₀, the maximum value of current, then
Amplitude of B = max. value of B = \(\frac{\mu_0 \mathrm{rI}_0}{2 \pi \mathrm{R}^2}\) = \(\frac{\mu_0 \mathrm{r} \sqrt{2} \mathrm{I}_{\mathrm{rms}}}{2 \pi \mathrm{R}^2}\)
= \(\frac{4 \pi \times 10^{-7} \times 0.03 \times \sqrt{2} \times 6.9 \times 10^{-6}}{2 \times 3.14 \times(0.06)^2}\) = 1.63 × 10^-11T.

Question 3.
What physical quantity is the same for X-rays of wavelength 10^-10m, red light of wavelength 6800 A and radiowaves of wavelength 500m?
Answer:
The speed in vacuum is same for all the given wavelengths, which is 3 × 10⁸ m/s.

Question 4.
A plane electromagnetic wave travels In vacuum aloñg z-direction. What can you say about the directions of its electric and magnetic field vectors ? If the frequency of the wave is 30 MHz, what is its wavelength?
Answer:
In electromagnetic wave, the electric field vector \(\overrightarrow{\mathrm{E}}\) and magnetic field vector \(\overrightarrow{\mathrm{B}}\) show their variations perpendicular to the direction of propagation of wave as well as perpendicular to each other. As the electromagnetic wave is travelling along z – direction, hence \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) show their variation in x – y plane.
wave length λ = \(\frac{\mathrm{c}}{\mathrm{v}}\) = \(\frac{3 \times 10^8 \mathrm{~m} / \mathrm{s}}{30 \times 10^6 \mathrm{~s}^{-1}}\) = 10m

Question 5.
A radio can tune into any station in the 7.5 MHz to 12MHz band. What is-the corresponding wavelength band?
Answer:
λ₁ = \(\frac{3 \times 10^8}{7.5 \times 10^6}\) = 40m
λ₂ = \(\frac{3 \times 10^8}{12 \times 10^6}\) = 25m
Thus wavelength band is 40m to 25m.

Question 6.
A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. What is the frequency of the electromagnetic waves produced by the oscillator ?
Answer:
The frequency of electromagnetic wave is same as that of oscillating cliarged particle about its equilibrium position; which is 10⁹Hz.

Question 7.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B₀ = 510 nT. What is the amplitude of the electric field part of the wave ?
Answer:
Here, B₀ = 510nT = 510 × 10^-9T
E₀ = CB₀ = 3 × 10⁸ × 510 × 10^-9 = 153 NC^-1.

Question 8.
Suppose that the electric field amplitude of an electromagnetic wave is E₀ = 120 N/C and that its frequency is v = 50.0 MHz.
(a) Determine. B₀, ω, k, and λ.
(b) Find expressions for E and B.
Answer:
a)
B₀ = \(\frac{E_0}{\mathrm{c}}\) = \(\frac{120}{3 \times 10^8}\) = 4 × 10^-7 T
ω = 2πv = 2 × 3.14 × (50 × 10⁶) = 3.14 × 10⁸ rad/s
K = \(\frac{\omega}{\mathrm{C}}\) = \(\frac{3.14 \times 10^8}{3 \times 10^8}\) = 1.05 rad/m
λ = \(\frac{C}{V}\) = \(\frac{3 \times 10^8}{50 \times 10^6}\) = 6.00 m

b) Expression for \(\overrightarrow{\mathrm{E}}\) is E = E₀ sin (kx – ωt)
= (120 N/c) Sin [(1.05 rad/m) x – (3.14 × 108 rad /s)t] \(\hat{\mathrm{j}}\)
Expression for \(\overrightarrow{\mathrm{B}}\) is B = B₀ sin (kx – ωt)
= (4 × 10^-7 T) sin [(1.05 rad/m) x – (3.14 × 10⁸ rad/s)t] \(\hat{\mathrm{k}}\).

Question 9.
The terminology of different parts of the electromagnetic spectrum is given in the text. Use the formula E = hv (for energy of a quantum of radiation: photon) and obtain the photon energy in units of eV for different parts of the electromagnetic spectrum, in what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation ?
Answer:
Energy of a photon of frequency v is given by E = hv joules = \(\frac{\mathrm{hv}}{1.6 \times 10^{-19} \mathrm{ev}}\)
Where h = 6.6 × 10^-34 J. The energy of photon of different parts of electromagnetic spectrum in joules and eV are shown in table below, along with their sources of origin.

Question 10.
In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0 × 10¹⁰ Hz and amplitude 48 V m^-1.
a) What is the wavelength of the wave ?
b) What is the amplitude of the oscillating magnetic field ?
c) Show that the average energy density of the E field equals the average energy density of the B field. [C = 3 × 10⁸ ms^-1].
Answer:
Here, v = 2.0 × 10¹⁰Hz, E₀ = 48 Vm^-1, C = 3 × 10⁸ m/s

a) wavelength of the wave, λ = \(\frac{C}{v}\) = \(\frac{3 \times 10^8}{2.0 \times 10^{10}}\) = 1.5 × 10^-2 m

b) Amplitude of oscillating magnetic field,
B₀ = \(\frac{E_0}{C}\) = \(\frac{48}{3 \times 10^8}\) = 1.6 × 10^-7T

c) For average energy density
U_E = \(\frac{1}{2} \varepsilon_0 \mathrm{E}_0^2\) …… (1)
We know that \(\frac{E_0}{B_0}\) = C
Putting in Eq (1)
U_E = \(\frac{1}{4} \varepsilon_0 \cdot C^2 \mathrm{~B}_0^2\) …. (2)
Speed of Electro magnetic waves, C = \(\frac{1}{\sqrt{\mu_0 \mathrm{E}_0}}\)
Putting in Eq (2) We get.
U_E = \(\frac{1}{4} \varepsilon_0 B_0^2 \cdot \frac{1}{\mu_0 \varepsilon_0}\)
U_E = \(\frac{1}{4} \cdot \frac{\mathrm{B}_{\mathrm{O}}^2}{\mu_0}=\frac{\mathrm{Bo}^2}{2 \mu_0}\) = μ_B
Thus, the average energy density of E field equals the average energy density of B field.

Additional Exercises

Question 1.
Suppose that the electric field part of an electromagnetic wave in vacuum is E = {(3.1 N/C) cos [(1.8 rad/m) y + {5.4 × 10⁶ rad /s} t]} i.
a) What is the direction of propagation ?
b) What is the wavelength λ ?
c) What is the frequency v ?
d) What is the amplitude of the magnetic field part of the wave ?
e) Write an expression for the magnetic field part of the wave.
Answer:
a) From the given question it is clear that direction of motion of e.m. wave is along negative y direction i.e along – \(\hat{\mathrm{j}}\)

b) Comparing the given question with equation E = E₀ cos (ky + ωt).
We have, K = 1.8 rad/m, ω = 5.4 × 10⁸ rad/s, E₀ = 3.1 N/C
λ = \(\frac{2 \pi}{\mathrm{k}}\) = \(\frac{2 \times(22 / 7)}{1.8}\) = 3.492 m ≈ 3.5m

c) V = \(\frac{\omega}{2 \pi}\) = \(\frac{5.4 \times 10^8}{2 \times\left(\frac{22}{7}\right)}\) = 85.9 × 10⁶ ≈ 86MHz

d) B₀ = \(\frac{\mathrm{E}_0}{\mathrm{C}}\) = \(\frac{3.1}{3 \times 10^8}\) = 1.03 × 10^-8T ≈ 10.3nT

e) B = B0 cos (ky + ωt) \(\hat{\mathbf{k}}\) = (10.3nT) cos [(1.8 rad/m/y + (5.4 × 10⁸ rad / s)t] \(\hat{\mathbf{k}}\)

Question 2.
About 5% of the power of a 100 W light bulb is converted to visible radiation. What is the average intensity of visible radiation
a) at a distance of lm from the bulb ?
b) at a distance of 10 m ?
Assume that the radiation is emitted isotropically and neglect reflection.
Answer:
a) Intensity,

b) I = \(\frac{100 \times(5 / 100)}{4 \pi(10)^2}\) = 4 × 10^-3 W/m²

Question 3.
Use the formula λ_m T = 0.29 cm K to obtain the characteristic temperature ranges for different parts of the electromagnetic spectrum. What do the numbers that you obtain tell you ?
Answer:
We know, every body at given temperature T₁ emits radiations of all wavelengths in certain range. For a black body, the wavelength corresponding to maximum intensity of radiation at a given temperature.
λ_m T = 0.29cmk or T = \(\frac{0.29}{\lambda_{\mathrm{m}}}\)
For λ_m = 10^-6m = 10^-4cm, T = \(\frac{0.29}{10^{-4}}\) = 2900 k.

Temperature for other wavelengths can be similarly found. These numbers tell us the temperature ranges required for obtaining radiations in different parts of e.m spectrum. Thus to obtain visible radiation, say, λ_m = 5 × 10^-5cm, the source should have a temperature
T = \(\frac{0.29}{5 \times 10^{-5}}\) = 6000 k
It is to be noted that, a body at lower temperature will also produce this wavelength but not with maximum intensity.

Question 4.
Given below are some famous numbers associated with electromagnetic radiations in different contexts in physics. State the part of the electromagnetic spectrum to which each belongs.
a) 21 cm (wavelength emitted by atomic hydrogen in interstellar space).
b) 1057 MHz (frequency of radiation arising from two close energy levels in hydrogen; known as Lamb shift).
c) 2.7 K [temperature associated with the isotropic radiation filling all space-thought to be a relic of the ‘big-bang’ origin of the universe].
d) 5890 A – 5896 A [double lines of sodium]
e) 14.4 keV [energy of a particular transition in ⁵⁷Fe nucleus associated with a famous high resolution spectroscopic method (Mossbauer spectroscopy).
Answer:
a) This wavelength corresponds to radiowaves.

b) This frequency also corresponds to radiowaves.

c) Given T = 2.7 K As λ_m T = 0.29cm °k
∴ λ_m = \(\frac{0.29}{\mathrm{~T}}\) = \(\frac{0.29}{2.7}\) ≈ 0.11cm
This wavelength corresponds to microwave region of the electromagnetic spectrum.

d) This wavelength lies in the visible region of the electromagnetic spectrum.

e) Here, Energy E = 14.4KeV = 14.4 × 10³ × 1.6 × 10^-19J
As E = hv
∴ v = \(\frac{E}{h}\) = \(\frac{14.4 \times 10^3 \times 1.6 \times 10^{-19}}{6.6 \times 10^{-34}}\) ≈ 3 × 10¹¹ MHz
This frequency lies in the X-ray region of electromagnetic spectrum.

Question 5.
Answer the following questions :
a) Long distance radio broadcasts use short-wave bands. Why ?
b) It is neccessary to use satellites for long distance TV transmission. Why ?
c) Optical and radio telescopes are built on the ground, but X-ray astronomy is possible only from satellites orbiting the earth. Why ?
d) The small ozone layer on top of the stratosphere is crucial for human survival. Why ?
e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now ?
f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe ‘nuclear winter’ with a devastating effect on life on earth. What might be the basis of this prediction ?
Answer:
a) It is so because ionosphere reflects the waves in these bands.

b) Yes, television signals being of high frequency are not reflected by ionosphere, Therefore to reflect them satellites are needed. That is why, satellites are used for long distance TV transmission.

c) Optical and radiowaves can penetrate the atmosphere where as X-rays being of much smaller wavelength are absorbed by the atmosphere. That is why we can work with optical and radio telescopes on earth’s surface but X-ray astronomical telescopes must be used on the satellite orbiting above the earth’s atmosphere.

d) The small ozone layer present on the top of the stratosphere absorbs most of ultraviolet radiations from the sun which are dangerous and cause genetic damage to living cells, prevents them from reaching the earth’s surface and thus helps in the survival of life.

e) The temperature of earth would be lower because the green house effect of atmosphere would be absent.

f) The clouds by a global nuclear war would perhaps cover most parts of sky preventing solar light from reaching many parts of globe. This would cause a winter.

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 10th Lesson Alternating Current Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 10th Lesson Alternating Current

Very Short Answer Questions

Question 1.
A transformer converts 200 V ac into 2000 V ac. Calculate the number of turns in the secondary if the primary has 10 turns. (A.P. Mar.’19; T.S. Mar. ’16 )
Answer:
\(\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{p}}}\) = \(\frac{N_s}{N_p}\)
V_p = 200V, V_s = 2000V, N_p = 10
N_s = \(\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{p}}} \times \mathrm{N}_{\mathrm{p}}\) = \(\frac{2000}{200} \times 10\)
N_s = 100.

Question 2.
What type of transformer is used in a 6V bed lamp ?
Answer:
Step down transformer is used in 6V bed lamp.

Question 3.
What is the phenomenon involved in the working of a transformer ? (T.S. Mar.19; A.P. Mar. 16, Mar. 14)
Answer:
Transformer works on the principle of mutual induction.

Question 4.
What is transformer ratio ?
Answer:
The ratio of secondary e.m.f to the primary e.m.f. (or) number of turns in secondary to the number of turns in the primary is called the transformer ratio.
Transformer ratio = \(\frac{V_s}{V_p}\) = \(\frac{N_s}{N_p}\).

Question 5.
Write the expression for the reactance of

1. an inductor and
2. a capacitor.

Answer:

1. Inductive reactance (X_L) = ωL
2. Capacitive reactance (X_C) = \(\frac{1}{\omega C}\)

Question 6.
What is the phase difference between A.C emf and current in the following: Pure resistor, pure inductor and pure capacitor.
Answer:

1. In pure resistor A.C. e.in.f and current are in phase with each other.
2. In pure inductor, current lags behind the e.m.f. by an angle of \(\frac{\pi}{2}\) (or) 90°.
3. In pure capacitor, current leads the e.m.f by an angle \(\frac{\pi}{2}\) (or) 90°.

Question 7.
Define power factor. On which factors does power factor depend ?
Answer:
The ratio of true power and apparent power (virtual power) in an a.c circuit is called as power factor of the circuit.
Power factor (cosϕ) = \(\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{rms}}}\). (∴ P_rms = V_rmsI_rms)
Power factor depends on r.m.s voltage, r.m.s current and average power (P).

Question 8.
What is meant by wattless component of current ?
Answer:
Average power (P) = V_rms(I_rms sinϕ)cos \(\frac{\pi}{2}\)
The average power consumed in the circuit due to I_rms sin ϕ) component of current is zero. This component of current is known as wattless current. (I_rms sin ϕ) is the wattless component of current.

Question 9.
When does a LCR series circuit have minimum impedance?
Answer:
In LCR series circuit, Impedance (Z) = \(\sqrt{R^2+\left(\frac{1}{\omega C}-\omega L\right)^2}\)
At a particular frequency, ωL = \(\frac{1}{\omega C}\)
The impedance is minimum (Z = R)
This frequency is called resonant frequency

Question 10.
What is the phase difference between voltage and current when the power factor in LCR series circuit is unity ?
Answer:
In LCR series circuit power factor (cos ϕ) = 1
∴ Phase difference between voltage and current is zero. (ϕ = 0)

Short Answer Questions

Question 1.
Obtain an expression for the current through an inductor when an AC emf is applied.
Answer:
Circuit consists of pure inductor of inductance L. Let an ac e.m.f V = V_m sin ωt is applied to it. Let i be the instantaneous current.
Back e.m.f developed across the inductor = -L\(\frac{\mathrm{di}}{\mathrm{dt}}\)

Total e.m.f = V_m sin ωt – L\(\frac{\mathrm{di}}{\mathrm{dt}}\) ——- (1)
According to ohms law this must be equal to iR = 0

This is the expression for the instantaneous current through inductor. Here current lags behind the e.m.f by \(\frac{\pi}{2}\) radian (or) 90°.

Question 2.
Obtain an expression for the current in a capacitor when an AC emf is applied.
Answer:
Circuit consists of pure capacitor of capacitance C. Let an A.C emf V = V_m sin ωt is applied to it. Let i and q be the instantaneous values of current and charge.
Potential difference across capacitor = –\(\frac{\mathrm{q}}{\mathrm{C}}\).
Total emf = V_m sin ωt –\(\frac{\mathrm{q}}{\mathrm{C}}\)

According to Ohms law this must be equal to iR = 0
V_m sin ωt –\(\frac{\mathrm{q}}{\mathrm{C}}\) = 0

i₀ is peak value of current. Here the current leads the applied e.m.f. by \(\frac{\pi}{2}\) or (or) 90°

Question 3.
State the principle on which a transformer works. Describe the working of a transformer with necessary theory.
Answer:
Transformer is a device to convert a low alternating current of high voltage into high alternating current of low voltage and vice versa.
Principle : It works on the principle of mutual induction between two coils.
Working : When an alternating emf is applied across the primary coil, the input voltage changes with time. Hence the magnetic flux through the primary also changes with time.
This changing magnetic flux will be linked with secondary through the core. An emf is induced in the secondary.

Theory: Let N₁ and N₂ be the number of turns in the primary and secondary. Let V_P and Vs be the emf s across the primary and secondary.

Efficiency of transformer:
It is the ratio of output power to the input power.

Long Answer Questions

Question 1.
Obtain on expression for impedance and current in series LCR circuit. Deduce an expresssion for the resonating frequency of an LCR series resonating circuit
Answer:
Circuit consists of resistor of resistance R, inductor of inductance L and capacitor of capacitance C connected in series with an a.c Voltage V = V_m sin ωt.
Let i be the current and q be the charge at any instant t.

Back e.m.f across inductor is -L\(\frac{\mathrm{di}}{\mathrm{dt}}\)
and across capacitor is \(\frac{-\mathrm{q}}{\mathrm{C}}\)
Total e.m.f = V_m sin ωt – L\(\frac{\mathrm{di}}{\mathrm{dt}}\) – \(\frac{\mathrm{q}}{\mathrm{C}}\)
According to Ohms law, this must be equal to iR
V_m sinωt – L\(\frac{\mathrm{di}}{\mathrm{dt}}\) – \(\frac{q}{C}\) = iR
L\(\frac{\mathrm{di}}{\mathrm{dt}}\) + iR + \(\frac{q}{C}\) = V_m sin ωt ——- (1)
The current i any instant in the circuit is
i = i_m sin(ωt – ϕ) if ωL > \(\frac{1}{\omega \mathrm{C}}\) which is possible at high frequencies.
i = i_m sin (ωt + ϕ) if ωL which is possible at low frequencies.
The maximum current (i_m) is given by

Let ϕ be the phase difference between current and e.m.f

Resonant frequency(f₀):
At this frequency, the impedance of LCR circuit is minimum and is equal to R. At this frequency current is maximum This frequency is called resonant frequency (f₀).

In frequency response curve, at resonant frequency (f₀), current is maximum. This series resonant circuit is called acceptor circuit.

Problems

Question 1.
An ideal inductor (no internal resistance for the coil) or 20 mH is connected in series with an AC ammeter to an AC source whose emf is given by e = 20\(\sqrt{2}\) sin(200t + π/3)V, where t is in seconds. Find the reading of the ammeter ?
Solution:
Given that L = 20 mH = 20 × 10^-3H

Question 2.
The instantaneous current and instantaneous voltage across a series circuit containing resistance and inductance
are given by i = \(\sqrt{2}\) sin (100t – π/4)A and υ = 40 sin (100t) V. Calculate the resistance ?
Solution:
i = \(\sqrt{2}\) sin (100t – π/4)A
(∵ i = i₀ sin(ωt – ϕ))
υ = 40 sin (100t)V (∵ V = V₀sin(ωt))
i₀ = \(\sqrt{2}\), V₀ = 40, ω = 100, ϕ = π/4
R = \(\frac{\mathrm{V}_0}{\mathrm{i}_0} \cos \phi\) = \(\frac{40}{\sqrt{2}} \cos \frac{\pi}{4}\)
R = \(\frac{40}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\)
R = 20Ω

Question 3.
In an AC circuit, a condenser, a resistor and a pure inductor are connected in series across an alternator (AC generator). If the voltages across them are 20 V, 35 V and 20 V respectively, find the voltage supplied by the alternator.
Solution:
V_C = 20V, V_R = 35V, V_L = 20V
V = \(\sqrt{\mathrm{V}_{\mathrm{R}}^2+\left(\mathrm{V}_{\mathrm{L}}^2-\mathrm{V}_{\mathrm{C}}^2\right)}\)
V = \(\sqrt{(35)^2+\left(20^2-20^2\right)}\)
V = \(\sqrt{35^2}\)
V = 35 Volt.

Question 4.
An AC circuit contains a resistance R, an inductance L and a capacitance C connected in series across an alternator of constant voltage and variable frequency. At resonant frequency, it is found that the inductive reactance, the capacitive reactance and the resistance are equal and the current in the circuit
is i₀. Find the current in the circuit at a frequency twice that of the resonant frequency.
Solution:
At Resonance R = ω₀L = \(\frac{1}{\omega_0 C}\)

Question 5.
A series resonant circuit contains L₁, R₁ and C₁. The resonant frequency is f. Another series resonant circuit contains L₂, R₂ and C₂. The resonant frequency is also f. If these two circuits are connected in series, calculate the resonant frequency.
Solution:
Given that resonant frequency (f)
= \(\frac{1}{2 \pi \sqrt{\mathrm{L}_1 C_1}}\) = \(\frac{1}{2 \pi \sqrt{\mathrm{L}_2 \mathrm{C}_2}}\)
L₁C₁ = L₂C₂
L₁ = \(\frac{\mathrm{L}_2 \mathrm{C}_2}{\mathrm{C}_1}\) —— (1)
When these two circuits are connected in series
The total inductance L = L₁ + L₂
Total capacitance is given by
\(\frac{1}{\mathrm{C}}\) = \(\frac{1}{C_1}\) + \(\frac{1}{C_2}\) (or) C = \(\frac{\mathrm{C}_1 \mathrm{C}_2}{\mathrm{C}_1+\mathrm{C}_2}\)
The resonant frequency of combined circuit is given by

Question 6.
In a series LCR circuit R = 200Ω and the voltage and the frequency of the mains supply is 200 V and 50 Hz respectively. On taking out the capacitance from the circuit the current lags behind the voltage by 45°. On taking out the inductor from the circuit the current leads the voltage by 45°. Calculate the power dissipated in the LCR circuit.
Solution:
R = 200Ω, V = 200V, f = 50Hz
ϕ = 45°, At resonance ωL = \(\frac{1}{\omega \mathrm{C}}\)
Power dissipated (P) = Vi = \(\frac{\mathrm{V}^2}{\mathrm{R}}\) (∵ i = \(\frac{V}{R}\))
P = \(\frac{(200)^2}{200}\) = 200ω

Question 7.
The primary of a transformer with primary to secondary turns ratio of 1: 2, is connected to an alternator of voltage 200 V. A current of 4A is flowing though the primary coil. Assuming that the transformer has no losses, find the secondary voltage and current are respectively.
Solution:
Given that \(\frac{\mathbf{N}_1}{\mathbf{N}_2}\) = \(\frac{1}{2}\)
E₁ = 200V, i₁ = 4A

i)
Transformer ratio = \(\frac{E_2}{E_1}\) = \(\frac{\mathrm{N}_2}{\mathrm{~N}_1}\)
\(\frac{E_2}{200}\) = \(\frac{2}{1}\)
E₂ = 400V

ii)
\(\frac{\mathrm{N}_2}{\mathrm{~N}_1}\) = \(\frac{i_1}{i_2}\)
\(\frac{2}{1}\) = \(\frac{4}{i_2}\)
i₂ = 2A

Textual Exercises

Question 1.
A 100Ω resistor is connected to a 220 V. 50 Hz ac supply.
(a) What is the rms value of current in the circuit ?
(b) What is the net power consumed over a full cycle ?
Solution:
Given resistance R = 100Ω
V_rms = 220V
Frequency f = 50Hz

a) Current in the circuit
I_rms = \(\frac{V_{r m s}}{R}\) = \(\frac{220}{100}\) = 2.2A

b) Net power consumed in full cycle
P = V_rms × I_rms
= 220 × 2.2
= 474 W

Question 2.
(a) The peak voltage of an ac supply is 300 V. What is the rms voltage ?
(b) The rms value of current in an ac circuit is 10A. What is the peak current ?
Solution:
a) Given, peak value of voltage V₀ = 300V
The rms value of current I_rms = 10A
The rms value of voltage
V_rms = \(\frac{\mathrm{V}_0}{\sqrt{2}}\) = \(\frac{300}{\sqrt{2}}\) = 212.1V

b) Using the formula
I_rms = \(\frac{\mathrm{I}_0}{\sqrt{2}}\)
The peak value of current
I₀ = \(\sqrt{2} \times \mathrm{I}_{\mathrm{rms}}\)
= \(\sqrt{2}\) × 10 = 1.414 × 10
I₀ = 14.14 A

Question 3.
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. Determine the rms value of current in the circuit.
Solution:
Given inductance
L = 44mH = 44 × 10^-3H
V_rms = 220V
Frequency of Inductor f = 50Hz
Inductive resistance X_L = 2πfL
= 2 × 3.14 × 50 × 44 × 10^-3
= 13.83Ω
The rms value of current in the circuit
I_rms = \(\frac{V_{\text {rms }}}{X_L}\) = \(\frac{220}{13.83}\)15.9A

Question 4.
A 60 μF capacitor is connected to a 110V, 60 Hz ac supply. Determine the rms value of the current in the circuit.
Solution:
Given, capacitance of the capacitor C
= 60μF
= 60 × 10^-6F
V_rms = 110
Frequency of AC supply f = 60Hz
Capacitive reactance
X_C = \(\frac{1}{2 \pi \mathrm{fC}}\) = \(\frac{1}{2 \times 3.14 \times 60 \times 60 \times 10^{-6}}\)
= 44.23Ω
The rms value of current in the circuit
V_rms = \(\frac{\mathrm{V}_{\mathrm{rms}}}{\mathrm{X}_{\mathrm{C}}}\) = \(\frac{110}{44.23}\) = 2.49A

Question 5.
In Exercises 3 and 4, what is the net power absorbed by each circuit over a complete cycle. Explain your answer.
Solution:
In Exercise 3 Average power P = V_rms, I_rms. cos ϕ

As we know that the phase difference between current and voltage in case of inductor is 90°.
P = V_rms. I_rms. cos 90° = 0
In Exercise 4 Average power
P = V_rms. I_rms. cos ϕ
We know that the phase difference between current and voltage in case of capacitor is 90°
P = V_rms. I_rms. cos 90° = 0

Question 6.
Obtain the resonant frequency ω_r of a series LCR circuit with L = 2.0H. C = 32 μF and R = 10Ω. What is the Q-value of this circuit ?
Solution:
Given, L = 2H, C = 32μF, R = 10Ω
Resonant angular frequency

Question 7.
A charged 30 μF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit ?
Solution:
Capacitance of capacitor C = 30μF = 30 × 10^-6F
Inductance L = 27mH = 27 × 10^-3H
For free oscillations, the angular frequency should be resonant frequency. Resonant angular frequency of oscillation of the circuit

Question 8.
Suppose the initial charge on the capacitor in Exercise 7 is 6 mC. What is the total energy stored in the circuit initially ? What is the total energy at later time ?
Answer:
Given, charge on the capacitor Q = 6mC = 6 × 10^-3
C = 30μF = 30 × 10^-6F
Energy stored in the circuit
E = \(\frac{Q^2}{2 C}\) = \(\frac{\left(6 \times 10^{-3}\right)^2}{2 \times 30 \times 10^{-2}}\) = \(\frac{36}{60}\) = 0.6J
After some time, the energy is shared between C and L, but the total energy remains constant.
So, we assume that there is no loss of energy.

Question 9.
A series LCR circuit with R = 20Ω, L = 1.5 H and C = 35µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle ?
Given resistance R = 200Ω
Inductance L = 1.5H, capacitance C = 35µF = 35 × 10^-6F and voltage V_rms = 200V
When, the frequency of the supply equal to the natural frequency of the circuit, this is the condition of resonance. At the condition of resonance, Impedance Z = R = 20Ω
The rms value of current in the circuit
I_rms = \(\frac{V_{r m s}}{Z}\) = \(\frac{200}{20}\) = 10A
ϕ = 0°
Power transferred to the circuit in one complete cycle.
P = I_rms V_rms cos ϕ
= 10 × 200 × cos0° = 2000 ω = 2Kω

Question 10.
A radio can tune over the frequency range o a portion of MW broadcast band: (800 kHz to 1200 kHz). If its LC circuit has an effective inductance of 200 μH, what must be the range of its variable capacitor?

(Hint: For tuning, the natural frequency i.e., the frequency of free oscillations of the LC circuit should be equal to the frequency of the radiowave.)
Solution:
Given, minimum frequency
f₁ = 800KHz = 8 × 10⁵HZ
Inductance
L = 200μH = 200 × 10^-5H = 2 × 10^-4H.
Maximum frequency
f₂ = 1200 KHz = 12 × 10⁵Hz for tuning, the natural frequency is equal to the frequency of oscillations that means it is the case of resonance.
Frequency of oscillations f = \(\frac{1}{2 \pi \sqrt{L C}}\)
For capacitance C₁, f₁ = \(\frac{1}{2 \pi \sqrt{L C_i}}\)
C₁ = \(\frac{1}{4 \pi^2 \mathrm{f}_1^2 \mathrm{~L}}\)
= \(\frac{1}{4 \times 3.14 \times 3.14 \times\left(8 \times 10^5\right)^2 \times 2 \times 10^{-4}}\)
= 197.7 × 10^-12F
= 197.7PF
for capacitance C₂, f₂ = \(\frac{1}{2 \pi \sqrt{L C_2}}\)
C₂ = \(\frac{1}{4 \pi^2 f_1^2 \mathrm{C}}\)
= \(\frac{1}{4 \times 3.14 \times 3.14 \times\left(12 \times 10^5\right)^2 \times 2 \times 10^{-4}}\)
= 87.8 × 10^-12F = 87.8pF
Thus, the range of capacitor is 87.8pF to 197.7pF.

Question 11.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80μF, R = 40Ω.

(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
Solution:
Given, the rms value of voltage
V_rms = 230V
Inductance L = 5H
Capacitance C = 80μf = 80 × 10^-6F
Resistance R = 40Ω

a) For resonance frequency of circuit
ω_r = \(\frac{1}{\sqrt{\mathrm{LC}}}\) = \(\frac{1}{\sqrt{5 \times 80 \times 10^{-6}}}\) = 50 rad/s
Source frequency at resonance, then
υ₀ = \(\frac{\omega_0}{2 \pi}\) = \(\frac{50}{2 \times 3.14}\) = 7.76 Hz

b) At the resonant frequency, X_L = X_C
So, impedance of the circuit Z = R
∴ Impedance Z = 40Ω
The rms value of current in the circuit
I_rms = \(\frac{V_{r m s}}{Z}\) = \(\frac{230}{40}\) = 5.75A
Amplitude of current I₀ = I_rms\(\sqrt{2}\)
= 5.75 × \(\sqrt{2}\)
= 8.13A

c) The rms potential drop across L
V_L = I_rms X_L
= I_rms ω_rL = 5.75 × 50 × 5 = 1437.5V
The rms potential drop across R
V_R = I_rms = R = 5.75 × 40 = 230V
The rms potential drop across C,

Potential drop across LC combinations
= I_rms(X_L – X_C)
= I_rms(X_L – X_L) = 0 (∵ X_L – X_C)

Additional Exercises

Question 1.
An LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during LC oscillations ?
(b) What is the natural frequency of the circuit ?
(c) At What time is the energy stored
(i) Completely electrical (i.e., stored in the capacitor) ?
(ii) completely magnetic (i.e., stored in the inductor) ?
(d) At what times is the total energy shared equally between the inductor and the capacitor ?
(e) As a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?
Solution:
Given Inductance L = 20mH = 20 × 10^-3H
Capacitance of capacitor
C = 50μf = 50 × 10^-6F
Initial charge on the capacitor,
Q_i = 10mc = 10 × 10³C

a) The total energy stored across the capacitor initially,

Yes, this energy is conserved during LC oscillations.

b) To get the natural frequency or resonant frequency,
f_r = \(\frac{1}{2 \pi \sqrt{L C}}\)
= \(\frac{1}{2 \times 3.14 \times \sqrt{20 \times 10^{-3} \times 50 \times 10^{-6}}}\)
= \(\frac{7 \times 10^3}{44}\) = 159.2 Hz.
The natural frequency of the circuit
ω = 2πV = 2π × 159.2
= 999.78 ≈ 1000 = 10³ rad/s

c)

i) Let at any instant the energy stored is completely electrical the charge on the capacitor Q = Q₀ cos ωt
Q = Q₀ cos \(\frac{2 \pi}{T} \cdot t\) —– (1)
Q is maximum as it is equal to Q₀, only if cos \(\frac{2 \pi}{T}\) t = ±1 = cosnπt or t
= \(\frac{\mathrm{nT}}{2}\), where n = 1, 2, 3. ..
t = 0, T/2, T, 3T/2, ………..
Thus, the energy stored is completely electrical at t = 0, T/2, T, 3/2……….

ii) Let at any instant, the energy stored is completely magnetic as when the electrical energy across the capacitor is zero.
q = 0
Q = Q₀cos \(\frac{2 \pi t}{T}\) = 0 (from eq(i))
∴ cos \(\frac{2 \pi}{T} \cdot t\) = 0 = \(\frac{\mathrm{n} \pi}{2}\) or t = \(\frac{\mathrm{nT}}{4}\) = cos.
It happens if t = T/4, 3T/4, \(\frac{\mathrm{5T}}{4}\),………..
Thus, the energy stored is completely magnetic at
t = T/4, 3T/4, 5T/4………..

d) Equal sharing of energy between inductor and capacitor means the energy stored in capacitor = \(\frac{1}{2}\) × Maximum energy

or cos(2n + 1)π/4 = cos \(\frac{2 \pi \mathrm{t}}{\mathrm{T}}\)
\(\frac{(2 n+1) \pi}{4}\) = \(\frac{2 \pi t}{T}\)
t = T/8(2n + 1) (n = 0, 1, 2, 3, ……..)
Hence the energy will be shared half on capacitor and half on inductor.
t = \(\frac{T}{8}\), \(\frac{3 \mathrm{~T}}{8}\), \(\frac{5 \mathrm{~T}}{8}\), ………..

e) As a resistor is inserted in the circuit, all of the energy loss during heating. Energy loss = 1J. The oscillations becomes damped and becomes disappear after sometime as the total energy loss in the form of heat.

Question 2.
A coil of inductance 0.50 H and resistance 100Ω is connected to a 240 V, 50Hz ac supply.
a) What is the maximum current in the coil ?
b) What is the time lag between the voltage maximum and the current maximum ?
Solution:
Given, Inductance L = 0.50H
Resistance R = 100Ω
The rms value of voltage
V_rms = 240V, f = 50Hz

a) Impedance of circuit

the rms value of current
I_rms = \(\frac{\mathrm{V}_{\mathrm{rms}}}{\mathbf{Z}}\) = \(frac{240}{31400.15}\) = 0.00764
the maximum value of current in the circuit
I₀ = \(\sqrt{2}\) I_rms = 1.414 × 0.00764 = 1.824A

b) Using the formula of time lag,
t = \(\frac{\phi}{\omega}\)
tan ϕ = \(\frac{X_L}{R}\) = \(\frac{\omega \mathrm{L}}{\mathrm{R}}\) = \(\frac{2 \pi \mathrm{fL}}{\mathrm{R}}\) = \(\frac{2 \times 3.14 \times 50 \times 0.50}{100}\)
ϕ = tan^-6(1.571) = 57.5

Time lag t = \(\frac{\phi}{\omega}\) = \(\frac{57.5 \pi}{180 \times 2 \pi \mathrm{f}}\)
= \(\frac{57.5}{180 \times 2 \times 50}\)
= 3.19 × 10^-3S
Thus, the time lag between the voltage maximum and the current maximum is 3.19 × 10^-3S

Question 3.
Obtain the answers (a) to (b) in Exercise 13 if the circuit is connected to a high frequency supply (240V, 10 kHz). Hence, explain the statement that at very high frequency an inductor in a circuit nearly amounts to an open circuit. How does an inductor behave in a dc circuit after the steady state?
Answer:
Given frequency f = 10kHz = 10⁴Hz
the rms value of voltage V_rms = 240v
from Exercise 13
Resistance R = 100Ω
Inductance L = 0.5H

Question 4.
A 100μF capacitor in series with a 40Ω resistance is connected to a 110V. 60 Hz supply.
(a) What is the maximum current in the circuit?
(b) What is the time lag between the current maximum and the voltage maximum?
Answer:
Given capacitance of capacitor
C = 100µF= 100 × 10^-6F
Resistance R = 40Ω
the rms value of voltage V_rms = 110V
Frequency f = 60Hz

(a) Impedance Z

(b) Time lag (t) = \(\frac{\phi}{\omega}\)

Thus, the time lag between the voltage maximum and the current maximum is 1.55 × 10^-3S.

Question 5.
Obtain the answers to (a) and (b) in Exercise 15 if the circuit is connected to a 110 V, 12 kHz supply? Hence, explain the statement that a capacitor is a conductor at very high frequencies. Compare this behaviour with that of a capacitor in a dc circuit after the steady state.
Answer:
Given, the rms value of voltage,
V_rms = 110V
The frequency of capacitor
f = 12kHz = 12000 Hz.
Capacitance of conductor C = 10^-4F.
Resistance R = 40Ω
Capacitive Resistance
X_C = \(\frac{1}{2 \pi \mathrm{fC}}\) = \(\frac{1}{2 \times 3.14 \times 12000 \times 10^{-4}}\)
= 0.133Ω
The rms value of current

The maximum value of current,
I₀ = \(\sqrt{2}\) I_rms
= 1.414 × 2.75
= 3.9A
Here, the value of X_C is very small, so term containing C is negligible.
tan ϕ = \(\frac{1}{\omega \mathrm{CR}}\)
= \(\frac{1}{2 \times 3.14 \times 12000 \times 10^{-4} \times 40}\)
= \(\frac{1}{96 \pi}\)
It is very very small.
In DC circuits, ω = 0
X_C = \(\frac{1}{\omega C}\) = ∞
So, it behaves like an open circuit.

Question 6.
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified in Exercise 11 for this frequency.
Solution:
As they are corrected in the parallel combination
\(\frac{1}{Z}\) = \(\frac{1}{R}\) + (\(\frac{1}{X_L}\) + \(\frac{1}{X_C}\))
As the reactance (X_C – X_L) is perpendicular to the ohmic resistance R, therefore we can write as

That means \(\frac{1}{Z}\) = minimum and thus Z = maximum. As Z is maximum, current will be minimum, current through inductor

Question 7.
A circuit containing a 80 mH inductor and a 60μF capacitor in series is connected to a 230 V 50 Hz supply. The resistance of the circuit is negligible.
(a) Obtain the current amplitude and rms values.
(b) Obtain the rms values of potential drops across each element.
(c) What is the average power transferred to the inductor?
(d) What is the average power transferred to the capacitor?
(e) What is the total average power absorbed by the circuit? [‘Average’ implies ‘averaged over one cycle’]
Answer:
Given Inductance
L = 80mH = 80 × 10^-3H
Capacitance of capacitor
C = 60μF = 60 × 10^-6F .
The rms value of voltage
V_rms = 230V
Frequency f = 50Hz; Resistance R = 0

a) Impedance of circuit

As ZCO, means X_L < X_C, emf lags by current by 90°
The rms value of current
I_rms = \(\frac{\mathrm{V}_{\mathrm{rms}}}{\mathrm{Z}}\) = \(\frac{230}{27.95}\) = 8.29A
The maximum value of current
I₀ = \(\sqrt{2} I_{\text {rms }}\) = 1.414 × 8.29 = 11.64A

b) Potentiál drop acrõss L
V_rmsL = I_rms × X_L = 8.29 × 2 × 3.14 × 50 × 80 × 10^-3
= 208.25 V
Potential drop across C
V_rmsC = I_rms × X_C
= 8.29 × \(\frac{1}{2 \times 3.14 \times 50 \times 60 \times 10^{-6}}\)
= 440.02 V
∴ Applied rms voltage = V_C – V_L
= 440 – 208.25 = 231.75V

c) Average power transferred to the inductor
P = I_rms V_rms. cosϕ
As the phase difference is 90°, So P = 0

d) Average power transferred to the capacitor.
P = I_rms V_rms. cosϕ
As the phase difference is 90°, So P = 0

e) As there is no resistance in the circuit, so average power is equal to sum of average power due to inductor and capacitor. That means the average power consumed is zero.

Question 8.
Suppose the circuit in Exercise 18 has a resistance of 15Ω. Obtain the average power transferred to each element of the circuit, and the total power absorbed.
Solution:
Given, the rms value of voltage V = 230V
V_rms = 230V
Resistance R = 15Ω
Frequency f = 50Hz
Average power across inductor and capacitor is zero as the phase difference between current and voltage is 90°.
Total power absorbed = power absorbed in resistor, P_av

Total power absorbed = 790.6W

Question 9.
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23Ω is connected to a 230 V variable frequency supply.
a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency ? what is the current amplitude at these frequencies ?
d) What is the Q-factor of the given circuit ?
Answer:
Inductance L = 0.12H,
Capacitance C = 480nF = 480 × 10^-9F
Resistance R = 23Ω
The rms value of voltage
I_rms = \(\frac{V_{r m s}}{Z}\) = \(\frac{230}{23}\) = 10A
The maximum value of current I₀ = \(\sqrt{2}\)
I_rms = 1.414 × 10 = 14.14A.
At natural frequency, the current amplitude is maximum.
ω = \(\frac{1}{\sqrt{\mathrm{LC}}} \frac{1}{2 \pi \sqrt{0.12 \times 480 \times 10^{-9}}}\) = 4166.6
= 4167 rad/s

b) Average power is maximum for resonance.
P_av(max) = I²_rms R = 10 × 10 × 23 = 2300W.

c) Power transferred to the circuit is half the power at resonant frequency
Δω = \(\frac{\mathrm{R}}{2 \mathrm{~L}}\) = \(\frac{23}{2 \times 0.12}\) = 95.83 rad/s
ΔV = \(\frac{\Delta \mathrm{W}}{2 \pi}\) = 15.2Hz
The frequencies at which power transferred is half .
V = V₀ ± ΔV = 663.48 ± 15.26
So, frequencies are 448.3Hz and 678.2Hz, the maximum current
I = \(\frac{\mathrm{I}_0}{\sqrt{2}}\) = \(\frac{14.14}{\sqrt{2}}\) = 10A

d) Q-factor = \(\frac{\omega_{\mathrm{r}}}{\mathrm{R}}\) = \(\frac{4166.7 \times 0.12}{23}\) = 21.74

Question 10.
Obtain the resonant frequency and Q-factor of series LCR circuit with L = 3.0 H, C = 27μF, and R = 10.4Ω. It is desired to improved the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.
Solution:
Given, inductance L = 3H
Capacitance of capacitor
C = 27μF = 27 × 10^-6F
Resistance R = 7.4Ω
the resonant frequency of circuit
ω_r = \(\frac{1}{\sqrt{\mathrm{LC}}}\) = \(\frac{1}{\sqrt{3 \times 27 \times 10^{-6}}}\) = \(\frac{1000}{9}\)
= 111.1 rad/s.
Q-factor of a series LCR circuit
Q-factor = \(\frac{\omega_{\mathrm{r}} \mathrm{L}}{\mathrm{R}}\) = \(\frac{111.1 \times 3}{7.4}\) = 45.04
To reduce the full width at half by factor Q, we have to reduce the value of R as R/2
\(\frac{R}{2}\) = \(\frac{7.4}{2}\) = 3.7Ω

Question 11.
Answer the following questions :
a) In any ac circuit, is the applied Instantaneous voltage equal to the algebraic sum of the instantaneous voltages across the series elements of the circuit ? Is the same true for rms voltage ?
Answer:
Yes, the applied voltage equal to the algebraic sum of the instantaneous voltages across the series elements of the circuit
No, it is not true for rms voltage because there is some phase differences across different elements of circuits.

b) A capacitor is used in the primary circuit of an induction coil.
Answer:
A capacitor is used in the primary circuit of an induction coil because when the circuit is broken, a large induced voltage is used up in charging the capacitor. So, the parking or any damages are avoided.

c) An applied voltage signal consists of a superposition of a dc voltage and an ac voltage of high frequency. The circuit consists of an inductor and a capacitor in series. Show that the dc signal will appear across C and the ac signal across L.
Solution:
As we know that
X_C = \(\frac{1}{2 \pi f c}\), X_L = 2πfL
f = 0, X_C = ∞, X_L = 0

d) A choke coil in series with a lamp is connected to a dc line. The lamp is seen to shine brightly. Insertion of an Iron core in the choke causes no change in the lamp’s brightness. Predict the corresponding observations if the connection is to an ac line.
Answer:
When the choke coil is connected to dc, there is no change in the brightness. Because f = 0, X_L = 6. So, no change in the brightness. In Ac, the choke offers impedance, so, it glows dim. As we insert an iron core the magnetic field increases and hence inductance increases.
BA = LI = ϕ
L ∝ B
So, X_L also increases and the brightness of bulb decreases.

e) Why is choke coil needed in the use of fluorescent tubes with ac mains ? Why can we not use an ordinary resistor instead of the choke coil ?
Answer:
We use the choke coil instead of resistance because the power loss across resistor is maximum while the power loss across choke is zero.
For resistor, ϕ = 0
P = I_rms. V_rms. cos ϕ
= I_rms. V_rms = maximum
For Inductor ϕ = 90°
P = I_rms. V_rms. cos 90° = 0

Question 12.
A power transmission line feeds input power at 2300 V to a stepdown transformer with its primary windings having 4000 turns, what should be the number of turns in the secondary in order to get output power at 230 V ?
Solution:
Given Primary voltage V_P = 2300V N_P = 4000 turns
Secondary voltage V_S = 230V
Using formula,
\(\frac{\mathrm{V}_{\mathrm{S}}}{\mathrm{V}_{\mathrm{P}}}\) = \(\frac{N_S}{N_P}\)
\(\frac{230}{2300}\) = \(\frac{\mathrm{N}_{\mathrm{S}}}{4000}\)
N_S = 400
∴ thus, the number of turns in secondary are 400.

Question 13.
At a hydroelectric power plant, the water, pressure head is at a height of 300 m and the water flow available is 100 m³s^-1. If the turbine generator efficiency is 60%, estimate the electric power available from the plant (q = 9.8 ms^-2).
Answer:
Given, height of water h = 300m
Rate of flow of water V = 100m³/s
efficiency η = 60%
g = 9.8m/s².
As we know that input power is required to raised the water up to height
h = 300 m

Suppose, the power output is P_out which is equal to the power available from the plant. The efficiency of generator
η = \(\frac{P_{\text {out }}}{P_{\text {in }}}\)

p_out = 176.4MW = 1764 × 10⁵W

Question 14.
A small town with a demand of 800 kW of electric power at 220 V is situated 15 km away from an electric plant generating power at 440 V. The resistance of the two wire line carrying power in 0.5 Ω per km. The town gets power from the line through a 4000 – 220V step-down transformer at a substation in the town.
(a) Estimate the line power loss in the form of heat.
(b) How much power must the plant supply, assuming there is negligible power loss due to leakage ?
(c) Characterise the step up transformer at the plant.
Answer:
Generating power of Electric plant = 800 kW at V = 220V
Distance = 15km,
Generating voltage = 440V
Resistance/length = 0.50Ω/km
Primary voltage V_P = 4000V
Secondary voltage V_S = 220V
(a) Power = I_p. V_p
800 × 1000 = I_p × 4000
I_p = 200A
Line power loss in form of heat
= (I_p)² × Resistance of line
= (I_p)² × 0.5 × 15 × 2
= (200)² × 0.5 × 15 × 2
= 60 × 10⁴W
= 600KW

(b) If there is no power loss due to leakage the plant supply should be =
800 + 600 = 1400KW

(c) Voltage drop across the line
= I_P. R
= 200 × 0.5 × 15 × 2
= 3000V
Voltage from transmission
= 3000 + 4000 = 7000V
As it is given that the power generated at 440V
So, the step-up transformer needed at the plant is 440V – 7000V

Question 15.
Do the same exercise as above with the replacement of the earlier transformer by a 40,000-220V step-down transformer (Neglect, as before, leakage losses though this may not be a good assumption any longer because of the very high voltage transmission involved). Hence, explain why high voltage transmission is preferred ?
Answer:
Given primary voltage V_P = 40,000V
Let the current in primary is I_P
∴ V_PI_P = P
800 × 1000 = 40000 × I_P
I_P = 20A
a) Line power loss = (I_P)² × R
= (20)² × 2 × 0.5 × 15
= 6000W = 6KW

b) Power supply by plant
= 800 + 6 = 806KW

Voltage drop of line = I_P.R
= 20 × 2 × 0.5 × 15
= 300V
Voltage for transmission
= 40000 + 300 = 40300V
Power loss at higher voltage
= \(\frac{6}{800}\) × 100 = 0.74%
Power loss at lower voltage
= \(\frac{600}{1400}\) × 100 = 42.8%
Hence, the power loss is minimum at higher voltage. So, the high voltage transmission is preferred.

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 9th Lesson Electromagnetic Induction Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 9th Lesson Electromagnetic Induction

Very Short Answer Questions

Question 1.
What did the experiments of Faraday and Henry show?
Answer:
The discovery and understanding of electromagnetic induction are based on a long series of experiments carried out by Faraday and Henry.

Question 2.
Define magnetic flux.
Answer:
Magnetic flux is defined as the number of magnetic lines of force crossing through the surface.
ϕ_B = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}\) = BA cos θ
C.G.S unit → Maxwell
S.I. unit → Weber (wb)
Magnetic flux is a scalar.

Question 3.
State Faraday’s law of electromagnetic induction.
Answer:
“Magnitude of induced e.m.f is directly proportional to the rate of change of magnetic flux”
ε ∝ \(-\frac{d \phi}{d t}\)

Question 4.
State Lenz’s law.
Answer:
The direction of induced e.m.f (or) current is such that it opposes the cause which produce it. Lenz’s law is in accordance with law of conservation of energy.

Question 5.
What happens to the mechanical energy (of motion) .when a conductor is moved in a uniform magnetic field ?
Answer:
Motional e.m.f is produced to the motion of the conductor,in a magnetic field.
Motion e.m.f (ε) = Blυ

Question 6.
What are Eddy currents ? (T.S. Mar. ’19; A.P. Mar. ’15)
Answer:
Eddy currents (or) Foucault currents : The induced circulating currents produced in a conductor itself due to change in magnetic flux linked with the conductor are called Eddy currents.
Due to Eddy currents, the energy is dissipated in the form of heat energy.

Question 7.
Define ‘inductance’.
Answer:
Inductance is a coefficient of electromagnetic induction and is an intrinsic property of a material just like capacitance.
Inductance is an important scalar quantity which depends upon the geometry (i.e, dimensions) of a coil.

Question 8.
What do you understand by ‘self inductance’ ?
Answer:
Self inductance of a coil is defined as the induced e.m.f produced in the coil through which the rate of change of current is unity.
ε = \(-\mathrm{L} \frac{\mathrm{dI}}{\mathrm{dt}}\) ; ε = -L, If \(\frac{\mathrm{dI}}{\mathrm{dt}}\) = 1 A/s.

Short Answer Questions

Question 1.
Obtain an expression for the emf induced across a conductor which is moved in a uniform magnetic field which is perpendicular to the plane of motion.
Answer:
Consider a conductor PQ of length l moving freely in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\) with uniform velocity u on a rectangular conductor ABCD. Let any arbitrary charge q in the conductor also move in the field with same velocity.

Magnitude of Lorentz force on this charge (F) = Bqυ —– (1)
Workdone in moving the charge from P to Q is given by
W = Force × displacement
W = Bqυ × l —– (2) (∵ Direction of force on the charge as per Fleming’s left hand rule)
Electromotive force (ε) = \(\frac{W}{Q}\)
ε = \(\frac{\mathrm{Bqv} l}{\mathrm{q}}\) ⇒ ε = Blυ —- (3)

Question 2.
Describe the ways in which Eddy currents are used to advantage. (A.P. Mar. ’16, AP & T.S. Mar. ’15)
Answer:
Eddy currents are used to advantage in

1. Magnetic braking in trains : A strong magnetic field is applied across the metallic drum rotating with the axle of the electric train. Thus large eddy currents are produced in the metallic drum. These currents oppose the motion of the drum and hence the axle of the train which ultimately makes the train come to rest.
2. Induction Motor: Eddy currents are used to rotate the short circuited rotor of an induction motor. Ceiling fans are also induction motors which run on single phase alternating current.
3. Electromagnetic damping : Certain galvanometers have a fixed core made of non magnetic metallic material. When the coil oscillates, the eddy currents generated in the core oppose the motion and bring the coil to rest quickly.
4. Induction furnace : Induction furnace can be used to produce high temperatures and can be utilised to prepare alloys, by melting the constituent metals. A high frequency alternating current is passed through a coil. The eddy currents generated in the metals produce high temperatures sufficient to melt it.
5. Analogue energy meters : Concept of eddy currents is used in energy meters to record
   the consumption of electricity. Aluminium disc used in these meters get induced due to varying magnetic field. It rotates due to eddy currents produced in it.

Question 3.
Obtain an expression for the mutual inductance of two long co-axial solenoids. (A.P. Mar. ’19)
Answer:
Consider two solenoids as shown in figure. The length of primary coil be l and are a of cross section A. Let N₁ and N₂ are the total number of turns in the primary and secondary solenoids. Let n₁ and n₂ be the number of turns per unit length

(n₁ = \(\frac{\mathrm{N}_1}{l}\) and n₂ = \(\frac{\mathrm{N}_2}{l}\)). Current in the primary coil is i.
∴ Magnetic field inside the primary (B) = μ₀n₁ I = μ₀\(\frac{\mathrm{N}_1}{l}\) I —– (1)
Magnetic flux through each turn of primary
ϕ_B = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}\) = μ₀\(\frac{\mathrm{N}_1}{l} \mathrm{I} \times \mathrm{A}\) —— (2)

The same magnetic flux is linked with the secondary coil.
∴ Total magnetic flux linked with secondary = μ₀\(\frac{\mathrm{N}_1 \mathrm{i}}{l} \times \mathrm{A} \times \mathrm{N}_2\) ——– (3)
If M be mutual inductance of the two coils, the total flux linked with the secondary is Mi

Question 4.
Obtain an expression for the magnetic energy stored a solenoid in terms of the magnetic field, area and length of the solenoid.
Answer:
When the current flows through the inductor of inductance L, an e.m.f is induced in it is given by
ε = -L\(\frac{\mathrm{dI}}{\mathrm{dt}}\) —– (1)

(-ve sign shows that e.m.f opposes the passage of current)
Let an infinite small charge dq be driven through the inductor. So the work done by the external voltage is given by

Total work done to maintain the maximum current (I₀) is given by

This work done is stored in the form of potential energy in the magnetic field (U)

In case of solenoid B = μ₀nI₀ (or) I₀ = \(\frac{\mathrm{B}}{\mu_0 \mathrm{n}}\) and L = μ₀n²Al

Long Answer Questions

Question 1.
Outline the path-breaking experiments of Faraday and Henry and highlight the contributions of these experiments to our understanding of electromagnetism.
Answer:
Faraday’s and Henry’s experiments :

Experiment 1: A magnet induces current due to relative motion

1. The apparatus consists of a coil with a galvanometer G and a bar magnet.
2. When the bar magnet (NS) was at rest, the galvanometer shows no deflection.
3. When North pole of the bar magnet moved towards the coil, galvanometer shows the deflection in one direction indicating the flow of current in the coil.
   
4. When North pole of the bar magnet moved away from the coil, galvanometer again showed the deflection but now in the opposite direction.
5. The deflection of the galvanometer was large when the bar magnet was moved faster towards (or) away from the coil.
6. When south pole of the magnet was brought near the coil (or) moved away from the coil, the deflections in the galvanometer are opposite to that observed with the north pole for similar movements.

Conclusion:

1. Whenever there is a relative motion between a coil and a magnet, induced current flows through the coil.
2. Large induced e.m.f. (or) current is produced in the coil if the relative motion between magnet and the coil is large.

Experiment 2 : Current induces current due to relative motion of coils :

1. The bar magnet is replaced by a secondary coil C₂ connected to a battery as shown in figure.
2. The steady current in the coil C₂ produces a steady magnetic field.
3. As coil C₂ is moved towards the coil C₁, the galvanometer shows a deflection. This indicates current is induced in the coil C₁.
4. When coil C₂ is moved away, the galvanometer shows a deflection again, but opposite direction.
5. The deflection lasts as long as coil C₂ is in motion.
6. When the coil C₂ is held fixed and C₁ is moved, the same effects are observed.

Conclusion : Induced e.m.f (or) current is produced, when there is a relative motion between the coils.

Experiment 3: Changing current, Induces current without relative motion:

1. Faraday showed that this relative motion is not an absolute requirement.
2. Figure shows two coils C₁ and C₂ held stationary.
3. Coil C₁ is connected to a battery through a tap key K and coil C₂ is connected to a galvanometer (G).
4. it is observed that the galvanometer shows a momentary deflection when the tap key K is pressed.
5. The pointer in the galvanometer returns to zero immediately.
6. If the key is held pressed continuously, there is no deflection in the galvanometer.
7. When the key is released, the galvanometer shows deflection again but in the opposite direction.
8. Deflection of the galvanometer increases a lot when wooden bar is replaced by iron bar.

Question 2.
Describe the working of a AC generator with the aid of a simple diagram and necessary expressions.
Answer:
“An electrical machine used to convert mechanical energy into electrical energy is known as A.C generator/altemator”.
Principle : It works on the principle of electromagnetic induction.

Construction :

1. Armature : Armature coil (ABCD) consists of a large number of turns of insulated copper wire wound over a soft iron core.
2. Strong field magnet : A strong permanent magnet (or) an electromagnet whose poles (N and S) are cylindrical in shape used as a field magnet. The armature coil rotates between the pole pieces of the field magnet.
   
3. Slip rings: The two ends of the armature coil are connected to two brass slip rings R₁ and R₂. These rings rotate along with the armature coil.
4. Brushes : Two carbon brushes B₁ and B₂ are pressed against the slip rings. The brushes remain fixed while slip rings rotate along with the armature. These brushes are connected to the load through which the out put is obtained.

Working : When the armature coil ABCD rotates is the magnetic field provided by the strong field magnet, it cuts the magnetic line of force. The magnetic flux linked with the coil changes due to the rotation of the armature and hence induced e.m.f is set up in the coil.

The current flows out through the brush B in one direction of half of revolution and through the brush B₂ in the next half revolution in the reverse direction. This process is repeated, therefore e.m.f produced is of alternating nature.

Theory:

1. When the coil is rotated with a constant angular velocity (ω)
2. The angle between the normal to the coil and magnetic field \(\overrightarrow{\mathrm{B}}\) at any instant is given by θ = ωt —— (1)
3. The component of magnetic field normal to the plane of the coil = B cos θ = B cosωt —— (2)
4. Magnetic flux linked with the single turn of the coil = (B cos ωt) A —— (3)
   where A is the area of the coil, if the coil has n turns
5. Total magnetic flux linked with the coil (ϕ) = n(B cos ωt) A —– (4)
   According to Faraday’s law,

ε = \(-\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(-\frac{\mathrm{d}}{\mathrm{dt}}\)(nBA cos ωt) = -nBA(-ω sin ωt)
ε = nBA ω sin ωt —— (5)
Where nBAω is the maximum value of e.m.f. (ε₀)
ε = ε₀ sin ωt —– (6) (∵ ω = 2πυ)

Instantaneous current is the circuit is given by
I = \(\frac{\varepsilon}{\mathrm{R}}\) = \(\frac{\varepsilon_0}{\mathrm{R}}\) sin ωt [∵ i = \(\frac{\varepsilon_0}{\mathrm{R}}\)]
I = I₀ sin ωt
The direction of the current changes periodically and therefore the current is called alternating current (a.c.).

Textual Exercises

Question 1.
Predict the direction of induced current in the situations described by the following (a) to (f).

Answer:
a) Here south pole is moving towards the coil, so according to Lenz’s law this end becomes s-pole. (To oppose the motion of south pole by repelling it). Hence, the direction of current is clockwise (by using clock rule) and the current flows from p to q.

b) In coil p-q at the end q ⇒ s-pole is moving towards end q, so it behaves like a south pole (by lenz’s law). The direction of current is clockwise (by clock rule) i.e. from p to q. North pole is moving away so this end will behave like south pole (To oppose its away motion by attracting it). In coil x-y, S-pole is induced (by Lenz’s law) and the direction of current is clockwise i.e. x to y.

c) As the tapping key is just, closed, the current in coil increases so, the magnetic flux and field increases. According to Maxwell’s right hand grip rule, the direction of magnetic field is left wards. Thus, the direction of induced current in the neighbouring coil is such that it try to decrease the field, thus the direction of field in the neighbouring coil should be rightwards i.e., according to Maxwell’s right hand rule the direction of induced current is anti clock wise i.e. xyz.

d) As the rheostat setting is changed, the current is changed. The direction of field due to the coil is leftwards according to Maxwell’s right hand grip rule. The direction of induced current in the left coil is such that the magnetic field produced by it in rightwards, thus the direction of current in left coil is Anticlockwise i.e from zyx.

e) As the key is just released, the current which is flowing anticlockwise goes on decreasing. Thus, the induced current developed in such a sense the magnetic field due to left coil increases (which is towards right). So, the magnetic field due to the right coil should also towards right and hence the induced current is in anticlockwise, i.e., x to yx – direction.

f) The magnetic field lines due to the current carrying wire are in the plane of the loop. Hence, no induced current is produced in the loop (because no flux lines crosses the area of loop).

Question 2.
Use Lenz’s law to determine the direction of induced current in the situations described by fig. a, b.

(a) A wire of irregular shape turning into a circular shape.
(b) A circular loop being deformed into a narrow straight wire.
Answer:
a) Here, the direction of magnetic field is perpendicularly inwards to the plane of paper. If a wire of irregular shape turns into a circular shape then its area increases (∵ the circular loop has greater area than the loop of irregular shape) so that the magnetic flux linked also increases. Now, the induced current is produced in a direction such that it decreases the magnetic field (i.e.) the current will flow in such a direction so that the wire forming the loop is pulled inwards in all directions (to decreases the area) i.e., current is in anticlockwise direction, i.e., adcba

b) When a circular loop deforms into a narrow straight wire, the magnetic flux linked with it also decreases. The current induced due to change in flux will flow in such a direction that it will oppose the decrease in magnetic flux so it will flow anti clockwise i.e along a’d’c’b’a’, due to which the magnetic field produced will be out of the plane of paper.

Question 3.
A long solenoid with 15 turns per cm has a small loop of area 2.0 cm² placed inside the solenoid normal to its axis. If the current carried by the solenoid changes steadily from 2.0 A to 4.0 A in 0.1 s, what is the induced emf in the loop while the current is changing ?
Solution:
Given number of turns (n) = 15 per cm = 1500 per metre. .
Area of small loop A = 2 cm² = 2 × 10^-4m²
Change in current \(\frac{\mathrm{dI}}{\mathrm{dt}}\) = \(\frac{4-2}{0.1}\) = \(\frac{2}{0.1}\) = 20 A/s
Let e be the induced emf, According to Faraday’s law,
e = \(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(\frac{\mathrm{d}}{\mathrm{dt}}\)(BA) or e = \(\text { A. } \frac{\mathrm{dB}}{\mathrm{dt}}\) (∵ ϕ = BA)
e = A. \(\frac{\mathrm{d}}{\mathrm{dt}}\left(\mu_0 \mathrm{nI}\right)\) (∵ Magnetic field inside the solenoid B = μ₀nI)
or e = Aμ₀n\(\frac{\mathrm{dI}}{\mathrm{dt}}\)
e = 2 × 10^-4 × 4 × 3.14 × 10^-7 × 1500 × 20
e = 7.5 × 10⁶v (∵ μ₀ = 4π × 10^-7) Thus, the induced emf in the loop is 7.5 × 10⁶V.

Question 4.
A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of region of uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 cm s^-1 in a direction normal to the (a) longer side, (b) shorter side of the loop ? For how long does the induced voltage last in each case ?
Solution:
Given length of the loop l = 8 cm = 8 × 10^-2 m.
Width of the loop b = 2 cm = 2 × 10^-2 m.
Velocity of the loop = 1 cm/s = 0.01 m/s.
Magnitude of magnetic field (B) = 0.3

a) When velocity is normal to the longer side .
(l = 8 cm = 8 × 10^-2 m)
In this case, motional emf
e = B/υ = 0.3 × 8 × 10^-2 × 0.01 = 2.4 × 10^-4 V

b) When velocity is normal to the shorter side
(l = 2cm = 2 × 10^-2 m)
In this case, the developed emf
e = Blυ = 0.3 × 2 × 10^-2 × 0.01
e = 0.6 × 10^-4 V.

Question 5.
A 1.0 m long metallic rod is rotated with an angular frequency of 400 rad s^-1 about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring.
Solution:
Length of rod l = 1 m
Angular frequency of rod ω = 400 rad/s
Magnetic field B = 0.5 T
The linear velocity of fixed end = 0
The linear velocity of other end = lω (∵ V = rω)

Average linear velocity V = \(\frac{0+l \omega}{2}\)
V = \(\frac{l \omega}{2}\) —– (i) By using the formula of motional emf,
e = Bυl = \(\frac{\mathrm{B} l \omega}{2}\) (from equation (i)), e = \(\frac{0.5 \times 1 \times 400 \times 1}{2}\), e = 100.
Thus, the emf developed between the centre and ring is 100 V

Question 6.
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular speed of 50 rad s^-1 in a uniform horizontal magnetic field of magnitude 3.0 × 10^-2 T. Obtain the maximum and average emf induced in the coil. If the coil forms a closed loop of resistance 10Ω, calculate the maximum value of current in the coil. Calculate the average power loss due to Joule heating. Where does this power come from ?
Solution:
Given radius of coil = 8 cm = 0.08 m, Number of turns = 20
Resistance of closed loop = 10Ω, Angular speed ω = 50 rad/s
Magnitude of magnetic field B = 3 × 10^-2 T
Induced emf produced in the coil e = NBA W sin ωt
For maximum emf, sin ωt = 1
∴ Maximum emf e₀ = NBAω

The source of power dissipated as heat in the coil is the external rotar. The current induced in the coil causes a torque which opposes the rotation of the coil, so the external agent rotar counter this torque to keep the coil rotating uniformly.

Question 7.
A horizontal straight wire 10 m long extending from east to west is falling with a speed of 5.0 m s^-1, at right angles to the horizontal component of the earth’s magnetic field, 0.30 × 10^-4 Wb m².
(a) What is the instantaneous value of the emf induced in the wire ?
(b) What is the direction of the emf ?
(c) Which end of the wire is at the higher electrical potential ?
Solution:
Given, velocity of straight wire = 5 m/s
Magnetic field of straight wire,
B = 0.30 × 10^-4 Wb/m²
length of wire l = 10m

a) Emf induced in the wire e = B/υsin θ
Here, θ = 90°
∴ sin θ = 1 .
(∴ wire is falling at right angle to earth’s horizontal magnetic field component)
= 0.3 × 10^-4 × 10 × 5 = 1.5 × 10^-3 V.

b) According to the Fleming’s right hand rule, the force is downward, then the direction of induced emf will be from west to east.

c) As the direction of induced emf or current is from west to east, the west end of the wire is at higher potential.
(∵ current always flows from a point at higher potential to a point at lower potential).

Question 8.
Current in a circuit falls from 5.0 A to 0.0 A in 0.1 s. If an average emf of 200 V induced, give an estimate of the self-inductance of the circuit. (T.S. Mar. ’16, Mar. ’14)
Solution:
Change in current, dI = 5 – 0 = 5A, Time taken in current change dt = 0.1 s
Induced average emf e_av = 200 V
Induced emf in the circuit e = L. \(\frac{\mathrm{dI}}{\mathrm{dt}}\) ⇒ 200 = L\(\left(\frac{5}{0.1}\right)\) or L = \(\frac{200}{50}\) = 4H

Question 9.
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil ?
Solution:
Given, mutual inductance of coil M = 1.5 H, Current change in coil dl = 20 – 0 = 20 A
Time taken in change dt = 0.5s, Induced emf in the coil e = M\(\frac{\mathrm{dI}}{\mathrm{dt}}\) = \(\frac{\mathrm{d} \phi}{\mathrm{dt}}\)
dϕ = M.dl = 1.5 × 20, dϕ = 30 Wb, Thus the change of flux linkage is 30 Wb.

Question 10.
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10^-4 T and the dip angle is 30°.
Solution:
Speed of jet plane V = 1800 km/h = 1800 × \(\frac{5}{18}\) = 500 m/s
l = Distance between the ends of wings = 25 m
The magnitude of magnetic field B = 5 × 10^-4 T
Angle of dip γ = 30°.
Use the formula of motional emf
e = B_vVl, e = B sin γ Vl (B_v = B sin γ),
e = 5 × 10^-4 × sin 30° × 500 × 25, e = 3.1 V
Thus, the voltage difference developed between the ends is 3.1 V

Additional Question

Question 1.
Obtain an expression for the self inductance of a solenoid.
Answer:
i) Consider a long solenoid of length l, area of cross-section A. Let n be the number of turns per unit length (n = \(\frac{\mathrm{N}}{l}\))

ii) Let i be the current flows through it. The magnetic field inside the solenoid is given by
B = μ₀ni —— (1)

iii) Magnetic flux linked with each turn of the solenoid = B.A = μ₀niA —— (2)

iv) Total magnetic flux linked with whole solenoid
ϕ = μ₀niA × N (∵ N = nl)
ϕ = μ₀ni A × nl (Where N Total number of turns in the solenoid)
ϕ = μ₀n²iAl —— (3) Also, ϕ = Li —– (4) From eq’s (3) & (4), Li = μ₀n²iAl
L = μ₀n²Al —– (5) (or) L = μ₀\(\frac{\mathrm{N}^2}{l}\)A —– (6)

Additional Exercises

Question 1.
Suppose the loop in Textual Exercise 4 is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02 T s^-1. If the cut is joined and the loop has a resistance of 1.6Ω how much power is dissipated by the loop as heat ? What is the source of this power ?
Solution:
Area of loop = 8 × 2 = 16 cm²
Rate of change of magnetic field \(\frac{\mathrm{dB}}{\mathrm{dt}}\) = 0.02 T/S,
Resistance of loop R = 1.6Ω
Induced emf of loop e = \(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{BA})\) (∵ ϕ = BA)
e = A. \(\frac{\mathrm{dB}}{\mathrm{dt}}\) ⇒ e = 16 × 10^-4 × 0.02 ⇒ e = 0.32 × 10^-4V
Induced current in the loop I = \(\frac{e}{R}\) = \(\frac{0.32 \times 10^{-4}}{1.6}\) = 0.2 × 10^-4A
Power of source as heat P = I²R = (0.2 × 10^-4)² × 1.6 = 6.4 × 10^-10 W ⇒ P = 6.4 × 10^-10W
The agency which changing the magnetic field with time is the source of this power.

Question 2.
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s^-1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10^-3 T cm^-1 along the negative x-direction (that is it increases by 10^-3 T cm^-1 as one moves in the negative x-direction), and it is decreasing in time at the rate of 10^-3 Ts^-1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
Solution:
Given, side of loop a = 12 cm
∴ Area of loop (A) = a² = (12)² = 144 cm² = 144 × 10^-4 m² (∵ Area of square = (side)²)
Velocity v = 8 cm/s = 8 × 10^-2 m/s.
Rate of change of magnetic field with distance \(\frac{\mathrm{dB}}{\mathrm{dx}}\) = 10^-3 T/cm
Rate of change of magnetic field with time \(\frac{\mathrm{dB}}{\mathrm{dt}}\) = 10^-3 T/s
Resistance of the loop R = 4.5 mΩ = 4.5 × 10^-3Ω
Rate of change of magnetic flux with respect to time
\(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(\frac{\mathrm{d}(\mathrm{BA})}{\mathrm{dt}}\) = \(\left(\frac{\mathrm{dB}}{\mathrm{dt}}\right) \mathrm{A}\) = 10^-3 × 144 × 10^-4
= 1.44 × 10^-5 Wb/s

Rate of change of magnetic flux due to the motion of loop
\(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(\frac{\mathrm{dB}}{\mathrm{dx}} \cdot \mathrm{A} \cdot \frac{\mathrm{dx}}{\mathrm{dt}}\) = 10^-3 × 144 × 10^-4 × 8 = 11.52 × 10^-5 Wb/s
Both of the effects cause a decrease in magnetic flux along the positive z-direction.
Total induced emf in the loop e = 1.44 × 10^-5 + 11.52 × 10^-5
e = 12.96 × 10^-5 V
Induced current in the loop = \(\frac{\mathrm{e}}{\mathrm{R}}\) = \(\frac{12.96 \times 10^{-5}}{4.5 \times 10^{-3}}\) = 2.88 × 10^-2A.
The direction of induced current is such as to increase the flux through the loop along positive z-direction.

Question 3.
It is desired to measure the magnitude of field between the poles of a powerful loud speaker magnet. A small flat search coil of area 2 cm² with 25 closely wound turns, is positioned normal to the field direction and then quickly snatched out of the field region. Equivalently, one can give it a quick 90° turn to bring its plane parallel to the field direction). The total charge flown in the coil (measured by a ballistic galvanometer connected to coil) is 7.5 mC. The combined resistance of the coil and the galvanometer is 0.50Ω Estimate the field strength of magnet.
Solution:
Area of coil A = 2cm² = 2 × 10^-4 m², Number of turns N = 25
Total charge in the coil θ = 7.5 mC (1 mC = 10^-3 C) = 7.5 × 10^-3 C
Resistance of coil R = 0.5Ω
When the coil is removed from the field, the flux is zero ϕ_f = 0. Induced current in the coil

Thus, the strength of magnetic field is 0.75 T.

Question 4.
Following figure shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod and the magnetic field are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod = 9.0 mΩ. Assume the field to be uniform.
(a) Suppose K is open and the rod is moved with a speed of 12 cm s^-1 in the direction shown. Give the polarity and magnitude of the induced emf.
(b) Is there an excess charge built up at the ends of the rods when K is open ? What if K is closed ?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed ?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed (= 12 cm s^-1) when K is closed ? How much power is required when K is open ?
(f) How much power is dissipated as heat in the closed circuit ? What is source of this power ?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular ?
Solution:
Given, length of the rod l = 15 cm = 15 × 10^-2, Magnetic field B = 0.50 T
Resistance of the closed – loop containing the rod, R = 9mΩ ⇒ 9 × 10^-3Ω
Velocity of rod V = 12 cm/s = 12 × 10^-2 m/s,
a) The magnitude of the motional emf
e = BVl = 0.50 × 12 × 10^-2 × 15 × 10^-2, e = 9 × 10^-3 V.
According to the Fleming’s left hand rule, the direction of Lorentz force (f = -e(V × B)) on electrons in PQ is from P to Q. So, p would acquire positive charge and Q would acquire negative charge.

b) Yes, an excess positive charge developes at P and the same amount of negative charge developes at Q as the key is open. When the key K is closed, the induced current flows and maintains the excess charge.

c) When key is open, there is no net force on the electrons because the presence of excess charge at P and Q sets up an electric field and magnetic force on the electrons is balanced by force on them due to force by the electric field. So, there is no net force on the rod.

d) When the key K is closed, current flow in the loop and the current carrying wise experience a retarding force in the magnetic field which is given by
Force = BIl = B . \(\frac{\mathrm{e}}{\mathrm{R}}\) . l = \(\frac{0.5 \times 9 \times 10^{-3} \times 15 \times 10^{-12}}{9 \times 10^{-3}}\) = 7.5 × 10^-2 N.

e) To keep the rod moving at the same speed the required power
= retarding force × velocity = 7.5 × 10^-2 × 12 × 10^-2 = 9 × 10^-3 W

f) Power dissipated in closed circuit due to flow of current = I²R
= \(\left(\frac{\mathrm{e}}{\mathrm{R}}\right)^2\) × R = \(\frac{\left(9 \times 10^{-3}\right)^2}{9 \times 10^{-3}}\) = 9 × 10^-3 W₂ The source of this power is the external agent.

g) When the field is parallel to length of rails θ = 0°, induced emf = e = BVl sin θ = 0 (∵ sin θ° = 0). In this situation, the moving rod will not cut the field lines so that flux change is zero and hence induced emf is zero.

Question 5.
An air-cored solenoid with length 30 cm, area of cross-section 25 cm² and number of turns 500, carries a current of 2.5 A. The current is suddenly switched off in a brief time of 10^-3s. How much is the average back emf induced across the ends of the open switch in the circuit? Ignore the variation in magnetic field near the ends of the solenoid.
Solution:
Given, length of solenoid I = 30 cm = 30 × 10^-2 m
Area of cross-section A = 25 cm² = 25 × 10^-4 m²
Number of turns N = 500, Current I₁ = 2.5A, I₂ = 0, Brief time dt = 10^-3s.
Induced emf in the solenoid e = \(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(\frac{\mathrm{d}(\mathrm{BA})}{\mathrm{dt}}\) (∵ ϕ = BA)
Magnetic field induction B at a point well inside the long solenoid carring current I is

Question 6.
Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, υ = 10 m/s. Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take α = 0.1 m and assume that the loop has a large resistance.

Solution:
a) Let us assume that an elementary strip of width dx a at distance x from the wire carring current I.
Side of square = a.
The magnetic field due to current carring wire at a distance x from the wire is
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 I}{x}\) —— (i)
Small amount of magnetic flux associated with the strip

As we know that ϕ = MI —— (iii)
where, M is mutual inductance. From equations (ii) and (iii) we get

This is mutual inductance between wire and square loop.

b) Given current I = 50 A, Velocity V = 10 m/s, x = 0.2 m and a = 0.1 m

Question 7.
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (figure). A uniform magnetic field extends over a circular region within the rim. It is given by,
B = B₀k (r ≤ a, a < R)
= 0 (otherwise)

What is the angular velocity of the wheel after the field is suddenly switched off?
Solution:
Given Linear charge density

Radius of rim = R,
Mass of rim = M,
Magnetic field extends over a circular region
B = -B₀ (r ≤ a, a < R) = O (otherwise).
Let the angular velocity of the wheel be w, then induced emf e = \(\frac{-\mathrm{d} \phi}{\mathrm{dt}}\)
E exist along circumference of radius a due to change in magnetic flux.

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 8th Lesson Magnetism and Matter Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 8th Lesson Magnetism and Matter

Very Short Answer Questions

Question 1.
A magnetic dipole placed in a magnetic field experiences a net force. What can you say about the nature of the magnetic field?
Answer:
The nature of the magnetic field is uniform, magnetic dipole (bar magnet) experiences a net force (or torque).

Question 2.
What happens to compass needles at the Earth’s poles?
Answer:
At the poles, the earth’s field is exactly vertical. So, the compass needles are free to rotate in a horizontal plane only, it may point out in any direction.

Question 3.
What do you understand by the ‘magnetization’ of a sample? (A.P. Mar. ’16)
Answer:
When a magnetic sample is placed in a magnetic field, its magnetic moments add up in the direction of the magnetic field. Hence the sample get a net magnetic moment (m_net ≠ 0)
Magnetisation is defined as the net magnetic moment per unit volume i.e., M = \(\frac{m_{\text {net }}}{V}\)

Question 4.
What is the magnetic moment associated with a solenoid?
Answer:
Magnetic dipole moment in a solinoid m = NIA
Where ‘N’ is the number of turns in the loop, ‘I’ the current and A the area vector.

Question 5.
What are the units of magnetic moment, magnetic induction and magnetic filed ?
Answer:
Unit of

1. magnetic moment m is Am² or J T^-1.
2. Magnetic induction – wb m^-2 or Tesla (T)
3. magnetic field – Tesla.

Question 6.
Magnetic lines form continuous closed loops. Why ? (A.P. Mar. 16)
Answer:
Magnetic lines of force always start from north pole and forming curved path, enter south pole and travel to north pole inside the magnet. Thus lines of force are forming closed loops.

Question 7.
Define magnetic declination. (Mar. ’14)
Answer:
Magnetic Declinatin (D) : The angle between the true geographic north and the north shown by a compass needle is called magnetic declination or simply declination (D).

Question 8.
Define magnetic inclination or angle of dip. (A.P. & T.S. Mar. ’15)
Answer:
Inclination or Dip (I) : The angle which the total intensity of earth’s magnetic field makes with the horizontal at any place is called inclination (I).

Question 9.
Classify the following materials with regard to magnetism : Manganese, Cobalt, Nickel, Bismuth, Oxygen, Copper. (A.P. Mar. ’19 & T.S. Mar. ’16, ’15)
Answer:
Ferromagnetic materials → Cobalt, Nickel.
Paramagnetic materials → Oxygen, Manganese
Diamagnetic materials → Bismuth, Copper

Short Answer Questions

Question 1.
Derive an expression for the axial field of a solenoid of radius “a”, containing “n” turns per unit length and carrying current “i”.
Answer:
Expression for the axial field of a solenoid :

1. Consider a solinoid of length ‘2l’ and radius ‘a’ having ‘n’ turns per unit length.
2. Let ‘I’ be the current in the solenoid.
3. We have to calculate magnetic field at any point P on the axis of solenoid, where OP = r.
   
4. Consider a small element of thickness dx of the solenoid, at a distance ‘x’ from ‘O’.
5. Number of turns in the element = ndx.
6. Magnitude of magnetic field at P due to this current element is dB = \(\frac{\mu_0 \mathrm{ndx} \cdot \mathrm{Ia}^2}{2\left[(\mathrm{r}-\mathrm{x})^2+\mathrm{a}^2\right]^{3 / 2}}\)
7. If P lies at a very large distance from 0, i.e., r > > a and r > > x, then [(r – x)² + a²]^3/2 = r³.
   ⇒ dB = \(\frac{\mu_0 \mathrm{ndx} \mid \mathrm{a}^2}{2 \mathrm{r}^3}\)
8. To get total magnetic field, integrating the above equation between the limits from X = -l to X = +l.
   
9. The magnitude of the magnetic moment of the solenoid is, m = n(2l) I (πa²).
   B = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^3}\)
10. Therefore, magnetic moment of a bar magnet is equal to magnetic moment of an equivalent solenoid that produces the same magnetic field.

Question 2.
The force between two magnet poles separated by a distance’d’ in air is ‘F. At what distance between them does the force become doubled ?
Answer:
Force between two magnetic poles, F₁ = F;
Distance between two magnetic poles, d₁ = d
Force between two magnetic poles increased by double F₂ = 2F
Distance between two magnetic poles, d₂ = ?
From Coulombs law, \(\mathrm{F}_1 \mathrm{~d}_1^2\) = \(\mathrm{F}_2 \mathrm{~d}_2^2\)
Fd² = 2 F \(\mathrm{d}_2^2\)
⇒ \(\mathrm{d}_2^2\) = \(\frac{\mathrm{d}^2}{2}\)
∴ d₂ = \(\frac{\mathrm{d}}{\sqrt{2}}\)

Question 3.
Compare the properties of para, dia and ferromagnetic substances.
Answer:
Diamagnetic substances

a) When these materials placed in a magnetic field, they are magnetised feebly in the opposite direction to the applied external field.
b) When a rod of diamagnetic material is suspended freely in a uniform magnetic field, it comes to rest in the perpendicular direction to the magnetic field.
c) When they kept in a non uniform magnetic field, they moves from the region of greater field strength to the region of less field strength.
d) The relative permeability is less than 1. μ_r < 1 and negative.
e) The susceptibility \((\chi)\) is low and negative.
E.g. : Copper, Silver, Water, Gold, Antimony, Bismuth, Mercury Quartz Diamond etc.

Paramagnetic Substance

a) When these materials placed in a magnetic field, they are magnetised feebly in the direction of the applied magnetic field.
b) When a rod of paramagnetic material is suspended freely in a uniform magneticfield, it comes to rest in the direction of the applied magnetic field.
c) When they kept in a non-uniform magnetic field, they moves from the region of less field strength to the region of greater field strength.
d) The relative permeability is greater than 1. μ_r > 1 and positive.
e) The susceptibility \((\chi)\) is small and positive.
E.g. : Aluminium, Magnetiam, Tungsten, Platinum, Manganese, liquid oxygen, Ferric chloride, Cupric chloride etc.

Fêrromagnetic substances

a) When these materials placed in a magnetic field, they are magnetised strongly in the direction of the applied external field.
b) When a rod of ferromagnetic material is suspended freely in a uniform magnetic field, it comes to rest in the direction of the applied magnetic field.
c) When they kept in a non-uniform magnetic field they moves from the regions of lesser (magnetic field) strength to the regions of stronger (magnetic field) strength.
d) The relative permeability is much greater than μ_r >> 1 and positive.
e) The stisceptibility \((\chi)\) is high and positive.
E.g. : Iron, Cobalt, Nickel, Gadolinium and their alloys.

Question 4.
Explain the elements of the Earth’s magnetic field and draw a sketch showing the relationship between the vertical component, horizontal component and angle of dip.
Answer:
The magnetic field of the earth at a point on its surface can be specified by the declination D, the angle of dip or the inclination I and the horizontal component of the earth’s field H_E. These are known as the elements of the earth’s magnetic field.

Explanation:

1. The total magnetic field at P can be resolved into a horizontal component H_E and a vertical component Z_E.
2. The angle that B_E makes with H_E is the angle of dip, I.
3. Representing the vertical component by Z_E, we have
   Z_E = B_E Sin I
   H_E = B_E Cos I
   Which gives Tan I = \(\frac{\mathrm{Z}_{\mathrm{E}}}{\mathrm{H}_{\mathrm{E}}}\)

Question 5.
Define retentivity and coercivity. Draw the hysteresis curve for soft iron and steel. What do you infer from these curves ?
Answer:

1. Retentivity : The value of magnetic induction \(\overrightarrow{\mathrm{B}}\) left in the specimen, when the magnetising force (H) is reduced to zero is called Retentivity or Remanence or Residual magnetism.
2. Coercivity : To reduce the retentivity to zero, we have to apply a magnetising force in opposite direction. This value of magnetising force is called coercivity or coercive force.
3. Hysterisis eurve: The curve represents the relation between magnetic induction \(\overrightarrow{\mathrm{B}}\) (or) intensity of magnetization (I) of a ferromagnetic material with magnetizing force (or) magnetic intensity (\(\overrightarrow{\mathrm{H}}\)) is called Hystersis curve.
   
4. Hysterisis curve for soft Iron and steel is shown below.
   The hysterisis loops of soft iron and steel reveal that
   1. The retentivity of soft iron is greater than the retentivity of steel.
   2. Soft Iron is more strongly magnetised than steel.
   3. Coercivity of Soft Iron is less than coercivity of steel. It means soft Iron loses its magnetisation more rapidly than steel does.
   4. As area of I – H loop for soft Iron is smaller than the area of I – H loop for steel. Therefore hysterisis loss in case of soft Iron is smaller than the hysterisis loss in case of steel.

Question 6.
If B is the magnetic field produced at the centre of a circular coil of one turn of length L carrying current I then what is the magnetic field at the centre of the same coil which is made into 10 turns ?
Answer:
For first circular coil; B₁ = B, n₁ = 1; I₁ = I; a₁ = \(\frac{\mathrm{L}}{2 \pi}\)
For second circular coil, B₂ = ? n₂ = 10; I₂ = I; a₂ = \(\frac{\mathrm{L}}{2 \pi}\)
As B = \(\frac{\mu_0 \mathrm{n} I \mathrm{a}^2}{2 \mathrm{r}}\), B ∝ n
\(\frac{\mathrm{B}_2}{\mathrm{~B}_1}\) = \(\frac{\mathrm{n}_2}{\mathrm{n}_1}\)
\(\frac{\mathrm{B}_2}{\mathrm{~B}}\) = \(\frac{10}{1}\)
∴ B₂ = 10 B

Question 7.
If the number of turns of a solenoid is doubled, keeping the other factors constant, how does the magnetic field at the axis of the solenoid change?
Answer:
B₁ = B (say); n₁ = n; n₂ = 2n; B₂ =?
Magnetic field at the centre of a solinoid is given by B = \(\frac{\mu_0 \mathrm{nI} \mathrm{a}^2(2 l)}{2 \mathrm{r}^3}\)
⇒ \(\frac{\mathrm{B}_2}{\mathrm{~B}_1}\) = \(\frac{\mathrm{n}_2}{\mathrm{n}_1}\) ⇒ \(\frac{\mathrm{B}_2}{\mathrm{~B}}\) = \(\frac{2 \mathrm{n}}{\mathrm{n}}\)
∴ B₂ = 2 B

Long Answer Questions

Question 1.
Derive an expression for the magnetic field at a point on the axis of a current carrying circular loop.
Answer:
Expression for the magnetic field at a point on the axis of a current carrying circular loop:

1. Consider ‘O’ is the centre of a circular coil of one turn and radius ‘a’.
2. Let P is a point at a distance r from the centre, along the axis of coil.
3. The plane of the coil is ⊥^r to the plane of paper.
4. Consider two elements AB and AB’ each of length dl which are diametrically opposite.
5. Then, the magnetic fields at P due to these two elements will be dB and dB in the direction PM and PN respectively.
6. These directions are ⊥^r to the lines joining the mid-points of the elements with the point P
7. Resolve these fields into two components parallel (dB sin θ) and perpendicular (dB cos θ) to the axis of the coil.
8. The dB cos θ components cancel one another and dB sin θ components are in the same direction and add up due to the symmetric elements of the circular coil.
9. Therefore, the total magnetic field along the axis = B = \(\int \mathrm{dB}\) sin θ of the circular coil along PC —– (1)
10. The magnetic field at ‘P’ due to current element of length ‘dl’ is
    ‘dB’ = \(\frac{\mu_0}{4 \pi} \frac{I d l \sin \phi}{\left(a^2+x^2\right)}\) = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{Id} l}{\left(\mathrm{a}^2+\mathrm{r}^2\right)}\) —– (II) [∵ φ = 90°]
11. From equation (I) and (II), B = \(\int \frac{\mu_0}{4 \pi} \frac{\mathrm{Id} l}{\left(\mathrm{a}^2+\mathrm{r}^2\right)} \sin \theta\)
    From Δ^le OPE, sin θ = \(\frac{a}{\sqrt{\left(a^2+r^2\right)}}\)
    ⇒ B = \(\int \frac{\mu_0}{4 \pi} \frac{\mathrm{Id} l \mathrm{a}}{\left(\mathrm{a}^2+\mathrm{r}^2\right)^{3 / 2}}\) = \(\frac{\mu_0 \mathrm{Ia}}{4 \pi\left(\mathrm{a}^2+\mathrm{r}^2\right)^{3 / 2}} \int \mathrm{d} l\)
    But \(\int \mathrm{d} l\) = Circumference of the coil = 2πa
    ∴ B = \(\frac{\mu_0 \text { I a }}{4 \pi\left(a^2+r^2\right)^{3 / 2}}\) × 2πa = \(\frac{\mu_0 \mathrm{Ia}^2}{2\left(\mathrm{a}^2+\mathrm{r}^2\right)^{3 / 2}}\), Tesla along the direction of PC.
12. If the coil contains N turns, then B = \(\frac{\mu_0 \text { NIa }^2}{2\left(a^2+r^2\right)^{3 / 2}}\)
13. At the centre of the coil r = 0, B = \(\frac{\mu_0 \mathrm{NI} \mathrm{a}^2}{2 \mathrm{a}^3}\) = \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{a}}\)
    Note: If r >> a, B = \(\frac{\mu_0 \mathrm{NI}\left(\pi \mathrm{a}^2\right)}{2 \pi \mathrm{r}^3}\) = \(\frac{\mu_0 \mathrm{NI}_{\mathrm{A}}}{2 \pi^3}\)
    A = πa² = Area of current loop.

Question 2.
Prove that a bar magnet and a solenoid produce similar fields.
Answer:
Bar magnet produce similar field of Solenoid:

1. We know that the current loop acts as a magnetic dipole. According to Ampere’s all magnetic phenomena can be explained interms of circulating currents.
2. Cutting a bar magnet is like a solenoid. We get two similar solenoids with weaker magnetic properties.
3. The magnetic field lines remain continuous, emerging from one face of solenoid and entering into other face of solenoid.
4. If we were to move a small compass needle in the neighbourhood of a bar magnet and a current carrying solenoid, we would find that the deflections of the needle are similar in both cases as shown in diagrams.
   
   
   The axial field of a finite solenoid in order to demonstrate its similarity to that of a bar magnet –
5. The magnetic field at point P due to bar magnet in the form of solenoid is B = \(\frac{\mu_0}{4 \pi} \frac{2 m}{r^3}\)
6. The total magnetic field, at a point P due to solenoid is given by
7. The magnitude of the magnetic moment of the solenoid is, m = n(2l) I (πa²).
   ∴ B = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^3}\)
8. Therefore, magnetic moment of a bar magnet is equal to magnetic moment of an equivalent solenoid that produces the same magnetic field.

Question 3.
A small magnetic needle is set into oscillations in a magnetic field B obtain an expression for the time period of oscillation.
Answer:
Expression for time period of oscillation :

1. A small compass needle (magnetic dipole) of known magnetic moment m and moment of Inertia is placing in uniform magnetic field B and allowing it to oscillate in the magnetic field.
2. This arrangement is shown in Figure.
3. The torque on the needle is \(\tau\) = m × B
4. In magnitude \(\tau\) = mB sin θ.
   Here \(\tau\) is restoring torque and θ is the angle between m and B.
5. Therefore, in equilibrium
   
   Negative sign with mB sin θ implies that restoring torque is in opposition to deflecting torque.
   
6. For small values of θ in radians, we approximate sin θ ≈ θ and get
   
   
   This represents a simple harmonic motion.
7. From defination of simple harmonic motion, we have \(\) = -ω²θ ——– (II)
   From equation (1) and (II), we get ⇒ ω² = \(\frac{\mathrm{mB}}{\mathcal{J}}\)
   
8. Therefore, the time period is
   

Question 4.
A bar magnet, held horizontally, is set into angular oscillations in the Earth’s magnetic field. It has time periods T₁ and T₂ at two places, where the angles of dip are θ₁ and θ₂ respectively. Deduce an expression for the ratio of the resultant magnetic fields at the two places.
Answer:

1. Suppose, the resultant magnetic fields is to be compared at two places A and B.
2. A bar magnet, held horizontally at A and which is set into angular oscillatins in the Earths magnetic field.
3. Let time period of a bar magnet at place ‘A’ is T₁ and angular displacement or angle of dip is θ₁.
4. As the bar magnet is free to rotate horizontally, it does not remain vertical component (B₁sin θ₁) It can have only horizontal component (B₁ cos θ₁)
5. The time period of a bar magnet in uniform magnetic field is given by T = \(2 \pi \sqrt{\frac{\mathrm{I}}{\mathrm{mB}_{\mathrm{H}}}}\)
6. Now, in this case T = T₁ and B_H = B₁cosθ₁
   
7. Therefore time period of a bar magnet at place ‘A’ is given by
   T₁ = \(2 \pi \sqrt{\frac{I}{m B_1 \cos \theta_1}}\) —– (1) Where I is moment of Inertia of a barmagnet and m is magnitude of magnetic moment.
8. Similarly, the same bar magnet is placed at B and which is set into angular oscillations in the earths magnetic field.
9. Let time period of a bar magnet at place B is T₂ and angle of dip is θ₂.
10. Since horizontal component of earths field at B is B_H = B₂ cos θ₂, time period,
    T₂ = \(2 \pi \sqrt{\frac{1}{\mathrm{mB}_2 \cos \theta_2}}\) —— (2)
11. Dividing equation (1) by equation (2), we get \(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\) = \(\sqrt{\frac{\mathrm{mB}_2 \cos \theta_2}{\mathrm{mB}_1 \cos \theta_1}}\)
    Squaring on both sides, we have \(\frac{\mathrm{T}_1^2}{\mathrm{~T}_2^2}\) = \(\frac{\mathrm{B}_2 \cos \theta_2}{\mathrm{~B}_1 \cos \theta_1}\)
12. But B₁ = μ₀H₁ and B₂ = μ₀H₂
    \(\frac{\mathrm{T}_1^2}{\mathrm{~T}_2^2}\) = \(\frac{\mu_0 \mathrm{H}_2 \cos \theta_2}{\mu_0 \mathrm{H}_1 \cos \theta_1}\)
13. Therefore, \(\frac{\mathrm{H}_1}{\mathrm{H}_2}\) = \(\frac{\mathrm{T}_2^2 \cos \theta_2}{\mathrm{~T}_1^2 \cos \theta_1}\)
    H2 T?cosOi .
14. By knowing T₁, T₂ and θ₁, θ₂ at different places A and B, we can find the ratio of resultant magnetic fields.

Question 5.
Define magnetic susceptibility of a material. Name two elements one having positive susceptibility and other having negative susceptibility. (A.P. Mar. ’15)
Answer:

1. SusceptIbility: When a material is placed in a magnetic field, the ratio of the intensity of magnetization acquired by it to the intensity of the applied magnetic field is called its susceptibility.
   
2. The susceptibility of a material represents its ability to get magnetism.
3. Susceptibility is a dimension less quantity.
4. Relation between μ_r and \(\chi\):
   • Suppose that material is placed in a magnetic field of intensity H. Let I be the intensity of magnetisation acquired by it.
   • Then the magnetic induction with in the material is
     B = μ₀H + μ₀I ⇒ \(\frac{\mathrm{B}}{\mathrm{H}}\) = μ₀[1 + \(\frac{\mathrm{I}}{\mathrm{H}}\)]
     ⇒ μ = μ₀[1 + \(\chi\)] ⇒ \(\frac{\mu}{\mu_0}\) = 1 + \(\chi\)
     μ_r = 1 + \(\chi\) [∵ μ_r = \(\frac{\mu}{\mu_0}\)]
5. Negative susceptibility (y) of diamagnetic elements4are Bismuth (-1.66 × 10^-5) and copper (-9.8 × 10^-6).
6. Positive susceptibility of Ferromagnetic elements are Aluminium (2.3 × 10^-5) and oxygen at STP (2.1 × 10^-6).
7. Large and positive susceptibility of Ferromagnetic elements are Cobalt and Nickel.

Question 6.
Obtain Gauss Law for magnetism and explain it. (T.S. Mar. ’19)
Answer:
Gauss law for Magnetism:

1. According to Gauss’s law for magnetism, the net magnetic flux (ϕ_B) through any closed surface is always zero.
2. The law implies that the no. of magnetic field lines leaving any closed surface is always equal to the number of magnetic field lines entering it.
3. Suppose a closed surface S is held in a uniform magnetic field B. Consider a small vector area element ΔS of this surface as shown in figure.
4. Magnetic flux through this area element is defined as
   Δϕ_B = B. ΔS. Then the net flux ϕ_B, is,
   
5. If the area elements are really small, we can rewrite this equation as
   
   
6. Comparing this equation with Gauss’s law of electrostatics i.e., electric flux through a closed surface S is given by
   
   Where q is the electric charge enclosed by the surface.
7. In an electric dipole were enclosed by the surface equal and opposite charges in the dipole add upto zero. Therefore, ϕ_E would be zero.
8. The fact that ϕ_B = 0 indicates that the simplest magnetic element is a dipole or current loop.
9. The isolated magnetic poles, called magnetic monopoles are not known to exist.
10. All magnetic phenomena can be explained interms of an arrangement of magnetic dipoles and /or current loops.
11. Thus corresponding to equation (II) of Gauss’s theorem in electrostatics, we can visualize equation (I) as
    ϕ_B = \(\int_{S_{,}} B . d S\) = µ₀ (m) + µ₀ (-m) = 0 where m is strength of N-pole and -m is strength of S -pole of same magnet.
12. The net magnetic flux through any closed surface is zero.

Question 7.
What do you understand by “hysteresis” ? How does this propetry influence the choice of materials used in different appliances where electromagnets are used ?
Answer:

1. Cycle of magnetisation : When a fen or magnetic specimen is slowly magnetised, the intensity of magnetisation varies with magnetic field through a cycle is called cycle of magnetisation.
2. Hysterisis : The lagging of intensity of magnetisation (I) and magnetic induction (B) behind magnetic field intensity (H) when a magnetic specimen is subjected to a cycle of magnetisation is called hysterisis.
3. Retentivity : The value of I for which H = 0 is called retentivity or residual magnetism.
4. Coercivity: The value of magnetising force required to reduce I is zero in reverse direction of H is called coercive force or coercivity.
5. Hysterisis curve : The curve represents the relation between B or I of a ferromagnetic material with magnetising force or magnetic intensity H is known as Hysterisis curve.
6. Explanation of hysterisis loop or curve :
   • In fig, a closed curve ABCDEFA in H – I plane, called hysterisis loop is shown in fig.
   • When ferromagnetic specimen is slowly magnetised, I increases with H.
   • Part OA of the curve shows that I increases with H.
     
   • At point A, the value I becomes constant is called saturation value.
   • At B, I has some value while H is zero.
   • In fig. BO represents retentivity and OC represents coercivity.
7. Uses : The properties of hysterisis curve, i.e., saturation, retentivity, coercivity and hysterisis loss help us to choose the material for specific purpose.
   1. Permanent magnets : A permanent magnet should have both large retentivity and large coercivity. Permanent magnets are used in galvanometers, voltmeres, ammeters, etc.
   2. An electromagnet core : The electromagnet core material should have maximum induction field B even with small fields H, low hysterisis loss and high initial permeability.
   3. Transformer cores, Dynamocore, Chokes, Telephone diaphragms: The core material should have high initial permeability, low hysterisis loss and high specific resistance to reduce eddy currents. Soft iron is the best suited material.

Problems

Question 1.
What is torque acting on a plane coil of “n” turns carrying a current “i” and having an area A, when placed in a constant magnetic field B ?
Answer:

For Rectangular LOOP PQRS :
Length PR = QS = l
breadth PQ = RS = b
Current = i
Magnetic field Induction = B
Angle made by normal to plane of coil with B = θ
Forces on conductor PR and SQ, F = Bil sin θ
Force on conductor PQ and RS, F = 0
Torque on a rectangular coil, T – F × ⊥^r distnace (b) ⇒ \(\tau\) – Bil sin θ (b)
∴ \(\tau\) = BiA sinθ[∵ A = l × b]
If the loop has n turns, then \(\tau\) = B in A sin θ.

Question 2.
A coil of 20 turns has an area of 800 mm² and carries a current of 0.5A. If it is placed in a magnetic field of intensity 0.3T with its plane parallel to the field, what is the torque that it experiences ?
Answer:
n = 20; A = 800 mm² = 800 × 10^-6 m²; i = 0.5A; B = 0.3T; θ = 0°.
When the plane parallel to the field,
T = B in A cos θ = 0.3 × 0.5 × 20 × 800 × 10^-6 × cos 0°
\(\tau\) = 2.4 × 10^-3 Nm

Question 3.
In the Bohr atom model the electrons move around the nucleus in circular orbits. Obtain an expression the magnetic moment (μ) of the electron in a Hydrogen atom in terms of its angular momentum L.
Answer:
Consider an electron of charge e, moves with constant speed v in a circular orbit of radius ‘r’ in Hydrogen atom as shown in fig.
Time period of orbiting electron,


The current constitute by revolving electron in circular motion around a nucleus, I = \(\frac{\mathrm{e}}{\mathrm{T}}\).
orbital magnetic moment, μ = IA = I (πr²)
⇒ μ = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}}\left(\pi \mathrm{r}^2\right)=\frac{\mathrm{evr}}{2}\)
μ = \(\frac{\mathrm{e}}{2 \mathrm{~m}}(\mathrm{mvr})\) [∵ Multiplying and dividing with ‘m’ on right side]
∴ μ = \(\frac{\mathrm{e}}{2 \mathrm{~m}} \mathrm{~L}\) where L = mvr = angular momentum.

Question 4.
A solenoid of length 22.5 cm has a total of 900 turns and carries a current of 0.8 A. What is the magnetising field H near the centre and far away from the ends of the solenoid ?
Answer:
l = 22.5 cm = 22.5 × 10^-2 m = \(\frac{45}{2}\) × 10^-2m
N = 900; I = 0.8A ; H = ?
H = \(\frac{\mathrm{NI}}{l}\) = \(\frac{900 \times 0.8}{\left(\frac{45}{2}\right) \times 10^{-2}}\)
H = \(\frac{900}{45}\) × 0.8 × 10² × 2
∴ H = 3200Am^-1

Question 5.
A bar magnet of length 0.1 m and with a magnetic moment of 5Am² is placed in a uniform amagnetic field n of intensity 0.4T, with its axis making an angle of 60° with the field. What is the torque on the magnet ? (Mar. ’14)
Answer:
Given, 2l = 0.1m; m = 5A – m²; B = OAT; θ = 60°.
Torque, T = mB sin θ = 5 × 0.4 × sin 60° = 2 × \(\frac{\sqrt{3}}{2}\)
∴ T = 1.732 N-m

Question 6.
If the Earth’s magnetic field at the equator is about 4 × 10⁵T, What is its approximate magnetic dipole moment ?
Answer:
Given, B_E = 4 × 10^-5 T; r = 6.4 × 10⁶m; m = ?
B_E = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m}}{\mathrm{r}^3}\)
4 × 10^-5 = \(\frac{4 \pi \times 10^{-7}}{4 \pi}\) × \(\frac{\mathrm{m}}{\left(6.4 \times 10^6\right)^3}\)
m = 4 × 10² × (6.4 × 10⁶)³
∴ m = 1.05 × 10²³ Am² ≈ 1 × 10²³ Am²

Question 7.
The horizontal component of the earth’s magnetic field at a certain place is 2.6 × 10^-5T and the angle of dip is 60°. What is the magnetic field of the earth at this location ?
Answer:
Given H_E = 2.6 × 10^-5T;
D (or) δ = 60°
B_E = \(\frac{\mathrm{H}_{\mathrm{E}}}{\cos \mathrm{D}}\) = \(\frac{2.6 \times 10^{-5}}{\cos 60^{\circ}}\) = \(\frac{2.6 \times 10^{-5}}{(1 / 2)}\) = 5.2 × 10^-5T
∴ B_E = 5.2 × 10^-5T

Question 8.
A solenoid, of insulated wire, is wound on a core with relative permeability 400. If the number of turns per metre is 1000 and the solenoid carries a current of 2A, calculate H, B and the magnetisation M.
Answer:
Given, µ_r = 400, I = 2A, n = 1000
H = nI = 1000 × 2 = 2 × 10³ A/m
B = µ_rµ₀ H = 400 × 4π × 10^-7 × 2 × 10³ = 1.0 T Magnetisation M = (µ_r – 1) H = (400 – 1)H = 399 × 2 × 10³
∴ M \(\simeq\) 8 × 10⁵ A/m

Textual Exercises

Question 1.
Answer the following questions regarding earth’s magnetism :
a) A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.
Answer:
The three independent quantities used to specify earth’s magnetic field are, Magnetic declination (θ), Magnetic dip (δ) and Horizontal component of earth’s field (H).

b) The angle of dip at a location in southern India is about 18°. Would you expect a greater or smaller dip angle in Britain ?
Answer:
Yes, we expect greater dip angle in Britian, because it is located close to North pole; δ = 70° in Britain.

c) If you made a map of magnetic field lines at Melbourne in Australia, would the lines seem to go into the ground or come out of the ground ?
Answer:
As Melbourne is situated in Southern hemisphere where north pole of earth’s magnetic field lies, therefore, magnetic lines of foece seem to come out of the ground.

d) In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic north ro south pole ?
Answer:
At the poles, earth’s field is exactly vertical. As the compass needle is free to rotate in a horizontal plane only, it may point out in any direction.

e) The earth’s field, it is claimed, roughly approximates the field due to a dipole of magnetic moment 8 × 10²² J T^-1 located at its centre. Check the order of magnitude of this number in some way.
Answer:
Here, M = 8 × 10²² J T^-1.
Let us calculate magnetic field intensity at magnetic line of short mangetic dipole for which, d = R = radius of earth 6,400 km = 6.4 × 10⁶ m.
B = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{M}}{\mathrm{d}^3}\) = 10^-7 × \(\frac{8 \times 10^{22}}{\left(6.4 \times 10^6\right)^3}\) = 0.31 × 10^-4T.
= 0.31 gauss
This value is in good approximation with observed values of earth’s magnetic field.

f) Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all ?
Answer:
The earth’s magnetic field is only approximately a dipole field. Therefore, local N-S poles may exist oriented in different directions. This is possible due to deposits of magnetised minerals.

Question 2.
Answer the following questions :
a) The earth’s magnetic field varies from point to point in space. Does it also change with time ? If so, on what time scale does it change appreciably ?
Answer:
Yes, earth’s field undergoes a change with time. For example, daily changes, annual changes secular changes with period of the order of 960 years and irregular changes like magnetic storms. Time scale for appreciable change is roughly a few hundred years.

b) The earth’s core is known to contain iron. Yet geologists do not regard this as a source of the earth’s magnetism. Why ?
Answer:
The earth’s core does contain iron but in the molten form only. This is not ferromagnetic and hence it cannot be treated as a source of earth’s magnetism.

c) The charged currents in the outer conducting regions of the earth’s core are thought to be responsible for earth’s magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents ?
Answer:
One of the possibilities is radioactivity in the interior of the earth. But it is not certain.

d) The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth’s field in such distant past ?
Answer:
Earth’s magnetic field gets recorded weakly in certain rocks during their solidification. An analysis of these rocks may reveal the history of earth’s magnetism.

e) The earth’s field departs from its dipole shape substantially at large, distances (greater than about 30,000 km). What agencies may be responsible for this distortion?
Answer:
The earth’s magnetic field gets modified by the field produced by motion of ions in earth’s ionosphere.

f) Interstellar space has an extremely weak magnetic field of the order of 10^-12 T. Can such a weak field be of any significant consequence? Explain.
[Note : Exercise 2 is meant mainly to arouse your curiosity. Answers to some questions above are tentative or unknown. Brief answers wherever possible are given at the end. For details, you should consult a good text on geomagnetism.)
Answer:
When a charged particle moves in a magnetic field, it is deflected along a circular path such that BeV = \(\frac{\mathrm{mV}^2}{\mathrm{r}}\) ∴ r = \(\frac{\mathrm{mV}}{\mathrm{Be}}\)
When B is low, r is high i.e., radius of curvature of path is very large. Therefore, over the gigantic inter stellar distance, the deflection of charged particles becomes less noticeable.

Question 3.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.25 T experiences a troque of magnitude equal to 4.5 × 10^-2 J. What is the magnitude of magnetic moment of the magnet?
Answer:
Here θ = 30°, B = 0.25 T, r = 4.5 × 10^-2 J, M =?
As r = mB sin θ ∴ m = \(\frac{r}{B \sin \theta}\) = \(\frac{4.5 \times 10^{-2}}{0.25 \sin 30^{\circ}}\) = 0.36JT^-1

Question 4.
A short bar magnet of magnetic moment m = 0.32 JT^-1 is placed in a uniform magnetic field of 0.15T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium ? What is the potential energy of the magnet in each case?
Answer:
Here m = 0.32JT^-1, B = 0.15T

1. In stable equilibrium, the bar magnet is aligned along the magnetic field, i.e., θ = 0°.
   Potentiâl Energy = -mB cos θ° = -032 × 0.15 × 0 = -4.8 × 10^-2J.
2. In unstable equilibrium the magnet is so oriented that magnetic moment is at 180° to the magnetic field i.e., θ = 180°.
   Potential Energy = -mB cos 180° = – 0.32 × 0.15 (-1) = 4.8 × 10^-2 J.

Question 5.
A closely wound solenoid of 800 turns and area of cross section 2.5 × 10^-4 m² carries a
current of 3.0A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment ?
Answer:
Here n = 800, a = 2.5 × 10^-4 m², I = 3.0 A
A magnetic field develop along the axis of the solenoid. Therefore the current carrying solenoid behaves like a bar magnet m = N IA = 800 × 3.0 × 2.5 × 10^-4
= 0.6 JT^-1 along the axis of solenoid.

Question 6.
If the solenoid in Exercise 5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30° with the direction of applied field ?
Answer:
Here M = 0.6 JT^-1 (from Question 5)
B = 0.25 T r = ? q = 30°
As r = m B sin θ’ ∴ r = 0.6 × 0.25 sin 30° = 0.075 N.m.

Question 7.
A bar magnet of magnetic moment 1.5 JT^-1 lies aligned with the direction of a uniform magnetic field of 0.22T.
a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment:
(i) normal to the field direction,
(ii) opposite to the field direction ?
Answer:
Here m = 1.5 JT^-1, B = 0.22 T, W = ?

a) Here θ₁ = 0° (along the field)
θ₂ = 90° (⊥ to the field)
As W = -mB (cos θ₂ – cos θ₁)
W =-1.5 × 0.22 (cos 90° – cos 0°) = -0.33 (0 – 1)
= 0.33 f

ii) Here θ₁ = 0°, θ₂ = 180°
W = -1.5 × 0.22 (cos 180° – cos 0°)
= – 0.33 (-1 – 1) = 0.66 J.

b) What is the torque on the magnet in cases (i) and (ii) ?
Answer:
Torque r = mB sin θ
i) Here θ = 90°, r = 1.5 × 0.22 sin 90° = 0.33 Nm
ii) Here θ = 180°, r = 1.5 × 0.22 sin 180° = 0

Question 8.
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10^-4 m², carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
a) What is the magnetic moment associated with the solenoid ?
Answer:
N = 2000, A = 1.6 × 10^-4 m², I = 4 amp, M = ?
As m = NIA
∴ M = 2000 × 4 × 1.6 × 10^-4 = 1.28 JT^-1

b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10^-2 T is set up at an angle of 30° with the axis of the solenoid ?
Answer:
Net force on the solenoid = 0
Torque, r = m B sin θ = 1.28 × 7.5 × 10^-2 sin 30°
= 1.28 × 7.5 × 10^-2 × \(\frac{1}{2}\)
r = 4.8 × 10^-2 Nm.

Question 9.
A circular coil of 76 turns and radius 10 cm. carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 8.0 × 10^-2 T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s^-1. What is the moment of inertia of the coil about its axis of rotation.
Answer:
Here n = 16, r = 10 cm = 0.1 m, I = 0.75A, B = 5.0 × 10^-2T
v = 2.0 s^-1, I = ?

Question 10.
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 22° with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Answer:
Here θ = 22° 1 + 0.35 G, R = ?
As H = R cos θ
R = H/cos θ = \(\frac{0.35}{\cos 22^{\circ}}\) = \(\frac{0.35}{0.9272}\) = 0.38 G

Question 11.
At a certain location in Africa, a compass points 12° west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points 60° above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Answer:
Here declination θ = 12° west, dip θ = 60°
H = 0.16 gauss = 0.16 × 10^-4 tesla. R = ?
As H = R cos θ

R = \(\frac{\mathrm{H}}{\cos \theta}\) = \(\frac{0.16 \times 10^{-4}}{\cos 60^{\circ}}\)
R = \(\frac{0.16 \times 10^{-4}}{1 / 2}\) = 0.32 × 10^-4T
The earth’s field lies in a vertical plane 12° west of geographic meridian at an angle of 60° above the horizontal.

Question 12.
A short bar magnet has a magnetic moment of 0.48 J T^-1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equitorial lines (normal bisector) of the magnet.
Answer:
Here M = 0.48 J T^-1, B = ?
d = 10 cm = 0.1 m

a) On the axis of the magnet
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 M}{d^3}\) = 10^-7 × \(\frac{2 \times 0.48}{(0.1)^3}\)
= 0.96 × 10^T along S – N direction

b) On the equitorial line of the magnet
B = \(\frac{\mu_{\mathrm{0}}}{4 \pi} \times \frac{\mathrm{M}}{\mathrm{d}^3}\) = 10^-7 × \(\frac{0.48}{(0.1)^3}\) = 0.48 × 10^-4T, along N – S direction.

Question 13.
A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north-south direction. Null points are found on the axis of the magnet at 14 cm from the centre of the magnet. The earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null-point- (i.e., 14 cm) from the centre of the magnet ? (At null distants, field due to a magnet is equal and opposite to the horizontal component of earth’s magnetic field.)
Answer:
As null points are on the axis of the magnet, therefore
B₁ = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{\mathrm{d}^3}\) = H
On the equitorial line of magnet at same distance (d), field due to the magnet is
B₂ = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{M}}{\mathrm{d}^3}\) = \(\frac{B_1}{2}\) = \(\frac{\mathrm{H}}{2}\)

∴ Total Magnetic field at this point on equitorial line is
B = B₂ + H = H + \(\frac{\mathrm{H}}{2}\) = \(\frac{3}{2} \mathrm{H}\)
B = \(\frac{3}{2}\) × 0.36 = 0.54G

Question 14.
If the bar magnet in Exercise 13 is turned around by 180°, where will the new null points be located ?
Answer:
When the bar magnet is turned through 180°, neutral points would lie on equitorial line, so that
B₂ = \(\frac{\mu_0}{4 \pi} \frac{M}{d_2^3}\) = H
On the equitorial line of magnet at same direction (d), field due to the magnet is
B₂ = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{M}}{\mathrm{d}_2^3}\) = H
In the previous question
B₁ = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{\mathrm{d}_1^3}\)
\(\mathrm{d}_2^3\) = \(\frac{d_1^3}{2}\) = \(\frac{(14)^3}{2}\)
d₂ = \(\frac{14}{2^{1 / 3}}\) = 11.1 cm

Question 15.
A short bar magnet of magnetic movement 5.25 × 10^-2 J T^-1 is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45° with earth’s field on (a) its normal bisector and (b) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Answer:
Here M = 5.25 × 10^-2 J T^-1 r = ?

Earth’s field \(\overrightarrow{\mathrm{B}}_{\mathrm{e}}\) = 0.42 G = 0.42 × 10^-4 T
a) At a point P distant r on normal bisector, fig, field due to the magnet is
\(\overrightarrow{\mathrm{B}}_2\) = \(\frac{\mu_0}{4 \pi} \frac{M}{r^3}\) along PAI/NS.
The resultant field \(\overrightarrow{\mathrm{R}}\) will be inclined at 45° to the earth’s field along PQ only when
|\(\vec{B}_2\)| = |\(\overrightarrow{\mathrm{B}}_{\mathrm{e}}\)|
\(\frac{\mu_0}{4 \pi} \cdot \frac{M}{r^3}\) = 0.42 × 10^-4
which gives, r = 0.05 m = 5 cm

b) When the point P lies on axis of the magnet such that OP = r, field due to magnet [fig.] is

\(\overrightarrow{\mathrm{B}}_1\) = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{\mathrm{r}^3}\) along PO, Earth’s field \(\overrightarrow{\mathrm{B}}_{\mathrm{e}}\) is along \(\overrightarrow{\mathrm{PA}}\). The resultant field \(\overrightarrow{\mathrm{R}}\) will be inclined at 45° to Earth’s field [Figure.] only when
|\(\overrightarrow{\mathrm{B}}_1\)| = |\(\overrightarrow{\mathrm{B}_{\mathrm{e}}}\)|
\(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{\mathrm{r}^3}\) = 0.42 × 10^-4 which gives
r = 6.3 × 10^-2 m = 6.3 cm

Additional Exercises

Question 1.
Answer the following Questions :
a) Why does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled ?
Answer:
This is because at lower temperatures, the tendency to disrupt the alignment of dipoles (due to magnetising field) decreases on account of reduced random thermal motion.

b) Why is diamagnetism, in contrast, almost independent of temperature ?
Answer:
In a diamagnetic sample, each molecule is not a magnetic dipole in itself. Therefore, random thermal motion of molecules does not affect the magnetism of the specimen. This is why diamagnetism is independent of temperature.

c) If a toroid uses bismuth for its core,’ will the field in the core be (slightly) greater or (slightly) less than when the core is empty ?
Answer:
As bismuth is diamagnetic, therefore, the field in the core will be slightly less than when the core is empty.

d) Is the permeability of a ferromagnetic material independent of the magnetic field ? If not, is it more for lower or higher fields ?
Answer:
No, permeability of a ferromagnetic material is not independent of magnetic field. As is clear from the hysteresis curve, μ is greater for lower fields.

e) Magnetic field lines are always nearly normal to the surface of a ferromagnet at every point. (This fact is analogous to the static electric field lines being normal to the surface of a conductor at every point.) Why ?
Answer:
Magnetic field lines are always nearly normal to the surface of a ferromagnet at every point. The proof of this important fact is based on the boundary conditions of magnetic fields (B and H) at the interface of two media.

f) Would the maximum possible magnetisation of a paramagnetic sample be of the same order of magnitude as the magnetisation of a ferromagnet ?
Answer:
The magnetic permeability of a ferromagnetic material μ > > 1. That is why the field lines meet this medium normally.

Question 2.
Answer the following questions :
a) Explain qualitatively on the basis of domain picture the irreversibility in the magnetisation curve of a ferromagnet.
Answer:
Since, in a ferromagnetic substance the magnetic properties are due to alignment of domains, therefore on with drawing the magnetising field the original domain formation does not take place.

b) The hysteresis loop of a soft iron piece has a much smaller area than that of a carbon steel piece. If the material is to go through repeated cycles of magnetisation, which piece will dissipate greater heat energy ?
Answer:
Carbon steel piece, because heat lost per cycle is proportional to the area of the hysteresis loop.

c) A system displaying a hysterisis loop such as a ferromagnet, is a device for storing memory ?’ Explain the meaning of this statement.
Answer:
Magnetisation of a ferromagnet is not a single – valued function of the magnetizing field. Its value for a particular field depends both on the field and also on the history of magnetisatiop. In other words, the value of magnetisation is a record or ‘memory’ of its cycle of magnetisation. If information bits can be made to correspond these cycles, the system displaying such a hysterisis loop can act as a device for storing information.

d) What kind of ferromagnetic material is used for coating magnetic tapes in a cassette player, or for building ‘memory stores’ in a modern computer ?
Answer:
Ceramics (specially treated barium iron oxides) also called ferrites.

e) A certain region of space is to be shielded from magnetic fields. Suggest a method.
Answer:
Surround the region by soft iron rings. Magnetic field lines will be drawn into the rings, and the enclosed space will be free of magnetic field. But this shielding is only approximate, unlike the perfect electric shielding of a cavity in a conductor placed in an external electric field.

Question 3.
A long straight horizontal cable carries a current of 2.5 A in the direction 10° south of west to 10° north of east. The magnetic meridian of the place happens to be 10° west of the geographic meridian. The earth’s magnetic field at the location is 0.33 G, and the angle of dip is zero. Locate the line of neutral points (ignore the thickness of the cable) ? (At neutral points, magnetic field due to a current – carrying cable is equal and opposite to the horizontal component of earth’s magnetic field).
Answer:
Here i = 2.5 amp
R = 0.33G = 0.33 × 10^-4 T; θ = 0°
Horizontal component of earth’s field
H = R cos θ = 0.39 × 10^-4 cos 35°
= 0.39 × 10^-4 × 0.8192
= 3.9 × 10^-5 tesla.
Vertical component of earth’s field.
H = R cos θ = 0.33 × 10^-4 cos 0°
= 0.33 × 10^-4 tesla.
Let the neutral points lie at a distance r from the cable
Strength of magnetic field on this line due to current in the cable = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\)

At neutral point,
\(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) = H
r = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{H}}\) = \(\frac{4 \pi \times 10^{-7} \times 2.5}{2 \pi \times 0.33 \times 10^{-4}}\) = 1.5 × 10^-2m
Hence neutral points lie on a straigt line parallel to the cable at a perpendicular distance of 1.5 cm above te plane of the paper.

Question 4.
A telephone cable at a place has four long straight horizontal wires carrying a current of 1.0 A in the same direction east to west. The earth’s magnetic field at the place is 0.39 G, and the angle of dip is 35°. The magnetic declination is nearly zero. What are the resultant magnetic fields at points 4.0 cm below the cable ?
Answer:
There, no. of wires, n = 4, i = 1.0 amp
Earth’s field R = 0.39 G = 0.39 × 10^-4 T
dip, θ = 35 declination θ = 0°
R₁ = ?, R₂ = ?

r = 4 cm each 4 × 10^-2 m
Magnetic field at 4 cm due to currents in 4 wires
B = 4 × \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) = 4 × \(\frac{4 \pi \times 10^{-7} \times 1}{2 \pi \times 4 \times 10^{-2}}\)
Horizontal component of earth’s field
H = R cos θ = 0.39 × 10^-4 cos 35°
= 0.39 × 10^-4 × 0.8192 = 3.19 × 10^-5tesla
Vertical component of Earth’s field
V = R sin θ = 0.39 × 10^-4 sin 35°
= 0.39 × 10^-4 × 0.5736 = 2.2 × 10^-5 tesla.
At point Q, 4 cm below the wire, horizontal component due to Earth’s field and field due to current are in opposite directions (fig.)
H₁ = H – B
∴ H₁ = 3.19 × 10^-5 – 2 × 10^-5
= 1.19 × 10^-5 tesla.
Hence R₁ = \(\sqrt{\mathrm{H}_1^2+\mathrm{V}^2}\)
= \(\sqrt{\left(1.19 \times 10^{-5}\right)^2+\left(2.2 \times 10^{-5}\right)^2}\)
= 2.5 × 10^-5 tesla.
At point P, 4 cm above the wire, horizontal component of Earth’s field and field due to current are in the same direction [fig.]
H₂ = H + B = 3.19 × 10^-5 + 2 × 10^-5 = 5.19 × 10^-5 T
R₂ = \(\sqrt{\mathrm{H}_2^2+\mathrm{V}^2}\) = \(\sqrt{\left(5.19 \times 10^{-5}\right)^2+\left(2.2+10^{-5}\right)^2}\) = 5.54 × 10^-5 tesla.

Question 5.
A compass needle free to turn in a horizontal plane is placed at the centre of circular coil of 30 turns and radius 12 cm. The coil is in a vertical plane making an angle of 45° with the magnetic meridian. When the current in the coil is 0.35 A, the needle points west to east.
a) Determine the horizontal component of the earth’s magnetic field at the location.
b) The current in the coil is reversed, and the coil is rotated about its vertical axis by an angle of 90° in the anticlockwise sense looking from above. Predict the direction of the needle. Take the magnetic declination at the places to be zero.
Answer:
a) Here n = 30, r = 12 cm = 12 × 10^-2 m
i = 0.35 amp, H = ?
As is clear from fig. 11 the needle can point west to east only when H = B sin 45°
Where B = Magnetic field strength due to current in coil = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{ni}}{\mathrm{r}}\)

b) When current in coil is reversed and coil is turned through 90° anticlock wise, the direction of needle will reverse (i.e., it will point from East to West). This follow from the figure.

Question 6.
A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 60°, and one of the fields has a magnitude of 1.2 × 10^-2 T. If the dipole comes to stable equilibrium at an angle of 15° with this field, what is the magnitude of the other field ?
Answer:
Here θ = 60°; B₁ = 1.2 × 10^-2 tesla
θ₁ = 15°; θ₂ = 60° – 15° = 45°

In equilibrium, torque due to two fields must balance i.e., r₁ = r₂
MB₁ sin θ₁ = MB₂ sin θ₂
B₂ = \(\frac{B_1 \sin \theta_1}{\sin \theta_2}\) = \(\frac{1.2 \times 10^{-2} \sin 15^{\circ}}{\sin 45^{\circ}}\)
B₂ = \(\frac{1.2 \times 10^{-2} \times 0.2588}{0.7071}\) = 4.4 × 10^-3 tesla.

Question 7.
A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.04 G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (m_e = 9.11 × 10^-31 kg).
[Note : Data in this exercise are so chosen that the answer will give you an idea of the effect of earth’s magnetic field bn the motion of the electron beam from the electron gun to the screen in a TV set] .
Answer:
Here energy E = 18 KeV = 18 × 1.6 × 10^-19J
B = 0.40 G = 0.40 × 10^-4 T
x = 30 cm = 0.3 m
As E = \(\frac{1}{2}\) mυ² ∴ υ = \(\sqrt{\frac{2 E}{m}}\)
In a magnetic field electron beam is deflected along a circular arc of radius r, such that

BeV = \(\frac{m v^2}{r}\) or r = \(\frac{\mathrm{mv}}{\mathrm{Be}}\)
r = \(\frac{m}{B e} \sqrt{\frac{2 E}{m}}\) = \(\frac{1}{\mathrm{Be}} \sqrt{2 \mathrm{Em}}\) = 11.3 m
If y is the deflection at the end of the path it is clear from fig.
θ = \(\frac{\mathrm{x}}{\mathrm{r}}\) = \(\frac{\mathrm{y}}{\mathrm{x} / 2}\) = 2\(\frac{y}{x}\)
or y = \(\frac{x^2}{2 r}\) = \(\frac{0.30 \times(0.30)}{2 \times 11.3}\)m = 0.004m = 4mm

Question 8.
A sample of paramagnetic salt contains 2.0 × 10²⁴ atomic dipoles each of dipole moment 1.5 × 10^-23 J T^-1. The sample is placed under a homogeneous magnetic field of 0.64 T, and cooled to a temperature of 4.2 K. The degree of magnetic saturation achieved is equal to 15%. What is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K ? (Assume Curie’s law)
Answer:
Here no. of dipoles n = 2 × 10²⁴
Magnetic moment of each dipole M = 1.5 × 10^-23 J T^-1.
Total dipole moment of sample = n × M = 2 × 10²⁴ × 1.5 × 10^-23 = 30
As saturation achieved is 15% therefore, effective dipole moment
M₁ = \(\frac{15}{100}\) × 30 = 4.5 J T^-1; B₁ = 0.64T, T₁ = 4.2 k,
M₂ = ?; B₂ = 0.98 T,T₂ = 2.8 k

Question 9.
A Rowland ring of mean radius 15 cm has 3500 turns of wire wound on a ferromagnetic core of relative permeability 800. What is the magnetic field B in the core for a magnetising current of 1.2 A?
Answer:
Here r = 15 cm = 15 × 10^-2 m, N = 3500, M_r = 800
I = 1.2A, B =?
Number of turns, length, n = \(\frac{N}{2 \pi r}\) = \(\frac{3500}{2 \pi \times 15 \times 10^{-2}}\)
B = μ₀μ_rnI
= 4π × 10^-7 × 800 × \(\frac{3500 \times 1.2}{2 \pi \times 15 \times 10^{-2}}\)
= 4.48T

Question 10.
The magnetic moment vectors μ_s and μ_l associated with the intrinsic spin angular momentum S and orbital angular momentum 1, respectively, of an electron are predicted
by quantum theory (and verified experimentally to a high accuracy) to be given by:
m_s = -(e/m) S,
μ_l = -(e/2m)l
Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
Answer:
Out of the two relations given only one is in accordance with classical physics. This is
\(\vec{\mu}_1\) = \(-\left(\frac{\mathrm{e}}{2 \mathrm{~m}}\right) \vec{l}\)
It follows from the definitions of μ₁ and l.
μ = iA = \(\left(\frac{-\mathrm{e}}{\mathrm{T}}\right) \pi \mathrm{r}^2\)
l = mvr = \(\mathrm{m}\left(\frac{2 \pi \mathrm{r}}{\mathrm{T}}\right) \mathrm{r}\)
Where r is the radius of the circular orbit, which the electron of mass m and charge (-e) completes in time T.
Divide (i) by (ii) \(\frac{\mu_1}{l}\) = \(\frac{-\mathrm{e}}{\mathrm{T}} \pi \mathrm{r}^2 \times \frac{\mathrm{T}}{\mathrm{m}^2 \pi \mathrm{r}^2}=\frac{-\mathrm{e}}{2 \mathrm{~m}}\)
\(\vec{\mu}_1\) = \(\left(\frac{-\mathrm{e}}{2 \mathrm{~m}}\right) \vec{l}\)
‘Clearly \(\vec{\mu}_1\) and \(\vec{l}\) will be antiparallel (both being normal to the plane of the orbit)
In contrast \(\frac{\mu_{\mathrm{S}}}{\mathrm{S}}\) = \(\frac{\mathrm{e}}{\mathrm{m}}\). It is obtained on the basis of quantum mechanics.

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism

Very Short Answer Questions

Question 1.
What is the importance of Oersted’s experiment ?
Answer:
Importance of Oersted’s experiment is every current carrying conductor produces a magnetic field around it and which is perpendicular to current carrying conductor.

Question 2.
State Ampere’s law and Biot-Savart law. (T.S. Mar. ’19)
Answer:
Ampere’s law : The line integral of the intensity of magnetic induction around a closed path is equal to µ₀ times the total current enclosed in it.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = \(\mu_0 \mathrm{i}\)

Biot – Savart’s laws : Biot – Savart’s states that the intensity of magnetic induction (dB) due to a small element is directly proportional to the .

1. current (i)
2. length of the element (dl)
3. sine angle between radius vector (r) and dl and
4. Inversely proportional to the square of the point from current element.
   ∴ dB ∝ \(\frac{\mathrm{i} \mathrm{d} l \sin \theta}{\mathrm{r}^2}\)
   dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{i} d l \sin \theta}{r^2}\)

Question 3.
Write the expression for the magnetic induction at any point on the axis of a circular current-carrying coil. Hence, obtain an expression for the magnetic induction at the centre of the circular coil.
Answer:

1. Intensity of magnetic induction field on the axis of the circular coil B = \(\frac{\mu_0 n i r^2}{2\left(r^2+x^2\right)^{3 / 2}}\)
2. At the centre of the coil B = \(\frac{\mu_0 \mathrm{ni}}{2 \mathrm{r}}\)

Question 4.
A circular coil of radius V having N turns carries a current “i”. What is its magnetic moment ?
Answer:
Magnetic moment (M) = N i A
M = N i (πr²) (∵ A = πr²)
∴ M = n N i r²

Question 5.
What is the force on a conductor of length L carrying a current “i” placed in a magnetic field of induction B ? When does it become maximum ?
Answer:

1. Force on a conductor (F) = B i L sin θ
2. If θ = 90°, F_Max = B i L
   i.e., the direction of current and magnetic field are perpendicular to each other, then force is maximum.

Question 6.
What is the force on a charged particle of charge “q” moving with a velocity “v” in a uniform magnetic field of induction B ? When does it become maximum ?
Answer:

1. Force on a charged particle (F) = B q v sin θ.
2. If θ = 90°, F_Max = B q v.

Question 7.
Distinguish between ammeter and voltmeter. (A.P. Mar. ’15)
Answer:
Ammeter

1. It is used to measure current.
2. Resistance of an ideal Ammeter is zero.
3. It is connected in series in the circuits.

Voltmeter

1. It is used to measure P.D between two points.
2. Resistance of ideal voltmeter is infinity.
3. It is connected in parallel in the circuits.

Question 8.
What is the principle of a moving coil galvanometer ?
Answer:
Moving coil galvanometer is based on the fact that when a current carrying coil is placed in a uniform magnetic field, it experiences a torque.
∴ current in the coil (i) ∝ deflecting angle (θ).

Question 9.
What is the smallest value of current that can be measured with a moving coil galvanometer ?
Answer:
Moving coil galvanometer is sensitive galvanometer, it is used to measure very small current upto 10^-9A.

Question 10.
How do you convert a moving coil galvanometer into an ammeter ? (A.P. Mar. ’19)
Answer:
A small resistance is connected in parallel to the moving coil galvanometer, then it converts to Ammeter.
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)

Question 11.
How do you convert a moving coil galvanometer into a voltmeter? (T.S. & A.P. Mar. ’16, T.S. Mar. ’15 Mar. ’14)
Answer:
A high resistance is connected in series to the moving coil galvanometer, then it converts to voltmeter.
R = \(\frac{\mathrm{v}}{\mathrm{i}_{\mathrm{g}}}-\mathrm{G}\)

Question 12.
What is the relation between the permittivity of free space e₀, the permeability of free space m₀ and the speed of light in vacuum ?
Answer:
Speed of light in vacuum (C) = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\)
Here μ₀ = m₀ = permeability in vacuum
ε₀ = permittivity in vacuum.

Question 13.
A current carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic field be set up in such a manner that the loop turns about the vertical axis ?
Answer:
Torque \((\tau)\) = \(\overrightarrow{\mathrm{M}}\) × \(\overrightarrow{\mathrm{B}}\) = i\(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) (M = n i A)
where i is current, \(\overrightarrow{\mathrm{A}}\) is area vector, \(\overrightarrow{\mathrm{B}}\) is magnetic field. Area vector \(\overrightarrow{\mathrm{A}}\) acts normal to the loop, so torque \(\vec{\tau}\) cannot act along the vertical axis. The magnetic field is not set up to turn the loop around it self.

Question 14.
A current carrying circular loop is placed in a uniform external magnetic field. If the loop is free to turn, what is its orientation when it is achieves stable equilibrium ?
Answer:
The plane of the loop is perpendicular to the direction of magnetic field because the torque on the loop in this orientation is zero.

Question 15.
A wire loop of Irregular shape carrying current is placed In an external magnetic field. If the wire is flexible, what shape will the loop change to ? Why?
Answer:
For a given perimeter, a circle has maximum area among all geometrical shapes. So to maximise tie magnetic flux through it will assume a circular shape with its plane normal to the field.

Short Answer Questions

Question 1.
State and explain Biot-Savart law. (T.S. Mar. ’16, Mar. ’14)
Answer:
Consider a very small element of length dl of a conductor carrying current

Magnetic induction due to small element at a point P distance r form the element. Magnetic induction (dB) is directly proportional to

1. 1. current (i)
   2. Length of the element (dl)
   3.  sine angle between r and dl and
   4. Inversely proportional to the square of the distance from small element to point R
      
      dB ∝ \(\frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
      dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
      where μ = permeability in free space.
      \(\frac{\mu_0}{4 \pi}\) = 10^-7 Wb m^-1 A^-1

Question 2.
State and explain Ampere’s law.
Answer:
Ampere’s law : The line integral of the intensity of magnetic induction field around closed path is equal to μ₀ times the net current (i) enclosed by the path.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i
Proof: Consider a long” straight conductor carrying current i as shown in figure. Magnetic induction at a distance r from the conductor is given by

B = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) (from Biot-Savart’s law)
The value of B is same at all points on the circle.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = \(\oint \mathrm{Bd} l \cos \theta\)
= \(\mathrm{B} \oint \mathrm{d} l\) = B × 2πr (∵ θ = 0° Angle between \(\overrightarrow{\mathrm{B}}\) & \(\overrightarrow{\mathrm{d} l}\) is zero)
= \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) × 2πr
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i.
This proves Ampere’s circuital laws.

Question 3.
Find the magnetic induction due to a long current carrying conductor.
Answer:
Consider a long straight conductor carrying a current i. Let P be a point at a distance r from the conductor. Let r be the radius of the circle passing through point p.

(∵ \(\oint \mathrm{d} l\) = 2πr = circumference of the circle)
Magnetic induction is same at all points on the circle. Consider a small element of length dl.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = \(\oint \mathrm{Bd} l \cos \theta\)
Angle between B and dl is zero i.e. θ = 0
= B\(\oint \mathrm{dl}\)
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = B (2πr) ——> (1)
According to Ampere’s laws
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = µ₀i ——-> (2)
From equations (1) and (2), B (2πr) = µ₀ i
B = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\)

Question 4.
Derive an expression for the magnetic induction at the centre of a current carrying circular coil using Biot-Savart law.
Answer:
Consider a circular coil of radius r and carry a current i. Consider a small element ‘dl’. Let O is the centre of the coil. By using Biot – Savart’s law
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{i} d l \sin \theta}{\mathrm{r}^2}\)
Here angle \(\overrightarrow{\mathrm{d} t}\) and \(\overrightarrow{\mathrm{r}}\) is 90° (i.e. θ = 90°)
dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{id} l}{\mathrm{r}^2}\) — (1)

As the field due to all elements of the circular loop have the same direction.
The resultant magnetic field can be obtained by integrating equation (1)
\(\int \mathrm{dB}\) = \(\int \frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l}{\mathrm{r}^2}\)
B = \(\frac{\mu_0 \mathrm{i}}{4 \pi \mathrm{r}^2} \int \mathrm{d} l\) ∵ (\(\int\)dl = 2πr)
= \(\frac{\mu 0 \mathrm{i}}{4 \pi \mathrm{r}^2}\) × 2πr
B = \(\frac{\mu_0 \mathrm{i}}{2 \mathrm{r}}\)
If the circular coil has n turns.
B = \(\frac{\mu_0 \mathrm{ni}}{2 \mathrm{r}}\)

Question 5.
Derive an expression for the magnetic induction a point on the axis of a current carrying circular coil using
Answer:

Consider a circular coil of radius R and carrying a current i. Let P is a point on the axis at a distance x from the centre O. Let r be the distance of small element (dl) from P.
From Biot – savart’s law
dB = \(\frac{\mu_0}{4 \pi} \frac{\text { id } l \sin \theta}{r^2}\) = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l}{\mathrm{r}^2}\) —– (1) (∵ θ = 90° Angle between \(\overrightarrow{\mathrm{d} l}\) and \(\overrightarrow{\mathrm{r}}\))
dB can be resolved into two components dB cos θ and dB sinθ. If we consider another element diametrically opposite to AB.
This also resolved into dB cosθ and dB sinθ.
The components along the axis will add up and perpendicular to the axis will cancel.
∴ Resultant magnetic induction at P is
B = \(\int \frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
= \(\frac{\mu_0 i}{4 \pi^2} \int d / \sin \theta\) (∵ sin θ = \(\frac{R}{r}\))
= \(\frac{\mu_0 \mathrm{i}}{4 \pi \mathrm{r}^2}\) × 2πR × \(\frac{\mathrm{R}}{\mathrm{r}}\) (∵ \(\int dl\) = 2πr)
B = \(\frac{\mu_0 \mathrm{iR}^2}{2 \mathrm{r}^3}\) —–> (3)
From figure r = \(\sqrt{\mathrm{R}^2+\mathrm{x}^2}\)
B = \(\frac{\mu_0 i R^2}{2\left(R^2+x^2\right)^{3 / 2}}\) —–> (4)
If the coil contains N turns,
B = \(\frac{\mu_0 N i R^2}{2\left(R^2+x^2\right)^{3 / 2}}\) —–> (5)

Question 6.
Obtain an expression for the magnetic dipole moment of current loop.
Answer:
We know that magnetic induction on the axial line of a circular coil is B = \(\frac{\mu_0 N \mathrm{iR}^2}{2\left(\mathrm{R}^2+\mathrm{x}^2\right)^{3 / 2}}\)
where N = Number of turns in the coil
R = Radius of the coil
x = Distance from centre of the coil
i = Current in a coil
If x >> R, Then B = \(\frac{\mu_0 \mathrm{Ni} \mathrm{R}^2}{2 \mathrm{x}^3}\)
Multiplying and dividing with 2π
B = \(\frac{\mu_0 \mathrm{Ni} \mathrm{R}^2}{2 \mathrm{x}^3} \times \frac{2 \pi}{2 \pi}\)
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{Ni}\left(\pi \mathrm{R}^2\right)}{\mathrm{x}^3}\) (∵ A = πR²)
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{Ni} \mathrm{A}}{\mathrm{x}^3}\) —– (1)
We know that magnetic induction field on the axial line of a bar magnet
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{\mathrm{x}^3}\) —– (2)
Comparing the equations (1) and (2)
Magnetic moment (M) = N i A

Question 7.
Derive an expression for the magnetic dipole moment of a revolving electron. (Ã.P. Mar. ’16)
Answer:
Consider an electron revolving in a circular orbit of radius r with speed v and frequency υ.
If the electron cross a point P on the circle in every revolution, then distance travelled by electron to complete one revolution = 2πr.
No. of revolutions in one second (υ) = \(\frac{\mathrm{v}}{2 \pi r}\)
The electric current (i) = \(\frac{\text { charge }}{\text { time }}\) = charge × frequency
i = e × \(\frac{\mathrm{v}}{2 \pi \mathrm{r}}\)
∴ Magnetic dipole moment (M) = I A (∵ N = 1)
M = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}} \times \pi \mathrm{r}^2\) (∵ A = πr²)
M = \(\frac{\text { evr }}{2}\)

Question 8.
Explain how crossed E and B fields serve as a velocity selector.
Answer:
When a charged particle q moving with a velocity v in presence of both electric and magnetic fields.
The force experienced due to electric field F_E = q\(\overrightarrow{\mathrm{E}}\)
The force experienced due to magnetic field F_B = q \(\left(\begin{array}{l}
\vec{v} \times \vec{B}
\end{array}\right)\)
Consider electric and magnetic fields are perpendicular to each other and also perpendicular to the velocity of the particle.
E = E\(\hat{j}\), B = B\(\hat{k}\), v = v\(\hat{i}\)
F_E = qE\(\hat{j}\), F_B = q (v\(\hat{i}\) × B\(\hat{k}\)) = – qvB\(\hat{j}\)
∴ F = F_E + F_B
F = q (E – υB) \(\hat{j}\)

Thus electric and magnetic forces are in opposite directions.
We adjust E and B such that, the forces are equal
F_E = F_B
qE’ = q υ B
υ = \(\frac{E}{B}\)
This condition can be used to select charged particles of a particular velocity. The crossed field E and B serve as a velocity selector.

Question 9.
What are the basic components of a cyclotron ? Mention its uses ?
Answer:
Cyclotron is a device used to accelerate positively charged particles like protons, α – particles, deutrons etc.

Cyclotron mainly consists of

1. Two hollow D-shaped metallic chambers D₁ and D₂
2. High frequency oscillator
3. Strong electro magnet
4. Vacuum chamber.

Uses of cyclotron :

1. It is used for producing radioactive material for medical purposes i.e. diagnostics and treatment of chronic diseases.
2. It is used to improve the quality of solids by adding ions.
3. It is used to synthesise fresh substances.
4. It is used to bombard the atoms with highly accelerated particles to study the nuclear reactions.

Long Answer Questions

Question 1.
Deduce an expression for the force on a current carrying conductor placed in a magnetic field. Derive an expression for the force per unit length between two parallel current carrying conductors.
Answer:
Expression for the Force acting on a current carrying conductor :
Consider a straight conductor (wire) of length ‘l’, area of cross section ‘A’, carrying a current ’i’, ‘which is placed in a uniform magnetic field of induction B’ as shown in fig.
We know the external magnetic field exerts a force on the conductor.
The electrons in effect move with an average velocity called drift velocity V_d‘. The direction of conventional current will be opposite to the direction of drift velocity.

Let us assume that the current flows through the conductor from left ‘B’ in the plane of the paper makes an angle ‘θ’ with the direction of current ‘i’ as shown in fig.

If F’ is the force acting on the charge ‘q’ in B
∴ F = q V_d B sin θ
If ‘n’ represents number of moving electrons per unit volume (∵ n = \(\frac{\mathrm{N}}{\mathrm{V}}\))
∴ Current i = nqV_dA
If ‘N’ is the number of electrons in the length ‘l’
N = nlA .
Total force on conductor F = F’.N (∵ N = nV = n × A × l)
= (q V_dB sin θ) (nlA)
= (nqV_dA) (IB sin θ)
∴ F = ilB sin θ
Case (i) : If θ = 0°, F_Min = 0
Case (ii) : If θ = 90°, F_Max = Bil

Expression for the force between two Parallel conductors carrying conductors:
Consider two straight parallel conductors .‘AB and ‘CD’ carrying currents ‘i₁’ and “i₂’ and which are separated by a distance ‘r’ as shown in fig.

If B₁ and B₂ are magnetic inductions produced by the current carrying conductors AB and CD. Magnetic induction B₁ at a distance ‘r’ from the conductor ‘AB’ can be written as B₁ = \(\frac{\mu_0 i_1}{2 \pi r}\)
If ‘F is force acting on CD’ due to magnetic induction B₁ then
F_CD = i₂lB₁
Where l = length of the conductor
F_CD = \(\mathrm{i}_2 l\left(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\right)\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\) — (1)

The direction of the force can be determined by using Flemings left hand rule.
Similarly we can find the force acting on the conductor AB due to magnetic induction B₂.
F_AB = i₁lB₂
∴ F_AB = \(\mathrm{i}_1 l\left(\frac{\mu_0 \mathrm{i}_2}{2 \pi \mathrm{r}}\right)\) —– (2) [∵ B₂ = \(\frac{\mu_0 i_2}{2 \pi r}\)]
From the equations (1) and (2) F_AB = F_CD = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
∴ Force between two parallel, straight conductors carrying currents
F = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
Force per unit length \(\frac{\mathrm{F}}{l}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\)

Question 2.
Obtain an expression for the torque on a current carrying loop placed in a uniform magnetic field. Describe the construction and working of a moving coil galvanometer.
Answer:
Torque acting on a coil carrying a current kept in a uniform magnetic field : Let a rectangular current loop ABCD of length l = AB = CD and width b = AD = BC carrying a current “i” be suspended in a magnetic field of flux density B.
The normal ON drawn to the plane of the coil makes an angle ‘θ’ with the magnetic field B.

Force on arm AD = i\(\overline{\mathrm{b}}\) × \(\overrightarrow{\mathrm{B}}\) acting upwards along the axis of suspension
Force on arm BC = i\(\overline{\mathrm{b}}\) × \(\overrightarrow{\mathrm{B}}\) acting downwards along the axis of suspension
Hence these two forces cancel.

Force on arm AB = ilB acting perpendicular to the plane as shown.
Force on arm CD = ilB acting perpendicular to the plane as shown.
These two forces constitute a couple on the coil.
Moment of the couple = (Force) × (Perpendicular distance between the forces) = i/B (PQ sin θ)
Torque = ilB b sinθ
But l × b = Area of coil
∴ Torque = iAB sin θ
If the loop has n’ turns the torque on the coil
\(\tau\) = n i AB sinθ
If “ϕ’ is the deflection of the coil, that is the angle between the plane of the coil and magnetic field B
\(\tau\) = n i AB cos ϕ

Moving coil galvanometer:
Principle : When a current carrying coil is placed in the uniform magnetic field, it experiences a torque.

Construction: .

1. It consists of a coil wound on a non metallic frame.
2. A rectangular coil is suspended between two concave shaped magnetic poles with the help of phosphour Bronze wire.
3. The lower portion of the coil ‘is connected to a spring.
4. A small plane mirror M is fixed to the phosphour Bronze wire to measure the deflection of the coil.
5. A small soft iron cylinder is placed with in the coil without touching the coil. ‘The soft iron cylinder increases the induction field strength.
6. The concave shaped magnetic poles render the field radial. So maximum torque acting on it.
7. The whole of the apparatus is kept inside a brass case provided with a glass window.
   

Theory:
Consider a rectangular coil of length l and breadth b and carrying current i suspended in the induction field strength B.
Deflecting torque \((\tau)\) = B i A N —–> (5)

where A = Area of the coil
N = Total number of turns.
The restoring torque developed in the suspension = C θ —-> (2)
Where C is the couple per unit twist and θ is the deflection made by the coil. When the coil is in equilibrium position
Deflecting torque = Restoring torque
B i A N = C θ
i = \(\left(\frac{C}{\mathrm{BAN}}\right) \theta\)
Where K = \(\frac{\mathrm{C}}{\mathrm{BAN}}\) = Galvanometer constant
i = K θ —-> (3)
i ∝ θ
Thus deflection of the coil is directly proportional to the current flowing through it.
The deflection in the coil is measured using lamp and scale arrangement.

Question 3.
How can a galvanometer be converted fo an ammeter ? Why is the parallel resistance smaller that the galvanometer resistance ?
Answer:
Conversion of Galvanometer into Ammeter :
Galvanometer is converted into an ammeter by connecting a suitable resistance is parallel to it.
This arrangement decreases the effective resistance.

Ammeter is used for measuring the current in an electric circuit and it is connected in series in circuit.
The inclusion of the ammeter in the circuit should not alter the current or total resistance of the circuit so it has very low resistance.
The resistance of An ideal Ammeter is zero.
Let G and S be the Galvanometer and shunt resistances respectively.
Let ‘i’ be the total current, divided at A into i_g and i_s as shown in fig.
From Kirchhoff’s I^st law i = i_g + i_s
As ‘G’ and ‘S’ are parallel
PD. across Galvanometer = P.D. across shunt
i_g G = i_s S
S = \(\frac{\mathrm{i}_{\mathrm{g}}}{\mathrm{i}_{\mathrm{s}}} \mathrm{G}\)
= \(\frac{\mathrm{Gi}_{\mathrm{g}}}{\mathrm{i}-\mathrm{i}_{\mathrm{g}}}\) [∵ i_s = i – i_g]
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)
If \(\frac{\mathrm{i}}{\mathrm{i}_g}\) = n ⇒ i_g = \(\frac{i}{n}\)
∴ The current flowing through the galvanometer be \(\left(\frac{1}{n}\right)^{\text {th }}\) of total current.
∴ S = \(\frac{\mathrm{G}}{\mathrm{n}-1}\)
If ‘R is the effective resistance between points ‘A’ and ‘B’ then

Hence current through galvanometer is proportional to the total current. Since ‘S’ is small major portion of the current flows through it and a small portion of current flows through G. So shunt protects the galvanometer from high currents. Parallel resistance is smaller than Galvanometer resistance because to protect the Galvanometer from high (large) current (or) to pass. Large currents through shunt and small current passes through the galvanometer.

Question 4.
How can a galvanometer be converted to a voltmeter ? Why is the series resistance greater that the galvanometer resistance ?
Answer:
Conversion of Galvanometer into, Voltmeter: A galvanometer-is converted into voltmeter by connecting a high resistance (R) in series with it. Voltmeter is used to measure the RD. between any two points in circuit and it is connected in parallel to the component of the circuit.

Let V be the potential difference to be measured between the points ‘A’ and ‘B’.
∴ V = (R + G) i_g [∴ V = iR]

Where G = Galvanometer Resistance
i_g = Current passing through the galvanometer
\(\frac{\mathrm{V}}{\mathrm{i}_g}\) = R + G
∴ R = \(\frac{\mathrm{V}}{\mathrm{i}_g}\) – G —- (1)
The value of ‘R’ can be calculated by using the above formula. If V_g is the maximum P.D. across the galvanometer then V_g = i_g G
∴ i_g = \(\frac{V_g}{G}\) —— (2)
Substitute ‘i_g‘ in Equ (1)
R = \(\frac{V G}{V_g}\) – G = G\(\left(\frac{V}{V_g}-1\right)\)
If \(\frac{V}{V_g}\) = n ⇒ R = G(n – 1)
Note: n = \(\frac{V}{V_g}\) is the ratio of maximum voltage to be measured to the maximum voltage across the galvanometer
Series resistance is greater than galvanometer resistance because the current in external resistance and potential difference will be decreased and to increase the resistance of the galvanometer.

Question 5.
Derive an expression for the force acting between two very long parallel current-carrying conductors and hence define the Ampere.
Answer:
Force between two parallel conductors carrying current:

Let two long parallel conductors A and B seperated by a distance r carry currents i₁ and i₂ in the same directions.
The current i₁ produces magnetic induction around the conductor A and the current i₂ produces magnetic induction B₂ around the conductor B.
If l is the length of each conductor,
The magnetic induction B₁ at distance r from conductor A is
B₁ = \(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\) — (1)
The force on conductor B is given by
F₂ = i₂ l B₁ —- (2)
The direction of force is given by Fleming left hand rule
F₂ = i₂l × \(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\) —- (3)
The direction of force F₂ is towards conductor A. Similary the magnetic induction B₂ at distance r from conductor B is
B₂ = \(\frac{\mu_0 \mathrm{i}_2}{2 \pi \mathrm{r}}\) — (4)
The force on conductor A is given by
F₁ = i₁lB₂ —- (5)
Substituting B₂ value in equation (5)
F₁ = \(\frac{\mathrm{i}_1 l \times \mu_0 \mathrm{i}_2}{2 \pi \mathrm{r}}\)
F₁ = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\) — (6)
It can be seen that | F₁| = | F₂| = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
The force per unit length of the conductor is given by
\(\frac{F}{l}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\) —–>(7)

Definition of Ampere:
If i₁ = i₂ = 1A, r = 1m
F/l = \(\frac{4 \pi \times 10^{-7} \times 1 \times 1}{2 \pi \times 1}\) = 2 × 10^-7 Nm^-1
“When two infinitely long parallel conductors, carrying the same current are seperated by 2 × 10^-7 Nm^-1, then the current flowing through each conductor is said to be one Ampere”.

Problems

Question 1.
A current of 10A passes through two very long wires held parallel to each other and separated by a distance of 1m. What is the force per unit length between them ? (T.S. Mar. ’19 & A.P. & T.S. Mar. ’15)
Solution:
i₁ = i₂ = 10A
r = 1m
\(\frac{\mathrm{F}}{l}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\)
= \(\frac{4 \pi \times 10^{-7} \times 10 \times 10}{2 \pi \times 1}\)
\(\frac{\mathrm{F}}{\mathrm{l}}\) = 2 × 10^-5 Nm^-1.

Question 2.
A moving coil galvanometer can measure a current of 10^-6 A. What is the resistance of the shunt required if it is to measure 1A ?
Solution:
Galvanometer current (i_g) = 10^-6A
i = 1A
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)
= \(\frac{\mathrm{G}}{\frac{1}{10^{-6}}-1}\)
S = \(\frac{G}{10^6-1}\)
S = \(\frac{\mathrm{G}}{99,999} \Omega\)
Where G = Galvanometer resistance.

Question 3.
A circular wire loop of radius 30 cm carries a current of 3.5 A. Find the magnetic field at a point on its axis 40 cm away from the centre.
Solution:
Radius (r) = 30 cm = 30 × 10^-2m
Current (i) = 3.5 A
x = 40 cm = 40 × 10^-2m

Textual Exercises

Question 1.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil ?
Solution:
Here, n = 100, r = 8cm = 8 × 10^-2 m and I = 0.40 A
The magnetic field B at the centre
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{In}}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 3.14 \times 0.4 \times 100}{8 \times 10^{-2}}\) = 3.1 × 10^-4T
The direction of magnetic field depends on the direction of current if the direction of current is anticlockwise. According to Maxwell’s right hand rule, the direction of magnetic field at the centre of coil will be perpendicular outwards to the plane of paper.

Question 2.
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire ?
Solution:
Here, I = 35 A and r = 20 cm = 0.2 m
The wire is along and it is considered as an infinite length wire. The magnetic field
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 35}{0.2}\) = 3.5 × 10^-5T

Question 3.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Solution:
Given I = 50A and r = 2.5 m
The magnitude of magnetic field

B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 I}{r}\) = 10^-7 × \(\frac{2 \times 50}{2.5}\)
= 4 × 10^-6T
The direction of magnetic field at point P is given by Maxwell’s right hand rule.

Question 4.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line ?
Solution:

Given I = 90 A and r = 1.5m
The magnitude of magnetic field
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 90}{1.5}\)
= 1.2 × 10^-5 T
The direction of magnetic flux is given by Maxwell’s right hand rule. So, the direction of magnetic field at point P due to the following current is perpendicularly outwards to the plane of paper.

Question 5.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8A and making an angle of 300 with the direction of a uniform magnetic field of 0.15.T?
Solution:
According to the question
I = 8 A, θ = 30°, B = 0.15 T, l = 1 m
The magnitude of magnetic force

f = I(l × B) = I l B sin θ
= 8 × 1 × 0.15 × sin 30°
= \(\frac{8 \times 0.15}{2}\) = 4 × 0.15 = 0.6 N/m

Question 6.
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire ?
Solution:
Here, the angle between the magnetic field and the direction of flow of current is 90°. Because the magneitc field due to a solenoid is along the axis of solenoid and the wire is placed perpendicular to the axis.

Given, l = 3 cm = 3 × 10^-2 m, I = 10A, B = 0.27 T
f = I l B sin 90°
= 10 × 3 × 10^-2 × 0.27 = 8.1 × 10^-2 N
According to right hand palm rule, the direction of magnetic force is perpendicular to plane of paper inwards.

Question 7.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Solution:
Given I₁ = 8A, I₂ = 5A and r = 4 cm = 0.4m
F = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}_1 \mathrm{I}_2}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 8 \times 5}{0.04}\) = 2 × 10^-4N
The force on A of length 10 cm is F¹ = F × 0.1 (∵ 1m = 100 cm)
F¹ = 2 × 10^-4 × 0.1
F¹ = 2 × 10^-5N.

Question 8.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. It the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Solution:
The length of solenoid, l = 80 cm = 0.8 m
Number of layers = 5
Number of turns per layer = 400

Diameter of solenoid = 1.8 cm
Current in solenoid = I = 8 A
∴ The total number of turns N = 400 × 5 = 2000
and no. of turns / length, n = \(\frac{2000}{0.8}\) = 2500
The magnitude of magnetic field inside the solenoid
B = μ₀nl = 4 × 3 .14 10^-7 × 2500 × 8
= 2. 5 × 10^-2 T
The direction of magnetic field is along the axes of solenoid.

Question 9.
A square coil of side 10 cm consists of 20 turns and carries current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil ?
Solution:
Given, side of square coil = 10 cm = 0.1 m
Number of turns (n) = 20
current in square coil I = 12 A
Angle made by coil θ = 30°
Magnetic filed B = 0.80 T

The magnitude of torque experienced by the coil
\(\tau\) = NIAB sinθ
= 20 × 12 × (10 × 10^-2)² × 0.80 × sin 30°
= 0.96 N – m

Question 10.
Two moving coil meters, M₁ and M₂ have the following particulars :
R₁ = 10 Ω, n₁ = 30,
A₁ = 3.6 × 10^-3 m², B₁ = 0.25 T
R₂ = 14Ω, n₂ = 42,
A₂ = 1.8 × 10^-3 m², B₂ = 0.50 T, K₁ = K₂
(The spring constants are identical for the two meters).
Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M₂ and M₁.
Solution:
Given, R₁ = 10 Ω, N₁ = 30, A₁ = 3.6 × 10^-3 m², B₁ = 0.25 T
R₂ = 140Ω, n₂ = 42, A₂ = 1.8 × 10^-3 m², B₂ = 0.50 T, K₁ = K₂

Question 11.
In a chamber, a uniform magnetic field of 6.5 G (1 G = 10^-4 T) is maintained. An electron is shot into the field with a speed of 4.8 × 10⁶ m s^-1 normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.
(e = 1.5 × 10^-19 C, m_e = 9.1 × 10^-31 kg)
Solution:
Given, magnetic field B = 6.5 G = 6.5 × 10^-4 T
Charge e = -1.6 × 10^-19 C
Speed of electron V = 4.8 × 10⁶ m/s
Mass of electron m_e = 9.1 × 10^-31 kg
Angle between magnetic field and electron (θ) = 90°
The force on charge particle entering in the magnetic field
F = q (V × B) = e (V × b)
The electron attains a circular path and necessarily centripetal force is provided by magnetic force.
e (V × B) = \(\frac{m V^2}{r}\)
e V B sin 90° = \(\frac{\mathrm{m} \mathrm{V}^2}{\mathrm{r}}\)
r = \(\frac{\mathrm{mV}}{\mathrm{e} \mathrm{B} \times 1}\) = \(\frac{9.1 \times 10^{-31} \times 4.8 \times 10^6}{1.6 \times 10^{-19} \times 6.5 \times 10^{-4}}\) = 4.2 × 10^-2m = 4.2 cm

Question 12.
From Exercise 11 data, obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron ? Explain.
Solution:
Given
B = 6.5 G = 6.5 × 10^-4T, V = 4.8 × 10⁶ m/s, e = 1.6 × 10^-19C
m_e = 9.1 × 10^-3 kg
\(\frac{\mathrm{mV}^2}{\mathrm{r}}\) = q V B ⇒ \(\frac{\mathrm{mV}}{\mathrm{r}}\) = qB
If angular velocity of electron is ω, then
V = r ω
ω = \(\frac{\mathrm{qB}}{\mathrm{m}}\)
2πn = \(\frac{\mathrm{qB}}{\mathrm{m}}\) ⇒ n = \(\frac{\mathrm{qB}}{2 \pi \mathrm{m}}\)
Frequency of revolution of electron in orbit
υ = \(\frac{\mathrm{Bq}}{2 \pi \mathrm{m}}\) = \(\frac{\mathrm{Be}}{2 \pi \mathrm{m}_{\mathrm{e}}}\) = \(\frac{6.5 \times 10^{-4} \times 1.6 \times 10^{-19}}{2 \times 3.14 \times 9.1 \times 10^{-31}}\) = 18.18 × 10⁶ Hz.

Question 13.
(a) Circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniiorm horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil form turning.
(b) Would your answer change, If the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area ? (All other particular are also unaltered.)
Answer:
a) Given, no. of turns (n) = 30, radius (r) = 8 cm = 0.08 m
Current in coil (I) = 6A, Magnetic field (B) = 1.0 T,
Angle made by field with the normal of the coil, θ = 60°
\(\tau\) = n I A Bsinθ
= 30 × 6 × π (0.08)² × 1 × sin 60°
= 30 × 6 × 3.14 × 0.08 × 0.08 × \(\frac{\sqrt{3}}{2}\)
\(\tau\) = 3.133 N – m

b) From the formula, it is clear that the torque on the loop does not depend on the shape if area remains constant. So, the torque remains constant.

Additional Exercises

Question 1.
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X Is anticlockwise, and clockwise In Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
Solution:
For coil X
Radius of coil, r_x = 16 cm = 0.16 m
No. of turns n_x = 20
Current in the coil I_x = 16A (Anti clockwise) .
For coil Y
Radius of coil, r_y = 10 cm = 0.1 m
No. of turns n_y = 25
Current in the coil I_y = 18 A (clockwise)
The magnitude of the magnetic field at the centre of coil X
B_x = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 I_x \cdot \pi n_x}{r_x}\) = \(\frac{10^{-7} \times 2 \times 16 \times 3.14 \times 20}{0.16} \mathrm{~T}\)
B_x = 4π × 10^-4T
The magnitude field at the centre B =B_y – B_x
= (9π – 4π) × 10^-4 = 5π × 10^-4
= 1.6 × 10^-3T (towards west)

Question 2.
A magnetic field of 1oo G (1 G = 10^-4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10^-3 m². The maximum current carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a côre is at most 1000 turns m^-1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
Solution:
Magnetic field B = 100 G = 100 × 10^-4T = 10^-2 T
Maximum current I = 15A, n = 1000/m.
The magnitude of magnetic field B = μ₀ nI
nI = \(\frac{\mathrm{B}}{\mu_0}\) = \(\frac{10^{-2}}{4 \times 3.14 \times 10^{-7}}\)
⇒ nI = 7961 ≈ 8000
Here; the product of n I is 8000. So,
Current I = 8A and no. of turns = 1000
The other design is I = 10A and n = 800/m. This is the most appropriate design as the requirement.

Question 3.
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from Its centre is given by,
B = \(\frac{\mu_0 \mathbf{I R}^2 \mathbf{N}}{2\left(\mathbf{x}^2+\mathbf{R}^2\right)^{3 / 2}}\)
a) Show that this reduces to the familiar result for field at the centre of the coil.
Solution:
Given, magnetic field at distance x :
B = \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{x}^2+\mathrm{R}^2\right)^{3 / 2}}\) (∵ x = 0)
∴ The magnetic field at the centre B = \(\frac{\mu_0 \mathrm{~N} \mathrm{I} \mathrm{R}^2}{2 \mathrm{R}^3}\)
B = \(\frac{\mu_0 \mathrm{~N} \mathrm{I}}{2 \mathrm{R}}\)
This result is same as the magnetic field due to current loop at its centre.

b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated bya distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = 072\(\frac{\mu_0 \mathrm{NI}}{\mathrm{R}}\) approximately.
ISuch an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.] :
Solution:
Radius of two parallel co-axial coils = R, number of turns = N Current = I
Let the mid points between the coils is at point O and P be the pomt around the mid point O.
Suppose, the distance between OP = d which is very less than R (d < < R)
For the Coil A,
O_AP = \(\frac{R}{2}\) + d
the magnetic field at point P due to coil A.


as according to the question d < <R, so neglect turn d².

The direction of B_A is along PO_B. According to Maxwell’s right hand rule
for the coil B, O_BP = (Rl₂ – d)
The magnetic field at point P due to coil B

The direction of magnetic field B_B is towards PO_B. So, the resultant magnetic field at P due to coil A and coil B is

Now, use binomial theorem and neglect higher power as d < < R

Question 4.
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around whIch 3500 turns of a wire are wound. If the current in the wire Is 11 A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid.
Solution:
a) For outside the toroid, the magnetic field is zero, because the magnetic field due to toroid is only inside it and along the length of toroid.

b) Inner radius of toroid, r₁ = 25 cm = 0.25 m
Outer radius of toroid, r₂ = 26 cm = 0.26 m
Number of turns N = 3500
current in the wire, I = 11A
The mean radius of toroid r = \(\left(\frac{\mathrm{r}_1+\mathrm{r}_2}{2}\right)\) = \(\frac{2}{2}\)(0.25 + 0.26) = 0.51
∴ length of toroid = 2πr = 2π × 0.51
the magnetic field strength due to toroid is B = µ₀ n I
where n is number of turns per unit length
n = \(\frac{N}{I}\)
B = 4π × 10^-7 × \(\frac{3500}{\pi \times 0.51}\) × 11 = 3.02 × 10^-2 T

c) The magnetic field in the empty space surrounded by toroid is also zero, because the
magnetic field due to toroid is only along its length.

Question 5.
Answer the following questions.
a) A magnetic field that varies in magnitude form point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
Answer:
The magnetic field is in constant direction from east to west. According to the question, a charged particle travels undeflected along a striaght path with constant speed. It is only possible, if the magnetic force experienced by the charged particle is zero. The magnitude of magnetic force on a moving charged particle in a magnetic field is given by F = qvB sin θ. Here F = 0, if and only if sinθ. This indicates the angle between the velocity and magnetic fled is 0° or 180°. Thus, the charged particle moves parallel or antiparallel to the magnetic field B.

b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory Would its final speed equal the initial speed lilt suffered no collisions with the environment?
Answer:
Yes, the final speed be equal to its initial speed as the magnetic force acting on the charged particle only changes the direction of velocity of charged particle but cannot change the magnitude of velocity of charged particle.

c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.
Solution:
B should be in a vertically downward direction.

Question 6.
An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of 30° with the initial velocity.
Solution:
a) Since magnetic field is perpendicular to initial velocity of electron therefore, the electron will move in circular path.
B = 0.15 T,PD = 200 V
K. E. of electron = eV = \(\frac{1}{2}\)mv²
V² = \(\frac{2 \mathrm{ev}}{\mathrm{m}}\)
V = \(\sqrt{\frac{2 \times 1.6 \times 10^{-19} \times 2000}{9.1 \times 10^{-31}}}\)
V = \(\frac{8}{3}\) (e = charge of electron)
V = 2.66 × 10⁷ m/s
Also
BqV = \(\frac{\mathrm{m} \mathrm{V}^2}{\mathrm{Br}}\)
∴ r = \(\frac{\mathrm{mv}}{\mathrm{Bq}}\)
or r = \(\frac{9.1 \times 10^{-31} \times 2.66 \times 10^7}{0.15 \times 1.6 \times 10^{-19}}\)
= \(\frac{91 \times 83.86 \times 10^{-5}}{15 \times 1.6}\) = 10^-3 m = 1 mm

b) When magnetic field makes an angle 30° with the initial velocity i.e. θ = 30°
Then V¹ = V sin θ = \(\sqrt{\frac{2 \mathrm{ev}}{\mathrm{m}}}\) = sin 30°
V¹ = \(\frac{8}{3}\) × 10⁷ × \(\frac{1}{2}\) = \(\frac{4}{3}\) × 10⁷ m/s
The radius of the helical path is
r = \(\frac{\mathrm{m} \mathrm{V}^{\prime}}{\mathrm{Be}}\)
= \(\frac{9 \times 10^{-31} \times\left(\frac{4}{3} \times 10^7\right)}{0.15 \times 1.6 \times 10^{-19}}\) = 0.5 mm

Question 7.
A magnetic field set up using Helmholtz coils (described in Exercise 16) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10^-5 V m^-1, make a simple guess as to what the beam contains. Why is the answer not unique ?
Solution:
B = 0.75 T, E = 9 × 10⁵ Vm^-1
V = \(\frac{E}{B}\) = \(\frac{9 \times 10^5}{0.75}\) = 12 × 10⁶ m/s
K. E of charged particle
= \(\frac{1}{2} \mathrm{mv}^2\) = eV
or \(\frac{\mathrm{e}}{\mathrm{m}}\) = \(\frac{v^2}{2 v}\) = \(\frac{144 \times 10^{12}}{2 \times 15000}\) = 4.8 × 10⁷C kg^-1
Particle is deuteron; the answer is not unique because only the ratio of charge to mass is determined. Other possibe answers are He⁺⁺, Li⁺⁺⁺ etc.
∴ He⁺⁺ and Li⁺⁺⁺ also have the same value of
e/m (∵ e/m = \(\frac{2 \mathrm{e}}{2 \mathrm{~m}}\) = \(\frac{3 \mathrm{e}}{3 \mathrm{~m}}\))

Question 8.
A straight horizontal conducting rod of length 0.45 m and mass 6 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.

a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?
Solution:
Rod carrying current placed in uniform magnetic field expëriences a force Bu which is balanced by weigth of rod
F = B I l
mg = B I l
B = \(\frac{\mathrm{m} \mathrm{g}}{\mathrm{I} l}\) = \(\frac{60 \times 9.8}{1000 \times 0.45 \times 5}\) = 0.26 T

b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) g = 9.8 m s^-2.
Solution:
Force due to magnetic field = B I l
= 0.26 × 5 × 0.45 = 5.85 N
Weight of rod = \(\frac{60}{1000}\) × 9.8 = 0.588 N
Total force = 0.588 + 0.585 = 1.173 N

Question 9.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Solution:
F = \(\frac{\mu_0}{4 \pi} \times \frac{2 I_1 I_2}{r}\)
= 10^-7 × \(\frac{2 \times 300 \times 300 \times 100}{1.5 \times 10^{-2}}\) = 1.2 Nm^-1 (Repulsive force)

Question 10.
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,

a) the wire intersects the axis,
Solution:
F = BI 1 sin 900 = 1.5 × 7 × \(\frac{20}{100}\) = 2.1 N acting vertically downwards.

b) The wire is turned form N-S to north-east-northwest direction,
Solution:
Now θ = 45°, and length of the wire in the cylindrical region of the magnetic field is l, and is given by
l = l₁ sin 45°
l₁ = \(\frac{l}{\sin 45^{\circ}}\) = \(\sqrt{2 l}\)
So force F₁ = BI l sin 45°
= 1.5 × 7.0 × \(\sqrt{2} l\) × \(\frac{l}{\sqrt{2}}\)
= 10.5 × 0.2 = 2.1 N

c) The wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
Solution:
When the wire is lowered through a distance 6.0 cm and reaches at CD then length of wire in magnetic field
l₂ = 2x
x.x = 4 × (10 + 6) = 64
x = 8 cm
∴ l₂ = 8 × 2 = 16 cm = \(\frac{16}{100}\)m
∴ Force on the wire
F₂ = BI l₂
= \(\frac{1.5 \times 7 \times 16}{100}\) = 1.68 N (Vertically downwards)

Question 11.
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. ? What is the force on each case ? Which case corresponds to stable equilibrium?

Solution:
a) Torque = 300, G = 3000 × 10^-4 T
Area A = 10 × 5 = 50 cm² = \(\frac{50}{100 \times 100}\)m²
\(\tau\) = BIA = \(\frac{3}{10}\) × 12 × \(\frac{50}{100 \times 100}\) = 18 × 10^-2 Nm along Y-axis
b) Same as in (a)
c) 1.8 × 10^-2 Nm along x – direction
d) 1.8 × 10^-2 Nm at an angle 240° with the +x direction :
e) Zero
f) Zero
Force is zero in each case. Case (e) corresponds to stable and case (f) to unstable equilibrium.

Question 12.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. 1f the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10^-5 m², and the free electron density in copper is given to be about 10²⁹ m^-3.)
Solution:
n = 20, r = 10 cm, B = 0.10 T, I = 50 A
a) Torque acting on the coil = nBIA sinθ = 0
b) Force acting on the coil = BIl sinθ = 0
e) Force on each electron
n = No. of electrons per unit volume
A = Area of cross – section of wire
F = Be V = \(\frac{\mathrm{BI}}{\mathrm{nA}}\) = \(\frac{0.1 \times 5}{10^{29} \times 10^{-5}}\) = 5 × 10^-25N

Question 13.
A solenoid 60 cm long and of radius 7.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two lead parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire ? g = 9.8 m s^-2.
Solution:
B = μ₀n I
Force acts on the wire normal to its length
∴ F = BI¹ l
= μ₀n I I¹ l and n = \(\frac{\frac{900}{60}}{100}\) = 1500
= μ₀n I I¹ l = mg
I = \(\frac{2.5 \times 9.8}{1000 \times 4 \pi \times 10^{-7} \times 1500 \times 6 \times \frac{1}{15}}\) = 108 A.

Question 14.
A galvanometer coil has a resistance of 12 Ω and the metre shows full scale deflection for a current of 3 mA How will you convert the metre into a voltameter of range 0 to 18V ?
Solution:
Here G = 12Ω, Ig = 3mA = 3 × 10^-3A, V = 18V
R = \(\frac{v}{I_g}\) – G = \(\frac{18}{3 \times 10^{-3}}\) – 12 = (6000 – 12)Ω = 5988 Ω.

Question 15.
A galvanometer coil has a resistance of 15 Ω and the meter shows full scale deflection for a current of 4 mA. How will you convert the meter into an ammeter of range 0 to 6 A?
Solution:
Here G = 15Ω, I_g = 4 mA = 0.004 A, I = 6A
shunt S = \(\frac{\mathrm{I}_{\mathrm{g}} \mathrm{G}}{\mathrm{I}-\mathrm{I}_{\mathrm{g}}}\) = \(\frac{0.004 \times 15}{6-0.004}\) = \(\frac{0.06}{5.996}\) = ≈ 10 × 10^-3Ω = 10 m Ω
So shunt resistance = 10 m \(\simeq\) 10 mΩ

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(e) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(e)

I. Evaluate the following integrals.

Question 1.
∫\(\frac{x-1}{(x-2)(x-3)}\)dx
Solution:

Question 2.
∫\(\frac{x^2}{(x+1)(x+2)^2}\)dx
Solution:
∫\(\frac{x^2}{(x+1)(x+2)^2}\) ≡ \(\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\)
⇒ x² = A(x + 2)² + B(x + 1)(x + 2) + (x + 1) …………….. (1)
Put x = -2 in (1)
(-2)² = A(0) + B(0) + C(-2 + 1) ⇒ C = -4
Put x = -1 in (1)
(-1)² = A(-1 + 2)² + B(0) + C(0)
⇒ A = 1
Equation coeffs. of x² in (1)
1 = A + B
⇒ B = 1 – A = 1 – 1 = 0
∴ \(\frac{x^2}{(x+1)(x+2)^2}=\frac{1}{x+1}+\frac{0}{x+2}+\frac{(-4)}{(x+2)^2}\)
∴ ∫\(\frac{x^2}{(x+1)(x+2)^2}\)dx
= ∫\(\frac{1}{x+1}\)dx – 4∫\(\frac{1}{(x+2)^2}\)dx
= log|x + 1| – 4\(\frac{(-1)}{x+2}\)
= log|x + 1| + \(\frac{4}{x+2}\) + C

Question 3.
∫\(\frac{x+3}{(x-1)(x^2+1)}\)dx
Solution:
Let \(\frac{x+3}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}\)
⇒ (x + 3) = A(x² + 1) + (Bx + C)(x – 1) …………….. (1)
Put x = 0 in (1)
3 = A(1) + C(-1)
⇒ A – C = 3 ⇒ C = A – 3 = 2 – 3 = -1
Equation coefficient of x² in (1)
0 = A + B
⇒ B = -A = -2
∴ \(\frac{x+3}{(x-1)(x^2+1)}=\frac{+2}{(x-1)}+\frac{-2x-1}{x^2+1}\)
∫\(\frac{x+3}{(x-1)(x^2+1)}\)dx = 2∫\(\frac{1}{x-1}\)dx
-∫\(\frac{2x}{x^2+1}\)dx – ∫\(\frac{1}{x^2+1}\)dx
= 2 log |x – 1| – log |x² + 1| – tan^-1(x) + C

Question 4.

Solution:

Question 5.
∫\(\frac{dx}{(e^x+e^{2x}}\)
Solution:

Question 6.
∫\(\frac{dx}{(x+1)(x+2)}\)
Solution:

Question 7.
∫\(\frac{1}{(e^x-1}\)dx
Solution:

Question 8.
∫\(\frac{1}{(1-x)(4+x^2)}\)dx
Solution:
Let \(\frac{1}{(1-x)(4+x^2)}=\frac{A}{1-x}+\frac{Bx+C}{4+x^2}\)
⇒ 1 = A(4 + x²) + (Bx + C)(1 – x) ………….. (1)
Put x = 1 in (1)
1 = A(4 + 1) ⇒ A = \(\frac{1}{5}\)
Put x = 0 in (1)
1 = A(4) + C(1)
⇒ C = 1 – 4A = 1 – 4(\(\frac{1}{5}\)) = \(\frac{5-4}{5}\) = \(\frac{1}{5}\)
0 = A – B
⇒ B = A = \(\frac{1}{5}\)

Question 9.
∫\(\frac{2x+3}{x^3+x^2-2x}\)dx
Solution:

Put x = 0 in (1), then
3 = A(2)(-1) + B(0) + C(0)
⇒ A = –\(\frac{3}{2}\)
Put x = 1 in (1). Then
2 + 3 = A(0) + B(0) + C(1)(3)
⇒ C = \(\frac{5}{3}\)
Put x = -2 in (1). Then
2(-2) + 3 = A(0) + B(-2)(-2 – 1) + C(0)
⇒ -1 = 6B ⇒ B = \(\frac{-1}{6}\)

II. Evaluate the following integrals.

Question 1.
∫\(\frac{dx}{6x^2-5x+1}\)
Solution:

Question 2.
∫\(\frac{dx}{x(x+1)(x+2)}\)
Solution:
\(\frac{1}{x(x+1)(x+2)}\) ≡ \(\frac{A}{x}+\frac{B}{x+1}+\frac{C}{x+2}\)
⇒ 1 ≡ A(x + 1)(x + 2) + B(x)(x + 2) + C(x)(x + 1)
Put x = 0
1 = A(1)(2) + B(0) + C(0) ⇒ A = \(\frac{1}{2}\)
Put x = -1
1 = A(0) + B(0) + C(-2)(-2 + 1)
⇒ C = \(\frac{1}{2}\)

Question 3.
∫\(\frac{3x-2}{(x-1)(x+2)(x-3)}\)dx
Solution:
\(\frac{3x-2}{(x-1)(x+2)(x-3)}\) ≡ \(\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{x-3}\)
⇒ 3x – 2 = A(x + 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x + 2)
Put x = 1
3(1) – 2 = A(1 + 2)(1 – 3) + B(0) + C(0)
⇒ A = \(\frac{-1}{6}\)
Put x = 3
3(3) – 2 = A(0) + B(0) + C(3 – 1)(3 + 2)
C = \(\frac{7}{10}\)
Put x = -2
3(-2) – 2 = A(0) + B(-2 – 1)(-2 – 3) + C(0) – 8
= 15B ⇒ B = \(\frac{-8}{15}\)

Question 4.
∫\(\frac{7x-4}{(x-1)^2(x+2)}\)dx
Solution:
\(\frac{7x-4}{(x-1)^2(x+2)}\) ≡ \(\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+2}\)
⇒ 7x – 4 = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)² ………….. (1)
Put x = 1 in (1)
7 – 4 = A(0) + B(1 + 2) ⇒ B = 1
Put x = -2 in (1)
7(-2) – 4 = A(0) + B(0) + C(-2 – 1)²
⇒ -18 = 9C ⇒ C = -2
Equating coeffs. of x² in (1)
0 = A + C ⇒ A = -C = 2

III. Evaluate the following integrals.

Question 1.
∫\(\frac{1}{(x-a)(x-b)(x-c)}\)dx
Solution:

Question 2.
∫\(\frac{2x+3}{(x+3)(x^2+4)}\)dx
Solution:
\(\frac{2x+3}{(x+3)(x^2+4)}\) = \(\frac{A}{x+3}+\frac{Bx+C}{x^2+4}\)
2x + 3 = A(x² + 4) + (Bx + C)(x + 3)
x = -3 ⇒ -3 = A(9 + 4) = 13A
A = –\(\frac{3}{13}\)
Equating the coefficient of x²
0 = A + B ⇒ B = -A = \(\frac{3}{13}\)
Equating the constants
3 = 4A + 3C

Question 3.
∫\(\frac{2x^2+x+1}{(x+3)(x-2)^2}\)dx
Solution:
Let \(\frac{2x^2+x+1}{(x+3)(x-2)^2}\) = \(\frac{A}{x+3}+\frac{B}{x-2}+\frac{C}{(x-2)^2}\)
2x² + x + 1 = A(x – 2)² + B(x + 3)(x – 2) + C(x + 3)
x = 2 ⇒ 8 + 2 + 1 = C(2 + 3) = 5C
⇒ C = \(\frac{11}{5}\)
x = -3 ⇒ 18 – 3 + 1
= A(-5)² = 25 A ⇒ A = \(\frac{16}{25}\)
Equating the coefficients of x²
2 = A + B ⇒ B = 2 – A = 2 – \(\frac{16}{25}\) = \(\frac{34}{25}\)

Question 4.
∫\(\frac{dx}{x^3+1}\)dx
Solution:
\(\frac{1}{x^3+1}\) = \(\frac{1}{(x+1)(x^2-x+1)}\)
Let \(\frac{1}{x^3+1}\) = \(\frac{1}{x+1}+\frac{1}{x^2-x+1}\)
⇒ 1 = A(x² – x + 1) + (Bx + C)(x + 1) ……………. (1)
Put x = -1 in (1)
1 = A(1 + 1 + 1) + (-B + C)(0)
⇒ 3A = 1 ⇒ A = \(\frac{1}{3}\)
Put x = 0 in (1)
1 = A(1) + C(1)
⇒ C = 1 – A = 1 – \(\frac{1}{3}=\frac{2}{3}\)
Equating the coefficients of x²
O = A + B ⇒ B = -A = –\(\frac{1}{3}\)

Question 5.
∫\(\frac{\sin x \cos x}{\cos^2 x+3cos x+2}\)dx
Solution:
Put cos x = t ⇒ – sin x dx = dt
∫\(\frac{\sin x \cos x}{\cos^2 x+3cos x+2}\)dx = ∫\(\frac{-t dt}{t^2+3t+2}\)
= -∫\(\frac{t}{t^2+3t+2}\)dt …………. (1)
Let \(\frac{t}{t^2+3t+2}\) = \(\frac{t}{(t+1)(t+2)}\)
= \(\frac{A}{t+1}+\frac{B}{t+2}\)
⇒ t = A(t + 2) + B(t + 1) ………… (2)
Put t = -1 in (2)
-1 = A(-1 + 2) ⇒ A = -1
Put t = -2 in (2)
-2 = B(-2 + 1) ⇒ B = 2
∴ \(\frac{t}{t^2+3t+2}\) = \(\frac{-1}{t+1}+\frac{2}{t+2}\) ……….. (3)
∴ From (1) & (2)
∫\(\frac{\sin x.\cos x}{\cos^2 x+3cos x+2}\)dx
= -[∫\(\frac{-1}{t+1}\)dt+2∫\(\frac{1}{t+2}\)]
= ∫\(\frac{1}{t+1}\) – 2∫\(\frac{1}{t+2}\)
= log|t + 1| – 2log|t + 2| + C
= log|1 + cos x| – 2log|2 + cos x| + C
= log|1 + cos x| – log(2 + cos x)² + C
= log|\(\frac{1+\cos x}{(2+\cos x)^2}\)| + C

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(d)

I. Evaluate the following integrals.

Question 1.
∫\(\frac{dx}{\sqrt{2x-3x^2+1}}\)
Solution:

Question 2.
∫\(\frac{\sin \theta}{\sqrt{2-\cos^2 \theta}}\)dθ
Solution:

Question 3.
∫\(\frac{\cos x}{\sin^2 x+4sin x+5}\)dx
Solution:
t = sin x ⇒ dt = cos x dx
I = ∫\(\frac{dt}{t^2+4t+5}\) = ∫\(\frac{dt}{(t+2)^2+1}\)
= tan^-1(t + 2) + C
= tan^-1(sin x + 2) + C

Question 4.
∫\(\frac{dx}{1+\cos^2 x}\)
Solution:

Question 5.
∫\(\frac{dx}{2\sin^2 x+3\cos^2 x}\)
Solution:

Question 6.
∫\(\frac{1}{1+\tan x}\)dx
Solution:

Question 7.
∫\(\frac{1}{1-\cot x}\)dx
Solution:

II. Evaluate the following integrals.

Question 1.
∫\(\sqrt{1+3x-x^2}\)dx
Solution:

Question 2.
∫\(\frac{9\cos x-\sin x}{4\sin x+5\cos x}\)dx
Solution:

Question 3.
∫\(\frac{2\cos x+3\sin x}{4\cos x+5\sin x}\)dx
Solution:
Let 2 cos c + 3 sin x = A(4 cos x + 5 sin x) + B(-4 sin x + 5 cos x)
Equating the co-efficient of sin x and cos x,
we get
4A + 5B = 2
5A – 4B = 3

Question 4.
∫\(\frac{1}{1+\sin x+\cos x}\)dx
Solution:

Question 5.
∫\(\frac{1}{3x^2+x+1}\)dx
Solution:

Question 6.
∫\(\frac{dx}{\sqrt{5-2x^2+4x}}\)
Solution:

III. Evaluate the following integrals.

Question 1.
∫\(\frac{x+1}{\sqrt{x^2-x+1}}\)
Solution:

Question 2.
∫(6x + 5)\(\sqrt{6-2x^2+x}\)dx
Solution:
Let 6x + 5 = A(1 – 4x) + B
Equating the constants
A + B = 5
B = 5 – A = 5 + \(\frac{3}{2}\) = \(\frac{13}{2}\)
∫(6x + 5)\(\sqrt{6-2x^2+x}\)dx

Question 3.
∫\(\frac{dx}{4+5\sin x}\)
Solution:
t = tan \(\frac{x}{2}\) ⇒ dt = sec² \(\frac{x}{2}\) . \(\frac{1}{2}\)dx

Question 4.
∫\(\frac{1}{2-3\cos 2x}\)dx
Solution:
t = tan x ⇒ dt = sec² x dx
= (1 + tan² x)dx
= (1 +t²)dx
dx = \(\frac{dt}{1+t^2}\)

Question 5.
∫x\(\sqrt{1+x-x^2}\)dx
Solution:
Let x = A(1 – 2x) + B
Equating the coefficients of x
1 = -2 A ⇒ A = –\(\frac{1}{2}\)
Equating the constants
0 = A + B ⇒ B = -A = \(\frac{1}{2}\)
∫x\(\sqrt{1+x-x^2}\)dx
= –\(\frac{1}{2}\)∫(1 – 2x)\(\sqrt{1+x-x^2}\)dx + \(\frac{1}{2}\)∫\(\sqrt{1+x-x^2}\)dx

Question 6.
∫\(\frac{dx}{(1+x)\sqrt{3+2x-x^2}}\)
Solution:

Question 7.
∫\(\frac{dx}{4\cos x+3\sin x}\)
Solution:
Let t = tan\(\frac{x}{2}\) so that dx = \(\frac{2dt}{1+t^2}\)

Question 8.
∫\(\frac{1}{\sin x+\sqrt{3} \cos x}\)dx
Solution:
Let t = tan \(\frac{x}{2}\) so that dx = \(\frac{2dt}{1+t^2}\)
sin x = \(\frac{2t}{1+t^2}\), cos x = \(\frac{1-t^2}{1+t^2}\)

Question 9.
∫\(\frac{dx}{5+4\cos 2x}\).
Solution:

Question 10.
∫\(\frac{2\sin x+3\cos x+4}{3\sin x+4\cos x+5}\)dx.
Solution:
Let 2 sin x + 3 cos x + 4
= A(3 sin x + 4 cos x + 5) + 3(3 cos x – 4 sin x) + C
Equating the co-efficient of
sin x, we get 3A – 4B = 2
cos x, we get 4A + 3B = 3

Equating the constants
4 = 5A + C
C = 4 – 5A = 4 – 5.\(\frac{18}{25}\) = \(\frac{2}{5}\)

Substituting in (1)
I = \(\frac{18}{25}\). x + \(\frac{1}{25}\) log|3 sin x + 4 cos x + 5| – \(\frac{4}{5\left(3+\tan \frac{x}{2}\right)}\) + C

Question 11.
∫\(\sqrt{\frac{5-x}{x-2}}\) dx on (2, 5).
Solution:

Let 5 – x = A. \(\frac{d}{dx}\)(7x – 10 – x²) + B
⇒ 5 – x = A(7 – 2x) + B
Equating coffs. of like terms
-2A = -1 ⇒ A = \(\frac{1}{2}\)
7A + B = 5
7(+\(\frac{1}{2}\)) + B = 5 ⇒ B = 5 – \(\frac{7}{2}\) = \(\frac{3}{2}\)
∴ 5 – x = \(\frac{1}{2}\)(7 – 2x) + \(\frac{3}{2}\)

Question 12.
∫\(\sqrt{\frac{1+x}{1-x}}\) dx on (-1, 1).
Solution:

Question 13.
∫\(\frac{dx}{(1 – x)\sqrt{3-2x+x^2}}\) on (-1, 3).
Solution:
Put 1 – x = \(\frac{1}{1}\) ⇒ 1 – \(\frac{1}{1}\) = x\(\frac{1}{1-x}\) = t
dx = \(\frac{1}{t^2}\)dt
3 – 2x – x² = 3 – 2(\(\frac{1-1}{1}\)) – (\(\frac{1-1}{1}\))²

Question 14.
∫\(\frac{dx}{(x + 2)\sqrt{x+1}}\) on (-1, ∞).
Solution:
Put = x + 1 = t² ⇒ dx = 2t dt and
x + 2 = 1 + t²

Question 15.
∫\(\frac{dx}{(2x + 3)\sqrt{x+2}}\) on I ⊂ (-2, ∞)\{\(\frac{-3}{2}\)}.
Solution:
Put x + 2 = t² ⇒ dx = 2t dt and
2x + 3 = 2(t² – 2) + 3 = 2t² – 1

Question 16.
∫\(\frac{1}{(1+\sqrt{x}) \sqrt{x-x^2}}\)dx on (0, 1).
Solution:

Question 17.
∫\(\frac{dx}{(x + 1)\sqrt{2x^2+3x+1}}\) on
Solution:

Question 18.
∫\(\sqrt{e^x-4}\) dx on [log_e 4, ∞]
Solution:
Put e^x – 4 = t² ⇒ e^x dx = 2t dt

Question 19.
∫\(\sqrt{1+\sec x}\) dx on [(2n – \(\frac{1}{2}\))π – (2n + \(\frac{1}{2}\))π], (n ∈ Z).
Solution:

Question 20.
∫\(\frac{dx}{1+x^4}\) on R.
Solution:

Students get through AP Inter 2nd Year Physics Important Questions 16th Lesson Communication Systems which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 16th Lesson Communication Systems

Very Short Answer Questions

Question 1.
What are the basic blocks of a communication system?
Answer:
Basic blocks in a communication system are

1. Transmitter
2. Receiver
3. Channel

Question 2.
What is the ‘World Wide Web” (WWW)?
Answer:
Tern Berners -Lee invented the World Wide Web.
It is an encyclopedia of knowledge accessible to everyone round the clock throughout the year.

Question 3.
Mention the frequency range of speech signals.
Answer:
Speech signals frequency range is 300 Hz to 3100 Hz.

Question 4.
What is sky wave propagation ?
Answer:
In the frequency range from a MHz upto about 30 MHz, long distance communication can be achieved by ionospheric reflection of radio waves back towards the earth. This mode of propagation is called sky wave propagation.

Question 5.
Mention the various parts of the ionosphere ?
Answer:
Parts of ionosphere are

1. D Part of stratosphere (65-70 km day only),
2. E Part of stratosphere (100 km day only),
3. F₁ Part of mesosphere (170 km – 190 km),
4. F₂ Part of thermosphere [300 km at night 250 – 400 km during day time].

Question 6.
Define modulation. Why is it necessary ? [A.P. 17; A.P., T.S. Mar. 16, T.S. Mar. 15, Mar. 14]
Answer:
Modulation : The process of combining low frequency audio signal with high frequency carrier wave is called modulation.
Necessary: Low frequency signals cannot transmit directly. To reduce size of the antenna and to avoid mixing up of signal from different transmitters modulation is necessary.

Question 7.
Mention the basic methods of modulation. [T.S. Mar. 15, 17, A.P. Mar. 16]
Answer:
The basic methods of modulation are :

1. Amplitude modulation (AM)
2. Frequency modulation (FM)
3. Phase modulation (PM)

Question 8.
Which type of communication is employed in Mobile Phones ? [A.P. Mar. 15]
Answer:
Space wave mode of propagation is employed in mobile phones.

Textual Examples

Question 1.
A transmitting antenna at the top of a tower has a height 32 m and the height of the receiving antenna Is 50 m. What is the maximum distance between them for satisfactory communication in LOS mode? Given radius of earth 6.4 × 10⁶ m.
Solution:
d_m = \(\sqrt{2 \mathrm{Rh}_{\mathrm{T}}}+\sqrt{2 \mathrm{Rh}_{\mathrm{R}}}\)
d_m = \(\sqrt{2 \times 64 \times 10^5 \times 32}+\sqrt{2 \times 64 \times 10^5 \times 50 \mathrm{~m}}\)
=64 × 10² × \(\sqrt{10}\) +8 × 10³ × \(\sqrt{10}\)m = 144 × 10² × \(\sqrt{10}\)m
= 45.5 km.

Question 2.
A message signal of frequency 10 kHz and peak voltage of 10 volts Is used to modulate a carrier of frequency 1 MHz and peak voltage of 20 volts. Determine
(a) modulation index
(b) the side bands produced.
Solution:
a) Modulation index = \(\frac{10}{2}\) = 0.5
b) The side bands are at (1000 + 10 kHz) = 1010 kHz and (1000 – 10 kHz) = 990 kHz.

Students get through AP Inter 2nd Year Physics Important Questions 13th Lesson Atoms which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 13th Lesson Atoms

Very Short Answer Questions

Question 1.
What is the physical meaning of negative energy of an electron’ ?
Answer:
The ‘negative energy of an electron’ indicates that the electron is bound to the nucleus due to force of attraction.

Question 2.
Sharp lines are present in the spectrum of a gas. What does this indicate ?
Answer:
Sharp lines in the spectrum of gas, indicates bright lines against dark background.

Question 3.
Name a physical quantity whose dimensions are the same as those of angular momentum.
Answer:
Planck’s constant.

Question 4.
What is the difference between α – particle and helium atom ?
Answer:
Alpha particle

1. It is a + 2e charged Helium nucleus.
2. It contains 2 protons and 2 neutrons.

Helium atom

1. It has no charge.
2. It contains 2 protons, 2 electrons and 2 neutrons.

Question 5.
Among alpha, beta and gamma radiations, which get affected by the electric field ?
Answer:
Alpha and Beta radiations are get affected by the electric field.

Question 6.
What do you understand by the phrase ground state atom ?
Answer:
If the electron is present in the ground state, it is called ground state atom.

Question 7.
Why does the mass of the nucleus not have any significance in scattering in Rutherford’s experiment ?
Answer:
The size of the atom is 10^-10 m and size of the nucleus is 10^-15 m. Hence atom has large empty space. So the mass of nucleus has no significance in Rutherford’s scattering experiment.

Question 8.
The Lyman series of hydrogen spectrum lies in the ultraviolet region. Why ? [A.P. Mar. 15]
Answer:
The calculated values of wavelengths lie in the ultraviolet region of the spectrum will agree with the values of wavelengths observed experimentally by Lyman.

Question 9.
Write down a table giving longest and shortest wavelengths of different spectral series.
Answer:
Wavelength limits of some spectral series of hydrogen.

Question 10.
Give two drawbacks of Rutherford’s atomic model.
Answer:
Drawbacks of Rutherford’s atomic model:

1. As the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. But matter .is stable, we cannot expect the atom collapse.
2. The atoms should emit continuous spectrum, but what we observe is only a line spectrum.

Question 11.
If the kinetic energy of revolving electron in an orbit is K, what is its potential energy and total energy ?
Answer:
For an electron revolving round the nucleus, total energy is always negative and it is numerically equal to kinetic energy.
∴ Total energy = -Kinetic energy = -K
Potential energy is always negative and PE = 2 × TE = -2K

Short Answer Questions

Question 1.
What is impact parameter and angle of scattering ? How are they related to each other ?
Answer:

1. Impact parameter (b) : Impact parameter is defined as the perpendicular distance of the initial velocity vector of the alpha particle from the central line of the nucleus, when the particle is far away from the nucleus of the atom.
2. Scattering angle (θ) : The scattering angle (θ) is the angle between the asymtotic direction of approach of the α – particle and the asymtotic direction in which it receeds.
3. The relation between b and θ is b = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Ze}^2}{\mathrm{E}}\) cot \(\frac{\theta}{2}\) where E = K.E of α – particle = \(\frac{1}{2}\) mυ².

Question 2.
Explain the distance of closest approach and impact parameter.
Answer:
Distance of closest approach :

1. Suppose an α-particle with initial kinetic energy (K.E) is directed towards the centre of the nucleus of an atom.
2. On account of Coulomb’s repulsive force between nucleus and alpha particle, kinetic energy of alpha particle goes on decreasing and in turn, electric potential energy of the particle goes on increasing.
3. At certain distance d’ from the nucleus, K. E of α-particle reduces to zero. The particle stops and it cannot go closer to the nucleus. It is repelled by the nucleus and therefore it retraces its path, turning through 180°.
4. Therefore, the distance d is known as the distance of closest of approach.
   
   The closest distance of approach,
   d = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{Z e^2}{\left(\frac{1}{2} m v^2\right)}\)
5. Impact parameter (b) : Impact parameter is defined as the ⊥^r distance of the initial velocity vector of the α – particle from the central line of the nucleus, when the particle is far away from the nucleus of the atom.
   

Question 3.
Describe Rutherford atom model. What are the draw backs of this model ?
Answer:
Rutherford atom model: The essential features of Rutherford’s nuclear model of the atom or planetary model of the atom are as follows :

1. Every atom consists of tiny central core, called the atomic nucleus, in which the entire positive charge and almost entire mass of the atom are concentrated.
2. The size of nucleus is of the order of 10^-15m, which is very small as compared to the size of the atom which is of the order of 10^-10 m.
3. The atomic nucleus is surrounded by certain number of electrons. As atom on the whole is electrically neutral, the total negative charge of electrons surrounding the nucleus is equal to total positive charge on the nucleus.
4. These electrons revolve around the nucleus in various circular orbits as do the planets around the sun. The centripetal force required by electron for revolution is provided by the electrostatic force of attraction between the electrons and the nucleus.

Drawbacks : According to classical E.M. theory,

1. the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. As matter is stable, we cannot expect the atoms to collapse.
2. since the frequency of radiation emitted is the same as the frequency of revolution, the atom should radiate a continuous spectrum, but what we observe is only a line spectrum.

Question 4.
What are the limitations of Bohr’s theory of hydrogen atom ? [A.P. Mar. 17; Mar. 14]
Answer:
Limitations of Bohr’s theory of Hydrogen atom :

1. This theory is applicable only to simplest atom like hydrogen, with z = 1. The theory fails in case of atoms of other elements for which z > 1.
2. The theory does not explain why orbits of electrons are taken as circular, while elliptical orbits are also possible.
3. Bohr’s theory does not say anything about the relative intensities of spectral lines.
4. Bohr’s theory does not take into account the wave properties of electrons.

Question 5.
Write a short note on Debroglie’s explanation of Bohr’s second postulate of quantization. [T.S. Mar. 17]
Answer:
Debroglie’s explanation of Bohr’s second postulate of quantization :

1. The second postulate of Bohr atom model says that angular momentum of electron orbiting around the nucleus is quantized i.e., mυr = \(\frac{\mathrm{nh}}{2 \pi}\) where n = 1, 2, 3,….
2. According to Debroglie, the electron in its circular orbit, as proposed by Bohr, must be seen as a particle wave.
3. When a string fixed at two ends is plucked, a large number of wavelengths are excited and standing wave is formed.
4. It means that in a string, standing waves form when total distance travelled by a wave down the string and back is an integral number of wavelengths.
5. According to Debroglie, a stationary orbit is that which contains an integral number of Debrogile waves associated with the revolving electron.
6. For an electron revolving in n^th circular orbit of radius r_n, total distance covered = circumference of the orbit = 2πr_n
   ∴ For permissible orbit, 2πr_n = nλ
7. According to Debrogile, λ = \(\frac{h}{m v_n}\)
   Where υ_n is speed of electron revolving in n^th orbit
   ∴ 2πr_n = \(\frac{\mathrm{nh}}{\mathrm{m} v_{\mathrm{n}}}\)
   mυ_nr_n = \(\frac{\mathrm{nh}}{2 \pi}=\mathrm{n}\left(\frac{\mathrm{h}}{2 \pi}\right)\)
   i.e., angular momentum of electron revolving in n^th orbit must be an integral multiple of \(\frac{\mathrm{h}}{2 \pi}\), which is the quantum condition proposed by Bohr in second postulate.

Question 6.
Explain the different types of spectral series in hydrogen atom. [T.S. Mar. 16, A.P. Mar. 15]
Answer:
The atomic hydrogen emits a line spectrum consisting of five series.

1. Lyman series : v = Rc \(\left(\frac{1}{1^2}-\frac{1}{n^2}\right)\) where n = 2, 3, 4
2. Balmer series : v = Rc \(\left(\frac{1}{2^2}-\frac{1}{n^2}\right)\) where n = 3, 4, 5.
3. Paschen series : v = Rc \(\left(\frac{1}{3^2}-\frac{1}{n^2}\right)\) where n = 4, 5, 6
4. Brackett series: v = Rc \(\left(\frac{1}{4^2}-\frac{1}{n^2}\right)\) where n = 5, 6, 7
5. Pfund series: v = Rc \(\left(\frac{1}{5^2}-\frac{1}{n^2}\right)\) where n = 6, 7, 8

Long Answer Questions

Question 1.
State the basic postulates of Bohr’s theory of atomic spectra. Hence obtain an expression for the radius of orbit and the energy of orbital electron in a hydrogen atom. [A.P. Mar. 16]
Answer:
a) Basic postulates of Bohr’s theory are

1. The electron revolves round a nucleus in an atom in various orbits known as stationary orbits. The electrons cannot emit radiation when moving in their own stationary levels.
2. The electron can revolve round the nucleus only in allowed orbits whose angular momentum is the integral multiple of \(\frac{\mathrm{h}}{2 \pi}\)
   i.e., mυ_nr_n = \(\frac{\mathrm{nh}}{2 \pi}\) …………… (1)
   where n = 1, 2, 3 …………..
   If an electron jumps from higher energy (E₂) orbit to the lower energy (E₁) orbit, the difference of energy is radiated in the form of radiation.
   i.e., E = hv = E₂ – E₁ ⇒ v = \(\frac{E_2-E_1}{h}\) …………… (2)

b) Energy of emitted radiation: In hydrogen atom, a single electron of charge – e, revolves around the nucleus of charge e in a circular orbit of radius r_n.
1) K.E. of electron : For the electron to be in circular orbit, centripetal force = The electrostatic force of attraction between the electron and nucleus.

3) Radius of the oribit: Substituting the value of (6) in (2),
\(\frac{\mathrm{m}}{\mathrm{r}_{\mathrm{n}}}\left(\frac{\mathrm{n}^2 \mathrm{~h}^2}{4 \pi^2 \mathrm{r}_{\mathrm{n}}^2 \mathrm{~m}^2}\right)=\frac{\mathrm{Ke}^2}{\mathrm{r}_{\mathrm{n}}^2}\)
r_n = \(\frac{n^2 h^2}{4 \pi^2 m K e^2}\) ……………. (1)
∴ r_n = 0.53 n²

4) Total energy (E_n) : Revolving electron possess K.E. as well as P.E.

Problems

Question 1.
The radius of the first electron orbit of a hydrogen atom is 5.3 x HTum. What is the radius of the second orbit ?
Solution:
∴ r_n ∝ n²
\(\) ⇒ r₂ = 4r₁
∴ r₂ = 4 × 5.3 × 10^-11 = 2.12 × 10^-10m.

Question 2.
The total energy of an electron in the first excited state of the hydrogen atom is -3.4eV. What is the potential energy of the electron in this state?
Solution:
In 1^st orbit, E = -3.4 eV
Total energy E = \(\frac{\mathrm{KZe}^2}{2 \mathrm{r}}-\frac{\mathrm{KZe}^2}{\mathrm{r}}\)
\(\frac{\mathrm{KZe}^2}{\mathrm{r}}\) = U(say)
E = \(\frac{\mathrm{U}}{2}\) – u = \(\frac{\mathrm{-U}}{2}\)
U = -2E
∴ U = -2 × -3.4 = 6.8 eV.

Question 3.
The total energy of an electron in the first excited state of hydrogen atom is -3.4eV. What is the kinetic energy of the electron in this state ?
Solution:
In Hydrogen like atom, we know that
K = – Total energy E
Here E = – 3.4eV
∴ K = -(-3.4) = 3.4 eV . . ,

Question 4.
Prove that the ionisation energy of hydrogen atom is 13.6 eV.
Solution:
n = 1 corresponds to ground state.
E = \(\frac{-13.6}{\mathrm{n}^2}\) eV
E = \(\frac{-13.6}{\mathrm{1}^2}\) eV
E = -13.6 eV
The minimum energy required to free the electron from the ground state of hydrogen atom = 13.6 eV.
∴ Ionisation energy of hydrogen atom = 13.6 eV

Question 5.
Calculate the ionization energy for a lithium atom.
Solution:
For 3^Li7 atom, Z = 3, n = 2 [∵Li = 1s² 2s¹]
E_n = \(\frac{13.6 \mathrm{Z}^2}{\mathrm{n}^2}\) eV
= \(\frac{13.6 \times(3)^2}{4}\) = 30.6 eV
∴ Ionization energy of Lithium = 30.6eV

Question 6.
The wavelength of the first member of Lyman series is 1216 A. Calculate the wavelength of second member of Balmer series.
Solution:

Textual Examples

Question 1.
In the Rutherford’s nuclear model of the atom, the nucleus (radius about 10^-15m) is analogous to the sun about which the electron move in orbit (radius ≈ 10^-10m) like the earth orbits around the sun. If the dimensions of the solar system had the same proportions as those of the atom, would the earth be closer to or farther away from the sun than actually it is ? The radius of earth’s orbit is about 1.5 × 10¹¹m. The radius of sun is taken as 7 × 10⁸ m.
Solution:
The ratio of the radius of electron’s orbit to the radius of nucleus is (10^-10 m)/(10^-15 m) = 105, that is, the radius of the electron’s orbit is 10⁵ times larger than the radius of nucleus. If the radius of the earth’s orbit around the sun were 10⁵ times larger than the radius of the sun, the radius of the earth’s orbit would be 10⁵ × 7 × 10⁸ m = 7 × 10¹³ m. This is more than 100 times greater than the actual orbital radius of earth. Thus, the earth would be much farther away from the sun.

It implies that an atom contains a much greater fraction of empty space than our solar system does.

Question 2.
In a Geiger-Marsden experiment, what is the distance of closest approach to the nucleus of a 7.7 MeV α-particle before it comes momentarily to rest and reverses its direction?
Solution:
The key idea here is that throughout the scattering process, the total mechanical energy of the system consisting of an α-particle and a gold nucleus is conserved. The system’s initial mechanical energy is E_i; before the particle and nucleus interact, and it is equal to its mechanical energy E_f when the α-particle momentarily stops. The initial energy E_t is just the kinetic energy K of the incoming α-particle. The final energy E_f is just the electric potential energy U of the system. The potential energy U can be calculated from Equation.
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{r}^2}\)
Let d be the centre-to-centre distance between the α-particle and the gold nucleus when the α-particle is at its stopping point. Then we can write the conservation of energy
E_i = E_f as
K = \(\frac{1}{4 \pi \varepsilon_0} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{d}}=\frac{2 \mathrm{Ze}^2}{4 \pi \varepsilon_0 \mathrm{~d}}\)
Thus the distance of closest approach d is given by
d = \(\frac{2 \mathrm{Ze}^2}{4 \pi \varepsilon_0 \mathrm{~K}}\)
The maximum kinetic energy found in α-particles of natural origin is 7.7 MeV or 1.2 × 10^-12 J. Since 1/4πε₀ = 9.0 × 10⁹N m²/C². Therefore with e = 1.6 × 10^-19C, we have,
d = \(\frac{(2)\left(9.0 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)^2 \mathrm{Z}}{1.2 \times 10^{-12} \mathrm{~J}}\)
= 3.84 × 10^-16 Zm
The atomic number of foil material gold is Z = 79, so that
d (Au) = 3.0 × 10^-14m = 30 fm. (1 fm (i.e. fermi) = 10^-15m.)
The radius of gold nucleus is, therefore, less than 3.0 × 10^-14 m. This is not in very good agreement with the observed result as the actual radius of gold nucleus is 6 fm. The cause of discrepancy is that the distance of closest approach is considerably larger than the sum of the radii of the gold nucleus and the a-particle. Thus, the α-particle reverses its motion without ever actually touching the gold nucleus.

Question 3.
It is found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
Solution:
Total energy of the electron in hydrogen atom is – 13.6 eV = -13.6 × 1.6 × 10^-19J
= -2.2 × 10^-18 J.
Thus from equation, E = – \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) we have
– \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) = 2.2 10^-18 J
This gives the orbital radius
r = – \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) = \(\frac{\left(9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)^2}{(2)\left(-2.2 \times 10^{-18} \mathrm{~J}\right)}\)
= 5.3 × 10^-11 m.
The velocity of the revolving electron can be computed from Equation r = –\(\frac{e^2}{4 \pi \varepsilon_0 r m v^2}\)
with
m = 9.1 × 10^-31kg,
υ = \(\frac{\mathrm{e}}{\sqrt{4 \pi \varepsilon_0 \mathrm{mr}}}\) = 2.2 × 10⁶ m/s

Question 4.
According to the classical electromagnetic theory, calculate the initial frequency of the light emitted by the electron revolving around a proton in hydrogen atom.
Solution:
From Examjple 3 we know that velocity of electron moving around a proton in hydrogen atom in an orbit of radius 5.3 × 10^-11 m is 2.2 × 10^-6 m/s. Thus, the frequency of the electron moving around the proton is
v = \(\frac{v}{2 \pi \mathrm{r}}=\frac{2.2 \times 10^6 \mathrm{~m} \mathrm{~s}^{-1}}{2 \pi\left(5.3 \times 10^{-11} \mathrm{~m}\right)}\)
≈ 6.6 × 10¹⁵ Hz.
According to the classical electromagnetic theory we know that the frequency of the electromagnetic waves emitted by the revolving electrons is equal to the frequency of its revolution around the nucleus. Thus the initial frequency of the light emitted is 6.6 × 10¹⁵Hz.

Question 5.
A 10 kg satellite circles earth once every 2 h in an orbit having a radius of 8000 km. Assuming that Bohr’s angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, find the quantum number of the orbit of the satellite.
Solution:
From equation, we have
mυ_nr_n = nh/2π
Here m = 10 kg and r_n = 8 × 10⁶ m. We have the time period T of the circling satellite as 2h. That is T = 7200 s.
Thus the velocity υ_n = 2π r_n/T
The quantum number of the orbit of satellite
n = (2π r_n)² × m(T × h)
Substituting the values,
n = (2π × 8 × 10⁶m)² × 10/(7200 s × 6.64 × 10^-34 J s)
= 5.3 × 10⁴⁵
Note that the quantum number for the satellite motion is extremely large. In fact for such large quantum numbers the results of quantisation conditions tend to those of classical physics.

Question 6.
Using the Rydberg formula, calculate the wavelengths of the first four spectral lines in the Lyman series of the hydrogen spectrum.
Solution:
The Rydberg formula is
hc/λ_if = \(\left(\frac{1}{n_{\mathrm{f}}^2}-\frac{1}{\mathrm{n}_{\mathrm{i}}^2}\right)\)
The wavelengths of the first four lines in the Lyman series correspond to transitions from n_i = 2, 3, 4, 5 to n_f = 1. We know that
\(\frac{\mathrm{me}^4}{8 \varepsilon_0^2 \mathrm{~h}^2}\) = 13.6 eV = 21.76 × 10^-19 J
Therefore,

Substituting, n_i = 2, 3, 4, 5 we get λ₂₁ = 1218 Å, λ₃₁ = 1028 Å, λ₄₁ = 974.3 Å, and λ₅₁ = 951.4 Å.

Students get through AP Inter 2nd Year Physics Important Questions 12th Lesson Dual Nature of Radiation and Matter which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 12th Lesson Dual Nature of Radiation and Matter

Very Short Answer Questions

Question 1.
What are “cathode rays”? [A.P. Mar. 17]
Answer:
Cathode rays are streams of fast-moving electrons or negatively charged particles.

Question 2.
What important fact did Millikan’s experiment establish?
Answer:
Millikan’s experiment established that electric charge is quantized. That means the charge on anybody (oil drop) is always an integral multiple of the charge of an electron, i.e., Q = ne.

Question 3.
What is “work function”? [T.S. Mar. 17, 15]
Answer:
The minimum energy required to liberate an electron from a photo metal surface is called the work function, Φ₀.

Question 4.
What is “photoelectric effect” ?
Answer:
When light of sufficierit energy is incident on the photometal surface, electrons are emitted. This phenomenon is called photoelectric effect.

Question 5.
Give examples of “photosensitive substances”. Why are they called so ?
Answer:
Examples of photosensitive substances are Li, Na, K, Rb and Cs etc.
The work function of alkali metals is very low. Even the ordinary visible light, alkali metals can produce photoelectric emission. Hence they are called photosensitive substances.

Question 6.
Write down Einstein’s photoelectric equation. [A.P. Mar. 15]
Answer:
Einstein’s photoelectric equation is given by K_max = \(\frac{1}{2}\) mv²_max = hυ – Φ₀

Question 7.
Write down de-Broglie’s relation and explain the terms therein. [T.S. & A.P. Mar. 16]
Answer:
The de-Broglie wave length (λ) associated with a moving particle is related to its momentum (p) is λ = \(\frac{h}{p}=\frac{h}{m v}\), where h is planck’s constant.

Question 8.
State Heisenberg’s Uncertainity Principle. [Mar. 14]
Answer:
Uncertainity principle states that “it is impossible to measure both position (∆x) and momentum of an electron (∆p) [or any other particle] at the same time exactly”, i.e., ∆x . ∆p ≈ h where ∆x is uncertainty in the specification of position and ∆p is uncertainty in the specification of momentum.

Question 9.
The photoelectric cut off voltage in a certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted ? [Mar. 11]
Answer:
Cut off voltage, V₀ = 1.5 V; Maximum kinetic energy, (KE)_max = eV₀ = e × 1.5 = 1.5eV

Question 10.
An electron, an α-particle and a proton have the same kinetic energy. Which of these particles has the shortest de Broglie wavelength ? [T.S. Mar. 15]
Answer:
For a particle,
de Broglie wavelength, λ = h/p
Kinetic energy, K = p²/2m
Then, λ = h/\(\sqrt{2 \mathrm{mK}}\)
For the same kinetic energy K, the de Broglie wavelength associated with the particle is inversely proportional to the square root of their masses.A proton is 1836 times massive than an electron and an a-particle \(\left({ }_2^4 \mathrm{He}\right)\) four times that of a proton.
Hence, α-particle has the shortest de Broglie wavelength.

Qeustion 11.
What is-the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts ? [A.P. Mar. 15]
Solution:
Accelerating potential V = 100 V The de Broglie wavelngth λ is
λ = h/p = \(\frac{1.227}{\sqrt{\mathrm{V}}}\) nm
λ = \(\frac{1.227}{\sqrt{100}}\) nm = 0.123 nm
The de Broglie wavelength associated with an electron in this case is of the order of X-ray wavelengths.

Question 12.
If the wave length of electro magnetic radiation is doubled, what happens to energy of photon ? [IPE 2015 (TS)]
Answer:
E = \(\frac{\mathrm{hc}}{\lambda}\) ⇒ E ∝ \(\frac{1}{\lambda}\), since wave length of photon is doubled, its energy becomes halved.

Question 13.
In an experiment on photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 × 10^-15 V s. Calculate the value of Planck’s constant.
Solution:
Given, slope of graph tan θ = 4.12 × 10^-15 V – s;

For slope of graph, tan θ = \(\frac{\mathrm{V}}{\mathrm{v}}\)
We know that hv = eV
\(\frac{\mathrm{V}}{\mathrm{v}}=\frac{\mathrm{h}}{\mathrm{e}} \Rightarrow \frac{\mathrm{h}}{\mathrm{e}}\) = 4.12 × 10^-15; h = 4.12 × 10^-15 × 1.6 × 10^-19 = 6.592 × 10^-34 J – s.

Question 14.
The energy flux of sunlight reaching the surface of the earth is 1.388 × 10³ W/m². How many photons (nearly) per square metre are incident on the Earth per second ? Assume that the photons in the sunlight have an average wavelength of 550 nm.
Solution:
Given, P = 1.388 × 10³ W/m²; λ = 550 nm = 550 × 10^-9 m ,
h = 6.63 × 10^-34 J-s; c = 3 × 10⁸ m/s
Energy of each photon E = \(\frac{\text { hc }}{\lambda}=\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{550 \times 10^{-9}}\) = 3.616 × 10^-19 J
No. of photons incident on the earth’s surface, N = \(\frac{\mathrm{P}}{\mathrm{E}}=\frac{1.388 \times 10^3}{3.66 \times 10^{-19}}\)
∴ N = 3.838 × 10²¹ photons/m² – s.

Question 15.
Show that the wavelength of electromagnetic radiation is equal to the de-Brogile wavelength of its quantum (photon). [Mar. 14]
Answer:
Wave length of electromagnetic wave of frequency v and velocity C is given by,
λ = \(\frac{\mathrm{C}}{\mathrm{v}} \Rightarrow \lambda=\frac{\mathrm{C}}{\mathrm{v}} \times \frac{\mathrm{h}}{\mathrm{h}}=\frac{\mathrm{h}}{\left(\frac{\mathrm{hv}}{\mathrm{C}}\right)}=\frac{\mathrm{h}}{\mathrm{p}}\)    (∵ \(\frac{\mathrm{hv}}{\mathrm{C}}\) = p)
Hence, we can say wavelength of electromagnetic radiation is equal to the de-Brogile wavelength.

Sample Problem :

Question 1.
Calculate the (a) momentum and (b) dE-Brogile wavelength of the electrons accelerated through a potential difference of 56 V. [Mar. 14]
Answer:
a) Mass of the electron, m = 9 × 10^-31 kg;
Potential difference, V = 56V
Momentum of electron, mv = \(\sqrt{2 \mathrm{eVm}}=\sqrt{2 \times\left(1.6 \times 10^{-19}\right) \times 56 \times 9 \times 10^{-31}}\) = 4.02 × 10^-24kg ms^-1

b) de-Broglie wavelength, λ = \(\frac{\mathrm{h}}{\mathrm{p}}=\frac{\mathrm{h}}{\mathrm{mv}}=\frac{6.62 \times 10^{-34}}{4.04 \times 10^{-24}}\) = 1.64 × 10^-10m

Short Answer Questions

Question 1.
Describe an experiment to study the effect of frequency of incident radiation on ‘stopping potential’.
Answer:
Experimental study of the effect of frequency of incident radiation on stopping potential:

1. The experimental set up is shown in fig.
   
2. Monochromatic light of sufficient energy (E = hv) from source ‘s’ is incident on photosensitive plate ‘C’ (emitter), electrons are emitted by it.
3. The electrons are collected by the plate A (collector), by the electric field created by the battery.
4. The polarity of the plates C and A can be reversed by a commutator.
5. For a particular frequency of incident radiation, the minimum negative (retarding) potential V0 given to the plate A for which the photo current stops or becomes zero is called stopping potential.
6. The experiment is repeated with different frequencies, and their different stopping potential are measured with voltmeter.
7. From graph, we note that
   
   • The values of stopping potentials are different for different frequencies.
   • The value of stopping potential is more negative for radiation of highef incident frequency.
   • The value of saturation current depends on the intensity of incident radiation but it is independent of the frequency of the incident radiation.

Question 2.
What is the deBroglie wavelength of a ball of mass 0.12 Kg moving with a speed of 20 ms^-1? What can we infer from this result ?
Answer:
Given, m = 0.12 kg; υ = 20 m/s; h = 6.63 × 10^-34 J-s;
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}=\frac{6.63 \times 10^{-34}}{0.12 \times 20}=\frac{6.63 \times 10^{-34}}{2.4}\)
∴ λ = 2.762 × 10^-34 m = 2762 × 10^-21 Å.
The wave length of ball is very very small. Hence, its motion can be observed.

Question 3.
What is the effect of (i) intensity of light (ii) potential on photoelectric current ?
Answer:
(i) Effect of intensity of light on photoelectric current:
1) When the intensity (I) of incident light, with frequency greater than the threshold frequency (υ > υ₀) is increased then the number of photoelectrons emitted increases i.e., the value of photoelectric current (i) increases, ie., i ∝ I.

ii) The effect of potential on photoelectric current:

1. On increasing the positive potential on collecting electrode, the photoelectric current increases. At a particular positive potential, the photocurrent becomes maximum which is known as saturated current.
   
2. On increasing the value of negative potential on collecting electrode, the photoelectric current gradually goes on decreasing. At a particular negative potential the value of photoelectric current becomes zero. This is known as stopping potential.
3. Stopping potential does not depend on the intensity of incident light. On increasing intensity, the value of saturated current increases, whereas the stopping potential remains unchanged.

Sample Problem :

Question 1.
The work function of caesium metal is 2.14 eV When light of frequency 6 × 10¹⁴ Hz is incident on the metal surface, photoemission of electrons occurs. What is the (a) maximum kinetic energy of the emitted electrons, (b) stopping potential and (c) maximum speed of the emitted photoelectrons ? [A.P. Mar. 16]
Solution:
Given, Φ₀ = 2.14 eV; v = 6 × 10¹⁴ Hz
a) KE_max = hv – Φ₀ = \(\frac{6.63 \times 10^{-34} \times 6 \times 10^{14}}{1.6 \times 10^{-19}}\) – 2.14
∴ KE_max = 0.35 eV

b) KE_max = eV₀ ⇒ 0.35 eV = eV₀
∴ V₀ = 0.35 V

Long Answer Questions

Question 1.
How did Einstein’s photoelectric equation explain the effect of intensity and potential on photoelectric current ? How did this equation account for the effect of frequency of ‘ incident light on stopping potential ?
Answer:

1. Einstein postulated that a beam of light consists of small energy packets called photons or quanta.
2. The energy of photon is E = hv. Where ‘h1 is Planck’s constant; v is frequency of incident light (or radiation).
3. If the absorbed energy of photon is greater than the work function (Φ₀ = hυ₀), the electron is emitted with maximum kinetic energy i.e., k_max = \(\frac{1}{2} \mathrm{mv}_{\max }^2\) = eV₀ = hv – Φ₀. This equation is known as Einstein’s photoelectric equation.
4. Effect of intensity of light on photoelectric current:
   When the intensity (I) of incident light, with frequency greater than the threshold frequency (υ > υ₀) is increased then the number of photoelectrons emitted decreases i.e., the value of photoelectric current (i) increases, ie., i ∝ I.
   
5. The effect of potential on photoelectric current:
   • On increasing the positive potential on collecting electrode, the photoelectric current increases. At a particular positive potential, the photocurrent becomes maximum which is known as saturated current.
     
   • On increasing the value of negative potential on collecting electrode, the photoelectric current gradually goes on decreasing. At a particular negative potential the value of photoelectric current becomes zero. This is known as stopping potential (v₀).
   • Stopping potential does not depend on the intensity of incident light. On increasing intensity, the value of saturated current increases, whereas the stopping potential remains unchanged.
6. The effect of frequency of incident radiation on stopping potential:
   On increasing the frequency of incident light, the value of stopping potential goes on increasing gradually as shown in fig. That means k_max increases eV₀ also increases.
   
7. From the graph, we note that
   • For a given photosensitive metal, the cut off potential (v₀) varies linearly with the frequency of the incident radiation.
   • For a given photosensitive metal, there is a certain minimum cut off frequency υ₀ (called threshold frequency) for which the stopping potential is zero.
     
8. From the graph we note that
   • The value of cut-off potential is different for radiation of different frequency.
   • The value of stopping potential is more negative for radiation of higher incident frequency.
9.  From above experiments, it is found that, if the incident radiation is of higher frequency than that of threshold frequency, the photoelectric emission is. possible.

Textual Examples

Question 1.
Monochromatic light of frequency 6.0 × 10¹⁴ Hz is produced by a laser. The power emitted is 2.0 × 10^-3 W. (a) What is the energy of a photon in the light beam ? (b) How many photons per second, on an average, are emitted by the source ?
Solution:
a) Each photon has an energy
E = hv = (6.63 × 10^-34 J s) (6.0 × 10¹⁴ Hz)
= 3.98 × 10^-19 J

b) If N is the number of photons emitted by the source per second, the power P transmitted in the beam equals N times the energy per photon E, so that P = NE.
Then N = \(\frac{\mathrm{P}}{\mathrm{E}}=\frac{2.0 \times 10^{-3} \mathrm{~W}}{3.98 \times 10^{-19} \mathrm{~J}}\)
= 5.0 × 10¹⁵ photons per second.

Question 2.
The work function of caesium is 2.14 eV. Find (a) the threshold frequency for caesium, and (b) the wavelength of the incident light if the photocurrent is brought to zero by a stopping potential of 0.60 V. [A.P. Mar. 16]
Solution:
a) For the cut-off or threshold frequency, the energy hv₀ of the incident radiation must be equal to work function Φ₀, so that
v₀ = \(\frac{\phi_0}{\mathrm{~h}}=\frac{2.14 \mathrm{eV}}{6.63 \times 10^{-34} \mathrm{Js}}\)
= \(\frac{2.14 \times 1.6 \times 10^{-19} \mathrm{~J}}{6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s}}\) = 5.16 × 10¹⁴ Hz
Thus, for frequencies less than this threshold frequency, no photoelectrons are ejected.

b) Photocurrent reduces to zero, when maximum kinetic energy of the emitted photoelectrons equals the potential energy e V₀ by the retarding potential V₀. Einstein’s Photoelectric equation is
eV₀ = hv – Φ₀ = \(\frac{\mathrm{hc}}{\lambda}\) – Φ₀
or λ = hc/(eV₀ + Φ₀)
= \(\frac{\left(6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s}\right) \times\left(3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)}{(0.60 \mathrm{eV}+2.14 \mathrm{eV})}\)
= \(\frac{19.89 \times 10^{-26} \mathrm{~J} \mathrm{~m}}{(2.74 \mathrm{eV})}\)
λ = \(\frac{19.89 \times 10^{-26} \mathrm{~J} \mathrm{~m}}{2.74 \times 1.6 \times 10^{-19} \mathrm{~J}}\) = 454 nm

Question 3.
The wavelength of light in the visible region is about 390 nm for violet colour, about 550 nm (average wavelength) for yellow-green colour and about 760 nm for red colour.
(a) What are the energies of photons in (eV) at the (i) violet end, (ii) average wavelength, yellow-green colour, and (iii) red end of the visible spectrum ? (Take h = 6.63 × 10^-34 J s and 1 eV = 1.6 × 10^-19 J.)
(b) From which of the photosensitive materials with work functions listed in table and using the results of (i), (ii) and (iii) of (a) can you build a photoelectric device that operates with visible light ?

Solution:
a) Energy of the incident photon,
E = hv = hc/λ
E = (6.63 × 10^-34 J s) (3 × 10⁸ m/s)/λ.
= \(\frac{1.989 \times 10^{-25} \mathrm{~J} \mathrm{~m}}{\lambda}\)
i) For violet light,
λ₁ = 390 nm (lower wavelength end)
Incident photon energy,
E₁ = \(\frac{1.989 \times 10^{-25} \mathrm{~J} \mathrm{~m}}{390 \times 10^{-9} \mathrm{~m}}\)
5.10 × 10^-19 J = \(\frac{5.10 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\)
= 3.19 eV

ii) For yellow-green light,
λ₂ = 550 nm (average wavelength)
Incident photon energy,
E₂ = \(\frac{1.989 \times 10^{-25} \mathrm{~J} \mathrm{~m}}{550 \times 10^{-9} \mathrm{~m}}\)
= 3.62 × 10^-19 J = 2.26 eV.

iii) For red light,
λ₃ = 760 nm (higher wavelength end)
Incident photon energy,
E₃ = \(\frac{1.989 \times 10^{-25} \mathrm{~J} \mathrm{~m}}{760 \times 10^{-9} \mathrm{~m}}\)
= 2.62 × 10^-19 J = 1.64 eV

b) For a photoelectric device to operate, we require incident light energy E to be equal to or greater than the work function Φ₀ of the material. Thus, the photoelectric device will operate with violet light (with E = 3.19 eV) photosensitive material Na (with Φ₀ = 2.75 eV), K (with Φ₀ = 2.30 eV) and Cs (with Φ₀ = 2.14 eV). It will also operate with yellow-green light (with E = 2.26 eV) for Cs (with Φ₀ = 2.14 eV) only. However, it will not operate with red light (with E = 1.64 eV) for any of these photosensitive materials.

Question 4.
What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4 × 10⁶ m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s ?
Solution:
a) For the electron :
Mass m= 9.11 × 10^-31 kg, speed υ = 5.4 × 10⁶ m/s. Then, momentum
P = mυ = 9.11 × 10^-31 (kg) × 5.4 × 10⁶ (m/s)
P = 4.92 × 10^-24 kg m/s
de Broglie wavelength, λ = h/p
= \(\frac{6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s}}{4.92 \times 10^{-24} \mathrm{~kg} \mathrm{~m} / \mathrm{s}}\)
λ = 0.135 nm

b) For the ball:
Mass m’ = 0.150 kg, speed υ’ = 30.0 m/s.
Then momentum
p’ = m’υ’ = 0.150 (kg) × 30.0 (m/s)
p’ = 4.50 kg m/s
de Broglie wavelength λ’ = h/p’.
= \(\frac{6.63 \times 10^{\pm 34} \mathrm{Js}}{4.50 \times \mathrm{kg} \mathrm{m} / \mathrm{s}}\)
λ’ = 1.47 × 10^-34 m
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10^-19 times the size of the proton, quite beyond experimental measurement.

Question 5.
An electron, an a-particle and a proton have the same kinetic energy. Which of these particles has the shortest de Broglie wavelength ? [T.S. Mar. 15]
Solution:
For a particle,
de Broglie wavelength, λ = h/p
Kinetic energy, K = p²/2m
Then, λ = h /\(\sqrt{2 \mathrm{mK}}\)
For the same kinetic energy K, the de Broglie wavelength associated with the particle is inversely proportional to the square root of their masses. A proton \(\left({ }_1^1 \mathrm{He}\right)\) is 1836 times massive than an electron and an a-particle \(\left({ }_2^4 \mathrm{He}\right)\) four times that of a proton
Hence, α-particle has the shortest de Broglie wavelength.

Question 6.
A particle is moving three times as fast as an electron. The ratio of the de Broglie wavelength of the particle to that of the electron is 1.813 × 10^-4. Calculate the particle’s mass and identify the particle.
Solution:
de Broglie wavelength of a moving particle, having mass m and velocity υ :
λ = \(\frac{\mathrm{h}}{\mathrm{p}}=\frac{\mathrm{h}}{\mathrm{mv}}\)
Mass, m = h/A.
For an electron, mass m_e = h/λ_e υ_e
Now, we have υ/υ_e = 3 and
λ/λ_e = 1.813 × 10^-4
Then, mass of the particle,
m = m_e \(\left(\frac{\lambda_{\mathrm{e}}}{\lambda}\right)\left(\frac{v_{\mathrm{e}}}{v}\right)\)
m = (9.11 × 10^-31 kg) × (1/3) × (1/1.813 × 10^-4)
m = 1.675 × 10^-27 kg.
Thus, the particle, with this mass could be a proton or a neutron.

Question 7.
What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts? [A.P. Mar. 15]
Solution:
Accelerating potential V = 100 V The de Broglie wavelength λ is
λ = h/p = \(\frac{1.227}{\sqrt{\mathrm{V}}}\) nm
λ = \(\frac{1.227}{\sqrt{100}}\) nm = 0.123 nm
The de Broglie wavelength associated with an electron in this case is of the order of X-ray wavelengths.