Mahesh

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(d)

Question 1.
Find the coefficient of x³ in the power series expansion of \(\frac{5 x+6}{(x+2)(1-x)}\) specifying the region in which the expansion is valid.
Solution:

Question 2.
Find is the coefficient of x⁴ in the power series expansion of \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}\) specifying the interval in which the expansion is valid.
Solution:
Let \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}=\frac{A}{x-3}+\frac{B x+C}{x^2+2}\)
Multiplying with (x² + 2) (x – 3)
3x² + 2x = A(x² + 2) + (Bx + C) (x – 3)
x = 3
⇒ 27 + 6 = A(9 + 2)
⇒ 33 = 11A
⇒ A = 3
Equating the coefficients of x²
3 = A + B
⇒ B = 3 – A = 3 – 3 = 0
Equating the constants,
2A – 3C = 0
⇒ 3C = 2A = 6
⇒ C = 2

Question 3.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x-4}{x^2-5 x+6}\) specifying the region in which the expansion is valid.
Solution:
Let \(\frac{x-4}{x^2-5 x+6}=\frac{A}{x-2}+\frac{B}{x-3}\)
Multiplying with (x – 2) (x – 3)
x – 4 = A(x – 3) + B(x – 2)
x = 2
⇒ -2 = A(2 – 3) = -A
⇒ A = 2
x = 3
⇒ -1 = B(3 – 2) = B
⇒ B = -1

Question 4.
Find the coefficient of xⁿ in the power series expansion of \(\frac{3 x}{(x-1)(x-2)^2}\)
Solution:

∴ 3x = A(x – 2)² + B(x – 1) (x – 2) + C(x – 1) ……..(1)
putting x = 1,
3 = A(1 – 2)²
⇒ A = 3
putting x = 2,
6 = C(2 – 1)
⇒ C = 6
Now equating the co-efficient of x² terms in (1)
0 = A + B
⇒ B = -A
⇒ B = -3

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(c)

Resolve the following into partial fractions.

Question 1.
\(\frac{x^2}{(x-1)(x-2)}\)
Solution:
Let \(\frac{x^2}{(x-1)(x-2)}=1+\frac{A}{x-1}+\frac{B}{x-2}\)
Multiplying with (x – 1) (x – 2)
x² = (x – 1) (x – 2) + A(x – 2) + B(x – 1)
Put x = 1, 1 = A(-1) ⇒ A = -1
Put x = 2, 4 = B(1) ⇒ B = 4
∴ \(\frac{x^2}{(x-1)(x-2)}=1-\frac{1}{x-1}+\frac{4}{x-2}\)

Question 2.
\(\frac{x^3}{(x-1)(x+2)}\)
Solution:

Question 3.
\(\frac{x^3}{(2 x-1)(x-1)^2}\)
Solution:
Let \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{A}{2 x-1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\)
Multiplying with 2(2x – 1) (x – 1)²
2x³ = (2x – 1) (x – 1)² + 2A(x – 1)² + 2B(2x – 1) (x – 1) + 2C(2x – 1)
Put x = \(\frac{1}{2}\),
⇒ 2(\(\frac{1}{8}\)) = 2A(\(\frac{1}{4}\))
⇒ A = \(\frac{1}{2}\)
Put x = 1,
⇒ 2(1) = 2C(1)
⇒ C = 1
Put x = 0,
0 = (-1) (1) + 2A(1) + 2B(-1) (-1) + 2C(-1)
⇒ 2A + 2B – 2C = 1
⇒ 2B = 1 + 2C – 2A
⇒ 2B = 1 + 2 – 1 = 2
⇒ B = 1
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{(x-1)}+\frac{1}{(x-1)^2}\)

Question 4.
\(\frac{x^3}{(x-a)(x-b)(x-c)}\)
Solution:
Let \(\frac{x^3}{(x-a)(x-b)(x-c)}\) = \(1+\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
Multiplying with (x – a)(x – b) (x – c),
x³ = (x – a)(x – b) (x – c) + A(x – b) (x – c) + B(x – a) (x – c) + C(x – a) (x – b)
Put x = a,
a³ = A(a – b) (a – c)
⇒ A = \(\frac{a^3}{(a-b)(a-c)}\)
Put x = b,
b³ = B(b – a) (b – c)
⇒ B = \(\frac{b^3}{(b-a)(b-c)}\)
Put x = c, c³ = C(c – a) (c – b)
⇒ C = \(\frac{c^3}{(c-a)(c-b)}\)
∴ \(\frac{x^3}{(x-a)(x-b)(x-c)}\) = \(1+\frac{a^3}{(a-b)(a-c)(x-a)}+\frac{b^3}{(b-a)(b-c)(x-b)}\) + \(\frac{c^3}{(c-a)(c-b)(x-c)}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(b)

Resolve the following into partial fractions.

Question 1.
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\)
Solution:
Let \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\)
Multiplying with (x – 1) (x² + 2)
2x² + 3x + 4 = A(x² + 2) + (Bx + C) (x – 1)
x = 1
⇒ 2 + 3 + 4 = A(1 + 2)
⇒ 9 = 3A
⇒ A = 3
Equating the coefficients of x²
2 = A + B
⇒ B = 2 – A = 2 – 3 = -1
Equating constants
4 = 2A – C
⇒ C = 2A – 4 = 6 – 4 = 2
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{-x+2}{x^2+2}\)

Question 2.
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\)
Solution:
Let \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{A}{2+x}+\frac{B x+C}{1-x+x^2}\)
Multiplying with (2 + x) (1 – x + x²)
3x – 1 = A(1 – x + x²) (Bx + C) (2 + x)
x = -2
⇒ -7 = A(1 + 2 + 4) = 7A
⇒ A = -1
Equating the coefficients of x²
0 = A + B ⇒ B = -A = 1
Equating the constants
-1 = A + 2C
⇒ 2C = -1 – A = -1 + 1 = 0
⇒ C = 0
∴ \(\frac{3 x-1}{\left(1-x+x^2\right)(2+x)}=-\frac{1}{2+x}+\frac{x}{1-x+x^2}\)

Question 3.
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\)
Solution:
Let \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\)
Multiplying with (x + 2) (x² + 1)
x² – 3 = A(x² + 1) + (Bx + C) (x + 2)
x = -2
⇒ 4 – 3 = A(4 + 1)
⇒ 1 = 5A
⇒ A = \(\frac{1}{5}\)
Equating the coefficients of x²
1 = A + B
⇒ B = 1 – A = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Equating the constants
-3 = A + 2C
⇒ 2C = -3 – A
⇒ 2C = -3 – \(\frac{1}{5}\)
⇒ 2C = \(-\frac{16}{5}\)
⇒ C = \(-\frac{8}{5}\)
∴ \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\)

Question 4.
\(\frac{x^2+1}{\left(x^2+x+1\right)^2}\)
Solution:
Let \(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{A x+B}{x^2+x+1}+\frac{C x+D}{\left(x^2+x+1\right)^2}\)
Multiplying with (x² + x + 1)²
x² + 1 = (Ax + B) (x² + x + 1) + (Cx + D)
Equating the coefficients of x³,
A = 0
Equating the coefficients of x²,
A + B = 1 ⇒ B = 1
Equating the coefficients of x,
A + B + C = 0
⇒ 1 + C = 0
⇒ C = -1
Equating the constants,
B + D = 1
⇒ D = 1 – B = 1 – 1 = 0
∴ Ax + B = 1, Cx + D = -x
∴ \(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{1}{x^2+x+1}-\frac{x}{\left(x^2+x+1\right)^2}\)

Question 5.
\(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\)
Solution:

∴ x³ + x² + 1 = A(x – 1) (x² + x + 1) + B(x² + x + 1) + (Cx + D) (x – 1)² …….(2)
Put x = 1 in (2)
1 + 1 + 1 = A(0) + B(1 + 1 + 1) + (C(1) + D) (0)
⇒ 3B = 3
⇒ B = 1
Equating the coefficients of x³ in (2)
1 = A + C ………(3)
Equating the coefficients of x² in (2)
1 = A(1 – 1) + B(1) + C(-2) + D(1)
⇒ 1 = B – 2C + D
∵ B = 1,
⇒ 1 = 1 – 2C + D
⇒ 2C = D ………(4)
Put x = 0 in (2)
1 = A(-1)(1) + B(1) + D(-1)²
⇒ -A + B + D = 1
⇒ -A + 1 + D = 1
⇒ A = D ………(5)
From (3), (4) and (5)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(a)

Resolve the following into partial fractions.

I.

Question 1.
\(\frac{2 x+3}{(x+1)(x-3)}\)
Solution:
Let \(\frac{2 x+3}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}\)
Multiplying with (x + 1) (x – 3)
2x + 3 = A(x – 3) + B(x + 1)
x = -1 ⇒ 1 = A(-4) ⇒ A = \(-\frac{1}{4}\)
x = 3 ⇒ 9 = B(4) ⇒ B = \(\frac{9}{4}\)
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{-1}{4(x+1)}+\frac{9}{4(x-3)}\)

Question 2.
\(\frac{5 x+6}{(2+x)(1-x)}\)
Solution:
Let \(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\)
Multiplying with (2 + x) (1 – x)
5x + 6 = A(1 – x) + B(2 + x)
Put x = -2,
-10 + 6 = A(1 + 2)
⇒ A = \(-\frac{4}{3}\)
Put x = 1,
5 + 6 = B(2 + 1)
⇒ B = \(\frac{11}{3}\)
∴ \(\frac{5 x+6}{(2+x)(1-x)}=-\frac{4}{3(2+x)}+\frac{11}{3(1-x)}\)

II.

Question 1.
\(\frac{3 x+7}{x^2-3 x+2}\)
Solution:
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\)
Multiplying with x² – 3x + 2
3x + 7 = A(x – 2) + B(x – 1)
x = 1 ⇒ 10 = -A ⇒ A = -10
x = 2 ⇒ 13 = B ⇒ B = 13
∴ \(\frac{3 x+7}{x^2-3 x+2}=\frac{-10}{x-1}+\frac{13}{x-2}\)

Question 2.
\(\frac{x+4}{\left(x^2-4\right)(x+1)}\)
Solution:
\(\frac{x+4}{\left(x^2-4\right)(x+1)}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{x-2}\)
Multiplying with (x² – 4) (x + 1)
x + 4 = A(x² – 4) + B(x + 1) (x – 2) + C(x + 1) (x + 2)
x = -1
⇒ 3 = A(1 – 4)
⇒ 3 = -3A
⇒ A = -1
x = -2
⇒ 2 = B(-2 + 1) (-2 – 2)
⇒ 2 = 4B
⇒ B = \(\frac{1}{2}\)
x = 2
⇒ 6 = C(2 + 1)(2 + 2)
⇒ 6 = 12C
⇒ C = \(\frac{1}{2}\)
∴ \(\frac{x+4}{\left(x^2-4\right)(x+1)}=-\frac{1}{x+1}+\frac{1}{2(x+2)}\) + \(\frac{1}{2(x-2)}\)

Question 3.
\(\frac{2 x^2+2 x+1}{x^3+x^2}\)
Solution:
Let \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
Multiplying with x²(x + 1)
2x² + 2x + 1 = Ax(x + 1) + B(x + 1) + Cx²
Put x = 0, 1 = B
Put x = -1, 2 – 2 + 1 = C(1) ⇒ C = 1
Equating the coefficients of x²,
2 = A + C
⇒ A = 2 – C = 2 – 1 = 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\)

Question 4.
\(\frac{2 x+3}{(x-1)^3}\)
Solution:
\(\frac{2 x+3}{(x-1)^3}\)
Put x – 1 = y ⇒ x = y + 1
⇒ \(\frac{2 x+3}{(x-1)^3}=\frac{2(y+1)+3}{y^3}=\frac{2 y+5}{y^3}\)
⇒ \(\frac{2 x+3}{(x-1)^3}\) = \(\frac{2}{y^2}+\frac{5}{y^3}=\frac{2}{(x-1)^2}+\frac{5}{(x-1)^3}\)
∴ \(\frac{2 x+3}{(x-1)^3}=\frac{2}{(x-1)^2}+\frac{5}{(x-1)^3}\)

Question 5.
\(\frac{x^2-2 x+6}{(x-2)^3}\)
Solution:
Let x – 2 = y then x = y + 2

III.

Question 1.
\(\frac{x^2-x+1}{(x+1)(x-1)^2}\)
Solution:
Let \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\)
Multiplying with (x + 1) (x – 1)²
x² – x + 1 = A(x – 1)² + B(x + 1) (x – 1) + C(x + 1)
Put x = -1,
1 + 1 + 1 = A(4)
⇒ A = \(\frac{3}{4}\)
Put x = 1,
1 – 1 + 1 = C(2)
⇒ C = +\(\frac{1}{2}\)
Equating the coefficients of x²,
A + B = 1
⇒ B = 1 – A
⇒ B = 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{3}{4(x+1)}+\frac{1}{4(x-1)}\) + \(\frac{1}{2(x-1)^2}\)

Question 2.
\(\frac{9}{(x-1)(x+2)^2}\)
Solution:
Let \(\frac{9}{(x-1)(x+2)^2}=\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\)
Multiplying with (x – 1) (x + 2)²
9 = A(x + 2)² + B(x – 1) (x + 2) + C(x – 1)
x = 1
⇒ 9 = 9A
⇒ A = 1
x = -2
⇒ 9 = -3C
⇒ C = -3
Equating the coefficients of x²
A + B = 0 ⇒ B = -A = -1
∴ \(\frac{9}{(x-1)(x+2)^2}=\frac{1}{x-1}-\frac{1}{x+2}-\frac{3}{(x+2)^2}\)

Question 3.
\(\frac{1}{(1-2 x)^2(1-3 x)}\)
Solution:
Let \(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{A}{1-3 x}+\frac{B}{1-2 x}+\frac{C}{(1-2 x)^2}\)
Multiplying with (1 – 2x)² (1 – 3x)
1 = A(1 – 2x)² + B(1 – 3x) (1 – 2x) + C(1 – 3x)

Question 4.
\(\frac{1}{x^3(x+a)}\)
Solution:
Let \(\frac{1}{x^3(x+a)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+a}\) = \(\frac{A \cdot x^2(x+a)+B(x)(x+a)+C(x+a)+D x^3}{x^3(x+a)}\)
∴ 1 = A (x²) (x + a) + Bx (x + a) + C(x + a) + Dx³ ……..(1)
Put x = 0 in (1)
1 = A(0) + B(0) + C(0 + a) + D(0)
⇒ 1 = C(a)
⇒ C = \(\frac{1}{a}\)

Question 5.
\(\frac{x^2+5 x+7}{(x-3)^3}\)
Solution:
Let x – 3 = y ⇒ x = y + 3
\(\frac{x^2+5 x+7}{(x-3)^3}=\frac{(y+3)^2+5(y+3)+7}{y^3}\)

Question 6.
\(\frac{3 x^3-8 x^2+10}{(x-1)^4}\)
Solution:
Put x – 1 = y ⇒ x = y + 1

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(c)

Question 1.
Find an approximate value of the following corrected to 4 decimal places.
(i) \(\sqrt[5]{242}\)
Solution:

(ii) \(\sqrt[7]{127}\)
Solution:

(iii) \(\sqrt[5]{32.16}\)
Solution:

(iv) \(\sqrt{199}\)
Solution:

(v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)
Solution:

(vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
Solution:

Question 2.
If |x| is so small that x² and higher powers of x may be neglected then find the approximate values of the following.
(i) \(\frac{(4+3 x)^{1 / 2}}{(3-2 x)^2}\)
Solution:

(ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{3 / 2}(32+5 x)^{1 / 5}}{(3-x)^3}\)
Solution:

(iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)
Solution:

(iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{-1 / 3}}\)
Solution:

(v) \(\frac{(8+3 x)^{2 / 3}}{(2+3 x) \sqrt{4-5 x}}\)
Solution:

Question 3.
Suppose s and t are positive and t is very small when compared to s. Then find an approximate value of \(\left(\frac{s}{s+t}\right)^{1 / 3}-\left(\frac{s}{s-t}\right)^{1 / 3}\)
Solution:
Since t is very small when compared with s, \(\frac{t}{s}\) is very very small.

Question 4.
Suppose p, q are positive and p is very small when compared to q. Then find an approximate value of \(\left(\frac{q}{q+p}\right)^{1 / 2}+\left(\frac{q}{q-p}\right)^{1 / 2}\)
Solution:

Question 5.
By neglecting x⁴ and higher powers of x, find an approximate value of \(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\)
Solution:

Question 6.
Expand 3√3 in increasing powers of \(\frac{2}{3}\).
Solution:

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(b)

I.

Question 1.
Find the set of values of x for which the binomial expansions of the following are valid.
(i) (2 + 3x)^-2/3
(ii) (5 + x)^3/2
(iii) (7 + 3x)^-5
(iv) \(\left(4-\frac{x}{3}\right)^{-1 / 2}\)
Solution:
(i) (2 + 3x)^-2/3 = \(\left[2\left(1+\frac{3}{2} x\right)\right]^{-2 / 3}\)

Question 2.
Find the
(i) 6th term of \(\left(1+\frac{x}{2}\right)^{-5}\)
Solution:

(ii) 7th term of \(\left(1-\frac{x^2}{3}\right)^{-4}\)
Solution:

(iii) 10th term of (3 – 4x)^-2/3
Solution:

(iv) 5th term of \(\left(7+\frac{8 y}{3}\right)^{7 / 4}\)
Solution:

Question 3.
Write down the first 3 terms in the expansion of
(i) (3 + 5x)^-7/3
Solution:

(ii) (1 + 4x)^-4
Solution:

(iii) (8 – 5x)^2/3
Solution:

(iv) (2 – 7x)^-3/4
Solution:

Question 4.
Find the general term (r + 1)^th term in the expansion of
(i) (4 + 5x)^-3/2
Solution:

(ii) \(\left(1-\frac{5 x}{3}\right)^{-3}\)
Solution:

(iii) \(\left(1+\frac{4 x}{5}\right)^{5 / 2}\)
Solution:

(iv) \(\left(3-\frac{5 x}{4}\right)^{-1 / 2}\)
Solution:

II.

Question 1.
Find the coefficient of x¹⁰ in the expansion of \(\frac{1+2 x}{(1-2 x)^2}\)
Solution:

Question 2.
Find the coefficient of x⁴ in the expansion of (1 – 4x)^-3/5
Solution:

Question 3.
(i) Find the coefficient of x⁵ in \(\frac{(1-3 x)^2}{(3-x)^{3 / 2}}\)
Solution:

(ii) Find the coefficient of x⁸ in \(\frac{(1+x)^2}{\left(1-\frac{2}{3} x\right)^3}\)
Solution:

(iii) Find the coefficient of x⁷ in \(\frac{(2+3 x)^3}{(1-3 x)^4}\)
Solution:

Question 4.
Find the coefficient of x³ in the expansion of \(\frac{\left(1+3 x^2\right)^{3 / 2}}{(3+4 x)^{1 / 3}}\)
Solution:

III.

Question 1.
Find the sum of the infinite series
(i) \(1+\frac{1}{3}+\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\ldots\)
Solution:

(ii) \(1-\frac{4}{5}+\frac{4.7}{5.10}-\frac{4.7 .10}{5.10 .15}+\ldots \ldots\)
Solution:

(iii) \(\frac{3}{4}+\frac{3.5}{4.8}+\frac{3.5 .7}{4.8 .12}+\ldots\)
Solution:

(iv) \(\frac{3}{4.8}-\frac{3.5}{4.8 .12}+\frac{3.5 .7}{4.8 .12 .16}-\ldots \ldots\)
Solution:

Question 2.
If t = \(\frac{4}{5}+\frac{4.6}{5.10}+\frac{4.6 .8}{5.10 .15}+\ldots \ldots \ldots \infty\), then prove that 9t = 16.
Solution:

Question 3.
If x = \(\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\frac{1.3 .5 .7}{3.6 .9 .12}+\ldots \ldots\) then prove that 9x² + 24x = 11.
Solution:

⇒ 3x + 4 = 3√3
Squaring on both sides
(3x + 4)² = (3√3)²
⇒ 9x² + 24x + 16 = 27
⇒ 9x² + 24x = 11

Question 4.
If x = \(\frac{5}{(2 !) \cdot 3}+\frac{5 \cdot 7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots\) then find the value of x² + 4x.
Solution:

Question 5.
Find the sum of the infinite series \(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1.3}{1.2} \cdot \frac{1}{10^4}+\frac{1.3 .5}{1.2 .3} \cdot \frac{1}{10^6}+\ldots .\right)\)
Solution:

Question 6.
Show that \(1+\frac{x}{2}+\frac{x(x-1)}{2.4}+\frac{x(x-1)(x-2)}{2.4 .6}+\ldots .\) = \(1+\frac{x}{3}+\frac{x(x+1)}{3.6}+\frac{x(x+1)(x+2)}{3.6 .9}+\ldots\)
Solution:

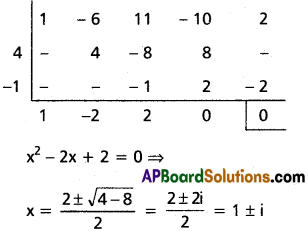
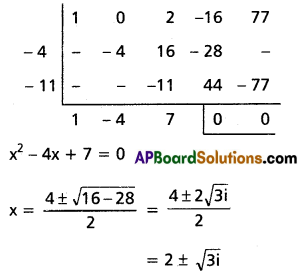
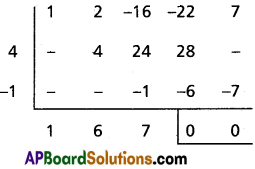
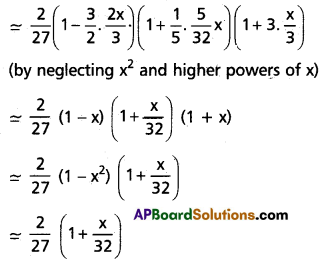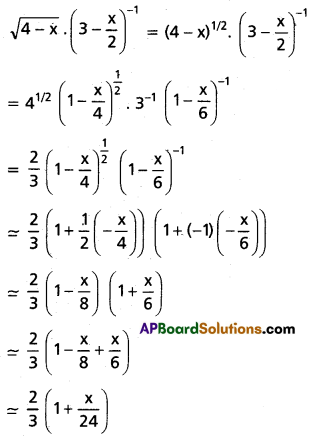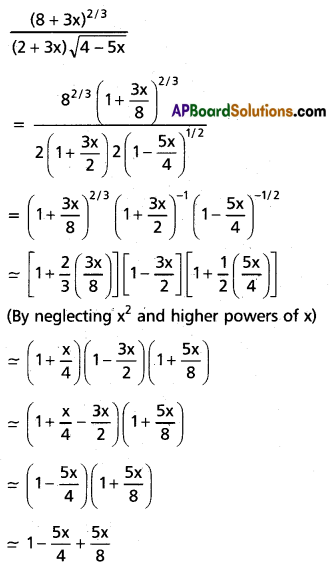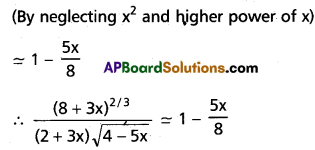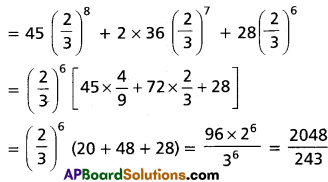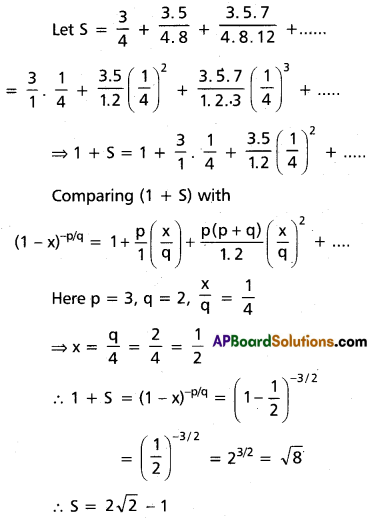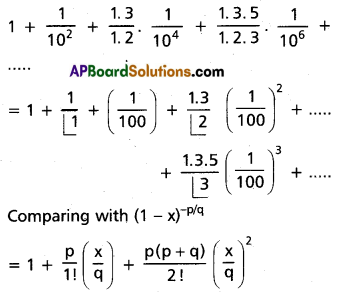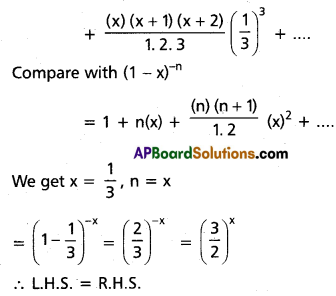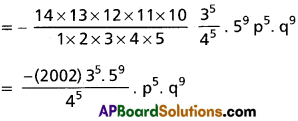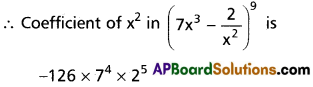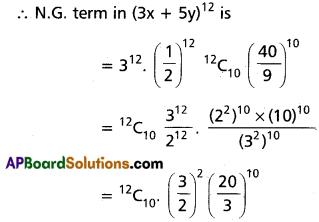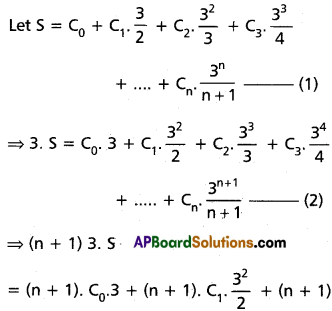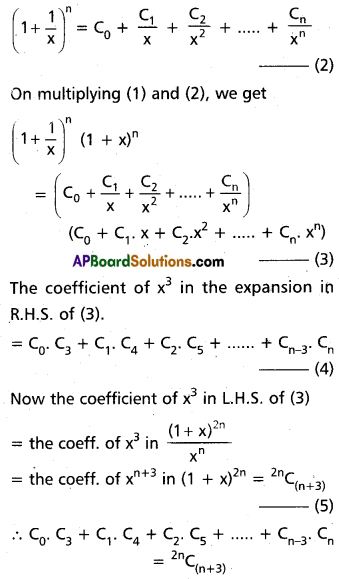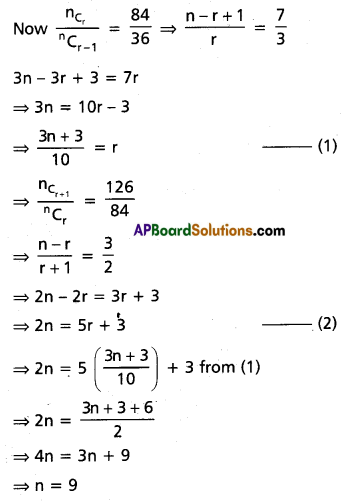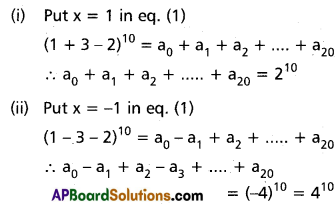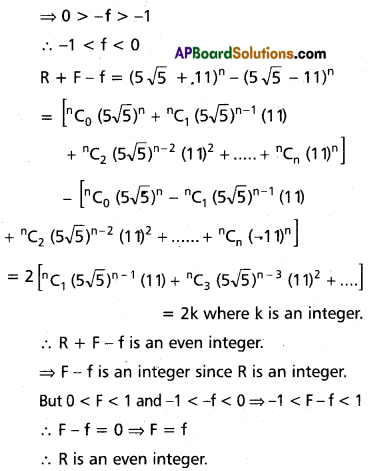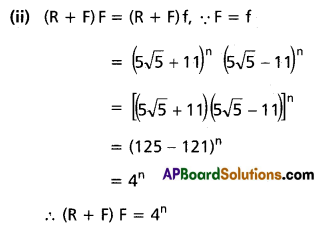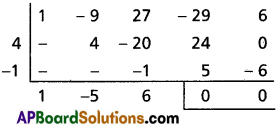Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(a)

I.

Question 1.
Expand the following using the binomial theorem.
(i) (4x + 5y)⁷
Solution:

(ii) \(\left(\frac{2}{3} x+\frac{7}{4} y\right)^5\)
Solution:

(iii) \(\left(\frac{2 p}{5}-\frac{3 q}{7}\right)^6\)
Solution:

\(\sum_{r=0}^6(-1)^{r \cdot 6} C_r\left(\frac{2 p}{5}\right)^{6-r}\left(\frac{3 q}{7}\right)^r\)

(iv) (3 + x – x²)⁴
Solution:

Question 2.
Write down and simplify
(i) 6th term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\)
Solution:
6th term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\)
The general term in \(\left(\frac{2 x}{3}+\frac{3 y}{2}\right)^9\) is

(ii) 7th term in (3x – 4y)¹⁰
Solution:
7th term in (3x – 4y)¹⁰
The general term in (3x – 4y)¹⁰ is

(iii) 10th term in \(\left(\frac{3 p}{4}-5 q\right)^{14}\)
Solution:
10th term in \(\left(\frac{3 p}{4}-5 q\right)^{14}\)
General term in \(\left(\frac{3 p}{4}-5 q\right)^{14}\) is

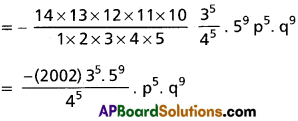
(iv) r^th term in \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) (1 ≤ r ≤ 9)
Solution:
r^th term in \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\)
The general term in \(\left(\frac{3 a}{5}+\frac{5 b}{7}\right)^8\) is

Question 3.
Find the number of terms in the expansion of
(i) \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\)
Solution:
The number of terms in (x + a)ⁿ is (n + 1), where n is a positive integer.
Hence number of terms in \(\left(\frac{3 a}{4}+\frac{b}{2}\right)^9\) are 9 + 1 = 10

(ii) (3p + 4q)¹⁴
Solution:
Number of terms in (3p + 4q)¹⁴ are 14 + 1 = 15

(iii) (2x + 3y + z)⁷
Solution:
Number of terms in (a + b + c)ⁿ are \(\frac{(n+1)(n+2)}{2}\), where n is a positive integer.
Hence number of terms in (2x + 3y + z)⁷ are = \(\frac{(7+1)(7+2)}{2}=\frac{8 \times 9}{2}\) = 36

Question 4.
Find the number of terms with non-zero coefficients in (4x – 7y)⁴⁹ + (4x + 7y)⁴⁹.
Solution:

∴ The number of terms with non-zero coefficient in (4x – 7y)⁴⁹ + (4x + 7y)⁴⁹ is 25.

Question 5.
Find the sum of the last 20 coefficients in the expansions of (1 + x)³⁹.
Solution:

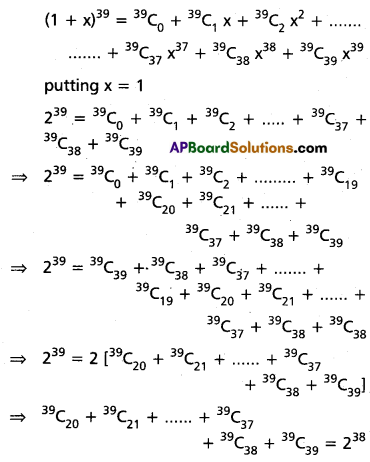
∴ The sum of the last 20 coefficients in the expansion of (1 + x)³⁹ is 238.

Question 6.
If A and B are coefficients of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^2n-1 respectively, then find the value of \(\frac{A}{B}\)
Solution:
Given A and B are the coefficient of xⁿ in the expansion of (1 + x)²ⁿ and (1 + x)^2n-1 respectively.

II.

Question 1.
Find the coefficient of
(i) x^-6 in \(\left(3 x-\frac{4}{x}\right)^{10}\)
Solution:

(ii) x¹¹ in \(\left(2 x^2+\frac{3}{x^3}\right)^{13}\)
Solution:

(iii) x² in \(\left(7 x^3-\frac{2}{x^2}\right)^9\)
Solution:

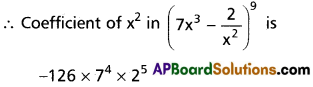
(iv) x^-7 in \(\left(\frac{2 x^2}{3}-\frac{5}{4 x^5}\right)^7\)
Solution:

Question 2.
Find the term independent of x in the expansion of
(i) \(\left(\frac{\sqrt{x}}{3}-\frac{4}{x^2}\right)^{10}\)
Solution:

(ii) \(\left(\frac{3}{\sqrt[3]{x}}+5 \sqrt{x}\right)^{25}\)
Solution:

(iii) \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\)
Solution:
The general term in \(\left(4 x^3+\frac{7}{x^2}\right)^{14}\) is

For term independent of x,
put 42 – 5r = 0
⇒ r = \(\frac{42}{5}\) which is not an integer.
Hence term independent of x in the given expansion is zero.

(iv) \(\left(\frac{2 x^2}{5}+\frac{15}{4 x}\right)^9\)
Solution:

Question 3.
Find the middle term(s) in the expansion of
(i) \(\left(\frac{3 x}{7}-2 y\right)^{10}\)
Solution:
The middle term in (x + a)ⁿ when n is even and is \(\frac{T_{n+1}}{2}\), when n is odd, we have two middle terms, i.e., \(\frac{T_{n+1}}{2}\) and \(\frac{T_{n+3}}{2}\)
∵ n = 10 is even,
we have only one middle term (i.e.,) \(\frac{10}{2}\) + 1 = 6th term.

(ii) \(\left(4 a+\frac{3}{2} b\right)^{11}\)
Solution:
Here n = 11 is an odd integer,
we have two middle terms, i.e., \(\frac{n+1}{2}\) and \(\frac{n+3}{2}\) terms
= 6th and 7th terms are middle terms.
T₆ in \(\left(4 a+\frac{3}{2} b\right)^{11}\) is \({ }^{11} C_5(4 a)^6\left(\frac{3}{2} b\right)^5\)

(iii) (4x² + 5x³)¹⁷
Solution:
(4x² + 5x³)¹⁷ = [x²(4 + 5x)]¹⁷ = x³⁴(4 + 5x)¹⁷ ……..(1)
Consider (4 + 5x)¹⁷
∵ n = 17 is an odd positive integer, we have two middle terms.
They are \(\left(\frac{17+1}{2}\right)^{\text {th }}\) and \(\left(\frac{17+3}{2}\right)^{\text {th }}\) (i.e.,) 9th and 10th terms are middle terms.

(iv) \(\left(\frac{3}{a^3}+5 a^4\right)^{20}\)
Solution:
Here n = 20 is an even positive integer, we have only one middle term

Question 4.
Find the numerically greatest term(s) in the expansion of
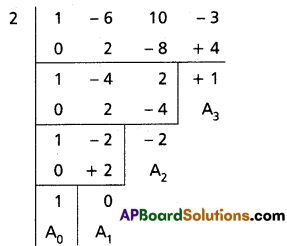
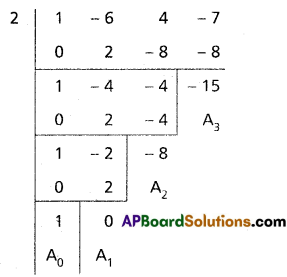
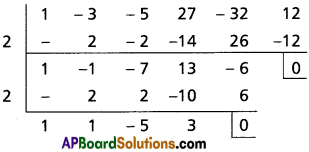
(i) (4 + 3x)¹⁵ when x = \(\frac{7}{2}\)
Solution:

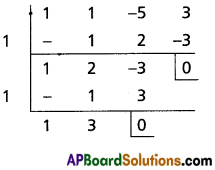
(ii) (3x + 5y)¹² when x = \(\frac{1}{2}\), y = \(\frac{4}{3}\)
Solution:

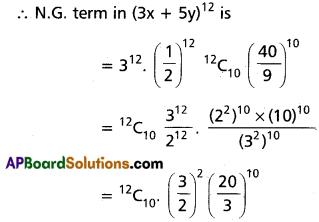
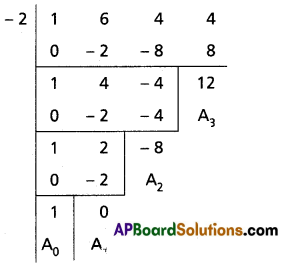
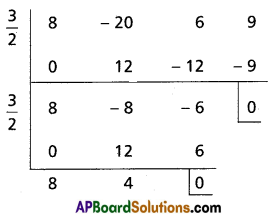
(iii) (4a – 6b)¹³ when a = 3, b = 5
Solution:

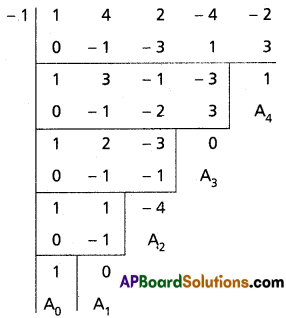
(iv) (3 + 7x)ⁿ when x = \(\frac{4}{5}\), n = 15
Solution:

Question 5.
Prove the following.
(i) 2 . C₀ + 5 . C₁ + 8 . C₂ + ……… + (3n+2) . C_n = (3n + 4) . 2^n-1
Solution:

(ii) C₀ – 4 . C₁ + 7 . C₂ – 10 . C₃ + ……… = 0, if n is an even positive integer.
Solution:

(iii) \(\frac{C_1}{2}+\frac{C_3}{4}+\frac{C_5}{6}+\frac{C_7}{8}+\ldots \ldots=\frac{2^n-1}{n+1}\)
Solution:

(iv) \(C_0+\frac{3}{2} \cdot C_1+\frac{9}{3} \cdot C_2+\frac{27}{4} \cdot C_3\) + ……… + \(\frac{3^n}{n+1} \cdot C_n=\frac{4^{n+1}-1}{3(n+1)}\)
Solution:

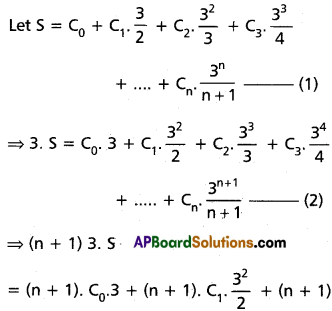
(v) C₀ + 2 . C₁ + 4 . C₂ + 8 . C₃ + ….. + 2ⁿ . C_n = 3ⁿ
Solution:

Question 6.
Find the sum of the following.
(i) \(\frac{{ }^{15} C_1}{{ }^{15} C_0}+2 \frac{{ }^{15} C_2}{{ }^{15} C_1}+3 \frac{{ }^{15} C_3}{{ }^{15} C_2}\) + …….. + \(15 \frac{{ }^{15} C_{15}}{{ }^{15} C_{14}}\)
Solution:

(ii) C₀ . C₃ + C₁ . C₄ + C₂ . C₅ + …….. + C_n-3 . C_n
Solution:
We know that
(1 + x)ⁿ = C₀ + C₁ x + C₂ x² + ……. + C_n . xⁿ ……….(1)
On replacing x by \(\frac{1}{x}\), we get

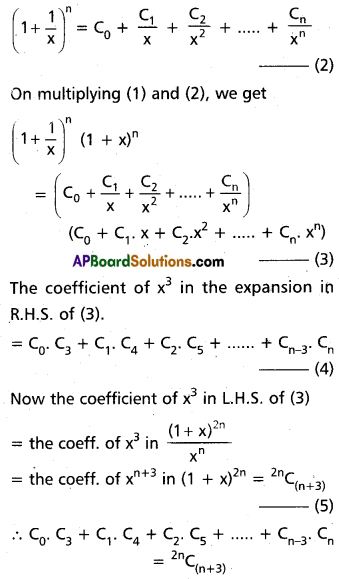
(iii) 2² . C₀ + 3² . C₁ + 4² . C₂ + ……… + (n + 2)² C_n
Solution:

(iv) 3C₀ + 6C₁ + 12C₂ + ……… + 3 . 2ⁿ . C_n
Solution:

Question 7.
Using the binomial theorem, prove that 50ⁿ – 49n – 1 is divisible by 492 for all positive integers n.
Solution:

= 49² [a positive integer]
Hence 50ⁿ – 49n – 1 is divisible by 49² for all positive integers of n.

Question 8.
Using the binomial theorem, prove that 5⁴ⁿ + 52n – 1 is divisible by 676 for all positive integers n.
Solution:

∴ 5⁴ⁿ + 52n – 1 is divisible by 676, for all positive integers n.

Question 9.
If (1 + x + x²)ⁿ = a₀ + a₁ x + a₂ x² + ……… + a_2n x²ⁿ, then prove that
(i) a₀ + a₁ + a₂ + ……… + a_2n = 3ⁿ
(ii) a₀ + a₂ + a₄ + …… + a_2n = \(\frac{3^n+1}{2}\)
(iii) a₁ + a₃ + a₅ + ……… + a_2n-1 = \(\frac{3^n-1}{2}\)
(iv) a₀ + a₃ + a₆ + a₉ + ……….. = 3^n-1
Solution:

Question 10.
If (1 + x + x² + x³)⁷ = b₀ + b₁x + b₂x² + ………. b₂₁ x²¹, then find the value of
(i) b₀ + b₂ + b₄ + …….. + b₂₀
(ii) b₁ + b₃ + b₅ + ………. + b₂₁
Solution:

Question 11.
If the coefficient of x¹¹ and x¹² in the binomial expansion of \(\left(2+\frac{8 x}{3}\right)^n\) are equal, find n.
Solution:
The general term of \(\left(2+\frac{8 x}{3}\right)^n\) is \(T_{r+1}={ }^n C_r(2)^{n-r}\left(\frac{8 x}{3}\right)^r\)

Question 12.
Find the remainder when 22013 is divided by 17.
Solution:
We know 2⁴ = 16
The remainder when 24 is divided by 17 is 1
22013 = (24)⁵⁰³ . 2¹
∴ The remainder when 22013 is divided by 17 is (-1)⁵⁰³ . 2 = (-1) . 2 = -2

Question 13.
If the coefficients of (2r + 4)^th term and (3r + 4)^th term in the expansion of (1 + x)²¹ are equal, find r.
Solution:

III.

Question 1.
If the coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in A.P., then prove that n² – 41n + 398 = 0.
Solution:
The coefficients of x⁹, x¹⁰, x¹¹ in (1 + x)ⁿ are

⇒ (n – 9) (n – 21) = 11(n – 19)
⇒ n² – 9n – 21n + 189 = 11n – 209
⇒ n² – 41n + 398 = 0

Question 2.
If 36, 84, 126 are three successive binomial coefficients in the expansion of (1 + x)ⁿ, find n.
Solution:
Let ⁿC_r-1, ⁿC_r, ⁿC_r+1 are three successive binomial coefficients in (1 + x)ⁿ.
Then ⁿC_r-1 = 36; ⁿC_r = 84 and ⁿC_r+1 = 126

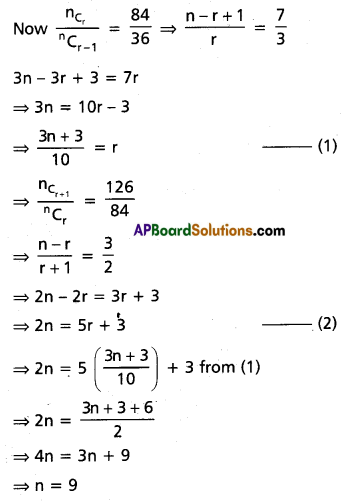
Question 3.
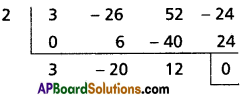
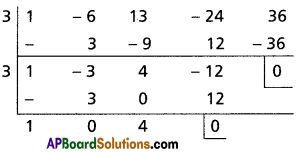
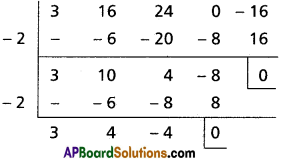
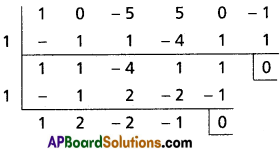
If the 2nd, 3rd and 4th terms in the expansion of (a + x)ⁿ are respectively 240, 720, 1080, find a, x, n.
Solution:

Question 4.
If the coefficients of rth, (r + 1)th and (r + 2)nd terms in the expansion of (1 + x)ⁿ are in A.P. then show that n² – (4r + 1)n + 4r² – 2 = 0.
Solution:
Coefficient of Tr = ⁿC_r-1

Question 5.
Find the sum of the coefficients of x³² and x^-18 in the expansion of \(\left(2 x^3-\frac{3}{x^2}\right)^{14}\)
Solution:

Question 6.
If P and Q are the sums of odd terms and the sum of even terms respectively in the expansion of (x + a)ⁿ then prove that
(i) P² – Q² = (x² – a²)ⁿ
(ii) 4PQ = (x + a)²ⁿ – (x – a)²ⁿ
Solution:

Question 7.
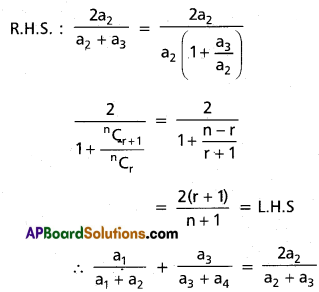
If the coefficients of 4 consecutive terms in the expansion of (1 + x)ⁿ are a₁, a₂, a₃, a₄ respectively, then show that \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\)
Solution:
Given a₁, a₂, a₃, a₄ are the coefficients of 4 consecutive terms in (1 + x)ⁿ respectively.
Let a₁ = ⁿC_r-1, a₂ = ⁿC_r, a₃ = ⁿC_r+1, a₄ = ⁿC_r+2

Question 8.
Prove that (²ⁿC₀)² – (²ⁿC₁)² + (²ⁿC₂)² – (²ⁿC₃)² + ……… + (²ⁿC_2n)² = (-1)^{n 2n}C_n
Solution:

Question 9.
Prove that (C₀ + C₁)(C₁ + C₂)(C₂ + C₃) ………… (C_n-1 + C_n) = \(\frac{(n+1)^n}{n !}\) . C₀ . C₁ . C₂ ……… C_n
Solution:

Question 10.
Find the term independent of x in \((1+3 x)^n\left(1+\frac{1}{3 x}\right)^n\)
Solution:

Question 11.
Show that the middle term in the expansion of (1 + x)²ⁿ is \(\frac{1.3 .5 \ldots(2 n-1)}{n !}(2 x)^n\)
Solution:
The expansion of (1 + x)²ⁿ contains (2n + 1) terms.
middle term = ²ⁿC_n xⁿ

Question 12.
If (1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² + …….. + a₂₀ x²⁰ then prove that
(i) a₀ + a₁ + a₂ + ……… + a₂₀ = 2¹⁰
(ii) a₀ – a₁ + a₂ – a₃ + ……….. + a₂₀ = 4¹⁰
Solution:
(1 + 3x – 2x²)¹⁰ = a₀ + a₁x + a₂x² + ……… + a₂₀ x²⁰

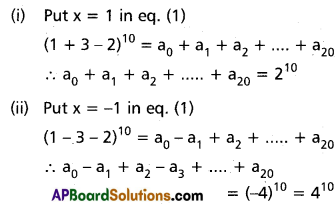
Question 13.
If (3√3 + 5)²ⁿ⁺¹ = x and f = x – [x] where ([x] is the integral part of x), find the value of x.f.
Solution:

Question 14.
If R, n are positive integers, n is odd, 0 < F < 1 and if (5√5 + 11)ⁿ = R + F, then prove that
(i) R is an even integer and
(ii) (R + F) . F = 4ⁿ
Solution:
(i) Since R, n are positive integers, 0 < F < 1 and (5√5 + 11)ⁿ = R + F
Let (5√5 – 11)ⁿ = f
Now, 11 < 5√5 < 12
⇒ 0 < 5√5 – 11 < 1
⇒ 0 < (5√5 – 11)ⁿ < 1
⇒ 0 < f < 1

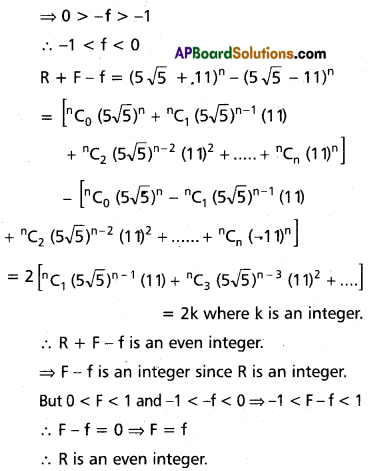
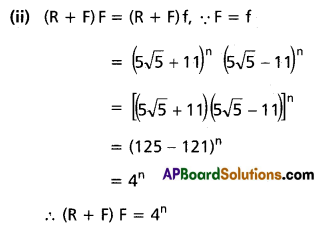
Question 15.
If I, n are positive integers, 0 < f < 1 and if (7 + 4√3 )ⁿ = I + f, then show that
(i) I is an odd integer and
(ii) (I + f) (1 – f) = 1
Solution:
Given I, n are positive integers and
(7 + 4√3)ⁿ = I + f, 0 < f < 1
Let 7 – 4√3 = F
Now 6 < 4√3 < 7
⇒ -6 > -4√3 > -7
⇒ 1 > 7 – 4√3 > 0
⇒ 0 < (7 – 4√3)ⁿ < 1
∴ 0 < F < 1
I + f + F = (7 + 4√3)ⁿ + (7 – 4√3)ⁿ

= 2k where k is an integer.
∴ I + f + F is an even integer.
⇒ f + F is an integer since I is an integer.
But 0 < f < 1 and 0 < F < 1
⇒ 0 < f + F < 2
∴ f + F = 1 ………..(1)
⇒ I + 1 is an even integer.
∴ I is an odd integer.
(I + f) (I – f) = (I + f) F …..[By (1)]
= (7 + 4√3)ⁿ (7 – 4√3)ⁿ
= [(7 + 4√3) (7 – 4√3)]ⁿ
= (49 – 48)ⁿ
= 1

Question 16.
If n is a positive integer, prove that \(\sum_{r=1}^n r^3\left(\frac{{ }^n C_r}{{ }^n C_{r-1}}\right)^2=\frac{(n)(n+1)^2(n+2)}{12}\)
Solution:

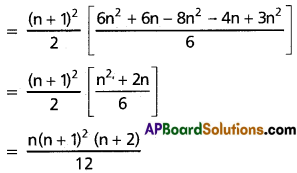
Question 17.
Find the number of irrational terms in the expansion of (5^1/6 + 2^1/8)¹⁰⁰.
Solution:
General term
T_r+1 = \({ }^{100} C_r\left(5^{1 / 6}\right)^{100-r}\left(2^{1 / 8}\right)^r\) = \({ }^{100} C_r 5^{\frac{100-r}{6}} \cdot 2^{\frac{r}{8}}\)
\(\frac{100-r}{6}\) is an integer in the span
or 0 ≤ r ≤ 100 if r = 4, 10, 16, 22, 28, 34, 40, 46, 52, 58, 64, 70, 76, 82, 88, 94, 100
\(\frac{r}{8}\) is an integer in the span of 0 ≤ r ≤ 100
if r = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, \(\frac{100-r}{6}\), \(\frac{r}{8}\) both an integers
If r = 16, 40, 64, 88
∴ The number of rational terms in the expansion of (5^1/6 + 2^1/8)^r is 4.
∴ The number of irrational terms in the expansion of (5^1/6 + 2^1/8)^r is 101 – 4 = 97 terms.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(c)

I.

Question 1.
Find the number of ways of arranging 7 persons around a circle.
Solution:
Number of persons, n = 7
∴ The number of ways of arranging 7 persons around a circle = (n – 1)!
= 6!
= 720
Hint: The no. of circular permutations of n dissimilar things taken all at a time is (n – 1)!

Question 2.
Find the number of ways of arranging the chief minister and 10 cabinet ministers at a circular table so that the chief minister always sits in a particular seat.
Solution:
Total number of persons = 11
The chief minister can be occupied a separate seat in one way and the remaining 10 seats can be occupied by the 10 cabinet ministers in (10)! ways.
∴ The number of required arrangements = (10)! × 1
= (10)!
= 36,28,800

Question 3.
Find the number of ways to prepare a chain with 6 different coloured beads.
Solution:
Hint: The number of circular permutations like the garlands of flowers, chains of beads, etc., of n things = \(\frac{1}{2}\)(n – 1)!
The number of ways of preparing a chain with 6 different coloured beads = \(\frac{1}{2}\)(6 – 1)!
= \(\frac{1}{2}\) × 5!
= \(\frac{1}{2}\) × 120
= 60

II.

Question 1.
Find the number of ways of arranging 4 boys and 3 girls around a circle so that all the girls sit together.
Solution:
Treat all the 3 girls as one unit. Then we have 4 boys and 1 unit of girls. They can be arranged around a circle in 4! ways. Now, the 3 girls can be arranged among themselves in 3! ways.
∴ The number of required arrangements = 4! × 3!
= 24 × 6
= 144

Question 2.
Find the number of ways of arranging 7 gents and 4 ladies around a circular table if no two ladies wish to sit together.
Solution:
First, arrange the 7 gents around a circular table in 6! ways.
Then we can find 7 gaps between them. The 4 ladies can be arranged in these 7 gaps in ⁷P₄ ways.

∴ The number of required arrangements = 6! × ⁷P₄
= 720 × 7 × 6 × 5 × 4
= 6,04,800

Question 3.
Find the number of ways of arranging 7 guests and a host around a circle if 2 particular guests wish to sit on either side of the host.
Solution:
Number of guests = 7
Treat the two particular guests along with the host as one unit. Then we have 5 guests and one unit of 2 particular guests along with the host.
They can be arranged around a circle in 5! ways.
The two particular guests can be arranged on either side of the host in 2! ways.
∴ The number of required arrangements = 5! × 2!
= 120 × 2
= 240

Question 4.
Find the number of ways of preparing a garland with 3 yellow, 4 white, and 2 red roses of different sizes such that the two red roses come together.
Solution:
Treat that 2nd rose of different sizes as one unit. Then we have 3 yellow, 4 white, and one unit of red roses.
Then they can be arranged in garland form in \(\frac{1}{2}\) (8 – 1)! = \(\frac{1}{2}\) (7!) ways.
Now 2 red roses in one unit can be arranged among themselves in 2! ways.
∴ The number of ways of preparing a garland = \(\frac{1}{2}\) (7!) × (2!)
= \(\frac{1}{2}\) × 5040 × 2
= 5040

III.

Question 1.
Find the number of ways of arranging 6 boys and 6 girls around a circular table so that
(i) all the girls sit together
(ii) no two girls sit together
(iii) boys and girls sit alternately
Solution:
(i) Treat all 5 girls as one unit. Then we have 6 boys and 1 unit of girls. They can be arranged around a circular table in 6! ways.
Now, the 6 girls can be arranged among themselves in 6! ways.
∴ The number of required arrangements = 6! × 6!
= 720 × 720
= 5,18,400

(ii) First arrange the 6 boys around a circular table in 5! ways. Then we can find 6 gaps between them.
The 6 girls can be arranged in these 6 gaps in 6! ways.

∴ The number of required arrangements = 5! × 6!
= 120 × 720
= 86,400

(iii) Here the number of girls and number of boys are the same.

Hence the arrangements of boys and girls sit alternatively in the same as the arrangements of no two girls sitting together or arrangements of no two boys sitting together.
First, arrange the 6 girls around a circular table in 5! ways. Then we can find 6 gaps between them.
The 6 boys can be arranged in these 6 gaps in 6! ways.
∴ The number of required arrangements = 5! × 6!
= 120 × 720
= 86,400

Question 2.
Find the number of ways of arranging 6 red roses and 3 yellow roses of different sizes into a garland. In how many of them
(i) all the yellow roses are together
(ii) no two yellow roses are together
Solution:
Hint: The number of circular permutations like the garlands of flowers, chains of beads, etc., of n things = \(\frac{1}{2}\)(n – 1)!
Total number of roses = 6 + 3 = 9
∴ The number of ways of arranging 6 red roses and 3 yellow roses of different sizes into a garland = \(\frac{1}{2}\)(9 – 1)!
= \(\frac{1}{2}\) × 8!
= \(\frac{1}{2}\) × 40,320
= 20,160
(i) Treat all the 3 yellow roses as one unit. Then we have 6 red roses and one unit of yellow roses. They can be arranged in garland form in (7 – 1)! = 6! ways.
Now, the 3 yellow roses can be arranged among themselves in 3! ways.
But in the case of garlands, clockwise arrangements look alike.
∴ The number of required arrangements = \(\frac{1}{2}\) × 6! × 3!
= \(\frac{1}{2}\) × 720 × 6
= 2160

(ii) First arrange the 6 red roses in garland form in 5! ways. Then we can find 6 gaps between them.
The 3 yellow roses can be arranged in these 6 gaps in ⁶P₃ ways.
But in the case of garlands, clockwise and anti-clockwise arrangements look alike.
∴ The number of required arrangements = \(\frac{1}{2}\) × 5! × ⁶P₃
= \(\frac{1}{2}\) × 120 × 6 × 5 × 4
= 7200

Question 3.
A round table conference is attended by 3 Indians, 3 Chinese, 3 Canadians, and 2 Americans. Find a number of ways of arranging them at the round table so that the delegates belonging to the same country sit together.
Solution:
Since the delegates belonging to the same country sit together, first arrange the 4 countries in a round table in 3! ways.
Now, 3 Indians can be arranged among themselves in 3! ways,
3 Chinese can be arranged among themselves in 3! ways,
3 Canadians can be arranged among themselves in 3! ways,
and 2 Americans can be arranged among themselves in 2! ways.
∴ The number of required arrangements = 3! × 3! × 3! × 3! × 2!
= 6 × 6 × 6 × 6 × 2
= 2592

Question 4.
A chain of beads is to be prepared using 6 different red coloured beads and 3 different blue coloured beads. In how many ways can this be done so that no two blue-coloured beads come together?
Solution:
First, arrange the 6 red-coloured beads in the form of a chain of beads in (6 – 1)! = 5! ways.
Then there are 6 gaps between them. The 3 blue coloured beads can be arranged in these 6 gaps in ⁶P₃ ways.
Then the total number of circular permutations = 5! × ⁶P₃
But in the case of a chain of beads, clockwise and anti-clockwise arrangements look alike.
∴ The number of required arrangements = \(\frac{1}{2}\) × 5! × ⁶P₃
= \(\frac{1}{2}\) × 120 × 6 × 5 × 4
= 7200

Question 5.
A family consists of a father, a mother, 2 daughters, and 2 sons. In how many different ways can they sit at a round table if the 2 daughters wish to sit on either side of the father?
Solution:
Total number of persons in a family = 6
Treat the 2 daughters along with a father as one unit. Then we have a mother, 2 sons, and one unit of daughters along with the father in a family.
They can be seated around a table in (4 – 1)! = 3! ways.
The 2 daughters can be arranged on either side of the father in 2! ways.
∴ The number of required arrangements = 3! × 2!
= 6 × 2
= 12

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(b)

I.

Question 1.
Find the number of 4-digited numbers that can be formed using the digits 1, 2, 4, 5, 7, 8 when repetition is allowed.
Solution:
The number of 4 digited numbers that can be formed using the digits 1, 2, 4, 5, 7, 8 when repetition is allowed = 6⁴ = 1296

Question 2.
Find the number of 5-letter words that can be formed using the letters of the word RHYME if each letter can be used any number of times.
Solution:
The number of 5 letter words that can be formed using the letters of the word RHYME if each letter can be used any number of times = 5⁵ = 3125

Question 3.
Find the number of functions from a set A containing 5 elements into a set B containing 4 elements.
Solution:
Set A contains 5 elements.
Set 8 contains 4 elements.
Hint: The total number of functions from set A containing m elements to set B containing n elements is n^m.
For the image of each of the 5 elements of the set, A has 4 choices.
∴ The number of functions from set A containing 5 elements into a set B containing 4 elements = 4 × 4 × 4 × 4 × 4 (5 times)
= 4⁵
= 1024

II.

Question 1.
Find the number of palindromes with 6 digits that can be formed using the digits
(i) 0, 2, 4, 6, 8
(iii) 1, 3, 5, 7, 9
Solution:
Palindromes mean first digit, sixth digit and second digit, fifth digit and third digit, and the fourth digit are the same numbers.
That is we have filled the first three digits only and then the remaining digits are the same.

(i) Given numbers are 0, 2, 4, 6, 8
For the required 6-digit palindromes first digit can be filled 4 ways except ‘0’.
The second digit can be filled in 5 ways and the third can be filled in 5 ways.
∴ The number of 6-digit palindromes using the digits 0, 2, 4, 6, 8 are 4 × 5² = 100

(ii) Given numbers are 1, 3, 5, 7, 9
For the required 6-digit palindromes first digit can be filled in 5 ways, the second digit can be filled in 5 ways and the third digit can be filled in 5 ways.
∴ The number of 6-digit palindromes using the digits 1, 3, 5, 7, 9 are 5³ = 125

Question 2.
Find the number of 4-digit telephone numbers that can be formed using the digits 1, 2, 3, 4, 5, 6 with atleast one digit repeated.
Solution:
The number of 4 digited numbers formed using the digits 1, 2, 3, 4, 5, 6 when repetition is allowed = 6⁴
The number of 4 digited numbers formed using the digits 1, 2, 3, 4, 5, 6 when repetition is not allowed = ⁶P₄
The number of 4 digited telephone numbers in which atleast one digit is repeated = 6⁴ – ⁶P₄
= 6⁴ – 6 × 5 × 4 × 3
= 1296 – 360
= 936

Question 3.
Find the number of bijections from a set A containing 7 elements onto itself.
Solution:
Hint: The number of bijections from set A with n elements to set B with the same number of elements in A is n!
Let A = [a₁, a₂, a₃, a₄, a₅, a₆, a₇]
For a bijection, the element a₁ has 7 choices
for its image, the element a₂ has 6 choices
for its image, the element a₃ has 5 choices
for its image, the element a₄ has 4 choices
for its image, the element a₅ has 3 choices
for its image, the element a₆ has 2 choices
for its image and the element, a₇ has 1 choice for its image.
∴ The number of bijections from set A with 7 elements onto itself = 7!
= 7 × 6 × 5 × 4 × 3 × 2 × 1
= 5040

Question 4.
Find the number of ways of arranging ‘r’ things in a line using the given ‘n’ different things in which atleast one thing is repeated.
Solution:
The number of ways of arranging, r things in a line using the given n different things
(i) when repetition is allowed is n^r
(ii) when repetition is not allowed is ⁿP_r
∴ The number of ways of arranging ‘r’ things in a line using the ‘n1 different things in which atleast one thing is repeated = n^r – ⁿP_r

Question 5.
Find the number of 5-letter words that can be formed using the letters of the word NATURE that begin with N when repetition is allowed.
Solution:
First, we can fill up the first place with N in one way.

The remaining 4 places can be filled with any one of the 6 letters in 6 × 6 × 6 × 6 = 6⁴ ways.
∴ The number of 5 letter words that can be formed using the letters of the word NATURE that begin with N when repetition is allowed = 1 × 6⁴ = 1296

Question 6.
Find the number of 5-digit numbers divisible by 5 that can be formed using the digits 0, 1, 2, 3, 4, 5 when repetition is allowed.
Solution:
The unit place of 5 digited numbers which can be divisible by 5 using the given digits can be filled by either 0 or 5 in two ways.
The first place can be filled in any one of the given digits except ‘0’ in 5 ways.
The remaining 3 places can be filled by any one of the given digits in 6 × 6 × 6 ways (∵ repetition is allowed)

∴ The number of 5 digited numbers divisible by 5 that can be formed using the given digits when repetition is allowed = 2 × 5 × 6 × 6 × 6 = 2160 ways.

Question 7.
Find the number of numbers less than 2000 that can be formed using the digits, 1, 2, 3, 4 if repetition is allowed.
Solution:
All the single digited numbers, two digited numbers, three digited numbers and the four digited numbers started with 1 are the numbers less than 2000 using the digits 1, 2, 3, 4.
The number of single digited numbers formed using the given digits = 4

The number of two digited numbers formed using the given digits when repetition is allowed = 4 × 4 = 16

The number of three digited numbers formed using the given digits = 4 × 4 × 4 = 64

The number of 4 digited numbers started with 1 formed using the given digits = 4 × 4 × 4 = 64

∴ The total number of numbers less than 2000 that can be formed using the digits 1, 2, 3, 4 if repetition is allowed = 4 + 16 + 64 + 64 = 148

III.

Question 1.
9 different letters of an alphabet are given. Find the number of 4 letter words that can be formed using these 9 letters which have
(i) no letter is repeated
(ii) At atleast one letter is repeated
Solution:
The number of 4 letter words can be formed using the 9 different letters of an alphabet when repetition is allowed = 9⁴
(i) The number of 4 letter words can be formed using the 9 different letters of an alphabet in which no letter is repeated = ⁹P₄
= 9 × 8 × 7 × 6
= 3024
(ii) The number of 4 letter words can be formed using the 9 different letters of an alphabet in which atleast one letter is repeated = 9⁴ – ⁹P₄
= 6561 – 3024
= 3537

Question 2.
Find the number of 4-digit numbers which can be formed using the digits 0, 2, 5, 7, 8 that are divisible by (i) 2 (ii) 4 when repetition is allowed.
Solution:
(i) First place can be filled by either 2 or 5 or 7 or 8 in 4 ways.

Second place can be filled by any one of the given digits in 5 ways.
Third place can be filled by any one of the given digits in 5 ways.
Last place (or units place) can be filled by either 0 or 2 or 8 in 3 ways.
∴ The number of 4 digited divisible by 2 numbers that can be formed using the digits 0, 2, 5, 7, 8 when repetition is allowed = 4 × 5 × 5 × 3 = 300
(ii) Since a number is divisible by 4, the last two places should be filled with one of the 00, 08, 20, 28, 52, 72, 80, 88 in 8 ways.
The first place can be filled 4 ways except 0. Second place can be filled in 5 ways.

Question 3.
Find the number of 4-digit numbers that can be formed using the digits 0, 1, 2, 3, 4, 5 which are divisible by 6 when repetition of the digits is allowed.
Solution:
Since a number is divisible by 4, the last two places should be filled with one of the 00, 04, 12, 20, 24, 32, 40, 44 = 8 ways

The first place can be filled in any one of the given digits except ‘0’ in 4 ways. The remaining 2 places can be filled by anyone the given digits in 5 × 5 ways.
∴ The number of 5 digited numbers that can be formed using the digits 0, 1, 2, 3, 4 that are divisible by 4 when repetition is allowed = 4 × 5² × 8 = 800

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(d)

I.

Question 1.
Find the algebraic equation whose roots are 3 times the roots of x³ + 2x² – 4x + 1 = 0
Solution:
Given equation is f(x) = x³ + 2x² – 4x + 1 = 0
We require an equation whose roots are 3 times the roots of f(x) = 0
i,e., Required equation is f(\(\frac{x}{3}\)) = 0
⇒ \(\left(\frac{x}{3}\right)^{3}+2\left(\frac{x}{3}\right)^{2}-\frac{4 x}{3}+1=0\)
⇒ \(\frac{x^{3}}{27}+\frac{2}{9} x^{2}-\frac{4}{3} x+1=0\)
Multiplying with 27, required equation is x³ + 6x² – 36x + 27 = 0

Question 2.
Find the algebraic equation whose roots are 2 times the roots of x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0
Solution:
Given equation is f(x) = x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0
We require an equation whose roots are 2 times the roots of f(x) = 0
Required equation is f(\(\frac{x}{2}\)) = 0
⇒ \(\left(\frac{x}{2}\right)^{5}-2\left(\frac{x}{2}\right)^{4}+3\left(\frac{x}{2}\right)^{3}-2\left(\frac{x}{2}\right)^{2}+4\left(\frac{x}{2}\right)\) + 3 = 0
⇒ \(\frac{x^{5}}{32}-2 \cdot \frac{x^{4}}{16}+3 \cdot \frac{x^{3}}{8}-2 \cdot \frac{x^{2}}{4}+4 \cdot \frac{x}{2}+3=0\)
Multiplying with 32, the required equation is
⇒ x⁵ – 4x⁴ + 12x³ – 16x² + 64x + 96 = 0

Question 3.
Find the transformed equation whose roots are the negative of the roots of x⁴ + 5x³ + 11x + 3 = 0
Solution:
Given f(x) = x⁴ + 5x³ + 11x + 3 = 0
We want an equation whose roots are -α₁, -α₂, -α₃, -α₄
Required equation f(-x) = 0
⇒ (-x)⁴ + 5(-x)³ + 11(-x) + 3 = 0
⇒ x⁴ – 5x³ – 11x + 3 = 0

Question 4.
Find the transformed equation whose roots are the negatives of the roots of x⁷ + 3x⁵ + x³ – x² + 7x + 2 = 0
Solution:
Given f(x) = x⁷ + 3x⁵ + x³ – x² + 7x + 2 = 0
We want an equation whose roots are -α₁, -α₂, ………., -α_n
Required equation is f(-x) = 0
⇒ (-x)⁷ + 3(-x)⁵ + (-x)³ – (-x)² + 7(-x) + 2 = 0
⇒ -x⁷ – 3x⁵ – x³ – x² – 7x + 2 = 0
⇒ x⁷ + 3x⁵ + x³ + x² + 7x – 2 = 0

Question 5.
Find the polynomial equation whose roots are the reciprocals of the roots of x⁴ – 3x³ + 7x² + 5x – 2 = 0
Solution:
Given equation is f(x) = x⁴ – 3x³ + 7x² + 5x – 2 = 0
Required equation is f(\(\frac{1}{x}\)) = 0
i.e., \(\frac{1}{x^{4}}-\frac{3}{x^{3}}+\frac{7}{x^{2}}+\frac{5}{x}-2=0\)
Multiplying with x⁴
⇒ 1 – 3x + 7x² + 5x³ – 2x⁴ = 0
⇒ 2x⁴ – 5x³ – 7x² + 3x – 1 = 0

Question 6.
Find the polynomial equation whose roots are the reciprocals of the roots of x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0
Solution:
Given equation is f(x) = x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0
Required equation is f(\(\frac{1}{x}\)) = 0
\(\frac{1}{x^5}+\frac{11}{x^4}+\frac{1}{x^3}+\frac{4}{x^2}-\frac{13}{x}+6=0\)
Multiplying by x⁵
⇒ 1 + 11x + x² + 4x³ – 13x⁴ + 6x⁵ = 0
⇒ 6x⁵ – 13x⁴ + 4x³ + x² + 11x + 1 = 0

II.

Question 1.
Find the polynomial equation whose roots are the squares of the roots of x⁴ + x³ + 2x² + x + 1 = 0
Solution:
Given equation is f(x) = x⁴ + x³ + 2x² + x + 1 = 0
Required equation f(√x) = 0
⇒ x² + x√x + 2x + √x + 1 = 0
⇒ √x(x + 1) = -(x² + 2x + 1)
Squaring both sides,
⇒ x(x + 1)² = (x² + 2x + 1)²
⇒ x(x² + 2x + 1) = x⁴ + 4x² + 1 + 4x³ + 4x + 2x²
⇒ x³ + 2x² + x = x⁴ + 4x³ + 6x² + 4x + 1
⇒ x⁴ + 3x³ + 4x² + 3x + 1 = 0

Question 2.
Form the polynomial equation whose roots are the squares of the roots of x³ + 3x² – 7x + 6 = 0
Solution:
Given equation is f(x) = x³ + 3x² – 7x + 6 = 0
Required equation is f(√x) = 0
⇒ x√x + 3x – 7√x + 6 = 0
⇒ √x(x – 7) = -(3x + 6)
Squaring on both sides,
⇒ x(x – 7)² = (3x + 6)²
⇒ x(x² – 14x + 49) = 9x² + 36 + 36x
⇒ x³ – 14x² + 49x – 9x² – 36x – 36 = 0
⇒ x³ – 23x² + 13x – 36 = 0

Question 3.
Form the polynomial equation whose roots are cubes of the roots of x³ + 3x² + 2 = 0
Solution:
Given equation is x³ + 3x² + 2 = 0
Put y = x³ so that x = y^1/3
∴ y + 3y^2/3 + 2 = 0
∴ 3y^2/3 = -(y + 2)
Cubing on both sides,
27y² = -(y + 2)³ = -(y³ + 6y² + 12y + 8)
∴ y³ + 6y² + 12y + 8 = 0
⇒ y³ + 33y² + 12y + 8 = 0
Required equation is x³ + 33x² + 12x + 8 = 0

III.

Question 1.
Find the polynomial equation whose roots are the translates of those of the equation x⁴ – 5x³ + 7x² – 17x + 11 = 0 by -2.
Solution:
Given equation is f(x) = x⁴ – 5x³ + 7x² – 17x + 11 = 0
The required equation is f(x + 2) = 0
(x + 2)⁴ – 5(x + 2)³ + 7(x + 2)² – 17(x + 2) + 11 = 0

Required equation is x⁴ + 3x³ + x² – 17x – 19 = 0

Question 2.
Find the polynomial equation whose roots are the translates of those of x⁵ – 4x⁴ + 3x² – 4x + 6 = 0 by -3.
Solution:
Given equation is f(x) = x⁵ – 4x⁴ + 3x² – 4x + 6 = 0
Required equation is f(x + 3) = 0
(x + 3)⁵ – 4(x + 3)⁴ + 3(x + 3)²

Required equation is x⁵ + 11x⁴ + 42x³ + 57x² – 13x – 60 = 0

Question 3.
Find the polynomial equation whose roots are the translates of the roots of the equation x⁴ – x³ – 10x² + 4x + 24 = 0 by 2.
Solution:
Given f(x) = x⁴ – x³ – 10x² + 4x + 24 = 0
Required equation is f(x – 2) = 0
(x – 2)⁴ – (x – 2)³ – 10(x – 2)² + 4(x – 2) + 24 = 0

Required equation is x⁴ – 9x³ + 20x² = 0

Question 4.
Find the polynomial equation whose roots are the translates of the equation 3x⁵ – 5x³ + 7 = 0 by 4.
Solution:
Given f(x) = 3x⁵ – 5x³ + 7 = 0
Required equation is f(x – 4) = 0
3(x – 4)⁵ – 5(x – 4)³ + 7 = 0

Required equation is x⁵ – 60x⁴ + 475x³ – 1860x² + 3600x – 2745 = 0

Question 5.
Transform each of the following equations into ones in which of the coefficients of the second highest power of x is zero and also find their transformed equations.
(i) x³ – 6x² + 10x – 3 = 0
Solution:
Given equation is x³ – 6x² + 10x – 3 = 0
To remove the second term diminish the roots by \(-\frac{a_1}{n a_0}=\frac{6}{3}=2\)

Required equation is x³ – 2x + 1 = 0

(ii) x⁴ + 4x³ + 2x² – 4x – 2 = 0
Solution:
Given equation is x⁴ + 4x³ + 2x² – 4x – 2 = 0
Diminishing the roots by \(-\frac{a_1}{n a_0}=\frac{-4}{4}=-1\)

Required equation is x⁴ – 4x² + 1 = 0

(iii) x³ – 6x² + 4x – 7 = 0
Solution:
Given equation is x³ – 6x² + 4x – 7 = 0
Diminishing the roots by \(-\frac{a_1}{n a_0}=\frac{6}{3}=2\)

Required equation is x³ – 8x – 15 = 0

(iv) x³ + 6x² + 4x + 4 = 0
Solution:
Given equation is x³ + 6x² + 4x + 4 = 0
To remove the second term diminish the roots by \(\frac{-a_1}{n a_0}=-\frac{6}{3}=-2\)

Required equation is x³ – 8x + 12 = 0

Question 6.
Transform each of the following equations into ones in which the coefficients of the third highest power of x are zero.
Hint: To remove the r^th term in an equation f(x) = 0 of degree n diminish the roots by ‘h’ such that \(f^{(n-r+1)}(h)=0\)
(i) x⁴ + 2x³ – 12x² + 2x – 1 = 0
Solution:
Let f(x) = x⁴ + 2x³ – 12x² + 2x – 1
To remove the 3^rd term, diminish the roots by h such that f”(h) = 0
f'(x) = 4x³ + 6x² – 24x + 2
f”(x) = 12x² + 12x – 24
f”(h) = 0
⇒ 12h² + 12h – 24 = 0
⇒ h² + h – 2 = 0
⇒ (h + 2) (h – 1) = 0
⇒ h = -2 or 1
Case (i):

Transformed equation is x⁴ – 6x³ + 42x – 53 = 0
Case (ii):

Transformed equation is x⁴ – 6x³ – 12x – 8 = 0
∴ The required equation is x⁴ – 6x³ + 42x – 53 = 0
or x⁴ + 6x³ – 12x – 8 = 0

(ii) x³ + 2x² + x + 1 = 0
Solution:
Let f(x) = x³ + 2x² + x + 1
To remove the 3^rd term, diminish the roots by h such that f'(h) = 0, f'(x) = 3x² + 4x + 1
f'(h) = 0
⇒ 3h² + 4h + 1 = 0
⇒ (3h + 1) (h + 1)
⇒ h = -1, \(-\frac{1}{3}\)
Case (i):

Transformed equation is x³ – x² + 1 = 0
Case (ii):

Transformed equation is x³ + x² + \(\frac{23}{27}\) = 0
⇒ 27x³ + 27x² + 23 = 0
∴ The required equation is x³ – x² + 1 = 0 or 27x³ + 27x² + 23 = 0

Question 7.
Solve the following equations.
(i) x⁴ – 10x³ + 26x² – 10x + 1 = 0
Solution:
This is a standard reciprocal equation.
Dividing with x²
\(x^2-10 x+26-\frac{10}{x}+\frac{1}{x^2}=0\)
\(\left(x^2+\frac{1}{x^2}\right)-10\left(x+\frac{1}{x}\right)+26=0\) …….(1)
put a = x + \(\frac{1}{x}\)
\(x^2+\frac{1}{x^2}=\left(x+\frac{1}{x}\right)^2-2\) = a² – 2
Substituting in (1)
a² – 2 – 10a + 26 = 0
⇒ a² – 10a + 24 = 0
⇒ (a – 4)(a – 6) = 0
⇒ a = 4 or 6
Case (i): a = 4
x + \(\frac{1}{x}\) = 4
⇒ x² + 1 = 4x
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}=\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
Case (ii): a = 6
x + \(\frac{1}{x}\) = 6
⇒ x² + 1 = 6x
⇒ x² – 6x + 1 = 0
⇒ x = \(\frac{6 \pm \sqrt{36-4}}{2}\)
⇒ x = \(\frac{2(3 \pm 2 \sqrt{2)}}{2}\)
⇒ x = 3 ± 2√2
∴ The roots are 3 ± 2√2, 2 ± √3

(ii) 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
Solution:
Given f(x) = 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
This is an odd-degree reciprocal equation of the first type.
∴ -1 is a root.
Dividing f(x) with x + 1

Dividing f(x) by (x + 1), we get
2x⁴ – x³ – 11x² – x + 2 = 0
Dividing by x²
\(2 x^2-x-11-\frac{1}{x}+\frac{2}{x^2}=0\)
\(2\left(x^2+\frac{1}{x^2}\right)-\left(x+\frac{1}{x}\right)-11=0\) ……..(1)
Put a = x + \(\frac{1}{x}\) so that
\(x^2+\frac{1}{x^2}=a^2-2\)
Substituting in (1), the required equation is
⇒ 2(a² – 2) – a – 11 = 0
⇒ 2a² – 4 – a – 11 = 0
⇒ 2a² – a – 15 = 0
⇒ (a – 3) (2a + 5) = 0
⇒ a = 3 or \(-\frac{5}{2}\)
Case (i): a = 3
x + \(\frac{1}{x}\) = 3
⇒ x² + 1 = 3x
⇒ x² – 3x + 1 = 0
⇒ x = \(\frac{3 \pm \sqrt{9-4}}{2}=\frac{3 \pm \sqrt{5}}{2}\)
Case (ii): a = \(-\frac{5}{2}\)
⇒ \(x+\frac{1}{x}=-\frac{5}{2}\)
⇒ \(\frac{x^2+1}{x}=-\frac{5}{2}\)
⇒ 2x² + 2 = -5x
⇒ 2x² + 5x + 2 = 0
⇒ (2x + 1) (x + 2) = 0
⇒ x = \(-\frac{1}{2}\), -2
∴ The roots are -1, \(-\frac{1}{2}\), -2, \(\frac{3 \pm \sqrt{5}}{2}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(c)

I.

Question 1.
Form the polynomial equation whose roots are
(i) 2 + 3i, 2 – 3i, 1 + i, 1 – i
Solution:
The required equation is [x – (2 + 3i)] [x – (2 – 3i)] [x – (1 + i)][x – (1 – i)] = 0
⇒ [(x – 2) – 3i)] [(x – 2) + 3i] [(x – 1) – i] [(x – 1) + i] = 0
⇒ [(x – 2)² – 9i²] [(x – 1)² – i²] = 0
⇒ (x² – 4x + 4 + 9) (x² – 2x + 1 + 1) = 0
⇒ (x² – 4x + 13) (x² – 2x + 2) = 0
⇒ x⁴ – 4x³ + 13x² – 2x³ + 8x² – 26x + 2x² – 8x + 26 = 0
⇒ x⁴ – 6x³ + 23x² – 34x + 26 = 0

(ii) 3, 2, 1 + i, 1 – i
Solution:
Required equation is (x – 3) (x – 2) [x – (1 + i)] [ x – (1 – i)] = 0
⇒ (x² – 5x + 6) [(x – 1) – i] [(x – 1) + i] = 0
⇒ (x² – 5x + 6) [(x – 1)² – i²] = 0
⇒ (x² – 5x + 6) (x² – 2x + 1 + 1) = 0
⇒ (x² – 5x + 6) (x² – 2x + 2) = 0
⇒ x⁴ – 5x³ + 6x² – 2x³ + 10x² – 12x + 2x² – 10x + 12 = 0
⇒ x⁴ – 7x³ + 18x² – 22x + 12 = 0

(iii) 1 + i, 1 – i, -1 + i, -1 – i
Solution:
Required equation is [x – (1 + i)] [x – (1 – i)] [x – (-1 + i)] [x – (-1 – i)] = 0
⇒ [(x – 1) – i][(x – i) + i] [(x + 1) – i] [(x + 1) + i] = 0
⇒ [(x – 1)² – i²] [(x + 1)² – i²] = 0
⇒ (x² – 2x + 1 + 1) (x² + 2x + 1 + 1) = 0
⇒ (x² – 2x + 2) (x² + 2x + 2) = 0
⇒ x⁴ – 2x³ + 2x² + 2x³ – 4x² + 4x + 2x² – 4x + 4 = 0
⇒ x⁴ + 4 = 0

(iv) 1 + i, 1 – i, 1 + i, 1 – i
Solution:
Required equation is [x – (1 + i)] [x – (1 – i)] [x – (1 + i)] [x – (1 – i)] = 0
⇒ [(x – 1) – i]² [(x – 1) + i]² = 0
⇒ [(x – 1)² – i²] = 0
⇒ (x² – 2x + 1 + 1)² = 0
⇒ x⁴ + 4x² + 4 – 4x³ + 4x² – 8x = 0
⇒ x⁴ – 4x³ + 8x² – 8x + 4 = 0

Question 2.
Form the polynomial equation with rational coefficients whose roots are
(i) 4√3, 5 + 2i
Solution:
For the polynomial equation with rational coeffs. the roots are conjugate surds and conjugate complex numbers.
4√3, 5 + 2i
Let α = 4√3 then β = -4√3, and γ = 5 + 2i then δ = 5 – 2i
α, β, γ, δ are the roots
α + β = 0, αβ = -48
γ + δ = 10, γδ = 25 + 4 = 29
The required equation is [x² – (α + β)x + αβ] [x² – (γ + δ)x + γδ] = 0
⇒ (x² – 48) (x² – 10x + 29) = 0
⇒ x⁴ – 10x³ + 29x² – 48x² + 480x – 1932 = 0
⇒ x⁴ – 10x³ – 19x² + 480x – 1932 = 0

(ii) 1 + 5i, 5 – i
Solution:
For the polynomial equation with rational coeffs. the roots are conjugate surds and conjugate complex numbers.
Let α = 1 + 5i then β = 1 – 5i,
and γ = 5 + i then δ = 5 – i
α + β = 2, αβ = 26
γ + δ = 10, γδ = 26
The required equation is [x² – (α + β)x + αβ] [x² – (γ + δ)x + γδ] = 0
⇒ (x² – 2x + 26) (x² – 10x + 26) = 0
⇒ x⁴ – 12x³ + 72x² – 312x + 676 = 0

(iii) i – √5
Solution:
For the polynomial equation with rational coeffs. the roots are conjugate surds and conjugate complex numbers.
Let α = i – √5, β = i + √5, γ = -i – √5, δ = -i + √5 are the roots
α + β = 2i, αβ = -6
γ + δ = -2i, γδ = -6
The required equation is [x² – (α + β)x + αβ][x² – (γ + δ)x + γδ] = 0
⇒ (x² – 2ix – 6) (x² + 2ix – 6) = 0
⇒ [(x² – 6) – 2ix] [(x² – 6) + 2ix] = 0
⇒ (x² – 6)² + 4x² = 0
⇒ x⁴ + 36 – 12x² + 4x² = 0
⇒ x⁴ – 8x² + 36 = 0

(iv) -√3 + i√2
Solution:
Let α = -√3 + i√2, β = -√3 – i√2, γ = √3 – i√2, γ = √3 + i√2
α + β = -2√3
αβ = (-√3)² – (i√2)²
= 3 – i² (2)
= 5
γ + δ = 2√3
γδ = 5
The required equation is [(x² – (α + β)x + αβ)] [(x² – (γ + δ)x + γδ)] = 0
⇒ (x² + 2√3x + 5) (x² – 2√3x + 5) = 0
⇒ (x² + 5)² – (2√3x)² = 0
⇒ x⁴ + 25 + 10x² – 12x² = 0
⇒ x⁴ – 2x² + 25 = 0

II.

Question 1.
Solve the equation x⁴ + 2x³ – 5x² + 6x + 2 = 0 given that 1 + i is one of its roots.
Solution:
Let 1 + i be one root ⇒ 1 – i be another root
The equation having roots 1 ± i is x² – 2x + 2 = 0
∴ x² – 2x + 2 is a factor of x⁴ + 2x³ – 5x² + 6x + 2 = 0

∴ The roots of the given equation are 1 ± i, -2 + √3

Question 2.
Solve the equation 3x³ – 4x² + x + 88 = 0 which has 2 – √-7 as a root.
Solution:
Let 2 – √-7 (i.e) 2 – √7i is one root
⇒ 2 + √7i is another root.
The equation having roots 2 ± √7i is x² – 4x + 11 = 0
∴ x² – 4x + 11 is a factor of the given equation.

3x + 8 = 0
⇒ x = \(-\frac{8}{3}\)
∴ The roots of the given equation are 2 ± √7i, \(-\frac{8}{3}\)

Question 3.
Solve x⁴ – 4x² + 8x + 35 = 0, given that 2 + i√3 is a root.
Solution:
Let 2 + i√3 be one root
⇒ 2 – i√3 is another root.
The equation having roots 2 ± i√3 is x² – 4x + 7 = 0
∴ x² – 4x + 7 is a factor of x⁴ – 4x² + 8x + 35

∴ The roots of the given equation are 2 ± i√3, -2 ± i

Question 4.
Solve the equation x⁴ – 6x³ + 11x² – 10x + 2 = 0, given that 2 + √3 is a root of the equation.
Solution:
2 + √3 is one root
⇒ 2 – √3 is another root.
The equation having the roots of 2 ± √3 is x² – 4x + 1 = 0
∴ x² – 4x + 1 is a factor of x⁴ – 6x³ + 11x² – 10x + 2 = 0

∴ The roots of the required equation are 2 ± √3, 1 ± i

Question 5.
Given that -2 + √-7 is a root of the equation x⁴ + 2x² – 16x + 77 = 0, solve it completely.
Solution:
-2 – √-7 (i.e) -2 + i√7 is one root
⇒ -2 – i√7 is another root.
The equation having the roots of -2 ± i√7 is x² + 4x + 11 = 0
∴ x² + 4x + 11 is a factor of x⁴ + 2x² – 16x + 77

∴ The roots of the required equation are -2 ± i√7, 2 ± √3i

Question 6.
Solve the equations x⁴ + 2x³ – 16x² – 22x + 7 = 0, given that 2 – √3 is a root of it.
Solution:
2 + √3 is a root ⇒ 2 – √3 is also a root.
The equation having roots 2 ± √3 is
x² – (2 + √3 + 2 – √3)x + (2 + √3) (2 – √3) = 0
⇒ x² – 4x + 1 = 0

x² + 6x + 7 = 0
⇒ x = \(\frac{-6 \pm \sqrt{36-28}}{2}\)
⇒ x = -3 ± √2
∴ Roots are 2 ± √3, -3 ± √2

Question 7.
Solve the equation 3x⁵ – 4x⁴ – 42x³ + 56x² + 27x – 36 = 0 given that √2 + √5 is one of its roots.
Solution:
√2 + √5 is a root
⇒ -√2 – √5, -√2 + √5, -√2 – √5 are also roots.
The equation haying roots √2 + √5 is
x² – (√2 + √5 + √2 – √5) + (√2 + √5) (√2 – √5) = 0
⇒ x² – 2√2x – 3 = 0
The equation having roots -√2 ± √5 is
x² – (-√2 + √5 – √2 – √5) + (√2 + √5)(-√2 – √5) = 0
⇒ x² + 2√x – 3 = 0
The equation having roots ±√2 ± √5 is (x² + 2√2x – 3) (x² – 2√2x – 3) = 0
⇒ (x² – 3)² – (2√2x)² = 0
⇒ x⁴ – 6x² + 9 – 8x² = 0
⇒ x⁴ – 14x² + 9 = 0
∴ 3x⁵ – 4x⁴ – 42x³ + 56x² + 27x – 36 = 0
⇒ 3x(x⁴ – 14x² + 9) – 4(x⁴ – 14x² + 9) = 0
⇒ (x⁴ – 14x² + 9) (3x – 4) = 0
⇒ x = ±√2 ± √5 or 4/3
∴ The roots are ±√2 ± √5, 4/3

Question 8.
Solve the equation x⁴ – 9x³ + 27x² – 29x + 6 = 0, given that one root of it is 2 – √3.
Solution:
2 – √3 is one root ⇒ 2 + √3 is another root.
The equation having the roots of 2 ± √3 is x² – 4x + 1 = 0
∴ x² – 4x + 1 is a factor of the given equation.

x² – 5x + 6 = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, 3
∴ The roots of the required equations are 2 ± √3, 2, 3

Question 9.
Show that the equation \(\frac{a^{2}}{x-a^{\prime}}+\frac{b^{2}}{x-b^{\prime}}+\frac{c^{2}}{x-c^{\prime}}+\ldots+\frac{k^{2}}{x-k^{\prime}}\)= x – m Where a, b, c ….k, m, a’, b’, c’…. k’ are all real numbers, cannot have a non-real root.
Solution:
Let α + iβ be the root of the given equation.
Suppose if β ≠ 0, then α – iβ is also a root of the given equation.
Substitute α + iβ in the given equation, and we get

\(\left[\frac{a^{2}}{\left(\alpha-a^{\prime}\right)^{2}+\beta^{2}}+\frac{b^{2}}{\left(\alpha-b^{\prime}\right)^{2}+\beta^{2}}+\ldots \frac{k^{2}}{\left(\alpha-k^{\prime}\right)^{2}+\beta^{2}}+1\right]\)
= 0
⇒ β = 0
This is a contradiction.
∴ The given equation cannot have non-real roots.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(b)

I.

Question 1.
Solve x³ – 3x² – 16x + 48 = 0, given that the sum of two roots is zero.
Solution:
Let α, β, γ are the roots of x³ – 3x² – 16x + 48 = 0
α + β + γ = 3
Given α + β = 0 (∵ Sum of two roots is zero)
∴ γ = 3
i.e. x – 3 is a factor of x³ – 3x² – 16x + 48 = 0

x² – 16 = 0
⇒ x² = 16
⇒ x = ±4
∴ The roots are -4, 4, 3

Question 2.
Find the condition that x³ – px² + qx – r = 0 may have the sum of its roots zero.
Solution:
Let α, β, γ be the roots of x³ – px² + qx – r = 0
α + β + γ = p ………(1)
αβ + βγ + γα = q ………..(2)
αβγ = r ………..(3)
Given α + β = 0 (∵ Sum of two roots is zero)
From (1), γ = p
∴ γ is a root of x³ – px² + qx – r = 0
γ³ – pγ² + qγ – r = 0
But γ = p
p³ – p(p²) + q(p) – r = 0
p³ – p² + qp – r = 0
∴ qp = r is the required condition.

Question 3.
Given that the roots of x³ + 3px² + 3qx + r = 0 are in
(i) A.P., show that 2p³ – 3qp + r = 0
(ii) G.P., show that p³r = q³
(iii) H.P., show that 2q³ = r(3pq – r)
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
(i) The roots are in A.P.
Suppose a – d, a, a + d are the roots
Sum = a – d + a + a + d = -3p
⇒ 3a = -3p
⇒ a = -p ……….(1)
∵ ‘a’ is a root of x³ + 3px² + 3qx + r = 0
⇒ a³ + 3pa² + 3qa + r = 0
But a = -p
⇒ p³ + 3p(-p)² + 3q(-p) + r = 0
⇒ 2p³ – 3pq + r = 0 is the required condition

(ii) The roots are in G.P.
Suppose the roots be \(\frac{a}{R}\), a, aR
Given (\(\frac{a}{R}\)) (a) (aR) = -r
⇒ a = -r
⇒ a = (-r)^1/3
∵ ‘a’ is a root of x³ + 3px² + 3qx + r = 0
⇒ (-r^1/3)³ + 3p(-r^1/3)² + 3q(-r^1/3) + r = 0
⇒ -r + 3pr^2/3 – 3qr^1/3 + r = 0
pr^2/3 = qr^1/3
⇒ pr^1/3 = q
⇒ p^1/3r = q is the required condition

(iii) The roots of x³ + 3px² + 3qx + r = 0 are in H.P.
x³ + 3px² + 3qx + r = 0 ……..(1)
Let y = \(\frac{1}{x}\) so that \(\frac{1}{y^{3}}+\frac{3 p}{y^{2}}+\frac{3 q}{y}+r\) = 0
Roots of ry³ + 3qy² + 3py + 1 = 0 are in A.P.
ry³ + 3qy² + 3py + 1 = 0 ……..(2)
Suppose a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = \(-\frac{3 q}{r}\)
3a = \(-\frac{3 q}{r}\)
a = \(-\frac{q}{r}\) ………(1)
∵ ‘a’ is a root of ry³ + 3qy² + 3py + 1 = 0
⇒ ra³ + 3qa² + 3pa + 1 = 0
But a = \(-\frac{q}{r}\)
⇒ \(r\left(-\frac{q}{r}\right)^{3}+3 q\left(-\frac{q}{r}\right)^{2}+3 p\left(-\frac{q}{r}\right)+1=0\)
⇒ \(\frac{-q^{3}}{r^{2}}+\frac{3 q^{3}}{r^{2}}-\frac{3 p q}{r}+1=0\)
⇒ -q³ + 3q³ – 3pqr + r² = 0
⇒ 2q³ = r(3pq – r) is the required condition.

Question 4.
Find the condition that x³ – px² + qx – r = 0 may have the roots in G.P.
Solution:
Let \(\frac{a}{R}\), a, aR be the roots of x³ – px² + qx – r = 0
The product of the roots = \(\frac{a}{R}\) . a . aR = a³
product of the roots = r
⇒ a = r^1/3
∵ a is a root of x³ – px² + qx – r = 0
⇒ a³ – pa² + qa – r = 0
But a = r^1/3
⇒ (r^1/3)³ – p(r^1/3)² + q(r^1/3) – r = 0
⇒ r – p . r^2/3 + q . r^1/3 – r = 0
⇒ p . r^2/3 = qr^1/3
By cubing on both sides
⇒ p³r² = q³r
⇒ p³r = q³ is the required condition

II.

Question 1.
Solve 9x³ – 15x² + 7x – 1 = 0, given that two of its roots are equal.
Solution:
Suppose α, β, γ are the roots of 9x³ – 15x³ + 7x – 1 = 0
α + β + γ = \(\frac{15}{9}=\frac{5}{3}\)
αβ + βγ + γα = \(\frac{7}{9}\)
αβγ = \(\frac{1}{9}\)
Given α = β (∵ two of its roots are equal)
2α + γ = \(\frac{5}{3}\)
⇒ γ = \(\frac{5}{3}\) – 2α
α² + 2αγ = \(\frac{7}{9}\)
⇒ α² + 2α (\(\frac{5}{3}\) – 2α) = \(\frac{7}{9}\)
⇒ α² + \(\frac{2 \alpha(5-6 \alpha)}{3}=\frac{7}{9}\)
⇒ 9α² + 6α(5 – 6α) = 7
⇒ 9α² + 30α – 36α² = 7
⇒ 27α² – 30α + 7 = 0
⇒ (3α – 1)(9α – 7) = 0
⇒ α = \(\frac{1}{3}\) or \(\frac{7}{9}\)

The roots are \(\frac{1}{3}\), \(\frac{1}{3}\), 1

Question 2.
Given that one root of 2x³ + 3x² – 8x + 3 = 0 is double of another root, find the roots of the equation.
Solution:
Suppose α, β, γ are the roots of 2x³ + 3x² – 8x + 3 = 0
α + β + γ = \(-\frac{3}{2}\) ……..(1)
αβ + βγ + γα = -4 ……..(2)
αβγ = \(-\frac{3}{2}\)
Given α = 2β (∵ one root is double the other)
Substituting in (1)
3β + γ = \(-\frac{3}{2}\)
⇒ γ = \(-\frac{3}{2}\) – 3β …….(4)
Substituting in (2)
αβ + γ(α + β) = -4
⇒ 2β² + 3βγ = -4
⇒ 2β² + 3β(\(-\frac{3}{2}\) – 3β) = -4
⇒ 2β² – \(\frac{3 \beta(3+6 \beta)}{2}\) = -4
⇒ 4β² – 9β – 18β² = -8
⇒ 14β² + 9β – 8 = 0
⇒ (2β – 1)(7β + 8) = 0
⇒ 2β – 1 = 0 or 7β + 8 = 0
⇒ β = \(\frac{1}{2}\) or β = \(-\frac{8}{7}\)

∴ The roots are \(\frac{1}{2}\), 1 and -3

Question 3.
Solve x³ – 9x² + 14x + 24 = 0, given that two of the roots are in the ratio 3 : 2.
Solution:
Suppose α, β, γ are the roots of x³ – 9x² + 14x + 24 = 0
α + β + γ = 9 ………(1)
αβ + βγ + γα = 14 ……….(2)
αβγ = -24 ……….(3)
∵ two roots are in the ratio 3 : 2
Let α : β = 3 : 2
⇒ β = \(\frac{2 \alpha}{3}\)
Substituting in (1)
\(\frac{5 \alpha}{3}\) + γ = 9
⇒ γ = 9 – \(\frac{5 \alpha}{3}\) ………(4)
Substituting in (2)
⇒ \(\frac{2}{3}\) α² + γ(α + β) = 14
⇒ \(\frac{2}{3} \alpha^{2}+\left(9-\frac{5 \alpha}{3}\right) \cdot \frac{5 \alpha}{3}\) = 14
⇒ 2α² + 5α(9 – \(\frac{5 \alpha}{3}\)) = 42
⇒ 2α² + 5α \(\frac{(27-5 \alpha)}{3}\) = 42
⇒ 6α² + 135α – 25α² = 126
⇒ 19α² – 135α + 126 = 0
⇒ 19α² – 114α – 21α + 126 = 0
⇒ 19α(α – 6) – 21(α – 6) = 0
⇒ (19α – 21)(α – 6) = 0
⇒ 19α – 21 = 0 or α – 6 = 0
⇒ α = \(\frac{21}{19}\) or α = 6
Case (i): α = 6
β = \(\frac{2 \alpha}{3}\)
= \(\frac{2}{3}\) × 6
= 4
γ = 9 – \(\frac{5 \alpha}{3}\)
= 9 – \(\frac{5}{3}\) × 6
= 9 – 10
= -1
α = 6, β = 4, γ = -1 satisfy αβγ = -24
∴ The roots are 6, 4, -1

Case (ii): α = \(\frac{21}{19}\)
β = \(\frac{2}{3} \times \frac{21}{19}=\frac{14}{19}\)
γ = 9 – \(\frac{5 \alpha}{3}\)
= 9 – \(\frac{5}{3} \cdot \frac{21}{19}\)
= \(\frac{136}{19}\)
These values do not satisfy αβγ= -24
∴ The roots are 6, 4, -1.

Question 4.
Solve the following equations, given that the roots of each are in A.P.
(i) 8x³ – 36x² – 18x + 81 = 0
Solution:
Given the roots of 8x³ – 36x² – 18x + 81 = 0 are in A.P.
Let the roots be a – d, a, a + d
Sum of the roots = \(\frac{36}{8}\)
⇒ a – d + a + a + d = \(\frac{9}{2}\)
⇒ 3a = \(\frac{9}{2}\)
⇒ a = \(\frac{3}{2}\)
∴ (x – \(\frac{3}{2}\)) is a factor of 8x³ – 36x² – 18x + 81 = 0

⇒ 8x² – 24x – 54 = 0
⇒ 4x² – 12x – 27 = 0
⇒ 4x² – 18x + 6x – 27 = 0
⇒ 2x(2x – 9) + 3(2x – 9) = 0
⇒ (2x + 3) (2x – 9) = 0
⇒ x = \(-\frac{3}{2}, \frac{9}{2}\)
∴ The roots are \(-\frac{3}{2}, \frac{3}{2}, \frac{9}{2}\)

(ii) x³ – 3x² – 6x + 8 = 0
Solution:
The roots of x³ – 3x² – 6x + 8 = 0 are in A.P
Suppose a – d, a, a + d be the roots
Sum = a – d + a + a + d = 3
⇒ 3a = 3
⇒ a = 1
∴ (x – 1) is a factor of x³ – 3x² – 6x + 8 = 0

⇒ x² – 2x – 8 = 0
⇒ x² – 4x + 2x – 8 = 0
⇒ x(x – 4)+ 2(x – 4) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x = 4, -2
∴ The roots are -2, 1, 4

Question 5.
Solve the following equations, given that the roots of each are in G.P.
(i) 3x³ – 26x² + 52x – 24 = 0
Solution:
Given equation is 3x³ – 26x² + 52x – 24 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar are the roots.
Product = \(\frac{a}{r}\) . a . ar = \(-\left(-\frac{24}{3}\right)\)
⇒ a³ = 8
⇒ a = 2
∴ (x – 2) is a factor of 3x³ – 26x² + 52x – 24

Hint: 3 × 12 = 3 ×6 × 2 = (-18)(-2)
⇒ 3x² – 20x + 12 = 0
⇒ 3x² – 18x – 2x + 12 = 0
⇒ 3x(x – 6) – 2(x – 6) = 0
⇒ (3x – 2) (x – 6) = 0
⇒ x = \(\frac{2}{3}\), 6
∴ The roots are \(\frac{2}{3}\), 2, 6.

(ii) 54x³ – 39x² – 26x + 16 = 0
Solution:
Given equation is 54x³ – 39x² – 26x + 16 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar be the roots.
Product = \(\frac{a}{r}\) . a . ar = \(-\frac{16}{54}\)

Hint: 18 × 8 = 9 × 2 × 8 = (-9) (-16)
⇒ 54x² – 75x + 24 = 0
⇒ 18x² – 25x + 8 = 0
⇒ 18x² – 9x – 16x + 8 = 0
⇒ 9x(2x – 1) – 8(2x- 1) = 0
⇒ (9x – 8) (2x – 1) = 0
⇒ x = \(\frac{8}{9}, \frac{1}{2}\)
∴ The roots are \(\frac{8}{9},-\frac{2}{3}, \frac{1}{2}\)

Question 6.
Solve the following equations, given that the roots of each are in H.P.
(i) 6x³ – 11x² + 6x – 1 = 0
Solution:
Given equation is 6x³ – 11x² + 6x – 1 = 0 …….(1)
Put y = \(\frac{1}{x}\) so that \(\frac{6}{\mathrm{y}^{3}}-\frac{11}{\mathrm{y}^{2}}+\frac{6}{\mathrm{y}}-1\) = 0
⇒ 6 – 11y + 6y² – y³ = 0
⇒ y³ – 6y² + 11y – 6 = 0 ………(2)
Roots of (1) are in H.P.
⇒ Roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = 6
⇒ 3a = 6
⇒ a = 2
Product = a(a² – d²) = 6
⇒ 2(4 – d²) = 6
⇒ 4 – d² = 3
⇒ d² = 1
⇒ d = 1
a – d = 2 – 1 = 1,
a = 2
a + d = 2 + 1 = 3
The roots of (2) are 1, 2, 3
The roots of (1) are 1, \(\frac{1}{2}\), \(\frac{1}{3}\)

(ii) 15x³ – 23x² + 9x – 1 = 0
Solution:
Given equation is 15x³ – 23x² + 9x – 1 = 0 …….(1)
Put y = \(\frac{1}{x}\) so that \(\frac{15}{y^{3}}-\frac{23}{y^{2}}+\frac{9}{y}-1\) = 0
⇒ 15 – 23y + 9y² – y³ = 0
⇒ y³ – 9y² + 23y – 15 = 0 ………(2)
Roots of (1) are in H.P. So that roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = 9
⇒ 3a = 9
⇒ a = 3
Product = a(a² – d²) = 15
⇒ 3(9 – d²) = 15
⇒ 9 – d² = 5
⇒ d² = 4
⇒ d = 2
a – d = 3 – 2 = 1
a = 3
a + d = 3 + 2 = 5
Roots of (2) are 1, 3, 5
Hence roots of (1) are 1, \(\frac{1}{3}\), \(\frac{1}{5}\)

Question 7.
Solve the following equations, given that they have multiple roots.
(i) x⁴ – 6x³ + 13x² – 24x + 36 = 0
Solution:
(i) Let f(x) = x⁴ – 6x³ + 13x² – 24x + 36
⇒ f'(x) = 4x³ – 18x² + 26x – 24
⇒ f'(3) = 4(27) – 18(9) + 26(3) – 24
⇒ f'(3) = 108 – 162 + 78 – 24
⇒ f'(3) = 0
f(3) = 81 – 162 + 117 – 72 + 36 = 0
Hint: Choose the value of x from the factors of the G.C.D of constant terms in f(x) and f'(x).
∴ x – 3 is a factor of f'(x) and f(x)
∴ 3 is the repeated foot of f(x)

x² + 4 = 0
⇒ x = ±2i
∴ The roots of the given equation are 3, 3, ±2i

(ii) 3x⁴ + 16x³ + 24x² – 16 = 0
Solution:
Let f(x) = 3x⁴ + 16x³ + 24x² – 16
f(x) = 12x³ + 48x² + 48x
= 12x(x² + 4x + 4)
= 12x (x + 2)²
f'(-2) = 0
f(-2) = 3(16) + 16(-8) + 24(4) – 16 = 0
∴ x + 2 is a factor of f'(x) and f(x)
∴ -2 is a multiple root of f(x) = 0

3x² + 4x – 4 = 0
⇒ 3x² + 6x – 2x – 4 = 0
⇒ 3x(x + 2) – 2(x + 2) = 0
⇒ (x + 2) (3x – 2) = 0
⇒ x = -2, \(\frac{2}{3}\)
∴ The roots of the given equation are -2, -2, -2, \(\frac{2}{3}\)

III.

Question 1.
Solve x⁴ + x³ – 16x² – 4x + 48 = 0, given that the product of two of the roots is 6.
Solution:
Suppose α, β, γ, δ are the roots of
x⁴ + x³ – 16x² – 4x + 48 = 0 ………..(1)
Sum of the roots = -1
⇒ α + β + γ + δ = -1
and Product of the roots = αβγδ = 48
∵ Product of two roots is 6
Let αβ = 6
From (1), γδ = \(\frac{48}{\alpha \beta}=\frac{48}{6}\) = 8
Let α + β = p and γ + δ = q
The equation having roots α, β is x² – (α + β) x + αβ = 0
⇒ x² – px + 6 = 0 ………..(2)
The equation having the roots γ, δ is x² – (γ + δ) x + γδ = 0
⇒ x² – qx + 8 = 0 ……….(3)
∴ From (1), (2) and (3)
x⁴ + x³ – 16x² – 4x + 48 = (x² – px + 6) (x² – qx + 8)
= x⁴ – (p + q) x³ + (pq + 14) x² – (8p + 86q) x + 48
Comparing the like terms,
p + q = -1
8p + 6q = 4 ⇒ 4p + 3q = 2
Solving, q = -6
∴ p = -1 + 6 = 5
Substitute the value of p in eq. (2),
x² – 5x + 6 = 0 ⇒ x = 2, 3
Substitute/the value of q in eq. (3),
x² + 6x + 8 = 0 ⇒ x = -2, – 4
∴ The roots of the given equation are -4, -2, 2, 3

Question 2.
Solve 8x⁴ – 2x³ – 27x² + 6x + 9 = 0 given that two roots have the same absolute value, but are opposite in signs.
Solution:
Suppose α, β, γ, δ are the roots of the equation
8x⁴ – 2x³ – 27x² + 6x + 9 = 0
⇒ \(x^{4}-\frac{1}{4} x^{3}-\frac{27}{8} x^{2}+\frac{3}{4} x+\frac{9}{8}=0\) …………(1)
Sum of the roots = α + β + γ + δ = \(\frac{1}{4}\) and
Product of the roots = αβγδ = \(\frac{9}{8}\)
Given β = -α
⇒ α + β = 0
∴ 0 + γ + δ = \(\frac{1}{4}\)
⇒ γ + δ = \(\frac{1}{4}\)
Let αβ = p, γδ = q, so that pq = \(\frac{9}{8}\)
The equation having the roots α, β is x² – (α + β)x + αβ = 0
⇒ x² + p = 0 ……….(2)
The equation having the roots γ, δ is x² – (γ + δ)x + γδ = 0
⇒ x² – \(\frac{1}{4}\) x + q = 0 ……..(3)
From (1), (2) and (3)
\(x^{4}-\frac{1}{4} x^{3}-\frac{27}{8} x^{2}+\frac{3}{4} x+\frac{9}{8}\) = (x² + p) \(\left(x^{2}-\frac{1}{4} x+q\right)\)
= \(x^{4}-\frac{1}{4} x^{3}+(p+q) x^{2}-\frac{p}{4} x+p q\)
Comparing the coefficients of x and constants
\(\frac{-p}{4}=\frac{3}{4}\) ⇒ p = -3
pq = \(\frac{9}{8}\)
⇒ q = \(\frac{9}{8} \times \frac{-1}{3}=\frac{-3}{8}\)
Substitute the value of p in eq. (2),
x² – 3 = 0 ⇒ x = ±√3
Substitute the value of q in eq. (3),
\(x^{2}-\frac{1}{4} x-\frac{3}{8}=0\)
⇒ 8x² – 2x – 3 = 0
⇒ (2x + 1) (4x – 3) = 6
⇒ x = \(-\frac{1}{2}, \frac{3}{4}\)
∴ The roots of the given equation are -√3, \(-\frac{1}{2}, \frac{3}{4}\), √3

Question 3.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots.
Solution:
Suppose α, β, γ are the roots of 18x³ + 81x² + 121x + 60 = 0
sum = α + β + γ = \(\frac{-81}{18}=\frac{-9}{2}\) ……….(1)
αβ + βγ + γα = \(\frac{121}{18}\) …………(2)
αβγ = \(\frac{-60}{18}=\frac{-10}{3}\) ………(3)
∵ One root is equal to half of the sum of the remaining two,
Let α = \(\frac{1}{2}\) (β + γ)
Substitute in (1)

Question 4.
Find the condition in order that the equation ax⁴ + 4bx³ + 6cx² + 4dx + e = 0 may have a pair of equal roots.
Solution:
Let α, α, β, β are the roots of the equation.
ax⁴ + 4bx³ + 6cx² + 4dx + e = 0
⇒ \(x^{4}+\frac{4 b}{a} x^{2}+\frac{6 c}{a} x^{2}+\frac{4 d}{a} x+\frac{e}{a}=0\)
Sum of the roots, 2(α + β) = \(-\frac{4 b}{a}\)
⇒ α + β = \(-\frac{2 b}{a}\)
⇒ αβ = k (say)
Equation having roots α, β is x² – (α + β) x + αβ = 0

Question 5.
(i) Show that x⁵ – 5x³ + 5x² – 1 = 0 has three equal roots and find this root.
Solution:
Let f(x) = x⁵ – 5x³ + 5x² – 1
f'(x) = 5x⁴ – 15x² + 10x = 5x(x³ – 3x + 2)
f'(1) = 5(1) (1 – 3 + 2) = 0
f(1) = 1 – 5 + 5 – 1 = 0
x – 1 is a factor of f'(x) and f(x)
∴ 1 is a repeated root of f(x).

x³ + 2x² – 2x – 1 = 0
⇒ 1 is a root of the above equation (∵ sum of the coefficients is zero)
∴ 1 is the required root.

(ii) Find the repeated roots of x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12 = 0
Solution:
Let f(x) = x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12
f'(x) = 5x⁴ – 12x³ – 15x² + 54x – 32
f'(2) = 5(2)⁴ – 12(2)³ – 15(2)² + 54(2) – 32
= 80 – 96 – 60 + 108 – 32
= 0
f(2) = (2)⁵ – 3(2)⁴ – 5(2)³ + 27(2)² – 32(2) + 12
= 32 – 48 – 40 + 108 – 64 + 12
= 152 – 152
= 0
∴ x – 2 is a common factor of f'(x) and f(x)
2 is a multiple root of f(x) = 0

Let g(x) = x³ + x² – 5x + 3
g'(x) = 3x² + 2x – 5 = (3x + 5) (x – 1)
g(1) = 1 + 1 – 5 + 3 = 0
∴ x – 1 is a common factor of g'(x) and g(x)
∴ 1 is a multiple root of g(x) = 0

x + 3 = 0 ⇒ x = -3
∴ The roots are 2, 2, 1, 1, -3

Question 6.
Solve the equation 8x³ – 20x² + 6x + 9 = 0 given that the equation has multiple roots.
Solution:
Let f(x) = 8x³ – 20x² + 6x + 9
f'(x) = 24x² – 40x + 6
= 2 (12x² – 20x + 3)
= 2[12x² – 18x – 2x + 3]
= 2[6x(2x – 3) – 1(2x – 3)]
= 2(2x – 3) (6x – 1)
f'(x) = 0
⇒ x = \(\frac{3}{2}\), x = \(\frac{1}{6}\)
\(f\left(\frac{3}{2}\right)=8\left(\frac{3}{2}\right)^{3}-20\left(\frac{3}{2}\right)^{2}+6\left(\frac{3}{2}\right)+9\)
= 27 – 45 + 9 + 9
= 0
Hence x – \(\frac{3}{2}\) is a factor of f(x) and f'(x)
∴ \(\frac{3}{2}\) is a multiple root of f(x) = 0

8x – 4 = 0
⇒ x = \(\frac{4}{8}=\frac{1}{2}\)
∴ The roots of the equation f(x) = 0 are \(\frac{3}{2}, \frac{3}{2}, \frac{1}{2}\)