Srinivas

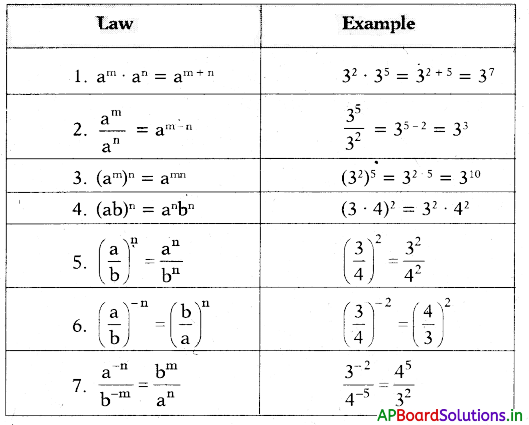
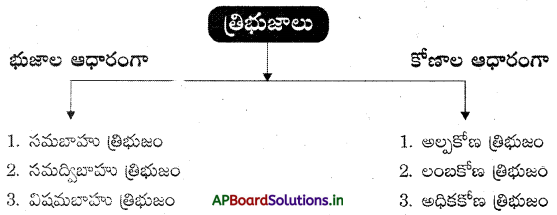
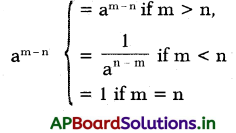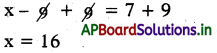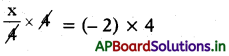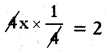Students can go through AP Board 7th Class Maths Notes 6th Lesson దత్తాంశ నిర్వహణ to understand and remember the concept easily.

AP Board 7th Class Maths Notes 6th Lesson దత్తాంశ నిర్వహణ

→ Dr. కాలియంపూడి రాధాకృష్ణరావు (C.R. రావు) – భారతదేశం : ప్రముఖ సాంఖ్యక శాస్త్రజ్ఞుడు. ఈయన రచించిన “థియరీ ఆఫ్ ఎస్టిమేషన్” అనే గ్రంథము ప్రాచుర్యము పొందినది. ఈయన క్రామర్ – రావు ఇనీక్వాలిటీ మరియు ఫిషర్ – రావు సిద్ధాంతా లను రూపొందించారు. గూడూరు, నూజివీడు, నందిగామ, విశాఖపట్నంలో ఆయన పాఠశాల విద్యను పూర్తి చేసారు. ఆంధ్ర విశ్వవిద్యాలయం నుండి గణితశాస్త్రంలో .M.A. చేసారు. ఆయన సర్ ఆర్.ఎ.ఫిషర్ ఆధ్వర్యంలో Ph.D. డిగ్రీ పొందారు.

→ సంఖ్యలు, పదాలు లేదా చిత్రాల రూపంలో సేకరించిన సమాచారమే “చత్తాంశము”.

→ సమాచారాన్ని సేకరించే పద్ధతిని బట్టి దత్తాంశాన్ని “ప్రాథమిక దత్తాంశము” మరియు “గౌణ (ద్వితీయ) దత్తాంశము” అనే రెండు రకాలుగా విభజించవచ్చు.

→ ఇచ్చిన దత్తాంశములోని గరిష్ఠ మరియు కనిష్ఠ విలువల మధ్య భేదాన్నే “వ్యాప్తి” అంటారు.

→ సర్వసాధారణంగా ప్రాతినిధ్య విలువ లేదా కేంద్రీయ స్థాన విలువగా “సగటు” లేదా “అంకగణిత సగటు”ను ఉపయోగిస్తారు.

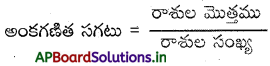
→ అంకగణిత సగటు ఎల్లప్పుడూ అత్యల్ప మరియు అత్యధిక పరిశీలనా విలువల మధ్య ఉంటుంది.

→ దత్తాంశములో ఎక్కువ సార్లు పునరావృతం అయ్యే రాశిని “బాహుళకం” అంటారు.

→ ఒకే ఒక రాశి బాహుళకముగా గల దత్తాంశమును “ఏక బాహుళక దత్తాంశము” అని మరియు రెండు రాశులు బాహుళకముగా గల దత్తాంశమును “ద్వి బాహుళక దత్తాంశము” అంటారు.

→ దత్తాంశములోని రాశులను ఆరోహణ లేదా అవరోహణ క్రమములో అమర్చగా, ఆ అమరికలోని మధ్యమ విలువను . “మధ్యగతం” అంటారు.

→ దత్తాంశములో రాశుల సంఖ్య (బ) బేసి సంఖ్య అయిన మధ్యగతము \(\left(\frac{\mathrm{n}+1}{2}\right)\) వ పదము అగును.

→ ఇచ్చిన దత్తాంశములో రాశుల సంఖ్య (n) సరి సంఖ్య అయిన మధ్యగతము \(\left(\frac{\mathrm{n}}{2}\right)\) వ పదము \(\left(\frac{\mathrm{n}}{2}+1\right)\) వ పదాల సరాసరి.

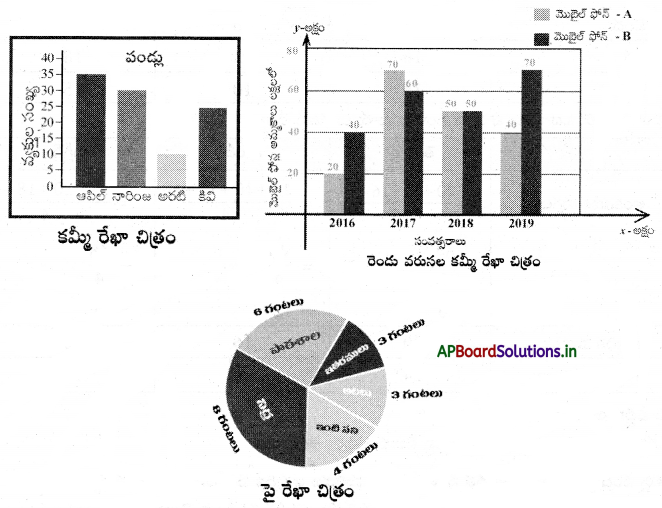
→ దత్తాంశమును సమాన వెడల్పు గల ఉన్న కమ్మీల రూపములో ప్రదర్శించుటనే కమ్మీ చిత్రం అంటారు.

→ ఏకరీతి వెడల్పు కలిగిన కమ్మీలను ఉపయోగించడం ద్వారా ఒకే గ్రాఫ్ మీద రెండు విభిన్న దత్తాంశములను ప్రదర్శించుటను డబుల్ బార్ గ్రాఫ్ లేదా రెండు వరుసల కమ్మీ చిత్రం అంటారు.

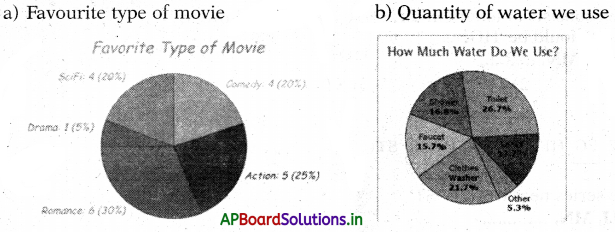
→ వృత్తంను సెక్టార్లుగా విభజించుట ద్వారా దత్తాంశమును ప్రదర్శించుటనే వృత్తరేఖా చిత్రము లేదా పై చిత్రము – అంటాము. పై చిత్రంలో ప్రతీ సెక్టారు వృత్త కేంద్రం వద్ద చేసే కోణము (సెక్టారు వైశాల్యము) అది సూచించే అంశ విలువకు అనులోమానుపాతంలో ఉంటుంది.

→ ప్రాథమిక దత్తాంశము : వ్యక్తిగత అనుభవాలు, ఇంటర్వ్యూలు, ప్రత్యక్ష పరిశీలనలు, భౌతిక పరీక్ష మొదలైన పద్ధతుల ద్వారా ప్రత్యక్షంగా సేకరించిన దత్తాంశమును ప్రాథమిక దత్తాంశము అంటారు. దీనినే ముడిదత్తాంశము అని కూడా అంటారు. ఉదా : తరగతి ఉపాధ్యాయుడు వ్యక్తిగత మార్కుల రిజిష్టర్ లో నమోదు చేసిన మార్కులు.

→ గౌణ దత్తాంశము లేదా ద్వితీయ దత్తాంశము : గతంలో వేరొకరు సేకరించిన సమాచారాన్ని ప్రస్తుత అవసరాలకు పరిశోధకుడు ఉపయోగించుకున్న దత్తాంశమును గౌణ లేదా ద్వితీయ దత్తాంశం అని అంటారు.
ఉదా : గ్రామ జనాభా వివరాలను జనాభా లెక్కల రిజిష్టరు నుండి సేకరించడము.

→ కేంద్రీయ స్థాన మాపనములు : విభిన్న రూపములోని దత్తాంశములకు విభిన్న ప్రాతినిధ్య విలువలు అవసరమవుతాయి. ఈ ప్రాతినిధ్య విలువలను కేంద్రీయ స్థాన విలువలు అంటాము.
ఇవి : 1. అంకగణిత సగటు 2. బాహుళకము 3. మధ్యగతము.

1. అంకగణిత సగటు (లేదా) సరాసరి : అంకగణిత సగటు (సరాసరి) అనేది ఒక సంఖ్య. ఇది దత్తాంశములోని అన్ని పరిశీలనల యొక్క కేంద్రీయ స్థాన విలువను సూచిస్తుంది.

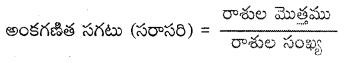
ఉదా : 32, 37, 25, 49, 36, 31 రాశుల సరాసరి ఎంత ?
జవాబు:

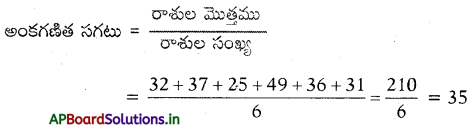
అంకగణిత సగటు (సరాసరి) దత్తాంశములోని అత్యల్ప మరియు అత్యధిక పరిశీలనా విలువల మధ్య ఉంటుంది. ఇది ఆ దత్తాంశంలోని పరిశీలనా విలువ కావచ్చు, కాకపోవచ్చును.

2. బాహుళకము : ఇవ్వబడిన దత్తాంశములో ఎక్కువసార్లు పునరావృతం అయ్యేరాశిని బాహుళకం అంటారు.
ఉదా – 1 : 6, 8, 5, 6, 6, 5, 7, 5, 6, 5, 4, 7, 6 ల బాహుళకం ఎంత ?
జవాబు:
ఇచ్చిన రాశులను ఒకే విలువ గల రాశులను ఒక క్రమ పద్ధతిలో అమర్చగా
4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, 7, 8.
మిగతా వాని కన్నా 6 ఎక్కువసార్లు పునరావృతం అయినది.
బాహుళకం = 6

ఉదా – 2 : 3, 5, 4, 3, 6, 5, 8, 5, 6, 3, 2 రాశుల బాహుళకం ఎంత ?
జవాబు:
2, 3, 3, 3, 4, 5, 5, 5, 6, 6, 8.
మిగతా అన్నింటికన్నా ఎక్కువసార్లు 3 మరియు 5 లు సమానంగా రావడం జరిగినది.
బాహుళకం = 3 మరియు 5

→ ఒక దత్తాంశమునకు ఒకటి లేదా అంతకన్నా ఎక్కువ బాహుళకాలు ఉండవచ్చును. అలాగే ఒక్కొక్కసారి బాహుళకం ఉండకనూ పోవచ్చును.
ఉదా -1 :
మొదటి 10 సహజసంఖ్యల బాహుళకం ఎంత ?
జవాబు:
మొదటి 10 సహజ సంఖ్యలు : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
ఇందులో ఏ రాశి కూడా ఎక్కువసార్లు పునరావృతం కాలేదు. కాబట్టి ఈ దత్తాంశమునకు బాహుళకం లేదు.

ఉదా – 2 :
2, 3, 5, 4, 4, 2, 5, 3, 4, 3, 2, 5 రాశుల బాహుళకం ఎంత ?
జవాబు:
2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5 (దత్తాంశంలోని రాశులను క్రమపద్ధతిలో అమర్చగా)
దత్తాంశంలోని రాశులు అన్ని సమానంగా పునరావృతం అవుతున్నాయి. ఈ సందర్భంలో ఇచ్చిన దత్తాంశమునకు బాహుళకం లేదు. ఇలాంటి దత్తాంశాన్ని బాహుళకరహిత దత్తాంశం అంటారు.

→ బాహుళకంగా ఒకే ఒక రాశిగల దత్తాంశమును “ఏక బాహుళక దత్తాంశం” అని, బాహుళకముగా రెండు రాశులు గల దత్తాంశాన్ని “ద్వి బాహుళక దత్తాంశము” అని అంటారు.

3. మధ్యగతము : దత్తాంశములోని రాశులను ఆరోహణ లేదా అవరోహణ క్రమంలో అమర్చగా, ఆ అమరికలోని
మధ్యమ విలువను మధ్యగతం అంటారు. మధ్యగతం దత్తాంశమును రెండు సమాన భాగాలుగా విభజిస్తుంది.
ఇచ్చిన దత్తాంశములోని రాశుల సంఖ్య (n) బేసి సంఖ్య అయిన మధ్యగతవ \(\left(\frac{\mathrm{n}+1}{2}\right)\)
వ రాశి అవుతుంది.
అలాగే దత్తాంశములోని రాశుల సంఖ్య (n) సరిసంఖ్య అయిన మధ్యగతము \(\left(\frac{n}{2}\right)\) వ రాశి మరియు \(\left(\frac{\mathrm{n}}{2}+1\right)\) వ రాశుల సరాసరి అవుతుంది.

ఉదా -1 :
20, 15, 17, 14, 21, 18, 19 రాశుల మధ్యగతము ఎంత ?
జవాబు:
ఇచ్చిన రాశులు ఆరోహణ క్రమములో అమర్చితే 14, 15, 17, 18, 19, 20, 21 పరిశీలనల సంఖ్య 7 ఒక బేసి సంఖ్య.
కావున, \(\frac{\mathrm{n}+1}{2}=\frac{7+1}{2}=\frac{8}{2}\) = 4వ రాశి మధ్య పదం అగును.
∴ మధ్యగతం = 18.

ఉదా – 2 :
13, 10, 12, 11, 14, 15 రాశుల మధ్యగతము ఎంత ?
జవాబు:
ఇచ్చిన రాశులు ఆరోహణ క్రమములో అమర్చితే 10, 11, 12, 13, 14, 15
పరిశీలనల సంఖ్య 6 ఒక సరి సంఖ్య. కావున, \(\left(\frac{n}{2}\right)\) వ మరియు \(\left(\frac{\mathrm{n}}{2}+1\right)\) పదాల సరాసరి మధ్యగతము ; n = 6
= \(\left(\frac{6}{2}\right),\left(\frac{6}{2}+1\right)\)
= 3, 4 పదాల సరాసరి అగును.
∴ మధ్యగతం = \(\frac{12+13}{2}=\frac{25}{2}\) = 12.5

→ వ్యాప్తి : దత్తాంశములోని గరిష్ఠ, కనిష్ఠ విలువల భేదాన్ని వ్యాప్తి అంటారు.
ఉదా :
6, 9, 3, 7, 11, 14, 2, 15 ల వ్యాప్తిని కనుగొనండి.
జవాబు:
వ్యాప్తి = గరిష్ఠ విలువ – కనిష్ఠ విలువ
దత్తాంశాన్ని ఆరోహణ క్రమంలో రాయగా
2, 3, 6, 7, 9, 11, 14, 15
వ్యాప్తి = 15 – 2 = 13
వ్యాప్తి కేంద్రీయ స్థాన విలువ కాదు.
అంకగణిత సగటు, బాహుళకం, మధ్యగతంలు కేంద్రీయ, స్థాన విలువలు.

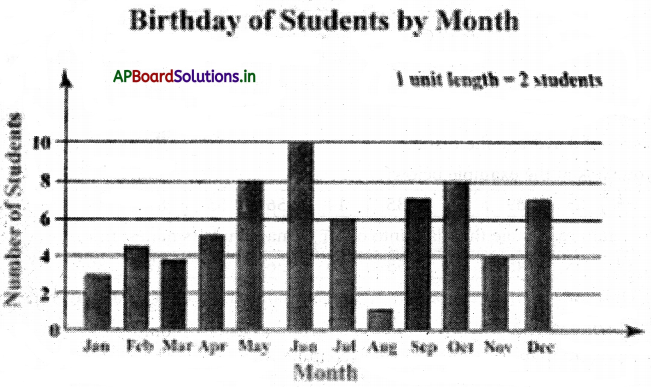
→ కమ్మీ రేఖా చిత్రం : ఇచ్చిన సంఖ్యా దత్తాంశాన్ని సమాన వెడల్పు గల కమ్మీల రూపంలో ప్రదర్శించటాన్ని “కమ్మీ రేఖా చిత్రము” అంటారు. కమ్మీ రేఖా చిత్రంలోని కమ్మీల వెడల్పు సమానంగా ఉండును. మరియు కమ్మీల ఎత్తు (పొడవు) అది సూచించే అంశం యొక్క విలువకు అనులోమానుపాతంలో ఉంటుంది.

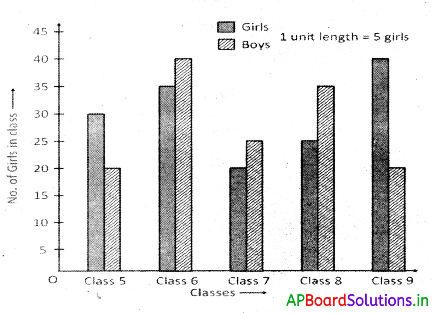
→ రెండు వరుసల కమ్మీ రేఖా చిత్రం (డబుల్ బార్ గ్రాఫ్) : ఏకరీతి వెడల్పు కలిగిన కమ్మీలను ఉపయోగించడం ద్వారా ఒకే గ్రాఫ్ (రేఖాచిత్రం) మీద రెండు విభిన్న దత్తాంశములను ప్రదర్శించుటను రెండు వరుసల కమ్మీ రేఖా చిత్రం (లేదా) డబుల్ బార్ గ్రాఫ్ అంటారు.

→ పై (π) రేఖా చిత్రం (లేదా) వృత్త రేఖా చిత్రము : వృత్తమును సెక్టార్లుగా విభజించుట ద్వారా దత్తాంశమును ప్రదర్శించుటనే వృత్త. రేఖాచిత్రము లేదా పై (π) రేఖా చిత్రము అంటారు.

Students can go through AP Board 7th Class Maths Notes 10th Lesson Construction of Triangles to understand and remember the concept easily.

AP Board 7th Class Maths Notes 10th Lesson Construction of Triangles

→ The triangles can be constructed given the following cases :

• Three sides of a triangle.
• The lengths of any two sides and the measure of the angle between these sides.
• The measures of two angles and the lengths of side included between them.

→ To Construct a triangle we need at least the measure of one side.
Construct a triangle ABC given that AB = 4 cm, BC = 6 cm and AC = 5 cm.

Steps of construction:

• Draw a line segment BC = 6 cm.
• With B as centre and radius 4 cm, draw an arc.
• With C as centre and radius 5 cm, draw another arc, cutting the previous arc atA.
• Join BA and CA.
• ∆ABC is formed.

→ Construction of a triangle given two sides and an included angle.
Construct triangle PQR given that PQ = 4cm,QR = 6.5cm and ∠Q = 60°.

Steps of construction:

• Draw a line segment QR = 6.5 cm.
• Using a protractor, draw ∠PQR = 60°.
• With Q as centre and radius 4 cm, draw an arc, cutting the ray \(\overrightarrow{\mathrm{QX}}\) at P
• Join RP
• ∆PQR is formed.

→ Construction of a right angled triangle given a base and hypotenuse.
Construct a right angled triangle ABC given that AB = 4 cm, ∠A = 90°, AC = 3 cm.

For making angle 90:

• Take A as center and with any radius, draw an arc intersecting AB at O.
• Now O as center and same radius as before, draw an arc intersecting previous arc at P.
• Now P as center and same radius as before, draw an arc intersecting previous arc at Q.

Steps of Construction:

• Draw a line segment AB = 4 cm. .
• At A, draw an angle of 90° and name the line as AX;
• With A as centre and radius 3 cm, draw an arc cutting the line AX at C.
• Join BC.
• ∆ABC is formed.

→ Construction of a triangle given two angles and a side included between them.
Construct a triangle XYZ in which ∠X = 30°, ∠Y = 100° and XY = 6 cm.

Steps of Construction:

• Draw a line segment XY of length 6 cm.
• Using a protractor, draw ∠YXP = 30° at point X.
• Again using the protractor, draw ∠XYQ = 100° at point Q, intersecting the ray PX at Z.
• ∆XYZ is formed.

→ Counting of Triangles

Students can go through AP Board 7th Class Maths Notes 8th Lesson Exponents and Powers to understand and remember the concept easily.

AP Board 7th Class Maths Notes 8th Lesson Exponents and Powers

→ To make large numbers easy to read, write and understand in a simple man¬ner exponents help us in doing so
Ex: 2 × 2 × 2 × 2× 2 × 2 = 26
a × a × a … ‘n’ times = an

→ Laws of exponents :
For any non-zero integers ‘a’ and ‘b’ and integers ‘m’ and ‘n

• a^m × aⁿ = a^m+n
• (a^m)ⁿ = a^mn

• a^m × b^m = (ab)^m
• a^m ÷ b^m = \(\left(\frac{a}{b}\right)^{m}\)
• a⁰ = 1 (where a ≠ 0)
• (-1)^{even number} = 1
• (-1 )^{odd number} = -1

→ In standard form a number is expressed as the product of largest integer exponent of 10 and any decimal number from 1 to 9.

→ Repeated addition can be expressed as multiplication i.e., if a number ‘a’ is added to itself for n-times we write it as na.
a + a + a + a + ………………… a (n-times) = n.a = na

→ If a number a is multiplied by itself n- number of times, We can express in exponential form.
a . a . a . a . a . a . a . a . a ……………….. (n-times) = aⁿ. This is read as a to the power of n. Here a is called base and n is called exponent.

→ Exponential Form:
Example:

→ A natural number can be expressed in exponential form using its prime factors. Write the given number as product of primes and the express in, exponential form.
Example : 72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
405 = 3 × 3 × 3 × 3 × 5 = 34 × 5

→ Laws of Exponents:

→ Standard form: In standard form, a number is expressed as a product of integer exponent of 10 and a decimal number from 1 to 9.
Example: 8569 = 8.569 × 1000 = 8.569 × 10³

Students can go through AP Board 7th Class Maths Notes 7th Lesson Ratio and Proportion to understand and remember the concept easily.

AP Board 7th Class Maths Notes 7th Lesson Ratio and Proportion

→ Compound Ratio of a: b and c: d is ac: bd.

→ a, b are two quantities if a increases, b also increases or a decreases, b also decreases then a and b are said to be in direct proportion.

→ a and b are in direct proportion, then \(\frac{a}{b}\) = k, where k is proportional constant.

→ a, b are two quantities, if ‘a’ increases, ‘b’ decreases or ‘a’ decreases, ‘b’ increases, then ‘a’ and ‘b’ are said to be in inverse proportion.

→ a and b are in inverse proportion, then a × b = k, where k is proportional constant.

→ Sometimes change in one quantitiy depends upon the change in two or more quantities in some proportion, which is called compound proportion.
1% = 1/100 = 0.01 = 1:100

→ Profit = Selling price – Cost price
Loss = Cost price – Selling price
Profit percentage = \(\frac{\text { profit }}{\text { C.P }}\) × 100

→ Loss percentage = \(\frac{\text { loss }}{\text { C.P }}\) × 100

→ Discount always calculated on marked price

→ Discount = Marked price – Selling

→ Simple Interest I = \(\frac{P \times T \times R}{100}\)

→ Ratio: Comparing two quantities of the same kind by virtue of division is called ‘Ratio’ of these two quantities.

• The ratio of ‘a’ and ‘b’ is a ÷ b or \(\frac{a}{b}\) and is denoted by a: b. and read as ‘a’ is to ‘b’.
• In a: b the first term ‘a’ is called antecedent and the second term ‘b’ is called consequent.
• The terms of the ratio should be expressed in same units.
• Generally a ratio is expressed in its simplest form.
  Ex: The ratio of 200 ml and 3l is?
  200: 3000 = 1: 15

→ Compound ratio: For two or more ratios, if we take antecedent as product of antecedents of the ratios and conse-quent as product of consequents of the ratios, then the ratio thus formed is called mixed or compound ratio.

• When two or more ratios are multiplied term-wise; the ratio thus obtained is called compound ratio.
• The compound ratio of a: b and c: d is ac: bd.
• The compound ratio of a: b, c: d and e: f is ace: bdf and so on.

→ Direct proportion:
Direct proportion is the relationship between two variables whose ratio is equal to a constant value. In other words, the direct proportion is a situation where an increase in one quantity causes a corresponding increase in the other quantity, or a decrease in one quantity results in a decrease in the other quantity.

→ If a and b are in direct proportion, then an increase (decrease) in a causes an increase (decrease) in b at the same rate. This is represented by a ∝ b
\(\frac{a}{b}\) = k or a = kb where k is proportionality constant.

Example:

• If the number of individuals visiting a restaurant increases, earning of the restaurant also increases and vice versa.
• Speed is directly proportional to distance.
• The cost of the fruits or vegetable increases as the weight for the same increase. Indirect proportion: Two quantities a and b are said to be in inverse proportion if an increase in the quantity a, there will be a decrease in the quantity b, and vice-versa. In other words, the product of their corresponding values should remain constant. Sometimes, it is also known as inverse variation.

→ The statement ‘a is inversely proportional to b’ is written as
a ∝ \(\frac{1}{b}\)
ab = k, where k is called proportionality constant.
That is, if ab = k, then a and b are said to vary inversely. In this case, if b₁, b₂ are the values of b corresponding to the values a₁ > a₂ of a respectively, then a₁ b₁ = a₂ b₂ or a₁ / a₂ = b₂ / b₁

Example:

• If speed increases, then the time taken to cover the same distance decreases.
• If number of men increases, then time taken to complete a given work decreases.

→ Compound proportion:
The proportion involving two or more quantities is called Compound propor¬tionality. The quantities could be directlly related or inversely related or both.

Ex.: 195 men working 10 hours a day can finish a job in 20 days. How many men are employed,to finish the job in 15 days if they work 13 hours a day ?
Answer:
Let x be the no. of men required

20 × 10 × 195 = 15 × 13 × x
x = \(\frac{20 \times 10 \times 195}{15 \times 13}\)
= 200 men

→ CASE – 1: If quantity 1 and quantity 2 are directly related and quantity 2 and quantity 3 are also directly related, then we use the following rule:
\(\frac{\mathrm{a} \times \mathrm{b}}{\mathrm{c}}=\frac{\mathrm{d} \times \mathrm{e}}{\mathrm{x}}\)

→ CASE – 2: If quantity 1 and quantity 2 are directly related and quantity 2 and quantity 3 are inversely related, then we use the following rule:
\(\frac{b \times c}{a}=\frac{e \times x}{d}\)

→ CASE – 3: If quantity 1 and quantity 2 are inversely related and quantity 2 and quantity 3 are directly related, then we use the following rule:
\(\frac{a \times b}{c}=\frac{d \times e}{x}\)

→ CASE – 4: If quantity 1 and quantity 2 are inversely related and quantity 2 and quantity 3 are also inversely related, then we use the following rule:
a × b × c = d × e × x

→ Application of percentages: A percentage is a number or ratio that can be expressed as a fraction of 100. If we have to calculate percent of a number, divide the number by whole and multiply by 100. Hence, the percentage means, a part per hundred. The word per cent means per 100. It represented by the symbol %.

• Percentages have no units. Hence it is called a dimensionless/unitless number.
• If we say, 50% of a number, then it means 50 per cent of its whole.

→ Percentage formula: The formula to calculate percentage of a number out of another number is:
Percentage = (Original number/ Another number) × 100
Express the given number as a part of whole or equivalent fraction. Multiply the fraction with 100.
Assign the symbol %.

→ What is the percentage of 45 out of 150?
Answer:
(45/150) × 100 = 30%

→ What is 40% of 120 ?
Answer:
40% of 120
= 40/100 × 120 = 48

→ Cost Price: It is the price at which a product is purchased. It is commonly abbreviated as C.P.
Example: A shopkeeper has bought 1 kg of apples for Rs.100, then C.P of apples is Rs. 100.

→ Selling Price: It is the price at which a product is sold. It is commonly abbre-viated as S.P.
Example:

• A shopkeeper has bought 1 kg of apples for Rs.100. And sold it for Rs. 120 per kg.
• The S.P of apples is Rs.120

→ Profit or gain: If the selling price of a product is more than the cost price, there will be profit in the deal.
Therefore, Profit or Gain = S.P. – C.P

Example: A shopkeeper has bought 1 kg of apples for Rs.100 and sold it for Rs. 120 per kg, then the profit is
S.P. – C.P. = 120 – 100 = Rs. 20

→ Loss: If the selling price of a product is less than the cost price, the seller will incur a loss. Therefore,
Loss = C.P – S.P.

Example: A shopkeeper has bought 1 kg of apples for Rs.100 and sold it for Rs. 80 per kg, then the loss is
C.P. – S.P = 100 – 80 = Rs. 20.
The profit percent or loss percent is always calculated as some percent of cost price.

→ Profit percentage = (Profit/Cost Price) × 100
Example: A shopkeeper has bought 1 kg of apples for Rs. 100 and sold it for Rs. 120 per kg then the profit percent is?
= (Loss / Cost price) × 100

Example: A shopkeeper has bought 1 kg of apples for Rs.100 and sold it for Rs. 80 per kg. then the loss percent is ?
Loss percent = \(\frac{\text { C.P-S.P. }}{\text { C.P. }}\) × 100%
= \(\frac{100-80}{100}\) × 100%
= \(\frac{20}{100}\) × 100% = 20%

→ Marked Price Formula (M.P): The price shown on an item is called its marked price. This is basically labelled by shop-keepers to offer a discount.

→ Discount: Discount is often given as a percent on C.P.
Discount = Marked Price – Selling Price

Discount percent = \(\frac{\text { M.P. }-\text { S.P. }}{\text { M.P. }}\) × 100%

→ Simple Interest: Sum lent or borrowed is called the Principle denoted by P. Time after which a loan is repaid is called the Time Period denoted by T.
The extra amount to be paid on a loan at the end of agreed time period is always expressed as a percent on P and is known as Rate of interest denoted by R%.

So Interest = R% of P for T years
= R × \(\frac{\mathrm{P}}{100}\) × T = \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}\)

Amount = Principle + Interest
= P + \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}\) = P\(\left(1+\frac{\mathrm{TR}}{100}\right)\)

Students can go through AP Board 7th Class Maths Notes 5th Lesson త్రిభుజాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 5th Lesson త్రిభుజాలు

→ మూడు సరళ రేఖలచే ఏర్పడిన సరళ సంవృత సమతల పటమును త్రిభుజం అంటారు.

→ భుజముల ఆధారంగా, త్రిభుజములు మూడు రకములు. అవి :

1. సమబాహు త్రిభుజం,
2. సమద్విబాహు త్రిభుజం,
3. విషమబాహు త్రిభుజం.

→ కోణములు ఆధారంగా త్రిభుజములు మూడు రకములు. అవి :

1. అల్పకోణ త్రిభుజం,
2. అధికకోణ త్రిభుజం,
3. లంబకోణ త్రిభుజం.

→ త్రిభుజములో అంతర కోణముల మొత్తము 180°.

→ ఒక త్రిభుజంలో బాహ్యకోణం, దాని అంతరాభిముఖ కోణముల మొత్తమునకు సమానము.

→ త్రిభుజములో భుజముల కొలతల ధర్మాలు :

• ఒక త్రిభుజంలో ఏవైనా రెండు భుజముల మొత్తము, మూడవ భుజం కన్నా ఎక్కువ.
• ఒక త్రిభుజములో ఏ రెండు భుజముల భేదమైన మూడవ భుజం కన్నా తక్కువ.

→ త్రిభుజము : మూడు రేఖా ఖండాలతో ఏర్పడిన సరళ సంవృత పటాన్ని త్రిభుజము అంటారు.

త్రిభుజంలోని భాగాలు : మూడు శీర్షాలు, మూడు కోణాలు, మూడు భుజాలు.
త్రిభుజం ABC లో (AABCలో)
మూడు శీర్షాలు : A, B మరియు C
మూడు కోణాలు : A, B మరియు ∠C (లేదా) ∠BAC, ∠ABC మరియు ∠BCA
మూడు భుజములు : \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}\) మరియు \(\overline{\mathrm{CA}}\)

→ త్రిభుజాల వర్గీకరణ : త్రిభుజాలను

• భుజాల కొలతను బట్టి,
• కోణాలను బట్టి రెండు విధాలుగా విభజిస్తారు.

→ భుజాల కొలతల ఆధారంగా, త్రిభుజాలను మూడు రకాలుగా వర్గీకరించవచ్చు. అవి :
1. సమబాహు త్రిభుజం : అన్ని భుజాలు సమానంగా ఉన్న త్రిభుజమును సమబాహు త్రిభుజం అంటారు.
ఉదా :
(i) ∆ARC లో.
AB = BC = CA = 3 సెం.మీ.

(ii) ∆PQRలో PQ = QR = RP

2. సమద్విబాహు త్రిభుజం : రెండు భుజాలు సమానంగా ఉన్న త్రిభుజమును సమద్విబాహు త్రిభుజం అంటారు.
ఉదా :
(i) ∆KLM లో KM = ML = 2.5 సెం.మీ.

(ii) ∆XYZ లో,
XY = XZ

→ విషమబాహు త్రిభుజం : ఏ రెండు భుజాలు సమానంగా లేని త్రిభుజమును విషమబాహు త్రిభుజము అంటారు.
ఉదా :
(i) ∆DEF లో
DE ≠ EF ≠ FD

(ii) ∆STU లో
ST ≠ TU ≠ US

→ కోణాల కొలతల ఆధారంగా త్రిభుజాలను మూడు రకాలుగా వర్గీకరించవచ్చును. అవి :
1. అల్పకోణ త్రిభుజం : త్రిభుజము యొక్క అన్ని కోణాలు అల్పకోణములుగా గల త్రిభుజమును అల్పకోణ త్రిభుజం అంటారు. ఉదా :

2. లంబకోణ త్రిభుజం : త్రిభుజములో ఒక కోణం లంబకోణం గల త్రిభుజమును లంబకోణ త్రిభుజం అంటారు.
ఉదా

3. అధికకోణ త్రిభుజం : త్రిభుజములో ఒక కోణం అధిక కోణంగా గల త్రిభుజమును అధిక కోణ త్రిభుజం అంటారు.
ఉదా :

→ త్రిభుజ అంతరకోణాల మొత్తము-ధర్మము : త్రిభుజం లోని మూడు అంతర కోణాల మొత్తం 180°.
∆ABC లో ∠A + ∠B + ∠C = 180°.

ఒక లంబకోణ త్రిభుజంలో లంబకోణేతర కోణాలు రెండూ అల్పకోణాలు మరియు ఆ రెండు కోణాలు పూరకాలు. అనగా ఆ రెండు కోణాల మొత్తము 90°. ∆ABC లో, ∠B = 90°. కనుక ∆ABC ఒక లంబకోణ త్రిభుజము.

∆ABC లో ∠A + ∠C = 90°.

→ త్రిభుజ బాహ్యకోణ ధర్మము : ఒక త్రిభుజంలోని బాహ్య కోణము, దాని యొక్క అంతరాభిముఖ కోణాల మొత్తమునకు సమానము.

∆ABC లో ∠ACD = ∠A + ∠B

→ త్రిభుజము యొక్క భుజాల అసమానత్వ ధర్మాలు :
i) ఒక త్రిభుజంలోని ఏవైనా రెండు భుజాల మొత్తం మూడవ భుజం కన్నా ఎక్కువ.

∆ABC లో,

• AB + AC > BC
• BC + AC > AB
• AB + BC > AC

(ii) ఒక త్రిభుజంలోని ఏ రెండు భుజాల భేదము, మూడవ భుజం కన్నా తక్కువ.

• AB – BC < AC
• BC – AC < AB
• AC – AB < BC

→ త్రిభుజ భుజాలకు మరియు కోణాలకు మధ్య గల సంబంధము :
(i) ఏ త్రిభుజంలో అయిన అతి చిన్న కోణమునకు ఎదురుగా ఉన్న భుజము, మిగిలిన రెండు భుజాల కన్నా చిన్నది. అలాగే

(ii) ఏ త్రిభుజంలో అయిన అతి పెద్ద కోణమునకు ఎదురుగా గల భుజము మిగిలిన రెండు భుజాల కన్నా పెద్దది.

∆ABC లో, ∠A = 120°, ∠B = 35°, ∠C = 25°
∠C కోణము అతి చిన్నది. కావున ∠C కి ఎదురుగా గల భుజము BC మిగిలిన AC, AB కన్నా చిన్నదిగా ఉంటుంది.
∠C < ∠B కావున \(\overline{\mathrm{AB}}<\overline{\mathrm{AC}}\) మరియు
∠C < ∠A కావున \(\overline{\mathrm{AB}}<\overline{\mathrm{BC}}\) అలాగే ∠A కోణము అతి పెద్ద కోణము. కావున ∠A కు ఎదురుగా గల భుజం \(\overline{\mathrm{BC}}\) మిగిలిన రెండు భుజాల కన్నా పెద్దది. ∠A > ∠B కావున \(\overline{\mathrm{BC}}<\overline{\mathrm{AC}}\) మరియు ∠A > ∠C కావున \(\overline{\mathrm{BC}}<\overline{\mathrm{AB}}\).

→ లంబకోణ త్రిభుజంలో లంబకోణము (90°) మిగిలిన కోణాల కన్నా పెద్దది. కావున 90° గా గల కర్ణము. మిగిలిన రెండు భుజాల కన్నా పెద్దది.
∆ABC లో,
∠B = 90° కావున ∠B కి ఎదురుగా గల భుజం AC (కర్ణము) అతి పెద్ద భుజము అవుతుంది.

(iii) ఒక త్రిభుజంలో సమాన కోణాలకు ఎదురుగా గల భుజాలు సమానము. అలాగే సమాన భుజాలకు ఎదురుగా గల కోణాలు సమానము.

3 cm సమద్విబాహు త్రిభుజం సమద్విబాహు త్రిభుజంలో, PQ = PR కావున ∠R = ∠Q అలాగే ∠Q = ∠R కావున PQ = PR అవుతుంది.

సమబాహు త్రిభుజం సమబాహు త్రిభుజంలో ప్రతికోణము సమానము. అనగా ప్రతికోణము .60. ∠A = ∠B = ∠C = 60° మరియు BC = AC = AB

Students can go through AP Board 7th Class Maths Notes 4th Lesson రేఖలు మరియు కోణాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 4th Lesson రేఖలు మరియు కోణాలు

→ యూక్లిడ్ (323 – 283 BC) ఒక .గ్రీకు గణిత శాస్త్రవేత్త. ఆయన “రేఖాగణిత పితామహుడు”గా ప్రసిద్ధి చెందాడు. ఆయన “ఎలిమెంట్స్” అనే పేరుతో ఒక పుస్తకాన్ని రచించెను. ఇది రేఖాగణితాన్ని గురించి వివరించే 13 పుస్తకాల సమాహారం. గణిత శాస్త్ర చరిత్రలో “ఎలిమెంట్స్” అత్యంత ప్రభావితమైన రచన. ఆయన తన పుస్తకాల్లో అనేక స్వీకృతాలను ఉపయోగించి అనేక సిద్ధాంతాలను వివరించారు. ఈ సిద్ధాంతాలు యూక్లిడియన్ జ్యామితి అధ్యయనంలో ఇప్పటికీ ఉపయోగించబడుతున్నాయి.

→ రెండు కోణాల మొత్తం 90° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి పూరక కోణాలు అంటారు.

→ రెండు కోణాల మొత్తం 180° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంపూరక కోణాలు అంటారు.

→ రెండు కోణాల మొత్తం 360° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంయుగ్మ కోణాలు అంటారు.

→ రెండు కోణాలు ఉమ్మడి శీర్షం, ఉమ్మడి భుజం కలిగి ఆ రెండు కోణాలు ఉమ్మడి భుజానికి చెరోవైపున ఉన్నచో వాటిని ఆసన్న కోణాలు అంటారు.

→ రెండు ఆసన్న కోణాల మొత్తం 180° అయినచో వాటిని రేఖీయ కోణాల జత లేదా రేఖీయ ద్వయం అని అంటారు.

→ రెండు సరళరేఖలు ఒకదానికొకటి ఖండించుకొన్నప్పుడు, ఆ ఖండన బిందువు వద్ద ఏర్పడిన అభిముఖ కోణాల – జతను శీర్షాభిముఖ కోణాలు అని అంటారు.

→ శీర్షాభిముఖ కోణాలు సమానం.

→ రెండు లేదా అంతకంటే ఎక్కువ సరళరేఖలను విభిన్న బిందువుల వద్ద ఖండించే సరళరేఖను తిర్యక్ రేఖ అంటారు.

→ ఒక జత సమాంతర రేఖలు p, q లను ఒక తిర్యగ్రేఖ r ఖండించినప్పుడు, ఏర్పడిన కోణాలు ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 మరియు ∠8 అని అనుకొనుము.

→ ఒక తిర్యక్ రేఖ ఒక జత సరళరేఖలను ఖండించినపుడు,

→ పూరక కోణాలు : రెండు కోణాల మొత్తం 90° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి పూరక కోణాలు అంటారు.
ఉదా : 50° కు పూరకకోణం 40°
అలాగే 40° కు పూరక కోణం 50°
(ఎందుకనగా 50° + 40° = 90°)
x° కు పూరకకోణము 90 – x° అవుతుంది.

→ సంపూరక కోణాలు : రెండు కోణాల మొత్తం 180° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంపూరక కోణాలు అంటారు.
ఉదా : 50° కు సంపూరకకోణం 130°
అలాగే 130° కు సంపూరకకోణం 50°
(ఎందుకనగా 50° + 130° = 180°)
x°కు సంపూరక కోణము 180 – x అవుతుంది.

→ సంయుగ్మ కోణాలు : రెండు కోణాల మొత్తం 360° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంయుగ్మ కోణాలు అంటారు.
ఉదా : 50° కు సంయుగ్మకోణము 310°
అలాగే 310° కు సంయుగ్మకోణము 50°
x° కు సంయుగ్మకోణము 360 – x° అవుతుంది.

→ ఆసన్న కోణాలు : రెండు కోణాలకు ఉమ్మడి శీర్షం, ఉమ్మడి భుజం కలిగి ఆ రెండు కోణాలు ఉమ్మడి భుజానికి చెరోవైపున ఉన్నచో వాటిని ఆసన్న కోణాలు అంటారు.
ఉదా 1:

∠AOX మరియు ∠BOXలకు ఉమ్మడి శీర్షము – ‘O’
ఉమ్మడి భుజం – OX
ఉమ్మడి భుజం OXకు ∠AOX మరియు ∠BOX లు చెరొకవైపు కలవు.
కావున ∠AOX మరియు ∠BOX లు ఆసన్న కోణాలు.

ఉదా 2:

పటం – 1 లో ‘O’ ఉమ్మడి శీర్షం అయితే ∠AOB మరియు ∠XOY లకు ఉమ్మడి భుజం లేదు. కావున ఈ రెండు కోణాలు ఆసన్న కోణాలు కావు.

పటం – 2 లో ఉమ్మడి భుజం PM మరియు ∠KPM, ∠MQL లు భుజం PM కు చెరొకవైపు కలవు. కాని రెండు కోణాలకు ఉమ్మడి శీర్చం లేదు.
కావున ∠KPM మరియు ∠MQL లు ఆసన్న కోణాలు కావు.

→ రేఖీయ కోణాల జత (లేదా) రేఖీయ ద్వయం : రెండు ఆసన్న కోణాల మొత్తం 180° అయినచో వాటిని రేఖీయ కోణాల జత లేదా రేఖీయ ద్వయం అని అంటారు.
∠AOB మరియు ∠BOC లు ఆసన్న కోణాలు BO మరియు వాని మొత్తం 45° + 135° = 180°.
కావున, ∠AOB మరియు ∠BOC లు రేఖీయ కోణాల జత లేదా రేఖీయ ద్వయం.
ఉదా :

→ శీర్షాభిముఖ కోణాలు : రెండు సరళరేఖలు ఒకదానికొకటి ఖండించుకొన్నప్పుడు, ఆ ఖండన బిందువు వద్ద ఏర్పడిన అభిముఖ (ఆసన్నం కానటువంటి) కోణాలను శీర్షాభిముఖ కోణాలు అని అంటారు.
ఉదా :

∠AOB, ∠COD లు ఒక జత ∠BOC, ∠AOD లు మరొక జత శీర్షాభిముఖ కోణాలు. శీర్షాభిముఖ కోణాలు ఎప్పటికీ ఆసన్నకోణాల జత కావు. c శీర్షాభిముఖ కోణాలు ఎల్లప్పుడూ సమానము.

→ తిర్యక్ రేఖ : రెండు లేదా అంతకంటే ఎక్కువ సరళరేఖలను విభిన్న బిందువుల వద్ద ఖండించే సరళరేఖను తిర్యక్ రేఖ అంటారు.
ఉదా :

l, m సరళరేఖలను n సరళరేఖ, P మరియు Q అనే వేర్వేరు బిందువుల వద్ద ఖండిస్తున్నది. కావున n తిర్యక్ రేఖ.

→ తిర్యక్ రేఖతో ఏర్పడే కోణాలు, కోణాల జతలు :

→ సమాంతర రేఖలపై తిర్యగ్రేఖలో ఏర్పడే కోణాల ధర్మాలు :
(i) సదృశ కోణాల ధర్మం : ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన సదృశ కోణాలు సమానము.
(∠1, ∠5) మరియు (∠2, ∠6) లు రెండు జతల సదృశ కోణాలు.
∠1 = ∠5 మరియు 22 = 26.

(ii) ఏకాంతర కోణాల ధర్మం : ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన ఏకాంతర కోణాలు సమానము. ప్రక్కపటంలో (∠3, ∠5) మరియు (∠4, ∠6) లు రెండు జతల ఏకాంతర కోణాలు.

∠3 = ∠5 మరియు ∠4 = ∠6.

→ తిర్యగ్రేఖకు ఒకేవైపు గల అంతరకోణాల ధర్మం : “ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన తిర్యగ్రేఖకు, ఒకేవైపు గల అంతరకోణాలు సంపూరకాలు”. అనగా ఆ రెండు కోణాల మొత్తం 180°.

∠3 + ∠6 = 180°
∠4 + ∠5 = 180°
అలాగే తిర్యగ్రేఖకు ఒకేవైపు గల బాహ్య కోణాలు సంపూరకాలు.

∠1 + ∠8 = 180°
∠2 + ∠7 = 180°

→ ఒక జత రేఖలను తిర్యగ్రేఖ ఖండించడం వలన ఏర్పడే

• సదృశకోణాల జత సమానం అయితే అవి సమాంతరాలు.
• ఏకాంతర కోణాల జత సమానం అయితే అవి సమాంతరాలు.
• ఏక బాహ్య కోణాల జత సమానం అయితే అవి సమాంతరాలు అలాగే
• సహ అంతర కోణాలు సంపూరకాలు అయిన అవి సమాంతరాలు.
• సహ బాహ్య అంతర కోణాలు సంపూరకాలు అయిన అవి సమాంతర రేఖలు.

Students can go through AP Board 7th Class Maths Notes 3rd Lesson సామాన్య సమీకరణాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 3rd Lesson సామాన్య సమీకరణాలు

→ భాస్కర – 2 : ప్రాచీన భారతదేశపు ప్రసిద్ధ గణిత శాస్త్రజ్ఞుడు. అతను 1150 A.D. లో 36 సంవత్సరాల వయస్సులో సిద్ధాంత శిరోమణి రాశాడు మరియు ఈ’ రచన (సుమారు 1450 శ్లోకాలను కలిగి ఉంది). నాలుగు భాగాలుగా విభజించబడింది.

1. లీలావతి (ARITHMETIC) లో 278 శ్లోకాలు ఉన్నాయి.
2. జగణితం (ALGEBRA) గణితంలో 213 శ్లోకాలు ఉన్నాయి.
3. గోలాధ్యయ (గోళ | ఖగోళ భూగోళం) 451 శ్లోకాలను కలిగి ఉంది. మరియు
4. గ్రహగణిత్ (గ్రహాల గణితం)లో 501 శ్లోకాలు ఉన్నాయి.

ఒక చరరాశిలో రేఖీయ సమీకరణాలు (సామాన్య సమీకరణాలు), ఒకటి కంటే ఎక్కువ చరరాసులలో రేఖీయ సమీకరణాలు వాటి సాధనాల మీద ఎక్కువ పరిశోధనలు చేసారు.

→ భాస్కర – 2 లీలావతి గణితంలో వ్రాసిన ఒక సమస్య :
“తేనెటీగల సమూహంలో ఐదవ భాగం కదంబ పువ్వు మీద, మూడవవంతు సిలిండా పువ్వు మీద విశ్రాంతి తీసుకుంది. ఈ రెండు సంఖ్యల మధ్య తేడాకు మూడు రెట్లు తేనె టీగలు క్రుతాజా పువ్వుపైకి ఎగిరాయి. మరియు ఒక తేనెటీగ ఒంటరిగా గాలిలో ఉండిపోయింది. అయిన సమూహంలో ఎన్ని తేనెటీగలు ఉన్నాయి ?

→ ‘ = ‘ గుర్తును కలిగిన అనిశ్చిత వాక్యాన్ని సమీకరణం అంటారు.

→ ఒకే చరరాశి గల సమీకరణంలో గరిష్ఠ ఘాతాంకం 1 అయితే అటువంటి సమీకరణాన్ని సామాన్య సమీకరణం అంటారు.

→ సమీకరణంను తృప్తిపరచే చరరాశి యొక్క విలువను సాధన లేదా సమీకరణం యొక్క మూలం అంటారు.

→ సామాన్య సమీకరణాలు సాధించేటపుడు పాటించే నియమాలు :
(a) సమీకరణం ఇరువైపులా ఒకే విలువను కలుపడం వలన సమీకరణంలో ఎటువంటి మార్పు ఉండదు.
(b) సమీకరణం ఇరువైపులా ఒకే విలువను తీసివేయడం వలన సమీకరణంలో ఎటువంటి మార్పు ఉండదు.
(c) సమీకరణం ఇరువైపులా ఒకే విలువతో గుణించడం వలన సమీకరణంలో ఎటువంటి మార్పు ఉండదు.
(d) సమీకరణం ఇరువైపులా ఒకే విలువ (0 శూన్యేతర సంఖ్య)తో భాగించడం వలన సమీకరణంలో ఎటువంటి మార్పు ఉండదు.

→ సమీకరణంలో ఒక వైపునున్న పదాన్ని మరొక వైపుకు మార్చే ప్రక్రియను పక్షాంతరం అంటారు. పక్షాంతరం చెందినపుడు గుర్తును మార్చి, సమీకరణం యొక్క మరొక వైపుకు తీసుకువెళతాము.
ఈ విధంగా, LHS నుండి RHS కు పదాలను మార్చడంలో

• ‘ + పరిమాణం’ ‘ – పరిమాణం’ అవుతుంది.
• ‘-‘ పరిమాణం’ ‘ +’ పరిమాణం’ అవుతుంది.
• ‘×’ పరిమాణం’ ‘ ÷’ పరిమాణం’ అవుతుంది.
• ‘÷’ పరిమాణం’ ‘ ×’ పరిమాణం’ అవుతుంది.

→ సమీకరణం : సమానత్వపు గుర్తు ‘=’ ను కలిగిన అనిశ్చిత వాక్యాన్ని సమీకరణం అంటారు.
ఉదా :

• 3x + 5 = 20
• x² + 4x + 5 = 3x³ -9 .
• 3x + 4y = 9
• x – 2y = 37

→ సామాన్య (సరళ) సమీకరణం : ఒకే చరరాశి గల సమీకరణంలో చరరాశి గరిష్ఠ ఘాతాంకం 1 అయితే అటువంటి సమీకరణాన్ని సామాన్య సమీకరణం అంటారు.
ఉదా :

• x + 5 = 12
• 2y + 9 = 3y + 1
• 3m – 15 = 3
• p + 2 =6

→ సాధన లేదా మూలం : ఒక సమీకరణమును తృప్తిపరిచే చరరాశి యొక్క విలువను ఆ సమీకరణం యొక్క సాధన లేదా మూలం అంటారు.
ఉదా : x + 3 = 5
x = 2 అయినపుడు (2) + 3 = 5 అవుతుంది.
అనగా x + 3 = 5 సమీకరణం X = 2 అయినపుడు సత్యమవుతుంది. కావున, x + 3 = 5 సమీకరణం యొక్క సాధన లేదా మూలం 2 అవుతుంది.

→ L.H.S (Left Hand Side) : సమీకరణంలో సమానత్వపు గుర్తుకు ఎడమవైపు గల సమీకరణ భాగాన్ని L.H.S అంటారు.
ఉదా : 2x-3 = x + 4 సమీకరణంలో 2x-3 అనేది L.H.S అవుతుంది.

→ R.H.S (Right Hand Side) : సమీకరణంలో సమానత్వపు గుర్తుకు కుడివైపు గల సమీకరణ భాగాన్ని R.H.S అంటారు.
ఉదా : 2X – 3 = x + 4 సమీకరణంలో x + 4 అనేది R.H.S అవుతుంది.

→ సామాన్య సమీకరణాన్ని సాధించు పద్ధతులు :

1. చరరాశిని వేరు చేసి సాధించడం.
2. పడ్డాంతర పద్ధతి.

(1) చరరాశిని వేరు చేసి సాధించు పద్ధతిలో పాటించే నియమాలు :
() సమీకరణం ఇరువైపులా ఒకే విలువను కలుపడం వలన సమీకరణంలోని సమానత్వపు గుర్తులో ఎటువంటి మార్పు రాదు.
ఉదా : x – 9 = 71
ఇరువైపులా 9ని కలుపగా

(ii) సమీకరణం ఇరువైపులా ఒకే విలువను తీసివేయడం వలన సమీకరణంలోని సమానత్వపు గుర్తులో ఎటువంటి మార్పు రాదు.
ఉదా : x + 4 = 9
ఇరువైపులా 4ను తీసివేయగా .

(iii) సమీకరణంలో ఇరువైపులా ఒకే విలువతో గుణించడం వలన సమీకరణంలోని సమానత్వపు గుర్తులో ఎటువంటి మార్పు ఉండదు.
ఉదా : \(\frac{x}{4}\) = -2
ఇరువైపులా 4తో గుణించగా

∴ x = -8

(iv) సమీకరణంలో ఇరువైపులా ఒకే విలువ (‘0’ కాని సంఖ్య)తో భాగించడం వలన సమీకరణంలోని సమానత్వపు గుర్తు మారదు.
ఉదా : 4x = 8
ఇరువైపులా 4తో భాగించగా
4x ÷ 4 = 8 ÷ 4

x = 2

(2) పక్షాంతర పద్ధతి (Method of transposition) : సమీకరణంలో సమానత్వపు గుర్తుకు ఒక వైపు గల పదాన్ని లేదా రాశి మరొక వైపుకు మార్చే ప్రక్రియను పక్షాంతరం అంటారు. ఈ విధంగా సాధనను కనుగొను పద్దతిని పక్షాంతర పద్దతి అంటారు. పదాన్ని లేదా రాశిని పక్షంతరం చేసినపుడు పదం లేదా రాశి యొక్క గుర్తులు క్రింది విధంగా మారుతాయి.

→ పదాన్ని లేదా రాశిని i) LHS నుండి RHS కు లేదా ii) RHS నుండి LHS కు మార్చడంలో

• ‘+’ గుర్తు గల పదం, ‘ ‘ గుర్తు గల పదంగా
• ‘-‘ గుర్తు గల పదం, ‘+’ గుర్తు గల పదంగా,
• ‘×’ గుర్తు గల రాశి, ‘÷’ గుర్తు గల రాశిగా
• ‘÷’ గుర్తు గల రాశి, “×” గుర్తు గల రాశిగా మారుతుంది.

ఉదా : 5x + 8 = 2x-7 ను సాధించండి.
5x = 2x-1-8 (+8 ని LHS నుండి RHS కు పక్షాంతరం చేశాము..)
5x = 2x – 15
5x – 2x = -15 (+ 2x ను RHS నుండి LHS కు పక్షాంతరం చేశాము.)
3x = -15
x =- 15 ÷ 3 (×3 ని LHS నుండి RHS కు పక్షాంతరం చేశాము. )

∴ x = -5

→ తుల్య సమీకరణాలు : ఒకే సాధనను కలిగిన సమీకరణాలను తుల్య సమీకరణాలు అంటారు.
ఉదా :

• x – 4 = 2
• 2x = 12

పై మూడు సమీకరణాలకు సాధన x = 6. కావున, పై మూడు సమీకరణాలను తుల్య సమీకరణాలు అంటారు.

Students can go through AP Board 7th Class Maths Notes 2nd Lesson భిన్నాలు మరియు దశాంశాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 2nd Lesson భిన్నాలు మరియు దశాంశాలు

→ జాన్ నేపియర్ (1550 – 1617): మెర్కిస్టన్‌కు చెందిన జాన్ నేపియర్ 1550వ సంవత్సరంలో జన్మించాడు. ఆనాటి సంప్రదాయం ప్రకారం అతను 13 సంవత్సరాల వయస్సులో తన సాధారణ విద్యను అభ్యసించాడు. అయినప్పటికీ అతను కొద్ది కాలంలోనే పాఠశాలకు వెళ్లడం మానివేసి యూరప్ వెళ్ళాడు. అతను 21 సంవత్సరాల వయస్సులో స్కాట్లాండుకు తిరిగి వచ్చాడు.

‘జాన్ నేపియర్’ ఖగోళశాస్త్రం యొక్క సుదీర్ఘ గణనలు చేయుటలో ఎక్కువ గంటలు గడుపుట వున్న సమస్యలను అధిగమించే క్రమంలో ‘లాగరిథం’లను కనుగొన్నాడు. అతను ‘నేపియర్ పట్టీలు’ అని పిలవబడే వాటిని కనుగొన్నాడు. అవి కాలిక్యులేటర్లుగా ఉపయోగించబడే పరికరాలు. ‘నేపియర్’ దశాంశ బిందువు వాడకాన్ని ప్రారంభించడం ద్వారా దశాంశ భిన్నం యొక్క ఆలోచనలను విస్తృతం చేశాడు. ఈ పద్ధతి బ్రిటన్ అంతటా చాలా సాధారణమైంది. ‘నేపియర్’ గణితం మరియు ఖగోళ శాస్త్రంలో చేసిన కృషికి ప్రత్యేకంగా గుర్తింపు పొందాడు. అతను 1617 సంవత్సరంలో మరణించాడు.

→ భిన్నాలను కలపడానికి లేదా తీసివేత చేయుటకు అవి ఒకే హారం కలిగి ఉండాలి. (సజాతి భిన్నాలు)

→ భిన్నాల గుణకారం చేయుట కొరకు, మనం వాటి లవాలను లవాలతోను మరియు హారాలను హారాలతోను గుణిస్తాం.

→ ఒక భిన్నాన్ని మరో భిన్నంతో భాగించాలంటే, ఒక భిన్నాన్ని మరో భిన్నం యొక్క గుణకార విలోమంతో గుణించాల్సి ఉంటుంది.

→ దశాంశ సంఖ్యలను 10, 100, 1000తో గుణించాలంటే, సంఖ్య మరియు భాగఫలం యొక్క అంకెలు ఒకే విధంగా ఉంటాయి. అయితే, 1 తరువాత సున్నాల సంఖ్యకు సమానంగా దశాంశ బిందువును కుడివైపుకు మార్చండి.

→ రెండు దశాంశ సంఖ్యలను గుణించినపుడు లబ్దంలో దశాంశ స్థానాల సంఖ్య, గుణించబడిన సంఖ్యల దశాంశ స్థానాల సంఖ్యల మొత్తానికి సమానం.

→ ఒక దశాంశ సంఖ్యను 10, 100 లేదా 1000 తో భాగించేటప్పుడు, సంఖ్య మరియు భాగఫలం యొక్క అంకెలు ఒకే విధంగా ఉంటాయి. అయితే, 1 తరువాత సున్నాల సంఖ్యకు సమానంగా దశాంశ బిందువును ఎడమ వైపుకు మార్చండి.

→ భిన్నం: భిన్నం అనగా మొత్తంలో కొంత భాగం.

→ క్రమభిన్నం: హారం కన్నా లవము చిన్నదిగా గల భిన్నము.
ఉదా: \(\frac{1}{4}, \frac{5}{7}, \frac{12}{17}\)…………….

→ అపక్రమ భిన్నం: హారం కన్నా లవము పెద్దదిగా గాని, సమానంగా గాని గల భిన్నము.
ఉదా: \(\frac{7}{5}, \frac{17}{12}, \frac{3}{3}\)…………….

→ మిశ్రమ భిన్నము: పూర్ణాంకము మరియు క్రమ భిన్నములను కలిగిన భిన్నము.
ఉదా: \(2 \frac{1}{3}, 3 \frac{2}{5}, 10 \frac{4}{7}\)…………..

→ సజాతి భిన్నాలు: ఒకే హారాన్ని కలిగిన భిన్నాలు.
ఉదా: \(\frac{7}{5}, \frac{3}{5}, \frac{14}{5}\)………….

→ భిన్నాల సంకలనం మరియు వ్యవకలనం:
(i) భిన్నాలను కలపడానికి లేదా తీసివేత చేయుటకు అవి ఒకే హారాన్ని కలిగి ఉండాలి. అనగా అవి సజాతి భిన్నాలై ఉండాలి.
ఉదా: \(\frac{3}{4}+\frac{2}{4}=\frac{3+2}{4}=\frac{5}{4}\)
\(\frac{3}{4}-\frac{2}{4}=\frac{3-2}{4}=\frac{1}{4}\)

(ii) సజాతి భిన్నాలు కానిచో మొదట ఇచ్చిన భిన్నాలను సజాతి భిన్నాలుగా మార్చి తరువాత కలపడం లేదా తీసివేయడం చేయాలి.
ఉదా: \(\frac{3}{4}+\frac{1}{6}\)
(హారాన్ని 4, 6 ల క.సా.గు. 12 కు పెంచాలి).
\(\frac{3 \times 3}{4 \times 3}+\frac{1 \times 2}{6 \times 2}=\frac{9}{12}+\frac{2}{12}=\frac{9+2}{12}=\frac{11}{12}\)

→ భిన్నాల గుణకారం: భిన్నాల గుణకారం చేయుట కొరకు మనం వాటి లవాలను గుణించి, లబ్దం భిన్నం యొక్క లవంగాను, హారాలను గుణించి ఫలిత భిన్నం హారంగాను రాస్తాము.
ఉదా:

• \(\frac{3}{4} \times \frac{1}{6}=\frac{3 \times 1}{4 \times 6}=\frac{3}{24}\)
• \(\frac{3}{4} \times \frac{2}{7} \times \frac{5}{3}=\frac{3 \times 2 \times 5}{4 \times 7 \times 3}=\frac{30}{84}\)

→ భిన్నాల భాగహారం: ఒక భిన్నాన్ని మరొక భిన్నంతో భాగించాలంటే, భాగింపబడుతున్న భిన్నాన్ని భాగిస్తున్న భిన్నం యొక్క గుణకార విలోమంతో (వ్యుత్తమం)తో గుణించాలి.

ఉదా:
\(\frac{3}{4} \div \frac{2}{5}\) (\(\frac{3}{4}\) ను \(\frac{2}{5}\) యొక్క గుణకార విలోమం \(\frac{5}{2}\) తో గుణించాలి).

→ దశాంశ భిన్నాలు: హారం 10, 100, 1000 (10 యొక్క ఘాత సంఖ్యలు) …………. గా గల భిన్నాలు.

ఉదా:
\(\frac{3}{10}, \frac{7}{100}, \frac{834}{1000}, \frac{76}{10}\),…………..
\(\frac{3}{10}\) = 0.3, \(\frac{7}{100}\) = 0.07, \(\frac{834}{1000}\) = 0.834, \(\frac{76}{10}\) = 7.6, ……….

దశాంశ భిన్నాలను దశాంశ సంఖ్యలు అని కూడా అనవచ్చును.

→ దశాంశ సంఖ్యలు – స్థానవిలువలు:

ఉదా: 495.836 = 4 × 100 + 9 × 10 + 5 × 1 + 8 × \(\frac{1}{10}\) + 3 × \(\frac{1}{100}\) + 6 × \(\frac{1}{1000}\)
= 400 + 90 + 5 + \(\frac{8}{10}+\frac{3}{100}+\frac{6}{1000}\)
దీనినే మనం దశాంశ సంఖ్యల విస్తరణ రూపం అని అంటాము.
495.836 లో 3 యొక్క స్థాన విలువ \(\frac{3}{100}\)

→ దశాంశ సంఖ్యల గుణకారం: రెండు దశాంశ సంఖ్యలను గుణించినపుడు లబ్దంలో దశాంశ స్థానాల సంఖ్య గుణించబడిన సంఖ్యల దశాంశ స్థానాల సంఖ్యల మొత్తానికి సమానం.

ఉదా:
2.64 × 3.6 = 9.504 (రెండు దశాంశ సంఖ్యలలోని దశాంశ స్థానాలు 2 మరియు 1. కావున, లబ సంఖ్యలోని దశాంశ స్థానాలు, 2 + 1 = 3)

→ దశాంశ సంఖ్యలను 10, 100, 1000 లతో గుణించాలంటే, సంఖ్య మరియు లబ్దం యొక్క అంకెలు ఒకే విధంగా ఉంటాయి. అయితే 1 తరువాత సున్నాల సంఖ్యకు సమానంగా దశాంశ బిందువును కుడివైపుకు మార్చాలి.

ఉదా:
253.746 × 100 = 25374.6
1 తరువాత రెండు సున్నాలు కలవు. కావున, దశాంశ బిందువును రెండు అంకెలు కుడివైపుకు జరపాలి. అనగా 4 తరువాత దశాంశ బిందువును ఉంచాలి.

→ దశాంశ సంఖ్యలను 10, 100, 1000, …………….. లతో భాగించినపుడు సంఖ్య మరియు భాగఫలం యొక్క అంకెలు ఒకే విధంగా ఉంటాయి. అయితే 1 తరువాత సున్నాల సంఖ్యకు సమానంగా దశాంశ బిందువును ఎడమవైపుకు మార్చాలి.

ఉదా:
253.746 ÷ 100 = 2.53746

Students can go through AP Board 7th Class Maths Notes 6th Lesson Data Handling to understand and remember the concept easily.

AP Board 7th Class Maths Notes 6th Lesson Data Handling

→ Dr. Caiyampudi Radhakrishna Rao (C.R. Rao) – India:
A wellknown statistician, famous for his theory of estimations. He worked on Cramer – Rao Inequality and Fisher – Rao theorem. His schooling was completed in Gudur, Nuzvid, Nandigama and Visakhapatnam. He studied M.A (Mathematics) in Andhra University. He obtained a Ph.D.Degree under the guidance of Sir R.A. Fisher.

→ The information either in form of pictures, numbers or words is called ‘Data’.

→ Based on the method of collecting information the data is divided into two different types namely ‘Primary, data’ and ‘Secondary data’.

→ The difference between maximum and minimum values of data is its ‘Range’.

→ The most common representative or Central Tendency Value of a grouped data is average or Arithmetic Mean.

→ Arithmetic Mean = \(\frac{\text { Sum of observations }}{\text { Number of observations }}\)

→ Arithmetic Mean of given data always lies between the lowest and highest observations in the data.

→ The observation which occurs most frequently in the given data is ‘Mode’.

→ Data having only one mode is Unimodal data and data having two modes is Bimodal data.

→ The middle most value of the data when the observations are arranged in either ascending or descending order is called Median.

→ If number of observations(n) is odd, then Median is \(\left(\frac{\mathrm{n}+1}{2}\right)^{\text {th }}\) observations.

→ If number of observations(n) is even, then median is average of \(\left(\frac{\mathrm{n}}{2}\right)^{\text {th }}\) and \(\left(\frac{\mathrm{n}}{2}+1\right)^{\mathrm{th}}\) observations.

→ Representation of numerical data by using bars of uniform width is Bar graph.

→ Representation of two sets of numerical data on the same graph by using bars of uniform width is Double bar graph.

→ A Pie chart is the representation of the numerical data by sectors of the circle such that angle of each sector (area of sector) is proportional to value of the given data.

→ Angle of sector = \(\frac{\text { Value of the item }}{\text { Sum of the values of all items }}\) × 360°

→ Data : The information which collected either in the form of numbers, words or pictures is called Data.
Example : Marks obtained by a class at EA are 23, 35, 48, 30, 25, 46, 13, 27, 32, 38,

→ Primary data : The data collected directly through personal experiences, interviews, direct observations, physical testing etc., is called primary data. It is also described as raw data or first hand information.

Example :

• Performance of your class in Mathematics.
• Performance of India in football or in cricket.
• Number of children below the age of five in the families around you.

→ Secondary data : Secondary data is the information which has been collected in the past by someone else but used by the investigator for his own purpose. The sources of secondary data are books, journals, newspapers, websites etc.

Example :

• Collection of village population details from census register.
• Female literacy rate in a given area.

→ Measures of Central Tendency : A measure of central tendency is a single value that attempts to describe a set of data by identifying the central position within that set of data. The mean, median and mode are all valid measures of central tendency, but under different conditions, some measures of central tendency become more appropriate to use than others.

→ Arithmetic Mean: The mean (or average) is the most popular and well known measure of central tendency. The average or Arithmetic Mean (A.M.) or simply mean is defined as follows:
Mean = \(\frac{\text { Sum of all observations }}{\text { Number of observations }}\)

Example : Sita studies for 4 hours, 5 hours and 3 hours respectively on three consecutive days. How many hours does she study daily on an average? ‘
Answer:
The average study time of Sita = \(\frac{\text { Total number of study hours }}{\text { Number of days for which she studied }}\)
= \(\frac{4+5+3}{3}=\frac{12}{3}\)
= 4 hours per day.
Thus, we can say that Sita studies for 4 hours daily on an average.

In general, mode is used to find the representative value of verbal data.
Example: To know the most popular game among the students of a class.
Find the mode of the data 5, 9, 6, 8, 6, 3, 6, 7, 2, 1, 17, 8 & 3.
Answer:
As 6 occurs more frequently than other observations, Mode = 6.

• Data having only one mode is called unimodal data.
• Data having two modes is called bimodal data.
• If no observation in the data is repeated then we say that the given data has no mode.
• If each observation in the data is repeated an equal number of times, then we say that the given data has no mode.

→ Median: In some situations, arithmetic mean is an appropriate measure of central tendency whereas in some other situations, mode is the appropriate measure of central tendency. Let us now look into the situations where median is appropriate measure of central tendency.

The median is the middle score for a given data that has been arranged in order of magnitude i.e. either in ascending order or in descending order. The median is less affected by maximum and minimum values of the data.

Let us consider the data below:

We first need to rearrange that data into order of magnitude (smallest first):

Our median mark is the middle mark – in this case, 56 (highlighted in bold). It is the middle mark because there are 5 scores before it and 5 scores after it.
If the number of observations is even then we simply have to take the middle twro scores and average the result.

Now look at the example below:

We again rearrange that data into order of magnitude (smallest first):

Only now we have to take the 5th and 6th score in our data set and average them to get a median of 55.5.
If there are n-observations in the given data, then
Median = \(\left(\frac{n+1}{2}\right)^{t h}\) observation, if n is odd
= average of \(\left(\frac{\mathrm{n}}{2}\right)\) and \(\left(\frac{\mathrm{n}}{2}+1\right)\) observations.

→ The 3 most common measures of central, tendency are the mean, median and mode. The mode is the most frequent value. The median is the middle number in an ordered data set. The mean is the sum of all values divided by the total number of values.

→ Visual representation of the data: Data represented in the form of pictures, graphs or charts is visual data.

→ Bar graphs: Representation of numerical data by using bars of uniform width is called “Bar. Graph”.
In bar graphs the width of all bars or rectangles is equal and the height of each bar is proportional to the data that it represents.
Example : Bar graph showing the dates of births of a class during the months of a year.

→ Double bar graph :

• A double bar graph is used to display two sets of data on the same graph.
• From a double bar graph we can compare the two groups of observations in a single look.

Example: A double bar graph showing the number of boys and girls in a primary school.

→ Pie charts: A circle is divided into sectors to represent the given data is called a pie diagram or pie chart.
Or
Pie chart is the visual representation of the numerical data by sectors of a circle such that angle of each sector (area of sector) is proportional to the value of data that it represents.

Example :
Pie charts showing

Angle of sector = \(\frac{\text { Value of the item }}{\text { Sum of values of all item }}\) × 360

→ Letter Series :
Letter series is a logical arrangement of English alphabetical letters arranged in a specific pattern. In this series of letters, groups of letters, combination of letters and numbers are given. Each letter or group is called term. The terms of a series are arranged in a particular order or pattern. We have to identify the pattern and find the missing term (next term) from the alternatives, which will satisfy the pattern. Assigning numbers to the alphabets is very useful to practice letter series.

Example 1.
B, D, F, H, ________
(1)1
(2) K
(3) J
Answer:
(3) J

Explanation:

Example 2.
A, B, D, E, G, ________
(1) H
(2) I
(3) K
Answer:
(1) H

Explanation:

Example 3.
Z,X, U, Q, ________
(1) M
(2) K
(3) N
(4) L
Answer:
(4) L

Explanation:

Example 4.
QPO, NML, KJI, ________, EDC
(1) KL
(2) GHI
(3) CAB
(4) HGF
Answer:
(4) HGF

Explanation:
This series consists of letters in a reverse alphabetical order.
So, answer should be ‘HGF’.

Example 5.
AB, DE, HI, MN, ________
(1) TV
(2) TU
(3) ST
(4) RS
Answer:
(3) ST

Explanation:

So, in the series next word is ‘ST’.

Example 6.
AB, EF, IJ, MN, ________
(1) QR
(2) OP
(3) XY
(4) PQ
Answer:
(1) QR

Explanation:

So, in the series next word is ‘QR.

Example 7.
B2, D4, F6, H8, J10, ________
(1) L12
(2) K11
(3) N14
(4) M13
Answer:
(1) L12

Explanation:
Alternate letters with their assigned numbers. So, answer is L12.

Example 8.
AFK, BGL, CHM, DIN, ________
(1) GJO
(2) FIO
(3) EJO
(4) GJN
Answer:
(3) EJO

Explanation:
Each group next letter is forwarding 5th letter.
So, answer is ‘EJO’.

Students can go through AP Board 7th Class Maths Notes 5th Lesson Triangles to understand and remember the concept easily.

AP Board 7th Class Maths Notes 5th Lesson Triangles

→ A triangle is a simple closed plane figure made up of three line segments. .

→ Based on the sides triangles are of three types.

1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle

→ Based on the angles, triangles are of three types.

1. Acute angled triangle
2. Obtuse angled triangle
3. Right angled triangle

→ The sum of the three interior angles in a triangle is 180°.

→ The exterior angle of a triangle is equal to the sum of it’s opposite interior angles.

→ Properties of the lengths of the sides of a triangle:

• The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
• The difference between the lengths of any two sides of a triangle is smaller than the length of the third side.

→ Triangle: A simple closed figure formed by three line segments is called a triangle. In the figure ABC is a triangle.

• A, B, C are its corners known as vertices.
• ∠A, ∠B & ∠C are called its interior angles,
• AB, BC & CA are called its sides.
• Side opposite to ∠A is BC, also denoted by a.
• Side opposite to ∠B is AC, also denoted by b,
• Side opposite to ∠C is AB, also denoted by c.

→ Types of Triangles:
(i) Equilateral triangle: All 3 sides and angles are equal.

(ii) Isosceles triangle: 2 equal sides and 2 equal angles.

(iii) Scalene triangle: Has no equal sides or angles.

(iv) Acute angled triangle: All 3 angles re acute.

(v) Right angled triangle: Has 1 right angle.

(vi) Obtuse angled triangle: Has 1 Abtuse angle.

Note: The sides with equal lengthifBfS! denoted by same number of strokes (/), similarly for equal angles also.

• In an equilateral triangle all the three sides and each angle is equal to 60°.
• In an isosceles triangle two sides are equal.
• In an isosceles triangle angles opposite to equal sides are equal.
• Conversely in an isosceles triangle sides opposite to equal angles are equal.
• In a right angled triangle the side opposite to right angle is called hypotenuse.
• Hypotenuse is the longest side of a right triangle.

→ Angle sum property of a triangle:
The sum of three interior angles of a triangle is equal to 180°

∠A + ∠B + ∠C = 180°

→ Exterior angle property of a triangle:
If in a triangle any side is produced angle, then formed is called its exterior angle.

In ∆ABC, BC is produced to D, then ∠ACD is called exterior angle.

→ Exterior Angle Theorem: The exterior angle of a triangle is equal to the sum of the two opposite interior angles.

Example:

→ Inequality properties of a triangle:

→ In any ∆ABC, sum of any two sides is always greater than the third side. If AB, BC & CA are the sides of the triangle, then

• AB + BC > CA c + a > b
• BC + CA > AB a + b > c
• CA + AB > BC b + c > a

→ Also the difference between any two sides of a triangle is always less than the third side.

• AB – BC < CA c – a < b
• BC – CA < AB a – b < c
• CA – AB < BC b – c < a

→ In a triangle, if two sides are given, then the side opposite to greater angle is greater than the other.

→ In a triangle, if two sides are given, then the side opposite to smaller angle is smaller than the other.

→ Also in a triangle, if two angles are given,.then the angle opposite to greater side is greater than the other.

→ In a triangle, if two angles are given, then the angle opposite to smaller side is smaller than the other.

→ The perpendicular line segment from any vertex to its opposite side is called altitude.

Height = length of the altitude
Area = space inside the triangle

Students can go through AP Board 7th Class Maths Notes 4th Lesson Lines and Angles to understand and remember the concept easily.

AP Board 7th Class Maths Notes 4th Lesson Lines and Angles

→ Euclid (323 – 283 BC) was a Greek mathematician. He is well known as ‘Father of Geometry.’ He wrote a book named ‘Elements’ which was a collection of 13 volumes, dealing with geometry. ‘Elements’ was most influenced work in the history of mathematics. In his books he deduced many theorems using axioms. These theorems are being used in the study of Euclidean geometry.

→ If the sum of two angles is 90°, then the angles are called as complementary angles to each other.

→ If the sum of two angles is 180°, then the angles are called as supplementary angles to each other.

→ If the sum of the two angles is 360°, then the angles are called as conjugate angles to each other.

→ Two angles are said to be adjacent angles, if they have a common vertex, common arm and lie on either side of the common arm.

→ A pair of adjacent angles whose sum is 180° are called as linear pair of angles.

→ When two straight lines intersect, the opposite angles at the point of intersection are called as vertically opposite angles.

→ Vertically opposite angles are equal.

→ A transversal is a straight line that intersects two or more straight lines at distinct points.

→ When a transversal intersects a pair of parallel lines p and q, let the angles formed be ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.

→ When a transversal intersects two lines,

→ Types of angles:

→ Parallel lines: Two or more lines are said to be parallel if they never meet each other however long they are produced.

→ Intersecting lines: Two lines are said to be intersecting if they meet at a point or meet at a point if they are produced.

→ Perpendicular lines: Two lines are said to be perpendicular if they meet at right angles. In other words the angle between them is 900.

→ Pairs of Lines in a Plane:
Intersecting Lines: Lines that cross each other \(\overleftrightarrow{\mathrm{AB}}\) intersects \(\overleftrightarrow{\mathrm{PQ}}\) at C.

→ Parallel Lines: Lines that do not touch. They are always the same distance apart. \(\overrightarrow{\mathrm{AB}} \| \overleftrightarrow{\mathrm{PQ}}\)

→ Perpendicular Lines: Lines that cross a right angles. \(\overrightarrow{\mathrm{AB}} \perp \overleftrightarrow{\mathrm{PQ}}\)

→ Pair of angles:
(i) Complementary angles:

Two angles whose sum is 90°.
Examples: (52°, 38°), (50°, 406), (68°, 22°) 180°

(ii) Supplementary angles: Two angles whose sum is 180°

Examples: (52°, 128°), (50°, 130°), (68°, 112°)

(iii) Explementary or Conjugate angles: Two angles whose sum is 360°.

Examples: (132°, 228°), (150°, 210°), (168°, 192°)

• Complementary angles are always acute.
• In a pair of complementary angles no angle is obtuse.
• Two acute angles can’t be supplementary.
• Two obtuse angles can’t be supplementary.

→ In a pair of supplementary angles one angle must be obtuse or both are right angles.

→ Adjacent angles: Two angles are said to be adjacent if they have

• a common vertex
• a common arm
• and the two angles lie on either side of the common arm.

Example:

Angle ADB and Angle BDC share a common vertex of D and have a common side of DB.

• The interior of adjacent angles must have no common points.
• The adjacent angles need not be complementary or supplementary.

→ Linear pair of angles: A pair of adjacent angles whose sum is 180° is called a pair of linear angles.

• A linear pair of angles must be supplementary.
• A pair of supplementary angles need not necessarily be a linear pair.

→ Vertically opposite angles: When a pair of straight lines intersect each other, the pairs of opposite angles thus formed at the point of intersection are called vertically opposite angles.

→ When a pair of lines intersects each other, the pairs of vertically opposite angles thus formed are equal.

→ Transversal: A transversal is a straight line that intersects two or more straight lines at distinct points. Here are two lines l₁ and l₂ is a transversal.

→ Two or more lines are said to be con current if they pass through a common point i.e., they intersect at a point.

• Here the lines AB, CD and EF are concurrent lines since they intersect at a common point O.
• If two or more lines do not intersect at a common point, then they are non-concurrent.

→ Angles made by a transversal: When a transversal t intersects a pair of lilies ‘l’ and ‘m’, there form eight angles.

→ Interior angles: Angles lying between the two lines are called interior angles. Here, ∠3, ∠4, ∠5 and ∠6 are interior angles.

→ Exterior angles: Angles lying outside the two lines are called exterior angles. Here ∠1, ∠2, ∠7 and ∠8 are exterior angles.

→ Corresponding angles: Two angles are said to form a pair of corresponding angles if

• One is interior and other is exterior
• They are not adjacent
• They lie on the same side of the transversal.

Here the pairs are (∠1 and ∠5), (∠2 and ∠6), (∠3 and ∠7), (∠4 and ∠8).

→ If lines are parallel then the pairs of corresponding angles become equal. (∠1 = ∠5), (∠2 = ∠6), (∠3 = ∠7), (∠4 = ∠8)
Conversely if a transversal intersects a pair of straight lines making corresponding angles equal, then the lines are parallel.

→ Alternate interior angles: Two angles are said to form a pair of alternate interior angle, if

• both are interior
• they are not adjacent
• they lie on the either side of the transversal.

Here the pairs are (∠1 and ∠7), (∠2 and ∠8).
If lines are parallel, then the pairs of alternate interior angles become equal.
(∠1 = ∠7), (∠2 = ∠8).

Conversely, if a transversal intersects a pair of straight lines making alternate exterior angles equal, then the lines are parallel.

→ Alternate exterior angles: Two angles are said to form a pair of alternate exterior angle if

• both are exterior
• they are not adjacent
• they lie on the either side of the transversal.

Here the pairs are (∠3 and ∠4), (∠5 and ∠6).
If lines are parallel, then the pairs of co-interior angles become supplementary.
(∠3 + ∠4 = 180°), (∠5 + ∠6 = 180°). Conversely if a transversal intersects a pair of straight lines making co-interior angles supplementary, then the lines are parallel.

→ Co-interior angles: Interior angles on same side of transversal are co-interior angles.

• both are interior
• they are adjacent
• they lie on the either side of the transversal.

Here the pairs are (∠3 and ∠5), (∠4 and ∠6).
If lines are parallel, then the pairs of alternate interior angles become equal.
(∠3 = ∠5), (∠4 = ∠6).
Conversely, if a transversal intersects a pair of straight lines making alternate interior angles equal, then the lines are parallel.

Students can go through AP Board 7th Class Maths Notes 3rd Lesson Simple Equations to understand and remember the concept easily.

AP Board 7th Class Maths Notes 3rd Lesson Simple Equations

→ Bhaskara-II: Bhaskara-II is a famous mathematician of ancient India. He wrote Siddhanta Shiromani at the age of 36 in 1150 A.D. and this work (consisting of about 1450 verses) was divided into four parts.

• Lilavati (ARITHMETIC) has 278 verses.
• Bijaganit (ALGEBRA) has 213 verses.
• Goladhyaya (sphere/celestial globe) has 451 verses.
• Grahaganit (mathematics of the planets) has 501 verses.

Linear equations in one variable and several variables were one of the equations that Bhaskara II was interested in, and he presented many problems below one problem is an example to illustrate it.

MA fifth part of a swarm of bees came to rest on the flower of Kadamba, a third on the flower of Silinda. Three times the difference between these two numbers flew over a flower of Krutaja, and one bee alone remained in the air, attracted by the perfume of a jasmine in bloom. Tell me, beautiful girl, how many bees were in the swarm ?

→ An open sentence which contain sign “ = ” is called an equation.

→ An equation which involves only one variable whose highest power 1 is known as simple equation.

→ Solution of simple equation or root of simple equation: The value of the variable for which equation becomes true is called the solution or the root of the equation.

→ The equation remains unchanged if:
(a) The same number is added to both sides of the equation.
(b) The same number is subtracted from both sides of the equation.
(c) The same number is multiplied to both sides of the equation.
(d) The same non-zero number divides both sides of the equation.

→ The process of changing the term from one side of the equation to other side is called transposition.

→ So, by transposing a term we simply change its sign and carry it to the other side of the equation. Thus, in transposing terms from LHS to RHS.

• ‘+ quantity’ becomes ‘-‘ quantity’
• ‘-‘ quantity’ becomes ‘+’ quantity’
• ‘×’ quantity’ becomes ‘÷’ quantity’
• ‘÷’ quantity’ becomes ‘×’ quantity’.

→ Open sentence: A mathematical sentence whose truth value can’t be determined is called as open sentence.
Example: The age of GOPI is more than 12 years.

→ Equation: An open sentence containing an equality (=) symbol is called an equation.
Example: The age of GOPI =12 years.

An equation involving only one variable whose highest power is 1 is known as a simple equation.
Example: 7 + x = 15
a + 3 = 8
8 – y = 3

→ Solution of a simple equation: The value of variable for which the equation becomes
true or equal on both sides is called the solution or root of the simple equation.
Example: 7 + x = 15 becomes true or qqual on both sides when x = 8. Here 8 is called the solution of the simple equation 7 + x = 15.

→ Rules of simple equations:

• The equation remains unchanged if the same number is added on both sides of the equation.
  Example: 7 + x = 15 is same as 10 + x = 18 (adding 3 on both sides)
• The equation remains unchanged if the same number is subtracted from both sides of the equation.
  Example: 7 + x = 15 is same as 4 + x = 12 (subtracting 3 from both sides)
• The equation remains unchanged if both sides of the equation are multiplied by the
  same positive number. ‘
  Example: 7 + x – 15 is same as 14 + 2x = 30 (multiplied by 2 on both sides)
• The equation remains unchanged if the both sides of the equation are divided by a non-zero positive number.
  Example: 7+x = 15 is same as \(\frac{7}{2}+\frac{x}{2}=\frac{15}{2}\) (divided by 2 on both sides).

→ Transposition: The process of transferring the terms of a simple equation from one side to other is called transposition of term.

• When a term is transposed.
• It gets opposite sign.
• It means a positive quantity when transposed it gets a negative sign.
• Similarly, a negative quantity when transposed it gets a positive sign.
• Also when a term multiplying one side of a simple equation is transposed it divides the other side.
• Similarly when a term dividing one side of a simple equation is transposed it multiplies the other side.

→ Solving a real life problem:

• Read the problem carefully and separate knowns and unknowns i.e. identify what is given and what is to be found.
• Represent the unknowns by variables such as x, y, z, …….
• Translate the problem to the language of mathematical statements.
• Form the simple equations using the conditions given in the problem.
• Solve the simple equations.
• Verify the answer.