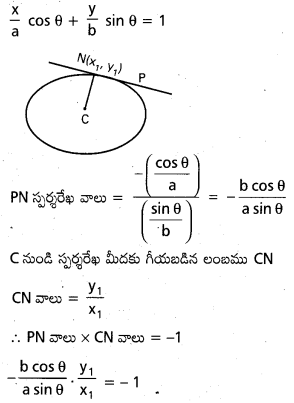
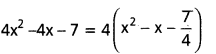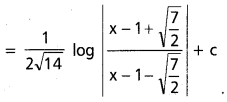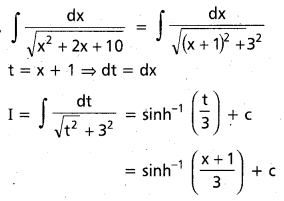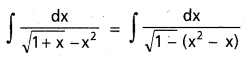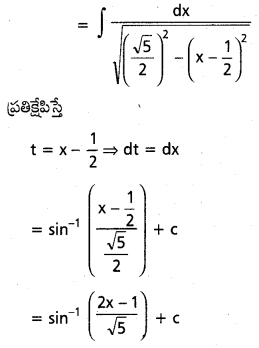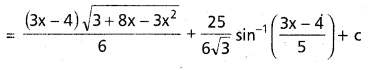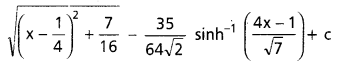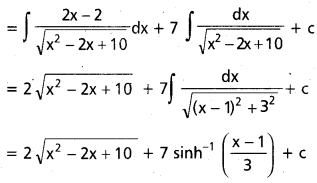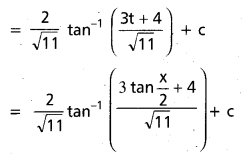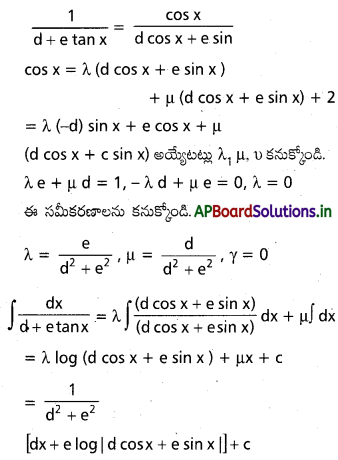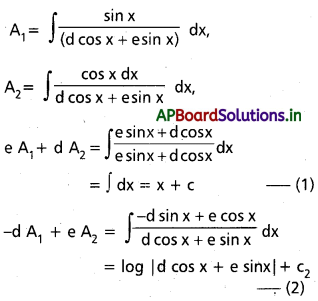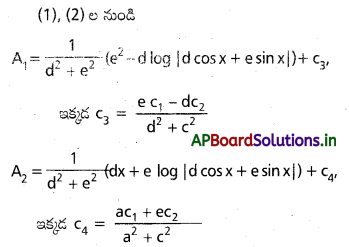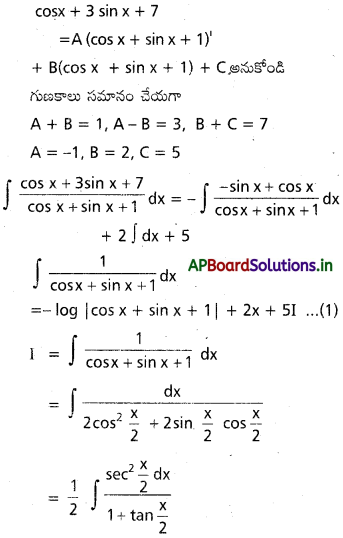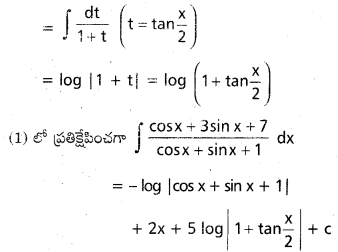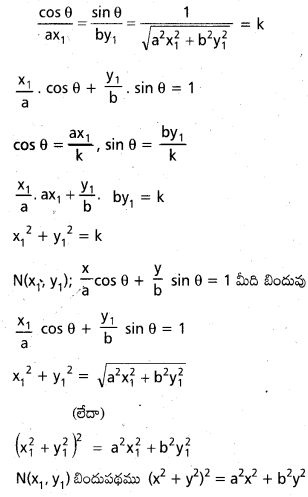Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 1 వృత్తం which are most likely to be asked in the exam.
AP Inter 2nd Year Maths 2B Important Questions Chapter 1 వృత్తం
ప్రశ్న 1.
(1,4) కేంద్రంగా, 5 వ్యాసార్ధంగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
ఇక్కడ (h,k) = (1,4), r = 5 కాబట్టి,
Darodo (x-h)2+(y-k)2
= (x-1)2+(y-4)2 = 52 అంటే,
x2+ y2-2x-8y-8=0.

ప్రశ్న 2.
x2+ y2+2x – 4y – 4 = 0 సూచించే వృత్త కేంద్రాన్న వ్యాసార్ధాన్ని కనుక్కోండి.
సాధన:
ఇక్కడ 2 g=2,2 f=-4, c=-4
∴ g = 1, f = -2,
కాబట్టి వృత్త కేంద్రం = (−g, −f) = (−1, 2)
వ్యాసార్ధాలను \(=\sqrt{g^2+f^2-c}=\sqrt{1+4-(-4)}=3\)
ప్రశ్న 3.
3x2+3y2-6 x+4y – 4 = 0 సూచించే వృత్త కేంద్రం, వ్యాసార్ధాలను కనుక్రోండి.
సాధన:
దత్త సమీకరణము 3 x2+3y2 – 6 x + 4y – 4 = 0
3 తో బించగా

ప్రశ్న 4.
వృత్త కేంద్రం(-1, 2)గా ఉంటూ (5, 6) గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
C = (−1, 2) వృత్త కేంద్రం అనుకొందాం.
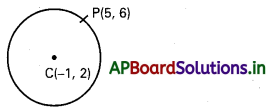
P(5,6) వృత్తము మీది బిందువు కనుక CP = r
CP2 = r 2 ⇒ r2 =(-1-5)2 + (2-0)2
= 36 +16=52
వృత్త సమీకరణము (x + 1)2 + (y – 2)2 = 52
x2 + 2x + 1 + y2 = 4y + 4 – 52 – 0
x2 + y2 + 2x – 4y – 47 = 0

ప్రశ్న 5.
(2,3) బిందువు ద్వారా పోతూ x + y + 8x + 12y + 15 = 0 వృత్తంలో ఏక కేంద్రంగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
కావలసిన వృత్తం దత్త వృత్తానికి ఏక కేంద్రము
x2 + y2 + 8x + 12y + 15 = 0
∴ కావలసిన వృత్త సమీకరణము
x2 + y2 + 8x + 12y + c’ = 0
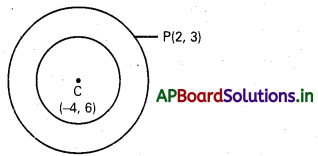
P(2, 3) గుండా వృత్తం పోతుంది.
∴ 4+9+16 +36 + c = 0
c’ = – 65
కావలసిన వృత్త సమీకరణము
x2 + y2 + 8x + 12y – 65 = 0
ప్రశ్న 6.
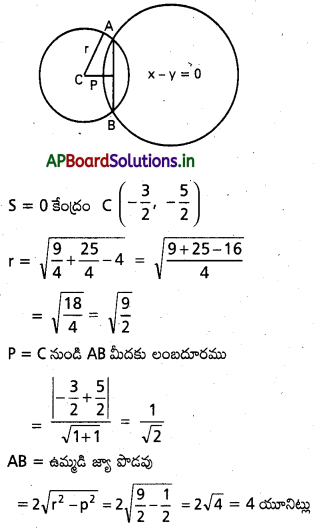
(x2 + 4x + (y – 3)2 = 0 వృత్తంపై ఉన్న బిందువు A(0, 3) నుంచి వృత్తానికి AB అనే జ్యాను గీసి M వరకు AM = 2AB అయ్యేటట్లు పొడిగించబడింది. M బిందువు బిందు పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
M = (x’, y’) అనుకొందాం.
దత్తాంశం ప్రకారం AM = 2AB అని ఇవ్వబడినది.
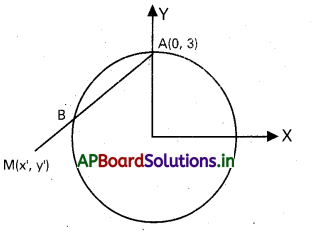
AB + BM = 2AB + AB BM = AB
AM మధ్య బిందువు B

M ( X’ , Y’) బిందు పథము x2+y2+8x-6 y+9=0 ఇది ఒక వృత్తము.

ప్రశ్న 7.
x2+y2+ax+by-12=0 వృత కేంద్రం (2,3) అయితే a, b విలువలను, వృత్త వ్యాసార్థాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము

ప్రశ్న 8.
x2+y2 – 4 x+6 y+a=0 సూచించే వృత్త వ్యాసార్ధం 4 అయితే a విలువను కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
X2 + y2– 4x + 6y +a = 0
2g= – 4, 2f = 6,c = a
g = – 2, f = 3, c = a
వ్యాసార్ధం = 4 ⇒ \(\sqrt{g^2+f^2-c}=4\)
\(\sqrt{4+9-a}=4\)
13 – a = 16
a = 13 – 16 = – 3
ప్రశ్న 9.
(4,1),(6,5) బిందువుల గుండా పోతూ 4 x+y-16=0 రేఖపై కేంద్రం ఉండే వృత్త సమీకరణమును కనుక్కోండి.
సాధన:
కావలసిన వృత్త సమీకరణము
x2+y2+2gx+2fy+c=0
ఈ వృత్తం A(4,1) గుండా పోతుంది.
16+1+8 g+2f+c=0
8g+2f+c=-17
వృత్తం B(6,5) గుండా పోతుంది.
36+25+12 g+10 f+c=0
12g+10 f+c=-61
కేంద్రం (-g,-f), 4 x+y-16=0 రేఖమీద ఉంది
-4 g-f-16=0
4 g+f+16=0
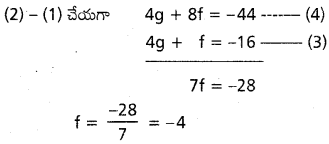
(3) నుండి 4g – 4=-16
4 g=-12 ⇒ g=-3
(1) నుండి 8(-3)+2(-4)+c=-17
c=-17+24+8=15
కావలసిన వృత్త సమీకరణము
x2+y2-6x-8y+15=0

ప్రశ్న 10.
g, f, c వాస్తవ సంఖ్యలి అయి (x1,y1) బిందువు x2+y2+2g x+2 f y+c=0 ను తృప్తిపరిచినట్లంితే ఈ సమీకరణం వృత్తాన్ని సూచిస్తుందని చూపండి.
సాధన:
రెండవ తరగతి సాధారణ సమీకరణంతో పోల్చగా x2 గుణఃమము =y2 గుణకము మరియు xy గుణకం =0 దత్త సమీకాణము వృత్తాన్ని సూచిస్తుంది.
g2+f2-c ≥ 0
(x1,y1) దత్త సమీకరణం మీది బిందువు
x2+y2+2gx+2 f y+c=0,
x12+y12 +2gx1+2fy1+c=0
g2+f2-c=g2+f2+x12+y12
+2g x1+2fy1=0
= (x1 + g)2 + (y1 + f)2≥ 0
g, f, c వాస్తవాలు
∴ దత్త సమీకరణము వృత్తాన్ని సూచిస్తుంది.
ప్రశ్న 11.
(1,2),(4,5)లు వ్యాసాగ్రాలుగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
(x1-y1) = (1,2) మరియు (x2-y2) =(4,5)
వృత్త సమీకరణము
(x-1)(x-4)+(y-2)(y-5)=0
x2-5x+4+y2-7 y+10=0
x2+y2-5 x-7 y+14=0
ప్రశ్న 12.
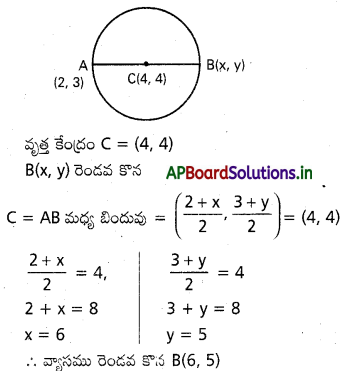
x2+y2-8 x-8 y+27=0 వృత్తం ఒక వ్యాసప ఒక కొన (2,3) అయేతే దీని మరో కొన కనుక్రోండి.
సాధన:
A=(2,3) C వృత్త కేంద్రం అనుకుందాం.
x2+y2-8 x-8y+27=0

ప్రశ్న 13.
ax+by+c=0 (abc ≠ 0) రేఖ అక్షాలతో ఏర్పిిచే త్రిభుజపు పరి:కృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
a x+b y+c=0 రేఖ A మరియు B ల వద్ద నిరూపకాక్షాలను ఖందడి్తుఁడి.
O, A, B నిరూపకాలు 0: (0,0)
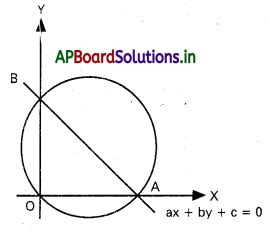
\(A\left(-\frac{c}{a}, 0\right) \quad B\left(0,-\frac{c}{b}\right)\)
కావలసిన వృత్త సమీకరణము x2+y2+2gx+ fy+c=0
ఈ వృత్తం 0(0,0) గుండా పోతుంది
c=0
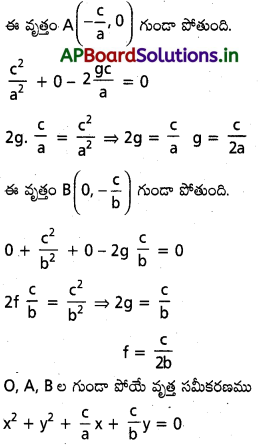
a b(x2+y2)+c(b x+ay)=0
ఇది OAB పరివృత్త సమీకరణము.
ప్రశ్న 14.
L1=x+y+1=0, L2=3 x+y-5=0, L3=2 x+y-5=0 రేఖలతో ఏర్పడే త్రిభుపు శీర్షాల గుండా పోమే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన.:
L1, L2 ; L2, L3 మరియు L3, L1 రేఖలు A, B, C ల వద్ద ఖండించుకోంటున్నాయి. ఇది O, A, B పరివృత్త సమీకరణము క్రింది సమీకరణము గల వక్రాన్ని తీసుకొందాం.
k(x+y+1)(3 x+y-5)+l(3 x+y-5)
(2 x+y-5)+m(2 x+y-5)(x+y+1)=0 …………… (1)
ఈ సమీకరణము వృత్తాన్ని సూచిస్తుంది.
x2 గుణకము = y2 గుణకము
3k + 6l+ 2m k +l+ m
2k+5l+m=0 ………….. (2)
xy గుణకము =0 ………….. (3)
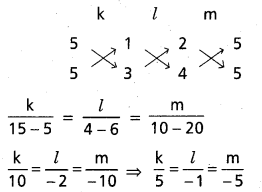
(1) లో ప్రతిక్షేపిస్తే. కావలసిన వృత్త సమీకరణము
5(x+y+ 1)(3x+y-5)-1(3x+y-5)
(2x+y-5)-5(2x+y-5)(x+y+1)=0
(i.e. x2 +y2– 30x – 10y+25 =0
Note : త్రిభుజ శీర్షాలు కనుగొని సమస్యను సాధించవచ్చు.

ప్రశ్న 15.
(0,0),(2,0),(0,2)ల బిందువుల గుండా ఏోయే వృత్త కేంద్రాన్ని కనుక్రోండి.
సాధన.
కావలసిన వృత సమీకరణము
x2+y2+2g x+2fy+c=0
ఈ వృత్తం 0(0,0) c=0 గుండా పోతుంది.
ఈ వృత్తం A(2,0) గుండా పోతుంది.
4+4g=0 ⇒ g =-1
ఈ వృత్తం B(0,2) గుండా పోతుంది.
4+4f=0 ⇒ f=-1
వృత్త కేంద్రం (-g,-f)=(1,1)
ప్రశ్న 16.
x2+y2=1 వృత్తం షొక్కపరామితీయ సమీకరణాలను కనుక్కోండి.
సాధన:
వృత్త సమీకరరణము x2+y2=1
కేంద్రం (0,0), వ్యాసార్ధం =r=1
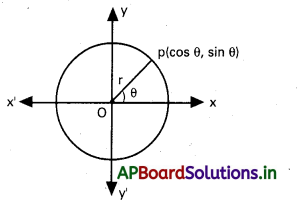
x2+y2=1 పరామితీయ నిరాపకాలు
X = 1 . cos θ = cos θ
y=1. sinθ=sinθ. θ≤θ≤2π
గమనిక : వృత్తం మీది ఏదేని బిందువు నిరూపకాలు
(cosθ , sinθ)
ప్రశ్న 17.
x2+y2+6 x+8 y-96=0 వృత్తానికి పరామితీయ సమీకరణాలు రాయండి.
సాధన.
వృత్త కేంద్రం (-3,-4)
వ్యాసార్ధము =\(\sqrt{9+16+96}=\sqrt{121}=11\)
పరామితీయ సమీకరణాలు
x = h + rcosθ = -3 + 11 cosθ
y=k+r sinθ = -4+11 sin θ
(0 ≤ θ ≤ 2π)
ప్రశ్న 18.
x2+ y2-4x-6y+ 11 = 0 వృత్తం దృష్ట్యా (2,4) బిందువు యొక్క స్థితిని తెలపండి.
సాధన.
(x1, y1) = (2, 4) మరియు
5 ≡ x2+ y2-4x-6y+ 11
S11= 4+16-8-24 +11
= 31- 32 – 1 <0
∴ (2, 4) బిందువు S = 0 లోపల ఉంటుంది.
ప్రశ్న 19.
బిందువు (1, 3) నుంచి x2 + y2 – 2x + 4y 11 =0 వృత్తానికి గీసిన స్పర్శరేఖ పొడవును కనుక్కోండి..
సాధన.
(x1, y1) = (1, 3) మరియు
S = x2 + y2-2x+4y-11 = 0
స్పర్శరేఖ పొడవు \(=\sqrt{S_{11}}\)
\(=\sqrt{1+9-2+12-11}=\sqrt{9}=3\)

ప్రశ్న 20.
P బిందువు నుంచి x2 + y2-2x+4y-20 = 0, x2 + y2-2x-8y + 1 = 0 వృత్తాలకు గీసిన స్పర్శ రేఖల పొడవుల నిష్పత్తి 2:1 అయ్యేటట్లు P చలిస్తుంటే, P బిందు పథ సమకరణము x2 + y2 – 2x – 12y + 8 = 0 అని చూపండి.
సాధన:
(X1, y1) బిందుపథము మీది బిందువులు \(\overline{\mathrm{PT}_1}, \overline{\mathrm{PT}_2}\) నుండి

ప్రశ్న 21.
S ≡ x2+y2+2gx+2fy+c=0 వృత్తాన్ని సూచిస్తే L=lx+my+n=0 సరళేేఖ
(i) s=0 వృత్తాన్ని స్పృశించడానికి నియమము
\(\left(g^2+f^2-c\right)=\frac{(g l+m f-n)^2}{\left(l^2+m^2\right)}\)
(ii) s = 0 వృత్తాన్ని రెండు బిందువులో ఖండించడానికి నియమము
\(g^2+f^2-c>\frac{(g l+m f-n)^2}{\left.l^2+m^2\right)}\)
(iii) s = 0 వృత్తాన్ని స్పృశించకుండా ఖండించకుండా నిహమం ఉండటానికి
\(g^2+f^2-c<\frac{(g l+m f-n)^2}{\left(l^2+m^2\right)}\)
సాధన:
s = 0 సూచించే వృత్త కేంద్రం ఁ అని వ్యాసార్ధం అని అనుకొందాం.
ఇప్పుడు c = (−g, –f), r = \(\sqrt{g^2+f^2-c}\)
(i) s = 0 వృత్తాన్ని దత్త రేఖ స్పృశించడానికి నియమము.
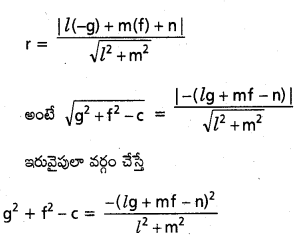
(ii) ఇలాగే దత్త రేఖ lx + my + n = 0 వృత్తం s = 0 రెండో బిందువుతో ఖండించడానికి నియమం
\(\left(\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}\right)>\frac{(\mathrm{g} l+\mathrm{mf}-\mathrm{n})^2}{l^2+\mathrm{m}^2}\)
(iii) lx + my + n = 0 రేఖ s = 0 వృత్తాన్ని స్పృశించకుండా, ఖండించకుండా ఉండటానికి నియమము
\(\left(\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}\right)>\frac{(\mathrm{g} l+\mathrm{mf}-\mathrm{n})^2}{l^2+\mathrm{m}^2}\)
ప్రశ్న 22.
x’ + y + Bx – 4y – 16 = 0 వృత్తం పై 3x − y + 4 = 0 రేఖ ఏర్పరచే జ్యా పొడవును కనుక్కోండి.
సాధన. వృత్త కేంద్రం C= ( 4, 2)
వ్యాసార్ధం r = \(\sqrt{16+4+16}\) = 6
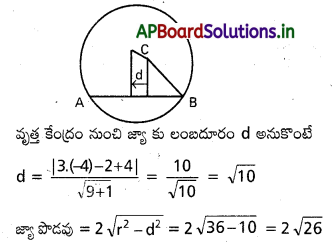
ప్రశ్న 23.
x2+y2-4 x+6 y-12=0 వృత్తానికి x+2 y-8=0 రేఖకు సమాంతరంగా రేఖకు సమాంతరంగా ఉఁడే స్పర్శరేఖ (లు) కనుకోండి.
సాధన:
g = -2, f = 3, c = -12


ప్రశ్న 24.
S ≡ x2+y2+2gx+2fy+c=0 వృత్తం
(i) g2 = C అయితే X అక్షాన్ని స్పృశిస్తుంది.
(ii) f2 = C అయితే Y అక్షాన్ని స్పృతిస్తుంది అని చూపండి.
సాధన:
g2-c>0 అయితే x2+y2+2gx+2fy+c=0
s=0 వృత్తం X – అక్షంపై చేసే అంతరం \(2 \sqrt{g^2-c}\)
ఈ వృత్తం X- అక్షాన్ని స్పృతిస్తే \(2 \sqrt{g^2-c}=0 \mathrm{~g}^2=\mathrm{c}\)
ఇదే విధంగా (ii) నిరూపించవచ్చు.
ప్రశ్న 25.
x2 + y2 – 6x + 4y – 12 = 0 వృత్తానికి (− 1, 1) వద్ద స్పర్శరేఖా సమీకరణాన్ని కనుక్కోండి.
సాధన:
(x1 y1) = (− 1, 1) మరియు
S ≡ x2 + y2– 6x + 4y – 12 = 0
స్పర్శరేఖ సమీకరణము
x (−1) + y . 1 – 3(x 1) + 2(y + 1) 12 = 0
− x + y – 3x + 3 + 2y + 2 – 12 = 0
– 4x + 3y – 7 = 0
(లేదా) 4x – 3y + 7 = 0
ప్రశ్న 26.
(3,-1) బిందువు వద్ద x2+y2-2 x+4y=0 వృత్తానికి స్రర్శరేఖ సమీకరణం కనుక్రొని ఇదే వృత్తానికి దీనికి సమాంతరంగా ఉండే స్ర్శరేఖ సమీకరణం కూడా కనుక్రోండి.
సాధన:
ఇక్కడ (x1, y1)=(3,-1)
S ≡ x2+y2-2 x+4 y=0
స్పర్శరేఖ సమీకరణము (3,-1) వద్ద
x.3 + y (-1)- (x + 3) + 2(y- 1) = 0
3x – y – x – 3 + 2y – 2 = 0
2x + y – 5 = 0
స్పర్శరేఖ వాలు =m=-2, వృత్తానికి g=-1, f=2, c=0
r = \(\sqrt{1+4-0}=\sqrt{5}\)
స్పర్శరేఖల సమీకరణాలు
y+f =m(x+g)±\(\pm r \sqrt{1+m^2}\)
y+2 =-2(x-1)\(\pm \sqrt{5} \sqrt{1+4}\)
y+2 =-2x+2 ± 5
2x + y= ± 5
స్పర్శరరీఖలు
2 x+y+5=0 మరియు 2 x+y-5=0
సమాంతర స్పర్శరేఖ సమీకరణము
2 x+y-5=0

ప్రశ్న 27.
x2+y2-6 x+4 y-12=0$ వృత్తానికి 4 x-3 y+7=0స్పర్శ రేఖ అయితే దీని స్పర్ళ బిందువును కనుక్కోండి.
సాధన.
(x1, y1) స్పర్శ బిందువు అనుకాందాం.
స్పర్శరేఖ సమీకరణము
x(x1 + g) + y(y1 + f) + (gx1 + fy1 + c) = 0
x(x1 – 3) + y (y1 + 2) + (-3x1 + 2y1 -12) = 0 ………………….(1)
దత్త రేఖ సమీకరణము
4 x-3 y+7=0 ………………….(2)
(1) మరియు (2) సమీకరణాలను సరిపోల్చగా

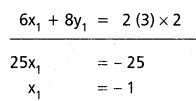
సమీ|| (3) నుండి -3+4 y1=1 ⇒ 4 y1=4y1=1 స్పర్య బిందువు (-1,1)
ప్రశ్న 28.
2 x-3 y+1=0 సరళ రీఖని (1,1) వద్ద స్ప్లశించే \(\sqrt{13}\) యానిట్ల వ్యాసార్ధంతో గల వృత్తాల సమీకరణాలు కనుక్రోండి.
సాధన.
వృత్త కేంద్రాలు (1,1) గుండా పోతూ 2 x-3 y+1=0 రేఖకు లంబంగా ఉండే రేఖ మీద ఉంటాయి.
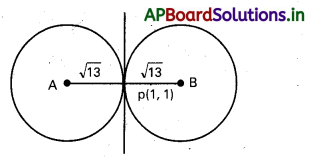
కేంద్రాలు కలిగిన రేఖ
3 x+2 y+k=0
ఈ రేఖ (1,1) గుండా పోతుంది.
3+2+k=0 ⇒ k=-5
AB సమీకరణాలు 3x+2 y-5=0
ఈ కేంద్రాలు (1,1) నుంచి \(\sqrt{13}\)యానిట్ల దూరంలో ఉంటూ 3 x+2 y-5=0 రేఖపై ఉంటాయి. కాబట్టి ఈ కేంద్రాలు
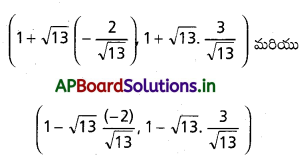
(i.e.) (1-2,1+3) మరియు (1+2,1 – 3) (-1,4) మరియు (3,-2)
సందర్భం (i) :
కేంద్రం (-1,4), r=\(\sqrt{13}\)
వృత్త సమీకరణము
(x + 1)2 + (y-4)2 = 13
x2+2x+1+y2-8y+16-13=0
X2 + y2 + 2x – 8y + 4 = 0
సందర్భం (ii) :
కేంద్రం (3,-2), r=\(\sqrt{13}\)
వృత్త సమీకరణము
(x-3)2 + (y + 2)2 = 13
x2-6x + 9 + y2 + 4y + 4-13 = 0
x2 + y2-6x + 4y = 0
ప్రశ్న 29.
29 x + y – 6x + 4y + 12 = 0 వృత్తాన్ని 5x + 12y – 4 = 0 రేఖ స్పృశిస్తుందని చూపండి.
సాధన.
వృత్త సమీకరణము
x2 + y2 – 6x + 4y + – 12 = 0
కేంద్రము (3, −2), r = \(\sqrt{9+4-12}=1\)
దత్తరేఖ వృత్తాన్ని స్పృశిస్తే కేంద్రం నుండి
లంబదూరము = వ్యాసార్ధము
d= నుండి లంబదూరము (3, -2)
\(=\frac{|5(3)+12(-2)-4|}{\sqrt{25+144}}\)
\(=\frac{13}{13}=1\)= వృత్తంయొక్క వ్యాసార్థం
∴ 5x + 12y – 4 = 0 వృత్తాన్ని స్పృశిస్తుంది.

ప్రశ్న 30.
x + y – 6x + 4y – 12 = 0 వృత్తంపై ఉన్న 30°, 60° ల బిందువులను కలిపే జ్యా సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
x2 + y2 – 6x + 4y – 12 = 0
θ2 – θ1 బిందువులను కలిపే జ్యా సమీకరణము

ప్రశ్న 31.
x2 + y2 + 4x + 6y – 39 = 0 పై బిందువు 30° వద్ద స్పర్శరేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన.
వృత్త సమీకరణము
x2 + y2+4x+6y-39 = 0
g = 2, f = 3, r = \(\begin{aligned}
& =\sqrt{4+9+39} \\
& =\sqrt{52}=2 \sqrt{13}
\end{aligned}\)
θ =30°
స్పర్శరేఖ సమీకరణము
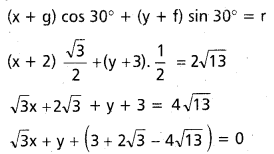
ప్రశ్న 32.
x1 y1 ≠ 0 అయి, x2 + y2 = a2 వృత్తం పై ఉన్న బిందువు P(x1, y1,) వద్ద గీసిన స్పర్శరేఖ నిరూపకాక్షాలతో ఏర్పరిచే త్రిభుజ వైశాల్యాన్ని కనుక్కోండి.
సాధన.
వృత్త సమీకరణము ×2 + y2 = a2
P(x1, y1) వద్ద స్పర్శరేఖ సమీకరణము
xx1 + yy1 = a2 …………………….. (1)
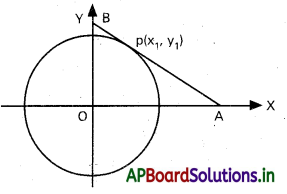
ఈ స్పర్శరేఖ X – అక్షాన్ని A వద్ద, Y- అక్షాన్ని B వద్ద ఖండిస్తుంది.
అంతరఖండ రూపంలోనికి మార్చగా


ప్రశ్న 33.
x2 + y2 – 4x – 6y + 11 = 0 వృత్తానికి (3,2) వద్ద అభిలంబ రేఖ సమీకరణాన్ని కనుక్కోండి. ఇంకా ఈ అభిలంబరేఖ వృత్తాన్ని ఖండించే మరో బిందువును కనుక్కోండి.
సాధన.
వృత్త సమీకరణము
x2+y2+4x+6y+11=O
g = -2, f = – 3, c = 11
వ్యాసార్ధము \(=\sqrt{g^2+f^2-c}\)
\(=\sqrt{4+9-11}=\sqrt{2}\)
అఖిలంబరేఖ సమీకరణము
(x-x1) (y1+f)-(y-y1) (x1+g) = 0
A (3, 2) వద్ద అభిలంబరేఖ
(x-3) (2-3)-(y-2) (3-2)=0
-x+3y+2=0
x+y-5=0
A వద్ద అభిలంబరేఖ వృత్తాన్ని B వద్ద ఖండిస్తే C, AB మధ్య బిందువు
కేం(దం =C(-g,-f)=(2,3)
B(x, y) అయితే
C సిరూపకాలు

ప్రశ్న 34.
x2+y2-22 x-4 y+25=0 వృత్తానికి (3,-4) వద్ద గీసిన అభిలంబరేఖ, అక్షాలతో ఏర్పడే త్ిభజ వైశాల్యాన్ని కనుక్రోండి.
సాధన.
2 g=-22, 2 f=-4, అక్షం
g =-11, f=-2
x1 = 3, y1 = -4
(3, -4) వద్ద అభిలంబ రేఖ సమీకరణము
(x-x1)(y1 + f)-(y-y1)(x1 +g) =0
(x-3) (-4-2)–(y + 4)(3-11) = 0
– 6x + 18 + 8y + 32 = 0
6x-8y-50 = 0
3x-4y-25 = 0 ………………. (1)
3x-4y=25
\(\frac{3 x}{25}+\frac{4 y}{25}=1\)

ప్రశ్న 35.
S = x2+ y2+ 2gx + 2fy + c = 0 lx + my + n =0 రేఖ అఫిలంబ రేఖ కావడానికి ఆవశ్యక, పర్యాప్త నియమము gl + mf = n అని చూపండి.
సాధన.
lx + y + n = 0 రేఖ వృత్తానికి అభిలంబరేఖ
S = x2 + y2+2gx + 2fy + c = 0
⇒ కేం(దం (-g, -f)
lx + my + n = 0 మీద ఉంటుంది.
l(-g)+m(-f) + n = 0
gl + fm = n
ప్రశ్న 36.
S = x2+ y2+2gx + 2fy + c = 0 బాహ్య బిందువు (g, f) నుంచి గీసిన స్పర్శరేఖలు లంబంగా ఉండటానికి నియమం కనుక్కోండి.
సాధన.
P(x1, y1) నుండి 5 = 0 కు గీయబడిన స్పర్శరేఖ
మధ్యశ్లోకోణము 8 అయితే tan \(\left(\frac{\theta}{2}\right)=\frac{r}{\sqrt{s_1}}\)
వృత్త సమీకరణము

Note : ఇక్కడ C<0

ప్రశ్న 37.
x2 +y2 =a2 వృత్తానికి P గుండా గీసిన స్చర్రరీణలుల X – అక్షం గుండా θ1 ,θ2 కోణాలు చేస్తున్నాయి. cot θ1+ cot θ2=k అయ్యే P బిండు పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము x2 +y2 =a2
స్పర్శరేఖ వాలు m అయితే P(x1, y1) గుండా పోమే స్వర్శరేఖ సమీకరణము

P(x1, y1) బిందు పథము 2xy = kiya )
విపర్యంగా P(x1 ,y1) 2xy = k(y2 – a2) నియమాన్ని తృప్తిపరుస్తుంది.
cot θ1 + cot θ2 = k అని చూపవచ్చును.
P బిందు పథము 2xy = k(y2 – a2)
ప్రశ్న 38.
x2 + y2 – 5x + 4y-2 = 0 వృత్తం దృష్ట్వా (2, 5) కు స్పర్శ జ్యా సమీకరణాలను కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
x2 + y2 – 5x + 4y – 2 = 0
S1 = 0 స్పర్శ జ్యా సమీకరణము
P(2, 5) యొక్క స్పర్శరేఖ
x. 2 + y.5 – \(\frac{5}{2}\)(x + 2) + 2 (y + 5) – 20
4x+10y-5x-10+4y+ 20-40
-x+14y+60
(లేదా)x-14y-6 = 0
ప్రశ్న 39.
x2 + y2 = a2 వృత్తం దృష్ట్యా P బిందువు స్పర్శ జ్యా వృత్తాన్ని A,B ల వద్ద ఖండిస్తూ \(\text { AÔB }\) = 90° అయ్యే P బిందువులు x2 + y2 = a2 వృత్తంపై ఉంటాయని చూపండి.
సాధన:
వృత్త సమీకరణము x2 + y2 = a2 ……………… (1)
P(x1, y1) బిందు పథం మీది బిందువు
P స్పర్శ జ్యా సమీకరణము xx1 + yy1 =a2
\(\frac{x_1+y y_1}{a^2}=1\) ……………… (2)
(2) సహాయంతో (1) ని సమఘాతపరిస్తే OA, OB ల ఉమ్మడి సమీకరణము


ప్రశ్న 40.
x2 + y2 + 6x+8y-96=0 వృత్తం దృష్ట్రా P(2, 3) బిందువుకు ధృవరేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
(x1, y1)=(2, 3) ⇒ x1 2, y1 = 3
వృత్త సమీకరణము
x2 + y2+6x+8y-96 = 0
ధృవ రేఖ సమీకరణము S1 = 0
(2, 3) యొక్క ద్యృ రేఖ x. 2 + y. 3 + 3(x+2) +4(y+3)-960
2x + 3y + 3x + 6 + 4y + 12 -96 = 0
5x + 7y-78 = 0
ప్రశ్న 41.
x2 + y2-4x+6y 120 వృత్తం దృష్ట్రా x + y + 2 = 0 రేఖకు ధృవాన్ని కనుక్కోండి.
సాధన:
lx+my+ n = 0 ను x + y + 2 = 0 పోల్చగా
l = 1, m = 1, n = 2
వృత్త సమీకరణము
S ≡ x2 + y24x+6y-12 = 0

ప్రశ్న 42.
x2+y2=a2 వృత్తం స్ర్శరేఖలు (x+a)2+y2 =2 a2 దృష్టాల ధృవరేఖలు అయితే వీటి ధృవాలు y2 +4 a x=0 పై ఉంటాయని చూపండి.
సాధన.
దత్త వృత్తాల సమీకరణాలు
x2+y2=a2 …………….. (1)
మరియు (x+a)2+y2=2a2…………….. (2)
(2) వృత్తం దృష్ట్ల (1) వృత్తం మొక్క స్పర్శరేఖ P(x1, y1) ధృవం అనుకొందాం.
(2) వృత్తం దృష్ట్రా P యొక్క ధృవరేఖ సమీకరణము
xx1+yy1 +a(x+x1) – a2=0
x(x1 +a) + yy1 + (ax1 – a2) = 0
ఈ రేఖలకి స్పర్శరేఖ (1)


ప్రశ్న 43.
x2+y2-24=0 వృత్తం దృష్ట్లా (4,-2),(3,-6) సంయుగ్ళ పిందువులు అని చూపండి.
సాధన.
(x1, y1)=(4,-2) మరియు (x2, y2)=(3,-6) మరియు
S ≡ x2 +y2 2-24=0
(X1, y1), (x2, y2) బిందువులు S=0 దృష్ట్లా సంయుగ్ళ
బిందువులయిత్ S12=0
x1 x2 + Y1 Y2 – 24 = 0
12 = + (-2)(-6)-24
= 12 + 12-24 = 0
∴ దత్త బిందువులు దత్త వృత్తం దృష్ట్రా సంఝుగ్ర బిందువులు
ప్రశ్న 45.
x2+ y2 + 4x + 6y + 12 = 0 వృత్తం దృష్ట్యా 2x + 3y + 11 = 0, 2x – 2y – 1 = 0 రేఖలు సంయుగ్మ రేఖలు అని చూపండి.
సాధన:
l1 = 2, m1 = 3, n1 = 11
l2 = 2, m2 =2, n2 = -1
మరియు g =2, f = 3, c = 12
r =\(\sqrt{9+4-12}\)=1

(2.2 +3.3-11) (2.2-2.3 +11)
=2(-1)=-2
L.H.S. = R.H.S.
సంయుగ్మ రేఖల నియమము తృప్తి పడింది.
∴ దత్తరేఖలు సంయుగ్మరేఖలు
ప్రశ్న 46.
S ≡ x2 + y2 + 2gx + 2fy + c = 0 వృత్తానికి బాహ్య బిందువు అయిన P(x1, y1) నుంచి గీసిన స్పర్శరేఖలు, వీటి స్పర్శ జ్యాతో ఏర్పడే త్రిభుజ వైశాల్యం \(\frac{r\left(S_{11}\right)^{3 / 2}}{S_{11}+r^2}\) (r వృత్త వ్యాసార్ధం) అని చూపండి.
సాధన:
S = 0 కు P నుండి గీయబడిన స్పర్శరేఖలు PA, PB. AB స్పర్శ జ్యా


ప్రశ్న 47.
వృత్తం x2+y2-2 x-10 y+1=0, x-2 y+ 7 =0 రేఖపై ఏర్పరచే జ్యా మర్య బిందువును కనుక్రోండి.
సాధన:
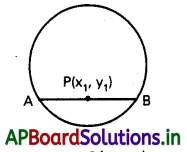
AB జ్యా మధ్య బిందువు P(x1, y1)
జ్యా సమీకరణము S1=S11
xx1+yy1-1(x+x1) – 5(y+y1)+1
= x +y -2x1 – 10y1+1

ప్రశ్న 48.
lx + my + n = 0 రేఖపై ఉన్న బిందువుల నుంచి x2 + y2 = a2 వృత్తానికి గీసిన స్పర్శజ్యాల మధ్య బిందువుల బిందు పథాన్ని కనుక్కోండి.
సాధన:
P = (x1,y1) బిందు పథము P మీది బిందువు
x2 + y2 = a2
జ్యా సమీకరణము
lx+my+ n = 0 ………………… (1)
వృత్త సమీకరణము x2 + y2 = a2
(x1 y1) మధ్య బిందువుగా గల జ్యాసమీకరణము
S1 = S11
xx1 + yy1 = x1 2+ y1 2
xx1 + yy1 – (x1 2+ y1 2) = 0 ………………… (2)


ప్రశ్న 49.
x2+y2– 14 x+6 y+33=0, x2+y2+30 x-2 y+1=0 eకు నాలుగు ఉమ్మడ స్ర్య రేఖలి ఉంటాయని చూపి వీటికి సరూప అంతర కేంద్రం సరూప బాహ్య కేంద్రాలను కనుక్కోండి.
సాధన.
వృత్తాల సమీకరణాలు
x2+y2-14 x+6 y+33=0
మరియు x2+y2+30 x-2 y+1=0
కేంధ్రాలు A(7,-3), B(-15,1)

\(=\left(\frac{6}{4}, \frac{1-9}{4}\right)=\left(\frac{3}{2},-2\right)\)
బాహ్య స్వరూప కేంద్రం S, A B ని బాహ్యంగా 1: 3 నిష్తత్తిలో విభజిస్తుంది.
S నిరూపకాలు
ప్రశ్న 50.
x2+y2 -8 x-6 y+21=0
x2+y2-2y-15=0 వృత్లాలకు రెండే రెండు ఉమ్మడి స్రర్శరేఖలుంటాయని చూపండి. ఇంకా వీటి ఖండన బిందువలను కనుక్రోండి.
సాధన:
C1, C2 లు కేంద్రాలు మరియు r1, r2 లు వ్యాసార్ధాలు వృత్తాల సమీకరణాలు
x2+y2– 8x- 6y+21 =0
k+y2-2y-15 =0
మరియు
C1(4,3), & C2(0,1)


ప్రశ్న 51.
x2+y2-4 x-6 y-12=0 ,x2+y2+6 x+18 y+26=0 వృత్తాల స్పృశించుకుంటాయని చావండి. ఇంకా స్ర్శ బిందువును, స్రాశబిందువు వద్ద ఉమ్మడి స్రర్శరేళను కనుక్కోండి.
సాధన:
వృత్తాల సమీకరణాలు
x2+y2-4x-6y-12 =0
మరియు x2+y2+6x+18y+26 =0
కేంధ్రాలు C1(2; 3), C2(-3, -9)

ప్రశ్న 52.
x2+y2-4 x-6 y-12=0, 5(x2+y2)-8 x-14 y-32=0 వృత్తాల స్పృశించుకుంటాయని చూప స్పర్శ పిందువును కనుక్కోండి.
సాధన:
వృత్లాల సమీకరణాలు
x2+y2-4 x-6 y-12=0

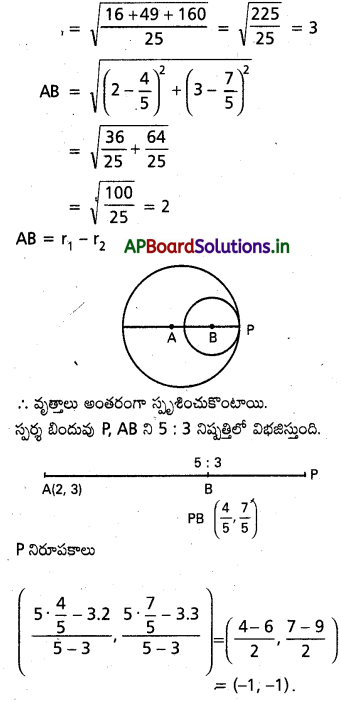

ప్రశ్న 53.
బిందువు (10,4) నుంచి x2+y2=25 వృత్తానికి గీసిన స్పర్శ రేఖా యుగ్మ సమీకరణాన్ని కనుక్కోండి.
సాధన:
(x1, y1)=(10,4)
వృత్త సమీకరణము x2+y2-25=0
స్పర్శరేఖల ఉమ్మడి సమీకరణాలు S1= S.S11
(10x + 4y-25)2
= (100 + 16-25)(x2 +y2– 25)
100x2+ 16y2+625+80xy – 500x – 200y
= 91x2 + 91y2 – 2275
9x2 + 80xy – 75y2 – 500x – 200y + 2900=0
ప్రశ్న 54.
x2 + y2 − 2x – 6y + 6 = 0, x2 + y2 = 1 వృత్తాలకు గల అన్ని ఉమ్మడి స్పర్శరేఖల సమీకరణాలను కనుక్కోండి.
సాధన:
వృత్తాల సమీకరణాలు
x2+ y2 – 2x – 6y + 6 = 0
మరియు x2 + y2 = 1
కేంద్రాలు A(1,3), B(0,0),
r1= \(\sqrt{1+9-6}\) = 2
r2=1
బాహ్యసరూప కేంద్రం S, AB ని బాహ్యంగా 2 1 నిష్పత్తిలో
విభజిస్తుంది.
S నిరూపకాలు
\(\left(\frac{2.0-1.1}{2-1}, \frac{2.0-1.3}{2-1}\right)=(-1,-3)\)
ప్రత్యక్ష ఉమ్మడి స్పర్శరేఖల సమీకరణము
(x2 + y2 – 1) (1 + 9 – 1) = (x + 3y + 1)2
దీనిని క్రింది విధంగా వ్రాయవచ్చును.
(y – 1) (4y + 3x − 5) = 0,
ప్రత్యక్ష ఉమ్మడి స్పర్శరేఖల సమీకరణాలు
y – 1 = 0 మరియు 3x + 4y – 5 = 0
అంతర్ స్వరూప కేంద్రం S‘, AB ని అంతరంగా 21 నిష్పత్తిలో విభజిస్తుంది.
S’ నిరూపకాలు

దీనిని క్రింది విధంగా వ్రాయవచ్చును.
(x + 1)(4x – 3y – 5) = 0
తిర్యక్ ఉమ్మడి స్పర్శరేఖల సమీకరణాలు
x + 1 = 0 మరియు 4x – 3y 5 = 0.
![]()


![]()



![]()
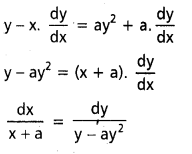
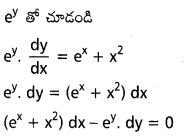

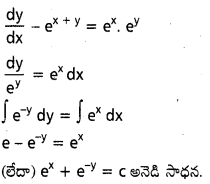
![]()
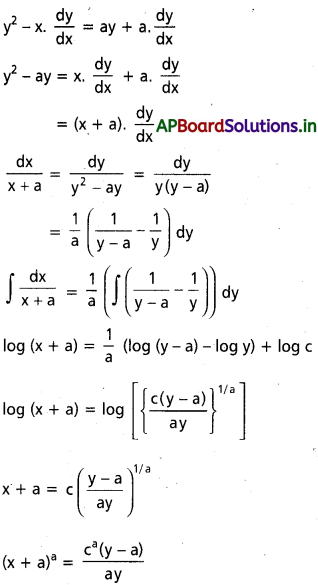
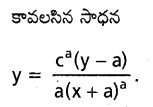
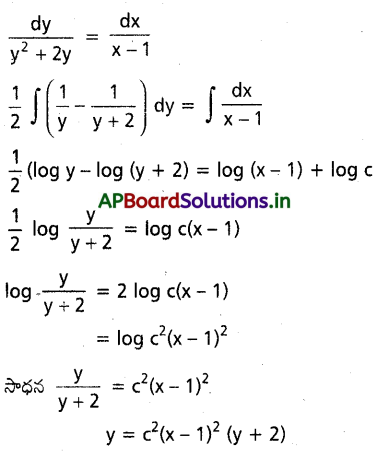

![]()
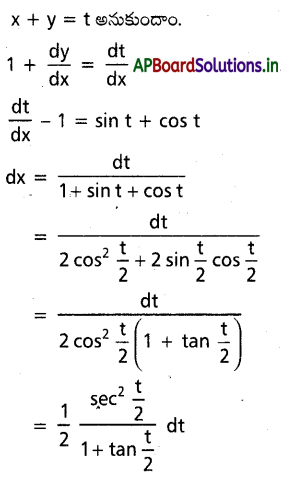
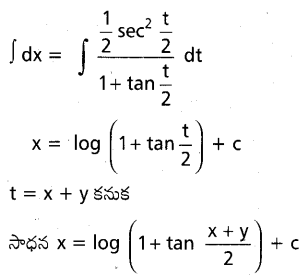

![]()
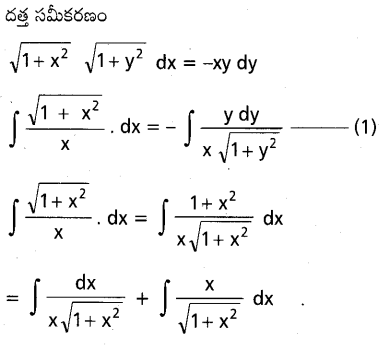
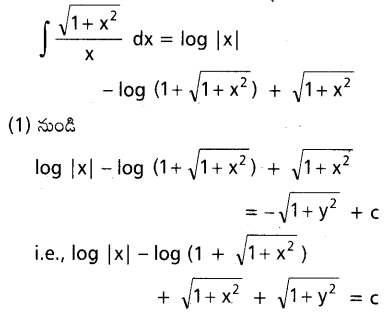

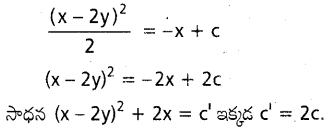
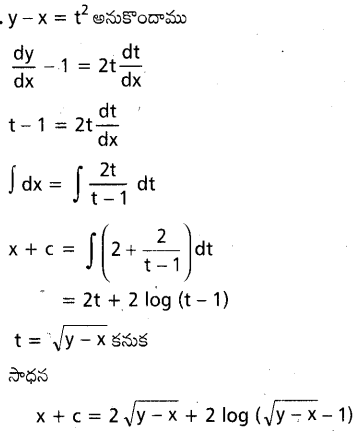
![]()


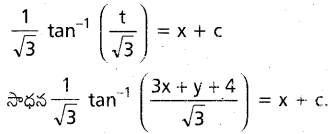

![]()

![]()
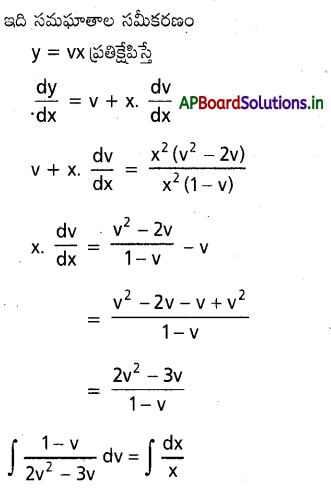
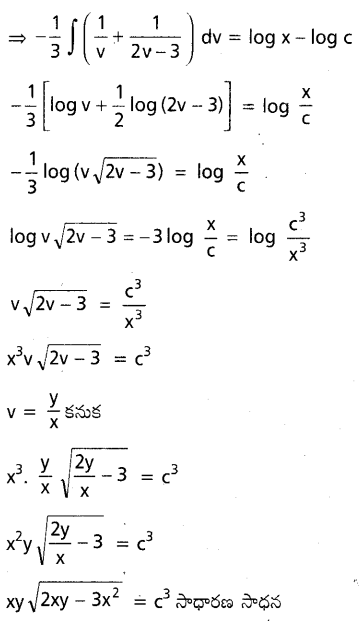


![]()

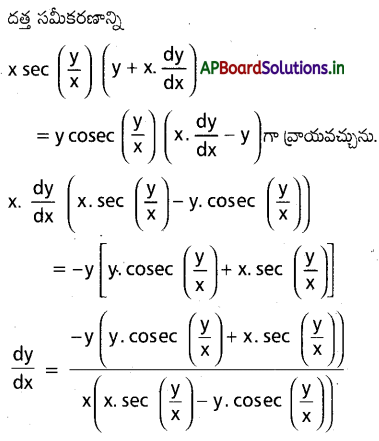
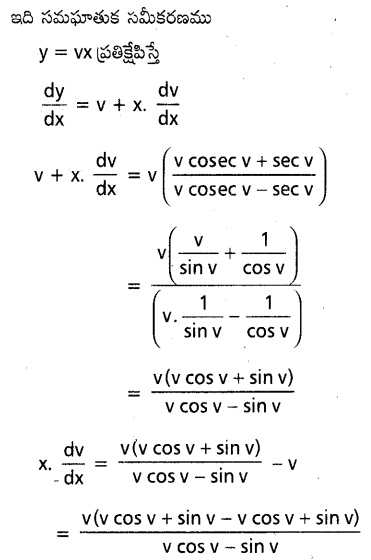
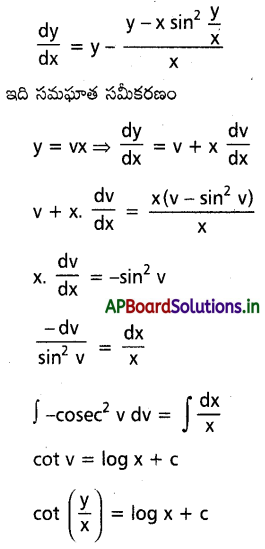
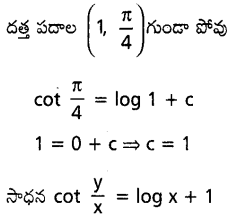
![]()

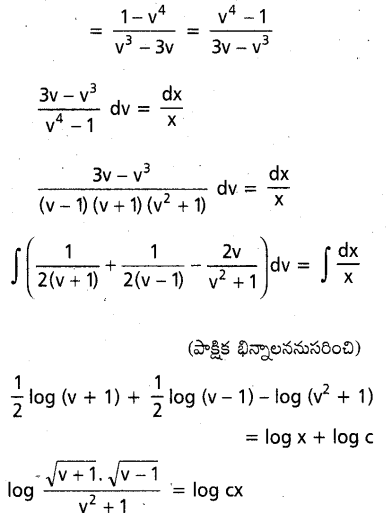
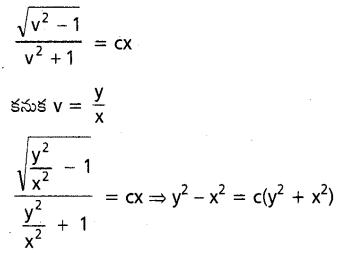
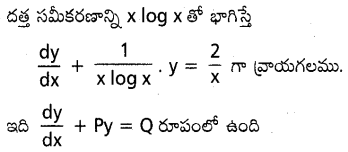



![]()



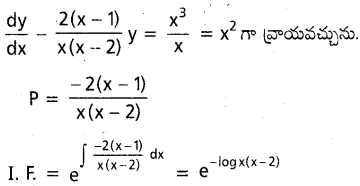
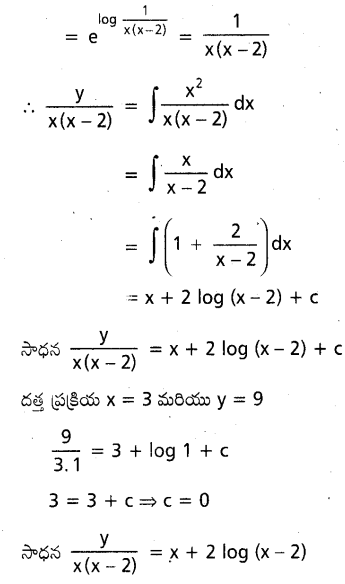
![]()









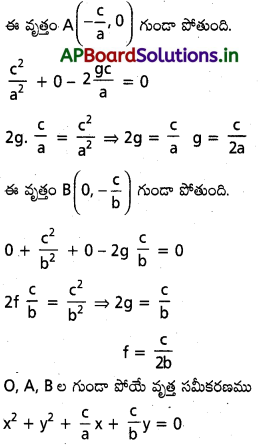


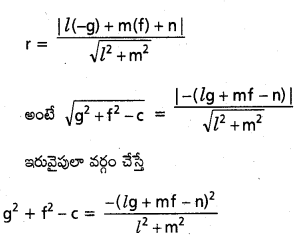



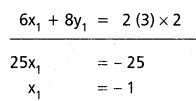



























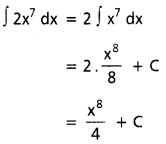



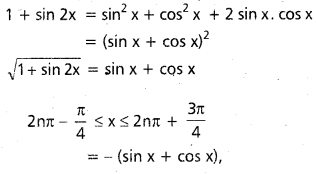



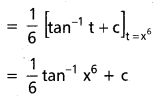


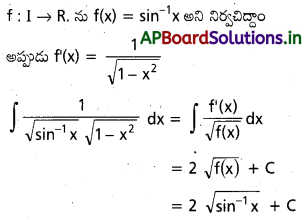
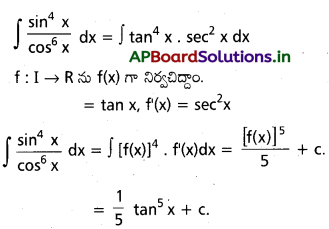
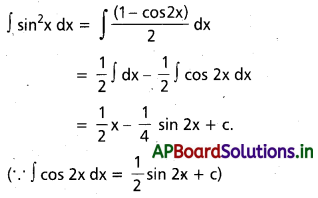

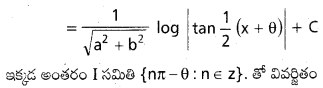


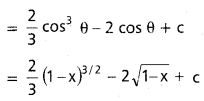



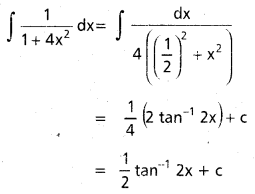
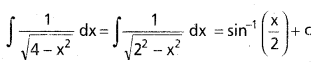




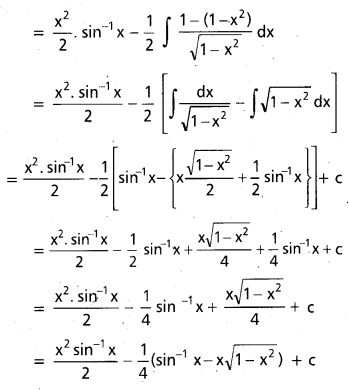
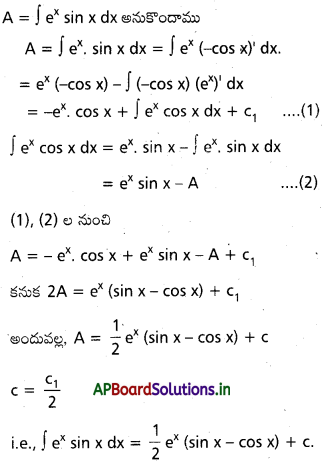
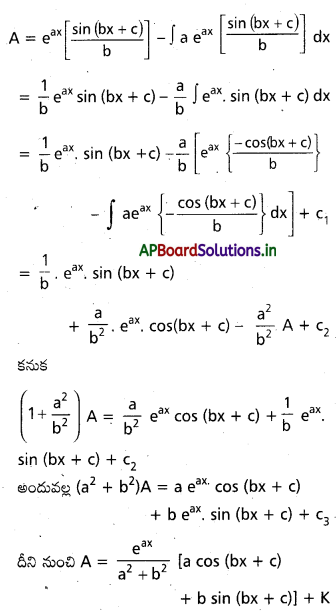
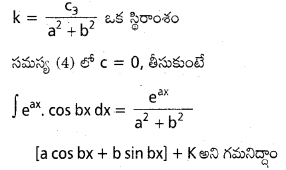

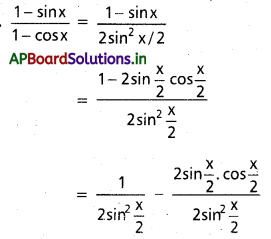
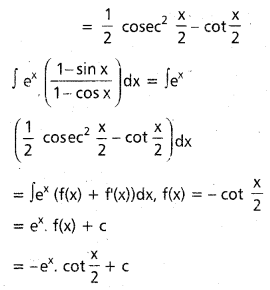
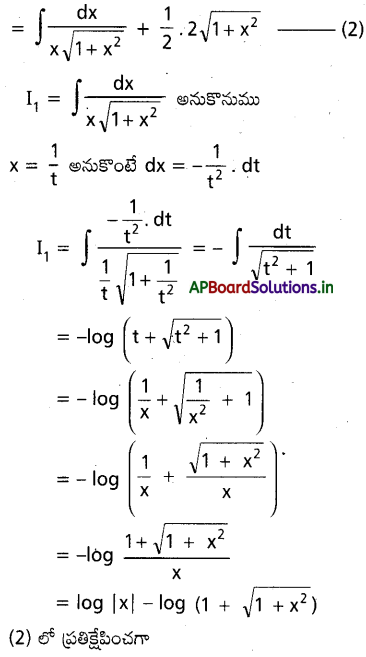
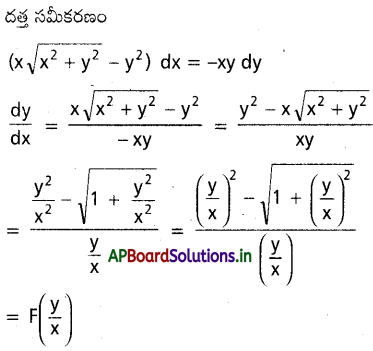
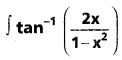 dx ను గణించండి.
dx ను గణించండి.

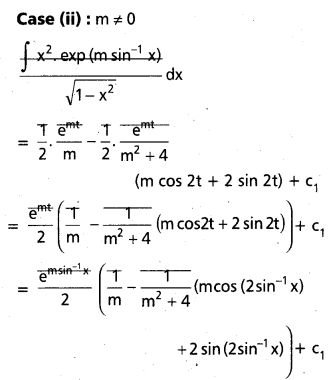
 ను గణించండి.
ను గణించండి.