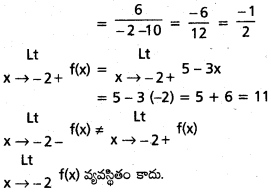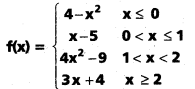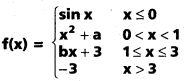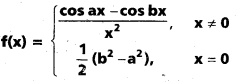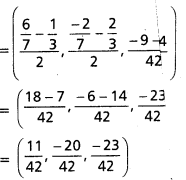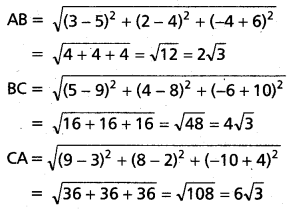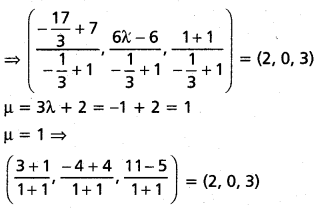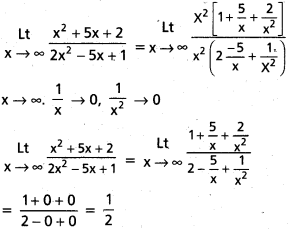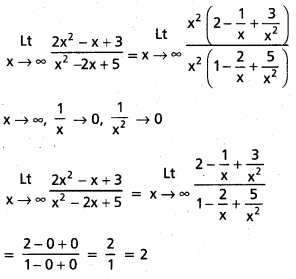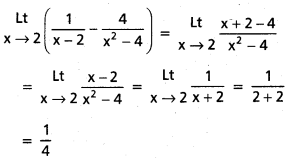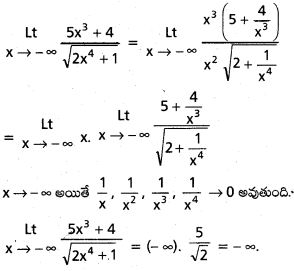Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 6 దిక్ కొసైన్లు, దిక్ సంఖ్యలు Exercise 6(b) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1B Solutions Chapter 6 దిక్ కొసైన్లు, దిక్ సంఖ్యలు Exercise 6(b)
అభ్యాసం – 6(బి)
I.
ప్రశ్న 1.
(3, 4, 0), (4, 4, 4) బిందువులను కలిపే రేఖ దిక్ సంఖ్యలు రాయండి.
సాధన:
A(3, 4, 0), B(4, 4, 4) లో దత్త బిందువులు
AB యొక్క d.rs x2 – x1, y2 – y1, z2 – z1
4 – 3, 4 – 4, 4 – 0 i.e., 1, 0, 4
ప్రశ్న 2.
ఒక రేఖ దిక్ సంఖ్యలు (-6, 2, 3) అయితే, దాని దిక్ కొసైన్లు కనుక్కోండి.
సాధన:
రేఖ D.R లు – 6, 2, 3
\(\sqrt{36+4+9}\) = 7 తో భాగించగా
రేఖ దిక్ కోసైన్లు – \(\frac{6}{7}\), \(\frac{2}{7}\), \(\frac{3}{7}\)

ప్రశ్న 3.
(1, 1, 2) (\(\sqrt{3}\), –\(\sqrt{3}\), 0) దిక్ కొసైన్లుగా గల రేఖల మధ్య కోణానికి కొసైన్లు విలువను కనుక్కోండి.
సాధన:
cos θ = l1l2 + m1 m2 + n1 n3
= \(\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}\) . 0
= \(\frac{\hat{i}+1}{\sqrt{6}}=\frac{2}{\sqrt{6}}=\sqrt{\frac{4}{6}}=\sqrt{\frac{2}{3}}\)
ప్రశ్న 4.
(1, 1, 2) (\(\sqrt{3}\), –\(\sqrt{3}\), 0) దిక్ సంఖ్యలుగా గల రేఖల మధ్య కోణం కనుక్కోండి.
సాధన:
cos θ = \(\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_i^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\)
= \(\frac{1 \cdot \sqrt{3}+1(-\sqrt{3})+2 \cdot 0}{\sqrt{1+1+4} \sqrt{3+3}}=\frac{0}{6}\) = 0
θ = \(\frac{\pi}{2}\)
ప్రశ్న 5.
\(\left(\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13}\right)\), \(\left(\frac{4}{13}, \frac{12}{13}, \frac{3}{13}\right)\) దిక్ కొసైన్లుగా గల రేఖల పరస్పరం లంబంగా ఉంటాయని చూపండి.
సాధన:
రెండు రేఖలు లంబంగా ఉంటే
l1l2 + m1m2 + n1n2
l1l2 + m1m2 + n1n2
= \(\frac{12}{13}\) . \(\frac{4}{13}\) – \(\frac{3}{13}\) . \(\frac{12}{13}\) – \(\frac{4}{13}\) . \(\frac{3}{13}\)
= \(\frac{48-36-12}{169}\) = 0
∴ దత్త రేఖలు లంబంగా ఉన్నాయి.

ప్రశ్న 6.
O మూలబిందువు, P(2, 3, 4), Q(1, k, 1) బిందువులు \(\overline{\mathrm{OP}}\) ⊥ \(\overline{\mathrm{OQ}}\) అయ్యేట్లుంటే, k విలువ ఎంత ?
సాధన:
OP యొక్క d.r లు 2, 3, 4
OQ యొక్క d.r లు 1, k, 1
OP, OQ లు లంబంగా ఉన్నాయి.
⇒ a1a2 + b1b2 + c1c2 = 0
2 + 3k + 4 = 0
3k = – 6
k = -2.
II.
ప్రశ్న 1.
ఒక రేఖ దిక్ సంఖ్యలు (3, 4, 0) అయితే దాని దిక్ కొసైన్లు, ఇంకా ఆ రేఖ నిరూపకాక్షాలతో చేసే కోణాలు కనుక్కోండి.
సాధన:
రేఖ నిష్పత్తి దిక్ సంఖ్యలు (3, 4, 0)
\(\sqrt{9+16+0}\) = 5తో భాగించగా
రేఖ దిక్ కొసైన్లు \(\left(\frac{3}{5}, \frac{4}{5}, 0\right)\)
α, β, γ లు ఈ రేఖ నిరూపకాక్షాలతో చేసే కోణాలు అయితే,
cos α = \(\frac{3}{5}\) cos β = \(\frac{4}{5}\) cos γ = 0
α = cos-1 \(\left(\frac{3}{5}\right)\), β = cos-1 \(\left(\frac{4}{5}\right)\), γ = \(\frac{\pi}{2}\)
రేఖ నిరూపకాక్షాలతో చేసే కోణం
cos-1 \(\left(\frac{3}{5}\right)\), cos-1 \(\left(\frac{4}{5}\right)\), \(\frac{\pi}{2}\)

ప్రశ్న 2.
(1, -1, 2) (3, 4, -2) బిందువులను కలిపేరేఖ (0, 3, 2), (3, 5, 6)లను కలిపే రేఖకు లంబంగా ఉంటుందని చూపండి.
సాధన:
A(1, -1, 2) B(3, 4, -2) C(0, 3, 2)
D(3, 5, 6) లు దత్త బిందువులు
AB యొక్క d.r లు 3 – 1, 4 + 1, -2 – 2 i. e., 2, 5, -4
CD యొక్క d.r లు 3 – 0, 5 – 3, 6 – 2 i.e., 3, 2, 4
a1a2 + b1b2 + c1c2 = 2.3 + 5.2 – 4.4
= 6 + 10 – 16 = 0
AB, CD లు లంబంగా ఉన్నాయి.
ప్రశ్న 3.
A = (3, 4, 5), B = (4,6, 3) C = (-1, 2, 4), D(1, 0, 5) బిందువులైతే \(\overline{\mathrm{D C}}\), \(\overline{\mathrm{A B}}\) రేఖా ఖండాల మధ్య కోణం కనుక్కోండి.
సాధన:
A(3, 4, 5), B(4, 6, 3), C(-1, 2, 4), D (1, 0, 5)లు దత్త బిందువులు ఎంత ?
AB యొక్క d.r లు 4 – 3, 6 – 4, 3 – 5 i.e., 1, 2, -2
CD యొక్క d.r లు 1 + 1, 0 – 2, 5 – 4 i.e., 2, – 2, 1
cos θ = \(\frac{\left|a_1 a_2+b_1 b_2+c_1 c_2\right|}{\sqrt{a_1^2+b_1^2+c_1^2} \cdot \sqrt{a_2^2+b_2^2+c_2^2}}\)
= \(\frac{1.2+2(-2)+(-2) \cdot 1}{\sqrt{1+4+4} \sqrt{4+4}}\)
= \(\frac{4}{9}\) ⇒ θ = cos-1\(\left(\frac{4}{9}\right)\)

ప్రశ్న 4.
(1, −1, 2), (2, 1, −1) దిక్ సంఖ్యలుగా గల రేఖలకు లంబంగా ఉండే రేఖ దిక్ కొసైన్లు కనుక్కొండి.
సాధన:
కావలసిన రేఖ D.C లు l, m, n అనుకుంటే
(1, -1, 2), (2, 1, −1) యొక్క d.rs గల రేఖలకు లంబంగా ఉంది.
l – m + 2n = 0
2l + m – n = 0
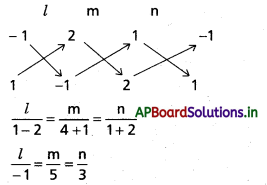
రేఖ యొక్క d.rs -1, 5, 3
\(\sqrt{1+25+9}=\sqrt{35}\) తో భాగించగా
D.C రేఖ యొక్క దిక్కా సైన్లు
\(-\frac{1}{\sqrt{35}}, \frac{5}{\sqrt{35}}, \frac{3}{\sqrt{35}}\)
ప్రశ్న 5.
(2, 3, 4), (1, -2, 3), (3, 8, -11) బిందువులు సరేఖీయాలని చూపండి.
సాధన:
A(2, 3, 4), B(1, 2, 3), C(3, 8, -11) లు దత్త బిందువులు

∴ A, B, C లు సరేఖీయాలు

ప్రశ్న 6.
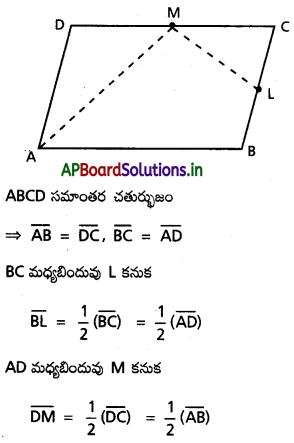
(4, 7, 8), (2, 3, 4), (-1, -2, 1), (1, 2, 5) బిందువులు ఒక సమాంతర చతుర్భుజం శీర్షాలని చూపండి.
సాధన:
A(4, 7, 8), B(2, 3, 4), C(-1, -2, 1) మరియు D (1, 2, 5) లు దత్త బిందువులు.

∴ AB = CD మరియు BC = DA
∴ A, B, C, D సమాంతర చతుర్భుజ శీర్షాలు.
III.
ప్రశ్న 1.
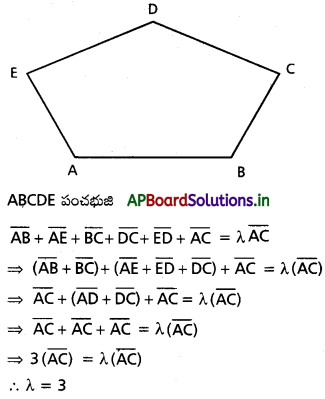
l + m + n = 0, 2mn + 3nl – 5lm = 0 సమీకరణాలను తృప్తి పరిచే దిక్ కొసైన్లు గల రేఖలు ఒక దానికొకటి లంబంగా ఉంటాయని చూపండి. [Mar. ’12]
సాధన:
దత్తాంశం ప్రకారం l + m + n = 0. …………… (1)
2mn + 3nl – 5lm = 0 …………….. (2)
(1) నుండి, l = -(m + n)
(2) లో ప్రతిక్షేపించగా
2mn – 3n(m + n) + 5m(m + n) = 0
2mn – 3mn – 3n2 + 5m2 + 5mn = 0
5m2 + 4mn – 3n2 = 0
\(\frac{m_1 m_2}{n_1 n_2}=-\frac{3}{5} \Rightarrow \frac{m_1 m_2}{-3}=\frac{n_1 n_2}{5}\) ……………..
(1) నుండి n = -(l + m)
(2) లో ప్రతిక్షేపించగా
– 2m (l + m) – 3l (l + m) – 5lm = 0
-2lm – 2m2 – 3l2 – 3lm – 5lm = 0
3l2 + 10lm + 2m2 = 0
\(\frac{l_1 l_2}{m_1 m_2}=\frac{2}{3} \Rightarrow \frac{l_1 l_2}{2}=\frac{m_1 m_2}{3}\) …………… (2)
(1), (2) ల నుండి,
\(\frac{l_1 l_2}{2}=\frac{m_1 m_2}{3}=\frac{n_1 n_2}{-5}\) = 1
l1l2 = 2k, m1m2 = 3k, n1n2 = -5k
∴ l1l2 + m1m2+ n1n2 = 2k + 3k – 5k = 0
ఈ రేఖలు లంబంగా ఉన్నాయి.

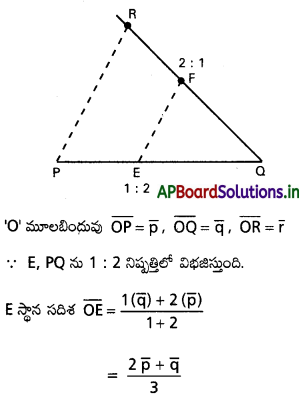
ప్రశ్న 2.
రెండు రేఖల దిక్ కొసైన్లు l + m + n = 0, l2 + m2 – n2 = 0. సమీకరణాలను తృప్తిపరిస్తే వాటి మధ్య కోణాన్ని కుసుకోండి. [Mar. ’13, ’07; May ’11, ’07; June ’04]
సాధన:
దత్తాంశం ప్రకారం l + m + n = 0 …………….. (1)
l2 + m2 – n2 = 0 ……………. (2)
(1) నుండి l = − (m + n)
(2) లో ప్రతిక్షేపించగా
(m + n)2 + m2 – n2 = 0
m2 + n2 + 2mn + m2 – n2 = 0
2m2 + 2mn = 0
2m (m + n) = 0
∴ m = 0 లేదా m + n = 0
సందర్భము (i) : m = 0, (1) లో ప్రతిక్షేపించగా l + n = 0
l = -n ⇒ \(\frac{l}{1}=\frac{n}{-1}\)
l1 రేఖ D.R లు (1, 0, – 1)
సందర్భము (ii) : m + n = 0 ⇒ m = -n ⇒ \(\frac{m}{1}=\frac{n}{-1}\)
(1) లో ప్రతిక్షేపించగా l = 0
l2 యొక్క DR లు (0, 1 – 1)
ఈ రేఖల మధ్య కోణం 9 అయితే
cos θ = \(\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\)
= \(\frac{|0+0+1|}{\sqrt{2} \cdot \sqrt{2}}=\frac{1}{2}=\cos \frac{\pi}{3}\)
θ = \(\frac{\pi}{3}\)

ప్రశ్న 3.
ఒక కిరణం, సమఘనం యొక్క నాలుగు కర్ణాలతో α, β, γ కోణాలు చేస్తే, cos2 α + cos2 β + cos2 γ + cos2 δ విలువ ఎంత ? [Mar. ’05; May ’05]
సాధన:
ఘనము యొక్క భుజము పొడవు ఘనము ఒక శీర్షాన్ని మూల , \(\overline{\mathrm{OA}}, \overline{\mathrm{OB}}, \overline{\mathrm{OC}}\) భుజాలను నిరూపకాక్షాలుగా తీసుకుందాం. \(\overline{\mathrm{OP}}, \overline{\mathrm{CD}}, \overline{\mathrm{AE}}, \overline{\mathrm{BF}}\) లు కర్ణాలు. వీటి దిక్ సంఖ్యలు వరుసగా (a, a, a), (a, a, a), (-a, a, a), (a, -a, a).
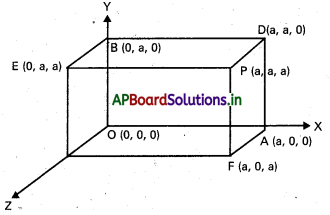
దత్తరేఖ దిక్ కొసైనులు (l, m, n) మరియు ఈ రేఖ ఘనము యొక్క కర్ణాలతో α, β, γ మరియు & కోణాలు చేస్తుంది అనుకుందాం.
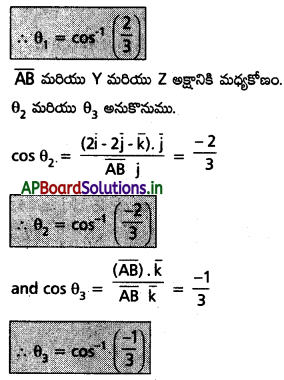
cos α = \(\frac{|\mathrm{a} \times l+\mathrm{a} \times \mathrm{m}+\mathrm{a} \times \mathrm{n}|}{\sqrt{\mathrm{a}^2+\mathrm{a}^2+\mathrm{a}^2}}=\frac{|l+\mathrm{m}+\mathrm{n}|}{\sqrt{3}}\)
ఇదే విధంగా cos β = \(\frac{|l+\mathrm{m}-\mathrm{n}|}{\sqrt{3}}\)
cos γ = \(\frac{|-l+\mathrm{m}+\mathrm{n}|}{\sqrt{3}}\) మరియు
cos δ = \(\frac{|l-\mathrm{m}+\mathrm{n}|}{\sqrt{3}}\)
cos2 α + cos2 β + cos2 γ + cos2 δ
\(\frac{1}{3}\) {|l + m + n|2 + |l + m – n|2 + |-l + m + n|2 + |l – m + n|2}
\(\frac{1}{2}\) [(l + m + n)2 + (l + m – n)2 + (-l + m + n)2 + (l – m + n)2]
\(\frac{1}{2}\) [4(l2 + m2 + n2)] = \(\frac{4}{3}\) (∵ l2 + m2 + n2 = 1)

ప్రశ్న 4.
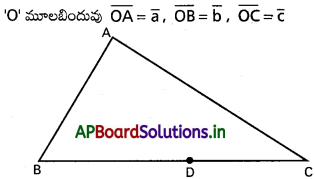
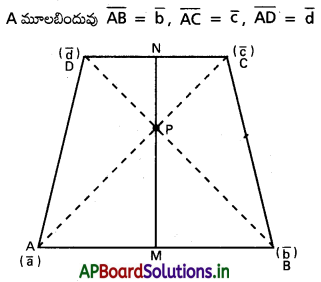
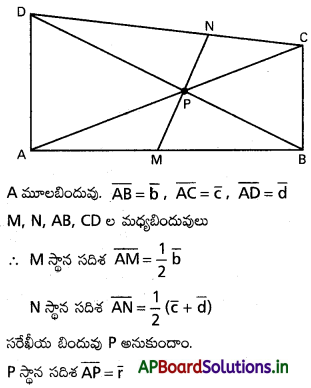
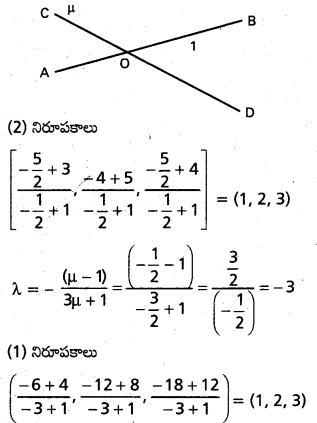
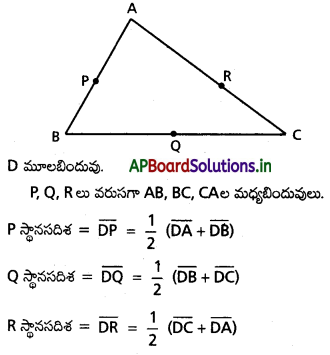
(l1, m1, n1), (l2, m2, n2) లు రెండు ఖండించుకొనే రేఖల దిక్ కొసైన్లయితే, వాటి మధ్య కోణ సమద్విఖండన రేఖల దిక్ కొసైన్లు l1 ± l2, m1 ± m2, n1 ± n2 లకు అనుపాతంలో ఉంటాయని చూపండి.
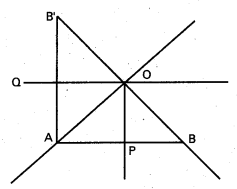
సాధన:
OA, OB లు దత్త రేఖలు
A, B లు O నుండి యూనిట్ దూరంలో గల బిందువు
A నిరూపకాలు (l1, m1, n1)
B నిరూపకాలు (l2, m2, n2)
AB మధ్య బిందువు P
P నిరూపకాలు \(\left(\frac{l_1+l_2}{2}, \frac{m_1+m_2}{2}, \frac{n_1+n_2}{2}\right)\)
∴ OP రేఖ ∠AOB కోణ సమద్విఖండన రేఖ.
OP యొక్క D.R లు l1 + l2, m1 + m2, n1 + n2
OB’ = OB = 1 అయ్యే విధంగా B బిందువు OB మీద వుంది.
B’ నిరూపకాలు (-l2, -m2, -n2)
AB’ మధ్య బిందువు Q
Q నిరూపకాలు \(\left(\frac{l_1-l_2}{2}, \frac{m_1-m_2}{2}, \frac{n_1-n_2}{2}\right)\)
OQ రేఖ ∠AOB
OQ యొక్క D.Rs l1 – l2, m1 – m2, n1 – n2.

ప్రశ్న 5.
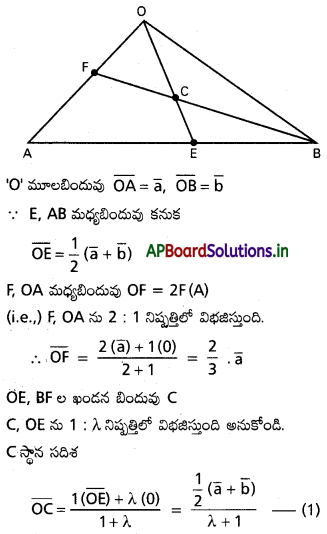
A (-1, 2, -3), B (4, 0, -6), C(0, 4, -1) బిందువులు, ∠BAC కోసమద్విఖండన రేఖల దిక్ కొసైన్లు (25, 8, 5), (-11, 20, 23)లకు అనుపాతంలో ఉంటాయని చూపండి.
సాధన:
A (-1, 2, -3), B (5,0, -6), C (0, 4, -1) లు దత్త బిందువులు
AB యొక్క D.R లు 5 +, 0 – 2, -6 + 3 i.e., 6, -2, -3
AB యొక్క D.R లు \(\frac{6}{7}\), \(\frac{2}{7}\), \(\frac{-3}{7}\)
AC యొక్క D.R లు 0 +, 4 – 2, -1 + 3 i.e 1, 2, 2
AC యొక్క D. R లు \(\frac{1}{3}\), \(\frac{-2}{3}\), \(\frac{2}{3}\)
ఒక కోణ సమద్విఖండన రేఖD. R లు
= \(\left(\frac{\frac{6}{7}+\frac{1}{3}}{2}, \frac{\frac{-2}{7}+\frac{2}{3}}{2}, \frac{\frac{3}{2}+\frac{2}{3}}{2}\right)\)
= \(\left(\frac{18+7}{42}, \frac{-6+14}{42}, \frac{-9+14}{42}\right)\)
= \(\left(\frac{25}{42}, \frac{8}{42}, \frac{5}{42}\right)\)
ఒక కోణ సమద్విఖండన రేఖలు (25, 8, 5)
రెండవ కోణ సమద్విఖండన రేఖ). R లు
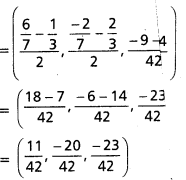
రెండవ సమద్విఖండన రేఖ D.R లు (-11, 20, 23)

ప్రశ్న 6.
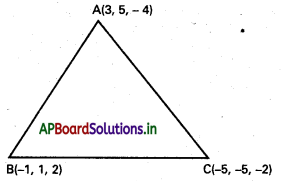
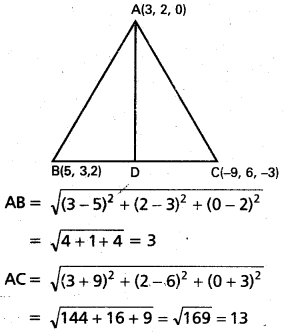
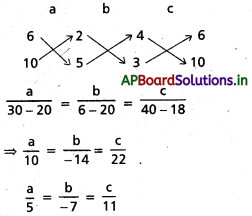
(6, 10, 10), (1, 0, -5), (6, -10, 0) లు ఒక త్రిభుజం శీర్షాలైతే, త్రిభుజం భుజాల దిక్ సంఖ్యలను కనుక్కోండి. ఇది లంబకోణ త్రిభుజమా, సమద్విబాహు త్రిభుజమా నిర్ధారించండి.
సాధన:
A (6, 10, 10), B (1, 0, -5), C (6, -10, 0) లు
∆ABC త్రిభుజ శీర్షాలు
AB యొక్క D.R లు 5, 10, 15 i.e., 1, 2, 3
BC యొక్క D.Rలు -5, 10, -5 i.e., 1, -2, 1
AC యొక్క D.R లు 0, 20, 10, i.e., 0, 2, 1
cos ∠ABC = \(\frac{|1.1+2(-2)+3.1|}{\sqrt{1+4+9} \sqrt{1+4+1}}\) = 0
⇒ ∠B = \(\frac{\pi}{2}\)
∴ దత్త త్రిభుజం లంబకోణ త్రిభుజం.
ప్రశ్న 7.
ఒక త్రిభుజం శీర్షాలు వరసగా A (1, 4, 2), B (-2, 1, 2), C (2, 3,-4). అయితే A, B, C లను కనుక్కోండి. [Mar. ’14]
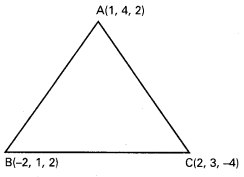
సాధన:
A (1, 4, 2), B (–2, 1, 2), C (2, 3, –4) లు OABC
యొక్క త్రిభుజ శీర్షాలు,
AB యొక్క D.R లు 3, 3, 0 i.e., 1, 1, 0
BC యొక్క D.R లు -4, -2, 6 i.e., 2, 1, -3
AC యొక్క D.R లు -1, 1, 6.

ప్రశ్న 8.
3l + m + 5n = 0, 6mn – 2nl + 5lm = 0 సమీకరణాలతో సూచించబడే దిక్ కొసైన్లు గల రేఖల మధ్య కోణం కనుక్కోండి. [T.S Mar’ 15; May ’12, ’06]
సాధన:
దత్తాంశం 3l + m + 5 = 0 …………….. (1)
6mn – 2nl + 5lm ……………… (2)
(1) నుండి, m = – (3l + 5n)
(2) లో ప్రతిక్షేపించగా
-6n(3l + 5n) – 2nl – 5l (3l + 5n) = 0
-18ln – 30n2 – 2nl – 15l2 – 25ln = 0
-15l2 – 45ln – 30n2 = 0
l2 + 3ln + 2n2 = 0
(l + 2n) (l + n) = 0
l + 2n = 0 లేదా l + n = 0

సందర్భం (i) : l1 + n1 = 0 ⇒ n1 = -l1;
⇒ \(\frac{l_1}{1}=\frac{n_1}{-1}\)
కానీ m1 – (3l1 + 5n1) = (-3n1 + 5n1) = -2n1
∴ \(\frac{m_1}{+2}=\frac{n_1}{-1}\)
∴ \(\frac{l_1}{1}=\frac{m_1}{2}=\frac{n_1}{-1}\)
l1 యొక్క D.R లు (1, 2, -1)
సందర్భం (ii) : l2 + 2n2 = 0
l2 = −2n2 ⇒ \(\frac{l_2}{-2}=\frac{n_2}{1}\)
m2 = (3l2 + 5n2) = -(-6n2 + 5n2) = n2
\(\frac{m_2}{1}=\frac{n_2}{1}\)
∴ \(\frac{l_2}{-2}=\frac{m_2}{1}=\frac{n_2}{1}\)
l2 యొక్క D.R లు (-2, 1, 1)
l1, l2 రేఖల మధ్య కోణం ‘θ’ అనుకుందాం.
cos θ = \(\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\)
= \(\frac{|1(-2)+2.1+(-1) .1|}{\sqrt{1+4+1} \sqrt{4+1+1}}\)
= \(\frac{1}{6}\) ⇒ θ = cos-1 (1/6)

ప్రశ్న 9.
రెండు ఆసన్న స్థానాలలో ఒక చలరేఖ దిక్ కొసైన్లు (l, m, n), (2 + δl, m + δm, n + δn), ఈ రెండు స్థానాల మధ్య గల స్వల్ప కోణం δθ, (δθ)2 = (δl)2 + (δm)2 + (δn)2 తృప్తిపరుస్తుందని చూపండి.
సాధన:
(l, m, n), (l + δl, m + δn, n + δn) లు దిక్ కొసైన్లు
l2 + m2 + n2 = 1 ……………… (1)
(l + δl)2 + (m + δm)2 + (n + δn)2
(2) − (1) ⇒ (l + δl )2 + (m + δm)2 + (n + δn)2 (l2 + m2 + n2) = 0
2(l . δl + m . δm + n . δ)
= −((δl)2 + (δm)2 + (δn)2) ……………….. (3)
cos θ . δθ = l (l + δl)+ m (m + δm) + n (n + δn)
= (l2 + m2 + n2) + (l . δl + m . δm + n . δn)
= 1 – \(\frac{1}{2}\) [(δl)2 + (δm)2 + (δn)2]
(δl)2 + (δm)2 + (δr2 = 1 = 2 (1 cos θ . δθ)
δθ చిన్నది కనుక sin \(\frac{\delta}{2}=\frac{\delta \theta}{2}\)
∴ 4 sin2 θ \(\frac{\delta \theta}{2}=\left(\frac{\delta \theta}{2}\right)^2\) = (δθ)2
∴ (δθ)2 = (δl)2 – (δm)2 + (δn)2
![]()
![]()
![]()
![]()
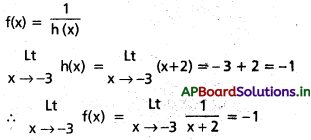
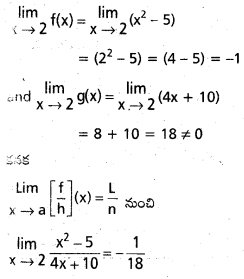
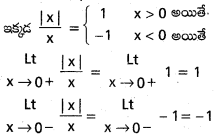
 ద్వారా నిర్వచితమనుకోండి. అప్పుడు \(\stackrel{L t}{x \rightarrow 3}\) f(x) = 5 అని చూపండి.
ద్వారా నిర్వచితమనుకోండి. అప్పుడు \(\stackrel{L t}{x \rightarrow 3}\) f(x) = 5 అని చూపండి.
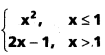 , అయితే \(\underset{\mathbf{x} \rightarrow 1+}{\text { Lt }}\) f(x) \(\underset{\mathbf{x} \rightarrow 1-}{\text { Lt }}\) f(x) లను కనుక్కోండి.
, అయితే \(\underset{\mathbf{x} \rightarrow 1+}{\text { Lt }}\) f(x) \(\underset{\mathbf{x} \rightarrow 1-}{\text { Lt }}\) f(x) లను కనుక్కోండి.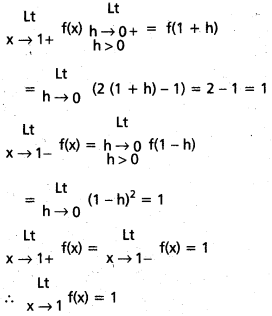
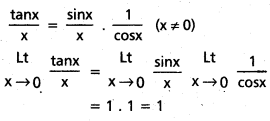

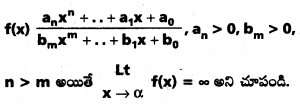
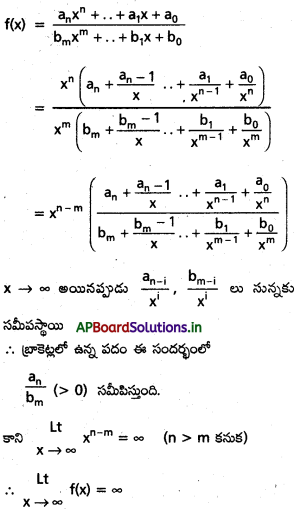
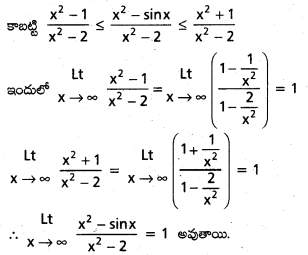
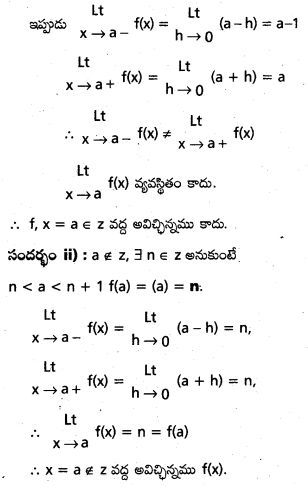
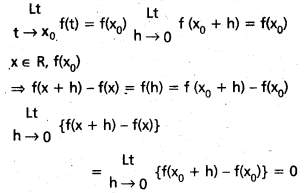
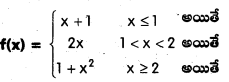

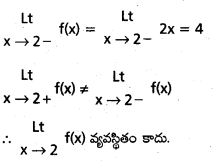



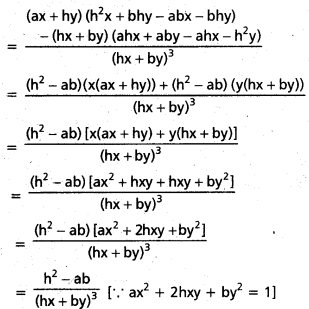

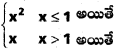 ద్వారా నిర్వచితమైన ప్రమేయం f, R పై అవిచ్ఛిన్నమా ? [May ‘ 11]
ద్వారా నిర్వచితమైన ప్రమేయం f, R పై అవిచ్ఛిన్నమా ? [May ‘ 11]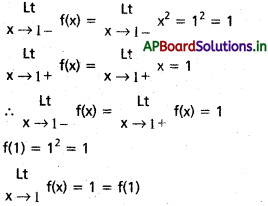
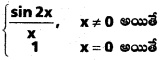 ద్వారా నిర్వచితమైన ప్రమేయం f, 0 పై అవిచ్ఛిన్నామా ? [May ’12]
ద్వారా నిర్వచితమైన ప్రమేయం f, 0 పై అవిచ్ఛిన్నామా ? [May ’12]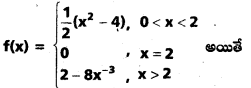

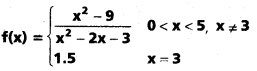
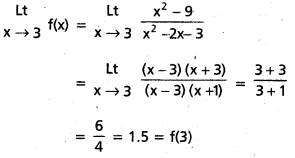
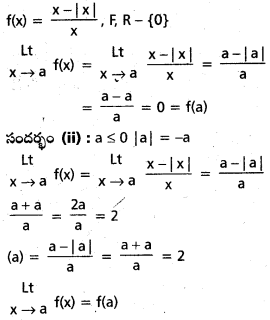
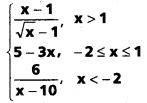 తో నిర్వచితమైతే f అవిచ్ఛిన్నతను చర్చించండి.
తో నిర్వచితమైతే f అవిచ్ఛిన్నతను చర్చించండి.