AP State Board Syllabus AP SSC 10th Class Telugu Important Questions Chapter 4 వెన్నెల
AP State Syllabus SSC 10th Class Telugu Important Questions 4th Lesson వెన్నెల
10th Class Telugu 4th Lesson వెన్నెల 2 Marks Important Questions and Answers
ఈ క్రింది ప్రశ్నలకు నాలుగైదు వాక్యాల్లో సమాధానాలు రాయండి.
ప్రశ్న 1.
రాత్రి అనే ఆలోచన రానీక చీకటి అనే పేరు విననీక ‘వెన్నెల’ ను వర్ణించిన కవిని గురించి తెల్పండి. (March 2017)
(లేదా)
చంద్రోదయాన్ని అత్యంత మనోహరంగా వర్ణించిన “వెన్నెల” పాఠ్యభాగ ‘కవి పరిచయం’ వ్రాయండి. (March 2019)
జవాబు:
వెన్నెల పాఠ్యభాగం ఎఱ్ఱన గారు రచించారు. ఆయన తల్లి పేరు పోతమాంబిక, తండ్రి పేరు సూరనార్యుడు. ఆయన 14వ శతాబ్దం ప్రథమార్ధంలో జీవించారు. ఎఱ్ఱన గురువుగారి పేరు శంకరస్వామి. ఎఱ్ఱనకు ప్రబంధ పరమేశ్వరుడు, శంభుదాసుడు అనే బిరుదులు కలవు.
ప్రశ్న 2.
ఎఱ్ఱన రచనల గురించి వ్రాయండి.
జవాబు:
ఎఱ్ఱన ఆంధ్రమహాభారతంలోని అరణ్యపర్వశేషం రచించాడు. హరివంశం, నృసింహపురాణం, రామాయణం మొ||నవి రచించాడు.
ఆంధ్రమహాభారతంలోని అరణ్య పర్వశేషాన్ని రాజరాజ నరేంద్రునికి అంకితమిచ్చాడు. హరివంశం, రామాయణాలను ప్రోలయవేమారెడ్డికి అంకితమిచ్చాడు. నృసింహపురాణమును అహోబిల నృసింహస్వామికి అంకితమిచ్చాడు.

ప్రశ్న 3.
ఎఱ్ఱన రచనా వైశిష్ట్యాన్ని వివరించండి.
జవాబు:
ఎఱ్ఱన రచనలలో వర్ణనలు అధికంగా కనిపిస్తాయి. ఆయన రచించిన నృసింహపురాణంలో ‘అష్టాదశ (18) వర్ణనలు’ ఉన్నాయి. తరువాతి కాలంలో వర్ణనాత్మక కావ్యాలు రావడానికి ఎఱ్ఱన వర్ణనలే కారణం. అందుచేతనే ఎఱ్ఱనను ‘ప్రబంధ పరమేశ్వరుడు’ అని సాహితీలోకం గౌరవించింది.
ఎఱ్ఱన నృసింహపురాణం యొక్క ప్రభావం బమ్మెర పోతన భాగవతంపై ఎక్కువగా కనిపిస్తుంది. పోతన భాగవతంలోని ప్రహ్లాద చరిత్రలో ఎఱ్ఱన ప్రభావం స్పష్టంగా కనిపిస్తుందని పరిశోధకులు నిరూపించారు.
ప్రశ్న 4.
‘కాటుక గ్రుక్కినట్టి కరవటంబున జగదండ ఖండమమెరె’ ఈ మాటలు కవి ఏ సందర్భంలో పేర్కొన్నాడో వివరించండి. ఈ పోలికను విశ్లేషించండి.
జవాబు:
సంధ్యా సమయం తర్వాత విశ్వమంతా చీకటి వ్యాపించిందని చెబుతున్న సందర్భంలో కవి ఈ మాటలను పేర్కొన్నాడు.
చీకటిలో భూమి, ఆకాశం, దిక్కులూ అన్నీ కలిసి పోయాయి. అప్పుడు బ్రహ్మాండ ఖండం కాటుక నింపిన పెద్ద భరిణెలా ఉందన్నాడు. బ్రహ్మాండంలో 14 లోకాలుంటాయి. పై లోకాలు 7. క్రింది లోకాలు 7. మధ్యలోనిది భూలోకం. చీకటి కేవలం భూగోళానికి మాత్రమే ఏర్పడింది. అందుకే పైన, క్రింద సమానమైన మూతలు గల భరిణెతో భూగోళాన్ని పోల్చాడు. దీనిద్వారా ఎఱ్ఱనగారి పరిశీలనా దృష్టి, లోకజ్ఞానం వ్యక్తమౌతున్నాయి.
ప్రశ్న 5.
ఈ పాఠంలో కవి వెన్నెలను వర్ణించడానికి ఏయే అంశాలను ఎన్నుకొన్నాడు?
జవాబు:
ఆకాశమనే చెట్టు దిక్కులనే కొమ్మలతో, వెలుగులీనే నక్షత్రాలనే పూలతో ప్రకాశిస్తోందన్నాడు. అప్పుడే ఉదయిస్తున్న చంద్రుడు తన కిరణములనే చేతులతో ఆ ఆకాశపు చెట్టుకున్న నక్షత్రాలనే పూలను కోయడానికి ప్రయత్నిస్తున్నాడని పేర్కొన్నాడు. ఈ పద్యంలో వెన్నెలను వర్ణించడానికి చెట్టు, కొమ్మలు, పూలు, బాల్యచేష్టలు అనే అంశాలను కవి ఎన్నుకొన్నాడు.
‘వెన్నెల వెల్లి ….’ అనే పద్యంలో వెన్నెల ప్రవాహాన్ని పాలసముద్రంతో పోల్చాడు. చంద్రుడిని ఆదిశేషువుతో పోల్చాడు. చంద్రునిలోని మచ్చను శ్రీమహావిష్ణువుతో పోల్చాడు.
ఈ పద్యంలో తెల్లని వెన్నెలను తెల్లటి పాలసముద్రం ఎన్నుకొని పోల్చాడు. అలాగే తెల్లని చందమామను పోల్చడానికి నల్లటి మచ్చను పోల్చడానికి నల్లని విష్ణువును ఎన్నుకొన్నాడు.
ప్రశ్న 6.
పతిభక్తికి ఆదర్శం పద్మిని అని ఎలా చెప్పగలవు?
జవాబు:
మహా తేజస్సంపన్నుడైన సూర్యుని చూసిన కంటితో అల్పమైన తేజస్సు గల ఇతరులను చూడడానికి మనస్సు అంగీకరించదు. అందుకే కదిలెడి తుమ్మెదలనెడు కనుగ్రుడ్లు గల గొప్పదైన పద్మము అనెడు తన కంటిని వెంటనే మూసుకొన్నది.
ఎంతటి మహా పతివ్రతయైన పరపురుషుని కనీసం చూడనైనా చూస్తుంది. కానీ, పద్మిని మాత్రం కనీసం పరపురుషుని చూడడానికి కూడా అంగీకరించలేదు. అందుకే పద్మిని పతిభక్తికి ఆదర్శం. సూర్యోదయంకాగానే కమలాలు వికసిస్తాయి. సూర్యాస్తమయం కాగానే పద్మాలు ముడుచుకొంటాయి. ఇది లోక సహజం.
ప్రశ్న 7.
బాలచంద్రుడెలా ఉన్నాడు?
జవాబు:
పిల్లలకు ప్రాకడం సహజ లక్షణం. ఎక్కడైనా మెరుస్తున్నవి కనిపిస్తే, అవి లాగడం కూడా సహజమే.
అలాగే ఆకాశంలోని చంద్రుడు కూడా ఉన్నాడు. ఆకాశమే పెద్ద చెట్టులాగ ఉంది. దిక్కులు దానికి కొమ్మలులా ఉన్నాయి. నక్షత్రాలు కొమ్మల చివర పువ్వులులా ఉన్నాయి. అప్పుడే ఉదయించిన బాలచంద్రుడు తన పొడవైన కరములతో ఆ నక్షత్రాలనే పువ్వులు కోయడానికి ప్రయత్నిస్తున్నట్లున్నాడు.

ప్రశ్న 8.
వెన్నెలెలా ఉంది?
జవాబు:
వెన్నెల పాలసముద్రంలాగా తెల్లగా ఉంది. అది విజృంభించి దిక్కులన్నీ ముంచుతోంది. రజనీకరబింబం ఆదిశేషువులాగా తెల్లగా ఉంది. చంద్రునిలోని నల్లని మచ్చ ఆదిశేషునిపై పవ్వళించిన శ్రీమహావిష్ణువులా ఉంది.
పాలసముద్రంలో శ్రీమహావిష్ణువు ఆదిశేషునిపై పవ్వళిస్తాడు. ఈ సందర్భాన్ని వెన్నెలతో సమన్వయం చేస్తూ ఎఱ్ఱనగారు అద్భుతమైన కల్పన చేశారు.
ప్రశ్న 9.
పడమటి దిక్కును ఎఱ్ఱని తెరతో పోల్చడం సరైనదేనా? ఎందుకు?
జవాబు:
సాయం సమయంలో సూర్యుడు అస్తమిస్తాడు. సూర్యాస్తమయం సమయంలో సూర్యుడు పడమటి దిక్కుకు వెడతాడు. అప్పుడు సూర్యబింబం చాలా ఎర్రగా ఉంటుంది. అప్పుడు సూర్యుని కాంతి కిరణాలు కూడా ఎరుపురంగులో ఉంటాయి. ఆ సూర్యకాంతికి పడమటి దిక్కంతా ఎర్రగా అవుతుంది. .
సాధారణంగా తెరలు తెలుపురంగులో ఉంటాయి. ఆయా సన్నివేశాలకు తగినట్లు తెరపైకి కాంతిని ప్రసరింపచేస్తూ, రంగులు మార్చడం నాటకాలలో సహజం. ఇక్కడ కూడా నాట్యం చేసే నిశాసతికి తగినట్లుగా పడమటి దిక్కు అనే తెర ఎరుపురంగులో ఉంది అనడం’ అద్భుతమైన ఊహ.
ప్రశ్న 10.
లోకంలో చీకటి అలుముకున్న సందర్భాన్ని కవి ఎలా వర్ణించాడు?
జవాబు:
కవి ఎట్టా ప్రెగ్గడ ‘వెన్నెల’ పాఠంలో చీకటి యొక్క వ్యాప్తిని ఇలా వర్ణించాడు. సంధ్యాకాలం తరువాత చీకట్లు లోకమంతా వ్యాపించాయి. ఆ చీకటిలో భూమి, ఆకాశం, దిక్కులు అన్నీ ఒకటిగా కలిసిపోయాయి. అప్పుడు బ్రహ్మాండ ఖండము, కాటుక నింపిన పెద్ద బరిణె ఏమో అన్నట్లు ఉంది. అంటే అధికమైన చీకట్ల రాశీ వల్ల, దిక్కులు, భూమి, ఆకాశం ఒకదానిలో ఒకటి కలిసి పోయాయి. విశ్వము బాగా కాటుక నింపిన బరిణె ఏమో అన్నట్లు నల్లగా కనిపించిందని కవి వర్ణించాడు.
10th Class Telugu 4th Lesson వెన్నెల 4 Marks Important Questions and Answers
ఈ క్రింది ప్రశ్నలకు 10 లేక 12 వాక్యాల్లో జవాబులు రాయండి.
ప్రశ్న 1.
రాత్రి అనే ఆలోచన రానీయక, చీకటి అనే పేరును విననీయక ఆనంద తరంగంలా విస్తరించిన వెన్నెల విజృంభణను మీ సొంతమాటల్లో రాయండి.
జవాబు:
చంద్రుడు ఉదయించాడు. వెన్నెల ప్రవాహం పాలసముద్రంలా పొంగి ఆకాశాన్ని ముంచెత్తింది. చంద్రబింబం ఆ పాలసముద్రంలో గుండ్రంగా చుట్టుకొన్న ఆదిశేషుడి శయ్యలా, చంద్రుడిలోని మచ్చ ఆ శయ్య మధ్యన ఉన్న విష్ణువులా కనబడింది.
ఆ వెన్నెలలో కలువల రేకులు విచ్చుకున్నాయి. కలువ పూలలో తేనెలు పొంగి కెరటాలుగా విజృంభించాయి. తుమ్మెదలకు విందు చేస్తూ పూల పరిమళాలు బయలుదేరాయి.
చంద్రకాంత శిలల వానలతో, చకోరాల రెక్కల స్పర్శలతో, స్త్రీల చిరునవ్వుల కాంతులతో అతిశయించి, దిక్కులన్నింటినీ ముంచెత్తి వెన్నెల సముద్రంలా వ్యాపించింది. ఆ వెన్నెల అనే సముద్రపు నీటి నుండి చంద్రుడు ఆవిర్భవించాడు.
ఆ విధంగా అందంగా, గంభీరంగా, నిండుగా చంద్రుని వెన్నెల వ్యాపించింది.
అది రాత్రి అనే ఆలోచనను రానీయలేదు. చీకటి అనే పేరు విననీయలేదు. అవ్యక్తం అనే అనుమానాన్ని కలిగించలేదు. ఆ వెన్నెల కళ్ళకు అమృతపు జల్లులా, శరీరానికి మంచి గంధంలా, మనసుకు ఆనంద తరంగంలా విజృంభించింది.

ప్రశ్న 2.
పద్యభావాలను ఆధారంగా చేసుకొని పాఠ్యభాగ సారాంశాన్ని ఇరవై వాక్యాలకు కుదించి రాయండి.
జవాబు:
- సాటిలేని కాంతి గల సూర్యుని చూచినట్లుగా అల్ప తేజస్సు కలవానిని చూడలేనని సాయంసంధ్యలో కమలం కళ్లు (రేకులు) మూసుకొన్నది.
- నక్షత్రాలనే పూలతో అలంకరింపబడిన ఆకాశమనే వేదికపై నాట్యం చేయడానికి రాత్రి అనే స్త్రీకి ఏర్పరచిన ఎఱ్ఱని పరదా వలె పడమటి దిక్కు శోభించింది.
- ఇంతలో ఆకాశం, భూమి, దిక్కులు ఒక్కటి చేస్తూ చీకటి, ప్రపంచాన్ని కాటుక భరిణిగా మార్చింది.
- అంతలో తూర్పున చంద్రుడు ఉదయించాడు. అప్పుడు చంద్రబింబం చీకటి అనే పిశాచపు బాధా నివారణకు ముల్లోకాలనెడు స్త్రీ ధరించిన ఎఱ్ఱని బొట్టువలె ఉంది.
- రాత్రి అనెడు స్త్రీ తూర్పు దిక్కుకు ఇచ్చిన ఎఱ్ఱని గురువింద పూసల దండవలే శశిబింబం ఉంది.
- ఐరావతం మూపురంపై ఉన్న ఎఱ్ఱని అలంకారంలా, ఇంద్రసభలోని మాణిక్యదీపంలా నెలవంక గోచరించింది.
- తెల్లకలువ అనురాగ రసంతో నింపిన మాత్రవలె కన్పించింది.
- స్త్రీలకు ఉత్సాహం పెంచే ఔషధపు ముద్దలా మెరిసింది.
- అలా అలా చంద్రుడు పెరుగుతూ ఉన్నాడు.
- ఆకాశమనే వృక్షానికి గల దిక్కులనే కొమ్మలలోని నక్షత్రాలనే పూలు కోయడానికి తన కరములతో ఉత్సాహంగా ఆకాశంలో పాకుతున్నాడు.
- వెన్నెలనే పాల సముద్రంతో దిశలు, ఆకాశం ముంచుతున్న నెలవంక శేషపాన్పులా కనువిందు చేసింది.
- చంద్రునిలోని మచ్చ విష్ణువువలె కన్పించింది.
- ఆ పండు వెన్నెలలో కలువలు బాగా వికసించి, వెన్నెలకు పరవశిస్తూ కొంట్రొత్త సువాసనలు వెదజల్లుతూ నేత్రపర్వం చేస్తున్నాయి.
- వెన్నెల అనే సముద్రం చంద్రకాంత శిలలను తడుపుతూ, చక్రవాకపక్షుల రెక్కల వేగం పెంచుతూ, విరబూసిన కలువలను ఆకర్షిస్తూ, అనేక విధాల అందగించింది.
- అందంతో రాత్రి అనే ఆలోచన రానివ్వక వెన్నెల చూచేవారి కళ్లకు అమృతాభిషేకం చేస్తోంది.
- వెన్నెల తన గంభీరతతో చీకటి అనే పేరు విననివ్వక శరీరానికి గంధపు వర్షం అవుతోంది.
- ధీరమైన వెన్నెలను చూస్తే పరమాత్మ కూడా గుర్తుకు రాడు.
- ఎందుకంటే వెన్నెలను చూస్తుంటే అంతరాత్మకు బ్రహ్మానందం కలుగుతుంది.
- ఈ విధంగా కళ్లకు, శరీరానికి, ఆత్మకు ఆనందకారకమైంది వెన్నెల.
- ఈ వర్ణన ఎఱ్ఱన కవిత్వంలో కలికితురాయి.
ప్రశ్న 3.
సాయం సంధ్యా సమయంలో ఆకాశం ఎలా ఉందని కవి వర్ణించాడు? అది ఎంతవరకు సమంజసం?
జవాబు:
సూర్యుడు అస్తమించేటపుడు ప్రకృతిని పరిశీలిస్తే మొదట జరిగేది కమలాలు ముడుచుకొంటాయి. అస్తమించే సూర్యునికాంతి వన్నె తగ్గుతుంది. ఆ కాంతిలో వెచ్చదనం తగ్గుతుంది. అందుకే కమలాలు ముడుచుకొంటాయి.
ప్రకృతి సహజమైన దీనిని కవిగారు భార్యాభర్తల సంబంధంతో పోల్చారు. మహా తేజోవంతుడైన సూర్యుని చూసిన కంటితో అల్పతేజస్కులను చూడడానికి అంగీకరించదన్నట్లు పద్మిని తన కమలపు కంటిని మూసుకొన్నది అని చక్కగా వర్ణించారు.
సూర్యుడు పూర్తిగా పడమటి దిక్కుకు చేరి క్రిందకు అస్తమిస్తుంటే పడమటి దిక్కు ఎర్రబారుతుంది. పడమటి దిక్కు ఒక ఎర్రని తెరలా కవిగారు ఊహించారు. ఆ తేర వద్ద నటించడానికి రాత్రి అనే స్త్రీకి ఆకాశమనే వేదిక అలంకరించబడింది. కాలపురుషుడే సూత్రధారి, దిక్పాలకులే ప్రేక్షకులు.
అంటే సూర్యాస్తమయంతో ఒక అంకం ముగిసిపోయింది. క్రొత్త అంకానికి తెరలేచింది. ఇది ఒక అత్యద్భుతమైన నాటక రంగంగా కవి కల్పించాడు. సూర్యుడి అస్తమయంతో ఒక పెద్ద వెలుగు ఆకాశమనే రంగస్థలం నుండి ఖాళీ చేసి వెళ్ళిపోయింది.
రంగస్థలంపై ఎవరైనా కళాకారుడు ఉండాలి తప్ప, వేదిక ఖాళీగా ఉండకూడదు. వెలుగు ఖాళీ చేస్తే ఆ ప్రదేశాన్ని చీకటి ఆక్రమించడం సహజం.
క్రమేణా చీకటి దట్టంగా అలుముకొంది. ఆకాశం, నేల, దిక్కులు అన్నీ చీకటితో నిండిపోయాయి. బ్రహ్మాండంలో , భాగమైన భూగోళం ఒక కాటుక నిండిన భరిణెలా ఉందని ఎఱ్ఱనగారు ఊహించారు.
కవిగారి ఊహ చాలా సమంజసంగా ఉంది.
ప్రశ్న 4.
వెన్నెల వ్యాపించిన విధానాన్ని విశ్లేషించండి.
జవాబు:
వెన్నెల వ్యాపించిన విధానాన్ని ఎఱ్ఱనగారు చక్కగా వర్ణించారు. చంద్రుని ఒక చిన్నబాలుడుగా వర్ణించాడు. చిన్న పిల్లలకు చెట్లెక్కడం సరదా. పూలు, పళ్ళు కోయాలని చేతులు చాపడం సహజం. అది బాల్య చాపల్యం.
ఇక్కడ చంద్రుడు కూడా పుట్టి కొద్దికాలమే అయింది. అందుచే ఆకాశమనే చెట్టు పైకి ప్రాకాడు. దిక్కులనే కొమ్మలకు పూసిన నక్షత్రాలనే చుక్కలను కోయడానికి తన కరములు చాపాడు అని ఎర్రనగారు వర్ణించారు.
చీకటి పడగానే నక్షత్రాలు ఆకాశంలో రావడం సహజం. ఆ తరువాత చంద్రకిరణాలు ఆకాశంలోకి వ్యాపిస్తాయి. చంద్రకిరణాలు వ్యాపించే కొద్దీ వెన్నెల కాంతి పెరుగుతూ ఉంటుంది. వెన్నెల కాంతి పెరుగుతుంటే నక్షత్రాల కాంతి మసకబారుతూ ఉంటుంది. ఇది సహజం. దీనినే ఎర్రనగారు తన ఊహాబలంతో చాలా చక్కగా వర్ణించారు.
తరువాత పద్యంలో వెన్నెలను పాల సముద్రంతో పోల్చారు. చంద్రుడిని ఆదిశేషువుతో పోల్చారు. చంద్రుడిలోని నల్లని మచ్చను శ్రీమహావిష్ణువుతో పోల్చారు.
నిజానికి చంద్రుడి వలన వెన్నెల వ్యాపించింది. అది చంద్రుడిని మించిపోతుంది. చంద్రుడు ఆకాశంలో మాత్రమే కనిపిస్తాడు. వెన్నెల ప్రపపంచమంతా నిండిపోతుంది. దేనికైనా ఆవలి ఒడ్డు, ఈవలి ఒడ్డు ఉంటుంది. కాని అనంతమైనది సముద్రం. సముద్రంలో ఎటుచూసినా నీరే కనిపిస్తుంది. పాలసముద్రంలో ఎటుచూసినా తెల్లదనమే కనిపిస్తుంది. అలాగే ప్రపంచమంతా తెల్లటి వెన్నెలతో నిండిపోయింది.
పాలసముద్రంలో ఆదిశేషుడులా చంద్రుడు కనిపించాడు. ఆదిశేషువు తెలుపు. చంద్రుడు తెలుపే. కాని, చంద్రునిలో నల్లటి మచ్చను కూడా కవి వదలలేదు. అదే మహాకవుల లక్షణం. ఆ మచ్చను శ్రీమహావిష్ణువుతో పోల్చి తన చతురత నిరూపించారు ఎఱ్ఱనగారు.

ప్రశ్న 5.
వెన్నెల పాఠ్యాంశం ఆధారంగా ఎఱ్ఱన రచనా శైలిని విశ్లేషించండి.
జవాబు:
ఎఱ్ఱన వర్ణనలకు గీటురాయి వంటిది వెన్నెల పాఠం. సూర్యాస్తమయం జరిగినపుడు పద్మాలు ముడుచుకోవడం ప్రకృతిలో సాధారణమైన విషయం. కాని, అసమానమైన సూర్యుని చూసిన కంటితో ఇతరులను చూడడానికి అంగీకరించని పద్మిని తన పద్మమనే కంటిని మూసుకొన్నదని చక్కటి వర్ణన చేశాడు. పద్మాన్ని పద్మినీ జాతి స్త్రీతో పోల్చాడు. భార్యాభర్తల సంబంధాన్ని చక్కగా వర్ణించాడు.
‘సురుచిర తారకాకుసుమ శోభి’ అనే పద్యంలో సంధ్యాసమయంలో ఎఱ్ఱబడిన పడమటి దిక్కును పెద్ద తెరతో పోల్చాడు. ఆకాశాన్ని వేదికగా ఊహించాడు. నక్షత్రాలను పుష్పాలుగా ఊహించాడు. కాలమును సూత్రధారిగా భావించాడు. దిక్పాలకులను ప్రేక్షకులను చేశాడు. రాత్రిని నాట్యకత్తెగా మార్చాడు. ఈ పద్యంలో కూడా ఎఱ్ఱన వర్ణనాత్మక శైలిని ప్రదర్శించాడు.
‘దట్టమైన చీకటిని కాటుక భరిణెతో పోల్చి తన పరిశీలనాదృష్టిని ప్రదర్శించాడు.
అప్పుడే ఉదయిస్తున్న చంద్రుడు తన కరములతో ఆకాశమనే వృక్షమునకు గల దిక్కులనే కొమ్మలకు ప్రాకుతూ నక్షత్రాలనే పూలను కోయడానికి ప్రయత్నిస్తున్నాడని వెన్నెల రావడాన్ని చక్కగా వర్ణించాడు.
ఇదే విధంగా ప్రతి పద్యంలోనూ ఎఱ్ఱనగారు తన ప్రత్యేకతను నిరూపించుకొన్నారు.
ప్రశ్న 6.
సూర్యాస్తమయానికి, చంద్రోదయానికి మధ్య కాలాన్ని కవి ఎలా వర్ణించాడు?
జవాబు:
“పద్మిని, తన ప్రియుడయిన గొప్ప తేజస్సు కల సూర్యుడిని చూసిన తన కళ్ళతో, అల్ప కాంతికల పరపురుషులను చూడడం తగదన్నట్లుగా, కదలుతున్న తుమ్మెద అనే నల్లగ్రుడ్డు కల పద్మం వంటి తన కన్నును మూసుకుందని” కవి వర్ణించాడు. అంటే సూర్యాస్తమయం కాగానే పద్మాలు ముడుచుకున్నాయని పద్మాలలో తుమ్మెదలు చిక్కుకున్నాయని భావం. పద్మాలు ముడుచుకోవడం, అవి తమ పతి భక్తిని ప్రదర్శించడానికా అన్నట్లు ఉందని కవి వర్ణించాడు.
- రాత్రి అనే స్త్రీ చేయబోయే నాట్యానికి, రంగస్థలం మీద కట్టిన ఎఱ్ఱరంగు తోపు తెరవలె, పడమటి దిక్కున ఆకాశంలో సంధ్యారాగం కనబడింది.
- చుక్కలతో కూడిన ఆకాశం, పువ్వులతో అలంకరించిన నాట్య రంగస్థలం వలె కన్పడింది.
- రాత్రి అనే స్త్రీ ‘నర్తకి’ వలె ఉంది.
- కాలము అనేది నాటక సూత్రధారుడు వలె ఉంది. అంటే సంధ్యాకాలమయ్యింది. పడమటి దిక్కున ఆకాశం ఎఱుపురంగులో కనబడుతోంది. ఆకాశంలో నక్షత్రాలు ఉదయించాయి. రాత్రి వస్తోంది. రాత్రి తన చీకటిని అంతా వ్యాపింప చేస్తుందని కవి తెలిపాడు.
ప్రశ్న 7.
చంద్రోదయానికి ముందు ప్రకృతి ఎలా ఉందో వివరించండి.
జవాబు:
1) చంద్రుడు, దిక్కులు అనే కొమ్మలను, తన పొడవైన కిరణాలు అనే చేతులతో పట్టుకొని, పైకి లేచి, ఆకాశము అనే చెట్టు యొక్క నక్షత్రాలు అనే పువ్వులను కోయడం కోసమేమో అన్నట్టు ఆకాశంలోకి పాకాడు. అంటే చంద్రుడి , కాంతి, ఆకాశం అంతా వ్యాపించిందని భావము.
2) వెన్నెల ప్రవాహం పాలసముద్రంలా పొంగి అన్ని దిక్కులనూ, ఆకాశాన్ని ముంచెత్తింది. అప్పుడు చంద్రబింబం, ఆ పాలసముద్రంలో గుండ్రంగా చుట్టుకొన్న ఆదిశేషుడి శయ్యను ఏర్పాటు చేసినట్లు ఉంది. చంద్రుడిలోని నల్లని మచ్చ ఆదిశేషువు శయ్యపై మధ్యలో ఉన్న విష్ణుమూర్తివలె కనబడింది.
అంటే చంద్రుడి వెన్నెల పాలసముద్రంలా కనబడింది. చంద్రబింబం, పాలసముద్రంలో విష్ణుమూర్తి నిద్రించే శేషుని పానుపు వలె కనిపించింది. చంద్రుడిలోని నల్లని మచ్చ, ఆదిశేషువుపై నిద్రించిన నీలవర్ణుడైన విష్ణువువలె కన్పించిందన్న మాట.
ప్రశ్న 8.
కవి వెన్నెలను ఏయే అంశాల ఆధారంగా వర్ణించాడు?
జవాబు:
కవి ఎట్టి ప్రెగ్గడ, వెన్నెలను వర్ణించడానికి క్రింది వస్తువులను ఎన్నుకొన్నాడు.
- వెన్నెల పాలసముద్రంలా తెల్లగా వ్యాపించిందన్నాడు.
- నిండు వెన్నెలలో కలువ పువ్వురేకులు విచ్చుకున్నాయని చెప్పాడు.
- వెన్నెలకు చంద్రకాంత శిలలు కరిగి, జడివానలు కురిశాయన్నాడు.
- చకోరపక్షులు, తమ రెక్కలతో వెన్నలను స్పృశించాయన్నాడు.
- వెన్నెల, స్త్రీల అందమైన చిఱునవ్వుల కాంతి వలే ఉందన్నాడు.
- వెన్నెల, సముద్రజలంలా వ్యాపించిందన్నాడు.
- చూసే వారి కళ్ళకు వెన్నెల, అమృతపు జల్లులా, శరీరానికి పూసిన మంచిగంధపు పూతలా ఉందన్నాడు.
- వెన్నెల చూసే వారి మనస్సులకు ఆనంద తరంగము వలె ఉందన్నాడు.
ప్రశ్న 9.
వెన్నెల వ్యాపించినపుడు ప్రకృతిలో కలిగిన మార్పులేమి?
జవాబు:
చంద్రోదయము :
- చంద్రుడు ఉదయించాడు. వెన్నెల ప్రవాహం, పాలసముద్రంలా పొంగి ఆకాశాన్ని ముంచెత్తింది.
- చంద్రబింబం, ఆ పాలసముద్రములో గుండ్రంగా చుట్టుకొన్న ఆదిశేషుడి పానుపులా, చంద్రుడిలోని మచ్చ, ఆ శయ్యపై ఉన్న విష్ణువులా కనబడింది.
- ఆ వెన్నెలలో కలువటేకులు విచ్చుకున్నాయి. కలువపూలలో తేనెలు పొంగి, కెరటాలుగా విజృంభించాయి. తుమ్మెదలకు విందు చేస్తూ పూల పరిమళాలు వ్యాపించాయి.
- చంద్రకాంత శిలలు కరిగిన జడివానలతో, చకోరాల టెక్కల స్పర్శలతో, స్త్రీల చిఱునవ్వుల కాంతులతో అతిశయించి, దిక్కులన్నింటిలో ముంచెత్తి, వెన్నెల సముద్రంలా వ్యాపించింది. ఈ విధంగా అందంగా, గంభీరంగా, నిండుగా చంద్రుని వెన్నెల వ్యాపించింది.

ప్రశ్న 10.
చంద్రోదయానికి ముందు, తరువాత జరిగిన మార్పులను వివరించండి.
జవాబు:
చంద్రోదయానికి ముందు మార్పులు :
- సూర్యుడు అస్తమించాడు.
- పద్మములు ముడచుకున్నాయి.
- తుమ్మెదలు ఆ పద్మాలలో చిక్కుపడ్డాయి.
- పడమటి దిక్కున సంధ్యారాగం కనబడింది.
- ఆకాశంలో నక్షత్రాలు ఉదయించాయి.
- చీకటి బాగా పెరిగి, దిక్కులూ, భూమ్యాకాశాలు దానిలో కలిసి పోయాయి.
- విశ్వం, కాటుక నింపిన బరిణెయా అన్నట్లు కనబడింది.
చంద్రోదయము తరువాత జరిగిన మార్పులు :
- చంద్రుడు ఉదయించగానే, వెన్నెల ప్రవాహం పాలసముద్రం వలె పొంగి ఆకాశాన్ని ముంచెత్తింది.
- చంద్రబింబం, ఆ పాలసముద్రంలో చుట్టచుట్టుకొన్న ఆదిశేషువు శయ్యవలె కనిపించింది.
- చంద్రుడిలోని మచ్చ, ఆ శయ్య మధ్యన ఉన్న విష్ణువువలె కనబడింది.
- వెన్నెలలో కలువరేకులు విచ్చుకున్నాయి. కలువలలో తేనెలు ఉప్పొంగాయి.
- పువ్వుల పరిమళాలు వ్యాపించాయి. 6) చంద్రకాంత శిలలు కరిగి జడివానలు కురిశాయి.
- చకోరాల లెక్కల స్పర్శలతో, స్త్రీల చిరునవ్వుల కాంతులతో అతిశయించి, వెన్నెల దిక్కులన్నింటినీ ముంచెత్తి, సముద్రంలా వ్యాపించింది.
10th Class Telugu 4th Lesson వెన్నెల Important Questions and Answers
ప్రశ్న 1.
నీకు నచ్చిన ప్రకృతి దృశ్యాన్ని వర్ణిస్తూ ఒక కవిత రాయండి.
జవాబు:
చంద్రోదయము
1) “చెరువులో నీరు గాలికి తిరుగుచుండె
కలువపుష్పాలు వికసించి కనులు తెరిచె
పూల గంధాల మధుపాలు మురియుచుండె
చంద్రకాంతులు వ్యాపించే జగము నిండ”
2) దివిని చుక్కల పూవులు తేజరిల్లె
రాత్రి సతికట్టె నల్లని రంగు చీర
చంద్రుని రాకకు జగమంత సంతసించె
విశ్వమంతకు వెన్నెల విందు చేసె
ప్రశ్న 2.
మీ పాఠం (వెన్నెల) ఆధారంగా ఎఱ్ఱన రచనా శైలిని వివరిస్తూ మీ తండ్రిగారికి లేఖ రాయండి.
జవాబు:
విశాఖపట్టణము,
x x x x x. పియ్రమైన నాన్నగార్కి, నమస్కారములు. ఉభయకుశలోపరి. అమ్మకు నమస్కారాలు చెప్పండి. ఈ మధ్య మాకు ఎఱ్ఱన కవి రచించిన నృసింహపురాణంలోని వెన్నెల పాఠాన్ని చెప్పారు. వెన్నెల పాఠంలో అద్భుతమైన వర్ణనలు ఉన్నాయి. ఈ పద్యాలలో ఎఱ్ఱా ప్రెగ్గడ కవి, సంధ్యాకాలాన్ని, చంద్రోదయాన్ని బాగా వర్ణించాడు. మీకు కవిత్వం అంటే ఇష్టమని ఇది రాస్తున్నా. సూర్యుడిని చూసిన కళ్ళతో పరపురుషులను చూడ్డానికి ఇష్టపడని పద్మిని, కళ్ళు మూసుకుందని పద్మము, సాయంత్రం వేళ ముడుచుకోవడాన్ని చక్కగా ఎఱ్ఱన వర్ణించాడు. మరో పద్యంలో ఆకాశాన్ని రంగస్థలంతో పోల్చాడు. కాలాన్ని నాటకంలో సూత్రధారిగా చెప్పాడు. దిక్పాలకులను నాటక ప్రేక్షకులుగా వర్ణించాడు. సంధ్యాకాలంలోని ఆకాశాన్ని తోపురంగు నాటకం తెరగా వర్ణించాడు. ఎఱ్ఱన గారి వర్ణన శైలి అద్భుతము. అందుకే ఎఱ్ఱన గారిని ‘ప్రబంధ పరమేశ్వరుడు’ అంటారు. వర్ణనలు చేయడంలో ఎఱ్ఱన కవికి సాటి మరి లేరని నా నమ్మకం. మీరు కూడా చదవండి. లేఖ రాయండి. ఉంటా. మీ ప్రియపుత్రుడు, / పుత్రిక,
రంగనాథ్. / శ్యామల. చిరునామా:
కె. రమణగారు,
ఇంటినెంబరు 3. 216,
గాంధీనగర్, శ్రీకాకుళం, ఆంధ్రప్రదేశ్. |
ప్రశ్న 3.
వెన్నెలను వర్ణిస్తూ కవిత వ్రాయండి.
జవాబు:
“వెన్నెలా ! కన్నెపిల్లల చిన్నారి ముద్దుల చెల్లెలా !
వెన్నెలా ! ప్రేమికుల మనసుల మల్లెచెండులా
వెన్నెలా ! చంద్రుని చిరునవ్వుల పన్నీరులా
వెన్నెలా ! పసిపాపల ముద్దుల బోసి నవ్వులా
వెన్నెలా ! కన్నతల్లుల కమనీయ రాగవెల్లిలా
వెన్నెలా ! మా చిన్నారి పొన్నారి చెల్లెలా
వెన్నెలా ! కలువల చుట్టపు చూపులా
వెన్నెలా ఉన్నావు, చల్లావు చంద్రికలు
నయనారవిందాల నయగార మధురిమలు”
ప్రశ్న 4.
వర్ణన ఎలా ఉంటుందో తెలిసింది కదా! ఉషోదయ కాలం నుండి రాత్రి నిండుపున్నమి వెన్నెల వచ్చే వరకు రోజంతా ఆకాశంలో జరిగే మార్పుల్ని గురించి వర్ణిస్తూ రాయండి.
జవాబు:
ఉషోదయ కాలంలో ఆకాశంలో వేగుచుక్క కనిపిస్తుంది. అక్కడక్కడ చుక్కలు కనబడతాయి. క్రమంగా తూర్పు దిక్కున సూర్యబింబం ఎఱ్ఱని పెద్ద బంతిలా కనబడుతుంది. తెల్లవారేక సూర్యోదయం తూర్పుదిశలో జరుగుతుంది.
ఎండ ఎక్కిన కొద్దీ సూర్యకిరణాలు కరకరలాడుతాయి. మధ్యాహ్నం వేళ సూర్యుడు నడినెత్తిమీదికి వస్తాడు. క్రమంగా సూర్యుడు పడమటి దిశకు జారుతాడు. అక్షాశంలో పడమటి దిశలో పేదరాశి పెద్దమ్మ కుంకుమ ఆరబోసుకున్నట్లు ఆకాశం ఎరుపెక్కుతుంది. సూర్యబింబం ఎరుపు ఎక్కుతుంది.
సాయంత్రం 7 గంటలకు ఆకాశంలోని నక్షత్రాలు ఉదయిస్తాయి. చంద్రబింబం ఎఱుపుగా కనబడుతుంది. చంద్రోదయం కాగానే చల్లదనం ప్రాణాలకు హాయిని ఇస్తుంది. మేఘాల కదలికలో చంద్రబింబం ప్రయాణిస్తున్నట్లు ఉంటుంది.

ప్రశ్న 5.
ఎఱ్ఱన రచించిన వెన్నెల పాఠంలోని వర్ణనలు నీకెందుకు నచ్చిందో వివరిస్తూ నీ మిత్రునికి లేఖ వ్రాయి.
జవాబు:
అమలాపురం,
x x x x x ప్రియమిత్రుడు శేఖర్ కు,
నీ మిత్రుడు రాజేష్ వ్రాయులేఖ. నేను బాగా చదువుచున్నాను. నీవు కూడా బాగా చదువుతున్నావనుకొంటున్నాను. నేను ఈ లేఖలో ‘వెన్నెల’ పాఠం గురించి వ్రాస్తున్నాను. వెన్నెల పాఠంలోని ఎఱ్ఱన గారి వర్ణనలు చాలా బాగున్నాయి. ముఖ్యంగా మొదటి పద్యంలో సూర్యుడిని చూసిన కళ్ళతో ఇతరులను చూడడానికి ఇష్టం లేని పద్మిని తన కమలపు కన్నును మూసుకొందని వర్ణించిన తీరు నాకు చాలా నచ్చింది. సూర్యస్తమయం అయినపుడు కమలాలు ముడుచుకోవడం సహజం. దానిని చక్కగా భార్యాభర్తల అనురాగంతో పోల్చిన ఎఱ్ఱనగారి చతురత నాకు నచ్చింది. రెండవ పద్యంలో ఆకాశాన్ని రంగస్థలంతో పోల్చారు. కాలమును సూత్రధారిగా ఊహించారు. దిక్పాలకులను ప్రేక్షకులను చేశారు. రాత్రిని నాట్యకత్తెగా భావించారు. ఎఱ్ఱబారిన పడమటి దిక్కును పెద్ద తెరగా ఊహించారు. సాయంకాలపు సంధ్యా సమయాన్ని ఇంత బాగా ఊహించిన కవి మరొకరు లేరేమో అనిపిస్తుంది. నాకు మాత్రం వెన్నెల పాఠంలోని ప్రతి పద్యం చాలా సచ్చింది. ఆ అద్భుతమైన వర్ణనలు ఎవరికైనా నచ్చుతాయిలే. అందుకే ఎఱ్ఱనను ప్రబంధ పరమేశ్వరుడన్నారని మా గురువుగారు చెప్పారు. నీకు ఏ పాఠం నచ్చిందో వ్రాయి. ఎందుకు నచ్చిందో వివరంగా వ్రాయి. ఇక ఉంటా మరి. ఇట్లు
నీ స్నేహితుడు,
పి. రాజేష్, చిరునామా:
కె. శేఖర్, నెం. 8,
బి. సెక్షన్, 10వ తరగతి,
జి.ప. ఉ. పాఠశాల,
సత్తెనపల్లి, గుంటూరు జిల్లా. |
10th Class Telugu 4th Lesson వెన్నెల 1 Mark Bits
1. దేవతలు దివి నుండి భువికి దిగి వచ్చారు – గీత గీసిన పదానికి అర్థం గుర్తించండి. (June 2017).
A) సముద్రం
B) పాతాళం
C) ఆకాశం
D) చీకటి
జవాబు:
C) ఆకాశం
2. నెమలి ఎగిరి వచ్చి పామును పట్టి చంపింది – గీత గీసిన పదాలకు నానార్థ పదాన్ని గుర్తించండి. (June 2017)
A) వనం
B) ఫలం
C) కులం
D) కుండలి
జవాబు:
D) కుండలి
3. వెన్నెల అన్ని దెసలకు వ్యాపించింది – గీత గీసిన పదానికి ప్రకృతి పదాన్ని గుర్తించండి. (June 2017)
A) దిశ
B) దేశం
C) దివాణం
D) దిక్కు
జవాబు:
A) దిశ
4. ‘UUU’ గుర్తులు గల గణమేది ? (June 2017)
A) య గణం
B) ర గణం
C) మ గణం
D) త గణం
జవాబు:
C) మ గణం

5. రజనీకర బింబమును చూస్తే పిల్లలు ఆనందిస్తారు – (గీత గీసిన పదమునకు అర్థమును గుర్తించుము.) (March 2017)
A) సూర్యబింబము
B) చంద్రబింబము
C) ప్రతిబింబము
D) ఆకాశం
జవాబు:
B) చంద్రబింబము
6. విద్యార్థులు చదువు పట్ల శ్రద్ధాసక్తులు కల్గియుండాలి – (గీత గీసిన పదము ఏ సమాసమో గుర్తించుము. ) (March 2017)
A) కర్మధారయం
B) బహుబ్లిహి
C) తత్పురుషం
D) ద్వంద్వము
జవాబు:
D) ద్వంద్వము
7. ఉత్పలమాల పద్యంలో యతిస్థానం గుర్తించండి. (March 2017)
A) 14వ అక్షరం
B) 10వ అక్షరం
C) 13వ అక్షరం
D) 11వ అక్షరం
జవాబు:
B) 10వ అక్షరం
8. దెసలను కొమ్మ లొయ్య నతిదీర్ఘములైన కరంబులన్ బ్రియం – ఏ పద్యపాదమో గుర్తించండి. (March 2017)
A) ఉత్పలమాల
B) శార్దూలం
C) చంపకమాల
D) మత్తేభం
జవాబు:
C) చంపకమాల
9. భూరుహములు జీవులకు ప్రాణవాయువును ఇస్తున్నాయి – గీత గీసిన పదానికి సరియైన అర్థాన్ని గుర్తించండి. (June 2018)
A) నదులు
B) సముద్రాలు
C) చెట్లు
D) పర్వతాలు
జవాబు:
C) చెట్లు
10. కష్టాలు మిక్కుటమైనందున, రైతులు ప్రభుత్వ సహాయం కొరకు ఎదురుచూస్తున్నారు – గీత గీసిన పదానికి పర్యాయపదాలను గుర్తించండి. (June 2018)
A) అధికం, సమానం
B) క్షామం, మితం
C) ఎక్కువ, అధికం
D) తక్కువ, పరిమితం
జవాబు:
C) ఎక్కువ, అధికం
11. దినకరుడు రాగానే లోకమంతా చైతన్యమౌతుంది. అందుకే సూర్యుడు మనకు ప్రత్యక్ష దైవం – గీత గీసిన పదాలకు పర్యాయపదాన్ని గుర్తించండి. (June 2018)
A) స్నేహితుడు
B) చంద్రుడు
C) ధనికుడు
D) ఇనుడు
జవాబు:
D) ఇనుడు

12. ప్రతి పాదంలో ఒక సూర్యగణం + రెండు ఇంద్రగణములు + రెండు సూర్యగణములు క్రమముగా ఉండే పద్యము పేరు గుర్తించండి. (June 2018)
A) కందం
B) సీసము
C) తేటగీతి
D) ఆటవెలది
జవాబు:
C) తేటగీతి
13. వెన్నెల పిండారబోసినట్లుండటం శరత్కాలపు లక్షణం – గీత గీసిన పదానికి పర్యాయపదాలను గుర్తించండి. (March 2018)
A) కౌముది, జ్యోత్స్న
B) చీకటి, తమస్సు
C) కోరిక, కాంక్ష
D) నిశి, నుసి
జవాబు:
A) కౌముది, జ్యోత్స్న
14. ఎటువంటి పరిస్థితిలోనైన ధర్మం వీడరాదు. (వికృతి గుర్తించండి) (S.N. I – 2018-19)
A) దమ్మం
B) దరమం
C) దరుమం
D) దరువుం
జవాబు:
A) దమ్మం
15. మానవునిచే ప్రకృతి ఒడి పాఠశాలగా చేసుకోబడింది. (కర్తరి వాక్యం గుర్తించండి.) (June 2017)
A) మానవుడు ప్రకృతి ఒడిని పాఠశాలగా చేసుకున్నాడు.
B) మానవుడు ప్రకృతి ఒడిని పాఠశాలగా చేసుకోలేదు.
C) మానవునిచే ప్రకృతి,పాఠశాలగా చేసుకోబడింది.
D) మానవుడు ప్రకృతిలో పాఠశాల నిర్మించాడు.
జవాబు:
A) మానవుడు ప్రకృతి ఒడిని పాఠశాలగా చేసుకున్నాడు.
16. చంద్రుడిలోని మచ్చ విష్ణువులాగ కనిపిస్తూ అలరింపబడుతున్నది – కర్తరి వాక్యం గుర్తించండి. (June 2018)
A) చంద్రుడిలోని మచ్చ విష్ణువులాగా కనిపిస్తూ అలరిస్తున్నది.
B) చంద్రుడిలోని మచ్చ విష్ణువులాగ అలరించడం లేదు.
C) చంద్రుడిలోని మచ్చ శివునిలాగ కనిపిస్తోంది.
D) చంద్రుడిలోని మచ్చ విష్ణువనే భ్రాంతి కలిగిస్తోంది.
జవాబు:
A) చంద్రుడిలోని మచ్చ విష్ణువులాగా కనిపిస్తూ అలరిస్తున్నది.
17. వెన్నెల రాత్రిని పగలుగా మారుస్తున్నది – వ్యతిరేకార్థక వాక్యాన్ని గుర్తించండి. (June 2018)
A) చీకటి రాత్రిని పగలుగా మారుస్తున్నది.
B) వెన్నెల రాత్రిని పగలుగా మార్చడం లేదు.
C) వెన్నెల పగలును రాత్రిగా మారుస్తున్నది.
D) వెన్నెల రాత్రిని రాత్రిగానే ఉంచుతుంది.
జవాబు:
B) వెన్నెల రాత్రిని పగలుగా మార్చడం లేదు.

18. వెన్నెల కాలంలో రాత్రింబవళ్లు వెలుగుంటుంది. (ఇది ఏ రకమైన వాక్యమో గుర్తించండి) (S.N. I – 2018-19)
A) చేదగ్ధక వాక్యం
B) సంక్లిష్ట వాక్యం
C) సంయుక్త వాక్యం
D) నిషేధార్థక వాక్యం
జవాబు:
C) సంయుక్త వాక్యం
19. వానలు వస్తే పంటలు పండుతాయి. (ఇది ఏ రకమైన వాక్యమో గుర్తించండి) (S.I. I – 2018 -19)
A) సంయుక్తం
B) చేదర్థకం
C) సామర్థ్యార్థకం
D) విధ్యర్థకం
జవాబు:
B) చేదర్థకం

![]()

![]()
![]()
![]()
![]()
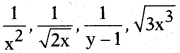 , etc. are not polynomials.
, etc. are not polynomials.