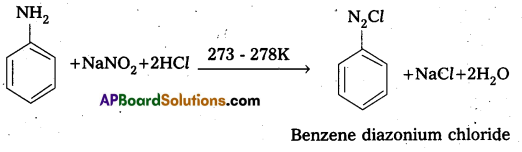
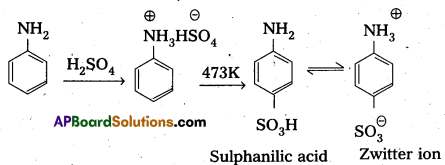
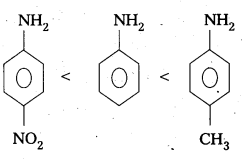
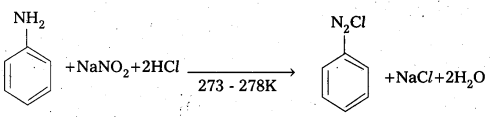
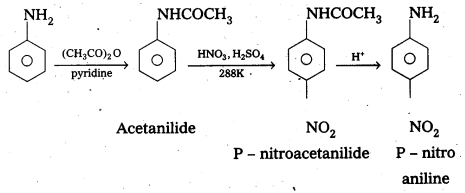
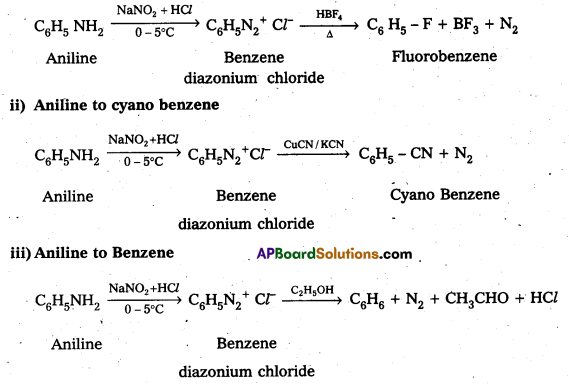
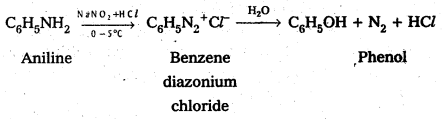
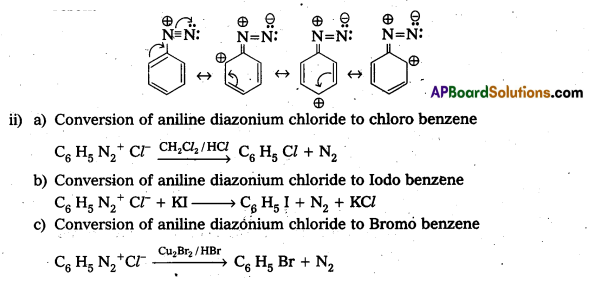
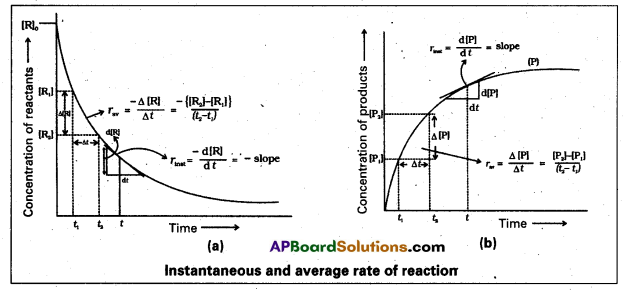
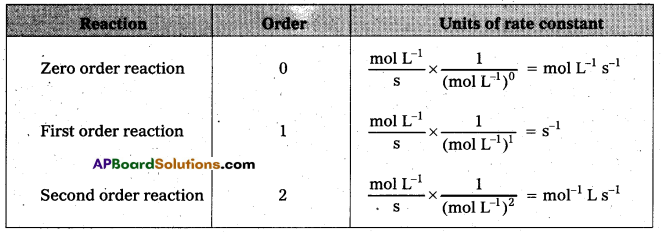
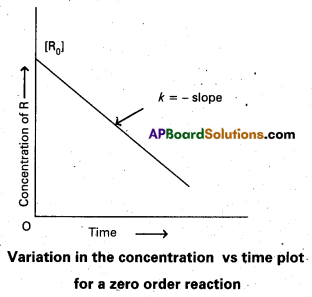
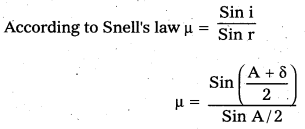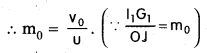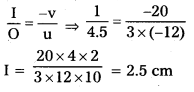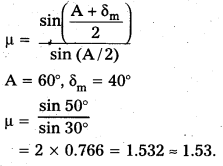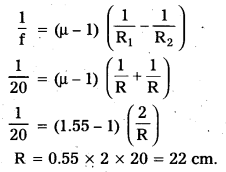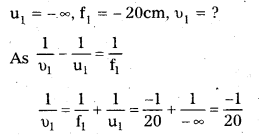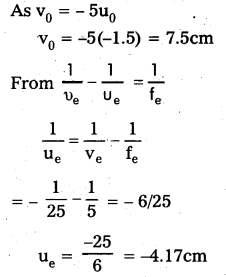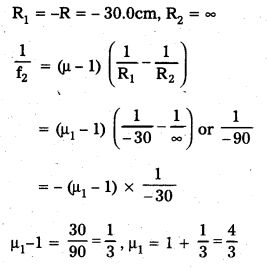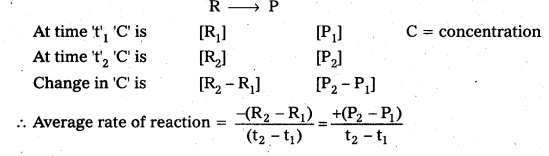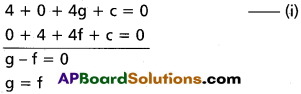Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 2nd Lesson Ray Optics and Optical Instruments Textbook Questions and Answers.
AP Inter 2nd Year Physics Study Material 2nd Lesson Ray Optics and Optical Instruments
Very Short Answer Questions
Question 1.
Define focal length and radius of curvature of a concave lens.
Answer:
Focal length (f) : The distance of principal focus from the optical centre of the lens is called focal length of the lens. The focal length (f) = CF
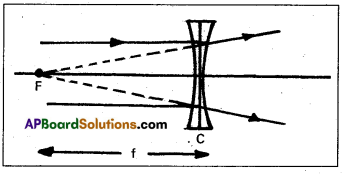
Radius of curvature : Radius of curvature is the radius of the sphere from which the curved surface is taken a part.
Question 2.
What do you understand by the terms ‘focus’ and ‘principal focus’ in the context of lenses ?
Answer:
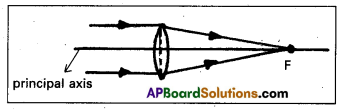
Focus : The point where image of an object placed at infinity is formed is called the focus of the lens.
Principal focus: A narrow beam of light incident on a lens in a direction parallel to its principal axis, after refraction through the lens, the rays converge to a point on the principal axis. This point is called principal focus.
Question 3.
What is optical density and how is it different from mass density ? (T.S. Mar. ’16)
Answer:
Optical density: Optical density is defined as the ratio of the speed of light in media.
Mass density: Mass per unit volume is defined as mass density.
Mass density of an optically denser medium less than that of optically rarer medium.
Question 4.
What are the laws of reflection through curved mirrors ?
Answer:
- “The angle of reflection equals to the angle of incidence”.
- “The incident ray, reflected ray and the normal to the reflecting surface at the point of incidence lie in the same plane”.
Question 5.
Define ‘power’ of a convex lens. What is its unit ?
Answer:
Power of a lens : Power of a lens is defined as its bending ability and is measured as reciprocal of focal length in metre.
∴ Power of a lens (P) = \(\frac{1}{\text { f(in metres) }}\) = \(\frac{100}{\mathrm{f}(\text { in } \mathrm{cms})}\)
Unit → Dioptre (D)
Question 6.
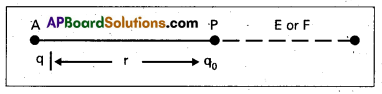
A concave mirror of focal length 10 cm is placed at a distance 35 cm from a wall. How far from the wall should an object be placed so that its real image is formed on the wall ?
Answer:
f = 10 cm, υ = 35 cm
\(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{-u}\) (using sign convention)
\(\frac{1}{\mathrm{u}}\) = \(\frac{1}{v}\) – \(\frac{1}{f}\) = \(\frac{1}{35}\) – \(\frac{1}{10}\)
\(\frac{1}{\mathrm{u}}\) = \(\frac{10-35}{35 \times 10}\) = \(\frac{-1}{14}\)
U = – 14 cm.
Distance of the object from the wall = 35 – 14 = 21cm.
Question 7.
A concave mirror produces an image of a long vertical pin, placed 40cm from the mirror, at the position of the object. Find the focal length of the mirror.
Answer:
Give u = υ = 40cm]
\(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{u}\)
\(\frac{1}{f}\) = \(\frac{1}{40}\) + \(\frac{1}{40}\)
\(\frac{1}{f}\) = \(\frac{2}{40}\)
f = 20 cm.
Question 8.
A small angled prism of 40 deviates a ray through 2.48°. Find the refractive index of the prism. (A.P. Mar. ’19)
Answer:
A = 4°, Dm = 2.48°
Dm = A(μ – 1)
μ – 1 = \(\frac{D_m}{A}\) = \(\frac{2.48}{4}\) = 0.62
μ = 1 + 0.62
μ = 1.62
Question 9.
What is dispersion ? Which colour gets relatively more dispersed?
Answer:
Dispersion : The phenomenon of splitting of white light into its constituent colours, on passing through a prism is called dispersion of light.
The deviation is maximum for violet colour.
Question 10.
The focal length of a concave lens is 30 cm. Where should an object be placed so that its image is 1/10 of its size? (T.S. Mar. ‘19)
Answer:
f = 30 cm, h1 = h, h2 = \(\frac{\mathrm{h}}{10}\)
Question 11.
What is myopia ? How can it be corrected ? (T.S. Mar. ’15)
Answer:
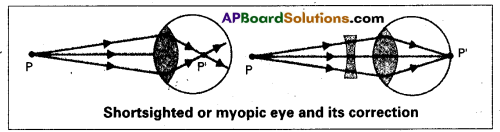
Myopia (or) Near sightedness :
The light from a distant object arriving at the eye-lens may get converged at a point infront of the retina. This type of defect is called myopia.
To correct this, we interpose a concave lens between the eye and the object.
Question 12.
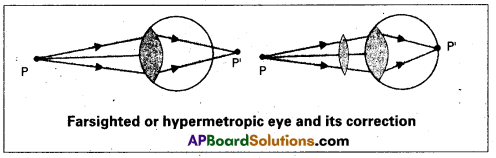
What is hypermetropia ? How can it be corrected ? (A.P. Mar. ’16)
Answer:
Hypermetropia (or) Farsightedness :
The light from a distant object arriving at the eye-lens may get converged at a point behind the retina. This type of defect is called Hypermetropia.
To correct this, we interpose a convex lens (Convergent lens) between the eye and the object.
Short Answer Questions
Question 1.
A light ray passes through a prism of angle A in a position of minimum deviation. Obtain an expression for (a) the angle of incidence in terms of the angle of the prism and the angle of minimum deviation (b) the angle of refraction in terms of the refractive index of the prišm.
Answer:
In the quadrilateral AQNR
∠A + ∠QNR = 180° ……… (1)
From Δle QNR, r1 + r2 + ∠QNR = 180° ………. (2)
r1 + r2 = A …….. (3)
Total deviation δ = (i – r1) + (e – r2)
δ = i + e – A ……. (4)
a) At minimum deviation position M
δ = Dm, i = e and r1 = r2 = r
∴ From eq(4), Dm = 2i – A
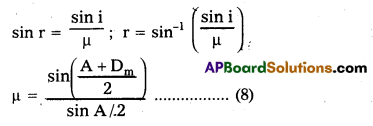
i = \(\frac{\mathrm{A}+\mathrm{D}_{\mathrm{m}}}{2}\) …… (5)
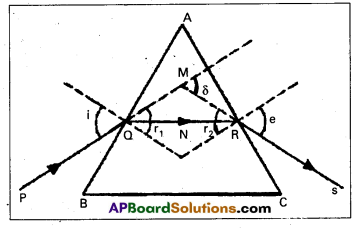
b) From eq (3), r + r = A
r = A/2 ……. (6)
Refractive index of the prism μ = \(\frac{\sin i}{\sin r}\) …… (8)
Question 2.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length. (A.P. Mar. ’19)
Answer:
Focal length of concave mirror:
The distance between the focus F and the pole P of the mirror is called the focal length of the concave mirror.
Consider a ray AB parallel to principal axis incident on a concave mirror at B and is reflected along BF. The line CB is normal to the mirror.
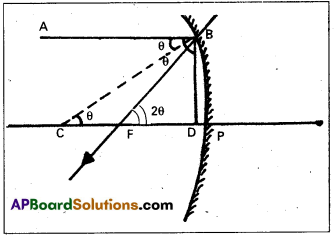
Let θ be the angle of incidence, ∠ABC = ∠BCP = θ
Draw BD ⊥ CP
In right angled Δle BCD
Tan θ = \(\frac{\mathrm{BD}}{\mathrm{CD}}\) ….. (1)
From Δle BFD, Tan2θ = \(\frac{\mathrm{BD}}{\mathrm{FD}}\) ……. (2)
Dividing eq (2) by eq (1)
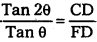…….. (3)
If θ is very small, them tan θ ≈ θ and tan 2θ ≈ 2θ since the aperture of the lens is small
∴ The point B lies very close to p.
CD ≈ CP and FD ≈ FP
From eq (3), \(\frac{2 \theta}{\theta}\) = \(\frac{C P}{F P}\) = \(\frac{R}{f}\) ⇒ 2 = \(\frac{R}{f}\)
R = 2f
Question 3.
A mobile phone lies along the principal axis of a concave mirror longitudinally. Explain why the magnification is not uniform.
Answer:
The ray diagram for the formation of image of the phone is shown in figure. The image of part which is on the plane perpendicular to principal axis will be on the same plane. It will be the same size i.e, B’C = BC.
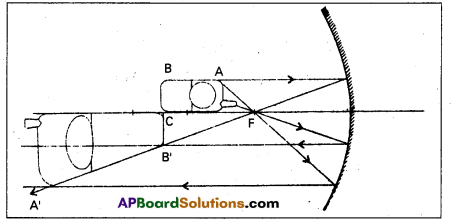
Question 4.
Explain the cartesian sign convention for mirrors.
Answer:
According to cartesian sign convention:
- All distances are measured from the pole of the mirror (or) the optical centre of the lens.
- The distances measured in the same direction as incident light are taken as positive.
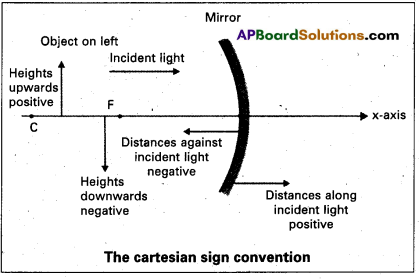
- The distances measured in the direction opposite to the incident light are taken as negative.
- The heights measured upwards with respect to x-axis and normal to the x-axis are taken as positive.
- The heights measured downwards are taken as negative.
Question 5.
Define critical angle. Explain total internal reflection using a neat diagram.(T.S. Mar. ’15)
Answer:
Critical angle:
When light ray travelling from denser medium to rarer medium, then the angle of inci-dence for which angle of refraction in air is 90° is called critical angle.
C = sin-1 \(\left(\frac{1}{\mu}\right)\)
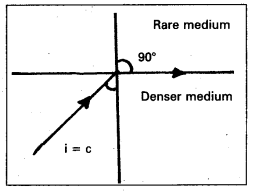
Total internal reflection:
When a light ray travels from denser to rarer medium, the angle of incidence is greater than the critical angle, then it reflects into the same medium is called total internal reflection.
Explanation:
Consider an object in the denser medium. A ray OA incident on XY bends away from the normal. As the angle of incidence is increased, the angle of refraction goes on increasing. For certain angle of incidence, the refracted ray parallel to XY surface (r = 90°)
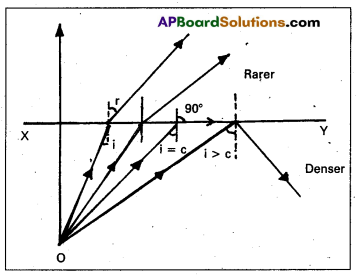
When the angle of incidence is further increased, the ray is not refracted but is totally reflected back in the denser medium. This phenomenon is called total internal reflection.
Question 6.
Explain the formation of a mirage. (T.S. Mar. 19 & A.P. Mar. ’16)
Answer:
In a desert, the sand becomes very hot during the day time and it rapidly heats the layer of air which is in its contact. So density of air decreases. As a result the successive upward layers are denser than lower layers.
When a beam of light travelling from the top of a tree enters a rarer layer, it is refracted away from the normal. As a result at the surface of layers of air, each time the angle of incidence increases and ultimately a stage is reached, when the angle of incidence becomes greater than the critical angle between the two layers, the incident ray suffers total internal reflection.
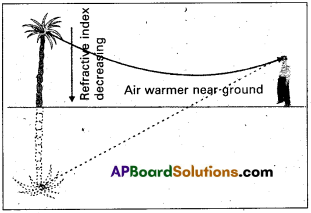
So it appears as inverted image of the tree is formed and the same looks like a pool of water to the observer.
Question 7.
Explain the formation of a rainbow.
Answer:
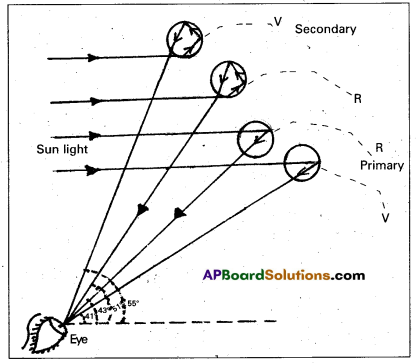
Figure shows how sun light is broken into its segments in the process and a rainbow appears. The dispersion of the violet and the red rays after internal reflection in the drop is shown in figure.
The red rays emerge from the drops of water at one angle (43°) and the violet rays emerge at another angle (41°). The large number of water drops in the sky makes a rainbow. The rainbow appears semicircular for an observer on earth.
Question 8.
Why does the setting sun appear red ? (Mar. ’14)
Answer:
As sunlight travels through the earths atmosphere, gets scattered by the large number of molecules present. This scattering of sun light is responsible for the colour of the sky, during sunrise and sunset etc.
The light of shorter wave length is scattered much more than light of larger wavelength. Scattering ∝ \(\frac{1}{\lambda^4}\).
Most of blue light is scattered, hence the bluish colour of sky predominates.
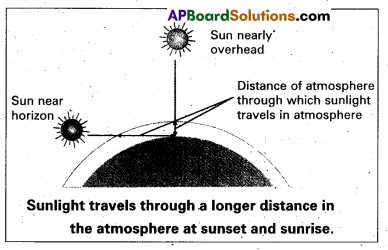
At sunset (or) sunrise, sun rays must pass through a larger atmospheric distance. More of the blue colour is scattered away only red colour which is least scattered appears to come from sun. Hence it appears red.
Question 9.
With a neat labelled diagram explain the formation of image in a simple microscope. (T.S. Mar. 16 & A.P. Mar. 15)
Answer:
Simple microscope : It consists a single short focus convex lens. It increases the visual angle to see an object clearly. It is also called magnifying glass (or) reading glass.
Working : The object is adjusted within the principal focus of the convex lens to form the image at the near point. The image is formed on same side of the object and it is virtual, erect and magnified as shown in fig.
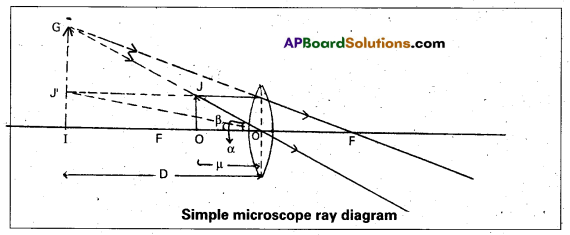
Magnifying power: The ratio of the angle subtended by the image at the eye to the angle subtended by the object at the eye is called magnifying power of a simple microscope.
It is denoted by ‘m’
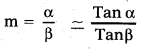
Question 10.
What is the position of the object for a simple microscope ? What is the maximum magnification of a simple microscope for a realistic focal length?
Answer:
When an object is placed between principal focus and optical centre of a convex lens, a virtual and erect image will be formed on the same side of the object.
Magnifying power: It is defined as the ratio of the angle subtended at the eye by the image to the angle subtended by the object at the eye.
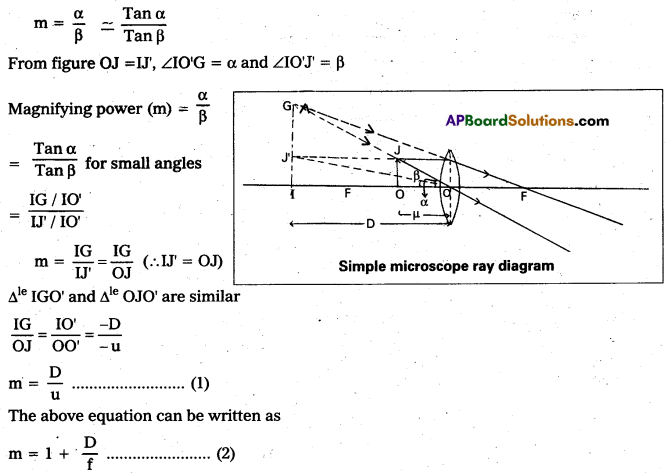
This shows that smaller the focal length of the lens, greater will be the magnifying power of microscope.
Long Answer Questions
Question 1.
a) What is the cartesian sign convention ? Applying this convention and using a neat diagram, derive an expression for finding the image distance using the mirror equation.
b) An object of 5 cm height is placed at a distance of 15 cm from a concave mirror of radius of curvature 20cm. Find the size of the image.
Answer:
According to cartesian sign convention:
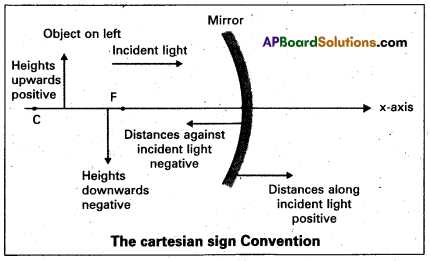
- All distances are measured from the pole of the mirror (or) the optical centre of the lens.
- The distances measured in the same direction as incident light are taken as positive.
- The distances measured in the direction opposite to the incident light are taken as negative.
- The heights measured upwards with respect to x-axis and normal to the x-axis are taken as positive.
- The heights measured downwards are taken as negative.
Image distance using mirror equation :
Consider an object AB is placed beyond centre of curvature of a concave mirror, on its principal axis.
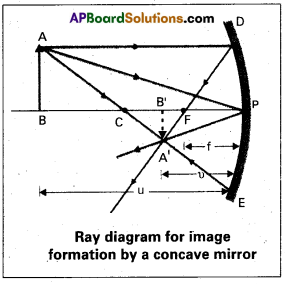
A ray AD parallel to principal axis incident on the mirror at point D and is reflected to pass through F. Another ray AE passing through centre of curvature C is reflected along the same path. Two rays of light intersect at point A’. Thus A’B’ is real, inverted and diminished image of AB formed between C and F.
Δle DPF and Δle A’B’ F are similar
\(\frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{PD}}\) = \(\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{FP}}\)
(or) \(\frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{BA}}\) = \(\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{FP}}\) …… (1) (∴ PD = AB)
Since ∠APB = ∠A’P’V’
The right angle triangles A’B’P and ABP are similar
\(\frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{BA}}\) = \(\frac{B^{\prime} P}{B P}\) …….. (2)
From equations (1) and (2), \(\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{FP}}\) = \(\frac{\mathrm{B}^{\prime} \mathrm{P}}{\mathrm{BP}}\) = \(\frac{\mathrm{B}^{\prime} \mathrm{P}-\mathrm{FP}}{\mathrm{FP}}\) ….. (3)
Now applying the sign convention
B’P = -v, FP = -f, BP = -u
\(\frac{-v+f}{-f}\) = \(\frac{-\mathrm{V}}{-\mathrm{u}}\) ⇒ \(\frac{v-f}{f}\) = \(\frac{\mathrm{v}}{\mathrm{u}}\)
\(\frac{v}{\mathrm{f}}\) – 1 = \(\frac{v}{\mathrm{u}}\) ⇒ \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) + \(\frac{v}{\mathrm{u}}\)
b) Given that h1 = 5 cm
u = -15cm
R = 20cm
f = \(\frac{-\mathrm{R}}{2}\) = \(\frac{-20}{2}\) = -10cm
Question 2.
a) Using a neat labelled diagram derive the mirror equation. Define linear magnification.
b) An object is placed at 5cm from a convex lens of focal length 15cm. What is the position and nature of the image ?
Answer:
a) Derivation of mirror equation: Consider an object AB is placed beyond centre of curvature of a concave mirror, on its principal axis.
A ray AD parallel to principal axis incident on the mirror at point D and is reflected to pass through F.
Another ray AE passing through centre of curvature C is reflected along the same path. Two rays of light intersect at point A’. Thus A’ B’ is real, inverted and diminished image of AB formed between C and F.
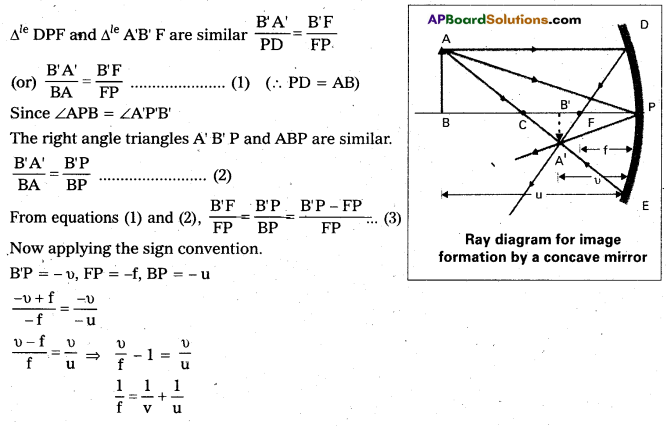
Linear magnification:
Linear magnification is the ratio of the size of the image formed by the mirror to the size of the object.
Nature of the image is virtual.
Question 3.
a) Derive an expression for a thin double convex lens. Can you apply the same to a double concave lens too?
b) An object is placed at a distance of 20cm from a thin double convex lens of focal length 15cm. Find the position and magnification of the image.
Answer:
a)
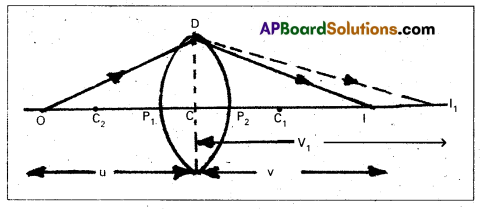
- A convex lens is made up of two spherical refracting surfaces of radii of curvatures, R1 and R2 and μ is the refractive index of the lens.
- P1, P2 are the poles, C1, C2 are the centres of curvatures of two surfaces with optical centre C.
- Consider a point object O lying on the principal axis of the lens and I1 is the real image of the object.
If CI1 ≈ P1 I1 = v1
and CC1 ≈ PC1 = R1
CO ≈ P1 = u - As refraction is taking place from rarer to denser medium
\(\frac{\mu_1}{-u}\) + \(\frac{\mu_2}{v_1}\) = \(\frac{\mu_2-\mu_1}{R_1}\) ……. (1) - The refracted ray suffers further refraction
Therefore I is the final real image of O. - For refraction at second surface, I1 as virtual object, whose real image is formed at I.
∴ u ≈ CI1 ≈ P2I1 = V1
Let CI ≈ P2 I = V - Now refraction taking place from denser to rarer medium
When the object on the left of the lens is at infinity (∝), image is formed at principal focus of the lens.
∴ u = ∝, υ = f = focal length of the lens
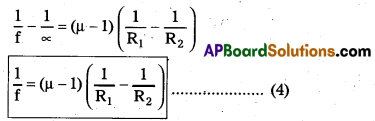
This is the lens maker’s formula
Yes, same formula applies to double concave lens too.
b) Given that u = 20 cm, f = 15 cm
\(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{u}\)
\(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\) = \(\frac{1}{15}\) – \(\frac{1}{20}\)
\(\frac{1}{v}\) = \(\frac{20-15}{15 \times 20}\) + \(\frac{5}{15 \times 20}\)
\(\frac{1}{v}\) = \(\frac{1}{60}\)
v = 60 cm.
Magnification (m) = \(\frac{-\mathbf{v}}{\mathbf{u}}\)
m = \(\frac{-60}{-20}\) (u = -20cm)
m = 3
Question 4.
Obtain an expression for the combined focal length for two thin convex lenses kept in contact and hence obtain an expression for the combined power of the combination of the lenses.
Answer:
- Consider two lenses A and B of focal lengths f1 and f2 placed in contact with each other.
- Let the object be placed at a point O, the first lens forms the image at I1, it is real. It serves as the virtual object of lens B, Producing final image at I.
- For the image formed by lens A, we get
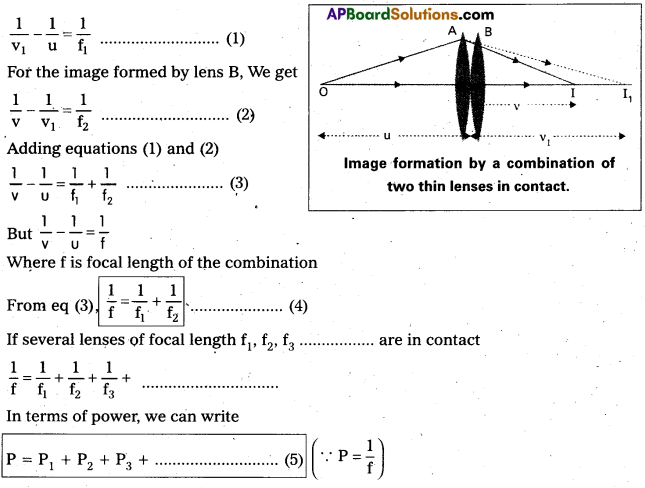
Question 5.
a) Define Snell’s Law. Using a neat labelled diagram derive an expression for the refractive index of the material of an equilateral prism.
b) A ray of light, after passing through a medium, meets the surface separating the medium from air at an angle of 45° and is just not refracted. What is the refractive index of the medium ?
Answer:
a) Snell’s law:
The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant, called the refractive index of the medium.
\(\frac{\sin i}{\sin r}\) = μ (constant).
Let ABC be the glass prism. Its angle of prism is A. The refractive index of the material of the prism is μ. Let AB and AC be the two refracting surfaces PQ = incident ray, RS = emergent ray.
Let angle of incidence = i1
angle of emergence = i2
angle of refraction = r1
angle of refraction at R = r2
After travelling through the prism it falls on AC and emerges as RS.
The D = angle of deviation.
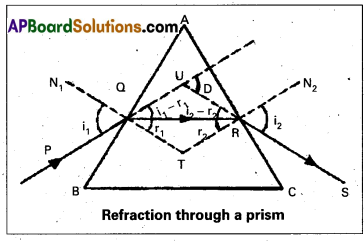
From the Δ QRT
r1 + r2 + ∠T = 180° —— (1)
From the quadrilateral AQTR
∠A + ∠T = 180°
∠T = 180° – A ……. (2)
From the equations (1) and (2)
r1 + r2 + ∠T = 180° we get
r1 + r2 + 180° – A = 180°
r1 + r2 = A …… (3)
from the Δ QUR
i1 – r1 + i2 – r2 + 180° – D = 180°
i1 + i2 – (r1 + r2) = D
i1 + i2 – A = D [∵ r1 + r2 = A]
i1 + i2 = A + D …. (4)
Minimum deviation: Experimentally it is found that as the angle of incidence increased the angle of deviation decreases till it reaches a minimum value and then it increases. This least value of deviation is called angle of minimum deviation ‘δ’ as shown in the fig.
When D decreases the two angles i1 and i2 become closer to each other at the angle of minimum deviation, the two angles of incidence are same i.e, i1 = i2
As i1 = i2, r1 = r2
∴ i1 = i2 = r1 = r2 = r
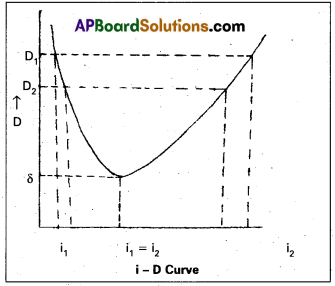
substituting this in (1) and (2) we get
2r = A ⇒ r = A/2
i + i = A + δ ⇒ i = \(\frac{\mathrm{A}+\delta}{2}\)
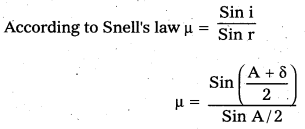
Note :The minimum deviation depends on the refractive index of the prism material and the angle of the prism.
b) Given that i = C = 45°
μ = \(\frac{1}{\sin c}\) ⇒ μ = \(\frac{1}{\sin 45^{\circ}}\)
μ = \(\frac{1}{1 / \sqrt{2}}\) = \(\sqrt{2}\)
μ = 1.414
Question 6.
Draw a neat labelled diagram of a compound microscope and explain its working. Derive an expression for its magnification.
Answer:
Description: It consists of two convex lenses separated by a distance. The lens near the object is called objective and the lens near the eye is called eye piece. The objective lens has small focal length and eye piece has of Idrger focal length. The distance of the object can be adjusted by means of a rack and pinion arrangement.
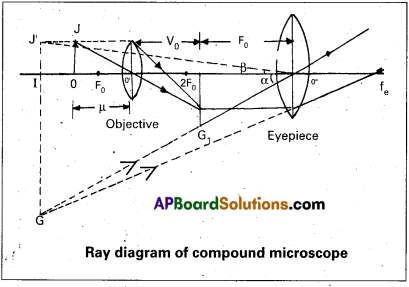
Working: The object OJ is placed outside the principal focus of the objective and the real image is formed on the other side of it. The image I1 G1 is real, inverted and magnified.
This image acts as the object for the eyepiece. The position of the eyepiece is so adjusted that the image due to the objective is between the optic centre and principal focus to form the final image at the near point. The final image IG is virtual, inverted and magnified.
Magnifying Power : It is defined as the ratio of the angle subtended by the final image at the eye when formed at near point to the angle subtended by the object at the eye when imagined to be at near point.
Imagining that the eye is at the optic centre, the angle subtended by the final image is α. When the object is imagined to be taken at near point it is represented by IJ’ and OJ = IJ’. The angle made by I J’ at the eye is β. Then by the definition of magnifying power
Magnifying power of the objective (me) = I1 G1 / OJ = Height of the image due to the objective / Height of its object.
Magnifying power of the eye piece (me) = IG/I1G1 = Height of the final image / Height of the object for the eyepiece.
∴ m = mo × me ….. (1)
To find mo : In figure OJ O’ and I1 G1 O’ are similar triangles. \(\left(\frac{\mathrm{I}_1 \cdot \mathrm{G}_1}{\mathrm{OJ}}\right)\) = \(\frac{O^{\prime} I_1}{O^{\prime} O}\)
Using sign convention, we find that O’I1 = + v0 and O’O = -u where v0 is the image distance due to the objective and u is the object distance for the objective or the compound microscope.
I1G1 is negative and OJ is positive.
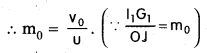
To find me : The eyepiece behaves like a simple microscope. So the magnifying power of the eye piece.
∴ me = \(\left(1+\frac{D}{f_e}\right)\)
Where fe is the focal length of the eyepiece.
Substituting m0 and me in equation (1),
m = \(+\frac{\mathrm{v}_0}{\mathrm{u}}\left(1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right)\)
When the object is very close to the principal focus F0 of the objective, the image due to the objective becomes very close to the eyepiece.
u ≈ f0 and v0 ≈ L
Where L is the length of the microscope. Then
m = \(-\frac{L}{f_0}\left(1+\frac{D}{f_e}\right)\)
Problems
Question 1.
A light wave of frequency 4 × 1014 Hz and a wavelength of 5 × 10-7 m passes through a medium. Estimaté the refractive index of the medium.
Answer:
υ = 4 × 1014 Hz
A = 5 × 10-7 m
v = υλ = 4 × 1014 × 5 × 10-7 = 20 × 107
= 2 × 108 m fs
we know that C = 3 × 108 m/s
µ = \(\frac{C}{v}\)
µ = \(\frac{3 \times 10^8}{2 \times 10^8}\)
µ = \(\frac{3}{2}\) = 1.5
Question 2.
A ray of light is incident at an angle of 60° on the face of a prism of angle 30°. The emergent ray makes an angle of 30° with the incident ray. Calculate the refractive index of the material of the prism.
Answer:
i1 = 60°, r = 30°, i2 = 30° .
µ = \(\frac{\sin i}{\sin r}\)
µ = \(\frac{\sin 60^{\circ}}{\sin 30^{\circ}}\)
µ = \(\frac{\sqrt{3}}{2 \times \frac{1}{2}}\)
µ = \(\sqrt{3}\)
µ = 1.732
Question 3.
Two lenses of power – 1.75D and +2.25D respectivetly, are placed in contact. Calculate the focal length of the combination.
Answer:
P1 = – 1.75 D, P2 = + 2.25 D.
P = P1 + P2
P = -1.75 + 2.25
P = 0.5
\(\frac{1}{\mathrm{~F}}\) = P
F = \(\frac{1}{p}\) = \(\frac{1}{0.5}\) = 2m
F = 200cm
Question 4.
Some rays falling on a converging lens are focussed 20cm from the lens. When a diverging lens is placed in contad with the converging lens, the rays are focussed 30cm from the combination. What is the focal length of the diverging lens?
Answer:
u = -20 cm
υ = 30cm
\(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{\mathrm{u}}\) ⇒ \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{30}}\) – \(\frac{1}{\mathrm{20}}\)
\(\frac{1}{\mathrm{f}}\) = \(\frac{20-30}{30 \times 20}\) = \(\frac{-10}{30 \times 20}\)
\(\frac{1}{\mathrm{f}}\) = \(-\frac{1}{60}\)
f = -60cm.
Question 5.
A double convex lens of focal length 15cm is used as a magnifying glass in order to produce an erect image which
is 3 times magnified. What is the distance between the object and the lens?
Answer:
f = 15cm
m = 3
Magnifying power (m) = \(\frac{-v}{\mathbf{u}}\) = \(\frac{f}{f-u}\)
3 = \(\frac{15}{15-u}\)
45 – 3u = 15
3u = 45 – 15
3u = 30
u = \(\frac{30}{3}\) = 10cm.
Question 6.
A compound microscope consists of an object lens of focal length 2cm and an eyepiece of focal length 5cm. When an object is placed at 2.2cm from the object lens, the final Image is at 25cm from the eye lens. What is the distance between the lenses ? What is the total linear magnification?
Answer:
Given that f0 = 2, fe = u0 = 2.2, D = 25cm
\(\frac{1}{\mathrm{f}_0}\) = \(\frac{1}{\mathrm{u}_0}\) + \(\frac{1}{\mathrm{v}_0}\)
\(\frac{1}{\mathrm{v}_0}\) = \(\frac{1}{\mathrm{f}_0}\) – \(\frac{1}{\mathrm{u}_0}\) = \(\frac{1}{2}\) – \(\frac{1}{2.2}\) ⇒ \(\frac{1}{v_0}\) = \(\frac{2.2-2}{2 \times 2.2}\)
v0 = 22 cm
For the eye-piece, the distance of the image Ve = 25cm
\(\frac{1}{f_e}\) = \(\frac{1}{\mathrm{u}_{\mathrm{e}}}\) – \(\frac{1}{v_e}\) (For virtual image)
\(\frac{1}{u_e}\) = \(\frac{1}{f_e}\) + \(\frac{1}{v_e}\) = \(\frac{1}{5}\) + \(\frac{1}{25}\)
⇒ \(\frac{1}{u_e}\) = \(\frac{25+5}{5 \times 25}\)
ue = 4.166
i) The distance between the two lenses
L = v0 + ue
L = 22 + 4.166
L = 26.166
Question 7.
The distance between two point sources of light is 24cm. Where should you place a converging lens, of focal length 9 cm, so that the images of both sources are formed at the same point ?
Answer:
Distance between two point sources of light = 24cm Focal length (f) = 9cm Radius of curvature (R) = 2f
R = 2 × 9 = 18cm
∴ Converging lens is placed at 18 cm (or) Second position of converging
lens = 24 – 18 = 6cm.
∴ position of converging lens = 18 cm (or) 6cm.
Question 8.
Find two positions of an object, placed in front of a concave mirror of focal length 15cm, so that the image formed is 3 times the size of the object.
Answer:
f = 15cm
m = 3
i) m = \(\frac{-v}{u}\) = \(\frac{f}{f-u}\)
3 = \(\frac{15}{15-u}\)
45 – 3u = 15
3u = 30
u = 10 cm
ii) m = \(\frac{\mathrm{f}}{\mathrm{u}-\mathrm{f}}\)
3 = \(\frac{15}{\mathrm{u}-15}\)
3u – 45 = 15
3u = 60
u = 20
Question 9.
When using a concave mirror, the magnification is found to be 4 times as much when the object is 25cm from the mirror as it is with the object at 40cm from the mirror, the image being real in each case. What is the focal length of the mirror?
Answer:
Given that m = 4
u = 25cm
m = \(\frac{f}{u-f}\)
4 = \(\frac{f}{25-f}\)
100 – 4f = f
100 = 5f
f = \(\frac{100}{5}\) = 20cm.
Question 10.
The focal length of the objective and eyepiece of a compound microscope are 4cm and 6cm respectively. If an object is placed at a distance of 6cm from the objective, what is the magnification produced by the microscope ?
Answer:
Given that f0 = -4cm, fe = 6cm, u0 = 6
\(\frac{1}{\mathrm{f}_0}\) = \(\frac{1}{\mathrm{v}_0}+\frac{1}{\mathrm{u}_0}\)
\(\frac{1}{v_0}\) = \(\frac{1}{\mathrm{f}_0}\) – \(\frac{1}{\mathrm{u}_0}\) = \(\frac{1}{4}-\frac{1}{6}\)
\(\frac{1}{v_0}\) = \(\frac{2}{24}\)
υ0 = 12 cm.
Magnifying power m = \(\frac{\mathrm{v}_0}{\mathrm{u}_0}\left(1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right)\)
= \(\frac{12}{6}\left[1+\frac{25}{6}\right]\) = \(2\left[\frac{31}{6}\right]\) = \(\frac{62}{6}\)
m = 10.33
Textual Exercises
Question 1.
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved ?
Answer:
u = – 27cm, R = – 36cm, f = – 18cm
\(\frac{1}{\mathrm{u}}\) + \(\frac{1}{v}\) = \(\frac{1}{\mathrm{f}}\) ⇒ \(\frac{-1}{27}+\frac{1}{v}\) = \(\frac{-1}{18}\)
\(\frac{1}{v}\) = \(\frac{1}{27}-\frac{1}{18}\) ⇒ \(\frac{1}{\mathrm{v}}\) = \(\frac{-1}{54}\)
v = – 54 cm.
The Screen should be placed 54cm from the mirror
m = \(\frac{\mathrm{I}}{\mathrm{O}}\) = \(\frac{-\mathrm{V}}{\mathrm{u}}\) ⇒ \(\frac{\mathrm{I}}{2.5}\) = \(\frac{-54}{27}\)
U = – 5cm
∴ The image is real, inverted and magnified. If the candle is moved closer, the screen would have moved farther and farther. Closer than 18cm from the mirror, the image gets virtual and cannot be collected on the screen.
Question 2.
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification.
Answer:
O = 4.5 cm, u = -12cm, f = 15cm
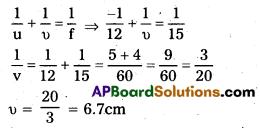
Image is virtual and erect and is formed behind the mirror.
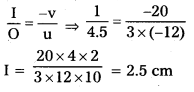
As the needle is moved further from the mirror, the image moves towards the focus and gets progressively diminished in size.
Question 3.
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 2.4 cm. What is the refractive index of water ? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again ?
Answer:
Distance by which image becomes raised = 9.4 – 7.67 = 1.73 = 1.7cm the microscope will be moved up by 1.7cm to focus on the needle again.
Question 4.
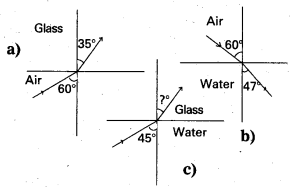
The above 3 Figures (a) and (b) show refraction of a ray in air incident at 60° with the normal to a glass-air and water- air figures interface respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45° with, the normal to a water-glass interface [Fig. (c)]
Answer:
1st Case:
Angle of incidence i = 60°
Angle of refraction r = 35°
3rd Case :
Angle of incidence i = 45°
Angle of refraction = ?
wrg = \(\frac{\sin i}{\sin r}\) = \(\frac{\sin i}{\sin r}\) = 1.28
Sin r = \(\frac{\sin 45^{\circ}}{1.28}\) = 0.5525
sin r = sin 33°54′
r = 33°44′
Question 5.
A small bulb is placed at the bottom of a tank containing water to a depth of 80cm. What is the area of the surface of water through which light from the bulb can emerge out ? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
Answer:
If r is the radius of the large circle from which light comes out, C is the critical angle for water – air interface, then
tan C = \(\frac{\mathrm{DB}}{\mathrm{DO}}\) = \(\frac{\mathbf{r}}{\mathbf{d}}\)
r = d tan C
Area of circle,
A = πr²
A = π(d tan C)2
A = πd².\(\frac{\sin ^2 C}{\cos ^2 C}\)
A = πd².\(\frac{\sin ^2 C}{1-\sin ^2 C}\)
But Sin C = \(\frac{1}{\mu}\) = \(\frac{1}{1.33}\) ≈ 0.75
A = \(\frac{\pi(0.8)^2(0.75)^2}{1-(0.75)^2}\) = 2.6m2
Question 6.
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism ? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
Answer:
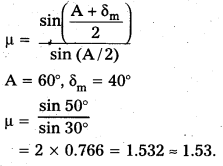
Question 7.
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20cm ?
Answer:
\(\frac{\mu_2}{\mu_1}\) = μ = 1.55
R1 = R, R2 = -R
f = 20
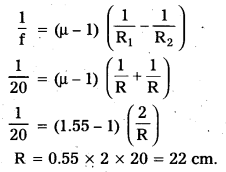
Question 8.
A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm, and (b) a concave lens of focal length 16 cm ?
Answer:
Here the object is virtual and the image is real u = + 12 cm (object on right and virtual)
a) f = + 20cm
Lens formula is \(\frac{-1}{\mathrm{u}}\) + \(\frac{1}{v}[latex] = \)\frac{1}{f}[/latex]
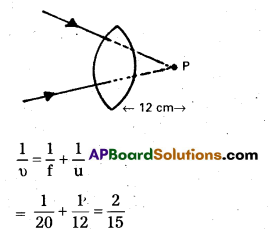
i. e., u = 7.5 cm (image on right and real) It is located 7.5 cm from the lens,
b) f = – 16cm
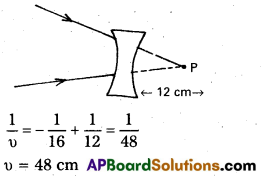
Image will be located 48cm from the lens.
Question 9.
An object of size 3.0cm is placed 14cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens ?
Answer:
‘O’ = 3.0cm
u = – 14cm, f = -21cm
\(\frac{1}{v}+\frac{1}{u}\) = \(\frac{1}{f}\) ⇒ \(\frac{1}{v}+\frac{1}{14}\) = \(\frac{-1}{21}\)
\(\frac{1}{v}\) = \(\frac{-1}{21}-\frac{1}{14}\)
υ = \(\frac{-42}{5}\) = – 8.4 cm
Image is erect, virtual and located 8.4cm from the lens on the same side as the object. Using the relation,
\(\frac{I}{O}\) = \(\frac{\mathrm{v}}{\mathrm{u}}\)
υ = \(\frac{8.4}{15}\) × 5 = 1.8cm
As the object is moved away from the lens, the virtual image moves towards the focus of the lens and progressively diminishes in size. (When u = 21 cm, v = -10.5 cm and when u = ∞, v = -21 cm)
Question 10.
What is the focal length of a convex lens of focal length 30cm in contact with a concave lens of focal length 20cm ? Is the system a converging or a diverging lens ? Ignore thickness of the lenses.
Answer:
Given f1 = 30 cm, f2 = -20 cm, f = ?
f = \(\frac{\mathrm{f}_1 \mathrm{f}_2}{\mathrm{f}_1+\mathrm{f}_2}\)
f = \(\frac{30 \times(-20)}{30-20}\) = -60cm
Thus the system is a diverging lens of focal length 60cm.
Question 11.
A compound microscope consists of an objective lens of focal length 2.0cm and an eyepiece of focal length 6.2 5cm separated by a distance of 15cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (2 5cm), and (b) at infinity? What is the magnifying power of the microscope in each case?
Answer:
a) Ve = 25 cm
fe = 6.25 cm.
Using lens formula,
Question 12.
A person with a normal near point (25cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5 cm can bring an object placed at 2.0 mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope.
Answer:
Angular magnification of the eye piece for image at 25 cm
u = –\(\frac{25}{11}\) = -2.27 cm
∴ Distance between objective and eye piece
= v + |u| = 7.2 + 2.27 = 9.47cm
Magnifying power of microscope
= \(\frac{7.2}{0.9} \times \frac{-25}{\frac{-25}{11}}\) = 88
Question 13.
A small telescope has an objective lens of focal length 144 cm and an eyepiece of focal length 6.0 cm. What is the magnifying power of the telescope ? What is the separation between the objective and the eyepiece?
Answer:
a) For normal adjustment
M.P of telescope = \(\frac{f_0}{f_e}\) = \(\frac{144}{6}\) = 24
b) The length of the telescope in normal adjustment
L = f0 + fe = 144 + 6
= 150 cm.
Question 14.
a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of
focal length 1.0 cm is used, what is the angular magnification of the telescope?
b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens ? The diameter of the moon is 3.48 × 106m, and radius of lunar orbit is 3.8 × 108m.
Answer:
a) Anglular magnification
= \(\frac{f_0}{f_e}\) = \(\frac{15}{0.01}\) = 1500
b) if d is the diameter of the image (in cm)
\(\frac{\mathrm{d}}{1500}\) = \(\frac{3.48 \times 10^6}{3.8 \times 10^8}\)
d = 13.7
Question 15.
Use the mirror equation to deduce that:
a) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
b) a convex mirror always produces a virtual image independent of the location of the object.
c) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
d) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
[Note : This exercise helps you deduce algebraically properties of images that one obtains from explicit ray diagrams.]
Answer:
Since for concave mirror, f is negative, υ becomes negative.
It means image produced is real and beyond 2f.
b) For mirror formula,
υ = \(\frac{\mathbf{u f}}{\mathbf{u}-\mathbf{f}}\)
since for a convex mirror, fis positive and u is always negative, u will be always positive image and will always be formed behind the mirror and will be virtual.
c) For relation, m = \(\frac{v-f}{f}\) positive for convex mirror, m will always be negative and less than one. Hence virtual image formed will always be diminished.
For relation, m = \(\frac{v-f}{f}\) and m being negative, υ will always be less than f. Hence image will be formed between pole and focus.
d) When u > 0 < f we get m = \(\frac{f}{u-f}\) = \(\frac{f}{(>0<f)-f}\) = \(\frac{f}{(>-f<0)}\) = > -1
(∵ m is negative, image is virtual and enlarged because is numerically >1).
Question 16.
A small pin fixed on a table top is viewed from above from a distance of 50 cm. By What distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table ? Refractive index of glass = 1.5. Does the answer depend on the location of the slab ?
Answer:
μ = 1.5; real thickness = 15 cm
∴ Apparent Depth = \(\frac{15}{1.5}\) = 10 cm
∴ Pin appears raised by 15 – 10 = 5 cm.
The result is independent of the location of the slab.
Question 17.
a) Figure shows a cross-section of a light pipe made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
b) What is the answer if there is no outer covering of the pipe ?
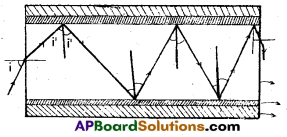
Answer:
a)
μ = \(\frac{1.68}{1.44}\) = \(\frac{1}{\sin C}\)
Sin C = \(\frac{1.44}{1.68}\) = 0.8571
C = 59°
Total internal reflection takes place when i > 59° or angle r may have value between 0 to 31°
rmax = 31°
Now \(\frac{\sin \mathrm{i}_{\max }}{\sin \mathrm{r}_{\max }}\) = 1.68
\(\frac{\sin i_{\max }}{\sin 31^{\circ}}\) = 1.68
sin imax = 0.8562, i<sub.max = 60°
Thus all incident rays of angles in the range 0 < i < 60° will suffer total internal reflections in the pipe.
b) If there is no outer covering of the pipe
Sin C = \(\frac{1}{\mu}\)
= \(\frac{1}{1.68}\) = 0.5962
sin C = sin 36.5°
C = 36.5°
Question 18.
Answer the following questions :
a) You have learnt that plane and convex mirrors produce virtual images of objects. Can they produce, real images under some circumstances ? Explain.
b) A virtual image, we always say, cannot be caught on a screen. Yet when we ‘see’ a virtual image, we are obviously bringing it on to the ‘screen’ (i.e., the retina) of our eye. Is there a contradiction ?
c) A diver under water, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is ?
d) Does the apparent depth of a tank of water change if viewed obliquely ? If so, does the apparent depth increase or decrease ?
e) The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter ?
Answer:
a) Rays converging to a point (behind) a plane or convex mirror are reflected to a point infront of the mirror on the screen. In other words a plane or convex mirror can produce a real image if the object is virtual
b) When the reflected or refracted rays are divergent, the image is virtual. The divergent rays can be converged on to a screen by means of an appropriate converging lens. The convex lens of the eye does just that the virtual image here serves as a object for the lens to produce a real image. The screen here is not located at the position of the virtual image. There is no contradiction.
c) The rays starting from the head of the fisherman and incident on water become bent towards normal and appear to come from a higher point.
AF is real height of fisherman. Rays starting from A, bend towards normal. For diver they appear to come from A1, A1 F becomes apparent height of fisherman, which is more than real height.
d) The apparent depth for oblique viewing decreases from its value for near-normal viewing.
e) Refractive index of diamond is about 2.42, much larger than that of ordinary glass. The critical angle for diamond is above 24°, much less than that of glass. A skilled diamond cutter exploits the large range of angles of incidence (in the diamond) 24° to 90° to ensure that light entering the diamond is totally reflected from many faces before getting out thus producing a sparkling effect.
Question 19.
The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3m away by means of a large convex lens: What is the maximum possible focal length of the lens required for the purpose ?
Answer:
Let,
υ = + υ
∴ u = -(3 – υ)
fmax = ?
Now, \(\frac{1}{f}\) = \(\frac{1}{v}-\frac{1}{u}\) = \(\frac{1}{v}-\frac{1}{-(3-v)}\)
\(\frac{1}{f}\) = \(\frac{1}{v}+\frac{1}{3-v}\) ⇒ \(\frac{1}{f}\) = \(\frac{3-v+v}{(3-v) v}\)
3υ – υ2 = 3f
For f to be maximum d(f) = 0
i.e d(3υ – υ2) = 0
3 – 2 υ = 0
υ = 3/2 = 1.5 m
Hence, u = -(3 – 1.5)
= -1.5m
and
\(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{1.5}\) – \(\frac{1}{-1.5}\) = \(\frac{1+1}{1.5}\)
= \(\frac{2}{1.5}\) = 0.75m
Question 20.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
Answer:
a) Distance between object and image D = 90 cm = u + υ
Distance between two’ positions of lens d = 20 = u = υ
u = 55 cm and υ = 35 cm.
For lens formula,
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{55}\) + \(\frac{1}{35}\) = \(\frac{18}{385}\)
f = \(\frac{385}{18}\) = 21.4
Question 21.
a) Determine the ‘effective focal length’ of the combination of the two lenses in Exercise 10, if they are placed 8.0cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident ? Is the notion of effective focal length of this system useful at all ?
b) An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40cm. Determine the magni-fication produced by the two-lens is 40cm.
Answer:
a) Here f1 = 30cm, f2 = -20cm,
d = 8.0cm, f = ?
i) Let a parallel beam be incident on the convex lens first. If 2nd lens were absent, then
u1 = ∞ and f1 = 30cm
As \(\frac{1}{v_1}-\frac{1}{\mathrm{u}_1}\) = \(\frac{1}{f_1}\)
\(\frac{1}{v_1}\) = \(\frac{1}{\infty}\) = \(\frac{1}{30}\)
υ1 = 30 cm
The image would now act as a virtual object for 2nd lens.
υ2 = + (30 – 8) = + 22 cm
υ2 = ? f2 = – 20 cm
As \(\frac{1}{v_2}\) = \(\frac{1}{\mathrm{f}_2}+\frac{1}{\mathrm{u}_2}\)
\(\frac{1}{v_2}\) = \(\frac{1}{-20}+\frac{1}{22}\) = \(\frac{-11+10}{220}\) = \(\frac{-1}{220}\)
υ2 = -220 cm
∴ Parallel incident beam would appear to diverge from a point 220 – 4 = 216 cm from the centre of the two lens system,
ii) Suppose a parallel beam of light from the left is incident first on the concave lens.
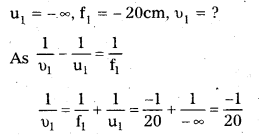
This image acts as a real object for the 2nd lens.
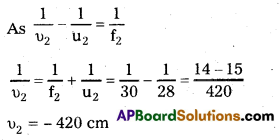
∴ The parallel beam appears to diverge from a point 420 – 4 = 416 cm, on the left of the centre of the two lens system From the above discussion, we observe that the answer depends on which side of the lens system the parallel beam is incident. Therefore, the notion of effective focal length does not seem to be useful here.
b) Here, h1 = 1.5 cm, u1 = 40 cm, m = ?, h2 = ? for the 1st lens, \(\frac{1}{v_1}-\frac{1}{u_1}\) = \(\frac{1}{f_1}\)
\(\frac{1}{v_1}\) = \(\frac{1}{p_1}+\frac{1}{u_1}\) = \(\frac{1}{30}-\frac{1}{40}\) = \(\frac{1}{120}\)
υ1 = 120 cm
Magnitude of magnification produced by first lens,
m1 = \(\frac{v_1}{u_1}=\frac{120}{40}\) = 3
The image formed by 1st lens as virtual object for the 2nd lens.
υ2 = 120 – 8 = 112 cm, f2 = – 20cm
υ2 = ?
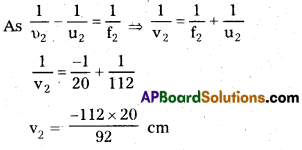
Magnitude of Magnification produced by second lens
m2 = \(\frac{\mathrm{v}_2}{\mathrm{u}}\) = \(\frac{112 \times 20}{92 \times 112}\) = \(\frac{20}{92}\)
Net magnification produced by the combination
m = m1 × m2
= 3 × \(\frac{20}{92}\) = \(\frac{60}{92}\) = 0.652
∴ size of image h2 = mh1
= 0.652 × 1.5
= 0.98 cm
Question 22.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
Answer:
i1 = ?, A = 60°, μ = 1.524
μ = \(\frac{1}{\sin C}\)
C = r2
sin C = sin r2 = \(\frac{1}{\mu}=\frac{1}{1.524}\) = 0.6561
r2 = 41°
As r1 + r2 = A
r1 = A – r2 = 60° – 41° = 19°
μ = \(\frac{\sin i_1}{\sin r_1}\)
sin i1 = 1.524 sin 19°
= 1.524 × 0.3256
= 0.4962
i1 = 29°451
Question 23.
You are given prisms made of crown glass and flint glass with a wide variety of angles. Suggest a combination of prisms which will
a) deviate a pencil of white light without much dispersion.
b) disperse (and displace) a pencil of white light without much deviation.
Answer:
i) For no dispersion, angular dispersion produced by two prisms should be zero
i.e. (μb – μ) A + (μb – μ’r) A’ = 0
As (μ’b – μ’r) for flint glass is more than that for grown glass, therefore A’ < A i.e ., flint glass prism of smaller angle has to be suitably combined with crown glass prism of larger angle.
ii) For almost no deviation (μv – 1) A + (μ’y – 1) A’ = 0
Taking crown glass prism of certain angle, we go on-increasing angle of flint glass prism till this condition is met. In the final combination however, angle of flint glass prism will be smaller than the angle of crown glass prism as μ’y for flint glass is more than μy for crown glass.
Question 24.
For a normal eye, the far point is at infinity and the near point of distinct vision is about 25cm in front of the eye. The cornea of the eye provides a converging power of about 40 diopters, and the least converging power of the eye- lens behind the cornea is about 20 diopters. From this rough data estimate the range of accommodation (i.e., the range of converging power of the eye-lens) of a normal eye. ”
Answer:
To observe objects at infinity, the eye uses its least converging power = 40 + 20 = 60D
∴ Distance between cornea eye lens and retina
focal length of eye lens = \(\frac{100}{p}\) = \(\frac{100}{60}\) = \(\frac{5}{3}\) cm
To focus an object at the near point u = -25cm, v = 5/3 cm f = ? –
\(\frac{1}{f}\) = \(-\frac{1}{\mathrm{u}}+\frac{1}{v}\) ⇒ \(\frac{1}{f}\) = \(\frac{1}{25}+\frac{3}{5}\) = \(\frac{1+15}{25}\)
= 16/25
f = 25/16 cm
Power = \(\frac{100}{f}\) = \(\frac{100}{25 / 16}\) = 64D
Power of eye lens = 64 – 40 = 24D
Hence range of accommodation of eye lens is roughly 20 to 24 dioptre.
Question 25.
Does short-sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodation? If not, what might cause these defects of vision?
Answer:
No, a person may have normal ability of accommodation and yet he may be myopic or hyper metropic. Infact, myopia arises when length of eye ball gets shortened.
However, when eye ball has normal length, but the eye lens loses partially its power of accommodation, the defect is called Presbiopia.
Question 26.
A myopic person has been using spectacles of power – 1.0 dioptre for distant vision. During old age he also needs to use separate reading glass of power + 2.0 dioptres. Explain whàt may have happened.
Answer:
Here u = -25cm, y = -50cm, f = ?
\(\frac{1}{v}-\frac{1}{u}\) = \(\frac{1}{\mathrm{f}}\) ⇒ –\(\frac{1}{50}\) + \(\frac{1}{25}\) = \(\frac{1}{f}\)
\(\frac{-1+2}{50}\) = \(\frac{1}{\mathrm{f}}\) or f = 50 cm
As P = \(\frac{100}{f}\) = \(\frac{100}{50}\) = + 2 dioptres.
Question 27.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to ? How is such a defect of vision corrected ?
Answer:
This defect is called Astigmatism. It arises because curvature of cornea plus eye lens refracting system is-not the same in diffreht planes. As vertical lines are seen distinctly, the curvature in the vertical plane is enough, but in the horizontal , plane, curvature is insufficient.
This defect is removed by using a cylindrical lens with its axis along the vertical.
Question 28.
A man with normal near point (25 cm) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5 cm.
a) What is the closest and the farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass ?
b) What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope ?
Answer:
a) Here, f = 5 cm, u = ?
For the closest distance; v = – 25cm
As \(\frac{1}{f}\) = \(\frac{1}{v}-\frac{1}{u}\)
\(\frac{1}{u}\) = \(\frac{1}{v}-\frac{1}{f}\) = \(\frac{1}{-25}-\frac{1}{5}\) = \(\frac{-1-5}{25}\)
u’ = \(\frac{25}{-6}\) – 4.2 cm
This is the closest distance at which he can read the book.
For the farthest distance, v’ = ∞, u’ = ?
As \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}^{\prime}}-\frac{1}{\mathrm{u}^{\prime}}\)
\(\frac{1}{v^{\prime}}\) = \(\frac{1}{v^i}-\frac{1}{f}\) = \(\frac{1}{\infty}-\frac{1}{5}\) = \(\frac{-1}{5}\)
u’ = -5cm
This is the farthest distance at which he can real the book.
b) Max. Angular magnification
m = \(\frac{\mathrm{d}}{\mathrm{u}}\) = \(\frac{25}{25 / 6}\) = 6
Min. Angular magnification
m’ = \(\frac{\mathrm{d}}{\mathrm{u}^{\prime}}\) = \(\frac{25}{5}\) = 5
Question 29.
A card sheet divided into squares each of size 1 mm2 is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9cm) held close to the eye.
a) What is the magnification in produced by the lens ? How much is the area of each square in the virtual image ?
b) What is the angular magnification (magnifying power) of the lens ?
c) Is the magnification in (a) equal to the magnifying power in (b) ? Explain.
Answer:
a) Here, area of each (object) square 1mm2,
u – 9cm, f = 10cm
\(\frac{1}{v}\) = \(\frac{1}{f}+\frac{1}{u}\) = \(\frac{1}{10} \frac{-1}{9}\) = \(\frac{-1}{90}\)
v = -90cm
Magnification, m = \(\frac{v}{|u|}=\frac{90}{9}=10\)
∴ Area of each square in virtual image = (10)2 × 1 = 100 sq,mm
b) Magnifying power = \(\frac{\mathrm{d}}{\mathrm{u}}\) = 25/9 = 2.8
c) No, Magnification in (a) which is (υ/u) cannot be equal to magnifying power in (b) which is (dlu) unless v = d ie., image is located at the least distance of distinct vision.
Question 30.
a) At what distance should the lens be held from the figure in Exercise 2.29 in order to view the squares distinctly with the maximum possible magnifying power ?
b) What is the magnification in this case ?
c) Is the magnification equal to the magnifying power in this case ? Explain.
Answer:
i) Here, υ = -25cm, f = 10cm, u = ?
Yes, the magnification and magnify-ing power in this case are equal, because image is formed at the least distance of distinct vision.
Question 31.
What should be the distance between the object in Exercise 30 and the magnifying glass if the virtual image of each square in the figure is to have an , area of 6.25 mm2. Would you be able to see the squares distinctly with your eyes very close to the magnifier ?
[Note : Exercises 29 to31 will help you clearly understand the difference between magnification in absolute size ‘ and the angular magnification (or magnifying power) of an instrument.]
Answer:
Here, magnification in area = 6.25
linear magnification m = \(\sqrt{6.25}\) = 2.5
As m = \(\frac{v}{u}\) or v = mu = 2.5u
As \(\frac{1}{v}\) – \(\frac{1}{\mathrm{u}}\) = \(\frac{1}{\mathrm{f}}\)
\(\frac{1}{2.5 \mathrm{u}}\) – \(\frac{1}{\mathrm{u}}\) = \(\frac{1}{10}\)
\(\frac{1-2.5}{2.5 u}\) = \(\frac{1}{10}\)
u = -6cm
y = 2.5u = 2.5 (-6) = -15cm
as the virtual image is at 15cm; where as distance of distinct vision is 25cm, therefore, the image cannot be seen distinctly by the eye.
Question 32.
Answer the following questions :
a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification ?
b) In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back ?
c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power ?
d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths ?
e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why ? How much should be that short distance between the eye and eyepiece ?
Answer:
a) It is true that angular size of image is equal to the angular size of the object. By using magnifying glass, we keep the object far more closer to the eye than at 25cm, its normal position without use of glass. The closer object has larger angular size than the same object at 25cm. It is in this sense that angular magnification is achieved.
b) yes, the angluar magnification changes, if the eye is moved back. This is because angle subtended at the eye would be slightly less than the angle subtended at the lens. The effect is negligible when image is at much larger distance.
c) Theoretically, it is true, However, when we decrease focal length, observations both spherical and chromatic become more pronounced. Further, it is difficult to grind lenses of very small focal lengths.
d) Angular magnification of eye piece is \(\left(1+\frac{d}{f_e}\right)\). This increase as fe decreases. Further, magnification if objective lens is \(\frac{v}{u}\). As object lies close to focus of objective lens u ≈ f0. To increase this magnification (υ/f0), f0 should be smaller.
e) The image of objective lens in eye pie is called ‘eye ring’ All the rays from the object refracted by the objective go through the eye ring. Therefore, ideal position for our eyes for viewing is this eye ring only.
When eye is too close to the eye piece, field of view reduces and eyes do not collect much of the light. The precise, location of the eye ring would depend upon the separation between the objective and eye piece, and also on focal length of the eye piece.
Question 33.
An angular magnification (magnifying power) of 30X is desired using an objective of focal length 1.25 cm and an eyepiece of focal length 5cm. How will you set up the compound microscope ?
Answer:
In normal ajustment, image is formed at least distance of distinet vision, d = 25cm Angular Magnification of eye piece = \(\left(1+\frac{d}{f_e}\right)=\left(1+\frac{25}{5}\right)\) = 6 As total Magnification is 30, Magnification of objective lens.
i.e. object should be held at 1.5cm in-front of objective lens
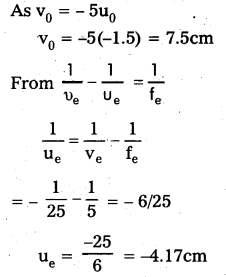
∴ Seperation between the objective lens and eye piece
= |ue| + |v0|
= 4.17 + 7.5.
= 11.67cm
Question 34.
A small telescope has an objective lens of focal length 140cm and an eyepiece of focal length 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when
a) the telescope is in normal adjustment (i.e., when the final image is at infinity) ?
b) the final image is formed at the least distance of distinct vision (25 cm) ?
Answer:
Here, f0 = 140cm, fe = 5.0cm
Magnifying power = ?
a) In normal adjustment,
Magnifying power
= \(\frac{f_0}{-f_e}\) = \(\frac{140}{-5}\) = -28
b) When final image is at the least distance of distinct vision, Magnifying power
= \(\frac{-\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\left(1+\frac{\mathrm{f}_{\mathrm{e}}}{\mathrm{d}}\right)\) = \(\frac{-140}{5}\left(1+\frac{5}{25}\right)\) = -33.6
Question 35.
a) For the telescope described in Exercise 34 (a), what is the separation between the objective lens and the eyepiece ?
b) If this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens ?
c) What is the height of the final image of the tower if it is formed at 25 cm ?
Answer:
a) Here, in normal adjustment, seperation between objective lens and eye lens = f0 + fe = 140 + 5 = 145cm
b) Angle subtended by tower 100m tall at 3km
α = \(\frac{100}{3 \times 1000}\) = \(\frac{1}{30}\) radian
if his the height of image formed by the objective, then
α = \(\frac{\mathrm{h}}{\mathrm{f}_0}\) = \(\frac{h}{140}\)
∴ \(\frac{\mathrm{h}}{140}\) = \(\frac{\mathrm{1}}{30}\)
h = \(\frac{\mathrm{140}}{30}\) = 4.7 cm
c) Magnifying produced by eye piece
= (1 + \(\frac{d}{f e}\)) = 1 + \(\frac{25}{5}\) = 6
∴ Height of final image = 4.7 × 6 = 28.2cm
Question 36.
A cassegrain telescope is built with the mirrors 20mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140mm. where will the final image of an object at infinity be ?
Answer:
Here, radius of curvature of objective mirror R1 = 220 mm radius of curvature of secondary mirror R2 = 140mm;
f2 = \(\frac{\mathrm{R}_2}{2}=\frac{140}{2}\) = 70mm
Distance between the two mirrors, d = 20mm. When object is at infinity, parallel rays falling on objective mirror, on reflection, would collect at its focus at
f1 = \(\frac{\mathrm{R}_1}{2}=\frac{220}{2}\) = 110mm
Instead, they fall on secondary mirror at 20mm from objective mirror.
∴ For secondary mirror, u = f1 – d = 110 – 20 = 90 mm
From \(\frac{1}{v}+\frac{1}{u}\) = \(\frac{1}{\mathrm{f}_2}\)
υ = \(\frac{1}{\mathrm{f}_2} \frac{-1}{\mathrm{u}}\) = \(\frac{1}{70}-\frac{1}{90}\) = \(\frac{9-7}{630}\) = \(\frac{2}{630}\)
υ = \(\frac{630}{2}\) = 315 mm = 31.5 cm to the right of secondary mirror
Question 37.
Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?
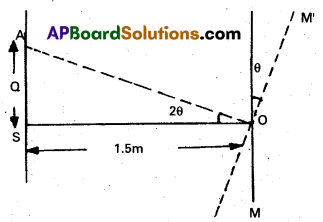
Answer:
Here, θ = 3.5°
x = 1.5m, d = ?
When the mirror turns through an angle θ, the reflected ray turns through double the angle.
2θ = 2 × 3.5° = 7° = \(\frac{7 \pi}{180}\) rad
from figure,
tan 2θ = \(\frac{\text { SA }}{\mathrm{OS}}\) = \(\frac{\mathrm{d}}{1.5} \times \mathrm{d}\)
= 1.5 × \(\frac{7 \pi}{180} \mathrm{~m}\) = 0.18m
d = 1.5 tan 2θ
≈ 1.5(2θ)
= 1.5 × \(\frac{7 \pi}{180} \mathrm{~m}\) = 0.18m
Question 38.
Figure shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A
small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid?
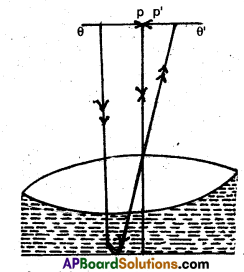
Answer:
Let focal length of convex lens of glass = f1 = 30cm focal length of plano concave lens of liquid = f2 combined focal length, F = 45.0cm
For liquid lens
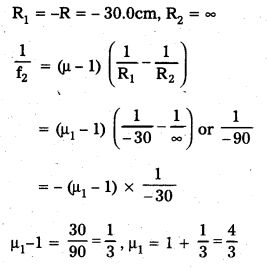
. What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the YZ plane ?
CH3 – CH2 – NC + 3KCl + 3H2O
