Mahesh

SCERT AP Board 6th Class Social Solutions 1st Lesson Our Earth in the Solar System Textbook Questions and Answers.

AP State Syllabus 6th Class Social Studies Solutions 1st Lesson Our Earth in the Solar System

6th Class Social Studies 1st Lesson Our Earth in the Solar System Textbook Questions and Answers

Improve Your Learning

Question 1.
How does a planet differ from a star?
Answer:
Stars have their own heat and light and planets have to depend on stars for light and heat.

Question 2.
What is meant by the ‘Solar system’?
Answer:
The eight planets which revolve around the sun, satellites, and other celestial bodies are together known as‘Solar System’.

Question 3.
Why is life not possible on all planets?
Answer:
The Earth has all the three components such as lithosphere, hydrosphere, and atmosphere which makes life possible. The remaining planets do not consist of these components. So life is not possible on all planets.

Question 4.
Why do we always see only one side of the moon?
Answer:
The moon moves around the earth and spin on its own also. So we can see only one side of the moon always.

Question 5.
What is the Universe?
Answer:
Millions of Milkyway galaxies including the solar system together are called the Universe.

Question 6.
Air and water are essential to life on the earth. But now they are being polluted by humans. What happens to the life of humans on this earth if pollution increases further?
Answer:
Pollution contains toxins that adversely impact living creatures within them. Rising pollution will lead to premature aging. Human exposure to toxins will increase to a great extent if pollution is not controlled. This pollution is directly linked to cancer and heart diseases.

Question 7.
Scientists are now trying to explore more about the moon and other planets. Do you think their efforts benefit us?
Answer:
The efforts of scientists in exploring the moon and other planets definitely useful to us. Space exploration alone provides us a significant amount of knowledge which is important for the education of people also about our planet and universe. It increases the knowledge about space and the discovery of distant planets and galaxies and gives us an insight into the beginnings of our universe.

Question 8.
Observe figure 1.4 (text book Page No. 5) and fill in the table.

Answer:

Project Work

Prepare a model of the solar system.
Answer:
Student Activity.

Choose the correct answer.
1. Though tremendous heat is emitted by the Sun, why do we receive only limited heat?
A) Sun is very far from the Earth
B) Sun is very small when compared with the Earth
C) Sun is very close to the Earth
D) None of these
Answer:
A) Sun is very far from the Earth

2. The planet is known as the “Earth’s Twin” is
A) Jupiter
B) Saturn
C) Venus
D) Aries
Answer:
C) Venus

3. Which is the third nearest planet to the sun?
A) Venus
B) Earth
C) Mercury
D) Jupiter
Answer:
B) Earth

4. All the planets move around the Sun in a
A) Circular path
B) Rectangular path
C) Elongated path
D) Square path
Answer:
C) Elongated path

5. Asteroids are found in between the orbits of
A) Saturn and Jupiter
B) Mars and Jupiter
C) The Earth and Mars
D) Uranus & Neptune
Answer:
B) Mars and Jupiter

Match the following:

1. Blue Planet                        [ ]          a) Mars
2. Farthest Planet to Sun       [ ]          b) Neptune
3. Fourth Planet from Sun     [ ]          c) Mercury
4. Nearest Planet to Sun       [ ]          d) Earth
Answer:
1. Blue Planet                            [ D ]          a) Mars
2. Farthest Planet to Sun           [ B ]          b) Neptune
3. Fourth Planet from Sun         [ A ]          c) Mercury
4. Nearest Planet to Sun           [ C ]           d) Earth

Let’s do

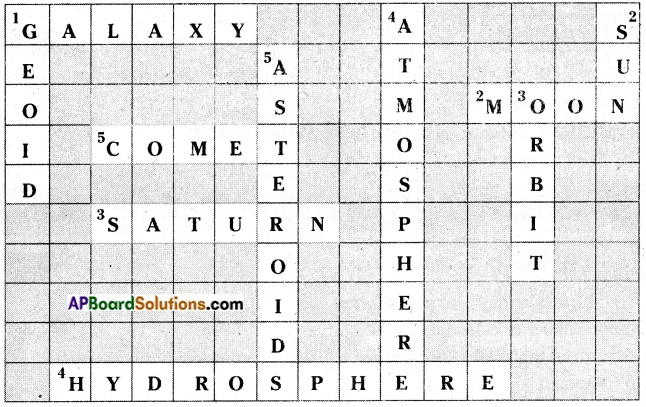
Solve the puzzle with the terms defined in the following statements.

CROSS:

1. The cluster of millions of Stars. – Galaxy
2. The natural satellite of the Earth. – Moon
3. The ringed planet (See figure 1.4). – Saturn
4. The sphere of water. – Hydrosphere
5. The celestial object is made up of a head and a tail. – Comet

DOWN:

1. The shape of the Earth. – Geoid
2. The closest star to the earth. – Sun
3. The path of the planets that move around the Sun. – Orbit
4. The sphere of gases that surrounds the Earth. – Atmosphere
5. The small pieces of celestial bodies, move around the Sun between Mars and Jupiter.

Answer:

Let’s do

You might have heard that people make human chains and run for world peace etc. You can also make a Solar system and run for fun by using the following steps.
Step – 1: All children of your class can play this game. Assemble in a big hall or on a playground.
Step – 2: Now draw eight circles on the ground. Draw all circles in the same manner.
Step – 3: Prepare 10 placards. Name them as Sun, Moon, Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune.
Step – 4: Select 10 children in the following order and give each one of them a placard.
Order of placard distribution

• The Sun – tallest, The Moon – smallest; Mercury, Mars, Venus, and Earth(almost equal heights); Neptune, Uranus, Saturn, and Jupiter taller than the earlier four Planets but smaller than the Sun.
• Now ask the children holding placards to take their places with the Sun in the cent rein their orbits. Ask the child holding the Moon placard to keep the hand of the child holding the Earth placard always.
• Now your Solar system is almost ready to go into action.
• Now make everybody move slowly in the anti-clockwise direction. Your class has turned into a small human replica of the Solar system.
• While moving in your orbit you can also turn around. For every celestial body, the spin should be anti-clockwise except for Venus and Uranus who will make the spin in the clockwise direction.

Answer:
Student Activity.

Field Visit

Question 1.
Observe the video of Planetarium in the QR Code. Describe your experiences.

Answer:
Student Activity.

Question 2.
Visit SHAR which is located in SPSR Nellore District.
Answer:
Student Activity.

6th Class Social Studies 1st Lesson Our Earth in the Solar System InText Questions and Answers

Let’s Do

(Textbook Page No. 3)

Question 1.
To know how days and nights occur
Answer:
Let us observe celestial bodies:
Required material: Torch, a sheet of plain paper, pencil and a needle.
Process:

1. Place the torch in the centre of the paper with its glass front touching the paper.
2. Now draw a circle around the torch.
3. Perforate the paper with the needle within the circled area.
4. Now place the perforated circle part of the paper on the glass front and wrap the paper around the torch with a rubber band.
5. In a dark room, stand at some distance facing a plain wall. Switch off all other lights. Now flash the torchlight on the wall. You will see numerous dots of light on the wall, which look like stars at night.
6. Switch on all the lights in the room. All dots of light will be almost invisible.
7. You may now compare the situation with what happens to the bright objects of the night sky after the Sun rises in the morning.

Answer:
Student Activity.

Question 2.
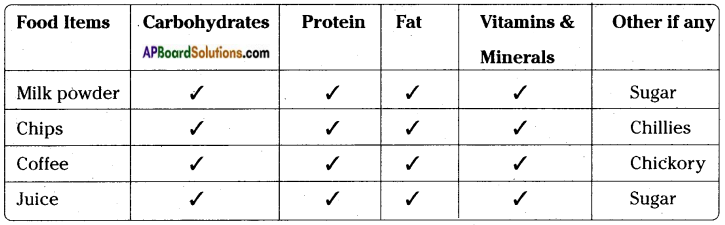
Observe the following picture and name the planets in the boxes given below. (Textbook Page No. 6)

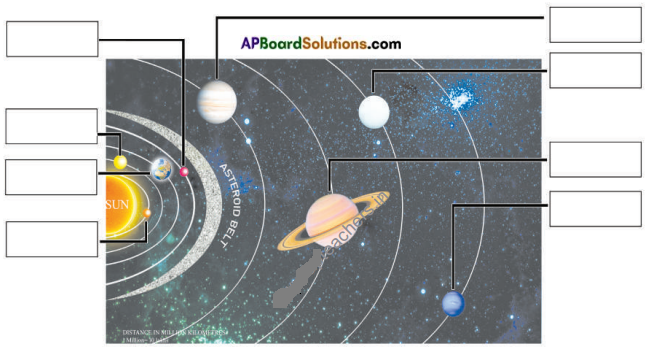
Answer:

Think and Respond

Question 1.
From ancient times people worship the Sim as God. Give reasons. (Textbook Page No. 4)
Answer:
Sun is glorified in the Vedas of ancient India as an all-seeing god who observes both good and evil victims. The Sun is the source of all life on our planet. Without the Sun we couldn’t be here. Sun is the only natural source of energy. So people in ancient times treated the Sun as a god and we worship him.

Question 2.
What do animals and plants require in order to grow and survive? (Textbook Page No. 6)
Answer:
To grow and survive animals need air, water, food and shelter. To grow and survive plants require air, water, nutrients and light.

Question 3.
How can you say that our earth is a unique planet in the solar system? (Textbook Page No. 7)
Answer:
Earth is a unique planet for many reasons. They are:

1. Earth is the only planet that supports animal or plants life.
2. Earth’s location maintains the right temperature which is important for life forms.
3. Human beings in-universe is found only on the Earth,

Question 4.
How is man-made satellites useful to mankind? Discuss. (Textbook Page No. 9)
Answer:
A satellite is an object that orbits another object. They are natural and man-made. Moon is a natural satellite of the Earth. Satellites are used for many purposes. They are weather satellites, communication satellites, navigation satellites, astronomy satellites and many other kinds.

1. They are used for communication purposes.
2. Carry instruments or passengers to perform experiments in space.
3. For weather forecasting system.
4. For global positioning system. (GPS).

Question 5.
Can you relate yourself to the Universe now? You are on the Earth and the Earth is a part of the Solar system. Our Solar system is a part of the Milky Way or Galaxy which is part of the Universe. Think of the fact that the Universe contains millions of such galaxies. How do you fit in the picture? How tiny you are? Think a while. (Textbook Page No. 11)

Answer:
Student Activity.

Explore

Question 1.
Browse the following website and know more about the solar system. (Textbook Page No. 5) https://spaceplace.nasa.gov/menu/solarsystem/.
Answer:
Student Activity.

Question 2.
Up to 2006, there were 9 planets in our Solar system. But now we have only 8 planets. What was the 9th planet? What happened to it? Find out the reasons with the help of your teacher? (Textbook Page No. 6)
Answer:
Up to 2006, we considered there are 9 planets in our solar system.
They are:

1. Mercury,
2. Venus,
3. Earth,
4. Mars,
5. Jupiter,
6. Saturn,
7. Uranus,
8. Neptune,
9. Pluto.

In 2006 the International Astronomical Union decided that Pluto is not having the technical qualities of a planet and reduced the number of planets from 9 to 8.

Question 3.
Who is the first Indian astronaut to go into space? (Textbook Page No. 8)
Answer:
Rakesh Sharma was the first Indian Astronaut to travel into space. He was part of the Soviet Union’s Soyuz T-11 expedition, which was launched on April 2, 1984.

Question 4.
Have you heard of Chandrayan-1 and Chandrayan-2? Try to know about them and discuss them in class. (Textbook Page No. 8)
Answer:
Chandrayaan is India’s moon mission. Chandra means the moon and yarn is a vehicle. Chandrayaan means Lunar Space Craft.
Chandrayaan -1 was India’s first moon mission. Chandrayaan -1 was launched in 2008 from Satish Dhawan Space Centre, Sriharikota.
Chandrayaan – 2 is the second moon mission developed by the Indian Space Research Organisation. It was launched in September 2019 from Satish Dhawan Space Centre, Sriharikota.

AP State Syllabus AP Board 7th Class Science Important Questions Chapter 1 Food Components

AP State Syllabus 7th Class Science Important Questions 1st Lesson Food Components

7th Class Science 1st Lesson Food Components Important Questions and Answers

Question 1.
What type of food is required to keep us healthy?
Answer:

1. Generally every food item contains all the components of food.
2. But some components may be more while some may be less.
3. We require different quantities of carbohydrates, proteins and fats according to age and need of individuals.
4. Growing children and adolescents need more protein-containing food like milk, meat, pulses etc.
5. We also need minute quantities of some other components called vitamins and minerals to keep us healthy.

Question 2.
What are roughages? In what way are they useful to us?
Answer:

1. There are some components of food that are necessary for our body called roughages or dietary fibres.
2. Vegetables like a ribbed gourd, bunch beans, lady’s finger or some boiled sweet potato etc. are called roughages.
3. Roughages are a kind of carbohydrate that our body fails to digest.
4. They help in free bowel movement in the digestive tract and prevent constipation.

Question 3.
Mention some sources of roughages.
Answer:
Sources of Roughages:

1. Bran, shredded wheat, cereals, fruits and vegetables, sweet and plain potato, peas and berries, pumpkins, palak, apples, banana, papaya and many kinds of beans are the sources of roughages.
2. We must take care to include sufficient fibre foods in our daily diet.

Question 4.
Why should we eat fruits with peels? What should be done before eating them.
Answer:

1. Generally we have a habit of eating some fruits without peels.
2. We eat banana without peel but fruits like apples, grapes, sapota are eaten along with peels.
3. Most of the vegetable are also used along with peels, sometimes we make some special dishes like chutneys etc., with peels.
4. So don’t peel or discard outer layers of fruits or vegetables.
5. They are rich in nutrients.
   
6. Peel contains fibre which helps in digestion.
7. But now a days farmers use many pesticides in the fields.
8. They are very dangerous for our health so we must wash fruits and vegetables with salt water thoroughly.
9. Then only it becomes safe to eat them along with peels.

Question 5.
Do fruits and vegetables contain water in them? Give some examples of such fruits.
Answer:

1. Water is also an essential component needed by our body.
2. We should drink sufficient water for our body.
3. We get water from fruits and vegetables also.
   
4. Most fruits and vegetables contain water.
5. Cut these fruits and vegetables. We find water in them.
6. Most vegetables like potatoes, beans, kheera, tomatoes, gourds and fruits like apples, papaya and melons etc., contain water.

Question 6.
Why does our body need water? Explain with an example.
Answer:

1. Take a piece of sponge and try to move it in a pipe.
2. It moves with some difficulty. Remove the sponge from the pipe, dip it in water and try to move it again in the pipe.
   
3. It moves freely or smoothly.
4. Water is food and it also helps the food to move easily in the digestive tract.
5. Water helps in many other processes in our body as well.
6. Hence, we must drink plenty of water.

Question 7.
How would you make your diet a balanced one?
Answer:

1. Taking green salads and vegetables everyday.
2. Taking foods like cereals, pulses, milk etc., adequately.
3. Taking a bit of fat (Oil, Ghee, Butter etc.)
4. Don’t forget to supplement your daily diet with green salads and vegetables.

Question 8.
Write the history of food and nutrition.
Answer:
History of food and nutrition:

1. Until about 170 years ago there was little scientific knowledge in the West about nutrition.
2. The founder of modern science of nutrition was Frenchman named Lavoisier (1743 to 1793) whose contribution paved new ways to nutrition research.
   
3. In the year 1752 James Lind’s discovered “Scurvy” which could be cured or prevented by eating fresh fruits and vegetables.
4. It was known that diseases could be cured by eating certain kinds of foods.
5. In 19th century it was known that the body obtains food from three substances namely proteins, fats and carbohydrates.

Question 9.
How do you test the presence of starch in the food item given to you.
Answer:
Test for Starch: N – line Preparation of dilute iodine solution

1. Take a test tube or a cup and add few drops of Iodine solution to it.
2. Then dilute it with water till it becomes light yellow / brown in colour.
   
3. Take a sample of food item in the test tube.
4. Add a few drops of dilute Iodine solution on the sample we have collected.
5. Observe the change in colour.
6. If the substance turns dark-blue or black, it contains starch.

Question 10.
Describe how do you test the presence of fats in the food item given to you.
Answer:
Test for fats:

1. Take a small quantity of each sample.
   
2. Rub it gently on a piece of paper.
3. If the paper turns translucent the substance contains fats.

Question 11.
What test do you conduct to detect the presence of proteins in the food item given to you?
Answer:
A) Preparation of solutions:

1. Preparation of 2% copper sulphate solution: To make 2% copper sulphate solution dissolve 2 gms of copper sulphate in 100 ml. of water.
2. To make 10% of sodium hydroxide solution: Dissolve 10 gms of sodium hydroxide in 100 ml. of water.

B) Test for proteins:

1. If the substance to test is a solid, grind it into powder or paste.
2. Add a little of it in the test tube and add 10 drops of water to the powder and stir well.
3. Add 10 drops of this solution in a clean test tube. Add 2 drops of copper sulphate solution and 10 drops of sodium hydroxide solution to the test tube and shake well.
4. Change of colour to violet or purple confirms presence of protein.

Question 12.
What do the above tests confirm?
Answer:

1. The above tests show the presence of components of food which are usually present in larger amounts as compared to others,
2. All types of food that we eat contain all the above-mentioned food components.
3. The quantity of each component varies from type to type.

Question 13.
Collect some food packets like chips, coffee, milk, juice … etc., and put a tick mark if you find the listed food components present in food items.
Answer:
Table: Food items and components

Question 14.
What are the components found in biscuits?
Answer:
In biscuits the following components are present.

1. carbohydrates
2. proteins
3. fat
4. sugars
5. saturated fatty acids
6. mono unsaturated fatty acids
7. poly unsaturated fatty acids
8. trans-fatty acids
9. cholesterol
10. calcium
11. iron
12. iodine
13. vitamins.

Question 15.
What components are most common in your list?
Answer:
The common components in the list are

1. carbohydrates
2. proteins
3. fats
4. sugars
5. minerals and
6. vitamins.

Question 16.
Do you find any vitamins and minerals in the biscuits? What are they?
Answer:

1. I find vitamins and minerals in the biscuits.
2. They are
   a) Vitamin – D, Vitamins B, B₆ and B₁₂
3. a) Calcium, b) Iron, c) Iodine are the minerals present.

Question 17.
Where do you write salt and sugar? Why?
Answer:

1. Salt and sugar are written separately.
2. These two components are not present in all the food items as common.

Question 18.
Are there any food items with similar components?
Answer:
Many ready made food items packed will have similar components.

Question 19.
What are the essential components of food?
Answer:

1. Our food consists of carbohydrates, proteins, fats, vitamins and minerals.
2. Besides these, water and fibres are also present.

Question 20.
Different food items are given in the table below. Find out the type of components in them and fill the information on the basis of your observations.
Answer:
Table: Testing of food items for carbohydrates, proteins, fats

Question 21.
Which foods show the presence of starch?
Answer:

1. Rice (78.2%)
2. Potato (22.6%)
3. Milk (5%)
4. Curd (3%)
5. Egg (0%)

Question 22.
What nutrients are present in milk?
Answer:
In buffalo’s milk

1. Minerals are present (0.8%)
2. Calcium (210 mg per 100 g) is present
3. Phosphorus (130 mg per 100 g) is present
4. Iron (0.2 mg per 100 g) is present.

Question 23.
Which components of food could you identify in potatoes?
Answer:
The following components are identified in potatoes.
a) (1.6 gm per 100 gm) proteins.
b) (0.1 gm per 100 gm) fat
c) (0.6 gm per 100 gm) minerals
d) (0.4 gm per 100 gm) fibre
e) (22.6 gm per 100 gm) carbohydrates
f) (10 mg per 100 gm) calcium
g) (40 mg per 100 gm) phosphorus
h) (0.48 mg per 100 gm) iron

Question 24.
Which food item contain more fat?
Answer:
Buffalo’s milk contains more fat (6.5 gm / 100 gm)

Question 25.
Which food items contain more protein?
Answer:
a) Rice contains proteins of 6.8 gm / 100 gm
b) Potato contains proteins of 1.6 gm / 100 gm.
c) Milk contains proteins of 4.3 gm / 100 gm
d) Curd contains proteins of 3.1 gm / 100 gm.
e) Egg contains proteins of 13.3 gm / 100 gm.
So egg and milk contain more proteins compared to other food items.

Question 26.
Why should we eat food?
Answer:
We should eat food because food supplies the energy we need to do many tasks in our day to day activities.

Question 27.
Do we need energy while sleeping?
Answer:

1. While we are sleeping, we breathe.
2. The circulation of blood in our body goes on.
3. So we need energy while we are sleeping.

Question 28.
Suppose you do not get food for lunch how do you feel?
Answer:

1. If I do not get food for lunch, I shall be very much tired and exhausted with lack of supply of energy at the end of the day.
2. I shall feel very weak. The hunger will be in an alarming condition.
3. I shall be ready to eat anything that is available.

Question 29.
If you do not get food for many days what will happen to you?
Answer:

1. If I do not get food for many days, I shall become very weak and the resistive power of my body decreases very much.
2. The energy resources in my body will also be exhausted.
3. There will be a danger to my life.

Question 30.
Mention some food items which keep you healthy.
Answer:
Dry fruits like dates, plums, raisins, cashew nuts, pistachios, etc., also keep us healthy.

Question 31.
Is balanced diet cheap? Explain.
Answer:

1. Scientists have found out that a balanced diet need not necessarily be costly.
2. Everyone can afford it, even the poor.
3. If a person eats dal, rice, rotis, green vegetables, little oil and jaggery all the food requirements of the body are fulfilled.
4. Just balancing our diet with different kinds of foods is not enough.
5. It should be cooked in a proper way.

Question 32.
List the food items eaten by you yesterday from breakfast to dinner.
a) Does your diet contain all necessary components of food in it.
Answer:
Following is the list of the food items eaten by me yesterday.

a) Yes, my food contains all necessary components of food.

Question 33.
Look at the food ‘THAU’ with many food items and list out the food items and food components in it. You need not eat all items as shown in the “THAU” rather you should ensure that your food contains all food components everyday in adequate quantity. For example, a diet containing food items having more of carbohydrates and protein along with a little fat, vitamins and minerals makes a balanced diet.

Answer:

Question 34.
How and why the nutrients in the food are lost?
Answer:
You know many nutrients are lost by over cooking, re-heating many times, washing the vegetables after cutting them into small pieces.

Question 35.
Write which foods are to be eaten moderately, adequately, plenty and sparingly.
Answer:

1. Foods like cereals, pulses, milk etc. should be taken adequately.
2. Fruits, leafy vegetables and other vegetables should be used in plenty.
3. Cooking oils and animal foods should be used moderately.
4. Vanaspathi, Ghee, Butter, Cheese must be used sparingly.

Question 36.
Why should we avoid Junk foods?
Answer:

1. If we are eating only pizzas and sandwiches daily.
   
2. Our body is being deprived of other food substances.
3. Junk food causes damages to our digestive system.
4. It is better to avoid eating junk food.

Question 37.
On what factors do the food habits of people depend?
Answer:

1. Food habits of the people depend upon climatic conditions and cultural practices of the particular place.
2. We eat rice in large quantities but people living in north India eat chapathies as daily food.
3. Because wheat is grown widely in that region.
4. The way of cooking and eating food also reflects the cultural practices of people.

Question 38.
Kiran wants to know about nutrients in the milk. He added 2 drops of Copper Sulphate solution and 10 drops of Sodium Hydroxide solution to the Milk. What colour he may have observed in it? Which nutrient does he find in the milk?
Answer:

1. Take 10 drops of milk in a clean test tube.
2. Add 2 drops of Copper Sulphate solution and 10 drops of Sodium Hydroxide solution to the test tube and shake well.
3. We observe the change of colour to violet or purple.
4. The colour confirms presence of proteins in milk.

Question 39.
Who need the highest proportion of Proteins in their daily diet-a 15 year old boy, a 55 year old female writer and 35 year old male bank officer? Explain why.
Answer:

1. The boy with an age of 15, requires high quantity of proteins in his diet.
2. Because proteins are very essential for his physical growth.
3. The boy is in adolescence, hence he has rapid physical growth. So, he needs high quantity of proteins in his diet.

Question 40.
We are suffering from various gastro intestinal diseases. What precautions do you take to avoid these diseases?
Answer:

1. We should take healthy nutritious diet.
2. We should consume high fibre content food like leafy vegetables. They have roughages. They are very helpful in preventing constipation.
3. Avoid junk foods completely.
4. We should cultivate healthy food habits.

Question 41.
You did an experiment in your classroom to test the proteins. In that
i) What apparatus did you use in that experiment?
ii) What are the solutions you prepared?
iii) What change did you observe in the colour?
iv) What precautions did you take in this experiment?
Answer:
a) Test tubes, Dropper.
b) 2% Copper Sulphate solution and 10% Sodium Hydroxide solution.
c) Violet or purple colour.
d) Take care of measuring chemicals while preparing the solutions.

Question 42.
What are the major nutrients found in our food?
Answer:
There are three major nutrients present in our body. They are: 1) Carbohydrates, 2) Proteins and 3) Fats.

Question 43.
Define the term balanced diet. Which food items are to be eaten moderately, ade¬quately, plenty and sparingly to make our diet a balanced one?
Answer:

1. The diet that is with all the required nutrients in adequate quantities is called balanced diet.
2. Energy is required according to the age and nature of work.
3. Carbohydrates provide energy and are present in cereals, pulses, milk etc. They should be taken adequately.
4. Vitamins, minerals available in vegetables, fruits and leafy vegetables should be used in plenty.
5. Fats present in cooking oils and animal foods should be used moderately.
6. Vanaspati, ghee, butter and cheese must be used sparingly.

Question 44.
Madhavi eats only biryani and chicken daily. Do you think it is a balanced diet? Why? If not, write a few suggestions to make her diet a balanced diet.
Answer:

1. Madhavi’s diet is not a balanced diet.
2. We should take a balanced diet containing all the nutrients.
3. Madhavi can get only carbohydrates, proteins and fats in large quantities through her meal.
4. This diet leads to obesity in future.
5. Madhavi should take fruits, vegetables, in order to get vitamins and minerals as well as roughages.

Question 45.
How do you test the presence of starch in the food item given to you? (OR) Write the procedure of test for carbohydrates conducted in your classroom.
Answer:
Test for Starch: N – line Preparation of dilute iodine solution

1. Take a test tube or a cup and add few drops of Iodine solution to it.
2. Then dilute it with water till it becomes light yellow/brown in colour.
   
3. Take a sample of food item in the test tube.
4. Add a few drops of dilute Iodine solution on the sample we have collected.
5. Observe the change in colour.
6. If the substance turns dark-blue or black, it contains starch.

Students can go through AP SSC 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle

→ The locus of points which are joined by a curve and are equidistant from a fixed point is called a circle. The fixed point here is called the centre of the circle.
(or)
A simple closed curve consisting of all points in a plane which are equidistant from a fixed point is called a circle. The fixed point is its centre and the fixed distance is its radius.

→ The path followed by a circular object is a straight line.

→ The line segment joining any two points on a circle is called a ‘chord’. The longest of all chords of a circle passes through the centre and is called a diameter.

\(\overline{\mathrm{AB}}\) is a chord and \(\overline{\mathrm{PQ}}\) is a diameter.
\(\overline{\mathrm{OP}}\) is the radius of the circle,
diameter = 2 × radius d = 2r
r = \(\frac{d}{2}\)

→ There are three different possibilities for a given line and a circle.

Case (i): The line PQ and the circle have no point in common (or) they do not touch each other.
Case (ii): The line PQ and the circle have two common points (or)
The line PQ intersects the circle at two distinct points A and B. Here the line PQ is a “secant” of the circle.
Case (iii): The line PQ touches the circle at an unique point A (or) there is one and only one point common to both the line and circle.
Here \(\stackrel{\leftrightarrow}{\mathrm{PQ}}\) is called a tangent to the circle at ‘A’.

→ The word tangent is derived from the Latin word “TANGERE” which means “to touch” and was introduced by Danish mathematician“Thomas Fineke” in 1583.

→ There is only one tangent to the circle at one point.

→ The tangent at any point of a circle is perpendicular to the radius through the point of contact.

The radius OP is perpendicular to \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) at P.
i.e, OP ⊥ AB.

→ Construction of a tangent to a circle:
Draw a circle with centre ‘O’.
Take a point ‘P’ on it. Join OP.
Draw a perpendicular line to OP through ‘P’.

Let it be \(\stackrel{\leftrightarrow}{\mathrm{XY}}\)
XY is the required tangent to the given circle passing through P.

→ Let ‘O’ be the centre of the given circle and \(\overline{\mathrm{AP}}\) is a tangent through A where OA is the radius, then the length of the tangent AP = \(\sqrt{\mathrm{OP}^{2}-\mathrm{OA}^{2}}\).

→ Two tangents can be drawn to a circle from an external point.

→ Let ‘O’ be the centre of the circle and P is an exterior point. There are exactly two tangents to the circle through P.
\(\overline{\mathrm{PA}}\) and \(\overline{\mathrm{PB}}\) are the tangents.

Here the lengths of the two tangents drawn from the external points are equal.
\(\overline{\mathrm{PA}}\) = \(\overline{\mathrm{PB}}\)

→ Construction of tangents to a circle from an external point:
Step – 1: Draw a circle with centre ‘O’ and with given radius.
Step – 2: Mark a point ‘P’ in the exterior of the circle and join ‘OP’.
Step – 3: Draw the perpendicular bisector \(\stackrel{\leftrightarrow}{\mathrm{XY}}\) to \(\overline{\mathrm{OP}}\), intersecting at M.
Step – 4: Taking M as centre, MP or OM as radius, draw a circle which intersects the given circle at A and B.

Step – 5: Join PA and PB. PA and PB are the required tangents.

→ Consider a circle with centre ‘O’. PA and PB are the tangents from an exterior point ‘P’. Then, the centre of the circle lies on the bisector of the angle between two tangents drawn from the exterior point P.
∠OPA = ∠OPB

→ Consider two concentric circles with centre ‘O’. Let the chord \(\overline{\mathrm{AB}}\) of the larger/ bigger circle just touches the smaller circle, then it is bisected at the point of contact with the smaller circle.
In the figure, \(\overline{\mathrm{AB}}\) is the chord of bigger circle touching the smaller circle at P then AP = PB.

→ If AP and AQ are two tangents to a circle with centre ‘O’, then ∠PAQ = 2∠OPQ = 2∠OQP.

→ If a circle touches the sides of a quadrilateral ABCD at points P, Q, R and S then AB + CD = BC + DA.
i.e., sum of the opposite sides are equal.

→ The region enclosed by a secant/chord and an arc is called a ‘segment of the circle’.

Case (i): If the arc is a minor arc then the segment is a minor segment.
Case (ii): If the arc is a semi arc then the segment is a semi circle.
Case (iii): If the arc is a major arc then the segment is a major segment.

→ Area of a segment between the chord AB and whose arc makes an angle ‘x’ at the centre = \(\frac{x}{360}\) × πr²

i.e., Area of the segment APB = (Area of the corresponding sector OAPB) – (Area of the corresponding triangle OAB).

Students can go through AP SSC 10th Class Maths Notes Chapter 3 Polynomials to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 3 Polynomials

→ Polynomial: An algebraic expression in which the variables involved have only non-negative integer power is called a polynomial.
Ex: 2x + 5, 3x² + 5x + 6, -5y, x³, etc.

→ Polynomials are constructed using constants and variables.

→ Coefficients operate on variables, which can be raised to various powers of non negative integer exponents.
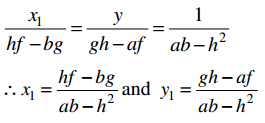
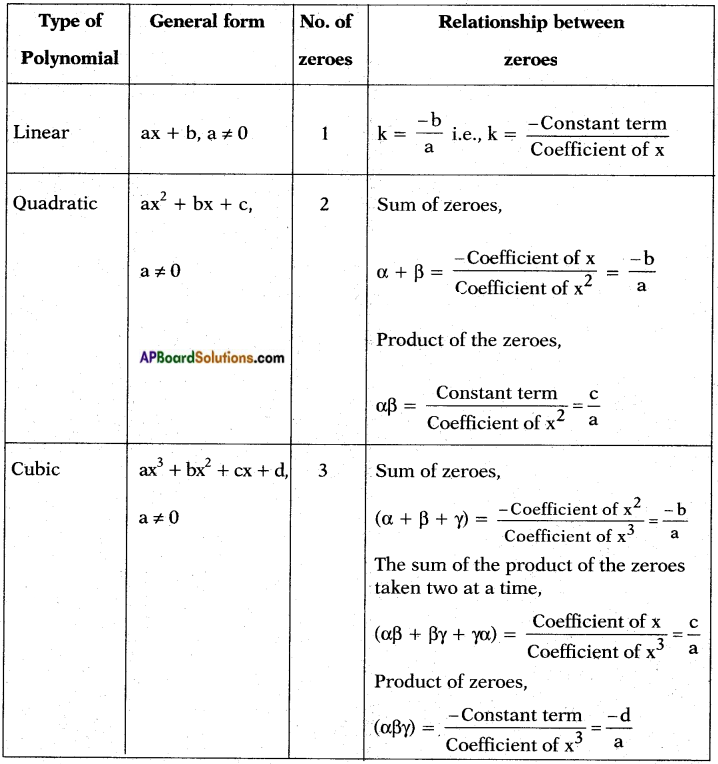
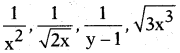, etc. are not polynomials.

→ General form of a polynomial having n^th degree is p(x) = a₀xⁿ + a₁x^n-1 + a₂x^n-2 …….. + a_n-1x + a_n where a₀, a₁, a₂,…… a_n-1, a_n are real coefficients and a₀ ≠ 0.

→ Degree of a polynomial:
The exponent of the highest degree term in a polynomial is known as its degree.
In other words, the highest power of x in a polynomial f(x) is called the degree of a polynomial f(x).
Example:
i) f(x) = 5x + \(\frac{1}{3}\) is a polynomial in the variable x of degree 1.
ii) g(y) = 3y² – \(\frac{5}{2}\)y + 7 is a polynomial in the variable y of degree 2.

→ Zero polynomial: A polynomial of degree zero is called zero polynomial that are having only constants.
Ex: f(x) = 8, f(x) = –\(\frac{5}{2}\)

→ Linear polynomial: A polynomial of degree one is called linear polynomial.
Ex: f(x) = 3x + 5, g(y) = 7y – 1, p(z) = 5z – 3.
More generally, any linear polynomial in variable x with real coefficients is of the form f(x) = ax + b, where a and b are real numbers and a ≠ 0.
Note: A linear polynomial may be a monomial or a binomial because linear polynomial f(x) = \(\frac{7}{5}\)x – \(\frac{5}{2}\) is a binomial, whereas the linear polynomial g(x) = \(\frac{2}{5}\) x is a monomial.

→ Quadratic polynomial: A polynomial of degree two is called quadratic polynomial.
Ex: f(x) = 5x², f(x) = 7x² – 5x, f(x) = 8x² + 6x + 5.
More generally, any quadratic polynomial in variable x with real coefficients is of the form f(x) = ax² + bx + c, where a, b and c are real numbers and a ≠ 0.
Note: A quadratic polynomial may be a monomial or a binomial or a trinomial.
Ex: f(x) = \(\frac{1}{5}\)x² is a monomial, g(x) = 3x² – 5 is a binomial and
h(x) = 3x² – 2x + 5 is a trinomial.

→ Cubic polynomial: A polynomial of degree three is called cubic polynomial.
Ex: f(x) = 8x³, f(x) = 9x³ + 5x²
f(y) = 11y³ – 9y² + 7y,
f(z) = 13z³ – 12z² + 11z + 5.

→ Polynomial of degree ‘n’ in standard form: A polynomial in one variable x of degree n is an expression of the form f(x) = a_nxⁿ + a_n-1x^n-1 + …….. + a₁x + a₀ where a₀, a₁, a₂,…… a_n, a_n are constants and a_n ≠ 0.
In particular, if a₀ = a₁ = a₂ = …… = a_n = 0 (all the constants are zero; we get the constants zero), we get the zero polynomial which is not defined.

→ Value of a polynomial at a given point: If p(x) is a polynomial in x and α is a real number. Then the value obtained by putting x = a in p(x) is called the value of p(x) at x = α.
Ex : Let p(x) = 5x² – 4x + 2, then its value at x = 2 is given by
p(2) = 5(2)² – 4(2) + 2 = 5(4) – 8 + 2 = 20 – 8 + 2 = 14 Thus, the value of p(x) at x = 2 is 14.

→ Graph of a polynomial: In algebraic or in set theory language, the graph of a polynomial f(x) is the collection (or set) of all points (x, y) where y = f(x).
i) Graph of a linear polynomial ax + b is a straight line.
ii) The graph of a quadratic polynomial (ax² + bx + c) is U – shaped, called parabola.

→ If a > 0 in ax² + bx + c, the shape of parabola is opening upwards ‘∪’.

→ If a < 0 in ax² + bx + c, the shape of parabola is opening downwards ‘∩’

→ Relationship between the zeroes and the coefficient of a polynomial:

Note: Formation of a cubic polynomial : Let α, β, and γ be the zeroes of the polynomial.
∴ Required cubic polynomial = (x – α) (x – β) (x – γ).

→ How to make a quadratic polynomial with the given zeroes : Let the zeroes of a quadratic polynomial be α and β.
∴ x = α, x = β
Then, obviously the quadratic polynomial is (x – α) (x – β) i.e., x² – (α + β)x 4- ap.
i.e., x² – (sum of the zeroes) x + product of the zeroes.

→ Division Algorithm : If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that, p(x) = g(x) × q(x) + r(x)
i.e., Dividend = Divisor × Quotient + Remainder
where, r(x) = 0 or degree of r(x) < degree of g(x). This result is known as the division algorithm for polynomials.

→ Some useful relations:
α² + β² = (α + β)² – 2αp
(α – β)² = (α + β)² – 4αβ
α² – β² = (α + β) (α – β) = (α + β)\(\sqrt{(\alpha+\beta)^{2}-4 \alpha \beta}\)
α³ + β³ = (α + β)³ – 3αβ(α + β)
α³ – β³ = (α – β)³ + 3αβ(α – β)

AP State Syllabus AP Board 8th Class English Textbook Solutions Chapter 1B My Mother Textbook Questions and Answers.

AP State Syllabus 8th Class English Solutions Chapter 1B My Mother

8th Class English Chapter 1B My Mother Textbook Questions and Answers

Comprehension

Answer the following questions.

Question 1.
How does the poet feel the presence of his mother?
Answer:
The poet feels the presence of his mother when he plays with his play things. When he plays with his play things, he seems to be able to hear a tune which reminds him his mother. He also feels the presence of his mother when he smells the fragrance of shiuli flowers in autumn and when he sees the blue sky through this bedroom window.

Question 2.
What do you understand from the statement – ‘I cannot remember my mother’?
Answer:
The poet’s mother passed away when he was still young. Hence, he can’t be able to recall his mother.

Question 3.
Does the poem convey sadness? If yes, pick out the suggestive expressions.
Answer:
Yes, this poem conveys some kind of sadness. The expression “I cannot remember my mother”, suggests this. The poet can’t remember his mother because she passed away when he was young.

Question 4.
What imagery do you find in each stanza? How does it appeal to you?

Answer:

Question 5.
Read the poem ‘My Mother’ again and complete the table.

Answer:

Question 6.
We all love our mother, don’t we? We love her because of certain qualities. Think and write about her qualities.
Answer:
We love mother as:
i) She gives birth to her children.
ii) She gives her children her love and care.
iii) She understands her children’s needs.
iv) She makes her children ready to live a happy life.
v) She defends her children.
vi) She supports her children’s dreams even when they seem impossible.
vii) She loves her children though they hurt and neglect her.

Question 7.
How would you choreograph the first stanza? (Group work)
(a) What settings do you arrange ?
Answer:

(b) What are the characters and their actions ?
Answer:

(c) What is the sequence of actions ?
Answer:

Each group may choreograph different stanzas of the song.

Figurative language: The use of words to express meaning beyond the literal meaning of the words themselves.
Imagery: Language which describes something in detail, using words to substitute for and create sensory stimulation, including visual imagery and sound imagery, e.g: Mother rocking the cradle. Here child senses with eyes and ears.
Metaphor: The comparison of two unlike things in which no words of comparison (like or as) are used.
e.g: Harry was a lion in the fight.
Simile: A figure of speech involving a comparison between unlike things using like, as, or as though.
e.g: as cool as a cucumber, as white as snow, life is just like an ice-cream. Personification: Giving non-human objects human characteristics, e.g: The moon danced mournfully over the water.

My Mother Summary in English

‘My Mother’ is a gentle nostalgic poem written by ‘Guru’ Rabindranath Tagore. He is one of the greatest poets of modern India. His mother passed away when he was young. In this poem, he expresses his inability to recall the face or the features of his mother. When he looks at his playthings, he seems to be able to hear a tune. Perhaps his mother often sang the same song when she moved his cradie gently. In autumn, the shiuli tree blossoms into fragrant tiny flowers. His mother would string the flowers for the morning service in the temple. When he smells the scent of shiuli flowers, he recalls his mother. When he sees from his bedroom window into the blue of the distant sky, he feels the stillness of his mother’s gaze. This poem eloquently reveals the emotional bonding between the poet and his mother. She has a great impact on the poet.

About the Poet

Rabindranath Tagore (1861-1941) is popularly known as Vishwa Kavi and Gurudev. He was the founder of Shantiniketan, an experimental school. He was awarded the Nobel Prize in literature for his ‘Gitanjali’, the Song of Offerings. Each of his poems reflects Indian vision and love towards his Mother Land. He is considered the Voice of Indian Heritage and Spiritualism.

My Mother Glossary

hover (v): remain in the air

shiuli (n): small, white or orange flowers that bloom in autumn

scent (n): perfume/good smell

rock (v): move gently

hum (v): sing with closed lips

gaze (v): look fixedly

morning service (n.phr): a religious service

AP State Syllabus AP Board 8th Class English Textbook Solutions Chapter 5C I Can Take Care of Myself Textbook Questions and Answers.

AP State Syllabus 8th Class English Solutions Chapter 5C I Can Take Care of Myself

8th Class English Chapter 5C I Can Take Care of Myself Textbook Questions and Answers

Comprehension

Answer the following questions.

Question 1.
What do you think is the most important thing to learn to live well?
Answer:
The most important thing to learn to live well is that one should not depend upon others. One should take care of oneself. One should stand on one’s own feet.

Question 2.
What are the skills or qualities that would help you to be independent in your life?
Answer:
The skills or qualities that would help us to be independent in our life are:

1. One needs to know how to take care of oneself.
2. One needs to be able to protect oneself.
3. One needs to learn to be strong and work hard.
4. One needs to be powerful oneself.
5. One needs to stand on one’s own feet.
6. One needs to learn more about the world and learn to live in it as a good creature.
7. One needs to depend on the power within oneself to seek the target in one’s life.

Question 3.
Do you agree/disagree with the daughter of the mother rat? Give reasons for your response.
Answer:
I agree with the daughter of the mother rat. Depending on another person’s power, position or prosperity does not promise peace and security in the long run. To be safe, one needn’t get someone married. One should work hard to achieve one’s goal. The married woman, who doesn’t stand on her own feet has to depend upon her husband for everything.

I. Observe the data given in the bar diagrams related to male and female infant mortality rates (IMR) in India over the years 1990 to 2008 and answer the questions given.

(Source: Ministry of Statistics and Programme Implementation National Statistical Organisation – Website : www.mospi.gov.in)

Question 1.
In which year is the difference in infant mortality rates between male and female the highest?
Answer:
In the year 2003, the difference in infant mortality rates between male and female is the highest.

Question 2.
In which case and in which year do we find a sudden decrease in the IMR?
Answer:
We find sudden decrease in the case of male IMR in the year 2003.

Question 3.
What will happen if there is a wide gap in IMR between male and female?
Answer:
If there is a wide gap in IMR between male and female, one of them (either male or female) will be left unmarried. There will be an imbalance in the ratio between the male and female.

Question 4.
What, according to you, may the reasons be for the female IMR being higher than the male IMR?.
Answer:
I think the reason may be that the parents think that girl children are burdensome. They think it is very difficult to educate them and get them married to the males. They have to give dowry to the males. So, most of the parents don’t want female children. Hence, the female IMR is higher than the male IMR.

Question 5.
What may be the reasons for the decrease in IMR rates over the years?
Answer:
The reasons for the decrease in IMR rates over the years.

1. The attitude of the parents is changed with the times.
2. Increasing medical facilities.
3. Increase in the literacy rate among the girls (women).
4. Women empowerment.

Question 6.
Do you think there could be a further decrease in the IMR after 5 years?
Answer:
Yes. I think there would be a further decrease in the IMR after 5 years.

Question 7.
What, according to you, may the reasons be for the death of more than half of both male and female infants?
Answer:
The reasons for the death of more than half of both male and female infants.

1. The superstitious beliefs of the parents. (Village parents)
2. Lack of proper medical facilities.
3. In some cases the young couples don’t want the children in the earlier days after their marriage. They think that the children will obstruct their privacy.

II. Group Work :
Discuss the above questions in your group and write an analytical report on the Infant Mortality Rates in India.
Answer:
When we observe the bar diagram, there has been a gradual decrease in both the female IMR and the male IMR. There is a sudden fall in the male IMR in 2003. The difference in infant mortality rates between male and female is the highest in 2003. The decrease in the IMR shows us the changed views of the parents with the times. If there is a wide gap in IMR between male and female, one of genders will be left unmarried and there is an imbalance in the family system. The parents think that females are burdensome. They feel it difficult to educate and get them married. They are not in a position to give dowry to the males. So, most of the parents don’t want female children. Hence, the female IMR is higher than the male IMR. The main reason for the decrease in IMR over the years is that the parents have changed their attitude with the times. The advanced medical facilities and the increase in the literacy rate among the girl children are also reasons for it. I think there will be a further decrease in the IMR after 5 years.

Oral Activity

Work in pairs and debate on the following proposition.
“Reservation in education, employment and legislature will empower the women.”
Answer:
Argument for the statement:
There is no doubt, surely reservation in education, employment and legislature will empower the women. As all of us know, today most of the women’s lives are confined to the kitchen. They have to depend upon their husbands for everything. They can’t protect themselves. If they have reservation, most of the women get good education and employment. Then they don’t have to beg anyone for anything. They will be able to lead a dignified life. If there is reservation in legislature, there will be more women participation in politics and society. It is expected to create equal opportunities for women along with men with reservation for women. Our society is a male dominated one. Reservation in education, employment and legislature would amount to a positive discrimination. Reservation for women not only empowers them but also helps the society.
Argument against the statement:
Can reservations for women be an effective measure and do the women really require such special treatment and will they be really empowered with reservations ? The intelligent male persons will lose the opportunities if the women are given reservations. Instead of providing any solution to this problem, giving reservations to women may give rise to social, political and psychological tensions. Besides, it is debatable if more women will attend schools, colleges or offices merely because of reservations. Reservation for women can be a temporary sort of relief and it won’t empower them. There should be a broader political, social and economic policy for the upliftment and empowerment of women.

Project work

A. Interview some female members in your family and neighbourhood with the following questions.
Would you like the girls in the family to take up a job after they have received education?
If yes, give some reasons.
Yes, I would like the girls in the family to take up a job after they have received education. The girl child is an equal partner in sharing the responsibilities and duties. An educated girl can render financial assistance to the father and later to the husband. The woman can take care of herself if she is employed. She doesn’t need to depend on others. She is able to lead a dignified life. So, the girls should take up a job after they have received education.
If no, give some reasons.
No, I would not like the girls in the family to take up a job after they have received education. The girl child’s primary duty in the later part of life is to look after the family and children. So, she doesn’t need to take up a job. If she takes up a job, she can’t find time to look after the family and children when she gets married.

B. Work on the following items.
Note down whether the woman you have interviewed is educated or uneducated; working/not working; married/unmarried.

Answer:

C. Based on the above information write a paragraph on ‘Woman Empowerment’.
Answer:
I have interviewed five women. Of them three women are married the rest of the two are unmarried. Three women are employed and the rest of the two are unemployed. All the five women opined that the women should be empowered. The employed women opined that they couldn’t find time to serve their families. The unemployed women want to stand on their feet. They want financial independence. They want jobs to get the stability and share the responsibilities and duties along with men. A woman is dynamic in
many roles she plays. She has to face many challenges and find out practical solutions. She is facing the challenges of economic inequality, gender-based violence, limited leadership and political participation and other issues. So, the women should be provided with more opportunities which could empower them to improve their lives, their rights and their future.

Grammar Family

Parts of Speech

There is a family in London whose surname is grammar. There is a couple, Mr. Noun and Mrs. Verb. The couple has three children-one son pronoun and two daughters adverb and adjective. The son (pronoun) has to do all the work of his father in his absence. The two daughters love each other but there is a difference in them. Adjective loves her father and brother and keeps praising them. Adverb loves her mother more she always modifies her when there is a need. There are two servants in the family, preposition and conjunction. The preposition is the chief servant. He is the official servant of his master. He is the family servant and looks after every member of the family. The interjection joins the family in times of joy and sorrow.

I Can Take Care of Myself Summary in English

Once, a mother rat wanted to get her young daughter married to the most powerful being that she could find. She thought that the sun god was the most powerful being on earth. So, she asked the sun god if he was the most powerful being on earth. The sun god smiled and replied that the rain was greater than him as there would be no water on earth or no crop or tree without the rain. So, the mother rat asked the rain god if he was the most powerful being on earth. The rain god smiled and replied that the mountain was greater than him as he would protect the creatures. He blocked the clouds and let the water flow safely. The mother rat asked the mountain god if he was the most powerful being on earth. The mountain god smiled and replied that the worm was greater than him. He also told that the earthworm was the greatest friend of the living beings. The mother rat’s daughter came to her and asked her what she was doing. The mother replied that she was looking for the most powerful being on earth to get her married. She also told her daughter that she would be safe if she married the most powerful being on earth. The daughter replied why she would need to marry to be safe. She also told that she would need to know how to take care of herself if she wanted to be safe. To protect herself, she needed to learn to be strong and work hard. She wanted to be powerful herself, so that she could take care of herself and those that she loved. She wanted to stand on her own feet. She opined that she needed to learn more about the world and learn to live in it as a good creature. She asked for her mother’s help. She wanted her mother’s support. She was not interested in marrying anybody. She didn’t want to depend on others. She wanted to believe her power only.

Students can go through AP SSC 10th Class Maths Notes Chapter 8 Similar Triangles to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 8 Similar Triangles

→ The geometrical figures which have the same shape but are not necessarily of the same size are called similar figures.

→ The heights and distances of distant objects can be found using the principles of similar figures.

→ Two polygons with same number of sides are said to be similar if their corresponding angles are equal and their corresponding sides are in proportion.

→ A polygon in which all sides and all its angles are equal is called a regular polygon. Eg.:

→ The ratio of the corresponding sides is referred to as scale factor or representative factor.

→ All squares are similar.

→ All circles are similar.

→ All equilateral triangles are similar.

→ Two congruent figures are similar but two similar figures need not be congruent.

→ A square ABCD and a rectangle PQRS are of equal corresponding angles, but their corre¬sponding sides are not in proportion.

∴ The square ABCD and the rectangle PQRS are not similar.

→ The corresponding sides of a square ABCD and a rhombus PQRS are equal but their corresponding angles are not equal. So they are not similar.

→ If a line is drawn parallel to one side of a triangle intersecting the other two sides at two distinct points then the other two sides are divided in the same ratio.

In △ABC; DE // BC then \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\).
This is called Basic proportionality theorem (or) Thale’s theorem.

→ If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.

In △ABC, a line ‘l’ intersecting AB in D and AC in E
such that \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) then l // BC.
This is converse of Thale’s theorem.

→ Two triangles are similar, if
i) their corresponding angles are equal.
ii) their corresponding sides are in the same ratio.

→ If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio or proportional and hence the two triangles are similar.

In △ABC, △DEF
∠A = ∠D
∠B = ∠E
∠C = ∠F
⇒ \(\frac{AB}{DE}\) = \(\frac{BC}{EF}\) = \(\frac{AE}{DF}\)
∴ △ABC ~ △DEF (A.A.A)

→ If in two triangles, sides of one triangle are proportional to the sides of other triangle, then their corresponding angles are equal and hence the two triangles are similar.

In △ABC, △DEF
if \(\frac{AB}{DE}\) = \(\frac{BC}{EF}\) = \(\frac{AE}{DF}\)
⇒ ∠A = ∠D
∠B = ∠E
∠C = ∠F
Hence, △ABC ~ △DEF (S.S.S)

→ If two angles of a triangle are equal to two corresponding angles of another triangle then the two triangles are similar.

In △ABC, △DEF
if ∠A = ∠D
∠B = ∠E
⇒ ∠C = ∠F (By Angle Sum property)
∴ △ABC ~ △DEF (A.A)

→ If one angle of a triangle is equal to one angle of other triangle and the sides including these angles are proportional, then the two triangles are similar.

In △ABC, △DEF if ∠A = ∠D, and
\(\frac{AB}{DE}\) = \(\frac{AC}{DF}\)
⇒ △ABC ~ △DEF (S.A.S)

→ The ratio of areas of two similar triangles is equal to the ratio corresponding sides.

→ If a perpendicular is drawn from the vertex, containing the right angle of a right angled – triangle to the hypotenuse, then the triangles on each side of perpendicular are similar to one another and to the original triangle. Also the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
In △ABC, ∠B = 90°
BD ⊥ AC

Then △ADB ~ △BDC ~ △ABC and
BD² = AD . DC

→ Pythagoras theorem: In a right angled triangle, the square of hypotenuse is equal to the sum of the squares of other two sides.

In △ABC; ∠A = 90°
AB² + AC² = BC²

→ In a triangle, if square of one side is equal to sum of squares of the other two sides, then the angle opposite to the first side is right angle.

In △ABC, if
AC² = AB² + BC² then ∠B = 90°
This is converse of Pythagoras theorem.

→ Baudhayan Theorem (about 800 BC):
The diagonal of a rectangle produces itself the same area as produced by its both sides (i.e., length and breadth).
In rectangle ABCD,

area produced by the diagonal AC = AC • AC
= AC²
area produced by the length = AB • BA = AB
area produced by the breadth = BC • CB = BC²
Hence, AC² = AB² + BC².

→ A sentence which is either true or false but not both is called a simple statement.

→ A statement formed by combining two or more simple statements is called a compound statement.

→ A compound statement of the form “If …… then ……” is called a Conditional or Implication.

→ A statement obtained by modifying the given statement by ‘NOT’ is called its negation.

AP State Syllabus AP Board 8th Class English Textbook Solutions Chapter 3C The Garden Within Textbook Questions and Answers.

AP State Syllabus 8th Class English Solutions Chapter 3C The Garden Within

8th Class English Chapter 3C The Garden Within Textbook Questions and Answers

Look at the pictures given and answer the questions that follow.

Comprehension

Question 1.
What is the central idea of the poem?
Answer:
There is a garden in the poet’s heart. She wants to tend it beautifully. She wants to be grateful to achieve her goal. She wants to be good to others. When one is good to others, one will get respect. When one is thankful, one will reach one’s goal.

Question 2.
What features of the garden in the poet’s heart are mentioned in stanza 1?
Answer:
The feature of the garden in the poet’s heart that is mentioned in stanza 1 is that beauty grows in fits and starts.

Question 3.
What is the mood of the poet? Put a tick (✓) mark,
a. sad b. hopeful c. thankful
Answer:
b) hopeful ( ✓)

Question 4.
Explain the word ‘gratitude’ as used in the poem.
Answer:
‘Gratitude’ means thankfulness. The poetess wants to be thankful to achieve her goal and it will comfort her soul.

Simile, Metaphor and Personification:

Observe the following sentences.

1. Here and there over the grass stood beautiful flowers like stars.
In this sentence “flowers are compared to stars” such a comparison using ‘like’ and ‘as’ is called ‘simile’.
e.g.: a. He roared like a lion.
b. Her face is as white as snow.

2. Life is a journey. Enjoy the ride.
In the above sentence the word ‘journey’ is used to describe/compare the word ‘life’. Such words are called ‘metaphor’. They are used to show that two things have same qualities. They make the description more powerful, e.g.: a. Rudramadevi was a lioness in battle, b. Her home was a prison.

3. Spring has forgotten his garden.
Here, though ‘spring’ is a season, it is represented as a human being and given the qualities of forgetting, etc. Such usage in literature is called ‘personification’, e.g.: a. The stars danced playfully in the moonlit sky.
b. The snow covered up the grass with her great white cloak.

Project work

Collect a few story books and fill in the table with details and present it before the class.

Answer:

The Garden Within Summary in English

The poetess finds that there is a garden in her heart. Like the gardener who lovingly tends his garden for the pleasures of bloom, the poetess nourishes the memories because they comfort her soul. In the garden of her heart beauty doesn’t grow continuously. She wants to give her smiles to others like the petals of the flowers in the garden of her heart. Then the others will respond in the same way and respect her feelings. There is a good hope in her and it results in good seeds to comfort her spirit. She wants to reach her goal with thankfulness and it will touch her soul. Here the soul of the poetess is compared with beautiful garden.

The Garden Within Glossary

petal (n): a delicate coloured part of a flower

bestowed (v): gave, showed respect

bowers (n): a pleasant place in the shade of tree

nutritious (adj): good

reaps (v): gives

spirit (n): inner feeling or mood

gratitude (n): thankfulness

goal (n): something that you hope to achieve

in fits and starts (phr): in a sudden and irregular manner

AP State Syllabus AP Board 8th Class English Textbook Solutions Chapter 1A The Tattered Blanket Textbook Questions and Answers.

AP State Syllabus 8th Class English Solutions Chapter 1A The Tattered Blanket

8th Class English Chapter 1A The Tattered Blanket Textbook Questions and Answers

Look at the pictures given and answer the questions that follow.

Question 1.
What do you observe in the pictures?
Answer:
In picture A, we observe a nuclear family that consists of a pair of adults and their children. In picture B, we observe a joint family that consists of a man (the head), his wife, their children, daughters-in-law and their grandchildren.

Question 2.
Do we find many joint families in our society? Yes/No? Give reasons.
Answer:
We don’t find many joint families in our society. The joint family system has been breaking up in India as a result of the increasing individualistic and independent attitudes of grown up children. Nuclear families provide more privacy. Today youngsters want financial independence. Hence, the system of joint family has been gradually disappearing.

Comprehension

I. Answer the following questions.

Question 1.
Why didn’t the mother recognise Gopi and how did he feel?
Answer:
Gopi’s mother did not recognize him as she might have lost her memory. He didn’t visit her very often. He was very disappointed at that. He tried to convience her that he was Gopi, her son but of no use.

Question 2.
Why do you think Gopi didn’t get anything for his mother?
Answer:
I think Gopi didn’t have any love and affection for his Amma. Actually he didn’t have any feelings for her. He spent all his time in money making. He didn’t have any values. He didn’t give any importance to human relations. He forgot his mother. So, I think, he didn’t get anything for his mother.

Question 3.
The mother could not remember Gopi. Do you think Gopi remembered his mother? What does it suggest?
Answer:
No, I don’t think Gopi remembered his mother. It suggests us that he didn’t have any moral values. He didn’t care for human relations. He was the man of money. He forgot her service and sacrifice. He only looked for the status.

Question 4.
What is meant by the expression ‘the tattered blanket’?
Answer:
The expression “the tattered blanket” means the torn blanket. It symbolizes the life of the Amma. Here the old woman is compared to the torn blanket. Amma is very old and she is in her last stage. No one has any use of her. In the same way, the blanket is a tattered one which is not very useful.

Question 5.
Why didn’t Gopi answer his sister’s question, ‘Do you remember your Amma?’?
Answer:
Gopi knew what he had done to his mother. He came after a very long time to his mother. He didn’t remember his mother. He didn’t even write a letter to her. He came there only for selling his share of the family property but not with love and affection. He valued money and status only. So, Gopi didn’t answer his sister’s question.

Question 6.
If you were Gopi’s sister, how would you respond to his behaviour?
Answer:
If I were Gopi’s sister, I would make him know that he was doing wrong. I would make him know a son’s responsibility towards his mother. I would make him recall Amma’s service and sacrifice for him. I would make him realize that one day he too would become old and face the same situation. I would really hate him.

Vocabulary

I. Fill in the blanks with the most appropriate words from the box. Remember, the box has some extra words.

1. All my attempts to make him happy proved ———–.
2. It was very cold. So, I ———– in a corner.
3. Forced by her parents, Sita ———– took the diploma course.
4. What are you ———–? I can’t hear you.
5. The news that he was denied promotion caused ———– to him.

II. Tick (✓) the words that are similar in meaning to the underlined words.

1. His mother made a futile attempt to get up.
a. barren
b. limited
c. useless
d. empty
Answer:
c. useless

2. It’s all tattered now.
a. spoiled
b. old
c. dirty
d. torn
Answer:
d. torn

3. There is a cold mist in the mornings,
a. ice
b. snow
c. fog
d. win
Answer:
c. fog

4. It’s just like a ball of knotted yarn.
a. very small
b. rounded tightly
c. joined
d. tied
Answer:
d. tied

5. I can’t make both ends meet with my salary.
a. earn a lot of money
b. spend a lot of money
c. earn just enough money
d. give all that one has
Answer:
c. earn just enough money

Grammar

Phrases, Noun Phrase and Noun Phrase Apposition

I. Look at the following sentences from the text and observe the underlined part in each sentence.

She saw a bald, fat, middle-aged man.

Discussion:

• Which word in the underlined part is important?
• The underlined part in the above sentence has more than one word. It is called a phrase. The underlined part ‘a bald, fat middle-aged man’ functions as a Noun Phrase.

Here the word ‘man’ is important and all other words add more information to that word. So it is called a Noun Phrase.
Identify some more noun phrases from the story and write them below.
Answer:
1) The tattered blanket
2) A thin bath towel
3) His office jeep
4) Her wrinkled cheeks
5) A ball of knotted yarn

Complete the sentences with noun phrases using the words given in brackets.

1. I bought ———– (beautiful/a/umbrella/red)
2. We saw ———–in the zoo. (baby/a/elephants/of/couple)
3. Our grand father lives in ———– (big/house/a/stone-built)
4. Ramya has ———– (nice/a/sari/silk)
Answer:
1. a beautiful red umbrella.
2. a couple of baby elephants
3. a big stone-built house.
4. a nice silk sari.

II. Noun Phrase in Apposition.

Look at the following sentences and observe the underlined part in each sentence.

1. Kamala, her eldest daughter, a widow, got up reluctantly.
2. Don’t you remember Vimala, District Collector Nambiar’s eldest daughter?

The underlined parts in the above sentences refer to the nouns that occur before them. The underlined parts are called Noun phrases in Apposition.

Rewrite the following sentences using Noun Phrase in Apposition.
1. Mahesh is my elder brother. He lives in Delhi.
Mahesh, ———–, lives in Delhi.
2. Sarojini Naidu is popularly known as the Nightingale of India. She wrote many poems in English.
Sarojini Naidu, ———–, wrote many poems in English.
3. Rabindranath Tagore is called Gurudev. He was awarded the Nobel Prize for literature in 1913.
Rabindranath Tagore, ———–, was awarded the Nobel Prize for literature in 1913.
4. Mount Everest is the highest peak in the world. It is located in Nepal.
Mount Everest, ———–, is located in Nepal.
Answer:
1. my elder brother
2. the Nightingale of India
3. Gurudev
4. the highest peak in the world

Writing

I. Read the following paragraph, taken from the story.

Delhi is too expensive. You know I have four children to look after now. I can’t make both ends meet with my salary. And one has to keep up one’s status. It will be a great help if I can raise some money by selling my share of the family property. I came to talk it over with you.
Now, write a paragraph on how to keep up family ties despite economic pressures (You may use the hints given below).

• Impact of economic pressures
• Lack of time to spend with the family
• Lack of love and affection
• Absence of human relationships

Answer:
People lead a very busy life in the present society. They work like machines. They even don’t find time to sit together. They forget their families. They don’t have any enjoyment. Because of the economic pressures they have to earn more and more money. They don’t give any importance to the human relations. Everyone tries to keep up his/her status. They don’t show any love and affection on their family members. The younger ones forget the selfless service rendered by their parents. They don’t have any feelings to them. They forget the sacrifice made by their par¬ents in the process of giving them good education, providing them good facilities and giving them good lives. In the hunting of money, they don’t find time to spend with their family members. They neglect their parents. The old people are equal to the little children. They need help, service, money, etc. from their offspring. So, the younger ones must provide them to their parents. Despite their economic pressures, they must find some time to spend with their parents. They should remember that one day they too will become old. If they don’t show any love and affection, they too will have to face the same situation. Though the younger ones are busy with their work, they should maintain family ties and show the right path to the next generations.

Listening

Listen to your teacher making an announcement and answer the following questions.

An Announcement on the Radio

Prashanth, a thirteen year old boy has been missing since last Sunday. The boy is in blue trousers and pink T-shirt. He can speak Telugu, Hindi and English. He has fair complexion. He is fond of movies. His parents are much worried about him. Whoever finds Prashanth will be rewarded. You may contact the Sub- Inspector of Police, Vidya Nagar, Thiruvananthapuram. (Mobile No. 99xxxxxx00)

Question 1.
What is the announcement about?
Answer:
The announcement is about the missing boy, Prashanth.

Question 2.
What are the features of Prashanth?
Answer:
Prashanth is a thirteen year old boy. He is in blue trousers and pink T-shirt. He can speak Telugu, Hindi and English. He has fair complexion. He is fond of movies.

Question 3.
Where do you generally listen to such announcements?
Answer:
We generally listen to such announcements :
(i) On the radio (ii) On the television (iii) Over the loudspeakers, etc.

Question 4.
Think of some announcement you may make or listen at school.
Answer:
As you are aware, we are going to celebrate the Children’s Day celebrations in our school on the 14th of this month. We are going to organize a number of cultural programmes on the occasion. So, I would like to request the students who are interested to give their names to the SPL. The selected events are : Dances, Skits, Songs and Plays.

Question 5.
What are the other ways to trace the missing persons or things?
Answer:
The other ways to trace the missing persons or things are :
(i) Announcement on TV.
(ii) Announcement in dailies, weeklies and other magazines.
(iii) Announcement over loudspeakers.
(iv) Announcement through wall posters, pamphlets, etc.

Study Skills

Family related information.

Is yours a nuclear or joint family?
Now write a paragraph describing the types of families using the information given in the above tree diagram.
Write which type of family you prefer and why.
Answer:
Ours is a nuclear family. But I prefer to be a member of a joint family. There are two types of families. They are (i) Joint family and (ii) Nuclear family. A joint family consists of father, mother, their children and their families. A nuclear family consists of father, mother and their children. I really can’t see any disadvantages with a joint family. In every sense it is a convenient arrangement for everyone – morally, emotionally, mentally, financially, etc. With everyone putting his or her efforts, joint family system benefits everyone. The children are well taken care of. They learn to give and take, to be patient, cooperative, tolerant and to adjust with the other family members in a joint family. The joint family gives security, health and prosperity to everyone of its members. The joint family system is one that could help us to live a less stressful life as there are a lot of people around to help us and to share joys and sorrows. The eleders handle the financial matters. So there is no stress on the younger ones. The elders show the right path to younger ones. The younger ones develop the virtues like co-operation, sympathy, sacrifice, selfless ser­vice, obedience, etc. in a joint family. We find love and affection among the members of a joint family. Hence I prefer the joint family system.

The Tattered Blanket Summary in English

Gopi was a government officer living in Delhi. He married Vimala. district collector Nambiar’s eldest daughter. They had four children. Gopi’s old mother was living in the countryside along with her eldest daughter Kamala, a widow. After attending a meeting in Thiruvananthapuram, he dropped in on his way back. His mother saw him getting down at the gate and asked Kamala to see who he was. Kamala walked slowly to the gate reluctantly. She recognised Gopi and asked him unpleasantly why he made a sudden unexpected visit. But Amma did not recognize him. Gopi tried to tell her that he was her son. Kamala told Gopi that that Amma was often like that those days. She didn’t recognize anybody. When Amma asked Kamala if her son (Gopi) had sent a letter, Kamala told her everything was fine with him. But Gopi didn’t write any letter to her. When Kamala told Gopi all these things, he replied that he was on his toes always as he got promotion the previous year. So he didn’t get any time to write letters. Again Amma asked who he was. Gopi told her that he was her son Gopi and he had come from Delhi. She even forgot his wife’s name. She used to think that Gopi wrote letters to him every day. So she asked Kamala if he wrote a letter that day. Gopi kept his briefcase on the thinna, opened it and pulled out his contents such as clothes, files, a shaving set, etc. Amma told Gopi that her son Gopi was a government officer in Delhi and had Kesariyogam. She asked him to send her a new red blanket to protect herself from a cold mist. Her old blanket, which was brought by Gopi when he was studying in Madras, was all tattered. Actually Gopi didn’t come to the village too see her Amma. He didn’t have any affection and love towards his Amma. He gave more importance to status. He wanted to raise some money by selling his share of the family property. He came to talk it over with his sister. Kamala knew that he would never come there anymore after selling his land. When she told Gopi the same, he answered that he would come when he got time. He said that Amma couldn’t remember who he was. Actually it was he who didn’t remember his Amma.

About the Author

Kamala Das (1932-2009) is the daughter of the famous Malayalam poet- Balamani Amma and V.M. Nair. She is an internationally known poet, short story writer and novelist who writes effortlessly both in English and Malayalam. She has received many awards for her literary work. Some of them are Asian Poetry Prize, Kent Award for English Writing from Asian Countries, Asian World Prize, Sahitya Academy Award and Vayalar Rama Varma Sahitya Award.

The Tattered Blanket Glossary

thinna (n): sit out (elevated place on the verandas)

futile (adj): unsuccessful

huddled (v): held arms and legs close because of fear or cold.

reluctantly (adv): not willing to do something

screwing up eyes (v): narrowing the eyes to look more carefully

on toes (idm): busy, ready to work

mumbling (v): speaking unclearly and quietly

exasperatedly (adv): very annoyed

kesariyogam (n): well settled (in Malayalam)

tattered (adj): torn

irritation (n): annoyance

peer (v): to look closely or carefully at something or somebody

grating (adj): unpleasant to Listen to

scared (adj): frightened

awkwardly (adv): uncomfortably

wrinkled (adj): having folds in one’s skin.

knotted yarn (n.phr): tied threads

nod (v) : move one’s head up and down to show agreement

make both ends meet (idiom): to earn just enough money to be able to buy the things you need

look after (phr. v): to take care of somebody/something

feebly (adv): weakly

Students can go through AP SSC 10th Class Maths Notes Chapter 2 Sets to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 2 Sets

→ Set theory is comparatively a new concept in mathematics.

→ This theory was developed by George Cantor.

→ A well defined collection of objects or ideas is known as “set”.

→ Well defined means that:
i) All the objects in the set should have a common feature or property.
ii) It should be possible to decide whether any given object belongs to the set or not.
Example or comparision of well defined and not well defined collections:

→ Some more examples of well defined collections:
i) Vowels of English alphabets, namely a, e, i, o, u.
ii) Odd natural numbers less than 11, namely 1, 3, 5, 7, 9.
iii) The roots of the equation x² – 3x + 2 = 0, i.e., 1 and 2.

→ Objects, elements and members of a set are synonymous words.

→ Sets are usually denoted by the capital letters like A, B, C, X, Y, Z, etc.

→ An object belonging to a set is known as a member/element/individual of the set.

→ The elements of a set are represented by small case letters,
i.e., a, b, c, , x, y, z, etc.

→ If ‘b’ is an element of a set A, then we say that ‘b’ belongs to A.

→ The word ‘belongs to’ is denoted by the Greek symbol ‘∈’.

→ Thus, in a notation form, ‘b’ belongs to A is written as b ∈ A and ‘c’ does not belong to ‘A’ is written as c ∉ A.

→ Representation of sets: Sets are generally represented by the following two methods.
i) Roster (or) Tabular form
ii) Rule method (or) Set builder form.

→ Roster (or) Tabular form: In this form, all elements of the set are written, separated by commas, within curly brackets.
Example:
i) The set of all natural numbers less than 5 is represented as N = {l,2,3,4}
ii) The set of all letters in the word “JANUARY” is represented as B = {A, J, N, R, U, Y}
Note:
a) In a set notation, order is not important.
b) The elements of a set are generally not repeated in a particular set.

→ Set builder form (or) Rule method: In this method, a set is described by using a representative and stating the property (or) properties which the elements of the set satisfy, through the representative.
Example:
i) Set of all natural numbers less than 5.
A = {x : x ∈ N, x < 5}
ii) Set of vowels of the English alphabet.
V = {x : x is a vowel in the English alphabet)
Note: It may be observed that we describe the set by using a symbol (x or y or z etc.) for elements of the set.

→ Types of set:

→ Empty set (or) Null set (or) Void set: A set, which does not contain any element is called an empty set (or) a null set (or) a void set.

→ Empty set is denoted by ∅ (or) { }

Example :
A = (x : x is a natural number smaller than 1}
B = {x : x² – 2 = 0 and x is a rational number}
C = (x : x is a man living on the moon}
Note: ∅ and { 0 } are two different sets. {0} is a set containing the single element ‘0’ while { } is a null set.

→ Singleton set: A set consisting of a single element is called a singleton set.
Examples:
{ 0 }, {- 7} are singleton sets.

→ Finite set: A set which is possible to count the number of elements of that set is called finite set.
Example – 1 : The set {3, 4, 5, 6} is a finite set, because it contains a definite number of elements i.e., only 4 elements.
Example – 2 : The set of days in a week is a finite set.

Example – 3 : An empty set, which does not contain any element (no element) is also a finite set.

→ Infinite set: A set whose elements cannot be listed, that type of set is called infinite set.

Example : i) B = {x : x is an even number}
ii) J = {x : x is a multiple of 7}
iii) The set of all points in a plane. s|s A set is infinite if it is not finite.

→ Equal sets: Two sets are said to be equal, if they have exactly the same elements.
For example: The set A and B are having same elements i.e., watch, ring, flower are said to be equal sets.

→ Cardinal number: The number of elements in a set is called the cardinal number of the set.
Example: Consider the finite set A = {1, 2, 4}
Number of elements in set ‘A’ is 3.
It is represented by n(A) = 3

→ Universal set: A set which consists of all the sets under consideration (or) discussion is called the universal set. (or) A set containing all objects or elements and of which all other sets or subsets.
It is usually denoted by ∪ (or) μ.

The universal set is usually represented by rectangles.
Example:
i) The set of real numbers is universal set for number theory.
Here ‘R’ is a universal set.
ii) If we want to study various groups of people of our state, universal set is the set of all people in Andhra Pradesh.

→ Subset: If every element of first set (A) is also an element of second set (B), then first set (A) is said to be a subset of second set (B).

→ It is represented as A ⊂ B.
Example :
Set A = {2, 4, 6, 8} is a subset of .
Set B = {1,2, 3, 4,5, 6, 7, 8}

→ Empty set is a subset of every set.

→ Every set is a subset of itself.

→ Consider ‘A’ and ‘B’ are two sets, if A ⊂ B and B ⊂ A ⇔ A = B.

→ A set doesn’t change if one or more elements of the set are repeated.

→ If A ⊂ B, B ⊂ C ⇒ A ⊂ C.

→ Venn Diagrams: Venn-Euler diagram or simply Venn diagram is a way of representing the relationships between sets.

→ These diagrams consist of rectangles and closed curves usually circles.
Example: Consider that U = {1, 2, 3, ……, 10} is
the universal set of which, A = {2, 4, 6, 8, 10} is a subset.
Then the Venn diagram is as:

→ Basic operations on sets: In sets, we define the operations of union, intersection and difference of sets.

→ Union of sets: The union of two or more sets is the set of all those elements which are either individual (or) both in common.

→ In symbolic form, union of two sets A and B is written as A ∪ B and usually read as “A union B”.

→ Set builder form of A ∪ B is A ∪ B = (x : x ∈ A or x ∈ B}

→ The union of the sets can be represented by a Venn diagram as shown (shaded portion).

→ It is evident from the definition that A ⊆ A ∪ B; B ⊆ A ∪ B.

→ Roster form of union of sets : Let A = {a, e, i, o, u} and B = (a, i, u} then A ∪ B = {a, e, i, o, u} ∪ { a, i, u} = {a, e, i, o, u}

→ Intersection of sets: The intersection of two sets A and B is the set of all those elements which belong to both A and B.

→ We denote intersection by A ∩ B.

→ We read A ∩ B as “A intersection B”.

→ Symbolically, we write A ∩ B = (x : x ∈ A and x ∈ B}

→ The intersection of A and B can be illustrated in the Venn diagram as shown in the shaded portion in the adjacent figure.

→ The intersection of A and B can be illustrated in the Roster form:
If A = {5, 6, 7, 8} and B = {7, 8, 9, 10} then A ∩ B = {7, 8}

→ Disjoint set: Consider A and B are two finite sets and if there are no common element in both A and B. Such set is known as disjoint set (or A ∩ B = ∅).
(or)
Two sets (finite) are said to be disjoint sets if they have no common elements. That is if the intersection of two sets is a null set they are disjoint sets.

→ The disjoint sets can be represented by means of the Venn diagrams as shown in the adjacent figure.

→ Difference of sets: The difference of sets A and B is the set of elements which belong to ‘A’ but do not belong to ‘B’.

→ We denote the difference of A and B by A – B or simply “A minus B”.

→ Set builder form of A – B is (x : x ∈ A and ∉ B}

→ Venn-diagram of A – B is

→ Venn-diagram of B – A is

→ A – B ≠ B – A

→ Fundamental theorem on sets:
If A and B are any two sets then n (A ∪ B) = n (A) + n (B) – n (A ∩ B) where
n (A ∪ B) = number of elements in the set (A ∪ B), also called cardinal number of A ∪ B
n (A) = number of elements in the set A also called cardinal number of A
n (B) = number of elements in the set B also called cardinal number of B