AP State Board Notes

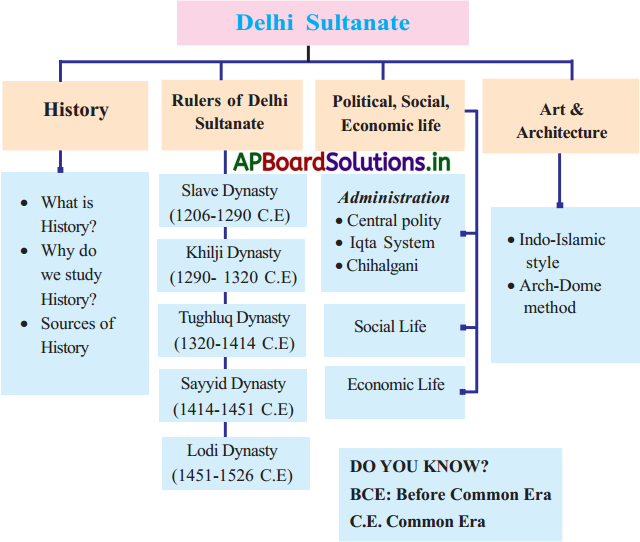
Students can go through AP Board 7th Class Maths Notes 9th Lesson బీజీయ సమాసాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 9th Lesson బీజీయ సమాసాలు

→ ఒక చరరాశి వివిధ విలువలను తీసుకోగలదని మరియు దాని విలువ స్థిరంగా వుండదని మనం తెలుసుకున్నాం. ఉదాహరణ a, b, x, y, Z మొదలైనవి అదే విధంగా స్థిరరాశులు స్థిర విలువను కలిగి ఉంటాయి. ఉదాహరణకు 6, 8, -10 మొదలైనవి కొన్ని స్థిరాంకాలు.

→ ఒక సమాసము యొక్క ప్రతి పదం కూడా ఒక స్థిరపదం అయితే, ఆ సమాసాన్ని సంఖ్యా సమాసము అని అంటారు.

→ ఒక సమాసములో కనీసం ఒక బీజీయ పదం ఉన్నట్లయితే అప్పుడు ఆ సమాసాన్ని బీజీయ సమాసము అని అంటారు.

→ ఒకే బీజీయ కారణాంకాలు కలిగిన పదాలను సజాతి పదాలని అంటారు. వేరు వేరు బీజీయ కారణాంకాలు కలిగిన పదాలను విజాతి పదాలని అంటారు.

→ ఒకే ఒక పదాన్ని కలిగి ఉన్న బీజీయ సమాసాన్ని ఏకపద సమాసము లేదా ఏకపది అని అంటారు. రెండు పదాలు ఉండే బీజీయ సమాసాన్ని ద్విపది అని అంటారు. మూడు పదాలు ఉండే బీజీయ సమాసాన్ని త్రిపది అని అంటారు.

→ ఒక బీజీయ సమాసములో చరరాశి యొక్క ఘాతాంకము, ఋణేతర పూర్ణసంఖ్య అయినపుడు దానిని బహుపది అంటారు.

→ ఒక సమాసములో, పదాలలోని చరరాశుల ఘాతాలు అవరోహణ క్రమంలో ఉండే విధంగా పదాలను అమర్చినట్లయితే, ఆ సమాసము ప్రామాణిక రూపంలో ఉంటుందని చెప్పబడుతుంది.

→ ఒక బీజీయ సమాసములో ఏ రెండు పదాలు జాతి పదాలు కానపుడు, అది సూక్ష్మరూపంలో ఉంది అని అంటాము.

→ రెండు లేదా అంతకంటే ఎక్కువ సమాసాల మొత్తం, అందులోని అన్ని పదాల యొక్క సంఖ్యాగుణకాల యొక్క మొత్తమునకు సమానము.

→ రెండు లేదా అంతకంటే ఎక్కువ సమాసాల భేదం, అందులోని అన్ని పదాల సంఖ్యా గుణకాల భేదానికి సమానము.

→ సమాసము యొక్క విలువ, అందులో ఉన్న చరరాశులకు తీసుకోబడ్డ విభిన్న విలువలపై ఆధారపడి ఉంటుంది.

→ స్థిరరాశి : విలువ స్థిరంగాగల రాశులను స్థిరరాశులు అంటారు. ఉదా : 2, 8, -10,

→ చరరాశి (చలరాశి) : విలువ స్థిరంగా లేకుండా సందర్భాన్ని బట్టి వివిధ విలువలను తీసుకొనే రాశిని చరరాశి అంటారు. వీటిని సాధారణంగా చిన్న ఆంగ్ల అక్షరాలతో సూచిస్తారు. ఉదా : 2, x, y. …….

→ పదము : స్థిరరాశులు లేదా చరరాశులు లేదా గుణకారం, భాగహారంతో కూడిన ఈ రెండింటి కలయిక అనేది ఒక పదము.
ఉదా : 5, x, 4x, -11x²y, \(\frac{12 x^{2}}{5}\), 13\(\frac{\mathrm{ab}}{\mathrm{c}}\), 13, …….
వీటిలో 5, 13, ….. లను సంఖ్యాపదాలు అని, x, 4x, – 11x²y, \(\frac{12 x^{2}}{5}\),13\(\frac{\mathrm{ab}}{\mathrm{c}}\) ….. లను బీజీయ పదాలు అని అంటారు.

→ సమాసము : సమాసము సంఖ్యాపదాలు, బీజీయ పదాలు లేదా +, – లతో కూడిన ఈ రెండింటి కలయికను సమాసము అంటారు.
ఉదా : 5, \(\frac{9}{7}\), x, y + 9, 2 + 3 – 6, 5c – 4, \(\frac{5}{x}\) + 7y – z, 3x² – 4x + 9……

→ ఒక సమాసంలోని అన్ని పదాలు సంఖ్యాపదాలైన దానిని సంఖ్యా సమాసం అంటారు.
ఉదా : 5, \(\frac{9}{7}\), 2 + 3 – 6, ………

→ బీజీయ సమాసం : ఒక సమాసంలో కనీసం ఒకటైన బీజీయ పదము ఉన్నట్లయితే ఆ సమాసాన్ని బీజీయ సమాసం అంటారు.
ఉదా : x, y + 9, 5C – 4, \(\frac{5}{x}\) +7y – z, ………..

→ గుణకము : ఒక బీజీయ పదంలో ఒక సంఖ్య లేదా ఒక బీజీయ కారణాంకము లేదా ఆ రెండింటి లబ్దము ఆ పదం యొక్క “గుణకము” అవుతుంది.

ఉదా : 7xy లో

• xy గుణకము లేదా సంఖ్యా గుణకము 7.
• y గుణకము = 7x
• x గుణకము = 7y
• 7X గుణకము =y
• 7y గుణకము = x
• 7 యొక్క గుణకము లేదా బీజీయ గుణకం = xy

→ సజాతి పదాలు : ఒకే బీజీయ గుణకమును కలిగిన పదాలను సజాతి పదాలు అంటారు.
ఉదా :

• 6X, – 8x, x సజాతి పదాలు (అన్ని పదాల యొక్క బీజీయ గుణకం = x)
• -7x²y, 5x²y, 3x²y సజాతి పదాలు (అన్ని పదాల యొక్క బీజీయ గుణకం x²y)

→ విజాతి పదాలు : ఒకే బీజీయ గుణకమును కలిగి ఉండనటువంటి పదాలను విజాతి పదాలు అంటారు.
ఉదా :

• 6x, – 8y, Z లు జాతి పదాలు.
• -7x²y, 5x²y², 3xy లు విజాతి పదాలు.

→ బీజీయ సమాసాల రకాలు : బీజీయ సమాసాలను ఆ సమాసంలోని పదాల సంఖ్యను బట్టి ఏకపది, ద్విపది, త్రిపది, బహుళపది, …….. గా విభజించవచ్చును.

• ఏకపది : ఒకే ఒక పదంను కలిగిన బీజీయ సమాసాన్ని ఏకపది అంటారు.
  ఉదా : 5x²y, 11\(\frac{x}{y}\), – 8t, ……..
• ద్విపది : రెండు విజాతి పదాలను కలిగిన బీజీయ సమాసాన్ని ద్విపది అంటారు.
  ఉదా : x + y, 5 + p, 6y + \(\frac{7}{x}\) a – 7b ……
• త్రిపది : మూడు విజాతి పదాలను కలిగిన బీజీయ సమాసాన్ని త్రిపది అంటారు.
  ఉదా : x + y + 2, 7a – \(\frac{8}{b}\) + c, 8m – 7n + 6. ……

→ బహుళపది : ఒకటి కన్నా ఎక్కువ బీజీయ పదాలు కలిగిన బీజీయ సమాసాన్ని బహుళపది అంటారు.
ఉదా :

• x + y, 7x² – \(\frac{4}{y}\) + 8, 3x^2/3 + 9y² + 3x – 9
• x² + y² + z³ + 9, ……….

→ బహుపది : ఒక బీజీయ సమాసంలో చరరాశి యొక్క ఘాతాంకము రుణేతర పూర్ణసంఖ్య అయితే దానిని బహుపది అంటారు.
ఉదా : x + y, x² + y² + z³ + 9, – 3xy + y² + x³, …………

• 7x² – \(\frac{4}{y}\) + 8 అనునది బహుళపది అవుతుంది. కాని బహుపది కాదు. ఎందుకనగా 7x² – + + 8 =
  7x² – 4y^-1 + 8 గా రాయవచ్చు. ఇందులో y యొక్క ఘాతాంకము ‘-1’. ఇది ఒక రుణ సంఖ్య.
• 3x^2/3 + 9y² + 3x – 9 కూడా బహుళపది, కాని బహుపది కాదు. ఎందుకనగా 3x^2/3 లో X యొక్క ఘాతాంకము పూర్ణసంఖ్య కాదు.

గమనిక : బహుపదులు అన్నీ బహుళపదులు అవుతాయి.. కాని, బహుళపదులు అన్నీ బహుపదులు కావు.

→ బీజీయ సమాసాల సూక్ష్మరూపం : ఒక బీజీయ సమాసంలో ఏ రెండు పదాలు సజాతి పదాలు కానపుడు, అది సూక్ష్మరూపంలో ఉంది అని అంటాము.
ఉదా :

• 7x + 8y + 9, సూక్ష్మరూపంలో కలదు.
• 9x + 8y – 2x + 9 సూక్ష్మరూపంలో లేదు. ఎందుకనగా ఇందులో 9x, – 2x అనే రెండు సజాతి పదాలు కలవు.

బీజీయ సమాసాలను సూక్ష్మరూపంలో రాయడానికి మనం సజాతి పదాలను కూడడం లేదా తీసివేయడం అనే పరిక్రియలను ఉపయోగిస్తాము.

→ బీజీయ సమాసాల కూడిక (సంకలనం) : బీజీయ సమాసంలోని సజాతి పదాల సంఖ్యా గుణకాలను కలిపి మొత్తం యొక్క సంఖ్యా గుణకంగా రాసి బీజీయ గుణకాన్ని అలాగే రాస్తాము.
ఉదా-1: 7x మరియు 8x లను కూడుము.
7x + 8x
(7 + 8 = 15)
7x + 8x = 15x

ఉదా-2 : 7x² + 9y మరియు 2x² – 5y లను కూడండి.
7x² + 9y + 2x² – 5y
7x² + 2x² + 9y – 5y (సజాతి పదాలను ఒకచోట రాయడం)
(7 + 2 = 9, 9 + (-5) = 4)
= 9x² + 4y

బీజీయ సమాసాల సంకలనానికి రెండు పద్ధతులు కలవు. అవి :

• అడ్డు వరుస పద్ధతి (పంక్తి పద్ధతి)
• నిలువు వరుస పద్ధతి (దొంతి పద్ధతి)

ఉదా-1: 7x మరియు 8x లను కూడండి.
అడ్డు వరుస పద్దతి : 7x + 8x = 15x

ఉదా-2 : 7x² + 9y మరియు 2x² – 5y ల మొత్తంను కనుగొనుము.
అడ్డు వరుస పద్ధతి : (7x² + 9y) + (2x² – 5y)
7x² + 9y + 2x² – 5y
7x² + 2x² + 9y – 5y
9x² + 4y.

నిలువు వరుస పద్దతి : 2 (సజాతి పదాలను సజాతి పదాల కింద రాయాలి.)

→ బీజీయ సమాసాల తీసివేత (వ్యవకలనం) : ఒక బీజీయ సమాసాన్ని మరొక బీజీయ సమాసం నుండి తీసివేయడం అనగా దాని సంకలన విలోమాన్ని కూడడము.

ఉదా-1:
7x నుండి 3x ను తీసివేయడం అనగా 7x కు 3x యొక్క సంకలన విలోమం – 3x ను కూడడము.
7x – 3x = 7x + (- 3x) = 4x .

ఉదా-2 :
7a + 6b + 4 నుండి 5a – 2b – 5 ను తీసివేద్దాము .
5a – 2b – 5 యొక్క సంకలన విలోమం
– (5a – 2b – 5) = – 5a + 2b + 5

ఇప్పుడు 7a + 6b + 4 నుండి 5a – 2b – 5 ను తీసివేయడానికి
7a + 6b + 4 నకు 5a – 2b – 5 యొక్క సంకలన విలోమాన్ని కూడవలెను.
(7a + 6b + 4) – (5a – 2b – 5)
= (7a + 6b + 4) + (-5a + 2b + 5)
= 7a + (-5a) + 6b + 2b + 4 + 5
= 2a + 8b + 9

→ బీజీయ సమాస ప్రామాణిక రూపం : ఒక బీజీయ సమాసంలోని పదాల యొక్క ఘాతాంకాలు అవరోహణ క్రమంలో ఉండే విధంగా పదాలను అమర్చితే అప్పుడు ఆ సమాసము ప్రామాణిక రూపంలో ఉంది అంటారు. ఉదా : 2x + 3x³ – 2 + 8×2 సమాసాన్ని ప్రామాణిక రూపంలో రాయగా 3x³ + 8x² + 2x – 2.

→ బీజీయ సమాస విలువ : బీజీయ సమాసంలోని చరరాశిని ఇచ్చిన విలువలో ప్రతిక్షేపించడము వలన వచ్చు సంఖ్యావిలువ ఆ సమాసము యొక్క విలువ అవుతుంది.
ఉదా : x = 2 అయిన 2x + 3 సమాస విలువ
2(2) + 3 = 4 + 3 = 7

Students can go through AP Board 7th Class Maths Notes 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు

→ పెద్ద సంఖ్యలను సరళమైన రీతిలో చదవడం, రాయడం, అర్థం చేసుకోవటంలో ఘాతాంకాలు దోహదపడతాయి.
ఉదా : 2 × 2 × 2 × 2 × 2 × 2 = 26
a × a × a … ‘n’ సార్లు = aⁿ

→ ఘాతాంక న్యాయాలు :
‘n’ మరియు ‘m’ లు ఏవైనా రెండు శూన్యేతర పూర్ణసంఖ్యలు, ‘a’ మరియు ‘b’ లు పూర్ణసంఖ్యలైన ,

• a^m × aⁿ = a^m+n
• (a^m)ⁿ = a^mn

• a^m × b^m = (ab)^m
• a^m ÷ b^m = \(\left(\frac{a}{b}\right)^{m}\)
• a⁰ = 1 (where a ≠ 0)
• (-1)^{సరిసంఖ్య} = 1
• (-1 )^{బేసిసంఖ్య} = -1

→ ఒక సంఖ్యను 1 నుండి 9 మధ్యగల దశాంశ భిన్నంగా మరియు 10 యొక్క ఘాతాలతో లబ్దం చేయటాన్ని ప్రామాణిక రూపంలో వ్యక్తపరచడం అంటాం.

→ ఘాతరూపం : ఒక సంఖ్య యొక్క పునరావృత గుణకారాన్ని సరళమైన రీతిలో వ్యక్తపరచడాన్ని ఘాతరూపం
అంటారు.
ఉదా : 2 × 2 × 2 = 2³
10 × 10 × 10 × 10 = 10⁴
10⁴ లో 10ని భూమి అని, 4 ను ఘాతాంకం అని అంటారు.

→ ఘాతాంక సాధారణ రూపం : a × a × a × ……. n సార్లు = aⁿ ను ఘాతాంక సాధారణ రూపం అని
అంటారు. ఇక్కడ a భూమి, n ఘాతాంకం.

→ ప్రామాణిక రూపం : ఒక సంఖ్యను 1 నుండి 9 వరకు గల దశాంశ భిన్నం మరియు 10 యొక్క పూర్ణాంక ఘాతాల లబ్దంగా వ్రాయుటను ప్రామాణిక రూపంలో వ్యక్తపరచడం అంటాం.
ఉదా : 59 = 5.9 × 10
590 = 5.9 × 10²
5904 = 5.904 × 10³

Students can go through AP Board 7th Class Social Notes 8th Lesson Bhakthi – Sufi to understand and remember the concept easily.

AP Board 7th Class Social Notes 8th Lesson Bhakthi – Sufi

→ The Bhakti movement reached its prominence in 8th century and continued to grow ever after.

→ Bhakti means a path of loving devotion to a particular deity.

→ It has the characteristics like universal brotherhood and equality of all in the society.

→ Bhakti movement was started by Adi Shankaracharya.

→ Ramanujacharya promoted Vishishtadvaita and Madhvacharya has promoted Dvaita philosophy.

→ Sankaracharya was born in Kaladi in Kerala.

→ Shankaracharya established four Shakti Peethas in all the four corners of India.

→ Ramanujacharya preached everyone could attain salvation by completely surrendering to the will of the Almighty.

→ Vallabhacharya’s teachings are also known as Pushtimarga or the Path of Grace.

→ Basaveswara was popularised the Veerasaivism.

→ The credit for the spread of Vaishnava religion in North India goes to Ramananda.

→ Kabir advocated “all are equal before God”.

→ Sant Ravidas cardial quote was “Hari is in all and all in Hari”.

→ Mira Bai was another important woman saint of the medieval times.

→ Sankaradeva succeeded in preaching Vaishnavism among all people including tribal people.

→ Guru Nanak believed in the oneness of God and the brotherhood of men.

→ Jnaneswar used Marathi to convey his thoughts.

→ Tallapaka Annamacharya is popularly known as Annamayya.

→ Annamayya Sankeerthanas are very popular among telugu people.

→ The Sufi movement was a socio-religious movement in Islam.

→ Khwaja Moinuddin Chishti was a great Sufi Saint of India.

→ Bhakti Movement : The trend that was brought forward by a number of Hindu saints in medieval Hinduism that sought to bring religious reforms by adopting the method of devotion to achieve salvation.

→ Sufi Movement : It is the mystical movement against orthodox practice in Islam with an aim to adhere the direct perception of mankind to God without any mediator.

→ Inferences from the Poetry of Bhakti and Sufi saints about existing social order : The saints of Bhakti and Sufi – spread message of friendship, emity tolerance peace and equality among all.

→ Upanishads : They are known as Vedanta. These are the last parts of Vedas.

→ Esoteric : The philosophical knowledge attained by few saints with dedicative effort.

→ Egalitarian : The concept of equalness.

→ Ecstasy : A trance or trance like state in which a person transcends.

→ Salvation : Deliverance of the soul from earthly matters and reach the abode of God.

Students can go through AP Board 7th Class Social Notes 7th Lesson Mughal Empire to understand and remember the concept easily.

AP Board 7th Class Social Notes 7th Lesson Mughal Empire

→ Red Fort was built by Shahjahan.

→ The Rise of the Mughals has brought a great change in medieval Indian History.

→ Babur established Mughal Empire after during Ibrahim Lodi the last ruler of Delhi Sultanate at Panipat in 1526 CE.

→ Babur’s son Humayun came to throne after Babur, but Humayun’s brothers did not help him at the right time.

→ Shershah Sur was an Afghan leader.

→ Shershah was not only a great warrior but also an administrator.

→ Many Rajputs surrendered to Akbar and married of their daughters.

→ Salim the successor of Akbar came to the throne with the title Jahangir.

→ Shajahan’s period was much known for the construction of buildings.

→ Aurangzeb was a devout Muslim and led his life as per the principles of Quran.

→ The Mughals had a centralised administration.

→ Akbar introduced the Mansabdari system in his military policy.

→ Mughals are Sunni Muslims.

→ The Mughals were responsible for building an extensive road system, creation of uniform currency, and the unification of the country.

→ Indian Agricultural production increased under the Mughal Empire.

→ The textile industry developed in the Mughal Empire.

→ A new tradition of architecture was started during the Mughal era.

→ Persian language was the dominant and official language of the empire.

→ A new school of art known as miniature painting emerged during the Mughal period.

→ The decline of Mughal Empire started with Shahjahan and ended with Aurangzeb.

→ The contemporary rulers during Mughals were Afghans, Rajputs, Marathas and Bahman kings.

→ Shivaji was the founder of the Maratha kingdom.

→ Though Shivaji was a devout Hindu, he respected other religions.

→ Shivaji developed naval force.

→ In Shivaji’s administration, to assist him ‘Ashta Pradhans1 are there (Eight Ministers).

→ Rulers of Mughal Empire : The Mughal emperors built and ruled the Mughal Empire on the Indian Subcontinent.

→ Political, Social and Economic life
Political life : The Mughals had a centralised administration.

→ Social life : Mughals are Sunni Muslims.

→ Economic life : The Indian Economy prospered under the Mughal Empire.

→ Art and Architecture : A new tradition of architecture was started during the Mughal era.

→ Contemporary Kingdom to Mughal empire : Happening, existing, living or coming into being during the same period of time.

→ Warrior : a brave or experienced soldier or fighter.

→ Regent : a person appointed to administer a state because the monarch is a minor or is absent or incapacitated.

→ Heretic : a person believing in or practicing religious heresy.

→ Guerrilla warfare : a surprise attack of hit and run tactic by a group of soldiers.

→ Agrarian : relating to the ownership and use of farmland.

Students can go through AP Board 7th Class Social Notes 6th Lesson Vijayanagara Empire to understand and remember the concept easily.

AP Board 7th Class Social Notes 6th Lesson Vijayanagara Empire

→ When Muhammad-Bin-Tughlaq was loosing his power in the Deccan, two new kingdoms were emerged in South India.
They are: Vijayanagara and Bahmani Kingdoms.

→ The founders of Vijayanagara empire were Hari Hara Raya and Bukkaraya.

→ The capital of Vijayanagara was Hampi.

→ Vijayanagara was the richest kingdom in the world during 14th and 15th centuries.

→ The struggle between Vijayanagara and Sultanate of Madurai lasted for about 4 decades. □I The greatest ruler of the Sangam dynasty was Devaraya II.

→ Saluva dynasty was founded by Saluva Narasimharaya.

→ Krishna Devaraya was a very powerful ruler of Vijayanagara. ‘

→ The founder of Tuluva dynasty was Narasa Nayaka. He was the father of Krishnadevaraya. □I Sri Krishna Devaraya maintained friendly relations with the Portuguese and Arab traders.

→ “Desa Bhasalandu Telugu Lessa” said by Sri Krishna Devaraya.

→ Allasani Peddana was called Andhra Kavita Pitamaha.

→ The king enjoyed absolute authority in executive, judicial and legislative matters.

→ The empire was divided into different administrative units called Mandalas, Nadus, Sthalas and Gramas. .

→ The Amara Nayaka system was a major political innovation of Vijayanagara empire.

→ The society was systemized.

→ Women occupied a high position and took an active part in all aspects.

→ Vijayanagara was also a great center of trade.

→ The art of shipbuilding developed.

→ The Carnatic music was developed.

→ Bharatanatyam was famous.

→ The Reddy kingdom was established by Prolaya Verna Reddy.

→ The founder of Bahamani kingdom was Alauddin Hasan Bahman Shah.

→ Mahmud Gawan was a Persian merchant.

→ Rulers of Vijayanagara : Who ruled the Vijayanagara empire.

→ Political life : The administration under Vijayanagara empire was well organised.

→ Social life : The society was systemized.

→ Economic life : Vijayanagara empire was one of the wealthiest parts of the world at that time.

→ Art and Architecture : Is defined as the art and science of designing building and structures.

→ Contemporary Kingdoms (Bahamanis, Reddies) : The kindoms existing at the same time.

→ Doab : The land lying between two rivers.

→ Artillery : Large caliber guns used in warfare, weapon.

→ Nayakas : Who discharge civil and military functions on behalf of the emperor.

→ Merchant : A person doing trade.

→ Invade : An armed force attack, conquer, capture.

1.

2.

Students can go through AP Board 7th Class Social Notes 5th Lesson Kakatiya Kingdom to understand and remember the concept easily.

AP Board 7th Class Social Notes 5th Lesson Kakatiya Kingdom

→ During the medieval period five important kingdoms emerged in South India.

→ These are 1. The Chalukyas of Kalyani, 2. The Yadav&s 3. The Kakatiyas 4. The Hoyasalas and 5. The Pandyas.

→ Thailapa II was the founder of Chalukyas of Kalyani.

→ Yadavas of Devagiri originally served as subordinates to Chalukyas to Kalyani.

→ Hoyasalas belong to Dwarasamudra.

→ Pandyas ruled from Madurai.

→ Early Kakatiyas served as a feudatories to the Rashtrakutas and the Western Chalukya kings.

→ The Kakatiya kingdom emerged after the fall of the Western Chalukyas.

→ Rudra deva, the Kakatiya king built a new capital Orugallu.

→ The reign of the Praia II, was a land mark in the history of the Kakatiyas.

→ Rudra Deva’s achievements were described in Hanumakonda.inscription.

→ Ganapati deva was the most powerful of the Kakatiya sovereigns.

→ Rudrama Devi came to th% throne in 1262 CE.

→ The Kakatiyas divided their territories among a number of military chiefs known as Nayankara.

→ Land revenue was the major source of income to the Kakatiya kingdom.

→ The Kakatiyas brought large tracts of forest land under cultivation.

→ The Kakatiya kings gave much importance to foreign trade.

→ The Kakatiya rulers extended liberat patronage to Sanskrit.

→ Kakatiya temple architecture shows fantastic smooth carving of black marble stone.

→ Regional kingdoms during Medieval Period : These are basically local or small kingdoms ruling a small town and are found in a particular region.

→ The Kakatiya Dynasty : This dynasty was a South Indian dynasty. It ruled most of Eastern Deccan region comprising present day Telangana and Andhra Pradesh and parts of Eastern Karnataka and Southern Odisa.

Political, Social and Economic Life
→ Political life : With the leading officials, their interactions, any documents, laws, treaties etc.

→ Social life : The way that laws, government actions, events etc.

→ Economic life : Specific to the financial implications of laws and events, how they affect trade, job availability and the flow of money.

→ Art and Architecture : Is defined as the art and science of designing building and structures.

→ Feudatory : Subordinates to king, that obediently follow the kings’ orders or instructions.

→ Patronized : To give help and support promoting culture and heritage.

→ Veera Saivam : One of the reform branch in the Hindu religion.

→ Inscription : The fact of writing or a small bit of writing.

→ Splendour : Brilliant appearance or great brightness.

→ Dynasty : A succession of rulers of the same line of descent.

→ Recalcitrant : A person who has an obstinately uncooperative attitude towards authority.

→ Sue : To proceed with and follow up to proper termination.

→ Heir-apparent : An heir apparent is a person who is first in an order of succession.

→ Clan : A group of people tracing descent from a common ancestor.

1.

2.

3.

Students can go through AP Board 7th Class Social Notes 4th Lesson Delhi Sultanate to understand and remember the concept easily.

AP Board 7th Class Social Notes 4th Lesson Delhi Sultanate

→ History is considered as the record of the past factual events.

→ We have to study History as it reveals how the people lived in that society, their rules and regulations, cultures and traditions in a chronological order i.e., from past to present.

→ The sources of History are broadly classified into two categories. They are: 1. Archaeological Sources which include material remains and 2. Literary Sources which include all texts.

→ Tomara or Tomar Rajputs built Dhillika or Dhillika pura (modern day Delhi) and made it capital of their kingdom.

→ Delhi became an important commercial centre under the Tomaras and Chauhans.

→ Muhammad Ghori defeated Prithviraj Chauhan at Tarain in 1192 CE. and occupied Delhi. Jl The Slave dynasty was established by Qutbuddin Aibak in 1206 CE.

→ lltutmish was the first sovereign ruler from Delhi and the real founder of the Delhi Sultanate.

→ Sultan Raziyya was the only woman ruler of Delhi Sultanate.

→ Alauddin Khalji was the successor of Jalaluddin Khalji.

→ Ghiyasuddin Tughlaq was the founder of Tughlaq dynasty.

→ Muhammad bin Tughlaq changed the capital from Delhi to Devagiri (Daulatabad).

→ The Sultan was the head of the empire.

→ Delhi Sultanate was divided into Iqtas (provinces).

→ Agriculture was the main occupation.

→ Tanka (silver) and Jital (copper) were the basic coins in usage.

→ A combination of Arabic and Indian style of art and architecture developed during this period.

→ Qutub Minar was built by Qutubuddin Aibak.

→ Literature was produced in Persian, Sanskrit and other regional languages.

→ Alberuni, Amir Khusrav and Zia-ud-din Barani were some of the great scholars.

→ The rule of the Delhi Sultanate came to an end during the reign of Lodi dynasty.

→ The Mughal ruler, Babur defeated Ibrahim Lodi in the first battle of Panipat in 1526 A.D.

→ What is History? : History is considered as the record of the past factural events.

→ Why do we study History? : We have to study history as it reveals how the people lived in that society, their rules and regulations, cultures and traditions in a chronological order i.e., from past to present.

→ Sources of History : 1. Archaeological sources. 2. Literary sources.

→ Rulers of Delhi Sultanate : Various Muslim dynasties that ruled in India.

→ Social, Political and Economic life
Social : The way that laws, government actions, events etc.

→ Political : With the leading officials, their interactions, any documents, laws, treaties etc.

→ Economic life : Specific to the financial implications of laws and events, how they affect trade, job availability and the flow of money.

→ Art and Architecture : Is defined as the art and science of designing building and structures.
(OR)
A combination of Arabic and Indian style of art and architecture developed during that period.

1. Dynasty : A line of hereditary rulers.

2. Proclaimed : Officially announced.

3. Couplets : Two lined verses of same rhyming and length.

4. Karkhanas : Workshops.

5. Shariat : Rule according to Islamic principles.

Students can go through AP Board 7th Class Social Notes 3rd Lesson Learning Through Maps to understand and remember the concept easily.

AP Board 7th Class Social Notes 3rd Lesson Learning Through Maps

→ Maps make our travel easier and accurate in guiding us towards the destination.

→ Vasco Da Gama reached Calicut in 1498 AD.

→ Magellan was the first person who voyaged across the Globe.

→ The Sailors and travellers had a great contribution in map – making.

→ The Sumerians, Babylonians used clay tablets as maps.

→ The Greek map makers Anaximander, Hacataeus, Herodotus prepared maps from arranging the places from West to East.

→ Gerardus Mercator introduced a method called projection that brought a great change in map making.

→ Scale, directions, symbols and colours are parts of a map.

→ Title of the map says about the theme or subject of the map.

→ Colours used in physical maps, thematic maps convey specific information.

→ Map makers use symbols to show their location in a map.

→ Maps are the key resources to know the details of a place.

→ Political map shows the administrative units, neighbouring countries, boundaries, capitals etc.

→ The map that shows the information about the physical features of a place like mountain ranges, hills, plateaus, plains, rivers, deserts, lakes, highlands etc. is called a physical map.

→ The imaginary lines that connect the places of equal heights are known as Contour lines.

→ Maps that are prepared for a special purpose or on theme are called thematic maps.

→ The map that shows historical details are known as Historical maps.

→ Index of a Map : A list of some kind of feature shown on the map, which either helps users to interpret the map, or to locate.

→ Types of Maps : Maps are classified based on the scale theme/content/ concepts and methods of preparation.
Ex:

1. Political map
2. Physical map.

→ Political Maps : Political map shows the administrative units, neighbouring countries, capitals etc.

→ Physical Maps : The map that shows the information about the physical features of a place like mountain ranges, hills, plateaus, plains, rivers, deserts, lakes, high lands etc. is called a physical map.

→ Thematic Maps : Maps that are prepared fora special purpose or on theme are called thematic maps.

→ Historical Maps : The map that shows historical details are known as Historical maps.

1. Spatial Information : Information with direct or indirect reference to a specific location.

2. Cartographer : A person who draws maps.

3. Edicts : Inscriotions; The official order or proclamation issused by a person in authority.

4. Toposheets : Maps that represent the natural and cultural features of a particular area.

5. Union Territories : An administrative unit of our country, governed by the central goverment.

6. Conventional Symbol : These are the small pictures that stand for different features on a map used by Survey of India.

7. Voyage : A long journey involving travel by sea or in space.

8. Drainage : The flow of water, particularly the river systems.

Students can go through AP Board 6th Class Maths Notes 1st Lesson మన చుట్టూ ఉండే సంఖ్యలు to understand and remember the concept easily.

AP Board 6th Class Maths Notes 1st Lesson మన చుట్టూ ఉండే సంఖ్యలు

→ శ్రీనివాస రామానుజన్ (22.12.1887 – 26.04.1920),
సంఖ్య సిద్ధాంతంలో భారతీయ మేధావి. ఫెలో ఆఫ్ రాయల్ సొసైటీ (ఇంగ్లాండ్) కు ఎన్నికైన మొదటి భారతీయుడు. 1729 రామానుజన్’ సంఖ్య, ప్రతి సంవత్సరం జాతీయ గణిత దినోత్సవం అతని పుట్టినరోజు (డిసెంబరు 22) న జరుపుకుంటారు.

→ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 లను అంకెలు అంటాం. ఈ 10 అంకెలను ఉపయోగించి అన్ని సంఖ్యలను రాస్తాము.

→ సంఖ్యలోని ప్రతి అంకె విలువ, అది సంఖ్యలోని స్థానంను బట్టి ఆధారపడి ఉంటుంది. కుడినుండి ఎడమకు జరిగిన అంకెస్థాన విలువ 10 రెట్లు పెరుగుతుంది.

→ స్థాన విలువల పట్టిక (లక్షల వరకు) :

→ సంఖ్యలను క్రమం అమర్చడం కూడా స్థాన విలువల ఆధారంగానే చేస్తాము. సంఖ్యలను ఆరోహణ క్రమం, అవరోహణ క్రమంలలో అమర్చుతారు.

→ ఆరోహణ క్రమం : సంఖ్యలను కనిష్ఠ సంఖ్య నుండి గరిష్ఠ సంఖ్యకు అమర్చడం.
ఉదాహరణ : 9, 576, 28, 106, 28, 116, 37, 596, 1,25,765

→ అవరోహణక్రమం : సంఖ్యలను గరిష్ఠ సంఖ్య నుండి కనిష్ఠ సంఖ్యకు అమర్చడం.
ఉదాహరణ : 1, 25, 765, 37, 596, 28, 116, 28, 106, 9,576

→ సంఖ్యామానం – పద్ధతులు :

• హిందూ సంఖ్యామానం
• అంతర్జాతీయ సంఖ్యామానం

పై రెండు పద్ధతులలోను సంఖ్యలను రాయడానికి 0, 1, 2, 3, 4, 5, 6, 7, 8 మరియు 9 అనే అంకెలనే ఉపయోగిస్తారు.

→ హిందూ సంఖ్యామానం-స్థాన విలువల పట్టిక :

1 కోటి = 10 పది లక్షలు
= 100 లక్షలు
1000 పదివేలు
= 10,000 వేలు
= 1,00,000 వందలు
= 10,00,000 పదులు
= 1,00,00,000 ఒకట్లు

→ అంతర్జాతీయ సంఖ్యామానం – స్థాన విలువల పట్టిక :

హిందూ సంఖ్యామానం = అంతర్జాతీయ సంఖ్యామానం

• 1 లక్ష = 100 వేలు
• 10 లక్షలు, = 1 మిలియన్
• 1 కోటి = 10 మిలియన్లు
• 10 కోట్లు = 100 మిలియన్లు
• 100 కోట్లు = 1 బిలియన్

→ ఒక సంఖ్యను ఒక స్థానానికి సవరించడం లేదా అంచనా వేయడం ఆ సంఖ్యలోని కుడివైపుగల అంకె పై ఆధారపడి ఉంటుంది. ఒక సంఖ్యను పదులకు సవరించుటకు :

• ఒకట్ల స్థానంలోని అంకె 5 కన్నా తక్కువైనచో ఒకట్ల స్థానాన్ని సున్నతో పూరించండి. మిగతా అంకెలను అలాగే ఉంచండి.
  ఉదా : 5,473 ను దగ్గరి పదులకు సవరించి 5,470గా రాస్తాము.
• ఒకట్ల స్థానంలోని అంకె 5 లేదా 5 కన్నా ఎక్కువైన పదులస్థానంలోని అంకెకు ‘1’ కలిపి ఒకట్ల స్థానంలో ‘0’ను రాయాలి.
  ఉదా : 5,637ను దగ్గరి పదులకు సవరించి 5, 640గా రాస్తాము.

→ ఒక సంఖ్యను వందలకు సవరించుటకు :
(i) పదుల స్థానంలోని అంకె 5 కన్నా తక్కువ అయినచో వందల స్థానంలోని అంకెను అలాగే ఉంచి, పదులు, ఒకట్ల స్థానంలోని అంకెల స్థానంలో ‘0’ను రాయాలి.
ఉదా : 64,329ని దగ్గరి వందలకు సవరించి 64,300గా రాస్తాము.

(ii) పదులస్థానంలో 5 గాని, 5 కన్నా ఎక్కువగాని ఉన్నచో వందలస్థానంలోని అంకెకు ‘1’ కలపాలి. పదులు, ఒకట్ల స్థానాలలో సున్నా రాయాలి.
ఉదా :

• 64,356ను దగ్గరి వందలకు సవరించి 64,400గా రాస్తాము.
• 64,365ను దగ్గరి వందలకు సవరించి 64,400 గా రాస్తాము.

→ చతుర్విద ప్రక్రియలైన సంకలనం (+), వ్యవకలనం (-), గుణకారం (×), భాగహారముల ఫలితాలను సవరించడం ద్వారా అంచనా వేయవచ్చును.

→ నీటి ప్రవాహాన్ని కొలవడానికి మనం క్యూసెక్ మరియు టి.యం. సిలను వాడతాం. ‘ క్యూసెక్ = క్యూబిక్ ఫీట్ పర్ సెకండ్
= 28.316 లీటర్ల ప్రవాహం సెకనుకు ఒక వెయ్యి మిలియన్ క్యూబిక్ ఫీట్ = 1 టి.యం.సి.
= 2831.6 కోట్ల లీటర్లు.

→ బరువులను కొలవడానికి సాధారణంగా గ్రాము, కిలోగ్రాము, క్వింటాల్ లను ఉపయోగిస్తాము.

• 1 గ్రాం = 1 గ్రా.
• 1 కిలోగ్రాం = 1000 గ్రా.
• 1 క్వింటాలు = 100 కి.గ్రా. = 1,00,000 గ్రా.
• 1 టన్ను = 1000 కి.గ్రా. = 10,00,000 గ్రా.
• 1 మెగాటన్ను = 1,00,00,00,000 కి.గ్రా. = 10,00,00,00,00,000 గ్రా.
• 1 గిగాటన్ను = 10,00,00,00,00,000 కి.గ్రా. = 1,00,00,00,00,00,00,000 గ్రా.

→ పొడవులను కొలచుటకు మనం మిల్లీమీటరు (మి.మీ.), సెంటీమీటరు (సెం.మీ.), మీటరు (మీ.) మొదలగు ప్రమాణాలను ఉపయోగిస్తాము.

• 10 మిల్లీమీటర్లు = 1 సెం.మీ.
• 100 సెంటీమీటర్లు = 1 మీటరు
• 1000 మీటర్లు = 1 కి.మీ.

→ క్రింది పట్టికను గమనించి ఖాళీలను సరియైన సంఖ్యలతో పూరించి, అక్షరాలలో రాయండి. (జి నెం. 2) సందర్భం సంఖ్య.

Students can go through AP Board 10th Class Maths Notes 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత to understand and remember the concept easily.

AP Board 10th Class Maths Notes 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత

→ ఆర్యభట్ట క్రీ.శ. 476 మార్చి 21

• ఆర్యభట్ట క్రీ.శ. 476 మార్చి 21 న పాటలీపుత్రంలో జన్మించాడు. ఆర్యభట్ట భారతీయ గణిత శాస్త్రజ్ఞులలో అతిప్రసిద్ధుడు. ఆర్యభట్టీయం గ్రంథ రచనతో ఇతడు ప్రసిద్ధికెక్కాడు.
• π = \(\frac{62832}{20000}\) = 3.1416 అని, అది ఎల్లప్పుడు స్థిరమని, అయితే ఆ π విలువ ఉజ్జాయింపు మాత్రమేనని చెప్పడం ద్వారా విలువను మొదటి నాలుగు దశాంశాల వరకు ఇవ్వడమే గాక, అది అకరణీయ సంఖ్యకాదు అని ప్రపంచానికి మొదటి సారిగా తెలియజేశాడు.
• ఇతడు ax + by = c (a, b, c లు పూర్ణసంఖ్యలు) వంటి సాధారణ సమీకరణాలను “పల్వరైజర్” అనే పద్ధతి ద్వారా సాధించాడు. ఆర్యభట్టకు ముందే మనకు గణితం ఉన్నప్పటికి, ఆ కాలం తర్వాత భారతీయ గణిత పునర్జీవనం ఆర్యభటతోనే ప్రారంభమైనదనవచ్చును. ఒక ప్రామాణిక గణిత గ్రంథ రచనకు ఆద్యుడు ఆర్యభట్ట.
• భారతదేశం ప్రయోగించిన మొదటి ఉపగ్రహానికి ఇతని పేరునే “ఆర్యభట్ట”గా నామకరణం చేశారు.

→* రెండు చరరాశులలో రేఖీయ సమీకరణం : రెండు చరరాశులతో కూడియున్న ప్రథమ పరిమాణ సమీకరణాన్ని రెండు చరరాశులలో రేఖీయ సమీకరణం అంటారు.
ఉదా : 5x + 7y = 3 సాధారణంగా ax + by + c = 0 రూపంలో ఉండి a, b,c లు వాస్తవ సంఖ్యలై a² + b² ≠ 0 అయ్యేటట్లు
ఉన్న సమీకరణాన్ని రెండు చరరాశులు x, y లలో రేఖీయ సమీకరణం అంటారు. (a² + b² ≠ 0, a, b ∈ R , కావాలంటే a, b లలో కనీసం ఒకటైనా సున్న కాకూడదు.)

→ రెండు చరరాశులలో రేఖీయ సమీకరణాల జత : a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + C₂ = 0. a₁, a₂, b₁, , b₂, c₁, c₂, లు వాస్తవ సంఖ్యలు మరియు a₁² + b₁² ≠ 0, a₂² + b₂² ≠ 0 రూపంలో గల రేఖీయ సమీకరణాల ద్వయాన్ని రెండు చరరాశులలో రేఖీయ సమీకరణాల జత అంటారు.

→ రేఖీయ సమీకరణాల జత సాధన : రెండు చరరాశులలోని, రేఖీయ సమీకరణాల జతను ఉమ్మడిగా తృప్తిపరచే x, y విలువలను రేఖీయ సమీకరణాల జతకు సాధన అంటారు.

ఉదా : x + 2y = 8 మరియు 3x – 4y = 4.
పై రెండు రేఖీయ సమీకరణాలు రెండు చరరాశులలో ఒక రేఖీయ సమీకరణాల జతను సూచిస్తాయి.

• x = 4, y = 2 విలువలు x + 2y = 8లో రాయగా 4 + 2(2)= 8 అలాగే, 3x – 4y = 4 లో రాయగా 3(4) – 4(2) = 12 – 8 = 4.
• x = 4, y = 2, రేఖీయ సమీకరణాల జతలోని రెండు సమీకరణాలను తృప్తి పరుస్తున్నాయి. కావున X = 4, y = 2.
• x + 2y = 8 మరియు 3x – 4y = 4 అనే రెండు చరరాశులలో రేఖీయ సమీకరణాల జతకు సాధన అవుతుంది.

→ రెండు చరరాశులలో రేఖీయ సమీకరణాల జత-రకాలు : రెండు చరరాశులలో రేఖీయ సమీకరణాల జతలు రెండు రకాలు.

1. సంగత రేఖీయ సమీకరణాలు
2. అసంగత రేఖీయ సమీకరణాలు

→ సంగత రేఖీయ సమీకరణాల జత : కనీసం ఒక సాధననైనా కలిగివున్న రేఖీయ సమీకరణాల జతను సంగత రేఖీయ సమీకరణాల జత అంటారు. సంగత సమీకరణాలు రెండు రకాలు : అవి :

1. పరస్పర స్వతంత్ర సమీకరణాల జత
2. పరస్పరాధారిత సమీకరణాల జత

→ పరస్పర స్వతంత్ర సమీకరణాల జత ఒకే ఒక సాధనను కలిగి ఉంటుంది. a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + c₂ = 0 లు పరస్పర స్వతంత్ర సమీకరణాల జత అయితే \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)

→ ‘పరస్పరాధారిత రేఖీయ సమీకరణాల జత అనంతమైన సాధనలు కలిగి ఉంటుంది. a₁x + b₁y + c₁ = 0 మరియు a₁x + b₁y + c₁ = 0 లు పరస్పరాధారితాలైతే ఆ \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\) పరస్పరాధారిత సమీకరణాలలో ఒక సమీకరణాన్ని ఒక స్థిరసంఖ్యతో గుణించడం వలన మరొకటి వస్తుంది.
ax + by + c = 0 మరియు kax + kby + kc = 0, k ≠ 0 లు పరస్పరాధారిత రేఖీయ సమీకరణాల జత అవుతుంది. పరస్పం ఖీ య సమీకరణాల జత ax + by + c = 0 మరియు k (ax + by + c) = 0 రూపంలో ఉంటుంది.

→ పరస్పర స్వతంత్ర సమీకరణాల జత రెండు ఖండన రేఖలను సూచిస్తే, పరస్పరాధారిత సమీకరణాల జత ఏకీభవించే రెండు రేఖలను సూచిస్తుంది.

→ అసంగత రేఖీయ సమీకరణాల జత : సాధన లేనటువంటి రేఖీయ సమీకరణాల జతను అసంగత రేఖీయ సమీకరణాల జత అంటారు. a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + c₂ = 0 లు ఒక అసంగత రేఖీయ సమీకరణాల జతను సూచిస్తే a
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
అసంగత రేఖీయ సమీకరణాల జత రెండు సమాంతర రేఖలను సూచిస్తుంది.
అసంగత రేఖీయ సమీకరణాల జత యొక్క సాధన సమితి శూన్యసమితి అవుతుంది.

→ రెండు చరరాశులలో రేఖీయ సమీకరణాల జత యొక్క సాధనను కనుగొనే పద్ధతులు :

1. జ్యా మితీయ పద్ధతి లేక గ్రాఫ్ పద్ధతి
2. బీజీయ పద్ధతులు
   • ప్రతిక్షేపణ పద్ధతి
   • చరరాశిని తొలగించు పద్ధతి
   • చరరాశిని పోల్చు పద్ధతి
   • సూత్రపద్ధతి (అడ్డ గుణకార పద్ధతి) మొదలగు పద్ధతులలో రేఖీయ సమీకరణాల జత యొక్క సాధనను కనుగొంటారు.

→ జ్యా మితీయ పద్ధతి (లేక) గ్రాఫ్ పద్ధతి : ax + by + C= 0 అనే రేఖీయ సమీకరణం జ్యా మితీయంగా ఒక సరళరేఖను సూచిస్తుంది. ఈ రేఖపై గల వాస్తవ సంఖ్యాక్రమయుగ్మాలు (x, y) అన్నీ రేఖీయ సమీకరణం యొక్క సాధనలు అవుతాయి.
a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + c₂ = 0 అనే సమీకరణాల జత, ఒక తలంలో రెండు సరళరేఖలను సూచిస్తుంది. ఈ రెండు సరళరేఖలపై ఉమ్మడిగా గల క్రమయుగ్మాలు (x, y) రేఖీయ సమీకరణాల జతకు సాధనలు అవుతాయి.
ఒక తలంలో రెండు సరళరేఖలు ఉంటే క్రింది మూడు సందర్భాలలో ఒకటి మాత్రమే సాధ్యము.

→ సందర్భం 1 – ఖండనరేఖలు :

రెండు చరరాశులలో రేఖీయ సమీకరణాల జత ఖండించుకొనే రేఖలను సూచిస్తుంది. ఈ రేఖల ఖండ బిందువు (x, y) రేఖీయ సమీకరణాల జతకు ఏకైక సాధన అవుతుంది. ఈ సందర్భంలో ు a₁x + by₁+c₁ మరియ a₂x + b₂y + c = 0 సంగత రేఖీయ సమీకరణాల జత అవుతుంది \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) అవుతుంది.

→ సందర్భం 2 – సమాంతర రేఖలు :

రెండు చరరాశులలో రేఖీయ సమీకరణాల జత ఒక సమాంతర రేఖల జతను సూచిస్తుంది. ఇటువంటి రేఖలకు . ఉమ్మడి బిందువులు ఉండవు. అనగా రేఖీయ సమీకరణాల జతకు సాధన ఉండదు. కావున రేఖీయ సమీకరణాల జత a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + c₂ = 0 -అసంగత రేఖీయ సమీకరణాల జత \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\) అవుతుంది.

→ సందర్భం 3 – ఏకీభవించే రేఖలు :

రెండు చరరాశులలో రేఖీయ సమీకరణాల జత ఏకీభవించే రెండు రేఖలను సూచిస్తుంది. ఈ సందర్భంలో సరళరేఖపై గల ప్రతి బిందువు రేఖీయ సమీకరణాల జతకు సాధన అవుతుంది. అనగా రేఖీయ సమీకరణాల జతకు అనంతమైన సాధనలు ఉంటాయి. a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + c₂ = 0లు సంగత రేఖీయ సమీకరణాల జతను సూచిస్తాయి. మరియు పరస్పరాధారిత రేఖీయ సమీకరణాల జత అవుతుంది. \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) అవుతుంది.
L₁ = ax + by + c = 0 అయి L₁, L₂లు పరస్పరాధారిత రేఖీయ సమీకరణాల జత అయితే L₂ = KL₁అవుతుంది. K ∈ R
∴ L₂ = k (ax + by + c) = 0.

→ గ్రాఫ్ పద్ధతిలో రెండు చరరాశులలో రేఖీయ సమీకరణాలను సాధించే సోపాన క్రమము :
L₁ = a₁x + b₁y + c₁ = 0 మరియు L₂ = a₂x + b₂y + c₂ = 0 రేఖీయ సమీకరణాల జత అయితే.

→ సోపానం 1 : y ని X పదాలలో రాయాలి.
y = \(\frac{-\left(a_{1} x+c_{1}\right)}{b_{1}}\)
y = \(\frac{-\left(a_{2} x+c_{2}\right)}{b_{2}}\)

సోపానం 2 : x యొక్క కనీసం రెండు విలువలకు సోపానం 1 నుండి y యొక్క విలువను రెండు సమీకరణాలకు . వేర్వేరుగా లెక్కించి ప్రతి రేఖ యొక్క క్రమయుగ్మాలు (x,y) రాయాలి.

సోపానం 3 : 2వ సోపానంలో పొందిన బిందువులను గ్రాఫ్ పై గుర్తించి రెండు సరళరేఖలు L₁, మరియు L₂ లను గీయాలి.

సోపానం 4 :

• సోపానం 3లోని సరళరేఖలు L₁ మరియు L₂లు ఖండన రేఖలు అయి ఖండన బిందువు (α, β) అయితే (x = α) అయితే మరియు (y = β)ను సాధనగా రాయాలి.
• L₁, L₂ రేఖలు సమాంతరాలైతే ఉమ్మడిబిందువులు ఉండవు కావున సాధన లేదని గుర్తించాలి.
• L₁, L₂ లు ఏకీభవించే రేఖలైతే రేఖ పై గల ప్రతి బిందువు సాధన అవుతుంది. అనంత సాధనలు కలిగి ఉంటాయని గుర్తించాలి.

గమనిక : సరళరేఖ గీయడానికి మూడు బిందువులను కనుగొనడం ఒక ఉత్తమ పద్ధతి.

→ బీజీయ పద్దతులు : a) ప్రతిక్షేపణ పద్దతి : రెండు చరరాశులలో రేఖీయ సమీకరణాల జతలోని ఒక సమీకరణంలోని ఒక చరరాశిని మరొక చరరాశి పదాలలో రాసి, తద్వారా రెండవ సమీకరణాన్ని ఉపయోగించి సాధనను కనుగొంటాము.

ఈ విధానంలోని సోపానాలక్రమం :

• సోపానం 1 : ఒక సమీకరణంలో ఒక చరరాశిని వేరొక చరరాశి పదాలలో రాయాలి. అనగా ‘ ని x పదాలలో లేదా x ని y పదాలలో రాయాలి.
• సోపానం 2 : సోపానం 1లో వచ్చిన చరరాశి లేదా x విలువను రెండవ సమీకరణంలో ప్రతిక్షేపించాలి.
• సోపానం 3 : సోపానం 2లో వచ్చిన సమీకరణాన్ని సూక్ష్మీకరించి x లేదా y విలువను కనుగొనాలి.
• సోపానం 4 : సోపానం 3లో వచ్చిన x లేదా y విలువలను ఇచ్చిన ఏదో ఒక సమీకరణంలో ప్రతిక్షేపించి y లేదా x ను సాధించాలి.
• సోపానం 5 : వచ్చిన సాధన x, y విలువలు రెండవ సమీకరణంలో ప్రతిక్షేపించి సరిచూసుకోవాలి.

ఉదాహరణ : x + 2y – 7 = 0, 4x – 3y – 6 = 0 రేఖీయ సమీకరణాల జతను ప్రతిక్షేపణ పద్ధతిలో సాధిద్దాము.
సాధన : x + 2y – 7 = 0. ………………. (1)
4x – 3y- 6 = 0 ……………… (2)
(1) నుండి x = 7-2y (సోపానం 1)
x = 7 – 2yని (2) లో ప్రతిక్షేపించగా
4(7- 2y) – 3y- 6 = 0 (సోపానం 2)
28 – 8y – 3y – 6 = 0
22 – 11y = 0
-11y = -22
11y = 22,

y= 2 ను (2) లో ప్రతిక్షేపించగా

4x – 3 (2) – 6 = 0
4x – 6 – 6 = 0
4x – 12 = 0
4x = 12

సాధన : x = 3, y = 2
సరిచూడటం :
x = 3, y = 2 ను (1) లో రా యగా
3 + 2(2) – 7 = 0
3 + 4 -7 = 0
7 – 7 = 0
0 = 0 (సోపానం 5)
∴ సాధన X= 3, y = 2 (1) ని సంతృప్తిపరుస్తున్నది.

(b) చరరాశిని తొలగించు పద్ధతి :
రెండు చరరాశులలో రేఖీయ సమీకరణాల జతలోని రెండు సమీకరణాలలోను ఒక చరరాశి గుణకాలను సమానం చేయడం ద్వారా ఆ చరరాశిని తొలగిస్తాము. దీని వలన ఏక చరరాశిలో ఒకే రేఖీయ సమీకరణం ఏర్పడుతుంది. దీనిని సాధించడం ద్వారా రెండవ చరరాశి వస్తుంది. ఈ చరరాశి సహాయంతో మొదట తొలగించిన చరరాశిని కనుగొంటాము.

గమనిక : సాధారణంగా రెండు సమీకరణాలలోను తొలగించాల్సిన చరరాశి యొక్క గుణకాలను, గుణకాల యొక్క క.సా.గు.కు సమానం అయ్యేటట్లు పెంచుతాము. ఈ పద్ధతి మోడల్ పద్ధతిని పోలి ఉంటుంది.

ఈ విధానంలో సోపాన క్రమం :

• సోపానం 1 : ఇచ్చిన రేఖీయ సమీకరణాలను
  a₁x + b₁y = c₁
  a₂x + b₂y = c₂, గా రా యాలి.
• సోపానం 2 : రెండు సమీకరణాలను సరియగు వాస్తవసంఖ్యతో గుణించి తొలగించాల్సిన చరరాశి గుణకాలను వాని క.సా.గుకు సమానం చేయాలి.
• సోపానం 3 : 2వ సోపానంలోని రెండు సమీకరణాలలోని తొలగించాల్సిన చరరాశి గుణకాలు ఒకే గుర్తును కలిగి ఉంటే ‘ఒక సమీకరణం నుండి మరొక సమీకరణాన్ని తీసివేయడం ద్వారా మనకు ఏక చరరాశి రేఖీయ సమీకరణం వస్తుంది. అదే గుణకాలకు వ్యతిరేక గుర్తులు ఉంటే కూడాలి.
• సోపానం 4 : సోపానం 3 లోని ఏక చరరాశి రేఖీయ సమీకరణాన్ని సాధించి చరరాశి విలువను రాబట్టాలి.
• సోపానం 5 : సోపానం 4లో వచ్చిన చరరాశి. సహాయంతో ఇచ్చిన ఏదో ఒక సమీకరణంలో ప్రతిక్షేపించి 3వ సోపానంలో తొలగించిన చరరాశిని రాబట్టాలి.
• సోపానం 6 : చరరాశి విలువలను రెండవ సమీకరణాలలో ప్రతిక్షేపించి సరిచూసుకోవాలి.

ఉదాహరణ : x + 2y – 7 = 0, 4x – 3y — 6 = 0
లను చరరాశి తొలగింపు పద్ధతిలో సాధిద్దాము.
సాధన : x + 2y = 1 …………… (1)
4x – 3y = 6 …………… (2)
రెండు సమికరణాల నుండి y ని తొలగిద్దాము y గుణకాలు 2, 3 ల క.సా.గు 6. . . . .

X = 3ను (1) లో ప్రతిక్షేపించగా –
3 + 2y = 7
2y = 7 – 3 ⇒ 2y = 4
y = \(\frac{4}{2}\) = 2
సాధన X = 3, V = 2. . (సోపానం 5)

సరిచూడటం :
x = 3, y = 2ను (2) లో ప్రతిక్షేపించగా
4(3) – 3 (2) = 6
12 – 6 = 6
6 = 6
∴ సాధన x = 3, y = 2 (2)వ సమీకరణాన్ని సంతృప్తి పరుస్తున్నది.

గమనిక : సోపానం 2, సోపానం 3 లను సోపానం 4 (సోపానం 1) లోని కనుగొన్న చరరాశి తర్వాత కనుగొనాల్సిన మరొక రెండు సమీకరణాల నుండి ని తొలగిద్దాము. చరరాశికి కూడా పునరావృతం చేసి రెండవ చరరాశిని కనుగొనవచ్చును. ఇది సోపానం 5 అవుతుంది.

ఉదాహరణ : పై ఉదాహరణలో 4వ సోపానంలో x = 3 కనుగొన్న తర్వాత y కోసం క్రింది విధంగా కూడా ప్రయత్నించవచ్చును.

∴ సాధన x = 3, y = 2.

* c) చరరాశిని పోల్చు పద్దతి : రెండు చరరాశులలో రేఖీయ సమీకరణాల జతలో రెండు సమీకరణాలోని ఒక చరరాశిని మరొక చరరాశి పదాలలో రాశి పోల్చడం ద్వారా సాధిస్తాము.
సాధన సోపాన క్రమము .
a₁x + b₁y + c₁ = o …………..(1)
a₂x + b₂y + c₂ = 0 ………….. (2)

సోపానం 1 : ఇచ్చిన సమీకరణాల నుండి
(1) ⇒ y = \(\frac{-\left(a_{1} x+c_{1}\right)}{b_{1}}\)
(2) ⇒ y = \(\frac{\left(a_{2} x+c_{2}\right)}{b_{2}}\) గా రాయాలి
సోపానం 2 : సోపానం 1 లోని y విలువలను సమానం చేసి Xలో ఏక చరరాశి సమీకరణాన్ని రాబట్టాలి.
సోపానం 3 : సోపానం 2లోని ఏక చరరాశి సమీకరణాల నుండి X విలువను కనుగొనాలి.
సోపానం 4: X విలువ సహాయంతో (1) వ సోపానంలోని ఏదేని సమీకరణం నుండి y విలువను కనుగొనాలి. సోపానం 5 : సాధనను సరిచూసుకోవాలి.
ఉదాహరణ : x + 2y – 7 = 0, 4x – 3y – 6 = 0 లను చరరాశి పోల్చు పద్ధతిలో సాధిద్దాము.

సాధన : x + 2y-7 = 0. ………… (1)
4x – 3y – 6 = 0 …………(2)
(1) ⇒ 2y = 7 – x
y = \(\frac{7-x}{2}\) …………(3)
(2) ⇒ 3y = 6 – 4x
3y = 4x – 6
x = \(\frac{4 x-6}{3}\)………. (4) (1వ సోపానం)
(3) మరియు (4) ల నుండి
3 (7 – x) = 2 (4x – 6)
21 – 3x = 8x – 12 (2వ సోపానం)
11x = 33
x = \(\frac{33}{11}\) = 3 (3వ సోపానం)
3 ను (3) లో రాయగా
\(\frac{7-3}{2} \quad \frac{4}{2}\) = 2 (4వ సోపానం) .
సాధన x = 3 , y = 2
సరిచూడటం ఇంతకు మునుపు పద్ధతులలో లాగానే ‘ చేయాలి. (5వ సోపానం)

(d) సూత్ర పద్ధతి (అడ్డగుణకార పద్ధతి)
a₁x + b₁y + c₁ = 0 మరియు a₂x + b₂y + c₂ = 0 లు రెండు రేఖీయ సమీకరణాలు అయితే
x = \(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)
y = \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)
a₁b₂ – a₂b₁ # 0 అనే సూత్రాన్ని ఉపయోగించి సాధనను కనుగొంటాము.
(లేదా )
x, y గుణాకాలను కింది విధంగా రాసుకొని అడ్డ గుణాకార పద్ధతిలో సాధిస్తాము

దీని నుండి సూక్ష్మీకరిస్తే పై సూత్రాలు వస్తాయి

ఉదాహరణ : x + 2y – 7 = 0
4x – 3y – 6 = 0
సమీకరణాల జతను సూత్ర పద్ధతిలో సాధిద్దాము

సాధన : a, = 1, b, = 2, c = -7
a = 4, b) = -3, c, = -6

\(\frac{y}{-22}=\frac{1}{-11} \Rightarrow y=\frac{-22}{-11}\) = 2
సాధన x = 3, y = 2.

→ రెండు చరరాశులలో రేఖీయ సమీకరణాల జతలుగా మార్చగలిగే సమీకరణాల సాధన :
a₁x +b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 రూపంలో లేని కొన్ని సమీకరణాల జతలను కొన్ని ప్రత్యేక ప్రతిక్షేపణలు లేదా సూక్ష్మీకరణాల ద్వారా వాటిని రేఖీయ సమీకరణాలుగా మార్చి సాధించవచ్చును.

ఉదా : \(\frac{3}{x}-\frac{1}{y}\) = -9 మరియు \(\frac{2}{x}+\frac{3}{y}\) =5
\(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v గా తీసుకొని పై సమీకరణాలలో రాయగా,. పై సమీకరణాలు 3u – v = -9 మరియు 2u + 3v = 5 అనే u, v లలో రేఖీయ సమీకరణాల జతలుగా మారుతాయి.

ఉదా : \(\frac{x+y}{x y}\) = 2 మరియు \(\frac{x-y}{x y}\) = 6 లను సాధిద్దాము.
సాధన. \(\frac{x}{x y}+\frac{-y}{x y}\) = 2 మరియు \(\frac{x}{x y}-\frac{-y}{x y}\) = 6 గా రాసి సూక్ష్మీకరిస్తాము.

అపుడు \(\frac{1}{y}+\frac{1}{x}\) = 2 మరియు\(\frac{1}{y}-\frac{1}{x}\) – 6
\(\frac{1}{y}\) =u, \(\frac{1}{x}\) = v అనుకొందాం. అపుడు u + v = 2 మరియు u – V = 6 అనే u, v లలో రేఖీయ సమీకరణాల జతగా మారుతాయి.

Students can go through AP Board 10th Class Maths Notes 3rd Lesson బహుపదులు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 3rd Lesson బహుపదులు

→ పావులూరి మల్లన 11వ శతాబ్దం :

• పావులూరి మల్లన ప్రముఖ గణిత శాస్త్రజ్ఞుడు. ఇతడు 11వ శతాబ్దానికి చెందిన తూర్పు .
• చాళుక్యరాజైన రాజరాజనరేంద్రుని ఆస్థాన పండితుడు. ఇతను నన్నయ భట్టుకు సమకాలికుడు.
• పావులూరి మల్లన మహావీరాచార్యునిచే రచింపబడిన ‘గణితసార సంగ్రహం’ అనే ఆ సంస్కృత భాషలోని గణితగ్రంథాన్ని స్వతంత్ర అనువాద పద్దతిలో తెలుగు భాషలోకి అనువదించాడు. దీని పేరు “సారసంగ్రహ గణితం”. చాలా సరళమైన శైలిలోని ఈ గణిత గ్రంథము ఒక పద్యకావ్యంలా ఉంటుంది. ఆ కాలం ఆ మూల గంథమైన ‘గణిత సారసంగ్రహం ‘లో పరికర్మ, భిన్న, ప్రకీర్ల, తైరాశిక, మిత్ర క్షేత్ర, ఖాత, ఛాయవ్యవహారములు అని 8 ప్రకరణాలుగా ఉంటే మల్లన మిశ్ర గణితాన్ని సూత్ర గణితం, సువర్ణ గణితం అని రెండు భాగాలుగా చేశాడు.
• మూలములోని గణిత విధానములను మాత్రమే తీసుకొని సమస్యలు, ఉదాహరణలు, తనదైన పద్ధతిలో స్వతంత్రముగా ఇచ్చాడు. భిన్నాంకముల సమస్యలలో ‘ఇష్టకర్మము’ , అనే గణిత వ్యవహారంలో కూడా మల్లన అనేకమైన ఉదాహరణలు ఇచ్చాడు.
• సార సంగ్రహ గణితం’ గ్రంధాన్ని పాటి గణితం, క్షేత్ర గణితం మరియు బీజ గణితం – అనే మూడు విభాగాలుగా వ్రాశాడు. పావులూరి గణితంగా ప్రసిద్ది చెందిన “సార సంగ్రహగణితం” తొలి తెలుగు గ్రంథం. తొలి తెలుగు గణిత గ్రంథం వ్రాసిన ఘనత – పావులూరి మల్లనకు దక్కింది.

→ బహుపది . చరరాశుల యొక్క ఘాతాంకాలు రుణేతర పూర్ణసంఖ్యలుగా గల బీజీయ సమాసాలను ‘బహుపదులు అంటారు.

ఉదా :

• 3x + 9
• 4x²y + 3xy² – 7xy + 7
• x³ – √3 x² + 7x – 9

→ బహుపది పరిమాణం : బహుపది వివిధ పరిమాణాలలో గరిష్ఠ పరిమాణమే బహుపది పరిమాణము.
ఉదా : p(x) = 7x⁴ – 3×3 + 5×2 + 9x + 3 యొక్క పరిమాణం :  4
ply) = 9×3 – 7×5 – 8 + 7×2 – Q యొక్క పరినూణం : 5

సూచన : p(x) ఒక బహుపది అయిన X యొక్క గరిష్ఠ ఘాతాంకము p(x) యొక్క పరిమాణం అవుతుంది.

→ n వ పరిమాణ బహుపది యొక్క సాధారణ రూపం :
p(x) = a₀xⁿ + a₁ x^n-1 + a₂ x^n-2 + …. + a_n-1 x + a_n. ఇక్కడ a₀, a₁, a₂, . . a_n-1, a లు వాస్తవ సంఖ్యలు మరియు a₀ ≠ 0.

• స్థిర బహుపది : ‘సున్న’ పరిమాణంగా గల బహుపది
  ఉదా : p(x) = 8
  p(y) = – 4 .
• రేఖీయ బహుపది : పరిమాణం ‘1’ గా గల బహుపది
  ఉదా : p(x) = 5x – 4
  p(x) = 9z + 27 .
• వర్గ బహుపది : పరిమాణం ‘2’ గా గల బహుపది
  ఉదా : p(x) = x² + 5x + 6 .
  p(y) = 4y² – 12y + 9
• ఘన బహుపది : పరిమాణం ‘3’ గా గల బహుపది
  ఉదా : p(x) = 8x³ – 4x² + 9x + 8
  p(y) = y³ + 8y² – 3y + 4

సూచన : బహుపది యొక్క పరిమాణం ఆ బహుపదిలోని పదాలకన్నా 1 తక్కువ p(x) లో n పదాలు ఉంటే p(x) యొక్క పరిమాణం : n – 1.

→ బహుపది విలువ : బహుపది p(x) లోని చరరాశి x కు k ను ప్రతిక్షేపించగా వచ్చే విలువను x = k వద్ద p(x) యొక్క బహుపది విలువ అంటారు. దీనిని p(k) తో సూచిస్తారు.
ఉదా : p(x) = x² – 5x + 6
x = 1 వద్ద p(x) విలువ
p(1) = (1)² 5 (1) + 6
= 1 – 5 + 6 = 2
x = 1 వద్ద p(x) విలువ p(1) = 2

→ బహుపది శూన్య విలువ : బహుపది p(x) లోని చరరాశి x యొక్క ఏ విలువకు p(x) బహుపది విలువ శూన్యం (‘0’) అవుతుందో. x యొక్క ఆ విలువను బహుపది p(x) శూన్య విలువ అంటారు
ఉదా :

(1) p(x) = 5x – 10
x = 2 అయిన p(2) = 5(2)
10 = 10
10 = 0
p(2) = 0
కావున p(x) = 5x
10 యొక్క శూన్య విలువ ‘2’ అవుతుండ

(2) p(x) = x² – 3x + 2
x = 3 అయిన
p(3) = (3)² – 3(3) + 2 = 2
p(3) = 2
p(3) ≠ 0 కావున p(x) కు 3 శూన్య విలువ కాదు.

(1) రేఖీయ బహుపది p(x) = ax + b ఒకే ఒక శూన్య విలువ x =-b/a ను కలిగి ఉంటుంది.

(2) (i) వర్గ బహుపది p(x) = ax² + bx + c గరిష్ఠంగా రెండు శూన్య విలువలను కలిగి ఉంటుంది.
(ii) p(x) = ax² + bx + c వర్ణ బహుపది కావున

• D = b² – 4ac > 0 అయిన రెండు శూన్య విలువలు (α ≠ β), α, β ∈ R ను కలిగి ఉంటుంది.
• D = b² – 4ac = 0 అయిన ఒకే ఒక శూన్య విలువ (α = β), α ∈ R ను కలిగి ఉంటుంది.
• D = b² – 4ac < 0 అయినప్పుడు p(x) కు వాస్తవ శూన్య విలువలు ఉండవు.

(iii) వర్గ బహుపది p(x) యొక్క శూన్య విలువలు

• D = b² – 4ac > 0 అయినప్పుడు α ≠ β
  α = \(\frac{-b+\sqrt{D}}{2 a}\) మరియు β = \(\frac{-b-\sqrt{D}}{2 a}\)
• D = b² – 4ac = 0 అయినప్పుడు α = β
  α = \(\frac{-b}{2 a}\)

(3) ఘన బహుపది p(x) = ax³ + bx² + cx + d గరిష్ఠంగా 3 శూన్య విలువలను కలిగి ఉంటుంది.

(4) 1వ పరిమాణ బహుపది గరిష్ఠంగా n శూన్య విలువలను కలిగి ఉంటుంది.

→ బహుపదులను రేఖీయ చిత్రాలుగా చూపడం :

• రేఖీయ బహుపది p(x) = ax + bని జ్యా మితీయంగా చిత్రించినపుడు ‘వచ్చే గ్రాఫ్ ఒక సరళరేఖను సూచిస్తుంది.
  y = p(x) = ax + b, a ≠ 0 గ్రాఫ్ సూచించే సరళరేఖ
  X – అక్షాన్ని ఒకే ఒక బిందువు ( \(\frac{-b}{a}\), 0) వద్ద ఖండిస్తుంది. ఈ ఖండన బిందువులోని X – నిరూపకం \(\frac{-b}{a}\), p(x) = ax + b యొక్క శూన్య విలువ అవుతుంది.
• వర్గ బహుపది y = p(x) = ax² + bx + c రేఖీయ చిత్రం ఒక పరావలయాన్ని సూచిస్తుంది. p(x) లో x² గుణకం a > 0 అయిన పరావలయం పైవైపు వివృతంగాను a < 0 అయిన క్రిందివైపు వివృతంగాను ( ) ఉంటుంది. ఈ రెండు రకాల పరావలయాలు X – అక్షాన్ని గరిష్ఠంగా రెండు బిందువుల వద్ద ఖండిస్తాయి. ఈ రెండు బిందువులలోని X – నిరూపకాలే p(x) యొక్క శూన్య విలువలు అవుతాయి.

సూచన :
p(x) = ax² + bx + c, X- అక్షాన్ని (\(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\), 0) మరియు (\(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\), o) అనే బిందువుల వద్ద ఖండిస్తుంది.

→ ఘన బహుపది : ఘన బహుపది p(x) = ax³ + bx² + cx + d రేఖాచిత్రం X – అక్షాన్ని గరిష్టంగా మూడు బిందువుల వద్ద ఖండిస్తుంది. ఈ మూడు బిందువులలోని X- నిరూపకాలు p(x) యొక్క శూన్య విలువలు అవుతాయి.

→ ఘన బహుపది రేఖాచిత్రము – వివిధ సందర్భాలలో : p(x) = ax³ + bx² + cx + d:

→ బహుపదుల భాగహార అల్ గారిథమ్ (బహుపదుల భాగహార నియమం) : p(x) మరియు g(x) లు రెండు బహుపదులు, g(x) = 0 అయిన p(x) = g(x) × q(x) + r(x) అయ్యేటట్లు q(x) మరియు r(x) అనే బహుపదులను కనుగొనవచ్చును. ఈ ఫలితాన్నే ‘బహుపదుల భాగహార అల్గారిథమ్’ అంటారు. ఇక్కడ r(x) = 0 లేదా r(x) పరిమాణం < g(x) పరిమాణం .

పై నియమం నుండి మనం క్రింది విషయాలు తెలుసుకొనవచ్చును.

• g(x) రేఖీయ బహుపది అయితే r(x) = స్థిరాంకము.
• q(x) పరిమాణం 1 అయిన p(x) పరిమాణం = 1 + g(x) పరిమాణం.
• q{x} పరిమాణం n అయిన p(x) పరిమాణం = n + g(x) పరిమాణం
• p(x) ను X – a చే భాగించగా వచ్చే శేషము p(a) అవుతుంది.
• శేషము r = 0 అయితే p(x) కు g(x) కారణాంకము అవుతుంది.
  అనగా p(x) = g(x) × q(x) అవుతుంది.

Students can go through AP Board 10th Class Maths Notes 12th Lesson త్రికోణమితి అనువర్తనాలు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 12th Lesson త్రికోణమితి అనువర్తనాలు

→ వరాహమిహిరుడు (505 – 587)

• మిహిరుడని కూడా పిలవబడే వరాహమిహిరుడు ఉజ్జయినిలో జన్మించిన ఖగోళ శాస్త్రజ్ఞుడు, గణిత మేధావి.
• ఆర్యభట్ట, వరాహమిహిరుల చిత్రపటాలు భారత పార్లమెంటు భవనంలో ఉన్నాయి.
• వరాహమిహిరుడు విక్రమాదిత్య చక్రవర్తి ఆస్థానంలో ఉన్న నవరత్నాలలో ఒకడు.
• 0′ వరాహమిహిరుడు పాస్కల్ త్రిభుజాన్ని కనుక్కొన్నాడు. మాయా చదరాల మీద కృషి చేశాడు. “పంచ సిద్ధాంతిక” (క్రీ.శ. 575) అనే గ్రంథం ఇతని ప్రముఖ రచన.

→ సర్వేయర్లు చాలా వందల యేండ్ల నుండియే త్రికోణమితిని వాడుతూ ఉన్నారు. వారు సర్వే చేసే ప్రక్రియలో ఊర్థ్వకోణం, నిమ్నకోణాలను కనుక్కోవడానికి “థియోడలైట్” అనే పరికరాన్ని వాడతారు. 19వ శతాబ్దంలో “గ్రేట్ ట్రిగనా మెట్రిక్ సర్వే” పేరుతో బ్రిటిష్ ఇండియా భారతదేశంలో సర్వే చేయడానికి రెండు పెద్ద “థియోడలైట్”లను తయారు చేయించింది. ఆ సర్వే జరుగుతుండగా, 1852లో ప్రపంచంలోనే ఒక అతి, పెద్ద పర్వత శిఖరాన్ని భారతదేశంలో కనుగొన్నారు. 160 కి.మీ. దూరం నుండి చుట్టూ ఉన్న ఆరు విభిన్న కూడళ్ల నుండి పరిశీలించి పర్వతం యొక్క ఎత్తును కనుగొన్నారు. 1856లో ఆ సర్వే చేసిన అధికారియైన “సర్ జార్జ్ ఎవరెస్ట్” గౌరవార్థం ఆ శిఖరానికి అతని పేరు పెట్టడం జరిగింది. మొట్టమొదటగా అతడు ఉపయోగించిన ఆ థియోడలైట్లను డెహ్రాడూన్లోని “సర్వే ఆఫ్ ఇండియా మ్యూజియం’లో సందర్శనార్థం పెట్టారు.

→ ఒక వస్తువు యొక్క ఎత్తును గాని, పొడవును గాని కనుగొనడానికి, రెండు వస్తువుల మధ్య దూరాన్ని లెక్కించుటకు త్రికోణమితీయ నిష్పత్తులను వాడుతూ ఉంటాం.

→ త్రికోణమితిని ఉపయోగించేందుకు క్రింది పదములపై అవగాహన అవసరము.

→ ఆ పదములు దృష్టిరేఖ, క్షితిజ సమాంతర రేఖ, ఊర్థ్వకోణము మరియు నిమ్నకోణములు.

→ క్షితిజ సమాంతర రేఖ : పరిశీలన ‘బిందువు నుండి వస్తువుకు సమాంతరంగా ఉండు రేఖ.

→ దృష్టిరేఖ : పరిశీలకుని కంటి నుండి వస్తువుకి గీయబడిన దృష్టి యొక్క రేఖను “దృష్టిరేఖ” అంటారు.
(లేదా)
ఒక వస్తువుపై ఒక బిందువు నుండి పరిశీలకుని కంటిని కలిపే సరళరేఖ.

→ ఊర్ద్వకోణము : క్షితిజ సమాంతర రేఖకు, దృష్టిరేఖ పైన ఉన్నప్పుడు వాటి మధ్య ఏర్పడే కోణాన్ని “ఊర్ధ్వకోణము” అంటారు. ఈ సందర్భంలో పరిశీలకుడి తల పైకెత్తబడుతుంది.

→ నిమ్నకోణము : క్షితిజ సమాంతర రేఖకు, దృష్టిరేఖ ‘క్రింద ఉన్నప్పుడు వాటి మధ్య ఏర్పడే కోణాన్ని “నిమ్నకోణం” అంటారు. ఈ సందర్భంలో పరిశీలకుడి తల క్రింది వైపుకు చూస్తుంది.

→ గుర్తుంచుకోవలసినవి :
I. లంబకోణ త్రిభుజములో త్రికోణమితీయ నిష్పత్తులు :

II. కొన్ని త్రికోణమితీయ నిష్పత్తుల విలువలు :

→ సమస్యల సాధన పద్ధతులు : ఎత్తులు మరియు దూరాలకు సంబంధించిన సమస్యలు సాధించడానికి కింది విషయాలను దృష్టిలో పెట్టుకోవాలి.

• గణితపరంగా సౌలభ్యం కొరకు టవర్లు, చెట్లు, భవనాలు, ఓడలు, పర్వతాలు మొ||లగు వాటిని రేఖీయంగానే పరిగణనలోనికి తీసుకోవాలి.
• ఊర్థ్వకోణం లేదా నిమ్నకోణాన్ని క్షితిజ సమాంతరరేఖ ఆధారంగానే తీసుకోవాలి.
• సమస్యలో పరిశీలిస్తున్న వ్యక్తి ఎత్తు ఇవ్వనట్లైతే, అతడి ఎత్తును లెక్కించకుండానే సమస్యను సాధించాలి.
• ఊర్థ్వ, నిమ్న కోణాలతో ఆ సాధన సందర్భాలను జ్యామితీయంగా ఊహించాల్సి ఉంటుంది.
• సమస్యలను సాధించడానికి వాటికి సంబంధించిన పటాలను గీయడం చాలా ముఖ్యము. వాటి ఆధారంగా సమస్యలను సులభంగా సాధించవచ్చు.