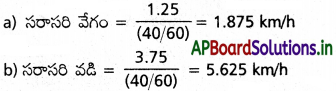Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 3rd Lesson సరళరేఖాత్మక గమనం Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 3rd Lesson సరళరేఖాత్మక గమనం
అతిస్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
గమన, నిశ్చల స్థితులు సాపేక్షం వివరించండి.
జవాబు:
నిశ్చల స్థితి మరియు గమనస్థితి సాపేక్షం.
ఉదా : ఒక నిర్ధేశకం పరంగా వస్తువు నిశ్చల స్థితిలోగాని లేదా గమనంలోగాని ఉండవచ్చు. గమనంలో ఉన్న ఒక రైలులో ఒకవ్యక్తి తన సహప్రయాణికుని పరంగా నిశ్చల స్థితిలో, భూమిపై గల వ్యక్తి పరంగా గమనంలో ఉంటాడు.
ప్రశ్న 2.
సగటు వేగం ఏవిధంగా తత్కాల వేగంతో విభేదిస్తుంది? [Mar. ’13]
జవాబు:
సగటు వేగం చలించే కణం యొక్క ఫలిత గమనాన్ని తెల్పును.
తత్కాల వేగం, ఏదైనా నిర్దిష్ట సమయం వద్ద కణం వేగంను కూడా తెల్పును. ఏకరీతి చలనంలో తత్కాల వేగం, సగటు వేగం రెండు సమానమవుతాయి.
ప్రశ్న 3.
ఒక వస్తువు వేగం శూన్యమై దాని త్వరణం శూన్యం కాని సందర్భానికి ఒక ఉదాహరణ ఇవ్వండి. [Mar. ’13]
జవాబు:
నిట్టనిలువుగా పైకి విసిరిన వస్తువు, గరిష్ట ఎత్తు వద్ద సున్నా వేగం కల్గి, త్వరణం (a) సున్నాకాదు (i.e a = g)
ప్రశ్న 4.
ఒక వాహనం ప్రయాణించిన దూరం L లో సగం దూరం వడి υ1, తోనూ, రెండవ సగం దూరం వడి v2 తోనూ ప్రయాణించింది. ఆ వాహనం సగటు వడి ఎంత?
జవాబు:

ప్రశ్న 5.
కింది దిశలో ప్రయాణిస్తూ ఒక లిఫ్టు భూ అంతస్తు (ground floor) కు చేరబోతున్నది. భూ అంతస్తును మూల బిందువుగానూ, ఊర్ధ్వ దిశను ధన దిశగానూ అన్ని రాశులకూ ఎంపిక చేసుకొంటే కింది ఇచ్చిన వాటిలో ఏది సరియైనది?
a) x < 0, v < 0, a > 0,
c) x > 0, v < 0, a > 0,
b) x > 0, v < 0, a < 0, d) x > 0, V > 0, a > 0
జవాబు:
లిఫ్ట్, గ్రౌండ్ ఫ్లోర్ (మూలబిందువు) వైపు చలిస్తూ ఉన్నప్పుడు, దానిస్థానం X తగ్గును, వేగం తగ్గును, కావున x < 0, v <0 కాని a > 0 కావున (a) సరియైన సమాధానము.

ప్రశ్న 6.
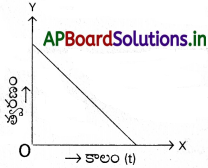
ఏకరీతి (సమరీతి) గమనం గల ఒక క్రికెట్ బంతి చాలా స్వల్పకాలం పాటు ఒక బ్యాట్ తో కొట్టగా వెనకకు మరలింది. తిరోదిశలో త్వరణాన్ని ధనాత్మకంగా తీసుకొని కాలంపరంగా త్వరణంలో మార్పుకు గ్రాఫు గీయండి.
జవాబు:
ప్రశ్న 7.
ధన x—దిశలో అక్షం వెంబడి ఏకమితీయ గమనాన్ని కలిగి ఉండి, ఆవర్తకంగా నిశ్చలస్థితికి వచ్చి ముందుకు పోతూ ఉండే ఒక కణం గమనానికి ఉదాహరణ ఇవ్వండి.
జవాబు:
సరళహరాత్మక డోలని ఎడమ అంత్యస్థానం నుండి బయలుదేరి, అదే బిందువు వద్దకు ఆవర్తకంగా నిశ్చలస్థితికి వచ్చి ధన X- అక్ష దిశలో ముందుకు చలిస్తుంది.
ప్రశ్న 8.
ఒక (ద్రవంలో) ప్రవాహిలో పతనం చెందే ఒక వస్తువు a = g-bv త్వరణం కలిగి ఉందని పరిశీలించడం జరిగింది. ఇక్కడ g గురుత్వ త్వరణం, b ఒక స్థిరాంకం. కొంత కాలం తరువాత వస్తువు స్థిర వేగంతో పతనం చెందుతుందని తెలుసుకొన్నారు. ఆ స్థిరవేగం విలువ ఎంతై ఉండవచ్చు?
జవాబు:
త్వరణం, a = g – bv

వస్తువు ప్రవాహి ద్వారా స్థిర వేగంతో చలిస్తే, dv = 0
0 = g – bv ∴ v = \(\frac{g}{b}\)
ప్రశ్న 9.
ఒక నిర్దేశ చట్రం పరంగా ఒక వస్తువు గమన పథం పరావలయం. ఈ నిర్దేశ చట్రం పరంగా స్థిరవేగంతో గమనంలో ఉన్న వేరొక నిర్దేశ చట్రం పరంగా వస్తువు గమన పథం పరావలయం అవుతుందా? కాకపోతే మరేమై ఉండవచ్చు?
జవాబు:
కాదు, వస్తువు’ యొక్క పథం నిలువు సరళరేఖాత్మక మార్గంలో ఉంటుంది.
ప్రశ్న 10.
ఒక స్ప్రింగు ఒక కొనను ద్రుఢ ఆధారానికి బిగించి, రెండో కొనకు ఒక ద్రవ్యరాశిని వేలాడదీసి, లాగి వదిలారు. ఎప్పుడు త్వరణం పరిమాణం గరిష్ఠంగా ఉంటుంది?
జవాబు:
అంత్యస్థానం వద్ద త్వరణ పరిమాణం గరిష్టము.
స్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
త్వరణం కాలంతోపాటు మారుతూ ఉన్నప్పుడు శుద్ధగతి శాస్త్రంలోని సమీకరణాలను ఉపయోగించవచ్చా? ఉపయోగించ వీలులేకపోతే ఆ సమీకరణాలు ఏ రూపాన్ని సంతరించుకొంటాయి ?
జవాబు:
కాలంతో త్వరణం మారితే, శుద్ధగతిక సమీకరణాలు ఉపయోగించలేము.
ఒక వస్తువు ఏకరీతి త్వరణం (a) తో సరళరేఖ వెంట చలిస్తున్నప్పుడు, శుద్ధగతిక సమీకరణాలు
1) v = vo + at; 2) x = vot + \(\frac{1}{2}\) at²; 3) v² = v0² + 2ax
ఇచ్చట ‘X’ స్థానభ్రంశం, t = 0 వద్ద వేగం v0, కాలం t వద్ద వేగం ‘v’, ‘a’ త్వరణము.
స్థిరత్వరణంతో, సరళ పథం గమనంలో ఈ సమీకరణాలను, శుద్ధగతిక సమీకరణాలు అంటారు.

ప్రశ్న 2.
ఒక కణం ఒక సరళరేఖ వెండి సమత్వరణంతో గమనంలో ఉంది. t = 0 వద్ద కణం వేగం v., t = t వద్ద వేగం vz ఆ కణం సగటు వేగం, ఈ కాలవ్యవధిలో (v1 + v2)/2 అని తెలిపితే, అది సరియైనదేనా? మీ సమాధానానికి తగిన వివరణ ఇవ్వండి.
జవాబు:
సరియైనది.
వివరణ :
ఒక కణం, ఏకరీతి త్వరణం ‘a’ తో గమనంలో ఉందని భావిద్దాం.

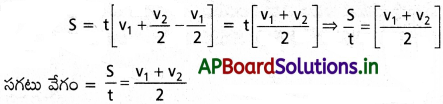
ప్రశ్న 3.
ఒక కణం వేగ దిశ, కణ త్వరణ దిశతో పోల్చితే వేరుగా ఉండవచ్చా? అవును అయితే ఉదాహరణ ఇవ్వండి.
జవాబు:
ఒక కణం యొక్క వేగం, త్వరణంలు భిన్న దిశలలో ఉండవచ్చును.
ఉదా : నిట్టనిలువుగా పైకి విసిరిన కణం వేగం మరియు త్వరణంలు వ్యతిరేక దిశలలో ఉండును. వాని మధ్య కోణం 180° ఉండును. కణం ప్రయాణంలో వేగదిశ ఊర్థ్వదిశలో, త్వరణదిశ అథోదిశలో ఉండును.
ప్రశ్న 4.
ఎగురుతూ ఉన్న విమానం నుంచి పారాచూట్ సహాయంతో ఒక వ్యక్తి భూమి నుంచి 3 km ఎత్తు నుంచి దూకాడు. అతడు భూమి నుంచి 1 km ఎత్తులో ఉన్నప్పుడు పారాచూటును పూర్తిగా విప్పాడు. అతడి గమనాన్ని వివరించండి.
జవాబు:
- భూమి నుండి 3 km ఎత్తులో ఎగురుతూ గమనంలో ఉన్న విమానం నుండి పారాచూట్తో ఒకవ్యక్తి దూకితే, భూమి నుండి 1 km ఎత్తు వరకు స్వేచ్ఛా వస్తువు వలె, 9.8 ms-2 స్థిర గురుత్వ త్వరణంతో చలిస్తాడు.
- భూమి నుండి 1 km ఎత్తు వద్ద, పారాచూటన్ను వ్యక్తి పూర్తిగా తెరిస్తే, దానిపై గురుత్వాకర్షణ బలం క్రిందికి, గాలి నిరోధ బలం పైకి పనిచేయును. పారాచూట్ ఫలిత త్వరణం, a = g – bv అనుసరించి క్రమంగా తగ్గును.
- పారాచూటైపై ఊర్థ్వదిశలో గాలి నిరోధ బలం, అథోదిశలో గురుత్వాకర్షణ బలంనకు సమానమై, వ్యక్తి చరమ వేగాన్ని పొందుతాడు.
- ఈ చరమ వేగం తక్కువగా ఉంటే, పారాచుటిస్టు ఎక్కువ కష్టం లేకుండా భూమిపై క్షేమంగా చేరతాడు.
ప్రశ్న 5.
ఒక పక్షి తన ముక్కును ఒక పండు కరుచుకుని భూమికి సమాంతరంగా ఎగురుతున్నది. ఒకానొక ఎత్తు అది పండును జారవిడిచింది (a) పక్షిపరంగానూ (b) భూమిపై నిలబడిన వ్యక్తి పరంగానూ కిందపడుతున్న పండు గమన పథాన్ని వివరించండి.
జవాబు:
ఒక పక్షి పండును ముక్కున కరచుకుని, భూమికి క్షితిజ సమాంతరంగా ఎగురుతూ, పండును వదిలితే

(a) పక్షిపరంగా పండు యొక్క పథం సరళరేఖ
(b) భూమిపై నిలబడిన వ్యక్తి పరంగా పండు పథం పరావలయం
ప్రశ్న 6.
ఒకడు ఎత్తైన భవన ఉపరితలంపై పరిగెడుతూ, పక్కనే కొద్దిగా తక్కువ ఎత్తున్న ఇంకొక భవనం పైకి క్షితిజ సమాంతరంగా దూకాడు. అతడి వేగం 9 ms 1. రెండు భవనాల మధ్య దూరం 10m భవనాల ఎత్తులలో తేడా9 m అయితే అతడు రెండవ భవనం పైకి దూకగలడా ? (g = 10 ms-2).
జవాబు:

రెండు భవనాల మధ్య ఎత్తుల తేడా h = 9 m; g = 10 ms-2
మనిషి గమన కాలం t = \(\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times9}{10}}\) = 1.341 sec
మనిషి క్షితిజ సమాంతర వడి, u = 9 ms-1
మనిషి ప్రయాణించిన క్షితిజ సమాంతర దూరం,
d3 = క్షితిజ సమాంతర వడి × గమన కాలం = u × t = 9 × 1.341 12.07 m
రెండు భవనాల మధ్య క్షితిజ సమాంతర దూరం db = 10 m అని ఇవ్వబడినది.
∴ మనిషి రెండవ భవనంపైకి దూకగలడు. కారణము dm > db
ప్రశ్న 7.
ఒక ఎత్తైన భవనంపై నుంచి ఒక బంతిని జారవిడిచారు. అదే క్షణంలో ఇంకొక బంతిని కొంత వేగంతో క్షితిజ సమాంతరంగా విసిరారు. ఏ బంతి మొదటగా భూమిని చేరుతుంది? మీ సమాధానాన్ని
వివరించండి.
జవాబు:
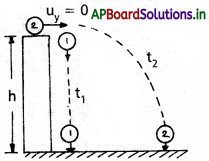
భవంతి ఎత్తు = బంతి స్థానంభ్రంశం = h
మొదటి బంతికి, u = 0; S = h, a = g; t = t1
ఈ విలువలను S = ut + \(\frac{1}{2}\) at² లో ప్రతిక్షేపిస్తే,
h = 0 + \(\frac{1}{2}\) gt1²
∴ t1 = \(\sqrt{\frac{2h}{g}}\) ………….. (1)
రెండవ బంతికి, uX = u; uY = 0, aY = g, SY = h; t = t2
ఈ విలువలను SY = uYt + \(\frac{1}{2}\)aYt² లో ప్రతిక్షేపిస్తే,
h = 0 + \(\frac{1}{2}\) gt2²
∴ t2 = \(\sqrt{\frac{2h}{g}}\) …………… (2)
(1) మరియు (2) సమీకరణాల నుండి, t, = t,
∴ రెండు బంతులు ఒకేసారి భూమిని చేరతాయి.

ప్రశ్న 8.
ఒక భవనంపై నుంచి ఒక బంతిని జారవిడిచారు. అదే క్షణంలో ఇంకొక బంతిని నిట్టనిలువుగా పైకి కొంత వేగంతో విసిరారు. ఆ బంతుల సాపేక్ష వేగాలలోమార్పును కాలం ప్రమేయంగా వివరించండి.
జవాబు:
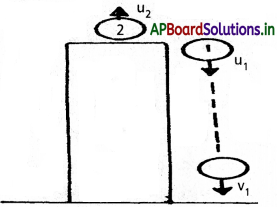
మొదటి బంతికి u = u1; v = v1; a = g; t = t
ఈ విలువలను v = u + at లో ప్రతిక్షేపిస్తే
v1 = u1 + gt1 ……………. (1)
రెండవ బంతికి, u = u2; v = v2; a = − g; t = t2
ఈ విలువలను v = u + at లో ప్రతిక్షేపిస్తే,
v2 = u2 + gt2 ………. (2)
(1) − (2) ⇒ (v1 − v2) = (u1 − u2) + g(t1 + t2)
∴ (v1 − v2) − (u1 − u2) = g(t1 + t2)
∴ (v1 – v2) – (0 – u2) = g(t1 + t2)[∵ u1 = 0]
∴ రెండు బంతుల తుది సాపేక్ష మరియు తొలి సాపేక్ష వేగంల మధ్య భేదం = కాలంలో ప్రమేయము.
ప్రశ్న 9.
ఒకనొక వర్ష బిందువు వ్యాసం 4 mm. భూమి నుంచి 1 km ఎత్తున గల మేఘం నుంచి ఆ వర్షం బిందువు జారిపడితే అది భూమిని ఎంత ద్రవ్యవేగంతో తాకుతుంది?
జవాబు:
వర్షపు బిందువు వ్యాసము, D = 4 mm
వర్షపు బిందువు వ్యాసార్థం, r = 2 mm = 2 × 10-3 m
వర్షపు బిందువు ఘనపరిమాణం, V = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\times\frac{22}{7}\) × (2 × 10-3)³
నీటి సాంద్రత, d = 10³ kg/m³
నీటి బిందువు ద్రవ్యరాశి, M = Vd = \(\frac{4}{3}\times\frac{22}{7}\) × 8 × 10-9 × 10³ = 33.5 × 2 × 10-6 kg
మేఘం నుండి పడు వర్షపు బిందువు ఎత్తు, h = 1 km = 1000 m
భూమిని తాకే ముందు వర్షపు బిందువు వేగం V = \(\sqrt{2gh}=\sqrt{2\times9.8\times1000}\) = 140 ms-1
భూమిని తాకేటప్పుడు వర్షపు బిందువు ద్రవ్యవేగం P = mV = 33.52 × 10-6 × 140 = 469.28 × 10-5
= 0.004692 kg ms-1
ప్రశ్న 10.
క్షితిజంతో 45° కోణంతో ప్రక్షిప్తం చేసిన ప్రక్షేపకం చేరే గరిష్ట ఎత్తు దాని వ్యాప్తిలో నాలుగోవంతు ఉంటుందని చూపండి.
జవాబు:
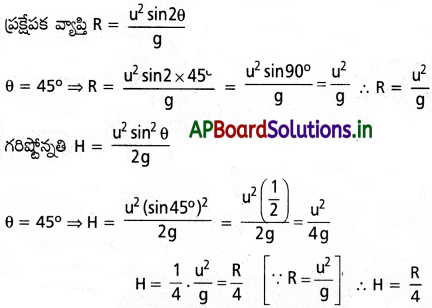
లెక్కలు (Problems)
ప్రశ్న 1.
ఒకడు ఒక తిన్నని రోడ్డు వెంట తన ఇంటి నుంచి 2.5 km దూరాన ఉన్న మార్కెట్కు 5 km h-1 వడితో నడిచాడు. మార్కెట్ మూసి ఉండటం గమనించి, వెంటనే వెనుదిరిగి ఇంటికి 7.5 km h-1 వేగంతో చేరాడు. 0 నుంచి 50 నిమిషాల కాలవ్యవధిలో అతడి (a) సగటు వేగ పరిమాణం, (b) సగటు వడి ఎంత?
సాధన:
ఇంటినుండి మార్కెట్కు :
X1 = 2.5 km; v1 = 5 km h-1;

ప్రశ్న 2.
ఒక కారు మొదటి మూడు వంతుల దూరాన్ని 10 kmph వేగంతోనూ, రెండవ మూడు వంతుల దూరాన్ని 20 kmph వేగంతోనూ, చివరి మూడు వంతుల దూరాన్ని 60 kmph వేగంతోనూ ప్రయాణిస్తే, మొత్తం దూరాన్ని పూర్తి చేయడంలో కారు సగటు వడి ఎంత ?
సాధన:
v1 = 10 kmph; v2 = 20 kmph;
v3 = 60 kmph; v = ?
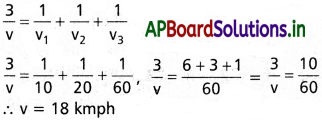
ప్రశ్న 3.
ఒక తుపాకి గుండు 150 ms-1 వడితో ప్రయాణిస్తూ చెట్టును తాకి 3.5 cm దూరం దూసుకొని పోయి ఆగిపోయింది. చెట్టు కాండంలో గుండు రుణత్వరణం పరిమాణం, చెట్టును తాకిన తరువాత గుండు ఆగిపోవడానికి పట్టిన కాలం ఎంత?
సాధన:
u 150 m/s, s = 3.5 cm = 0.035 m, v = 0
v² – u² = 2as
0 – 150² = 2 × a × 0.035


ప్రశ్న 4.
ఒక మోటారు వాహకుడు మోటారును 35 min నిమిషాలపాటు 85 km/h వేగంతో ఉత్తర దిశగా నడిపి 15 నిమిషాలపాటు ఆగిపోయాడు. తరువాత ఉత్తరదిశలోనే ప్రయాణించి 2 గంటలలో 130 km దూరం వెళ్ళాడు. అతడి మొత్తం స్థానభ్రంశం, సగటు వేగం ఎంత?
సాధన:
v1 = 85 kmph, t = 35.0 min, S2 = 130 km
S1 = స్థానభ్రంశం = \(\frac{85}{60}\) × 30 = 42.5 km
S2 = 130 km
a) S = S1 + S2 = 42.5 + 130 = 172.50 km
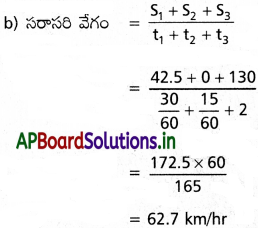
ప్రశ్న 5.
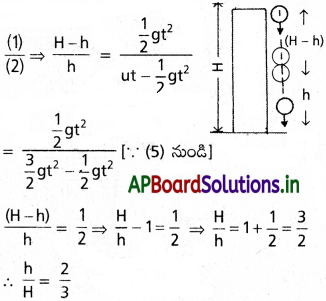
ఒక భవనంపైకప్పు నుంచి ఒక బంతి A ని జారవిడిచిన క్షణంలోనే, అలాంటిదే బంతి B ను భూమిపై నుంచి నిట్టనిలువుగా పైకి విసిరారు. బంతులు ఢీకొట్టుకున్న క్షణంలో బంతి Aవడి, బంతి B వడికి రెట్టింపు ఉంది. బంతులు అభిఘాతం జరుపుకొన్న ఎత్తు, భవనం ఎత్తులో ఎన్నో వంతు ఉంటుంది?
సాధన:
బిల్డింగ్ ఎత్తు = H గా తీసుకుందాము
రెండు బంతులు అభిఘాతం జరిగిన ఎత్తు = h
బంతి A కు, u = : 0; V = VA; s = H – h; t = t; a = g
ఈ విలువలు 5 = ut + \(\frac{1}{2}\) at² లో ప్రతిక్షేపించగా
H- h = 0 + \(\frac{1}{2}\)gt²
H – h = \(\frac{1}{2}\)gt² ………… (1)
మరియు VA = gt ………….. (2)
బంతి B కు, u = u; V= VB; s = h; a = -g
ఈ విలువలు s = ut + \(\frac{1}{2}\)at² లో ప్రతిక్షేపించగా
⇒ h = ut – \(\frac{1}{2}\)gt² ………….. (3)
మరియు VB = u – gt ………….. (4)
ఇచ్చినది VA = 2VB
gt = 2(u – gt)
u = \(\frac{3}{2}\) gt ………….. (5)
ప్రశ్న 6.
16 m ఎత్తు గల ఒక భవనం పై కప్పు నుంచి క్రమ కాలవ్యవధులలో నీటి బిందువులు పడుతున్నాయి. మొదటి నీటి బిందువు భూమిని తాకిన క్షణంలో, అయిదవ నీటి బిందువు పైకప్పును వదిలింది. వరస నీటి బిందువుల మధ్య దూరం కనుక్కోండి.
సాధన:
H = 16 m
మొదటి నీటి బిందువు భూమిని తాకుటకు పట్టుకాలం
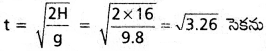
= 1.8 సెకను.
ప్రతి నీటి బిందువుకు మధ్య కాలవ్యవధి = \(\frac{t}{n – 1}\)
ఇచ్చట n = నీటి బిందువుల సంఖ్య
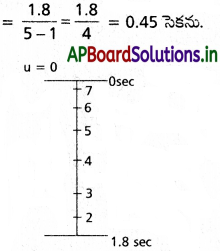
రెండవ నీటి బిందువుకు h2 = \(\frac{1}{2}\) gt²
\(\frac{1}{2}\) × 9.8 × 1.35 × 1.35 = 8.93 m
d12 = 16 – 8.93 = 7.06 = 7 m
మూడవ నీటి బిందువుకు h3 = \(\frac{1}{2}\) × 9.8 × 0.90 × 0.90
= 3.97
d23 = 8.93 – 3.97 = 4.961 = 5 m
నాల్గవ నీటి బిందువుకు h4 = \(\frac{1}{2}\) × 9.8 × 0.45 × 0.45
= 0.9922
d34 = 3.97 – 0.9922
d34 = 2.9778 = 3 m
అదేవిధంగా d45 = 0.9922 – 0 = 0.9922 =1 m
ప్రశ్న 7.
ఒక వేటగాడు తనకు కొంత దూరంలో ఉన్న చెట్టు నుంచి వేలాడుతున్న ఒక కోతికి తుపాకీ గురిపెట్టాడు. వేటగాడు తుపాకీ పేల్చిన క్షణాన, గుండు తగలకుండా తప్పించుకోవాలని కోతి కొమ్మను విడిచి జారిపడింది. కోతిది తప్పుడు నిర్ణయం అని వివరించండి.
సాధన:
ఒక వేటగాడు తన నుంచి ‘d’ దూరంలో ఉన్న చెట్టుపై కొమ్మనుంచి వేలాడుతున్న ఒక కోతి వైపు తుపాకీ గురిపెట్టాడనుకుందాము. తుపాకీ గుండు వెలుగును గమనించిన అది చెట్టు నుండి క్రింద పడుతుంది. తుపాకీ వేగం ఎంతైనప్పటికీ అది కోతిని తాకుతుంది.
కోతి భూమిని చేరుటకు పట్టుకాలం t1 = \(\sqrt{\frac{2h}{g}}\) ……….. (1)
తుపాకీ నుండి తూటా గమనం క్షితిజ సమాంతర ప్రక్షిప్త వస్తువువలె ఉంటుంది.
లంబదిశలో వేగం uy = 0
తూటా భూమిని చేరుటకు పట్టుకాలం t2 అనుకుందాము.
∴ S= ut + \(\frac{1}{2}\)at²1
S = 0 × t + \(\frac{1}{2}\)at²2
∴ h = \(\frac{1}{2}\)ht²2
t2 = \(\sqrt{\frac{2h}{g}}\) ……….. (2)
(1) మరియు (2) ల నుండి, t1 = t2
తూటా మరియు కోతి ఒకేసారి భూమిని చేరును.
కావున కోతిని తూటా తాకుతుంది.
కోతి పొరపాటు పడింది.
ప్రశ్న 8.
భూమి నుంచి 500 m ఎత్తున 360 kmph వడితో క్షితిజ సమాంతర దిశలో ప్రయాణిస్తున్న విమానం నుంచి ఆహారపు పొట్లాన్ని జార విడిచారు. (i) పొట్లం అవరోహణ కాలం, (ii) జారవిడిచిన బిందువు నుంచి క్షితిజ సమాంతరంగా ఎంత దూరంలో పొట్లం భూమిని చేరుతుందో కనుక్కోండి.
సాధన:
విమానం వేగం v = 360 kmph
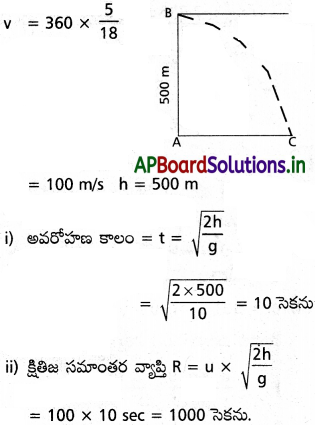
ప్రశ్న 9.
ఒక భవనం కిటికీ నుంచి, క్షితిజానికి 20° కిందగా, 8 ms−1 వేగంతో ఒక బంతిని విసి రారు. బంతి భూమిని 3 s తరువాత తాకింది. బంతిని ఎంత ఎత్తు నుంచి విసిరారు ? భవనం పునాది నుంచి ఎంత దూరంలో బంతి భూమిని తాకుతుంది ?
సాధన:
u = 8 m/s, θ = 20°, t = 35
a) క్షితిజ సమాంతర దూరం (u cos θ) t = 8
cos 20° × 3 = 8 × 0.9397 × 3 = 22.6 m
b) ఎత్తు h = (u sin θ)t + \(\frac{1}{2}\) gt²
= 8 sin 20° × 3 + \(\frac{1}{2}\) × 9.8 × 9
= 8.208 + 44.1 = 52.31 m
c) 44.1 m ఎత్తు నుండి బంతిని విసిరారు.
h1 = (u sin θ)t1 + \(\frac{1}{2}\) gt1²
10 = (8 sin 20°)t1 + \(\frac{1}{2}\)9.8 t1²
= 2.736 t1 + 4.9 t1²
⇒ 4.9 t1² + 2.736 t1 – 10 = 0
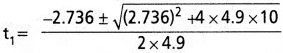

ప్రశ్న 10.
క్షితిజంతో 30°, 60° చేసే దిశలలో, ఒకే బిందువు నుంచి రెండు బంతులను ప్రక్షిప్తం చేశారు. ఆ రెండు బంతులూ (a) ఒకే ఎత్తును చేరితే, (b) ఒకే వ్యాప్తిని కలిగి ఉంటే వాటి తొలి వేగాల నిష్పత్తి ఎంత?
సాధన:
θ1 = 30°, θ2 = 60°
మొదటి వస్తువు గరిష్ట ఎత్తు
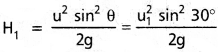
రెండవ వస్తువు గరిష్ట ఎత్తు H2

అదనపు లెక్కలు (Additional Problems)
ప్రశ్న 1.
కింద ఇచ్చిన గమన సంబంధ ఉదాహరణలలో దేనిలో వస్తువును బిందు వస్తువుగా ఉజ్జాయింపు చేయవచ్చు.
a) రెండు స్టేషన్ల మధ్య కుదుపులు లేకుండా ప్రయాణించే రైలు కారేజ్.
b) వృత్తాకార మార్గంలో సైకిల్ తొక్కే వ్యక్తి తలపై కూర్చున్న కోతి.
c) స్పిన్ తిరుగుతూ భూమిని తాకి హఠాత్తుగా మలుపు తిరిగిన క్రికెట్ బంతి.
d) టేబుల్ అంచు నుంచి జారిపడి అటూ ఇటూ దొర్లుతున్న బీకర్.
సాధన:
a) రైల్వే క్యారేజి పరిమాణం, రెండు స్టేషన్ల మధ్య దూరంతో పోల్చిన చాలా తక్కువ. కావున క్యారేజిని బిందు వస్తువుగా పరిగణిస్తారు.
b) కోతి పరిమాణం, సైక్లిస్ట్, హెచ్చు వ్యాసార్థంగల వృత్తాకార ట్రాక్ వెంట తిరుగుతున్నప్పుడు, ప్రయాణించు దూరం కంటే చాలా తక్కువ. కావున వృత్తాకార ట్రాక్ సైక్లిస్ట్ పై కూర్చున్న కోతిని బిందు వస్తువుగా పరిగణిస్తారు.
c) భ్రమణ క్రికెట్ బంతి పరిమాణం, అది భూమిని తాకి ప్రయాణించు దూరంతో విస్మరించలేము. కావున క్రికెట్ బంతిని బిందు వస్తువుగా పరిగణిస్తారు.
d) టేబుల్ అంచునుండి జారిపడిన బీకరు పరిమాణం, టేబుల్ ఎత్తులో పోల్చి విస్మరించలేము. కావున బీకరును బిందు వస్తువుగా పరిగణించలేము.
ప్రశ్న 2.
ఇద్దరు పిల్లలు A, B లు వారి స్కూలు 0 నుంచి వారి ఇళ్ళు P, Q లకు తిరిగి ప్రయాణమయ్యే సందర్భంలో వారి గమనాన్ని సూచించే స్థానం- కాలం (x – t) గ్రాఫు పటంలో చూపడం జరి గింది. కింద ఇచ్చిన బ్రాకెట్లలో సరియైన ఎంపికచేయండి.
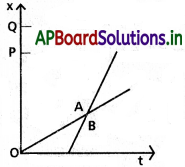
a) (A/B) స్కూలుకు (B/A) కంటే దగ్గరగా ఉంటాడు.
b) (A/B) స్కూలుకు (B/A) కంటే ముందుగా బయలుదేరుతాడు.
c) (A/B), (B/A) కంటే వేగంగా నడుస్తాడు.
d) A, B లు ఇంటికి (ఒకే సమయంలో/ వేరు వేరు సమయాలలో) చేరుతారు.
e) (A/B) ప్రయాణంలో (B/A) ను (ఒకసారి/ రెండు సార్లు) దాటి వెళతాడు.
సాధన:
a) OP < OQ కావున A పిల్లవాడు B పిల్లవాని కన్న స్కూలు దగ్గరగా నివసించుచున్నాడని చెప్పవచ్చు.
b) Aకు x = 0, t = 0. B కొంత నిర్ణీత t విలువ కల్గి ఉన్నాడు. కావున A స్కూల్ నుండి B కన్నా ముందుగా బయలుదేరును.
c) ఏకరీతి చలన సందర్భంలో x – t గ్రాఫ్ వాలు వేగంనకు సమానము మరియు B కు x – t గ్రాఫ్ వాలు A కన్నా ఎక్కువ. కావున B, A కన్నా వేగంగా నడుచును.
d) x – t గ్రాఫ్ల నుండి t విలువ A మరియు B కు సమానము. t అక్షంనకు సమాంతరంగా గీసిన రేఖలు
P మరియు Q లకు సమానం. కావున A, B లు ఒకేసారి ఇళ్లను చేరును.
e) A మరియు B, X-t గ్రాఫ్లు ఒకే ఒకచోట ఖండించు కొనును. స్కూల్ వదిలిన తరువాత B బయలుదేరిన తరువాత A ను ఒకసారి అతిక్రమించును.

ప్రశ్న 3.
ఒక స్త్రీ ఇంటి వద్ద 9.00 amకు బయలుదేరి, కాలి నడకన 5 km h-1 వడితో తిన్నని రోడ్డుపై 2.5 km దూరంలో ఉన్న కార్యాలయానికి చేరి, 5.00 pm వరకు అక్కడ ఉండిపోయి, ఆటోలో 25 km h-1 వడితో తిరిగి ఇంటికి చేరింది. తగిన స్కేలు తీసుకొని ఆ స్త్రీ గమనానికి సంబంధించి x-t గ్రాఫు గీయండి.
సాధన:
ఆఫీస్ ను చేరుటకు పట్టుకాలము
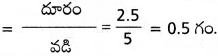
ఆఫీస్ నుండి తిరిగి వచ్చుటకు పట్టుకాలం
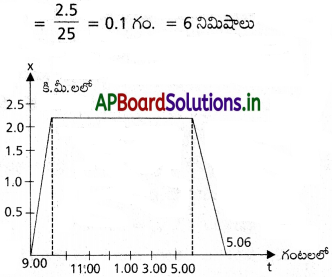
మహిళ ఆఫీస్ను 9.30 am కు చేరును మరియు 5.06 p.m. ను తిరిగి ఇంటికి చేరును. ఈ చలనంనకు సంబంధించిన x – t గ్రాఫ్ పటంలో చూడండి.
ప్రశ్న 4.
ఒక వ్యక్తి సన్నని వీధిలో 5 అడుగులు ముందుకు, 3 అడుగులు వెనక్కి, మరల 5 అడుగులు ముందుకు, 3 అడుగులు వెనక్కి.. ఇలా నడిచాడు. ప్రతి అడుగులో అతడు 1 m దూరం, 1 సెకనులో ప్రయాణిస్తే, అతని గమనానికి x t గ్రాఫు గీయండి. వ్యక్తి తాగినవాడైతే బయలుదేరిన చోటు నుంచి 13 m దూరంలో ఉన్న గుంతలో పడడానికి ఎంత సమయం పడుతుందో గ్రాఫు ద్వారా కనుక్కోండి. సాధన:
త్రాగిన వ్యక్తి 8 స్టెప్స్ ప్రయాణించు ప్రభావ దూరం = 5 – 3 = 2 m.
∴ 8m లు చలించుటకు 32 స్టెప్స్ తీసుకొనును.
గుంటను చేరుటకు 5 m కన్నా ఎక్కువ దూరం ప్రయాణించాల్సి ఉంటుంది. అందుకు అతడు ముందుకు 5 స్టెప్స్ తీసుకొనును.
∴ అతడు 13m ప్రయాణించుటకు తీసుకున్న స్టెప్లు
= 32 + 5 = 37
కావున అతడు 37 స్టెప్స్ తీసుకున్న తరువాత బయలుదేరిన 37 సెకనుల తరువాత గుంటలో పడిపోవును.
ప్రశ్న 5.
500 km h-1 వడితో పోతున్న ఒక జెట్ విమానం పరంగా దాని నుంచి దగ్ధం చెందిన ఇంధన వాయువులు 1500 km h వడితో వెలువడుతున్నాయి. భూమిపై నుంచి పరి శీలించి వ్యక్తికి వాయువులు ఎంత వడితో వెలువడుతున్నట్లు అనిపిస్తుంది?
సాధన:
భూమి సాపేక్షంగా ఉత్పత్తుల వేగం vp. ధన X-అక్ష దిశలో విమాన చలనదిశను భావిద్దాం.
జెట్ విమానం వడి, vA = 500 km h-1
జెట్ విమానం పరంగా దహన ఉత్పత్తుల సాపేక్ష వడి VPA= -1500 km h-1.
విమాన పరంగా ఉత్పత్తుల సాపేక్ష వేగం,
VPA = VP – VA = −1500
VP = VA – 1500 = 500 – 1500
= 1000 km h-1
ఇచ్చట రుణగుర్తు విమాన చలన దిశకు వ్యతిరేకంగా దహన ఉత్పత్తుల దిశ ఉండునని తెల్పును. కావున సాపేక్ష వేగం పరిమాణం 1000 km h-1.
ప్రశ్న 6.
ఒక తిన్నని రహదారి వెంట ఒక కారు 126 km h-1 వడితో ప్రయాణిస్తూ 200 m దూరంలో నిశ్చలస్థితిలోకి వచ్చింది. కారు రుణ త్వరణం (త్వరణం సమరీతి త్వరణం అని భావించండి) ఎంత? నిశ్చలస్థితికి రావడానికి కారు తీసుకున్న సమయం ఎంత?
సాధన:

ప్రశ్న 7.
400 m పొడవున్న రెండు రైళ్ళు A, Bలు రెండు సమాంతర రైలు మార్గాలపై 72 km h-1 సమవడితో ఒకేదిశలో ప్రయాణిస్తున్నాయి. రైలు A, రైలు B కంటే ముందు ఉంది. రైలు B డ్రైవరు, రైలు Aను దాటిపోవాలని నిర్ణయించి తన రైలుకు 1 ms-2 త్వరణం కలిగించాడు. 50 s తరువాత రైలు Bలో గార్డు, రైలు A డ్రైవరును దాటి రెండు రైళ్ళ మధ్య ఉన్న అసలు దూరం ఎంత?
సాధన:
రైలు A కు : u = 72 km h-1 = \(\frac{72\times1000}{60\times60}\)
= 20 m s-2; t = 50s; a = 0 s = sA ;
s = ut + \(\frac{1}{2}\)at²
∴ SA = 20 × 50 + \(\frac{1}{2}\) × 0 × 50²
= 1000 m
రైలు Bకు : u = 72 kms-1 = 20 ms -2;
a = 1 ms-2; t = 50/S, s = s-B
∴ SB = 20 × 50 + \(\frac{1}{2}\) × 1 × 50²
= 2250 m
రైలు B చివరి పెట్టెలో గార్డ్ ఉంటే, రెండు రైళ్ళ మధ్య యదార్థ దూరం + A రైలు పొడవు + B రైలు పొడవు = SB – SA.
లేక రెండు రైళ్ళ మధ్య యదార్ధ దూరం + 400 + 400
= 2250 – 1000 = 1250 m
లేక రెండు రైళ్ళ మధ్య యదార్ధ దూరం
= 1250 – 800 = 450m.
ప్రశ్న 8.
రెండు వరుసలున్న (two-lane) రోడ్డుపై కారు A 36 km h-1 వడితో పోతున్నది. రెండు కార్లు B, Cలు వ్యతిరేక దిశల్లో 54 km h-1 వడితో A వైపు ప్రయాణిస్తున్నాయి. ఒకానొక క్షణాన, దూరాలు AB, AC లు1 kmకు సమానమై నప్పుడు, C కంటే ముందుగా A ని దాటి పోవాలని B నిర్ణయించడం జరిగింది. ప్రమాదాన్ని నివారించడానికి కారు B కి ఉండాల్సిన కనీస త్వరణం ఎంత?
సాధన:
కారు A వేగం = 36 km h-1 = 10 ms-1
కారు B లేక C వేగం = 54 km h-1 = 15 ms-1
A రంగ B సాపేక్ష వేగం
A = 15 – 10 – 5 ms-1
A పరంగ C సాపేక్ష వేగం
A = 15 + 10 = 25 ms-1
AB = AC = 1 km = 1000 m
A దాటుటకు B లేక కు అవసరమయ్యే కాలం
= \(\frac{1000}{25}\) = 40 sec.
కారు ( కన్నా ముందు కారు A ను దాటుటకు, కారు B, a త్వరణంతో ప్రయాణిస్తే, అప్పుడు
u = 5 ms-1, t = 40s, s = 1000 m, a = ?
Using s = ut + \(\frac{1}{2}\)at²
1000 = 5 × 40 + \(\frac{1}{2}\) × a × 40² (లేక)
1000 – 200 800 a (లేక)
a = 1 m/s²
ప్రశ్న 9.
రెండు పట్టణాలు A, Bల నుంచి ప్రతి T నిమిషాలకు రెండు దిశల్లోనూ బస్సులు బయలుదేరేటట్లు రవాణా సౌకర్యంతో వాటిని సంధానించారు. A నుంచి Bకు 20 km h-1 వడితో సైకిల్పై ప్రయాణించే వ్యక్తిని, అతని గమన దిశలో, ప్రతి 18 నిమిషాలకు ఒక బస్సు దాటుతుంది. వ్యతిరేక దిశలో ప్రతి 6 నిమిషాలకు ఒక బస్సు దాటుతుంది. రవాణా వ్యవస్థలో రెండు వరస బస్సుల మధ్య కాల వ్యవధి Tబస్సుల వడి (స్థిర వడిగా భావించండి) ఎంత?
సాధన:
v km h-1 స్థిర వడితో A మరియు B టౌన్ల మధ్య ప్రయాణించినవని తీసుకుందాం. సైక్లిస్ట్ దృష్ట్యా (A నుండి B వైపు) సాపేక్ష వేగం (i.e., సైక్లిస్ట్ వెళ్ళే దిశలో)
= (v – 20) kmh-1. సైక్లిస్ట్ దృష్ట్యా B నుండి A వైపు బస్సు సాపేక్ష వేగం = (v + 20) kmh-1.
T (మినిట్) కాలంలో బస్సు ప్రయాణించు దూరం
= VT ప్రశ్న పరంగా = \(\frac{vT}{v – 20}\) = 18 లేక vT
= 18v – 18 × 20 …………. (i)
మరియు \(\frac{vT}{v + 20}\) = 6 లేక vT = 6v + 20 × 6 ……… (ii)
(i) మరియు (ii) లను సమానం చేయగా
18v – 18 × 20 = 6v + 20 × 6 (లేక)
12v = 20 × 6 + 18 × 20 = 480
(లేక) υ = 40 kmh-1
υ విలువను (i) లో ప్రతిక్షేపించగా
40 T = 18 × 40 – 18 × 20 = 18 × 20
(లేక) T = 18 × 20/40 9 min.
ప్రశ్న 10.
ఒక క్రీడాకారుడు ఒక బంతిని 29.4 m s తొలి వేగంతో నిట్టనిలువుగా విసిరాడు.
a) బంతి ఊర్ధ్వ దిశలో. గమనంలో ఉన్న కాలంలో త్వరణం దిశ ఏమిటి?
b) బంతి గరిష్ట ఎత్తు వద్ద గల బిందువును చేరినప్పుడు బంతి వేగం, త్వరణాల విలువలు ఎంతెంత?
c) బంతి గరిష్ఠ ఎత్తు వద్ద x = 3 0 m t = 0 s గా స్థానం, కాలం విలువలను ఎన్నుకొని, నిమ్నదిశను ధన x – అక్షం దిశగా భావించి, స్థానం, వేగం, త్వరణం సంజ్ఞలను బంతి ఊర్ధ్వ దిశలో గమనంలో ఉన్నప్పుడు, నిమ్న దిశలో గమనంలో ఉన్నప్పుడు ఎలా ఉంటాయో తెలపండి.
d) బంతి ఎంత ఎత్తుకు చేరుతుందో, ఎంత కాలం తరువాతక్రీడాకారుని చేతిలోకి తిరిగి వస్తుందో తెలపండి. (g = 9.8 ms-2 గాను, గాలి నిరోధం లేనట్లుగానూ భావించండి.)
సాధన:
a) గురుత్వాకర్షణవల్ల బంతి చలించును. గురుత్వ త్వరణం ఎల్లప్పుడు నిలువుగా క్రింది దిశలో పని చేయును.
b) గరిష్ఠ బిందువు వద్ద బంతి వేగం శూన్యం. గురుత్వ త్వరణం = 9.8 ms-2 క్రింది దిశలో పనిచేయును.
c) గరిష్ఠ బిందువును (x = 0 మరియు t = 0) మూల బిందువుగా పరిగణిస్తే, క్రింది నిలువు దిశలో x – అక్ష దిశను ధనాత్మకంగా మరియు ఊర్ధ్వ దిశలో x-అక్ష దిశను రుణాత్మకంగా తీసుకుంటారు. ఊర్ధ్వ దిశ చలనంలో, స్థానం గుర్తు ధనాత్మకం, వేగం గుర్తు ధనాత్మకం మరియు త్వరణం గుర్తు ధనాత్మకం.
d) భూమి 5 నుండి గరిష్ఠ బిందువును బంతి చేరుటకు పట్టు కాలం t. బంతి ఊర్ధ్వ నిలువు చలనంలో,
u = -29.4 m/s-1, a = 9.8 m/s-2,
v = 0, S = 5, t = 2
v² – u² = 2as
0 – (29.4)² = 2 × 9.8 × s (Or)
S = \(\frac{-(29.4)^2}{2\times9.8}\) = – 44.1 m
ఇచ్చట రుణగుర్తు ఊర్ధ్వ దిశలో ప్రయాణించు దూరంను తెల్పును.
As v = u + at
∴ 0 = -29.4 + 9.8 × t లేదా t = \(\frac{29.4}{9.8}\)
ఆరోహణ కాలం = 3s
వస్తువు ఒక్క గురుత్వాకర్షణ ప్రభావం వల్ల చలిస్తే, ఆరోహణ కాలం ఎల్లప్పుడు అవరోహణ కాలంనకు సమానము.
ఆటగాడు చేతిలోనికి తిరిగి వచ్చుటకు పట్టు మొత్తం కాలం = 3 + 3 = 6s.

ప్రశ్న 11.
కింది వాక్యాలను జాగ్రత్తగా చదివి, అవి తప్పో, ఒప్పో తెలిపి తగిన కారణాలను, ఉదాహరణ లను పేర్కొనండి. ఒక కణం ఏకమితీయ గమనంలో ఉంది.
a) ఒకానొక క్షణంలో దాని వడి శూన్యమై, ఆ క్షణంలో త్వరణం శూన్యేతర విలువ కలిగి ఉండవచ్చు.
b) దాని వడి శూన్యమై, వేగం శూన్యేతర విలువ కలిగి ఉండవచ్చు.
c) అది స్థిరపడి కలిగి ఉండి తప్పక త్వరణం శూన్యమై ఉండి తీరాలి.
d) దాని త్వరణం విలువ ధనాత్మకమై తప్పక వడి వృద్ధి కలిగి ఉండాలి.
సాధన:
a) వస్తువును అంతరాళంలోనికి ఊర్ధ్వ లోనికి విసిరితే, గరిష్ట బిందువు వద్ద సున్నా వడి కలిగి, త్వరణం గురుత్వ త్వరణానికి సమానమగును. కావున ఇచ్చిన స్టేట్మెంట్ నిజము.
b) వస్తు వడి దిశలో వేగం ఉండును. వడి సున్నా అయిన వస్తు వేగ పరిమాణం సున్న. వేగం సున్న. కావున ఇచ్చిన స్టేట్మెంట్ తప్పు,
c) కణం సరళరేఖా మార్గంలో స్థిర వడిలో చలిస్తే, కాలంతోపాటు వేగము స్థిరము. త్వరణం
 నిజము.
నిజము.
d) వస్తువు స్టేట్మెంట్ క్షణిక కాలంపై ఆధారపడును. సరళరేఖలో ధన త్వరణంతో ప్రయాణించునపుడు, క్షణిక కాలం t వద్ద వస్తు వేగము v = u + at. క్షణిక కాలము మూల బిందువుగా తీసుకుంటే, a ధనాత్మకమైతే, u రుణాత్మకం అగును. ఇచ్చిన స్టేట్మెంట్ నిజము కాదు.
క్షణిక కాలంనకు ముందు అన్ని కాలాలకు ఉండదు. కణం నెమ్మదిగా క్రిందికి చలిస్తున్నప్పుడు, కణం వడి కాలంతో క్రమంగా తగ్గును.
వస్తువును నిలువుగా పైకి ప్రక్షిప్తం చేసినపుడు u ధనాత్మకం మరియు a ధనాత్మకం. కావున ఇచ్చిన స్టేట్మెంట్ నిజము.
ప్రశ్న 12.
90 m ఎత్తు నుంచి ఒక బంతిని నేలపైకి జారవిడిచారు. నేలతో అభిఘాతం జరిపిన ప్రతిసారి బంతి తన వేగంలో 10వవంతు కోల్పోతుంది. t = 0,12 s మధ్య బంతి గమనానికి సంబంధించి వడి కాలం గ్రాఫు గీయండి.
సాధన:
90 m ఎత్తు నుండి బంతి నిలువు అధో చలనంను భావిస్తే,
u = 0, a = 10 m/s², S = 90 m, t = ?, v = ?
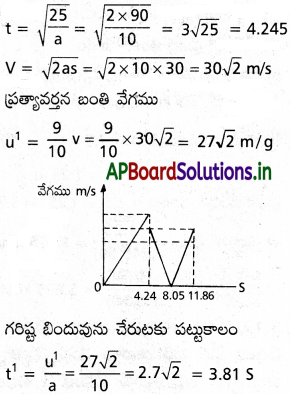
మొత్తం కాలం = = t + t¹ = 4.24 + 3.81 = 8.05 S
నేల = 2.7√2 m/s.
నేలకు తిరిగి రావటానికి పట్టుకాలం = 3.81 S
t¹ = \(\frac{u^1}{a}=\frac{27 \sqrt{2}}{10}\) = 2.7√2 m/s.
మొత్తం కాలం = t + t¹ = 4.24 + 3.81 = 8.05 S
నేలను తాకే ముందు బంతి వేగం = 2.7√2 m/s.
నేలను తాకిన తరువాత బంతి వేగం
= \(\frac{9}{10}\) × 27√2=24.3√2 m/s.
బంతి ఊర్ధ్వ చలనంనకు పట్టు మొత్తం కాలం
= 8.05 3.81 = 11.86 S
ఈ చలనంనకు సంబంధించిన వడి కాలం గ్రాఫ్ పటంలో చూపబడింది.
ప్రశ్న 13.
కింద ఇచ్చిన అంశాల మధ్య భేదాలను తగిన ఉదాహరణలతో స్పష్టంగా వివరించండి.
a) ఒకానొక కాలవ్యవధిలో స్థానభ్రంశపు పరిమాణం (ఒక్కొక్కప్పుడు దూరం అంటారు) ఆ కాలవ్యవధిలో కణం ప్రయాణించిన పథం పొడవు;
b) ఒకానొక కాలవ్యవధిలో సగటు వేగం పరిమాణం, అదే కాలవ్యవధిలో సగటు వడి. (ఒకానొక కావవ్యధిలో కణం ప్రయాణించిన మొత్తం పథం పొడవును ఆ కాలవ్యవధితో భాగించగా వచ్చే భాగఫలాన్ని సగటు వడిగా నిర్వచించడమైనది) (a), (b) లలో రెండవ రాశి (పథం పొడవు, సగటు వడి) మొదటి రాశి (స్థానభ్రంశ పరిమాణం, సగటు వేగ పరిమాణం) కంటే తక్కువ లేదా సమానంగా ఉంటుందని చూపండి. (సరళత కోసం, ఏకమితీయ గమనాన్ని మాత్రమే పరి గణించండి.)
సాధన:
a) కణం స్థాన భ్రంశ పరిమాణం, ఇచ్చిన కాలంలో తొలిమరియు తుది స్థానాల మధ్య కనిష్ట దూరంనకు సమానము. అదేకాలంలో కణం ప్రయాణించిన వాస్తవ మార్గంను మొత్తం పొడవుగా చెప్పవచ్చు. పటంలో చూపినట్లు కణం A నుండి Bకు మరియు B నుండి C కు t కాలంలో చలిస్తే, అప్పుడు స్థానభ్రంశ పరిమాణం = దూరం AC.
మొత్తం పదం పొడవు = దూరం AB + దూరం AC కావున మొత్తం పదం పొడవు (AB + AC) స్థాన భ్రంశం (AC) పరిమాణం కన్నా ఎక్కువ.
కణం చలనంను ఒకే దిశలో i. e., సరళరేఖ వెంట తీసుకుంటే, స్థానభ్రంశ పరిమాణం, కణం ప్రయాణించిన మొత్తం పొడవుకు సమానం.
b) సరాసరి వేగం పరిమాణం

మరియు సరాసరి వడి
(AB + AC) AC, కావున సరాసరి వడి, సరాసరి వేగ పరిమాణం కన్నా ఎక్కువ. కణం సరళరేఖ వెంట చలిస్తే, ఇచ్చిన కాలంలో స్థానభ్రంశ పరిమాణం, అదే సమయంలో కణం ప్రయాణించిన మొత్తం పొడవుకు సమానం. కావున సరాసరి వడి, సరాసరి వేగంనకు సమానము.

ప్రశ్న 14.
ఒక వ్యక్తి తిన్ననని రోడ్డుపై తన ఇంటి నుంచి 2.5 kmల దూరం ఉన్న మార్కెట్కు 5 km h-1. వడితో నడిచాడు. మార్కెట్ మూసి ఉండటం వల్ల వెంటనే వెనుదిరిగి ఇంటికి 7.5 km h-1. వడితో నడిచాడు. అతడి
a) సగటు వేగ పరిమాణం,
b) సగటు వడి (i) 0 నుంచి 30 నిమిషాల కాలవ్యవధిలో (ii) 0 నుంచి 50 నిమిషాల కాలవ్యవధిలో, (iii) 0 నుంచి 40 నిమిషాల కాలవ్యవధిలో ఎంతెంత ? [గమనిక : ఈ అభ్యాసం ద్వారా సగటు వేగ పరిమాణం కాకుండా, సగటు వడిని మొత్తం పథం పొడువు, కాలవ్యవధుల భాగఫలంగా నిర్వచించడం ఎందువల్ల ఉచితమో మీరు చక్కగా అవగాహన చేసుకొంటారు.]
సాధన:
ఇంటి నుండి మార్కెట్ను చేరుటకు పట్టుకాలం,

iii) 0 to 40 min
30 min లో ప్రయాణించు దూరం
(ఇంటి నుండి ‘మార్కెట్కు) = 2.5 km
10 min లో 7.5 km/h వడితో ప్రయాణించు దూరం
(మార్కెట్ నుండి ఇంటికి) = 7.5 × \(\frac{10}{60}\) = 12.5 km
స్థానభ్రంశం 2.5 – 1.25 = 1.25 km
ప్రయాణించిన దూరం = 2.5 + 1.25 = 3.75 km
ప్రశ్న 15.
3.13, 3.14 అభ్యాసాల ద్వారా సగటు వడి, సగటు వేగ పరిమాణాల మధ్య వ్యత్యాసాన్ని జాగ్రత్తగా అవగాహన చేసుకొని ఉంటారు. అయితే ఈ రకపు వ్యత్యాసాన్ని తత్కాల వడి, తత్కాల వేగాల మధ్య గుర్తించ వలసిన అవసరం లేదు. తత్కాల వడి ఎప్పుడూ తత్కాల వేగ పరిమాణానికి సమానం అవుతుంది. ఎందువల్ల?
సాధన:
ఏ క్షణానైన క్షణిక వడి దూరంలోని మార్పు రేటుకు కణం స్వల్పకాల సమానం. ie., vక్షణిక = \(\frac{dx}{dt}\) ప్రయాణంలో, దిశలో మార్పు లేకపోతే, dt కాలంలో ప్రయాణించిన మొత్తం పొడవు, స్థానభ్రంశ. పరిమాణంనకు సమానమగును. కావున క్షణిక వడి ఎల్లప్పుడు క్షణికవేగ పరిమాణంనకు సమానము.
ప్రశ్న 16.
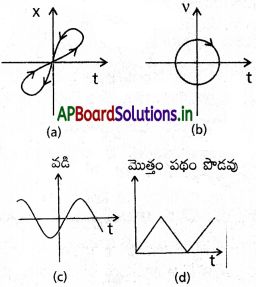
పటం లోని గ్రాఫులు (a) నుంచి (d) వరకు జాగ్రత్తగా గమనించండి. ఏ గ్రాపు కణం ఏకమితీయ గమనాన్ని సూచించదో కారణాలతో సహా తెలపండి.
సాధన:
a) ఈ గ్రాఫ్ ఏకమితీయ చలనంను సూచించదు. ఏదైనా కాలంలో కణం రెండు స్థానాలను కల్గి ఉండుట వల్ల ఏకమితీయ చలనం సాధ్యం కాదు.
b) ఈ గ్రాఫ్ ఏకమితీయ చలనంను సూచించదు. ఏదైనా కాలంలో కణం ధనాత్మక వేగం, రుణాత్మక దిశను కల్గి ఉండుట వల్ల ఏకమితీయ చలనం సాధ్యం కాదు.
c) ఈ గ్రాఫ్ ఏకమితీయ చలనంను సూచించదు. గ్రాఫ్ రుణాత్మక వడి కల్గి ఉండుటను చెబుతుంది. కాని కణం వడి ఎప్పుడు రుణాత్మకం కాదు.
d) ఈ గ్రాఫ్ ఏకమితీయ చలనంను సూచించదు. గ్రాఫ్ నిర్ణీత కాలం తరువాత మొత్తం పదం పొడవును తెల్పుతుంది. కాని కణం మొత్తం పదం పొడవు కాలంతో ఎప్పుడు తగ్గదు.
ప్రశ్న 17.
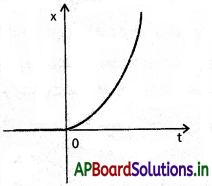
పటం లో ఒక కణం ఏకమితీయ గమనానికి x – t గ్రాఫ్ చూపడం జరిగింది. గ్రాఫ్ ద్వారా t < 0 అయినపుడు కణం సరళరేఖా మార్గంలో గమనంలో ఉన్నదనీ, t > 0 అయినపుడు పరావలయపథంలో గమనంలో వున్నదనీ అనడం సరియైనదేనా ? ఒక వేళ సరికాక పోతే, గ్రాఫ్ సూచించే తగిన భౌతిక సందర్భాన్ని తెలపండి.
సాధన:
కణం అనుసరించి పదంను x – t గ్రాఫ్ సూచించదు. గ్రాఫ్ నుండి t = 0, x 0 కావున కణం సరళరేఖలో ప్రయాణించదు.
కంటెస్ట్ :
పై గ్రాఫ్ శిఖరం నుండి స్వేచ్ఛగా గురుత్వాకర్షణకు లోనై చలించు వస్తువుకు సంబంధించిన గ్రాఫ్ను
సూచించును.

ప్రశ్న 18.
రహదారిపై 30 km h-1 వడితో గమనంలో ఉన్న పోలీసు వ్యాను నుంచి అదే దిశలో 192 km h-1 వడితో కారులో పారిపోతున్న దొంగలపైకి తుపాకీ గుండ్లను పేల్చారు. తుపాకి నుంచి వెలువడినగుండ్ల వడి 150 ms-1 అయితే, ఎంత వడితో తుపాకి గుండు దొంగల కారును తాకుతుంది? (గమనిక : దొంగల కారుకు హాని చేకూర్చే వడిని రాబట్టండి)
సాధన:
బుల్లెట్ వడి, υb = 150 m/s = 540 km h-1
పోలీస్ వాహనం వడి, υp = 30 km/h
దొంగ యొక్క కారు వడి υT = 192 km/h
పోలీస్ వాహనం దృష్ట్యా బుల్లెట్ సాపేక్ష వేగం
VB = υB + υp = 540 + 30 570 km/h
దొంగ కారు దృష్ట్యా అదే దిశలో చలించు బుల్లెట్ వడి
VBT = VB – υT
= \(\frac{378\times1000}{60\times60}\) = 105 m/s
ప్రశ్న 19.
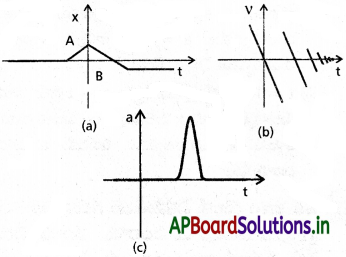
పటం లోని ప్రతి గ్రాపు ద్వారా సూచించే భౌతిక సందర్భాన్ని సూచించండి.
సాధన:
(a) పటంలో x – t గ్రాఫ్ x సున్నాను (i.e విరామస్థితి) సూచించును. కాలంతో పాటు దాని విలువ పెరిగి స్థిర విలువను చేరి, ఆ తరువాత కాలంతో తగ్గుతూ మరల సున్న చేరి, ఆ తరువాత వ్యతిరేకదిశలో అది స్థిర విలువను చేరి విరామస్థితికి వచ్చును.
(b) పటంలో, వేగం కాలంతో మరల, మరల వేగం మార్పు గుర్తు మారి మరియు ప్రతిసారి కొంత వడి కోల్పోవును.
(c) పటంలో, వస్తువు ఏకరీతి వేగంతో చలించుటను తెల్పును. స్వల్పకాలంలో త్వరణం పెరిగి, మరల సున్నకు తగ్గి, ఆ తరువాత వస్తువు స్థిరవేగంతో చలించుటను తెల్పును.
ప్రశ్న 20.
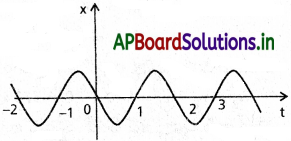
పటం ఏకమితీయ సరళహరత్మక గమనంలో ఉన్న ఒక x – t గ్రాపును చూపిస్తోంది. t = 0.3s, 1.2s,−1.2s వద్ద కణం చరరాశులు స్థానం, వేగం, త్వరణాల సంజ్ఞలను తెలపండి.
సాధన:
స.హ.చ.లో, త్వరణం a = ω²x, ఇచ్చట ω (i.e., కోణీయ పౌనఃపున్యం) స్థిరాంకం.
i) కాలం t = 0.35 వద్ద, × రుణాత్మకం, x – t వాలు రుణాత్మకం, కావున స్థానం మరియు వేగంలు రుణాత్మకం. a = ω²x, కావున త్వరణం ధనాత్మకం.
ii) t = 1.25 వద్ద, × ధనాత్మకము, x – t వాలు ధనాత్మకం, కావున స్థానం మరియు వేగంలు ధనాత్మకము. a = ω²x కావున త్వరణం
iii) t = 1.25 వద్ద, × రుణాత్మకం, x – t గ్రాఫ్ కూడ రుణాత్మకం. కాని x మరియు t లు రుణాత్మకము. కావున వేగం ధనాత్మకము. చివరకు ‘a’ కూడ ధనాత్మకము.
ప్రశ్న 21.
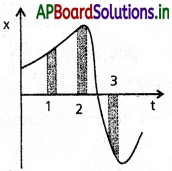
ఒక కణం యొక్క ఏకమితీయ గమనానికి x – t గ్రాపును పటంలోచూపించారు. మూడు వేరు వేరు సమాన కాలవ్యవధులను సూచించారు. ఏ కాలవ్యవధిలో సగటువడి గరిష్ఠం, ఏ కాలవ్యవధిలో సగటు వడి కనిష్ఠం? ప్రతి కాలవ్యవధిలో సగటు వేగపు సంజ్ఞను తెలపండి.
సాధన:
స్వల్పకాలవ్యవధిలో x – t గ్రాఫ్ వాలు, అదేకాలవ్యవధిలో సరాసరి వడికి సమానం. కాలవ్యవధిలో 3 లో సరాసరి వడి ఎక్కువ కారణం వాలు ఎక్కువ మరియు కాలవ్యవధి 2 లో సరాసరి వడి తక్కువ కారణం వాలు తక్కువ.
కాలవ్యవధి 1 మరియు 2ల మధ్య, x – t వాలు ధనాత్మకం. కావున సరాసరి వడి ధనాత్మకము. కాలవ్యవధి 3లో, x-tవాలు రుణాత్మకం. కావున సరాసరి వడి రుణాత్మకం.
ప్రశ్న 22.
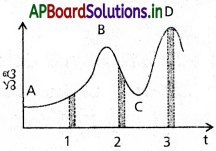
స్థిరమైన (ఒకే) దిశ వెంబడి గమనంలో ఉన్న ఒక కణం గమనానికి వడి-కాలం గ్రాఫ్ పటంలో చూపించారు. మూడు సమాన కాల వ్యవధులు చూపించారు. ఏ కాలవ్యవధిలో సగటు త్వరణం పరిమాణం గరిష్ఠం ఝ ఏ కాలవ్యవధిలో సగటు వడి గరిష్ఠం? (స్థిర దిశ గల) గమన దిశను ధన దిశగా ఎంచుకుని v, a ల సంజ్ఞలను మూడు కాలవ్యవధులలోనూ తెలపండి. A, B, C, D బిందువుల వద్ద త్వరణాలు ఏమిటి?
సాధన:
స్వల్పకాల వ్యవధిలో వేగం-కాలం వాలు సరాసరి త్వరణంనకు సమానం. వ్యవధులు 1 మరియు 3 లతో” పోల్చిన వ్యవధి 2 లో వేగం-కాలం గ్రాఫ్ వాలు గరిష్టం. కావున సరాసరి త్వరణ పరిమాణం వ్యవధి 2 లో ఎక్కువ. సరాసరి వడి వ్యవధి 3లో ఎక్కువ.
వ్యవధి 1లో, వేగం -కాలం గ్రాఫ్ వాలు ధనాత్మకం, కావున త్వరణం a ధనాత్మకం. వడి u, ఈ కాలవ్యవధిలో ధనాత్మకం. వ్యవధిలో2, వేగం-కాలం గ్రాఫ్ వాలు రుణాత్మకం, కావున త్వరణం రుణాత్మకం. వడి u, ఈ కాలవ్యవధిలో ధనాత్మకం. వ్యవధి 3 లో, వేగం -కాలం గ్రాఫ్ కాలం అక్షంనకు సమాంతరం. త్వరణం సున్న కాని v ధనాత్మకం.
A, B, C మరియు D బిందువుల వద్ద, వేగం-కాలం గ్రాఫ్ కాలం అక్షంనకు సమాంతరం. అన్ని నాల్గు బిందువుల వద్ద త్వరణం a సున్న.
అదనపు లెక్కలు (Additional Problems)
ప్రశ్న 23.
ఒక ఆటో (మూడు చక్రాల వాహనం) నిశ్చల స్థితి నుంచి బయలుదేరి, తిన్నని రోడ్డుపై, 10 5 పాటు 1 ms-2 సమత్వరణంతోను, అటుపై సమవేగంతో గమనంలో ఉంది. వాహనం n వ సెకనులో (n = 1, 2, 3, ………….) ప్రయాణించిన దూరానికీ n కూ మద్య గ్రాపు గీయండి. వాహనం త్వరణంతో ప్రయాణించిన కాలంలో గ్రాపు ఆకారం ఎలా ఉండవచ్చో ఊహించండి. ఒక సరళరేఖా? లేదా ఒక పరావలయమా?
సాధన:
ఇక్కడ u = 0, a = 1 m/s²
n వ సెకండ్లో ప్రయాణించిన దూరం
Dn = u + \(\frac{a}{2}\)(2n – 1) = 0 + \(\frac{1}{2}\) (2n – 1) = 0.5
(2n – 1)
n = 1, 2, 3, …………… ప్రతిక్షేపించి Dn విలువ కనుక్కోవచ్చును. n వేర్వేరు విలువలు మరియు వానికి సంబంది Dn విలువలు పట్టికలో క్రింద చూపబడినవి.
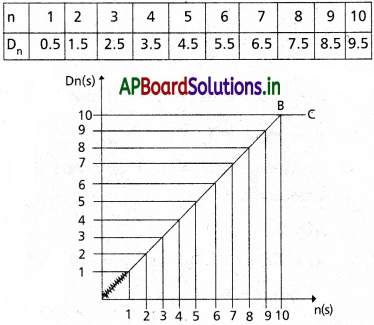
Dn మరియు n లకు గ్రాఫ్ గీసి పటంలో చూపినట్లు AB సరళరేఖను పొందవచ్చును. (1) నుండి, Dn∝n గ్రాఫ్ సరళరేఖ. 10S తరువాత గ్రాఫ్ కాలం అక్షానికి సమాంతరంగా ఉన్న సరళరేఖ BC.
ప్రశ్న 24.
నిశ్చలంగా ఉన్న పై కప్పు లేని లిఫ్ట్ లో నిలబడిన ఒక బాలుడు ఒక బంతిని నిట్టనిలువుగా అతడు విసరగలిగిన గరిష్ఠ తొలి వడి 49 ms-1 తో విసిరాడు. అతని చేతిలోకి తిరిగి చేరడానికి బంతికి ఎంత సమయం పడుతుంది? లిఫ్టు, సమవడి 5 ms-1తో పై దిశలో కదులుతూ ఉన్నప్పుడు తిరిగి ఆ బాలుడు అతడు విసర గలిగిన గరిష్ఠ వడితో (49 ms-1) బంతిని పైకి విసిరితే అతని చేతిలోకి తిరిగి చేరడానికి బంతి తీసుకొనే సమయం ఎంత?
సాధన:
నిలువు ఊర్ధ్వదిశను X అక్షం ధనాత్మక దిశగ తీసుకుందాము. లిఫ్ట్ నిశ్చలంగా ఉన్నప్పుడు, బంతి నిలువుగా ఊర్ధ్వ దిశలో చలించి బాలుని చేతిలోనికి చేరినట్లు భావిద్దాము.
u = 49 m/s, a = 9.8m/s², t = ? x – x0 = S = 0
S = ut + \(\frac{1}{2}\) at²
0 = 49 t + \(\frac{1}{2}\)(-9.8)t² లేదా 49t = 4.9 t² లేదా
t = 49/4.9 = 10 sec
లిఫ్ట్ స్థిరవడితో చలించినపుడు :
లిఫ్ట్ స్థిరవడి 5 m/s తో ఊర్వదిశలో చలిస్తే, బాలుని దృష్ట్యా బంతి సాపేక్ష వేగం మారదు. అది 49 ms1. కల్గి ఉండును. కావున, ఈ సందర్భంలో, బంతి 10 సెకండ్ల తరువాత బంతి బాలుని చేతిలోనికి చేరును.
ప్రశ్న 25.
ఒక పొడవైన, క్షితిజ సమాంతరంగా కదిలే, బెల్ట్ (పటం) పైన 50m దూరంలో నిలబడిన తన తండ్రి, తల్లి స్థానాల మధ్య ముందుకూ, వెననకూ బెల్ట్ పరంగా 9 km h-1 వడితో ఒక బిడ్డ పరుగెడుతున్నాడు. బెల్ట్ 4 km h-1 వడితో కదులుతున్నది. బెల్టు ఆవల స్థిరమైన ప్లాట్ ఫాంపై నిలబడి ఉన్న పరిశీలకుడికి,
a) బెల్ట్ గమన దిశలో బిడ్డ పరుగెడుతున్నప్పుడు బిడ్డ వడి ఎంత?
b) బెల్ట్ గమనదిశకు వ్యతిరేక దిశలో బిడ్డ పరెగెడుతున్నప్పుడు బిడ్డ వడి ఎంత?
c) (a), (b) లలో తీసుకొనే సమయమెంత? తల్లి లేదా తండ్రి పరంగా చూసినప్పుడు పై ప్రశ్నల సమాధానాలలో దేని సమాధానం మారుతుంది?
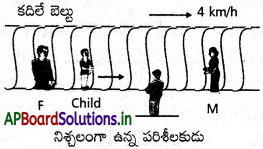
సాధన:
ఎడమ నుండి కుడివైపు x-అక్షం ధనాత్మక దిశగ భావిద్దాం.
a) బెల్టు వేగం, υB = + 4 km/h-1;
బెల్టు దృష్ట్యా పిల్లవాని వడి,
υC= + 9 km/h = \(\frac{5}{2}\)m/s-1
నిశ్చల పరిశీలనకుని దృష్ట్యా పిల్లవాని వడి,
υC¹ = υC + υB = 9 + 4 = 13 km/h-1
b) ఇక్కడ υB = + 4 km/h, υC = -9 km/h
నిశ్చల పరిశీలకుని దృష్ట్యా పిల్లవాని వడి,
υC¹ = υC + υB = -9 + 4 = -5 km/h-1
బెల్టుచలనదిశకు వ్యతిరేకంగా పిల్లవాడు పరిగెత్తుటకు రుణగుర్తు సూచించును.
c) తల్లిదండ్రుల మధ్యదూరం, S = 540 m
తల్లిదండ్రులు మరియు పిల్లవాడు అదే బెల్టుపై ఉన్నప్పుడు, నిశ్చలంగా ఉన్న పరిశీలకుని దృష్ట్యా (తల్లివైపు లేక తండ్రి వైపు నుండి), పిల్లవాని వడి 9 km/h.
(a) మరియు (b) సందర్భంలో పిల్లవానికి పట్టుకాలం
t = \(\frac{50}{(5/2)}\) = 20 S
తల్లిదండ్రులలో ఒకరు చలనంను పరిశీలిస్తే సందర్భము (a) లేక సందర్భం (b) సమాధానాలు ఒకదానికొకటి మారును. అందువల్ల తల్లి లేక తండ్రి దృష్ట్యా పిల్లవాని వడి 9 km/h కాని సమాధానం (C) మారదు. కారణం తల్లి, తండ్రి మరియు పిల్లవాడు అదే బెల్టుపై ఉండుట వల్ల, బెల్టు చలనం వల్ల అందరు ఒకే ప్రభావంను కల్గి ఉంటారు.

ప్రశ్న 26.
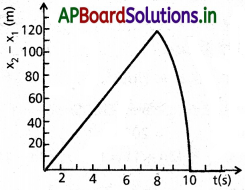
200m ఎత్తున ఒక కొండచరియ అంచు నుంచి రెండు రాళ్ళను ఏకకాలంలో నిట్టనిలువుగా, వరసగా 15 ms-1, 30 ms-1 వడులతో పైకి విసిరారు.మొదటి రాయితో పోల్చినపుడు రెండవ రాయి సాపేక్ష స్థానం కాలంతో ఎలా మార్పు చెందుతున్నదో సూచించే గ్రాఫ్ను పటంలో చూపించారు. ఈగ్రాఫ్ సరిగా ఉందని నిరూపిం చండి. గాలి నిరోధాన్ని ఉపేక్షించి, భూమికి తాకిన రాయి తిరిగి వెనక్కి ప్రయాణించదు అని భావించండి. g = 10 ms-2 గా తీసుకోండి. గ్రాఫ్లోని సరళరేఖా భాగానికి, వక్ర భాగానికి సమీకరణాలు తెలపండి.
సాధన:
నిలువు ఊర్థ్వ దిశలో మొదటి రాయి t కాలం చలనం తీసుకుందాము.
x0 = 200 m, u = 15 m/s, a = -10 m/s², t = t1,
x = x1
x = x0 + \(\frac{1}{2}\)ut²
x1 = 200 + 15t + \(\frac{1}{2}\)(-10)t² లేదా
x1 = 200 + 15 t – 5t² ………… (i)
నిలువు ఊర్ధ్వ దిశలో రెండవ రాయి t కాలం చలనం తీసుకుందాము.
అప్పుడు
x0 = 200 m, u = 30 m/s-1, a = = -10 m/s-2,
t = t1, x = x2
అప్పుడు x2 = 200 + 30 t – \(\frac{1}{2}\) × 10 t²
= 200 + 30 t – 5t²
మొదటి రాయి భూమిని తాకితే,
x1 = 0, So t² – 3t – 40 = 0
లేదా (t – 8) (t + 5) = 0 ………… (ii)
∴ t = 8 S లేదా – 5S
t = 0 రాయి ప్రక్షిప్తం చేసిన కాలంనకు సంబంధించినది. కావున రుణకాలంనకు అర్థం లేదు. ఈ సందర్భంలో t = 8S.
రెండవ రాయి భూమిని తాకితే, x2 = 0.
0 = 200 + 30 t – 5t² (లేదా) t² – 6t – 40 = 0
(లేదా) (t – 10) (t + 4) = 0
t = -4s కు అర్థం లేదు. కావున t = 10 s
మొదటిరాయి దృష్ట్యా రెండవరాయి సాపేక్షస్థానం
= x2 – x1 = 15 t ………….. (ii)
(i) మరియు (ii) నుండి
(x2 – x1) మరియు t లు రేఖియ సంబంధంను కల్గి ఉండును. గ్రాఫ్ t = 8s వరకు సరళరేఖను ఇస్తుంది.
t = 8 S లకు రెండు రాయిల మధ్య గరిష్ట దూరం = 15 × 8 = 120 m
8 సెకనుల తరువాత రెండవ రాయి 2 సెకనుల వరకు చలనంలో ఉండి, కాలవ్యవధి 8 సెకనుల నుండి 10 సెకనుల వరకు x = 200 + 30 – 5t² వర్గ సమీకరణం గ్రాఫ్ను కల్గి ఉండును.
ప్రశ్న 27.
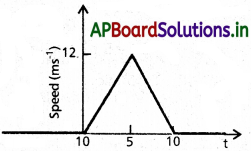
ఒక స్థిర దిశ కలిగి సరళరేఖపై గమనంలో ఉన్న ఒక కణం గమనాన్ని తెలిపే వడి కాలం గ్రాఫ్ను పటంలో చూపించారు. (a) t = 0 s to 10 s, (b) t = 2s నుంచి 6s. మధ్య కణం ప్రయాణించిన దూరాలను లెక్కగట్టండి. (a), (b) లలో (ఆ కాలవ్యవధిలలో) కణం సగటు వడి ఎంత?
సాధన:
a) 0 నుండి 10 సెకనుల మధ్య కణం ప్రయాణించు దూరం
= ఆధారం 10s మరియు ఎత్తు 12 ms-1 గల
∆ OAB వైశాల్యం.
\(\frac{1}{2}\) × 10 × 12 = 60 m
సరాసరి వడి = \(\frac{60}{10}\) = 6mS-1
b) t1 = 2S నుండి 5s మరియు t2 = 5s నుండి 6s వరకు కణం ప్రయాణించిన దూరాలు వరుసగా s1 మరియు s2 t = 2s నుండి 6s వ్యవధిలో మొత్తం ప్రయాణించు దూరం s = s1 + s2 …………… (i)
s1 కనుగొనుట :
2 సెకనుల తరువాత కణం వేగం 4, మరియు కాలం సున్న నుండి 5 సెకనుల వ్యవధిలో కణం త్వరణం a1.
అప్పుడు u1 = 0, v = 12 m/s,
a = a1 మరియు t = 5s
a1 = \(\frac{v-u}{t}=\frac{12-0}{5}=\frac{12}{5}\)
= 2.4 m/s²
∴ u1 = υ + a1t = 0 + 2.4 × 2 = 4.8 m/s-1
కణం 3s లలో ప్రయాణించిన దూరం
(i.e., కాలవ్యవధి 2s నుండి 5s).
∴ u1 = 4.8 m/s, t1 = 3s, a1 = 2.4 m/s², s1 = ?
s1 = u1t1 + \(\frac{1}{2}\)a1t1²
S1 = 4.8 + 3 × \(\frac{1}{2}\) × 2.4 × 3² = 25.2 m
s2 కనుగొనుట :
t = 5s నుండి t = 10s ల మధ్య కణం త్వరణం a2.
a2 = \(\frac{0-12}{10-5}\) = -2.4 m/s²
t = 5s నుండి t = 6s ల మధ్య కణం చలనం తీసుకుందాము.
u1 = 12 m/s-1, a2 = -2.4 m/s²
t2 = 1s, s2 = ?
s2 = u2t + \(\frac{1}{2}\)a2t2²
s2 = 12 × 1 + \(\frac{1}{2}\)(-2.4) 1² = 10.8 m
∴ మొత్తం ప్రయాణించిన దూరం,
s = 25.2 + 10.8 = 36 m
సరాసరి వేగం = \(\frac{36}{6-2}=\frac{36}{4}\) = 9 m/s
ప్రశ్న 28.
ఏకమితీయ గమనంలో ఉన్న ఒక కణం వేగం- కాలం గ్రాపును పటం 3.29లో ఇచ్చారు. t1 నుంచి t2 కాలవ్యవధిలో కణం గమనాన్ని వర్ణించే సరియైన ఫార్ములాను కింది వాటి నుంచి ఎంపిక చేయండి.
a) x(t2) = x(t1) + v(t1) (t2 – t1) + \(\frac{1}{2}\)a(t2 – t1)²
b) v(t2) = v(t1) + a(t2 – t1)
c) vసగటు = (x(t2) − x(t1)) / (t2 – t1)
d) vసగటు = (v(tz) – v(t,)) / (t) – t, )
e) x(t2) = x(t1) + vసగటు (t2 – t1) + (\(\frac{1}{2}\))సగటు(t2 – t1)²
f) x(t2) = x(t1) = t-అక్షం, చుక్కల గీత మధ్య v – t వక్రంతో ఆవరించిన వైశాల్యం.
సాధన:
గ్రాఫ్ నుండి వాలు స్థిరం కాదు మరియు ఏకరీతిగా ఉండదు. కావున (i), (ii) మరియు (v) ల సంబంధాలు నిజము కాదు. కాని (iii), (iv), మరియు (vi) లు నిజము.
సాధించిన సమస్యలు (Solved Problems)
ప్రశ్న 1.
ఒక కారు ఒక సరళరేఖ వెంబడి OP అనుకుందాం, గమనంలో ఉన్నది. అది 18s లలో O నుంచి P బిందువును చేరి మరల P నుంచి బిందువు Q ను 6.0sలలో చేరింది. (a) O నుంచి P ను చేరినప్పుడు, (b) O నుంచి P ను, అటు నుంచి వెనుదిరిగి Q ను చేరినప్పుడు వస్తువు సగటు వేగం, సగటు వడి విలువ లేమిటి?
సాధన:
ఈ సందర్భంలో సగటు వడి సగటు వేగ పరిమాణానికి సమానం
b) ఈ సందర్భంలో


ప్రశ్న 2.
x అక్షం వెంబడి గమనంలో ఉన్న ఒక వస్తువు స్థానం x = a + bt² గా ఇవ్వడమైనది. ఇక్కడ a = 8.5 m, b = 2.5 ms-2, t ను సెకండ్లలో కొలిచారు. t = 0s, t = 2.0s వద్ద వేగం ఎంత? t = 2.0s, t = 4.0s మధ్య సగటు వేగం ఎంత?
సాధన:
అవకలన కలన గణితం సంకేత పద్ధతిలో వేగం

ప్రశ్న 3.
కలన గణిత పద్ధతిని ఉపయోగించి స్థిర త్వరణం గల గమనానికి సమీకరణాలను ఉత్పాదించండి.
సాధన:
నిర్వచనాన్నిబట్టి a = \(\frac{dυ}{dt}\)
dυ = a dt
ఇరువైపులా సమాకలనం చేస్తే


ప్రశ్న 4.
ఒక బహుళ అంతస్థు పై భాగం నుంచి ఒక బంతిని నిట్టనిలువుగా పైకి 20 ms-1 వేగంతో విసిరారు. బంతిని విసిరిన బిందువు భూమి నుంచి 25.0 m ఎత్తున ఉంది. (a) బంతి ఎంత ఎత్తుకు ఎగురుతుంది? (b) విసిరిన తరువాత బంతి భూమిని తాకడానికి ఎంత కాలం పడుతుంది? g = 10 ms-2 గా తీసుకోండి. (g నిజవిలువ 9.8 ms-2).
సాధన:
a) నిట్టనిలువు దిశలో y-అక్షాన్ని, భూమి సున్నా నిరూపకంగా పటంలో చూపించినట్లు తీసుకొందాం.
ఇప్పుడు υ0 = + 20 ms-1
a = -g = -10 ms-2,
υ = 0 ms-1
విసిరిన బిందువు నుంచి బంతి y ఎత్తును చేరింది అనుకొంటే
υ² + υo² + 2a(y − yo) సమీకరణాన్ననుసరించి 0 = (20)² + 2(−10) (y – yo) ను పొందుతాం.
దీన్ని సాధిస్తే (y – yo) = 20 m వస్తుంది.
b) సమస్యలోని ఈ భాగాన్ని మనం రెండు పద్ధతులలో సాధించవచ్చు. పద్ధతులను చాలా జాగ్రత్తగా గమనించండి.
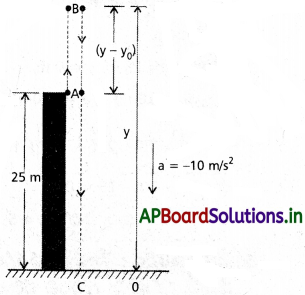
మొదటి పద్ధతి :
ఈ పద్ధతిలో మార్గాన్ని రెండు భాగాలుగా విడదీస్తాం. పై దిశలో గమనం (A నుంచి Bవరకు), కింది దిశలో గమనం (B నుంచి C వరకు). ఈ గమనాలకు సంబంధించిన కాలాలు t1, t2 లను లెక్కిస్తాం. B వద్ద వేగం శూన్యం అవుతుంది. కాబట్టి :
υ = υo + at
0 = 20 – 10 t1
(∵ a = −g = – 10 ms-2)
లేదా t1 = 2s వస్తుంది.
ఈ కాలాన్ని A నుంచి Bని చేరడానికి తీసుకొంటుంది. బిందువు B నుంచి లేదా గరిష్ఠ ఎత్తు వద్ద బిందువు నుంచి, బంతి స్వేచ్ఛగా గురుత్వత్వరణంతో కిందికి పడుతుంది. బంతి రుణ y-అక్షము దిశలో కదులుతుంది.
y = yo + υot + \(\frac{1}{2}\)at² సమీకరణాన్ని ఉపయోగిస్తాం.
yo = 45 m, y = 0, υo = 0, a = -g = -10 ms-2 అని మనకు తెలుసు.
0 = 45 + (\(\frac{1}{2}\))(-10) t2²
సాధిస్తే, t2 = 3s వస్తుంది.
అందువల్ల విసిరిన తరువాత బంతి బూమిని చేరేలోపు పట్టిన కాలం = t1 + t2 = 2s + 3s = 5s
రెండవ పద్ధతి (Second Method) :
ఎంచుకొన్న మూలబిందువు పరంగా బంతి తొలి, తుది స్థానాల నిరూపకాలను గుర్తించి బంతి భూమిని చేరడానికి తీసుకొన్న మొత్తం కాలాన్ని
y = yo + υot + \(\frac{1}{2}\) at² సమీకరణాన్ని ఉపయోగించి లెక్కించవచ్చు.
ఇప్పుడు yo = 25 m, y = 0 m
υo = 20 ms-1, a = -10 ms-2, t = ?
0 = 25 + 20t + (\(\frac{1}{2}\))(-10)t²
లేదా 5t² – 20t – 25 = 0
ఈ వర్గ సమీకరణాన్ని సాధిస్తే, t = 5s వస్తుంది.

ప్రశ్న 5.
స్వేచ్ఛాపతనం : స్వేచ్ఛగా పతనం చెందే ఒక వస్తువు గమనాన్ని గురించి చర్చించండి. గాలి నిరోధాన్ని ఉపేక్షించండి.
సాధన:
భూ ఉపరితలం పై నుంచి ఒక వస్తువును జారవిడిస్తే అది గురుత్వబల ప్రభావం వల్ల నిమ్న చెందుతుంది. గురుత్వత్వరణం పరిమాణాన్ని 9 తో సూచిస్తారు. గాలి నిరోధాన్ని ఉపేక్షించినట్లయితే వస్తువు స్వేచ్ఛాపటనం చెందుతున్నదని అంటారు. వస్తువు ఎంత ఎత్తు నుంచి పతనం చెందుతున్నదో ఆ ఎత్తును భూ వ్యాసార్ధంతో పోల్చినప్పుడు చాలా తక్కువగా ఉంటే g విలువను స్థిరాంకంగా 9.8 ms-2 కు సమానంగా తీసుకోవచ్చు. అందువల్ల స్వేచ్ఛాపతన గమనాన్ని ఏకరీతి (సమరీతి) త్వరణం గల గమనంగా తీసుకోవచ్చు. గమనం y-దిశలో, ఇంకా కచ్చితంగా రుణ y దిశలో ఉన్నట్లుగా అనుకొందాం. ఎందువల్ల అంటే ఊర్ధ్వ దిశను ధనాత్మకంగా ఎంచుకొందాం. గురుత్వ త్వరణం ఎప్పటికీ నిమ్నదిశలోనే ఉండటం వల్ల అది రుణ దిశలోనే ఉంటుంది. అందువల్ల
a = – g = -9.8 ms-2
y = 0 నుంచి, వస్తువును నిశ్చల స్థితి నుంచి జారవిడిచారు. అందువల్ల υo = 0 అప్పుడు గమన సమీకరణాలు కింద ఇచ్చినట్లుగా మారతాయి.
υ = 0 – gt = -9.8 t ms-1
y = 0 – \(\frac{1}{2}\)gt² = -4.9 t² m
υ² = 0 – 2 gy = -19.6 ym²s-2
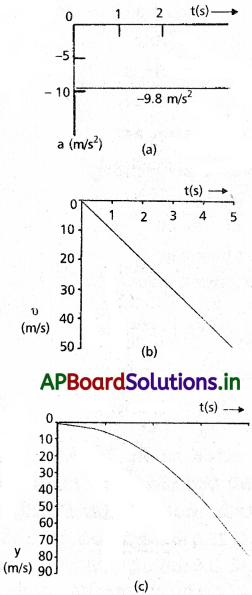
మొదటి సమీకరణం వేగాన్ని కాలప్రమేయంగా రెండవ సమీకరణం ప్రయాణించిన దూరాన్ని కాల ప్రమేయంగా తెలుపుతున్నాయి. మూడవ సమీకరణం వేగాన్ని దూరం ప్రమేయంగా తెలుపుతున్నది. కాలంతో త్వరణంలో మార్పును, వేగంలో మార్పును, దూరంలో మార్పును వరసగా పటాలు (a), (b), (c) లలోని వక్రాలు సూచిస్తున్నాయి.
ప్రశ్న 6.
గెలీలియో బేసి సంఖ్యల నియమం (Galileo’s | సాధన. law of odd numbers) : “నిశ్చల స్థితి నుంచి స్వేచ్ఛగా పతనం చెందే వస్తువు వరస సమానకాలవ్యవధులలో ప్రయాణించే దూరాల నిష్పత్తి ఒకటితో మొదలయ్యే బేసి సంఖ్య నిష్పత్తికి సమానం దీన్ని నిరూపించండి.
సాధన:
ఒక వస్తువు స్వేచ్ఛగా పతనం చెందిన కాలవ్యవధిని అనేక సమాన కాలవ్యవధులు τ విభజించి, వరస కాలవ్యవధుల్లో ప్రయాణించిన దూరాలను లెక్కించండి. తొలి వేగం శూన్యం కాబట్టి y = –\(\frac{1}{2}\)gt² అవుతుంది. ఈ సమీకరనాన్ని ఉపయోగించి వివిధ కాలవ్యవధుల, 0, τ, τ2, τ3 .. తరువాత వస్తువు స్థానాన్ని లెక్కించి రెండ నిలువు వరసలో పొందు పరచడమైంది. yo (-1/2) gτ² ను మొదటి కాలవ్యవధి τ తరువాత స్థాన నిరూపకం (y0) గా తీసుకొంటే, మూడవ నిలువ వరుస (yo) ప్రమాణాల్లో వస్తువు స్థానాలను ఇస్తుంది. వరస కాలవ్యవధులు τs లలో వస్తువు ప్రయాణించిన దూరాలను నాలుగో నిలువు వరుస సూచిస్తుంది. పట్టికలోని చివరి వరసలో దూరాల నిష్పత్తి సరళంగా 1 : 3 : 5 : 7 : 9 : 11 ……….గా ఉంటుందని గుర్తిస్తాం.
వస్తువుల స్వేచ్ఛా పతన గమనాన్ని గుణాత్మకంగా మొదటగా అధ్యయనం చేసిన గెలీలియా గలీలీ (Galileo Galilei) (1564–1642) ఈ నియమాన్ని రుజువు చేశాడు.
ప్రశ్న 7.
వాహనాల నిలిచే దూరం (Stopping distance of vehicles) : బ్రేకు పడిన తరవాత నిలిచిపోయే ముందు వాహనం ప్రయాణించిన దూరాన్ని నిలిచే దూరం అంటారు. రోడ్డు రవాణా భద్రతకు అత్యంత ప్రాముఖ్యంగల ఈ దూరం వాహనం తొలి (బ్రేకు వేయడానికి పూర్వం) వేగం (υo), బ్రేకింగ్ సామర్థ్యం లేదా బ్రేకు వేయడం వల్ల కలిగే రుణత్వరణం (-a) పై ఆధారపడి ఉంటుంది. ఒక వాహనం నిలిచే దూరానికి υo, a పదాలలో సమాసాన్ని రాబట్టండి.
సాధన:
వాహనం నిలిచిపోవడానికి ముందు అది ప్రయాణించిన దూరం (నిలిచే దూరం) ds అనుకొందాం. గమన సమీకరణం υ = υo² + 2 ax నుంచి υ = 0 అని గుర్తిస్తే, నిలిచే దూరం
ds = \(\frac{-v_0^2}{2 a}\)
ఈవిధంగా నిలిచే దూరం తొలివేగం (υo) వర్గానికి అనులోమానుపాతంలో ఉంటుంది. తొలివేగాన్ని రెట్టింపు చేస్తే నిలిచే దూరం (అదే రుణ త్వరణం విలువకు) 4 రెట్లు అవుతుంది.
ఒక నిర్దిష్టమైన పద్ధతిలో తయారయిన కారుకు 11, 15,20, 25 m/s వేగాలకు అనురూపంగా బ్రేకులు వేసినప్పుడు ఆగిన దూరాలు వరసగా 10 m, 20 m, 34 m, 50 m అని కనుక్కోవడం జరిగింది. ఈ విలువలు పైన ఉత్పాదించిన సమాసానికి దాదాపు అనుగుణంగాను ఉన్నాయి.
ప్రశ్న 8.
ప్రతిస్పందన కాలం (Reaction time) : పరిస్థితిని అనుసరించి తక్షణ చర్య తీసుకోవలసిన అవసరం ఏర్పడినప్పుడు చర్య తీసుకోవడానికి కొంత సమయం పడుతుంది. ఒక వ్యక్తి అక్కడ ఉన్నస్థితిని గమనించడానికి, ఆపై ఆలోచించి, తగిన చర్య తీసుకోవడం ప్రారంభించడానికి పట్టే కాలాన్ని ప్రతిస్పందన కాలం అంటారు. ఉదాహరణకు కారు నడిపే వ్యక్తి హఠాత్తుగా దారికి అడ్డంగా వచ్చిన బాలుణ్ణి చూసి దభాలున బ్రేకులు వేసేలోపు గడిచిన కాలమే ప్రతిస్పందన కాలం. ప్రతిస్పందన కాలం పరిస్థితి సంక్లిష్టతమైనా, పరిస్థితిని ఎదురుకొనే వ్యక్తిపైనా ఆధారపడి ఉంటుంది.
మీరు మీ ప్రతిస్పందన కాలాన్ని ఒక సులభమైన ప్రయోగం ద్వారా లెక్కించవచ్చు. ఒక రూళ్ళ కర్రను మీ స్నేహితునికిచ్చి, దానిని మీ చేతి బొటనవేలు, చూపుడు వేలు మధ్య ఉన్న ఖాళీ ద్వారా నిట్టనిలువుగా జారవిడవమని చెప్పండి (పటం). అలా విడిచిన రూళ్ళ కర్రను మీరు పట్టుకొన్న తరవాత అది ప్రయాణించిన దూరం d కనుక్కోండి. ఒక ప్రత్యేక ప్రయోగంలో d. విలువ21:0 cm గా కనుక్కొన్నారు. ప్రతిస్పందన కాలం లెక్కించండి.

సాధన:
రూళ్ళకర్ర స్వేచ్ఛగా పతనం చెందుతుంది. అందువల్ల, υo = 0 and a = -g = -9.8 ms-2. రూళ్ళకర్ర ప్రయాణించిన దూరం d, ప్రతిస్పందన కాలం t, ల మధ్య సంబంధం తెలిపే సమాసం
d = –\(\frac{1}{2}\) gt²r లేదా tr = \(\sqrt{\frac{2d}{g}}\)s.
ప్రయోగం ద్వారా తెలిసిన d విలువ 21.0 cm,
g = 0.8 ms-2
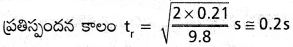

ప్రశ్న 9.
ఉత్తర – దక్షిణ దిశలో రెండు సమాంతర రైలు మార్గాలున్నాయి. రైలు A 54 km h-1 వడితో ఉత్తరం వైపు, రైలు B 90 kmh-1 వడితో దక్షిణం వైపు ప్రయాణిస్తున్నాయి.
a) A పరంగా B వేగం ఎంత?
b) B పరంగా భూమి వేగం ఎంత?
c) రైలు A పైకప్పుపై 18 kmh-1 వేగంతో రైలు వేగానికి వ్యతిరేక దిశలో పరుగెడుతున్న కోతి సాపేక్ష వేగం భూమిపై నిల్చున్న పరిశీలకుడి పరంగా ఎంత?
సాధన:
దక్షిణం నుంచి ఉత్తరం వైపు ధన x-axis దిశగా ఎంచుకొందాం. అప్పుడు,
υA = + 54 km h-1 = 15 ms-1
υB = – 90 km h-1 = -25ms-1
A పరంగా B సాపేక్ష వేగం = υB – υA = – 40 ms-1, అంటే రైలు A పరంగా రైలు B 40 ms1 వడితో ఉత్తరం నుంచి దక్షిణంవైపు ప్రయాణిస్తున్నట్లు అనిపిస్తుంది. రైలు B పరంగా భూమి సాపేక్ష వేగం
= 0 – υB = 25 ms-1.
భాగం (c) లో భూమి పరంగా కోతి వేగం υM అనుకొందాం. రైలు A పరంగా కోతి సాపేక్షవేగం
υMA = υM – υA = – 18 km h– = -5 ms-1
అందువల్ల υM = (15 – 5)ms-1 = 10 ms-1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
































































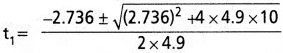

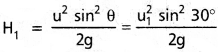




 నిజము.
నిజము.