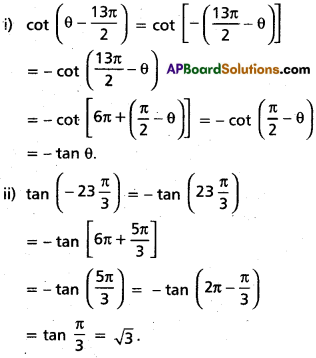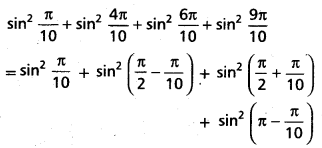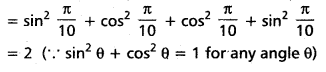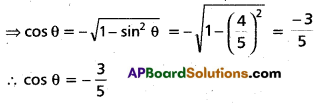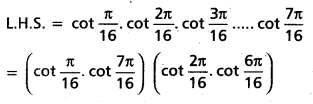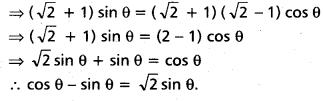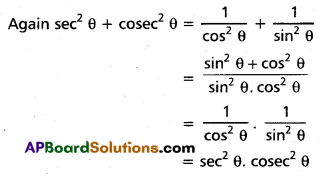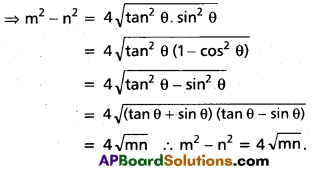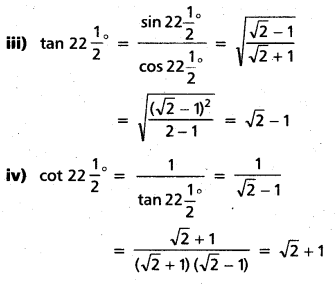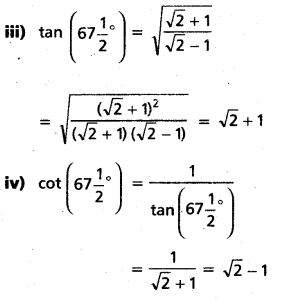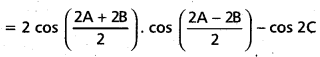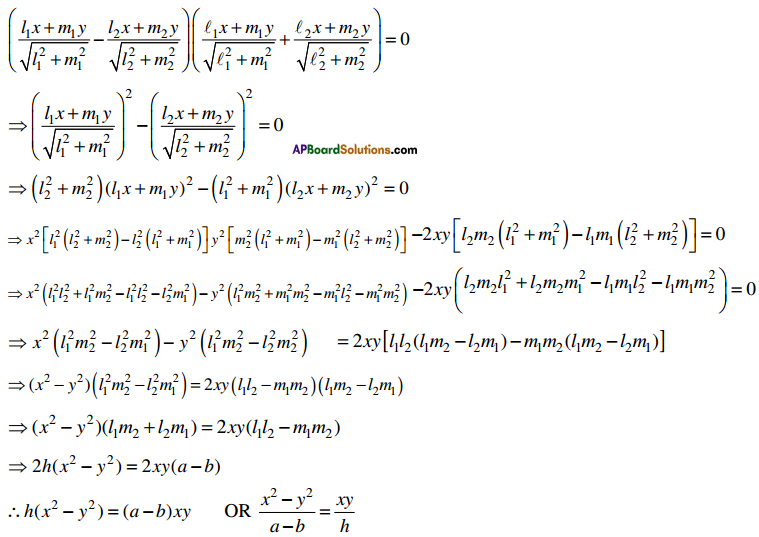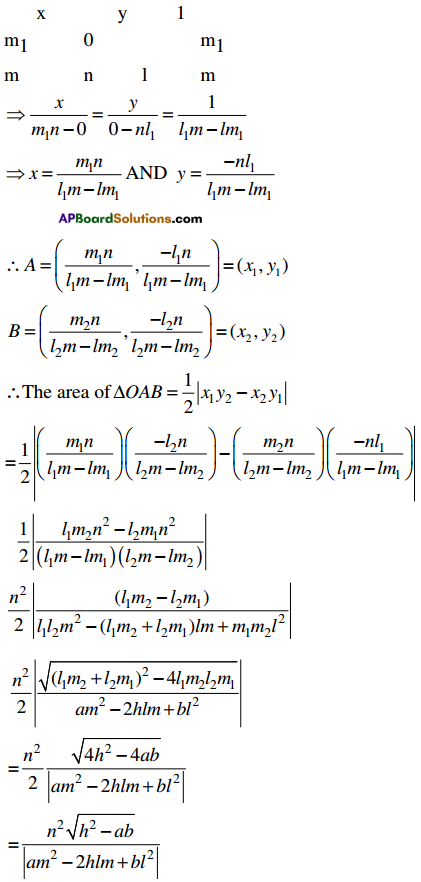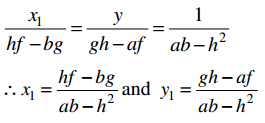Inter 1st Year

Students can go through AP Inter 1st Year Botany Notes 7th Lesson పుష్పించే మొక్కలలో లైంగిక ప్రత్యుత్పత్తి will help students in revising the entire concepts quickly.

AP Inter 1st Year Botany Notes 7th Lesson పుష్పించే మొక్కలలో లైంగిక ప్రత్యుత్పత్తి

→ లైంగిక ప్రత్యుత్పత్తి కొరకు రూపాంతరము చెందిన ప్రకాండంను పుష్పం అంటారు.

→ పుష్పంలో కేసరావళిని పురుష ప్రత్యుత్పత్తి భాగమని, అండకోశంను స్త్రీప్రత్యుత్పత్తి భాగమని అంటారు.

→ ఒక ఆవృత బీజ పరాగకోశం ద్విలంబికంగా ఉండి, ప్రతి లంబికలో 2 గదులు కల్గి ఉంటుంది.

→ మందారలో పరాగకోశం ఏకలంబికము, దానిని ఏక కక్ష్య యుత పరాగకోశం అంటారు.

→ పరాగకోశము అడ్డుకోతలో 4 పార్శ్వాలుగా ఉండి వాటిలో సూక్ష్మసిద్ధ బీజశయాలు ఉంటాయి.

→ ప్రతి సూక్ష్మ సిద్ధబీజాశయము గుండ్రంగా ఉండి 4 పొరలతో ఉన్న కుడ్యంతో కప్పబడి ఉంటుంది. అవి బాహ్యచర్మం, ఎండోథీషియమ్, మధ్య వరుసలు, టపెటమ్.

→ టపెటమ్ అభివృద్ధి చెందే పరాగ రేణువులకు పోషణనిస్తుంది.

→ సిద్ధబీజ జనక కణజాలము క్షయకరణ విభజన చెంది సూక్ష్మ సిద్ధబీజ చతుష్కాలు ఏర్పడుటను సూక్ష్మసిద్ధబీజ జననము అంటారు.

→ పరాగరేణువులు గోళాకారంలో రెండు పొరలతో ఉంటాయి. వెలుపలి పొర ఎత్తైన్, స్పోరోపొలెనిన్ ను, లోపలిపొర, ఇంటైన్ పెక్టిన్ సెల్యులోస్లతోను నిర్మితమై ఉంటాయి.

→ 60 శాతం ఆవృత బీజాలలో పరాగరేణువులు 2 కణాలదశలో (పెద్ద శాకీయ కణము, చిన్న ఉత్పాదక కణము) విడుదల అవుతాయి.

→ 40 శాతం ఆవృత బీజాలలో పరాగ రేణువులు 3 కణాల దశలో (1 శాకీయకణం, 2 పురుషబీజాలు) విడుదల అవుతాయి.

→ పరాగరేణువులో పోషకాలు ఎక్కువగా ఉండుటవల్ల, పాశ్చాత్యదేశాలలో ఇవి టాబ్లెట్లు, సిరప్ రూపంలో లభిస్తున్నాయి.

→ పరాగరేణువులు కీలాగ్రంపై పడి మొలకెత్తుతాయి.

→ లొరాంథస్ లో అండం చుట్టూ అండకవచాలు ఉండవు.

→ హీలియంథస్, దత్తురలలో అండాలు ఏకకవచయుతాలు.

→ పాలిపెటాలే జాతులు, ఏకదళబీజాలలో అండాలు ద్వికవచయుతాలు.

→ పాలీగోనంలో అండద్వారం, చలాజా, అండవృంతం, మూడు ఒక నిలువ వరుసలో ఉంటాయి. దానిని నిర్వక్ర అండం అంటారు.

→ సూర్యకాంతం, అండదేహం 180° కోణంలో వంపుతిరిగి ఉంటుంది. దీనిని వక్ర అండం అంటారు.

→ చిక్కుడులో అండదేహం మూత్రపిండాకారంలో ఉంటుంది. దానిని కాంపైలోట్రోపస్ అండం అంటారు.

→ స్థూలసిద్ధ బీజమాతృకణం నుండి స్థూలసిద్ధ బీజాలు ఏర్పడుటను స్థూలసిద్ధ బీజ జననము అంటారు.

→ 7 కణాలు, 8 కేంద్రకాలతో ఉన్న పిండకోశము ఒక స్థూల సిద్ధబీజం నుండి ఏర్పడుతుంది కావున దానిని ఏకసిద్ధబీజ వర్థక రకము అంటారు.

→ పిండకోశంలో స్త్రీబీజ పరికరం, ప్రతిపాదకణాలు, 2ధ్రువ కేంద్రకాలు ఉంటాయి.

→ పరాగకోశం నుండి పరాగరేణువులు కీలాగ్రంను చేరుటను పరాగసంపర్కం అంటారు.

→ ఒక పుష్పంలోని పరాగరేణువులు అదే పుష్పంలో కీలాగ్రంను చేరుటను ఆత్మపరాగసంపర్కము అని, వేరొక పుష్పంలోని కీలాగ్రంను చేరుటను పరపరాగ సంపర్కము అంటారు.

→ గాలి ద్వారా జరిగే పరాగసంపర్కంను ఎనిమోఫిలీ అంటారు.

→ నీరు ద్వారా జరిగే పరాగసంపర్కంను హైడ్రోఫిలీ అంటారు.

→ జంతువుల ద్వారా జరిగే పరాగసంపర్కంను జూఫిలీ అంటారు.

→ పక్షుల ద్వారా జరిగే పరాగసంపర్కంను ఆర్నిథోఫిలీ అంటారు.

→ గబ్బిలాల ద్వారా జరిగే పరాగసంపర్కంను కీరోష్టిరి ఫిలీ అంటారు.

→ ఉడతల ద్వారా జరిగే పరాగసంపర్కంను లెరోఫిలీ అంటారు.

→ సరీసృపాల ద్వారా జరిగే పరాగసంపర్కంను ఒఫియోఫిలీ అంటారు.

→ సూర్యకాంతంలో పుంభాగప్రథమోత్పత్తి వల్ల పరపరాగ సంపర్కం జరుగుతుంది.

→ దతూర, సొలానమ్లలో స్త్రీ భాగ ప్రథమోత్పత్తి వల్ల పరపరాగసంపర్కం జరుగుతుంది.

→ హైబిదాస్కస్ లో పరాగ కోశాలు, కీలాగ్రాలు వేరు వేరు స్థానాలలో ఉంటాయి. దానిని హెర్కొగమి అంటారు.

→ అబూటిలాన్ ఆత్మవంధ్యత్వం కనిపిస్తుంది.

→ పురుష, స్త్రీ పుష్పాలు ఒకే మొక్క పై ఉంటే ఆ స్థితిని ద్విలింగాశ్రయ స్థితి అంటారు. ఉదా: ఆముదం, మొక్కజొన్న,

→ పురుష, స్త్రీ పుష్పాలు వేరువేరు మొక్కలపై ఉంటే ఆ స్థితిని ఏకలింగాశ్రయ స్థితి అంటారు. ఉదా : బొప్పాయి

→ ఒకే జాతికి చెందిన పుప్పొడిని స్వీకరించే శక్తి కీలాగ్రంనకు ఉన్నది.

→ పరాగనాళం అండంలోనికి అండద్వారం లేక, చలాజా ద్వారా లేక అండకవచాల ద్వారా చేరుతుంది.

→ ద్విలింగపుష్పంలోని (స్త్రీజనకులు) కేసరాలను తొలగించుటను విపుంసీకరణ అంటారు.

→ విపుంసీకరణ చేసిన పుష్పాలను పాలిథిన్ సంచులు (బట్టర్ పేపర్) తో మూసివేయుటను బాగింగ్ అంటారు.

→ ఒక పురుషబీజం, స్త్రీబీజంతో కలియుటను సంయుక్త సంయోగము అంటారు. రెండవ పురుషబీజము ద్వితీయ కేంద్రకంతో కలియుటను త్రిసంయోగం అంటారు.

→ సంయుక్త బీజం అభివృద్ధి చెంది హృదయాకారంలో ఉన్న పిండమును ఇస్తుంది.

→ ఫలదీకరణ లేకుండా విత్తనాలు ఏర్పడుటను అసంయోగజననం అంటారు.

→ ఫలదీకరణ లేకుండా అండాశయం నుండి ఫలాలు ఏర్పడుటను అనిషేకఫలాల జననం అంటారు.

→ విత్తనంలో ఒకటికంటే ఎక్కువ పిండాలు ఉంటే దానిని బహుపిండత అంటారు.

→ పరపరాగసంపర్కం (అల్లోగమి) : ఒక పుష్పంలోని పరాగ రేణువులు వేరొక పుష్పాన్ని చేరడం.

→ వాయు పరాగ సంపర్కం : గాలి ద్వారా జరిగే సంపర్కం

→ ఆటోగమి : ఒకే పుష్పంలో జరిగే పరాగ రేణువుల రవాణా.

→ ప్రతిపాద కణాలు : పిండకోశంలో చలాజా వైపున ఉండే మూడు కణాలు.

→ అసంయోగజననం (Apomixis) : సాధారణ లైంగిక ప్రత్యుత్పత్తికి బదులుగా ఫలదీకరణ లేకుండా జరిగే లైంగిక ప్రత్యుత్పత్తి లేదా విత్తనాభివృద్ధి.

→ వివృత సంయోగం : వికసించే పుష్పాలలో పరాగ సంపర్కం జరగడం.

→ కీరోఫ్టిరి ఫెలీ : గబ్బిలాల వల్ల జరిగే పరపరాగ సంపర్కం.

→ సంవృత సంయోగం : ఎప్పుడూ వికసించని పుష్పాలలో జరిగే పరాగ సంపర్కం.

→ క్లోన్ : లైంగిక ప్రత్యుత్పత్తి ద్వారా కాకుండా యితర ప్రత్యుత్పత్తి విధానాల ద్వారా ఏర్పడి స్వరూపాత్మకంగా, జన్యుపరంగా ఒకే విధంగా ఉండే సంతతి.

→ చలాజా : అండంలోని అండాంతఃకణజాలం పీఠభాగం. ఇక్కడ నుంచి అండకవచాలు ఏర్పడతాయి.

→ చలజో సంయోగం : పరాగనాళం అండంలోని చలాజా ద్వారా పిండకోశంలోనికి ప్రవేశించడం.

→ మూలాంకుర కంచుకం (Coleorhiza) : పిండాక్షంలోని ప్రథమ మూలం, దాన్ని ఆవరించి ఉన్న వేరు తొడుగును కప్పుతూ ఉండే విభేదనం చూపని పొర.

→ ప్రాంకుర కంచుకం (Coleoptile) : పిండాక్షంలోని ఉపరి బీజదళంలోని, ప్రకాండపు మొగ్గ, పత్ర ఆద్యాలను కప్పుతూ బోలుగా ఉండే పొర.

→ భిన్నకాలిక పక్వత (Dichogamy) : పుప్పొడి విడుదల, కీలాగ్రం పక్వదశకు చేరడం అనేది సమకాలికంగా ఉండదు.

→ ఏకలింగాశ్రయి (Heterothallic) : పురుష, స్త్రీ ప్రత్యుత్పత్తి అవయవాలు వేరువేరు థాలస్లపై అభివృద్ధి చెందడం. ద్విఫలదీకరణ : రెండు ఫలదీకరణ ప్రక్రియలు
(a) ఒక పురుష సంయోగబీజం + స్త్రీ బీజకణం
(b) రెండవ పురుష సంయోగబీజం + ద్వితీయ కేంద్రకం, ఆవృత బీజాల ప్రత్యేక లక్షణం.

→ కీటక పరాగ సంపర్కం : కీటకాల సహాయంతో జరిగే పరాగ సంపర్కం

→ స్త్రీబీజ కణ పరికరం : అండద్వారం కొనవైపున ఉండే పిండకోశంలోని మూడు కణాలు.

→ పిండం : పిండాక్షం (ప్రథమ మూలం, ప్రథమ కాండం), బీజదళాలతో ఉండే అతిచిన్న మొక్క దీన్ని కప్పుతూ బీజకవచాలు ఉంటాయి.

→ పిండోత్పత్తి శాస్త్రం : సంయోగ బీజాల అభివృద్ధి, నిర్మాణం ఫలదీకరణ విధానం, పిండాభివృద్ధి మొదలైన అంశాలు అధ్యయనం చేసే విజ్ఞాన శాస్త్రశాఖ.

→ పిండకోశం : స్త్రీబీజ కణ పరికరం, ద్వితీయ కేంద్రకం/ ధ్రువకేంద్రకాలు, ప్రతిపాద కణాలు ఉండే స్త్రీ సంయోగ బీజదం. ఆవృత బీజాలలో ఇది 7 కణాలలో (8- కేంద్రకాలలో), ఉంటుంది.

→ అంకురచ్ఛదం : అభివృద్ధి చెందుతున్న పిండాన్ని చుట్టి ఉండి పోషణనిచ్చే కణజాలం. ఆవృత బీజాలలో ఇది త్రయస్థితికంగా ఉంటుంది.

→ ఎండోథీసియమ్ : పరాగకోశపు గోడోలోని బాహ్యచర్మ కిందనున్న పొర, దీనిలో స్పర్శరేఖీయ గోడలు తంతుయుత మందాలలో (fibrous thickenings) ఉండి పరాగకోశాల స్ఫోటనానికి సహాయపడతాయి.

→ ఫలదీకరణ : పురుష సంయోగబీజం, స్త్రీ బీజకణంతో సంయోగం చెందే ప్రక్రియ.

→ ఫ్లోరికల్చర్ : పుష్పాలనిచ్చే మొక్కలను సాగు చేసే విధానం.

→ అండవృంతం : అండానికి ఉండే కాడ వంటి భాగం.

→ సంయోగబీజదం : మొక్క జీవిత చక్రంలో ఏకస్థితికంగా ఉన్న, సంయోగ బీజాన్ని ఏర్పరచే (లైంగిక) దశ.

→ ఏకవృక్ష పరపరాగ సంపర్కం (geitonogamy) : ఒక పుష్పంలోని పరాగ రేణువులు అదే మొక్కపై ఉన్న వేరొక పుష్ప కీలాగ్రం మీద పడటం.

→ హెర్కోగమి : పరాగకోశాలు, కీలాగ్రాలు వేర్వేరు ఎత్తులో లేదా వేర్వేరు దిశలలో ఉండటం.

→ భిన్న సంయోగ బీజాలు : స్వరూపాత్మకంగా రెండుగా విభేదనం చూపే సంయోగ బీజాలు (పురుష, స్త్రీ).

→ ఏకకాలపక్వత (homogamy) : పుష్పంలోని పరాగ కోశాలు, కీలాగ్రం ఒకే సమయాన పక్వదశకు చేరుకోవడం.

→ జల పరాగ సంపర్కం : నీటి ద్వారా జరిగే పరాగ సంపర్కం

→ అండకవచాలు : అండంలోని అండాంతఃకణ జాలాన్ని కప్పుతూ ఉండే బహుకణయుత కవచాలు.

→ సమసంయోగబీజాలు : నిర్మాణాత్మకంగా, క్రియాత్మకంగా ఒకేవిధంగా / రకంగా ఉండే రెండు సంయోగ బీజాలు.

→ శైశవ దశ (Juvenile phase) : పెరుగుదల, అభివృద్ధి చూపే దశ.

→ మెలకోఫిలి (malacophily) : నత్తల ద్వారా జరిగే పరాగ సంపర్కం.

→ ద్విలింగాశ్రయ మొక్క (monoecious) : పురుష, స్త్రీ పుష్పాలు ఒకే మొక్కపై ఏర్పడటం.

→ స్థూలసిద్ధ బీజాలు : ఏకస్థితిక కణం – స్త్రీ సంయోగ బీజదం లేదా పిండకోశంగా అభివృద్ధి చెంతుంది.

→ మధ్య సంయోగం (mesogamy) : అండకవచం ద్వారాగాని, అండ వృంతం ద్వారా గాని లేదా అండం పీఠభాగం నుంచి గాని, పరాగ నాళాలు అండంలోనికి ప్రవేశించడం.

→ అండద్వారం : అండకవచాలు అండాతఃకణజాలాన్ని పూర్తిగా కప్పి వేయకుండా అండంకొనభాగంలో ఏర్పడే రంధ్రం.

→ సూక్ష్మసిద్ధబీజము : పురుష సంయోగబీజదంగా (3 కణాలతో) వృద్ధి చెందే పరాగ రేణువు.

→ అండాతఃకణజాలం : అండంలోపల, పలుచని కవచాలతో ఉండే మృదు కణజాలం.

→ పక్షిపరాగ సంపర్కం : పక్షుల ద్వారా జరిగే పరాగ సంపర్కం.

→ అండం : పుష్పించే మొక్కల్లోని స్థూల సిద్ధబీజాశయం.

→ ఫలకవచం : ఫలకుడ్యం. కండగల ఫలంలో వెలుపలవైపు బాహ్యఫలకవచం, మధ్యలో మధ్యఫలకవచం, లోపలివైపు అంతఃఫలకవచం అనే విభేదనం చూపుతుంది.

→ పరిచ్ఛదం : మిగిలిపోయిన దీర్ఘకాలిక అండాంతఃకణజాలం.

→ పుప్పొడి బ్యాంక్ (Pollen Bank) : జీవించే శక్తి ఉన్న పుప్పొడి రేణువులను సేకరించి రాబోయే తరాల కొరకు భద్రపరిచే విధానం. ప్రజనన ప్రయోగాల కొరకు ఏకస్థితిక మొక్కలను రూపొందించటం కొరకు ఇవి ప్రాముఖ్యత పొందినవి. పుప్పొడి/మకరందం దోపిడి దొంగలు : పరాగ సంపర్కానికి తోడ్పడకుండా పుప్పొడి/మకరందాన్ని వినియోగించుకునే కీటకాలు.

→ పరాగసంపర్కం : పరాగకోశంలోని పరాగరేణువులు కీలాగ్రాన్ని చేరడం.

→ పరాగసంపర్క సహకారులు : పరాగసంపర్కం జరగడానికి తోడ్పడే సహకారులు.

→ పుంభాగ ప్రథమోత్పత్తి (protandry) : ఒకే పుష్పంలోని కీలాగ్రం కంటే పరాగ కోశాలు ముందుగా పక్వానికి రావడం.

→ స్త్రీభాగ ప్రథమోత్పత్తి (Protogyny) : ఒకే పుష్పంలో పరాగకోశాల కంటే కీలాగ్రం ముందు పక్వానికి రావడం.

→ బహుపిండత : ఒక విత్తనంలో, ఒకటి కంటే ఎక్కువ పిండాలు వృద్ధి చెందుట.

→ రంధ్రసంయోగం : పరాగనాళం అండంలోనికి అండ ద్వారం ద్వారా ప్రవేశించడం.

→ ప్రాథమిక ‘అంకురచ్ఛద కేంద్రకం : రెండవ పురుష సంయోగ బీజ కేంద్రకం, రెండు ధృవకేంద్రాలతో సంయోగం చెంది, ఏర్పడే త్రయస్థితిక కేంద్రకం.

→ రాఫే (Raphe) : వక్రఅండంలో అండదేహం పక్క భాగానంతటా, విత్తుచారను దాటి అతుక్కొని ఉండే అండవృంతం భాగం. స్కూటెల్లమ్ : ఏకదళ బీజ మొక్కల్లోని బీజదళాలు (గడ్డిజాతి కుటుంబం)

→ ద్వితీయకేంద్రకం : రెండు ధృవకేంద్రాల సంయోగం ద్వారా ఏర్పడిన కేంద్రకం. విత్తనబ్యాంక్ (Seed Bank) మొలకెత్తే శక్తి కలిగి ఉన్న విత్తనాలను సేకరించి ముందుతరాల కొరకు భద్రపరచడం. లైంగిక ప్రత్యుత్పత్తి జరిపే మొక్కలలోని ఈ భాగాలను (విత్తనాలను) స్థానేతరపద్ధతులలో సమర్ధవంతంగా భద్రపరచడం.

→ ఆత్మవంధ్యత్వం (self-sterility) : ఒక పుష్పంలోని పరాగ రేణువులు అదే పుష్పంలోని కీలాగ్రంపై పడినపుడు మొలకెత్తలేకపోవడం.

→ సిద్ధబీజదం : మొక్క జీవితచక్రంలో ద్వయస్థితికంగా ఉండి సిద్ధబీజాలను ఏర్పరిచే అలైంగిక దశ. ఇది సిద్ధబీజ మాతృకణాలలో జరిగే క్షయకరణ విభజన ద్వారా ఏకస్థితిక బీజాలను ఏర్పరుస్తుంది.

→ సహాయకణాలు : స్త్రీ బీజకణ పరికరంలో, స్త్రీబీజ కణానికి ఇరువైపులా ఉండే రెండు కణాలు.

→ టపెటమ్ : పరాగకోశపు కుడ్యము అన్నిటికన్నా లోపల ఉండే పొర. ఇది అభివృద్ధి చెందుతున్న సూక్ష్మ సిద్ధబీజాలకు పోషణనిస్తుంది.

→ వివిపారి (Vivipary) : విత్తనం తల్లి మొక్కను అంటిపెట్టుకొని ఉండగానే అంకురించి పిల్ల మొక్కగా వృద్ధి చెందుట.

→ భిన్న వృక్షపరపరాగ సంపర్కం (Xenogamy) : ఒక పుష్పంలోని పరాగరేణువులు అదే జాతికి చెందిన వేరొక మొక్కపై ఉన్న పుష్పం కీలాగ్రం మీద పడడం.

→ జంతు పరాగసంపర్కం (zoophily) : జంతువుల సహాయంతో జరిగే పరాగ సంపర్కం.

→ సంయుక్త బీజం : పురుష సంయోగ బీజం, స్త్రీ బీజకణం సంయోగం చెందడం ద్వారా ఏర్పడే ద్వయ స్థితిక కణం

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(c)

I.

Question 1.
Find the derivatives of the following functions.
i) sin^-1 (3x – 4x³)
Solution:
Put x = sin θ
y = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3 θ) = 3 θ = 3 sin^-1 x.
\(\frac{dy}{dx}\) = \(\frac{3}{\sqrt{1-x^{2}}}\)

ii) cos^-1 (4X3 – 3x)
Solution:
Put x = cos θ
y = cos^-1 (4 cos³ θ – 3 cos θ)
= cos^-1 (cos 3θ) = 3θ = 3 cos^-1 x
\(\frac{dy}{dx}\) = \(\frac{3}{\sqrt{1-x^{2}}}\)

iii) sin^-1 \(\frac{3}{{1-x^{2}}}\)
Solution:
Put x tan θ ⇒ y

iv) tan^-1 \(\frac{a-x}{1+ax}\)
Solution:
Put a tan α, x = tan θ
y = tan^-1 \(\left(\frac{\tan \alpha-\tan \theta}{1+\tan \alpha \tan \theta}\right)\)
= tan^-1 (tan (α – θ)) = α – θ
= tan^-1 a – tan^-1 x;
\(\frac{dy}{dx}\) = 0 – \(\frac{1}{1+x^{2}}\) = – \(\frac{1}{1+x^{2}}\)

v) tan^-1 \(\sqrt{\frac{1-\cos x}{1+\cos x}}\)
Solution:

Differentiating w.r.to x; \(\frac{dy}{dx}\) = \(\frac{1}{2}\)

vi) sin [cos (x²)]
Solution:
\(\frac{dy}{dx}\) = cos [cos (x²)]\(\frac{d}{dx}\) [cos (x²)]
= cos [cos (x²)]. [-sin (x²)] \(\frac{d}{dx}\) (x²)
= cos [cos (x²)] [- sin (x²)]. 2x
= -2x . sin (x²).cos [cos (x²)]

vii) sec^-1 (\(\frac{1}{2x^{2}-1}\)) (0 < x < \(\frac{1}{\sqrt{2}}\))
Solution:
x = cos θ
2x² – 1 = 2 cos² θ – 1 = cos 2θ

viii) sin^-1 [tan^-1 (e^-x)]
Solution:
\(\frac{dy}{dx}\) = cos [tan^-1 (e^-x)]. [tan^-1 (e^-x)]¹
= cos (tan^-1 (e^-x)]x – \(\frac{1}{1+\left(e^{-x}\right)^{2}}\) (e^-x)¹
= \(\frac{-e^{-x}}{1+e^{-2 x}}\) . cos [tan^-1 (e^-x)]

Question 2.
Differentiate f(x) with respect to g(x) for the following.
i) f(x) = e^x, g(x) = √x
Solution:
Let y = e^x and z = √x

ii) f(x) = e^{sin x}, g(x) = sin x.
Solution:
Let y = e^{sin x} and z = sin x.

iii) f(x) = tan^-1 \(\frac{2x}{1-x^{2}}\), g(x) sin^-1 = \(\frac{2x}{1+x^{2}}\)
Solution:
Lety = tan^-1 \(\frac{2x}{1-x^{2}}\), and z = sin^-1 = \(\frac{2x}{1+x^{2}}\)
Put x = tan θ

Question 3.
If y = e^a sin^-1x the prove that \(\frac{dy}{dx}\) = \(\frac{a y}{\sqrt{1-x^{2}}}\)
Solution:
y = e^{a sin-1x}
\(\frac{dy}{dx}\) = e^{a sin-1x} (a sin^-1 x)¹
= e^{a sin-1x} . a \(\frac{1}{\sqrt{1-x^{2}}}\) = \(\frac{a y}{\sqrt{1-x^{2}}}\)

II.

Question 1.
Find the derivatives of the following function.
i) tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a\left(a^{2}-3 x^{2}\right)}\right)\)
Solution:
Put x = a tan θ

ii) tan^-1 (sec x + tan x)
Solution:

iii) tan^-1 \(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\)
Solution:
Put x = tan θ

iv) (logx)^{tan x}
Solution:
log y = log (log x)^{tan x}
= (tan x). log (log x)
Differentiating w.r.to x
\(\frac{1}{y}\) . \(\frac{dy}{dx}\) = tan x . \(\frac{d}{dx}\) (log(log x)) + log(logx) \(\frac{d}{dx}\) (tan x)
= tan x. \(\frac{1}{log x}\) . \(\frac{1}{x}\) + log(log x). sec² x

v) (x^x)^x = x^x²
Solution:
log y = log x^x² = x². log x
\(\frac{1}{y}\) . \(\frac{dy}{dx}\) = x² . \(\frac{d(\log x)}{d x}\) + (log x ) \(\frac{d}{dx}\) (x²)
= x². \(\frac{1}{x}\) + 2x. log x
= x + 2x log x = x (1 + 2 log x).
= x (log e + log x²)
= x. log (ex²)
\(\frac{dy}{dx}\) = y. x. log (ex²)
= x^x² . x. log (ex²)
= x^{x² +1} log (ex²)

vi) 20^{log (tan x)}
Solution:
log y = log (20)^{log (tan x)}
= log (tan x) log 20
Differentiating w. r. to x

\(\frac{dy}{dx}\) = y. (2 log 20). cosec 2x
= 20^{log (tan x)} (2 log 20). cosec 2x

vii) x^x + e^ex
Solution:
Let y₁ = x^x and y₂ = e^ex so that y = y₁ + y₂.
y₁ = x^x ⇒ log y₁ = log x^x = x log x

viii) x. log x. log (log x)
Solution:
\(\frac{dy}{dx}\) = x. log x \(\frac{d}{dx}\) (log. (log x)) + log (log x) logx. 1 + x. log (log x) \(\frac{1}{x}\).
= x log x. \(\frac{1}{log x}\) . \(\frac{1}{x}\) + log x. log (log x) + log (log x)
= 1 + log (logx) (1 + logx) = 1 + log (logx) + log x log (log x)
= log e + log (log x) + log x. log (log x)
= log (e log x) + log x. log (log x)

ix) e^-ax² sin (x log x)
Solution:
\(\frac{dy}{dx}\) = e^-ax² . \(\frac{d}{dx}\) (sin (x log x)) dx + sin (x log x) \(\frac{d}{dx}\) (e^-ax²)
= e^-ax² cos (x log x). (x . \(\frac{1}{x}\) + log x) + sin (x log x) e^-ax² (-2ax)
= e^-ax² [(cos (x log x) (1 + log x) – 2 ax. sin (x log x)]
= e^-ax² (cos (x log x) (log ex) -2 ax. sin (x log x))

x) sin^-1\(\left(\frac{2^{x+1}}{1+4^{x}}\right)\) (Put 2ⁿ = tan θ)
Solution:
sin^-1\(\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
Put 2^x = tan θ.

Question 2.
Find \(\frac{dy}{dx}\) for the following functions.
i) x = 3 cos t – 2 cos³ t,
y = 3 sin t – 2 sin³ t
Solution:
\(\frac{dx}{dt}\) = – 3 sin t – 2(3 cos² t) (- sin t)
= – 3 sin t + 6 cos² t (sin t)
= 3 sin t (2 cos² t – 1)
= 3 sin t. cos 2t
y = 3 sin t – 2 sin³ t
\(\frac{dy}{dt}\) = 3 cos t – 2 (3 sin² t) (- cos t)
= 3 cos t (1 – 2 sin² t)
= 3 cos t. cos 2t
\(\frac{dy}{dx}\) = \(\frac{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}{\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)}=\frac{3 \cos t \cos 2 t}{3 \sin t \cos 2 t}\) = cot t

ii) x = \(\frac{3 a t}{1+t^{3}}\), y = \(\frac{3 a t^{2}}{1+t^{3}}\)
Solution:

iii) x = a (cos t + t sin t), y = a (sin t – t cos t)
Solution:
\(\frac{dx}{dt}\) = a (- sin t + t cos t + sin t) = at cos t
∴ y = a (sin t – t cos t)
\(\frac{dy}{dt}\) = a (cos t – cos t + t sin t) = at sin t
\(\frac{dy}{dx}\) = \(\frac{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}{\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)}=\frac{at\cos t}{at\cos t}\) = tan t

iv) x = a\(\left[\frac{\left(1-t^{2}\right)}{1+t^{2}}\right], \mathbf{y}=\frac{2 b t}{1+t^{2}}\)
Solution:

Question 3.
Differentiate f(x) with respect to g(x) for the following.
i) f(x) = log_a^x, g(x) = a^x.
Solution:
y = log_a^x = \(\frac{\log x}{\log _{c}^{a}}\)

ii) f(x) = sec^-1 (\(\frac{1}{2x^{2}-1}\)) g(x) = \(\sqrt{1-x^{2}}\)
Solution:
Let y = sec^-1 (\(\frac{1}{2x^{2}-1}\)) and z = \(\sqrt{1-x^{2}}\)
Put x = cos θ

iii) f(x) = tan^-1\(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\), g(x) = tan^-1 x.
Solution:
Let y = tan^-1\(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) and z = tan^-1 x
x = tan z

Question 4.
Find the derivative of the function y defined implicitly by each of the following equations.
i) x⁴ + y⁴ – a² xy = 0
Solution:
Differentiate w.r.to x
4x³ + 4y³ . \(\frac{dy}{dx}\) – a²(x. \(\frac{dy}{dx}\) + y . 1 = 0)
4x³ + 4y³ . \(\frac{dy}{dx}\) – a²x\(\frac{dy}{dx}\) – a²y = 0
4y³ – a²x) \(\frac{dy}{dx}\) = a²y – 4x³ ; \(\frac{dy}{dx}\) = \(\frac{a^{2} y-4 x^{3}}{4 y^{3}-a^{2} x}\)

ii) y = x^y
Solution:
log y = log x^y = y log x
Differentiate w.r.to x

iii) y^x = x^{sin y}
Solution:
Take log on both sides
log y^x = log x^{sin y} ⇒ x. log y = (sin y) log x.
Differentiating w.r.to x

Question 5.
Establish the following.
i) If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}\) = a(x – y), than \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\)
Solution:
Given \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}\) = a(x – y)
Put x = sin θ, y = sin Φ
Differentiating w.r. to x

ii) If y = x \(\sqrt{a^{2}+x^{2}}\) + a² log (x + \(\sqrt{a^{2}+x^{2}}\)), then \(\frac{dy}{dx}\) = 2 \(\sqrt{a^{2}+x^{2}}\)
Solution:
y ⇒ x\(\sqrt{a^{2}+x^{2}}\) + a² log (x + \(\sqrt{a^{2}+x^{2}}\))

iii) If x^{log y} = log x, then
Solution:
Given x^{log y} = log x, log x^{log y} = log log x
(log y) (log x) = log(logx).
Differentiating w.r.to x

iv) If y = Tan^-1 \(\frac{2x}{1-x^{2}}\) + Tan^-1 \(\frac{3x-x^{3}}{1-3x^{2}}\) – tan^-1 \(\frac{4x-4x^{3}}{1-6x^{2}+x^{4}}\) than \(\frac{dy}{dx}\) = \(\frac{1}{1+x^{2}}\)
Solution:
Put x = tan θ

= tan^-1 (tan 2θ) + tan^-1 (tan 3θ) – tan^-1 (tan 4θ)
= 2θ + 3θ – 4θ = θ = tan^-1 x
∴ \(\frac{dy}{dx}\) = \(\frac{1}{1+x^{2}}\)

v) If x^y = y^x, then \(\frac{dy}{dx}\) = \(\frac{y(x log y – y)}{x(y log x – x)}\)
Solution:
Given x^y = y^x ; log x^y = log y^x
y log x = x log y
Differentiating w.r.to x

vi) If x^2/3 + y^2/3 = a^2/3 then \(\frac{dy}{dx}\) = -3 √y/x
Solution:
Given x^2/3 + y^2/3 = a^2/3
Differentiating w.r.to x

Question 6.
Find the derivative \(\frac{dy}{dx}\) of each of the following functions.
i) y = \(\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\)
Solution:
log y = log \(\left\{\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\right\}\)
= log (1 – 2x)^2/3 + log (1 + 3x)^-3/4 – log (1 – 6x)^5/6 – log (1 + 7x)^-6/7
= \(\frac{2}{3}\) log (1 – 2x) – \(\frac{3}{4}\) log (1 + 3x) – \(\frac{5}{6}\) log (1 – 6x) + \(\frac{6}{7}\) log (1 + 7x)
Differentiating w.r.to x
\(\frac{1}{y}\).\(\frac{dy}{dx}\) = \(\frac{2}{3}\) . \(\frac{1(-2)}{1-2x}\) – \(\frac{3}{4}\) . \(\frac{1}{1+3x}\) . 3

ii)

Solution:
log y = log x⁴ + log (x² + 4)^1/3 – log (4x² – 7)^1/2
= 4 log x + \(\frac{1}{3}\) log (x² + 4) – \(\frac{1}{2}\) log (4x² – 7)
Differentiating w.r.to x

iii) y = \(\frac{(a-x)^{2}(b-x)^{3}}{(c-2 x)^{3}}\)
Solution:
log y = log \(\frac{(a-x)^{2}(b-x)^{3}}{(c-2 x)^{3}}\)
= log (a – x)² + log (b – x)³ – log (c – 2x)³
= 2 log (a – x) + 3 log (b – x) – 3 log (c – 2x)
Differentiating w.r.to x

iv)

Solution:
log y = log \(\frac{x^{3}(2+3 x)^{1 / 2}}{(2+x)(1-x)}\)
= log x³ + log (2 + 3x)^1/2 – log (2 + x) – log (1 – x)
= 3 log x + \(\frac{1}{2}\) log (2 + 3x) – log (2 + x) – log (1 – x)
Differentiating w.r. to x

v) y = \(\sqrt{\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}}\)
Solution:
log y = log(\(\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}\))^1/2
= \(\frac{1}{2}\) log \(\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}\)
= \(\frac{1}{2}\) (log (x – 3) + log (x² + 4) – log (3x² + 4x + 5))

III.

Question 1.
Find the derivatives of the following functions.
i) y = (sin x)^logx + x^{sin x}
Solution:
Let y₁ =(sinx)^logx, y₂ = x^{sin x} so that y = y₁ + y₂
y₁ = (sin x)^logx
log y₁= log{ (Sin x)^logx} = log x. log (sin x)
Differentiating w.r. to x

y₂ = x^{sin x}
log y₂ = (log x)^{sin x} = sin x. logx

ii) x^xx
Solution:
log y = log x(x^xx) = x^x. log X
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = x^x. \(\frac{1}{x}\) + (log x). x^x (1 + log x)
[\(\frac{d}{dx}\)(x^x) = x^x (1 + log x)]
= x^x-1 [1+ x log x (log e + log x)]
= x^x-1 (1 + x. log x. log ex)
\(\frac{dy}{dx}\) = y.x^x-1 (1 + x log x. log ex)
= x^(xx) . x^x-1 (1 + x log x. log ex)
= x^xx+x-1 (1 + x log x. log ex)

iii) (sin x)^x + x^{sin x}
Solution:
Let y₁ = (sin x)^x and y₂ = x^{sin x}
so that y = y₁ + y₂
log y₁ = log (sin x)^x = x. log sin x

iv) x^x + (cot x)^x
Solution:
Let y₁ = x^x and y₂ = (cot x)^x
log y₁ = log x^x = x log x

Question 2.
Establish the following
i) If x^y + y^x = a^b then
\(\frac{dy}{dx}\) = \(-\left(\frac{y \cdot x^{y-1}+y^{x} \cdot \log y}{x^{y} \cdot \log x+x \cdot y^{x-1}}\right)\)
Solution:
Let y₁ = x^y and y₂ = y^x. so that y₁ + y₂ = a^b
logy₁ = log x^y = y logx

ii) If f(x) = sin^-1\(\sqrt{\frac{x-\beta}{\alpha-\beta}}\) and
g(x) = tan \(\sqrt{\frac{x-\beta}{\alpha-x}}\) than
f'(x) = g'(x) (β < x < α)
Solution:

iii) If a > b > 0 and 0 < x < π
f(x) = (a – b)^-1/2 . cos^-1\(\left(\frac{a \cos x+b}{a+b \cos x}\right)\), than f'(x) = (a + b cos x)^-1
Solution:
Let u = cos^-1\(\left(\frac{a \cos x+b}{a+b \cos x}\right)\)

Question 3.
Differentiate (x² – 5x + 8) (x³ + 7x + 9) by
i) Using product
ii) Obtaining a single polynomial expanding the product
iii) Logarithmic differentiation do they all give the same answer?
Solution:
Do Product rule:
y = (x² – 5x + 8) (x³ + 7x + 9)
\(\frac{dy}{dx}\) = (x² – 5x + 8) \(\frac{d}{dx}\)(x³ + 7x + 9) + (x³ + 7x + 9) \(\frac{d}{dx}\)(x² – 5x + 8)
= (x² – 5x + 8)(3x² + 7) + (x³ + 7x + 9)(2x – 5)
= 3x⁴ – 15x³ + 24x² + 7x² – 35x + 56 + 2x⁴ + 14x² + 18x – 15x³ – 35x – 45
= 5x⁴ – 20x³ + 45x² – 52x + 11 ……….. (1)

ii) Expanding the product :
Solution:
y = (x² – 5x + 8) (x³ + 7x + 9)
= 5x⁵ + 7x³ + 9x² – 5x⁴ -35x² – 45x + 8x³ + 56x + 72
= x⁵ – 5x⁴ + 15x³ – 26x² + 11x +72
\(\frac{dy}{dx}\) = 5x⁴ – 20x³ + 45x² – 52x + 11 ……….. (2)

iii) y = (x² – 5x + 8) (x³ + 7x + 9)
Solution:
log y = log (x² – 5x + 8) (x³ + 7x + 9)
= log (x² – 5x + 8) + log (x³ + 7x + 9)

= (2x – 5)(x³ + 7x + 9) + (x² – 5x + 8)(3x² + 7)
= 2x⁴ + 14x² + 18x – 5x³ – 35x – 45 + 3x⁴ -15x³ + 24x² + 7x² – 35x + 56
= 5x⁴ – 20x³ +45x² – 52x + 11 ……….. (3)
From (1), (2) and (3) we observe that all the three give same answer.

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 9th Lesson Gravitation Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 9th Lesson Gravitation

Very Short Answer Questions

Question 1.
State the unit and dimension of the universal gravitational constant (G).
Answer:
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{~d}^2}\)
units of G = Nm² Kg^-2
dimensional formula of G = \(\frac{\left[\mathrm{MLT}^{-2}\right]\left[\mathrm{L}^2\right]}{[\mathrm{M}][\mathrm{M}]}\) = [M^-1 L³ T^-2]

Question 2.
State the vector form of Newtons’s law of gravitation.
Answer:
Vector form of Newton’s law of gravitation is
F = \(\frac{-G m_1 m_2}{r^3} \hat{r}\) where \(\hat{r}\) is unit vector.

Question 3.
If the gravitational force of Earth on the Moon is F, what is the gravitational force of moon on earth ? Do these forces to attraction-reaction pair ?
Answer:
F. Yes, they form action and reaction pair.

Question 4.
What would be the change in acceleration due to gravity (g) at the surface, if the radius of Earth decreases by 2% keeping the mass of Earth constant ?
Answer:
g₁r₁², l = g₂r₂², r₂ = \(\frac{98}{100}\) r₁
\(\frac{g_2}{g_1}=\frac{r_1^2}{r_2^2}=\frac{r_1^2}{\left(\frac{98}{100}\right) r_1^2}=\frac{100 \times 100}{98 \times 98}\)
\(\frac{g_2}{g_1}\) = 1.04
\(\frac{g_2}{g_1}\) – 1 = 1.04 – 1
\(\frac{g_2-g_1}{g_1}\) = 0.04

Question 5.
As we go from one planet to another, how will
a) the mass and
b) the weight of a body change ?
Answer:
a) The mass remains constant.
b) The weight (w = mg), changes from one planet to another planet.

Question 6.
Keeping the length of a simple pendulum constant, will the time period be the same on all planets ? Support your answer with reason.
Answer:
No, Time period depends on acceleration due to gravity (g).
T = 2π \(\sqrt{\frac{l}{g}}\)
g value varies from planet to planet. So time period changes.

Question 7.
Give the equation for the value of g at a depth ‘d’ from the surface of Earth. What is the value of ‘g’ at the centre of Earth ?
Answer:

1. g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) where d = Depth
   R = Radius of the Earth
2. At the centre of the Earth g = 0.

Question 8.
What are the factors that make ‘g’ the least at the equator and maximum at the poles ? > .
Answer:

1. g value is maximum at poles due to
   a) Rotation of the Earth
   b) Earth is flattened at the poles
   c) The equatorial radius is less at the poles.
2. g value minimum at equator due to
   a) Rotation of the earth
   b) Bulging near the equator.

Question 9.
“Hydrogen is in abundance around the sun but not around Earth”. Explain.
Answer:
The escape velocity on the sun is 620 km/s and escape velocity on the Earth is 11.2 km/s. The r.m.s velocities of hydrogen (2 km/s) is less than escape velocity on the Sun. So hydrogen is more abundant around the Sun and less around the Earth.

Question 10.
What is the time period of revolution of a geostationary satellite ? Does it rorate from West to East or from East to West ?
Answer:
Time period of geo-stationary satellite is 24 hours. It can rotate from west to east.

Question 11.
What are polar satellites ?
Answer:
Polar satellites are low altitude satellites (500 to 800 km), but they go around the poles of the earth in a north-south direction. Its time period is around 100 minutes.

Short Answer Questions

Question 1.
State Kepler’s laws of planetary motion.
Answer:
The three laws of Kepler can be stated as follows.

1. Law of orbits : All planets move in elliptical orbits with the sun situated at one of the foci.
   
2. Law of areas : The line that joins any planet to the sun sweeps equal areas in equal intervals of time.
3. Law of periods : The square of the time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.
   T² ∝ R³

Question 2.
Derive the relation between acceleration due to gravity (g) at the surface of a planet and Gravitational constant (G).
Answer:
Consider a body of mass m on the surface of the planet. Let R be the radius of the Earth and M be the mass of the Earth.
Force acting on the body due to gravitational pull of the planet is
F = m g → (1)
According to Newton’s gravitational law, Force on the body is F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) → (2)

From eq’s (1) and (2), we have
m g = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\)
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
This is the relation between g and G
Mass of the earth (M) = Volume × density of the earth
M = \(\frac{4}{3}\) π R² × ρ
g = \(\frac{4}{3}\) π G R ρ

Question 3.
How does the acceleration due to gravity (g) change for the same values of height(h) and depth (d).
Answer:
a) g_h = g(1 – \(\frac{2 \mathrm{~h}}{\mathrm{R}}\)), g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
Same values of height and depth, h = d
g_h = g (1 – \(\frac{2 \mathrm{~d}}{\mathrm{R}}\)) and g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
∴ g_d > g_h

b) For large height and large depth
g_h = \(\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^2}\) and g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
If h = d = R
g_h = \(\frac{\mathrm{g}}{\left(1+\frac{\mathrm{R}}{\mathrm{R}}\right)^2}\) and g_d = g(1 – \(\frac{\mathrm{R}}{\mathrm{R}}\)) = 0
∴ g_h > g_d

Question 4.
What is orbital velocity ? Obtain an expression for it. [Mar. 14]
Answer:
Orbital velocity (V₀) : The horizontal velocity required for an object to revolve around a planet in a circular orbit is called orbital velocity.

Expression for orbital velocity :
Consider a body (satellite) of mass m, revolves round the earth in a circular orbit. Let h be the height of the satellite from the surface of the earth. Then (R + h) is the radius of the orbit.
The Gravitational force of attraction of the earth on the body is given by F = \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^2}\) ………….. (1)
Where M = Mass of the earth, R = Radius of the earth, G = universal gravitational constant. If V₀ is the orbital velocity of the body.
The centripetal force on the body is given by F = \(\frac{\mathrm{mv}_{\mathrm{o}}^2}{(\mathrm{R}+\mathrm{h})}\) …………… (2)
In order to make the body revolve in the same orbit, its centripetal force must be equal to the gravitational force

Question 5.
What is escape velocity ? Obtain an expression for it.
Answer:
Escape velocity : It is the minimum velocity with which a body should be projected, so that it moves into the space by overcoming the earth’s gravitational field.

Expression for escape velocity :
Consider a body of mass m thrown with a velocity v₂
Then K.E = \(\frac{1}{2}\) m v_e² …………. (1)
The gravitational force of attraction of the earth of mass M and Radius R on a body of mass m at its surface is F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) ……………… (2)
Gravitational P. E. = work done on the body
∴ P. E. = F × R = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) × R
P.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\) …………….. (3)
A body just escapes when its K. E. = P. E
\(\frac{1}{2}\) m v_e² = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\)
v_e² = \(\frac{2 \mathrm{GM}}{\mathrm{R}}\) (∵ g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\))
v_e = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)
v_e = \(\sqrt{2 g R}\) (gR = \(\frac{\mathrm{GM}}{\mathrm{R}}\))
v_e = \(\sqrt{2} \times \sqrt{g R}\) (∵ v₀ = \(\sqrt{g R}\))
v_e = \(\sqrt{2}\) × v₀
∴ Escape velocity is \(\sqrt{2}\) times the orbital velocity.

Question 6.
What is a geostationary satellite ? State its uses. [T.S. Mar. 18, 15; A.P. Mar. 16]
Answer:
Geo-stationary satellite : If the period of revolution of an artificial satellite is equal to the period of rotation of earth, then such a satellite is called geo-stationary satellite.
Time period of geo-stationary satellite is 24 hours.
Uses :

1. Study the upper layers of atmosphere
2. Forecast the changes in atmosphere
3. Know the shape and size of the earth.
4. Identify the minerals and natural resources present inside and on the surface of the earth.
5. Transmit the T. V. programmes to distant objects
6. Under take space research i.e. to know about the planets, satellites, comets etc.

Question 7.
If two places are at the same height from the mean sea level; One is a mountain and other is in air at which place will ‘g’ be greater ? State the reason for your answer.
Answer:
The acceleration due to gravity on mountain is greater than that of air.
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) ………….. (1)
Mass (M) = volume × density (ρ)
M = \(\frac{4}{3}\)π R³ × ρ
g = \(\frac{\mathrm{G}}{\mathrm{R}^2}\) × \(\frac{4}{3}\) π R³ ρ
g = – \(\frac{4}{3}\) π R G ρ …………….. (2)
g ∝ ρ
So density is more at mountains. So g is more on mountain.

Question 8.
The weight of an object is more at the poles than at the equator. At which of these can we get more sugar for the same weight ? State the reason for your answer.
Answer:
Weight of the object at poles = m_p g_p (∵ w = mg)
Weight of the object at equator = m_e g_e
Given weight of the object at poles > weight of the object at equator
m_p g_p > m_eg_e
We know that g_p > g_e
Then m_p < m_e
Hence we can get more sugar at equator.

Question 9.
If a nut becomes loose and gets detached form a satellite revolving around the earth, will it fall down to earth or will it revolve around earth ? Give reasons for your answer.
Answer:
When a nut is detached from a satellite revolving around the earth, the nut is also moving with the speed of the satellite as the orbit of a satellite does not depend upon its mass. Hence nut is moving in the same orbit under centripetal force.

Question 10.
An object projected with a velocity greater than or equal to 11.2 kms it will not return to earth. Explain the reason.
Answer:
The escape velocity on the surface of the earth (v_e) = 11.2 km/s. Any object projected with the velocity greater then (or) equal to 11.2 km/s it will not come back. Because it has overcome the earth’s gravitational pull.
So an object never come back to earth.

Long Answer Questions

Question 1.
Define gravitational potential energy and derive an expression for it associated with two particles of masses m₁ and m₂.
Answer:
Gravitational potential energy : Gravitational potential energy of a body at a point in a gravitational field of another body is defined as the amount of work done in brining the given body from infinity to that point without acceleration.

Expression for gravitational potential energy : Consider a gravitational field due to earth of mass M, radius R. The mass of the earth can be supposed to be concentrated at its centre 0. Let us calculate the gravitational the potential energy of the body of mass m placed at point p in the gravitational field, where OP = r and r > R. Let OA = x and AB = dx.
The gravitational force on the body at A will be
F = \(\frac{\mathrm{GMm}}{\mathrm{X}^2}\) ……………… (1)
Small amount of work done in bringing the body without acceleration through a small distance dx is given by
dw = Force × displacement
dw = F × dx
dw = \(\frac{\mathrm{GMm}}{\mathrm{X}^2}\) × dx ……………… (2)
Total work done in bringing the body from infinity to point P is given by

This work done is stored in the body as its gravitational potential energy (u)
∴ Gravitational potential energy (u) = \(\frac{\mathrm{GMm}}{\mathrm{r}}\) ……………….. (4)
Gravitational potential energy associated with two particles of masses m, and m2 separated by a distance r is given by
u = –\(\frac{G m_1 m_2}{r}\) ……………….. (5) (if we choose u = 0 as r → ∞).

Question 2.
Derive an expression for the variation of acceleration due to gravity (a) above and (b) below the surface of the Earth.
Answer:
i) Variation of g with height:
When an object is on the surface of the earth, it will be at a distance r = R radius of the earth, then we have g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
Where G = universal gravitational constant, M = Mass of the earth
When the object is at a height h above the surface of the earth, Then r = R + h

g value decreases with altitude.

ii) Variation of g with depth :
Let us assume that the earth to be a homogeneous uniform sphere of radius R, mass M and of uniform density ρ.
We know that g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) = \(\frac{4}{3}\) π ρ G R ………………… (1)
Consider a body of mass m be placed at a depth d.

The value of g decreases with depth.

Question 3.
State Newton’s Universal Law of gravitation. Explain how the value of the Gravitational constant (G) can be determined by Cavendish method.
Answer:
Newton’s law of gravitation :
“Every body in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversly proportional to the square of the distance between them”
Determination of G value by cavendish method :

1. In 1798 Henry Cavendish determined the value of G experimentally.
2. The bar AB has two small lead spheres attached at its ends.
3. The bar is suspended from a rigid support by a fine wire.
4. Two large lead spheres are brought close to the small ones but on opposite sides as shown in figure.
5. The big spheres attract the nearby small ones by equal and opposite force as shown in figurer.
6. There is no net force on the bar but only a torque which is clearly equal to F times the length of the bar. When F is the force of attraction between a big sphere and its neighbouring small sphere.
7. Due to this torque, the suspended wire gets twisted till such time as the restoring torque of the wire equals the gravitational torque.
   Restoring torque = τ θ ………………… (1)
   Where τ is restoring couple per unit twist 0 is the angle
8. If d is the seperation between big and small balls having masses M and m.
   Gravitational force (F) = \(\frac{\mathrm{GMm}}{\mathrm{d}^2}\) ……………… (2)
   ix) If L is the length of the bar A B, then the torque arising out of F is F multiplied by L. At equilibrium, this is equal to the restoring torque.
   \(\frac{\mathrm{GMm}}{\mathrm{d}^2}\) = τ θ
   observations of θ thus enables one to calculate G.
   The measurement of G = 6.67 × 10^-11 Nm²/ Kg²

Problems

(Gravitational Constant ‘G’ = 6.67 × 10^-11 Nm²/ Kg^-2; Radius of earth ‘R’ = 6400 km; Mass of earth ‘ME’ = 6 × 10²⁴ kg)

Question 1.
Two spherical balls each of mass 1 kg are placed 1 cm apart. Find the gravitational force of attraction between them.
Solution:
m₁ = m₂ = 1 kg, d = 1 cm = 1 × 10^-2 m
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{~d}^2}\)
F = \(\frac{6.67 \times 10^{-11} \times 1 \times 1}{\left(1 \times 10^{-2}\right)^2}\) = 6.67 × 10^-7N

Question 2.
The mass of a ball is four times the mass of another ball. When these balls are separated by a distance of 10 cm, the force of gravitation between them is 6.67 × 10^-7 N. Find the masses of the two balls.
Solution:
m₁ = m, m₂ = 4m, d = 10 cm = 10 × 10^-2 m,
F = 6.67 × 10^-7 N
G = 6.67 × 10^-11 Nm²/kg ²
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{~d}^2}\)
6.67 × 10^-7 = \(\frac{6.67 \times 10^{-11} \times \mathrm{m} \times 4 \mathrm{~m}}{\left(10 \times 10^{-2}\right)^2}\)
4 m² = 10²
m² = \(\frac{100}{4}\) = 25
m = 5 kg
∴ m₁ = m = 5 kg
m₂ = 4m = 4 × 5 = 20 kg

Question 3.
Three spherical balls of masses 1 kg, 2kg and 3 kg are placed at the corners of an equilateral triangle of side 1 m. Find the magnitude of gravitational force exerted by the 2 kg and 3kg masses on the 1 kg mass.
Solution:
The force of attraction at 2 kg on the 1 kg particle
F₂ = \(\frac{\mathrm{Gmn}{\mathrm{~d}^2}\) = \(\frac{\mathrm{G} \times 1 \times 2}{1^2}\)
F₂ = 2 G

Question 4.
At a certain height above the earth’s surface, the acceleration due to gravity is 4% of its value at the surface of earth. Determine the height.
Solution:
g_h = 4% of g = \(\frac{4}{100}\)g, R = 6400 km
g_h = \(\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^2}\)
\(\frac{4 \mathrm{~g}}{100}=\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^2}\)
\(\left(1+\frac{h}{R}\right)^2=\frac{100}{4}\) = 25
1 + \(\frac{h}{R}\) = 5
\(\frac{h}{R}\) = 4
h = 4 × R = 4 × 6400 = 25,600 km.

Question 5.
A satellite is orbiting the earth at a height of 1000km. Find its orbital speed.
Solution:
h = 1000 km
Oribital velocity (v₀) = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\)
G = 6.67 × 10^-11 Nm²/kg ², M = 6 × 10²⁴ kg
R + h = 6400 + 1000 = 7400 km
= 7400 × 10³m
v₀ = \(\sqrt{\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{7400 \times 10^3}}\)
v₀ = \(\sqrt{0.5408 \times 10^{10}}\) = 73.54 × 10³ m/s
v₀ = 7.354km/s

Question 6.
A satellite orbits the earth at a height equal to the radius of earth. Find it’s
(i) orbital speed and
(ii) Period of revolution
Solution:
Height h = R

Question 7.
The gravitational force of attraction between two objects decreases by 36% when the distance between them is increased by 4 m. Find the original distance between them.
Solution:
F₁ = F, F₂ = \(\frac{64}{100}\) F
d₁ = d, d₂ = (d + 4) m

5d = 4d + 16
d = 16 m.

Question 8.
Four identical masses of m are kept at the corners of a square of side a. Find the gravitational force exerted on one of the masses by the other masses.
Solution:

Question 9.
Two spherical balls of 1 kg and 4kg are separated by a distance of 12 cm. Find the distance of a point from the 1 kg mass at which the gravitational force on any mass becomes zero.
Solution:
m₁ = 1 kg, m₂ = 4kg, r = 12 cm
∴ x = \(\frac{r}{\sqrt{\frac{m_2}{m_1}}+1}\) from m₁
= \(\frac{12}{\sqrt{\frac{4}{1}}+1}=\frac{12}{2+1}=\frac{12}{3}\) = 4 cm
At x = 4 cm the gravitational force is zero.

Question 10.
Three uniform spheres each of mass m and radius R are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any one of the spheres due to the other two.
Solution:

Question 11.
Two satellites are revolving round the earth at different heights. The ratio of their orbital speeds ¡s 2 : 1. If one of them is at a height of 100 km, what is the height of the other satellite ?
Solution:

4R + 400 = R + h₂
h₂ = 3R + 400 = 3 × 6400 + 400
= 19200 + 400
h₂ = 19,600 km.

Question 12.
A satellite is revolving round in a circular orbit with a speed of 8 km s-1 at a height where the value of acceleration due to gravity is 8 m s-2. How high is the satellite from the Earth’s surface ? (Radius of planet = 6000 km)
Solution:
v₀ = 8 km/s = 8000 m/s
g_h = 8 m/s², R = 6000 km = 6000 × 10³ m
∴ v₀ = \(\sqrt{\frac{G M}{R+h}}=\sqrt{g(R+h)}\)
v₀² = g(R + h)
(8000)² = 8(6000 × 10³ + h)
6000 × 10³ + h = 8 × 10⁶
h = (8 – 6) 10⁶
h = 2 × 10⁶m
h = 2000 × 10³ = 2000 km.

Question 13.
(a) Calculate the escape velocity of a body from the Earth’s surface, (b) If. the Earth were made of wood, its mass would be 10% of its current mass. What would be the escape velocity, if the Earth were made of wood ?
Solution:
R = 6400 × 10³m,

Additional Problems

Question 1.
Answer the following :
a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
b) An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity ?
c) If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the moon’s pull, (you can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the moon’s pull is greater than the tidal effect of sun. Why ?
Solution:
a) We cannot shield a body from the gravitational influence of nearby matter because the gravitational force on the body due to near by matter is independent of the presence of other matter, whereas it is not so in the case of electrical forces it means the gravitational screens are not possible.

b) Yes, if the size of the spaceship orbiting around the earth is large enough, an astronaut inside the spaceship can detect the variation in g.

c) Tidal effect depends inversly on the cube of the distance, unlike force which depends inversly on the square of the distance. Since the distance of moon from the ocean water is very small as compared to the distance of sun from the ocean water on earth. Therefore, the tidal effect of moon’s pull is greater than the tidal effect of the sun.

Question 2.
Choose the correct alternative :
a) Acceleration due to gravity increase^ decreases with increasing altitude.
b) Acceleration due to gravity increases/decreases with increas¬ing depth (assume the earth to be a sphere of uniform density).
c) Acceleration due to gravity is independent of mass of the earth/ mass of the body.
d) The formula – G Mm (1/r₂ – 1/r₁) is more/less accurate than the formula mg (r₂ – r₁) for the difference of potential energy between two points r2 and r1 distance away from the centre of the earth.
Solution:
a) decreases
b) decreases
c) mass of the body
d) more

Question 3.
Suppose there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth ?
Solution:
Here, T_e = 1 year; T_p = \(\frac{T_c}{2}=\frac{1}{2}\) year; r_e = 1
A.U.; r_p = ?
Using Kepler’s third law, we have
r_p = r_e\(\left(\frac{T_p}{T_e}\right)^{2 / 3}\) = \(1\left(\frac{1 / 2}{1}\right)^{2 / 3}\)
= 0.63 AU

Question 4.
Io, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is 4.22 × 10⁸m. Show that the mass of Jupiter is about-one-thousandth that of the sun.
Solution:
For a satellite of Jupiter, orbital period,
T₁ = 1.769 days = 1.769 × 24 × 60 × 60 s
Radius of the orbit of satellite,
r₁ = 4.22 × 10⁸ m
mass of Jupiter, M₁ is given by M₁
= \(\frac{4 \pi^2 \times\left(4.22 \times 10^8\right)^3}{G \times(1.769 \times 24 \times 60 \times 60)^2}\)
= \(\frac{4 \pi^2 r_1^3}{\mathrm{GT}_1^2}\) ……………. (1)
We know that the orbital period of earth around the sun,
T = 1 year = 365.25 × 24 × 60 × 60 s
Oribital radius, r = 1 A.U = 1.496 × 10¹¹ m

Question 5.
Let us assume that our galaxy consists of 2.5 × 10¹¹ stars each of one solar mass. How long will a star at a distance of 50,000ly from the galactic centre take to complete one revolution ? Take the diameter of the Milky Way to be 105 ly.
Solution:
Here, r = 50,000 ly =50,000 × 9.46 × 10¹⁵m
= 4.73 × 10²⁰m.
M = 2.5 × 10¹¹ solar, mass = 2.5 × 10¹¹ × (2 × 10³⁰) kg
= 5.0 × 10⁴¹ kg
We know that, M = \(\frac{4 \pi^2 r^3}{\mathrm{GT}^2}\)
or T = \(\left(\frac{4 \pi^2 r^3}{G M}\right)^{1 / 2}\)
= \(\left[\frac{4 \times(22 / 7)^2 \times\left(4.73 \times 10^{20}\right)^3}{\left(6.67 \times 10^{11}\right) \times\left(5.0 \times 10^{41}\right)}\right]^{1 / 2}\)
= 1.12 × 10¹⁶S.

Question 6.
Choose the correct alternative :
a) If the zero of potential energy is at infinity, the total energy of an orbiting satellite is negative of its kinetic/potentia! energy.
b) The energy required to launch an orbiting .satellite out of earth’s gravitational influence is more/less than the energy required to project a stationary object at the same height (as the satellite) out of earth’s influence.
Solution:
a) Kinetic energy
b) Less.

Question 7.
Does the escape speed of a body from the earth depend on (a) the mass of the body, (b) the Ideation from where it is projected, (c) the direction of projection, (d) the height of the location from where the body is launched ?
Solution:
The escape velocity is independent of mass of the body and the direction of projection it depends upon the gravitational potential at the point from where the body is launched. Since this potential depends slightly on the latitude and height of the point, therefore, the escape velocity depends slightly on these factors.

Question 8.
A comet orbits the sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit ? Neglect any mass loss of the comet when it comes very close to the Sun.
Solution:
A comet while going on elliptical orbit around the sun has constant angular momentum and total energy at all locations but other quantities vary with locations.

Question 9.
Which of the following symptoms is likely to afflict an astronaut in space
(a) swollen feet,
(b) swollen face,
(c) headache,
(d) orientational problem.
Solution:
a) We know that the legs carry the weight of the body in the normal position due to gravity pull. The astronaut in space is in weightless state. Hence, swollen feet may not affect his working.

b) In the conditions of weightless, the face of the astronaut is expected to get more supply. Due to it, the astronaut may develop swollen face. As eyes, ears, nose, mouth etc. are all embedded in the face, hence, swollen face may affect to great extent the seeing / hearing / eating / smelling capabilities of the astronaut in space.

c) Headache is due to metal strain it will persist whether a person is an astronaut in space or he is on earth it means headache will have the same effect on the astronaut in space as on a person on earth.

d) Space also has orientation. We also have the frames of reference in space. Hence, orientational problem will affect the astronaut in space.

Question 10.
In the following two exercises, choose the correct answer from among the given ones : The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig) (i) a, (ii) b, (iii) c, (iv) 0.

Solution:
We know that the gravitational potential is constant at all points upside a spherical shell. Therefore, the gravitational potential gradient at all points inside the spherical shell is zero [i.e as v is constant, \(\frac{\mathrm{dv}}{\mathrm{dr}}\) = 0].

Since gravitational intensity is equal to negative of the gravitational potential gradient, hence the gravitational intensity is zero at all points inside a hollow spherical shell. This indicates that the gravitational forces acting on a particle at any point inside a spherical shell, will be symmetrically placed. Therefore if we remove the upper hemispherical shell, the net gravitational forces acting on the particle at the centre Q or at some other point P will be acting downwards which will also be the direction of gravitational intensity it is so because, the gravitational intensity at a point is the gravitational force per unit mass at that point. Hence the gravitational intensity at the centre Q will be along c, i.e., option (iii) is correct.

Question 11.
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g. .
Solution:
As per explanation given in the answer of Q. 10, the direction of gravitational intensity at P will be along e i.e., option (ii) is correct.

Question 12.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero ? Mass of the sun = 2 × 10³⁰ kg, mass of the earth 6 × 10²⁴ kg. Neglect the effect of other planets etc. (orbital radius 1.5 × 10¹¹ m).
Solution:
Here M_s = 2 × 10³⁰ kg ; M_c = 6 × 10²⁴ kg ; r = 1.5 × 10¹¹ m .
Let x be the distance of a point from the earth where gravitational forces on the rocket due to sun and earth become equal and opposite. Then distance of rocket from the sun
= (r – x). If m is the mass of rocket then
\(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{m}}{(\mathrm{r}-\mathrm{x})^2}=\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{x}^2} \text { or } \frac{(\mathrm{r}-\mathrm{x})^2}{\mathrm{x}^2}=\frac{\mathrm{M}_{\mathrm{s}}}{\mathrm{M}_{\mathrm{e}}}\)

Question 13.
How will you ‘weigh the sun1, that is estimate its mass ? The mean orbital radius of the earth around the sun is 1.5 × 10⁸ km.
Solution:
To estimate the mass of the sun, we require, the time period of revolution T of one of its planets (say the earth). Let M_s, M_e be the masses of sun and earth respectively and r be the mean orbital radius of the earth around the sun. The gravitational force acting on earth due to sum is
F = \(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{M}_{\mathrm{e}}}{\mathrm{r}^2}\)
Let, the earth be moving in circular orbit around the sun, with a uniform angular velocity ω, the centripetal force acting on earth is.
F¹ = M_erω² = M_er \(\frac{4 \pi^2}{T^2}\)
As this centripetal force is provided by the gravitational pull of sun on earth, So
\(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{M}_{\mathrm{e}}}{\mathrm{r}^2}=\mathrm{M}_{\mathrm{e}} \mathrm{r} \frac{4 \pi^2}{\mathrm{~T}^2} \text { or } \mathrm{M}_{\mathrm{s}}=\frac{4 \pi^2 \mathrm{r}^3}{G \mathrm{~T}^2}\)
Knowing r and T, mass M_s of the sun can be estimated.
In this Question, we are given, r = 1.5 × 10⁸ km
= 1.5 × 10¹¹ m
T = 365 days = 365 × 24 × 60 × 60 s
∴ M_s = \(\frac{4 \times(22 / 7)^2 \times\left(1.5 \times 10^{11}\right)^3}{\left(6.67 \times 10^{-11}\right) \times(365 \times 24 \times 60 \times 60)^2}\)
= 2 × 10³⁰ kg.

Question 14.
A saturn year is 29.5 times the earth year. How far is the saturn from the sun if the earth is 1.50 × 10⁸ km away from the sun ?
Solution:
Here, T_s = 29.5 T_e; R_e = 1.5 × 10⁸ km; R_s =?
Using the relation, \(\frac{\mathrm{T}_{\mathrm{s}}^2}{\mathrm{R}_{\mathrm{s}}^3}=\frac{\mathrm{T}_{\mathrm{e}}^2}{\mathrm{R}_{\mathrm{e}}^3}\)
or R = Re \(\left(\frac{\mathrm{T}_{\mathrm{s}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\)
= 1.5 × 10⁸ \(\left(\frac{29.5 \mathrm{~T}_{\mathrm{e}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\)
= 1.43 × 10⁹ km.

Question 15.
A body weighs 63 N on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?
Solution:
Weight of the body = mg = 63N
At height h, the value of g is given by
g’ = \(\frac{g R^2}{(R+h)^2}=\frac{g R^2}{(R+R / 2)^2}\) = 4/9 g
Gravitational force on body at height h is
F = mg’ = m × \(\frac{4}{9}\) g = \(\frac{4}{9}\) mg
= \(\frac{4}{9}\) × 63 = 28N

Question 16.
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighed 250 N on the surface ?
Solution:
wt. of body at a depth d = mg¹
= m × g \(\left(1-\frac{d}{R}\right)\)
= 250 \(\left(1-\frac{R / 2}{R}\right)\)
= 125 N

Question 17.
A rocket is fired vertically with a speed of 5 km s^-1 from the earth’s surface. How far from the earth does the rocket go before returning to the earth ? Mass of the earth = 6.0 × 10²⁴ kg; mean radius of the earth = 6.4 × 10⁶ m; G = 6.67 × 10^-11 N m² kg^-2.
Solution:
Let the rocket be fired with velocity v from the surface of earth and it reaches a height h from the surface of earth where its velocity becomes zero.
Total energy of rocket at the surface of energy

or h = \(\frac{\mathrm{Rv}^2}{2 \mathrm{gR}-\mathrm{v}^2}\)
= \(\frac{\left(6.4 \times 10^6\right) \times\left(5 \times 10^3\right)^2}{2 \times 9.8 \times\left(6.4 \times 10^6\right)-\left(5 \times 10^3\right)^2}\)
= 1.6 × 10⁶m

Question 18.
The escape speed of a projectile on the earth’s surface is 11.2 km s-1. A body is projected out with thrice this speed. What is the speed of the body far away from the earth ? Ignore the presence of the sun and other planets.
Solution:
Here, v_e = 11.2 kms^-1, velocity of projection of the body v = 3ve. Let m be the mass of the projectile and v₀ be the velocity of the projectile when far away from the earth (i.e) out of gravitational field of earth) then from the law of conservation of energy
\(\frac{1}{2}\) mv₀² = \(\frac{1}{2}\) mv² – \(\frac{1}{2}\) mv_e²
or v₀ = \(\sqrt{v^2-v_e^2}\)
= \(\sqrt{(3 v e)^2-v_e^2}\)
= \(\sqrt{8} v_e=\sqrt{8}\) × 11.2 = 31.68 kms^-1

Question 19.
A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence ? Mass of the satellite = 200 kg; mass of the earth = 6.0 × 1024 kg; radius of the earth = 6.4 × 10⁶ m; G = 6.67 × 10^-11 N m² kg^-2.
Solution:
Total energy of orbiting satellite at a hight h.
= – \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}+\frac{1}{2} \mathrm{mv}^2\)
= – \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}+\frac{1}{2} m \frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}\)
= \(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)
energy expended to rocket the satellite out of the earth’s gravitational field.
= – (total energy of orbiting satellite)
= \(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)
= \(\frac{\left(6.67 \times 10^{-11}\right) \times\left(6 \times 10^{24}\right) \times 200}{2\left(6.4 \times 10^6+4 \times 10^5\right)}\)
= 5.9 × 10⁹J

Question 20.
Two stars each of one solar mass (= 2 × 10^30< kg) are approaching each other for a head on collision. When they are a distance i09 km, their speeds are negligible. What is the speed with which they collide? The radius of each star is 10^4< km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
Solution:
Here, mass of each star, M = 2 × 10^30< kg
initial distance between two stars, r = 10^9<
km = 10^12< m.
initial potential energy of the system = – \(\frac{\text { GMM }}{r}\)
Total K.E. of the stars = \(\frac{1}{2}\) mv^2< + \(\frac{1}{2}\) mv^2<
= Mv^2<
Where v is the speed of stars with which they collide. When the stars are about to collide, the distance between their centres, r^1< = 2R.
∴ Final potential energy of two starts = \(\frac{-\mathrm{GMM}}{2 \mathrm{R}}\)
since gain in K.E. is at the cost of loss in P.E

Question 21.
Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the mid point of the line joining the centres of the spheres ? Is an object placed at that point in equilibrium ? If so, is the equilibrium stable or unstable ?
Solution:
Gravitational field at the mid – point of the line joining the centres of the two spheres.
= \(\frac{\mathrm{GM}}{(r / 2)^2}(-\hat{r})+\frac{\mathrm{GM}}{(r / 2)^2} \hat{r}=0\)
Gravitational potential at the mid point of the list joining the centres of the two spheres is
v = \(\frac{-\mathrm{GM}}{r / 2}+\left(\frac{-\mathrm{GM}}{r / 2}\right)=\frac{-4 \mathrm{GM}}{r}\)
\(\frac{-4 \times 6.67 \times 10^{-11} \times 100}{1.0}\) = -2.7 × 10^-8< J/kg
As the effective force on the body placed at mid-point is zero, so the body is in equilibrium. If the body is displaced a little towards either mass body from its equilibrium position, it will not return back to its initial position of equilibrium. Hence, the body is in unstable equilibrium.

Question 22.
As you have learnt in the text, a geo-stationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth’s gravity at the site of this satellite ? (Take the potential energy at infinity to be zero). Mass of the earth = 6.0 × 10²⁴ kg, radius = 6400 km.
Solution:
Gravitational potential at height h from the surface of earth is
v = \(\frac{-\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}\)
= \(\frac{-6.67 \times 10^{-11} \times\left(6 \times 10^{24}\right)}{\left(6.4 \times 10^6+36 \times 10^6\right)}\)
= -9.4 × 10⁶ J/kg.

Question 23.
A star 2.5 times the mass of the sun and collapsed to a size of 12 km rotates with a speed of 1.2 rev. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity ? (mass of the sun = 2 × 10^30< kg).
Solution:
The object will remain struck to the surface of star due to gravity, if the accerlation due to gravity is more than the centrifugal accerlation due to its rotation.
Accerlation due to gravity, g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
= \(\frac{6.67 \times 10^{-11} \times 2.5 \times 2 \times 10^{30}}{(12000)^2}\)
= 2.3 × 10¹² m/s²
centrifugal accerlation = rw²
= r(2πv)²
= 12000 (2π × 1.5)²
= 1.1 × 10⁶ ms^-2
since g > rω² , therefore the body will remain struck with the surface of star.

Question 24.
A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system ? Mass of the space ship = 1000 kg; mass of the sun = 2 × 10³⁰ kg; mass of mars = 6.4 × 10^23< kg; radius of mars = 3395 km; radius of the orbit of mars = 2.28 × 10^8< km; G = 6.67 × 10^-11< N m² kg ² .
Solution:
Let R, be the radius of the orbit of mars and R be the radius of the mars. M be the mass of the sun and M’ be the mass of mars. If m is the mass of the space ship, then potential energy of space-ship due to gravitational attraction of the sun = \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
potential energy of space – ship due to gravitational attraction of mars = – \(\frac{\mathrm{GM}^1 \mathrm{~m}}{\mathrm{R}^1}\)
since K.E of space ship is zero, therefore total energy of spaceship
= \(\frac{-\mathrm{GMm}}{\mathrm{R}}\) – \(\frac{\mathrm{GM}^1 \mathrm{~m}}{\mathrm{R}^1}\)
= – Gm \(\left(\frac{M}{R}+\frac{M^1}{R^1}\right)\)
∴ energy required to rocket out the spaceship from the solar system = – (total energy of space ship)

Question 25.
A rocket is fired ‘vertically’ from the surface of mars with a speed of 2 km s^-1. If 20% of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of mars before returning to it ? Mass of mars = 6.4 × 10^23< kg; radius of mars = 3395 km; G = 6.67 × 10^-11< N m² kg^-2.
Solution:
Let m = mass of the rocket, M = mass of the mars and
R = radius of mars. Let v be the initial velocity of rocket.
Initial K.E = \(\frac{1}{2}\) mv²; Initial P.E = – \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
Total initial energy = \(\frac{1}{2}\) mv² – \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
since 20% of K.E is lost, only 80% is left behind to reach the height. Therefore
Total energy available = \(\frac{80}{100} \times \frac{1}{2}\) mv²
– \(\frac{-\mathrm{GMm}}{\mathrm{R}}\) = 0.4 mv² – \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
If the rocket reaches the higher point which is at a height h from the surface of Mars, its
K.E. is zero and P.E. = \(\frac{-\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
using principle of conservation of energy, we have
0.4 mv² – \(\frac{\mathrm{GMm}}{\mathrm{R}}=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
or \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}=\frac{\mathrm{GM}}{\mathrm{R}}\) – 0.4 v²

Textual Examples

Question 1.
Let the speed of the planet at the perihelion P in Fig. be υ_p and the Sun- planet distance SP be r_p. Relate {r_p, υ_p} to the corresponding quantities at the aphelion {r_A, υ_A}. Will the planet take equal times to traverse BAC and CPB ?

(a) An ellipse traced out by a planet around the sun. The colsest point is P and the farthest point is A. P is called the perihelion and A the aphelion. The semimajor axis (a) is half the distance AP
Answer:
The magnitude of the angular momentum at P is L_p = m_p r_p υ_p. Similarly, L_A = m_p r_A υ_A. From angular momentum conservation
m_p r_p υ_p = m_p r_A υ_A
or \(\frac{v_p}{v_A}=\frac{r_A}{r_p}\)

Question 2.
Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC. (a) What is the force acting on a mass,2m placed at the centroid O of the triangle ? (b) What is the force if the mass at the vertex A is doubled ?
Take AO = BO = CO = 1 m (see Fig)

Three equal masses are placed at the three vertices of the ∆ABC. A mass 2m is placed at the centroid O.
Answer:
(a) The angle between OC and the positive x- axix is 30° and so is the angle between OB and the negative x-axis. The individual forces a vector notation are

From the principle of superposition and the law of vector addition, the resultant gravitational force F_R on (2m) at O is
F_R = F_OA + F_OB + F_OC
F_R = 2Gm² \(\hat{\mathrm{j}}\) + 2Gm² \(-\hat{\mathrm{i}}\) cos 30° – \(\hat{\mathrm{j}}\) sin 30°) + 2Gm² (\(\hat{\mathrm{i}}\) cos 30° – \(\hat{\mathrm{j}}\) sin 30°) = 0
Alternatively, one expects on the basis of symmetry that the resultant force ought to be zero.

(b) By symmetry the x-component of the force cancels out. The y-component survives.
F_R = 4Gm² \(\hat{\mathrm{j}}\) – 2Gm² \(\hat{\mathrm{j}}\) = 2Gm² \(\hat{\mathrm{j}}\)

Question 3.
Find the potential energy of a system of four particles placed at the vertices of a square of side l. Also obtain the potential at the centre of the square.
Answer:
We have four mass pairs at distance l and two diagonal pairs at distance \(\sqrt{2}\)1 Hence,

= \(\frac{2 \mathrm{Gm}}{1}\left(2+\frac{1}{\sqrt{2}}\right)\) = -5.41 \(\frac{\mathrm{Gm}^2}{l}\)
The gravitational potential U(r) at the centre of the square (r = \(\sqrt{2}\) l / 2) is
U(r) = \(-4 \sqrt{2} \frac{\mathrm{Gm}}{\mathrm{l}}\)

Question 4.
Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in Fig. The two spheres are held fixed A projeetile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.

Answer:
If ON = r, we have
\(\frac{\mathrm{GMm}}{\mathrm{r}^2}=\frac{4 \mathrm{GMm}}{\left(6 \mathrm{R}-\mathrm{r}^2\right)}\)
(6R – r)² = 4r²
6R – r = ±2r
r = 2R or – 6R.
The neutral point r = -6R does not concern us in this example. Thus ON = r = 2R.
Thereafter, the greater gravitational pull of 4M would suffice. The mechanical energy at the surface of M is
E_i = \(\frac{1}{2} \mathrm{~m} v^2-\frac{\mathrm{GMm}}{\mathrm{R}}-\frac{4 \mathrm{GMm}}{5 \mathrm{R}}\)
The mechanical energy at N is purely potential.
E_N = \(-\frac{\mathrm{GMm}}{\mathrm{R}}-\frac{4 \mathrm{GMm}}{4 \mathrm{R}}\)
From the principle of conservation of mechanical energy
\(\frac{1}{2} v^2-\frac{G M}{R}-\frac{4 G M}{5 R}=-\frac{G M}{2 R}-\frac{G M}{R}\)
υ² = \(\frac{2 G M}{R}\left(\frac{4}{5}-\frac{1}{2}\right)\)
υ² = \(\left(\frac{3 \mathrm{GM}}{5 R}\right)^{1 / 2}\)

Question 5.
The planet Mars has two moons, phobos and delmos. (i) phobos has a period 7 hours, 39 minutes and an orbital radius of 9.4 × 10³ km. Calculate the mass of Mars, (ii) Assume that Earth and Mars move in circular orbits around the sun, with the Martian orbits being 1.52 times the orbital radius of the earth. What is the length of the Martain year in days ?
Answer:
(i) We employ T² = K (R_E + h)³ (where K = 4π² / GM_E) with the Earth’s mass replaced by the Martian mass M_m

(ii) Once again Kepler’s third law comes to our aid,
\(\frac{T_M^2}{T_E^2}=\frac{R_{M S}^3}{R_{E S}^3}\)
Where R_MS is the Mars-Sun distance and R_ES is the Earth-Sun distance.
∴ T_M = (1.52)^3/2 × 365
= 684 days
For example. the ratio of the semi-minor to semi-major axis for our Earth is, b/a = 0.99986.

Question 6.
Weighing the Earth : You are given the following data g = 9.81 ms² R_E = 6.37 x106 m the distance to the moon R = 3.4 × 10⁸ m and the time period of the moons revolution is 27.3 days. Obtain the mass of the Earth M_E in two different ways.
Answer:
(1) From g = \(\frac{F}{m}=\frac{G M_E}{R_E^2}\)
M_E = \(\frac{g R_E^2}{G}\)
= \(\frac{9.81 \times\left(6.37 \times 10^6\right)^2}{6.67 \times 10^{-11}}\)
= 5.97 × 10²⁴kg. (by Method – 1)

(2) The moon is a satellite of the Earth. From the derivation of Kepler’s third law

= 6.02 × 10²⁴kg (by Method – 2)
Both methods yield almost the same answer the difference between them being less than 1%.

Question 7.
Express the constant k T² = K (R_E + h)² where K = 4π²/GM_E of in days and kilometres. Given k = 10^-13 s² m^-3. The moon is at a distance of 3.84 × 10⁵ km from the earth. Obtain its time period of revolution in days.
Answer:
Given
k = 10^-13 s² m^-3 (d = day)
= 10^-13 \(\left[\frac{1}{(24 \times 60 \times 60)^2} d^2\right]\)
\(\left[\frac{1}{(1 / 1000)^3 \mathrm{~km}^3}\right]\) = 1.33 × 10^-14 d² km^-3
Using T² = K (R_E + h)³ (where k = 4π²/ GM_E) and the given value of k the time period of the moon is
T² = (1.33 × 10^-14) (3.84 × 10⁵)³
T = 27.3 d

Question 8.
A 400 kg satellite is in a circular orbit of radius 2R_E about the Earth. How much energy is required to transfer it to a circular orbit of radius 4R_E? What are the changes in the kinetic and potential energies ?
Answer:
Initially,
E₁ = \(\)
While finally
E_f = \(\)
The change in the total energy is
∆E = E_f – E_i
= \(\frac{\mathrm{GM}_E \mathrm{~m}}{8 R_E}=\left(\frac{\mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}^2}\right) \frac{\mathrm{mR} \mathrm{R}_{\mathrm{E}}}{8}\)
∆E = \(\frac{\mathrm{gm} \mathrm{R}_{\mathrm{E}}}{8}=\frac{9.81 \times 400 \times 6.37 \times 10^6}{8}\)
= 3.13 × 10⁹J
The kinetic enegy is reduced and it mimics ∆E, namely, ∆K = K_f – K_i = -3.13 × 10⁹ J.
The change in potential energy is twice the change in the total energy, namely
∆V = V_f – V_i= -6.25 × 10⁹ J

Use these Inter 1st Year Maths 1A Formulas PDF Chapter 1 Functions to solve questions creatively.

Intermediate 1st Year Maths 1A Functions Formulas

Function:
Let A and B be non – empty sets and f be a relation from A to B. If for each element a e A, there exists a unique element b e B such that (a,b) ∈ f, then f is called a function or mapping from A to B (or A into B). It is denoted by f: A → B. The set A is called the domain of f and B is called co-domain off.

Illustration: Let A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25}. Consider the relation f(x) = x², then f(1) = 1, f(2) = 4, f(3) = 9, f(4) = 16. Clearly each element in A has unique image in B. So, f: A → B.
f = {(1, 1) (2, 4) (3, 9) (4, 16)} is a function from A to. B.
Clearly Domain (f) = {1,2, 3, 4} and Range (f) = {1, 4, 9, 16}
Note : The number of functions that can be defined from, a non-empty finite set A into a non-empty finite set B is [n(B)]^n(A).

If f: A → B a function then f(A) = {f(a) / a ∈ A} is called the range off. It is a subset of B (ie) f(A) ≤ B.

One – one function (Injection):
Let f: A B, then f is said to be one-one function if different elements of A have different f- images in B. Thus f: A → B is one-one. (μ) f: A B is an injection <=> ay a2 e A and f(a7) = f(aj implies that a₁ = a₂

Illustration:
LetA = {1, 2, 3} and B = {2, 4, 6}. Consider f: A → B. f(x) = 2x then f(1) = 2, f(2) = 4 and f(3) = 6. Clearly f is a function from A to B such that different elements in A have different f – images in B.
∴ f: {(1, 2) (2, 4) (3, 6)} is one – one.

Note : The number of one-one functions that can be defined from a non-empty finite set A into a non-empty finite set B is n(B) P_n(A) if n(B) ≥ n(A) and zero if n(B) < n(A).

Onto function (Surjection):
Let f: A → B. If every element of B occurs as the image of at least one element of in A, then fis an onto function. Thus f: A → B is surjection iff for each b e B, 3 a e A such that f(a) = b. Clearly fis onto ⇔ Range (f) = B.

Illustration; Let A = {-1, 7, 2, -2}, B = {1, 4} and Let f: A → B, be a function defined by f(x) = x² then fis onto because f(A) = {f(-1), f(1), f(2), f(-2)} = {1, 4} = B.
Note : The number of onto functions that can be defined from a non – empty finite set A onto a two element set B is 2^n(A) – 2 if n(A) ≥ 2 and zero if n(A) < 2.

Bijective function :
A function f: A → B is a bijection if

• It is one – one i.e., f(a) – f(b) ⇒ a = b ∀ a, b ∈ A.
• It is onto i.e., ∀ b ∈ B ∃ a ∈ A such that f(a) = b.

Note : Number of bijections that can be defined from A to B is [n(A)]!, [n(A) = n(B)].

If f: A → B is a bijection then the relation f^-1 = {(b, a) / (a, b) ∈ f} is a function from B to A and is called the inverse function off.

Constant function :
Let f: A B defined in such a way that all the elements of A have the same f- image in B, then f is said to be a constant function.

Illustration : Let A – {1, 2, 3} and B = {6, 7, 8}. Let f: A → B
f(x) = 6 ∀ x ∈ A i.e., f = {(1, 6) (2, 6) (3, 6)} is a constant function.
The range of a constant function is a singleton set.

Identity function :
Let A be a non-empty set then the function f: A → A defined by, f(x) = x ∀ x ∈ I_A is called the identity function on A and is denoted by I_A. The identity function is bijective.

Let f: A → B, g: B → C be functions. Then gof: A → C is a function and (gof) (a) = g If (a)] ∀ a ∈ A, is called composite of ‘g’ with ‘f.

If f : A → B, g B → C are bijections so is (go f) : A → C and (gof)^-1 = f^-1o g^-1.

• If f: A → B is a bijection, then fof^-1 = I_B and f^-1of = I_A.
• If f: A → B, g: B → C such that go f = I_A fog = I_B then f is a bijection and g = f^-1

Let A be a non-empty subset of R such that – x ∈ A, for all x ∈ A and f: A → R.

• If f(-x) = f(x), ∀ x ∈ A then fis called an EVEN function.
• If f(-x) = – f(x), ∀ x ∈ A then f is called an ODD function.

Functions:
Def 1:
A relation f from a set A into a set B is said to be a function or mapping from A into B if for each x ∈ A there exists a unique y ∈ B such that (x, y) ∈ f. It is denoted
by f : A → B.
Note: Example of a function may be represented diagrammatically. The above example can be written diagrammatically as follows.

Def 2:
A relation f from a set A into a set B is a said to be a function or mapping from a into B if
i) x ∈ A ⇒ f (x) ∈ B
ii) x₁, x₂ ∈ A, x₂ ⇒ f (x₁) = f (x₂)

Def 3:
If f : A → B is a function, then A is called domain, B is called codomain and f (A) = {f (x): x ∈ A} is called range of f.

Def 4:
A function f : A → B if said to be one one function or injection from A into B if different element in A have different f-images in B.
Note:

• A function f : A → B is one one if f(x₁, y) ∈ f,(x₂, y) ∈ f ⇒ x₁ = x₂.
• A function f : A → B is one one iff x₁, x₂ ∈ A, x₁ ≠ x₂ ⇒ f (x₁) ^ f (x₁)
• A function f : A → B is one one iff x₁, x₂ ∈ A, f (x₁) = f (x₂) ⇒ x₁ = x₂
• A function f : A → B which is not one one is called many one function
• If f : A → B is one one and A, B are finite then n(A) < n(B).

Def 5:
A function f : A → B is said to be onto function or surjection from A onto B if f(A) = B.

Note:

• A function f : A → B is onto if y e B U ⇓ ∃x ∈ A ∋ f (x) = y .
• A function f : A → B which is not onto is called an into function.
• If A, B are two finite sets and f : A → B is onto then n(B) ≤ n(A).
• If A, B are two finite sets and n (B) = 2, then the number of onto functions that can be defined from A onto B is 2^{n( A)} – 2.

Def 6:
A function f : A → B is said to be one one onto function or bijection from A onto B if f : A → B is both one one function and onto function.

Theorem: If f : A → B, g : B → C are two functions then the composite relation gof is a function a into C.
Theorem: If f : A → B, g : B → C are two one one onto functions then gof : A → C is also one one be onto.
i) Let x₁, x₂ ∈ A and f (x₁) = f (x₂).
x₁,x₂ ∈ A, f : A → B ⇒ f (x₁), f (x₂) ∈ B
f (x₁), f (x₂) ∈ B → C, f (x₂) ⇒ g[f (x₁)] = g[f (x₂)] ⇒ (gof)(x₁) = (gof)(x₂)
x₁, x₂ ∈ A,(gof)(x₁) = (gof): A → C is one one ⇒ x₁ = x₂
x₁, x₂ ∈ A, f (x₁) = f (x₂) ⇒ x₁ = x₂.
∴ f: A → B Is one one.

ii) Proof: let z ∈ C,g : B → C is onto B y ∈ B ∃:g (y) = z y ∈ Bf : A → B is onto
∃x ∈ A ∋ f (x) = y
G {f(x)} = t
(g o f) x = t
∀ z ∈ CB x ∈ A ∋ (gof)(x) = z.
∴ g is onto.

Def 7:
Two functions f : A → B, g : C → D are said to be equal if

• A = C, B = D
• f (x) = g (x) ∀ x ∈ A. It is denoted by f = g

Theorem:
If f : A → B, g : B → C , h: C → D are three functions, then ho(gof) = (hof )of

Theorem:
if A is set, then the identify relation I on A is one one onto.

Def 8:
If A is a set, then the function I on A defined by I(x) = x ∀ x ∈ A, is called identify function on A. it is denoted by IA.

Theorem: If f : A → B and IA, IB are identify functions on A, B respectively then
foIA = IBof = f .
Proof:
I_A: A → A , f: A → B ⇒ foI_A: A → B
f : A → B , I_B : B → B ⇒ I_Bof: A → B
(foIA)(x) = f {IA(x)} = f (x), ∀x ∈ A ∴ f0I_A = f
(IBof)(x) = IB{f (x)} = f (x), ∀ x ∈ A ∴ I_Bof = f
∴ foI_A = I_Bof = f

Def 9:
If f : A → B is a function then {(y, x) ∈ B × A:(x, y) ∈ f} is called inverse of f. It is denoted by f^-1.

Def 10:
If f : A → B is a bijection, then the function f^-1: B → A defined by f^-1(y) = x iff f (x) = y ∀ y ∈ B is called inverse function of f.

Theorem:
If f : A → B is a bijection, then f^-1 of = IA, fof^-1 = IB
Proof:
Since f : A → B is a bijection f^-1: B → A is also a bijection and
f^-1 (y) = x ⇔ f (x) = y ∀ y ∈ B
f : A → B, f^-1: B → A ⇒ f^-1 of: A → A
Clearly I_A : A → A such that I_A (x) = x, ∀ x ∈ A.

Let x ∈ A
x ∈ A, f : A → B ⇒ f (x) ∈ B
Let y = f(x)
y = f (x) ⇒ f^-1(y) = x
(f -1 of)(x) = f ^-1[ f (x) = f^-1( y) = x = I_A (x)
(f^-1 of) (x) = IA (x) ∀ x ∈ A f^-1of = I_A
f^-1: B → A, f: A → B ⇒ fof^-1: B → B

Clearly I_B : B → B such that I_B (y) = y ∀ y ∈ B
Let y ∈ B
y ∈ B, f^-1: B → A = f^-1(y) ∈ A
Let f^-1(y) = x
f^-1(y) = x ⇒ f (x) = y
(fof’)(y) = f [ f ^-1( y)] = f (x) = y = I_B (y)
∴ (fof^-1)(y) = I_B (y) ∀ y ∈ B
∴ fof^-1 = I_B

Theorem: If f : A → B, g : B → C are two bijections then (gof )^-1 = f^-1og^-1.
Proof:
f : A → B, g : B →C are bijections gof: A → C is bijection (gof )^-1: C → A is a bijection.
f : A → B is a bijection f^-1: B → A is a bijection
g : B → C Is a bijection ⇒ g^-1: C → B is a bijection
g^-1:C → B , g^-1: B → A are bijections ⇒ f^-1 og^-1: C → A is a bijection

Let z ∈ C
z ∈ C, g : B → C is onto ⇒ ∃ y ∈ B ∋ g (y) = z ⇒ g^-1(z) = y
y e B, f: A → B is onto ⇒ ∃ x ∈ A ∋ f (x) = y ⇒ f^-1(y) = x
(gof) (x) = g[ f (x)] = g (y) = z ⇒ (gof )^-1(z) = x
∴ (gof)^-1 (z) = x = f^-1( y) = f^-1 [ g^-1 (z) ] = (f ^-1og^-1)(z)
∴ (gof )^-1 = f^-1og^-1

Theorem:
If f : A → B, g : B → A are two functions such that gof = I_A and fog = I_B then f : A → B is a bijection and f^-1 = g .
Proof:
Let x₁, x₂ ∈ A, f (x₁) = f (x₂)
x₁, x₂ ∈ A, f : A → B ⇒ f (x₁), f (x₂) ∈ B
f (x₁), f (x₂) ∈ B, f (x₁) = f (x₂), g = B → A
⇒ g [ f (x₁)] = g[ f (x₂)]
⇒ (gof)(x₁) = (gof)(x₁) ⇒ I_A (x₂) ⇒ x₁ = x₂
x₁,x₂ ∈ A, f (x₁) = f (x₂) ⇒ x₁ = x₂.
∴ f : A → B is one one

Let y ∈ B .
y ∈ B, g : B → A ⇒ g(y) ∈ A

Def 11:
A function f : A → B is said tobe a constant function if the range of f contain only one element i.e., f (x) = c ∀ x ∈ A where c is a fixed element of B

Def 12:
A function f : A → B is said to be a real variable function if A ⊆ R.

Def 13:
A function f : A → B is said to be a real valued function iff B ⊆ R.

Def 14:
A function f : A → B is said to be a real function if A ⊆ R, B ⊆ R.

Def 15:
If f : A → R, g : B → R then f + g : A ∩ B → R is defined as (f + g)(x) = f (x) + g (x) ∀ x ∈ A ∩ B

Def 16:
If f : A → R and k e R then kf : A → R is defined as (kf)(x) = kf (x), ∀ x ∈ A

Def 17:
If f : A → B, g : B → R then fg : A n B → R is defined as (fg)(x) = f (x)g(x) ∀ x ∈ A ∩ B .

Def 18:
If f : A → R, g : B → R then : C → R is defined as
C = {x ∈ A n B: g(x) ≠ 0}.

Def 19:
If f : A → R then |f| (x) =| f (x)|, ∀ x ∈ A

Def 20:
If n ∈ Z , n ≥ 0, a₀, a₁, a₂, ………….. a_n ∈ R, a_n ≠ 0, then the function f : R → R defined by
f (x) = a₀ + a₁x + a₂x² + + a_nxⁿ ∀ x ∈ R is called a polynomial function of degree n.

Def 21:
If f : R → R, g : R → R are two polynomial functions, then the quotient f/g is called a rational function.

Def 22:
A function f : A → R is said to be bounded on A if there exists real numbers k1, k2 such that k1 < f (x) < k2 ∀ x ∈ A Def 23: A function f : A → R is said to be an even function if f (-x) = f (x) ∀ x ∈ A Def 24: A function f : A → R is said to be an odd function if f (-x) = – f (x) ∀ x ∈ A .  Def 25: If a ∈ R, a > 0 then the function f : R → R defined as f (x) = ax is called an exponential function.

Def 26:
If a ∈ R, a > 0, a ≠ 1 then the function f : (0, ∞) → R defined as f (x) = log_a x is called a logarithmic function.

Def 27:
The function f : R → R defined as f(x) = n where n ∈ Z such that n ≤ x < n + 1 ∀ x ∈ R is called step function or greatest integer function. It is denoted by f (x) = [x]

Def 28:
The functions f(x) = sin x, cos x, tan x, cot x, sec x or cosec x are called trigonometric functions.

Def 29:
The functions f (x) = sin^-1 x ,cos^-1x,tan^-1 x,cot^-1x,sec^-1x or cos ec^-1 x are called inverse trigonometric functions.

Def 30:
The functions f(x) = sinh x, cosh x, coth x, sech x or cosech x are called hyperbolic functions.

Def 30:
The functions f(x) = sinh^-1x, cosh^-1x, coth^-1x, sech^-1x or cosech^-1x are called Inverse hyperbolic functions.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(b)

I.

Question 1.
If the quadratic equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0, (b ≠ c) have a common root, then show that a + 4b + 4c = 0
Solution:
Let α be the common roots of the equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0
aα² + 2bα + c = 0
aα² + 2cα + b = 0
on Subtracting,
2α(b – c) + c – b = 0
2α(b – c) = b – c
2α = 1 (b ≠ c)
α = \(\frac{1}{2}\)
Substitute α = \(\frac{1}{2}\) in ax² + 2bx + c = 0 is
\(a\left(\frac{1}{4}\right)+2 b \frac{1}{2}+c=0\)
⇒ a + 4b + 4c = 0
∴ a + 4b + 4c = 0

Question 2.
If x² – 6x + 5 = 0 and x² – 12x + p = 0 have a common root, then find p.
Solution:
Given x² – 6x + 5 = 0, x² – 12x + p = 0 have a common root.
If α is the common root then
α² – 6α + 5 = 0, α² – 12α + p = 0
α² – 6α + 5 = 0
⇒ (α – 1) (α – 5) = 0
⇒ α = 1 or 5
If α = 1 then α² – 12α + p = 0
⇒ 1 – 12 + p = 0
⇒ p = 11
If α = 5 then α² – 12α + p = 0
⇒ 25 – 60 + p = 0
⇒ p = 35
∴ p = 11 or 35

Question 3.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
The roots of the equation x² – 6x + 5 = 0 are
(x – 1) (x – 5) = 0
⇒ x = 1, x = 5
Case (i): x = 1 is a common root then it is also root for the equation x² – 3ax + 35 = 0
⇒ 1 – 3a(1) + 35 = 0
⇒ a = 12
Case (ii): x = 5 is a common root then
(5)² – 3a(5) + 35 = 0
⇒ 60 – 15a = 0
⇒ a = 4
∴ a = 12 (or) a = 4

Question 4.
If the equation x² + ax + b = 0 and x² + cx + d = 0 have a common root and the first equation has equal roots, then prove that 2(b + d) = ac.
Solution:
Let α be the common root.
∴ x² + ax + b = 0 has equal roots.
Its roots are α, α
α + α = -a
⇒ α = \(-\frac{a}{2}\)
α . α = b
⇒ α² = b
∴ α is a root of x² + cx + d = 0
⇒ α² + cα + d = 0
⇒ b + c(\(-\frac{a}{2}\)) + d = 0
⇒ 2(b + d) = ac

Question 5.
Discuss the signs of the following quadratic expressions when x is real.
(i) x² – 5x + 4
Solution:
x² – 5x + 4 = (x – 1) (x – 4)
a = 1 > 0
The expression x² – 5x + 2 is positive if x < 1 or x > 4 and is negative if 1 < x < 4

(ii) x² – x + 3
Solution:
∆ = b² – 4ac
= (-1)² – 4 (1) (3)
= 1 – 12
= -11 < 0
a = 1 > 0, ∆ < 0
⇒ The given expression is positive for all real x.

Question 6.
For what values of x, the following expressions are positive?
(i) x² – 5x + 6
Solution:
x² – 5x + 6 = (x – 2) (x – 3)
Roots of x² – 5x + 6 = 0 are 2, 3 which are real.
The expression x² – 5x + 6 is positive if x < 2 or x > 3
∴ a = 1 > 0

(ii) 3x² + 4x + 4
Solution:
Here a = 3, b = 4, c = 4
∆ = b² – 4ac
= 16 – 48
= -32 < 0
∴ 3x² + 4x + 4 is positive ∀ x ∈ R
∴ a = 3 > 0 and ∆ < 0
ax² + bx + c and ‘a’ have same sign ∀ x ∈ R, if ∆ < 0

(iii) 4x – 5x² + 2
Solution:
Roots of 4x – 5x² + 2 = 0 are \(\frac{-4 \pm \sqrt{16+40}}{-10}\)
i.e., \(\frac{2 \pm \sqrt{14}}{5}\) which is real
∴ The expression 4x – 5x² + 2 is positive when
\(\frac{2-\sqrt{14}}{5}<x<\frac{2+\sqrt{14}}{5}\) [∵ a = -5 < 0]

(iv) x² – 5x + 14
Solution:
Here a = 1, b = -5, c = 14
∆ = b² – 4ac
= 25 – 56
= -31 < 0
∴ ∆ < 0 ∵ a = 1 > 0 and ∆ < 0
⇒ x² – 5x + 14 is positive ∀ x ∈ R.

Question 7.
For what values of x, the following expressions are negative?
(i) x² – 7x + 10
Solution:
x² – 7x + 10 = (x – 2)(x – 5)
Roots of x² – 7x + 10 = 0 are 2, 5 which are real.
∴ The expression x² – 7x + 10 is negative if 2 < x < 5, ∵ a = 1 > 0

(ii) 15 + 4x – 3x²
Solution:
The roots of 15 + 4x – 3x² = 0 are \(\frac{-4 \pm \sqrt{16+180}}{-6}\)
i.e., \(\frac{-5}{3}\), 3
∴ The expression 15 + 4x – 3x² is negative if
-5x < \(\frac{-5}{3}\) or x > 3, ∵ a = -3 < 0

(iii) 2x² + 5x – 3
Solution:
The roots of 2x² + 5x – 3 = 0 are \(\frac{-5 \pm \sqrt{25+24}}{4}\)
i.e., -3, \(\frac{1}{2}\)
∴ The expression 2x² + 5x – 3 is negative if -3 < x < \(\frac{1}{2}\), ∵ a = 2 > 0

(iv) x² – 5x – 6
Solution:
x² – 5x – 6 = (x – 6) (x + 1)
Roots of x² – 5x – 6 = 0 are -1, 6 which are real.
∴ The expression x² – 5x – 6 is negative if -1 < x < 6, ∵ a = 1 > 0

Question 8.
Find the changes in the sign of the following expressions and find their extreme values.
Hint: Let α, β are the roots of ax² + bx + c = 0 and α < β
(1) If x < α or x > β, ax² + bx + c and ‘a’ have same sign.
(2) If α < x < β, ax² + bx + c and ‘a’ have opposite sign.

(i) x² – 5x + 6
Solution:
x² – 5x + 6 = (x – 2) (x – 3)
(1) If 2 < x < 3, the sign of x² – 5x + 6 is negative, ∵ a = 1 > 0
(2) If x < 2 or x > 3, the sign of x² – 5x + 6 is positive, ∵ a = 1 > 0
Since a > 0, the minimum value of x² – 5x + 6 is \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{4(1)(6)-(-5)^{2}}{4(1)}\)
= \(\frac{24-25}{4}\)
= \(-\frac{1}{4}\)
Hence the extreme value of the expression x² – 5x + 6 is \(-\frac{1}{4}\)

(ii) 15 + 4x – 3x²
Solution:
15 + 4x – 3x² = 15 + 9x – 5x – 3x²
= 3(5 + 3x) – x(5 + 3x)
= (3 – x) (5 + 3x)
(1) If \(-\frac{5}{3}\) < x < 3 the sign of 15 + 4x – 3x² is positive, ∵ a = -3 < 0
(2) If x < \(-\frac{5}{3}\) or x > 3, the sign of 15 + 4x – 3x² is negative, ∵ a = -3 < 0
Since a < 0, the maximum value of 15 + 4x – 3x² is \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{4(-3)(15)-16}{4(-3)}\)
= \(\frac{49}{3}\)
Hence the extreme value of the expression 15 + 4x – 3x² is \(\frac{49}{3}\)

Question 9.
Find the maximum or minimum of the following expressions as x varies over R.
(i) x² – x + 7
Solution:
a = 1 > 0,
minimum value = \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{28-1}{4}\)
= \(\frac{27}{4}\)

(ii) 12x – x² – 32
Solution:
a = -1 < 0,
maximum value = \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{128-144}{-4}\)
= 4

(iii) 2x + 5 – 3x²
Solution:
a = -3 < 0,
maximum value = \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{(4)(-3)(5)-(2)^{2}}{4 \times-3}\)
= \(\frac{16}{3}\)

(iv) ax² + bx + a
Solution:
If a < 0, then maximum value = \(\frac{4 a \cdot a-b^{2}}{4 a}\) = \(\frac{4 a^{2}-b^{2}}{4 a}\)
If a > 0, then minimum value = \(\frac{4 a \cdot a-b^{2}}{4 a}\) = \(\frac{4 a^{2}-b^{2}}{4 a}\)

II.

Question 1.
Determine the range of the following expressions.
(i) \(\frac{x^{2}+x+1}{x^{2}-x+1}\)
Solution:
Let y = \(\frac{x^{2}+x+1}{x^{2}-x+1}\)
⇒ x²y – xy + y = x² + x + 1
⇒ x²y – xy + y – x² – x – 1 = 0
⇒ x² (y – 1) – x(y + 1) + (y – 1) = 0
∴ x is real ⇒ b² – 4ac ≥ 0
⇒ (y + 1 )² – 4(y – 1 )² ≥ 0
⇒ (y + 1)² – (2y – 2)² ≥ 0
⇒ (y + 1 + 2y – 2) (y + 1 – 2y + 2) ≥ 0
⇒ (3y – 1) (-y + 3) ≥ 0
⇒ -(3y – 1) (y – 3) ≥ 0
a = Coeff of y² = -3 < 0
But The expression ≥ 0
⇒ y lies between \(\frac{1}{3}\) and 3
∴ The range of \(\frac{x^{2}+x+1}{x^{2}-x+1}\) is [\(\frac{1}{3}\), 0]

(ii) \(\frac{x+2}{2 x^{2}+3 x+6}\)
Solution:
Let y = \(\frac{x+2}{2 x^{2}+3 x+6}\)
Then 2yx² + 3yx + 6y = x + 2
⇒ 2yx² + (3y – 1)x + (6y – 2) = 0
∴ x is real ⇒ discriminant ≥ 0
⇒ (3y – 1)² – 4(2y)(6y – 2) ≥ 0
⇒ 9y² + 1 – 6y – 48y² + 16y ≥ 0
⇒ -39y² + 10y + 1 ≥ 0
⇒ 39y² – 10y – 1 < 0
⇒ 39y² – 13y + 3y – 1 < 0
⇒ 13y(3y – 1) + 1(3y – 1) ≤ 0
⇒ (3y – 1) (13y + 1) ≤ 0
∴ a = Coeff of y² = 39 > 0 and the exp ≤ 0
⇒ y lies between \(\frac{-1}{13}\) and \(\frac{1}{3}\)
∴ Range of \(\frac{x+2}{2 x^{2}+3 x+6}\) is \(\left[-\frac{1}{13}, \frac{1}{3}\right]\)

(iii) \(\frac{(x-1)(x+2)}{x+3}\)
Solution:
Let y = \(\frac{(x-1)(x+2)}{x+3}\)
⇒ yx + 3y = x² + x – 2
⇒ x² + (1 – y)x – 3y – 2 = 0
x ∈ R ⇒ (1 – y²) – 4(-3y – 2) ≥ 0
⇒ 1 + y² – 2y + 12y + 8 ≥ 0
⇒ y² + 10y + 9 ≥ 0
y² + 10y + 9 = 0
⇒ (y + 1) (y + 9) = 0
⇒ y = -1, -9
y² + 10y + 9 ≥ 0
∴ a = Coeff of y² = 1 > 0 and exp ≥ 0
⇒ y ≤ -9 or y ≥ -1
∴ Range = (-∞, -9] ∪ [-1, ∞)

(iv) \(\frac{2 x^{2}-6 x+5}{x^{2}-3 x+2}\)
Solution:
Let y = \(\frac{2 x^{2}-6 x+5}{x^{2}-3 x+2}\)
⇒ yx² – 3yx + 2y = 2x² – 6x + 5
⇒ (y – 2)x² + (6 – 3y)x + (2y – 5) = 0
x ∈ R ⇒ (6-3y)² – 4(y – 2) (2y – 5) ≥ 0
⇒ 36 + 9y² – 36y – 4(2y² – 9y + 10) ≥ 0
⇒ 36 + 9y² – 36y – 8y² + 36y – 40 ≥ 0
⇒ y² – 4 ≥ 0
y² – 4 = 0
⇒ y² = 4
⇒ y = ±2
y² – 4 ≥ 0
⇒ y ≤ -2 or y ≥ 2
⇒ y does not lie between -2, 2,
∵ y² Coeff is > 0 and exp is also ≥ 0
∴ Range of \(\frac{2 x^{2}-6 x+5}{x^{2}-3 x+2}\) is (-∞, -2] ∪ [2, ∞)

Question 2.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real.
Solution:
Let y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
⇒ y = \(\frac{x+1+3 x+1-1}{(3 x+1)(x+1)}\)
⇒ y = \(\frac{4 x+1}{3 x^{2}+4 x+1}\)
⇒ 3yx² + 4yx + y = 4x + 1
⇒ 3yx² + (4y – 4)x + (y – 1) = 0
x ∈ R ⇒ (4y – 4)² – 4(3y)(y – 1) ≥ 0
⇒ 16y² + 16 – 32y – 12y² + 12y ≥ 0
⇒ 4y² – 20y + 16 ≥ 0
4y² – 20y + 16 = 0
⇒ y² – 5y + 4 = 0
⇒ (y – 1)(y – 4) = 0
⇒ y = 1, 4
4y² – 20y + 16 ≥ 0
⇒ y ≤ 1 or y ≥ 4
⇒ y does not lie between 1 and 4
Since y² Coeff is the and exp ≥ 0.

Question 3.
If x is real, prove that \(\frac{x}{x^{2}-5 x+9}\) lies between 1 and \(\frac{-1}{11}\).
Solution:
Let y = \(\frac{x}{x^{2}-5 x+9}\)
⇒ yx² + (-5y – 1)x + 9y = 0
x ∈ R ⇒ (5y – 1)² – 4y(9y) ≥ 0
⇒ 25y² + 1 + 10y – 36y² ≥ 0
⇒ -11y² + 10y + 1 ≥ 0 ……….(1)
-11y² + 10y + 1 = 0
⇒ -11y² + 11y – y + 1 = 0
⇒ 11y(-y + 1) + 1(-y + 1) = 0
⇒ (-y + 1) (11y + 1) = 0
⇒ y = 1, \(\frac{-1}{11}\)
-11y² + 10y + 1 ≥ 0
∴ y² Coeff is -ve, but the exp is ≥ 0 from (1)
⇒ \(\frac{-1}{11}\) ≤ y ≤ 1
⇒ y lies between 1 and \(\frac{-1}{11}\)

Question 4.
If the expression \(\frac{x-p}{x^{2}-3 x+2}\) takes all real value for x ∈ R, then find the bounts for p.
Solution:
Let y = \(\frac{x-p}{x^{2}-3 x+2}\), given y is real
Then yx² – 3yx + 2y = x – p
⇒ yx² + (-3y – 1)x + (2y + p) = 0
∵ x is real ⇒ (-3y – 1)² – 4y(2y + p) ≥ 0
⇒ 9y² + 6y + 1 – 8y² – 4py ≥ 0
⇒ y² + (6 – 4p)y + 1 ≥ 0
∵ y is real ⇒ y² + (6 – 4p)y + 1 ≥ 0
⇒ The roots are imaginary or real and equal
⇒ ∆ ≤ 0
⇒ (6 – 4p)² – 4 ≤ 0
⇒ 4(3 – 2p)² – 4 ≤ 0
⇒ (3 – 2p)² – 1 ≤ 0
⇒ 4p² – 12p + 8 ≤ 0
⇒ p² – 3p + 2 ≤ 0
⇒ (p – 1)(p – 2) ≤ 0
If p = 1 or p = 2 then \(\frac{x-p}{x^{2}-3 x+2}\) is not defined.
∴ 1 < p < 2

Question 5.
If c² ≠ ab and the roots of (c² – ab)x² – 2(a² – bc)x + (b² – ac) = 0 are equal, then show that a³ + b³ + c³ = 3abc or a = 0.
Solution:
Given equation is (c² – ab)x² – 2(a² – bc)x + (b² – ac) = 0
Discriminant = 4(a² – bc)² – 4(c² – ab) (b² – ac)
= 4[(a² – bc)² – (c² – ab) (b² – ac)]
= 4(a⁴ + b²c² – 2a²bc – b²c² + ac³ + ab³ – a²bc)
= 4(a⁴ + ab³ + ac³ – 3a²bc)
= 4a(a³ + b³ + c³ – 3abc)
The roots are equal ⇒ discriminant = 0
4a(a³ + b³ + c³ – 3abc) = 0
a = 0 or a³ + b³ + c³ – 3abc = 0
i.e., a = 0 or a³ + b³ + c³ = 3abc

Andhra Pradesh BIEAP AP Inter 1st Year Economics Study Material 5th Lesson Theory of Value Textbook Questions and Answers.

AP Inter 1st Year Economics Study Material 5th Lesson Theory of Value

Essay Questions

Question 1.
Explain the classification of Markets. [March 18, 17]
Answer:
Edwards defiried “Market , as a mechanism by which buyers and sellers are brought together”. Hence market means where selling and buying transactions take place. The classification of markets is’ based on three factors.

1. On the basis of area
2. On the basis of time
3. On the basis of competition.

I. On the basis of area : According to the area, markets can be of three types.

1. Local market : When a commodity is sold at particular locality. It is called a local market. Ex : Vegetables, flowers, fruits etc.
2. National market : When a commodity is demanded and supplied throughout the country is called national market. Ex : Wheat, rice etc.
3. International market: When a commodity is demanded and supplied all over the world is called international market. Ex : Gold, silver etc.-

II. On the basis of time : It can be further classified into three types.

1. Market period or very short period : In this period where producer cannot make any changes in supply of a commodity. Here supply remains constant. Ex : Perishable goods. .
2. Short period : In this period supply can be change to some extent by changing the variable factors of production.
3. Long period : In this period-supply can be adjusted in according change in demand. In long run all factors will become variable.

III. On the basis of competition : This can be classified into two types.

1. Perfect market: A perfect market is one in which the number of buyers and sellers is very large, all engaged in buying and selling a homogeneous products without any restrictions.
2. Imperfect market: In this market, competition is imperfect among the buyers and sellers. These markets are divided into
   1. Monopoly
   2. Duopoly
   3. Oligopoly
   4. Monopolistic competition.

Question 2.
Elucidate the features of perfect competition.
Answer:
Perfect competitive market is one in which the number of buyers and sellers is very large, all engaged in buying and selling a homogeneous products without any restrictions.
The following are the features of perfect competition :
1) Large number of buyers and sellers : Under perfect competition the number of buyers and sellers are large. The share of each seller and buyer in total supply or total demand is small. So no buyer and seller cannot influence the price. The price is determine only demand and supply. Thus the firm is price taker.

2) Homogeneous product: The commodities produced by all the firm of an industry are homogeneous or identical. The cross elasticity of products of sellers is infinite. As a result, single price will rule in the industry.

3) Free entry and exit: In this competition there is a freedom of free entry and exit. If existing firms are getting profits. New firms enter into the market. But when a firm getting losses, it would leave to the market.

4) Perfect mobility of factors of production : Under perfect competition the factors of production are freely mobile between the firms. This is useful for free entry and exits of firms.

5) Absence of transport cost: There are no transport cost. Due to this, price of the commodity will be the same throughout the market.

6) Perfect knowledge of the economy : All the buyers and sellers have full information regarding the prevailing and future prices and availability of the commodity. Information regarding market conditions is availability of commodity.

Question 3.
Describe Price determination in the imperfect competition.
Answer:
Monopoly is one of the market in the imperfect competition. The word Mono’ means single and Poly means seller. Thus monopoly means single seller market.
In the words of Bilas “Monopoly is represented by a market situation in which there is a single seller of a product for which there are no close substitutes, this single seller is unaffected by and does not affect, the prices and outputs of other products sold in the economy”. Monopoly exists under the following conditions.

1. There is a single seller of product.
2. There are no close substitutes.
3. Strong barriers to entry into the industry exist.

Features of monopoly :

1. There is no single seller in the market.
2. No close substitutes.
3. There is no difference between firm and industry.
4. The monopolist either fix the price or output.

Price determination : Under monopoly the monopolist has complete control over the supply of the product. He is price maker who can set the price to attain maximum profit. But he cannot do both things simultaneously. Either he can fix the price and leave the output to be determined by consumer demand at a particular price. Or he can fix the output to be produced and leave the price to be determined by the consumer demand for his product. This can be shown in the diagram.

In the above diagram on ‘OX’ axis measures output and OY axis measures cost. AR is Average Revenue curve, AC is Average Cost curve. In the above diagram at E point where MC = MR at that point the monopolist determine the output. Price is determine where this output line touches the AR line. In the above diagram for producing OQ quantity cost of production is OCBQ and revenue is OPAQ.
Profit = Revenue – Cost
= PACB shaded area is profit under monopoly.

Short Answer Questions

Question 1.
What are the main features of perfect competition ?
Answer:
Perfect competitive market is one in which the number of buyers and sellers is very large, all engaged in buying and selling a homogeneous products without any restrictions.
The following are the features of perfect competition :
1) Large number of buyers and sellers : Under perfect competition the number of buyers and sellers are large. The share of each seller and buyer in total supply or total demand is small. So no buyer and seller cannot influence the price. The price is determine only demand and supply. Thus the firm is price taker.

2) Homogeneous product: The commodities produced by all the firm of an industry are homogeneous or identical. The cross elasticity of products of sellers is infinite. As a result, single price will rule in the industry.

3) Free entry and exit: In this competition there is a freedom of free entry and exit. If existing firms are getting profits. New firms enter into the market. But when a firm getting losses, it would leave to the market.

4) Perfect mobility of factors of production : Under perfect competition the factors of production are freely mobile between the firms. This is useful for free entry and exits of firms.

5) Absence of transport cost: There are no transport cost. Due to this, price of the commodity will be the same throughout the market.

6) Perfect knowledge of the economy : All the buyers and sellers have full information regarding the prevailing and future prices and availability of the commodity. Information regarding market conditions is availability of commodity.

Question 2.
What is meant by price discrimination ? Explain various methods of price discrimination.
Answer:
Price discrimination refers to the practice of a monopolist charging different prices for different customers of. the same product.
In the words of Joan Robinson “The act of selling the same article, produced under single control at different prices to different buyers is known as price discrimination”. Price discrimination is of three types. 1. Personal 2. Local 3. Use or trade discrimination.

1. Personal discrimination : When a seller charges different prices from different persons.
   Ex : A book is sold ₹ 15/- to one person and other person at discount rate of ?
2. Local discrimination : When a seller charges different prices from people of different localities or places.
   Ex : Dumping.
3. Use discrimination : When different prices of commodity are charged according to the uses to which the commodity is put is known discrimination is according to use.
   Ex : Electricity is sold at a cheaper rate for uses of domestic purposes than for industrial purposes.

Question 3.
Define Oligopoly.
Answer:
The term ‘Oligopoly’ is derived from two Greek word “Oligoi” meaning a few and “Pollein” means to sell. Oligopoly refers to a market situation in which the number of sellers dealing in a homogeneous or differentiated product is small. It is called competition among the few. The main features of oligopoly are the following.

1. Few sellers of the product.
2. There is interdependence in the determination of price.
3. Presence of monopoly power.
4. There is existence of price rigidity.
5. There is excessive selling cost or advertisement cost.

Question 4.
Compare Perfect competition and Monopoly.
Answer:
Perfect competition

1. There is large number of sellers.
2. All products are homogeneous.
3. There is freedom of free entry and exists.
4. There is difference between industry and firm.
5. Industry determines the price and firm receives the price.
6. There is universal price.
7. The AR, MR curves are parallel to ‘X, axis.

Monopoly

1. There is only one seller.
2. No close substitutes.
3. There is no freedom of free entry and exists.
4. Industry and firm both are same.
5. Firm alone determine the price.
6. Price discrimination is possible.
7. The AR, MR curves are different and slopes downs from left to right.

Additional Questions

Question 5.
Define Monopolistic competition. Explain the important characteristics of Monopolistic competition.
Answer:
It is a market with many sellers for a product but the products are different in certain respects. It is mid way of monopoly and perfect competition. Prof. E.H. Chamberlin and Mrs. Joan Robinson pioneered this market analysis.
Characteristics of Monopolistic competition :

1. Relatively small number of firms : The number of firms in this market are less than that of perfect competition. No one should not control the output in the market as a result of high competition.
2. Product differentiation : One of the features of monopolistic competition is product
   differentiation. It take the form of brand names, trade marks etc. It cross elasticity of demand is very high.
3. Entry and exit: Entry into the industry is unrestricted. New firms are able to commence production of very close substitutes for the existing brands of the product.
4. Selling cost: Advertisement or sales promotion technique is the important feature of Monopolitic competition. Such costs are called selling costs.
5. More Elastic Demand : Under this competition the demand curve slopes downwards from left to the right. It is highly elastic.

Question 6.
Explain the price determination under perfect competition ?
Answer:
Perfect competition is a competition in which the number of buyers and sellers is very large. All enged in buying and selling a homogeneous without any restrictions.

Under this competition there are large no. of by buyers and sellers no buyer is.a seller can’t influence market price all products are homogeneous there is a freedom of free entry and exit. There is a perfect mobility of factors are production. There is no transport cost these are the main features are perfect competition.

Price determination:
Under perfect competition sellers and buyers can’t decide the price industry decides the price of the good in the supply and demand determined the price these can shown in the following table.

In this competition where demand supply both are equal at that point price and output determine the table changes in price always lead to a change in supply and demand as price increases there is a fall in the quantity demanded. The relation between price and demand is negative. The relation between price and supply is positive. It can be observe the table price 1 ₹ market demand 60 and supply is 20. When price increases 5 ₹ supply increases’ 60 and demand decreases 20. When the price is 3 ₹ the demand supply are equal that is 40 these price called equilibrium price. This process is explain with help of the diagram.

In the diagram ‘OX’ axis shown demand and supply OY’ axis represented price. DD demand curve, ‘SS’ is supply curve. In the diagram the demand curve and supply curve intersect at point E. Where the price is ‘OP’ and output is ‘OQ’.

Very Short Answer Questions

Question 1.
Market
Answer:
Market is place where commodities are brought and sold and where buyers and sellers meet. Communication facilities help us today to purchase and sell without sell without going to the market. All the activities take place is now called as market.

Question 2.
Local Market
Answer:
A product is said to have local market, when buyers and sellers of the product carry on the business in a particular locality. These goods are highly perishable cannot to take to distant places. They cannot even stored for a longer time.
Ex : Vegetables, milk, fruits etc.

Question 3.
National Market
Answer:
A National Market is said to exist when a commodity is demanded and supplies all over our country.
Ex : Rice, wheat, sugar etc. .

Question 4.
Monopoly
Answer:
Mono means single, Poly means seller. In this market single seller and there is no close substitutes. The monopolist is a price maker.

Question 5.
Monopolistic Competitions
Answer:
It is a market where several firms produce same commodity with small differences is called monopolistic competition. In this market producers to produce close substitute goods.
Ex : Soaps, cosmetics etc.

Question 6.
Oligopoly
Answer:
A market with a small number of producer is called oligopoly. The product may be homogeneous or may be differences. This market exists in automobiles, electricals etc.

Question 7.
Duopoly [march 16]
Answer:
When there are only two sellers of a product, there exist -duopoly. Each seller under duopoly must consider the other firms reactions to any changes that he make in price or output. They make decisions either independently or together.

Question 8.
Equilibrium Price
Answer:
Equilibrium price is that price where demand and supply are equal in the market.

Question 9.
Price discrimination [March 18, 17, 16]
Answer:
Monopolist will charge different prices for the same commodity or service in the market. This is known as discriminating monopoly or price discrimination.

Question 10.
Selling Costs [March 18, 17]
Answer:
An important feature of monopolistic market is every firm makes expenditure to sell more output. Advertisements through newspapers, journals, electronic media etc., these methods are used to attract more consumers by each firm.

Additional Question

Question 11.
Perfect competition
Answer:
In this market large number of buyers and sellers who promote competition. In this market goods are homogeneous. There is no transport fares and publicity costs. So price is uniform of any market.

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 1st Lesson Physical World Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 1st Lesson Physical World

Very Short Answer Questions

Question 1.
What is Physics ?
Answer:
Physics is a branch of science which deals with the study of nature and natural phenomena.

Question 2.
What is the discovery of C.V.Raman ? [T.S. Mar. 17, 16; Mar. 14]
Answer:
In elastic scattering of light by molecules.

Question 3.
What are the fundamental forces in nature ?
Answer:

1. Gravitational force
2. Electromagnetic force
3. strong nuclear force
4. weak nuclear force

Question 4.
Which of the following has symmetry ?
(a) Acceleration due to gravity
(b) Law of gravitation.
Answer:
Law of gravitation. For example, the acceleration due to gravity at the moon is one-sixth that at the earth, but the law of gravitation is same both on the moon and the earth.

Question 5.
What is the contribution of S. Chandra Sekhar to physics ? [AP – Mar. ’17, ’16, ’15; TS – Mar. – ’15]
Answer:
While studying the constitution of the stars, he has proved that the maximum mass that a white dwarf can have is 1.4 times the solar mass. This mass is known as Chandrasekhar limit. If a star crosses this limit, it has to face a catostropic collapse.

Additional Exercises

Question 1.
Some of the most profound statements on the nature of science have come from Albert Einstein, one of the greatest scientists of all time. What do you think Einstein meant when he said : “The most incomprehensible thing about the world is that it is comprehensible” ?
Answer:
The physical world when seen by a layman, presents us with such a wide diversity of things. It seems incomprehensible, ie as if it can not be understood. On study and analysis, the scientists find that the physical phenomena from atomic to astronomical ranges can be understood interms of only a few basic concepts i.e., the physical world becomes comprehensible. This is what is meant by Einsteins statement mode above.

Question 2.
“Every great physical theory starts as a heresy and ends as a dogma”. Give some examples from the history of science of the validity of this incisive remark.
Answer:
The statement is true. For example, in ancient times, ptolemy postulated that earth is stationary and all heavy bodies like sum, stars, planets etc revolve around the earth, Later an Italian Scientist Galileo was postulated that sun is stationary and earth along with other planets is revolving around the sun. Galileo was punished by the authorities for spreading wrong concepts. How ever later on newton and kepler supported Galileo’s theory and now it is no more than a dogma.

Question 3.
“Politics is the art of the possible”. Similarly. “Science is the art of the soluble”. Explain this beautiful aphorism on the nature and practice of science.
Answer:
It is well known that to win over vots, politicians would make anything and everything possible even when they are least sure of the same. The statement that science is the art of the soluble implies that a wide variety of physical phenomena are understood in terons of only a few basic concepts ie there appears to be unity in diversity as if widely different phenomena are soluble and can be explained in terms of only a few fundamental laws.

Question 4.
Though India now has a large base in science and technology, which is fast expanding, it is still a long way from realising its potential of becoming a world leader in science. Name some important factors which in your view have hindered the advancement of science in India.
Answer:
In my view some important factors which have hindered the advancement of science in india are

1. Lack of education.
2. Poverty, which leads to lack of resources and lack of infrastructure.
3. Pressure of increasing population.
4. lack of scientific planning.
5. Lack of development of work culture and self discipline.

Question 5.
No physicist has ever “seen” an electron. Yet, all physicists believe in the existence of electrons. An intelligent but superstitious man advances this analogy to argue that ‘ghosts’ exist even though no one has ‘seen’ one. How will you refute his argument ?
Answer:
No physicist has every seen an electron. This is true. But there is so much of Evidence that establishes the existance of electrons, on the contrary, there is hardly any evidence, direct (or) indirect to establish the existance of ghosts’.

Question 6.
The shells of crabs found around a particular coastal location in Japan seem mostly to resemble that legendary face of Samurai. Given below are two explanations of this observed fact. Which of these strikes you as a scientific explanation ?
(a) A tragic sea accident several centuries ago drowned a young Samurai. As a tribute to his bravery, nature through its inscrutable ways immortalised his face by imprinting it on the crab shells in that area.
(b) After the sea tragedy, fishermen in that area, in a gesture of honour to their dead hero, let free any crab shell caught by them which accidentally had a shape resembling the face of a Samurai. Consequently, the particular shape of the crab shell survived longer and therefore in course of time the shape was genetically propagated. This is an example of evolution by artificial selection.
[Note : This interesting illustration taken from Carl Sagan’s The Cosmos’ highlights the fact that often strange and inexplicable facts which on the first sight appear ‘supernatural’ actually turn out to have simple scientific explanations. Try to think out other examples of this kind).
Answer:
Explanation (b) is a scientific explanation of the observed fact.

Question 7.
The industrial revolution in England and Western Europe more than two centuries ago was triggered by some key scientific and technological advances. What were these advances ?
Answer:
Industrial revolution in England and western Europe in 1750 A.D. was triggered by some key scientific and technological advances. Development of steam engine, blast furnace and cotton gin and power loom are some of the examples.

Question 8.
It is often said that the world is witnessing now a second industrial revolution, which will transform the society as radically as did the first. List some key contemporary areas of science and technology,which are responsible fo this revolution.
Answer:
Some of the key contemparary areas of science and technology which may transform the society radically are

1. Development of superconducting materials at room temperature –
2. Development of superfast computers
3. Information explosion and advances in information technology
4. Developments in biotechnology
5. Developments of robots.

Question 9.
Write in about 1000 words is fiction piece on the science and technology of the twenty second century.
Answer:
Imagine a space ship heading towards a star about 100.light years away. It is propelled by electric current generated by electromagnetic induction, as the space ship crosses the magnetic fields in space the current is given to an electric motor made of super conducting wires. Thus no energy would be required to propagate the space ship over it extire journey.

In a particular region of the space, suppose the temperature becomes so high that the super conducting property of the wires of the motor is destroyed. This causes a panic in the space ship because no power is generated by the motor.

In a split second, another space ship filled with matter and antimatter stored in different compartments to produce energy for the first ship comes to its rescue. And the first ship continues its onward Journey.

Question 10.
Attempt to formulate your ‘moral’ views on the practice of science. Imagine yourself stumbling upon a discovery, which has great academic interest but is certain to have nothing but dangerous consequences for the human society. How, it at all, will you resolve your dilemma ?
Answer:
Science is search for truth. If a discovery is of great academic interest, but is sure to have dangerous consequences for the human society, it must be made public. To reveal the truth and the means to prevent its misuse, both are the responsibilities of the scientist. For example, discovery of nuclear fission led to generation of electric power, and also to the development of an atom bomb, a weapon of mass destruction . The humanity at large has to be educated to use nuclear energy for peaceful purposes.

Question 11.
Science, like any knowledge, can be put to good or bad use, depending on the user. Given below are some of the applications of science. Formulate your views on whether the particular application is good, bad or something that cannot be so clearly categorised:
a) Mass vaccination against small pox to curb and finally eradicate this disease from the population. (This has already been successfully done in India).
b) Television for eradication of illiteracy and for mass communication of news and ideas.
c) Prenatal sex determination
d) Computers for increase in work efficiency
e) Putting artificial satellites into orbits around the Earth
f) Development of nuclear weapons
g) Development of new and powerful techniques of chemical and biological warfare).
h) Purification of water for drinking
i) Plastic surgery
j) Cloning
Answer:
a) Mass Vaccination is good
b) Television for eradication of illeteracy and for mass communication of news and ideas is really good.
c) Prenatal sex determination is not bad, but people are misusing it. they must be educated to avoid its misuse in creating inbalance between the male arid female population.
d) computers for increase in work efficiency are good.
e) Putting artificial satellites in to orbits around the earth is a good development.
f) Development of nuclear weapons is bad as they are the weapons of mass destruction.
g) Development of new and powerful techniques of chemical and biological warfare is real bad as these weapons are destruction of mankind.
h) purification of water for drinking is good.
i) Plastic surgery is good.
j) Cloning is also good.

Question 12.
India has had a long and unbroken tradition of great scholarship – in mathematics, astronomy, linguistics, logic and ethics. Yet, in parallel with this, several superstitious and obscurantistic attitudes and practices flourished in our society and unfortunately continue even today – among many educated people too. How will you use your knowledge of science to develop strategies to counter these attitudes ?
Answer:
Educating the common man is the only way to get rid of superstitious and obscurantistic attitudes. The mass media like news papers, magazines, radio, T.V. etc can play vital role school and colleges curricula can be suitably developed and teachers can take this responsibility.

Question 13.
Though the law gives women equal status in India, many people hold unscientific views on a woman’s innate nature, capacity and intelligence, and in practice give them a secondary status and role. Demolish this view using scientific arguments, and by quoting examples of great women in science and other spheres; and persuade yourself and others that, given equal opportunity, women are on par with men.
Answer:
Given equal opportunity, women are at par with men. Development of human mind depends basically on nutrition content of prenatal and postnatal diet, and also on the care and use of the mind. There is no gender bias involved. Anything which can be achieved by man’s mind can also be achieved by women’s mind. Madam curie won Nobel Prize in physics. Mother teresa proved herself a saint. In politics Mrs. Indira Gandhi, Mr. Margarettheatcher, Mr’s. Bhandarnaike excelled others.

Question 14.
“It is more important to have beauty in the equations of physics than to have them agree with experiments”. The great British physicist. P. A. M. Dirac held this view. Criticize this statement. Look out for some equations and results in this book which strike you as beautiful.
Answer:
The statement of great British physicist P.A.M. Dirac is partially true. For example f = ma; E = mc² are some of simple and beautiful equations of physics which have universal application.

However, there is not the case always. The equations involved in general theory of relativity, some of the least works of higher physics are neither simple nor beautiful, they are rather difficult to understand.

Question 15.
Thought the statement quoted above may be disputed, most physicists do have a feeling that the great laws of physics are at once simple and beautiful. Some of the notable physicists, besides Dirac, who have articulated this feeling, are : Einstein, Bohr. Heisenberg, Chandrasekhar and Feynman: You are urged to make special efforts to get access to the general books and writings by these and other great masters of physics. (See th§ Bibliography at the end of this book.) Their writings are truly inspiring !
Answer:
General books on physics make an interesting reading, students are advised to consult a good library. Surely you are Joking Mr. Feynman by Feynman is one of the books that would amuse the students. Some other interesting books are : physics for the inquiring mind by E.M, Rogers; physics. Foundations and frontiers by G. Gamow; thirty years that shook physics by G. Gamow; physics can be fun by perelman.

Question 16.
Textbooks on science may give you a wrong impression that studying science is dry and all too serious and that scientists are absent-minded introverts who never laugh or grin. This image of science and scientists is patently false. Scientists, like any other group of humans, have their share of humorists, and many have led their lives with a great sense of fun and adventure, even as they seriously pursued their scientific work. Two great physicists of this genre are Gamow and Feynman. You will enjoy reading their books listed in the Bibliography.
Answer:
True, scientists like any other group of humans have their share of humorists ; lively, jovial, fun loving, adventurist people, some of them are absent minded introvert too. Students are advised to go through books by two great physicists, Feynman and Gamow to realise this view.

Andhra Pradesh BIEAP AP Inter 1st Year Economics Study Material 3rd Lesson Theory of Demand Textbook Questions and Answers.

AP Inter 1st Year Economics Study Material 3rd Lesson Theory of Demand

Essay Questions

Question 1.
Explain the Law of Demand and examine Exceptions to it.
Answer:
Demand means a desire which is backed up by ability to buy and willingness to pay the price is called demand in Economics. Thus demand will be always to a price and time. Demand has the following features.

1. Desire for the commodity
2. Ability to buy the commodity
3. Willing to pay the price of commodity
4. Demand is always at a price
5. Demand is per unit of time i.e, per day, week etc.

Therefore the price demand may be expressed in the form of small equation.
D_x = f(P_x)
Price demand explains the relation between price and quantity demanded of a commodity. Price demand states that there is an inverse relationship between price and demand.

Law of demand : Marshall defines the law of demand as, “The amount demanded increases with a fall in price and diminishes with arise in price when other things remain the same”. So, the law of demand explains the inverse relationship between the price and quantity demanded of a commodity.

Demand schedule : It means a list of the quantities demanded at various prices in a given period of time in a market. An imaginary example given below.

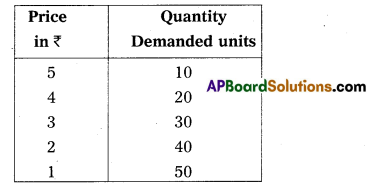
The table shows that as the price falls to ₹ 1/- the quantity demanded 50 units, when price ₹ 5/- he is buying 10 units. So, there is inverse relationship between price and demand. Price is low demand will be high and price is high demand will be low. We can illustrate the above schedule in a diagram.

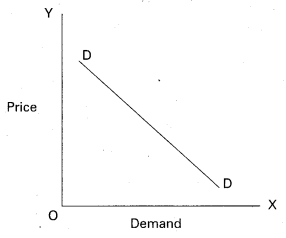
In the above diagram on X-axis demand is shown and price is on Y-axis. DD is the ad curve. Demand curves slopes downward from left to right.
Assumptions :

1. No change in the income of consumer
2. The taste and preferences consumers remain same.
3. The prices of related goods remain the same.
4. New substitutes are not discovered.
5. No expectation of future price changes.

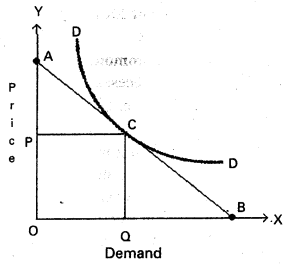
Exceptions : In certain situations, more will be demanded at higher price and less will be demanded at a lower price. In such cases the demand curve slopes upward from left to right which is called an exceptional demand curve. This can be shown in the following diagram.

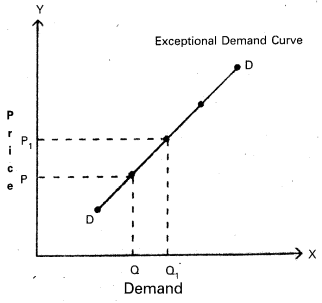
In the diagram when price increases from OP to OP₁, demand also increases from OQ to OQ₁. This is opposite to law of demand.
1) Giffen’s Paradox: This was stated by Sir Robert Giffen. He observed that poor people will demand more of inferior goods, if their prices raise. Inferior goods are known as Giffen goods.
Ex : Ragee, Jowar etc. He pointed out that in case of the English workers, the law of demand does not apply to bread. Giffen noticed that workers spend a major portion of their income on bread and only small portion on meat.

2) Veblen Effect (Prestigious goods) : This exception was stated by Veblen. Costly goods like diamonds and precious stones are called prestige goods or veblen goods. Generally rich people purchase those goods for the sake of prestige. Hence rich people may buy more such goods when their prices rise.

3) Speculation : When the price of a commodity rises the group of speculators expect that it will rise still further. Therefore, they buy more of that commodity. If they expect that there is a fall in price, the demand may not expand.
Ex : Shares in the stock market.

4) Illusion : Some times, consumer develop to false idea that a high priced good will have a better quality instead of low priced good. If the price of such good falls, demand decreases, which is contrary to the law of demand.

Question 2.
What is Demand Function ? What are the factors that determine the demand for a good ? [March 16]
Answer:
The functional relationship between the demand for a commodity and its various determinants may be explained mathematically in terms of a demand function.
D_x = f(P_x,P₁, ………… P_n, Y, T)
Where D_x = Demand for good X;
P_x = price of X;
P₁ …. P_n = Prices of substitutes and complementaries
Y = Income,
T = Taste of the consumer.
Determinants of demand :

1. Price of commodity: The demand for any good depends on its price, more will be demanded at lower price and vice-versa.
2. Prices of substitutes and complementaries : Demand is influenced by changes in price of related goods either substitutes or complementary goods.
   Ex: Increase in the price of coffee leads an increase in the demand for tea in the case of substitutes positive relation and complementaries negative relationship between price and demand.
3. Income of the consumer : Demand always changes with a change in the incomes of the people. When income increases the demand for several commodities increases and vice-versa.
4. Population : A change in the size and composition of population will effect the demand for certain goods like food grains, clothes etc.
5. Taste and preferences: A change in the taste and the fashions bring about a change in the demand for a commodity.
6. Technological changes: Due to economic progress technological changes the quantity the quality of goods available to the consumers increase.
   Ex : Demand for cell phones reduced the demand for landline phones.
7. Change in the weather : Demand for commodity may change due to change in a climatic condition.
   Ex : During summer demand for cool drinks, in winter demand for wollen clothes.
8. State of business : During the period of prosperity demand for commodities will expand and during depression demand will contract.

Question 3.
Explain the Concept of Demand and various types of Demand.
Answer:
The concept of demand has immerse significance in economics. In general language demand means a desire but in economics the desire backed up by ability to buy and willingness to pay the price.
Types of demands :
The demand may be classified into 3 types.

1. Price demand
2. Income demand
3. Cross demand

1) Price demand : Price demand explains the relation between price and quantity demanded by a commodity it shows the inverse relationship between price and demand when the other things like consumers income, taste etc., remains constant. It means the price falls demand extends and the price raises demand contracts. The price demand can be expressed D_x = f(P_x).
whereD_x = Demand for X commodity
P_x = Price of X
F = Function.

2) Income demand: It explains the relationship between consumers income and various quantities of various levels of income assuming other factors like price of goods, related goods, taste etc; remain the same. It means if income increases quantity demand increases and vice versa. This can be shown in the following form.
D_x = F(Y)
Where D_x = demand of X good;
Y = income of consumer.

3) Cross demand: It refers to change in demand for a commodity as a result of change in prices of its related commodities when other factors remains constant. This can be shown
D_x = f(P_y)
D_x = demand of X good;
P_y = Price of Y commodity;
F = function
Related goods are 2 types,

1. Substitutes : Goods which satisfy same want called substitutes.
   Ex : Coffee and tea. Here there is a positive relation between price and demand.
2. Complementary goods : These goods which satisfy the same want jointly.
   Ex : Car and petrol, shoes and sockes etc; are complementary goods.
   Here there exists inverse relation between complementary goods.

Question 4.
Explain the three Forms of Demand with suitable diagrams.
Answer:
The concept of demand has great significance in economics. In general language demand means a desire but in economics the desire backed up by ability to buy and willingness to pay the price.
Types of demand : The demand may be classified into three types.

1. Price demand
2. Income demand
3. Cross demand

1) Price demand : Price demand explains the relationship between price and quantity demanded of a commodity it shows the inverse relationship between price and demand when the other things like consumers income, taste etc., remains constant. It means the price falls demand extends and price raises demand contracts. The price demand can be expressed D_x = f(P_x)
Price demand can be explained with the help of demand schedule.

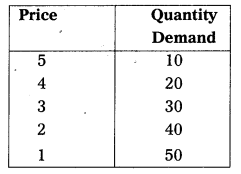
As price falls to ₹ 1/- the quantity demand is 50 units, when price of apple is ₹ 5/- he is buying 10 units. So, the table shows inverse relationship between price and demand. Price demand can be explained with the help of the demand curve.

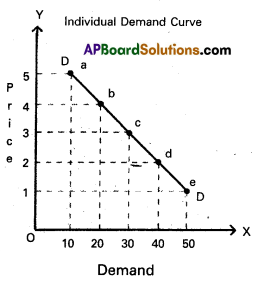
On OX axis shows demand, OY axis shows price. We can obtain the demand curve ‘DD’ by joining all the points A, B, C, D, E which represents various quantities of demand at various prices. ‘DD’ is demand curve. It slopes downwards from left to right. It shows the inverse relationship between price and demand.

2) Income demand: It explains the relationship between consumers income and various quantities of various levels of income assuming other factors like price of goods, related goods, taste etc; remain the same. It means if income increases quantity demand increases and vice versa. This can be shown in the following form.
D_x = f(Y)
The functional relationship between income and demand may be inverse or direct depending on the nature of the commodity. This can be shown in the following table.

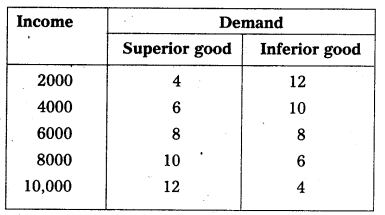
Superior goods : In case of superior goods quantity demanded will increase when there is an increase in the income of consumers.
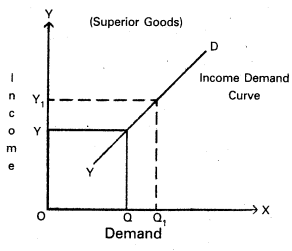
In the diagram ‘X’ axis represents demand, OY axis represents income, YD represents the income demand curve. It showing positive slope whenever income increased from OY to OY₁; the demand of superior or normal goods increases from OQ to OQ₁.
This may happens in case of Veblen goods.

Inferior goods : On the contrary quantity demanded of inferior goods decreases with the increase in incomes of consumers.
In the diagram on ‘OX’ axis measures demand and OY axis represents income of the consumer. When the consumer income increases from OY to OY₁ the demand for a commodity decreases from OQ to OQ₁ So the YD’ curve is negative sloping.

3) Cross demand: Cross demand refers to the relationship between any two goods which are either complementary to each other or substitute for each other. It explains the functional relationship between the price of one commodity and quantity demanded of another commodity is called cross demand.
D_x = f(Py)
Where D_x – demand for ‘X’ commodity
P_y Price of Y’ commodity
f = function
Substitutes : The goods which satisfy the same want are called substitutes.
Ex : Tea and coffee; pepsi and coca-cola etc. In the case of substitutes, the demand curve has a positive slope.

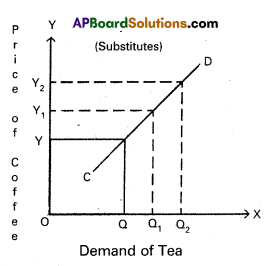
In the diagram ‘OX’ axis represents demand tea and OY axis represents price of coffee. Increase in the price of coffee from OY to OY₂ leads to increase in the demand of tea from OQ to OQ₂.

Complementaries : In case of complementary goods, with the increase in price of one commodity, the quantity demanded of another commodity falls.
Ex : Car and Petrol. Hence the demand curve of these goods slopes downward to the right.

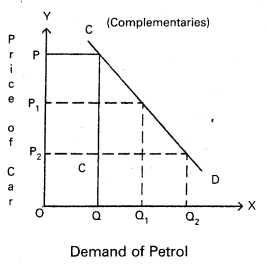
In the diagram if price of car decreases from OP to OP₂ the quantity demand of petrol increases from OQ to OQ₂. So cross demand i.e., CD curve is downward slopes.

Question 5.
Define the Concept of Elasticity of Demand and explain the concepts of price, income and cross elasticity of demand.
Answer:
The concept of elasticity demand was first introduced by Cournot and Mill. Later it was developed in a scientific manner by Marshall. Elasticity of demand means the degree of sensitiveness or responsiveness of demand to a change in its price.

According to Marshall “The elasticity of demand in a market is great or small according as the amount demanded increases much or little for a given fall in price”.

The concept of elasticity of demand explains how much or to what extent a change in any one of the independent variables leads to change in the dependent variable.
There are three kinds of elasticity of demand.

1. Price elasticity of demand
2. Income elasticity of demand
3. Cross elasticity of demand

1) Price Elasticity of Demand : Alfred Marshall developed the concept of price elasticity of demand. Price elasticity of demand is generally defined as the degree of responsiveness or sensitiveness of demand for a commodity to the changes in its price. Thus price elasticity of demand is the ratio of percentage change in quantity demanded of a good and percentage change in its price. The following formula to measure price elasticity of demand.
E_p = \(\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change in price }}\)
= \(\frac{\text { Change in quantity demanded }}{\text { Original quantity demanded }} \times \frac{\text { Original price }}{\text { Change in price }}\)
= \(\frac{\Delta \mathrm{q}}{\mathrm{q}} \times \frac{\mathrm{p}}{\Delta \mathrm{p}}=\frac{\Delta \mathrm{q}}{\Delta \mathrm{p}} \times \frac{\mathrm{p}}{\mathrm{q}}\)
where q = quantity;
p = price;
∆q = change in quantity demanded;
∆p = change in price.
There are five kinds of price elasticity of demand. They are :

1. Perfectly Elastic demand (Ed = α)
2. Perfectly Inelastic demand (Ed = 0)
3. Unitary Elastic demand (Ed = 1)
4. Relatively Elastic demand (Ed > 1)
5. Relatively Inelastic demand (Ed < 1)

2) Income Elasticity of Demand : Income elasticity of demand shows the degree of responsiveness of quantity demanded of a commodity to a change in the income of the consumer, other things remain constant.
E_y = \(=\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change inconsumer’s income }}\)
= \(=\frac{\text { Change in quantity demanded }}{\text { Original quantity demanded }} \times \frac{\text { Original income }}{\text { Change in income }}\)
= \(\frac{\Delta \mathrm{q}}{\mathrm{q}} \times \frac{\mathrm{y}}{\Delta \mathrm{y}}=\frac{\Delta \mathrm{q}}{\Delta \mathrm{y}} \times \frac{\mathrm{y}}{\mathrm{q}}\)
where q = Quantity;
y = income;
∆Q = change in quantity demanded;
∆y = change in income.
Income elasticity of demand will be positive in case of superior goods like milk and meat and negative in case of inferior goods like porridge and broken rice.

3) Cross Elasticity of Demand : Cross elasticity of demand refers to change in the quantity demanded of one good in response to change in the price of related good, other things remaining constant. There are certain goods whose demand depend not only to their price but also on the prices of related goods.
Ec = \(\frac{\text { Percentage change in quantity demanded of X }}{\text { Percentage change in the price of } Y}\)
Ec = \(\frac{\Delta \mathrm{Qx}}{\mathrm{Qx}} \div \frac{\Delta \mathrm{Py}}{\mathrm{Py}}=\frac{\Delta \mathrm{Qx}}{\mathrm{Qx}} \times \frac{\mathrm{Py}}{\Delta \mathrm{Py}}=\frac{\Delta \mathrm{Qx}}{\Delta \mathrm{Px}} \times \frac{\mathrm{Py}}{\mathrm{Px}}\)
Where Q(x) = Quantity demanded for X; P(y) = price of commodity (Y), ∆Q(x) = change in quantity demanded of X commodity, ∆P(y) = change in price of commodity Y.
Substitute goods like tea and coffee have positive cross elasticity demand where as complementary goods like shoes and socks have negative cross elasticity of demand.

Question 6.
What is Price Elasticity of Demand ? Explain the various types of Price Elasticity of Demand.
Answer:
Alfred Marshall developed the concept of price elasticity of demand. Price elasticity measures, other things remaining constant, change in the demanded of a good in response to a change in its price. Thus price elasticity of demand is the ratio of percentage change in quantity demanded of a good and percentage change in its price. Price elasticity can be written as stated below.
Ep = \(\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change in price }}\)
= \(\frac{\text { Change in demand }}{\text { Original demand }} \times \frac{\text { Original price }}{\text { Change in price }}\)
= \(\frac{\Delta \mathrm{q}}{\mathrm{q}} \times \frac{\mathrm{p}}{\Delta \mathrm{p}}=\frac{\Delta \mathrm{q}}{\Delta \mathrm{p}} \times \frac{\mathrm{p}}{\mathrm{q}}\)
Where q = quantity; p = price; ∆q = change in demand; ∆p = change in price
Types of price elasticity of demand : Based on numerical value, price elasticity of demand can be five types.

1. Perfectly Elastic demand (Ed = ∞)
2. Perfectly Inelastic demand (Ed = 0)
3. Unitary Elastic demand (Ed = 1)
4. Relatively Elastic demand (Ed > 1)
5. Relatively Inelastic demand (Ed < 1)

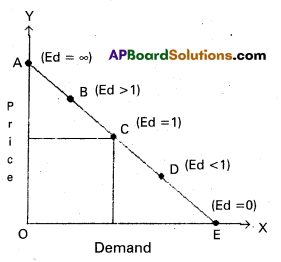
1) Perfectly Elastic demand : It is also known as “infinite elastic demand”. A small change in price leads to an infinite change in demand is called perfectly elastic demand. It is horizontal straight line to ‘X’ axis. The numerical value of perfectly elastic demand is infinite (Ed = ∞). It can be shown in the diagram.

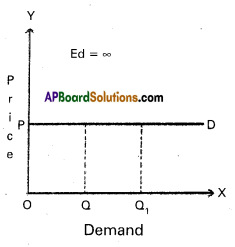
In the diagram, Ed = \(\frac{\mathrm{OQQ}_1}{\mathrm{OQ}} \div \frac{\mathrm{O}}{\mathrm{OP}}\)
= \(\frac{\mathrm{QQ}_1}{\mathrm{OQ}} \times \frac{\mathrm{OP}}{\mathrm{O}}\) = ∞

2) Perfectly Inelastic demand: It is also known as “zero elastic demand”. In this case even a great rise ‘or fall in price does not lead to any change in quantity demanded is known as perfectly inelastic demand. The ‘demand curve will be vertical to the Y axis. The numerical value is ‘OE. This can be shown in the following diagram.

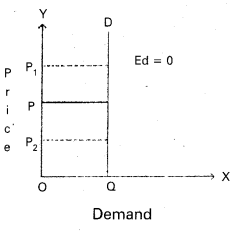
In the diagram, Ed = \(\frac{\text { Zero }}{\mathrm{OQ}} \div \frac{\mathrm{PP}_1}{\mathrm{OP}}\) = 0
∴ Ed = 0

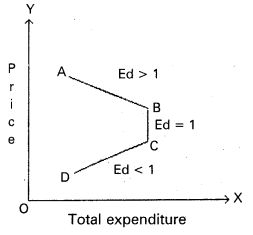
3) Unitary Elastic demand: The percentage change in price leads to same percentage change in demand is called unitary elastic demand. In this case the elasticity of demand is equal to one. The shape of demand curve is “Rectangular Hyperbola”. This can be shown in the following.

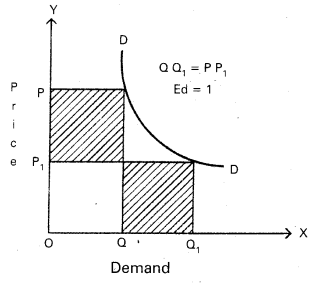
In the diagram, Ed = OP₁Q₁ = OPQ
(or) OQ₁ = PP₁
∴ Ed = 1

4) Relatively Elastic demand: When a percentage change in price leads to more than percentage change in quantity demand is called relatively elastic demand. In this case the numerical value of Ed is greater than one (Ed > 1)

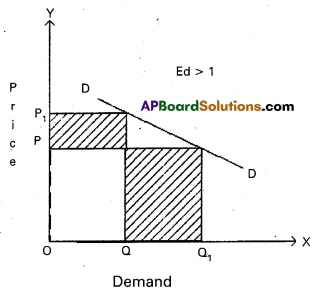
In the diagram, Ed = OQ₁ > PP₁
∴ Ed > 1

5) Relatively Inelastic demand : When the percentage change in price leads to a less than percentage change in quantity demand is called relatively inelastic demand. Here the numerical value is less than one (Ed < 1) . This can be shown to following diagram.

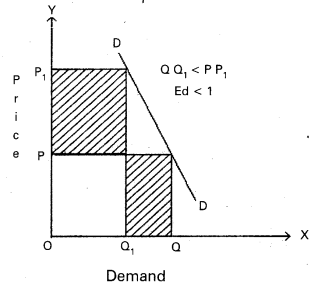
In the diagram, Ed = QQ₁ < PP₁
∴ Ed < 1

Question 7.
Explain the three methods of Measuring Price Elasticity of Demand.
Answer:
The concept of elasticity of demand is one of the original contributions of Dr.Marshall. The concepts of elasticity of demand clearly explains ‘how much’ demand increases due to a certain fall in price and ‘how much’ demand decreases due to certain rise in price.

According to Mrs. Joan Robinson, “The elasticity of demand at any price or at any output is the proportional change of amount purchased in response to a small change in price, divided by the proportional change in price”.

Methods of measurements of Price Elasticity of demand :
The Elasticity of demand can be measured mainly in three ways.

1. Total outlay (or) Expenditure method
2. Point method and
3. Arc method.

1) Total outlay (or) Expenditure method : This method was introduced by Alfred Marshall. Price elasticity of demand can be measured on the basis of change in the total outlay due to a change in the price of a commodity. This method helps us to compare the total expenditure from a buyer or total revenue from the seller before and after the change in price.
Total outlay = Price × Quantity demanded
According to this method the price elasticity of demand is expressed in three forms, they are elastic demand, unitary elastic and inelastic demand. This can be explained with the help of table.

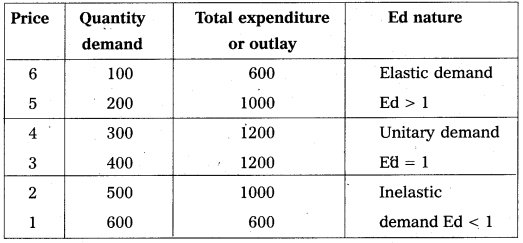
In this table shows that

1. If the total expenditure increases due to a fall in price is known as relatively elastic demand.
2. If total expenditure remains constant even the price falls is known as unitary elastic demand.
3. If the total expenditure decreases due to a fall in price is known as relatively inelastic demand.

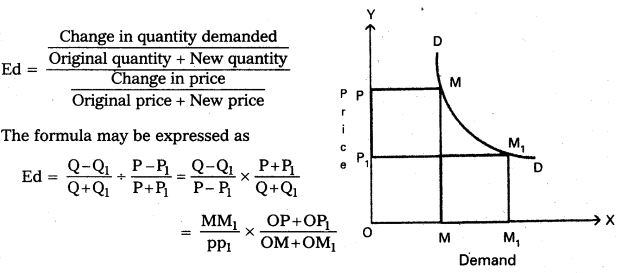
2) Point method : This method is introduced by Marshall. In this method elasticity of demand is measured at a point on the demand curve. So, this method is also called as “geometrical method”. In this method to measure elasticity at a point on demand curve the following formula is applied.
Ed = \(\frac{\text { The distance from the point to the } \mathrm{X} \text {-axis }}{\text { The distance from the point to the } \mathrm{Y} \text {-axis }}\)
In the below diagram ‘AE’ is straight line demand curve. Which is 10 cm length. Applying the formula we get
Ed = 1 Ed < 1 Ed = 0

Elasticity at point A, Ed = \(\frac{\mathrm{AE}}{\mathrm{A}}=\frac{10}{0}\) = 0
Elasticity at point B, Ed = \(\frac{\mathrm{BE}}{\mathrm{BA}}=\frac{7.5}{2.5}\) = 3 > 1
Elasticity at point C, Ed = \(\frac{\mathrm{CE}}{\mathrm{CA}}=\frac{5}{5}\) = 1
Elasticity at point D, Ed = \(\frac{\mathrm{DE}}{\mathrm{DA}}=\frac{1}{3}\) = < 1
Elasticity at point E, Ed = \(\frac{\mathrm{E}}{\mathrm{DA}}=\frac{0}{10}\) = 0
if the demand curve is non-linear. It means if the demand curve is not straight line will be drawn at the point on the demand curve where to measure elasticity.

In the diagram at C point where Elasticity of demand will be equal to \(\frac{\mathrm{CB}}{\mathrm{CA}}\).

3) Arc method : The word ‘ArC means a portion or a segment of a demand curve. In this method mid points between the old and new price and quantities demanded are used. This method used to known small changes in price. This method is also known as ‘Average Elasticity of demand”. This method studies a segment of the demand curve between two points the formula for measuring elasticity is given below.

Suppose we take price of the commodity is ₹ 4/- demand is 300 units. If price falls ₹ 3/ – demand increases 400 units.
Then applying above formula Arc elasticity of demand is
\(\frac{100}{300+400} \div \frac{1}{4+3}=\frac{100}{700} \div \frac{1}{7}\)
= \(\frac{100}{700} \times \frac{7}{1}=\frac{700}{700}\) = 1
∴ Ed = 1

Question 8.
What are the factors that determine Price Elasticity of Demand ?
Answer:
The term elasticity refers to the measure of extent of relationship between two related variables. The elasticity of demand is the measure of responsiveness or sensitiveness of demand for a commodity to the change in it demand.
Determinants of Elasticity of Demand : The. elasticity of demand varies from commodity to commodity.
1) Nature of commodity: Commodities can be grouped as necessaries, comforts and luxuries. In case of necessaries, the elasticity of demand will be inelastic.
Ex : Rice, salt etc. On the other hand in case of luxuries the demand will be more elastic.
Ex : Diamonds & gold etc.

2) Availability of substitutes : Prices of substitutes influence the demand for a com-modity upto a certain extent. The closer the substitute, the greater the elasticity of demand for the commodity. For Ex : Cool drinks, soaps etc. but in case of non-availability of substitutes the elasticity of demand will be low.

3) Complementary goods: Price elasticity for a good is also depends on the nature of price elasticity of jointly demand goods. If the demand for car is elastic, then the demand for petrol will also be elastic.

4) Multiple uses of the commodity : The wider the range of alternative uses of a product, the higher the elasticity of demand and vice-versa.
Ex : Coal and electricity have multiple uses and will have elastic demand.

5) Proportion of income spent: If proportion of income spent on commodity is very small, its demand will be less elastic and vice-versa.

6) Period of time : In the long run, demand will be more elastic. Longer the time period considered, greater will be the possibility of substitution. For a cheaper good.
Ex : If the price of petrol increases in the short run, it may not be possible to replace the petrol engines with diesel engines but in the long run it can be possible.

7) Price level: Goods which are in very high range or in very low range have inelastic demand but it is high at moderate price.

8) Habit : The demand for a commodity to which the consumer is accustomed is generally inelastic.
Ex : Tobacco and alcohol.

9) Income group : The demand of higher income groups will be inelastic as they do not bother about price changes. On the other hand, the demand of middle and lower income groups will be elastic.

10) Postponement of purchase: The demand for a commodity, the consumption of which can be postponed is more eiastic than that of the use of the commodity cannot be postpone the purchases of such goods like life saving medicines.

Question 9.
Explain importance of Elasticity of Demand.
Answer:
The term elasticity refers to the measure of extent of relationship between two related variable. The elasticity of demand is the measure of responsiveness or sensitiveness of demand for a commodity to the change in it demand.
Importance :
1) Useful to monopolist: Monopolist should study the elasticity of demand for his commodity before fixing up the price. Monopolist will fix a higher price when the commodity inelastic demand, but he will fix a lower price when the commodity has elastic demand.

2) Useful to joint products : It is useful in the price fixation of joint goods like meat and fur. In such case the producer wall be guided by elasticity of demand to fix the prices of the joint goods.

3) Useful to the government: The concept of elasticity can be used in formulating government policies relating public utility service like Railways, drug industry etc.

4) Useful to international trade : In calculating the terms of trade both countries have to take into account the mutual elasticities of demand for the products.

5) Useful to finance minister : The concept of elasticity is useful to the Finance Minister in imposing taxes on goods. The finance minister studies the elasticity of commodities before he imposes new taxes or enhances old taxes.

6) Useful to Management: Before asking for higher wages trade union leaders must know the elasticity of demand of the product produced by them. Trade union leaders may demand for higher wages only when the goods produced by them have inelastic demand.

7) Useful to producers : Volume of goods must be produced in accordance with demand for the commodity. Whenever the demand for the commodity is inelastic, the producer will produce more commodities to take advantage of higher price. So, it helps in determining the volume of output.

Short Answer Questions

Question 1.
Explain the Law of Demand or Price Demand.
Answer:
Demand means a desire which is backed up by ability to buy and willingness to pay the price is called demand in Economics. Thus demand will be always to a price and time. Demand has the following features.

1. Desire for the commodity
2. Ability to buy the commodity
3. Willing to pay the price of commodity
4. Demand is always at a price ‘
5. Demand is per unit of time i.e, per day, week etc.

Therefore the price demand may be expressed in the form of small equation.
D_x = f(P_x)
Price demand explains the relation between price and quantity demanded of a commodity. Price demand states that there is an inverse relationship between price and demand.

Law of demand : Marshall defines the law of demand as, “The amount demanded increases with a fall in price and diminishes with arise in price when other things remain the same”. So, the law of demand explains the inverse relationship between the price and quantity demanded of a commodity.

Demand schedule : It means a list of the quantities demanded at various prices in a given period of time in a market. An imaginary example given below.

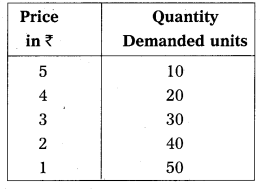
The table shows that as the price falls to ₹ 1/- the quantity demanded 50 units, when price ₹ 5/- he is buying 10 units. So, there is inverse relationship between price and demand. Price is low demand will be high and price is high demand will be low. We can illustrate the above schedule in a diagram.

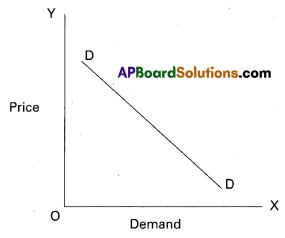
In the above diagram on X-axis demand is shown and price is on Y-axis. DD is the demand curve. Demand curves slopes downward from left to right.
Assumptions :

1. No change in the income of consumer
2. The taste and preferences consumers remain same.
3. The prices of related goods remain the same.
4. New substitutes are not discovered.
5. No expectation of future price changes.

Exceptions : In certain situations, more will be demanded at higher price and less will be demanded at a lower price. In such cases the demand curve slopes upward from left to right which is called an exceptional demand curve. This can be shown in the following diagram.

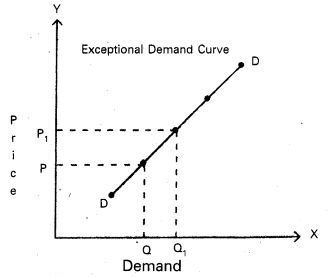
In the diagram when price increases from OP to OP₁, demand also increases from OQ to OQ₁. This is opposite to law of demand.

Question 2.
Explain the Exceptions to the Law of Demand or Price Demand.
Answer:
In Economics demand means a desire which is backed up by ability to buy and willingness to pay the price. Thus demand will be always at a price and time.

According to Marshal “The amount demanded increases with a fall in price and diminishes with rise in price when other things remain the same”.

Exceptions : In certain situations, more will be demanded at higher price and less will be demanded at a lower price. In such cases the demand curve slopes upward from left to right which is called an exceptional demand curve. This can be shown in the following diagram.

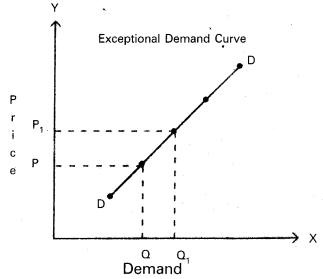
In the diagram when price increases from OP to OP₁, demand also increases from OQ to OQ₁. This is opposite to law of demand.

Question 3.
Why a Demand Curve has a negative slope or why Demand Curve slopes downward ? [March 18]
Answer:
According to Marshall “The amount demanded increases with a fall in price and diminishes with a rise in price when other things remain the same”.

The law of demand explains inverse relationship between the price and quantity demanded of a commodity. Therefore the demand curve slopes downward from left to right.

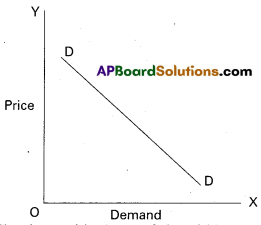
There are some other reasons also responsible for downward sloping demand curve.
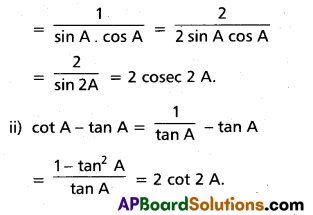
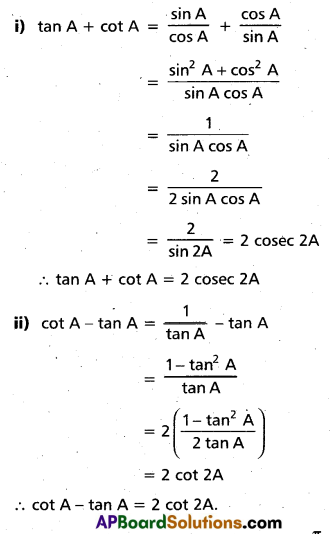
1) Old and new buyers : If the price of a good falls, the real income of the old buyers will increase. Hence the demand for the good will increase. In the same way, the fall in price attracts new buyers and will be able to built after a fall in its price. So the demand curve slopes downards from left to right.

2) Income effect: Fall in price of commodity the real income of its consumers increase. The increase in real income encourages demand for the commodity with reduced price. The increase in demand on account of increased in real income is known as income effect.

3) Substitution effect: When the price of commodity falls, it will become relatively cheaper than its substitutes. The increase in demand on account of increased in real income is known as income effect.

4) Law of diminishing marginal utility: According to this law, if consumer goes on consuming more units of the commodity, the additional utility goes on diminishing. Therefore, the consumer prefers to buy at a lower price. As a result the demand curve has a negative slope.

Question 4.
Explain the concept of Income Demand.
Answer:
Income demand : It explains the relationship between consumers income and various quantities of various levels of income assuming other factors like price of goods, related goods, taste etc; remain the same. It means if income increases quantity demand increases and vice versa. This can be shown in the following form.
D_x = f(Y)
The functional relationship between income and demand may be inverse or direct depending on the nature of the commodity. This can be shown in the following table.

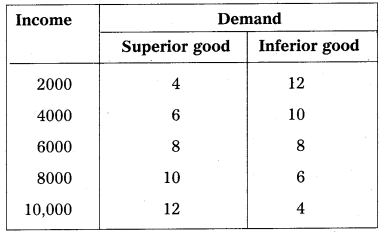
Superior goods : In case of superior goods quantity demanded will increase when there is an increase in the income of consumers.

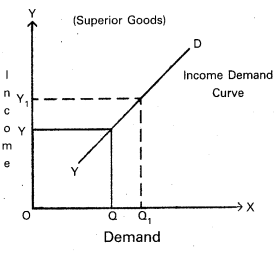
In the diagram ‘X’ axis represents demand, OY axis represents income, YD represents the income demand curve. It showing positive slope whenever income increased from OY to OY₁ the demand of superior or normal goods increases from OQ to OQ₁.
This may happens in case of Veblen goods.

Inferior goods : On the contrary quantity demanded of inferior goods decreases with the increase in incomes of consumers.

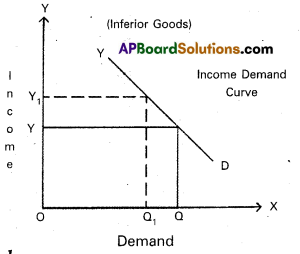
In the diagram on ‘OX’ axis measures demand and OY axis represents income of the consumer. When the consumer income increases from OY to OY₁ the demand for a commodity decreases from OQ to OQ₁ So the YD’ curve is negative sloping.

Question 5.
Explain the concept of Cross Demand.
Answer:
Cross demand: Cross demand refers to the relationship between any two goods which are either complementary to each other or substitute for each other. It explains the functional relationship between the price of one commodity and quantity demanded of another commodity is called cross demand.
D_x = f(P_y)
Where D_x = demand for ‘X’ commodity
P_x = Price of ‘y’ commodity
f = function
Substitutes : The goods which satisfy the same want are called substitutes.
Ex : Tea and coffee; pepsi and coca-cola etc. In the case of substitutes, the demand curve has a positive slope.

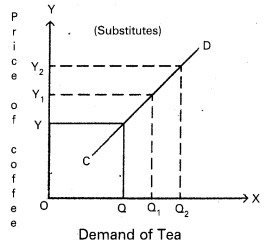
In the diagram ‘OX’ axis represents demand of tea and OY axis represents price of coffee. Increase in the price of coffee from OY to OY₂ leads to increase in the demand of tea from OQ to OQ₂.

Complementaries: In case of complementary goods, with the increase in price of one commodity, the quantity demanded of another commodity falls.
Ex : Car and Petrol. Hence the demand curve of these goods slopes downward to the right.

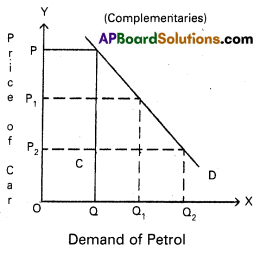
In the diagram if price of car decreases from OP to OP₂ the quantity demand of petrol increases from OQ to OQ₂. So cross demand i.e., CD curve is down ward slopes.

Question 6.
What are the factors that determine Demand ? [March 18, 17]
Answer:
The functional relationship between the demand for a commodity and its various determinants may be explained mathematically in terms of a demand function.
D_x = f(P_x,P₁, ………… P_n, Y, T)
Where D_x = Demand for good X;
P_x = price of X;
P₁ …. P_n = Prices of substitutes and complementaries
Y = Income,
T = Taste of the consumer.
Determinants of demand :
1) Price of commodity: The demand for any good depends on its price, more will be demanded at lower price and vice-versa.

2) Prices of substitutes and complementaries : Demand is influenced by changes in price of related goods either substitutes or complementary goods.
Ex: Increase in the price of coffee leads an increase in the demand for tea in the case of substitutes positive relation and complementaries negative relationship between price and demand.

3) Income of the consumer : Demand always changes with a change in the incomes of the people. When income increases the demand for several commodities increases and vice-versa.

4) Population : A change in the size and composition of population will effect the demand for certain goods like food grains, clothes etc.

5) Taste and preferences: A change in the taste and the fashions bring about a change in the demand for a commodity.

6) Technological changes: Due to economic progress technological changes the quantity the quality of goods available to the consumers increase.
Ex : Demand for cell phones reduced the demand for landline phones.

7) Change in the weather : Demand for commodity may change due to change in a climatic condition.
Ex : During summer demand for cool drinks, in winter demand for wollen clothes.

8) State of business : During the period of prosperity demand for commodities will expand and during depression demand will contract.

Question 7.
What is Elasticity of Demand ?
Answer:
In Economic theory, the concept of elasticity of demand has a significant role. Elasticity of demand means the percentage change in quantity demanded in response to the percentage change in one of the variables on which demand depends.
Elasticity of demand changes from person to person, place to place, time to time and one commodity to another.
Accoridng to Marshall “The elasticity of demand in a market is great or small according as the amount demanded increases much or little for a given fall in price”.
The concept of elasticity of demand explains how much or to what extent a change in any one of the independent variables leads to a change in the dependent variable.
There are three kinds of elasticity of demand.

1. Price Elasticity of demand
2. Income Elasticity of demand .
3. Cross Elasticity of demand

Question 8.
Explain the three types of Elasticity of Demand.
Answer:
The concept of elasticity demand was first introduced by Cournot and Mill. Later it was developed in a scientific manner by Marshall. Elasticity of demand means the degree of sensitiveness or responsiveness of demand to a change in its price.

According to Marshall “The elasticity of demand in a market is great or small according as the amount demanded increases much or little for a given fall in price”.

The concept of elasticity of demand explains how much or to what extent a change in any one of the independent variables leads to change in the dependent variable.
There are three kinds of elasticity of demand.

1. Price elasticity of demand
2. Income elasticity of demand
3. Cross elasticity of demand

1) Price Elasticity of Demand : Alfred Marshall developed the concept of price elasticity of demand. Price elasticity of demand is generally defined as the degree of responsiveness or sensitiveness of demand for a commodity to the changes in its price. Thus price elasticity of demand is the ratio of percentage change in quantity demanded of a good and percentage change in its price. The following formula to measure price elasticity of demand.
E_p = \(\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change in price }}\)
= \(\frac{\text { Change in quantity demanded }}{\text { Original quantity demanded }} \times \frac{\text { Original price }}{\text { Change in price }}\)
= \(\frac{\Delta \mathrm{q}}{\mathrm{q}} \times \frac{\mathrm{p}}{\Delta \mathrm{p}}=\frac{\Delta \mathrm{q}}{\Delta \mathrm{p}} \times \frac{\mathrm{p}}{\mathrm{q}}\)
where q = quantity;
p = price;
∆q = change in quantity demanded;
∆p = change in price.
There are five kinds of price elasticity of demand. They are :

1. Perfectly Elastic demand (Ed = α)
2. Perfectly Inelastic demand (Ed = 0)
3. Unitary Elastic demand (Ed = 1)
4. Relatively Elastic demand (Ed > 1)
5. Relatively Inelastic demand (Ed < 1)

2) Income Elasticity of Demand : Income elasticity of demand shows the degree of responsiveness of quantity demanded of a commodity to a change in the income of the consumer, other things remain constant.
E_y = \(=\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change inconsumer’s income }}\)
= \(=\frac{\text { Change in quantity demanded }}{\text { Original quantity demanded }} \times \frac{\text { Original income }}{\text { Change in income }}\)
= \(\frac{\Delta \mathrm{q}}{\mathrm{q}} \times \frac{\mathrm{y}}{\Delta \mathrm{y}}=\frac{\Delta \mathrm{q}}{\Delta \mathrm{y}} \times \frac{\mathrm{y}}{\mathrm{q}}\)
where q = Quantity;
y = income;
∆Q = change in quantity demanded;
∆y = change in income.
Income elasticity of demand will be positive in case of superior goods like milk and meat and negative in case of inferior goods like porridge and broken rice.

3) Cross Elasticity of Demand : Cross elasticity of demand refers to change in the quantity demanded of one good in response to change in the price of related good, other things remaining constant. There are certain goods whose demand depend not only to their price but also on the prices of related goods.
Ec = \(\frac{\text { Percentage change in quantity demanded of X }}{\text { Percentage change in the price of } Y}\)
Ec = \(\frac{\Delta \mathrm{Qx}}{\mathrm{Qx}} \div \frac{\Delta \mathrm{Py}}{\mathrm{Py}}=\frac{\Delta \mathrm{Qx}}{\mathrm{Qx}} \times \frac{\mathrm{Py}}{\Delta \mathrm{Py}}=\frac{\Delta \mathrm{Qx}}{\Delta \mathrm{Px}} \times \frac{\mathrm{Py}}{\mathrm{Px}}\)
Where Q(x) = Quantity demanded for X; P(y) = price of commodity (Y), ∆Q(x) = change in quantity demanded of X commodity, ∆P(y) = change in price of commodity Y.
Substitute goods like tea and coffee have positive cross elasticity demand where as complementary goods like shoes and socks have negative cross elasticity of demand.

Quantity 9.
Define Price Elasticity of Demand. Explain briefly various types of Price Elasticity of Demand.
Answer:
Alfred Marshall developed the concept of price elasticity of demand. Price elasticity measures, other things remaining constant, change in the demanded of a good in response to a change in its price. Thus price elasticity of demand is the ratio of percentage change in quantity demanded of a good and percentage change in its price. Price elasticity can be written as stated below.
Ep = \(\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change in price }}\)
= \(\frac{\text { Change in demand }}{\text { Original demand }} \times \frac{\text { Original price }}{\text { Change in price }}\)
= \(\frac{\Delta \mathrm{q}}{\mathrm{q}} \times \frac{\mathrm{p}}{\Delta \mathrm{p}}=\frac{\Delta \mathrm{q}}{\Delta \mathrm{p}} \times \frac{\mathrm{p}}{\mathrm{q}}\)
Where q = quantity; p = price; ∆q = change in demand; ∆p = change in price
Types of price elasticity of demand : Based on numerical value, price elasticity of demand can be five types.

1. Perfectly Elastic demand (Ed = ∞)
2. Perfectly Inelastic demand (Ed = 0)
3. Unitary Elastic demand (Ed = 1)
4. Relatively Elastic demand (Ed > 1)
5. Relatively Inelastic demand (Ed < 1)

1) Perfectly Elastic demand : It is also known as “infinite elastic demand”. A small change in price leads to an infinite change in demand is called perfectly elastic demand. It is horizontal straight line to ‘X’ axis. The numerical value of perfectly elastic demand is infinite (Ed = ∞). It can be shown in the diagram.

In the diagram, Ed = \(\frac{\mathrm{OQQ}_1}{\mathrm{OQ}} \div \frac{\mathrm{O}}{\mathrm{OP}}\)
= \(\frac{\mathrm{QQ}_1}{\mathrm{OQ}} \times \frac{\mathrm{OP}}{\mathrm{O}}\) = ∞

2) Perfectly Inelastic demand: It is also known as “zero elastic demand”. In this case even a great rise ‘or fall in price does not lead to any change in quantity demanded is known as perfectly inelastic demand. The ‘demand curve will be vertical to the Y axis. The numerical value is ‘OE. This can be shown in the following diagram.

In the diagram, Ed = \(\frac{\text { Zero }}{\mathrm{OQ}} \div \frac{\mathrm{PP}_1}{\mathrm{OP}}\) = 0
∴ Ed = 0

3) Unitary Elastic demand: The percentage change in price leads to same percentage change in demand is called unitary elastic demand. In this case the elasticity of demand is equal to one. The shape of demand curve is “Rectangular Hyperbola”. This can be shown in the following.

In the diagram, Ed = OP₁Q₁ = OPQ
(or) OQ₁ = PP₁
∴ Ed = 1

4) Relatively Elastic demand: When a percentage change in price leads to more than percentage change in quantity demand is called relatively elastic demand. In this case the numerical value of Ed is greater than one (Ed > 1)

In the diagram, Ed = OQ₁ > PP₁
∴ Ed > 1

5) Relatively Inelastic demand : When the percentage change in price leads to a less than percentage change in quantity demand is called relatively inelastic demand. Here the numerical value is less than one (Ed < 1) . This can be shown to following diagram.

In the diagram, Ed = QQ₁ < PP₁
∴ Ed < 1

Question 10.
Explain the Total Outaly method of Measuring Elasticity of Demand.
Answer:
Total Outlay (or) Expenditure method : This method was introduced by Alfred Marshall. Price elasticity of demand can be measured on the basis of change in the total outlay due to a change in the price of a commodity. This method helps us to compare the total expenditure from a buyer or total revenue from the seller before and after the change in price.
Total outlay = Price × Quantity demanded
According to this method the price elasticity of demand is expressed in three forms, they are elastic demand, unitary elastic and inelastic demand. This can be explained with the help of table.


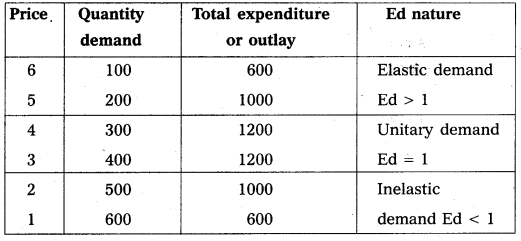
In this table shows that

1. If the total expenditure increases due to a fall in price is known as relatively elastic demand.
2. If total expenditure remains constant even the price falls is known as unitary elastic demand.
3. If the total expenditure decreases due to a fall in price is known as relatively inelastic demand.

In the diagram on ‘OX’ axis measure total expenditure and ‘OY axis measures price. The total outlay curve AD is shown in three parts i.e., A to B; B to C and C to D.

Question 11.
Explain the Point method of Measuring Price Elasticity of Demand or How do you measure Elasticity of Demand on straight line Demand Curve ?
Answer:
Point method : This method is introduced by Marshall. In this method elasticity of demand is measured at a point on the demand curve. So, this method is also called as “geometrical method”. In this method to measure elasticity at a point on demand curve the following formula is applied.
Ed = \(\frac{\text { The distance from the point to the } \mathrm{X} \text {-axis }}{\text { The distance from the point to the } \mathrm{Y} \text {-axis }}\)
In the below diagram ‘AE’ is straight line demand curve. Which is 10 cm length. Applying the formula we get
Ed = 1 Ed < 1 Ed = 0

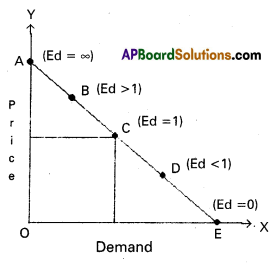
Elasticity at point A, Ed = \(\frac{\mathrm{AE}}{\mathrm{A}}=\frac{10}{0}\) = 0
Elasticity at point B, Ed = \(\frac{\mathrm{BE}}{\mathrm{BA}}=\frac{7.5}{2.5}\) = 3 > 1
Elasticity at point C, Ed = \(\frac{\mathrm{CE}}{\mathrm{CA}}=\frac{5}{5}\) = 1
Elasticity at point D, Ed = \(\frac{\mathrm{DE}}{\mathrm{DA}}=\frac{1}{3}\) = < 1
Elasticity at point E, Ed = \(\frac{\mathrm{E}}{\mathrm{DA}}=\frac{0}{10}\) = 0
If the demand curve is non-linear. It means if the demand curve is not straight line will be drawn at the point on the demand curve where to measure elasticity.

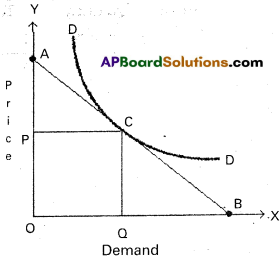
In the diagram at C point where Elasticity of demand will be equal to \(\frac{\mathrm{CB}}{\mathrm{CA}}\).

Question 12.
What are the basic determinants of Elasticity of Demand ?
Answer:
The term elasticity refers to the measure of extent of relationship between two related variables. The elasticity of demand is the measure of responsiveness or sensitiveness of demand for a commodity to the change in it demand.
Determinants of Elasticity of Demand : The. elasticity of demand varies from commodity to commodity.
1) Nature of commodity: Commodities can be grouped as necessaries, comforts and luxuries. In case of necessaries, the elasticity of demand will be inelastic.
Ex : Rice, salt etc. On the other hand in case of luxuries the demand will be more elastic.
Ex : Diamonds & gold etc.

2) Availability of substitutes : Prices of substitutes influence the demand for a com-modity upto a certain extent. The closer the substitute, the greater the elasticity of demand for the commodity. For Ex : Cool drinks, soaps etc. but in case of non-availability of substitutes the elasticity of demand will be low.

3) Complementary goods: Price elasticity for a good is also depends on the nature of price elasticity of jointly demand goods. If the demand for car is elastic, then the demand for petrol will also be elastic.

4) Multiple uses of the commodity : The wider the range of alternative uses of a product, the higher the elasticity of demand and vice-versa.
Ex : Coal and electricity have multiple uses and will have elastic demand.

5) Proportion of income spent: If proportion of income spent on commodity is very small, its demand will be less elastic and vice-versa.

6) Period of time : In the long run, demand will be more elastic. Longer the time period considered, greater will be the possibility of substitution. For a cheaper good.
Ex : If the price of petrol increases in the short run, it may not be possible to replace the petrol engines with diesel engines but in the long run it can be possible.

7) Price level: Goods which are in very high range or in very low range have inelastic demand but it is high at moderate price.

8) Habit : The demand for a commodity to which the consumer is accustomed is generally inelastic.
Ex : Tobacco and alcohol.

9) Income group : The demand of higher income groups will be inelastic as they do not bother about price changes. On the other hand, the demand of middle and lower income groups will be elastic.

10) Postponement of purchase: The demand for a commodity, the consumption of which can be postponed is more eiastic than that of the use of the commodity cannot be postpone the purchases of such goods like life saving medicines.

Question 13.
Explain the importance of the Concept of Elasticity of Demand.
Answer:
The term elasticity refers to the measure of extent of relationship between two related variable. The elasticity of demand is the measure of responsiveness or sensitiveness of demand for a commodity to the change in it demand.
Importance :
1) Useful to monopolist: Monopolist should study the elasticity of demand for his commodity before fixing up the price. Monopolist will fix a higher price when the commodity inelastic demand, but he will fix a lower price when the commodity has elastic demand.

2) Useful to joint products : It is useful in the price fixation of joint goods like meat and fur. In such case the producer wall be guided by elasticity of demand to fix the prices of the joint goods.

3) Useful to the government: The concept of elasticity can be used in formulating government policies relating public utility service like Railways, drug industry etc.

4) Useful to international trade : In calculating the terms of trade both countries have to take into account the mutual elasticities of demand for the products.

5) Useful to finance minister : The concept of elasticity is useful to the Finance Minister in imposing taxes on goods. The finance minister studies the elasticity of commodities before he imposes new taxes or enhances old taxes.

6) Useful to Management: Before asking for higher wages trade union leaders must know the elasticity of demand of the product produced by them. Trade union leaders may demand for higher wages only when the goods produced by them have inelastic demand.

7) Useful to producers : Volume of goods must be produced in accordance with demand for the commodity. Whenever the demand for the commodity is inelastic, the producer will produce more commodities to take advantage of higher price. So, it helps in determining the volume of output.

Very Short Answer Question

Question 1.
Demand
Answer:
The desire backed up by willingness and ability to pay a sum of money for some quantity of a good or service.

Question 2.
Demand Schedule [March 17]
Answer:
It shows the functional relationship between the quantity of commodity demanded and its price. The demand schedule may be two types.

1. Individual demand schedule
2. Market demand schedule

Question 3.
Individual Demand Schedule
Answer:
It explains the relationship between various quantities purchased at various prices by a single consumer in the market.

Question 4.
Market Demand Schedule
Answer:
It shows the total demand for a group at a particular time at different prices in the market.

Question 5.
Demand Function
Answer:
Demand function shows the functional relationship between quantity demanded at various factors that determine the demand for a commodity. It can be expressed as follows.
D_x = f(P_x, P₁, ………… P_n, Y, T)
Where
D_x = Demand for good X
P_x = price of X
P₁ …. P_n = Prices of substitutes and complementary
Y = Income of consumer
T = Tastes
f = Functional relationship

Question 6.
Giffen’s Paradox (or) Giffen Goods [March 18, 16]
Answer:
It means necessary goods Sir Robert Giffen in mid 19th century observed that the low paid workers in England purchased more bread when its price increase by decrease in the purchase of meat. The increase in demand for bread when price increased is an exception to the law of demand, it is known as Giffen’s paradox.

Question 7.
Veblen Goods (or) Prestigious Goods
Answer:
This is associated with the name of T.Veblen costly goods like diamonds and cars are called Veblen goods generally rich people purchase those goods. For the sake of prestage. Hence rich people may buy more such goods when their prises rise.

Question 8.
Speculation
Answer:
When the price of commodity rises the group of speculats except that be rise still further. Therefore, they buy more of the commodity. If they expect that there is a fallen price, the demand may not expand. Ex : shares.

Question 9.
Price Demand
Answer:
It explains the functional relationship between price of good and quantity of demanded when the remaining factors constant. It shows inverse relationship between price and demand.
D_x = f(P_x)
D_x = Demand for X commodity
P_x = Price of X

Question 10.
Income Demand [March 17]
Answer:
It shows the direct relationship between the income of the consumer and quantity demanded when the other factors remain constant. There is direct relationship between income and demand for superior goods. Inverse relationship between income and demand for inferior goods.
D_x = f(Y)

Question 11.
Cross Demand [March 18]
Answer:
Cross demand refers to the relationship between any two goods which are either complementary to each other or substitute of each other at different prices.
D_x = f(P_y)

Question 12.
Substitutes
Answer:
These are goods which satisfy the same want.
Ex : tea and coffee. In this case the relationship between demand for a product and the price of its substitute is positive in its nature.

Question 13.
Complementaries
Answer:
These are goods which satisfy the same wants jointly.
Ex : Shoes and socks, car and petrol. The relationship between complementary goods is inverse.

Question 14.
Inferior Goods
Answer:
The goods whose income elasticity of demand is negative for levels of income are termed as inferior goods. In case of inferior goods if income increases demand decreases and vice-versa. The income demand for inferior goods has a negative slope.

Question 15.
Elasticity of Demand
Answer:
It means the degree of responsiveness of demand or the sensitiveness of demand to change in price. This was developed by Marshall It explains how much demand increases due to fall in price and how much demand decreases due to rise in price.

Question 16.
Price Elasticity of Demand
Answer:
It is the percentage change in quantity demanded of a commodity as a result of percentage change in price of a commodity.
Ed = \(\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change in price }}\)

Question 17.
Income Elasticity of Demand
Answer:
It is the percentage change in quantity demanded of a commodity as a result of percentage change in the income of the consumer.
Ey = \(\frac{\text { Percentage change in quantity demanded }}{\text { Percentage change in consumer’s income }}\)

Question 18.
Cross Elasticity of Demand
Answer:
It is the percentage change in the quantity demanded of a commodity as a result of proportional change in the price of related commodity.
Ec = \(\frac{\text { Percentage change in quantity demanded of } \mathrm{X}}{\text { Percentage change in the price of } \mathrm{Y}}\)

Question 19.
Perfectly Elastic Demand
Answer:
If a negligible change in price leads to an infinite change in demand is called perfectly elastic demand. In this case the demand curve is horizontal to ‘X’ axis.

Question 20.
Perfectly Inelastic Demand [March 16]
Answer:
Even a great rise or fall in price does not lead and change in quantity demanded is known as perfectly inelastic demand. The demand curve is vertical to ‘Y’ axis.

Question 21.
Unitary Elastic Demand
Answer:
The proportionate change demand is equal to the proportionate change in price. In this case the demand curve will be a rectangular hyperbola.

Question 22.
Relatively Elastic Demand
Answer:
When a proportionate change in price leads to more than proportionate change in quantity demand is called relatively elastic demand.

Question 23.
Relatively Inelastic Demand
Answer:
When the proportionate change in price leads to a less than proportionate change in quantity demand is called relatively inelastic demand.

Question 24.
Arc method
Answer:
Arc method is the elasticity of the mid point of an arc of a demand curve. It studies a portion of the demand curve between two points. This is used when the change in price is not very large.

Question 25.
Importance of Price Elasticity of Demand.
Answer:

1. It is useful to finance minister in imposing taxes.
2. Useful to monopolist for fixing the price.
3. Useful in determination of wages.
4. Useful in determination of prices of factors of production.

Additional Questions

Question 26.
Terms of Trade
Answer:
It is the ratio of an index of a country’s export price to an index of its important price.

Question 27.
Tax
Answer:
Tax is a compulsory payment collected from individuals or firms by central, state and local governments.

Andhra Pradesh BIEAP AP Inter 1st Year Commerce Study Material 1st Lesson Concept of Business Textbook Questions and Answers.

AP Inter 1st Year Commerce Study Material 1st Lesson Concept of Business

Essay Answer Questions

Question 1.
Define Business. What are its characteristics? [A.P. Mar. 2019, 17]
Answer:
The term Business refers to “the state of being busy”. Every individual is engaged in some activities to fulfill his/her set of needs and wants. All these activities are intended to satisfy human needs. Business is one of the human economic activities.

Business – Definitions :
“A human activity directed towards producing or acquiring wealth through buying and selling of goods.” -L.H. Haney

“Business is an institution organized and operated to provide goods and services to society under the incentive of private gain.” -B.O. Wheeler

“Business is a sum of all activities involved in the production and distribution of goods and services for private profits.” – Keith and Carlo

Business – Characteristics :
Following are the essential characteristics of business.

1. Creation of utilities
2. Deals with goods and services
3. Continuity in dealings
4. Sale, transfer or exchange
5. Profit motive
6. Risk and uncertainty
7. Economic activity
8. Art as well as science

1) Creation of utilities :
Business makes goods more useful to satisfy human wants. It adds to production, the utilities of person, time, place, form, knowledge, etc. Businessman is able to satisfy the customer’s demands effectively and economically with the help of business transactions.

2) Deals with goods and services :
Business deals with goods and services. The goods may be consumer goods such as cloths, soaps, milk, shoes, furniture, etc. They may be industrial goods such as machinery, equipment, etc. which are used for further production. Business also deals with services such as transport, warehousing, banking, insurance, etc.

3) Continuity in dealings :
Dealings in goods and services become business only if undertaken on a regular basis. A single isolated transaction of purchase and sale does not constitute business. Recurring or repeated transactions of purchase and sale constitutes business. E.g.: If a person sells his old scooter or a car, it is not business though the seller gets money in exchange. But if he opens a shop and sells scooters or cars regularly, it will become business. Therefore, regularity of dealings in an essential feature of business.

4) Sale, transfer or exchange :
In a business activity there should be two parties i.e. a buyer and a seller. There should be exchange, sale, transfer of goods or services between these two parties for money. For instance, cooking food for personal consumption does not constitute business. But cooking food and selling it to others for a price becomes business. E.g.: Students’ mess.

5) Profit motive:
The primary objective of business is to earn profits. Profits are essential for the survival as well as growth of business. Profits must, however, be earned through legal and fair means. Business should never exploit society to make money.

6) Risk and uncertainty :
Profit is the reward for assuming risk. Risk implies uncertainty of profit or the possibility of loss. Risk is a part and parcel of business. Business enterprises function in uncertain and uncontrollable environment. E.g.: Changes in customers’ tastes and fashions, demand, competition, government policies, etc. create risk. Flood, fire, earthquake, strike by employees, theft, etc. also cause loss. A businessman can reduce risks through correct forecasting and insurance. But all risks cannot be eliminated.

7) Economic activity:
Business is primarily an economic function. It involves production and distribution of goods and services for the satisfaction of human wants. However, business is a part of society and it reflects on aspiration, values and beliefs of people. Therefore, business may be described as a socio-economic function.

8) Art as well as science :
Business is an art because it requires personal skills and experience. It is also a science because it is based on certain principles and laws.
The above mentioned features are common to all business enterprises irrespec¬tive of their nature, size and form of ownership.

Question 2.
Explain the objectives of a business.
Answer:
Objectives of business mean the purposes for which business is established and carried on. Proper selection of objectives is essential for the success of a business. Therefore, every businessman must select and define his business objectives carefully and clearly.

Objectives of business are classified as given below.

1) Economic Objectives:
Business is basically an economic activity. Therefore, its primary objectives are economic in nature. The main economic objectives of business are as follows.

i) Earning profits :
Every business enterprise’s main object is profit. It is the hope of earning profits that inspires people to start business. Profit is essential for the survival of every business unit. Profit also serves as the barometer of stability, efficiency and progress of a business enterprise.

ii) Creating customers :
Profits arise from the businessman’s efforts to satisfy the needs and wants of customers. A businessman can earn profits only when there are enough customers to buy and pay for his goods and services. The customer is the foundation of business and keeps it in existence. Business exists to satisfy the wants, tastes and preferences of customers.

iii) Innovation :
Innovation refers to “creation of new things resulting from the study and experimentation, research and development”. In these days of competition a business can be successful only when it creates new designs, better machines, improved techniques, new varieties, etc. Modern science and technology have created a great scope for innovation in the business world.

2) Social Objectives:
Business does not exist in a vaccum. It is a part of society. It cannot survive and grow without the support of society. So, business must have some social objectives. They are given below.

i) Supplying desired goods at reasonable prices :
Business is expected to supply the goods and services required by the society. Goods and services should be of good quality and these should be supplied at reasonable prices. It is also the social obligation of business toaKoid malpractices tike smuggling, black makreting and misleading advertising.

ii) Fair Remuneration to employees:
Employees must be given fair compensation for their work. In addition to wages and salary a reasonable part of profits should be distribuited among employees by way of bonus. Such sharing of profits will help to increase the motivation and efficiency of employees.

It is the obligation of business to provide healthy and safe work environment for employees. Employees work day and night to ensure smooth functioning of business. It is, therefore, the duty of employers to provide hygienic working and living conditions for workers.

iii) Employment generation :
Business should provide opportunities for gainful employment to members of the society. In a country like India unemployment has become a serious problem and no government can offer jobs to all. Therefore, provision of adequate and full employment opportunities is a significant service to society.

iv) Social welfare :
Business should provide support to social, cultural and reli¬gious organisations. Business enterprises can build schools, colleges, libraries, dharamshalas, hospitals, sports bodies and research institutions. They can help non-government organisations (NGOs) like CRY (Child Relief and You), Help Age, and others which render services to weaker sections of society.

v) Payment of government dues :
A business should not shut its eyes to its obligations towards the government. Therefore, business owes it to the government to pay its tax dues honestly and in time. It must also dutifully abide by the laws of the land.

3) Human Objectives:
i) Labour welfare :
Business must recognise the dignity of labour and human factor should be given due recognition. Adequate provisions should be made for their health, safety and social security.

ii) Developing human resources :
Employees must be provided with the opportunities for developing new skills and attitudes. This can be done by training the employees and conducting workshops on skill development and attitude. Human resources are the most valuable asset of business and their development will help in the growth of business.

iii) Participative management :
Employees should be allowed to take part in decision making process of business. This will help in the development of employees. Workers’ participation in management will usher in industrial democracy.

iv) Labour – Management cooperation :
Business should strive for creating and maintaining cordial employer- employee relations so as to ensure peace and progress, in industry.

4) National Objectives:
i) Optimum utilisation of resources :
Business should use the nation’s resources in the best possible manner. Judicious allocation and optimum utilisation of scarce resources is essential for rapid and balanced economic growth of the country. Business should produce goods in accordance with national priorities and interests. It should minimise the wastage of scarce natural resources.

ii) National self-reliance :
It is the duty of business to help the government in increasing exports and in reducing dependence on imports. This will help a country to achieve economic independence. .

iii) Development of small scale industries :
Big business firms are expected to encourage growth of small scale industries which are necessary for generating employment. Small scale firms can be developed as ancillaries which provide inputs to large scale industries.

iv) Development of backward areas :
Business is expected to give preference to the industrialisation of backward regions of the country. Balanced regional development is necessary for peace and progress in the country. It will also help to raise standard of living in backward areas. Government offers special incen¬tives to the businessmen who set up factories in notified backward areas.

Question 3.
Discuss the social responsibility of business.
Answer:
Business organisations are obliged to consider social impact of their decisions. The obligation of any business to protect and serve public interest is known as social responsibility of business. Any responsibility business has, particularly towards members of the society with whom they interact or towards the society in general called is social responsibility.

The Concept of Social Responsibility:
Every business operates within a society. It uses the resources of the society and depends on the society for its functioning. This creates an obligation on the part of business to look after the welfare of society. Therefore, all the activities of the business should be such that they will not harm, rather they will protect and contribute to the interests of the society.

Social responsibility of business refers to all such duties and obligations of business directed towards the welfare of society. So, every business must contribute in some way or the other for their benefit. E.g. : Every business must ensure a satisfactory rate of return to investors, provide good salary, security and proper working condition to its employees, make available quality products at reasonable price to its consumers, maintain the environment properly, etc. Social responsibility implies that a business should not do anything harmful to the society in course of business activities of a businessman.

Social Responsibility Towards Different Interest Groups :
The business generally interacts with owners, investors, employees, suppliers, customers, competitors, gov-ernment and society. They are called interest groups. Such interest groups are given below.

Social responsibility towards different interest groups

• Responsibility towards owners
• Responsibility towards employees
• Responsibility towards suppliers
• Responsibility towards customers
• Responsibility towards government
• Responsibility towards society

1) Responsibility towards owners :
Owners are the persons who own the business. They contribute capital and bear the business risks. The primary responsibilities of business towards its owners are to :

1. Run the business efficiently.
2. Proper utilisation of capital and other resources.
3. Growth and appreciation of capital.
4. Regular and fair return on capital invested by way of dividends.

2) Responsibility towards employees :
Business needs employees or workers to work for it. These employees put their best effort for the benefit of the business. The responsibility of business towards its employees include:

1. Timely and regular payment of wages and salaries.
2. Proper working conditions and welfare amenities.
3. Opportunity for better career prospects.
4. Job security as well as social security like facilities of provident fund, group insurance, pension, retirement benefits, etc.

3) Responsibility towards suppliers :
Suppliers are businessmen who supply raw materials and other items required by manufacturers and traders. Certain suppliers, called distributors, supply finished products to the customers. The responsibilities of business towards these suppliers are :

1. Giving qualitative goods at reasonable prices.
2. Dealing on fair terms and conditions.
3. Availing reasonable credit period.
4. Timely payment of dues.

4) Responsibility towards customers :
No business can survive without customers. As a part of the responsibility of business towards them the business should provide the following facilities.

1. Products and services must be qualitative
2. Giving delivery of goods within stipulated time
3. Reasonable price
4. There must be proper after-sales services.
5. Complaints and grievances of the customers, if any, must be settled quickly.
6. Unfair means like underweighing the product, adulteration, etc. must be avoided.

5) Responsibility towards government:
Business activities are governed by the rules and regulations framed by the government. The various social responsibilities of the government are:

1. Setting up units as per guidelines of the government.
2. Payment of fees, duties and taxes regularly as well as honestly.
3. Conforming to pollution control norms set up by government.
4. Not to indulge in corruption through bribing and other unlawful activities.

6) Responsibility towards society :
A society consists of individuals, groups, organizations, families, etc. They all are the members of the society. Thus, it has certain responsibilities towards society, which may be as follows :

1. to help the weaker and backward sections of the society
2. to preserve and promote social and cultural values
3. to generate employment
4. to protect the environment
5. to conserve natural resources and wildlife
6. to promote sports and culture

Question 4.
Classify and describe each type of Economic activities.
Answer:
All the activities in which the people participate from morning till night are called human activities. Every individual is engaged in some activities to fulfil his/her set of needs and wants. All these activities are intended to satisfy human needs.

All the activities of human beings can be classified into two types. They are :

Non – economic Activities :
Those human activities do not involve money or money’s worth, such activities are termed as non-economic activities. Human beings engage themselves in non-economic activities due to love, affection, patriotism, charity, sympathy, and other such sentiments.
E.g. : A mother looks after her children, young man helps a blind man to cross the road, etc.

Economic Activities:
Human beings undertake certain economic activities for earning money or livelihood. Working as a teacher in a school, a doctor in a hospital, a worker in a factory, a farmer in a field, an emloyee in an office, a merchant selling goods, etc.

In other words, an human being involves in any activity together with money or money’s worth, such activities are termed as human economic activities. Such human economic activities are classified into three types. They are given below ;

1. Profession
2. Employment
3. Business

1) Profession:
An activity which involves the rendering of personalized services of a specialized nature based on professional knowledge, education and training is called a profes¬sion. Services rendered by doctors, lawyers, chartered accountants, engineers, etc. come under this category.

2) Employment:
An employment is a contract of service. A person who works under the contract for a salary is called an employee and the person who has given the job to the employee is called employer. An employee works under an agreement as per the rules of service and performs tasks assigned to him by the employer. The relationship between the employer and the employee is that of a ‘Master’ and ‘Servant’.

3) Business:
Business is one of the human economic activities. Business is an economic activity involving production, exchange, distribution and sale of goods and services with an objective of making profits.

Short Answer Questions

Quelition 1.
Business objectives.
Answer:
Objectives of business mean the purposes for which business is established and carried on. Proper selection of objectives is essential for the success of a business. Objectives serve as the guidelines for the future direction and management of business. Therefore, every businessman must select and define his business objectives carefully and clearly.

Objectives of business may be classified into four broad categories. They are :

1. Economic objectives
2. Social objectives
3. Human objectives
4. National objectives

Every businessman seeks to earn profits by satisfying the wants of people. It is the hope of earning profits which induce people to enter into business. No business can survive without making adequate profits. Thus profit is the fundamental economic objective of business.

If profit maximization is regarded as the sole objective of business, it is likely to result in unfair practices such as hoarding, black marketing, etc. The profit making and social service objectives are not contradictory to each other.

Business must discharge social responsibilities in addition to earning profits. It should aim at servicing the community.

Quelition 2.
Social objectives.
Answer:
Business does not exist in a vacuum. It is a part of society. It cannot survive and grow without the support of society. Business must therefore discharge social responsibilities in addition to earning profits.

Social objectives – Definition :
“The primary aim of business should be service and subsidiary aim should be earning of profit.” – Henry Ford

Some important social objectives are given below :

1. Business is expected to supply the goods and services required by the society. Goods and services should be of good quality and these should be supplied at reasonable prices.
2. Employees must be given fair compensation for their work. In addition to wages and salary a reasonable part of profits should be distributed among employees by way of bonus. Such sharing of profits will help to increase the motivation and efficiency of employees. So, fair remuneration to employees is an important social objective.
3. Business should provide job opportunities to the members of the society. In a country like India unemployment has become a serious problem and no government can offer jobs to all. So, employment generation is also one of the social objectives.
4. Business should provide support to social, cultural and religious organisations. Business enterprises can build schools, colleges, libraries, hospitals, etc.
5. Every business enterprise should pay tax dues to the government honestly and at the right time. These direct and indirect taxes provide revenue to the government for spending on public welfare. So, payment of government dues is also one of the important social objectives.

Quelition 3.
Role of profit in business.
Answer:
A business enterprise is established for earning some income. It is the hope of earning profits that inspires people to start business. Profit is essential for the survival of every business unit. Just as a person cannot live without food, a business firm cannot survive without profit. Profits enable a businessman to stay in business by maintaining intact the wealth producing capacity of its resources.

Profit is also necessary for the expansion and growth of business. Profits ensure continuous flow of capital for the modernisation and extension of business operations in future. Profit also serves as the barometer of stability, efficiency and progress of a business enterprise.

Quelition 4.
Brief explaination of economic activities.
Answer:
The term business refers to “the state of being busy”. Every business individual is engaged in some activities to fulfil his/her set of needs and wants. All these activities are intended to satisfy human needs. E.g.: A farmer engages himself in agricultural activities and an employee works in the office, a teacher teaches in the classroom, etc. for satisfying his needs, comforts and luxuries.

All the activities of human being can be divided into two types. They are :

1. Economic Activities
2. Non-economic Activities

Economic activities :
Those human activities that are involved in money, such activities are termed as economic activities. Human beings undertake certain economic activities for earning money or livelihood. Working as a teacher in a school, a doctor in a hospital, a worker in a factory, a merchant selling goods or an industrialist manufacturing goods, all these are economic activities. These economic activities are concerned with production, exchange and distribution of goods and services.

Very Short Answer Questions

Quelition 1.
Define Business. [Mar. 2018, 17 ; May 17 – A.P.]
Answer:
A business is an economic institution. It is concerned with production and distribution of goods and rendering of service in order to earn profits and acquire wealth. Business may be defined as “a human activity directed towards producing or acquiring wealth through buying and selling of goods”. – L.H. Haney

Profits are consideration of Business.

Quelition 2.
What is a Profession?
Answer:
Profession is one of the human economic activities. An activity which involves the rendering of personalised services of a specialized nature based on professional knowledge, education and training is called a profession. E.g. : Doctors, Lawyers, Chartered Accountants, Engineers, etc.

Remuneration is consideration of Profession.

Quelition 3.
What is Employment?
Answer:
Employment is also one of human economic activities. Any activity assigned to a person by the employer under an agreement or rules of services comes under the category of employment.

A person who undertakes such activity is called employee.

Salary is consideration of Employment.

Andhra Pradesh BIEAP AP Inter 1st Year Accountancy Study Material 9th Lesson Bank Reconciliation Statement Textbook Questions and Answers.

AP Inter 1st Year Accountancy Study Material 9th Lesson Bank Reconciliation Statement

Short Answer Questions

Question 1.
What is meant by Bank Reconciliation Statement? (May ’17 – T.S.)
Answer:
Bank Reconciliation Statement is a statement prepared to reconcile the difference between the balances as per the bank column of the cash book and the pass book on any given date.

Question 2.
What do you mean by Favourable Balance ? (Mar. ’17 – T.S.)
Answer:
It means cash book shows debit balance at the same time pass book shows credit balance. Favourable balance means our money is in the Bank Account. Hence cash book debit balance and pass book credit balance is called favourable balance.

Question 3.
What do you mean by Unfavourable Balance ?
Answer:
Sometimes a businessman withdraws/excess amount from the bank account and the closing bank balance of a month is a debit balance. This balance amount is called unfavourable balance or overdraft balance.

Question 4.
Describe the Overdraft. (Mar. 2019, ’18 – T.S.; Mar ’15 – A.P.)
Answer:
When withdrawals exceed deposits, cash book bank column shows credit balance and the pass book shows debit balance. It is called unfavourable or overdraft balance. Sometimes business¬man is allowed by the bank to withdraw the amount, in excess of what he has in his bank account after moving prior agreement with banker. This facility is called overdraft.

Question 5.
Cheques deposited with a bank for collection, what is the impact on Cash Book?
Answer:
When the cheques are deposited with a bank for collection, that the cheques amount was debited in the cash book, before sending them for collection. Hence the impact on cash book is the cash balance increased.

Essay Type Questions

Question 1.
Explain the nature and importance of the Bank Reconciliation Statement.
Answer:
A statement prepared to reconcile the balance of cash book and pass book is called the ‘Bank Reconciliation Statement’.
Generally the business concerns would like to maintain an account with a bank and prepare a Bank Reconciliation Statement.

Importance:

1. Locating the mistakes or errors either side of both cash book and pass book.
2. Preventing any fraud and misappropriations.
3. Enabling the business concern to get up-to-date record of transactions from the bank.
4. Ensuring a proper evidence of payment.
5. Help to know exact cash balance at bank.

Question 2.
Enumerate the reasons for differences between the balance shown in the Cash Book and Pass Book.
Answer:
I. Items entered in the bank columns of the Cash Book, but not entered in Pass Book or bank statement.

1. Cheques sent for collection, but not collected by the bank. This will appear only on the debit side of the cash book.
2. Cheques issued but not yet presented for payment. This appears only on credit side of the cash book.

II. Items entered in the bank statement or bank Pass Book, but not in Cash Book:

1. Direct payment into the bank by a customer. This appears only on the credit side of the bank statement.
2. Bank charges : Charges paid by the business for using some of the bank services. This will appear on the debit side of the pass book.
3. When the business instructs the bank to make regular payments of fixed amounts, rent, insurance premium, etc. These will appear on the debit side of the bank statement.
4. Interest on overdrafts or loans appears on the debit side of the bank statement.
5. Interest on deposits appears on the credit side of the bank statement.
6. Dishonour of cheques and bills – first appears on the debit side of the bank statement. But the firm records the same when it receives the information from the bank. As a result, the balance as per cash book and that of pass book will differ.

III. Difference caused by Errors:

1. Errors committed in recording transactions by the firm in cash book : Omission of transaction, wrong recording, wrong totaling, over / under casting, etc.
2. Errors committed in recording transactions by the bank : Sometimes bank may also commit errors. E.g. Omission or wrong recording of transaction, wrong totaling, over/ under casting, etc.

Question 3.
Explain the procedure of preparing the Bank Reconciliation Statement by taking imaginary items and figures.
Answer:
Bank reconciliation statement is prepared to reconcile the two balances of Cash Book and Pass Book. The preparation of Bank Reconciliation Statement starts with banking adjustments to one balance to reach the other balance, which ensures agreement between both the balances.

The BRS is prepared usually at the end of the period, i.e. a month, a quarter, half a year or a year whichever is convenient to the firm. When both the books, cash book and pass book are given in problem, then see whether the two books are related to the same period or different periods. If the books are for different periods, then common items should be considered and if it is for same period, then items not appearing in both the books should be taken into consideration.

The way how to prepare BRS may be illustrated as follows.
Bank Reconciliation Statement of …… as on …….

Problems

Question 1.
Pass Book of a trader shows a balance of Rs. 12,600. On comparing the Pass Book with the cash Book, the following discrepancies were noted. (Mar. 2018 – A.P.)
a) Cheques deposited in bank but not collected Rs. 2,100
b) Cheques issued but not presented for payment Rs. 1,800
c) Bank Charges Rs. 175
d) Bank paid insurance premium Rs. 1,500
e) The Debtor paid directly into bank account Rs. 1200
Answer:
Bank Reconciliation Statement

Question 2.
Murthy and Son’s Pass Book showed a balance of Rs. 21,700 as on 30^th September, 2013. On comparing the Cash Book the following discrepancies were noted.
a) Cheques issued but not yet presented for payment Rs. 2,500
b) Directly deposited by a customer Rs. 3,000
c) Interest credited by bank is found in Pass Book only Rs. 575
d) Cheques deposited in bank but not credited Rs. 3,500
e) Bank Charges Rs. 150
Prepare a Bank Reconciliation Statement showing balance as per Cash Book.
Answer:
Bank Reconciliation Statement of Murthy and Son as on 30th September 2013

Question 3.
Giri Ind Ltd’s bank balance as per Pass Book is Rs. $,900. There is disagreement between Cash Book and Pass Book balances as, on 31.3.2014. Prepare Bank Reconciliation statement by considering following transactions.
a) Cheque issued but not yet presented for payment Rs. 2100
b) Cheque deposited for collection, but not yet realized Rs. 900
c) A wrong debit given by bank in Pass Book Rs. 500
d) Bank charges debited only in Pass Book Rs. 210
e) Direct payment of insurance premium as per standing instructions Rs. 600
Answer:
Bank Reconciliation Statement of Giri lnd Ltd’s as on 31.03.2014

Question 4.
On comparing the bank Pass Book of BBR Ltd., with its Cash Book (bank column), the following differences were noticed. Prepare BRS with the help of Cash Book Balance Rs. 15,000.
a) Cheque sent for collection, notyet realized Rs. 5,600
b) Cheques issued but not yet presented for payment Rs. 4,200
c) The receipts side of Cash Book has been overcast by Rs. 300
d) A cheque drawn on firm’s current a/c, wrongly debited in its savings a/c, Rs. 2,100
e) A cheque ofRs. 900 deposited into bank, bit forgot to enter in Cash Book
Answer:
Bank Reconciliation Statement of BBR Ltd

Question 5.
Reddy’s Cash Book shows a favourable balance ofRs. 25,500 as on 31^st December, 2013. On comparing the same with his Pass Book following differences were noticed. Calculate bank balance as per Pass Book.
a) A cheque for Rs. 2,450 received from Saritha & Co was entered twice in the Cash Book.
b) The receipts column of the Cash Book has been over added by Rs. 1940.
c) Several cheques, totaling Rs. 6,000 were issued to different suppliers. Of these, cheques worth Rs. 1,500 were debited in Pass Book on 2nd January, 2014 and Rs. 2,500 on 4th January. The balance being debited before 31st December, 2013.
d) Bills discounted, got dishonored Rs. 750.
e) A cheque ofRs. 400 was credited in Pass Book, but was not recorded in Cash Book.
f) Uncredited cheque Rs. 1,000
Answer:
Bank Reconciliation Statement of Reddy’s as on 31^st December 2013

Question 6.
On 31^st December, 2013 the Cash Book showed an unfavourable balance Rs. 29,000. Prepare a Reconciliation Statement with the following information.
a) Cheques had been deposited into the bank but were not collected Rs, 4,530
b) A cheque issued to Karthik Reddy, the supplier, has not been encashed Rs. 5,040.
c) There was a debit entry in the Pass Book ofRs. 600 for bank charges.
d) Bills worth Rs. 2000 were discounted but dishonored.
Answer:
Bank Reconciliation Statement as on 31^st December 2013

Question 7.
From the following particulars prepare a Bank Reconciliation Statement.
a) Bank Overdraft as per Cash Book Rs. 16,100
b) Debit side of the bank column of Cash Book cast short Rs. 200
c) Bills collected directly by bank Rs. 3,500
d) Bank charges recorded twice in the Cash Book Rs. 240
e) A cheque deposited as per bank statement but not recorded in the Cash Book Rs. 1100
f) The cheques of 6,000 deposited but collections as per statement Rs. 2,600
g) Interest on investment collected by the banker, same was shown only in Pass Book Rs. 2,000
Answer:
Bank Reconciliation Statement

Question 8.
From the following particulars prepare Bank Reconciliation Statement as on 31^st March, 2014.
a) Overdraft balance as on 31-3-2014 as per Bank statement Rs. 22,470.
b) As per standing instructions given to bank, Chamber of Commerce fee Rs. 2,530 was paid by the bank but was not recorded in the Cash Book.
c) On 23-3-2014, the credit side of the bank column of the Cash Book was cast Rs. 1,900 short.
d) Cheque deposited into the bank but not recorded in Cash Book Rs. 2,500
e) In the Cash Book, a Bank charge ofRs. 290 was recorded twice while another bank charge of Rs. 120 was not recorded at all.
f) Divided on shares Rs. 3,200 was collected by bank directly the trader has no information.
g) Two cheques ofRs. 1850 and Rs. 1,500 were issued but out of them only one cheque ofRs. 1850 was presented for payment up to reconcile day.
Answer:
Bank Reconciliation Statement as on 31.03.2014

Question 9.
Prepare Bank Reconciliation statement ofKarthik as on 31 – 03 – 2014.
a) Bank overdraft as per Pass Book Rs. 6,500
b) Cheques deposited into bank Rs. 5,000, but only Rs. 2,000 was collected.
c) Cheques issued but not presented for payment Rs. 1500
d) A customer directly deposited in our bank Rs. 1200
e) Bank charges Rs. 200; Insurance premium Rs. 300 has debited in the Pass Book only
f) Divided Rs. 300 collected by the bank has credited in the Pass Book only
Answer:
Bank Reconciliation Statement of Karthik as on 31.03.2014

Question 10.
Prepare Bank Reconciliation Statement of P.R.G. Rao & Sons as on 31.03.2014
a) Bank overdraft as per Cash Book Rs. 14,500
b) Cheques issued but not yet presented for payment Rs. 4,500
c) Directly deposited by a Customer in our bank account Rs. 3,500.
d) Cheques deposited in bank but not credited Rs. 7,500
e) Bank charges debited in pass book only Rs. 200
f) Interest debited in the pass book only Rs. 500
Answer:
Bank Reconciliation Statement of P.R.G. Rao as on 31.03.2014

Student Activity

Visit any business careers and enquire about what discrepancies generally they notice in the items. Make a list of the discrepancies and show the effect on the bank balance.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(f) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(f)

I.

Question 1.
Verify Rolle’s theorem for the following functions.
i) x² – 1 on [-1, 1]
Solution:
Let f(x) = x² – 1
f is continuous on [-1,1]
since f(-1) = f(1) = 0 and
f is differentiable on [-1, 1]
∴ By Rolle’s theorem ∃ c ∈ (-1, 1) such that f'(c) = 0
f'(x) = 2x = 0
∴ = f'(c) = 0
2c = 0
c = 0
The point c = 0 ∈ (-1, 1)
Then Rolle’s theorem is verified.

ii) sin x – sin 2x on [0, π].
Solution:
Let f(x) = sin x – sin 2x
f is continuous on [0, π]
since f(0) = f(π)= 0 and
f is differentiable on [0, π]
By Rolle’s theorem ∃ c ∈ (0, π)
such that f'(c) = 0
f'(x) = cos x – 2 cos 2x
f'(c) = 0 ⇒ cosc – 2 cos 2c = 0
⇒ cosc – 2(2cos²c – 1):
cosc – 4 cos²c + 2=0 2
4 cos² c – cosc – 2 = 0

iii) log (x² + 2) – log 3 on [-1, 1]
Solution:
Let f(x) = log (x² + 2) – log 3
f is continuous on [-1, 1]
Since f(-1) = f(1) = 0 and f is
Differentable on [-1, 1]
By Rolle’s theorem ∃ c ∈ (-1, 1)
Such that f'(c) = 0
f'(x) = \(\frac{1}{x^{2}+2}\) = (2x)
f'(x) = \(\frac{2c}{c^{2}+2}\) = 0
2c = 0
c = 0
c = 0 ∈ (-1, 1).

Question 2.
It is given that Rolle’s theorem holds for the function f(x) = x³ + bx² + ax on [1, 3] with c = 2t + \(\frac{1}{\sqrt{3}}\). Find the values of a and b.
Solution:
Given f(x) = x³ + bx² + ax
f'(x) = 3x² + 2bx + a
∴ f'(c) = 0 6 ⇔ 3c² + 2bc + a = 0

⇔ b = 6 and b² – 3a = 3
36 – 3 = 3a
33 = 3a
a = 11
Hence a = 11 and b = -6.

Question 3.
Show that there is no real number k, for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1].
Solution:
Clearly f(0) = f(c)
0 – 0 + k = 1 – 3 + k
0 = -2
Which is not possible
∴ There is no real number K.

Question 4.
Find a point on the graph of the curve y = (x – 3)², where the tangent is parallel to the chord joining (3, 0) and (4, 1).
Solution:
Given points (3, 0) and (4, 1)
The slope of chord = \(\frac{1-0}{4-3}\) = 1
Given y = (x- 3)²
\(\frac{dy}{dx}\) = 2(x – 3)
⇒ Slope = 2(x – 3)
1 = 2(x – 3)
\(\frac{1}{2}\) = x – 3
x = \(\frac{1}{2}\) + 3 = \(\frac{7}{2}\)
y = (x – 3)² = (\(\frac{7}{2}\) – 3)² = \(\frac{1}{4}\)
∴ The point on the curve is (\(\frac{7}{2}\), \(\frac{1}{4}\))

Question 5.
Find a point on the graph of the curve y = x³, where the tangent is parallel to the chord joining (1, 1) and (3, 27).
Solution:
Given points (1, 1) and (3, 27)
Slope of chord = \(\frac{27-1}{3-1}\) = 13
Given y = x³
\(\frac{dy}{dx}\) = 3x²
⇒ Slope = 3x²
13 = 3x²

∴ The point on the curve is (\(\frac{\sqrt{39}}{3}\), \(\frac{13\sqrt{39}}{9}\))

Question 6.
Find ‘c’, so that f'(c) = \(\frac{f(b)-f(a)}{b-a}\) in the following cases.
i) f(x) = x² – 3x – 1, a = \(\frac{-11}{7}\), b = \(\frac{13}{7}\).
Solution:

f'(x) = 2x – 3
f'(c) = 2c – 3
Given f'(c)= \(\frac{f(b)-f(a)}{b-a}\)

ii) f(x) = e^x ; a = 0, b = 1
Solution:
f(b) = f(1) = e’ = e
f(a) = f(0) = e° = 1
Given f(x) = e^x
f'(x) = e^x
Given condition f'(c) = \(\frac{f(b)-f(a)}{b-a}\)

Question 7.
Verify the Rolle’s theorem for the function (x² – 1) (x – 2) on [-1, 2]. Find the point in the interval where the derivate vanishes.
Solution:
Let f(x) = (x² – 1) (x- 2) = x³ – 2x² – x + 2
f is continous on [-1, 2]
since f(-1) = f(2) = 0 and f is
Differentiable on [-1, 2]
By Rolle’s theorem ∃ C ∈ (-1, 2)
Let f'(c) = 0
f'(x) = 3x² – 4x – 1
3c² – 4c – 1 = 0

Question 8.
Verify the conditions of the Lagrange’s mean value theorem for the following functions. In each case find a point ‘c’ in the interval as stated by the theorem
i) x² -1 on [2, 3]
Solution:
Solution:
Let f(x) = x² – 1
f is continous on [2, 3]
and f is differentiable
Given f(x) = x² – 1
f'(x) = 2x
By Lagrange’s mean value theorem ∃ C ∈ (2, 3) such there

ii) sin x – sin 2x on [0, π]
Solution:
Let f(x) = sin x – sin 2x
f is continuous on [0, π] and f is differentiable
Given f(x) = sin x – sin 2x
f'(x) = cos x – 2 cos 2x
By Lagrange’s mean value than ∃ C ∈ (0, π) such there
f'(c) = \(\frac{f(\pi)-f(0)}{\pi-0}\)
cosc – 2 cos 2c = 0
cosc 2(2cos² – 1) = 0
cosc – 4 cos²c + 2 = 0
4 cos² c – cos c – 2 = 0

iii) log x on [1, 2].
Solution:
Let f(x) = log x
f is continuous on [1, 2] and f is differentiable
Given f(x) = log x
f'(x) = \(\frac{1}{x}\)
By Lagrange’s mean value theorem ∃ c ∈ (1, 2) such that

Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Important Questions which are most likely to be asked in the exam.

Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Important Questions

Question 1.
Find the values of
(i) sin \(\frac{5 \pi}{3}\)
(ii) tan (855°)
(iii) sec \(\left(\frac{13 \pi}{3}\right)\)
Solution:
i) sin \(\frac{5 \pi}{3}\) = sin \(\left(2 \pi-\frac{\pi}{3}\right)\) = -sin \(\frac{\pi}{3}\) = \(-\frac{\sqrt{3}}{2}\)

ii) tan (855°) = tan (2 × 360° + 135°)
= tan (135°)
= tan (180° – 45°)
= -tan 45° = -1

iii) sec \(\left(13 \frac{\pi}{3}\right)\) = sec \(\left(4 \pi+\frac{\pi}{3}\right)\)
= sec \(\frac{\pi}{3}\) = 2

Question 2.
Simplify.
i) Cot (θ – \(\frac{13 \pi}{2}\))
ii) tan \(\left(-23 \frac{\pi}{3}\right)\)
Solution:

Question 3.
Find the value of sin² \(\frac{\pi}{10}\) + sin² \(\frac{4 \pi}{10}\) + sin² \(\frac{6 \pi}{10}\) + sin² \(\frac{9 \pi}{10}\)
Solution:

Question 4.
If sin θ = \(\frac{4}{5}\) and θ is not in the first qua-drant, find the value of cos θ.
Solution:
∵ sin θ = \(\frac{4}{5}\) and θ is not in the first quadrant
⇒ θ lies in 2^nd quadrant, ∵ sin θ is +ve

Question 5.
If sec θ + tan θ = \(\frac{2}{3}\), find the value of sin θ and determine the quadrant in which θ lies.
Solution:
∵ sec θ + tan θ = \(\frac{2}{3}\)

∵ tan θ is negative, sec θ is positive
⇒ θ lies in fourth quadrant.

Question 6.
Prove that
cot\(\frac{\pi}{16}\).cot\(\frac{2 \pi}{16}\).cot\(\frac{3 \pi}{16}\)…..cot\(\frac{7 \pi}{16}\) = 1
Solution:

Question 7.
If 3 sin θ + 4 cos θ = 5, then find the value of 4 sin θ – 3 cos θ.
Solution:
Given 3 sin θ + 4 cos θ = 5 and let 4 sin θ – 3 cos θ = x
By squaring and adding, we get
(3 sin θ + 4 cos θ)² + (4 sin θ – 3 cos θ)² = 5² + x²
⇒ 9 sin² θ + 16 cos² θ + 24 sin θ cos θ + 16 sin² θ + 9 cos² θ – 24 sin θ cos θ = 25 + x²
⇒ 9 + 16 = 25 + x²
⇒ x² = 0 ⇒ x = 0
∴ 4 sin θ – 3 cos θ = 0.

Question 8.
If cos θ + sin θ = \(\sqrt{2}\) cos θ, prove that cos θ – sin θ = \(\sqrt{2}\) sin θ. (May ’11)
Solution:
Given cos θ + sin θ = \(\sqrt{2}\) cos θ
⇒ sin θ = (\(\sqrt{2}\) – 1) cos θ
Now multiplying both sides by (\(\sqrt{2}\) + 1)

Question 9.
Find the value of 2(sin² θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ)
Solution:
2 (sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ)
= 2[(sin² θ)³ + (cos² θ)³] – 3[(sin² θ)² + (cos² θ)²]
= 2[(sin² θ + cos² θ)³ – 3 sin² θ cos² θ (sin² θ + cos² θ)] – 3[(sin² θ + cos² θ)² – 2 sin² θ cos² θ]
= 2[1 – 3 sin² θ cos² θ] – 3[1 – 2 sin² θ cos² θ]
= 2 – 6 sin² θ cos² θ – 3 + 6 sin² θ cos² θ
= -1

Question 10.
Prove that (tan θ + cot θ)² = sec² θ + cosec² θ = sec² θ cosec² θ.
Solution:
(tan θ + cot θ)²
=tan² θ + cot ² θ + 2 tan θ cot θ
= tan² θ + cot² θ + 2
= (1 + tan² θ) + (1 + cot² θ)
= sec² θ + cosec² θ

Question 11.
If cos θ > 0, tan θ + sin θ = m and tan θ – sin θ = n, then show that m² – n² = n, then show that m² – n² = 4\(\sqrt{m n}\)
Solution:
Given that m = tan θ + sin θ
n = tan θ – sin θ
⇒ m + n = 2 tan θ and m – n = 2 sin θ
Now(m + n)(m – n) = 4 tan θ sin θ

Question 12.
If tan 20° = λ, then show that \(\frac{\tan 160^{\circ}-\tan 110^{\circ}}{1+\tan 160^{\circ} \cdot \tan 110^{\circ}}\) = \(\frac{1-\lambda^{2}}{2 \lambda}\) (A.P.) Mar. ’16
Solution:
Given tan 20° = λ

Question 13.
Find the values of sin 75°, cos 75°, tan 75° and cot 75°.
Solution:
i) sin 75° = sin (45° + 30°)
= sin 45°. cos 30° + cos 45°. sin 30°

ii) cos (75°) = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°

Question 14.
If 0 < A, B < 90°.cos A = \(\frac{5}{13}\) and sin B = \(\frac{4}{5}\)-then find sin(A + B).
Solution:
0 < A < 90°and cos A = \(\frac{5}{13}\) ⇒ sin A = \(\frac{12}{13}\)
0 < B < 90°and sin B = \(\frac{4}{5}\) ⇒ cos B = \(\frac{3}{5}\)
∴ sin (A + B) = sin A cos B + cos A sin B
= \(\frac{12}{13}\) • \(\frac{3}{5}\) + \(\frac{5}{13}\) • \(\frac{4}{5}\) = \(\frac{56}{65}\)

Question 15.
Prove that
sin² \(\left(52 \frac{1}{2}\right)^{\circ}\) – sin² \(\left(22 \frac{1}{2}\right)^{\circ}\) = \(\frac{\sqrt{3}+1}{4 \sqrt{2}}\)
Solution:

Question 16.
Prove that tan 70° – tan 20° = 2 tan 50°.
Solution:
tan 50° = tan (70° – 20°)
= \(\frac{\tan 70^{\circ}-\tan 20^{\circ}}{1+\tan 20^{\circ} \cdot \tan 70^{\circ}}\)
⇒ tan 70° – tan 20°
= tan 50° [1 + tan 20° . tan (90° – 20°)]
= tan 70° – tan 20° = tan 50°[1 + tan 20° cot 20°]
⇒ tan 70° – tan 20° = 2 tan 50°.

Question 17.
If A + B = π/4, then prove that
i)(1 + tan A)(1 + tan B) = 2. (May ’11; Mar. ’07)
ii) (cot A – 1)(cot B – 1) = 2
Solution:
i) Given that A + B = π/4 (T.S) (Mar. ’16)
⇒ tan (A + B) = tan (π/4)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = 1
⇒ tan A + tan B = 1 – tan A tan B
⇒ tan A + tan B + tan A tan B = 1
Add 1 on both sides
⇒ 1 + tan A + tan B + tan A tan B = 1 + 1
⇒ (1 + tan A)(1 + tan B) = 2

ii) Given A + B = π/4
⇒ cot (A + B) = cot π/4
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}\) = 1
⇒ cot A cot B – 1 = çot B + cot A
⇒ cot A cot B – cot A – cot B = 1
Again add 1 on both sides
cot A cot B – cot A – cot B + 1 = 1 + 1
∴ (cot A – 1) (cot B – 1) = 2.

Question 18.
If sin α = \(\frac{1}{\sqrt{10}}\), sin β = \(\frac{1}{\sqrt{5}}\) and α, β are acute, show that α + β = π/4.
Solution:
Given α is acute and sin α = \(\frac{1}{\sqrt{10}}\)
⇒ tan α = \(\frac{1}{3}\)
β is acute and sin β = \(\frac{1}{\sqrt{5}}\) ⇒ tan β = \(\frac{1}{2} .\)

Question 19.
If sin A = \(\frac{12}{13}\), cos B = \(\frac{3}{5}\) and neither A nor B is in the first quadrant, then find the quadrant in which A + B lies.
Solution:
sin A = \(\frac{12}{13}\) and A is not in first quadrant
⇒ A lies in second quadrant, ∵ sin A is +ve
cos B = \(\frac{3}{5}\) and B is not in first quadrant
⇒ B lies in fourth quadrant, cos B is +ve
∵ sin A = \(\frac{12}{13}\) ⇒ cos A = –\(\frac{5}{13}\)
cos B = \(\frac{3}{5}\) ⇒ sin B = –\(\frac{4}{5}\)
sin (A + B) = sin A cos B + cos A sin B

cos (A + B) = cos A cos B – sin A sin B

∵ sin (A + B) and cos (A + B) are positive
⇒ (A + B) lies in first quadrant.

Question 20.
Find (i) tan \(\left(\frac{\pi}{4}+\mathbf{A}\right)\) interms of tan A
and (ii) cot \(\left(\frac{\pi}{4}+\mathbf{A}\right)\) interms of cot A.
Solution:

Question 21.
Prove that \(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}\) = cot 36°. (A.P) (Mar ’15, Mar. ’11)
Solution:

Question 22.
Show that
cos 42° + cos 78° + cos 162° = 0 (May. ’11)
Solution:
L.H.S. = cos 42° + cos 78° + cos 162°
= 2 cos \(\left(\frac{42^{\circ}+78^{\circ}}{2}\right)\). cos \(\left(\frac{42^{\circ}-78^{\circ}}{2}\right)\) + cos (180° – 18°)
= 2 cos 60° . cos (-18°) + cos (180° – 18°)
= 2\(\left(\frac{1}{2}\right)\) cos 18° – cos 18° = 0
∴ cos 42° + cos 78° + cos 162° = 0

Question 23.
Express \(\sqrt{3}\) sin θ + cos θ as a sine of an angle.
Solution:
\(\sqrt{3}\) sin θ + cos θ = 2(\(\frac{\sqrt{3}}{2}\) sin θ + cos θ)
= 2(cos \(\frac{\pi}{6}\) sin θ + sin \(\frac{\pi}{6}\) cos θ)
= 2. sin[θ + \(\frac{\pi}{6}\)]

Question 24.
Prove that sin² θ + sin² [θ – \(\frac{\pi}{3}\)] + sin² [θ – \(\frac{\pi}{3}\)] = \(\frac{3}{2} .\)
Solution:

Question 25.
If A, B, C are angles of a triangle and if none of them is equal to \(\frac{\pi}{2}\), then prove that
i) tan A + tan B + tan C = tan A tan B tan C
ii) cot A cot B + cot B cot C + cot C cot A = 1
Solution:
i) ∵ A, B, C are angles of a triangle
⇒ A + B + C = 180°
⇒ A + B = 180° – C
⇒ tan (A + B) = tan (180° – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = -tan C
⇒ tan A + tan B = -tan C + tan A tan Btan C
⇒ tan A + tan B + tan C = tan A tan B tan C

ii) ∵ A + B + C = 180°
⇒ A + B = 180° – C
⇒ cot (A + B) = cot (180° – C)
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}\) = -cot C
⇒ cot A cot B – 1 = -cot B cot C – cot C. cot A
⇒ cot A cot B + cot B cot C + cot C cot A = 1

Question 26.
Let ABC be a triangle such that cot A + cot B + cot C = \(\sqrt{3}\). Then prove that ABC is an equilateral triangle.
Solution:
Given that A + B + C = 180°
Then we know that
cot A cot B + cot B cot C + cot C cot A = 1
i.e., Σ(cot A cot B) = 1 —– (1)
Now Σ (cot A – cot B)²
= Σ (cot² A + cot² B – 2 cot A cot B)
= 2 cot² A + 2 cot² B + 2 cot² C – 2 cot A cot B – 2 cot B cot C – 2 cot C cot A
= 2 [cot A + cot B + cot C]² – 6 (cot A cot B + cot B cot C + cot C cot A)
= 2
= 6 – 6 = 0
∴ Σ (cot A – cot B)² = 0 .
⇒ cot A = cot B = cot C
⇒ cot A = cot B = cot C = \(\frac{\sqrt{3}}{3}\) = \(\frac{1}{\sqrt{3}}\)
(∵ cot A + cot B + cot C = \(\sqrt{3})\))
⇒ A = B = C = 60°
∴ ΔABC is an equilateral triangle.

Question 27.
Suppose x = tan A, y = tan B, z = tan C. Suppose none of A, B, C, A – B, B – C, C – A is an odd multiple of \(\frac{\pi}{2}\).Then prove that \(\sum\left(\frac{x-y}{1+x y}\right)\) = \(\pi\left(\frac{x-y}{1+x y}\right)\)
Solution:
∵ x = tan A, y = tan B, z = tan C

Write P = A – B, Q = B – C, R = C – A.
Then P + Q + R = O
⇒ tan (P + Q) = tan (-R)
⇒ \(\frac{\tan P+\tan Q}{1-\tan P \tan Q}\) = -tan R
⇒ tan P + tan Q = -tan R + tan P tan Q tan R
⇒ tan P + tan Q + tan R = tan P tan Q tan R
⇒ Σ(tan P) = π (tan P)
⇒ Σtan (A – B) = π tan (A – B)
∴ Σ\(\left(\frac{x-y}{1+x y}\right)\) = π\(\left(\frac{x-y}{1+x y}\right)\)

Question 28.
Find the values of
i) sin 22\(\frac{1}{2}\)°
ii) cos 22\(\frac{1}{2}\)°
iii) tan 22\(\frac{1}{2}\)°
iv) cot 22\(\frac{1}{2}\)°
Solution:

Question 29.
Find the values of
i) sin 67\(\frac{1}{2}\)°
ii) cos 67\(\frac{1}{2}\)°
iii) tan 67\(\frac{1}{2}\)°
iv) cot 67\(\frac{1}{2}\)°
Solution:
Let A = 67\(\frac{1}{2}\)° ⇒ = 2A = 135°

Question 30.
Simplify: \(\frac{1-\cos 2 \theta}{\sin 2 \theta}\)
Solution:
\(\frac{1-\cos 2 \theta}{\sin 2 \theta}\) = \(\frac{2 \sin ^{2} \theta}{2 \sin \theta \cos \theta}\) = \(\frac{\sin \theta}{\cos \theta}\) = tan θ

Question 31.
If cos A = \(\sqrt{\frac{\sqrt{2}+1}{2 \sqrt{2}}}\), find the value of cos 2A.
Solution:
cos 2A = 2 cos²A – 1 = 2 \(\left(\frac{\sqrt{2}+1}{2 \sqrt{2}}\right)\) – 1
= \(\frac{\sqrt{2}+1}{\sqrt{2}}\) – 1 = \(\frac{1}{\sqrt{2}}\)

Question 32.
If cos θ = \(\frac{-5}{13}\) and \(\frac{\pi}{2}\) < θ < π, find the value of sin 2θ.
Solution:
\(\frac{\pi}{2}\) < θ < π ⇒ sin θ > 0 and cos θ = –\(\frac{5}{13}\)
⇒ Sin θ = \(\frac{12}{13}\)
∴ sin 2θ = 2 sin θ cos θ
= 2 . \(\frac{12}{13}\)(-\(\frac{5}{13}\)) = –\(\frac{120}{169}\)

Question 33.
For what values of x in the first quadrant \(\frac{2 \tan x}{1-\tan ^{2} x}\) is positive?
Solution:
\(\frac{2 \tan x}{1-\tan ^{2} x}\) > 0 ⇒ tan 2x > 0
⇒ 0 < 2x < \(\frac{\pi}{2}\) (since x is in the first quadrant)
⇒ 0 < x < \(\frac{\pi}{4}\)

Question 34.
If cos θ = \(\frac{-3}{5}\) and π < θ < \(\frac{3 \pi}{2}\), find the value of tan θ/2.
Solution:

Question 35.
If A is not an integral multiple of \(\frac{\pi}{2}\), prove that
i) tan A + cot A = 2 cosec 2A
ii) cot A – tan A = 2 cot 2A
Solution:
i) tan A + cot A = \(\frac{\sin A}{\cos A}\) + \(\frac{\cos A}{\sin A}\)
= \(\frac{\sin ^{2} A+\cos ^{2} A}{\sin A \cos A}\)

Question 36.
If A is not an integral multiple of prove that
i) tan A + cot A = 2 cosec 2A
ii) cot A – tan A = 2 cot 2A
Solution:

Question 37.
If θ is not an integral multiple of \(\frac{\pi}{2}\), prove that tan θ + 2 tan 2θ + 4 tan 4θ +
8 cot 8θ = cot θ.
Solution:
From cot A – tan A = 2 cot 2A above tan A = cot A – 2 cot 2A ….(1)
∴ tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = (cot θ – 2 cot 2θ) + 2 (cot 2θ – 2 cot 4θ) + 4 (cot 4θ – 2 cot 8θ) + 8 cot 8θ (by (1) above)
= cot θ

Question 38.
For A ∈ R, prove that
i) sin A.sin(π/3 +A).sin(π/3 – A) = \(\frac{1}{4}\) . sin3A
ii) cosA . cos (π/3 + A). cos(π/3 – A)
= \(\frac{1}{4}\) cos 3A and hence deduce that
iii) sin 20° sin 40° sin 60° sin 80° = \(\frac{3}{16}\)
iv) cos \(\frac{\pi}{9}\), cos \(\frac{2 \pi}{9}\), cos \(\frac{3 \pi}{9}\). cos \(\frac{4 \pi}{9}\) = \(\frac{1}{16}\).
Solution:
i) sin A. sin (π/3 + A). sin (π/3 – A)
= sin A [sin² π/3 – sin² A]


iii) ∵ sin A. sin (60° + A). sin (60° – A)
= \(\frac{1}{4}\) sin 3A
Put A = 20°
⇒ sin 20°. sin (60° + 20°). sin (60° – 20°)
= \(\frac{1}{4}\). sin(3 × 20°) .
⇒ sin 20°. sin 40°. sin 80° = \(\frac{1}{4}\) sin 60°
Multiplying on both sides with sin 60°
We get, sin 20° sin 40° sin 60° sin 80°
= \(\frac{1}{4}\) sin² 60°
= \(\frac{1}{4}\left(\frac{\sqrt{3}}{2}\right)^{2}[latex] = [latex]\frac{3}{16}\)

iv) ∵ cos A. cos (60° + A). cos (60° – A) = \(\frac{1}{4}\)cos 3A
Put A = 20°
⇒ cos 20°. cos (60° + 20°) cos (60° – 20°)
= \(\frac{1}{4}\). cos(3 × 20°)
⇒ cos 20°. cos 40°. cos 80° = cos 60°
On multiplying both sides by cos 60°, we get cos 20°. cos 40°. cos 60°. cos 80°
= \(\frac{1}{4}\). cos² 60°

Question 39.
If 3A is not an odd multiple of \(\frac{\pi}{2}\), prove that tan A. tan (60° + A). tan (60° – A)
= tan 3A and hence find the value of tan 6°. tan 42°. tan 66°. tan 78°.
Solution:

∴ tan A . tan \(\left(\frac{\pi}{3}+\mathrm{A}\right)\) tan \(\left(\frac{\pi}{3}-A\right)\) = tan 3A
i.e., tan A tan (60° – A) tan (60° + A) = tan 3A —— (1)
Put A = 6°
⇒ tan 6° tan 54° tan 66° = tan 18° ——- (2)
Put A = 18° in (1)
tan 18° tan 42° tan 78° = tan 54° ——- (3)
put (2) in (3),
(tan 6° tan 54° tan 66°) tan 42° tan 78°
= tan 54
⇒ tan 6° tan 42° tan 66° tan 78° = 1

Question 40.
For α, β ∈ R, prove that (cos α + cos β)² + (sin α + sin β)² = 4 cos² \(\left(\frac{\alpha-\beta}{2}\right)\).
Solution:
LH.S. = (cos α + cos β)² + (sin α + sin β)²
= (cos² α + cos² β + 2 cos α cos β + (sin² α + sin² β + 2 sin α sin β)
= 1 + 1 + 2 (cos α cos β + sin α sin β)
= 2 + 2 cos (α – β) = 2 (1 + cos (α – β)]
= 2[2cos²\(\left(\frac{\alpha-\beta}{2}\right)\)]
= 4.cos²\(\left(\frac{\alpha-\beta}{2}\right)\); [∵ 1 + cos θ = 2 cos² \(\frac{\theta}{2}\)]

Question 43.
If a, b, c are non zero real numbers and α, β are solutions of the equation a cos θ + b sin θ = c then show that
(i) sin α + sin β = \(\frac{2 b c}{a^{2}+b^{2}}\) and
(ii) sin α. sin β = \(\frac{c^{2}-a^{2}}{a^{2}+b^{2}}\)
Solution:
∵ a cos θ + b sin θ = c
= a cos θ = c – b sin θ
⇒ (a cos θ)² = (c – b sin θ)²
⇒ a² cos² θ = c² + b² sin² θ – 2bc sinθ
⇒ a² (1 – sin² θ) = c² + b² sin² θ – 2bc sin θ
⇒ (a² + b²) sin² θ – 2bc sin θ + (c² – a²) = 0
This is a quadratic equatioñ in sin θ, whose roots are sin α and sin β (given that α, β are two solutions of θ)
∴ Sum of the roots sin α + sin β = \(\frac{2 b c}{a^{2}+b^{2}}\)
Product of the roots sin α sin β = \(\frac{c^{2}-a^{2}}{a^{2}+b^{2}}\)

Question 42.
If θ is not an odd multiple of \(\frac{\pi}{2}\) and cos θ ≠ \(\frac{-1}{2}\), prove that
\(\frac{\sin \theta+\sin 2 \theta}{1+\cos \theta+\cos 2 \theta}\) = tan θ.
Solution:

Question 43.
Prove that sin⁴ \(\frac{\pi}{8}\) + sin⁴ \(\frac{3 \pi}{8}\) + sin⁴ \(\frac{5 \pi}{8}\) + sin⁴ \(\frac{7 \pi}{8}\) = \(\frac{3}{2}\)
Solution:

Question 44.
If none of 2A and 3A is an odd multiple of \(\frac{\pi}{2}\), then prove that tan 3A. tan 2A. tanA = tan 3A – tan 2A – tan A.
Solution:
∵ tan 3A = tan (2A + A)
= \(\frac{\tan 2 A+\tan A}{1-\tan 2 A \tan A}\)
⇒ tan 3A(1 – tan 2A tan A) = tan 2A + tan A
⇒ tan 3A – tan A tan 2A tan 3A
= tan 2A + tan A
∴ tan 3A – tan 2A – tan A
= tan A tan 2A tan 3A

Question 45.
Prove that sin 78° + cos 132° = \(\frac{\sqrt{5}-1}{4}\).
Solution:
L.H.S. = sin 78° + cos 132°
= sin 78° + cos (90° + 42°)
= sin 78° – sin 42°

Question 46.
Prove that sin 21° cos 9° – cos 84° cos 6° = \(\frac{1}{4}\).
Solution:
LH.S. = sin 21° cos 9° – cos 84° cos 6°
= \(\frac{1}{2}\)[2 sin 21° cos 9° – 2 cos 84° cos 6°]
= \(\frac{1}{2}\)[sin (21° + 9°) + sin (21° – 9°) – 2 cos (90° – 6°) cos 6°]
= \(\frac{1}{2}\)[sin 30° + sin 12° – 2 sin 6° cos 6°]
= \(\frac{1}{2}\)[\(\frac{1}{2}\) + sin 12° – sin (2 × 16°)
= \(\frac{1}{4}\) = R.H.S.

Question 47.
Find the value of sin 34° + cos 64° – cos 4°.
Solution:
sin 34° + (cos 64° – cos 4°)

Question 48.
Prove that cos² 76° + cos² 16° – cos 76° cos 16° = \(\frac{3}{4} .\)
Solution:
L.H.S. = cos² 76° + cos² 16° – cos 76° cos 16°
= cos² 76° + (1 – sin² 16°) – \(\frac{1}{2}\)(2 cos 76° cos 16°)
= 1 + (cos² 76° – sin² 16°) – \(\frac{1}{2}\)[cos (76° + 16°) + cos (76° – 16°)]
= 1 + cos (76° + 16°). cos (76° – 16°) – \(\frac{1}{2}\)[cos 92° + cos 60°]
= 1 + cos (92°). cos 60° – \(\frac{1}{2}\)cos 92° – \(\frac{1}{2}\)cos 60°
= 1 + \(\frac{1}{2}\). cos 92° – \(\frac{1}{2}\). cos 92° – \(\frac{1}{2}\) × \(\frac{1}{2}\)
= 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\) = R.H.S.

Question 49.
If a, b, ≠ 0 and sin x + sin y = a and cos x + cos y = b, find two values of
i) tan \(\left(\frac{x+y}{2}\right)\)
ii) sin \(\left(\frac{x-y}{.2}\right)\) interms of a and b.
Solution:

First method:

ii) a² + b² = (sin x + sin y)² + (cos x + cos y)²
= sin² x + sin² y + 2 sin x sin y + cos² x + cos² y + 2 cos x cos y
= 2 + 2(cos x cos y + sin x sin y)
= 2 + 2 cos (x – y)
= 2[1 + cos (x – y)]
a² + b² – 2 = 2 cos (x – y)

Second method:

Question 50.
Prove that cos 12° + cos 84° + cos 132° + cos 156° = –\(\frac{1}{2}\).
Solution:
L.H.S. = cos 12° + cos 84° + cos 132° + cos 156°

Question 51.
Show that for any θ ∈ R
4 sin \(\frac{5 \theta}{2}\) cos \(\frac{3 \theta}{2}\) cos 3θ = sin θ – sin 2θ + sin 4θ + sin 7θ
Solution:
R.H.S. = 4 sin \(\frac{5 \theta}{2}\) cos \(\frac{3 \theta}{2}\) cos 3θ

= 2 [(sin 4θ + sin θ) cos 3θ]
= 2 sin 4θ cos 3θ + 2 sinθ cos 3θ
= sin (4θ + 3θ) + sin (4θ – 3θ) + sin (θ + 3θ) + sin(θ – 3θ)
= sin 7θ + sin θ + sin 4θ – sin 2θ = R.H.S.

Question 52.
If none of A, B, A + B is an integral multiple of π, then prove that

Solution:

Question 53.
For any α ∈ R, provethat cos² (α – π/4) + cos² (α + π/12) – cos² (α – π/12) = \(\frac{1}{2}\).
Solution:

Question 54.
Suppose (α – β) is not an odd multiple of \(\frac{\pi}{2}\), m is a non – zero real number such that m ≠ -1 and \(\frac{\sin (\alpha+\beta)}{\cos (\alpha-\beta)}\) = \(\frac{1-m}{1+m}\), Then prove that tan \(\left(\frac{\pi}{4}-\alpha\right)\) = m. tan \(\left(\frac{\pi}{4}+\beta\right)\)
Solution:

Question 55.
If A, B, C are the angles of a triangle, prove that
i) sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
ii) sin 2A + sin 2B – sin 2C = 4 cos A cos B sin C
Solution:
i) ∵ A, B, C are angles of a triangle
⇒ A + B + C = 180° ——- (1)
L.H.S. = sin 2A + sin 2B + sin 2C

= 2 sin (A + B) cos (A – B) + sin 2C
= 2 sin (180° – C) cos (A – B) + sin 2C
By(1)
= 2 sin C. cos (A — B) + 2 sin C. cos C
= 2 sin C [cos (A — B) + cos C]
= 2 sin C [cos (A — B) + cos (180° — \(\overline{A+B}\))]
= 2 sin C [cos (A – B) — cos (A + B)]
= 2 sin C (2 sin A sin B)
= 4 sin A sin B sin C = R.H.S.

ii) LH.S. = sin 2A + sin 28 — sin 2C

= 2 sin(A+ B)cos(A—B)—sin2C
= 2 sin (180° — C) cos (A — B) — sin 2C
= 2 sin C. cos(A – B) – 2 sin C cos C
= 2 sin C [cos (A – B) – cos C]
= 2 sin C [cos (A — B)—cos (180°— \(\overline{A+B}\))]
By(1)
= 2 sin C [cos (A — B) + cos (A + B)]
= 2 sin C [2 cos A cas B]
= 4 cos A cos B sin C = R.H.S.

Question 56.
If A, B, C are angles of a triangle, prove that
i) cos 2A + cos 2B + cos 2C
= -4 cos A cos B cos C – 1

ii) cos 2A + cos 2B – cos 2C
= 1 – 4 sin A sin B cos C
Solution:
i) ∵ A, B, C are angles of a triangle
⇒ A + B + C = 180° ———— (1)
L.H.S. = (cos 2A + cos 2B) + cos 2C
= 2 cos(A + B) cos (A – B) + 2 cos² C – 1
= -2 cos C cos (A – B) – 2 cos C cos (A + B) – 1
[∵ cos (A + B) = -cos C]
= – 1 – 2 cos C[cos (A – B) + cos(A – B)]
= – 1 – 2 cos C[2 cos A cos B]
= -1 – 4 cos A cos B cos C = R.H.S.

ii) L.H.S. = cos 2A + cos 2B – cos 2C

= 2 cos (A + B). cos (A – B) – (2 cos² C – 1)
= 2 cos (180° – C) cos (A – B) – 2 cos² C + 1
= 1 – 2 cos C cos (A – B) – 2 cos² C
= 1 – 2 cos C [cos (A – B) + cos C]
= 1 – 2 cos C[cos(A – B) + cos(180° – \(\overline{\mathrm{A}+\mathrm{B}}\))]
= 1 – 2 cos C [cos (A – B) – cos (A + B)]
= 1 – 2 cos C [2 sin A sin B]
= 1 – 4 sin A sin B cos C = R.H.S.

Question 57.
If A B, C are angles in a triangle, then prove that
i) sin A + sin B + sin C = 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)
ii) cos A + cos B + cos C = 1 + 4 sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) sin \(\frac{C}{2}\)
Solution:

Question 58.
If A + B + C = π/2, then show that
i) sin² A + sin² B + sin² C = 1 – 2 sin A sin B sin C
ii) sin 2A + sin 2B + sin 2C = 4 cos A cos B cos C
Solution:
A + B + C = π/2 ——– (1)
L.H.S. = sin² A + sin² B + sin² C
= \(\frac{1}{2}\)(1 – cos2A + 1 – cos 2B + 1 – cos 2C]
= \(\frac{1}{2}\)[3 – (cos 2A + cos 2B + cos 2C)]
= \(\frac{1}{2}\)[3 – (1 + 4 sin A sin B sin C)
(By Problem No. 57(ii)]
(∵ 2A + 2B + 2C = 180°)
= \(\frac{1}{2}\)[2 – 4 sin A sin B sin C]
= 1 – 2 sin A sin B sin C

ii) A + B + C = 90°
⇒ 2A + 2B + 2C = 180°
2A + 2B + 2C 180°
sin 2A + sin 2B + sin 2C
= 4 cos A cos B cos C
By Problem No. 57(i).

Question 59.
If A + B + C = 3π/2, prove that cos 2A + cos 2B + cos 2C = 1 – 4 sin A sin B sin C.
Solution:
A + B + C = 3π/2 —— (1)
L.H.S. = cos 2A + cos 2B + cos 2C
= 2 cos (A + B). cos(A – B) +1 – 2 sin² C
= 2 cos (270° – C). cos (A – B) + 1 – 2 sin² C
= 1 – 2 sin C cos (A – B) – 2 sin²C
= 1 – 2 sin C [cos(A – B) + sin C]
= 1 – 2 sin C[cos (A – B) + sin (270° – \(\overline{A+B}\))]
= 1 – 2 sin C[cos(A – B) – cos(A + B)]
= 1 – 2 sin C[2 sin A sin B]
= 1 – 4 sin A sin B sin C

Question 60.
If A B, C are angles of a triangle, then prove that
sin² \(\frac{A}{2}\) + sin² \(\frac{B}{2}\) – sin² \(\frac{C}{2}\) = 1 – 2 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\) (Mar. ’16, May ’12, ’11)
Solution:

Question 61
If A. B, C are angles of a triangle, then prove that sin \(\frac{\mathbf{A}}{\mathbf{2}}\) + sin \(\frac{\mathbf{B}}{\mathbf{2}}\) + sin \(\frac{\mathbf{C}}{\mathbf{2}}\) = 1 + 4 sin \(\frac{\pi-\mathbf{A}}{4}\) sin \(\frac{\pi-B}{4}\) sin \(\frac{\mathrm{C}}{2}\)
Solution:
A + B + C = 180° ——- (1)

Question 62.
If A + B + C = 0, then prove that cos² A + cos² B + cos² C = 1 + 2 cos A cos B cos C.
Solution:
A + B + C = 0 —— (1)
L.H.S. = cos² A + cos² B + cos² C
= cos² A + (1 – sin² B) + cos² C
= 1 + (cos² A – sin² B) + cos² C
= 1 + cos (A + B) cos (A – B) + cos² C
= 1 + cos(-C) cos(A – B) + cos² C
By (1)
= 1 + cos C cos (A – B) + cos² C
= 1 + cos C [cos (A – B) + cos c]
= 1 + cos C[cos(A – B) + cos(-B – A)]
By (1)
1 + cos C[cos (A – B) + cos(A + B)]
= 1 + cos C (2 cos A cos B)
= 1 + 2 cos A cos B cos C = R.H.S.

Question 63.
If A + B + C = 25, then prove that cos (S – A) + cos (S – B) + cos (S – C) + cos (S) = 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\).
Solution: