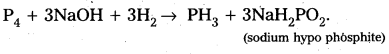Inter 2nd Year

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 4 Theory of Equations to solve questions creatively.

Intermediate 2nd Year Maths 2A Theory of Equations Formulas

→ If n is a non-negative integer and a₀, a₁, a₂, ……….. a_n are real or complex numbers and a₀ ≠ 0, then the expression f(x) = a₀xⁿ + a₁x^{n – 1} + a₂x^{n – 2} + ……. + a_n is called a polynomial in x of degree n.

→ f(x) = a₀xⁿ + a₁x^{n – 1} + a₂x^{n – 2} + ……. + a_n = 0 is called a polynomial equation in x of degree n (a₀ ≠ 0). Every non-constant polynomial equation has atleast one root.

→ If f(α) = 0 then α is called a root of the equation f(x) = 0.

→ If f(α) = 0 then (x – α) is a factor of f(x).

Relation between roots and coefficients of an equation:
→ If α β γ are the roots of x³ + p₁x² + p₂x + p₃ = 0 then sum of the roots s₁ = α + β + γ = – p₁.
Sum of the products of two roots taken at a time s₂ = αβ + βγ + γα = p₂.
Product of all the roots, s₃ = αβγ = – p₃.

→ If α, β, γ, δ are the roots of x⁴ + p₁x³ + p₂x² + p₃x + p₄ = 0 then sum of the roots s₁ = α + β + γ + δ = – p₁.
Sum of the products of roots taken two at a time
s₂ = αβ + αγ + αδ + βγ + βδ + γδ = p₂.
Sum of the products of roots taken three at a time .
s₃ = αβγ + βγδ + γδα + δαβ = – p₃.
Product of the roots, s₄ = αβγδ = p₄.

→ For a cubic equation, when the roots are

• In A.P., then they are taken as a – d, a, a + d.
• In G.P., then they are taken as \(\frac{a}{r}\), a, ar.
• In H.P., then they are taken as \(\frac{1}{a-d}, \frac{1}{a^{\prime}}, \frac{1}{a+d}\).

→ For a bi quadratic equation, if the roots are

• In A.P., then they are taken as a – 3d, a – d, a + d, a + 3d.
• In C.P., then they are taken as \(\frac{1}{a-3 d}, \frac{1}{a-d}, \frac{1}{a+d}, \frac{1}{a+3 d}\).

→ In an equation with real coefficients, imaginary roots occur in conjugate pairs.

→ In an equation with rational coefficients, irrational roots occur in pairs of conjugate surds.

→ The equation whose roots are those of the equation f(x) = 0 with contrary signs is f(- x) = 0.

→ The equation whose roots are multiplied by kfa 0) of those of the proposed equation f(x) = 0 is f \(\left(\frac{x}{k}\right)\) = 0.

→ The equation whose roots are reciprocals of the roots of f(x) = 0 is f \(\left(\frac{1}{x}\right)\) = 0.

→ The equation whose roots are exceed by h than those of f(x) = 0 is f(x – h) = 0.

→ The equation whose roots are diminished by h than those of f(x) 0 is f(x + h) = 0.

→ The equation whose roots are the square of the roots of f(x) = 0 is obtained by eliminating square root from f(√x) = 0.

→ If f(x) = p₀xⁿ + p₁x^{n – 1} + p₂x^{n – 2} + ……. + p_n = 0 then to eliminate the second term,
f(x) = 0 can be transformed to f(x + h) = 0 where h = \(\frac{-p_{1}}{n \cdot p_{0}}\).

→ If an equation is unaltered by changing x into \(\frac{1}{x}\) then it is a reciprocal equation.

→ A reciprocal equation f(x) = p₀xⁿ + p₁x^{n – 1} + …… + pⁿ = 0 is said to be a reciprocal equation of first class p_i = p_{n – i} for all i.

→ A reciprocal equation f(x) = p₀xⁿ + p₁x^{n – 1} + …… + pⁿ = 0 is said to be a reciprocal equation of second class if p_i = – p_{n – i} for all i.

→ For an odd degree reciprocal equation of class one, – 1 is a root and for an odd degree reciprocal equation of class two, 1 is a root.

→ For an even degree reciprocal equation of class two, 1 and – 1 are roots.

→ If f(x) = 0 is an equation of degree ‘n’ then to eliminate r^th term, f(x) = 0 can be transformed to f(x + h) = 0 where h is a constant such that f^{(n – r + 1)}(h) = 0 i.e.,(n – r + 1)^th derivative of f(h) is zero.

→ Every n^th degree equation has exactly n roots real or imaginary.

→ Relation between, roots and coefficients of an equation.

(i) If α, β, γ are the roots of x³ + p₁x² + p₂x + p₃ = 0 the sum of the roots s₁ = α + β + γ = -p₁.
Sum of the products of two roots taken at a time s₂ = αβ + βγ + γα = -p₂
Product of all the roots, s₃ = αβγ= – p₃.

(ii) If α, β, γ, δ are the roots of x⁴ + p₁x³ + p₂x² + p₃x + p₄ = 0 then

• Sum of the roots s₁ = a+P+y+S = -p₁.
  s₂ = αβ + αγ + αδ + βα + βδ + γδ = p₂.
• Sum of the products of roots taken three at a time
  s₃ = αβγ + βγδ + γδα + δαβ = – p₃.
• Product of the roots, s₄ = αβγδ = p₄

→ For the equation xⁿ + p₁x^n-1 + p₂x^n-2 + ……… + p_n = 0

• Σ α₂ = p₁² – 2p₂
• Σ α₃ = -p₁³ + 3p₁p₂ – 3p₃
• Σ α₄ =p₁⁴ – 4p₁²p² + 2p₂² + 4p₁p₃ – 4p₄
• Σ α₂β = 3p₃ – p₁p₂
• Σ α₂βγ = p₁p₃ – 4p₄

Note: For the equation x³ + p₁x² + p₂x + p₃ = 0 Σα₂β₂ — p₂ -2p₁p₃

→ To remove the second term from a nth degree equation, the roots must be diminished by \(\frac{-\mathrm{a}_{1}}{\mathrm{na}_{0}}\) and the resultant equation will not contain the term with x^n-1.

→ If α₁ , α₂ ………………. , α_n are the roots of f(x) = 0, the equation

• Whose roots are \(\) is f\(\left(\frac{1}{x}\right)\) = 0
• Whose roots are kα₁, kα₂ …,kα_n is f\(\left(\frac{x}{h}\right)\) = 0
• Whose roots are α₁ – h, α₂ – h, …. α_n – h is f(x + h) = 0.
• Whose roots are α₁ + h, α₂ + h, ………….. α_n + h is f(x – h) = 0
• Whose roots are α₁², α₂²…. α₁² is f (f√y) = 0

→ In any equation with rational coefficients, irrational roots occur in conjugate pairs.

→ In any equation with real coefficients, complex roots occur in conjugate pairs.

→ If α is r – multiple root of f(x) = 0, then a is a (r – 1) – multiple root of f¹(x) = 0 and (r-2) – Multiple root of f ¹¹(x) = 0 and non multiple root of f^r-1(x) =0.

→ If f(x) = xⁿ + p₁x^n-1 + …………. + p_n-1x + p_n and f(a) and f(b) are of opposite sign, then at least
one real root of f(x) =0 lies between a and b.

(a) For a cubic equation, when the roots are

• In A.P., then they are taken as a – d, a, a + d
• In G.P., then are taken as \(\frac{a}{r}\), a, ar
• In H.P., then they are taken as \(\frac{1}{a-d}, \frac{1}{a}, \frac{1}{a+d}\)

(b) For a bi quadratic equation, if the roots are

• In A.P., then they are taken as a – 3d, a + d, a + 3d
• In G.P., then they are \(\frac{a}{d^{3}}, \frac{a}{d}\), ad, ad³
• In H.P., then they are taken as \(\frac{1}{a-3 d}, \frac{1}{a-d}, \frac{1}{a+d}, \frac{1}{a+3 d}\)

→ It an equation is unaltered by changing x into \(\frac{1}{x}\), then it is a reciprocal equation.

• A reciprocal equation f (x) = p₀xⁿ + p₁x^n-1 + ……………….. + p_n = 0 is said to be a reciprocal equation of first class p_i = p_n-i for all i.
• A reciprocal equation f (x) = p₀xⁿ + p₁x^n-1 + ……………….. + p_n = 0 = 0 is said to be a reciprocal equation of second class p_i = p_n-i for all i.
• For an odd degree reciprocal equation of class one, -1 is a root and for an odd degree reciprocal equation of class two, 1 is a root.
• For an even degree reciprocal equation of class two, 1 and -1 are roots.

→ If f(x) = 0 is an equation of degree ‘n’ then to eliminate rth term, .f(x) = 0 can be transformed to f(x+h) = 0 where h is a constant such that f^(n-r+1)(h) =0 i.e., (n – r + 1)^th derivative of f(h) is zero.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 3 Quadratic Expressions to solve questions creatively.

Intermediate 2nd Year Maths 2A Quadratic Expressions Formulas

→ If a, b, c are real or complex numbers and a ≠ 0, then the expression ax² + bx + c is called a quadratic expression in the variable x.
Eg: 4x² – 2x + 3

→ If a, b, c are real or complex numbers and a ≠ 0, then ax² + bx + c = 0 is called a quadratic equation in x.
Eg: 2x² – 5x + 6 = 0

→ A complex number α is said to be a root or solution of the quadratic equation ax² + bx + c = 0 if aα² + bα + c = 0

→ The roots of ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

→ If α, β are roots of ax² + bx + c = 0, then α + β = \(\frac{-b}{a}\) and αβ = \(\frac{C}{a}\)

→ The equation of whose roots are α, β is x² – (α + β)x + αβ = 0

→ Nature of the roots: ∆ = b² – 4ac is called the discriminant of the quadratic equation ax² + bx + c = 0. Let α, β be the roots of the quadratic equation ax² + bx + c = 0
Case 1: If a, b, c are real numbers, then

• ∆ = 0 ⇔ α = β = \(\frac{-b}{2 a}\) (a repeated root or double root)
• ∆ > 0 ⇔ α and β are real and distinct.
• ∆ < 0, ⇔ α and β are non- real complex numbers conjugate to each other.

Case 2: If a, b, c are rational numbers, then

• ∆ = 0 ⇔ α and β are rational and equal (ei) α = \(\frac{-b}{2 a}\), a double root or a repeated root.
• ∆ > 0 and is a square of a rational number ⇔ α and β are rational and distinct.
• ∆ > 0 but not a square of a rational number ⇔ α and β are conjugate surds.
• ∆ < 0, ⇔ α and β are non- real ⇔ α and β are non-real con conjugate complex numbers.

→ Let a, b and c are rational numbers, α and β be the roots of the equations ax² + bx + c = 0. Then

• α, β are equal rational numbers if ∆ = 0.
• α, β are distinct rational numbers if ∆ is the square of a non zero rational numbers.
• α, β are conjugate surds if ∆ > 0 and ∆ is not the square of a nonzero square of a rational number.

→ If a₁x² + b₁x + c₁ = 0, a₂x² + b₂x + c₂ = 0 have two same roots, then \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ If α, β are roots of ax² + bx + c = 0,

• the equation whose roots are \(\frac{1}{\alpha}, \frac{1}{\beta}\) is f \(\left(\frac{1}{x}\right)\) = 0. If c ≠ 0 (ie) αβ ≠ 0
• the equation whose roots are α + k, β + k is f(x – k) = 0
• the equation whose roots are kα and kβ is f\(\left(\frac{x}{k}\right)\) = 0
• the equation whose roots are equal but opposite in sign is f(-x) = 0
  (ie) the equation whose roots are – α, – β is f(-x) = 0.

→ If the roots of ax² + bx + c = 0 are complex roots then for x ∈ R, ax² + bx + c and ‘a’ have the same sign.

→ If α and β (α < β) are the roots of ax² + bx + c = 0 then

• ax² + bx + c and ‘a’ are of opposite sign when α < x < β
• ax² + bx + c and ‘a’ are of the same sign if x < α or x > β.

→ Let f(x) = ax² + bx + c be a quadratic function

• If a > 0 then f(x) has minimum value at x = \(\frac{-b}{2 a}\) and the minimum value is given by \(\frac{4 a c-b^{2}}{4 a}\)
• If a < 0 then f(x) has maximum value at x = \(\frac{-b}{2 a}\) and the maximum value is given by \(\frac{4 a c-b^{2}}{4 a}\)

→ A necessary and sufficient condition for the quadratic equation a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0 to have a common root is (c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁).

→ If a₁b₂ – a₂b₁ = 0 then common root of a₁x² + b₁x + c₁ = 0, a₂x² + b₂x + c₂ = 0 is \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\).

→ The standard form of a quadratic ax² + bx + c = 0 where a, b, c ∈ R and a ≠ 0

→ The roots of ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

→ For the equation ax² + bx + c = 0, sum of the roots = \(-\frac{b}{a}\), product of the roots = \(\frac{c}{a}\).

→ If the roots of a quadratic are known, the equation is x² – (sum of the roots)x +(product of the roots)= 0

→ “Irrational roots” of a quadratic equation with “rational coefficients” occur in conjugate pairs. If p + √q is a root of ax² + bx + c = 0, then p – √q is also a root of the equation.

→ “Imaginary” or “Complex Roots” of a quadratic equation with “real coefficients” occur in conjugate pairs. If p + iq is a root of ax² + bx + c = 0. Then p – iq is also a root of the equation.

→ Nature of the roots of ax² + bx + c = 0

→ Two equations a₁x² + b₁x + c₁ = 0, a₂x² + b₂x + c₂ = 0 have exactly the same roots if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ The equations a₁x² + b₁x + c₁ = 0, a2x² + b₂x + c₂ = 0 have a common root, if (c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁)(b₁c₂ – b₂c₁) and the common root is \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\) if a₁b₂ ≠ a₂b₁

→ If f(x) = 0 is a quadratic equation, then the equation whose roots are

• The reciprocals of the roots of f(x) = 0 is f\(\left(\frac{1}{x}\right)\) = 0
• The roots of f(x) = 0, each ‘increased’ by k is f(x – k) = 0
• The roots of f(x) = 0, each ‘diminished’ by k is f(x + k) = 0
• The roots of f(x) = 0 with sign changed is f(-x) = 0
• The roots of f(x) = 0 each multiplied by k(≠0) is f\(\left(\frac{x}{k}\right)\) = 0

→ Sign of the expression ax² + bx + c = 0

• The sign of the expression ax² + bx + c is same as that of ‘a’ for all values of x if b² – 4ac ≤ 0 i.e. if the roots of ax² + bx + c = 0 are imaginary or equal.
• If the roots of the equation ax² + bx + c = 0 are real and different i.e b² – 4ac > 0, the sign of the expression is same as that of ‘a’ if x does not lie between the two roots of the equation and opposite to that of ‘a’ if x lies between the roots of the equation.

→ The expression ax² + bx + c is positive for all real values of x if b² – 4ac < 0 and a > 0.

→ The expression ax² + bx + c has a maximum value when ‘a’ is negative and x = –\(\frac{\mathrm{b}}{2 \mathrm{a}}\). Maximum value of the expression = \(\frac{4 a c-b^{2}}{4 a}\)

→ The expression ax² + bx + c has a maximum value when ‘a’ is positive and x = –\(\frac{\mathrm{b}}{2 \mathrm{a}}\). Minimum value of the expression = \(\frac{4 a c-b^{2}}{4 a}\)

Theorem 1:
If the roots of ax² + bx + c = 0 are imaginary, then for x ∈ R , ax² + bx + c and a have the same sign.
Proof:
The root are imaginary
b² – 4ac < 0 4ac – b² > 0
\(\frac{a x^{2}+b x+c}{a}=x^{2}+\frac{b}{a} x+\frac{c}{a}=\left(x+\frac{b}{2 a}\right)^{2}+\frac{c}{a}-\frac{b^{2}}{4 a^{2}}=\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\)
∴ For x ∈ R, ax² + bx + c = 0 and a have the same sign.

Theorem 2.
If the roots of ax² + bx + c = 0 are real and equal to α = \(\frac{-b}{2 a}\), then α ≠ x ∈ R ax² + bx + c and a will have same sign.
Proof:
The roots of ax² + bx + c = 0 are real and equal
⇒ b² = 4ac ⇒ 4ac – b² = 0
\(\frac{a x^{2}+b x+c}{a}\) = x + \(\frac{b}{a}\)x + \(\frac{c}{a}\)
= \(\left(x+\frac{b}{2 a}\right)^{2}+\frac{c}{a}-\frac{b^{2}}{4 a^{2}}\)
= \(\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a^{2}}\)
= \(\left(x+\frac{b}{2 a}\right)^{2}\) > 0 for x ≠ \(\frac{-b}{2 a}\) = α
For α ≠ x ∈ R, ax² + bx + c and a have the same sign.

Theorem 3.
Let be the real roots of ax² + bx + c = 0 and α < β. Then
(i) x ∈ R, α < x< β ax² + bx + c and a have the opposite signs
(ii) x ∈ R, x < α or x> β ax² + bx + c and a have the same sign.
Proof:
α, β are the roots of ax² + bx + c = 0
Therefore, ax² + bx + c = a(x – α)(x – β)
\(\frac{a x^{2}+b x+c}{a}\) = (x – α)(x – β)

(i) Suppose x ∈ R, α < x < β
⇒ x < α < β then x – α < 0, x – β < 0 ⇒ (x – α)(x – β) > 0 ⇒ \(\frac{a x^{2}+b x+c}{a}\) > 0
⇒ ax² + bx + c, a have a same sign

(ii) Suppose x ∈ R, x > β, x > β > α then x – α > 0, x – β > 0
⇒ (x – α)(x – β) > 0 ⇒ \(\frac{a x^{2}+b x+c}{a}\) > 0
⇒ ax² + bx + c, a have same sign
∴ x ∈ R, x < α or x > β ⇒ ax² + bx + c and a have the same sign.

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 2 De Moivre’s Theorem to solve questions creatively.

Intermediate 2nd Year Maths 2A De Moivre’s Theorem Formulas

Statement:
→ If ‘n’ is an integer, then (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ
If n’ is a rational number, then one of the values of
(cos θ + i sin θ)ⁿ is cos nθ + i sin nθ

n^th roots of unity:
→ n^th roots of unity are {1, ω, ω² …….. ω^{n – 1}}.
Where ω = \(\left[\cos \frac{2 k \pi}{n}+i \sin \frac{2 k \pi}{n}\right]\) k = 0, 1, 2 ……. (n – 1).
If ω is a n^th root of unity, then

• ωⁿ = 1
• 1 + ω + ω² + ………… + ω^{n – 1} = 0

Cube roots of unity:
→ 1, ω, ω² are cube roots of unity when

• ω³ = 1
• 1 + ω + ω² = 0
• ω = \(\frac{-1+i \sqrt{3}}{2}\), ω² = \(\frac{-1-i \sqrt{3}}{2}\)
• Fourth roots of unity roots are 1, – 1, i, – i

→ If Z₀ = r₀ cis θ₀ ≠ 0, then the n^th roots of Z₀ are α_k = (r₀)^1/n cis\(\left(\frac{2 k \pi+\theta_{0}}{n}\right)\) where k = 0, 1, 2, ……… (n – 1)

→ If n is any integer, (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ

→ If n is any fraction, one of the values of (cosθ + i sinθ)ⁿ is cos nθ + i sin nθ.

→ (sinθ + i cosθ)ⁿ = cos(\(\frac{n \pi}{2}\) – nθ) + i sin(\(\frac{n \pi}{2}\) – nθ)

→ If x = cosθ + i sinθ, then x + \(\frac{1}{x}\) = 2 cosθ, x – \(\frac{1}{x}\) = 2i sinθ

→ xⁿ + \(\frac{1}{x^{n}}\) = 2cos nθ, xⁿ – \(\frac{1}{x^{n}}\) = 2i sin nθ

→ The nth roots of a complex number form a G.P. with common ratio cis\(\frac{2 \pi}{n}\) which is denoted by ω.

→ The points representing n^th roots of a complex number in the Argand diagram are concyclic.

→ The points representing n^th roots of a complex number in the Argand diagram form a regular polygon of n sides.

→ The points representing the cube roots of a complex number in the Argand diagram form an equilateral triangle.

→ The points representing the fourth roots of complex number in the Argand diagram form a square.

→ The nth roots of unity are 1, w, w²,………. , w^n-1 where w = cis\(\frac{2 \pi}{n}\)

→ The sum of the nth roots of unity is zero (or) the sum of the nth roots of any complex number is zero.

→ The cube roots of unity are 1, ω, ω² where ω = cis\(\frac{2 \pi}{3}\), ω² = cis\(\frac{4 \pi}{3}\) or
ω = \(\frac{-1+i \sqrt{3}}{2}\)
ω² = \(\frac{-1-i \sqrt{3}}{2}\)
1 + ω + ω² = 0
ω³ = 1

→ The product of the n^th roots of unity is (-1)^n-1 .

→ The product of the n^th roots of a complex number Z is Z(-1)^n-1 .

→ ω, ω² are the roots of the equation x² + x + 1 = 0

Use these Inter 2nd Year Maths 2A Formulas PDF Chapter 1 Complex Numbers to solve questions creatively.

Intermediate 2nd Year Maths 2A Complex Numbers Formulas

Definition of a complex number:
→ A number of the type z = x + yi, where x, y ∈ R and i = √- 1 i.e., i² = – 1 is called a complex number ‘x’ is called real part of z, and ‘y’ is called imaginary part of z. We write x = Re(z) and y = Im(z). A number z = x + yi is said to be purely real iff y = 0 (x ≠ 0) and purely imaginary iff x = 0 (y ≠ 0)
A complex number a + ib is an ordered pair of real numbers. It is denoted by (a, b), a ∈ R, b ∈ R.

→ Two complex numbers z₁ = (a, b), z₂ = (c, d) are said to be equal iff a = c and b = d.

→ If z₁ = (a, b), z₂ = (c, d) then

• z₁ + z₁ = (a + c, b + d)
• z₁ – z₂ = (a – c, b – d)
• z₁. Z₂ = (ac – bd, ad + bc) and
• \(\frac{z_{1}}{z_{2}}=\left(\frac{a c+b d}{c^{2}+d^{2}}, \frac{b c-a d}{c^{2}+d^{2}}\right)\)

Modulus and Amplitude:
→ The modulus of a complex number z = x + iy is defined as a non-negative real number r = \(\sqrt{x^{2}+y^{2}}\). It is denoted by |z|.

→ Any real number θ satisfying the equation cos θ = \(\frac{x}{r}\), sin θ = \(\frac{y}{r}\) is called an amplitude or argument of z. The unique argument θ of z satisfying – π < θ ≤ π is called the principal argument of z and is denoted by Arg z.

→ The polar form or modulus amplitude form of the complex number
z = x + iy is r(cos θ + i sin θ)

Conjugate of a complex number:
→ If z = x + iy i.e., x, y ∈ R, then the complex number x – iy is called conjugate of z and is written as z̅. The sum and product of a complex number and its Conjugate is always purely real.

Some properties of modulus, amplitude and conjugate:

• (z̅) = z
• z + z̅ = 2 Re (z) and z – z̅ = 2 Im (z)
• \(\overline{Z_{1} Z_{2}}\) = \(\overline{Z_{1}}\) \(\overline{Z_{2}}\)
• \(\) and \(\) (z₂ ≠ 0) and |z₁z₂| = |z₁| |z₂|
• zz̅ = |z|²
• |z| = |z̅|;
• |z₁ + z₂| ≤ |z₁| + |z₂|, |z₁ – z₂| ≤ |z₁| + |z₂|
• |z₁ – z₂| > | |z₁| – |z₂| |
  In (vii) and (viii) equality holds iff amp (z₁) – amp (z₂) is an integral multiple of 2π.
• amp (z₁ z₂) = amp (z₁) + amp (z₂) + nπ, for some n ∈ {- 1, 0, 1}
• amp \(\left(\frac{Z_{1}}{Z_{2}}\right)\) = amp (z₁) – amp (z₂) + nπ, for some n ∈ {- 1, 0, 1}
• \(\frac{1}{{cis} \alpha}\) = cis(- α)
• cis α cis β = cis (α + β)
• \(\frac{{cis} \alpha}{{cis} \beta}\) = cis (α – β)

De-Moivre’s theorem:

• If n is any integer, then (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ
• If n = \(\frac{p}{q}\), where p and q are integers having no common factor and q > 1, then cos nθ + i sin nθ is one of the q values of (cos θ + i sin θ)ⁿ
• If z₀ = r₀ cis θ₀ ≠ 0, then the n^th roots of z₀ are α_k = r₀^1/n cis \(\left(\frac{2 k \pi+\theta_{0}}{n}\right)\),
  k = 0, 1, 2, 3 … (n-1)

Cube roots of unity:

• The cube roots of unity are 1, ω = \(\frac{-1+\sqrt{3 i}}{2}\) and ω² = \(\frac{-1-\sqrt{3 i}}{2}\)
• 1 + ω + ω² = 0 and w³ = 1; 1 + ω = – ω ², 1 + ω² = – ω, ω + ω² = – 1
• Either of the two non-real cube roots of unity is square of the other.
• For either of the two non – real cube roots a.and of unity α + β = – 1, αβ = – 1, α² = β, β² = α and α³ = β³ = 1
• (-1)^1/3 = – 1, – ω – ω²
• The n^th roots of unity are cis\(\left(\frac{2 k \pi}{n}\right)\), k = 0, 1, 2, ….. (n – 1)

Formulae:

→ Modulus of Z = \(\sqrt{x^{2}+y^{2}}\)

→ If \(\sqrt{a+i b}\) = (x + iy), then x = \(\sqrt{\frac{\sqrt{a^{2}+b^{2}}+a}{2}}\) and y = \(\sqrt{\frac{\sqrt{a^{2}+b^{2}}-a}{2}}\)

→ Conjugate of a + ib = a – ib

→ Conjugate of a – ib = a + ib

→ Any number of the form x + iy where x, y ∈ R and i² = -1 is called a Complex Number.

→ In the complex number x + iy, x is called the real part and y is called the imaginary part of the complex number.

→ A complex number is said to be purely imaginary if its real part is zero and is said to be purely real if its imaginary part is zero.
(a) Two complex numbers are said to be equal if their real parts are equal and their imaginary parts are equal.
(b) In the set of complex numbers, there is no meaning to the phrase one complex is greater than or less than another i.e. If two complex numbers are not equal, we say they are unequal.
(c) a+ ib > c + id is meaningful only when b = 0, d = 0.

→ Two complex numbers are conjugate if their sum and product are both real. They are of the form a + ib, a – ib.

→ cisθ₁ cisθ₂ = cis(θ₁ + θ₂), \(\frac{{cis} \theta_{1}}{{cis} \theta_{2}}\) = cis(θ₁ – θ₂), \(\frac{1}{\cos \theta+i \sin \theta}\) = cosθ – isinθ

→ \(\frac{a_{1}+i b_{1}}{a_{2}+i b_{2}}=\frac{\left(a_{1} a_{2}+b_{1} b_{2}\right)+i\left(a_{2} b_{1}-a_{1} b_{2}\right)}{a_{2}^{2}+b_{2}^{2}}\)

→ \(\frac{1+i}{1-i}\) = i, \(\frac{1-i}{1+i}\) = i

→ \(\sqrt{x^{2}+y^{2}}\) is called the modulus of the complex number x + iy and is denoted by r or |x + iy|

→ Any value of 0 obtained from the equations cos θ = \(\frac{x}{r}\), sin θ = \(\frac{y}{r}\) is called an amplitude of the complex number.

→ The amplitude lying between -π and π is called the principal amplitude of the complex number. Rule for choosing the principal amplitude.

→ If θ is the principal amplitude, then -π < 0 < π

→If α is the principle amplitude of a complex number, general amplitude = 2nπ + α where n ∈ Z.

• Amp (Z₁ Z₂) = Amp Z₁ + AmpZ₂
• Amp z + Amp z̅ = 2π (when z is a negative real number) = 0 (otherwise)

→ r(cos θ + i sin θ) is the modulus amplitude form of x + iy.

→ If the amplitude of a complex number is \(\frac{\pi}{2}\), its real part is zero.

→ If the amplitude of a complex number is \(\frac{\pi}{4}\), its real part is equal to its imaginary part.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(c)

I.

Question 1.
Solve the following inequations by the algebraic method.
(i) 15x² + 4x – 4 ≤ 0
Solution:
15x² + 4x – 4 ≤ 0
⇒ 15x² – 6x + 10x – 4 ≤ 0
⇒ 3x(5x – 2) + 2(5x – 2) ≤ 0
⇒ (3x + 2) (5x – 2) ≤ 0
Co-efficient of x² = 15 > 0,
Given Expression is ≤ 0
⇒ x lies between \(\frac{-2}{3}\) and \(\frac{2}{5}\)
i.e., \(\frac{-2}{3} \leq x \leq \frac{2}{5}\)

(ii) x² – 2x + 1 < 0
Solution:
x² – 2x + 1 < 0
⇒ (x – 1)² < 0
There is no real value of ‘x’ satisfying this inequality
Solution set = Φ (or) Solution does not exist.

(iii) 2 – 3x – 2x² ≥ 0
Solution:
-(2x² + 3x – 2) ≥ 0
⇒ -(2x² + 4x – x – 2) ≥ 0
⇒ -[2x(x + 2) – 1(x + 2)] ≥ 0
⇒ -(2x – 1) (x + 2) ≥ 0
Co-efficient of x² = -2 < 0,
The given expression is ≥ 0
⇒ x lies between -2 and \(\frac{1}{2}\)
i.e., -2 ≤ x ≤ \(\frac{1}{2}\)

(iv) x² – 4x – 21 ≥ 0
Solution:
x² – 4x – 21 ≥ 0
⇒ x² – 7x + 3x – 21 ≥ 0
⇒ x(x – 7) + 3(x – 7) ≥ 0
⇒ (x + 3) (x – 7) ≥ 0
Co-efficient of x² = 1 > 0,
The given expression is ≥ 0
x does not lie between -3 and 7
i.e., {x/x ∈ (-∞, -3] ∪ [7, ∞)}

II.

Question 1.
Solve the following inequations by graphical method.
(i) x² – 7x + 6 > 0
Solution:
f(x) = x² – 7x + 6

f(x) > 0 ⇒ y > 0
Solutions are given by x < 1 and x > 6

(ii) 4 – x² > 0
Solution:
Let f(x) = 4 – x²

f(x) > 0 ⇒ y > 0
Solution set = {x/-2 < x < 2}

(iii) 15x² + 4x – 4 < 0
Solution:
Let f(x) = 15x² + 4x – 4

f(x) ≤ 0 ⇒ y ≤ 0
Solution set = \(\left\{x / \frac{-2}{3} \leq x \leq \frac{2}{5}\right\}\)

(iv) x² – 4x – 21 ≥ 0
Solution:
Let f(x) = x² – 4x – 21

f(x) ≥ 0 ⇒ y ≥ 0
Solution set = {x/x ∈ (-∞, -3] ∪ [7, ∞)}

Question 2.
Solve the following inequations.
(i) \(\sqrt{3 x-8}\) < -2
Solution:
L.H.S. is positive and R.H.S. is negative.
∴ The given inequality holds for no real x.
Solution set = Φ (or) Solution does not exist.

(ii) \(\sqrt{-x^{2}+6 x-5}\) > 8 – 2x
Solution:
\(\sqrt{-x^{2}+6 x-5}\) > 8 – 2x
⇔ -x² + 6x – 5 > 0
and (i) 8 – 2x < 0 (or) (ii) 8 – 2x ≥ 0
We have -x² + 6x – 5 = -(x² – 6x + 5) = -(x – 1) (x – 5)
Hence -x² + 6x – 5 ≥ 0 ⇔ x ∈ [1, 5]
(i) -x² + 6x – 5 ≥ 0 and 8 – 2x < 0
⇔ x ∈ [1, 5] and x > 4
⇔ x ∈ [4, 5] ………(1)
(ii) -x² + 6x – 5 ≥ 0 and 8 – 2x ≥ 0
∵ \(\sqrt{\left(-x^{2}+6 x-5\right)}\) > 8 – 2x
⇔ -x² + 6x – 5 > (8 – 2x)² and 8 – 2x ≥ 0
⇔ -x² + 6x – 5 > 64 + 4x² – 32x and x ≤ 4
⇔ -5x² + 38x – 69 > 0 and x ≤ 4
⇔ 5x² – 38x + 69 < 0 and x ≤ 4
⇔ 5x² – 15x – 23x + 69 < 0 and x ≤ 4
⇔ (5x – 23)(x – 3) < 0 and x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) and x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) ∩ (-∞, 4)
⇔ x ∈ (3, 4)
Hence the solution set of the given equation is x ∈ (4, 5) ∪ (3, 4)
⇒ x ∈ (3, 5) (or) 3 < x ≤ 5.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(a)

I.

Question 1.
Find the roots of the following equations.
(i) x² – 7x + 12 = 0
Solution:
a = 1, b = -7, c = 12

∴ The roots are 4, 3

(ii) -x² + x + 2 = 0
Solution:
a = -1, b = 1, c = 2

∴ The roots are 2, -1

(iii) 2x² + 3x + 2 = 0
Solution:
a = 2, b = 3, c = 2

(iv) √3x² + 10x – 8√3 = 0
Solution:
a = √3 , b = 10, c = -8√3

∴ The roots are \(\frac{2}{\sqrt{3}}\), -4√3

(v) 6√5x² – 9x – 3√5 = 0
Solution:
a = 6√5 , b = -9, c = -3√5

∴ The roots are \(\frac{\sqrt{5}}{2},-\frac{1}{\sqrt{5}}\)

Question 2.
Form a quadratic equation whose roots are:
(i) 2, 5
Solution:
α + β = 2 + 5 = 7
αβ = 2 × 5 = 10
The required equation is x² – (α + β)x + αβ = 0
⇒ x² – 7x + 10 = 0

(ii) \(\frac{m}{n},-\frac{n}{m}\), (m ≠ 0, n ≠ 0)
Solution:

(iii) \(\frac{p-q}{p+q}, \frac{-p+q}{p-q}\), (p ≠ ±q)
Solution:

(iv) 7 ± 2√5
Solution:
α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – 20
= 29
The required equation is x² – (α + β)x + αβ = 0
⇒ x² – 14x + 29 = 0

(v) -3 ± 5i
Solution:
α + β = -3 + 5i – 3 – 5i = -6
αβ = (-3 + 5i) (-3 – 5i)
= 9 + 25
= 34
The required equation is x² – (α + β)x + αβ = 0
⇒ x² + 6x + 34 = 0

Question 3.
Find the nature of the roots of the following equation, without finding the roots.
(i) 2x² – 8x + 3 = 0
Solution:
a = 2, b = -8, c = 3
b² – 4ac = 64 – 24 = 40 > 0
∴ The roots are real and distinct.

(ii) 9x² – 30x + 25 = 0
Solution:
a = 9, b = -30, c = 25
b² – 4ac = 900 – 900 = 0
∴ The roots are rational and equal.

(iii) x² – 12x + 32 = 0
Solution:
a = 1, b = -12, c = 32
b² – 4ac = 144 – 128
= 16
= (4)²
= perfect square
∴ The roots are rational and distinct.

(iv) 2x² – 7x + 10 = 0
Solution:
a = 2, b = -7, c = 10
b² – 4ac = 49 – 80 = -31 < 0
∴ The roots are complex conjugate numbers.

Question 4.
If α, β are the roots of the equation ax² + bx + c = 0, find the values of the following expressions in terms of a, b, c.
(i) \(\frac{1}{\alpha}+\frac{1}{\beta}\)
(ii) \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\)
(iii) α⁴β⁷ + α⁷β⁴
(iv) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^{2}\), if c ≠ 0
(v) \(\frac{\alpha^{2}+\beta^{2}}{\alpha^{-2}+\beta^{-2}}\)
Solution:
α, β are the roots of the equation ax² + bx + c = 0
α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)

Question 5.
Find the values of m for which the following equations have equal roots.
(i) x² – 15 – m(2x – 8) = 0
Solution:
Given equation is x² – 15 – m(2x – 8) = 0
⇒ x² – 2mx + 8m – 15 = 0
a = 1, b = -2m, c = 8m – 15
b² – 4ac = (-2m)² – 4(1) (8m – 15)
= 4m² – 32m + 60
= 4(m² – 8m + 15)
= 4(m – 3) (m – 5)
If the equation ax² + bx + c = 0 has equal roots then its discriminant is zero.
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ 4(m – 3) (m – 5) = 0
⇒ m – 3 = 0 or m – 5 = 0
⇒ m = 3 or 5

(ii) (m + 1)x² + 2(m + 3)x + (m + 8) = 0
Solution:
Given equation is (m + 1 )x² + 2(m + 3)x + (m + 8) = 0
a = m + 1, b = 2(m + 3), c = m + 8
b² – 4ac = [2(m + 3)]² – 4(m + 1) (m + 8)
= 4(m² + 6m + 9) – 4(m² + 8m + m + 8)
= 4m² + 24m + 36 – 4m² – 36m – 32
= -12m + 4
= -4(3m – 1)
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ -4(3m – 1) = 0
⇒ 3m – 1 = 0
⇒ 3m = 1
⇒ m = \(\frac{1}{3}\)

(iii) x² + (m + 3)x + m + 6 = 0
Solution:
Given equation is x² + (m + 3)x + m + 6 = 0
a = 1, b = m + 3, c = m + 6
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ (m + 3)² – 4(1) (m + 6) = 0
⇒ m² + 6m + 9 – 4m – 24 = 0
⇒ m² + 2m – 15 – 0
⇒ m² + 5m – 3m – 15 = 0
⇒ m(m + 5) – 3(m + 5) = 0
⇒ (m + 5) (m – 3) = 0
⇒ m = -5, 3

(iv) (3m + 1)x² + 2(m + 1)x + m = 0
Solution:
Given equation is (3m + 1)x² + 2(m + 1)x + m = 0
a = 3m + 1, b = 2(m + 1), c = m
b² – 4ac = 4(m + 1)² – 4m(3m + 1)
= 4[(m + 1)² – m(3m + 1)]
= 4(m² + 2m + 1 – 3m² – m)
= 4(-2m² + m + 1)
= -4(2m² – m – 1)
= -4(m – 1) (2m + 1)
∴ The roots are equal
⇒ discriminant = 0
⇒ b² – 4ac = 0
⇒ -4(m – 1) (2m + 1) = 0
⇒ m – 1 = 0 or 2m + 1 = 0
⇒ m = 1 or m = \(\frac{-1}{2}\)

(v) (2m + 1)x² + 2(m + 3)x + (m + 5) = 0
Solution:
Given equation is (2m + 1)x² + 2(m + 3)x + m + 5 = 0
a = 2m + 1, b = 2(m + 3), c = m + 5
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ 4(m + 3)² – 4(2m + 1) (m + 5) = 0
⇒ 4(m² + 6m + 9 – 2m² – 10m – m – 5) = 0
⇒ -m² – 5m + 4 = 0
⇒ m² + 5m – 4 = 0
⇒ m = \(\frac{-5 \pm \sqrt{25+16}}{2}\)
⇒ m = \(\frac{-5 \pm \sqrt{41}}{2}\)

Question 6.
If α and β are the roots of x² + px + q = 0, form a quadratic equation whose roots are (α – β)² and (α + β)².
Solution:
∵ α, β are the roots of the equation x² + px + q = 0
α + β = -p, αβ = q
(α – β)² + (α + β)² = 2(α² + β²)
= 2[(α + β)² – 2αβ]
= 2[p² – 2q]
(α – β)² (α + β)² = [(α + β)² – 4αβ)] (α + β)²
= (p² – 4q) (p²)
∴ The required equation is x² – (sum of the roots) x + product of the roots = 0
∴ x² – 2(p² – 2q)x + p²(p² – 4q) = 0

Question 7.
If x² + bx + c = 0, x² + cx + b = 0 (b ≠ c) have a common root, then show that b + c + 1 = 0.
Solution:
If α is a common root of x² + bx + c = 0, x² + cx + b = 0 then
α² + bα + c = 0 ………..(1)
α² + cα + b = 0 ……….(2)
(1) – (2) ⇒ (b – c)α + (c – b) = 0
⇒ α – 1 = 0
⇒ α = 1
From (1), 1 + b + c = 0
Hence b + c + 1 = 0

Question 8.
Prove that the roots of (x – a) (x – b) = h² are always real.
Solution:
Given equation is (x – a) (x – b) = h²
x² – (a + b)x + (ab – h²) = 0
Discriminant = (a + b)² – 4(ab – h²)
= (a + b)² – 4ab + 4h²
= (a – b)² + (2h)² > 0
∴ The roots are real.

Question 9.
Find the condition that one root of the quadratic equation ax² + bx + c = 0 shall be n times the other, where n is a positive integer.
Solution:
Let the roots of the equation ax² + bx + c = 0 be α, nα

Question 10.
Find two consecutive positive even integers, the sum of whose squares is 340.
Solution:
Let the two consecutive positive even integers be 2λ, 2λ + 2
Sum of squares = 340
⇒ (2λ)² + (2λ + 2)² = 340
⇒ λ² + (λ + 1)² = 85
⇒ λ² + λ² + 2λ + 1 – 85 = 0
⇒ 2λ² + 2λ – 84 = 0
⇒ λ² + λ – 42 = 0
⇒ (λ + 7) (λ – 6) = 0
⇒ λ = 6, λ = -7
∵ Given numbers are positive λ = 6
∴ The two consecutive positive even integers are
2λ = 2(6) = 12 and 2λ + 2 = 12 + 2 = 14

II.

Question 1.
If x₁, x₂ are the roots of the quadratic equation ax² + bx + c = 0 and c ≠ 0, find the value of (ax₁ + b)^-2 + (ax₂ + b)^-2 terms of a, b, c.
Solution:
x₁, x₂ are the roots of the equation ax² + bx + c = 0

Question 2.
If α, β are the roots of the quadratic equation ax² + bx + c = 0, form a quadratic equation whose roots are α² + β² and α^-2 + β^-2.
Solution:
α, β are the roots of ax² + bx + c = 0, then

Question 3.
Solve the following equation:
2x⁴ + x³ – 11x² + x + 2 = 0
Solution:
2x⁴ + x³ – 11x² + x + 2 = 0
Dividing by x²

Substituting in (1)
2(a² – 2) + a – 11 = 0
⇒ 2a² – 4 + a – 11 = 0
⇒ 2a² + a – 15 = 0
⇒ (a + 3) (2a – 5) = 0
⇒ a + 3 = 0 or 2a – 5 = 0
⇒ a = -3 or 2a = 5
⇒ a = -3 or a = \(\frac{5}{2}\)

⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0
⇒ (2x – 1) (x – 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ x = \(\frac{1}{2}\), 2
∴ The roots are \(\frac{1}{2}\), 2, \(\frac{-3 \pm \sqrt{5}}{2}\)

Question 4.
Solve 3^1+x + 3^1-x = 10
Solution:
3^1+x + 3^1-x = 10
\(\text { 3. } 3^{x}+\frac{3}{3^{x}}=10\)
Put a = 3^x so that 3a + \(\frac{3}{a}\) = 10
⇒ 3a² + 3 = 10a
⇒ 3a² – 10a + 3 = 0
⇒ (a – 3) (3a – 1) = 0
⇒ a – 3 = 0 or 3a – 1 = 0
⇒ a = 3 or a = \(\frac{1}{3}\)
Case (i): a = 3
⇒ 3^x = 3¹
⇒ x = 1
Case (ii): a = \(\frac{1}{3}\)
⇒ 3^x = 3^-1
⇒ x = -1
∴ The roots are 1, -1

Question 5.
Solve 4^x-1 – 3 . 2^x-1 + 2 = 0
Solution:
4^x-1 – 3 . 2^x-1 + 2 = 0
Put a = 2^x-1 so that a² = (2^x-1)² = 4^x-1
∴ a² – 3a + 2 = 0
⇒ (a – 2) (a – 1) = 0
⇒ a – 2 = 0 or a – 1 = 0
⇒ a = 2 or 1
Case (i): a = 2
2^x-1 = 2¹
⇒ x – 1 = 1
⇒ x = 2
Case (ii): a = 1
2^x-1 = 2⁰
⇒ x – 1 = 0
⇒ x = 1
∴ The roots are 1, 2

Question 6.
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\), when x ≠ 0 and x ≠ 3
Solution:
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\)
Put a = \(\sqrt{\frac{x}{x-3}}\)
\(a+\frac{1}{a}=\frac{5}{2}\)
⇒ \(\frac{a^{2}+1}{a}=\frac{5}{2}\)
⇒ 2a² + 2 = 5a
⇒ 2a² – 5a + 2 = 0
⇒ (2a – 1) (a – 2) = 0
⇒ 2a – 1 = 0 or a – 2 = 0
⇒ a = \(\frac{1}{2}\) or 2
Case (i): a = 2
\(\sqrt{\frac{x}{x-3}}\) = 2
⇒ \(\frac{x}{x-3}\) = 4
⇒ x = 4x – 12
⇒ 3x = 12
⇒ x = 4
Case (ii): a = \(\frac{1}{2}\)
\(\sqrt{\frac{x}{x-3}}=\frac{1}{2}\)
⇒ \(\frac{x}{x-3}=\frac{1}{4}\)
⇒ 4x = x – 3
⇒ 3x = -3
⇒ x = -1
∴ The roots are -1, 4.

Question 7.
\(\sqrt{\frac{3 x}{x+1}}+\sqrt{\frac{x+1}{3 x}}=2\), when x ≠ 0 and x ≠ -1
Solution:
Put a = \(\sqrt{\frac{3 x}{x+1}}\)
\(a+\frac{1}{a}=2\)
⇒ \(\frac{a^{2}+1}{a}\) = 2
⇒ a² + 1 = 2a
⇒ a² – 2a + 1 = 0
⇒ (a – 1)² = 0
⇒ a – 1 = 0
⇒ a = 1, 1
∴ \(\sqrt{\frac{3 x}{x+1}}\) = 1
⇒ \(\frac{3 x}{x+1}\)
⇒ 3x = x + 1
⇒ 2x = 1
⇒ x = \(\frac{1}{2}\)
∴ The root is \(\frac{1}{2}\)

Question 8.
Solve \(2\left(x+\frac{1}{x}\right)^{2}-7\left(x+\frac{1}{x}\right)+5=0\), when x ≠ 0.
Solution:
\(2\left(x+\frac{1}{x}\right)^{2}-7\left(x+\frac{1}{x}\right)+5=0\)
Put a = x + \(\frac{1}{x}\)
⇒ 2a² – 7a + 5 = 0
⇒ (2a – 5)(a – 1) = 0
⇒ 2a – 5 = 0 or a -1 = 0
⇒ a = \(\frac{5}{2}\) or 1
Case (i): a = \(\frac{5}{2}\)
x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ \(\frac{x^{2}+1}{x}=\frac{5}{2}\)
⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0
⇒ (2x – 1) (x – 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ x = \(\frac{1}{2}\) or 2
Case (ii): a = 1
\(x+\frac{1}{x}=1\)
⇒ \(\frac{x^{2}+1}{x}\)
⇒ x² + 1 = x
⇒ x² – x + 1 = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm \sqrt{3 i}}{2}\)
∴ The roots are \(\frac{1 \pm \sqrt{3 i}}{2}, \frac{1}{2}\), 2

Question 9.
Solve \(\left(x^{2}+\frac{1}{x^{2}}\right)-5\left(x+\frac{1}{x}\right)+6=0\), when x ≠ 0
Solution:
Put a = x + \(\frac{1}{x}\)
⇒ a² = \(\left(x+\frac{1}{x}\right)^{2}\)
⇒ a² = \(x^{2}+\frac{1}{x^{2}}+2\)
⇒ \(x^{2}+\frac{1}{x^{2}}\) = a² – 2
∴ a² – 2 – 5a + 6 = 0
⇒ a² – 5a + 4 = 0
⇒ (a – 1) (a – 4) = 0
⇒ a = 1 or 4
Case (i): a = 1
x + \(\frac{1}{x}\) = 1
⇒ \(\frac{x^{2}+1}{x}\) = 1
⇒ x² + 1 = x
⇒ x² – x + 1 = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm \sqrt{3 i}}{2}\)
Case (ii): a = 4
x + \(\frac{1}{x}\) = 4
⇒ \(\frac{x^{2}+1}{x}\) = 4
⇒ x² + 1 = 4x
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}\)
⇒ x = \(\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
∴ The roots are 2 ± √3, \(\frac{1 \pm \sqrt{3 i}}{2}\)

Question 10.
Find a quadratic equation for which the sum of the roots is 7 and the sum of the squares of the roots is 25.
Solution:
Let α, β be the roots of quadratic equation
α + β = 7, α² + β² = 25
⇒ (α + β)² – 2αβ = 25
⇒ 49 – 25 = 2αβ
⇒ αβ = 12
The required equation is x² – (α + β)x + αβ = 0
⇒ x² – 7x + 12 = 0

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(d) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(d)

I.

Question 1.
(i) Find the equation of the perpendicular bisector of the line segment joining the points 7 + 7i, 7 – 7i in the Argand diagram.
Solution:
A(7, 7); B(7, -7) represents the given complex numbers in the Argand diagram.

O is the mid-point of AB.
Co-ordinates of O are \(\left(\frac{7+7}{2}, \frac{7-7}{2}\right)\) = (7, 0)
Slope of \(\overleftrightarrow{\mathrm{AB}}=\frac{7+7}{7-7}=\frac{14}{0}\) = ∞
AB is parallel to Y-axis
PQ is perpendicular to AB
PQ is parallel to X-axis
Slope of PQ = 0
Equation of PQ is y – 0 = 0(x – 7)
i.e., y = 0

(ii) Find the equation of the straight line joining the point -9 + 6i, 11 – 4i in the Argand plane.
Solution:
Given points are -9 + 6i, 11 – 4i
Let A = (-9, 6); B = (11, -4)
Equation of the straight line AB is y – 6 = \(\frac{-4-6}{11+9}\) (x + 9)
⇒ y – 6 = \(\frac{-1}{2}\) (x + 9)
⇒ 2y – 12 = -x – 9
⇒ x + 2y – 3 = 0

Question 2.
If Z = x + iy and if the point P in the Argand plane represents Z, then describe geometrically the locus of z satisfying the equation.
(i) |z – 2 – 3i| = 5
(ii) 2|z – 2| = |z – 1|
(iii) Img z² = 4
(iv) \({Arg}\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
Solution:
(i) z = x + iy and |z – 2 – 3i| = 5
|z – 2 – 3i| = 5
⇒ |x + iy – 2 – 3i| = 5
⇒ |(x – 2) + i(y – 3)| = 5
⇒ \(\sqrt{(x-2)^{2}+(y-3)^{2}}\) = 5
⇒ (x – 2)² + (y – 3)² = 25
⇒ x² – 4x + 4 + y² – 6y + 9 = 25
∴ Locus of P is x² + y² – 4x – 6y – 12 = 0

(ii) 2|z – 2| = |z – 1|
2|x + iy – 2| = |x + iy – 1|
⇒ 2|(x – 2) + iy| = |(x – 1) + iy|
⇒ \(2 \sqrt{(x-2)^{2}+y^{2}}=\sqrt{(x-1)^{2}+y^{2}}\)
Squaring both sides
⇒ 4[(x – 2)² + y²] = (x – 1)² + y²
⇒ 4(x² – 4x + 4 + y²) = x² – 2x + 1 + y²
⇒ 4x² + 4y² – 16x + 16 = x² + y² – 2x + 1
∴ Locus of P is 3x² + 3y² – 14x + 15 = 0

(iii) Img z² = 4
∵ z = x + iy
⇒ z² = (x + iy)²
⇒ z² = x² + i²y² + 2ixy
⇒ z² = (x² – y²) + i(2xy)
∴ Img (z²) = 2xy = 4
∴ The locus of P is xy = 2

(iv) \({Arg}\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)

Since \({Arg}\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
∴ \(\frac{2 y}{x^{2}+y^{2}-1}=\tan \frac{\pi}{4}\)
⇒ 2y = x² + y² – 1
⇒ x² + y² – 2y – 1 = 0
∴ The locus of z is x² + y² – 2y – 1 = 0.

Question 3.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i, -2 – 2i, 2√3 + 2√3 i are the vertices of an equilateral triangle.
Solution:
A(2, 2), B(-2, -2), C(-2√3, 2√3) represent the given complex number in the Argand diagram.

AB² = (2 + 2)² + (2 + 2)²
= 16 + 16
= 32
BC² = (-2 + 2√3)² + (-2 – 2√3)²
= 4 + 12 – 8√3 + 4 + 12 + 8√3
= 32
AC² = (-2√3 – 2)² + (2√3 – 2)²
= 12 + 4 + 8√3 + 12 + 4 – 8√3
= 32
AB² = BC² = AC²
⇒ AB = BC = CA
∴ ∆ABC is an Equilateral triangle.

Question 4.
Find the eccentricity of the ellipse whose equation is |z – 4| + |z – \(\frac{12}{5}\)| = 10
Solution:
SP + S’P = 2a
S = (4, 0), S’ = (\(\frac{12}{5}\), 0)
2a = 10 ⇒ a = 5
SS’ = 2ae
⇒ 4 – \(\frac{12}{5}\) = 2 × 5e
⇒ \(\frac{8}{5}\) = 10e
⇒ e = \(\frac{4}{25}\)

II.

Question 1.
If \(\frac{z_{3}-z_{1}}{z_{2}-z_{1}}\) is a real number, show that the points represented by the complex numbers z₁, z₂, z₃ are collinear.
Solution:
Let z₁ = x₁ + iy₁; z₂ = x₂ + iy₂; z₃ = x₃ + iy₃

Given \(\frac{z_{3}-z_{1}}{z_{2}-z_{1}}\) is a real number.
Imaginary part = 0
⇒ (y₃ – y₁) (x₂ – x₁) – (x₃ – x₁) (y₂ – y₁) = 0
⇒ (y₃ – y₁) (x₂ – x₁) = (x₃ – x₁) (y₂ – y₁)
⇒ \(\frac{y_{3}-y_{1}}{x_{3}-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
The points A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) represents the complex numbers z₁, z₂, z₃ respectively.
Slope of \(\stackrel{\leftrightarrow}{\mathrm{AC}}\) = Slope of \(\stackrel{\leftrightarrow}{\mathrm{AB}}\)
∴ A, B, C are collinear.

Question 2.
Show that the points in the Argand plane represented by the complex numbers 2 + i, 4 + 3i, 2 + 5i, 3i are the vertices of a square.
Solution:
A(2, 1), B(4, 3) C(2, 5), D(0, 3) represent the given complex number in the Argand plane

AB² = (2 – 4)² + (1 – 3)² = 4 + 4 = 8
BC² = (4 – 2)² + (3 – 5)² = 4 + 4 = 8
CD² = (2 – 0)² + (5 – 3)² = 4 + 4 = 8
DA² = (0 – 2)² + (3 – 1)² = 4 + 4 = 8
AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA ………(1)
AC² = (2 – 2)² + (1 – 5)² = 0 + 16 = 16
BD² = (4 – 0)² + (3 – 3)² = 16 + 0 = 16
AC² = BD²
⇒ AC = BD …….(2)
By (1), (2)
A, B, C, D are the vertices of a square.

Question 3.
Show that the points in the Argand plane represented by the complex numbers -2 + 7i, \(-\frac{3}{2}+\frac{1}{2} i\), 4 – 3i, \(\frac{7}{2}\)(1 + i) are the vertices of a rhombus.
Solution:
A(-2, 7), B(\(-\frac{3}{2}\), \(\frac{1}{2}\)), C(4, -3), D(\(\frac{7}{2}\), \(\frac{7}{2}\)) represents the given complex numbers in the Argand diagram.

∴ AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA ……….(1)
AC² = (-2 – 4)² + (7 + 3)²
= 36 + 100
= 136
BD² = \(\left(-\frac{3}{2}-\frac{7}{2}\right)^{2}+\left(\frac{1}{2}-\frac{7}{2}\right)^{2}\)
= 25 + 9
= 34
AC ≠ BD ……..(2)
∴ A, B, C, D are the vertices of a Rhombus.

Question 4.
Show that the points in the Argand diagram represented by the complex numbers z₁, z₂, z₃ are collinear, if and only if there exist three real numbers p, q, r not all zero, satisfying pz₁ + qz₂ + rz₃ = 0 and p + q + r = 0.
Solution:
pz₁ + qz₂ + rz₃ = 0
⇔ rz₃ = -pz₁ – qz₂
⇔ z₃ = \(\frac{-p z_{1}-q z_{2}}{r}\) [∵ r ≠ 0]
∵ p + q + r = 0
⇔ r = -p – q
⇔ z₃ = \(-\frac{\left(p z_{1}+q z_{2}\right)}{-(p+q)}\)
⇔ z₃ = \(\frac{p z_{1}+q z_{2}}{p+q}\)
⇔ z₃ divides the line segment joining z₁, z₂ in the ratio q : p
⇔ z₁, z₂, z₃ are collinear

Question 5.
The points P, Q denotes the complex numbers z₁, z₂ in the Argand diagram. O is the origin. If \(\bar{z}_{1} \bar{z}_{2}+\bar{z}_{2} \bar{z}_{1}=0\), show that POQ = 90°.
Solution:
Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂
Then P(x₁, y₁), Q(x₂, y₂), O(0, 0)
\(\overline{\mathbf{z}}_{1}\) = x1 – iy1, \(\overline{\mathbf{z}}_{2}\) = x₂ – iy₂
\(\bar{z}_{1} \bar{z}_{2}+\bar{z}_{2} \bar{z}_{1}\) = (x₁ + iy₁) (x₂ – iy₂) + (x₂ + iy₂) (x₁ – iy₁) = 0
⇒ x₁x₂ + y₁y₂ – ix₁y₂ + ix₂y₁ + x₁x₂ + y₁y₂ – ix₂y₁ + ix₁y₂ = 0
⇒ 2(x₁x₂ + y₁y₂) = 0
⇒ x₁x₂ + y₁y₂ = 0
⇒ x₁x₂ = -y₁y₂
⇒ \(\left(\frac{-x_{1}}{y_{1}}\right)\left(-\frac{x_{2}}{y_{2}}\right)=-1\)
Slope of OP × Slope of OQ = -1
∴ OP, OQ are perpendicular
⇒ ∠POQ = 90°

Question 6.
The complex number z has argument θ, 0 < θ < \(\frac{\pi}{2}\) and satisfy the equation |z – 3i| = 3. Then prove that (cot θ – \(\frac{6}{z}\)) = i
Solution:
Let z = cos θ + i sin θ
Given |z – 3i| = 3.
⇒ |(cos θ + i sin θ) – 3i| = 3
⇒ |cos θ + i(sin θ – 3)| = 3
⇒ \(\sqrt{\cos ^{2} \theta+(\sin \theta-3)^{2}}\) = 3
⇒ cos²θ + sin²θ – 6 sin θ + 9 = 9
⇒ 1 – 6 sin θ = 0
⇒ 6 sin θ = 1
⇒ sin θ = \(\frac{1}{6}\)
since 0 < θ < \(\frac{\pi}{2}\)

∴ cos θ = \(\frac{\sqrt{35}}{6}\)
cot θ = √35
∴ cot θ – \(\frac{6}{z}\) = cot θ – \(\frac{6}{\cos \theta+i \sin \theta}\)
= cot θ – 6(cos θ – i sin θ)
= √35 – 6\(\left[\frac{\sqrt{35}}{6}-i \cdot \frac{1}{6}\right]\)
= √35 – √35 + i
= i
Hence cot θ – \(\frac{6}{z}\) = i

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(b)

I.

Question 1.
Write the following complex numbers in the form A + iB.
(i) (2 – 3i) (3 + 4i)
(ii) (1 + 2i)³
(iii) \(\frac{a-i b}{a+i b}\)
(iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)
(v) (-√3 + √-2) (2√3 – i)
(vi) (-5i) \(\left(\frac{i}{8}\right)\)
(vii) (-i) 2i
(viii) i⁹
(ix) i^-19
(x) 3(7 + 7i) + i(7 + 7i)
(xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)
Solution:
(i) (2 – 3i) (3 + 4i) = 6 + 8i – 9i – 12i²
= 6 – i + 12
= 18 – i
= 18 + i(-1)

(ii) (1 + 2i)³ = 1 + 3 . i² . 2i + 3 . 1 . 4i² + 8i³
= 1 + 6i – 12 – 8i
= -11 – 2i
= (-11) + i(-2)

(v) (-√3 + √-2) (2√3 – i) = (-√3 + i√2) (2√3 – i)
= -6 + i√3 + i2√6 + √2
= (-6 + √2) + i(√3 + 2√6)

(vi) (-5i) \(\left(\frac{i}{8}\right)\) = \(\frac{-5 i^{2}}{8}\)
= \(\frac{5}{8}\) + i(0)

(vii) (-i)(2i) = -2i²
= -2(-1)
= 2
= 2 + i(0)

(viii) i⁹ = i⁴ . i⁴ . i
= 1 . 1 . i
= i
= 0 + i(1)

(ix) i^-19 = \(\frac{1}{i^{19}}\)
= \(\frac{i}{i^{20}}\)
= \(\frac{i}{\left(i^{4}\right)^{5}}\)
= \(\frac{\mathrm{i}}{\mathrm{i}^{5}}\)
= i
= 0 + i(1)

(x) 3(7 + 7i) + i(7 + 7i)
= 21 + 21i + 7i – 7
= 14 + 28i

Question 2.
Write the conjugate of the following complex numbers.
(i) 3 + 4i
(ii) (15 + 3i) – (4 – 20i)
(iii) (2 + 5i) (-4 + 6i)
(iv) \(\frac{5 i}{7+i}\)
Solution:
(i) Let z = 3 + 4i
\(\bar{z}\) = 3 – 4i

(ii) Let z = (15 + 3i) – (4 – 20i)
= 15 + 3i – 4 + 20i
= 11 + 23i
\(\bar{z}\) = 11 – 23i

(iii) Let z = (2 + 5i) (-4 + 6i)
= -8 + 12i – 20i – 30
= -38 – 8i
\(\bar{z}\) = -38 + 8i

Question 3.
Simplify
(i) i² + i⁴ + i⁶ + …….. + (2n + 1) terms
(ii) i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (-i)²⁶
Solution:
(i) i² + i⁴ + i⁶ + …….. + (2n + 1) terms
= -1 + 1 – 1 + (2n + 1) terms
= -1

(ii) i¹⁸ – 3i² + i² (1 + i⁴) (-i)²⁶
= i¹⁶ . i² – 3 . i⁴ . i³ + i² (1 + 1) i²⁴ . i²
= 1 . (-1) – 3 . 1 . (-i) + (-1) (2) (1) (-1)
= -1 + 3i + 2
= 1 + 3i

Question 4.
Find a square root for the following complex numbers.
(i) 7 + 24i
(ii) -8 – 6i
(iii) (3 + 4i)
(iv) (-47 + i8√3)
Solution:

Question 5.
Find the multiplicative inverse of the following complex numbers.
(i) √5 + 3i
(ii) -i
(iii) i^-35
Solution:
(i) √5 + 3i
The multiplicative inverse of x + iy is \(\frac{x-i y}{x^{2}+y^{2}}\)

II.

Question 1.
(i) If (a + ib)² = x + iy, find x² + y²
Solution:
(a + ib)² = x + iy
⇒ a² + i(2ab) – b² = x + iy
⇒ (a² – b²) + i(2ab) = x + iy
⇒ (a² – b²) + i(2ab) = x + iy
Equating real and imaginary parts on both sides, we have
x = a² – b² and y = 2ab
x² + y² = (a² – b²)² + (2ab)²
= a⁴ – 2a²b² + b⁴ + 4a²b²
= a⁴ + 2a²b² + b⁴
= (a² + b²)²

(ii) If x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) then show that x² + y² = 4x – 3
Solution:
x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) \(\frac{(2+\cos \theta)-i \sin \theta}{(2+\cos \theta)-i \sin \theta}\)

(iii) If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\), show that 4x² – 1 = 0.
Solution:

Equating real parts on both sides, we have
x = \(\frac{1}{2}\)
⇒ 2x = 1
⇒ 4x² = 1
⇒ 4x² – 1= 0

(iv) If u + iv = \(\frac{2+i}{z+3}\) and z = x + iy, find u, v.
Solution:

Question 2.
(i) If z = 3 – 5i Show that z³ – 10z² + 58z – 136 = 0.
Solution:
Given z = 3 – 5i
⇒ z – 3 = -5i
⇒ (z – 3)² = 25i²
⇒ z² – 6z + 9 = -25
⇒ z² – 6z + 34 = 0
∴ z³ – 10z² + 58z – 136 = z(z² – 6z + 34) – 4z² + 24z – 136
= z(0) – 4(z² – 6z + 34)
= 0 – 4(0)
= 0
∴ z³ – 10z² + 58z – 136 = 0

(ii) If z = 2 – i√7 , then show that 3z³ – 4z² + z + 88 = 0.
Solution:
Given z = 2 – i√7
⇒ z – 2 = -i√7
⇒ (z – 2)² = (-i√7)²
⇒ z² – 4z + 4 = 7i²
⇒ z² – 4z + 4 = -7
⇒ z² – 4z + 11 = 0
∴ 3z³ – 4z² + z + 88 = 3z(z² – 4z + 11) + 8z² – 32z + 88
= 3z(0) + 8(z² – 4z + 11)
= 0 + 8(0)
= 0
∴ 3z³ – 4z² + z + 88 =0

(iii) Show that \(\frac{2-i}{(1-2 i)^{2}}\) and \(\left(\frac{-2-11 i}{25}\right)\) conjugate to each other.
Solution:

Question 3.
(i) If (x – iy)^1/3 = a – ib then show that \(\frac{x}{a}+\frac{y}{b}\) = 4(a² – b²)
Solution:
Given (x – iy)^1/3 = (a – ib)
⇒ x – iy = (a – ib)³
⇒ x – iy = a³ – 3a²ib + 3ai²b² – i³b³
⇒ x – iy = (a³ – 3ab²) – i(3a²b – b³)
Equating real and imaginary parts
x = a³ – 3ab²
⇒ \(\frac{x}{a}\) = a² – 3b²
y = 3a²b – b³
⇒ \(\frac{y}{b}\) = 3a² – b²
∴ \(\frac{x}{a}+\frac{y}{b}\) = a² – 3b² + 3a² – b²
= 4a² – 4b²
= 4(a² – b²)
∴ \(\frac{x}{a}+\frac{y}{b}\) = 4(a² – b²)

(ii) Write \(\left(\frac{a+i b}{a-i b}\right)^{2}-\left(\frac{a-i b}{a+i b}\right)^{2}\) in the form of x + iy.
Solution:

(iii) If x and y are real numbers such that \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-1}=i\), then determine the values of x and y.
Solution:

Question 4.
(i) Find the least positive integer n, satisfying \(\left(\frac{1+i}{1-i}\right)^{n}\) = 1
Solution:

(ii) If \(\left(\frac{1+i}{1-i}\right)^{3}-\left(\frac{1-i}{1+i}\right)^{3}\) = x + iy, find x and y.
Solution:

(iii) Find real values of ‘θ’ in order that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is a
(a) real numbers
(b) Purely imaginary number
Solution:

(iv) Find the real values of x and y if \(\frac{x-1}{3+i}+\frac{y-1}{3-i}=i\)
Solution:
Given \(\frac{x-1}{3+i}+\frac{y-1}{3-i}=i\)
⇒ \(\frac{(x-1)(3-i)+(y-1)(3+i)}{9-i^{2}}=i\)
⇒ 3x – xi – 3 + i + 3y – iy – 3 – i = 10i
⇒ (3x + 3y – 6) + i(-x + y) = 0 + 10i
Now equating real and imaginary parts
3x + 3y – 6 = 0
⇒ x + y – 2 = 0 ……..(1)
-x + y = 10
⇒ x – y + 10 = 0 ………(2)
(1) + (2) ⇒ 2x + 8 = 0
⇒ x = -4
From (1),
-4 + y – 2 = 0
⇒ y = 6
∴ x = -4, y = 6

Students get through AP Inter 2nd Year Chemistry Important Questions 11th Lesson Haloalkanes And Haloarenes which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions 11th Lesson Haloalkanes And Haloarenes

Very Short Answer Questions

Question 1.
Write the structures of the following compounds. [IPE – 2015 (AP), 2016 (TS)]
i) 2-chloro-3-methylpentane,
ii) 1 -B romo4-sec-butyl-2-methylbenzene.
Answer:
i) 2-chloro-3-methyl pentane
Structure:

ii) 1-Bromo-4-sec-butyl 2-methyl benzene
Structure:

Question 2.
Which compound in each of the following pairs will react faster in S_N² reaction with -OH?
i) CH₃Br or CH₃I
ii) (CH₃)₃CCl or CH₃Cl.
Answer:
i) Among CH₃Br and CH₃I, CH₃ – I reacts faster in S_N2 reaction with OH^⊖ because bond dissociation energy of C -1 is less than the bond dissociation energy of C – Br.

ii) Among CH₃Cl and (CH₃)₃CCl, CH₃ – Cl reacts faster in S_N2 reaction with OH^⊖ because (CH₃)₃CCl has high steric hindrance than CH₃Cl.

Question 3.
Out of C₆H₅CH₂Cl and C₆H₅CHClC₆H₅, which is more easily hydrolysed aqueous KOH ?
Answer:

• Out of C₆H₅CH₂Cl and C₆H₅CHClC₆H₅ the 2nd one i.e., C₆H₅CHClC₆H₅ gets hydrolysed more easily than C₆H₅CH₂Cl.
• This can be explained by considering S_N1 reaction mechanism. In case of S_N1 reactions reactivity depends upon the stability of carbo cations.
• C₆H₅CHClC₆H₅ forms more stable carbo cation than C₆H₅CH₂Cl.
  

Question 4.
Treatment of alkyl halides with aq.KOH leads to the formation of alcohols, while in presence of alc.KOH what products are formed ?
Answer:
Treatment of alkyl halides with aq. KOH leads to the formation of alcohols. Here Nucleophillic substitution reaction takes place.
Eg. : C₂H₅Cl + aq.KOH → C₂H₅OH + KCl
Treatment of alkyl halides with alc.KOH leads to the formation of alkenes. Here elimination reaction takes place.
Eg. : C₂H₅Cl + alc. KOH → C₂H₄ + KCl + H₂O

Question 5.
What is Grignard’s reagents. How it is prepared.
Answer:
Alkyl magnesium halide is called Grignard reagent. It is prepared by the action of Mg on alkyl halide in ether solvent.
R – X + Mg → RMgX

Question 6.
What is the stereochemical result of S_N1 and S_N2 reactions? [T.S. Mar. 17 IPE 2015 (AP)]
Answer:

• The stereochemical result of S_N1 reaction is racemisation product.
• The stereochemical result of S_N2 reaction is inversion product.

Short Answer Questions

Question 1.
Define the following [A.P. Mar. 17] [IPE – 2014, 2016 (AP)]
i) Racemic mixture
ii) Retention of configuration
iii) Enantiomers.
Answer:
i) Racemic mixture: Equal portions of Enantiomers combined to form an optically inactive mixture. This mixture is called racemic mixture.

• Here rotation due to one isomer will be exactly cancelled by the rotation of due to other isomer.
• The process of conversion of enantiomer into a racemic mixture is called as racemisation.
  

ii) Retention of configuration: The preservation of integrity of the spatial arrangement of . bonds to an asymmetric centre during a chemical reaction (or) transformation is called Retention of configuration.
General Eg : Conversion of XC_abc chemical species into YC_abc.

Eg : (-) 2 – Methyl 1 – butanol conversion into (+) 1 – chloro 2. Methyl butane

Enantiomers : The stereo isomers related to each other as non-superimposable mirror images are called enantiomers. [A.P. Mar. 16]
These have identical physical properties like melting point, boiling points refractive index etc.
They differ in rotation of plane polarised light.

Question 2.
Explain the mechanism of Nucleophilic bimolecular substitution (S_N2) reaction with one example. [A.P. Mar. 18. 16] [Mar. 14]
Answer:
Nucleophilic Bimolecular substitution Reaction S_N2 :

1. The nucleophilic substitution reaction in which rate depends upon concentration of both reactants is called S_N2 reaction.
2.  It follows 2nd order kinetics. So it is called bimolecular reaction.
   Eg.: Methyl chloride reacts with hydroxide ion and forms methanol and chloride ion.
3. Here the rate of reaction depends upon the concentration of two reactants.
   
4. In the above mechanism the configuration of carbon atom under attack inverts in much the same way as an umbrella is turned inside out when caught in a strong wind. This process is called inversion of configuration.
5. In transition state the carbon atom is simultaneously bonded to the incoming nucleophile and out going group. It is very unstable.
6. The order of reactivity for SN2 reactions follows : 1°-alkyl halides > 2°-alkyl halides > 3°-alkyl halides.

Question 3.
Explain why allylic and benzylic halides are more reactive towards S_N1 substitution while 1-halo and 2-halobutanes preferentially undergoes S_N2 substitution.
Answer:

1. Allylic and benzylic halides show high reactivity towards the S_N1 reaction.
   Reason : The carbocation thus formed gets stabilised through resonance phenomenon as shown below.
   
2. 1-halo and 2-halo butanes preferentially undergoes S_N2 substitute.
   Reason : S_N2 reactions involve transition state formation. Higher the steric hindrance lesser the stability of transition state. The given 1 -halo and 2-halo butanes have less steric hindrance. So these are preferentially undergo S_N2 reaction.

Question 4.
Write the preparations of Alkyl halides.
Answer:

Preparation ofAlkyl Halides :
i) From Alcohols : Alkyl halides are prepared by the action of HX, PX₃, PX₃, PX₅, X₂ & red phosphurs or SOCl on alcohols.

Question 5.
Explain SN¹ and SN² reactions. [T.S. Mar. 18] [IPE – 2016, 2015, 2014 (TS)]
Answer:
i) SN¹: Substitution nucleophilic unimolecular reaction: In this reaction the first step is the formation of stable carbonium ion. This step is slow and is the rate determining step. The alkyl halides which form stable carbonium ion follow SN¹ reaction.

The order of reactivity of alkyl halides towards SN¹ reaction.
Tertiary halide > Secondary halide > Primary halide > CH₃ – X.
Benzyl halide and allyl halides are primary halides but participate in SN¹ mechanism due to the formation of stable benzyl and allyl carbonium ions (Benzyl and allyl carbonium ions are stabilised due to resonance).

ii) SN²: Substitution nucleophilic bimolecular reaction: In this reaction the rate of reaction depends on the concentration of alkyl halide and also on the concentration of nucleophile hence it is a bimolecular reaction.

The order of reactivity of alkyl halides towards SN2 reaction.
CH₃ – X > Primary halide> Secondary halide > Tertiary halide
For a given alkyl group, the reaction of the alkyl halide, R – X follows the same order in both the mechanisms R – I > R – Br> R – Cl > R – F

Question 6.
What is Wurtz reaction ? Give equation.
Answer:
Wurtz Reaction : Alkyl halides react with sodium in dry ether solvent give alkanes.

Question 7.
Explain different chemical properties of Alkyl halide. [IPE 2016 (TS)]
Answer:

Question 8.
Explain Wurtz – Fittig and Fittig reactions. [A.P. Mar. 17]
Answer:
i) Wurtz – Fittig reaction : The reaction of aryl halide with alkyl halide in the presence of sodium in ether to give alkyl benzene is called Wurtz Fittig reaction.

ii) Fittig reaction : Aryl halides react vith sodium in dry ether solvent to give diphenyl is called fitting reaction.

Question 9.
Write any one method for the preparation of chloro benzene.
Answer:
Chlorination of benzene in the pressence of Lewis acid like AlCl₃, FeCl₃ gives chioro benzene.

Question 10.
Explain electrophilic substitution reactions of chioro benzene.
Answer:
Electrophilic Substitution Reaction : Halogen atom is electron releasing group. it activates the benzene ring hence electrophilic substitution takes place at ortho and para positions.

Question 11.
Write the structures of the following organic halides. [IPE 2016 (T.S)]
i) 1 -Bromo-4-sec-butyl-2-methylbenzene,
ii) 2-Chioro- 1 -phenylbutane
iii) p-bromochlorobenzene,
iv) 4-t-butyl-3-iodoheptane.
Answer:
i) 1 -Bromo-4-sec-butyl-2-methylbenzene,
Structure :

ii) 2-Chioro- 1 -phenylbutane
Structure :

iii) p-bromochlorobenzene,
Structure :

iv) 4-t-butyl-3-iodoheptane.
Structure :

Students get through AP Inter 2nd Year Chemistry Important Questions Lesson 6(a) Group-15 Elements which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions Lesson 6(a) Group-15 Elements

Very Short Answer Questions

Question 1.
Nitrogen molecule is highly stable – Why? (IPE 2014)
Answer:
Nitrogen Molecule is more stable because in between two nitrogen atoms of N₂, a triple bond is present. To break this triple bond high energy is required (941.4KJ/mole).

Question 2.
Why are the compounds of bismuth more stable in +3 oxidation state ?
Answer:
Bismuth compounds are more stable in +3 oxidation state because ‘Bi’ exhibits +3 stable oxidation state instead of +5 due to inert pair effect.

Question 3.
What is allotropy ? Explain the different allotropic forms of phosphorus. (IPE 2016(TS))
Answer:
Allotropy: The existence of an element in different physical forms having similar chemical properties is called allotropy.
→ Allotropes of ‘P’: → White ‘P’ (or) Yellow P.

• Red P
• Scarlet ‘P’
• Violet P
• α – black P’
• β – black ‘P’.

White phosphorus :

• It is poisonous and insoluble in water and soluble in carbon disulphide and glows in dark.
• It is a translucent white waxy solid.
• It dissolves in boiling NaOH solution and gives PH₃.
  
• It is more reactive than other solid phases.
• Bond angle is 60° and it readily catches fire,

Red phosphorus :

• Red P possesses iron grey lustre.
• In it odour less, non poisonous and insoluble in water as well as CS₂.
• Red P is much less reactive than white P.

Black P’:

• α – Black P : It is formed when red P is heated in a sealed tube 803K.
• β – Black P : It is prepared by heating white P at 473 K under high pressure.

Question 4.
Explain the difference in the structures of white and red phosphorus.
Answer:
White ‘P’ molecule has tetrahedral structure (discrete molecule). Discrete ‘P’ molecules are held by vander waal’s forces.

Red ‘P’ is polymeric consisting of chains of P₄ tetrahedron linked together through covalent bonds.

Question 5.
What is inert pair effect ?
Answer:
Inert pair effect: The reluctance of ns pair of electrons to take part in bond formation is called inert pair effect.

• Bi exhibits +3 oxidation state instead of +5 due to inert pair effect.

Question 6.
How do calcium phosphide and heavy water react ?
Answer:
Calcium phosphide reacts with heavy water to form Deutero phosphine.
Ca₃P₂ + 6D₂O → 3 Ca (OD)₂ + 2PD₃

Question 7.
Ammonia is a good complexing agent – Explain with an example.
Answer:
NH₃ is a lewis base and it donates electron pair to form dative bond with metal ions. This results in the formation of complex compound.
Eg :

Question 8.
NO is paramagnetic in gaseous state but diamagnetic in liquid and solid states – Why ?
Answer:
In gaseous state NO₂ exists as a Monomer and contains one unpaired electron but in solid state it dimerises to N₂O₄ so it doesnot contain unpaired electron.
Hence NO₂ is para magnetic in geseous state but diamagnetic in solid state.

Question 9.
Iron becomes passive in cone. HNO₃ – Why ?
Answer:
Iron becomes passive in cone. HNO₃ due to formation of a passive film of oxide on the surface of iron.

Question 10.
Give the neutral oxides of nitrogen.
Answer:
Nitrous oxide (N₂O) and Nitric oxide (NO) are neutral oxides of nitrogen.

Question 11.
Give the paramagnetic oxides of nitrogen.
Answer:
Nitric oxide (NO) and nitrogen dioxide (NO₂) are the paramagnetic oxides of nitrogen due to the presence of odd number of electrons.

Question 12.
Why is white phosphorus is more reactive than red phosphorus ?
Answer:
In white phosphorus the P – P – P bond angle is 60° hence the bonds are in strain. As a result the bonds are broken easily. In red phosphorus the bond angle is 120°, hence it is stable and less reactive.

Question 13.
What happens when white phosphorus is heated with conc. NaOH solution in an inert atmosphere of CO₂ ?
Answer:
When white phosphorus heated with con. NaOH solution in an inert atmosphere of CO₂ forms PH₃.
P₄ + 3NaoH + 3H₂O → PH₃ + 3NaH₂PO₂.

Question 14.
Give the uses of
a) nitric acid and
b) ammonia.
Answer:
Nitric acid : It is used in the manufacture of fertilizers, explosives, nitro glycerine, nitro toluence etc.,
Ammonia : It is used to produce fertilizers like urea liquid NH₃ is used as a refrigerant.

Question 15.
Give the disproportionation reaction of H₃PO₃.
Answer:
Orthophosphoric acid (H₃PO₃) on heating disproportionates to give orthophosphoric acid and phosphine.
4H₃PO₃ → 3H₃PO₄ + PH₃.

Question 16.
Nitrogen exists as diatomic molecule and phosphorus as P₄ – Why ?
Answer:
Nitrogen exists as diatomic molecule :

• Nitrogen has small size and high electronegativity and nitrogen atom forms Pπ – Pπ multiple bonds with itself (triplebond). So it exists as a discrete diatomic molecule in elementary state.

Phosphorus exists as tetra atomic molecule :

• Phosphorus has large size and less electronegative and it forms P-P single bonds. So it exists as tetra atomic i.e., P₄.

Question 17.
Arrange the hydrides of group – 15 elements in the increasing order of basic strength and decreasing order of reducing character.
Answer:

• Increasing order of basic strength of Group – 15 elements hydrides is
  BiH₃ < SbH₃ < AsH₃ < PH₃ < NH₃.
• Decreasing order of reducing character of Group – 15 elements hydrides is
  BiH₃ > SbH₃ > AsH₃ > PH₃ > NH₃.

Question 18.
PH₃ is a weaker base than NH₃ – Explain.
Answer:
PH₃ is a weaker base than NH₃.

• In NH₃ nitrogen atom undergoes sp³ hybridisation and due to small size it has high electron density than in’P of PH₃.
• Due to large size of ‘P’ atom and availability of large surface area, lone pair of electron spread in PH₃. Hence PH₃ is weaker base than NH₃.

Question 19.
A mixture of Ca₃P₂ and CaC₂ is used in making Holme’s signal – Explain.
Answer:
A mixture of Ca₃P₂ and CaC₂ is used in Holme’s signal. This Mixture containing containers are pierced and thrown in the sea, when the gas is evolved bum and serve as a signal.
The spontaneous combustion of PH₃ is the technical use of Holme’s signal.

Question 20.
Which chemical compound is formed in the brown ring test of nitrate ions ?
Answer:
In the brown ring test of nitrate salts a brown ring is formed. It’s formula is [Fe(H₂O)₅NO]⁺².

Question 21.
Why does NH₃ act as a Lewis base ?
Answer:
Nitrogen atom in NH₃ has one lone pair of electrons with is available for donation. Therefore, it acts as a Lewis base.

Question 22.
Why does NO₂ dimerise ?
Answer:
NO₂ contains of odd number of electrons. It behaves as a typical odd molecule. On dimerisation, it is converted to stable N₂O₄ molecule with even number of electrons.

Question 23.
Why does PCl₃ fume in moisture ?
Answer:
PCl₃ hydrolyses in the presence of moisture giving fumes of HCl.
PCl₃ + 3H₂O → H₃PO₃ + 3HCl

Question 24.
Are all the five bonds in PCl₅ molecule equivalent ? Justify your answer.
Answer:
PCl₅ has a trigonal bipyramidal structure and the three equatorial P-Cl bonds are equivalent. While the two axial bonds are different and longer than equatorial bonds.

Question 25.
How is nitric oxide (NO) prepared ?
Answer:
Nitric oxide (NO) is prepared by the action of dilute nitric acid on copper.

Question 26.
Explain the following .
a) reaction of alkali with red phosphorus.
b) reaction between PCl₃ and H₂O.
Answer:
a) Red phosphorus reacts with alkalies slowly and forms phosphine and hypophosphite.
P₄ + 3NaOH + 3 H₂O → PH₃ + 3 NaH₂ PO₂
b) PCl₃ is hydrolysed by water and gives H₃PO₃

Question 27.
Write the oxidation states of phosphorus in solid PCl₅.
Answer:
In solid state PCl₅ exists as an ionic solid [PCl₄)⁺ [PCl₆]^–

• ‘P’ exhibits +5 oxidation state in [PCl₄)⁺ and [PCl₆]

Question 28.
Illustrate how copper metal can give different products on reaction with HNO₃.
Answer:

Question 29.
H₃PO₂ is a good reducing agent – Explain with an example.
Answer:
In H₃PO₂, two H-atoms are bonded directly to P-atom which imparts reducing character to the acid.

Question 30.
NH₃ forms hydrogen bonds but PH₃ does not – Why ?
Answer:
NH₃ forms hydrogen bonds but PH₃ does not.
Reason : Ammonia forms hydrogen bonds because it is a polar molecule and N-H bond is highly polar. Nitrogen has more electronegativity than phosphorus. In case of PH₃, P-H bond polarity decreases.

Question 31.
PH₃ has lower boiling point than NH₃. Why ?
Answer:
Unlike NH₃, PH₃ molecules are not associated through inter molecular hydrogen bonding. That is why the boiling point of PH₃ is lower than NH₃.

Long Answer Questions

Question 1.
How is ammonia manufactured by Haber’s process ? Explain the reactions of ammonia with
a) ZnSO_4(aq)
b) CuSO_4(aq)
c) AgCl_(s) (TS Mar. ’17 IPE 2015(AP))
Answer:
In Haber process ammonia is directly synthesised from elements (nitrogen and hydrogen). The principle involved in this is

This is a reversible exothermic reaction.
According to Le Chatelier’s principle favourable conditions for the better yield of ammonia are low temperature and high pressure. But the optimum conditions are :
Temperature : 720k
Pressure : 200 atmospheres
Catalyst: Finely divided iron in the presence of molybdenum (Promoter).
Procedure : A mixture of nitrogen and hydrogen in the volume ratio 1 : 3 is heated to 725 – 775K at a pressure of 200 atmospheres is passed over hot finely divided iron mixed with small amount of molybdenum as promotor. The gases coming out of the catalyst chamber consists of 10 – 20% ammonia. Gases are cooled and compressed, so that ammonia gas is liquified and the uncondensed gases are sent for recirculation.

a) Aq. ZnSO₄ reacts with ammonia aqueous solution to form white ppt of Zinc hydroxide.

Question 2.
How is nitric acid manufactured by Ostwald’s process ? How does it react with the following ? (A.P. Mar. ’17)
a) Copper
b) Zn
c) S₈
d) P₄
Answer:
Ostwald’s process : Ammonia, mixed with air in 1 : 7 or 1 : 8, when passed over a hot platinum gauze catalyst, is oxidised to NO mostly (about 95%).
The reaction is

The liberated heat keeps the catalyst hot. The ’NO’ is cooled and is mixed with oxygen to give the dioxide, in large empty towers (oxidation chamber). The product is then passed into warm water, under pressure in the presence of excess of air, to give HNO₃.
4NO₂ + O₂ + 2H₂O → 4HNO₃.
The acid formed is about 61% concentrated.

a) Copper reacts with dil. HNO₃ and cone. HNO₃ and liberates Nitric Oxide and Nitrogen dioxide respectively
3 Cu + 5 HNO₃ (dil) → 3 Cu (NO₃)₂ + 2 NO + 4 H₂O
Cu + 4 HNO₃ (conc.) → Cu (NO₃)₂ + 2 NO₂ + 2 H₂O

b) Zn reacts with dil. HNO₃ and Cone. HNO₃ and liberates Nitrous oxide and Nitrogen
dioxide respectively.
4 Zn + 10 HNO₃ (dil) → 4 Zn (NO₃)₂ + 5 H₂O + N₂O.
Zn + 4 HNO₃ (conc.) → Zn (NO₃)₂ + 2 H₂O + 2 NO₂

c) S₈ reacts with cone, nitric acid to form Sulphuric acid, NO₂ gas.
S₈ + 48 HNO₃ → 8 H₂SO₄ + 48 NO₂ + 16 H₂O
d) P₄ reacts with cone, nitric acid to form phosphoric acid and NO₂ gas.
P₄ + 20 HNO₃ → 4 H₃PO₄ + 20 NO₂ + 4 H₂O

Students get through AP Inter 2nd Year Physics Important Questions 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits

Very Short Answer Questions

Question 1.
What is an n-type semiconductor? What are the majority and minority charge carriers in it?
Answer:

• If a pentavalent impurity is added to a pure tetravalent semiconductor, it is called an n-type semiconductor.
• In n-type semiconductor majority, of charge carriers are electrons and the minority charge carriers are holes.

Question 2.
What are intrinsic and extrinsic semiconductors? [A.P. Mar. 15]
Answer:

• Pure form of semiconductors are called intrinsic semiconductors.
• When impure atoms are added to increase their conductivity, they are called extrinsic semiconductors.

Question 3.
What is a p-type semiconductor ? What are the majority and minority charge carriers in it ? [A.P. & T.S. Mar. 17]
Answer:
If a trivalent impurity is added to a tetravalent semiconductor, it is called p-type semi-conductor.

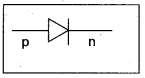
In p-type semiconductor majority charge carriers are holes and minority charge carriers are electrons.

Question 4.
What is a p-n junction diode ? Define depletion’ layer.
Answer:
When an intrinsic semiconductor crystal is grown with one side doped with trivalent element and on the other side doped with pentavalent element, a junction is formed in the crystal. It is called p-n junction diode.

A thin narrow region is formed on either side of the p-n junction, which is free from charge carriers is called depletion layer.

Question 5.
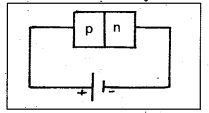
How is a battery connected to a junction diode in i) forward and ii) reverse bias ?
Answer:
i) In p-n junction diode, if p-side is connected to positive terminal of a cell and n-side to negative terminal, it is called forward bias.

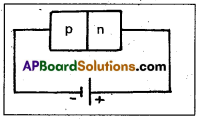
ii) In a p-n junction diode, p-side is connected to negative terminal of a cell and n-side to positive terminal, it is called reverse bias.

Question 6.
What is the maximum percentage of rectification in half wave and full wave rectifiers ?
Answer:

1. The percentage of rectification in half-wave rectifier is 40.6%.
2. The percentage of rectification in full-wave rectifiers is 81.2%.

Question 7.
What is Zener voltage (V_z) and how will a Zener diode be connected in circuits generally ?
Answer:

1. When Zener diode is in reverse biased, at a particular voltage current increases suddenly is called Zener (or) break down voltage.
2. Zener diode always connected in reverse bias.

Question 8.
Write the expressions for the efficiency of a full wave rectifier and a half wave rectifier.
Answer:

1. Efficiency of half wave rectifier (η) = \(\frac{0.406 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}\)
2. Efficiency of full wave rectifier (η) = \(\frac{0.812 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}\)

Question 9.
What happens to the width of the depletion layer in a p-n junction diode when it is
i) forward-biased and ii) reverse biased ?
Answer:
When a p-n junction diode is forward bias, thickness of depletion layer decreases and in reverse bias, thickness of depletion layer increases.

Question 10.
Draw the circuit symbols for p-n-p and n-p-n transistors. [Mar. 14]
Answer:

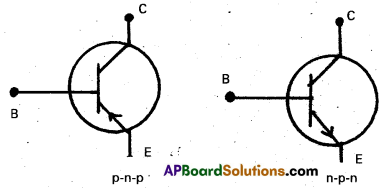
Question 11.
Define amplifier and amplification factor.
Answer:

1. Rising the strength of a weak signal is known as amplification and the device is called amplifier.
2. Amplification factor is the ratio between output voltage to the input voltage.
   A = \(\frac{\mathrm{V}_0}{\mathrm{~V}_{\mathrm{i}}}\)

Question 12.
In which bias can a Zener diode be used as voltage regulator ?
Answer:
In reverse bias Zener diode can be used as voltage regulator.

Question 13.
Which gates are called universal gates ? [T.S. Mar. 15]
Answer:
NAND gate and NOR gates are called universal gates.

Question 14.
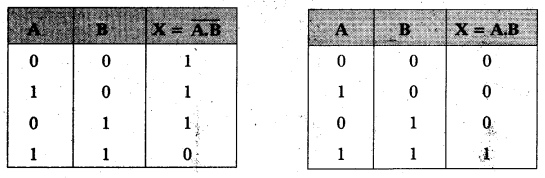
Write the truth table of NAND gate. How does it differ from AND gate ?
Answer:

Short Answer Questions

Question 1.
What is a rectifier ? Explain the working of half wave and full Wave rectifiers with diagrams. [A.P. Mar. 17]
Answer:
Rectifier: It is a circuit which converts ac into d.c. A p-n junction diode is used as a rectifier.
Half-wave rectifier:

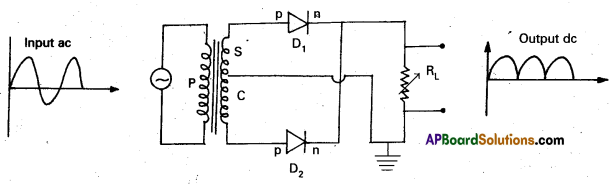
1. A half wave rectifier can be constructed with a single diode. The ac input signal is fed to the primary coil of a transformer. The output signal is taken across the load resistance R_L.
2. During positive half cycle, the diode is forward biased and current flows through the diode.
3. During negative half cycle, diode is reverse biased and no current flows through the load resistance.
4. This means current flows through the diode only during positive half cycles and negative half cycles are blocked. Hence in the output we get only positive half cycles.
5. Rectifier efficiency is defined as the ratio of output dc power to the input ac power.
   η = \(\frac{\mathrm{P}_{\mathrm{dc}}}{\mathrm{P}_{\mathrm{ac}}}=\frac{0.406 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}\)
   Where r_f = Forward resistance of a diode; R_L = Load resistance
   The maximum efficiency of half wave rectifier is 40.6%.

Full wave rectifier : The process of converting an alternating current into a direct current is called rectification.
The device used for this purpose is called rectifier.

1. A full wave rectifier can be constructed with the help of two diodes D₁ and D₂.
2. The secondary transformer is centre tapped at C and its ends are connected to the p regions of two diodes D₁ & D₂.
3. The output voltage is measured across the load resistance R_L.
4. During positive half cycles of ac, the diode D₁ is forward biased and current flows through the load resistance R_L. At this time D₂ will be reverse biased and will be in switch off position.
5. During negative half cycles of ac, the diode D₂ is forward biased and the current flows through R_L. At this time D₁ will be reverse biased and will be in switch off position.
6. Hence positive output is obtained for all the input ac signals.
7. The efficiency of a rectifier is defined as the ratio between the output dc power to the input ac power.
   η = \(\frac{\mathrm{P}_{\mathrm{dc}}}{\mathrm{P}_{\mathrm{ac}}}=\frac{0.812 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}\)
   The maximum efficiency of a full wave rectifier is 81.2%.

Question 2.
What is a junction diode ? Explain the formation of depletion region at the junction. Explain the variation of depletion region in forward and reverse-biased condition.
Answer:
p-n junction diode: When a p-type semiconductor is suitablyjoined to n-type semiconductor, a p-n junction diode is formed. ’
The circuit symbol of p-n junction diode is shown in figure.

Formation of depletion layer at the junction: When p-n junction is formed, the free electrons on n-side diffuse over to p-side, they combine with holes and become neutral. Similarly holes on p-side diffuse over to n-side and combihe with electrons become neutral.

This results in a narrow region formed on either side of the junction. This region is called depletion layer. Depletion layer is free from charge carriers.

The n-type material near the junction becomes positively charged due to immobile donor ions and p-type material becomes negatively charged due to immobile acceptor ions. This creates an electric field near the junction directed from n-region to p-region and cause a potential barrier.

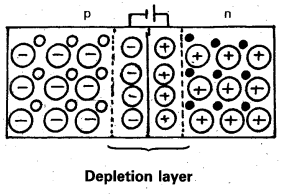
The potential barrier stops further diffusion of holes and electrons across the* junction. The value of the potential barrier depends upon the nature of the crystal, its temperature and the amount of doping.

Forward bias :
“When a positive terminal of a battery is connected to p-side and negative terminal is connected to n-side; then p-n junction diode is said to be forward bias”.

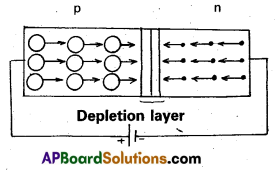
The holes in the p-region are repelled by the positive polarity and move towards the junction. Similarly electrons in the n-region are repelled by the negative polarity and move towards the junction.

As a result, the width of the depletion layer decreases. The charge carriers cross the junction apd electric current flows in the circuit.
Hence in forward bias resistance of diode is low. This position is called switch on position.
Reverse bias:

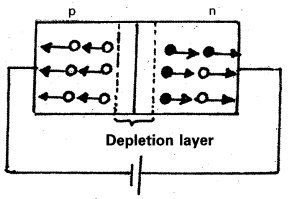
“When the negative terminal of the battery is connected to p-side and positive terminal of the battery is connected to n-side of the p-n junction, then the diode is said to be reverse bias”.

The holes in the p-region are attracted towards negative polarity and move away from the junction. Similarly the electrons in the n-region are attracted towards positive polarity and move away from the junction.

So, width of the depletion layer and potential barrier increases. Hence resistance of p-n junction diode increases. Thus the reverse biased diode is called switch off position.

Question 3.
What is a Zener diode ? Explain how it is used as a voltage regulator.
Answer:
Zener diode : Zener diode is a heavily doped germanium (or) silicon p-n junction diode. It works on reverse bias break down region.
The circuit symbol of zener diode is shown in figure.

Zener diode can be used as a voltage regulator. In- general zener diode is connected in reverse bias in the circuits.

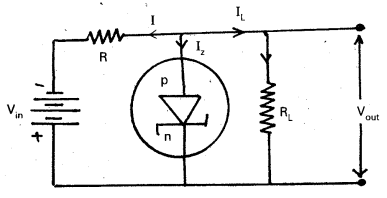
1. The zener diode is connected to a battery, through a resistance R. The battery reverse biases the zener diode.
2. The load resistance R_L is connected across the terminals of the zener diode.
3. The value of R is selected in such away that In the absence of load R_L maximum safe current flows in the diode.
4. Now consider that load is connected across the diode. The load draws a current.
5. The current through the diode falls by the same amount but the voltage drops across the load remains constant.
6. The series resistance ‘R’ absorbs the output voltage fluctuations, so as to maintain constant voltage across the load.
7. The voltage across the zener diode remains constant even if the load R_L varies. Thus, zener diode works as voltage regulator.
8. If I is the input current, I_Z and I_L are zener and load currents.
   I = I_Z + I_L; V_in = IR + V_Z
   But V_0ut = V_Z
   ∴ V_out = V_in – IR

Question 4.
Explain the working of LED and what are its advantages over conventional incandescent low power lamps.
Answer:
Light emitting diode (LED) : It is a photoelectronic device which converts electrical energy into light energy.

It is a heavily doped p-n junction diode which under forward bias emits spontaneous radiation. The diode is covered with a transparent cover so that the emitted light may not come out. Working : When p-n junction diode is forward biased, the movement of majority charge carriers takes place across the junction. The electrons move from n-side to p-side through the junction and holes move from p-side to n-side.

As a result of it, concentration of majority carriers increases rapidly at the junction.

When there is no bias across the junction, therefore there are excess minority carriers on either side of the junction, which recombine with majority carriers near the junction.

On recombination of electrons and hole, the energy is given out in the form of heat and light.
Advantages of LED’s over incandescent lamp :

1. LED is cheap and easy to handle.
2. LED has less power and low operational voltage.
3. LED has fast action and requires no warm up time.
4. LED can be used in burglar alarm system.

Question 5.
Define NAND and NOR gates. Give their truth tables. [T.S. Mar. 17]
Answer:
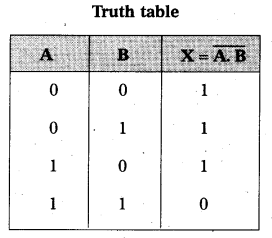
NAND gate : NAND gate is a combination of AND gate and NOT gate.

NAND gate can be obtained by connecting a NOT gate in the output of an AND gate. NAND gates are called universal gates.

1. If both inputs are low, output is high.
   A = 0, B = 0, X = 1
2. If any input is low, output is high.
   A = 0, B = 1, X = 1
   A = 1, B = 0, X =1
3. If both inputs are high, output is low.
   A = 1, B = 1, X = 0
   

NOR gate : NOR gate is a combination of OR gate and NOT gate when the output of OR gate is connected to NOT gate. It has two (or) more inputs and one output.

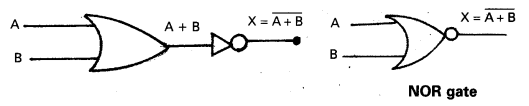
1. If both inputs are low, output is high.
   A = 0, B = 0, X = 1
2. If any input is high, the output is low.
   A = 0, B = 1, X = 0
   A = 1, B = 0, X = 0
3. If both inputs are high, the output is low.
   A = 1, B = 1, X = 0
   NOR gate is also a universal gate.
   

Question 6.
Explain the working of a solar cell and draw its I-V characteristics.
Answer:
Solar cell is a p-n junction device which converts solar energy into electric energy.
It consists of a silicon (or) gallium – arsenic p-n junction diode packed in a can with glass window on top. The upper layer is of p- type semiconductor. It is very thin so that the incident light photons may easily reach the p-n junction.

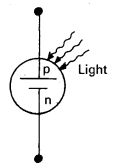
Working : When light (E = hv) falls at the junction, electron – hole pairs are generated near the junction. The electrons and holes produced move in opposite directions due to junction field. They will be collected at the two sides of the junction giving rise to a photo voltage between top and bottom metal electrodes. Top metal acts as positive electrode and bottom metal acts as a negative electrode. When an external load is connected across metal electrodes a photo current flows.

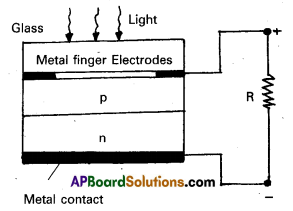
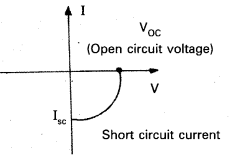
I-V characteristics : I – V characteristics of solar cell is drawn in the fourth quadrant of the coordinate axes. Because it does not draw current.

Uses : They are used in calculators, wrist watches, artificial satellites etc.

Question 7.
Explain the operation of a NOT gate and give its truth table. [IPE 15, T.S.]
Answer:
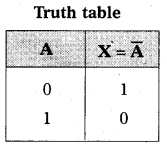
NOT gate: NOT gate is the basic gate. It has one input and one output. The NOT gate is also called an inverter. The circuit symbol of NOT gate is shown in figure.

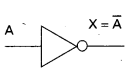
1. If input is low, output is high.
   A = 0, X = \(\overline{0}\) = 1
2. If input is high, output is low.
   A = 1, X = \(\overline{1}\) = 0
   

Question 8.
Draw an OR gate using two diodes and explain its operation. Write the truth table and logic symbol of OR gate.
Answer:
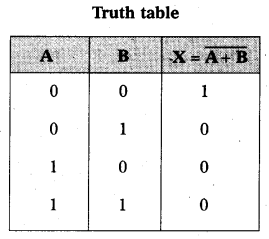
OR Gate : It has two input terminals and one output terminal. If both inputs are low the output is low. If one of the inputs is high, or both the inputs are high then the output of the gate is high. The truth tables of OR gate.

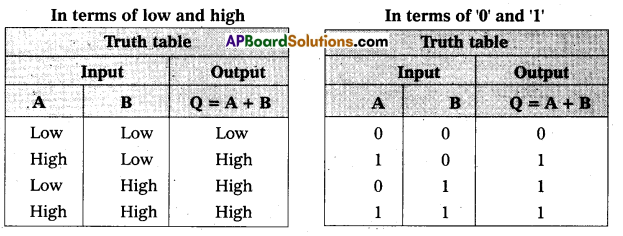
In truth table logic function is written as A or B ‘OR’ logic function is represented by the symbol ‘plus’.
Q = A + B
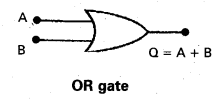
Logic gate ‘OR’ is shown given below.

Implementation of OR gate using diodes :
Let D₁ and D₂ be two diodes.

A potential of 5V represents the logical value 1.
A potential of OV represents the logical value 0.

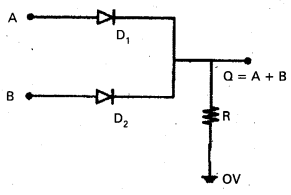
When A = 0, B = 0 both the diodes are reverse biased and there is no current through the resistance. So, the potential at Q is zero i.e., Q = 0. When A = 0 or B = 0 and the other equal to a potential of 5 V the diode whose anode is at a potential of 5 V is forward – biased and that diode behaves like a closed switch. The output potential then becomes 5 V i.e., Q = 1. When both A and B are 1, both the diodes are forward-biased and the potential at Q is same as that at A and B which is 5 V i.e., Q = 1. The output is same as that of the OR gate.

Question 9.
Sketch a basic AND circuit with two diodes and explain its operation. Explain how doping increases the conductivity in semiconductors ?
Answer:
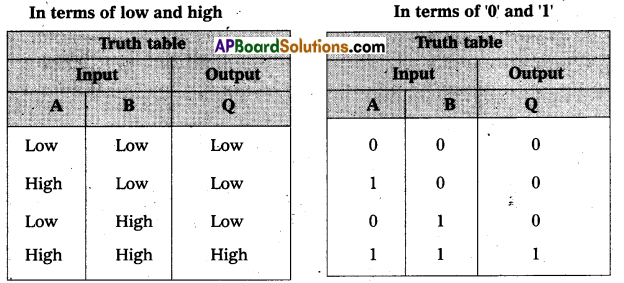
AND gate : It has two input terminals and one output terminal.

• If both the inputs are low (or) one of the inputs is low.
  • The output is low in an AND gate.
• If both the inputs .are high
  • The output of the gate is high.
• Note : If A and B are the inputs of the gate and the output is ‘Q’ then ‘Q’ is a logical function of A and B.
  AND gate Truth Tables
  
  The logical function AND is represented by the symbol dot so that the output, Q = A.B and the circuit symbol used for the logic gate AND is shown in Fig.
  
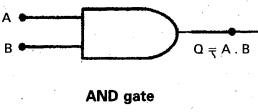
  The logical function AND is similar to the multiplication.

Implementation of AND gate using diodes : Let D₁ and D₂ represents two diodes. A potential of 5 V represents the logical value 1 and a potential of 0 V represents the logical value zero (0). When A = 0, B = ,0 both the diodes D₁ and D₂ are forward-biased and they behave like closed switches. Hence, the output Q is same as that A or B (equal to zero.) When A = 0 or B = 0, D₁ or D₂ is forward – biased and Q is zero. When A = 1 and B = T both the diodes are reverse – biased and they behave like open switches. There is no current through the resistance R making the potential at Q equal to 5V i.e., Q = 1. The output is same as that of an AND gate.

Doping increases the conductivity in Semiconductors: If a pentavalent impurity (Arsenic) is added to a pure tetravalent semiconductor it is called n-type semiconductor. Arsenic has 5 valence electrons, but only 4 electrons are needed to form covalent bonds with the adjacent Germanium atoms. The fifth electron is very loosely bound and become a free electron. Therefore excess electrons are available for conduction and conductivity of semiconductor increases.

Similarly when a trivalent impurity Indium is added to pure Germanium it is called p-type semi-conductor. In this excess holes in addition to those formed due to thermal energy are available for conduction in the valence band and the conductivity of semiconductor increases.

Question 10.
Explain how transistor can be used as a switch ?
Answer:
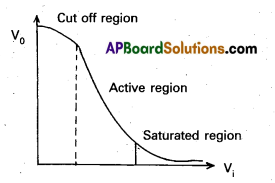
To understand the operation of transistor as a switch.

1. As long as V_i is low and unable to forward bias the transistor, V₀ is high (at V_cc).
2. If V_i is high enough to drive the transistor into saturation then V₀ is low, very near to zero.
   
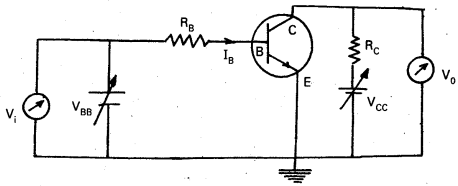
3. When the transistor is not conducting it is said to be switched off and when it is driven into saturation it is said to be switched on.
4. We can say that a low input to the transistor gives a high output and high input gives a low output.
5. When the transistor is used in the cutoff (or) saturation state it acts as a switch.
   

Problems

Question 1.
In a half wave rectifier, a p-n junction diode with internal resistance 20 ohm is used. If the load resistance of 2 ohm is used in the circuit, then find the efficiency of this half wave rectifier.
Solution:
Internal resistance (r_f) = 20Ω
R_L = 2kΩ = 2000 Ω
η = \(\frac{0.406 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}=\frac{0.406 \times 2000}{20+2000} \times 100=\frac{812 \times 100}{2020}\)
η = 40.2%.

Question 2.
A full wave p-n junction diode rectifier uses a load resistance of 1300 ohm. The internal resistance of each diode is 9 ohm. Find the efficiency of this full wave rectifier.
Solution:
Given that R_L = 1300 Ω
r_f = 9Ω
η = \(\frac{0.812 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}=\frac{0.812 \times 1300}{9+1300} \times 100 ; \eta=\frac{8120 \times 13}{1309}\)
η = 80.64%.

Question 3.
Calculate the current amplification factor β(beta) when change in collector current is 1mA and change in base current is 20μA.
Solution:
Change in collector current (∆I_C) = 1mA = 10^-3 A
Change in base current (∆I_B) = 20 μA = 20 × 10^-6 A
β = \(\frac{\Delta \mathrm{I}_{\mathrm{C}}}{\Delta \mathrm{I}_{\mathrm{B}}}=\frac{10^{-3}}{20 \times 10^{-6}}\); β = \(\frac{1000}{20}\)
β = 50

Question 4.
For a transistor amplifier, the collector load resistance R_L = 2k ohm and the input resistance R_i = 1 k ohm. If the current gain is 50, calculate voltage gain of the amplifier.
Solution:
R_L = 2kΩ = 2 × 10³ Ω
R_i = 1kΩ = 1 × 10³ Ω
β = 50.
Voltage gain (A_V) = β × \(\frac{\mathrm{R}_{\mathrm{L}}}{\mathrm{R}_{\mathrm{i}}}=\frac{50 \times 2 \times 10^3}{1 \times 10^3}\)

A_V = 100.

Textual Examples

Question 1.
C, Si and Ge have same lattice structure. Why is C insulator while Si and Ge intrinsic semiconductors ?
Solution:
The 4 bonding electrons of C, Si or Ge lie, respectively, in the second, third and fourth orbit. Hence, energy required to take out and electron from these atoms(i.e., ionisation energy E_g) will be least for Ge, following by Si and highest for C. Hence, number of free electrons for conduction in Ge and Si are significant but negligibly small for C.

Question 2.
Suppose a pure Si crystal has 5 × 10²⁸ atoms m^-3. It is doped by 1 ppm concentration of pentavalent As. Calculate the number of electrons and holes. Given that n. = 1.5 × 10¹⁶ m^-3.
Solution:
Note that thermally generated electrons (n_i ~ 10¹⁶ m^-3) are negligibly small as compared to those produced by doping.
Therefore, n_i ≈ N_D.
Since n_en_h = n_i², The number of holes, n_h = (1.5 × 10¹⁶)² / 5 × 10²⁸ × 16^-6
n_h = (2.25 × 10³²)/(5 × 10²²) ~ 4.5 × 10⁹m^-3

Question 3.
Can we take one slab of p-type semiconductor and physically join it to another n-type semiconductor to get p-n junction ?
Solution:
No ! Any slab, howsoever flat, will have roughness much large than the inter-atomic crystal spacing(~2 to 3 A°) and hence continuous contact at the atomic level will not be possible. The junction will behave as a discontinuity for the flowing charge carriers.

Question 4.
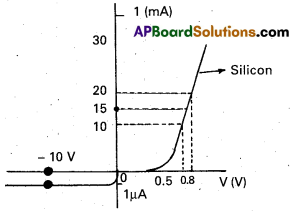
The V-I characteristics of a silicon diode are shown in the Fig. Calculate the resistance of the diode at (a) I_D = 15 mA and (b) V_D = -10 V.

Solution:
Considering the diode characteristics as a straight line between I = 10 mA to I = 20 mA passing through the origin, we can calculate the resistance using Ohm’s law.
a) From the curve, at I = 20 mA, V = 0.8 V, I = 10 mA, V = 0.7 V
r_fb = ∆V/∆I = 0.1V/10mA = 10Ω
b) From the curve at V = -10 V, I = -1 µA.
Therefore r_rb = 10V/1µA = 1.0 × 10⁷ Ω

Question 5.
In a Zener regulated power supply a Zener diode’with V_z = 6.0 V is used for regulation. The load current is to be 4.0 mA and the unregulated input is 10,0 V. What should be the value of series resistor R_s?
Solution:
The value of Rs should be such that the current through the Zener diode is much larger than the load current. This is to have good load regulation. Choose Zener current as five times the load current, i.e., I_z = 20 mA. The total current through R_S is , therefore, 24 mA. The voltage drop across R_S is 10.0 – 6.0 = 4.0 V This gives R_S = 4.0V/(24 × 10^-3) A = 167Ω. The nearest value of carbon resistor is 150 Ω. So, a series resistor of 150 Ω is appropriate. Note that slight variation in the value of the resistor does not matter, what is important is that the current I_Z should be sufficiently larger than I_L.

Question 6.
The current in the forward bias is known to be more (~mA) than the current in the reverse bias (~µA). What is the reason then to operate the photodiodes in reverse bias ?
Solution:
Consider the case of an n-type semiconductor. Obviously, the majority carrier density (n) is considerably larger than the minority hole density p (i.e., n> > p). On illumination, let the excess eletrons and holes generated be ∆n and ∆p, respectively,
n’ = n + ∆n
p’ = p + ∆p
Here n’ and p’ are the electron and hole concentrations at any particular illumination and n and p are carriers concentration when there is no illumination. Remember ∆n = ∆p and n > > p. Hence, the fractional change in the majority carriers (i.e., ∆n/n) would be much less than that in the minority carriers (i.e,, ∆p/p). In general, we can state that the fractional change due to the photo-effects on the minority carrier dominated reverse bias current is more easily measurable than the fractional change in the forward bias current. Hence, photodiodes-are preferably used in the reverse bias condition for measuring light intensity.

Question 7.
Why are Si and GaAs are preferred materials for solar cells ?
Solution:
The solar radiation spectrum received by us is shown in figure.

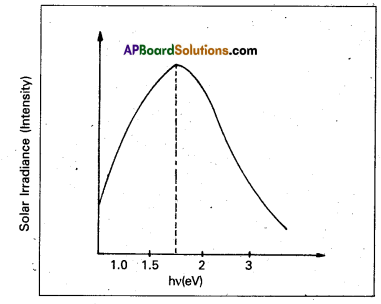
The maxima is near 1.5 eV. For photo-excitation, hv > E_g. Hence, semiconductor with band gap ~1.5 eV or lower is likely to give better solar conversion efficiency. Silicon has E_g ~ 1.1 eV while for GaAS it is ~ 1.53 eV. In fact, GaAs is better On spite of its higher band gap) than Si because of its relatively higher absorption coefficient. If we choose materials like CdS or CdSe(E_g ~ 2.4 eV), we can use only the high energy component of the solar energy for photo-conversion and a significant part of energy will be of no use.

The question arises: why we do not use material like pbS(E_g ~ 0.4 eV) which satisfy the condition hv > E_g for v maxima corresponding to the solar radiation spectra ? if we do so, most of the solar radiation will be absorbed on the top-layer of solar cell mid will not reach in or near the depletion region. For effective electron-hole separation, due to the junction field, we want the photo-generation to occur in the junction region only.

Question 8.
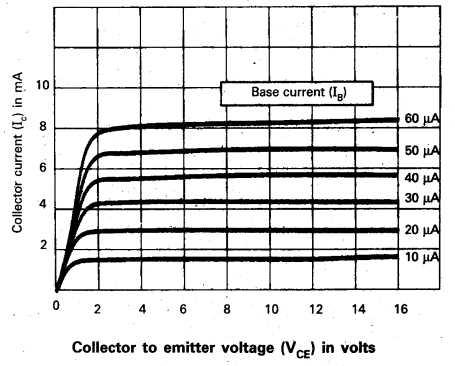
From the output charactristics shown in fig, calculate the values of β_ac and β_dc of the transistor when V_CE is 10 V and I_C = 4.0 mA.

Solution:
β_ac = \(\left(\frac{\Delta \mathrm{I}_{\mathrm{C}}}{\Delta \mathrm{I}_{\mathrm{B}}}\right)_{\mathrm{V}_{\mathrm{CE}}}\) ; β_dc = \(\frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{B}}}\)
For determining β_ac and β_dc at the stated values of V_CE and I_C one can proceed as follows. Consider any two characteristics for two values of I_B which lie above and below the given value of I_C. Here I_C = 4.0 mA. (Choose characteristics for I_B = 30 and 20μA.) At V _CE = 10V
we read the two values of Ic from the graph. Then
∆I_B = (30 – 20)μA = 10μA. ∆I_C
= (4.5 – 3.0) mA = 1.5 mA
Therefore, β_ac =1.5 mA/ 10μA = 150
For determining β_dc either estimate the value of I_B corresponding to I_C = 4.0 mA at V_CE = 10V or calculate the two values of β_dc for the two characteristics chosen and find their mean.
Therefore, for I_C = 4.5 mA and I_B = 30 μA
β_dc = 4.5 mA/30 μA = 150 and for I_C = 3.0 mA/ and I_B = 20 μA
β_dc = 3.0 mA / 20 μA= 150
Hence, β_dc = (150 + 150)/ 2 = 150

Question 9.
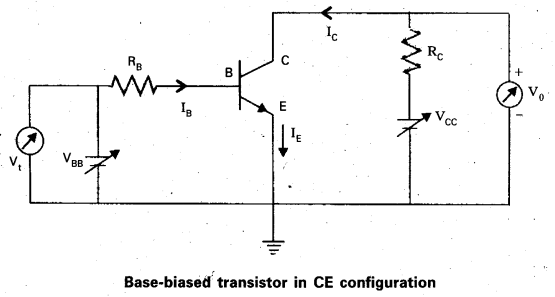
In Fig. the V_BB supply can be varied from OV to 5.0 V. The Si transistor has β_dc = 250 and R_B = 100 kΩ, R_C = 1 KΩ, V_CC = 5.0V. Assume that when the transistor is saturated, V_CE = 0V and V_BE = 0.8V. Calculate
(a) the minimum base current, for which the transistor will reach saturation. Hence,
(b) determine V₁ for when the transistor is ‘switched on’,
(c) find the ranges of V₁ for which the transistor is ‘switched of and ‘switched on’.

Solution:
Given at stauration
V_CE = OV, V_BE = 0.8V
V_CE = V_CC – I_CR_C
I_C = V_CC / R_C = 5.0V/1/0 kΩ = 5.0mA
Therefore, I_B = I_C/β
= 5.0 mA/250 = 20μA
The input voltage at which the transistor will go into saturation is given by
V_IH = V_BB = I_BR_B + V_BE
= 20μA × 100 kΩ + 0.8V = 2.8V
The value of input voltage below which the transistor remains cutoff is given by
V_IL = 0.6V, V_IH = 2.8V
Between 0.0V and 0.6V the transistor will be in the ‘switched off-state. Between 2.8V and 5.0V, it will be in ‘switched on’ state.
Note that the transistor is in active state when I_B varies from 0.0mA to 20mA. In this range, I_C = βI_B is valid. In the saturation range I_C ≤ βI_B.

Question 10.
For a CE transistor amplifier, the audio signal voltage across the collector resistance of 2.0 kΩ is 2.0 V. Suppose the current amplification factor of the transistor is 100, what should be the value of R_B in series with V_BB supply of 2.0 V if the dc base current has to be 10 times the signal current. Also calculate the dc drop across the collector resistance. (Refer to Fig)

Solution:
The output ac voltage is 2.0 V. So, the ac collector current i_C= 2.0/2000 = 1.0 mA. The signal current through the base is, therefore given by i_B = i_C/β = 1.0 mA/100 = 0.010 mA. The dc base current has to be 10 × 0.010 = 0.10 mA
From V_BB = V_BE+ I_B R_B R_B = (V_BB – V_BE)/I_B. Assuming V_BE = 0.6V
R_B = (2.0 – 0.6)/0.10 = 14kΩ
The dc collector current I_C = 100 × 0.10 = 10 mA.

Question 11.
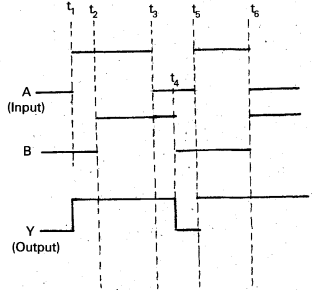
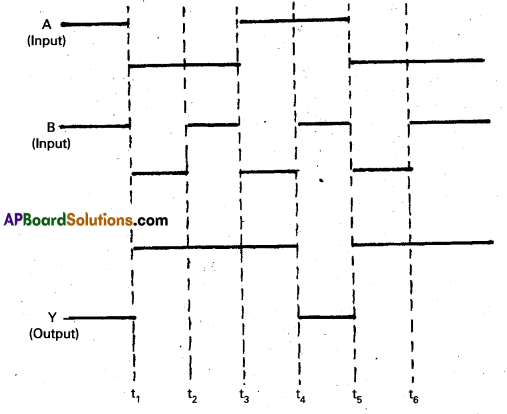
Justify the output waveform (Y) of the OR gate for the following inputs A and B given in fig.

Solution:
Note the following :

• At t ≤ t₁; A = 0, B = 0; Hence Y = 0
• For t₁ to t₂; A = 1, B = 0; Hence Y = 1
• For t₂ to t₃; A = 1, B = 1; Hence Y = 1
• For t₃ to t₄; A = 0, B = 1; Hence Y = 1
• For t₄ to t₅; A = 0, B = 0; Hence Y = 0
• For t₅ to t₆; A = 1, B = 0; Hence Y = 1
• For t > t₆; A = 0,B = 1; Hence Y = 1

Therefore the waveform Y will be as shown in the Fig.

Question 12.
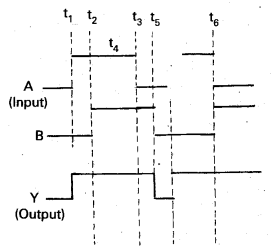
Take A and B input waveforms similar to that in Example 11. Sketch the output waveform obtained from AND gate.
Solution:

• For t ≤ t₁; A = 0, B = 0; Hence Y = 0
• For t₁ to t₂; A = 1, B = 0; Hence Y = 0
• For t₂ to t₃; A = 1, B = 1; Hence Y = 1
• For t₃ to t₄; A = 0, B = 1; Hence Y = 0
• For t₄ to t₅; A = 0, B = 0; Hence Y = 0
• For t₅ to t₆; A = 1, B = 0; Hence Y = 0
• For t > t₆; A = 0,B = 1; Hence Y = 0

Based on the above, the output waveform for AND gate can be drawn as given below.

Question 13.
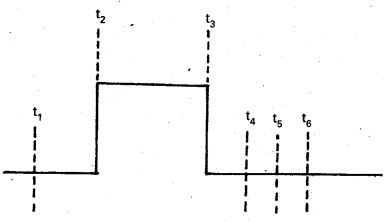
Sketch the output Y from a NAND gate having inputs A and B given below :
Solution:

• For t ≤ t₁; A = 1, B = 1; Hence Y = 0
• For t₁ to t₂; A = 0, B = 0; Hence Y = 1
• For t₂ to t₃; A = 0, B = 1; Hence Y = 1
• For t₃ to t₄; A = 1, B = 0; Hence Y = 1
• For t₄ to t₅; A = 1, B = 1; Hence Y = 0
• For t₅ to t₆; A = 0, B = 0; Hence Y = 1
• For t > t₆; A = 0,B = 1; Hence Y = 1
  

Students get through AP Inter 2nd Year Physics Important Questions 5th Lesson Electrostatic Potential and Capacitance which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 5th Lesson Electrostatic Potential and Capacitance

Short Answer Questions

Question 1.
Derive an expression for the electric potential due to a point charge. [T.S. Mar. 16]
Answer:
Expression for the electric potential due to a point charge:

1. Electric potential at a point is defined as the amount of workdone in moving a unit + ve charge from infinity to that point.
   
2. Consider a point P at a distance r from the point charge having charge + q. The electric field at P = E = \(\frac{q}{4 \pi \varepsilon_0 x^2}\)
3. Workdone in taking a unit +ve charge from B to A = dV = -E.dx (-ve sign shows that the workdone is +ve in the direction B to A, whereas the potential difference is +ve in the direction A to B.
4. Therefore, potential at P = The amount of workdone in taking a unit +ve charge from infinity to P
   

Question 2.
Derive an expression for the electrostatic potential energy of a system of two point charges and find its relation with electric potential of a charge.
Answer:
Expression for the electrostatic potential energy of a system of two point charges :

1. Let two point charges q₁ and q₂ are separated by distance ‘r’ in space.
2. An electric field will develop around the charge q₁.
3. To bring a charge q₂ from infinity to the point B some work must be done.
   
   Workdone = q₂ v_B
   But v_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r}\)
   W = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
4. This amount of workdone is stored as electrostatic potential energy (U) of a system of two charged particles. Its unit is joule.
   ∴ U = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
5. If the two charges are similar then ‘U’ is positive. This is in accordance with the fact that two similar charges repel one another and positive work has to be done on the system to bring the charges nearer.
6. Conversely if the two charges are of opposite sign, they attract one another and potential energy is negative.

Question 3.
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field.
Answer:
Expression for potential energy of an electric dipole placed in a uniform electric field :

1. Consider a electric dipole of length 2a having charges + q and -q.
2. The electric dipole is placed in uniform electric field E and it’s axis makes an angle θ with E.
3. Force on charges are equal but opposite sign. They constitute torque on the dipole.
   
   Torque τ = one of its force (F) × ⊥^r distance (BC)
   F = qE and sinθ = \(\frac{\mathrm{BC}}{2 \mathrm{a}} \) ⇒ BC = 2a sinθ
   ∴ Torque τ = qE × 2a sinθ = PE sin θ [∴ p = 2aq]
4. Suppose the dipole is rotated through an angle dθ, the workdone dw is given by
   dw = τdθ = PE sinθ dθ
5. For rotating the dipole from angle θ₁ to θ₂
   workdone W = \(\int_{\theta_1}^{\theta_2}\) PE sinθdθ = PE(cosθ₁ – cosθ₂)
6. This workdone (W) is then stored as potential energy(U) in the dipole.
   ∴ U = PE(cosθ₁ – cosθ₂)
7. If θ₁ = 90° and θ₂ = 0°, U = – PE cos₁.
   In vector form U = –\(\overrightarrow{\mathrm{P}} \cdot \overrightarrow{\mathrm{E}}\)

Question 4.
Derive an expression for the capacitance of a parallel plate capacitor. [A.P. Mar. 16; T.S. Mar. 14]
Answer:
Expression for the capacitance of a parallel plate capacitor:

1. P and Q are two parallel plates of a capacitor separated by a distance of d.
2. The area of each plate is A. The plate P is charged and Q is earth connected.
3. The charge on P is + q and surface charge density of charge = σ
   ∴ q = Aσ
   
4. The electric intensity at point x , E = \(\frac{|\sigma|}{\varepsilon_0}\)
5. Potential difference between the plates P and Q,
   \(\int {\mathrm{dV}}=\int_{\mathrm{d}}^0-\mathrm{Edx}=\int_{\mathrm{d}}^0 \frac{-\sigma}{\varepsilon_0} \mathrm{dx}=\frac{\sigma \mathrm{d}}{\varepsilon_0}\)
6. Capacitance of the capacitor C = \(\frac{\mathrm{Q}}{\mathrm{V}}=\frac{\mathrm{A} \sigma}{\frac{\sigma \mathrm{d}}{\varepsilon_0}}=\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) Farads (In air)
   Note : Capacity of a capacitor with dielectric medium is C = \(\frac{\varepsilon_0 \mathrm{~A}}{\left[\mathrm{~d}-\mathrm{t}+\frac{\mathrm{t}}{\mathrm{k}}\right]}\) Farads.

Question 5.
Explain the behaviour of dielectrics in an external field.
Answer:

1. When an external field is applied across dielectrics, the centre of positive charge distribution shifts in the direction of electric field and that of the negative charge distribution shifts
   
   opposite to the electric field and induce a net electric field within the medium opposite to the external field. In such situation the molecules are said to be polarised.
2. Now consider a capacitor with a dielectric between the plates. The net field in the dielectric becomes less.
3. If E₀ is the external field strength and E_i is the electric field strength induced, then the net field, \(\overrightarrow{\mathrm{E}}_{\text {net }}=\overrightarrow{\mathrm{E}}_0+\overrightarrow{\mathrm{E}}_{\mathrm{i}}\)
   (E_net) = E₀ – E_i = \(\frac{E}{K}\) where K is the dielectric constant of the medium.

Question 6.
Define electric potential. Derive an expression for the electric potential due to an electric dipole and hence the electric potential at a point (a) the axial line of electric dipole (b) on the equatorial line of electric dipole.
Answer:
Electric potential (V) : The workdone by a unit positive charge from infinite to a point in an electric field is called electric potential.

Expression for the potential at a point due to a dipole:

1. Consider A and B having -q and + q charges separated by a distance 2a.
2. The electric dipole moment P = q × 2a along AB
3. The electric potential at the point’P’is to be calculated.
4. P is at a distance ‘r’ from the point ‘O’. θ is the angle between the line OP and AB.
5. BN and AM are perpendicular to OP.
6. Potential at ‘P’ due to charge +q at B,
   V₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{BP}}\right]\)
   ∴ V₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{NP}}\right]\) [∵ BP = NP]
7. Potential at P due to charge -q at A, V₂ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{-q}}{\mathrm{AP}}\right]\)
   ∴ V₂ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{MP}}\right]\) [∵ AP = MP]
8. Therefore, Resultant potential at P is V = V₁ + V₂
   V = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{NP}}-\frac{\mathrm{q}}{\mathrm{MP}}\right]\) ………… (1)
9. In △le ONB, ON = OB cos0 = a cosθ; ∴NP = OP – ON = r – a cosθ ………………… (2)
10. In △le AMO, OM = AO cos0 = a cosθ; ∴ MP = MO + OP = r + a cosθ ………………. (3)
11. Substituting (2) and (3) in (1), we get
    
12. As r > >a, a² cos²θ can be neglected with comparision of r².
    ∴ V = \(\frac{\mathrm{P} \cos \theta}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
13. (a) Electric potential on the axial line of dipole:
    
    • When θ = 0°, point p lies on the side of + q. ____
      ∴ V = \(\frac{\mathrm{P}}{4 \pi \varepsilon_0 \mathrm{r}^2}\) [∵ cos 0° = 1]
    • When θ = 180°, point p lies on the side of — q.
      ∴ V = \(\frac{\mathrm{-P}}{4 \pi \varepsilon_0 \mathrm{r}^2}\) [∵ cos 180° = -1]

Qeustion 7.
What is series combination of capacitors. Derive the formula for equivalent capacitance in series combination. [A.P.& T.S. Mar.15]
Answer:
Series combination : If a number of condensers are connected end to end between the fixed points then such combination is called series.
In this combination

1. Charge on each capacitor is equal.
2. P.D’s across the capacitors is not equal.

Consider three capacitors of capacitances C₁, C₂ and C₃ are connected in series across a battery of P.D V as shown in figure.

Let ‘Q’ be the charge on each capacitor.
Let V₁, V₂ and V₃ be the P.D’s of three
V = V₁ + V₂ + V₃ ……………… (1)
RD across I^st condenser V₁ = \(\frac{\mathrm{Q}}{\mathrm{C}_1}\)
RD across III^nd condenser V₂ = \(\frac{\mathrm{Q}}{\mathrm{C}_2}\)
RD across IIII^rd condenser V₃ = \(\frac{\mathrm{Q}}{\mathrm{C}_3}\)
∴ From the equation (1),V = V₁ + V₂ + V₃
= \(\frac{\mathrm{Q}}{\mathrm{C}_1}+\frac{\mathrm{Q}}{\mathrm{C}_2}+\frac{\mathrm{Q}}{\mathrm{C}_3}=\mathrm{Q}\left[\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\right]\)
\(\frac{\mathrm{V}}{\mathrm{Q}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\)
\(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\) [∵ \(\frac{1}{C}=\frac{V}{Q}\)
For ‘n’ number of capacitors, the effective capacitance
\(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}+\ldots+\frac{1}{\mathrm{C}_{\mathrm{n}}}\)

Question 8.
What is parallel combination of capacitors. Derive the formula for equivalent capacitance in parallel combination. [T.S. Mar. 17; A.P.& T.S. Mar. 15]
Answer:
Parallel Combination: The first plates of different capacitors are connected at one terminal and all the second plates of the capacitors are connected at another terminal then the two terminals are connected to the two terminals of battery is called parallel combination.

In this combination,
1. The P.D’s between each capacitor is equal (or) same.
2. Charge on each capacitor is not equal.
Consider three capacitors of capacitance C₁, C₂ and C₃ are connected in parallel across a P.D V as shown in fig.
The charge on Ist capacitor Q₁ = C₁ V
The charge on IInd capacitor Q₂ = C₂ V
The charge on IIIrd capacitor Q₃ = C₃ V
∴ The total charge Q = Q₁ + Q₂ + Q₃
= C₁ V + C₂ V + C₃ V
Q = V(C₁ + C₂ + C₃) ⇒ \(\frac{\mathrm{Q}}{\mathrm{V}}\) = C₁ + C₂ + C₃
C = C₁ + C₂ + C₃ [∵ C = \(\frac{\mathrm{Q}}{\mathrm{V}}\)]
for ‘n’ number of capacitors connected in parallel, the equivalent capacitance can be written as
C = C₁ + C₂ + C₃ + ……………. + C_n

Question 9.
Derive an expression for the energy stored in a capacitor.
Answer:
Expression for the energy stored in a capacitor : Consider an uncharged capacitor of capacitance ‘c’ and its initial will be zero. Now it is connected across a battery for charging then the final potential difference across the capacitor be V and final charge on the capacitor be ‘Q’
∴ Average potential difference V_A = \(\frac{\mathrm{O}+\mathrm{V}}{2}=\frac{\mathrm{V}}{2}\)
Hence workdone to move the charge Q = W = V_A × Q = \(\frac{\mathrm{VQ}}{2}\)
This is stored as electrostatic potential energy ‘U’
∴ U = \(\frac{\mathrm{QV}}{2}\)
We know Q = CV then ‘U’ can be written as given below.
U = \(\frac{\mathrm{QV}}{2}=\frac{1}{2}\) CV² = \(\frac{Q^2}{2 C}\)
∴ Energy stored in a capacitor
U = \(\frac{\mathrm{QV}}{2}=\frac{1}{2}\) CV² = \(\frac{1}{2} \frac{\mathrm{Q}^2}{\mathrm{C}}\)

Qeustion 10.
What is the energy stored when the space between the plates is filled with dielectric.
a) With charging battery disconnected ?
b) With charging battery connected in the circuit ?
Answer:
Effect of Dielectric on energy stored :
Case (a) : When the charging battery is disconnected from the circuit:
Let the capacitor is charged by a battery and disconnected from the circuit. Now the space between the plates is filled with a dielectric of dielectric constant ‘K’ then potential decreases by \(\frac{1}{\mathrm{~K}}\) times and charge remains constant.
Capacity increases by’K’ times.
New capacity C’ = \(\frac{Q}{V}\) = \(\frac{\frac{Q}{V}}{K}\) = K\(\frac{Q}{V}\) = KC [V’ = \(\frac{V}{K}\); C = \(\frac{Q}{V}\)]
∴ C’ = KC
Energy stored U’ = \(\frac{1}{2}\) QV = \(\frac{1}{2}\) Q \(\frac{V}{K}\) = \(\frac{U}{K}\)
U’ = \(\frac{U}{K}\)
∴ Energy stored decreases by \(\frac{1}{\mathrm{~K}}\) times.

Case (b) : When the charging battery is connected in the circuit:
Let the charging battery is continue the supply of charge. When the dielectric is introduced then potential decreases by \(\frac{1}{\mathrm{~K}}\) times and charge on the plates increases until the potential difference attains the original value = V
New charge on the plates Q’= KQ
Hence new capacity C’ = \(\frac{Q^{\prime}}{V}=\frac{K Q}{V}\) = KC
Energy stored in the capacitor U’ = \(\frac{1}{2}\) QV; = \(\frac{1}{2}\) (KQ) V = KU
U = KU
∴ Energy stored in the capacitor increases by ‘K times.

Problems

Question 1.
(a) Calculate the potential at a point P due to a charge of 4 × 10^-7 C located 9 cm away,
(b) Hence obtain the work done in bringing a charge of 2 × 10^-9 C from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
Solution:
(a) V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}}\)
= 9 × 10⁹ Nm² C^-2 \(\frac{4 \times 10^{-7} \mathrm{C}}{0.09 \mathrm{~m}}\)
= 4 × 10⁴ V

(b) W = qV = 2 × 10^-9 C × 4 × 10⁴V
= 8 × 10^-5 J
No, work done will be path independent. Any arbitrary infinitesimal path can be resolved into two perpendicular displacements. One along r and another perpendicular to r. The work done corresponding to the later will be zero.

Qeustion 2.
Two charges 3 × 10^-8 C and -2 × 10^-8 C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Thke the potential at infinity to be zero.
Solution:
Let us take the origin O at the location of the positive charge. The line joining the two charges is taken to be x-axis; the negative charge is taken to be on the right side of the origin fig.

Let P be the required point on the x-axis where the potential is zero. If x is the x – coordinate of P, obviously x must be positive. (There is no possibility of potentials due to the two charges adding up to zero for x < 0.) If x lies between O and A, we have
\(\frac{1}{4 \pi \varepsilon_0}\left[\frac{3 \times 10^{-8}}{x \times 10^{-2}}-\frac{2 \times 10^{-8}}{(15-x) \times 10^{-2}}\right]\) = 0
where x is in cm. That is \(\frac{3}{x}-\frac{2}{15-x}\) = 0
which gives x = 9 cm
If x lies on the extended line OA, the required condition is \(\frac{3}{x}-\frac{2}{x-15}\) = 0
Which gives x = 45 cm
Thus, electric potential is zero at 9 cm and 45 cm away from the positive charge on the side of the negative charge. Note that the formula for potential used in the calculation required choosing potential to be zero at infinity.

Question 3.
A slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickness (3/4)d, where d is the separation of the plates. How is the capacitance changed when die slab is inserted between the plates ?
Solution:
Let E₀ = V_g/d be the electric field between the plates when there is no dielectric and the potential difference is V₀. If the dielectric is now inserted, the electric field in the dielectric will be E = E₀/K. The potential difference will then be
V = \(E_0\left(\frac{1}{4} d\right)+\frac{E_0}{K}\left(\frac{3}{4} d\right)\)
= \(\mathrm{E}_0 \mathrm{~d}\left(\frac{1}{4}+\frac{3}{4 \mathrm{~K}}\right)=\mathrm{V}_0 \frac{\mathrm{K}+3}{4 \mathrm{~K}}\)
The potential difference decreases by the factor (K + 3)/K while the free charge Q₀ on the plates remains unchanged. The capacitance thus increases,
C = \(\frac{\mathrm{Q}_0}{\mathrm{~V}}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \frac{\mathrm{Q}_0}{\mathrm{~V}_0}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \mathrm{C}_0\)

Question 4.
Four charges are arranged at the corners of a square ABCD of side d. as shown in fig. Find the work required to put together this arrangement, (b) A charge q₀ is brought to the centre of the square, the four charges being held fixed at its comers. How much extra work is needed to do this ?

Solution:
(a) Since the work done depends on the final arrangement of the charges, and not on how they are put together, we calculate work needed for one way of putting the charges at A, B, C and D. Suppose, first the charge +q is brought to A and then the charges -q, +q, and -q are brought to B, C and D, respectively. The total work needed can be calculated in steps.

1. Work needed to bring charge +q to A when no charge is present elsewhere: this is zero.
2. Work needed to bring -q to B when + q is at A. This is given by (charge at B) × (electrostatic potential at B due to change +q at A) = -q × \(\left(\frac{q}{4 \pi \varepsilon_0 d}\right)\)
3. Work needed to bring charge +q to C when +q is at A and -q is at B. This is given by – (charge at Q × (potential at C due to charges at A and B) .
   
4. Work needed to bring -q to D when +q at A, -q at B, and +q at C.
   This is given by (charge at D) × (potential at D due to charges at A, B and C)
   
   Add the work done is steps (i), (ii), (iii) and (iv). The total work required is
   
   The work done depends only on the arrangement of the charges, and not how they are assembled. By definition, this is the total electrostatic energy of the charges.
   (Students may try calculating same work/energy by taking charges in any other order they desire and convince themselves that the energy will remain the same.)

b) The extra work necessary to bring a charge q₀ to the point E when the four charges are at A, B, C and D is q₀ × (electrostatic potential at E due to the charges at A, B, C and D). The electrostatic potential at E is clearly zero since potential due to A and C is cancelled by that due to B and D.Hence no work is required to bring any charge to point E.

Question 5.
a) Determine the electrostatic potential energy of a system consisting of two charges 7μC and -2μC (and with no external field) placed at (-9 cm, 0,0) and (9cm, 0, 0) respectively.
b) How much work is required to separate the two charges infinitely away from each ‘ other?
Solution:
(a) U = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
= 9 × 10⁹ × \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\) = -0.7 J.

(b)W = U₂ – U₁ = 0 – U = 0 – (-0.7)
= 0.7J.

Question 6.
There is a uniform electric field in the XOY plane represented by (\(40 \hat{\mathrm{i}}+30 \hat{\mathrm{j}}\)) Vm^-1. If the electric potential at the origin is 200 V, the electric potential at the point with coordinates (2m, 1m) is
Answer:
Given, uniform Electric field intensity,
\(\overrightarrow{\mathrm{E}}\) = (\(40 \hat{\mathrm{i}}+30 \hat{\mathrm{j}}\)) Vm^-1
Electric potential at the origin = 200V
Position vector \(\mathrm{d} \overrightarrow{\mathrm{r}}=(2 \hat{\mathrm{i}}+1 \hat{\mathrm{j}})\) m
We know that,

dV = \(-\vec{E} \cdot d \vec{r}=-(40 \hat{i}+30 \hat{j}) \cdot(2 \hat{i}+\hat{j})\)
V_p – V₀ = -(80 + 30) = -110Volt. ’
V_p = V₀ – 110 = (200 – 110) Volt = 90 Volt
∴ Potential at point P, V_p = 90Volt.

Question 7.
An equilateral triangle has a side length L. A charge +q is kept at the centroid of the triangle. P is a point on the perimeter of the triangle. The ratio of the minimum and maximum possible electric potentials for the point P is
Answer:
Charge at the centroid of an equilateral triangle = +q
The charge + q divides the line segment in ratio 2 : 1.
That means r_max = 2 and r_min = 1

Question 8.
A condenser of certain capacity is charged to a potential V and stores some energy. A second condenser of twice the capacity is to store half the energy of the first, find to what potential one must be charged ?
Solution:
(For first capacitor, C₁ = C; V₁ = V
And U₁ = \(\frac{1}{2}\) C₁V₁² = \(\frac{1}{2}\) CV² …………………. (1)
For second capacitor, C₂ = 2C₁ = 2C;
U₂ = \(\frac{\mathrm{U}_1}{2}=\frac{1}{4}\)CV²; Let potential difference across the capacitor = V₂

Then, U₂ = \(\frac{1}{2}\) C₂V₂²
⇒ \(\frac{1}{4}\) CV² = \(\frac{1}{2}\) × 2C × V₂²
⇒ V₂² = \(\frac{\mathrm{V}^2}{4}\)
∴ V₂ = \(\frac{V}{2}\)

Question 9.
Three Capacitors each of capaitance 9 pF are connected in series.
a) What is the total capacitance of the combination ?
b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply ?
Solution:
a) Resultant capacitance in series combination \(\frac{1}{C_s}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3} \Rightarrow \frac{1}{C_S}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}\)
C_S = 3pF

b) Rd across each capacitor = \(\frac{\mathrm{V}}{3}=\frac{120}{3}\) = 40V

Question 10.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. [A.P. Mar. 17]
a) What is the total capacitance of the combination ?
b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Solution:
a) C_p = C₁ + C₂ + C₃ = 2 + 3 + 4 = 9pF
b) For each capacitor, V is same = 100 Volt
q₁ = C₁V = 2 × 100 = 200pC
q₂ = C₂V = 3 × 100 = 300pC
q₂ = C₃V = 4 × 100 = 400pC

Textual Examples

Question 1.
(a) Calculate the potential at a point P due to a charge of 4 × 10^-7C located 9 cm away.
(b) Hence obtain the work done in bringing a charge of 2 × 10^-9C from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
Solution:
(a) V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}}\)
= 9 × 10⁹ Nm² C^-2 \(\frac{4 \times 10^{-7} \mathrm{C}}{0.09 \mathrm{~m}}\)
= 4 × 10⁴ V

(b) W = qV = 2 × 10^-9 C × 4 × 10⁴V
= 8 × 10^-5 J
No, work done will be path independent. Any arbitrary infinitesimal path can be resolved into two perpendicular displacements. One along r and another perpendicular to r. The work done corresponding to the later will be zero.

Question 2.
Two charges 3 × 10^-8 C and -2 × 10^-8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
Solution:
Let us take the origin O at the location of the positive charge. The line joining the two charges is taken to be x-axis; the negative charge is taken to be on the right side of the origin fig.

Let P be the required point on the x-axis where the potential is zero. If x is the x – coordinate of P, obviously x must be positive. (There is no possibility of potentials due to the two charges adding up to zero for x < 0.) If x lies between O and A, we have
\(\frac{1}{4 \pi \varepsilon_0}\left[\frac{3 \times 10^{-8}}{x \times 10^{-2}}-\frac{2 \times 10^{-8}}{(15-\mathrm{x}) \times 10^{-2}}\right]\) = 0
where x is in cm. That is \(\frac{3}{x}-\frac{2}{15-x}\) = 0
which gives x = 9 cm.
If x lies on the extended line OA, the required condition is \(\frac{3}{x}-\frac{2}{x-15}\) = 0
Which gives x. = 45 cm
Thus, electric potential is zero at 9 cm and 45 cm away from the positive charge on the side of the negative charge. Note that the formula for potential used in the claculation required choosing potential to be zero at infinity.

Question 3.
Figure (a) and (b) shows the field lines of a positive and negative point charge respectively.

(a) Give the signs of the potential difference V_p – V_Q; V_B – V_A.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P; A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B And A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A ?
Solution:
(a) As V ∝ \(\frac{1}{\mathrm{r}}\), V_p > V_Q. Thus, (V_p – V_Q) is positive. Also VB is less negative than V_A. Thus, V_B > V_A or (V_B – V_A) is positive.

(b) A small negative charge will be attracted towards positive charge. The negative charge moves from higher potential energy to lower potential energy. Therefore the sign of potential energy difference of a small negative charge between Q and P is positive. Similarly. (PE.)_A > (P.E.)_B and hence sign of potential energy differences is positive.

(c) In moving a small positive charge from Q to P, work has to be done by an external agency against the eletric field. Therefore, work done by the field is negative.

(d) In moving a small negative charge from B to A work has to be done by the external agency. It is positive.

(e) Due to force of repulsion on the negative charge, velocity decreases and hence the kinetic energy decreases in going form B to A.

Question 4.
Four charges are arranged at the comets of a square ABCD of side d. as shown in fig. 5.15.(a) Find the work required to put together this arrangement, (b) A charge q0 is brought to the centre of the square, the four charges being held fixed at its comers. How much extra work is needed to do this ?

Solution:
(a) Since the work done depends on the final arrangement of the charges, and not on how they are put together, we calculate work needed for one way of putting the charges at A, B, C and D. Suppose, first the charge +q is brought to A, and then the charges -q, +q, and -q are brought to B, C and D, respectively The total work needed can be calculated in steps.

1. Work needed to bring charge +q to A when no charge is present elesewhere: this is zero.
2. Work needed to bring -q to B when +q is at A. This is given by (charge at B) x (electrostatic .potential at B due to charge +q at A) = -q × \(\left(\frac{\mathrm{q}}{4 \pi \varepsilon_0 \mathrm{~d}}\right)\)
3. Work needed to bring charge +q to C when +q is at A and -q is at B. This is given by – (charge at Q × (potential at C due to charges at A and B) .
   
4. Work needed to bring -q to D when +q at A, -q at B, and +q at C.
   This is given by (charge at D) × (potential at D due to charges at A, B and C)
   
   Add the work done is steps (i), (ii), (iii) and (iv). The total work required is
   
   The work done depends only on the arrangement of the charges, and not how they are assembled. By definition, this is the total electrostatic energy of the charges.
   (Students may try calculating same work/energy by taking charges in any other order they desire and convince themselves that the energy will remain the same.)

b) The extra work necessary to bring a charge q0 to the point E when the four charges are at A, B, C and D is q₀ × (electrostatic potential at E due to the charges at A, B, C and D). The electrostatic potential at E is clearly zero since potential due to A and C is cancelled by that due to B and D.Hence no work is required to bring any charge to point E.

Question 5.
a) Determine the electrostatic potential energy of a system consisting of two charges 7µC and -2µC (and with no external field) placed at (-9 cm, 0,0) and (9cm, 0, 0) respectively.
b) How much work is required to separate the two charges infinitely away from each other ?
c) Suppose that the same system of charges is now placed in an external electric field E = A(1/r²); A = 9 × 10⁵ C m^-2. What would the electrostatic energy of the configuration be ?
Solution:
(a) U = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
= 9 × 10⁹ × \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\) = -0.7 J.

(b)W = U₂ – U₁ = 0 – U = 0 – (-0.7)
= 0.7J.

c) The mutual interaction energy of the two charges remains unchanged. In addition, there is the energy of interaction of the two charges with the external electric field. We find,
q₁V(r₁) + q₂V(r₂) = A \(\frac{7 \mu \mathrm{C}}{0.09 \mathrm{~m}}\) + A \(\frac{-2 \mu \mathrm{C}}{0.09 \mathrm{~m}}\)
and the net electrostatic energy is
q₁V(r₁) + q₂V(r₂) + \(\frac{q_1 q_2}{4 \pi \varepsilon_0 r_{12}}\)
= A \(\frac{7 \mu \mathrm{C}}{0.09 \mathrm{~m}}\) + A \(\frac{-2 \mu \mathrm{C}}{0.09 \mathrm{~m}}\)
= 70 – 20 – 0.7 = 49.3J

Question 6.
A molecule of a substance has a perma-nent electric dipole moment of magnitude 10^-29C m. A mole of this substance is polarised (at low temperature) by applying a strong electrostatic field of magnitude 10⁶ V m^-1. The direction of the field is suddenly changed by an angle of 60°. Estimate the heat released by the substance in aligning its dipoles along the new direction of the field. For simplicity, assume 100% polarisation of the sample.
Solution:
Here, dipole moment of each molecules = 10^-29C m
As 1 mole of the substance contains 6 × 10²³ molecules,
total dipole moment of all the molecules, p = 6 × 10²³ × 10^-29 Cm
= 6 × 10^-6 C m
Initial potential energy, U_t = -pE cos θ
=-6 × 10^-6 × 10⁶ cos 0° = -6 J
Final potential energy (when θ = 60°),
U_f = -6 × 10^-6 × 10⁶ × cos 60° = – 3J
Change in potential energy
= -3 J – (-6j) = 3 J
So, there is loss in potential energy. This must be the energy released by the substance in the form of heat in aligning its dipoles.

Question 7.
(a) A comb run through one’s dry hair attracts small bits of paper. Why ? What happens if the hair is wet or if it is a rainy day ? (Remember, a paper does not conduct electricity.)
(b) Ordinary rubber is an insulator. But special rubber types of aircraft are made slightly conducting. Why is this necessary ?
(c) Vehicles carrying inflammable materials usually have metallic ropes touching the ground during motion. Why?
(d) A bird perches on a bare high power line, and nothing happens to the bird. A man standing on the ground touches the same line and gets a fatal shock. Why ?
Solution:
(a) This is because the comb gets charged by friction. The molecules in the paper gets polarised by the charged comb, resulting in a net force of attraction, if the hair is wet, or if it is a rainy day. friction between hair and the comb reduces. The comb does not get charged and thus it will not attract small bits of paper.

(b) To enable them to conduct charge (produced by friction) to the ground; as too much of static electricity accumulated may result in spark and result in fire.

(c) Reason similar to (b).

(d) Current passes only when there is difference in potential.

Question 8.
A slab of material of dielectric constant K has the same area as the plates of a parallelplate capacitor but has a thickness (3/4)d, where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates ?
Solution:
Let E₀ = V_g/d be the electric field between the plates when there is no dielectric and the potential difference is V₀. If the dielectric is now inserted, the electric field in the dielectric will be E = E₀/K. The potential difference will then be
V = \(E_0\left(\frac{1}{4} d\right)+\frac{E_0}{K}\left(\frac{3}{4} d\right)\)
= \(\mathrm{E}_0 \mathrm{~d}\left(\frac{1}{4}+\frac{3}{4 \mathrm{~K}}\right)=\mathrm{V}_0 \frac{\mathrm{K}+3}{4 \mathrm{~K}}\)
The potential difference decreases by the factor (K + 3)/K while the free charge Q₀ on the plates remains unchanged. The capacitance thus increases,
C = \(\frac{\mathrm{Q}_0}{\mathrm{~V}}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \frac{\mathrm{Q}_0}{\mathrm{~V}_0}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \mathrm{C}_0\)

Question 9.
A network of four 10μF capacitors is connected to a 500V supply, as shown in Fig. Determine
(a) the equivalent capacitance of the network and
(b) the charge on each capacitor, (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

Solution:
(a) In the given network, C₁, C₂ and C₃ are connected in series. The effective capacitance C’ of these three capacitors isgivgftby
\(\frac{1}{\mathrm{C}^{\prime}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\)
For C₁ = C₂ = C₃ = 10 μF. C = (10/3) μF. The network has C and C₄ connected in parallel. Thus, the equivalent capacitance C of the network is
C = C’ + C₄ = (\(\frac{10}{3}\) + 10) μF = 13.3 μF

(b) Clearly, from the figure, the charge on each of the capacitors, C₁, C₂ and C₃ is the same, say Q. Let the charge on C₄ be Q. Now, since the potential difference c across AB is Q/C₁ across BC is Q/C₂. across CD is Q/C₃, we have
\(\frac{\mathrm{Q}}{\mathrm{C}_1}+\frac{\mathrm{Q}}{\mathrm{C}_2}+\frac{\mathrm{Q}}{\mathrm{C}_3}\) = 500 V
Also Q’/C₄ = 500V.
This gives for the given value of the capacitances,
Q = 500 V × \(\frac{10}{3}\) μF = 1.7 × 10^-3C and
Q’ = 500 V × 10μF = 5.0 × 10^-3C

Question 10.
(a) A 900pF capacitor is charged by 100 V battery [Fig.a]. How much electrostatic energy is stored by the capacitor ?
(b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor. What is the electrostatic y energy stored by the system ?

Solution:
The charge on the capacitor is
Q = CV = 900 × 10^-12F × 100 V
= 9 × 10^-8C
The energy stored by the capacitor is
= (1/2) CV² = (1/2) QV
= (1/2) × 9 × 10^-8C × 100 V
= 4.5 × 10^-6 J

(b) In the steady situation, the two capacitors have their positive plates at the same potential, and their negative plates at the same potential. Let the common potential difference be V. The charge on each capacitor is then Q’ = CV’. By charge conservation, Q’ = Q/2. This implies V’ = V/2. The total energy of the system is
= 2 × \(\frac{1}{2}\)Q’V’ = \(\frac{1}{4}\)QV = 2.25 × 10⁶J
Thus in going from (a) to (b), though no charge is lost; the final energy is only half the initial energy. Where has the remaining energy gone ?
There is a transient period before the system settles to the situation (b). During this period, a transient current flows from the first capacitor to the second. Energy is lost during this time in the form of heat and electromagnetic radiation.