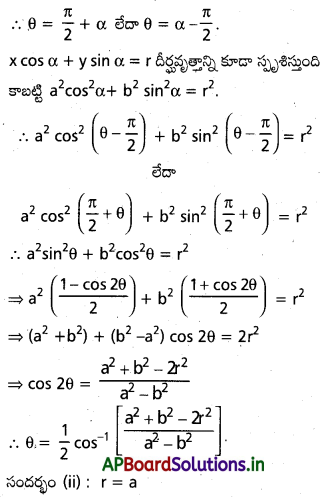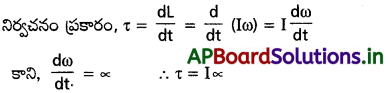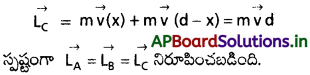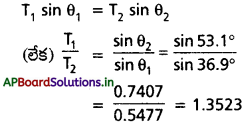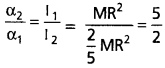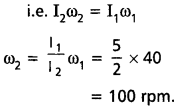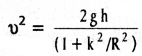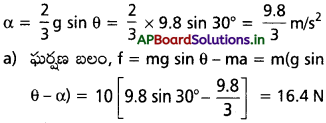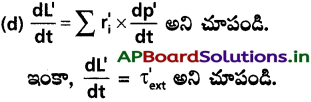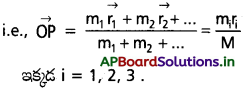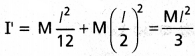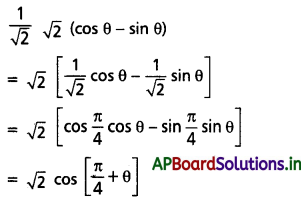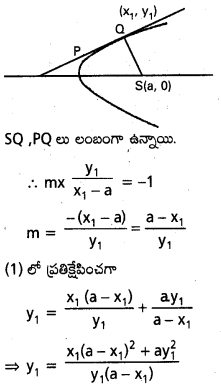Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం
అతిస్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
ఏ వ్యవస్థకైనా దాని ద్రవ్యరాశి కేంద్రం వద్ద ద్రవ్యరాశి తప్పక ఉండవలసిన అవసరం ఉందా?
జవాబు:
ద్రవ్యరాశి కేంద్రం వద్ద ద్రవ్యరాశి ఉండవలసిన అవసరం లేదు.
ఉదా : బోలుగోళం యొక్క కేంద్రం వద్ద ద్రవ్యరాశి ఉండదు.
ప్రశ్న 2.
ఒక అమ్మాయి బరువులున్న ఒక సంచీని ఒక చేతిలో పట్టుకొని నిలుచున్నది. ఇంకొక అమ్మాయి అంతే బరువు ఉన్న రెండు సంచులను తన రెండు చేతులతో పట్టుకొని నిలుచున్నది. ఆ అమ్మాయిల ద్రవ్యరాశి కేంద్ర స్థానాలలో మార్పులెలా ఉంటాయి?
జవాబు:
ఒక చేతిలో బరువున్న సంచీ గల అమ్మాయి, ద్రవ్యరాశి కేంద్ర స్థానం, సంచీ ఉన్నవైపుకు జరుగును. కాని రెండు చేతులలో ఒకే బరువులున్న సంచులు గల అమ్మాయి, ద్రవ్యరాశి కేంద్ర స్థానంలో మార్పు ఉండదు.
ప్రశ్న 3.
రెండు దృఢ వస్తువుల జఢత్వ భ్రామకాలు, వాటి సౌష్ఠవాక్షాల పరంగా సమానం. ఆ రెండింటిలో దేని గతిజశక్తి అధికంగా ఉంటుంది?
జవాబు:
వస్తువు భ్రమణ గతిజశక్తి E = \(\frac{1}{2}\)I ω² = \(\frac{1}{2}\frac{L^2}{l}\)
⇒ E ∝ \(\frac{l}{l}\) (∵ L = స్థిరం)
జడత్వ భ్రామకం తక్కువున్న వస్తువు, అధిక గతిజశక్తిని కలిగి ఉండును.
ప్రశ్న 4.
సైకిల్ చక్రాలకు కమ్మీలు (spokes) ఎందుకు అమర్చుతారు?
జవాబు:
సైకిల్ చక్రాలకు కమ్మీలు (spokes) కల్పితే, చక్రం ద్రవ్యరాశి రిమ్ వెంట ఎక్కువగా ఉండి, జడత్వ భ్రామకంను పెంచును. ఫలితంగా సైకిల్ ఏకరీతి చలనంను కలిగి ఉండును.
ప్రశ్న 5.
మడత బందుల (hinges) వద్ద బలాన్ని ప్రయోగించి ఒక తలుపును తెరవడం లేదా మూయడం సాధ్యం కాదు. ఎందువల్ల?
జవాబు:
మడత బందు వద్ద బలంను ప్రయోగిస్తే, బలరేఖా చర్య, మడత బందు భ్రమణ అక్షం ద్వారా పోవును. కావున మడత బందు వద్ద బలంను ప్రయోగించి ఒక తలుపును తెరవలేము లేక మూయలేము.

ప్రశ్న 6.
భుజం పొట్టిగా ఉన్న స్పానర్ (మరను త్రిప్పడానికి వాడే ఉపకరణం) కంటే భుజం పొడవుగా ఉన్న స్పానర్ను మనమెందుకు ఎక్కువగా ఎంచుకొంటాం?
జవాబు:
స్పానర్ ప్రయోగించు టార్క్ (T) = rF sin θ
భుజం పొడవుగా ఉన్న స్పానర్ (rL), భుజం పొట్టిగా ఉన్న స్పానర్ (rs) కన్నా ఎక్కువ. రెండింటి టార్క్లు సమానం కావటానికి, భుజం పొడవుగా ఉన్న స్పానర్కు, తక్కువ బలం, భుజం తక్కువ పొడవున్న స్పానర్కు ఎక్కువ బలం అవసరం. కావున భుజం పొడవుగా ఉన్న స్పానర్ను ఎంచుకుంటాం.
ప్రశ్న 7.
టేబుల్ తలంపై ఒక గుడ్డును బొంగరంవలె తిప్పి అది ఉడికినదీ లేనిదీ ఎలా నిర్ధారించగలం? [Mar. ’13]
జవాబు:
ఉడకని గుడ్డు కోణీయ ద్రవ్యవేగం Lr = Irωr
ఉడికిన గుడ్డు కోణీయ ద్రవ్యవేగం Lb = Ibωb
ఉడకని గుడ్డును తిప్పితే అపకేంద్రబలం వల్ల, ద్రవ కణాలను అంచువైపుకు నెట్టి, జడత్వ భ్రామకంను పెంచును.
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం L, స్థిరం అయిన ω ∝ \(\frac{1}{l}\) కావున ωb > ωr. ఉడికిన గుడ్డు కోణీయ వేగం,
ఉడకని గుడ్డు కోణీయ వేగం కన్నా ఎక్కువ.
∴ ఉడకని గుడ్డు అయితే తిప్పిన తరువాత త్వరగా ఆగుతుంది.
అదే ఉడికిన గుడ్డు అయితే తిప్పిన తరువాత నిదానంగా ఆగుతుంది.
ప్రశ్న 8.
ఒక హెలికాప్టర్కు ఎందుకు రెండు ప్రొపెల్లర్లు (propellers – ముందుకు నడిపే యంత్రం) తప్పక ఉండి తీరాలి?
జవాబు:
హెలికాఫ్టర్ ఒకే ఒక ప్రొపెల్లర్ కల్గి ఉంటే, కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమం వల్ల, హెలికాఫ్టర్ తనంతట తాను వ్యతిరేక దిశలో తిరుగును. కావున హెలికాప్టర్ను క్షేమంగా ముందుకు నడపాలంటే, రెండు ప్రొపెల్లర్లు తప్పనిసరి.
ప్రశ్న 9.
భూగోళ ధ్రువాల వద్ద ఉన్న మంచు పూర్తిగా కరిగిపోతే ఒకరోజు కాలవ్యవధి ఏ విధంగా ప్రభావిత మౌతుంది?
జవాబు:
భూమి తన ధృవ అక్షం వెంట భ్రమణం చెందుతుంది.
భూమి ధృవాల వద్ద మంచు పర్వతాలు ద్రవీభవనం చెందితే, భ్రమణాక్షం వెంట కేంద్రీకృతమైన ద్రవ్యరాశి వెలుపలకు నెట్టబడును. కావున జఢత్వ భ్రామకము పెరుగును.
బాహ్య టార్క్ పనిచేయకపోతే, L = I × ω = I(\(\frac{2 \pi}{T}\)) = స్థిరాంకము. I పెరుగుదలతో, T కూడ పెరుగును. i.e., రోజులో కాలం పెరుగుదల ఉండును.

ప్రశ్న 10.
కదిలే సైకిల్ను సులభంగా అటూ, ఇటూ ఒరగకుండా నిలుపవచ్చు. ఎందుకు ?
జవాబు:
సైకిల్ చలనంలో ఉన్నప్పుడు, కోణీయ ద్రవ్యవేగ నిత్యత్వ సూత్రం వల్ల, సైకిల్ను తేలికగా బ్యాలన్స్ చేయవచ్చును.
స్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
ఒక వ్యవస్థ ద్రవ్యరాశి కేంద్రం, గరిమనాభుల మధ్య భేదాలను గుర్తించండి. [Mar. ’14, ’13; May ;’13]
జవాబు:
| ద్రవ్యరాశి కేంద్రం | గరిమనాలి |
| 1. ద్రవ్యరాశి కేంద్రం అనేది కణాల వ్యవస్థ లేదా వస్తువు మొత్తం ద్రవ్యరాశి కేంద్రీకృతమయ్యేటట్లు ప్రవర్తించే బిందువు. | 1. కణ వ్యవస్థ యొక్క గరిమనాభి, ఆ కణాల భారాల యొక్క ఫలిత భారం పనిచేసే స్థానం. |
| 2. వస్తు ద్రవ్యరాశిని సూచిస్తుంది. | 2. ఇది వస్తు భారంను సూచిస్తుంది. |
| 3. సమరీతి గురుత్వక్షేత్రంలో ద్రవ్యరాశి కేంద్రం మరియు గరిమనాభులు ఏకీభవిస్తాయి. | 3. అసమరీతి క్షేత్రంలో గరిమనాభి, ద్రవ్యరాశి కేంద్రం ఏకీభవించవు. |
| 4. వస్తు ద్రవ్యరాశి కేంద్రము వస్తువు మొత్తం చలన స్వభావాన్ని వివరిస్తుంది. | 4. గురుత్వకేంద్రము వస్తు స్థిరత్వంను తెల్పును. |
ప్రశ్న 2.
బాహ్య బల ప్రభావానికి గురయిన ఒక కణవ్యవస్థ, ఆ బలం వ్యవస్థ ద్రవ్యరాశి కేంద్రం వద్ద ప్రయోగించినట్లుగా గమనంలో ఉంటుందని చూపండి.
జవాబు:
m1, m2, m3, ………… mn ద్రవ్యరాశులు గల n కణాల వ్యవస్థ భావిద్దాం. వాని స్థాన సదిశలు r1, r2, r3, ….. rn. ద్రవ్యరాశి కేంద్ర నిర్వచనం ప్రకారం

ఇక్కడ Fబాహ్య కణాల వ్యవస్థపై పనిచేయు బాహ్య బలాల మొత్తంను సూచించును.
బాహ్య బల ప్రభావానికి గురయిన ఒక కణ వ్యవస్థ, ఆ బలం వ్యవస్థ ద్రవ్యరాశి కేంద్రం వద్ద ప్రయోగించినట్లుగా గమనంలో ఉంటుంది.
ప్రశ్న 3.
భూమి – చంద్రుడు వ్యవస్థ ద్రవ్యరాశి కేంద్రం పరంగా సూర్యుని చుట్టూ దాని భ్రమణాలను వివరించండి.
జవాబు:
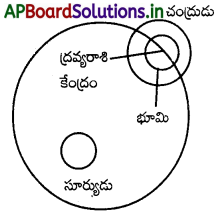
సౌర వ్యవస్థలో గ్రహాలు వేర్వేరు వేగాలతో, సంక్లిష్ట ద్విమితీయ చలనం కల్గి ఉండును. కాని గ్రహం ద్రవ్యరాశి కేంద్ర చలనం సరళం మరియు స్థానాంతరణము. భూమి మరియు చంద్రుని వ్యవస్థ భావిద్దాము.
భూమి సూర్యుని చుట్టూ దీర్ఘవృత్తాకార కక్ష్యలో తిరుగుచున్నదనుకొనుము. చంద్రుడు, భూమి చుట్టూ వృత్తాకార కక్ష్యలో తిరుగును. భూమి చంద్రుని యొక్క ద్రవ్యరాశి కేంద్రం ‘కూడా సూర్యుని చుట్టూ దీర్ఘ వృత్తాకార కక్ష్యలోనే తిరుగును.
భూమి, చంద్రుని యొక్క ద్రవ్యరాశి కేంద్రం కూడా సూర్యుని చుట్టూ దీర్ఘ వృత్తాకార కక్ష్యలోనే తిరుగును.
భూమికి, చంద్రునికి మధ్య గల గురుత్వాకర్షణ బలాలు, అంతర బలాలు అవుతాయి. కావున ఇవి ద్రవ్యరాశి కేంద్రాన్ని ప్రభావితం చేయవు. కాని సూర్యునికి, భూమికి మధ్య లేదా సూర్యునికి, చంద్రునికి మధ్య గల గురుత్వాకర్షణ బలాలు, బాహ్య బలాలవుతాయి. కావున ఇవి ద్రవ్యరాశి కేంద్రాన్ని ప్రభావితం చేస్తాయి.

ప్రశ్న 4.
సదిశాలబ్దాన్ని నిర్వచించండి. సదిశా లబ్ద ధర్మాలను రెండు ఉదాహరణలతో వివరించండి.
జవాబు:
సదిశ లబ్దము :
రెండు సదిశల యొక్క పరిమాణాన్ని, ఆ రెండు సదిశల మధ్య కోణము యొక్క sin విలువకు గల లబ్దాన్ని సదిశ లబ్దము అంటారు. దీనినే వజ్ర లబ్దం అంటారు.

ప్రశ్న 5.
కోణీయ వేగానికి నిర్వచనం తెలపండి. v = r ω రాబట్టండి.
జవాబు:
కోణీయ వేగం(ω) :
ఒక వస్తువు కోణీయ స్థానభ్రంశంలోని మార్పు రేటును కోణీయ వేగం అంటారు.
i.e., ω = \(\frac{d \theta}{dt}\)
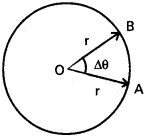
v = rω ఉత్పాదన :
ఒక దృఢ వస్తువు r వ్యాసార్థం ఉన్న వృత్త పరిధిపై V ఏకరీతి వడితో చలిస్తుందనుకొందాము. వస్తువు స్వల్పకాలం ∆t లో A నుండి B కు స్థానభ్రంశం చెందితే కేంద్రము వద్ద కోణము ∆θ. A నుండి Bకు రేఖీయ స్థానభ్రంశం ∆x.
వృత్త ధర్మం ప్రకారం, ∆x = r ∆θ

ప్రశ్న 6.
కోణీయ త్వరణాన్ని, టార్క్ను నిర్వచించండి. ఈ రెండు రాశుల మధ్య సంబంధాన్ని తెలిపే సమాసాన్ని రాబట్టండి.
జవాబు:
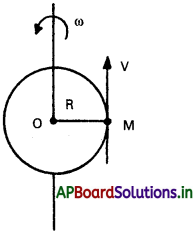
కోణీయ త్వరణము : కోణీయ వేగంలోని మార్పు రేటును కోణీయ త్వరణం అంటారు.
i.e., α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)
టార్క్ :
కోణీయ ద్రవ్య వేగంలోని మార్పు రేటును టార్క్ అంటారు.
కోణీయ త్వరణము మరియు టార్క్ మధ్య సంబంధము :
M ద్రవ్యరాశి ఉన్న దృఢ వస్తువు R. వ్యాసార్థం గల వృత్తపథంలో, ఆ కోణీయ వేగంతో స్థిర అక్షం వెంట భ్రమణం చెందుతుందని భావిద్దాం.
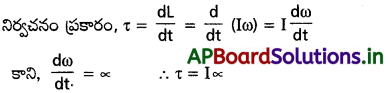
ప్రశ్న 7.
ఒక స్థిర అక్షం పరంగా భ్రమణం చేస్తున్న కణం గమన సమీకరణాలను రాయండి. జ. స్థిర అక్షం వెంట భ్రమణం చెందుతున్న కణం చలన సమీకరణాలు
జవాబు:

ప్రశ్న 8.
సమతలంపై నిశ్చల స్థితి నుంచి స్లిప్కకుండా దొర్లుతూ ఉన్న ఒక వస్తువు తుది వేగం, మొత్తం శక్తికి సమాసాలను రాబట్టండి.
జవాబు:
వాలు తలంపై కిందికి దొర్లుతున్న ఒక వస్తువు వేగ సమీకరణము :
M ద్రవ్యరాశి, R వ్యాసార్థం గల ఒక దృఢ వస్తువు, h ఎత్తు నుండి వాలుతలంపై క్రిందికి దొర్లుతున్నట్లు భావిద్దాం. వస్తువు తలం వెంట క్రిందకు v రేఖీయ వడితో చేరినట్లు తీసుకుందాము. దాని భ్రమణ వ్యాసార్థం K.
శక్తి నిత్యత్వ నియమం ప్రకారం, వాలు తలంపైన వస్తువు స్థితిజశక్తి (P.E) = వాలు తలం క్రింద వస్తువు యొక్క గతిజశక్తి (K.E).
h ఎత్తు గల వాలు తలం నుండి ఒక వస్తువు దొర్లుతూ ఉన్నప్పుడు, శక్తినిత్యత్వ నియమాన్ని అనువర్తింపవచ్చును.
i. e., వాలుతలంపైన P.E = స్థానాంతరణ K.E + భ్రమణ K.E
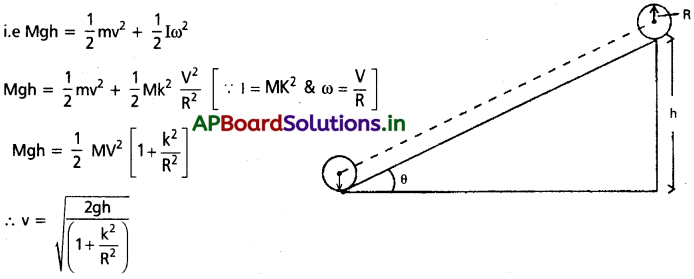
వాలు తలంపై క్రిందికి దొర్లుతున్న వస్తువు యొక్క మొత్తం శక్తికి సమాసం :
ఒక వస్తువు (గోళం) తలంపై దొర్లుతుందని భావిద్దాం. దాని చలనంను, ద్రవ్యరాశి కేంద్ర స్థానాంతరణ మరియు ద్రవ్యరాశి కేంద్రం ద్వారా పోవు అక్షం వెంట భ్రమణ చలనాల సంయోగముగా తీసుకోవచ్చును. మొత్తం శక్తి Eని క్రింది విధంగా వ్రాయవచ్చును.

దీర్ఘ సమాధాన ప్రశ్నలు
ప్రశ్న 1.
a) సమాంతరాక్షాల సిద్ధాంతాన్ని తెలిపి నిరూపించండి.

b) పలుచని వృత్తాకార బిళ్ళకు, దాని వ్యాసం పరంగా భ్రమణ వ్యాసార్థం k. పటంలో చూపినట్లు బిళ్ళను వ్యాసం AB వెంబడి రెండు ముక్కలుగా కత్తిరించినప్పుడు, AB పరంగా ప్రతి ముక్క భ్రమణ వ్యాసార్థం కనుక్కోండి.
జవాబు:
a) నిర్వచనం :
ఏదైనా అక్షం పరంగా దృఢ వస్తువు యొక్క జఢత్వ భ్రామకము, ఆ అక్షానికి సమాంతరంగా ఉంటూ ద్రవ్యరాశి కేంద్రం గుండా పోయే అక్షం పరంగా జఢత్వ భ్రామకము మరియు దృఢ వస్తు ద్రవ్యరాశి మరియు ఆ రెండు అక్షముల దూర వర్గముల లబ్దానికి సమానం.
i.e., I0 = Ig + Mr²
Ig = ‘O’ గుండా పోయే అక్షం పరంగా జఢత్వ భ్రామకము
M = ∑m = వస్తువు ద్రవ్యరాశి
r = అక్షముల మధ్య దూరము
Ig = ‘G’ గుండా పోయే అక్షం పరంగా జఢత్వ భ్రామకము
నిరూపణ :
వస్తువులో P వద్ద ‘m’ ద్రవ్యరాశి గల కణమును తీసుకొనుము. PO ను PG లను కలుపవలెను. OG ను కలుపగా వచ్చిన గీతకు లంబంగా P నుండి రేఖ PQను గీయవలెను.
‘O’ గుండా గల అక్షం పరంగా ‘P’ వద్ద కణం జఢత్వ భ్రామకం = m × OP².
‘O’ గుండా గల అక్షం పరంగా కణం యొక్క జఢత్వ భ్రామకం = m × PG².
‘G’ గుండా గల అక్షం పరంగా కణం యొక్క జఢత్వ భ్రామకం = Ig = ∑m.PG²
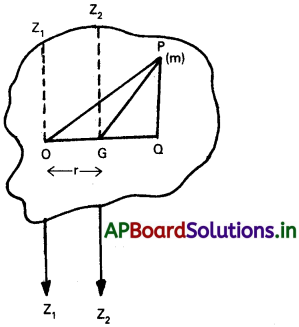
OPQ త్రిభుజంలో OP² = OQ² + PQ²
OP² = (OG² + GQ²)+ PQ² [∵ OQ = OG + GQ]
OP² = OG² + GQ² + 2OG. GQ + PQ²
OP² = OG² + GP² + 2OG.GQ [∵ GQ2 + PQ² = GP²]
కానీ I0 = ∑m OP²
I0 = Σm (OG² + GP² + 2 OG. GQ)
I0 = ∑m (OG² + GP² + 2 OG. GQ)
I0 = Σm.OG² +Σm. Gp² + Σm. 2OG. GQ
I0 = Mr² + IG + Σm. 2.OG. GQ
ఇక్కడ Σm = M, OG = r
IG = Σm PG²
∴ I0 = IG + Mr² + 2 OG. Σm. GQ
కాని ద్రవ్యరాశి కేంద్రం పరంగా వస్తువులోని అన్ని కణాల గురుత్వాకర్షణ బలాల భ్రామకాల బీజీయాల మొత్తం శూన్యం.
కావున Σm. GQ = 0
∴ I0 = IG + Mr²
(b) పలుచని వృత్తాకార బిళ్ళ (డిస్క్) వ్యాసం, AB వెంట భ్రమణ వ్యాసార్థం
K = \(\sqrt{\frac{1}{M}}\)
ఇక్కడ M = బిళ్ళ ద్రవ్యరాశి; I = బిళ్ళ జఢత్వ భ్రామకము
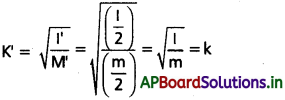
AB వెంట బిళ్ళను రెండు సగభాగాలుగా కత్తిరించిన, ఒక్కొక్క ముక్క ద్రవ్యరాశి M’ = \(\frac{M}{2}\) మరియు ఒక్కొక్క ముక్క
జఢత్వ భ్రామకము, I’ = \(\frac{1}{2}\)
ప్రతి ముక్క భ్రమణ వ్యాసార్థం,
ప్రశ్న 2.
a) లంబాక్షాల సిద్ధాంతాన్ని తెలిపి నిరూపించండి.
అధ్యాయం కణాల వ్యవస్థలు, భ్రమణ గమనం
b) ఒక సన్నని వృత్తాకార కంకణం, ఒక పలుచని చదునైన వృత్తాకార బిళ్ళలు సమాన ద్రవ్యరాశి, వాటి వాటి వ్యాసాల పరంగా సమాన జఢత్వ భ్రామకాన్ని కలిగి ఉంటే వాటి వ్యాసార్థాల నిష్పత్తి కనుక్కోండి.
జవాబు:
a) నిర్వచనం :
ఒక సమతల పటలానికి లంబంగా ఒక బిందువు గుండా పోయే అక్షంపరంగా దాని జఢత్వ భ్రామకము, అదే బిందువు గుండా పోతూ పరస్పరం లంబంగా ఉన్న అక్షముల పరంగా ఉన్న జఢత్వ భ్రామకాల మొత్తంనకు సమానము.
i.e., Iz = Ix + Iy
ఇక్కడ Iz = z – అక్షం పరంగా జఢత్వ భ్రామకము
Ix = X – అక్షం పరంగా జఢత్వ భ్రామకము
Iy = Y – అక్షం పరంగా జఢత్వ భ్రామకము
నిరూపణ :
‘m’ ద్రవ్యరాశి గల కణము P వద్ద XOY తలంలో ఉన్నదనుకొనుము.
దీని నిరూపకాలు (x, y). ఈ కణం Y – అక్షం నుండి ‘x’ లంబ దూరంలో, X – అక్షం నుండి ‘y’ లంబదూరంలో, Z – అక్షం నుండి ‘r’ లంబ దూరంలో ఉన్నదనుకొనుము.
Y – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము mx²
Y – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = Iy = Σmx² ……………. (1)
X – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = my²
X – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = Ix = Σmy² ……………. (2)
Z – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = mr²
Z – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = Iz = Σmz² ……………. (3)
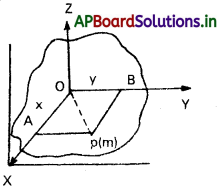
పటం నుండి, r² = x² + y²
Iz = Σmr² = Σm (x² + y²) = Σm x² + Σmy²
(1), (2) సమీకరణముల నుండి Iy = Imx²; Ly = Σmy²
Iz = Iy + Ix
∴ Iz = Iy + Ix ∴ లంబాక్ష సిద్ధాంతం నిరూపించబడింది.

ప్రశ్న 3.
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని తెలిపి నిరూపించండి. ఈ నియమాన్ని ఉదాహరణలతో వివరించండి.
జవాబు:
నిర్వచనం :
ఒక వ్యవస్థపై పనిచేసే బాహ్య టార్క్ శూన్యమైన, ఆ వ్యవస్థ కోణీయ ద్రవ్యవేగం స్థిరంగా ఉంటుంది.
L = Iω = స్థిరాంకము (లేక) I1 ω1 = I2 ω2
ఒక వస్తువు యొక్క జఢత్వ భ్రామకం (I) తగ్గిన, ఆ వస్తువు యొక్క కోణీయ వేగం (ω) పెరుగును.
నిరూపణ :
కోణీయ ద్రవ్య వేగంలోని మార్పు రేటును టార్క్ అంటారు.

ఉదా :
1) ఒక వ్యక్తి భ్రమణాలు చేయుచున్న పలకపై నిలుచుని, అతని చేతులు చాచి (డంబెల్స్) సమాన బరువులను పట్టుకొని ఉన్నాడనుకొనుము. అతడు పలకపై భ్రమణాలు స్థిర కోణీయ వేగంతో చేయుచున్నాడు. చేతులు చాచినపుడు జఢత్వ భ్రామకం I1, కోణీయ వేగం ω1. అతడు తన చేతులను ముడుచుకొన్నచో (బరువుల నుండి భ్రమణాక్షానికి గల దూరం తగ్గి) జఢత్వ భ్రామకం (I2) తగ్గి, దానికి అనుగుణంగా వ్యక్తి యొక్క కోణీయ వేగము (ω2) పెరుగును.
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం,
I1 ω1 = I2 ω2
కాని I1 > I2
∴ ω1 < ω2
నాట్యము చేయువారు, స్కేటర్లు, నీటిలోనికి డైవ్ చేయువారు కోణీయ ద్రవ్యవేగ నియమం ఉపయోగించుకొని స్థిరత్వమును పొందుతారు.
ఉదా – 2 :
నిలువు అక్షంపై స్వేచ్ఛగా భ్రమణాలు చేయుచున్న గుండ్రని బల్లపై ఒక పరిశీలకుడు నిశ్చలంగా కూర్చొని ఉన్నాడు. అతని చేతిలో నిలువు అక్షంపై స్వేచ్ఛగా సవ్యదిశలో భ్రమణాలు చేయుచున్న సైకిలు చక్రం చట్రం ఉంది. ఇప్పుడు అతడు చట్రాన్ని తలక్రిందులుగా త్రిప్పితే చక్రం ఈసారి అపసవ్య దిశలో తిరుగుతూ ఉంటుంది. బల్ల, వ్యక్తి, చక్రం, ఒకే వ్యవస్థ కాబట్టి దీనికి కోణీయ ద్రవ్యవేగ నిత్యత్వం వర్తిస్తుంది. కోణీయ ద్రవ్యవేగం స్థిరంగా ఉంచేందుకు బల్ల సవ్య దిశలో తిరుగుతుంది. బల్లను తిరిగా ఆపాలంటే చక్రాన్ని తలక్రిందులుగా చేసి తొలి దశలో తిరిగేటట్లు చేయాలి.
లెక్కలు (Problems)
ప్రశ్న 1.
a. (b × c) పరిమాణం a, b, c సదిశలు భుజాలుగా గల సమానాంతర చతుర్భుజ ఘనం (parallele-piped) ఘనపరిమాణానికి సమానం అని చూపండి.
సాధన:
ఒక దీర్ఘఘనాకారం మూడు సదిశలను ఏర్పరు స్తుందని తీసుకుందాము.
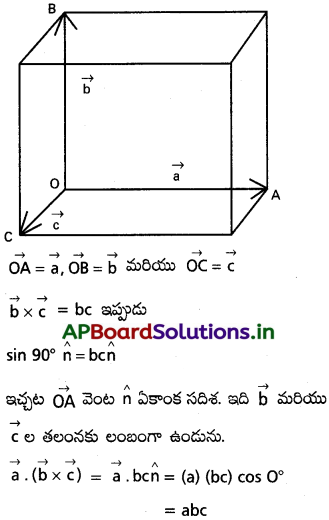
ఇది దీర్ఘఘనాకారం ఘనపరిమాణ పరిమాణంనకు సమానం.

ప్రశ్న 2.
3kg ద్రవ్యరాశి, 40 cm వ్యాసార్ధం ఉన్న ఒక బోలు స్థూపం చుట్టూ దాదాపు ద్రవ్యరాశి లేని ఒక తాడు చుట్టారు. 30 N బలంతో తాడును లాగితే స్థూపం ఎంత కోణీయ త్వరణాన్ని పొందుతుంది? తాడు రేఖీయ త్వరణం ఎంత అవుతుంది? తాడు స్థూపంపై జారదు అని భావించండి.
సాధన:
ఇచ్చినవి M = 3kg, R = 40 cm = 0.4 m
బోలు స్థూపం అక్షం వెంట జఢత్వ భ్రామకం
I = MR² = 3(0.4)² = 0.48 kgm²
ప్రయోగించిన బలం F = 30 N
∴ టార్క్, τ = F × R= 30 × 0.4 = 12 N – m
కోణీయ స్థానభ్రంశం α ఏర్పడితే, అప్పుడు τ = Iα
α = \(\frac{\tau}{1}=\frac{12}{0.48}\) = 25 rads-2
రేఖీయ త్వరణం, a = Rα = 0.48 × 25 = 10 m/s².
ప్రశ్న 3.
క్షితిజ తలంలో భ్రమణం చెందే తిరుగుడు బల్లపై దాని కేంద్రం నుంచి 10 cm దూరంలో ఒక నాణాన్ని ఉంచారు. తిరుగుడు బల్ల, నాణాల మధ్య స్థితిక ఘర్షణ గుణకం 0.8 అయితే, నాణెం బల్లపై జారడం మొదలు పెట్టడానికి తిరుగుడు బల్ల భ్రమణ పౌనఃపున్యం ఎంత ఉండాలి?
సాధన:
ఇచ్చినవి, వ్యాసార్థం r = 10cm 0.1m;
µs = 0.8; F = µmg
mrω² = µmg
rω² = μg

n = 1.409 × 60 = 84.54 rpm = 84.54 rpm
ప్రశ్న 4.
ఒక మీటర్ స్కేలుపై 1cm, 2cm, 3cm…… 100cm ల గుర్తుల వద్ద వరుసగా 1g, 2g, 3g, ….100g ద్రవ్యరాశులు గల కణాలను ఉంచారు. మీటర్ స్కేలు మధ్యలంబరేఖ పరంగా ఈ వ్యవస్థ జఢత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
అన్ని కణాల ద్రవ్యరాశులను కూడగా,
M 5050g = 5.050 kg = 5.1 kg
మరియు L = 1m
స్కేలు యొక్క జఢత్వ భ్రామకం \(\frac{Ml^2}{12}= \frac{5.1\times1^2}{12}\)
= 0.425kg m²
= 0.43kg -m²
ప్రశ్న 5.
10 cm భుజం కలిగిన ఒక సమబాహు త్రిభుజ శీర్షాల వద్ద ప్రతిది 100g ద్రవ్యరాశి ఉన్న మూడు కణాలను ఉంచారు. ఆ త్రిభుజ కేంద్రాభం ద్వారా పోతూ, త్రిభుజ తలానికి లంబంగా ఉన్న అక్షం పరంగా ఈ వ్యవస్థ జఢత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
m = 100 g = 100 × 10-3 kg
భుజం a = 10 cm
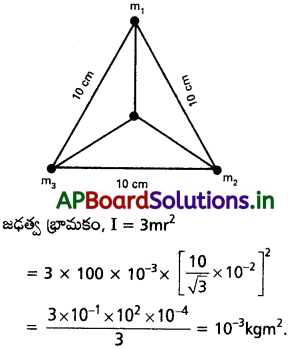
ప్రశ్న 6.
10 cm భుజం ఉన్న చతురస్ర శీర్షాల వద్ద ప్రతిది 100g ద్రవ్యరాశి ఉన్న నాలుగు కణాలను ఉంచారు. చతురస్రం మధ్య బిందువు ద్వారా పోతూ, దాని తలానికి లంబంగా ఉన్న అక్షం పరంగా వ్యవస్థ జఢత్వ భ్రామకాన్ని కనుక్కోండి. వ్యవస్థ భ్రమణ వ్యాసార్థాన్ని కనుక్కోండి.
సాధన:
ద్రవ్యరాశి m = 100g
= 100 × 10-3kg
m = 4m = 400 × 10-3kg
వ్యాసార్థం = 10cm
= 10 × 10-2m
జఢత్వ భ్రామకం
I = mr²
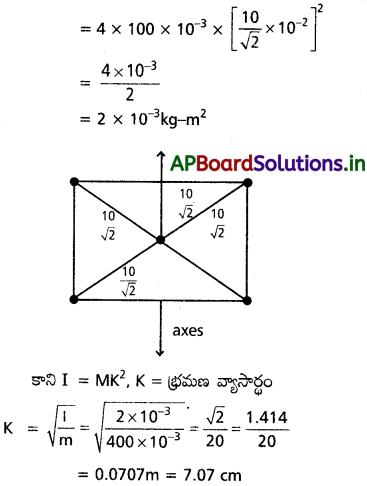
ప్రశ్న 7.
1 kg ద్రవ్యరాశి, 20 cm వ్యాసార్థం ఉన్న రెండు ఏకరీతి వృత్తాకార దిమ్మెలు ఒకదానినొకటి స్పృశించుకునేటట్లుగా స్పర్శారేఖ స్పర్శా బిందువు ద్వారా పోయేటట్లు అమర్చారు. స్పర్శా బిందువు ద్వారా పోయే స్పర్శారేఖ పరంగా ఈ వ్యవస్థ జఢత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
ద్రవ్యరాశి m = 1kg
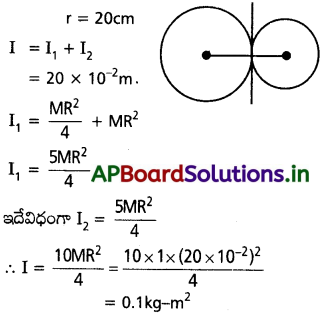
ప్రశ్న 8.
2a వ్యాసం, ‘m’ ద్రవ్యరాశి ఉన్న నాలుగు గోళాల కేంద్రాలను b భుజంగా ఉన్న ఒక చతురస్ర నాలుగు శీర్షాల వద్ద ఉంచారు. ఒకే భుజం భ్రమణ అక్షంగా ఈ వ్యవస్థ జఢత్వ భ్రామకాన్ని లెక్కించండి.
సాధన:
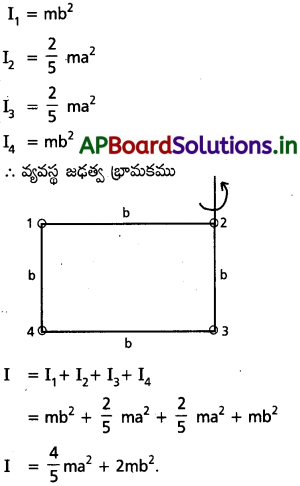
ప్రశ్న 9.
ఒక యంత్రం భ్రమణ భాగానికి (rotor) 200 rad s-1 ఏకరీతి కోణీయ వడిని సమకూర్చడానికి యంత్రం 180 Nm టార్క్ను అందించవలసి ఉంది. యంత్రానికి అవసరమయ్యే సామర్థ్యం ఎంత? (గమనిక : మర్షణ లేనప్పుడు సమకోణీయ వేగం కలిగి ఉండటమంటే టార్క్ శూన్యం అని అర్థం. వాస్తవానికి ప్రయోగించిన టార్క్ ఘర్షణ వల్ల కలిగే టార్క్ను వ్యతిరేకిస్తుంది) యంత్రం 100% దక్షత కలిగి ఉన్నదని భావించండి.
సాధన:
ఇచ్చినవి ω = 200 rad/s
టార్క్, τ = 180 N – m, సామర్థ్యం p = ?
p = τ ω
∴ p = 180 × 200
= 3600 watt
= 36 kw.

ప్రశ్న 10.
ఒక మీటరు స్కేలును దాని కేంద్రం వద్ద కత్తి మొన ఉంచి తుల్య స్థితిలో నిలిపారు. ఒక్కొక్కటి 5g ద్రవ్యరాశి ఉన్న రెండు నాణాలను ఒకదానిపై ఒకటి అమర్చేటట్లుగా స్కేలుపై 12.0 cm విభాగం వద్ద ఉంచారు. అప్పుడు కత్తిమొన 45.0 cm విభాగం వద్ద ఉన్నప్పుడు స్కేలు తుల్య స్థితికి వచ్చింది. మీటర్ స్కేలు ద్రవ్యరాశి ఎంత?
సాధన:
ఒక మీటర్ స్టిక్ ద్రవ్యరాశి M, L = 50 cm
గుర్తు వద్ద కేంద్రీకరించినట్లు భావిద్దాం.
స్టిక్, G’ = 45 cm గుర్తు వద్ద సమతాస్థితిలో ఉంటే
10g (45-12) = Mg(50 – 45)
10 g × 33 = mg × 5
M = \(\frac{10\times33}{5}\) = 66 gram.
ప్రశ్న 11.
వృత్త పరిధిపై ఏదో ఒక బిందువు ద్వారా పోతూ, తలానికి లంబంగా ఉన్న అక్షం పరంగా 60 rpm వడితో భ్రమణం చెందే ఒక వృత్తాకార దిమ్మె గతిజశక్తిని కనుక్కోండి. దిమ్మె ద్రవ్యరాశి 5kg, వ్యాసార్థం 1m.
సాధన:
ఇచ్చట M = 5kg; R = 1m;
ω
0 = 2π × \(\frac{N}{t}\)
= 2π × \(\frac{60}{60}\)rad/s = 2π rad/s
వృత్తాకార పరిధిపై ఏదైనా బిందువు గుండాపోవు, సమాంతర అక్షం పరంగా బిళ్ళ జఢత్వ భ్రామకం

ప్రశ్న 12.
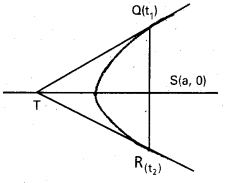
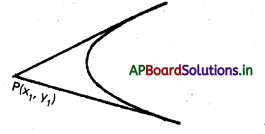
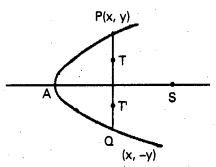
ఒక్కొక్కటి m ద్రవ్యరాశి గల రెండు కణాలు, వ్యతిరేక దిశలో, d దూరంలో ఉన్న సమాంతర రేఖలపై U వడితో గమనంలో ఉన్నాయి. ఏ బిందువు పరంగా కోణీయ ద్రవ్యవేగాన్ని కొలిచినా, ఈ ద్వికణ వ్యవస్థ కోణీయ ద్రవ్యవేగ సదిశ సమానమని చూపండి.
సాధన:
ఇచ్చినవి m1 = m2 = m;
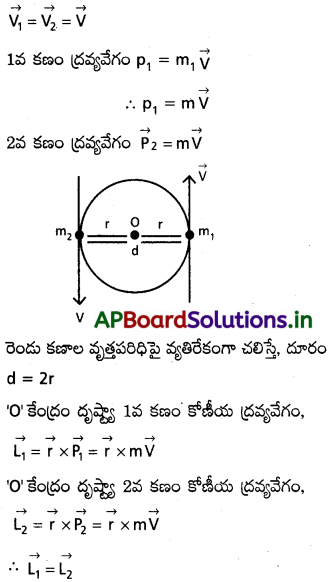
ప్రశ్న 13.
నిమిషానికి 300 భ్రమణాలు చేసే ఒక గతిపాలక చక్రం (fly wheel) జఢత్వ భ్రామకం 0.3 kgm² 20 సెకన్లలో దీన్ని నిశ్చల స్థితికి తీసుకు రావడానికి అవసరమైన టార్ను కనుక్కోండి.
సాధన:


ప్రశ్న 14.
ఒక గతిపాలకచక్రం (fly wheel) పై 100J పని జరిగినప్పుడు దాని కోణీయవేగం 60 rpm నుంచి180 rpm కి పెరిగింది. చక్రం జఢత్వ భ్రామకాన్ని లెక్కించండి.
సాధన:
తొలి పౌనఃపున్యము,
n1 = \(\frac{60}{60}\) = 1Hz
తొలి కోణీయ వేగం ω1 = 2π n1
= 2π rad/sec
తుది పౌనఃపున్యం,
n2 = \(\frac{180}{60}\) = 3Hz
తుది కోణీయ వేగం
ω2 = 2π n2 = 2π × 3 = 6π rad/sec
జరిగిన పని = 100 j
పని-శక్తి సిద్ధాంతం ప్రకారము,
జరిగిన పని = K.E. లో మార్పు

అదనపు లెక్కలు (Additional Problems)
ప్రశ్న 1.
ఏకరీతి సాంద్రత ఉన్న (i) గోళం, (ii) స్థూపం, (iii) కంకణం, (iv) ఘనాల ద్రవ్యరాశి కేంద్ర స్థానాన్ని గుర్తించండి. వస్తువు ద్రవ్యరాశి కేంద్రం తప్పక ఆ వస్తువులో ఉండి తీరాలా?
జవాబు:
అన్ని నాలుగు సందర్భాలలో, ద్రవ్యరాశి సాంద్రత ఏకరీతిగా ఉండును. జ్యామితీయ కేంద్రాల వద్ద ద్రవ్యరాశి కేంద్రం ఉంటుంది.
వస్తువుపై ద్రవ్యరాశి కేంద్రం ఉండాల్సిన అవసరం లేదు. ఉదాహరణకు, వృత్తాకార రింగ్ సందర్భంలో రింగ్ కేంద్రం వద్ద ద్రవ్యరాశి లేకపోయినా, ద్రవ్యరాశి కేంద్రం ఉంటుంది.

ప్రశ్న 2.
HCl అణువులో రెండు పరమాణువుల కేంద్రకాల మధ్య దూరం దాదాపు 1.27Å (1 Å = 10 10m). ఈ అణువు ద్రవ్యరాశి కేంద్ర స్థానాన్ని ఉజ్జాయింపుగా కనుక్కోండి. హైడ్రోజన్ పరమాణువుతో పోలిస్తే క్లోరీన్ పరమాణువు ద్రవ్యరాశి సుమారు 35.5 రెట్లు ఉంటుంది. పరమాణు ద్రవ్యరాశి అంతా కేంద్రకం వద్దనే కేంద్రీకృతమవుతుందని ఊహించండి.
సాధన:
H పరమాణువు ద్రవ్యరాశి = m యూనిట్
Cl పరమాణువు ద్రవ్యరాశి = 35.5 m యూనిట్స్
H పరమాణువు నుండి xÅ దూరం వద్ద c.mను తీసుకుందాము.
∴ Cl పరమాణువు నుండి c.m దూరం = (1.27 – x)Å
మూలబిందువు వద్ద c.m తీసుకుంటే, అప్పుడు
mx + (1.27 – x) 55.5m = 0
mx = (1.27 – x) 35.5m.
c.mకు కుడివైపున Cl పరమాణువు ధనాత్మక గుర్తును, ఎడమవైపున ఋణగుర్తును సూచించును. ఋణగుర్తును వదిలెస్తే,
x + 35.5 x = 1.27 x 35.5
36.5 x = 45.085
x = \(\frac{45.085}{36.5}\)
= 1.235
x = 1.235 Å
H మరియు cl పరమాణువుల కేంద్రాలను కలుపు రేఖపై H నుండి 1.235 Å వద్ద c.m ఉంటుంది.
ప్రశ్న 3.
నున్నని క్షితిజ సమాంతర నేలపై V వడితో సమరీతి గమనం కలిగిన ఒక ట్రాలీ (trolley – చక్రాలున్న పొడవైన బండి) మీద ఒక చివర ఒక బాలుడు నిశ్చలంగా కూర్చుని ఉన్నాడు. బాలుడు లేచి ట్రాలీపై ఏ విధంగా పరిగెత్తినా ట్రాలీ – బాలుడు వ్యవస్థ ద్రవ్యరాశి కేంద్రం వడి ఎంత?
సాధన:
పిల్లవాడు ట్రాలీపై లేచి పరుగెత్తితే, వ్యవస్థ (ట్రాలీ + పిల్లవాడు) ద్రవ్యరాశి కేంద్రం వడి మారదు. బలాలు అంతర్గత బలాలే. వ్యవస్థపై బాహ్యబలం పని చేయదు. వ్యవస్థ వేగంలో మార్పు ఉండదు.
ప్రశ్న 4.
సదిశలు a, bలు భుజాలుగా కలిగి ఉన్న త్రిభుజ వైశాల్యం a × b పరిమాణంలో సగం ఉంటుందని చూపండి.
సాధన:
\(\overrightarrow{OP}\) మరియు \(\overrightarrow{O Q}\) లు \(\overrightarrow{a}\) మరియు \(\overrightarrow{b}\) ను సూచించునట్లు తీసుకుందాం.
∠POQ = θ సమాంతర చతుర్భుజం
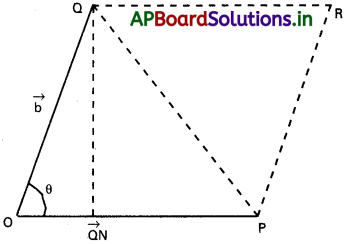
OPRQ ను పూర్తిచేద్దాం.
PQ ను కలుపుదాం. ON ⊥ OP

ప్రశ్న 5.
a. (b × c) పరిమాణం a, b, cసదిశలు భుజాలుగా గల సమానాంతర చతుర్భుజ ఘనం (parallele- piped) ఘన పరిమాణానికి సమానం అని చూపండి.
సాధన:
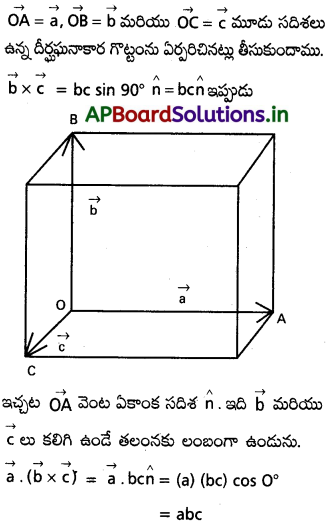
దీర్ఘఘనాకార గొట్టం ఘనపరిమాణం, పరిమాణంనకు సమానము.
ప్రశ్న 6.
ఒక కణం కోణీయ ద్రవ్యవేగం 1 x, y, z అక్షాల వెంబడి అంశాలను కనుక్కోండి. కణం స్థాన సదిశ r అంశాలు x, y, z లు. రేఖీయ ద్రవ్యవేగం p అంశాలు px py, pz ఒకవేళ కణం కేవలం x−y తలంలోనే గమనంలో ఉంటే కోణీయ ద్రవ్యవేగం z-అంశాన్ని మాత్రమే కలిగి ఉంటుందని చూపండి.
సాధన:
3D చలనంలో, స్థానభ్రంశ సదిశ \(\overrightarrow{r}\) మరియు రేఖీయ ద్రవ్యవేగ సదిశ \(\overrightarrow{p}\) ను క్రింది దీర్ఘచతురస్ర అంశాలుగా వ్రాయవచ్చును.

Lz = xpy – ypx·
∴ కణం x – y తలంలో చలించును.
కోణీయ ద్రవ్యవేగం మాత్రం ఒకే z–అంశాన్ని కలిగి ఉండును.
ప్రశ్న 7.
ఒక్కొక్కటి m ద్రవ్యరాశి గల రెండు కణాలు, వ్యతిరేక దిశలో d దూరంలో ఉన్న సమాంతర రేఖలపై V వడితో గమనంలో ఉన్నాయి. ఏ బిందువు పరంగా కోణీయ ద్రవ్యవేగాన్ని కొలిచినా, ఈ ద్వికరణ వ్యవస్థ కోణీయ ద్రవ్యవేగ సదిశ సమానమని చూపండి.
సాధన:
x1 y1 పై ఏదైనా బిందువు A వెంట రెండు కణాల వ్యవస్థ కోణీయ ద్రవ్యవేగం సదిశ,
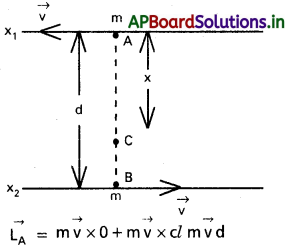
x2y2 పై ఏదైనా బిందువు B వెంట రెండు కణాల వ్యవస్థ కోణీయ ద్రవ్యవేగం సదిశ,
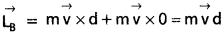
AC = x అయ్యేటట్లు, ABపై మరియొక బిందువు ఁను భావిద్దాం.
∴ c వెంట రెండు కణాల వ్యవస్థ కోణీయ ద్రవ్యవేగం సదిశ
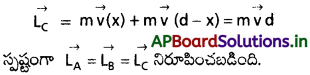
ప్రశ్న 8.
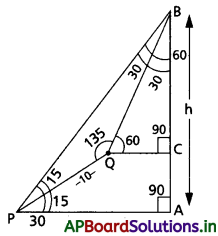
ఒక అసమరీతి, Wభారం ఉన్న కడ్డీని ఉపేక్షించ దగ్గ ద్రవ్యరాశి ఉన్న రెండు దారాలతో, పటంలో చూపినట్లు నిశ్చల స్థితిలో ఉండేటట్లు వేలాడ దీశారు. క్షితిజ లంబరేఖతో దారాలు చేసే కోణాలు వరుసగా 36.99, 53.1°. కడ్డీ పొడవు 2 m. కడ్డీ ఎడమ చివర నుంచి గరిమనాభి ఉండే దూరం dని లెక్కించండి.
సాధన:
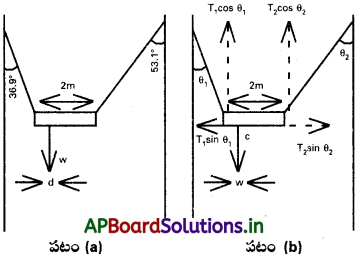
పటం నుండి స్పష్టంగా,
θ1 = 36.9°, θ2 = 53.1°
రెండు తీగలలో తన్యతలు T1, T2
తీగ క్షితిజ సమాంతరంగా సమతాస్థితిలో ఉంటే
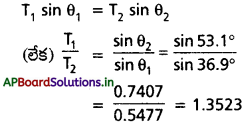
కడ్డీ ఎడమ చివరి నుండి d దూరంలో ద్రవ్యరాశి కేంద్రం d తీసుకుందాము.
c వెంట భ్రమణ సమతాస్థితిలో,
T1 cos θ1 Xd = T2 cos θ2 (2 – d)
T1 cos 36.9° × d = T2 cos 53.1° (2 – d)
T1 × 0.8366 d = T2 × 0.6718 (2 – d)
T1 = 1.3523 T2 ను ఉంచి సాధించగా
d = 0.745 m.

ప్రశ్న 9.
ఒక కారు 1800 kg బరువుంది. ముందు వెనకాల ఇరుసుల మధ్య దూరం 1.8 m. కారు గరిమనాభి, ముందు ఇరుసు వెనక 1.05 m దూరంలో ఉంది. సమతలంగా ఉన్న భూమి వల్ల ముందు వెనక గల చక్రాలొక్కక్కటి పై ప్రయోగించే బలాన్ని కనుక్కోండి.
సాధన:
m = 1800 kg
ముందు మరియు వెనుక యాక్సిల్స్ మధ్యదూరం = 1.8m
ముందు యాక్సిల్ వెనుక గురుత్వాకేంద్రం (C) దూరం = 1.05 m
ముందు మరియు వెనుక యాక్సిల్స్పై సమాంతరంగా భూమి ప్రయోగించు బలాలు R1 మరియు R2. స్పష్టంగా పటం నుండి
R1 + R2 = mg = 1800 × 9.8
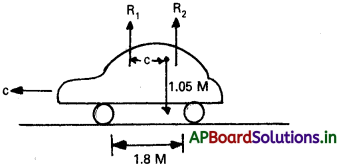
C వెంట భ్రమణ సమతాస్థితిలో

ప్రశ్న 10.
(a) ఘన గోళానికి స్పర్శరేఖ పరంగా దాని జఢత్వ భ్రామకాన్ని కనుక్కోండి. గోళం వ్యాసంపరంగా జఢత్వ భ్రామకం 2 MR²/5 గా ఇచ్చారు. M గోళం ద్రవ్యరాశి, R దాని వ్యాసార్థం.
(b) M ద్రవ్యరాశి, వ్యాసార్థం ఉన్న వృత్తాకార దిమ్మె జఢత్వ భ్రామకం, వ్యాసం పరంగా MR²/4, దిమ్మె ఒక అంచునుంచి పోతూ దిమ్మె తలానికి లంబంగా ఉండే అక్షం పరంగా జఢత్వ భ్రామకాన్ని కనుగొనుము.
సాధన:
a) ఏదైనా వ్యాసం వెంట గోళం జఢత్వ భ్రామకం = \(\frac{2}{5}\)MR²
సమాంతర అక్ష సిద్ధాంతంను అనువర్తింపచేయగా,
గోళం స్పర్శరేఖ వెంట గోళం జఢత్వ భ్రామకం
= \(\frac{2}{5}\)MR² + M(R)² = \(\frac{7}{5}\)MR²
b) ఏదైనా వ్యాసం వెంట డిస్క్ జఢత్వ భ్రామకము = \(\frac{1}{4}\)MR².
i) లంబాక్ష సిద్ధాంతం ఉపయోగించి, డిస్క్ కేంద్రం గుండాపోతూ తలంనకు లంబంగా పోవు అక్షం పరంగా జఢత్వ భ్రామకం
= 2 × \(\frac{1}{4}\) MR²
= \(\frac{1}{2}\)MR².
ii) సమాంతర అక్ష సిద్ధాంతం ఉపయోగించి, డిస్ అంచుపై ఉన్న బిందువు గుండాపోతూ, డిస్కు లంబంగా ఉన్న అక్షంపరంగా జఢత్వ భ్రామకం
= \(\frac{1}{2}\) MR² + MR² = \(\frac{3}{2}\)MR².
ప్రశ్న 11.
సమాన ద్రవ్యరాశి, సమాన వ్యాసార్థం ఉన్న ఒక బోలు స్తూపం, ఒక ఘనగోళంపై సమాన పరిమాణం ఉన్న టార్క్ ను ప్రయోగించారు. స్తూపం దాని సౌష్టవాక్షం పరంగా స్వేచ్ఛగా భ్రమణం చేయగలుగుతుంది. గోళం దాని కేంద్రం ద్వారా పోయే అక్షం పరంగా స్వేచ్ఛగా భ్రమణం చేయగలుగుతుంది. వీటిల్లో, ఇచ్చిన కాల వ్యవధిలో, ఏది అధిక కోణీయ వేగాన్ని పొందుతుంది?
సాధన:
బోలు స్థూపం మరియు ఘనస్థూపం ద్రవ్యరాశి M మరియు వ్యాసార్థము R.
సౌష్ఠవ అక్షం వెంట బోలు స్థూపం జఢత్వ భ్రామకం, I1 = MR²
కేంద్రం ద్వారా పోవు అక్షం పరంగా ఘనగోళం జఢత్వ భ్రామకం, I2 = \(\frac{2}{5}\)MR²
ప్రయోగించిన టార్క్, τ = I1 α1 = I2 α2
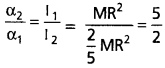
α2 > α1
ω = ω0 +αt నుండి, ω0 మరియు tలను కనుగొంటే, ω2 > ω1 i.e., ఘనగోళం కోణీయ వడి, బోలు స్థూపం కోణీయ వడి కన్నా ఎక్కువ.
ప్రశ్న 12.
20 kg ద్రవ్యరాశి ఉన్న ఒక ఘన స్థూపం దాని అక్షంపరంగా 100 rad s-1 కోణీయ వడితో భ్రమణాలు చేస్తుంది. స్థూపం వ్యాసార్థం 0.25m. స్తూపం గతిజశక్తి ఎంత ? స్థూపం అక్షంపరంగా కోణీయ ద్రవ్యవేగ పరిమాణం ఎంత?
సాధన:
M = 20 kg, R = 0.25 m, w = 100 g-1
ఘనస్థూపం జఢత్వ భ్రామకము

ప్రశ్న 13.
(a) ఒక తిరుగుడు బల్ల కేంద్రం వద్ద ఒక బాలుడు తన చేతులను బయటకు చాచి నిలబడి ఉన్నాడు. తిరుగుడు బల్ల 40 భ్రమణాలు / నిమిషం కోణీయ వడితో భ్రమణం చేసేట్లు దాన్ని తిప్పారు. ఇలా తిరుగుతున్న బల్ల మీద బాలుడు తన చేతులను అతని జఢత్వ భ్రామకం తొలి విలువకు 2/5 వంతులు అయ్యేట్లు ముడిస్తే అతని కోణీయ వడి ఎంత? తిరుగుడు బల్ల ఘర్షణ లేకుండా భ్రమణాలు చేస్తుందని భావించండి.
సాధన:
తొలి కోణీయ వడి, ω1 = 40 rev/min,
ω2 = ?
తుది జఢత్వ భ్రామకం, I2 = \(\frac{2}{5}\)I,
ఈ ప్రక్రియలో బాహ్య టార్క్ పనిచేయకపోతే,
L = స్థిరాంకం
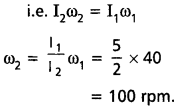
b) బాలుని కొత్త భ్రమణ గతిజశక్తి తొలి గతిజశక్తి కంటే ఎక్కువ అని చూపండి. అతని భ్రమణ గతిజశక్తి పెరుగుదలకు కారణాన్ని వివరించండి.

∴ భ్రమణ K.E పెరుగును. ఇది చేతులను వెనుకకు మడవటంలో పిల్లవానికి అంతరిక శక్తి ఖర్చు అగును.
ప్రశ్న 14.
3kg ద్రవ్యరాశి, 40 cm వ్యాసార్థం ఉన్న ఒక బోలు స్తూపం చుట్టూ దాదాపు ద్రవ్యరాశి లేని ఒక తాడు చుట్టారు. 30 N బలంతో తాడును లాగితే స్తూపం ఎంత కోణీయ త్వరణాన్ని పొందుతుంది? తాడు రేఖీయ త్వరణం ఎంత అవుతుంది? తాడు స్తూపంపై స్లిప్ కాదు అని భావించండి.
సాధన:
M = 3kg, R = 40 cm = 0.4 m
బోలు స్థూపం దాని అక్షం వెంట జఢత్వ భ్రామకం
I = MR² = 3(0.4)² = 0.48 kgm²
ప్రయోగించిన బలం F = 30 N
∴ టార్క్, τ = F × R = 30 × 0.4
= 12 N – m
α కోణీయ త్వరణం అయితే,
అప్పుడు τ = Iα
రేఖీయ త్వరణం, a = Rα
= 0.4 × 25
= 10m/s².
ప్రశ్న 15.
ఒక యంత్రం భ్రమణ భాగానికి (rotor) 200 rad s-1 ఏకరీతి కోణీయ వడిని సమకూర్చడానికి యంత్రం 180 Nm టార్క్ను అందించవలసి ఉంది. యంత్రానికి అవసరమయ్యే సామర్థ్యం ఎంత? (గమనిక : ఘర్షణ లేనప్పుడు సమ కోణీయ వేగం కలిగి ఉండటమంటే టార్క్ శూన్యం అని అర్థం. వాస్తవానికి ప్రయోగించిన టార్క్ ఘర్షణ వల్ల కలిగే టార్క్ను వ్యతిరేకిస్తుంది.) యంత్రం 100% దక్షత కలిగి ఉన్నదని భావించండి.
సాధన:
ω = 200 rad/s,
టార్క్ τ = 180 N
సామర్థ్యం p = ?
p = ω
∴ p = 180 × 200
= 36 kw.
ప్రశ్న 16.
R వ్యాసార్థం ఉన్న ఒక ఏకరీతి వృత్తాకార దిమ్మె నుంచి R/2 వ్యాసార్ధం గల వృత్తాకార ముక్కను వేరుచేసి రంధ్రాన్ని చేశారు. రంధ్రం కేంద్రం అసలు దిమ్మె కేంద్రం నుంచి R/2 దూరంలో
ఉంది. ఫలితంగా ఏర్పడిన చదును వస్తువు గరిమనాభి స్థానాన్ని తెలపండి.
సాధన:
డిస్క్ ప్రమాణ వైశాల్యంపై ద్రవ్యరాశి = M
∴ డిస్క్ యదార్థ ద్రవ్యరాశి M = πR² × m
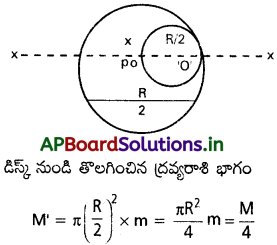
పటంలో, M ద్రవ్యరాశి O వద్ద కేంద్రీకృతమవుతుంది.
మరియు M’ ద్రవ్యరాశి ‘ వద్ద కేంద్రీకృతమవుతుంది.
OO’ = \(\frac{R}{2}\)
M’ ద్రవ్యరాశి వృత్తాకార డిస్క్న తొలగించిన తరువాత, మిగిలిన భాగం రెండు ద్రవ్యరాశుల వ్యవస్థ 0 వద్ద M మరియు -M’గా పరిగణిద్దాం.
O’ వద్ద ద్రవ్యరాశి = \(\frac{-M}{4}\)
మిగిలిన భాగం నుండి ద్రవ్యరాశి కేంద్ర దూరం X అయితే, అప్పుడు
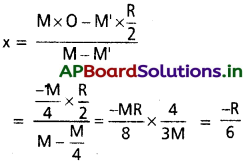
ఋణగుర్తు p, O కు ఎడమవైపు ఉండుటను సూచిస్తుంది.
ప్రశ్న 17.
ఒక మీటరు స్కేలును దాని కేంద్రం వద్ద కత్తి మొన ఉంచి తుల్య స్థితిలో నిలిపారు. ఒక్కొక్కటి 5g ద్రవ్యరాశి ఉన్న రెండు నాణాలను ఒకదానిపై ఒకటి అమరేట్లుగా స్కేలుపై 12.0 cm విభాగం వద్ద ఉంచారు. అప్పుడు కత్తి మొన 45.0 cm విభాగం వద్ద ఉన్నప్పుడు స్కేలు తుల్య స్థితికి వచ్చింది. మీటర్ స్కేలు ద్రవ్యరాశి ఎంత?
సాధన:
పుల్ల c (50 cm) వద్ద m ద్రవ్యరాశి కేంద్రీకృత మయినట్లు తీసుకుందాము.
(45 cm)c’ వెంట సమతాస్థితిలో ఉంటే,
10g (45 – 12) = mg(50 – 45)
10 g × 33 = mg × 5
m = \(\frac{10\times33}{5}\)
= 66 gram.

ప్రశ్న 18.
ఒక ఘనగోళం వరుస క్రమంలో, సమాన ఎత్తులున్న రెండు భిన్న వాలు కోణాలున్న వాలు తలాలపై కిందికి దొర్లింది. (a) ప్రతి వాలు తలంపై దొర్లుతూ అడుగు భాగానికి చేరినప్పుడు గోళం సమాన వడి కలిగి ఉంటుందా? (b) ఒక వాలు తలంపై దొర్లడానికి తీసుకునే కాలం, రెండవ దానిపై తీసుకొన్న కాలం కంటే ఎక్కువగా ఉంటుందా? (c) అలా అయితే ఏ వాలు తలంపై ఎక్కువ సమయం తీసుకుంటుంది? ఎందుకు?
సాధన:
వాలుతలం అడుగున ఘనగోళం వడి v.
శక్తి నిత్యత్వ సూత్రంను అనువర్తించగా

రెండు సందర్భాలలో h సమానం, v సమానం. తలాల వెంబడి దొర్లుటకు పట్టుకాలాలు సమానం.
ప్రశ్న 19.
2m వ్యాసార్థం ఉన్న ఒక కంకణం 100 kgల బరువు కలిగి ఉంది. అది ఒక క్షితిజ సమాంతర తలంపై, దాని ద్రవ్యరాశి కేంద్రం 20 cm/s వడితో గమనంలో ఉండేటట్లు దొర్లుతున్నది. దీన్ని నిశ్చలస్థితికి తేవడానికి ఎంతపని చేయవలసి ఉంటుంది?
సాధన:
R = 2m, M = 100 kg
v = 20 cm/s = 0.2 m/s
హూప్ మొత్తం శక్తి = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)Iw²
= \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)(MR)² w² = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)mv²
= mv²
హూప న్ను ఆపుటకు కావాల్సిన పని =హూప్ మొత్తం శక్తి
w = mv² = 100(0.2)² = 4 joule.
ప్రశ్న 20.
ఆక్సిజన్ అణువు ద్రవ్యరాశి 5.30 × 10-26 kg. ఈ అణువులోని పరమాణువులను కలిపే రేఖకు గల మధ్య లంబరేఖ పరంగా దాని జఢత్వ భ్రామకం 1.94 × 10-46kg m². ఇటువంటి అణువులున్న ఒక వాయువులో అణువు సగటు వడి 500 m/s, అణువు భ్రమణ గతిజశక్తి దాని స్థానాంతరణ గతిజశక్తిలో 2/3 వంతులు ఉన్నది అనుకొంటే అణువు సగటు కోణీయ వేగం ఎంత?
సాధన:
m = 5.30 × 10-26 kg
I = 1.94 × 10-46 kgm²
v = 500 m/s
ప్రతి ఆక్సిజన్ పరమాణువు ద్రవ్యరాశి \(\frac{m}{2}\). రెండు ఆక్సిజన్ పరమాణువుల మధ్యదూరం 2r
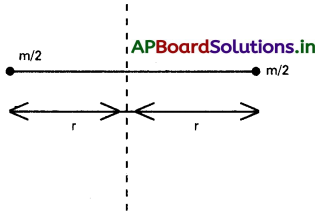

ప్రశ్న 21.
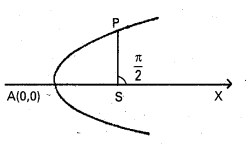
ఒక ఘన స్తూపం 30° వాలు కోణం ఉన్న ఒక వాలు తలంపై కింది నుంచి పైకి దొర్లుతోంది. వాలుతలం కింది అంచువద్ద స్తూపం ద్రవ్యరాశి కేంద్ర వడి 5 m/s.
a) స్తూపం ఎంత దూరం వాలుతలం మీద పైకి దొర్లుతుంది?
b) మళ్ళీ అడుగుకు చేరడానికి ఎంత సమయం పడుతుంది?
సాధన:
θ = 30°, v = θm/s
స్థూపం వాలుతలంపైకి h ఎత్తుకు చేరినట్లు తీసుకుందాము.

అదనపు అభ్యాసాలు (Additional Exercises)
ప్రశ్న 1.
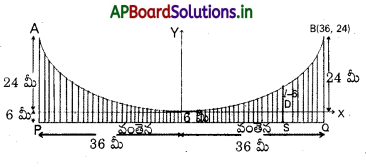
A వద్ద మడత బందుతో కలిపి రెండు భాగాలున్న ఒక నిచ్చెన పటంలో చూపినట్లు ఉంది. నిచ్చెన భాగాలు BA, CA ల పొడవు 1.6 m. BA, CA ల మధ్య బిందువులకు 0.5 m ల పొడవు ఉన్న ఒక తాడు DE కట్టారు. BA నిచ్చెన భాగానికి B నుంచి 1.2 m దూరంలో F బిందువు వద్ద 40 kg బరువు వేలాడదీశారు. నిచ్చెన భారం ఉపేక్షించదగినదనీ, నిచ్చెనకూ నేలకూ మధ్య ఘర్షణ లేదనీ భావించి, తాడులోని తన్యతనూ, నేల నిచ్చెనపై ప్రయోగించే బలాలనూ కనుక్కోండి. (g = 9.8 m/s²) గా తీసుకోండి.)
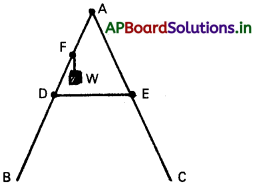
(Hint : నిచ్చెన రెండు భాగాలకూ విడివిడిగా సమతాస్థితిని పరిగణించండి.)
సాధన:
దత్తాంశం పూర్తిగా ఇవ్వలేదు.
ప్రశ్న 2.
ఒక వ్యక్తి తన ప్రతి చేతిలోనూ 5 kg ల బరువును పట్టుకొని, చేతులను క్షితిజ సమాంతరంగా చాచి భ్రమణం చేస్తున్న ఒక వేదిక (ప్లాట్ఫాం)పై దాని కేంద్రం వద్ద నిలబడ్డాడు. ప్లాట్ఫాం కోణీయ వడి 30 భ్రమణాలు / నిమిషం. భ్రమణాక్షం నుంచి చేతిలోని ప్రతి బరువు దూరం 90cm నుంచి 20 cm కు మారేటట్లుగా వ్యక్తి తన చేతులను దేహానికి దగ్గరగా తీసుకువచ్చాడు. ప్లాట్ఫాంతో పాటుగా వ్యక్తి జఢత్వ భ్రామకం స్థిరం అనీ, దాని విలువ 7.6 kg m² అనుకొంటే (a) వ్యక్తి కోణీయ వడి (కొత్త విలువ) ఎంత? (ఘర్షణను ఉపేక్షించండి.)
b) ఈ ప్రక్రియలో గతిజశక్తి నిత్యత్వమౌతుందా? ఒకవేళ నిత్యత్వం కాకపోతే మార్పు ఏ కారణంగా వస్తుంది?
సాధన:
ఇక్కడ l1 = 7.6 × 2 × 5 (0.9) 2 = 15.7 kgm²
ω1 = 30 rpm
l2 = 7.6 + 2 × 5(0.2)² = 8.0 kgm²
ω2 = ?
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమము ప్రకారము
l2ω2 = l1ω1
ω2 = \(\frac{l_1}{l_2}\)ω1 = \(\frac{15.7\times30}{8.0}\) = 58.88 rpm.
ఈ ప్రక్రియలో గతిజశక్తి నిత్యత్వం కాదు. వాస్తవంగా జఢత్వ భ్రామకం తగ్గును. భ్రమణ K.E పెరుగును. ఈ మార్పు వ్యక్తి చేతులను అతని శరీరం దగ్గరకు తెచ్చుటలో జరిగిన పనికి సమానం.
ప్రశ్న 3.
10 g ద్రవ్యరాశి ఉన్న ఒక తుపాకి గుండును 500 m/s వేగంతో ఒక తలుపువైపు పేల్చితే అది సరిగ్గా తలుపు కేంద్రం వద్ద దానిలో ఇమిడి పోయింది. తలుపు 1.0 m వెడల్పు, ద్రవ్యరాశి 12 kg కలిగి ఉంది. తలుపు ఒక అంచువద్ద మడత బందులతో, నిట్టనిలువు అక్షం పరంగా ఘర్షణ లేకుండా భ్రమణం చెందగలదు. తుపాకి గుండు తలుపులో ఇమిడిన వెంటనే తలుపు కోణీయ వడిని కనుక్కోండి.
(Hint : తలుపు జఢత్వ భ్రామకం, ఒక అంచు నుంచి పోయే నిట్టనిలువు అక్షం పరంగా ML³/3.)
సాధన:
బుల్లెట్ కోణీయ ద్రవ్యవేగం

ప్రశ్న 4.
వాటివాటి అక్షాల పరంగా (తలాలకు లంబంగా, కేంద్రం నుంచి పోయే) రెండు వృత్తాకార దిమ్మెల జఢత్వ భ్రామకాలు వరుసగా 14,12. 0, 002 కోణీయ వడులతో భ్రమణంలో ఉన్న ఈ దిమ్మెలను వాటి అక్షాలు ఏకీభవించేట్లు వాటి ముఖ తలాలను ఒకదానినొకటి తాకునట్లు ఉంచారు. (a) రెండు దిమ్మెల వ్యవస్థ కోణీయ వడి ఎంత? (b) దిమ్మెల సంయోగ వ్యవస్థ గతిజ శక్తి ఆ రెండు దిమ్మెల తొలి గతిజ శక్తుల మొత్తానికంటే తక్కువగా ఉంటుందని చూపండి. శక్తిలో తరుగుదలకు కారణమేమిటి? (ω1 ≠ ω2 అని తీసుకోండి.)
సాధన:
a) రెండు డిస్క్లల మొత్తం తొలి కోణీయ ద్రవ్యవేగం
L1 = I1ω1 + I2ω2
ఇచ్చిన షరతులకు లోబడి, రెండు డిస్క్ వ్యవస్థ
జఢత్వభ్రామకం = (I1 + I2)
సంయోగ వ్యవస్థ కోణీయ వడి ω, వ్యవస్థ కోణీయ ద్రవ్యవేగం

E1 > E2 లేక E2 < E1
ఈ ప్రక్రియలో K.Eలో నష్టం కలిగి ఉండును.
శక్తిలో నష్టము = E1 – E2.
రెండు డిస్క్లను స్పృశించుటలో ఘర్షణ వల్ల నష్టం కలిగి ఉండును. ఘర్షణ వల్ల టార్క్, ఒక్క ఆంతరిక టార్క్ కోణీయ ద్రవ్యవేగం నిత్యత్వం అగును.

ప్రశ్న 5.
a) లంబాక్షాల సిద్ధాంతాన్ని నిరూపించండి. (Hint : x −yతలంలో ఉన్న ఒక బిందువు (x, y) దూరం వర్గం, తలానికి లంబంగా మూలబిందువు నుంచి పోయే అక్షం నుంచి x² + y²
b) సమాంతరాక్షాల సిద్ధాంతాన్ని నిరూపించండి.
(Hint : ద్రవ్యరాశి కేంద్రాన్ని మూల బిందువుగా తీసుకుంటే ∑miri = 0).
సాధన:
నిర్వచనం :
ఒక సమతల పటలానికి లంబంగా ఒక బిందువు గుండా పోయే అక్షంపరంగా దాని జఢత్వ భ్రామకము, అదే బిందువు గుండా పోతూ పరస్పరం లంబంగా ఉన్న అక్షముల పరంగా ఉన్న జఢత్వ భ్రామకాల మొత్తంనకు సమానము.
ie., Iz = Ix + Iy
ఇక్కడ Iz = Z – అక్షం పరంగా జఢత్వ భ్రామకము
Ix = X – అక్షం పరంగా జఢత్వ భ్రామకము
Iy = Y – అక్షం పరంగా జఢత్వ భ్రామకము
నిరూపణ :
‘m’ ద్రవ్యరాశి గల కణము P వద్ద XOY తలంలో ఉన్నదనుకొనుము.
దీని నిరూపకాలు (x, y). ఈ కణం Y – అక్షం నుండి ‘x’ లంబ దూరంలో, X – అక్షం నుండి ‘y’ లంబదూరంలో, 2 – అక్షం నుండి ‘r’ లంబ దూరంలో ఉన్నదనుకొనుము.
Y – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = mx²
Y – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = Iy = ∑mx² …………. (1)
X – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = my²
X – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = Ix = ∑my² …………. (2)
Z – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = mr²
Z – అక్షం పరంగా కణము యొక్క జఢత్వ భ్రామకము = Iz = ∑mr² …………. (3)
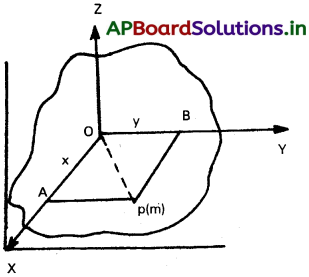
పటం నుండి, r² = x² + y²
Iz = Σmr² = Σm (x² + y²) = Σm x² + Σmy²
(1), (2) సమీకరణముల నుండి
Iy = Σmx² ; Iy = Σmy²
Iz = Iy + Ix
∴ Iz = Ix + Iy
∴ లంబాక్ష సిద్ధాంతం నిరూపించబడింది.
నిర్వచనం :
ఏదైనా అక్షం పరంగా దృఢ వస్తువు యొక్క జఢత్వ భ్రామకము, ఆ అక్షానికి సమాంతరంగా ఉంటూ ద్రవ్యరాశి కేంద్రం గుండా పోయే అక్షం పరంగా జఢత్వ భ్రామకము మరియు దృఢ వస్తు ద్రవ్యరాశి మరియు ఆ రెండు అక్షముల దూర వర్గముల లబ్దానికి సమానం.
I0 = Ig + Mr²
Ig = ‘O’ గుండా పోయే అక్షం పరంగా జఢత్వ భ్రామకము
M = Σm = వస్తువు ద్రవ్యరాశి
r = అక్షముల మధ్య దూరము
IG = ‘G’ గుండా పోయే అక్షం పరంగా జఢత్వ భ్రామకము
నిరూపణ :
వస్తువులో P వద్ద ‘m’ ద్రవ్యరాశి గల కణమును తీసుకొనుము. PO ను PG లను కలుపవలెను. OG ను కలుపగా వచ్చిన గీతకు లంబంగా P నుండి రేఖ PQను గీయవలెను.
‘O’ గుండా గల అక్షం పరంగా ‘P’ వద్ద కణం జఢత్వ భ్రామకం = m × OP².
‘O’ గుండా గల అక్షం పరంగా కణం యొక్క జఢత్వ భ్రామకం = m × PG².
‘G’ గుండా గల అక్షం పరంగా కణం యొక్క జఢత్వ భ్రామకం = IG = ∑m. PG²
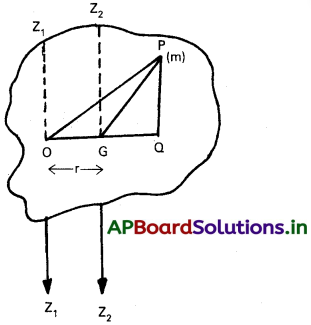
OPQ త్రిభుజంలో OP² = OQ² + PQ²
OP² = (OG² + GQ²)+ PQ² [∵ OQ = OG + GQ]
OP² = OG² + GQ² + 2OG. GQ + PQ²
OP² = OG² + GP² + 20G.GQ [∵ GQ² + PQ² = GP²]
కానీ I0 = Σm Op²
I0 = Σm (OG² + GP² + 2 OG. GQ)
I0 = Σm (OG² + GP² + 20G. GQ)
I0 = Σm.OG² +Σm. Gp² + Σm. 20G. GQ
I0 = Mr² + IG + Σm. 2.OG. GQ
ఇక్కడ Σm M, OG = r
IG = Σm PG²
∴ I0 = IG + Mr² + 2 OG. Σm. GQ
కాని ద్రవ్యరాశి కేంద్రం పరంగా వస్తువులోని అన్ని కణాల గురుత్వాకర్షణ బలాల భ్రామకాల బీజీయాల మొత్తం శూన్యం.
కావున Σm. GQ = 0
∴ I0 = IG + Mr²
ప్రశ్న 6.
h ఎత్తున్న వాలుతలంపై దొర్లుతున్న వస్తువు (కంకణం, వృత్తాకార దిమ్మె, స్తూపం లేదా గోళం) వాలుతలం అడుగు భాగం చేరినప్పుడు దాని స్థానాంతరణ వేగం υ అయితే
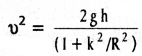
అని గతికశాస్త్ర భావనలు (బలాలూ, టార్క్లూ) ఉపయోగించి నిరూపించండి. వస్తువు సౌష్ఠవాక్షం పరంగా భ్రమణ వ్యాసార్థం k, వస్తువు వ్యాసార్థం R. వస్తువు వాలుతలం పై భాగం నుంచి నిశ్చల స్థితి నుంచి గమనం ప్రారంభించిందని ఊహించండి.
సాధన:
h ఎత్తు గల వాలు తలం క్రింది దిశలో వస్తువు దొర్లుతూ ఉన్నప్పుడు, శక్తి నిత్యత్వసూత్రంను అనువర్తింపచేద్దాము.
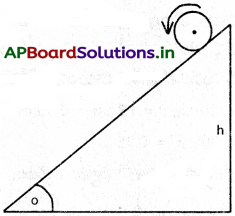

ప్రశ్న 7.
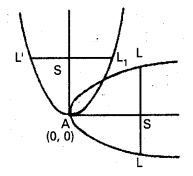
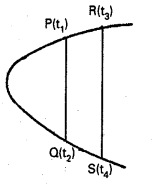
ఘర్షణ లేని ఒక బల్లపై ఏ విధమైన తోపుడు లేకుండా, తన అక్షం పరంగా ω0 కోణీయ వడితో భ్రమణం చెందుతున్న వృత్తాకార బిళ్ళను ఉంచారు. దిమ్మె వ్యాసార్థం R దిమ్మెలోని బిందువులు A, B, C ల రేఖీయ వేగాలు ఎంతెంత ? పటంలో సూచించిన దిశలో దిమ్మె దొర్లుతుందా?
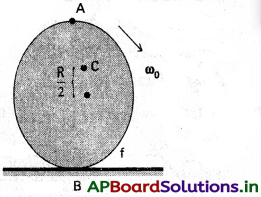
సాధన:
v = rω సంబంధంను ఉపయోగించి,
బిందువుకు, VA = Rωo, AX వెంబడి
B బిందువుకు, VB = Rωo, BX వెంబడి
C బిందువు, VC (\(\frac{1}{2}\))ωo, AXకు సమాంతరంగా
డిస్క్ భ్రమణం చెందదు, కారణం ఘర్షణలేని బల్లపై ఉంచబడింది. ఘర్షణ లేకుండా, దొర్లుడు సాధ్యం కాదు.
ప్రశ్న 8.
పటంలో సూచించిన దిశలో దిమ్మె దొర్లడానికి ఘర్షణ ఎందుకు అవసరమో వివరించండి.
(a) శుద్ద దొర్లుడు గమనానికి ముందు బిందువు B, ఘర్షణ బలం దిశ, ఘర్షణ వల్ల టార్క్ దిశలను ఇవ్వండి.
(b) శుద్ధ దొర్లుడు గమనం ప్రారంభమైన తరువాత ఘర్షణ బలాన్ని కనుక్కోండి.
సాధన:
డిస్క్ దొర్లుటకు, టార్క్ కావాలి, దీనిని స్పర్శియ బలం సమకూరుస్తుంది. ఈ సందర్భంలో ఘర్షణ బలం, స్పర్శీయ బలం మాత్రమే, ఇది అవసరము.
(a) B వద్ద ఘర్షణ బలంను; వేగం ఎడమవైపు వ్యతిరేకించును. ఘర్షణ బలం కుడివైపు పని చేయును. ఘర్షణ టార్క్ డిస్క్ తలంనకు లంబంగా వెలుపల వైపుకు పని చేయును.
(b) B వద్ద ఘర్షణ బలం, Bతో తాకిన తలం బిందువు వద్ద వేగంను తగ్గించును. బిందువు B వేగం సున్నా అయిన తరువాత దొర్లుట మొదలవుతుంది. ఈ స్టేజిలో ఘర్షణ బలం కూడా శూన్యమగును.

ప్రశ్న 9.
10 π rad s-1 తొలి కోణీయ వడితో భ్రమణం చేస్తున్న ఒక ఘన వృత్తాకార బిళ్ళ, ఒక కంకణం ఏకకాలంలో క్షితిజ సమాంతర బల్లపై ఉంచడం జరిగింది. వాటి వ్యాసార్థాలు 10 cm. ఈ రెండింటిలో ఏది మొదటగా దొర్లడం ప్రారంభిస్తుంది గతిక ఘర్షణ గుణకం µ k= 0.2.
సాధన:
ద్రవ్యరాశి కేంద్ర తొలివేగం సున్నా ie, u = ఘర్షణ బలం
ద్రవ్యరాశి కేంద్రం త్వరణానికి కారణమగును.
μk mg = ma ∴ a = µk g
v = u + at ∴ v = 0 + μkgt
ఘర్షణ వల్ల టార్క్ అపత్వరణానికి కారణం. తొలికోణీయ వడి ω0.


(vi) మరియు (vii) పోల్చగా, డిస్క్ రింగ్ కన్నా ముందు దొర్లుట ప్రారంభించును.
μk, g, R మరియు ω0 తెలిసిన విలువలను ఉపయోగించి (vi) మరియు (vii) నుండి t విలువలను గణించవచ్చును.
ప్రశ్న 10.
10kg ద్రవ్యరాశి, 15 cm వ్యాసార్థం ఉన్న ఒక స్తూపం 30° వాలు కోణం ఉన్న ఒక వాలు తలంపై శుద్ధ దొర్లుడు గమనంలో ఉంది. స్థితిక ఘర్షణ గుణకం μs = 0.25.
(a) ఎంత ఘర్షణ బలం స్తూపంపై ఉంటుంది?
(b) దొర్లుతూ ఉన్నప్పుడు ఘర్షణకు వ్యతిరేకంగా ఎంతపని జరుగుతుంది?
(c) వాలు కోణం 6 ను పెంచితే ఏ 6 విలువ వద్ద స్తూపం జారుతుంది, గమనం శుద్ధ దొర్లుడు గమనం కాకుండా పోతుంది?
సాధన:
m = 10 kg, r = 15 cm = 0.15 cm
θ = 30°, μs = 0.25
వాలుతలం క్రింది దిశలో స్థూపం త్వరణం,
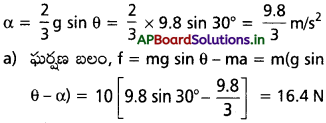
b) దొర్లుతున్నప్పుడు, స్పర్శబిందువు విరామస్థితిలో ఉండును. ఘర్షణబలంనకు వ్యతిరేకంగా జరిగిన పని సున్నా.
c) జారకుండా దొర్లుటకు μ = \(\frac{1}{2}\) tan θ
tan θ = 3μ = 3 × 0.25
θ = 37°
ప్రశ్న 11.
కింద ఇచ్చిన వాక్యాలను జాగ్రత్తగా చదివి, తగిన కారణాలతో అవి ఒప్పో, తప్పో తెలపండి.
(a) దొర్లుడు గమనంలో ఘర్షణ బలం వస్తువు ద్రవ్యరాశి కేంద్ర గమన దిశలోనే పని చేస్తుంది.
(b)దొర్లుడు గమనంలో స్పర్శా బిందువు తాక్షణిక వడి శూన్యం.
(c) దొర్లుడు గమనంలో స్పర్శా బిందువు తాక్షణిక త్వరణం శూన్యం.
(d) శుద్ధ దొర్లుడు గమనానికి, ఘర్షణకు వ్యతిరేకంగా చేసిన పని శూన్యం.
(e) ఘర్షణ రహిత వాలు తలం వెంట కిందికి గమనంలో ఉన్న ఒక చక్రం స్లిప్ అవుతుంది. (శుద్ధ దొర్లుడు గమనం కలిగి ఉండదు).
సాధన:
a) ఇచ్చిన స్టేట్మెంట్ తప్పు.
b) ఇచ్చిన స్టేట్మెంట్ ఒప్పు. దొర్లుతున్నప్పుడు భూమితో స్పృశిస్తున్న బిందువు వడి సున్నా.
c) ఇచ్చిన స్టేట్మెంట్ తప్పు. కారణం దొర్లుడు వస్తు క్షణిక త్వరణం సున్నాకాదు.
d) ఇచ్చిన స్టేట్మెంట్ ఒప్పు. దీనికి కారణం పరిపూర్ణ దొర్లుడు ఆరంభమయిన, ఘర్షణబలం సున్నా. కావున ఘర్షణకు వ్యతిరేకంగా పని జరుగును.
e) ఇచ్చిన స్టేట్మెంట్ ఒప్పు. దొర్లుడుకు అవసరమైన ఘర్షణను, స్పర్శబలం టార్క్ వల్ల ఏర్పరచును. వాలుతలం పరిపూర్ణంగా నున్నగా ఉంటే, దాని భారం వల్ల జారును.
ప్రశ్న 12.
ఒక కణవ్యవస్థ గమనాన్ని – ఆ వ్యవస్థ ద్రవ్యరాశి కేంద్ర గమనంగా, ద్రవ్యరాశి కేంద్రపరమైన గమనంగా విభజించడం.
(a) p = p’i; + mi V అని చూపండి.
pii వ కణం (m; ద్రవ్యరాశి గల) రేఖీయ ద్రవ్యవేగం p’i = miv’i. ఇక్కడ v’i ద్రవ్యరాశి కేంద్రంపరంగా iవ కణం వేగమని గుర్తించండి. ‘అలాగే ద్రవ్యరాశి కేంద్ర నిర్వచనాన్ని బట్టి ∑P’i = 0 అని నిరూపించండి.
(b) K = K’ + ½MV² అని చూపండి.
K కణ వ్యవస్థ మొత్తం గతిజశక్తి, K’ ద్రవ్యరాశి కేంద్రం పరంగా కణాల వేగాలను తీసుకొంటే వ్యవస్థ మొత్తం గతిజశక్తి, MV²/2 వ్యవస్థను ఏక మొత్తంగా తీసుకొన్నప్పుడు (అంటే వ్యవస్థ ద్రవ్యరాశి కేంద్రం) దాని స్థానాంతరణ గతిజశక్తి విభాగం 7.14 లో ఈ ఫలితాన్ని ఉపయోగించాం.
(c) L = L’ + R × MV అని చూపండి.
L’ = ∑r’1 P’1, వ్యవస్థ కోణీయ ద్రవ్యవేగం ద్రవ్యరాశి కేంద్రం పరంగా (అంటే కణాల వేగాలను ద్రవ్యరాశి కేంద్రపరంగా లెక్కిస్తే), r’1 = r1 – R అని గుర్తుంచుకోండి. మిగతా సంకేతనాలు (notations) ఈ అధ్యాయంలో ఉపయోగించిన ప్రామాణిక సంకేతనాలే. L’, MR × V లు వరుసగా ద్రవ్యరాశి కేంద్రం పరంగా కణవ్యవస్థ కోణీయ ద్రవ్యవేగం, వ్యవస్థ ద్రవ్యరాశి కేంద్ర ద్రవ్యవేగాలు.
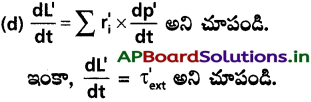
τext = ద్రవ్యరాశి కేంద్రంపరంగా వ్యవస్థపై గల బాహ్య టార్క్లన్నింటి మొత్తం.
(Hint : ద్రవ్యరాశి కేంద్రం నిర్వచనాన్ని, న్యూటన్ మూడో గమన నియమాన్ని ఉపయోగించండి. రెండు కణాల మధ్య అంతర బలాలు ఆ రెండు కణాలను కలిపే రేఖ వెంబడి ఉంటాయని భావించండి).
సాధన:
a) మూలబిందువు ‘O’ పరంగా, m1, m2, …… mi
ద్రవ్యరాశులు గల కణాల స్థాన సదిశలు \(\overrightarrow{r_1},\overrightarrow{r_2},\overrightarrow{r_i}\)1,2, గా తీసుకుందాం.
ద్రవ్యరాశి కేంద్ర స్థానసదిశ \(\overrightarrow{O P}\)గా తీసుకుంటే
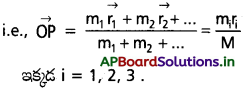
ఇక్కడ మూలబిందువును O’కు మారిస్తే ద్రవ్యరాశి కేంద్రం p’ వద్ద ఉందని ఊహిద్దాం. అప్పుడు
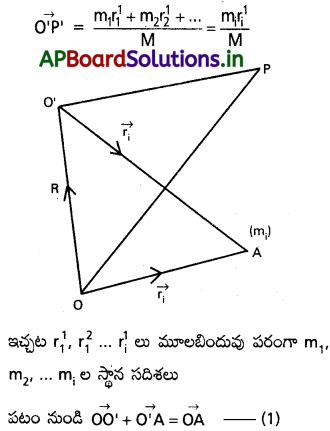
(1) వ సమీకరణాన్ని m; తో గుణించి, ఆ తరువాత
కాలం దృష్ట్యా అవకలనం చేయగా,

మూలబిందువు మార్చినప్పటికి ద్రవ్యరాశి కేంద్ర స్థానంలో
మార్పు ఉండదు. ∴ ∑ P’i = 0
b) భ్రమణ శుద్ధగతికశాస్త్రం ప్రకారం, కణాల వ్యవస్థ మొత్తం గతిజశక్తి = K.ET. ద్రవ్యరాశి కేంద్రపరంగా తీసుకున్న వ్యవస్థ కణాల మొత్తం గతిజశక్తి + వ్యవస్థ స్థానాంతరణ గతిజశక్తి


సాధించిన సమస్యలు (Solved Problems)
ప్రశ్న 1.
0.5 m భుజం ఉన్న ఒక సమబాహు త్రిభుజం శీర్షాల వద్ద ఉన్న మూడు కణాల ద్రవ్యరాశి కేంద్రాన్ని కనుక్కోండి. కణాల ద్రవ్యరాశులు వరుసగా 100g, 150 g, 200g
సాధన:
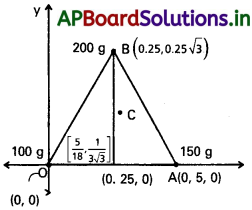
పటంలో చూపినట్లు X -, y- అక్షాలను ఎంచుకొంటే సమబాహు త్రిభుజాన్ని ఏర్పరచే బిందువులు 0, A, B ల నిరూపకాలు వరుసగా (0, 0), (0, 5, 0), (0.25,0:25 √3) . 100 g, 150g, 200g ద్రవ్యరాశులు వరుసగా O, A, B ల వద్ద ఉన్నాయనుకొంటే,

ద్రవ్యరాశి కేంద్రం ( ను పటంలో చూపడమైంది. ఈ బిందువు త్రిభుజం OAB జ్యామితీయ కేంద్రం కాదని గమనించండి.
ప్రశ్న 2.
ఒక త్రిభుజాకార పటలం (lamina) (పలక) ద్రవ్యరాశి కేంద్రాన్ని కనుక్కోండి.
సాధన:
భూమి (MN) కి సమాంతరంగా ఉండే సన్నటి పట్టీలుగా పటలం (∆LMN) ను పటంలో చూపినట్లు విభజించ వచ్చు. ప్రతి పట్టీ ద్రవ్యరాశి కేంద్రం, సౌష్టవాన్ని అనుసరించి, పట్టీ మధ్య బిందువు వద్ద ఉంటుంది. అన్ని పట్టీల మధ్య బిందువులను కలుపుతూ ఒక రేఖను గీస్తే అది త్రిభుజ మధ్యగత రేఖ (median) అవుతుంది. మొత్తం మీద, త్రిభుజ పటలం ద్రవ్యరాశి కేంద్రం ఈ మధ్యగత రేఖపై ఉండాలి.
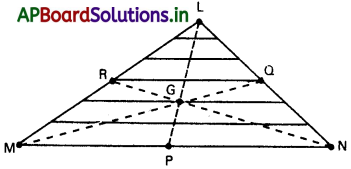
అదే విధంగా ద్రవ్యరాశి కేంద్రం మధ్యగత రేఖలు MQ, NR లపై ఉంటుందని నిరూపించవచ్చు. అంటే ఈ మధ్యగత రేఖల ఖండన బిందువు వద్ద ద్రవ్యరాశి కేంద్రం ఉంటుంది. అంటే త్రిభుజ కేంద్రాభం వద్ద ద్రవ్యరాశి కేంద్రం ఉంటుందన్నమాట.
ప్రశ్న 3.
L – ఆకారంలో ఉన్న పల్చని ఏకరీతి పలక (పటలం) ద్రవ్యరాశి కేంద్రాన్ని కనుక్కోండి. దాని కొలతలు పటంలో చూపడమైనది. పలక ద్రవ్యరాశి 3 kg.
సాధన:
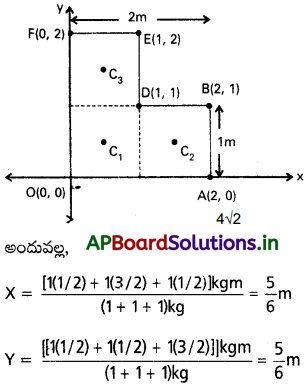
పటంలో చూపినట్లు X, Y అక్షాలను తీసుకుంటే L – ఆకారం ఉన్న పటలం శీర్షాలు 0(0, 0), A(2, 0), B(2, 1), D(1, 1), E(1, 2), F(0, 2) అవుతాయి. ఈ పటలాన్ని 1m భుజం ఉన్న మూడు చతుస్రాలుగా భావించ వచ్చు. ఈ చతురస్రాల ద్రవ్యరాశి కేంద్రాలు C1, C2, C3లు సౌష్టవం వల్ల, ఆయా చతురస్రాల జ్యామితీయ కేంద్రాలవుతాయి. వాటి నిరూపకాలు వరుసగా (1/2, 1/2), (3/2, 1/2), (1/2, 3/2) అని తెలుసుకోవచ్చు.
చతురస్రాల ద్రవ్యరాశులు ఈ బిందువుల వద్ద కేంద్రీకృత మైనట్లుగా మనం భావించవచ్చు. ఈ మూడు ద్రవ్యరాశి ‘బిందువుల ద్రవ్యరాశి కేంద్రమే, మొత్తంగా L. ఆకారం ఉన్న పటలం ద్రవ్యరాశి కేంద్రం (X, Y) అవుతుంది.
ప్రశ్న 4.
20 kg ద్రవ్యరాశి, 3m పొడవు ఉన్న ఒక నిచ్చెన ఘర్షణలేని ఒక గోడకు వాలి ఉంది. నిచ్చెన కింది కొన నేలపై గోడనుంచి 1 m దూరంలో, (పటంలో చూపినట్లు) గోడ, నేలల ప్రతిచర్య బలాలను కనుక్కోండి.
సాధన:
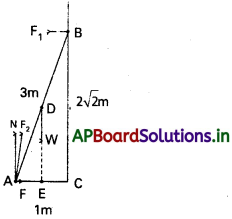
నిచ్చెన AB పొడవు 3 m, దీని కింద కొన A, గోడ నుంచి AC = 1m దూరంలో ఉంది. పైథాగరస్ సిద్ధాంతాన్ని అనుసరించి BC = 2√2 m. నిచ్చెనపై బలాలు గరిమనాభి D ద్వారా ఉండే నిచ్చెన భారం W, గోడ, నేలల వల్ల కలిగే ప్రతిచర్య బలాలు వరుసగా F1, F2. గోడవల్ల ఘర్షణ లేనందున బలం F1 గోడకు లంబంగా ఉంటుంది.
బలం F2 ను రెండు అంశాలుగా, ఒకటి అభిలంబ ప్రతిచర్య N గానూ, రెండవ అంశం ఘర్షణ బలం F గానూ విభజించవచ్చు. బలం F నిచ్చెన గోడ నుంచి దూరంగా జారిపోకుండా నిరోధిస్తుంది. అందువల్ల F దిశ గోడవైపు ఉంటుంది.
స్థానాంతరణ సమతాస్థితి కోసం,
క్షితిజ లంబదిశలో బలాలు తీసుకొంటే
N – W = 0 ………….. (i)
క్షితిజ సమాంతర బలాలు తీసుకొంటే
F – F1 = 0 ………….. (ii)
భ్రమణ సమతాస్థితి కోసం, A బిందువు పరంగా బల భ్రామకాలను తీసుకొంటే,
2√2 F, – (1/2) W = 0 ………….. (iii)
ఇప్పుడు W = 20 g = 20 ×9.8 N = 196.0 N
(i) నుంచి N 196.0
(iii) నుంచి F1 = W/ 4√2 = 196.0/4√2
= 34.6 N
(ii) నుంచి F = F1 = 34.6 N
F2 = \(\sqrt{F^2+N^2}\)\sqrt{F^2+N^2}= 199.0 N
బలం F2 క్షితిజంతో α కోణం చేస్తుంది.
tan α = N/F = 4√2, α = tan-1(4√2)>80°
ప్రశ్న 5.
రెండు సదిశలు
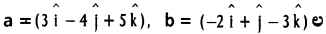
ల అదిశ, సదిశా లబ్దాలను కనుక్కోండి.
సాధన:

ప్రశ్న 6.
ω = ω + αt ను ప్రాథమిక సూత్రాల నుంచి రాబట్టండి.
సాధన:
కోణీయ త్వరణం ఏకరీతిగా ఉంటే,
\(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) = α = : స్థిరాంకం …….. (i)
ఈ సమీకరణాన్ని సమాకలనం చేయగా,
ω = ∫αdt + c = at + c (α స్థిరాంకం)
t = 0 వద్ద, ω = ω0 (ఇచ్చారు)
(i) నుంచి t = 0 వద్ద, ω = c = ω0
ఆ విధంగా, ω = αt + ω0 అవుతుంది.
ω = \(\frac{d \theta}{dt}\) నిర్వచనంతో పాటు ω = ω0 + αt ను సమాకలనం చేస్తే θ = θ0 + ω0t + αt² మీకై ఒక అభ్యాసంగా వదిలేస్తున్నాం.

ప్రశ్న 7.
ఒక మోటారు చక్రం కోణీయ వడిని 1200 rpm నుంచి 3120 rpm కు 16 సెకన్లలో పెంచారు. (i) కోణీయ త్వరణం స్థిరమని భావించి, కోణీయ త్వరణాన్ని లెక్కించండి. (ii) ఈ సమయంలో ఇంజను ఎన్ని భ్రమణాలు చేస్తుంది?
సాధన:
(i) ω = ω0 + αt ను ఉపయోగించాలి.
ω0 = తొలి కోణీయ (వేగం) వడి rad/s

(ii) t కాలం తరువాత కోణీయ స్థానభ్రంశం

ప్రశ్న 8.
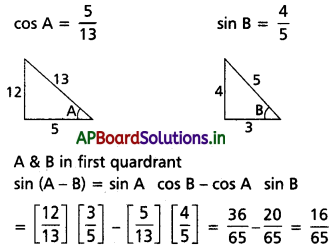
బలం (\(7\hat{\mathbf{i}}+3\hat{\mathbf{j}}-5\hat{\mathbf{k}}\)) వల్ల, మూలబిందువు పరంగా టార్క్ను కనుక్కోండి. బలం ప్రయోగించిన కణం స్థానసదిశ \(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\) [Mar. ’14, ’13; May ’13]
సాధన:

ప్రశ్న 9.
స్థిర వేగంతో గమనంలో ఉన్న ఒక కణం కోణీయ ద్రవ్యవేగం, ఏ బిందువు పరంగానైనా, దాని గమనమంతటా స్థిరంగా ఉంటుందని చూపండి.
సాధన:
ఒకానొక కాలం వద్ద, కణం P బిందువు వద్ద ఉందనీ, దాని వేగం V అనీ అనుకొందాం. ఏదైనా ఒక బిందువు ౦ పరంగా ఆ కణం కోణీయ ద్రవ్యవేగాన్ని కనుక్కోవాలని మనం అనుకొంటున్నాం.
కణం కోణీయ ద్రవ్యవేగం l = r × mv. దీని పరిమాణం mvr sin θ. r, v ల మధ్య కోణం θ. కణం స్థానం కాలంతోపాటు మారుతున్నా, వేగం దిశ స్థిరంగా ఉండటం వల్ల OM = r sin θ స్థిరంగా ఉంటుంది.
ప్రశ్న 10.
బలభ్రామకాలను ఏ బిందువు పరంగా లెక్కిస్తామో ఆ బిందువు స్థానంపై బలయుగ్మ భ్రామకం ఆధారపడదని చూపండి.
సాధన:

పటంలో చూపినట్లు ఒక దృఢ వస్తువుపై ప్రయోగించిన బలయుగ్మాన్ని ఊహించండి. F, -F బలాలను వరుసగా బిందువులు B, A ల వద్ద ప్రయోగించారు. మూల బిందువు O పరంగా A, Bల స్థానసదిశలు r1, r2. మూలబిందువు పరంగా బలభ్రామకాలను లెక్కిద్దాం.
బలయుగ్మభ్రామకం = బలయుగ్మాన్ని ఏర్పరచే బలాల బలభ్రామకాల మొత్తం
= r1 × (-F) + r2 × F
= r2 × F – r1 × F
= (r2 − r1) × F
కాని r1 + AB = r2 కాబట్టి AB = r2 – r1.
అందువల్ల బలయుగ్మ భ్రామకం AB × F.
ఈ ఫలితం మూలబిందువు స్థానంతో సంబంధం లేకుండా స్వతంత్రంగా ఉంది (ఏ బిందువు పరంగా బలభ్రామకాలను కొలిచామో ఆ స్థానంతో సంబంధం లేదు).
ప్రశ్న 11.
ఒక వృత్తాకార పళ్ళెం (disc) జఢత్వ భ్రామకం, దాని ఏదైనా ఒక వ్యాసం పరంగా ఎంత?
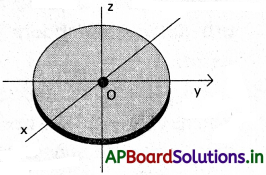
పళ్ళెం తలానికి లంబంగా ఉంటూ, దాని కేంద్రం ద్వారా పోయే అక్షం పరంగా జఢత్వ భ్రామకం ఇచ్చినప్పుడు, పళ్ళెం, జఢత్వ భ్రామకాన్ని, దాని వ్యాసం వరంగా కనుక్కోవడం.
సాధన:
పళ్ళెం తలానికి లంబంగా ఉండి, దాని కేంద్రం నుంచి పోయే అక్షం పరంగా పళ్ళెం జఢత్వ భ్రామకం మనకు తెలుసు అనుకొందాం. ఆ విలువ MR²/2, M పళ్ళెం ద్రవ్యరాశి, R దాని వ్యాసార్థం.
పళ్ళెం ఒక పలక వంటిదని భావించవచ్చు. అందువల్ల లంబాక్షాల సిద్ధాంతం ఈ సందర్భంలో అనువర్తనీయం. పటంలో చూపినట్లు మనం మూడు అనుషక్త అక్షాలు, x, y z అక్షాలను • బిందువు ద్వారా పోతున్నాయి అనుకొందాం. x, y – అక్షాలు పళ్ళెం తలంలోనే ఉన్నాయి. z అక్షం పళ్ళెం తలానికి లంబంగా ఉంది. లంబాక్షాల సిద్ధాంతం ప్రకారం
Iz = Ix = Iy
x, y అక్షాలు పళ్ళెం వ్యాసం వెంబడి ఉన్న అక్షాలు; సౌష్ఠవాన్ని అనుసరించి ఏ వ్యాసం పరంగానైనా పళ్ళెం జఢత్వ భ్రామకం సమానంగానే ఉండాలి. అందువల్ల
Ix = Iy
Iz = 2Ix
కాని Iz = MR²/2
అందువల్ల, చివరగా Ix = Iz/2 = MR²/4
ఆ విధంగా పళ్ళెం (ఏదైనా) వ్యాసం పరంగా దాని జఢత్వ భ్రామకం MR²/4.
ప్రశ్న 12.
M ద్రవ్యరాశి, l పొడవు ఉన్న ఒక కడ్డీకి లంబంగా, ఒక కొన ద్వారా పోయే అక్షం పరంగా జఢత్వ భ్రామకం ఎంత?
సాధన:
M ద్రవ్యరాశి, l పొడవు ఉన్న కడ్డీకి I = Ml² / 12.
సమాంతరాక్ష సిద్ధాంతం ప్రకారం
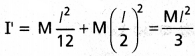
2M ద్రవ్యరాశి, 21 పొడవు ఉన్న కడ్డీ మధ్య బిందువు నుంచి పోతూ, పొడవుకు లంబంగా ఉండే అక్షం పరంగా జఢత్వ భ్రామకంలో సగం I’ అవ్వడం వల్ల ఈ ఫలితాన్ని స్వతంత్రంగానే సరిచూడవచ్చు.
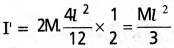
ప్రశ్న 13.
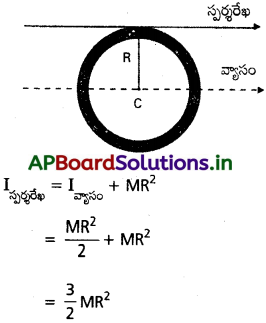
ఒక కంకణం స్పర్శరేఖ పరంగా కంకణ జఢత్వ భ్రామకాన్ని కనుక్కోండి.
సాధన:
కంకణ తలానికి సమాంతరంగా ఉన్న కంకణం స్పర్శరేఖ ఒకానొక కంకణ వ్యాసానికి సమాంతరంగా ఉంటుంది. (పటం). ఈ రెండు సమాంతర అక్షాల మధ్య దూరం, కంకణ వ్యాసార్థం R అవుతుంది.
ప్రశ్న 14.
20 kg ద్రవ్యరాశి, 20 cm వ్యాసార్థం ఉన్న ఒక గతిపాలక చక్రం అంచువెంట తేలికైన దారం చుట్టడమైంది. వేలాడే దారం చివర ఒక లాగే బలాన్ని 25 N ల పరిమాణం కలది. పటంలో చూపినట్లు ప్రయోగించారు. గతిపాలక చక్రాన్ని క్షితిజ సమాంతర ఇరుసుకు ఘర్షణ లేని బేరింగులతో అమర్చారు.
(a) చక్రీయ కోణీయ త్వరణం లెక్కకట్టండి.
(b) 2m పొడవు దారం విచ్చుకొనేటట్లు లాగడానికి చేయవలసిన పనిని కనుక్కోండి.
(c) (b) లోని స్థితిని చేరడంలో గతిజ శక్తి కనుక్కోండి. చక్రం నిశ్చల స్థితి నుంచి
తిరగటం ప్రారంభించిందని భావించండి.
(d) (b), (c) లోని సమాధానాలను పోల్చండి.
సాధన:
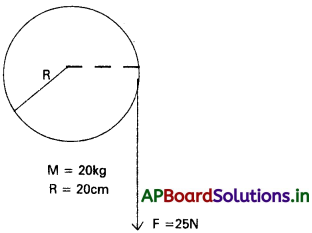
(a) Iα = τ
టార్క్ τ = FR
25 × 0.20 Nm(R = 0.20m)
= 5.0 Nm
I = దాని అక్షం పరంగా గతిపాలక చక్రం జడత్వభ్రామకం = \(\frac{MR^2}{2}\)
= \(\frac{20.0\times(0.2)^2}{2}\)
= 0.4kg m²
α = కోణీయ త్వరణం
= 5.0 Nm/0.4_kg m² 12.5 C-2
(b) 2m దారం చుట్టు విప్పడానికి జరిగిన పని
= 25 N × 2m = 50 J
(c) తుది కోణీయ వేగం ॥ అనుకొందాం. పొందిన గతిజశక్తి = \(\frac{1}{2}\) Iω²
నిశ్చల స్థితి నుంచి భ్రమణం ప్రారంభమైనది కాబట్టి ఇప్పుడు
ω2 = ω²0 +2αθ, ω0 = θ
కోణీయ స్థానభ్రంశం θ =
(విచ్చుకున్న దారం పొడవు) / (చక్రం వ్యాసార్థం)
= 2m/0.2 m = 10 rad
ω² = 2 × 12.5 ×10.0 = 250 (rad/s)²
పొందిన గతిజ శక్తి (K.E) = \(\frac{1}{2}\) × 0.4 × 250
= 50 J
(d) రెండింటి సమాధానం ఒకటే, అంటే చక్రం పొందిన గతిజశక్తి = బలం వల్ల జరిగిన పని. ఘర్షణ వల్ల శక్తి నష్టం జరగలేదు.

ప్రశ్న 15.
మూడు వస్తువులు, ఒక కంకణం, ఒక ఘన స్తూపం, ఒక ఘన గోళం, ఒకే వాలుతలంపై స్లిప్ కాకుండా దొర్లుతున్నాయి. అవి అన్నీ నిశ్చల స్థితి నుంచి దొర్లడం ప్రారంభించాయి. అన్నింటి వ్యాసార్థాలూ సమానం. ఏ వస్తువు గరిష్ఠ వేగంతో భూమిని (వాలు తలం కింది అంచును) చేరుతుంది?
సాధన:
దొర్లే వస్తువులకు శక్తి నిత్యత్వ సూత్రం వర్తిస్తుందని భావిద్దాం. అంటే ఘర్షణ వంటి బలాల వల్ల శక్తి నష్టం ఉండదని అనుకొందాం. అందువల్ల వాలుతలం వెంబడి కిందికి దొర్లే వస్తువు స్థితిజశక్తిలో తగ్గుదల (= mgh) వస్తువు గతిజశక్తిలో పెరుగుదలకు సమానం కావాలి (పటంలో చూడండి). వస్తువులు నిశ్చల స్థితి నుంచి బయలుదేరాయి. కాబట్టి అవి పొందిన గతిజశక్తి వాటి తుది గతిజశక్తికి సమానం.

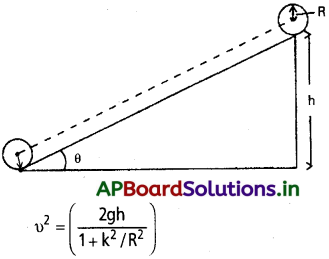
υ² విలువ దొర్లే వస్తువు ద్రవ్యరాశిపై ఆధారపడదు;
కంకణానికి, k² = R²

పై ఫలితాల నుంచి క్షితిజ తలాన్ని చేరినప్పుడు మూడు వస్తువుల్లోనూ గోళానికి వేగం గరిష్టంగా, కంకణానికి ద్రవ్యరాశి కేంద్ర వేగం కనిష్టంగా ఉంటుందని తెలుస్తోంది. వస్తువులు సమాన ద్రవ్యరాశి కలిగి ఉన్నాయనుకోండి.


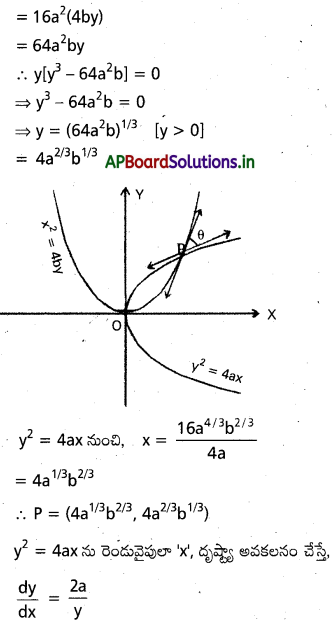
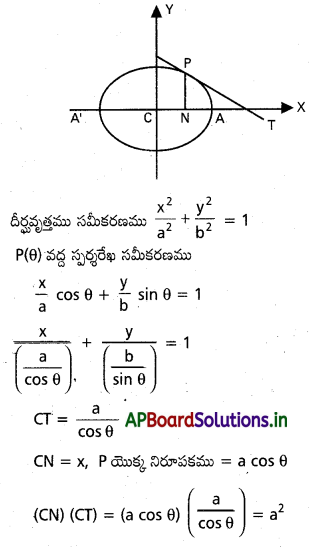
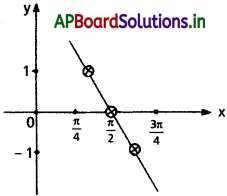
![]()




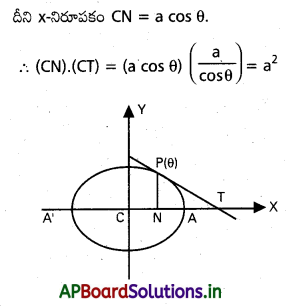
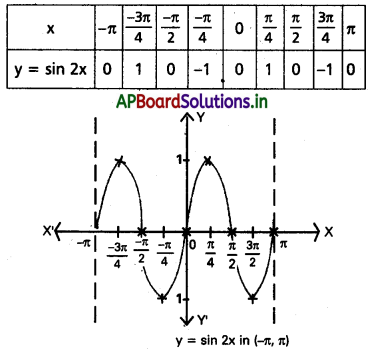
![]()

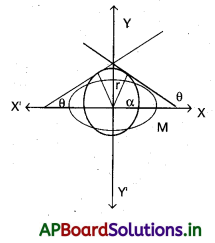
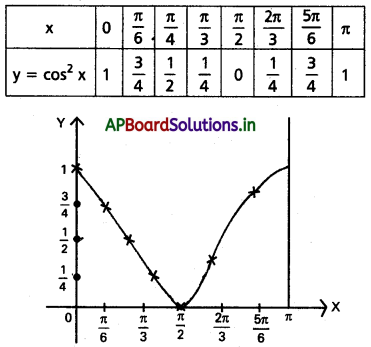
![]()




















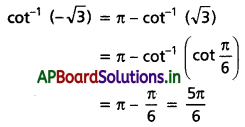

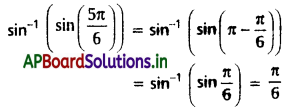

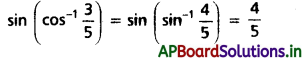
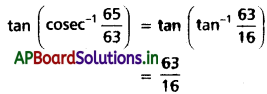

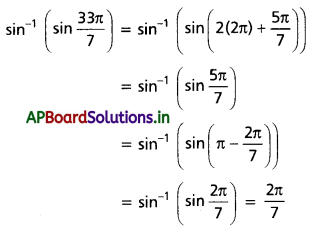
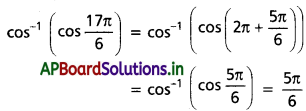
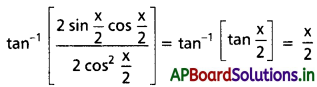
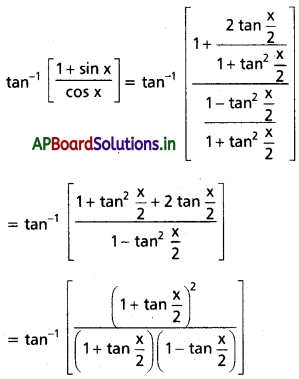
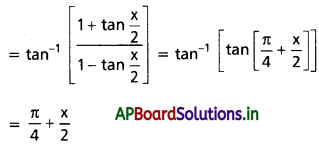
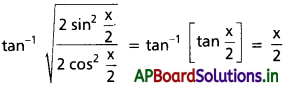
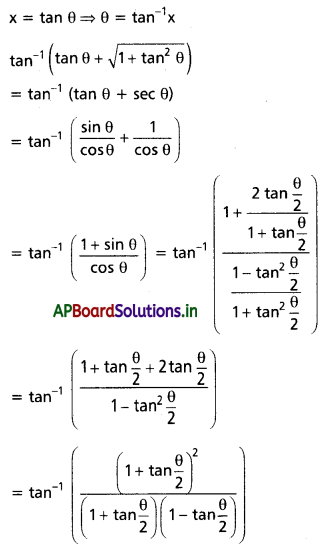
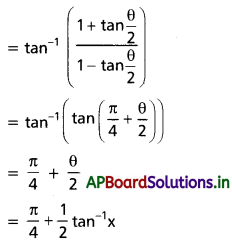














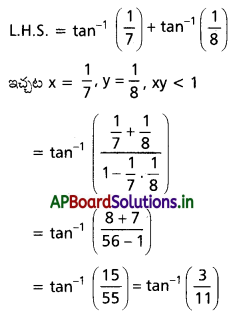


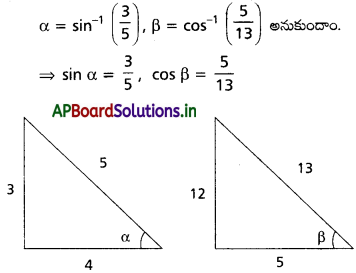

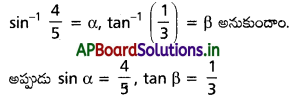


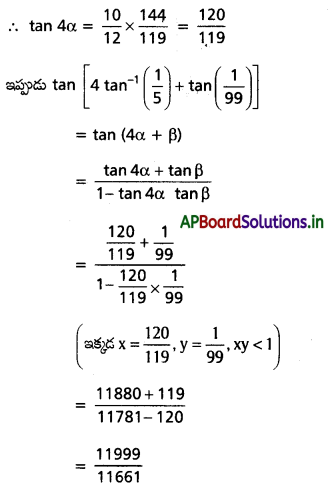

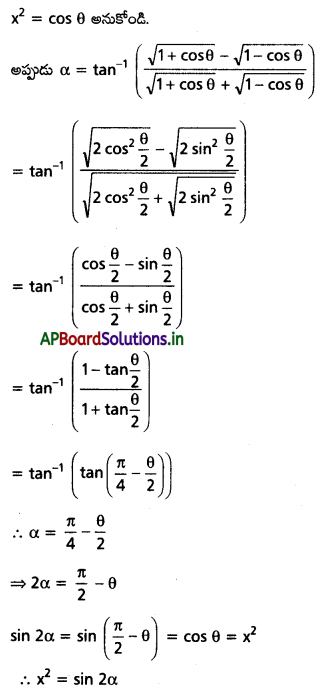
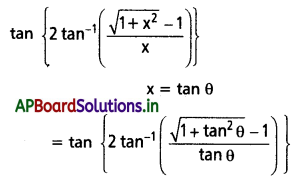






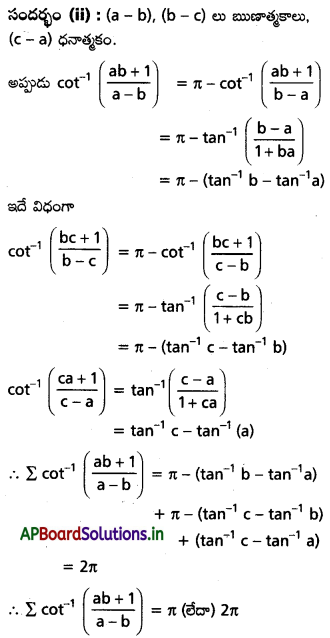
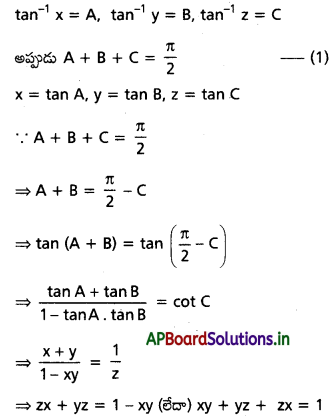














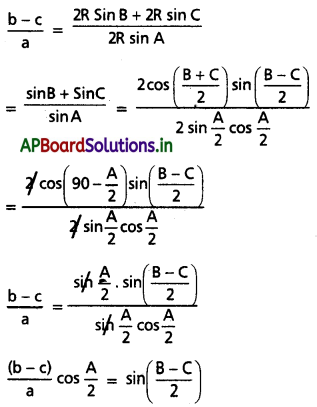
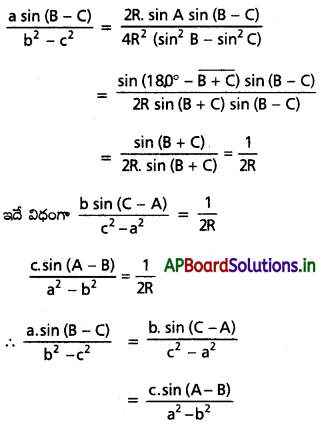



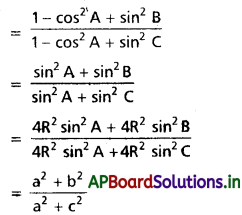





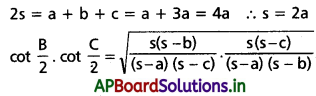








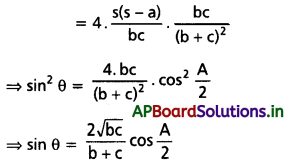
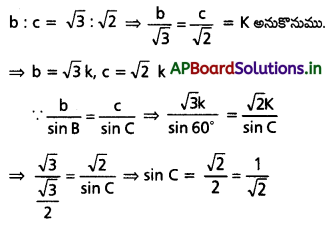
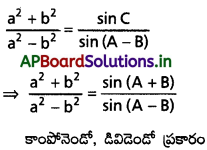



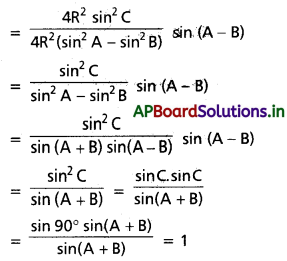






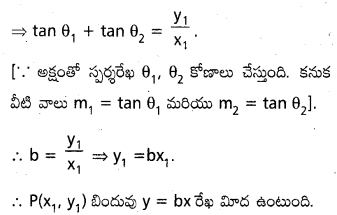

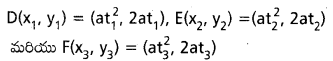

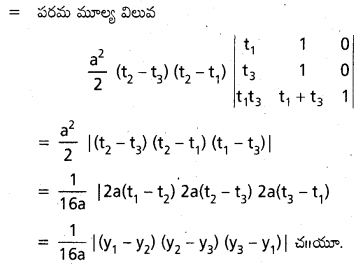
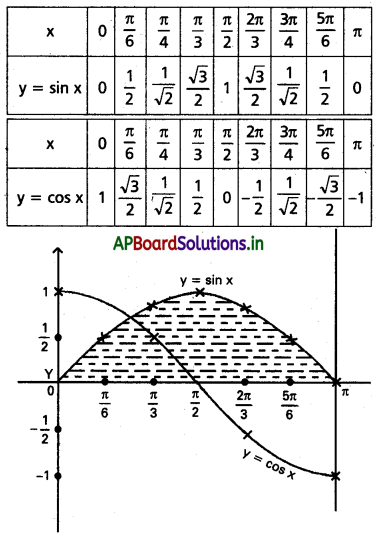
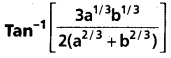 అని చూపండి.
అని చూపండి.