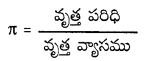AP State Board Notes

Students can go through AP Board 6th Class Maths Notes 12th Lesson దత్తాంశ నిర్వహణ to understand and remember the concept easily.

AP Board 6th Class Maths Notes 12th Lesson దత్తాంశ నిర్వహణ

→ P.C. మహలనోబిస్ (భారతదేశం) (1893 – 1972):
ఈయన భారత సాంఖ్యక శాస్త్ర పితామహుడిగా ఖ్యాతిగాంచారు. కోల్‌కతాలో గల భారత సాంఖ్యక శాస్త్ర పరిశోధనా సంస్థను ఈయన స్థాపించారు. ఈయన ‘నేషనల్ శాంపిల్ సర్వేలు’ ప్రపంచ ఖ్యాతిని పొందాయి.

→ దత్తాంశము : ఒక నిర్ణయం తీసుకోవడానికి సహాయపడు సంఖ్యాత్మక లేదా వివరణాత్మక సమాచారాన్ని దత్తాంశం అంటారు.

→ పౌనఃపున్య విభాజన పట్టిక : దత్తాంశంలోని వివిధ అంశాలను, వాటి పౌనఃపున్యాలను (అంశాల సంఖ్యను) సూచించు పట్టికను పౌనఃపున్య విభాజన పట్టిక అంటారు.

→ దత్తాంశాన్ని సూచించు చిత్రాలు : పౌనఃపున్య విభాజన పట్టికలో చూపిన దత్తాంశాన్ని దృశ్య రూపంలో చూపటానికి పట చిత్రాలు, కమ్మీ రేఖాచిత్రాలు, వలయ చిత్రాలు మొదలగునవి ఉపయోగిస్తారు.

→ పట చిత్రాలు : పౌనఃపున్య విభాజనంలోని దత్తాంశాన్ని సూచించుటకు బొమ్మలకు ఉపయోగించే చిత్రాలు. దత్తాంశంలోని అంశాల పౌనఃపున్యం అనుగుణంగా కొన్ని అంశాలకు ఒక బొమ్మ ప్రాతినిథ్యం వహించే విధంగా స్కేలును నిర్ణయించి, పటచిత్రాలు గీస్తాము.

→ కమ్మీ రేఖా చిత్రాలు : కమ్మీ రేఖా చిత్రాలు గీయడానికి గ్రాఫ్ కాగితాన్ని ఉపయోగిస్తాము. ఇవి రెండు రకాలుగా గీస్తాము.
అవి : 1. నిలువు కమ్మీ రేఖా చిత్రాలు,
2. అడ్డు కమ్మీ రేఖా చిత్రాలు. కమ్మీ రేఖా చిత్రాలలోని కమ్మీల వెడల్పులు మరియు కమ్మీల మధ్య దూరం సమానంగా ఉంటాయి. కమ్మీలు దీర్ఘచతురస్రాకారంలో ఉంటాయి. మరియు కమ్మీల పొడవులు అవి సూచించే రాశుల పౌనఃపున్యాలకు అనులోమానుపాతంలో ఉంటాయి.

Students can go through AP Board 6th Class Maths Notes 11th Lesson చుట్టుకొలత – వైశాల్యం to understand and remember the concept easily.

AP Board 6th Class Maths Notes 11th Lesson చుట్టుకొలత – వైశాల్యం

→ చుట్టుకొలత : ఒక బహుభుజి యొక్క అన్ని భుజాల పొడవుల మొత్తాన్ని దాని చుట్టుకొలత అంటాము.
(i) త్రిభుజం చుట్టుకొలత :

త్రిభుజం చుట్టుకొలత = BC + AC + AB = (a + b + C) యూనిట్లు

(ii) చతురస్రం చుట్టుకొలత :

చతురస్రం చుట్టుకొలత = AB + BC + CD + DA
= a + a + a + a
= 4a యూనిట్లు = 4 × భుజము

(iii) దీర్ఘ చతురస్ర చుట్టుకొలత :

దీర్ఘ చతురస్ర చుట్టుకొలత = AB + BC + CD + DA
= l + b + l + b = 2l + 2b
= 2 × పొడవు + 2 × వెడల్పు

iv) వృత్తం యొక్క చుట్టుకొలతను వృత్త పరిధి అంటారు. దీనిని ‘C’ తో సూచిస్తారు.

వృత్త పరిధి C = 2πr యూనిట్లు (ఇక్కడ r – వృత్త వ్యాసార్ధం, π = \(\frac{22}{7}\))
π : వృత్త పరిధి మరియు వ్యాసముల యొక్క నిష్పత్తిని π విలువగా నిర్వచిస్తాము. ఈ విలువ ఎల్లప్పుడు స్థిరము. ఈ స్థిర విలువ \(\frac{22}{7}\)కు సమానము.

π = \(\frac{C}{d}\)
∴ C = πd
వృత్త పరిధి = π × వ్యాసము
C = π × 2 × వ్యాసార్ధం
C = 2π × వ్యాసార్ధం
C = 2πr.

వైశాల్యం : ఒక వస్తువు ఆవరించిన ప్రాంతాన్ని దాని వైశాల్యము అంటాం.
చతురస్ర వైశాల్యం A = భుజం × భుజం
దీర్ఘచతురస్ర వైశాల్యం A = పొడవు × వెడల్పు

Students can go through AP Board 6th Class Maths Notes 10th Lesson ప్రాయోజిక జ్యామితి to understand and remember the concept easily.

AP Board 6th Class Maths Notes 10th Lesson ప్రాయోజిక జ్యామితి

→ జ్యామితీయ ఉపకరణాల పెట్టెలోని పరికరాలు – ఉపయోగాలు :
స్కేలు, వృత్తలేఖిని, కోణమానిని, విభాగిని మరియు రెండు మూలమట్టాలుంటాయి.
ఈ మూలమట్టాలలో ఒకటి 459, 459, 90°ల మూలమట్టం, మరొకటి 309, 60, 90°ల మూలమట్టము.

ఉపయోగాలు :

• స్కేలు : రేఖలు, రేఖాఖండాలు గీయడం మరియు రేఖాఖండాల పొడవులను కొలవడం.
• వృత్తలేఖిని : వృత్తాలు, చాపరేఖలు గీయడం.
• కోణమానిని : కోణాలను కొలవడం, కోణాలను గీయడం.
• విభాగిని : రేఖాఖండాన్ని సమభాగాలుగా విభజించడం, రేఖపై బిందువులను గుర్తించడం.
• మూలమట్టాలు : 159, 30°, 459, 75°, 90°, 1059, 135° కోణాలను గీయడానికి ఇచ్చిన రేఖ పై ఇచ్చిన బిందువు వద్ద సమాంతర, లంబరేఖలను గీయడానికి ఉపయోగిస్తారు.

→ రేఖాఖండానికి లంబ సమద్విఖండన రేఖ : ఇచ్చిన రేఖాఖండాన్ని రెండు సమాన భాగాలుగా విభజిస్తూ, ఆ రేఖాఖండానికి లంబంగా ఉండే రేఖను లంబ సమద్విఖండన రేఖ అంటారు.

→ కోణ సమద్విఖండనరేఖ : :ఇచ్చిన కోణాన్ని రెండు సమాన కోణాలుగా విభజించే రేఖ (కిరణం)ను ఆ కోణం యొక్క కోణ సమద్విఖండన రేఖ అంటారు.

ఉదా :
ప్రక్కపటంలో ∠BOC = ∠COA
∠AOB ని \(\overrightarrow{\mathrm{OC}}\) రెండు సమాన కోణాలు ∠BOC
మరియు ∠COA లుగా విభజిస్తున్నది.
కావున ∠AOB యొక్క కోణ సమద్విఖండనరేఖ \(\overrightarrow{\mathrm{OC}}\) అవుతుంది.

Students can go through AP Board 8th Class Maths Notes 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు to understand and remember the concept easily.

AP Board 8th Class Maths Notes 4th Lesson ఘాతాంకాలు మరియు ఘాతాలు

→ a × a × a …… m సార్లు = a^m.

→ a^m ను భూమి అని, m ను ఘాతాంకం అని అంటారు.

→ a^m × aⁿ = a^m+n

→ \(\frac{a^{m}}{a^{n}}\) = a^m-n (m > n) = \(\frac{1}{a^{n-m}}\) (m < n)

→ (ab)^m = a^m . b^m

→ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)

→ a⁰ = 1

→ (a^m)ⁿ = a^mn

→ a^-n = \(\frac{1}{a^{n}}\)

→ \(\sqrt[n]{a}\) = (a)^1/n

→ aⁿ = \(\frac{1}{a^{-n}}\)

Students can go through AP Board 8th Class Maths Notes 3rd Lesson చతుర్భుజాల నిర్మాణాలు to understand and remember the concept easily.

AP Board 8th Class Maths Notes 3rd Lesson చతుర్భుజాల నిర్మాణాలు

→ఒక చతుర్భుజం నాలుగు భుజాలు, నాలుగు కోణాలు, నాలుగు శీర్షాలు, రెండు కర్ణాలు కలిగి ఉంటుంది.

→ చతుర్భుజంలో 4 కోణాల మొత్తం 360°.

→ చతుర్భుజాలు – రకాలు :

→ ఏకైక చతుర్భుజం నిర్మించాలంటే అయిదు స్వతంత్ర కొలతలు అవసరం.

→ చతుర్భుజాలు ఏకైకంగా నిర్మించడానికి మనం వాడే కొలతలు
a) నాలుగు భుజాల పొడవులు, ఒక కోణం కొలత ఇచ్చినపుడు
b) నాలుగు భుజాల పొడవులు, ఒక కర్ణం కొలత ఇచ్చినపుడు
c) మూడు భుజాల పొడవులు మరియు రెండు కర్ణాల కొలతలు ఇచ్చినపుడు
d) రెండు ఆసన్న భుజాలు మరియు మూడు కోణాల కొలతలు ఇచ్చినపుడు
e) మూడు భుజాల పొడవులు మరియు రెండు ఉమ్మడి కోణాలు ఇచ్చినపుడు

→ ప్రత్యేక చతుర్భుజాలైన రాంబస్ మరియు చతురస్రాలను వాటి రెండు కర్ణాల కొలతలు ఇచ్చినపుడు నిర్మించవచ్చు.

Students can go through AP Board 8th Class Maths Notes 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు to understand and remember the concept easily.

AP Board 8th Class Maths Notes 2nd Lesson ఏకచరరాశిలో రేఖీయ సమీకరణాలు

→ ఒక బీజీయ సమీకరణం అనేది స్థిరరాశులు, చరరాశులు గల బీజీయ సమాసాల సమానత్వంను తెలుపుతుంది.

→ ‘ =’ గుర్తు గలిగిన గణిత వాక్యాన్ని సమీకరణం అంటారు.

→ ‘=’ గుర్తునకు ఎడమవైపున ఉండే పదాన్ని L.H.S అని, కుడివైపున ఉండే పదాన్ని R.H.S అని అంటారు.

→ ఒక సర్వసమీకరణం L.H.S = R.H.S అవుతుంది.

→ ఒక రేఖీయ సమీకరణంలో ఒకే ఒక చరరాశి ఉన్న దానిని ఏక చరరాశిలో రేఖీయ సమీకరణం అంటారు.

→ గమనించండి :

• ‘+’ రాశి పక్షాంతరం చెందిన ‘-‘ రాశి గానూ
• ‘-‘ రాశి పక్షాంతరం చెందిన ‘+’ రాశి గానూ
• ‘×’ రాశి పక్షాంతరం చెందిన ‘÷’ రాశి గానూ
• ‘÷’ రాశి పక్షాంతరం చెందిన ‘×’ రాశి గానూ మార్పు చెందును.

Students can go through AP Board 10th Class Maths Notes 14th Lesson సాంఖ్యక శాస్త్రం to understand and remember the concept easily.

AP Board 10th Class Maths Notes 14th Lesson సాంఖ్యక శాస్త్రం

→ రోనాల్డ్. ఎ. ఫిషర్ – (1890-1962):

• సాంఖ్యకశాస్త్ర పితామహుడు “సర్.రోనాల్డ్.ఎ.ఫిషర్ ఫ్రెంచ్)”.
• స్టాటిస్టిక్స్ అను ఆంగ్ల పదం “స్టారుస్టా” అను ఇటాలియన్ పదం మరియు “స్టాటిస్టిక్” అను గ్రీకు పదం నుండి ఉద్భవించింది.
• స్టాటిస్టిక్స్ అనగా ‘సంఖ్యల గురించి సమాచారం సేకరించుట’.

→ అవర్గీకృల బత్తాంశ సగటు : ఇవ్వబడిన రాశులు (observations) యొక్క మొత్తాన్ని రాశుల సంఖ్యచే భాగిస్తే – సగటు” వస్తుంది. x₁, x₂, , …… x_n, రాశుల యొక్క పౌనఃపున్యాలు వరుసగా f₁, f₂, ……. f_n, అనగా x₁, అనే రాశి f₁, సార్లు, x₂, అనే రాశి {, సార్లు పునరావృతం అయిందని అదే విధంగా x₃, …, x_n, లు కూడా.
ఇపుడు, రాశుల మొత్తము = f₁x₁ + f₂x₂ + ….. + f_nx_n
మరియు రాశుల సంఖ్య = f₁ + f₂ + …. + f_n.

కాబట్టి, ఇవ్వబడిన దత్తాంశం యొక్క సగటు (x̄)
x̄ = \(\frac{f_{1} x_{1}+f_{2} x_{2}+\ldots \ldots \ldots+f_{n} x_{n}}{f_{1}+f_{2}+\ldots \ldots \ldots+f_{n}}\)
పై ‘సగటు’ను సంక్షిప్తంగా గ్రీకు అక్షరం (సిగ్మా) ‘Σ’ (Σ అనగా మొత్తం) నుపయోగించి
x̄ = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)గా రాస్తాము.

→ ఒక వర్గీకృత విభాజనము యొక్క అంకమధ్యమము లెక్కించుటకు సూత్రాలు :
(i) ప్రత్యక్ష పద్ధతి : x̄ = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) f – పౌనఃపున్యము, x – తరగతి మధ్య విలువ

(ii) విచలన పద్ధతి (ఊహించిన సగటు పద్ధతి) : x̄ = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
a = ఊహించిన తరగతి అంకమధ్యమం
d = x_i – a,
x_i – తరగతి మధ్య విలువ
Σf_i = పౌనఃపున్యాల మొత్తం

(iii) సంక్షిప్త విచలన పద్ధతి : x̄ = a + \(\left(\frac{\Sigma f_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\right)\) × h
a = ఊహించిన తరగతి సగటు
µ_i = \(\frac{\mathrm{x}_{\mathrm{i}}-\mathrm{a}}{\mathrm{h}}\)
x_i = తరగతి మధ్య విలువ
h = తరగతి అంతరం
Σf_i = పౌనఃపున్యాల మొత్తం

→ వర్గీకృత పౌనఃపున్య విభాజనంనకు బాహుళక సూత్రం :
బాహుళకము = l + \(\left(\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}}\right)\) × h
ఇచ్చట, l = బాహుళక తరగతి యొక్క దిగువహద్దు
h = బాహుళక తరగతి పొడవు
f₁ = బాహుళక తరగతి యొక్క పౌనఃపున్యము
f₀ = బాహుళక తరగతికి ముందున్న తరగతి యొక్క పౌనఃపున్యము
f₂ = బాహుళక తరగతికి తరువాత నున్న తరగతి యొక్క పౌనఃపున్యము.

→ వర్గీకృత దత్తాంశం యొక్క మధ్యగతము (Median) : ‘మధ్యగతము’ అనేది కేంద్రస్థాన విలువలు (Measure of central tendency)లో ఒకటి, ఇది ఇవ్వబడిన దత్తాంశములోని రాశుల లేదా పరిశీలనాంశాల యొక్క మధ్య విలువ’ను ఇస్తుంది. అవర్గీకృత దత్తాంశానికి ‘మధ్యగతాన్ని కనుగొనే విధానాన్ని ఒకసారి గుర్తుకు తెచ్చుకుందాం. అవర్గీకృత దత్తాంశానికి ‘మధ్యగతం’ను కనుగొనుటకు, ముందుగా , దత్తాంశంలోని రాశులను లేదా పరిశీలనాంశాలను ‘ఆరోహణక్రమం’లో అమర్చుకోవాలి.

అపుడు, ఒకవేళ రాశులసంఖ్య ‘n’ బేసిసంఖ్య అయితే, మధ్యగతము అనేది \(\left(\frac{\mathrm{n}+1}{2}\right)\) వ రాశి లేదా పరిశీలనాంశము అవుతుంది.

ఒకవేళ, ‘n’ సరిసంఖ్య అయితే ‘మధ్యగతం’ అనేది \(\left(\frac{n}{2}\right)\) వ రాశి మరియు \(\left(\frac{\mathrm{n}}{2}+1\right)\) రాశుల సరాసరి అవుతుంది.
ఇచ్చిన దత్తాంశము యొక్క మధ్యగతమును క్రింది సూత్రమును ఉపయోగించి కనుగొంటాము.

→ వర్గీకృత దత్తాంశం యొక్క మధ్యగతమునకు సూత్రం : పదాల వివరణ :
మధ్యగతము M = l + \(\left(\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\right)\) × h
ఇందులో l = మధ్యగత తరగతి దిగువహద్దు
n = దత్తాంశంలోని రాశుల సంఖ్య
cf = మధ్యగత తరగతికి ముందు తరగతి యొక్క సంచిత పౌనఃపున్యము
f = మధ్యగత తరగతి యొక్క పౌనఃపున్యము
h = మధ్యగత తరగతి పొడవు

→ ఓజీవ్ వక్రాలు గీయుటలో X-అక్షముపై తరగతి హద్దులను, Y-అక్షముపై సంచిత పౌనఃపున్యములను తీసుకొనవలెను.

→ రెండు అక్షములపై తీసుకొను స్కేలు సమానంగా ఉండనవసరం లేదు.

→ ఒకే దత్తాంశము యొక్క రెండు ‘ఓజీవ్ వక్రాలు పరస్పరం ఖండించుకొన్న బిందువు నుండి X-అక్షం మీదికి గీచిన లంబపాదము ఆ దత్తాంశము యొక్క మధ్యగతమును తెలుపుతుంది. ‘ అనగా ఖండన బిందువులోని X-నిరూపకం మధ్యగతము అవుతుంది.

Students can go through AP Board 10th Class Maths Notes 13th Lesson సంభావ్యత to understand and remember the concept easily.

AP Board 10th Class Maths Notes 13th Lesson సంభావ్యత

→ పియర్ సిమ్సన్ లాప్లేస్ (1749-1827)

• “సంభావ్యత” అను నిర్వచనాన్ని మొదటగా పియర్ సిమ్సన్ లాప్లేస్ 1795లో ఇచ్చారు.
• “ది బుక్ ఆన్ గేమ్స్ ఆఫ్ ఛాన్స్” అనే పుస్తకంలో సంభావ్యతకు చెందిన సిద్ధాంతాన్ని ఇటాలియన్ ఫిజీషియన్ మరియు గణిత శాస్త్రవేత్త అయిన జె. కార్డన్ 16వ శతాబ్దములో ఇచ్చారు.
• ఇంకా సంభావ్యతపై విశేష కృషిగావించినవారు జేమ్స్ బెర్నౌలి. ఎ.డి. మావియర్ మరియు పియర్ సిమ్సన్ లాప్లేన్లు.
• ప్రస్తుత కాలంలో సంభావ్యతను జీవశాస్త్రం, అర్థశాస్త్రం, భౌతికశాస్త్రం, సామాజికశాస్త్రం, భౌతికశాస్త్రం, ఆర్థికశాస్త్రం మొదలైన రంగాలలో విశేషంగా వాడుతున్నారు.

→ సంభావ్యతకు చెందిన సిద్ధాంతం 16వ శతాబ్ద కాలానిది.

→ “ది బుక్ ఆన్ గేమ్స్ ఆఫ్ ఛాన్స్” అనే పుస్తకాన్ని ఇటాలియన్ ఫిజీషియన్ మరియు గణితవేత్త అయిన జె. కార్డన్ రచించారు.

→ జేమ్స్ బెర్నౌలి, ఎ. డి. మావియర్ మరియు పియర్ సిమ్సన్ లాప్లేన్లు సంభావ్యత సిద్ధాంతంపై విశేషమైన కృషిచేశారు.

→ ప్రయోగిక సంభావ్యత : ప్రయోగపూర్వక ఫలితాలను ఆధారం చేసుకొని లెక్కించిన సంభావ్యతను “ప్రయోగిక సంభావ్యత” అంటారు. ఉదా : ఒక నాణేన్ని 1000 సార్లు ఎగురవేసినపుడు 455సార్లు బొమ్మ, 545 సార్లు బొరుసు పడినది. బొమ్మపడే సంభవాన్ని ప్రమాణీకరణము చేస్తే 1000కి 455 సార్లు అనగా \(\frac{455}{1000}\) = 0.455.

మొత్తం పర్యవసానాల సంఖ్య సైద్ధాంతిక (లేదా) సాంప్రదాయక సంభావ్యత : ప్రయోగం చేయకుండానే అన్ని పర్యవసానాలను బట్టి ఒక ఘటన యొక్క సంభావ్యతను అంచనావేయుటను సైద్ధాంతిక సంభావ్యత లేదా సాంప్రదాయక సంభావ్యత అంటారు. పియర్ సిమ్సన్ లాప్లేస్ ఈ క్రింది నిర్వచనాన్ని ఇచ్చారు.

ఉదా : ఒక నాణేన్ని ఎగురవేసిన బొమ్మ పడు సంభావ్యత
ఒక నాణేన్ని ఎగురవేసినపుడు బొమ్మ పడుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 1
మొత్తం పర్యవసానాల సంఖ్య = 2 (బొమ్మ, బొరుసు)

గమనిక : ఒక ప్రయోగాన్ని అనేకసార్లు నిర్వచించినపుడు ప్రయోగిక సంభావ్యత దాదాపుగా సైద్ధాంతిక సంభావ్యతను సమీపించును. అనగా రెండింటి విలువలు ఒకే విధంగా ఉండును (దాదాపుగా సమానంగా ఉండును).

→ కచ్చిత ఘటన యొక్క సంభావ్యత 1.

→ అసంభవ ఘటన యొక్క సంభావ్యత ‘0’.

→ ఒక ఘటన (E) యొక్క సంభావ్యత P(E) అయిన 0 ≤ P(E) ≤ 1 అగును.

→ P(E) + P(\(\overline{\mathrm{E}}\)) = 1.

→ కొన్ని పరిశీలనలు :

• ఒక ప్రయోగములో ఒక ఘటనకు అనుకూల పర్యవసానము ఒక్కటి మాత్రమే అయిన దానిని ప్రాథమిక ఘటన (Elementary event) అంటారు.
• ఒక ప్రయోగంలో Y, R, B లు ప్రాథమిక ఘటనలు అయితే P(Y) + P(R) + P(B) = 1. – ఒక ప్రయోగంలో అన్ని ప్రాథమిక ఘటనల యొక్క సంభావ్యతల మొత్తము 1 అవుతుంది.
• పాచికను దొర్లించుటలో 3 కన్నా తక్కువ పడు ఘటనలు కానీ, 3 లేక అంతకన్నా ఎక్కువ పడు ఘటనలు కానీ ఈ ప్రాథమిక ఘటనలు కావు. కానీ రెండు నాణెములను ఎగురవేసినప్పుడు {HH}, {HT}, {TH}, {TT}లు ప్రాథమిక ఘటనలు.

→ పేక ముక్కలు (కార్డులు) – సంభావ్యత (Playing Cards – Probability):
మీరు ఎప్పుడైనా పేక ముక్కలను చూశారా? ఒక కట్టలో 52 కార్డులు ఉంటాయి. వాటిలో ఒక్కొక్కటి 13 కార్డులు గల 4 విభాగాలు ఉంటాయి. ఆ విభాగాల గుర్తులు నలుపు స్పేట్లు , ఎరుపు హృదయం గుర్తులు , ఎరుపు డైమండులు మరియు నలుపు కళావరులు మరలా ఒక్కొక్క విభాగంలో ఏస్, రాజు, రాణి, జాకీలకు 10, 9, 8, 7, 6, 5, 4, 3, 2 గుర్తించబడిన 13 కార్డులు ఉంటాయి. రాజు, రాణి, జాక్ కార్డులను ముఖకార్డులంటారు. ఒక కట్టలోని అన్ని కార్డులు, కొన్ని కార్డులు లేక రెండు కట్టలను ఉపయోగించి రకరకాల ఆటలను ఆడుతారు. ఈ కార్డులను పంచుటలో, ఎదుటివారి వద్ద ఉన్న కార్డులను ఊహించుటలో, గెలుచుటకు ఎత్తులు వేయుటలో సంభావ్యత ఎంతగానో ఉపయోగపడుతుంది.

ఉదా : ఒక పేక కట్ట నుండి ఒక పేక ముక్కను తీసిన అది ఎరుపు లేదా నలుపు ముక్క అగుట-సమ సంభవ ఘటన.
→ ఏస్ లేదా రాజు ‘కార్డు పొందుట – పరస్పర వర్జిత ఘటన.


→ ఏస్ లేదా హృదయాకార కార్డు పొందుట – ఇది పరస్పర వర్జిత ఘటన కాదు. ఎందుకనగా హృదయాకార కార్డులు ఏస్ ను కూడా కలిగి ఉంటాయి.

→ ఒక నాణేన్ని ఎగురవేస్తే వచ్చు పర్యవసానాలు H, T.

→ ఒక పాచికను దొర్లిస్తే వచ్చు పర్యవసానాలు 1, 2, 3, 4, 5 & 6.

→ ఒక నాణేన్ని ‘n’ సార్లు ఎగురవేస్తే వచ్చు మొత్తం పర్యవసానాల సంఖ్య = 2ⁿ.

→ ఒక పాచికను ‘n’ సార్లు ఎగురవేస్తే వచ్చు మొత్తం పర్యవసానాల సంఖ్య = 6ⁿ.

Students can go through AP Board 6th Class Maths Notes 9th Lesson ద్విమితీయ – త్రిమితీయ ఆకారాలు to understand and remember the concept easily.

AP Board 6th Class Maths Notes 9th Lesson ద్విమితీయ – త్రిమితీయ ఆకారాలు

→ ద్విమితీయ ఆకారాలు (2D ఆకారాలు) :
చదునైన ఉపరితలంపై ఉండే కాగితం, బోర్డు, చాప మొదలైన వాటిని ద్విమితీయ ఆకారాలు లేదా 2D ఆకారాలు అంటారు.
ద్విమితీయ ఆకారాలు లేదా 2D ఆకారాలు పొడవు, వెడల్పు అనే రెండు కొలతలను కలిగి ఉంటాయి.

→ త్రిమితీయ లేదా 3D – ఆకారాలు :
త్రిమితీయ లేదా 3D – ఆకారాలు పొడవు, వెడల్పు, ఎత్తు (లేదా లోతు) అనే మూడు కొలతలను కలిగి ఉంటాయి. ఉదాహరణ : ఇటుక, సోపు.

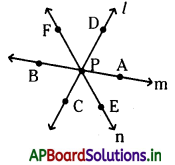
→ తలం : చదునుగా ఉండే ఉపరితలంపై ఉండే బిందు సముదాయాన్ని ‘తలం’ అంటారు. తలం అన్ని దిశలా వ్యాపించి ఉంటుంది.

→ బహుభుజులు : పరిమిత సంఖ్య గల రేఖాఖండాలతో ఏర్పడిన సరళ సంవృత పటాలను ‘బహుభుజులు’ అంటాము. భుజాల సంఖ్యను బట్టి బహుభుజులకు వేర్వేరు పేర్లు కలవు.

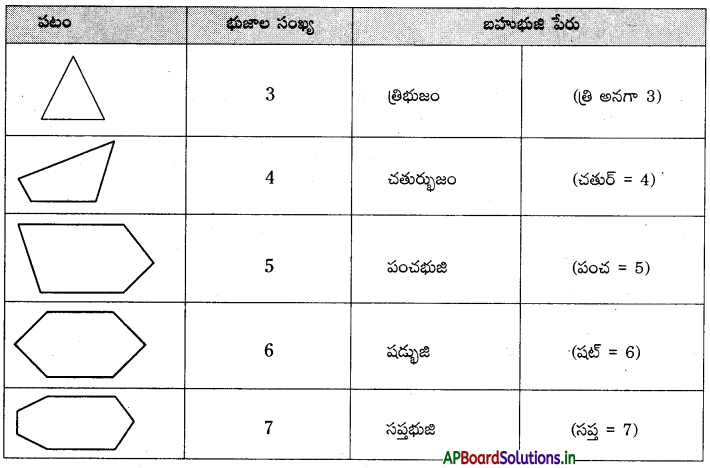
బహుభుజి ఏర్పడటానికి కావలసిన కనీస భుజాల సంఖ్య -3.

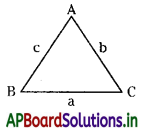
→ త్రిభుజాలు : మూడు రేఖాఖండాలతో ఏర్పడిన సరళ సంవృత పటాన్ని త్రిభుజం అంటారు. ఈ రేఖాఖండాలను త్రిభుజ భుజాలంటారు. త్రిభుజాన్ని “∆” గుర్తుతో సూచిస్తాము.
త్రిభుజం మూడు భుజాలను, మూడు కోణాలను, మూడు శీర్షాలను కలిగి ఉంటుంది.

→ త్రిభుజ భాగాలు :

భుజాలు : \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\)
కోణాలు : ∠BAC లేదా ∠A, ∠ABC లేదా ∠B, ∠BCA లేదా ∠C.
శీర్షాలు : A, B, C

→ ఒక తలంలోని త్రిభుజం ఆ తలంలోని బిందువులను మూడు భాగాలుగా విభజిస్తుంది.

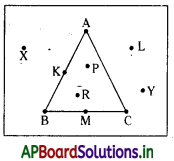
అవి :

• త్రిభుజం అంతరంలోని బిందువులు
• త్రిభుజం మీది బిందువులు
• త్రిభుజానికి బాహ్యంగా ఉన్న బిందువులు.
  P, R లు అంతర బిందువులు.
  A, B, C, K, M లు త్రిభుజం పై బిందువులు.
  M L, X, Y లు బాహ్యబిందువులు.

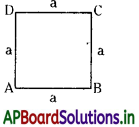
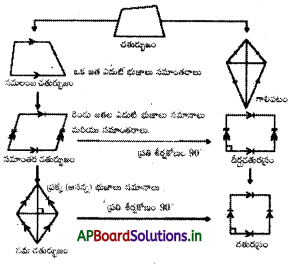
→ చతుర్భుజం : నాలుగు భుజాలతో ఏర్పడే సరళ సంవృతపటాన్ని చతుర్భుజం అంటారు. చతుర్భుజం నాలుగు భుజాలను, నాలుగు కోణాలను, నాలుగు శీర్షాలను కలిగి ఉంటుంది. ఎదురెదురు శీర్షాలను కలిపే రేఖాఖండాలను కర్ణాలు అంటారు. ABCD చతుర్భుజం యొక్క

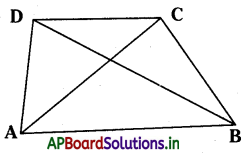
• భుజాలు : \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DA}}\)
• కోణాలు :
  • ∠DAB లేదా ∠A
  • ∠ABC లేదా ∠B
  • ∠BCD లేదా ∠C
  • ∠CDA లేదా ∠D
• శీర్షాలు : A, B, C, D.
• కర్ణాలు : \(\overline{\mathrm{AC}}, \overline{\mathrm{BD}}\)
  చతుర్భుజంలో ప్రక్కప్రక్కన ఉండే కోణాలను చతుర్భుజ ఆసన్నకోణాలు అంటారు.
  ∠A కు ఆసన్నకోణాలు ∠D మరియు ∠B.

→ వృత్తం : ఒక స్థిరబిందువు నుండి సమాన దూరంలో గల బిందువులను కలుపగా ఏర్పడే సరళసంవృత పటాన్ని వృత్తం అంటారు. స్థిర బిందువును వృత్త కేంద్రం అంటాము. స్థిరబిందువు నుండి వృత్తం పై గల బిందువుకు గల దూరాన్ని వృత్తకేంద్రం అని, ఆ వృత్తం యొక్క అంచు పొడవును వృత్తపరిధి అని అంటారు.

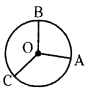
O – వృత్తకేంద్రము
\(\overline{\mathrm{OA}}, \overline{\mathrm{OB}}, \overline{\mathrm{OC}}\) లు వృత్త వ్యాసార్ధాలు

→ జ్యా, వ్యాసము : వృత్తం పై గల ఏ రెండు బిందువులనైనా కలిపే రేఖాఖండాన్ని వృత్త జ్యా అంటారు. కేంద్రం గుండా పోవు జ్యాను ఆ వృత్త వ్యాసం అంటారు. ఒక వృత్త జ్యాలన్నింటిలోను వ్యాసం పెద్దది. ప్రక్కతలంలో,

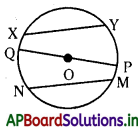
O – వృత్తకేంద్రము
\(\overline{\mathrm{XY}}, \overline{\mathrm{PQ}}, \overline{\mathrm{MN}}\) లు జ్యాలు
PQ – వ్యాసము

→ వృత్తచాపము : ఒక వృత్తంపై ఉండే రెండు బిందువుల మధ్య ‘ , “ఉండే వృత్త భాగాన్ని “చాపం” అని అంటారు. ప్రక్కపటంలో చూపిన వృత్తభాగాన్ని \(\widehat{\mathrm{CD}}\) గా రాస్తాము.

→ సౌష్ఠవం :
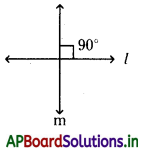
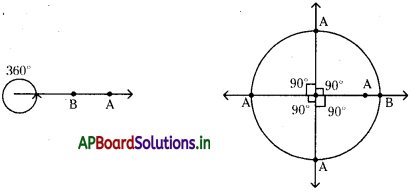
రేఖాసౌష్ఠవం : ఏ గీత వెంబడి మనం చిత్రాన్ని మడిచినప్పుడు రెండు భాగాలు ఒకదానితో ఒకటి సరిగ్గా ఏకీభవిస్తాయో దానిని రేఖాసౌష్టవమని, ఏ రేఖ వెంబడి కాగితాన్ని మడిచామో ఆ రేఖను సౌష్ఠవరేఖ లేదా సౌష్ఠవాక్షం అని అంటారు.

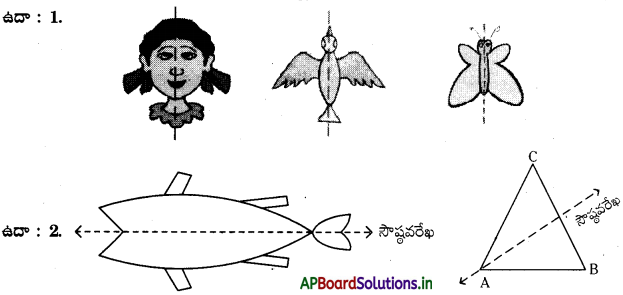
పై ఉదాహరణల నుండి మనం సౌష్ఠవ రేఖ నిలువుగా లేదా అడ్డంగా లేదా ఒక మూలగా కూడా ఉండవచ్చును. ఒక పటానికి ఒకటి లేదా ఒకటికన్నా ఎక్కువ సౌష్ఠవ రేఖలు ఉండవచ్చును.

→ త్రిమితీయ లేదా 3-D ఆకారాలు :
పొడవు (l), వెడల్పు (b), ఎత్తు లేదా లోతు (h) కలిగిన వస్తువులను త్రిమితీయ లేదా 3-D ఆకారాలు అంటారు.
ఉదా : దీర్ఘఘనం, ఘనం, స్థూపం, …….. . 3D – వస్తువులు తలాలు, అంచులు, శీర్షాలను కలిగి ఉంటాయి.

→ దీర్ఘఘనం (Cuboid) :

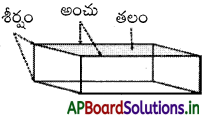
అగ్గిపెట్టె, ఇటుక ఆకారంలో గల వస్తువులు దీర్ఘఘనానికి చక్కటి ఉదాహరణలు. శీర్షం కుతలం దీర్ఘఘనం 6 తలాలు, 12 అంచులు, 8 శీర్షాలను కలిగి ఉంటుంది. (తలంను ముఖం అని కూడా అంటారు. )

→ ఘనం (Cube) :

పొడవు, వెడల్పు, ఎత్తులు సమానంగా గల దీర్ఘఘనమే ఘనము. . ఘనం కూడా 6 తలాలు, 12 అంచులు, 8 శీర్షాలను కలిగి ఉంటుంది.

→ పట్టకం (Prism):

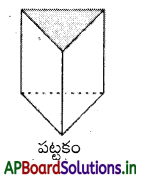
పట్టక త్రిభుజాకార ముఖాలు, మిగిలిన ముఖాలు దీర్ఘచతురస్రాకారంలోగాని, చతురస్రాకారంలో గాని ఉంటాయి. దీనిని త్రిభుజాకార పట్టకం అంటారు.
త్రిభుజాకార పట్టకం 5 ముఖాలు, 9 అంచులు, 6 శీర్షాలను కలిగి ఉంటుంది.

→ పిరమిడ్ (Pyramid):

భూమి బహుభుజిగాను, ముఖాలు త్రిభుజాకారంలో ఉంటాయి.
పట్టకం భూమి చతురస్రాకారం అయితే దానిని చతురస్రాకార పిరమిడ్ అంటారు. చతురస్రాకార పిరమిడ్ 5 ముఖాలు, 8 అంచులు, 5 శీర్షాలను కలిగి ఉంటుంది.

పిరమిడ్ స్థూపం (Cylinder) :

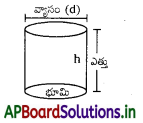
స్థూపం వక్రతలాన్ని, భూమిని కలిగి ఉంటుంది. దానికి ఎత్తు, వ్యాసంలను పటంలో చూడవచ్చును.

→ శంఖువు (Cone) :

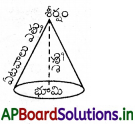
శంఖువు చదునైన వృత్తాకార భూమిని కలిగి, చదునైన వక్రతలాన్ని కలిగి, ఆ వక్రతలం ఒక బిందువు వద్దకు కొనసాగి అంతమవుతుంది. ఈ బిందువును శీర్షం అంటారు.

→ గోళం (Sphere) :

గోళం అన్ని వైపుల నుండి సులువుగా దొర్లే త్రిమితీయ వస్తువు. బంతి, గోళీలు గోళమునకు చక్కటి ఉదాహరణలు. గోళాన్ని అడ్డుకోతగా రెండు సమాన భాగాలుగా కోస్తే ఒక్కొక్క భాగం ఒక అర్ధగోళంగా ఏర్పడుతుంది.

→ 3D – ఆకారాల ముఖాలు (తలాలు) (Faces), అంచులు (Edges), శీర్షాల (Vertices) మధ్య సంబంధం (ఆయిలర్ సూత్రం) (Euler’s Formula) :
F+ V = E + 2

ముఖాల సంఖ్య + శీర్షాల సంఖ్య = అంచుల సంఖ్య + 2
దీనినే ఆయిలర్ సూత్రం అంటారు.

Students can go through AP Board 6th Class Maths Notes 8th Lesson జ్యామితీయ భావనలు to understand and remember the concept easily.

AP Board 6th Class Maths Notes 8th Lesson జ్యామితీయ భావనలు

→ బిందువు : పొడవు, వెడల్పులు లేని జ్యామితీయ ఆకారం బిందువు. బిందువులను సూచించుటకు మనం సాధారణంగా ఆంగ్ల పెద్ద అక్షరాలు A, B, C, …. లతో సూచిస్తాము.

→ స్కేలు, విభాగిని, వృత్తలేఖిని సహాయంతో మనం రేఖాఖండం పొడవును కొలుస్తాము.

→ రేఖ : రెండు వైపులా అనంతంగా విస్తరించిన రెండు కిరణాల సమ్మేళనం. దీనిని \(\overrightarrow{\mathrm{AB}}\) లేదా l, m అనే చిన్న అక్షరాలతో సూచిస్తారు.

→ ఖండన రేఖలు : సమతలంలోనే రెండు రేఖలకు ఒకే ఉమ్మడి బిందువు ఉంటే వాటిని ఖండన రేఖలు అంటారు. ఉదాహరణ : ‘m’ రేఖపై A, B, C బిందువులు, ‘l’ రేఖపై D, A,E బిందువులు కలవు. A బిందువు రెండు రేఖలపై కలదు. అనగా A ఉమ్మడిబిందువు. l, m లు ఖండనరేఖలు అవుతాయి.

→ సమాంతర రేఖలు : సమతలంలో రెండు రేఖలకు ఉమ్మడి బిందువు లేకుంటే వాటిని సమాంతర రేఖలు అంటారు.

l, m రేఖలకు ఉమ్మడిబిందువులు లేవు. l m లు సమాంతర రేఖలు.
సమాంతరరేఖలను ∥ గుర్తుతో సూచిస్తాము.
పై l, m రేఖలను l ∥ m లేదా \(\overrightarrow{\mathrm{AB}} / / \overrightarrow{\mathrm{CD}}\) గా సూచిస్తాము.

→ మిళిత రేఖలు : రెండు కన్నా ఎక్కువ రేఖలకు ఒకే ఉమ్మడి బిందువు ఉంటే, ఆ రేఖలను మిళిత రేఖలు అంటారు. ఆ ఉమ్మడి బిందువును మిళిత బిందువు అంటారు.

పై పటంలో l, m, n రేఖల ఉమ్మడి బిందువు P. (అనగా l, m, n రేఖలు ఒకదానికొకటి P వద్ద ఖండించుకొంటున్నాయి)

→ లంబరేఖలు : ఖండనరేఖలలో ఒక ప్రత్యేక సందర్భమే లంబరేఖలు. ఈ లంబరేఖలకు పుస్తకం పక్కపక్క అంచులు, నల్లబల్ల పక్క పక్క అంచులు, తలుపు పక్కపక్క అంచులను ఉదాహరణలుగా మనం చెప్పవచ్చును. లంబరేఖలను ‘⊥’ గుర్తుతో సూచిస్తాము.

→ రెండు లంబరేఖల మధ్యకోణము 90°.

పై పటంలోని l, m రేఖలు లంబరేఖలు. వీనిని l ⊥ m గా రాస్తాము.

→ కోణాలు, అందులో రకాలు : కోణము : ఒకే తొలిబిందువును కలిగిన రెండు విభిన్న కిరణాల సమ్మేళనాన్ని కోణం అంటారు. ఉమ్మడి తొలి బిందువును శీర్షం అని, కోణం ఏర్పరిచిన కిరణాలను కోణ భుజాలు అని అంటారు. ప్రక్క పటంలో ‘O’ కోణశీర్షము.

\(\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}}\) లు కోణ భుజాలు. శీర్షమును ఆధారంగా చేసుకొని ఒక భుజం నుండి మరొక భుజం చేసే భ్రమణ (తిరిగిన) పరిమాణాన్ని కొలవడమే కోణాన్ని కొలవడము.
కోణాన్ని సూచించడానికి వివిధ పద్ధతులు కలవు.

• శీర్షం ఆధారంగా పై పటంలో కోణం ∠O,
• కోణశీర్షం, భుజాలపై గల బిందువుల ఆధారంగా ∠AOB లేదా ∠BOA.
• సంఖ్య ఆధారంగా ∠1 గా సూచిస్తాము.

→ కోణాన్ని కొలవడం – షష్ట్యంశమానం :
కోణాలను మనం కోణమానిని అనే పరికరాన్ని ఉపయోగించి కొలుస్తాము. మూల మట్టాలను ఉపయోగించి కొన్ని ప్రత్యేక కోణాలను కొలవవచ్చును (15°, 30°, 45°, 60°, 75°, 90°,….). శీర్షం ఆధారంగా కోణం యొక్క ఒక భుజం, మరొక భుజంతో ఒక పూర్తి భ్రమణం పూర్తి చేసిన అది చేసే కోణము 360° గా పరిగణిస్తాము. ఈ పూర్తిభ్రమణాన్ని 360 సమభాగాలు చేయగా అందులో ఒక భాగాన్ని 1° అంటారు.

→ లంబకోణము : పూర్తి భ్రమణాన్ని 4 సమభాగాలు చేయగా ప్రతి భాగం యొక్క కోణము ఒక లంబ కోణము అవుతుంది. లంబకోణం విలువ = \(\frac{360^{\circ}}{4}\) = 90°

→ అల్పకోణము : 90° కన్నా తక్కువగా గల కోణాన్ని అల్పకోణము అంటారు.

→ అధికకోణము : 90° కన్నా ఎక్కువ, 180° కన్నా తక్కువ గల కోణాన్ని అధిక కోణం అంటారు.

→ అధికతర లేదా పరావర్తన కోణము : 180° కన్నా ఎక్కువ, 360° కన్నా తక్కువ గల కోణాన్ని అధికతర లేదా పరావర్తన కోణం అంటారు.

→ సరళకోణం : 180° గల కోణాన్ని సరళకోణం అంటారు.

→ సంపూర్ణ లేదా పరిపూర్ణ కోణం : 360° కోణాన్ని సంపూర్ణ లేదా పరిపూర్ణ కోణం అంటారు.

Students can go through AP Board 6th Class Maths Notes 7th Lesson బీజ గణిత పరిచయం to understand and remember the concept easily.

AP Board 6th Class Maths Notes 7th Lesson బీజ గణిత పరిచయం

→ చరరాశి : బీజగణితంలో మనం ప్రధానంగా తెలియని రాశులను బీజీయ అక్షరాలతో సూచిస్తాము. ఈ బీజీయ అక్షరాలను చరరాశులు అంటారు. ఈ చరరాశులను ఆంగ్ల అక్షరాలు l, m, n, p, q, x, y, Z, ………… లతో సూచిస్తాము.

→ చరరాశిని ఏదేని ఒక అక్షరంతో ఏదేని ఒక సంఖ్య కోసం ఉపయోగిస్తారు.

→ చరరాశి వేర్వేరు సందర్భాలలో వేర్వేరు విలువలను కలిగి ఉంటుంది. చరరాశికి ఖచ్చితమైన విలువ ఉండదు అయితే ఇవి కూడా సంఖ్యలే.

→ సంఖ్యా పరిక్రియలైన సంకలనం (+), వ్యవకలనం(-), గుణకారం (×), భాగహారం (+) వీటికి కూడా వర్తిస్తాయి.

→ రేఖాగణితం, క్షేత్రమితి, అంకగణితమునకు సంబంధించిన సూత్రాలలో చరరాశులను ఉపయోగిస్తాము. ఉదా : దీర్ఘచతురస్ర వైశాల్యం A = l × b
ఇక్కడ A వైశాల్యానికి, దీర్ఘచతురస్ర పొడవుకు, పే దీర్ఘచతురస్ర వెడల్పుకు ప్రాతినిథ్యం వహిస్తాయి.

→ సామాన్య సమీకరణాలు : బీజగణితంలోని నిబంధనను సమానత్వ గుర్తును ఉపయోగించి రాయడాన్ని సమీకరణం అంటారు.

ఉదా :
(1) x కన్నా 4 పెద్దదైన సంఖ్య 6.
x + 4 = 6
(2) ఒక సంఖ్య యొక్క 3 రెట్లు 15 అవుతుంది. .
3x = 15

→ సమీకరణానికి L.H.S మరియు R.H.S :
పై x + 4 = 6 అనే సమీకరణంలో మనం సమానత్వ గుర్తును చూడవచ్చును.
ఈ సమానత్వ గుర్తుకు ఎడమ చేతివైపు గల సమాసాన్ని LHS (Left Hand Side) అని, కుడిచేతివైపు గల సమాసాన్ని RHS (Right Hand Side) అని అంటారు. సమీకరణం అనగా LHS విలువ, RHS విలువ సమానం అయ్యేది. . . . . x + 4 = 6 లో LHS = x + 4
RHS = 6

→ ఏ చరరాశి విలువకు ఒక సమీకరణం యొక్క LHS మరియు RHS లు సమానం అగునో దానిని సమీకరణ సాధన అంటారు. దీనినే సమీకరణ మూలం అని కూడా అంటారు.
x + 4 = 6 లో x = 2 అయిన
2 + 4 = 6
6 = 6
L.H.S = R.H.S
కావున x + 4 = 6 యొక్క
సాధన (మూలం) x = 2

Students can go through AP Board 6th Class Maths Notes 6th Lesson ప్రాథమిక అంకగణితం to understand and remember the concept easily.

AP Board 6th Class Maths Notes 6th Lesson ప్రాథమిక అంకగణితం

→ నిష్పత్తి : ఒకే రకమైన రెండు రాశులను సరిపోల్చుటను నిష్పత్తి అంటారు. ఈ రెండు రాశులను ఒకదానితో మరొకటి భాగించినను, ఆ రాశులను నిష్పత్తి రూపంలో రాయు విధం అంటారు.
a, b అనే రాశుల నిష్పత్తిని a : b లేదా a + b లేదా \(\frac{a}{b}\) గా సూచించవచ్చును.
a : b లో a ని మొదటి పదం లేదా పూర్వపదం (Antecedent) అని, b ని ద్వితీయ పదం లేదా పరపదం (consequent) అని అంటారు.

→ నిష్పత్తిలోని రెండు పదాలను ఒకే సంఖ్యతో భాగించినా, లేదా గుణించినా ఆ నిష్పత్తి విలువ మారదు.
ఉదా : 3:2 = 3 × 3:2 × 3 = 9 : 6
9:6 = 9 ÷ 3 : 6 ÷ 3 = 3:2

→ నిష్పత్తి యొక్క కనిష్ఠ రూపం :
a : b అనే నిష్పత్తిలో పూర్వపదం a కు, పరపదం b కు ‘1’ తప్ప మరే ఉమ్మడి కారణాంకం లేకపోతే a : b కనిష్ట రూపంలో ఉంది అంటాము. దీనినే నిష్పత్తి యొక్క సామాన్య రూపం అని కూడా అంటాము.
ఉదా : 8:4 అనునది నిష్పత్తి యొక్క కనిష్ఠ రూపం కాదు. ఎందుకనగా పూర్వపదం 8 మరియు పరపదం 4లకు 2 మరియు 4లు ఉమ్మడి కారణాంకాలుగా కలవు. ఈ నిష్పత్తిలో పూర్వ, పరపదాలను 4తో భాగించగా,
8 ÷ 4 : 4 ÷ 4
\(\frac{8}{4}: \frac{4}{4}\) = 2:1
8 : 4 యొక్క కనిష్ఠ రూపాన్ని 2 :1 గా రాస్తాము.

→ సమనిష్పత్తులు లేదా సమాననిష్పత్తులు : నిష్పత్తి యొక్క పూర్వపదాన్ని మరియు పరపదాన్ని ఒకే శూన్యేతర సంఖ్యతో గుణించగా లేదా భాగించగా ఏర్పడే నిష్పత్తులను సమనిష్పత్తులు లేదా సమాన నిష్పత్తులు అంటారు.
ఉదా : 1 : 2 = 1 × 2:2 × 2 = 2 : 4
= 1 × 3:2 × 3 = 3:6
1:2, 2 : 4, 3 : 6 లు సమాన నిష్పత్తులు.

→ నిష్పత్తులను సరిపోల్చుట :
రెండు, అంతకన్నా ఎక్కువ నిష్పత్తులను పోల్చుటకు మనం కింది సోపానాలను అనుసరించాలి.

• ఇవ్వబడిన నిష్పత్తులను రాయాలి.
• ప్రతి నిష్పత్తిని భిన్న రూపంలో రాసి, దానిని సూక్ష్మరూపం (కనిష్ఠ రూపం)లోకి మార్చాలి.
• హారాల క.సా.గు. కనుగొనాలి.
• క.సా.గు. హారాలుగా గల సజాతి భిన్నాలుగా మార్చాలి.
• ఈ సజాతి భిన్నాల లవాలను సరిపోల్చాలి.
  లవం ఏ భిన్నానికైతే ఎక్కువ వుంటుందో ఆ భిన్నం రెండవ భిన్నం కన్నా పెద్దది.

ఉదా : 3:4; 5 : 6 లలో ఏది పెద్దదో పరిశీలిద్దాము .
3:4; 5:6 (సోపానం 1)
3.5 7 6 (సోపానం 2)
హారాలు 4, 6 ల కసాగు = 12 (సోపానం 3)
\(\frac{3 \times 3}{4 \times 3}=\frac{9}{12} ; \frac{5 \times 2}{6 \times 2}=\frac{10}{12}\) (సోపానం 4)
\(\frac{10}{12}>\frac{9}{12}\), కావున 5 : 6-పెద్దది (సోపానం 5)

→ అనుపాతము :
నిష్పత్తుల సమానత్వమును అనుపాతము అంటారు. a మరియు b ల నిష్పత్తి C మరియు C ల నిష్పత్తికి సమానం అయిన అవి అనుపాతంలో కలవు అంటారు.
దీనిని a : b:: c:d (a ఈజ్ టు b ఈజ్ ఏజ్ C ఈజ్ టు d) గా చదువుతాము . దీనిని a : b = c:d గా కూడా రాస్తాము.

. a, b, c, d లు అనుపాతంలో ఉంటే,
a: b :: c: d ఇక్కడ a, d లను అంత్యములని, b, c లను మధ్యములు అని అంటారు. మరియు a × d = b × c అనగా అంత్యముల లబ్ధం = మధ్యముల లబ్ధం అవుతుంది. అలాగే రెండు నిష్పత్తుల యొక్క అంత్యముల లబ్ధం, మధ్యముల
లబ్దానికి సమానమైన అవి రెండు అనుపాతంలో ఉంటాయి.

→ ఏకవస్తు పద్దతి : ఒక వస్తువు యొక్క విలువను కనుగొని, తద్వారా కావలసిన వస్తువుల విలువలని కనుగొనే పద్ధతిని ఏకవస్తు పద్ధతి అంటారు.
ఉదా : 5 పెన్నుల ఖరీదు ₹ 60 అయిన 3 పెన్నుల ఖరీదు ఎంత ?
సాధన. 5 పెన్నుల ఖరీదు = ₹ 60
1 పెన్ను ఖరీదు = ₹ 60 ÷ 5 = ₹ 12
3 పెన్నుల ఖరీదు = ₹ 12 × 3 = ₹ 36 శాతం : శాతం అనగా నూటికి (100కి) అని అర్ధము. అనగా ఒక వస్తువును 100 భాగాలు చేస్తే ఒక్కొక్క భాగం 1 శాతం అవుతుంది.
శాతమును సూచించుటకు “%” గుర్తుని ఉపయోగిస్తాము.

ఉదా : 1% = \(\frac{1}{100}\) = 0.01 లేదా 1 : 100 గా రాయవచ్చును.
25 % = \(\frac{25}{100}\) = 0.25 లేదా 25 : 100 గా రాయవచ్చును.

→ శాతంను భిన్న రూపంలోకి మార్చడానికి శాతంలోని ‘%’ గుర్తును తీసివేసి 100 చే భాగించాలి. ”
ఉదా : 30% ను భిన్నరూపంలో రాయడానికి 30% = \(\frac{30}{100}=\frac{3}{10}\)

→ భిన్నంను శాతంగా మార్చడానికి ఇచ్చిన భిన్నాన్ని 100చే గుణించి వచ్చిన ఫలితానికి % గుర్తును రాయాలి.