AP State Board Notes

Students can go through AP Board 10th Class Maths Notes 11th Lesson త్రికోణమితి to understand and remember the concept easily.

AP Board 10th Class Maths Notes 11th Lesson త్రికోణమితి

→ ఆర్యభట్ట 500 A.D:
ఈ రోజుల్లో మనం ఉపయోగించే ‘sine’ అనే భావన యొక్క ఉపయోగం మొట్టమొదటగా 500 A.D. లో ఆర్యభట్ట ద్వారా రాయబడిన “ఆర్యభట్టీయం” లో కనిపిస్తుంది. అందులో ఇది “అర్ధ-జ్యా”గా వాడబడింది. తర్వాత అది “జ్యా”గా లేదా “జివా”గా కాలక్రమేణా మారింది. అరబిక్ భాషలో అనువదింపబడిన ఆర్యభట్టీయంలో “జివా” యొక్క ప్రయోగం కనిపిస్తుంది. తర్వాత లాటిన్ భాషలో అనువదింపబడిన “ఆర్యభట్టీయం” లో “జివా”, “sine (సైన్)”గా మారింది. ఆంగ్ల ఖగోళ శాస్త్ర ఆచార్యుడు ఎడ్మండ్ గుంటర్(1581-1626)మొట్టమొదటగా ‘sine’ ను సూక్ష్మంగా ‘sin’ గా ఉపయోగించాడు.

→ మన నిత్యజీవితంలో వివిధ కట్టడాల ఎత్తులు, దూరాలు మరియు వివిధ సందర్భాల్లో ఏర్పడే కోణాలను త్రిభుజ ధర్మాల ఆధారంగా కనుగొనవచ్చును.

→ ఈ రకమైన సమస్యలను గణితంలో ఒక భాగమైన త్రికోణమితి ఆధారంగా సాధించవచ్చును.

→ త్రికోణమితి అనగా త్రిభుజంలో భుజాలకు మరియు కోణాలకు మధ్యన గల సంబంధంను తెలుపు గణితశాస్త్రము.

→ లంబకోణ త్రిభుజంలో భుజాలకు పేర్లు పెట్టటం :
ఒక లంబకోణ త్రిభుజం ABC ని తీసుకొనుము. పటంలో ‘B’ వద్ద లంబకోణము కలదు. A పరంగా ఎదురుగా వున్న భుజము BC కావున దీనిని ∠A కు “ఎదుటి భుజము” గరి అని అంటారు. మిగిలిన భుజము AB ని ∠A కు “ఆసన్న భుజము” అంటారు. ∠B కు ఎదురుగా ఉన్న భుజమును ‘కర్ణము” అంటారు.

→ త్రికోణమితీయ నిష్పత్తులు : ఒక లంబకోణ త్రిభుజంలో లంబకోణం మినహా మిగిలిన అల్పకోణాలకు, వాటి భుజాలకు మధ్యన గల నిష్పత్తిని “త్రికోణమితీయ నిష్పత్తులు” అంటారు, పటంలో చూపినట్లుగా ‘B’ వద్ద లంబకోణం కలిగిన లంబకోణ త్రిభుజం ABC లో ∠A కు A. త్రికోణమితీయ నిష్పత్తులు


→ “sine A” Dušxomaso as too “cosec A”, sin A : cosec A = 1.
“cosine A” యొక్క గుణకార విలోమం “secant A”, cos A ‘ sec A = 1
“tangent A” యొక్క గుణకార విలోమం “cot A”, tan A . cot A = 1

→ త్రికోణమితీయ నిష్పత్తుల యొక్క విలువలు

Note: 0 ≤ A ≤ 90 అయిన

• sinA మరియు CosA విలువలు ‘0’ మరియు ‘1’ ల మధ్యన ఉండును.
• tanA విలువ ‘0’ నుండి పెరిగి ‘∞’ అగును.
• cotA విలువ ‘co’ నుండి తగ్గి ‘0’ అగును.
• coseCA విలువ ‘o’ నుండి తగ్గి ‘1’ అగును.
• secA విలువ ‘1’ నుండి పెరిగి ‘∞’ అగును.
• పూరక కోణాల త్రికోణమితీయ నిష్పత్తుల మధ్య సంబంధం :

రెండు కోణాల మొత్తం 90° అయిన వాటిని “పూరక కోణాలు” అంటారు.
→ ఒక లంబకోణ త్రిభుజంలో B వద్ద లంబకోణమున్న ∠A + ∠C = 90° అగును. ∠C = 90° – 2A అగును.

→ ‘θ’ అల్పకోణమైన sin (90 – θ) = cos θ

• cot (90 – θ) = tanθ
• cos (90 – θ) = sin θ
• sec (90 – θ) = cosec θ
• tan (90 – θ) = cot θ
• cosec (90 – θ) = sec θ అగును

→ కోణమితీయ సర్వసమీకరణం : త్రికోణమితీయ నిష్పత్తుల ఆధారంగా ఏర్పడే అన్ని కోణాలకు సత్యమగు సమీకరణంను “త్రికోణమితీయ సర్వసమీకరణం” అంటారు. .

• sinA + cos- A = 1
• sec – A – tan: A = 1
• cosec – A – cot A = 1

Note : sin² A = (sinA)² కాని sinA² ≠ (sinA)²

Students can go through AP Board 10th Class Maths Notes 10th Lesson క్షేత్రమితి to understand and remember the concept easily.

AP Board 10th Class Maths Notes 10th Lesson క్షేత్రమితి

→ హెరాన్ క్రీ.శ. 10 – క్రీశ. 70 :

• అలెగ్జాండ్రియాకు చెందిన హెరాన్ (క్రీ.శ. 10 – క్రీ.శ. 70) ఒక ప్రాచీన గ్రీకు గణిత శాస్త్రజ్ఞుడు మరియు ఇంజినీర్.
• హెరాన్ వర్గమూలాన్ని దశదశల పద్ధతిలో గణించే పద్ధతిని వర్ణించాడు.
• త్రిభుజ వైశాల్యాన్ని దాని భుజ పొడవుల నుండి కనుగొన్నందుకు ఆయన పేరుతో హెరాన్ ఫార్ములా రూపొందింది. ఇక
• దృక్ శాస్త్రంలో ప్రిన్సిపల్ ఆఫ్ షార్టెస్ట్ పాథ్ ఆఫ్ లైట్’ను హెరాన్ రూపొందించాడు.
• ఆయన వాస్తవ రచనలు మరియు నమూనాలు చాలా వరకు లభ్యమగుట లేదు. అయితే కొన్ని రచనలు అరబిక్ రాత ప్రతులలో భద్రపరచబడినవి.
• ట్యూబ్ నర్ పబ్లిషింగ్ హౌస్ 1903లో లీగ్ లో హెరాన్ ప్రసిద్ధ రచనలను – 5 సంపుటాలుగా వెలువరించింది.

→ మూడు కొలతలు కలిగిన రేఖీయ ఘనాకృతులు ఈ క్రింది విధంగా కలవు.

→ ఘనాకృతులు ఈ క్రింది వైశాల్యాలు కలిగి ఉండును. అవి :

• ప్రక్కతల / ఉపరితల వైశాల్యాలు,
• సంపూర్ణతల వైశాల్యాలు.

→ దీర్ఘఘనం యొక్క ప్రక్కతల వైశాల్యం = 2h(l + b)
స్థూపం యొక్క ప్రక్కతల వైశాల్యం = 2πrh.

→ స్థూపం యొక్క సంపూర్ణతల వైశాల్యం = స్థూపం యొక్క ప్రక్కతల వైశాల్యం + 2 × భూ వైశాల్యము
= 2πrh + 2πr²- = 2πr(r + h)

సమఘనం యొక్క ఘనపరిమాణం V = a² × a²; V = a³

సూపం యొక్క ఘనపరిమాణం V = πr² × h; V = πr²h.
సూచన : ఘనాకార వస్తు సముదాయ ఉపరితల వైశాల్యము ఆ ఆకృతిలోని ఘనాకార వస్తువుల ఉపరితల వైశాల్యముల మొత్తమునకు సమానము కాదు. దీనికి గల కారణము కొన్ని ఉపరితలములు, వస్తువులను జతపరిచినప్పుడు ఏకీభవిస్తాయి. కనుక వాటిని పరిగణనలోనికి తీసుకోలేము, కాని ఘనపరిమాణము మాత్రము ఆ వస్తువులోని ఘనాకార ఆకృతుల ఘనపరిమాణముల మొత్తమునకు సమానం.

→ వివిధ ఘనాకృతులు, వాటి ఉపరితల వైశాల్యములు, ఘనపరిమాణములు :

→ కొన్ని ఘనాకృతులు మరియు వాని సమ్మేళన ఆకారాలు :

Students can go through AP Board 10th Class Maths Notes 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు

→ థామస్ ఫిస్కీ 15వ శతాబ్దం :

• థామస్ ఫిస్కీ “స్పర్శరేఖ” (Tangent) అను పదాన్ని 1583 సం||లో ప్రవేశ పెట్టాడు .
• ఇతను డెన్మార్క్ దేశస్థుడు.
• టాన్జెంట్ (స్పర్శరేఖ) అను పదం “టాన్ గ్రీ” అను “లాటిన్” పదం నుండి తీసుకొనబడినది.

→ ఒక స్థిర బిందువు నుండి సమాన దూరంలో గల బిందువులను వక్రంచే కలుపగా ఏర్పడిన దానిని ‘వృత్తం’ అంటారు. ఆ స్థిర బిందువును వృత్తానికి కేంద్ర బిందువు అంటారు. దీనిని ‘O’ అను అక్షరంచే సూచిస్తారు.

వృత్తంపై ఏవేని రెండు బిందువులను ఒక రేఖాఖండంచే కలుపగా ఏర్పడు దానిని “జ్యా” అంటారు. వృత్తంలోని అతి పొడవైన జ్యాను “వ్యాసము” అంటారు.
ప్రక్క పటం నుండి

\(\overline{\mathrm{AB}}\) ఒక జ్యా, \(\overline{\mathrm{PQ}}\) వ్యాసము. వృత్త వ్యాసం ఎల్లప్పుడూ కేంద్రం గుండా పోతుంది.

→ \(\overline{\mathrm{OP}}\) = \(\overline{\mathrm{OQ}}\) = వ్యాసార్థం (r) = \(\frac{d}{2}\) లేదా d = 2r

→ ఒక వృత్తము మరియు రేఖ మధ్య ఈ క్రింది సందర్భాలు కలవు.

• సందర్భం (i) : (i) వ పటంలో వృత్తానికి, సరళరేఖకు మధ్య ఉమ్మడి బిందువు లేదు. అనగా అవి రెండూ స్పృశించుకొనుటలేదు.
• సందర్భం (ii) : (ii) వ పటంలో \(\overline{\mathrm{AB}}\) అను సరళరేఖ వృత్తాన్ని P, Q బిందువుల వద్ద ఖండిస్తున్నది. కావున \(\overline{\mathrm{AB}}\) సరళరేఖ ఆ వృత్తానికి ఛేదనరేఖ అగును.
• సందర్భం (iii) : (iii) వ పటంలో \(\overline{\mathrm{AB}}\) అను సరళరేఖ వృత్తాన్ని ఒకే ఒక బిందువు P వద్ద తాకుచున్నది. కావున \(\overline{\mathrm{AB}}\) వృత్తానికి ఒక స్పర్శరేఖ అగును.

→ వృత్తానికి ఒక బిందువు వద్ద ఒకే ఒక స్పర్శరేఖ ఉంటుంది.

→ వృత్తానికి గీచిన స్పర్శరేఖకు స్పర్శబిందువు వద్ద దాని వ్యాసార్ధం లంబంగా ఉండును. ”

→ స్పర్శరేఖ పొడవు : స్పర్శరేఖ పొడవు AP = \(\sqrt{\mathrm{OP}^{2}-\mathrm{OA}^{2}}\)

OA = వ్యాసార్థం
OP = వృత్తకేంద్రం నుండి బాహ్య బిందువు ‘P’ కు గల దూరం.

→ బాహ్య బిందువు నుండి వృత్తానికి రెండు స్పర్శరేఖలు గీయగలం.

→ బాహ్య బిందువు నుండి వృత్తానికి గీచిన స్పర్శరేఖల పొడవులు సమానాలు. అనగా PA = PB.

→ ‘O’ కేంద్రంగా గల వృత్తానికి ‘P’ అను బాహ్య బిందువు నుండి PA, PB లు గీయబడిన స్పర్శరేఖలు అయిన ∠OPA = ∠OPB.

→ ‘O’ కేంద్రంగా గల ఏకకేంద్ర వృత్తాలలో చిన్న వృత్తానికి \(\overline{\mathrm{AB}}\), P వద్ద స్పర్శరేఖ మరియు పెద్ద వృత్తానికి జ్యా అయిన AP = PB అగును.

→ పటం నుండి ‘O’ కేంద్రంగా గల వృత్తానికి ‘A’ అను బాహ్య బిందువు నుండి గీయబడిన స్పర్శరేఖలు \(\overline{\mathrm{AP}}\), \(\overline{\mathrm{AQ}}\)లు
అయిన ∠PAQ = 2∠OPQ = 2∠OQP.

→ ABCD అను చతుర్భుజంలో ఒక వృత్తం అంతర్లిఖించబడినది. ఆ వృత్తం చతుర్భుజాన్ని, P, Q, R, S వద్ద ఖండించినచో AB + CD = BC + DA అగును. అనగా ఎదురెదురు భుజాల మొత్తాలు సమానాలు.

→ వృత్త ఖండము యొక్క వైశాల్యమును అంచనావేయుటకు వృత్తానికి ఛేదనరేఖలను గీచి వృత్త ఖండాలను ఏర్పరచవచ్చు.

వృత్త చాపము చేతను, జ్యా చేతను ఏర్పడే ప్రదేశమును వృత్త ఖండము అంటారు. దీని వైశాల్యము షేడ్ చేసిన భాగం తెలుపుతుంది. పటము (i) లో అల్ప వృత్తఖండము, పటము (ii) లో అర్ధవృత్తఖండము మరియు పటము (iii) లో అధిక వృత్తఖండము తెలుపుతాయి.

→ ‘O’ కేంద్రంగా గల వృత్తానికి OA, OB లు వ్యాసార్ధాలు (r). x అనునది AB చాపం వృత్తకేంద్రం వద్ద చేయు కోణం అయిన ABP వృత్త ఖండ వైశాల్యం
= AOB సెక్టార్ వైశాల్యం – ∆AOB వైశాల్యం = \(\frac{x}{360}\) – πr² – (\(\frac{1}{2}\)bh).

Students can go through AP Board 10th Class Maths Notes 8th Lesson సరూప త్రిభుజాలు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 8th Lesson సరూప త్రిభుజాలు

→ పైథాగరస్ (570-495 B.C.)

• పైథాగరస్ క్రీ.పూ. 570-495) ఒక గ్రీకు తత్త్వవేత్త మరియు గణిత శాస్త్రజ్ఞుడు.
• ఆయన గ్రీస్లోని సామోస్ ద్వీపంలో జన్మించారు. యువకుడిగా నా ఉన్నప్పుడు విజ్ఞాన సముపార్జన కోసం విస్తృతంగా పర్యటిస్తూ ఈజిప్టును మరియు ఇతర ప్రాంతాలను సందర్శించారు.
• ఆయన వేదాంతము, సంకేతము, గణితము, నీతి శాస్త్రము, రాజనీతి శాస్త్రములలో ఆసక్తిని కనబరచేవారు.
• ఆయన ఖగోళ శాస్త్రంలోను ముఖ్యమైన ఆవిష్కరణలు చేశారు. రి ఆయన గొప్ప గణిత శాస్త్రజ్ఞుడే కాదు గూఢ మతవాది, శాస్త్రవేత్త కూడా,
• క్రీ.పూ. 6వ శతాబ్దం చివరిలో తత్త్వశాస్త్రానికి, మతానికి ఎనలేని సేవలు చేశారు.
• ఆయన పేరు మీదనే పైథాగరస్ సిద్ధాంతం పేరుగాంచింది.
• పైథాగరస్ ఆలోచనలు, అభిప్రాయాలు తత్త్వవేత్త ప్లేటోపై, పాశ్చాత్య తత్త్వ శాస్త్రంపై గొప్ప ప్రభావం కనబరచాయి.

→ ఒకే ఆకారమును కలిగి ఉండి ఒకే పరిమాణము కలిగి ఉండనవసరములేని పటాలను సరూప పటాలు అంటారు.

→ వస్తువుల యొక్క ఎత్తులు మరియు దూరాలను సరూప పటాల నియమాలపై ఆధారపడి కనుగొంటారు.

→ జ్యామితిలో, భుజాల సంఖ్య సమానంగా ఉన్న రెండు బహుభుజులు సరూపాలు కావలెనన్న వాటి అనురూప కోణాలు సమానంగాను, అనురూప భుజాలు ఒకే నిష్పత్తిలో (లేదా) అనుపాతంలోనూ ఉండాలి.

→ ఒక బహుభుజిలో భుజాలన్నీ మరియు కోణాలన్నీ సమానంగా ఉంటే దానిని క్రమ బహుభుజి అంటారు. → అనురూప భుజాల నిష్పత్తిని సాధారణంగా స్కేలు (లేదా) స్కేలు గుణకం (లేదా) ప్రత్యామ్నాయ గుణకం అంటారు.

→ సమాన సంఖ్యలో భుజాలు కల్గిన రెండు బహుభుజులు సరూపాలు కావాలంటే

• వాటి అనురూప కోణాలు సమానంగా ఉండాలి.
• వాటి అనురూప భుజాలు ఒకే నిష్పత్తిలో ఉండాలి (అనుపాతంలో ఉండాలి). ఈ బహుభుజుల సరూపకతకు పై రెండు నియమాలలో ఏదో ఒక నియమము సరిపోదు. కాని త్రిభుజాలకు మాత్రం పై రెండింటిలో ఏదో ఒక నియమం సరిపోతుంది.

→ రెండు త్రిభుజాలు సరూపాలు కావాలంటే

1. వాటి అనురూప కోణాలు సమానంగా ఉండాలి.
2. వాటి అనురూప భుజాలు ఒకే నిష్పత్తిలో ఉండాలి.

→ ‘K’, స్కేలు గుణకము విలువ అయిన
K> 1 అయిన పెద్దవి చేయబడిన పటాలు
K= 1 అయిన సర్వసమాన పటాలు
K<1 అయిన చిన్నవి చేయబడిన పటాలు ఏర్పడతాయి.
ప్రాథమిక అనుపాత సిద్ధాంతము (థేల్స్ సిద్ధాంతము)

→ ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరు వేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి.

∆ABC లో; DE ∥ BC అయిన \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\). దీనినే ‘థేల్స్’ సిద్ధాంతము (లేక) ప్రాథమిక అనుపాత సిద్ధాంతము అంటారు.

→ ఒక త్రిభుజములో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు . .. సరళరేఖ, మూడవ భుజానికి సమాంతరంగా ఉండును.
∆ABCలో, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) అయిన l ∥ BC అగును.

దీనినే ‘థేల్స్ సిద్ధాంతపు విపర్యయము’ లేదా ‘ప్రాథమిక సిద్ధాంతపు విపర్యయము’ అంటారు. కో.కో.కో. నియమం :

→ రెండు త్రిభుజాలలో అనురూపక కోణాలు సమానంగా ఉంటే, వాటి అనురూప భుజాల నిష్పత్తులు సమానంగా ఉంటాయి (అనుపాతంలో వుంటాయి), ఇంకా ఆ రెండు త్రిభుజాలు సరూప త్రిభుజాలు అవుతాయి.

→ ∆ABC, ∆DEFలలో
∠A = ∠D, ∠B = ∠E, ∠C = ∠F అయిన
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) అగును.

∴ ∆ABC ~ ∆DEF (కో.కో.కో. సరూపకత).

→ రెండు త్రిభుజాలలో, ఒక త్రిభుజములోని భుజాలు వేరొక త్రిభుజములోని భుజాలకు అనుపాతములో ఉన్న ఆ రెండు త్రిభుజాలలోని అనురూప కోణాలు సమానము మరియు ఆ రెండు త్రిభుజాలు సరూఫాలు.

→ ∆ABC, ∆DEF లలో,
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) కావున
∠A = ∠D, ∠B = ∠E, మరియు∠C = ∠F

∴ ∆ABC ~ ∆DEF (కో.కో.కో సరూపకత). భు.భు. భు. సరూపత నియమం :

→ ఒక త్రిభుజములోని ఒక కోణము, వేరొక త్రిభుజములోని ఒక కోణమునకు సమానమై, ఈ కోణాలను కల్గి వున్న భుజాలు అనుపాతంలో ఉంటే ఆ రెండు త్రిభుజాలు సరూపాలు.

→ ∆ABC మరియు ∆DEF లలో \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) మరియు
∠A = ∠D అయిన

∆ABC ~ ∆DER (భు. కో. భు సరూపకత).

→ రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము.

→ ఒక లంబకోణ త్రిభుజములో, లంబకోణము కల్గిన శీర్షము నుండి కర్ణానికి లంబము గీసిన, ఆ లంబానికి ఇరువైపులా ఏర్పడిన త్రిభుజాలు, ఇచ్చిన త్రిభుజానికి సరూపాలు మరియు అవి ఒకదానికొకటి కూడా సరూపాలు.

∆ABCలో, ∠B = 90°, BD ⊥ AC అయిన
∆ADB ~ ∆BDC ~ ∆ABC మరియు BD² = AD . DC

పైథాగరస్ సిద్ధాంతము :

→ ఒక లంబకోణ త్రిభుజములో కర్ణము మీది వర్గము, మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానము.
∆ABCలో; ∠A = 90° అయిన AB² + AC² = BC²

పైథాగరస్ సిద్ధాంత విపర్యము : –
→ ఒక త్రిభుజములో ఒక భుజము మీది వర్గము మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానమైన, మొదటి భుజానికి ఎదురుగా ఉండే కోణము లంబకోణము అనగా త్రిభుజము లంబకోణ త్రిభుజమవుతుంది.

→ ఒక వాక్యము సత్యముగాని, అసత్యముగాని ఏదో ఒకటి మాత్రమే అగునటువంటి వాక్యమును “ప్రవచనము” అంటారు.

→ ఒక ప్రవచనముకు చివరన “కాదు” చేర్చడం వలన ఏర్పడు కొత్త ప్రవచనమును వ్యతిరేక ప్రవచనము అంటారు.

→ ‘p’ అను ప్రవచనము యొక్క వ్యతిరేక ప్రవచనమును “~p” తో సూచిస్తారు.

→ రెండు సరళ ప్రవచనాలను కలుపగా ఏర్పడు నూతన ప్రవచనమును సంయుక్త ప్రవచనం అంటారు.

→ రెండు సరళ ప్రవచనాలను “అయినచో” చే కలుపగా ఏర్పడిన సంయుక్త ప్రవచనాన్ని “అనుషంగికము” లేదా “నియత ప్రవచనము” అంటారు.

→ రెండు సరళ ప్రవచనాలను p మరియు q లను “అయినచో” కలుపగా “p అయినచో q” అని వస్తుంది. దీనిని మనం p ⇒ q అని రాస్తాము.

→ p ⇒ q లో మనము p, q లను తారుమారు చేయగా q ⇒ p ఏర్పడును. దీనినే మనం ప్రవచన విపర్యయము అంటాము.
ఉదా : ∆ABC లో AB = AC అయితే C = ∠B, ఈ ప్రవచనపు విపర్యయము ∆ABC లో C = ∠B అయితే AB = AC అగును.

Students can go through AP Board 10th Class Maths Notes 7th Lesson నిరూపక రేఖాగణితం to understand and remember the concept easily.

AP Board 10th Class Maths Notes 7th Lesson నిరూపక రేఖాగణితం

→ రెనె డెకార్టి (1596 – 1650)

• గణిత శాస్త్రవేత్త ఆ రెనె డెకార్టె 31-3-1596వ తేదీన ఫ్రాన్లోని లాహై నగరంలో ఒక ఆ సామాన్య కుటుంబంలో జన్మించాడు. ఆధునిక గణితానికి, తత్వ శాస్త్రానికి పితామహునిగా పేరొందాడు.
• విశ్వసనీయమైన జ్ఞానాన్నిచ్చే నూతన పద్దతి కోసం అన్వేషణ, విశ్వ పునర్నిర్మాణానికి కృషి చేశాడు. గణిత పద్దతులను అధ్యయనం చేసి, వాటి నుంచి పరిశుద్ధమైన జ్ఞానాన్ని అన్ని క్షేత్రాలలో రూపొందించే పద్ధతిగా “విశ్వగణితాన్ని” ఆవిష్కరించేందుకు కొన్ని సార్వత్రిక నియమాల అన్వేషణ రెనె డెకార్ట్ సాగించాడు. 1596-1650
• తలంలోని బిందువులను వాస్తవ సంఖ్యా క్రమయుగ్మాలతో అనుసంధానం చేయడం వల్ల రేఖాగణితానికి, బీజగణితానికి మధ్య అంతరం పోయి రెండింటిని కలిపి ఒకటిగానే అధ్యయనం చేయడం సాధ్యమైనది.
• రేఖాగణిత, బీజగణితాలను ఏకం చేసే ప్రయత్నంలో నిరూపక రేఖాగణితం లేదా వైశ్లేషిక జ్యామితి అనే గణిత శాఖకు మూల పురుషుడయ్యాడు. ఇతని గౌరవార్థం ఈ శాఖకు కార్టీజియన్ రేఖాగణితం అని పేరు పెట్టారు.
• తత్వశాస్త్రం, జ్యామెట్రీ, డయాప్టిక్స్ అనే మూడు అంశాల వ్యాస సంపుటిగా “దిస్ కో ఆన్ మెథడ్” అనే ప్రసిద్ధ గ్రంథాన్ని రచించాడు. వర్గమూలానికి మొదటిసారిగా ‘ √ ‘ గుర్తును ఉపయోగించాడు.
• డెకార్టెతత్వ శాస్త్రానికి, వైశ్లేషిక రేఖా గణితానికి ప్రజాదరణ పెరగడంతో హాలెండ్ రాజు డెకార్టెను ఆహ్వానించి యువరాణి క్రిష్టినాకు బోధకునిగా నియమించాడు. ఆమె దినచర్య కారణంగా ఉదయం 5 గం||లకే చలిలో డెకార్టెరాజ ప్రాసాదానికి వెళ్ళవలసి వచ్చేది. ఆ వాతావరణం పడక న్యుమోనియా వ్యాధికి గురై 54 ఏళ్ళ వయస్సులో 11-2-1650వ తేదీన మరణించాడు.
• “సత్యాన్వేషణ కోసం మనం జీవితంలో ఒకసారి అన్నింటిని శంకించవలసి వస్తుంది”.. అంకు – రెనె డెకార్టి

→ ఒకే తలంలో గల క్షితిజ సమాంతర మరియు క్షితిజ లంబరేఖలు ఆ తలాన్ని నాలుగు భాగాలుగా విభజిస్తాయి. క్షితిజ సమాంతరరేఖను X – అక్షం అని, క్షితిజ లంబరేఖను Y – అక్షం అని, ఈ రెండు రేఖల ఖండన బిందువును మూలబిందువు అని అంటారు.

→ X, Y అక్షాలతో ఏర్పడిన నాలుగు భాగాలను వరుసగా 1వ పాదం (Q₁), 2వ పాదం (Q₂), 3వ పాదం (Q₃), 4వ పాదం (Q₄)లుగా పిలుస్తారు. ఈ తలాన్ని ‘కార్టిజియన్ తలం’ (రెనెడెకార్ట్ పేరుతో) లేదా నిరూపక | x < 0, y < 0 1 x > 0, y < 0. తలం లేదా XY తలం అని అంటారు.

→ నిరూపక తలంలోని రెండు బిందువుల మధ్య దూరం :
(i) నిరూపక అక్షాలకు సమాంతరంగా ఉన్న రేఖ పైగల రెండు బిందువుల మధ్య దూరం :
(a) X – అక్షానికి సమాంతరంగా గల రేఖ పై గల బిందువులలో y – నిరూపకాలు సమానంగా ఉంటాయి.
A(x₁, y₁) B (x₂, y₂) లు X – అక్షానికి సమాంతరంగా గల రేఖపై గల బిందువులు అవుతాయి.
A, B ల మధ్య దూరం = |x₂ – x₁| అనగా వాని X – నిరూపకాల మధ్య వ్యత్యాసమునకు సమానము.

(b) ఇదే విధంగా A(x₁, y₁), B(x₂, y₂) లు Y – అక్షానికి సమాంతరంగా గల రేఖ పై బిందువులు అవుతాయి. ఆ
A, B ల మధ్య దూరం = |y₂ – Y₁| అనగా Y నిరూపకాల మధ్య తేడాకు సమానము.

(ii) నిరూపక తలంలోని ఏవేని రెండు బిందువుల మధ్య దూరం :

A(x₁, y₁) B (x₂, y₂) లు నిరూపక తలంలో రెండు బిందువులు అనుకొందాం.
OP = x₁ OQ = x₂ అలాగే QB = y₂, QR = y₁
∴ PQ = AR = x₂ – x₁ ……………(1)
ఇదే విధంగా, BR = y₂ – y₁ …………….(2)
∆ARB ఒక లంబకోణ త్రిభుజము.
AB² = AR² + RB² (పైథాగరస్ సిద్ధాంతము)
AB² = (x² – x₁)² + (y² – y₁)²
∴ AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
∴ A(x₁, y₁), B(x₂, y₂) బిందువుల మధ్య దూరం.
AB = d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Note:
(i) a) మూలబిందువు (0, 0) నుండి A (x₁, y₁) బిందువుకు గల దూరం \(\sqrt{x_{1}^{2}+y_{1}^{2}}\) అవుతుంది.
b) A (x₁, 0), B (0, y₁) లు X, Y – అక్షాలపై గల బిందువులు. A, B ల మధ్య దూరం = \(\sqrt{x_{1}^{2}+y_{1}^{2}}\)

(ii) A, B, C బిందువులు సరేఖీయాలైతే
AB + BC = AC లేదా AC + CB = AB లేదా AB + AC = BC అవుతుంది.

(iii) A, B, C లు త్రిభుజ శీర్షాలైతే .
AB = BC = AC అయితే ∆ABC సమబాహు త్రిభుజాన్ని, AB, BC, ACలలో ‘ఏ రెండు భుజాలు , సమానమైన సమద్విబాహు త్రిభుజాన్ని, AB² + BC² = AC² లేదా AB² + AC² = BC² లేదా AC² + CB² = AB² అయితే లంబకోణ త్రిభుజాన్ని ఏర్పరుస్తాయి.

(iv) A, B, C, D బిందువులు చతుర్భుజ శీర్షాలైతే
(a) ఎదురెదురు భుజాలు సమానాలు మరియు కర్ణాలు కూడా సమానాలు అయితే ABCD దీర్ఘ చతురస్రం అవుతుంది. AB = CD, BC = AD మరియు AC = BD.
(b) నాలుగు భుజాలు సమానము మరియు కర్ణాలు సమానం అయితే ABCD చతురస్రం అవుతుంది. AB = BC = CD = AD మరియు AC = BD
(c) ఎదురెదురు భుజాలు సమానమైన సమాంతర చతుర్భుజం అవుతుంది. AB = CD, BC = AD.
(d) ఎదురెదురు భుజాలు సమానమై, కర్ణాలు సమానం కాకపోతే అది దీర్ఘ చతురస్రం కానటువంటి సమాంతర చతుర్భుజం అవుతుంది. AB = CD, BC = AD మరియు AC ≠ BD.
(e) నాలుగు భుజాలు సమానం అయితే రాంబస్ అవుతుంది. AB = BC = CD = AD. f) నాలుగు భుజాలు సమానం అయి కర్ణాలు సమానం కాకపోతే అది చతురస్రం కానటువంటి రాంబస్ అవుతుంది. (ఇక్కడ AB అనగా భుజం AB పొడవు అని అర్థం)

→ విభజన సూత్రం :
(i) \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) రేఖపై A, B ల మధ్య P అనే బిందువు AB రేఖాఖండాన్ని P బిందువు అంతరంగా AP : PB నిష్పత్తిలో విభజిస్తుంది అంటారు.
AP = m₁, PB = m₂, గా తీసుకొంటే A, B లను Pm₁: m₂, నిష్పత్తిలో అంతరంగా విభజిస్తుంది అంటాము.

(ii) \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) రేఖపై A, B బిందువుల మధ్య కాకుండా P బిందువు ఉంటే AB రేఖాఖండాన్ని P బిందువు బాహ్యంగా
AP : BP నిష్పత్తిలో విభజిస్తుంది అంటారు.

(iii) A (x₁, y₁), B(x₂, y₂) బిందువులను అంతరంగా విభజించే. బిందువు P యొక్క నిరూపకాలను కనుగొందాము.

A(x₁, y₁), B(x₂, y₂) ఏవేని రెండు బిందువులు. P(x, y) అనేది AB ని అంతరంగా m₁ : m₂
నిష్పత్తిలో విభజిస్తుంది అనుకొందాం. \(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}\)
∆PAQ ~ ∆BPC (కో.కో.కో. నియమం) .
∴ \(\frac{\mathrm{PA}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{PC}}=\frac{\mathrm{PQ}}{\mathrm{BC}}\) ……..(1)
ప్రక్క పటం నుండి , AQ = RS = OS – OR = x – x₁
PC = ST = OT – OS = x₂ – x
PQ = PS – QS = y – y₁
BC = BT – CT =y₂ – y₁
పై విలువలు (1)లో రాయగా

ఇదే విధంగా \(\frac{m_{1}}{m_{2}}=\frac{y-y_{1}}{y_{2}-y_{1}}\) తీసుకొంటే y = \(\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\) కాబట్టి A(x₁, y₁), B(x₂, y₂) లచే ఏర్పడే రేఖాఖండాన్ని m₁ : m₂డి నిష్పత్తిలో అంతరంగా విభజించే బిందువు
p(x, y) = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

Note:

• AB రేఖను P బిందువు k : 1 నిష్పత్తిలో అంతరంగా విభజిస్తున్నట్లయితే అప్పుడు P బిందువు నిరూపకాలు \(\left(\frac{\mathrm{kx}_{2}+\mathrm{x}_{1}}{\mathrm{k}+1}, \frac{\mathrm{ky}_{2}+\mathrm{y}_{1}}{\mathrm{k}+1}\right)\)
• \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) పై A, B బిందువులకు బాహ్యంగా P ఉంటే అప్పుడు m) ను -m,గా తీసుకొంటాము అలాంటి సందర్భంలో P నిరూపకాలు \(\left(\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}, \frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}\right)\)
• \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) పై A : B బిందువుకు P మధ్య బిందువు అయితే m, = m) అయి విభజన నిష్పత్తి 1 : 1 అవుతుంది. అప్పుడు P యొక్క నిరూపకాలు \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

→ త్రిభుజం యొక్క గురుత్వ కేంద్రము. : త్రిభుజం యొక్క మధ్యగత రేఖల మిళిత బిందువును ఆ త్రిభుజం యొక్క గురుత్వ కేంద్రము అంటాము. త్రిభుజ శీర్షం నుండి ఎదుటి భుజం మధ్య బిందువును కలిపే రేఖాఖండము మధ్యగతం అవుతుందని, మధ్యగతరేఖను గురుత్వ కేంద్రం 2 : 1 నిష్పత్తిలో విభజిస్తుందని మనకు తెలుసు. A(x¹, y¹), B(x², y²), C(x³, y³) లు ∆ABC యొక్క శీర్షాలు.. AD, BE, CF లు ∆ABC యొక్క మధ్యగతరేఖలు, 6 గురుత్వ కేంద్రం అనుకొందాం.

AD మధ్యగతరేఖ భూమి BC, మధ్య బిందువు AD గుండా పోతుంది.

∴ D = BC మధ్య బిందువు = \(\left(\frac{\mathrm{x}_{2}+\mathrm{x}_{3}}{2}, \frac{\mathrm{y}_{2}+\mathrm{y}_{3}}{2}\right)\)
AD మధ్యగతరేఖను గురుత్వ కేంద్రం G, 2 : 1 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
G(x, y) అనుకొంటే A(x₁, y₁), D = \(\left(\frac{\mathrm{x}_{2}+\mathrm{x}_{3}}{2}, \frac{\mathrm{y}_{2}+\mathrm{y}_{3}}{2}\right)\)

గురుత్వ కేంద్రాన్ని ‘కేంద్రాభాసం గరిమనాభి’ అని కూడా అంటారు.

→ ఒక రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు : ఒక రేఖాఖండమును మూడు సమాన భాగాలుగా విభజించు బిందువులను త్రిథాకరణ బిందువులు అంటారు.

AB రేఖాఖండం యొక్క ప్రాథాకరణ బిందువులు P, Q లు అయితే AP = PQ = QB అవుతుంది. . AB రేఖాఖండాన్ని P బిందువు AP : PB = 2 : 1 నిష్పత్తిలోను, Q బిందువు AQ : QB = 2 : 1 నిష్పత్తిలోను విభజిస్తుంది.

→ త్రిభుజ వైశాల్యము : ఏదేని త్రిభుజం ABC యొక్క శీర్షాలు A(x₁, y₁), B(x₂, y₂), C (x₃, y₃) అనుకొందాం.

A, B మరియు C ల నుండి X – అక్షంపైకి AP, BQ మరియు CR అనే లంబరేఖలు గీయాలి. ఇప్పుడు.
BQ = y₂, PQ = OP – 0Q = x₁ – x₂
AP =y₁, PR = OR – OP = x₃ -x₁
CR = y₃, QR = OR – 0Q = x₃ – x₂
పటం నుండి ∆ABC వైశాల్యం = ట్రెపీజియం ABOP వైశాల్యం + ట్రెపీజియం APRC వైశాల్యం – ట్రెపీజియం BQRC వైశాల్యం. ట్రెపీజియం వైశాల్యం A = \(\frac{1}{2}\)(a + b) h లు సమాంతర భుజాలు, a, b లు సమాంతర భుజాలు, h వాని మధ్య దూరం.

∆ABC వైశాల్యం = \(\frac{1}{2}\)(BQ + AP) PQ + \(\frac{1}{2}\)(AP + CR) PR – \(\frac{1}{2}\)(BQ + CR) QR
= \(\frac{1}{2}\)(y₂ + y₁) (x₁ – x₂) + (y₁ + y₃) (x₃ – x₁) – (y₂ + y₃) (x₃ – x₂)
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂|

∴ (x₁, y₁), (x₂, y₂), (x₃, y₃) శీర్షాలుగా గల త్రిభుజ వైశాల్యము
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂|

గమనిక :
(i) A(x₁, y₁), B(x₂, y₂), C (x₃, y₃), D (x₄, y₄) లు చతుర్భుజ శీర్షాలైతే ఆ చతుర్భుజ వైశాల్యము :

ABCD చతుర్భుజాన్ని కర్ణం సహాయంతో రెండు త్రిభుజాలుగా విభజించి త్రిభుజ వైశాల్య సూత్రాన్ని ఉపయోగించి చతుర్భుజ వైశాల్యాన్ని కనుగొంటాము.
రెండు త్రిభుజాలుగా విభజించుటకు ఏ కర్ణాన్నైనా (AC లేదా BD) తీసుకొనవచ్చును.

చతుర్భుజం ABCD వైశాల్యం = ∆ABC వైశాల్యం + ∆ACD వైశాల్యం
(లేదా)
= ∆ABD వైశాల్యం + ∆BDC వైశాల్యం

(ii) a) బిందువుల సరేఖీయత వైశాల్యము : A(x₁, y₁), B(x₂, y₂), C (x₃, y₃)లు సరేఖీయాలైతే ఆ మూడు బిందువుల ఒకే రేఖపై ఉండటం వలన త్రిభుజాన్ని ఏర్పరచలేవు. కావున ∆ABC వైశాల్యము సున్నా అవుతుంది. మూడు బిందువులతో ఏర్పడే త్రిభుజ వైశాల్యం సున్న అయితే ఆ మూడు బిందువులు సరేఖీయాలు అవుతాయి.
A, B, C లు సరేఖీయాలు ⇔∆ABC వైశాల్యము సున్న.
b) నాలుగు బిందువులు A, B, C, D లు సరేఖీయాలైతే చతుర్భుజం ABCD వైశాల్యము సున్నా అవుతుంది.

(iii) త్రిభుజ వైశాల్యము – హెరాన్ సూత్రం : a, b, c లు భుజాలుగాగల త్రిభుజ వైశాల్యం కనుగొనుటకు “హెరాన్” అనే గ్రీకు గణిత శాస్త్రవేత్త ఒక సూత్రాన్ని కనుగొన్నాడు. ఆ సూత్రం త్రిభుజ వైశాల్యం A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
ఇక్కడ S = \(\frac{a+b+c}{2}\)

సరళరేఖ వాలు : రెండు చరరాసులు x, y లలో ఏకఘాత సమీకరణం యొక్క సాధనలు ఒక సరళరేఖను ఏర్పరుస్తాయి. ఈ సరళరేఖ X – అక్షం యొక్క ధన దిశలో (అపసవ్య దిశ) చేసే కోణాన్ని ఆ సరళరేఖ యొక్క ఏటవాలు తనం అని, ఆ కోణం యొక్క Tan విలువను ఆ సరళరేఖ వాలు అని అంటారు.

ax + by + c = 0 సరళరేఖ X – అక్షం అపసవ్య దిశలో చేసే కోణం θ అయిన ‘θ’ ను ax + by + c = 0 రేఖ యొక్క వాలుతనం అని, tan θ విలునను ax + by + c = 0 రేఖ వాలు అని అంటారు. .
ఒక రేఖపై నున్న బిందువుల నిరూపకాలలో Y నిరూపకాల భేదం మరియు X నిరూపకాల భేదంకు గల నిష్పత్తి వాలు (tan θ) కు సమానం అవుతుంది.

→ రెండు బిందువులను కలిపే రేఖవాలు : A(x₁, y₁), B(x₂, y₂) బిందువులను కలిపే రేఖ యొక్క వాలు m = tanθ = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

గమనిక :

• X – అక్షము మరియు X – అక్షానికి సమాంతరంగా గల రేఖ యొక్క వాలు సున్న.
  Y- అక్షము మరియు Y – అక్షానికి సమాంతరంగా గల రేఖ యొక్క వాలు నిర్వచింపబడదు.
• వాలు అధారంగా సరేఖీయత :
  A, B, C లు ఏవేని మూడు బిందువులై AB వాలు = BC వాలు = AC వాలు అయిన A, B, C బిందువులు సరేఖీయాలు అవుతాయి.

→ A, B, C బిందువులు సరేఖీయాలు అయితే

• A, B, C బిందువులతో ఏర్పడే ఏ రెండు రేఖాఖండాలైనా మూడవ రేఖాఖండానికి సమానం.
  AB + BC = AC లేదా AB + AC = BC లేదా AC + BC = AB
• A, B, C లతో ఏర్పడే త్రిభుజ వైశాల్యము సున్న.
• AB వాలు = BC వాలు = AC వాలు.

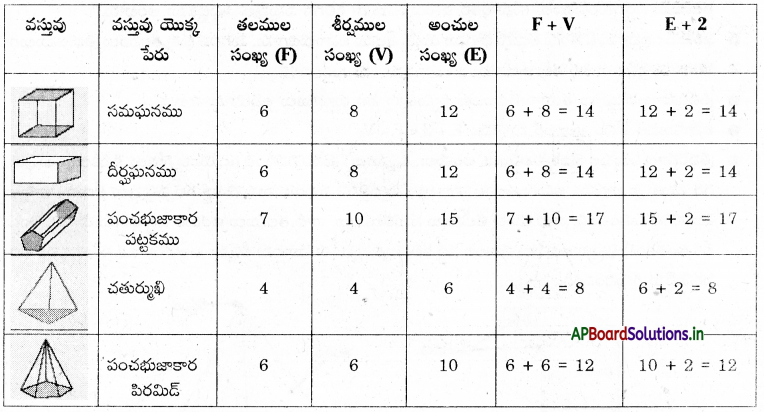
Students can go through AP Board 10th Class Maths Notes 2nd Lesson సమితులు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 2nd Lesson సమితులు

→ జార్జి కాంటర్: 1845 -1918:

• జార్జికాంటర్ మార్చి 3, 1845న రష్యాలో జన్మించి, పదకొండేళ్ళ వయస్సులో తండ్రితో పాటు జర్మనీకి వలస వెళ్ళాడు.
• కాంటర్ ఆధునిక గణితం అనేక శాఖలుగా అభివృద్ధి చెందడానికి ఆధారమైన సమితి వాదాన్ని ప్రతిపాదించి, అభివృద్ధిపరచి ఆధునిక గణిత భాషకు ఆద్యుడైనాడు. కాంటర్ సమితివాద శక్తి గణిత శాఖలన్నింటిని ఏకీకృతం చేయడంలో ప్రధానపాత్ర వహిస్తోంది.
• “ఊహించగల, సంభవించగల ఆలోచనల రూపమే సమితి” అన్న కాంటర్ భావనను ఆనాటి సాంప్రదాయవాదులు ఒక నూతన గణితానికి ఆరంభంగా అంగీకరించలేక పోయారు. అదసలు గణితమే కాదన్నారు. కాంటర్ ప్రతిపాదనలు, ఆలోచనలు కొత్తవిగాను, వింతగాను భావించిన సహచరులు నిరుత్సాహపరచడం, అగౌరవపరచడం చేసేవారు.
• కోవలోనే తన గురువు క్రోనేకర్ కూడా ఉండటంతో సున్నితమనస్కుడైన కాంటర్ తట్టుకోలేకపోయాడు. తన సిద్ధాంతాలపట్ల సమకాలీన గణిత ప్రపంచంలో ఏర్పడిన వైరుధ్యాల ఒత్తిడికి నిలవలేక మానసిక ఆరోగ్యం కోల్పోయి, చివరకు జనవరి 6, 1918లో మరణించాడు. “కాంటర్ మనకోసం గణిత ప్రపంచంలో ఓ స్వర్గం సృష్టించి, అనుభవించ లేక పిచ్చివాడయ్యా డు”. – డేవిడ్ హిలిబర్ట్

→ సమితి’: సునిర్వచిత వస్తువుల సముదాయాన్ని సమితి అంటారు.
సునిర్వచితం అనగా : 1. సమితిలోని వస్తువులన్నీ ఒకే విధమైన సామాన్య పోలిక లేదా ధర్మం కలిగి ఉండాలి. మరియు 2. ఏదైనా ఒక వస్తువు సమితికి చెందినది, లేనిదీ నిర్ధారించేటట్లు ఉండాలి.

→ సమితులను ఆంగ్ల భాషలోని పెద్ద అక్షరాలతో సూచిస్తారు.
ఉదా : A అనేది 6 కన్నా తక్కువైన సహజ సంఖ్యల సమితి. A = {1, 2, 3, 4, 5}

→ సమితికి చెందిన వస్తువులను ఆ సమితి యొక్క మూలకాలు అంటారు.
ఉదా : A = {1, 2, 3, 4, 5} అయిన 1, 2, 3, 4, 5 అనేవి సమితి A యొక్క మూలకాలు.

→ ఒక మూలకము ఒక సమితికి చెందినది అని తెలుపుటకు 6 (belonging to) గుర్తుని ఉపయోగిస్తారు.
B = {2, 4, 6, 8} అయిన 2 ∈ B, 4 ∈ B, 6 ∈ B, 8 ∈ B,
10 ∉ B అనగా B అనే సమితికి 10 చెందదు అని అర్థం.

→ సమితులను సూచించే /రాసే పద్ధతులు : సమితులను సాధారణంగా

• రోస్టర్ రూపం (జాబితా రూపం),
• సమితి నిర్మాణ రూపం (లాక్షణిక రూపం) మరియు
• వెన్ చిత్రాల రూపంలో సూచిస్తారు.

→ రోస్టర్ రూపం : సమితిలోని మూలకాలన్నింటిని వరుసగా కామా (,) లతో వేరు చేస్తూ జాబితాగా రాసి ఫ్లవర్ బ్రాకెట్ { } ల మధ్యలో రాసే పద్ధతి.

→ రోస్టర్ రూపంలో మూలకాలను ఏ క్రమంలోనైనా రాయవచ్చును మరియు ఒకే మూలకాన్ని మళ్ళీ మళ్ళీ రాయకూడదు.
ఉదా : A అనే సమితి SCHOOL లోని అక్షరాలతో ఏర్పడే సమితి.

• A = {S, C, H, O, L} లేదా
• A = {C, H, L, O, S} లేదా
• A = {L, 0, H, C, S} …… గా రాయవచ్చు.
• A = {S, C, H, 0, 0, L} గా రాయకూడదు.

→ సమితి నిర్మాణ రూపం : సమితికి చెందిన మూలకాల సామాన్య లక్షణం లేదా ధర్మాలను తెలియజేస్తూ రాసే పద్ధతిని ‘సమితి నిర్మాణ రూపం అంటారు. సమితిలోని మూలకాన్ని x గా సూచిస్తూ, .x ప్రక్కన / గాని, : గాని ఉంచి ఆ సమితికి చెందిన మూలకాల యొక్క లక్షణాలు లేదా ధర్మాలను గాని రాస్తాము. మొత్తాన్ని ఫ్లవర్ బ్రాకెట్లలో { } ఉంచుతాము. ఉదా : సమితి P 13 కన్నా తక్కువైన ప్రధాన సంఖ్యల సమితి.
P= {x/ X అనేది 13 కన్నా తక్కువైన ప్రధాన సంఖ్య } లేదా
P = {x : X అనేది 13 కంటే తక్కువైన ప్రధాన సంఖ్య }

→ సమితుల రకాలు :
శూన్య సమితి : ఎలాంటి మూలకాలు లేనటువంటి సమితిని శూన్యసమితి అంటారు. శూన్యసమితిని (phi) లేదా { } తో సూచిస్తారు.
ఉదా : A = {x : X అనేది 1 కన్నా తక్కువైన సహజ సంఖ్య}
B = {x: X అనేది సంవత్సరంలో 35 రోజులు గల నెల}
C = {x : x = 3, X ఒక అకరణీయ సంఖ్య }
సూచన : Φ, {Φ} మరియు {0} లు వేర్వేరు సమితులు. {Φ}, {0} అనేవి శూన్య సమితులు కావు. ఎందుకనగా {Φ} లో ‘Φ’ అనే మూలకము, { 0 } లో ‘0’ అనే మూలకము ఉన్నాయి.

→ పరిమిత సమితి : పరిమిత సంఖ్యలో మూలకాలను కలిగిన సమితిని పరిమిత సమితి అంటారు. అంటే పరిమిత సమితిలోని మూలకాలను లెక్కించగలమన్న మాట.

ఉదా : A = {తరగతిలోని విద్యార్థులు}
B = {a, b, c, d, e, ………., x, y, z}
C = {x : X అనేది 10 కన్నా తక్కువైన సహజసంఖ్య }

→ అపరిమిత సమితి : మూలకాల సంఖ్య అపరిమితంగా గల సమితిని అపరిమిత సమితి అంటారు.

ఉదా : E = {x: X ఒక సరిసంఖ్య }
G = {x : X అనేది 5 యొక్క గుణిజము}
గమనిక : ఒక సమితి పరిమిత సమితి కాకపోతే అపరిమిత సమితి అవుతుంది.

→ కార్డినల్ సంఖ్య : పరిమిత సమితిలోని మూలకాల సంఖ్యను ఆ సమితి యొక్క కార్డినల్ సంఖ్య అంటారు.
ఉదా : A = {1, 2, 4, 8, 16} అయిన
A యొక్క కార్డినల్ సంఖ్య = 5 A సమితి యొక్క కార్డినల్ సంఖ్యను n(A) గా సూచిస్తాము.

గమనిక :

• శూన్య సమితి యొక్క కార్డినల్ సంఖ్య సున్న (n (Φ) = 0).
• అపరిమిత సమితి యొక్క కార్డినల్ సంఖ్యను నిర్ణయించలేము.

→ ఉపసమితి, ఉన్నత సమితి : A సమితిలోనున్న ప్రతి మూలకము సమితి B లో . ఉంటే A సమితిని B యొక్క ఉపసమితి అని, B ని A యొక్క ఉన్నత సమితి అని అంటారు. దీనిని A ⊆ B గా రాస్తాము. A ⊆ B ని B ⊆ A గా కూడా రాయవచ్చును. ఉపసమితిని క్రింది విధంగా కూడా నిర్వచించవచ్చును.

A, B లు రెండు సమితులు. a ∈ A అయిన A ⊆ B ⇒ a ∈ B. a, A కి మూలకం అయి A, B కి ఉపసమితి అయితే a అనేది B కి కూడా మూలకం అవుతుంది.

ఉదా : A = {2, 4, 6}, B = {1, 2, 3, 4, 5, 6, 7} .
2 ∈ A, 2 ∈ B
4 ∈ A, 4 ∈ B
6 ∈ A, 6 ∈ B సమితి Aలోని మూలకాలన్నీ సమితి B లో కలవు. కావున A ⊂ B.

→ క్రమ ఉపసమితి (శుద్ధ ఉపసమితి) : A ⊆ B అయి A ≠ B అయితే ‘A’ ని Bకి క్రమ ఉపసమితి లేదా శుద్ధ ఉపసమితి అంటారు. దీనిని A ⊂ B గా సూచిస్తారు. A; B కి క్రమ ఉపసమితి కావాలంటే A లోని అన్ని మూలకాలు B లో ఉంటూ A లో లేనటువంటి కనీసం ఒక మూలకం B లో ఉండాలి.

ఉదా : A = {2, 4, 6}, B = {2, 4, 6, 8} A లోని మూలకాలన్నీ B లో కలవు మరియు Aలో లేని 8 అనే మూలకం B లో కలదు. కావున A సమితి B కి క్రమ ఉపసమితి అవుతుంది.
A ⊂ B. Ac B అయిన n(A) < n(B).

సూచన :

• శూన్యసమితి ప్రతి సమితికి ఉపసమితి.
• ప్రతి సమితి దానికదే ఉపసమితి.
• n మూలకాలు కలిగిన సమితికి సాధ్యమయ్యే ఉపసమితుల సంఖ్య 2″ అవుతుంది.
• n మూలకాలు కలిగిన సమితికి సాధ్యమయ్యే క్రమ ఉపసమితుల సంఖ్య 2″ – 1 అవుతుంది.

→ విశ్వసమితి (సార్వత్రిక సమితి) : ఒక పరిశీలనలోకి తీసుకొన్న సతులన్నింటిని ఉపసమితులుగా కలిగిన సమితిని విశ్వసమితి లేదా సార్వత్రిక సమితి అంటారు. విశ్వసమితిని ∪ లేదా μ తో సూచిస్తారు.

ఉదా – 1: A = {8వ తరగతి విద్యార్థులు}
B = {9వ తరగతి విద్యార్థులు}
C = {10వ తరగతి విద్యార్థులు}
D = {పాఠశాలలోని విద్యార్థులు} అనుకొనుము.

A ⊂ D, B ⊂ D మరియు C ⊂ D. Dని విశ్వసమితి అంటారు.
ఉదా – 2: A = {2, 3, 5, 7}
B = {2, 4, 6, 8}
C = {1, 3, 5, 7, 9} అయితే విశ్వసమితి μ = {1, 2, 3, 4, 5, 6, 7, 8, 9} అవుతుంది.

→ సమసమితులు : A మరియు Bలలో ఒకే మూలకాలున్నట్లయితే A, B లను సమసమితులు అంటారు. A, B లు సమసమితులైతే, సమితి A లో గల మూలకాలన్నీ సమితి B లో, సమితి B లోని మూలకాలన్నీ సమితి A లో ఉంటాయి. A ⊂ B మరియు B ⊂ A ↔ A = B
A, B లు సమసమితులైతే n(A) = n(B).

ఉదా : A = {x: x అనేది 11 లోపు సరి సహజసంఖ్య}
B = {x : x అనేది 12 కన్నా తక్కువైన 2 యొక్క గుణిజం}.
A మరియు B సమితులు ఒకే మూలకాలు 2, 4, 6, 8, 10 లను కలిగి ఉంటాయి. A = B మరియు n(A) = n(B).
సూచన : n(A) = n(B) అయితే A, B లు సమసమితులు కాకపోవచ్చును.

→ వెన్ చిత్రాలు : సమితిని సంవృత వక్రంగా సూచిస్తూ, సమితిలోని మూలకాలన్నింటిని వక్రం లోపలి బిందువులుగా చూపిస్తాము. వీటిని “జాన్వెన్” అనే ఆంగ్ల గణితశాస్త్రవేత్త మొదటిసారిగా ఉపయోగించాడు. స్విట్జర్లాండ్ కు చెందిన లెనార్డు ఆయిలర్ కూడా వీటిని ఉపయోగించాడు. కావున వీనిని వెన్-ఆయిలర్ చిత్రాలు అని కూడా అంటారు.
సమితులను సూచించడానికి మనం ఏ సరళ సంవృత పటాన్నైనా ఉపయోగించవచ్చును. సాధారణంగా వెన్ చిత్రాలుగా దీర్ఘచతురస్రాలు, చతురస్రాలు, త్రిభుజాలు, సంవృతవక్రాలు, వృత్తాలు, దీర్ఘవృత్తాలను ఉపయోగిస్తాము. విశ్వసమితి (μ) ను సాధారణంగా దీర్ఘచతురస్రంగా సూచిస్తాము.
(i) A = {1, 2, 3, 4, 5} అయితే సమితి Aని వెన్ చిత్రంగా ప్రక్క విధంగా సూచిస్తాము.

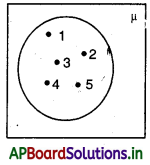
(ii) A ⊂ B ని వెన్ చిత్రంగా చూపడం :

→ సమితుల ప్రాథమిక పరిక్రియలు : సమితుల సమ్మేళనం, ఛేదనం, భేదాలను సమితుల ప్రాథమిక పరిక్రియలు అంటారు.

→ సమితుల సమ్మేళనం : A సమితిలోని మూలకాలతోపాటు ‘B సమితిలోని మూలకాలు చేర్చి వ్రాయగా వచ్చే నూతన సమితిని A, B ల సమ్మేళనం అంటారు. దీనిని A ∪ B తో సూచిస్తూ A యూనియన్ B అని చదువుతారు. అనగా A లో కాని లేక B లో కాని లేక రెండింటిలోకాని ఉన్న మూలకాలన్నింటిని కలిగిన సమితి A ∪ B.
A ∪ B = {x : x ∈ A లేదా x ∈ B}
A మరియు B సమితుల సమ్మేళనాన్ని వెన్ చిత్రంగా క్రింది విధంగా చూపిస్తాము.

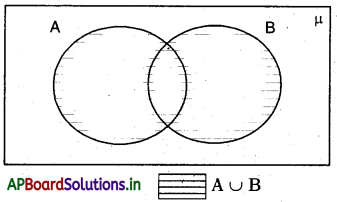
షేడ్ చేయబడిన ప్రాంతం A ∪ B ని సూచిస్తుంది.

ఉదాహరణ : A = {1, 3, 5, 7, 9}, B = {2, 3, 5, 7} అయిన A ∪ B = {1, 2, 3, 5, 7, 9}

సూచన :

• A ∪ B = B ∪ A
• A ∪ Φ = Φ ∪ A = A
• A ∪ μ = μ ∪ A = μ
• ACB అయితే A ∪ B = B
• A ⊂ A ∪ B మరియు B ⊂ A ∪ B

→ సమితుల ఛేదనం : A సమితి మరియు B సమితులలోని ఉమ్మడి మూలకాలతో ఏర్పడే నూతన సమితిని A, B ల ఛేదనం అంటారు. దీనిని A ∩ B తో సూచిస్తూ, A ఇంటర్ సెక్షన్ B గా చదువుతారు. అనగా A ∩ B అనే సమితి A మరియు B సమితులలోని ఉమ్మడి మూలకాలను కలిగి ఉంటుంది.
A ∩ B = {x : x ∈ A మరియు x ∈ B}

A మరియు B సమితుల ఛేదన వెన్ చిత్రం :

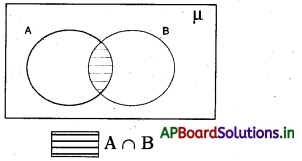
షేడ్ చేసిన ప్రాంతం A ∩ B ని సూచిస్తుంది.
BAB ఉదా : A = {1, 3, 5, 7, 9}, B = {2, 3, 5, 7} అయిన A ∩ B = {3, 5, 7}. . .

సూచన :

• A ∩ B = B ∩ A
• A ∩ Φ = Φ ∩ A = 0
• A ∩ u = A
• A ⊂ B అయితే A ∩ B = A.
• A ∩ BCA మరియు A ∩ B ⊂ B

→ వియుక్త సమితులు : A, B సమితులలో ఉమ్మడి మూలకాలు లేకుంటే A, B సమితులను వియుక్త సమితులు అంటారు.
A, B లు వియుక్త సమితులైతే A ∩ B = d.
వియుక్త సమితుల వెన్ చిత్రం :

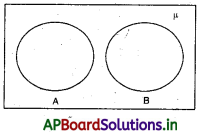
ఉదా : A = {1, 3, 5, 7}, B = {2, 4, 6, 8} A, B లలో కనీసం ఒక ఉమ్మడి మూలకం కూడా
∴ A, B లు వియుక్త సమితులు.

→ సమితుల భేదం : సమితి A కు మాత్రం చెంది, సమితి B కి చెందకుండా ఉండే మూలకాలతో ఏర్పడే సమితిని A, Bల భేదం అంటారు. అనగా A – B లోని మూలకాలు A లో మాత్రమే ఉంటాయి. కాని B లో ఉండవు.
A – B = {x: x ∈ A మరియు x ∉ B}

A, B ల భేదం – వెన్ చిత్రం :

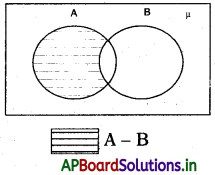
షేడ్ చేసిన ప్రాంతం A – B ని సూచిస్తుంది.

B, A ల భేదం – వెన్ చిత్రం

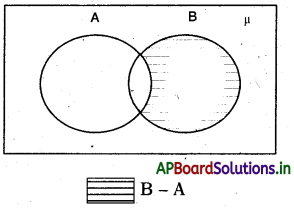
షేడ్ చేసిన ప్రాంతం B – A ని సూచిస్తుంది.

సూచన :

• A – B ≠ B – A
• A – Φ = A
• Φ – A = Φ
• A ⊂ B.అయితే A – B = Φ
• A, B లు వియుక్త సమితులైతే A – B = A మరియు B – A = B.
• A – B; B – A మరియు A ∩ B లు వియుక్త సమితులు అవుతాయి.

కావున
(a) (A – B) ∩ (B – A) = Φ
(b) (A – B) ∩ (A ∩ B) = Φ
(c) (B – A) ∩ (A ∩ B) = Φ

→ n(A), n(B), n(A ∪ B), n (A ∩ B) ల మధ్యగల సంబంధము :

• n(A ∪ B) = n(A) + n(B) – n (A ∩ B)
• A, B లు వియుక్త సమితులైతే n(A ∩ B) = 0 అవుతుంది.
  ∴ n (A ∪ B) = n (A) + n(B).

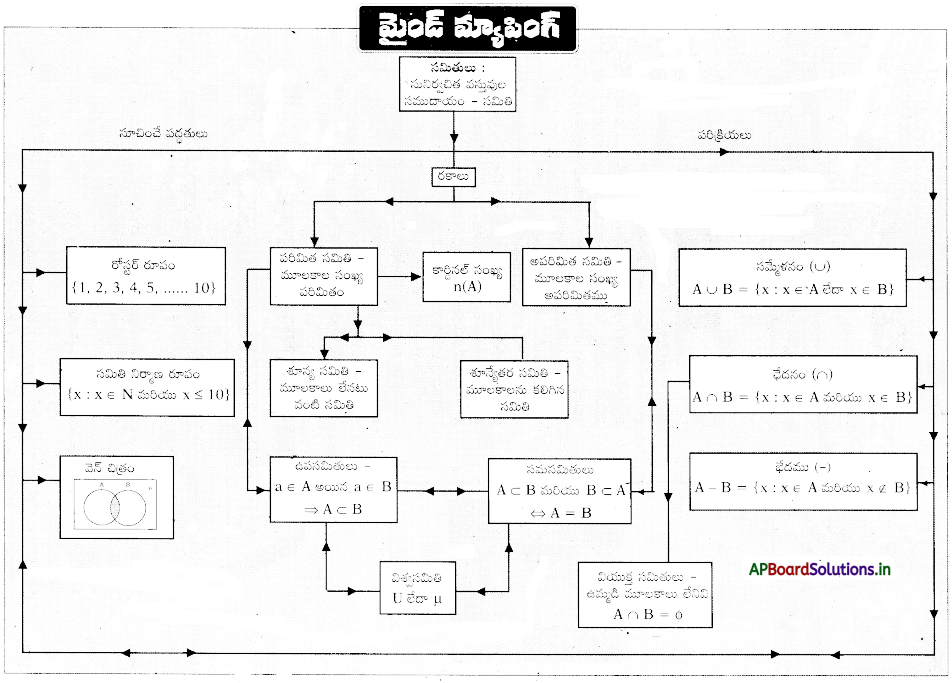
Students can go through AP Board 10th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు

→ యూక్లిడ్ (క్రీ.పూ. 330 – 275):

• యూక్లిడ్ అలెగ్జాండ్రియా రాజు విశ్వవిద్యాలయంలో గణిత బోధకుడిగా పనిచేశాడు. యూక్లిడ్ ను “ఫాదర్ ఆఫ్ జామెట్రీగా” పిలుస్తారు.
• ఇతను అందుబాటులోని గణితాంశాలన్నింటిని సేకరించి, నిర్వచనాలు, స్వీకృతాలు, సిద్ధాంతాలుగా వర్గీకరించి చరిత్ర ప్రసిద్ధి పొందిన గ్రంథం “ఎలిమెంట్స్”ను రచించాడు. ప్రపంచంలో బైబిల్ తర్వాత అత్యధికంగా అమ్ముడు పోయిన గ్రంథం ఇదే.
• యూక్లిడ్ అల్గారిథమ్, సాపేక్ష ప్రధాన సంఖ్యలు, ఒకటి కన్నా పెద్దదైన ఏ పూర్ణ సంఖ్యనైనా ప్రధాన సంఖ్యల లబ్ధంగా ఏకైకం రాయవచ్చు.
• కరణీయ సంఖ్యలు మొదలగునవి ఎలిమెంట్స్ గ్రంథంలోనివే. ఈ నాటికీ పాఠశాలల్లో గణితంగా బోధిస్తున్న దానిలో అధిక భాగం “ఎలిమెంట్స్” ను అనుసరించేవే. యూక్లిడ్ , క్రీ.పూ. 330 – 275

→ వస్తువులను లెక్కించుటకు (count చేయుటకు) అవసరమయ్యే సంఖ్యలను ‘సహజ సంఖ్యలు’ అంటారు. ఈ సంఖ్యా సమితిని N తో సూచిస్తారు. N = {1, 2, 3, ………}

→ గణిత అవసరాలను తీర్చుటకు సహజ సంఖ్య సమితి పూర్తి స్థాయిలో సరిపోవుటలేదనే విషయాన్ని గ్రహించుట ద్వారా “0” (సున్న) ను సహజ సంఖ్యా సమితికి చేర్చుట వల్ల నూతనంగా ఏర్పడే సంఖ్యా సమితిని పూర్ణాంకాలు అంటాం. దీనిని ‘W’ తో సూచిస్తాం. . పూర్ణాంకాలు W = {0, 1, 2, 3, ………….} గణితశాస్త్రానికి “0” సున్నాను పరిచయం చేసినది మన భారతీయులే.

→ సున్నా కంటే తక్కువ విలువ కలిగినవి ఋణపూర్ణాంకాలు. పూర్ణాంకాల సమితి (W) కు ఋణ పూర్ణాంకాలు చేర్చుట ద్వారా ఏర్పడిన సంఖ్యాసమితిని “పూర్ణ సంఖ్యలు” అంటాం. ‘Z’ తో సూచిస్తాం.
Z = {……… -4, -3, -2, -1, 0, 1, 2, 3, …………}

→ పూర్ణ సంఖ్యలు మరియు,” అంతమయ్యే దశాంశాలు, అంతంకాకపోయినా ఆవర్తనమయ్యే దశాంశాలు అన్నింటిని అకరణీయ సంఖ్యలు అంటారు. ఈ అకరణీయ సంఖ్యా సమితిని Q తో సూచిస్తాం. ఈ అకరణీయ సంఖ్యా సమితి పైన చెప్పిన అన్ని సంఖ్యాసమితులు (N, W, Z) కంటే కూడా పెద్ద సంఖ్యా సమితి. ఈ అకరణీయ సంఖ్యలను \(\frac{p}{q}\) రూపంలో వ్రాయగలుగుతాము. p, q లనేవి ‘Z’ కు చెంది ఉంటాయి. q ≠ 0 అవ్వాలి.
Q = {\(\frac{p}{q}\), q ≠ 0; p, q ∈ Z} * అంతములేని, ఆవర్తనముకాని (దశాంశ రూపంలో గల) సంఖ్యలను కరణీయ సంఖ్యలు అంటాం. వీటిని Q’ లేదా S తో సూచిస్తాం. ఉదా : √2, √3, √5, √7 ,………………..

→ కరణీయ సంఖ్యలు, అకరణీయ సంఖ్యలను కలిపి వ్రాయగా ఏర్పడే సంఖ్యాసమితిని వాస్తవసంఖ్యలు అంటాం. దీనిని R తో సూచిస్తాం. R = Q ∪ Q’

→ ప్రధాన సంఖ్యలు : 1 మరియు అదే సంఖ్య మాత్రమే కారణాంకాలుగా గల 1 కన్నా పెద్దవైన సహజసంఖ్యలు. ఉదా : 2, 3, 5, 7, ………….

→ ప్రధాన సంఖ్య నిర్ధారణ పరీక్ష : p ఒక సంఖ్య మరియు n² > p అయ్యేటట్లు ఉండే కనిష్ఠ సంఖ్య n అయిన n కన్నా చిన్నది లేదా “సమానమైన ఏ ప్రధాన సంఖ్యతోను p భాగింపబడకపోతే p ఒక ప్రధాన సంఖ్య అవుతుంది. ఉదా : 1: 319

• 18² > 319. 18 కన్నా తక్కువైన ప్రధాన సంఖ్యలు 2, 3, 5, 7, 11, 13, 17లలో ఏ సంఖ్యతోను 319 భాగింపబడదు. కావున 319 ప్రధాన సంఖ్య అవుతుంది. ఉదా : 2 : 253
• 16² > 253. 16 కన్నా చిన్నవైన ప్రధాన సంఖ్యలలో ఒకటైన 11 తో 253 భాగింపబడుతుంది.
  ∴ 253 ప్రధానసంఖ్య కాదు.

→ సంయుక్త సంఖ్యలు : 1 మరియు అదే సంఖ్యతోపాటు ఇతర సంఖ్యలతో కూడా భాగింపబడే సహజ సంఖ్యలు.
ఉదా : 4, 6, 9, …………

→ యూక్లిడ్ భాగహార న్యాయము : a = bq + r,0 ≤ r < b అయ్యే విధంగా a మరియు b ల జతకు అనుగుణంగా q మరియు r లు ఏకైక పూర్ణసంఖ్యలు వ్యవస్థితం అవుతాయి. అంకగణిత ప్రాథమిక సిద్ధాంతము : ప్రతి సంయుక్త సంఖ్యను ప్రధాన కారణాంకాల లబ్దంగా రాయవచ్చును మరియు ప్రధాన కారణాంకాల క్రమం ఏదైనప్పటికీ ఈ కారణాంకాల లబ్ధము ఏకైకము.

(i) గ.సా. కా లేదా గ.సా.భా : ఇచ్చిన సంఖ్యల యొక్క సామాన్య ప్రధాన కారణాంకాల యొక్క కనిష్ఠ ఘాతాల లబ్ధం వాని యొక్క గ.సా.5 అగును.
ఉదా : 60, 168 సంఖ్యలను కారణాంకాల లబ్దంగా వ్రాయగా
60 = 22 × 3 × 5; 168 = 22 × 3 × 7
60, 168 ల యందుగల సామాన్య కారణాంకాలు = 2, 3
వాని యొక్క కనిష్ఠ ఘాతాలు = 2², 3¹
∴ 60, 168 ల గ.సా. కా = వాని సామాన్య కారణాంకాల కనిష్ఠ ఘాతాల లబ్దం = 2² × 3 = 4 × 3 = 12

(ii) క.సా.గు : ఇచ్చిన సంఖ్యల యొక్క ప్రతీ ప్రధాన కారణాంకాల గరిష్ఠ ఘాతాల లబ్ధం వాని క.సా.గు (కనిష్ఠ సామాన్య గుణిజం) అగును.
ఉదా : 60, 168 సంఖ్యలను వాని కారణాంకాల లబ్దంగా వ్రాయగా
60 = 2² × 3 × 5; 168 = 2² × 3 × 7
60, 168 గల యొక్క అన్ని ప్రధాన కారణాంకాలు = 2, 3, 5, 7,
వాని యొక్క గరిష్ఠ ఘాతాలు = 2², 3¹, 5¹, 7¹
∴ 60, 168 ల క.సా.గు వాని గరిష్ఠ (ప్రతి కారణాంకం యొక్క ఘాతాల లబ్దం = 2² × 3 × 5 × 7 = 840.

→ ఒక సంఖ్య యొక్క ఒకట్ల స్థానంలో సున్న (0) ఉంటే ఆ సంఖ్య యొక్క ప్రధాన కారణాంకాల లబ్దంలో 2 మరియు 5 ఆ ఉంటాయి. దీని విపర్యయము కూడా నిజము.
ఒక సంఖ్య యొక్క ఒకట్ల స్థానంలో 5 ఉంటే ఆ సంఖ్య యొక్క ప్రధాన కారణాంకాలలో 5 ఉంటుంది.

ఉదా :

• 510 = 2 × 5 × 3 × 17;
• 620 = 2² × 5 × 31;
• 45 = 3² × 5;
• 455 = 5 × 7 × 13

→ x అనేది ఒక అకరణీయ సంఖ్య మరియు దీని దశాంశ రూపం ఒక అంతమయ్యే దశాంశము అయినప్పుడు x ను p, q లు పరస్పర ప్రధానాంకాలు అయివున్న \(\frac{p}{q}\) రూపంలో వ్యక్తపరచవచ్చు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్దం 20 5m అవుతుంది. ఇందులో n, m లు రుణేతర పూర్ణసంఖ్యలు. దీని విపర్యయము కూడా నిజము. విపర్యయము : ‘n, m లు రుణేతర పూర్ణసంఖ్యలు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్ధరూపం 215m కలిగినటువంటి అకరణీయ సంఖ్య x = \(\frac{p}{q}\) అయిన X యొక్క దశాంశ రూపం ఒక అంతమయ్యే దశాంశం అవుతుంది. (p, q లు సాపేక్ష ప్రధాన సంఖ్యలు)

→ x ఒక అకరణీయ సంఖ్య, p, q లు సాపేక్ష ప్రధాన సంఖ్యలు అయి x = \(\frac{p}{q}\) అంతమవు దశాంశము అయితే q = 2ⁿg^m రూపంలో ఉంటుంది. ఈ దశాంశము n, m లలో పెద్దదైన సంఖ్యకు సమానమైన అంకెల వద్ద అంతం అవుతుంది.

ఉదా : \(\frac{13}{40}=\frac{13}{2^{3} \times 5}\) ; n = 3, m = 1 మరియు n > m.
\(\frac{13}{40}\) మూడు దశాంశాల తర్వాత అంతం అవుతుంది. ..
\(\frac{13}{40}\) = 0.325

→ n, m లు రుణేతర పూర్ణసంఖ్యలు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్దము 2ⁿg^m రూపంలో లేకుంటే అకరణీయ సంఖ్య x = \(\frac{p}{q}\) యొక్క దశాంశ రూపం ఒక అంతంకాని.ఆవర్తన దశాంశము అవుతుంది.

→ p అనేది ఒక ప్రధాన సంఖ్య మరియు a ఒక ధనపూర్ణ సంఖ్య అయితే a² ను p నిశ్శేషంగా భాగిస్తే, a ను p నిశ్శేషంగా
భాగిస్తుంది. సంవర్గమానాలు : a మరియు N లు ధన పూర్ణసంఖ్యలై a > 1, N > 0 అవుతూ a^x = N అయిన దీనిని సంవర్గమాన రూపంలో log_a N = x అని వ్రాస్తాము. ఇచ్చట a, N ∈ R

గమనిక : ధన పూర్ణసంఖ్యలకు మాత్రమే సంవర్గమానాలు నిర్వచించబడ్డాయి.

• log_a 1 = 0 (ఏ ఆధారానికైనా 1 యొక్క సంవర్గమానం ‘0’.)
• log_a = 1

→ ఒక సంఖ్య యొక్క సంవర్గమానాలు విభిన్న భూములకు (ఆధారాలకు) వేర్వేరుగా ఉంటాయి.
ఉదా :

• 64 = 8² యొక్క సంవర్గమాన రూపం log₈ 64 = 2
• 64 = 4³ యొక్క సంవర్గమాన రూపం log₄ 64 = 3
• 64 = 2⁶ యొక్క సంవర్గమాన రూపం log₂ 64 = 6

→ సంవర్గమాన న్యాయాలు : లబ్ధ సూత్రం

• log_a xy = log_ax + log_ay భాగఫల సూత్రం
• log_a \(\frac{x}{y}\) = log_ax – log_ay

→ ఘాత సూత్రాలు :

• log_a x^m = m log_a x,
• log_aⁿ n x = \(\frac{1}{n}\) log_a x;
• log_aⁿ n x^m = \(\frac{m}{n}\) log_a x
• a log_a x = x

→ ఆధార మార్పిడి సూత్రాలు :

• log_ax = log_bx. log_ab;
• log_ax = \(\frac{1}{\log _{x} a}\)

→ సంఖ్యల సంవర్గమానాలు పూర్ణాంక, దశాంశ భాగాలను కలిగి ఉంటాయి. పూర్ణాంక భాగాన్ని లాక్షణిక అని, దశాంశ భాగాన్ని మాంటిస్సా అని అంటారు.
ఒక అంకె సంఖ్య సంవర్గమానాల లాక్షణిక సున్న.
రెండు అంకెల సంఖ్య సంవర్గమానాల లాక్షణిక 1.
– మూడు అంకెల సంఖ్య సంవర్గమానాల లాక్షణిక 2.

→ ఒక సంఖ్యలో n అంకెలుంటే ఆ సంఖ్య యొక్క లాక్షణికలో (n- 1) అంకెలుంటాయి. విపర్యయంగా, ఒక సంవర్గమాన లాక్షణిక n అయిన, ఆ సంఖ్యలో (n + 1) అంకెలుంటాయి.

ఉదా : ఒక తేనెటీగల గుంపు రెండు పువ్వులపై సమాన సంఖ్యలో వాలినపుడు ఒక తేనెటీగ మిగులుతుంది. అదే గుంపు మూడు పూవులపై సమాన సంఖ్యలో వాలినపుడు రెండు తేనెటీగలు మిగులుతాయి. అదే గుంపు నాలుగు పూవులపై సమాన సంఖ్యలో వాలినపుడు 3 మిగులుతాయి. అదే గుంపు ఐదు పూవులపై సమాన సంఖ్యలో వాలినపుడు మరి మిగలవు. ఆ గుంపులో గరిష్టంగా 50 వరకు తేనెటీగలు కలిగి ఉండవచ్చు. అయిన వాటి ఖచ్చిత సంఖ్య కనుగొనుము.

→ సాధన. ఈ గుంపులో గల తేనెటీగలు = x అనుకుందాం
రెండు పూవులపై సమానంగా వాలిన 1 మిగులును

• కావున x = 2a + 1 గా వ్రాయవచ్చును. ……………………….(1)
• మూడు పూవులపై సమానంగా వాలిన 2 తేనెటీగలు మిగులును. కావున x = 3b + 2 ………………(2)
• నాలుగు పూవులపై సమానంగా వాలిన 3 తేనెటీగలు మిగులును. కావున x = 4c + 3.0 ……………….(3)
• ఐదు పూవులపై సమాన సంఖ్యలో వాలిన మరి మిగలవు. కావున x = 5d + 0 ……………..(4)

మరియు x ≤ 50 (ఎందుకనగా అవి గరిష్ఠంగా 50)
x అనునది 5 గుణజం అని 4వ సమీకరణం నుండి అర్థమగును కావున x యొక్క సాధ్య విలువలు = 5, 10, 15, 20, 25, 30, 35, 40 మరియు 45. మొదటి సమీకరణం నుండి x బేసి సంఖ్య అని అర్థమగును. కావున ఇపుడు ‘x’ యొక్క సాధ్య విలువలు = 5, 15, 25, 35, 45 (పై వాటి నుండి సరిసంఖ్యలు తొలగించాం). సమీకరణ (2) ప్రకారం 3చే భాగిస్తే శేషం 2 రావాలి.

కావున ఇపుడు ‘x’ యొక్క సాధ్య విలువలు = (5, 35). సమీకరణ (3) ప్రకారం 4చే భాగిస్తే శేషం 3 రావాలి. కావున 5, 35 లలో 35 మాత్రమే 4 చే భాగించినపుడు 3 శేషాన్ని ఇవ్వగలుగుతుంది.
∴ ఆ గుంపులో 35 తేనెటీగలు కలవని అర్థమవుచున్నది.

సరిచూచుట :

• 35 తేనెటీగలు 5 పూవుల పై వాలిన \(\frac{35}{5}\) = 7 (శేషం – 0)
• 35 తేనెటీగలు 4 పూవుల పై వాలిన \(\frac{35}{4}\) = 8 (శేషం – 3)
• 35 తేనెటీగలు 3 పూవులపై వాలిన \(\frac{35}{3}\) =11 (శేషం – 2)
• 35 తేనెటీగలు 2 పూవులపై వాలిన \(\frac{35}{2}\) =17 (శేషం – 1)

Students can go through AP Board 8th Class Maths Notes 15th Lesson సంఖ్యలతో ఆడుకుందాం to understand and remember the concept easily.

AP Board 8th Class Maths Notes 15th Lesson సంఖ్యలతో ఆడుకుందాం

→ ఒక సంఖ్య ‘a’ మరొక సంఖ్య ‘b’ను భాగించడం అంటే నిశ్శేషంగా భాగించుట అని అర్థం. దీనినే b, a చే భాగింపబడును అంటారు.

→ అంకెల స్థాన విలువ 12,34,56,789

→ సంఖ్యలను విస్తరణ రూపంలో వ్రాయుట :
3456 = 3 × 1000 + 4 × 100 + 5 × 10 + 6 × 1
= 3 × 10³ + 4 × 10² + 5 × 10¹ + 6 × 10°

→ 10 యొక్క భాజనీయతా నియమం : ఒక సంఖ్య యొక్క ఒకట్ల స్థానమందు అంకె ‘0’ అయినచో అది ’10’ చే నిశ్శేషంగా భాగింపబడుతుంది.

→ 5 యొక్క భాజనీయతా నియమం : ఒక సంఖ్య యొక్క ఒకట్ల స్థానమందు అంకె 0, 5 అయినచో ఆ సంఖ్య ‘5’చే నిశ్శేషంగా భాగింపబడుతుంది.

→ 2 యొక్క భాజనీయతా నియమం : ఒక సంఖ్య యొక్క ఒకట్ల స్థానమందు గల అంకె 0, 2, 4, 6, 8 అయినచో అది ‘2’చే నిశ్శేషంగా భాగింపబడుతుంది.

→ ఒక సంఖ్య యొక్క అంకెల మొత్తం, 3 యొక్క గుణిజం అయిన ఆ సంఖ్య ‘3’చే నిశ్శేషంగా భాగింపబడుతుంది.

→ ఒక సంఖ్య యొక్క అంకెల మొత్తం, 9 యొక్క గుణిజం అయిన ఆ సంఖ్య ‘9’చే నిశ్శేషంగా భాగింపబడుతుంది.

→ 2 మరియు 3చే భాగింపబడే అన్ని సంఖ్యలు ‘6’చే నిశ్శేషంగా భాగింపబడును.

→ ఒక సంఖ్య యొక్క చివరి రెండంకెలు 4చే భాగింపబడిన ఆ సంఖ్య 4చే నిశ్శేషంగా భాగింపబడును.

→ ఒక సంఖ్యలోని చివరి మూడంకెలు 8చే భాగింపబడిన ఆ సంఖ్య ‘8’చే నిశ్శేషంగా భాగింపబడును.

→ ఒక సంఖ్య 7చే నిశ్శేషంగా భాగించబడవలెనన్న, (2a + 3b + c) 7తో భాగింపబడవలెను. –
(ఇక్కడ a = వందల స్థానంలోని అంకె, b = పదుల స్థానంలోని అంకె, C = ఒకట్ల స్థానంలోని అంకె)

→ ఒక సంఖ్యలోని సరి స్థానములలోని అంకెల మొత్తం మరియు బేసి స్థానాలలోని అంకెల మొత్తముల భేదం 11 యొక్క గుణిజం లేక ‘0’ అయిన ఆ సంఖ్య ’11’చే నిశ్శేషంగా భాగింపబడును.

→ ప్రతి పాలిండ్రోమ్ సంఖ్య ’11’చే నిశ్శేషంగా భాగింపబడును.

Students can go through AP Board 8th Class Maths Notes 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) to understand and remember the concept easily.

AP Board 8th Class Maths Notes 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము)

→ దీర్ఘఘనం యొక్క పొడవు, వెడల్పు, ఎత్తులు వరుసగా l, b, h లు అయిన

దీర్ఘఘనం యొక్క ప్రక్కతల వైశాల్యము = 2h (l + b)
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2(lb + bh + lh)

→ ‘a’ భుజంగా గల సమఘనం యొక్క ప్రక్కతల వైశాల్యము = 4a²

సమఘనం యొక్క సంపూర్ణతల వైశాల్యము = 6a²

→ దీర్ఘఘనం యొక్క ఘనపరిమాణం (V) = పొడవు × వెడల్పు × ఎత్తు = l × b × h = lbh
సమఘనం యొక్క ఘనపరిమాణం (V) = (s)³ = a³ (a = సమఘనం యొక్క భుజం)

→ 1 cm³ = 1 మిల్లీ లీటరు
1 లీటరు = 1000 ఘ. సెం.మీ.
1 మీ ³ = 1000000 ఘ. సెం.మీ. = 1000 లీటర్లు = 1 కిలోలీటరు

Students can go through AP Board 8th Class Maths Notes 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట to understand and remember the concept easily.

AP Board 8th Class Maths Notes 13th Lesson త్రిమితీయ వస్తువులను ద్విమితీయంగా చూపుట

→త్రిరిపరిమాణ వస్తువుల ఆకారములు సమాన మాపము గల చుక్కల కాగితముపై గీయు విధానము.

→ త్రిపరిమాణ వస్తువులను పై నుండి, ప్రక్క నుండి, ఎదుటి నుండి చూసినపుడు కనబడు వివిధ ఆకారములు.

→ బహుముఖి : సమతలములు కలిగిన వస్తువులు.

→ పట్టకము : బహుముఖి నందు సమాంతరముగా ఎదురెదురుగా గల రెండు తలములు సర్వసమానముగాను, మిగిలిన తలములు దీర్ఘచతురస్రములు (సమాంతర చతుర్భుజము)గా కలిగిన వస్తువులను పట్టకము అంటారు.

→ పిరమిడ్ : బహుముఖి నందు అడుగు భాగము యొక్క తలము బహుభుజిగాను, మిగిలిన ప్రక్కతలములు త్రిభుజములుగా కలిగిన వస్తువులను పిరమిడ్ అంటారు.

→ త్రిపరిమాణ వస్తువులు తయారుచేయుటకు ద్విమితీయ వల రూపములు ఉపయోగించుట.

→ బహుముఖిల కోసం ఆయిలర్ సూత్రము E + 2 = F + V

→ త్రిపరిమాణ వస్తువుల యొక్క తలములు, అంచులు, శీర్షములు : మనం నివసించే గది యొక్క గోడలు, కిటికీలు, తలుపులు, గది యొక్క పై భాగము, అడుగు తలము, మూలలు మొదలైనవి మరియు మన చుట్టూ గల వస్తువులు టేబుల్స్,
బాలు మొ||నవి గమనించండి. వాటి యొక్క తలములు సమతలములు. వాటి తలములు అంచుల వద్ద కలియుచున్నవి. రెండు లేక అంతకంటే ఎక్కువ అంచులు మూలల వద్ద కలియుచున్నవి. ఈ మూలను శీర్షము అంటారు. ఒక సమఘనము లేదా పిరమిడ్ ను గమనించండి.

→ ప్లేటోనిక్ వస్తువుల వలరూపాలు :

బహుముఖి పేరు	బహుభుజి తలాలు	వలరూపము
చతుర్ముఖీయం	4 త్రిభుజాలు
అష్టముఖీయం	8 త్రిభుజాలు
షష్టిముఖీయం	6 చతురస్రాలు
ఇరవై ముఖాలు కలది	20 త్రిభుజాలు
ద్వాదశముఖీయం	6 పంచభుజిలు

→ బహుముఖి యొక్క అంచులు, తలములు, శీర్షముల సంఖ్య
ప్రక్క పటంలో బహుముఖి యొక్క అంచులు, తలములు, శీర్షములను లెక్కించెదము.

తలముల సంఖ్య – 5
అంచుల సంఖ్య – 9
శీర్షముల సంఖ్య – 6

→ కింది పట్టికను గమనించండి.

పై పట్టిక యొక్క చివరి రెండు నిలువు వరుసలు పరిశీలిస్తే అన్ని బహుముఖిలకు మనము F + V = E + 2 అని గమనించగలము.

Students can go through AP Board 8th Class Maths Notes 12th Lesson కారణాంక విభజన to understand and remember the concept easily.

AP Board 8th Class Maths Notes 12th Lesson కారణాంక విభజన

→ ఒక సంఖ్యను ప్రధానసంఖ్యల లబ్ధంగా వ్యక్తపరిచే పద్ధతిని “ప్రధాన కారణాంక విభజన పద్ధతి” అంటారు.

→ ఇచ్చిన సమాసమును దాని కారణాంకాల లబ్ధంగా వ్రాయటాన్ని కారణాంక విభజన అందురు.

→ సూక్ష్మీకరణ సాధ్యం కాని కారణాంకమును అవిభాజ్య కారణాంకం అంటారు.

→ (a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
(a + b) (a – b) = a² – b²

→ (x + a) (x + b) = x² + x(a + b) + ab

→ గోల్డ్ బాక్ ఊహ : ప్రతి బేసిసంఖ్య, ప్రధానసంఖ్యగానో లేదా కొన్ని ప్రధాన సంఖ్య మరియు వర్గ సంఖ్యకు రెట్టింపు సంఖ్యల మొత్తంగానే ఉంటుంది.
ఉదా : 21 (ఒక బేసి సంఖ్య); 21 = 19 + 2 (లేదా) 21 = 13 + 2(4) (లేదా) 21 = 3 + 2(9) గా వ్రాయవచ్చు

Students can go through AP Board 8th Class Maths Notes 11th Lesson బీజీయ సమాసాలు to understand and remember the concept easily.

AP Board 8th Class Maths Notes 11th Lesson బీజీయ సమాసాలు

→ ఒక ఏకపదిలోని చరరాశుల ఘాతాంకాల మొత్తాన్ని ఆ ఏకపది పరిమాణం అంటారు.

→ ఒక బీజీయ సమాసంలోని వివిధ పదాల పరిమాణాల్లో గరిష్ఠ పరిమాణాన్ని ఆ బీజీయ సమాస పరిమాణం అంటారు.

→ రెండు ఏకపదుల లబ్ధం ఒక ఏకపది అవుతుంది.

→ ఒక బహుపదిని ఏకపదిచే గుణించాలంటే బహుపదిలోని అన్ని పదాలను ఆ ఏకపదిచే గుణించాలి.

→ సర్వసమానం అనునది ఒక సమానత. సమీకరణంలోని సమానత్వం, చరరాశిలోని అన్ని విలువలకు సత్యమైనపుడు సర్వసమానత్వం అవుతుంది. ఇంకోవైపు సమీకరణం కొన్ని విలువలకే సత్యం అయితే సర్వసమానత్వంలో అన్ని విలువలకు సత్యం అవుతాయి.

→ కొన్ని సర్వసమీకరణాలు

• (a + b)² = a² + 2ab + b²
• (a – b)2² = a² – 2ab + b²
• (a + b) (a – b) = a² – b²
• (x + a) (x + b) = x² + x(a + b) + ab .
• (a + b)² + (a – b)² = 2(a² + b²)
• (a + b)² – (a – b)² = 4ab

గమనిక :

• రెండు ధనసంఖ్యల లబ్ధము ధనసంఖ్య
• రెండు ఋణ సంఖ్యల లబ్ధము ధనసంఖ్య
• ఒక ధన మరియు ఒక ఋణ సంఖ్యల లబ్దము ఋణసంఖ్య